A Comparison of Marine Pilots' Planning and Manoeuvring Skills: Uncovering Mental Models to Assess Shiphandling and Explore Expertise

Abstract

This paper introduces an assessment methodology that can underpin the objective measurement of shiphandling skills and permit comparative analysis of manoeuvring plans against their execution in a full mission bridge simulator. It was hypothesised that expert shiphandlers would have shown a strong consistency between the initial plan provided and the following execution. Ten marine pilots participated in the study. Their performance was evaluated across several variables using data gathered during the planning and objective measurements completed during the execution on a simulator. A significant capability to match execution against the plan was evidenced by the group of pilots. The mathematical analysis proposed represents an objective approach that can assure a valid and reliable assessment when applied across different contexts and needs such as: selection, training and certification of pilots, port development, optimisation of bridge procedures and improvement of equipment design.

1. INTRODUCTION

The aim of this study was to better depict the complexity underlying shiphandling expertise in a port environment, with an emphasis on the human element relating to the safety, accuracy and efficacy of ship movements. The study investigated individual competence in a group of marine pilots, to plan and forecast future operational needs in different contexts and manoeuvring conditions. Such competence is considered to be of critical importance, since pilots have to decide if a vessel can safely operate in a port, basing their decision on the vessel's manoeuvring characteristics and contingent environmental conditions. Inaccurate evaluations could expose the vessel to critical consequences. The “mental model” concept helps to better contextualise pilots' planning competence in a theoretical background (Mohammed et al., 2010). Mental models have been defined as “mechanisms whereby humans are able to generate descriptions of system purpose and form, explanations of system functioning and observed system states, and predictions of future states” (Rouse and Morris, 1986). They are generally used to describe a person's mental representations and beliefs of some physical system, with a particular focus on how the individual's interactions with the system lead to the outcome of interest (Hinsz, 1995). Mental models can also be used to describe abstract dynamics or concepts as deductive reasoning and inference (Aronson, 1997), they could refer to individual or distributed cognitive processes among team members (Banks and Millward, 2000). Effective planning increases shared mental models, allowing team members to better perform during high workload conditions (Stout et al., 1999). Mental models can be seen as knowledge structures which are formed of stored long term static information (Johnson-Laird, 1983) that can be exploited to explain, interact and direct problem solving (Al-Diban and Ifenthaler, 2011). When complex, novel, high risk problems are presented, people rely on mental models as a guide (Mumford et al., 2012) or as a map (Fiol and Huff, 1992). Evaluating how well mental representations are able to forecast future outcomes implies evaluating the prediction validity of the proposed methodology. This approach could improve specific aspects of performance, correcting and refining inaccurate assumptions derived from a partial or erroneous initial understanding. Trainers could adopt different forms of evidence from those they would usually seek to assess performance, modifying learning and assessment events. The current study explored the relationship between pilots' competency to plan several manoeuvres and the execution of those manoeuvres in a simulated environment. This can be seen as the translation in practical terms of their manoeuvring mental models into a simulated “reality”. Mental models and outcomes in the simulators were quantified, in order to obtain, through such comparison, a performance measurement. We expected that participant pilots, being “proficient” (Benner, 1984) or “expert” (Dreyfus and Dreyfus, 1980), were able to formulate plans sufficiently close to execution. In order to contain possible influence of other interfering factors ensuring validity of measurements, participants were also compared with the original company group on several aspects better described in Section 2.1.

2. METHODOLOGY

2.1. Participants

The participants of this study were a group of ten marine pilots coming from the same pilot company. They were all males in good health, as required by professional medical standards (AMSA, 2010). At the time of data collection (December 2013) the company had a total of 39 pilots with an average age of 51·2 years at a standard deviation of 7·0 years. All the pilots had an average of 10·8 years of service with the company with a standard deviation of 6·8 years. The group of ten participating pilots were 51·8 years of age on average with a deviation standard of 5·9 years. On average these pilots had been with the company for 10·6 years with a standard deviation of 7·8 years. An Analysis of Variance (ANOVA) for age and service confirmed no significant difference between the participants and the rest of the pilots working for the same company. All the pilots involved in the research had more than ten years of previous experience in pilotage, even if not in the same company.

The experiment was divided into two phases. During Phase 1 participants were required to complete a thorough and comprehensive planning of the manoeuvres that would later be undertaken on the simulator. Phase 2 consisted of observed performance and data collection by the assessor while the pilot executed the previously planned manoeuvres in a simulator. The authors assert that all procedures contributing to this work comply with the ethical standards of our university and the relevant national and institutional committees on human experimentation and with the Helsinki Declaration of 1975, as revised in 2008.

2.2. Phase 1 – Planning

The first phase included the planning of four proposed manoeuvres. Each manoeuvre included the whole process necessary to transfer the ship from a defined initial position to a berth within constrained port waters, with the use of own and/or external means of propulsion (i.e. tugs, when allowed). These four manoeuvres were controlled on three main factors: (a) “port familiarity” (from now on referred as “port”), (b) “difficulty”, and (c) “phase”. The first factor, “port”, took into account whether the manoeuvre was conducted in the participant pilot's homeport (the port where they were regularly working) or in a different port. The other port chosen for the experiment was Vorbasse, a virtual port only present in the simulator software. This port was chosen to avoid any possibility of learning effect associated with previous manoeuvring experience the subjects may have possessed and to provide support for methodology reliability. Vorbasse was also chosen to investigate how “pilots' expertise” could be “bounded”, i.e. related to pilots' local knowledge of the port where they normally operate.

The pilots' homeport in the tables and graphs presented will be coded “B”, while Vorbasse will be coded “V”. For the factor “difficulty” the easy level will be coded “1” while the difficulty level will be coded “2”. To control the level of difficulty, specific manoeuvres' parameters were altered as summarised in Table 1.

Table 1. Levels of Difficulty – Adopted in both Ports.

Level 1 reproduced a comparable level of difficulty of routine operations. Level 2 aimed to engage pilots with a level of difficulty slightly exceeding the safety limits established in the pilots' homeport, without losing construct validity. Each manoeuvre required the pilot to complete a mooring using the side of the ship opposite to the berth position on commencement of the exercise. This implied that for each manoeuvre the ship had to swing (rotate 180°) before she could be moored. Each manoeuvre therefore developed through three main sections that provided an additional factor for the analysis; (1) the “approach” (from the initial position until the start of the swing), (2) the “swing” (from the start of the swing until the rotation was completed and stabilised), and (3) the “closing” (from the end of the swing until a defined distance from the berth). In the graphs and tables presented, the phases will be coded: “1” for the approach, “2” for the swing and “3” for the closing.

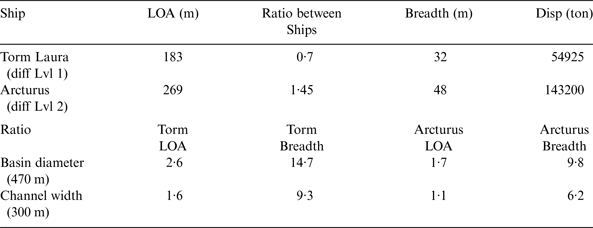
Manoeuvres were also coupled across the “port” factor (grouped for the same level of difficulty); i.e. the easy manoeuvres in the two ports (as well as the difficult manoeuvres) were, as much as possible, kept technically similar (e.g., vessels used, distances to be covered, etc.) to promote data baseline formation on pilot performance and assure reliability of the assessment process. Spatial constraints due to port dimensions were purposely maintained to be similar, modifying Vorbasse in order to match homeport dimensions as summarised in Table 2.

Table 2. Proportions between vessels and port dimensions.

Phase 1 required participants to explain extensively how they would have performed the manoeuvres in the simulator, meaning that the plan provided would have been their intended, preferred and expected course of action. Any difference recorded in the following execution would have been considered unexpected and deemed necessary as the best possible option available at the time to maintain the safety of the vessel while achieving the goal of berthing. In order to create and to obtain the record of such explanation in a numerical form, a Detailed Manoeuvre Plan (DMP) table was compiled by each participant for each manoeuvre, before performing such a manoeuvre in the simulator. Such a table can be seen as a more detailed version of the routine passage plan normally discussed by pilots and ship masters before a ship enters into a port (Wild and Constable, 2013). The initial material provided by the researcher to pilots included a facsimile of port navigational charts at the appropriate scale for each manoeuvre. Pilots were able to use the charts to sketch the exact expected ship movement and highlight elements of interest. For each sequential position sketched on the charts, the pilot had to forecast in the DMP details such as:

• • ship's speed in knots;

• • ship's main engine power in percentage of maximum power available;

• • ship's bow thruster power (when available) in percentage of maximum power available;

• • tug's force (when available) in percentage of maximum bollard pull available.

Prepared prior to the simulations these plans formed a comparative basis that were used to assess outcomes generated in the simulator. In reality a full mission bridge simulator can record all the previously mentioned parameters (and more) with a high degree of accuracy at several samples per second.

2.3. Phase 2 – Execution

For this research, the Maritime Safety Queensland Simulator located in Brisbane was used (Smartship® Simulator www.smartshipaustralia.com.au). This “Full Mission Bridge” simulator is classified as Class A (NAV) according to the standards issued by DNV (Veritas, 2011). It is capable of simulating a total shipboard bridge operation situation, including the capability for advanced manoeuvring in restricted waterways. Before the experimental manoeuvres, pilots were required to perform a very simple mooring with a vessel different from those used in the experimental runs. This first manoeuvre was used as a familiarisation run to ensure participants had a standardised level of familiarity with the bridge environment and the navigation equipment available. The manoeuvres planned in Phase 1 were then used in random order to record all the data. To provide realism to the manoeuvres, during their execution, the researcher was present on the simulator bridge and he was generally acting as the ship's Master or the bridge member most suitable for the specific interaction.

Performance outcomes were obtained calculating the following dependent variables:

• • XTD – Cross Track Distance: Distance from the intended track as per positions obtained from the planning charts and the ship track provided by the simulator;

• • SpdEst – Speed Estimation: Difference between the intended speed over the ground (SOG) as per DMP (expressed in knots) and the recorded speed provided by the simulator.

• • EngEst – Engine Power Estimation: Difference between the absolute value of the intended use of engine power as per DMP (expressed in percentage) and the absolute value of the recorded engine power provided by the simulator.

• • ThrEst – Bow Thruster Power Estimation: Difference between the absolute value of the intended bow thruster power (expressed in percentage) as per DMP and the recorded absolute value of the bow thruster power provided by the simulator (when applicable).

• • Tug(n)Est – Tug Force Estimation: Difference between the absolute value of the forecasted tug's bollard pull as per DMP (expressed in percentage, based on the maximum bollard pull that tugs could provide) and the recorded absolute value of the tug's bollard pull provided by the simulator (when applicable, with (n) differentiating each tug used).

Figure 1 shows two screenshots taken from the simulator interface showing two different manoeuvres (B2 on the left and V1 on the right). It is possible to notice in light grey the outline of two vessels used (Arcturus in the homeport on the left and Torm Laura in Vorbasse on the right). The empty outlines creating the shaded area represent the swept path covered by the vessel during its movement. In the middle of the basins it is possible to note as a segmented line the pilot's intended path from which the XTD was measured.

Figure 1. Examples of Manoeuvres as shown by the simulator interface.

3. RESULTS

Results against the above parameters were calculated for each manoeuvre completed by a participant. The results obtained were averaged across all participants and within each phase previously identified as “approach”, “swing” and “closing”. During the simulations not all the runs were completed by the pilots. A total of four crashes were recorded (three during the manoeuvres in Vorbasse and one in the homeport). A “crash” was an impact or a grounding that required the interruption of the simulation and data collection. All the crashes were experienced during the manoeuvres at Level 2 of difficulty. Three impacts were also experienced (one in Vorbasse with difficulty level 1 and two during the swing in both ports at difficulty Level 2). An “impact” was classified as a contact of the vessel with another ship or port infrastructures that did not impede the continuation of the manoeuvre. Note that Level 2 of difficulty implied that the safety limits currently adopted in pilots' homeport were exceeded. All the pilots clearly stated during the planning phase that they would have chosen not to conduct those manoeuvres should the stated conditions have occurred in the workplace. For all the variables described in Section 2.3. A Univariate Analysis of Variance (ANOVA) was performed, using the statistical package IBM SPSS (IBM_Corp., 2010), on the factors “difficulty”, “port” and “phase” (as defined in Section 2.2.), obtaining the results reported in Table 3 (showing only significant results with alpha < = 0.05 are reported, all results are reported in the Appendix):

Table 3. Summary Table for ANOVA – Significance of Results.

(1) Bow Thruster was available only in the easy manoeuvres

(2) Tugs were available only in the difficult manoeuvres

In XTD the comparison of the means was significant only on the factor phase (Sig = 0·000). To specifically identify which of the three phases was significantly different from the others, a post hoc analysis using a Tukey's Honestly Significant Difference Test (Tukey HSD) (Abdi and Williams, 2010) was carried out. A significant difference (Sig = 0·04) was found between the phases swing (mean = 55·51) with approach (mean = 26·04) and swing (mean = 55·51) with closing (mean = 38·20). Considering all the manoeuvres performed, pilots showed an averaged XTD of between 21 and 50 metres during the approach and the closing phases and between 38 and 69 metres during the swing. Even though results may suggest that this group of pilots were able to remain, on average, within 40 metres of the intended track across all the exercises, further analysis highlighted other elements of interest. A different perspective was achieved considering the Cumulative Distribution Function (CDF) of the variable XTD. Figure 2(a) shows the cumulative distribution functions of XTD across the whole manoeuvres, while Figure 2(b) graphs those distributions only in the phase swing. Results will be further discussed in Section 4.1.

Figure 2. XTD Cumulative distribution function – (a) All manoeuvres – (b) Swing phase.

In the rest of the independent variables that will be explored later, positive values suggest an “overestimation”, i.e. the plan provided by a pilot had estimates that exceeded values achieved in the simulator. Conversely, negative values indicate an “underestimation”, i.e. the values recorded in the simulator were above those provided by the pilot.

The SpdEst, reported in Figure 3, provided a main significant effect on the port factor (Sig. = 0·044). Pilots showed a deeper underestimation of the vessel's speed in Vorbasse (mean = −0·26) than in their homeport (mean = −0·07). There was also a significant interaction (Sig. = 0·000) between the factor's difficulty per phase. There was an overestimation during the approach of the difficult manoeuvres (B2 and V2; mean = 0·19) compared to the easier ones (B1 and V1; mean = −0·71) in the same phase.

Figure 3. Comparison between SpdEst values in the easy and in the difficult manoeuvres.

The EngEst, shown in Figure 4, was obtained according to the same rules as the speed calculation. The difference was in the use of the absolute value of the measurements in the comparison. The engine power used was provided by the simulator with positive or negative values depending on whether the engine was running ahead or astern. Since our focus was on the strain put on the engine in terms of power utilisation and not on the direction induced by the propeller on the water flow, we adopted the absolute value. EngEst, had the main effect (Sig = 0·000) on the factor phase, requiring a post hoc analysis using a Tukey HSD test. Significant differences were found between closing (mean = 0·10) and approach (mean = −0·06) (Sig = 0·001) and then between closing (mean = 0·10) and swing (mean = −0·05) (Sig = 0·006). It also highlighted a marginal interaction (Sig = 0·061) between factors difficulty and phase. In the swing an underestimation was recorded during the most difficult manoeuvres (B2 and V2; mean = −0·13) while in the easier ones the use of the engine was overestimated (B1 and V1; mean = 0·35).

Figure 4. Comparison between EngEst values in the easy and in the difficult manoeuvres.

Adopting an analogous approach to the one used for the engine estimation, ThrEst was calculated as the difference between the plan and the real use (see Figure 5) of the bow thruster. The bow thruster was available to pilots only in the easier manoeuvres (Homeport and Vorbasse, level of difficulty 1). A Univariate Analysis of ThrEst showed no significant effects on the factors port and phase.

Figure 5. Comparison Plan and Real Use of Bow Thruster in the easy manoeuvres.

Tugs were available to pilots only in the most difficult manoeuvres (Homeport and Vorbasse, level of difficulty 2). In order to uniquely identify the tugs throughout the duration of the whole manoeuvre, a number was initially assigned depending on their position around the hull at the very beginning. Tug 1 was the tug made fast on the shoulder of the vessel, Tug 2 on the quarter, while Tug 3 was made fast through the centre lead aft. Even though the disposition of the tugs could have changed throughout the manoeuvre according to pilots' orders, the initial number assigned would have remained the same. As shown in Figure 6(a), only Tug1Est (estimation on Tug 1) reported a significant difference (Sig = 0·001) on the phase factor. A Tukey HSD test showed a significant difference between closing (mean = 0·22) and approach (mean = −0·07) (Sig = 0·008) and significant difference between closing (mean = 0·22) and swing (mean = −0·15) (Sig = 0·001).

Figure 6. Comparison between Tug1Est Tug2Est and Tug3Est in the difficult manoeuvres.

Pearson coefficients were calculated for each manoeuvre, to obtain the correlation between the provided values in the DMP and the values recorded by the simulator. The curves representing plan and execution that were compared were obtained through a moving average across pilots. In addition, Pearson correlation coefficients were also used to compare the independent variables' outcomes (with the exception of XTD) across manoeuvres with the same level of difficulty (B1 with V1 and B2 with V2). All the correlations reported in Table 4 provided significant values (alpha <= 0·05) with one exception (see note (3) in Table 4):

Table 4. Summary Table for Pearson correlation coefficients.

(1) Bow Thruster was available only in the easy manoeuvres

(2) Tugs were available only in the difficult manoeuvres

(3) Not Significant

4. DISCUSSION

4.1. XTD – Cross Track Distance

After performing an ANOVA we were able to isolate only one statistically significant result that occurred in the factor phase. The swing was the phase that showed a statistical difference from the approach and closing phases. This empirical result suggests that pilots were generally able to show consistency in their ability to maintain their intended track despite working in different ports and at different levels of difficulty, with a decreased performance only evident when engaged in the swing. This result becomes more evident looking at the graphs reported in Figure 2. Figure 2(a) reports the cumulative distributions of the XTD scores for the whole manoeuvres while Figure 2(b) is specifically for the swing. A CDF obtained from an ensemble of measurements, provides, for any given score, the number of remaining scores that would be lower in value. In a CDF such a number is provided on the Y axis as a fraction of 1, meaning what percentage of scores would be lower than the score chosen on the X axis. That ordinate value, expressed as a fraction, can also be considered a percentage or a probability. In this case, the scores we are referring to are the cross track distances from the intended track (XTD). These curves show that if the pilotage organisation chose 80% as the target probability to remain within a certain distance from the intended track (ordinate 0·8), this requires a distance of 100 metres during the swing, while for the rest of the manoeuvre 50 metres would be sufficient. This implies that if a distance of 75 metres from the intended track was targeted as safe, in the rest of the manoeuvre there would be a less than 20% probability of reaching and exceeding such a distance, while during the swing such probability would increase to around 40%.

In Figure 2(b), it is shown how scores in the easy manoeuvres (B1S and V1S) reported with a dotted line, exceeded in their maximum values the abscissa of the 200 metres, while the most difficult manoeuvres remained below 200 metres. The explanation for this counter-intuitive result could reside in the fact that in the easier manoeuvres the ratio between the dimensions of the vessel used and the dimension of the available swinging basin was more favourable (2·6) compared to the one available for the more difficult manoeuvres (1·7). Pilots were able to exploit more space in the easier manoeuvres (for example to allow more time to reduce speed) while in the more difficult ones a similar range would have resulted in an impact or grounding. It has to be remembered that the scores collected during the swing and during the closing only occurred with those manoeuvres that were successfully completed without crashes.

4.2. SpdEst – Speed Estimation

Results show that pilots estimated the speed in the two ports differently. Pilots underestimated the speed in the port of Vorbasse (−0.26) slightly more than in their homeport (−0·068). In this case, the lack of familiar lateral visual cues in Vorbasse could have reduced the capability of pilots to perceive such differences. Moreover, evaluating the interaction between factors phase and difficulty (see Figure 3), it can be seen that in the easy manoeuvres the speed during the approach was higher than the one forecasted (underestimation with a mean = −0·714 knots), while during the difficult manoeuvres the speed in the same phase was lower than the estimated one (overestimation with a mean = 0·191 knots). The difference between the types of vessels employed for the manoeuvres could have determined the difference in the speed management during the approach. In the easy manoeuvres a controllable pitch propeller tanker was used. Since in this type of propulsion the shaft never stops its rotational movement, it induces a rotation to the heading of the vessel especially when the longitudinal thrust is stopped (stern transversal thrust effect enhanced when setting the propeller pitch to zero). Therefore pilots had to maintain a higher speed than forecasted in order to counteract this effect through active use of propeller thrust on the rudder. This active use of propeller thrust, on average, did not allow the expected reduction of speed to satisfy the original plan. In addition the current was coming from the stern of the vessel in that phase, helping to increase the speed over the ground. In the more difficult manoeuvres an alternate explanation for the observed lower speed than forecasted could be found in the reduced under keel clearance. Such reduced under keel clearance (down to 1·5 metres with a draft of 14 metres), enhanced the dragging effect of the two knots of current coming in that phase from the bow (possibly more than pilots expected). Moreover, even if there was no significant difference between the rest of the phases, it is interesting to note that in the more difficult manoeuvres a slight underestimation of the speed is present during the swing and the closing. A further explanation for this may be found in the action of the two knots of current interacting more significantly than pilots expected.

4.3. EngEst – Engine Power Estimation

Considering the competency of pilots to forecast the use of the main engine power (variable EngEst), a significant difference was apparent only for the factor phase. The closing phase shows a significant difference compared to the other two phases (see Figure 4). Pilots accounted in their plans for a higher use of the main engine during the closing phase (mean = 0·10). In the other two phases (approach mean = −0·064 and swing mean = −0·048), the planning estimation was slightly lower than the actual use. Moreover, a marginal interaction (Sig = 0·061) between the factors phase and difficulty was encountered (compare Figure 4(a) with 4(b), abscissa from 2 to 3). In the swing phase, pilots planned a higher need of engine than the actual use in the easier manoeuvres (mean = 0·035) but a lower need of the engine for the more difficult manoeuvres (mean = −0·131).

It is worth reiterating that these numbers are percentages. This means that the value – 0·131 expresses a difference between planned and effective use of the main engine of −13·1%. This value represents an average calculated for the entire duration of the phase. This value alone, being a difference, would not be able to define the level of power at which the main engine was working (−13% could be the result of 37% planned minus 50% effective as well as 87% planned minus 100% effective). A critical underestimation could happen for example when the power effectively required could already be close to the engine's working limits. To better explain this consideration, we can refer to the graphs obtained from manoeuvre B2 in Figure 7.

Figure 7. Manoeuvre B2 - Detailed analysis of the engine estimation.

In Figure 7(a) three functions are reported. The continuous bold line shows the mean of all the pilots' EngEst scores. The dotted lines represent the upper and lower limits of the standard error of the mean with a probability of 95%. Such error was calculated using the standard deviation and considering ten subjects (see Figure 7(c)). The averaged planned and recorded engine power are reported in Figure 7(b), as fractions of 1, where 1 means 100% of available power. EngEst, reported in Figure 7(a) can be seen as the difference between those two curves graphed in Figure 7(b). Considering abscissa values from 2·5 to 3 (second half of the swing phase), in Figure 7(a) and 7(b), it can be seen how pilots expected to use the engine much less than was experienced in the simulation. The difference between the planned and the effective use reached values of 50% when the engine was working already up to 80% of its maximum power. Pilots' plans did not consider they would use the main engine that much, nor so close to its maximum availability. This may suggest that the manoeuvre could have required a different approach in that particular section to increase safety margins. This example and analysis of results not only improves understanding of shiphandling but can help pilot companies to better identify critical sections, allowing the development of more effective and safer techniques.

4.4. ThrEst – Bow Thruster Power Estimation

No significant results were found on performing an ANOVA on ThrEst. The absence of significant results in the ANOVA suggested that pilots showed a limited difference between plan and effective use of bow thruster, as confirmed also by the correlations reported in Table 4. Both B1 (Figure 5(a)) and V1 (Figure 5(b)) reported a significant correlation between plan and execution, confirming that pilots were able to follow their plans. The correlation between the variable ThrEst across the two easy manoeuvres was considered. The aim was to evaluate if the two manoeuvres showed similarities in the way pilots performed. Results confirmed pilots showed a similar performance in the two manoeuvres (r = 0·574; Sig = 0·00). This outcome supports the conclusion that the two manoeuvres, even if carried out in different ports, were essentially similar in the use of the bow thruster, showing underestimation or overestimation consistently in the same sections of these manoeuvres. This is another result that might be exploited by pilot companies to better direct the development or training activities associated with new manoeuvres.

4.5. TugEst – Tug Force Estimation

Pilots were free to decide the number of tugs that they wanted to use and their initial position. Pilots also had discretionary control over the position of the tugs during the execution. Only Tug1Est (the difference between the force expected as stated in the plan and the force effectively developed by Tug 1 during the manoeuvre) reported a significant main effect (Sig = 0·001) on the factor phase. The closing phase (see Figure 6(a), abscissa from 3 to 4) was significantly different from the other two (closing and approach (Sig = 0·06), closing and swing (Sig = 0·01)). In this case the plans prepared by the pilots forecasted a higher use of Tug 1 compared to data recorded during the simulations. The lack of other significant results in the ANOVA again suggested a general matching between plan and execution that was subsequently confirmed by the analysis of Pearson correlation coefficients. Tug 1 (Figure 6(a), abscissa from 3 to 4) shows a clear overestimation of the bollard pull needed in the closing phase. With the help of graphs and as shown by results, it is also possible to observe that there is a generally sensitive fit between plan and execution for all three tugs. Specifically referring to Tug 2 and Tug 3, Pearson coefficients reported a lower (even if significant) correlation in manoeuvre B2 than manoeuvre V2. It should be reiterated that in manoeuvre V2, pilots experienced three crashes. This might have helped higher correlations, since data remaining was only coming from pilots that adopted a more efficient strategy and successfully completed the manoeuvre. Similarly to findings associated with the variable ThrEst, it was considered the correlation between the variable TugEst (one for each tug) measured across the two manoeuvres B2 and V2. As shown in Table 4, significant correlations were obtained. These correlations may numerically support how the strategies adopted in the use of tugs were similar in the two manoeuvres.

4.6. Study Limitations

The number of participants could represent a limitation of this study. Nevertheless, pilots spent an average of eight hours in the simulator performing these tasks, allowing a deep and detailed data collection. We recognise the value of larger data sets, and suggest that increasing the number of participants in future studies would provide more definitive results in specific manoeuvres. We acknowledge also the difficulties related to the somewhat unusual task that required pilots to unpack their manoeuvring mental model in a more quantifiable form represented by the Detailed Manoeuvre Plan.

5. CONCLUSIONS

In this paper, an analytical approach, comparing pilots' planned and simulated ship manoeuvres was introduced in order to more deeply understand the participant's mental models. A group of ten proficient marine pilots participated in the study. For the purposes of this paper, several variables were defined. Our expectation was that proficient pilots would have been able to provide plans that had a high degree of consistency with execution. Our aim was also to objectively quantify this matching in order to develop a methodology that could be profitably applied in other future comparative studies. Results obtained in the performance variables defined in Section 2.2, overall confirmed this expectation: pilots were generally able to perform according to their plans, showing only a limited number of differences in the scores recorded in the different ports, at different levels of difficulty and during different phases of the manoeuvres. Pearson correlation coefficients calculated between plans and execution also supported the expectation. Correlation coefficients between manoeuvres with the same level of difficulty further showed consistency in the way those exercises were designed, hence approached and performed. Significant differences instead pointed our attention to possible areas of improvement where pilots' approach to the manoeuvres could be discussed, reconsidered and modified. Research results confirm forecasting vessel's position was significantly more difficult for pilots during the swing than during other phases. Additional elements could have influenced these outcomes such as speed management, influenced by a different vessel's propulsion type in the easy manoeuvres and the interaction with the current in the more difficult ones. Data analysis also evidenced another marginally significant effect in the swing phase related to the estimation of the engine power. Pilots showed a tendency to slightly underestimate the use of the main engine during the most difficult manoeuvres. This was possibly related to the need in those manoeuvres to immediately respond and undertake effective actions to keep the vessel in a safe position during the rotation within a relatively smaller basin. This is just an example of how exploiting the results provided by the methodology introduced in this paper, it was possible to better analyse and unpack the complexity of shiphandling dynamics.

Ship manoeuvring requires an understanding and manipulation of complex interactions of masses and forces. It is rare that the effects of these interactions observe linear laws. This makes their appreciation and prediction a considerable task, especially when carried out without the support of appropriate tools and training. This very fact has led other researchers to explore the possibility, through fast time simulations, of making more accurate real time predictions of a vessel's behaviour while manoeuvring (Benedict, 2012). Nevertheless, the seamless integration of operators and state of the art technology (when available on ships' bridges) continues to evolve. Pilots perform their job with different types of vessels, each of them with its unique configuration of bridge equipment and personnel. They have to quickly adapt to the situation, making critical judgements as to the feasibility and the safety of the manoeuvre that they will immediately execute. In this study it was shown and quantified how such judgement could be sensitive to inaccuracies. Those inaccuracies may become more relevant as the situation departs from relatively stable and more linear conditions, as highlighted by the results obtained in the swing phase.

5.1. Future Applications and Added Value

The method described in this paper, if systematically adopted, provides a valid and reliable basis to better develop training and test manoeuvring techniques. Analysing results with this methodology could help to clearly identify optimal ranges of distances, speeds or use of available means, thus allowing the development of safer and more efficient manoeuvres. Remembering that the comparisons and the results obtained are based on simulated results, this research argues that it will be of the utmost importance in the future to apply the same methodology to real life shiphandling contexts. Using systematic feedback from similar manoeuvres in real situations, it will be possible to refine reliability and further validate simulated models.

Portable Pilotage Units (PPUs) and ships' Voyage Data Recorders (VDRs), engine logs, video and audio recordings can be exploited in order to collect this data in a workplace context. Within this naturalistic approach, it will not be possible to decide a priori the level of difficulty of the berthings so performed. Mooring operations, once recorded, can be grouped in different levels, comparing the conditions encountered, according for example to a “level matrix” similar to the one used for the simulator assessment here introduced. Such an approach may open the opportunity for new avenues of research and provide applications that may include: (a) the creation of standardised simulated exercises to select, train, evaluate and certify pilots based on national standards; (b) identification of more realistic construction criteria for actual/future port developments; (c) more reliable port operations safety criteria through more accurate risk assessments.

Based on the findings and the methodological approach reported in this initial foundation research, further empirical analysis on data differently sourced needs to be carried out. Comparative studies with different groups of shiphandlers at different levels of experience and engaged in different manoeuvres, used as models, would help to standardise scales able to better define the dimensions of shiphandling expertise.