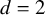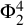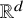1 Introduction
1.1 Log-correlated Gibbs measures
In this paper, we study the Gibbs measure
![]() $\rho $
on the d-dimensional torus on
$\rho $
on the d-dimensional torus on
![]() ${\mathbb {T}}^d = ({\mathbb {R}}/2\pi \mathbb {Z})^d$
, formally written asFootnote
1
${\mathbb {T}}^d = ({\mathbb {R}}/2\pi \mathbb {Z})^d$
, formally written asFootnote
1
 $$ \begin{align} d\rho(u) = Z^{-1} \exp \bigg(\frac{\lambda}{k} \int_{{\mathbb{T}}^d} u^k dx\bigg) d\mu(u), \end{align} $$
$$ \begin{align} d\rho(u) = Z^{-1} \exp \bigg(\frac{\lambda}{k} \int_{{\mathbb{T}}^d} u^k dx\bigg) d\mu(u), \end{align} $$
where
![]() $k \geq 3$
is an integer and the coupling constant
$k \geq 3$
is an integer and the coupling constant
![]() $\lambda \in {\mathbb {R}}\setminus \{0\}$
denotes the strength of interaction, which is repulsive (i.e., defocusing) when
$\lambda \in {\mathbb {R}}\setminus \{0\}$
denotes the strength of interaction, which is repulsive (i.e., defocusing) when
![]() $\lambda < 0$
and k is even, and is attractive (i.e., focusing) when
$\lambda < 0$
and k is even, and is attractive (i.e., focusing) when
![]() $\lambda> 0$
or k is odd.Footnote
2
Here,
$\lambda> 0$
or k is odd.Footnote
2
Here,
![]() $\mu $
is the log-correlated Gaussian free field on
$\mu $
is the log-correlated Gaussian free field on
![]() ${\mathbb {T}}^d$
, formally given by
${\mathbb {T}}^d$
, formally given by
 $$ \begin{align} d \mu = Z^{-1} e^{-\frac 12 \| u\|_{H^{d/ 2} }^2 } du & = Z^{-1} \prod_{n \in \mathbb{Z}^d} e^{-\frac 12 \langle n \rangle^{d} |\widehat u(n)|^2} d\widehat u(n) , \end{align} $$
$$ \begin{align} d \mu = Z^{-1} e^{-\frac 12 \| u\|_{H^{d/ 2} }^2 } du & = Z^{-1} \prod_{n \in \mathbb{Z}^d} e^{-\frac 12 \langle n \rangle^{d} |\widehat u(n)|^2} d\widehat u(n) , \end{align} $$
where
![]() $\langle \,\cdot \, \rangle = (1+|\,\cdot \,|^2)^{\frac {1}{2}}$
and
$\langle \,\cdot \, \rangle = (1+|\,\cdot \,|^2)^{\frac {1}{2}}$
and
![]() $\widehat u(n)$
denotes the Fourier coefficient of u. When
$\widehat u(n)$
denotes the Fourier coefficient of u. When
![]() $d = 2$
,
$d = 2$
,
![]() $\mu $
corresponds to the massive Gaussian free field on
$\mu $
corresponds to the massive Gaussian free field on
![]() ${\mathbb {T}}^2$
. Recall that this Gaussian measure
${\mathbb {T}}^2$
. Recall that this Gaussian measure
![]() $\mu $
is nothing but the induced probability measure under the map:Footnote
3
$\mu $
is nothing but the induced probability measure under the map:Footnote
3
 $$ \begin{align} \omega\in \Omega \longmapsto u(\omega) = \sum_{n \in {\mathbb{Z}}^d } \frac{g_n(\omega)}{\langle n \rangle^{\frac{d}{2}}} e_n, \end{align} $$
$$ \begin{align} \omega\in \Omega \longmapsto u(\omega) = \sum_{n \in {\mathbb{Z}}^d } \frac{g_n(\omega)}{\langle n \rangle^{\frac{d}{2}}} e_n, \end{align} $$
where
![]() $e_n=e^{i n\cdot x}$
and
$e_n=e^{i n\cdot x}$
and
![]() $\{ g_n \}_{n \in \mathbb {Z}^d}$
is a sequence of mutually independent standard complex-valued Gaussian random variables on a probability space
$\{ g_n \}_{n \in \mathbb {Z}^d}$
is a sequence of mutually independent standard complex-valued Gaussian random variables on a probability space
![]() $(\Omega ,\mathcal {F},\mathbb {P})$
conditioned that
$(\Omega ,\mathcal {F},\mathbb {P})$
conditioned that
![]() $g_{-n} = \overline {g_n}$
.Footnote
4
See Remark 1.1. It is well known that a typical function u in the support of
$g_{-n} = \overline {g_n}$
.Footnote
4
See Remark 1.1. It is well known that a typical function u in the support of
![]() $\mu $
is merely a distribution and thus a renormalization on the potential energy
$\mu $
is merely a distribution and thus a renormalization on the potential energy
![]() $\frac \lambda k \int _{{\mathbb {T}}^d} u^k dx$
is required for the construction of the Gibbs measure
$\frac \lambda k \int _{{\mathbb {T}}^d} u^k dx$
is required for the construction of the Gibbs measure
![]() $\rho $
.
$\rho $
.
Our main goal in this paper is to study the Gibbs measure
![]() $\rho $
in (1.1) in the focusing case. In particular, we prove the nonnormalizability of the focusing Gibbs measure
$\rho $
in (1.1) in the focusing case. In particular, we prove the nonnormalizability of the focusing Gibbs measure
![]() $\rho $
with the quartic interaction (
$\rho $
with the quartic interaction (
![]() $\lambda> 0$
and
$\lambda> 0$
and
![]() $k = 4$
). See Theorem 1.4. We also present a brief discussion on the construction of the Gibbs measure with the cubic interaction. See Theorem 1.9.
$k = 4$
). See Theorem 1.4. We also present a brief discussion on the construction of the Gibbs measure with the cubic interaction. See Theorem 1.9.
Before proceeding further, let us first go over the defocusing case:
![]() $\lambda < 0$
and
$\lambda < 0$
and
![]() $k \geq 4$
is an even integer. When
$k \geq 4$
is an even integer. When
![]() $d = 2$
, the defocusing Gibbs measure
$d = 2$
, the defocusing Gibbs measure
![]() $\rho $
in (1.1) corresponds to the well-studied
$\rho $
in (1.1) corresponds to the well-studied
![]() $\Phi ^k_2$
-measure whose construction follows from the hypercontractivity of the Ornstein–Uhlenbeck semigroup (see Lemma 2.3) and Nelson’s estimate [Reference Nelson39]. See [Reference Simon60, Reference Glimm, Jaffe and Physics26, Reference Da Prato and Tubaro21, Reference Oh and Thomann47]. For a general dimension
$\Phi ^k_2$
-measure whose construction follows from the hypercontractivity of the Ornstein–Uhlenbeck semigroup (see Lemma 2.3) and Nelson’s estimate [Reference Nelson39]. See [Reference Simon60, Reference Glimm, Jaffe and Physics26, Reference Da Prato and Tubaro21, Reference Oh and Thomann47]. For a general dimension
![]() $d \geq 1$
, the same argument allows us to construct the defocusing Gibbs measure
$d \geq 1$
, the same argument allows us to construct the defocusing Gibbs measure
![]() $\rho $
in (1.1) for any
$\rho $
in (1.1) for any
![]() $\lambda < 0$
and any even integer
$\lambda < 0$
and any even integer
![]() $k \ge 4$
. Let us briefly go over the procedure.
$k \ge 4$
. Let us briefly go over the procedure.
Given
![]() $N \in \mathbb {N}$
, we define the frequency projectorFootnote
5
$N \in \mathbb {N}$
, we define the frequency projectorFootnote
5
![]() $\pi _N$
by
$\pi _N$
by
For u as in (1.3), set
![]() $u_N = \pi _N u$
. Then, for each fixed
$u_N = \pi _N u$
. Then, for each fixed
![]() $x \in {\mathbb {T}}^d$
,
$x \in {\mathbb {T}}^d$
,
![]() $u_N(x)$
is a mean-zero real-valued Gaussian random variable with variance
$u_N(x)$
is a mean-zero real-valued Gaussian random variable with variance
 $$ \begin{align} \sigma_N = {\mathbb{E}}\big[u_N^2(x)\big] = \sum _{|n| \le N} \frac{1}{\langle n \rangle^d} \sim \log N \longrightarrow \infty, \end{align} $$
$$ \begin{align} \sigma_N = {\mathbb{E}}\big[u_N^2(x)\big] = \sum _{|n| \le N} \frac{1}{\langle n \rangle^d} \sim \log N \longrightarrow \infty, \end{align} $$
as
![]() $N \to \infty $
. Note that
$N \to \infty $
. Note that
![]() $\sigma _N$
is independent of
$\sigma _N$
is independent of
![]() $x \in {\mathbb {T}}^d$
in the current translation invariant setting. We then define the renormalized power (= Wick power)
$x \in {\mathbb {T}}^d$
in the current translation invariant setting. We then define the renormalized power (= Wick power)
![]() $:\! u_N^k\!:$
by setting
$:\! u_N^k\!:$
by setting
where
![]() $H_k(x;\sigma )$
is the Hermite polynomial of degree k with a variance parameter
$H_k(x;\sigma )$
is the Hermite polynomial of degree k with a variance parameter
![]() $\sigma $
defined through the following generating function:Footnote
6
$\sigma $
defined through the following generating function:Footnote
6
 $$ \begin{align} F(t, x; \sigma) \stackrel{\mathrm{def}}{=} e^{tx - \frac{1}{2}\sigma t^2} = \sum_{k = 0}^\infty \frac{t^k}{k!} H_k(x;\sigma). \end{align} $$
$$ \begin{align} F(t, x; \sigma) \stackrel{\mathrm{def}}{=} e^{tx - \frac{1}{2}\sigma t^2} = \sum_{k = 0}^\infty \frac{t^k}{k!} H_k(x;\sigma). \end{align} $$
For readers’ convenience, we write out the first few Hermite polynomials:
See, for example, [Reference Kuo32], for further properties of the Hermite polynomials. We then define the following renormalized truncated potential energy:
where the coupling constant
![]() $\lambda < 0 $
denotes the strength of repulsive interaction. A standard computation allows us to show that
$\lambda < 0 $
denotes the strength of repulsive interaction. A standard computation allows us to show that
![]() $\{R_N \}_{N \in \mathbb {N}}$
forms a Cauchy sequence in
$\{R_N \}_{N \in \mathbb {N}}$
forms a Cauchy sequence in
![]() $L^p(\mu )$
for any finite
$L^p(\mu )$
for any finite
![]() $p \geq 1$
, thus converging to some random variable
$p \geq 1$
, thus converging to some random variable
![]() $R(u)$
:
$R(u)$
:
in
![]() $L^p(\mu )$
and almost surely See, for example, Proposition 1.1 in [Reference Oh and Thomann47].Footnote
7
$L^p(\mu )$
and almost surely See, for example, Proposition 1.1 in [Reference Oh and Thomann47].Footnote
7
Define the renormalized truncated Gibbs measure
![]() $\rho _{N}$
by
$\rho _{N}$
by
Then, a standard application of Nelson’s estimateFootnote
8
yields the following uniform exponential integrability of the density; given any finite
![]() $ p \ge 1$
, there exists
$ p \ge 1$
, there exists
![]() $C_{p, d}> 0$
such that
$C_{p, d}> 0$
such that
See, for example, Proposition 1.2 in [Reference Oh and Thomann47]. Then, the uniform bound (1.10) together with softer convergence in measure (as a consequence of (1.9)) implies the following
![]() $L^p$
-convergence of the density:
$L^p$
-convergence of the density:
See, for example, Remark 3.8 in [Reference Tzvetkov66]. This allows us to construct the defocusing Gibbs measure:
as a limit of the truncated defocusing Gibbs measure
![]() $\rho _N$
.
$\rho _N$
.
As mentioned above, our main goal is to study the Gibbs measure
![]() $\rho $
with the log-correlated Gaussian field
$\rho $
with the log-correlated Gaussian field
![]() $\mu $
in the focusing case (
$\mu $
in the focusing case (
![]() $\lambda> 0$
). Before doing so, we present a brief discussion on dynamical problems associated with these Gibbs measures in Subsection 1.2. We then present the nonnormalizability of the focusing log-correlated Gibbs measure with the quartic interaction (Theorem 1.4) and the construction of the focusing log-correlated Gibbs measure with the cubic interaction (Theorem 1.9).
$\lambda> 0$
). Before doing so, we present a brief discussion on dynamical problems associated with these Gibbs measures in Subsection 1.2. We then present the nonnormalizability of the focusing log-correlated Gibbs measure with the quartic interaction (Theorem 1.4) and the construction of the focusing log-correlated Gibbs measure with the cubic interaction (Theorem 1.9).
Remark 1.1. Recall from [Reference Aronszajn and Smith2, (4,2)] that the Green’s function
![]() $G_{{\mathbb {R}}^d}$
for
$G_{{\mathbb {R}}^d}$
for
![]() $(1 - \Delta )^{\frac {d}{2}}$
on
$(1 - \Delta )^{\frac {d}{2}}$
on
![]() ${\mathbb {R}}^d$
satisfies
${\mathbb {R}}^d$
satisfies
as
![]() $x \to 0$
for some
$x \to 0$
for some
![]() $c_d> 0$
. Here, in view of the translation invariance, we view G as a function of one variable through
$c_d> 0$
. Here, in view of the translation invariance, we view G as a function of one variable through
![]() $G(x) \equiv G(x, 0)$
. It is a smooth function on
$G(x) \equiv G(x, 0)$
. It is a smooth function on
![]() ${\mathbb {R}}^d \setminus \{0\}$
and decays exponentially as
${\mathbb {R}}^d \setminus \{0\}$
and decays exponentially as
![]() $|x| \to \infty $
; see [Reference Grafakos28, Proposition 1.2.5].
$|x| \to \infty $
; see [Reference Grafakos28, Proposition 1.2.5].
Now, let G be the Green’s function for
![]() $(1-\Delta )^{\frac {d}{2}}$
on
$(1-\Delta )^{\frac {d}{2}}$
on
![]() ${\mathbb {T}}^d$
. Then, we have
${\mathbb {T}}^d$
. Then, we have
 $$ \begin{align} G \stackrel{\mathrm{def}}{=} (1-\Delta)^{-\frac{d}{2}} \delta_0 = \sum_{n\in\mathbb{Z}^d}\frac 1{\langle n \rangle^{d}}e_n = \lim_{N \to \infty} \sum_{|n|\leq N}\frac 1{\langle n \rangle^{d}}e_n. \end{align} $$
$$ \begin{align} G \stackrel{\mathrm{def}}{=} (1-\Delta)^{-\frac{d}{2}} \delta_0 = \sum_{n\in\mathbb{Z}^d}\frac 1{\langle n \rangle^{d}}e_n = \lim_{N \to \infty} \sum_{|n|\leq N}\frac 1{\langle n \rangle^{d}}e_n. \end{align} $$
Recall the Poisson summation formula ([Reference Grafakos27, Theorem 3.2.8]):
for any function f on
![]() ${\mathbb {R}}^d$
such that
${\mathbb {R}}^d$
such that
![]() $|f(x)|\lesssim \langle x \rangle ^{-d-\delta }$
for some
$|f(x)|\lesssim \langle x \rangle ^{-d-\delta }$
for some
![]() $\delta> 0$
and
$\delta> 0$
and
![]() $\sum _{n \in \mathbb {Z}^d} |\mathcal {F}_{{\mathbb {R}}^d} (f)(n)| < \infty $
. The Poisson summation formula (1.13) is a typical tool to pass information from
$\sum _{n \in \mathbb {Z}^d} |\mathcal {F}_{{\mathbb {R}}^d} (f)(n)| < \infty $
. The Poisson summation formula (1.13) is a typical tool to pass information from
![]() ${\mathbb {R}}^d$
to a periodic torus
${\mathbb {R}}^d$
to a periodic torus
![]() ${\mathbb {T}}^d$
; see [Reference Bényi and Oh4, Reference Oh and Wang50, Reference Bényi, Oh and Zhao5] for example. Here,
${\mathbb {T}}^d$
; see [Reference Bényi and Oh4, Reference Oh and Wang50, Reference Bényi, Oh and Zhao5] for example. Here,
![]() $\mathcal {F}_{{\mathbb {R}}^d} (f)(n)$
denotes the Fourier transform of f on
$\mathcal {F}_{{\mathbb {R}}^d} (f)(n)$
denotes the Fourier transform of f on
![]() ${\mathbb {R}}^d$
given by
${\mathbb {R}}^d$
given by
where
![]() $dx = dx_{{\mathbb {R}}^d}$
is the standard Lebesgue measure on
$dx = dx_{{\mathbb {R}}^d}$
is the standard Lebesgue measure on
![]() ${\mathbb {R}}^d$
. Then, by applying (1.13) (with a frequency truncation
${\mathbb {R}}^d$
. Then, by applying (1.13) (with a frequency truncation
![]() $\pi _N$
and taking
$\pi _N$
and taking
![]() $N \to \infty $
) together with the asymptotics (1.11), we conclude that there exists a smooth function
$N \to \infty $
) together with the asymptotics (1.11), we conclude that there exists a smooth function
![]() $ R$
such that
$ R$
such that
for any
![]() $x \in {\mathbb {T}}^d \setminus \{0\}$
. See [Reference Oh, Robert, Sosoe and Wang44, Section 2] for a related discussion. Finally, from (1.3), (1.12) and (1.15), we obtain
$x \in {\mathbb {T}}^d \setminus \{0\}$
. See [Reference Oh, Robert, Sosoe and Wang44, Section 2] for a related discussion. Finally, from (1.3), (1.12) and (1.15), we obtain
for any
![]() $x, y \in {\mathbb {T}}^d$
with
$x, y \in {\mathbb {T}}^d$
with
![]() $x\ne y$
.
$x\ne y$
.
1.2 Dynamical problems associated with the log-correlated Gibbs measures
From the viewpoint of mathematical physics such as Euclidean quantum field theory, the construction of the Gibbs measures
![]() $\rho $
in (1.1) is of interest in its own right. In this subsection, we briefly discuss some examples of dynamical problems associated with these log-correlated Gibbs measures. These examples show the importance of studying the log-correlated Gibbs measure
$\rho $
in (1.1) is of interest in its own right. In this subsection, we briefly discuss some examples of dynamical problems associated with these log-correlated Gibbs measures. These examples show the importance of studying the log-correlated Gibbs measure
![]() $\rho $
in (1.1) from the (stochastic) partial differential equation (PDE) point of view.
$\rho $
in (1.1) from the (stochastic) partial differential equation (PDE) point of view.
The associated energy functionalFootnote
9
for the Gibbs measure
![]() $\rho $
in (1.1) is given by
$\rho $
in (1.1) is given by
The study of the Gibbs measures for Hamiltonian PDEs, initiated by [Reference Friedlander25, Reference Lebowitz, Rose and Speer33, Reference Bourgain8, Reference McKean38, Reference Bourgain11], has been an active field of research over the last decade. We first list examples of the Hamiltonian PDEs generated by this energy functional
![]() $E(u)$
in (1.16) along with the references.
$E(u)$
in (1.16) along with the references.
-
(i) fractional nonlinear Schrödinger equation (for complex-valued u):
(1.17)Equation (1.17) corresponds to the nonlinear half-wave equation (also known as the semirelativistic nonlinear Schrödinger equation (NLS)) when $$ \begin{align} i\partial_t u + (1-\Delta)^{{\frac{d}{2}}}u -\lambda | u |^{k-2}u=0. \end{align} $$
$$ \begin{align} i\partial_t u + (1-\Delta)^{{\frac{d}{2}}}u -\lambda | u |^{k-2}u=0. \end{align} $$
 $ d= 1$
, to the well-studied cubic NLS when
$ d= 1$
, to the well-studied cubic NLS when
 $d = 2$
([Reference Bourgain11, Reference Oh and Thomann47, Reference Deng, Nahmod and Yue23]), and to the biharmonic NLS when
$d = 2$
([Reference Bourgain11, Reference Oh and Thomann47, Reference Deng, Nahmod and Yue23]), and to the biharmonic NLS when
 $d = 4$
.
$d = 4$
.
In Appendix A, we also provide a brief discussion on the Gibbs measure for the Zakharov system when
 $d = 2$
.
$d = 2$
. -
(ii) fractional nonlinear wave equation (NLW):Footnote 10
(1.18)Equation (1.18) corresponds to the NLW equation (or the nonlinear Klein–Gordon equation) when $$ \begin{align} \partial_t^2 u + (1- \Delta)^{\frac{d}{2}} u - \lambda u^{k-1} = 0. \end{align} $$
$$ \begin{align} \partial_t^2 u + (1- \Delta)^{\frac{d}{2}} u - \lambda u^{k-1} = 0. \end{align} $$
 $d = 2$
([Reference Oh and Thomann48]), and to the nonlinear beam equation when
$d = 2$
([Reference Oh and Thomann48]), and to the nonlinear beam equation when
 $d = 4$
.
$d = 4$
.
-
(iii) generalized Benjamin–Ono equation (with
 $d = 1$
):Footnote
11
(1.19)where
$d = 1$
):Footnote
11
(1.19)where $$ \begin{align} \partial_t u+\mathcal{H}\partial_x^2u -\lambda \partial_x (u^{k-1})=0, \end{align} $$
$$ \begin{align} \partial_t u+\mathcal{H}\partial_x^2u -\lambda \partial_x (u^{k-1})=0, \end{align} $$
 $\mathcal H$
denotes the Hilbert transform defined by
$\mathcal H$
denotes the Hilbert transform defined by
 $\widehat {\mathcal H f}(n) = -i \text {sgn}(n) \widehat f(n)$
with the understanding that
$\widehat {\mathcal H f}(n) = -i \text {sgn}(n) \widehat f(n)$
with the understanding that
 $\widehat {\mathcal H f}(0) = 0$
. Equation (1.19) is known as the Benjamin–Ono equation when
$\widehat {\mathcal H f}(0) = 0$
. Equation (1.19) is known as the Benjamin–Ono equation when
 $k = 3$
([Reference Tzvetkov67, Reference Deng22]) and the modified Benjamin–Ono equation when
$k = 3$
([Reference Tzvetkov67, Reference Deng22]) and the modified Benjamin–Ono equation when
 $k = 4$
.
$k = 4$
.
Next, we list stochastic PDEs associated with the Gibbs measure
![]() $\rho $
in (1.1).
$\rho $
in (1.1).
-
(iv) parabolic stochastic quantization equation [Reference Parisi and Wu52]:
(1.20) $$ \begin{align} \partial_t u + (1 - \Delta)^{\frac{d}{2}} u -\lambda u^{k-1} = \sqrt 2\xi. \end{align} $$
$$ \begin{align} \partial_t u + (1 - \Delta)^{\frac{d}{2}} u -\lambda u^{k-1} = \sqrt 2\xi. \end{align} $$
Here,
 $\xi $
denotes the space-time white noise on
$\xi $
denotes the space-time white noise on
 ${\mathbb {T}}^d \times {\mathbb {R}}_+$
. When
${\mathbb {T}}^d \times {\mathbb {R}}_+$
. When
 $d = 2$
and
$d = 2$
and
 $\lambda < 0$
, (1.20) corresponds to the standard parabolic
$\lambda < 0$
, (1.20) corresponds to the standard parabolic
 $\Phi ^k_2$
-model ([Reference Da Prato and Debussche20, Reference Röckner, Zhu and Zhu56, Reference Tsatsoulis and Weber65]).
$\Phi ^k_2$
-model ([Reference Da Prato and Debussche20, Reference Röckner, Zhu and Zhu56, Reference Tsatsoulis and Weber65]). -
(v) canonical stochastic quantization equation [Reference Ryang, Saito and Shigemoto57]:
(1.21) $$ \begin{align} \partial_t^2 u + \partial_t u + (1 - \Delta)^{\frac{d}{2}} u -\lambda u^{k-1} = \sqrt{2} \xi.\end{align} $$
$$ \begin{align} \partial_t^2 u + \partial_t u + (1 - \Delta)^{\frac{d}{2}} u -\lambda u^{k-1} = \sqrt{2} \xi.\end{align} $$
Equation (1.21) corresponds to the stochastic damped NLW when
 $d = 2$
([Reference Gubinelli, Koch and Oh29, Reference Gubinelli, Koch, Oh and Tolomeo30, Reference Tolomeo63]), and to the stochastic damped nonlinear beam equation when
$d = 2$
([Reference Gubinelli, Koch and Oh29, Reference Gubinelli, Koch, Oh and Tolomeo30, Reference Tolomeo63]), and to the stochastic damped nonlinear beam equation when
 $d = 4$
.
$d = 4$
.
When
![]() $d = 2$
, the conservative stochastic Cahn–Hilliard equation is known to (formally) preserve the Gibbs measure
$d = 2$
, the conservative stochastic Cahn–Hilliard equation is known to (formally) preserve the Gibbs measure
![]() $\rho $
in (1.1) ([Reference Röckner, Yang and Zhu55]).
$\rho $
in (1.1) ([Reference Röckner, Yang and Zhu55]).
For the equations listed above, once we establish local well-posedness almost surely with respect to the Gibbs measure initial data, Bourgain’s invariant measure argument [Reference Bourgain8, Reference Bourgain11] allows us to construct almost sure global dynamics and to prove invariance of the Gibbs measure. However, since functions on the support of the log-correlated Gibbs measure
![]() $\rho $
in (1.1) almost surely belong to the
$\rho $
in (1.1) almost surely belong to the
![]() $L^p$
-based Sobolev spaces
$L^p$
-based Sobolev spaces
![]() $W^{s, p}({\mathbb {T}}^d) \setminus L^p({\mathbb {T}}^d)$
only for
$W^{s, p}({\mathbb {T}}^d) \setminus L^p({\mathbb {T}}^d)$
only for
![]() $ s < 0$
with any
$ s < 0$
with any
![]() $1 \le p \le \infty $
, there are only a handful of the well-posedness results [Reference Bourgain11, Reference Deng22, Reference Oh and Thomann48, Reference Gubinelli, Koch and Oh29, Reference Deng, Nahmod and Yue23] for the Hamiltonian PDEs mentioned above (including (1.21)).
$1 \le p \le \infty $
, there are only a handful of the well-posedness results [Reference Bourgain11, Reference Deng22, Reference Oh and Thomann48, Reference Gubinelli, Koch and Oh29, Reference Deng, Nahmod and Yue23] for the Hamiltonian PDEs mentioned above (including (1.21)).
Remark 1.2. We point out that as long as we can construct the Gibbs measure, a compactness argument with invariance of the truncated Gibbs measures and Skorokhod’s theorem allows us to construct (nonunique) global-in-time dynamics along with invariance of the Gibbs measure in some mild sense. See [Reference Albeverio and Cruzeiro1, Reference Da Prato and Debussche19, Reference Burq, Thomann and Tzvetkov14, Reference Oh and Thomann47, Reference Oh, Richards and Thomann43]. In our current setting, this almost sure global existence result holds for (i) the defocusing case (
![]() $\lambda < 0$
and even
$\lambda < 0$
and even
![]() $k \geq 4$
; see the discussion in Subsection 1.1) and (ii) the quadratic nonlinearity (i.e.,
$k \geq 4$
; see the discussion in Subsection 1.1) and (ii) the quadratic nonlinearity (i.e.,
![]() $k = 3$
). See Theorem 1.9 for the latter case.
$k = 3$
). See Theorem 1.9 for the latter case.
Remark 1.3. Given
![]() $\delta> 0$
, consider the intermediate long wave equation (ILW) on
$\delta> 0$
, consider the intermediate long wave equation (ILW) on
![]() ${\mathbb {T}}$
:
${\mathbb {T}}$
:
where the dispersion operator
![]() $\mathcal {G}_{\delta } $
is given by
$\mathcal {G}_{\delta } $
is given by
Equation (1.22) models the internal wave propagation of the interface in a stratified fluid of finite depth
![]() $\delta> 0$
, providing a natural connection between the Benjamin–Ono regime (
$\delta> 0$
, providing a natural connection between the Benjamin–Ono regime (
![]() $\delta = \infty $
) and the Korteweg–de Vries (KdV) regime (
$\delta = \infty $
) and the Korteweg–de Vries (KdV) regime (
![]() $\delta = 0$
). Indeed, there are results establishing convergence of ILW to the Benjamin–Ono equation (and the KdV equation) as
$\delta = 0$
). Indeed, there are results establishing convergence of ILW to the Benjamin–Ono equation (and the KdV equation) as
![]() $\delta \to \infty $
(and
$\delta \to \infty $
(and
![]() $\delta \to 0$
, respectively); see [Reference Li34, Reference Chapouto, Forlano, Li, Oh and Pilod15, Reference Chapouto, Li, Oh and Pilod16] and the references therein. While it is not obvious from the rather complicated dispersive symbol in (1.23), the Gibbs measure associated to ILW is indeed log-correlated, and the results in this paper apply to the Gibbs measure associated to the generalized ILW (where the nonlinearity
$\delta \to 0$
, respectively); see [Reference Li34, Reference Chapouto, Forlano, Li, Oh and Pilod15, Reference Chapouto, Li, Oh and Pilod16] and the references therein. While it is not obvious from the rather complicated dispersive symbol in (1.23), the Gibbs measure associated to ILW is indeed log-correlated, and the results in this paper apply to the Gibbs measure associated to the generalized ILW (where the nonlinearity
![]() $\partial _x (u^2)$
in (1.22) is replaced by
$\partial _x (u^2)$
in (1.22) is replaced by
![]() $\lambda \partial _x (u^{k-1})$
). Furthermore, as
$\lambda \partial _x (u^{k-1})$
). Furthermore, as
![]() $\delta \to \infty $
(and
$\delta \to \infty $
(and
![]() $\delta \to 0$
), the Gibbs measure for the (generalized) ILW converges to that for the (generalized) Benjamin–Ono equation (and the (generalized) KdV equation, respectively) in an appropriate sense. See a recent work [Reference Li, Oh and Zheng35] for a further discussion. See also [Reference Chapouto, Li and Oh17] for the construction and convergence of invariant measures for ILW associated with higher order conservation laws.
$\delta \to 0$
), the Gibbs measure for the (generalized) ILW converges to that for the (generalized) Benjamin–Ono equation (and the (generalized) KdV equation, respectively) in an appropriate sense. See a recent work [Reference Li, Oh and Zheng35] for a further discussion. See also [Reference Chapouto, Li and Oh17] for the construction and convergence of invariant measures for ILW associated with higher order conservation laws.
1.3 Nonnormalizability of the focusing Gibbs measure
We now turn our attention to the focusing case. In this subsection, we study the Gibbs measure
![]() $\rho $
in (1.1) with the focusing quartic interaction (
$\rho $
in (1.1) with the focusing quartic interaction (
![]() $\lambda> 0$
and
$\lambda> 0$
and
![]() $k = 4$
). In this case, we prove the following nonnormalizability of the (renormalized) focusing Gibbs measure
$k = 4$
). In this case, we prove the following nonnormalizability of the (renormalized) focusing Gibbs measure
![]() $\rho $
.
$\rho $
.
Theorem 1.4. Let
![]() $\lambda> 0$
and
$\lambda> 0$
and
![]() $k = 4$
. Then, given any
$k = 4$
. Then, given any
![]() $K> 0$
, we have
$K> 0$
, we have
where
![]() $R_N$
is the renormalized potential energy defined in (1.8) with
$R_N$
is the renormalized potential energy defined in (1.8) with
![]() $k = 4$
. Moreover, the divergence rate of
$k = 4$
. Moreover, the divergence rate of
![]() $Z_{K,N}$
is given by
$Z_{K,N}$
is given by
as
![]() $N\to \infty $
. Here,
$N\to \infty $
. Here,
![]() $C_B$
is the optimal constant in Bernstein’s inequality:
$C_B$
is the optimal constant in Bernstein’s inequality:
where P is the sharp Fourier projection onto the unit ball:
and
![]() $\sigma _N$
is defined in (1.5). Moreover, we have
$\sigma _N$
is defined in (1.5). Moreover, we have
where
![]() $R(u)$
is the limit of
$R(u)$
is the limit of
![]() $R_N(u)$
defined in (1.9). In particular, the focusing Gibbs measure (even with a Wick-ordered
$R_N(u)$
defined in (1.9). In particular, the focusing Gibbs measure (even with a Wick-ordered
![]() $L^2$
-cutoff) cannot be defined as a probability measure.
$L^2$
-cutoff) cannot be defined as a probability measure.
When
![]() $d = 2$
, Theorem 1.4 provides an alternative proof of the nonnormalizability result for of the focusing
$d = 2$
, Theorem 1.4 provides an alternative proof of the nonnormalizability result for of the focusing
![]() $\Phi ^4_2$
-measure due to Brydges and Slade [Reference Brydges and Slade13] whose proof is based on analysis of a model closely related to the Berlin–Kac spherical model. Furthermore, Theorem 1.4 provides a precise rate (1.25) of divergence of the partition function
$\Phi ^4_2$
-measure due to Brydges and Slade [Reference Brydges and Slade13] whose proof is based on analysis of a model closely related to the Berlin–Kac spherical model. Furthermore, Theorem 1.4 provides a precise rate (1.25) of divergence of the partition function
![]() $Z_{K, N}$
. Our strategy for proving the divergence rate (1.25) is straightforward and thus is expected to be applicable to a wide range of models.
$Z_{K, N}$
. Our strategy for proving the divergence rate (1.25) is straightforward and thus is expected to be applicable to a wide range of models.
Our proof of Theorem 1.4 is based on the variational approach due to Barashkov and Gubinelli [Reference Barashkov and Gubinelli3]. More precisely, we will rely on the Boué–Dupuis variational formula [Reference Boué and Dupuis7, Reference Üstünel68]; see Lemma 3.1. Our main task is to construct a drift term which achieves the desired divergence (1.24). Our argument is inspired by recent works by the third author with Weber [Reference Tolomeo and Weber64] and by the first and third authors with Okamoto [Reference Oh, Okamoto and Tolomeo41, Reference Oh, Okamoto and Tolomeo42]. In particular, our presentation closely follows but refines that in [Reference Oh, Okamoto and Tolomeo41], where an analogous nonnormalizability is shown for focusing Gibbs measures on
![]() ${\mathbb {T}}^3$
with a quartic interaction of Hartree-type. We point out that the argument in [Reference Oh, Okamoto and Tolomeo41] shows nonnormalizability only for large
${\mathbb {T}}^3$
with a quartic interaction of Hartree-type. We point out that the argument in [Reference Oh, Okamoto and Tolomeo41] shows nonnormalizability only for large
![]() $K \gg 1$
and thus we need to refine the argument to prove the divergence (1.24) for any
$K \gg 1$
and thus we need to refine the argument to prove the divergence (1.24) for any
![]() $K> 0$
. The main new ingredient (as compared to [Reference Oh, Okamoto and Tolomeo41]) is the construction a drift term which approximates a blowup profile, such that the Wick-ordered
$K> 0$
. The main new ingredient (as compared to [Reference Oh, Okamoto and Tolomeo41]) is the construction a drift term which approximates a blowup profile, such that the Wick-ordered
![]() $L^2$
-cutoff does not exclude this blowup profile for any cutoff size
$L^2$
-cutoff does not exclude this blowup profile for any cutoff size
![]() $K>0$
. See, in particular, Lemma 3.4 and the proof of (3.42). We also mention related works [Reference Lebowitz, Rose and Speer33, Reference Brydges and Slade13, Reference Rider53, Reference Bourgain and Bulut12, Reference Oh, Sosoe and Tolomeo46, Reference Robert, Seong, Tolomeo and Wang54] on the nonnormalizability (and other issues) for focusing Gibbs measures.
$K>0$
. See, in particular, Lemma 3.4 and the proof of (3.42). We also mention related works [Reference Lebowitz, Rose and Speer33, Reference Brydges and Slade13, Reference Rider53, Reference Bourgain and Bulut12, Reference Oh, Sosoe and Tolomeo46, Reference Robert, Seong, Tolomeo and Wang54] on the nonnormalizability (and other issues) for focusing Gibbs measures.
Remark 1.5. As a direct consequence of (1.24), we have
 $$ \begin{align*} \sup_{N \in \mathbb{N}} {\mathbb{E}}_{\mu} \Big[ e^{ R_N (u)} \Big] & \ge \sup_{N \in \mathbb{N}} {\mathbb{E}}_{\mu} \Big[ \mathbf 1_{\{\int_{{\mathbb{T}}^d} \, :u_N^2: \, dx \, \leq K\}} e^{ R_N (u)} \Big]\\ & \ge \sup_{N \in \mathbb{N}} {\mathbb{E}}_{\mu} \Big[ \mathbf 1_{\{|\int_{{\mathbb{T}}^d} \, :u_N^2: \, dx| \, \leq K\}} e^{ R_N (u)} \Big] = \infty. \end{align*} $$
$$ \begin{align*} \sup_{N \in \mathbb{N}} {\mathbb{E}}_{\mu} \Big[ e^{ R_N (u)} \Big] & \ge \sup_{N \in \mathbb{N}} {\mathbb{E}}_{\mu} \Big[ \mathbf 1_{\{\int_{{\mathbb{T}}^d} \, :u_N^2: \, dx \, \leq K\}} e^{ R_N (u)} \Big]\\ & \ge \sup_{N \in \mathbb{N}} {\mathbb{E}}_{\mu} \Big[ \mathbf 1_{\{|\int_{{\mathbb{T}}^d} \, :u_N^2: \, dx| \, \leq K\}} e^{ R_N (u)} \Big] = \infty. \end{align*} $$
Remark 1.6. In the one-dimensional setting studied in [Reference Lebowitz, Rose and Speer33, Reference Oh, Sosoe and Tolomeo46], the sharp Gagliardo–Nirenberg inequality on
![]() ${\mathbb {R}}$
plays an important role in determining (non-)normalizability of the focusing Gibbs measure with a sextic interaction. In our current problem with a quartic interaction, Bernstein’s inequality (1.26) on
${\mathbb {R}}$
plays an important role in determining (non-)normalizability of the focusing Gibbs measure with a sextic interaction. In our current problem with a quartic interaction, Bernstein’s inequality (1.26) on
![]() ${\mathbb {R}}^d$
, which is essentially a frequency-localized version of Sobolev’s inequality, plays a crucial role in determining the precise divergence rate (1.25). We point out that this particular form of Bernstein’s inequality appears due to the form of the regularization we use for our problem (namely, the sharp frequency truncation onto the frequencies
${\mathbb {R}}^d$
, which is essentially a frequency-localized version of Sobolev’s inequality, plays a crucial role in determining the precise divergence rate (1.25). We point out that this particular form of Bernstein’s inequality appears due to the form of the regularization we use for our problem (namely, the sharp frequency truncation onto the frequencies
![]() $\{|n|\le N\}$
). In the current singular setting where a renormalization is required, we need to start with a regularized problem. However, there are different ways to regularize a problem, and different regularizations lead to different divergence rates. For example, if we instead use a smooth frequency truncation, we would obtain a divergence rate with a different constant (while the essential rate
$\{|n|\le N\}$
). In the current singular setting where a renormalization is required, we need to start with a regularized problem. However, there are different ways to regularize a problem, and different regularizations lead to different divergence rates. For example, if we instead use a smooth frequency truncation, we would obtain a divergence rate with a different constant (while the essential rate
![]() $N^d (\log N)^2$
in (1.25) remains the same).
$N^d (\log N)^2$
in (1.25) remains the same).
Remark 1.7. (i) An analogous nonnormalizability result holds for a focusing Gibbs measure with the quartic interaction even if we endow it with taming by the Wick-ordered
![]() $L^2$
-norm. See Remark 1.12.
$L^2$
-norm. See Remark 1.12.
(ii) By controlling combinatorial complexity, we can extend the nonnormalizability result in Theorem 1.4 to the higher-order interactions
![]() $k \geq 5$
in the focusing case (i.e., either k is odd or
$k \geq 5$
in the focusing case (i.e., either k is odd or
![]() $\lambda> 0$
when k is even).
$\lambda> 0$
when k is even).
(iii) In terms of dynamical problems, Theorem 1.4 states that Gibbs measures associated with the equations listed in Subsection 1.2 do not exist for (i)
![]() $\lambda> 0$
and
$\lambda> 0$
and
![]() $k \ge 4$
or (ii) odd
$k \ge 4$
or (ii) odd
![]() $k \ge 5$
. This list in particular includes
$k \ge 5$
. This list in particular includes
-
• the focusing
 $L^2$
-(super)critical fractional NLS (1.17) (including the focusing (super)cubic NLS on
$L^2$
-(super)critical fractional NLS (1.17) (including the focusing (super)cubic NLS on
 ${\mathbb {T}}^2$
),
${\mathbb {T}}^2$
), -
• the focusing
 $L^2$
-(super)critical fractional NLW (1.18) (including the focusing (super)cubic NLW on
$L^2$
-(super)critical fractional NLW (1.18) (including the focusing (super)cubic NLW on
 ${\mathbb {T}}^2$
and the focusing (super)cubic nonlinear beam equation on
${\mathbb {T}}^2$
and the focusing (super)cubic nonlinear beam equation on
 ${\mathbb {T}}^4$
),
${\mathbb {T}}^4$
), -
• the focusing modified Benjamin–Ono equation (1.19) (and the focusing generalized Benjamin–Ono equation with
 $k \ge 5$
).
$k \ge 5$
).
See also Appendix A for a brief discussion on the two-dimensional Zakharov system.
Remark 1.8. In a recent work [Reference Oh, Sosoe and Tolomeo46], the first and third authors with Okamoto studied the construction of the
![]() $\Phi ^3_3$
-measure on
$\Phi ^3_3$
-measure on
![]() ${\mathbb {T}}^3$
(i.e., (1.1) with
${\mathbb {T}}^3$
(i.e., (1.1) with
![]() $d = 3$
and
$d = 3$
and
![]() $k = 3$
) and established the following phase transition: normalizability in the weakly nonlinear regime (
$k = 3$
) and established the following phase transition: normalizability in the weakly nonlinear regime (
![]() $|\lambda |\ll 1$
) and nonnormalizability in the strongly nonlinear regime (
$|\lambda |\ll 1$
) and nonnormalizability in the strongly nonlinear regime (
![]() $|\lambda |\gg 1$
), where the latter result was obtained based on the strategy in the current paper. In particular, in view of the nonnormalizability of the
$|\lambda |\gg 1$
), where the latter result was obtained based on the strategy in the current paper. In particular, in view of the nonnormalizability of the
![]() $\Phi ^3_3$
-measure in the strongly nonlinear regime, we expect that the same approach would yield nonnormalizability of the focusing
$\Phi ^3_3$
-measure in the strongly nonlinear regime, we expect that the same approach would yield nonnormalizability of the focusing
![]() $\Phi ^k_3$
-measure for
$\Phi ^k_3$
-measure for
![]() $k \ge 4$
(namely, (i) for even
$k \ge 4$
(namely, (i) for even
![]() $k \ge 4$
with
$k \ge 4$
with
![]() $\lambda> 0$
or (ii) for odd
$\lambda> 0$
or (ii) for odd
![]() $k \ge 5$
with
$k \ge 5$
with
![]() $\lambda \ne 0$
).
$\lambda \ne 0$
).
1.4 Gibbs measure with the cubic interaction
Let us first go over the focusing Gibbs measure construction in the two-dimensional setting. In [Reference Bourgain10], Bourgain reported Jaffe’s construction of a
![]() $\Phi ^3_2$
-measure endowed with a Wick-ordered
$\Phi ^3_2$
-measure endowed with a Wick-ordered
![]() $ L^2$
-cutoff:
$ L^2$
-cutoff:
Note that the measure in (1.28) is not suitable to generate any NLS / NLW / heat dynamics since (i) the renormalized cubic power
![]() $:\!u^3 \!:$
makes sense only in the real-valued setting and hence is not suitable for the Schrödinger equation and (ii) NLW and the heat equation do not preserve the
$:\!u^3 \!:$
makes sense only in the real-valued setting and hence is not suitable for the Schrödinger equation and (ii) NLW and the heat equation do not preserve the
![]() $L^2$
-norm of a solution and thus are incompatible with the Wick-ordered
$L^2$
-norm of a solution and thus are incompatible with the Wick-ordered
![]() $L^2$
-cutoff. In [Reference Bourgain10], Bourgain instead proposed to consider the Gibbs measure of the form:Footnote
12
.
$L^2$
-cutoff. In [Reference Bourgain10], Bourgain instead proposed to consider the Gibbs measure of the form:Footnote
12
.
(for sufficiently large
![]() $A>0$
) in studying NLW dynamics on
$A>0$
) in studying NLW dynamics on
![]() ${\mathbb {T}}^2$
.Footnote
13
${\mathbb {T}}^2$
.Footnote
13
We now extend the construction of the Gibbs measures in (1.28) and (1.29) to a general dimension
![]() $d \geq 1$
. Given
$d \geq 1$
. Given
![]() $N \in \mathbb {N}$
, let
$N \in \mathbb {N}$
, let
 $$ \begin{align} R_N^\diamond (u) &= \frac \lambda 3\int_{{\mathbb{T}}^d} :\! u_N^3 \!: dx - A \, \bigg( \int_{{\mathbb{T}}^d} :\! u_N^2 \!: dx\bigg)^2, \end{align} $$
$$ \begin{align} R_N^\diamond (u) &= \frac \lambda 3\int_{{\mathbb{T}}^d} :\! u_N^3 \!: dx - A \, \bigg( \int_{{\mathbb{T}}^d} :\! u_N^2 \!: dx\bigg)^2, \end{align} $$
where the coupling constant
![]() $\lambda \in {\mathbb {R}}\setminus \{0\} $
denotes the strength of cubic interaction, and define the truncated renormalized Gibbs measure
$\lambda \in {\mathbb {R}}\setminus \{0\} $
denotes the strength of cubic interaction, and define the truncated renormalized Gibbs measure
![]() $\rho _{N}$
by
$\rho _{N}$
by
Then, we have the following result for the focusing Gibbs measure with a cubic interaction.
Theorem 1.9. Let
![]() $\lambda \in {\mathbb {R}}\setminus \{0\}$
. Given any finite
$\lambda \in {\mathbb {R}}\setminus \{0\}$
. Given any finite
![]() $ p \ge 1$
, there exists sufficiently large
$ p \ge 1$
, there exists sufficiently large
![]() $A = A(\lambda , p)> 0$
such that
$A = A(\lambda , p)> 0$
such that
![]() $R_N^\diamond $
in (1.30) converges to some limit
$R_N^\diamond $
in (1.30) converges to some limit
![]() $R^\diamond $
in
$R^\diamond $
in
![]() $L^p(\mu )$
. Moreover, there exists
$L^p(\mu )$
. Moreover, there exists
![]() $C_{p, d, A}> 0$
such that
$C_{p, d, A}> 0$
such that
In particular, we have
As a consequence, the truncated renormalized Gibbs measure
![]() $\rho _{N}$
in (1.31) converges, in the sense of (1.33), to the focusing Gibbs measure
$\rho _{N}$
in (1.31) converges, in the sense of (1.33), to the focusing Gibbs measure
![]() $\rho $
given by
$\rho $
given by
Furthermore, the resulting Gibbs measure
![]() $\rho $
is equivalent to the log-correlated Gaussian field
$\rho $
is equivalent to the log-correlated Gaussian field
![]() $\mu $
.
$\mu $
.
As for the convergence of
![]() $R_N^\diamond $
, we omit details since the argument is standard. See, for example, [Reference Oh and Thomann47, Proposition 1.1], [Reference Oh and Tzvetkov49, Proposition 3.1], [Reference Gunaratnam, Oh, Tzvetkov and Weber31, Lemma 4.1] and [Reference Oh, Okamoto and Tolomeo41, Lemma 5.1] for related details. As mentioned in Subsection 1.1, the main task is to prove the uniform integrability bound (1.32). Once this is done, the rest follows from a standard argument. In Section 4, we establish the bound (1.32) by using the variational formulation.
$R_N^\diamond $
, we omit details since the argument is standard. See, for example, [Reference Oh and Thomann47, Proposition 1.1], [Reference Oh and Tzvetkov49, Proposition 3.1], [Reference Gunaratnam, Oh, Tzvetkov and Weber31, Lemma 4.1] and [Reference Oh, Okamoto and Tolomeo41, Lemma 5.1] for related details. As mentioned in Subsection 1.1, the main task is to prove the uniform integrability bound (1.32). Once this is done, the rest follows from a standard argument. In Section 4, we establish the bound (1.32) by using the variational formulation.
Remark 1.10. Note that
for any
![]() $K, A , \gamma> 0$
. Then, the following uniform bound for the focusing cubic interaction:
$K, A , \gamma> 0$
. Then, the following uniform bound for the focusing cubic interaction:
for any
![]() $K> 0$
follows as a direct consequence of the uniform bound (1.32) and (1.34) with
$K> 0$
follows as a direct consequence of the uniform bound (1.32) and (1.34) with
![]() $\gamma = 2$
, where
$\gamma = 2$
, where
![]() $R_N$
is as in (1.8) with
$R_N$
is as in (1.8) with
![]() $\lambda \in {\mathbb {R}}\setminus \{ 0\}$
and
$\lambda \in {\mathbb {R}}\setminus \{ 0\}$
and
![]() $k = 3$
. This allows us to construct the log-correlated Gibbs measure with the cubic interaction (with a Wick-ordered
$k = 3$
. This allows us to construct the log-correlated Gibbs measure with the cubic interaction (with a Wick-ordered
![]() $ L^2$
-cutoff):
$ L^2$
-cutoff):
as a limit of its truncated version (for any
![]() $\lambda \in {\mathbb {R}}\setminus \{0\}$
and
$\lambda \in {\mathbb {R}}\setminus \{0\}$
and
![]() $ K> 0$
).
$ K> 0$
).
Remark 1.11. In [Reference Tzvetkov67], Tzvetkov constructed the Gibbs measure (with a Wick-ordered
![]() $ L^2$
-cutoff) for the Benjamin–Ono equation (1.19) with
$ L^2$
-cutoff) for the Benjamin–Ono equation (1.19) with
![]() $k = 3$
. Theorem 1.9 and Remark 1.10 provide an alternative proof of the construction of the Gibbs measure for the Benjamin–Ono equation.
$k = 3$
. Theorem 1.9 and Remark 1.10 provide an alternative proof of the construction of the Gibbs measure for the Benjamin–Ono equation.
Remark 1.12. (i) It follows from Theorem 1.4 and (1.34) that an analogue of Theorem 1.9 fails for the quartic interaction (
![]() $k = 4$
). More precisely, we have
$k = 4$
). More precisely, we have
 $$ \begin{align*} \sup_{N\in \mathbb{N}} \bigg\| \exp \bigg( \frac \lambda 4 \int_{{\mathbb{T}}^d} :\! u_N^4 \!: dx - A \, \Big| \int_{{\mathbb{T}}^d} :\! u_N^2 \!: dx\Big|^\gamma \bigg)\bigg\|_{L^p(\mu)} = \infty \end{align*} $$
$$ \begin{align*} \sup_{N\in \mathbb{N}} \bigg\| \exp \bigg( \frac \lambda 4 \int_{{\mathbb{T}}^d} :\! u_N^4 \!: dx - A \, \Big| \int_{{\mathbb{T}}^d} :\! u_N^2 \!: dx\Big|^\gamma \bigg)\bigg\|_{L^p(\mu)} = \infty \end{align*} $$
for any
![]() $\lambda , A, \gamma> 0$
.
$\lambda , A, \gamma> 0$
.
(ii) If we consider a smoother base Gaussian measure
![]() $\mu _\alpha $
, then we can prove the following uniform exponential integrability bound; given any
$\mu _\alpha $
, then we can prove the following uniform exponential integrability bound; given any
![]() $\lambda> 0$
,
$\lambda> 0$
,
![]() $\alpha> {\frac {d}{2}}$
and finite
$\alpha> {\frac {d}{2}}$
and finite
![]() $p \geq 1$
, there exists sufficiently large
$p \geq 1$
, there exists sufficiently large
![]() $A = A(\lambda , \alpha , p)> 0$
and
$A = A(\lambda , \alpha , p)> 0$
and
![]() $\gamma = \gamma (\alpha )> 0$
such that
$\gamma = \gamma (\alpha )> 0$
such that
 $$ \begin{align} \sup_{N\in \mathbb{N}} \bigg\| \exp \bigg( \frac \lambda 4 \int_{{\mathbb{T}}^d} u_N^4 dx - A \, \Big( \int_{{\mathbb{T}}^d} u_N^2 dx\Big)^\gamma \bigg)\bigg\|_{L^p(\mu_\alpha)} \leq C_{p, d, A} < \infty. \end{align} $$
$$ \begin{align} \sup_{N\in \mathbb{N}} \bigg\| \exp \bigg( \frac \lambda 4 \int_{{\mathbb{T}}^d} u_N^4 dx - A \, \Big( \int_{{\mathbb{T}}^d} u_N^2 dx\Big)^\gamma \bigg)\bigg\|_{L^p(\mu_\alpha)} \leq C_{p, d, A} < \infty. \end{align} $$
Here,
![]() $\mu _\alpha $
denotes the Gaussian measure with a formal density
$\mu _\alpha $
denotes the Gaussian measure with a formal density
See Appendix B for the proof of (1.35). The bound (1.35) allows us to construct the focusing Gibbs measure with a focusing quartic interaction of the form:
Moreover, in view of (1.34), we can also construct the following focusing Gibbs measure with an
![]() $L^2$
-cutoff:
$L^2$
-cutoff:
for any
![]() $K> 0$
.
$K> 0$
.
In [Reference Sun and Tzvetkov61, Reference Sun and Tzvetkov62], Sun and Tzvetkov recently studied the following fractional NLS on
![]() ${\mathbb {T}}$
:
${\mathbb {T}}$
:
in the defocusing case (
![]() $\lambda < 0$
). They proved almost sure local well-posedness of (1.39) with respect to the Gaussian measure
$\lambda < 0$
). They proved almost sure local well-posedness of (1.39) with respect to the Gaussian measure
![]() $\mu _\alpha $
in (1.36) for
$\mu _\alpha $
in (1.36) for
![]() $\alpha> \frac {31- \sqrt {233}}{28} \approx 0.562 \ ( \, > \frac 12)$
,Footnote
14
which in turn yielded almost sure global well-posedness with respect to the defocusing Gibbs measure (namely,
$\alpha> \frac {31- \sqrt {233}}{28} \approx 0.562 \ ( \, > \frac 12)$
,Footnote
14
which in turn yielded almost sure global well-posedness with respect to the defocusing Gibbs measure (namely,
![]() $\rho _\alpha $
in (1.38) without an
$\rho _\alpha $
in (1.38) without an
![]() $L^2$
-cutoff) and invariance of the defocusing Gibbs measure. Since their local result also holds in the focusing case (
$L^2$
-cutoff) and invariance of the defocusing Gibbs measure. Since their local result also holds in the focusing case (
![]() $\lambda>0$
), our construction of the focusing Gibbs measure
$\lambda>0$
), our construction of the focusing Gibbs measure
![]() $\rho _\alpha $
in (1.38) implies almost sure global well-posedness of (1.39) with respect to the focusing Gibbs measure
$\rho _\alpha $
in (1.38) implies almost sure global well-posedness of (1.39) with respect to the focusing Gibbs measure
![]() $\rho _\alpha $
in (1.38) and its invariance under the dynamics of (1.39) for the same range of
$\rho _\alpha $
in (1.38) and its invariance under the dynamics of (1.39) for the same range of
![]() $\alpha $
.
$\alpha $
.
(iii) Theorem 1.4 and Part (ii) of this remark show that in the case of the focusing quartic interaction, there is no phase transition, depending on the value of
![]() $\lambda> 0$
. Compare this with the situation in [Reference Oh, Okamoto and Tolomeo41, Reference Oh, Okamoto and Tolomeo42], where such a phase transition (as described in Remark 1.8) was established in the critical case. It may be of interest to pursue the issue of a possible phase transition for a higher-order focusing interaction, in the nonsingular regime
$\lambda> 0$
. Compare this with the situation in [Reference Oh, Okamoto and Tolomeo41, Reference Oh, Okamoto and Tolomeo42], where such a phase transition (as described in Remark 1.8) was established in the critical case. It may be of interest to pursue the issue of a possible phase transition for a higher-order focusing interaction, in the nonsingular regime
![]() $\alpha> {\frac {d}{2}}$
.
$\alpha> {\frac {d}{2}}$
.
2 Preliminary lemmas
In this section, we recall basic definitions and lemmas used in this paper.
Let
![]() $s \in {\mathbb {R}}$
and
$s \in {\mathbb {R}}$
and
![]() $1 \leq p \leq \infty $
. We define the
$1 \leq p \leq \infty $
. We define the
![]() $L^2$
-based Sobolev space
$L^2$
-based Sobolev space
![]() $H^s({\mathbb {T}}^d)$
by the norm:
$H^s({\mathbb {T}}^d)$
by the norm:
We also define the
![]() $L^p$
-based Sobolev space
$L^p$
-based Sobolev space
![]() $W^{s, p}({\mathbb {T}}^d)$
by the norm:
$W^{s, p}({\mathbb {T}}^d)$
by the norm:
When
![]() $p = 2$
, we have
$p = 2$
, we have
![]() $H^s({\mathbb {T}}^d) = W^{s, 2}({\mathbb {T}}^d)$
.
$H^s({\mathbb {T}}^d) = W^{s, 2}({\mathbb {T}}^d)$
.
2.1 Deterministic estimates
We first recall the following interpolation and fractional Leibniz rule. As for the second estimate (2.1), see [Reference Gubinelli, Koch and Oh29, Lemma 3.4].
Lemma 2.1. The following estimates hold.
(i) (interpolation) For
![]() $0 < s_1 < s_2$
, we have
$0 < s_1 < s_2$
, we have
(ii) (fractional Leibniz rule) Let
![]() $0\le s \le 1$
. Suppose that
$0\le s \le 1$
. Suppose that
![]() $1<p_j,q_j,r < \infty $
,
$1<p_j,q_j,r < \infty $
,
![]() $\frac 1{p_j} + \frac 1{q_j}= \frac 1r$
,
$\frac 1{p_j} + \frac 1{q_j}= \frac 1r$
,
![]() $j = 1, 2$
. Then, we haveFootnote
15
$j = 1, 2$
. Then, we haveFootnote
15
where
![]() $\langle \nabla \rangle = \sqrt {1 - \Delta }$
.
$\langle \nabla \rangle = \sqrt {1 - \Delta }$
.
The next lemma states almost optimal Bernstein’s inequality on
![]() ${\mathbb {T}}^d$
.
${\mathbb {T}}^d$
.
Lemma 2.2. Given
![]() $N \in \mathbb {N}$
, let
$N \in \mathbb {N}$
, let
![]() $\pi _N$
be the frequency projector as in (1.4). Then, we have
$\pi _N$
be the frequency projector as in (1.4). Then, we have
as
![]() $N \to \infty $
, where
$N \to \infty $
, where
![]() $C_B$
is the optimal constant for Bernstein’s inequality (1.26) on
$C_B$
is the optimal constant for Bernstein’s inequality (1.26) on
![]() ${\mathbb {R}}^d$
.
${\mathbb {R}}^d$
.
Proof. Given
![]() $N \in \mathbb {N}$
, let
$N \in \mathbb {N}$
, let
![]() $C_{B,N}$
be the optimal constant for the following inequality on
$C_{B,N}$
be the optimal constant for the following inequality on
![]() ${\mathbb {T}}^d$
:
${\mathbb {T}}^d$
:
and let
![]() $f_N$
be an optimizer for (2.2) with
$f_N$
be an optimizer for (2.2) with
![]() $\|f_N\|_{L^2({\mathbb {T}}^d)} = 1$
and
$\|f_N\|_{L^2({\mathbb {T}}^d)} = 1$
and
![]() $\pi _N f_N = f_N$
. In particular, we have
$\pi _N f_N = f_N$
. In particular, we have
Note that such an optimizer exists since the set
![]() $\{f_N: \|f_N\|_{L^2({\mathbb {T}}^d)} = 1, \, \pi _N f_N = f_N\}$
is compact. Moreover, by Sobolev’s inequality on the torus, we have
$\{f_N: \|f_N\|_{L^2({\mathbb {T}}^d)} = 1, \, \pi _N f_N = f_N\}$
is compact. Moreover, by Sobolev’s inequality on the torus, we have
uniformly in
![]() $N \in \mathbb {N}$
. Then, in view of (2.3), it suffices to show that
$N \in \mathbb {N}$
. Then, in view of (2.3), it suffices to show that
Fix small
![]() $\varepsilon> 0$
. Let
$\varepsilon> 0$
. Let
![]() $ \chi _\varepsilon \in C^\infty _c({\mathbb {R}}^d; [0, 1])$
be a smooth bump function which is compactly supported on
$ \chi _\varepsilon \in C^\infty _c({\mathbb {R}}^d; [0, 1])$
be a smooth bump function which is compactly supported on
![]() $[-\pi ,\pi )^d\cong {\mathbb {T}}^d$
such that
$[-\pi ,\pi )^d\cong {\mathbb {T}}^d$
such that
![]() $\chi _\varepsilon \equiv 1$
on
$\chi _\varepsilon \equiv 1$
on
![]() $[-\pi +c_0 \varepsilon ,\pi -c_0\varepsilon ]^d$
for some small
$[-\pi +c_0 \varepsilon ,\pi -c_0\varepsilon ]^d$
for some small
![]() $c_0 = c_0> 0$
to be chosen later. Recalling that
$c_0 = c_0> 0$
to be chosen later. Recalling that
![]() $dx_{{\mathbb {T}}^d} = (2\pi )^{-d} dx$
is the normalized Lebesgue measure on
$dx_{{\mathbb {T}}^d} = (2\pi )^{-d} dx$
is the normalized Lebesgue measure on
![]() ${\mathbb {T}}^d$
, we see that
${\mathbb {T}}^d$
, we see that
![]() $\|f_N\|_{L^4({\mathbb {T}}^d)}^4$
is the average of
$\|f_N\|_{L^4({\mathbb {T}}^d)}^4$
is the average of
![]() $|f(x)|^4$
on
$|f(x)|^4$
on
![]() ${\mathbb {T}}^d$
. Hence, by suitably translating
${\mathbb {T}}^d$
. Hence, by suitably translating
![]() $f_N$
(that does not affect its optimality) and choosing
$f_N$
(that does not affect its optimality) and choosing
![]() $c_0 = c_0> 0$
sufficiently small (independent of small
$c_0 = c_0> 0$
sufficiently small (independent of small
![]() $\varepsilon> 0$
and
$\varepsilon> 0$
and
![]() $N \in \mathbb {N}$
), we have
$N \in \mathbb {N}$
), we have
uniformly in
![]() $N \in \mathbb {N}$
. In the following, when we view
$N \in \mathbb {N}$
. In the following, when we view
![]() $f_N$
as a function on
$f_N$
as a function on
![]() ${\mathbb {R}}^d$
, we simply view it as a periodic function:
${\mathbb {R}}^d$
, we simply view it as a periodic function:
![]() $f(x) = f(x + 2\pi m)$
,
$f(x) = f(x + 2\pi m)$
,
![]() $m \in \mathbb {Z}^d$
.
$m \in \mathbb {Z}^d$
.
Let
![]() $\theta \in C^\infty _c({\mathbb {R}}^d; [0, 1])$
be a smooth radial bump function on
$\theta \in C^\infty _c({\mathbb {R}}^d; [0, 1])$
be a smooth radial bump function on
![]() ${\mathbb {R}}^d$
such that
${\mathbb {R}}^d$
such that
![]() $\theta (\xi ) = 1$
for
$\theta (\xi ) = 1$
for
![]() $|\xi |\le 1$
and
$|\xi |\le 1$
and
![]() $\theta (\xi ) = 0$
for
$\theta (\xi ) = 0$
for
![]() $|\xi |> 2$
. Given
$|\xi |> 2$
. Given
![]() $M> 0$
, set
$M> 0$
, set
![]() $\theta _M(\xi ) = \theta \big (\frac \xi M\big )$
. Now, we set
$\theta _M(\xi ) = \theta \big (\frac \xi M\big )$
. Now, we set
where
![]() $\mathcal {F}^{-1}_{{\mathbb {R}}^d}$
is the inverse Fourier transform on
$\mathcal {F}^{-1}_{{\mathbb {R}}^d}$
is the inverse Fourier transform on
![]() ${\mathbb {R}}^d$
. Namely,
${\mathbb {R}}^d$
. Namely,
![]() $\chi _{\varepsilon ,M}$
is the frequency-localized version of
$\chi _{\varepsilon ,M}$
is the frequency-localized version of
![]() $\chi _\varepsilon $
onto the frequencies
$\chi _\varepsilon $
onto the frequencies
![]() $\{\xi \in {\mathbb {R}}^d: |\xi |\le 2 M\}$
. Then, by choosing
$\{\xi \in {\mathbb {R}}^d: |\xi |\le 2 M\}$
. Then, by choosing
![]() $M = M(\varepsilon , N)> 0$
sufficiently large, we have
$M = M(\varepsilon , N)> 0$
sufficiently large, we have
Since
![]() $\chi _\varepsilon $
is a Schwartz function, we have
$\chi _\varepsilon $
is a Schwartz function, we have
![]() $M(\varepsilon ,N) = o(N)$
for each fixed
$M(\varepsilon ,N) = o(N)$
for each fixed
![]() $\varepsilon> 0$
.
$\varepsilon> 0$
.
By the definition (2.7) of
![]() $\chi _{\varepsilon , M}$
and choosing
$\chi _{\varepsilon , M}$
and choosing
![]() $M = M(\varepsilon , N) = o(N)$
possibly larger, we have
$M = M(\varepsilon , N) = o(N)$
possibly larger, we have
 $$ \begin{align} \nonumber \| \chi_{\varepsilon,M}(\,\cdot + 2\pi m) \|_{L^\infty([-\pi,\pi)^d)} & = \sup_{x \in [-\pi,\pi)^d} M^{d} \int_{{\mathbb{R}}^d}\chi_\varepsilon(x+2\pi m - y) \mathcal{F}_{{\mathbb{R}}^d}^{-1}(\theta)(M y) dy \\ & \lesssim \frac {M^d }{\langle Mm \rangle^{2d+1} } \ll \frac{\varepsilon}{\langle m \rangle^{d}}, \end{align} $$
$$ \begin{align} \nonumber \| \chi_{\varepsilon,M}(\,\cdot + 2\pi m) \|_{L^\infty([-\pi,\pi)^d)} & = \sup_{x \in [-\pi,\pi)^d} M^{d} \int_{{\mathbb{R}}^d}\chi_\varepsilon(x+2\pi m - y) \mathcal{F}_{{\mathbb{R}}^d}^{-1}(\theta)(M y) dy \\ & \lesssim \frac {M^d }{\langle Mm \rangle^{2d+1} } \ll \frac{\varepsilon}{\langle m \rangle^{d}}, \end{align} $$
uniformly in
![]() $m \in \mathbb {Z}^d\setminus \{0\}$
, where the penultimate step follows from
$m \in \mathbb {Z}^d\setminus \{0\}$
, where the penultimate step follows from
![]() $\operatorname *{\mathrm {supp}} \chi _\varepsilon \subset [- \pi , \pi )^d$
and the fact that
$\operatorname *{\mathrm {supp}} \chi _\varepsilon \subset [- \pi , \pi )^d$
and the fact that
![]() $\theta $
is a Schwartz function. Then, from the periodicity of
$\theta $
is a Schwartz function. Then, from the periodicity of
![]() $f_N$
,
$f_N$
,
![]() $\operatorname *{\mathrm {supp}} \chi _\varepsilon \subset [- \pi , \pi )^d$
, (2.8) and (2.9), we obtain
$\operatorname *{\mathrm {supp}} \chi _\varepsilon \subset [- \pi , \pi )^d$
, (2.8) and (2.9), we obtain
 $$ \begin{align*} & \| (\chi_{\varepsilon} - \chi_{\varepsilon,M})f_N \|_{L^4({{\mathbb{R}}}^d, \frac{dx}{(2\pi)^d)}}\\ & = \bigg(\frac{1}{(2\pi)^d}\sum_{m \in {\mathbb{Z}}^d} \int_{[-\pi,\pi)^d} (\chi_{\varepsilon} - \chi_{\varepsilon,M})^4(x + 2\pi m) | f_N(x)|^4 dx\bigg)^{\frac{1}{4}}\\ & \le \| f_N \|_{L^4({{\mathbb{T}}}^d)} \bigg( \|\chi_\varepsilon - \chi_{\varepsilon, M}\|_{L^\infty([-\pi,\pi)^d)}^4 + \sum_{m \in {\mathbb{Z}}^d\setminus\{0\}} \| \chi_{\varepsilon,M}^4(\,\cdot + 2\pi m) \|_{L^\infty([-\pi,\pi)^d)}^4 \bigg)^{\frac{1}{4}} \\ & \ll \varepsilon \| f_N \|_{L^4({{\mathbb{T}}}^d)}. \end{align*} $$
$$ \begin{align*} & \| (\chi_{\varepsilon} - \chi_{\varepsilon,M})f_N \|_{L^4({{\mathbb{R}}}^d, \frac{dx}{(2\pi)^d)}}\\ & = \bigg(\frac{1}{(2\pi)^d}\sum_{m \in {\mathbb{Z}}^d} \int_{[-\pi,\pi)^d} (\chi_{\varepsilon} - \chi_{\varepsilon,M})^4(x + 2\pi m) | f_N(x)|^4 dx\bigg)^{\frac{1}{4}}\\ & \le \| f_N \|_{L^4({{\mathbb{T}}}^d)} \bigg( \|\chi_\varepsilon - \chi_{\varepsilon, M}\|_{L^\infty([-\pi,\pi)^d)}^4 + \sum_{m \in {\mathbb{Z}}^d\setminus\{0\}} \| \chi_{\varepsilon,M}^4(\,\cdot + 2\pi m) \|_{L^\infty([-\pi,\pi)^d)}^4 \bigg)^{\frac{1}{4}} \\ & \ll \varepsilon \| f_N \|_{L^4({{\mathbb{T}}}^d)}. \end{align*} $$
As a consequence, we have
 $$ \begin{align} \nonumber & \| (\chi_{\varepsilon}^2 - \chi_{\varepsilon,M}^2 )f_N \|_{L^4({\mathbb{R}}^d, \frac{dx}{(2\pi)^d})\cap L^2({\mathbb{R}}^d, \frac{dx}{(2\pi)^d})}\\ \nonumber & \le \| \chi_{\varepsilon} - \chi_{\varepsilon,M} \|_{L^\infty({\mathbb{R}}^d)\cap L^4({\mathbb{R}}^d, \frac{dx}{(2\pi)^d} )}\\ & \quad \times \bigg(2 \| \chi_{\varepsilon} f_N \|_{L^4({\mathbb{R}}^d, \frac{dx}{(2\pi)^d})}+ \| (\chi_{\varepsilon} - \chi_{\varepsilon,M})f_N \|_{L^4({\mathbb{R}}^d, \frac{dx}{(2\pi)^d})}\bigg)\\ \nonumber & \ll \varepsilon N^{-\frac{d}{4}} \| f_N \|_{L^4({\mathbb{T}}^d)}. \end{align} $$
$$ \begin{align} \nonumber & \| (\chi_{\varepsilon}^2 - \chi_{\varepsilon,M}^2 )f_N \|_{L^4({\mathbb{R}}^d, \frac{dx}{(2\pi)^d})\cap L^2({\mathbb{R}}^d, \frac{dx}{(2\pi)^d})}\\ \nonumber & \le \| \chi_{\varepsilon} - \chi_{\varepsilon,M} \|_{L^\infty({\mathbb{R}}^d)\cap L^4({\mathbb{R}}^d, \frac{dx}{(2\pi)^d} )}\\ & \quad \times \bigg(2 \| \chi_{\varepsilon} f_N \|_{L^4({\mathbb{R}}^d, \frac{dx}{(2\pi)^d})}+ \| (\chi_{\varepsilon} - \chi_{\varepsilon,M})f_N \|_{L^4({\mathbb{R}}^d, \frac{dx}{(2\pi)^d})}\bigg)\\ \nonumber & \ll \varepsilon N^{-\frac{d}{4}} \| f_N \|_{L^4({\mathbb{T}}^d)}. \end{align} $$
Hence, from (2.6) and (2.10), we have
for any small
![]() $\varepsilon> 0$
, uniformly in
$\varepsilon> 0$
, uniformly in
![]() $N \in \mathbb {N}$
.
$N \in \mathbb {N}$
.
Define the function
![]() $g_N, g_{N,M}:{\mathbb {R}}^d \to \mathbb {C}$
by setting
$g_N, g_{N,M}:{\mathbb {R}}^d \to \mathbb {C}$
by setting
Then, from (2.11) and (2.12), we have
By Hölder’s inequality and (2.10) with (2.3) and (2.4), we have
 $$ \begin{align*} \|g_N - g_{N,M}\|_{L^2({\mathbb{R}}^d, \frac{dx}{(2\pi)^d)}} &= \| (\chi_\varepsilon^2 - \chi_{\varepsilon,M}^2)f_N \|_{L^2({\mathbb{R}}^d, \frac{dx}{(2\pi)^d)}} \\ & \ll \varepsilon. \end{align*} $$
$$ \begin{align*} \|g_N - g_{N,M}\|_{L^2({\mathbb{R}}^d, \frac{dx}{(2\pi)^d)}} &= \| (\chi_\varepsilon^2 - \chi_{\varepsilon,M}^2)f_N \|_{L^2({\mathbb{R}}^d, \frac{dx}{(2\pi)^d)}} \\ & \ll \varepsilon. \end{align*} $$
Noting that
![]() $\|g_N\|_{L^2({\mathbb {R}}^d, \frac {dx}{(2\pi )^d)}} = \|\chi _\varepsilon ^2f_N \|_{L^2({\mathbb {T}}^d)} \le 1$
, we then obtain
$\|g_N\|_{L^2({\mathbb {R}}^d, \frac {dx}{(2\pi )^d)}} = \|\chi _\varepsilon ^2f_N \|_{L^2({\mathbb {T}}^d)} \le 1$
, we then obtain
Finally, recalling that the Fourier support of
![]() $f_N = \pi _N f $
(as a function on
$f_N = \pi _N f $
(as a function on
![]() ${\mathbb {T}}^d$
) is contained in
${\mathbb {T}}^d$
) is contained in
![]() $\{n \in \mathbb {Z}^d |n| \le N\}$
and the Fourier support of
$\{n \in \mathbb {Z}^d |n| \le N\}$
and the Fourier support of
![]() $\chi _{\varepsilon ,M}$
(as a function on
$\chi _{\varepsilon ,M}$
(as a function on
![]() ${\mathbb {R}}^d$
is contained in
${\mathbb {R}}^d$
is contained in
![]() $\{\xi \in {\mathbb {R}}^d: |\xi | \le 2M\}$
and that
$\{\xi \in {\mathbb {R}}^d: |\xi | \le 2M\}$
and that
![]() $M(\varepsilon ,N) = o(N)$
, it follows from (2.12) that
$M(\varepsilon ,N) = o(N)$
, it follows from (2.12) that
 $$ \begin{align} \operatorname*{\mathrm{supp}}(\widehat g_{N,M}) \subset \bigg\{ \xi \in {\mathbb{R}}^d : |\xi| \le \frac{N+2M}{N}\bigg\} \subset \big\{ \xi \in {\mathbb{R}}^d : |\xi| \le 1 + o(1) \big\}. \end{align} $$
$$ \begin{align} \operatorname*{\mathrm{supp}}(\widehat g_{N,M}) \subset \bigg\{ \xi \in {\mathbb{R}}^d : |\xi| \le \frac{N+2M}{N}\bigg\} \subset \big\{ \xi \in {\mathbb{R}}^d : |\xi| \le 1 + o(1) \big\}. \end{align} $$
Therefore, from (2.13) and (the scaled version of) (1.26) with (2.15) followed by (2.14), we conclude that
 $$ \begin{align*} N^{-d}\|f_N\|_{L^4({\mathbb{T}}^d)}^4 & \le (1 -2 \varepsilon)^{-4} \|g_{N,M}\|_{L^4({\mathbb{R}}^d, \frac{dx}{(2\pi)^d})}^4 \\ & \le (1-2\varepsilon)^{-4}4 C_B (1 +o(1)) \|g_{N,M}\|_{L^2({\mathbb{R}}^d, \frac{dx}{(2\pi)^d})}^4 \\ & \le \bigg(\frac{1+\varepsilon}{1-2\varepsilon}\bigg)^4 C_B (1 +o(1)). \end{align*} $$
$$ \begin{align*} N^{-d}\|f_N\|_{L^4({\mathbb{T}}^d)}^4 & \le (1 -2 \varepsilon)^{-4} \|g_{N,M}\|_{L^4({\mathbb{R}}^d, \frac{dx}{(2\pi)^d})}^4 \\ & \le (1-2\varepsilon)^{-4}4 C_B (1 +o(1)) \|g_{N,M}\|_{L^2({\mathbb{R}}^d, \frac{dx}{(2\pi)^d})}^4 \\ & \le \bigg(\frac{1+\varepsilon}{1-2\varepsilon}\bigg)^4 C_B (1 +o(1)). \end{align*} $$
Since
![]() $\varepsilon>0 $
is arbitrary, by taking the
$\varepsilon>0 $
is arbitrary, by taking the
![]() $\limsup $
as
$\limsup $
as
![]() $N\to \infty $
, we obtain (2.5).
$N\to \infty $
, we obtain (2.5).
2.2 Tools from stochastic analysis
Next, we recall the Wiener chaos estimate (Lemma 2.3). For this purpose, we first recall basic definitions from stochastic analysis; see [Reference Bogachev6, Reference Shigekawa59]. Let
![]() $(H, B, \nu )$
be an abstract Wiener space. Namely,
$(H, B, \nu )$
be an abstract Wiener space. Namely,
![]() $\nu $
is a Gaussian measure on a separable Banach space B with
$\nu $
is a Gaussian measure on a separable Banach space B with
![]() $H \subset B$
as its Cameron–Martin space. Given a complete orthonormal system
$H \subset B$
as its Cameron–Martin space. Given a complete orthonormal system
![]() $\{e_j \}_{ j \in \mathbb {N}} \subset B^*$
of
$\{e_j \}_{ j \in \mathbb {N}} \subset B^*$
of
![]() $H^* = H$
, we define a polynomial chaos of order k to be an element of the form
$H^* = H$
, we define a polynomial chaos of order k to be an element of the form
![]() $\prod _{j = 1}^\infty H_{k_j}(\langle x, e_j \rangle )$
, where
$\prod _{j = 1}^\infty H_{k_j}(\langle x, e_j \rangle )$
, where
![]() $x \in B$
,
$x \in B$
,
![]() $k_j \ne 0$
for only finitely many j’s,
$k_j \ne 0$
for only finitely many j’s,
![]() $k= \sum _{j = 1}^\infty k_j$
,
$k= \sum _{j = 1}^\infty k_j$
,
![]() $H_{k_j}$
is the Hermite polynomial of degree
$H_{k_j}$
is the Hermite polynomial of degree
![]() $k_j$
as in (1.7), and
$k_j$
as in (1.7), and
![]() $\langle \cdot , \cdot \rangle = \vphantom {|}_B \langle \cdot , \cdot \rangle _{B^*}$
denotes the B-
$\langle \cdot , \cdot \rangle = \vphantom {|}_B \langle \cdot , \cdot \rangle _{B^*}$
denotes the B-
![]() $B^*$
duality pairing. We then denote the closure of polynomial chaoses of order k under
$B^*$
duality pairing. We then denote the closure of polynomial chaoses of order k under
![]() $L^2(B, \nu )$
by
$L^2(B, \nu )$
by
![]() $\mathcal {H}_k$
. The elements in
$\mathcal {H}_k$
. The elements in
![]() $\mathcal {H}_k$
are called homogeneous Wiener chaoses of order k. We also set
$\mathcal {H}_k$
are called homogeneous Wiener chaoses of order k. We also set
 $$ \begin{align*} \mathcal{H}_{\leq k} = \bigoplus_{j = 0}^k \mathcal{H}_j \end{align*} $$
$$ \begin{align*} \mathcal{H}_{\leq k} = \bigoplus_{j = 0}^k \mathcal{H}_j \end{align*} $$
for
![]() $k \in \mathbb {N}$
.
$k \in \mathbb {N}$
.
Let
![]() $L = \Delta -x \cdot \nabla $
be the Ornstein–Uhlenbeck operator.Footnote
16
Then, it is known that any element in
$L = \Delta -x \cdot \nabla $
be the Ornstein–Uhlenbeck operator.Footnote
16
Then, it is known that any element in
![]() $\mathcal H_k$
is an eigenfunction of L with eigenvalue
$\mathcal H_k$
is an eigenfunction of L with eigenvalue
![]() $-k$
. Then, as a consequence of the hypercontractivity of the Ornstein–Uhlenbeck semigroup
$-k$
. Then, as a consequence of the hypercontractivity of the Ornstein–Uhlenbeck semigroup
![]() $U(t) = e^{tL}$
due to Nelson [Reference Nelson39], we have the following Wiener chaos estimate [Reference Simon60, Theorem I.22].
$U(t) = e^{tL}$
due to Nelson [Reference Nelson39], we have the following Wiener chaos estimate [Reference Simon60, Theorem I.22].
Lemma 2.3. Let
![]() $k \in \mathbb {N}$
. Then, we have
$k \in \mathbb {N}$
. Then, we have
for any
![]() $p \geq 2$
and any
$p \geq 2$
and any
![]() $X \in \mathcal {H}_{\leq k}$
.
$X \in \mathcal {H}_{\leq k}$
.
Lemma 2.4. Let
![]() $\nu _N$
be the law of
$\nu _N$
be the law of
![]() $I_N \stackrel {\mathrm {def}}{=} \int _{{\mathbb {T}}^d}:\! u_N^2(x) \!: dx$
, where u is as in (1.3) and
$I_N \stackrel {\mathrm {def}}{=} \int _{{\mathbb {T}}^d}:\! u_N^2(x) \!: dx$
, where u is as in (1.3) and
![]() $u_N = \pi _N u$
. Then, for every
$u_N = \pi _N u$
. Then, for every
![]() $N \in \mathbb {N}$
,
$N \in \mathbb {N}$
,
![]() $\nu _N$
is absolutely continuous with respect to the Lebesgue measure
$\nu _N$
is absolutely continuous with respect to the Lebesgue measure
![]() $\lambda $
on
$\lambda $
on
![]() ${\mathbb {R}}$
. Moreover, we have
${\mathbb {R}}$
. Moreover, we have
 $$ \begin{align} \bigg\|\frac{d\nu_N}{d\lambda} \bigg\|_{L^\infty({\mathbb{R}})} \lesssim 1, \end{align} $$
$$ \begin{align} \bigg\|\frac{d\nu_N}{d\lambda} \bigg\|_{L^\infty({\mathbb{R}})} \lesssim 1, \end{align} $$
uniformly in
![]() $N \in \mathbb {N}$
. As a consequence, we have
$N \in \mathbb {N}$
. As a consequence, we have
 $$ \begin{align} \mu \bigg(\int_{{\mathbb{T}}^d}:\! u^2(x) \!: dx = K\bigg) = 0 \end{align} $$
$$ \begin{align} \mu \bigg(\int_{{\mathbb{T}}^d}:\! u^2(x) \!: dx = K\bigg) = 0 \end{align} $$
for any
![]() $K \in {\mathbb {R}}$
, where
$K \in {\mathbb {R}}$
, where
![]() $\mu $
is the log-correlated Gaussian free field defined in (1.2).
$\mu $
is the log-correlated Gaussian free field defined in (1.2).
Proof. By the definition (1.6) of
![]() $:\! u_N^2 \!: \,$
with (1.3), we have
$:\! u_N^2 \!: \,$
with (1.3), we have
 $$ \begin{align*} \int_{{\mathbb{T}}^d} :\! u_N^2(x) \!: dx & = \sum_{0 \le |n|\le N} \frac{|g_n|^2 - 1}{\langle n \rangle^d} \\ & = \sum_{0\le|n|\le 1} \frac{|g_n|^2-1}{\langle n \rangle^d}+ \sum_{2\le|n|\le N} \frac{|g_n|^2-1}{\langle n \rangle^d} \\& =: A_1 + A_{2, N} \end{align*} $$
$$ \begin{align*} \int_{{\mathbb{T}}^d} :\! u_N^2(x) \!: dx & = \sum_{0 \le |n|\le N} \frac{|g_n|^2 - 1}{\langle n \rangle^d} \\ & = \sum_{0\le|n|\le 1} \frac{|g_n|^2-1}{\langle n \rangle^d}+ \sum_{2\le|n|\le N} \frac{|g_n|^2-1}{\langle n \rangle^d} \\& =: A_1 + A_{2, N} \end{align*} $$
with the understanding that
![]() $A_{2, N} = 0$
when
$A_{2, N} = 0$
when
![]() $N = 1$
. Because of independence of the Gaussians
$N = 1$
. Because of independence of the Gaussians
![]() $\{g_n\}_{|n|>2}$
from
$\{g_n\}_{|n|>2}$
from
![]() $g_0$
and
$g_0$
and
![]() $g_1$
, the random variables
$g_1$
, the random variables
![]() $A_1$
and
$A_1$
and
![]() $A_{2, N}$
are independent. Note that the law
$A_{2, N}$
are independent. Note that the law
![]() $\mu _1$
of
$\mu _1$
of
![]() $A_1$
(and
$A_1$
(and
![]() $\mu _{2, N}$
of
$\mu _{2, N}$
of
![]() $A_{2, N}$
when
$A_{2, N}$
when
![]() $N \ge 2$
, respectively) is absolutely continuous with respect to the Lebesgue measure
$N \ge 2$
, respectively) is absolutely continuous with respect to the Lebesgue measure
![]() $\lambda $
on
$\lambda $
on
![]() ${\mathbb {R}}$
. Thus, we have
${\mathbb {R}}$
. Thus, we have
![]() $d \mu _1 = \sigma _1 d\lambda $
for some
$d \mu _1 = \sigma _1 d\lambda $
for some
![]() $\sigma _1 \in L^1({\mathbb {R}})$
(and
$\sigma _1 \in L^1({\mathbb {R}})$
(and
![]() $d \mu _{2, N} = \sigma _{2, N} d\lambda $
for some
$d \mu _{2, N} = \sigma _{2, N} d\lambda $
for some
![]() $ \sigma _{2, N} \in L^1({\mathbb {R}})$
when
$ \sigma _{2, N} \in L^1({\mathbb {R}})$
when
![]() $N \ge 2$
, respectively).
$N \ge 2$
, respectively).
We have
 $$ \begin{align*} \sum_{0\le|n|\le 1} \frac{|g_n|^2-1}{\langle n \rangle^d} = (g_0^2- 1) + 2^{1-{\frac{d}{2}}}(|g_1|^2 -1). \end{align*} $$
$$ \begin{align*} \sum_{0\le|n|\le 1} \frac{|g_n|^2-1}{\langle n \rangle^d} = (g_0^2- 1) + 2^{1-{\frac{d}{2}}}(|g_1|^2 -1). \end{align*} $$
Letting
![]() $\sigma _{10}$
(and
$\sigma _{10}$
(and
![]() $\sigma _{11}$
) be the density for
$\sigma _{11}$
) be the density for
![]() $g_0^2- 1$
(and
$g_0^2- 1$
(and
![]() $ 2^{1-{\frac {d}{2}}}(|g_1|^2 -1)$
, respectively), we have
$ 2^{1-{\frac {d}{2}}}(|g_1|^2 -1)$
, respectively), we have
Note that
![]() $g_0^2$
is a chi-square distribution of one degree of freedom and thus the density
$g_0^2$
is a chi-square distribution of one degree of freedom and thus the density
![]() $\sigma _{10}$
for
$\sigma _{10}$
for
![]() $g_0^2- 1$
is unbounded.Footnote
17
On the other hand,
$g_0^2- 1$
is unbounded.Footnote
17
On the other hand,
![]() $2|g_1|^2 = 2(\operatorname *{\mathrm {Re}} g_1)^2 + 2(\operatorname *{\mathrm {Im}} g_1)^2$
is a chi-square distribution of two degrees of freedom and thus the density
$2|g_1|^2 = 2(\operatorname *{\mathrm {Re}} g_1)^2 + 2(\operatorname *{\mathrm {Im}} g_1)^2$
is a chi-square distribution of two degrees of freedom and thus the density
![]() $\sigma _{11}$
for
$\sigma _{11}$
for
![]() $ 2^{1-{\frac {d}{2}}}(|g_1|^2 -1)$
is bounded. Hence, by Young’s inequality, we have
$ 2^{1-{\frac {d}{2}}}(|g_1|^2 -1)$
is bounded. Hence, by Young’s inequality, we have
which proves (2.16), when
![]() $N = 1$
. Next, we consider the case
$N = 1$
. Next, we consider the case
![]() $N \ge 2$
. Denoting by
$N \ge 2$
. Denoting by
![]() $\sigma _{2n}$
the density for
$\sigma _{2n}$
the density for
![]() $ 2\langle n \rangle ^{-d}(|g_n|^2 -1)$
, by Young’s inequality, we have
$ 2\langle n \rangle ^{-d}(|g_n|^2 -1)$
, by Young’s inequality, we have
 $$ \begin{align} \|\sigma_{2, N}\|_{L^1({\mathbb{R}})} = \| \sigma_{22} * \sigma_{23} * \cdots \sigma_{2N}\|_{L^1({\mathbb{R}})} \le \prod_{n = 2}^N \|\sigma_{2n}\|_{L^1({\mathbb{R}})} = 1, \end{align} $$
$$ \begin{align} \|\sigma_{2, N}\|_{L^1({\mathbb{R}})} = \| \sigma_{22} * \sigma_{23} * \cdots \sigma_{2N}\|_{L^1({\mathbb{R}})} \le \prod_{n = 2}^N \|\sigma_{2n}\|_{L^1({\mathbb{R}})} = 1, \end{align} $$
where the last equality holds since
![]() $\sigma _{2n}$
is a density of a probability measure. Hence, by Young’s inequality with (2.18), we have
$\sigma _{2n}$
is a density of a probability measure. Hence, by Young’s inequality with (2.18), we have
 $$ \begin{align*} \bigg\|\frac{d\nu_N}{d\lambda}\bigg\|_{L^\infty({\mathbb{R}})} &= \bigg\|\frac{d\operatorname{\mathrm{Law}}( A_1 + A_{2, N})}{d\lambda}\bigg\|_{L^\infty({\mathbb{R}})} \\ &= \| \sigma_1 \ast \sigma_{2, N}\|_{L^\infty({\mathbb{R}})} \\ &\le \| \sigma_1 \|_{L^\infty({\mathbb{R}})} \|\sigma_{2, N}\|_{L^1({\mathbb{R}})} \\ &= \| \sigma_1 \|_{L^\infty({\mathbb{R}})} \\ &\lesssim 1, \end{align*} $$
$$ \begin{align*} \bigg\|\frac{d\nu_N}{d\lambda}\bigg\|_{L^\infty({\mathbb{R}})} &= \bigg\|\frac{d\operatorname{\mathrm{Law}}( A_1 + A_{2, N})}{d\lambda}\bigg\|_{L^\infty({\mathbb{R}})} \\ &= \| \sigma_1 \ast \sigma_{2, N}\|_{L^\infty({\mathbb{R}})} \\ &\le \| \sigma_1 \|_{L^\infty({\mathbb{R}})} \|\sigma_{2, N}\|_{L^1({\mathbb{R}})} \\ &= \| \sigma_1 \|_{L^\infty({\mathbb{R}})} \\ &\lesssim 1, \end{align*} $$
uniformly in
![]() $N \ge 2$
. This proves (2.16).
$N \ge 2$
. This proves (2.16).
Let
![]() $I_\infty = \int _{{\mathbb {T}}^d}:\! u^2(x) \!: dx$
. Since
$I_\infty = \int _{{\mathbb {T}}^d}:\! u^2(x) \!: dx$
. Since
![]() $I_N$
converges to
$I_N$
converges to
![]() $I_\infty $
in law (see, for example, [Reference Oh and Thomann47, Proposition 1.1]), it follows from the Portmanteau theorem and (2.16) that
$I_\infty $
in law (see, for example, [Reference Oh and Thomann47, Proposition 1.1]), it follows from the Portmanteau theorem and (2.16) that
 $$ \begin{align*} \mathbb{P}(I_\infty = K) & \le \mathbb{P}\big(I_\infty \in (K-\varepsilon, K+\varepsilon)\big) \le \liminf_{N\to \infty} \mathbb{P}\big(I_N \in (K-\varepsilon, K+\varepsilon)\big) \\ & = \liminf_{N\to \infty} \nu_N\big( (K-\varepsilon, K+\varepsilon)\big)\\ & \le \sup_{N \in \mathbb{N}} \bigg\|\frac{d\nu_N}{d\lambda}\bigg\|_{L^\infty({\mathbb{R}})} \cdot \lambda \big( (K-\varepsilon, K+\varepsilon)\big)\\ & \lesssim \varepsilon \end{align*} $$
$$ \begin{align*} \mathbb{P}(I_\infty = K) & \le \mathbb{P}\big(I_\infty \in (K-\varepsilon, K+\varepsilon)\big) \le \liminf_{N\to \infty} \mathbb{P}\big(I_N \in (K-\varepsilon, K+\varepsilon)\big) \\ & = \liminf_{N\to \infty} \nu_N\big( (K-\varepsilon, K+\varepsilon)\big)\\ & \le \sup_{N \in \mathbb{N}} \bigg\|\frac{d\nu_N}{d\lambda}\bigg\|_{L^\infty({\mathbb{R}})} \cdot \lambda \big( (K-\varepsilon, K+\varepsilon)\big)\\ & \lesssim \varepsilon \end{align*} $$
for any
![]() $\varepsilon> 0$
. Since the choice of
$\varepsilon> 0$
. Since the choice of
![]() $\varepsilon> 0$
was arbitrary, we then conclude (2.17).
$\varepsilon> 0$
was arbitrary, we then conclude (2.17).
3 Nonnormalizability of the focusing Gibbs measure with the quartic interaction
In this section, we present the proof of the nonnormalizability of the log-correlated Gibbs measure with the focusing quartic interaction (Theorem 1.4).
3.1 Variational formulation
In order to prove (1.24) and (1.27), we use a variational formula for the partition function as in [Reference Tolomeo and Weber64, Reference Oh, Okamoto and Tolomeo41]. Let us first introduce some notations. Fix a a probability space
![]() $(\Omega , \mathcal {F}, \mathbb P)$
. Let
$(\Omega , \mathcal {F}, \mathbb P)$
. Let
![]() $W(t)$
be a cylindrical Brownian motion in
$W(t)$
be a cylindrical Brownian motion in
![]() $L^2({\mathbb {T}}^d)$
. Namely, we have
$L^2({\mathbb {T}}^d)$
. Namely, we have
where
![]() $\{B_n\}_{n \in \mathbb {Z}^d}$
is a sequence of mutually independent complex-valuedFootnote
18
Brownian motions such that
$\{B_n\}_{n \in \mathbb {Z}^d}$
is a sequence of mutually independent complex-valuedFootnote
18
Brownian motions such that
![]() $\overline {B_n}= B_{-n}$
,
$\overline {B_n}= B_{-n}$
,
![]() $n \in \mathbb {Z}^d$
. Then, define a centered Gaussian process
$n \in \mathbb {Z}^d$
. Then, define a centered Gaussian process
![]() $Y(t)$
by
$Y(t)$
by
Note that we have
![]() $\operatorname {\mathrm {Law}}(Y(1)) = \mu $
, where
$\operatorname {\mathrm {Law}}(Y(1)) = \mu $
, where
![]() $\mu $
is the log-correlated Gaussian measure in (1.2). By setting
$\mu $
is the log-correlated Gaussian measure in (1.2). By setting
![]() $Y_N = \pi _NY $
, we have
$Y_N = \pi _NY $
, we have
![]() $\operatorname {\mathrm {Law}}(Y_N(1)) = (\pi _N)_*\mu $
, that is, the pushforward of
$\operatorname {\mathrm {Law}}(Y_N(1)) = (\pi _N)_*\mu $
, that is, the pushforward of
![]() $\mu $
under
$\mu $
under
![]() $\pi _N$
. In particular, we have
$\pi _N$
. In particular, we have
![]() ${\mathbb {E}} [Y_N^2(1)] = \sigma _N$
, where
${\mathbb {E}} [Y_N^2(1)] = \sigma _N$
, where
![]() $\sigma _N$
is as in (1.5). Here, the expectation
$\sigma _N$
is as in (1.5). Here, the expectation
![]() ${\mathbb {E}}$
is with respect to the underlying probability measure
${\mathbb {E}}$
is with respect to the underlying probability measure
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
Next, let
![]() $\mathbb {H}_a$
denote the space of drifts, which are progressively measurableFootnote
19
processes belonging to
$\mathbb {H}_a$
denote the space of drifts, which are progressively measurableFootnote
19
processes belonging to
![]() $L^2([0,1]; L^2({\mathbb {T}}^d))$
,
$L^2([0,1]; L^2({\mathbb {T}}^d))$
,
![]() $\mathbb {P}$
-almost surely. We now state the Boué–Dupuis variational formula [Reference Boué and Dupuis7, Reference Üstünel68]; in particular, see Theorem 7 in [Reference Üstünel68].
$\mathbb {P}$
-almost surely. We now state the Boué–Dupuis variational formula [Reference Boué and Dupuis7, Reference Üstünel68]; in particular, see Theorem 7 in [Reference Üstünel68].
Lemma 3.1. Let Y be as in (3.2). Fix
![]() $N \in \mathbb {N}$
. Suppose that
$N \in \mathbb {N}$
. Suppose that
![]() $F:C^\infty ({\mathbb {T}}^d) \to {\mathbb {R}}$
is measurable such that
$F:C^\infty ({\mathbb {T}}^d) \to {\mathbb {R}}$
is measurable such that
![]() ${\mathbb {E}}\big [|F(\pi _NY(1))|^p\big ] < \infty $
and
${\mathbb {E}}\big [|F(\pi _NY(1))|^p\big ] < \infty $
and
![]() ${\mathbb {E}}\big [|e^{-F(\pi _NY(1))}|^q \big ] < \infty $
for some
${\mathbb {E}}\big [|e^{-F(\pi _NY(1))}|^q \big ] < \infty $
for some
![]() $1 < p, q < \infty $
with
$1 < p, q < \infty $
with
![]() ${\frac {1}{p}} + {\frac {1}{q}} = 1$
. Then, we have
${\frac {1}{p}} + {\frac {1}{q}} = 1$
. Then, we have
 $$ \begin{align} - \log {\mathbb{E}}\Big[e^{-F(\pi_N Y(1))}\Big] = \inf_{\theta \in \mathbb H_a} {\mathbb{E}}\bigg[ F(\pi_N Y(1) + \pi_N I(\theta)(1)) + {\frac{1}{2}} \int_0^1 \| \theta(t) \|_{L^2_x}^2 dt \bigg], \end{align} $$
$$ \begin{align} - \log {\mathbb{E}}\Big[e^{-F(\pi_N Y(1))}\Big] = \inf_{\theta \in \mathbb H_a} {\mathbb{E}}\bigg[ F(\pi_N Y(1) + \pi_N I(\theta)(1)) + {\frac{1}{2}} \int_0^1 \| \theta(t) \|_{L^2_x}^2 dt \bigg], \end{align} $$
where
![]() $I(\theta )$
is defined by
$I(\theta )$
is defined by
 $$ \begin{align} I(\theta)(t) = \int_0^t \langle \nabla \rangle^{-{\frac{d}{2}}} \theta(t') dt' \end{align} $$
$$ \begin{align} I(\theta)(t) = \int_0^t \langle \nabla \rangle^{-{\frac{d}{2}}} \theta(t') dt' \end{align} $$
and the expectation
![]() ${\mathbb {E}} = {\mathbb {E}}_{\mathbb {P}}$
is an expectation with respect to the underlying probability measure
${\mathbb {E}} = {\mathbb {E}}_{\mathbb {P}}$
is an expectation with respect to the underlying probability measure
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
In the following, we construct a drift
![]() $\theta $
depending on Y and the Boué–Dupuis variational formula (Lemma 3.1) is suitable for this purpose since an expectation in (3.3) is taken with respect to the underlying probability measure
$\theta $
depending on Y and the Boué–Dupuis variational formula (Lemma 3.1) is suitable for this purpose since an expectation in (3.3) is taken with respect to the underlying probability measure
![]() $\mathbb {P}$
. Compare this with the variational formula in [Reference Gunaratnam, Oh, Tzvetkov and Weber31], where an expectation is taken with respect to a shifted measure.
$\mathbb {P}$
. Compare this with the variational formula in [Reference Gunaratnam, Oh, Tzvetkov and Weber31], where an expectation is taken with respect to a shifted measure.
Before proceeding to the proof of Theorem 1.4, we state a lemma on the pathwise regularity bounds of
![]() $Y(1)$
and
$Y(1)$
and
![]() $I(\theta )(1)$
.
$I(\theta )(1)$
.
Lemma 3.2.
(i) Let
![]() $\varepsilon> 0$
. Then, given any finite
$\varepsilon> 0$
. Then, given any finite
![]() $p \ge 1$
, we have
$p \ge 1$
, we have
uniformly in
![]() $N \in \mathbb {N}$
.
$N \in \mathbb {N}$
.
(ii) For any
![]() $\theta \in \mathbb {H}_a$
, we have
$\theta \in \mathbb {H}_a$
, we have
 $$ \begin{align} \| \hspace{0.5mm}\text{I}\hspace{0.5mm}(\theta)(1) \|_{H^{{\frac{d}{2}}}}^2 \leq \int_0^1 \| \theta(t) \|_{L^2}^2dt. \end{align} $$
$$ \begin{align} \| \hspace{0.5mm}\text{I}\hspace{0.5mm}(\theta)(1) \|_{H^{{\frac{d}{2}}}}^2 \leq \int_0^1 \| \theta(t) \|_{L^2}^2dt. \end{align} $$
Before proceeding to the proof of Lemma 3.2, recall the following orthogonality result [Reference Nualart40, Lemma 1.1.1]; let f and g be jointly Gaussian random variables with mean zero and variances
![]() $\sigma _f$
and
$\sigma _f$
and
![]() $\sigma _g$
. Then, we have
$\sigma _g$
. Then, we have
where
![]() $H_k (x,\sigma )$
denotes the Hermite polynomial of degree k with variance parameter
$H_k (x,\sigma )$
denotes the Hermite polynomial of degree k with variance parameter
![]() $\sigma $
.
$\sigma $
.
Proof. Part (i) is a direct consequence of pathwise regularities of the log-correlated Gaussian process Y (and its Wick powers) whose law at time
![]() $t = 1$
is given by
$t = 1$
is given by
![]() $\mu $
in (1.2). See, for example, [Reference Oh and Thomann48, Proposition 2.3] and [Reference Gubinelli, Koch and Oh29, Proposition 2.1] for related results when
$\mu $
in (1.2). See, for example, [Reference Oh and Thomann48, Proposition 2.3] and [Reference Gubinelli, Koch and Oh29, Proposition 2.1] for related results when
![]() $d = 2$
. For readers’ convenience, we present details. Given
$d = 2$
. For readers’ convenience, we present details. Given
![]() $\varepsilon> 0$
and finite
$\varepsilon> 0$
and finite
![]() $p \ge 1$
, let
$p \ge 1$
, let
![]() $r \ge p$
such that
$r \ge p$
such that
![]() $\varepsilon r> 2d$
. Then, from the Sobolev embedding theorem and Minkowski’s integral inequality, we have
$\varepsilon r> 2d$
. Then, from the Sobolev embedding theorem and Minkowski’s integral inequality, we have
 $$ \begin{align} \nonumber \Big\|\|:\!Y_N^k(1)\!:\|_{W^{-\varepsilon, \infty}}\Big\|_{L^p(\Omega)} & \lesssim \Big\|\|:\!Y_N^k(1)\!:\|_{W^{-{\frac{\varepsilon}{2}}, r}}\Big\|_{L^p(\Omega)}\\ & \leq\Big\|\|\langle \nabla \rangle^{-{\frac{\varepsilon}{2}}}:\!Y_N^k(1, x)\!:\|_{L^p(\Omega)}\Big\|_{L^r_x}. \end{align} $$
$$ \begin{align} \nonumber \Big\|\|:\!Y_N^k(1)\!:\|_{W^{-\varepsilon, \infty}}\Big\|_{L^p(\Omega)} & \lesssim \Big\|\|:\!Y_N^k(1)\!:\|_{W^{-{\frac{\varepsilon}{2}}, r}}\Big\|_{L^p(\Omega)}\\ & \leq\Big\|\|\langle \nabla \rangle^{-{\frac{\varepsilon}{2}}}:\!Y_N^k(1, x)\!:\|_{L^p(\Omega)}\Big\|_{L^r_x}. \end{align} $$
On the other hand, from (1.6) and (3.7) with (3.1) and (3.2), we have
 $$ \begin{align*} {\mathbb{E}}\big[:\!Y_N^k(1, x)\!:\, :\!Y_N^k(1, y)\!:\big] & = k! \big\{{\mathbb{E}}[Y_N(1, x) Y_N(1, y)]\big\}^{k}\\ & = k!\sum_{\substack{n_1, \dots, n_k \in \mathbb{Z}^d\\ |n_j|\le N}} \prod_{j = 1}^k \frac{1}{\langle n_j \rangle^d} e_{n_1+ \cdots + n_k} (x - y). \end{align*} $$
$$ \begin{align*} {\mathbb{E}}\big[:\!Y_N^k(1, x)\!:\, :\!Y_N^k(1, y)\!:\big] & = k! \big\{{\mathbb{E}}[Y_N(1, x) Y_N(1, y)]\big\}^{k}\\ & = k!\sum_{\substack{n_1, \dots, n_k \in \mathbb{Z}^d\\ |n_j|\le N}} \prod_{j = 1}^k \frac{1}{\langle n_j \rangle^d} e_{n_1+ \cdots + n_k} (x - y). \end{align*} $$
By applying the Bessel potentials
![]() $\langle \nabla \rangle _x^{-{\frac {\varepsilon }{2}}}$
and
$\langle \nabla \rangle _x^{-{\frac {\varepsilon }{2}}}$
and
![]() $\langle \nabla \rangle _y^{-{\frac {\varepsilon }{2}}}$
of order
$\langle \nabla \rangle _y^{-{\frac {\varepsilon }{2}}}$
of order
![]() $-\frac \varepsilon 2$
and then setting
$-\frac \varepsilon 2$
and then setting
![]() $x = y$
, we have
$x = y$
, we have
 $$ \begin{align} {\mathbb{E}}\big[|\langle \nabla \rangle^{-{\frac{\varepsilon}{2}}} :\!Y_N^k(1, x)\!:|^2\big] & = k!\sum_{\substack{n_1, \dots, n_k \in \mathbb{Z}^d\\ |n_j|\le N}} \prod_{j = 1}^k \frac{1}{\langle n_j \rangle^d\langle n_1+ \cdots + n_k \rangle^\varepsilon} \lesssim 1, \end{align} $$
$$ \begin{align} {\mathbb{E}}\big[|\langle \nabla \rangle^{-{\frac{\varepsilon}{2}}} :\!Y_N^k(1, x)\!:|^2\big] & = k!\sum_{\substack{n_1, \dots, n_k \in \mathbb{Z}^d\\ |n_j|\le N}} \prod_{j = 1}^k \frac{1}{\langle n_j \rangle^d\langle n_1+ \cdots + n_k \rangle^\varepsilon} \lesssim 1, \end{align} $$
uniformly in
![]() $N \in \mathbb {N}$
. Then, (3.5) follows from (3.8), Lemma 2.3 and (3.9).
$N \in \mathbb {N}$
. Then, (3.5) follows from (3.8), Lemma 2.3 and (3.9).
As for Part (ii), the estimate (3.6) follows from (3.4), Minkowski’s inequality and Cauchy–Schwarz’s inequality. See the proof of Lemma 4.7 in [Reference Gunaratnam, Oh, Tzvetkov and Weber31] .
3.2 Proof of Theorem 1.4
In this subsection, we present the proof of Theorem 1.4. Let us first discuss the divergence (1.27) for any
![]() $K>0$
. Given
$K>0$
. Given
![]() $K, L> 0$
and
$K, L> 0$
and
![]() $N \in \mathbb {N}$
, define
$N \in \mathbb {N}$
, define
![]() $Z_{K,L,N}$
and
$Z_{K,L,N}$
and
![]() $Z_{K,L}$
by
$Z_{K,L}$
by
and
Then, by the monotone convergence theorem, we have
Moreover, by the dominated convergence theorem together with the almost sure convergenceFootnote
20
of
![]() $R_N(u)$
(and
$R_N(u)$
(and
![]() $\int _{{\mathbb {T}}^d} : \! u_N^2 \!: dx$
) to
$\int _{{\mathbb {T}}^d} : \! u_N^2 \!: dx$
) to
![]() $R(u)$
(and
$R(u)$
(and
![]() $\int _{{\mathbb {T}}^d} : \! u^2 \!: dx$
, respectively) and Lemma 2.4 (which guarantees almost sure convergence of
$\int _{{\mathbb {T}}^d} : \! u^2 \!: dx$
, respectively) and Lemma 2.4 (which guarantees almost sure convergence of
![]() $\mathbf 1_{\{ |\int _{{\mathbb {T}}^d} \, : \, u_N^2 :\, dx | \le K\}}$
to
$\mathbf 1_{\{ |\int _{{\mathbb {T}}^d} \, : \, u_N^2 :\, dx | \le K\}}$
to
![]() $\mathbf 1_{\{ |\int _{{\mathbb {T}}^d} \, : \, u^2 :\, dx | \le K\}}$
), we obtain
$\mathbf 1_{\{ |\int _{{\mathbb {T}}^d} \, : \, u^2 :\, dx | \le K\}}$
), we obtain
Therefore, (1.27) follows once we prove the following divergence:
where
![]() $R_N(u)$
is as in (1.8) with
$R_N(u)$
is as in (1.8) with
![]() $\lambda> 0$
and
$\lambda> 0$
and
![]() $k = 4$
.
$k = 4$
.
Noting that
the divergence (3.10) (and thus (1.24)) follows once we prove
By the Boué–Dupuis variational formula (Lemma 3.1), we have
 $$ \begin{align} \nonumber - \log & \, {{\mathbb{E}}_\mu \Big[\exp\Big(\min{( R_N(u),L)} \cdot \mathbf 1_{\{ |\int_{{\mathbb{T}}^d} \, : u_N^2 :\, dx | \le K\}}\Big) \Big]} \\ \nonumber &= \inf_{\theta \in \mathbb H_a} {\mathbb{E}}\bigg[ -\min\big( R_N(Y(1) + I(\theta)(1)),L\big)\\ &\hphantom{XXXXX} \times \mathbf 1_{\{ |\int_{{\mathbb{T}}^d} : (\pi_N Y(1))^2: + 2 (\pi _N Y(1)) (\pi_N I(\theta)(1)) + (\pi_N I(\theta)(1))^2 dx | \le K\}} \\ &\hphantom{XXXXX} \nonumber + {\frac{1}{2}} \int_0^1 \| \theta(t)\|_{L^2_x} ^2 dt \bigg], \end{align} $$
$$ \begin{align} \nonumber - \log & \, {{\mathbb{E}}_\mu \Big[\exp\Big(\min{( R_N(u),L)} \cdot \mathbf 1_{\{ |\int_{{\mathbb{T}}^d} \, : u_N^2 :\, dx | \le K\}}\Big) \Big]} \\ \nonumber &= \inf_{\theta \in \mathbb H_a} {\mathbb{E}}\bigg[ -\min\big( R_N(Y(1) + I(\theta)(1)),L\big)\\ &\hphantom{XXXXX} \times \mathbf 1_{\{ |\int_{{\mathbb{T}}^d} : (\pi_N Y(1))^2: + 2 (\pi _N Y(1)) (\pi_N I(\theta)(1)) + (\pi_N I(\theta)(1))^2 dx | \le K\}} \\ &\hphantom{XXXXX} \nonumber + {\frac{1}{2}} \int_0^1 \| \theta(t)\|_{L^2_x} ^2 dt \bigg], \end{align} $$
where
![]() $Y(1)$
is as in (3.2). Here,
$Y(1)$
is as in (3.2). Here,
![]() ${\mathbb {E}}_\mu $
and
${\mathbb {E}}_\mu $
and
![]() ${\mathbb {E}}$
denote expectations with respect to the Gaussian field
${\mathbb {E}}$
denote expectations with respect to the Gaussian field
![]() $\mu $
in (1.2) and the underlying probability measure
$\mu $
in (1.2) and the underlying probability measure
![]() $\mathbb {P}$
, respectively. In the following, we show that the right-hand side of (3.13) tends to
$\mathbb {P}$
, respectively. In the following, we show that the right-hand side of (3.13) tends to
![]() $-\infty $
as
$-\infty $
as
![]() $N, L \to \infty $
. The main idea is to construct a drift
$N, L \to \infty $
. The main idea is to construct a drift
![]() $\theta $
such that
$\theta $
such that
![]() $I(\theta )$
looks like ‘
$I(\theta )$
looks like ‘
![]() $- Y(1) + $
a perturbation’, where the perturbation term is bounded in
$- Y(1) + $
a perturbation’, where the perturbation term is bounded in
![]() $L^2({\mathbb {T}}^d)$
but has a large
$L^2({\mathbb {T}}^d)$
but has a large
![]() $L^4$
-norm.Footnote
21
$L^4$
-norm.Footnote
21
![]() $\bullet $
Part 1: We first present several preliminary results. The proofs of Lemmas 3.3 and 3.4 are presented in Subsection 3.3. We first construct a perturbation term in the next lemma. Fix a large parameter
$\bullet $
Part 1: We first present several preliminary results. The proofs of Lemmas 3.3 and 3.4 are presented in Subsection 3.3. We first construct a perturbation term in the next lemma. Fix a large parameter
![]() $M \gg 1$
. Let
$M \gg 1$
. Let
![]() $f: {\mathbb {R}}^d \to {\mathbb {R}}$
be a real-valued Schwartz function with
$f: {\mathbb {R}}^d \to {\mathbb {R}}$
be a real-valued Schwartz function with
![]() $\|f\|_{L^2({\mathbb {R}}^d, \frac {dx}{(2\pi )^d})} = 1$
such that its Fourier transform
$\|f\|_{L^2({\mathbb {R}}^d, \frac {dx}{(2\pi )^d})} = 1$
such that its Fourier transform
![]() $\widehat f$
is supported on
$\widehat f$
is supported on
![]() $\{\xi \in {\mathbb {R}}^d: |\xi | \le 1 \}$
with
$\{\xi \in {\mathbb {R}}^d: |\xi | \le 1 \}$
with
![]() $\widehat f(0) = 0$
. Define a function
$\widehat f(0) = 0$
. Define a function
![]() $f_M$
on
$f_M$
on
![]() ${\mathbb {T}}^d$
by
${\mathbb {T}}^d$
by
 $$ \begin{align} f_M = M^{-{\frac{d}{2}}} \sum_{\substack{n \in \mathbb{Z}^d \\ |n| \le M}} \widehat f\Big( {\frac{n}{M}} \Big) e_n, \end{align} $$
$$ \begin{align} f_M = M^{-{\frac{d}{2}}} \sum_{\substack{n \in \mathbb{Z}^d \\ |n| \le M}} \widehat f\Big( {\frac{n}{M}} \Big) e_n, \end{align} $$
where
![]() $\widehat f = \mathcal {F}_{{\mathbb {R}}^d}(f)$
denotes the Fourier transform on
$\widehat f = \mathcal {F}_{{\mathbb {R}}^d}(f)$
denotes the Fourier transform on
![]() ${\mathbb {R}}^d$
defined in (1.14). Then, a direct computation yields the following lemma.
${\mathbb {R}}^d$
defined in (1.14). Then, a direct computation yields the following lemma.
Lemma 3.3. Let
![]() $\alpha> 0$
. Then, we have
$\alpha> 0$
. Then, we have
 $$ \begin{align} \nonumber\int_{\mathbb{T}^d} (\langle \nabla \rangle^{-\alpha} f_M)^2 dx &\le C(f) M^{-d-2 + \max(d+ 2 -2\alpha, 0)}\\ & = \begin{cases} M^{-2\alpha}, & \text{for }\alpha \le {\frac{d}{2}} + 1,\\ M^{-d-2}, & \text{for }\alpha> {\frac{d}{2}} + 1. \end{cases} \end{align} $$
$$ \begin{align} \nonumber\int_{\mathbb{T}^d} (\langle \nabla \rangle^{-\alpha} f_M)^2 dx &\le C(f) M^{-d-2 + \max(d+ 2 -2\alpha, 0)}\\ & = \begin{cases} M^{-2\alpha}, & \text{for }\alpha \le {\frac{d}{2}} + 1,\\ M^{-d-2}, & \text{for }\alpha> {\frac{d}{2}} + 1. \end{cases} \end{align} $$
for any
![]() $M \gg 1$
and some constant
$M \gg 1$
and some constant
![]() $C(f)> 0$
.
$C(f)> 0$
.
See Lemma 5.13 in [Reference Oh, Okamoto and Tolomeo41] for an analogous result on the construction of a perturbation term. While Lemma 3.3 follows from a similar consideration, we present some details of the proof in Subsection 3.3.
In the next lemma, we construct an approximation
![]() $\zeta _M$
to Y in (3.2) by solving stochastic differential equations. Note that, in [Reference Oh, Okamoto and Tolomeo41], such an approximation of
$\zeta _M$
to Y in (3.2) by solving stochastic differential equations. Note that, in [Reference Oh, Okamoto and Tolomeo41], such an approximation of
![]() $Y(1)$
was constructed essentially by (a suitable frequency truncation of)
$Y(1)$
was constructed essentially by (a suitable frequency truncation of)
![]() $Y(\frac {1}{2})$
, which was sufficient to prove a divergence analogous to (3.12) for large
$Y(\frac {1}{2})$
, which was sufficient to prove a divergence analogous to (3.12) for large
![]() $K \gg 1 $
. In order to prove the divergence (3.12) for any
$K \gg 1 $
. In order to prove the divergence (3.12) for any
![]() $K> 0$
, we need to establish a more refined approximation argument. For simplicity, we denote
$K> 0$
, we need to establish a more refined approximation argument. For simplicity, we denote
![]() $Y(1)$
and
$Y(1)$
and
![]() $\pi _N Y(1)$
by Y and
$\pi _N Y(1)$
by Y and
![]() $Y_N$
, respectively, in the following.
$Y_N$
, respectively, in the following.
Lemma 3.4. Given
![]() $ M\gg 1$
, define
$ M\gg 1$
, define
![]() $\zeta _M$
by its Fourier coefficients as follows. For
$\zeta _M$
by its Fourier coefficients as follows. For
![]() $|n| \leq M$
,
$|n| \leq M$
,
![]() $\widehat \zeta _M(n, t)$
is a solution of the following differential equation:
$\widehat \zeta _M(n, t)$
is a solution of the following differential equation:
 $$ \begin{align} \begin{cases} d \widehat \zeta_{M}(n, t) = \langle n \rangle^{-{\frac{d}{2}}} M^{\frac{d}{2}} (\widehat Y(n, t)- \widehat \zeta_{M}(n, t)) dt \\ \widehat \zeta_{M}|_{t = 0} =0, \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} d \widehat \zeta_{M}(n, t) = \langle n \rangle^{-{\frac{d}{2}}} M^{\frac{d}{2}} (\widehat Y(n, t)- \widehat \zeta_{M}(n, t)) dt \\ \widehat \zeta_{M}|_{t = 0} =0, \end{cases} \end{align} $$
and we set
![]() $\widehat \zeta _{M}(n, t) \equiv 0$
for
$\widehat \zeta _{M}(n, t) \equiv 0$
for
![]() $|n|> M$
. Then,
$|n|> M$
. Then,
![]() $\zeta _M(t)$
is a centered Gaussian process in
$\zeta _M(t)$
is a centered Gaussian process in
![]() $L^2({\mathbb {T}}^d)$
, which is frequency localized on
$L^2({\mathbb {T}}^d)$
, which is frequency localized on
![]() $\{|n| \le M \}$
, satisfying
$\{|n| \le M \}$
, satisfying
 $$ \begin{align} &{\mathbb{E}}\bigg[ 2 \int_{{\mathbb{T}}^d} Y_N \zeta_M dx - \int_{{\mathbb{T}}^d} \zeta_M^2 dx \bigg] = \sigma_M(1 + o(1)) \sim \log M, \end{align} $$
$$ \begin{align} &{\mathbb{E}}\bigg[ 2 \int_{{\mathbb{T}}^d} Y_N \zeta_M dx - \int_{{\mathbb{T}}^d} \zeta_M^2 dx \bigg] = \sigma_M(1 + o(1)) \sim \log M, \end{align} $$
 $$ \begin{align} &{\mathbb{E}} \bigg[ \Big| \int_{{\mathbb{T}}^d} :\! ( Y_N-\zeta_M)^2 \!: dx \Big|^2 \bigg] \lesssim M^{-d}\log M, \end{align} $$
$$ \begin{align} &{\mathbb{E}} \bigg[ \Big| \int_{{\mathbb{T}}^d} :\! ( Y_N-\zeta_M)^2 \!: dx \Big|^2 \bigg] \lesssim M^{-d}\log M, \end{align} $$
 $$ \begin{align} &{\mathbb{E}}\bigg[\Big( \int_{{\mathbb{T}}^d} Y_N f_M dx \Big)^2\bigg] + {\mathbb{E}}\bigg[\Big( \int_{{\mathbb{T}}^d} \zeta_M f_M dx \Big)^2\bigg] \lesssim M^{-d}, \end{align} $$
$$ \begin{align} &{\mathbb{E}}\bigg[\Big( \int_{{\mathbb{T}}^d} Y_N f_M dx \Big)^2\bigg] + {\mathbb{E}}\bigg[\Big( \int_{{\mathbb{T}}^d} \zeta_M f_M dx \Big)^2\bigg] \lesssim M^{-d}, \end{align} $$
 $$ \begin{align} &{\mathbb{E}}\bigg[\int_0^1 \Big\| {\frac{d}{ds}} \zeta_M(s) \Big\|^2_{H^{\frac{d}{2}}}ds\bigg] \lesssim M^d \end{align} $$
$$ \begin{align} &{\mathbb{E}}\bigg[\int_0^1 \Big\| {\frac{d}{ds}} \zeta_M(s) \Big\|^2_{H^{\frac{d}{2}}}ds\bigg] \lesssim M^d \end{align} $$
for any
![]() $N \ge M \gg 1$
, where
$N \ge M \gg 1$
, where
![]() $\zeta _M =\zeta _M|_{t = 1}$
and
$\zeta _M =\zeta _M|_{t = 1}$
and
Here, (3.19) is independent of
![]() $x \in {\mathbb {T}}^d$
.
$x \in {\mathbb {T}}^d$
.
We now define
![]() $ \alpha _{M, N}$
by
$ \alpha _{M, N}$
by
 $$ \begin{align} \alpha_{M, N}= \frac{{\mathbb{E}} \bigg[ 2 \int_{{\mathbb{T}}^d}Y_N\zeta_M dx-\int_{{\mathbb{T}}^d}\zeta_M^2 dx \bigg]}{\int_{{\mathbb{T}}^d} f_M^2 dx} \end{align} $$
$$ \begin{align} \alpha_{M, N}= \frac{{\mathbb{E}} \bigg[ 2 \int_{{\mathbb{T}}^d}Y_N\zeta_M dx-\int_{{\mathbb{T}}^d}\zeta_M^2 dx \bigg]}{\int_{{\mathbb{T}}^d} f_M^2 dx} \end{align} $$
for
![]() $N\ge M \gg 1$
. Then, from (3.15) and (3.20), we have
$N\ge M \gg 1$
. Then, from (3.15) and (3.20), we have
for any
![]() $N \ge M\gg 1$
.
$N \ge M\gg 1$
.
![]() $\bullet $
Part 2: In this part, we prove the divergence (3.12). For
$\bullet $
Part 2: In this part, we prove the divergence (3.12). For
![]() $M \gg 1$
, we set
$M \gg 1$
, we set
![]() $f_M$
,
$f_M$
,
![]() $\zeta _M$
and
$\zeta _M$
and
![]() $ \alpha _{M, N}$
as in (3.14), Lemma 3.4 and (3.25). For the minimization problem (3.13), we set a drift
$ \alpha _{M, N}$
as in (3.14), Lemma 3.4 and (3.25). For the minimization problem (3.13), we set a drift
![]() $\theta = \theta ^0$
by
$\theta = \theta ^0$
by
 $$ \begin{align} \theta^0 (t) & = \langle \nabla \rangle^{{\frac{d}{2}}} \bigg( -\frac{d}{dt} \zeta_M(t) + \sqrt{ \alpha_{M, N}} f_M \bigg) \end{align} $$
$$ \begin{align} \theta^0 (t) & = \langle \nabla \rangle^{{\frac{d}{2}}} \bigg( -\frac{d}{dt} \zeta_M(t) + \sqrt{ \alpha_{M, N}} f_M \bigg) \end{align} $$
such that
 $$ \begin{align} \Theta^0 = I(\theta^0)(1) = \int_0^1 \langle \nabla \rangle^{-{\frac{d}{2}}} \theta^0(t) \, dt = - \zeta_M + \sqrt{ \alpha_{M, N}} f_M. \end{align} $$
$$ \begin{align} \Theta^0 = I(\theta^0)(1) = \int_0^1 \langle \nabla \rangle^{-{\frac{d}{2}}} \theta^0(t) \, dt = - \zeta_M + \sqrt{ \alpha_{M, N}} f_M. \end{align} $$
We also define
![]() $Q(u$
) by
$Q(u$
) by
for
![]() $u \in L^4({\mathbb {T}}^d)$
and
$u \in L^4({\mathbb {T}}^d)$
and
![]() $v\in L^4({\mathbb {R}}^d)$
, respectively.
$v\in L^4({\mathbb {R}}^d)$
, respectively.
Let us first make some preliminary computations. By Cauchy’s inequality, we have
 $$ \begin{align} \nonumber |\zeta_M(\sqrt{ \alpha_{M, N}} f_M)^3| &\le {\frac{\delta}{4}} \alpha_{M, N}^2 f_M^4 +\frac{1}{\delta} \alpha_{M, N} \zeta_M^2 f_M^2, \\ |\zeta_M^3 \sqrt{ \alpha_{M, N}} f_M | &\le {\frac{\delta}{4}} \zeta_M^4+\frac{ 1}{\delta} \alpha_{M, N}\zeta_M^2 f_M^2 \end{align} $$
$$ \begin{align} \nonumber |\zeta_M(\sqrt{ \alpha_{M, N}} f_M)^3| &\le {\frac{\delta}{4}} \alpha_{M, N}^2 f_M^4 +\frac{1}{\delta} \alpha_{M, N} \zeta_M^2 f_M^2, \\ |\zeta_M^3 \sqrt{ \alpha_{M, N}} f_M | &\le {\frac{\delta}{4}} \zeta_M^4+\frac{ 1}{\delta} \alpha_{M, N}\zeta_M^2 f_M^2 \end{align} $$
for any
![]() $0<\delta <1$
. Then, from (3.28), (3.29) and (3.30), we have
$0<\delta <1$
. Then, from (3.28), (3.29) and (3.30), we have
 $$ \begin{align} \nonumber Q(\Theta^0) & - \alpha_{M, N}^2 Q(f_M) \\ &= - \int_{{\mathbb{T}}^d} \zeta_M(\sqrt{ \alpha_{M, N}} f_M)^3 dx + {\frac{3}{2}} \int_{{\mathbb{T}}^d} \zeta_M^2 (\sqrt{ \alpha_{M, N}} f_M)^2 dx \\ &\quad \nonumber - \int_{{\mathbb{T}}^d} \zeta_M^3 \sqrt{ \alpha_{M, N}} f_M dx + Q(\zeta_M) \\ \nonumber &\ge -\delta \alpha_{M, N}^2 Q(f_M) - C_\delta \alpha_{M, N}\int_{{\mathbb{T}}^d} \zeta_M^2 f_M^2 dx +(1-\delta) Q(\zeta_M) \\ \nonumber &\ge -\delta \alpha_{M, N}^2 Q(f_M) - C_\delta \alpha_{M, N} \int_{{\mathbb{T}}^d} \zeta_M^2f_M^2 dx\end{align} $$
$$ \begin{align} \nonumber Q(\Theta^0) & - \alpha_{M, N}^2 Q(f_M) \\ &= - \int_{{\mathbb{T}}^d} \zeta_M(\sqrt{ \alpha_{M, N}} f_M)^3 dx + {\frac{3}{2}} \int_{{\mathbb{T}}^d} \zeta_M^2 (\sqrt{ \alpha_{M, N}} f_M)^2 dx \\ &\quad \nonumber - \int_{{\mathbb{T}}^d} \zeta_M^3 \sqrt{ \alpha_{M, N}} f_M dx + Q(\zeta_M) \\ \nonumber &\ge -\delta \alpha_{M, N}^2 Q(f_M) - C_\delta \alpha_{M, N}\int_{{\mathbb{T}}^d} \zeta_M^2 f_M^2 dx +(1-\delta) Q(\zeta_M) \\ \nonumber &\ge -\delta \alpha_{M, N}^2 Q(f_M) - C_\delta \alpha_{M, N} \int_{{\mathbb{T}}^d} \zeta_M^2f_M^2 dx\end{align} $$
for any
![]() $0<\delta <1$
. From (3.26), (3.19) in Lemma 3.4 and (3.15) in Lemma 3.3, we have
$0<\delta <1$
. From (3.26), (3.19) in Lemma 3.4 and (3.15) in Lemma 3.3, we have
 $$ \begin{align} \nonumber {\mathbb{E}} \bigg[ \alpha_{M, N} \int_{{\mathbb{T}}^d} \zeta_M^2 f_M^2 dx \bigg] & = \alpha_{M, N} \int_{{\mathbb{T}}^d} {\mathbb{E}} [\zeta_M^2(x)] f_M^2(x) dx \\ &\sim (\log M)^2 \| f_M \|_{L^2}^2 \lesssim (\log M )^2 \end{align} $$
$$ \begin{align} \nonumber {\mathbb{E}} \bigg[ \alpha_{M, N} \int_{{\mathbb{T}}^d} \zeta_M^2 f_M^2 dx \bigg] & = \alpha_{M, N} \int_{{\mathbb{T}}^d} {\mathbb{E}} [\zeta_M^2(x)] f_M^2(x) dx \\ &\sim (\log M)^2 \| f_M \|_{L^2}^2 \lesssim (\log M )^2 \end{align} $$
for any
![]() $N \ge M \gg 1$
. Therefore, it follows from (3.31), (3.32) and (3.26) with (3.29) and (3.16) that for any measurable set E with
$N \ge M \gg 1$
. Therefore, it follows from (3.31), (3.32) and (3.26) with (3.29) and (3.16) that for any measurable set E with
![]() $\mathbb {P}(E)>0$
and any
$\mathbb {P}(E)>0$
and any
![]() $L \gg \lambda \cdot \alpha _{M, N}^2 Q(f_M)$
, we have
$L \gg \lambda \cdot \alpha _{M, N}^2 Q(f_M)$
, we have
 $$ \begin{align} \nonumber {\mathbb{E}} \Big[\min\big( \gamma \lambda Q(\Theta^0), L\big) \cdot \mathbf 1_E\Big] &\ge \gamma \lambda (1-\delta) \alpha_{M, N}^2 Q(f_M) \mathbb{P}(E) - \gamma C^{\prime}_\delta (\log M )^2 \\ &= \gamma \lambda (1-\delta) \sigma_M^2 M^d Q_{{\mathbb{R}}^d}(f)\mathbb{P}(E) (1 + o(1)) \end{align} $$
$$ \begin{align} \nonumber {\mathbb{E}} \Big[\min\big( \gamma \lambda Q(\Theta^0), L\big) \cdot \mathbf 1_E\Big] &\ge \gamma \lambda (1-\delta) \alpha_{M, N}^2 Q(f_M) \mathbb{P}(E) - \gamma C^{\prime}_\delta (\log M )^2 \\ &= \gamma \lambda (1-\delta) \sigma_M^2 M^d Q_{{\mathbb{R}}^d}(f)\mathbb{P}(E) (1 + o(1)) \end{align} $$
for any
![]() $N \ge M \gg 1$
.
$N \ge M \gg 1$
.
Recall from (3.14) that
![]() $\widehat f_M$
is supported on
$\widehat f_M$
is supported on
![]() $\{|n|\leq M\}$
. Then, by Lemma 3.2 (ii) with (3.28), (3.27), (3.23) in Lemma 3.4, (3.26) and (3.15) in Lemma 3.3, we have
$\{|n|\leq M\}$
. Then, by Lemma 3.2 (ii) with (3.28), (3.27), (3.23) in Lemma 3.4, (3.26) and (3.15) in Lemma 3.3, we have
 $$ \begin{align} \nonumber {\mathbb{E}} \big[ \| \Theta^0\|_{H^{\frac{d}{2}}}^2 \big] &\le {\mathbb{E}} \bigg[ \int_0^1 \|\theta^0(t)\|_{L^2}^2 dt \bigg] \\ &\lesssim {\mathbb{E}}\bigg[\int_0^1 \Big\| \frac{d}{ds} \zeta_M(s) \Big\|^2_{H^{\frac{d}{2}}}ds\bigg] + M^d \alpha_{M,N} \|f_M \|_{L^2}^2 \\ \nonumber &\lesssim M^d \log M. \end{align} $$
$$ \begin{align} \nonumber {\mathbb{E}} \big[ \| \Theta^0\|_{H^{\frac{d}{2}}}^2 \big] &\le {\mathbb{E}} \bigg[ \int_0^1 \|\theta^0(t)\|_{L^2}^2 dt \bigg] \\ &\lesssim {\mathbb{E}}\bigg[\int_0^1 \Big\| \frac{d}{ds} \zeta_M(s) \Big\|^2_{H^{\frac{d}{2}}}ds\bigg] + M^d \alpha_{M,N} \|f_M \|_{L^2}^2 \\ \nonumber &\lesssim M^d \log M. \end{align} $$
Lastly, recall the following identity (see [Reference Oh and Thomann48, (1.18)]):
 $$ \begin{align} H_k(x+y; \sigma ) & = \sum_{\ell = 0}^k \begin{pmatrix} k \\ \ell \end{pmatrix} x^{k - \ell} H_\ell(y; \sigma), \end{align} $$
$$ \begin{align} H_k(x+y; \sigma ) & = \sum_{\ell = 0}^k \begin{pmatrix} k \\ \ell \end{pmatrix} x^{k - \ell} H_\ell(y; \sigma), \end{align} $$
which follows from a Taylor expansion with the differentiation rule [Reference Kuo32, p. 159]:
![]() $H_k(x;\sigma ) = k H_{k-1}(x;\sigma )$
. Then, from (1.8) with
$H_k(x;\sigma ) = k H_{k-1}(x;\sigma )$
. Then, from (1.8) with
![]() $k = 4$
and (3.35), we have
$k = 4$
and (3.35), we have
 $$ \begin{align} \nonumber R_N (Y + \Theta^0) & = {\frac{\lambda}{4}}\int_{{\mathbb{T}}^d} :\! Y_N^4 \!: dx + \lambda \int_{{\mathbb{T}}^d} :\! Y_N^3 \!: \Theta^0 dx+\frac {3\lambda}2\int_{{\mathbb{T}}^d} :\! Y_N^2 \!: (\Theta^0)^2 dx \\ &\hphantom{X} + \lambda\int_{{\mathbb{T}}^d} Y_N (\Theta^0)^3 dx + {\frac{\lambda}{4}}\int_{{\mathbb{T}}^d} (\Theta^0)^4 dx, \end{align} $$
$$ \begin{align} \nonumber R_N (Y + \Theta^0) & = {\frac{\lambda}{4}}\int_{{\mathbb{T}}^d} :\! Y_N^4 \!: dx + \lambda \int_{{\mathbb{T}}^d} :\! Y_N^3 \!: \Theta^0 dx+\frac {3\lambda}2\int_{{\mathbb{T}}^d} :\! Y_N^2 \!: (\Theta^0)^2 dx \\ &\hphantom{X} + \lambda\int_{{\mathbb{T}}^d} Y_N (\Theta^0)^3 dx + {\frac{\lambda}{4}}\int_{{\mathbb{T}}^d} (\Theta^0)^4 dx, \end{align} $$
where we used
for
![]() $N \ge M \ge 1$
. We now state a lemma, controlling the second, third and fourth terms on the right-hand side of (3.36). We present the proof of this lemma in Subsection 3.3.
$N \ge M \ge 1$
. We now state a lemma, controlling the second, third and fourth terms on the right-hand side of (3.36). We present the proof of this lemma in Subsection 3.3.
Lemma 3.5. There exist small
![]() $\varepsilon>0$
and a constant
$\varepsilon>0$
and a constant
![]() $c_0=c_0(\varepsilon )>0$
such that for any
$c_0=c_0(\varepsilon )>0$
such that for any
![]() $\delta>0$
, we have
$\delta>0$
, we have
 $$ \begin{align} \bigg| \int_{{\mathbb{T}}^d} :\! Y_N^3 \!: \Theta^0dx \bigg| &\le c(\delta) \| :\! Y_N^3 \!: \|_{W^{-\varepsilon,\infty}}^2 + \delta \| \Theta^0\|_{ H^{{\frac{d}{2}}}}^2, \end{align} $$
$$ \begin{align} \bigg| \int_{{\mathbb{T}}^d} :\! Y_N^3 \!: \Theta^0dx \bigg| &\le c(\delta) \| :\! Y_N^3 \!: \|_{W^{-\varepsilon,\infty}}^2 + \delta \| \Theta^0\|_{ H^{{\frac{d}{2}}}}^2, \end{align} $$
 $$ \begin{align} \bigg| \int_{{\mathbb{T}}^d} :\! Y_N^2 \!: (\Theta^0)^2 dx \bigg| &\le c(\delta) \| :\! Y_N^2 \!: \|_{W^{-\varepsilon,\infty}}^4 + \delta \Big( \| \Theta^0\|_{ H^{{\frac{d}{2}}}}^2 + \| \Theta^0 \|_{L^4}^4 \Big), \end{align} $$
$$ \begin{align} \bigg| \int_{{\mathbb{T}}^d} :\! Y_N^2 \!: (\Theta^0)^2 dx \bigg| &\le c(\delta) \| :\! Y_N^2 \!: \|_{W^{-\varepsilon,\infty}}^4 + \delta \Big( \| \Theta^0\|_{ H^{{\frac{d}{2}}}}^2 + \| \Theta^0 \|_{L^4}^4 \Big), \end{align} $$
 $$ \begin{align} \bigg| \int_{{\mathbb{T}}^d} Y_N (\Theta^0)^3 dx\bigg| &\le c(\delta) \| Y_N \|_{W^{-\varepsilon,\infty}}^{c_0}+ \delta \Big( \| \Theta^0\|_{ H^{{\frac{d}{2}}}}^2 + \| \Theta^0 \|_{L^4}^4 \Big), \end{align} $$
$$ \begin{align} \bigg| \int_{{\mathbb{T}}^d} Y_N (\Theta^0)^3 dx\bigg| &\le c(\delta) \| Y_N \|_{W^{-\varepsilon,\infty}}^{c_0}+ \delta \Big( \| \Theta^0\|_{ H^{{\frac{d}{2}}}}^2 + \| \Theta^0 \|_{L^4}^4 \Big), \end{align} $$
uniformly in
![]() $N \in \mathbb {N}$
.
$N \in \mathbb {N}$
.
Fix small
![]() $\delta _0> 0$
. Then, from (3.36) and Lemma 3.5, we have
$\delta _0> 0$
. Then, from (3.36) and Lemma 3.5, we have
 $$ \begin{align} \nonumber R_N(Y + \Theta^0) &\ge (1-\delta_0) \lambda Q(\Theta^0) \\ & \quad - c(\delta_0)\lambda \Big( \| :\! Y_N^3 \!: \|_{W^{-\varepsilon,\infty}}^2 + \|:\! Y_N^2 \!:\|_{W^{-\varepsilon,\infty}}^4 + \|Y_N\|_{W^{-\varepsilon,\infty}}^{c_0} \Big) \\ \nonumber &\quad -c\delta_0 \lambda \|\Theta^0\|_{H^{\frac{d}{2}}}^2- |R_N(Y)|. \end{align} $$
$$ \begin{align} \nonumber R_N(Y + \Theta^0) &\ge (1-\delta_0) \lambda Q(\Theta^0) \\ & \quad - c(\delta_0)\lambda \Big( \| :\! Y_N^3 \!: \|_{W^{-\varepsilon,\infty}}^2 + \|:\! Y_N^2 \!:\|_{W^{-\varepsilon,\infty}}^4 + \|Y_N\|_{W^{-\varepsilon,\infty}}^{c_0} \Big) \\ \nonumber &\quad -c\delta_0 \lambda \|\Theta^0\|_{H^{\frac{d}{2}}}^2- |R_N(Y)|. \end{align} $$
We are now ready to put everything together. With (3.37) in mind, suppose that for any
![]() $K>0$
and small
$K>0$
and small
![]() $\delta _1>0$
, there exists
$\delta _1>0$
, there exists
![]() $M_0=M_0(K,\delta _1) \geq 1$
such that
$M_0=M_0(K,\delta _1) \geq 1$
such that
 $$ \begin{align} \mathbb{P}\bigg( \Big|\int_{{\mathbb{T}}^d} (:{Y_N^2}: + 2 Y_N \Theta^0 + (\Theta^0)^2) dx \Big| \le K \bigg) \ge 1 - \delta_1, \end{align} $$
$$ \begin{align} \mathbb{P}\bigg( \Big|\int_{{\mathbb{T}}^d} (:{Y_N^2}: + 2 Y_N \Theta^0 + (\Theta^0)^2) dx \Big| \le K \bigg) \ge 1 - \delta_1, \end{align} $$
uniformly in
![]() $N \ge M \ge M_0$
. Then, it follows from (3.13), (3.41), (3.33), Lemma 3.2 (3.34), (1.9) (controlling
$N \ge M \ge M_0$
. Then, it follows from (3.13), (3.41), (3.33), Lemma 3.2 (3.34), (1.9) (controlling
![]() $|R_N(Y)|$
, uniformly in
$|R_N(Y)|$
, uniformly in
![]() $N \in \mathbb {N}$
), and (3.26) with (3.37) that there exist constants
$N \in \mathbb {N}$
), and (3.26) with (3.37) that there exist constants
![]() $C_1, C_2> 0 $
such that
$C_1, C_2> 0 $
such that
 $$ \begin{align} -\log & \, {\mathbb{E}}_\mu\Big[\exp\Big(\min{( R_N(u),L)} \cdot \mathbf 1_{\{ |\int_{{\mathbb{T}}^d} \, : u_N^2 :\, dx | \le K\}}\Big) \Big] \notag \\ &\le {\mathbb{E}}\bigg[ -\min\big( R_N(Y + \Theta^0),L\big)\notag \\ & \hphantom{XXX}\times \mathbf 1_{\{ |\int_{{\mathbb{T}}^d} ( :{Y_N^2}: + 2 Y_N \Theta^0 + (\Theta^0)^2) dx | \le K\}} + {\frac{1}{2}} \int_0^1 \| \theta^0(t)\|_{L^2_x} ^2 dt \bigg] \notag \\ &\le {\mathbb{E}}\bigg[ -\min\big((1-\delta_0) \lambda Q(\Theta^0),L\big) \cdot \mathbf 1_{\{ |\int_{{\mathbb{T}}^d} ( :{Y_N^2}: + 2 Y_N \Theta^0 + (\Theta^0)^2) dx | \le K\}} \notag \\ &\hphantom{XXX} + c(\delta_0)\lambda \Big( \| :\! Y_N^3 \!: \|_{W^{-\varepsilon,\infty}}^2 + \|:\! Y_N^2 \!:\|_{W^{-\varepsilon,\infty}}^4 + \|Y_N\|_{W^{-\varepsilon,\infty}}^{c_0} \Big) \notag \\ &\hphantom{XXX} + c\delta_0\lambda\|\Theta^0\|_{H^{{\frac{d}{2}}}}^2 + |R_N(Y)| + {\frac{1}{2}} \int_0^1 \| \theta^0(t)\|_{L^2_x} ^2 dt \bigg] \notag \\ &\le -(1-\delta_0)(1-\delta)(1-\delta_1)\lambda \alpha_{M,N}^2M^d Q_{{\mathbb{R}}^d}(f)(1+o(1)) \notag \\ & \quad + C_1(\delta_0,\lambda) M^d \log M+ C_2(\delta_0,\lambda) \notag \\ &= -(1-\delta_0)(1-\delta)(1-\delta_1)\lambda \sigma_M^2M^dQ_{{\mathbb{R}}^d}(f)(1+o(1)) \end{align} $$
$$ \begin{align} -\log & \, {\mathbb{E}}_\mu\Big[\exp\Big(\min{( R_N(u),L)} \cdot \mathbf 1_{\{ |\int_{{\mathbb{T}}^d} \, : u_N^2 :\, dx | \le K\}}\Big) \Big] \notag \\ &\le {\mathbb{E}}\bigg[ -\min\big( R_N(Y + \Theta^0),L\big)\notag \\ & \hphantom{XXX}\times \mathbf 1_{\{ |\int_{{\mathbb{T}}^d} ( :{Y_N^2}: + 2 Y_N \Theta^0 + (\Theta^0)^2) dx | \le K\}} + {\frac{1}{2}} \int_0^1 \| \theta^0(t)\|_{L^2_x} ^2 dt \bigg] \notag \\ &\le {\mathbb{E}}\bigg[ -\min\big((1-\delta_0) \lambda Q(\Theta^0),L\big) \cdot \mathbf 1_{\{ |\int_{{\mathbb{T}}^d} ( :{Y_N^2}: + 2 Y_N \Theta^0 + (\Theta^0)^2) dx | \le K\}} \notag \\ &\hphantom{XXX} + c(\delta_0)\lambda \Big( \| :\! Y_N^3 \!: \|_{W^{-\varepsilon,\infty}}^2 + \|:\! Y_N^2 \!:\|_{W^{-\varepsilon,\infty}}^4 + \|Y_N\|_{W^{-\varepsilon,\infty}}^{c_0} \Big) \notag \\ &\hphantom{XXX} + c\delta_0\lambda\|\Theta^0\|_{H^{{\frac{d}{2}}}}^2 + |R_N(Y)| + {\frac{1}{2}} \int_0^1 \| \theta^0(t)\|_{L^2_x} ^2 dt \bigg] \notag \\ &\le -(1-\delta_0)(1-\delta)(1-\delta_1)\lambda \alpha_{M,N}^2M^d Q_{{\mathbb{R}}^d}(f)(1+o(1)) \notag \\ & \quad + C_1(\delta_0,\lambda) M^d \log M+ C_2(\delta_0,\lambda) \notag \\ &= -(1-\delta_0)(1-\delta)(1-\delta_1)\lambda \sigma_M^2M^dQ_{{\mathbb{R}}^d}(f)(1+o(1)) \end{align} $$
for any
![]() $N \ge M \ge M_0(K,\delta _1)$
and
$N \ge M \ge M_0(K,\delta _1)$
and
![]() $L \gg \lambda \cdot \alpha _{M, N}^2 Q(f_M)\sim \lambda M^d (\log M)^2$
. Therefore, we obtain
$L \gg \lambda \cdot \alpha _{M, N}^2 Q(f_M)\sim \lambda M^d (\log M)^2$
. Therefore, we obtain
 $$ \begin{align} \nonumber \lim_{L \to \infty} & \liminf_{N \to \infty} {\mathbb{E}}_\mu\Big[\exp\Big(\min{(\lambda R_N(u),L)} \Big) \cdot \mathbf 1_{\{ |\int_{{\mathbb{T}}^d} \, : u_N^2 :\, dx | \le K\}} \Big] \\ \ge&~ \exp\Big( (1-\delta_0)(1-\delta)(1-\delta_1)\lambda \sigma_{M}^2M^dQ_{{\mathbb{R}}^d}(f) (1+o(1))\Big) \longrightarrow \infty, \end{align} $$
$$ \begin{align} \nonumber \lim_{L \to \infty} & \liminf_{N \to \infty} {\mathbb{E}}_\mu\Big[\exp\Big(\min{(\lambda R_N(u),L)} \Big) \cdot \mathbf 1_{\{ |\int_{{\mathbb{T}}^d} \, : u_N^2 :\, dx | \le K\}} \Big] \\ \ge&~ \exp\Big( (1-\delta_0)(1-\delta)(1-\delta_1)\lambda \sigma_{M}^2M^dQ_{{\mathbb{R}}^d}(f) (1+o(1))\Big) \longrightarrow \infty, \end{align} $$
as
![]() $M \to \infty $
. This proves (3.12) by assuming (3.42).
$M \to \infty $
. This proves (3.12) by assuming (3.42).
It remains to prove (3.42) for any
![]() $K> 0$
and small
$K> 0$
and small
![]() $\delta _1>0$
. From (3.28), we have
$\delta _1>0$
. From (3.28), we have
 $$ \begin{align} \nonumber &{\mathbb{E}} \bigg[ \Big|\int_{{\mathbb{T}}^d} \Big( :{Y_N^2}: + 2 Y_N \Theta^0 + (\Theta^0)^2 \Big) dx \Big|^2 \bigg]\\ &= {\mathbb{E}} \bigg[ \Big|\int_{{\mathbb{T}}^d} :{Y_N^2}: dx - 2 \int_{{\mathbb{T}}^d} Y_N \zeta_M dx+\int_{{\mathbb{T}}^d} \zeta_M^2 dx+ \alpha_{M, N} \int_{{\mathbb{T}}^d} f_M^2 dx \\ &\hphantom{X} \nonumber+ 2 \sqrt{ \alpha_{M, N}} \int_{{\mathbb{T}}^d} (Y_N-\zeta_M)f_M dx \Big|^2 \bigg]. \end{align} $$
$$ \begin{align} \nonumber &{\mathbb{E}} \bigg[ \Big|\int_{{\mathbb{T}}^d} \Big( :{Y_N^2}: + 2 Y_N \Theta^0 + (\Theta^0)^2 \Big) dx \Big|^2 \bigg]\\ &= {\mathbb{E}} \bigg[ \Big|\int_{{\mathbb{T}}^d} :{Y_N^2}: dx - 2 \int_{{\mathbb{T}}^d} Y_N \zeta_M dx+\int_{{\mathbb{T}}^d} \zeta_M^2 dx+ \alpha_{M, N} \int_{{\mathbb{T}}^d} f_M^2 dx \\ &\hphantom{X} \nonumber+ 2 \sqrt{ \alpha_{M, N}} \int_{{\mathbb{T}}^d} (Y_N-\zeta_M)f_M dx \Big|^2 \bigg]. \end{align} $$
From (3.26) and (3.22) in Lemma 3.4, we have
 $$ \begin{align} {\mathbb{E}} \bigg[ \Big| \sqrt{ \alpha_{M, N}} \int_{{\mathbb{T}}^d} (Y_N-\zeta_M)f_M dx \Big|^2 \bigg] \lesssim M^{-d} \log M. \end{align} $$
$$ \begin{align} {\mathbb{E}} \bigg[ \Big| \sqrt{ \alpha_{M, N}} \int_{{\mathbb{T}}^d} (Y_N-\zeta_M)f_M dx \Big|^2 \bigg] \lesssim M^{-d} \log M. \end{align} $$
On other hand, from (3.25) and (3.24), we have
 $$ \begin{align} \nonumber \int_{{\mathbb{T}}^d} & :\!Y_N^2\!: dx - 2 \int_{{\mathbb{T}}^d} Y_N \zeta_M dx+\int_{{\mathbb{T}}^d} \zeta_M^2 dx+ \alpha_{M, N} \int_{{\mathbb{T}}^d} f_M^2 dx \\ & =\int_{{\mathbb{T}}^d} (Y_N-\zeta_M)^2 -{\mathbb{E}} \big[(Y_N-\zeta_M )^2 \big] dx \\ \nonumber & =\int_{{\mathbb{T}}^d} :\! ( Y_N-\zeta_M)^2 \!: dx. \end{align} $$
$$ \begin{align} \nonumber \int_{{\mathbb{T}}^d} & :\!Y_N^2\!: dx - 2 \int_{{\mathbb{T}}^d} Y_N \zeta_M dx+\int_{{\mathbb{T}}^d} \zeta_M^2 dx+ \alpha_{M, N} \int_{{\mathbb{T}}^d} f_M^2 dx \\ & =\int_{{\mathbb{T}}^d} (Y_N-\zeta_M)^2 -{\mathbb{E}} \big[(Y_N-\zeta_M )^2 \big] dx \\ \nonumber & =\int_{{\mathbb{T}}^d} :\! ( Y_N-\zeta_M)^2 \!: dx. \end{align} $$
Hence, from (3.45), (3.46) and (3.47) with (3.21) in Lemma 3.4, we obtain
 $$ \begin{align*} {\mathbb{E}} \bigg[ \Big|\int_{{\mathbb{T}}^d} \Big( :{Y_N^2}: + 2 Y_N \Theta^0 + (\Theta^0)^2 \Big) dx \Big|^2 \bigg]\lesssim M^{-d }\log M. \end{align*} $$
$$ \begin{align*} {\mathbb{E}} \bigg[ \Big|\int_{{\mathbb{T}}^d} \Big( :{Y_N^2}: + 2 Y_N \Theta^0 + (\Theta^0)^2 \Big) dx \Big|^2 \bigg]\lesssim M^{-d }\log M. \end{align*} $$
Therefore, by Chebyshev’s inequality, given any
![]() $K{\kern-1pt}>{\kern-1pt} 0$
and small
$K{\kern-1pt}>{\kern-1pt} 0$
and small
![]() $\delta _1{\kern-1pt}>{\kern-1pt} 0$
, there exists
$\delta _1{\kern-1pt}>{\kern-1pt} 0$
, there exists
![]() $M_0 {\kern-1pt}={\kern-1pt} M_0(K, \delta _1) {\kern-1pt}\geq{\kern-1pt} 1$
such that
$M_0 {\kern-1pt}={\kern-1pt} M_0(K, \delta _1) {\kern-1pt}\geq{\kern-1pt} 1$
such that
 $$ \begin{align*} \mathbb{P}\bigg( \Big|\int_{{\mathbb{T}}^d} (:{Y_N^2}: + 2 Y_N \Theta^0 + (\Theta^0)^2) dx \Big|> K \bigg) &\le C\frac{M^{-d} \log M}{K^2} < \delta_1 \end{align*} $$
$$ \begin{align*} \mathbb{P}\bigg( \Big|\int_{{\mathbb{T}}^d} (:{Y_N^2}: + 2 Y_N \Theta^0 + (\Theta^0)^2) dx \Big|> K \bigg) &\le C\frac{M^{-d} \log M}{K^2} < \delta_1 \end{align*} $$
for any
![]() $M \ge M_0 (K,\delta _1)$
. This proves (3.42).
$M \ge M_0 (K,\delta _1)$
. This proves (3.42).
![]() $\bullet $
Part 3: In this last part, we establish the exact divergence rate (1.25) of
$\bullet $
Part 3: In this last part, we establish the exact divergence rate (1.25) of
![]() $Z_{K, N}$
. From (3.44) with
$Z_{K, N}$
. From (3.44) with
![]() $M=N$
, we already have
$M=N$
, we already have
as
![]() $N\to \infty $
, for any small
$N\to \infty $
, for any small
![]() $\delta ,\delta _0,\delta _1> 0$
and any Schwartz function f with
$\delta ,\delta _0,\delta _1> 0$
and any Schwartz function f with
![]() $\|f\|_{L^2({\mathbb {R}}^d, \frac {dx}{(2\pi )^d})} = 1$
,
$\|f\|_{L^2({\mathbb {R}}^d, \frac {dx}{(2\pi )^d})} = 1$
,
![]() $\operatorname *{\mathrm {supp}}(\widehat {f}) \subset \{ |\xi |\le 1\}$
and
$\operatorname *{\mathrm {supp}}(\widehat {f}) \subset \{ |\xi |\le 1\}$
and
![]() $\widehat f(0) = 0$
. Since Schwartz functions with
$\widehat f(0) = 0$
. Since Schwartz functions with
![]() $\operatorname *{\mathrm {supp}}(\widehat {f}) \subset \{ |\xi |\le 1\}$
and
$\operatorname *{\mathrm {supp}}(\widehat {f}) \subset \{ |\xi |\le 1\}$
and
![]() $\widehat f(0) = 0$
are dense in
$\widehat f(0) = 0$
are dense in
![]() $L^2({\mathbb {R}}^d) \cap \big \{f: \operatorname *{\mathrm {supp}}(\widehat {f}) \subset \{ |\xi |\le 1\}\big \}$
, there exists a sequence
$L^2({\mathbb {R}}^d) \cap \big \{f: \operatorname *{\mathrm {supp}}(\widehat {f}) \subset \{ |\xi |\le 1\}\big \}$
, there exists a sequence
![]() $\{f_n\}_{n \in \mathbb {N}}$
of Schwartz functions with
$\{f_n\}_{n \in \mathbb {N}}$
of Schwartz functions with
![]() $\|f_n\|_{L^2({\mathbb {R}}^d, \frac {dx}{(2\pi )^d})} = 1$
and
$\|f_n\|_{L^2({\mathbb {R}}^d, \frac {dx}{(2\pi )^d})} = 1$
and
![]() $\operatorname *{\mathrm {supp}}(\widehat f_n) \subset \{ |\xi |\le 1\}$
which are almost optimizers for Bernstein’s inequality (1.26) on
$\operatorname *{\mathrm {supp}}(\widehat f_n) \subset \{ |\xi |\le 1\}$
which are almost optimizers for Bernstein’s inequality (1.26) on
![]() ${\mathbb {R}}^d$
, namely, we have
${\mathbb {R}}^d$
, namely, we have
Therefore, by inserting
![]() $f_n$
in (3.48) and taking
$f_n$
in (3.48) and taking
![]() $n \to \infty $
and
$n \to \infty $
and
![]() $\delta ,\delta _0,\delta _1 \to 0$
, we obtain
$\delta ,\delta _0,\delta _1 \to 0$
, we obtain
 $$ \begin{align} \liminf_{N\to\infty} \frac{\log Z_{K, N}}{\sigma_N^2 N^d} \ge \lambda \frac{C_B}{4}. \end{align} $$
$$ \begin{align} \liminf_{N\to\infty} \frac{\log Z_{K, N}}{\sigma_N^2 N^d} \ge \lambda \frac{C_B}{4}. \end{align} $$
Hence, it remains to prove the upper bound. In view of (3.13), we have
 $$ \begin{align} \nonumber \log Z_{K, N}&\le \sup_{\theta \in \mathbb{H}_a}{\mathbb{E}}\bigg[ R_N(Y + \Theta)\\ \nonumber &\hphantom{XXX} \times \mathbf 1_{\{ |\int_{{\mathbb{T}}^d} ( :{Y_N^2}: + 2 Y_N \Theta_N + \Theta_N^2) dx | \le K\}} - {\frac{1}{2}} \int_0^1 \| \theta(t)\|_{L^2_x} ^2 dt \bigg]\\ \nonumber & \le \sup_{\theta \in \mathcal{L}^2_{t,x}} {\mathbb{E}}\bigg[ R_N(Y+\Theta) \\ &\hphantom{XXX} \times \mathbf 1_{\{ |\int_{{\mathbb{T}}^d} ( :{Y_N^2}: + 2 Y_N \Theta_N + (\Theta_N)^2) dx | \le K\}} - {\frac{1}{2}} \int_0^1 \| \theta(t)\|_{L^2_x} ^2 dt \bigg]\\ \nonumber & \le \sup_{\Theta \in \mathcal{H}_x^{{\frac{d}{2}}} } {\mathbb{E}}\bigg[ R_N(Y+\Theta) \cdot \mathbf 1_{\{ |\int_{{\mathbb{T}}^d} ( :{Y_N^2}: + 2 Y_N \Theta_N + (\Theta_N)^2) dx | \le K\}} - {\frac{1}{2}} \| \Theta_N \|^2_{H^{{\frac{d}{2}}}} \bigg], \end{align} $$
$$ \begin{align} \nonumber \log Z_{K, N}&\le \sup_{\theta \in \mathbb{H}_a}{\mathbb{E}}\bigg[ R_N(Y + \Theta)\\ \nonumber &\hphantom{XXX} \times \mathbf 1_{\{ |\int_{{\mathbb{T}}^d} ( :{Y_N^2}: + 2 Y_N \Theta_N + \Theta_N^2) dx | \le K\}} - {\frac{1}{2}} \int_0^1 \| \theta(t)\|_{L^2_x} ^2 dt \bigg]\\ \nonumber & \le \sup_{\theta \in \mathcal{L}^2_{t,x}} {\mathbb{E}}\bigg[ R_N(Y+\Theta) \\ &\hphantom{XXX} \times \mathbf 1_{\{ |\int_{{\mathbb{T}}^d} ( :{Y_N^2}: + 2 Y_N \Theta_N + (\Theta_N)^2) dx | \le K\}} - {\frac{1}{2}} \int_0^1 \| \theta(t)\|_{L^2_x} ^2 dt \bigg]\\ \nonumber & \le \sup_{\Theta \in \mathcal{H}_x^{{\frac{d}{2}}} } {\mathbb{E}}\bigg[ R_N(Y+\Theta) \cdot \mathbf 1_{\{ |\int_{{\mathbb{T}}^d} ( :{Y_N^2}: + 2 Y_N \Theta_N + (\Theta_N)^2) dx | \le K\}} - {\frac{1}{2}} \| \Theta_N \|^2_{H^{{\frac{d}{2}}}} \bigg], \end{align} $$
where
![]() $\Theta = I(\theta )(1)$
in the first two lines and
$\Theta = I(\theta )(1)$
in the first two lines and
![]() $\Theta _N = \pi _N \Theta $
. Here, the space
$\Theta _N = \pi _N \Theta $
. Here, the space
![]() $\mathcal {L}^2_{t,x}$
denotes the space of drifts, which are stochastic processes belonging to
$\mathcal {L}^2_{t,x}$
denotes the space of drifts, which are stochastic processes belonging to
![]() $ L^2([0,1]; L^2({\mathbb {T}}^d)) \mathbb {P}$
-almost surely (namely, they do not have be adapted), and the space
$ L^2([0,1]; L^2({\mathbb {T}}^d)) \mathbb {P}$
-almost surely (namely, they do not have be adapted), and the space
![]() $\mathcal {H}_x^{{\frac {d}{2}}}$
denotes the space of
$\mathcal {H}_x^{{\frac {d}{2}}}$
denotes the space of
![]() $H^{{\frac {d}{2}}}({\mathbb {T}}^d)$
-valued random variables.
$H^{{\frac {d}{2}}}({\mathbb {T}}^d)$
-valued random variables.
For any
![]() $\Theta \in \mathcal {H}_x^{\frac {d}{2}} $
, let
$\Theta \in \mathcal {H}_x^{\frac {d}{2}} $
, let
![]() $V = Y+ \Theta $
. Then, with
$V = Y+ \Theta $
. Then, with
![]() $V_N = \pi _N V$
, we have
$V_N = \pi _N V$
, we have
and thus we see that
where
![]() $\sigma _N={\mathbb {E}}\big [Y_N^2\big ]$
is as in (1.5). Hence, from (3.50), a change of variables
$\sigma _N={\mathbb {E}}\big [Y_N^2\big ]$
is as in (1.5). Hence, from (3.50), a change of variables
![]() $\Theta _N=-Y_N+V_N$
, (3.52) and the almost optimal Bernstein inequality (Lemma 2.2), we have
$\Theta _N=-Y_N+V_N$
, (3.52) and the almost optimal Bernstein inequality (Lemma 2.2), we have
 $$ \begin{align} \nonumber \log Z_{K, N} &\le \sup_{\Theta \in \mathcal{H}_x^{\frac{d}{2}} } {\mathbb{E}}\bigg[ R_N(Y+\Theta) \cdot \mathbf 1_{\{ |\int_{{\mathbb{T}}^d} ( :{Y_N^2}: + 2 Y_N \Theta_N + (\Theta_N)^2) dx | \le K\}} \bigg]\\ & \le \sup_{V_N \in \mathcal{H}_x^{\frac{d}{2}}} {\mathbb{E}}\bigg[ R_N(V) \nonumber \cdot \mathbf 1_{\{ \int_{{\mathbb{T}}^d} V_N^2 dx \le K +\sigma_N \}} \bigg] \\ & \le \sup_{V_N \in \mathcal{H}_x^{\frac{d}{2}}} {\mathbb{E}}\bigg[ \lambda \frac{C_{\text{B}} }{4} N^d (1+o(1)) \| V_N \|_{L^2}^4 \cdot \mathbf 1_{\{ \int_{{\mathbb{T}}^d} V_N^2 dx \le K +\sigma_N \}} \bigg] + O(\lambda \sigma_N^2) \\ \nonumber & \le \lambda \frac{C_{B}}{4} N^d (1+o(1)) (K+\sigma_N)^2 + O(\lambda \sigma_N^2) = \lambda \frac{C_{B}}{4} N^d \sigma_N^2(1+o(1)) \end{align} $$
$$ \begin{align} \nonumber \log Z_{K, N} &\le \sup_{\Theta \in \mathcal{H}_x^{\frac{d}{2}} } {\mathbb{E}}\bigg[ R_N(Y+\Theta) \cdot \mathbf 1_{\{ |\int_{{\mathbb{T}}^d} ( :{Y_N^2}: + 2 Y_N \Theta_N + (\Theta_N)^2) dx | \le K\}} \bigg]\\ & \le \sup_{V_N \in \mathcal{H}_x^{\frac{d}{2}}} {\mathbb{E}}\bigg[ R_N(V) \nonumber \cdot \mathbf 1_{\{ \int_{{\mathbb{T}}^d} V_N^2 dx \le K +\sigma_N \}} \bigg] \\ & \le \sup_{V_N \in \mathcal{H}_x^{\frac{d}{2}}} {\mathbb{E}}\bigg[ \lambda \frac{C_{\text{B}} }{4} N^d (1+o(1)) \| V_N \|_{L^2}^4 \cdot \mathbf 1_{\{ \int_{{\mathbb{T}}^d} V_N^2 dx \le K +\sigma_N \}} \bigg] + O(\lambda \sigma_N^2) \\ \nonumber & \le \lambda \frac{C_{B}}{4} N^d (1+o(1)) (K+\sigma_N)^2 + O(\lambda \sigma_N^2) = \lambda \frac{C_{B}}{4} N^d \sigma_N^2(1+o(1)) \end{align} $$
as
![]() $N\to \infty $
, where, in the third step, we used
$N\to \infty $
, where, in the third step, we used
Therefore, combining this with (3.49), we conclude (1.25).
Remark 3.6. The perturbation (at the level of
![]() $\Theta ^0$
in (3.28)) is given by
$\Theta ^0$
in (3.28)) is given by
![]() $f_M$
(modulo the logarithmic factor
$f_M$
(modulo the logarithmic factor
![]() $\sqrt {\alpha _{M, N}}$
). We point out that Lemma 3.3 shows that
$\sqrt {\alpha _{M, N}}$
). We point out that Lemma 3.3 shows that
![]() $f_M$
looks like a highly concentrated profile whose
$f_M$
looks like a highly concentrated profile whose
![]() $L^4$
-norm (in fact, any
$L^4$
-norm (in fact, any
![]() $L^p$
-norm for
$L^p$
-norm for
![]() $p> 2$
) blows up while its
$p> 2$
) blows up while its
![]() $L^2$
-norm is
$L^2$
-norm is
![]() $O(1)$
as
$O(1)$
as
![]() $M \to \infty $
. Note that the blowup of
$M \to \infty $
. Note that the blowup of
![]() $L^4$
-norm (3.16) was crucially used in (3.33), which led to the desired divergence rate
$L^4$
-norm (3.16) was crucially used in (3.33), which led to the desired divergence rate
![]() $M^d (\log M)^2$
in (3.44). Moreover, the uniform (in M) bound (3.15) on the
$M^d (\log M)^2$
in (3.44). Moreover, the uniform (in M) bound (3.15) on the
![]() $L^2$
-norm
$L^2$
-norm
![]() $f_M$
played an essential role in (3.32) and (3.34) to guarantee that the terms in (3.32) and (3.34) grow at a slower rate than
$f_M$
played an essential role in (3.32) and (3.34) to guarantee that the terms in (3.32) and (3.34) grow at a slower rate than
![]() $M^d (\log M)^2$
.
$M^d (\log M)^2$
.
3.3 Proofs of the auxiliary lemmas
In this subsection, we present the proofs of Lemmas 3.3, 3.4 and 3.5.
We first briefly discuss the proof of Lemma 3.3.
Proof of Lemma 3.3.
Define a function
![]() $F_M$
on
$F_M$
on
![]() ${\mathbb {R}}^d$
by setting
${\mathbb {R}}^d$
by setting
Then, from the Poisson summation formula (1.13) with (3.14), we have
where
![]() $T_m f(x) = M^{\frac {d}{2}} f(M(x+2\pi m))$
.
$T_m f(x) = M^{\frac {d}{2}} f(M(x+2\pi m))$
.
Recall our convention of the normalized Lebesgue measure on
![]() ${\mathbb {T}}^d$
. Since f is a Schwartz function, we have
${\mathbb {T}}^d$
. Since f is a Schwartz function, we have
 $$ \begin{align} \nonumber \int_{{\mathbb{T}}^d} (T_0f(x))^k dx & = \frac{M^{d( {\frac{k}{2}} - 1)}}{(2\pi)^d}\int_{{\mathbb{R}}^d} \mathbf 1_{[-\pi M, \pi M)^d}(x)f^k(x) dx\\[5pt] & = \frac {M^{d( {\frac{k}{2}} - 1)}}{(2\pi)^d}\int_{{\mathbb{R}}^d}f^k(x) dx + O(M^{-\alpha}) \end{align} $$
$$ \begin{align} \nonumber \int_{{\mathbb{T}}^d} (T_0f(x))^k dx & = \frac{M^{d( {\frac{k}{2}} - 1)}}{(2\pi)^d}\int_{{\mathbb{R}}^d} \mathbf 1_{[-\pi M, \pi M)^d}(x)f^k(x) dx\\[5pt] & = \frac {M^{d( {\frac{k}{2}} - 1)}}{(2\pi)^d}\int_{{\mathbb{R}}^d}f^k(x) dx + O(M^{-\alpha}) \end{align} $$
for any
![]() $\alpha> 0$
. On the other hand, from (3.54), for
$\alpha> 0$
. On the other hand, from (3.54), for
![]() $k \in \mathbb {N}$
, we have
$k \in \mathbb {N}$
, we have
 $$ \begin{align} \nonumber \int_{{\mathbb{T}}^d} f_M^k(x) dx & = \int_{{\mathbb{T}}^d} \bigg(\sum_{m \in \mathbb{Z}^d} T_mf(x)\bigg)^k dx\\[5pt] & = \int_{{\mathbb{T}}^d} (T_0f)^k(x) dx + \text{l.o.t.}. \end{align} $$
$$ \begin{align} \nonumber \int_{{\mathbb{T}}^d} f_M^k(x) dx & = \int_{{\mathbb{T}}^d} \bigg(\sum_{m \in \mathbb{Z}^d} T_mf(x)\bigg)^k dx\\[5pt] & = \int_{{\mathbb{T}}^d} (T_0f)^k(x) dx + \text{l.o.t.}. \end{align} $$
Here, l.o.t. consists of the sum of the terms of the form
 $$\begin{align*}\int_{{\mathbb{T}}^d} \prod_{j = 1}^k T_{m_j} f(x) dx,\end{align*}$$
$$\begin{align*}\int_{{\mathbb{T}}^d} \prod_{j = 1}^k T_{m_j} f(x) dx,\end{align*}$$
where
![]() $m_j \ne 0$
for at least one j. It follows from the fast decay of the Schwartz function f that, for any
$m_j \ne 0$
for at least one j. It follows from the fast decay of the Schwartz function f that, for any
![]() $\kappa> 0$
, there exists
$\kappa> 0$
, there exists
![]() $C> 0$
such that
$C> 0$
such that
for any
![]() $m \in \mathbb {Z}^d\setminus \{0\}$
; see the proof of Lemma 5.13 in [Reference Oh, Okamoto and Tolomeo41]. As a consequence, by summing over
$m \in \mathbb {Z}^d\setminus \{0\}$
; see the proof of Lemma 5.13 in [Reference Oh, Okamoto and Tolomeo41]. As a consequence, by summing over
![]() $m_j \in \mathbb {Z}^d$
,
$m_j \in \mathbb {Z}^d$
,
![]() $j = 1, \dots , k$
(not all zero), we obtain
$j = 1, \dots , k$
(not all zero), we obtain
Therefore, from (3.55), (3.56) and (3.57) with
![]() $\|f\|_{L^2({\mathbb {R}}^d, \frac {dx}{(2\pi )^d})} = 1$
, we conclude (3.15) and (3.16).
$\|f\|_{L^2({\mathbb {R}}^d, \frac {dx}{(2\pi )^d})} = 1$
, we conclude (3.15) and (3.16).
Next, we prove (3.17). Since f is a Schwartz function with
![]() $\widehat f (0) = 0$
, it follows from the fundamental theorem of calculus that
$\widehat f (0) = 0$
, it follows from the fundamental theorem of calculus that
for any
![]() $\xi \in {\mathbb {R}}^d$
. By Plancherel’s identity with (3.14) and (3.58), we have
$\xi \in {\mathbb {R}}^d$
. By Plancherel’s identity with (3.14) and (3.58), we have
 $$ \begin{align*} \int_{{\mathbb{T}}^d} (\langle \nabla \rangle^{-\alpha} f_M)^2 dx & = M^{-d} \sum_{\substack{n \in \mathbb{Z}^d\\|n|\le M}}\Big|\widehat f\Big({\frac{n}{M}}\Big)\Big|^2 \frac{1}{\langle n \rangle^2\alpha}\\[5pt] & \le C^2_f M^{-d-2} \sum_{\substack{n \in \mathbb{Z}^d\\|n|\le M}} \frac{1}{\langle n \rangle^{2(\alpha-1)}}\\[5pt] & \lesssim C^2_f M^{-d-2 + \max(d+ 2 -2\alpha, 0)}. \end{align*} $$
$$ \begin{align*} \int_{{\mathbb{T}}^d} (\langle \nabla \rangle^{-\alpha} f_M)^2 dx & = M^{-d} \sum_{\substack{n \in \mathbb{Z}^d\\|n|\le M}}\Big|\widehat f\Big({\frac{n}{M}}\Big)\Big|^2 \frac{1}{\langle n \rangle^2\alpha}\\[5pt] & \le C^2_f M^{-d-2} \sum_{\substack{n \in \mathbb{Z}^d\\|n|\le M}} \frac{1}{\langle n \rangle^{2(\alpha-1)}}\\[5pt] & \lesssim C^2_f M^{-d-2 + \max(d+ 2 -2\alpha, 0)}. \end{align*} $$
This prove (3.17).
Next, we present the proof of the approximation lemma (Lemma 3.4).
Proof of Lemma 3.4.
Let
Then, from (3.2) and (3.18), we see that
![]() $X_n(t)$
satisfies the following stochastic differential equation:
$X_n(t)$
satisfies the following stochastic differential equation:
 $$ \begin{align*} \begin{cases} dX_n(t)=-\langle n \rangle^{-\frac{d}{2}}M^{\frac{d}{2}} X_n(t) dt +\frac{1}{\langle n \rangle^{\frac{d}{2}}}dB_n(t)\\ X_n(0)=0 \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} dX_n(t)=-\langle n \rangle^{-\frac{d}{2}}M^{\frac{d}{2}} X_n(t) dt +\frac{1}{\langle n \rangle^{\frac{d}{2}}}dB_n(t)\\ X_n(0)=0 \end{cases} \end{align*} $$
for
![]() $|n|\le M$
. By solving this stochastic differential equation, we have
$|n|\le M$
. By solving this stochastic differential equation, we have
 $$ \begin{align} X_n(t)=\frac{1}{\langle n \rangle^{\frac{d}{2}}}\int_0^t e^{-\langle n \rangle^{-\frac{d}{2}}M^{\frac{d}{2}}(t-s)}dB_n(s). \end{align} $$
$$ \begin{align} X_n(t)=\frac{1}{\langle n \rangle^{\frac{d}{2}}}\int_0^t e^{-\langle n \rangle^{-\frac{d}{2}}M^{\frac{d}{2}}(t-s)}dB_n(s). \end{align} $$
Then, from (3.59) and (3.60), we have
 $$ \begin{align} \widehat \zeta_{M}(n, t)= \widehat Y_N(n, t)-\frac{1}{\langle n \rangle^{\frac{d}{2}} }\int_0^t e^{-\langle n \rangle^{-{\frac{d}{2}}}M^{\frac{d}{2}} (t-s)}dB_n(s) \end{align} $$
$$ \begin{align} \widehat \zeta_{M}(n, t)= \widehat Y_N(n, t)-\frac{1}{\langle n \rangle^{\frac{d}{2}} }\int_0^t e^{-\langle n \rangle^{-{\frac{d}{2}}}M^{\frac{d}{2}} (t-s)}dB_n(s) \end{align} $$
for
![]() $|n|\le M$
. Hence, from (3.61), the independence of
$|n|\le M$
. Hence, from (3.61), the independence of
![]() $\{B_n \}_{n \in \mathbb {Z}^d}$
,Footnote
22
Ito’s isometry and (3.2), we have
$\{B_n \}_{n \in \mathbb {Z}^d}$
,Footnote
22
Ito’s isometry and (3.2), we have
 $$ \begin{align} \nonumber{\mathbb{E}} \big[ |\zeta_M(x)|^2 \big]&=\sum_{|n| \le M} \bigg( {\mathbb{E}} \big[ | \widehat Y_N(n) |^2 \big] -\frac{2}{\langle n \rangle^d}\int_0^1 e^{-\langle n \rangle^{-\frac{d}{2}}M^{\frac{d}{2}} (1-s)}ds \\ & \hphantom{XXXXX} +\frac{1}{\langle n \rangle^d}\int_0^1 e^{-2\langle n \rangle^{-{\frac{d}{2}}}M^{\frac{d}{2}} (1-s)}ds \bigg)\\ \nonumber & = \sigma_M + O\Big(\sum_{|n|\le M }\frac{1}{\langle n \rangle^{\frac{d}{2}}}\cdot \frac{1}{M^{\frac{d}{2}}}\Big)\\ \nonumber & = \sigma_M(1 + o(1)) \end{align} $$
$$ \begin{align} \nonumber{\mathbb{E}} \big[ |\zeta_M(x)|^2 \big]&=\sum_{|n| \le M} \bigg( {\mathbb{E}} \big[ | \widehat Y_N(n) |^2 \big] -\frac{2}{\langle n \rangle^d}\int_0^1 e^{-\langle n \rangle^{-\frac{d}{2}}M^{\frac{d}{2}} (1-s)}ds \\ & \hphantom{XXXXX} +\frac{1}{\langle n \rangle^d}\int_0^1 e^{-2\langle n \rangle^{-{\frac{d}{2}}}M^{\frac{d}{2}} (1-s)}ds \bigg)\\ \nonumber & = \sigma_M + O\Big(\sum_{|n|\le M }\frac{1}{\langle n \rangle^{\frac{d}{2}}}\cdot \frac{1}{M^{\frac{d}{2}}}\Big)\\ \nonumber & = \sigma_M(1 + o(1)) \end{align} $$
for any
![]() $M\gg 1$
. This proves (3.19).
$M\gg 1$
. This proves (3.19).
By Parseval’s theorem, (3.61), (3.19) and proceeding as in (3.62), we have
 $$ \begin{align*} {\mathbb{E}}\bigg[ 2 \int_{{\mathbb{T}}^d} Y_N & \zeta_M dx - \int_{{\mathbb{T}}^d} \zeta_M^2 dx \bigg] ={\mathbb{E}} \bigg[ 2 \sum_{|n| \le M }\widehat Y_N(n) \overline{ \widehat \zeta_M(n)} -\sum_{|n |\le M }| \widehat \zeta_M(n) |^2 \bigg]\\ &={\mathbb{E}} \bigg[ \sum_{|n | \le M } | \widehat \zeta_M(n) |^2+\sum_{|n|\leq M } \bigg( \frac{2}{\langle n \rangle^{\frac{d}{2}}} \int_0^1 e^{-\langle n \rangle^{-\frac{d}{2}}M^{\frac{d}{2}} (1-s) }dB_n(s) \bigg) \overline{\widehat \zeta_M(n)} \bigg]\\ &= \sigma_M(1 + o(1)) + O\Big(\sum_{|n| \le M } \frac{1}{\langle n \rangle^{\frac{d}{2}}}\cdot \frac{1}{M^{\frac{d}{2}}}\Big)\\ & = \sigma_M(1 + o(1)) \end{align*} $$
$$ \begin{align*} {\mathbb{E}}\bigg[ 2 \int_{{\mathbb{T}}^d} Y_N & \zeta_M dx - \int_{{\mathbb{T}}^d} \zeta_M^2 dx \bigg] ={\mathbb{E}} \bigg[ 2 \sum_{|n| \le M }\widehat Y_N(n) \overline{ \widehat \zeta_M(n)} -\sum_{|n |\le M }| \widehat \zeta_M(n) |^2 \bigg]\\ &={\mathbb{E}} \bigg[ \sum_{|n | \le M } | \widehat \zeta_M(n) |^2+\sum_{|n|\leq M } \bigg( \frac{2}{\langle n \rangle^{\frac{d}{2}}} \int_0^1 e^{-\langle n \rangle^{-\frac{d}{2}}M^{\frac{d}{2}} (1-s) }dB_n(s) \bigg) \overline{\widehat \zeta_M(n)} \bigg]\\ &= \sigma_M(1 + o(1)) + O\Big(\sum_{|n| \le M } \frac{1}{\langle n \rangle^{\frac{d}{2}}}\cdot \frac{1}{M^{\frac{d}{2}}}\Big)\\ & = \sigma_M(1 + o(1)) \end{align*} $$
for any
![]() $N\ge M\gg 1$
. This proves (3.20).
$N\ge M\gg 1$
. This proves (3.20).
Note that
![]() $\widehat Y(n)-\widehat \zeta _M(n)$
is a mean-zero Gaussian random variable. Then, from (3.61) and Ito’s isometry, we have
$\widehat Y(n)-\widehat \zeta _M(n)$
is a mean-zero Gaussian random variable. Then, from (3.61) and Ito’s isometry, we have
 $$ \begin{align} \nonumber {\mathbb{E}} \bigg[ \Big( |\widehat Y_N(n)- & \widehat \zeta_M(n)|^2-{\mathbb{E}}\big[ |\widehat Y(n)-\widehat \zeta_M(n)|^2 \big] \Big)^2 \bigg] \lesssim \Big({\mathbb{E}}\big[ |\widehat Y_N(n)-\widehat \zeta_M(n)|^2 \big] \Big)^2 \\ & = \frac{1}{\langle n \rangle^{2d} } \bigg(\int_0^1 e^{-2\langle n \rangle^{-\frac{d}{2}}M^{{\frac{d}{2}}}(1-s) } ds \bigg)^2 \sim \frac 1 {\langle n \rangle^{d} } \cdot \frac{1}{M^d}. \end{align} $$
$$ \begin{align} \nonumber {\mathbb{E}} \bigg[ \Big( |\widehat Y_N(n)- & \widehat \zeta_M(n)|^2-{\mathbb{E}}\big[ |\widehat Y(n)-\widehat \zeta_M(n)|^2 \big] \Big)^2 \bigg] \lesssim \Big({\mathbb{E}}\big[ |\widehat Y_N(n)-\widehat \zeta_M(n)|^2 \big] \Big)^2 \\ & = \frac{1}{\langle n \rangle^{2d} } \bigg(\int_0^1 e^{-2\langle n \rangle^{-\frac{d}{2}}M^{{\frac{d}{2}}}(1-s) } ds \bigg)^2 \sim \frac 1 {\langle n \rangle^{d} } \cdot \frac{1}{M^d}. \end{align} $$
Hence, from Plancherel’s identity, (3.24), the independence of
![]() $\{B_n \}_{n \in \mathbb {Z}^d}$
, the independence of
$\{B_n \}_{n \in \mathbb {Z}^d}$
, the independence of
![]() $\big \{ |\widehat Y_N(n) |^2- {\mathbb {E}} \big [ | \widehat Y_N(n)|^2 \big ]\big \}_{M < |n|\le N}$
and
$\big \{ |\widehat Y_N(n) |^2- {\mathbb {E}} \big [ | \widehat Y_N(n)|^2 \big ]\big \}_{M < |n|\le N}$
and
 $$ \begin{align*} {\mathbb{E}} \bigg[ & \Big| \int_{{\mathbb{T}}^d} :\! ( Y_N-\zeta_M)^2 \!: dx \Big|^2 \bigg] \notag \\ &= \sum_{M<|n|\le N } {\mathbb{E}} \bigg[ \Big( |\widehat Y_N(n) |^2- {\mathbb{E}} \big[ | \widehat Y_N(n)|^2 \big] \Big)^2 \bigg]\notag \\ &\hphantom{XX}+ \sum_{|n|\le M} {\mathbb{E}} \bigg[ \Big( |\widehat Y_N(n)-\widehat \zeta_M(n)|^2-{\mathbb{E}}\big[ |\widehat Y_N(n)-\widehat \zeta_M(n)|^2 \big] \Big)^2 \bigg]\notag \\ &\lesssim \sum_{M<|n|\le N}\frac{1}{\langle n \rangle^{2d}} +\sum_{|n|\le M } \frac{1}{\langle n \rangle^{d}} \frac{1}{M^d} \lesssim M^{-d}\log M. \end{align*} $$
$$ \begin{align*} {\mathbb{E}} \bigg[ & \Big| \int_{{\mathbb{T}}^d} :\! ( Y_N-\zeta_M)^2 \!: dx \Big|^2 \bigg] \notag \\ &= \sum_{M<|n|\le N } {\mathbb{E}} \bigg[ \Big( |\widehat Y_N(n) |^2- {\mathbb{E}} \big[ | \widehat Y_N(n)|^2 \big] \Big)^2 \bigg]\notag \\ &\hphantom{XX}+ \sum_{|n|\le M} {\mathbb{E}} \bigg[ \Big( |\widehat Y_N(n)-\widehat \zeta_M(n)|^2-{\mathbb{E}}\big[ |\widehat Y_N(n)-\widehat \zeta_M(n)|^2 \big] \Big)^2 \bigg]\notag \\ &\lesssim \sum_{M<|n|\le N}\frac{1}{\langle n \rangle^{2d}} +\sum_{|n|\le M } \frac{1}{\langle n \rangle^{d}} \frac{1}{M^d} \lesssim M^{-d}\log M. \end{align*} $$
This proves (3.21).
From (3.17) and (3.2), we have
 $$ \begin{align} \nonumber {\mathbb{E}}\bigg[ \Big( \int_{{\mathbb{T}}^d} Y_N f_M dx \Big)^2\bigg] &= {\mathbb{E}} \bigg[ \Big( \sum_{|n| \le M} \widehat Y_N(n) \overline{ \widehat f_M(n)} \Big)^2 \bigg] = \sum_{|n| \le M} \frac{1}{\langle n \rangle^d} |\widehat f_M(n)|^2 \\ &\le \int_{{\mathbb{T}}^d} \big(\langle \nabla \rangle^{-{\frac{d}{2}}} f_M (x)\big)^2 dx \lesssim M^{-d}. \end{align} $$
$$ \begin{align} \nonumber {\mathbb{E}}\bigg[ \Big( \int_{{\mathbb{T}}^d} Y_N f_M dx \Big)^2\bigg] &= {\mathbb{E}} \bigg[ \Big( \sum_{|n| \le M} \widehat Y_N(n) \overline{ \widehat f_M(n)} \Big)^2 \bigg] = \sum_{|n| \le M} \frac{1}{\langle n \rangle^d} |\widehat f_M(n)|^2 \\ &\le \int_{{\mathbb{T}}^d} \big(\langle \nabla \rangle^{-{\frac{d}{2}}} f_M (x)\big)^2 dx \lesssim M^{-d}. \end{align} $$
From (3.60), Ito’s isometry and (3.17), we have
 $$ \begin{align} \nonumber {\mathbb{E}} \bigg[ \Big( \sum_{|n| \le M} X_n(1) \overline{ \widehat f_M(n)} \Big)^2 \bigg] &={\mathbb{E}} \Bigg[ \bigg|\sum_{|n|\leq M} \bigg( \frac{1}{\langle n \rangle^{\frac{d}{2}}} \int_0^1 e^{-\langle n \rangle^{-\frac{d}{2}} M^{{\frac{d}{2}}}(1-s) } dB_n(s) \bigg) \widehat f_M(n) \bigg|^2 \Bigg]\\ &\lesssim M^{-{\frac{d}{2}}}\sum_{|n| \leq M} \frac{1}{\langle n \rangle^{\frac{d}{2}} }| \widehat f_M(n)|^2\\ \nonumber & \lesssim M^{-d}. \end{align} $$
$$ \begin{align} \nonumber {\mathbb{E}} \bigg[ \Big( \sum_{|n| \le M} X_n(1) \overline{ \widehat f_M(n)} \Big)^2 \bigg] &={\mathbb{E}} \Bigg[ \bigg|\sum_{|n|\leq M} \bigg( \frac{1}{\langle n \rangle^{\frac{d}{2}}} \int_0^1 e^{-\langle n \rangle^{-\frac{d}{2}} M^{{\frac{d}{2}}}(1-s) } dB_n(s) \bigg) \widehat f_M(n) \bigg|^2 \Bigg]\\ &\lesssim M^{-{\frac{d}{2}}}\sum_{|n| \leq M} \frac{1}{\langle n \rangle^{\frac{d}{2}} }| \widehat f_M(n)|^2\\ \nonumber & \lesssim M^{-d}. \end{align} $$
Hence, (3.22) follows from (3.64) and (3.65) with (3.61).
Lastly, from (3.18), (3.59) and (3.60) and Ito’s isometry, we have
 $$ \begin{align*} {\mathbb{E}}\bigg[\int_0^1 \Big\| \frac{d}{ds} \zeta_M(s) \Big\|^2_{H^{\frac{d}{2}}}ds\bigg] &= M^d {\mathbb{E}}\bigg[\int_0^1 \Big\| \pi_M(Y_N(s)) - \zeta_M(s) \Big\|^2_{L^2}ds\bigg] \\ &= M^d {\mathbb{E}}\bigg[ \int_0^1 \Big(\sum_{|n| \le M} |X_n(s)|^2\Big) ds\bigg]\\ &=M^d \sum_{|n| \le M} \frac{1}{\langle n \rangle^{d}} \int_0^1 \int_0^s e^{-2\langle n \rangle^{-{\frac{d}{2}}}M^{{\frac{d}{2}}}(s-s')} d s' ds \\ & \lesssim M^d \sum_{|n| \le M } \frac{1}{\langle n \rangle^{{\frac{d}{2}}}}\cdot \frac{1}{M^{{\frac{d}{2}}}}\\ & \lesssim M^d, \end{align*} $$
$$ \begin{align*} {\mathbb{E}}\bigg[\int_0^1 \Big\| \frac{d}{ds} \zeta_M(s) \Big\|^2_{H^{\frac{d}{2}}}ds\bigg] &= M^d {\mathbb{E}}\bigg[\int_0^1 \Big\| \pi_M(Y_N(s)) - \zeta_M(s) \Big\|^2_{L^2}ds\bigg] \\ &= M^d {\mathbb{E}}\bigg[ \int_0^1 \Big(\sum_{|n| \le M} |X_n(s)|^2\Big) ds\bigg]\\ &=M^d \sum_{|n| \le M} \frac{1}{\langle n \rangle^{d}} \int_0^1 \int_0^s e^{-2\langle n \rangle^{-{\frac{d}{2}}}M^{{\frac{d}{2}}}(s-s')} d s' ds \\ & \lesssim M^d \sum_{|n| \le M } \frac{1}{\langle n \rangle^{{\frac{d}{2}}}}\cdot \frac{1}{M^{{\frac{d}{2}}}}\\ & \lesssim M^d, \end{align*} $$
Finally, we present the proof of Lemma 3.5.
Proof of Lemma 3.5.
From the duality and Cauchy’s inequality, we have
 $$ \begin{align} \nonumber \bigg| \int_{{\mathbb{T}}^d} :\! Y_N^3 \!: \Theta^0 dx \bigg| &\le \| :\! Y_N^3 \!:\|_{W^{-\varepsilon,\infty}} \| \Theta^0\|_{W^{\varepsilon,1} }\le \| :\! Y_N^3 \!:\|_{W^{-\varepsilon,\infty}} \| \Theta^0\|_{H^{\frac{d}{2}}}\\ &\le c(\delta)\| :\! Y_N^3 \!:\|_{W^{-\varepsilon,\infty}}^2 + \delta \| \Theta^0\|_{H^{\frac{d}{2}}}^2. \end{align} $$
$$ \begin{align} \nonumber \bigg| \int_{{\mathbb{T}}^d} :\! Y_N^3 \!: \Theta^0 dx \bigg| &\le \| :\! Y_N^3 \!:\|_{W^{-\varepsilon,\infty}} \| \Theta^0\|_{W^{\varepsilon,1} }\le \| :\! Y_N^3 \!:\|_{W^{-\varepsilon,\infty}} \| \Theta^0\|_{H^{\frac{d}{2}}}\\ &\le c(\delta)\| :\! Y_N^3 \!:\|_{W^{-\varepsilon,\infty}}^2 + \delta \| \Theta^0\|_{H^{\frac{d}{2}}}^2. \end{align} $$
This yields (3.38).
From the fractional Leibniz rule (Lemma 2.1 (ii)), we have
 $$ \begin{align} \nonumber \bigg| \int_{{\mathbb{T}}^d} :\! Y_N^2 \!: (\Theta^0)^2 dx \bigg| & \le \| :\! Y_N^2 \!:\|_{W^{-\varepsilon,\infty}} \|(\Theta^0)^2\|_{W^{\varepsilon, 1}}\\ & \leq \| :\! Y_N^2 \!:\|_{W^{-\varepsilon,\infty}} \|(\Theta^0)^2\|_{W^{\varepsilon, \frac{4}{3}}}\\ \nonumber & \lesssim \| :\! Y_N^2 \!:\|_{W^{-\varepsilon,\infty}}\|\Theta^0\|_{H^{\frac{d}{2}}}\|\Theta^0\|_{L^4}. \end{align} $$
$$ \begin{align} \nonumber \bigg| \int_{{\mathbb{T}}^d} :\! Y_N^2 \!: (\Theta^0)^2 dx \bigg| & \le \| :\! Y_N^2 \!:\|_{W^{-\varepsilon,\infty}} \|(\Theta^0)^2\|_{W^{\varepsilon, 1}}\\ & \leq \| :\! Y_N^2 \!:\|_{W^{-\varepsilon,\infty}} \|(\Theta^0)^2\|_{W^{\varepsilon, \frac{4}{3}}}\\ \nonumber & \lesssim \| :\! Y_N^2 \!:\|_{W^{-\varepsilon,\infty}}\|\Theta^0\|_{H^{\frac{d}{2}}}\|\Theta^0\|_{L^4}. \end{align} $$
Then, the second estimate (3.39) follows from Young’s inequality.
Lastly, we consider (3.40). From the fractional Leibniz rule (Lemma 2.1 (ii)) (with
![]() $\frac {1}{1+\delta } = \frac {1}{2+\delta _0} + \frac {1}{4} + \frac {1}{4}$
for small
$\frac {1}{1+\delta } = \frac {1}{2+\delta _0} + \frac {1}{4} + \frac {1}{4}$
for small
![]() $\delta , \delta _0> 0$
), Sobolev’s inequality, and the interpolation (Lemma 2.1 (i)), we have
$\delta , \delta _0> 0$
), Sobolev’s inequality, and the interpolation (Lemma 2.1 (i)), we have
 $$ \begin{align} \nonumber \bigg| \int_{{\mathbb{T}}^d} Y_N (\Theta_N^0)^3 dx \bigg| &\le \| Y_N \|_{W^{-\varepsilon,\infty}} \| \langle \nabla \rangle^{\varepsilon} (\Theta_N^0)^3\|_{L^{1+\delta}}\\ &\lesssim\| Y_N \|_{W^{-\varepsilon,\infty}} \| \Theta_N^0 \|_{W^{\varepsilon, 2+\delta_0}} \| \Theta_N^0 \|_{L^4}^2\\ \nonumber &\lesssim\| Y_N \|_{W^{-\varepsilon,\infty}} \| \Theta_N^0 \|_{H^{\frac{d}{2}}}^\beta \| \Theta_N^0 \|_{L^4}^{3-\beta} \end{align} $$
$$ \begin{align} \nonumber \bigg| \int_{{\mathbb{T}}^d} Y_N (\Theta_N^0)^3 dx \bigg| &\le \| Y_N \|_{W^{-\varepsilon,\infty}} \| \langle \nabla \rangle^{\varepsilon} (\Theta_N^0)^3\|_{L^{1+\delta}}\\ &\lesssim\| Y_N \|_{W^{-\varepsilon,\infty}} \| \Theta_N^0 \|_{W^{\varepsilon, 2+\delta_0}} \| \Theta_N^0 \|_{L^4}^2\\ \nonumber &\lesssim\| Y_N \|_{W^{-\varepsilon,\infty}} \| \Theta_N^0 \|_{H^{\frac{d}{2}}}^\beta \| \Theta_N^0 \|_{L^4}^{3-\beta} \end{align} $$
for some small
![]() $\beta> 0$
. Then, the third estimate (3.40) follows from Young’s inequality since
$\beta> 0$
. Then, the third estimate (3.40) follows from Young’s inequality since
![]() $\frac {\beta }2 + \frac {3-\beta }4 < 1$
for small
$\frac {\beta }2 + \frac {3-\beta }4 < 1$
for small
![]() $\beta> 0$
. This completes the proof of Lemma 3.5.
$\beta> 0$
. This completes the proof of Lemma 3.5.
4 Construction of the Gibbs measure with the cubic interaction
In this section, we present the proof of Theorem 1.9. We prove the uniform exponential integrability (1.32) via the variational formulation. Since the argument is identical for any finite
![]() $p \geq 1$
, we only present details for the case
$p \geq 1$
, we only present details for the case
![]() $p =1$
. Moreover, the precise value of
$p =1$
. Moreover, the precise value of
![]() $\lambda \in {\mathbb {R}}\setminus \{0\}$
does not play any role and thus we set
$\lambda \in {\mathbb {R}}\setminus \{0\}$
does not play any role and thus we set
![]() $\lambda = 3$
in the following.
$\lambda = 3$
in the following.
In view of the Boué–Dupuis formula (Lemma 3.1), it suffices to establish a lower bound on
 $$ \begin{align} \mathcal{W}_N(\theta) = {\mathbb{E}} \bigg[-R_N^\diamond(Y(1) + I(\theta)(1)) + \frac{1}{2} \int_0^1 \| \theta(t) \|_{L^2_x}^2 dt \bigg], \end{align} $$
$$ \begin{align} \mathcal{W}_N(\theta) = {\mathbb{E}} \bigg[-R_N^\diamond(Y(1) + I(\theta)(1)) + \frac{1}{2} \int_0^1 \| \theta(t) \|_{L^2_x}^2 dt \bigg], \end{align} $$
uniformly in
![]() $N \in \mathbb {N}$
and
$N \in \mathbb {N}$
and
![]() $\theta \in \mathbb {H}_a$
. We set
$\theta \in \mathbb {H}_a$
. We set
![]() $Y_N = \pi _N Y = \pi _N Y(1)$
and
$Y_N = \pi _N Y = \pi _N Y(1)$
and
![]() $\Theta _N = \pi _N \Theta = \pi _N I(\theta )(1)$
.
$\Theta _N = \pi _N \Theta = \pi _N I(\theta )(1)$
.
From (1.30) and (3.35), we have
 $$ \begin{align} \nonumber R_N^\diamond (Y + \Theta) & = \int_{{\mathbb{T}}^d} :\! Y_N^3 \!: dx + 3\int_{{\mathbb{T}}^d} :\! Y_N^2 \!: \Theta_N dx+3 \int_{{\mathbb{T}}^d} Y_N \Theta_N^2 dx \\ &\hphantom{X} + \int_{{\mathbb{T}}^d} \Theta_N^3 dx - A \bigg\{ \int_{{\mathbb{T}}^d} \Big( :\! Y_N^2 \!: + 2 Y_N \Theta_N + \Theta_N^2 \Big) dx \bigg\}^2. \end{align} $$
$$ \begin{align} \nonumber R_N^\diamond (Y + \Theta) & = \int_{{\mathbb{T}}^d} :\! Y_N^3 \!: dx + 3\int_{{\mathbb{T}}^d} :\! Y_N^2 \!: \Theta_N dx+3 \int_{{\mathbb{T}}^d} Y_N \Theta_N^2 dx \\ &\hphantom{X} + \int_{{\mathbb{T}}^d} \Theta_N^3 dx - A \bigg\{ \int_{{\mathbb{T}}^d} \Big( :\! Y_N^2 \!: + 2 Y_N \Theta_N + \Theta_N^2 \Big) dx \bigg\}^2. \end{align} $$
Hence, from (4.1) and (4.2), we have
 $$ \begin{align} \nonumber \mathcal{W}_N(\theta) &={\mathbb{E}} \bigg[ -\int_{{\mathbb{T}}^d} :\! Y_N^3 \!: dx -3\int_{{\mathbb{T}}^d} :\! Y_N^2 \!: \Theta_N dx -3\int_{{\mathbb{T}}^d} Y_N \Theta_N^2 dx \\ &\hphantom{XXX} -\int_{{\mathbb{T}}^d} \Theta_N^3 dx + A \bigg\{ \int_{{\mathbb{T}}^d} \Big( :\! Y_N^2 \!: + 2 Y_N \Theta_N + \Theta_N^2 \Big) dx \bigg\}^2\\ \nonumber &\hphantom{XXX} + \frac{1}{2} \int_0^1 \| \theta(t) \|_{L^2_x}^2 dt \bigg]. \end{align} $$
$$ \begin{align} \nonumber \mathcal{W}_N(\theta) &={\mathbb{E}} \bigg[ -\int_{{\mathbb{T}}^d} :\! Y_N^3 \!: dx -3\int_{{\mathbb{T}}^d} :\! Y_N^2 \!: \Theta_N dx -3\int_{{\mathbb{T}}^d} Y_N \Theta_N^2 dx \\ &\hphantom{XXX} -\int_{{\mathbb{T}}^d} \Theta_N^3 dx + A \bigg\{ \int_{{\mathbb{T}}^d} \Big( :\! Y_N^2 \!: + 2 Y_N \Theta_N + \Theta_N^2 \Big) dx \bigg\}^2\\ \nonumber &\hphantom{XXX} + \frac{1}{2} \int_0^1 \| \theta(t) \|_{L^2_x}^2 dt \bigg]. \end{align} $$
In the following, we first state a lemma, controlling the terms appearing in (4.3). We present the proof of this lemma at the end of this section.
Lemma 4.1.
(i) There exist small
![]() $\varepsilon>0$
and a constant
$\varepsilon>0$
and a constant
![]() $c>0$
such that
$c>0$
such that
 $$ \begin{align} \bigg| \int_{{\mathbb{T}}^d} :\! Y_N^2 \!: \Theta_N dx \bigg| &\le c \| :\! Y_N^2 \!: \|_{W^{-\varepsilon,\infty}}^2 + \frac{1}{100} \| \Theta_N \|_{H^{\frac{d}{2}}}^2, \end{align} $$
$$ \begin{align} \bigg| \int_{{\mathbb{T}}^d} :\! Y_N^2 \!: \Theta_N dx \bigg| &\le c \| :\! Y_N^2 \!: \|_{W^{-\varepsilon,\infty}}^2 + \frac{1}{100} \| \Theta_N \|_{H^{\frac{d}{2}}}^2, \end{align} $$
 $$ \begin{align} \bigg| \int_{{\mathbb{T}}^d} Y_N \Theta_N^2 dx \bigg| &\le c \| Y_N \|_{W^{-\varepsilon,\infty}}^{6} + \frac{1}{100} \Big( \| \Theta_N \|_{H^{\frac{d}{2}}}^2 + \| \Theta_N \|_{L^2}^4 \Big), \end{align} $$
$$ \begin{align} \bigg| \int_{{\mathbb{T}}^d} Y_N \Theta_N^2 dx \bigg| &\le c \| Y_N \|_{W^{-\varepsilon,\infty}}^{6} + \frac{1}{100} \Big( \| \Theta_N \|_{H^{\frac{d}{2}}}^2 + \| \Theta_N \|_{L^2}^4 \Big), \end{align} $$
 $$ \begin{align} \bigg| \int_{{\mathbb{T}}^d} \Theta_N^3 dx \bigg| &\le \frac{1}{100} \| \Theta_N \|_{H^{\frac{d}{2}}}^2 + \frac{A}{100} \| \Theta_N \|_{L^2}^{4 } \end{align} $$
$$ \begin{align} \bigg| \int_{{\mathbb{T}}^d} \Theta_N^3 dx \bigg| &\le \frac{1}{100} \| \Theta_N \|_{H^{\frac{d}{2}}}^2 + \frac{A}{100} \| \Theta_N \|_{L^2}^{4 } \end{align} $$
for any sufficiently large
![]() $A>0$
, uniformly in
$A>0$
, uniformly in
![]() $N \in \mathbb {N}$
.
$N \in \mathbb {N}$
.
(ii) Let
![]() $A> 0$
. Given any small
$A> 0$
. Given any small
![]() $\varepsilon> 0$
, there exists
$\varepsilon> 0$
, there exists
![]() $c = c(\varepsilon , A)>0$
such that
$c = c(\varepsilon , A)>0$
such that
 $$ \begin{align} \nonumber A\bigg\{ \int_{{\mathbb{T}}^d}& \Big( :\! Y_N^2 \!: + 2 Y_N \Theta_N + \Theta_N^2 \Big) dx \bigg\}^2 \\ &\ge {\frac{A}{4}} \| \Theta_N \|_{L^2}^4 - \frac{1}{100} \| \Theta_N \|_{H^{\frac{d}{2}}}^2 - c\bigg\{ \| Y_N \|_{W^{-\varepsilon,\infty}}^c + \bigg( \int_{{\mathbb{T}}^d} :\! Y_N^2 \!: dx \bigg)^2 \bigg\}, \end{align} $$
$$ \begin{align} \nonumber A\bigg\{ \int_{{\mathbb{T}}^d}& \Big( :\! Y_N^2 \!: + 2 Y_N \Theta_N + \Theta_N^2 \Big) dx \bigg\}^2 \\ &\ge {\frac{A}{4}} \| \Theta_N \|_{L^2}^4 - \frac{1}{100} \| \Theta_N \|_{H^{\frac{d}{2}}}^2 - c\bigg\{ \| Y_N \|_{W^{-\varepsilon,\infty}}^c + \bigg( \int_{{\mathbb{T}}^d} :\! Y_N^2 \!: dx \bigg)^2 \bigg\}, \end{align} $$
uniformly in
![]() $N \in \mathbb {N}$
.
$N \in \mathbb {N}$
.
As in [Reference Barashkov and Gubinelli3, Reference Gunaratnam, Oh, Tzvetkov and Weber31, Reference Oh, Robert, Sosoe and Wang45, Reference Oh, Okamoto and Tolomeo41], the main strategy is to establish a pathwise lower bound on
![]() $\mathcal {W}_N(\theta )$
in (4.3), uniformly in
$\mathcal {W}_N(\theta )$
in (4.3), uniformly in
![]() $N \in \mathbb {N}$
and
$N \in \mathbb {N}$
and
![]() $\theta \in \mathbb {H}_a$
, by making use of the positive terms:
$\theta \in \mathbb {H}_a$
, by making use of the positive terms:
 $$ \begin{align} \mathcal{U}_N(\theta) = {\mathbb{E}} \bigg[\frac{A}{4}\| \Theta_N\|_{L^2}^4 + \frac{1}{2} \int_0^1 \| \theta(t) \|_{L^2_x}^2 dt\bigg] \end{align} $$
$$ \begin{align} \mathcal{U}_N(\theta) = {\mathbb{E}} \bigg[\frac{A}{4}\| \Theta_N\|_{L^2}^4 + \frac{1}{2} \int_0^1 \| \theta(t) \|_{L^2_x}^2 dt\bigg] \end{align} $$
coming from (4.3) and (4.7). From (4.3) and (4.8) together with Lemmas 4.1 and 3.2, we obtain
Then, the uniform exponential integrability (1.32) follows from (4.9) and Lemma 3.1. This proves Theorem 1.9.
We conclude this section by presenting the proof of Lemma 4.1.
Proof of Lemma 4.1.
(i) The estimate (4.4) follows from replacing
![]() $:\! Y_N^3 \!:$
in (3.66) by
$:\! Y_N^3 \!:$
in (3.66) by
![]() $:\! Y_N^2 \!:$
.
$:\! Y_N^2 \!:$
.
With small
![]() $\delta> 0$
, it follows from the fractional Leibniz rule (Lemma 2.1 (ii)) and Sobolev’s inequality as in (3.68) that
$\delta> 0$
, it follows from the fractional Leibniz rule (Lemma 2.1 (ii)) and Sobolev’s inequality as in (3.68) that
 $$ \begin{align*} \bigg| \int_{{\mathbb{T}}^d} Y_N \Theta_N^2 dx \bigg| & \le \| Y_N\|_{W^{-\varepsilon,\infty}} \|\Theta_N^2\|_{W^{\varepsilon, 1+\delta}}\\ & \leq \| Y_N\|_{W^{-\varepsilon,\infty}} \|\Theta_N\|^2_{H^\varepsilon}\\ & \lesssim \| Y_N\|_{W^{-\varepsilon,\infty}} \|\Theta_N\|_{H^{\frac{d}{2}}}^{\beta} \|\Theta_N\|_{L^2}^{2-\beta} \end{align*} $$
$$ \begin{align*} \bigg| \int_{{\mathbb{T}}^d} Y_N \Theta_N^2 dx \bigg| & \le \| Y_N\|_{W^{-\varepsilon,\infty}} \|\Theta_N^2\|_{W^{\varepsilon, 1+\delta}}\\ & \leq \| Y_N\|_{W^{-\varepsilon,\infty}} \|\Theta_N\|^2_{H^\varepsilon}\\ & \lesssim \| Y_N\|_{W^{-\varepsilon,\infty}} \|\Theta_N\|_{H^{\frac{d}{2}}}^{\beta} \|\Theta_N\|_{L^2}^{2-\beta} \end{align*} $$
for some small
![]() $\beta> 0$
. Then, the second estimate (4.5) follows from Young’s inequality since
$\beta> 0$
. Then, the second estimate (4.5) follows from Young’s inequality since
![]() $\frac {\beta }{2} + \frac {2-\beta }{4} < 1$
.
$\frac {\beta }{2} + \frac {2-\beta }{4} < 1$
.
As for the third estimate (4.6), it follows from Sobolev’s inequality, Lemma 2.1 (i) and Cauchy’s inequality that
 $$ \begin{align*} \bigg| \int_{{\mathbb{T}}^d} \Theta_N^3 dx \bigg| &\le C \| \Theta_N \|_{H^{\frac{d}{6}}}^3 \le C \| \Theta_N \|_{H^{\frac{d}{2}}}\| \Theta_N \|_{L^2}^2 \\ &\le \frac{1}{100}\| \Theta_N \|_{H^{\frac{d}{2}}}^2 + \frac{A}{100} \| \Theta_N \|_{L^2}^4, \end{align*} $$
$$ \begin{align*} \bigg| \int_{{\mathbb{T}}^d} \Theta_N^3 dx \bigg| &\le C \| \Theta_N \|_{H^{\frac{d}{6}}}^3 \le C \| \Theta_N \|_{H^{\frac{d}{2}}}\| \Theta_N \|_{L^2}^2 \\ &\le \frac{1}{100}\| \Theta_N \|_{H^{\frac{d}{2}}}^2 + \frac{A}{100} \| \Theta_N \|_{L^2}^4, \end{align*} $$
where
![]() $A>0$
is sufficiently large.
$A>0$
is sufficiently large.
(ii) The bound (4.7) follows from a slight modification of Lemma 5.8 in [Reference Oh, Okamoto and Tolomeo41]. Noting that
for any
![]() $a,b,c \in {\mathbb {R}}$
, we have
$a,b,c \in {\mathbb {R}}$
, we have
 $$ \begin{align} \nonumber A\bigg\{ & \int_{{\mathbb{T}}^d} \Big( :\! Y_N^2 \!: + 2 Y_N \Theta_N + \Theta_N^2 \Big) dx \bigg\}^2 \\ &\ge \frac{A}{2} \bigg( \int_{{\mathbb{T}}^d} \Theta_N^2dx \bigg)^2 - 2A \bigg\{ \bigg( \int_{{\mathbb{T}}^d} :\! Y_N^2 \!: dx \bigg)^2 + \bigg( \int_{{\mathbb{T}}^d} Y_N \Theta_N dx \bigg)^2 \bigg\}. \end{align} $$
$$ \begin{align} \nonumber A\bigg\{ & \int_{{\mathbb{T}}^d} \Big( :\! Y_N^2 \!: + 2 Y_N \Theta_N + \Theta_N^2 \Big) dx \bigg\}^2 \\ &\ge \frac{A}{2} \bigg( \int_{{\mathbb{T}}^d} \Theta_N^2dx \bigg)^2 - 2A \bigg\{ \bigg( \int_{{\mathbb{T}}^d} :\! Y_N^2 \!: dx \bigg)^2 + \bigg( \int_{{\mathbb{T}}^d} Y_N \Theta_N dx \bigg)^2 \bigg\}. \end{align} $$
From Lemma 2.1 (i) and Young’s inequality, we have
 $$ \begin{align} \nonumber \bigg| \int_{{\mathbb{T}}^d} Y_N \Theta_N dx \bigg|^2 &\le \| Y_N \|_{W^{-\varepsilon,\infty}}^2 \| \Theta_N \|_{W^{\varepsilon,1}}^2 \le \| Y_N \|_{W^{-\varepsilon,\infty}}^2 \| \Theta_N \|_{H^\varepsilon}^2\\ &\lesssim \| Y_N \|_{W^{-\varepsilon,\infty}}^2 \| \Theta_N \|_{L^2}^{2-\frac{4\varepsilon}{d} } \| \Theta_N \|_{H^{\frac{d}{2}}}^{\frac {4\varepsilon}d} \\ \nonumber &\le c \| Y_N \|_{W^{-\varepsilon,\infty}}^{\frac{2d}{d-2\varepsilon}} + \frac 1{8} \| \Theta_N \|_{L^2}^4 + \frac1{200 A} \| \Theta_N \|_{H^{\frac{d}{2}}}^2. \end{align} $$
$$ \begin{align} \nonumber \bigg| \int_{{\mathbb{T}}^d} Y_N \Theta_N dx \bigg|^2 &\le \| Y_N \|_{W^{-\varepsilon,\infty}}^2 \| \Theta_N \|_{W^{\varepsilon,1}}^2 \le \| Y_N \|_{W^{-\varepsilon,\infty}}^2 \| \Theta_N \|_{H^\varepsilon}^2\\ &\lesssim \| Y_N \|_{W^{-\varepsilon,\infty}}^2 \| \Theta_N \|_{L^2}^{2-\frac{4\varepsilon}{d} } \| \Theta_N \|_{H^{\frac{d}{2}}}^{\frac {4\varepsilon}d} \\ \nonumber &\le c \| Y_N \|_{W^{-\varepsilon,\infty}}^{\frac{2d}{d-2\varepsilon}} + \frac 1{8} \| \Theta_N \|_{L^2}^4 + \frac1{200 A} \| \Theta_N \|_{H^{\frac{d}{2}}}^2. \end{align} $$
Remark 4.2. In considering the construction of the Gibbs measure with the cubic interaction, it is possible to consider the following renormalized potential energy with a general power
![]() $\gamma> 0$
on the Wick-ordered
$\gamma> 0$
on the Wick-ordered
![]() $L^2$
-norm:
$L^2$
-norm:
 $$ \begin{align} R_N^{\diamond, \gamma} (u) &= \frac \lambda 3\int_{{\mathbb{T}}^d} :\! u_N^3 \!: dx - A \, \bigg( \int_{{\mathbb{T}}^d} :\! u_N^2 \!: dx\bigg)^\gamma, \end{align} $$
$$ \begin{align} R_N^{\diamond, \gamma} (u) &= \frac \lambda 3\int_{{\mathbb{T}}^d} :\! u_N^3 \!: dx - A \, \bigg( \int_{{\mathbb{T}}^d} :\! u_N^2 \!: dx\bigg)^\gamma, \end{align} $$
where the coupling constant
![]() $\lambda \in {\mathbb {R}}\setminus \{0\} $
denotes the strength of cubic interaction as in (1.30). When
$\lambda \in {\mathbb {R}}\setminus \{0\} $
denotes the strength of cubic interaction as in (1.30). When
![]() $\gamma = 2$
,
$\gamma = 2$
,
![]() $R_N^{\diamond , \gamma } (u)$
reduces to
$R_N^{\diamond , \gamma } (u)$
reduces to
![]() $R_N^\diamond (u)$
in (1.30).
$R_N^\diamond (u)$
in (1.30).
In the following, let us briefly discuss the optimality of the power
![]() $\gamma = 2$
in Theorem 1.9. In view of (4.5) and (4.6), we need to control the term
$\gamma = 2$
in Theorem 1.9. In view of (4.5) and (4.6), we need to control the term
![]() $\| \Theta _N \|_{L^2}^4$
, which forces us to choose
$\| \Theta _N \|_{L^2}^4$
, which forces us to choose
![]() $\gamma \ge 2$
in (4.12). When
$\gamma \ge 2$
in (4.12). When
![]() $\gamma = 2$
, it is also necessary to choose A sufficiently large because of (4.5). When
$\gamma = 2$
, it is also necessary to choose A sufficiently large because of (4.5). When
![]() $\gamma <2$
or when
$\gamma <2$
or when
![]() $\gamma =2$
and A is sufficiently small, the taming by the Wick-ordered
$\gamma =2$
and A is sufficiently small, the taming by the Wick-ordered
![]() $L^2$
-norm in (4.12) is too weak to control the terms mentioned above, and thus we expect an analogous nonnormalizability result to hold by repeating the proof of Theorem 1.4.
$L^2$
-norm in (4.12) is too weak to control the terms mentioned above, and thus we expect an analogous nonnormalizability result to hold by repeating the proof of Theorem 1.4.
A On the Gibbs measure for the two-dimensional Zakharov system
In this appendix, we give a brief discussion on Gibbs measures for the following scalar Zakharov system on
![]() ${\mathbb {T}}^d$
:
${\mathbb {T}}^d$
:
 $$ \begin{align} \begin{cases} i \partial_t u +\Delta u = uw\\ c^{-2} \partial_t^2 w - \Delta w = \Delta(|u|^2). \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} i \partial_t u +\Delta u = uw\\ c^{-2} \partial_t^2 w - \Delta w = \Delta(|u|^2). \end{cases} \end{align} $$
This is a coupled system of Schrödinger and wave equations. The unknown u for the Schrödinger part is complex-valued, while the unknown w for the wave part is real-valued. By introducing the velocity field
![]() $\vec v$
:
$\vec v$
:
we can rewrite (A.1) as
 $$ \begin{align} \begin{cases} i \partial_t u +\Delta u = uw\\ \partial_t w = - c^{2}\nabla \cdot \vec v\\ \partial_t \vec v = -\nabla w - \nabla (|u|^2). \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} i \partial_t u +\Delta u = uw\\ \partial_t w = - c^{2}\nabla \cdot \vec v\\ \partial_t \vec v = -\nabla w - \nabla (|u|^2). \end{cases} \end{align} $$
Note that (A.2) is a Hamiltonian system with the Hamiltonian
 $$ \begin{align} H(u, w, \vec v) = \frac{1}{2} \int_{{\mathbb{T}}^d} \big( |\nabla u|^2 + |u|^2 w \big) dx + \frac{1}{4} \int_{{\mathbb{T}}^d} w^2 dx + \frac{c^2}{4} \int_{{\mathbb{T}}^d} |\vec v|^2 dx. \end{align} $$
$$ \begin{align} H(u, w, \vec v) = \frac{1}{2} \int_{{\mathbb{T}}^d} \big( |\nabla u|^2 + |u|^2 w \big) dx + \frac{1}{4} \int_{{\mathbb{T}}^d} w^2 dx + \frac{c^2}{4} \int_{{\mathbb{T}}^d} |\vec v|^2 dx. \end{align} $$
Moreover, the wave energy, namely, the
![]() $L^2$
-norm of the Schrödinger component:
$L^2$
-norm of the Schrödinger component:
is known to be conserved. See [Reference Cher, Czubak and Sulem18].
By setting
![]() $W {\kern-1pt}={\kern-1pt} \frac {1}{\sqrt 2}w$
and
$W {\kern-1pt}={\kern-1pt} \frac {1}{\sqrt 2}w$
and
![]() $\vec V {\kern-1pt}={\kern-1pt} (V_1, \dots , V_d) {\kern-1pt}={\kern-1pt} \frac {c}{\sqrt 2}\vec v$
, we can rewrite the Hamiltonian in (A.3) as
$\vec V {\kern-1pt}={\kern-1pt} (V_1, \dots , V_d) {\kern-1pt}={\kern-1pt} \frac {c}{\sqrt 2}\vec v$
, we can rewrite the Hamiltonian in (A.3) as
Then, the Gibbs measure for the system (A.2) is formally given by
 $$ \begin{align} \nonumber d \rho & = Z^{-1} e^{- H(u, W, \vec V) - \frac 12 M(u)} du \, dW \, d \vec V\\ & = Z^{-1} e^{Q(u, W)} d\mu_{1}(u) d\mu_0(W) \prod_{j = 1}^d d \mu_0(V_j), \end{align} $$
$$ \begin{align} \nonumber d \rho & = Z^{-1} e^{- H(u, W, \vec V) - \frac 12 M(u)} du \, dW \, d \vec V\\ & = Z^{-1} e^{Q(u, W)} d\mu_{1}(u) d\mu_0(W) \prod_{j = 1}^d d \mu_0(V_j), \end{align} $$
where the potential
![]() $Q(u, W)$
is given by
$Q(u, W)$
is given by
the measure
![]() $\mu _{1}$
denotes the complex-valued version of the massive Gaussian free field on
$\mu _{1}$
denotes the complex-valued version of the massive Gaussian free field on
![]() ${\mathbb {T}}^d$
with the density formally given by
${\mathbb {T}}^d$
with the density formally given by
 $$ \begin{align*} d \mu_1 = Z^{-1} e^{-\frac 12 \| u\|_{H^{1} }^2 } du & = Z^{-1} \prod_{n \in \mathbb{Z}^d} e^{-\frac 12 \langle n \rangle^2 |\widehat u(n)|^2} d\widehat u(n), \end{align*} $$
$$ \begin{align*} d \mu_1 = Z^{-1} e^{-\frac 12 \| u\|_{H^{1} }^2 } du & = Z^{-1} \prod_{n \in \mathbb{Z}^d} e^{-\frac 12 \langle n \rangle^2 |\widehat u(n)|^2} d\widehat u(n), \end{align*} $$
and
![]() $\mu _0$
denotes the white noise measure defined as the pushforward measure
$\mu _0$
denotes the white noise measure defined as the pushforward measure
![]() $\mu _0 = (\langle \nabla \rangle ^{\frac {d}{2}})_*\mu $
, with
$\mu _0 = (\langle \nabla \rangle ^{\frac {d}{2}})_*\mu $
, with
![]() $\mu $
as in (1.2). In view of the conservation of the Hamiltonian
$\mu $
as in (1.2). In view of the conservation of the Hamiltonian
![]() $H(u, W, \vec V)$
and the wave energy
$H(u, W, \vec V)$
and the wave energy
![]() $M(u)$
, the Gibbs measure
$M(u)$
, the Gibbs measure
![]() $\rho $
in (A.5) expected to be invariant under the Zakharov dynamics.
$\rho $
in (A.5) expected to be invariant under the Zakharov dynamics.
As in the case of the focusing NLS, the main issue in constructing the Gibbs measure
![]() $\rho $
in (A.5) comes from the focusing nature of the potential, that is, the potential
$\rho $
in (A.5) comes from the focusing nature of the potential, that is, the potential
![]() $Q(u, W)$
is unbounded from above. In a seminal paper [Reference Lebowitz, Rose and Speer33], Lebowitz, Rose and Speer constructed the Gibbs measure
$Q(u, W)$
is unbounded from above. In a seminal paper [Reference Lebowitz, Rose and Speer33], Lebowitz, Rose and Speer constructed the Gibbs measure
![]() $\rho $
when
$\rho $
when
![]() $d = 1$
, by inserting a cutoff in terms of the conserved wave energy
$d = 1$
, by inserting a cutoff in terms of the conserved wave energy
![]() $M(u) = \|u\|_{L^2}^2$
, which was then proved to be invariant under (A.2) on
$M(u) = \|u\|_{L^2}^2$
, which was then proved to be invariant under (A.2) on
![]() ${\mathbb {T}}$
(and thus (A.1)) by Bourgain [Reference Bourgain9].
${\mathbb {T}}$
(and thus (A.1)) by Bourgain [Reference Bourgain9].
Then, a natural question is to consider the construction of the Gibbs measure
![]() $\rho $
in the two-dimensional setting.Footnote
23
Before doing this, let us recall the relation between the Zakharov system and the focusing cubic NLS. By sending the wave speed c in (A.1) to
$\rho $
in the two-dimensional setting.Footnote
23
Before doing this, let us recall the relation between the Zakharov system and the focusing cubic NLS. By sending the wave speed c in (A.1) to
![]() $\infty $
, the Zakharov system converges, at a formal level, to the focusing cubic NLS. See, for example, [Reference Ozawa and Tsutsumi51, Reference Masmoudi and Nakanishi37] for rigorous convergence results on
$\infty $
, the Zakharov system converges, at a formal level, to the focusing cubic NLS. See, for example, [Reference Ozawa and Tsutsumi51, Reference Masmoudi and Nakanishi37] for rigorous convergence results on
![]() ${\mathbb {R}}^d$
. When
${\mathbb {R}}^d$
. When
![]() $d = 2$
, Theorem 1.4 states that the (renormalized) Gibbs measure for the focusing cubic NLS on
$d = 2$
, Theorem 1.4 states that the (renormalized) Gibbs measure for the focusing cubic NLS on
![]() ${\mathbb {T}}^2$
is not normalizable, even with a Wick-ordered
${\mathbb {T}}^2$
is not normalizable, even with a Wick-ordered
![]() $L^2$
-cutoff. This suggests that, when
$L^2$
-cutoff. This suggests that, when
![]() $d = 2$
, the Gibbs measure
$d = 2$
, the Gibbs measure
![]() $\rho $
in (A.5) for the Zakharov system may not be constructible even with a Wick-ordered
$\rho $
in (A.5) for the Zakharov system may not be constructible even with a Wick-ordered
![]() $L^2$
-cutoff on the Schrödinger component u.
$L^2$
-cutoff on the Schrödinger component u.
Given
![]() $N \in \mathbb {N}$
, define the following renormalized truncated potential energy:
$N \in \mathbb {N}$
, define the following renormalized truncated potential energy:
where
![]() $u_N = \pi _N u $
as in Subsection 1.1 and
$u_N = \pi _N u $
as in Subsection 1.1 and
![]() $:\! | u_N|^2 \!: \, = | u_N|^2 -\sigma _N$
. We then define the renormalized truncated Gibbs measure
$:\! | u_N|^2 \!: \, = | u_N|^2 -\sigma _N$
. We then define the renormalized truncated Gibbs measure
![]() $\rho _{N}$
on
$\rho _{N}$
on
![]() ${\mathbb {T}}^2$
, endowed with a Wick-ordered
${\mathbb {T}}^2$
, endowed with a Wick-ordered
![]() $L^2$
-cutoff, by
$L^2$
-cutoff, by
 $$ \begin{align*} d \rho_N & = Z_N^{-1} \mathbf 1_{ \{|\int_{{\mathbb{T}}^2} : | u_N|^2 : dx| \le K\}} e^{Q_N(u, W)} d\mu_{1}(u) d\mu_0(W) \prod_{j = 1}^2 d \mu_0(V_j). \end{align*} $$
$$ \begin{align*} d \rho_N & = Z_N^{-1} \mathbf 1_{ \{|\int_{{\mathbb{T}}^2} : | u_N|^2 : dx| \le K\}} e^{Q_N(u, W)} d\mu_{1}(u) d\mu_0(W) \prod_{j = 1}^2 d \mu_0(V_j). \end{align*} $$
By integrating in
![]() $(V_1, V_2)$
and then in W, we have
$(V_1, V_2)$
and then in W, we have
 $$ \begin{align} \nonumber \iint & \mathbf 1_{ \{|\int_{{\mathbb{T}}^2} : | u_N|^2 : dx| \le K\}} e^{Q_N(u, W)} d\mu_0(W) \prod_{j = 1}^2 d \mu_0(V_j) \\ \nonumber & = \mathbf 1_{ \{|\int_{{\mathbb{T}}^2} : | u_N|^2 : dx| \le K\}} \int \exp\bigg(-\frac{1}{\sqrt 2} \sum_{n \in \mathbb{Z}^2} \mathcal{F}(: \!| u_N|^2 \!: )(n)\, \overline{\widehat W(n)} \bigg) d\mu_0(W) \\ & = \mathbf 1_{ \{|\int_{{\mathbb{T}}^2} : | u_N|^2 : dx| \le K\}} \int_{{\mathbb{R}}} \exp\bigg(-\frac{1}{\sqrt 2} \mathcal{F}(: \!| u_N|^2 \!: )(0)\, g_0\bigg) \frac{e^{-\frac 12 g_0^2}}{\sqrt {2\pi}} dg_0\\ \nonumber & \hphantom{X} \times \prod_{n \in \Lambda} \frac{1}{\pi}\int_{\mathbb{C}} \exp\bigg(-\sqrt 2 \operatorname*{\mathrm{Re}}\Big( \mathcal{F}( | u_N|^2 )(n)\, \overline{ g_n }\Big) \bigg) e^{-|g_n|^2}d g_n, \end{align} $$
$$ \begin{align} \nonumber \iint & \mathbf 1_{ \{|\int_{{\mathbb{T}}^2} : | u_N|^2 : dx| \le K\}} e^{Q_N(u, W)} d\mu_0(W) \prod_{j = 1}^2 d \mu_0(V_j) \\ \nonumber & = \mathbf 1_{ \{|\int_{{\mathbb{T}}^2} : | u_N|^2 : dx| \le K\}} \int \exp\bigg(-\frac{1}{\sqrt 2} \sum_{n \in \mathbb{Z}^2} \mathcal{F}(: \!| u_N|^2 \!: )(n)\, \overline{\widehat W(n)} \bigg) d\mu_0(W) \\ & = \mathbf 1_{ \{|\int_{{\mathbb{T}}^2} : | u_N|^2 : dx| \le K\}} \int_{{\mathbb{R}}} \exp\bigg(-\frac{1}{\sqrt 2} \mathcal{F}(: \!| u_N|^2 \!: )(0)\, g_0\bigg) \frac{e^{-\frac 12 g_0^2}}{\sqrt {2\pi}} dg_0\\ \nonumber & \hphantom{X} \times \prod_{n \in \Lambda} \frac{1}{\pi}\int_{\mathbb{C}} \exp\bigg(-\sqrt 2 \operatorname*{\mathrm{Re}}\Big( \mathcal{F}( | u_N|^2 )(n)\, \overline{ g_n }\Big) \bigg) e^{-|g_n|^2}d g_n, \end{align} $$
where
![]() $\{ g_n \}_{n \in \mathbb {Z}^2}$
is as in (1.3)Footnote
24
and
$\{ g_n \}_{n \in \mathbb {Z}^2}$
is as in (1.3)Footnote
24
and
![]() $\Lambda $
denotes the index set given by
$\Lambda $
denotes the index set given by
![]() $\Lambda = (\mathbb {Z}\times \mathbb {Z}_+)\cup (\mathbb {Z}_+\times \{0\})$
such that
$\Lambda = (\mathbb {Z}\times \mathbb {Z}_+)\cup (\mathbb {Z}_+\times \{0\})$
such that
![]() $\mathbb {Z}^2 = \Lambda \cup (-\Lambda ) \cup \{0\}$
. Here, we used the fact that
$\mathbb {Z}^2 = \Lambda \cup (-\Lambda ) \cup \{0\}$
. Here, we used the fact that
![]() $\mathcal {F}(: \!| u_N|^2 \!: )(n) = \mathcal {F}(| u_N|^2 )(n)$
for
$\mathcal {F}(: \!| u_N|^2 \!: )(n) = \mathcal {F}(| u_N|^2 )(n)$
for
![]() $n \ne 0$
. Then, recalling the moment generating function
$n \ne 0$
. Then, recalling the moment generating function
![]() ${\mathbb {E}}[e^{tX}] = e^{\frac 12 \sigma t^2}$
for
${\mathbb {E}}[e^{tX}] = e^{\frac 12 \sigma t^2}$
for
![]() $X \sim \mathcal {N}_{{\mathbb {R}}}(0, \sigma )$
, we have
$X \sim \mathcal {N}_{{\mathbb {R}}}(0, \sigma )$
, we have
 $$ \begin{align} \nonumber ({A.8}) & = \mathbf 1_{ \{|\int_{{\mathbb{T}}^2} : | u_N|^2 : dx| \le K\}} \exp\bigg( \frac 14 \big(\mathcal{F}(: \!| u_N|^2 \!: )(0)\big)^2 \bigg)\\ \nonumber & \hphantom{X} \times \prod_{n \in \Lambda} \frac{1}{\pi}\int_{\mathbb{C}} \exp\bigg(-\sqrt 2 \operatorname*{\mathrm{Re}} \! \big(\mathcal{F}( | u_N|^2 )(n)\big) \operatorname*{\mathrm{Re}} g_n \\ & \hphantom{XXXXXXXXXl} - \sqrt 2 \operatorname*{\mathrm{Im}}\! \big(\mathcal{F}( | u_N|^2 )(n) \big) \operatorname*{\mathrm{Im}} g_n \bigg) e^{-|g_n|^2}d g_n\\ \nonumber & \geq \mathbf 1_{ \{|\int_{{\mathbb{T}}^2} : | u_N|^2 : dx| \le K\}} \exp\bigg( \frac 14 \big\| \pi_{\ne 0} |u_N|^2 \big\|_{L^2}^2 - CK^2 \bigg), \end{align} $$
$$ \begin{align} \nonumber ({A.8}) & = \mathbf 1_{ \{|\int_{{\mathbb{T}}^2} : | u_N|^2 : dx| \le K\}} \exp\bigg( \frac 14 \big(\mathcal{F}(: \!| u_N|^2 \!: )(0)\big)^2 \bigg)\\ \nonumber & \hphantom{X} \times \prod_{n \in \Lambda} \frac{1}{\pi}\int_{\mathbb{C}} \exp\bigg(-\sqrt 2 \operatorname*{\mathrm{Re}} \! \big(\mathcal{F}( | u_N|^2 )(n)\big) \operatorname*{\mathrm{Re}} g_n \\ & \hphantom{XXXXXXXXXl} - \sqrt 2 \operatorname*{\mathrm{Im}}\! \big(\mathcal{F}( | u_N|^2 )(n) \big) \operatorname*{\mathrm{Im}} g_n \bigg) e^{-|g_n|^2}d g_n\\ \nonumber & \geq \mathbf 1_{ \{|\int_{{\mathbb{T}}^2} : | u_N|^2 : dx| \le K\}} \exp\bigg( \frac 14 \big\| \pi_{\ne 0} |u_N|^2 \big\|_{L^2}^2 - CK^2 \bigg), \end{align} $$
where
![]() $\pi _{\ne 0}$
is the projection onto nonzero frequencies.
$\pi _{\ne 0}$
is the projection onto nonzero frequencies.
Let
![]() $\{ h_n \}_{n \in \mathbb {Z}^2}$
be a sequence of mutually independent standard complex-valued Gaussian random variables. Then, we have
$\{ h_n \}_{n \in \mathbb {Z}^2}$
be a sequence of mutually independent standard complex-valued Gaussian random variables. Then, we have
 $$ \begin{align} \int\big\| \pi_{\ne 0} |u_N|^2 \big\|_{L^2}^2 d \mu_1 \nonumber & = {\mathbb{E}}\Bigg[ \sum_{\substack{n_1 - n_2 + n_3 - n_4 = 0\\ |n_j| \leq N\\ n_1 - n_2 \ne 0}} \frac{h_{n_1}}{\langle n_1 \rangle} \frac{\overline{h_{n_2}}}{\langle n_2 \rangle} \frac{h_{n_3}}{\langle n_3 \rangle} \frac{\overline{h_{n_4}}}{\langle n_4 \rangle}\Bigg]\\ & = \sum_{|n_1 |\leq N} \frac{1}{\langle n_1 \rangle^2} \sum_{\substack{|n_3|\leq N\\n_3 \ne n_1}} \frac{1}{\langle n_3 \rangle^2} \sim (\log N)^2 \longrightarrow \infty, \end{align} $$
$$ \begin{align} \int\big\| \pi_{\ne 0} |u_N|^2 \big\|_{L^2}^2 d \mu_1 \nonumber & = {\mathbb{E}}\Bigg[ \sum_{\substack{n_1 - n_2 + n_3 - n_4 = 0\\ |n_j| \leq N\\ n_1 - n_2 \ne 0}} \frac{h_{n_1}}{\langle n_1 \rangle} \frac{\overline{h_{n_2}}}{\langle n_2 \rangle} \frac{h_{n_3}}{\langle n_3 \rangle} \frac{\overline{h_{n_4}}}{\langle n_4 \rangle}\Bigg]\\ & = \sum_{|n_1 |\leq N} \frac{1}{\langle n_1 \rangle^2} \sum_{\substack{|n_3|\leq N\\n_3 \ne n_1}} \frac{1}{\langle n_3 \rangle^2} \sim (\log N)^2 \longrightarrow \infty, \end{align} $$
as
![]() $N \to \infty $
. Then, from (A.10), the interpolation of the
$N \to \infty $
. Then, from (A.10), the interpolation of the
![]() $L^p$
-spaces and Lemma 2.3, we have
$L^p$
-spaces and Lemma 2.3, we have
 $$ \begin{align} \nonumber \log N & \sim \big\| \| \pi_{\ne 0} |u_N|^2 \|_{L^2}\big\|_{L^2(\mu_1)} \ge \big \| \| \pi_{\ne 0} |u_N|^2 \|_{L^2}\big\|_{L^1(\mu_1)}\\ & \ge \frac{\big \| \| \pi_{\ne 0} |u_N|^2 \|_{L^2}\big\|_{L^2(\mu_1)}^3}{\big \| \| \pi_{\ne 0} |u_N|^2 \|_{L^2}\big\|_{L^4(\mu_1)}^2} \sim \log N. \end{align} $$
$$ \begin{align} \nonumber \log N & \sim \big\| \| \pi_{\ne 0} |u_N|^2 \|_{L^2}\big\|_{L^2(\mu_1)} \ge \big \| \| \pi_{\ne 0} |u_N|^2 \|_{L^2}\big\|_{L^1(\mu_1)}\\ & \ge \frac{\big \| \| \pi_{\ne 0} |u_N|^2 \|_{L^2}\big\|_{L^2(\mu_1)}^3}{\big \| \| \pi_{\ne 0} |u_N|^2 \|_{L^2}\big\|_{L^4(\mu_1)}^2} \sim \log N. \end{align} $$
Also, from Lemma 2.3 and (1.5), we have
Hence, given sufficiently small
![]() $ \varepsilon \gg \eta> 0$
, it follows from Lemma 3.1, Cauchy’s inequality, Sobolev’s inequality, (A.11) and (A.12) that
$ \varepsilon \gg \eta> 0$
, it follows from Lemma 3.1, Cauchy’s inequality, Sobolev’s inequality, (A.11) and (A.12) that
 $$ \begin{align*} -\log & \bigg(\int \exp\Big(-\eta\big\|\pi_{\ne 0} |u_N|^2 \big\|_{L^2}\Big) d \mu_1(u)\bigg)\\ & = \inf_{\theta \in \mathbb H_a} {\mathbb{E}}\bigg[ \eta \big\| \pi_{\ne 0} |\pi_N Y(1) + \pi_N I(\theta)(1)|^2\big\|_{L^2} + {\frac{1}{2}} \int_0^1 \| \theta(t) \|_{L^2_x}^2 dt \bigg]\\ & \ge \inf_{\theta \in \mathbb H_a} {\mathbb{E}}\bigg[ \eta \Big(\big\| \pi_{\ne 0} |\pi_N Y(1)|^2 \big\|_{L^2} - 2\| \pi_N Y(1) \pi_N I(\theta)(1)\|_{L^2} \\ & \hphantom{XXXXX} - \|\pi_N I(\theta)(1)\|_{L^4}^2\Big) + {\frac{1}{2}} \int_0^1 \| \theta(t) \|_{L^2_x}^2 dt \bigg] \\ & \ge \inf_{\theta \in \mathbb H_a} {\mathbb{E}}\bigg[ \eta \Big(\big\| \pi_{\ne 0} |\pi_N Y(1)|^2 \big\|_{L^2} - \varepsilon \| \pi_N Y(1)\|_{L^4}^2\Big) + {\frac{1}{4}} \int_0^1 \| \theta(t) \|_{L^2_x}^2 dt \bigg]\\ & \gtrsim \eta (\log N). \end{align*} $$
$$ \begin{align*} -\log & \bigg(\int \exp\Big(-\eta\big\|\pi_{\ne 0} |u_N|^2 \big\|_{L^2}\Big) d \mu_1(u)\bigg)\\ & = \inf_{\theta \in \mathbb H_a} {\mathbb{E}}\bigg[ \eta \big\| \pi_{\ne 0} |\pi_N Y(1) + \pi_N I(\theta)(1)|^2\big\|_{L^2} + {\frac{1}{2}} \int_0^1 \| \theta(t) \|_{L^2_x}^2 dt \bigg]\\ & \ge \inf_{\theta \in \mathbb H_a} {\mathbb{E}}\bigg[ \eta \Big(\big\| \pi_{\ne 0} |\pi_N Y(1)|^2 \big\|_{L^2} - 2\| \pi_N Y(1) \pi_N I(\theta)(1)\|_{L^2} \\ & \hphantom{XXXXX} - \|\pi_N I(\theta)(1)\|_{L^4}^2\Big) + {\frac{1}{2}} \int_0^1 \| \theta(t) \|_{L^2_x}^2 dt \bigg] \\ & \ge \inf_{\theta \in \mathbb H_a} {\mathbb{E}}\bigg[ \eta \Big(\big\| \pi_{\ne 0} |\pi_N Y(1)|^2 \big\|_{L^2} - \varepsilon \| \pi_N Y(1)\|_{L^4}^2\Big) + {\frac{1}{4}} \int_0^1 \| \theta(t) \|_{L^2_x}^2 dt \bigg]\\ & \gtrsim \eta (\log N). \end{align*} $$
Therefore, we obtain
for some constant
![]() $c> 0$
. Then, by Chebyshev’s inequality, we conclude that, for any
$c> 0$
. Then, by Chebyshev’s inequality, we conclude that, for any
![]() $M> 0$
,
$M> 0$
,
as
![]() $N \to \infty $
.
$N \to \infty $
.
We also note that, given any
![]() $K> 0$
, there exists a constant
$K> 0$
, there exists a constant
![]() $c_K> 0$
such that
$c_K> 0$
such that
 $$ \begin{align} \mu_1\bigg(\Big|\int_{{\mathbb{T}}^2} : | u_N|^2 : dx \Big|\le K\bigg) \ge c_K, \end{align} $$
$$ \begin{align} \mu_1\bigg(\Big|\int_{{\mathbb{T}}^2} : | u_N|^2 : dx \Big|\le K\bigg) \ge c_K, \end{align} $$
uniformly in
![]() $N \in \mathbb {N}$
. Indeed, for
$N \in \mathbb {N}$
. Indeed, for
![]() $L = L(K)> 0$
(to be chosen later), as in (3.11), we have
$L = L(K)> 0$
(to be chosen later), as in (3.11), we have
Now, by repeating the argument in Subsection 3.2, in particular, (3.34) and (3.42) with
![]() $M = M_0(K)$
, we have
$M = M_0(K)$
, we have
 $$ \begin{align} \nonumber -\log & \, {\mathbb{E}}_{\mu_1} \Big[ \exp\big(L\cdot \mathbf 1_{ \{|\int_{{\mathbb{T}}^2} : | u_N|^2 : dx| \le K\}}\big) \Big] \\ &\le {\mathbb{E}}\bigg[ -L\cdot \mathbf 1_{\{ |\int_{{\mathbb{T}}^d} ( :{Y_N^2}: + 2 Y_N \Theta^0 + (\Theta^0)^2) dx | \le K\}} + \frac 12 \int_0^1 \| \theta^0(t)\|_{L^2_x} ^2 dt \bigg] \\ \nonumber &\le - \frac 12 L + C M_0^d \log M_0 \le - \frac 14 L \end{align} $$
$$ \begin{align} \nonumber -\log & \, {\mathbb{E}}_{\mu_1} \Big[ \exp\big(L\cdot \mathbf 1_{ \{|\int_{{\mathbb{T}}^2} : | u_N|^2 : dx| \le K\}}\big) \Big] \\ &\le {\mathbb{E}}\bigg[ -L\cdot \mathbf 1_{\{ |\int_{{\mathbb{T}}^d} ( :{Y_N^2}: + 2 Y_N \Theta^0 + (\Theta^0)^2) dx | \le K\}} + \frac 12 \int_0^1 \| \theta^0(t)\|_{L^2_x} ^2 dt \bigg] \\ \nonumber &\le - \frac 12 L + C M_0^d \log M_0 \le - \frac 14 L \end{align} $$
by choosing
![]() $L = L(M_0) = L(K) \gg 1$
sufficiently large. From (A.15) and (A.16), we then obtain
$L = L(M_0) = L(K) \gg 1$
sufficiently large. From (A.15) and (A.16), we then obtain
 $$ \begin{align*} \mu_1\bigg(\Big|\int_{{\mathbb{T}}^2} : | u_N|^2 : dx \Big|\le K\bigg) \ge \frac{e^{\frac 14 L} - 1}{e^L} =: c_K, \end{align*} $$
$$ \begin{align*} \mu_1\bigg(\Big|\int_{{\mathbb{T}}^2} : | u_N|^2 : dx \Big|\le K\bigg) \ge \frac{e^{\frac 14 L} - 1}{e^L} =: c_K, \end{align*} $$
yielding (A.14).
Therefore, from (A.8), (A.9), (A.13) and (A.14), we obtain, for any
![]() $K> 0$
,
$K> 0$
,
 $$ \begin{align*} \lim_{N \to \infty} & \iiint \mathbf 1_{ \{|\int_{{\mathbb{T}}^2} : | u_N|^2 : dx| \le K\}} e^{Q_N(u, W)} d\mu_{1}(u) d\mu_0(W) \prod_{j = 1}^2 d \mu_0(V_j)\\ & \ge \liminf_{N \to \infty} \int \mathbf 1_{ \{|\int_{{\mathbb{T}}^2} : | u_N|^2 : dx| \le K\}} \exp\bigg( \frac 14 \big\| \pi_{\ne 0} |u_N|^2 \big\|_{L^2}^2 - CK^2 \bigg) d\mu_{1}(u) \\ & \ge \liminf_{N \to \infty} \Big(c_K - \exp\big(\eta(M- c \log N)\big) \Big) \exp\bigg(\frac14 M^2 - CK^2\bigg) \\ & = c_K \exp\bigg(\frac14 M^2 - CK^2\bigg) \longrightarrow \infty \end{align*} $$
$$ \begin{align*} \lim_{N \to \infty} & \iiint \mathbf 1_{ \{|\int_{{\mathbb{T}}^2} : | u_N|^2 : dx| \le K\}} e^{Q_N(u, W)} d\mu_{1}(u) d\mu_0(W) \prod_{j = 1}^2 d \mu_0(V_j)\\ & \ge \liminf_{N \to \infty} \int \mathbf 1_{ \{|\int_{{\mathbb{T}}^2} : | u_N|^2 : dx| \le K\}} \exp\bigg( \frac 14 \big\| \pi_{\ne 0} |u_N|^2 \big\|_{L^2}^2 - CK^2 \bigg) d\mu_{1}(u) \\ & \ge \liminf_{N \to \infty} \Big(c_K - \exp\big(\eta(M- c \log N)\big) \Big) \exp\bigg(\frac14 M^2 - CK^2\bigg) \\ & = c_K \exp\bigg(\frac14 M^2 - CK^2\bigg) \longrightarrow \infty \end{align*} $$
by taking
![]() $M \to \infty $
. This shows the nonnormalizability of the Gibbs measure for the Zakharov system on
$M \to \infty $
. This shows the nonnormalizability of the Gibbs measure for the Zakharov system on
![]() ${\mathbb {T}}^2$
even if we apply the Wick renormalization on the potential energy
${\mathbb {T}}^2$
even if we apply the Wick renormalization on the potential energy
![]() $Q(u, W)$
in (A.6) and endow the measure with a Wick-ordered
$Q(u, W)$
in (A.6) and endow the measure with a Wick-ordered
![]() $L^2$
-cutoff on the Schrödinger component.
$L^2$
-cutoff on the Schrödinger component.
Another way would be to apply a change of variables as in the one-dimensional case due to Bourgain [Reference Bourgain9]. Namely, rewrite the Hamiltonian in (A.4) as in the one-dimensional case by Bourgain [Reference Bourgain9]:
By introducing a new variable
![]() $\widetilde W = W+ \sqrt 2|u|^2$
, we arrive at
$\widetilde W = W+ \sqrt 2|u|^2$
, we arrive at
Then, we apply the Wick renormalization to the potential energy.
In this formulation, we consider the renormalized truncated Gibbs measure
![]() $\widetilde \rho _{N}$
defined by
$\widetilde \rho _{N}$
defined by
 $$ \begin{align*} d \widetilde \rho_N & = Z_N^{-1} \mathbf 1_{ \{|\int_{{\mathbb{T}}^2} : | u_N|^2 : dx| \le K\}} e^{R_N(u)} d\mu_{1}(u) d\mu_0(\widetilde W) \prod_{j = 1}^2 d \mu_0(V_j), \end{align*} $$
$$ \begin{align*} d \widetilde \rho_N & = Z_N^{-1} \mathbf 1_{ \{|\int_{{\mathbb{T}}^2} : | u_N|^2 : dx| \le K\}} e^{R_N(u)} d\mu_{1}(u) d\mu_0(\widetilde W) \prod_{j = 1}^2 d \mu_0(V_j), \end{align*} $$
where the renormalized truncated potential energy
![]() $R_N$
is defined by
$R_N$
is defined by
Note that, in the complex-valued setting, the Wick-ordered fourth power is given by
See [Reference Oh and Thomann47]. Then, by integrating in
![]() $\widetilde W$
and
$\widetilde W$
and
![]() $\vec V$
and then by applying Theorem 1.4 (in the complex-valued setting), we have
$\vec V$
and then by applying Theorem 1.4 (in the complex-valued setting), we have
 $$ \begin{align*} \sup_{N \in \mathbb{N}} & \iiint \mathbf 1_{\{|\int : | u_N|^2 : dx| \le K\}} e^{R_N(u)} d\mu_{1}(u) d\mu_0(\widetilde W) \prod_{j = 1}^2 d \mu_0(V_j)\\ & = \sup_{N \in \mathbb{N}} \int \mathbf 1_{\{|\int : | u_N|^2 : dx| \le K\}} e^{R_N(u)} d\mu_{1}(u) = \infty \end{align*} $$
$$ \begin{align*} \sup_{N \in \mathbb{N}} & \iiint \mathbf 1_{\{|\int : | u_N|^2 : dx| \le K\}} e^{R_N(u)} d\mu_{1}(u) d\mu_0(\widetilde W) \prod_{j = 1}^2 d \mu_0(V_j)\\ & = \sup_{N \in \mathbb{N}} \int \mathbf 1_{\{|\int : | u_N|^2 : dx| \le K\}} e^{R_N(u)} d\mu_{1}(u) = \infty \end{align*} $$
for any
![]() $K> 0$
. This shows the nonnormalizability of the limiting Gibbs measure in this formulation.
$K> 0$
. This shows the nonnormalizability of the limiting Gibbs measure in this formulation.
Remark A.1. In the renormalization (A.7), we added the term
![]() $\frac {\sigma _N}{\sqrt 2}\int _{{\mathbb {T}}^2}Wdx = \frac {\sigma _N}{2}\int _{{\mathbb {T}}^2}wdx$
. Note that the spatial mean of w is conserved under the flow of the system (A.2). Thus, by imposing the spatial mean-zero condition on w, we can write
$\frac {\sigma _N}{\sqrt 2}\int _{{\mathbb {T}}^2}Wdx = \frac {\sigma _N}{2}\int _{{\mathbb {T}}^2}wdx$
. Note that the spatial mean of w is conserved under the flow of the system (A.2). Thus, by imposing the spatial mean-zero condition on w, we can write
![]() $Q_N(u, W)$
in (A.7) as
$Q_N(u, W)$
in (A.7) as
showing that this term is self-renormalizing, and thus the renormalization (A.7) does not affect the system (A.2).
B Focusing quartic Gibbs measures with smoother Gaussian fields
In this appendix, we briefly discuss the construction of the focusing Gibbs measure
![]() $\rho _\alpha $
in (1.37) with a smoother base Gaussian measure
$\rho _\alpha $
in (1.37) with a smoother base Gaussian measure
![]() $\mu _\alpha $
in (1.36). We only discuss the uniform exponential integrability bound (1.35). Since the precise value of
$\mu _\alpha $
in (1.36). We only discuss the uniform exponential integrability bound (1.35). Since the precise value of
![]() $\lambda \in {\mathbb {R}}\setminus \{0\}$
does not play any role, we set
$\lambda \in {\mathbb {R}}\setminus \{0\}$
does not play any role, we set
![]() $\lambda = 4$
in the following. As before, we also assume
$\lambda = 4$
in the following. As before, we also assume
![]() $p = 1$
for simplicity.
$p = 1$
for simplicity.
Fix
![]() $\alpha> \frac {d}{2}$
. The Gaussian measure
$\alpha> \frac {d}{2}$
. The Gaussian measure
![]() $\mu _\alpha $
in (1.37) is the induced probability measure under the map:
$\mu _\alpha $
in (1.37) is the induced probability measure under the map:
 $$ \begin{align*} \omega\in \Omega \longmapsto u(\omega) = \sum_{n \in \mathbb{Z}^d } \frac{ g_n(\omega)}{\langle n \rangle^\alpha} e_n, \end{align*} $$
$$ \begin{align*} \omega\in \Omega \longmapsto u(\omega) = \sum_{n \in \mathbb{Z}^d } \frac{ g_n(\omega)}{\langle n \rangle^\alpha} e_n, \end{align*} $$
where
![]() $\{ g_n \}_{n \in \mathbb {Z}^d}$
is as in (1.3). In particular, a typical function u in the support of
$\{ g_n \}_{n \in \mathbb {Z}^d}$
is as in (1.3). In particular, a typical function u in the support of
![]() $\mu $
belongs to
$\mu $
belongs to
![]() $L^\infty ({\mathbb {T}}^d)$
.
$L^\infty ({\mathbb {T}}^d)$
.
We define
![]() $Y^\alpha $
by
$Y^\alpha $
by
where W is as in (3.1). Then, in view of the Boué–Dupuis formula (Lemma 3.1), it suffices to establish a lower bound on
 $$ \begin{align} \mathcal{W}_N^\alpha(\theta) = {\mathbb{E}} \bigg[-R^{\diamond, \gamma}_N(Y^\alpha(1) + I^\alpha(\theta)(1)) + \frac{1}{2} \int_0^1 \| \theta(t) \|_{L^2_x}^2 dt \bigg], \end{align} $$
$$ \begin{align} \mathcal{W}_N^\alpha(\theta) = {\mathbb{E}} \bigg[-R^{\diamond, \gamma}_N(Y^\alpha(1) + I^\alpha(\theta)(1)) + \frac{1}{2} \int_0^1 \| \theta(t) \|_{L^2_x}^2 dt \bigg], \end{align} $$
uniformly in
![]() $N \in \mathbb {N}$
and
$N \in \mathbb {N}$
and
![]() $\theta \in \mathbb {H}_a$
, where
$\theta \in \mathbb {H}_a$
, where
![]() $R^{\diamond , \gamma }_N (u)$
and
$R^{\diamond , \gamma }_N (u)$
and
![]() $I^\alpha (\theta )$
are defined by
$I^\alpha (\theta )$
are defined by
 $$ \begin{align} R^{\diamond, \gamma}_N (u) &= \int_{{\mathbb{T}}^d} u_N^4 dx - A \, \bigg( \int_{{\mathbb{T}}^d} u_N^2 dx\bigg)^\gamma \end{align} $$
$$ \begin{align} R^{\diamond, \gamma}_N (u) &= \int_{{\mathbb{T}}^d} u_N^4 dx - A \, \bigg( \int_{{\mathbb{T}}^d} u_N^2 dx\bigg)^\gamma \end{align} $$
for some
![]() $\gamma>0$
(to be chosen later) and
$\gamma>0$
(to be chosen later) and
 $$ \begin{align*} I^\alpha(\theta)(t) = \int_0^t \langle \nabla \rangle^{-\alpha} \theta(t') dt'. \end{align*} $$
$$ \begin{align*} I^\alpha(\theta)(t) = \int_0^t \langle \nabla \rangle^{-\alpha} \theta(t') dt'. \end{align*} $$
For simplicity of notation, we set
![]() $Y_N^\alpha = \pi _N Y^\alpha = \pi _N Y^\alpha (1)$
and
$Y_N^\alpha = \pi _N Y^\alpha = \pi _N Y^\alpha (1)$
and
![]() $\Theta _N^\alpha = \pi _N \Theta ^\alpha = \pi _N I^\alpha (\theta )(1)$
.
$\Theta _N^\alpha = \pi _N \Theta ^\alpha = \pi _N I^\alpha (\theta )(1)$
.
 $$ \begin{align*} \mathcal{W}_N^{\alpha}(\theta) &={\mathbb{E}} \bigg[ -\int_{{\mathbb{T}}^d} (Y_N^\alpha)^4 dx -4\int_{{\mathbb{T}}^d} (Y_N^\alpha)^3 \Theta_N^\alpha dx -6\int_{{\mathbb{T}}^d} (Y_N^\alpha)^2 (\Theta_N^\alpha)^2 dx\\ &\hphantom{XXX} -4\int_{{\mathbb{T}}^d} Y_N^\alpha (\Theta_N^\alpha)^3 dx -\int_{{\mathbb{T}}^d} (\Theta_N^\alpha)^4 dx + A \bigg\{ \int_{{\mathbb{T}}^d} \big (Y_N^\alpha + \Theta_N^\alpha\big)^2 dx \bigg\}^2\\ &\hphantom{XXX} + \frac{1}{2} \int_0^1 \| \theta(t) \|_{L^2_x}^2 dt \bigg]. \end{align*} $$
$$ \begin{align*} \mathcal{W}_N^{\alpha}(\theta) &={\mathbb{E}} \bigg[ -\int_{{\mathbb{T}}^d} (Y_N^\alpha)^4 dx -4\int_{{\mathbb{T}}^d} (Y_N^\alpha)^3 \Theta_N^\alpha dx -6\int_{{\mathbb{T}}^d} (Y_N^\alpha)^2 (\Theta_N^\alpha)^2 dx\\ &\hphantom{XXX} -4\int_{{\mathbb{T}}^d} Y_N^\alpha (\Theta_N^\alpha)^3 dx -\int_{{\mathbb{T}}^d} (\Theta_N^\alpha)^4 dx + A \bigg\{ \int_{{\mathbb{T}}^d} \big (Y_N^\alpha + \Theta_N^\alpha\big)^2 dx \bigg\}^2\\ &\hphantom{XXX} + \frac{1}{2} \int_0^1 \| \theta(t) \|_{L^2_x}^2 dt \bigg]. \end{align*} $$
Let us first state a lemma, analogous to Lemma 4.1.
Lemma B.1.
(i) Let
![]() $\alpha> {\frac {d}{2}}$
. Then, there exists
$\alpha> {\frac {d}{2}}$
. Then, there exists
![]() $c>0$
such that
$c>0$
such that
 $$ \begin{align} \bigg| \int_{{\mathbb{T}}^d} ( Y_N^\alpha)^3 \Theta_N^\alpha dx \bigg| &\le c \| Y_N^\alpha \|_{L^\infty}^6 + \frac 1{100} \| \Theta_N^\alpha \|_{L^2}^2, \end{align} $$
$$ \begin{align} \bigg| \int_{{\mathbb{T}}^d} ( Y_N^\alpha)^3 \Theta_N^\alpha dx \bigg| &\le c \| Y_N^\alpha \|_{L^\infty}^6 + \frac 1{100} \| \Theta_N^\alpha \|_{L^2}^2, \end{align} $$
 $$ \begin{align} \bigg| \int_{{\mathbb{T}}^d} (Y_N^\alpha)^2 (\Theta_N^\alpha)^2 dx \bigg| &\le c \| Y_N^\alpha \|_{L^\infty}^{4} + \frac 1{100} \| \Theta_N^\alpha \|_{L^2}^4, \end{align} $$
$$ \begin{align} \bigg| \int_{{\mathbb{T}}^d} (Y_N^\alpha)^2 (\Theta_N^\alpha)^2 dx \bigg| &\le c \| Y_N^\alpha \|_{L^\infty}^{4} + \frac 1{100} \| \Theta_N^\alpha \|_{L^2}^4, \end{align} $$
 $$ \begin{align} \bigg| \int_{{\mathbb{T}}^d} Y_N^\alpha (\Theta_N^\alpha)^3 dx \bigg| &\le c \| Y_N^\alpha \|_{L^\infty}^{4} + \frac 1{100} \| \Theta_N^\alpha \|_{L^4}^4, \end{align} $$
$$ \begin{align} \bigg| \int_{{\mathbb{T}}^d} Y_N^\alpha (\Theta_N^\alpha)^3 dx \bigg| &\le c \| Y_N^\alpha \|_{L^\infty}^{4} + \frac 1{100} \| \Theta_N^\alpha \|_{L^4}^4, \end{align} $$
 $$ \begin{align} \bigg| \int_{{\mathbb{T}}^d} (\Theta_N^\alpha)^4 dx \bigg| &\le \frac 1{100} \| \Theta_N^\alpha \|_{H^\alpha}^2 + \frac{A}{100} \| \Theta_N^\alpha \|_{L^2}^{\frac{8\alpha - 2d}{2\alpha - d}} \end{align} $$
$$ \begin{align} \bigg| \int_{{\mathbb{T}}^d} (\Theta_N^\alpha)^4 dx \bigg| &\le \frac 1{100} \| \Theta_N^\alpha \|_{H^\alpha}^2 + \frac{A}{100} \| \Theta_N^\alpha \|_{L^2}^{\frac{8\alpha - 2d}{2\alpha - d}} \end{align} $$
for any sufficiently large
![]() $A>0$
, uniformly in
$A>0$
, uniformly in
![]() $N \in \mathbb {N}$
.
$N \in \mathbb {N}$
.
(ii) Let
![]() $A, \gamma> 0$
. Then, there exists
$A, \gamma> 0$
. Then, there exists
![]() $c = c(A, \gamma )>0$
such that
$c = c(A, \gamma )>0$
such that
 $$ \begin{align} A\bigg\{ \int_{{\mathbb{T}}^d}& \big (Y_N^\alpha + \Theta_N^\alpha\big)^2 dx \bigg\}^\gamma \ge \frac A4 \| \Theta_N^\alpha \|_{L^2}^{2\gamma} - c \| Y_N^\alpha \|_{L^\infty}^{2\gamma}, \end{align} $$
$$ \begin{align} A\bigg\{ \int_{{\mathbb{T}}^d}& \big (Y_N^\alpha + \Theta_N^\alpha\big)^2 dx \bigg\}^\gamma \ge \frac A4 \| \Theta_N^\alpha \|_{L^2}^{2\gamma} - c \| Y_N^\alpha \|_{L^\infty}^{2\gamma}, \end{align} $$
uniformly in
![]() $N \in \mathbb {N}$
.
$N \in \mathbb {N}$
.
Set
Then, by arguing as in Section 4 with Lemma B.1,Footnote
25
the almost sure
![]() $L^\infty $
-regularity of
$L^\infty $
-regularity of
![]() $Y^\alpha $
and a variant of (3.6) for
$Y^\alpha $
and a variant of (3.6) for
![]() $ \Theta ^\alpha = I^\alpha (\theta )(1)$
:
$ \Theta ^\alpha = I^\alpha (\theta )(1)$
:
 $$ \begin{align*} \| \Theta^\alpha \|_{H^{\alpha}}^2 \leq \int_0^1 \| \theta(t) \|_{L^2}^2dt, \end{align*} $$
$$ \begin{align*} \| \Theta^\alpha \|_{H^{\alpha}}^2 \leq \int_0^1 \| \theta(t) \|_{L^2}^2dt, \end{align*} $$
we obtain the following uniform lower bound:
Then, the uniform exponential integrability (1.35) follows from (B.9) and Lemma 3.1.
We now present the proof of Lemma B.1.
Proof of Lemma B.1.
(i) The estimates (B.3), (B.4) and (B.5) follow from Hölder’s and Young’s inequalities. As for the fourth estimate (B.6), it follows from Sobolev’s inequality, Lemma 2.1 (i) and Young’s inequality that
 $$ \begin{align*} \bigg| \int_{{\mathbb{T}}^d} (\Theta_N^\alpha)^4 dx \bigg| &\le C \| \Theta_N^\alpha \|_{H^{\frac{d}{4}}}^4 \le C \| \Theta_N^\alpha \|_{H^\alpha}^{\frac{d}{\alpha}} \| \Theta_N^\alpha \|_{L^2}^{4 - \frac{d}{\alpha}} \\ &\le \frac{1}{100}\| \Theta_N^\alpha \|_{H^\alpha}^2+ \frac{A}{100} \| \Theta_N^\alpha \|_{L^2}^{\frac{8\alpha - 2d}{2\alpha - d}} \end{align*} $$
$$ \begin{align*} \bigg| \int_{{\mathbb{T}}^d} (\Theta_N^\alpha)^4 dx \bigg| &\le C \| \Theta_N^\alpha \|_{H^{\frac{d}{4}}}^4 \le C \| \Theta_N^\alpha \|_{H^\alpha}^{\frac{d}{\alpha}} \| \Theta_N^\alpha \|_{L^2}^{4 - \frac{d}{\alpha}} \\ &\le \frac{1}{100}\| \Theta_N^\alpha \|_{H^\alpha}^2+ \frac{A}{100} \| \Theta_N^\alpha \|_{L^2}^{\frac{8\alpha - 2d}{2\alpha - d}} \end{align*} $$
for sufficiently large
![]() $A> 0$
.
$A> 0$
.
(ii) Note that
for any
![]() $a,b,c \in {\mathbb {R}}$
. Then, the bound (B.7) follows from (B.10) and
$a,b,c \in {\mathbb {R}}$
. Then, the bound (B.7) follows from (B.10) and
 $$ \begin{align*} \bigg| \int_{{\mathbb{T}}^d} Y_N^\alpha \Theta_N^\alpha dx \bigg|^\gamma &\le c \| Y_N^\alpha \|_{L^\infty}^{2\gamma} + \frac{1}{100C_\gamma} \| \Theta_N^\alpha \|_{L^2}^{2\gamma}.\\[-42pt] \end{align*} $$
$$ \begin{align*} \bigg| \int_{{\mathbb{T}}^d} Y_N^\alpha \Theta_N^\alpha dx \bigg|^\gamma &\le c \| Y_N^\alpha \|_{L^\infty}^{2\gamma} + \frac{1}{100C_\gamma} \| \Theta_N^\alpha \|_{L^2}^{2\gamma}.\\[-42pt] \end{align*} $$
Remark B.2. Let
![]() $\gamma $
be as in (B.8). Then, we have
$\gamma $
be as in (B.8). Then, we have
![]() $\gamma> 2$
. Moreover, we have
$\gamma> 2$
. Moreover, we have
![]() $\gamma \to \infty $
as
$\gamma \to \infty $
as
![]() $\alpha \to {\frac {d}{2}}+$
, indicating an issue at
$\alpha \to {\frac {d}{2}}+$
, indicating an issue at
![]() $\alpha = {\frac {d}{2}}$
even if we disregard a renormalization required for
$\alpha = {\frac {d}{2}}$
even if we disregard a renormalization required for
![]() $\alpha = {\frac {d}{2}}$
.
$\alpha = {\frac {d}{2}}$
.
Acknowledgments
K.S. would like to express his gratitude to the School of Mathematics at the University of Edinburgh for its hospitality during his visit, where this manuscript was prepared. The authors would like to thank the anonymous referees for the helpful comments which improved the quality of the paper.
Competing interest
The authors have no competing interest to declare.
Financial support
T.O. was supported by the European Research Council (grant no. 864138 ‘SingStochDispDyn’). K.S. was partially supported by National Research Foundation of Korea (grant NRF-2019R1A5A1028324). L.T. was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy-EXC-2047/1-390685813 through the Collaborative Research Centre (CRC) 1060.