Introduction: conceptual origin in living systems
Programmable active matter (PAM) is the synthesis of programmable materials (Florijn et al., Reference Florijn, Coulais and van Hecke2014; Rubenstein et al., Reference Rubenstein, Cornejo and Nagpal2014; Cademartiri and Bishop, Reference Cademartiri and Bishop2015; Jones et al., Reference Jones, Seeman and Mirkin2015) and active matter (Marchetti et al., Reference Marchetti, Joanny, Ramaswamy, Liverpool, Prost, Rao and Simha2013; Needleman and Dogic, Reference Needleman and Dogic2017; Bowick et al., Reference Bowick, Fakhri, Marchetti and Ramaswamy2022). Being programmable means being able to modify material characteristics such as compositions, structures, properties, or functions based on external input. Being active means consuming free energy to maintain an out-of-equilibrium state. The synergy of being programmable and being active endows PAM with the ability to process information from external inputs to produce corresponding outputs. The term ‘active’ has different meanings in different fields. For example, in mechanics, soft materials endowed with active characters undergo deformation in response to external stimuli (Suo, Reference Suo2012). In biomaterials, active materials elicit physiological responses in animal or human bodies, such as forming chemical bonds between tissues and the materials (Hench and Polak, Reference Hench and Polak2002). Here, we follow the usage in soft matter and use it to denote specifically the out-of-equilibrium character of a system.
The concept of PAM overlaps with the idea of intelligent materials and can trace its root to biology (X. Zhang et al., Reference Zhang, Chen, Lim, Gonuguntla, Lim, Pranantyo, Yong, Yam, Low, Teo, Nien, Loh and Soh2019; Kaspar et al., Reference Kaspar, Ravoo, van der Wiel, Wegner and Pernice2021). Biological cells are PAM: they are active because they metabolise nutrients to stay alive; they are programmable because they adapt to their environments either via stimulus-responsive behaviours at the individual level or via evolution over generations at the population level. Environmental stimuli can be considered as the inputs of cells’ information processing, and the outputs are their behaviour changes or the adaptations in their genetic codes.
That a PAM can receive inputs, process information, and produce outputs necessitates a certain internal structure or organisation of components in a PAM. These components are often independent units that interact with each other, and their interactions obey physical and chemical laws. Many of the behaviours, properties, and functions of these systems emerge as a result of the self-organisation of these interacting units. Although the programmability and hence the capability to process information are rudimentary in many of the current systems, engineering interactions in PAMs can lead to more advanced capabilities.
Here, we review PAMs from the molecular scale to the centimetre scale from the perspective of interactions that enable the programmability. They include supramolecular systems, DNA assemblies, colloidal systems, bacteria swarms, droplet assemblies, millimetre-scale interfacial systems, and centimetre-scale robotic swarms (Figure 1). We present the scientific significance of PAMs both in the context of the long historical tradition of studying the relationship between matter and geometry and in the context of the study of complexity and emergence. Finally, we present the opportunities and challenges of using PAM to build a soft-matter brain.

Figure 1. Programmable active matter systems across scales with various degrees of complexity.
Programmable interactions across scales
Supramolecular systems
Supramolecular systems use interactions between molecules to drive equilibrium self-assembly processes (Lehn, Reference Lehn1995; Giuseppone and Walther, Reference Giuseppone and Walther2021) and non-equilibrium self-assembly processes (Mattia and Otto, Reference Mattia and Otto2015; Grzybowski and Huck, Reference Grzybowski and Huck2016; ‘Self-Assembling Life’, 2016). These interactions include noncovalent interactions such as hydrogen bonding, dipole–dipole interactions, π–π stacking, and hydrophobic effects (Eğe, Reference Eğe2004; Israelachvili, Reference Israelachvili2011a) and covalent interactions such as disulphide bonds (Table 1). The applications of supramolecular self-assembly include biomedicine (Donau et al., Reference Donau, Späth, Sosson, Kriebisch, Schnitter, Tena-Solsona, Kang, Salibi, Sattler, Mutschler and Boekhoven2020), molecule assembly (Engwerda and Fletcher, Reference Engwerda and Fletcher2020), drug delivery (H. Wang et al., Reference Wang, Wang, Shen, Liu and Lee2019; Z. Zheng et al., Reference Zheng, Geng, Xu and Guo2019), catalysis (Biagini et al., Reference Biagini, Fielden, Leigh, Schaufelberger, Di Stefano and Thomas2019; Grzelczak et al., Reference Grzelczak, Liz-Marzán and Klajn2019), sensing (Leira-Iglesias et al., Reference Leira-Iglesias, Tassoni, Adachi, Stich and Hermans2018; Morrow et al., Reference Morrow, Colomer and Fletcher2019), and molecular imaging (Qi et al., Reference Qi, Gao, Wang and Wang2018; Q. Zhang et al., Reference Zhang, Catti and Tiefenbacher2018).
Table 1. Common interactions in supramolecular self-assembly

The programmability of supramolecules is mostly due to the variety of molecular building blocks and the versatility of combinations of basic intermolecular interactions. In equilibrium self-assembly, different molecular building blocks can be considered as the input and the self-assembled structure as the output. In non-equilibrium self-assembly, the exchange of both matter and energy between the self-assembling structure and the environment provides more design space in constructing programmable supramolecular systems, such as energy-driven molecular machines (Kudernac et al., Reference Kudernac, Ruangsupapichat, Parschau, Maciá, Katsonis, Harutyunyan, Ernst and Feringa2011; Jalani et al., Reference Jalani, Dhiman, Jain and George2017), transient supramolecular materials driven by chemical fuels (Boekhoven et al., Reference Boekhoven, Brizard, Kowlgi, Koper, Eelkema and van Esch2010, Reference Boekhoven, Hendriksen, Koper, Eelkema and van Esch2015), and self-replicating processes driven by mechanical energy (Carnall et al., Reference Carnall, Waudby, Belenguer, Stuart, Peyralans and Otto2010; Colomb-Delsuc et al., Reference Colomb-Delsuc, Mattia, Sadownik and Otto2015; Sadownik et al., Reference Sadownik, Mattia, Nowak and Otto2016; Schwille et al., Reference Schwille, Spatz, Landfester, Bodenschatz, Herminghaus, Sourjik, Erb, Bastiaens, Lipowsky, Hyman, Dabrock, Baret, Vidakovic-Koch, Bieling, Dimova, Mutschler, Robinson, Tang, Wegner and Sundmacher2018; Liu et al., Reference Liu, Wu, Geerts, Markovitch, Pappas, Liu and Otto2022). We refer interested readers to comprehensive reviews in this area for detailed analyses (England, Reference England2015; Amabilino et al., Reference Amabilino, Smith and Steed2017; van Rossum et al., Reference van Rossum, Tena-Solsona, van Esch, Eelkema and Boekhoven2017; Weißenfels et al., Reference Weißenfels, Gemen and Klajn2021). In this section, we select three examples to illustrate how non-equilibrium supramolecular systems can be programmed using means other than molecular building blocks.
A pioneering example of nonequilibrium supramolecular system is the chemically fuelled dissipative self-assembly (DSA) developed by van Esch group (Figure 2a) (Boekhoven et al., Reference Boekhoven, Brizard, Kowlgi, Koper, Eelkema and van Esch2010, Reference Boekhoven, Hendriksen, Koper, Eelkema and van Esch2015). The building blocks of the DSA system are molecular gelators with two carboxylate groups (blue blocks). Alkylation of the carboxylate groups into esters activates the gelators (red blocks). Different fuel molecules, methyl iodine and dimethyl sulphate ((CH3)2SO4), produce different degrees of alkylation and different fibre structures. Spontaneous hydrolysis of esters in aqueous environments reverts the alkylation reaction, produces alcohol wastes, and disassembles the fibre structures. The fuel molecules – rather than the molecular building blocks – serve as the molecular input, and they program the intermolecular interactions to produce different fibre structures as output.

Figure 2. Dissipative supramolecular systems as programmable active matter. (a) The same building blocks produce different fibres depending on different input fuels (Boekhoven et al., Reference Boekhoven, Brizard, Kowlgi, Koper, Eelkema and van Esch2010, Reference Boekhoven, Hendriksen, Koper, Eelkema and van Esch2015). (b) Mixture of different building blocks gives rise to species. One species could serve as a template, or ancestor, for another species (Sadownik et al., Reference Sadownik, Mattia, Nowak and Otto2016). (c) The outcome of a self-replication process could depend on the type of mechanical agitation (Carnall et al., Reference Carnall, Waudby, Belenguer, Stuart, Peyralans and Otto2010).
Otto group first investigated self-replicating peptide-derived molecules that emerge from a dynamic combinatorial library (DCL). The building blocks of the DCL system are peptides with alternating hydrophobic and hydrophilic amino acid sequences. Peptide-functionalised self-replicators exhibit exponential growth when subjected to agitation (Carnall et al., Reference Carnall, Waudby, Belenguer, Stuart, Peyralans and Otto2010; Colomb-Delsuc et al., Reference Colomb-Delsuc, Mattia, Sadownik and Otto2015). Mechanical agitation breaks existing fibres, producing more fibre ends that serve as seeds for the exponential growth. Different information inputs such as the concentration of building blocks, the presence or absence of seeds (Figure 2b), and agitation conditions (stirring or shaking) (Figure 2c) produce different peptide-functionalised macrocyclic self-replicators and elongated fibres.
Moreover, self-replicating systems based on two building blocks exhibit information transfer analogous to biological inheritance (second row in Figure 2b) (Sadownik et al., Reference Sadownik, Mattia, Nowak and Otto2016). The formation of hexamers dominated by Building Block 1 templates the formation of hexamers dominated by Building Block 2. The transfer of information on the size of macrocycles is analogous to the transfer of genetic information from ancestors to descendants. These examples show the promise of using kinetic-controlled dissipative supramolecular self-assembly to discover self-replicating materials with programmability and information processing capability.
DNA-based systems
DNA, as a biological macromolecule, carries the genetic information encoded in the sequence of nucleotide bases under the principle of complementary Watson–Crick base pairing (Watson and Crick, Reference Watson and Crick1953). This information is transcribed to the RNA sequence and further translated to the structure of proteins. In addition to encoding the genetic information, the complementarity of the two single strands of DNA provides a means to achieve spatial and temporal distribution of matter at the nanometre scale (Seeman, Reference Seeman2010; Seeman and Sleiman, Reference Seeman and Sleiman2018). This DNA-based nanotechnology can be further divided into structural DNA nanotechnology (Seeman, Reference Seeman2007) and dynamic DNA nanotechnology (D. Y. Zhang and Seelig, Reference Zhang and Seelig2011), each with different functions and applications (Seeman, Reference Seeman2007, Reference Seeman2010; D. Y. Zhang and Seelig, Reference Zhang and Seelig2011; Seeman and Sleiman, Reference Seeman and Sleiman2018; DeLuca et al., Reference DeLuca, Shi, Castro and Arya2020). We select a few examples to illustrate the potential of DNA-based systems as PAM for information processing.
Structural DNA nanotechnology prepares complex structures from specific DNA motifs pioneered by Seeman (Seeman, Reference Seeman1982, Reference Seeman2010; Ma et al., Reference Ma, Kallenbach, Sheardy, Petrillo and Seeman1986; T. J. Fu and Seeman, Reference Fu and Seeman1993; X. Wang and Seeman, Reference Wang and Seeman2007). It enables the construction of two- or three-dimensional lattices (H. Yan et al., Reference Yan, Park, Finkelstein, Reif and LaBean2003; He et al., Reference He, Chen, Liu, Ribbe and Mao2005; J. Zheng et al., Reference Zheng, Birktoft, Chen, Wang, Sha, Constantinou, Ginell, Mao and Seeman2009), three-dimensional polyhedrons (J. Chen and Seeman, Reference Chen and Seeman1991; Y. Zhang and Seeman, Reference Zhang and Seeman1994; Goodman et al., Reference Goodman, Berry and Turberfield2004), and other complex objects (Mitchell et al., Reference Mitchell, Harris, Malo, Bath and Turberfield2004; Mathieu et al., Reference Mathieu, Liao, Kopatsch, Wang, Mao and Seeman2005; Lin et al., Reference Lin, Liu, Rinker and Yan2006), with applications in intelligent materials, DNA-based multi-functional devices, and DNA-based computation.
While structural DNA nanotechnology builds static structures, dynamic DNA nanotechnology constructs dynamic processes to respond to input signals, such as specific DNA strands, and generate corresponding output. It provides a method to process information, and its dynamic characteristic broadens the range of applications and permits the development of DNA-based nanoscale devices for sensing, drug delivery, molecular diagnostics, logic gate, and nanorobotics (Seeman and Sleiman, Reference Seeman and Sleiman2018; DeLuca et al., Reference DeLuca, Shi, Castro and Arya2020). One essential tool to implement the dynamic process is the toehold-mediated DNA strand displacement (TMSD) (D. Y. Zhang and Seelig, Reference Zhang and Seelig2011): a single input strand first hybridises with a short exposed segment (toehold) of a second single strand that is part of a double helix and eventually replaces the previous paired single strand to form a new double helix. TMSD was first introduced to create a DNA tweezer, a dynamic DNA structure that opens and closes via the control of a single input strand (Figure 3a) (Yurke et al., Reference Yurke, Turberfield, Mills, Simmel and Neumann2000). TMSD enables programmable and precise control of dynamic processes, which can lead to reconfigurable and autonomous devices.

Figure 3. Dynamic and dissipative DNA-based systems as programmable active matter. (a) Reversible DNA tweezers by toehold-mediated DNA strand displacement (Yurke et al., Reference Yurke, Turberfield, Mills, Simmel and Neumann2000). (b) A DNA-based computer with various DNA logic gates (Fan et al., Reference Fan, Wang, Wang and Dong2020). (c) DNA-based convolutional neural networks that classify the language and meaning of symbols (Xiong et al., Reference Xiong, Zhu, Zhu, Cao, Xiao, Li, Wang, Fan and Pei2022). (d) Autonomous dynamic control of the assembly of a DNA nanotube using a transcriptional molecular oscillator (Del Grosso et al., Reference Del Grosso, Prins and Ricci2020). (e) Programmable dynamic steady states of DNA chains via the control of reversible covalent bonds (Heinen and Walther, Reference Heinen and Walther2019). (f) Using redox reactions of disulphide invaders to control the assembly and disassembly of DNA nanotube (Green et al., Reference Green, Subramanian, Mardanlou, Kim, Hariadi and Franco2019).
When the output of a previous DNA strand displacement is used as the input of a downstream displacement, a strand-displacement cascade is formed, and these cascades can serve as the building blocks of a DNA circuit (Figure 3b). Such circuits can perform biological or computational tasks, and their advantages include low energy consumption, excellent biocompatibility, and high programmability (Fan et al., Reference Fan, Wang, Wang and Dong2020). Adleman (Reference Adleman1994) pioneered the use of DNA to solve a Hamiltonian path problem, thereby opening the door to DNA computation. Seelig et al. (Reference Seelig, Soloveichik, Zhang and Winfree2006) designed DNA-based logic gates (AND, OR, and NOT gates) and constructed larger circuits to demonstrate signal restoration, amplification, feedback, and cascading (Seelig et al., Reference Seelig, Soloveichik, Zhang and Winfree2006). Qian et al. (Reference Qian, Winfree and Bruck2011) have made significant progress on the strand displacement circuitry over the past decade (Qian and Winfree, Reference Qian and Winfree2011a, Reference Qian and Winfree2011b; Cherry and Qian, Reference Cherry and Qian2018). They use simple DNA gates to construct multilayer circuits that act like small neural networks to perform complex computations (Qian et al., Reference Qian, Winfree and Bruck2011). This system used DNA strand displacement cascades to play the role of linear threshold gate and can recognise four DNA patterns after training. They then improved the neural network using the winner-takes-all model and increased the number of classifications to nine (Cherry and Qian, Reference Cherry and Qian2018). The improved neural network shows excellent potential for DNA-based molecular machines responsive to environmental signals, such as complex disease profiles containing mRNA. Recently, Xiong et al. (Reference Xiong, Zhu, Zhu, Cao, Xiao, Li, Wang, Fan and Pei2022) produced even larger DNA circuits based on 512 DNA strands using convolutional neural networks. The circuits can be scaled up to classify patterns into 32 categories, with a sequential classification scheme to detect languages and then the symbols (Figure 3c). Taken together, these works show the evolution of DNA computation from simple to complex and its great potential for next-generation molecular computers to surpass the limit of traditional silicon-based computers.
Building on dynamic DNA nanotechnology, dissipative DNA nanotechnology introduces energy dissipation in dynamic processes (Del Grosso et al., Reference Del Grosso, Franco, Prins and Ricci2022). In dissipative DNA nanotechnology, the input fuel strands are degraded by some fuel-consuming components, like nuclease, which manifests explicitly as a reduction in the chemical potential energy. Like dynamic DNA nanotechnology, dissipative DNA systems can act as a dynamic network to form circuits to perform computation or to form reconfigurable structures. To mimic the function of the cytoskeleton, Zhan et al. (Reference Zhan, Jahnke, Liu and Göpfrich2022) synthesised DNA-based cytoskeletons by self-assembling DNA tiles into filament networks; these filament networks display the characteristics of biological cytoskeletons, such as reversible assembly, compartmentalisation, and cargo-transport. Green et al. (Reference Green, Subramanian, Mardanlou, Kim, Hariadi and Franco2019) achieved autonomous dynamic control of DNA nanotube self-assembly (Figure 3d). The nanotubes disassemble upon the addition of RNA invaders; the gradual digestion of RNA invaders by RNase reassembles the nanotubes. A molecular transcriptional oscillator is introduced to control the assembly–disassembly cycle autonomously. Heinen and Walther (Reference Heinen and Walther2019) demonstrated programmable dynamic steady states of covalently bonded DNA chains (Figure 3e). The dynamic steady states continuously consume chemical energy through the conversion of ATP. The DNA ligase is responsible for the ligation, and the endonuclease for the cleavage. Together, they regulate the dynamic cycle’s transformation rate and determine the dynamic steady state’s chain length and lifetime. Del Grosso et al. (Reference Del Grosso, Prins and Ricci2020) used redox fuels as a new control mechanism in the reversible assembly of tubular DNA structures (Figure 3f). The addition of disulphide invaders inactivates the tiles and drives the disassembly, whereas the addition of a reducing agent breaks the disulphide bond, reactivates the tiles, and reassembles the nanotubes. The length of the disulphide invaders and the concentration of the reducing agent determine the lifetime of the assembly–disassembly cycle.
These dissipative systems with a single function can be integrated to form a larger system with complex functions, just as various tissues in an organism form an organ; they operate under dissipative conditions that have biological relevance. They show the potential to develop complex life-like PAMs that integrate multiple subsystems, respond to different signal inputs, and possess information processing capabilities for applications in biomedicine, drug delivery, molecular computers, and beyond.
Colloidal systems
Active colloidal systems include self-propelled microparticles (W. Wang et al., Reference Wang, Duan, Ahmed, Sen and Mallouk2015; Pan and He, Reference Pan and He2017; Bär et al., Reference Bär, Großmann, Heidenreich and Peruani2020) and external field-driven microparticles (Shields and Velev, Reference Shields and Velev2017; Y. Chen et al., Reference Chen, Chen, Liang, Dai, Bai, Song, Zhang, Chen and Feng2021; Q. Wang and Zhang, Reference Wang and Zhang2021). They not only serve as model systems for the research on non-equilibrium physics (Theurkauff et al., Reference Theurkauff, Cottin-Bizonne, Palacci, Ybert and Bocquet2012; Cates and Tailleur, Reference Cates and Tailleur2015; Y. Fu et al., Reference Fu, Yu, Zhang, Malgaretti, Kishore and Wang2022), but also are used as microrobots for biomedical and environmental applications (Nelson et al., Reference Nelson, Kaliakatsos and Abbott2010; Aziz et al., Reference Aziz, Pane, Iacovacci, Koukourakis, Czarske, Menciassi, Medina-Sánchez and Schmidt2020; H. Chen et al., Reference Chen, Zhang, Xu and Yu2021). As active microparticles form colloidal swarms, collective properties and functions emerge as a result of the interactions among individual particles. These interactions include magnetic and electric dipole–dipole, hydrodynamic, phoretic, capillary, and van der Waals interactions (Table 2 and Supplementary Table 1). We show below how tuning these interactions endows programmability to active colloidal systems.
Table 2. Main interactions in active colloidal systems

Abbreviations: C-L, Casimir–Lifshitz interactions; D-L, electric double-layer interactions; DLVO, Derjaguin–Landau–Verwey–Overbeek.
1 The hydrodynamic force is proportional to velocity in low Reynolds number environment.
The programmability of active magnetic microparticles is due to the tunable magnetic dipole–dipole interactions under alternating magnetic fields. This programmability and the easy penetration of magnetic fields in most biological tissues make the magnetic manipulation of colloidal particles widely used in biomedical applications (Z. Yang and Zhang, Reference Yang and Zhang2020; Nelson et al., Reference Nelson, Gervasoni, PWY, Zhang and Zemmar2022). Swarms of magnetic colloidal particles could be steered and reconfigured into several typical patterns: dispersed state, aggregated state, chain state, and ribbon state (Figure 4a). Yu et al. (Reference Yu, Wang, Du, Wang and Zhang2018) used a horizontal oscillating field and a perpendicular uniform field to generate ribbon-like swarms. The swarms display reversible elongation, merging, and splitting via the change in the amplitude and the frequency of the horizontal field. They could be navigated to pass narrow channels and deliver cargo. Xie et al. (Reference Xie, Sun, Fan, Lin, Chen, Wang, Dong and He2019) used a rotating field to realise fast and reversible transformation among all four states and demonstrated collective locomotion, navigation, and manipulation. Yigit et al. (Reference Yigit, Alapan and Sitti2019) used a precessing magnetic field to assemble microparticles into chains and demonstrated the locomotion of the chains. Moreover, Law et al. (Reference Law, Chen, Wang, Yu and Sun2022) use dual-axis oscillating magnetic field-induced interaction to realise dynamic self-assembly in 3D. The colloidal particles display tunable configurations and collective locomotion, such as climbing slopes or stairs and crossing gaps or obstacles.

Figure 4. Active colloidal systems as programmable active matter. (a) Dynamic patterns of colloidal particles manipulated by the alternating magnetic field. (b) Active states of Janus colloidal spheres controlled by AC electric field of different frequencies (J. Yan et al., Reference Yan, Han, Zhang, Xu, Luijten and Granick2016). (c) The transition between dispersed and aggregated states of colloidal particles by light or NH3. (d) Collective behaviours of active particles mimicking quorum-sensing behaviours (left) and visual perceptions (right) (Bäuerle et al., Reference Bäuerle, Fischer, Speck and Bechinger2018; Lavergne et al., Reference Lavergne, Wendehenne, Bäuerle and Bechinger2019).
The electric dipole–dipole interactions between polarised dielectric particles could be similarly programmed via the configuration of electric fields. Because of the nonuniform dielectric properties of Janus particles, the patterns of the swarms could be tuned by the change in the frequencies of the oscillating electric field (J. Yan et al., Reference Yan, Han, Zhang, Xu, Luijten and Granick2016). These patterns (Figure 4b) bear resemblances to the ones generated in the magnetic colloid systems. Moreover, Z. Wang et al. (Reference Wang, Wang, Li, Tian and Wang2020) achieved the selective, directional, and strength-adjustable bonds between particles by adjusting particle shape, size, and AC electric field parameters. The precise programmability of dynamic colloidal bonds significantly improves the control over steering, reconfiguration, and other collective behaviours. The combination of activity and shape anisotropy provides even more parameters to orchestrate the structures and behaviours of colloidal systems. B. Zhang et al. (Reference Zhang, Sokolov and Snezhko2020) used pear-shaped dielectric particles to generate various chiral patterns, including gas-like phases, aster-like vortices, and rotating flocks, under different DC electric fields. Similarly, Alapan et al. (Reference Alapan, Yigit, Beker, Demirörs and Sitti2019) used the shape-encoded dielectrophoretic interaction to build micromachines consisting of active magnetic colloidal particles and a non-magnetic body. The shape of the non-magnetic body encodes a local electric field gradient and controls the dielectrophoretic force for the dynamic assembly. Even though some of the above strategies were used to build individual micromachines, they could inspire the dynamic assembly of swarms using electric fields.
Aside from the magnetic and electric dipole–dipole interaction, programmability could also come from diffusiophoresis interaction. The primary type of diffusiophoresis interaction is electrolyte diffusiophoresis (EDP). EDP is due to the different diffusive coefficients of cations and anions produced by hydrolysis or chemical reaction near particles and consists of parallel processes of electrophoresis and chemophoresis (Velegol et al., Reference Velegol, Garg, Guha, Kar and Kumar2016). For Janus particles with catalysts on one side, the stimuli could be the chemicals that trigger the reaction and produce a local chemical gradient. For photoactivated colloids, UV light is a common stimulus that endows motility. Duan et al. (Reference Duan, Liu and Sen2013)] used NH3 and UV light as stimuli to achieve the reversible transformation between clustering and dispersion of Ag3PO4 microparticles (Figure 4c). Palacci et al. (Reference Palacci, Sacanna, Steinberg, Pine and Chaikin2013) demonstrated that photoactivated colloidal particles could self-organise into ‘living crystals’. Singh et al. (Reference Singh, Choudhury, Fischer and Mark AG2017) used a small amount of active TiO2–SiO2 Janus particles propelled by UV light illumination to trigger the crystallisation of passive silica colloids. The cluster size and pattern could be tuned by light intensity and active–passive particle size ratio. Although the patterns of particles driven by diffusiophoresis often only transform between clustered and dispersed states and are not as versatile as magnetic/electric systems, light as a stimulus is comparatively simple and may be used to drive swarms on a large scale.
The hydrodynamic interactions are solvent-mediated long-range interactions and play an important role in both self-propelled and external field-driven microswimmers. The previous cases of magnetic, electric, and diffusiophoretic driving mechanisms all contain hydrodynamic interactions. The hydrodynamic laws are time-invariant at the micrometre scale, and the flow becomes laminar in a low Reynolds number (Re) environment, which permits controllable manipulation and tunable interactions. Boundaries strongly affect the dynamics of motile particles in a low Re environment. For example, gas/liquid and solid/liquid interfaces could induce opposite propelling directions because a liquid–air interface is a slip boundary, whereas a solid/liquid interface is a no-slip boundary. Stokes equations describe the fluid behaviours in a low Re environment, and the solution produces the Stokeslet singularity (scales with
![]() $1/r$
). Moreover, the derivatives of Stokeslet singularity give higher-order solutions, including force–dipole (scales with
$1/r$
). Moreover, the derivatives of Stokeslet singularity give higher-order solutions, including force–dipole (scales with
![]() $1/{r}^2$
), force–quadrupole (scales with
$1/{r}^2$
), force–quadrupole (scales with
![]() $1/{r}^3$
), and source–quadrupole (scales with
$1/{r}^3$
), and source–quadrupole (scales with
![]() $1/{r}^3$
) (Spagnolie and Lauga, Reference Spagnolie and Lauga2012; Lauga, Reference Lauga2020; T. H. Tan et al., Reference Tan, Tian, Zhang, Zhu, Liu, Cheng and Shi2022). Interactions between real microswimmers are complex and are often the superpositions of many singularities. As a result, many phenomenological laws have been proposed to guide our intuition in the design of microswimmers and their interactions. For example, the fluidic vortex forces caused by microswimmers’ rotation could impose long-range attraction and short-range repulsion (L. Yang and Zhang, Reference Yang and Zhang2021; Jin and Zhang, Reference Jin and Zhang2022). Nevertheless, how to program purely hydrodynamic interactions without coupling with magnetic, electric, or other interactions remains challenging. Microorganisms such as bacteria and algae could serve as an inspiration. For example, designing microswimmers that could change their swimming modes between pusher (bacteria) and puller (algae) could lead to programmable anisotropic hydrodynamic interactions and possible new collective properties and functions (Martínez-Pedrero and Tierno, Reference Martínez-Pedrero and Tierno2018).
$1/{r}^3$
) (Spagnolie and Lauga, Reference Spagnolie and Lauga2012; Lauga, Reference Lauga2020; T. H. Tan et al., Reference Tan, Tian, Zhang, Zhu, Liu, Cheng and Shi2022). Interactions between real microswimmers are complex and are often the superpositions of many singularities. As a result, many phenomenological laws have been proposed to guide our intuition in the design of microswimmers and their interactions. For example, the fluidic vortex forces caused by microswimmers’ rotation could impose long-range attraction and short-range repulsion (L. Yang and Zhang, Reference Yang and Zhang2021; Jin and Zhang, Reference Jin and Zhang2022). Nevertheless, how to program purely hydrodynamic interactions without coupling with magnetic, electric, or other interactions remains challenging. Microorganisms such as bacteria and algae could serve as an inspiration. For example, designing microswimmers that could change their swimming modes between pusher (bacteria) and puller (algae) could lead to programmable anisotropic hydrodynamic interactions and possible new collective properties and functions (Martínez-Pedrero and Tierno, Reference Martínez-Pedrero and Tierno2018).
The Casimir–Lifshitz force extends the Van der Waals force between molecules to macroscopic bodies (Parsegian, Reference Parsegian2006). The Derjaguin–Landau–Verwey–Overbeek theory combines the Casimir–Lifshitz force and electric double-layers force to describe the interaction between charged colloidal particles in solutions (Israelachvili, Reference Israelachvili2011b). Both forces can be tuned by changing the composition and the geometry of the particles. Even the sign of the Casimir–Lifshitz force could even be tuned by a suitable choice of interacting materials (Munday et al., Reference Munday, Capasso and Parsegian2009). However, existing examples of tuning both of these interactions are rare, probably because their range of interactions is relatively short.
Physical interactions among colloids can also be augmented by algorithm-based rules via external feedback loops (Figure 4d). Bechinger’s group constructed an imaging-feedback system with scanning lasers to control the motility of individual light-activated particles (Bäuerle et al., Reference Bäuerle, Fischer, Speck and Bechinger2018). Using this system, they could mimic the behaviour of quorum sensing by detecting the number of neighbours of each particle. They also found that a motility change of the individuals in response to the visual perception of their peers induces group formation and cohesion (Lavergne et al., Reference Lavergne, Wendehenne, Bäuerle and Bechinger2019). Since the interactions between particles can be programmed via algorithms, this system may not only give us insights into how communications between active colloidal particles affect their collective properties but also provide guidance in designing autonomous robotic systems.
The selected cases show that tunable interactions among active colloids could generate diverse patterns and other collective behaviours. Different stimuli produce different behaviours of colloids, which can be considered as a form of information processing: the stimuli are the inputs, and the responses are the outputs. This form of information processing could be enriched to achieve complex functions in the future.
Droplets, bacteria, and embryos
At the scale of a few hundred micrometres, PAM systems consist of droplets and biological organisms. Droplets and micro-organisms share similarities in their interactions among units. This section will present case studies in a sequence of increasing numbers of units, from small clusters to large populations.
For small clusters consisting of less than 10 units, systems are programmed via the compositions of units. Meredith et al. (Reference Meredith, Moerman, Groenewold, Chiu, Kegel, van Blaaderen and Zarzar2020) used net directional, micelle-mediated oil transport between different emulsion droplets to create an interfacial tension gradient that leads to the predator–prey type of asymmetric and non-reciprocal interactions. Significantly, the state of motions can be programmed by the different configurations of the multiple droplet clusters (Figure 5a). Z. Yang et al. (Reference Yang, Wei, Sobolev and Grzybowski2018) covered droplets with multi-responsive surfactants; these droplets show diverse assemblies and respond to different stimuli. Figure 5b shows light-triggered mechanical gears and droplet clustering behaviours.
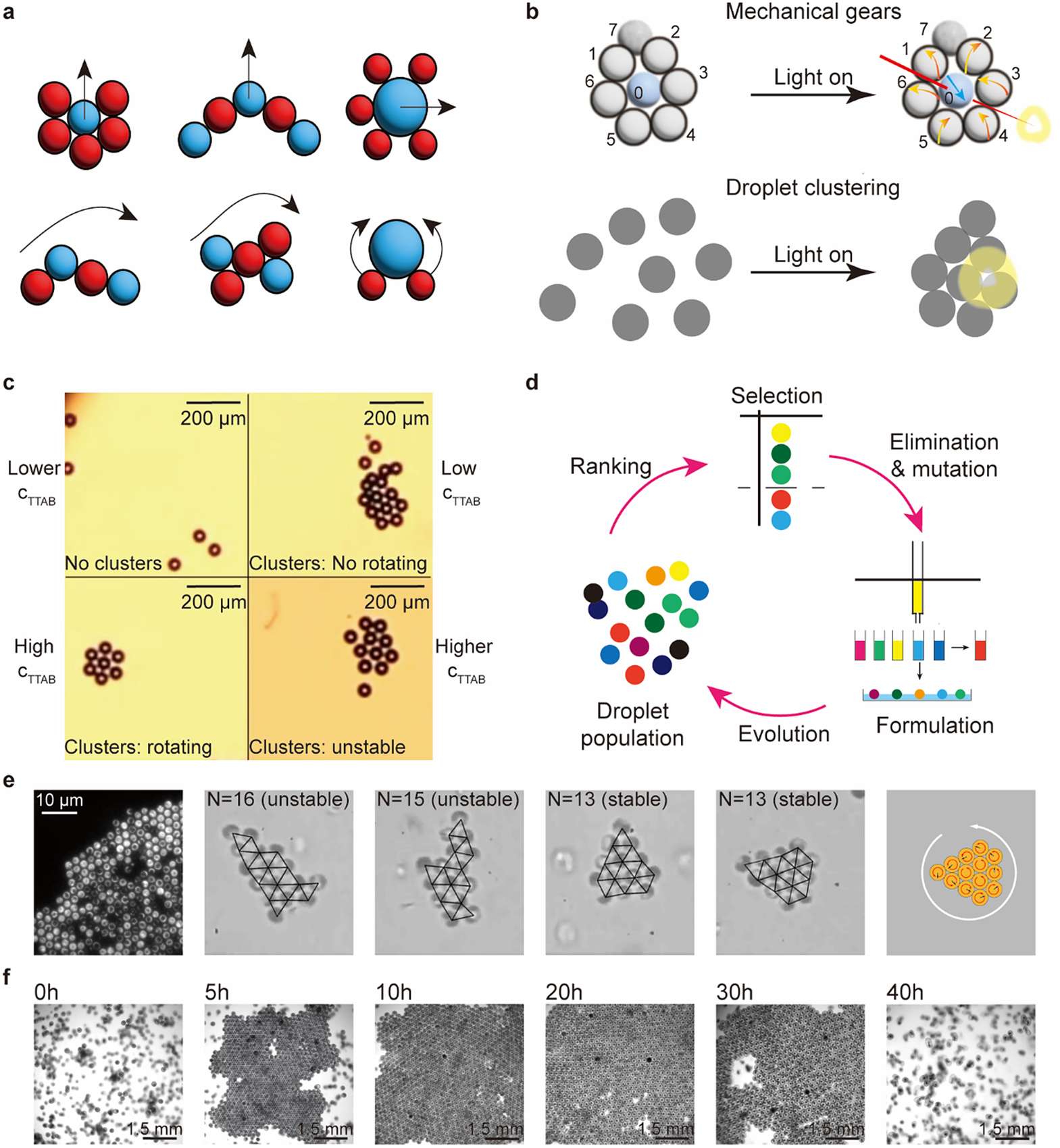
Figure 5. Programmable active matter based on droplets, bacteria, and embryos. (a) Emergent behaviours of clusters of droplets based on the mimics of the predator–prey interaction between red (predator) and blue (prey) droplets (Meredith et al., Reference Meredith, Moerman, Groenewold, Chiu, Kegel, van Blaaderen and Zarzar2020). (b) Multi-responsive droplets respond to light signals to exhibit mechanical gears-like and droplet clustering behaviours (Z. Yang et al., Reference Yang, Wei, Sobolev and Grzybowski2018). (c) Self-propelled droplets rotate to form rotating clusters. The stability of clusters and the state of rotation depend on
![]() ${c}_{TTAB}$
(the surfactant concentration) (Hokmabad et al., Reference Hokmabad, Nishide, Ramesh, Krügera and Maass2022). (d) An artificial evolution system based on droplet populations (Parrilla-Gutierrez et al., Reference Parrilla-Gutierrez, Hinkley, Taylor, Yanev and Cronin2014). Large ordered living crystals formed by (e) bacteria (Petroff et al., Reference Petroff, Wu and Libchaber2015) and (f) spinning starfish embryos (T. H. Tan et al., Reference Tan, Mietke, Li, Chen, Higinbotham, Foster, Gokhale, Dunkel and Fakhri2022). The red arrows in the last scheme in € are the rotation direction of the units, the black arrows are the force direction, and the white arrow is the rotation direction of the whole period.
${c}_{TTAB}$
(the surfactant concentration) (Hokmabad et al., Reference Hokmabad, Nishide, Ramesh, Krügera and Maass2022). (d) An artificial evolution system based on droplet populations (Parrilla-Gutierrez et al., Reference Parrilla-Gutierrez, Hinkley, Taylor, Yanev and Cronin2014). Large ordered living crystals formed by (e) bacteria (Petroff et al., Reference Petroff, Wu and Libchaber2015) and (f) spinning starfish embryos (T. H. Tan et al., Reference Tan, Mietke, Li, Chen, Higinbotham, Foster, Gokhale, Dunkel and Fakhri2022). The red arrows in the last scheme in € are the rotation direction of the units, the black arrows are the force direction, and the white arrow is the rotation direction of the whole period.
For large clusters consisting of a few dozen units, complex behaviour emerges from simple interactions among units. Hokmabad et al. (Reference Hokmabad, Nishide, Ramesh, Krügera and Maass2022) reported an active oil-in-water emulsion system; the dynamic modes of individual droplets induce cooperative behaviour, such as ascending and rotation, in active clusters (Figure 5c). The dynamics and stability of the clusters depend on the cluster size and activity. The activity of a droplet is regulated by the concentration of the surfactant: low surfactant concentration leads to low activity and results in no cluster formation or non-rotating clusters, whereas high concentration leads to high activity and results in rotating or even unstable clusters. Parrilla-Gutierrez et al. (Reference Parrilla-Gutierrez, Hinkley, Taylor, Yanev and Cronin2014, Reference Parrilla-Gutierrez, Tsuda, Grizou, Taylor, Henson and Cronin2017) reported artificial evolution in a system of interacting motile oil droplets driven by the Marangoni effect (Figure 5d). This platform creates selection pressure based on the motility of the droplets and analyses the motion of the droplets via a computer vision feedback loop. This work introduced artificial intelligence in an inanimate system to study the origin of life.
For populations of hundreds of units, we select two biological examples: bacteria and embryos. The hydrodynamic interactions between individual biological entities are similar to colloidal systems. When one single organism is swimming, it will create a flow field around it, and the field gradients influence the motion of nearby organisms (Spagnolie and Lauga, Reference Spagnolie and Lauga2012). The hydrodynamic interaction is responsible for most collective behaviours in the biological microswimmers, such as clustering. Clustering was initially observed on spherical alga Volvox, which shows flow-induced self-assembly and stable bound states in suspensions near the wall (Drescher et al., Reference Drescher, Leptos, Tuval, Ishikawa, Pedley and Goldstein2009). Petroff et al. (Reference Petroff, Wu and Libchaber2015) investigated the collective dynamics of active crystals formed by Thiovulum majus, a type of fast-swimming bacterium; they converge to a rotating hexagonal configuration, in which the period of rotation is proportional to the size of the crystal. The stability of the configurations is related to the period of rotation, which in turn depends on the number of bacteria (Figure 5e). T. H. Tan et al. (Reference Tan, Tian, Zhang, Zhu, Liu, Cheng and Shi2022) showed living chiral crystals composed of thousands of starfish embryos that exhibit collective dynamics (Figure 5f). The crystals undergo formation and dissolution at different stages of embryonic growth. The morphological changes of the embryos lead to changes in the flow field, which in turn affects the hydrodynamic interactions. They observed the odd elasticity in the chiral crystals. Topological defects can locally deform the living chiral crystals and encode information about the effective odd material properties in the deformation field. These two examples show the potential for information processing in the collectives of biological microswimmers: tunable interactions among individual units serve as inputs to produce different configurations and properties of the collectives as outputs. These tunable interactions are worth exploring and emulating in biomimetic artificial systems.
The examples in this section show that at the scale of hundreds of micrometres, PAM systems offer opportunities to study collective dynamics in nature and to address fundamental questions about the origin of life and artificial cells. They can also contribute to the construction of programmable micromachines to be deployed in clinical and industrial settings.
Millimetre-scale interfacial systems
The capillary interaction between objects floating at fluidic interfaces can be programmed via objects’ shapes and wettability. This idea dates back to pioneering works by Whitesides’s group, who demonstrated the static self-assembly of millimetre-scale objects at the perfluorodecalin–water interface using lateral capillary forces (Bowden et al., Reference Bowden, Terfort, Carbeck and Whitesides1997, Reference Bowden, Choi, Grzybowski and Whitesides1999, Reference Bowden, Oliver and Whitesides2000).
Building on their pioneering work, Whiteside’s group demonstrated dynamic self-assembly of millimetre-scale discs under a rotating magnetic field (Figure 6a) (Grzybowski et al., Reference Grzybowski, Stone and Whitesides2000). The magnetic attraction due to the overall potential of the magnetic field is balanced against the repulsion from the hydrodynamic lift force (Grzybowski et al., Reference Grzybowski, Stone and Whitesides2002). The overall patterns depend on the number of objects, spinning speeds, and the chirality of the objects (Figure 6b) (Grzybowski and Whitesides, Reference Grzybowski and Whitesides2002).
Figure 6. Millimetre-scale interfacial systems as PAM. (a) Patterns of the spinning discs under bar magnet at the air–water interface (Grzybowski et al., Reference Grzybowski, Stone and Whitesides2000). (b) Patterns of chiral spinners at the ethylene glycol–water interface under a magnetic field with different rotation speeds in unit of revolutions per minute (Grzybowski and Whitesides, Reference Grzybowski and Whitesides2002). (c) Patterns of spinning micro-rafts at the air–water interface under a magnetic field of different rotating speeds in units of revolutions per second (W. Wang et al., Reference Wang, Phan, Li, Wang, Peng, Chen, Qu, Goldman, Levin, Pienta, Amend, Austin and Liu2022). (d) Optocapillary-driven assembly of two shape-programmed actuators at the air–water interface (Hu et al., Reference Hu, Fang, Li, Feng and Lv2020). (e) Dynamic assembly of light-induced shape-morphing hydrogel nano-composite actuator at the air–water interface (Kim et al., Reference Kim, Kang, Zhou, Kuenstler, Kim, Chen, Emrick and Hayward2019). (f) Self-sorting of macroscopic supramolecular assembly with coupled magnetic and capillary interactions. (M. Tan et al., Reference Tan, Tian, Zhang, Zhu, Liu, Cheng and Shi2022).
The capillary interaction could be programmed explicitly via the design of floating objects’ boundaries. W. Wang et al. (Reference Wang, Giltinan, Zakharchenko and Sitti2017) designed a cosinusoidal edge profile for 100-micrometre discs to induce directional capillary interaction. This programmable capillary interaction is combined with tunable magnetic interactions to produce dynamic and programmable self-assembly of the microdiscs. Extending the disc size to 300 micrometres increased the magnitude of the hydrodynamic lift force in the balance of forces and generated an even wider range of patterns (Figure 6c) (W. Wang et al., Reference Wang, Phan, Li, Wang, Peng, Chen, Qu, Goldman, Levin, Pienta, Amend, Austin and Liu2022). This system can be used as a reconfigurable microrobotic system for manipulating small-scale objects at the air–water interface (Gardi et al., Reference Gardi, Ceron, Wang, Petersen and Sitti2022).
Apart from tuning the edge shape during fabrication, external stimuli could adjust the capillary interaction in situ. Lv group reported that rectangular actuators of photoresponsive azobenzene-functionalised liquid crystal polymer could dynamically transform their shapes between bending and flat upon UV/visible light irradiation (Figure 6d) (Hu et al., Reference Hu, Fang, Li, Feng and Lv2020). Hayward group embedded nanoparticles as photothermal heaters within thermally responsive hydrogel discs and used UV illumination to induce wrinkling and program the capillary interaction between hydrogel discs to generate different configurations (Figure 6e) (Kim et al., Reference Kim, Kang, Zhou, Kuenstler, Kim, Chen, Emrick and Hayward2019). Shi group combined magnetic and capillary effects between building blocks whose surface was modified with different molecules (A: polycations; B: polyanions) to realise self-sorting macroscopic supramolecular self-assembly (MSA) (M. Tan et al., Reference Tan, Tian, Zhang, Zhu, Liu, Cheng and Shi2022). MSA is challenging with capillary or magnetic interaction alone because the short-range molecular recognition is not strong enough in the long-range to distinguish AB, AA, or BB block combinations, and pure magnetic interaction will make blocks form clusters but lack local alignment (Figure 6f).
These cases present the diverse programmable interactions at the interface. They may inspire more discoveries and applications, such as using morphologically controllable swarm robots to realise the 3D assembly of biological tissues at liquid interfaces. Moreover, the tiling of building blocks at the interface could lead to complex computation. This idea could date back more than a decade ago: Rothemund showed that applying specific matching rules leads to specific structures representing different values, thereby proving the computational capacity of tiling (Rothemund, Reference Rothemund2000). Even though it is not as powerful as DNA-based computation yet, it provides a platform to investigate the link between computation and tiling.
Robotic swarms at the centimetre scale and above
Compared with the smaller systems in the preceding sections, swarm robotic systems at the scale of centimetres and above possess more complex interactions and larger parameter spaces to achieve information processing and display outputs, such as a change of collective patterns. The advantage of a swarm over a single robot mainly comes from the distributed sensing and computation capability that makes the function of a swarm more robust. The applications of these swarm robotic systems include transporting and escorting (Vásárhelyi et al., Reference Vásárhelyi, Virágh, Somorjai, Tarcai, Szörenyi, Nepusz and Vicsek2014; Zhou et al., Reference Zhou, Wen, Wang, Gao, Li, Wang, Yang, Lu, Cao, Xu and Gao2022), searching and rescuing (Naghsh et al., Reference Naghsh, Gancet, Tanoto and Roast2008; Stirling et al., Reference Stirling, Wischmann and Floreano2010), exploring (Vásárhelyi et al., Reference Vásárhelyi, Virágh, Somorjai, Nepusz, Eiben and Vicsek2018; McGuire et al., Reference McGuire, De Wagter, Tuyls, Kappen and de Croon2019), and mapping (Sergiyenko and Tyrsa, Reference Sergiyenko and Tyrsa2021; Zhou et al., Reference Zhou, Wen, Wang, Gao, Li, Wang, Yang, Lu, Cao, Xu and Gao2022). In this section, we will showcase examples of large-scale robotic swarms that either possess direct physical interactions, such as magnetic interactions, or interact according to algorithm-defined rules using pairwise communications (Table 3).
Table 3. Design of centimetre-scale robotic swarms

Two-dimensional robotic swarms could interact via direct contact and magnetic forces. For example, a particle robot can connect with its neighbours using its T-shaped magnetic connectors around its body, making one robot loosely coupled to another (Li et al., Reference Li, Batra, Brown, Chang, Ranganathan, Hoberman, Rus and Lipson2019). A cluster containing coupled particle robots can achieve locomotion if the particle robots coordinate the expansion–contraction cycles of their connectors. The phase offsets of the expansion–contraction cycles of the members in a cluster determine the movement characteristics of the cluster (Figure 7a). If a light is used to induce the phase offsets, the cluster will show phototaxis. Robots with swinging arms interact with direct physical contact (Savoie et al., Reference Savoie, Berrueta, Jackson, Pervan, Warkentin, Li, Murphey, Wiesenfeld and Goldman2019; Chvykov et al., Reference Chvykov, Berrueta, Vardhan, Savoie, Samland, Murphey, Wiesenfeld, Goldman and England2021). The arms are controlled by servomotors and hit other robots to exert a repulsive force. When a few of such robots are confined in a ring, the diffusive characteristics of the ring at a short time scale depend on the activity of the robots: if all robots are activated, the ring displays normal diffusion; if one robot is inactivated, the ring displays ballistic motion. At the long-time scale, both display super-diffusive behaviours (Figure 7b). BOBbots by Li et al. (Reference Li, Dutta, Cannon, Daymude, Avinery, Aydin, Richa, Goldman and Randall2021) use loose magnetic beads placed in the robot chambers to provide attractive interactions between robots. The strength of the interactions F affects the behaviours of the swarm: small and large Fs lead to small and large clusters, respectively; a large cluster can transport a big object that smaller clusters cannot transport (Figure 7c).
Local communication can achieve pattern formation of swarms of kilobots (Rubenstein et al., Reference Rubenstein, Cornejo and Nagpal2014). With the information of the final shape and relative positions within a swarm, a thousand kilobots can form arbitrary shapes such as a star, letter ‘K’, and a wrench shape (left of Figure 7d). Instead of the hierarchical control scheme used by Rubenstein et al., Slavkov et al. (Reference Slavkov, Carrillo-Zapata, Carranza, Diego, Jansson, Kaandorp, Hauert and Sharpe2018) adopted a reaction–diffusion scheme to form patterns that mimic the morphogenesis process in biological systems. Virtual activators and inhibitors react and diffuse in the swarm via local communication and guide the movement of kilobots (right of Figure 7d). The patterns formed in this scheme are robust to external disturbance and can self-heal. Berlinger et al. (Reference Berlinger, Gauci and Nagpal2021) developed a fish-inspired underwater robot swarm that uses only vision-based local communication and coordination. The fish-like robot has two cameras as eyes to capture the positions and states of other robots and a pair of colour-coded LED lights near its tail to broadcast its position and state. This system displays multiple collective behaviours and functions, including synchronisation, aggregation, dispersion, milling, and a complex task involving transitions between search, alert, and gather states (Figure 7e).

Figure 7. Centimetre-scale robotic swarms as programmable active matter. (a) The movement directions of particle robot clusters depend on the phase offsets of individuals (Li et al., Reference Li, Batra, Brown, Chang, Ranganathan, Hoberman, Rus and Lipson2019). (b) Smarticle robot with swinging arms. The diffusive characteristics of a ring containing smarticle robots depends on the activity of the robots (Chvykov et al., Reference Chvykov, Berrueta, Vardhan, Savoie, Samland, Murphey, Wiesenfeld, Goldman and England2021). (c) BOBbots’ swarm behaviours affected by the strength of the magnetic attractive forces F (Li et al., Reference Li, Dutta, Cannon, Daymude, Avinery, Aydin, Richa, Goldman and Randall2021). (d) Pattern formations of kilobots in a hierarchical control scheme (left) (Rubenstein et al., Reference Rubenstein, Cornejo and Nagpal2014) and a reaction–diffusion scheme (right) (Slavkov et al., Reference Slavkov, Carrillo-Zapata, Carranza, Diego, Jansson, Kaandorp, Hauert and Sharpe2018). (e) Underwater fish-inspired robotic swarms achieve different collective behaviours using vision-based local coordination among robots (Berlinger et al., Reference Berlinger, Gauci and Nagpal2021). (f) Light field-driven robots that use light as ‘food’ for movement. Robot clusters have different phases as the robot density changes (G. Wang et al., Reference Wang, Phan, Li, Wombacher, Qu, Peng, Chen, Goldman, Levin, Austin and Liu2021). (g) A light-field-driven robotic swarm displays complex behaviours that mimic biological evolution. The colours of the lights encode information that passes between robots (G. Wang et al., Reference Wang, Phan, Li, Wang, Peng, Chen, Qu, Goldman, Levin, Pienta, Amend, Austin and Liu2022).
Environmental conditions can be used as information input to program a swarm. G. Wang et al. (Reference Wang, Phan, Li, Wombacher, Qu, Peng, Chen, Goldman, Levin, Austin and Liu2021) built a light-responsive robotic swarm that displays different phases such as gas, liquid, crystal, and jammed phases under different light conditions. The robots consume light as they move in a light field and leave a dark trail. The light field can recover light strength gradually. By gradually shrinking the light area, the density of the robots increases, and the system displays phase transitions among different phases (Figure 7f). Using similar robotic systems, G. Wang et al. (Reference Wang, Gardi, Malgaretti, Kishore, Koens, Son, Gilbert, Wu, Harwani, Lauga, Holm and Sitti2022) built another evolving system in which robots can undergo the progress of life, death, and mutation, as well as rebirth based on genes from parents’ generations. They represent different states of the robots using RGB colours and use the colours as genes to mimic gene delivery. During the birth of robots, the gene or colour information obtained from the RGB sensor will change and trigger mutations by varying the environmental lights of an LED light board on which the robots move. Different evolution results were obtained in different environments, as in real biological evolution (Figure 7g).
Significance
We delineate two broad areas where PAM would contribute significant fundamental scientific understanding: the relationship between geometry and matter, and the study of complexity and emergence. We present these two broad areas from a historical perspective, with an emphasis on their applications in materials sciences. We then outline how a new kind of mechanics – computational mechanics – could provide insights and guidance in exploring the role of information in PAM.
Ubi materia, ibi geometria
‘Ubi materia, ibi geometria’ (where there is matter, there is geometry), uttered by Johannes Kepler in the seventeenth century, conveys the notion that the arrangement of the building blocks of the universe – the celestial objects in Kepler’s study – obeys the rules of geometry (Sihvola, Reference Sihvola2000). Kepler’s motto follows a long tradition that goes back to the Greek philosopher Democritus in 460 BC, who proposed the concept of atoms as the fundamental building block of matter and tried to understand the universe in terms of the arrangement and interactions of atoms (Mackay, Reference Mackay2002).
The most conspicuous success of Kepler’s motto in materials science is arguably crystallography. The advent of X-ray diffraction in the early twentieth century precipitated our understanding of the periodic arrangement of atoms in crystals. The sharp diffraction peaks in X-ray diffractograms were seen as clear experimental evidence of the ordered 3D arrangement of atoms, perfectly and completely described in terms of 14 Bravais lattices and 230 space groups. The discovery of quasicrystals challenged this understanding of the relationship between X-ray diffraction and periodic order and led to the redefinition of crystals as ‘any solids having an essentially discrete diffraction diagram’ (‘Report of the Executive Committee for 1991’, 1992). (The idea of quasi-periodicity, however, precedes the discovery of quasi-crystals. Penrose (Reference Penrose1979) invented quasiperiodic tiling in the 1970s by drawing inspiration from Kepler.)
The arrangement of components of materials is certainly not limited to periodic or quasiperiodic ordering. Amorphous materials (‘A Classy Material’, 2022) and living organisms (Haeckel, Reference Haeckel1866; Thompson, Reference Thompson1949) follow vastly different rules and form structures and patterns with various degrees of discernible order. These observations call for a generalised study of structures and patterns beyond the boundaries of traditional crystallography. Indeed, crystallographers have called for a generalised crystallography since at least the 1960s, and its most recent proponent is Alan Mackay (Mackay, Reference Mackay1986, Reference Mackay2002). Mackay noted that the periodic repetition of unit cells in three dimensions suggests that crystals can be described as ‘group(motif) = pattern’, meaning that group symmetry operations on the motif of unit cells produce the structural patterns of crystals. He argued that this equation restricts the description of structures only to those allowed by group symmetry operations. He thus generalised this equation to ‘program(motif) = structure’, where the programme represents the rules by which neighbouring elements or units interact. In other words, the new function ‘program(motif)’ is like a computer programme that prescribes how a structure emerges from the interactions of the constituting elements or units. This idea, we argue, can serve as the foundation for the rational design of PAM.
Taking the analogy between structures and computer programmes further, a programme contains information, and so does a structure – a notion that could be traced back to the concept of ‘aperiodic crystals’ by Schrödinger in the 1940s (Schrödinger, Reference Schrödinger1944). Most programmes have redundancies and thus can be compressed. Likewise, structures contain information and often have redundancy too. In the case of DNA, the sequence itself carries the information for subsequent transcription and translation; in the case of crystals, the periodic repetition represents redundancy, and hence the information of crystals is much shorter than the sequence that contains all the repeating units. The shortest description of a programme represents its algorithmic complexity, or the so-called Kolmogorov–Chaitin (KC) complexity (Kolmogorov, Reference Kolmogorov1965; Chaitin, Reference Chaitin1966). It quantifies the amount of information the programme carries. Similarly, Mackay and Cartwright have proposed the assembly complexity to measure the complexity of a structure (Cartwright and Mackay, Reference Cartwright and Mackay2012):
where
![]() $a$
is the assembly algorithm that builds the structure and
$a$
is the assembly algorithm that builds the structure and
![]() $d(a)$
is the description of the algorithm.
$d(a)$
is the description of the algorithm.
In the last decade, the confluence of (traditional) crystallography and information theory has given rise to chaotic crystallography (Varn and Crutchfield, Reference Varn and Crutchfield2015). Chaotic crystallography applies the tools of computational mechanics (Crutchfield, Reference Crutchfield2012), notably ε-machine – which consists of the states of a system and their dynamics – to describe the structures of matter. One of its successes is the explanation of the X-ray diffraction diagram of polytypic zinc sulphide (Varn et al., Reference Varn, Canright and Crutchfield2007). Chaotic crystallography analyses not only the structures of a system but also how the structures are formed. More broadly, with the analogy between structures and programmes in mind, it analyses how a structure stores and processes information (Crutchfield, Reference Crutchfield2012). In this sense, it closely aligns with Mackay’s proposal of assembly complexity. The difference, however, is that while the assembly complexity deals with one structure, computational mechanics – and by extension, chaotic crystallography – deals with an ensemble of structures and extracts the statistical properties of the ensemble.
Concretely, computational mechanics uses the representation of ε-machine (instead of a universal Turing machine as the KC complexity does) and defines the statistical complexity of a system as
where
![]() $\Pr \left(\sigma \right)$
is the distribution over causal states
$\Pr \left(\sigma \right)$
is the distribution over causal states
![]() $\mathcal{S}$
(a form of state space that can relate the current state to the next state).
$\mathcal{S}$
(a form of state space that can relate the current state to the next state).
![]() ${C}_{\mu }$
has the same form as Shannon entropy, and it quantifies the amount of information stored in the causal states
${C}_{\mu }$
has the same form as Shannon entropy, and it quantifies the amount of information stored in the causal states
![]() $\mathcal{S}$
. As we make repeated measurements of a system while the system evolves according to its dynamics (equation of states), the measurement
$\mathcal{S}$
. As we make repeated measurements of a system while the system evolves according to its dynamics (equation of states), the measurement
![]() $x$
forms a time series
$x$
forms a time series
![]() $\left\{x\right\}$
. If we consider the system as a signal source that generates the time series, the source entropy rate
$\left\{x\right\}$
. If we consider the system as a signal source that generates the time series, the source entropy rate
![]() ${h}_{\mu }$
quantifies the system’s degree of randomness:
${h}_{\mu }$
quantifies the system’s degree of randomness:
where
![]() $\Pr \left(x|\sigma \right)$
is the probability of transitioning from state
$\Pr \left(x|\sigma \right)$
is the probability of transitioning from state
![]() $\sigma$
(or leaving state
$\sigma$
(or leaving state
![]() $\sigma$
) on measurement
$\sigma$
) on measurement
![]() $x$
. It relates to how compressible the system as an information source is.
$x$
. It relates to how compressible the system as an information source is.
KC complexity can be related to statistical complexity and the Shannon entropy rate via the following relation:
where
![]() $KC(l)$
is the ensemble average of the KC complexity, and
$KC(l)$
is the ensemble average of the KC complexity, and
![]() $l$
is the length of the time series.
$l$
is the length of the time series.
In the light of the long tradition of Democritus, Kepler, and Mackay, given the quantitative insights offered by computational mechanics, particularly in the area of chaotic crystallography, we foresee a fertile ground for scientific inquiry in the study of PAM from the perspective of generalised crystallography. The main motivation for this approach is rooted in the common emphasis on the interaction among structural elements or units. The other motivation is based on the realisation that many patterns generated by PAM at different scales share similar features, which begs for a universal description and understanding.
Our recent work in using the entropy of the pairwise distance distribution between topological neighbours
![]() ${H}_{NDist}$
to measure the degree of order and disorder and to characterise the phases of the spinning disc system (W. Wang et al., Reference Wang, Phan, Li, Wang, Peng, Chen, Qu, Goldman, Levin, Pienta, Amend, Austin and Liu2022) is a step in this direction. The fundamental questions we ask are about the interplay between information and spatiotemporal structures or patterns: what are the possible manifestations of information in spatiotemporal patterns; how to quantify the information in spatiotemporal patterns; what is the relationship between information and other physical properties of spatiotemporal patterns. We think that local measures such as entropy by neighbour distances
${H}_{NDist}$
to measure the degree of order and disorder and to characterise the phases of the spinning disc system (W. Wang et al., Reference Wang, Phan, Li, Wang, Peng, Chen, Qu, Goldman, Levin, Pienta, Amend, Austin and Liu2022) is a step in this direction. The fundamental questions we ask are about the interplay between information and spatiotemporal structures or patterns: what are the possible manifestations of information in spatiotemporal patterns; how to quantify the information in spatiotemporal patterns; what is the relationship between information and other physical properties of spatiotemporal patterns. We think that local measures such as entropy by neighbour distances
![]() ${H}_{NDist}$
are particularly effective in characterising the patterns of PAMs because the range of interactions between units is often short-ranged and local. A local measure, therefore, can be an effective descriptor for PAMs.
${H}_{NDist}$
are particularly effective in characterising the patterns of PAMs because the range of interactions between units is often short-ranged and local. A local measure, therefore, can be an effective descriptor for PAMs.
Another related work by Martiniani, Chaikin, and Levine follows more closely the spirits of Kolmogorov and Chaitin and proposes computable information density (CID) to measure the hidden order in out-of-equilibrium systems (Martiniani et al., Reference Martiniani, Chaikin and Levine2019):
where
![]() $\mathcal{L}(x)$
is the binary code length of the sequence compressed by a lossless data compression algorithm and
$\mathcal{L}(x)$
is the binary code length of the sequence compressed by a lossless data compression algorithm and
![]() $L$
is the length of the original sequence. Even though a sequence is 1D, patterns in 2D and 3D can be transformed into 1D sequences by appropriate linearisation protocols. Therefore, CID is generalisable to 2D and 3D systems too.
$L$
is the length of the original sequence. Even though a sequence is 1D, patterns in 2D and 3D can be transformed into 1D sequences by appropriate linearisation protocols. Therefore, CID is generalisable to 2D and 3D systems too.
We point out that both
![]() ${H}_{NDist}$
and CID can be used to identify phase transitions in non-equilibrium systems, a feature that will be explored further in the next section.
${H}_{NDist}$
and CID can be used to identify phase transitions in non-equilibrium systems, a feature that will be explored further in the next section.
More is different
Anderson (Reference Anderson1972) laid the philosophical foundation of emergence in his 1972 essay ‘More Is Different’. He used the broken symmetry in the phase transition of matter as an example to argue for a hierarchical structure of science. He postulated that a large number of interacting components at one level of the hierarchy would create a new level in the hierarchy, and new fundamental laws would emerge to describe the behaviours of the system at this new level.
In materials sciences, a case in point is the change of symmetry in phase transitions. As Anderson pointed out, even though individual atoms are isotropic and possess the highest symmetry, the crystallisation of atoms into crystals breaks the symmetry and gives rise to properties not seen at the atomic level. The understanding of crystal properties necessitates new rules that describe crystal symmetries.
Moreover, intensive properties of materials – density, melting point, boiling point, specific heat, and so forth – are mostly determined by local interactions, such as the types (ionic, covalent, van der Waals, etc.) and the strengths of bonds (Israelachvili, Reference Israelachvili2011b). Tuning the local interactions – for example, by doping heterogeneous atoms or by changing the ratios of elements in alloys – will change material properties and thus provides opportunities to engineer materials.
Similarly, many phenomena and behaviours of PAM emerge from the interactions of structural elements or units. For example, even though individual motile colloidal particles move in all directions, densely packed colloid particles will move collectively in one direction (Bricard et al., Reference Bricard, Caussin, Desreumaux, Dauchot and Bartolo2013). As another example, motile colloids become stationary when forming clusters and separate from the randomly moving gas-like phase, a phenomenon termed motility-induced phase separation (Cates and Tailleur, Reference Cates and Tailleur2015). Perhaps the most miraculous example of emergence is the creation of life forms from the synergistic interactions of an Avogadro number of individually non-living molecules (Mann, Reference Mann2012).
Using the language of computational mechanics, the emergence of collective behaviours and properties from the interacting units can be seen as the divergence of statistical complexity
![]() ${C}_{\mu }$
at the unit level. Going from the individual unit to the collective whole represents a step-up in the levels of complexity, which in theory can be described by the hierarchical ε-machine reconstruction (Crutchfield, Reference Crutchfield1994, Reference Crutchfield2012). How the machinery of computational mechanics could translate this hierarchical ε-machine reconstruction into detailed understandings of specific systems remain to be seen.
${C}_{\mu }$
at the unit level. Going from the individual unit to the collective whole represents a step-up in the levels of complexity, which in theory can be described by the hierarchical ε-machine reconstruction (Crutchfield, Reference Crutchfield1994, Reference Crutchfield2012). How the machinery of computational mechanics could translate this hierarchical ε-machine reconstruction into detailed understandings of specific systems remain to be seen.
Another critical component in understanding the interaction between matter and information is the thermodynamics of information (JMR et al., Reference JMR, Horowitz and Sagawa2015). The thermodynamics of information has its root in the thought experiments of Maxwell’s demon and Szilard’s engine (Maxwell, Reference Maxwell1871; Leo Szilard, Reference Szilard1929; Leff and Rex, Reference Leff and Rex1990). Recent advances in this field are largely within the framework of stochastic thermodynamics (Jarzynski, Reference Jarzynski2011; Seifert, Reference Seifert2012). In stochastic thermodynamics, the randomness comes from the coarse-graining procedure that converts the deterministic microscopic dynamics into stochastic mesoscopic dynamics. This coarse-graining procedure loses some information about the system and therefore requires a probabilistic description. This transition from microscopic dynamics to mesoscopic dynamics resembles the hierarchical ε-machine reconstruction in computational mechanics, and their precise links beg further investigation. Similarly, the hydrodynamic thinking – exemplified by the construction of the Toner–Tu model (Toner and Tu, Reference Toner and Tu1995) from the Vicsek model (Vicsek et al., Reference Vicsek, Czirók, Ben-Jacob, Cohen and Shochet1995) – requires selections of information to move from discrete agent-level description to continuum description. It also poses opportunities for further exploration from the perspective of computational mechanics.
Conclusion and outlook
In the Introduction, we have used biological cells as the inspiration for our idea of information processing in PAM. We have considered the stimulus-responsive behaviour of single cells as a simple form of information processing and the evolution of genetic codes of cell populations as a complex form of information processing. The case studies in the second section illustrate various forms of information processing of PAMs across scales with varying degrees of complexity. The information inputs can be changes in building blocks, the number of units, or external conditions; the outputs could be changes of spatiotemporal patterns or collective functions or properties. Studying the relationship between information inputs and outputs is to understand the mechanism of information processing in the systems of PAM. Knowledge gained in such studies will further our understanding in the relationship between geometry and matter and provide insights into complexity and emergence, as we have argued in the third section.
Apart from the scientific significance, PAMs across scales have existing or potential applications in many areas. In biomedicine, PAMs are often cast as micromachines with specific structures and functions and can perform the diverse tasks, including drug delivery and in vivo imaging. PAMs can be used as cargo carriers, and the type of cargos depends on the size of the carriers: For example, supermolecular systems can transfer nanoparticles, and colloidal systems can transfer microparticles. At the centimetre scale, PAMs can realise cargo pick-up, transport, and delivery in diverse settings such as clinical environments or warehouses. In addition, the programmable characters in some PAMs, such as DNA and the interfacial systems, allow them to perform logic operations: they use matching rules to form complex structures as logic gates and neural networks, and they can usher in the next-generation molecular computers. Moreover, in the prebiotic chemistry, the droplet-based PAMs can serve as protocells and mimic the possible prebiotic evolution processes in order to study the origin of life. Lastly, the diverse patterns generated by PAMs across all scales can serve as research models to study the collective dynamics and emergence in nature.
In the Introduction, we have used biological cells as an inspiration for PAMs. Besides biological cells, another inspiration for PAM is biological brains. While we know that cells store their genetic information in DNA and unfold their genetic programs through steps of transcription and translation, we are much less certain of how brains store and process information. One of the chief current fascinations about biological brains is their low power consumption, about ~20 W for human brains (Raichle and Gusnard, Reference Raichle and Gusnard2002; Flamholz et al., Reference Flamholz, Phillips and Milo2014), compared with ~100 W per processing unit in personal computers. This efficiency may be attributed to the fact that biological brains operate at temperatures close to room temperature, and therefore their energy dissipation per calculation is closer to the theoretical Landauer’s limit ~kTln2 (Landauer, Reference Landauer1961). Concepts such as the self-organised criticality (Mora and Bialek, Reference Mora and Bialek2011) and coherent resonance (X. Zhang et al., Reference Zhang, Song and Jiang2022) have been proposed to rationalise our empirical observations about the efficiency in biological brains, but the progress remains slow and the evidence thin. To really understand how brains work, we will need to build them from scratch.
Engineering PAM to build artificial brains from bottom-up is perhaps the ultimate challenge in PAM, and it presents both scientific and technological opportunities. Although electrical engineering and computer science communities have been building neuromorphic solid-state devices for decades (Sandamirskaya et al., Reference Sandamirskaya, Kaboli, Conradt and Celikel2022), these solid-state devices bear little or no resemblance to the soft tissues that constitute biological brains and the biological neural networks. It is, therefore, difficult to conceive how these solid-state devices built on the paradigm of digital computation and Boolean algebra could mimic realistically how brains work. By contrast, many of the PAMs, particularly at the millimetre scale and below, are made of soft materials – supramolecules, colloids, and gels. Exploring their capacity for information processing could illuminate our way to build artificial soft-matter brains. Such an effort will require expertise from diverse disciplines such as chemistry, physics, and materials sciences, as well as information sciences, mechatronics, and robotics. We anticipate that merging concepts and techniques across these diverse disciplines will generate breakthroughs in the near future.
Supplementary material
The supplementary material for this article can be found at http://doi.org/10.1017/pma.2023.6.
Data availability statement
Data sharing is not applicable to this article as no new data were created or analysed in this study.
Acknowledgments
We thank Dr. Koens, Dr. Gardi, Dr. Kishore, and Dr. Malgaretti for discussion.
Funding statement
This work was supported by the National Natural Science Foundation of China (Grant No. 22175115).
Competing interest
The authors declare no competing interests.
Authorship contribution
W.W. conceived the project. All authors contributed to the writing of the original draft (Introduction, Significance, Conclusion and outlook: W.W.; Figure 1, DNA-based system and Droplets, bacteria, and embryos: H.Y. and J.S.; Colloidal systems and Millimetre-scale interfacial systems: Y.F.; Robotic swarms at the centimetre scale and above: X.Z and D.Q.; Supramolecular systems: L.C.); H.Y., Y.F., X.Z., L.C., and W.W. contributed to the editing of the manuscript. All authors have read and agreed to the submitted version of the manuscript. H.Y., Y. F., and X. Z. contributed equally to this work.














