1. INTRODUCTION
Terahertz (THz) frequency regime has become one of the thrust areas of research due to the variety of applications it offers. Application areas include information and communication technology (Hirata et al., Reference Hirata, Kosugi, Takahashi, Yamaguchi, Nakajima, Furuta, Ito, Sugahara, Sato and Nagatsuma2006; Krumbholz et al., Reference Krumbholz, Gerlach, Rutz, Koch, Piesiewicz, Kurner and Mittleman2006), biology and medical sciences (Brucherseifer et al., Reference Brucherseifer, Nagel, Bolivar, Kurz, Bosserhoff and Büttner2000; Davis et al., Reference Davis, Linfield and Johnston2002; Han et al., Reference Han, Cho and Zhang2002; Wallace et al., Reference Wallace, Anthony, Pickwell, Pye, Taday, Flanagan and Thomas2006), nondestructive evaluation (Kawase et al., Reference Kawase, Ogawa, Watanabe and Inoue2003; Zhong et al., Reference Zhong, Jingzhou, Xie, Yuan, Reightler, Madaras and Zhang2005), homeland security and explosive detection (Shen et al., Reference Shen, Lo, Taday, Cole, Tribe and Kemp2005; Karpowicz et al., Reference Karpowicz, Zhong, Zhang, Lin, Hwang, Xu and Zhang2005; Federici et al., Reference Federici, Huang, Gary, Barat, Oliveira and Zimdars2005; Kemp et al., Reference Kemp, Baker, Gregory, Schubert and Rimski2006; Ying et al., Reference Ying, Huang, Guo, Wang and Zhang2006), quality control of food and agricultural products, global environment monitoring (Tonouchi, Reference Tonouchi2007), ultrafast computing (Clery, Reference Clery2002), remote sensing (Waters et al., Reference Waters, Froidevaux, Harwood, Jarnot, Pickett, Read, Siegel, Cofield, Filipiak, Flower, Holden, Lau, Livesey, Manney, Pumphrey, Santee, Wu, Cuddy, Lay, Loo, Perun, Schwartz, Stek, Thurstans, Boyles, Chandra, Chavez, Chen, Chudasama, Dodge, Fuller, Girard, Jiang, Jiang, Knosp, Labelle, Lam, Lee, Miller, Oswald, Patel, Pukala, Quintero, Scaff, Snyder, Tope, Wagner and Walch2006), material characterization (Jiang et al., Reference Jiang, Li and Zhang2000), and semiconductor studies (Xu, Reference Xu1997). There is no strict definition for any wave to qualify as THz but the waves having frequencies in between microwave and far infrared of the electromagnetic spectrum are broadly considered as THz radiation. Typically, 0.1–10 THz is referred as THz region but the region is extending up to 40–50 THz (Wang, Reference Wang2001). A number of schemes have been employed to produce THz radiation (Hafizi et al., Reference Hafizi, Sprangle and Serafim1992; Hashimshony et al., Reference Hashimshony, Zigler and Papadopoulos1999; Muggli et al., Reference Muggli, Liou, Lai, Hoffman, Katsouleas and Joshi1998; Leemans et al., Reference Leemans, Tilborg, Faure, Geddes, Toth, Schroeder, Esarey, Fubiani and Dugan2004; Sheng et al., Reference Sheng, Mima, Zhang and Sanuki2005; Alekseev et al., Reference Alekseev, Gorkunov, Demarina, Hyart, Alexeeva and sorokov2006; Ma et al., Reference Ma, Tang, Kitaeva and Naumova2006; Kukushkin, Reference Kukushkin2008). Currently, the powerful sources of THz radiation are large accelerator-based sources and the lack of compact high-power sources limits the exploitation of full potential of THz radiation. For the development of practical high-power THz sources, schemes based on laser–plasma interaction have been proposed (Hamster et al., Reference Hamster, Sullivan, Gordon and Falcon1993; Yugami et al., Reference Yugami, Higashiguchi, Gao, Sakai, Takahashi, Ito, Nishida and Katsouleas2002; Gildenburg & Vvedenskii, Reference Gildenburg and Vvedenskii2007; Sharma et al., Reference Sharma, Monika, Sharma, Chauhan and Ji2010; Jha et al., Reference Jha, Sarochand and Mishra2011; Chen Reference Chen2013).
Filamentation (phenomena of periodic self-focusing and defocusing) is another process from which THz can be generated. THz radiation can be generated from the plasma filament created by short intense laser pulse. The mechanism of generation has been studied by some researchers (Wu et al., Reference Wu, Meyer-Ter-Vehn, Ruhland and Sheng2011). The generation of broadband THz within the plasma filaments formed by a femtosecond laser has been investigated by Ladouceur et al. (Reference Ladouceur, Baronnavski, Lohrmann, Grounds and Girardi2001). Orders of magnitude enhancement of THz energy has been achieved because of filamentation of a femtosecond laser in air in the presence of a transverse static electric field (Houard et al., Reference Houard, Liu, Prade, Tikhonchuk and Mysyrowicz2008). As the plasma is capable of handling high-power, these schemes generate THz radiation with high-electric fields without any physical damage to the medium used. In some studies, THz generation by focusing femtosecond bichromic laser pulses in a gas or plasma has been reported (Chizhov et al., Reference Chizhov, Volkov, Bukin, Ushakov, Garnov and Salvel'ev2013). Experimental studies have also been done to generate intense THz pulses using two color laser filamentation using TW lasers. High-energy (>1 μJ), high average power (>1 mW), intensity (>1 MV cm−1), and broadband (0.01–60 THz) THz via two color filamentations have been reported (Oh et al., Reference Oh, You, Jhajj, Rosenthal, Milchberg and Kim2013). There are several techniques available for the study of self-focusing in the plasma. One of the simplest methods has been given originally by Akhmanov et al. (Reference Akhmanov, Sukhorukov and Khokhlov1968) for the paraxial regime and later developed by Sodha et al. (Reference Sodha, Salimullah and Sharma1980).
The role of density ripple in the plasma in THz generation has been discussed by several researchers (Tripathi et al., Reference Tripathi, Bhasin, Uma and Tripathi2010; Singh et al., Reference Singh, Singh and Sharma2013). The importance of density ripple in the plasma has also been discussed by some authors in context of other phenomena taking place in the laser–plasma interaction (Singh et al., Reference Singh, Sharma and Tripathi2010; Xia & Xu, Reference Xia and Xu2013; Xia, Reference Xia2014). Significant amount of research is going into the fabrication of such kind of structure due to their other applications such as in the development plasma photonic devices.
Different spatial laser profiles (such as fundamental Gaussian, cosh-Gaussian, etc.) have been used to generate THz (Tripathi et al., Reference Tripathi, Bhasin, Uma and Tripathi2010; Singh et al., Reference Singh, Singh and Sharma2013). As the propagation and focusing properties of Gaussian laser beam in plasma have been studied extensively (Sodha et al., Reference Sodha, Ghatak and Tripathi1974; Reference Sodha, Sinha and Sharma1979), it is one of the most preferred beam profiles used in laser– plasma interaction studies.
In the present paper, we have studied the effect of self-focusing on the THz generation by amplitude-modulated Gaussian laser beam propagating in rippled density plasma. Because of the variation in intensity in the direction transverse to the laser propagation, a component of ponderomotive force is exerted on electrons, which gives rise to a stronger transient current driving THz radiation. The ripple in plasma density provides the necessary condition for phase matching (Singh et al., Reference Singh, Singh and Sharma2013) and plays the main role for the extraction of THz radiation. In the absence of ripple density, the THz cannot be generated by the present scheme. In Section 2, we discuss the self-focusing of an amplitude-modulated Gaussian laser having frequency of modulation in the THz region. In the subsequent section, we derive the nonlinear current density, generated THz amplitude, and intensity. We discuss the results in Section 4 and then conclude.
2. SELF-FOCUSING OF AMPLITUDE-MODULATED GAUSSIAN LASER BEAM
We consider an amplitude-modulated Gaussian laser (Gaussian in space) beam of frequency ω0, propagating in the z-direction and polarized along the x-direction in a collisionless, unmagnetized, hot, and homogeneous plasma. The laser field, at z = 0 is given by
where Ω is the frequency of modulation and μ is the index of modulation. r 0 is the initial pulse width of the laser. Because of the nonuniform spatial intensity distribution of the laser pulse, a ponderomotive force is exerted on the electrons in the plane transverse to the direction of propagation (z-direction). The ponderomotive force in the presence of laser pulse is given by Sodha et al. (Reference Sodha, Ghatak and Tripathi1976).
 $${\bf F}_{\rm P} = - \displaystyle{{e^2} \over {4m{\rm \omega} _0^2}} \left( {{\bf \nabla} ({\bf E}_0 \cdot {\bf E}_0 ^* )} \right). $$
$${\bf F}_{\rm P} = - \displaystyle{{e^2} \over {4m{\rm \omega} _0^2}} \left( {{\bf \nabla} ({\bf E}_0 \cdot {\bf E}_0 ^* )} \right). $$
This ponderomotive force leads to the redistribution of electrons. Assuming ![]() ${\rm \Omega} \ll {\rm \omega} _0 $, the modified electron density can be written as (Sodha et al., Reference Sodha, Salimullah and Sharma1980),
${\rm \Omega} \ll {\rm \omega} _0 $, the modified electron density can be written as (Sodha et al., Reference Sodha, Salimullah and Sharma1980),
 $$N = N_0 \,{\rm exp}\left[ { - \displaystyle{{e^2} \over {8mk_{\rm B} T_0 {\rm \omega} _0^2}} \left( {{\bf E}_0 \cdot {\bf E}_0 ^ *} \right)} \right], $$
$$N = N_0 \,{\rm exp}\left[ { - \displaystyle{{e^2} \over {8mk_{\rm B} T_0 {\rm \omega} _0^2}} \left( {{\bf E}_0 \cdot {\bf E}_0 ^ *} \right)} \right], $$where, T 0 is the temperature of the plasma and k B is the Boltzmann constant.
The propagation of laser pulse in the plasma is governed by the wave equation:
where J is the total current density in the plasma in the presence of laser pulse. Assuming E0 to be varying in space and time as:
and
 $$A_0 = \displaystyle{{E_{00} \left[ {1 + {\rm \mu} \cos {\rm \Omega} t} \right]} \over {\,f^{1/2} (x,z,t)}}{\rm exp}\left[ {\displaystyle{{ - x^2} \over {2r_0^2 f^2 (x,z,t)}} - ikS(x,z,t)} \right], $$
$$A_0 = \displaystyle{{E_{00} \left[ {1 + {\rm \mu} \cos {\rm \Omega} t} \right]} \over {\,f^{1/2} (x,z,t)}}{\rm exp}\left[ {\displaystyle{{ - x^2} \over {2r_0^2 f^2 (x,z,t)}} - ikS(x,z,t)} \right], $$where f and S are dimensionless beam width parameter and eikonal of the laser beam, respectively. The eikonal shows the slightly converging/diverging behavior of the laser beam in the plasma (Sodha et al., Reference Sodha, Ghatak and Tripathi1974). The eikonal (S) is given by S = 1/2x 2β(z, t)+Φ(z, t), where [β(z, t)]−1 and Φ(z, t) represent the radius of the curvature of the wavefront and initial phase, respectively. The current density in the plasma can be written as (Sodha et al., Reference Sodha, Salimullah and Sharma1980)
 $${\bf J} \cong \hat{x} \displaystyle{{Ne^2} \over {mi{\rm \omega} _0}} \left( {A_0 + \displaystyle{i \over {{\rm \omega} _0}} \displaystyle{{{\partial} A_0} \over {{\partial} t}}} \right) \times {\rm exp}[i({\rm \omega} _0 t - kz)]. $$
$${\bf J} \cong \hat{x} \displaystyle{{Ne^2} \over {mi{\rm \omega} _0}} \left( {A_0 + \displaystyle{i \over {{\rm \omega} _0}} \displaystyle{{{\partial} A_0} \over {{\partial} t}}} \right) \times {\rm exp}[i({\rm \omega} _0 t - kz)]. $$Substituting the expressions for E0 and J from Eqs. (5) and (7), respectively, in Eq. (4) and using the method adopted by Sodha et al. (Reference Sodha, Salimullah and Sharma1980), we obtain the equation governing the dimensionless beam width parameter (f) as
 $$\eqalign{\displaystyle{{d^2 f} \over {d {\rm \eta} ^2}} &= \displaystyle{1 \over {\,f^3}} - \left( {\displaystyle{{{\rm \omega} _{\rm p} r_0} \over c}} \right)^2 \displaystyle{{{\rm \alpha} E_{00}^2} \over {\,f^2}} \left( {1 + {\rm \mu} \cos {\rm \Omega} \xi} \right)^2 \cr & \quad \times\ {\rm exp}\left\{ { - \displaystyle{{{\rm \alpha} E_{00}^2} \over f}\left( {1 + {\rm \mu} \cos {\rm \Omega} \xi} \right)^2} \right\}},$$
$$\eqalign{\displaystyle{{d^2 f} \over {d {\rm \eta} ^2}} &= \displaystyle{1 \over {\,f^3}} - \left( {\displaystyle{{{\rm \omega} _{\rm p} r_0} \over c}} \right)^2 \displaystyle{{{\rm \alpha} E_{00}^2} \over {\,f^2}} \left( {1 + {\rm \mu} \cos {\rm \Omega} \xi} \right)^2 \cr & \quad \times\ {\rm exp}\left\{ { - \displaystyle{{{\rm \alpha} E_{00}^2} \over f}\left( {1 + {\rm \mu} \cos {\rm \Omega} \xi} \right)^2} \right\}},$$
where ![]() $z = {\rm \eta} kr_0^2 $, ξ = t−z/υg,
$z = {\rm \eta} kr_0^2 $, ξ = t−z/υg, ![]() ${\rm \upsilon} _{\rm g} = c \in _0^{{1 / 2}} $ and
${\rm \upsilon} _{\rm g} = c \in _0^{{1 / 2}} $ and ![]() ${\rm \alpha} = (e^2 /(8\,mk_{\rm B} T_0 {\rm \omega} _0^2 ))$.
${\rm \alpha} = (e^2 /(8\,mk_{\rm B} T_0 {\rm \omega} _0^2 ))$.
Equation (8) is solved numerically to study the self-focusing with initial condition, f = 1 at z = 0.
3. THz RADIATION GENERATION
We consider the propagation of amplitude-modulated Gaussian laser beam whose field is given by Eq. (1), through rippled density plasma. Plasma density is given by
where n q and k q are the amplitude and the wave number of the density ripple. This kind of density ripple can be created by different techniques (Hazra et al., Reference Hazra, Chini, Sanyal, Grenzer and Pietsch2004; Pai et al., Reference Pai, Huang, Kuo, Lin, Wang, Chen, Lee and Lin2005; Layer et al. Reference Layer, York, Antonson, Varma, Chen, Leng and Milchberg2007; Liu et al., Reference Liu and Tripathi2008). The laser propagates in the z-direction and polarized in the x-direction. Laser field is given by Eq. (5) and ponderomotive force is evaluated using Eq. (2) which comes out to be
 $${\bf F}_{\rm P} = - \displaystyle{{e^2} \over {4m{\rm \omega} _0^2}} {\bf {\rm \nabla}} \left( {\displaystyle{{E_{00}^2} \over f}(1 + {\rm \mu} \cos {\rm \Omega} {\rm \xi} )^2 {\rm exp}( - {{x^2} / {r_0^2 f^2 )}}} \right). $$
$${\bf F}_{\rm P} = - \displaystyle{{e^2} \over {4m{\rm \omega} _0^2}} {\bf {\rm \nabla}} \left( {\displaystyle{{E_{00}^2} \over f}(1 + {\rm \mu} \cos {\rm \Omega} {\rm \xi} )^2 {\rm exp}( - {{x^2} / {r_0^2 f^2 )}}} \right). $$The analysis is consistent with that made in Section 1. This ponderomotive force imparts an oscillatory velocity (perpendicular to the direction of propagation) to the electrons at modulation frequency Ω. The nonlinear velocity of the electrons is given by
When this nonlinear velocity couples with the density ripple, a nonlinear current is generated at a frequency Ω and wave number k q in the direction perpendicular to the propagation of the laser beam. The nonlinear current is evaluated by
 $$\eqalign{{\bf J}_{\rm \Omega}^{\rm NL} &= \displaystyle{{i{\rm \mu} n_q e^3 E_{00}^2 \,e^{( - x^2/r_0^2 f^2 )}} \over {4m^2 {\rm \omega} _0^2}} \left[ {\displaystyle{{2x} \over {r_0^2 f^3}} \displaystyle{1 \over \Omega} {\hat x }}\right. \cr & \quad \left. - \left\{ {\displaystyle{1 \over {{\rm \upsilon} _{\rm g} f}} + \displaystyle{1 \over {f^2 {\rm \Omega}}} \left( {\displaystyle{{2x^2} \over {r_0^2 f^2}} - 1} \right) \displaystyle{{\partial f} \over {\partial z}}} \right\}{\hat z} \right] e^{i\left\{ {{\rm \Omega} t - \left( {{{\rm \Omega} \over {{\rm \upsilon} _{\rm g}}} + k_q} \right)z} \right\}}}.$$
$$\eqalign{{\bf J}_{\rm \Omega}^{\rm NL} &= \displaystyle{{i{\rm \mu} n_q e^3 E_{00}^2 \,e^{( - x^2/r_0^2 f^2 )}} \over {4m^2 {\rm \omega} _0^2}} \left[ {\displaystyle{{2x} \over {r_0^2 f^3}} \displaystyle{1 \over \Omega} {\hat x }}\right. \cr & \quad \left. - \left\{ {\displaystyle{1 \over {{\rm \upsilon} _{\rm g} f}} + \displaystyle{1 \over {f^2 {\rm \Omega}}} \left( {\displaystyle{{2x^2} \over {r_0^2 f^2}} - 1} \right) \displaystyle{{\partial f} \over {\partial z}}} \right\}{\hat z} \right] e^{i\left\{ {{\rm \Omega} t - \left( {{{\rm \Omega} \over {{\rm \upsilon} _{\rm g}}} + k_q} \right)z} \right\}}}.$$This nonlinear current gives rise to THz wave at frequency Ω and wave number Ω/υ g+k q, which is governed by the wave equation
where
As the nonlinear current given by Eq. (14), is responsible for the THz generation, the THz field will also vary as ~ei (Ωt −kTz). Using Eqs. (14) and (15), the x-component of Eq. (15) is obtained as
 $$\eqalign{& 2ik_T \displaystyle{{{\partial} E_{Tx}} \over {{\partial} z}} + \left[ {\displaystyle{{{\rm \Omega} ^2} \over {c^2}} \left( {1 - \displaystyle{{{\rm \omega} _{\rm P}^2} \over {{\rm \Omega} ^2}}} \right) - k_T^2} \right]E_{Tx} \cr & \quad \cong \displaystyle{{ - 1} \over 2}\left( {\displaystyle{{n_q} \over {n_0}}} \right)\left( {\displaystyle{{{\rm \omega} _{\rm P}^2} \over {{\rm \omega} _0^2}}} \right)\displaystyle{{eE_{00}^2 {\rm \mu} x} \over {mc^2 r_0^2 f^3}} e^{ - \displaystyle{{x^2} \over {r_0^2 f^2}}} e^{ - i({{\rm \Omega} / {\upsilon _{\rm g} + k_q}} - k_T )z}}. $$
$$\eqalign{& 2ik_T \displaystyle{{{\partial} E_{Tx}} \over {{\partial} z}} + \left[ {\displaystyle{{{\rm \Omega} ^2} \over {c^2}} \left( {1 - \displaystyle{{{\rm \omega} _{\rm P}^2} \over {{\rm \Omega} ^2}}} \right) - k_T^2} \right]E_{Tx} \cr & \quad \cong \displaystyle{{ - 1} \over 2}\left( {\displaystyle{{n_q} \over {n_0}}} \right)\left( {\displaystyle{{{\rm \omega} _{\rm P}^2} \over {{\rm \omega} _0^2}}} \right)\displaystyle{{eE_{00}^2 {\rm \mu} x} \over {mc^2 r_0^2 f^3}} e^{ - \displaystyle{{x^2} \over {r_0^2 f^2}}} e^{ - i({{\rm \Omega} / {\upsilon _{\rm g} + k_q}} - k_T )z}}. $$
Using ![]() $k_T = ({\rm \Omega} /c)\left( {1 - \left( {{\rm \omega} _{\rm P}^2 /{\rm \Omega} ^2} \right)} \right)^{{1 / 2}} $, and applying exact phase-matching condition k T = Ω/υ g+k q, Eq. (17) becomes
$k_T = ({\rm \Omega} /c)\left( {1 - \left( {{\rm \omega} _{\rm P}^2 /{\rm \Omega} ^2} \right)} \right)^{{1 / 2}} $, and applying exact phase-matching condition k T = Ω/υ g+k q, Eq. (17) becomes
 $$\displaystyle{{\partial} \over {{\partial} z}}\left( {\displaystyle{{E_{Tx}} \over {E_{00}}}} \right) = \displaystyle{i \over 4}\left( {\displaystyle{{n_q} \over {n_0}}} \right)\left( {\displaystyle{{\omega _{\rm P}^2} \over {{\rm \omega} _0^2}}} \right)\left( {\displaystyle{{eE_{00}} \over {mc^2}}} \right)\left( {\displaystyle{{{\rm \mu} x} \over {r_0^2 k_T}}} \right)\displaystyle{{e^{\left( { - \displaystyle{{x^2} \over {r_0^2 f^2}}} \right)}} \over {\,f^3}}. $$
$$\displaystyle{{\partial} \over {{\partial} z}}\left( {\displaystyle{{E_{Tx}} \over {E_{00}}}} \right) = \displaystyle{i \over 4}\left( {\displaystyle{{n_q} \over {n_0}}} \right)\left( {\displaystyle{{\omega _{\rm P}^2} \over {{\rm \omega} _0^2}}} \right)\left( {\displaystyle{{eE_{00}} \over {mc^2}}} \right)\left( {\displaystyle{{{\rm \mu} x} \over {r_0^2 k_T}}} \right)\displaystyle{{e^{\left( { - \displaystyle{{x^2} \over {r_0^2 f^2}}} \right)}} \over {\,f^3}}. $$4. RESULTS AND DISCUSSION
Equation (8) describes the variation in beam width parameter with normalized distance, η where, η = z/R d and 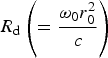 $R_{\rm d} \left( { = {{{\rm \omega} _0 r_0^2} \over c}} \right)$ is the diffraction length. To solve Eq. (8), the following laser–plasma parameters were used: ω 0 = 1.78 × 1014, ω p = 2.5 × 1013, Ω = 3 × 1013 rad s, T 0 = 106 K, n q = 0.3n 0, intensity of laser beam, I = 1014 W cm−2, and initial radius of the laser beam, r 0 = 40 μm.
$R_{\rm d} \left( { = {{{\rm \omega} _0 r_0^2} \over c}} \right)$ is the diffraction length. To solve Eq. (8), the following laser–plasma parameters were used: ω 0 = 1.78 × 1014, ω p = 2.5 × 1013, Ω = 3 × 1013 rad s, T 0 = 106 K, n q = 0.3n 0, intensity of laser beam, I = 1014 W cm−2, and initial radius of the laser beam, r 0 = 40 μm.
The beam width parameter f is plotted with the distance at different times. Plots are shown in Figures 1a and 1b corresponding to modulation indices μ = 0.05 and 0.1, respectively. The beam self-focuses and defocuses in the course of its propagation and the degree of focusing changes with time. Equation (18) was solved numerically and THz amplitude was evaluated at different times and compared with result obtained without considering the effect of self-focusing (i.e., f = 1). The amplitude was found to be enhanced significantly when self-focusing occurs. Further the enhancement was found to be time dependent as expected because of transient focusing of laser beam. Figure 2 shows schematic representation for THz radiation generation in the presence of ripple density plasma. Figures 3a and 3b exhibit the radial profile of the generated THz field amplitude (corresponding to values of modulation indices μ = 0.05 and 0.1, respectively) at different times for n q = 0.3n 0. The peak THz field is obtained at different values of transverse distances at different times. THz amplitude depends upon the generated nonlinear current density which in turn depends on the gradient of intensity of the laser beam. Since the laser beam has the spatial Gaussian profile, the gradient of intensity at the propagation axis is zero. It increases along the radial direction and after attaining the maximum value again starts decreasing. Thus the spatial profile of generated THz amplitude will follow the same trend as shown in Figures 3a and 3b. The line shown in black corresponds to the case without self-focusing [f(z) = 1, i.e., without focusing/defocusing], whereas colored lines correspond to the case with self-focusing at different times. Figures 4a and 4b show the power spectra of generated THz radiation at different times corresponding to the values of modulation indices 0.05 and 0.1, respectively. The lines shown in black and in colors correspond to the cases without and with self-focusing as before. The enhancement in the generated THz amplitude is primarily due to three factors: Modulation index (μ), ripple density amplitude (n q), and dimensionless beam width parameter (f).

Fig. 1. (a) Variation of beam width parameter with normalized distance along the direction of laser propagation for μ = 0.05. (b) Variation of beam width parameter with normalized distance along the direction of laser propagation for μ = 0.1.

Fig. 2. Schematic representation for THz radiation generation in the presence of ripple density plasma.
The efficiency of THz generation that is, the ratio of the energy of the generated THz to the energy of the laser used for the generation, which comes out to be of the order of ~10−4 for the parameters used. As amplitude of the generated THz depends on μ, n q, and f, the choice of their values will play an important role in optimizing the conversion efficiency to the best possible value. It is a matter of choosing these parameters as realistically as possible. Some of the best conversion efficiencies reported so far are ~10−5 (Hamster et al., Reference Hamster, Sullivan, Gordon and Falcon1993), ~5 × 10−4 (Wang et al., Reference Wang, Kawata, Sheng, Li and Zhang2011), ~10−4 (Chen, Reference Chen2013b), and ~10−5 (Wu et al., Reference Wu, Sheng, Dong, Xu and Zhang2007). Thus, the efficiency achieved in the proposed scheme is of the order of those achieved by other researchers using other mechanisms.
5. CONCLUSION
We can conclude that amplitude-modulated Gaussian laser beam self-focuses and defocuses when it propagates in the plasma. In the absence of density ripple, the phase-matching condition for the generated THz wave is not satisfied and hence the generated wave will not be able to propagate even if the dispersion relation is satisfied. The appropriate phase-matching condition is provided by the ripple density plasma. Accordingly, focusing changes with time and THz amplitude get enhanced. We observe significant enhancement in the THz amplitude in comparison with that generated without using self-focusing of the laser. Comparison of the predicted conversion efficiency with the best reported values shows that the THz generation by self-focusing of amplitude-modulated Gaussian laser beam can be a potential scheme for the efficient generation of the radiation.
ACKNOWLEDGMENT
This research was partially supported by the Department of Science and Technology (DST), India and University Grant Commission (UGC), India.








