1. Introduction
The accumulation areas of the Greenland and Antarctic ice sheets are covered with firn, the transitional product as snow metamorphoses into ice. Firn can be regarded as snow that has persisted through the melt season. The firn layer responds to variability and temporal trends of its surface boundary conditions: surface temperature, accumulation rate and surface density (Reference Arthern and WinghamArthern and Wingham, 1998; Reference Ligtenberg, Helsen and Van den BroekeLigtenberg and others, 2011). As a result of such changes, the vertical density and temperature profiles change, and the total thickness of the firn layer (defined as the vertical distance between the surface and the firn/ice interface) also varies. The timescale at which these variations take place is of the order of decades (e.g. Reference HelsenHelsen and others, 2008), so that observations of firn changes are the consequence of many decades of previous changes and variability in the surface climate.
In Greenland, firn is an important link in the chain from surface meltwater production to runoff into the ocean. Firn is a porous medium that provides storage space for percolating surface meltwater. The meltwater can either refreeze, depending on the firn temperature and the capillary capacity between the firn grains; or it can percolate further until it reaches an impermeable interface near the firn/ice transition along which it can run off into the englacial drainage system. Regional modelling studies suggest that ~40–45% of the surface melt in Greenland refreezes in the firn, rather than running off into the ocean (Reference Van AngelenVan Angelen and others, 2012; Reference FettweisFettweis and others, 2013). However, the storage capacity of the firn is still poorly constrained (Reference Harper, Humphrey, Pfeffer, Brown and FettweisHarper and others, 2012; Reference Koenig, Miège, Forster and BruckerKoenig and others, 2014). Careful modelling of the firn hydrology is needed to assess by how much and with what delay a projected increase in surface melt would contribute to sea-level rise.
Also, firn processes are crucial to take into account when converting altimetric estimates of ice-sheet volume change into mass change, both in Greenland and in Antarctica. The density of the firn is modulated by accumulation variability, and by trends in refreezing and densification rate, all depending on temperature. Remote-sensing and in situ observations reveal that both the Antarctic and Greenland firn layers exhibit variability and change. In Antarctica, the firn exhibits an annual cycle of surface elevation change (Reference Ligtenberg, Horwath, Van den Broeke and LegrésyLigtenberg and others, 2012), and multi-decadal variability (Reference Arthern and WinghamArthern and Wingham, 1998; Reference Zwally and LiZwally and Li, 2002; Reference HelsenHelsen and others, 2008). Satellite altimeters observe thinning of ice shelves in the Antarctic Peninsula. It has been suggested that the thinning in this particular region is attributable to thinning of the firn layer rather than thinning of the ice column below (Reference Pritchard, Ligtenberg, Fricker, Vaughan, Van den Broeke and PadmanPritchard and others, 2012), following strong atmospheric warming in that region over recent decades (Reference VaughanVaughan and others, 2003).
In Greenland, there is a discernible change in surface height, with radar altimetry detecting a pattern of thickening in the interior and thinning around the margins (Reference Thomas, Frederick, Krabill, Manizade and MartinThomas and others, 2006). The thinning in parts of the accumulation zone has both an ice-dynamical and a firn-related origin (Reference HurkmansHurkmans and others, 2014). These effects need to be separated carefully to provide an accurate assessment of current mass loss. Over the past 30 years, strong atmospheric warming has been observed both at coastal stations (Reference Hanna, Mernild, Cappelen and SteffenHanna and others, 2012) and on the ice sheet proper (Reference Box, Yang, Bromwich and BaiBox and others, 2009). As a consequence, the percolation zone has moved inland (Reference Fettweis, Tedesco, Van den Broeke and EttemaFettweis and others, 2011; Reference Hall, Comiso, DiGirolamo, Shuman, Box and KoenigHall and others, 2013). Associated meltwater lakes have also migrated inland to higher elevations (Reference Howat, De la Peña, Van Angelen, Lenaerts and Van den BroekeHowat and others, 2013). These developments imply that the firn in the percolation zone is undergoing changes. Surface meltwater production is increasing in the percolation zone, and at the edge of the dryfirn zone a transition is occurring from dry to wet firn.
Not all firn processes act on the same timescale. It is conceivable that an increase in melt and refreezing can achieve a more rapid and larger response of the firn than a temperature increase in the dry-firn zone. In this study, we investigate the response of firn to temperature change in a series of idealized model experiments. Our aim is to determine the fundamental transient behaviour of a firn layer, with an emphasis on the typical timescales for a change in the surface climate to propagate into the firn layer. The response of dry firn to stepwise changes in the surface forcing was studied by Reference Arthern and WinghamArthern and Wingham (1998). They found that the firn requires more time to adapt to changes in surface temperature than to changes in accumulation rate or surface density. Here we expand on these modelling efforts and we also discuss the behaviour of firn experiencing surface melt.
2. The Firn Model
We use a one-dimensional (1-D), time-dependent firn model that divides the firn pack into discrete vertical layers of 4.5–10.5 cm thickness. The total depth of the firn layer is always sufficient to capture the pore close-off density of 830 kg m−3. As fresh snow is added to the surface, layers move down the firn pack in a Lagrangian way, i.e. the properties of each layer (temperature, mass, density, liquid water content) are advected vertically together with the numerical layer. The model is described extensively by Reference Ligtenberg, Helsen and Van den BroekeLigtenberg and others (2011) and Reference Kuipers Munneke, Ligtenberg, Van den Broeke, Van Angelen and ForsterKuipers Munneke and others (2014). For detailed formulas and a discussion on the model assumptions, we refer to those papers. Here we present the model details necessary for understanding the analysis presented here.
For dry-firn compaction, we use the expressions from Reference Arthern, Vaughan, Rankin, Mulvaney and ThomasArthern and others (2010), with a modification factor that depends on the accumulation rate (Reference Ligtenberg, Helsen and Van den BroekeLigtenberg and others, 2011). Meltwater produced at the surface is allowed to percolate into the firn pack, where it will refreeze in any subsurface layer that can accommodate the release of latent heat upon refreezing and has sufficient pore space. Each layer can hold a maximum amount of liquid water, the irreducible water content W c (in mass-%), taken from Reference Coléou and LesaffreColéou and Lesaffre (1998):
where P is the firn porosity defined as P = 1 –(ρ/ρ i), ρ is the snow density and ρ i is the ice density. The downward percolation of meltwater is modelled as a so-called tipping bucket, in which water tips from one layer to the next (within one time step) until a layer is encountered with a liquid water content smaller than the irreducible water content for that layer. This approach is identical to the treatment of percolating liquid water in the snow model Crocus (Reference VionnetVionnet and others, 2012). When meltwater reaches the layer below which the density of all layers exceeds the pore close-off density, it runs off instantaneously.
The thermodynamical part of the model describes (1) the conduction of heat following a 1-D heat-transfer equation; and (2) the heat released upon refreezing of meltwater in the firn. The conductivity of the firn ks (Wm−1 K−1) is a function of density ρ (kg m−3) (Reference AndersonAnderson, 1976):
As in Reference Kuipers Munneke, Ligtenberg, Van den Broeke, Van Angelen and ForsterKuipers Munneke and others (2014), the surface climate is defined by three variables: ḃ (annual accumulation; mm w.e. a−1), T a (mean annual surface temperature; °C) and ΔT (amplitude of a sinusoidal annual cycle of surface temperature T; °C). The surface melt M (mm w.e.) is a function of surface temperature only, using positive degree-days:
where DDFs is a degree-day factor (mm w.e. d−1 °C−1), T 0 is a threshold temperature for melting and Δt is a time period. For DDFs and T 0, we adopt values of 1.5 mm w.e. d−1 °C−1 and –5°C, respectively (Reference Van den Broeke, Bus, Ettema and SmeetsVan den Broeke and others, 2010). Finally, the annual accumulation rate ḃ is distributed evenly over the year. When the surface temperature exceeds the melting point, the accumulation falls as rain, and the liquid water of the rain flux is added to the melt flux.
For each density profile ρ(z), the firn air content F (m) is defined as
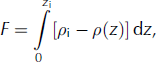
and equals the vertically integrated height of the air column in the firn. We define a response time, τ, as a metric of the time it takes for the firn to reach a new equilibrium after a stepwise increase in the surface temperature. It is defined here as the period of time it takes to complete a fraction ξ of the total change in firn air content ΔF = F(∞) – F(0) after the stepwise temperature change:
Here we use ξ = 0:9, i.e. our response time indicates the time it takes for 90% of the total change in F to occur. Reference Arthern and WinghamArthern and Wingham (1998) took ξ = 0:5 and used the term 'half time', but it will appear that in the case of wet firn, the firn response is not necessarily exponential-like, and in those cases a half time would not be representative of the timescale of the equilibrium change.
3. Firn Without Surface Melt
For a firn layer in steady state, and without surface melt, density increases with depth, from the surface density up to the ice density ρi at the depth of the ice density Z i. In the particular densification expressions by Reference Arthern, Vaughan, Rankin, Mulvaney and ThomasArthern and others (2010), the compaction rate is higher for ρ < 550 kg m−3 than for ρ > 550 kg m−3 for identical firn temperature. This is seen as an inflection in the density profiles in Figure 1b. An oscillation is superimposed on the vertical density profile. This reflects the increased compaction rate of the near-surface layers during summer. The amplitude of the surface temperature is dampened with depth (Fig. 1c and d), and the deep-firn temperature equals T a, the annual mean surface temperature.

Fig. 1. Example of a dry firn layer experiencing a stepwise surface temperature increase of 1°C at t = 10 years. (a) Density (kg m−3); (b) density profile before temperature increase (black) and in steady state after the temperature increase (red); (c) temperature (°C); and (d) firn temperature profile before temperature increase (black) and 70 years after the temperature increase (red).
To study the reaction of the firn layer to a change in surface climate, we perturbed the surface temperature with a stepwise change of 1°C, at time t = 10 years in the model simulation. Figure 1a and c show the subsequent evolution of density and firn temperature. In this example, ḃ = 300 mm w.e. a−1, T a = –20°C and ΔT = 12°C. As a result of increasing temperature, the densification rate increases. Due to both advection and conduction, the heat travels downward into the firn pack. Temperature profiles at t = 0 and t = 80 years are shown in Figure 1d. After 70 years (at t = 80 years), the firn has heated to ~14 m depth. Ultimately, the firn will have heated by 1°C along its entire vertical extent.
The results of a series of warming experiments for different accumulation rates are shown in Figure 2. The response time decreases with increasing accumulation rate (under the same temperature forcing): the higher accumulation rate enables a faster downward advection of warmer firn (black dots in Fig. 2a). Additionally, we performed a series of experiments in which we returned to the original climate by a stepwise temperature decrease (red dots in Fig. 2a). The return to the colder climate takes place a little faster than in the warming experiment, by ~5–10%. There are at least three explanations for this behaviour. First, the compaction rate of the warmer firn is higher, helping to adjust the warmer layer to a new equilibrium more rapidly. Second, the conductivity of the firn is higher for higher density (Eqn (2)). The warmer firn has a higher density, hence the conductivity is increased. The stepwise cooling of the warm firn layer is thus conducted more rapidly into the firn than the stepwise warming of the initial, cool firn. Third, the warmer firn layer is thinner because of the increased density, reducing the vertical distance the cooling signal has to travel.
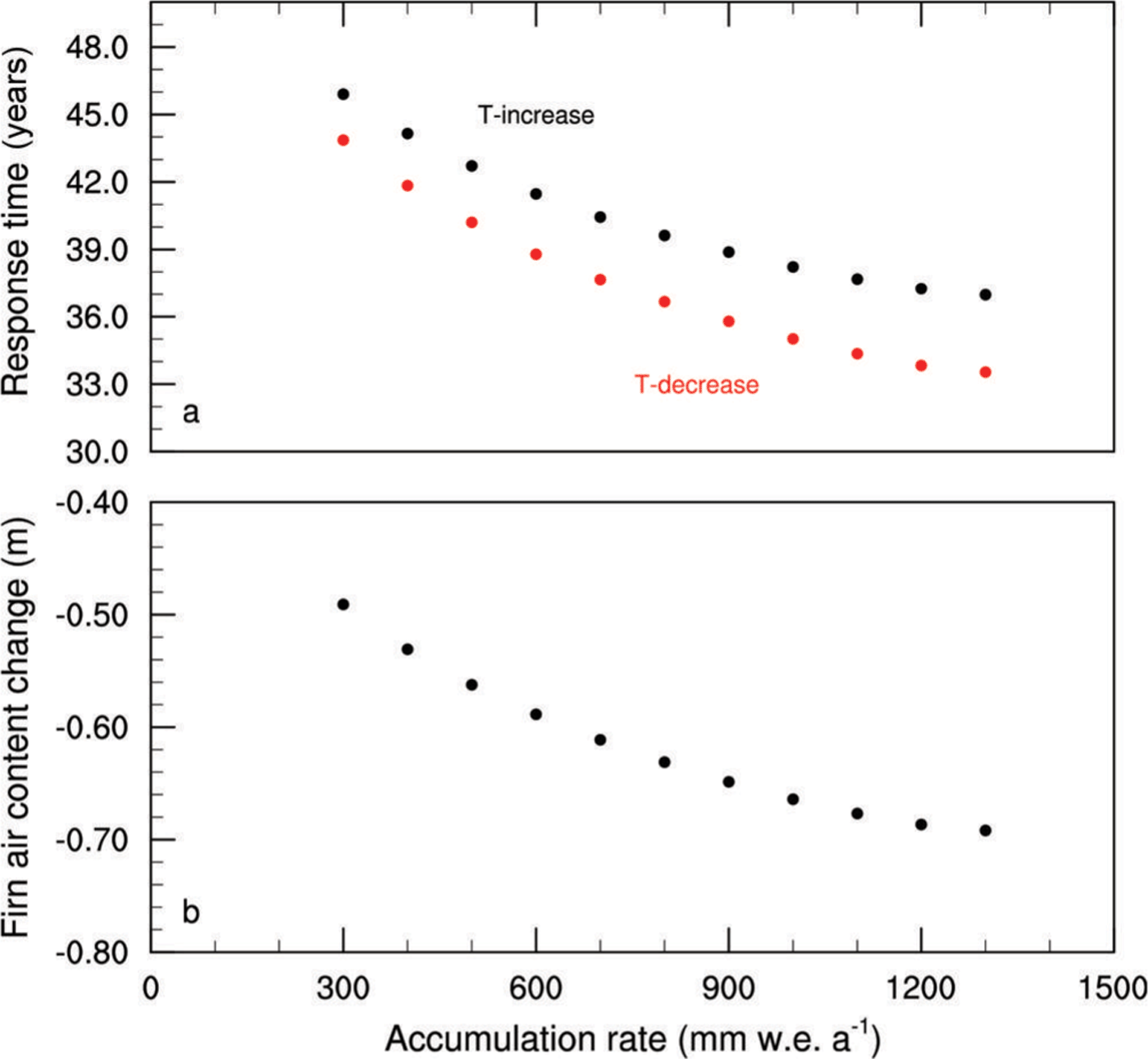
Fig. 2. (a) Response time of the firn layer after a stepwise temperature increase (black) or decrease (red) of 1°C, as a function of accumulation rate. (b) Equilibrium change in firn air content after warming.
Figure 2b shows that the absolute value of the equilibrium change, F(∞) – F(0), increases with accumulation rate. For higher accumulation rates, the mean density of the firn is reduced and the thickness of the firn is increased. The adjustment for higher accumulation rates is therefore larger.
We also found that the change in firn air content after the return to the colder climate (not shown) was equal and of opposite sign to the change following the warming shown in Figure 2b. It thus appears that the response of dry firn to changes in the surface forcing is linear and does not point to the existence of multiple equilibrium states.
4. Firn With Surface Melt
In dry firn, the vertical temperature profile is determined mainly by vertical conductive heat transfer (Reference Arthern and WinghamArthern and Wingham, 1998). At sufficient depth, the constant firn temperature equals the climatological mean surface temperature. Meltwater percolation, however, represents a mechanism to greatly increase the vertical advective heat transfer, raising the deep-firn temperature when the meltwater refreezes. Experimental evidence of this process is provided by a study employing thermistor strings along a transect from low to high elevation in the western percolation zone of the Greenland ice sheet (Reference Humphrey, Harper and PfefferHumphrey and others, 2012). They find that firn temperature at 10 m depth is higher than the annual mean surface temperature, by values in excess of 11°C. In observations of the Greenland firn aquifer, the deep-firn temperature is at the melting point (Reference Koenig, Miège, Forster and BruckerKoenig and others, 2014).
4.1. Deep-firn Temperature
We investigate the relation between the annual accumulation rate, melt rate and the deep-firn temperature (>15 m), given a fixed mean annual surface temperature. In Figure 3, we show the results for the particular example of T a = –12°C, melt rates M ranging from 100 to 300 mm w.e. a−1, and accumulation rates ḃ in the range 500–3000 mm w.e. a−1. Looking at the results in Figure 3, we make the following observations:
-
1. Almost everywhere, an increasing melt rate leads to a higher deep-firn temperature, for all accumulation rates;
-
2. For M = 100 mm w.e. a−1 (red line), the deep-firn temperature is around –11°C, and this value slightly increases for increasing accumulation rate;
-
3. For melt rates of 220 mm w.e. a−1 and higher (darkgreen, blue and violet lines), there is a sharp transition in deep-firn temperature for accumulation rates around 900–1200 mm w.e. a−1. For lower accumulation rates, the deep-firn temperature is in the range 10 to –7°C, and for higher accumulation rates the range is –5 to 0°C;
-
4. When the melt rate is 300 mm w.e. a−1 (violet line), the deep firn is at the melting point for accumulation rates between 1500 and 2500 mm w.e. a−1. For even higher accumulation rates, the deep-firn temperature falls below freezing again.

Fig. 3. Equilibrium deep-firn temperature as a function of accumulation rate, for Ta = –12°C. The melt rate varies for each line, and is indicated with the labels at the right (in mm w.e. a−1).
To explain these observations, we need to realize that the vertical temperature profile of a wet firn layer is determined by two processes: the release of latent heat upon refreezing of percolating meltwater, and the vertical diffusion of heat, both upward and downward. Additionally, the accumulation rate determines the rate at which a refrozen layer (with its associated release of latent heat) is buried below the surface. When the accumulation rate is low, the refreezing occurs close to the surface, and a large fraction of the released latent heat is able to diffuse upward, and then out of the firn into the atmosphere. For high accumulation rates, however, more released latent heat gets trapped in the firn and is advected downward. This process is closely related to the explanation for the formation of firn aquifers, i.e. perennial bodies of liquid water in the firn pack (Reference ForsterForster and others, 2014; Reference Kuipers Munneke, Ligtenberg, Van den Broeke, Van Angelen and ForsterKuipers Munneke and others, 2014): liquid water is isolated from the winter cold by sufficiently large accumulation rates.
The influence of accumulation rate on the vertical profiles of density, temperature and liquid water is demonstrated in Figure 4. Figure 4a–c show vertical profiles for an accumulation rate of 600 mm w.e. a−1 and a melt rate of 220 mm w.e. a−1. Figure 4d–f show the same profiles for an accumulation rate of 1500 mm w.e. a−1. Of particular interest is the difference in liquid water profiles, with percolating meltwater extending up to 3.5 m below the surface in the high-accumulation case (Fig. 4c), whereas liquid water does not penetrate deeper than 1.5 m below the surface in the low-accumulation case (Fig. 4f). For the high-accumulation case, it causes the delivery of latent heat sufficiently deep to isolate it from the winter cold. As a consequence, the deep-firn temperature for the high-accumulation scenario (Fig. 4e) is >4°C higher than for the low-accumulation scenario (Fig. 4b).

Fig. 4. Effect of accumulation rate on (a, d) density, (b, e) temperature and (c, f) liquid water content, for M = 220 mm w.e. a−1, and ḃ = 600 mm w.e. a−1 (a–c) and 1500 mm w.e. a−1 (d–f). Note that the vertical scales in (c) and (f) differ from those in the other panels.
The explanation for observation 1 follows from a larger release of latent heat for higher melt rates. Observation 2 can now be explained because some released latent heat of refreezing is buried in the firn. The deep-firn temperature is therefore ~1°C higher than the mean annual surface temperature. This confirms the field observations made by Reference Humphrey, Harper and PfefferHumphrey and others (2012) and Reference Koenig, Miège, Forster and BruckerKoenig and others (2014). The deep-firn temperature increases for higher accumulation rate, as more released latent heat is buried.
However, there are some remarkable transitions in the deep-firn temperature as the accumulation increases (observation 3). For low accumulation rates, most refreezing occurs close to the surface, and most of the upward-diffused latent heat is lost to the atmosphere. For higher accumulation rates, the released latent heat is advected downward faster, leading to a higher deep-firn temperature.
Observation 4 relates to the presence of a firn aquifer. The amount of released latent heat is so large that the melting point is reached in the deep firn. No more refreezing can occur, and liquid water can remain in the firn at depth. For even higher accumulation rates (3500 mm w.e. a−1 in this example), the cold content of the winter accumulation becomes so large that all meltwater is eventually refrozen, allowing for deep-firn temperatures below the melting point again (see also Reference Kuipers Munneke, Ligtenberg, Van den Broeke, Van Angelen and ForsterKuipers Munneke and others, 2014).
4.2. Response time
The response of wet firn to warming consists of several processes. First, the densification rate increases at higher temperatures (as with dry firn), which will lead to a denser and shallower firn column. However, the introduction of melt constitutes an additional mechanism that reduces the depth of the firn/ice interface. Increased melt increases the firn density, and leads to an increase in runoff, such that the new equilibrium firn layer consists of both less and denser firn. But there is an additional feedback process: the deep-firn temperature increases because of burial of the latent heat released upon refreezing (see Section 4.1). This temperature increase results in an additional increase in densification rate, which itself is a function of temperature. It can thus be expected that a larger increase in deep-firn temperature leads to a larger response of the firn layer (in terms of firn air or surface height).
The complicated relation between accumulation rate and deep-firn temperature, explained in Section 3, has implications for the response of a firn layer experiencing surface melt to a change in surface temperature. We present the response time (defined in Eqn (5)) of a firn layer with T a = 12−1°C and an initial melt rate M = 100 mm w.e. a−1 in Figure 5a, both for a stepwise temperature increase of 1°C and for the subsequent stepwise return to the colder climate. Figure 5b shows the equilibrium deep-firn temperatures before and after the temperature increase. Figure 5c shows the equilibrium change in firn air content after warming. In Figure 5d, the response of the firn to a stepwise warming (expressed in the firn air content F) is shown for different accumulation rates. The stepwise temperature increase of 1°C at t = 10 years leads to a new T a of –11°C, and a corresponding melt rate M = 220 mm w.e. a−1.
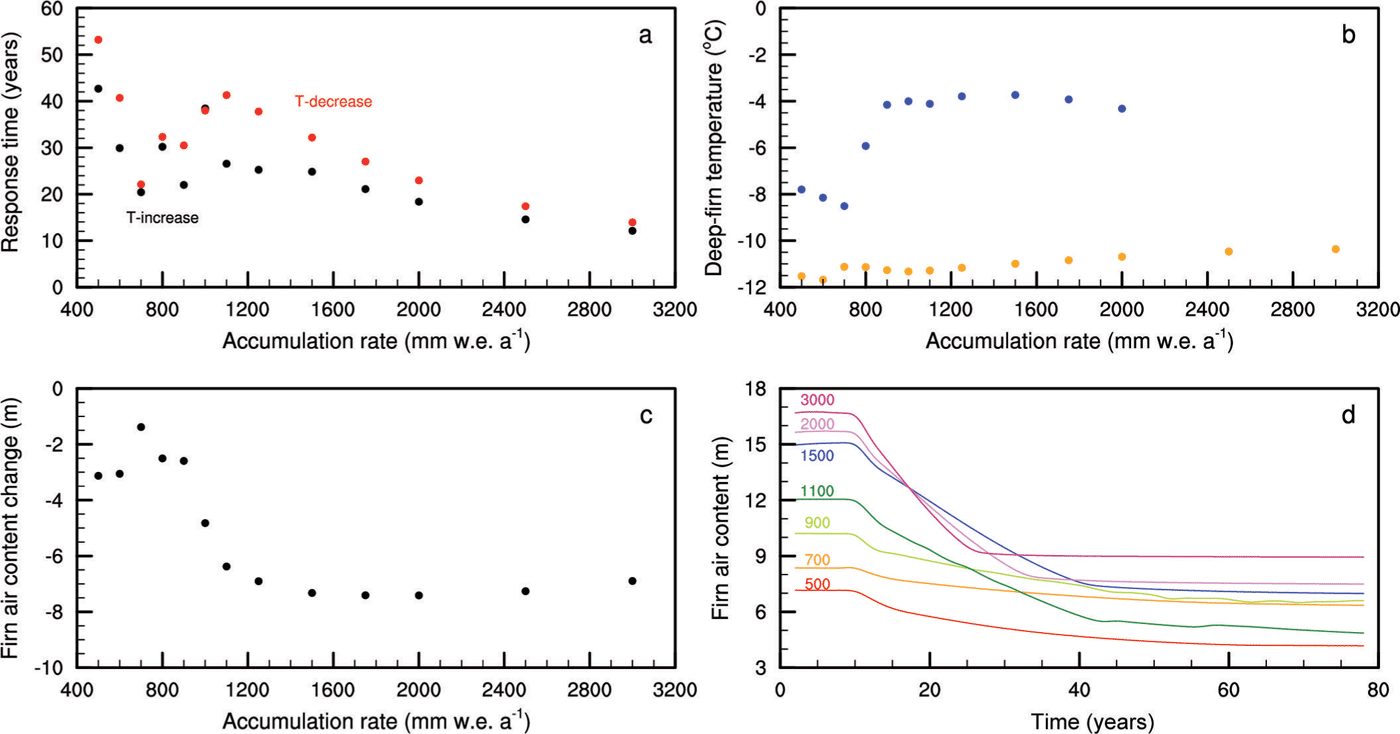
Fig. 5. Results of the idealized experiment in which an initial firn layer with T a = –12°C and M = 100 mm w.e.a−1 is subject to a stepwise warming of 1°C, leading to a new melt rate of 220 mm w.e. a−1. (a) Response time for stepwise warming (black) and cooling (red). (b) Deep-firn temperature before (orange) and after (blue) the stepwise warming. (c) Equilibrium change in the firn air content before and after the warming. (d) Change in firn air content as a function of time for selected accumulation rates (given in the coloured labels, in mm w.e. a−1). The lines in (d) are low-pass filtered to remove the annual signal in firn-air content, for clarity.
Above ḃ = 1100 mm w.e. a−1, the response time decreases with increasing accumulation rate, as in the case of dry firn. In this range of accumulation rates, the difference in equilibrium deep-firn temperature is approximately constant at ~7°C. The higher accumulation rate ensures a more rapid adaptation from the firn to the new climate state. For accumulation rates below 1000 mm w.e. a−1, one would expect an even longer response time. However, for those accumulation rates, the deep firn does not heat up as much, by a mere 3–4°C. As a result, both the magnitude of the response (measured in firn air content F) and the response time are reduced.
Contrary to dry firn, the response to stepwise warming is considerably faster than the return to the original climate by a stepwise cooling of the same magnitude (by up to 40% in the example provided in Fig. 5). We propose that the downward percolation of meltwater allows for increased downward transport of heat, which enhances the adjustment to a warmer climate. Percolation, under the influence of gravity, is a one-way process, so the return to a colder climate will take longer. Also, the rate of build-up of firn is limited by the accumulation rate, whereas the depletion is not. This may explain why the difference in build-up and depletion decreases as the accumulation rate increases. In general, the infilling and depletion of firn occurs at shorter timescales than its build-up.
5. Discussion and Conclusions
5.1. Model limitations and sensitivity to experiment set-up
The modelling of polar firn including dynamic meltwater hydrology is still relatively novel (Reference Ligtenberg, Helsen and Van den BroekeLigtenberg and others, 2011; Reference GasconGascon and others, 2014; Reference Kuipers Munneke, Ligtenberg, Van den Broeke, Van Angelen and ForsterKuipers Munneke and others, 2014; Reference PolashenskiPolashenski and others, 2014). The seasonal snow community has been studying snow hydrology with relatively sophisticated models for a longer time (Reference Bartelt and LehningBartelt and Lehning, 2002; Reference VionnetVionnet and others, 2012; Reference Wever, Fierz, Mitterer, Hirashima and LehningWever and others, 2014), and the polar firn community is rapidly catching up by including more advanced techniques in its models. The model in the current study can be improved, and we discuss a few examples of such improvements below. We try to assess how such model improvements impact the results presented above. The first three points deal with the set-up of the firn modelling experiments; the final two points pertain to the model physics.
5.1.1. Degree-day formulation
Reference Kuipers Munneke, Ligtenberg, Van den Broeke, Van Angelen and ForsterKuipers Munneke and others (2014) have found that the approximation of the annual temperature by a sinusoidal function leads to an overestimation of summer temperature and hence summer melt. Also, due to the presence of a melting surface in summer, it can be expected that an actual temperature increase over the Greenland ice sheet will be smaller in summer than in the other seasons. For the wet-firn experiments, this means that the warming by 1°C likely leads to a larger melt increase than could be expected from an annual mean temperature increase of 1°C. It implies that the wet-firn response may be smaller than presented in this study, given a certain increase in annual mean temperature.
5.1.2. Diurnal temperature variations
In the present study, we assume an annual temperature cycle in surface temperature, but no diurnal cycle. This could inhibit the formation of night-time ice layers close to the surface, and thus influence the temperature and density profiles. We tested the effect of including day- and nighttime temperatures by superimposing a sinusoidal diurnal cycle with an amplitude of 3°C on top of the surface temperature T a. Its effect on the steady-state deep-firn temperatures is shown in Figure 6 (solid lines with solid circle markers). While the daily and annual mean T a remains unchanged, it appears that the deep-firn temperature is higher by 1–2.5°C compared to the situation in which the diurnal cycle was omitted. The continuous melting and refreezing in the top layers leads to a somewhat denser and thicker summer melt layer (not shown). The enhanced conductivity enables a more rapid downward diffusion of temperature.

Fig. 6. Equilibrium deep-firn temperature as a function of accumulation rate for T a = 12°C. The melt rate varies for each line, and is indicated with the labels at the right (mm w.e. a−1), the label colours corresponding to the line colours. Dashed lines signify reference experiment (identical to the lines in Fig. 3). Solid lines with circle markers signify the experiment with daily temperature cycle. Solid lines with open square markers signify the experiment with annual density cycle.
5.1.3. Varying fresh snow density
In polar snow, the co-occurrence of high fresh-snow density and low temperature is well known. As an experiment, we modulated the annual mean density of 300 kg m−3 by an annual cycle with an amplitude of 75 kg m−3, with the highest density occurring in midwinter. Its effect on the modelled deep-firn temperature is shown in Figure 6 (solid line with open square markers). Deep-firn temperatures are generally lower by 0.5–2.0°C. In this experiment, the low-density summer snow has more capacity to hold and refreeze surface meltwater. As a consequence, the meltwater does not percolate as deep as in the reference experiment. As a result, latent heat of refreezing is released closer to the surface, so that the deep firn remains colder.
5.1.4. Saturated snow layers
The current model does not allow for the presence of liquid water above the irreducible water content W c. This means that the snowpack is free-draining and cannot be saturated (e.g. above an impermeable ice layer). Detailed observations in the percolation zone of the Greenland ice sheet (H. Machguth, unpublished information) reveal that an ice layer that can sustain standing water needs to be quite thick (1 m to several metres). Otherwise, the meltwater manages to find a way down, presumably through cracks and openings in a horizontally heterogeneous ice layer. This means that our assumption of free drainage is probably valid for the climate under consideration in this study.
5.1.5. Heterogeneous percolation
The response of wet firn is complicated, because of the feedback between refreezing, firn temperature and density. Both the amount and the depth of refreezing therefore impact the model results. In our study, the vertical transport of meltwater is described as a tipping-bucket method, which is essentially a variant of homogeneous wetting-front motion. No heterogeneous vertical water transport is allowed: a process also known as piping (Reference Marsh and WooMarsh and Woo, 1984). Field observations show that piping is a widespread phenomenon in Greenland firn (Reference Humphrey, Harper and PfefferHumphrey and others, 2012). It presents a mechanism by which meltwater can be transported downward (and eventually evacuated at the bottom of the firn layer) without the necessity to heat up the entire firn layer to the melting point first. The introduction of heterogeneous meltwater flow causes little change to the timing and magnitude of runoff in seasonal snow covers (Reference Wever, Fierz, Mitterer, Hirashima and LehningWever and others, 2014). For firn, however, the percolation scheme determines the vertical distribution of refreezing, and the associated latent heat release. The model results may thus change when a different formulation for meltwater percolation is chosen.
From the above discussion and sensitivity tests, it is clear that the findings in this paper are qualitatively robust. However, the precise numerical results depend on the choice of model and experiment set-up. A variation in the surface boundary conditions (fresh-snow density, surface temperature forcing) is shown to affect the vertical temperature and density profiles, and therewith the response of the firn layer to a change in the surface forcing. The main caveat in this study is likely the modelling of meltwater percolation. A more sophisticated treatment of percolation is required to further constrain the possible response of percolation-zone firn to climate change.
5.2. Conclusions
We have studied the response of firn with and without surface melting to a stepwise temperature change, using a firn model that includes simple meltwater hydrology. The model is driven by an idealized surface climate that is characterized by a positive degree-day relation between temperature and melt, and a constant accumulation rate.
In dry firn, we found that the response of the firn to a stepwise warming is slower than the response to a subsequent cooling to the original climate, by ~5–10%. We attribute this difference in response time to three effects: First, the densification rate is higher for warmer snow, enabling a more rapid response. Second, the conductivity of the warmer firn is higher because the density is higher. And third, the warmer firn layer is thinner, allowing for a faster response. The response time decreases for increasing accumulation rate, as higher accumulation allows for a faster replacement of firn.
In wet firn, we find that the response to warming is complicated by an interplay between refreezing, firn temperature and firn density. It stands out that, for a given temperature change, the equilibrium response of firn air content is much larger for wet firn than for dry firn. A particular temperature increase will thus lead to a much larger response in the percolation zones than in the dry-snow zone. The response time of wet firn generally decreases for higher accumulation rates, but is complicated by the behaviour of the deep-firn temperature. If the deep firn is heated significantly due to the surface temperature increase, the response time is increased. The depletion of firn following warming is faster than the build-up following cooling. Increased percolation of meltwater can enhance the downward transport of latent heat in the case of warming, while there is no such mechanism that can enhance the downward transport of a cooling signal. Also, the build-up rate of the firn layer is limited by the accumulation rate, while the depletion is not. This means that the wastage of the firn layer and the disappearance of firn occurs at shorter timescales than a full recovery of the firn layer after a cooling back to the original climate.
Acknowledgements
We thank two anonymous reviewers for suggestions that helped to improve the paper. This work was funded by the Netherlands Polar Programme (NPP) grant 866.10.112, provided by the Netherlands Institute for Scientific Research (NWO). Graphics were made using the NCAR Command Language (version 6.1.3, 2013).








