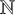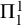1 Introduction
1.1 Motivation
Mathematicians often face the need to express very large quantities for one reason or another. In some extreme occasions, these numbers are incomprehensibly large. Examples include Graham’s number
![]() $g_{64}$
(see Gardner [Reference Gardner10]; see also Graham-Rothschild [Reference Graham and Rothschild14]) or Friedman’s tree number
$g_{64}$
(see Gardner [Reference Gardner10]; see also Graham-Rothschild [Reference Graham and Rothschild14]) or Friedman’s tree number ![]() (see Friedman [Reference Friedman9]). These immense numbers are completely foreign to our everyday experience, and so we would naturally like to attempt to provide a sense of scale for them. The way this is usually done is via fast-growing hierarchies, collections of functions
(see Friedman [Reference Friedman9]). These immense numbers are completely foreign to our everyday experience, and so we would naturally like to attempt to provide a sense of scale for them. The way this is usually done is via fast-growing hierarchies, collections of functions
![]() $f_\alpha :\mathbb {N}\to \mathbb {N}$
, where
$f_\alpha :\mathbb {N}\to \mathbb {N}$
, where
![]() $\alpha $
ranges over elements of
$\alpha $
ranges over elements of
![]() $\mathbb {N}$
, or possibly even over transfinite numbers, and each
$\mathbb {N}$
, or possibly even over transfinite numbers, and each
![]() $f_\alpha $
eventually dominates
$f_\alpha $
eventually dominates
![]() $f_\beta $
, for all
$f_\beta $
, for all
![]() $\beta <\alpha $
. One is mainly interested in fast-growing hierarchies obtained through a given recursive construction which usually generalizes the process that produces multiplication as iterated addition, exponentiation as iterated multiplication, etc. A commonly known example of such a hierarchy is given by Knuth’s arrow hierarchy (see Knuth [Reference Knuth17]):
$\beta <\alpha $
. One is mainly interested in fast-growing hierarchies obtained through a given recursive construction which usually generalizes the process that produces multiplication as iterated addition, exponentiation as iterated multiplication, etc. A commonly known example of such a hierarchy is given by Knuth’s arrow hierarchy (see Knuth [Reference Knuth17]):
 $$\begin{align*}f_n(a,b) = a \underbrace{\uparrow\uparrow\cdots\uparrow\,}_{n\ \text{times}} b.\end{align*}$$
$$\begin{align*}f_n(a,b) = a \underbrace{\uparrow\uparrow\cdots\uparrow\,}_{n\ \text{times}} b.\end{align*}$$
Fast-growing functions are really the ‘canonical’ way to express the magnitude of large integers and place them into perspective. Knuth’s and other related hierarchies (some of which will be discussed below) have proven to be effective for this purpose and indeed can be used to give bounds for the numbers
![]() $g_{64}$
and
$g_{64}$
and ![]() which illustrate their magnitude to the greatest extent one could perhaps hope for.
which illustrate their magnitude to the greatest extent one could perhaps hope for.
For completely different purposes, logicians – and, in particular, proof theorists – often face the need to talk about large countably infinite ordinal numbers (in fact, large computable ordinal numbers) such as the Bachmann-Howard ordinal
![]() $\psi (\varepsilon _{\aleph _1+1})$
. There is also a ‘canonical’ way to express these via what are known as ordinal collapsing functions. These allow us to make use of uncountable numbers to express large countably infinite (and indeed computable) numbers. In this article, we will prove an isomorphism theorem (Theorem 14 on p. 12) according to which the two constructions – ordinal collapsing functions and fast-growing hierarchies – can be regarded as one and the same.
$\psi (\varepsilon _{\aleph _1+1})$
. There is also a ‘canonical’ way to express these via what are known as ordinal collapsing functions. These allow us to make use of uncountable numbers to express large countably infinite (and indeed computable) numbers. In this article, we will prove an isomorphism theorem (Theorem 14 on p. 12) according to which the two constructions – ordinal collapsing functions and fast-growing hierarchies – can be regarded as one and the same.
1.2 Fast-growing hierarchies
Let us focus our attention on hierarchies of unary functions. Fast-growing hierarchies can be defined in various ways, and doing so often results in one hierarchy being a refinement of another. Another example is the Hardy hierarchy (introduced by Wainer [Reference Wainer25], though implicit in G. H. Hardy’s [Reference Hardy15] construction of a subset of
![]() $\mathbb {R}$
of cardinality
$\mathbb {R}$
of cardinality
![]() $\aleph _1$
), the iterative fast-growing hierarchy and the binary fast-growing hierarchy. Let us focus on the latter one, for the sake of definiteness, though we remark that the constructions in this article could be adapted to the other hierarchies. It is defined by transfinite induction according to the following construction:
$\aleph _1$
), the iterative fast-growing hierarchy and the binary fast-growing hierarchy. Let us focus on the latter one, for the sake of definiteness, though we remark that the constructions in this article could be adapted to the other hierarchies. It is defined by transfinite induction according to the following construction:
 $$ \begin{align*} B_0(n) &= n+1&\\ B_{\alpha+1}(n) &= B_\alpha\circ B_\alpha(n)&\\ B_\lambda(n) &= B_{\lambda[n]}(n), &\text{ at limit stages,} \end{align*} $$
$$ \begin{align*} B_0(n) &= n+1&\\ B_{\alpha+1}(n) &= B_\alpha\circ B_\alpha(n)&\\ B_\lambda(n) &= B_{\lambda[n]}(n), &\text{ at limit stages,} \end{align*} $$
where for each limit ordinal
![]() $\lambda $
,
$\lambda $
,
![]() $\{\lambda [n]:n\in \mathbb {N}\}$
is a sequence which converges to
$\{\lambda [n]:n\in \mathbb {N}\}$
is a sequence which converges to
![]() $\lambda $
, fixed in advance. The precise functions defined depend on the sequences chosen, but for natural choices of sequences, the functions behave very regularly. The ordinal
$\lambda $
, fixed in advance. The precise functions defined depend on the sequences chosen, but for natural choices of sequences, the functions behave very regularly. The ordinal
![]() $\varepsilon _0$
is defined by
$\varepsilon _0$
is defined by
![]() $B_{\varepsilon _0}$
is a total recursive function whose totality cannot be proved in Peano Arithmetic (or, equivalently, Arithmetical Comprehension,
$B_{\varepsilon _0}$
is a total recursive function whose totality cannot be proved in Peano Arithmetic (or, equivalently, Arithmetical Comprehension,
![]() ${\mathsf {ACA_0}}$
). The foundational significance of fast-growing functions was observed by Ackermann and, later, by Kreisel [Reference Kreisel18].
${\mathsf {ACA_0}}$
). The foundational significance of fast-growing functions was observed by Ackermann and, later, by Kreisel [Reference Kreisel18].
Theorem 1 (Kreisel 1952, essentially).
There is a canonical well-ordering W of
![]() $\mathbb {N}$
of length
$\mathbb {N}$
of length
![]() $\varepsilon _0$
such that the following theories prove the same
$\varepsilon _0$
such that the following theories prove the same
![]() $\Pi ^0_2$
theorems:
$\Pi ^0_2$
theorems:
-
1. Arithmetical Comprehension;
-
2. Primitive Recursive Arithmetic +
 $\{B_\alpha $
is total
$\{B_\alpha $
is total
 $:\alpha \in W\}$
.
$:\alpha \in W\}$
.
In particular, the two theories are equiconsistent.
Kreisel’s theorem is a computational analysis of arithmetic in the sense that it gives an explicit characterization of the recursive functions which are provably total.
1.3 Fast-growing functions and ordinal denotation systems
Kreisel’s result is of great foundational significance and has led to a great deal of metamathematical and combinatorial results in the context of arithmetic, as well as generalizations to stronger systems. For instance, one can prove a version of Kreisel’s theorem for the subsystem
![]() $\Pi ^1_1$
-
$\Pi ^1_1$
-
![]() ${\mathsf {CA_0}}$
of analysis where
${\mathsf {CA_0}}$
of analysis where
![]() $B_{\varepsilon _0}$
is replaced by
$B_{\varepsilon _0}$
is replaced by
![]() $B_{\psi _0(\aleph _\omega )}$
(see Buchholz [Reference Buchholz4]). Here,
$B_{\psi _0(\aleph _\omega )}$
(see Buchholz [Reference Buchholz4]). Here,
![]() $\psi _0(\aleph _\omega )$
is the Takeuti ordinal, a recursive ordinal that is most easily described by ordinal collapsing functions for the uncountable cardinals
$\psi _0(\aleph _\omega )$
is the Takeuti ordinal, a recursive ordinal that is most easily described by ordinal collapsing functions for the uncountable cardinals
![]() $\aleph _n$
, where
$\aleph _n$
, where
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
![]() $\Pi ^1_1$
-
$\Pi ^1_1$
-
![]() ${\mathsf {CA_0}}$
is a historically and mathematically important theory, and is the strongest of the ‘big five’ subsystems of Second-Order Arithmetic commonly studied in Reverse Mathematics. Ordinal collapsing functions were introduced by Bachmann [Reference Bachmann3] and are a powerful method in proof theory involved in the description of large recursive ordinals, such as the Bachmann-Howard ordinal
${\mathsf {CA_0}}$
is a historically and mathematically important theory, and is the strongest of the ‘big five’ subsystems of Second-Order Arithmetic commonly studied in Reverse Mathematics. Ordinal collapsing functions were introduced by Bachmann [Reference Bachmann3] and are a powerful method in proof theory involved in the description of large recursive ordinals, such as the Bachmann-Howard ordinal
![]() $\psi (\varepsilon _{\aleph _1+1})$
, the Takeuti ordinal and other larger numbers such as the proof-theoretic ordinals of
$\psi (\varepsilon _{\aleph _1+1})$
, the Takeuti ordinal and other larger numbers such as the proof-theoretic ordinals of
![]() ${\mathsf {KPi}}$
and
${\mathsf {KPi}}$
and
![]() ${\mathsf {KP}}$
+
${\mathsf {KP}}$
+
![]() $\Pi _3$
-reflection. These ordinals involve collapsing functions for inaccessible and weakly compact cardinals, respectively; see Rathjen [Reference Rathjen, Cooper and Truss20] for an overview. Indeed, ordinal collapsing functions are the canonical method of speaking about large countable ordinals.
$\Pi _3$
-reflection. These ordinals involve collapsing functions for inaccessible and weakly compact cardinals, respectively; see Rathjen [Reference Rathjen, Cooper and Truss20] for an overview. Indeed, ordinal collapsing functions are the canonical method of speaking about large countable ordinals.
The first observation we make is that fast-growing hierarchies can be regarded as functors on the category of natural numbers with strictly increasing functions as morphisms. This fact was perhaps underpinning the main result of [Reference Aguilera, Freund, Rathjen and Weiermann2]. Let us say more about this observation.
For our purposes, it will be convenient to shift our focus to the norm-based presentation of fast-growing hierarchies. This presentation goes back to [Reference Buchholz, Cichon and Weiermann5] and, for our purposes, is described as follows: suppose that we are given a denotation system D for ordinals. We will use D to index a fast-growing hierarchy. The definition of ‘denotation system’ is recalled in the next section, where these are defined as a particular kind of dilator. The reader unfamiliar with denotation systems might temporarily think of D as a system for representing ordinals in some way using natural numbers as parameters. For example, we may think of representing ordinals
![]() ${<}\omega ^\omega $
as sums of powers of
${<}\omega ^\omega $
as sums of powers of
![]() $\omega $
using integers as parameters together with the symbol ‘
$\omega $
using integers as parameters together with the symbol ‘
![]() $\omega $
’; for example,
$\omega $
’; for example,
The norm
![]() $N\alpha $
of an ordinal
$N\alpha $
of an ordinal
![]() $\alpha $
is the strict supremum of the natural number parameters which occur in the denotation. We define
$\alpha $
is the strict supremum of the natural number parameters which occur in the denotation. We define
Natural numbers can be represented by repeated applications of functions in the hierarchy:
If n is fixed and some constraints are imposed on the values ![]() , then the resulting representation is unique. We define
, then the resulting representation is unique. We define
Making use of the representation of natural numbers in terms of iterations of the fast-growing hierarchy, we can regard
![]() $B_D$
as a functor on the category of natural numbers with strictly increasing functions as morphisms. This is proved in §3.
$B_D$
as a functor on the category of natural numbers with strictly increasing functions as morphisms. This is proved in §3.
From the fact that
![]() $B_D$
is a functor on the category of natural numbers, it follows that
$B_D$
is a functor on the category of natural numbers, it follows that
![]() $B_D$
can be uniquely extended to a finitary functor on the category of linear orders. In particular, expressions of the form (1) can be given transfinite parameters and construed as denotations for elements of some linear order. In §4, we give an alternative (isomorphic) definition of the functor
$B_D$
can be uniquely extended to a finitary functor on the category of linear orders. In particular, expressions of the form (1) can be given transfinite parameters and construed as denotations for elements of some linear order. In §4, we give an alternative (isomorphic) definition of the functor
![]() $B_D$
as a term system performing a formal ordinal collapse of D. Thus, the main contribution of this work is captured by the following:
$B_D$
as a term system performing a formal ordinal collapse of D. Thus, the main contribution of this work is captured by the following:
Fundamental Observation. Binary fast-growing functors are naturally isomorphic to ordinal denotation systems given by ordinal collapses.
This insight is made precise by Theorem 14 on p. 12, which, together with Proposition 9 on p. 10, asserts that the ‘canonical’ method used to refer to large countable numbers is derived from a functorialization of the ‘canonical’ method used to refer to large finite numbers. In particular, we have an object
![]() $B_{D}$
which can be simultaneously viewed through the lenses of two fundamental concepts in Proof Theory (fast-growing functions and ordinal collapses), connecting the two fields of study. For example, we can use fast-growing functors to express the Bachmann-Howard ordinal as
$B_{D}$
which can be simultaneously viewed through the lenses of two fundamental concepts in Proof Theory (fast-growing functions and ordinal collapses), connecting the two fields of study. For example, we can use fast-growing functors to express the Bachmann-Howard ordinal as
where
and where
![]() $\exp $
is the natural exponential functor mapping a linear order X to
$\exp $
is the natural exponential functor mapping a linear order X to
![]() $\omega ^X$
and
$\omega ^X$
and
![]() $\textrm {Add}(1)$
is the addition functor mapping X to
$\textrm {Add}(1)$
is the addition functor mapping X to
![]() $X+1$
.
$X+1$
.
1.4 An application
In §5, we use functorial fast-growing hierarchies to prove a result in Reverse Mathematics. We first show that the ordinal collapses given by
![]() $B_D$
are well-foundedness-preserving, so that if A is a well-order, then so too is
$B_D$
are well-foundedness-preserving, so that if A is a well-order, then so too is
![]() $B_D(A)$
. This justifies us calling
$B_D(A)$
. This justifies us calling
![]() $B_D$
an ‘ordinal denotation system’ rather than a denotation system for elements of some linear order.
$B_D$
an ‘ordinal denotation system’ rather than a denotation system for elements of some linear order.
In fact,
![]() $B_D$
is a functor on the category of ordinal numbers and indeed a dilator. The proof of this fact requires the use of a powerful set-existence principle called
$B_D$
is a functor on the category of ordinal numbers and indeed a dilator. The proof of this fact requires the use of a powerful set-existence principle called
![]() $\Pi ^1_1$
-
$\Pi ^1_1$
-
![]() ${\mathsf {CA_0}}$
, and this is unavoidable: the fact that
${\mathsf {CA_0}}$
, and this is unavoidable: the fact that
![]() $B_D$
is well-foundedness-preserving, in turn, implies
$B_D$
is well-foundedness-preserving, in turn, implies
![]() $\Pi ^1_1$
-
$\Pi ^1_1$
-
![]() ${\mathsf {CA_0}}$
. This way, we obtain a restatement of
${\mathsf {CA_0}}$
. This way, we obtain a restatement of
![]() $\Pi ^1_1$
-
$\Pi ^1_1$
-
![]() ${\mathsf {CA_0}}$
in terms of fast-growing hierarchies and abstract ordinal collapses. We state the theorem; for all undefined terms, we refer the reader to the following section.
${\mathsf {CA_0}}$
in terms of fast-growing hierarchies and abstract ordinal collapses. We state the theorem; for all undefined terms, we refer the reader to the following section.
Theorem 2. The following are equivalent over
![]() ${\mathsf {ACA_0}}$
:
${\mathsf {ACA_0}}$
:
-
1.
 $\Pi ^1_1$
-
$\Pi ^1_1$
-
 ${\mathsf {CA_0}}$
;
${\mathsf {CA_0}}$
; -
2. for every dilator D,
 $B_D$
is a dilator.
$B_D$
is a dilator.
To establish the reversal in Theorem 2, it suffices to consider so-called weakly finite dilators. Theorem 2 fits within the family of results known as well-ordering principles. Most commonly, these are principles of the form ‘if X is a well-order, then
![]() $f(X)$
is a well-order’, where f is some transformation. These principles have been extensively studied in Reverse Mathematics and have led to reformulations of several subsystems of analysis. Some examples are the works of Girard [Reference Girard13], Friedman (unpublished), Hirst [Reference Hirst16], Afshari-Rathjen [Reference Afshari and Rathjen1], Marcone-Montalbán [Reference Marcone and Montalbán19], Rathjen-Valencia Vizcaíno [Reference Rathjen, Vizcaíno, Kahle and Rathjen21], Thomson-Rathjen [Reference Thomson, Rathjen, Kahle and Rathjen23] and [Reference Rathjen, Weiermann, Cooper and Sorbi22]. Higher-type well-ordering principles were used by Girard [Reference Girard11] and Freund [Reference Freund7] to characterize
$f(X)$
is a well-order’, where f is some transformation. These principles have been extensively studied in Reverse Mathematics and have led to reformulations of several subsystems of analysis. Some examples are the works of Girard [Reference Girard13], Friedman (unpublished), Hirst [Reference Hirst16], Afshari-Rathjen [Reference Afshari and Rathjen1], Marcone-Montalbán [Reference Marcone and Montalbán19], Rathjen-Valencia Vizcaíno [Reference Rathjen, Vizcaíno, Kahle and Rathjen21], Thomson-Rathjen [Reference Thomson, Rathjen, Kahle and Rathjen23] and [Reference Rathjen, Weiermann, Cooper and Sorbi22]. Higher-type well-ordering principles were used by Girard [Reference Girard11] and Freund [Reference Freund7] to characterize
![]() $\Pi ^1_1$
-
$\Pi ^1_1$
-
![]() ${\mathsf {CA_0}}$
. Freund’s theorem is an ingredient of our proof of Theorem 2. Freund’s principle maps dilators to well-orderings, while ours and Girard’s map dilators to dilators. Girard’s characterization of
${\mathsf {CA_0}}$
. Freund’s theorem is an ingredient of our proof of Theorem 2. Freund’s principle maps dilators to well-orderings, while ours and Girard’s map dilators to dilators. Girard’s characterization of
![]() $\Pi ^1_1$
-
$\Pi ^1_1$
-
![]() ${\mathsf {CA_0}}$
asserts the totality of the functor
${\mathsf {CA_0}}$
asserts the totality of the functor
![]() $\Lambda $
, which itself is reminiscent of fundamental-sequence–based fast-growing hierarchies. Well-ordering principles for theories such as
$\Lambda $
, which itself is reminiscent of fundamental-sequence–based fast-growing hierarchies. Well-ordering principles for theories such as
![]() $\Pi ^1_1$
-
$\Pi ^1_1$
-
![]() ${\mathsf {CA_0}}$
which are not
${\mathsf {CA_0}}$
which are not
![]() $\Pi ^1_2$
-axiomatizable require the use of higher-type objects such as dilators.
$\Pi ^1_2$
-axiomatizable require the use of higher-type objects such as dilators.
Although throughout this article we focus on the binary fast-growing hierarchy
![]() $B_D$
, we mention that the statement of Theorem 2 applies to many of the other usual fast-growing hierarchies as well. The use of
$B_D$
, we mention that the statement of Theorem 2 applies to many of the other usual fast-growing hierarchies as well. The use of
![]() $B_D$
is merely for convenience and to simplify the computations involved.
$B_D$
is merely for convenience and to simplify the computations involved.
2 Preliminaries
We deal with the category
![]() ${\mathsf {LO}}$
. The objects of
${\mathsf {LO}}$
. The objects of
![]() ${\mathsf {LO}}$
are linear orders whose domains are subsets of
${\mathsf {LO}}$
are linear orders whose domains are subsets of
![]() $\mathbb {N}$
. The morphisms are strictly increasing maps between these orders. We shall work within the subsystem
$\mathbb {N}$
. The morphisms are strictly increasing maps between these orders. We shall work within the subsystem
![]() ${\mathsf {ACA_0}}$
of second-order arithmetic. This is the system in the language of second-order arithmetic (which contains sorts for natural numbers and sets of natural numbers) whose principal axioms are the induction axiom and the schema asserting that every arithmetically definable set exists. When it leads to no confusion, we shall leave the precise formalization of statements to the reader and work informally.
${\mathsf {ACA_0}}$
of second-order arithmetic. This is the system in the language of second-order arithmetic (which contains sorts for natural numbers and sets of natural numbers) whose principal axioms are the induction axiom and the schema asserting that every arithmetically definable set exists. When it leads to no confusion, we shall leave the precise formalization of statements to the reader and work informally.
In the language of second-order arithmetic, one cannot generally speak of functors from
![]() ${\mathsf {LO}}$
to
${\mathsf {LO}}$
to
![]() ${\mathsf {LO}}$
; thus, we shall restrict to dealing with finitary functors (i.e., functors preserving co-limits of upward directed diagrams (direct limits in the model-theoretic sense)). These can be coded by sets of natural numbers:
${\mathsf {LO}}$
; thus, we shall restrict to dealing with finitary functors (i.e., functors preserving co-limits of upward directed diagrams (direct limits in the model-theoretic sense)). These can be coded by sets of natural numbers:
We consider
![]() ${\mathsf {Nat}}$
, the full subcategory of
${\mathsf {Nat}}$
, the full subcategory of
![]() ${\mathsf {LO}}$
where objects are natural numbers n, which we identify with the orders
${\mathsf {LO}}$
where objects are natural numbers n, which we identify with the orders
![]() $([0,n),<)$
. Since both
$([0,n),<)$
. Since both
![]() $\mathsf {Ob}_{\mathsf {Nat}}$
and
$\mathsf {Ob}_{\mathsf {Nat}}$
and
![]() $\mathsf {Mor}_{\mathsf {Nat}}$
are countable, each functor from
$\mathsf {Mor}_{\mathsf {Nat}}$
are countable, each functor from
![]() ${\mathsf {Nat}}$
to
${\mathsf {Nat}}$
to
![]() ${\mathsf {LO}}$
can be coded by a set of natural numbers. Each functor
${\mathsf {LO}}$
can be coded by a set of natural numbers. Each functor
![]() $D\colon {\mathsf {Nat}}\to {\mathsf {LO}}$
can be uniquely extended to a finitary functor
$D\colon {\mathsf {Nat}}\to {\mathsf {LO}}$
can be uniquely extended to a finitary functor
![]() $D\colon {\mathsf {LO}}\to {\mathsf {LO}}$
as follows:
$D\colon {\mathsf {LO}}\to {\mathsf {LO}}$
as follows:
Below, we write
![]() $A'\subseteq _{\mathsf {fin}} A$
if
$A'\subseteq _{\mathsf {fin}} A$
if
![]() $A'$
is a finite subset (or substructure) of A. Given a linear order A, we consider an upward directed diagram
$A'$
is a finite subset (or substructure) of A. Given a linear order A, we consider an upward directed diagram
![]() $H_A$
consisting of all finite suborders
$H_A$
consisting of all finite suborders
![]() $A'\subseteq _{\mathsf {fin}}A$
and all morphisms
$A'\subseteq _{\mathsf {fin}}A$
and all morphisms
![]() $\mathsf {id}_{A'\to A"}$
, for
$\mathsf {id}_{A'\to A"}$
, for
![]() $A'\subseteq _{\mathsf {fin}}A"\subseteq _{\mathsf {fin}}A$
, where
$A'\subseteq _{\mathsf {fin}}A"\subseteq _{\mathsf {fin}}A$
, where
![]() $\mathsf {id}_{A'\to A"}\colon A'\to A"$
denotes the inclusion map given by
$\mathsf {id}_{A'\to A"}\colon A'\to A"$
denotes the inclusion map given by
![]() $\mathsf {id}_{A'\to A"}(x)=x$
. Let
$\mathsf {id}_{A'\to A"}(x)=x$
. Let
![]() $H^{\prime }_A$
be the naturally isomorphic diagram in which all objects are orders in
$H^{\prime }_A$
be the naturally isomorphic diagram in which all objects are orders in
![]() $\mathsf {Ob}_{\mathsf {Nat}}$
. Applying D to all morphisms and objects in
$\mathsf {Ob}_{\mathsf {Nat}}$
. Applying D to all morphisms and objects in
![]() $H^{\prime }_A$
, we obtain a diagram
$H^{\prime }_A$
, we obtain a diagram
![]() $D[H^{\prime }_A]$
and define
$D[H^{\prime }_A]$
and define
where
![]() $\varinjlim D[H^{\prime }_A]$
denotes the co-limit of the diagram. The value
$\varinjlim D[H^{\prime }_A]$
denotes the co-limit of the diagram. The value
![]() $D(f)$
, for an
$D(f)$
, for an
![]() ${\mathsf {LO}}$
-morphism
${\mathsf {LO}}$
-morphism
![]() $f\colon A\to C$
is recovered in the natural way.
$f\colon A\to C$
is recovered in the natural way.
A finitary functor D on
![]() ${\mathsf {LO}}$
coded by a set of natural numbers is called a pre-dilator if it preserves pullbacks. Clearly, D preserves pullbacks if and only if its restriction to
${\mathsf {LO}}$
coded by a set of natural numbers is called a pre-dilator if it preserves pullbacks. Clearly, D preserves pullbacks if and only if its restriction to
![]() ${\mathsf {Nat}}$
preserves pullbacks.
${\mathsf {Nat}}$
preserves pullbacks.
It will be convenient for our purposes to work with inclusion-preserving (or
![]() $\subseteq $
-preserving) functors. These are the functors D such that for any order A and any suborder B of A,
$\subseteq $
-preserving) functors. These are the functors D such that for any order A and any suborder B of A,
-
1.
 $D(B)$
is a suborder of
$D(B)$
is a suborder of
 $D(A)$
, and furthermore,
$D(A)$
, and furthermore, -
2.
 $D(\mathsf {id}_{B\to A})=\mathsf {id}_{D(B)\to D(A)}$
.
$D(\mathsf {id}_{B\to A})=\mathsf {id}_{D(B)\to D(A)}$
.
Finitary
![]() $\subseteq $
-preserving functors were called
$\subseteq $
-preserving functors were called
![]() $\omega $
-local functors by S. Feferman [Reference Feferman6].Footnote
1
For
$\omega $
-local functors by S. Feferman [Reference Feferman6].Footnote
1
For
![]() $\subseteq $
-preserving functors, there are convenient reformulations of the conditions of being a finitary functor and a pre-dilator. Namely, a
$\subseteq $
-preserving functors, there are convenient reformulations of the conditions of being a finitary functor and a pre-dilator. Namely, a
![]() $\subseteq $
-preserving functor D is finitary if and only if for any order A, we have
$\subseteq $
-preserving functor D is finitary if and only if for any order A, we have
An
![]() $\subseteq $
-preserving finitary functor D is a pre-dilator iff for any order A and its suborders
$\subseteq $
-preserving finitary functor D is a pre-dilator iff for any order A and its suborders
![]() $B,C\subseteq A$
we have
$B,C\subseteq A$
we have
![]() $D(B\cap C)=D(B)\cap D(C)$
.
$D(B\cap C)=D(B)\cap D(C)$
.
Working in
![]() ${\mathsf {ACA_0}}$
, we code
${\mathsf {ACA_0}}$
, we code
![]() $\subseteq $
-preserving finitary functors as follows. We consider the full subcategory
$\subseteq $
-preserving finitary functors as follows. We consider the full subcategory
![]() ${\mathsf {FO}}$
of
${\mathsf {FO}}$
of
![]() ${\mathsf {LO}}$
, where objects are finite linear orders. As in the case of
${\mathsf {LO}}$
, where objects are finite linear orders. As in the case of
![]() ${\mathsf {Nat}}$
, both
${\mathsf {Nat}}$
, both
![]() $\mathsf {Ob}_{\mathsf {FO}}$
and
$\mathsf {Ob}_{\mathsf {FO}}$
and
![]() $\mathsf {Mor}_{\mathsf {FO}}$
are countable, so
$\mathsf {Mor}_{\mathsf {FO}}$
are countable, so
![]() $\subseteq $
-preserving functors D from
$\subseteq $
-preserving functors D from
![]() ${\mathsf {FO}}$
to
${\mathsf {FO}}$
to
![]() ${\mathsf {LO}}$
can each be coded naturally by a set of natural numbers. We extend any such D to a functor with domain
${\mathsf {LO}}$
can each be coded naturally by a set of natural numbers. We extend any such D to a functor with domain
![]() ${\mathsf {LO}}$
by putting
${\mathsf {LO}}$
by putting
Here, for
![]() $f\colon A\to C$
and
$f\colon A\to C$
and
![]() $A'\subseteq A$
,
$A'\subseteq A$
,
![]() $f\upharpoonright A'\colon A'\to C$
is the restriction of f.
$f\upharpoonright A'\colon A'\to C$
is the restriction of f.
A pre-dilator is called a dilator if it maps well-orders to well-orders. Dilators were introduced by Girard [Reference Girard12], to whom we refer the reader for further background. The fundamental theorem of dilators states that every pre-dilator D is naturally isomorphic to a denotation system, a special kind of
![]() $\subseteq $
-preserving predilators.
$\subseteq $
-preserving predilators.
Each denotation system D consists of a set of terms ![]() and comparison rules establishing, for each pair of terms
and comparison rules establishing, for each pair of terms
![]() $t(\vec x)$
and
$t(\vec x)$
and
![]() $s(\vec y)$
, which one is greater, depending on the relative ordering of the constants
$s(\vec y)$
, which one is greater, depending on the relative ordering of the constants
![]() $\vec x$
and
$\vec x$
and
![]() $\vec y$
. Note that we do not allow
$\vec y$
. Note that we do not allow
![]() $t(\vec x) = s(\vec y)$
unless
$t(\vec x) = s(\vec y)$
unless
![]() $t(\vec x)$
and
$t(\vec x)$
and
![]() $s(\vec y)$
are syntactically the same term. This allows us to define a binary relation
$s(\vec y)$
are syntactically the same term. This allows us to define a binary relation
![]() $D(A)$
for each linear order A as follows: the domain of
$D(A)$
for each linear order A as follows: the domain of
![]() $D(A)$
is the set of all expressions
$D(A)$
is the set of all expressions
![]() $t(a_1,\ldots ,a_n)$
, where
$t(a_1,\ldots ,a_n)$
, where
![]() $a_1>\ldots >a_n$
are elements of A and
$a_1>\ldots >a_n$
are elements of A and
![]() $t(x_1,\ldots ,x_n)$
is a D-term. The relative ordering of elements of the domain of
$t(x_1,\ldots ,x_n)$
is a D-term. The relative ordering of elements of the domain of
![]() $D(A)$
is determined by the comparison rules for each pair of terms.
$D(A)$
is determined by the comparison rules for each pair of terms.
Given a strictly increasing map
![]() $f\colon A\to C$
between finite orderings A and C, we define
$f\colon A\to C$
between finite orderings A and C, we define
 $$ \begin{align*} D(f)\colon D(A) &\to D(C)\\ D(f)\colon t(a_1,\ldots,a_n)&\mapsto t(f(a_1),\ldots,f(a_n)). \end{align*} $$
$$ \begin{align*} D(f)\colon D(A) &\to D(C)\\ D(f)\colon t(a_1,\ldots,a_n)&\mapsto t(f(a_1),\ldots,f(a_n)). \end{align*} $$
We shall sometimes identify the values of terms ![]() with the ordinals they denote. If
with the ordinals they denote. If ![]() , we call the set
, we call the set ![]() the support of
the support of
![]() $\alpha $
and denote it by
$\alpha $
and denote it by
![]() ${\text {supp}}(\alpha )$
. Given ordinals
${\text {supp}}(\alpha )$
. Given ordinals
![]() $\alpha ,\beta $
, we write
$\alpha ,\beta $
, we write
2.1 Conventions
Whenever we deal with a linear order L, we will write
![]() $<_L$
to indicate the ordering. If no confusion arises, we may occasionally omit reference to L and simply write
$<_L$
to indicate the ordering. If no confusion arises, we may occasionally omit reference to L and simply write
![]() $<$
.
$<$
.
When dealing with functions
![]() $f(x)$
, we will sometimes omit brackets and simply write
$f(x)$
, we will sometimes omit brackets and simply write
![]() $fx$
. The purpose of this is to avoid cluttering when dealing with nested application of functions.
$fx$
. The purpose of this is to avoid cluttering when dealing with nested application of functions.
3 The functoriality of fast-growing hierarchies
In this section, we fix a dilator D and investigate the functorial structure of
![]() $B_D$
. All the constructions in this section are formalizable in
$B_D$
. All the constructions in this section are formalizable in
![]() ${\mathsf {ACA_0}}$
. Note that the norms
${\mathsf {ACA_0}}$
. Note that the norms
![]() $N\alpha $
– and hence the B-hierarchy on
$N\alpha $
– and hence the B-hierarchy on
![]() $D(\omega )$
– are unaffected if we replace D by a naturally isomorphic denotation system. Hence, in order to simplify notation, we will assume that D is a denotation system (in fact, we will only use that it is
$D(\omega )$
– are unaffected if we replace D by a naturally isomorphic denotation system. Hence, in order to simplify notation, we will assume that D is a denotation system (in fact, we will only use that it is
![]() $\subseteq $
-preserving). If so,
$\subseteq $
-preserving). If so,
![]() $N \alpha = \min \{n\mid \alpha \in D(n)\}$
.
$N \alpha = \min \{n\mid \alpha \in D(n)\}$
.
Definition 3. Let n be a natural number and
![]() $\alpha \in D(\omega )\cup \{D(\omega )\}$
. An
$\alpha \in D(\omega )\cup \{D(\omega )\}$
. An
![]() $(n,\alpha )$
-normal form term is an expression of one of the following forms:
$(n,\alpha )$
-normal form term is an expression of one of the following forms:
-
1. m, where
 $m<n$
is a natural number, or
$m<n$
is a natural number, or -
2.
 $B_{\alpha _k}\dots B_{\alpha _1}(n)$
, where
$B_{\alpha _k}\dots B_{\alpha _1}(n)$
, where-
(a)
 $\alpha _k <_{D(\omega )} \dots <_{D(\omega )} \alpha _1<_{D(\omega )} \alpha $
; and
$\alpha _k <_{D(\omega )} \dots <_{D(\omega )} \alpha _1<_{D(\omega )} \alpha $
; and -
(b)
 $N\alpha _{i+1} \leq B_{\alpha _i}\dots B_{\alpha _1}(n)$
for all i with
$N\alpha _{i+1} \leq B_{\alpha _i}\dots B_{\alpha _1}(n)$
for all i with
 $0\leq i<k$
.
$0\leq i<k$
.
-
Normal form terms denote natural numbers obtained simply by evaluating the functions. If
![]() $m = B_{\alpha _k}\dots B_{\alpha _1}(n)$
is as above, we may omit reference to
$m = B_{\alpha _k}\dots B_{\alpha _1}(n)$
is as above, we may omit reference to
![]() $\alpha $
and call this expression the n-normal form of m; if so, we may write
$\alpha $
and call this expression the n-normal form of m; if so, we may write
For finite sequences of ordinals
![]() $(\alpha _1,\ldots ,\alpha _k)\in (D(\omega ))^{<\omega }$
, the lexicographical comparision
$(\alpha _1,\ldots ,\alpha _k)\in (D(\omega ))^{<\omega }$
, the lexicographical comparision
![]() $<_{\mathsf {lex}}$
is defined in the usual manner: by putting
$<_{\mathsf {lex}}$
is defined in the usual manner: by putting
if there exists
![]() $0\le n\le \min (k,l)$
such that
$0\le n\le \min (k,l)$
such that
![]() $\alpha _i=\beta _i$
, for
$\alpha _i=\beta _i$
, for
![]() $1\le i\le n$
and either
$1\le i\le n$
and either
![]() $n=k<l$
or
$n=k<l$
or
![]() $n<\min (k,l)$
and
$n<\min (k,l)$
and
![]() $\alpha _{n+1}<_{D(\omega )}\beta _{n+1}$
.
$\alpha _{n+1}<_{D(\omega )}\beta _{n+1}$
.
Lemma 4 (
 ${\mathsf {ACA_0}}$
).
${\mathsf {ACA_0}}$
).
Suppose
![]() $\alpha \in D(\omega )\cup \{D(\omega )\}$
and
$\alpha \in D(\omega )\cup \{D(\omega )\}$
and
![]() $n\in \mathbb {N}$
. Then,
$n\in \mathbb {N}$
. Then,
-
1. each number smaller than
 $B_{\alpha }(n)$
is the value of a unique
$B_{\alpha }(n)$
is the value of a unique
 $(n,\alpha )$
-normal form; and
$(n,\alpha )$
-normal form; and -
2. for any two
 $(n,\alpha )$
-normal forms
$(n,\alpha )$
-normal forms
 $B_{\alpha _k}\ldots B_{\alpha _1} (n)$
and
$B_{\alpha _k}\ldots B_{\alpha _1} (n)$
and
 $B_{\beta _l}\ldots B_{\beta _1} (n)$
, we have
$B_{\beta _l}\ldots B_{\beta _1} (n)$
, we have  $$ \begin{align*}B_{\alpha_k}\ldots B_{\alpha_1} (n)< B_{\beta_l}\ldots B_{\beta_1} (n)\iff (\alpha_1,\ldots,\alpha_k)<_{\mathsf{lex}}(\beta_1,\ldots,\beta_l).\end{align*} $$
$$ \begin{align*}B_{\alpha_k}\ldots B_{\alpha_1} (n)< B_{\beta_l}\ldots B_{\beta_1} (n)\iff (\alpha_1,\ldots,\alpha_k)<_{\mathsf{lex}}(\beta_1,\ldots,\beta_l).\end{align*} $$
Proof. We prove the lemma by transfinite induction on
![]() $\alpha $
. If there are no
$\alpha $
. If there are no
![]() $\alpha '<_{D(\omega )}\alpha $
with
$\alpha '<_{D(\omega )}\alpha $
with
![]() $N\alpha '\le n$
, then
$N\alpha '\le n$
, then
![]() $B_\alpha (n)=n+1$
and the only
$B_\alpha (n)=n+1$
and the only
![]() $(n,\alpha )$
-normal forms are constants
$(n,\alpha )$
-normal forms are constants
![]() $\le n$
, and hence, the lemma holds.
$\le n$
, and hence, the lemma holds.
Otherwise, choose
![]() $\alpha '<_{D(\omega )}\alpha $
such that
$\alpha '<_{D(\omega )}\alpha $
such that
![]() $N\alpha '\leq n$
and
$N\alpha '\leq n$
and
![]() $B_\alpha (n)=B_{\alpha '}(B_{\alpha '}(n))$
. Let
$B_\alpha (n)=B_{\alpha '}(B_{\alpha '}(n))$
. Let
![]() $s=B_{\alpha '}(n)$
. By induction hypothesis,
$s=B_{\alpha '}(n)$
. By induction hypothesis,
-
1. any number
 $<B_{\alpha '}(s)$
is the value of a unique
$<B_{\alpha '}(s)$
is the value of a unique
 $(s,\alpha ')$
-normal form;
$(s,\alpha ')$
-normal form; -
2. any number
 $<s$
is the value of a unique
$<s$
is the value of a unique
 $(n,\alpha ')$
-normal form.
$(n,\alpha ')$
-normal form.
Combining these two facts, we observe that each number
![]() $<B_{\alpha }(n)$
is the value of the unique term of one of the following three forms:
$<B_{\alpha }(n)$
is the value of the unique term of one of the following three forms:
-
1. m, for
 $m<n$
;
$m<n$
; -
2.
 $B_{\alpha _k}\dots B_{\alpha _1}(n)$
, where
$B_{\alpha _k}\dots B_{\alpha _1}(n)$
, where
 $\alpha _k <_{D(\omega )} \dots <_{D(\omega )} \alpha _1<_{D(\omega )}\alpha '$
and
$\alpha _k <_{D(\omega )} \dots <_{D(\omega )} \alpha _1<_{D(\omega )}\alpha '$
and
 $N\alpha _{i+1} \leq B_{\alpha _i}\dots B_{\alpha _1}(n)$
for all i with
$N\alpha _{i+1} \leq B_{\alpha _i}\dots B_{\alpha _1}(n)$
for all i with
 $0\leq i<k$
;
$0\leq i<k$
; -
3.
 $B_{\alpha _k}\dots B_{\alpha _1}(B_{\alpha '}(n))$
, where
$B_{\alpha _k}\dots B_{\alpha _1}(B_{\alpha '}(n))$
, where
 $\alpha _k <_{D(\omega )} \dots <_{D(\omega )} \alpha _1<_{D(\omega )}\alpha '$
and
$\alpha _k <_{D(\omega )} \dots <_{D(\omega )} \alpha _1<_{D(\omega )}\alpha '$
and
 $N\alpha _{i+1} \leq B_{\alpha _i}\dots B_{\alpha _1}(B_{\alpha '}(n))$
for all i with
$N\alpha _{i+1} \leq B_{\alpha _i}\dots B_{\alpha _1}(B_{\alpha '}(n))$
for all i with
 $0\leq i<k$
.
$0\leq i<k$
.
Since
![]() $\alpha '<_{D(\omega )}\alpha $
and
$\alpha '<_{D(\omega )}\alpha $
and
![]() $N\alpha ' \leq n$
, it follows that any number
$N\alpha ' \leq n$
, it follows that any number
![]() $<B_\alpha (n)$
is indeed the value of an
$<B_\alpha (n)$
is indeed the value of an
![]() $(n,\alpha )$
-normal form. To prove that
$(n,\alpha )$
-normal form. To prove that
![]() $(n,\alpha )$
-normal forms are compared as prescribed, we simply need to consider the cases of the forms (2) and (3). If both normal forms are of the same form, then we get the comparison property directly by induction hypothesis. The fact that the comparison property holds for terms of different forms follows from the fact that any term of the form (2) has smaller value than any term of the form (3). This is because, by construction, every term of the form (2) has value
$(n,\alpha )$
-normal forms are compared as prescribed, we simply need to consider the cases of the forms (2) and (3). If both normal forms are of the same form, then we get the comparison property directly by induction hypothesis. The fact that the comparison property holds for terms of different forms follows from the fact that any term of the form (2) has smaller value than any term of the form (3). This is because, by construction, every term of the form (2) has value
![]() $<s$
and every term of the form (3) has value
$<s$
and every term of the form (3) has value
![]() $\ge s$
.
$\ge s$
.
Definition 5. Let
![]() $f:n \to n'$
be a strictly increasing function. We define the function
$f:n \to n'$
be a strictly increasing function. We define the function
![]() $B_D(f):B_D(n) \to B_D(n')$
to be the unique strictly increasing function such that
$B_D(f):B_D(n) \to B_D(n')$
to be the unique strictly increasing function such that
-
1. if
 $m<n$
, then
$m<n$
, then
 $B_D(f)(m) = f(m)$
;
$B_D(f)(m) = f(m)$
; -
2. if
 $n\le m<B_D(n)$
and
$n\le m<B_D(n)$
and
 $m \stackrel {NF}{=} B_{\alpha _{k}}\dots B_{\alpha _1}(n)$
, then where
$m \stackrel {NF}{=} B_{\alpha _{k}}\dots B_{\alpha _1}(n)$
, then where $$\begin{align*}B_D(f)(m)=B_{\alpha^{\prime}_{k}}\dots B_{\alpha^{\prime}_1}(n'),\end{align*}$$
$$\begin{align*}B_D(f)(m)=B_{\alpha^{\prime}_{k}}\dots B_{\alpha^{\prime}_1}(n'),\end{align*}$$
 $\alpha ^{\prime }_i=D(B_D(f))(\alpha _i)$
for each i.
$\alpha ^{\prime }_i=D(B_D(f))(\alpha _i)$
for each i.
Lemma 6 (
 ${\mathsf {ACA_0}}$
).
${\mathsf {ACA_0}}$
).
Let
![]() $f:n \to n'$
be a strictly increasing function. Then, there is a unique strictly increasing function
$f:n \to n'$
be a strictly increasing function. Then, there is a unique strictly increasing function
![]() $B_D(f)$
satisfying Definition 5.
$B_D(f)$
satisfying Definition 5.
Proof. By induction on
![]() $s\leq B_D(n)$
, we define a sequence of strictly increasing maps
$s\leq B_D(n)$
, we define a sequence of strictly increasing maps
such that
![]() $g_{s+1}$
extends
$g_{s+1}$
extends
![]() $g_s$
for each s. The map
$g_s$
for each s. The map
![]() $g_0\colon 0 \to B_D(n')$
is simply the empty map.
$g_0\colon 0 \to B_D(n')$
is simply the empty map.
Assume that we already have defined maps
![]() $g_0,\ldots ,g_s$
and established that they are an increasing family of strictly increasing functions. We define the map
$g_0,\ldots ,g_s$
and established that they are an increasing family of strictly increasing functions. We define the map
as follows:
-
1. if
 $m<n$
, then we put
$m<n$
, then we put
 $g_{m+1}(m)=m$
;
$g_{m+1}(m)=m$
; -
2. if
 $n \leq m \stackrel {NF}{=} B_{\alpha _{k}}\dots B_{\alpha _1}(n)$
, then we put
$n \leq m \stackrel {NF}{=} B_{\alpha _{k}}\dots B_{\alpha _1}(n)$
, then we put
 $g_{s+1}(m)=B_{\alpha ^{\prime }_{k}}\dots B_{\alpha ^{\prime }_1}(n')$
, where
$g_{s+1}(m)=B_{\alpha ^{\prime }_{k}}\dots B_{\alpha ^{\prime }_1}(n')$
, where
 $\alpha ^{\prime }_{i}=D(g_s)(\alpha _{i})$
for each i.
$\alpha ^{\prime }_{i}=D(g_s)(\alpha _{i})$
for each i.
Note that in the second clause, the values
![]() $D(g_s)(\alpha _i)$
are well defined. This is because, by the condition on n-normal forms, we have
$D(g_s)(\alpha _i)$
are well defined. This is because, by the condition on n-normal forms, we have
and hence,
![]() $\alpha _i\in D(s)$
.
$\alpha _i\in D(s)$
.
Let us check that the expression
![]() $g_{s+1}(m)$
in (2) is an
$g_{s+1}(m)$
in (2) is an
![]() $n'$
-normal form. The fact that
$n'$
-normal form. The fact that
![]() $\alpha ^{\prime }_k<_{D(\omega )}\ldots <_{D(\omega )}\alpha ^{\prime }_1$
simply follows from the functoriality of D. We show that
$\alpha ^{\prime }_k<_{D(\omega )}\ldots <_{D(\omega )}\alpha ^{\prime }_1$
simply follows from the functoriality of D. We show that
![]() $N \alpha _i'\le B_{\alpha ^{\prime }_{i-1}}\dots B_{\alpha ^{\prime }_1}(n')$
. By definition,
$N \alpha _i'\le B_{\alpha ^{\prime }_{i-1}}\dots B_{\alpha ^{\prime }_1}(n')$
. By definition,
![]() $\alpha ^{\prime }_i=D(g_s)(\alpha _i)$
. Thus,
$\alpha ^{\prime }_i=D(g_s)(\alpha _i)$
. Thus,
![]() $\alpha ^{\prime }_i$
is the value of a D-term where all the constants result from shifting constants
$\alpha ^{\prime }_i$
is the value of a D-term where all the constants result from shifting constants
![]() ${\leq }N\alpha _i$
according to
${\leq }N\alpha _i$
according to
![]() $g_s$
. Hence,
$g_s$
. Hence,
![]() $\alpha ^{\prime }_i$
is the value of a D-term with constants
$\alpha ^{\prime }_i$
is the value of a D-term with constants
![]() $\leq {g_s(N\alpha _i)}$
. In other words,
$\leq {g_s(N\alpha _i)}$
. In other words,
![]() $D(g_s)(\alpha _i) \in D(g_s(N\alpha _i))$
. By the definition of N, it follows that
$D(g_s)(\alpha _i) \in D(g_s(N\alpha _i))$
. By the definition of N, it follows that
as desired. Hence, all the values produced in (2) are indeed normal forms.
Now, the comparision algorithm for n-normal forms provided by Lemma 4 implies that
![]() $g_{s+1}$
is strictly increasing. If
$g_{s+1}$
is strictly increasing. If
![]() $s=0$
, then
$s=0$
, then
![]() $g_{s+1}$
extends
$g_{s+1}$
extends
![]() $g_{s}$
simply because
$g_{s}$
simply because
![]() $g_0$
is the empty map. If
$g_0$
is the empty map. If
![]() $s>0$
, then we immediately obtain that
$s>0$
, then we immediately obtain that
![]() $g_{s+1}$
extends
$g_{s+1}$
extends
![]() $g_s$
from their definitions and the fact that
$g_s$
from their definitions and the fact that
![]() $g_{s}$
extends
$g_{s}$
extends
![]() $g_{s-1}$
.
$g_{s-1}$
.
Consider
given by
From the definition, it is clear that g satisfies properties (1) and (2) of the definition of
![]() $B_D(f)$
. By a straightforward induction on m, we show that if
$B_D(f)$
. By a straightforward induction on m, we show that if
is any other function satisfying properties (1) and (2) of the definition of
![]() $B_D(f)$
, then
$B_D(f)$
, then
![]() $g(m)=g'(m)$
. Therefore, the definition of
$g(m)=g'(m)$
. Therefore, the definition of
![]() $B_D(f)$
indeed defines a unique strictly increasing function.
$B_D(f)$
indeed defines a unique strictly increasing function.
Corollary 7.
![]() $B_D$
is a functor on the category
$B_D$
is a functor on the category
![]() $\mathsf {Nat}$
.
$\mathsf {Nat}$
.
Commenting on an earlier draft of this article, Wainer has brought to our attention an earlier result of his [Reference Wainer24] in which he establishes functoriality for a version of the binary fast-growing hierarchy in the context of tree-ordinals.
4 Fast-growing hierarchies as ordinal collapses
In this section, we give an alternate definition of
![]() $B_D$
in terms of formal ‘ordinal collapses’ which will directly result in a
$B_D$
in terms of formal ‘ordinal collapses’ which will directly result in a
![]() $\subseteq $
-preserving dilator. These are orderings defined formally using the notation of ordinal collapsing functions in a way that results in them having similar properties. This will become clearer in the following section; cf. for example, Lemma 20; see also the comment following Definition 8.
$\subseteq $
-preserving dilator. These are orderings defined formally using the notation of ordinal collapsing functions in a way that results in them having similar properties. This will become clearer in the following section; cf. for example, Lemma 20; see also the comment following Definition 8.
We will show that the new construction, as a functor, is naturally isomorphic to the one constructed in the previous section. It will be clear from the construction that this definition coincides with the previous one when applied to (finite) natural numbers with the usual ordering. As a consequence of this and Corollary 7, it follows that the new definition coincides with the previous one for arbitrary linear orderings A. Again, all the constructions will be formalizable in
![]() $\mathsf {ACA}_0$
.
$\mathsf {ACA}_0$
.
Recall that for a linear order A,
![]() $2^A$
is the linear order consisting of formal base-
$2^A$
is the linear order consisting of formal base-
![]() $2$
Cantor normal forms
$2$
Cantor normal forms
with
![]() $a_1>_A\ldots >_Aa_n$
. These formal sums are compared in the natural way – that is,
$a_1>_A\ldots >_Aa_n$
. These formal sums are compared in the natural way – that is,
![]() $2^{a_1}+\ldots +2^{a_n}<_{2^A}2^{b_1}+\ldots +2^{b_m}$
if
$2^{a_1}+\ldots +2^{a_n}<_{2^A}2^{b_1}+\ldots +2^{b_m}$
if
![]() $(a_1,\ldots ,a_n)<_{\mathsf {lex}}(b_1,\ldots ,b_m)$
. Here, the empty sum is allowed and identified with the term
$(a_1,\ldots ,a_n)<_{\mathsf {lex}}(b_1,\ldots ,b_m)$
. Here, the empty sum is allowed and identified with the term
![]() $0$
. This construction naturally extends to a dilator: given a strictly increasing function
$0$
. This construction naturally extends to a dilator: given a strictly increasing function
![]() $f\colon A\to B$
, we define
$f\colon A\to B$
, we define
 $$ \begin{align*} 2^f\colon 2^A &\to 2^B\\ 2^f\colon 2^{a_1}+\ldots+2^{a_n}&\mapsto 2^{f(a_1)}+\ldots+2^{f(a_n)}. \end{align*} $$
$$ \begin{align*} 2^f\colon 2^A &\to 2^B\\ 2^f\colon 2^{a_1}+\ldots+2^{a_n}&\mapsto 2^{f(a_1)}+\ldots+2^{f(a_n)}. \end{align*} $$
Below, if A is a linear ordering and
![]() $a \in A$
, we denote by
$a \in A$
, we denote by
![]() $A\upharpoonright a$
the initial segment
$A\upharpoonright a$
the initial segment
![]() $\{x\in A: x<a\}$
, viewed as a linear order.
$\{x\in A: x<a\}$
, viewed as a linear order.
Definition 8. Let A be a linear ordering.
![]() $B_D(A)$
is defined to be the (inclusion-)least linear ordering C such that the following hold:
$B_D(A)$
is defined to be the (inclusion-)least linear ordering C such that the following hold:
-
1. C contains the term
 $a^\star $
, for any
$a^\star $
, for any
 $a\in A$
.
$a\in A$
. -
2. C contains the term
 $\psi (0)$
.
$\psi (0)$
. -
3. Suppose that
-
(a)
 $\alpha _1,\ldots ,\alpha _k,\alpha _{k+1}\in D(C)$
,
$\alpha _1,\ldots ,\alpha _k,\alpha _{k+1}\in D(C)$
, -
(b)
 $\psi (2^{\alpha _1}+\ldots +2^{\alpha _k})\in C$
,
$\psi (2^{\alpha _1}+\ldots +2^{\alpha _k})\in C$
, -
(c)
 $\alpha _{k+1}<_{D(C)}\alpha _k$
, and
$\alpha _{k+1}<_{D(C)}\alpha _k$
, and -
(d)
 $\alpha _{k+1}\in D(C\upharpoonright \psi (2^{\alpha _1}+\ldots +2^{\alpha _k}))$
;
$\alpha _{k+1}\in D(C\upharpoonright \psi (2^{\alpha _1}+\ldots +2^{\alpha _k}))$
;
then,
 $\psi (2^{\alpha _1}+\ldots +2^{\alpha _k}+2^{\alpha _{k+1}})\in C$
.
$\psi (2^{\alpha _1}+\ldots +2^{\alpha _k}+2^{\alpha _{k+1}})\in C$
. -
-
4. if
 $a<_Ab$
, then
$a<_Ab$
, then
 $a^{\star }<_Cb^\star $
.
$a^{\star }<_Cb^\star $
. -
5.
 $a^\star <_C\psi (t)$
, for any
$a^\star <_C\psi (t)$
, for any
 $a^\star ,\psi (t)\in C$
.
$a^\star ,\psi (t)\in C$
. -
6. if
 $\psi (t), \psi (u)\in C$
,
$\psi (t), \psi (u)\in C$
,
 $t,u\in 2^{D(C)}$
, and
$t,u\in 2^{D(C)}$
, and
 $t<_{2^{D(C)}}u$
, then
$t<_{2^{D(C)}}u$
, then
 $\psi (t)<_C\psi (u)$
.
$\psi (t)<_C\psi (u)$
.
We shall refer to
![]() $B_D$
as the collapsing functor built over D. This is because Definition 8 could be regarded as a term system performing formal ordinal collapsing which admit a variation of the usual semantics for ordinal collapsing functions familiar from Ordinal Analysis.
$B_D$
as the collapsing functor built over D. This is because Definition 8 could be regarded as a term system performing formal ordinal collapsing which admit a variation of the usual semantics for ordinal collapsing functions familiar from Ordinal Analysis.
Proposition 9 (
 ${\mathsf {ZFC}}$
).
${\mathsf {ZFC}}$
).
Let
![]() $\alpha $
be an ordinal and D be an
$\alpha $
be an ordinal and D be an
![]() $\subseteq $
-preserving dilator. Let
$\subseteq $
-preserving dilator. Let
![]() $\Omega $
be a regular cardinal such that
$\Omega $
be a regular cardinal such that
![]() $\max (|\alpha |,|D|) < \Omega $
. We define a partial function
$\max (|\alpha |,|D|) < \Omega $
. We define a partial function
by recursion on
![]() $2^{D(\Omega )}$
as follows:
$2^{D(\Omega )}$
as follows:
Suppose
![]() $\alpha _n < \alpha _{n-1} < \dots < \alpha _1$
. Then,
$\alpha _n < \alpha _{n-1} < \dots < \alpha _1$
. Then,
![]() $\Omega +2^{\alpha _1}+\ldots +2^{\alpha _n}<2^{D(\Omega )}$
is in the domain of
$\Omega +2^{\alpha _1}+\ldots +2^{\alpha _n}<2^{D(\Omega )}$
is in the domain of
![]() $\tilde \psi ^\alpha $
if for each
$\tilde \psi ^\alpha $
if for each
![]() $i<n$
,
$i<n$
,
![]() $\alpha _{i+1}\in D(\tilde \psi ^\alpha ( \Omega + 2^{\alpha _1}+\ldots +2^{\alpha _i}))$
. Additionally, we add
$\alpha _{i+1}\in D(\tilde \psi ^\alpha ( \Omega + 2^{\alpha _1}+\ldots +2^{\alpha _i}))$
. Additionally, we add
![]() $\Omega +2^{D(\Omega )}$
to the domain of
$\Omega +2^{D(\Omega )}$
to the domain of
![]() $\tilde \psi ^\alpha $
. For
$\tilde \psi ^\alpha $
. For
![]() $\beta \in {\text {dom}}(\tilde \psi ^\alpha )$
, we put
$\beta \in {\text {dom}}(\tilde \psi ^\alpha )$
, we put
 $$ \begin{align*}\tilde\psi^\alpha(\beta)=\min\bigg\{\Omega\setminus \Big(\alpha\cup\big\{\tilde\psi^\alpha(\beta')\mid \beta'\in \beta\cap\mathsf{dom}(\tilde\psi^\alpha)\big\}\Big)\bigg\}.\end{align*} $$
$$ \begin{align*}\tilde\psi^\alpha(\beta)=\min\bigg\{\Omega\setminus \Big(\alpha\cup\big\{\tilde\psi^\alpha(\beta')\mid \beta'\in \beta\cap\mathsf{dom}(\tilde\psi^\alpha)\big\}\Big)\bigg\}.\end{align*} $$
Then,
![]() $\tilde \psi ^\alpha (\Omega +2^{D(\Omega )})$
is a well-order isomorphic to
$\tilde \psi ^\alpha (\Omega +2^{D(\Omega )})$
is a well-order isomorphic to
![]() $B_D(\alpha )$
.
$B_D(\alpha )$
.
Proof. First, using the fact that
![]() $\max (|\alpha |, |D|) < \Omega $
, a simple induction shows that
$\max (|\alpha |, |D|) < \Omega $
, a simple induction shows that
and hence,
![]() $\tilde \psi ^\alpha (\beta )$
is defined.
$\tilde \psi ^\alpha (\beta )$
is defined.
Given this, the isomorphism is essentially immediate from the definition of
![]() $B_D(\alpha )$
. Note that the conditions on the domain of
$B_D(\alpha )$
. Note that the conditions on the domain of
![]() $\tilde \psi ^\alpha $
correspond to the term-formation rules of
$\tilde \psi ^\alpha $
correspond to the term-formation rules of
![]() $B_D$
in Definition 8(1)–8(3); that the range of the function
$B_D$
in Definition 8(1)–8(3); that the range of the function
![]() $\tilde \psi ^\alpha $
takes values in
$\tilde \psi ^\alpha $
takes values in
![]() $(\alpha ,\Omega )$
, corresponding to Definition 8(4) and 8(5); and indeed that
$(\alpha ,\Omega )$
, corresponding to Definition 8(4) and 8(5); and indeed that
![]() $\tilde \psi ^\alpha (\beta )$
is precisely the least ordinal greater than
$\tilde \psi ^\alpha (\beta )$
is precisely the least ordinal greater than
![]() $\tilde \psi ^\alpha (\beta ')$
for
$\tilde \psi ^\alpha (\beta ')$
for
![]() $\beta '<\beta $
in the domain of
$\beta '<\beta $
in the domain of
![]() $\tilde \psi ^\alpha $
, corresponding to Definition 8(6). From this, it follows that the function
$\tilde \psi ^\alpha $
, corresponding to Definition 8(6). From this, it follows that the function
 $$ \begin{align*} \iota_\alpha: B_D(\alpha) &\to \tilde\psi^\alpha(\Omega+2^{D(\Omega)})\\ \gamma &\mapsto \gamma, & (\gamma<\alpha)\\ \psi(2^{\alpha_1} + \dots + 2^{\alpha_n}) &\mapsto \tilde\psi^\alpha(\Omega +2^{\alpha_1} + \dots + 2^{\alpha_n}) \end{align*} $$
$$ \begin{align*} \iota_\alpha: B_D(\alpha) &\to \tilde\psi^\alpha(\Omega+2^{D(\Omega)})\\ \gamma &\mapsto \gamma, & (\gamma<\alpha)\\ \psi(2^{\alpha_1} + \dots + 2^{\alpha_n}) &\mapsto \tilde\psi^\alpha(\Omega +2^{\alpha_1} + \dots + 2^{\alpha_n}) \end{align*} $$
is an isomorphism.
The function
![]() $\tilde \psi ^{\alpha }$
in Proposition 9 is a ‘pure’ variant of collapsing function, where the ordinals
$\tilde \psi ^{\alpha }$
in Proposition 9 is a ‘pure’ variant of collapsing function, where the ordinals
![]() $<\Omega $
are not closed under any ordinal functions (e.g., addition or the Veblen functions) as part of the construction; these are represented either as constants or values of
$<\Omega $
are not closed under any ordinal functions (e.g., addition or the Veblen functions) as part of the construction; these are represented either as constants or values of
![]() $\tilde \psi ^{\alpha }$
. The ordinals
$\tilde \psi ^{\alpha }$
. The ordinals
![]() $\ge \Omega $
are represented according to the dilator D.
$\ge \Omega $
are represented according to the dilator D.
While Proposition 9 gives a natural semantics for the collapsing functor
![]() $B_D$
, it requires access to uncountable cardinals. We now establish the totality of
$B_D$
, it requires access to uncountable cardinals. We now establish the totality of
![]() $B_D$
in the weak system
$B_D$
in the weak system
![]() ${\mathsf {ACA_0}}$
.
${\mathsf {ACA_0}}$
.
Lemma 10 (
 ${\mathsf {ACA_0}}$
).
${\mathsf {ACA_0}}$
).
Suppose D is an
![]() $\subseteq $
-preserving pre-dilator and A is a linear ordering. Then,
$\subseteq $
-preserving pre-dilator and A is a linear ordering. Then,
![]() $B_D(A)$
exists.
$B_D(A)$
exists.
Proof. The idea is to construct
![]() $B_D(A)$
as the limit of an inductive definition of length
$B_D(A)$
as the limit of an inductive definition of length
![]() $\omega $
. We construct linear orders
$\omega $
. We construct linear orders
Recursively, we denote by
![]() $B_{D,<n}(A)$
the already defined linear order
$B_{D,<n}(A)$
the already defined linear order
![]() $\bigcup \limits _{m<n}B_{D,m}(A)$
and define
$\bigcup \limits _{m<n}B_{D,m}(A)$
and define
![]() $B_{D,n}(A)$
to contain the following terms:
$B_{D,n}(A)$
to contain the following terms:
-
1.
 $a^\star $
, for
$a^\star $
, for
 $a\in A$
;
$a\in A$
; -
2.
 $\psi (0)$
;
$\psi (0)$
; -
3.
 $\psi (2^{\alpha _1}+\ldots +2^{\alpha _k}+2^{\alpha _{k+1}})$
, whenever
$\psi (2^{\alpha _1}+\ldots +2^{\alpha _k}+2^{\alpha _{k+1}})$
, whenever
 $\alpha _1,\ldots ,\alpha _k,\alpha _{k+1}\in D(B_{D,<n}(A))$
are such that
$\alpha _1,\ldots ,\alpha _k,\alpha _{k+1}\in D(B_{D,<n}(A))$
are such that-
(a)
 $\psi (2^{\alpha _1}+\ldots +2^{\alpha _k})\in B_{D,<n}(A)$
,
$\psi (2^{\alpha _1}+\ldots +2^{\alpha _k})\in B_{D,<n}(A)$
, -
(b)
 $\alpha _{k+1}<_{D(B_{D,<n}(A))}\alpha _k$
, and
$\alpha _{k+1}<_{D(B_{D,<n}(A))}\alpha _k$
, and -
(c)
 $\alpha _{k+1}\in D( B_{D,<n}(A){\upharpoonright } \psi (2^{\alpha _1}+\ldots +2^{\alpha _k}))$
.
$\alpha _{k+1}\in D( B_{D,<n}(A){\upharpoonright } \psi (2^{\alpha _1}+\ldots +2^{\alpha _k}))$
.
-
The order on these terms is defined in the same way as above (i.e.,
![]() $a^\star <_{B_{D,<n}(A)}b^\star $
if and only if
$a^\star <_{B_{D,<n}(A)}b^\star $
if and only if
![]() $a<_Ab$
); we always have
$a<_Ab$
); we always have
![]() $a^\star <_{B_{D,<n}(A)}\psi (t)$
; and
$a^\star <_{B_{D,<n}(A)}\psi (t)$
; and
![]() $\psi (t)<_{B_{D,n}(A)}\psi (u)$
if and only if
$\psi (t)<_{B_{D,n}(A)}\psi (u)$
if and only if
![]() $t<_{2^{D(B)}}u$
. It is straightforward to check that, provably in
$t<_{2^{D(B)}}u$
. It is straightforward to check that, provably in
![]() $\mathsf {ACA}_0$
, the order
$\mathsf {ACA}_0$
, the order
![]() $B_D(A)$
constructed as the union of the chain
$B_D(A)$
constructed as the union of the chain
![]() $\{B_{D, <n}(A):n\in \mathbb {N}\}$
satisfies the definition of
$\{B_{D, <n}(A):n\in \mathbb {N}\}$
satisfies the definition of
![]() $B_D(A)$
, for any linear ordering A.
$B_D(A)$
, for any linear ordering A.
Definition 11. Let A and
![]() $A'$
be linear orders and
$A'$
be linear orders and
![]() $f: A\to A'$
be a morphism. We define
$f: A\to A'$
be a morphism. We define
to be the unique map
![]() $g\colon B_D(A)\to B_D(B)$
such that
$g\colon B_D(A)\to B_D(B)$
such that
-
1.
 $g(a^{\star }) = (f(a))^{\star }$
, and
$g(a^{\star }) = (f(a))^{\star }$
, and -
2.
 $g(\psi (t))=\psi (2^{D(g)}(t))$
.
$g(\psi (t))=\psi (2^{D(g)}(t))$
.
Lemma 12 (
 ${\mathsf {ACA_0}}$
).
${\mathsf {ACA_0}}$
).
Suppose that A and
![]() $A'$
are linear orders and
$A'$
are linear orders and
![]() $f:A \to A'$
is a morphism. Then,
$f:A \to A'$
is a morphism. Then,
![]() $B_D(f)$
exists.
$B_D(f)$
exists.
Proof. This is similar to the previous proof. By induction, we define a sequence of embeddings
![]() $B_{D,n}(f)\colon B_{D,n}(A)\to B_{D,n}(B)$
. Letting
$B_{D,n}(f)\colon B_{D,n}(A)\to B_{D,n}(B)$
. Letting
we put
-
1.
 $B_{D,n}(f)(a^{\star }) = (f(a))^{\star }$
, and
$B_{D,n}(f)(a^{\star }) = (f(a))^{\star }$
, and -
2.
 $B_{D,n}(f)(\psi (t))=\psi (2^{D(B_{D,<n}(f))}(t))$
.
$B_{D,n}(f)(\psi (t))=\psi (2^{D(B_{D,<n}(f))}(t))$
.
Clearly,
![]() $B_{D,<\omega }(f)$
satisfies the definition of
$B_{D,<\omega }(f)$
satisfies the definition of
![]() $B_D(f)$
. By induction on n, one shows that for any
$B_D(f)$
. By induction on n, one shows that for any
![]() $g\colon B_D(A)\to B_D(B)$
satisfying the definition of
$g\colon B_D(A)\to B_D(B)$
satisfying the definition of
![]() $B_D(f)$
, we have
$B_D(f)$
, we have
Thus, indeed there is a unique mapping satisfying the definition of
![]() $B_D(f)$
.
$B_D(f)$
.
Lemma 13 (
 $\mathsf {ACA}_0$
).
$\mathsf {ACA}_0$
).
Suppose D is a
![]() $\subseteq $
-preserving pre-dilator. Then, so too is
$\subseteq $
-preserving pre-dilator. Then, so too is
![]() $B_D$
.
$B_D$
.
Proof. The functoriality and
![]() $\subseteq $
-preservation of
$\subseteq $
-preservation of
![]() $B_D$
are immediate from the definition. In order to check that
$B_D$
are immediate from the definition. In order to check that
![]() $B_D$
is finitary, it is enough to show that for any A, we have
$B_D$
is finitary, it is enough to show that for any A, we have
This is done by showing, via a straightforward induction on n, that
By a straightforward induction on n, we also show that for any order A and any suborders
![]() $A',A"$
of A, we have
$A',A"$
of A, we have
This implies that for any order A and its suborders
![]() $A',A"$
, we have
$A',A"$
, we have
(i.e., that
![]() $B_D$
preserves pullbacks). This concludes the proof that
$B_D$
preserves pullbacks). This concludes the proof that
![]() $B_D$
is a
$B_D$
is a
![]() $\subseteq $
-preserving pre-dilator.
$\subseteq $
-preserving pre-dilator.
For an arbitrary pre-dilator D, we may define the pre-dilator
![]() $B_D$
to be
$B_D$
to be
![]() $B_{D'}$
, where
$B_{D'}$
, where
![]() $D'$
is some fixed
$D'$
is some fixed
![]() $\subseteq $
-preserving pre-dilator naturally isomorphic to D. Below, a pre-dilator D is weakly finite if it maps finite orders to finite orders.
$\subseteq $
-preserving pre-dilator naturally isomorphic to D. Below, a pre-dilator D is weakly finite if it maps finite orders to finite orders.
Together with Proposition 9, Theorem 14 below asserts (in particular) that if D is a denotation system for ordinals, then the binary fast-growing functor given by D is isomorphic to an ordinal collapsing function; hence, it can be regarded as a precise formulation of the fundamental observation on p. 4.
Theorem 14 (
 $\mathsf {ACA}_0$
).
$\mathsf {ACA}_0$
).
Suppose D is a weakly finite dilator. Let
![]() $B_D$
be the collapsing functor over D as in Definition 8 and let
$B_D$
be the collapsing functor over D as in Definition 8 and let
![]() $\hat B_D$
be the fast-growing functor over D defined in §3. Then, there is a natural isomorphism
$\hat B_D$
be the fast-growing functor over D defined in §3. Then, there is a natural isomorphism
Proof. Let
![]() $\theta _D\colon D\to D'$
be the natural isomorphism given by the definition of
$\theta _D\colon D\to D'$
be the natural isomorphism given by the definition of
![]() $B_D$
for arbitrary pre-dilators D. For each
$B_D$
for arbitrary pre-dilators D. For each
![]() $n\in \mathbb {N}$
, let
$n\in \mathbb {N}$
, let
be the function given by
 $$ \begin{align*} m &\mapsto m^\star, &\text{ if } m < n,\\ B_{\alpha_k}\dots B_{\alpha_1}(n) &\mapsto \psi(2^{\alpha_1'} + \dots + 2^{\alpha_k'}),\text{ where }\alpha_i'=\theta_{B_D(n)}(\alpha_i), &\text{ otherwise.} \end{align*} $$
$$ \begin{align*} m &\mapsto m^\star, &\text{ if } m < n,\\ B_{\alpha_k}\dots B_{\alpha_1}(n) &\mapsto \psi(2^{\alpha_1'} + \dots + 2^{\alpha_k'}),\text{ where }\alpha_i'=\theta_{B_D(n)}(\alpha_i), &\text{ otherwise.} \end{align*} $$
It is clear that the collection of
![]() $\eta _n$
for
$\eta _n$
for
![]() $n\in \mathbb {N}$
forms a natural isomorphism between
$n\in \mathbb {N}$
forms a natural isomorphism between
![]() $\hat B_D\colon {\mathsf {Nat}}\to {\mathsf {LO}}$
to
$\hat B_D\colon {\mathsf {Nat}}\to {\mathsf {LO}}$
to
![]() $B_D\upharpoonright {\mathsf {Nat}}$
, the restriction of
$B_D\upharpoonright {\mathsf {Nat}}$
, the restriction of
![]() $B_D$
to the category
$B_D$
to the category
![]() ${\mathsf {Nat}}$
. Indeed, suppose that
${\mathsf {Nat}}$
. Indeed, suppose that
![]() $f: n\to n'$
is strictly increasing. Then, for each number
$f: n\to n'$
is strictly increasing. Then, for each number
![]() $B_{\alpha _k}\dots B_{\alpha _1}(n) < \hat B_D(n)$
, and letting
$B_{\alpha _k}\dots B_{\alpha _1}(n) < \hat B_D(n)$
, and letting
![]() $\alpha ^{\prime }_i$
be as above, we have
$\alpha ^{\prime }_i$
be as above, we have
 $$ \begin{align*} B_D(f) \circ \eta_n \big(B_{\alpha_k}\dots B_{\alpha_1}(n)\big) &= B_D(f) \big(\psi(2^{\alpha_1'} + \dots + 2^{\alpha_k'}) \big)\\ &= \psi(2^{D(B_D(f))(\alpha_1')} + \dots + 2^{D(B_D(f))(\alpha_k')}) \\ &= \eta_{n'}\big( B_{D(\hat B_D(f))(\alpha_k)}\dots B_{D(\hat B_D(f))(\alpha_1)}(n') \big) \\ &= \eta_{n'} \circ \hat B_D(f)\big(B_{\alpha_k}\dots B_{\alpha_1}(n)\big). \end{align*} $$
$$ \begin{align*} B_D(f) \circ \eta_n \big(B_{\alpha_k}\dots B_{\alpha_1}(n)\big) &= B_D(f) \big(\psi(2^{\alpha_1'} + \dots + 2^{\alpha_k'}) \big)\\ &= \psi(2^{D(B_D(f))(\alpha_1')} + \dots + 2^{D(B_D(f))(\alpha_k')}) \\ &= \eta_{n'}\big( B_{D(\hat B_D(f))(\alpha_k)}\dots B_{D(\hat B_D(f))(\alpha_1)}(n') \big) \\ &= \eta_{n'} \circ \hat B_D(f)\big(B_{\alpha_k}\dots B_{\alpha_1}(n)\big). \end{align*} $$
Since both
![]() $\hat B_D$
and
$\hat B_D$
and
![]() $B_D$
are finitary, this natural transformation extends to a natural isomorphism between the extension of
$B_D$
are finitary, this natural transformation extends to a natural isomorphism between the extension of
![]() $\hat B_D$
to
$\hat B_D$
to
![]() ${\mathsf {LO}}$
and
${\mathsf {LO}}$
and
![]() $B_D$
, as desired.
$B_D$
, as desired.
Remark 15. We note, without giving details, that, in fact, the operation
could be extended to a pullback-preserving functor on the category of pre-dilators; in other words, B is a preptyx and – as we will see in the next section – indeed it is a ptyx. Furthermore, if we treat the category of pre-dilators as a category of structures (denotation systems can be regarded as structures), then, in fact, the definition of B in terms of formal ‘ordinal collapses’ will be a
![]() $\subseteq $
-preserving functor.
$\subseteq $
-preserving functor.
Remark 16. The construction of
![]() $B_D(A)$
, in fact, works for all
$B_D(A)$
, in fact, works for all
![]() $\subseteq $
-preserving finitary functors
$\subseteq $
-preserving finitary functors
![]() $D\colon {\mathsf {LO}}\to {\mathsf {LO}}$
. We decided not to cover the extension to finitary functors in this paper for the following reason: The fact that any dilator is naturally isomorphic to a
$D\colon {\mathsf {LO}}\to {\mathsf {LO}}$
. We decided not to cover the extension to finitary functors in this paper for the following reason: The fact that any dilator is naturally isomorphic to a
![]() $\subseteq $
-preserving one is a known fact following from Girard’s fundamental theorem of dilators. There is an unpublished result by the second author that establishes an analog of Girard’s theorem for finitary functors on
$\subseteq $
-preserving one is a known fact following from Girard’s fundamental theorem of dilators. There is an unpublished result by the second author that establishes an analog of Girard’s theorem for finitary functors on
![]() ${\mathsf {LO}}$
that, in particular, implies that any finitary functor on
${\mathsf {LO}}$
that, in particular, implies that any finitary functor on
![]() ${\mathsf {LO}}$
is naturally isomorphic to a
${\mathsf {LO}}$
is naturally isomorphic to a
![]() $\subseteq $
-preserving one. This result shall appear in a forthcoming article by the second and third authors.
$\subseteq $
-preserving one. This result shall appear in a forthcoming article by the second and third authors.
In order to make sense of
![]() $B_D$
in the case when D is not
$B_D$
in the case when D is not
![]() $\subseteq $
-preserving, it suffices to choose a denotation system
$\subseteq $
-preserving, it suffices to choose a denotation system
![]() $D'$
and put
$D'$
and put
![]() $B_{D}=B_{D'}$
.
$B_{D}=B_{D'}$
.
5
 $\Pi ^1_1$
-Comprehension from fast-growing hierarchies
$\Pi ^1_1$
-Comprehension from fast-growing hierarchies
In this section, we present a characterization of the system
![]() $\Pi ^1_1$
-
$\Pi ^1_1$
-
![]() ${\mathsf {CA_0}}$
in terms of fast-growing hierarchies.
${\mathsf {CA_0}}$
in terms of fast-growing hierarchies.
Theorem 17. The following are equivalent over
![]() ${\mathsf {ACA_0}}$
:
${\mathsf {ACA_0}}$
:
-
1.
 $\Pi ^1_1$
-
$\Pi ^1_1$
-
 ${\mathsf {CA_0}}$
;
${\mathsf {CA_0}}$
; -
2. for every weakly finite dilator D,
 $B_D$
is a weakly finite dilator;
$B_D$
is a weakly finite dilator; -
3. for every dilator D,
 $B_D$
is a dilator.
$B_D$
is a dilator.
Lemma 18 (
 $\Pi ^1_1$
-
$\Pi ^1_1$
-
 ${\mathsf {CA_0}}$
).
${\mathsf {CA_0}}$
).
For any dilator D and any well-ordering A,
![]() $B_D(A)$
is well-ordered.
$B_D(A)$
is well-ordered.
Proof. By the definition of
![]() $B_D$
, it suffices to consider the case that D is
$B_D$
, it suffices to consider the case that D is
![]() $\subseteq $
-preserving.
$\subseteq $
-preserving.
Let
![]() $\Omega $
be the largest well-ordered initial segment of
$\Omega $
be the largest well-ordered initial segment of
![]() $B_D(A)$
. This exists by
$B_D(A)$
. This exists by
![]() $\Pi ^1_1$
-
$\Pi ^1_1$
-
![]() ${\mathsf {CA_0}}$
. By hypothesis, D is a dilator, so
${\mathsf {CA_0}}$
. By hypothesis, D is a dilator, so
![]() $D(\Omega )$
is well-ordered. By induction on ordinals
$D(\Omega )$
is well-ordered. By induction on ordinals
![]() $\alpha \in D(\Omega )$
, we show that for every
$\alpha \in D(\Omega )$
, we show that for every
![]() $\psi (2^{\alpha _1} + \dots + 2^{\alpha _k}) \in \Omega $
, if
$\psi (2^{\alpha _1} + \dots + 2^{\alpha _k}) \in \Omega $
, if
![]() $\psi (2^{\alpha _1} + \dots + 2^{\alpha _k} + 2^\alpha ) \in B_D(A)$
, then
$\psi (2^{\alpha _1} + \dots + 2^{\alpha _k} + 2^\alpha ) \in B_D(A)$
, then
Suppose that
![]() $x <_{B_D(A)} a$
. Then, either
$x <_{B_D(A)} a$
. Then, either
or else there are
![]() $l\in \mathbb {N}$
and
$l\in \mathbb {N}$
and ![]() with
with
![]() $\beta _l <_{D(B_D(A))} \dots <_{D(B_D(A))} \beta _1 < \alpha $
such that
$\beta _l <_{D(B_D(A))} \dots <_{D(B_D(A))} \beta _1 < \alpha $
such that
We show by induction on
![]() $i \leq l$
that
$i \leq l$
that
-
1.
 $\beta _i \in D(\Omega )$
, and
$\beta _i \in D(\Omega )$
, and -
2.
 $\psi (2^{\alpha _1} + \dots + 2^{\alpha _k} + 2^{\beta _1} + \dots + 2^{\beta _i}) \in \Omega $
.
$\psi (2^{\alpha _1} + \dots + 2^{\alpha _k} + 2^{\beta _1} + \dots + 2^{\beta _i}) \in \Omega $
.
By the definition of
![]() $B_D$
, we have
$B_D$
, we have
By the induction hypothesis on i,
![]() $\psi (2^{\alpha _1} + \dots + 2^{\alpha _k} + 2^{\beta _1} + \dots + 2^{\beta _i}) \in \Omega $
(this is immediate by the assumption on
$\psi (2^{\alpha _1} + \dots + 2^{\alpha _k} + 2^{\beta _1} + \dots + 2^{\beta _i}) \in \Omega $
(this is immediate by the assumption on
![]() $\alpha _1, \ldots , \alpha _k$
in the case
$\alpha _1, \ldots , \alpha _k$
in the case
![]() $i =0$
) and
$i =0$
) and
![]() $\Omega $
is an initial segment of
$\Omega $
is an initial segment of
![]() $B_D(A)$
, so the first claim follows. The second follows from the induction hypothesis on
$B_D(A)$
, so the first claim follows. The second follows from the induction hypothesis on
![]() $\alpha $
. We have shown that every element
$\alpha $
. We have shown that every element
![]() $x <_{B_D(A)} a$
belongs to
$x <_{B_D(A)} a$
belongs to
![]() $\Omega $
, and thus,
$\Omega $
, and thus,
![]() $a \in \Omega $
, as desired.
$a \in \Omega $
, as desired.
By a straightforward induction on k, it follows that
for all
![]() $\psi (2^{\alpha _1} + \dots + 2^{\alpha _k}) \in B_D(A)$
– that is, that
$\psi (2^{\alpha _1} + \dots + 2^{\alpha _k}) \in B_D(A)$
– that is, that
![]() $B_D(A) = \Omega $
, and thus,
$B_D(A) = \Omega $
, and thus,
![]() $B_D(A)$
is well ordered.
$B_D(A)$
is well ordered.
Lemma 19 (
 ${\mathsf {ACA_0}}$
).
${\mathsf {ACA_0}}$
).
Suppose that for every weakly finite dilator D,
![]() $B_D$
is a weakly finite dilator. Then, for every dilator D,
$B_D$
is a weakly finite dilator. Then, for every dilator D,
![]() $B_D$
is a dilator.
$B_D$
is a dilator.
Proof. If D and
![]() $D'$
are naturally isomorphic pre-dilators, then so too are
$D'$
are naturally isomorphic pre-dilators, then so too are
![]() $B_D$
and
$B_D$
and
![]() $B_{D'}$
. Hence, it suffices to prove the theorem for denotation systems D. Let D be a denotation system and enumerate all ordinal terms of D by
$B_{D'}$
. Hence, it suffices to prove the theorem for denotation systems D. Let D be a denotation system and enumerate all ordinal terms of D by ![]() ; write
; write
![]() $n_i$
for the arity of
$n_i$
for the arity of
![]() $d_i$
. We define a new dilator
$d_i$
. We define a new dilator
![]() $\hat D$
consisting of terms
$\hat D$
consisting of terms
![]() $\hat d_i$
of arity
$\hat d_i$
of arity
![]() $n_i+i$
. Clearly,
$n_i+i$
. Clearly,
![]() $\hat D$
will be weakly finite. The comparison rules for
$\hat D$
will be weakly finite. The comparison rules for
![]() $ \hat D$
are given by
$ \hat D$
are given by
if and only if one of the following holds:
-
1.
 , or else
, or else -
2.
 , and
, and  .
.
It is easy to check that
![]() $<_{\hat D}$
is a linear order. And it is easy to see that for any A, we have an embedding of
$<_{\hat D}$
is a linear order. And it is easy to see that for any A, we have an embedding of
![]() $\hat D (A)$
into
$\hat D (A)$
into
![]() $2^{A}\cdot D(A)$
:
$2^{A}\cdot D(A)$
:
Thus,
![]() $\hat D$
is a dilator. Observe that for each finite order A, the order
$\hat D$
is a dilator. Observe that for each finite order A, the order
![]() $\hat D(A)$
contains only terms of the form
$\hat D(A)$
contains only terms of the form
![]() $\hat d_i(\ldots )$
, where
$\hat d_i(\ldots )$
, where
![]() $i\le |A|$
, and hence,
$i\le |A|$
, and hence,
![]() $\hat D(A)$
is finite. Therefore,
$\hat D(A)$
is finite. Therefore,
![]() $\hat D$
is a weakly finite dilator. Thus,
$\hat D$
is a weakly finite dilator. Thus,
![]() $B_{\hat D}$
is a dilator.
$B_{\hat D}$
is a dilator.
In order to show that
![]() $B_D$
preserves well-foundedness, it is enough to find a strictly increasing map
$B_D$
preserves well-foundedness, it is enough to find a strictly increasing map
for an arbitrary well-order A. We fix a well-order A and define, by recursion on n,
-
1.
 $e_n(a^\star )=(\omega +a)^\star $
;
$e_n(a^\star )=(\omega +a)^\star $
; -
2.
 $e_n(\psi (2^{\alpha _1}+\ldots +2^{\alpha _k}))=\psi (2^{\alpha _1'}+\ldots +2^{\alpha _k'})$
, where if
$e_n(\psi (2^{\alpha _1}+\ldots +2^{\alpha _k}))=\psi (2^{\alpha _1'}+\ldots +2^{\alpha _k'})$
, where if
 $\alpha _i=d_j(a_{1},\ldots ,a_{n_{j}})$
, then
$\alpha _i=d_j(a_{1},\ldots ,a_{n_{j}})$
, then
 $\alpha _i'=\hat d_{j}(e_{n-1}(a_{1}),\ldots ,e_{n-1}(a_{n_j}), (j-1)^\star , \ldots , 0^\star )$
.
$\alpha _i'=\hat d_{j}(e_{n-1}(a_{1}),\ldots ,e_{n-1}(a_{n_j}), (j-1)^\star , \ldots , 0^\star )$
.
By a straightforward induction on n, we show that
![]() $e_n$
’s form a sequence of expanding strictly increasing maps. We finish the proof by defining
$e_n$
’s form a sequence of expanding strictly increasing maps. We finish the proof by defining
![]() $e=\bigcup \limits _{n<\omega } e_n$
.
$e=\bigcup \limits _{n<\omega } e_n$
.
In order to complete the proof, we have to show that if
![]() $B_D$
is a dilator for every dilator D, then
$B_D$
is a dilator for every dilator D, then
![]() $\Pi ^1_1$
-
$\Pi ^1_1$
-
![]() ${\mathsf {CA_0}}$
holds. This will be done by appealing to a theorem of Freund [Reference Freund7] whereby
${\mathsf {CA_0}}$
holds. This will be done by appealing to a theorem of Freund [Reference Freund7] whereby
![]() $\Pi ^1_1$
-
$\Pi ^1_1$
-
![]() ${\mathsf {CA_0}}$
is equivalent to a higher-order fixed-point principle. Using the terminology of Freund [Reference Freund7], this is the statement that every dilator D has a well-founded Bachmann-Howard fixed point (we recall this definition during the course of the forthcoming proof).
${\mathsf {CA_0}}$
is equivalent to a higher-order fixed-point principle. Using the terminology of Freund [Reference Freund7], this is the statement that every dilator D has a well-founded Bachmann-Howard fixed point (we recall this definition during the course of the forthcoming proof).
Lemma 20 (
 ${\mathsf {ACA_0}}$
).
${\mathsf {ACA_0}}$
).
Suppose that
![]() $B_D$
is a dilator for every dilator D. Then, every dilator has a well-founded Bachmann-Howard fixed point.
$B_D$
is a dilator for every dilator D. Then, every dilator has a well-founded Bachmann-Howard fixed point.
Proof. It suffices to restrict to the case where D is a denotation system and, in particular,
![]() $\subseteq $
-preserving. We need to find a Bachmann-Howard fixed point: a well-ordering A and a function
$\subseteq $
-preserving. We need to find a Bachmann-Howard fixed point: a well-ordering A and a function
such that the following hold:
-
1. whenever we have
 $\alpha <_{D(A)}\beta $
and
$\alpha <_{D(A)}\beta $
and
 ${\text {supp}}(\alpha )<_A \theta (\beta )$
, then we have
${\text {supp}}(\alpha )<_A \theta (\beta )$
, then we have
 $\theta (\alpha ) <_A \theta (\beta )$
, and
$\theta (\alpha ) <_A \theta (\beta )$
, and -
2.
 ${\text {supp}}(\alpha ) <_A \theta (\alpha )$
for every
${\text {supp}}(\alpha ) <_A \theta (\alpha )$
for every
 $\alpha \in D(A)$
.
$\alpha \in D(A)$
.
Consider the dilator
![]() $F=(\omega +1)D +\omega $
. This is defined as follows: Given a linear order B, the order
$F=(\omega +1)D +\omega $
. This is defined as follows: Given a linear order B, the order
![]() $F(B)$
consists of terms of two types:
$F(B)$
consists of terms of two types:
-
3.
 $(\omega +1)\alpha +a$
, where
$(\omega +1)\alpha +a$
, where
 $\alpha \in D(B)$
and
$\alpha \in D(B)$
and
 $a\le \omega $
;
$a\le \omega $
; -
4.
 $\Lambda +n$
, where
$\Lambda +n$
, where
 $n<\omega $
.
$n<\omega $
.
The terms are compared according to the following rules:
-
5. terms of the first type are always smaller than the terms of the second type;
-
6.
 $(\omega +1)\alpha +a$
is smaller than
$(\omega +1)\alpha +a$
is smaller than
 $(\omega +1)\beta +b$
if and only if either
$(\omega +1)\beta +b$
if and only if either
 $\alpha <\beta $
or
$\alpha <\beta $
or
 $\alpha =\beta $
and
$\alpha =\beta $
and
 $a<b$
;
$a<b$
; -
7.
 $\Lambda +n$
is smaller than
$\Lambda +n$
is smaller than
 $\Lambda +m$
if and only if
$\Lambda +m$
if and only if
 $n<m$
.
$n<m$
.
For a strictly increasing function
![]() $f\colon B\to C$
, we put
$f\colon B\to C$
, we put
 $$ \begin{align*} F(f):F(B) &\to F(C)\\ (\omega+1)\alpha+a &\mapsto (\omega+1)(D(f)(\alpha))+a;\\ \Lambda + n &\mapsto \Lambda + n. \end{align*} $$
$$ \begin{align*} F(f):F(B) &\to F(C)\\ (\omega+1)\alpha+a &\mapsto (\omega+1)(D(f)(\alpha))+a;\\ \Lambda + n &\mapsto \Lambda + n. \end{align*} $$
It is easy to see that F is indeed a dilator.
We put
![]() $A=B_{F}(0)$
. This is a well-ordering since
$A=B_{F}(0)$
. This is a well-ordering since
![]() $B_F$
is a dilator by hypothesis. Note that all elements of A are of the form
$B_F$
is a dilator by hypothesis. Note that all elements of A are of the form
![]() $\psi (2^{\alpha _1}+\ldots +2^{\alpha _n})$
, where
$\psi (2^{\alpha _1}+\ldots +2^{\alpha _n})$
, where
![]() $\alpha _i\in F(A)$
. We define
$\alpha _i\in F(A)$
. We define
to be the function that maps
![]() $\alpha \in D(A)$
to the least element of A of the form
$\alpha \in D(A)$
to the least element of A of the form
This function is well defined (i.e., for any
![]() $\alpha \in D(A)$
, there is some element of A as above). Indeed, the elements of the form
$\alpha \in D(A)$
, there is some element of A as above). Indeed, the elements of the form
![]() $\psi (2^{\Lambda +n})$
are cofinal in A. Thus, for any
$\psi (2^{\Lambda +n})$
are cofinal in A. Thus, for any
![]() $\alpha \in D(A)$
, one can find n large enough so that
$\alpha \in D(A)$
, one can find n large enough so that
![]() $\alpha \in D(A{\upharpoonright }\psi (2^{\Lambda +n}))$
, and hence,
$\alpha \in D(A{\upharpoonright }\psi (2^{\Lambda +n}))$
, and hence,
Let us verify that
![]() $\theta $
satisfies property (1): we suppose
$\theta $
satisfies property (1): we suppose
![]() $\alpha <_{D(A)}\beta $
and
$\alpha <_{D(A)}\beta $
and
![]() ${\text {supp}}(\alpha )<_A \theta (\beta )$
and claim that
${\text {supp}}(\alpha )<_A \theta (\beta )$
and claim that
![]() $\theta (\alpha ) <_A \theta (\beta )$
. Let
$\theta (\alpha ) <_A \theta (\beta )$
. Let
![]() $\beta _1$
,
$\beta _1$
, ![]() ,
,
![]() $\beta _n$
be such that
$\beta _n$
be such that
Observe that all elements of the form
are in A and are cofinal below
![]() $\theta (\beta )$
. It follows that, since
$\theta (\beta )$
. It follows that, since
is a finite set, we can find
![]() $m\in \mathbb {N}$
large enough so that
$m\in \mathbb {N}$
large enough so that
For such an m,
![]() $\psi (2^{\beta _1}+\ldots +2^{\beta _n}+2^{(\omega +1)\beta +m}+2^{(\omega +1)\alpha +\omega })$
is in A, by (3) and since
$\psi (2^{\beta _1}+\ldots +2^{\beta _n}+2^{(\omega +1)\beta +m}+2^{(\omega +1)\alpha +\omega })$
is in A, by (3) and since
follows from
![]() $\alpha <_{D(A)}\beta $
. Therefore,
$\alpha <_{D(A)}\beta $
. Therefore,
 $$ \begin{align*} \theta(\alpha) &\le \psi(2^{\beta_1}+\ldots+2^{\beta_n}+2^{(\omega+1)\beta+m}+2^{(\omega+1)\alpha+\omega})\\ &<\psi(2^{\beta_1}+\ldots+2^{\beta_n}+2^{(\omega+1)\beta+\omega})\\ &=\theta(\beta). \end{align*} $$
$$ \begin{align*} \theta(\alpha) &\le \psi(2^{\beta_1}+\ldots+2^{\beta_n}+2^{(\omega+1)\beta+m}+2^{(\omega+1)\alpha+\omega})\\ &<\psi(2^{\beta_1}+\ldots+2^{\beta_n}+2^{(\omega+1)\beta+\omega})\\ &=\theta(\beta). \end{align*} $$
The fact that
![]() $\theta $
satisfies (2) is immediate from the construction. Indeed, for any
$\theta $
satisfies (2) is immediate from the construction. Indeed, for any
![]() $\alpha \in D(A)$
, the value
$\alpha \in D(A)$
, the value
![]() $\theta (\alpha )$
is of the form
$\theta (\alpha )$
is of the form
![]() $\psi (2^{\alpha _1}+\ldots +2^{\alpha _n}+2^{(\omega +1)\alpha +\omega })\in A$
and by the definition of
$\psi (2^{\alpha _1}+\ldots +2^{\alpha _n}+2^{(\omega +1)\alpha +\omega })\in A$
and by the definition of
![]() $B_F(A)$
, we have
$B_F(A)$
, we have
as desired.
Putting together the lemmata in this section, the proof of Theorem 17 is now complete.
Remark 21. By appealing to the main theorem of Freund [Reference Freund8] and carefully formalizing the definition of
![]() $B_D$
in Section 4, the equivalence in Theorem 17 can be proved in
$B_D$
in Section 4, the equivalence in Theorem 17 can be proved in
![]() ${\mathsf {RCA_0}}$
.
${\mathsf {RCA_0}}$
.
Competing interest
The authors have no competing interest to declare.
Funding statement
J.P.A. was partially supported by FWF grants ESP-3N and P36837 and FWO grant 0E3017319; F.P. was supported by FWO grant G0F8421N; A.W. was partially supported by FWO grants G0E2121N and G030620N. The authors acknowledge TU Wien Bibliothek for financial support through its Open Access Funding Programme.