1. Introduction
The Boltzmann equation is the fundamental equation describing the collective motion of gas molecules from the continuum-fluid to the free-molecular flow regimes (Chapman & Cowling Reference Chapman and Cowling1970; Cercignani Reference Cercignani1990). It underpins a broad range of research areas from aerodynamics to microfluidics. While at small Knudsen numbers (i.e. when the molecular mean free path is much smaller than the characteristic flow length) macroscopic equations, such as the Navier–Stokes, Burnett, and Grad equations, can be used in some instances (Galkin & Rusakov Reference Galkin and Rusakov2005; Greenshields & Reese Reference Greenshields and Reese2007; Garcia-Colin, Velasco & Uribe Reference Garcia-Colin, Velasco and Uribe2008; Gu & Emerson Reference Gu and Emerson2009; Rana, Torrilhon & Struchtrup Reference Rana, Torrilhon and Struchtrup2013; Rahimi & Struchtrup Reference Rahimi and Struchtrup2014), in the transition and free-molecular regimes the Boltzmann equation itself should be solved. However, its intricate collision operator makes a solution difficult to obtain by deterministic numerical methods. For monatomic gases, the computational cost of the Boltzmann collision operator (BCO) is usually of the order of
![]() $N_{v}^{7}$
, although this can be reduced to
$N_{v}^{7}$
, although this can be reduced to
![]() $O(M^{2}N_{v}^{3}\log N_{v})$
using the fast spectral method for some special collision kernels (Mouhot & Pareschi Reference Mouhot and Pareschi2006; Wu et al.
Reference Wu, White, Scanlon, Reese and Zhang2013; Wu, Reese & Zhang Reference Wu, Reese and Zhang2014), where
$O(M^{2}N_{v}^{3}\log N_{v})$
using the fast spectral method for some special collision kernels (Mouhot & Pareschi Reference Mouhot and Pareschi2006; Wu et al.
Reference Wu, White, Scanlon, Reese and Zhang2013; Wu, Reese & Zhang Reference Wu, Reese and Zhang2014), where
![]() $M^{2}$
and
$M^{2}$
and
![]() $N_{v}$
are the number of discrete solid angles and velocity grid points in each velocity direction, respectively.
$N_{v}$
are the number of discrete solid angles and velocity grid points in each velocity direction, respectively.
The problem becomes even more serious if the internal degrees of freedom (such as rotation and vibration) of a polyatomic gas are considered in the framework of the Wang-Chang–Uhlenbeck (WCU) equation (Wang-Chang & Uhlenbeck Reference Wang-Chang and Uhlenbeck1951). Buet (Reference Buet1997) proposed conservative and entropy schemes for the polyatomic collision operator; however these have never been used because of their prohibitive computational cost. Tcheremissine & Agarwal (Reference Tcheremissine, Agarwal and Abe2008) solved the WCU equation for normal shock waves in nitrogen, and found that the computational cost is larger by about two orders of magnitude than for a monatomic gas. Recently, a spectral-Lagrangian method with computational memory and cost of the order of
![]() $N_{e}^{4}N_{v}^{6}$
has been proposed (Munafò et al.
Reference Munafò, Haack, Gamba and Magin2014), where
$N_{e}^{4}N_{v}^{6}$
has been proposed (Munafò et al.
Reference Munafò, Haack, Gamba and Magin2014), where
![]() $N_{e}$
is the number of discrete internal energy levels; for
$N_{e}$
is the number of discrete internal energy levels; for
![]() $N_{e}=5$
and
$N_{e}=5$
and
![]() $N_{v}=16$
, the memory needed is approximately 88 GB, while the time needed for calculating the collision operators once is approximately 3 s using 12 compute threads, which restricts its suitability when applied to real problems.
$N_{v}=16$
, the memory needed is approximately 88 GB, while the time needed for calculating the collision operators once is approximately 3 s using 12 compute threads, which restricts its suitability when applied to real problems.
The direct simulation Monte Carlo (DSMC) method proposed by Bird (Reference Bird1994), using the Larsen–Borgnakke collision rule (Borgnakke & Larsen Reference Borgnakke and Larsen1975) for the translational–internal energy exchange, is a good alternative because of its linear computational cost with the number of simulated particles and far smaller memory requirements. It is efficient for hypersonic flows, but becomes time-consuming for microflow simulations when the flow velocity is well below the speed of sound (Hadjiconstantinou et al. Reference Hadjiconstantinou, Garcia, Bazant and He2003).
These concerns have stimulated researchers to develop kinetic models with simplified collision operators for polyatomic gases (Morse Reference Morse1964; Holway Reference Holway1966; Rykov Reference Rykov1975; Andries et al. Reference Andries, Le Tallec, Perlat and Perthame2000; Fernandes & Marques Reference Fernandes and Marques2007). In these models, the gain part of the BCO is modelled by the Gauss, ellipsoidal Gauss, and Gauss–Hermite polynomials, while the loss part describes the exponential decay of the distribution function with a rate independent of molecular velocity. Recently, Gorji and co-workers have also proposed a model replacing the BCO by the Fokker–Planck collision operator (Gorji, Torrilhon & Jenny Reference Gorji, Torrilhon and Jenny2011; Gorji & Jenny Reference Gorji and Jenny2013), which models the drift and diffusion in velocity space. Although this model is faster than the DSMC method near the continuum-fluid regime, for microflow simulations it suffers the same slowness as the DSMC method because of its particulate nature.
A common drawback of all these kinetic models for polyatomic gases is that they do not reduce to the Boltzmann equation for monatomic gases when translational–internal energy exchange is absent. Also, they cannot capture the differences in flow properties for different molecular models even in isothermal flows. For instance, for monatomic gases, the Shakhov kinetic model (Shakhov Reference Shakhov1968) predicts the same mass flow rate for linearized Poiseuille flow with various viscosity indices, while the Boltzmann equation shows different mass flow rates for different molecular models (viscosity indices) (Sharipov & Bertoldo Reference Sharipov and Bertoldo2009; Wu et al. Reference Wu, Reese and Zhang2014).
In this paper, we present a new kinetic model for non-vibrating polyatomic gases, in which elastic collisions are modelled by the BCO for a monatomic gas, while inelastic collisions are the same as those in the Rykov model (Rykov Reference Rykov1975). Our model exactly recovers the Jeans’ relaxation equation for the translational–rotational energy exchange, and it reduces to the Boltzmann equation for monatomic gases when translational–rotational energy exchange is absent. Importantly, it can capture the influence of different molecular models on the flow properties, and the computational efficiency is nearly the same as that of the Boltzmann equation for monatomic gases.
This paper is organized as follows. In § 2, the Rykov kinetic model of the Boltzmann equation for non-vibrating diatomic gases is introduced, and then extended to polyatomic gases. A new kinetic model for non-vibrating polyatomic gases, which recovers the elastic velocity-dependent collision frequency, is then proposed. In § 3, the kinetic model equations are solved by the fast spectral method and the discrete velocity method. Numerical results for normal shock waves and planar Fourier/Couette flows are compared with DSMC results and experimental data. In § 4, the mass and heat flow rates in Poiseuille and thermal creep flows of polyatomic gases are calculated. In § 5, the spectra of both spontaneous and coherent Rayleigh–Brillouin scattering (RBS) in polyatomic gases are obtained, and the influence of the molecular model is analysed. We conclude in § 6.
2. Kinetic modelling of polyatomic gases
We consider polyatomic gases in which the vibrational degrees of freedom are not excited and the rotational degrees of freedom can be treated classically; for nitrogen, this corresponds to a temperature range of 100–600 K (Nyeland & Billing Reference Nyeland and Billing1988). In this case, the gas molecule has three translational degrees of freedom and
![]() $d$
rotational degrees of freedom, where
$d$
rotational degrees of freedom, where
![]() $d=2$
and 3 for diatomic and nonlinear polyatomic gases, respectively. For the rotational degrees of freedom, only the rotational energy is relevant (Kuščer Reference Kuščer1991). Therefore, the system state can be described by the distribution function
$d=2$
and 3 for diatomic and nonlinear polyatomic gases, respectively. For the rotational degrees of freedom, only the rotational energy is relevant (Kuščer Reference Kuščer1991). Therefore, the system state can be described by the distribution function
![]() $f(t,\boldsymbol{x},\boldsymbol{v},I)$
, where
$f(t,\boldsymbol{x},\boldsymbol{v},I)$
, where
![]() $t$
is the time,
$t$
is the time,
![]() $\boldsymbol{x}=(x_{1},x_{2},x_{3})$
is the spatial coordinate,
$\boldsymbol{x}=(x_{1},x_{2},x_{3})$
is the spatial coordinate,
![]() $\boldsymbol{v}=(v_{1},v_{2},v_{3})$
is the molecular translational velocity, and
$\boldsymbol{v}=(v_{1},v_{2},v_{3})$
is the molecular translational velocity, and
![]() $I^{2/d}$
is the rotational energy with
$I^{2/d}$
is the rotational energy with
![]() $I\geqslant 0$
. Macroscopic quantities, such as the molecular number density
$I\geqslant 0$
. Macroscopic quantities, such as the molecular number density
![]() $n(t,\boldsymbol{x})$
, the bulk velocity
$n(t,\boldsymbol{x})$
, the bulk velocity
![]() $\boldsymbol{U}(t,\boldsymbol{x})$
, the pressure tensor
$\boldsymbol{U}(t,\boldsymbol{x})$
, the pressure tensor
![]() $\unicode[STIX]{x1D617}_{ij}(t,\boldsymbol{x})$
, the translational temperature
$\unicode[STIX]{x1D617}_{ij}(t,\boldsymbol{x})$
, the translational temperature
![]() $T_{t}(t,\boldsymbol{x})$
, the rotational temperature
$T_{t}(t,\boldsymbol{x})$
, the rotational temperature
![]() $T_{r}(t,\boldsymbol{x})$
, and the heat fluxes
$T_{r}(t,\boldsymbol{x})$
, and the heat fluxes
![]() $\boldsymbol{q}_{t}(t,\boldsymbol{x})$
and
$\boldsymbol{q}_{t}(t,\boldsymbol{x})$
and
![]() $\boldsymbol{q}_{r}(t,\boldsymbol{x})$
produced by the transfer of translational and rotational energies, are defined as:
$\boldsymbol{q}_{r}(t,\boldsymbol{x})$
produced by the transfer of translational and rotational energies, are defined as:
where
![]() $k$
is the Boltzmann constant,
$k$
is the Boltzmann constant,
![]() $m$
is the molecular mass, and
$m$
is the molecular mass, and
![]() $\boldsymbol{c}=\boldsymbol{v}-\boldsymbol{U}$
is the peculiar velocity. The equilibrium temperature is
$\boldsymbol{c}=\boldsymbol{v}-\boldsymbol{U}$
is the peculiar velocity. The equilibrium temperature is
![]() $T=(3T_{t}+dT_{r})/(d+3)$
and the total heat flux is
$T=(3T_{t}+dT_{r})/(d+3)$
and the total heat flux is
![]() $\boldsymbol{q}=\boldsymbol{q}_{t}+\boldsymbol{q}_{r}$
. We also define the pressures
$\boldsymbol{q}=\boldsymbol{q}_{t}+\boldsymbol{q}_{r}$
. We also define the pressures
![]() $p_{t}=nkT_{t}$
,
$p_{t}=nkT_{t}$
,
![]() $p_{r}=nkT_{r}$
, and
$p_{r}=nkT_{r}$
, and
![]() $p=nkT$
in terms of the translational, rotational, and total degrees of freedom, respectively.
$p=nkT$
in terms of the translational, rotational, and total degrees of freedom, respectively.
The evolution of the polyatomic gas distribution function is governed by the WCU equation. The additional rotational degrees of freedom make the WCU equation much more complicated than the Boltzmann equation for monatomic gases. Kinetic model equations are therefore needed to simplify the complicated BCO. In the following, we first introduce the Rykov kinetic model (Rykov Reference Rykov1975) for diatomic gases because it can predict density profiles in normal shock waves (Larina & Rykov Reference Larina and Rykov2010; Liu et al. Reference Liu, Yu, Xu and Zhong2014). We then extend the Rykov model to model polyatomic gases. Finally, we propose a kinetic model with modified elastic collision operators, in order to improve the accuracy of rarefied gas flow simulations.
2.1. The Rykov kinetic model and its extension
Like most kinetic models for polyatomic gases (Morse Reference Morse1964; Holway Reference Holway1966), elastic and inelastic collisions are treated separately in the Rykov model (Rykov Reference Rykov1975). The original Rykov model was for non-vibrating diatomic gases, but the method of construction can be extended straightforwardly to nonlinear polyatomic gases. In the absence of an external force, the evolution of the distribution function is described by the following equation:
 $$\begin{eqnarray}\frac{\partial f}{\partial t}+\boldsymbol{v}\boldsymbol{\cdot }\frac{\partial f}{\partial \boldsymbol{x}}=\underbrace{\frac{g_{t}-f}{{\it\tau}}}_{elastic}+\underbrace{\frac{g_{r}-g_{t}}{Z{\it\tau}}}_{inelastic},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\partial f}{\partial t}+\boldsymbol{v}\boldsymbol{\cdot }\frac{\partial f}{\partial \boldsymbol{x}}=\underbrace{\frac{g_{t}-f}{{\it\tau}}}_{elastic}+\underbrace{\frac{g_{r}-g_{t}}{Z{\it\tau}}}_{inelastic},\end{eqnarray}$$
where the terms on the right describe elastic and inelastic collisions. The elastic collision conserves the translational energy, while the inelastic collision exchanges the translational and rotational energies. The relaxation time
![]() ${\it\tau}$
and the parameter
${\it\tau}$
and the parameter
![]() $Z$
are independent of the molecular velocity. The reference distribution functions
$Z$
are independent of the molecular velocity. The reference distribution functions
![]() $g_{t}$
and
$g_{t}$
and
![]() $g_{r}$
characterize the energy distributions of the particles that have undergone elastic and inelastic collisions, and are given by
$g_{r}$
characterize the energy distributions of the particles that have undergone elastic and inelastic collisions, and are given by
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}rcl@{}}g_{t}\, & =\, & \displaystyle n\left(\frac{m}{2{\rm\pi}kT_{t}}\right)^{3/2}\exp \left(\frac{-mc^{2}}{2kT_{t}}\right)\frac{2\left(kT_{r}\right)^{-d/2}}{d{\rm\Gamma}(d/2)}\exp \left(-\frac{I^{2/d}}{kT_{r}}\right)\\ \, & \, & \times \,\displaystyle \left[1+\frac{2m\boldsymbol{q}_{t}\boldsymbol{\cdot }\boldsymbol{c}}{15kT_{t}p_{t}}\left(\frac{mc^{2}}{2kT_{t}}-\frac{5}{2}\right)+\frac{2(1-{\it\delta})}{d}\frac{m\boldsymbol{q}_{r}\boldsymbol{\cdot }\boldsymbol{c}}{kT_{t}p_{r}}\left(\frac{I^{2/d}}{kT_{r}}-\frac{d}{2}\right)\right],\\ g_{r}\, & =\, & \displaystyle n\left(\frac{m}{2{\rm\pi}kT}\right)^{3/2}\exp \left(\frac{-mc^{2}}{2kT}\right)\frac{2\left(kT\right)^{-d/2}}{d{\rm\Gamma}(d/2)}\exp \left(-\frac{I^{2/d}}{kT}\right)\\ \, & \, & \times \,\displaystyle \left[1+{\it\omega}_{0}\frac{2m\boldsymbol{q}_{t}\boldsymbol{\cdot }\boldsymbol{c}}{15kTp}\left(\frac{mc^{2}}{2kT}-\frac{5}{2}\right)+\frac{2{\it\omega}_{1}(1-{\it\delta})}{d}\frac{m\boldsymbol{q}_{r}\boldsymbol{\cdot }\boldsymbol{c}}{kTp}\left(\frac{I^{2/d}}{kT}-\frac{d}{2}\right)\right],\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}rcl@{}}g_{t}\, & =\, & \displaystyle n\left(\frac{m}{2{\rm\pi}kT_{t}}\right)^{3/2}\exp \left(\frac{-mc^{2}}{2kT_{t}}\right)\frac{2\left(kT_{r}\right)^{-d/2}}{d{\rm\Gamma}(d/2)}\exp \left(-\frac{I^{2/d}}{kT_{r}}\right)\\ \, & \, & \times \,\displaystyle \left[1+\frac{2m\boldsymbol{q}_{t}\boldsymbol{\cdot }\boldsymbol{c}}{15kT_{t}p_{t}}\left(\frac{mc^{2}}{2kT_{t}}-\frac{5}{2}\right)+\frac{2(1-{\it\delta})}{d}\frac{m\boldsymbol{q}_{r}\boldsymbol{\cdot }\boldsymbol{c}}{kT_{t}p_{r}}\left(\frac{I^{2/d}}{kT_{r}}-\frac{d}{2}\right)\right],\\ g_{r}\, & =\, & \displaystyle n\left(\frac{m}{2{\rm\pi}kT}\right)^{3/2}\exp \left(\frac{-mc^{2}}{2kT}\right)\frac{2\left(kT\right)^{-d/2}}{d{\rm\Gamma}(d/2)}\exp \left(-\frac{I^{2/d}}{kT}\right)\\ \, & \, & \times \,\displaystyle \left[1+{\it\omega}_{0}\frac{2m\boldsymbol{q}_{t}\boldsymbol{\cdot }\boldsymbol{c}}{15kTp}\left(\frac{mc^{2}}{2kT}-\frac{5}{2}\right)+\frac{2{\it\omega}_{1}(1-{\it\delta})}{d}\frac{m\boldsymbol{q}_{r}\boldsymbol{\cdot }\boldsymbol{c}}{kTp}\left(\frac{I^{2/d}}{kT}-\frac{d}{2}\right)\right],\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where
![]() ${\rm\Gamma}$
is the gamma function,
${\rm\Gamma}$
is the gamma function,
![]() ${\it\omega}_{0}$
and
${\it\omega}_{0}$
and
![]() ${\it\omega}_{1}$
are constants to recover the thermal conductivity coefficients of polyatomic gases (see appendix A), and
${\it\omega}_{1}$
are constants to recover the thermal conductivity coefficients of polyatomic gases (see appendix A), and
![]() ${\it\delta}={\it\mu}(T_{t})/mnD$
, with
${\it\delta}={\it\mu}(T_{t})/mnD$
, with
![]() ${\it\mu}$
and
${\it\mu}$
and
![]() $D$
being the coefficients of the shear viscosity and diffusion, respectively.
$D$
being the coefficients of the shear viscosity and diffusion, respectively.
In numerical computations, it is useful to use the following reduced velocity distribution functions (VDFs):
![]() $G(t,\boldsymbol{x},\boldsymbol{v})=\int _{0}^{\infty }f(t,\boldsymbol{x},\boldsymbol{v},I)\text{d}I$
and
$G(t,\boldsymbol{x},\boldsymbol{v})=\int _{0}^{\infty }f(t,\boldsymbol{x},\boldsymbol{v},I)\text{d}I$
and
![]() $R(t,\boldsymbol{x},\boldsymbol{v})=\int _{0}^{\infty }f(t,\boldsymbol{x},\boldsymbol{v},I)I^{2/d}\text{d}I$
, in order to eliminate the rotational energy variable to save computational memory and cost. Multiplying (2.3) by 1 and
$R(t,\boldsymbol{x},\boldsymbol{v})=\int _{0}^{\infty }f(t,\boldsymbol{x},\boldsymbol{v},I)I^{2/d}\text{d}I$
, in order to eliminate the rotational energy variable to save computational memory and cost. Multiplying (2.3) by 1 and
![]() $I^{2/d}$
and integrating the resulting equations with respect to
$I^{2/d}$
and integrating the resulting equations with respect to
![]() $I$
from zero to infinity, (2.3) can be transformed into the following two coupled equations:
$I$
from zero to infinity, (2.3) can be transformed into the following two coupled equations:
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\displaystyle G_{t}=n\left(\frac{m}{2{\rm\pi}kT_{t}}\right)^{3/2}\exp \left(\frac{-mc^{2}}{2kT_{t}}\right)\left[1+\frac{2m\boldsymbol{q}_{t}\boldsymbol{\cdot }\boldsymbol{c}}{15kT_{t}p_{t}}\left(\frac{mc^{2}}{2kT_{t}}-\frac{5}{2}\right)\right],\\ \displaystyle G_{r}=n\left(\frac{m}{2{\rm\pi}kT}\right)^{3/2}\exp \left(\frac{-mc^{2}}{2kT}\right)\left[1+{\it\omega}_{0}\frac{2m\boldsymbol{q}_{t}\boldsymbol{\cdot }\boldsymbol{c}}{15kTp}\left(\frac{mc^{2}}{2kT}-\frac{5}{2}\right)\right],\\ \displaystyle R_{t}=\frac{dkT_{r}}{2}G_{t}+\left(\frac{m}{2{\rm\pi}kT_{t}}\right)^{3/2}\exp \left(\frac{-mc^{2}}{2kT_{t}}\right)(1-{\it\delta})\frac{m\boldsymbol{q}_{r}\boldsymbol{\cdot }\boldsymbol{c}}{kT_{t}},\\ \displaystyle R_{r}=\frac{dkT}{2}G_{r}+\left(\frac{m}{2{\rm\pi}kT}\right)^{3/2}\exp \left(\frac{-mc^{2}}{2kT}\right){\it\omega}_{1}(1-{\it\delta})\frac{m\boldsymbol{q}_{r}\boldsymbol{\cdot }\boldsymbol{c}}{kT},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\displaystyle G_{t}=n\left(\frac{m}{2{\rm\pi}kT_{t}}\right)^{3/2}\exp \left(\frac{-mc^{2}}{2kT_{t}}\right)\left[1+\frac{2m\boldsymbol{q}_{t}\boldsymbol{\cdot }\boldsymbol{c}}{15kT_{t}p_{t}}\left(\frac{mc^{2}}{2kT_{t}}-\frac{5}{2}\right)\right],\\ \displaystyle G_{r}=n\left(\frac{m}{2{\rm\pi}kT}\right)^{3/2}\exp \left(\frac{-mc^{2}}{2kT}\right)\left[1+{\it\omega}_{0}\frac{2m\boldsymbol{q}_{t}\boldsymbol{\cdot }\boldsymbol{c}}{15kTp}\left(\frac{mc^{2}}{2kT}-\frac{5}{2}\right)\right],\\ \displaystyle R_{t}=\frac{dkT_{r}}{2}G_{t}+\left(\frac{m}{2{\rm\pi}kT_{t}}\right)^{3/2}\exp \left(\frac{-mc^{2}}{2kT_{t}}\right)(1-{\it\delta})\frac{m\boldsymbol{q}_{r}\boldsymbol{\cdot }\boldsymbol{c}}{kT_{t}},\\ \displaystyle R_{r}=\frac{dkT}{2}G_{r}+\left(\frac{m}{2{\rm\pi}kT}\right)^{3/2}\exp \left(\frac{-mc^{2}}{2kT}\right){\it\omega}_{1}(1-{\it\delta})\frac{m\boldsymbol{q}_{r}\boldsymbol{\cdot }\boldsymbol{c}}{kT},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
with macroscopic quantities calculated as:
![]() $n=\int G\text{d}\boldsymbol{v}$
,
$n=\int G\text{d}\boldsymbol{v}$
,
![]() $\boldsymbol{U}=\int G\boldsymbol{v}\text{d}\boldsymbol{v}/n$
,
$\boldsymbol{U}=\int G\boldsymbol{v}\text{d}\boldsymbol{v}/n$
,
![]() $\unicode[STIX]{x1D617}_{ij}=\int Gmc_{i}c_{j}\text{d}\boldsymbol{v}$
,
$\unicode[STIX]{x1D617}_{ij}=\int Gmc_{i}c_{j}\text{d}\boldsymbol{v}$
,
![]() $T_{t}=\int Gmc^{2}\text{d}\boldsymbol{v}/(3nk)$
,
$T_{t}=\int Gmc^{2}\text{d}\boldsymbol{v}/(3nk)$
,
![]() $T_{r}=2\int R\text{d}\boldsymbol{v}/(n\text{d}k)$
,
$T_{r}=2\int R\text{d}\boldsymbol{v}/(n\text{d}k)$
,
![]() $\boldsymbol{q}_{t}=\int Gmc^{2}\boldsymbol{c}\text{d}\boldsymbol{v}/2$
, and
$\boldsymbol{q}_{t}=\int Gmc^{2}\boldsymbol{c}\text{d}\boldsymbol{v}/2$
, and
![]() $\boldsymbol{q}_{r}=\int R\boldsymbol{c}\text{d}\boldsymbol{v}$
.
$\boldsymbol{q}_{r}=\int R\boldsymbol{c}\text{d}\boldsymbol{v}$
.
If
![]() $G$
is the VDF for a monatomic gas, the elastic collision operator
$G$
is the VDF for a monatomic gas, the elastic collision operator
![]() $(G_{t}-G)/{\it\tau}$
in (2.5) is just the Shakhov simplification of the BCO for monatomic gases. In the limit of no translational–rotational energy exchange (i.e.
$(G_{t}-G)/{\it\tau}$
in (2.5) is just the Shakhov simplification of the BCO for monatomic gases. In the limit of no translational–rotational energy exchange (i.e.
![]() $Z\rightarrow \infty$
), (2.5) reduces to the Shakhov model equation for monatomic gases (Shakhov Reference Shakhov1968). In this sense, the Rykov kinetic model can be viewed as an extension to polyatomic gases of the Shakhov kinetic model for monatomic gases.
$Z\rightarrow \infty$
), (2.5) reduces to the Shakhov model equation for monatomic gases (Shakhov Reference Shakhov1968). In this sense, the Rykov kinetic model can be viewed as an extension to polyatomic gases of the Shakhov kinetic model for monatomic gases.
2.2. A kinetic model for non-vibrating polyatomic gases
The Rykov kinetic model has been applied to normal shock wave problems (Larina & Rykov Reference Larina and Rykov2010; Liu et al.
Reference Liu, Yu, Xu and Zhong2014). It predicts density profiles in nitrogen with a viscosity index of 0.74; however, the translational temperature profiles are not in good agreement with DSMC results, especially at large Mach numbers (Liu et al.
Reference Liu, Yu, Xu and Zhong2014). Note that the early rising of the translational temperature in normal shock waves has also been observed when using the Shakhov kinetic model for monatomic gas simulations (Xu & Huang Reference Xu and Huang2011). The reason for this is the use of a single relaxation time
![]() ${\it\tau}$
, while in the Boltzmann equation the relaxation time depends on the molecular velocity. For monatomic Maxwell molecules, the relaxation time is independent of the molecular velocity, and we find that the Shakhov model gives temperature profiles in good agreement with those of the Boltzmann equation (not shown here).
${\it\tau}$
, while in the Boltzmann equation the relaxation time depends on the molecular velocity. For monatomic Maxwell molecules, the relaxation time is independent of the molecular velocity, and we find that the Shakhov model gives temperature profiles in good agreement with those of the Boltzmann equation (not shown here).
To improve the model accuracy, we introduce a relaxation time that depends on the molecular velocity. It has already been shown that this can improve predictions for a monatomic gas flow (Mieussens & Struchtrup Reference Mieussens and Struchtrup2004). Here, we recover the realistic elastic relaxation time by replacing the elastic collision operator
![]() $(G_{t}-G)/{\it\tau}$
in the Rykov model (2.5) with the BCO
$(G_{t}-G)/{\it\tau}$
in the Rykov model (2.5) with the BCO
![]() $Q(G,G)$
for monatomic gases:
$Q(G,G)$
for monatomic gases:
For more information about the deflection angle
![]() ${\it\theta}$
, collision kernel
${\it\theta}$
, collision kernel
![]() $B$
, and post-collision velocity
$B$
, and post-collision velocity
![]() $v^{\prime }$
, see Wu et al. (Reference Wu, White, Scanlon, Reese and Zhang2013).
$v^{\prime }$
, see Wu et al. (Reference Wu, White, Scanlon, Reese and Zhang2013).
From
![]() $(G_{t}-G)/{\it\tau}=Q$
we have
$(G_{t}-G)/{\it\tau}=Q$
we have
![]() $G_{t}={\it\tau}Q+G$
. Then the elastic collision operator
$G_{t}={\it\tau}Q+G$
. Then the elastic collision operator
![]() $(R_{t}-R)/{\it\tau}$
in (2.6) is reduced to
$(R_{t}-R)/{\it\tau}$
in (2.6) is reduced to
![]() $(R^{\prime }-R)/{\it\tau}$
, where
$(R^{\prime }-R)/{\it\tau}$
, where
This new kinetic model for polyatomic gases, which treats translational and rotational degrees of freedom, is therefore:
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \frac{\partial G}{\partial t}+\boldsymbol{v}\boldsymbol{\cdot }\frac{\partial G}{\partial \boldsymbol{x}}=Q(G,G)+\frac{G_{r}-G_{t}}{Z{\it\tau}},\\ \displaystyle \frac{\partial R}{\partial t}+\boldsymbol{v}\boldsymbol{\cdot }\frac{\partial R}{\partial \boldsymbol{x}}=\frac{R^{\prime }-R}{{\it\tau}}+\frac{R_{r}-R_{t}}{Z{\it\tau}},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \frac{\partial G}{\partial t}+\boldsymbol{v}\boldsymbol{\cdot }\frac{\partial G}{\partial \boldsymbol{x}}=Q(G,G)+\frac{G_{r}-G_{t}}{Z{\it\tau}},\\ \displaystyle \frac{\partial R}{\partial t}+\boldsymbol{v}\boldsymbol{\cdot }\frac{\partial R}{\partial \boldsymbol{x}}=\frac{R^{\prime }-R}{{\it\tau}}+\frac{R_{r}-R_{t}}{Z{\it\tau}},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
which, in the limit of no translational–rotational energy exchange, reduces to the Boltzmann equation for monatomic gases. Note that the transport coefficients derived according to the Chapman–Enskog expansion from the kinetic model (2.10) are the same as from the Rykov model (considering that for monatomic gases, if the BCO is replaced by the Shakhov collision operator we can obtain the same shear viscosity and thermal conductivity).
The parameters
![]() ${\it\tau}$
,
${\it\tau}$
,
![]() $Z$
,
$Z$
,
![]() ${\it\delta}$
,
${\it\delta}$
,
![]() ${\it\omega}_{0}$
, and
${\it\omega}_{0}$
, and
![]() ${\it\omega}_{1}$
remain to be determined. First, according to (A 6), the relaxation time
${\it\omega}_{1}$
remain to be determined. First, according to (A 6), the relaxation time
![]() ${\it\tau}$
is determined by the shear viscosity, the molecular number density, and the translational temperature. Second, the parameter
${\it\tau}$
is determined by the shear viscosity, the molecular number density, and the translational temperature. Second, the parameter
![]() ${\it\delta}$
depends on the intermolecular potential. For example,
${\it\delta}$
depends on the intermolecular potential. For example,
![]() ${\it\delta}=1/1.33$
for nitrogen if the Lennard-Jones potential is considered; for inverse power-law potentials, as the viscosity index
${\it\delta}=1/1.33$
for nitrogen if the Lennard-Jones potential is considered; for inverse power-law potentials, as the viscosity index
![]() ${\it\omega}$
increases from 0.5 to 1,
${\it\omega}$
increases from 0.5 to 1,
![]() ${\it\delta}$
decreases from
${\it\delta}$
decreases from
![]() $1/1.2$
to
$1/1.2$
to
![]() $1/1.55$
. Third, it follows from (2.10) that the relaxation of the rotational temperature in spatially-homogeneous problems is described by:
$1/1.55$
. Third, it follows from (2.10) that the relaxation of the rotational temperature in spatially-homogeneous problems is described by:
while in kinetic theory the Jeans’ equation
![]() $\partial T_{r}/\partial t=(T_{t}-T_{r})/(Z_{rot}{\rm\pi}{\it\tau}/4)$
is frequently used, where
$\partial T_{r}/\partial t=(T_{t}-T_{r})/(Z_{rot}{\rm\pi}{\it\tau}/4)$
is frequently used, where
![]() $Z_{rot}$
is the rotational collision number. Therefore, the parameter
$Z_{rot}$
is the rotational collision number. Therefore, the parameter
![]() $Z$
is related to the rotational collision number
$Z$
is related to the rotational collision number
![]() $Z_{rot}$
as:
$Z_{rot}$
as:
Fourth, according to the kinetic theory of Mason & Monchick (Reference Mason and Monchick1962) regarding the thermal conductivity coefficients due to the transfer of translational and rotational energies,
![]() ${\it\omega}_{0}$
and
${\it\omega}_{0}$
and
![]() ${\it\omega}_{1}$
may be determined from the following two equations:
${\it\omega}_{1}$
may be determined from the following two equations:
3. Validation cases
For practical calculations it is convenient to use dimensionless variables. The following are therefore introduced:
![]() $\widetilde{G}=v_{m}^{3}G/n_{0}$
,
$\widetilde{G}=v_{m}^{3}G/n_{0}$
,
![]() $\widetilde{R}=v_{m}^{3}R/n_{0}kT_{0}$
,
$\widetilde{R}=v_{m}^{3}R/n_{0}kT_{0}$
,
![]() $\widetilde{\boldsymbol{x}}=\boldsymbol{x}/\ell$
,
$\widetilde{\boldsymbol{x}}=\boldsymbol{x}/\ell$
,
![]() $(\widetilde{\boldsymbol{v}},\widetilde{\boldsymbol{c}},\widetilde{\boldsymbol{U}})=(\boldsymbol{v},\boldsymbol{c},\boldsymbol{U})/v_{m}$
,
$(\widetilde{\boldsymbol{v}},\widetilde{\boldsymbol{c}},\widetilde{\boldsymbol{U}})=(\boldsymbol{v},\boldsymbol{c},\boldsymbol{U})/v_{m}$
,
![]() $\widetilde{t}=tv_{m}/\ell$
,
$\widetilde{t}=tv_{m}/\ell$
,
![]() $\widetilde{n}=n/n_{0}$
,
$\widetilde{n}=n/n_{0}$
,
![]() $(\widetilde{T},\widetilde{T}_{t},\widetilde{T}_{r})=(T,T_{t},T_{r})/T_{0}$
,
$(\widetilde{T},\widetilde{T}_{t},\widetilde{T}_{r})=(T,T_{t},T_{r})/T_{0}$
,
![]() $\widetilde{\unicode[STIX]{x1D617}}_{ij}=\unicode[STIX]{x1D617}_{ij}/n_{0}k_{B}T_{0}$
, and
$\widetilde{\unicode[STIX]{x1D617}}_{ij}=\unicode[STIX]{x1D617}_{ij}/n_{0}k_{B}T_{0}$
, and
![]() $(\widetilde{\boldsymbol{q}},\widetilde{\boldsymbol{q}}_{t},\widetilde{\boldsymbol{q}}_{r})=(\boldsymbol{q},\boldsymbol{q}_{t},\boldsymbol{q}_{r})/n_{0}k_{B}T_{0}v_{m}$
, where
$(\widetilde{\boldsymbol{q}},\widetilde{\boldsymbol{q}}_{t},\widetilde{\boldsymbol{q}}_{r})=(\boldsymbol{q},\boldsymbol{q}_{t},\boldsymbol{q}_{r})/n_{0}k_{B}T_{0}v_{m}$
, where
![]() $n_{0}$
and
$n_{0}$
and
![]() $T_{0}$
are the reference molecular number density and temperature, respectively,
$T_{0}$
are the reference molecular number density and temperature, respectively,
![]() $\ell$
is the characteristic flow length, and
$\ell$
is the characteristic flow length, and
![]() $v_{m}=\sqrt{2k_{B}T_{0}/m}$
is the most probable molecular speed. The dimensionless kinetic model equations (2.10) can then be written as follows:
$v_{m}=\sqrt{2k_{B}T_{0}/m}$
is the most probable molecular speed. The dimensionless kinetic model equations (2.10) can then be written as follows:
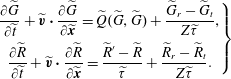 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \frac{\partial \widetilde{G}}{\partial \widetilde{t}}+\widetilde{\boldsymbol{v}}\boldsymbol{\cdot }\frac{\partial \widetilde{G}}{\partial \widetilde{\boldsymbol{x}}}=\widetilde{Q}(\widetilde{G},\widetilde{G})+\frac{\widetilde{G}_{r}-\widetilde{G}_{t}}{Z\widetilde{{\it\tau}}},\\ \displaystyle \frac{\partial \widetilde{R}}{\partial \widetilde{t}}+\widetilde{\boldsymbol{v}}\boldsymbol{\cdot }\frac{\partial \widetilde{R}}{\partial \widetilde{\boldsymbol{x}}}=\frac{\widetilde{R}^{\prime }-\widetilde{R}}{\widetilde{{\it\tau}}}+\frac{\widetilde{R}_{r}-\widetilde{R}_{t}}{Z\widetilde{{\it\tau}}}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \frac{\partial \widetilde{G}}{\partial \widetilde{t}}+\widetilde{\boldsymbol{v}}\boldsymbol{\cdot }\frac{\partial \widetilde{G}}{\partial \widetilde{\boldsymbol{x}}}=\widetilde{Q}(\widetilde{G},\widetilde{G})+\frac{\widetilde{G}_{r}-\widetilde{G}_{t}}{Z\widetilde{{\it\tau}}},\\ \displaystyle \frac{\partial \widetilde{R}}{\partial \widetilde{t}}+\widetilde{\boldsymbol{v}}\boldsymbol{\cdot }\frac{\partial \widetilde{R}}{\partial \widetilde{\boldsymbol{x}}}=\frac{\widetilde{R}^{\prime }-\widetilde{R}}{\widetilde{{\it\tau}}}+\frac{\widetilde{R}_{r}-\widetilde{R}_{t}}{Z\widetilde{{\it\tau}}}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
Here, the dimensionless BCO for inverse power-law intermolecular potentials (Wu et al. Reference Wu, White, Scanlon, Reese and Zhang2013) is
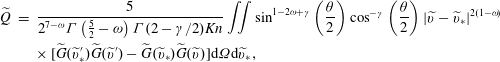 $$\begin{eqnarray}\displaystyle \widetilde{Q} & = & \displaystyle \frac{5}{2^{7-{\it\omega}}{\rm\Gamma}\left({\textstyle \frac{5}{2}}-{\it\omega}\right){\rm\Gamma}(2-{\it\gamma}/2)\mathit{Kn}}\iint \sin ^{1-2{\it\omega}+{\it\gamma}}\left(\frac{{\it\theta}}{2}\right)\cos ^{-{\it\gamma}}\left(\frac{{\it\theta}}{2}\right)|\widetilde{v}-\widetilde{v}_{\ast }|^{2(1-{\it\omega})}\nonumber\\ \displaystyle & & \displaystyle \times \,[\widetilde{G}(\widetilde{v}_{\ast }^{\prime })\widetilde{G}(\widetilde{v}^{\prime })-\widetilde{G}(\widetilde{v}_{\ast })\widetilde{G}(\widetilde{v})]\text{d}{\it\Omega}\text{d}\widetilde{v}_{\ast },\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{Q} & = & \displaystyle \frac{5}{2^{7-{\it\omega}}{\rm\Gamma}\left({\textstyle \frac{5}{2}}-{\it\omega}\right){\rm\Gamma}(2-{\it\gamma}/2)\mathit{Kn}}\iint \sin ^{1-2{\it\omega}+{\it\gamma}}\left(\frac{{\it\theta}}{2}\right)\cos ^{-{\it\gamma}}\left(\frac{{\it\theta}}{2}\right)|\widetilde{v}-\widetilde{v}_{\ast }|^{2(1-{\it\omega})}\nonumber\\ \displaystyle & & \displaystyle \times \,[\widetilde{G}(\widetilde{v}_{\ast }^{\prime })\widetilde{G}(\widetilde{v}^{\prime })-\widetilde{G}(\widetilde{v}_{\ast })\widetilde{G}(\widetilde{v})]\text{d}{\it\Omega}\text{d}\widetilde{v}_{\ast },\end{eqnarray}$$
![]() $\widetilde{R}^{\prime }=(d/2)\widetilde{T}_{r}(\widetilde{{\it\tau}}\widetilde{Q}+\widetilde{G})+2(1-{\it\delta})({\rm\pi}\widetilde{T}_{t})^{-3/2}\exp (-\widetilde{c}^{\,2}/\widetilde{T}_{t})\widetilde{\boldsymbol{q}}_{r}\boldsymbol{\cdot }\widetilde{\boldsymbol{c}}/\widetilde{T}_{t}$
, and the four normalized reference VDFs are
$\widetilde{R}^{\prime }=(d/2)\widetilde{T}_{r}(\widetilde{{\it\tau}}\widetilde{Q}+\widetilde{G})+2(1-{\it\delta})({\rm\pi}\widetilde{T}_{t})^{-3/2}\exp (-\widetilde{c}^{\,2}/\widetilde{T}_{t})\widetilde{\boldsymbol{q}}_{r}\boldsymbol{\cdot }\widetilde{\boldsymbol{c}}/\widetilde{T}_{t}$
, and the four normalized reference VDFs are
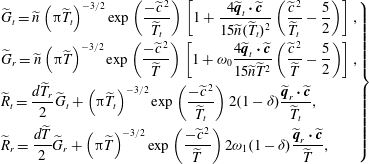 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\displaystyle \widetilde{G}_{t}=\widetilde{n}\left({\rm\pi}\widetilde{T}_{t}\right)^{-3/2}\exp \left(\frac{-\widetilde{c}^{\,2}}{\widetilde{T}_{t}}\right)\left[1+\frac{4\widetilde{\boldsymbol{q}}_{t}\boldsymbol{\cdot }\widetilde{\boldsymbol{c}}}{15\widetilde{n}(\widetilde{T}_{t})^{2}}\left(\frac{\widetilde{c}^{\,2}}{\widetilde{T}_{t}}-\frac{5}{2}\right)\right],\\ \displaystyle \widetilde{G}_{r}=\widetilde{n}\left({\rm\pi}\widetilde{T}\right)^{-3/2}\exp \left(\frac{-\widetilde{c}^{\,2}}{\widetilde{T}}\right)\left[1+{\it\omega}_{0}\frac{4\widetilde{\boldsymbol{q}}_{t}\boldsymbol{\cdot }\widetilde{\boldsymbol{c}}}{15\widetilde{n}\widetilde{T}^{2}}\left(\frac{\widetilde{c}^{\,2}}{\widetilde{T}}-\frac{5}{2}\right)\right],\\ \displaystyle \widetilde{R}_{t}=\frac{d\widetilde{T}_{r}}{2}\widetilde{G}_{t}+\left({\rm\pi}\widetilde{T}_{t}\right)^{-3/2}\exp \left(\frac{-\widetilde{c}^{\,2}}{\widetilde{T}_{t}}\right)2(1-{\it\delta})\frac{\widetilde{\boldsymbol{q}}_{r}\boldsymbol{\cdot }\widetilde{\boldsymbol{c}}}{\widetilde{T}_{t}},\\ \displaystyle \widetilde{R}_{r}=\frac{d\widetilde{T}}{2}\widetilde{G}_{r}+\left({\rm\pi}\widetilde{T}\right)^{-3/2}\exp \left(\frac{-\widetilde{c}^{\,2}}{\widetilde{T}}\right)2{\it\omega}_{1}(1-{\it\delta})\frac{\widetilde{\boldsymbol{q}}_{r}\boldsymbol{\cdot }\widetilde{\boldsymbol{c}}}{\widetilde{T}},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\displaystyle \widetilde{G}_{t}=\widetilde{n}\left({\rm\pi}\widetilde{T}_{t}\right)^{-3/2}\exp \left(\frac{-\widetilde{c}^{\,2}}{\widetilde{T}_{t}}\right)\left[1+\frac{4\widetilde{\boldsymbol{q}}_{t}\boldsymbol{\cdot }\widetilde{\boldsymbol{c}}}{15\widetilde{n}(\widetilde{T}_{t})^{2}}\left(\frac{\widetilde{c}^{\,2}}{\widetilde{T}_{t}}-\frac{5}{2}\right)\right],\\ \displaystyle \widetilde{G}_{r}=\widetilde{n}\left({\rm\pi}\widetilde{T}\right)^{-3/2}\exp \left(\frac{-\widetilde{c}^{\,2}}{\widetilde{T}}\right)\left[1+{\it\omega}_{0}\frac{4\widetilde{\boldsymbol{q}}_{t}\boldsymbol{\cdot }\widetilde{\boldsymbol{c}}}{15\widetilde{n}\widetilde{T}^{2}}\left(\frac{\widetilde{c}^{\,2}}{\widetilde{T}}-\frac{5}{2}\right)\right],\\ \displaystyle \widetilde{R}_{t}=\frac{d\widetilde{T}_{r}}{2}\widetilde{G}_{t}+\left({\rm\pi}\widetilde{T}_{t}\right)^{-3/2}\exp \left(\frac{-\widetilde{c}^{\,2}}{\widetilde{T}_{t}}\right)2(1-{\it\delta})\frac{\widetilde{\boldsymbol{q}}_{r}\boldsymbol{\cdot }\widetilde{\boldsymbol{c}}}{\widetilde{T}_{t}},\\ \displaystyle \widetilde{R}_{r}=\frac{d\widetilde{T}}{2}\widetilde{G}_{r}+\left({\rm\pi}\widetilde{T}\right)^{-3/2}\exp \left(\frac{-\widetilde{c}^{\,2}}{\widetilde{T}}\right)2{\it\omega}_{1}(1-{\it\delta})\frac{\widetilde{\boldsymbol{q}}_{r}\boldsymbol{\cdot }\widetilde{\boldsymbol{c}}}{\widetilde{T}},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where
is the unconfined Knudsen number,
![]() $\widetilde{{\it\tau}}=2(\widetilde{T}_{t})^{{\it\omega}-1}\mathit{Kn}/\sqrt{{\rm\pi}}\widetilde{n}$
is the normalized relaxation time, and
$\widetilde{{\it\tau}}=2(\widetilde{T}_{t})^{{\it\omega}-1}\mathit{Kn}/\sqrt{{\rm\pi}}\widetilde{n}$
is the normalized relaxation time, and
![]() ${\it\gamma}$
is a free parameter. Usually we choose
${\it\gamma}$
is a free parameter. Usually we choose
![]() ${\it\gamma}=0$
, but to solve the linearized BCO we choose
${\it\gamma}=0$
, but to solve the linearized BCO we choose
![]() ${\it\gamma}=(2{\it\omega}-1)/2$
to double the computational efficiency (Wu et al.
Reference Wu, White, Scanlon, Reese and Zhang2013, Reference Wu, Reese and Zhang2014). Finally, the macroscopic quantities are calculated as:
${\it\gamma}=(2{\it\omega}-1)/2$
to double the computational efficiency (Wu et al.
Reference Wu, White, Scanlon, Reese and Zhang2013, Reference Wu, Reese and Zhang2014). Finally, the macroscopic quantities are calculated as:
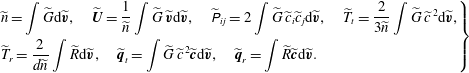 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\displaystyle \widetilde{n}=\int \widetilde{G}\text{d}\widetilde{\boldsymbol{v}},\quad \widetilde{\boldsymbol{U}}=\frac{1}{\widetilde{n}}\int \widetilde{G}\,\widetilde{\boldsymbol{v}}\text{d}\widetilde{\boldsymbol{v}},\quad \widetilde{\unicode[STIX]{x1D617}}_{ij}=2\int \widetilde{G}\,\widetilde{c}_{i}\widetilde{c}_{j}\text{d}\widetilde{\boldsymbol{v}},\quad \widetilde{T}_{t}=\frac{2}{3\widetilde{n}}\int \widetilde{G}\,\widetilde{c}^{\,2}\text{d}\widetilde{\boldsymbol{v}},\\ \displaystyle \widetilde{T}_{r}=\frac{2}{d\widetilde{n}}\int \widetilde{R}\text{d}\widetilde{\boldsymbol{v}},\quad \widetilde{\boldsymbol{q}}_{t}=\int \widetilde{G}\,\widetilde{c}^{\,2}\widetilde{\boldsymbol{c}}\text{d}\widetilde{\boldsymbol{v}},\quad \widetilde{\boldsymbol{q}}_{r}=\int \widetilde{R}\widetilde{\boldsymbol{c}}\text{d}\widetilde{\boldsymbol{v}}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\displaystyle \widetilde{n}=\int \widetilde{G}\text{d}\widetilde{\boldsymbol{v}},\quad \widetilde{\boldsymbol{U}}=\frac{1}{\widetilde{n}}\int \widetilde{G}\,\widetilde{\boldsymbol{v}}\text{d}\widetilde{\boldsymbol{v}},\quad \widetilde{\unicode[STIX]{x1D617}}_{ij}=2\int \widetilde{G}\,\widetilde{c}_{i}\widetilde{c}_{j}\text{d}\widetilde{\boldsymbol{v}},\quad \widetilde{T}_{t}=\frac{2}{3\widetilde{n}}\int \widetilde{G}\,\widetilde{c}^{\,2}\text{d}\widetilde{\boldsymbol{v}},\\ \displaystyle \widetilde{T}_{r}=\frac{2}{d\widetilde{n}}\int \widetilde{R}\text{d}\widetilde{\boldsymbol{v}},\quad \widetilde{\boldsymbol{q}}_{t}=\int \widetilde{G}\,\widetilde{c}^{\,2}\widetilde{\boldsymbol{c}}\text{d}\widetilde{\boldsymbol{v}},\quad \widetilde{\boldsymbol{q}}_{r}=\int \widetilde{R}\widetilde{\boldsymbol{c}}\text{d}\widetilde{\boldsymbol{v}}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
The BCO (3.2) can be solved by the fast spectral method (Wu et al.
Reference Wu, White, Scanlon, Reese and Zhang2013) with a computational cost of
![]() $O(M^{2}N_{v}^{3}\log (N_{v}))$
, while the other collision operators in (3.1) can be solved by the discrete velocity method (Huang & Giddens Reference Huang, Giddens and Brundin1967) with a cost of
$O(M^{2}N_{v}^{3}\log (N_{v}))$
, while the other collision operators in (3.1) can be solved by the discrete velocity method (Huang & Giddens Reference Huang, Giddens and Brundin1967) with a cost of
![]() $O(N_{v}^{3})$
. Since we have two VDFs, the computational memory required is twice that for monatomic gases; however, the computational cost only increases slightly.
$O(N_{v}^{3})$
. Since we have two VDFs, the computational memory required is twice that for monatomic gases; however, the computational cost only increases slightly.
To validate this kinetic model, we compare numerical solutions of shock waves and planar Fourier/Couette flows with DSMC solutions and experimental data. With the exception of the DSMC results for normal shock waves in § 3.1, the DSMC results reported in this paper have been obtained using the dsmcFoam solver (Scanlon et al. Reference Scanlon, Roohi, White, Darbandi and Reese2010). This is a parallelized, open source solver developed within the OpenFOAM framework by OpenCFD Ltd in collaboration with researchers at the University of Strathclyde. The in-house version of the dsmcFoam solver we use enables us to model polyatomic gases and to measure a much wider range of gas properties than the standard OpenFOAM release.
Note that in the dsmcFoam solver, when the variable hard-sphere model is used (Haas et al.
Reference Haas, Hash, Bird, Lumpkin and Hassan1994),
![]() $\partial T_{r}/\partial t=(T-T_{r})/[{\rm\pi}Z_{DSMC}{\it\tau}(7-2{\it\omega})(5-2{\it\omega})/96]$
. Thus, we have
$\partial T_{r}/\partial t=(T-T_{r})/[{\rm\pi}Z_{DSMC}{\it\tau}(7-2{\it\omega})(5-2{\it\omega})/96]$
. Thus, we have
3.1. Normal shock waves in gases
For normal shock wave simulations, the characteristic length is chosen to be the upstream mean free path (
![]() $16{\it\mu}/5n\sqrt{2{\rm\pi}mkT}$
), where the reference molecular number density
$16{\it\mu}/5n\sqrt{2{\rm\pi}mkT}$
), where the reference molecular number density
![]() $n$
, gas viscosity
$n$
, gas viscosity
![]() ${\it\mu}$
, and temperature
${\it\mu}$
, and temperature
![]() $T$
are all measured upstream of the shock. Therefore, the unconfined Knudsen number is
$T$
are all measured upstream of the shock. Therefore, the unconfined Knudsen number is
![]() $\mathit{Kn}=5{\rm\pi}/16$
. In the DSMC simulations, nitrogen has a viscosity index
$\mathit{Kn}=5{\rm\pi}/16$
. In the DSMC simulations, nitrogen has a viscosity index
![]() ${\it\omega}=0.74$
and rotational collision number
${\it\omega}=0.74$
and rotational collision number
![]() $Z_{DSMC}=3.5$
. We choose
$Z_{DSMC}=3.5$
. We choose
![]() ${\it\delta}=1/1.33$
, hence according to (2.13), (2.14) and (3.6), we obtain
${\it\delta}=1/1.33$
, hence according to (2.13), (2.14) and (3.6), we obtain
![]() $Z=2.226$
,
$Z=2.226$
,
![]() ${\it\omega}_{0}=0.477$
and
${\it\omega}_{0}=0.477$
and
![]() ${\it\omega}_{1}=1.919$
, for both the Rykov model (2.3) and our kinetic model (3.1). The Eucken factor is 1.96.
${\it\omega}_{1}=1.919$
, for both the Rykov model (2.3) and our kinetic model (3.1). The Eucken factor is 1.96.
With a shock wave travelling in the
![]() $x_{1}$
direction, the kinetic model equations (3.1) can be solved in the following iterative manner (for simplicity, the tildes are omitted):
$x_{1}$
direction, the kinetic model equations (3.1) can be solved in the following iterative manner (for simplicity, the tildes are omitted):
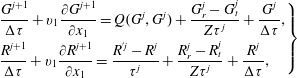 $$\begin{eqnarray}\left.\begin{array}{@{}l@{}}\displaystyle \frac{G^{j+1}}{{\rm\Delta}{\it\tau}}+v_{1}\frac{\partial G^{j+1}}{\partial x_{1}}=Q(G^{j},G^{j})+\frac{G_{r}^{j}-G_{t}^{j}}{Z{\it\tau}^{j}}+\frac{G^{j}}{{\rm\Delta}{\it\tau}},\\ \displaystyle \frac{R^{j+1}}{{\rm\Delta}{\it\tau}}+v_{1}\frac{\partial R^{j+1}}{\partial x_{1}}=\frac{R^{^{\prime }j}-R^{j}}{{\it\tau}^{j}}+\frac{R_{r}^{j}-R_{t}^{j}}{Z{\it\tau}^{j}}+\frac{R^{j}}{{\rm\Delta}{\it\tau}},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}\displaystyle \frac{G^{j+1}}{{\rm\Delta}{\it\tau}}+v_{1}\frac{\partial G^{j+1}}{\partial x_{1}}=Q(G^{j},G^{j})+\frac{G_{r}^{j}-G_{t}^{j}}{Z{\it\tau}^{j}}+\frac{G^{j}}{{\rm\Delta}{\it\tau}},\\ \displaystyle \frac{R^{j+1}}{{\rm\Delta}{\it\tau}}+v_{1}\frac{\partial R^{j+1}}{\partial x_{1}}=\frac{R^{^{\prime }j}-R^{j}}{{\it\tau}^{j}}+\frac{R_{r}^{j}-R_{t}^{j}}{Z{\it\tau}^{j}}+\frac{R^{j}}{{\rm\Delta}{\it\tau}},\end{array}\right\}\end{eqnarray}$$
where
![]() $j$
is the iteration step,
$j$
is the iteration step,
![]() ${\rm\Delta}{\it\tau}$
is the local time step (usually three times smaller than the local relaxation time
${\rm\Delta}{\it\tau}$
is the local time step (usually three times smaller than the local relaxation time
![]() ${\it\tau}$
), and the spatial derivative is approximated by the second-order upwind finite difference. The Rykov model can be solved in the same way. Given the molecular number density, temperature, and Mach number
${\it\tau}$
), and the spatial derivative is approximated by the second-order upwind finite difference. The Rykov model can be solved in the same way. Given the molecular number density, temperature, and Mach number
![]() $\mathit{Ma}$
at the upstream end, the equivalent quantities at the downstream end can be found by the Rankine–Hugoniot relations. The VDFs at the upstream and downstream ends are Maxwellian.
$\mathit{Ma}$
at the upstream end, the equivalent quantities at the downstream end can be found by the Rankine–Hugoniot relations. The VDFs at the upstream and downstream ends are Maxwellian.
Figure 1 compares the normal shock profiles obtained by the two kinetic models with DSMC results. As expected, our kinetic model resolves the problem of early rising of the temperatures, and produces results in good agreement with the DSMC data.

Figure 1. Comparisons of kinetic model results and DSMC data (Liu et al.
Reference Liu, Yu, Xu and Zhong2014) for normal shock waves in nitrogen: (a)
![]() $\mathit{Ma}=4$
; (b)
$\mathit{Ma}=4$
; (b)
![]() $\mathit{Ma}=5$
; (c)
$\mathit{Ma}=5$
; (c)
![]() $\mathit{Ma}=7$
. The squares, circles, stars and triangles are the normalized translational temperature in the
$\mathit{Ma}=7$
. The squares, circles, stars and triangles are the normalized translational temperature in the
![]() $x_{1}$
direction, the translational temperature, the rotational temperature, and the molecular number density, respectively, all obtained from the DSMC simulations. The solid and dashed lines are, respectively, the results of our kinetic model (3.1) and the Rykov kinetic model (2.3). Here
$x_{1}$
direction, the translational temperature, the rotational temperature, and the molecular number density, respectively, all obtained from the DSMC simulations. The solid and dashed lines are, respectively, the results of our kinetic model (3.1) and the Rykov kinetic model (2.3). Here
![]() $Q$
represents the value of the macroscopic quantity, and subscripts
$Q$
represents the value of the macroscopic quantity, and subscripts
![]() $u$
and
$u$
and
![]() $d$
represent the upstream and downstream values, respectively.
$d$
represent the upstream and downstream values, respectively.
We now compare our model results with experimental data for normal shock waves in nitrogen (Robben & Talbot Reference Robben and Talbot1966). Two upstream Mach numbers are considered. The rotational collision number is given by the formula proposed by Parker (Reference Parker1959):
where we take
![]() $T^{\ast }=91.5~\text{K}$
and
$T^{\ast }=91.5~\text{K}$
and
![]() $Z_{rot}^{\infty }=18$
(Gorji & Jenny Reference Gorji and Jenny2013).
$Z_{rot}^{\infty }=18$
(Gorji & Jenny Reference Gorji and Jenny2013).
Figure 2 shows the profiles of the normalized density and rotational temperature. Excellent agreement between our kinetic model (3.1) and the experimental data can be observed.

Figure 2. Comparisons of normal shock wave profiles in nitrogen from our kinetic model and the experimental data of Robben & Talbot (Reference Robben and Talbot1966): (a)
![]() $\mathit{Ma}=7$
; (b)
$\mathit{Ma}=7$
; (b)
![]() $\mathit{Ma}=12.9$
. Here
$\mathit{Ma}=12.9$
. Here
![]() $L^{\ast }$
is the mean free path based on the sonic temperature.
$L^{\ast }$
is the mean free path based on the sonic temperature.
3.2. Planar Fourier flow
Consider nitrogen gas between two parallel plates a distance
![]() $\ell$
apart. The normalized temperature of the lower plate at
$\ell$
apart. The normalized temperature of the lower plate at
![]() $x_{2}=0$
is
$x_{2}=0$
is
![]() $T_{l}=2/3$
, while that of the upper plate at
$T_{l}=2/3$
, while that of the upper plate at
![]() $x_{2}=\ell$
is
$x_{2}=\ell$
is
![]() $T_{u}=4/3$
. We choose
$T_{u}=4/3$
. We choose
![]() $n_{0}$
to be the average molecular number density, and test two different Knudsen numbers:
$n_{0}$
to be the average molecular number density, and test two different Knudsen numbers:
![]() $\mathit{Kn}=0.1$
and
$\mathit{Kn}=0.1$
and
![]() $\mathit{Kn}=1$
. Diffuse boundary conditions are adopted; for example, at
$\mathit{Kn}=1$
. Diffuse boundary conditions are adopted; for example, at
![]() $x_{1}=0$
we have
$x_{1}=0$
we have
for
![]() $v_{2}\geqslant 0$
, where
$v_{2}\geqslant 0$
, where
![]() $n_{w}=-2\sqrt{{\rm\pi}/T_{l}}\int _{v_{2}<0}v_{2}G(x_{2}=0,\boldsymbol{v})\text{d}\boldsymbol{v}$
. The boundary condition at
$n_{w}=-2\sqrt{{\rm\pi}/T_{l}}\int _{v_{2}<0}v_{2}G(x_{2}=0,\boldsymbol{v})\text{d}\boldsymbol{v}$
. The boundary condition at
![]() $x_{2}=\ell$
can be given in a similar way.
$x_{2}=\ell$
can be given in a similar way.
Figure 3 shows the resulting density and translational temperature profiles (the rotational temperatures are not shown because they are very close to the translational ones) in this planar Fourier flow. Excellent agreement between the results of our model and the DSMC simulations can be seen.

Figure 3. Comparisons of (a) density and (b) translational temperature between our kinetic model (lines) and our DSMC simulations for planar Fourier flows. The squares and circles are the dsmcFoam results at
![]() $\mathit{Kn}=0.1$
and
$\mathit{Kn}=0.1$
and
![]() $\mathit{Kn}=1$
, respectively. The working gas is nitrogen.
$\mathit{Kn}=1$
, respectively. The working gas is nitrogen.
3.3. Planar Couette flow
The planar Couette flow configuration is the same as for the planar Fourier flow above, although the two plates now have the same temperature
![]() $T_{0}$
, and the top plate moves in the
$T_{0}$
, and the top plate moves in the
![]() $x_{1}$
direction with a speed
$x_{1}$
direction with a speed
![]() $v_{m}$
while the bottom plate moves in the opposite direction at the same speed. In addition to nitrogen, we consider methane gas with a viscosity index
$v_{m}$
while the bottom plate moves in the opposite direction at the same speed. In addition to nitrogen, we consider methane gas with a viscosity index
![]() ${\it\omega}=0.84$
. In the DSMC simulations, we choose
${\it\omega}=0.84$
. In the DSMC simulations, we choose
![]() $Z_{DSMC}=3.5$
. For methane,
$Z_{DSMC}=3.5$
. For methane,
![]() $Z=2.023$
, and from (2.13) and (2.14) we obtain
$Z=2.023$
, and from (2.13) and (2.14) we obtain
![]() ${\it\omega}_{0}=0.316$
and
${\it\omega}_{0}=0.316$
and
![]() ${\it\omega}_{1}=1.774$
. The resulting Eucken factor 1.74 is close to the experimentally measured value. Good agreement between our model predictions and the DSMC results can be seen in figure 4.
${\it\omega}_{1}=1.774$
. The resulting Eucken factor 1.74 is close to the experimentally measured value. Good agreement between our model predictions and the DSMC results can be seen in figure 4.

Figure 4. Comparisons between our kinetic model (lines) and our DSMC simulations (squares) for planar Couette flows of (a) nitrogen and (b) methane gases at
![]() $\mathit{Kn}=1$
.
$\mathit{Kn}=1$
.
4. Application to Poiseuille and thermal creep flows
Calculating the mass and heat flow rates in Poiseuille and thermal creep flows between two parallel plates can be extremely slow using the DSMC method when the temperature and pressure gradients are small. Here we solve these two classical flows using our deterministic method.
The configuration is the same as for planar Fourier flow. The pressure and temperature gradients along the plates are
![]() $K_{P}=\ell \text{d}\ln p/\text{d}x_{1}$
and
$K_{P}=\ell \text{d}\ln p/\text{d}x_{1}$
and
![]() $K_{T}=\ell \text{d}\ln T/\text{d}x_{1}$
. When
$K_{T}=\ell \text{d}\ln T/\text{d}x_{1}$
. When
![]() $K_{P}$
and
$K_{P}$
and
![]() $K_{T}$
are small, the kinetic model equations can be linearized. We express the two VDFs as
$K_{T}$
are small, the kinetic model equations can be linearized. We express the two VDFs as
![]() $G=G_{0}+h_{0}$
and
$G=G_{0}+h_{0}$
and
![]() $R=R_{0}+h_{1}$
, where
$R=R_{0}+h_{1}$
, where
![]() $G_{0}={\rm\pi}^{-3/2}\exp (-v^{2})$
and
$G_{0}={\rm\pi}^{-3/2}\exp (-v^{2})$
and
![]() $R_{0}=(d/2)G_{0}$
are equilibrium VDFs. The VDFs
$R_{0}=(d/2)G_{0}$
are equilibrium VDFs. The VDFs
![]() $h_{0}$
and
$h_{0}$
and
![]() $h_{1}$
describe the deviations from the corresponding equilibrium states and satisfy
$h_{1}$
describe the deviations from the corresponding equilibrium states and satisfy
![]() $|h_{0}/G_{0}|,|h_{1}/R_{0}|\ll 1$
. In the following, the VDF
$|h_{0}/G_{0}|,|h_{1}/R_{0}|\ll 1$
. In the following, the VDF
![]() $h_{2}=h_{1}-(d/2)h_{0}$
is used instead of
$h_{2}=h_{1}-(d/2)h_{0}$
is used instead of
![]() $h_{1}$
, for convenience.
$h_{1}$
, for convenience.
When the Rykov kinetic model is considered, the evolution of
![]() $h_{0}$
and
$h_{0}$
and
![]() $h_{2}$
is governed by the following two linear equations (Titarev & Shakhov Reference Titarev and Shakhov2012):
$h_{2}$
is governed by the following two linear equations (Titarev & Shakhov Reference Titarev and Shakhov2012):
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\displaystyle h_{0}^{+}=2U_{1}v_{1}G_{0}+\frac{4}{15}q_{t1}v_{1}G_{0}\left(1-\frac{1-{\it\omega}_{0}}{Z}\right)\left(v^{2}-\frac{5}{2}\right),\\ \displaystyle h_{2}^{+}=2q_{r1}v_{1}G_{0}\left(1-\frac{1-{\it\omega}_{1}}{Z}\right)(1-{\it\delta}).\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\displaystyle h_{0}^{+}=2U_{1}v_{1}G_{0}+\frac{4}{15}q_{t1}v_{1}G_{0}\left(1-\frac{1-{\it\omega}_{0}}{Z}\right)\left(v^{2}-\frac{5}{2}\right),\\ \displaystyle h_{2}^{+}=2q_{r1}v_{1}G_{0}\left(1-\frac{1-{\it\omega}_{1}}{Z}\right)(1-{\it\delta}).\end{array}\right\} & & \displaystyle\end{eqnarray}$$
When the kinetic model (3.1) is considered, (4.1) and (4.2) remain unchanged, but
![]() $h_{0}^{+}$
in (4.3) becomes
$h_{0}^{+}$
in (4.3) becomes
where
![]() $\mathscr{L}(h_{0})=\mathscr{L}_{g}(h_{0})-{\it\nu}_{eq}h_{0}$
is the linearized BCO. A detailed expression for
$\mathscr{L}(h_{0})=\mathscr{L}_{g}(h_{0})-{\it\nu}_{eq}h_{0}$
is the linearized BCO. A detailed expression for
![]() $\mathscr{L}(h_{0})$
and its fast spectral approximation can be found in Wu et al. (Reference Wu, Reese and Zhang2014).
$\mathscr{L}(h_{0})$
and its fast spectral approximation can be found in Wu et al. (Reference Wu, Reese and Zhang2014).
The macroscopic quantities of interest are
![]() $U_{1}=\int h_{0}v_{1}\text{d}v$
,
$U_{1}=\int h_{0}v_{1}\text{d}v$
,
![]() $q_{t1}=\int h_{0}v_{1}(v^{2}-5/2)\text{d}v$
, and
$q_{t1}=\int h_{0}v_{1}(v^{2}-5/2)\text{d}v$
, and
![]() $q_{r1}=\int h_{2}v_{1}\text{d}v$
. The mass flow rate
$q_{r1}=\int h_{2}v_{1}\text{d}v$
. The mass flow rate
![]() $\mathscr{M}$
, translational heat flow rate
$\mathscr{M}$
, translational heat flow rate
![]() $\mathscr{Q}_{t}$
, and rotational heat flow rate
$\mathscr{Q}_{t}$
, and rotational heat flow rate
![]() $\mathscr{Q}_{r}$
can be calculated as
$\mathscr{Q}_{r}$
can be calculated as
As with (3.7), (4.1) and (4.2) can be solved by an implicit method iteratively. Diffuse boundary conditions are adopted, so that the values of VDFs
![]() $h_{0}$
and
$h_{0}$
and
![]() $h_{2}$
entering the domain are zero. We set
$h_{2}$
entering the domain are zero. We set
![]() $K_{P}=1$
and
$K_{P}=1$
and
![]() $K_{T}=0$
for Poiseuille flow, and
$K_{T}=0$
for Poiseuille flow, and
![]() $K_{P}=0$
and
$K_{P}=0$
and
![]() $K_{T}=1$
for thermal creep flow.
$K_{T}=1$
for thermal creep flow.
Some observations can be made before discussion of the numerical results. First, the mass and translational heat flow rates are determined by
![]() $h_{0}$
, which is governed by (4.1). The expressions for
$h_{0}$
, which is governed by (4.1). The expressions for
![]() $h_{0}^{+}$
suggest that the mass and translational heat flow rates are different for the Rykov model and our model. However, for both the Rykov model and our model there is no difference in flow rates between diatomic and nonlinear polyatomic gases with the same
$h_{0}^{+}$
suggest that the mass and translational heat flow rates are different for the Rykov model and our model. However, for both the Rykov model and our model there is no difference in flow rates between diatomic and nonlinear polyatomic gases with the same
![]() $Z$
and
$Z$
and
![]() ${\it\omega}_{0}$
values. Second, the rotational heat flow rate is related to
${\it\omega}_{0}$
values. Second, the rotational heat flow rate is related to
![]() $h_{2}$
, which is governed by (4.2). It is always zero in Poiseuille flow. In thermal creep flows, since the Rykov and our kinetic models have the same equation for
$h_{2}$
, which is governed by (4.2). It is always zero in Poiseuille flow. In thermal creep flows, since the Rykov and our kinetic models have the same equation for
![]() $h_{2}$
they produce the same rotational heat flow rates. Also, since the source term in (4.2) is proportional to the number of rotational degrees of freedom, the rotational heat flow rates of nonlinear polyatomic gases are one-and-a-half times larger than those of diatomic gases, provided the values of
$h_{2}$
they produce the same rotational heat flow rates. Also, since the source term in (4.2) is proportional to the number of rotational degrees of freedom, the rotational heat flow rates of nonlinear polyatomic gases are one-and-a-half times larger than those of diatomic gases, provided the values of
![]() $Z,{\it\omega}_{1},{\it\delta}$
for diatomic and nonlinear polyatomic gases are the same. Third, (4.3) is independent of the viscosity index
$Z,{\it\omega}_{1},{\it\delta}$
for diatomic and nonlinear polyatomic gases are the same. Third, (4.3) is independent of the viscosity index
![]() ${\it\omega}$
, so the molecular model has no influence on the flow rates when using the Rykov model. When our model (3.1) is used, the linearized BCO in (4.4) shows that different molecular models have different flow rates, according to the results in Sharipov & Bertoldo (Reference Sharipov and Bertoldo2009) and Wu et al. (Reference Wu, Reese and Zhang2014) for monatomic gases.
${\it\omega}$
, so the molecular model has no influence on the flow rates when using the Rykov model. When our model (3.1) is used, the linearized BCO in (4.4) shows that different molecular models have different flow rates, according to the results in Sharipov & Bertoldo (Reference Sharipov and Bertoldo2009) and Wu et al. (Reference Wu, Reese and Zhang2014) for monatomic gases.
For these reasons, only the mass and heat flow rates in Poiseuille and thermal creep flows of diatomic gases are presented below. We consider hard-sphere molecules with
![]() $Z=1$
and
$Z=1$
and
![]() $Z=5$
. Values of
$Z=5$
. Values of
![]() ${\it\omega}_{0}$
and
${\it\omega}_{0}$
and
![]() ${\it\omega}_{1}$
are chosen according to (2.13) and (2.14) with
${\it\omega}_{1}$
are chosen according to (2.13) and (2.14) with
![]() ${\it\delta}=1/1.33$
.
${\it\delta}=1/1.33$
.
Table 1 shows the numerical results for Poiseuille flow of a diatomic gas. The mass flow rates from our model are nearly the same as those for a monatomic gas. However, the translational heat flow rates are affected by diatomicity: for a fixed
![]() $\mathit{Kn}$
,
$\mathit{Kn}$
,
![]() $\mathscr{Q}_{t}$
increases with
$\mathscr{Q}_{t}$
increases with
![]() $Z$
and, in the limit of
$Z$
and, in the limit of
![]() $Z\rightarrow \infty$
,
$Z\rightarrow \infty$
,
![]() $\mathscr{Q}_{t}$
approaches that of a hard-sphere monatomic gas. This behaviour may be related to the magnitude of the translational thermal conductivity
$\mathscr{Q}_{t}$
approaches that of a hard-sphere monatomic gas. This behaviour may be related to the magnitude of the translational thermal conductivity
![]() ${\it\kappa}_{t}$
, see (A 7). That is, from (2.13) we see that
${\it\kappa}_{t}$
, see (A 7). That is, from (2.13) we see that
![]() ${\it\kappa}_{t}$
decreases with
${\it\kappa}_{t}$
decreases with
![]() $Z$
; as a consequence,
$Z$
; as a consequence,
![]() $\mathscr{Q}_{t}$
decreases with
$\mathscr{Q}_{t}$
decreases with
![]() $Z$
. At high Knudsen number, however, the difference between the translational heat flow rates in the
$Z$
. At high Knudsen number, however, the difference between the translational heat flow rates in the
![]() $Z=1$
and the
$Z=1$
and the
![]() $Z=5$
cases is very small, and both are very close to the monatomic gas value. This is because there are not enough collisions for the exchange of translational and rotational energies in the free-molecular regime. Comparisons between the Rykov and our models are also shown in this table: the Rykov model overpredicts the mass flow rates, and underpredicts the translational heat flow rate at large
$Z=5$
cases is very small, and both are very close to the monatomic gas value. This is because there are not enough collisions for the exchange of translational and rotational energies in the free-molecular regime. Comparisons between the Rykov and our models are also shown in this table: the Rykov model overpredicts the mass flow rates, and underpredicts the translational heat flow rate at large
![]() $\mathit{Kn}$
. This observation is consistent with the monatomic gas result when the Shakhov model is used (Sharipov & Bertoldo Reference Sharipov and Bertoldo2009).
$\mathit{Kn}$
. This observation is consistent with the monatomic gas result when the Shakhov model is used (Sharipov & Bertoldo Reference Sharipov and Bertoldo2009).
Table 1. Mass
![]() $(\mathscr{M})$
and translational heat
$(\mathscr{M})$
and translational heat
![]() $(\mathscr{Q}_{t})$
flow rates in Poiseuille flow of a hard-sphere diatomic gas between parallel plates. Note that the rotational heat flux is zero.
$(\mathscr{Q}_{t})$
flow rates in Poiseuille flow of a hard-sphere diatomic gas between parallel plates. Note that the rotational heat flux is zero.

Next we consider thermal creep flows. Figure 5 shows that the Onsager–Casimir relation holds for the diatomic gases we consider, that is, the heat flow rates in Poiseuille flows are identical to the mass flow rates in thermal creep flows. Table 2 shows the predicted heat flow rates in thermal creep flows of diatomic gases. As with Poiseuille flow,
![]() $\mathscr{Q}_{t}$
and
$\mathscr{Q}_{t}$
and
![]() ${\it\kappa}_{t}$
decrease with
${\it\kappa}_{t}$
decrease with
![]() $Z$
. However,
$Z$
. However,
![]() $\mathscr{Q}_{r}$
increases as
$\mathscr{Q}_{r}$
increases as
![]() $Z$
decreases, because the rotational thermal conductivity
$Z$
decreases, because the rotational thermal conductivity
![]() ${\it\kappa}_{r}$
increases with decreasing
${\it\kappa}_{r}$
increases with decreasing
![]() $Z$
; see (A 7) and (2.14).
$Z$
; see (A 7) and (2.14).

Figure 5. Onsager–Casimir relation for the hard-sphere diatomic gas: comparison between the heat flow rate in Poiseuille flow and the mass flow rate in thermal creep flow.
Table 2. Heat flow rates in thermal creep flow of a hard-sphere diatomic gas between parallel plates. Note that the rotational heat flow rates for both the Rykov model and our kinetic model are the same.

Finally, we investigate the influence of the molecular model on the mass flow rate in thermal creep flow. We only consider hard-sphere and Maxwell gases; for a gas interacting through inverse power-law potentials with a viscosity index between 0.5 and 1, the mass flow rates lie between those of the hard-sphere and Maxwell cases. As for monatomic gases (Wu et al.
Reference Wu, Reese and Zhang2014), figure 6 shows that at large
![]() $\mathit{Kn}$
the mass flow rate increases when the viscosity index decreases. Although the Rykov model underpredicts the mass flow rates relative to our model for a hard-sphere gas, it gives almost the same mass flow rate as Maxwell gases when
$\mathit{Kn}$
the mass flow rate increases when the viscosity index decreases. Although the Rykov model underpredicts the mass flow rates relative to our model for a hard-sphere gas, it gives almost the same mass flow rate as Maxwell gases when
![]() $\mathit{Kn}<4$
and larger mass flow rates when
$\mathit{Kn}<4$
and larger mass flow rates when
![]() $\mathit{Kn}>4$
.
$\mathit{Kn}>4$
.

Figure 6. Mass flow rates in thermal creep flow between parallel plates, varying with the Knudsen number.
5. Application to Rayleigh–Brillouin scattering
An important application for kinetic models of non-vibrating polyatomic gases is the calculation of the Rayleigh–Brillouin scattering (RBS) spectra. RBS is an invaluable non-destructive optical diagnostic technique for measuring the properties of gases and liquids, such as the sound speed, temperature, and bulk viscosity. This information can be extracted by comparing the experimental and theoretical spectra, where the accuracy of the obtained information depends on how reliable the experimental and theoretical results are. Recently, rapid improvements in the experimental resolution have been achieved (Vieitez et al. Reference Vieitez, van Duijn, Ubachs, Witschas, Meijer, de Wijn, Dam and van de Water2010; Gerakis, Shneider & Barker Reference Gerakis, Shneider and Barker2013; Gu & Ubachs Reference Gu and Ubachs2013); however, accurate theoretical line shapes are lacking, although several kinetic models have been proposed (Tenti, Boley & Desai Reference Tenti, Boley and Desai1974; Pan, Shneider & Miles Reference Pan, Shneider and Miles2002, Reference Pan, Shneider and Miles2004; Marques Reference Marques2007).
In RBS experiments, the light is scattered due to gas density variations, which either arise spontaneously or are induced by external optical potentials. Correspondingly, we have spontaneous RBS and coherent RBS. The spectrum of the scattered light depends on the Knudsen number, intermolecular interactions, and rotational collision number; in the hydrodynamic or free-molecular regimes, the spectrum can be calculated analytically. In the transition regime, a kinetic model must be used. Due to the high oscillation frequency of the optical field, the vibrational modes of the rarefied gas molecules are not excited, which justifies the use of kinetic models (2.3) and (3.1). For monatomic gases, theory and experiment have demonstrated that intermolecular interactions have little influence on the spectra of spontaneous RBS (Sugawara, Yip & Sirovich Reference Sugawara, Yip and Sirovich1968; Clark Reference Clark1975; Ghaem-Maghami & May Reference Ghaem-Maghami and May1980). However, for polyatomic gases and for coherent RBS, the role of the intermolecular interaction has never been studied. The current prevailing model is the s6 model (Tenti et al. Reference Tenti, Boley and Desai1974; Pan et al. Reference Pan, Shneider and Miles2004), which is derived for Maxwell molecules only. In the following, through our kinetic model (3.1), we investigate the influence of the molecular model on both the spontaneous and coherent RBS spectra.
5.1. Spontaneous Rayleigh–Brillouin scattering
The scattering of light due to spontaneous density fluctuations in gases is called spontaneous RBS. The light spectrum can be quantitatively interpreted by solutions of the linearized Boltzmann equation. Suppose scattered light with wavelength
![]() ${\it\lambda}$
propagates along the
${\it\lambda}$
propagates along the
![]() $x_{2}$
direction, and let the characteristic length be equal to
$x_{2}$
direction, and let the characteristic length be equal to
![]() ${\it\lambda}$
. The spectrum
${\it\lambda}$
. The spectrum
![]() $S(\,f_{s})$
of the scattered light is determined by the density fluctuation spectrum (Sugawara et al.
Reference Sugawara, Yip and Sirovich1968) as
$S(\,f_{s})$
of the scattered light is determined by the density fluctuation spectrum (Sugawara et al.
Reference Sugawara, Yip and Sirovich1968) as
where
![]() $\text{Re}$
denotes the real part of a complex number,
$\text{Re}$
denotes the real part of a complex number,
![]() $\text{i}$
is the imaginary unit,
$\text{i}$
is the imaginary unit,
![]() $f_{s}$
is the shifted frequency normalized by
$f_{s}$
is the shifted frequency normalized by
![]() $v_{m}/{\it\lambda}$
, and
$v_{m}/{\it\lambda}$
, and
![]() ${\rm\Delta}n_{0}(x_{2},t)=\int h_{0}(x_{2},t)\text{d}\boldsymbol{v}$
denotes the density variation.
${\rm\Delta}n_{0}(x_{2},t)=\int h_{0}(x_{2},t)\text{d}\boldsymbol{v}$
denotes the density variation.
According to our kinetic model, the evolution of
![]() $h_{0}$
and
$h_{0}$
and
![]() $h_{1}$
is governed by the two coupled equations:
$h_{1}$
is governed by the two coupled equations:
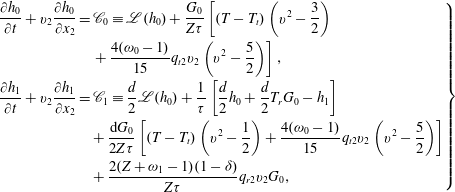 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}rcl@{}}\displaystyle \frac{\partial h_{0}}{\partial t}+v_{2}\frac{\partial h_{0}}{\partial x_{2}}\, & =\, & \displaystyle \mathscr{C}_{0}\equiv \mathscr{L}(h_{0})+\frac{G_{0}}{Z{\it\tau}}\left[(T-T_{t})\left(v^{2}-\frac{3}{2}\right)\right.\\ \, & \, & \left.+\,\displaystyle \frac{4({\it\omega}_{0}-1)}{15}q_{t2}v_{2}\left(v^{2}-\frac{5}{2}\right)\right],\\ \displaystyle \frac{\partial h_{1}}{\partial t}+v_{2}\frac{\partial h_{1}}{\partial x_{2}}\, & =\, & \displaystyle \mathscr{C}_{1}\equiv \frac{d}{2}\mathscr{L}(h_{0})+\frac{1}{{\it\tau}}\left[\frac{d}{2}h_{0}+\frac{d}{2}T_{r}G_{0}-h_{1}\right]\\ \, & \, & +\,\displaystyle \frac{\text{d}G_{0}}{2Z{\it\tau}}\left[(T-T_{t})\left(v^{2}-\frac{1}{2}\right)+\frac{4({\it\omega}_{0}-1)}{15}q_{t2}v_{2}\left(v^{2}-\frac{5}{2}\right)\right]\\ \, & \, & +\,\displaystyle \frac{2(Z+{\it\omega}_{1}-1)(1-{\it\delta})}{Z{\it\tau}}q_{r2}v_{2}G_{0},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}rcl@{}}\displaystyle \frac{\partial h_{0}}{\partial t}+v_{2}\frac{\partial h_{0}}{\partial x_{2}}\, & =\, & \displaystyle \mathscr{C}_{0}\equiv \mathscr{L}(h_{0})+\frac{G_{0}}{Z{\it\tau}}\left[(T-T_{t})\left(v^{2}-\frac{3}{2}\right)\right.\\ \, & \, & \left.+\,\displaystyle \frac{4({\it\omega}_{0}-1)}{15}q_{t2}v_{2}\left(v^{2}-\frac{5}{2}\right)\right],\\ \displaystyle \frac{\partial h_{1}}{\partial t}+v_{2}\frac{\partial h_{1}}{\partial x_{2}}\, & =\, & \displaystyle \mathscr{C}_{1}\equiv \frac{d}{2}\mathscr{L}(h_{0})+\frac{1}{{\it\tau}}\left[\frac{d}{2}h_{0}+\frac{d}{2}T_{r}G_{0}-h_{1}\right]\\ \, & \, & +\,\displaystyle \frac{\text{d}G_{0}}{2Z{\it\tau}}\left[(T-T_{t})\left(v^{2}-\frac{1}{2}\right)+\frac{4({\it\omega}_{0}-1)}{15}q_{t2}v_{2}\left(v^{2}-\frac{5}{2}\right)\right]\\ \, & \, & +\,\displaystyle \frac{2(Z+{\it\omega}_{1}-1)(1-{\it\delta})}{Z{\it\tau}}q_{r2}v_{2}G_{0},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
with the macroscopic quantities
![]() $T_{t}=\int (2v^{2}/3-1)h_{0}\text{d}\boldsymbol{v}$
,
$T_{t}=\int (2v^{2}/3-1)h_{0}\text{d}\boldsymbol{v}$
,
![]() $T_{r}=\int (2h_{1}/d-h_{0})\text{d}\boldsymbol{v}$
,
$T_{r}=\int (2h_{1}/d-h_{0})\text{d}\boldsymbol{v}$
,
![]() $q_{t2}=\int (v^{2}-(5/2))v_{2}h_{0}\text{d}\boldsymbol{v}$
, and
$q_{t2}=\int (v^{2}-(5/2))v_{2}h_{0}\text{d}\boldsymbol{v}$
, and
![]() $q_{r2}=\int v_{2}(h_{1}-dh_{0}/2)\text{d}\boldsymbol{v}$
. Similar equations can be written for the Rykov kinetic model.
$q_{r2}=\int v_{2}(h_{1}-dh_{0}/2)\text{d}\boldsymbol{v}$
. Similar equations can be written for the Rykov kinetic model.
The initial conditions describing the density impulse are
![]() $h_{0}=G_{0}$
and
$h_{0}=G_{0}$
and
![]() $h_{1}=(d/2)G_{0}$
at
$h_{1}=(d/2)G_{0}$
at
![]() $x_{2}=0$
, and
$x_{2}=0$
, and
![]() $h_{0},h_{1}=0$
at
$h_{0},h_{1}=0$
at
![]() $x_{2}\neq 0$
. Applying the Laplace–Fourier transform to (5.2) in the temporal–spatial domains, we obtain
$x_{2}\neq 0$
. Applying the Laplace–Fourier transform to (5.2) in the temporal–spatial domains, we obtain
![]() $2{\rm\pi}\text{i}(\,f_{s}-v_{2}){\hat{h}}_{0}=\hat{\mathscr{C}}_{0}+G_{0}$
and
$2{\rm\pi}\text{i}(\,f_{s}-v_{2}){\hat{h}}_{0}=\hat{\mathscr{C}}_{0}+G_{0}$
and
![]() $2{\rm\pi}\text{i}(\,f_{s}-v_{2}){\hat{h}}_{1}=\hat{\mathscr{C}}_{1}+(d/2)G_{0}$
, where quantities with a hat denote the Laplace–Fourier transform of the corresponding quantities. The two algebraic equations are rewritten as
$2{\rm\pi}\text{i}(\,f_{s}-v_{2}){\hat{h}}_{1}=\hat{\mathscr{C}}_{1}+(d/2)G_{0}$
, where quantities with a hat denote the Laplace–Fourier transform of the corresponding quantities. The two algebraic equations are rewritten as
![]() $2{\rm\pi}\text{i}(\,f_{s}-v_{2}){\hat{h}}_{0}+{\it\nu}{\hat{h}}_{0}=\hat{\mathscr{C}}_{0}+G_{0}+{\it\nu}{\hat{h}}_{0}$
and
$2{\rm\pi}\text{i}(\,f_{s}-v_{2}){\hat{h}}_{0}+{\it\nu}{\hat{h}}_{0}=\hat{\mathscr{C}}_{0}+G_{0}+{\it\nu}{\hat{h}}_{0}$
and
![]() $2{\rm\pi}\text{i}(\,f_{s}-v_{2}){\hat{h}}_{1}+{\it\nu}{\hat{h}}_{1}=\hat{\mathscr{C}}_{1}+(d/2)G_{0}+{\it\nu}{\hat{h}}_{1}$
with
$2{\rm\pi}\text{i}(\,f_{s}-v_{2}){\hat{h}}_{1}+{\it\nu}{\hat{h}}_{1}=\hat{\mathscr{C}}_{1}+(d/2)G_{0}+{\it\nu}{\hat{h}}_{1}$
with
![]() ${\it\nu}=2/{\it\tau}$
, which can then be solved in an iterative manner:
${\it\nu}=2/{\it\tau}$
, which can then be solved in an iterative manner:
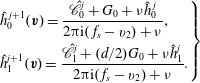 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\displaystyle {\hat{h}}_{0}^{\,j+1}(\boldsymbol{v})=\frac{\hat{\mathscr{C}}_{0}^{j}+G_{0}+{\it\nu}{\hat{h}}_{0}^{\,j}}{2{\rm\pi}\text{i}(\,f_{s}-v_{2})+{\it\nu}},\\ \displaystyle {\hat{h}}_{1}^{j+1}(\boldsymbol{v})=\frac{\hat{\mathscr{C}}_{1}^{j}+(d/2)G_{0}+{\it\nu}{\hat{h}}_{1}^{j}}{2{\rm\pi}\text{i}(\,f_{s}-v_{2})+{\it\nu}}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\displaystyle {\hat{h}}_{0}^{\,j+1}(\boldsymbol{v})=\frac{\hat{\mathscr{C}}_{0}^{j}+G_{0}+{\it\nu}{\hat{h}}_{0}^{\,j}}{2{\rm\pi}\text{i}(\,f_{s}-v_{2})+{\it\nu}},\\ \displaystyle {\hat{h}}_{1}^{j+1}(\boldsymbol{v})=\frac{\hat{\mathscr{C}}_{1}^{j}+(d/2)G_{0}+{\it\nu}{\hat{h}}_{1}^{j}}{2{\rm\pi}\text{i}(\,f_{s}-v_{2})+{\it\nu}}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
The spectrum of the spontaneous RBS, according to (5.1), is calculated by
Given the Knudsen number
![]() $\mathit{Kn}$
, viscosity index
$\mathit{Kn}$
, viscosity index
![]() ${\it\omega}$
, and frequency shift
${\it\omega}$
, and frequency shift
![]() $f_{s}$
, the iterations are terminated when the difference in the spectrum between two consecutive steps is smaller than
$f_{s}$
, the iterations are terminated when the difference in the spectrum between two consecutive steps is smaller than
![]() $10^{-6}$
. Our method takes about one minute to produce a line shape, which is much faster than the DSMC method used by Bruno et al. (Reference Bruno, Capitelli, Longo and Minelli2006).
$10^{-6}$
. Our method takes about one minute to produce a line shape, which is much faster than the DSMC method used by Bruno et al. (Reference Bruno, Capitelli, Longo and Minelli2006).
We first compare the spontaneous RBS spectra obtained from both the Rykov model and our kinetic model with those from the s6 kinetic model (Pan et al.
Reference Pan, Shneider and Miles2004). We choose
![]() ${\it\delta}=1/1.33$
and
${\it\delta}=1/1.33$
and
![]() ${\it\omega}_{0}$
in the Rykov model and our kinetic model according to (2.13), while we choose
${\it\omega}_{0}$
in the Rykov model and our kinetic model according to (2.13), while we choose
![]() ${\it\omega}_{1}$
to make the Eucken factor equal to 1.9 and 1.75 for diatomic and nonlinear polyatomic gases, respectively. The s6 model is derived for a Maxwell gas, and in figure 7 we see that for this gas the three models yield almost identical results. When a hard-sphere gas is considered, the Rykov model produces the same results as for the Maxwell gas, while our kinetic model (3.1) predicts a relatively higher spectrum near the Rayleigh peak (
${\it\omega}_{1}$
to make the Eucken factor equal to 1.9 and 1.75 for diatomic and nonlinear polyatomic gases, respectively. The s6 model is derived for a Maxwell gas, and in figure 7 we see that for this gas the three models yield almost identical results. When a hard-sphere gas is considered, the Rykov model produces the same results as for the Maxwell gas, while our kinetic model (3.1) predicts a relatively higher spectrum near the Rayleigh peak (
![]() $f_{s}\sim 0$
) when
$f_{s}\sim 0$
) when
![]() $\mathit{Kn}=0.06$
and a relatively lower spectrum near the Brillouin peak (
$\mathit{Kn}=0.06$
and a relatively lower spectrum near the Brillouin peak (
![]() $f_{s}\sim 0.8$
) when
$f_{s}\sim 0.8$
) when
![]() $\mathit{Kn}=0.08$
. We conclude that the intermolecular potential does indeed influence the spontaneous RBS spectrum of polyatomic gases.
$\mathit{Kn}=0.08$
. We conclude that the intermolecular potential does indeed influence the spontaneous RBS spectrum of polyatomic gases.

Figure 7. Spontaneous RBS spectra for different kinetic models and gas molecular models. In this and the following figures, the spectrum is normalized by its maximum value. (a) Diatomic gas
![]() $\mathit{Kn}=0.06$
; (b) diatomic gas
$\mathit{Kn}=0.06$
; (b) diatomic gas
![]() $\mathit{Kn}=0.08$
; (c) nonlinear polyatomic gas
$\mathit{Kn}=0.08$
; (c) nonlinear polyatomic gas
![]() $\mathit{Kn}=0.06$
; (d) nonlinear polyatomic gas
$\mathit{Kn}=0.06$
; (d) nonlinear polyatomic gas
![]() $\mathit{Kn}=0.08$
.
$\mathit{Kn}=0.08$
.
Experimentally, the bulk viscosity is obtained by comparing the experimental spectra with those from the s6 model (Vieitez et al. Reference Vieitez, van Duijn, Ubachs, Witschas, Meijer, de Wijn, Dam and van de Water2010; Gu & Ubachs Reference Gu and Ubachs2013). If the viscosity index of the gas is 0.5, some errors will be introduced. For instance, using the s6 model, the bulk viscosity is overpredicted by approximately 33 % and 50 %, respectively, in figure 7(a,b) for hard-sphere diatomic gases, and 20 % and 33 %, respectively, in figure 7(c,d) for hard-sphere nonlinear polyatomic gases. Further numerical simulations show that the closer the viscosity index is to one, the smaller the error that is introduced when comparing experimental spontaneous RBS spectra with those of the s6 model.
Figure 8 compares the spontaneous RBS spectra of nitrogen produced by our model with the experimental data of Gu & Ubachs (Reference Gu and Ubachs2013). The experimental spectrum is the convolution of the spectrum
![]() $S$
and the instrumental spectral response function, which can be found in Vieitez et al. (Reference Vieitez, van Duijn, Ubachs, Witschas, Meijer, de Wijn, Dam and van de Water2010). In our simulation, we use
$S$
and the instrumental spectral response function, which can be found in Vieitez et al. (Reference Vieitez, van Duijn, Ubachs, Witschas, Meijer, de Wijn, Dam and van de Water2010). In our simulation, we use
![]() ${\it\omega}=0.7383$
,
${\it\omega}=0.7383$
,
![]() ${\it\mu}=1.656\times 10^{-5}~\text{kg}~{\text{m}^{-1}~\text{s}}^{-1}$
at
${\it\mu}=1.656\times 10^{-5}~\text{kg}~{\text{m}^{-1}~\text{s}}^{-1}$
at
![]() $T=273.15~\text{K}$
, and the effective wavelength
$T=273.15~\text{K}$
, and the effective wavelength
![]() ${\it\lambda}=259.4~\text{nm}$
. Therefore, the shear viscosities in figure 8(a–d) are
${\it\lambda}=259.4~\text{nm}$
. Therefore, the shear viscosities in figure 8(a–d) are
![]() $(1.57,1.67,1.76,1.93)\times 10^{-5}~\text{kg}~{\text{m}^{-1}~\text{s}}^{-1}$
, respectively. To extract the bulk viscosity, the convolved spectrum from our theory is multiplied by
$(1.57,1.67,1.76,1.93)\times 10^{-5}~\text{kg}~{\text{m}^{-1}~\text{s}}^{-1}$
, respectively. To extract the bulk viscosity, the convolved spectrum from our theory is multiplied by
![]() $c_{1}$
and then added to
$c_{1}$
and then added to
![]() $c_{2}$
, where
$c_{2}$
, where
![]() $c_{1}$
and
$c_{1}$
and
![]() $c_{2}$
are obtained by least-squares fitting; the standard error in the fitting is a function of
$c_{2}$
are obtained by least-squares fitting; the standard error in the fitting is a function of
![]() $Z$
. We choose the value of
$Z$
. We choose the value of
![]() $Z$
when the standard error is minimum. The resulting bulk viscosities in figure 8(a–d) are
$Z$
when the standard error is minimum. The resulting bulk viscosities in figure 8(a–d) are
![]() $(0.75,1.02,1.22,1.70)\times 10^{-5}~\text{kg}~{\text{m}^{-1}~\text{s}}^{-1}$
, respectively.
$(0.75,1.02,1.22,1.70)\times 10^{-5}~\text{kg}~{\text{m}^{-1}~\text{s}}^{-1}$
, respectively.

Figure 8. Spontaneous RBS spectra for nitrogen, comparing our model (lines) to the experimental data (dots) of Gu & Ubachs (Reference Gu and Ubachs2013). (a)
![]() $T=254.7~\text{K}$
,
$T=254.7~\text{K}$
,
![]() $P=2.563~\text{bar}$
; (b)
$P=2.563~\text{bar}$
; (b)
![]() $T=275.2~\text{K}$
,
$T=275.2~\text{K}$
,
![]() $P=2.784~\text{bar}$
; (c)
$P=2.784~\text{bar}$
; (c)
![]() $T=296.7~\text{K}$
,
$T=296.7~\text{K}$
,
![]() $P=3.000~\text{bar}$
; (d)
$P=3.000~\text{bar}$
; (d)
![]() $T=336.6~\text{K}$
,
$T=336.6~\text{K}$
,
![]() $P=3.400~\text{bar}$
. The fitted values of
$P=3.400~\text{bar}$
. The fitted values of
![]() $Z$
are (a) 1.8, (b) 2.3, (c) 2.6 and (d) 3.3.
$Z$
are (a) 1.8, (b) 2.3, (c) 2.6 and (d) 3.3.
5.2. Coherent Rayleigh–Brillouin scattering
In coherent RBS experiments (Grinstead & Barker Reference Grinstead and Barker2000; Pan et al. Reference Pan, Shneider and Miles2002; Vieitez et al. Reference Vieitez, van Duijn, Ubachs, Witschas, Meijer, de Wijn, Dam and van de Water2010; Cornella et al. Reference Cornella, Gimelshein, Shneider, Lilly and Ketsdever2012), an individual molecule is subject to an external optical dipole force. When the beam intensities are small, the spectrum can be obtained by solving the linearized Boltzmann equation. Since the density fluctuations are induced by the external optical dipole force, the coherent RBS spectra are different to the spontaneous ones.
With the characteristic flow length being the effective wavelength
![]() ${\it\lambda}$
, (3.1) with the external optical potential is linearized to
${\it\lambda}$
, (3.1) with the external optical potential is linearized to
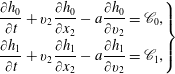 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\displaystyle \frac{\partial h_{0}}{\partial t}+v_{2}\frac{\partial h_{0}}{\partial x_{2}}-a\frac{\partial h_{0}}{\partial v_{2}}=\mathscr{C}_{0},\\ \displaystyle \frac{\partial h_{1}}{\partial t}+v_{2}\frac{\partial h_{1}}{\partial x_{2}}-a\frac{\partial h_{1}}{\partial v_{2}}=\mathscr{C}_{1},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\displaystyle \frac{\partial h_{0}}{\partial t}+v_{2}\frac{\partial h_{0}}{\partial x_{2}}-a\frac{\partial h_{0}}{\partial v_{2}}=\mathscr{C}_{0},\\ \displaystyle \frac{\partial h_{1}}{\partial t}+v_{2}\frac{\partial h_{1}}{\partial x_{2}}-a\frac{\partial h_{1}}{\partial v_{2}}=\mathscr{C}_{1},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where
![]() $a=\cos (x_{2}-f_{d}t)$
is the acceleration from the external optical potential, and
$a=\cos (x_{2}-f_{d}t)$
is the acceleration from the external optical potential, and
![]() $f_{d}$
is the frequency difference between the two pump beams, which has been normalized by the characteristic frequency
$f_{d}$
is the frequency difference between the two pump beams, which has been normalized by the characteristic frequency
![]() $v_{m}/{\it\lambda}$
. Similar equations can be written for the Rykov model.
$v_{m}/{\it\lambda}$
. Similar equations can be written for the Rykov model.
To find the coherent RBS spectrum, the Fourier transform is applied to (5.5) in both the spatial and temporal directions, and the resultant equations are solved in an iterative manner. That is, given the frequency difference
![]() $f_{d}$
, Knudsen number
$f_{d}$
, Knudsen number
![]() $\mathit{Kn}$
, and viscosity index
$\mathit{Kn}$
, and viscosity index
![]() ${\it\omega}$
, we have the following iterative scheme:
${\it\omega}$
, we have the following iterative scheme:
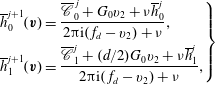 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\displaystyle \overline{h}_{0}^{j+1}(\boldsymbol{v})=\frac{\overline{\mathscr{C}}_{0}^{\,j}+G_{0}v_{2}+{\it\nu}\overline{h}_{0}^{j}}{2{\rm\pi}\text{i}(\,f_{d}-v_{2})+{\it\nu}},\\ \displaystyle \overline{h}_{1}^{j+1}(\boldsymbol{v})=\frac{\overline{\mathscr{C}}_{1}^{j}+(d/2)G_{0}v_{2}+{\it\nu}\overline{h}_{1}^{j}}{2{\rm\pi}\text{i}(\,f_{d}-v_{2})+{\it\nu}},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\displaystyle \overline{h}_{0}^{j+1}(\boldsymbol{v})=\frac{\overline{\mathscr{C}}_{0}^{\,j}+G_{0}v_{2}+{\it\nu}\overline{h}_{0}^{j}}{2{\rm\pi}\text{i}(\,f_{d}-v_{2})+{\it\nu}},\\ \displaystyle \overline{h}_{1}^{j+1}(\boldsymbol{v})=\frac{\overline{\mathscr{C}}_{1}^{j}+(d/2)G_{0}v_{2}+{\it\nu}\overline{h}_{1}^{j}}{2{\rm\pi}\text{i}(\,f_{d}-v_{2})+{\it\nu}},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where an overline denotes a spatial–temporal Fourier transformation. Since the intensity of the scattered light is proportional to the square of the gas density variations (Pan et al. Reference Pan, Shneider and Miles2004), the spectrum of the coherent RBS is then given by:
Starting from
![]() $\tilde{h}_{0}=\tilde{h}_{1}=0$
, the iterations are terminated when the relative error of
$\tilde{h}_{0}=\tilde{h}_{1}=0$
, the iterations are terminated when the relative error of
![]() $S$
between two consecutive iteration steps is less than
$S$
between two consecutive iteration steps is less than
![]() $10^{-6}$
. We consider hard-sphere and Maxwell gases. The accuracy and efficiency of our kinetic model is outlined in appendix B.
$10^{-6}$
. We consider hard-sphere and Maxwell gases. The accuracy and efficiency of our kinetic model is outlined in appendix B.
Figure 9 shows the coherent RBS line shapes for polyatomic gases at
![]() $\mathit{Kn}=0.08$
. The influence of the molecular model is clear: the spectrum near the Rayleigh peak increases as the viscosity index decreases. The Rykov model, as expected, gives results that are independent of the molecular model and agree only with the Maxwell gas case.
$\mathit{Kn}=0.08$
. The influence of the molecular model is clear: the spectrum near the Rayleigh peak increases as the viscosity index decreases. The Rykov model, as expected, gives results that are independent of the molecular model and agree only with the Maxwell gas case.

Figure 9. Coherent RBS spectra for hard-sphere and Maxwell gases, at
![]() $\mathit{Kn}=0.08$
: (a) and (b) diatomic gases; (c) and (d) nonlinear polyatomic gases.
$\mathit{Kn}=0.08$
: (a) and (b) diatomic gases; (c) and (d) nonlinear polyatomic gases.
The difference in spectra between different molecular models greatly affects the accuracy when measuring the bulk viscosity of polyatomic gases. Suppose the viscosity index of a gas is 0.5; if we compare the experimental line shape with that obtained from the s6 model (Pan et al.
Reference Pan, Shneider and Miles2004) to extract the bulk viscosity, then the bulk viscosities in figure 9(a,c) are overpredicted by 43 %, while the bulk viscosities in figure 9(b,d) are overpredicted by 100 %. Generally speaking, the larger the
![]() $Z$
value, the larger the overprediction. At room temperature, nitrogen and oxygen have viscosity indices close to 0.75. If one obtains
$Z$
value, the larger the overprediction. At room temperature, nitrogen and oxygen have viscosity indices close to 0.75. If one obtains
![]() $Z=3$
and
$Z=3$
and
![]() $Z=6$
by comparing the experimental line shapes with those from the s6 kinetic model, then by comparing with our kinetic model the actual values are
$Z=6$
by comparing the experimental line shapes with those from the s6 kinetic model, then by comparing with our kinetic model the actual values are
![]() $Z=2.5$
and
$Z=2.5$
and
![]() $Z=4$
, respectively.
$Z=4$
, respectively.
Figure 10 compares the coherent RBS spectra of our model with the experimental data of Vieitez et al. (Reference Vieitez, van Duijn, Ubachs, Witschas, Meijer, de Wijn, Dam and van de Water2010) for nitrogen at
![]() $T=293~\text{K}$
and
$T=293~\text{K}$
and
![]() ${\it\lambda}=266~\text{nm}$
. Our kinetic model predicts a bulk viscosity of
${\it\lambda}=266~\text{nm}$
. Our kinetic model predicts a bulk viscosity of
![]() $1.21\times 10^{-5}~\text{kg}~{\text{m}^{-1}~\text{s}}^{-1}$
, which agrees well with the literature value
$1.21\times 10^{-5}~\text{kg}~{\text{m}^{-1}~\text{s}}^{-1}$
, which agrees well with the literature value
![]() $1.28\times 10^{-5}~\text{kg}~{\text{m}^{-1}~\text{s}}^{-1}$
(Prangsma, Alberga & Beenakker Reference Prangsma, Alberga and Beenakker1973).
$1.28\times 10^{-5}~\text{kg}~{\text{m}^{-1}~\text{s}}^{-1}$
(Prangsma, Alberga & Beenakker Reference Prangsma, Alberga and Beenakker1973).

Figure 10. Coherent RBS spectra for nitrogen, comparing our model with
![]() $Z=2.6$
(lines) to the experimental data (dots) of Vieitez et al. (Reference Vieitez, van Duijn, Ubachs, Witschas, Meijer, de Wijn, Dam and van de Water2010): (a)
$Z=2.6$
(lines) to the experimental data (dots) of Vieitez et al. (Reference Vieitez, van Duijn, Ubachs, Witschas, Meijer, de Wijn, Dam and van de Water2010): (a)
![]() $P=2~\text{bar}$
, (b)
$P=2~\text{bar}$
, (b)
![]() $P=3~\text{bar}$
.
$P=3~\text{bar}$
.
6. Conclusions
We have proposed a kinetic model for the Boltzmann equation for non-vibrating polyatomic gases, based on the Rykov model for diatomic gases with a Jeans’ relaxation model for the translational–rotational energy exchange. Transport coefficients, such as shear viscosity, bulk viscosity and thermal conductivities, derived by the Chapman–Enskog technique, were used to determine the model parameters. Comparisons with DSMC simulations showed that the new kinetic model improves the accuracy of the Rykov model. This is due to the introduction of a realistic elastic relaxation time that is dependent on the molecular velocity. With this kinetic model, we investigated the flow rates in both Poiseuille and thermal creep flows of polyatomic gases, and the spectra of both spontaneous and coherent RBS. In Poiseuille/thermal creep flows, we found that the proposed kinetic model satisfies Onsager’s reciprocity relations. We also showed how the molecular model affects flow properties, and evaluated the error in extracting the bulk viscosity from RBS experiments. The present model may therefore be useful in gas microflow simulations where the molecular model plays an important role, for instance thermally driven flows (Wu et al. Reference Wu, Reese and Zhang2014).
Acknowledgements
Y.H.Z. thanks the UK’s Royal Academy of Engineering (RAE) and the Leverhulme Trust for the award of an RAE/Leverhulme Senior Research Fellowship. This work is financially supported by the UK’s Engineering and Physical Sciences Research Council (EPSRC) under grants EP/I036117/1 and EP/I011927/1. We thank Z. Gu and W. Ubachs for the experimental data on spontaneous Rayleigh–Brillouin scattering.
Appendix A. Transport coefficients from kinetic model equations
We use the Chapman–Enskog expansion (Chapman & Cowling Reference Chapman and Cowling1970) to obtain transport coefficients (such as the shear viscosity, bulk viscosity and thermal conductivities) from the Rykov kinetic model (2.3) for non-vibrating polyatomic gases.
When the system is close to equilibrium, the distribution function can be expanded as
![]() $f=f_{0}+f_{1}$
, where
$f=f_{0}+f_{1}$
, where
is the global equilibrium distribution function and
![]() $f_{1}$
is the perturbed distribution function satisfying
$f_{1}$
is the perturbed distribution function satisfying
![]() $|\,f_{1}|\ll 1$
. Linearizing the reference distribution functions
$|\,f_{1}|\ll 1$
. Linearizing the reference distribution functions
![]() $g_{t}$
and
$g_{t}$
and
![]() $g_{r}$
around the equilibrium temperature
$g_{r}$
around the equilibrium temperature
![]() $T$
, and considering the fact that
$T$
, and considering the fact that
![]() $|T_{t}-T|\ll 1$
, and
$|T_{t}-T|\ll 1$
, and
![]() $\boldsymbol{q}_{t}$
and
$\boldsymbol{q}_{t}$
and
![]() $\boldsymbol{q}_{r}$
are small, it is found that
$\boldsymbol{q}_{r}$
are small, it is found that
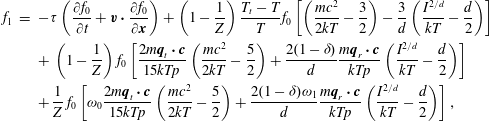 $$\begin{eqnarray}\displaystyle f_{1} & = & \displaystyle -{\it\tau}\left(\frac{\partial f_{0}}{\partial t}+\boldsymbol{v}\boldsymbol{\cdot }\frac{\partial f_{0}}{\partial \boldsymbol{x}}\right)+\left(1-\frac{1}{Z}\right)\frac{T_{t}-T}{T}f_{0}\left[\left(\frac{mc^{2}}{2kT}-\frac{3}{2}\right)-\frac{3}{d}\left(\frac{I^{2/d}}{kT}-\frac{d}{2}\right)\right]\nonumber\\ \displaystyle & & \displaystyle +\,\left(1-\frac{1}{Z}\right)f_{0}\left[\frac{2m\boldsymbol{q}_{t}\boldsymbol{\cdot }\boldsymbol{c}}{15kTp}\left(\frac{mc^{2}}{2kT}-\frac{5}{2}\right)+\frac{2(1-{\it\delta})}{d}\frac{m\boldsymbol{q}_{r}\boldsymbol{\cdot }\boldsymbol{c}}{kTp}\left(\frac{I^{2/d}}{kT}-\frac{d}{2}\right)\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{Z}\,f_{0}\left[{\it\omega}_{0}\frac{2m\boldsymbol{q}_{t}\boldsymbol{\cdot }\boldsymbol{c}}{15kTp}\left(\frac{mc^{2}}{2kT}-\frac{5}{2}\right)+\frac{2(1-{\it\delta}){\it\omega}_{1}}{d}\frac{m\boldsymbol{q}_{r}\boldsymbol{\cdot }\boldsymbol{c}}{kTp}\left(\frac{I^{2/d}}{kT}-\frac{d}{2}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{1} & = & \displaystyle -{\it\tau}\left(\frac{\partial f_{0}}{\partial t}+\boldsymbol{v}\boldsymbol{\cdot }\frac{\partial f_{0}}{\partial \boldsymbol{x}}\right)+\left(1-\frac{1}{Z}\right)\frac{T_{t}-T}{T}f_{0}\left[\left(\frac{mc^{2}}{2kT}-\frac{3}{2}\right)-\frac{3}{d}\left(\frac{I^{2/d}}{kT}-\frac{d}{2}\right)\right]\nonumber\\ \displaystyle & & \displaystyle +\,\left(1-\frac{1}{Z}\right)f_{0}\left[\frac{2m\boldsymbol{q}_{t}\boldsymbol{\cdot }\boldsymbol{c}}{15kTp}\left(\frac{mc^{2}}{2kT}-\frac{5}{2}\right)+\frac{2(1-{\it\delta})}{d}\frac{m\boldsymbol{q}_{r}\boldsymbol{\cdot }\boldsymbol{c}}{kTp}\left(\frac{I^{2/d}}{kT}-\frac{d}{2}\right)\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{Z}\,f_{0}\left[{\it\omega}_{0}\frac{2m\boldsymbol{q}_{t}\boldsymbol{\cdot }\boldsymbol{c}}{15kTp}\left(\frac{mc^{2}}{2kT}-\frac{5}{2}\right)+\frac{2(1-{\it\delta}){\it\omega}_{1}}{d}\frac{m\boldsymbol{q}_{r}\boldsymbol{\cdot }\boldsymbol{c}}{kTp}\left(\frac{I^{2/d}}{kT}-\frac{d}{2}\right)\right],\end{eqnarray}$$
where, according to Chapman & Cowling (Reference Chapman and Cowling1970), we have
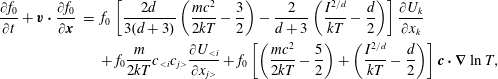 $$\begin{eqnarray}\displaystyle \frac{\partial f_{0}}{\partial t}+\boldsymbol{v}\boldsymbol{\cdot }\frac{\partial f_{0}}{\partial \boldsymbol{x}} & = & \displaystyle f_{0}\left[\frac{2d}{3(d+3)}\left(\frac{mc^{2}}{2kT}-\frac{3}{2}\right)-\frac{2}{d+3}\left(\frac{I^{2/d}}{kT}-\frac{d}{2}\right)\right]\frac{\partial U_{k}}{\partial x_{k}}\nonumber\\ \displaystyle & & \displaystyle +\;f_{0}\frac{m}{2kT}c_{{<}i}c_{j>}\frac{\partial U_{{<}i}}{\partial x_{j>}}+f_{0}\left[\left(\frac{mc^{2}}{2kT}-\frac{5}{2}\right)+\left(\frac{I^{2/d}}{kT}-\frac{d}{2}\right)\right]\boldsymbol{c}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\ln T,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\partial f_{0}}{\partial t}+\boldsymbol{v}\boldsymbol{\cdot }\frac{\partial f_{0}}{\partial \boldsymbol{x}} & = & \displaystyle f_{0}\left[\frac{2d}{3(d+3)}\left(\frac{mc^{2}}{2kT}-\frac{3}{2}\right)-\frac{2}{d+3}\left(\frac{I^{2/d}}{kT}-\frac{d}{2}\right)\right]\frac{\partial U_{k}}{\partial x_{k}}\nonumber\\ \displaystyle & & \displaystyle +\;f_{0}\frac{m}{2kT}c_{{<}i}c_{j>}\frac{\partial U_{{<}i}}{\partial x_{j>}}+f_{0}\left[\left(\frac{mc^{2}}{2kT}-\frac{5}{2}\right)+\left(\frac{I^{2/d}}{kT}-\frac{d}{2}\right)\right]\boldsymbol{c}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\ln T,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
with
![]() $c_{{<}i}c_{j>}=c_{i}c_{j}-c^{2}{\it\delta}_{ij}/3$
,
$c_{{<}i}c_{j>}=c_{i}c_{j}-c^{2}{\it\delta}_{ij}/3$
,
![]() $\partial U_{{<}i}/\partial x_{j>}=(\partial U_{i}/\partial x_{j})+(\partial U_{j}/\partial x_{i})-2/3(\partial U_{k}/\partial x_{k}){\it\delta}_{ij}$
, and
$\partial U_{{<}i}/\partial x_{j>}=(\partial U_{i}/\partial x_{j})+(\partial U_{j}/\partial x_{i})-2/3(\partial U_{k}/\partial x_{k}){\it\delta}_{ij}$
, and
![]() ${\it\delta}_{ij}$
being the Kronecker delta function.
${\it\delta}_{ij}$
being the Kronecker delta function.
The pressure tensor
![]() $\unicode[STIX]{x1D617}_{ij}=\int (\,f_{0}+f_{1})mc_{i}c_{j}\text{d}\boldsymbol{v}\text{d}I$
is
$\unicode[STIX]{x1D617}_{ij}=\int (\,f_{0}+f_{1})mc_{i}c_{j}\text{d}\boldsymbol{v}\text{d}I$
is
Taking the trace of
![]() $\unicode[STIX]{x1D617}_{ij}$
, we obtain
$\unicode[STIX]{x1D617}_{ij}$
, we obtain
![]() $p-p_{t}=(2dZ/3(d+3))p{\it\tau}(\partial U_{k}/\partial x_{k})$
. Substituting this expression into (A 4), we obtain
$p-p_{t}=(2dZ/3(d+3))p{\it\tau}(\partial U_{k}/\partial x_{k})$
. Substituting this expression into (A 4), we obtain
So the shear viscosity is
![]() ${\it\mu}=p{\it\tau}$
, while the bulk viscosity is
${\it\mu}=p{\it\tau}$
, while the bulk viscosity is
![]() ${\it\varpi}=2dZ{\it\mu}/3(d+3)$
. Note that the shear viscosity is derived under the assumption
${\it\varpi}=2dZ{\it\mu}/3(d+3)$
. Note that the shear viscosity is derived under the assumption
![]() $|T_{t}-T|\ll 1$
and, physically, the relaxation time is related to the translational temperature instead of the rotational temperature. Therefore, the shear viscosity and the bulk viscosity are expressed as follows:
$|T_{t}-T|\ll 1$
and, physically, the relaxation time is related to the translational temperature instead of the rotational temperature. Therefore, the shear viscosity and the bulk viscosity are expressed as follows:
Similarly, the heat fluxes
![]() $\boldsymbol{q}_{t}$
and
$\boldsymbol{q}_{t}$
and
![]() $\boldsymbol{q}_{r}$
, which are related to the transfer of translational and rotational energies, are given by
$\boldsymbol{q}_{r}$
, which are related to the transfer of translational and rotational energies, are given by
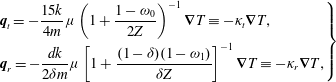 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\displaystyle \boldsymbol{q}_{t}=-\frac{15k}{4m}{\it\mu}\left(1+\frac{1-{\it\omega}_{0}}{2Z}\right)^{-1}\boldsymbol{{\rm\nabla}}T\equiv -{\it\kappa}_{t}\boldsymbol{{\rm\nabla}}T,\\ \displaystyle \boldsymbol{q}_{r}=-\frac{dk}{2{\it\delta}m}{\it\mu}\left[1+\frac{(1-{\it\delta})(1-{\it\omega}_{1})}{{\it\delta}Z}\right]^{-1}\boldsymbol{{\rm\nabla}}T\equiv -{\it\kappa}_{r}\boldsymbol{{\rm\nabla}}T,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\displaystyle \boldsymbol{q}_{t}=-\frac{15k}{4m}{\it\mu}\left(1+\frac{1-{\it\omega}_{0}}{2Z}\right)^{-1}\boldsymbol{{\rm\nabla}}T\equiv -{\it\kappa}_{t}\boldsymbol{{\rm\nabla}}T,\\ \displaystyle \boldsymbol{q}_{r}=-\frac{dk}{2{\it\delta}m}{\it\mu}\left[1+\frac{(1-{\it\delta})(1-{\it\omega}_{1})}{{\it\delta}Z}\right]^{-1}\boldsymbol{{\rm\nabla}}T\equiv -{\it\kappa}_{r}\boldsymbol{{\rm\nabla}}T,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where
![]() ${\it\kappa}_{t}$
and
${\it\kappa}_{t}$
and
![]() ${\it\kappa}_{r}$
are the coefficients of the translational and rotational thermal conductivity, respectively. Finally, the Eucken factor is
${\it\kappa}_{r}$
are the coefficients of the translational and rotational thermal conductivity, respectively. Finally, the Eucken factor is
For diatomic gases, the transport coefficients are the same as those found by Rykov & Skobelkin (Reference Rykov and Skobelkin1978).
Appendix B. Accuracy of our model for coherent RBS
We validate our kinetic model by comparing the coherent RBS line shape with those produced by the DSMC method and by Pan’s s6 model (Pan et al. Reference Pan, Shneider and Miles2004).
We solve the nonlinear Boltzmann equation using the DSMC method with the Larsen–Borgnakke translational–rotational energy exchange scheme. Unlike the DSMC method used by Cornella et al. (Reference Cornella, Gimelshein, Shneider, Lilly and Ketsdever2012), which solves at each frequency difference, we solve for the whole line shape in a single run using dsmcFoam. The key point is to use the broadband acceleration where each frequency difference has equal amplitude:
where
![]() $a_{0}$
is a constant and
$a_{0}$
is a constant and
![]() $f_{m}$
is the maximum frequency difference. We choose
$f_{m}$
is the maximum frequency difference. We choose
![]() $a_{0}=0.07$
to keep a relatively high signal-to-noise ratio that still enables us to linearize the Boltzmann equation (this is validated for monatomic gases by solving the nonlinear Boltzmann equation using DSMC and comparing the obtained spectra with those from the linearized Boltzmann equation solved by the fast spectral method). To cover all frequency differences,
$a_{0}=0.07$
to keep a relatively high signal-to-noise ratio that still enables us to linearize the Boltzmann equation (this is validated for monatomic gases by solving the nonlinear Boltzmann equation using DSMC and comparing the obtained spectra with those from the linearized Boltzmann equation solved by the fast spectral method). To cover all frequency differences,
![]() $f_{m}$
is set to be approximately 10 times the characteristic frequency.
$f_{m}$
is set to be approximately 10 times the characteristic frequency.
In the DSMC simulations, approximately 10 million simulated particles are uniformly distributed in the spatial domain from
![]() $x_{2}=0$
to
$x_{2}=0$
to
![]() ${\it\lambda}$
. The initial Maxwellian distribution is sampled at a given molecular number density, zero bulk velocity and equilibrium temperature. The length of the spatial cell is about a quarter of the molecular mean free path, and periodic boundary conditions are employed. The variable hard-sphere model is used to model the binary collisions. We record
${\it\lambda}$
. The initial Maxwellian distribution is sampled at a given molecular number density, zero bulk velocity and equilibrium temperature. The length of the spatial cell is about a quarter of the molecular mean free path, and periodic boundary conditions are employed. The variable hard-sphere model is used to model the binary collisions. We record
![]() ${\it\rho}(t)=\int _{0}^{{\it\lambda}}n(x_{2},t)\cos (2{\rm\pi}x_{2}/{\it\lambda})\text{d}x_{2}$
at each time step. When the simulation is finished, we take the Fourier transformation of
${\it\rho}(t)=\int _{0}^{{\it\lambda}}n(x_{2},t)\cos (2{\rm\pi}x_{2}/{\it\lambda})\text{d}x_{2}$
at each time step. When the simulation is finished, we take the Fourier transformation of
![]() ${\it\rho}(t)$
to obtain the spectrum, i.e.
${\it\rho}(t)$
to obtain the spectrum, i.e.
Figure 11(a) shows that our kinetic model (3.1) can predict accurate coherent RBS spectra, as compared to those from the DSMC method. Since the spatial variable has been eliminated, and (5.6) is solved using the fast spectral method, we obtain one line shape in about one minute (on a PC with an Intel Xenon 3.3 GHz CPU). However, the DSMC method takes approximately 5 h on the same PC to obtain a line shape. This demonstrates the accuracy of our kinetic model and efficiency of the numerical method: our method is approximately 300 times faster than the DSMC method.

Figure 11. Coherent RBS spectra generated by DSMC, the s6 model, and our kinetic model for (a) hard-sphere and (b) Maxwell diatomic gases, at
![]() $\mathit{Kn}=0.1$
.
$\mathit{Kn}=0.1$
.
We have also compared our model results with those from the s6 kinetic model. Note that the s6 model is derived for Maxwell molecules, so we choose the viscosity index
![]() ${\it\omega}=1$
in our kinetic model. Good agreement between the s6 model and our model can be seen in the results in figure 11(b).
${\it\omega}=1$
in our kinetic model. Good agreement between the s6 model and our model can be seen in the results in figure 11(b).
















