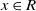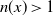1. Introduction
Boolean algebras play a significant role not only in mathematics but are also important tools in logic and computer science. Moreover, there is a natural correspondence between Boolean algebras and so-called Boolean rings: from a Boolean algebra, one may canonically construct a Boolean ring and vice versa (for details and an introduction to the subject, see [Reference Givant and Halmos4]). We recall that an associative ring R is Boolean provided every member of R is idempotent, that is,
![]() $x^2=x$
for every
$x^2=x$
for every
![]() $x\in R$
. It is well-known (and an exercise in many undergraduate algebra texts) that every Boolean ring is commutative (see [Reference Herstein5], for example). In fact, if one replaces the exponent 2 in the previous equation with 3, R is still commutative. Indeed, one can replace 2 with any integer greater than 1, and commutativity is guaranteed. Continuing to generalize, if one assumes only the existence of some such
$x\in R$
. It is well-known (and an exercise in many undergraduate algebra texts) that every Boolean ring is commutative (see [Reference Herstein5], for example). In fact, if one replaces the exponent 2 in the previous equation with 3, R is still commutative. Indeed, one can replace 2 with any integer greater than 1, and commutativity is guaranteed. Continuing to generalize, if one assumes only the existence of some such
![]() $n>1$
for every
$n>1$
for every
![]() $x\in R$
(which may depend on x), R must be commutative. This beautiful result is due to Nathan Jacobson and generalizes Wedderburn’s theorem that every finite division ring is a field ([Reference Wedderburn13]).
$x\in R$
(which may depend on x), R must be commutative. This beautiful result is due to Nathan Jacobson and generalizes Wedderburn’s theorem that every finite division ring is a field ([Reference Wedderburn13]).
Proposition 1 (Jacobson’s theorem [Reference Jacobson8]). Let R be an associative ring and suppose that for every
![]() $x\in R$
, there is an integer
$x\in R$
, there is an integer
![]() $n(x)>1$
such that
$n(x)>1$
such that
![]() $x^{n(x)}=x$
(that is, R is a potent ring). Then, R is commutative.
$x^{n(x)}=x$
(that is, R is a potent ring). Then, R is commutative.
We refer the reader to [Reference Buckley and MacHale2, Reference Dolan3], and [Reference Herstein6] for further reading, and to [Reference Anderson and Danchev1] for a recent generalization of Jacobson’s theorem.
Changing gears temporarily, the theory of idempotents contributes significantly to the theory of both commutative and non-commutative rings. Indeed, the number of different kinds of idempotents defined in the literature (orthogonal, central, primitive, local, irreducible, etc.) as well as rings defined in terms of idempotents (Baer, semisimple, von Neumann regular, Zorn, Rickart, etc.) indicates the utility of this notion in the structure theory of rings (see [Reference Lam11] for details). The purpose of this short note is to identify potency with a natural condition on the existence of idempotents. Specifically, we prove that an associative ring R is potent if and only if every nonzero subring of R contains a nonzero idempotent. We mention the classic texts [Reference Herstein5] and [Reference Hungerford7] as references for some standard algebraic results utilized in the paper such as the Chinese remainder theorem, the division algorithm for polynomials over a field, and Lagrange’s theorem.
Throughout, a ring is assumed only to be associative and not to be commutative nor to contain an identity unless specified; subrings are also not assumed unital, even in rings with identity.
2. Main result
Before presenting the main result of this paper, we prove the following lemma. For brevity, let us agree to call a ring with the property that every nonzero subring contains a nonzero idempotent idempotent-rich.Footnote 1
Lemma 1. The following hold:
-
(1) Every subring of an idempotent-rich ring is idempotent-rich.
-
(2) Every idempotent-rich ring is reduced.
-
(3) If R is a nonzero reduced ring, then the polynomomial ring
 $XR[X]\;:\!=\;\{Xf(X)\colon f(X)\in R[X]\}$
in the (commuting) variable X is not idempotent-rich.
$XR[X]\;:\!=\;\{Xf(X)\colon f(X)\in R[X]\}$
in the (commuting) variable X is not idempotent-rich. -
(4) If R is idempotent-rich and
 $e\in R$
is idempotent, then the additive order of e is a square-free integer.
$e\in R$
is idempotent, then the additive order of e is a square-free integer.
Proof. We establish each in succession.
-
(1) Trivial.
-
(2) Suppose by way of contradiction that R is idempotent-rich but not reduced. Then, there is some nonzero
 $\alpha\in R$
such that
$\alpha\in R$
such that
 $\alpha^2=0$
. But now
$\alpha^2=0$
. But now
 $\mathbb{Z}\alpha$
is a nonzero subring of R with no nonzero idempotent, a contradiction.
$\mathbb{Z}\alpha$
is a nonzero subring of R with no nonzero idempotent, a contradiction. -
(3) Let R be a nonzero reduced ring. We claim XR[X] has no nonzero idempotents. Indeed, consider an arbitrary
 $f\;:\!=\;a_1X+\cdots+a_nX^n\in XR[X]$
, where
$f\;:\!=\;a_1X+\cdots+a_nX^n\in XR[X]$
, where
 $a_n\neq 0$
. Then because R is reduced, it is easy to see that
$a_n\neq 0$
. Then because R is reduced, it is easy to see that
 $f^2$
has degree 2n and thus
$f^2$
has degree 2n and thus
 $f^2\neq f$
.
$f^2\neq f$
. -
(4) Let R be idempotent-rich and let
 $e\in R$
be an idempotent. Then
$e\in R$
be an idempotent. Then
 $\mathbb{Z}e$
is a subring of R and, moreover,
$\mathbb{Z}e$
is a subring of R and, moreover,
 $\mathbb{Z}e\cong\mathbb{Z}/\langle n\rangle$
for some non-negative integer n. If
$\mathbb{Z}e\cong\mathbb{Z}/\langle n\rangle$
for some non-negative integer n. If
 $n=0$
, then by (1), we see that
$n=0$
, then by (1), we see that
 $\mathbb{Z}$
is idempotent-rich, but this is absurd as the subring
$\mathbb{Z}$
is idempotent-rich, but this is absurd as the subring
 $2\mathbb{Z}$
of
$2\mathbb{Z}$
of
 $\mathbb{Z}$
has no nonzero idempotent. Thus,
$\mathbb{Z}$
has no nonzero idempotent. Thus,
 $n>0$
(and hence
$n>0$
(and hence
 $n=\mathrm{ord}(e)$
). Suppose that n is not square-free, and write
$n=\mathrm{ord}(e)$
). Suppose that n is not square-free, and write
 $n=m^2q$
, where m,q are integers and
$n=m^2q$
, where m,q are integers and
 $m>1$
. Then, mq (mod n) is a nonzero nilpotent element of
$m>1$
. Then, mq (mod n) is a nonzero nilpotent element of
 $\mathbb{Z}/\langle n\rangle$
, a contradiction to (1) and (2) above.
$\mathbb{Z}/\langle n\rangle$
, a contradiction to (1) and (2) above.
We are now ready to prove the main result of this note.
Theorem 1. Let R be a ring. Then, R is potent if and only if every nonzero subring of R contains a nonzero idempotent.
Proof. Let R be a ring. Suppose first that R is potent. We will show that R is idempotent-rich. Indeed, suppose that S is a nonzero subring of R, and let
![]() $s\in S$
be nonzero. By our assumption, there is an integer
$s\in S$
be nonzero. By our assumption, there is an integer
![]() $n>1$
such that
$n>1$
such that
![]() $s^n=s$
. Then,
$s^n=s$
. Then,
![]() $s^n(s^{n-2})=s(s^{n-2})$
, that is,
$s^n(s^{n-2})=s(s^{n-2})$
, that is,
![]() $(s^{n-1})^2=s^{2n-2}=s^{n-1}$
. As
$(s^{n-1})^2=s^{2n-2}=s^{n-1}$
. As
![]() $s^n=s$
and
$s^n=s$
and
![]() $s\neq 0$
, clearly
$s\neq 0$
, clearly
![]() $s^{n-1}\neq 0$
; since
$s^{n-1}\neq 0$
; since
![]() $n>1$
,
$n>1$
,
![]() $s^{n-1}\in S$
. Hence, S contains a nonzero idempotent.
$s^{n-1}\in S$
. Hence, S contains a nonzero idempotent.
Conversely, suppose that every nonzero subring of R contains a nonzero idempotent. We shall prove that R is potent. Suppose that
![]() $\alpha\in R$
is nonzero. We will show that
$\alpha\in R$
is nonzero. We will show that
We first verify that the ring
![]() $X\mathbb{Z}[X]$
is Noetherian (that is, every ascending chain of ideals stabilizes). Indeed, notice that every ideal of
$X\mathbb{Z}[X]$
is Noetherian (that is, every ascending chain of ideals stabilizes). Indeed, notice that every ideal of
![]() $X\mathbb{Z}[X]$
is also an ideal of
$X\mathbb{Z}[X]$
is also an ideal of
![]() $\mathbb{Z}[X]$
. As
$\mathbb{Z}[X]$
. As
![]() $\mathbb{Z}[X]$
is Noetherian,
$\mathbb{Z}[X]$
is Noetherian,
![]() $X\mathbb{Z}[X]$
is as well. Next, since
$X\mathbb{Z}[X]$
is as well. Next, since
![]() $\alpha\mathbb{Z}[\alpha]$
is a homomorphic image of
$\alpha\mathbb{Z}[\alpha]$
is a homomorphic image of
![]() $X\mathbb{Z}[X]$
, we conclude that
$X\mathbb{Z}[X]$
, we conclude that
![]() $\alpha\mathbb{Z}[\alpha]$
is a Noetherian ring. It now follows immediately that
$\alpha\mathbb{Z}[\alpha]$
is a Noetherian ring. It now follows immediately that
![]() $\alpha\mathbb{Z}[\alpha]$
does not contain an infinite internal direct sum of nonzero ideals. Therefore (see Lemma 4 of [Reference Oman and Stroud12]),
$\alpha\mathbb{Z}[\alpha]$
does not contain an infinite internal direct sum of nonzero ideals. Therefore (see Lemma 4 of [Reference Oman and Stroud12]),
Next, fix k with
![]() $1\leq k\leq n$
, and set
$1\leq k\leq n$
, and set
![]() $I\;:\!=\;I_k$
. Then, I is a nonzero subring of
$I\;:\!=\;I_k$
. Then, I is a nonzero subring of
![]() $\alpha\mathbb{Z}[\alpha]$
and thus contains a nonzero idempotent e. Let
$\alpha\mathbb{Z}[\alpha]$
and thus contains a nonzero idempotent e. Let
![]() $J\;:\!=\;\{ie-i\colon i\in I\}$
. Observe that J is a subideal of I and that
$J\;:\!=\;\{ie-i\colon i\in I\}$
. Observe that J is a subideal of I and that
![]() $Ie+J=I$
. We claim that the sum is direct: suppose that
$Ie+J=I$
. We claim that the sum is direct: suppose that
![]() $xe=ye-y$
for some
$xe=ye-y$
for some
![]() $x,y\in I$
. Multiplying through by e and using the fact that e is idempotent, we see that
$x,y\in I$
. Multiplying through by e and using the fact that e is idempotent, we see that
![]() $xe=ye-ye=0$
, proving the directness of the sum. Because e is a nonzero element of Ie, and since I is indecomposable, we have
$xe=ye-ye=0$
, proving the directness of the sum. Because e is a nonzero element of Ie, and since I is indecomposable, we have
![]() $Ie=I$
. By (4) of Lemma 1, the additive order of e is a square-free integer. As
$Ie=I$
. By (4) of Lemma 1, the additive order of e is a square-free integer. As
![]() $\alpha\mathbb{Z}[\alpha]$
is commutative, this clearly implies that the additive order of every member of
$\alpha\mathbb{Z}[\alpha]$
is commutative, this clearly implies that the additive order of every member of
![]() $Ie=I$
is also a square-free integer. Since k was arbitrary, it follows easily from (2.2) above that the order of every member of
$Ie=I$
is also a square-free integer. Since k was arbitrary, it follows easily from (2.2) above that the order of every member of
![]() $\alpha\mathbb{Z}[\alpha]$
is a square-free integer; in particular, the order of
$\alpha\mathbb{Z}[\alpha]$
is a square-free integer; in particular, the order of
![]() $\alpha$
is a square-free integer m. From this fact, we deduce thatFootnote
2
$\alpha$
is a square-free integer m. From this fact, we deduce thatFootnote
2
The map
![]() $\overline{a}_1X+\cdots+\overline{a}_nX^n\to a_1\alpha+\cdots+a_n\alpha^n$
is now a well-defined ring surjection of
$\overline{a}_1X+\cdots+\overline{a}_nX^n\to a_1\alpha+\cdots+a_n\alpha^n$
is now a well-defined ring surjection of
![]() $X\mathbb{Z}/\langle m\rangle[X]$
onto
$X\mathbb{Z}/\langle m\rangle[X]$
onto
![]() $\alpha\mathbb{Z}[\alpha]$
. Thus,
$\alpha\mathbb{Z}[\alpha]$
. Thus,
Write
![]() $m=p_1p_2\cdots p_n$
, where the
$m=p_1p_2\cdots p_n$
, where the
![]() $p_i$
are distinct primes (recall above that
$p_i$
are distinct primes (recall above that
![]() $\alpha\neq 0$
, and hence
$\alpha\neq 0$
, and hence
![]() $m>1$
). As is well-known, a simple application of The Chinese Remainder Theorem yields that, as rings,
$m>1$
). As is well-known, a simple application of The Chinese Remainder Theorem yields that, as rings,
![]() $\mathbb{Z}/\langle m\rangle\cong\mathbb{Z}/\langle p_1\rangle\oplus\cdots\oplus\mathbb{Z}/\langle p_n\rangle$
. We conclude that
$\mathbb{Z}/\langle m\rangle\cong\mathbb{Z}/\langle p_1\rangle\oplus\cdots\oplus\mathbb{Z}/\langle p_n\rangle$
. We conclude that
![]() $X\mathbb{Z}/\langle m\rangle[X]\cong X\mathbb{Z}/\langle p_1\rangle[X]\oplus\cdots\oplus X\mathbb{Z}/\langle p_n\rangle[X]$
. We may now view K as an ideal of
$X\mathbb{Z}/\langle m\rangle[X]\cong X\mathbb{Z}/\langle p_1\rangle[X]\oplus\cdots\oplus X\mathbb{Z}/\langle p_n\rangle[X]$
. We may now view K as an ideal of
![]() $X\mathbb{Z}/\langle p_1\rangle[X]\oplus\cdots\oplus X\mathbb{Z}/\langle p_n\rangle[X]$
. Via this identification,
$X\mathbb{Z}/\langle p_1\rangle[X]\oplus\cdots\oplus X\mathbb{Z}/\langle p_n\rangle[X]$
. Via this identification,
Next, for
![]() $1\leq i\leq n$
, let
$1\leq i\leq n$
, let
![]() $I_i\;:\!=\;K\cap X\mathbb{Z}/\langle p_i\rangle[X]$
. We claim that
$I_i\;:\!=\;K\cap X\mathbb{Z}/\langle p_i\rangle[X]$
. We claim that
![]() $I_i$
is nontrivial. If
$I_i$
is nontrivial. If
![]() $I_i$
is trivial, then the mapping
$I_i$
is trivial, then the mapping
![]() $y\mapsto K+y$
is a ring isomorphism of
$y\mapsto K+y$
is a ring isomorphism of
![]() $X_i\mathbb{Z}/\langle p_i\rangle[X]$
into
$X_i\mathbb{Z}/\langle p_i\rangle[X]$
into
![]() $(X\mathbb{Z}/\langle p_1\rangle[X]\oplus\cdots\oplus X\mathbb{Z}/\langle p_n\rangle[X])/K\cong\alpha\mathbb{Z}[\alpha]$
. But then by (1) of Lemma 1,
$(X\mathbb{Z}/\langle p_1\rangle[X]\oplus\cdots\oplus X\mathbb{Z}/\langle p_n\rangle[X])/K\cong\alpha\mathbb{Z}[\alpha]$
. But then by (1) of Lemma 1,
![]() $X\mathbb{Z}/\langle p_i\rangle[X]$
is idempotent-rich, contradicting (3) of Lemma 1. So we see that each
$X\mathbb{Z}/\langle p_i\rangle[X]$
is idempotent-rich, contradicting (3) of Lemma 1. So we see that each
![]() $I_i$
is a nonzero ideal of
$I_i$
is a nonzero ideal of
![]() $X\mathbb{Z}/\langle p_i\rangle[X]$
. But it is easy to see that
$X\mathbb{Z}/\langle p_i\rangle[X]$
. But it is easy to see that
![]() $I_i$
is also a nonzero ideal of the PID
$I_i$
is also a nonzero ideal of the PID
![]() $\mathbb{Z}/\langle p_i\rangle[X]$
. The Division Algorithm for polynomials over a field shows that
$\mathbb{Z}/\langle p_i\rangle[X]$
. The Division Algorithm for polynomials over a field shows that
![]() $\mathbb{Z}/\langle p_i\rangle[X]/I_i$
is finite and thus also
$\mathbb{Z}/\langle p_i\rangle[X]/I_i$
is finite and thus also
Now observe that
Invoking (2.6), it follows that
![]() $(X\mathbb{Z}/\langle p_1\rangle[X]\oplus\cdots\oplus X\mathbb{Z}/\langle p_n\rangle[X])/(I_1\oplus\cdots\oplus I_n)$
is finite. Since
$(X\mathbb{Z}/\langle p_1\rangle[X]\oplus\cdots\oplus X\mathbb{Z}/\langle p_n\rangle[X])/(I_1\oplus\cdots\oplus I_n)$
is finite. Since
![]() $I_1\oplus\cdots\oplus I_n\subseteq K$
,Footnote
3
it is immediate that
$I_1\oplus\cdots\oplus I_n\subseteq K$
,Footnote
3
it is immediate that
Thus, finally, we see that
![]() $\alpha\mathbb{Z}[\alpha]$
is a finite, reduced commutative ring. As is well-known (see p. 22 of [Reference Jans9], for example), this implies that
$\alpha\mathbb{Z}[\alpha]$
is a finite, reduced commutative ring. As is well-known (see p. 22 of [Reference Jans9], for example), this implies that
![]() $\alpha\mathbb{Z}[\alpha]$
has an identity. By the Chinese Remainder Theorem,
$\alpha\mathbb{Z}[\alpha]$
has an identity. By the Chinese Remainder Theorem,
![]() $\alpha\mathbb{Z}[\alpha]=F_1\oplus\cdots\oplus F_k$
for some finite fields
$\alpha\mathbb{Z}[\alpha]=F_1\oplus\cdots\oplus F_k$
for some finite fields
![]() $F_1,\ldots, F_k$
, establishing (2.1). We claim that
$F_1,\ldots, F_k$
, establishing (2.1). We claim that
showing that R is potent. To see this, fix i with
![]() $1\leq i\leq k$
, and let
$1\leq i\leq k$
, and let
![]() $\pi_i\colon\alpha\mathbb{Z}[\alpha]\to F_i$
be projection onto the ith coordinate. It clearly suffices to establish that
$\pi_i\colon\alpha\mathbb{Z}[\alpha]\to F_i$
be projection onto the ith coordinate. It clearly suffices to establish that
![]() $(\pi_i(\alpha))^{(|F_1|-1)(|F_2|-1)\cdots(|F_k|-1)+1}=\pi_i(\alpha)$
. If
$(\pi_i(\alpha))^{(|F_1|-1)(|F_2|-1)\cdots(|F_k|-1)+1}=\pi_i(\alpha)$
. If
![]() $\pi_i(\alpha)=0_i$
, this is patent, so assume that
$\pi_i(\alpha)=0_i$
, this is patent, so assume that
![]() $\pi_i(\alpha)\neq 0$
. Lagrange’s Theorem implies that
$\pi_i(\alpha)\neq 0$
. Lagrange’s Theorem implies that
![]() $\pi_i(\alpha)^{|F_i|-1}=1_i$
. Raising both sides to the power
$\pi_i(\alpha)^{|F_i|-1}=1_i$
. Raising both sides to the power
![]() $\prod_{j\neq i}|F_j|-1$
and then multiplying through by
$\prod_{j\neq i}|F_j|-1$
and then multiplying through by
![]() $\pi_i(\alpha)$
yields the desired equation, and (2.9) is established. The proof is now complete.
$\pi_i(\alpha)$
yields the desired equation, and (2.9) is established. The proof is now complete.![]()
The following equivalent formulation of Jacobson’s theorem is immediate.
Corollary 1 (Jacobson’s Theorem, Alternative Form). Let R be a ring. If every nonzero subring of R contains a nonzero idempotent of R, then R is commutative.
In [Reference Anderson and Danchev1], the authors show that if R is a ring with identity such that for every
![]() $x\in R$
, there are positive integers m(x) and n(x) of different parity such that
$x\in R$
, there are positive integers m(x) and n(x) of different parity such that
![]() $x^{m(x)}=x^{n(x)}$
, then R potent, and hence commutative. Note that the assumption that R is unital cannot be dropped completely, since every nil ring trivially has this property, and there are noncommutative nil rings. However, if R has no nonzero nilpotent elements, then we have the following stronger result.
$x^{m(x)}=x^{n(x)}$
, then R potent, and hence commutative. Note that the assumption that R is unital cannot be dropped completely, since every nil ring trivially has this property, and there are noncommutative nil rings. However, if R has no nonzero nilpotent elements, then we have the following stronger result.
Corollary 2. Let R be a reduced ring. Suppose that for every nonzero subring S of R, there exists a nonzero
![]() $x\in S$
and distinct positive integers m(x) and n(x) such that
$x\in S$
and distinct positive integers m(x) and n(x) such that
![]() $x^{m(x)}=x^{n(x)}$
. Then, R is commutative.
$x^{m(x)}=x^{n(x)}$
. Then, R is commutative.
Proof. Suppose that R is reduced with the above property. It suffices to prove that every nonzero subring of R contains a nonzero idempotent. Thus, let S be a nonzero subring and let
![]() $x\in S$
be nonzero and such that
$x\in S$
be nonzero and such that
![]() $x^m=x^n$
for some distinct positive integers m and n. Without loss of generality, we may assume that
$x^m=x^n$
for some distinct positive integers m and n. Without loss of generality, we may assume that
![]() $m>n$
. Let
$m>n$
. Let
![]() $l\;:\!=\;m-n$
. Then, it follows easily by induction that for every positive integer r, we have
$l\;:\!=\;m-n$
. Then, it follows easily by induction that for every positive integer r, we have
![]() $x^{m+rl}=x^n$
. Thus, we may assume without loss of generality that
$x^{m+rl}=x^n$
. Thus, we may assume without loss of generality that
![]() $m>2n$
. Now set
$m>2n$
. Now set
![]() $k\;:\!=\;m-2n$
. Then, observe that
$k\;:\!=\;m-2n$
. Then, observe that
![]() $(x^{n+k})^2=x^{2(n+k)}=x^{m+k}=x^{n+k}$
. As R is reduced,
$(x^{n+k})^2=x^{2(n+k)}=x^{m+k}=x^{n+k}$
. As R is reduced,
![]() $x^{n+k}$
is a nonzero idempotent of S, and the conclusion follows.
$x^{n+k}$
is a nonzero idempotent of S, and the conclusion follows.![]()
Conflicts of interest
The author declares none.