Tropical moments of tropical Jacobians

Abstract

Each metric graph has canonically associated to it a polarized real torus called its tropical Jacobian. A fundamental real-valued invariant associated to each polarized real torus is its tropical moment. We give an explicit and efficiently computable formula for the tropical moment of a tropical Jacobian in terms of potential theory on the underlying metric graph. We show that there exists a universal linear relation between the tropical moment, a certain capacity called the tau invariant, and the total length of a metric graph. To put our formula in a broader context, we relate our work to the computation of heights attached to principally polarized abelian varieties.

1 Introduction

1.1 Background and aim

A lattice is the datum of a finitely generated free abelian group H together with a positive definite bilinear form $[\cdot ,\cdot ]$ on the real vector space $H_{\mathbb R} = H \otimes _{\mathbb Z} {\mathbb R}$ . An alternative way of packaging the data $(H,[\cdot ,\cdot ])$ is to consider a real torus ${\mathbb T} = H_{\mathbb R} / H$ equipped with a polarization, that is, a positive definite bilinear form on its tangent space. A lattice $(H,[\cdot ,\cdot ])$ (or equivalently, a polarized real torus) canonically determines a compact convex region in $H_{\mathbb R}$ given by

$$\begin{align*}\operatorname{Vor}(0) =\left\{ z \in H_{\mathbb R} \, \colon \, \textrm{for all} \,\, \lambda \in H \, \colon \, [ z , z ] \leq [ z-\lambda,z-\lambda ] \right\}\kern-1.5pt,\end{align*}$$

known as the Voronoi polytope of $(H,[\cdot ,\cdot ])$ centered at the origin. Let $\mu _L$ denote a Lebesgue measure on $H_{\mathbb R}$ . In this work, we are interested in the second moment of $(H,[\cdot ,\cdot ])$ , defined as the value in ${\mathbb R}$ of the integral

(1.1) $$ \begin{align} \int_{\operatorname{Vor}(0)} [ z,z ] \, \mathrm{d} \mu_L(z), \end{align} $$

or rather its normalized version, which we call the tropical moment:

(1.2) $$ \begin{align} I(H,[\cdot,\cdot]) = I({\mathbb T})= \frac{ \int_{\operatorname{Vor}(0)} [ z,z ] \, \mathrm{d} \mu_L(z)}{\int_{\operatorname{Vor}(0)} \mathrm{d} \mu_L(z)}. \end{align} $$

The tropical moment is closely related to other lattice invariants such as the covering radius and the packing radius. The celebrated book [13] by Conway and Sloane contains an entire chapter (Chapter 21) devoted to the tropical moment, full of examples and of ways of computing it. In information theory, the tropical moment determines the quality of a lattice as a vector quantizer.

In this paper, we will study lattices canonically associated to metric graphs. Our purpose is to show that the tropical moment of these lattices allows an explicit expression in terms of the capacity attached to the effective resistance function. All ingredients of this expression are moreover efficiently computable. Up to dimension 3, every lattice arises from a metric graph, so that, in particular, one can recover the moment computations in [9, 13] from our expression. We mention that explicit formulas for the tropical moments of lattices in dimension $4$ were obtained by Zimmermann in [32].

A metric graph is a compact, connected length metric space $\Gamma $ homeomorphic to a topological graph. The lattice that we associate to a metric graph $\Gamma $ has as underlying abelian group H its first homology group $H=H_1(\Gamma ,{\mathbb Z})$ . The real vector space $H_{\mathbb R}=H_1(\Gamma ,{\mathbb R})$ is equipped with a standard inner product, determined by the lengths of the edges in a model of $\Gamma $ . See Section 3.3. The resulting “homology lattice” is independent of the choice of a model. The polarized real torus $H_{\mathbb R}/H$ associated to $\Gamma $ is commonly known as the tropical Jacobian of $\Gamma $ , and denoted by $\operatorname {Jac}(\Gamma )$ .

1.2 Main result

It is well known that one can think of a metric graph $\Gamma $ as an electrical network. For $x,y,z \in \Gamma $ , we define $j_z(x,y)$ to be the electric potential at x if one unit of current enters the network at y and exits at z, with z “grounded” (i.e., has zero potential). The j-function provides a fundamental solution of the Laplacian operator on $\Gamma $ , so naturally it is an important function in studying harmonic analysis on $\Gamma $ . The effective resistance between x and y is defined as $r(x,y) = j_y(x,x)$ , which has the expected physical meaning in terms of electrical networks. See Section 4.2.

It is convenient to fix a vertex set (which is a finite nonempty set containing all the branch points of $\Gamma $ ) and to think of the metric graph $\Gamma $ as being obtained from a finite (combinatorial) graph G. The metric data will be encoded by positive real numbers $\ell (e)$ for each edge e of G. We call the finite weighted graph arising in this way a model of $\Gamma $ . If e is an edge of G, the Foster coefficient of e is defined by $\mathsf F(e) = 1-{r(u, v)}/{\ell (e)}$ , where u and v are the two endpoints of the edge $e = \{u,v\}$ (see Definition 4.4).

Our main result is the following formula for the tropical moment of the homology lattice of $\Gamma $ .

Theorem A (=Theorem 8.1)

Let $\Gamma $ be a metric graph. Fix a model G of $\Gamma $ , and fix a vertex q of G. Then, for the tropical moment $I(\operatorname {Jac}(\Gamma ))$ of the tropical Jacobian of $\Gamma $ , one has

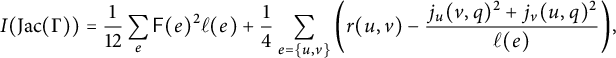$$\begin{align*}I(\operatorname{Jac}(\Gamma)) = \frac{1}{12}\sum_{e} {\mathsf F(e)^2 \ell(e) + \frac{1}{4}\sum_{e = \{u,v\}} \left(r(u,v) - \frac{j_{u}( v, q)^2 + j_{v}( u, q)^2}{\ell(e)}\right)}, \end{align*}$$

where the sums are over all edges $e \in E(G)$ .

As we explain in Remark 8.2(ii), the summands in this formula can all be computed in matrix multiplication time $O(n^\omega )$ , where n is the number of vertices in the given model G of $\Gamma $ , and $\omega $ is the exponent for matrix multiplication (currently $\omega < 2.38$ ). It is generally believed that to compute the second moment of a lattice is a hard problem. For example, if one wants to compute the tropical moment via the general “simplex method” (see, e.g., [13, Chapter 21, Section 2]), then one needs to know the set of vertices of $\operatorname {Vor}(0)$ . However, as is shown in [17], even computing the number of vertices of $\operatorname {Vor}(0)$ is already $\#$ P-hard. Interestingly, the example that is used to show this is given by the homology lattice of a graph.

1.3 Sketch of the proof of the main result

The proof of Theorem A is very subtle. Our strategy is as follows. To handle the integral in (1.2), we provide an explicit polytopal decomposition of $\operatorname {Vor}(0)$ . Given a base point $q\in V(G)$ , there is a full-dimensional polytope $\sigma _T + {\mathcal C}_T$ in our decomposition attached to each spanning tree T of G. Here, ${\mathcal C}_T$ is a centrally symmetric polytope, which makes $\sigma _T$ into the center of $\sigma _T + {\mathcal C}_T$ (see Theorem 7.5). The desired integral over $\operatorname {Vor}(0)$ is then a sum of integrals over each $\sigma _T + {\mathcal C}_T$ .

The contribution from the centrally symmetric polytopes ${\mathcal C}_T$ is rather easy to handle. The real difficulty comes in handling the contributions from the centers $\sigma _T$ . We introduce the notion of energy level of rooted spanning trees (see Definition 6.1). A crucial ingredient is the notion of cross ratio introduced in [16] for electrical networks. We prove that the weighted average of energy levels over all spanning trees has a remarkably simple expression in terms of values of the j-function (see Theorem 6.3). Proving this, in turn, uses some subtle computations related to functions arising from random spanning trees (see Section 5). We also repeatedly use our generalized (and quantitative) version of Rayleigh’s law in electrical networks, as developed in the companion paper [16].

Recall that the homology group of a graph naturally gives rise to a regular matroid. In principle, most of our approach leading to the computation of tropical moments should generalize to the setting of regular matroids. One can replace the subdivision in Theorem 7.5 with an arbitrary tight coherent subdivision in the sense of [10, Section 4]. We do not expect a clean expression as in Theorem 6.3 for general regular matroids. However, we note that already Lemma 6.5 yields an efficient algorithm for the weighted average of energy levels of bases of regular matroids.

1.4 Applications and context for our formula

Theorem A can be used to give a simple connection between $I(\operatorname {Jac}(\Gamma ))$ and a well-known potential theoretic capacity associated to $\Gamma $ called the tau invariant, denoted by $\tau (\Gamma )$ (see Section 11 for its definition). The invariant $\tau (\Gamma )$ can be traced back to the fundamental work of Chinburg and Rumely [11] in their study of the Arakelov geometry of arithmetic surfaces at non-archimedean places. We have the following result.

Theorem B (=Theorem 11.4)

Let $\Gamma $ be a metric graph. Let $\tau (\Gamma )$ denote the tau invariant of $\Gamma $ , and let $\ell (\Gamma )$ denote its total length. Then the identity

$$\begin{align*}\frac{1}{2}\tau(\Gamma)+I(\operatorname{Jac}(\Gamma)) = \frac{1}{8} \ell(\Gamma) \end{align*}$$

holds in ${\mathbb R}$ .

Next, we will explain in Section 9 how our work can be used for the computation of the stable Faltings height of principally polarized abelian varieties defined over number fields. For a discussion of an explicit example in this context, we refer to Section 10. As we will see there, our work gives a complete conceptual explanation of all entries in a table, found by Autissier [3], related to the calculation of local non-archimedean terms in a formula for the stable Faltings height of curves of genus 2.

Finally, we note that Theorem B may be thought of as an analogue, in the non-archimedean setting, of a remarkable identity established by Wilms [28, Theorem 1.1] between analytic invariants of Riemann surfaces. In fact, in [15, 29], Theorem B is used together with [28, Theorem 1.1] to derive a formula for the asymptotic behavior of the so-called Zhang–Kawazumi invariant [20, 21, 31] in arbitrary one-parameter semistable degenerations of Riemann surfaces.

1.5 Structure of the paper

In Section 2, we review the notion of polarized real tori and define the notion of tropical moments. In Section 3, we review the notions of weighted graphs and of metric graphs and their models. Moreover, we introduce the tropical Jacobian of a metric graph. In Section 4, we review potential theory and harmonic analysis on metric graphs, mainly from the perspective of our companion paper [16]. In Section 5, we study two functions that arise from the theory of random spanning trees. In Section 6, we introduce the notion of energy levels of rooted spanning trees, and prove that the average of energy levels has a simple expression in terms of the j-function. In Section 7, we study the combinatorics of the Voronoi polytopes arising from graphs, and present our suitable polytopal decomposition. In Section 8, we prove Theorem A. In Section 9 we discuss our application to the computation of stable Faltings heights. In Section 10, we elaborate upon an example related to Jacobian varieties in dimension  $2$ . In Section 11, we introduce the tau invariant and prove Theorem B.

2 Polarized real tori and tropical moments

The purpose of this section is to set notations and terminology related to polarized real tori and their tropical moments.

2.1 Polarized real tori

A (Euclidean) lattice is a pair $(H, [ \cdot ,\cdot ])$ consisting of a finitely generated free ${\mathbb Z}$ -module H and a positive definite symmetric bilinear form $[ \cdot ,\cdot ] $ on the real vector space $H_{\mathbb R}=H \otimes _{\mathbb Z} {\mathbb R}$ . Attached to each lattice $(H,[\cdot ,\cdot ])$ , one has a real torus ${\mathbb T}=H_{\mathbb R}/H$ , equipped with a natural structure of compact Riemannian manifold. We refer to the Riemannian manifold ${\mathbb T}$ as a polarized real torus. The tropical Jacobian of a metric graph (see Section 3.3) is an example of a polarized real torus. Clearly, “lattice” and “polarized real torus” are equivalent notions. We will mainly prefer the terminology of polarized real tori.

2.2 Voronoi decompositions and tropical moment

Let ${\mathbb T}$ be a polarized real torus coming from a lattice $(H,[\cdot ,\cdot ])$ as above. For each $\lambda \in H$ , we denote by $\operatorname {Vor}( \lambda )$ the Voronoi polytope of the lattice $(H,[ \cdot ,\cdot ])$ around $\lambda $ :

$$\begin{align*}\operatorname{Vor}(\lambda) := \{ z \in H_{{\mathbb R}} \, \colon \, \textrm{for all} \, \lambda' \in H \, \colon \, [ z - \lambda , z -\lambda ] \leq [ z-\lambda',z-\lambda' ] \}. \end{align*}$$

Note that, for each $\lambda \in H$ , we have $\operatorname {Vor}(\lambda ) = \operatorname {Vor}(0) + \lambda $ . Moreover, $\operatorname {Vor}(0)$ , up to some identifications on its boundary, is a fundamental domain for the translation action of H on $H_{{\mathbb R}}$ .

Definition 2.1 (cf. [13, Chapter 21])

The tropical moment of the polarized real torus ${\mathbb T}$ is set to be the value of the integral

(2.1) $$ \begin{align} I({\mathbb T}) := \, \int_{\operatorname{Vor}(0)} [ z,z ] \, \mathrm{d} \mu_L(z). \end{align} $$

Here, $\mu _L$ is the Lebesgue measure on $H_{{\mathbb R}}$ , normalized to have $\mu _L(\operatorname {Vor}(0)) = 1$ .

3 Metric graphs, models, and tropical Jacobians

The purpose of this section is to set notations and terminology related to weighted graphs, metric graphs, and their models. We also define the tropical Jacobian of a metric graph (see Section 3.3). Most of the material in this section is straightforward, and we leave details to the interested reader.

3.1 Weighted graphs

By a weighted graph, we mean a finite weighted connected multigraph G with no loop edges. The set of vertices of G is denoted by $V(G)$ , and the set of edges of G is denoted by $E(G)$ . We let $n = |V (G)|$ and $m = |E(G)|$ . An edge e is called a bridge if $G\backslash e$ is disconnected. The weights of edges are determined by a length function $ \ell \colon E(G) \to {\mathbb R}_{>0}$ . We let $\mathbb {E}(G) = \{e, \bar {e} \colon e \in E(G)\}$ denote the set of oriented edges. We have $\bar {\bar {e}} = e$ . For each subset ${\mathcal A} \subseteq {\mathbb E}(G)$ , we define $\overline {{\mathcal A}} = \{\bar {e} \colon e \in {\mathcal A}\} $ . An orientation ${\mathcal O}$ on G is a partition $\mathbb {E}(G) = {\mathcal O} \cup \overline {{\mathcal O}}$ . We have an obvious extension of the length function $\ell \colon \mathbb {E}(G) \rightarrow {\mathbb R}_{>0}$ by requiring $\ell (e) = \ell (\bar {e})$ . There is a natural map $\mathbb {E}(G) \rightarrow V(G) \times V(G)$ sending an oriented edge e to $(e^+, e^-)$ , where $e^- $ is the start point of e and $e^+$ is the end point of e.

Notation

For $e \in E(G)$ , we sometimes refer to its endpoints by $e^+,e^-$ even when an orientation is not fixed, so $e = \{e^+, e^-\}$ . We only allow ourselves to do this if the underlying expression is symmetric with respect to $e^+$ and $e^-$ , so there is no danger of confusion. The reader is welcome to fix an orientation ${\mathcal O}$ and think of $e^+$ and $e^-$ in the sense explained above.

A spanning tree T of G is a maximal subset of $E(G)$ that contains no circuit (closed simple path). Equivalently, T is a minimal subset of $E(G)$ that connects all vertices of G.

For a fixed $q \in V(G)$ and spanning tree T of G, we will refer to the pair $(T, q)$ as a spanning tree with a root at q (or just a rooted spanning tree). The choice of q imposes a preferred orientation on all edges of T. Namely, one can require that all edges are oriented away from q on the spanning tree T (see Figure 1c). We denote this orientation on T by ${\mathcal T}_q \subseteq \mathbb {E}(G)$ .

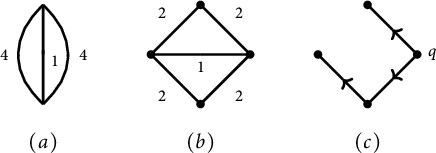
Figure 1: (a) A metric graph $\Gamma $ .(b) A weighted graph model G of $\Gamma $ .(c) A rooted spanning tree $(T, q)$ of G and the orientation ${\mathcal T}_q$ .

Given a commutative ring R, it is convenient to define the $1$ -chains with coefficients in R as the free module

$$\begin{align*}C_1(G,R) := \frac{\bigoplus_{e \in \mathbb{E}(G)} R e }{ \langle e+\bar{e} \colon e \in {\mathcal O} \rangle}. \end{align*}$$

Note that $\bar {e} = -e$ in $C_1(G,R)$ . For each orientation ${\mathcal O}$ on G, we have an isomorphism $ C_1(G,R) \simeq \bigoplus _{e \in {\mathcal O}} R e$ . For each subset ${\mathcal A} \subseteq {\mathbb E}(G)$ , we define its associated $1$ -chain as $\boldsymbol {\gamma }_{\mathcal A} = \sum _{e \in {\mathcal A}} e$ .

3.2 Metric graphs and models

A metric graph (or metrized graph) is a pair $(\Gamma ,d)$ consisting of a compact connected topological graph $\Gamma $ , together with an inner metric d. Equivalently, if $\Gamma $ is not a one-point space, then a metric graph is a compact connected metric space $\Gamma $ which has the property that every point has an open neighborhood isometric to a star-shaped set, endowed with the path metric.

The points of $\Gamma $ that have valency different from $2$ are called branch points of $\Gamma $ . A vertex set for $\Gamma $ is a finite set V of points of $\Gamma $ containing all the branch points of $\Gamma $ with the property that for each connected component c of $\Gamma \setminus V$ , the closure of c in $\Gamma $ is isometric with a closed interval.

A vertex set V for $\Gamma $ naturally determines a weighted graph G by setting $V(G)=V$ , and by setting $E(G)$ to be the set of connected components of $\Gamma \setminus V$ . We call G a model of $\Gamma $ . An edge segment (based on the choice of a vertex set V) is the closure in $\Gamma $ of a connected component of $\Gamma \setminus V$ . Note that there is a natural bijective correspondence between $E(G)$ and the edge segments of $\Gamma $ determined by V. By a small abuse of terminology, we will refer to the elements of $E(G)$ also as edge segments of $\Gamma $ . Given an edge segment $e\subset \Gamma $ (based on the choice of a vertex set V), we denote its boundary $\partial e \subset V$ by $\partial e =\{e^-,e^+\}$ . In particular, we will also use the notation $\{e^-,e^+\}$ for the boundary set of an edge segment e if there is no (preferred) orientation present. We hope that this does not lead to confusion.

Conversely, every weighted graph G naturally determines a metric graph $\Gamma _G$ containing $V(G)$ by gluing closed intervals $[0,\ell (e)]$ for $e \in E(G)$ according to the incidence relations. Note that $V(G)$ is naturally a vertex set of $\Gamma _G$ , and the associated model is precisely G. See Figure 1a,b.

3.3 Tropical Jacobians

Let $\Gamma $ be a metric graph. Fix a model G of $\Gamma $ . Let ${\mathcal O}=\{e_1,\ldots ,e_m\}$ be a labeling of an orientation ${\mathcal O}$ on G. The real vector space $ C_1(G,{\mathbb R}) \simeq \bigoplus _{i=1}^m {\mathbb R} e_i$ has a canonical inner product defined by $[ e_i,e_j ]=\delta _i(j)\ell (e_i)$ . Here, $\delta _i$ denotes the delta (Dirac) measure on $\{ 1, 2, \ldots , m\}$ centered at i. The resulting inner product space $\left ( C_1(G,{\mathbb R}), [\cdot , \cdot ] \right )$ is independent of the choice of ${\mathcal O}$ and its labeling.

The inner product $[ \cdot ,\cdot ]$ restricts to an inner product, also denoted by $[ \cdot ,\cdot ]$ , on the homology lattice $H =H_1(G,{\mathbb Z}) \subset C_1(G,{\mathbb Z})$ . The pair $(H,[ \cdot ,\cdot ])$ is a canonical lattice associated to $\Gamma $ (independent of the choice of the model G), and we have a canonical identification $H \simeq H_1(\Gamma ,{\mathbb Z})$ . Note that $H_{{\mathbb R}} \simeq H_1(\Gamma ,{\mathbb R})$ . The associated polarized real torus $H_1(\Gamma ,{\mathbb R})/H_1(\Gamma ,{\mathbb Z})$ is called the tropical Jacobian of $\Gamma $ [23, 25], and denoted by $\operatorname {Jac}(\Gamma )$ .

4 Potential theory on metric graphs

In this section, we closely follow [16] and review those results that are needed in this paper.

4.1 Graphs as electrical networks

Let $\Gamma $ be a metric graph, and let G be a model of $\Gamma $ . We may think of $\Gamma $ (or G) as an electrical network in which each edge $e \in E(G)$ is a resistor having resistance $\ell (e)$ . See Figure 2.

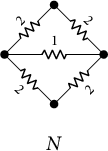
Figure 2: The electrical network N corresponding to the graphs in Figure 1a,b.

When studying the “potential theory” on a metric graph $\Gamma $ , it is convenient to always fix an (arbitrary) model G, and think of it as an electrical network.

4.2 Laplacians and j-functions

Let $\Gamma $ be a metric graph, and let G be a model of $\Gamma $ . We have the distributional Laplacian operator (see [16, Section 3.1])

$$\begin{align*}\Delta \colon \operatorname{PL}(\Gamma) \rightarrow \operatorname{DMeas}_{0}(\Gamma),\end{align*}$$

where $\operatorname {PL}(\Gamma )$ is the real vector space consisting of all continuous piecewise affine real valued functions on $\Gamma $ that can change slope finitely many times on each closed edge segment, and $\operatorname {DMeas}_{0}(\Gamma )$ is the real vector space of discrete measures $\nu $ on $\Gamma $ with $\nu (\Gamma ) = 0$ . We also have the combinatorial Laplacian operator (see [16, Section 3.2])

$$\begin{align*}\Delta \colon {\mathcal M}(G) \rightarrow \operatorname{DMeas}_{0}(G),\end{align*}$$

where ${\mathcal M}(G)$ is the real vector space of real-valued functions on $V(G)$ , and $\operatorname {DMeas}_{0}(G)$ is the real vector space of discrete measures $\nu $ on $V(G)$ with ${\nu (V(G)) = 0}$ . The distributional Laplacian $\Delta $ and the combinatorial Laplacian $\Delta $ are compatible in the sense described in [16, Section 3.3]. Moreover, the combinatorial Laplacian on G can be conveniently presented by its Laplacian matrix; let $\{v_1, \ldots , v_n\}$ be a labeling of $V(G)$ . The Laplacian matrix ${\mathbf Q}$ associated to G is the $n \times n$ matrix ${\mathbf Q} = (q_{ij})$ where, for $i \ne j$ , we have $ q_{ij} = - \sum _{e =\{v_i , v_j\} \in E(G)}{{1}/{\ell (e)}} $ . The diagonal entries are determined by forcing the matrix to have zero-sum rows.

The Laplacian matrix of G can also be expressed in terms of the incidence matrix of G. Let $\{v_1, \ldots , v_n\}$ be a labeling of $V(G)$ as before. Fix an orientation ${\mathcal O} = \{e_1, \ldots , e_m\}$ on G. The incidence matrix ${\mathbf B}$ associated to G is the $n \times m$ matrix ${\mathbf B}=(b_{ij})$ , where $b_{ij} = +1$ if $e_j^{+} = v_i$ and $b_{ij} = -1$ if $e_j^{-} = v_i$ and $b_{ij} = 0$ otherwise. Let ${\mathbf D}$ denote the $m \times m$ diagonal matrix with diagonal entries $\ell (e_i)$ for $e_i \in {\mathcal O}$ . We have ${\mathbf Q} = {\mathbf B} {\mathbf D}^{-1}{\mathbf B}^{\operatorname {T}}$ , where $(\cdot )^{\operatorname {T}}$ denotes the matrix transpose operation.

A fundamental solution of the Laplacian is given by j-functions. We follow the notation of [11]. See [16, Section 4] and the references therein for more details. Let $\Gamma $ be a metric graph and fix two points $y,z \in \Gamma $ . We denote by $j_z(\cdot \, , y; \Gamma )$ the unique function in $\operatorname {PL}(\Gamma )$ satisfying: (i) $\Delta \left (j_z(\cdot \, , y; \Gamma )\right )= \delta _y - \delta _z$ , and (ii) $j_z(z,y; \Gamma ) = 0$ . If the metric graph $\Gamma $ is clear from the context, we write $j_z(x,y)$ instead of $j_z(x,y; \Gamma )$ . The j-function exists and is unique, and satisfies the following basic properties:

• ◇ $j_z(x,y)$ is jointly continuous in all three variables $x,y,z \in \Gamma $ .

• ◇ $j_z(x,y) = j_z(y,x)$ .

• ◇ $0 \leq j_z(x,y) \leq j_z(x,x)$ .

• ◇ $j_z(x,x) = j_x(z,z)$ .

The effective resistance between two points $x, y \in \Gamma $ is $r(x,y) := j_y(x,x)$ . If we want to clarify the underlying metric graph $\Gamma $ , we use the notation $r(x,y; \Gamma )$ .

Let G be an arbitrary model of $\Gamma $ . One can explicitly compute the quantities $j_q(p,v) \in {\mathbb R}$ for $q,p,v \in V(G)$ using linear algebra (see [8, Section 3]) as follows. Fix a labeling of $V(G)$ as before, and let ${\mathbf Q}$ be the corresponding Laplacian matrix. Let ${\mathbf Q}_q$ be the $(n-1)\times (n-1)$ matrix obtained from ${\mathbf Q}$ by deleting the row and column corresponding to $q \in V(G)$ from ${\mathbf Q}$ . It is well known that ${\mathbf Q}_q$ is invertible. Let ${\mathbf L}_q$ be the $n \times n$ matrix obtained from ${\mathbf Q}_q^{-1}$ by inserting zeros in the row and column corresponding to q. One can easily check that $ {\mathbf Q}{\mathbf L}_q = {\mathbf I} + {\mathbf R}_q$ , where ${\mathbf I}$ is the $n \times n$ identity matrix and ${\mathbf R}_q$ has all $-1$ entries in the row corresponding to q and has zeros elsewhere. It follows from the compatibility of the two Laplacians that ${\mathbf L}_q = (j_q(p,v))_{p,v \in V(G)}$ . The matrix ${\mathbf L}_q$ is a generalized inverse of ${\mathbf Q}$ , in the sense that ${\mathbf Q}{\mathbf L}_q{\mathbf Q} = {\mathbf Q}$ .

Remark 4.1 Computing ${\mathbf L}_q$ takes time at most $O(n^\omega )$ , where $\omega $ is the exponent for matrix multiplication (currently $\omega < 2.38$ ).

4.3 Cross ratios

Let $\Gamma $ be a metric graph and fix $q \in \Gamma $ . As in [16], we define the cross ratio function (with respect to the base point q) $\xi _q \colon \Gamma ^4 \rightarrow {\mathbb R}$ by

$$\begin{align*}\xi_q(x,y , z,w) := j_q(x,z) +j_q(y,w) - j_q(x,w) - j_q(y,z). \end{align*}$$

If we want to clarify the graph $\Gamma $ , we use the notation $\xi _q(x,y , z,w; \Gamma )$ instead. As is observed in [16, Remark 6.1(i)], we have the identity

$$\begin{align*}-2\xi_q(x,y , z,w) = r(x, z) + r(y, w) - r(x, w) - r(y, z). \end{align*}$$

Remark 4.2 We borrowed the cross ratio terminology in [16] from the book of Baker and Rumely [7, Appendix B]. These cross ratios on the Berkovich hyperbolic space and on its natural extension to the Berkovich projective line also play an important role in the work of Favre and Rivera-Letelier [18, Section 6.3]. The terminology is also justified in the context of Gromov hyperbolic spaces, where this is sometimes called “cross difference” (see, for example, [27, Section 4.5]).

Cross ratios satisfy the following basic properties:

• ◇ $\xi (x,y , z,w) := \xi _q(x,y , z,w)$ is independent of the choice of q.

• ◇ $\xi (x,y , z,w) = \xi ( z,w,x,y)$ .

• ◇ $\xi (y,x , z,w) = - \xi ( x, y, z,w)$ .

• ◇ $\xi (x,y , z,w) = \langle \delta _x-\delta _y, \delta _z-\delta _w \rangle _{\operatorname {en}}$ , where $\langle \cdot , \cdot \rangle _{\operatorname {en}}$ denotes the energy pairing on $\operatorname {DMeas}_{0}(\Gamma )$ defined by

  (4.1) $$ \begin{align} \langle \nu_1 , \nu_2 \rangle_{\operatorname{en}} := \int_{\Gamma \times \Gamma} j_q (x,y) \mathrm{d} \nu_1(x) \mathrm{d} \nu_2(y). \end{align} $$

Example 4.3 The following identities will be useful for our computations.

It follows from $\xi _x(q,x,q,y) = \xi _y(q,x,q,y)$ that

(4.2) $$ \begin{align} r(x, q) - r(y, q) = j_{x}(y , q) - j_{y}(x , q). \end{align} $$

It follows from $\xi _x(x,y,x,q) = \xi _q(x,y,x,q)$ that

(4.3) $$ \begin{align} j_x(y,q) = j_q(x,x) - j_q(x,y). \end{align} $$

It follows from $\xi _x(x,y,x,q) = \xi _y(x,y,x,q)$ that

(4.4) $$ \begin{align} r(x,y) = j_{x}(y , q)+ j_y(x,q). \end{align} $$

It follows from $\xi _x(x,y,x,y) = \xi _q(x,y,x,y)$ that

(4.5) $$ \begin{align} r(x,y) = j_{q}(x , x)+ j_q(y,y) - 2j_q(x,y). \end{align} $$

4.4 Projections

Let G be a weighted graph. Fix an orientation ${\mathcal O}$ . Let T be a spanning tree of G. The weight of T is the product $ w(T) := \prod _{e \not \in T}{\ell (e)}$ . The coweight of T is the product $ w'(T) := \prod _{e \in T}{\ell ^{-1}(e)}$ . The weight and coweight of G are $w(G) := \sum _{T}{w(T)}$ and $w'(G) := \sum _{T}{w'(T)}$ , where the sums are over all spanning trees of G. The quantity $w(G)$ depends only on the underlying metric graph $\Gamma $ .

Let ${\mathbf M}_T$ be the $m \times m$ matrix whose columns are obtained from $1$ -chains $\operatorname {circ}(T,e)$ associated to fundamental circuits of T, and let ${\mathbf N}_T$ be the $m \times m$ matrix whose columns are obtained from $1$ -chains $\operatorname {cocirc}(T,e)$ associated to fundamental cocircuits of T (see [16, Section 7.2]). Consider the following matrix averages:

$$\begin{align*}{\mathbf P} = \sum_{T}{\frac{w(T)}{w(G)} {\mathbf M}_T}, \quad {\mathbf P}' = \sum_{T}{\frac{w'(T)}{w'(G)} {\mathbf N}_T}, \end{align*}$$

the sums being over all spanning trees T of G. It is a classical theorem of Kirchhoff [22] that the matrix of $\pi \colon C_1(G,{\mathbb R}) \twoheadrightarrow H_1(G, {\mathbb R})$ , with respect to ${\mathcal O}$ , is ${\mathbf P}$ . Similarly, the matrix of $\pi ' \colon C_1(G,{\mathbb R}) \twoheadrightarrow H_1(G, {\mathbb R})^{\perp }$ , with respect to ${\mathcal O}$ , is $({\mathbf P}')^{\operatorname {T}}$ .

Let ${\mathbf \Xi }$ be the $m \times m$ matrix of cross ratios:

$$\begin{align*}{\mathbf \Xi} := \left(\xi(e^-, e^+ , f^- , f^+) \right)_{e,f \in {\mathcal O}}. \end{align*}$$

Let ${\mathbf L}$ be any generalized inverse of ${\mathbf Q}$ (i.e., ${\mathbf Q}{\mathbf L}{\mathbf Q} = {\mathbf Q}$ ). Then we have ${\mathbf \Xi } = {\mathbf B}^{\operatorname {T}} {\mathbf L} {\mathbf B}$ . It is shown in [16, Theorem 7.5] that the matrix of $\pi \colon C_1(G,{\mathbb R}) \twoheadrightarrow H_1(G, {\mathbb R})$ , with respect to ${\mathcal O}$ , is ${\mathbf I}- {\mathbf D}^{-1} {\mathbf \Xi }$ , and the matrix of $\pi ' \colon C_1(G,{\mathbb R}) \twoheadrightarrow H_1(G, {\mathbb R})^{\perp }$ , with respect to ${\mathcal O}$ , is ${\mathbf D}^{-1} {\mathbf \Xi }$ . In particular, for each $f \in {\mathcal O}$ , we have

• ◇ $\pi (f) = \sum _{e \in {\mathcal O}} {\mathsf F(e,f) e}$ , where

  (4.6) $$ \begin{align} \mathsf F(e,f) := \begin{cases} 1-{r(e^-, e^+)}/{\ell(e)}, &\text{ if } e=f,\\ -{\xi(e^-, e^+ ,f^-, f^+)}/{\ell(e)}, &\text{ if } e \ne f. \end{cases} \end{align} $$

• ◇ $\pi '(f) = \sum _{e \in {\mathcal O}} {\mathsf F'(e,f) e}$ , where

  $$\begin{align*}\mathsf F'(e,f) = {\xi(e^-, e^+ ,f^-, f^+)}/{\ell(e)}. \end{align*}$$

Moreover, we have equalities:

(4.7) $$ \begin{align} {\mathbf P}= {\mathbf I}- {\mathbf D}^{-1} {\mathbf \Xi}, \quad {\mathbf P}' = {\mathbf \Xi} {\mathbf D}^{-1}. \end{align} $$

Definition 4.4 The Foster coefficient of $e \in \mathbb {E}(G)$ is, by definition,

$$\begin{align*}\mathsf F(e) := \mathsf F(e,e) = 1-\frac{r(e^-, e^+)}{\ell(e)}. \end{align*}$$

Clearly, $\mathsf F(e) = \mathsf F(\bar {e})$ , so $\mathsf F(e)$ is also well defined for $e \in E(G)$ .

Remark 4.5

1. (i) It follows from (4.7) that

   $$\begin{align*}\mathsf F(e) = \sum_{T \not \ni e} \frac{w(T)}{w(G)}, \end{align*}$$
   the sum being over all spanning trees T of G not containing e.

2. (ii) It is a consequence of “Rayleigh’s monotonicity law” that $0 \leq \mathsf F(e) < 1$ , and the equality $\mathsf F(e)=0$ holds if and only if e is a bridge. (See [16] and the references therein for more details.)

Fix an arbitrary path $\gamma $ from y to x. Let $\boldsymbol {\gamma }_{yx}$ denote the associated $1$ -chain. Then, by [16, Corollary 7.10], we have

(4.8) $$ \begin{align} r(x,y) = [\boldsymbol{\gamma}_{yx}, \pi'(\boldsymbol{\gamma}_{yx})]. \end{align} $$

Example 4.6 The following observation will be useful for computations. Let $e = \{u,v\}$ denote an edge segment in a metric graph $\Gamma $ , and let $p \in e$ be a point with distance x from u and distance $\ell (e) - x$ from v. Then, for each point $q \in \Gamma $ , we have

$$\begin{align*}r(p,q) = \frac{\ell(e)-x}{\ell(e)} r(u,q) + \frac{x}{\ell(e)}r(v,q) + \mathsf F(e) \frac{\left(\ell(e)-x\right)x}{\ell(e)}. \end{align*}$$

This follows, for example, by a direct computation using (4.8). We leave the details to the interested reader.

4.5 Generalized Rayleigh’s laws

We will need the following two corollaries of [16, Theorem B]. Let $\Gamma $ be a metric graph. Let e be an edge segment of $\Gamma $ with boundary points $\partial e = \{e^-, e^+\}$ . Let $\Gamma /e$ denote the metric graph obtained by contracting e (equivalently, by setting $\ell (e) = 0$ ). Then

(4.9) $$ \begin{align} j_z(x,y; \Gamma/e) = j_z(x,y; \Gamma) - \frac{\xi(x,z , e^-, e^+; \Gamma) \, \xi(y,z , e^-, e^+; \Gamma)}{r(e^-, e^+; \Gamma)}, \end{align} $$

and

(4.10) $$ \begin{align} r(x,y; \Gamma/e) =r(x,y; \Gamma) - \frac{\xi(x,y , e^-, e^+; \Gamma) ^2}{r(e^-, e^+; \Gamma)}. \end{align} $$

Note that (4.10) is, in fact, a special case of (4.9).

4.6 Contractions and models

Let G be a weighted graph, and let $e \in E(G)$ be an edge of G. We denote by $G/e$ the weighted graph obtained from G by contracting the edge e and removing all loops that might be created in the process. Assume that G is a model of the metric graph  $\Gamma $ . In particular, we may view e as an edge segment of $\Gamma $ . We then observe that, for $x, y, z, w \in V(G)$ , the cross ratio $\xi (x,y,z,w;\Gamma /e)$ measured on $\Gamma /e$ is equal to the cross ratio $\xi (x,y,z,w;G/e)$ measured on (the metric graph canonically associated to) $G/e$ . A similar remark pertains to the j-function $j_z(x,y;\Gamma /e)$ and the effective resistance function $r(x,y;\Gamma /e)$ . We leave the details to the reader.

5 Calculus of random spanning trees

In this section, we study two functions arising from random spanning trees.

Definition 5.1 Let G be a model of a metric graph $\Gamma $ . For edges $e = \{e^-, e^+\}$ and $f = \{f^-, f^+\}$ of G, we define

$$\begin{align*}\mathrm P (e,f) := \begin{cases} {r(e^-, e^+; G)}/{\ell(e)}, &\text{ if}\ e=f,\\ {r(e^-, e^+; G)}/{\ell(e)} \times {r(f^-, f^+; G/e)}/{\ell(f)}, &\text{ if}\ e\ne f. \end{cases} \end{align*}$$

We use the notation $\mathrm P(e):= \mathrm P (e,e)$ . If we want to clarify the underlying model G, we use the notations $\mathrm P(e,f; G)$ and $\mathrm P(e; G)$ .

By Definition 4.4 and Remark 4.5(i), we know

(5.1) $$ \begin{align} \mathrm P(e) = 1-\mathsf F(e) = \sum_{T \ni e} \frac{w(T)}{w(G)}, \end{align} $$

the sum being over all spanning trees T of G containing e. So $\mathrm P(e)$ is the probability of e being present in a random spanning tree, where a spanning tree T is chosen with probability ${w(T)}/{w(G)}$ .

A similar probabilistic interpretation holds for $\mathrm P (e,f)$ when $e\ne f$ . Namely, since $\mathrm P (e,f) = \mathrm P(e; G) \mathrm P(f; G/e)$ , it represents the probability of both e and f being present in a random spanning tree. In other words,

(5.2) $$ \begin{align} \mathrm P(e,f) = \sum_{T \ni e,f} \frac{w(T)}{w(G)}. \end{align} $$

It follows that $\mathrm P(e,f) = \mathrm P(f,e)$ . One can use (4.10) (alternatively, the “transfer–current theorem”—see [24, Section 4.2]) to compute $\mathrm P(e,f)$ directly in terms of invariants of G.

Definition 5.2

1. (i) Let ${\mathfrak s} \colon V(G) \rightarrow {\mathbb R}$ be the function defined by sending $p \in V(G)$ to

   $$\begin{align*}{\mathfrak s}(p) := \sum_{e=\{p , x\}} \mathrm P(e), \end{align*}$$
   the sum being over all edges e incident to p in G (i.e., the star of p).

2. (ii) Let ${\mathfrak t} \colon V(G) \times E(G) \rightarrow {\mathbb R}$ be the function defined by sending $(p , e)$ to

   $$\begin{align*}{\mathfrak t}(p, e) := \sum_{f=\{p , x\}} \mathrm P(e, f), \end{align*}$$
   the sum being over all edges f incident to p in G.

Proposition 5.3 Fix a vertex $q \in V(G)$ . We have

$$\begin{align*}{\mathfrak s}(p) = \sum_{e=\{p , x\}} \frac{r(x,q) - r(p,q)}{\ell(e)} + 2 - 2\, \delta_q(p), \end{align*}$$

the sum being over all edges $e \in E(G)$ incident to p.

Proof By (4.5), we may write $r(p,x) = j_q(x,x) - j_q(p,p) + 2 (j_q(p,p) - j_q(x,p))$ . Therefore,

$$\begin{align*}\begin{aligned} {\mathfrak s}(p) &= \sum_{e=\{p , x\}} \frac{r(p,x)}{\ell(e)} \\[4pt] &= \sum_{e=\{p , x\}} \frac{ j_q(x,x) - j_q(p,p)}{\ell(e)} + 2 \sum_{e=\{p , x\}}\frac{j_q(p,p) - j_q(x,p)}{\ell(e)} \\[4pt] &= \sum_{e=\{p , x\}} \frac{ j_q(x,x) - j_q(p,p)}{\ell(e)} + 2 \Delta \left( j_q(\cdot,p)\right) (p)\\[4pt] &= \sum_{e=\{p , x\}} \frac{ j_q(x,x) - j_q(p,p)}{\ell(e)} + 2 (\delta_p(p) - \delta_q(p)). \end{aligned}\\[-46pt] \end{align*}$$

▪

Recall from Section 4.6 the weighted graph $G/e$ obtained by contracting the edge $e=\{u,v\} \in E(G)$ and removing all loops that might be created in the process. Let $\mathrm {Par}(e) \subseteq E(G)$ denote the set of all edges parallel to e (i.e., connecting u and v). We make the identification $E(G/e) = E(G)\backslash \mathrm {Par}(e)$ , and the two vertices $u, v \in V(G)$ will be identified with a single vertex $v_e \in V(G/e)$ (see Figure 3), and $V(G) \backslash \{u,v\} = V(G/e) \backslash \{v_e\}$ .

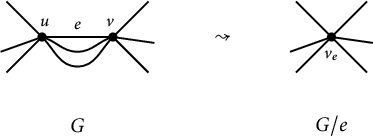
Figure 3: Contracting the edge $e = \{u,v\}$ .

Theorem 5.4 Fix a vertex $q \in V(G)$ . Let $p \in V(G)$ and $e= \{u,v\} \in E(G)$ . Then

$$\begin{align*}\begin{aligned} {\mathfrak t}(p,e) &= \frac{r(u,v; G)}{\ell(e)} \sum_{\substack{f=\{p , x\} \\ f \in E(G)\backslash \mathrm{Par}(e)}} \frac{r(x,q; G/e) - r(p,q; G/e)}{\ell(f)} \\[4pt] &\quad +2 \frac{r(u,v; G)}{\ell(e)} \left(1- \delta_q(p) - \frac{\xi(u,v,u,q; G)}{r(u,v; G)} \delta_u(p)- \frac{\xi(v,u,v,q; G)}{r(u,v; G)}\delta_v(p) \right). \end{aligned} \end{align*}$$

The sum is over all edges $f \in E(G) \backslash \mathrm {Par}(e)$ incident to p in G.

Proof By definition,

$$\begin{align*}\mathrm P (e,f) = \frac{r(u,v; G)}{\ell(e)} \mathrm P(f; G/e).\end{align*}$$

If $p \not \in \{u,v\}$ , the result follows immediately from Proposition 5.3:

$$\begin{align*}{\mathfrak t}(p,e) = \frac{r(u,v; G)}{\ell(e)} \left(\sum_{\substack{f=\{p , x\} \\ f \in E(G)}} \frac{r(x,q; G/e) - r(p,q; G/e)}{\ell(e)} + 2 - 2\, \delta_q(p)\right), \end{align*}$$

the sum being over all edges $f \in E(G)$ incident to p in G (equivalently, all edges $f \in E(G/e)$ incident to p in $G/e$ ).

So, by symmetry, it remains to show the equality for $p= u$ . Recall that we denote the vertex obtained by identifying u and v in $G/e$ by $v_e$ (Figure 3). As in the proof of Proposition 5.3, we first compute

(5.3) $$ \begin{align} \begin{aligned} {\mathfrak t}(u,e) &= \frac{r(u,v; G)}{\ell(e)} \left(\sum_{\substack{f=\{u , x\} \\ f \in E(G)\backslash \mathrm{Par}(e)}} \frac{ j_q(x,x;G/e) - j_q(v_e,v_e;G/e)}{\ell(f)} \right) \\[4pt] &\quad + 2 \frac{r(u,v; G)}{\ell(e)}\left(\sum_{\substack{f=\{u , x\} \\ f \in E(G)\backslash \mathrm{Par}(e)}}\frac{j_q(v_e,v_e;G/e) - j_q(x,v_e;G/e)}{\ell(f)} \right), \end{aligned} \end{align} $$

where the sums are over all edges $f \in E(G) \backslash \mathrm {Par}(e)$ incident to u in G. Unlike in the proof of Proposition 5.3, we cannot interpret the second sum as the Laplacian of the j-function on $G/e$ because the summation is not over all edges incident to $v_e$ in $G/e$ (e.g., in Figure 3, only edges on the left of $v_e$ appear in the summation). We proceed by “lifting” the problem to G using generalized Rayleigh’s laws (4.9) and (4.10). We find

$$\begin{align*}\begin{aligned} &\frac{j_q(v_e,v_e;G/e) - j_q(x,v_e;G/e)}{\ell(f)} = \frac{j_q(u,u;G) - j_q(x,u;G)}{\ell(f)}\\[4pt] &\quad + \frac{\xi(u,v,u,q;G)}{r(u,v;G)}\left( \frac{\xi(u,v,x,q;G) - \xi(u,v,u,q;G)}{\ell(f)}\right). \end{aligned} \end{align*}$$

It is easily checked that the right-hand side is zero for $x=v$ . Moreover, by the definition of cross ratios, we compute

$$\begin{align*}\xi(u,v,x,q;G) - \xi(u,v,u,q;G) = \xi(u,v,x,u;G).\end{align*}$$

So we have

(5.4) $$ \begin{align} \begin{aligned} &\sum_{\substack{f=\{u , x\} \\ f \in E(G)\backslash \mathrm{Par}(e)}}\frac{j_q(v_e,v_e;G/e) - j_q(x,v_e;G/e)}{\ell(f)} = \sum_{\substack{f=\{u , x\} \\ f \in E(G)}} \frac{j_q(u,u;G) - j_q(x,u;G)}{\ell(f)}\\[4pt] &\quad + \frac{\xi(u,v,u,q;G)}{r(u,v;G)} \sum_{\substack{f=\{u , x\} \\ f \in E(G)}} \frac{\xi(u,v,x,u;G)}{\ell(f)}. \end{aligned} \end{align} $$

As in the proof of Proposition 5.3, we have

(5.5) $$ \begin{align} \begin{aligned} \sum_{\substack{f=\{u , x\} \\ f \in E(G)}} \frac{j_q(u,u;G) - j_q(x,u;G)}{\ell(f)} &= \Delta\left(j_q (\cdot , u)\right)(u)\\ &= \delta_u(u)-\delta_q(u) = 1- \delta_q(u). \end{aligned} \end{align} $$

By expanding with respect to the base point q, we also compute

(5.6) $$ \begin{align} \begin{aligned} \sum_{\substack{f=\{u , x\} \\ f \in E(G)}} \frac{\xi(u,v,x,u;G)}{\ell(f)} &= \sum_{\substack{f=\{u , x\} \\ f \in E(G)}} \frac{j_q(v,u;G) - j_q(v,x;G)}{\ell(f)} \\[4pt] &\quad - \sum_{\substack{f=\{u , x\} \\ f \in E(G)}} \frac{j_q(u,u;G) - j_q(u,x;G)}{\ell(f)} \\[4pt] &= \Delta\left(j_q (v , \cdot)\right)(u) - \Delta\left(j_q (u , \cdot)\right)(u) \\[4pt] &= \left(\delta_v(u) - \delta_q(u) \right) - \left(\delta_u(u) - \delta_q(u) \right) \\[4pt] &= -1. \end{aligned} \end{align} $$

The result for $p=u$ follows by putting together (5.3)–(5.6).▪

6 Energy levels of rooted spanning trees

In this section, we prove a very subtle identity for cross ratios (Theorem 6.3).

6.1 Energy levels

Recall that a rooted spanning tree $(T, q)$ of G comes with a preferred orientation ${\mathcal T}_q \subseteq \mathbb {E}(G)$ , where all edges are oriented away from q on the spanning tree T (see Section 3.1).

Definition 6.1 We define the energy level of a rooted spanning tree $(T, q)$ to be

$$\begin{align*}\boldsymbol{\varrho}(T, q) := \sum_{e,f \in {\mathcal T}_q} \xi(e^-, e^+, f^-, f^+). \end{align*}$$

The following result is a justification for our terminology, and is useful in our later computation. Let $\deg _T(v)$ denote the number of edges incident with $v \in V(G)$ in the spanning tree T. Consider the canonical element $ \nu _{(T,q)} \in \operatorname {DMeas}_{0}(G)$ associated to the rooted spanning tree $(T, q)$ of G defined by

$$\begin{align*}\nu_{(T,q)} = \sum_{v\in V(G)} \left(\deg_T(v) - 2\right) \delta_v + 2 \delta_q. \end{align*}$$

Lemma 6.2 We have

(6.1) $$ \begin{align}\qquad \boldsymbol{\varrho}(T, q ) = \langle \nu_{(T,q)}, \nu_{(T,q)} \rangle_{\operatorname{en}} = \sum_{v,w \in V(G)} \left(\deg_T(v) - 2\right)\left(\deg_T(w) - 2\right) j_q(v,w). \end{align} $$

Proof By the definition of the preferred orientation ${\mathcal T}_q \subseteq \mathbb {E}(G)$ , we have

$$\begin{align*}\sum_{e \in {\mathcal T}_q} \left(\delta_{e^-} - \delta_{e^+}\right) = \nu_{(T,q)}. \end{align*}$$

This is because every vertex $v \ne q$ has exactly one incoming edge and $\deg _T(v) - 1$ outgoing edges in ${\mathcal T}_q$ . At q, however, there is no incoming edge in ${\mathcal T}_q$ .

The result now follows directly from bilinearity of the energy pairing:

$$\begin{align*}\begin{aligned} \boldsymbol{\varrho}(T, q) &= \sum_{e,f \in {\mathcal T}_q} \xi(e^-, e^+, f^-, f^+) =\sum_{e,f \in {\mathcal T}_q} \langle \delta_{e^-} - \delta_{e^+}, \delta_{f^-} - \delta_{f^+}\rangle_{\operatorname{en}} \\[4pt] &=\ \langle \, \sum_{e \in {\mathcal T}_q} \left(\delta_{e^-} - \delta_{e^+}\right),\sum_{f \in {\mathcal T}_q}\left( \delta_{f^-} - \delta_{f^+}\right) \, \rangle_{\operatorname{en}} = \langle \nu_{(T,q)}, \nu_{(T,q)} \rangle_{\operatorname{en}}. \end{aligned} \end{align*}$$

The second equality in (6.1) follows from (4.1), because $j_q(\cdot , q) = j_q (q, \cdot ) = 0$ .▪

6.2 The average of energy levels

We can now state the most technical ingredient in computing tropical moments of tropical Jacobians.

Theorem 6.3 Fix a vertex $q \in V(G)$ . We have the equality

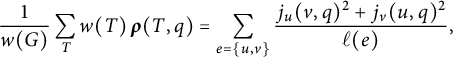$$\begin{align*}\frac{1}{w(G)}\sum_T {w(T) \, {\boldsymbol{\varrho}}(T, q)} = \sum_{e = \{u,v\}}\frac{j_{u}(v, q)^2 + j_{v}(u, q)^2}{\ell(e)}, \end{align*}$$

where the sum on the left is over all spanning trees T of G, and the sum on the right is over all edges $e \in E(G)$ .

Proof The result follows by putting together Lemmas 6.5–6.7.▪

Lemma 6.4 Let $(T,q)$ be a rooted spanning tree of G. We have the equality

$$\begin{align*}\begin{aligned} \boldsymbol{\varrho}(T, q) &= 4 \sum_{x,y \in V(G)} j_q(x,y) - 4 \sum_{e \in T} \sum_{x \in V(G)} \left(j_q(e^-, x)+j_q(e^+, x)\right) \\[4pt] &\quad + \sum_{e,f \in T}\left(j_q(e^-, f^-)+j_q(e^+, f^+)+j_q(e^-, f^+)+j_q(e^+, f^-) \right). \end{aligned} \end{align*}$$

Proof The result follows from Lemma 6.2, and an application of a (generalized) handshaking lemma: for each $\psi \in {\mathcal M}(G)$ , we have

$$\begin{align*}\sum_{x \in V(G)} \deg_T(x) \,\psi (x) = \sum_{e \in T} \left(\psi(e^-)+\psi(e^+)\right).\\[-48pt] \end{align*}$$

▪

Lemma 6.5 Fix a vertex $q \in V(G)$ . We have the equality

$$\begin{align*}\begin{aligned} & \frac{1}{w(G)}\sum_T {w(T) \, {\boldsymbol{\varrho}}(T, q)} = 4\!\! \!\!\!\! \!\sum_{x,y \in V(G)}\!\!\!\!\!\! j_q(x,y) -4\!\!\!\!\!\sum_{e \in E(G)} \sum_{x \in V(G)} \!\!\!\left(j_q(e^-, x)+j_q(e^+, x)\right) \mathrm P(e) \\[4pt] &\quad +\sum_{e,f \in E(G)}\left(j_q(e^-, f^-)+j_q(e^+, f^+)+j_q(e^-, f^+)+j_q(e^+, f^-)\right) \mathrm P(e,f). \end{aligned} \end{align*}$$

Proof This follows from Lemma 6.4: one only needs to change the order of summations and use (5.1) and (5.2).▪

To prove the next two results, it is convenient to work with matrices. We fix labelings $V(G) = \{v_1, \ldots , v_n\}$ and $E(G) = \{e_1, \ldots , e_m\}$ , and we introduce the following matrices:

• ◇ ${\mathbf 1}_n \in {\mathbb R}^n$ and ${\mathbf 1}_m \in {\mathbb R}^m$ denote the all-ones vectors.

• ◇ $\boldsymbol {\delta }_v \in {\mathbb R}^n$ (resp. $\boldsymbol {\delta }_e \in {\mathbb R}^m$ ) denotes the characteristic vector of $v \in V(G)$ (resp. $e \in E(G)$ ).

• ◇ ${\mathbf A} = (h_{ij})$ denotes the $n \times m$ unsigned incidence matrix of G, where $h_{ij} = 1$ if $e_j^+ = v_i$ or $e_j^- = v_i$ , and $h_{ij} = 0$ otherwise.

• ◇ ${\mathbf X}$ is the $n \times n$ diagonal matrix with diagonal $(i,i)$ -entries $j_q(v_i, v_i) = r(v_i, q)$ .

• ◇ ${\mathbf Y}$ is the $m \times m$ diagonal matrix with diagonal $(i,i)$ -entries $\mathrm P(e_i)$ .

• ◇ ${\mathbf Z}$ is the $m \times m$ matrix whose diagonal entries are zero, and the $(i,j)$ -entries ( $i\ne j$ ) are $\mathrm P(e_i, e_j)$ .

We will also use the matrices ${\mathbf Q}$ , ${\mathbf L}_q$ , ${\mathbf R}_q$ , and ${\mathbf I}$ introduced in Section 4.2.

Lemma 6.6 We have the equality

(6.2) $$ \begin{align} \sum_{e \in E(G)} \sum_{x \in V(G)} \left(j_q(e^-, x)+j_q(e^+, x)\right)\mathrm P(e) = 2 \sum_{x,y \in V(G)} j_q(x,y) - \sum_{x \in V(G)} j_q(x,x). \end{align} $$

Proof We start by writing the left-hand side of (6.2) in terms of our matrices:

$$\begin{align*}\sum_{e \in E(G)} \sum_{x \in V(G)} \left(j_q(e^-, x)+j_q(e^+, x)\right)\mathrm P(e) = {\mathbf 1}_n^{\operatorname{T}}{\mathbf L}_q {\mathbf A} {\mathbf Y} {\mathbf 1}_m. \end{align*}$$

By definitions, we observe ${\mathbf A} {\mathbf Y} {\mathbf 1}_m = \left ({\mathfrak s}(v_1), \ldots , {\mathfrak s}(v_n)\right )^{\operatorname {T}}$ . So, by Proposition 5.3, we have

$$\begin{align*}{\mathbf A} {\mathbf Y} {\mathbf 1}_m = -{\mathbf Q} {\mathbf X} {\mathbf 1}_n + 2\left({\mathbf 1}_n - \boldsymbol{\delta}_q\right). \end{align*}$$

Therefore,

$$\begin{align*}{\mathbf 1}_n^{\operatorname{T}}{\mathbf L}_q {\mathbf A} {\mathbf Y} {\mathbf 1}_m = - {\mathbf 1}_n^{\operatorname{T}}{\mathbf L}_q{\mathbf Q} {\mathbf X} {\mathbf 1}_n + 2 {\mathbf 1}_n^{\operatorname{T}}{\mathbf L}_q {\mathbf 1}_n -2{\mathbf 1}_n^{\operatorname{T}}{\mathbf L}_q \boldsymbol{\delta}_q. \end{align*}$$

Note that ${\mathbf L}_q \boldsymbol {\delta }_q = \mathbf {0}$ and ${\mathbf L}_q{\mathbf Q} = {\mathbf I}+{\mathbf R}_q^{\operatorname {T}}$ (see Section 4.2). We also have ${\mathbf R}_q^{\operatorname {T}} {\mathbf X} = \mathbf {0}$ . Therefore,

$$\begin{align*}{\mathbf 1}_n^{\operatorname{T}}{\mathbf L}_q {\mathbf A} {\mathbf Y} {\mathbf 1}_m = 2 {\mathbf 1}_n^{\operatorname{T}}{\mathbf L}_q {\mathbf 1}_n - {\mathbf 1}_n^{\operatorname{T}} {\mathbf X} {\mathbf 1}_n, \end{align*}$$

which is the right-hand side of (6.2).▪

For our next computation, it is convenient to use the notion of Hadamard–Schur products of matrices: for two $k \times m$ matrices $A , B$ , the Hadamard–Schur product, denoted by $A \circ B$ , is a matrix of the same dimension as A and B with entries given by $\left (A \circ B\right )_{ij} = (A)_{ij}(B)_{ij}$ .

One useful (and easy to prove) fact about Hadamard–Schur products is the following:

(6.3) $$ \begin{align} {\mathbf 1}_k^{\operatorname{T}} \left( A \circ B\right) {\mathbf 1}_m= \operatorname{Trace} \left({A^{\operatorname{T}}B}\right).\end{align} $$

Lemma 6.7 We have the equality

$$\begin{align*}\begin{aligned} &\sum_{e,f \in E(G)}\left(j_q(e^-, f^-)+j_q(e^+, f^+)+j_q(e^-, f^+)+j_q(e^+, f^-)\right) \mathrm P(e,f) \\[4pt] &\quad =\sum_{e = \{u,v\}}\frac{j_{u}(v, q)^2 + j_{v}(u, q)^2}{\ell(e)} +4 \sum_{x,y \in V(G)} j_q(x,y) -4 \sum_{x \in V(G)} j_q(x,x). \end{aligned} \end{align*}$$

Proof We first write

(6.4) $$ \begin{align} \begin{aligned} &\qquad\sum_{e,f \in E(G)} \left(j_q(e^-, f^-)+j_q(e^+, f^+)+j_q(e^-, f^+)+j_q(e^+, f^-)\right) \mathrm P(e,f)\\[4pt] &\qquad\quad = \sum_{e\in E(G)} \left(j_q(e^-, e^-)+j_q(e^+, e^+)+2j_q(e^-, e^+)\right) \mathrm P(e)\\[4pt] &\qquad\qquad + \sum_{\substack{e,f \in E(G)\\ e \ne f}} \left(j_q(e^-, f^-)+j_q(e^+, f^+)+j_q(e^-, f^+)+j_q(e^+, f^-)\right) \mathrm P(e,f). \end{aligned} \end{align} $$

We write the second sum in (6.4) in terms of our matrices:

(6.5) $$ \begin{align} \begin{aligned} & \sum_{\substack{e,f \in E(G)\\ e \ne f}} \left(j_q(e^-, f^-)+j_q(e^+, f^+)+j_q(e^-, f^+)+j_q(e^+, f^-)\right) \mathrm P(e,f) \\[4pt] &\quad = {\mathbf 1}_m^{\operatorname{T}}\left( \left({\mathbf A}^{\operatorname{T}} {\mathbf L}_q {\mathbf A} \right) \circ {\mathbf Z}\right) {\mathbf 1}_m. \end{aligned} \end{align} $$

By (6.3), we know

$$\begin{align*}{\mathbf 1}_m^{\operatorname{T}}\left( \left({\mathbf A}^{\operatorname{T}} {\mathbf L}_q {\mathbf A} \right) \circ {\mathbf Z}\right) {\mathbf 1}_m = \operatorname{Trace} \left( {\mathbf A}^{\operatorname{T}} {\mathbf L}_q {\mathbf A} {\mathbf Z} \right) = \sum_{e\in E(G)} \boldsymbol{\delta}_e^{\operatorname{T}} \left({\mathbf A}^{\operatorname{T}} {\mathbf L}_q {\mathbf A} {\mathbf Z} \right) \boldsymbol{\delta}_e. \end{align*}$$

By definitions, one observes ${\mathbf A} {\mathbf Z} \boldsymbol {\delta }_e = \left ({\mathfrak t}(v_1, e), \ldots , {\mathfrak t}(v_n, e)\right )^{\operatorname {T}}$ . Let

$$\begin{align*}e=\{u,v\} \ \ , \ \ \beta_u = \frac{\xi(u,v,u,q)}{r(u,v)} \ \ , \ \ \beta_v = \frac{\xi(v,u,v,q)}{r(u,v)} \ \ , \ \ \mathrm P(e) = \frac{r(u,v)}{\ell(e)}. \end{align*}$$

Theorem 5.4 states

$$\begin{align*}{\mathbf A} {\mathbf Z} \boldsymbol{\delta}_e = \mathrm P(e) \left(-{\mathbf Q} \widetilde{{\mathbf X}} {\mathbf 1}_n +2\left({\mathbf 1}_n - \boldsymbol{\delta}_q - \beta_u \boldsymbol{\delta}_u - \beta_v \boldsymbol{\delta}_v\right) \right). \end{align*}$$

Here, $\widetilde {{\mathbf X}}$ is the $n \times n$ diagonal matrix with diagonal $(i,i)$ -entries $j_q(v_i, v_i; G/e)$ for $v_i \not \in \{u,v\}$ . The diagonal entries corresponding to both u and v are $j_q(v_e, v_e; G/e)$ . Thus, we find

$$\begin{align*}\boldsymbol{\delta}_e^{\operatorname{T}} \left({\mathbf A}^{\operatorname{T}} {\mathbf L}_q {\mathbf A} {\mathbf Z} \right) \boldsymbol{\delta}_e = \mathrm P(e) \left(\boldsymbol{\delta}_u+\boldsymbol{\delta}_v\right)^{\operatorname{T}} {\mathbf L}_q \left(-{\mathbf Q} \widetilde{{\mathbf X}} {\mathbf 1}_n +2\left({\mathbf 1}_n - \boldsymbol{\delta}_q - \beta_u \boldsymbol{\delta}_u - \beta_v \boldsymbol{\delta}_v\right) \right). \end{align*}$$

Note that ${\mathbf L}_q \boldsymbol {\delta }_q = \mathbf {0}$ , ${\mathbf L}_q{\mathbf Q} = {\mathbf I}+{\mathbf R}_q^{\operatorname {T}}$ , and ${\mathbf R}_q^{\operatorname {T}} \widetilde {{\mathbf X}} = \mathbf {0}$ . We obtain

(6.6) $$ \begin{align} \begin{aligned} &\boldsymbol{\delta}_e^{\operatorname{T}} \left({\mathbf A}^{\operatorname{T}} {\mathbf L}_q {\mathbf A} {\mathbf Z} \right) \boldsymbol{\delta}_e =\mathrm P(e) \left(\boldsymbol{\delta}_u+\boldsymbol{\delta}_v\right)^{\operatorname{T}} \left(-\widetilde{{\mathbf X}} {\mathbf 1}_n + 2 {\mathbf L}_q \left({\mathbf 1}_n - \beta_u \boldsymbol{\delta}_u -\beta_v \boldsymbol{\delta}_v\right) \right) \\[4pt] &= -\mathrm P(e) \left(j_q(v_e,v_e; G/e)+j_q(v_e,v_e; G/e)\right) +2 \mathrm P(e) \! \! \sum_{x \in V(G)}\left(j_q(u,x) + j_q(v, x)\right)\\[4pt] &\ \ \ -2 \left(\frac{\xi(u,v,u,q)}{\ell(e)}\left(j_q(u,u) + j_q(v, u)\right) +\frac{\xi(v,u,v,q)}{\ell(e)} \left(j_q(u,v) + j_q(v, v)\right)\right). \end{aligned} \end{align} $$

We now use our generalized Rayleigh’s law (4.10) twice and write everything in terms of invariants of G:

(6.7) $$ \begin{align} \begin{aligned} j_q(v_e,v_e; G/e) &= j_q(u,u) - \frac{\xi(u,q,u,v)^2}{r(u,v)} = j_q(u,u) - \frac{j_u(v,q)^2}{r(u,v)},\\ j_q(v_e,v_e; G/e) &= j_q(v,v) - \frac{\xi(v,q,u,v)^2}{r(u,v)} = j_q(v,v) - \frac{j_v(u,q)^2}{r(u,v)}. \end{aligned} \end{align} $$

We also use the definition of cross ratios to compute

(6.8) $$ \begin{align} \xi(u,v,u,q) = j_q(u,u)- j_q(u,v) \ , \ \xi(v,u,v,q) = j_q(v,v)- j_q(u,v). \end{align} $$

Putting together (6.4)–(6.8), with a simple computation, we obtain

(6.9) $$ \begin{align} \begin{aligned} &\qquad\sum_{e,f \in E(G)} \left(j_q(e^-, f^-)+j_q(e^+, f^+)+j_q(e^-, f^+)+j_q(e^+, f^-)\right) \mathrm P(e,f) \\[4pt] &\quad\qquad = \sum_{e = \{u,v\}}\frac{j_{u}(v, q)^2 + j_{v}(u, q)^2}{\ell(e)} + 2 \sum_{e = \{u,v\}} \sum_{x \in V(G)} \mathrm P(e)\left( j_q(u,x)+j_q(v,x)\right) \\[4pt] &\quad\qquad\quad + 2 \sum_{e =\{u,v\}} \mathrm P(e) j_q(u,v) -2 \sum_{e = \{u,v\}} \frac{j_q(u,u)^2 +j_q(v,v)^2 -2j_q(u,v)^2}{\ell(e)}. \end{aligned} \end{align} $$

By Lemma 6.6, the second term in (6.9) is simplified as

(6.10) $$ \begin{align} \sum_{e = \{u,v\}} \sum_{x \in V(G)} \mathrm P(e)\left( j_q(u,x)+j_q(v,x)\right) = 2\sum_{x,y \in V(G)} j_q(x,y) - \sum_{x \in V(G)} j_q(x,x). \end{align} $$

The third and fourth terms in (6.9) are simplified as follows:

(6.11) $$ \begin{align} \\ & \sum_{e =\{u,v\}} \mathrm P(e) j_q(u,v) - \sum_{e = \{u,v\}} \frac{j_q(u,u)^2 +j_q(v,v)^2 -2j_q(u,v)^2}{\ell(e)} \nonumber \\[4pt] &= \!\! \sum_{e =\{u,v\}} \! \left(\frac{j_q(u,u)\!+\!j_q(v,v)\!-\!2j_q(u,v)}{\ell(e)}j_q(u,v) -\frac{j_q(u,u)^2 \!+\!j_q(v,v)^2 \!-\!2j_q(u,v)^2}{\ell(e)} \right) \nonumber \\&= - \sum_{e =\{u,v\}}\left( j_q(u,u) \frac{j_q(u,u)- j_q(u,v)}{\ell(e)} + j_q(v,v) \frac{j_q(v,v)- j_q(u,v)}{\ell(e)}\right) \nonumber \\[4pt] &= -\sum_{x \in V(G)} j_q(x,x) \sum_{f = \{x, y\}} \frac{j_q(x,x) -j_q(x,y)}{\ell(f)} = -\sum_{x \in V(G)} j_q(x,x) \Delta(j_q(x, \cdot))(x) \nonumber \\[4pt] &= -\sum_{x \in V(G)} j_q(x,x) \left(\delta_x(x) - \delta_q(x) \right) = -\sum_{x \in V(G)} j_q(x,x). \nonumber \end{align} $$

For the first equality, we used (4.5). The third equality is by a (generalized) handshaking lemma. The result now follows by putting together (6.9)–(6.11).▪

6.3 Average of energy levels, a variation

For our main application, we will need the following slight variation of Theorem 6.3. Let $\pi \colon C_1(G, {\mathbb R}) \twoheadrightarrow H_1(G, {\mathbb R})$ denote the orthogonal projection (as defined in Section 4.4).

Definition 6.8 We define the center of a rooted spanning tree $(T, q)$ to be

$$\begin{align*}\sigma_T := \frac{1}{2}\sum_{e \in {\mathcal T}_q} {\pi(e)}. \end{align*}$$

Theorem 6.9 We have the equality

$$\begin{align*}\frac{1}{w(G)}\sum_T w(T)[\sigma_T, \sigma_T] = \frac{1}{4}\sum_{e = \{u,v\}} \left(r(u,v) - \frac{j_{u}( v, q)^2 + j_{v}( u, q)^2}{\ell(e)}\right), \end{align*}$$

where the sum on the left is over all spanning trees T of G, and the sum on the right is over all edges $e \in E(G)$ .

Proof Using (4.6) and Definition 6.1, we compute

(6.12) $$ \begin{align} \\ &[\sigma_T, \sigma_T] = \frac{1}{4} [\sum_{e \in {\mathcal T}_q} {\pi(e)}, \sum_{e \in {\mathcal T}_q} {\pi(e)}]= \frac{1}{4} \left( \sum_{e \in {\mathcal T}_q} [\pi(e), \pi(e)] + \sum_{\substack{e,f \in {\mathcal T}_q\\ e \ne f}} [\pi(e), \pi(f)]\right) \nonumber \\[4pt] &=\frac{1}{4} \left( \! \sum_{e \in T} \mathsf F(e) \ell(e) + \!\!\! \sum_{\substack{e,f \in {\mathcal T}_q\\ e \ne f}} \mathsf F(e,f) \ell(e) \! \right) \! \! =\frac{1}{4} \left(\! \sum_{e \in T} \mathsf F(e) \ell(e) - \!\!\! \sum_{\substack{e,f \in {\mathcal T}_q\\ e \ne f}} \xi(e^-, e^+, f^-, f^+) \right) \nonumber \\[4pt] &=\frac{1}{4} \left( \sum_{e \in T} \mathsf F(e) \ell(e) +\sum_{e \in {\mathcal T}_q} r(e^-, e^+) - \!\!\!\sum_{\substack{e,f \in {\mathcal T}_q}} \xi(e^-, e^+, f^-, f^+) \right) \nonumber \\[4pt] &=\frac{1}{4} \sum_{\substack{e \in T\\ e=\{u,v\}}} \left(\mathsf F(e) \ell(e) +r(u, v)\right) - \frac{1}{4} {\boldsymbol{\varrho}}(T, q). \nonumber \end{align} $$

By Definition 4.4 and (5.1) and by changing the order of summations, we compute

(6.13) $$ \begin{align} \begin{aligned} & \sum_T \frac{w(T)}{w(G)} \sum_{\substack{e \in T\\ e=\{u,v\}}} \left(\mathsf F(e) \ell(e) +r(u, v)\right) = \sum_{e=\{u,v\}} \left(\mathsf F(e) \ell(e) +r(u, v)\right) \sum_{T \ni e} \frac{w(T)}{w(G)}\\[4pt] &\quad = \sum_{e=\{u,v\}} \left(\mathsf F(e) \ell(e) +r(u, v)\right) \mathrm P(e)=\sum_{e=\{u,v\}} r(u,v). \end{aligned} \end{align} $$

The result now follows from (6.12), (6.13), and Theorem 6.3.▪

7 Combinatorics of Voronoi polytopes

Throughout this section, we fix a metric graph $\Gamma $ and a model G. We are interested in the combinatorics of the lattice $\left (H_1(G, {\mathbb Z}), [\cdot , \cdot ]\right )$ . More specifically, we study the combinatorics of the Voronoi polytopes $\operatorname {Vor}(\lambda )$ (as defined in Section 2.2) for the lattice $\left (H_1(G, {\mathbb Z}), [\cdot , \cdot ]\right )$ . Since $\operatorname {Vor} ( \lambda ) = \operatorname {Vor}(0)+ \lambda $ for all $\lambda \in H_1(G, {\mathbb Z})$ , it suffices to understand the Voronoi polytope $\operatorname {Vor}(0)$ around the origin.

Let $\operatorname {Vol}\left (\cdot \right )$ denote the volume measure induced by the bilinear form $[ \cdot , \cdot ]$ on $H_1(G, {\mathbb R})$ . Let $w(G)$ be the weight of G (as in Section 4.4). Put $g=\dim _{\mathbb R} H_1(G,{\mathbb R})$ .

Lemma 7.1 $\operatorname {Vol}\left (\operatorname {Vor}(0)\right ) = \sqrt {w(G) }$ .

Proof The Voronoi polytopes $\{\operatorname {Vor}(0)+ \lambda \colon \lambda \in H_1(G, {\mathbb Z})\}$ induce a periodic polytopal decomposition of $H_1(G, {\mathbb R})$ . Therefore, $\operatorname {Vor}(0)$ , up to some identifications on its boundary, gives a fundamental domain for the translation action of $H_1(G, {\mathbb Z})$ on $H_1(G, {\mathbb R})$ . Therefore, $\operatorname {Vol}\left (\operatorname {Vor}(0)\right ) = \sqrt {\det ({\mathbf G})}$ where ${\mathbf G}$ is any Gram matrix for the lattice $\left (H_1(G, {\mathbb Z}), [\cdot , \cdot ]\right )$ .

Fix an orientation ${\mathcal O}$ on G, and fix a spanning tree T of G. It is well known that $\{\operatorname {circ}(T,e) \colon e \in {\mathcal O} \backslash T\}$ is a basis for $H_1(G, {\mathbb R})$ . Let ${\mathbf C}_T$ denote the totally unimodular $g \times m$ matrix whose rows correspond to these basis elements. Then a Gram matrix for the lattice $\left (H_1(G, {\mathbb Z}), [\cdot , \cdot ]\right )$ is ${\mathbf G}_T = {\mathbf C}_T {\mathbf D} {\mathbf C}_T^{\operatorname {T}}$ . The result now follows from a standard application of the Cauchy–Binet formula for determinants.▪

Remark 7.2 A geometric proof of Lemma 7.1 can be found in [2, Section 5].

Let $\pi \colon C_1(G, {\mathbb R}) \twoheadrightarrow H_1(G, {\mathbb R})$ denote the orthogonal projection (as defined in Section 4.4). Each finite collection of $1$ -chains $V = \{{\mathbf v}_1 , \ldots , {\mathbf v}_k\} \subset C_1(G,{\mathbb R})$ generates a zonotope ${\mathcal Z}(V)$ defined as

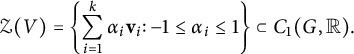$$\begin{align*}{\mathcal Z}(V) = \left\{ \sum_{i=1}^k \alpha_i {\mathbf v}_i \colon -1 \leq \alpha_i \leq 1 \right\} \subset C_1(G,{\mathbb R}). \end{align*}$$

Proposition 7.3 Fix an orientation ${\mathcal O}$ on G. Then

$$\begin{align*}\operatorname{Vor}(0) = \frac{1}{2} \, {\mathcal Z} \left(\{ \pi(e) \colon e \in {\mathcal O}\}\right). \end{align*}$$

Proof This is well known. To the best of our knowledge, this was first proved in [26, Proposition 5.2]. See also [17, Theorem 2] for a different proof.▪

Fix an orientation ${\mathcal O}$ on G. Let T be a spanning tree of G. We define

$$\begin{align*}{\mathcal C}_T := \frac{1}{2} {\mathcal Z} \left( \{ \pi(e) \colon e \in {\mathcal O} \backslash T \}\right). \end{align*}$$

Note that ${\mathcal C}_T$ is independent of the choice of ${\mathcal O}$ .

Lemma 7.4

1. (a) ${\mathcal C}_T$ is a g-dimensional parallelotope. Equivalently, $\{\pi (e) \colon e \in {\mathcal O} \backslash T\}$ is a basis for $H_1(G, {\mathbb R})$ .

2. (b) $\operatorname {Vol}({\mathcal C}_T) = w(T)/\sqrt {w(G)}$ .

Proof (a) Note that, for $e,e' \in {\mathcal O} \backslash T$ , we have $[\pi (e) , \operatorname {circ}(T,e')] = \ell (e) \delta _e(e')$ . It is well known that $\{\operatorname {circ}(T,e) \colon e \in {\mathcal O} \backslash T\}$ is a basis for $H_1(G, {\mathbb R})$ .

(b) This is proved in [2, Proposition 5.4].▪

Now, fix $q \in V(G)$ . Recall (see Section 3.1) that the rooted spanning tree $(T, q)$ comes with a preferred orientation ${\mathcal T}_q \subseteq \mathbb {E}(G)$ (where edges are oriented away from q on the spanning tree T). Let $\sigma _T := \frac {1}{2}\sum _{e \in {\mathcal T}_q} {\pi (e)}$ be the center of $(T,q)$ (Definition 6.8). We now state and prove the main result of this section.

Theorem 7.5 The collection of parallelotopes

$$\begin{align*}\{\sigma_T + {\mathcal C}_T \colon T \text{ is a spanning tree of } G\}\end{align*}$$

induces a polytopal decomposition of $\operatorname {Vor}(0)$ :

1. (i) $\operatorname {Vor}(0) = \bigcup _{T} \left (\sigma _T + {\mathcal C}_T \right )$ , the union being over all spanning trees T of G.

2. (ii) If $T \ne T'$ are two spanning trees such that

   $$\begin{align*}{\mathcal F} := \left(\sigma_T + {\mathcal C}_T \right) \cap \left(\sigma_{T'} + {\mathcal C}_{T'} \right)\end{align*}$$
   is nonempty, then $\mathcal {F} $ is a face of both $\left (\sigma _T + {\mathcal C}_T \right )$ and $\left (\sigma _{T'} + {\mathcal C}_{T'} \right )$ .

Proof It follows from Proposition 7.3 that, for all spanning trees T of G, we have

(7.1) $$ \begin{align} \sigma_T + {\mathcal C}_T \subseteq \operatorname{Vor}(0). \end{align} $$

Moreover, by Lemmas 7.1 and 7.4(b), we know

(7.2) $$ \begin{align} \sum_T{\operatorname{Vol}\left(\sigma_T + {\mathcal C}_T \right)} = \operatorname{Vol}\left(\operatorname{Vor}(0)\right), \end{align} $$

the sum being over all spanning trees T of G.

Next, we describe how these parallelotopes can intersect each other. Let $T \ne T'$ be two spanning trees. We choose an orientation ${\mathcal O}$ on G that agrees with ${\mathcal T}_q$ for $e\in T$ , disagrees with ${\mathcal T}^{\prime }_q$ for $e \in T' \backslash T$ , and is arbitrary outside $T \cup T'$ . We may partition ${\mathcal O}$ into the following (possibly empty) subsets:

$$\begin{align*}\begin{aligned} {\mathcal S}_1 := {\mathcal T}_q \, \backslash \left( {\mathcal T}^{\prime}_q \cup \overline{{\mathcal T}^{\prime}_q}\right), \,\, {\mathcal S}_2 &:= \overline{{\mathcal T}^{\prime}_q} \, \backslash \left( {\mathcal T}_q \cup \overline{{\mathcal T}_q}\right) , \,\, {\mathcal S}_3 := {\mathcal T}_q \, \cap \overline{{\mathcal T}^{\prime}_q} \,\, , \,\, {\mathcal S}_4 := {\mathcal T}_q \, \cap {\mathcal T}^{\prime}_q,\\ {\mathcal S}_5 &:= {\mathcal O} \backslash \left({\mathcal S}_1 \cup {\mathcal S}_2 \cup {\mathcal S}_3 \cup {\mathcal S}_4 \right)\kern-1.5pt. \end{aligned} \end{align*}$$

We can now describe the corresponding parallelotopes as follows:

$$\begin{align*}\sigma_T + {\mathcal C}_T = \frac{1}{2} \, {\mathcal Z} \left(\{ \pi(e) \colon e \in {\mathcal S}_2 \cup {\mathcal S}_5\}\right) + \frac{1}{2}\sum_{e \in {\mathcal S}_1 \cup {\mathcal S}_3 \cup {\mathcal S}_4} \pi(e), \end{align*}$$

$$\begin{align*}\sigma_{T'} + {\mathcal C}_{T'} = \frac{1}{2} \, {\mathcal Z} \left(\{ \pi(e) \colon e \in {\mathcal S}_1 \cup {\mathcal S}_5\}\right) - \frac{1}{2}\sum_{e \in {\mathcal S}_2 \cup {\mathcal S}_3} \pi(e) + \frac{1}{2}\sum_{e \in {\mathcal S}_4} \pi(e). \end{align*}$$

Consider the oriented subgraph ${\mathcal D} := {\mathcal S}_1 \cup {\mathcal S}_2 \cup {\mathcal S}_3$ . Note that the oriented subgraph ${\mathcal D}$ is obtained from the edge set $T\cup T'$ by deleting those edges in $T\cap T'$ that have the same orientation in ${\mathcal T}_q$ and in ${\mathcal T}^{\prime }_q$ , and by orienting the remaining edges according to  ${\mathcal O}$ . One can extend ${\mathcal D}$ to a totally cyclic (also known as strongly connected) subgraph of G, after possibly adding some oriented edges to ${\mathcal D}$ chosen from the (unoriented) edges of $\mathcal {S}_4$ . This is because ${\mathcal D}$ , by construction, has no directed cocircuit. This implies that there exists a vector ${\mathbf v} \in H_1(G, {\mathbb R})$ such that

$$\begin{align*}\begin{aligned} [{\mathbf v} , \pi(e)] &> 0, \quad \quad \text{if } e \in {\mathcal S}_1 \cup {\mathcal S}_2 \cup {\mathcal S}_3,\\ [{\mathbf v} , \pi(e)] &= 0, \quad \quad \text{if } e \in {\mathcal S}_5. \end{aligned} \end{align*}$$

To see this, consider the oriented (cographic) hyperplane arrangement with normal vectors $\{\pi (e) \colon e \in {\mathcal O}\}$ in the vector space $H_1(G, {\mathbb R})$ . It is well known (see, e.g., [19, Lemma 8.2]) that there is a one-to-one correspondence between cells of this hyperplane arrangement and totally cyclic subgraphs of G (see also [1]). Our desired vector ${\mathbf v}$ is any vector in the cell corresponding to any totally cyclic extension of ${\mathcal D}$ .

Consider the function ${\mathfrak h} \colon H_1(G, {\mathbb R}) \rightarrow {\mathbb R}$ defined by

$$\begin{align*}{\mathfrak h}(z) = [{\mathbf v} , z + \sum_{e \in {\mathcal S}_2}{\frac{1}{2}\pi(e)} - \sum_{e \in {\mathcal S}_1 \cup {\mathcal S}_4}{\frac{1}{2}\pi(e)}]. \end{align*}$$

Let ${\mathcal F}= \left (\sigma _T + {\mathcal C}_T \right ) \cap \left (\sigma _{T'} + {\mathcal C}_{T'} \right )$ . We compute

$$\begin{align*}{\mathfrak h}\left( \sigma_T + {\mathcal C}_T \right) = \{ 0 \leq x \leq \sum_{e \in {\mathcal S}_2} [{\mathbf v}, \pi(e) ] \} + \frac{1}{2}\sum_{e \in {\mathcal S}_3} [{\mathbf v}, \pi(e) ] \subseteq {\mathbb R}_{\geq 0}, \end{align*}$$

$$\begin{align*}{\mathfrak h}\left( \sigma_{T'} + {\mathcal C}_{T'} \right) = \{ - \sum_{e \in {\mathcal S}_1} [{\mathbf v}, \pi(e) ] \leq x \leq 0\} - \frac{1}{2}\sum_{e \in {\mathcal S}_3} [{\mathbf v}, \pi(e) ] \subseteq {\mathbb R}_{\leq 0}. \end{align*}$$

• • If ${\mathcal S}_3 \ne \emptyset $ , then ${\mathfrak h}\left ( \sigma _T + {\mathcal C}_T \right )\cap {\mathfrak h}\left ( \sigma _{T'} + {\mathcal C}_{T'} \right ) = \emptyset $ and, therefore, ${\mathcal F}= \emptyset $ .

• • If ${\mathcal S}_3 = \emptyset $ , then ${\mathfrak h}\left ( \sigma _T + {\mathcal C}_T \right ) \cap {\mathfrak h}\left ( \sigma _{T'} + {\mathcal C}_{T'} \right ) = \{0\}$ . Consider the hyperplane $\mathcal {H} = {\mathfrak h}^{-1}(0)$ in $H_1(G, {\mathbb R})$ . One computes

  $$\begin{align*}\begin{aligned} &\mathcal{H} \cap \left(\sigma_T + {\mathcal C}_T \right) = \mathcal{H} \cap \left(\sigma_{T'} + {\mathcal C}_{T'}\right) \\[4pt] &= \frac{1}{2} \, {\mathcal Z} \left(\{ \pi(e) \colon e \in {\mathcal S}_5\}\right) + \frac{1}{2}\sum_{e \in {\mathcal S}_1 \cup {\mathcal S}_4} \pi(e) - \frac{1}{2}\sum_{e \in {\mathcal S}_2} \pi(e)\\[4pt] &= {\mathcal F}. \end{aligned} \end{align*}$$

The result now follows from these intersection patterns, together with (7.1) and (7.2).▪

8 The tropical moment of a tropical Jacobian

In this section, we prove our promised potential theoretic expression for the tropical moment of a tropical Jacobian.

Theorem 8.1 Let $\Gamma $ be a metric graph. Fix a model G of $\Gamma $ , and fix a point $q \in V(G)$ . Then

$$\begin{align*}I(\operatorname{Jac}(\Gamma)) = \frac{1}{12}\sum_{e} {\mathsf F(e)^2 \ell(e) + \frac{1}{4}\sum_{e = \{u,v\}} \left(r(u,v) - \frac{j_{u}( v, q)^2 + j_{v}( u, q)^2}{\ell(e)}\right)}, \end{align*}$$

where the sums are over all edges $e \in E(G)$ .

Proof Recall

$$\begin{align*}I(\operatorname{Jac}(\Gamma)) = \int_{\operatorname{Vor}(0)} [ z,z ] \, \mathrm{d} \mu_L(z), \end{align*}$$

where $\mu _L$ is the Lebesgue measure on $H_1(G, {\mathbb R})$ , normalized to have $\mu _L(\operatorname {Vor}(0)) = 1$ . By Theorem 7.5, we obtain

(8.1) $$ \begin{align} I(\operatorname{Jac}(\Gamma)) = \sum_T \int_{\sigma_T + {\mathcal C}_T} [ z,z ] \, \mathrm{d} \mu_L(z), \end{align} $$

the sums being over all spanning trees T of G. We also have

(8.2) $$ \begin{align} \begin{aligned} \int_{\sigma_T + {\mathcal C}_T} [ z,z ] \, \mathrm{d} \mu_L(z) &= \int_{{\mathcal C}_T} [ y+\sigma_T, y+\sigma_T ] \, \mathrm{d} \mu_L(y)\\[4pt] &= \int_{{\mathcal C}_T} \left( [ y, y]+2[\sigma_T, y]+[\sigma_T, \sigma_T] \right) \, \mathrm{d} \mu_L(y)\\[4pt] &= \int_{{\mathcal C}_T} [ y, y] \, \mathrm{d} \mu_L(y) + \int_{{\mathcal C}_T} [\sigma_T, \sigma_T] \, \mathrm{d} \mu_L(y). \end{aligned} \end{align} $$

The last equality is because ${{\mathcal C}_T}$ is centrally symmetric and $[\sigma _T, y]$ is odd.

By Lemmas 7.1 and 7.4(b), we have

(8.3) $$ \begin{align} \int_{{\mathcal C}_T} [\sigma_T, \sigma_T] \, \mathrm{d} \mu_L(y) = \frac{\operatorname{Vol}({\mathcal C}_T)}{\operatorname{Vol}\left(\operatorname{Vor}(0)\right)} [\sigma_T, \sigma_T] = \frac{w(T)}{w(G)}[\sigma_T, \sigma_T]. \end{align} $$

On the other hand,

(8.4) $$ \begin{align} \begin{aligned} \int_{{\mathcal C}_T} [ y, y] \, \mathrm{d} \mu_L&(y)= \frac{\operatorname{Vol}({\mathcal C}_T)}{\operatorname{Vol}\left(\operatorname{Vor}(0)\right)} \int_{[-\frac{1}{2}, \frac{1}{2}]^g} [\sum_{e \not\in T} \alpha_e \pi(e) , \sum_{e \not\in T} \alpha_e \pi(e)] \, \mathrm{d} \boldsymbol{\alpha} \\[4pt] &= \frac{w(T)}{w(G)} \int_{[-\frac{1}{2}, \frac{1}{2}]^g} \left( \sum_{\substack{e,f \not\in T\\ e \ne f}} \alpha_e \alpha_{f} [\pi(e), \pi(f)] + \sum_{e\not \in T} \alpha_e^2 [\pi(e), \pi(e)] \right) \! \mathrm{d}\boldsymbol{\alpha} \\[4pt] &= \frac{w(T)}{w(G)} \sum_{e \not \in T} [\pi(e), \pi(e)] \int_{[-\frac{1}{2}, \frac{1}{2}]^g} \alpha_e^2 \mathrm{d}\boldsymbol{\alpha}.\end{aligned} \end{align} $$

Here, $\mathrm {d} \boldsymbol {\alpha } = \prod _{e \not \in T}\mathrm {d}\alpha _e$ denotes the usual Lebesgue measure on ${\mathbb R}^g$ . The first equality is by the change of variables theorem, and the last equality holds because $\alpha _e \alpha _{f}$ is an odd function on the symmetric domain $[-\frac {1}{2}, \frac {1}{2}]^g$ . Clearly (see Section 4.4),

(8.5) $$ \begin{align} [\pi(e), \pi(e)] = \mathsf F(e) \ell(e) , \quad \int_{[-\frac{1}{2}, \frac{1}{2}]^g} \alpha_e^2 \mathrm{d}\boldsymbol{\alpha} = \int_{-\frac{1}{2}}^{\frac{1}{2}} \alpha_e^2 \mathrm{d}\alpha_e = \frac{1}{12}. \end{align} $$

Putting (8.1)–(8.5) together, we obtain

(8.6) $$ \begin{align} I(\operatorname{Jac}(\Gamma)) = \frac{1}{12} \sum_T \frac{w(T)}{w(G)} \sum_{e \not \in T} \mathsf F(e) \ell(e) + \sum_T \frac{w(T)}{w(G)}[\sigma_T, \sigma_T]. \end{align} $$

The first sum is simplified immediately, after changing the order of summations (see Remark 4.5(i)):

(8.7) $$ \begin{align} \qquad\sum_T \frac{w(T)}{w(G)} \sum_{e \not \in T} \mathsf F(e) \ell(e) = \sum_{e \in E(G)} \mathsf F(e) \ell(e) \sum_{T \not \ni e} \frac{w(T)}{w(G)} = \sum_{e \in E(G)} \mathsf F(e)^2 \ell(e). \end{align} $$

The result now follows from (8.6), (8.7), and Theorem 6.9.▪

Remark 8.2

1. (i) If $e = \{u,v\}$ is a bridge, then one observes that $r(u, v)= \ell (e)$ and $\mathsf F(e)= 0$ and $\{j_{u}( v, q), j_{v}( u, q)\} = \{0,\ell (e)\}$ . So e contributes $0$ to $I(\operatorname {Jac}(\Gamma ))$ . This is expected, as bridges do not contribute to the first homology.

2. (ii) By (4.3)–(4.5), it is clear that everything in the formula for $I(\operatorname {Jac}(\Gamma ))$ in Theorem 8.1 can be expressed in terms of the entries of ${\mathbf L}_q$ and edge lengths. As mentioned in Remark 4.1, all entries of ${\mathbf L}_q$ can be computed in matrix multiplication time $O(n^\omega )$ , where n is the number of vertices in a model of $\Gamma $ , and $\omega $ is the exponent for matrix multiplication.

Example 8.3 Consider the metric graph $\Gamma $ in Figure 4.

Figure 4: A banana graph $\Gamma $ , consisting of two branch points and m edges $\{e_1, \ldots , e_m\}$ with $\ell (e_i) = x_i$ .

Fix the minimal model G whose vertex set consists of the two branch points u and v, and let $q=v$ . Let $\mathrm R$ denote the effective resistance between u and v:

$$\begin{align*}{\mathrm R}^{-1} = \sum_{i=1}^m {x_i}^{-1}. \end{align*}$$

Then, for each edge $e_i = \{u,v\}$ , we have

$$\begin{align*}\mathsf F(e_i) = 1 - {\mathrm R}/{x_i}, \quad r(u,v) = \mathrm R, \quad j_u(v,q) = \mathrm R, \quad j_v(u,q) = 0. \end{align*}$$

By Theorem 8.1, one computes

$$\begin{align*}I(\operatorname{Jac}(\Gamma)) = \frac{1}{12} \left( \sum_{i=1}^m x_i +\frac{m-2}{\sum_{i=1}^m {x_i}^{-1}}\right). \end{align*}$$

In the special case $x_1 = \cdots = x_m = 1$ , the lattice $\left (H_1(\Gamma , {\mathbb Z}), [\cdot , \cdot ] \right )$ corresponds to the root lattice $A_{m-1}$ . So one recovers the formula in [13, p. 460]:

$$\begin{align*}I(A_{m-1}) = \frac{m^2+m-2}{12m}. \end{align*}$$

We record two other special cases for our application in Section 10:

• • If $m=2$ , then the metric graph $\Gamma $ is just a circle, and

  $$\begin{align*}I(\operatorname{Jac}(\Gamma)) = \frac{1}{12} \ell ,\end{align*}$$
  where $\ell $ is the total length of the circle.

• • If $m=3$ , then we have

  $$\begin{align*}I(\operatorname{Jac}(\Gamma)) = \frac{1}{12}\left( x_1+x_2+x_3 + \frac{x_1x_2x_3}{x_1x_2+x_2x_3+x_3x_1}\right). \end{align*}$$

The case $m=3$ corresponds to a lattice of rank 2, with Gram matrix

$$\begin{align*}\left( \begin{array}{cc} x_1 + x_2 & x_1 \\ x_1 & x_1 + x_3 \end{array} \right) \end{align*}$$

on a suitable basis. As each two-dimensional lattice has a Gram matrix on a suitable basis of this shape, our formula gives a “quick” expression for the tropical moment of any two-dimensional lattice in terms of a Gram matrix.

9 Connection with arithmetic geometry

A metric graph may be canonically interpreted as a skeleton of a Berkovich curve, and the tropical Jacobian of a metric graph can be interpreted as the canonical skeleton of a Berkovich Jacobian variety [5]. More generally, one may view the canonical skeleton of any Berkovich polarized abelian variety as a polarized real torus in a canonical way, via non-archimedean uniformization. Based on this connection, our results can be applied in the study of polarized abelian varieties. For example, we have the following application concerning the computation of Arakelov heights attached to principally polarized abelian varieties defined over a number field. For more background and for terminology used in this section, we refer to [14].

Let k be a number field, and let $M(k)_0$ and $M(k)_\infty $ denote the set of non-archimedean places and the set of complex embeddings of k. Let $(A,\lambda )$ be a principally polarized abelian variety defined over k. Assume that A has semistable reduction over k. For $v \in M(k)_\infty $ , we let $I(A_v,\lambda _v)$ denote the I-invariant, as defined in [3], of the principally polarized complex abelian variety $(A_v,\lambda _v)$ obtained by extending scalars to $\bar {k}_v \simeq {\mathbb C}$ . For $v \in M(k)_0$ , we let $I(A_v,\lambda _v)$ denote the tropical moment of the canonical skeleton of the Berkovich analytification of $(A,\lambda )$ at v, viewed as a polarized real torus. Let $Nv$ be the cardinality of the residue field at $v \in M(k)_0$ .

Theorem [14, Theorem A]

Let $\varTheta $ be a symmetric effective divisor on A that defines the polarization $\lambda $ , and put $L=\mathcal {O}_A(\varTheta )$ . Let $\mathrm {h}^{\prime }_L(\varTheta )$ denote the Néron–Tate height of the cycle $\varTheta $ , and let $\mathrm {h}_F(A)$ denote the stable Faltings height of A. Set $g=\dim (A)$ . Then the equality

(9.1) $$ \begin{align} \mathrm{h}_F(A) = 2g \, \mathrm{h}^{\prime}_L(\varTheta) - \kappa_0 \, g + \frac{1}{[k:{\mathbb Q}]} \left( \sum_{v \in M(k)_0} I(A_v,\lambda_v) \log Nv + 2 \sum_{v \in M(k)_\infty} I(A_v,\lambda_v) \right) \end{align} $$

holds in ${\mathbb R}$ .

Assume that $v \in M(k)_0$ is a finite place such that the canonical skeleton of the Berkovich analytification of $(A,\lambda )$ at v can be realized as the tropical Jacobian of some (explicitly given) metric graph. For example, $(A,\lambda )$ could be the Jacobian variety of a smooth projective geometrically connected curve with semistable reduction over k. Then Theorem 8.1 can be applied to compute the local term $I(A_v,\lambda _v)$ efficiently. We shall illustrate this in Section 10 by discussing the case of Jacobian varieties of dimension $2$ in some detail.

10 Example: heights of Jacobians in dimension $\boldsymbol{2}$

In this section, we specialize (9.1) to the case where the principally polarized abelian variety $(A,\lambda )$ is a Jacobian variety of dimension $2$ . We use (9.1) together with Example 8.3 to give a conceptual explanation of a result due to Autissier [3].

Let k be a number field. Let X be a smooth projective geometrically connected curve of genus 2 with semistable reduction over k. Let $\operatorname {Jac}(X)$ be the Jacobian variety of X. As in Section 9, we denote by $M(k)_0$ and $M(k)_\infty $ the set of non-archimedean places and the set of complex embeddings of k. For each $v \in M(k)_0$ , we have a metric graph $\Gamma _v$ canonically associated to X at v by taking the dual graph of the geometric special fiber of the stable model of X at v (see, for example, [30]). The tropical Jacobian $\operatorname {Jac}(\Gamma _v)$ is canonically isometric with the canonical skeleton of the Berkovich analytification of $\operatorname {Jac}(X)$ at v.

Equation (9.1) specializes into the identity

(10.1) $$ \begin{align} \begin{aligned} \mathrm{h}_F(\operatorname{Jac}(X)) &= 4 \, \mathrm{h}^{\prime}_L (\Theta) - 2 \, \kappa_0 +\frac{1}{[k:{\mathbb Q}]} \sum_{v \in M(k)_0} I(\operatorname{Jac}(\Gamma_v)) \log Nv \\[4pt] &\quad + \frac{2}{[k:{\mathbb Q}]} \sum_{v \in M(k)_\infty} I(\operatorname{Jac}(X_v)). \end{aligned} \end{align} $$

In [3, Théorème 5.1], Autissier proves an identity

(10.2) $$ \begin{align} \begin{aligned} \mathrm{h}_F(\operatorname{Jac}(X)) &= 4 \, \mathrm{h}^{\prime}_L (\Theta) - 2 \, \kappa_0 +\frac{1}{[k:{\mathbb Q}]} \sum_{v \in M(k)_0} \alpha_v \log Nv \\[4pt] &\quad + \frac{2}{[k:{\mathbb Q}]} \sum_{v \in M(k)_\infty} I(\operatorname{Jac}(X_v)), \end{aligned} \end{align} $$

where, for each $v \in M(k)_0$ , the local invariant $\alpha _v$ is given explicitly in terms of the metric graph $\Gamma _v$ by means of a table. See the Remarque following the proof of [3, Théorème 5.1] where, for each of the seven possible topological types of stable dual graphs in genus 2, the invariant $\alpha _v$ is given in terms of the edge lengths of a minimal model of $\Gamma _v$ .

A simple explicit calculation using Example 8.3 shows that for all seven topological types as listed in Autissier’s table, the equality $\alpha _v = I(\operatorname {Jac}(\Gamma _v))$ is verified. For example, consider case VII in the last row of Autissier’s table, corresponding to a banana graph with three edges. The table in this case gives

$$\begin{align*}\alpha_v = \frac{1}{12}\left( x_1+x_2+x_3 + \frac{x_1x_2x_3}{x_1x_2+x_2x_3+x_3x_1}\right), \end{align*}$$

where $x_1, x_2, x_3$ are the three edge lengths. By Example 8.3, with $m=3$ , we see immediately that $\alpha _v = I(\operatorname {Jac}(\Gamma _v))$ for case VII. The cases I–VI are very similar, and in fact simpler, as the irreducible components of the corresponding graphs are either bridges, which by Remark 8.2(ii) contribute zero to $I(\operatorname {Jac}( \Gamma _v))$ , or circles, which by Example 8.3 with $m=2$ contribute ${1}/{12}$ of their total length to $I(\operatorname {Jac}(\Gamma _v))$ . We thus have a complete conceptual explanation of all entries in Autissier’s table.

11 Connection with the tau invariant of a metric graph

Let $\Gamma $ be a metric graph. The notion of Arakelov–Green’s function $g_\mu (x, y)$ associated to a measure $\mu $ on $\Gamma $ is introduced in [11, 30]. It can be shown [11, Theorem 2.11] that there exists a unique measure $\mu _{\operatorname {can}}$ on $\Gamma $ having total mass $1$ , such that $g_{\mu _{\operatorname {can}}}(x, x)$ is a constant. This constant is by definition $\tau (\Gamma )$ . Alternatively, $\tau (\Gamma )$ can be interpreted as a certain “capacity,” with equilibrium measure $\mu _{\operatorname {can}}$ and with potential kernel ( $1/2$ times) the effective resistance function $r(x,y)$ [6, Corollary 14.2]. See also [4, 6, 12] for more background, examples, and formulas.

We will work with the following definition (see, e.g., [6, Lemma 14.4]) in terms of the effective resistance function.

Definition 11.1 Fix a point $q \in \Gamma $ . Let $f(x) = \frac {1}{2} r(x, q)$ . We put

$$\begin{align*}\tau(\Gamma) := \int_{\Gamma}{\left(f'(x)\right)^2 \mathrm{d} x}, \end{align*}$$

where $\mathrm {d} x$ denotes the (piecewise) Lebesgue measure on $\Gamma $ .

It is elementary and well known that the real number $\tau (\Gamma )$ is independent of the choice of $q \in \Gamma $ .

We have the following explicit (and efficiently computable) formula for $\tau (\Gamma )$ . See also [12, Proposition 2.9] for an equivalent form of this formula. Our proof is somewhat different and avoids “circuit reduction theory.”

Theorem 11.2 Let $\Gamma $ be a metric graph. Fix a model G of $\Gamma $ , and fix a point $q \in V(G)$ . Then

$$\begin{align*}\tau(\Gamma) = \frac{1}{12} \sum_{e}\mathsf F(e)^2 \ell(e) +\frac{1}{4} \sum_{e= \{u,v\}} \frac{\left(r(u, q) - r(v, q)\right)^2}{\ell(e)}, \end{align*}$$

where the sums are over all edges $e \in E(G)$ .

Proof Let $f(x)$ be as in Definition 11.1. Let G be a model of $\Gamma $ . Then

$$\begin{align*}\tau(\Gamma) = \sum_{e \in E(G)} \int_e {\left(f'(x)\right)^2 \mathrm{d} x}. \end{align*}$$

We identify each edge segment e in $E(G)$ with an interval $[0,\ell (e)]$ and represent a point $x \in e$ by $x \in [0,\ell (e)]$ . By Example 4.6, we have

$$\begin{align*}2f'(x) = \mathsf F(e) -\frac{r(u,q) - r(v,q)}{\ell(e)} - 2 \frac{\mathsf F(e)}{\ell(e)} x. \end{align*}$$

With a direct computation, we obtain

$$\begin{align*}\int_e {\left(f'(x)\right)^2 \mathrm{d} x} = \int_0^{\ell(e)} {\left(f'(x)\right)^2 \mathrm{d} x} = \frac{1}{12} \mathsf F(e)^2 \ell(e) + \frac{1}{4} \frac{\left(r(u,q) - r(v,q) \right)^2}{\ell(e)}, \end{align*}$$

and the result follows.▪

The reader will notice the similarity between the right-hand side in Theorem 11.2 and the right-hand side in Theorem 8.1. In fact, we can now prove a simple linear relation between $\tau (\Gamma )$ , the tropical moment $I(\operatorname {Jac}(\Gamma ))$ , and the total length of $\Gamma $ . The result was announced as Theorem B in Section 1.

Definition 11.3 Let $\Gamma $ be a metric graph, and fix a model G of $\Gamma $ . The total length of $\Gamma $ is defined by

$$\begin{align*}\ell(\Gamma) := \sum_{e \in E(G)}{\ell(e)}.\end{align*}$$

It is easily seen that $\ell (\Gamma )$ is independent of the choice of the model G.

Theorem 11.4 Let $\Gamma $ be a metric graph. The identity

$$\begin{align*}\frac{1}{2}\tau(\Gamma)+I(\operatorname{Jac}(\Gamma)) = \frac{1}{8} \ell(\Gamma) \end{align*}$$

holds in ${\mathbb R}$ .

Proof Fix a model G of $\Gamma $ . By Theorem 11.2 and (4.2), we have

(11.1) $$ \begin{align} \tau(\Gamma) = \frac{1}{12} \sum_{e}\mathsf F(e)^2 \ell(e) +\frac{1}{4} \sum_{e= \{u,v\}} \frac{\left(j_{u}(v , q) - j_{v}(u , q)\right)^2}{\ell(e)}, \end{align} $$

where the sums are over all edges $e \in E(G)$ . The result follows from (4.4), (11.1), Theorem 8.1, and the following direct computation:

$$\begin{align*} &\frac{1}{2}\tau(\Gamma)+I(\operatorname{Jac}(\Gamma)) \\[4pt] &=\! \frac{1}{8} \! \sum_{e = \{u,v\}} \left( \mathsf F(e)^2 \ell(e) + \frac{\left(j_{u}(v , q) - j_{v}(u , q)\right)^2}{\ell(e)} + 2r(u,v) - 2\frac{j_{u}( v, q)^2 + j_{v}( u, q)^2}{\ell(e)} \!\right) \nonumber \\&=\! \frac{1}{8} \! \sum_{e = \{u,v\}} \left( \mathsf F(e)^2 \ell(e) + 2r(u,v) - \frac{\left(j_{u}(v , q) + j_{v}(u , q)\right)^2}{\ell(e)}\right)\\[4pt] &=\! \frac{1}{8} \! \sum_{e = \{u,v\}} \left( \left(1 -\frac{r(u,v)}{\ell(e)}\right)^2 \ell(e) + 2r(u,v) - \frac{r(u,v)^2}{\ell(e)}\right)\\[4pt] &=\! \frac{1}{8} \! \sum_{e = \{u,v\}} \ell(e) = \frac{1}{8}\, \ell(\Gamma). \\[-48pt] \end{align*}$$

▪