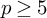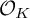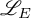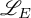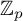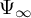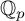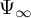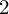1 Introduction
1.1
Since the seminal work of Coates and Wiles, Iwasawa theory of CM elliptic curves influences general Iwasawa theory. It continues to have applications to classical Diophantine problems. The nature of prime p is inherent to Iwasawa theory. For primes split in the CM field, CM Iwasawa theory is well-developed. In contrast, for non-split primes, new phenomena abound and CM Iwasawa theory is still incipient.
Let K be an imaginary quadratic field and
![]() $p\geq 5$
a rational prime which is inert in K. Let
$p\geq 5$
a rational prime which is inert in K. Let
![]() $K_{n}$
be the n-th layer of the anticyclotomic
$K_{n}$
be the n-th layer of the anticyclotomic
![]() ${\mathbb {Z}}_{p}$
-extension
${\mathbb {Z}}_{p}$
-extension
![]() $K_{\infty }$
of K. Let E be an elliptic curve defined over
$K_{\infty }$
of K. Let E be an elliptic curve defined over
![]() $\mathbb {Q}$
with complex multiplication by
$\mathbb {Q}$
with complex multiplication by
![]() $\mathcal {O}_K$
. In the early 1980s, R. Greenberg found the formula
$\mathcal {O}_K$
. In the early 1980s, R. Greenberg found the formula
for root numbers, where
![]() $\varphi $
denotes the Hecke character of E and
$\varphi $
denotes the Hecke character of E and
![]() $\chi $
an anticyclotomic finite character of K of order
$\chi $
an anticyclotomic finite character of K of order
![]() $p^n>1$
. It led him to the formula
$p^n>1$
. It led him to the formula
for all n sufficiently large (cf. [Reference Greenberg24], [Reference Greenberg26], see also Corollary 3.11). Here,
![]() $\varepsilon _{n}$
is
$\varepsilon _{n}$
is
![]() $0$
or
$0$
or
![]() $2$
and
$2$
and
![]() $\varepsilon _{n}=2$
if and only if
$\varepsilon _{n}=2$
if and only if
![]() $W(\varphi )=(-1)^{n}$
. So, new points of infinite order occur in the alternate anticyclotomic layers. This behavior of the Mordell–Weil rank is peculiar to the inert case. For example, for a split prime p, we have
$W(\varphi )=(-1)^{n}$
. So, new points of infinite order occur in the alternate anticyclotomic layers. This behavior of the Mordell–Weil rank is peculiar to the inert case. For example, for a split prime p, we have
![]() ${\mathrm {rank}}_{{\mathbb {Z}}} E(K_\infty )<+\infty $
if
${\mathrm {rank}}_{{\mathbb {Z}}} E(K_\infty )<+\infty $
if
![]() $W(\varphi )=+1$
. In the late 1980s K. Rubin envisioned an Iwasawa theory echoing such phenomena and made a fundamental conjecture on the structure of anticyclotomic local units (cf. [Reference Rubin47]). Recently, we proved the conjecture [Reference Burungale, Kobayashi and Ota12]. The resolution has unexpectedly led us to new developments in supersingular Iwasawa theory. This is the first of the series of papers of our study.
$W(\varphi )=+1$
. In the late 1980s K. Rubin envisioned an Iwasawa theory echoing such phenomena and made a fundamental conjecture on the structure of anticyclotomic local units (cf. [Reference Rubin47]). Recently, we proved the conjecture [Reference Burungale, Kobayashi and Ota12]. The resolution has unexpectedly led us to new developments in supersingular Iwasawa theory. This is the first of the series of papers of our study.
In [Reference Rubin47], Rubin constructed an anticyclotomic p-adic L-function
![]() $\mathscr {L}_{E}$
interpolating special values
$\mathscr {L}_{E}$
interpolating special values
![]() $L(\varphi \chi , 1)$
for finite anticyclotomic characters
$L(\varphi \chi , 1)$
for finite anticyclotomic characters
![]() $\chi $
of K with
$\chi $
of K with
![]() $W(\varphi \chi )=+1$
. If one expects a p-adic Birch and Swinnerton-Dyer conjecture for
$W(\varphi \chi )=+1$
. If one expects a p-adic Birch and Swinnerton-Dyer conjecture for
![]() $\mathscr {L}_{E}$
, the function should encode the rank behavior (1.1). The main result of this paper is a formula relating the value of
$\mathscr {L}_{E}$
, the function should encode the rank behavior (1.1). The main result of this paper is a formula relating the value of
![]() $\mathscr {L}_{E}$
at a finite anticyclotomic character
$\mathscr {L}_{E}$
at a finite anticyclotomic character
![]() $\chi $
of K with
$\chi $
of K with
![]() $W(\varphi \chi )=-1$
to the formal group logarithm of a rational point on
$W(\varphi \chi )=-1$
to the formal group logarithm of a rational point on
![]() $E(K_n)^\chi $
behind the phenomenon (1.1) (see Theorems 1.1 and 1.2). It has an application for the Birch and Swinnerton-Dyer (BSD) conjecture, namely a p-converse to the Gross–Zagier and Kolyvagin theorem (see Theorem 1.5).
$E(K_n)^\chi $
behind the phenomenon (1.1) (see Theorems 1.1 and 1.2). It has an application for the Birch and Swinnerton-Dyer (BSD) conjecture, namely a p-converse to the Gross–Zagier and Kolyvagin theorem (see Theorem 1.5).
1.2 Main results
Let
![]() $p\geq 5$
be a prime. Let
$p\geq 5$
be a prime. Let
![]() $\overline {{\mathbb {Q}}}$
be an algebraic closure of
$\overline {{\mathbb {Q}}}$
be an algebraic closure of
![]() ${\mathbb {Q}}$
. Fix embeddings
${\mathbb {Q}}$
. Fix embeddings
![]() $\iota _{\infty }:\overline {{\mathbb {Q}}}\hookrightarrow {\mathbb {C}}$
and
$\iota _{\infty }:\overline {{\mathbb {Q}}}\hookrightarrow {\mathbb {C}}$
and
![]() $\iota _{p}:\overline {{\mathbb {Q}}}\hookrightarrow {\mathbb {C}}_{p}$
.
$\iota _{p}:\overline {{\mathbb {Q}}}\hookrightarrow {\mathbb {C}}_{p}$
.
Let K be an imaginary quadratic field with p inert and
![]() ${\mathcal {O}}_{K}$
the integer ring. Let
${\mathcal {O}}_{K}$
the integer ring. Let
![]() $\mathcal O$
(resp.
$\mathcal O$
(resp.
![]() $\Phi $
) be the completion of
$\Phi $
) be the completion of
![]() ${\mathcal {O}}_{K}$
(resp. K) at p. In this introduction, we assume the class number
${\mathcal {O}}_{K}$
(resp. K) at p. In this introduction, we assume the class number
![]() $h_K$
of K equals
$h_K$
of K equals
![]() $1$
; however, the main text only assumes
$1$
; however, the main text only assumes
![]() $p \nmid h_K$
. Let
$p \nmid h_K$
. Let
![]() $K_{\infty }$
be the anticyclotomic
$K_{\infty }$
be the anticyclotomic
![]() ${\mathbb {Z}}_p$
-extension of K and
${\mathbb {Z}}_p$
-extension of K and
![]() $\Gamma ={\mathrm {Gal}}(K_{\infty }/K)$
. Let
$\Gamma ={\mathrm {Gal}}(K_{\infty }/K)$
. Let
![]() $\Xi $
be the set of finite characters of
$\Xi $
be the set of finite characters of
![]() $\Gamma $
. Let
$\Gamma $
. Let
 $$ \begin{align*} \Xi^+&={\{} \chi \in \Xi\ |\ \mathrm{cond^r} \chi\text{ is an even power of } p{\}},\\ \Xi^-&={\{} \chi \in \Xi\ |\ \mathrm{cond^r} \chi \text{ is an odd power of } p{\}}. \end{align*} $$
$$ \begin{align*} \Xi^+&={\{} \chi \in \Xi\ |\ \mathrm{cond^r} \chi\text{ is an even power of } p{\}},\\ \Xi^-&={\{} \chi \in \Xi\ |\ \mathrm{cond^r} \chi \text{ is an odd power of } p{\}}. \end{align*} $$
In particular,
![]() for
for
![]() the trivial Hecke character of K. Let
the trivial Hecke character of K. Let
![]() $\Lambda $
be the anticyclotomic Iwasawa algebra
$\Lambda $
be the anticyclotomic Iwasawa algebra
![]() $\mathcal O[\![\Gamma ]\!]$
.
$\mathcal O[\![\Gamma ]\!]$
.
Let E be an elliptic curve defined over
![]() ${\mathbb {Q}}$
with complex multiplication by
${\mathbb {Q}}$
with complex multiplication by
![]() ${\mathcal {O}}_{K}$
with good reduction at p (note that E has supersingular reduction at p since p is inert). Let T be the p-adic Tate module of E, which is an
${\mathcal {O}}_{K}$
with good reduction at p (note that E has supersingular reduction at p since p is inert). Let T be the p-adic Tate module of E, which is an
![]() $\mathcal O$
-module of rank
$\mathcal O$
-module of rank
![]() $1$
, and put
$1$
, and put
![]() $T^{\otimes -1}=\mathrm {Hom}_{\mathcal {O}}(T, \mathcal {O})$
. Fix a minimal Weierstrass model of E over
$T^{\otimes -1}=\mathrm {Hom}_{\mathcal {O}}(T, \mathcal {O})$
. Fix a minimal Weierstrass model of E over
![]() ${\mathbb {Z}}_{(p)}$
and let
${\mathbb {Z}}_{(p)}$
and let
![]() $\omega $
be the associated Néron differential form. Let
$\omega $
be the associated Néron differential form. Let
![]() $\Omega \in {\mathbb {C}}^{\times }$
be a CM period so that
$\Omega \in {\mathbb {C}}^{\times }$
be a CM period so that
![]() $\Omega {\mathcal {O}}_{K}$
is the period lattice. Let
$\Omega {\mathcal {O}}_{K}$
is the period lattice. Let
![]() $\varphi $
be the associated Hecke character of K. In particular,
$\varphi $
be the associated Hecke character of K. In particular,
Let
![]() $W(\varphi )$
be the root number of the Hecke L-function
$W(\varphi )$
be the root number of the Hecke L-function
![]() $L(\varphi ,s)$
.
$L(\varphi ,s)$
.
1.2.1 Rubin p-adic L-function
Here, we introduce Rubin’s theory in terms of Galois cohomology. The relation to Rubin’s original formulation is explained in Section 2.
Let
![]() $\Psi _\infty $
be the anticyclotomic
$\Psi _\infty $
be the anticyclotomic
![]() ${\mathbb {Z}}_p$
-extension of
${\mathbb {Z}}_p$
-extension of
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi _n$
the n-th layer. We denote the Iwasawa cohomology
$\Psi _n$
the n-th layer. We denote the Iwasawa cohomology
![]() $\varprojlim _n H^1(\Psi _n, T^{\otimes -1}(1))$
by
$\varprojlim _n H^1(\Psi _n, T^{\otimes -1}(1))$
by
![]() $\mathcal {H}^1$
. For
$\mathcal {H}^1$
. For
![]() $\chi \in \Xi $
, which factors through
$\chi \in \Xi $
, which factors through
![]() ${\mathrm {Gal}}(\Psi _m/\Phi )$
, the dual exponential map for
${\mathrm {Gal}}(\Psi _m/\Phi )$
, the dual exponential map for
![]() $\chi \otimes T^{\otimes -1}(1)$
normalized by
$\chi \otimes T^{\otimes -1}(1)$
normalized by
![]() $\omega $
defines a map
$\omega $
defines a map
![]() $\delta _\chi : \mathcal {H}^1 \longrightarrow \Psi _m(\mathrm {Im}\,\chi ) $
(cf. (2.9)). Then, we put
$\delta _\chi : \mathcal {H}^1 \longrightarrow \Psi _m(\mathrm {Im}\,\chi ) $
(cf. (2.9)). Then, we put
Rubin showed
![]() $\mathcal {H}^1_\pm $
is a free
$\mathcal {H}^1_\pm $
is a free
![]() $\Lambda $
-module of rank one (cf. [Reference Rubin47, Prop. 8.1] and (2.7)). Rubin’s conjecture, which is proved in [Reference Burungale, Kobayashi and Ota12], posits
$\Lambda $
-module of rank one (cf. [Reference Rubin47, Prop. 8.1] and (2.7)). Rubin’s conjecture, which is proved in [Reference Burungale, Kobayashi and Ota12], posits
We fix a generator
![]() $v_\pm =(v_{\pm ,n})_n$
of the local
$v_\pm =(v_{\pm ,n})_n$
of the local
![]() $\Lambda $
-module
$\Lambda $
-module
![]() $\mathcal {H}^1_\pm $
. Let
$\mathcal {H}^1_\pm $
. Let
![]() $\varepsilon \in \{+, -\}$
be the sign of the root number
$\varepsilon \in \{+, -\}$
be the sign of the root number
![]() $W(\varphi )$
and let
$W(\varphi )$
and let
be the associated Rubin p-adic L-function [Reference Rubin47, §10] (cf. §3.3.1). Let
![]() $\mathscr {L}_{E}(\chi )$
denote its evaluation at an anticyclotomic character
$\mathscr {L}_{E}(\chi )$
denote its evaluation at an anticyclotomic character
![]() $\chi $
.
$\chi $
.
For
![]() $\chi \in \Xi ^{\varepsilon }$
(resp.
$\chi \in \Xi ^{\varepsilon }$
(resp.
![]() $\chi \in \Xi ^{-\varepsilon }$
), the Hecke L-function
$\chi \in \Xi ^{-\varepsilon }$
), the Hecke L-function
![]() $L(\varphi \chi , s)$
is self-dual and
$L(\varphi \chi , s)$
is self-dual and
![]() $W(\varphi \chi )=+1$
(resp.
$W(\varphi \chi )=+1$
(resp.
![]() $W(\varphi \chi )=-1$
). The interpolation property of the Rubin p-adic L-function is given by
$W(\varphi \chi )=-1$
). The interpolation property of the Rubin p-adic L-function is given by
 $$ \begin{align} \mathscr{L}_{E}(\chi) =\frac{1}{\delta_{\chi^{-1}}(v_\varepsilon)}\cdot \frac{L_{p{\mathfrak{f}}}(\overline{\varphi\chi}, 1)}{\Omega} \quad (\chi \in \Xi^{\varepsilon}), \end{align} $$
$$ \begin{align} \mathscr{L}_{E}(\chi) =\frac{1}{\delta_{\chi^{-1}}(v_\varepsilon)}\cdot \frac{L_{p{\mathfrak{f}}}(\overline{\varphi\chi}, 1)}{\Omega} \quad (\chi \in \Xi^{\varepsilon}), \end{align} $$
where the non-vanishing of
![]() $\delta _{\chi ^{-1}}(v_\varepsilon )$
is a consequence of Rubin’s conjecture, and
$\delta _{\chi ^{-1}}(v_\varepsilon )$
is a consequence of Rubin’s conjecture, and
![]() $L_{p{\mathfrak {f}}}(\overline {\varphi \chi }, s)$
denotes the associated L-function whose Euler factors at the primes dividing
$L_{p{\mathfrak {f}}}(\overline {\varphi \chi }, s)$
denotes the associated L-function whose Euler factors at the primes dividing
![]() $p{\mathfrak {f}}$
are removed.
$p{\mathfrak {f}}$
are removed.
For
![]() $\chi \in \Xi ^{-\varepsilon }$
, note that
$\chi \in \Xi ^{-\varepsilon }$
, note that
![]() $L(\overline {\varphi \chi },1)= 0$
by the functional equation and
$L(\overline {\varphi \chi },1)= 0$
by the functional equation and
![]() $\mathscr {L}_{E}(\chi )$
is not related to
$\mathscr {L}_{E}(\chi )$
is not related to
![]() $L(\overline {\varphi \chi },1)$
directly. In light of the BSD conjecture, it is natural to seek:
$L(\overline {\varphi \chi },1)$
directly. In light of the BSD conjecture, it is natural to seek:
This question is due to Rubin [Reference Rubin47, p. 421].
1.2.2
Theorem 1.1. Let
![]() $E_{/{\mathbb {Q}}}$
be a CM elliptic curve with root number
$E_{/{\mathbb {Q}}}$
be a CM elliptic curve with root number
![]() $-1$
and K the CM field. Let
$-1$
and K the CM field. Let
![]() $p\geq 5$
be a prime of good supersingular reduction for
$p\geq 5$
be a prime of good supersingular reduction for
![]() $E_{/{\mathbb {Q}}}$
and
$E_{/{\mathbb {Q}}}$
and
![]() $\mathscr {L}_{E}$
the Rubin p-adic L-function as in (1.4). Then, there exists a rational point
$\mathscr {L}_{E}$
the Rubin p-adic L-function as in (1.4). Then, there exists a rational point
![]() $P\in E({\mathbb {Q}})$
with the following properties.
$P\in E({\mathbb {Q}})$
with the following properties.
-
(a) We have
forFootnote 1 some
 $c_{P}\in {\mathbb {Q}}^\times \mathcal {O}_K^\times $
.
$c_{P}\in {\mathbb {Q}}^\times \mathcal {O}_K^\times $
.
-
(b) P is non-torsion if and only if
 ${\mathrm {ord}}_{s=1}L(E_{/{\mathbb {Q}}},s)=1$
.
${\mathrm {ord}}_{s=1}L(E_{/{\mathbb {Q}}},s)=1$
. -
(c) If
 ${\mathrm {ord}}_{s=1}L(E_{/{\mathbb {Q}}},s)=1$
, then for
${\mathrm {ord}}_{s=1}L(E_{/{\mathbb {Q}}},s)=1$
, then for $$ \begin{align*}c_{P}=\frac{L'(E_{/{\mathbb {Q}}},1)}{\Omega\langle P, P \rangle_{\infty}} \end{align*} $$
$$ \begin{align*}c_{P}=\frac{L'(E_{/{\mathbb {Q}}},1)}{\Omega\langle P, P \rangle_{\infty}} \end{align*} $$
 $\langle \ , \ \rangle _{\infty }$
the Néron–Tate height pairing.
$\langle \ , \ \rangle _{\infty }$
the Néron–Tate height pairing.
See also Theorem 4.8 in a more general setting.
The formula is the principal result of this paper. It gives a p-adic criterion for E to have analytic rank one. For such curves, the p-adic L-value in turn leads to a p-adic construction of a rational point of infinite order which is independent of the choice of
![]() $v_{-}$
(cf. Corollary 4.9).
$v_{-}$
(cf. Corollary 4.9).
Our second result is an interpolation of the Rubin p-adic L-function at higher order characters in
![]() $\Xi ^{-\varepsilon }$
.
$\Xi ^{-\varepsilon }$
.
Theorem 1.2. Let
![]() $E_{/{\mathbb {Q}}}$
be a CM elliptic curve and K the CM field. Let
$E_{/{\mathbb {Q}}}$
be a CM elliptic curve and K the CM field. Let
![]() $\varphi $
be the associated Hecke character and
$\varphi $
be the associated Hecke character and
![]() $\varepsilon $
the sign of the root number of
$\varepsilon $
the sign of the root number of
![]() $\varphi $
. Let
$\varphi $
. Let
![]() $p\geq 5$
be a prime of good supersingular reduction for
$p\geq 5$
be a prime of good supersingular reduction for
![]() $E_{/{\mathbb {Q}}}$
and
$E_{/{\mathbb {Q}}}$
and
![]() $\mathscr {L}_{E}$
the Rubin p-adic L-function as in (1.4). Let
$\mathscr {L}_{E}$
the Rubin p-adic L-function as in (1.4). Let
![]() $\chi \in \Xi ^{-\varepsilon }$
be a Hecke character with conductor
$\chi \in \Xi ^{-\varepsilon }$
be a Hecke character with conductor
![]() $p^{n+1}$
. Let
$p^{n+1}$
. Let
![]() $z_{\chi } \in H^1(K_{n},T_pE)^{\chi }$
be the image of a system of elliptic units of E (cf. §3.1.2). Then,
$z_{\chi } \in H^1(K_{n},T_pE)^{\chi }$
be the image of a system of elliptic units of E (cf. §3.1.2). Then,
and it has the following properties.
-
(a) We have
 $$ \begin{align*} \mathscr{L}_{E}(\chi^{-1}) =\delta_\chi(v_{-\varepsilon}) \cdot \log_{\omega}(z_{\chi}). \end{align*} $$
$$ \begin{align*} \mathscr{L}_{E}(\chi^{-1}) =\delta_\chi(v_{-\varepsilon}) \cdot \log_{\omega}(z_{\chi}). \end{align*} $$
-
(b) If
 ${\mathrm {ord}}_{s=1}L(\varphi \chi ^{-1},s)=1$
, then
${\mathrm {ord}}_{s=1}L(\varphi \chi ^{-1},s)=1$
, then
 $z_{\chi }\in H^1_{\mathrm {{f}}}(K_{n},V_pE)^{\chi }$
is a generator of the
$z_{\chi }\in H^1_{\mathrm {{f}}}(K_{n},V_pE)^{\chi }$
is a generator of the
 $\mathbb {Q}_p(\chi )$
-vector space
$\mathbb {Q}_p(\chi )$
-vector space
 $(E(K_n)\otimes \mathbb {Q}_p(\chi ))^\chi $
.
$(E(K_n)\otimes \mathbb {Q}_p(\chi ))^\chi $
.
See also Theorem 3.16 in a more general setting.
Note that
![]() ${\mathrm {ord}}_{s=1}L(\varphi \chi ,s)=1$
for all but finitely many
${\mathrm {ord}}_{s=1}L(\varphi \chi ,s)=1$
for all but finitely many
![]() $\chi \in \Xi ^{-\varepsilon }$
(cf. [Reference Rohrlich45]). So, in view of Theorem 1.2 (b), the Rubin p-adic L-function leads to a construction of new points of infinite order in the alternate anticyclotomic layers (cf. (1.1)).
$\chi \in \Xi ^{-\varepsilon }$
(cf. [Reference Rohrlich45]). So, in view of Theorem 1.2 (b), the Rubin p-adic L-function leads to a construction of new points of infinite order in the alternate anticyclotomic layers (cf. (1.1)).
Remark 1.3. For
![]() $\chi \in \Xi ^{-\varepsilon }$
, one expects that if
$\chi \in \Xi ^{-\varepsilon }$
, one expects that if
![]() $z_{\chi ^{-1}}$
is non-zero, then
$z_{\chi ^{-1}}$
is non-zero, then
![]() ${\mathrm {ord}}_{s=1}L(\varphi \chi ,s)=1$
and
${\mathrm {ord}}_{s=1}L(\varphi \chi ,s)=1$
and
An evidence appears in [Reference Burungale, Kobayashi and Ota12, Thm. 2.4]. It seems interesting to compare Theorems 1.1 and 1.2 with the exceptional zero conjecture of Mazur, Tate and Teitelbaum [Reference Mazur, Tate and Teitelbaum39].
As a corollary of the above theorems, we obtain a refined (non-asymptotic) version of (1.1).
Corollary 1.4. Let
![]() $E_{/{\mathbb {Q}}}$
be a CM elliptic curve and K the CM field.
$E_{/{\mathbb {Q}}}$
be a CM elliptic curve and K the CM field.
-
(i) If
 $L(E_{/\mathbb {Q}}, 1)/\Omega $
is a p-adic unit, then for all
$L(E_{/\mathbb {Q}}, 1)/\Omega $
is a p-adic unit, then for all
 $n \geq 1$
, we have
$n \geq 1$
, we have  $$ \begin{align*}{\mathrm{corank}}_{{\mathbb {Z}}_{p}}{\mathrm{Sel}}_{p^\infty}(E_{/K_{n}}) -{\mathrm{corank}}_{{\mathbb {Z}}_{p}}{\mathrm{Sel}}_{p^{\infty}}(E_{/K_{n-1}}) =\varepsilon_{n}p^{n-1}(p-1), \end{align*} $$
$$ \begin{align*}{\mathrm{corank}}_{{\mathbb {Z}}_{p}}{\mathrm{Sel}}_{p^\infty}(E_{/K_{n}}) -{\mathrm{corank}}_{{\mathbb {Z}}_{p}}{\mathrm{Sel}}_{p^{\infty}}(E_{/K_{n-1}}) =\varepsilon_{n}p^{n-1}(p-1), \end{align*} $$
where
 $\varepsilon _{n}=0$
(resp.
$\varepsilon _{n}=0$
(resp.
 $2$
) for n odd (resp. even).
$2$
) for n odd (resp. even). -
(ii) Suppose that
 $\mathrm {ord}_{s=1}L(E_{/\mathbb {Q}},s)=1$
and there exists a rational point
$\mathrm {ord}_{s=1}L(E_{/\mathbb {Q}},s)=1$
and there exists a rational point
 $P \in E(\mathbb {Q})$
whose image generates the free
$P \in E(\mathbb {Q})$
whose image generates the free
 $\mathbb {Z}_p$
-module
$\mathbb {Z}_p$
-module
 $E(\mathbb {Q}_p)/E({\mathbb {Q}}_{p})_{{\mathrm {tor}}}$
of rank
$E(\mathbb {Q}_p)/E({\mathbb {Q}}_{p})_{{\mathrm {tor}}}$
of rank
 $1$
. If
$1$
. If  $$ \begin{align*}L'(E_{/\mathbb{Q}},1)/\Omega \langle P, P \rangle_\infty\end{align*} $$
$$ \begin{align*}L'(E_{/\mathbb{Q}},1)/\Omega \langle P, P \rangle_\infty\end{align*} $$
is a p-adic unit, then for all
 $n \geq 1$
, we have
$n \geq 1$
, we have  $$ \begin{align*}{\mathrm{corank}}_{{\mathbb {Z}}_{p}}{\mathrm{Sel}}_{p^\infty}(E_{/K_{n}}) -{\mathrm{corank}}_{{\mathbb {Z}}_{p}}{\mathrm{Sel}}_{p^{\infty}}(E_{/K_{n-1}}) =\varepsilon_{n}p^{n-1}(p-1), \end{align*} $$
$$ \begin{align*}{\mathrm{corank}}_{{\mathbb {Z}}_{p}}{\mathrm{Sel}}_{p^\infty}(E_{/K_{n}}) -{\mathrm{corank}}_{{\mathbb {Z}}_{p}}{\mathrm{Sel}}_{p^{\infty}}(E_{/K_{n-1}}) =\varepsilon_{n}p^{n-1}(p-1), \end{align*} $$
where
 $\varepsilon _{n}=0$
(resp.
$\varepsilon _{n}=0$
(resp.
 $2$
) for n even (resp. odd).
$2$
) for n even (resp. odd).
In particular, if
![]() is finite, then
is finite, then
A key to the proof of main results is a theory of local points, similarly as [Reference Kobayashi31, §8] underlies the cyclotomic signed Iwasawa theory [Reference Kobayashi31] (cf. Section 2.3.) In the case of cyclotomic deformation, such a theory is the core of Perrin-Riou theory. However, Perrin-Riou theory for the anticyclotomic
![]() ${\mathbb {Z}}_p$
-extension is not yet developed sufficiently to be applicable to our case. Instead, we use Rubin’s conjecture to construct local points. It may give some insight towards a Perrin-Riou theory for the anticyclotomic
${\mathbb {Z}}_p$
-extension is not yet developed sufficiently to be applicable to our case. Instead, we use Rubin’s conjecture to construct local points. It may give some insight towards a Perrin-Riou theory for the anticyclotomic
![]() ${\mathbb {Z}}_p$
-extension.
${\mathbb {Z}}_p$
-extension.
1.2.3 p-converse to a theorem of Gross–Zagier and Kolyvagin
Theorem 1.5. Let
![]() $E_{/{\mathbb {Q}}}$
be a CM elliptic curve with good supersingular reduction at
$E_{/{\mathbb {Q}}}$
be a CM elliptic curve with good supersingular reduction at
![]() $p\geq 5$
. If
$p\geq 5$
. If
![]() ${\mathrm {corank}}_{{\mathbb {Z}}_{p}}{\mathrm {Sel}}_{p^{\infty }}(E)=1$
and
${\mathrm {corank}}_{{\mathbb {Z}}_{p}}{\mathrm {Sel}}_{p^{\infty }}(E)=1$
and
![]() is finite, then
is finite, then
![]() ${\mathrm {ord}}_{s=1}L(E_{/{\mathbb {Q}}},s)=1$
.
${\mathrm {ord}}_{s=1}L(E_{/{\mathbb {Q}}},s)=1$
.
See also Theorem 4.18 in a more general setting. Just as the Bertolini–Darmon–Prasanna formula is employed in the proof of Skinner’s p-converse [Reference Skinner52], our approach is based on Theorem 1.1.
Remark 1.6.
-
(i) The first results towards the p-converse were due to Rubin [Reference Rubin51], which treated CM elliptic curves and ordinary primes p. The first general results for non-CM curves were independently due to Skinner [Reference Skinner52] and Zhang [Reference Zhang56] a few years back.
-
(ii) One may seek a refined p-converse:
(1.6) $$ \begin{align} {\mathrm{corank}}_{{\mathbb {Z}}_{p}}{\mathrm{Sel}}_{p^{\infty}}(E)=1 \implies {\mathrm{ord}}_{s=1}L(E_{/{\mathbb {Q}}},s)=1 \end{align} $$
$$ \begin{align} {\mathrm{corank}}_{{\mathbb {Z}}_{p}}{\mathrm{Sel}}_{p^{\infty}}(E)=1 \implies {\mathrm{ord}}_{s=1}L(E_{/{\mathbb {Q}}},s)=1 \end{align} $$
(cf. [Reference Zhang56], [Reference Burungale and Tian18], [Reference Burungale, Skinner and Tian16],[Reference Burungale, Castella, Skinner and Tian10], [Reference Burungale, Castella, Skinner and Tian11]). While it may be possible to approach Theorem 1.5 via the p-adic Gross–Zagier formula [Reference Kobayashi32], with a view to (1.6), our approach instead employs Theorem 1.1.
Background
An impetus to Theorems 1.1 and 1.2 is a formula of Rubin. For primes p split in an imaginary quadratic field K, Rubin proved an influential formula [Reference Rubin50] which links certain values of the Katz p-adic L-function of K to the formal group logarithm of rational points on elliptic curves with CM by K (cf. [Reference Perrin-Riou42], [Reference Perrin-Riou44]). The last decade has led to a revival of Rubin’s formula. For an arbitrary elliptic curve
![]() $E_{/{\mathbb {Q}}}$
and K an imaginary quadratic field satisfying Heegner hypothesis for E with p split, the Bertolini–Darmon–Prasanna (BDP) formula relates certain values of a Rankin–Selberg p-adic L-function
$E_{/{\mathbb {Q}}}$
and K an imaginary quadratic field satisfying Heegner hypothesis for E with p split, the Bertolini–Darmon–Prasanna (BDP) formula relates certain values of a Rankin–Selberg p-adic L-function
![]() $\mathscr {L}_{E}^{\mathrm {Gr}}$
of
$\mathscr {L}_{E}^{\mathrm {Gr}}$
of
![]() $E_{/K}$
with the formal group logarithm of Heegner points on E (cf. [Reference Bertolini, Darmon and Prasanna6], [Reference Kobayashi34]). Since its advent, the BDP formula has influenced the arithmetic of elliptic curves and inspired progress towards the BSD conjecture, with an instance being p-converse to the Gross–Zagier and Kolyvagin theorem due to Skinner (cf. [Reference Skinner52]), which is a p-adic criterion for
$E_{/K}$
with the formal group logarithm of Heegner points on E (cf. [Reference Bertolini, Darmon and Prasanna6], [Reference Kobayashi34]). Since its advent, the BDP formula has influenced the arithmetic of elliptic curves and inspired progress towards the BSD conjecture, with an instance being p-converse to the Gross–Zagier and Kolyvagin theorem due to Skinner (cf. [Reference Skinner52]), which is a p-adic criterion for
![]() $E_{/{\mathbb {Q}}}$
to have both algebraic and analytic rank one. The p-converse is based on the BDP formula and an Iwasawa theory of
$E_{/{\mathbb {Q}}}$
to have both algebraic and analytic rank one. The p-converse is based on the BDP formula and an Iwasawa theory of
![]() $\mathscr {L}_{E}^{\mathrm {Gr}}$
. Subsequently, Liu–Zhang–Zhang interpreted the BDP formula as a p-adic Waldspurger formula and generalised it to modular elliptic curves over totally real fields (cf. [Reference Liu, Zhang and Zhang37]).
$\mathscr {L}_{E}^{\mathrm {Gr}}$
. Subsequently, Liu–Zhang–Zhang interpreted the BDP formula as a p-adic Waldspurger formula and generalised it to modular elliptic curves over totally real fields (cf. [Reference Liu, Zhang and Zhang37]).
An emerging search is the analogue of the BDP formulaFootnote 2 over imaginary quadratic fields with p non-split, and a pertinent Iwasawa main conjecture (the conjectural backdrop of Iwasawa theory excludes such a non-split setting; cf. [Reference Greenberg25], [Reference Perrin-Riou44], [Reference Kobayashi31]). The ensuing CM case is perhaps the first instance, whose investigation we plan to continue (cf. [Reference Burungale, Kobayashi and Ota13], [Reference Burungale, Kobayashi, Ota and Yasuda14]).
1.3 Plan
Section 2 presents the local theory. In Section 3, certain global aspects appear, including (1.1) and Theorem 1.2. Then Section 4 treats Theorems 1.1 and 1.5.
The proof of Theorem 1.1 is based on the appendices to which the reader may refer prior to Section 4. Appendix A describes a variant of the p-adic Gross–Zagier formula [Reference Kobayashi32] in which the p-adic logarithm of Heegner points appears (see Theorem A.6). Appendix B exhibits another consequence: the Perrin-Riou conjecture [Reference Perrin-Riou42] for
![]() ${\mathrm {GL}}_2$
-type abelian varieties at primes of good non-ordinary reduction (see Theorem B.3).
${\mathrm {GL}}_2$
-type abelian varieties at primes of good non-ordinary reduction (see Theorem B.3).
2 Local points
2.1 The set-up
We introduce the module of anticyclotomic local units as well as its signed submodules following [Reference Rubin47], [Reference Burungale, Kobayashi and Ota12].
2.1.1 Notation
Let
![]() $p\ge 5$
be a prime. Let
$p\ge 5$
be a prime. Let
![]() $\Phi $
be the unramified quadratic extension of
$\Phi $
be the unramified quadratic extension of
![]() $\mathbb {Q}_p$
and
$\mathbb {Q}_p$
and
![]() ${\mathcal {O}}$
the integer ring. We fix a Lubin–Tate formal group
${\mathcal {O}}$
the integer ring. We fix a Lubin–Tate formal group
![]() $\mathscr {F}$
over
$\mathscr {F}$
over
![]() $\mathcal {O}$
for the uniformizing parameter
$\mathcal {O}$
for the uniformizing parameter
![]() $\pi :=-p$
. Let
$\pi :=-p$
. Let
![]() $\lambda $
denote the logarithm of
$\lambda $
denote the logarithm of
![]() $\mathscr {F}$
.
$\mathscr {F}$
.
For
![]() $n\ge 0$
, write
$n\ge 0$
, write
![]() $\Phi _n=\Phi ({\mathscr {F}}[\pi ^{n+1}])$
, the extension of
$\Phi _n=\Phi ({\mathscr {F}}[\pi ^{n+1}])$
, the extension of
![]() $\Phi $
in
$\Phi $
in
![]() ${\mathbb {C}}_{p}$
generated by the
${\mathbb {C}}_{p}$
generated by the
![]() $\pi ^{n+1}$
-torsion points of
$\pi ^{n+1}$
-torsion points of
![]() $\mathscr {F}$
, and put
$\mathscr {F}$
, and put
![]() $\Phi _{\infty }=\cup _{n\ge 0}\Phi _n.$
Let
$\Phi _{\infty }=\cup _{n\ge 0}\Phi _n.$
Let
be the natural isomorphism induced by the Galois action on the
![]() $\pi $
-adic Tate module
$\pi $
-adic Tate module
![]() $T_{\pi }{\mathscr {F}}=:T.$
Let
$T_{\pi }{\mathscr {F}}=:T.$
Let
![]() $\Theta _n$
be the subfield of
$\Theta _n$
be the subfield of
![]() $\Phi _{n}$
with
$\Phi _{n}$
with
![]() $[\Theta _n:\Phi ]=p^{2n}$
and
$[\Theta _n:\Phi ]=p^{2n}$
and
![]() $\Theta _{\infty }=\cup _{n\ge 1}\Theta _n$
the
$\Theta _{\infty }=\cup _{n\ge 1}\Theta _n$
the
![]() ${\mathbb {Z}}_p^2$
-extension of
${\mathbb {Z}}_p^2$
-extension of
![]() $\Phi $
. Let
$\Phi $
. Let
![]() $\Psi _\infty $
be the anticyclotomic
$\Psi _\infty $
be the anticyclotomic
![]() ${\mathbb {Z}}_p$
-extension of
${\mathbb {Z}}_p$
-extension of
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi _n$
the n-th layer. We put
$\Psi _n$
the n-th layer. We put
![]() $G:= {\mathrm {Gal}}(\Theta _{\infty }/\Phi ) \cong {\mathbb {Z}}_p^{2}$
,
$G:= {\mathrm {Gal}}(\Theta _{\infty }/\Phi ) \cong {\mathbb {Z}}_p^{2}$
,
![]() $G^{-}:={\mathrm {Gal}}(\Psi _{\infty }/\Phi )\cong {\mathbb {Z}}_{p}$
and
$G^{-}:={\mathrm {Gal}}(\Psi _{\infty }/\Phi )\cong {\mathbb {Z}}_{p}$
and
![]() $\Delta :={\mathrm {Gal}}(\Phi _{\infty }/ \Theta _{\infty })={\mathrm {Gal}}(\Phi _0/\Phi ) \cong ({\mathcal {O}}/p)^{\times }.$
Fix a topological generator
$\Delta :={\mathrm {Gal}}(\Phi _{\infty }/ \Theta _{\infty })={\mathrm {Gal}}(\Phi _0/\Phi ) \cong ({\mathcal {O}}/p)^{\times }.$
Fix a topological generator
![]() $\gamma $
of
$\gamma $
of
![]() $G^-$
.
$G^-$
.
Let
![]() $U_n$
be the group of principal units in
$U_n$
be the group of principal units in
![]() $\Phi _n$
, that is, the group of elements in
$\Phi _n$
, that is, the group of elements in
![]() ${\mathcal {O}}_{\Phi _n}^{\times }$
congruent to one modulo the maximal ideal. Let
${\mathcal {O}}_{\Phi _n}^{\times }$
congruent to one modulo the maximal ideal. Let
where the superscript
![]() $\Delta $
means the
$\Delta $
means the
![]() $\Delta $
-invariants. Define the Iwasawa algebras
$\Delta $
-invariants. Define the Iwasawa algebras
It is known that
![]() $U_{\infty }^{*}$
is a free
$U_{\infty }^{*}$
is a free
![]() $\Lambda _2$
-module of rank
$\Lambda _2$
-module of rank
![]() $2$
(cf. [Reference Wintenberger54]). A primary object is the anticyclotomic projection
$2$
(cf. [Reference Wintenberger54]). A primary object is the anticyclotomic projection
Let
![]() $\delta _n: U_{\infty }^{*} \to \Phi _n$
be the Coates–Wiles homomorphism as in [Reference Burungale, Kobayashi and Ota12, §2]. For a finite character
$\delta _n: U_{\infty }^{*} \to \Phi _n$
be the Coates–Wiles homomorphism as in [Reference Burungale, Kobayashi and Ota12, §2]. For a finite character
![]() $\chi $
of
$\chi $
of
![]() ${\mathrm {Gal}}(\Phi _{\infty }/\Phi )$
of conductor dividing
${\mathrm {Gal}}(\Phi _{\infty }/\Phi )$
of conductor dividing
![]() $p^{n+1}$
and
$p^{n+1}$
and
![]() $u \in U_{\infty }^*$
, let
$u \in U_{\infty }^*$
, let
 $$ \begin{align} \delta_{\chi}(u)= \frac{1}{\pi^{n+1}}\sum_{\sigma\in {\mathrm{Gal}}(\Phi_n/\Phi)}\chi(\sigma)\delta_n(u)^{\sigma}. \end{align} $$
$$ \begin{align} \delta_{\chi}(u)= \frac{1}{\pi^{n+1}}\sum_{\sigma\in {\mathrm{Gal}}(\Phi_n/\Phi)}\chi(\sigma)\delta_n(u)^{\sigma}. \end{align} $$
If
![]() $\chi $
factors through
$\chi $
factors through
![]() $G^-$
, then
$G^-$
, then
![]() $\delta _{\chi }$
factors through
$\delta _{\chi }$
factors through
![]() $V_{\infty }^*$
(cf. [Reference Rubin47, Lem. 2.1 (ii)]).
$V_{\infty }^*$
(cf. [Reference Rubin47, Lem. 2.1 (ii)]).
2.1.2 Rubin’s conjecture
Let
![]() $\Xi $
be the set of finite characters of
$\Xi $
be the set of finite characters of
![]() $G^-$
. Let
$G^-$
. Let
 $$ \begin{align*} \Xi^+&={\{}\chi \in \Xi\ | \text{ }\mathrm{cond^r}\chi \text{ is an even power of } p{\}},\\ \Xi^-&={\{}\chi \in \Xi\ | \text{ } \mathrm{cond^r}\chi \text{ is an odd power of } p{\}}. \end{align*} $$
$$ \begin{align*} \Xi^+&={\{}\chi \in \Xi\ | \text{ }\mathrm{cond^r}\chi \text{ is an even power of } p{\}},\\ \Xi^-&={\{}\chi \in \Xi\ | \text{ } \mathrm{cond^r}\chi \text{ is an odd power of } p{\}}. \end{align*} $$
Define
Rubin showed that
![]() $V^{*,\pm }_{\infty }$
is a free
$V^{*,\pm }_{\infty }$
is a free
![]() $\Lambda $
-module of rank one (cf. [Reference Rubin47, Prop. 8.1]).
$\Lambda $
-module of rank one (cf. [Reference Rubin47, Prop. 8.1]).
The following is central to the construction of local points.
Theorem 2.1. (Rubin’s conjecture) We have
This was proposed by Rubin as [Reference Rubin47, Conj. 2.2] and recently proved [Reference Burungale, Kobayashi and Ota12, Thm. 2.1].
2.2 Local cohomology
2.2.1 Kummer theory
We recast the modules of anticyclotomic local units in terms of the local Iwasawa cohomology.
Define a natural isomorphism of
![]() ${\mathcal {O}}[\![{\mathrm {Gal}}(\Phi _{\infty }/\Phi )]\!]$
-modules
${\mathcal {O}}[\![{\mathrm {Gal}}(\Phi _{\infty }/\Phi )]\!]$
-modules
as the composite
 $$ \begin{align*} \varprojlim_n(U_n\otimes {\mathcal {O}})\otimes T^{\otimes -1}&\cong \varprojlim_nH^1(\Phi_n, {\mathcal {O}}(1))\otimes T^{\otimes -1} \\ &\cong \varprojlim_nH^1(\Phi_n, {\mathcal {O}}/\pi^n(1))\otimes T^{\otimes -1} \\ &\cong \varprojlim_nH^1(\Phi_n, T^{\otimes -1}(1)/\pi^n) \\ &\cong \varprojlim_n H^1(\Phi_n, T^{\otimes -1}(1)). \end{align*} $$
$$ \begin{align*} \varprojlim_n(U_n\otimes {\mathcal {O}})\otimes T^{\otimes -1}&\cong \varprojlim_nH^1(\Phi_n, {\mathcal {O}}(1))\otimes T^{\otimes -1} \\ &\cong \varprojlim_nH^1(\Phi_n, {\mathcal {O}}/\pi^n(1))\otimes T^{\otimes -1} \\ &\cong \varprojlim_nH^1(\Phi_n, T^{\otimes -1}(1)/\pi^n) \\ &\cong \varprojlim_n H^1(\Phi_n, T^{\otimes -1}(1)). \end{align*} $$
Here, the first isomorphism is the Kummer map and the third is a consequence of the
![]() ${\mathrm {Gal}}(\Phi _{\infty }/\Phi _n)$
-action on
${\mathrm {Gal}}(\Phi _{\infty }/\Phi _n)$
-action on
![]() ${\mathcal {O}}(1)\otimes T^{\otimes -1}/\pi ^n$
being trivial. The
${\mathcal {O}}(1)\otimes T^{\otimes -1}/\pi ^n$
being trivial. The
![]() $\Delta $
-invariants of (2.3) give an isomorphism
$\Delta $
-invariants of (2.3) give an isomorphism
of
![]() $\Lambda _2$
-modules.
$\Lambda _2$
-modules.
For a finite extension L of
![]() $\Phi $
, let
$\Phi $
, let
be the dual exponential map which arises from the identification of
![]() $\mathrm {Fil}^0D_{\mathrm {dR}}(T^{\otimes -1}(1)\otimes {\mathbb {Q}}_p)$
with
$\mathrm {Fil}^0D_{\mathrm {dR}}(T^{\otimes -1}(1)\otimes {\mathbb {Q}}_p)$
with
![]() $\Phi $
so that the invariant differential
$\Phi $
so that the invariant differential
![]() $d\lambda $
corresponds to
$d\lambda $
corresponds to
![]() $1$
(cf. [Reference Kato29, §1.2.4, Ch. II]).
$1$
(cf. [Reference Kato29, §1.2.4, Ch. II]).
By the explicit reciprocity law of Wiles (cf. [Reference Kato29, Thm. 2.1.7, Ch. II]), note that the following diagram

commutes, where the upper horizontal map is (2.4). The anticyclotomic projection induces an isomorphism
as well as a commutative diagram

where
![]() $\delta _n^{\mathrm {ac}}:= \mathrm {Tr}_{\Phi _n/\Psi _{n}}\circ \delta _n$
. Hence, for a character
$\delta _n^{\mathrm {ac}}:= \mathrm {Tr}_{\Phi _n/\Psi _{n}}\circ \delta _n$
. Hence, for a character
![]() $\chi $
of
$\chi $
of
![]() ${\mathrm {Gal}}(\Psi _n/\Phi )$
and
${\mathrm {Gal}}(\Psi _n/\Phi )$
and
![]() $v=(v_m)_{m\ge 0} \in V_{\infty }^*=\varprojlim _m H^1(\Psi _m, T^{\otimes -1}(1))$
(cf. (2.7)), we have
$v=(v_m)_{m\ge 0} \in V_{\infty }^*=\varprojlim _m H^1(\Psi _m, T^{\otimes -1}(1))$
(cf. (2.7)), we have
 $$ \begin{align} \delta_{\chi}(v)= \sum_{\sigma \in {\mathrm{Gal}}(\Psi_n/\Phi)}\exp^*_{\Psi_n}(v_n^{\sigma})\chi(\sigma). \end{align} $$
$$ \begin{align} \delta_{\chi}(v)= \sum_{\sigma \in {\mathrm{Gal}}(\Psi_n/\Phi)}\exp^*_{\Psi_n}(v_n^{\sigma})\chi(\sigma). \end{align} $$
Therefore, we may naturally identify
![]() $V_{\infty }^{*, \pm }$
with the module
$V_{\infty }^{*, \pm }$
with the module
![]() $\mathcal {H}^1_{\pm }$
introduced in (1.2), and Theorem 2.1 implies the decomposition (1.3) of
$\mathcal {H}^1_{\pm }$
introduced in (1.2), and Theorem 2.1 implies the decomposition (1.3) of
![]() $\varprojlim _{m}H^1(\Psi _m, T^{\otimes -1}(1))$
.
$\varprojlim _{m}H^1(\Psi _m, T^{\otimes -1}(1))$
.
Let
![]() $H^1_{\mathrm {f}}(\Psi _{n}, T)$
and
$H^1_{\mathrm {f}}(\Psi _{n}, T)$
and
![]() $H^1_{\mathrm {f}}(\Psi _{n}, T^{\otimes -1}(1))$
denote the finite part of
$H^1_{\mathrm {f}}(\Psi _{n}, T^{\otimes -1}(1))$
denote the finite part of
![]() $H^1_{}(\Psi _{n}, T)$
and
$H^1_{}(\Psi _{n}, T)$
and
![]() $ H^1_{}(\Psi _{n}, T^{\otimes -1}(1))$
, respectively.
$ H^1_{}(\Psi _{n}, T^{\otimes -1}(1))$
, respectively.
Lemma 2.2.
-
(1) The quotient by the ideal
 $(\gamma ^{p^n}-1)\Lambda $
induces an isomorphism (2.10)
$(\gamma ^{p^n}-1)\Lambda $
induces an isomorphism (2.10) $$ \begin{align} V_{\infty}^{*}/(\gamma^{p^n}-1)\cong H^1(\Psi_{n}, T^{\otimes -1}(1)). \end{align} $$
$$ \begin{align} V_{\infty}^{*}/(\gamma^{p^n}-1)\cong H^1(\Psi_{n}, T^{\otimes -1}(1)). \end{align} $$
-
(2) The
 ${\mathcal {O}}$
-module
${\mathcal {O}}$
-module
 $H^1_{\mathrm {f}}(\Psi _{n}, T^{\otimes -1}(1))$
coincides with
$H^1_{\mathrm {f}}(\Psi _{n}, T^{\otimes -1}(1))$
coincides with
 $\mathrm {ker}(\delta ^{\mathrm {ac}}_{n})$
via (2.10).
$\mathrm {ker}(\delta ^{\mathrm {ac}}_{n})$
via (2.10).
Proof.
-
(1) By definition,
 $V_{\infty }^{*}/(\gamma ^{p^n}-1)$
is isomorphic to
$V_{\infty }^{*}/(\gamma ^{p^n}-1)$
is isomorphic to
 $\varprojlim _m H^1(\Psi _m, T^{\otimes -1}(1))/(\gamma ^{p^n}-1)$
. In light of the inflation-restriction sequence and [Reference Rubin47, Prop. 4.5 (ii)], it follows that
$\varprojlim _m H^1(\Psi _m, T^{\otimes -1}(1))/(\gamma ^{p^n}-1)$
. In light of the inflation-restriction sequence and [Reference Rubin47, Prop. 4.5 (ii)], it follows that
 $\varprojlim _m H^1(\Psi _m, T^{\otimes -1}(1))/(\gamma ^{p^n}-1)$
is isomorphic to the Pontryagin dual of The local duality thus implies (2.10).
$\varprojlim _m H^1(\Psi _m, T^{\otimes -1}(1))/(\gamma ^{p^n}-1)$
is isomorphic to the Pontryagin dual of The local duality thus implies (2.10). $$ \begin{align*}H^0(\Psi_n, H^1(\Psi_{\infty}, {\mathscr {F}}[\pi^{\infty}])) \cong H^1(\Psi_n, {\mathscr {F}}[\pi^{\infty}]).\end{align*} $$
$$ \begin{align*}H^0(\Psi_n, H^1(\Psi_{\infty}, {\mathscr {F}}[\pi^{\infty}])) \cong H^1(\Psi_n, {\mathscr {F}}[\pi^{\infty}]).\end{align*} $$
-
(2) Note that
 $H^1_{\mathrm {f}}(\Psi _{n}, T)$
coincides with the Kummer image of
$H^1_{\mathrm {f}}(\Psi _{n}, T)$
coincides with the Kummer image of
 ${\mathscr {F}}({\mathfrak {m}}_n)$
in
${\mathscr {F}}({\mathfrak {m}}_n)$
in
 $H^1(\Psi _{n}, T)$
, and that
$H^1(\Psi _{n}, T)$
, and that
 $H^1_{\mathrm {f}}(\Psi _{n}, T^{\otimes -1}(1))$
coincides with the kernel of
$H^1_{\mathrm {f}}(\Psi _{n}, T^{\otimes -1}(1))$
coincides with the kernel of
 $\exp ^*_{\Psi _n}: H^1_{}(\Psi _{n}, T^{\otimes -1}(1)) \to \Psi _n$
. Hence, by the commutative diagram (2.8), the proof concludes.
$\exp ^*_{\Psi _n}: H^1_{}(\Psi _{n}, T^{\otimes -1}(1)) \to \Psi _n$
. Hence, by the commutative diagram (2.8), the proof concludes.
In the following, (2.10) will be often treated as an identification.
2.2.2 An optimal basis
We introduce a basis of the submodule of signed anticyclotomic local units and duality pairings, which will be used in the construction of local points.
We fix a
![]() $\Lambda $
-basis
$\Lambda $
-basis
![]() $v_\pm $
of
$v_\pm $
of
![]() $V_{\infty }^{*, \pm }$
and regard it as an element of
$V_{\infty }^{*, \pm }$
and regard it as an element of
![]() $\varprojlim _n H^1(\Psi _n, T^{\otimes -1}(1))$
via (2.7).
$\varprojlim _n H^1(\Psi _n, T^{\otimes -1}(1))$
via (2.7).
For
![]() $n\ge 0$
, put
$n\ge 0$
, put
![]() $\Lambda _n={\mathcal {O}}[\mathrm {Gal}(\Psi _n/\Phi )]$
. Let
$\Lambda _n={\mathcal {O}}[\mathrm {Gal}(\Psi _n/\Phi )]$
. Let
![]() $v_{\pm , n}$
denote the image of
$v_{\pm , n}$
denote the image of
![]() $v_{\pm }$
in
$v_{\pm }$
in
![]() $H^1(\Psi _n, T^{\otimes -1}(1))$
via (2.10). Let
$H^1(\Psi _n, T^{\otimes -1}(1))$
via (2.10). Let
be the natural pairing.
Lemma 2.3.
-
(1)
 $\{v_{+, n}, v_{-,n}\}$
is a
$\{v_{+, n}, v_{-,n}\}$
is a
 $\Lambda _n$
-basis of
$\Lambda _n$
-basis of
 $H^1(\Psi _n, T^{\otimes -1}(1))$
.
$H^1(\Psi _n, T^{\otimes -1}(1))$
. -
(2)
 $(\ \ , \ \ )_n$
is a perfect pairing.
$(\ \ , \ \ )_n$
is a perfect pairing. -
(3)
 $H^1_{\mathrm {f}}(\Psi _{n}, T)$
and
$H^1_{\mathrm {f}}(\Psi _{n}, T)$
and
 $H^1_{\mathrm {f}}(\Psi _{n}, T^{\otimes -1}(1))$
are orthogonal complements of each other under the pairing.
$H^1_{\mathrm {f}}(\Psi _{n}, T^{\otimes -1}(1))$
are orthogonal complements of each other under the pairing.
Proof. The first assertion is a simple consequence of Theorem 2.1.
Note that
![]() $T^{\otimes -1}(1) \cong T^{\tau }$
as an
$T^{\otimes -1}(1) \cong T^{\tau }$
as an
![]() ${\mathcal {O}}[G_{\Phi }]$
-module, where
${\mathcal {O}}[G_{\Phi }]$
-module, where
![]() $T^{\tau }$
denotes conjugation of T by the complex conjugate. Then, by [Reference Rubin47, Prop. 4.5],
$T^{\tau }$
denotes conjugation of T by the complex conjugate. Then, by [Reference Rubin47, Prop. 4.5],
![]() $H^1(\Psi _n, T)$
and
$H^1(\Psi _n, T)$
and
![]() $H^1(\Psi _n, T^{\otimes -1}(1))\cong H^1(\Psi _n, T)$
are
$H^1(\Psi _n, T^{\otimes -1}(1))\cong H^1(\Psi _n, T)$
are
![]() ${\mathcal {O}}$
-free, and we have natural identifications
${\mathcal {O}}$
-free, and we have natural identifications
Hence, the local duality induces
where the isomorphism arises from the perfect pairing
It follows that the map
![]() $H^1(\Psi _n, T) \to {\mathrm {Hom}}_{{\mathcal {O}}}(H^1(\Psi _n, T^{\otimes -1}(1)),{\mathcal {O}})$
induced by
$H^1(\Psi _n, T) \to {\mathrm {Hom}}_{{\mathcal {O}}}(H^1(\Psi _n, T^{\otimes -1}(1)),{\mathcal {O}})$
induced by
![]() $(\ \ , \ \ )_n$
is an isomorphism. By replacing
$(\ \ , \ \ )_n$
is an isomorphism. By replacing
![]() $T $
with
$T $
with
![]() $T^{\otimes -1}(1)$
, the map
$T^{\otimes -1}(1)$
, the map
![]() $H^1(\Psi _n, T^{\otimes -1}(1)) \to {\mathrm {Hom}}_{{\mathcal {O}}}(H^1(\Psi _n, T),{\mathcal {O}})$
induced by
$H^1(\Psi _n, T^{\otimes -1}(1)) \to {\mathrm {Hom}}_{{\mathcal {O}}}(H^1(\Psi _n, T),{\mathcal {O}})$
induced by
![]() $(\ \ , \ \ )_n$
is also an isomorphism, and hence,
$(\ \ , \ \ )_n$
is also an isomorphism, and hence,
![]() $(\ \ , \ \ )_n$
is perfect.
$(\ \ , \ \ )_n$
is perfect.
The assertion (3) then follows from the fact that
![]() $H^1_{\mathrm {f}}(\Psi _{n}, T)\otimes \mathbb {Q}_p$
is the orthogonal complement of
$H^1_{\mathrm {f}}(\Psi _{n}, T)\otimes \mathbb {Q}_p$
is the orthogonal complement of
![]() $H^1_{\mathrm {f}}(\Psi _{n}, T^{\otimes -1}(1))\otimes \mathbb {Q}_p$
under the base change of
$H^1_{\mathrm {f}}(\Psi _{n}, T^{\otimes -1}(1))\otimes \mathbb {Q}_p$
under the base change of
![]() $(\ \ , \ \ )_n$
, and vice versa.
$(\ \ , \ \ )_n$
, and vice versa.
By Lemma 2.3, we have a perfect pairing
 $$ \begin{align} (\ \ , \ \ )_{\Lambda_n}: H^1(\Psi_n,T) \times H^1(\Psi_n, T^{\otimes -1}(1)) \to \Lambda_n,\quad (a,b) \mapsto \sum_{\sigma\in {\mathrm{Gal}}(\Psi_n/\Psi) }(a,b^{\sigma})_n\sigma, \end{align} $$
$$ \begin{align} (\ \ , \ \ )_{\Lambda_n}: H^1(\Psi_n,T) \times H^1(\Psi_n, T^{\otimes -1}(1)) \to \Lambda_n,\quad (a,b) \mapsto \sum_{\sigma\in {\mathrm{Gal}}(\Psi_n/\Psi) }(a,b^{\sigma})_n\sigma, \end{align} $$
which is sesquilinear with respect to the involution
![]() $\iota $
of
$\iota $
of
![]() $\Lambda _n$
induced by
$\Lambda _n$
induced by
![]() $\sigma \mapsto \sigma ^{-1}$
for
$\sigma \mapsto \sigma ^{-1}$
for
![]() $\sigma \in {\mathrm {Gal}}(\Psi _n/\Phi ).$
Let
$\sigma \in {\mathrm {Gal}}(\Psi _n/\Phi ).$
Let
![]() $\{v^{\perp }_{+, n}, v^{\perp }_{-,n}\} \subseteq H^1(\Psi _n,T)$
be the dual basis of
$\{v^{\perp }_{+, n}, v^{\perp }_{-,n}\} \subseteq H^1(\Psi _n,T)$
be the dual basis of
![]() $\{v_{-,n}, v_{+,n}\}$
with respect to
$\{v_{-,n}, v_{+,n}\}$
with respect to
![]() $(\ \ , \ \ )_{\Lambda _n}$
, that is,
$(\ \ , \ \ )_{\Lambda _n}$
, that is,
 $$ \begin{align} \sum_{\sigma \in {\mathrm{Gal}}(\Psi_n/\Phi)}(v^{\perp}_{\pm, n}, v_{\pm, n}^{\sigma} )_n\sigma =0,\qquad \sum_{\sigma \in {\mathrm{Gal}}(\Psi_n/\Phi)}(v^{\perp}_{\pm, n}, v_{\mp, n}^{\sigma} )_n\sigma=1. \end{align} $$
$$ \begin{align} \sum_{\sigma \in {\mathrm{Gal}}(\Psi_n/\Phi)}(v^{\perp}_{\pm, n}, v_{\pm, n}^{\sigma} )_n\sigma =0,\qquad \sum_{\sigma \in {\mathrm{Gal}}(\Psi_n/\Phi)}(v^{\perp}_{\pm, n}, v_{\mp, n}^{\sigma} )_n\sigma=1. \end{align} $$
Note that
![]() $v^{\perp }_{\pm , n}$
depends on the choice of
$v^{\perp }_{\pm , n}$
depends on the choice of
![]() $v_{\mp }$
but is independent of
$v_{\mp }$
but is independent of
![]() $v_{\pm }$
.
$v_{\pm }$
.
2.3 Local points
We introduce an optimal system of local points, which generate the signed submodules of the underlying Lubin–Tate group.
For
![]() $n\geq 0$
, let
$n\geq 0$
, let
![]() $\Xi ^{\pm }_n$
denote the set of
$\Xi ^{\pm }_n$
denote the set of
![]() $\chi \in \Xi ^{\pm }$
factoring through
$\chi \in \Xi ^{\pm }$
factoring through
![]() ${\mathrm {Gal}}(\Psi _n/\Phi )$
. For
${\mathrm {Gal}}(\Psi _n/\Phi )$
. For
![]() $\chi \in \Xi ^{\pm }_n$
, let
$\chi \in \Xi ^{\pm }_n$
, let
 $$ \begin{align*} \lambda_{\chi}(x)=\frac{1}{p^{n}} \sum_{\sigma\in {\mathrm{Gal}}(\Psi_n/\Phi)}\chi^{-1}(\sigma)\lambda(x)^{\sigma}. \end{align*} $$
$$ \begin{align*} \lambda_{\chi}(x)=\frac{1}{p^{n}} \sum_{\sigma\in {\mathrm{Gal}}(\Psi_n/\Phi)}\chi^{-1}(\sigma)\lambda(x)^{\sigma}. \end{align*} $$
Define
2.3.1
We put
for
![]() $\Phi _{p^k}(X)$
the
$\Phi _{p^k}(X)$
the
![]() $p^k$
-th cyclotomic polynomial, and we also put
$p^k$
-th cyclotomic polynomial, and we also put
![]() $\omega ^{+}_0=1$
and
$\omega ^{+}_0=1$
and
![]() $\omega ^{-}_0=\gamma -1$
.
$\omega ^{-}_0=\gamma -1$
.
Definition 2.4 (local points).
For
![]() $v_{\pm }$
and
$v_{\pm }$
and
![]() $\gamma $
as above, let
$\gamma $
as above, let
Lemma 2.5. For
![]() $n\ge 0$
,
$n\ge 0$
,
![]() $c_n^{\pm }$
lies in
$c_n^{\pm }$
lies in
![]() $H^1_{\mathrm {f}}(\Psi _n,T).$
$H^1_{\mathrm {f}}(\Psi _n,T).$
Proof. It suffices to show that for a finite character
![]() $\chi $
of
$\chi $
of
![]() ${\mathrm {Gal}}(\Psi _n/\Phi )$
, the image
${\mathrm {Gal}}(\Psi _n/\Phi )$
, the image
![]() $\chi (c_n^{\pm })$
of
$\chi (c_n^{\pm })$
of
![]() $c_n^{\pm }$
under the natural map
$c_n^{\pm }$
under the natural map
![]() $H^1(\Psi _n, T) \to H^1(\Phi , V (\chi ))$
lies in the finite part
$H^1(\Psi _n, T) \to H^1(\Phi , V (\chi ))$
lies in the finite part
![]() $H^1_{\mathrm {f}}(\Phi , V(\chi )),$
where
$H^1_{\mathrm {f}}(\Phi , V(\chi )),$
where
![]() $V(\chi ):=T\otimes \mathbb {Q}_p(\chi )$
denotes the twist of
$V(\chi ):=T\otimes \mathbb {Q}_p(\chi )$
denotes the twist of
![]() $T\otimes \mathbb {Q}_p$
by
$T\otimes \mathbb {Q}_p$
by
![]() $\chi $
.
$\chi $
.
If
![]() $\chi \in \Xi ^{\pm }$
, then
$\chi \in \Xi ^{\pm }$
, then
![]() $\chi (\omega _{n}^{\mp })=0,$
and so
$\chi (\omega _{n}^{\mp })=0,$
and so
![]() $\chi (c_n^{\pm }) \in H^1_{\mathrm {f}}(\Phi , V(\chi )).$
If
$\chi (c_n^{\pm }) \in H^1_{\mathrm {f}}(\Phi , V(\chi )).$
If
![]() $\chi \in \Xi ^{\mp },$
then
$\chi \in \Xi ^{\mp },$
then
![]() $\delta _{\chi }(v_{\pm })=0$
. Now, by Lemma 2.2 and (2.8), the image of
$\delta _{\chi }(v_{\pm })=0$
. Now, by Lemma 2.2 and (2.8), the image of
![]() $v_{\pm ,n}$
under
$v_{\pm ,n}$
under
lies in the finite part, and it gives rise to a generator of
![]() $H^1_{\mathrm {f}}(\Phi , V(\chi )^{\otimes -1}(1))$
over
$H^1_{\mathrm {f}}(\Phi , V(\chi )^{\otimes -1}(1))$
over
![]() $\Phi (\mathrm {Im}(\chi ))$
. Since
$\Phi (\mathrm {Im}(\chi ))$
. Since
![]() $H^1_{\mathrm {f}}(\Phi , V(\chi ))$
is the orthogonal complement of
$H^1_{\mathrm {f}}(\Phi , V(\chi ))$
is the orthogonal complement of
![]() $H^1_{\mathrm {f}}(\Phi , V(\chi )^{\otimes -1}(1))$
with respect to the local duality, it thus follows that
$H^1_{\mathrm {f}}(\Phi , V(\chi )^{\otimes -1}(1))$
with respect to the local duality, it thus follows that
![]() $\chi (c_n^{\pm })$
lies in the finite part.
$\chi (c_n^{\pm })$
lies in the finite part.
By Lemma 2.5, we may naturally regard
![]() $c_n^{\pm }$
as an element in
$c_n^{\pm }$
as an element in
![]() ${\mathscr {F}}({\mathfrak {m}}_n)$
. In particular,
${\mathscr {F}}({\mathfrak {m}}_n)$
. In particular,
Salient features of the local points are given by the following.
Lemma 2.6. Let
![]() $n\geq 1$
.
$n\geq 1$
.
-
(1) If
 $(-1)^{n+1}=\pm 1$
, then
$(-1)^{n+1}=\pm 1$
, then  $$ \begin{align*} \mathrm{Tr}_{n+1/{n}}c_{n+1}^{\pm}=c^{\pm}_{n-1},\quad c_{n}^{\pm}=\mathrm{Res}_{n,n-1}c_{n-1}^{\pm} \end{align*} $$
$$ \begin{align*} \mathrm{Tr}_{n+1/{n}}c_{n+1}^{\pm}=c^{\pm}_{n-1},\quad c_{n}^{\pm}=\mathrm{Res}_{n,n-1}c_{n-1}^{\pm} \end{align*} $$
for
 $\mathrm {Tr}_{n+1/{n}}: {\mathscr {F}}({\mathfrak {m}}_{n+1})\to {\mathscr {F}}({\mathfrak {m}}_n)$
the trace map and
$\mathrm {Tr}_{n+1/{n}}: {\mathscr {F}}({\mathfrak {m}}_{n+1})\to {\mathscr {F}}({\mathfrak {m}}_n)$
the trace map and
 $\mathrm {Res}_{n,n-1}: H^1(\Psi _{n-1}, T) \to H^1(\Psi _{n},T)$
the restriction.
$\mathrm {Res}_{n,n-1}: H^1(\Psi _{n-1}, T) \to H^1(\Psi _{n},T)$
the restriction. -
(2) We have
 $c_{n}^{\pm } \in {\mathscr {F}}({\mathfrak {m}}_{n})^{\pm }.$
$c_{n}^{\pm } \in {\mathscr {F}}({\mathfrak {m}}_{n})^{\pm }.$
Proof.
-
(1) First, note that an element x of
 $H^1(\Psi _n, T)$
is determined by the two elements
$H^1(\Psi _n, T)$
is determined by the two elements
 $(x, v_{+,n}^{\sigma })_{\Lambda _n}$
and
$(x, v_{+,n}^{\sigma })_{\Lambda _n}$
and
 $(x, v_{-,n}^{\sigma })_{\Lambda _n} \in \Lambda _n$
.
$(x, v_{-,n}^{\sigma })_{\Lambda _n} \in \Lambda _n$
.By definition,
 $$ \begin{align*} (\mathrm{Tr}_{n+1/{n}}c_{n+1}^{\pm}, v_{\pm,n})_{\Lambda_n}=(c_{n}^{\pm}, v_{\pm,n})_{\Lambda_n}=(\mathrm{Res}_{n, n-1}c_{n-1}^{\pm}, v_{\pm,n})_{\Lambda_n}=0. \end{align*} $$
$$ \begin{align*} (\mathrm{Tr}_{n+1/{n}}c_{n+1}^{\pm}, v_{\pm,n})_{\Lambda_n}=(c_{n}^{\pm}, v_{\pm,n})_{\Lambda_n}=(\mathrm{Res}_{n, n-1}c_{n-1}^{\pm}, v_{\pm,n})_{\Lambda_n}=0. \end{align*} $$
As
 $(c_{n}^{\pm }, v_{\mp ,n})_{\Lambda _n}=\omega _n^{\mp },$
it suffices to show that
$(c_{n}^{\pm }, v_{\mp ,n})_{\Lambda _n}=\omega _n^{\mp },$
it suffices to show that  $$ \begin{align*} (\mathrm{Tr}_{n+1/{n}}c_{n+1}^{\pm}, v_{\mp,n})_{\Lambda_n}=(c_{n-1}^{\pm}, v_{\mp,n})_{\Lambda_n}=\omega_n^{\mp}. \end{align*} $$
$$ \begin{align*} (\mathrm{Tr}_{n+1/{n}}c_{n+1}^{\pm}, v_{\mp,n})_{\Lambda_n}=(c_{n-1}^{\pm}, v_{\mp,n})_{\Lambda_n}=\omega_n^{\mp}. \end{align*} $$
Since
 $\omega _{n+1}^{\mp }=\omega _{n}^{\mp },$
we have
$\omega _{n+1}^{\mp }=\omega _{n}^{\mp },$
we have  $$ \begin{align*} (\mathrm{Tr}_{n+1/{n}}c_{n+1}^{\pm}, v_{\mp,n})_{\Lambda_n}\equiv (c_{n+1}^{\pm}, v_{\mp,n})_{\Lambda_{n+1}} \equiv\omega_n^{\mp} \bmod (\gamma^{p^n}-1). \end{align*} $$
$$ \begin{align*} (\mathrm{Tr}_{n+1/{n}}c_{n+1}^{\pm}, v_{\mp,n})_{\Lambda_n}\equiv (c_{n+1}^{\pm}, v_{\mp,n})_{\Lambda_{n+1}} \equiv\omega_n^{\mp} \bmod (\gamma^{p^n}-1). \end{align*} $$
Since
 $\omega _{n}^{\mp }=\omega _{n-1}^{\mp }\Phi _{n}(\gamma )$
and
$\omega _{n}^{\mp }=\omega _{n-1}^{\mp }\Phi _{n}(\gamma )$
and
 $\{v_{\mp ,n}\}_n$
is norm compatible,
$\{v_{\mp ,n}\}_n$
is norm compatible,  $$ \begin{align*} \kern-20pt (c_{n-1}^{\pm}, v_{\mp,n})_{\Lambda_n}&\equiv \sum_{\sigma \in {\mathrm{Gal}}(\Psi_n/\Phi)}(c_{n-1}^{\pm}, v^{\sigma}_{\mp, n-1})_{n-1}\sigma \equiv \omega_{n-1}^{\mp}\sum_{\sigma \in {\mathrm{Gal}}(\Psi_n/\Phi)}(v_{\pm, n-1}^{\perp}, v^{\sigma}_{\mp, n-1})_{n-1}\sigma \\ & \equiv \omega_{n-1}^{\mp}\sum_{\sigma \in {\mathrm{Gal}}(\Psi_n/\Psi_{n-1})}\sigma \equiv \omega_{n-1}^{\mp}\Phi_{n-1}(\gamma)=\omega_n^{\mp}. \end{align*} $$
$$ \begin{align*} \kern-20pt (c_{n-1}^{\pm}, v_{\mp,n})_{\Lambda_n}&\equiv \sum_{\sigma \in {\mathrm{Gal}}(\Psi_n/\Phi)}(c_{n-1}^{\pm}, v^{\sigma}_{\mp, n-1})_{n-1}\sigma \equiv \omega_{n-1}^{\mp}\sum_{\sigma \in {\mathrm{Gal}}(\Psi_n/\Phi)}(v_{\pm, n-1}^{\perp}, v^{\sigma}_{\mp, n-1})_{n-1}\sigma \\ & \equiv \omega_{n-1}^{\mp}\sum_{\sigma \in {\mathrm{Gal}}(\Psi_n/\Psi_{n-1})}\sigma \equiv \omega_{n-1}^{\mp}\Phi_{n-1}(\gamma)=\omega_n^{\mp}. \end{align*} $$
Therefore, the assertion follows.
-
(2) This is a simple consequence of (1).
2.3.2 The
 $\pm $
-subgroups
$\pm $
-subgroups
Theorem 2.7. Let
![]() $n\geq 0$
.
$n\geq 0$
.
-
(a) As
 $\Lambda _n$
-modules, we have
$\Lambda _n$
-modules, we have
 ${\mathscr {F}}({\mathfrak {m}}_n)={\mathscr {F}}({\mathfrak {m}}_n)^{+}\oplus {\mathscr {F}}({\mathfrak {m}}_n)^{-}$
.
${\mathscr {F}}({\mathfrak {m}}_n)={\mathscr {F}}({\mathfrak {m}}_n)^{+}\oplus {\mathscr {F}}({\mathfrak {m}}_n)^{-}$
. -
(b)
 ${\mathscr {F}}({\mathfrak {m}}_n)^{\pm }$
is generated by
${\mathscr {F}}({\mathfrak {m}}_n)^{\pm }$
is generated by
 $c_n^{\pm }$
.
$c_n^{\pm }$
.
Proof. By definition,
 $$ \begin{align} \sum_{\sigma \in {\mathrm{Gal}}(\Psi_n/\Phi)}(c_n^{\pm}, v_{\mp,n}^{\sigma})_n\sigma=\omega_n^{\mp} \in \Lambda_n. \end{align} $$
$$ \begin{align} \sum_{\sigma \in {\mathrm{Gal}}(\Psi_n/\Phi)}(c_n^{\pm}, v_{\mp,n}^{\sigma})_n\sigma=\omega_n^{\mp} \in \Lambda_n. \end{align} $$
-
(a) Let
 $x \in \mathscr {F}(\mathfrak {m}_n)$
and consider which livesFootnote 3 in
$x \in \mathscr {F}(\mathfrak {m}_n)$
and consider which livesFootnote 3 in $$ \begin{align*} \sum_{\sigma \in \mathrm{Gal}(\Psi_n/\Phi)} (x, v_{\mp,n}^\sigma)_n \sigma, \end{align*} $$
$$ \begin{align*} \sum_{\sigma \in \mathrm{Gal}(\Psi_n/\Phi)} (x, v_{\mp,n}^\sigma)_n \sigma, \end{align*} $$
 $\omega ^{\mp }_{n}\Lambda _n$
. Thus, by (2.14), there exists
$\omega ^{\mp }_{n}\Lambda _n$
. Thus, by (2.14), there exists
 $h_{\pm }(\gamma ) \in \Lambda _n$
such that Now, for
$h_{\pm }(\gamma ) \in \Lambda _n$
such that Now, for $$ \begin{align*} \sum_{\sigma \in \mathrm{Gal}(\Psi_n/\Phi)} (x-h_{\pm}(\gamma)c_n^{\pm}, v_{\mp,n}^\sigma)_n \sigma=0. \end{align*} $$
$$ \begin{align*} \sum_{\sigma \in \mathrm{Gal}(\Psi_n/\Phi)} (x-h_{\pm}(\gamma)c_n^{\pm}, v_{\mp,n}^\sigma)_n \sigma=0. \end{align*} $$
 $y:=h_+(\gamma )c_n^++h_-(\gamma )c_n^-$
, we have for arbitrary
$y:=h_+(\gamma )c_n^++h_-(\gamma )c_n^-$
, we have for arbitrary $$ \begin{align*} \sum_{\sigma \in \mathrm{Gal}(\Psi_n/\Phi)} (x-y, u^\sigma)_n \sigma=0 \end{align*} $$
$$ \begin{align*} \sum_{\sigma \in \mathrm{Gal}(\Psi_n/\Phi)} (x-y, u^\sigma)_n \sigma=0 \end{align*} $$
 $u \in H^1(\Psi _n, T^{\otimes -1}(1))$
. Hence,
$u \in H^1(\Psi _n, T^{\otimes -1}(1))$
. Hence,
 $x=y$
.
$x=y$
.
-
(b) If
 $x \in {\mathscr {F}}({\mathfrak {m}}_n)^{\pm }$
, then Thus, we may choose
$x \in {\mathscr {F}}({\mathfrak {m}}_n)^{\pm }$
, then Thus, we may choose $$ \begin{align*}\sum_{\sigma \in \mathrm{Gal}(\Psi_n/\Phi)} (x, v_{\pm,n}^\sigma)_n \sigma=0.\end{align*} $$
$$ \begin{align*}\sum_{\sigma \in \mathrm{Gal}(\Psi_n/\Phi)} (x, v_{\pm,n}^\sigma)_n \sigma=0.\end{align*} $$
 $h_{\mp }$
as above to be
$h_{\mp }$
as above to be
 $0$
.
$0$
.
Remark 2.8. The local points are also elemental to Iwasawa theory of the
![]() ${\mathbb {Z}}_p$
-anticyclotomic deformation of a non-CM elliptic curve over imaginary quadratic fields with p inert (cf. [Reference Burungale, Buyukboduk, Lei and Iwasawa9]).
${\mathbb {Z}}_p$
-anticyclotomic deformation of a non-CM elliptic curve over imaginary quadratic fields with p inert (cf. [Reference Burungale, Buyukboduk, Lei and Iwasawa9]).
3 Rubin p-adic L-function and global points
The main results are Theorems 3.9 and 3.16.
3.0.1 Notation
Let
![]() $\overline {{\mathbb {Q}}}$
be an algebraic closure of
$\overline {{\mathbb {Q}}}$
be an algebraic closure of
![]() $\mathbb {Q}$
. Fix
$\mathbb {Q}$
. Fix
![]() $\iota _{\infty }:\overline {\mathbb {Q}} \hookrightarrow {\mathbb {C}}$
and
$\iota _{\infty }:\overline {\mathbb {Q}} \hookrightarrow {\mathbb {C}}$
and
![]() $\iota _p:\overline {\mathbb {Q}} \hookrightarrow {\mathbb {C}}_p$
.
$\iota _p:\overline {\mathbb {Q}} \hookrightarrow {\mathbb {C}}_p$
.
For a number field L, let
![]() $G_{L}={\mathrm {Gal}}(\overline {{\mathbb {Q}}}/L)$
. For a finite dimensional
$G_{L}={\mathrm {Gal}}(\overline {{\mathbb {Q}}}/L)$
. For a finite dimensional
![]() ${\mathbb {Q}}_p$
-vector space V endowed with a continuous
${\mathbb {Q}}_p$
-vector space V endowed with a continuous
![]() $G_L$
-action and v a prime of L, the Bloch–Kato subgroup is given by
$G_L$
-action and v a prime of L, the Bloch–Kato subgroup is given by
 $$ \begin{align*} H^1_{\mathrm{f}}(L_{v},V)= \begin{cases} \mathrm{ker}\left(H^1(L_{v}, V) \to H^1_{}(L_{v},V\otimes B_{\mathrm{crys}})\right) & (v\mid p),\\ \mathrm{ker}\left(H^1(L_{v}^{}, V) \to H^1(L_{v}^{\mathrm{ur}}, V)\right) & (v\nmid p). \end{cases} \end{align*} $$
$$ \begin{align*} H^1_{\mathrm{f}}(L_{v},V)= \begin{cases} \mathrm{ker}\left(H^1(L_{v}, V) \to H^1_{}(L_{v},V\otimes B_{\mathrm{crys}})\right) & (v\mid p),\\ \mathrm{ker}\left(H^1(L_{v}^{}, V) \to H^1(L_{v}^{\mathrm{ur}}, V)\right) & (v\nmid p). \end{cases} \end{align*} $$
If M denotes V or a
![]() ${\mathbb {Z}}_p$
-lattice in V, then the Bloch–Kato Selmer group is defined as
${\mathbb {Z}}_p$
-lattice in V, then the Bloch–Kato Selmer group is defined as
 $$ \begin{align*} H^{1}_{\mathrm{{f}}}(L, M)=\mathrm{ker} \left(H^1_{}(L,M) \to \prod_{v} \frac{H^1_{}(L_{v}^{},V)}{H^1_{\mathrm{f}}(L_{v}^{},V)} \right). \end{align*} $$
$$ \begin{align*} H^{1}_{\mathrm{{f}}}(L, M)=\mathrm{ker} \left(H^1_{}(L,M) \to \prod_{v} \frac{H^1_{}(L_{v}^{},V)}{H^1_{\mathrm{f}}(L_{v}^{},V)} \right). \end{align*} $$
For an extension
![]() $N/L$
of number fields, let
$N/L$
of number fields, let
![]() ${\mathrm {Ind}}^{N}_{L}(\cdot )$
denote the induction
${\mathrm {Ind}}^{N}_{L}(\cdot )$
denote the induction
![]() ${\mathrm {Ind}}^{G_{N}}_{G_{L}}(\cdot )$
.
${\mathrm {Ind}}^{G_{N}}_{G_{L}}(\cdot )$
.
For an abelian variety A, let
![]() $T_p(A)$
denote the p-adic Tate module and put
$T_p(A)$
denote the p-adic Tate module and put
![]() $V_p(A)=T_p(A)\otimes _{{\mathbb {Z}}_p}{\mathbb {Q}}_p.$
$V_p(A)=T_p(A)\otimes _{{\mathbb {Z}}_p}{\mathbb {Q}}_p.$
3.1 Elements of Selmer groups
3.1.1 The set-up
Let K be an imaginary quadratic field of discriminant
![]() $-D_{K}<0$
and H the Hilbert class field. Suppose
$-D_{K}<0$
and H the Hilbert class field. Suppose
Let
![]() $K^{}_{\infty }$
be the anticyclotomic
$K^{}_{\infty }$
be the anticyclotomic
![]() ${\mathbb {Z}}_p$
-extension of K and
${\mathbb {Z}}_p$
-extension of K and
![]() $K_n^{}$
the n-th layer. Let
$K_n^{}$
the n-th layer. Let
![]() $G^-$
also denote
$G^-$
also denote
![]() ${\mathrm {Gal}}(K_{\infty }/K)$
.
${\mathrm {Gal}}(K_{\infty }/K)$
.
Let
![]() $\varphi $
be a Hecke character over K of infinity type
$\varphi $
be a Hecke character over K of infinity type
![]() $(1,0)$
such that the Hecke character
$(1,0)$
such that the Hecke character
![]() $\varphi \circ N_{H/K}$
is associated to a
$\varphi \circ N_{H/K}$
is associated to a
![]() ${\mathbb {Q}}$
-curve E over H which has good reduction at each prime of H above p. In particular, E satisfies the Shimura condition. Fix a minimal Weierstrass model of E over
${\mathbb {Q}}$
-curve E over H which has good reduction at each prime of H above p. In particular, E satisfies the Shimura condition. Fix a minimal Weierstrass model of E over
![]() ${\mathcal {O}}_{H,{\mathfrak {p}}} \cap H={\mathcal {O}}_{\Phi }\cap H$
for
${\mathcal {O}}_{H,{\mathfrak {p}}} \cap H={\mathcal {O}}_{\Phi }\cap H$
for
![]() ${\mathfrak {p}} \mid p$
the prime of H arising via
${\mathfrak {p}} \mid p$
the prime of H arising via
![]() $\iota _p$
and let
$\iota _p$
and let
![]() $\omega $
be the Néron differential. Pick a non-zero
$\omega $
be the Néron differential. Pick a non-zero
![]() $b_E\in H^1(E({\mathbb {C}}), {\mathbb {Z}}_{(p)}) \cong {\mathbb {Z}}_{(p)} \otimes {\mathcal {O}}_{K}$
and define a CM period
$b_E\in H^1(E({\mathbb {C}}), {\mathbb {Z}}_{(p)}) \cong {\mathbb {Z}}_{(p)} \otimes {\mathcal {O}}_{K}$
and define a CM period
![]() $\Omega \in {\mathbb {C}}^{\times }$
by
$\Omega \in {\mathbb {C}}^{\times }$
by
for
![]() $\mathrm {per}_{E/H}: \mathrm {coLie}(E) \to H^1(E({\mathbb {C}}), {\mathbb {Q}})\otimes _K {\mathbb {C}}$
the period map.
$\mathrm {per}_{E/H}: \mathrm {coLie}(E) \to H^1(E({\mathbb {C}}), {\mathbb {Q}})\otimes _K {\mathbb {C}}$
the period map.
In this section, let
![]() ${\mathcal {O}}$
denote the integer ring of a finite extension of
${\mathcal {O}}$
denote the integer ring of a finite extension of
![]() $\Phi $
which contains the Hecke field
$\Phi $
which contains the Hecke field
![]() $K(\varphi (\widehat {K}^{\times }))$
for
$K(\varphi (\widehat {K}^{\times }))$
for
![]() $\widehat {K}:=K\otimes \varprojlim _m {\mathbb {Z}}/m{\mathbb {Z}}$
. Let
$\widehat {K}:=K\otimes \varprojlim _m {\mathbb {Z}}/m{\mathbb {Z}}$
. Let
![]() ${\mathfrak {f}}$
be the conductor of
${\mathfrak {f}}$
be the conductor of
![]() $\varphi $
. Let T be the p-adic Galois representation of
$\varphi $
. Let T be the p-adic Galois representation of
![]() $G_{K}$
associated to
$G_{K}$
associated to
![]() $\varphi $
, which is an
$\varphi $
, which is an
![]() ${\mathcal {O}}$
-module free of rank one so that its restriction to
${\mathcal {O}}$
-module free of rank one so that its restriction to
![]() $G_{H}$
is
$G_{H}$
is
![]() $T_pE\otimes _{{\mathcal {O}}_\Phi }{\mathcal {O}}$
. Since
$T_pE\otimes _{{\mathcal {O}}_\Phi }{\mathcal {O}}$
. Since
as formal groups over
![]() ${\mathcal {O}}_{\Phi }$
, the results in §2 may be utilized by replacing
${\mathcal {O}}_{\Phi }$
, the results in §2 may be utilized by replacing
![]() ${\mathscr {F}}$
with
${\mathscr {F}}$
with
![]() $\hat {E}$
and identifying
$\hat {E}$
and identifying
![]() $T_pE $
with
$T_pE $
with
![]() $T_{\pi }E$
via
$T_{\pi }E$
via
We put
![]() $T^{\otimes -1}=\mathrm {Hom}_{{\mathcal {O}}}(T, {\mathcal {O}})$
and note that
$T^{\otimes -1}=\mathrm {Hom}_{{\mathcal {O}}}(T, {\mathcal {O}})$
and note that
![]() $T^{\otimes -1}(1)$
is identified with the complex conjugation of T as follows. Let
$T^{\otimes -1}(1)$
is identified with the complex conjugation of T as follows. Let
![]() $\tau $
be the complex conjugation. We have a natural decomposition
$\tau $
be the complex conjugation. We have a natural decomposition
where
![]() $\otimes _{{\mathcal {O}}_\Phi ,\tau }$
is the tensor product with respect to the map
$\otimes _{{\mathcal {O}}_\Phi ,\tau }$
is the tensor product with respect to the map
![]() ${\mathcal {O}}_\Phi \rightarrow {\mathcal {O}}$
induced by
${\mathcal {O}}_\Phi \rightarrow {\mathcal {O}}$
induced by
![]() $\tau $
and the natural inclusion. This decomposition and the base change of the Weil pairing over
$\tau $
and the natural inclusion. This decomposition and the base change of the Weil pairing over
![]() ${\mathcal {O}}$
induce a perfect
${\mathcal {O}}$
induce a perfect
![]() ${\mathcal {O}}$
-bilinear pairing
${\mathcal {O}}$
-bilinear pairing
Thus, we may naturally identify
![]() $T^{\otimes -1}(1)$
with
$T^{\otimes -1}(1)$
with
![]() $T_pE\otimes _{{\mathcal {O}}_\Phi , \tau }{\mathcal {O}}.$
Since
$T_pE\otimes _{{\mathcal {O}}_\Phi , \tau }{\mathcal {O}}.$
Since
![]() $\varphi (\tau ({\mathfrak {a}}))=\overline {\varphi ({\mathfrak {a}})}$
for an integral ideal
$\varphi (\tau ({\mathfrak {a}}))=\overline {\varphi ({\mathfrak {a}})}$
for an integral ideal
![]() ${\mathfrak {a}}$
of
${\mathfrak {a}}$
of
![]() ${\mathcal {O}}_K$
relatively prime to
${\mathcal {O}}_K$
relatively prime to
![]() ${\mathfrak {f}}$
(cf. [Reference Gross27, Lem. 11.1.1 ]),
${\mathfrak {f}}$
(cf. [Reference Gross27, Lem. 11.1.1 ]),
![]() $T_pE\otimes _{{\mathcal {O}}_\Phi , \tau }{\mathcal {O}}$
is naturally identified with the complex conjugation
$T_pE\otimes _{{\mathcal {O}}_\Phi , \tau }{\mathcal {O}}$
is naturally identified with the complex conjugation
![]() $T^{\tau }$
of the
$T^{\tau }$
of the
![]() $G_K$
-representation T. Hence, we have a natural isomorphism of
$G_K$
-representation T. Hence, we have a natural isomorphism of
![]() ${\mathcal {O}}[G_K]$
-modules
${\mathcal {O}}[G_K]$
-modules
![]() $T^{\otimes -1}(1)\cong T^{\tau },$
which induces an isomorphism
$T^{\otimes -1}(1)\cong T^{\tau },$
which induces an isomorphism
![]() $H^1(K_{n}, T^{\otimes -1}(1)) \cong H^1(K_n,T^{\tau })$
. Since the complex conjugation gives rise to an isomorphism
$H^1(K_{n}, T^{\otimes -1}(1)) \cong H^1(K_n,T^{\tau })$
. Since the complex conjugation gives rise to an isomorphism
![]() $H^1(K_n,T^{\tau })\cong H^1(K_n,T)^{\iota }$
of
$H^1(K_n,T^{\tau })\cong H^1(K_n,T)^{\iota }$
of
![]() $\Lambda $
-modules, we often identify
$\Lambda $
-modules, we often identify
where
![]() $\iota :\Lambda \to \Lambda $
denotes the involution induced by
$\iota :\Lambda \to \Lambda $
denotes the involution induced by
![]() $g \mapsto g^{-1}$
for
$g \mapsto g^{-1}$
for
![]() $g \in G^-$
and for a
$g \in G^-$
and for a
![]() $\Lambda $
-module M, we put
$\Lambda $
-module M, we put
![]() $M^{\iota }=M\otimes _{\Lambda ,\iota }\Lambda .$
$M^{\iota }=M\otimes _{\Lambda ,\iota }\Lambda .$
3.1.2 Construction of Selmer elements
Based on elliptic units, we associate a Selmer element to a Hecke character.
The following existence is due to Coates and Wiles [Reference Coates and Wiles20] (cf. [Reference Rubin46], [Reference Kato30, Prop. 15.9]).
Proposition 3.1. There exists an elliptic unit
associated to
![]() $b_E$
such that for a character
$b_E$
such that for a character
![]() $\chi $
of
$\chi $
of
![]() $\mathrm {Gal}(K_{n}/K)$
, we have
$\mathrm {Gal}(K_{n}/K)$
, we have
 $$ \begin{align} \sum_{\sigma\in {\mathrm{Gal}}(K_n/K)}\chi(\sigma)\exp^*_{K_n}({\mathrm{loc}}_{p}(z_n^{\sigma})) = \frac{L_{p{\mathfrak{f}}}(\overline{\varphi}\chi,1)}{\Omega_{}}\omega. \end{align} $$
$$ \begin{align} \sum_{\sigma\in {\mathrm{Gal}}(K_n/K)}\chi(\sigma)\exp^*_{K_n}({\mathrm{loc}}_{p}(z_n^{\sigma})) = \frac{L_{p{\mathfrak{f}}}(\overline{\varphi}\chi,1)}{\Omega_{}}\omega. \end{align} $$
Here,
is the dual exponential map,
![]() $K_p=K\otimes {\mathbb {Q}}_p=\Phi $
, and
$K_p=K\otimes {\mathbb {Q}}_p=\Phi $
, and
 $$ \begin{align*} {\mathrm{loc}}_{p}:H^1(K_n, T^{\otimes -1}(1)) \to H^1(K_{n}\otimes_K K_{p}, T^{\otimes -1}(1))=\prod_{w\mid p} H^1(\Psi_n,T^{\otimes -1}(1)) \end{align*} $$
$$ \begin{align*} {\mathrm{loc}}_{p}:H^1(K_n, T^{\otimes -1}(1)) \to H^1(K_{n}\otimes_K K_{p}, T^{\otimes -1}(1))=\prod_{w\mid p} H^1(\Psi_n,T^{\otimes -1}(1)) \end{align*} $$
is the localization as w varies over the places of
![]() $K_n$
above p.
$K_n$
above p.
We put
![]() ${\mathcal {O}}_{\chi }= {\mathcal {O}}[\mathrm {Im}(\chi )]$
and let
${\mathcal {O}}_{\chi }= {\mathcal {O}}[\mathrm {Im}(\chi )]$
and let
![]() ${\mathcal {O}}(\chi )$
denote the
${\mathcal {O}}(\chi )$
denote the
![]() ${\mathcal {O}}[G_{K}]$
-module with the underlying space
${\mathcal {O}}[G_{K}]$
-module with the underlying space
![]() ${\mathcal {O}}_{\chi }$
and the
${\mathcal {O}}_{\chi }$
and the
![]() $G_K$
-action being
$G_K$
-action being
![]() $\chi .$
For an
$\chi .$
For an
![]() ${\mathcal {O}}[G_{K}]$
-module M, let
${\mathcal {O}}[G_{K}]$
-module M, let
![]() $M(\chi )=M\otimes _{{\mathcal {O}}}{\mathcal {O}}(\chi )$
and
$M(\chi )=M\otimes _{{\mathcal {O}}}{\mathcal {O}}(\chi )$
and
Definition 3.2 (Selmer element).
For a character
![]() $\chi $
of
$\chi $
of
![]() ${\mathrm {Gal}}(K_n/K)$
, let
${\mathrm {Gal}}(K_n/K)$
, let
![]() $z_{\chi } \in H^1(K_n^{}, T^{\otimes -1}(1))^{\chi ^{-1}}$
denote the image of the elliptic unit
$z_{\chi } \in H^1(K_n^{}, T^{\otimes -1}(1))^{\chi ^{-1}}$
denote the image of the elliptic unit
![]() $z_n$
under the composite
$z_n$
under the composite
 $$ \begin{align} H^1(K^{}_n, T^{\otimes -1}(1)) \xrightarrow{\cong} &H^1(K^{}_n, T^{\otimes -1}(1)(\chi)) \to H^1(K, T^{\otimes -1}(1)(\chi))\nonumber\\ \xrightarrow{\cong} &H^0(K, H^1(K_n^{}, T^{\otimes -1}(1)(\chi))) = H^1(K_n^{}, T^{\otimes -1}(1))^{\chi^{-1}}. \end{align} $$
$$ \begin{align} H^1(K^{}_n, T^{\otimes -1}(1)) \xrightarrow{\cong} &H^1(K^{}_n, T^{\otimes -1}(1)(\chi)) \to H^1(K, T^{\otimes -1}(1)(\chi))\nonumber\\ \xrightarrow{\cong} &H^0(K, H^1(K_n^{}, T^{\otimes -1}(1)(\chi))) = H^1(K_n^{}, T^{\otimes -1}(1))^{\chi^{-1}}. \end{align} $$
Here, the second and third maps are corestriction and restriction, respectively.
Note that
 $$ \begin{align} z_{\chi}=\sum_{\sigma \in {\mathrm{Gal}}(K_{n}/K) } \chi(\sigma)z_n^{\sigma}. \end{align} $$
$$ \begin{align} z_{\chi}=\sum_{\sigma \in {\mathrm{Gal}}(K_{n}/K) } \chi(\sigma)z_n^{\sigma}. \end{align} $$
Since
![]() $(H^1(K_n^{}, T)^{\iota })^{\chi ^{-1}}=H^{1}(K_n,T)^{\chi }$
by (3.1), we regard
$(H^1(K_n^{}, T)^{\iota })^{\chi ^{-1}}=H^{1}(K_n,T)^{\chi }$
by (3.1), we regard
Lemma 3.3. If
![]() $L(\varphi \chi ^{-1},1)=0$
, then
$L(\varphi \chi ^{-1},1)=0$
, then
![]() $z_{\chi } \in H^{1}_{\mathrm {{f}}}(K_n^{}, T)^{\chi }$
.
$z_{\chi } \in H^{1}_{\mathrm {{f}}}(K_n^{}, T)^{\chi }$
.
Proof. By definition and [Reference Kato30, Prop. 15.9],
![]() $z_\chi $
lies in the image of
$z_\chi $
lies in the image of
where
![]() $K({\mathfrak {f}} p^m)$
denotes the ray class field of K of conductor
$K({\mathfrak {f}} p^m)$
denotes the ray class field of K of conductor
![]() ${\mathfrak {f}} p^m$
.
${\mathfrak {f}} p^m$
.
For a prime
![]() $v\nmid p$
of
$v\nmid p$
of
![]() $K_n$
and a prime
$K_n$
and a prime
![]() $w \mid v$
of
$w \mid v$
of
![]() $\cup _{m\ge 1}K({\mathfrak {f}} p^m)$
, note that the completion of
$\cup _{m\ge 1}K({\mathfrak {f}} p^m)$
, note that the completion of
![]() $\cup _mK({\mathfrak {f}} p^m)$
at w contains the maximal pro-p unramified extension of
$\cup _mK({\mathfrak {f}} p^m)$
at w contains the maximal pro-p unramified extension of
![]() $K_{n,v}$
, and so
$K_{n,v}$
, and so
![]() ${\mathrm {loc}}_{v}(z_{\chi })\in H^1_{\mathrm {f}}(K_{n,v}^{} ,T^{\otimes -1}(1)).$
Since
${\mathrm {loc}}_{v}(z_{\chi })\in H^1_{\mathrm {f}}(K_{n,v}^{} ,T^{\otimes -1}(1)).$
Since
![]() $L(\varphi \chi ^{-1},1)=0$
, by the explicit reciprocity law (3.3) and (3.5),
$L(\varphi \chi ^{-1},1)=0$
, by the explicit reciprocity law (3.3) and (3.5),
As the Bloch–Kato subgroup
![]() $\oplus _{v\mid p} H^1_{\mathrm {f}}(K_{n,v}, T^{\otimes -1}(1))$
coincides with the kernel of
$\oplus _{v\mid p} H^1_{\mathrm {f}}(K_{n,v}, T^{\otimes -1}(1))$
coincides with the kernel of
![]() $\exp ^*_{K_n}$
, the proof concludes.
$\exp ^*_{K_n}$
, the proof concludes.
3.2 Global points
3.2.1 Mordell–Weil groups over
 ${\mathbb {Q}}$
${\mathbb {Q}}$
In this subsection, for sufficiently large n with
![]() $(-1)^{n+1}=-W(\varphi )$
and
$(-1)^{n+1}=-W(\varphi )$
and
![]() $\chi $
an anticyclotomic character of conductor
$\chi $
an anticyclotomic character of conductor
![]() $p^{n+1}$
, the Selmer element
$p^{n+1}$
, the Selmer element
![]() $z_{\chi }$
is shown to arise from a rational point.
$z_{\chi }$
is shown to arise from a rational point.
Let
![]() $\chi $
be a finite character of
$\chi $
be a finite character of
![]() ${\mathrm {Gal}}(K_{\infty }/K)$
and
${\mathrm {Gal}}(K_{\infty }/K)$
and
![]() $f_{\chi } \in S_2(\Gamma _{0}(D_{K}N_{K/{\mathbb {Q}}}({\mathfrak {f}}{\mathfrak {c}}_{\chi })))$
the theta series attached to
$f_{\chi } \in S_2(\Gamma _{0}(D_{K}N_{K/{\mathbb {Q}}}({\mathfrak {f}}{\mathfrak {c}}_{\chi })))$
the theta series attached to
![]() $\varphi \chi ^{-1}$
, where
$\varphi \chi ^{-1}$
, where
![]() ${\mathfrak {c}}_{\chi }$
denotes the conductor of
${\mathfrak {c}}_{\chi }$
denotes the conductor of
![]() $\chi $
. In particular,
$\chi $
. In particular,
![]() $L(f_{\chi },s)=L(\varphi \chi ^{-1},s)$
. Let
$L(f_{\chi },s)=L(\varphi \chi ^{-1},s)$
. Let
![]() $F_{\chi }$
denote the Hecke field. Fix an abelian variety
$F_{\chi }$
denote the Hecke field. Fix an abelian variety
![]() $A_{\chi }$
over
$A_{\chi }$
over
![]() ${\mathbb {Q}}$
of dimension
${\mathbb {Q}}$
of dimension
![]() $[F_{\chi }:{\mathbb {Q}}]$
with an
$[F_{\chi }:{\mathbb {Q}}]$
with an
![]() ${\mathcal {O}}_{F_{\chi }}$
-action so that
${\mathcal {O}}_{F_{\chi }}$
-action so that
 $$ \begin{align*}L(A_{\chi},s)=\prod_{\sigma: F_{\chi}\hookrightarrow \overline{{\mathbb {Q}}}}L(f_{\chi}^{\sigma},s).\end{align*} $$
$$ \begin{align*}L(A_{\chi},s)=\prod_{\sigma: F_{\chi}\hookrightarrow \overline{{\mathbb {Q}}}}L(f_{\chi}^{\sigma},s).\end{align*} $$
In this subsection,
![]() ${\mathcal {O}}$
is enlarged to also contain the image of
${\mathcal {O}}$
is enlarged to also contain the image of
![]() $\chi $
, and
$\chi $
, and
![]() ${\mathfrak {m}}$
denotes the maximal ideal.
${\mathfrak {m}}$
denotes the maximal ideal.
We begin with a preliminary.
Lemma 3.4. We have
which is an irreducible
![]() $G_{{\mathbb {Q}}}$
-representation.
$G_{{\mathbb {Q}}}$
-representation.
Proof. Note that
![]() $T^{\otimes -1}(1)(\chi ) \cong T(\chi ^{-1})^{\tau }$
as an
$T^{\otimes -1}(1)(\chi ) \cong T(\chi ^{-1})^{\tau }$
as an
![]() ${\mathcal {O}}[G_{K}]$
-module, and so the first assertion follows.
${\mathcal {O}}[G_{K}]$
-module, and so the first assertion follows.
As for the irreducibility, in light of the proof of [Reference Kato30, Lem. 15.20], it suffices to show that for a finite character
![]() $\chi $
of
$\chi $
of
![]() ${\mathrm {Gal}}(K_{\infty }/K)$
, there exists an integral ideal
${\mathrm {Gal}}(K_{\infty }/K)$
, there exists an integral ideal
![]() ${\mathfrak {b}}$
of K relatively prime to
${\mathfrak {b}}$
of K relatively prime to
![]() $p{\mathfrak {f}}$
such that
$p{\mathfrak {f}}$
such that
We put
![]() ${\mathfrak {b}}=(1+f \sqrt {-D_K}){\mathcal {O}}_K$
for
${\mathfrak {b}}=(1+f \sqrt {-D_K}){\mathcal {O}}_K$
for
![]() $f=N_{K/{\mathbb {Q}}}({\mathfrak {f}}) \in {\mathbb {Z}}.$
As p is inert in K, note that p is relatively prime to
$f=N_{K/{\mathbb {Q}}}({\mathfrak {f}}) \in {\mathbb {Z}}.$
As p is inert in K, note that p is relatively prime to
![]() $N_{K/{\mathbb {Q}}}({\mathfrak {b}})=1+f^2D_K$
, i.e.
$N_{K/{\mathbb {Q}}}({\mathfrak {b}})=1+f^2D_K$
, i.e.
![]() $N_{K/{\mathbb {Q}}}({\mathfrak {b}})\in {\mathcal {O}}^{\times }$
. Since
$N_{K/{\mathbb {Q}}}({\mathfrak {b}})\in {\mathcal {O}}^{\times }$
. Since
![]() $p\nmid fD_K$
and
$p\nmid fD_K$
and
![]() $1+f \sqrt {-D_K} \equiv 1\ \mathrm {mod}\ {\mathfrak {f}}$
, we have
$1+f \sqrt {-D_K} \equiv 1\ \mathrm {mod}\ {\mathfrak {f}}$
, we have
![]() $\varphi ({\mathfrak {b}})-\varphi (\bar {{\mathfrak {b}}}) =2f\sqrt {-D_K}\in {\mathcal {O}}^{\times }$
, and so
$\varphi ({\mathfrak {b}})-\varphi (\bar {{\mathfrak {b}}}) =2f\sqrt {-D_K}\in {\mathcal {O}}^{\times }$
, and so
![]() $\varphi ({\mathfrak {b}})\gamma _{{\mathfrak {b}}}-\varphi (\bar {{\mathfrak {b}}})\gamma _{\bar {{\mathfrak {b}}}} \in \Lambda ^{\times }$
, from which (3.6) follows. (Here,
$\varphi ({\mathfrak {b}})\gamma _{{\mathfrak {b}}}-\varphi (\bar {{\mathfrak {b}}})\gamma _{\bar {{\mathfrak {b}}}} \in \Lambda ^{\times }$
, from which (3.6) follows. (Here,
![]() $\gamma _{{\mathfrak {a}}}\in G^{-}$
denotes the element which corresponds via the Artin map to an integral ideal
$\gamma _{{\mathfrak {a}}}\in G^{-}$
denotes the element which corresponds via the Artin map to an integral ideal
![]() ${\mathfrak {a}}$
of K relatively prime to
${\mathfrak {a}}$
of K relatively prime to
![]() $p{\mathfrak {f}}$
.)
$p{\mathfrak {f}}$
.)
Put
![]() $V=T\otimes {\mathbb {Q}}_p \cong {\mathcal {O}}[1/p]$
and
$V=T\otimes {\mathbb {Q}}_p \cong {\mathcal {O}}[1/p]$
and
![]() $V_p(A)=T_p(A_{\chi })\otimes {\mathbb {Q}}_p \cong (F_{\chi }\otimes {\mathbb {Q}}_p)^{\oplus 2}.$
We embed
$V_p(A)=T_p(A_{\chi })\otimes {\mathbb {Q}}_p \cong (F_{\chi }\otimes {\mathbb {Q}}_p)^{\oplus 2}.$
We embed
![]() $F_{\chi }$
into
$F_{\chi }$
into
![]() ${\mathcal {O}}[1/p]$
via
${\mathcal {O}}[1/p]$
via
![]() $\iota _p$
and notice an abstract isomorphism
$\iota _p$
and notice an abstract isomorphism
which follows from considering the action of Frobenius elements. By Lemma 3.4, there exists an isomorphism
![]() $\mathrm {Ind}^{K}_{{\mathbb {Q}}}(T(\chi ^{-1}))\cong T_p(A_{\chi })\otimes _{{\mathcal {O}}_{F_{\chi }}\otimes {\mathbb {Z}}_p } {\mathcal {O}}$
of
$\mathrm {Ind}^{K}_{{\mathbb {Q}}}(T(\chi ^{-1}))\cong T_p(A_{\chi })\otimes _{{\mathcal {O}}_{F_{\chi }}\otimes {\mathbb {Z}}_p } {\mathcal {O}}$
of
![]() ${\mathcal {O}}[G_{{\mathbb {Q}}}]$
-modules, and so we have an identification
${\mathcal {O}}[G_{{\mathbb {Q}}}]$
-modules, and so we have an identification
Proposition 3.5. Suppose that
![]() $\mathrm {ord}_{s=1} L(\varphi \chi ^{-1},s)=r\in \{0,1\}$
. Then,
$\mathrm {ord}_{s=1} L(\varphi \chi ^{-1},s)=r\in \{0,1\}$
. Then,
![]() $\mathrm {rank}_{{\mathcal {O}}_{F_{\chi }}} A_{\chi }({\mathbb {Q}})=r$
and the Tate–Shafarevich group
$\mathrm {rank}_{{\mathcal {O}}_{F_{\chi }}} A_{\chi }({\mathbb {Q}})=r$
and the Tate–Shafarevich group
![]() is finite. In particular, if
is finite. In particular, if
![]() $r=1$
, we have
$r=1$
, we have
Proof. Since
![]() $\mathrm {ord}_{s=1}L(f_{\chi },s)=r$
, by the main result of [Reference Bump, Friedberg and Hoffstein8], there exists an imaginary quadratic field L such that
$\mathrm {ord}_{s=1}L(f_{\chi },s)=r$
, by the main result of [Reference Bump, Friedberg and Hoffstein8], there exists an imaginary quadratic field L such that
-
(i)
 ${\mathrm {ord}}_{s=1}L(f_{\chi /L},s)=1$
and
${\mathrm {ord}}_{s=1}L(f_{\chi /L},s)=1$
and -
(ii) the pair
 $(f_{\chi }, L)$
satisfies the Heegner hypothesis.
$(f_{\chi }, L)$
satisfies the Heegner hypothesis.
Then, the Gross–Zagier formula [Reference Gross and Zagier28], [Reference Yuan, Zhang and Zhang55] implies that the Heegner point
![]() $y_{L} \in A_{\chi }(L)$
is non-torsion, and so the assertion is due to Kolyvagin [Reference Kolyvagin35] (see also [Reference Nekovář40]). As for the “in particular” part, note that
$y_{L} \in A_{\chi }(L)$
is non-torsion, and so the assertion is due to Kolyvagin [Reference Kolyvagin35] (see also [Reference Nekovář40]). As for the “in particular” part, note that
![]() $A_{\chi }({\mathbb {Q}})$
is p-torsion-free by Lemma 3.4.
$A_{\chi }({\mathbb {Q}})$
is p-torsion-free by Lemma 3.4.
Remark 3.6. The
![]() $r=0$
case is due to Coates–Wiles [Reference Coates and Wiles20] and Rubin [Reference Rubin46], [Reference Rubin48].
$r=0$
case is due to Coates–Wiles [Reference Coates and Wiles20] and Rubin [Reference Rubin46], [Reference Rubin48].
Let
![]() $z_{\chi }$
still denote the element of
$z_{\chi }$
still denote the element of
![]() $H^1(K, T(\chi ^{-1}))=H^1(K, T^{\otimes -1}(1)(\chi ) )$
which corresponds via (3.4) to the element
$H^1(K, T(\chi ^{-1}))=H^1(K, T^{\otimes -1}(1)(\chi ) )$
which corresponds via (3.4) to the element
![]() $z_{\chi }$
as in (3.5). Suppose
$z_{\chi }$
as in (3.5). Suppose
![]() $L(\varphi \chi ^{-1},1)=0$
. Then, by Lemma 3.3, we have
$L(\varphi \chi ^{-1},1)=0$
. Then, by Lemma 3.3, we have
![]() $z_{\chi } \in H^1_{\mathrm {{f}}}(K, T(\chi ^{-1}))$
. Let
$z_{\chi } \in H^1_{\mathrm {{f}}}(K, T(\chi ^{-1}))$
. Let
denote the corresponding element via (3.7). An immediate consequence of Proposition 3.5 is the following.
Corollary 3.7. If
![]() $\mathrm {ord}_{s=1}L(\varphi \chi ^{-1},s)=1$
, then
$\mathrm {ord}_{s=1}L(\varphi \chi ^{-1},s)=1$
, then
![]() $y_{\chi }$
arises from
$y_{\chi }$
arises from
![]() $A_{\chi }({\mathbb {Q}})\otimes _{{\mathcal {O}}_{F_{\chi }}} {\mathcal {O}}.$
$A_{\chi }({\mathbb {Q}})\otimes _{{\mathcal {O}}_{F_{\chi }}} {\mathcal {O}}.$
If
![]() $\mathrm {ord}_{s=1}(L(\varphi \chi ^{-1},s))=1$
, then
$\mathrm {ord}_{s=1}(L(\varphi \chi ^{-1},s))=1$
, then
![]() $y_{\chi }$
will be shown to be non-torsion (cf. Corollary 3.18). In our case, the latter is equivalent to being non-zeroFootnote
4
by Lemma 3.4.
$y_{\chi }$
will be shown to be non-torsion (cf. Corollary 3.18). In our case, the latter is equivalent to being non-zeroFootnote
4
by Lemma 3.4.
Remark 3.8. For any sufficiently large integer n with
![]() $(-1)^{n+1}=-W(\varphi )$
and
$(-1)^{n+1}=-W(\varphi )$
and
![]() $\chi $
a character of
$\chi $
a character of
![]() ${\mathrm {Gal}}(K_{n}/K)$
of conductor
${\mathrm {Gal}}(K_{n}/K)$
of conductor
![]() $p^{n+1}$
, Rohrlich proved that
$p^{n+1}$
, Rohrlich proved that
![]() $\mathrm {ord}_{s=1}L(\varphi \chi ^{-1} ,s)=1$
(cf. [Reference Rohrlich45]).
$\mathrm {ord}_{s=1}L(\varphi \chi ^{-1} ,s)=1$
(cf. [Reference Rohrlich45]).
3.2.2 Anticyclotomic Mordell–Weil groups
This independent subsection presents an anticyclotomic variation of the Mordell–Weil groups.
For the identity Hecke character
![]() , we put
, we put
![]() $A=A_{1}$
,
$A=A_{1}$
,
![]() $f=f_1$
and
$f=f_1$
and
![]() $F=F_{1}$
. Let
$F=F_{1}$
. Let
![]() $\chi $
be a finite character of
$\chi $
be a finite character of
![]() ${\mathrm {Gal}}(K_{\infty }/K)$
and n denote the maximum
${\mathrm {Gal}}(K_{\infty }/K)$
and n denote the maximum
![]() $\max \{0, \mathrm {ord}_p({\mathfrak {c}}_{\chi })-1\}.$
If
$\max \{0, \mathrm {ord}_p({\mathfrak {c}}_{\chi })-1\}.$
If
![]() $n=0$
, put
$n=0$
, put
![]() .
.
Theorem 3.9. Suppose that
![]() ${\mathrm {ord}}_{s=1}L(\varphi \chi ^{-1},s)=r \in \{0,1\}$
.
${\mathrm {ord}}_{s=1}L(\varphi \chi ^{-1},s)=r \in \{0,1\}$
.
-
(a) We have
 $$ \begin{align*} \mathrm{rank}_{{\mathcal {O}}_\chi}A(K_n)^{\chi}&= r[F:{\mathbb {Q}}], \\ (A(K_n)\otimes {\mathbb {Z}}_p)^{\chi} &= H^1_{\mathrm{{f}}}(K_n,T_{p}(A))^{\chi}. \end{align*} $$
$$ \begin{align*} \mathrm{rank}_{{\mathcal {O}}_\chi}A(K_n)^{\chi}&= r[F:{\mathbb {Q}}], \\ (A(K_n)\otimes {\mathbb {Z}}_p)^{\chi} &= H^1_{\mathrm{{f}}}(K_n,T_{p}(A))^{\chi}. \end{align*} $$
-
(b) In particular, the quotient
is finite.
Proof. Let
![]() $B_n$
denote the Weil restriction
$B_n$
denote the Weil restriction
![]() ${\mathrm {Res}}_{K_n/K}(A_{/K_n})$
of A over
${\mathrm {Res}}_{K_n/K}(A_{/K_n})$
of A over
![]() $K_{n}$
. By considering the Galois action on valued points of
$K_{n}$
. By considering the Galois action on valued points of
![]() $B_n$
, note that the Galois group
$B_n$
, note that the Galois group
![]() ${\mathrm {Gal}}(K_{n}/K)$
embeds into
${\mathrm {Gal}}(K_{n}/K)$
embeds into
![]() $\mathrm {End}\,B_n$
, which in turn implies
$\mathrm {End}\,B_n$
, which in turn implies
as algebras (cf. [Reference Diem and Naumann23, Thm. 3]).
In light of the decomposition
![]() ${\mathbb {Q}}[{\mathrm {Gal}}(K_{n}/K)] \cong {\mathbb {Q}}[\gamma ]/(\Phi _{p^n}(\gamma )) \times {\mathbb {Q}}[{\mathrm {Gal}}(K_{n-1}/K)]$
and factorisation of the underlying L-functions, we have an isogeny
${\mathbb {Q}}[{\mathrm {Gal}}(K_{n}/K)] \cong {\mathbb {Q}}[\gamma ]/(\Phi _{p^n}(\gamma )) \times {\mathbb {Q}}[{\mathrm {Gal}}(K_{n-1}/K)]$
and factorisation of the underlying L-functions, we have an isogeny
of abelian varieties over K. Here,
![]() $A_n$
is the abelian variety defined as a product of copies of
$A_n$
is the abelian variety defined as a product of copies of
![]() $A_{\chi }$
with
$A_{\chi }$
with
![]() $\dim (A_n)=[F:{\mathbb {Q}}](p^n-p^{n-1})$
. Note that the set of K-rational points is given by
$\dim (A_n)=[F:{\mathbb {Q}}](p^n-p^{n-1})$
. Note that the set of K-rational points is given by
Now, we consider
![]() ${\mathrm {Gal}}(K_{n}/K)$
-action which leads to
${\mathrm {Gal}}(K_{n}/K)$
-action which leads to
and
In light of the Gross–Zagier formula [Reference Gross and Zagier28], [Reference Yuan, Zhang and Zhang55] and Proposition 3.5, we have
and so
Hence, in conjunction with (3.10), it follows that
where
![]() $\chi _1$
ranges over the conjugates of
$\chi _1$
ranges over the conjugates of
![]() $\chi $
.
$\chi $
.
-
(a) Recall the short exact sequence
Now, as
 is p-torsion-free, (3.13) readily implies the second asserted equality of part (a).
is p-torsion-free, (3.13) readily implies the second asserted equality of part (a).
Since p is unramified in K, observe
 $K[\gamma ]/\Phi _{p^n}(\gamma )$
is a field with
$K[\gamma ]/\Phi _{p^n}(\gamma )$
is a field with
 $\mathrm {dim}_{K}(K[\gamma ]/ \Phi _{p^n}(\gamma ))=p^{n}-p^{n-1}$
. Naturally,
$\mathrm {dim}_{K}(K[\gamma ]/ \Phi _{p^n}(\gamma ))=p^{n}-p^{n-1}$
. Naturally,
 $(\gamma ^{p^{n-1}}-1)A(K_n)\otimes {\mathbb {Q}}$
is a
$(\gamma ^{p^{n-1}}-1)A(K_n)\otimes {\mathbb {Q}}$
is a
 $K[\gamma ]/\Phi _{p^n}(\gamma )$
-vector space. So, in view of (3.9) and (3.12), it follows that Hence, the evaluation at
$K[\gamma ]/\Phi _{p^n}(\gamma )$
-vector space. So, in view of (3.9) and (3.12), it follows that Hence, the evaluation at $$ \begin{align*} (\gamma^{p^{n-1}}-1)A(K_n)\otimes {\mathbb {Q}} \cong (K [\gamma]/(\Phi_{p^n}(\gamma)))^{\oplus [F:{\mathbb {Q}}]}. \end{align*} $$
$$ \begin{align*} (\gamma^{p^{n-1}}-1)A(K_n)\otimes {\mathbb {Q}} \cong (K [\gamma]/(\Phi_{p^n}(\gamma)))^{\oplus [F:{\mathbb {Q}}]}. \end{align*} $$
 $\chi $
yields the first asserted equality of part (a).
$\chi $
yields the first asserted equality of part (a).
-
(b) In view of (3.13), we have
i.e. part (b) holds.
Remark 3.10. The above argument is a variation of Rubin’s argument for [Reference Agboola and Howard3, Prop. A.8].
Corollary 3.11. Suppose E is defined over K. Then, for any sufficiently large n,
Here, if
![]() $W(\varphi )=+1$
, then
$W(\varphi )=+1$
, then
![]() $\varepsilon _{n}=0$
(resp.
$\varepsilon _{n}=0$
(resp.
![]() $2$
) for n odd (resp. even) and the reverse in the case
$2$
) for n odd (resp. even) and the reverse in the case
![]() $W(\varphi )=-1$
.
$W(\varphi )=-1$
.
The corollary implies that new points of infinite order appear in the alternate anticyclotomic layers. As shown in Corollary 3.18 below, these points correspond to the Selmer elements
![]() $y_{\chi }$
.
$y_{\chi }$
.
Remark 3.12.
-
(i) Corollary 3.11 is originally due to Greenberg (unpublished, cf. [Reference Greenberg26, (1.10)]).
-
(ii) An analogue of Corollary 3.11 for Selmer groups appears in [Reference Agboola and Howard2, Thm. A].
3.3 Rubin p-adic L-function and global points
The section presents a Rubin type special value formula for the Rubin p-adic L-function, which is a result towards the question (Q).
Assume that
Then, the Galois group
![]() ${\mathrm {Gal}}(K_{\infty }/K)$
is naturally identified with
${\mathrm {Gal}}(K_{\infty }/K)$
is naturally identified with
![]() ${\mathrm {Gal}}(\Psi _{\infty }/\Phi )$
. For
${\mathrm {Gal}}(\Psi _{\infty }/\Phi )$
. For
![]() $n\ge 0$
, let
$n\ge 0$
, let
![]() ${\mathfrak {p}}$
denote the prime of
${\mathfrak {p}}$
denote the prime of
![]() $K_n$
above p.
$K_n$
above p.
3.3.1 Rubin p-adic L-function
Let
![]() $\varepsilon $
be the sign of the root number
$\varepsilon $
be the sign of the root number
![]() $W(\varphi )$
of the functional equation of the Hecke L-function
$W(\varphi )$
of the functional equation of the Hecke L-function
![]() $L(\varphi ,s)$
. In light of (2.8) and (3.3), the image of
$L(\varphi ,s)$
. In light of (2.8) and (3.3), the image of
![]() ${\mathrm {loc}}_{{\mathfrak {p}}}(z) \in \varprojlim _{n}H^1(K_{n,{\mathfrak {p}}}, T^{\otimes -1}(1))$
in
${\mathrm {loc}}_{{\mathfrak {p}}}(z) \in \varprojlim _{n}H^1(K_{n,{\mathfrak {p}}}, T^{\otimes -1}(1))$
in
![]() $V_{\infty }^*$
via (2.7) lives in
$V_{\infty }^*$
via (2.7) lives in
![]() $V^{*,\varepsilon }_{\infty }$
.
$V^{*,\varepsilon }_{\infty }$
.
Following [Reference Rubin47, §10], we introduce the following.
Definition 3.13. A Rubin p-adic L-function
![]() $\mathscr {L}:=\mathscr {L}_{{b_E, v_\varepsilon }} \in \Lambda ^{}$
is defined by
$\mathscr {L}:=\mathscr {L}_{{b_E, v_\varepsilon }} \in \Lambda ^{}$
is defined by
For an anticyclotomic character
![]() $\chi $
, let
$\chi $
, let
![]() $\mathscr {L}(\chi )$
denote the evaluation at
$\mathscr {L}(\chi )$
denote the evaluation at
![]() $\chi $
. For
$\chi $
. For
![]() $\chi \in \Xi ^{\varepsilon }$
(resp.
$\chi \in \Xi ^{\varepsilon }$
(resp.
![]() $\chi \in \Xi ^{-\varepsilon }$
), note that
$\chi \in \Xi ^{-\varepsilon }$
), note that
![]() $W(\varphi \chi )=+1$
(resp.
$W(\varphi \chi )=+1$
(resp.
![]() $W(\varphi \chi )=-1$
, cf. [Reference Greenberg24, p. 247]).
$W(\varphi \chi )=-1$
, cf. [Reference Greenberg24, p. 247]).
Lemma 3.14. For
![]() $\chi \in \Xi ^{\varepsilon }$
, we have
$\chi \in \Xi ^{\varepsilon }$
, we have
 $$ \begin{align*}\mathscr{L}(\chi)=\frac{1}{\delta_{\chi^{-1}}(v_{\epsilon})} \cdot \frac{L_{p{\mathfrak{f}}}(\overline{\varphi\chi},1)}{\Omega}. \end{align*} $$
$$ \begin{align*}\mathscr{L}(\chi)=\frac{1}{\delta_{\chi^{-1}}(v_{\epsilon})} \cdot \frac{L_{p{\mathfrak{f}}}(\overline{\varphi\chi},1)}{\Omega}. \end{align*} $$
Proof. The non-vanishing of
![]() $\delta _{\chi ^{-1}}(v_{\varepsilon })$
is a consequence of Theorem 2.1 and [Reference Rubin47, Lem. 10.1]. Hence, the assertion follows by (2.8) and (3.3).
$\delta _{\chi ^{-1}}(v_{\varepsilon })$
is a consequence of Theorem 2.1 and [Reference Rubin47, Lem. 10.1]. Hence, the assertion follows by (2.8) and (3.3).
3.3.2 A Rubin type formula
The subsection explores
![]() $\mathscr {L}(\chi )$
for
$\mathscr {L}(\chi )$
for
![]() $\chi \in \Xi ^{-\varepsilon }.$
$\chi \in \Xi ^{-\varepsilon }.$
Let
![]() $\lambda _{E}: \hat {E}(\Psi _n)\otimes _{{\mathcal {O}}_{\Phi }} {\mathcal {O}} \to \Psi _n\otimes {\mathcal {O}}$
denote the homomorphism induced by the logarithm associated to
$\lambda _{E}: \hat {E}(\Psi _n)\otimes _{{\mathcal {O}}_{\Phi }} {\mathcal {O}} \to \Psi _n\otimes {\mathcal {O}}$
denote the homomorphism induced by the logarithm associated to
![]() $\hat {E}$
. For a character
$\hat {E}$
. For a character
![]() $\chi $
of
$\chi $
of
![]() ${\mathrm {Gal}}(\Psi _{n}/\Psi )$
and
${\mathrm {Gal}}(\Psi _{n}/\Psi )$
and
![]() $c \in \hat {E}(\Psi _{n})$
, let
$c \in \hat {E}(\Psi _{n})$
, let
 $$ \begin{align*}\lambda_{E,\chi}(c)=p^{-n}\sum_{\sigma\in {\mathrm{Gal}}(\Psi_n/\Phi)}\chi^{-1}(\sigma)\lambda_{E}(c^{\sigma}).\end{align*} $$
$$ \begin{align*}\lambda_{E,\chi}(c)=p^{-n}\sum_{\sigma\in {\mathrm{Gal}}(\Psi_n/\Phi)}\chi^{-1}(\sigma)\lambda_{E}(c^{\sigma}).\end{align*} $$
Recall that
![]() $T|_{G_{K_{{\mathfrak {p}}}}}$
is identified with
$T|_{G_{K_{{\mathfrak {p}}}}}$
is identified with
![]() $T_p(E)\otimes {\mathcal {O}}.$
$T_p(E)\otimes {\mathcal {O}}.$
As in (3.1), we identify
by which an element v of
![]() $H^1(\Psi _n,T^{\otimes -1}(1))$
will be regarded as an element of
$H^1(\Psi _n,T^{\otimes -1}(1))$
will be regarded as an element of
![]() $H^1(\Psi _n,T)$
. In view of the identifications the pairings
$H^1(\Psi _n,T)$
. In view of the identifications the pairings
![]() $(\ \ , \ \ )_{\Lambda _m}$
in (2.11) induce a perfect pairing
$(\ \ , \ \ )_{\Lambda _m}$
in (2.11) induce a perfect pairing
which is
![]() $\Lambda $
-bilinear (as the pairing (2.11) is sesquilinear). In the following, we regard
$\Lambda $
-bilinear (as the pairing (2.11) is sesquilinear). In the following, we regard
![]() $(\ \ , \ \ )_n$
and
$(\ \ , \ \ )_n$
and
![]() $(\ \ , \ \ )_{\Lambda _n}$
as pairings on
$(\ \ , \ \ )_{\Lambda _n}$
as pairings on
![]() $H^1(\Psi _n,T) \times H^1(\Psi _n,T).$
$H^1(\Psi _n,T) \times H^1(\Psi _n,T).$
Lemma 3.15. We have
Proof. As for the first assertion, by Nakayama’s lemma, it suffices to show that
![]() $(v_{+,0},v_{-,0})_0 \in {\mathcal {O}}^{\times }.$
$(v_{+,0},v_{-,0})_0 \in {\mathcal {O}}^{\times }.$
In view of Theorem 2.1,
where
![]() $v_{\pm ,0}$
is the image of
$v_{\pm ,0}$
is the image of
![]() $v^{\pm }$
in
$v^{\pm }$
in
![]() $V_{\infty }^{*}/(\gamma -1)$
. Note that
$V_{\infty }^{*}/(\gamma -1)$
. Note that
![]() $H^1_{\mathrm {f}}(\Phi , T) \cong {\mathscr {F}}({\mathfrak {m}}_0) \cong {\mathcal {O}}$
, and so by (3.16),
$H^1_{\mathrm {f}}(\Phi , T) \cong {\mathscr {F}}({\mathfrak {m}}_0) \cong {\mathcal {O}}$
, and so by (3.16),
As
![]() $\delta _{0}(v_{-})=0$
, observe
$\delta _{0}(v_{-})=0$
, observe
![]() $v_{-,0} \in H^1_{\mathrm {f}}(\Phi , T)$
by Lemma 2.2. Recall
$v_{-,0} \in H^1_{\mathrm {f}}(\Phi , T)$
by Lemma 2.2. Recall
![]() $(\ \ , \ \ )_0$
is perfect and
$(\ \ , \ \ )_0$
is perfect and
![]() $ H^1_{\mathrm {f}}(\Phi , T)$
is a maximal isotropic subgroup. Hence, (3.16) implies that
$ H^1_{\mathrm {f}}(\Phi , T)$
is a maximal isotropic subgroup. Hence, (3.16) implies that
![]() $(v_{+,0}, v_{-,0})_0 \in {\mathcal {O}}^{\times }$
.
$(v_{+,0}, v_{-,0})_0 \in {\mathcal {O}}^{\times }$
.
We now consider the second assertion. For any
![]() $\chi \in \Xi ^{\mp }$
, note that
$\chi \in \Xi ^{\mp }$
, note that
![]() $\delta _{\chi }(v_{\pm })=0,$
i.e. the image of
$\delta _{\chi }(v_{\pm })=0,$
i.e. the image of
![]() $v_{\pm }$
under
$v_{\pm }$
under
![]() $\varprojlim _{m}H^1(\Phi _m, T) \to H^1(\Phi , V(\chi ^{-1}))$
lies in the finite part
$\varprojlim _{m}H^1(\Phi _m, T) \to H^1(\Phi , V(\chi ^{-1}))$
lies in the finite part
![]() $H^1_{\mathrm {f}}(\Phi , V(\chi ^{-1}))$
. Since
$H^1_{\mathrm {f}}(\Phi , V(\chi ^{-1}))$
. Since
![]() $H^1_{\mathrm {f}}(\Phi , V(\chi ^{-1}))$
is the orthogonal complement of itself under
$H^1_{\mathrm {f}}(\Phi , V(\chi ^{-1}))$
is the orthogonal complement of itself under
![]() $(\ \ , \ \ )_n$
, we have
$(\ \ , \ \ )_n$
, we have
![]() $\chi \left ((v_{\pm },v_{\pm })_{\Lambda }\right )=0$
. This implies
$\chi \left ((v_{\pm },v_{\pm })_{\Lambda }\right )=0$
. This implies
![]() $(v_{\pm },v_{\pm })_{\Lambda }=0$
as
$(v_{\pm },v_{\pm })_{\Lambda }=0$
as
![]() $\Xi ^{\mp }$
is an infinite set.
$\Xi ^{\mp }$
is an infinite set.
From now, we fix
![]() $v_+,v_-$
so that
$v_+,v_-$
so that
and then
![]() $v^{\perp }_{\pm , n}$
in (2.12) is identified with
$v^{\perp }_{\pm , n}$
in (2.12) is identified with
![]() $v_{\pm ,n}$
via (3.15).
$v_{\pm ,n}$
via (3.15).
The main result of this subsection is the following.
Theorem 3.16. Let K be an imaginary quadratic field and
![]() $p\geq 5$
a prime satisfying (inr) and (cp). Let E be a
$p\geq 5$
a prime satisfying (inr) and (cp). Let E be a
![]() ${\mathbb {Q}}$
-curve with complex multiplication by
${\mathbb {Q}}$
-curve with complex multiplication by
![]() $\mathcal {O}_K$
with good reduction at p,
$\mathcal {O}_K$
with good reduction at p,
![]() $\varphi $
the associated Hecke character of K and
$\varphi $
the associated Hecke character of K and
![]() $\varepsilon $
the sign of the root number. Let
$\varepsilon $
the sign of the root number. Let
![]() $\mathscr {L}$
be the Rubin p-adic L-function as in (3.14).
$\mathscr {L}$
be the Rubin p-adic L-function as in (3.14).
-
(a) Let
 $\chi \in \Xi ^{-\varepsilon }$
be a Hecke character with conductor
$\chi \in \Xi ^{-\varepsilon }$
be a Hecke character with conductor
 $p^{n+1}$
. Let
$p^{n+1}$
. Let
 $z_{\chi ^{-1}} \in H^1(K_{n},T_pE)^{\chi ^{-1}}$
be the image of a system of elliptic units of E (cf. §3.1.2). Then, and we haveFootnote 5
$z_{\chi ^{-1}} \in H^1(K_{n},T_pE)^{\chi ^{-1}}$
be the image of a system of elliptic units of E (cf. §3.1.2). Then, and we haveFootnote 5 $$ \begin{align*} z_{\chi^{-1}}\in H^1_{\mathrm{{f}}}(K_{n},T_pE)^{\chi^{-1}} \end{align*} $$
where
$$ \begin{align*} z_{\chi^{-1}}\in H^1_{\mathrm{{f}}}(K_{n},T_pE)^{\chi^{-1}} \end{align*} $$
where $$ \begin{align*} \mathscr{L}(\chi)=\delta_{\chi^{-1}}(v_{-\varepsilon}) \cdot\lambda_{E}({\mathrm{loc}}_{{\mathfrak{p}}}(z_{\chi^{-1}})) =\frac{\omega^{-\varepsilon}_n(\chi(\gamma))}{\tau(\chi^{}, \lambda_{E}(c_n^{\varepsilon}))}\cdot \lambda_{E}({\mathrm{loc}}_{{\mathfrak{p}}}(z_{\chi^{-1}})), \end{align*} $$
$$ \begin{align*} \mathscr{L}(\chi)=\delta_{\chi^{-1}}(v_{-\varepsilon}) \cdot\lambda_{E}({\mathrm{loc}}_{{\mathfrak{p}}}(z_{\chi^{-1}})) =\frac{\omega^{-\varepsilon}_n(\chi(\gamma))}{\tau(\chi^{}, \lambda_{E}(c_n^{\varepsilon}))}\cdot \lambda_{E}({\mathrm{loc}}_{{\mathfrak{p}}}(z_{\chi^{-1}})), \end{align*} $$
 $\tau (\chi ^{}, \alpha ):=\sum _{\sigma \in {\mathrm {Gal}}(K_{n}/K) }\chi ^{}(\sigma )\alpha ^{\sigma }. $
$\tau (\chi ^{}, \alpha ):=\sum _{\sigma \in {\mathrm {Gal}}(K_{n}/K) }\chi ^{}(\sigma )\alpha ^{\sigma }. $
-
(b) If
 $\varepsilon =-1$
, then
$\varepsilon =-1$
, then 
Proof.
-
(a) By Definition 3.13, note that
where $$ \begin{align*} \sum_{\sigma \in {\mathrm{Gal}}(K_n^{}/K)}(v^{\perp}_{-\varepsilon, n}, z_n^{\sigma})_n\sigma=\mathscr{L}(\gamma^{-1}) \ \mathrm{mod}\ (\gamma^{p^n}-1), \end{align*} $$
$$ \begin{align*} \sum_{\sigma \in {\mathrm{Gal}}(K_n^{}/K)}(v^{\perp}_{-\varepsilon, n}, z_n^{\sigma})_n\sigma=\mathscr{L}(\gamma^{-1}) \ \mathrm{mod}\ (\gamma^{p^n}-1), \end{align*} $$
 $z_{n}$
also denotes
$z_{n}$
also denotes
 ${\mathrm {loc}}_{{\mathfrak {p}}}(z_{n})$
.
${\mathrm {loc}}_{{\mathfrak {p}}}(z_{n})$
.
In view of the explicit reciprocity law of Wiles (cf. [Reference Wiles53]) and [Reference Rubin47, Lem. 5.5], we have
(see also [Reference Rubin47, p. 413]). Here, $$ \begin{align*} \kern-25pt \sum_{\sigma \in {\mathrm{Gal}}(K_n^{}/K)}(v^{\perp}_{-\varepsilon, n}, z_n^{\sigma})_n\chi^{-1}(\sigma) &= ( v_{-\varepsilon,n}^{\perp}, \sum_{\sigma} z_{n}^{\sigma}\chi^{-1}(\sigma) )_{n}\\ &= \mathrm{Tr}_{\Psi_n(\mathrm{Im}(\chi))/\Phi(\mathrm{Im}(\chi))}\left[\exp^*(v_{-\varepsilon,n}^{\perp}), \log\left( \sum_{\sigma} z_{n}^{\sigma}\chi^{-1}(\sigma)\right)\right]\\ &= \left[\sum_{\sigma \in {\mathrm{Gal}}(\Psi_n/\Phi)}\exp^*(\sigma v_{-\varepsilon,n}^{\perp})\chi(\sigma), \log\left( \sum_{\sigma} z_{n}^{\sigma}\chi^{-1}(\sigma)\right)\right]\\ &=\delta_{\chi^{-1}}(v_{-\varepsilon})\cdot \lambda_{E}(z_{\chi^{-1}}) \end{align*} $$
denotes the natural pairing,
$$ \begin{align*} \kern-25pt \sum_{\sigma \in {\mathrm{Gal}}(K_n^{}/K)}(v^{\perp}_{-\varepsilon, n}, z_n^{\sigma})_n\chi^{-1}(\sigma) &= ( v_{-\varepsilon,n}^{\perp}, \sum_{\sigma} z_{n}^{\sigma}\chi^{-1}(\sigma) )_{n}\\ &= \mathrm{Tr}_{\Psi_n(\mathrm{Im}(\chi))/\Phi(\mathrm{Im}(\chi))}\left[\exp^*(v_{-\varepsilon,n}^{\perp}), \log\left( \sum_{\sigma} z_{n}^{\sigma}\chi^{-1}(\sigma)\right)\right]\\ &= \left[\sum_{\sigma \in {\mathrm{Gal}}(\Psi_n/\Phi)}\exp^*(\sigma v_{-\varepsilon,n}^{\perp})\chi(\sigma), \log\left( \sum_{\sigma} z_{n}^{\sigma}\chi^{-1}(\sigma)\right)\right]\\ &=\delta_{\chi^{-1}}(v_{-\varepsilon})\cdot \lambda_{E}(z_{\chi^{-1}}) \end{align*} $$
denotes the natural pairing, $$ \begin{align*}[\ \ , \ \ ] :D_{{\mathrm{dR}}}(V)\otimes_{\Phi} \Psi_n \times D_{{\mathrm{dR}}}(V^{\otimes -1}(1))\otimes_{\Phi}\Psi_n \to {\mathcal {O}}[1/p]\otimes_{\Phi}\Psi_n\end{align*} $$
$$ \begin{align*}[\ \ , \ \ ] :D_{{\mathrm{dR}}}(V)\otimes_{\Phi} \Psi_n \times D_{{\mathrm{dR}}}(V^{\otimes -1}(1))\otimes_{\Phi}\Psi_n \to {\mathcal {O}}[1/p]\otimes_{\Phi}\Psi_n\end{align*} $$
 $\exp ^*$
is the dual exponential map, and the last equality follows from (2.9) and the fact that
$\exp ^*$
is the dual exponential map, and the last equality follows from (2.9) and the fact that
 $\sigma v_{-\varepsilon , n}^{\perp }$
corresponds to
$\sigma v_{-\varepsilon , n}^{\perp }$
corresponds to
 $\sigma ^{-1} v_{-\varepsilon , n}$
under (3.15). Hence, (3.17)
$\sigma ^{-1} v_{-\varepsilon , n}$
under (3.15). Hence, (3.17) $$ \begin{align} \mathscr{L}(\chi(\gamma))= \delta_{\chi^{-1}}(v_{-\varepsilon}^{}) \cdot \lambda_{E}(z_{\chi^{-1}}) \end{align} $$
$$ \begin{align} \mathscr{L}(\chi(\gamma))= \delta_{\chi^{-1}}(v_{-\varepsilon}^{}) \cdot \lambda_{E}(z_{\chi^{-1}}) \end{align} $$
However,
and so $$ \begin{align*} \sum_{\sigma\in {\mathrm{Gal}}(K_n^{}/K)}(\sigma c_n^{\varepsilon}, v_{-\varepsilon,n})_n\sigma =\omega^{-\varepsilon}_n(\gamma^{}) \bmod (\gamma^{p^n}-1), \end{align*} $$
Hence, (3.17) concludes the proof.
$$ \begin{align*} \sum_{\sigma\in {\mathrm{Gal}}(K_n^{}/K)}(\sigma c_n^{\varepsilon}, v_{-\varepsilon,n})_n\sigma =\omega^{-\varepsilon}_n(\gamma^{}) \bmod (\gamma^{p^n}-1), \end{align*} $$
Hence, (3.17) concludes the proof. $$ \begin{align*}\delta_{\chi^{-1}}(v_{-\varepsilon})\cdot p^n\lambda_{E,\chi^{-1}}(c_n^{\varepsilon})= \omega^{-\varepsilon}_n(\chi(\gamma)). \end{align*} $$
$$ \begin{align*}\delta_{\chi^{-1}}(v_{-\varepsilon})\cdot p^n\lambda_{E,\chi^{-1}}(c_n^{\varepsilon})= \omega^{-\varepsilon}_n(\chi(\gamma)). \end{align*} $$
-
(b) This just follows by letting
 $n=0$
and
$n=0$
and
 in the above argument.
in the above argument.
Remark 3.17.
-
(i) In view of Theorem 3.16 (b), if
 $\varepsilon =-1$
, then (3.18)up to an element in
$\varepsilon =-1$
, then (3.18)up to an element in
 ${\mathcal {O}}^{\times }.$
${\mathcal {O}}^{\times }.$
-
(ii) One may seek a Coleman integration approach to Theorem 3.16. The preliminary study of a p-adic Eisenstein series in [Reference Bannai, Furusho and Kobayashi5] maybe relevant.
-
(iii) A natural problem is to investigate a special value formula
 $\mathscr {L}(\chi )$
for anticyclotomic characters
$\mathscr {L}(\chi )$
for anticyclotomic characters
 $\chi $
of infinity type
$\chi $
of infinity type
 $(j,-j)$
with
$(j,-j)$
with
 $j>0$
. It will be investigated in a forthcoming paper.
$j>0$
. It will be investigated in a forthcoming paper.
Corollary 3.18. Let
![]() $\chi $
be a primitive character of
$\chi $
be a primitive character of
![]() ${\mathrm {Gal}}(K_n/K)$
so that
${\mathrm {Gal}}(K_n/K)$
so that
![]() $\mathrm {ord}_{s=1} L(\varphi \chi ,s)=1.$
Then,
$\mathrm {ord}_{s=1} L(\varphi \chi ,s)=1.$
Then,
![]() $y_{\chi ^{-1}}\in A_{\chi ^{-1}}({\mathbb {Q}})\otimes {\mathcal {O}}_{\chi }$
, as in Corollary 3.7, has the following properties.
$y_{\chi ^{-1}}\in A_{\chi ^{-1}}({\mathbb {Q}})\otimes {\mathcal {O}}_{\chi }$
, as in Corollary 3.7, has the following properties.
-
(i)
 $y_{\chi ^{-1}}$
is nontorsion.
$y_{\chi ^{-1}}$
is nontorsion. -
(ii) We have
for a non-zero $$ \begin{align*} \mathscr{L}(\chi)=d_{\chi}\cdot\lambda_{A_{\chi^{-1}}}(y_{\chi^{-1}}) \end{align*} $$
$$ \begin{align*} \mathscr{L}(\chi)=d_{\chi}\cdot\lambda_{A_{\chi^{-1}}}(y_{\chi^{-1}}) \end{align*} $$
 $d_{\chi }\in {\mathcal {O}}_{\chi }[1/p]$
and
$d_{\chi }\in {\mathcal {O}}_{\chi }[1/p]$
and
 $\lambda _{A_{\chi ^{-1}}}$
a formal group logarithm of the Néron model of
$\lambda _{A_{\chi ^{-1}}}$
a formal group logarithm of the Néron model of
 $A_{\chi ^{-1}}$
over
$A_{\chi ^{-1}}$
over
 ${\mathbb {Z}}_{(p)}$
.
${\mathbb {Z}}_{(p)}$
.
Proof. The following is based on Iwasawa main conjectures [Reference Agboola and Howard2], [Reference Burungale, Kobayashi and Ota12], to which we refer for notation.
Let
![]() $\varepsilon $
denote the sign of the root number
$\varepsilon $
denote the sign of the root number
![]() $W(\varphi )$
. By [Reference Agboola and Howard2, Thm. 3.6], the Selmer group
$W(\varphi )$
. By [Reference Agboola and Howard2, Thm. 3.6], the Selmer group
![]() $\mathscr {X}_{\infty }^{\varepsilon }$
has
$\mathscr {X}_{\infty }^{\varepsilon }$
has
![]() $\Lambda $
-rank one. Let
$\Lambda $
-rank one. Let
![]() $\mathscr {X}_{\mathrm {str}}$
be the Pontryagin dual of the strict Selmer group
$\mathscr {X}_{\mathrm {str}}$
be the Pontryagin dual of the strict Selmer group
![]() $S_{\mathrm {{str}}}:=\mathrm {Sel}_{\mathrm {str}}(K_{\infty }, V/T)$
(cf. [Reference Agboola and Howard2, §2] or (4.1) below). Let
$S_{\mathrm {{str}}}:=\mathrm {Sel}_{\mathrm {str}}(K_{\infty }, V/T)$
(cf. [Reference Agboola and Howard2, §2] or (4.1) below). Let
![]() $\mathscr {X}_{\mathrm {rel}}$
be defined analogously.
$\mathscr {X}_{\mathrm {rel}}$
be defined analogously.
In light of Proposition 3.5 and [Reference Agboola and Howard2, Thm. 5.2], the latter being the main conjectureFootnote
6
, the
![]() $\chi ^{-1}$
-specialization of
$\chi ^{-1}$
-specialization of
![]() $\mathrm {char}_{\Lambda }(\mathscr {X}_{\infty ,{\mathrm {tor}}}^{\varepsilon })$
is non-zero, where
$\mathrm {char}_{\Lambda }(\mathscr {X}_{\infty ,{\mathrm {tor}}}^{\varepsilon })$
is non-zero, where
![]() $\mathrm {char}_{\Lambda }(\cdot )$
denotes the characteristic ideal. Observe that Proposition 3.5 also implies that the
$\mathrm {char}_{\Lambda }(\cdot )$
denotes the characteristic ideal. Observe that Proposition 3.5 also implies that the
![]() $\chi ^{-1}$
-specialization of
$\chi ^{-1}$
-specialization of
![]() $\mathrm {char}_{\Lambda }(\mathscr {X}_{\mathrm {str}})$
is non-zero and then so is the
$\mathrm {char}_{\Lambda }(\mathscr {X}_{\mathrm {str}})$
is non-zero and then so is the
![]() $\chi ^{-1}$
-specialization of
$\chi ^{-1}$
-specialization of
![]() $\mathrm {char}_{\Lambda }(\mathscr {X}_{\mathrm {rel}, \Lambda -\mathrm {tor}})$
(cf. [Reference Agboola and Howard2, Thm. 4.1]). Hence, in view of [Reference Agboola and Howard2, (4.1), (4.4)], it follows that
$\mathrm {char}_{\Lambda }(\mathscr {X}_{\mathrm {rel}, \Lambda -\mathrm {tor}})$
(cf. [Reference Agboola and Howard2, Thm. 4.1]). Hence, in view of [Reference Agboola and Howard2, (4.1), (4.4)], it follows that
![]() $z_{\chi ^{-1}}$
is non-torsion, and the proof concludes by Theorem 3.16 (b).
$z_{\chi ^{-1}}$
is non-torsion, and the proof concludes by Theorem 3.16 (b).
Remark 3.19.
-
(i) By Lemma 3.4,
 $A_{\chi }({\mathbb {Q}})\otimes {\mathcal {O}}_{\chi }$
is p-torsion-free.
$A_{\chi }({\mathbb {Q}})\otimes {\mathcal {O}}_{\chi }$
is p-torsion-free. -
(ii) If
 $\mathrm {ord}_{s=1}L(\varphi ,s)=1$
, then (3.19)up to an element in
$\mathrm {ord}_{s=1}L(\varphi ,s)=1$
, then (3.19)up to an element in
 ${\mathcal {O}}^{\times }$
.
${\mathcal {O}}^{\times }$
.
4 Rubin p-adic L-function and rational points
The main results are Theorems 4.8 and 4.18, and Proposition 4.14.
4.0.1 Notation
Let the setup be as in §3.3. In particular,
![]() $f\in S_{2}(\Gamma _{0}(N))$
denotes the theta series associated to the Hecke character
$f\in S_{2}(\Gamma _{0}(N))$
denotes the theta series associated to the Hecke character
![]() $\varphi $
. Let
$\varphi $
. Let
![]() $F\subset {\mathbb {C}}$
denote the Hecke field of f.
$F\subset {\mathbb {C}}$
denote the Hecke field of f.
Let
![]() $A_{/{\mathbb {Q}}}$
be a
$A_{/{\mathbb {Q}}}$
be a
![]() ${\mathrm {GL}}_2$
-type abelian variety so that
${\mathrm {GL}}_2$
-type abelian variety so that
(cf. §B.1). Let L denote the subfield of
![]() ${\mathbb {C}}$
generated by
${\mathbb {C}}$
generated by
![]() $\varphi (\widehat {K}^{\times })$
over K, a finite extension of K containing F. As in §3, let
$\varphi (\widehat {K}^{\times })$
over K, a finite extension of K containing F. As in §3, let
![]() ${\mathcal {O}}$
be the integer ring of the completion
${\mathcal {O}}$
be the integer ring of the completion
![]() $L_{{\mathfrak {p}}}$
at the prime
$L_{{\mathfrak {p}}}$
at the prime
![]() ${\mathfrak {p}}$
compatible with the embedding
${\mathfrak {p}}$
compatible with the embedding
![]() $\iota _p$
. Let
$\iota _p$
. Let
![]() $\lambda _f: A({\mathbb {Q}}_{p}) \to F_{{\mathfrak {p}}}$
be a formal group logarithm arising from the differential attached to the newform f as in §A.3.
$\lambda _f: A({\mathbb {Q}}_{p}) \to F_{{\mathfrak {p}}}$
be a formal group logarithm arising from the differential attached to the newform f as in §A.3.
Put
![]() $V(f)=V_p(A)\otimes _{F\otimes {\mathbb {Q}}_p} F_{{\mathfrak {p}}} \cong F_{{\mathfrak {p}}}^{\oplus 2}$
and
$V(f)=V_p(A)\otimes _{F\otimes {\mathbb {Q}}_p} F_{{\mathfrak {p}}} \cong F_{{\mathfrak {p}}}^{\oplus 2}$
and
![]() $V_{L_{{\mathfrak {p}}}}(f)=V(f)\otimes _{F_{{\mathfrak {p}}}} L_{{\mathfrak {p}}}$
. Our normalisation differs from [Reference Kato30]; namely, our
$V_{L_{{\mathfrak {p}}}}(f)=V(f)\otimes _{F_{{\mathfrak {p}}}} L_{{\mathfrak {p}}}$
. Our normalisation differs from [Reference Kato30]; namely, our
![]() $V_{L_{\mathfrak {p}}}(f)$
is isomorphic to
$V_{L_{\mathfrak {p}}}(f)$
is isomorphic to
![]() $V_{L_{\mathfrak {p}}}(f)(1)$
of [Reference Kato30, §8.3] as a
$V_{L_{\mathfrak {p}}}(f)(1)$
of [Reference Kato30, §8.3] as a
![]() $G_{{\mathbb {Q}}}$
-representation.
$G_{{\mathbb {Q}}}$
-representation.
Replacing A by an isogeny, we may assume that A has
![]() ${\mathcal {O}}_F$
-multiplication. For
${\mathcal {O}}_F$
-multiplication. For
![]() $W = A[{\mathfrak {p}}^{\infty }]$
(resp.
$W = A[{\mathfrak {p}}^{\infty }]$
(resp.
![]() $V/T $
) and a finite extension M of
$V/T $
) and a finite extension M of
![]() ${\mathbb {Q}}$
(resp. K), define
${\mathbb {Q}}$
(resp. K), define
 $$ \begin{align} {\mathrm{Sel}}_{\mathrm{str}}(M,W)= \mathrm{ker}\left(H^1(M,W) \to \prod_{v\mid p} H^1(M_v,W) \times \prod_{v\nmid p} \frac{H^1(M_{v}^{}, W )}{H^1_{\mathrm{f}}(M_{v}^{}, W )}\right). \end{align} $$
$$ \begin{align} {\mathrm{Sel}}_{\mathrm{str}}(M,W)= \mathrm{ker}\left(H^1(M,W) \to \prod_{v\mid p} H^1(M_v,W) \times \prod_{v\nmid p} \frac{H^1(M_{v}^{}, W )}{H^1_{\mathrm{f}}(M_{v}^{}, W )}\right). \end{align} $$
Put
![]() ${\mathrm {Sel}}_{\mathrm {str}}(K_{\infty }, V/T)=\varinjlim _n{\mathrm {Sel}}_{\mathrm {str}}(K_{n}, V/T).$
${\mathrm {Sel}}_{\mathrm {str}}(K_{\infty }, V/T)=\varinjlim _n{\mathrm {Sel}}_{\mathrm {str}}(K_{n}, V/T).$
4.1 p-adic Beilinson formula: a first form
4.1.1
Theorem 4.1. Let
![]() $A_{/{\mathbb {Q}}}$
be a
$A_{/{\mathbb {Q}}}$
be a
![]() ${\mathrm {GL}}_2$
-type CM abelian variety. Let K be the corresponding imaginary quadratic field and F the Hecke field. Suppose that the root number of the associated CM newform is
${\mathrm {GL}}_2$
-type CM abelian variety. Let K be the corresponding imaginary quadratic field and F the Hecke field. Suppose that the root number of the associated CM newform is
![]() $-1$
. Let
$-1$
. Let
![]() $p\geq 5$
be a prime of good non-ordinary reduction for
$p\geq 5$
be a prime of good non-ordinary reduction for
![]() $A_{/{\mathbb {Q}}}$
with
$A_{/{\mathbb {Q}}}$
with
![]() $p\nmid h_{K}$
and
$p\nmid h_{K}$
and
![]() $\mathscr {L}$
the Rubin p-adic L-function as in (3.14). Then, there exists a rational point
$\mathscr {L}$
the Rubin p-adic L-function as in (3.14). Then, there exists a rational point
![]() $P\in A({\mathbb {Q}})$
with the following properties.
$P\in A({\mathbb {Q}})$
with the following properties.
-
(a) We have
for some
 $c \in L^\times $
.
$c \in L^\times $
.
-
(b) P is non-torsion if and only if
 ${\mathrm {ord}}_{s=1}L(A,s)=[F:{\mathbb {Q}}].$
${\mathrm {ord}}_{s=1}L(A,s)=[F:{\mathbb {Q}}].$
4.1.2 Tools of the proof
We outline the strategy. Elliptic units and Beilinson–Kato elements. The following link between zeta elements is a key.
Theorem 4.2. Let
![]() $z=(z_n) \in \varprojlim _{n}H^1(K_n,T)$
be the elliptic unit as in (3.2) under the identification (3.1) and
$z=(z_n) \in \varprojlim _{n}H^1(K_n,T)$
be the elliptic unit as in (3.2) under the identification (3.1) and
![]() $z_{f}\in H^{1}({\mathbb {Q}},V(f))$
a Beilinson–Kato element associated to the newform f. Then, under the identification (4.2), we have
$z_{f}\in H^{1}({\mathbb {Q}},V(f))$
a Beilinson–Kato element associated to the newform f. Then, under the identification (4.2), we have
up to an element in
![]() $L^{\times }$
.
$L^{\times }$
.
Proof. This is [Reference Kato30, (15.16.1)].
Beilinson-Kato elements and rational points. The following connects Beilinson-Kato elements with Heegner points.
Theorem 4.3. If
![]() $L(f,1)=0$
, then there exists a rational point
$L(f,1)=0$
, then there exists a rational point
![]() $P\in A({\mathbb {Q}})$
with the following properties.
$P\in A({\mathbb {Q}})$
with the following properties.
-
(a) We have
for some $$ \begin{align*} \lambda_{f}({\mathrm{loc}}_{p}(z_{f})) = c_P \left(1-\frac{a_p(f)}{p}+\frac{1}{p}\right) \lambda_{f}(P)^{2} \end{align*} $$
$$ \begin{align*} \lambda_{f}({\mathrm{loc}}_{p}(z_{f})) = c_P \left(1-\frac{a_p(f)}{p}+\frac{1}{p}\right) \lambda_{f}(P)^{2} \end{align*} $$
 $c_{P}\in F^\times $
and
$c_{P}\in F^\times $
and
 $a_p(f)$
the p-th Fourier coefficient of f.
$a_p(f)$
the p-th Fourier coefficient of f.
-
(b) P is non-torsion if and only if
 ${\mathrm {ord}}_{s=1}L(f,s)=1.$
${\mathrm {ord}}_{s=1}L(f,s)=1.$
-
(c) If the equivalent conditions in (b)hold, then
for $$ \begin{align*}c_P=\frac{L'(f, 1)}{\Omega_f\langle P, P \rangle_{\infty}}\end{align*} $$
$$ \begin{align*}c_P=\frac{L'(f, 1)}{\Omega_f\langle P, P \rangle_{\infty}}\end{align*} $$
 $\langle \,,\,\rangle _\infty $
the Néron-Tate height pairing.
$\langle \,,\,\rangle _\infty $
the Néron-Tate height pairing.
This is an evidence towards a conjecture of Perrin-Riou [Reference Perrin-Riou42]. We refer to Appendix B for details (cf. Theorem B.3).
p-adic Gross-Zagier formula. Theorem 4.3 is based on the following interrelation between p-adic logarithm of a Heegner point and central derivative
![]() $\mathscr {L}^{\prime }_{p,\gamma }(f,1)$
of the cyclotomic p-adic L-function
$\mathscr {L}^{\prime }_{p,\gamma }(f,1)$
of the cyclotomic p-adic L-function
![]() $\mathscr {L}_{p,\gamma }(f,s)$
for
$\mathscr {L}_{p,\gamma }(f,s)$
for
![]() $\gamma \in \{\alpha ,\beta \}$
a root of the Hecke polynomial at p.
$\gamma \in \{\alpha ,\beta \}$
a root of the Hecke polynomial at p.
Theorem 4.4. Suppose that the root number of
![]() $L(f, s)$
is
$L(f, s)$
is
![]() $-1$
. Then, there exists a point
$-1$
. Then, there exists a point
![]() $P \in A(\mathbb {Q})$
and a non-zero constant
$P \in A(\mathbb {Q})$
and a non-zero constant
![]() $c_P \in \mathbb {Q}$
such that
$c_P \in \mathbb {Q}$
such that
 $$ \begin{align*} \left(1-\frac{1}{\alpha}\right)^{-2} \mathscr{L}^{\prime}_{p,\alpha}(f,1)- \left(1-\frac{1}{\beta}\right)^{-2}\mathscr{L}^{\prime}_{p,\beta}(f,1)=c_P\frac{(\beta-\alpha)}{[ \omega_f, \varphi\omega_f]}\lambda_f(P)^2. \end{align*} $$
$$ \begin{align*} \left(1-\frac{1}{\alpha}\right)^{-2} \mathscr{L}^{\prime}_{p,\alpha}(f,1)- \left(1-\frac{1}{\beta}\right)^{-2}\mathscr{L}^{\prime}_{p,\beta}(f,1)=c_P\frac{(\beta-\alpha)}{[ \omega_f, \varphi\omega_f]}\lambda_f(P)^2. \end{align*} $$
Moreover, P is non-torsion if and only if
![]() $\mathrm {ord}_{s=1}L(f, s)=1$
, and
$\mathrm {ord}_{s=1}L(f, s)=1$
, and
 $$ \begin{align*}c_P=\frac{L'(f, 1)}{\Omega_f\langle P, P \rangle_{\infty}}.\end{align*} $$
$$ \begin{align*}c_P=\frac{L'(f, 1)}{\Omega_f\langle P, P \rangle_{\infty}}.\end{align*} $$
This is a variant of the p-adic Gross–Zagier formula [Reference Kobayashi32] (cf. Appendix A). In combination with Proposition B.4, it yields Theorem 4.3.
4.1.3 Proof of Theorem 4.1
The approach is based on Theorem 3.16 (b) and a link between elliptic units and Heegner points (cf. Theorems 4.2 and 4.3).
Proof. Fix an isomorphism
![]() $\mathrm {Ind}^K_{{\mathbb {Q}}}(V) \cong V_{L_{{\mathfrak {p}}}}(f)$
of
$\mathrm {Ind}^K_{{\mathbb {Q}}}(V) \cong V_{L_{{\mathfrak {p}}}}(f)$
of
![]() $G_{\mathbb {Q}}$
-representations and let
$G_{\mathbb {Q}}$
-representations and let
be the induced identification. Let
be a Beilinson–Kato element as in [Reference Kato30, Thm. 12.5], which depends on a choice of an element in
![]() $H^1(A({\mathbb {C}}), {\mathbb {Q}})\cong F$
(cf. §B.2).
$H^1(A({\mathbb {C}}), {\mathbb {Q}})\cong F$
(cf. §B.2).
Since the root number of f is
![]() $-1$
,
$-1$
,
![]() $L(f,1)=0$
, and so
$L(f,1)=0$
, and so
![]() ${\mathrm {loc}}_p(z_f) \in H^1_{\mathrm {f}}({\mathbb {Q}}_p, V(f))$
by Kato’s reciprocity law [Reference Kato30, Thm. 12.5 (1)]. Now in view of Theorems 3.16 and 4.2, it follows that
${\mathrm {loc}}_p(z_f) \in H^1_{\mathrm {f}}({\mathbb {Q}}_p, V(f))$
by Kato’s reciprocity law [Reference Kato30, Thm. 12.5 (1)]. Now in view of Theorems 3.16 and 4.2, it follows that
up to an element in
![]() $L^\times $
. Hence, Theorem 4.3 concludes the proof.
$L^\times $
. Hence, Theorem 4.3 concludes the proof.
Remark 4.5. Theorem 4.1 concerns an anticyclotomic p-adic L-value, yet its proof relies on central derivative of cyclotomic p-adic L-functions.
4.2 p-adic Beilinson formula: a refined form
The main result is Theorem 4.8.
To consider a refinement of Theorem 4.1, we first specify an abelian variety A in the associated isogeny class (cf. §4.2.1), leading to an explicit form of Theorem 4.2 (cf. Proposition 4.12).
4.2.1 A CM abelian variety
We begin with a preliminary (cf. [Reference Gross27, §5.1]).
Lemma 4.6. Let E be a CM elliptic curve as in §3.1.1 and
![]() $j\in H$
denote its j-invariant. Then the following holds.
$j\in H$
denote its j-invariant. Then the following holds.
-
(1)
 $[H:{\mathbb {Q}}(j)]=2$
,
$[H:{\mathbb {Q}}(j)]=2$
, -
(2)
 ${\mathbb {Q}}(j)$
has at least one real place and
${\mathbb {Q}}(j)$
has at least one real place and -
(3)
 $H={\mathbb {Q}}(j)K$
.
$H={\mathbb {Q}}(j)K$
.
Suppose that
This holds if
![]() $j=j({\mathcal {O}}_K)$
or, equivalently,
$j=j({\mathcal {O}}_K)$
or, equivalently,
![]() $E({\mathbb {C}})\cong {\mathbb {C}}/{\mathcal {O}}_K$
(cf. [Reference Gross27, (5.1.4) and Thm. 10.1.3]).
$E({\mathbb {C}})\cong {\mathbb {C}}/{\mathcal {O}}_K$
(cf. [Reference Gross27, (5.1.4) and Thm. 10.1.3]).
Fix a minimal Weierstrass model of E at
![]() ${\mathfrak {p}}$
over
${\mathfrak {p}}$
over
![]() ${\mathcal {O}}_{H_{{\mathfrak {p}}}}\cap {\mathbb {Q}}(j)$
and let
${\mathcal {O}}_{H_{{\mathfrak {p}}}}\cap {\mathbb {Q}}(j)$
and let
![]() $\omega $
be the Néron differential.
$\omega $
be the Néron differential.
Lemma 4.7. The Weil restriction
is a
![]() ${\mathrm {GL}}_2$
-type abelian variety associated to f.
${\mathrm {GL}}_2$
-type abelian variety associated to f.
Proof. By [Reference Gross27, Thm. 15.2.5], A is a CM abelian varietyFootnote
7
defined over
![]() ${\mathbb {Q}}$
which is simple over K. Since
${\mathbb {Q}}$
which is simple over K. Since
(cf. [Reference Gross27, Thm. 18.1.7]), the assertion follows.
We now describe some structures on A arising from E.
The canonical identification
is compatible with the Hodge filtration, via which the Néron differential
![]() $\omega $
of E gives an element
$\omega $
of E gives an element
![]() $\omega _A$
of
$\omega _A$
of
![]() $\mathrm {coLie}(A_{/{\mathbb {Q}}})$
. Since
$\mathrm {coLie}(A_{/{\mathbb {Q}}})$
. Since
![]() $H={\mathbb {Q}}(j) K$
, we have
$H={\mathbb {Q}}(j) K$
, we have
So, the one-dimensional L-vector space
![]() $\mathrm {coLie}(A_{/{\mathbb {Q}}}) \otimes _F L$
leads to a one-dimensional subspace
$\mathrm {coLie}(A_{/{\mathbb {Q}}}) \otimes _F L$
leads to a one-dimensional subspace
![]() $S(\varphi )$
of
$S(\varphi )$
of
![]() $\mathrm {coLie}(E_{/H})\otimes _{K}L$
, namely its
$\mathrm {coLie}(E_{/H})\otimes _{K}L$
, namely its
![]() $\varphi $
-part. This induces an identification
$\varphi $
-part. This induces an identification
which is the same as the identification [Reference Kato30, (15.11.2)] (recall that our
![]() $V_{L_{{\mathfrak {p}}}}(f)$
is isomorphic to the
$V_{L_{{\mathfrak {p}}}}(f)$
is isomorphic to the
![]() $L_{{\mathfrak {p}}}$
-linear dual of that of [Reference Kato30]). In turn,
$L_{{\mathfrak {p}}}$
-linear dual of that of [Reference Kato30]). In turn,
![]() $\lambda _E: H^1_{\mathrm {f}}(\Phi , V) \to L_{{\mathfrak {p}}}$
is identified with the logarithm map
$\lambda _E: H^1_{\mathrm {f}}(\Phi , V) \to L_{{\mathfrak {p}}}$
is identified with the logarithm map
![]() $\lambda _f: H^1_{\mathrm {f}}({\mathbb {Q}}_p, V_{L_{{\mathfrak {p}}}}(f)) \to L_{{\mathfrak {p}}}$
associated to
$\lambda _f: H^1_{\mathrm {f}}({\mathbb {Q}}_p, V_{L_{{\mathfrak {p}}}}(f)) \to L_{{\mathfrak {p}}}$
associated to
![]() $\omega _A$
, where
$\omega _A$
, where
![]() $\omega _A \in \mathrm {coLie}(A_{/{\mathbb {Q}}})$
is regarded as an element of
$\omega _A \in \mathrm {coLie}(A_{/{\mathbb {Q}}})$
is regarded as an element of
![]() $\mathrm {Fil}^{0}(D_{\mathrm {dR}}(V_{L_{{\mathfrak {p}}}}(f)))=\mathrm {coLie}(A_{/{\mathbb {Q}}})\otimes _F L_{{\mathfrak {p}}}$
.
$\mathrm {Fil}^{0}(D_{\mathrm {dR}}(V_{L_{{\mathfrak {p}}}}(f)))=\mathrm {coLie}(A_{/{\mathbb {Q}}})\otimes _F L_{{\mathfrak {p}}}$
.
Fix
![]() $b_A \in H^1(A({\mathbb {C}}),{\mathbb {Q}})$
and define a period
$b_A \in H^1(A({\mathbb {C}}),{\mathbb {Q}})$
and define a period
![]() $\Omega _f \in {\mathbb {R}}^\times $
as in (B.3). Note that
$\Omega _f \in {\mathbb {R}}^\times $
as in (B.3). Note that
![]() $u:=\Omega _f/\Omega \in L^{\times }$
.
$u:=\Omega _f/\Omega \in L^{\times }$
.
4.2.2 Main result and applications
Theorem 4.8. Let
![]() $A_{/{\mathbb {Q}}}$
be a
$A_{/{\mathbb {Q}}}$
be a
![]() ${\mathrm {GL}}_2$
-type abelian variety associated to a CM newform f as in §4.2.1. Let K be the CM field and F the Hecke field. Suppose that (rt) holds and the root number of f equals
${\mathrm {GL}}_2$
-type abelian variety associated to a CM newform f as in §4.2.1. Let K be the CM field and F the Hecke field. Suppose that (rt) holds and the root number of f equals
![]() $-1$
. Let
$-1$
. Let
![]() $p\geq 5$
be a prime of good non-ordinary reduction for
$p\geq 5$
be a prime of good non-ordinary reduction for
![]() $A_{/{\mathbb {Q}}}$
with
$A_{/{\mathbb {Q}}}$
with
![]() $p\nmid h_{K}$
and
$p\nmid h_{K}$
and
![]() $\mathscr {L}$
the Rubin p-adic L-function as in (3.14). Then there exists a rational point
$\mathscr {L}$
the Rubin p-adic L-function as in (3.14). Then there exists a rational point
![]() $P\in A({\mathbb {Q}})$
with the following properties.
$P\in A({\mathbb {Q}})$
with the following properties.
-
(a) We have
for some
 $c_{P}\in F^\times $
.
$c_{P}\in F^\times $
.
-
(b) P is non-torsion if and only if
 $\mathrm {ord}_{s=1}L(f,s)=1$
.
$\mathrm {ord}_{s=1}L(f,s)=1$
. -
(c) If
 $\mathrm {ord}_{s=1}L(f,s)=1$
, then
$\mathrm {ord}_{s=1}L(f,s)=1$
, then  $$ \begin{align*} c_P=\frac{L^{\prime}(f,1)}{\Omega_{f} \langle P, P\rangle_{\infty}}. \end{align*} $$
$$ \begin{align*} c_P=\frac{L^{\prime}(f,1)}{\Omega_{f} \langle P, P\rangle_{\infty}}. \end{align*} $$
Part (a) leads to the following p-adic construction of a rational point of infinite order.
Corollary 4.9. Let
![]() $E_{/{\mathbb {Q}}}$
be a CM elliptic curve with root number
$E_{/{\mathbb {Q}}}$
be a CM elliptic curve with root number
![]() $-1$
. Let
$-1$
. Let
![]() $p\geq 5$
be a prime of good supersingular reduction for
$p\geq 5$
be a prime of good supersingular reduction for
![]() $E_{/{\mathbb {Q}}}$
and
$E_{/{\mathbb {Q}}}$
and
![]() $\mathscr {L}_{E}$
the Rubin p-adic L-function as in (3.14). Suppose that
$\mathscr {L}_{E}$
the Rubin p-adic L-function as in (3.14). Suppose that
![]() $\mathrm {ord}_{s=1}L(E,s)=1$
, and the Birch–Swinnerton-Dyer formula is true for
$\mathrm {ord}_{s=1}L(E,s)=1$
, and the Birch–Swinnerton-Dyer formula is true for
![]() $E_{/{\mathbb {Q}}}$
. Then,
$E_{/{\mathbb {Q}}}$
. Then,

is a rational point of infinite order, where
![]() $c_\ell $
denotes the Tamagawa number at
$c_\ell $
denotes the Tamagawa number at
![]() $\ell $
.
$\ell $
.
Remark 4.10.
-
(i) The BSD formula is known to be true up to an element in
 ${\mathbb {Z}}[\frac {1}{\#{\mathcal {O}}_{K}^{\times }\cdot N}]^{\times }$
(cf. [Reference Kobayashi32, Cor. 1.4]).
${\mathbb {Z}}[\frac {1}{\#{\mathcal {O}}_{K}^{\times }\cdot N}]^{\times }$
(cf. [Reference Kobayashi32, Cor. 1.4]). -
(ii) The rational point is independent of the choices involved, besides that of the square root.
-
(iii) Rubin initiated p-adic construction of rational points of infinite order (cf. [Reference Rubin50, Thm. 10.4].)
Another application is the following variant of Corollary 3.11.
Corollary 4.11. Let
![]() $E_{/{\mathbb {Q}}}$
be a CM elliptic curve and K the CM field. Let
$E_{/{\mathbb {Q}}}$
be a CM elliptic curve and K the CM field. Let
![]() $p\geq 5$
be a prime of good supersingular reduction for
$p\geq 5$
be a prime of good supersingular reduction for
![]() $E_{/{\mathbb {Q}}}$
and
$E_{/{\mathbb {Q}}}$
and
![]() $K_n$
the
$K_n$
the
![]() $n^{th}$
-layer of the anticyclotomic
$n^{th}$
-layer of the anticyclotomic
![]() ${\mathbb {Z}}_p$
-extension of K.
${\mathbb {Z}}_p$
-extension of K.
-
(i) If
 $L(E_{/\mathbb {Q}}, 1)/\Omega $
is a p-adic unit, then for all
$L(E_{/\mathbb {Q}}, 1)/\Omega $
is a p-adic unit, then for all
 $n \geq 1$
, where
$n \geq 1$
, where $$ \begin{align*}{\mathrm{corank}}_{{\mathbb {Z}}_{p}}{\mathrm{Sel}}_{p^\infty}(E_{/K_{n}}) -{\mathrm{corank}}_{{\mathbb {Z}}_{p}}{\mathrm{Sel}}_{p^\infty}(E_{/K_{n-1}}) =\varepsilon_{n}p^{n-1}(p-1), \end{align*} $$
$$ \begin{align*}{\mathrm{corank}}_{{\mathbb {Z}}_{p}}{\mathrm{Sel}}_{p^\infty}(E_{/K_{n}}) -{\mathrm{corank}}_{{\mathbb {Z}}_{p}}{\mathrm{Sel}}_{p^\infty}(E_{/K_{n-1}}) =\varepsilon_{n}p^{n-1}(p-1), \end{align*} $$
 $\varepsilon _{n}=0$
(resp.
$\varepsilon _{n}=0$
(resp.
 $2$
) for n odd (resp. even).
$2$
) for n odd (resp. even).
-
(ii) Suppose that
 $\mathrm {ord}_{s=1}L(E_{/\mathbb {Q}},s)=1$
and there exists a rational point
$\mathrm {ord}_{s=1}L(E_{/\mathbb {Q}},s)=1$
and there exists a rational point
 $P \in E(\mathbb {Q})$
whose image generates the
$P \in E(\mathbb {Q})$
whose image generates the
 $\mathbb {Z}_p$
-module
$\mathbb {Z}_p$
-module
 $E(\mathbb {Q}_p)/E({\mathbb {Q}}_{p})_{{\mathrm {tor}}}$
. If is a p-adic unit, then for all
$E(\mathbb {Q}_p)/E({\mathbb {Q}}_{p})_{{\mathrm {tor}}}$
. If is a p-adic unit, then for all $$ \begin{align*}L'(E_{/\mathbb{Q}},1)/\Omega \langle P, P \rangle_\infty\end{align*} $$
$$ \begin{align*}L'(E_{/\mathbb{Q}},1)/\Omega \langle P, P \rangle_\infty\end{align*} $$
 $n \geq 1$
, where
$n \geq 1$
, where $$ \begin{align*}{\mathrm{corank}}_{{\mathbb {Z}}_{p}}{\mathrm{Sel}}_{p^\infty}(E_{/K_{n}}) -{\mathrm{corank}}_{{\mathbb {Z}}_{p}}{\mathrm{Sel}}_{p^{\infty}}(E_{/K_{n-1}}) =\varepsilon_{n}p^{n-1}(p-1), \end{align*} $$
$$ \begin{align*}{\mathrm{corank}}_{{\mathbb {Z}}_{p}}{\mathrm{Sel}}_{p^\infty}(E_{/K_{n}}) -{\mathrm{corank}}_{{\mathbb {Z}}_{p}}{\mathrm{Sel}}_{p^{\infty}}(E_{/K_{n-1}}) =\varepsilon_{n}p^{n-1}(p-1), \end{align*} $$
 $\varepsilon _{n}=0$
(resp.
$\varepsilon _{n}=0$
(resp.
 $2$
) for n even (resp. odd).
$2$
) for n even (resp. odd).
In particular, if
![]() is finite, then
is finite, then
Proof. We first consider the case (i).
Since
![]() $L(\bar {\varphi },1)/\Omega $
is a p-adic unit, note that
$L(\bar {\varphi },1)/\Omega $
is a p-adic unit, note that
![]() $\varepsilon (\varphi )=+1$
and
$\varepsilon (\varphi )=+1$
and
For
![]() $\chi \in \Xi ^{+}$
, we then have
$\chi \in \Xi ^{+}$
, we then have
![]() $ L(\varphi \chi ,1)\neq 0 $
and so
$ L(\varphi \chi ,1)\neq 0 $
and so
![]() ${\mathrm {rank}}_{\mathcal O_{\chi }}E(K_{n})^{\chi ^{-1}}=0$
by Theorem 3.9 (a) where n denotes
${\mathrm {rank}}_{\mathcal O_{\chi }}E(K_{n})^{\chi ^{-1}}=0$
by Theorem 3.9 (a) where n denotes
![]() $\max \{0, \mathrm {ord}_p({\mathfrak {c}}_{\chi })-1\}$
. Now, let
$\max \{0, \mathrm {ord}_p({\mathfrak {c}}_{\chi })-1\}$
. Now, let
![]() $\chi \in \Xi ^{-}$
. In view of Theorem 3.16,
$\chi \in \Xi ^{-}$
. In view of Theorem 3.16,
Hence, the image of z in
![]() $S_{\mathrm {{rel}}}$
is a
$S_{\mathrm {{rel}}}$
is a
![]() $\Lambda _{{\mathfrak {q}}}$
-basis for
$\Lambda _{{\mathfrak {q}}}$
-basis for
![]() $S_{\mathrm {{rel}},{\mathfrak {q}}}$
up to tensoring with
$S_{\mathrm {{rel}},{\mathfrak {q}}}$
up to tensoring with
![]() ${\mathbb {Q}}_p$
, where
${\mathbb {Q}}_p$
, where
![]() $S_{\mathrm {{rel}}}$
denotes the relaxed compact Selmer group and
$S_{\mathrm {{rel}}}$
denotes the relaxed compact Selmer group and
![]() ${\mathfrak {q}}$
the prime ideal of
${\mathfrak {q}}$
the prime ideal of
![]() $\Lambda $
corresponding to the
$\Lambda $
corresponding to the
![]() $\chi ^{-1}$
-specialization. In turn,
$\chi ^{-1}$
-specialization. In turn,
![]() $\mathscr {X}_{\mathrm {{str},{\mathfrak {q}}}}$
is finite by [Reference Agboola and Howard2, Prop. 3.3] and then so is
$\mathscr {X}_{\mathrm {{str},{\mathfrak {q}}}}$
is finite by [Reference Agboola and Howard2, Prop. 3.3] and then so is
![]() $H^{2}(\mathcal O_{K}[\frac {1}{p}],T(\chi ))$
. Hence, Tate’s Euler characteristic formula implies
$H^{2}(\mathcal O_{K}[\frac {1}{p}],T(\chi ))$
. Hence, Tate’s Euler characteristic formula implies
Since
![]() $z_{\chi ^{-1}}\in H^1_{\mathrm {{f}}}(K,T(\chi ))$
by Lemma 3.3, we conclude that
$z_{\chi ^{-1}}\in H^1_{\mathrm {{f}}}(K,T(\chi ))$
by Lemma 3.3, we conclude that
![]() ${\mathrm {rank}}_{\mathcal O_{\chi }}H^{1}_{\mathrm {{f}}}(\mathcal O_{K}[\frac {1}{p}],T(\chi ))=1$
. The assertion follows from this.
${\mathrm {rank}}_{\mathcal O_{\chi }}H^{1}_{\mathrm {{f}}}(\mathcal O_{K}[\frac {1}{p}],T(\chi ))=1$
. The assertion follows from this.
The case (ii) is similarly proven by using Theorem 4.8.
4.2.3 Elliptic units and Beilinson–Kato elements
Proposition 4.12. Let
![]() $z=(z_n) \in \varprojlim _{n}H^1(K_n,T)$
be the elliptic unit as in (3.2) under the identification (3.1) and
$z=(z_n) \in \varprojlim _{n}H^1(K_n,T)$
be the elliptic unit as in (3.2) under the identification (3.1) and
![]() $z_{f,0}\in H^{1}({\mathbb {Q}},V(f))$
the Beilinson–Kato element associated to the newform f as in (4.8). Then, under the identification (4.7), we have
$z_{f,0}\in H^{1}({\mathbb {Q}},V(f))$
the Beilinson–Kato element associated to the newform f as in (4.8). Then, under the identification (4.7), we have
where
![]() $u:=\Omega _f/\Omega \in L^{\times }$
.
$u:=\Omega _f/\Omega \in L^{\times }$
.
Proof. By [Reference Kato30, Lem. 15.11 (2)], there is a unique isomorphism
of
![]() $L[\mathrm {Gal}({\mathbb {C}}/{\mathbb {R}})]$
-modules such that the following diagram
$L[\mathrm {Gal}({\mathbb {C}}/{\mathbb {R}})]$
-modules such that the following diagram

commutes. Here,
![]() $H^1(A({\mathbb {C}}), {\mathbb {Q}})$
is regarded as a
$H^1(A({\mathbb {C}}), {\mathbb {Q}})$
is regarded as a
![]() $\mathrm {Gal}({\mathbb {C}}/{\mathbb {R}})$
-module via the complex conjugation on
$\mathrm {Gal}({\mathbb {C}}/{\mathbb {R}})$
-module via the complex conjugation on
![]() $A({\mathbb {C}})$
,
$A({\mathbb {C}})$
,
![]() $\mathrm {per}_{\varphi }$
is the period map induced by that of E (cf. [Reference Kato30, §15.8]) and the right vertical map is the base change of (4.5) via
$\mathrm {per}_{\varphi }$
is the period map induced by that of E (cf. [Reference Kato30, §15.8]) and the right vertical map is the base change of (4.5) via
![]() $L \subseteq {\mathbb {C}}$
.
$L \subseteq {\mathbb {C}}$
.
Recall that
![]() $z\in \varprojlim _n H^1(K_n, T)$
is the image of an element
$z\in \varprojlim _n H^1(K_n, T)$
is the image of an element
![]() $\mathbf {z}^{\mathrm {ell}} \in \varprojlim _n H^1(K({\mathfrak {f}} p^n), T)$
associated to
$\mathbf {z}^{\mathrm {ell}} \in \varprojlim _n H^1(K({\mathfrak {f}} p^n), T)$
associated to
![]() $b_E$
as in [Reference Kato30, Prop. 15.9] under the corestriction map
$b_E$
as in [Reference Kato30, Prop. 15.9] under the corestriction map
where
![]() ${\mathfrak {f}}$
denotes the conductor of
${\mathfrak {f}}$
denotes the conductor of
![]() $\varphi $
and
$\varphi $
and
![]() $K({\mathfrak {f}} p^n)$
the ray class field of K of conductor
$K({\mathfrak {f}} p^n)$
the ray class field of K of conductor
![]() ${\mathfrak {f}} p^n$
(cf. [Reference Kato30, p. 254]). Let
${\mathfrak {f}} p^n$
(cf. [Reference Kato30, p. 254]). Let
![]() ${\mathbb {Q}}_n$
be the n-th layer of the cyclotomic
${\mathbb {Q}}_n$
be the n-th layer of the cyclotomic
![]() ${\mathbb {Z}}_p$
-extension
${\mathbb {Z}}_p$
-extension
![]() ${\mathbb {Q}}_{\infty }$
of
${\mathbb {Q}}_{\infty }$
of
![]() ${\mathbb {Q}}$
. Let
${\mathbb {Q}}$
. Let
denote the image of
![]() $\mathbf {z}^{\mathrm {ell}}$
under
$\mathbf {z}^{\mathrm {ell}}$
under
Here, the first map is induced by the corestriction maps with respect to
![]() $K\otimes {\mathbb {Q}}_{n} \subseteq K({\mathfrak {f}} p^n)$
, and the equality is a consequence of (4.4) and Shapiro’s lemma.
$K\otimes {\mathbb {Q}}_{n} \subseteq K({\mathfrak {f}} p^n)$
, and the equality is a consequence of (4.4) and Shapiro’s lemma.
Note that
![]() $b_E=\Omega ^{-1}\mathrm {per}_{\varphi }(\omega )$
maps to
$b_E=\Omega ^{-1}\mathrm {per}_{\varphi }(\omega )$
maps to
![]() $\Omega ^{-1}\mathrm {per}_f(\omega _A)$
under (4.5) and
$\Omega ^{-1}\mathrm {per}_f(\omega _A)$
under (4.5) and
![]() $\mathbf {z}^{\mathrm {ell}}$
is associated to
$\mathbf {z}^{\mathrm {ell}}$
is associated to
![]() $b_E$
. Thus, in light of (4.6) and [Reference Kato30, (15.16.1)], it follows that
$b_E$
. Thus, in light of (4.6) and [Reference Kato30, (15.16.1)], it follows that
![]() $z^{\mathrm {ell}}$
coincides with the system of Beilinson–Kato elements associated to
$z^{\mathrm {ell}}$
coincides with the system of Beilinson–Kato elements associated to
Since
![]() ${\mathbb {Q}}_{\infty }$
is a totally real field, the last assertion in [Reference Kato30, Thm. 12.5 (1)] implies that
${\mathbb {Q}}_{\infty }$
is a totally real field, the last assertion in [Reference Kato30, Thm. 12.5 (1)] implies that
![]() $z^{\mathrm {ell}}$
also coincides with the system of Beilinson–Kato elements associated to
$z^{\mathrm {ell}}$
also coincides with the system of Beilinson–Kato elements associated to
and that
![]() $\mathfrak {z}_f$
coincides with the one associated to
$\mathfrak {z}_f$
coincides with the one associated to
(cf. (B.3)), where
![]() $\iota $
denotes the involution induced by the complex conjugation on
$\iota $
denotes the involution induced by the complex conjugation on
![]() $A({\mathbb {C}})$
.
$A({\mathbb {C}})$
.
Therefore, we have
Since
![]() $z_0= z^{\mathrm {ell}}_{0}$
in
$z_0= z^{\mathrm {ell}}_{0}$
in
![]() $H^1(K, V)=H^1({\mathbb {Q}}, V_{L_{{\mathfrak {p}}}}(f))$
, the proposition follows.
$H^1(K, V)=H^1({\mathbb {Q}}, V_{L_{{\mathfrak {p}}}}(f))$
, the proposition follows.
4.2.4 Proof of Theorem 4.8
We proceed as in the proof of Theorem 4.1 (cf. §4.1.3). The additional ingredient is Proposition 4.12.
Proof. By (4.4) and Shapiro’s lemma, we have an identification
Let
![]() $T(f)$
be a Galois stable
$T(f)$
be a Galois stable
![]() ${\mathcal {O}}_{F_{{\mathfrak {p}}}}$
-lattice of
${\mathcal {O}}_{F_{{\mathfrak {p}}}}$
-lattice of
![]() $V(f)$
.
$V(f)$
.
Let
be the Beilinson–Kato element associated to
![]() $b_A$
as in [Reference Kato30, Thm. 12.5 (1)] (since our
$b_A$
as in [Reference Kato30, Thm. 12.5 (1)] (since our
![]() $V_{L_{{\mathfrak {p}}}}(f)$
is a Tate twist of that in [Reference Kato30],
$V_{L_{{\mathfrak {p}}}}(f)$
is a Tate twist of that in [Reference Kato30],
![]() ${\mathfrak {z}}_f$
is the corresponding twist of
${\mathfrak {z}}_f$
is the corresponding twist of
![]() $\mathbf {z}_{b_A}^{(p)}$
as in [Reference Kato30]). In particular,
$\mathbf {z}_{b_A}^{(p)}$
as in [Reference Kato30]). In particular,
![]() ${\mathfrak {z}}_{f}$
satisfies the explicit reciprocity law (B.4).
${\mathfrak {z}}_{f}$
satisfies the explicit reciprocity law (B.4).
Note that
![]() $L(f,1)=0$
, and so by Proposition 4.12,
$L(f,1)=0$
, and so by Proposition 4.12,
Hence, Theorem 4.8 is a consequence of Theorems 3.16 (b) and 4.3.
Remark 4.13. For a given
![]() $b_E$
or
$b_E$
or
![]() $\omega $
, note that
$\omega $
, note that
![]() is independent of the choices of
is independent of the choices of
![]() $\Omega $
and
$\Omega $
and
![]() $v_-$
. Moreover, the right-hand side of Theorem 4.8 (a) is independent of the choice of
$v_-$
. Moreover, the right-hand side of Theorem 4.8 (a) is independent of the choice of
![]() $b_A$
.
$b_A$
.
4.3 Towards a conjecture of Perrin-Riou: primes of bad reduction
The conjecture [Reference Perrin-Riou42] intertwines Beilinson–Kato elements and global arithmetic (cf. §B.1).
For a weight two elliptic newform g and
![]() $z_{g}\in H^{1}({\mathbb {Q}},V)$
an associated p-adic Beilinson–Kato element, the conjecture predicts
$z_{g}\in H^{1}({\mathbb {Q}},V)$
an associated p-adic Beilinson–Kato element, the conjecture predicts
(cf. (B.2)).
Proposition 4.14. Let
![]() $\varphi $
be a self-dual Hecke character of an imaginary quadratic field K of infinity type
$\varphi $
be a self-dual Hecke character of an imaginary quadratic field K of infinity type
![]() $(1,0)$
. Let
$(1,0)$
. Let
![]() $p\geq 5$
be a prime so that (inr) holds and
$p\geq 5$
be a prime so that (inr) holds and
![]() $p\nmid h_{K}\cdot \mathrm {cond^r}{\varphi }$
. Let
$p\nmid h_{K}\cdot \mathrm {cond^r}{\varphi }$
. Let
![]() $K_\infty $
be the anticyclotomic
$K_\infty $
be the anticyclotomic
![]() ${\mathbb {Z}}_p$
-extension of K. For a finite character
${\mathbb {Z}}_p$
-extension of K. For a finite character
![]() $\chi $
of
$\chi $
of
![]() ${\mathrm {Gal}}(K_{\infty }/K)$
, let g be the theta series associated to the Hecke character
${\mathrm {Gal}}(K_{\infty }/K)$
, let g be the theta series associated to the Hecke character
![]() $\varphi \chi ^{-1}$
. Let
$\varphi \chi ^{-1}$
. Let
![]() $z_{g}$
be an associated Beilinson–Kato element. Then,
$z_{g}$
be an associated Beilinson–Kato element. Then,
Proof. By Corollary 3.18, the localisation of the Selmer element
![]() $y_{\chi }$
is non-torsion. This element is defined using elliptic units as in (3.4). Hence, the assertion is a consequenceFootnote
8
of Theorem 4.2.
$y_{\chi }$
is non-torsion. This element is defined using elliptic units as in (3.4). Hence, the assertion is a consequenceFootnote
8
of Theorem 4.2.
Remark 4.15. For non-trivial
![]() $\chi $
, an abelian variety
$\chi $
, an abelian variety
![]() $A_{\chi }$
associated to g does not have semistable reduction at p. Accordingly, the proposition complements [Reference Bertolini, Darmon and Venerucci7], [Reference Burungale, Skinner and Tian17] and Theorem B.3. It is perhaps the first evidence towards Perrin-Riou’s conjecture at primes of non-semistable reduction.
$A_{\chi }$
associated to g does not have semistable reduction at p. Accordingly, the proposition complements [Reference Bertolini, Darmon and Venerucci7], [Reference Burungale, Skinner and Tian17] and Theorem B.3. It is perhaps the first evidence towards Perrin-Riou’s conjecture at primes of non-semistable reduction.
4.4 p-converse to a theorem of Gross–Zagier and Kolyvagin
Let the setting be as in §4.1.
4.4.1 Preliminary
Proposition 4.16. Suppose that
![]() $L(\varphi , 1)=0$
. Then, the element
$L(\varphi , 1)=0$
. Then, the element
![]() ${\mathrm {loc}}_{p} (z_0) \in H^1_{\mathrm {f}}(K_{p}, V)$
is non-zero if and only if
${\mathrm {loc}}_{p} (z_0) \in H^1_{\mathrm {f}}(K_{p}, V)$
is non-zero if and only if
![]() $\mathrm {ord}_{s=1}L(\varphi ,s)=1.$
$\mathrm {ord}_{s=1}L(\varphi ,s)=1.$
4.4.2 p-converse
Theorem 4.17. Let
![]() $A_{/{\mathbb {Q}}}$
be a
$A_{/{\mathbb {Q}}}$
be a
![]() ${\mathrm {GL}}_2$
-type CM abelian variety. Let K be the CM field and F the Hecke field. Suppose that (rt) holds and
${\mathrm {GL}}_2$
-type CM abelian variety. Let K be the CM field and F the Hecke field. Suppose that (rt) holds and
![]() $\mathcal O_{F}\hookrightarrow {\mathrm {End}}{A}$
. Let
$\mathcal O_{F}\hookrightarrow {\mathrm {End}}{A}$
. Let
![]() $p\geq 5$
be a prime of good non-ordinary reduction for
$p\geq 5$
be a prime of good non-ordinary reduction for
![]() $A_{/{\mathbb {Q}}}$
with
$A_{/{\mathbb {Q}}}$
with
![]() $p\nmid h_{K}$
, and
$p\nmid h_{K}$
, and
![]() ${\mathfrak {p}}$
a prime of F above p. If
${\mathfrak {p}}$
a prime of F above p. If
![]() ${\mathrm {Sel}}_{\mathrm {str}}({\mathbb {Q}}, A[{\mathfrak {p}}^{\infty }])$
is finite, then
${\mathrm {Sel}}_{\mathrm {str}}({\mathbb {Q}}, A[{\mathfrak {p}}^{\infty }])$
is finite, then
Proof. We have
![]() $A({\mathbb {Q}}_p)\otimes _{{\mathcal {O}}_F} F_{{\mathfrak {p}}}/{\mathcal {O}}_{F_{\mathfrak {p}}} \cong F_{{\mathfrak {p}}}/{\mathcal {O}}_{F_{\mathfrak {p}}}$
. So the exact sequence
$A({\mathbb {Q}}_p)\otimes _{{\mathcal {O}}_F} F_{{\mathfrak {p}}}/{\mathcal {O}}_{F_{\mathfrak {p}}} \cong F_{{\mathfrak {p}}}/{\mathcal {O}}_{F_{\mathfrak {p}}}$
. So the exact sequence
and the finiteness of
![]() ${\mathrm {Sel}}_{\mathrm {str}}({\mathbb {Q}}, A[{\mathfrak {p}}^{\infty }])$
imply that
${\mathrm {Sel}}_{\mathrm {str}}({\mathbb {Q}}, A[{\mathfrak {p}}^{\infty }])$
imply that
ObserveFootnote 9
 $$ \begin{align} \begin{aligned} {\mathrm{Sel}}_{\mathrm{str}}(K_{\infty}, V/T)^{\vee}\otimes {\mathbb {Q}}_p/(\gamma-1)&\cong {\mathrm{Sel}}_{\mathrm{str}}(K, V/T)^{\vee}\otimes {\mathbb {Q}}_p\\&\cong {\mathrm{Sel}}_{\mathrm{str}}({\mathbb {Q}}, A[{\mathfrak{p}}^{\infty}])^{\vee}\otimes_{{\mathcal {O}}_{F_{{\mathfrak{p}}}}} L_{{\mathfrak{p}}}\\ &= \{0\}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} {\mathrm{Sel}}_{\mathrm{str}}(K_{\infty}, V/T)^{\vee}\otimes {\mathbb {Q}}_p/(\gamma-1)&\cong {\mathrm{Sel}}_{\mathrm{str}}(K, V/T)^{\vee}\otimes {\mathbb {Q}}_p\\&\cong {\mathrm{Sel}}_{\mathrm{str}}({\mathbb {Q}}, A[{\mathfrak{p}}^{\infty}])^{\vee}\otimes_{{\mathcal {O}}_{F_{{\mathfrak{p}}}}} L_{{\mathfrak{p}}}\\ &= \{0\}. \end{aligned} \end{align} $$
Thus,
![]() $z_0 \in H^1(K,T) $
is non-torsion by [Reference Agboola and Howard2, Prop. 3.3 (ii)].
$z_0 \in H^1(K,T) $
is non-torsion by [Reference Agboola and Howard2, Prop. 3.3 (ii)].
We now show
To begin,
![]() ${\mathrm {Sel}}_{\mathrm {str}}(K, V/T)$
is finite by (4.12). Put
${\mathrm {Sel}}_{\mathrm {str}}(K, V/T)$
is finite by (4.12). Put
Since
![]() $z_0 \in H^1(K,T) $
is non-torsion, pick an integer m such that
$z_0 \in H^1(K,T) $
is non-torsion, pick an integer m such that
![]() $ p^{-m+a} z_0 \in H^1(K,V)$
does not lie in the image of
$ p^{-m+a} z_0 \in H^1(K,V)$
does not lie in the image of
![]() $H^1(K, T)$
. Suppose that
$H^1(K, T)$
. Suppose that
![]() ${\mathrm {loc}}_{{\mathfrak {p}}}(z_0) =0 \in H^1(K_{{\mathfrak {p}}}, V)$
. Then, as
${\mathrm {loc}}_{{\mathfrak {p}}}(z_0) =0 \in H^1(K_{{\mathfrak {p}}}, V)$
. Then, as
![]() $z_0$
is unramified outside
$z_0$
is unramified outside
![]() ${\mathfrak {p}}$
, the image
${\mathfrak {p}}$
, the image
![]() $w_m$
of
$w_m$
of
![]() $p^{-m}z_0$
in
$p^{-m}z_0$
in
![]() $H^1(K,V/T)$
lies in
$H^1(K,V/T)$
lies in
![]() ${\mathrm {Sel}}_{\mathrm {str}}(K, V/T)$
and so does
${\mathrm {Sel}}_{\mathrm {str}}(K, V/T)$
and so does
![]() $p^aw_m$
. However,
$p^aw_m$
. However,
This contradiction yields (4.13).
-
• The case
 $W(\varphi )=+1$
. In view of (3.3) and (4.13), we have
$W(\varphi )=+1$
. In view of (3.3) and (4.13), we have
 $L(\varphi , 1)\neq 0$
. Hence, by the theorem of Coates-Wiles [Reference Coates and Wiles20] and Rubin [Reference Rubin46],
$L(\varphi , 1)\neq 0$
. Hence, by the theorem of Coates-Wiles [Reference Coates and Wiles20] and Rubin [Reference Rubin46],  $$ \begin{align*} \mathrm{ord}_{s=1}L(A,s)=[F: {\mathbb {Q}}]\cdot \mathrm{corank}_{{\mathcal {O}}_{F,{\mathfrak{p}}}}{\mathrm{Sel}}_{{\mathfrak{p}}^{\infty}}(A)=0. \end{align*} $$
$$ \begin{align*} \mathrm{ord}_{s=1}L(A,s)=[F: {\mathbb {Q}}]\cdot \mathrm{corank}_{{\mathcal {O}}_{F,{\mathfrak{p}}}}{\mathrm{Sel}}_{{\mathfrak{p}}^{\infty}}(A)=0. \end{align*} $$
-
• The case
 $W(\varphi )=-1$
. In view of (4.13) and Lemma 3.3, the image of
$W(\varphi )=-1$
. In view of (4.13) and Lemma 3.3, the image of
 $p^{-m}z_0$
in
$p^{-m}z_0$
in
 $H^1(K,V/T)$
gives a non-zero element of
$H^1(K,V/T)$
gives a non-zero element of
 ${\mathrm {Sel}}(K, V/T)$
for a sufficiently large m. By (4.11), it then follows that Hence, the assertion is a consequence of Proposition 4.16.
${\mathrm {Sel}}(K, V/T)$
for a sufficiently large m. By (4.11), it then follows that Hence, the assertion is a consequence of Proposition 4.16. $$ \begin{align*}\mathrm{corank}_{{\mathcal {O}}_{F,{\mathfrak{p}}}}{\mathrm{Sel}}_{{\mathfrak{p}}^{\infty}}(A)=1.\end{align*} $$
$$ \begin{align*}\mathrm{corank}_{{\mathcal {O}}_{F,{\mathfrak{p}}}}{\mathrm{Sel}}_{{\mathfrak{p}}^{\infty}}(A)=1.\end{align*} $$
Finally, we have the following p-converse.
Theorem 4.18. Let
![]() $A_{/{\mathbb {Q}}}$
be a
$A_{/{\mathbb {Q}}}$
be a
![]() ${\mathrm {GL}}_2$
-type CM abelian variety. Let K be the CM field and F the Hecke field. Suppose that (rt) holds and
${\mathrm {GL}}_2$
-type CM abelian variety. Let K be the CM field and F the Hecke field. Suppose that (rt) holds and
![]() $\mathcal O_{F}\hookrightarrow {\mathrm {End}}{A}$
. Let
$\mathcal O_{F}\hookrightarrow {\mathrm {End}}{A}$
. Let
![]() $p\geq 5$
be a prime of good non-ordinary reduction for
$p\geq 5$
be a prime of good non-ordinary reduction for
![]() $A_{/{\mathbb {Q}}}$
with
$A_{/{\mathbb {Q}}}$
with
![]() $p\nmid h_{K}$
, and
$p\nmid h_{K}$
, and
![]() ${\mathfrak {p}}$
a prime of F above p. Suppose either of the following.
${\mathfrak {p}}$
a prime of F above p. Suppose either of the following.
-
(a)
 ${\mathrm {corank}}_{{\mathcal {O}}_{F,{\mathfrak {p}}}}{\mathrm {Sel}}_{{\mathfrak {p}}^{\infty }}(A)=1$
and
${\mathrm {corank}}_{{\mathcal {O}}_{F,{\mathfrak {p}}}}{\mathrm {Sel}}_{{\mathfrak {p}}^{\infty }}(A)=1$
and
 ${\mathrm {loc}}_p:{\mathrm {Sel}}_{{\mathfrak {p}}^{\infty }}(A)\to A({\mathbb {Q}}_p)\otimes _{{\mathcal {O}}_F} F_{{\mathfrak {p}}}/{\mathcal {O}}_{F_{\mathfrak {p}}}$
is a non-zero map.
${\mathrm {loc}}_p:{\mathrm {Sel}}_{{\mathfrak {p}}^{\infty }}(A)\to A({\mathbb {Q}}_p)\otimes _{{\mathcal {O}}_F} F_{{\mathfrak {p}}}/{\mathcal {O}}_{F_{\mathfrak {p}}}$
is a non-zero map. -
(b)
 ${\mathrm {corank}}_{{\mathcal {O}}_{F,{\mathfrak {p}}}}{\mathrm {Sel}}_{{\mathfrak {p}}^{\infty }}(A)=1$
and
${\mathrm {corank}}_{{\mathcal {O}}_{F,{\mathfrak {p}}}}{\mathrm {Sel}}_{{\mathfrak {p}}^{\infty }}(A)=1$
and
 is finite.
is finite.
Then,
Proof.
-
(a) In view of the assumption and (4.10),
 ${\mathrm {Sel}}_{\mathrm {str}}({\mathbb {Q}}, A[{\mathfrak {p}}^{\infty }])$
is finite. So, the assertion directly follows from Theorem 4.17.
${\mathrm {Sel}}_{\mathrm {str}}({\mathbb {Q}}, A[{\mathfrak {p}}^{\infty }])$
is finite. So, the assertion directly follows from Theorem 4.17. -
(b) Recall the exact sequence
(4.14)So, by the assumption, we have
 $A({\mathbb {Q}})\otimes _{{\mathcal {O}}_{F}} F_{{\mathfrak {p}}}/{\mathcal {O}}_{F_{{\mathfrak {p}}}} \cong F_{{\mathfrak {p}}}/{\mathcal {O}}_{F_{{\mathfrak {p}}}}$
. Hence, is a non-zero map.
$A({\mathbb {Q}})\otimes _{{\mathcal {O}}_{F}} F_{{\mathfrak {p}}}/{\mathcal {O}}_{F_{{\mathfrak {p}}}} \cong F_{{\mathfrak {p}}}/{\mathcal {O}}_{F_{{\mathfrak {p}}}}$
. Hence, is a non-zero map. $$ \begin{align*}{\mathrm{loc}}_{{\mathfrak{p}}}: A({\mathbb {Q}})\otimes_{{\mathcal {O}}_{F}} F_{{\mathfrak{p}}}/{\mathcal {O}}_{F_{{\mathfrak{p}}}} \to A({\mathbb {Q}}_p)\otimes_{{\mathcal {O}}_{F}} F_{{\mathfrak{p}}}/{\mathcal {O}}_{F_{{\mathfrak{p}}}}\end{align*} $$
$$ \begin{align*}{\mathrm{loc}}_{{\mathfrak{p}}}: A({\mathbb {Q}})\otimes_{{\mathcal {O}}_{F}} F_{{\mathfrak{p}}}/{\mathcal {O}}_{F_{{\mathfrak{p}}}} \to A({\mathbb {Q}}_p)\otimes_{{\mathcal {O}}_{F}} F_{{\mathfrak{p}}}/{\mathcal {O}}_{F_{{\mathfrak{p}}}}\end{align*} $$
Remark 4.19. The p-converse was initiated by Skinner and Zhang (cf. [Reference Skinner52], [Reference Zhang56]). The above approach is a variant of [Reference Skinner52], yet it does not rely on the parity conjecture.
Appendix A p-adic height pairings and logarithms
A basic reference is [Reference Kobayashi33, §3.2]. See also [Reference Kobayashi32], [Reference Perrin-Riou42] for elliptic curves.
A.1 p-adic height pairings on abelian varieties
We fix an embedding
![]() $\iota _p : \overline {\mathbb {Q}} \hookrightarrow \mathbb {C}_p$
. Let F be a finite extension of
$\iota _p : \overline {\mathbb {Q}} \hookrightarrow \mathbb {C}_p$
. Let F be a finite extension of
![]() $\mathbb {Q}$
. We choose a continuous homomorphism
$\mathbb {Q}$
. We choose a continuous homomorphism
![]() $\ell _F: \mathbb {A}_F^\times /F^\times \rightarrow \mathbb {Q}_p$
and denote by
$\ell _F: \mathbb {A}_F^\times /F^\times \rightarrow \mathbb {Q}_p$
and denote by
![]() $\ell _{F, v}$
or
$\ell _{F, v}$
or
![]() $\ell _v$
the v-th component for a place v of F (note that
$\ell _v$
the v-th component for a place v of F (note that
![]() $\ell _v=0$
if v is archimedean). The important example is the cyclotomic logarithm. Let
$\ell _v=0$
if v is archimedean). The important example is the cyclotomic logarithm. Let
![]() $\log _p$
be the p-adic logarithm on
$\log _p$
be the p-adic logarithm on
![]() $\mathbb {Z}_p^\times $
such that
$\mathbb {Z}_p^\times $
such that
![]() $\log _p p=0$
. We define the cyclotomic logarithm
$\log _p p=0$
. We define the cyclotomic logarithm
![]() $\ell _{F, v}^{c}$
on
$\ell _{F, v}^{c}$
on
![]() $F_v^\times $
at a non-archimedean place v by
$F_v^\times $
at a non-archimedean place v by
 $$ \begin{align*} \ell_{F, v}^c(x)= \begin{cases} -\log_p|x|_v=v(x) \log_p \mathbf{N}(v) \qquad &\text{if}\quad v \nmid p\\ -\log_p \mathbf{N}_{F_v/\mathbb{Q}_p}(x) \qquad &\text{if}\quad v \mid p, \end{cases} \end{align*} $$
$$ \begin{align*} \ell_{F, v}^c(x)= \begin{cases} -\log_p|x|_v=v(x) \log_p \mathbf{N}(v) \qquad &\text{if}\quad v \nmid p\\ -\log_p \mathbf{N}_{F_v/\mathbb{Q}_p}(x) \qquad &\text{if}\quad v \mid p, \end{cases} \end{align*} $$
where
![]() $\mathbf {N}(v)$
is the number of elements of the residue field of F at v and we normalize as
$\mathbf {N}(v)$
is the number of elements of the residue field of F at v and we normalize as
![]() $v(\pi )=1$
for a uniformizer
$v(\pi )=1$
for a uniformizer
![]() $\pi $
at v of F. We define the cyclotomic logarithm
$\pi $
at v of F. We define the cyclotomic logarithm
![]() $\ell ^c_F$
by
$\ell ^c_F$
by
![]() $\ell ^c_F:=\sum _v \ell ^c_{F, v}$
. Then,
$\ell ^c_F:=\sum _v \ell ^c_{F, v}$
. Then,
![]() $ \ell ^c_F(x)=0$
for
$ \ell ^c_F(x)=0$
for
![]() $x \in F^\times $
and it defines a homomorphism
$x \in F^\times $
and it defines a homomorphism
![]() $\mathbb {A}_F^\times /F^\times \rightarrow \mathbb {Q}_p$
.
$\mathbb {A}_F^\times /F^\times \rightarrow \mathbb {Q}_p$
.
Let A be an abelian variety defined over F with good reduction at all places over p and let
![]() $A^\vee $
be its dual. For simplicity, we also assume that F is unramified at all places over p. Let L be a finite extension of
$A^\vee $
be its dual. For simplicity, we also assume that F is unramified at all places over p. Let L be a finite extension of
![]() $\mathbb {Q}_p$
, which plays as the coefficient field. We choose a splitting of the Hodge filtration of
$\mathbb {Q}_p$
, which plays as the coefficient field. We choose a splitting of the Hodge filtration of
![]() $M_v(A)\otimes _{\mathbb {Q}_p} L$
for each place v over p. Here,
$M_v(A)\otimes _{\mathbb {Q}_p} L$
for each place v over p. Here,
![]() $M_v(A)$
is the weakly admissible filtered
$M_v(A)$
is the weakly admissible filtered
![]() $\varphi $
-module of A over
$\varphi $
-module of A over
![]() $F_v$
with Hodge-Tate weight
$F_v$
with Hodge-Tate weight
![]() $\{0,1\}$
(the Hodge-Tate weight of the cyclotomic character is normalized as
$\{0,1\}$
(the Hodge-Tate weight of the cyclotomic character is normalized as
![]() $-1$
). In other words, we fix an L-vector subspace
$-1$
). In other words, we fix an L-vector subspace
![]() $N_v$
of
$N_v$
of
![]() $M_v(A)\otimes _{\mathbb {Q}_p} L$
which is complementary to
$M_v(A)\otimes _{\mathbb {Q}_p} L$
which is complementary to
![]() $\mathrm {Fil}^1M_v(A)\otimes _{\mathbb {Q}_p} L$
. We put
$\mathrm {Fil}^1M_v(A)\otimes _{\mathbb {Q}_p} L$
. We put
![]() $N:=(N_v)_{v|p}$
.
$N:=(N_v)_{v|p}$
.
Let
![]() $\mathfrak {a}=\sum _i n_i (P_i)$
be a zero cycle on A of degree
$\mathfrak {a}=\sum _i n_i (P_i)$
be a zero cycle on A of degree
![]() $0$
defined over
$0$
defined over
![]() $F_v$
and let D be an algebraically trivial divisor over
$F_v$
and let D be an algebraically trivial divisor over
![]() $F_v$
prime to the support of
$F_v$
prime to the support of
![]() $\mathfrak {a}$
. Then, for a place
$\mathfrak {a}$
. Then, for a place
![]() $v \nmid p$
, there is a canonical way to define the local height pairing
$v \nmid p$
, there is a canonical way to define the local height pairing
![]() $\langle D, \mathfrak {a} \rangle _{\ell _{v}} \in \mathbb {Q}_p$
characterized by certain standard functorial properties (cf. [Reference Kobayashi33, Proposition 9]. The pairing is independent of the choice N). For a place v over p, depending on the choice of
$\langle D, \mathfrak {a} \rangle _{\ell _{v}} \in \mathbb {Q}_p$
characterized by certain standard functorial properties (cf. [Reference Kobayashi33, Proposition 9]. The pairing is independent of the choice N). For a place v over p, depending on the choice of
![]() $N_v$
, we can define the local p-adic height pairing
$N_v$
, we can define the local p-adic height pairing
![]() $ \langle D, \mathfrak {a} \rangle _{\ell _{v}, N_v} \in L. $
We recall the definition below.
$ \langle D, \mathfrak {a} \rangle _{\ell _{v}, N_v} \in L. $
We recall the definition below.
The global p-adic height pairing is defined as the sum of local p-adic height pairings:
 $$ \begin{align*} \langle \;, \; \rangle_{\ell_F, N}: A^\vee(F) \times A(F) \rightarrow L, \quad (d, a) \mapsto \sum_{v\nmid p} \langle D, \frak{a} \rangle_{\ell_v}+\sum_{v|p} \langle D, \frak{a} \rangle_{\ell_v, N_v}. \end{align*} $$
$$ \begin{align*} \langle \;, \; \rangle_{\ell_F, N}: A^\vee(F) \times A(F) \rightarrow L, \quad (d, a) \mapsto \sum_{v\nmid p} \langle D, \frak{a} \rangle_{\ell_v}+\sum_{v|p} \langle D, \frak{a} \rangle_{\ell_v, N_v}. \end{align*} $$
Here, D is an algebraically trivial divisor that represents d, and
![]() $\frak {a}$
is a zero cycle
$\frak {a}$
is a zero cycle
![]() $\sum n_i [P_i]$
of degree zero with
$\sum n_i [P_i]$
of degree zero with
![]() $\sum n_i P_i=a$
. We choose D and
$\sum n_i P_i=a$
. We choose D and
![]() $\frak {a}$
so that they have no point in common. The global pairing does not depend on the choice of D,
$\frak {a}$
so that they have no point in common. The global pairing does not depend on the choice of D,
![]() $\frak {a}$
.
$\frak {a}$
.
A.1.1 The local p-adic height at
 $v | p$
$v | p$
We assume that
![]() $v|p$
. As before, let
$v|p$
. As before, let
![]() $\mathfrak {a}=\sum _i n_i (P_i)$
be a zero cycle on A of degree
$\mathfrak {a}=\sum _i n_i (P_i)$
be a zero cycle on A of degree
![]() $0$
defined over
$0$
defined over
![]() $F_v$
and let D be an algebraically trivial divisor over
$F_v$
and let D be an algebraically trivial divisor over
![]() $F_v$
prime to the support of
$F_v$
prime to the support of
![]() $\mathfrak {a}$
. Let
$\mathfrak {a}$
. Let
![]() $\mathscr {A}/\mathcal {O}_{F_v}$
be the smooth model of
$\mathscr {A}/\mathcal {O}_{F_v}$
be the smooth model of
![]() $A/F_v$
and let
$A/F_v$
and let
![]() $\mathscr {A}^\vee $
be the smooth model of
$\mathscr {A}^\vee $
be the smooth model of
![]() $A^\vee $
. Then, the rational equivalence class of D defines a point in
$A^\vee $
. Then, the rational equivalence class of D defines a point in
![]() $A^{\vee }(F_v)=\mathscr {A}^\vee (\mathcal {O}_{F_v}) =\mathrm {Ext}^1_{fppf}(\mathscr {A}, \mathbb {G}_m)$
. Hence, we have an exact sequence as fppf sheaves
$A^{\vee }(F_v)=\mathscr {A}^\vee (\mathcal {O}_{F_v}) =\mathrm {Ext}^1_{fppf}(\mathscr {A}, \mathbb {G}_m)$
. Hence, we have an exact sequence as fppf sheaves
where
![]() $\mathscr {X}_{{D}}$
is a smooth separated commutative group scheme over
$\mathscr {X}_{{D}}$
is a smooth separated commutative group scheme over
![]() $\mathcal {O}_{F_v}$
. Over
$\mathcal {O}_{F_v}$
. Over
![]() $\mathrm {Spec}\,F_v$
, this exact sequence is isomorphic to
$\mathrm {Spec}\,F_v$
, this exact sequence is isomorphic to
where
![]() $X_D$
is the line bundle associated to
$X_D$
is the line bundle associated to
![]() $\mathcal {O}_{A}(D)$
minus zero section which has a group law since D is algebraically equivalent to zero. Hence, attached to D, there is a geometric section
$\mathcal {O}_{A}(D)$
minus zero section which has a group law since D is algebraically equivalent to zero. Hence, attached to D, there is a geometric section
![]() $s_D : A \setminus |D| \rightarrow X_D$
which is canonical up to a translation by an element of
$s_D : A \setminus |D| \rightarrow X_D$
which is canonical up to a translation by an element of
![]() $\mathbb {G}_m$
. We identify
$\mathbb {G}_m$
. We identify
![]() $\mathscr {X}_{{D}} \otimes F_v$
with
$\mathscr {X}_{{D}} \otimes F_v$
with
![]() $X_D$
.
$X_D$
.
We define a local section
First, we identify
and so for
![]() $\mathscr {X}_D(\mathcal {O}_{F_v})$
. Here,
$\mathscr {X}_D(\mathcal {O}_{F_v})$
. Here,
![]() $M_{\mathscr {A},L}=M_{v}(A){\otimes _{\mathbb {Q}_p}} L$
is the filtered
$M_{\mathscr {A},L}=M_{v}(A){\otimes _{\mathbb {Q}_p}} L$
is the filtered
![]() $\varphi $
-module with coefficients in
$\varphi $
-module with coefficients in
![]() $F_v\otimes _{\mathbb {Q}_p} L$
associated to
$F_v\otimes _{\mathbb {Q}_p} L$
associated to
![]() $\mathscr {A}/\mathcal {O}_{F_v}$
. Hence, it suffices to construct an L-linear map
$\mathscr {A}/\mathcal {O}_{F_v}$
. Hence, it suffices to construct an L-linear map
Since
![]() $M_{\mathscr {A},L}$
and
$M_{\mathscr {A},L}$
and
![]() $M_{\mathbb {G}_m,L}$
have different Frobenius eigenvalues, the exact sequence
$M_{\mathbb {G}_m,L}$
have different Frobenius eigenvalues, the exact sequence
splits as
![]() $F_v \otimes L[\varphi ]$
-modules. Hence, we have a left splitting
$F_v \otimes L[\varphi ]$
-modules. Hence, we have a left splitting
![]() $M_{\mathscr {X}_D,L}\rightarrow M_{\mathscr {A},L}$
. By composing it to the projection
$M_{\mathscr {X}_D,L}\rightarrow M_{\mathscr {A},L}$
. By composing it to the projection
![]() $M_{\mathscr {A},L} \rightarrow \mathrm {Fil}^1M_{\mathscr {A},L}$
by
$M_{\mathscr {A},L} \rightarrow \mathrm {Fil}^1M_{\mathscr {A},L}$
by
![]() $N_v$
, we obtain the map
$N_v$
, we obtain the map
![]() $t_{D, N_v}: M_{\mathscr {X}_D,L}\rightarrow \mathrm {Fil}^1M_{\mathscr {A},L}$
. By the restriction to
$t_{D, N_v}: M_{\mathscr {X}_D,L}\rightarrow \mathrm {Fil}^1M_{\mathscr {A},L}$
. By the restriction to
![]() $\mathrm {Fil}^1 M_{\mathscr {X}_D,L}$
, we obtain the desired map.
$\mathrm {Fil}^1 M_{\mathscr {X}_D,L}$
, we obtain the desired map.
The local height pairing at
![]() $v | p$
is defined as
$v | p$
is defined as
 $$ \begin{align*} \langle D, \mathfrak{a} \rangle_{\ell_{v}, N_v}:= \ell_{v}\left(\prod_i (s_D(P_i)/s_{D, N_v}(P_i))^{n_i }\right) \in L \end{align*} $$
$$ \begin{align*} \langle D, \mathfrak{a} \rangle_{\ell_{v}, N_v}:= \ell_{v}\left(\prod_i (s_D(P_i)/s_{D, N_v}(P_i))^{n_i }\right) \in L \end{align*} $$
(we write the group law on
![]() $X_D$
multiplicatively. Note that the image of
$X_D$
multiplicatively. Note that the image of
![]() $s_D/s_{D, N_v}$
lives in
$s_D/s_{D, N_v}$
lives in
![]() $\mathbb {G}_m$
).
$\mathbb {G}_m$
).
A.2 The dependence of the p-adic height on the splitting
Suppose that
![]() $N'=(N_v')_{v|p}$
is another splitting. Then,
$N'=(N_v')_{v|p}$
is another splitting. Then,
 $$ \begin{align} \langle d, a \rangle_{\ell_F, N'}- \langle d, a \rangle_{\ell_F, N}= \sum_{v|p} \ell_{v}\left(\prod_i (s_{D, N_v} (P_i)/s_{D, N^{\prime}_v} (P_i))^{n_i}\right). \end{align} $$
$$ \begin{align} \langle d, a \rangle_{\ell_F, N'}- \langle d, a \rangle_{\ell_F, N}= \sum_{v|p} \ell_{v}\left(\prod_i (s_{D, N_v} (P_i)/s_{D, N^{\prime}_v} (P_i))^{n_i}\right). \end{align} $$
Note that the image of
![]() $s_{D, N_v}/s_{D, N^{\prime }_v}$
lives in
$s_{D, N_v}/s_{D, N^{\prime }_v}$
lives in
![]() $ \mathcal {O}_{F_v}^\times \otimes _{\mathbb {Z}_p} L \subset \mathscr {X}_D(\mathcal {O}_{F_v}) \otimes _{\mathbb {Z}_p}L. $
We also remark that
$ \mathcal {O}_{F_v}^\times \otimes _{\mathbb {Z}_p} L \subset \mathscr {X}_D(\mathcal {O}_{F_v}) \otimes _{\mathbb {Z}_p}L. $
We also remark that
![]() $s_{D, N_v}/s_{D, N^{\prime }_v}$
does not depend on the choice of D for d (the geometric section
$s_{D, N_v}/s_{D, N^{\prime }_v}$
does not depend on the choice of D for d (the geometric section
![]() $s_D$
depends on the choice of the divisor D for d). The map
$s_D$
depends on the choice of the divisor D for d). The map
![]() $s_{D, N_v}/s_{D, N^{\prime }_v}$
is induced by the map
$s_{D, N_v}/s_{D, N^{\prime }_v}$
is induced by the map
Here,
![]() $\omega _{\mathbb {G}_m}^H \in \mathrm {Fil}^1 M_{\mathscr {X}_D,L}$
is a lift of
$\omega _{\mathbb {G}_m}^H \in \mathrm {Fil}^1 M_{\mathscr {X}_D,L}$
is a lift of
![]() $\omega _{\mathbb {G}_m}$
under
$\omega _{\mathbb {G}_m}$
under
(note that
![]() $t_{N_v}$
is identity on
$t_{N_v}$
is identity on
![]() $\mathrm {Fil}^1M_{\mathscr {A},L}$
). We note that the image of d by the logarithm
$\mathrm {Fil}^1M_{\mathscr {A},L}$
). We note that the image of d by the logarithm
![]() $\lambda _{\omega _{A^\vee }}$
for
$\lambda _{\omega _{A^\vee }}$
for
![]() $\omega _{A^\vee } \in \mathrm {Fil}^1M_{\mathscr {A}^\vee }$
is given by
$\omega _{A^\vee } \in \mathrm {Fil}^1M_{\mathscr {A}^\vee }$
is given by
Here,
![]() ${\omega }^\varphi _{\mathbb {G}_m}\in M_{\mathscr {X}_D,L}$
is the lift of
${\omega }^\varphi _{\mathbb {G}_m}\in M_{\mathscr {X}_D,L}$
is the lift of
![]() $\omega _{\mathbb {G}_m}$
compatible with the action of
$\omega _{\mathbb {G}_m}$
compatible with the action of
![]() $\varphi $
under (A.3), and
$\varphi $
under (A.3), and
![]() $[\;,\;]$
is the de Rham pairing on
$[\;,\;]$
is the de Rham pairing on
![]() $M_{\mathscr {A}^\vee }$
and
$M_{\mathscr {A}^\vee }$
and
![]() $M_{\mathscr {A}}$
. Let
$M_{\mathscr {A}}$
. Let
![]() $\omega _1^\vee , \dots , \omega _g^\vee $
be a basis of
$\omega _1^\vee , \dots , \omega _g^\vee $
be a basis of
![]() $\mathrm {Fil}^1M_{\mathscr {A}^\vee }$
and
$\mathrm {Fil}^1M_{\mathscr {A}^\vee }$
and
![]() $\eta _1, \dots , \eta _g$
a basis of a complementary subspace of
$\eta _1, \dots , \eta _g$
a basis of a complementary subspace of
![]() $\mathrm {Fil}^1M_{\mathscr {A}}$
such that
$\mathrm {Fil}^1M_{\mathscr {A}}$
such that
![]() $[\omega _i^\vee , \eta _j]=\delta _{ij}$
(the Kronecker Delta). Then, we have
$[\omega _i^\vee , \eta _j]=\delta _{ij}$
(the Kronecker Delta). Then, we have
for some
![]() $c_i \in F_v$
. Hence,
$c_i \in F_v$
. Hence,
where
![]() $t_{N_v}: M_{\mathscr {A}} \rightarrow \mathrm {Fil}^1M_{\mathscr {A}}$
is a splitting by
$t_{N_v}: M_{\mathscr {A}} \rightarrow \mathrm {Fil}^1M_{\mathscr {A}}$
is a splitting by
![]() $N_v$
.
$N_v$
.
Suppose that
![]() $\omega _{\mathbb {G}_m}$
is the canonical invariant differential of
$\omega _{\mathbb {G}_m}$
is the canonical invariant differential of
![]() $\mathbb {G}_m$
. Then, the map
$\mathbb {G}_m$
. Then, the map
is the logarithm map defined by the invariant differential
![]() $\ell _{d, N_v. N_v'}(\omega _{\mathbb {G}_m}) \in \mathrm {Fil}^1 M_{\mathscr {A},L}$
. Hence,
$\ell _{d, N_v. N_v'}(\omega _{\mathbb {G}_m}) \in \mathrm {Fil}^1 M_{\mathscr {A},L}$
. Hence,
 $$ \begin{align} \langle d, a \rangle_{\ell_F, N'}- \langle d, a \rangle_{\ell_F, N}= \sum_{v|p} \ell_{v}\left( \exp \circ \lambda_{d, N_v, N_v'}(a)\right). \end{align} $$
$$ \begin{align} \langle d, a \rangle_{\ell_F, N'}- \langle d, a \rangle_{\ell_F, N}= \sum_{v|p} \ell_{v}\left( \exp \circ \lambda_{d, N_v, N_v'}(a)\right). \end{align} $$
The difference between global p-adic height pairing is measured by logarithms on A.
Proposition A.1. Assume that
![]() $N_v \cap N^{\prime }_v=\{0\}$
. Then,
$N_v \cap N^{\prime }_v=\{0\}$
. Then,
![]() $s_{D, N_v}=s_{D, N^{\prime }_v}$
if and only if D is torsion in
$s_{D, N_v}=s_{D, N^{\prime }_v}$
if and only if D is torsion in
![]() $A^\vee $
.
$A^\vee $
.
Proof.
D is torsion if and only if (A.3) splits as filtered
![]() $\varphi $
-modules. In such a case,
$\varphi $
-modules. In such a case,
![]() $t_{D, N_v}$
does not depend on the choice of
$t_{D, N_v}$
does not depend on the choice of
![]() $N_v$
. Assume that
$N_v$
. Assume that
![]() $s_{D, N_v}=s_{D, N^{\prime }_v}$
. Then,
$s_{D, N_v}=s_{D, N^{\prime }_v}$
. Then,
![]() $\ell _{d, N_v, N_v'} (\omega _{\mathbb {G}_m})=0$
. Then, we have
$\ell _{d, N_v, N_v'} (\omega _{\mathbb {G}_m})=0$
. Then, we have
Hence, by our assumption, we have
This means that (A.3) splits as filtered
![]() $\varphi $
-modules.
$\varphi $
-modules.
A.3 Applications for modular abelian varieties
Let f be a normalized eigen newform of weight
![]() $2$
for
$2$
for
![]() $\Gamma _0(M)$
with
$\Gamma _0(M)$
with
![]() $p\nmid M$
. Let
$p\nmid M$
. Let
![]() $A_f$
be a modular abelian variety defined over
$A_f$
be a modular abelian variety defined over
![]() $\mathbb {Q}$
associated to f. We fix a polarization of
$\mathbb {Q}$
associated to f. We fix a polarization of
![]() $A_f$
compatible with the Hecke action and identify objects on
$A_f$
compatible with the Hecke action and identify objects on
![]() $A_f$
and
$A_f$
and
![]() $A^\vee _f$
by the pullback after tensoring L if necessary (e.g. differential forms, rational points). Let
$A^\vee _f$
by the pullback after tensoring L if necessary (e.g. differential forms, rational points). Let
![]() $K_f$
be the Hecke field of f. We apply our theory for
$K_f$
be the Hecke field of f. We apply our theory for
![]() $A=A_f/F$
for a number field F unramified over p and L containing
$A=A_f/F$
for a number field F unramified over p and L containing
![]() $K_f$
and roots of the Hecke eigen polynomial of f at p. Then, we have the decomposition
$K_f$
and roots of the Hecke eigen polynomial of f at p. Then, we have the decomposition
 $$ \begin{align*}M_{\mathscr{A}/F_v,L}=\bigoplus_{\sigma \in \mathrm{Gal}(K_f/\mathbb{Q})} M_{f^\sigma}\end{align*} $$
$$ \begin{align*}M_{\mathscr{A}/F_v,L}=\bigoplus_{\sigma \in \mathrm{Gal}(K_f/\mathbb{Q})} M_{f^\sigma}\end{align*} $$
as filtered
![]() $\varphi $
-modules by the Hecke action. Here,
$\varphi $
-modules by the Hecke action. Here,
![]() $M_{f^\sigma }$
is a filtered
$M_{f^\sigma }$
is a filtered
![]() $\varphi $
-module of dimension 2 as
$\varphi $
-module of dimension 2 as
![]() $F_v\otimes _{{\mathbb {Q}}_p}\!L$
-vector space and
$F_v\otimes _{{\mathbb {Q}}_p}\!L$
-vector space and
![]() $\mathrm {Fil}^1 M_{f^\sigma }=F_v\otimes _{{\mathbb {Q}}_p} \!L \,\omega _{f^\sigma }$
, where
$\mathrm {Fil}^1 M_{f^\sigma }=F_v\otimes _{{\mathbb {Q}}_p} \!L \,\omega _{f^\sigma }$
, where
![]() $\omega _{f^\sigma }$
is the differential form on
$\omega _{f^\sigma }$
is the differential form on
![]() $X_0(N)$
associated to
$X_0(N)$
associated to
![]() $f^\sigma $
. Let
$f^\sigma $
. Let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be distinct roots of the Hecke eigen polynomial of f at p in L. (cf. [Reference Coleman and Edixhoven21].) We consider a splitting
$\beta $
be distinct roots of the Hecke eigen polynomial of f at p in L. (cf. [Reference Coleman and Edixhoven21].) We consider a splitting
![]() $N_\alpha $
(resp.
$N_\alpha $
(resp.
![]() $N_\beta $
) of the Hodge filtration of
$N_\beta $
) of the Hodge filtration of
![]() $M_f$
generated by
$M_f$
generated by
![]() $\beta \omega _f-\varphi \omega _f$
(resp.
$\beta \omega _f-\varphi \omega _f$
(resp.
![]() $\alpha \omega _f-\varphi \omega _f$
). Note that if
$\alpha \omega _f-\varphi \omega _f$
). Note that if
![]() $F=\mathbb {Q}$
,
$F=\mathbb {Q}$
,
![]() $N_\alpha $
is an
$N_\alpha $
is an
![]() $\alpha $
-eigenspace of the Frobenius. We extend them (arbitrary) to splittings for
$\alpha $
-eigenspace of the Frobenius. We extend them (arbitrary) to splittings for
![]() $M_{\mathscr {A}/F_v,L}$
, which are also denoted by
$M_{\mathscr {A}/F_v,L}$
, which are also denoted by
![]() $N_\alpha $
and
$N_\alpha $
and
![]() $N_\beta $
. Then, by (A.6), we have
$N_\beta $
. Then, by (A.6), we have
for the cyclotomic height pairing (here,
![]() $\mathrm {Tr}_{F/\mathbb {Q}}\lambda _{d, N_\alpha , N_\beta }(a):= \sum _{\sigma : F \hookrightarrow {\mathbb {C}}_p} \lambda _{d^\sigma , N_\alpha , N_\beta }(a^\sigma )$
). We put
$\mathrm {Tr}_{F/\mathbb {Q}}\lambda _{d, N_\alpha , N_\beta }(a):= \sum _{\sigma : F \hookrightarrow {\mathbb {C}}_p} \lambda _{d^\sigma , N_\alpha , N_\beta }(a^\sigma )$
). We put
![]() $A(F)_f$
for the f-part of
$A(F)_f$
for the f-part of
![]() $A(F)\otimes L$
be the Hecke action. Let
$A(F)\otimes L$
be the Hecke action. Let
![]() $\lambda _f: A(F)_f \rightarrow {\mathbb {C}}_p$
be the logarithm associated to
$\lambda _f: A(F)_f \rightarrow {\mathbb {C}}_p$
be the logarithm associated to
![]() $\omega _f$
.
$\omega _f$
.
Theorem A.2. Assume that
![]() $[\varphi \omega _f, \omega _f]\not =0$
. Then, we have
$[\varphi \omega _f, \omega _f]\not =0$
. Then, we have
 $$ \begin{align*} \langle d, a \rangle_{\ell_{F}^c, N_\alpha}- \langle d, a \rangle_{\ell_{F}^c, N_\beta}=\frac{(\beta-\alpha)}{[ \omega_f, \varphi\omega_f]} \mathrm{Tr}_{F/\mathbb{Q}}(\lambda_{f}(d)\lambda_{f}(a)) \end{align*} $$
$$ \begin{align*} \langle d, a \rangle_{\ell_{F}^c, N_\alpha}- \langle d, a \rangle_{\ell_{F}^c, N_\beta}=\frac{(\beta-\alpha)}{[ \omega_f, \varphi\omega_f]} \mathrm{Tr}_{F/\mathbb{Q}}(\lambda_{f}(d)\lambda_{f}(a)) \end{align*} $$
for
![]() $d, a \in A(F)_f$
(note that A is self-dual). In particular,
$d, a \in A(F)_f$
(note that A is self-dual). In particular,
 $$ \begin{align*} \langle a, a \rangle_{{\ell^c_F}, N_\alpha}- \langle a, a \rangle_{{\ell^c_F}, N_\beta}=\frac{(\beta-\alpha)}{[ \omega_f, \varphi\omega_f]} \mathrm{Tr}_{F/\mathbb{Q}}\lambda_{f}(a)^2. \end{align*} $$
$$ \begin{align*} \langle a, a \rangle_{{\ell^c_F}, N_\alpha}- \langle a, a \rangle_{{\ell^c_F}, N_\beta}=\frac{(\beta-\alpha)}{[ \omega_f, \varphi\omega_f]} \mathrm{Tr}_{F/\mathbb{Q}}\lambda_{f}(a)^2. \end{align*} $$
Proof. Put
![]() $\eta _f:=\frac {1}{[ \omega _f, \varphi \omega _f]}\varphi \omega _f$
and extend
$\eta _f:=\frac {1}{[ \omega _f, \varphi \omega _f]}\varphi \omega _f$
and extend
![]() $\omega _f$
,
$\omega _f$
,
![]() $\eta _f$
to a symplectic basis of
$\eta _f$
to a symplectic basis of
![]() $M_{\mathscr {A}/F_v}$
. Since
$M_{\mathscr {A}/F_v}$
. Since
![]() $\beta \omega _f-\varphi \omega _f \in N_\alpha $
, we have
$\beta \omega _f-\varphi \omega _f \in N_\alpha $
, we have
![]() $t_{N_\alpha }(\eta )=\frac {\beta }{[ \omega _f, \varphi \omega _f]} \omega _f$
. Hence, the assertion follows from (A.5) and (A.6).
$t_{N_\alpha }(\eta )=\frac {\beta }{[ \omega _f, \varphi \omega _f]} \omega _f$
. Hence, the assertion follows from (A.5) and (A.6).
Corollary A.3. Assume that
![]() $[\varphi \omega _f, \omega _f]\not =0$
. The pairing
$[\varphi \omega _f, \omega _f]\not =0$
. The pairing
![]() $\langle \;, \; \rangle _{\ell _{\mathbb {Q}}^c, N_\alpha }$
or
$\langle \;, \; \rangle _{\ell _{\mathbb {Q}}^c, N_\alpha }$
or
![]() $\langle \;, \; \rangle _{\ell _{\mathbb {Q}}^c, N_\beta }$
is non-trivial. In particular, if the Hecke polynomial at p is irreducible over the p-adic completion of
$\langle \;, \; \rangle _{\ell _{\mathbb {Q}}^c, N_\beta }$
is non-trivial. In particular, if the Hecke polynomial at p is irreducible over the p-adic completion of
![]() $K_f$
, the height pairing
$K_f$
, the height pairing
![]() $\langle \;, \; \rangle _{\ell _{\mathbb {Q}}^c, N_\alpha }$
is non-trivial.
$\langle \;, \; \rangle _{\ell _{\mathbb {Q}}^c, N_\alpha }$
is non-trivial.
Proof. This follows from Theorem A.2 since
![]() $\lambda _f$
is non-trivial. The pairings
$\lambda _f$
is non-trivial. The pairings
![]() $\langle \;, \; \rangle _{\ell _{\mathbb {Q}}^c, N_\alpha }$
and
$\langle \;, \; \rangle _{\ell _{\mathbb {Q}}^c, N_\alpha }$
and
![]() $\langle \;, \; \rangle _{\ell _{\mathbb {Q}}^c, N_\beta }$
are conjugate if
$\langle \;, \; \rangle _{\ell _{\mathbb {Q}}^c, N_\beta }$
are conjugate if
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are.
$\beta $
are.
Corollary A.4. The p-adic Gross-Zagier formula of f holds for inert primes if f is non-ordinary at p. (cf. [Reference Kobayashi33, Theorem 3])
Proof. We first show that
![]() $[\varphi \omega _f, \omega _f]\not =0$
. We have a strongly divisible lattice D in
$[\varphi \omega _f, \omega _f]\not =0$
. We have a strongly divisible lattice D in
![]() $M_f$
by the Fontaine-Laffaille theory. Suppose that
$M_f$
by the Fontaine-Laffaille theory. Suppose that
![]() $[\varphi \omega _f, \omega _f]=0$
. Then,
$[\varphi \omega _f, \omega _f]=0$
. Then,
![]() $\mathrm {Fil}^1D$
is stable by
$\mathrm {Fil}^1D$
is stable by
![]() $\varphi $
. Hence,
$\varphi $
. Hence,
![]() $\varphi (\mathrm {Fil}^1D)\subset \mathrm {Fil}^1D \cap pD= p\mathrm {Fil}^1D$
. This implies that one of the eigenvalues
$\varphi (\mathrm {Fil}^1D)\subset \mathrm {Fil}^1D \cap pD= p\mathrm {Fil}^1D$
. This implies that one of the eigenvalues
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
is divisible by p, which contradicts the non-ordinary assumption. By Corollary A.3, choose
$\beta $
is divisible by p, which contradicts the non-ordinary assumption. By Corollary A.3, choose
![]() $\alpha $
for which
$\alpha $
for which
![]() $\langle \;, \; \rangle _{\ell _{\mathbb {Q}}^c, N_\alpha }$
is non-trivial. Then, see a remark after [Reference Kobayashi33, Theorem 3].
$\langle \;, \; \rangle _{\ell _{\mathbb {Q}}^c, N_\alpha }$
is non-trivial. Then, see a remark after [Reference Kobayashi33, Theorem 3].
Corollary A.5. Let p be a non-ordinary (good) prime for f. Suppose that
![]() $\mathrm {ord}_{s=1}L(f, s)=1$
and the Iwasawa main conjecture for f is true for p. Then, the p-part of the full Birch and Swinnerton-Dyer conjecture (Bloch-Kato’s tamagawa number conjecture) is true for f.
$\mathrm {ord}_{s=1}L(f, s)=1$
and the Iwasawa main conjecture for f is true for p. Then, the p-part of the full Birch and Swinnerton-Dyer conjecture (Bloch-Kato’s tamagawa number conjecture) is true for f.
Proof. Take
![]() $\alpha $
so that
$\alpha $
so that
![]() $\langle \;, \; \rangle _{\ell _{\mathbb {Q}}^c, N_\alpha }$
is non-trivial. Then, the assertion follows from similar arguments as [Reference Kobayashi33, Corollary 1.3 (iii)].
$\langle \;, \; \rangle _{\ell _{\mathbb {Q}}^c, N_\alpha }$
is non-trivial. Then, the assertion follows from similar arguments as [Reference Kobayashi33, Corollary 1.3 (iii)].
Let
 $$ \begin{align*} \mathscr{H}_L= \bigg{\{} \sum_{n\ge 0}a_n(\gamma-1)^n \in L[\![\gamma-1]\!] \big{|} \lim_n |a_n|_pn^{-1}=0 \bigg{\}}, \end{align*} $$
$$ \begin{align*} \mathscr{H}_L= \bigg{\{} \sum_{n\ge 0}a_n(\gamma-1)^n \in L[\![\gamma-1]\!] \big{|} \lim_n |a_n|_pn^{-1}=0 \bigg{\}}, \end{align*} $$
where
![]() $| \cdot |_p$
is the multiplicative valuation of L normalized by
$| \cdot |_p$
is the multiplicative valuation of L normalized by
![]() $|p|_p=1/p$
. For
$|p|_p=1/p$
. For
![]() $|\alpha |_p> 1/p$
, let
$|\alpha |_p> 1/p$
, let
![]() $L_{p,\alpha }(f)\in \mathscr {H}_L$
be the cyclotomic p-adic L-function as in [Reference Kato30, Theorem 16.2]. Fixing a real period
$L_{p,\alpha }(f)\in \mathscr {H}_L$
be the cyclotomic p-adic L-function as in [Reference Kato30, Theorem 16.2]. Fixing a real period
![]() $\Omega _f$
of f, we have the following interpolation property. For a finite character
$\Omega _f$
of f, we have the following interpolation property. For a finite character
![]() $\chi $
of
$\chi $
of
![]() ${\mathrm {Gal}}({\mathbb {Q}}_{\infty } /{\mathbb {Q}})$
of conductor
${\mathrm {Gal}}({\mathbb {Q}}_{\infty } /{\mathbb {Q}})$
of conductor
![]() $p^n>1$
,
$p^n>1$
,
 $$ \begin{align*} L_{p,\alpha}(f)(\chi)=\frac{p^n}{\alpha^n\tau(\chi^{-1}, \zeta_{p^n})}\cdot \frac{L(f,\chi^{-1},1)}{\Omega_f}, \end{align*} $$
$$ \begin{align*} L_{p,\alpha}(f)(\chi)=\frac{p^n}{\alpha^n\tau(\chi^{-1}, \zeta_{p^n})}\cdot \frac{L(f,\chi^{-1},1)}{\Omega_f}, \end{align*} $$
where
![]() $\zeta _{p^n}=e^{2\pi i /p^{n}}$
, and for the trivial character
$\zeta _{p^n}=e^{2\pi i /p^{n}}$
, and for the trivial character

If
![]() $|\beta |_p> 1/p$
, then replacing
$|\beta |_p> 1/p$
, then replacing
![]() $\alpha $
with
$\alpha $
with
![]() $\beta ,$
we see the interpolation property of
$\beta ,$
we see the interpolation property of
![]() $L_{p,\beta }(f).$
$L_{p,\beta }(f).$
Define
where
![]() $\chi ^{{\mathrm {cyc}}}: {\mathrm {Gal}}({\mathbb {Q}}_{\infty }/{\mathbb {Q}}) \to 1+p{\mathbb {Z}}_p$
is the cyclotomic character. We similarly define
$\chi ^{{\mathrm {cyc}}}: {\mathrm {Gal}}({\mathbb {Q}}_{\infty }/{\mathbb {Q}}) \to 1+p{\mathbb {Z}}_p$
is the cyclotomic character. We similarly define
![]() $\mathscr {L}_{p,\beta }^{\prime }(f,1).$
$\mathscr {L}_{p,\beta }^{\prime }(f,1).$
Theorem A.6. Let p be a non-ordinary (good) prime for f. Suppose that the root number of
![]() $L(f, s)$
is
$L(f, s)$
is
![]() $-1$
. Then, there exists a point
$-1$
. Then, there exists a point
![]() $P \in A(\mathbb {Q})_f$
and a non-zero constant
$P \in A(\mathbb {Q})_f$
and a non-zero constant
![]() $c_P \in \mathbb {Q}$
such that
$c_P \in \mathbb {Q}$
such that
 $$ \begin{align*} \left(1-\frac{1}{\alpha}\right)^{-2} \mathscr{L}^{\prime}_{p,\alpha}(f,1)- \left(1-\frac{1}{\beta}\right)^{-2}\mathscr{L}^{\prime}_{p,\beta}(f,1)=c_P\frac{(\beta-\alpha)}{[ \omega_f, \varphi\omega_f]}\lambda_f(P)^2. \end{align*} $$
$$ \begin{align*} \left(1-\frac{1}{\alpha}\right)^{-2} \mathscr{L}^{\prime}_{p,\alpha}(f,1)- \left(1-\frac{1}{\beta}\right)^{-2}\mathscr{L}^{\prime}_{p,\beta}(f,1)=c_P\frac{(\beta-\alpha)}{[ \omega_f, \varphi\omega_f]}\lambda_f(P)^2. \end{align*} $$
Moreover, P is non-torsion if and only if
![]() $\mathrm {ord}_{s=1}L(f, s)=1$
, and in such a case
$\mathrm {ord}_{s=1}L(f, s)=1$
, and in such a case
![]() $c_P=\frac {L'(f, 1)}{\Omega _f\langle P, P \rangle _{\infty }},$
where
$c_P=\frac {L'(f, 1)}{\Omega _f\langle P, P \rangle _{\infty }},$
where
![]() $\langle \,,\,\rangle _\infty $
is the Néron-Tate height pairing.
$\langle \,,\,\rangle _\infty $
is the Néron-Tate height pairing.
Proof. By [Reference Bump, Friedberg and Hoffstein8], there exists an imaginary quadratic field K satisfying the Heegner hypothesis and
![]() $L(f\otimes \varepsilon , 1)\not =0$
for the quadratic character
$L(f\otimes \varepsilon , 1)\not =0$
for the quadratic character
![]() $\varepsilon $
associated to K. Let z be a Heegner point associated to K. Since
$\varepsilon $
associated to K. Let z be a Heegner point associated to K. Since
![]() $L(f\otimes \varepsilon , 1)\not =0$
, the Heegner point z lives in
$L(f\otimes \varepsilon , 1)\not =0$
, the Heegner point z lives in
![]() $A({\mathbb {Q}})\otimes {\mathbb {Q}}$
up to a torsion element. Then, by Theorem A.2 for
$A({\mathbb {Q}})\otimes {\mathbb {Q}}$
up to a torsion element. Then, by Theorem A.2 for
![]() $F=K$
and by the p-adic Gross-Zagier formula, we have
$F=K$
and by the p-adic Gross-Zagier formula, we have
 $$ \begin{align} \left(1-\frac{1}{\alpha}\right)^{-4} \mathscr{L}_{p, \alpha}'(f/K, 1)- \left(1-\frac{1}{\beta}\right)^{-4}\mathscr{L}_{p, \beta}'(f/K, 1)=2u^{-2}\frac{(\beta-\alpha)}{[ \omega_f, \varphi\omega_f]}\lambda_f(z)^2, \end{align} $$
$$ \begin{align} \left(1-\frac{1}{\alpha}\right)^{-4} \mathscr{L}_{p, \alpha}'(f/K, 1)- \left(1-\frac{1}{\beta}\right)^{-4}\mathscr{L}_{p, \beta}'(f/K, 1)=2u^{-2}\frac{(\beta-\alpha)}{[ \omega_f, \varphi\omega_f]}\lambda_f(z)^2, \end{align} $$
where
![]() $\mathscr {L}_{p, -}(f/K, s)$
is the p-adic L-function of f over K (cf. [Reference Kobayashi32], [Reference Kobayashi33]) and
$\mathscr {L}_{p, -}(f/K, s)$
is the p-adic L-function of f over K (cf. [Reference Kobayashi32], [Reference Kobayashi33]) and
![]() . By the classical Gross-Zagier formula, z is non-torsion if and only if
. By the classical Gross-Zagier formula, z is non-torsion if and only if
![]() $\mathrm {ord}_{s=1}L(f, s)=1$
. Then, as in the proof of [Reference Kobayashi32, Corollary 1.3], we have the desired formula from (A.7) by using the complex and the p-adic Gross-Zagier formulae.
$\mathrm {ord}_{s=1}L(f, s)=1$
. Then, as in the proof of [Reference Kobayashi32, Corollary 1.3], we have the desired formula from (A.7) by using the complex and the p-adic Gross-Zagier formulae.
Appendix B Perrin-Riou conjecture
Rubin’s formula [Reference Rubin50] inspired the eponymous conjecture [Reference Perrin-Riou42, §3.3.2], which primarily concerns the arithmetic of Beilinson-Kato elements.
B.1 The conjecture
Let
![]() $f\in S_{2}(\Gamma _{0}(N))$
be an elliptic newform and
$f\in S_{2}(\Gamma _{0}(N))$
be an elliptic newform and
![]() $F \subseteq {\mathbb {C}}$
the Hecke field. Let A be an associated
$F \subseteq {\mathbb {C}}$
the Hecke field. Let A be an associated
![]() ${\mathrm {GL}}_2$
-type abelian variety over
${\mathrm {GL}}_2$
-type abelian variety over
![]() ${\mathbb {Q}}$
; that is, A is a simple,
${\mathbb {Q}}$
; that is, A is a simple,
![]() $[F:{\mathbb {Q}}]$
-dimensional abelian variety equipped with a homomorphism
$[F:{\mathbb {Q}}]$
-dimensional abelian variety equipped with a homomorphism
![]() $F \to \mathrm {End}(A)\otimes {\mathbb {Q}}$
of
$F \to \mathrm {End}(A)\otimes {\mathbb {Q}}$
of
![]() ${\mathbb {Q}}$
-algebras such that
${\mathbb {Q}}$
-algebras such that
 $$ \begin{align*} L(A,s)=\prod_{\sigma:F\hookrightarrow \overline{{\mathbb {Q}}}} L(f^{\sigma},s). \end{align*} $$
$$ \begin{align*} L(A,s)=\prod_{\sigma:F\hookrightarrow \overline{{\mathbb {Q}}}} L(f^{\sigma},s). \end{align*} $$
Let p be a prime number and
![]() ${\mathfrak {p}}$
the prime of the Hecke field F over p arising from the fixed embedding
${\mathfrak {p}}$
the prime of the Hecke field F over p arising from the fixed embedding
![]() $\iota _p: \overline {{\mathbb {Q}}} \hookrightarrow {\mathbb {C}}_p$
. Let
$\iota _p: \overline {{\mathbb {Q}}} \hookrightarrow {\mathbb {C}}_p$
. Let
![]() $V(f) \cong F_{{\mathfrak {p}}}^{\oplus 2}$
denote the
$V(f) \cong F_{{\mathfrak {p}}}^{\oplus 2}$
denote the
![]() ${\mathfrak {p}}$
-th component of the Galois representation
${\mathfrak {p}}$
-th component of the Galois representation
![]() $T_p(A)\otimes {\mathbb {Q}}_p\cong \prod _{v\mid p}F_v^{\oplus 2}$
. Let
$T_p(A)\otimes {\mathbb {Q}}_p\cong \prod _{v\mid p}F_v^{\oplus 2}$
. Let
![]() $z_{f} \in H^{1}({\mathbb {Q}},V(f))$
be a Beilinson-Kato element as in [Reference Kato30, Theorem 12.5]. By Kato’s reciprocity law [Reference Kato30, Theorem 12.5 (1)],
$z_{f} \in H^{1}({\mathbb {Q}},V(f))$
be a Beilinson-Kato element as in [Reference Kato30, Theorem 12.5]. By Kato’s reciprocity law [Reference Kato30, Theorem 12.5 (1)],
After Kato, if
![]() $L(f,1)\neq 0$
, then
$L(f,1)\neq 0$
, then
![]() $z_{f}$
is inherent to the arithmetic of f (cf. [Reference Kato30, Theorem 14.5]). If
$z_{f}$
is inherent to the arithmetic of f (cf. [Reference Kato30, Theorem 14.5]). If
![]() $L(f,1)=0$
, then Perrin-Riou [Reference Perrin-Riou42, §3.3.2] (for elliptic curves) conjectured the Beilinson-Kato element
$L(f,1)=0$
, then Perrin-Riou [Reference Perrin-Riou42, §3.3.2] (for elliptic curves) conjectured the Beilinson-Kato element
![]() $z_{f}$
to be still intertwined with the arithmetic as follows.
$z_{f}$
to be still intertwined with the arithmetic as follows.
Conjecture B.1. Let
![]() $f\in S_{2}(\Gamma _{0}(N))$
be an elliptic newform and
$f\in S_{2}(\Gamma _{0}(N))$
be an elliptic newform and
![]() $A_{/{\mathbb {Q}}}$
an associated
$A_{/{\mathbb {Q}}}$
an associated
![]() ${\mathrm {GL}}_2$
-type abelian variety. Suppose that
${\mathrm {GL}}_2$
-type abelian variety. Suppose that
![]() $L(f,1)=0$
. Let p be a prime. Then, there exists a rational point
$L(f,1)=0$
. Let p be a prime. Then, there exists a rational point
![]() $P\in A({\mathbb {Q}})$
with the following properties.
$P\in A({\mathbb {Q}})$
with the following properties.
-
(a) We have
for some $$ \begin{align*}\lambda_{f}({\mathrm{loc}}_{p}(z_{f})) = c \lambda_{f}(P)^{2} \end{align*} $$
$$ \begin{align*}\lambda_{f}({\mathrm{loc}}_{p}(z_{f})) = c \lambda_{f}(P)^{2} \end{align*} $$
 $c\in F^{\times }$
and
$c\in F^{\times }$
and
 $\lambda _{f}:H^{1}_{{\mathrm {f}}}({\mathbb {Q}}_{p},V(f)) \rightarrow F_{{\mathfrak {p}}}$
the logarithm map associated to a non-zero element
$\lambda _{f}:H^{1}_{{\mathrm {f}}}({\mathbb {Q}}_{p},V(f)) \rightarrow F_{{\mathfrak {p}}}$
the logarithm map associated to a non-zero element
 $\omega _A \in \mathrm {coLie}(A).$
$\omega _A \in \mathrm {coLie}(A).$
-
(b) P is non-torsion if and only if
 ${\mathrm {ord}}_{s=1}L(f,s)=1.$
${\mathrm {ord}}_{s=1}L(f,s)=1.$
The conjecture implies
B.2 The non-ordinary case
We prove Perrin-Riou’s Conjecture B.1 at the primes of good non-ordinary reduction. The main result is Theorem B.3, which shows a refinement of the conjecture.
B.2.1 Backdrop
Let the setting be as in §B.1.
Fix an element
![]() $b_A \in H^1(A({\mathbb {C}}), {\mathbb {Q}})$
such that
$b_A \in H^1(A({\mathbb {C}}), {\mathbb {Q}})$
such that
![]() $b^{+}_A:=2^{-1}(1+\iota )b_A \neq 0$
for
$b^{+}_A:=2^{-1}(1+\iota )b_A \neq 0$
for
![]() $\iota $
the involution of
$\iota $
the involution of
![]() $H^1(A({\mathbb {C}}), {\mathbb {Q}})$
induced by the complex conjugation c on
$H^1(A({\mathbb {C}}), {\mathbb {Q}})$
induced by the complex conjugation c on
![]() $A({\mathbb {C}})$
. Fix a non-zero element
$A({\mathbb {C}})$
. Fix a non-zero element
![]() $\omega _A \in \mathrm {coLie}(A) \cong F$
. Define
$\omega _A \in \mathrm {coLie}(A) \cong F$
. Define
![]() $\Omega _f \in {\mathbb {R}}$
by
$\Omega _f \in {\mathbb {R}}$
by
where
![]() $\mathrm {per}_f: \mathrm {coLie}(A) \to H^1(A({\mathbb {C}}), {\mathbb {Q}})\otimes _F {\mathbb {C}}$
denotes the F-linear map induced by the period map of A. (Since
$\mathrm {per}_f: \mathrm {coLie}(A) \to H^1(A({\mathbb {C}}), {\mathbb {Q}})\otimes _F {\mathbb {C}}$
denotes the F-linear map induced by the period map of A. (Since
![]() $\omega _A$
is defined over
$\omega _A$
is defined over
![]() ${\mathbb {Q}}$
, note that
${\mathbb {Q}}$
, note that
![]() $\mathrm {per}_f(\omega _A)$
lies in the
$\mathrm {per}_f(\omega _A)$
lies in the
![]() $(\iota \otimes c)$
-fixed part of
$(\iota \otimes c)$
-fixed part of
![]() $H^1(A({\mathbb {C}}), {\mathbb {Q}})\otimes _F {\mathbb {C}}$
, and so
$H^1(A({\mathbb {C}}), {\mathbb {Q}})\otimes _F {\mathbb {C}}$
, and so
![]() $\Omega _{f} \in {\mathbb {R}}$
.) Fix a polarization of A which is compatible with the F-action. Let
$\Omega _{f} \in {\mathbb {R}}$
.) Fix a polarization of A which is compatible with the F-action. Let
![]() $T(f)$
be a Galois stable
$T(f)$
be a Galois stable
![]() ${\mathcal {O}}_{F_{{\mathfrak {p}}}}$
-lattice of
${\mathcal {O}}_{F_{{\mathfrak {p}}}}$
-lattice of
![]() $V(f)$
.
$V(f)$
.
Let
be the Beilinson-Kato element associated to
![]() $b_A$
as in [Reference Kato30, Thm. 12.5 (1)]. The following explicit reciprocity law is due to Kato [Reference Kato30, Thm. 12.5].
$b_A$
as in [Reference Kato30, Thm. 12.5 (1)]. The following explicit reciprocity law is due to Kato [Reference Kato30, Thm. 12.5].
Proposition B.2. For a finite character
![]() $\chi $
of
$\chi $
of
![]() ${\mathrm {Gal}}({\mathbb {Q}}_n/{\mathbb {Q}})$
, we have
${\mathrm {Gal}}({\mathbb {Q}}_n/{\mathbb {Q}})$
, we have
 $$ \begin{align} \sum_{\sigma \in {\mathrm{Gal}}({\mathbb {Q}}_n/{\mathbb {Q}} )} \chi(\sigma)\exp^*_{n}({\mathrm{loc}}_{\tilde{{\mathfrak{p}}}}(z_{f,n}^{\sigma}))= \frac{L(f, \chi, 1)}{\Omega_f} \omega_A. \end{align} $$
$$ \begin{align} \sum_{\sigma \in {\mathrm{Gal}}({\mathbb {Q}}_n/{\mathbb {Q}} )} \chi(\sigma)\exp^*_{n}({\mathrm{loc}}_{\tilde{{\mathfrak{p}}}}(z_{f,n}^{\sigma}))= \frac{L(f, \chi, 1)}{\Omega_f} \omega_A. \end{align} $$
Here,
is the dual exponential map and
![]() $\tilde {{\mathfrak {p}}}$
the prime of
$\tilde {{\mathfrak {p}}}$
the prime of
![]() ${\mathbb {Q}}_n$
over p.
${\mathbb {Q}}_n$
over p.
B.2.2 The theorem
Theorem B.3. Let
![]() $f\in S_{2}(\Gamma _{0}(N))$
be an elliptic newform and p a prime of good non-ordinary reduction. Then, an explicit form of Conjecture B.1 is true: if
$f\in S_{2}(\Gamma _{0}(N))$
be an elliptic newform and p a prime of good non-ordinary reduction. Then, an explicit form of Conjecture B.1 is true: if
![]() $L(f,1)=0$
, then there exists a rational point
$L(f,1)=0$
, then there exists a rational point
![]() $P\in A({\mathbb {Q}})$
with the following properties.
$P\in A({\mathbb {Q}})$
with the following properties.
-
(a) We have
for some $$ \begin{align*} \lambda_{f}({\mathrm{loc}}_{p}(z_{f})) = c_P \left(1-\frac{a_p(f)}{p}+\frac{1}{p}\right) \lambda_{f}(P)^{2} \end{align*} $$
$$ \begin{align*} \lambda_{f}({\mathrm{loc}}_{p}(z_{f})) = c_P \left(1-\frac{a_p(f)}{p}+\frac{1}{p}\right) \lambda_{f}(P)^{2} \end{align*} $$
 $c_{P}\in F^\times $
, and
$c_{P}\in F^\times $
, and
 $z_f:=z_{f,0}$
,
$z_f:=z_{f,0}$
,
 $a_p(f)$
the p-th Fourier coefficient of f, and
$a_p(f)$
the p-th Fourier coefficient of f, and
 $\lambda _{f}:H^{1}_{{\mathrm {f}}}({\mathbb {Q}}_{p},V(f)) \rightarrow F_{{\mathfrak {p}}}$
the logarithm map associated to
$\lambda _{f}:H^{1}_{{\mathrm {f}}}({\mathbb {Q}}_{p},V(f)) \rightarrow F_{{\mathfrak {p}}}$
the logarithm map associated to
 $\omega _A$
.
$\omega _A$
.
-
(b) P is non-torsion if and only if
 ${\mathrm {ord}}_{s=1}L(f,s)=1.$
${\mathrm {ord}}_{s=1}L(f,s)=1.$
-
(c) If the equivalent conditions in (b)hold, then
for $$ \begin{align*}c_P=\frac{L'(f, 1)}{\Omega_f\langle P, P \rangle_{\infty}}\end{align*} $$
$$ \begin{align*}c_P=\frac{L'(f, 1)}{\Omega_f\langle P, P \rangle_{\infty}}\end{align*} $$
 $\langle \,,\,\rangle _\infty $
the Néron-Tate height pairing.
$\langle \,,\,\rangle _\infty $
the Néron-Tate height pairing.
Our proof is based on the following link between the logarithm of
![]() ${\mathrm {loc}}_p(z_{f}) \in H^1_{\mathrm {f}}({\mathbb {Q}}_p, V(f))$
and the first derivatives of the p-adic L-functions.
${\mathrm {loc}}_p(z_{f}) \in H^1_{\mathrm {f}}({\mathbb {Q}}_p, V(f))$
and the first derivatives of the p-adic L-functions.
Proposition B.4. Let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be the roots of the Hecke polynomial
$\beta $
be the roots of the Hecke polynomial
![]() $X^2-a_p(f)X+p$
of f. Then, we have
$X^2-a_p(f)X+p$
of f. Then, we have
where
![]() $\mathscr {L}_{p,\alpha }^{\prime }(f,1)$
and
$\mathscr {L}_{p,\alpha }^{\prime }(f,1)$
and
![]() $\mathscr {L}_{p,\beta }^{\prime }(f,1)$
are the derivatives of the cyclotomic p-adic L-functions as in §A.3, and
$\mathscr {L}_{p,\beta }^{\prime }(f,1)$
are the derivatives of the cyclotomic p-adic L-functions as in §A.3, and
is the natural pairing induced by the de Rham pairing. Here, under the last isomorphism, the basis of
![]() $D_{\mathrm {cris}}({\mathbb {Q}}_p(1))$
associated to
$D_{\mathrm {cris}}({\mathbb {Q}}_p(1))$
associated to
![]() $(\zeta _{p^n})_n=(e^{2\pi i/n})_n$
corresponds to
$(\zeta _{p^n})_n=(e^{2\pi i/n})_n$
corresponds to
![]() $1 \in F_{{\mathfrak {p}}},$
and
$1 \in F_{{\mathfrak {p}}},$
and
![]() $D^0_{\mathrm {cris}}(V(f))$
denotes
$D^0_{\mathrm {cris}}(V(f))$
denotes
![]() $\mathrm {Fil}^0D_{\mathrm {cris}}(V(f))$
.
$\mathrm {Fil}^0D_{\mathrm {cris}}(V(f))$
.
Proof. Define
![]() $\omega _{\alpha }, \omega _{\beta } \in D:= D_{\mathrm {cris}}(V(f))\otimes _{F_{{\mathfrak {p}}}} F_{{\mathfrak {p}}}(\alpha )$
by
$\omega _{\alpha }, \omega _{\beta } \in D:= D_{\mathrm {cris}}(V(f))\otimes _{F_{{\mathfrak {p}}}} F_{{\mathfrak {p}}}(\alpha )$
by
for
![]() $\varphi $
the Frobenius map of D. Then,
$\varphi $
the Frobenius map of D. Then,
![]() $\omega _\alpha $
and
$\omega _\alpha $
and
![]() $\omega _\beta $
are non-zero elements such that
$\omega _\beta $
are non-zero elements such that
![]() $\varphi \omega _{\alpha }=\alpha ^{-1} \omega _{\alpha }$
and
$\varphi \omega _{\alpha }=\alpha ^{-1} \omega _{\alpha }$
and
![]() $\varphi \omega _{\beta }=\beta ^{-1} \omega _{\beta }.$
Here, we note that D coincides with
$\varphi \omega _{\beta }=\beta ^{-1} \omega _{\beta }.$
Here, we note that D coincides with
![]() $M_{f}\otimes D_{\mathrm {cris}}({\mathbb {Q}}_p(1))$
in subsection A.3 with
$M_{f}\otimes D_{\mathrm {cris}}({\mathbb {Q}}_p(1))$
in subsection A.3 with
![]() $L=F_{{\mathfrak {p}}}(\alpha )$
.
$L=F_{{\mathfrak {p}}}(\alpha )$
.
Following [Reference Perrin-Riou42, §3.1.3], defineFootnote
10
![]() ${L}_p(f)\in \mathscr {H}_{F_{{\mathfrak {p}}}(\alpha )}\otimes _{F_{{\mathfrak {p}}}(\alpha )} D$
by
${L}_p(f)\in \mathscr {H}_{F_{{\mathfrak {p}}}(\alpha )}\otimes _{F_{{\mathfrak {p}}}(\alpha )} D$
by
and
![]() $\mathscr {L}_{p}^{\prime }(f,1)=\lim _{s\to 1}{L}_{p}(f)((\chi ^{\mathrm {cyc}})^{s-1})/(s-1) \in D$
.
$\mathscr {L}_{p}^{\prime }(f,1)=\lim _{s\to 1}{L}_{p}(f)((\chi ^{\mathrm {cyc}})^{s-1})/(s-1) \in D$
.
Then, by [Reference Perrin-Riou42, Proposition 2.2.2] and (B.4), we have
 $$ \begin{align*} &\log_{f}({\mathrm{loc}}_p(z_{f})) \equiv(1-p^{-1}\varphi^{-1})(1-\varphi)^{-1}\mathscr{L}_{p}^{\prime}(f,1)\\& \quad \equiv \frac{p}{\alpha-\beta} (1-p^{-1}\alpha)(1-\alpha^{-1})^{-1}\mathscr{L}_{p,\alpha}^{\prime}(f,1)\omega_{\alpha}- \frac{p}{\alpha-\beta} (1-p^{-1}\beta)(1-\beta^{-1})^{-1}\mathscr{L}_{p,\beta}^{\prime}(f,1)\omega_{\beta}\\&\quad \equiv \frac{1-a_p(f)+p}{\beta-\alpha}\left((1-\alpha^{-1})^2\mathscr{L}_{p,\alpha}^{\prime}(f,1) - (1-\beta^{-1})^2\mathscr{L}_{p,\beta}^{\prime}(f,1) \right)\varphi\omega_A \quad \ \mathrm{mod}\ \mathrm{Fil}^0D. \end{align*} $$
$$ \begin{align*} &\log_{f}({\mathrm{loc}}_p(z_{f})) \equiv(1-p^{-1}\varphi^{-1})(1-\varphi)^{-1}\mathscr{L}_{p}^{\prime}(f,1)\\& \quad \equiv \frac{p}{\alpha-\beta} (1-p^{-1}\alpha)(1-\alpha^{-1})^{-1}\mathscr{L}_{p,\alpha}^{\prime}(f,1)\omega_{\alpha}- \frac{p}{\alpha-\beta} (1-p^{-1}\beta)(1-\beta^{-1})^{-1}\mathscr{L}_{p,\beta}^{\prime}(f,1)\omega_{\beta}\\&\quad \equiv \frac{1-a_p(f)+p}{\beta-\alpha}\left((1-\alpha^{-1})^2\mathscr{L}_{p,\alpha}^{\prime}(f,1) - (1-\beta^{-1})^2\mathscr{L}_{p,\beta}^{\prime}(f,1) \right)\varphi\omega_A \quad \ \mathrm{mod}\ \mathrm{Fil}^0D. \end{align*} $$
Here,
![]() $\log _f:H^1_{\mathrm {f}}({\mathbb {Q}}_p, V(f))\to D_{\mathrm {cris}}(V(f))/D^0_{\mathrm {cris}}(V(f))$
denotes the Bloch-Kato logarithm of
$\log _f:H^1_{\mathrm {f}}({\mathbb {Q}}_p, V(f))\to D_{\mathrm {cris}}(V(f))/D^0_{\mathrm {cris}}(V(f))$
denotes the Bloch-Kato logarithm of
![]() $V(f)$
. Considering the product with
$V(f)$
. Considering the product with
![]() $\omega _A$
, the proposition follows.
$\omega _A$
, the proposition follows.
We now return to Theorem B.3.
Proof of Theorem B.3
Since
![]() $D_{\mathrm {cris}}(V(f)) \cong M_{f}\otimes D_{\mathrm {cris}}({\mathbb {Q}}_p(1))$
, note that
$D_{\mathrm {cris}}(V(f)) \cong M_{f}\otimes D_{\mathrm {cris}}({\mathbb {Q}}_p(1))$
, note that
![]() $p[\omega _A, \varphi \omega _A]_{D_{\mathrm {cris}}(V(f))}$
coincides with
$p[\omega _A, \varphi \omega _A]_{D_{\mathrm {cris}}(V(f))}$
coincides with
![]() $[\omega _A, \varphi \omega _A]$
in Theorem A.6.
$[\omega _A, \varphi \omega _A]$
in Theorem A.6.
Hence, the assertion is a consequence of Theorem A.6 and Proposition B.4.
Remark B.5.
-
(i) A recent progress towards Conjecture B.1 appears in [Reference Bertolini, Darmon and Venerucci7], [Reference Burungale, Skinner and Tian17], [Reference Buyukboduk, Pollack and Sasaki19]. The key tools are (variants of) the Beilinson-Flach element and the BDP formula. In the non-ordinary case, these results assume additional hypotheses such as p odd, while our independent approach treats the general non-ordinary case.
-
(ii) Theorem B.3 is a tool in the proof of yet another CM p-converse (cf. [Reference Burungale and Skinner15]), and in turn, a result towards the cube sum problem (cf. [Reference Alpoge, Bhargava and Shnidman1]).
Acknowledgement
It is a pleasure to thank Chris Skinner for stimulating discussions. We are grateful to the referee for valuable suggestions.
The paper owes its very existence to prescient works [Reference Rubin47], [Reference Rubin50] by Karl Rubin. The authors would like to express their sincere gratitude to him.
This work was partially supported by the NSF grant DMS 2001409 and the JSPS KAKENHI grants JP17H02836, JP18H05233, JP22H00096, JP17K14173, JP21K13774.
Competing Interests
The author declares none.