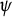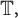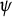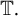1 Introduction
In 1955, Lehto [Reference Lehto4] showed that given an arbitrary measurable function
![]() $\psi $
on the interval
$\psi $
on the interval
![]() $[0,2\pi ),$
there exists a function f holomorphic in the unit disc
$[0,2\pi ),$
there exists a function f holomorphic in the unit disc
![]() $\mathbb D \subset \mathbb C $
such that
$\mathbb D \subset \mathbb C $
such that
Lehto’s theorem shows that the radial boundary values of holomorphic functions in the unit disc can be prescribed almost everywhere on the boundary of the disc. On the other hand, any attempt to prescribe angular boundary values fails dramatically due to the Luzin–Privalov uniqueness theorem [Reference Noshiro and Heft6]. This result asserts that if a meromorphic function f in the unit disc
![]() $\mathbb D $
has angular limit
$\mathbb D $
has angular limit
![]() $0$
at each point of a subset of the boundary having positive linear measure, then
$0$
at each point of a subset of the boundary having positive linear measure, then
![]() $f= 0.$
$f= 0.$
Having recalled this uniqueness result on angular limits, we recall the well-known existence result on angular limits. Namely, functions in Nevanlinna class, and in particular in Hardy spaces, have angular limits at almost all points of the unit circle.
For
![]() $p\in \mathbb C $
and
$p\in \mathbb C $
and
![]() $r>0,$
we denote by
$r>0,$
we denote by
![]() $B(p,r)$
the open disc of center p and radius r. We will denote the Lebesgue
$B(p,r)$
the open disc of center p and radius r. We will denote the Lebesgue
![]() $2$
-measure by m. Our main result is the following.
$2$
-measure by m. Our main result is the following.
Theorem 1.1 Given an arbitrary measurable function
![]() $\psi $
on the interval
$\psi $
on the interval
![]() $[0,2\pi ),$
whose restriction to some closed subset
$[0,2\pi ),$
whose restriction to some closed subset
![]() $S\subset [0,2\pi )$
is continuous, there exists a function f holomorphic in
$S\subset [0,2\pi )$
is continuous, there exists a function f holomorphic in
![]() $\mathbb D ,$
and for every
$\mathbb D ,$
and for every
![]() $\theta \in S$
and a.e.
$\theta \in S$
and a.e.
![]() $\theta \in [0,2\pi )$
, there is a set
$\theta \in [0,2\pi )$
, there is a set
![]() $E_\theta \subset \mathbb D ,$
such that
$E_\theta \subset \mathbb D ,$
such that
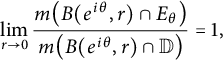 $$ \begin{align*}\lim_{r\to 0}\frac{m\big(B(e^{i\theta},r)\cap E_\theta\big)}{m\big(B(e^{i\theta},r)\cap\mathbb D \big)}=1, \end{align*} $$
$$ \begin{align*}\lim_{r\to 0}\frac{m\big(B(e^{i\theta},r)\cap E_\theta\big)}{m\big(B(e^{i\theta},r)\cap\mathbb D \big)}=1, \end{align*} $$
and
Notice that points
![]() $e^{i\theta }$
satisfying the first limit are necessarily accumulation points of the corresponding sets
$e^{i\theta }$
satisfying the first limit are necessarily accumulation points of the corresponding sets
![]() $E_\theta .$
$E_\theta .$
More generally, we shall present such a result for solutions of elliptic equations on manifolds. Our result applies, in particular, to harmonic functions on Riemannian manifolds and to holomorphic functions on Riemann surfaces.
Let M be an oriented real analytic manifold with countable base. We shall denote by
![]() $*$
the ideal point of the one-point compactification
$*$
the ideal point of the one-point compactification
![]() $M^*$
of
$M^*$
of
![]() $M.$
Fix a distance function d on M and a positive Borel measure
$M.$
Fix a distance function d on M and a positive Borel measure
![]() $\mu $
for which open sets have positive measure and compact sets have finite measure. Then,
$\mu $
for which open sets have positive measure and compact sets have finite measure. Then,
![]() $\mu $
is regular (see [Reference Rudin7, Theorem 2.18]). On M, the Lebesgue measure of a measurable set is not well defined, but because M is smooth, Lebesgue measure zero is invariant under change of coordinates, so the notion of absolute continuity of the measure
$\mu $
is regular (see [Reference Rudin7, Theorem 2.18]). On M, the Lebesgue measure of a measurable set is not well defined, but because M is smooth, Lebesgue measure zero is invariant under change of coordinates, so the notion of absolute continuity of the measure
![]() $\mu $
(with respect to Lebesgue measure) is well defined. We shall assume that our measure
$\mu $
(with respect to Lebesgue measure) is well defined. We shall assume that our measure
![]() $\mu $
is absolutely continuous. Let U be an open subset of
$\mu $
is absolutely continuous. Let U be an open subset of
![]() $M, p$
a boundary point of U, and F a closed subset of
$M, p$
a boundary point of U, and F a closed subset of
![]() $U.$
For
$U.$
For
![]() $\alpha \in [0,1]$
, we shall say that the set
$\alpha \in [0,1]$
, we shall say that the set
![]() $F\subset U$
has
$F\subset U$
has
![]() $\mu $
-density
$\mu $
-density
![]() $\alpha $
at p relative to
$\alpha $
at p relative to
![]() $U,$
if
$U,$
if
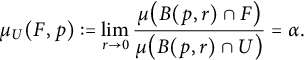 $$ \begin{align*}\mu_{U}(F,p):=\lim_{r\to 0}\frac{\mu\big( B(p,r)\cap F\big)}{\mu\big(B(p,r)\cap U\big)}=\alpha. \end{align*} $$
$$ \begin{align*}\mu_{U}(F,p):=\lim_{r\to 0}\frac{\mu\big( B(p,r)\cap F\big)}{\mu\big(B(p,r)\cap U\big)}=\alpha. \end{align*} $$
Denote by
![]() $\vartheta $
the trivial vector bundle
$\vartheta $
the trivial vector bundle
![]() $\vartheta =M\times \mathbb R ^k.$
For a (Borel) measurable subset
$\vartheta =M\times \mathbb R ^k.$
For a (Borel) measurable subset
![]() $S\subset M,$
denote by
$S\subset M,$
denote by
![]() $\mathcal M(S,\vartheta ),$
the family of measurable sections of
$\mathcal M(S,\vartheta ),$
the family of measurable sections of
![]() $\vartheta $
over
$\vartheta $
over
![]() $S.$
Thus, an element
$S.$
Thus, an element
![]() $u\in \mathcal M(S,\vartheta )$
can be identified with a k-tuple
$u\in \mathcal M(S,\vartheta )$
can be identified with a k-tuple
![]() $u=(u_1,\ldots ,u_k)$
of measurable functions
$u=(u_1,\ldots ,u_k)$
of measurable functions
![]() $u_j:S\to \mathbb R , \, j=1,\ldots ,k.$
For an open set
$u_j:S\to \mathbb R , \, j=1,\ldots ,k.$
For an open set
![]() $U\subset M,$
we denote by
$U\subset M,$
we denote by
![]() $C^\infty (U,\vartheta )$
the family of smooth sections on U endowed with the topology of uniform convergence on compact subsets of all derivatives. For
$C^\infty (U,\vartheta )$
the family of smooth sections on U endowed with the topology of uniform convergence on compact subsets of all derivatives. For
![]() $u\in C^\infty (U,\vartheta )$
and
$u\in C^\infty (U,\vartheta )$
and
![]() $x\in U,$
we denote
$x\in U,$
we denote
![]() $|u(x)|=\max \{|u_1(x)|,\ldots ,|u_k(x)|\}.$
Let
$|u(x)|=\max \{|u_1(x)|,\ldots ,|u_k(x)|\}.$
Let
![]() $P:\vartheta \to \eta $
be an elliptic operator on M with analytic coefficients, where
$P:\vartheta \to \eta $
be an elliptic operator on M with analytic coefficients, where
![]() $\eta $
is a real analytic vector bundle on M of the same rank
$\eta $
is a real analytic vector bundle on M of the same rank
![]() $k.$
$k.$
If
![]() $M=\mathbb R ^n$
and
$M=\mathbb R ^n$
and
where the
![]() $a_\alpha $
are analytic maps into the space of
$a_\alpha $
are analytic maps into the space of
![]() $s\times r$
matrices, then P is a linear differential operator on
$s\times r$
matrices, then P is a linear differential operator on
![]() $\mathbb R ^r.$
It maps an r-tuple
$\mathbb R ^r.$
It maps an r-tuple
![]() $u=(u_1,\ldots ,u_r)$
of functions on
$u=(u_1,\ldots ,u_r)$
of functions on
![]() $\mathbb R ^n$
to an s-tuple
$\mathbb R ^n$
to an s-tuple
![]() $Pu=v=(v_1,\ldots ,v_s)$
of functions on
$Pu=v=(v_1,\ldots ,v_s)$
of functions on
![]() $\mathbb R ^n.$
The operator P is of order
$\mathbb R ^n.$
The operator P is of order
![]() $m,$
if not all of the coefficients
$m,$
if not all of the coefficients
![]() $a_\alpha , |\alpha |=m$
vanish. The symbol of P is the expression
$a_\alpha , |\alpha |=m$
vanish. The symbol of P is the expression
Because the
![]() $a_\alpha (x)$
are
$a_\alpha (x)$
are
![]() $s\times r$
matrices and the
$s\times r$
matrices and the
![]() $\xi ^\alpha $
are scalars,
$\xi ^\alpha $
are scalars,
The operator P is elliptic, if for every
![]() $x\in \mathbb R ^n$
and every
$x\in \mathbb R ^n$
and every
![]() $\xi \in \mathbb R ^n\backslash \{0\}, \sigma _P(x,\xi )$
is injective as an element of
$\xi \in \mathbb R ^n\backslash \{0\}, \sigma _P(x,\xi )$
is injective as an element of
![]() $Hom(\mathbb R ^r,\mathbb R ^s),$
that is, if the matrix
$Hom(\mathbb R ^r,\mathbb R ^s),$
that is, if the matrix
![]() $\sigma _P(x,\xi )$
always has rank
$\sigma _P(x,\xi )$
always has rank
![]() $r.$
If
$r.$
If
![]() $a_0\equiv 0,$
then P annihilates constants. Such elliptic operators on
$a_0\equiv 0,$
then P annihilates constants. Such elliptic operators on
![]() $\mathbb R ^n$
with analytic coefficients and which annihilate constants are concrete examples of operators satisfying the hypotheses of the following theorem.
$\mathbb R ^n$
with analytic coefficients and which annihilate constants are concrete examples of operators satisfying the hypotheses of the following theorem.
Theorem 1.2 Let
![]() $M, d, \mu , \vartheta , \eta , P$
be as above, and suppose that P annihilates constants. Let
$M, d, \mu , \vartheta , \eta , P$
be as above, and suppose that P annihilates constants. Let
![]() $U\subset M$
be an arbitrary open subset and
$U\subset M$
be an arbitrary open subset and
![]() $\varphi \in \mathcal M(\partial U,\vartheta )$
an arbitrary Borel measurable section on the boundary
$\varphi \in \mathcal M(\partial U,\vartheta )$
an arbitrary Borel measurable section on the boundary
![]() $\partial U,$
whose restriction to some closed subset
$\partial U,$
whose restriction to some closed subset
![]() $S\subset \partial U$
is continuous. Then, for an arbitrary regular
$S\subset \partial U$
is continuous. Then, for an arbitrary regular
![]() $\sigma $
-finite Borel measure
$\sigma $
-finite Borel measure
![]() $\nu $
on
$\nu $
on
![]() $\partial U,$
there exists
$\partial U,$
there exists
![]() $ \widetilde \varphi \in C^\infty (U,\vartheta )$
with
$ \widetilde \varphi \in C^\infty (U,\vartheta )$
with
![]() $P \widetilde \varphi =0,$
such that, for
$P \widetilde \varphi =0,$
such that, for
![]() $\nu $
-almost every
$\nu $
-almost every
![]() $p\in \partial U$
, and for every
$p\in \partial U$
, and for every
![]() $p\in S, \widetilde \varphi (x)\to \varphi (p)$
, as
$p\in S, \widetilde \varphi (x)\to \varphi (p)$
, as
![]() $x\to p$
outside a set of
$x\to p$
outside a set of
![]() $\mu $
-density 0 at p relative to
$\mu $
-density 0 at p relative to
![]() $U.$
$U.$
Consider the two extremal situations, where S is empty and S is the entire boundary
![]() $\partial U$
, respectively. If
$\partial U$
, respectively. If
![]() $S=\emptyset ,$
then Theorem 1.2 solves an asymptotic measurable first boundary value problem. If
$S=\emptyset ,$
then Theorem 1.2 solves an asymptotic measurable first boundary value problem. If
![]() $S=\partial U,$
then Theorem 1.2 solves an asymptotic continuous first boundary value problem. The following two corollaries simply state that Theorem 1.2 applies, in particular, for harmonic functions of several variables and to holomorphic functions of a single complex variable.
$S=\partial U,$
then Theorem 1.2 solves an asymptotic continuous first boundary value problem. The following two corollaries simply state that Theorem 1.2 applies, in particular, for harmonic functions of several variables and to holomorphic functions of a single complex variable.
Corollary 1.3 Let M be a Riemannian manifold, and let
![]() $\mu $
be the associated volume measure on
$\mu $
be the associated volume measure on
![]() $M.$
Let
$M.$
Let
![]() $U\subset M$
be an arbitrary open subset and
$U\subset M$
be an arbitrary open subset and
![]() $\varphi $
an arbitrary Borel measurable function
$\varphi $
an arbitrary Borel measurable function
![]() $\varphi $
on the boundary
$\varphi $
on the boundary
![]() $\partial U,$
whose restriction to some closed subset
$\partial U,$
whose restriction to some closed subset
![]() $S\subset \partial U$
is continuous. Then, for an arbitrary regular
$S\subset \partial U$
is continuous. Then, for an arbitrary regular
![]() $\sigma $
-finite Borel measure
$\sigma $
-finite Borel measure
![]() $\nu $
on
$\nu $
on
![]() $\partial U,$
there exists a harmonic function
$\partial U,$
there exists a harmonic function
![]() $\widetilde \varphi $
on
$\widetilde \varphi $
on
![]() $U,$
such that, for
$U,$
such that, for
![]() $\nu $
-almost every
$\nu $
-almost every
![]() $p\in \partial U$
and for every
$p\in \partial U$
and for every
![]() $p\in S, \widetilde \varphi (x)\to \varphi (p)$
, as
$p\in S, \widetilde \varphi (x)\to \varphi (p)$
, as
![]() $x\to p$
outside a set of
$x\to p$
outside a set of
![]() $\mu $
-density 0 at p relative to
$\mu $
-density 0 at p relative to
![]() $U.$
$U.$
Corollary 1.4 Let M be an open Riemann surface,
![]() $\pi :M\rightarrow \mathbb C$
a holomorphic immersion, and
$\pi :M\rightarrow \mathbb C$
a holomorphic immersion, and
![]() $\mu $
the associated measure on
$\mu $
the associated measure on
![]() $M.$
Let
$M.$
Let
![]() $U\subset M$
be an arbitrary open subset and
$U\subset M$
be an arbitrary open subset and
![]() $\varphi $
an arbitrary Borel measurable function
$\varphi $
an arbitrary Borel measurable function
![]() $\varphi $
on the boundary
$\varphi $
on the boundary
![]() $\partial U,$
whose restriction to some closed subset
$\partial U,$
whose restriction to some closed subset
![]() $S\subset \partial U$
is continuous. Then, for an arbitrary regular
$S\subset \partial U$
is continuous. Then, for an arbitrary regular
![]() $\sigma $
-finite Borel measure
$\sigma $
-finite Borel measure
![]() $\nu $
on
$\nu $
on
![]() $\partial U,$
there exists a holomorphic function
$\partial U,$
there exists a holomorphic function
![]() $\widetilde \varphi $
on
$\widetilde \varphi $
on
![]() $U,$
such that, for
$U,$
such that, for
![]() $\nu $
-almost every
$\nu $
-almost every
![]() $p\in \partial U$
and for every
$p\in \partial U$
and for every
![]() $p\in S, \widetilde \varphi (x)\to \varphi (p)$
, as
$p\in S, \widetilde \varphi (x)\to \varphi (p)$
, as
![]() $x\to p$
outside a set of
$x\to p$
outside a set of
![]() $\mu $
-density 0 at p relative to
$\mu $
-density 0 at p relative to
![]() $U$
.
$U$
.
Proof Although the theorem is for real vector bundles and the
![]() $\overline \partial $
-operator on a Riemann surface is generally considered as an operator between complex vector bundles of rank 1, we may also consider it as an operator between real vector bundles of rank 2 (see [Reference Narasimhan5, Remark 3.10.10 and Theorem 3.10.11]).▪
$\overline \partial $
-operator on a Riemann surface is generally considered as an operator between complex vector bundles of rank 1, we may also consider it as an operator between real vector bundles of rank 2 (see [Reference Narasimhan5, Remark 3.10.10 and Theorem 3.10.11]).▪
Remark Riemann surfaces are complex manifolds of dimension 1. Our proof does not allow us to prove an analogue of Corollary 1.4 for holomorphic functions on higher-dimensional complex manifolds, because the proof of Theorem 1.2 is based on the Malgrange–Lax theorem [Reference Narasimhan5], which is for differential operators
![]() $P:\xi \to \eta $
between bundles of equal rank. On complex manifolds, the Cauchy–Riemann operator
$P:\xi \to \eta $
between bundles of equal rank. On complex manifolds, the Cauchy–Riemann operator
![]() $\overline \partial $
maps forms of type
$\overline \partial $
maps forms of type
![]() $(p,q)$
to forms of type
$(p,q)$
to forms of type
![]() $(p,q+1).$
Thus,
$(p,q+1).$
Thus,
![]() $\overline \partial :\mathcal E^{p,q}\to \mathcal E^{p,q+1}.$
For
$\overline \partial :\mathcal E^{p,q}\to \mathcal E^{p,q+1}.$
For
![]() $\overline \partial :\mathcal E^{p,0}\to \mathcal E^{0,1},$
it is elliptic, and, in particular, it is elliptic for the case
$\overline \partial :\mathcal E^{p,0}\to \mathcal E^{0,1},$
it is elliptic, and, in particular, it is elliptic for the case
![]() $\overline \partial :\mathcal E^{0,0}\to \mathcal E^{0,1},$
mapping functions to forms of type
$\overline \partial :\mathcal E^{0,0}\to \mathcal E^{0,1},$
mapping functions to forms of type
![]() $(0,1).$
On a complex manifold of dimension
$(0,1).$
On a complex manifold of dimension
![]() $n,$
this is a map between bundles of respective (complex) ranks
$n,$
this is a map between bundles of respective (complex) ranks
![]() $1$
and n (see [Reference Narasimhan5, Remark 3.10.10]). Thus, in order to have an operator between bundles of equal rank, we must restrict our attention to complex manifolds of dimension
$1$
and n (see [Reference Narasimhan5, Remark 3.10.10]). Thus, in order to have an operator between bundles of equal rank, we must restrict our attention to complex manifolds of dimension
![]() $1,$
that is, Riemann surfaces.
$1,$
that is, Riemann surfaces.
When
![]() $S=\partial U,$
Corollaries 1.3 and 1.4 were proved in [Reference Falcó and Gauthier2] and [Reference Falcó and Gauthier1], respectively. When
$S=\partial U,$
Corollaries 1.3 and 1.4 were proved in [Reference Falcó and Gauthier2] and [Reference Falcó and Gauthier1], respectively. When
![]() $M=\mathbb C , \, U=\mathbb D $
, and
$M=\mathbb C , \, U=\mathbb D $
, and
![]() $S=\emptyset ,$
Corollary 1.4 gives Theorem 1.1.
$S=\emptyset ,$
Corollary 1.4 gives Theorem 1.1.
2 Runge–Carleman approximation
A closed subset E of M is said to satisfy the open
![]() $K-Q$
-condition if, for every compact
$K-Q$
-condition if, for every compact
![]() $K\subset M$
, there is a compact
$K\subset M$
, there is a compact
![]() $Q\subset M$
such that
$Q\subset M$
such that
![]() $K\subset Q^\circ $
and
$K\subset Q^\circ $
and
![]() $E\cap Q$
is contained in
$E\cap Q$
is contained in
![]() $Q^\circ $
.
$Q^\circ $
.
An exhaustion
![]() $(K_j)_{j=1}^\infty $
of M is said to be regular if, for each n, the sets
$(K_j)_{j=1}^\infty $
of M is said to be regular if, for each n, the sets
![]() $K_{n}$
are compact,
$K_{n}$
are compact,
![]() $ K_{n}\subset K_{n+1}^\circ , M^*\backslash K_n$
is connected, and
$ K_{n}\subset K_{n+1}^\circ , M^*\backslash K_n$
is connected, and
![]() $M=\cup _{n=1}^{\infty } K_{n}^\circ $
. We say that an exhaustion
$M=\cup _{n=1}^{\infty } K_{n}^\circ $
. We say that an exhaustion
![]() $(K_j)_{j=1}^\infty $
of M is open compatible with a closed subset E of M if, for every
$(K_j)_{j=1}^\infty $
of M is open compatible with a closed subset E of M if, for every
![]() $j=1,2,\ldots , E\cap K_j$
is contained in
$j=1,2,\ldots , E\cap K_j$
is contained in
![]() $K_j^\circ .$
$K_j^\circ .$
Lemma 2.1 Let E be a closed subset of
![]() $M,$
satisfying the open
$M,$
satisfying the open
![]() $K-Q$
-condition, then there exists a regular exhaustion of M which is open compatible with
$K-Q$
-condition, then there exists a regular exhaustion of M which is open compatible with
![]() $E.$
$E.$
Proof Let
![]() $(K_j)_{j=1}^\infty $
be a regular exhaustion of M. We shall define recursively an exhaustion
$(K_j)_{j=1}^\infty $
be a regular exhaustion of M. We shall define recursively an exhaustion
![]() $(Q_{n})_{n=1}^{\infty }$
of M with certain properties. From the
$(Q_{n})_{n=1}^{\infty }$
of M with certain properties. From the
![]() $K-Q$
condition, we choose a compact set
$K-Q$
condition, we choose a compact set
![]() $Q_1,$
such that
$Q_1,$
such that
![]() $K_1\subset Q_1^\circ $
and
$K_1\subset Q_1^\circ $
and
![]() $E\cap Q_1\subset Q_1^\circ .$
Now, we may choose a compact set
$E\cap Q_1\subset Q_1^\circ .$
Now, we may choose a compact set
![]() $Q_2,$
such that
$Q_2,$
such that
![]() $K_1\cup Q_1\subset Q_2^\circ $
and
$K_1\cup Q_1\subset Q_2^\circ $
and
![]() $E\cap Q_2\subset Q_2^\circ .$
Suppose we have selected compact sets
$E\cap Q_2\subset Q_2^\circ .$
Suppose we have selected compact sets
![]() $Q_1,\ldots ,Q_{n},$
such that
$Q_1,\ldots ,Q_{n},$
such that
![]() $K_j\cup Q_j\subset Q_{j+1}^\circ $
and
$K_j\cup Q_j\subset Q_{j+1}^\circ $
and
![]() $E\cap Q_{j+1}\subset Q_{j+1}^\circ ,$
for
$E\cap Q_{j+1}\subset Q_{j+1}^\circ ,$
for
![]() $j=1,\ldots ,n-1.$
We may choose a compact set
$j=1,\ldots ,n-1.$
We may choose a compact set
![]() $Q_{n+1},$
such that
$Q_{n+1},$
such that
![]() $K_n\cup Q_n\subset Q_{n+1}^\circ $
and
$K_n\cup Q_n\subset Q_{n+1}^\circ $
and
![]() $E\cap Q_{n+1}\subset Q_{n+1}^\circ .$
Thus, we have inductively constructed an exhaustion
$E\cap Q_{n+1}\subset Q_{n+1}^\circ .$
Thus, we have inductively constructed an exhaustion
![]() $(Q_n)_{n=1}^\infty $
such that, for each
$(Q_n)_{n=1}^\infty $
such that, for each
![]() $n, K_n\cup Q_n\subset Q_{n+1}^\circ $
and
$n, K_n\cup Q_n\subset Q_{n+1}^\circ $
and
![]() $E\cap Q_n\subset Q_n^\circ .$
We denote by
$E\cap Q_n\subset Q_n^\circ .$
We denote by
![]() $Q_{n,*}^c$
the connected component of
$Q_{n,*}^c$
the connected component of
![]() $M^*\backslash Q_n$
that contains the point
$M^*\backslash Q_n$
that contains the point
![]() $*$
and put
$*$
and put
![]() $ L_n=M\backslash Q_{n,*}^c$
. Then,
$ L_n=M\backslash Q_{n,*}^c$
. Then,
![]() $(L_{n})_{n=1}^{\infty }$
is a regular exhaustion of M (see [Reference Narasimhan5, p. 224]). Furthermore, for each
$(L_{n})_{n=1}^{\infty }$
is a regular exhaustion of M (see [Reference Narasimhan5, p. 224]). Furthermore, for each
![]() $n, E\cap \partial Q_n=\emptyset ,$
so
$n, E\cap \partial Q_n=\emptyset ,$
so
![]() $E\cap L_n\subset L_n^\circ $
. Thus, the exhaustion
$E\cap L_n\subset L_n^\circ $
. Thus, the exhaustion
![]() $(L_n)_{n=1}^\infty $
is open compatible with
$(L_n)_{n=1}^\infty $
is open compatible with
![]() $E$
.▪
$E$
.▪
A closed set
![]() $E\subset M$
is said to be a set of Runge–Carleman approximation for an operator
$E\subset M$
is said to be a set of Runge–Carleman approximation for an operator
![]() $P,$
if for every open neighborhood U of
$P,$
if for every open neighborhood U of
![]() $E,$
every section
$E,$
every section
![]() $f\in C^\infty (U,\mathcal \vartheta ),$
with
$f\in C^\infty (U,\mathcal \vartheta ),$
with
![]() $Pf=0,$
and every positive continuous function
$Pf=0,$
and every positive continuous function
![]() $\varepsilon $
on
$\varepsilon $
on
![]() $E,$
there is a global section
$E,$
there is a global section
![]() $u\in C^\infty (M,\mathcal \vartheta ),$
with
$u\in C^\infty (M,\mathcal \vartheta ),$
with
![]() $Pu=0,$
such that
$Pu=0,$
such that
![]() $|u-f|<\varepsilon $
on
$|u-f|<\varepsilon $
on
![]() $E.$
$E.$
Theorem 2.2 Let P be an elliptic operator on M with analytic coefficients. Let E be a closed subset of M satisfying the open
![]() $K-Q$
condition, with
$K-Q$
condition, with
![]() $M^*\backslash E$
connected. Then, E is a set of Runge–Carleman approximation for the operator
$M^*\backslash E$
connected. Then, E is a set of Runge–Carleman approximation for the operator
![]() $P.$
$P.$
Proof By Lemma 2.1, let
![]() $(L_{n})_{n=1}^{\infty }$
be a regular exhaustion of M which is open compatible with E and set
$(L_{n})_{n=1}^{\infty }$
be a regular exhaustion of M which is open compatible with E and set
![]() $L_0=\emptyset $
. Fix an open neighborhood U of
$L_0=\emptyset $
. Fix an open neighborhood U of
![]() $E,$
and a section
$E,$
and a section
![]() $f\in C^\infty (U,\mathcal \vartheta ),$
with
$f\in C^\infty (U,\mathcal \vartheta ),$
with
![]() $Pf=0$
. Consider
$Pf=0$
. Consider
![]() $\varepsilon $
a continuous and positive function on
$\varepsilon $
a continuous and positive function on
![]() $E,$
which we may assume is continuous and positive on all of M, and set
$E,$
which we may assume is continuous and positive on all of M, and set
Now, we construct recursively a sequence
![]() $(u_n)_{n=0}^\infty $
of sections
$(u_n)_{n=0}^\infty $
of sections
![]() $u_{n}\in C^\infty (M,\vartheta )$
such that
$u_{n}\in C^\infty (M,\vartheta )$
such that
![]() $|u_{n}-u_{n-1}|<\varepsilon _{n}/2^{n}$
on
$|u_{n}-u_{n-1}|<\varepsilon _{n}/2^{n}$
on
![]() $ L_{n-1}$
and
$ L_{n-1}$
and
![]() $|u_{n}-f|<\varepsilon _{n}/2^{n}$
on
$|u_{n}-f|<\varepsilon _{n}/2^{n}$
on
![]() $E\cap (L_{n}\backslash L_{n-1})$
. Consider
$E\cap (L_{n}\backslash L_{n-1})$
. Consider
![]() $u_0=0$
. For
$u_0=0$
. For
![]() $n=1$
, we only need to check the second condition on
$n=1$
, we only need to check the second condition on
![]() $u_1$
, because the first condition is void. Note that
$u_1$
, because the first condition is void. Note that
![]() $U_1=L_1^\circ \cap U$
is an open set containing
$U_1=L_1^\circ \cap U$
is an open set containing
![]() $E\cap L_1$
such that
$E\cap L_1$
such that
![]() $M\backslash U_1$
has no compact connected components and
$M\backslash U_1$
has no compact connected components and
![]() $Pf=0$
on
$Pf=0$
on
![]() $U_1$
. By the Malgrange–Lax theorem (see [Reference Narasimhan5]), there exists a section
$U_1$
. By the Malgrange–Lax theorem (see [Reference Narasimhan5]), there exists a section
![]() $u_{1}\in C^\infty (M,\vartheta )$
with
$u_{1}\in C^\infty (M,\vartheta )$
with
![]() $Pu_{1}=0,$
such that
$Pu_{1}=0,$
such that
![]() $|u_1-f|<\varepsilon _{1}/2$
on
$|u_1-f|<\varepsilon _{1}/2$
on
![]() $E\cap L_{1}.$
$E\cap L_{1}.$
Assume now that we have fixed
![]() $(u_{n})_{n=1}^{N-1}$
satisfying the required conditions. Consider two open sets
$(u_{n})_{n=1}^{N-1}$
satisfying the required conditions. Consider two open sets
![]() $V_N, W_N$
such that
$V_N, W_N$
such that
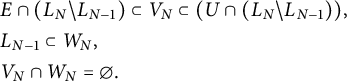 $$ \begin{align*} &E\cap (L_N\backslash L_{N-1})\subset V_N\subset (U\cap (L_N\backslash L_{N-1})),&\\ &L_{N-1}\subset W_N,&\\ &V_N\cap W_N=\emptyset.& \end{align*} $$
$$ \begin{align*} &E\cap (L_N\backslash L_{N-1})\subset V_N\subset (U\cap (L_N\backslash L_{N-1})),&\\ &L_{N-1}\subset W_N,&\\ &V_N\cap W_N=\emptyset.& \end{align*} $$
Because
![]() $M^*\backslash E$
is connected and
$M^*\backslash E$
is connected and
![]() $(L_n)_{n=1}^\infty $
is a regular exhaustion, without loss of generality, we can assume that
$(L_n)_{n=1}^\infty $
is a regular exhaustion, without loss of generality, we can assume that
![]() $M\backslash (V_N\cup W_N)$
has no compact connected components.
$M\backslash (V_N\cup W_N)$
has no compact connected components.
Define
![]() $g\in C^\infty (G,\vartheta ),$
by putting
$g\in C^\infty (G,\vartheta ),$
by putting
![]() $g=u_{N-1}$
on
$g=u_{N-1}$
on
![]() $ W_{N}$
and
$ W_{N}$
and
![]() $g=f$
on
$g=f$
on
![]() $V_{N}$
. Set
$V_{N}$
. Set
and
![]() $U_N=(V_N\cup W_n)\cap U$
. Then,
$U_N=(V_N\cup W_n)\cap U$
. Then,
![]() $Pg=0$
on
$Pg=0$
on
![]() $U_N$
and
$U_N$
and
![]() $M\backslash U_N$
has no compact connected components. By the Malgrange–Lax theorem again, there exists a section
$M\backslash U_N$
has no compact connected components. By the Malgrange–Lax theorem again, there exists a section
![]() $u_{N}\in C^\infty (M,\vartheta )$
with
$u_{N}\in C^\infty (M,\vartheta )$
with
![]() $Pu_{N}=0,$
such that
$Pu_{N}=0,$
such that
The section
![]() $u_N$
has the required properties, which completes the inductive construction of the sequence
$u_N$
has the required properties, which completes the inductive construction of the sequence
![]() $(u_n)_{n=0}^\infty .$
$(u_n)_{n=0}^\infty .$
For every
![]() $x\in M,$
the sequence
$x\in M,$
the sequence
![]() $\{u_n(x)\}_{n=0}^\infty $
is Cauchy, and hence u converges pointwise to a section
$\{u_n(x)\}_{n=0}^\infty $
is Cauchy, and hence u converges pointwise to a section
![]() $\vartheta .$
Let
$\vartheta .$
Let
![]() $u(x)=\lim _{n\to \infty }u_{n}(x)$
for every
$u(x)=\lim _{n\to \infty }u_{n}(x)$
for every
![]() $x\in M$
. Because, for every natural number
$x\in M$
. Because, for every natural number
![]() $j,$
the sequence
$j,$
the sequence
![]() $(u_{n})_{n=j}^{\infty }$
converges to u in
$(u_{n})_{n=j}^{\infty }$
converges to u in
![]() $C^\infty (L_j^\circ ,\vartheta )$
and
$C^\infty (L_j^\circ ,\vartheta )$
and
![]() $Pu_{n}=0$
on
$Pu_{n}=0$
on
![]() $M,$
we have that
$M,$
we have that
![]() $u\in C^\infty (L_j^\circ ,\vartheta )$
and also
$u\in C^\infty (L_j^\circ ,\vartheta )$
and also
![]() $Pu=0$
on
$Pu=0$
on
![]() $L_j^\circ .$
Because this holds for every
$L_j^\circ .$
Because this holds for every
![]() $j=1,2,\ldots ,$
we have that
$j=1,2,\ldots ,$
we have that
![]() $u\in C^\infty (M,\vartheta )$
and
$u\in C^\infty (M,\vartheta )$
and
![]() $Pu=0.$
$Pu=0.$
To finish, we show that
![]() $|u(x)-f(x)|\le \varepsilon (x)$
on E. Fix
$|u(x)-f(x)|\le \varepsilon (x)$
on E. Fix
![]() $x\in E.$
Then, there exists a unique natural number
$x\in E.$
Then, there exists a unique natural number
![]() $n=n(x),$
such that
$n=n(x),$
such that
![]() $x\in L_n\backslash L_{n-1}.$
We have
$x\in L_n\backslash L_{n-1}.$
We have
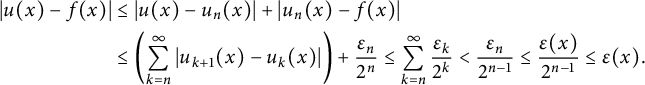 $$ \begin{align*} |u(x)-f(x)|&\le |u(x)-u_n(x)|+|u_n(x)-f(x)|\\ &\le \left( \sum_{k=n}^\infty|u_{k+1}(x)-u_k(x)|\right)+\frac{\varepsilon_n}{2^n} \le \sum_{k=n}^\infty\frac{\varepsilon_k}{2^k} < \frac{\epsilon_n}{2^{n-1}} \le \frac{\varepsilon(x)}{2^{n-1}}\le \varepsilon(x). \end{align*} $$
$$ \begin{align*} |u(x)-f(x)|&\le |u(x)-u_n(x)|+|u_n(x)-f(x)|\\ &\le \left( \sum_{k=n}^\infty|u_{k+1}(x)-u_k(x)|\right)+\frac{\varepsilon_n}{2^n} \le \sum_{k=n}^\infty\frac{\varepsilon_k}{2^k} < \frac{\epsilon_n}{2^{n-1}} \le \frac{\varepsilon(x)}{2^{n-1}}\le \varepsilon(x). \end{align*} $$
▪
Corollary 2.3 Let E be a subset of M that is a union of a locally finite family of disjoint continua, and suppose that
![]() $M^*\backslash E$
is connected. Then, E is a set of Runge–Carleman approximation.
$M^*\backslash E$
is connected. Then, E is a set of Runge–Carleman approximation.
Proof Notice that E is closed, because it is the union of a locally finite family of closed sets. We only need to show that E satisfies the open
![]() $K-Q$
condition. For this, fix a compact set K in M. We denote the connected components of E by
$K-Q$
condition. For this, fix a compact set K in M. We denote the connected components of E by
![]() $E_j$
, and we may assume that they are ordered, so that
$E_j$
, and we may assume that they are ordered, so that
![]() $E_1, \ldots , E_m$
are the connected components that meet
$E_1, \ldots , E_m$
are the connected components that meet
![]() $K.$
Set
$K.$
Set
![]() $L = K\cup E_1\cup \cdots \cup E_m$
, and let Q be a compact neighborhood of L disjoint from the closed set
$L = K\cup E_1\cup \cdots \cup E_m$
, and let Q be a compact neighborhood of L disjoint from the closed set
![]() $E_{m+1}\cup E_{m+2}\cup \cdots .$
Then, Q satisfies the required conditions.▪
$E_{m+1}\cup E_{m+2}\cup \cdots .$
Then, Q satisfies the required conditions.▪
3 Proof of Theorem 1.2
Lemma 3.1 Let U be a proper open subset of a manifold M and Q and K be disjoint compact subsets of
![]() $\partial U.$
Then, for each
$\partial U.$
Then, for each
![]() $\varepsilon>0,$
there exist
$\varepsilon>0,$
there exist
![]() $\delta>0$
and an open set
$\delta>0$
and an open set
![]() $V_\delta $
that is a
$V_\delta $
that is a
![]() $\delta $
-neighborhood of K in M disjoint from Q such that
$\delta $
-neighborhood of K in M disjoint from Q such that
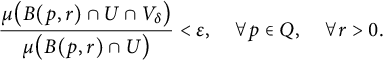 $$ \begin{align*} \frac{\mu\big(B(p,r)\cap U\cap V_\delta\big)}{\mu\big(B(p,r)\cap U\big)} < \varepsilon, \quad \forall p\in Q, \quad \forall r>0. \end{align*} $$
$$ \begin{align*} \frac{\mu\big(B(p,r)\cap U\cap V_\delta\big)}{\mu\big(B(p,r)\cap U\big)} < \varepsilon, \quad \forall p\in Q, \quad \forall r>0. \end{align*} $$
Furthermore,
![]() $\delta $
can be chosen, so that
$\delta $
can be chosen, so that
![]() $B(p,r)\cap V_\delta =\emptyset $
, for all
$B(p,r)\cap V_\delta =\emptyset $
, for all
![]() $p\in Q$
and
$p\in Q$
and
![]() $r<\delta $
.
$r<\delta $
.
Proof Set
![]() $r_0=d(Q,K)/2>0$
. We claim that
$r_0=d(Q,K)/2>0$
. We claim that
Assume that this was not the case and we have that
![]() $\rho =0$
. Then, by the compactness of Q, we could find a sequence of points
$\rho =0$
. Then, by the compactness of Q, we could find a sequence of points
![]() $(p_n)_{n=1}^\infty \subset Q$
convergent to a point
$(p_n)_{n=1}^\infty \subset Q$
convergent to a point
![]() $p_0\in Q$
, so that
$p_0\in Q$
, so that
![]() $\mu \big (B(p_n,r_0)\cap U\big )<1/n$
and
$\mu \big (B(p_n,r_0)\cap U\big )<1/n$
and
![]() $d(p_n,p_0)<r_0/2$
. But then, we would have that
$d(p_n,p_0)<r_0/2$
. But then, we would have that
![]() $\mu \big (B(p_0,r_0/2)\cap U\big )\leq \mu \big (B(p_n,r_0)\cap U\big )<1/n$
for every natural number n. Hence,
$\mu \big (B(p_0,r_0/2)\cap U\big )\leq \mu \big (B(p_n,r_0)\cap U\big )<1/n$
for every natural number n. Hence,
![]() $\mu \big (B(p_0,r_0/2)\cap U\big )=0$
, contradicting the fact that
$\mu \big (B(p_0,r_0/2)\cap U\big )=0$
, contradicting the fact that
![]() $\mu $
has positive measure on open sets. Thus, equation (3.1) holds.
$\mu $
has positive measure on open sets. Thus, equation (3.1) holds.
Consider
![]() $V_\delta $
a
$V_\delta $
a
![]() $\delta $
-neighborhood of K in M with
$\delta $
-neighborhood of K in M with
![]() $\delta <r_0$
and
$\delta <r_0$
and
![]() $\mu (U\cap V_\delta )<\varepsilon \rho $
. It is clear that, for such
$\mu (U\cap V_\delta )<\varepsilon \rho $
. It is clear that, for such
![]() $\delta $
, we have that
$\delta $
, we have that
![]() $V_\delta $
and Q are disjoint and
$V_\delta $
and Q are disjoint and
![]() $B(p,r)\cap V_\delta =\emptyset ,$
for all
$B(p,r)\cap V_\delta =\emptyset ,$
for all
![]() $p\in Q$
and all
$p\in Q$
and all
![]() $r<r_0.$
Thus, the last statement of the lemma is obvious by choosing
$r<r_0.$
Thus, the last statement of the lemma is obvious by choosing
![]() $\delta =r_0$
. Furthermore, for any
$\delta =r_0$
. Furthermore, for any
![]() $r\geq r_0$
, we have that
$r\geq r_0$
, we have that
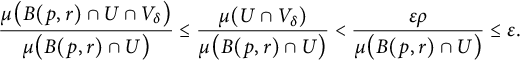 $$ \begin{align*} \hspace{3.2pc}\frac{\mu\big(B(p,r)\cap U\cap V_\delta\big)}{\mu\big(B(p,r)\cap U\big)}\leq \frac{\mu(U\cap V_\delta)}{\mu\big(B(p,r)\cap U\big)} < \frac{\varepsilon\rho}{\mu\big(B(p,r)\cap U\big)}\leq \varepsilon.\hspace{3.2pc} \end{align*} $$
$$ \begin{align*} \hspace{3.2pc}\frac{\mu\big(B(p,r)\cap U\cap V_\delta\big)}{\mu\big(B(p,r)\cap U\big)}\leq \frac{\mu(U\cap V_\delta)}{\mu\big(B(p,r)\cap U\big)} < \frac{\varepsilon\rho}{\mu\big(B(p,r)\cap U\big)}\leq \varepsilon.\hspace{3.2pc} \end{align*} $$
The following lemma was stated in [Reference Falcó and Gauthier2, Lemma 4] for volume measure on a Riemannian manifold, but the same proof yields the following more general version.
Lemma 3.2 Let U be a proper open subset of a manifold M and C a connected compact subset of U with
![]() $\mu (C)=0.$
Then, for each
$\mu (C)=0.$
Then, for each
![]() $\epsilon>0$
, there is a connected open neighborhood R of C in U such that
$\epsilon>0$
, there is a connected open neighborhood R of C in U such that
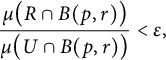 $$ \begin{align*} \frac{\mu\big(R\cap B(p,r)\big)}{\mu\big(U\cap B(p,r)\big)} < \epsilon, \end{align*} $$
$$ \begin{align*} \frac{\mu\big(R\cap B(p,r)\big)}{\mu\big(U\cap B(p,r)\big)} < \epsilon, \end{align*} $$
for every
![]() $p\in \partial U$
and every
$p\in \partial U$
and every
![]() $r>0.$
$r>0.$
We recall that an open subset W of a real manifold M is an open parametric ball if there is a chart
![]() $\varphi :W\to \mathbb B ,$
where
$\varphi :W\to \mathbb B ,$
where
![]() $\mathbb B $
is an open ball in the euclidean space and
$\mathbb B $
is an open ball in the euclidean space and
![]() $\varphi (W)=\mathbb B $
. A subset
$\varphi (W)=\mathbb B $
. A subset
![]() $H\subset M$
is a closed parametric ball if there is a parametric ball
$H\subset M$
is a closed parametric ball if there is a parametric ball
![]() $\varphi :W\to \mathbb B $
and a closed ball
$\varphi :W\to \mathbb B $
and a closed ball
![]() $\overline B\subset \mathbb B ,$
such that
$\overline B\subset \mathbb B ,$
such that
![]() $H=\varphi ^{-1}(\overline B).$
$H=\varphi ^{-1}(\overline B).$
Lemma 3.3 Under the hypotheses of Theorem 1.2, there exists a set
![]() $F,$
with
$F,$
with
![]() $S\subset F\subset \partial U$
and
$S\subset F\subset \partial U$
and
![]() $\nu (\partial U\backslash F)=0,$
and
$\nu (\partial U\backslash F)=0,$
and
![]() $u\in C(U,\xi )$
on
$u\in C(U,\xi )$
on
![]() $U,$
such that, for every
$U,$
such that, for every
![]() $p\in F$
,
$p\in F$
,
![]() $u(x)\to \varphi (p)$
, as
$u(x)\to \varphi (p)$
, as
![]() $x\to p$
outside a set of
$x\to p$
outside a set of
![]() $\mu $
-density 0 at p relative to
$\mu $
-density 0 at p relative to
![]() $U.$
$U.$
Proof In the following proof, we use the symbol
![]() $\dot \cup $
to denote the disjoint union. We start by showing that there exists a subset
$\dot \cup $
to denote the disjoint union. We start by showing that there exists a subset
![]() $F\subset \partial U$
containing S of the form
$F\subset \partial U$
containing S of the form
with
![]() $Q_n$
compact, so that the restriction of
$Q_n$
compact, so that the restriction of
![]() $\varphi $
is continuous on
$\varphi $
is continuous on
![]() $Q_n$
and
$Q_n$
and
![]() $\nu (\partial U\backslash F)=0$
.
$\nu (\partial U\backslash F)=0$
.
First, we assume that
![]() $\nu (\partial U\backslash S)<+\infty $
. By Lusin’s theorem (see [Reference Halmos3] and [Reference Wage8, Theorem 2]), there exists a compact set
$\nu (\partial U\backslash S)<+\infty $
. By Lusin’s theorem (see [Reference Halmos3] and [Reference Wage8, Theorem 2]), there exists a compact set
![]() $Q_1$
in
$Q_1$
in
![]() $\partial U\backslash S$
such that
$\partial U\backslash S$
such that
![]() $\nu \left ((\partial U\backslash S)\backslash Q_1\right )<2^{-1}$
and the restriction of
$\nu \left ((\partial U\backslash S)\backslash Q_1\right )<2^{-1}$
and the restriction of
![]() $\varphi $
to
$\varphi $
to
![]() $Q_1$
is continuous. Now, again by Lusin’s theorem, we can find a compact set
$Q_1$
is continuous. Now, again by Lusin’s theorem, we can find a compact set
![]() $Q_2$
in
$Q_2$
in
![]() $(\partial U\backslash S)\backslash Q_1$
with
$(\partial U\backslash S)\backslash Q_1$
with
![]() $\nu (\big ((\partial U\backslash S)\backslash Q_1)\backslash Q_2\big )<2^{-2}$
, so that the restriction of
$\nu (\big ((\partial U\backslash S)\backslash Q_1)\backslash Q_2\big )<2^{-2}$
, so that the restriction of
![]() $\varphi $
to
$\varphi $
to
![]() $Q_1\dot \cup Q_2$
is continuous. By induction, we can construct a sequence of compact sets
$Q_1\dot \cup Q_2$
is continuous. By induction, we can construct a sequence of compact sets
![]() $(Q_n)_{n=1}^\infty $
, so that
$(Q_n)_{n=1}^\infty $
, so that
![]() $Q_{n}\subset (\partial U\backslash S)\backslash \cup _{j=1}^{n-1} Q_j$
,
$Q_{n}\subset (\partial U\backslash S)\backslash \cup _{j=1}^{n-1} Q_j$
,
![]() $\nu ((\partial U\backslash S)\backslash \cup _{j=1}^{n} Q_j)<2^{-n}$
, and the restriction of
$\nu ((\partial U\backslash S)\backslash \cup _{j=1}^{n} Q_j)<2^{-n}$
, and the restriction of
![]() $\varphi $
to
$\varphi $
to
![]() $Q_1\dot \cup \cdots \dot \cup Q_n$
is continuous for
$Q_1\dot \cup \cdots \dot \cup Q_n$
is continuous for
![]() $n=1,2,3,\ldots $
. We set
$n=1,2,3,\ldots $
. We set
It is obvious that
![]() $(Q_n)_{n=1}^\infty $
is a family of pairwise disjoint compact sets and
$(Q_n)_{n=1}^\infty $
is a family of pairwise disjoint compact sets and
![]() $\nu (\partial U\backslash F)=0$
.
$\nu (\partial U\backslash F)=0$
.
If
![]() $\nu (\partial U\backslash S)$
is not finite, by the
$\nu (\partial U\backslash S)$
is not finite, by the
![]() $\sigma $
-finiteness of the measure
$\sigma $
-finiteness of the measure
![]() $\nu $
, there exists a pairwise disjoint sequence of measurable sets
$\nu $
, there exists a pairwise disjoint sequence of measurable sets
![]() $(R_l)_{l=1}^\infty $
with
$(R_l)_{l=1}^\infty $
with
![]() $\nu (R_l)<+\infty $
and
$\nu (R_l)<+\infty $
and
![]() $\partial U\backslash S=\dot {\bigcup }_{l=1}^\infty R_l$
. By the previous argument applied to the section
$\partial U\backslash S=\dot {\bigcup }_{l=1}^\infty R_l$
. By the previous argument applied to the section
![]() $\varphi $
restricted to the set
$\varphi $
restricted to the set
![]() $R_l$
, we can find a pairwise disjoint sequence of compact sets
$R_l$
, we can find a pairwise disjoint sequence of compact sets
![]() $(Q_{n,l})_{n=1}^\infty $
of
$(Q_{n,l})_{n=1}^\infty $
of
![]() $R_l,$
so that the restriction of
$R_l,$
so that the restriction of
![]() $\varphi $
is continuous on
$\varphi $
is continuous on
![]() $Q_{n,l}$
and
$Q_{n,l}$
and
![]() $\nu (R_l\backslash \dot \cup _{n=1}^\infty Q_{n,l})=0.$
Then,
$\nu (R_l\backslash \dot \cup _{n=1}^\infty Q_{n,l})=0.$
Then,
satisfies the desired result.
We now begin to extend the section
![]() $\varphi $
. For this, we shall construct inductively a sequence of increasing sets
$\varphi $
. For this, we shall construct inductively a sequence of increasing sets
![]() $(E_n)_{n=1}^\infty $
and a sequence of sections
$(E_n)_{n=1}^\infty $
and a sequence of sections
![]() $(f_n)_{n=1}^\infty $
. We can write
$(f_n)_{n=1}^\infty $
. We can write
![]() $S=\cup _{n=1}^\infty S_n$
and
$S=\cup _{n=1}^\infty S_n$
and
![]() $F=S\dot \cup \left (\dot \cup _{n=1}^\infty Q_n\right )$
, with
$F=S\dot \cup \left (\dot \cup _{n=1}^\infty Q_n\right )$
, with
![]() $S_n$
and
$S_n$
and
![]() $Q_n$
compact,
$Q_n$
compact,
![]() $S_n$
increasing, and
$S_n$
increasing, and
![]() $Q_n$
pairwise disjoint, so that the restriction
$Q_n$
pairwise disjoint, so that the restriction
![]() $\varphi _n$
of
$\varphi _n$
of
![]() $\varphi $
to
$\varphi $
to
![]() $F_n=S\cup Q_1\dot \cup \cdots \dot \cup Q_n$
is continuous. By Lemma 3.1, for
$F_n=S\cup Q_1\dot \cup \cdots \dot \cup Q_n$
is continuous. By Lemma 3.1, for
![]() $l=2,3,\ldots ,$
there is an open
$l=2,3,\ldots ,$
there is an open
![]() $\delta _{1,l}$
-neighborhood
$\delta _{1,l}$
-neighborhood
![]() $V_{1,l}$
of
$V_{1,l}$
of
![]() $Q_l$
in M such that
$Q_l$
in M such that
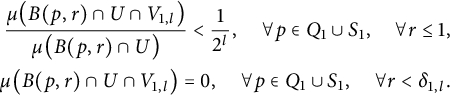 $$ \begin{align} \begin{aligned} \frac{\mu\big(B(p,r)\cap U\cap V_{1,l}\big)}{\mu\big(B(p,r)\cap U\big)} < \frac{1}{2^l}, \quad \forall p\in Q_{1}\cup S_1, \quad \forall r\le 1,\\ \mu\big(B(p,r)\cap U\cap V_{1,l}\big)=0, \quad \forall p\in Q_1 \cup S_1, \quad \forall r<\delta_{1,l}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \frac{\mu\big(B(p,r)\cap U\cap V_{1,l}\big)}{\mu\big(B(p,r)\cap U\big)} < \frac{1}{2^l}, \quad \forall p\in Q_{1}\cup S_1, \quad \forall r\le 1,\\ \mu\big(B(p,r)\cap U\cap V_{1,l}\big)=0, \quad \forall p\in Q_1 \cup S_1, \quad \forall r<\delta_{1,l}. \end{aligned} \end{align} $$
By the compactness of
![]() $Q_l$
, the sets
$Q_l$
, the sets
![]() $V_{1,l}$
can be chosen to be a finite union of open parametric balls in M. Let
$V_{1,l}$
can be chosen to be a finite union of open parametric balls in M. Let
Because
![]() $S\cup Q_1$
is closed in
$S\cup Q_1$
is closed in
![]() $E_1\cup S\cup Q_1,$
by the Tietze extension theorem, we can extend the section
$E_1\cup S\cup Q_1,$
by the Tietze extension theorem, we can extend the section
![]() $\varphi _1$
to a continuous section
$\varphi _1$
to a continuous section
![]() $f_1$
on
$f_1$
on
![]() $E_1\cup S\cup Q_1.$
$E_1\cup S\cup Q_1.$
Set
![]() $E_0=\emptyset $
, and assume that, for
$E_0=\emptyset $
, and assume that, for
![]() $j=1,\ldots ,n,$
we have fixed positive constants
$j=1,\ldots ,n,$
we have fixed positive constants
![]() $\delta _{j,l}<1/j,$
for
$\delta _{j,l}<1/j,$
for
![]() $l\ge j+1,$
sets
$l\ge j+1,$
sets
![]() $E_j=U\backslash \cup _{l=j+1}^\infty V_{j,l}$
with
$E_j=U\backslash \cup _{l=j+1}^\infty V_{j,l}$
with
![]() $V_{j,l}$
being an open
$V_{j,l}$
being an open
![]() $\delta _{j,l}$
-neighborhood of
$\delta _{j,l}$
-neighborhood of
![]() $Q_l$
in
$Q_l$
in
![]() $M\backslash E_j$
that is a finite union of open parametric balls in M, and sections
$M\backslash E_j$
that is a finite union of open parametric balls in M, and sections
![]() $f_j$
continuous on
$f_j$
continuous on
![]() $E_j\cup F_j$
such that
$E_j\cup F_j$
such that
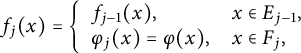 $$ \begin{align*}f_j(x) = \left\{ \begin{array}{ll} f_{j-1}(x), & x\in E_{j-1},\\ \varphi_j(x)=\varphi(x), & x\in F_j, \end{array} \right. \end{align*} $$
$$ \begin{align*}f_j(x) = \left\{ \begin{array}{ll} f_{j-1}(x), & x\in E_{j-1},\\ \varphi_j(x)=\varphi(x), & x\in F_j, \end{array} \right. \end{align*} $$
and
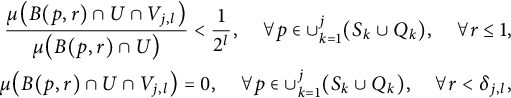 $$ \begin{align} \begin{aligned} \frac{\mu\big(B(p,r)\cap U\cap V_{j,l}\big)}{\mu\big(B(p,r)\cap U\big)} < \frac{1}{2^l}, \quad \forall p\in \cup_{k=1}^j(S_k\cup Q_k), \quad \forall r\le 1,\\ \mu\big(B(p,r)\cap U\cap V_{j,l}\big)=0, \quad \forall p\in \cup_{k=1}^j(S_k\cup Q_k), \quad \forall r<\delta_{j,l}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \frac{\mu\big(B(p,r)\cap U\cap V_{j,l}\big)}{\mu\big(B(p,r)\cap U\big)} < \frac{1}{2^l}, \quad \forall p\in \cup_{k=1}^j(S_k\cup Q_k), \quad \forall r\le 1,\\ \mu\big(B(p,r)\cap U\cap V_{j,l}\big)=0, \quad \forall p\in \cup_{k=1}^j(S_k\cup Q_k), \quad \forall r<\delta_{j,l}, \end{aligned} \end{align} $$
for
![]() $j=1,\ldots ,n$
and
$j=1,\ldots ,n$
and
![]() $l=j+1,j+2,\ldots $
. For the step
$l=j+1,j+2,\ldots $
. For the step
![]() $n+1$
, using Lemma 3.1 again, we have that, for every natural number
$n+1$
, using Lemma 3.1 again, we have that, for every natural number
![]() $l>n+1$
, there is an open
$l>n+1$
, there is an open
![]() $\delta _{n+1,l}$
-neighborhood
$\delta _{n+1,l}$
-neighborhood
![]() $V_{n+1,l}$
of
$V_{n+1,l}$
of
![]() $Q_l$
in
$Q_l$
in
![]() $M\backslash E_n$
such that
$M\backslash E_n$
such that
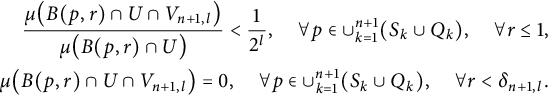 $$ \begin{align*} \begin{aligned} \frac{\mu\big(B(p,r)\cap U\cap V_{n+1,l}\big)}{\mu\big(B(p,r)\cap U\big)} < \frac{1}{2^l}, \quad \forall p\in \cup_{k=1}^{n+1}(S_k\cup Q_k), \quad \forall r\le 1,\\ \mu\big(B(p,r)\cap U\cap V_{n+1,l}\big)=0, \quad \forall p\in \cup_{k=1}^{n+1}(S_k\cup Q_k), \quad \forall r<\delta_{n+1,l}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{\mu\big(B(p,r)\cap U\cap V_{n+1,l}\big)}{\mu\big(B(p,r)\cap U\big)} < \frac{1}{2^l}, \quad \forall p\in \cup_{k=1}^{n+1}(S_k\cup Q_k), \quad \forall r\le 1,\\ \mu\big(B(p,r)\cap U\cap V_{n+1,l}\big)=0, \quad \forall p\in \cup_{k=1}^{n+1}(S_k\cup Q_k), \quad \forall r<\delta_{n+1,l}. \end{aligned} \end{align*} $$
Without loss of generality, we can assume that
![]() $\delta _{n+1,l}<1/(n+1)$
, and, by the compactness of
$\delta _{n+1,l}<1/(n+1)$
, and, by the compactness of
![]() $Q_l$
, the sets
$Q_l$
, the sets
![]() $V_{n+1,l}$
can be chosen to be a finite union of open parametric balls in M. Set
$V_{n+1,l}$
can be chosen to be a finite union of open parametric balls in M. Set
Note that
![]() $E_n\cup F_{n+1}$
is relatively closed in
$E_n\cup F_{n+1}$
is relatively closed in
![]() $E_{n+1}\cup F_{n+1}$
. Furthermore, the section
$E_{n+1}\cup F_{n+1}$
. Furthermore, the section
![]() $f_{n+1}$
defined as
$f_{n+1}$
defined as
![]() $f_{n+1}=f_{n}$
on
$f_{n+1}=f_{n}$
on
![]() $E_n$
and
$E_n$
and
![]() $f_{n+1}=\varphi _{n+1}=\varphi $
on
$f_{n+1}=\varphi _{n+1}=\varphi $
on
![]() $F_{n+1}$
is continuous on the set
$F_{n+1}$
is continuous on the set
![]() $E_n\cup F_{n+1}$
, because
$E_n\cup F_{n+1}$
, because
![]() $E_n\cap V_{n,n+1}=\emptyset $
. Therefore, by the Tietze extension theorem, we can extend the section
$E_n\cap V_{n,n+1}=\emptyset $
. Therefore, by the Tietze extension theorem, we can extend the section
![]() $f_{n+1}$
to a continuous section on
$f_{n+1}$
to a continuous section on
![]() $E_{n+1}\cup F_{n+1}$
that we denote in the same way.
$E_{n+1}\cup F_{n+1}$
that we denote in the same way.
Note also that
![]() $\cup _{n=1}^\infty E_n=U$
. Indeed, if
$\cup _{n=1}^\infty E_n=U$
. Indeed, if
![]() $x\in U$
, because U is open, there exists
$x\in U$
, because U is open, there exists
![]() $r_x>0$
, so that
$r_x>0$
, so that
![]() $B(x,r_x)\subset U$
. Fix a natural number
$B(x,r_x)\subset U$
. Fix a natural number
![]() $l_0$
, so that
$l_0$
, so that
![]() $\frac {1}{l_0}<r_x$
. Then, for every
$\frac {1}{l_0}<r_x$
. Then, for every
![]() $l>l_0$
, because
$l>l_0$
, because
![]() $V_{n,l}$
is a
$V_{n,l}$
is a
![]() $\frac {1}{l}$
-neighborhood of
$\frac {1}{l}$
-neighborhood of
![]() $Q_l\subset \partial U$
in M, we have that
$Q_l\subset \partial U$
in M, we have that
![]() $x\notin V_{n,l}$
for every natural number n. Thus, for
$x\notin V_{n,l}$
for every natural number n. Thus, for
![]() $n\geq l_0$
, we have that
$n\geq l_0$
, we have that
![]() $x\in E_{n}=U\backslash \cup _{l=n+1}^\infty V_{n,l}$
. Then, the section
$x\in E_{n}=U\backslash \cup _{l=n+1}^\infty V_{n,l}$
. Then, the section
![]() $u,$
defined on U as
$u,$
defined on U as
![]() $u(x)=f_n(x)$
if
$u(x)=f_n(x)$
if
![]() $x\in E_n,$
is continuous at
$x\in E_n,$
is continuous at
![]() $x.$
Because x is arbitrary, we have the u is continuous on U.
$x.$
Because x is arbitrary, we have the u is continuous on U.
There only remains to show that, for every
![]() $p\in F$
,
$p\in F$
,
![]() $u(x)\to \varphi (p)$
, as
$u(x)\to \varphi (p)$
, as
![]() $x\to p$
outside a set of
$x\to p$
outside a set of
![]() $\mu $
-density 0 at p relative to
$\mu $
-density 0 at p relative to
![]() $U.$
For this, fix
$U.$
For this, fix
![]() $p\in F.$
Then, we can find a natural number n, so that
$p\in F.$
Then, we can find a natural number n, so that
![]() $p\in F_n$
. Note that
$p\in F_n$
. Note that
![]() $f_n$
is continuous on
$f_n$
is continuous on
![]() $E_n\cup F_n$
, and we have defined
$E_n\cup F_n$
, and we have defined
![]() $u=f_n$
on
$u=f_n$
on
![]() $E_n$
and
$E_n$
and
![]() $f_n=\varphi _n=\varphi $
on
$f_n=\varphi _n=\varphi $
on
![]() $F_n.$
Therefore, for every
$F_n.$
Therefore, for every
![]() $p\in F$
,
$p\in F$
,
![]() $u(x)\to \varphi (p)$
, as
$u(x)\to \varphi (p)$
, as
![]() $x\to p$
in
$x\to p$
in
![]() $E_n.$
By construction,
$E_n.$
By construction,
![]() $U\backslash E_n$
has
$U\backslash E_n$
has
![]() $\mu $
-density
$\mu $
-density
![]() $0$
at p relative to
$0$
at p relative to
![]() $U$
.▪
$U$
.▪
Before we continue, we introduce some terminology. A compact subset
![]() $K\subset M$
is a parametric Mergelyan set if there is an open parametric ball
$K\subset M$
is a parametric Mergelyan set if there is an open parametric ball
![]() $\varphi :W\to \mathbb B $
, with
$\varphi :W\to \mathbb B $
, with
![]() $K\subset W$
, and a compact set
$K\subset W$
, and a compact set
![]() $Q\subset \mathbb B ,$
such that
$Q\subset \mathbb B ,$
such that
![]() $\mathbb B \backslash Q$
is connected and
$\mathbb B \backslash Q$
is connected and
![]() $K=\varphi ^{-1}(Q).$
A subset E of a manifold M is a Mergelyan chaplet, which we simply call a chaplet, if it is the countable disjoint union of a (possibly infinite) locally finite family
$K=\varphi ^{-1}(Q).$
A subset E of a manifold M is a Mergelyan chaplet, which we simply call a chaplet, if it is the countable disjoint union of a (possibly infinite) locally finite family
![]() $E_{j}$
of pairwise disjoint parametric Mergelyan sets
$E_{j}$
of pairwise disjoint parametric Mergelyan sets
![]() $E_j.$
We denote the chaplet by
$E_j.$
We denote the chaplet by
![]() $E=(E_j)_j.$
By Corollary 2.3, a chaplet is a Runge–Carleman set.
$E=(E_j)_j.$
By Corollary 2.3, a chaplet is a Runge–Carleman set.
Proof Proof of Theorem 1.2
By Lemma 3.3, there exists a set
![]() $F,$
with
$F,$
with
![]() $S\subset F\subset \partial U$
and
$S\subset F\subset \partial U$
and
![]() $\nu (\partial U\backslash F)=0,$
and
$\nu (\partial U\backslash F)=0,$
and
![]() $u\in C(U,\xi )$
on
$u\in C(U,\xi )$
on
![]() $U,$
such that, for every
$U,$
such that, for every
![]() $p\in F$
,
$p\in F$
,
![]() $u(x)\to \varphi (p)$
, as
$u(x)\to \varphi (p)$
, as
![]() $x\to p$
outside a set of
$x\to p$
outside a set of
![]() $\mu $
-density 0 at p relative to
$\mu $
-density 0 at p relative to
![]() $U.$
$U.$
Let
![]() $\mathcal S=\{S_l\}_{l=1}^{\infty }$
be a locally finite family of smoothly bounded compact parametric balls
$\mathcal S=\{S_l\}_{l=1}^{\infty }$
be a locally finite family of smoothly bounded compact parametric balls
![]() $S_l$
in U such that
$S_l$
in U such that
![]() $U=\cup _lS_l^0$
and
$U=\cup _lS_l^0$
and
![]() $|S_l|<dist(S_l,\partial U),$
where
$|S_l|<dist(S_l,\partial U),$
where
![]() $|S_l|$
denotes the diameter of
$|S_l|$
denotes the diameter of
![]() $S_l$
. Assume also that none of these balls contains another. We may also assume that the balls become smaller as we approach
$S_l$
. Assume also that none of these balls contains another. We may also assume that the balls become smaller as we approach
![]() $\partial U$
, so that the oscillation
$\partial U$
, so that the oscillation
![]() $\omega _l=\omega _l(u)$
of u on
$\omega _l=\omega _l(u)$
of u on
![]() $S_l$
is less than
$S_l$
is less than
![]() $1/l,$
for each
$1/l,$
for each
![]() $l.$
Let
$l.$
Let
![]() $s_l=\partial S_l$
for
$s_l=\partial S_l$
for
![]() $l\in \mathbb N$
. Because
$l\in \mathbb N$
. Because
![]() $\mu $
is absolutely continuous, Lemma 3.2 tells us that there is an open neighborhood
$\mu $
is absolutely continuous, Lemma 3.2 tells us that there is an open neighborhood
![]() $R_{j}$
of
$R_{j}$
of
![]() $s_j$
in U such that
$s_j$
in U such that
 $$ \begin{align} \frac{\mu\big(R_{j}\cap B(p,r)\big)}{\mu\big(U\cap B(p,r)\big)} < \frac{1}{2^j}, \quad \forall \, p\in \partial U, \quad \forall \, r>0. \end{align} $$
$$ \begin{align} \frac{\mu\big(R_{j}\cap B(p,r)\big)}{\mu\big(U\cap B(p,r)\big)} < \frac{1}{2^j}, \quad \forall \, p\in \partial U, \quad \forall \, r>0. \end{align} $$
Without loss of generality, we may assume that each
![]() $R_{j}$
is a smoothly bounded shell. That is, that in a local coordinate system,
$R_{j}$
is a smoothly bounded shell. That is, that in a local coordinate system,
![]() $R_{j}=\{x: 0<\rho _{j}<\|x\|<1\}$
. By the local finiteness of
$R_{j}=\{x: 0<\rho _{j}<\|x\|<1\}$
. By the local finiteness of
![]() $\mathcal S$
, we may also assume that if
$\mathcal S$
, we may also assume that if
![]() $s_j\cap s_l=\emptyset $
, then
$s_j\cap s_l=\emptyset $
, then
![]() $R_j\cap R_l=\emptyset $
.
$R_j\cap R_l=\emptyset $
.
Consider the closed set
![]() $A=U\backslash \bigcup _{k=1}^\infty R_{k}$
. Then, denoting by
$A=U\backslash \bigcup _{k=1}^\infty R_{k}$
. Then, denoting by
![]() $H_j=S_j^0\cap A$
and
$H_j=S_j^0\cap A$
and
![]() $A_j=H_j\backslash \bigcup _{k=1}^{j-1}S_k^0$
, we have that
$A_j=H_j\backslash \bigcup _{k=1}^{j-1}S_k^0$
, we have that
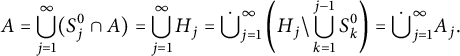 $$ \begin{align*} A = \bigcup_{j=1}^\infty( S_j^0\cap A) = \bigcup_{j=1}^\infty H_j = \dot{\bigcup}_{j=1}^\infty\left( H_j\backslash\bigcup_{k=1}^{j-1}S_k^0\right) = \dot{\bigcup}_{j=1}^\infty A_j. \end{align*} $$
$$ \begin{align*} A = \bigcup_{j=1}^\infty( S_j^0\cap A) = \bigcup_{j=1}^\infty H_j = \dot{\bigcup}_{j=1}^\infty\left( H_j\backslash\bigcup_{k=1}^{j-1}S_k^0\right) = \dot{\bigcup}_{j=1}^\infty A_j. \end{align*} $$
For each
![]() $j,$
the set
$j,$
the set
![]() $H_j$
is a parametric Mergelyan set in
$H_j$
is a parametric Mergelyan set in
![]() $S_j^0$
and the family
$S_j^0$
and the family
![]() $(H_j)_{j=1}^\infty $
is locally finite, but they may not be disjoint. However, the
$(H_j)_{j=1}^\infty $
is locally finite, but they may not be disjoint. However, the
![]() $(A_j)_{j=1}^\infty $
form a locally finite family of disjoint compacta, and hence
$(A_j)_{j=1}^\infty $
form a locally finite family of disjoint compacta, and hence
![]() $A=(A_j)_{j=1}^\infty $
is a Mergelyan chaplet.
$A=(A_j)_{j=1}^\infty $
is a Mergelyan chaplet.
Let us fix now a continuous function
![]() $\varepsilon :A\to (0,1]$
, so that
$\varepsilon :A\to (0,1]$
, so that
![]() $\varepsilon (x)\to 0,$
when
$\varepsilon (x)\to 0,$
when
![]() $x\to \partial U$
. Because
$x\to \partial U$
. Because
![]() $(A_j)_{j=1}^\infty $
is a locally finite family of compacta, we may construct a family
$(A_j)_{j=1}^\infty $
is a locally finite family of compacta, we may construct a family
![]() $(V_j)_{j=1}^\infty $
of disjoint open neighborhoods
$(V_j)_{j=1}^\infty $
of disjoint open neighborhoods
![]() $A_j\subset V_j, \, j=1,2,\ldots .$
For each
$A_j\subset V_j, \, j=1,2,\ldots .$
For each
![]() $A_j$
of A, we choose a point
$A_j$
of A, we choose a point
![]() $x_{A_{j}}\in A_{j}$
and define a function g on
$x_{A_{j}}\in A_{j}$
and define a function g on
![]() $V=\cup _jV_j$
as
$V=\cup _jV_j$
as
![]() $g(x)=\sum _{j}u(x_{A_{j}})\chi _{V_{j}}(x).$
Because the function g is constant in each connected component
$g(x)=\sum _{j}u(x_{A_{j}})\chi _{V_{j}}(x).$
Because the function g is constant in each connected component
![]() $V_j$
and P annihilates constants, we have that
$V_j$
and P annihilates constants, we have that
![]() $Pg=0$
on V.
$Pg=0$
on V.
We claim that
![]() $U^*\backslash A=\cup _kR_k$
is connected. Choose some
$U^*\backslash A=\cup _kR_k$
is connected. Choose some
![]() $R_j$
, and let
$R_j$
, and let
![]() $\mathcal R_j$
be the connected component of
$\mathcal R_j$
be the connected component of
![]() $\cup _kR_k$
containing
$\cup _kR_k$
containing
![]() $R_j.$
Then,
$R_j.$
Then,
![]() $\mathcal R_j$
is the union of a subfamily of
$\mathcal R_j$
is the union of a subfamily of
![]() $(R_k)_{k=1}^\infty .$
Let us show that this subfamily connects
$(R_k)_{k=1}^\infty .$
Let us show that this subfamily connects
![]() $R_j$
with
$R_j$
with
![]() $*$
in
$*$
in
![]() $U^*$
. Suppose this is not the case. Consider the sets
$U^*$
. Suppose this is not the case. Consider the sets
![]() $V=\cup _{s_l\subset \mathcal R_j} S_l^{\circ }$
and
$V=\cup _{s_l\subset \mathcal R_j} S_l^{\circ }$
and
![]() $W=\cup _{s_l\not \subset \mathcal R_j} S_l^{\circ }$
. Both sets are open because they are the union of open sets. Note that if
$W=\cup _{s_l\not \subset \mathcal R_j} S_l^{\circ }$
. Both sets are open because they are the union of open sets. Note that if
![]() $s_k\cap s_l=\emptyset $
, then
$s_k\cap s_l=\emptyset $
, then
![]() $R_k\cap R_l=\emptyset .$
Now, for every set
$R_k\cap R_l=\emptyset .$
Now, for every set
![]() $s_l$
, either
$s_l$
, either
![]() $s_l$
intersects some
$s_l$
intersects some
![]() $s_k\subset \mathcal R_j$
or it is disjoint from every
$s_k\subset \mathcal R_j$
or it is disjoint from every
![]() $s_k\subset \mathcal R_j,$
in which case
$s_k\subset \mathcal R_j,$
in which case
![]() $R_\ell $
is disjoint from every
$R_\ell $
is disjoint from every
![]() $R_k\subset \mathcal R_j.$
In the second case,
$R_k\subset \mathcal R_j.$
In the second case,
![]() $R_\ell $
cannot be in the bounded complementary component of any
$R_\ell $
cannot be in the bounded complementary component of any
![]() $R_k$
with
$R_k$
with
![]() $R_k\subset \mathcal R_j$
, for then
$R_k\subset \mathcal R_j$
, for then
![]() $S_\ell $
would be a subset of
$S_\ell $
would be a subset of
![]() $S_k^0$
which is forbidden. Therefore,
$S_k^0$
which is forbidden. Therefore,
![]() $R_\ell $
and consequently
$R_\ell $
and consequently
![]() $S_\ell ^0$
lie in the unbounded complementary component of every
$S_\ell ^0$
lie in the unbounded complementary component of every
![]() $R_k$
with
$R_k$
with
![]() $R_k\subset \mathcal R_j$
. This means that
$R_k\subset \mathcal R_j$
. This means that
![]() $S_ \ell \cap S_k=\emptyset .$
We have shown that, if
$S_ \ell \cap S_k=\emptyset .$
We have shown that, if
![]() $s_\ell \not \subset \mathcal R_j,$
then
$s_\ell \not \subset \mathcal R_j,$
then
![]() $S_\ell \cap S_k=\emptyset ,$
for every
$S_\ell \cap S_k=\emptyset ,$
for every
![]() $s_k\subset \mathcal R_j$
and consequently
$s_k\subset \mathcal R_j$
and consequently
![]() $V\cap W=\emptyset .$
If, as we supposed,
$V\cap W=\emptyset .$
If, as we supposed,
![]() $\mathcal R_j$
is bounded in
$\mathcal R_j$
is bounded in
![]() $U,$
both V and W are nonempty and this contradicts the assumption that U is connected. Thus, every
$U,$
both V and W are nonempty and this contradicts the assumption that U is connected. Thus, every
![]() $\mathcal R_j$
is unbounded in
$\mathcal R_j$
is unbounded in
![]() $U.$
Because
$U.$
Because
![]() $U^*\backslash A=\cup _j(\mathcal R_j\cup \{*\})$
is the union of a family of connected sets having point
$U^*\backslash A=\cup _j(\mathcal R_j\cup \{*\})$
is the union of a family of connected sets having point
![]() $*$
in common, it follows that
$*$
in common, it follows that
![]() $U^*\backslash A$
is connected as claimed.
$U^*\backslash A$
is connected as claimed.
By Corollary 2.3, there exists a function
![]() $\widetilde \varphi \in C^\infty (U,\vartheta )$
with
$\widetilde \varphi \in C^\infty (U,\vartheta )$
with
![]() $P\widetilde \varphi =0,$
such that
$P\widetilde \varphi =0,$
such that
![]() $|\widetilde \varphi -g|<\varepsilon $
on A. We show now that
$|\widetilde \varphi -g|<\varepsilon $
on A. We show now that
If
![]() $(x_n)_{n=1}^\infty $
is a sequence of points in A tending to
$(x_n)_{n=1}^\infty $
is a sequence of points in A tending to
![]() $p\in \partial U$
, then
$p\in \partial U$
, then
![]() $(x_{A_{j_n}})_{n=1}^\infty $
is also a sequence of points in A tending to
$(x_{A_{j_n}})_{n=1}^\infty $
is also a sequence of points in A tending to
![]() $p\in \partial U$
, where
$p\in \partial U$
, where
![]() $x_{A_{j_n}}$
is the previously fixed point in the
$x_{A_{j_n}}$
is the previously fixed point in the
![]() $A_{j_n}$
of A containing
$A_{j_n}$
of A containing
![]() $x_n$
. Indeed, this follows automatically, because
$x_n$
. Indeed, this follows automatically, because
when n goes to infinity.
Furthermore,
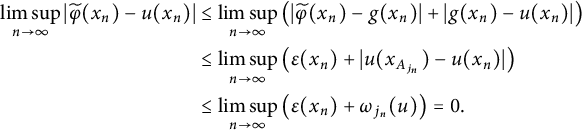 $$ \begin{align*} \limsup_{n\to\infty}\vert \widetilde \varphi(x_{n})-u(x_n)\vert & \leq\limsup_{n\to\infty}\big(\vert \widetilde \varphi(x_{n}) -g(x_n)\vert+\vert g(x_{n})-u(x_n)\vert\big)\\ & \leq\limsup_{n\to\infty}\big(\varepsilon(x_{n})+\vert u(x_{A_{j_{n}}})-u(x_n)\vert\big)\\ & \leq \limsup_{n\to\infty}\big(\varepsilon(x_{n})+ \omega_{j_n}(u)\big) =0. \end{align*} $$
$$ \begin{align*} \limsup_{n\to\infty}\vert \widetilde \varphi(x_{n})-u(x_n)\vert & \leq\limsup_{n\to\infty}\big(\vert \widetilde \varphi(x_{n}) -g(x_n)\vert+\vert g(x_{n})-u(x_n)\vert\big)\\ & \leq\limsup_{n\to\infty}\big(\varepsilon(x_{n})+\vert u(x_{A_{j_{n}}})-u(x_n)\vert\big)\\ & \leq \limsup_{n\to\infty}\big(\varepsilon(x_{n})+ \omega_{j_n}(u)\big) =0. \end{align*} $$
We now show that A satisfies that,
 $$ \begin{align} \mu_{U}(A,p)=\liminf_{r\rightarrow 0}\frac{\mu\big(B(p,r)\cap A\big)}{\mu\big(B(p,r)\cap U\big)}=1. \end{align} $$
$$ \begin{align} \mu_{U}(A,p)=\liminf_{r\rightarrow 0}\frac{\mu\big(B(p,r)\cap A\big)}{\mu\big(B(p,r)\cap U\big)}=1. \end{align} $$
For this, we shall show that
 $$ \begin{align*}\limsup_{r\rightarrow 0}\frac{\mu(B(p,r)\cap(U\backslash A))}{\mu(B(p,r)\cap U)}=0. \end{align*} $$
$$ \begin{align*}\limsup_{r\rightarrow 0}\frac{\mu(B(p,r)\cap(U\backslash A))}{\mu(B(p,r)\cap U)}=0. \end{align*} $$
For fixed
![]() $\varepsilon>0$
, consider
$\varepsilon>0$
, consider
![]() $j_\varepsilon $
, so that
$j_\varepsilon $
, so that
Consider
![]() $r_\varepsilon>0$
, so that
$r_\varepsilon>0$
, so that
![]() $B(p,r_\varepsilon )$
is disjoint from the neighborhoods
$B(p,r_\varepsilon )$
is disjoint from the neighborhoods
![]() $R_{j}$
of the sets
$R_{j}$
of the sets
![]() $s_j$
for
$s_j$
for
![]() $j\le j_\varepsilon $
. Then, for all
$j\le j_\varepsilon $
. Then, for all
![]() $r<r_\varepsilon $
, because
$r<r_\varepsilon $
, because
![]() $U\backslash A = \cup _j R_{j}$
, we have that
$U\backslash A = \cup _j R_{j}$
, we have that
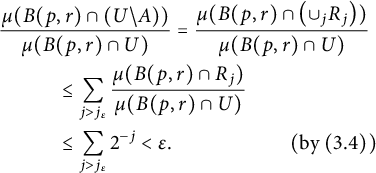 $$ \begin{align*} \hspace{1cm}&\hspace{-1cm}\frac{\mu(B(p,r)\cap(U\backslash A))}{\mu(B(p,r)\cap U)} = \frac{\mu(B(p,r) \cap\left( \cup_j R_{j}\right))}{\mu(B(p,r)\cap U)}\\ &\le\sum_{j>j_\varepsilon}\frac{\mu(B(p,r)\cap R_{j})}{\mu(B(p,r)\cap U)}\\ &\le \sum_{j>j_\varepsilon}2^{-j} <\varepsilon.\hspace{2cm}(\text{by } (3.4)) \end{align*} $$
$$ \begin{align*} \hspace{1cm}&\hspace{-1cm}\frac{\mu(B(p,r)\cap(U\backslash A))}{\mu(B(p,r)\cap U)} = \frac{\mu(B(p,r) \cap\left( \cup_j R_{j}\right))}{\mu(B(p,r)\cap U)}\\ &\le\sum_{j>j_\varepsilon}\frac{\mu(B(p,r)\cap R_{j})}{\mu(B(p,r)\cap U)}\\ &\le \sum_{j>j_\varepsilon}2^{-j} <\varepsilon.\hspace{2cm}(\text{by } (3.4)) \end{align*} $$
Thus, the
![]() $\mu $
-density of
$\mu $
-density of
![]() $U\backslash A$
relative to U at p is at most
$U\backslash A$
relative to U at p is at most
![]() $\varepsilon .$
Because p and
$\varepsilon .$
Because p and
![]() $\varepsilon $
are arbitrary, this proves (3.6).
$\varepsilon $
are arbitrary, this proves (3.6).
Note that the function u has all the properties desired in the theorem, except that of satisfying the differential equation
![]() $Pu=0.$
The function
$Pu=0.$
The function
![]() $\widetilde \varphi $
does satisfy the equation
$\widetilde \varphi $
does satisfy the equation
![]() $P\widetilde \varphi =0$
and also satisfies the desired properties, because of (3.5) and (3.6).▪
$P\widetilde \varphi =0$
and also satisfies the desired properties, because of (3.5) and (3.6).▪