1 Introduction
Throughout this paper, unless specified, M denotes a d-dimensional closed Riemannian manifold and
![]() $\mathrm {End}^1(M)$
the set of all
$\mathrm {End}^1(M)$
the set of all
![]() $C^1$
-maps from M into itself endowed with the
$C^1$
-maps from M into itself endowed with the
![]() $C^1$
-topology. The elements of
$C^1$
-topology. The elements of
![]() $\mathrm {End}^1(M)$
are called endomorphisms. Some of them exhibit critical points, that is, points on which the derivative is not a linear isomorphism; and the other ones, endomorphisms without critical points, are local diffeomorphisms or diffeomorphisms.
$\mathrm {End}^1(M)$
are called endomorphisms. Some of them exhibit critical points, that is, points on which the derivative is not a linear isomorphism; and the other ones, endomorphisms without critical points, are local diffeomorphisms or diffeomorphisms.
An endomorphism f is said to be robustly transitive if there exists a neighborhood
![]() $\mathcal {U}_f$
of f in
$\mathcal {U}_f$
of f in
![]() $\mathrm {End}^1(M)$
such that every
$\mathrm {End}^1(M)$
such that every
![]() $g \in \mathcal {U}_f$
is transitive, where transitive means the existence of a dense forward orbit.
$g \in \mathcal {U}_f$
is transitive, where transitive means the existence of a dense forward orbit.
It should be pointed out that we are actually defining
![]() $C^1$
robust transitivity. The
$C^1$
robust transitivity. The
![]() $C^r$
robust transitivity could also be defined using the
$C^r$
robust transitivity could also be defined using the
![]() $C^r$
-topology. Our approach cannot be extended for
$C^r$
-topology. Our approach cannot be extended for
![]() $C^r$
robust transitivity since many of the techniques used here do not work in
$C^r$
robust transitivity since many of the techniques used here do not work in
![]() $C^r$
-topology and, in [Reference Iglesias and Portela15], an example is constructed of a
$C^r$
-topology and, in [Reference Iglesias and Portela15], an example is constructed of a
![]() $C^2$
-robustly transitive endomorphism which is not
$C^2$
-robustly transitive endomorphism which is not
![]() $C^1$
-robustly transitive.
$C^1$
-robustly transitive.
The main purpose of this paper is to show that dominated splitting is a necessary condition for the existence of robustly transitive endomorphisms displaying critical points. Concretely, we prove the following result.
Theorem A. Every robustly transitive endomorphism displaying critical points admits a non-trivial dominated splitting.
An endomorphism f admits non-trivial dominated splitting of index
![]() $\kappa $
if for every orbit
$\kappa $
if for every orbit
![]() $(x_i)_i$
, that is, a sequence of points
$(x_i)_i$
, that is, a sequence of points
![]() $(x_i)_i$
in M such that
$(x_i)_i$
in M such that
![]() $f(x_{i})=x_{i+1}$
for each
$f(x_{i})=x_{i+1}$
for each
![]() $i \in \mathbb {Z}$
, there are two non-trivial families
$i \in \mathbb {Z}$
, there are two non-trivial families
![]() $(E(x_i))_i$
and
$(E(x_i))_i$
and
![]() $(F(x_i))_i$
of
$(F(x_i))_i$
of
![]() $\kappa $
and
$\kappa $
and
![]() $(d-\kappa )$
-dimensional subspaces, respectively, satisfying the following:
$(d-\kappa )$
-dimensional subspaces, respectively, satisfying the following:
Invariant splitting. For each
![]() $i \in \mathbb {Z}$
, one has that
$i \in \mathbb {Z}$
, one has that
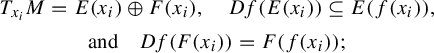 $$ \begin{align*} &T_{x_i}M=E(x_i)\oplus F(x_i), \quad Df(E(x_i)) \subseteq E(f(x_i)), \\ & \qquad\ \qquad \text{and}\quad Df(F(x_i))=F(f(x_i)); \end{align*} $$
$$ \begin{align*} &T_{x_i}M=E(x_i)\oplus F(x_i), \quad Df(E(x_i)) \subseteq E(f(x_i)), \\ & \qquad\ \qquad \text{and}\quad Df(F(x_i))=F(f(x_i)); \end{align*} $$
Domination property. There is an integer
![]() $\ell>0$
independent of any orbit such that
$\ell>0$
independent of any orbit such that
for every unit vectors
![]() $u \in E(x_i)$
and
$u \in E(x_i)$
and
![]() $v \in F(x_i)$
.
$v \in F(x_i)$
.
We will sometimes abuse notation and call the families of subspaces by E and F subbundles (cf. Remark 2.1). Further, we denote the domination property by
![]() $E\prec F$
or
$E\prec F$
or
![]() $E\prec _{\ell } F$
if we want to emphasize the role of
$E\prec _{\ell } F$
if we want to emphasize the role of
![]() $\ell $
. See §2 for further details about dominated splitting.
$\ell $
. See §2 for further details about dominated splitting.
The authors believe that, in general, robustly transitive endomorphisms displaying critical points require more than just dominated splitting. It is feasible that the dominated splitting
![]() $E\oplus F$
provided by Theorem A admits the finest dominated splitting such as
$E\oplus F$
provided by Theorem A admits the finest dominated splitting such as
![]() $E\oplus _{i=1}^k{F_i}$
where the derivative
$E\oplus _{i=1}^k{F_i}$
where the derivative
![]() $Df$
restricted to the extremal subbundle
$Df$
restricted to the extremal subbundle
![]() $F_k$
is volume expanding. (
$F_k$
is volume expanding. (
![]() $E_1\oplus \cdots \oplus E_k$
is the finest dominated splitting if
$E_1\oplus \cdots \oplus E_k$
is the finest dominated splitting if
![]() $E_1\prec E_2 \prec \cdots \prec E_k$
and none of the invariant subbundle
$E_1\prec E_2 \prec \cdots \prec E_k$
and none of the invariant subbundle
![]() $E_i$
admits a dominated splitting.) It was proved for a surface endomorphism in [Reference Lizana and Ranter17]. For higher dimension, it would be a similar result as that obtained for diffeomorphisms in [Reference Bonatti, Díaz and Pujals8] which states, in [Reference Bonatti, Díaz and Pujals8, Theorem 4], that every
$E_i$
admits a dominated splitting.) It was proved for a surface endomorphism in [Reference Lizana and Ranter17]. For higher dimension, it would be a similar result as that obtained for diffeomorphisms in [Reference Bonatti, Díaz and Pujals8] which states, in [Reference Bonatti, Díaz and Pujals8, Theorem 4], that every
![]() $C^1$
-robustly transitive diffeomorphism admits a finest dominated splitting such that the derivative
$C^1$
-robustly transitive diffeomorphism admits a finest dominated splitting such that the derivative
![]() $Df$
restricted to the extremal subbundles are volume contracting and volume expanding, respectively. See §1.1 for further discussion.
$Df$
restricted to the extremal subbundles are volume contracting and volume expanding, respectively. See §1.1 for further discussion.
As a consequence of the main result, we obtain the following topological obstruction. The proof is in §3.
Corollary 1.1. Even-dimensional spheres do not admit robustly transitive endomorphisms.
Note that the existence of robustly transitive diffeomorphisms in
![]() $S^3$
is a well-known open problem, and a negative answer is expected (see e.g. [Reference Díaz, Pujals and Ures11]). It makes sense to ask if examples of robustly transitive endomorphisms in
$S^3$
is a well-known open problem, and a negative answer is expected (see e.g. [Reference Díaz, Pujals and Ures11]). It makes sense to ask if examples of robustly transitive endomorphisms in
![]() $S^3$
may exist, while we expect this question to be difficult.
$S^3$
may exist, while we expect this question to be difficult.
We introduce now the following result that will be useful to prove Theorem A.
Theorem B. Let
![]() $f_0$
be a robustly transitive endomorphism displaying critical points and a neighborhood
$f_0$
be a robustly transitive endomorphism displaying critical points and a neighborhood
![]() $\mathcal {U}_0$
of
$\mathcal {U}_0$
of
![]() $f_0$
in
$f_0$
in
![]() $\mathrm {End}^1(M)$
such that every f in
$\mathrm {End}^1(M)$
such that every f in
![]() $\mathcal {U}_0$
is transitive. Then, there exist an integer
$\mathcal {U}_0$
is transitive. Then, there exist an integer
![]() $\ell \geq 1$
, a number
$\ell \geq 1$
, a number
![]() $\alpha>0$
, and subset
$\alpha>0$
, and subset
![]() $\mathcal {F}$
of
$\mathcal {F}$
of
![]() $\mathcal {U}_0$
such that the following hold:
$\mathcal {U}_0$
such that the following hold:
-
(a)
 $f_0$
is accumulated by the endomorphisms in
$f_0$
is accumulated by the endomorphisms in
 $\mathcal {F}$
; and
$\mathcal {F}$
; and -
(b) every
 $f \in \mathcal {F}$
admits a dominated splitting
$f \in \mathcal {F}$
admits a dominated splitting
 $E\oplus F$
such that
$E\oplus F$
such that
 $E\prec _{\ell } F$
and the angle between E and F is greater than
$E\prec _{\ell } F$
and the angle between E and F is greater than
 $\alpha $
. (It means that
$\alpha $
. (It means that  , for all vectors
, for all vectors
 $u \in E(x_i),v \in F(x_i),$
for each
$u \in E(x_i),v \in F(x_i),$
for each
 $x_i$
along the orbit
$x_i$
along the orbit
 $(x_i)_i \in \Lambda _f$
. For details, see §2.)
$(x_i)_i \in \Lambda _f$
. For details, see §2.)
Theorem B implies uniformity of the dominated splitting for endomorphisms in
![]() $\mathcal {F}$
which will allow us, since
$\mathcal {F}$
which will allow us, since
![]() $f_0$
is accumulated by
$f_0$
is accumulated by
![]() $\mathcal {F}$
, to extend the dominated splitting to
$\mathcal {F}$
, to extend the dominated splitting to
![]() $f_0$
.
$f_0$
.
1.1 A brief history of robust transitivity
Robust transitivity has been well studied in the diffeomorphism context. The first examples were given by Shub on
![]() $\mathbb {T}^4$
in [Reference Shub and Chillingworth25] and by Mañé on
$\mathbb {T}^4$
in [Reference Shub and Chillingworth25] and by Mañé on
![]() $\mathbb {T}^3$
in [Reference Mañé19], which have an underlying structure weaker than hyperbolic, known as partially hyperbolic. However, Mañé proved for surface diffeomorphisms in [Reference Mañé20] that robust transitivity implies hyperbolicity and, in particular, the only surface that admits such systems is the torus,
$\mathbb {T}^3$
in [Reference Mañé19], which have an underlying structure weaker than hyperbolic, known as partially hyperbolic. However, Mañé proved for surface diffeomorphisms in [Reference Mañé20] that robust transitivity implies hyperbolicity and, in particular, the only surface that admits such systems is the torus,
![]() $\mathbb {T}^2$
.
$\mathbb {T}^2$
.
Bonatti and Díaz, in [Reference Bonatti and Díaz7], construct a powerful geometric tool (called a blender) to produce robustly transitive partially hyperbolic diffeomorphisms. Later, in [Reference Bonatti and Viana9], Bonatti and Viana construct the first examples of robustly transitive diffeomorphisms with dominated splitting which are not partially hyperbolic. In [Reference Bonatti, Díaz and Pujals8, Reference Díaz, Pujals and Ures11], Bonatti et al prove for a diffeomorphism on three- and higher-dimensional manifolds that robust transitivity requires some weak form of hyperbolicity.
In view of this, a natural question arises. In general, do robustly transitive endomorphisms require some weak form of hyperbolicty?
In the local diffeomorphisms scenario, there are several advances. Based on the examples of robustly transitive diffeomorphisms, robustly transitive non-expanding endomorphisms were constructed. In [Reference Lizana and Pujals16], necessary and sufficient conditions for robustly transitive local diffeomorphisms were obtained. In particular, it is not necessary any weak form of hyperbolicity for the existence of a robustly transitive local diffeomorphism; a trivial example is an expanding linear endomorphism with complex eigenvalues, which does not admit a dominated splitting. That result shows a difference between the diffeomorphisms and local diffeomorphisms setting. We note however that one can think of an endomorphism as having a strong stable bundle consisting on pre-orbits, and with this point of view, the results bear a closer analogy to those of diffeomorphisms.
In the endomorphisms displaying a critical points setting, the first examples were given in [Reference Berger and Rovella3, Reference Iglesias, Lizana and Portela14]. Although these examples exhibit some form of weak hyperbolicity and are homotopic to a hyperbolic linear endomorphism on
![]() $\mathbb {T}^2$
, any result about necessary conditions was established only recently. In [Reference Lizana and Ranter17], it was proved for surface endomorphisms that a weak form of hyperbolicity is needed for robust transitivity, so-called partial hyperbolicity. Furthermore, it was also proved that only the Torus and the Klein bottle support a robustly transitive endomorphism exhibiting critical points; and that the action of such a map on the first homology group has at least an eigenvalue with modulus greater than one. Later, new classes of examples of robustly transitive endomorphisms were given in [Reference Lizana and Ranter18]. The examples are homotopic to an expanding linear endomorphism on the torus or the Klein bottle; and an example of a robustly transitive endomorphism of zero degree. In higher dimension, the first examples of robustly transitive endomorphisms displaying critical points were constructed only recently in [Reference Morelli22].
$\mathbb {T}^2$
, any result about necessary conditions was established only recently. In [Reference Lizana and Ranter17], it was proved for surface endomorphisms that a weak form of hyperbolicity is needed for robust transitivity, so-called partial hyperbolicity. Furthermore, it was also proved that only the Torus and the Klein bottle support a robustly transitive endomorphism exhibiting critical points; and that the action of such a map on the first homology group has at least an eigenvalue with modulus greater than one. Later, new classes of examples of robustly transitive endomorphisms were given in [Reference Lizana and Ranter18]. The examples are homotopic to an expanding linear endomorphism on the torus or the Klein bottle; and an example of a robustly transitive endomorphism of zero degree. In higher dimension, the first examples of robustly transitive endomorphisms displaying critical points were constructed only recently in [Reference Morelli22].
1.2 Comments about some previous approaches
Here, we briefly comment on the main ingredients used to show that some (weak) form of hyperbolicity is a necessary condition for the existence of robust transitivity.
1.2.1 Key obstructions for robust transitivity
In a broad sense, an obstruction for robust transitivity is some phenomenon which is incompatible with this feature.
Here, we discuss these phenomena which play an important role in the proof that robust transitivity requires some weak form of hyperbolicity. These phenomena are in some sense related to ‘the candidate for dominated splitting’. Let us define them.
-
• Source. A periodic point p for f, where
 $n_p \geq 1$
denotes its period, such that
$n_p \geq 1$
denotes its period, such that
 $Df^{n_p}_p$
is a matrix having all the eigenvalues with modulus greater than one.
$Df^{n_p}_p$
is a matrix having all the eigenvalues with modulus greater than one. -
• Sink. A periodic point p for f, where
 $n_p \geq 1$
denotes its period, such that
$n_p \geq 1$
denotes its period, such that
 $Df^{n_p}_p$
is a matrix having all the eigenvalues with modulus less than one.
$Df^{n_p}_p$
is a matrix having all the eigenvalues with modulus less than one.
The set of all critical points of an endomorphism f will be denoted by
![]() $\mathrm {Cr}(f)$
and its interior in M denoted by
$\mathrm {Cr}(f)$
and its interior in M denoted by
![]() $\mathrm {int}(\mathrm {Cr}(f))$
.
$\mathrm {int}(\mathrm {Cr}(f))$
.
-
• Full-dimensional kernel. There exist a point
 $x \in \mathrm {Cr}(f)$
and an integer
$x \in \mathrm {Cr}(f)$
and an integer
 $n\geq 1$
such that
$n\geq 1$
such that
 $\dim \ker (Df^n_x)=d$
.
$\dim \ker (Df^n_x)=d$
.
1.2.2 Key obstructions versus dominated splitting for diffeomorphisms
Here, we discuss the role of sources and sinks as obstructions to obtain that a robustly transitive diffeomorphism admits a dominated splitting. First, it is easy to see that transitive diffeomorphisms do not admit neither sources nor sinks, otherwise there is a small neighborhood such that its image by some (backward or forward) iterate goes into itself, which is incompatible with transitivity.
Let
![]() $\mathcal {U}_f$
be a neighborhood of f in
$\mathcal {U}_f$
be a neighborhood of f in
![]() $\mathrm {End}^1(M)$
, where all endomorphisms in
$\mathrm {End}^1(M)$
, where all endomorphisms in
![]() $\mathcal {U}_f$
are transitive diffeomorphisms. Let us start commenting on the approaches for surface diffeomorphisms in [Reference Mañé20] and on the higher-dimensional manifold in [Reference Bonatti, Díaz and Pujals8, Reference Díaz, Pujals and Ures11].
$\mathcal {U}_f$
are transitive diffeomorphisms. Let us start commenting on the approaches for surface diffeomorphisms in [Reference Mañé20] and on the higher-dimensional manifold in [Reference Bonatti, Díaz and Pujals8, Reference Díaz, Pujals and Ures11].
-
• In [Reference Mañé20], the fact that sources and sinks are obstructions for transitivity is used to prove that the set of all the periodic points of any surface diffeomorphism in
 $\mathcal {U}_f$
is hyperbolic, and so, it has a ‘natural’ splitting given by the stable and unstable directions. Later, it is proved that the lack of domination property allows to create, up to a perturbation, sinks or sources contradicting the robust transitivity. Finally, the classical result is used, the so-called closing lemma, to extend the dominated splitting to the whole surface. Consequently, every robustly transitive surface diffeomorphism admits a dominated splitting (weak hyperbolicity). More precisely, the following dichotomy is proved.In particular, every robustly transitive surface diffeomorphism is an Anosov diffeomorphism.
$\mathcal {U}_f$
is hyperbolic, and so, it has a ‘natural’ splitting given by the stable and unstable directions. Later, it is proved that the lack of domination property allows to create, up to a perturbation, sinks or sources contradicting the robust transitivity. Finally, the classical result is used, the so-called closing lemma, to extend the dominated splitting to the whole surface. Consequently, every robustly transitive surface diffeomorphism admits a dominated splitting (weak hyperbolicity). More precisely, the following dichotomy is proved.In particular, every robustly transitive surface diffeomorphism is an Anosov diffeomorphism.Theorem [Reference Mañé20]
Let M be a closed surface. Then there is a residual subset
 ${\mathcal {R} \subseteq \mathrm {Diff}^1(M)}$
(that is, the set of all the diffeomorphisms
${\mathcal {R} \subseteq \mathrm {Diff}^1(M)}$
(that is, the set of all the diffeomorphisms
 $\mathrm {Diff}^1(M)$
),
$\mathrm {Diff}^1(M)$
),
 $\mathcal {R}=\mathcal {R}_1\sqcup \mathcal {R}_2,$
such that every
$\mathcal {R}=\mathcal {R}_1\sqcup \mathcal {R}_2,$
such that every
 $f \in \mathcal {R}_1$
is an Axiom A and every
$f \in \mathcal {R}_1$
is an Axiom A and every
 $f \in \mathcal {R}_2$
has infinitely many sources and sinks.
$f \in \mathcal {R}_2$
has infinitely many sources and sinks.
Note that in higher-dimensional manifolds, even if each periodic point is hyperbolic, they could have different indexes (that is, unstable directions of different dimensions) which hamper the choice of a ‘natural’ splitting over the set of all the periodic points. Thus, the approach followed in [Reference Bonatti, Díaz and Pujals8, Reference Díaz, Pujals and Ures11] was slightly different.
-
• In this context, they consider a hyperbolic saddle point p of the diffeomorphism f and its homoclinic class, denoted by
 $H(p,f)$
. Then, one defines ‘naturally’ a splitting using the stable and unstable directions over
$H(p,f)$
. Then, one defines ‘naturally’ a splitting using the stable and unstable directions over
 $H(p,f)$
and proves that if such splitting is not dominated, one can create a source or a sink for some perturbation of f. Since any diffeomorphism in
$H(p,f)$
and proves that if such splitting is not dominated, one can create a source or a sink for some perturbation of f. Since any diffeomorphism in
 $\mathcal {U}_f$
admits neither sources nor sinks, one has that
$\mathcal {U}_f$
admits neither sources nor sinks, one has that
 $H(p,f)$
admits a dominated splitting. Finally, using classical results such as the closing lemma and connecting lemma, they extend the splitting to the whole manifold, proving that robust transitivity for diffeomorphisms requires dominated splitting (weak hyperbolicity).In fact, the result above follows as a consequence of the following.
$H(p,f)$
admits a dominated splitting. Finally, using classical results such as the closing lemma and connecting lemma, they extend the splitting to the whole manifold, proving that robust transitivity for diffeomorphisms requires dominated splitting (weak hyperbolicity).In fact, the result above follows as a consequence of the following.Theorem [Reference Bonatti, Díaz and Pujals8]
Let p be a hyperbolic saddle of a diffeomorphism f defined on M. Then:
-
– either the homoclinic class
 $H(p,f)$
of p admits a dominated splitting; or
$H(p,f)$
of p admits a dominated splitting; or -
– given any neighborhood U of
 $H(p,f)$
and any integer
$H(p,f)$
and any integer
 $\ell \geq 1$
, there exists g arbitrarily
$\ell \geq 1$
, there exists g arbitrarily
 $C^1$
-close to f having
$C^1$
-close to f having
 $\ell $
sources or sinks arbitrarily close to p, whose orbits are contained in U.
$\ell $
sources or sinks arbitrarily close to p, whose orbits are contained in U.
Even more, it was proved that every robustly transitive diffeomorphism is volume hyperbolic, which is a consequence of the following result.
Theorem [Reference Bonatti, Díaz and Pujals8, Reference Díaz, Pujals and Ures11]
Let
 $\Lambda _f(U)$
be a robustly transitive set and
$\Lambda _f(U)$
be a robustly transitive set and
 $E_1\oplus \cdots \oplus E_k$
,
$E_1\oplus \cdots \oplus E_k$
,
 $E_1\prec E_2 \prec \cdots \prec E_k$
, be its finest dominated splitting. (A compact set
$E_1\prec E_2 \prec \cdots \prec E_k$
, be its finest dominated splitting. (A compact set
 $\Lambda $
is a robustly transitive set for f if it is the maximal f-invariant set in some neighborhood U and if, for every
$\Lambda $
is a robustly transitive set for f if it is the maximal f-invariant set in some neighborhood U and if, for every
 $g C^1$
-close to f, the maximal g-invariant set
$g C^1$
-close to f, the maximal g-invariant set
 $\Lambda _g(U)=\bigcap _{n \in \mathbb {Z}}g^n(U)$
is also compact and
$\Lambda _g(U)=\bigcap _{n \in \mathbb {Z}}g^n(U)$
is also compact and
 $g:\Lambda _g \to \Lambda _g$
is transitive.) Then,
$g:\Lambda _g \to \Lambda _g$
is transitive.) Then,
 $\Lambda _f(U)$
is a volume hyperbolic set, that is, there exists an integer
$\Lambda _f(U)$
is a volume hyperbolic set, that is, there exists an integer
 $\ell \geq 1$
such that
$\ell \geq 1$
such that
 $Df^{\ell }$
uniformly contracts the volume in
$Df^{\ell }$
uniformly contracts the volume in
 $E_1$
and uniformly expands the volume in
$E_1$
and uniformly expands the volume in
 $E_k$
.
$E_k$
. -
1.2.3 Key obstructions versus dominated splitting for non-invertible endomorphisms
For the case of non-invertible endomorphisms, the situation changes dramatically. On the one hand, the existence of a source no longer is an obstruction, we can consider, for example, an expanding map. On the other hand, as it was said before, there are examples of local diffeomorphisms on surfaces without dominated splitting. Moreover, when endomorphisms having critical points are considered, the full-kernel obstruction (which was first introduced in [Reference Lizana and Ranter17]) plays an essential role.
Key Obstruction Lemma. There are no robustly transitive endomorphisms exhibiting a full-dimensional kernel.
To prove this, we use the following classical tool in
![]() $C^1$
-perturbative arguments introduced by Franks in [Reference Franks12] for diffeomorphisms that can be easily adapted for endomorphisms as follows.
$C^1$
-perturbative arguments introduced by Franks in [Reference Franks12] for diffeomorphisms that can be easily adapted for endomorphisms as follows.
Franks’ Lemma. Given
![]() $\mathcal {U}$
open set in
$\mathcal {U}$
open set in
![]() $\mathrm {End}^1(M)$
and
$\mathrm {End}^1(M)$
and
![]() $f \in \mathcal {U}$
, there exist
$f \in \mathcal {U}$
, there exist
![]() $\varepsilon>0$
such that for every finite collection of distinct points
$\varepsilon>0$
such that for every finite collection of distinct points
![]() $\Sigma =\{x_0,\ldots ,x_n\}$
in M, and linear maps
$\Sigma =\{x_0,\ldots ,x_n\}$
in M, and linear maps
there exist an endomorphism
![]() $\hat {f} \in \mathcal {U}$
, a neighborhood B of
$\hat {f} \in \mathcal {U}$
, a neighborhood B of
![]() $\Sigma $
, and a family of balls
$\Sigma $
, and a family of balls
![]() $\{B_i\}_{i=0}^n$
contained in B, where
$\{B_i\}_{i=0}^n$
contained in B, where
![]() $B_i$
is centered at
$B_i$
is centered at
![]() $x_i$
, verifying
$x_i$
, verifying
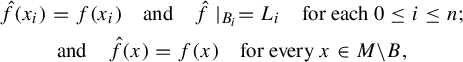 $$ \begin{align*} &\hat{f}(x_i)=f(x_i) \quad \text{and}\quad \hat{f}\mid_{B_i}=L_i \quad \text{for each } 0\leq i \leq n; \\& \qquad\!\quad \text{and}\quad \hat{f}(x)=f(x) \quad \text{for every } x \in M\backslash B, \end{align*} $$
$$ \begin{align*} &\hat{f}(x_i)=f(x_i) \quad \text{and}\quad \hat{f}\mid_{B_i}=L_i \quad \text{for each } 0\leq i \leq n; \\& \qquad\!\quad \text{and}\quad \hat{f}(x)=f(x) \quad \text{for every } x \in M\backslash B, \end{align*} $$
where, by abuse of notation,
![]() $\hat {f}\mid _{B_i}=L_i$
means the action of
$\hat {f}\mid _{B_i}=L_i$
means the action of
![]() $\hat {f}$
in each
$\hat {f}$
in each
![]() $B_i$
is equal to the linear map
$B_i$
is equal to the linear map
![]() $L_i$
.
$L_i$
.
Thus, we can conclude that the Key Obstruction Lemma follows from Franks’ Lemma applied to
![]() $\Sigma =\{x,f(x),\ldots ,f^{m-1}(x)\}$
and
$\Sigma =\{x,f(x),\ldots ,f^{m-1}(x)\}$
and
![]() $L_i=Df_{f^i(x)}$
for each
$L_i=Df_{f^i(x)}$
for each
![]() $i=0,1,\ldots ,m-1$
, where
$i=0,1,\ldots ,m-1$
, where
![]() $\ker (Df^m_x)$
is d-dimensional. Hence, there is an endomorphism
$\ker (Df^m_x)$
is d-dimensional. Hence, there is an endomorphism
![]() $\hat {f}$
arbitrarily close to f so that
$\hat {f}$
arbitrarily close to f so that
![]() $\hat {f}$
is equal to
$\hat {f}$
is equal to
![]() $L_i=Df_{f^i(x)}$
around
$L_i=Df_{f^i(x)}$
around
![]() $f^i(x)$
for each
$f^i(x)$
for each
![]() $i=0,1,\ldots ,m-1$
. In particular,
$i=0,1,\ldots ,m-1$
. In particular,
![]() $\hat {f}^m$
is equal to
$\hat {f}^m$
is equal to
![]() $Df^m_x$
around x and hence the image of such neighborhood of x by
$Df^m_x$
around x and hence the image of such neighborhood of x by
![]() $\hat {f}^m$
is exactly one point which contradicts transitivity. Therefore, f cannot be a robustly transitive endomorphism.
$\hat {f}^m$
is exactly one point which contradicts transitivity. Therefore, f cannot be a robustly transitive endomorphism.
1.2.4 Two-dimensional endormorphisms with critical points
Let us quickly comment about the approach in [Reference Lizana and Ranter17]. For a robustly transitive surface endomorphism f displaying critical points having non-empty interior, one can define the set
![]() $\Lambda $
consisting of all the orbits
$\Lambda $
consisting of all the orbits
![]() $(x_i)_i$
which get into the interior of the critical set infinitely many times for the past and the future. That is,
$(x_i)_i$
which get into the interior of the critical set infinitely many times for the past and the future. That is,
![]() $(x_i)_i \in \Lambda $
if and only if
$(x_i)_i \in \Lambda $
if and only if
![]() $x_i \in \mathrm {int}(\mathrm {Cr}(f))$
for infinitely many
$x_i \in \mathrm {int}(\mathrm {Cr}(f))$
for infinitely many
![]() $i<0$
and infinitely many
$i<0$
and infinitely many
![]() $i>0$
. To simplify the notation, let us also denote by f the map on the space of all the orbits defined by
$i>0$
. To simplify the notation, let us also denote by f the map on the space of all the orbits defined by
![]() $(x_i)_i \mapsto (f(x_i))_i=(x_{i+1})_i$
. Then, one has that
$(x_i)_i \mapsto (f(x_i))_i=(x_{i+1})_i$
. Then, one has that
![]() $\Lambda $
is f-invariant and, moreover, one can define for every
$\Lambda $
is f-invariant and, moreover, one can define for every
![]() $(x_i)_i$
in
$(x_i)_i$
in
![]() $\Lambda $
an invariant splitting of the tangent bundle over
$\Lambda $
an invariant splitting of the tangent bundle over
![]() $\Lambda $
as follows:
$\Lambda $
as follows:
where
![]() $\tau _i^{+}\geq 0$
is the time that
$\tau _i^{+}\geq 0$
is the time that
![]() $x_i$
takes to enter in the critical set for the first time, and
$x_i$
takes to enter in the critical set for the first time, and
![]() $\tau _i^{-} < 0$
is the time that
$\tau _i^{-} < 0$
is the time that
![]() $x_{i}$
takes to go back to the critical set along the orbit
$x_{i}$
takes to go back to the critical set along the orbit
![]() $(x_i)_i$
for the first time. In particular, we have
$(x_i)_i$
for the first time. In particular, we have
![]() $x_{i+\tau _i^{+}}$
and
$x_{i+\tau _i^{+}}$
and
![]() $x_{i+\tau _i^{-}}$
in
$x_{i+\tau _i^{-}}$
in
![]() $\mathrm {Cr}(f)$
.
$\mathrm {Cr}(f)$
.
The splitting
![]() $E\oplus F$
is well defined over
$E\oplus F$
is well defined over
![]() $\Lambda $
because the full-dimensional kernel obstruction guarantees that
$\Lambda $
because the full-dimensional kernel obstruction guarantees that
![]() $\ker (Df^n_{x_i})$
is at most one-dimensional for any
$\ker (Df^n_{x_i})$
is at most one-dimensional for any
![]() $n\geq 0$
. In particular, E is one-dimensional and
$n\geq 0$
. In particular, E is one-dimensional and
![]() $Df$
-invariant. Furthermore, the definition of
$Df$
-invariant. Furthermore, the definition of
![]() $\tau _i^{-}$
is used together with the fact that
$\tau _i^{-}$
is used together with the fact that
![]() $\dim \ker (Df^n_{x_i}) \leq 1$
, for all
$\dim \ker (Df^n_{x_i}) \leq 1$
, for all
![]() $n\geq 1$
, to show that F is
$n\geq 1$
, to show that F is
![]() $Df$
-invariant. Then, to get that
$Df$
-invariant. Then, to get that
![]() $E\oplus F$
is a dominated splitting, it is proved in [Reference Lizana and Ranter17] that the absence of domination property allows to create a point having full-dimensional kernel for some
$E\oplus F$
is a dominated splitting, it is proved in [Reference Lizana and Ranter17] that the absence of domination property allows to create a point having full-dimensional kernel for some
![]() $C^1$
-perturbation of f which is incompatible with robust transitivity. Thus,
$C^1$
-perturbation of f which is incompatible with robust transitivity. Thus,
![]() $E\oplus F$
is a dominated splitting and it can be extended to the closure of
$E\oplus F$
is a dominated splitting and it can be extended to the closure of
![]() $\Lambda $
which is the whole space. Finally, we use that every robustly transitive endomorphism displaying critical points is approximated by such kinds of endomorphisms having dominated splitting, which allows us to push the domination splitting to the limit to conclude Theorem A for surface endomorphisms.
$\Lambda $
which is the whole space. Finally, we use that every robustly transitive endomorphism displaying critical points is approximated by such kinds of endomorphisms having dominated splitting, which allows us to push the domination splitting to the limit to conclude Theorem A for surface endomorphisms.
In higher dimension, the kernel of
![]() $Df^n$
may have distinct dimensions depending on n, even if the kernel of
$Df^n$
may have distinct dimensions depending on n, even if the kernel of
![]() $Df$
has constant dimension. Moreover, the subbundles E and F on
$Df$
has constant dimension. Moreover, the subbundles E and F on
![]() $\Lambda $
may not have constant dimension along the orbit on
$\Lambda $
may not have constant dimension along the orbit on
![]() $\Lambda $
.
$\Lambda $
.
In the sequel, we explain our strategy to figure out that obstacle and then prove Theorem A.
1.3 Sketch of the proof of Theorem A
Let
![]() $f_0$
be a robustly transitive endomorphism displaying critical points and
$f_0$
be a robustly transitive endomorphism displaying critical points and
![]() $\mathcal {U}_0$
a neighborhood of
$\mathcal {U}_0$
a neighborhood of
![]() $f_0$
in
$f_0$
in
![]() $\mathrm {End}^1(M)$
such that every endomorphism in it is (robustly) transitive. Up to shrink
$\mathrm {End}^1(M)$
such that every endomorphism in it is (robustly) transitive. Up to shrink
![]() $\mathcal {U}_0$
, we can find
$\mathcal {U}_0$
, we can find
![]() $1\leq \kappa <d$
as the smallest integer satisfying
$1\leq \kappa <d$
as the smallest integer satisfying
where
![]() $\dim \ker (Df)=\max _{x \in M}\dim \ker (Df_x)$
. Otherwise, we could find
$\dim \ker (Df)=\max _{x \in M}\dim \ker (Df_x)$
. Otherwise, we could find
![]() $f \in \mathcal {U}_0$
and
$f \in \mathcal {U}_0$
and
![]() ${m\geq 1}$
such that
${m\geq 1}$
such that
![]() $\dim \ker (Df^m)=d$
, which by Key Obstruction Lemma is absurd since f is also a robustly transitive endomorphism.
$\dim \ker (Df^m)=d$
, which by Key Obstruction Lemma is absurd since f is also a robustly transitive endomorphism.
Since
![]() $\kappa $
is chosen as the smallest integer satisfying (1.2), it follows that
$\kappa $
is chosen as the smallest integer satisfying (1.2), it follows that
![]() $f_0$
can be approximated by
$f_0$
can be approximated by
![]() $f \in \mathcal {U}_0$
satisfying the equality for some
$f \in \mathcal {U}_0$
satisfying the equality for some
![]() $m\geq 1$
. Let us define
$m\geq 1$
. Let us define
![]() $m_f$
as the smallest positive integer m such that:
$m_f$
as the smallest positive integer m such that:
-
•
 $\{x \in M:\dim \ker (Df^m_x)=\kappa \}$
has non-empty interior; or
$\{x \in M:\dim \ker (Df^m_x)=\kappa \}$
has non-empty interior; or -
• if such a subset above has an empty interior, then we take
 $m_f$
as the smallest one such that
$m_f$
as the smallest one such that
 $\dim \ker (Df^m_x)=\kappa $
for some
$\dim \ker (Df^m_x)=\kappa $
for some
 $x \in M.$
$x \in M.$
To avoid any confusion, we point out that the second item must be considered if and only if the interior of
![]() $\{x \in M:\dim \ker (Df^m_x)=\kappa \}$
is empty.
$\{x \in M:\dim \ker (Df^m_x)=\kappa \}$
is empty.
From now on, let us define
![]() $\mathrm {Cr}_{\kappa }(f)$
as the set
$\mathrm {Cr}_{\kappa }(f)$
as the set
![]() $\{x \in M:\dim \ker (Df^{m_f}_x)=\kappa \}$
. This set plays an important role in our approach. Furthermore, we denote the set of all endomorphisms f in
$\{x \in M:\dim \ker (Df^{m_f}_x)=\kappa \}$
. This set plays an important role in our approach. Furthermore, we denote the set of all endomorphisms f in
![]() $\mathcal {U}_0$
where
$\mathcal {U}_0$
where
![]() $\mathrm {Cr}_{\kappa }(f)$
has non-empty interior by
$\mathrm {Cr}_{\kappa }(f)$
has non-empty interior by
![]() $\mathcal {F}_0$
.
$\mathcal {F}_0$
.
It should be noted that
![]() $\mathcal {F}_0$
is non-empty and accumulates at
$\mathcal {F}_0$
is non-empty and accumulates at
![]() $f_0$
. Indeed, given
$f_0$
. Indeed, given
![]() ${x \in \mathrm {Cr}_{\kappa }(f)}$
for some f close to
${x \in \mathrm {Cr}_{\kappa }(f)}$
for some f close to
![]() $f_0$
, we can apply Franks’ Lemma to
$f_0$
, we can apply Franks’ Lemma to
![]() $\Sigma =\{x,f(x),\ldots , f^{m_f-1}(x)\}$
and
$\Sigma =\{x,f(x),\ldots , f^{m_f-1}(x)\}$
and
![]() $L_i=Df_{f^i(x)}$
, for each
$L_i=Df_{f^i(x)}$
, for each
![]() $i=0,1,\ldots ,m_f-1$
, to get an endomorphism
$i=0,1,\ldots ,m_f-1$
, to get an endomorphism
![]() $\hat {f} C^1$
-close to f and, therefore, close to
$\hat {f} C^1$
-close to f and, therefore, close to
![]() $f_0$
, such that
$f_0$
, such that
![]() $ \ker (D\hat {f}^{m_f}_y)$
is
$ \ker (D\hat {f}^{m_f}_y)$
is
![]() $\kappa $
-dimensional for every y near x. Then, we conclude that
$\kappa $
-dimensional for every y near x. Then, we conclude that
![]() $\mathrm {Cr}_{\kappa }(\hat {f})$
has non-empty interior and, moreover,
$\mathrm {Cr}_{\kappa }(\hat {f})$
has non-empty interior and, moreover,
![]() $m_{\hat {f}}\leq m_f$
.
$m_{\hat {f}}\leq m_f$
.
We now define the set
![]() $\Lambda $
and the splitting
$\Lambda $
and the splitting
![]() $E\oplus F$
in our context of higher dimension. For
$E\oplus F$
in our context of higher dimension. For
![]() $f \in \mathcal {F}_0$
, we define
$f \in \mathcal {F}_0$
, we define
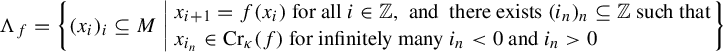 $$ \begin{align} \Lambda_f=\left\{(x_i)_i \subseteq M\left|\!\begin{array}{l}x_{i+1}=f(x_i) \text{ for all } i \in \mathbb{Z}, \text{ and } \text{ there exists } (i_n)_{n} \subseteq \mathbb{Z} \text{ such that}\!\!\! \\ x_{i_n} \in \mathrm{Cr}_{\kappa}(f) \text{ for infinitely many } i_n<0 \text{ and } i_n>0\end{array}\right.\right\} \end{align} $$
$$ \begin{align} \Lambda_f=\left\{(x_i)_i \subseteq M\left|\!\begin{array}{l}x_{i+1}=f(x_i) \text{ for all } i \in \mathbb{Z}, \text{ and } \text{ there exists } (i_n)_{n} \subseteq \mathbb{Z} \text{ such that}\!\!\! \\ x_{i_n} \in \mathrm{Cr}_{\kappa}(f) \text{ for infinitely many } i_n<0 \text{ and } i_n>0\end{array}\right.\right\} \end{align} $$
and
where
Note that
![]() $\tau ^{-}_i$
and
$\tau ^{-}_i$
and
![]() $\tau ^{+}_i$
are slightly different from those in [Reference Lizana and Ranter17] (recall definition in (1.1)). However, it should be noted that
$\tau ^{+}_i$
are slightly different from those in [Reference Lizana and Ranter17] (recall definition in (1.1)). However, it should be noted that
![]() $m_f$
is the time that
$m_f$
is the time that
![]() $\ker (Df^n)$
have maximal dimension in
$\ker (Df^n)$
have maximal dimension in
![]() $\mathcal {U}_0$
and
$\mathcal {U}_0$
and
![]() $\mathrm {Cr}_{\kappa }(f)$
is the set such that the kernel of
$\mathrm {Cr}_{\kappa }(f)$
is the set such that the kernel of
![]() $Df^{m_f}$
has maximal dimension. In particular, if f is a surface endomorphism, we have that
$Df^{m_f}$
has maximal dimension. In particular, if f is a surface endomorphism, we have that
![]() $m_f=1, \kappa =1$
,
$m_f=1, \kappa =1$
,
![]() $\mathrm {Cr}_1(f)$
is the critical set of f, and
$\mathrm {Cr}_1(f)$
is the critical set of f, and
![]() $\tau ^{\pm }_i$
are the same as in [Reference Lizana and Ranter17].
$\tau ^{\pm }_i$
are the same as in [Reference Lizana and Ranter17].
We remark that (up to taking a subset)
![]() $\mathcal {F}_0$
is the natural candidate to prove Theorem B. Then, it remains to show that there is an integer
$\mathcal {F}_0$
is the natural candidate to prove Theorem B. Then, it remains to show that there is an integer
![]() $\ell>0$
and a number
$\ell>0$
and a number
![]() $\alpha>0$
such that
$\alpha>0$
such that
![]() $E\oplus F$
is an
$E\oplus F$
is an
![]() $(\alpha ,\ell )$
-dominated splitting. To prove that, we will see in Lemma 3.1 that
$(\alpha ,\ell )$
-dominated splitting. To prove that, we will see in Lemma 3.1 that
![]() $\Lambda _f$
, given by (*), is dense in the inverse limit space (see §2) and, in Proposition 2.10,
$\Lambda _f$
, given by (*), is dense in the inverse limit space (see §2) and, in Proposition 2.10,
![]() $E\oplus F$
can be extended to the closure of
$E\oplus F$
can be extended to the closure of
![]() $\Lambda _f$
once provided that
$\Lambda _f$
once provided that
![]() $E\oplus F$
is an
$E\oplus F$
is an
![]() $(\alpha ,\ell )$
-dominated splitting.
$(\alpha ,\ell )$
-dominated splitting.
To prove such uniform behavior, we state a technical dichotomy as follows. However, before doing it, we would like to emphasize that to define E and F in (**), only the fact that
![]() $\Lambda _f\neq \emptyset $
is used and
$\Lambda _f\neq \emptyset $
is used and
![]() $\dim \ker (Df^m)\leq \kappa $
for all
$\dim \ker (Df^m)\leq \kappa $
for all
![]() $m\geq 1$
.
$m\geq 1$
.
Theorem C. Let
![]() $f_0$
be an endomorphism displaying critical points. Assume that there is an integer
$f_0$
be an endomorphism displaying critical points. Assume that there is an integer
![]() $1\leq \kappa <d$
and a set
$1\leq \kappa <d$
and a set
![]() $\mathcal {F}$
consisting of endomorphisms converging to
$\mathcal {F}$
consisting of endomorphisms converging to
![]() $f_0$
such that every
$f_0$
such that every
![]() $f \in \mathcal {F}$
satisfies that
$f \in \mathcal {F}$
satisfies that
![]() $\Lambda _f\neq \emptyset $
and
$\Lambda _f\neq \emptyset $
and
![]() $\dim \ker (Df^m)\leq \kappa \text { for all } m \in \mathbb {Z}$
. Then, only one of the following statements hold:
$\dim \ker (Df^m)\leq \kappa \text { for all } m \in \mathbb {Z}$
. Then, only one of the following statements hold:
-
• either there exist
 $\ell>0$
and
$\ell>0$
and
 $\alpha>0$
such that for each
$\alpha>0$
such that for each
 $f \in \mathcal {F}$
, the splitting
$f \in \mathcal {F}$
, the splitting
 $E\oplus F$
is an (
$E\oplus F$
is an (
 $\alpha ,\ell $
)-dominated splitting over
$\alpha ,\ell $
)-dominated splitting over
 $\Lambda _f$
; or
$\Lambda _f$
; or -
•
 $f_0$
is accumulated by endomorphisms g, where
$f_0$
is accumulated by endomorphisms g, where
 $\ker (Dg^m)$
has dimension greater than
$\ker (Dg^m)$
has dimension greater than
 $\kappa $
for some
$\kappa $
for some
 $m \geq 1$
.
$m \geq 1$
.
We have already shown that
![]() $\mathcal {F}_0$
satisfies the hypothesis of Theorem C and
$\mathcal {F}_0$
satisfies the hypothesis of Theorem C and
![]() $f_0$
cannot be approximated by endomorphisms whose kernel has dimension greater than
$f_0$
cannot be approximated by endomorphisms whose kernel has dimension greater than
![]() $\kappa $
. Then, Theorem B follows from Theorem C since Lemma 3.1 implies the density of
$\kappa $
. Then, Theorem B follows from Theorem C since Lemma 3.1 implies the density of
![]() $\Lambda _f$
, and in Proposition 2.10, we prove that the dominated splitting can be extended to the closure of
$\Lambda _f$
, and in Proposition 2.10, we prove that the dominated splitting can be extended to the closure of
![]() $\Lambda _f$
which is the space of all the orbits.
$\Lambda _f$
which is the space of all the orbits.
1.3.1 Novelties and new techniques
We want to emphasize the new approaches brought by the present paper that differ with those developed for diffeomorphisms and surface endomorphisms having critical points.
-
• The kernel of
 $Df$
is used at the critical set (that could be multidimensional and have different dimension at distinct points) to build a candidate for a dominated splitting on a dense set. On the one hand, this is substantially different from how the splitting is built for the case of diffeomorphisms where the splitting over the periodic points is used. On the other hand, the strategy goes beyond the approach for surface endomorphisms where the kernel of
$Df$
is used at the critical set (that could be multidimensional and have different dimension at distinct points) to build a candidate for a dominated splitting on a dense set. On the one hand, this is substantially different from how the splitting is built for the case of diffeomorphisms where the splitting over the periodic points is used. On the other hand, the strategy goes beyond the approach for surface endomorphisms where the kernel of
 $Df^n$
has dimension one for any point in the critical set and any iterated n.
$Df^n$
has dimension one for any point in the critical set and any iterated n. -
• A dominated splitting defined on an invariant non-compact set could not be extended to the closure (see Example 2.3). Therefore, a fine control on the angle between multidimensional subbundles has to be brought into consideration, an issue that is not present in previous approaches.
1.4 How the paper is organized
In §2, we discuss the notion of dominated splitting and some related properties, the equivalence of dominated splitting via cone criterion. In §3, we use Theorem B to prove Theorem A. Finally, §4 is devoted to the proof of Theorem C and to recall that Theorem B follows from Theorem C.
2 Weak form of hyperbolicity for endomorphisms
In this section, the notion of dominated splitting will be formalized in terms of invariant splitting for endomorphisms displaying critical points. Further, we will present some fundamental properties that will be useful throughout this paper.
Due to the fact that for an endomorphism, a point may exhibit more than one preimage, it is natural to consider the inverse limit space of M with respect to f,
It is a compact metric space and the natural projection
![]() $(x_i)_i \mapsto x_0$
is continuous. Moreover, an endomorphism
$(x_i)_i \mapsto x_0$
is continuous. Moreover, an endomorphism
![]() $f \in \mathrm {End}^1(M)$
induces a homeomorphism on
$f \in \mathrm {End}^1(M)$
induces a homeomorphism on
![]() $M_f$
defined by
$M_f$
defined by
![]() $(x_i)_i \mapsto (f(x_i))_i=(x_{i+1})_i$
, and whenever there is no confusion, it will also be denoted by f. The points in
$(x_i)_i \mapsto (f(x_i))_i=(x_{i+1})_i$
, and whenever there is no confusion, it will also be denoted by f. The points in
![]() $M_f$
are called the orbits of f. A subset
$M_f$
are called the orbits of f. A subset
![]() $\Lambda $
of
$\Lambda $
of
![]() $M_f$
is said to be f-invariant or simply, invariant if
$M_f$
is said to be f-invariant or simply, invariant if
![]() $f^{-1}(\Lambda )=\Lambda $
.
$f^{-1}(\Lambda )=\Lambda $
.
The concept of dominated splitting is established in the context of endomorphisms without critical points (that is, local diffeomorphisms and diffeomorphisms) and its definition is the following.
We say that an f-invariant set
![]() $\Lambda \subseteq M_f$
admits a dominated splitting of index
$\Lambda \subseteq M_f$
admits a dominated splitting of index
![]() $\kappa $
for f if for all
$\kappa $
for f if for all
![]() $(x_i)_i \in \Lambda $
, there exist two families
$(x_i)_i \in \Lambda $
, there exist two families
![]() $(E(x_i))_i$
and
$(E(x_i))_i$
and
![]() $(F(x_i))_i$
of
$(F(x_i))_i$
of
![]() $\kappa $
and
$\kappa $
and
![]() $(d-\kappa )$
-dimensional subspaces satisfying the following properties.
$(d-\kappa )$
-dimensional subspaces satisfying the following properties.
Invariant splitting. For each
![]() $i \in \mathbb {Z}$
, one has that
$i \in \mathbb {Z}$
, one has that
Domination property. There exists
![]() $\ell \geq 1$
such that for each
$\ell \geq 1$
such that for each
![]() $i \in \mathbb {Z}$
and unit vectors
$i \in \mathbb {Z}$
and unit vectors
![]() $u \in E(x_i)$
and
$u \in E(x_i)$
and
![]() $v \in F(x_i)$
, one has that
$v \in F(x_i)$
, one has that
When f is a diffeomorphism, M is used instead of
![]() $M_f$
in the definition above. Recall that the domination property is denoted by
$M_f$
in the definition above. Recall that the domination property is denoted by
![]() $E \prec F$
or
$E \prec F$
or
![]() $E\prec _{\ell } F$
if we want to emphasize the role of
$E\prec _{\ell } F$
if we want to emphasize the role of
![]() $\ell $
.
$\ell $
.
Remark 2.1. The families E and F are actually subbundles of the vector bundle of
![]() $M_f$
defined by
$M_f$
defined by
![]() $TM_f=\{((x_i)_i,v) : v \in T_{x_0}M\}$
. Moreover, the bundle E depends only on the forward orbit while F depends only on the backward orbit of a point in
$TM_f=\{((x_i)_i,v) : v \in T_{x_0}M\}$
. Moreover, the bundle E depends only on the forward orbit while F depends only on the backward orbit of a point in
![]() $M_f$
. This implies that the bundle E induces a subbundle of
$M_f$
. This implies that the bundle E induces a subbundle of
![]() $TM$
and this will be used in the proof of Corollary 1.1.
$TM$
and this will be used in the proof of Corollary 1.1.
Remark 2.2. Let W be any inner product space and
![]() $\Phi :W \to W$
be a linear map. For a subspace V of W, we denote
$\Phi :W \to W$
be a linear map. For a subspace V of W, we denote
![]() $\Phi $
restricted to V by
$\Phi $
restricted to V by
![]() $\Phi \mid _V$
and respectively define the norm and conorm of
$\Phi \mid _V$
and respectively define the norm and conorm of
![]() $\Phi \mid _V$
by
$\Phi \mid _V$
by
When V is the whole space, we simply say that
![]() $\|\Phi \|$
and
$\|\Phi \|$
and
![]() $\operatorname {{\mathfrak {m}}}(\Phi )$
are the norm and conorm of
$\operatorname {{\mathfrak {m}}}(\Phi )$
are the norm and conorm of
![]() $\Phi $
.
$\Phi $
.
From now on, by Remark 2.2, we rewrite the inequality in the domination property:
Some differences should be pointed out when the derivative is not invertible everywhere. For instance, suppose that
![]() $E \oplus F$
is a splitting over an f-invariant set
$E \oplus F$
is a splitting over an f-invariant set
![]() $\Lambda \subseteq M_f$
verifying all the properties of the definition above. Note that if
$\Lambda \subseteq M_f$
verifying all the properties of the definition above. Note that if
![]() $u_E+u_F \in \ker (Df_{x_i})$
, where
$u_E+u_F \in \ker (Df_{x_i})$
, where
![]() $u_E \in E(x_i)$
and
$u_E \in E(x_i)$
and
![]() $u_F \in F(x_i)$
, then
$u_F \in F(x_i)$
, then
![]() $Df(u_E)$
is parallel to
$Df(u_E)$
is parallel to
![]() $Df(u_F)$
which affects the invariance property. Moreover, if
$Df(u_F)$
which affects the invariance property. Moreover, if
![]() $u_F \in \ker (Df_{x_i})$
, then the domination property implies that
$u_F \in \ker (Df_{x_i})$
, then the domination property implies that
![]() $ E(x_i)$
is contained in
$ E(x_i)$
is contained in
![]() $\ker (Df_{x_i})$
, and so neither
$\ker (Df_{x_i})$
, and so neither
![]() $E(x_i)$
nor
$E(x_i)$
nor
![]() $F(x_i)$
are invariant. Therefore, to extend the notion of dominated splitting, we require the following:
$F(x_i)$
are invariant. Therefore, to extend the notion of dominated splitting, we require the following:
In addition, we also require that the angle between E and F is uniformly away from zero. This will allow to extend the dominated splitting to the closure of
![]() $\Lambda $
, see Proposition 2.10. Otherwise, an orbit
$\Lambda $
, see Proposition 2.10. Otherwise, an orbit
![]() $(x_i)_i$
may exist such that
$(x_i)_i$
may exist such that
![]() $E(x_i)=\ker (Df_{x_i})$
, and the angles of
$E(x_i)=\ker (Df_{x_i})$
, and the angles of
![]() $E(x_i)$
and
$E(x_i)$
and
![]() $F(x_i)$
go to zero as i goes to
$F(x_i)$
go to zero as i goes to
![]() $+\infty $
then, somewhere on the boundary of
$+\infty $
then, somewhere on the boundary of
![]() $\Lambda $
, the extensions of E and F have some intersection. See the following example.
$\Lambda $
, the extensions of E and F have some intersection. See the following example.
Example 2.3. Let
![]() $(A_n)_n$
be a sequence of square matrices defined by
$(A_n)_n$
be a sequence of square matrices defined by
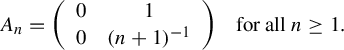 $$ \begin{align*}A_n=\left(\begin{array}{cc} 0 & 1\\ 0 & (n+1)^{-1} \end{array}\right)\! \quad \text{for all } n \geq 1.\end{align*} $$
$$ \begin{align*}A_n=\left(\begin{array}{cc} 0 & 1\\ 0 & (n+1)^{-1} \end{array}\right)\! \quad \text{for all } n \geq 1.\end{align*} $$
Take
![]() $E:=E_n$
and
$E:=E_n$
and
![]() $F_n$
as the subspaces generated by
$F_n$
as the subspaces generated by
![]() $v=(1,0)$
and
$v=(1,0)$
and
![]() $v_n=(1,1/n)$
, respectively. Then,
$v_n=(1,1/n)$
, respectively. Then,
![]() $E_n \oplus F_n$
is a dominated splitting for
$E_n \oplus F_n$
is a dominated splitting for
![]() $(A_n)_n$
since
$(A_n)_n$
since
![]() $A_n(E_n) \subseteq E_{n+1}$
and
$A_n(E_n) \subseteq E_{n+1}$
and
![]() $A_n(F_n)=F_{n+1}$
. Moreover,
$A_n(F_n)=F_{n+1}$
. Moreover,
for each
![]() $n \geq 1$
. However,
$n \geq 1$
. However,
![]() $E_n$
and
$E_n$
and
![]() $F_n$
converge to the same subspace E.
$F_n$
converge to the same subspace E.
This example shows the existence of a dominated splitting along an orbit which cannot be extended to the closure.
Thus, before proposing the definition of dominated splitting for an endomorphism displaying critical points, we should introduce the notion about the angle between subspaces.
The angle between the non-zero vectors
![]() $v,w \in T_xM$
with respect to the metric
$v,w \in T_xM$
with respect to the metric
![]() $\langle \cdot ,\cdot \rangle $
(where, for simplicity, we ignore the dependence of the inner product on x in M) is defined as the unique number
$\langle \cdot ,\cdot \rangle $
(where, for simplicity, we ignore the dependence of the inner product on x in M) is defined as the unique number ![]() in
in
![]() $[0,\pi ]$
satisfying
$[0,\pi ]$
satisfying ![]() . Then, given V and W, two non-trivial subspaces of
. Then, given V and W, two non-trivial subspaces of
![]() $T_xM$
, we define the angle between them by
$T_xM$
, we define the angle between them by
The angle between two subspace is a number contained in
![]() $[0,\pi /2]$
. We also write
$[0,\pi /2]$
. We also write ![]() to refer to the angle between the space generated by a non-zero vector v and the subspace W.
to refer to the angle between the space generated by a non-zero vector v and the subspace W.
We would like to emphasize that ![]() does not mean that
does not mean that
![]() $V=W$
, it just means that the intersection between V and W is non-trivial; and
$V=W$
, it just means that the intersection between V and W is non-trivial; and ![]() for some
for some
![]() $\alpha>0$
means that V and W are far away from each other. This notion of angle between two subspaces will be useful to extend the definition of dominated splitting in the context of endomorphisms displaying critical points. Furthermore, that angle allows us to define a distance on
$\alpha>0$
means that V and W are far away from each other. This notion of angle between two subspaces will be useful to extend the definition of dominated splitting in the context of endomorphisms displaying critical points. Furthermore, that angle allows us to define a distance on
![]() $\mathrm {Grass}_r(T_xM)$
, called the r-dimensional Grassmannian of
$\mathrm {Grass}_r(T_xM)$
, called the r-dimensional Grassmannian of
![]() $T_xM$
, which consists of all the r-dimensional subspaces of
$T_xM$
, which consists of all the r-dimensional subspaces of
![]() $T_xM$
. For all V and W in
$T_xM$
. For all V and W in
![]() $\mathrm {Grass}_r(T_xM)$
, we define the distance between them by
$\mathrm {Grass}_r(T_xM)$
, we define the distance between them by
where
![]() $V^{\perp }$
denotes the orthogonal complement of V. It is well known that the Grassmannian endowed with this distance is a compact metric space. For more details about the distance, see [Reference Bochi, Potrie and Sambarino6, Appendix A.1]
$V^{\perp }$
denotes the orthogonal complement of V. It is well known that the Grassmannian endowed with this distance is a compact metric space. For more details about the distance, see [Reference Bochi, Potrie and Sambarino6, Appendix A.1]
Now, we are able to define a dominated splitting for endomorphisms exhibiting critical points.
Definition 2.1. Let
![]() $f \in \mathrm {End}^1(M)$
be an endomorphism displaying critical points. An invariant subset
$f \in \mathrm {End}^1(M)$
be an endomorphism displaying critical points. An invariant subset
![]() $\Lambda $
of
$\Lambda $
of
![]() $M_f$
admits a dominated splitting of index
$M_f$
admits a dominated splitting of index
![]() $\kappa $
for f if for all
$\kappa $
for f if for all
![]() $(x_i)_i \in \Lambda $
, there exist two families
$(x_i)_i \in \Lambda $
, there exist two families
![]() $(E(x_i))_i$
and
$(E(x_i))_i$
and
![]() $(F(x_i))_i$
of
$(F(x_i))_i$
of
![]() $\kappa $
and
$\kappa $
and
![]() $(d-\kappa )$
-dimensional subspaces such that the following properties hold.
$(d-\kappa )$
-dimensional subspaces such that the following properties hold.
Invariant splitting. For each
![]() $i \in \mathbb {Z}$
, one has that
$i \in \mathbb {Z}$
, one has that
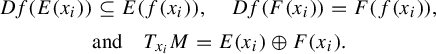 $$ \begin{align*} & Df(E(x_i))\subseteq E(f(x_i)), \quad Df(F(x_i))=F(f(x_i)),\\ & \qquad\qquad\!\!\quad \text{and} \quad T_{x_i}M=E(x_i)\oplus F(x_i). \end{align*} $$
$$ \begin{align*} & Df(E(x_i))\subseteq E(f(x_i)), \quad Df(F(x_i))=F(f(x_i)),\\ & \qquad\qquad\!\!\quad \text{and} \quad T_{x_i}M=E(x_i)\oplus F(x_i). \end{align*} $$
Uniform angle. There exists
![]() $\alpha>0$
such that
$\alpha>0$
such that ![]() for each
for each
![]() $i \in \mathbb {Z}$
.
$i \in \mathbb {Z}$
.
Domination property. There exists
![]() $\ell \geq 1$
such that
$\ell \geq 1$
such that
![]() $E\prec _{\ell } F$
.
$E\prec _{\ell } F$
.
We will say that
![]() $E\oplus F$
is an
$E\oplus F$
is an
![]() $(\alpha ,\ell )$
-dominated splitting if we want to emphasize the role of
$(\alpha ,\ell )$
-dominated splitting if we want to emphasize the role of
![]() $\ell $
and
$\ell $
and
![]() $\alpha $
. When
$\alpha $
. When
![]() $\Lambda =M_f$
, we also say that f has a dominated splitting. For simplicity, we will write
$\Lambda =M_f$
, we also say that f has a dominated splitting. For simplicity, we will write
![]() $E\prec F$
instead of
$E\prec F$
instead of
![]() $E\prec _{\ell } F$
when there is no confusion.
$E\prec _{\ell } F$
when there is no confusion.
Remark 2.4. Observe that if E and F satisfy the items in Definition 2.1, then
![]() $Df\mid _F$
is an isomorphism and
$Df\mid _F$
is an isomorphism and
![]() $\ker (Df_{x_i}^n) \subseteq E(x_i)$
for each
$\ker (Df_{x_i}^n) \subseteq E(x_i)$
for each
![]() $(x_i)_i \in \Lambda $
and
$(x_i)_i \in \Lambda $
and
![]() $n\geq 1$
.
$n\geq 1$
.
Remark 2.5. No uniform angle property is required to define dominated splitting for endomorphisms displaying critical points in the introduction. The uniformity of the angle follows from the fact that the manifold is compact and the subbundles are continuous.
More generally, an invariant subset
![]() $\Lambda $
of
$\Lambda $
of
![]() $M_f$
admits a dominated splitting of index
$M_f$
admits a dominated splitting of index
![]() $\kappa $
for f if for all
$\kappa $
for f if for all
![]() $(x_i)_i \in \Lambda $
, there exist non-trivial families
$(x_i)_i \in \Lambda $
, there exist non-trivial families
![]() $(E(x_i))_i$
and
$(E(x_i))_i$
and
![]() $(F_j(x_i))_i,\ {1\leq j \leq r}$
, of
$(F_j(x_i))_i,\ {1\leq j \leq r}$
, of
![]() $\kappa $
and
$\kappa $
and
![]() $d_j$
-dimensional subspaces with
$d_j$
-dimensional subspaces with
![]() $d_1+d_2+\cdots +d_r=d-\kappa $
satisfying the following properties.
$d_1+d_2+\cdots +d_r=d-\kappa $
satisfying the following properties.
Invariant splitting. For each
![]() $i \in \mathbb {Z}$
, one has that
$i \in \mathbb {Z}$
, one has that
Uniform angle. There exists
![]() $\alpha>0$
so that
$\alpha>0$
so that ![]() for each
for each
![]() $i \in \mathbb {Z}$
.
$i \in \mathbb {Z}$
.
Domination property.
![]() $E\prec F_1 \prec F_2 \prec \cdots \prec F_r$
.
$E\prec F_1 \prec F_2 \prec \cdots \prec F_r$
.
2.1 Dominated splitting properties
Throughout this section, we adapt some of the main properties about dominated splitting which appear in [Reference Crovisier and Potrie10] in the diffeomorphisms context to the context of endomorphisms displaying critical points.
Let f be an endomorphism displaying critical points and
![]() $E\oplus F$
be a dominated splitting over f-invariant subset
$E\oplus F$
be a dominated splitting over f-invariant subset
![]() $\Lambda $
of
$\Lambda $
of
![]() $M_f$
.
$M_f$
.
The uniqueness of the dominated splitting is guaranteed by the following.
Proposition 2.6. If
![]() $G\oplus H$
is a dominated splitting over
$G\oplus H$
is a dominated splitting over
![]() $\Lambda $
for f, which holds
$\Lambda $
for f, which holds
![]() ${\dim E=\dim G}$
, then
${\dim E=\dim G}$
, then
![]() $E(x_i)=G(x_i)$
and
$E(x_i)=G(x_i)$
and
![]() $F(x_i)=H(x_i)$
for all
$F(x_i)=H(x_i)$
for all
![]() $x_i$
in the orbit
$x_i$
in the orbit
![]() $(x_i)_i \in \Lambda $
.
$(x_i)_i \in \Lambda $
.
The proof needs some preliminaries.
Lemma 2.7. If
![]() $G\oplus H$
is a dominated splitting over
$G\oplus H$
is a dominated splitting over
![]() $\Lambda $
for f with
$\Lambda $
for f with
![]() $\dim E(x_i)\leq \dim G(x_i)$
for all
$\dim E(x_i)\leq \dim G(x_i)$
for all
![]() $(x_i)_i \in \Lambda $
, then
$(x_i)_i \in \Lambda $
, then
![]() $E(x_i)\subseteq G(x_i)$
. In particular,
$E(x_i)\subseteq G(x_i)$
. In particular,
![]() $E\oplus (G\cap F) \oplus H$
is a dominated splitting over
$E\oplus (G\cap F) \oplus H$
is a dominated splitting over
![]() $\Lambda $
for f.
$\Lambda $
for f.
Proof. We can, without loss of generality, choose
![]() $\ell \geq 1$
such that
$\ell \geq 1$
such that
![]() $E\prec _{\ell } F$
and
$E\prec _{\ell } F$
and
![]() $G\prec _{\ell } H$
. Moreover, it follows from Remark 2.4 that
$G\prec _{\ell } H$
. Moreover, it follows from Remark 2.4 that
![]() $Df\mid _{H}$
is an isomorphism and
$Df\mid _{H}$
is an isomorphism and
![]() $\ker (Df^m_{x_i})$
must be contained in
$\ker (Df^m_{x_i})$
must be contained in
![]() $E(x_i)$
and
$E(x_i)$
and
![]() $G(x_i)$
, for each
$G(x_i)$
, for each
![]() $(x_i)_i \in \Lambda $
and
$(x_i)_i \in \Lambda $
and
![]() $m\geq 1$
.
$m\geq 1$
.
To conclude the proof of the proposition, it remains to show that if
![]() $u \in E(x_i)$
such that
$u \in E(x_i)$
such that
![]() $Df^m(u)\neq 0$
, for every
$Df^m(u)\neq 0$
, for every
![]() $m\geq 1$
, then
$m\geq 1$
, then
![]() $u \in G(x_i)$
. Then, for every
$u \in G(x_i)$
. Then, for every
![]() $u \in E(x_i)$
, one can decompose
$u \in E(x_i)$
, one can decompose
![]() $u=u_G+u_H$
in a unique way where
$u=u_G+u_H$
in a unique way where
![]() $u_G \in G(x_i)$
and
$u_G \in G(x_i)$
and
![]() $u_H \in H(x_i)$
. Analogously, one can decompose
$u_H \in H(x_i)$
. Analogously, one can decompose
![]() $u_H=u^{\prime }_E+u^{\prime }_F$
, where
$u_H=u^{\prime }_E+u^{\prime }_F$
, where
![]() $u^{\prime }_E \in E(x_i)$
and
$u^{\prime }_E \in E(x_i)$
and
![]() $u^{\prime }_F \in F(x_i)$
. Then
$u^{\prime }_F \in F(x_i)$
. Then
![]() $u^{\prime }_F$
must be zero. Otherwise, we get that
$u^{\prime }_F$
must be zero. Otherwise, we get that
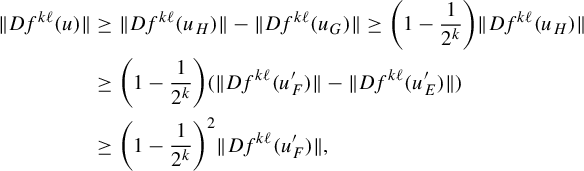 $$ \begin{align*} \|Df^{k\ell}(u)\|&\geq \|Df^{k\ell}(u_H)\|-\|Df^{k\ell}(u_G)\|\geq \bigg(1-\frac{1}{2^{k}}\bigg)\|Df^{k\ell}(u_H)\|\\ &\geq \bigg(1-\frac{1}{2^{k}}\bigg) (\|Df^{k\ell}(u^{\prime}_F)\|-\|Df^{k\ell}(u^{\prime}_E)\| )\\ &\geq \bigg(1-\frac{1}{2^{k}}\bigg)^2 \|Df^{k\ell}(u^{\prime}_F)\|, \end{align*} $$
$$ \begin{align*} \|Df^{k\ell}(u)\|&\geq \|Df^{k\ell}(u_H)\|-\|Df^{k\ell}(u_G)\|\geq \bigg(1-\frac{1}{2^{k}}\bigg)\|Df^{k\ell}(u_H)\|\\ &\geq \bigg(1-\frac{1}{2^{k}}\bigg) (\|Df^{k\ell}(u^{\prime}_F)\|-\|Df^{k\ell}(u^{\prime}_E)\| )\\ &\geq \bigg(1-\frac{1}{2^{k}}\bigg)^2 \|Df^{k\ell}(u^{\prime}_F)\|, \end{align*} $$
implying that
![]() $\|Df^{k\ell }(u)\|$
and
$\|Df^{k\ell }(u)\|$
and
![]() $\|Df^{k\ell }(u^{\prime }_F)\|$
have the same growth, which is impossible. Therefore,
$\|Df^{k\ell }(u^{\prime }_F)\|$
have the same growth, which is impossible. Therefore,
![]() $u_H \in E(x_i)\cap H(x_i)$
and
$u_H \in E(x_i)\cap H(x_i)$
and
![]() $u_G \in E(x_i)\cap G(x_i)$
. Symmetrically, we deduce that if
$u_G \in E(x_i)\cap G(x_i)$
. Symmetrically, we deduce that if
![]() $v \in G(x_i)$
whose
$v \in G(x_i)$
whose
![]() $v=v_E+v_F$
, then
$v=v_E+v_F$
, then
![]() $v_E \in G(x_i)\cap E(x_i)$
and
$v_E \in G(x_i)\cap E(x_i)$
and
![]() $v_F \in G(x_i)\cap F(x_i)$
. Moreover, since
$v_F \in G(x_i)\cap F(x_i)$
. Moreover, since
![]() $\dim E(x_i)\leq \dim G(x_i)$
, we have that either
$\dim E(x_i)\leq \dim G(x_i)$
, we have that either
![]() $G(x_i)=E(x_i)$
or
$G(x_i)=E(x_i)$
or
![]() $G(x_i)\cap F(x_i)\neq \{0\}$
.
$G(x_i)\cap F(x_i)\neq \{0\}$
.
Take non-zero vectors
![]() $u \in E(x_i)\cap H(x_i)$
and
$u \in E(x_i)\cap H(x_i)$
and
![]() $v \in G(x_i)\cap F(x_i)$
. Then, as
$v \in G(x_i)\cap F(x_i)$
. Then, as
![]() $G \prec H$
, we deduce that
$G \prec H$
, we deduce that
![]() $\|Df^{\ell }(u)\|$
grows faster than
$\|Df^{\ell }(u)\|$
grows faster than
![]() $\|Df^{\ell }(v)\|$
, which contradicts the fact that
$\|Df^{\ell }(v)\|$
, which contradicts the fact that
![]() ${E \prec F}$
. Thus, at least one of these intersections
${E \prec F}$
. Thus, at least one of these intersections
![]() $E(x_i)\cap H(x_i)$
and
$E(x_i)\cap H(x_i)$
and
![]() $G(x_i)\cap F(x_i)$
is trivial. Thus, we obtain that
$G(x_i)\cap F(x_i)$
is trivial. Thus, we obtain that
![]() $E(x_i)\cap H(x_i)=\{0\}$
. It implies that
$E(x_i)\cap H(x_i)=\{0\}$
. It implies that
![]() $E(x_i)$
is contained in
$E(x_i)$
is contained in
![]() $G(x_i)$
. To conclude the proof, we should observe that
$G(x_i)$
. To conclude the proof, we should observe that
![]() $G(x_i)\cap F(x_i)$
is invariant and
$G(x_i)\cap F(x_i)$
is invariant and
![]() ${E(x_i)\prec G(x_i)\cap F(x_i) \prec H(x_i)}$
.
${E(x_i)\prec G(x_i)\cap F(x_i) \prec H(x_i)}$
.
As a direct consequence of the previous lemma, we conclude the first part of the uniqueness of the dominated splitting.
Corollary 2.8. If
![]() $G\oplus H$
is a dominated splitting over
$G\oplus H$
is a dominated splitting over
![]() $\Lambda $
for f such that
$\Lambda $
for f such that
![]() ${\dim E=\dim G}$
, then
${\dim E=\dim G}$
, then
![]() $E(x_i)=G(x_i)$
for all
$E(x_i)=G(x_i)$
for all
![]() $x_i$
in the orbit
$x_i$
in the orbit
![]() $(x_i)_i \in \Lambda $
.
$(x_i)_i \in \Lambda $
.
To complete the proof of Proposition 2.6, we state the following.
Lemma 2.9. If
![]() $E\oplus F$
and
$E\oplus F$
and
![]() $E\oplus H$
are dominated splittings over
$E\oplus H$
are dominated splittings over
![]() $\Lambda $
for f, then
$\Lambda $
for f, then
![]() ${F(x_i)=H(x_i)}$
for all
${F(x_i)=H(x_i)}$
for all
![]() $x_i$
in the orbit
$x_i$
in the orbit
![]() $(x_i)_i$
in
$(x_i)_i$
in
![]() $\Lambda $
.
$\Lambda $
.
Proof. First, we assume that
![]() $(x_i)_i \in \Lambda $
with
$(x_i)_i \in \Lambda $
with
![]() $x_i \notin \mathrm {Cr}(f)$
for all
$x_i \notin \mathrm {Cr}(f)$
for all
![]() $i \in \mathbb {Z}$
. Then, since
$i \in \mathbb {Z}$
. Then, since
![]() $Df_{x_i}:T_{x_i}M \to T_{x_{i+1}}M$
is an isomorphism, one has that for every unit vectors
$Df_{x_i}:T_{x_i}M \to T_{x_{i+1}}M$
is an isomorphism, one has that for every unit vectors
![]() $u \in E(x_i)$
and
$u \in E(x_i)$
and
![]() $v \in F(x_i)$
,
$v \in F(x_i)$
,
In particular,
![]() $F\prec _{\ell } E$
for
$F\prec _{\ell } E$
for
![]() $Df^{-1}$
along the orbit
$Df^{-1}$
along the orbit
![]() $(x_i)_i$
and, similarly,
$(x_i)_i$
and, similarly,
![]() $H\prec _{\ell } E$
for
$H\prec _{\ell } E$
for
![]() $Df^{-1}$
. Therefore, applying Corollary 2.8, one concludes that
$Df^{-1}$
. Therefore, applying Corollary 2.8, one concludes that
![]() $F(x_i)=H(x_i)$
since
$F(x_i)=H(x_i)$
since
![]() ${\dim F=\dim H}$
.
${\dim F=\dim H}$
.
In the general case, for a non-zero vector
![]() $u \in F(x_i)$
, one deduces that there are two vectors
$u \in F(x_i)$
, one deduces that there are two vectors
![]() $w \in E(x_i)$
and
$w \in E(x_i)$
and
![]() $v \in H(x_i)$
, with
$v \in H(x_i)$
, with
![]() $v\neq 0$
, such that
$v\neq 0$
, such that
![]() $u=w+v$
. Assume without loss of generality that
$u=w+v$
. Assume without loss of generality that
![]() $i=0$
. Then, using that
$i=0$
. Then, using that
![]() $Df\mid _F$
and
$Df\mid _F$
and
![]() $Df\mid _H$
are isomorphisms, we can find the sequences
$Df\mid _H$
are isomorphisms, we can find the sequences
![]() $(u_j)_{j\leq 0}\subseteq F\backslash \{0\}, \, (w_i)_{j\leq 0} \subseteq E$
, and
$(u_j)_{j\leq 0}\subseteq F\backslash \{0\}, \, (w_i)_{j\leq 0} \subseteq E$
, and
![]() $(v_j)_{j\leq 0} \subseteq H\backslash \{0\}$
such that
$(v_j)_{j\leq 0} \subseteq H\backslash \{0\}$
such that
![]() ${u_j=w_j+v_j}$
and
${u_j=w_j+v_j}$
and
![]() $Df(u_{j-1})=u_j$
. Note that if
$Df(u_{j-1})=u_j$
. Note that if
![]() $Df^m(w_{j-1})=0$
, for some
$Df^m(w_{j-1})=0$
, for some
![]() $1\leq m\leq |j|$
, there is nothing to be proved since it directly implies that
$1\leq m\leq |j|$
, there is nothing to be proved since it directly implies that
![]() $u \in H(x_j)$
. Hence, we can assume that
$u \in H(x_j)$
. Hence, we can assume that
![]() $Df(\ast _{i-1})=\ast _i$
, where
$Df(\ast _{i-1})=\ast _i$
, where
![]() $\ast =u,v,\text { and }w$
and
$\ast =u,v,\text { and }w$
and
![]() $\ast _0=\ast $
.
$\ast _0=\ast $
.
Denote
![]() $V_i=\mathrm {span}\{w_i,v_i\}$
as the span of
$V_i=\mathrm {span}\{w_i,v_i\}$
as the span of
![]() $w_i,v_i$
; and define
$w_i,v_i$
; and define
![]() $A_i:V_{i-1} \to V_i$
as the restriction of
$A_i:V_{i-1} \to V_i$
as the restriction of
![]() $Df_{x_{i-1}}$
to
$Df_{x_{i-1}}$
to
![]() $V_{i-1}$
for each
$V_{i-1}$
for each
![]() $i\leq 0$
. Observe that defining
$i\leq 0$
. Observe that defining
![]() $A_i^n:V_i \to V_{i+n}$
by
$A_i^n:V_i \to V_{i+n}$
by
![]() $A_i^n=A_{i+n}^{-1}\cdots A_i^{- 1}$
for every
$A_i^n=A_{i+n}^{-1}\cdots A_i^{- 1}$
for every
![]() $n \leq 0$
, we can repeat the previous arguments to show that
$n \leq 0$
, we can repeat the previous arguments to show that
![]() $V_i$
admits two dominated splittings for
$V_i$
admits two dominated splittings for
![]() $A_i^{-1}$
, which are
$A_i^{-1}$
, which are
![]() $V_i=\mathrm {span}\{u_i\}\oplus \mathrm {span}\{w_i\}$
with
$V_i=\mathrm {span}\{u_i\}\oplus \mathrm {span}\{w_i\}$
with
![]() $\mathrm {span}\{u_i\}\prec _{\ell } \mathrm {span}\{w_i\}$
, and
$\mathrm {span}\{u_i\}\prec _{\ell } \mathrm {span}\{w_i\}$
, and
![]() $V_i=\mathrm {span}\{v_i\}\oplus \mathrm {span}\{w_i\}$
with
$V_i=\mathrm {span}\{v_i\}\oplus \mathrm {span}\{w_i\}$
with
![]() $\mathrm {span}\{v_i\}\prec _{\ell } \mathrm {span}\{w_i\}$
since
$\mathrm {span}\{v_i\}\prec _{\ell } \mathrm {span}\{w_i\}$
since
![]() $u_i \in V_i$
and the following holds:
$u_i \in V_i$
and the following holds:
 $$ \begin{align*}&\|A_i{\mid}_{\mathrm{span}\{w_i\}}{\kern-1.5pt}\|\leq \|Df{\mid}_{E}{\kern-1.5pt}\|, \ \|A_i{\mid}_{\mathrm{span}\{u_i\}}{\kern-1.5pt}\|\geq \operatorname{{\mathfrak{m}}}(Df{\mid}_{F}), \quad \text{and}\\ &\qquad\qquad\qquad\ \ \|A_i{\mid}_{\mathrm{span}\{v_i\}}{\kern-1.5pt}\|\geq \operatorname{{\mathfrak{m}}}(Df{\mid}_{H}).\end{align*} $$
$$ \begin{align*}&\|A_i{\mid}_{\mathrm{span}\{w_i\}}{\kern-1.5pt}\|\leq \|Df{\mid}_{E}{\kern-1.5pt}\|, \ \|A_i{\mid}_{\mathrm{span}\{u_i\}}{\kern-1.5pt}\|\geq \operatorname{{\mathfrak{m}}}(Df{\mid}_{F}), \quad \text{and}\\ &\qquad\qquad\qquad\ \ \|A_i{\mid}_{\mathrm{span}\{v_i\}}{\kern-1.5pt}\|\geq \operatorname{{\mathfrak{m}}}(Df{\mid}_{H}).\end{align*} $$
Therefore, we repeat the argument in the proof of Lemma 2.7 to get that
![]() $v_0$
and
$v_0$
and
![]() $u_0$
are parallel. This completes the proof.
$u_0$
are parallel. This completes the proof.
We can use the uniqueness of the dominated splitting to show the continuity and extend it to the closure.
Proposition 2.10. The subbundles E and F depend continuously with the point
![]() ${(x_i)_i \in \Lambda }$
and the closure
${(x_i)_i \in \Lambda }$
and the closure
![]() $\overline {\Lambda }$
in
$\overline {\Lambda }$
in
![]() $M_f$
admits a dominated splitting which coincides with
$M_f$
admits a dominated splitting which coincides with
![]() $E\oplus F$
in
$E\oplus F$
in
![]() $\Lambda $
. (Continuity means that when considering local coordinates so that the tangent bundle becomes trivial, the bundles depend on the point continuously as subspaces of
$\Lambda $
. (Continuity means that when considering local coordinates so that the tangent bundle becomes trivial, the bundles depend on the point continuously as subspaces of
![]() $\mathbb {R}^d$
.)
$\mathbb {R}^d$
.)
Proof. The proof is a standard argument once we have shown the uniqueness of the dominated splitting and the uniformity of the angle. This can be found in [Reference Crovisier and Potrie10].
Remark 2.11. It is well known and follows from the proof of uniqueness that if
![]() $E\oplus F$
is a dominated splitting, then the subbundle E only depends on the forward orbits. That is, for all points
$E\oplus F$
is a dominated splitting, then the subbundle E only depends on the forward orbits. That is, for all points
![]() $(x_i)_i$
and
$(x_i)_i$
and
![]() $(y_i)_i$
in
$(y_i)_i$
in
![]() $\Lambda $
, one has that
$\Lambda $
, one has that
In particular, by Propositions 2.6 and 2.10 together with (2.5), the subbundle E of
![]() $TM_f$
induces an invariant continuous subbundle of
$TM_f$
induces an invariant continuous subbundle of
![]() $TM$
which will also be denoted by E.
$TM$
which will also be denoted by E.
2.2 Cone criterion
In this section, we will show that the existence of dominated splitting for endomorphisms displaying critical points can also be characterized in terms of cone fields as well as in the diffeomorphisms context.
A cone-field
![]() $\mathscr {C}$
of dimension k on M is a continuous family of convex closed non-vanishing cones
$\mathscr {C}$
of dimension k on M is a continuous family of convex closed non-vanishing cones
![]() $\mathscr {C}(x)$
in
$\mathscr {C}(x)$
in
![]() $T_xM$
such that the subspaces of maximal dimension inside of
$T_xM$
such that the subspaces of maximal dimension inside of
![]() $\mathscr {C}(x)$
are k-dimensional. The closure of the complement of
$\mathscr {C}(x)$
are k-dimensional. The closure of the complement of
![]() $\mathscr {C}(x)$
in
$\mathscr {C}(x)$
in
![]() $T_xM$
is a cone of dimension
$T_xM$
is a cone of dimension
![]() $d-k$
, called a dual cone at x and denoted by
$d-k$
, called a dual cone at x and denoted by
![]() $\mathscr {C}^{\kern2pt\ast }(x)$
. We will call a dual cone-field of
$\mathscr {C}^{\kern2pt\ast }(x)$
. We will call a dual cone-field of
![]() $\mathscr {C}$
the family
$\mathscr {C}$
the family
![]() $\mathscr {C}^{\kern2pt\ast }=\{\mathscr {C}^{\kern2pt\ast }(x):x \in M\}$
. We say that a cone-field
$\mathscr {C}^{\kern2pt\ast }=\{\mathscr {C}^{\kern2pt\ast }(x):x \in M\}$
. We say that a cone-field
![]() $\mathscr {C}$
is invariant by an endomorphism f if there is an integer
$\mathscr {C}$
is invariant by an endomorphism f if there is an integer
![]() $\ell>0$
such that
$\ell>0$
such that
![]() $Df^{\ell }(\mathscr {C}(x))$
is contained in
$Df^{\ell }(\mathscr {C}(x))$
is contained in
![]() $\mathrm {int}(\mathscr {C}(f^{\ell }(x)))\cup \{0\}$
, where
$\mathrm {int}(\mathscr {C}(f^{\ell }(x)))\cup \{0\}$
, where
![]() $\mathrm {int}(\mathscr {C}(x))$
denotes the interior of
$\mathrm {int}(\mathscr {C}(x))$
denotes the interior of
![]() $\mathscr {C}(x)$
in
$\mathscr {C}(x)$
in
![]() $T_xM$
. We also can say that
$T_xM$
. We also can say that
![]() $\mathscr {C}$
is
$\mathscr {C}$
is
![]() $\ell $
-invariant if we want to emphasize the role of
$\ell $
-invariant if we want to emphasize the role of
![]() $\ell $
.
$\ell $
.
We next state an equivalent notion of dominated splitting for endomorphisms
![]() ${f:M\to M}$
exhibiting critical points.
${f:M\to M}$
exhibiting critical points.
Proposition 2.12. Let
![]() $E\oplus F$
be a dominated splitting for f with
$E\oplus F$
be a dominated splitting for f with
![]() $\kappa =\dim E$
. Then there is a
$\kappa =\dim E$
. Then there is a
![]() $(d-\kappa )$
-dimensional invariant cone-field
$(d-\kappa )$
-dimensional invariant cone-field
![]() $\mathscr {C}$
such that
$\mathscr {C}$
such that
![]() $E(x)\cap \mathscr {C}(x)=\{0\}$
for each
$E(x)\cap \mathscr {C}(x)=\{0\}$
for each
![]() $x \in M$
.
$x \in M$
.
In the proof, we will first define the cone-field, and then will prove that it is invariant and transversal to the kernel.
By Remark 2.11, E is an invariant continuous subbundle of
![]() $TM$
and, by Remark 2.4, we have that
$TM$
and, by Remark 2.4, we have that
![]() $\ker (Df^n_x)$
is contained in
$\ker (Df^n_x)$
is contained in
![]() $E(x)$
for all
$E(x)$
for all
![]() $x \in M$
. Then, for every
$x \in M$
. Then, for every
![]() $x \in M$
, we can define a cone-field
$x \in M$
, we can define a cone-field
![]() $\mathscr {C}_{E}$
on M of dimension
$\mathscr {C}_{E}$
on M of dimension
![]() $\kappa $
and length
$\kappa $
and length
![]() $\eta>0$
by
$\eta>0$
by
Note that
![]() $u=(u_1,u_2) \in E(x)\oplus E^{\perp }(x)$
satisfies that
$u=(u_1,u_2) \in E(x)\oplus E^{\perp }(x)$
satisfies that
then, using that cosine is decreasing on
![]() $[0,\pi /2]$
, the cone-field can be rewritten as
$[0,\pi /2]$
, the cone-field can be rewritten as
From now on, since
![]() $\arctan : (0,+\infty ) \to (0,\pi /2)$
is a homeomorphism preserving the orientation, we will make an abuse of notation rewriting, for each
$\arctan : (0,+\infty ) \to (0,\pi /2)$
is a homeomorphism preserving the orientation, we will make an abuse of notation rewriting, for each
![]() $\eta \in (0,\pi /2)$
,
$\eta \in (0,\pi /2)$
,
Recall that the dual cone-field of
![]() $\mathscr {C}_{E}(x,\eta )$
is the closure of
$\mathscr {C}_{E}(x,\eta )$
is the closure of
![]() $T_xM\backslash \mathscr {C}_{E}(x,\eta )$
which is a
$T_xM\backslash \mathscr {C}_{E}(x,\eta )$
which is a
![]() $(d-\kappa )$
-dimensional cone-field and will be written as
$(d-\kappa )$
-dimensional cone-field and will be written as
It is clear that
![]() $E(x) \subseteq \mathscr {C}_E(x,\eta )$
for each
$E(x) \subseteq \mathscr {C}_E(x,\eta )$
for each
![]() $x \in M$
and
$x \in M$
and
![]() $\eta \in (0,\pi /2)$
. Thus, we can conclude that
$\eta \in (0,\pi /2)$
. Thus, we can conclude that
![]() $\ker (Df_x^n)\cap \mathscr {C}_E^{\kern2pt\ast }(x,\eta )=\{0\}$
for each
$\ker (Df_x^n)\cap \mathscr {C}_E^{\kern2pt\ast }(x,\eta )=\{0\}$
for each
![]() $x \in M$
and
$x \in M$
and
![]() $n\geq 1$
, since
$n\geq 1$
, since
![]() ${\ker (Df_x^n) \subseteq E(x)}$
.
${\ker (Df_x^n) \subseteq E(x)}$
.
Therefore, to conclude the proof of Proposition 2.12, we state the following.
Claim. There is
![]() $\alpha>0$
such that the dual cone-field
$\alpha>0$
such that the dual cone-field
![]() $\mathscr {C}_E^{\kern2pt\ast }=\{\mathscr {C}_E^{\kern2pt\ast }(x,\alpha ):x\in M\}$
is invariant.
$\mathscr {C}_E^{\kern2pt\ast }=\{\mathscr {C}_E^{\kern2pt\ast }(x,\alpha ):x\in M\}$
is invariant.
Indeed, since the angle between E and F is bounded away from zero, there is a number
![]() $\alpha>0$
small enough satisfying
$\alpha>0$
small enough satisfying ![]() , for each
, for each
![]() $i \in \mathbb {Z}$
in all the orbit
$i \in \mathbb {Z}$
in all the orbit
![]() $(x_i)_i$
. In particular, we have that the direction
$(x_i)_i$
. In particular, we have that the direction
![]() $F(x_0)$
associated to any orbit
$F(x_0)$
associated to any orbit
![]() $(x_i)_i$
with
$(x_i)_i$
with
![]() $x_0=x$
is contained in
$x_0=x$
is contained in
![]() $\mathscr {C}_E^{\kern2pt\ast }(x,\alpha )$
. Moreover, there is a constant
$\mathscr {C}_E^{\kern2pt\ast }(x,\alpha )$
. Moreover, there is a constant
![]() $c>0$
(depending only on
$c>0$
(depending only on
![]() $\alpha $
) such that any decomposition of a vector
$\alpha $
) such that any decomposition of a vector
![]() $w \in \mathscr {C}_E^{\kern2pt\ast }(x,\alpha )$
as
$w \in \mathscr {C}_E^{\kern2pt\ast }(x,\alpha )$
as
![]() $w=w_E+w_F$
with
$w=w_E+w_F$
with
![]() $w_E \in E(x)$
and
$w_E \in E(x)$
and
![]() $w_F$
in direction F at x satisfies
$w_F$
in direction F at x satisfies
![]() $\|w_F\|\geq c\|w_E\|$
. Otherwise, w cannot belong to
$\|w_F\|\geq c\|w_E\|$
. Otherwise, w cannot belong to
![]() $\mathscr {C}_E^{\kern2pt\ast }(x,\alpha )$
. Thus, we obtain that
$\mathscr {C}_E^{\kern2pt\ast }(x,\alpha )$
. Thus, we obtain that
 $$ \begin{align*} \|Df^{k\ell}(w_E)\|&\leq \|Df^{k\ell}\!\mid_{E}\!\|\|w_E\|\leq\big(\tfrac{1}{2}\big)^k\operatorname{{\mathfrak{m}}}(Df^{k\ell}\!\mid_{F})\|w_E\|\\ &\leq \big(\tfrac{1}{2}\big)^k \|Df^{k\ell}(w_F)\|\dfrac{\|w_E\|}{\|w_F\|}\leq \big(\tfrac{1}{2}\big)^k c^{-1} \|Df^{k\ell}(w_F)\| \end{align*} $$
$$ \begin{align*} \|Df^{k\ell}(w_E)\|&\leq \|Df^{k\ell}\!\mid_{E}\!\|\|w_E\|\leq\big(\tfrac{1}{2}\big)^k\operatorname{{\mathfrak{m}}}(Df^{k\ell}\!\mid_{F})\|w_E\|\\ &\leq \big(\tfrac{1}{2}\big)^k \|Df^{k\ell}(w_F)\|\dfrac{\|w_E\|}{\|w_F\|}\leq \big(\tfrac{1}{2}\big)^k c^{-1} \|Df^{k\ell}(w_F)\| \end{align*} $$
and hence, we can take
![]() $k>0$
large enough such that
$k>0$
large enough such that
![]() $\mathscr {C}_E^{\kern2pt\ast }(x,\alpha )$
is k-invariant for every
$\mathscr {C}_E^{\kern2pt\ast }(x,\alpha )$
is k-invariant for every
![]() $x \in M$
. Taking
$x \in M$
. Taking
![]() $\mathscr {C}$
as the dual cone-field
$\mathscr {C}$
as the dual cone-field
![]() $\mathscr {C}_E^{\kern2pt\ast }$
, we conclude the proof.
$\mathscr {C}_E^{\kern2pt\ast }$
, we conclude the proof.
Conversely, we will show that the existence of an invariant cone-field transversal to the kernel is sufficient to get a dominated splitting. More precisely, we state the following.
Proposition 2.13. If
![]() $\mathscr {C}$
is an invariant
$\mathscr {C}$
is an invariant
![]() $(d-\kappa )$
-dimensional cone-field by f such that
$(d-\kappa )$
-dimensional cone-field by f such that
![]() $\ker (Df_x^n)\cap \mathscr {C}(x)=\{0\}$
for each
$\ker (Df_x^n)\cap \mathscr {C}(x)=\{0\}$
for each
![]() $x \in M$
and
$x \in M$
and
![]() $n\geq 1$
, then there exist two non-trivial subbundles E and F on
$n\geq 1$
, then there exist two non-trivial subbundles E and F on
![]() $M_f$
such that
$M_f$
such that
![]() $E\oplus F$
is a dominated splitting for f, where E is
$E\oplus F$
is a dominated splitting for f, where E is
![]() $\kappa $
-dimensional.
$\kappa $
-dimensional.
To prove Proposition 2.13, some preliminaries are needed. For a linear transformation
![]() $\Phi : V \to W$
, where V and W are d-dimensional vector spaces with an inner product, we denote by
$\Phi : V \to W$
, where V and W are d-dimensional vector spaces with an inner product, we denote by
![]() $\Phi ^{\ast }:W \to V$
its adjoint. It is well known that if the kernel of
$\Phi ^{\ast }:W \to V$
its adjoint. It is well known that if the kernel of
![]() $\Phi $
is r-dimensional, then there are
$\Phi $
is r-dimensional, then there are
![]() $\{v_1,\ldots ,v_d\}$
and
$\{v_1,\ldots ,v_d\}$
and
![]() $\{w_1,\ldots ,w_d\}$
orthonormal bases of V and W, respectively, such that
$\{w_1,\ldots ,w_d\}$
orthonormal bases of V and W, respectively, such that
![]() $\Phi (v_i)=0,\ \ \Phi ^{\ast }(w_i)=0$
for each
$\Phi (v_i)=0,\ \ \Phi ^{\ast }(w_i)=0$
for each
![]() $1\leq i \leq r$
; and
$1\leq i \leq r$
; and
![]() $\Phi (v_i)=\sigma _i w_i, \ \ \Phi ^{\ast }(w_i)=\sigma _i v_i$
with
$\Phi (v_i)=\sigma _i w_i, \ \ \Phi ^{\ast }(w_i)=\sigma _i v_i$
with
![]() $\sigma _i>0$
for each
$\sigma _i>0$
for each
![]() $r<i\leq d$
. Moreover, we have that
$r<i\leq d$
. Moreover, we have that
![]() $\sigma _i=\|\Phi (v_i)\|=\|\Phi ^{\ast }(w_i)\|$
for each
$\sigma _i=\|\Phi (v_i)\|=\|\Phi ^{\ast }(w_i)\|$
for each
![]() $i=1,\ldots ,d$
.
$i=1,\ldots ,d$
.
We call the
![]() $\sigma _i$
terms the singular values of
$\sigma _i$
terms the singular values of
![]() $\Phi $
. Note that the singular values of
$\Phi $
. Note that the singular values of
![]() $\Phi $
are the eigenvalues of
$\Phi $
are the eigenvalues of
![]() $\sqrt {\Phi ^{\ast }\Phi }$
associated to the eigenvectors
$\sqrt {\Phi ^{\ast }\Phi }$
associated to the eigenvectors
![]() $v_i$
, and we will order them as the following:
$v_i$
, and we will order them as the following:
When the kernel of
![]() $\Phi $
is trivial (that is,
$\Phi $
is trivial (that is,
![]() $r=0$
), we have
$r=0$
), we have
![]() $0<\sigma _1\leq \sigma _2 \leq \cdots \leq \sigma _d$
.
$0<\sigma _1\leq \sigma _2 \leq \cdots \leq \sigma _d$
.
Note that the
![]() $\sigma _i$
terms are also the singular values of
$\sigma _i$
terms are also the singular values of
![]() $\Phi ^{\ast }$
. Moreover, the singular values are typically ordered from largest to smallest, but we are taking the opposite convention. For more information, see [Reference Horn and Johnson13, Theorem 7.3.2].
$\Phi ^{\ast }$
. Moreover, the singular values are typically ordered from largest to smallest, but we are taking the opposite convention. For more information, see [Reference Horn and Johnson13, Theorem 7.3.2].
We would also like to introduce a useful ‘minimax’ characterization of the singular values, which appears in [Reference Bochi, Potrie and Sambarino6, Appendix A]:
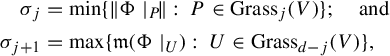 $$ \begin{align} \begin{split} \sigma_{j}&=\min\{\|\Phi\mid_{P}\!\!\|: \, P \in \mathrm{Grass}_j(V)\}; \quad \text{and} \\ \sigma_{j+1}&=\max\{\operatorname{{\mathfrak{m}}}(\Phi\mid_{U}): \, U \in \mathrm{Grass}_{d-j}(V)\}, \end{split} \end{align} $$
$$ \begin{align} \begin{split} \sigma_{j}&=\min\{\|\Phi\mid_{P}\!\!\|: \, P \in \mathrm{Grass}_j(V)\}; \quad \text{and} \\ \sigma_{j+1}&=\max\{\operatorname{{\mathfrak{m}}}(\Phi\mid_{U}): \, U \in \mathrm{Grass}_{d-j}(V)\}, \end{split} \end{align} $$
where
![]() $\mathrm {Grass}_r(V)$
denotes the r-dimensional Grassmannian of V.
$\mathrm {Grass}_r(V)$
denotes the r-dimensional Grassmannian of V.
From now on, we denote by
![]() $\sigma _1(x,n)\leq \cdots \leq \sigma _d(x,n)$
the singular values of
$\sigma _1(x,n)\leq \cdots \leq \sigma _d(x,n)$
the singular values of
![]() $Df^n_x$
and by
$Df^n_x$
and by
![]() $\{e_1^n(x),e_2^n(x),\ldots ,e_d^n(x)\}$
an orthogonal basis of
$\{e_1^n(x),e_2^n(x),\ldots ,e_d^n(x)\}$
an orthogonal basis of
![]() $T_xM$
so that
$T_xM$
so that
![]() $\|Df^n(e_i^n(x))\|=\sigma _i(x,n)$
for all
$\|Df^n(e_i^n(x))\|=\sigma _i(x,n)$
for all
![]() $x\in M, \, n\geq 1$
and
$x\in M, \, n\geq 1$
and
![]() $1\leq i \leq d$
. To simplify notation, we omit the dependence on x and write
$1\leq i \leq d$
. To simplify notation, we omit the dependence on x and write
![]() $e_i$
instead of
$e_i$
instead of
![]() $e_i(x)$
.
$e_i(x)$
.
To prove Proposition 2.13, we define
![]() $E_n(x)$
as the subspace of
$E_n(x)$
as the subspace of
![]() $T_xM$
spanned by the vectors
$T_xM$
spanned by the vectors
![]() $e_i^n$
on the basis such that
$e_i^n$
on the basis such that
![]() $\|Df^n(e_i^n)\|=\sigma _i(x,n)< \sigma _{\kappa +1}(x,n)$
; and
$\|Df^n(e_i^n)\|=\sigma _i(x,n)< \sigma _{\kappa +1}(x,n)$
; and
![]() $E^{\perp }_n(x)$
as the orthogonal complement of
$E^{\perp }_n(x)$
as the orthogonal complement of
![]() $E_n(x)$
. It should be noted that
$E_n(x)$
. It should be noted that
![]() $E_n(x)$
is at most
$E_n(x)$
is at most
![]() $\kappa $
-dimensional and
$\kappa $
-dimensional and
![]() $E^{\perp }_n(x)$
is the fastest direction of
$E^{\perp }_n(x)$
is the fastest direction of
![]() $Df^n$
, which means that
$Df^n$
, which means that
![]() $\operatorname {{\mathfrak {m}}}(Df^n\!\mid _{E^{\perp }_n(x)})\geq \|Df^n(v)\|$
for every unit vector
$\operatorname {{\mathfrak {m}}}(Df^n\!\mid _{E^{\perp }_n(x)})\geq \|Df^n(v)\|$
for every unit vector
![]() $v \notin E^{\perp }_n(x)$
.
$v \notin E^{\perp }_n(x)$
.
Since the cone-field
![]() $\mathscr {C}$
is
$\mathscr {C}$
is
![]() $(d-\kappa )$
-dimensional and
$(d-\kappa )$
-dimensional and
![]() $\ker (Df_x^n)\cap \mathscr {C}(x)=\{0\}$
for each
$\ker (Df_x^n)\cap \mathscr {C}(x)=\{0\}$
for each
![]() ${x \in M}$
and
${x \in M}$
and
![]() $n\geq 1$
, we obtain that
$n\geq 1$
, we obtain that
![]() $\dim \ker (Df^n_x) \leq \kappa $
for each
$\dim \ker (Df^n_x) \leq \kappa $
for each
![]() $x \in M$
and
$x \in M$
and
![]() $n\geq 1$
. Otherwise, the intersection between
$n\geq 1$
. Otherwise, the intersection between
![]() $\ker (Df^n_x)$
and the cone
$\ker (Df^n_x)$
and the cone
![]() $\mathscr {C}(x)$
would be non-trivial. Moreover, as
$\mathscr {C}(x)$
would be non-trivial. Moreover, as
![]() $\dim \ker (Df^n_x)=r$
implies that
$\dim \ker (Df^n_x)=r$
implies that
![]() $\sigma _i(x,n)=0$
for each
$\sigma _i(x,n)=0$
for each
![]() $1\leq i\leq r$
, we can conclude that
$1\leq i\leq r$
, we can conclude that
![]() $\ker (Df^n_x)$
is contained in
$\ker (Df^n_x)$
is contained in
![]() $E_n(x)$
.
$E_n(x)$
.
We will prove that for all
![]() $n\geq 1$
, the subspaces
$n\geq 1$
, the subspaces
![]() $E_n(x)$
are
$E_n(x)$
are
![]() $\kappa $
-dimensional, implying that they are in
$\kappa $
-dimensional, implying that they are in
![]() $\mathrm {Grass}_{\kappa }(T_xM)$
. After that, we will show that the family
$\mathrm {Grass}_{\kappa }(T_xM)$
. After that, we will show that the family
![]() $(E_n)_n$
is a Cauchy sequence and, recalling that
$(E_n)_n$
is a Cauchy sequence and, recalling that
![]() $\mathrm {Grass}_{\kappa }(T_xM)$
is a compact space with the usual distance (2.4), we will get the limit
$\mathrm {Grass}_{\kappa }(T_xM)$
is a compact space with the usual distance (2.4), we will get the limit
![]() $E(x)$
for each
$E(x)$
for each
![]() $x \in M$
. Finally, we will prove that E is
$x \in M$
. Finally, we will prove that E is
![]() $Df$
-invariant.
$Df$
-invariant.
Note that the subspace
![]() $E(x)$
which is limit of
$E(x)$
which is limit of
![]() $E_n(x)$
satisfies that
$E_n(x)$
satisfies that
![]() $\ker (Df^n_x) \subseteq E(x)$
for each
$\ker (Df^n_x) \subseteq E(x)$
for each
![]() $n\geq 1$
. Indeed, since
$n\geq 1$
. Indeed, since
![]() $\ker (Df^n_x) \subseteq E_n(x)$
and
$\ker (Df^n_x) \subseteq E_n(x)$
and
![]() $\ker (Df^j_x) \subseteq \ker (Df^{j+1}_x)$
, we have that
$\ker (Df^j_x) \subseteq \ker (Df^{j+1}_x)$
, we have that
![]() $\ker (Df^j_x) \subseteq E_n(x)$
for each
$\ker (Df^j_x) \subseteq E_n(x)$
for each
![]() $1\leq j \leq n$
and, then, we get that
$1\leq j \leq n$
and, then, we get that
![]() $\ker (Df^j_x) \subseteq E(x)$
for each
$\ker (Df^j_x) \subseteq E(x)$
for each
![]() $j\geq 1$
.
$j\geq 1$
.
To define the direction F, we observe that the assumptions
for each
![]() $x \in M$
and each
$x \in M$
and each
![]() $n\geq 1$
, allow us to claim the following, for which the proof can be found in [Reference Crovisier and Potrie10].
$n\geq 1$
, allow us to claim the following, for which the proof can be found in [Reference Crovisier and Potrie10].
Claim 1. For each orbit
![]() $(x_i)_i$
, there is a
$(x_i)_i$
, there is a
![]() $(d-\kappa )$
-dimensional subbundle F defined by
$(d-\kappa )$
-dimensional subbundle F defined by
Moreover, it is contained in
![]() $\mathrm {int}(\mathscr {C}(x_i))$
and is also
$\mathrm {int}(\mathscr {C}(x_i))$
and is also
![]() $Df^\ell $
-invariant.
$Df^\ell $
-invariant.
To complete the proof of Proposition 2.13, we will prove that the subbundle E is transversal to the cone-field, implying that
![]() $E\cap F=\{0\}$
; and, finally, we will show that
$E\cap F=\{0\}$
; and, finally, we will show that
![]() $E\prec F$
.
$E\prec F$
.
These arguments will be divided into a series of lemmas. Before stating the first one, we need to introduce some notation.
Since the subbundle F, as in Claim 1, is in the cone-field
![]() $\mathscr {C}$
away from the boundary, we can choose
$\mathscr {C}$
away from the boundary, we can choose
![]() $\delta _0>0$
small enough such that for every orbit
$\delta _0>0$
small enough such that for every orbit
![]() $(x_i)_i$
, the family of
$(x_i)_i$
, the family of
![]() $(d-\kappa )$
-dimensional cones
$(d-\kappa )$
-dimensional cones
![]() $\{\mathcal {K}(x_i,\delta _0):i \in \mathbb {Z}\}$
,
$\{\mathcal {K}(x_i,\delta _0):i \in \mathbb {Z}\}$
,
satisfies that
![]() $\mathcal {K}(x_i,\delta _0)$
is contained in the interior of
$\mathcal {K}(x_i,\delta _0)$
is contained in the interior of
![]() $\mathscr {C}(x_i)$
for each
$\mathscr {C}(x_i)$
for each
![]() $i \in \mathbb {Z}$
.
$i \in \mathbb {Z}$
.
We are getting this alternative family of cones because that family is centered in the direction F along the orbit
![]() $(x_i)_i$
, which does not necessarily happen for the cone-field
$(x_i)_i$
, which does not necessarily happen for the cone-field
![]() $\mathscr {C}$
, and this will be useful to make the computation.
$\mathscr {C}$
, and this will be useful to make the computation.
Now, we state the first lemma toward the proof of Proposition 2.13. Roughly speaking, the lemma guarantees that the directions out of the cone
![]() $\mathcal {K}(x_i,\delta )$
are dominated by the direction F.
$\mathcal {K}(x_i,\delta )$
are dominated by the direction F.
Lemma 2.14. For every
![]() $0<\delta <\delta _0$
and
$0<\delta <\delta _0$
and
![]() $\varepsilon>0$
small enough, there is an integer
$\varepsilon>0$
small enough, there is an integer
![]() $N>0$
such that every orbit
$N>0$
such that every orbit
![]() $(x_i)_i$
holds
$(x_i)_i$
holds
Moreover, for every
![]() $0<\unicode{x3bb} <1$
and every
$0<\unicode{x3bb} <1$
and every
![]() $0<\delta <\delta _0$
small enough, we can choose
$0<\delta <\delta _0$
small enough, we can choose
![]() $N>0$
such that if
$N>0$
such that if
![]() $w \notin \mathcal {K}(x_i,\delta )$
with
$w \notin \mathcal {K}(x_i,\delta )$
with
![]() $\|w\|=1$
, then at least one of the following holds:
$\|w\|=1$
, then at least one of the following holds:
-
(i)
 $Df^{N\ell }(w) \in \mathcal {K}(x_{i+N\ell },\delta )$
; or
$Df^{N\ell }(w) \in \mathcal {K}(x_{i+N\ell },\delta )$
; or -
(ii)
 $\|Df^{N\ell }(w)\|\leq \unicode{x3bb} \operatorname {{\mathfrak {m}}}(Df^{N\ell }\!\mid _{F(x_i)})$
.
$\|Df^{N\ell }(w)\|\leq \unicode{x3bb} \operatorname {{\mathfrak {m}}}(Df^{N\ell }\!\mid _{F(x_i)})$
.
Proof. Since
![]() $\mathcal {K}(x_i,\delta ) \subseteq \mathscr {C}(x_i)$
along the orbit
$\mathcal {K}(x_i,\delta ) \subseteq \mathscr {C}(x_i)$
along the orbit
![]() $(x_i)_i$
and by the definition of F, we have that for every
$(x_i)_i$
and by the definition of F, we have that for every
![]() $0<\varepsilon <\delta $
, there is a large number
$0<\varepsilon <\delta $
, there is a large number
![]() $N>0$
such that
$N>0$
such that
for each
![]() $i \in \mathbb {Z}$
. This proves the first part of the lemma.
$i \in \mathbb {Z}$
. This proves the first part of the lemma.
To prove the second part, let us fix any
![]() $\varepsilon $
where
$\varepsilon $
where
![]() $0<\varepsilon <({\delta }/({1+\delta }))({\delta \unicode{x3bb} }/ ({1+\delta \unicode{x3bb} }))$
and
$0<\varepsilon <({\delta }/({1+\delta }))({\delta \unicode{x3bb} }/ ({1+\delta \unicode{x3bb} }))$
and
![]() $N>0$
satisfying (2.10). We suppose by contradiction that there is a unit vector
$N>0$
satisfying (2.10). We suppose by contradiction that there is a unit vector
![]() $w \notin \mathcal {K}(x_i,\delta )$
such that
$w \notin \mathcal {K}(x_i,\delta )$
such that
Then, we will prove that (2.10) does not happen, contradicting the first part of the lemma.
Indeed, write
![]() $Df^{N\ell }(w)=au_1+bv_1$
, where
$Df^{N\ell }(w)=au_1+bv_1$
, where
![]() $u_1 \in F^{\perp }(x_{i+N\ell })$
and
$u_1 \in F^{\perp }(x_{i+N\ell })$
and
![]() $v_1 \in F(x_{i + N\ell })$
are unit vectors such that
$v_1 \in F(x_{i + N\ell })$
are unit vectors such that
![]() $|a|\geq \delta |b|$
. Then, we can bound
$|a|\geq \delta |b|$
. Then, we can bound
![]() $|a|$
from below and
$|a|$
from below and
![]() $|b|$
from above as follows:
$|b|$
from above as follows:
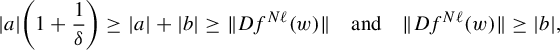 $$ \begin{align*}|a|\bigg(1+\dfrac{1}{\delta}\bigg)\geq|a|+|b|\geq \|Df^{ N\ell}(w)\| \quad \text{and} \quad \|Df^{ N\ell}(w)\|\geq |b|,\end{align*} $$
$$ \begin{align*}|a|\bigg(1+\dfrac{1}{\delta}\bigg)\geq|a|+|b|\geq \|Df^{ N\ell}(w)\| \quad \text{and} \quad \|Df^{ N\ell}(w)\|\geq |b|,\end{align*} $$
which gives
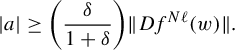 $$ \begin{align*}|a| \geq \bigg(\dfrac{\delta}{1+\delta}\bigg) \|Df^{ N\ell}(w)\|.\end{align*} $$
$$ \begin{align*}|a| \geq \bigg(\dfrac{\delta}{1+\delta}\bigg) \|Df^{ N\ell}(w)\|.\end{align*} $$
Take a unit vector
![]() $v \in F(x_i)$
satisfying
$v \in F(x_i)$
satisfying
![]() $\|Df^{N\ell }(v)\|=\operatorname {{\mathfrak {m}}}(Df^{N\ell }\!\mid _{F(x_i)})$
and choose a number
$\|Df^{N\ell }(v)\|=\operatorname {{\mathfrak {m}}}(Df^{N\ell }\!\mid _{F(x_i)})$
and choose a number
![]() $c \in \mathbb {R}$
such that
$c \in \mathbb {R}$
such that
![]() $w'=cw+v$
belongs to the boundary of
$w'=cw+v$
belongs to the boundary of
![]() $\mathcal {K}(x_i,\delta )$
, which is contained in
$\mathcal {K}(x_i,\delta )$
, which is contained in
![]() $\mathscr {C}(x_i)$
. Note that the constant c satisfies
$\mathscr {C}(x_i)$
. Note that the constant c satisfies
![]() $|c|\geq \delta $
, since w is a unit vector out of the cone
$|c|\geq \delta $
, since w is a unit vector out of the cone
![]() $\mathcal {K}(x_i,\delta )$
and v is a unit vector in
$\mathcal {K}(x_i,\delta )$
and v is a unit vector in
![]() $F(x_i)$
.
$F(x_i)$
.
We now decompose
![]() $Df^{N\ell }(w')=ca u_1+ cbv_1+\operatorname {{\mathfrak {m}}}(Df^{N\ell }\!\mid _{F(x_i)})v_0$
, where
$Df^{N\ell }(w')=ca u_1+ cbv_1+\operatorname {{\mathfrak {m}}}(Df^{N\ell }\!\mid _{F(x_i)})v_0$
, where
![]() $v_0=Df^{N\ell }(v)/\|Df^{N\ell }(v)\| \in F(x_{i+N\ell })$
and then we can get that
$v_0=Df^{N\ell }(v)/\|Df^{N\ell }(v)\| \in F(x_{i+N\ell })$
and then we can get that
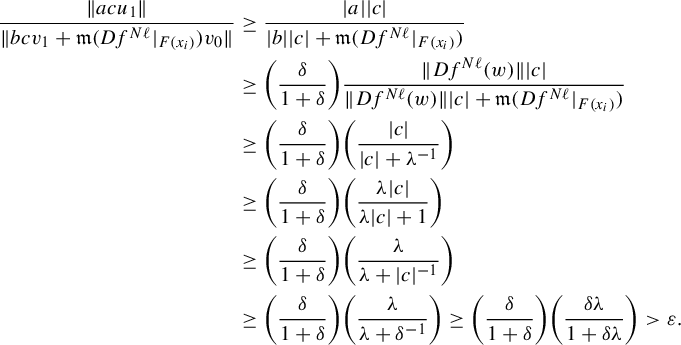 $$ \begin{align*} \dfrac{\|acu_1\|}{\|bcv_1+\operatorname{{\mathfrak{m}}}(Df^{N\ell}\!\mid_{F(x_i)})v_0\|}& \geq\dfrac{|a||c|}{|b||c|+\operatorname{{\mathfrak{m}}}(Df^{N\ell}\!\mid_{F(x_i)})}\\ &\geq\bigg(\dfrac{\delta}{1+\delta}\bigg) \dfrac{\|Df^{N\ell}(w)\||c|}{\|Df^{N\ell}(w)\||c|+\operatorname{{\mathfrak{m}}}(Df^{N\ell}\!\mid_{F(x_i)})}\\ &\geq \bigg(\dfrac{\delta}{1+\delta}\bigg)\bigg(\dfrac{|c|}{|c|+\unicode{x3bb}^{-1}}\bigg)\\ &\geq \bigg(\dfrac{\delta}{1+\delta}\bigg) \bigg(\dfrac{\unicode{x3bb}|c|}{\unicode{x3bb}|c|+1}\bigg)\\ &\geq \bigg(\dfrac{\delta}{1+\delta}\bigg) \bigg(\dfrac{\unicode{x3bb}}{\unicode{x3bb}+|c|^{-1}}\bigg)\\ & \geq \bigg(\dfrac{\delta}{1+\delta}\bigg) \bigg(\dfrac{\unicode{x3bb}}{\unicode{x3bb}+\delta^{-1}}\bigg) \geq \bigg(\dfrac{\delta}{1+\delta}\bigg)\bigg(\dfrac{\delta\unicode{x3bb}}{1+\delta\unicode{x3bb}}\bigg)>\varepsilon. \end{align*} $$
$$ \begin{align*} \dfrac{\|acu_1\|}{\|bcv_1+\operatorname{{\mathfrak{m}}}(Df^{N\ell}\!\mid_{F(x_i)})v_0\|}& \geq\dfrac{|a||c|}{|b||c|+\operatorname{{\mathfrak{m}}}(Df^{N\ell}\!\mid_{F(x_i)})}\\ &\geq\bigg(\dfrac{\delta}{1+\delta}\bigg) \dfrac{\|Df^{N\ell}(w)\||c|}{\|Df^{N\ell}(w)\||c|+\operatorname{{\mathfrak{m}}}(Df^{N\ell}\!\mid_{F(x_i)})}\\ &\geq \bigg(\dfrac{\delta}{1+\delta}\bigg)\bigg(\dfrac{|c|}{|c|+\unicode{x3bb}^{-1}}\bigg)\\ &\geq \bigg(\dfrac{\delta}{1+\delta}\bigg) \bigg(\dfrac{\unicode{x3bb}|c|}{\unicode{x3bb}|c|+1}\bigg)\\ &\geq \bigg(\dfrac{\delta}{1+\delta}\bigg) \bigg(\dfrac{\unicode{x3bb}}{\unicode{x3bb}+|c|^{-1}}\bigg)\\ & \geq \bigg(\dfrac{\delta}{1+\delta}\bigg) \bigg(\dfrac{\unicode{x3bb}}{\unicode{x3bb}+\delta^{-1}}\bigg) \geq \bigg(\dfrac{\delta}{1+\delta}\bigg)\bigg(\dfrac{\delta\unicode{x3bb}}{1+\delta\unicode{x3bb}}\bigg)>\varepsilon. \end{align*} $$
Therefore, we obtain that
![]() $Df^{N\ell }(w')$
does not belong to
$Df^{N\ell }(w')$
does not belong to
![]() $\mathcal {K}(x_{i+N\ell },\varepsilon )$
which contradicts (2.10) and therefore completes the proof of the lemma.
$\mathcal {K}(x_{i+N\ell },\varepsilon )$
which contradicts (2.10) and therefore completes the proof of the lemma.
From now on, we fix
![]() $\unicode{x3bb} , \delta $
, and
$\unicode{x3bb} , \delta $
, and
![]() $\varepsilon $
as in Lemma 2.14 and, to simplify notation, we will assume that
$\varepsilon $
as in Lemma 2.14 and, to simplify notation, we will assume that
![]() $N=1$
.
$N=1$
.
We will prove that there is an ‘exponential gap’ which means the quotient between
![]() $\sigma _{\kappa }(x,n)$
and
$\sigma _{\kappa }(x,n)$
and
![]() $\sigma _{\kappa +1}(x,n)$
decreases exponentially fast to zero. It will be useful to prove that
$\sigma _{\kappa +1}(x,n)$
decreases exponentially fast to zero. It will be useful to prove that
![]() $(E_n(x))_n$
is a Cauchy sequence.
$(E_n(x))_n$
is a Cauchy sequence.
Lemma 2.15. There is
![]() $c>0$
such that
$c>0$
such that
for all
![]() $x \in M$
and
$x \in M$
and
![]() $n\geq 1$
.
$n\geq 1$
.
Proof. We will first prove the lemma for n multiples of
![]() $\ell $
.
$\ell $
.
We will prove for an orbit
![]() $(x_i)_i$
that
$(x_i)_i$
that
for every
![]() $n\geq 1$
.
$n\geq 1$
.
Consider
![]() $P_0=E_{n\ell }(x_i)$
and
$P_0=E_{n\ell }(x_i)$
and
![]() $P_j=Df^{j\ell }(E_{n\ell }(x_i))$
for each
$P_j=Df^{j\ell }(E_{n\ell }(x_i))$
for each
![]() $1\leq j \leq n$
. We will first show that
$1\leq j \leq n$
. We will first show that
![]() $P_j \cap \mathcal {K}(x_{i+j\ell },\delta ) =\{0\}$
for each
$P_j \cap \mathcal {K}(x_{i+j\ell },\delta ) =\{0\}$
for each
![]() $0\leq j \leq n$
and, by invariance of the family
$0\leq j \leq n$
and, by invariance of the family
![]() $\{\mathcal {K}(x_i,\delta ):i \in \mathbb {Z}\}$
, it is enough to show this for
$\{\mathcal {K}(x_i,\delta ):i \in \mathbb {Z}\}$
, it is enough to show this for
![]() $P_n$
. Note that
$P_n$
. Note that
![]() $P_n$
is orthogonal to
$P_n$
is orthogonal to
![]() $Df^{n\ell }(E_{n\ell }^\perp (x_i))$
by definition and, since
$Df^{n\ell }(E_{n\ell }^\perp (x_i))$
by definition and, since
![]() $\dim E_{n\ell }^\perp (x_i)= \dim Df^{n\ell }(E_{n\ell }^\perp (x_i))$
is at least the dimension of the cone, it is enough to show that
$\dim E_{n\ell }^\perp (x_i)= \dim Df^{n\ell }(E_{n\ell }^\perp (x_i))$
is at least the dimension of the cone, it is enough to show that
![]() $Df^{n\ell }(E_{n\ell }^\perp (x_i)) \subset \mathcal {K}(x_{i+n\ell },\delta )$
. If this were not the case, we would find a unit vector
$Df^{n\ell }(E_{n\ell }^\perp (x_i)) \subset \mathcal {K}(x_{i+n\ell },\delta )$
. If this were not the case, we would find a unit vector
![]() $v \in E_{n\ell }^{\perp }(x)$
which does not belong to the cone
$v \in E_{n\ell }^{\perp }(x)$
which does not belong to the cone
![]() $\mathcal {K}(x_i,\delta )$
such that
$\mathcal {K}(x_i,\delta )$
such that
![]() $Df^{n\ell }(v)\notin \mathcal {K}(x_{i+n\ell },\delta )$
. We have that
$Df^{n\ell }(v)\notin \mathcal {K}(x_{i+n\ell },\delta )$
. We have that
![]() $\|Df^{n\ell }(v)\|\geq \sigma _{\kappa +1}(x_i,n\ell )\geq \operatorname {{\mathfrak {m}}}(Df^{n\ell }\mid _{F(x_i)})$
by definition of
$\|Df^{n\ell }(v)\|\geq \sigma _{\kappa +1}(x_i,n\ell )\geq \operatorname {{\mathfrak {m}}}(Df^{n\ell }\mid _{F(x_i)})$
by definition of
![]() $E_{n\ell }(x_i)^{\perp }$
. Then, a computation similar to that in Lemma 2.14 gives the contradiction that
$E_{n\ell }(x_i)^{\perp }$
. Then, a computation similar to that in Lemma 2.14 gives the contradiction that
![]() $Df^{n\ell }(\mathcal {K}(x_i,\delta ))$
is not contained in
$Df^{n\ell }(\mathcal {K}(x_i,\delta ))$
is not contained in
![]() $\mathcal {K}(x_{i+n\ell },\varepsilon ))$
.
$\mathcal {K}(x_{i+n\ell },\varepsilon ))$
.
To prove (2.11), we use the ‘minimax’ characterization in (2.9), which says
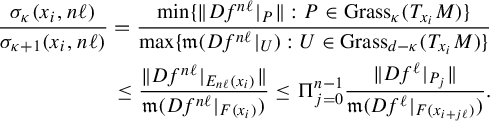 $$ \begin{align*} \dfrac{\sigma_{\kappa}(x_i,n\ell)} {\sigma_{\kappa+1}(x_i,n\ell)} =\dfrac{\min\{\|Df^{n\ell}\!\mid_{P}\!\|:P\in \mathrm{Grass}_{\kappa}(T_{x_{i}}M)\}} {\max\{\operatorname{{\mathfrak{m}}}(Df^{n\ell}\!\mid_{U}):U \in \mathrm{Grass}_{d-\kappa}(T_{x_{i}}M)\}}\\ \leq \dfrac{\|Df^{n\ell}\!\mid_{E_{n\ell}(x_{i})}\!\|} {\operatorname{{\mathfrak{m}}}(Df^{n\ell}\!\mid_{F(x_i)})}\leq \Pi_{j=0}^{n-1}\dfrac{\|Df^{\ell}\!\mid_{P_j}\!\|} {\operatorname{{\mathfrak{m}}}(Df^{\ell}\!\mid_{F(x_{i+j\ell})})}. \end{align*} $$
$$ \begin{align*} \dfrac{\sigma_{\kappa}(x_i,n\ell)} {\sigma_{\kappa+1}(x_i,n\ell)} =\dfrac{\min\{\|Df^{n\ell}\!\mid_{P}\!\|:P\in \mathrm{Grass}_{\kappa}(T_{x_{i}}M)\}} {\max\{\operatorname{{\mathfrak{m}}}(Df^{n\ell}\!\mid_{U}):U \in \mathrm{Grass}_{d-\kappa}(T_{x_{i}}M)\}}\\ \leq \dfrac{\|Df^{n\ell}\!\mid_{E_{n\ell}(x_{i})}\!\|} {\operatorname{{\mathfrak{m}}}(Df^{n\ell}\!\mid_{F(x_i)})}\leq \Pi_{j=0}^{n-1}\dfrac{\|Df^{\ell}\!\mid_{P_j}\!\|} {\operatorname{{\mathfrak{m}}}(Df^{\ell}\!\mid_{F(x_{i+j\ell})})}. \end{align*} $$
Thus, for every
![]() $w \in P_j$
, we have that
$w \in P_j$
, we have that
![]() $Df^{\ell }(w) \notin \mathcal {K}(x_{i+j\ell },{\delta })$
and, by Lemma 2.14, we obtain that
$Df^{\ell }(w) \notin \mathcal {K}(x_{i+j\ell },{\delta })$
and, by Lemma 2.14, we obtain that
![]() $\|Df^{\ell }\!\mid _{P_j}\!\|\leq \unicode{x3bb} \operatorname {{\mathfrak {m}}}(Df^{\ell }\!\mid _{F(x_{i+j\ell })})$
.
$\|Df^{\ell }\!\mid _{P_j}\!\|\leq \unicode{x3bb} \operatorname {{\mathfrak {m}}}(Df^{\ell }\!\mid _{F(x_{i+j\ell })})$
.
Finally, by continuity of
![]() $\mathscr {C}$
and by
$\mathscr {C}$
and by
![]() $\ker (Df^j)\cap \mathscr {C}=\{0\}$
, we can get a uniform constant
$\ker (Df^j)\cap \mathscr {C}=\{0\}$
, we can get a uniform constant
![]() $c>0$
such that
$c>0$
such that
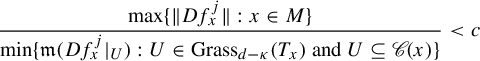 $$ \begin{align*}\frac{\max\{\|Df^j_x\|:x \in M\}}{\min\{\operatorname{{\mathfrak{m}}}(Df^j_{x}\!\mid_{U}):U\in \mathrm{Grass}_{d-\kappa}(T_x) \text{ and } U \subseteq \mathscr{C}(x)\}}<c\end{align*} $$
$$ \begin{align*}\frac{\max\{\|Df^j_x\|:x \in M\}}{\min\{\operatorname{{\mathfrak{m}}}(Df^j_{x}\!\mid_{U}):U\in \mathrm{Grass}_{d-\kappa}(T_x) \text{ and } U \subseteq \mathscr{C}(x)\}}<c\end{align*} $$
for each
![]() $1\leq j<\ell $
and then conclude that
$1\leq j<\ell $
and then conclude that
![]() $\sigma _{\kappa }(x_i,n)\leq c \unicode{x3bb} ^n \sigma _{\kappa +1}(x_i,n)$
.
$\sigma _{\kappa }(x_i,n)\leq c \unicode{x3bb} ^n \sigma _{\kappa +1}(x_i,n)$
.
The following result follows as immediate consequence of the previous lemma, since
![]() $\sigma _{\kappa }(x,n)< \sigma _{\kappa +1}(x,n)$
for every n large enough and
$\sigma _{\kappa }(x,n)< \sigma _{\kappa +1}(x,n)$
for every n large enough and
![]() $x \in M$
.
$x \in M$
.
Corollary 2.16. We have that
![]() $E_n(x)$
is
$E_n(x)$
is
![]() $\kappa $
-dimensional for every n large enough independently on
$\kappa $
-dimensional for every n large enough independently on
![]() $x \in M$
. Consequently,
$x \in M$
. Consequently,
![]() $E^{\perp }_n(x)$
is
$E^{\perp }_n(x)$
is
![]() $(d-\kappa )$
-dimensional.
$(d-\kappa )$
-dimensional.
Let us remind the reader what we have done so far to prove Proposition 2.13. By Corollary 2.16, we can suppose without loss of generality that
![]() $E_n(x)$
is
$E_n(x)$
is
![]() $\kappa $
-dimensional for all
$\kappa $
-dimensional for all
![]() $n\geq 1$
and we will next show that the sequence
$n\geq 1$
and we will next show that the sequence
![]() $(E_n(x))_n$
is of Cauchy on
$(E_n(x))_n$
is of Cauchy on
![]() $\mathrm {Grass}_{\kappa }(T_xM)$
endowed with the distance (2.4).
$\mathrm {Grass}_{\kappa }(T_xM)$
endowed with the distance (2.4).
We now state the following result (see [Reference Bochi, Potrie and Sambarino6, Lemma A.4] and also see [Reference Bochi and Gourmelon4, Reference Quas, Thieullen and Zarrabi24, Reference Zhu26] for related results).
Lemma 2.17. The sequence
![]() $(E_n(x))_n$
is of Cauchy.
$(E_n(x))_n$
is of Cauchy.
Before the proof of the lemma, we first need two useful lemmas.
Lemma 2.18. For large n, we have that
![]() $Df^n(E_n^{\perp }(x))\subseteq \mathscr {C}(f^n(x))$
for every
$Df^n(E_n^{\perp }(x))\subseteq \mathscr {C}(f^n(x))$
for every
![]() $x \in M$
.
$x \in M$
.
Proof. The proof will follow from item (ii) in Lemma 2.14. Indeed, suppose by contradiction that
![]() $Df^n(E_n^{\perp })$
is not contained in the cone. In particular, there is a vector
$Df^n(E_n^{\perp })$
is not contained in the cone. In particular, there is a vector
![]() $v \in E_n^{\perp }(x)$
such that
$v \in E_n^{\perp }(x)$
such that
![]() $Df^{j\ell }(Df^r(v))$
does not belongs to the cone with
$Df^{j\ell }(Df^r(v))$
does not belongs to the cone with
![]() $n=j\ell + r$
and
$n=j\ell + r$
and
![]() $0\leq r \leq \ell -1$
, satisfying:
$0\leq r \leq \ell -1$
, satisfying:
Thus, since j goes to
![]() $+\infty $
as n goes to
$+\infty $
as n goes to
![]() $+\infty $
, we can get n large enough such that
$+\infty $
, we can get n large enough such that
![]() $\|Df^n(v)\|<\operatorname {{\mathfrak {m}}}(Df^{j\ell }\!\mid _{F(x)})$
. This contradicts the definition of
$\|Df^n(v)\|<\operatorname {{\mathfrak {m}}}(Df^{j\ell }\!\mid _{F(x)})$
. This contradicts the definition of
![]() $E_n^{\perp }(x)$
to be the fastest direction of
$E_n^{\perp }(x)$
to be the fastest direction of
![]() $Df^n$
.
$Df^n$
.
Lemma 2.19. There is a constant
![]() $K_1>0$
such that for every
$K_1>0$
such that for every
![]() $x \in M$
and n large, the following inequality holds:
$x \in M$
and n large, the following inequality holds:
Proof. We take the constant
![]() $K_1=\min \{\|Df\!\mid _{\mathscr {C}(x)}\!\|: x \in M\}$
. Since the cone-field
$K_1=\min \{\|Df\!\mid _{\mathscr {C}(x)}\!\|: x \in M\}$
. Since the cone-field
![]() $\mathscr {C}$
depends continuously on x and is transversal to
$\mathscr {C}$
depends continuously on x and is transversal to
![]() $\ker (Df^n_x)$
for all
$\ker (Df^n_x)$
for all
![]() $n\geq 1$
, we have that
$n\geq 1$
, we have that
![]() $K_1>0$
.
$K_1>0$
.
We will first prove that
For that, we take V as the subspace of
![]() $T_xM$
generated by
$T_xM$
generated by
![]() $E_n(x)\cup \{e_{\kappa +1}^n\}$
. Then,
$E_n(x)\cup \{e_{\kappa +1}^n\}$
. Then,
 $$ \begin{align*} \|Df_{f^n(x)}\|\sigma_{\kappa+1}(x,n)&\geq \|Df_x^{n+1}\!\mid_V\!\|\\ &=\sigma_{\kappa+1}(x,n+1)\\ &\geq \operatorname{{\mathfrak{m}}}(Df^{n+1}_x\!\mid_{E^{\perp}_n(x)})\\ &\geq \operatorname{{\mathfrak{m}}}(Df_{f^n(x)}\!\mid_{Df^n(E^{\perp}_n(x))}) \operatorname{{\mathfrak{m}}}(Df^n_x\!\mid_{E^{\perp}_n(x)}). \end{align*} $$
$$ \begin{align*} \|Df_{f^n(x)}\|\sigma_{\kappa+1}(x,n)&\geq \|Df_x^{n+1}\!\mid_V\!\|\\ &=\sigma_{\kappa+1}(x,n+1)\\ &\geq \operatorname{{\mathfrak{m}}}(Df^{n+1}_x\!\mid_{E^{\perp}_n(x)})\\ &\geq \operatorname{{\mathfrak{m}}}(Df_{f^n(x)}\!\mid_{Df^n(E^{\perp}_n(x))}) \operatorname{{\mathfrak{m}}}(Df^n_x\!\mid_{E^{\perp}_n(x)}). \end{align*} $$
Thus, we conclude the proof using that
![]() $Df^n_x\!\mid _{E^{\perp }_n(x)}$
is contained in
$Df^n_x\!\mid _{E^{\perp }_n(x)}$
is contained in
![]() $\mathscr {C}(f^n(x))$
given by Lemma 2.18.
$\mathscr {C}(f^n(x))$
given by Lemma 2.18.
To complete the proof, it is sufficient to show that
![]() $\|Df_x\|\sigma _{\kappa +1}(f(x),n)\geq \sigma _{\kappa +1}(x, n+1)$
, since we have already known that
$\|Df_x\|\sigma _{\kappa +1}(f(x),n)\geq \sigma _{\kappa +1}(x, n+1)$
, since we have already known that
![]() $\sigma _{\kappa +1}(x,n+1)\geq K_1\sigma _{\kappa +1}(x,n)$
.
$\sigma _{\kappa +1}(x,n+1)\geq K_1\sigma _{\kappa +1}(x,n)$
.
To do that, we will use that
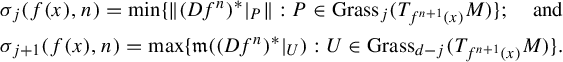 $$ \begin{align*} \sigma_j(f(x),n)=\min\{\|(Df^n)^{\ast}\!\mid_{P}\!\|: P \in \mathrm{Grass}_j(T_{f^{n+1}(x)}M)\}; \quad \text{and} \\ \sigma_{j+1}(f(x),n)=\max\{\operatorname{{\mathfrak{m}}}((Df^n)^{\ast}\!\mid_{U}): U \in \mathrm{Grass}_{d-j}(T_{f^{n+1}(x)}M)\}. \end{align*} $$
$$ \begin{align*} \sigma_j(f(x),n)=\min\{\|(Df^n)^{\ast}\!\mid_{P}\!\|: P \in \mathrm{Grass}_j(T_{f^{n+1}(x)}M)\}; \quad \text{and} \\ \sigma_{j+1}(f(x),n)=\max\{\operatorname{{\mathfrak{m}}}((Df^n)^{\ast}\!\mid_{U}): U \in \mathrm{Grass}_{d-j}(T_{f^{n+1}(x)}M)\}. \end{align*} $$
We consider two orthogonal bases
![]() $\{e_1^{n},\ldots ,e_d^{n}\}$
of
$\{e_1^{n},\ldots ,e_d^{n}\}$
of
![]() $T_{f(x)}M$
and
$T_{f(x)}M$
and
![]() $\{w_1^{n},\ldots ,w_d^{n}\}$
of
$\{w_1^{n},\ldots ,w_d^{n}\}$
of
![]() $T_{f^{n+1}(x)}M$
satisfying
$T_{f^{n+1}(x)}M$
satisfying
![]() $Df^{n}(e_j^{n})=\sigma _j(f(x),n)w_j^{n}$
and
$Df^{n}(e_j^{n})=\sigma _j(f(x),n)w_j^{n}$
and
![]() $(Df^{n})^{\ast }(w_j^{n})=\sigma _j(f(x),n)e_j^{n}$
. After that, taking
$(Df^{n})^{\ast }(w_j^{n})=\sigma _j(f(x),n)e_j^{n}$
. After that, taking
![]() $P=\{w_1^n,\ldots ,w_{\kappa +1}^n\}$
, we can verify that
$P=\{w_1^n,\ldots ,w_{\kappa +1}^n\}$
, we can verify that
![]() $\|Df_x\|=\|(Df_x)^{\ast }\|$
and
$\|Df_x\|=\|(Df_x)^{\ast }\|$
and
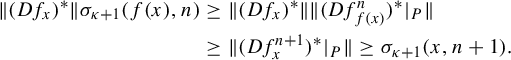 $$ \begin{align*} \|(Df_x)^{\ast}\|\sigma_{\kappa+1}(f(x),n)&\geq \|(Df_x)^{\ast}\|\|(Df_{f(x)}^n)^{\ast}\!\mid_{P}\!\|\\ &\geq\|(Df_x^{n+1})^{\ast}\!\mid_{P}\!\|\geq\sigma_{\kappa+1}(x,n+1).\\[-3pc] \end{align*} $$
$$ \begin{align*} \|(Df_x)^{\ast}\|\sigma_{\kappa+1}(f(x),n)&\geq \|(Df_x)^{\ast}\|\|(Df_{f(x)}^n)^{\ast}\!\mid_{P}\!\|\\ &\geq\|(Df_x^{n+1})^{\ast}\!\mid_{P}\!\|\geq\sigma_{\kappa+1}(x,n+1).\\[-3pc] \end{align*} $$
Finally, we can prove that
![]() $(E_n(x))_n$
is a Cauchy sequence.
$(E_n(x))_n$
is a Cauchy sequence.
Proof of Lemma 2.17
Suppose
![]() $n<m$
and observe that
$n<m$
and observe that
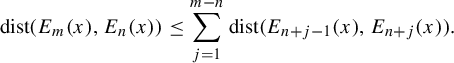 $$ \begin{align*}\mathrm{dist}(E_m(x),E_n(x)) \leq \sum_{j=1}^{m-n} \mathrm{dist}(E_{n+j-1}(x),E_{n+j}(x)).\end{align*} $$
$$ \begin{align*}\mathrm{dist}(E_m(x),E_n(x)) \leq \sum_{j=1}^{m-n} \mathrm{dist}(E_{n+j-1}(x),E_{n+j}(x)).\end{align*} $$
Then, to prove the lemma, it is sufficient to show that the distance
![]() $\mathrm {dist}(E_{n+1}(x),E_n(x))$
tends to zero exponentially fast with n and uniformly in x.
$\mathrm {dist}(E_{n+1}(x),E_n(x))$
tends to zero exponentially fast with n and uniformly in x.
We will omit the point x and simply rewrite
![]() $E_n$
and
$E_n$
and
![]() $E_n^{\perp }$
throughout the proof. To estimate the distance between
$E_n^{\perp }$
throughout the proof. To estimate the distance between
![]() $E_n$
and
$E_n$
and
![]() $E_{n+1}$
, we take
$E_{n+1}$
, we take
![]() $w\in E_n$
as the farthest unit vector from
$w\in E_n$
as the farthest unit vector from
![]() $E_{n+1}$
and decompose
$E_{n+1}$
and decompose
![]() $w=u+v$
in a unique way where
$w=u+v$
in a unique way where
![]() $u \in E_{n+1}$
and
$u \in E_{n+1}$
and
![]() $v \in E_{n+1}^{\perp }$
. Then, we obtain that
$v \in E_{n+1}^{\perp }$
. Then, we obtain that ![]() .
.
On the one hand, since the images of
![]() $E_{n+1}$
and
$E_{n+1}$
and
![]() $E_{n+1}^{\perp }$
by
$E_{n+1}^{\perp }$
by
![]() $Df^{n+1}$
are orthogonal, we have that
$Df^{n+1}$
are orthogonal, we have that
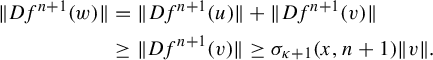 $$ \begin{align*} \|Df^{n+1}(w)\|&=\|Df^{n+1}(u)\|+\|Df^{n+1}(v)\|\\ &\geq \|Df^{n+1}(v)\|\geq \sigma_{\kappa+1}(x,n+1)\|v\|. \end{align*} $$
$$ \begin{align*} \|Df^{n+1}(w)\|&=\|Df^{n+1}(u)\|+\|Df^{n+1}(v)\|\\ &\geq \|Df^{n+1}(v)\|\geq \sigma_{\kappa+1}(x,n+1)\|v\|. \end{align*} $$
On the other hand,
where
![]() $K= \sup _x \|Df_x\| < \infty $
. Thus, by Lemmas 2.19 and 2.15, one concludes that
$K= \sup _x \|Df_x\| < \infty $
. Thus, by Lemmas 2.19 and 2.15, one concludes that
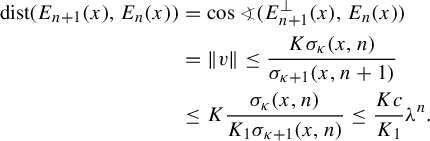
It should be noted that
![]() $(E_n(x))_n$
is a Cauchy for every
$(E_n(x))_n$
is a Cauchy for every
![]() $x \in M$
. Thus, we can define a continuous
$x \in M$
. Thus, we can define a continuous
![]() $\kappa $
-dimensional subbundle of
$\kappa $
-dimensional subbundle of
![]() $TM$
by
$TM$
by
Recall that
![]() $\ker (Df_x^j) \subseteq E(x)$
for all
$\ker (Df_x^j) \subseteq E(x)$
for all
![]() $x \in M$
and all
$x \in M$
and all
![]() $j\geq 1$
since
$j\geq 1$
since
![]() $\ker (Df_x^j)\subseteq E_n(x)$
for each
$\ker (Df_x^j)\subseteq E_n(x)$
for each
![]() $1\leq j\leq n$
.
$1\leq j\leq n$
.
We next prove that E is transversal to the cone-field
![]() $\mathscr {C}$
and is a
$\mathscr {C}$
and is a
![]() $Df$
-invariant subbundle.
$Df$
-invariant subbundle.
Lemma 2.20. For each
![]() $x \in M$
, we have that
$x \in M$
, we have that
![]() $E(x)\cap \mathscr {C}(x)=\{0\}$
and
$E(x)\cap \mathscr {C}(x)=\{0\}$
and
![]() $Df(E(x))\subseteq E(f(x))$
.
$Df(E(x))\subseteq E(f(x))$
.
Proof. We first prove that
![]() $E(x)\cap \mathscr {C}(x)=\{0\}$
. For that, recall that
$E(x)\cap \mathscr {C}(x)=\{0\}$
. For that, recall that
![]() $Df^n(E_n(x))$
and
$Df^n(E_n(x))$
and
![]() $Df^n(E_n^{\perp }(x))$
are perpendicular and, by Lemma 2.18,
$Df^n(E_n^{\perp }(x))$
are perpendicular and, by Lemma 2.18,
![]() $Df^n(E_n^{\perp }(x))$
is contained in
$Df^n(E_n^{\perp }(x))$
is contained in
![]() $\mathscr {C}(x)$
. Then, the intersection between
$\mathscr {C}(x)$
. Then, the intersection between
![]() $Df^n(E_n(x))$
and the cone-field is trivial, implying that
$Df^n(E_n(x))$
and the cone-field is trivial, implying that
![]() $E_n(x)\cap \mathscr {C}(x)=\{0\}$
. Thus, we can conclude that the intersection between
$E_n(x)\cap \mathscr {C}(x)=\{0\}$
. Thus, we can conclude that the intersection between
![]() $E(x)$
and
$E(x)$
and
![]() $\mathscr {C}(x)$
is also trivial.
$\mathscr {C}(x)$
is also trivial.
To show the invariance property, we will prove that the distance between
![]() $Df(E_{n+1}(x))$
and
$Df(E_{n+1}(x))$
and
![]() $E_n(f(x))$
goes to zero as n tends to infinity. Before, we fix
$E_n(f(x))$
goes to zero as n tends to infinity. Before, we fix
![]() $\rho>0$
such that
$\rho>0$
such that
for every
![]() $v \in \ker (Df_x)^{\perp }$
for every
$v \in \ker (Df_x)^{\perp }$
for every
![]() $x \in M$
.
$x \in M$
.
We start the proof of invariance, taking
![]() $v \in E(x)$
such that
$v \in E(x)$
such that
![]() $Df(v)=0$
. Then, clearly,
$Df(v)=0$
. Then, clearly,
![]() $Df(v) \in E(f(x))$
.
$Df(v) \in E(f(x))$
.
Now, we take a unit vector
![]() $v \in \ker (Df_x)^{\perp }\cap E(x)$
and choose a sequence of unit vectors
$v \in \ker (Df_x)^{\perp }\cap E(x)$
and choose a sequence of unit vectors
![]() $v_n \in E_{n+1}(x)\cap \ker (Df_x)^{\perp }$
such that
$v_n \in E_{n+1}(x)\cap \ker (Df_x)^{\perp }$
such that
![]() $v_n \to v$
. Then, we write
$v_n \to v$
. Then, we write
![]() $Df(v_n)=u_n+z_n$
, where
$Df(v_n)=u_n+z_n$
, where
![]() $u_n \in E_n(f(x))$
and
$u_n \in E_n(f(x))$
and
![]() $z_n \in E_n^{\perp }(f(x))$
.
$z_n \in E_n^{\perp }(f(x))$
.
Consider two orthogonal bases
![]() $\{e_1^n,\ldots ,e_d^n\}$
and
$\{e_1^n,\ldots ,e_d^n\}$
and
![]() $\{w_1^n,\ldots ,w_d^n\}$
of
$\{w_1^n,\ldots ,w_d^n\}$
of
![]() $T_{f(x)}M$
and
$T_{f(x)}M$
and
![]() $T_{f^{n+1}(x)}M$
, respectively, so that, for each
$T_{f^{n+1}(x)}M$
, respectively, so that, for each
![]() $1\leq i \leq d$
,
$1\leq i \leq d$
,
![]() $Df_{f(x)}^n(e_i^n)=\sigma _i(f(x),n) w_i^n$
and
$Df_{f(x)}^n(e_i^n)=\sigma _i(f(x),n) w_i^n$
and
![]() $(Df_{f(x)}^n)^{\ast }(w_i^n)=\sigma _i(f(x),n) e_i^n$
. Take a vector
$(Df_{f(x)}^n)^{\ast }(w_i^n)=\sigma _i(f(x),n) e_i^n$
. Take a vector
![]() $\tilde {z}_n \in \mathrm {span}\{w_{\kappa +1}^n,\cdots , w_d^n\}$
such that
$\tilde {z}_n \in \mathrm {span}\{w_{\kappa +1}^n,\cdots , w_d^n\}$
such that
![]() $(Df_{f(x)}^n)^{\ast }(\tilde {z}_n)=z_n$
and then,
$(Df_{f(x)}^n)^{\ast }(\tilde {z}_n)=z_n$
and then,
![]() $\|z_n\|\geq \sigma _{\kappa +1}(f(x),n)\|\tilde {z}_n\|$
. Thus, fixing
$\|z_n\|\geq \sigma _{\kappa +1}(f(x),n)\|\tilde {z}_n\|$
. Thus, fixing
![]() $K=\sup \|Df_x\|$
and using Lemma 2.19, we obtain that
$K=\sup \|Df_x\|$
and using Lemma 2.19, we obtain that
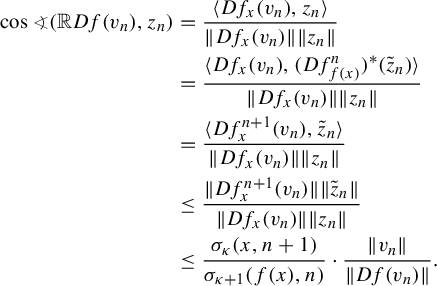
Then, by Lemmas 2.14 and 2.19, we obtain that
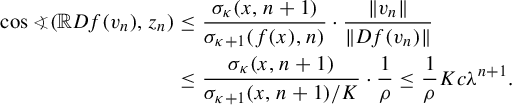
Since ![]() , we have that
, we have that
![]() $Df(v_n)$
and
$Df(v_n)$
and
![]() $E_n^{\perp }(f(x))$
are getting perpendicular when n tends to infinity. Thus,
$E_n^{\perp }(f(x))$
are getting perpendicular when n tends to infinity. Thus,
![]() $Df(v)=\lim Df(v_n)$
is perpendicular to
$Df(v)=\lim Df(v_n)$
is perpendicular to
![]() $E(f(x))^{\perp }$
and, consequently,
$E(f(x))^{\perp }$
and, consequently,
![]() $Df(v)$
belongs to
$Df(v)$
belongs to
![]() $E(f(x))$
.
$E(f(x))$
.
So far, we have shown that
![]() $E\oplus F$
is non-trivial splitting on
$E\oplus F$
is non-trivial splitting on
![]() $TM_f$
. Finally, we will next show that it is a dominated splitting for f and so prove Proposition 2.13.
$TM_f$
. Finally, we will next show that it is a dominated splitting for f and so prove Proposition 2.13.
Proof of Proposition 2.13
We have proved so far that under the assumption of Proposition 2.13, the splitting
![]() $E\oplus F$
satisfy for each orbit
$E\oplus F$
satisfy for each orbit
![]() $(x_i)_i$
that
$(x_i)_i$
that
![]() $Df(E(x_i)) \subseteq E(f(x_i))$
and
$Df(E(x_i)) \subseteq E(f(x_i))$
and
![]() $Df^{\ell }(F(x_i))=F(f^{\ell }(x_i))$
. Moreover, as the intersection between E and the cone-field
$Df^{\ell }(F(x_i))=F(f^{\ell }(x_i))$
. Moreover, as the intersection between E and the cone-field
![]() $\mathscr {C}$
is trivial, we conclude by item (ii) in Lemma 2.14 (recall that we are assuming
$\mathscr {C}$
is trivial, we conclude by item (ii) in Lemma 2.14 (recall that we are assuming
![]() $N=1$
) that
$N=1$
) that
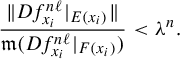 $$ \begin{align*}\dfrac{\|Df_{x_i}^{n\ell}\!\mid_{E(x_i)}\!\|}{\operatorname{{\mathfrak{m}}}(Df_{x_i}^{n\ell}\!\mid_{F(x_i)})}<\unicode{x3bb}^n.\end{align*} $$
$$ \begin{align*}\dfrac{\|Df_{x_i}^{n\ell}\!\mid_{E(x_i)}\!\|}{\operatorname{{\mathfrak{m}}}(Df_{x_i}^{n\ell}\!\mid_{F(x_i)})}<\unicode{x3bb}^n.\end{align*} $$
Thus,
![]() $E\oplus F$
is a dominated splitting for
$E\oplus F$
is a dominated splitting for
![]() $f^{\ell }$
.
$f^{\ell }$
.
To complete the proof, we use that
![]() $E\oplus Df(F)$
is also a dominated splitting for
$E\oplus Df(F)$
is also a dominated splitting for
![]() $f^{\ell }$
and get that
$f^{\ell }$
and get that
![]() $Df(F)=F$
by the uniqueness of dominated splitting (see Lemma 2.9).
$Df(F)=F$
by the uniqueness of dominated splitting (see Lemma 2.9).
Remark 2.21. It should be emphasized that the existence of a dominated splitting is an open property in the
![]() $C^1$
topology. That is, if f admits an invariant cone-field
$C^1$
topology. That is, if f admits an invariant cone-field
![]() $\mathscr {C}$
transversal to the kernel, then there exists a neighborhood
$\mathscr {C}$
transversal to the kernel, then there exists a neighborhood
![]() $\mathcal {U}$
of f in
$\mathcal {U}$
of f in
![]() $\mathrm {End}^1(M)$
such that the cone-field
$\mathrm {End}^1(M)$
such that the cone-field
![]() $\mathscr {C}$
is so for each
$\mathscr {C}$
is so for each
![]() $g \in \mathcal {U}$
.
$g \in \mathcal {U}$
.
3 Proof of Theorem A
Let us recall that
![]() $f_0: M \to M$
is a robustly transitive endomorphism displaying critical points and
$f_0: M \to M$
is a robustly transitive endomorphism displaying critical points and
![]() $\mathcal {F}_0$
is a subset of
$\mathcal {F}_0$
is a subset of
![]() $\mathcal {U}_0$
which accumulates on
$\mathcal {U}_0$
which accumulates on
![]() $f_0$
and for each
$f_0$
and for each
![]() $f \in \mathcal {F}_0$
, has
$f \in \mathcal {F}_0$
, has
![]() $\mathrm {int}(\mathrm {Cr}_{\kappa }(f))\neq \emptyset $
.
$\mathrm {int}(\mathrm {Cr}_{\kappa }(f))\neq \emptyset $
.
We next prove that
![]() $\Lambda _f$
is dense in
$\Lambda _f$
is dense in
![]() $M_f$
for every
$M_f$
for every
![]() $f \in \mathcal {F}_0$
.
$f \in \mathcal {F}_0$
.
Lemma 3.1. If f is a transitive endomorphism and
![]() $\mathrm {int}(\mathrm {Cr}_{\kappa }(f))\neq \emptyset $
, then
$\mathrm {int}(\mathrm {Cr}_{\kappa }(f))\neq \emptyset $
, then
![]() $\Lambda _f$
is a non-empty set. Moreover,
$\Lambda _f$
is a non-empty set. Moreover,
![]() $\Lambda _f$
is a dense subset of
$\Lambda _f$
is a dense subset of
![]() $M_f$
.
$M_f$
.
Proof. On the one hand, the transitivity of f on M implies that
![]() $f: (x_i)_i \mapsto (f(x_i))_i$
is a transitive homeomorphism on
$f: (x_i)_i \mapsto (f(x_i))_i$
is a transitive homeomorphism on
![]() $M_f$
(see [Reference Aoki and Hiraide1, Theorem 3.5.3]). Then, considering a base of open sets
$M_f$
(see [Reference Aoki and Hiraide1, Theorem 3.5.3]). Then, considering a base of open sets
![]() $\{B_n\}_n$
of
$\{B_n\}_n$
of
![]() $M_{f}$
, we have that
$M_{f}$
, we have that
![]() $A_n^{+}=\bigcup _{j\geq 0}f^j(B_n)$
and
$A_n^{+}=\bigcup _{j\geq 0}f^j(B_n)$
and
![]() $A_n^{-}=\bigcup _{j\geq 0}f^{-j}(B_n)$
are dense open sets in
$A_n^{-}=\bigcup _{j\geq 0}f^{-j}(B_n)$
are dense open sets in
![]() $M_{f}$
, for each n. By the Baire category theorem, we get that
$M_{f}$
, for each n. By the Baire category theorem, we get that
![]() $\bigcap _n (A_n^{+}\cap A_n^{-})$
is a residual set in
$\bigcap _n (A_n^{+}\cap A_n^{-})$
is a residual set in
![]() $M_f$
which consists of the points where their backward and forward orbits are dense in
$M_f$
which consists of the points where their backward and forward orbits are dense in
![]() $M_{f}$
. On the other hand, since
$M_{f}$
. On the other hand, since
![]() $\mathrm {Cr}_{\kappa }(f)$
has non-empty interior, we have that any orbit in
$\mathrm {Cr}_{\kappa }(f)$
has non-empty interior, we have that any orbit in
![]() $\bigcap _n A_n^{+}\cap A_n^{-}$
visits the interior of
$\bigcap _n A_n^{+}\cap A_n^{-}$
visits the interior of
![]() $\mathrm {Cr}_{\kappa }(f)$
infinitely many times for the past and the future and, hence, it belongs to
$\mathrm {Cr}_{\kappa }(f)$
infinitely many times for the past and the future and, hence, it belongs to
![]() $\Lambda _{f}$
. Thus,
$\Lambda _{f}$
. Thus,
![]() $\Lambda _f$
is non-empty and dense in
$\Lambda _f$
is non-empty and dense in
![]() $M_f$
.
$M_f$
.
We are now assuming that Theorem C holds. Then, we have that there are
![]() $\alpha>0$
and an integer
$\alpha>0$
and an integer
![]() $\ell>0$
such that
$\ell>0$
such that
![]() $E_f\oplus F_f$
is an
$E_f\oplus F_f$
is an
![]() $(\alpha ,\ell )$
-dominated splitting over
$(\alpha ,\ell )$
-dominated splitting over
![]() $\Lambda _f$
for every
$\Lambda _f$
for every
![]() $f \in \mathcal {F}_0$
. Since
$f \in \mathcal {F}_0$
. Since
![]() $\Lambda _f$
is dense on
$\Lambda _f$
is dense on
![]() $M_f$
by Lemma 3.1, we use Proposition 2.10 to conclude that
$M_f$
by Lemma 3.1, we use Proposition 2.10 to conclude that
![]() $E_f\oplus F_f$
is an
$E_f\oplus F_f$
is an
![]() $(\alpha ,\ell )$
-dominated splitting over
$(\alpha ,\ell )$
-dominated splitting over
![]() $M_f$
. This implies Theorem B, as we have already mentioned.
$M_f$
. This implies Theorem B, as we have already mentioned.
Now we will prove Theorem A. To do this, we will need to push the domination on
![]() $f \in \mathcal {F}_0$
to
$f \in \mathcal {F}_0$
to
![]() $f_0$
.
$f_0$
.
By the equivalence in Proposition 2.12, we can use the uniformity of the dominated splitting to obtain the cone-field
![]() $\mathscr {C}_{E_f}:=\{\mathscr {C}_{E_f}(x, \alpha ):x \in M\}$
where its dual cone-field
$\mathscr {C}_{E_f}:=\{\mathscr {C}_{E_f}(x, \alpha ):x \in M\}$
where its dual cone-field
![]() $\mathscr {C}_{E_f}^{\kern2pt\ast }$
is
$\mathscr {C}_{E_f}^{\kern2pt\ast }$
is
![]() $\ell $
-invariant uniformly in
$\ell $
-invariant uniformly in
![]() $f \in \mathcal {F}_0$
, up to increasing the constant
$f \in \mathcal {F}_0$
, up to increasing the constant
![]() $\ell $
. Then, we consider a sequence of
$\ell $
. Then, we consider a sequence of
![]() $f_n \in \mathcal {F}_0$
converging to
$f_n \in \mathcal {F}_0$
converging to
![]() $f_0$
, and we define
$f_0$
, and we define
![]() $E_0(x)$
and
$E_0(x)$
and
![]() $\mathscr {C}_{E_0}^{\kern2pt\ast }(x,\alpha )$
respectively as the limit of
$\mathscr {C}_{E_0}^{\kern2pt\ast }(x,\alpha )$
respectively as the limit of
![]() $E_n(x)$
and
$E_n(x)$
and
![]() $\mathscr {C}_{E_n}^{\kern2pt\ast }(x,\alpha )$
, which satisfy
$\mathscr {C}_{E_n}^{\kern2pt\ast }(x,\alpha )$
, which satisfy
![]() $E_0(x)\cap \mathscr {C}_{E_0}^{\kern2pt\ast }(x,\alpha )=\{0\}$
.
$E_0(x)\cap \mathscr {C}_{E_0}^{\kern2pt\ast }(x,\alpha )=\{0\}$
.
Finally, it remains to show that
![]() $\mathscr {C}_{E_0}^{\kern2pt\ast }(x,\alpha )$
is invariant and
$\mathscr {C}_{E_0}^{\kern2pt\ast }(x,\alpha )$
is invariant and
![]() $\ker (Df_0^m)\subseteq E_0(x)$
for every
$\ker (Df_0^m)\subseteq E_0(x)$
for every
![]() $x\in M$
and
$x\in M$
and
![]() $m\geq 1$
. For that, we first use that
$m\geq 1$
. For that, we first use that
![]() $\mathscr {C}_{E_n}^{\kern2pt\ast }(x,\alpha )$
is
$\mathscr {C}_{E_n}^{\kern2pt\ast }(x,\alpha )$
is
![]() $\ell $
-invariant for every n to conclude that
$\ell $
-invariant for every n to conclude that
![]() $\mathscr {C}_{E_0}^{\kern2pt\ast }(x,\alpha )$
is also
$\mathscr {C}_{E_0}^{\kern2pt\ast }(x,\alpha )$
is also
![]() $\ell $
-invariant. Second, to show that
$\ell $
-invariant. Second, to show that
![]() $\ker (Df^m_0)$
at
$\ker (Df^m_0)$
at
![]() $x \in M$
is contained in
$x \in M$
is contained in
![]() $E_0(x)$
, it is enough to prove that if
$E_0(x)$
, it is enough to prove that if
![]() $u \in \ker (Df_0^m)$
at
$u \in \ker (Df_0^m)$
at
![]() $x \in M$
, then
$x \in M$
, then
![]() $u \in E_n(x)$
for large
$u \in E_n(x)$
for large
![]() $n\geq 1$
since
$n\geq 1$
since
![]() $E_0(x)$
is the limit of
$E_0(x)$
is the limit of
![]() $E_n(x)$
. Thus, suppose that
$E_n(x)$
. Thus, suppose that
![]() $u \notin E_n(x)$
for infinitely many n. Considering
$u \notin E_n(x)$
for infinitely many n. Considering
![]() $E_n\oplus F_n$
as an
$E_n\oplus F_n$
as an
![]() $(\alpha ,\ell )$
-dominated splitting for
$(\alpha ,\ell )$
-dominated splitting for
![]() $f_n$
, we can conclude that for k large enough,
$f_n$
, we can conclude that for k large enough,
![]() $\|Df_n^{k\ell }(u)\|\approx \operatorname {{\mathfrak {m}}}(Df_n^{k\ell }\mid _{F_n})$
, which is away from zero independently on n. This contradicts the fact that
$\|Df_n^{k\ell }(u)\|\approx \operatorname {{\mathfrak {m}}}(Df_n^{k\ell }\mid _{F_n})$
, which is away from zero independently on n. This contradicts the fact that
![]() $Df_n^{k\ell }(u)$
must have to converge to
$Df_n^{k\ell }(u)$
must have to converge to
![]() $Df_0^{k\ell }(u)=0$
for
$Df_0^{k\ell }(u)=0$
for
![]() $k\ell \geq m$
.
$k\ell \geq m$
.
3.1 Proof of Corollary 1.1
Let
![]() $M=S^{2n}$
be an even-dimensional sphere and a robustly transitive map
$M=S^{2n}$
be an even-dimensional sphere and a robustly transitive map
![]() $f: M \to M$
. Let
$f: M \to M$
. Let
![]() $E \subseteq TM$
be a
$E \subseteq TM$
be a
![]() $\kappa $
-dimensional subbundle, that is, a map
$\kappa $
-dimensional subbundle, that is, a map
![]() $E: M \to \mathrm {Grass}_{\kappa }(TM)$
so that
$E: M \to \mathrm {Grass}_{\kappa }(TM)$
so that
![]() $E(x) \in \mathrm {Grass}_{\kappa }(T_xM)$
for every
$E(x) \in \mathrm {Grass}_{\kappa }(T_xM)$
for every
![]() $x \in M$
. Note that we can associate an Euler class to E which is an element of
$x \in M$
. Note that we can associate an Euler class to E which is an element of
![]() $H^{\kappa }(M),$
the
$H^{\kappa }(M),$
the
![]() $\kappa $
th-dimensional de Rham cohomology of M. Suppose
$\kappa $
th-dimensional de Rham cohomology of M. Suppose
![]() $E\neq TM$
(or equivalently,
$E\neq TM$
(or equivalently,
![]() $\kappa \neq 2n=\dim (M)$
), then we have that its Euler class is zero since all intermediate homologies vanish on spheres. However, we have that
$\kappa \neq 2n=\dim (M)$
), then we have that its Euler class is zero since all intermediate homologies vanish on spheres. However, we have that
![]() $E^\perp $
is another subbundle of dimension
$E^\perp $
is another subbundle of dimension
![]() $2n-\kappa $
complementary to E in
$2n-\kappa $
complementary to E in
![]() $TM$
, then it follows that
$TM$
, then it follows that
![]() $E \oplus E^\perp = TM$
. Therefore, the Euler class of
$E \oplus E^\perp = TM$
. Therefore, the Euler class of
![]() $TM$
(which is the Euler characteristic of M times the class of the volume form M in
$TM$
(which is the Euler characteristic of M times the class of the volume form M in
![]() $H^{2n}(M)$
) is the product of the Euler classes of E and
$H^{2n}(M)$
) is the product of the Euler classes of E and
![]() $E^\perp $
. Hence, the Euler characteristic of M is zero, but this is a contradiction since the Euler characteristic of an even-dimensional sphere is
$E^\perp $
. Hence, the Euler characteristic of M is zero, but this is a contradiction since the Euler characteristic of an even-dimensional sphere is
![]() $2$
. This argument shows that even-dimensional spheres do not admit non-trivial subbundles. This argument is classical and is taken from [Reference Avila and Bochi2], but it can be also found in [Reference Milnor and Stasheff21, Property 9.6].
$2$
. This argument shows that even-dimensional spheres do not admit non-trivial subbundles. This argument is classical and is taken from [Reference Avila and Bochi2], but it can be also found in [Reference Milnor and Stasheff21, Property 9.6].
Now, we can apply Theorem A which implies that if an endomorphism f is robustly transitive, then it cannot have critical points as it would imply the existence of a non-trivial subbundle. Therefore, we conclude that it is a local diffeomorphism (covering map) on M. However, since M is simply connected, the endomorphism f should be a diffeomorphism. We can use now [Reference Bonatti, Díaz and Pujals8] to conclude the corollary.
4 Proof of Theorem C
Here, let
![]() $f_0$
be an endomorphism displaying critical points and
$f_0$
be an endomorphism displaying critical points and
![]() $\mathcal {F}$
be a family of endomorphisms converging to
$\mathcal {F}$
be a family of endomorphisms converging to
![]() $f_0$
satisfying:
$f_0$
satisfying:
First, let us recall that for each
![]() $f \in \mathcal {F}$
and for each
$f \in \mathcal {F}$
and for each
![]() $x_i$
in the orbit
$x_i$
in the orbit
![]() $(x_i)_i \in \Lambda _f$
, we have defined the candidate to dominated splitting by
$(x_i)_i \in \Lambda _f$
, we have defined the candidate to dominated splitting by
where
The next statement will be useful to prove that E and F are invariant subbundles over
![]() $\Lambda _f$
.
$\Lambda _f$
.
Lemma 4.1. If
![]() $x \in \mathrm {Cr}_{\kappa }(f)$
and
$x \in \mathrm {Cr}_{\kappa }(f)$
and
![]() $n\geq m_f$
, then
$n\geq m_f$
, then
![]() $\ker (Df^n_x)$
and
$\ker (Df^n_x)$
and
![]() $\operatorname {\mathrm {Im}}(Df^n_x)$
are
$\operatorname {\mathrm {Im}}(Df^n_x)$
are
![]() $\kappa $
- and
$\kappa $
- and
![]() $(d-\kappa )$
-dimensional, respectively. Moreover, if
$(d-\kappa )$
-dimensional, respectively. Moreover, if
![]() $x_j=f^j(x)$
, for each
$x_j=f^j(x)$
, for each
![]() $0\leq j\leq n$
with
$0\leq j\leq n$
with
![]() ${n\geq m_f}$
such that
${n\geq m_f}$
such that
![]() $x_0,\, x_n \in \mathrm {Cr}_{\kappa }(f)$
, then
$x_0,\, x_n \in \mathrm {Cr}_{\kappa }(f)$
, then
![]() $T_{x_j}M=\ker (Df^{m_f+{n-j}}_{x_j})\oplus \operatorname {\mathrm {Im}}(Df^j_{x_0})$
for each
$T_{x_j}M=\ker (Df^{m_f+{n-j}}_{x_j})\oplus \operatorname {\mathrm {Im}}(Df^j_{x_0})$
for each
![]() $m_f\leq j \leq n$
.
$m_f\leq j \leq n$
.
Proof. By the assumption (4.1) and
![]() $Df^{m+n}_{y}=Df^{m}_{f^n(y)} \cdot Df^n_{y}$
, we can get that
$Df^{m+n}_{y}=Df^{m}_{f^n(y)} \cdot Df^n_{y}$
, we can get that
Then, when y or
![]() $f^n(y)$
belongs to
$f^n(y)$
belongs to
![]() $\mathrm {Cr}_{\kappa }(f)$
, we have that
$\mathrm {Cr}_{\kappa }(f)$
, we have that
In particular,
![]() $\ker (Df^m_x)$
is
$\ker (Df^m_x)$
is
![]() $\kappa $
-dimensional for every
$\kappa $
-dimensional for every
![]() $x \in \mathrm {Cr}_{\kappa }(f)$
and
$x \in \mathrm {Cr}_{\kappa }(f)$
and
![]() $m\geq m_f$
, and so,
$m\geq m_f$
, and so,
![]() $\operatorname {\mathrm {Im}}(Df^m_x)$
is
$\operatorname {\mathrm {Im}}(Df^m_x)$
is
![]() $(d-\kappa )$
-dimensional by the theorem of kernel and image. To prove the second part, we assume that there exists a non-zero vector
$(d-\kappa )$
-dimensional by the theorem of kernel and image. To prove the second part, we assume that there exists a non-zero vector
![]() $v \in T_{x_0}M$
such that
$v \in T_{x_0}M$
such that
![]() ${u=Df^j_{x_0}(v)}$
is a non-zero vector in
${u=Df^j_{x_0}(v)}$
is a non-zero vector in
![]() $\ker (Df^{m_f+n-j}_{x_j})\cap \operatorname {\mathrm {Im}}(Df^j_{x_0})$
. Note that
$\ker (Df^{m_f+n-j}_{x_j})\cap \operatorname {\mathrm {Im}}(Df^j_{x_0})$
. Note that
![]() $v \notin \ker (Df^j_{x_0})$
and
$v \notin \ker (Df^j_{x_0})$
and
![]() $v \in \ker (Df^{m_f+n}_{x_0})$
. It contradicts the assumption (4.1) since
$v \in \ker (Df^{m_f+n}_{x_0})$
. It contradicts the assumption (4.1) since
![]() $\ker (Df^{m_f+n}_{x_0})$
contains
$\ker (Df^{m_f+n}_{x_0})$
contains
![]() $\ker (Df^{j}_{x_0})\oplus \mathrm {span}\{v\}$
that is
$\ker (Df^{j}_{x_0})\oplus \mathrm {span}\{v\}$
that is
![]() $(\kappa +1)$
-dimensional for any
$(\kappa +1)$
-dimensional for any
![]() $m_f \leq j \leq n$
.
$m_f \leq j \leq n$
.
Lemma. (Invariance property)
The following statements hold:
-
(i) the subbundles E and F are
 $\kappa $
and
$\kappa $
and
 $(d-\kappa )$
-dimensional, respectively;
$(d-\kappa )$
-dimensional, respectively; -
(ii) for every orbit
 $(x_i)_i \in \Lambda _f$
, one has that
$(x_i)_i \in \Lambda _f$
, one has that
 $T_{x_i}M=E(x_i)\oplus F(x_i) \text { for all } i \in \mathbb {Z}$
;
$T_{x_i}M=E(x_i)\oplus F(x_i) \text { for all } i \in \mathbb {Z}$
; -
(iii) the subbundles E and F are invariant.
Proof. The statements (i) and (ii) follow from Lemma 4.1 since for each
![]() $x_i$
in the orbit
$x_i$
in the orbit
![]() $(x_i)_i$
, we have that
$(x_i)_i$
, we have that
![]() $x_{i+\tau _i^{-}}, x_{i+\tau _i^{+}}$
belong to
$x_{i+\tau _i^{-}}, x_{i+\tau _i^{+}}$
belong to
![]() $\mathrm {Cr}_{\kappa }(f)$
and
$\mathrm {Cr}_{\kappa }(f)$
and
![]() $|\tau _i^{-}|\geq m_f$
.
$|\tau _i^{-}|\geq m_f$
.
To prove statement (iii), we shall observe that
![]() $\tau _{i}^{-}= \tau _{i+1}^{-}+1$
and
$\tau _{i}^{-}= \tau _{i+1}^{-}+1$
and
![]() $|\tau _{i+1}^{-}|=|\tau _{i}^{-}|+1$
if
$|\tau _{i+1}^{-}|=|\tau _{i}^{-}|+1$
if
![]() $x_{i+1-m_f} \notin \mathrm {Cr}_{\kappa }(f)$
. Thus,
$x_{i+1-m_f} \notin \mathrm {Cr}_{\kappa }(f)$
. Thus,
However, if
![]() $x_{i+1-m_f} \in \mathrm {Cr}_{\kappa }(f)$
, then
$x_{i+1-m_f} \in \mathrm {Cr}_{\kappa }(f)$
, then
![]() $\tau _{i+1}^{-}=-m_f$
and hence
$\tau _{i+1}^{-}=-m_f$
and hence
![]() $\tau _i^{-}<~\tau _{i+1}^{-}$
. By Lemma 4.1, we have that
$\tau _i^{-}<~\tau _{i+1}^{-}$
. By Lemma 4.1, we have that
since
![]() $x_{i+1+\tau _{i+1}^{-}}=x_{i+1-m_f}=f^{|\tau _i^{-}|+1-m_f}(x_{i+\tau _i^{-}})$
. Therefore,
$x_{i+1+\tau _{i+1}^{-}}=x_{i+1-m_f}=f^{|\tau _i^{-}|+1-m_f}(x_{i+\tau _i^{-}})$
. Therefore,
The invariance of E follows from the assumption (4.1) and from the fact that E is
![]() $\kappa $
-dimensional.
$\kappa $
-dimensional.
The following lemma will be often used throughout this paper.
Lemma 4.2. There exists a small real number
![]() $\varepsilon>0$
such that if
$\varepsilon>0$
such that if
![]() $f \in \mathcal {U}$
, whose
$f \in \mathcal {U}$
, whose
![]() ${\Lambda _f \neq \emptyset }$
, then for every finite collection
${\Lambda _f \neq \emptyset }$
, then for every finite collection
![]() $\Sigma $
in
$\Sigma $
in
![]() $(x_i)_i \in \Lambda _f$
, say
$(x_i)_i \in \Lambda _f$
, say
![]() $\Sigma =\{x_0,\ldots ,x_{n-1}\}$
, and every collection of linear maps
$\Sigma =\{x_0,\ldots ,x_{n-1}\}$
, and every collection of linear maps
![]() $L_i:T_{x_i}M \to T_{f(x_i)}M$
for
$L_i:T_{x_i}M \to T_{f(x_i)}M$
for
![]() $i=0,1,\ldots ,n-1$
, satisfying the following two conditions:
$i=0,1,\ldots ,n-1$
, satisfying the following two conditions:
there exists an endomorphism
![]() $\hat {f} \in \mathcal {U}$
and a neighborhood B of
$\hat {f} \in \mathcal {U}$
and a neighborhood B of
![]() $\{x_0,\ldots ,x_{n-1}\}$
so that
$\{x_0,\ldots ,x_{n-1}\}$
so that
![]() $\dim \ker (D\hat {f}^m)\geq k+1$
for some positive integer m.
$\dim \ker (D\hat {f}^m)\geq k+1$
for some positive integer m.
Proof. Let
![]() $\varepsilon>0$
be given by Franks’ Lemma. Then, up to shrinking the neighborhood
$\varepsilon>0$
be given by Franks’ Lemma. Then, up to shrinking the neighborhood
![]() $\mathcal {U}$
, let us recall the orbit
$\mathcal {U}$
, let us recall the orbit
![]() $(x_i)_i \in \Lambda _f$
hits on
$(x_i)_i \in \Lambda _f$
hits on
![]() $\mathrm {Cr}_{\kappa }(f)$
infinitely many times for the past and for the future. Hence, assume without loss of generality that
$\mathrm {Cr}_{\kappa }(f)$
infinitely many times for the past and for the future. Hence, assume without loss of generality that
![]() $\tau _0^{-}$
and
$\tau _0^{-}$
and
![]() $\tau _0^{+}$
, defined for the orbit
$\tau _0^{+}$
, defined for the orbit
![]() $(x_i)_i$
, satisfy
$(x_i)_i$
, satisfy
![]() $\tau _0^{-}\leq 0 < n\leq \tau _0^{+}$
. Also by Franks’ Lemma, there exists
$\tau _0^{-}\leq 0 < n\leq \tau _0^{+}$
. Also by Franks’ Lemma, there exists
![]() $\hat {f} \in \mathcal {U}$
such that the neighborhood B of
$\hat {f} \in \mathcal {U}$
such that the neighborhood B of
![]() $\Sigma $
verifies
$\Sigma $
verifies
Then, there is
![]() $w \in F(x_{\tau _0^{-}})$
such that
$w \in F(x_{\tau _0^{-}})$
such that
![]() $Df^{|\tau _0^{-}|}(w)=v$
, and taking
$Df^{|\tau _0^{-}|}(w)=v$
, and taking
![]() $m=m_f+\tau _0^{+}+|\tau _0^{-}|$
, we get that
$m=m_f+\tau _0^{+}+|\tau _0^{-}|$
, we get that
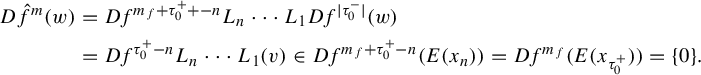 $$ \begin{align*} D\hat{f}^m(w)&=Df^{m_f+\tau_0^{+}+-n}L_n\cdots L_1 Df^{|\tau_0^{-}|}(w)\\ &=Df^{\tau_0^{+}-n}L_n\cdots L_1(v)\in Df^{m_f+\tau_0^{+}-n}(E(x_n))=Df^{m_f}(E(x_{\tau_0^{+}}))=\{0\}. \end{align*} $$
$$ \begin{align*} D\hat{f}^m(w)&=Df^{m_f+\tau_0^{+}+-n}L_n\cdots L_1 Df^{|\tau_0^{-}|}(w)\\ &=Df^{\tau_0^{+}-n}L_n\cdots L_1(v)\in Df^{m_f+\tau_0^{+}-n}(E(x_n))=Df^{m_f}(E(x_{\tau_0^{+}}))=\{0\}. \end{align*} $$
Therefore,
![]() $E(x_{\tau _0^{-}})\oplus \mathrm {span}\{ w\}$
is contained in
$E(x_{\tau _0^{-}})\oplus \mathrm {span}\{ w\}$
is contained in
![]() $\ker (D\hat {f}^m)$
. This completes the proof.
$\ker (D\hat {f}^m)$
. This completes the proof.
From now on, to prove Theorem C, we suppose that there is a neighborhood
![]() $\mathcal {U}_0$
of
$\mathcal {U}_0$
of
![]() $f_0$
such that
$f_0$
such that
In other words, we are assuming that the second item of Theorem C cannot happen.
Furthermore, we can also assume that
Throughout the rest of this paper, we fix
![]() $\varepsilon _0>0$
as in Lemma 4.2, and choose
$\varepsilon _0>0$
as in Lemma 4.2, and choose
![]() $\alpha>0$
small enough so that for all rotation R on
$\alpha>0$
small enough so that for all rotation R on
![]() $T_{f(x)}M$
of angle smaller than
$T_{f(x)}M$
of angle smaller than
![]() $\alpha $
satisfies:
$\alpha $
satisfies:
We would like the reader to keep in mind that the existence of a family of rotations
![]() $R_1,\ldots ,R_n$
of angles smaller than
$R_1,\ldots ,R_n$
of angles smaller than
![]() $\alpha $
such that
$\alpha $
such that
![]() $L_i=R_i\circ Df_{x_{i-1}}$
for
$L_i=R_i\circ Df_{x_{i-1}}$
for
![]() $1\leq i \leq n$
, satisfying the hypothesis of Lemma 4.2, is incompatible with (4.3). In the course of this section, we will evoke this incompatibility.
$1\leq i \leq n$
, satisfying the hypothesis of Lemma 4.2, is incompatible with (4.3). In the course of this section, we will evoke this incompatibility.
We now are devoted to prove the first item in Theorem C. More precisely, we will prove there are
![]() $\ell>0$
and
$\ell>0$
and
![]() $\alpha>0$
such that
$\alpha>0$
such that
![]() $E\oplus F$
is an
$E\oplus F$
is an
![]() $(\alpha ,\ell )$
-dominated splitting over
$(\alpha ,\ell )$
-dominated splitting over
![]() $\Lambda _f$
for every
$\Lambda _f$
for every
![]() $f \in \mathcal {F}$
.
$f \in \mathcal {F}$
.
Lemma. (Uniform angle)
For every
![]() $f \in \mathcal {F}$
and each
$f \in \mathcal {F}$
and each
![]() $(x_i)_i \in \Lambda _f$
, it holds that
$(x_i)_i \in \Lambda _f$
, it holds that
Proof. Otherwise, there is a unit vector
![]() $w \in F(f(x))$
for some x in
$w \in F(f(x))$
for some x in
![]() $(x_i)_i \in \Lambda _f$
, so that
$(x_i)_i \in \Lambda _f$
, so that ![]() . Thus, we take a rotation
. Thus, we take a rotation
![]() $R: T_{f(x)}M \to T_{f(x)}M$
of angle
$R: T_{f(x)}M \to T_{f(x)}M$
of angle
![]() $<\alpha $
such that
$<\alpha $
such that
![]() $R(w) \in E(f(x))$
, which contradicts the assumption (4.3) since
$R(w) \in E(f(x))$
, which contradicts the assumption (4.3) since
![]() $\Sigma =\{f(x)\}$
and
$\Sigma =\{f(x)\}$
and
![]() ${L_1=R\circ Df_x}$
satisfy the hypothesis of Lemma 4.2.
${L_1=R\circ Df_x}$
satisfy the hypothesis of Lemma 4.2.
To conclude the proof of Theorem C, it remains to show the following.
Lemma. (Uniform domination property)
There exists an integer
![]() $\ell>0$
such that for every
$\ell>0$
such that for every
![]() $f \in \mathcal {F}$
, the splitting
$f \in \mathcal {F}$
, the splitting
![]() $E\oplus F$
over
$E\oplus F$
over
![]() $\Lambda _f$
satisfies
$\Lambda _f$
satisfies
![]() $E\prec _{\ell } F$
.
$E\prec _{\ell } F$
.
The proof of this lemma, in some sense, carries the same ideas used in the context of diffeomorphisms, where the lack of domination property allows us to create a point exhibiting some obstruction for the robust transitivity. However, for endomorphisms displaying critical points, the proof is more subtle.
Let us make some comments to clarify how we are proceeding with the proof of the domination property lemma. We will assume by contradiction that the splitting
![]() $E\oplus F$
does not satisfy the domination property, and hence there are some unit vectors
$E\oplus F$
does not satisfy the domination property, and hence there are some unit vectors
![]() $v \in E(x)$
and
$v \in E(x)$
and
![]() $w \in F(x)$
so that for some point x and large positive integer
$w \in F(x)$
so that for some point x and large positive integer
![]() $\ell $
, the following holds:
$\ell $
, the following holds:
for each
![]() $1\leq j \leq \ell $
. Note that as
$1\leq j \leq \ell $
. Note that as
![]() $Df^j(w)\neq 0$
, we have that
$Df^j(w)\neq 0$
, we have that
![]() $Df^j$
restricts to the bidimensional subspace
$Df^j$
restricts to the bidimensional subspace
![]() $V_0=\mathrm {span}\{v,w\}$
an isomorphism onto its image,
$V_0=\mathrm {span}\{v,w\}$
an isomorphism onto its image,
![]() $V_j\subseteq T_{f^j(x)}M$
. Let us call
$V_j\subseteq T_{f^j(x)}M$
. Let us call
![]() $Df\mid _{V_{j-1}}:V_{j-1} \to V_j$
by
$Df\mid _{V_{j-1}}:V_{j-1} \to V_j$
by
![]() $A_j$
. Then, we provide some control over the norms of
$A_j$
. Then, we provide some control over the norms of
![]() $A_j$
and
$A_j$
and
![]() $A_j^{-1}$
for each
$A_j^{-1}$
for each
![]() $1\leq j\leq \ell $
to apply Lemma 4.9 to mix the subbundles E and F to increase the dimension of the critical set, which is incompatible with (4.3). However, the control over the norms of
$1\leq j\leq \ell $
to apply Lemma 4.9 to mix the subbundles E and F to increase the dimension of the critical set, which is incompatible with (4.3). However, the control over the norms of
![]() $A_j$
and
$A_j$
and
![]() $A_j^{-1}$
for each
$A_j^{-1}$
for each
![]() $1\leq j \leq \ell $
is the subtle part of the proof since
$1\leq j \leq \ell $
is the subtle part of the proof since
![]() $Df^{-1}$
is not necessarily defined due to the existence of critical points.
$Df^{-1}$
is not necessarily defined due to the existence of critical points.
To obtain such norm control of
![]() $Df^{-1}$
, we divide our approach into two cases. For the first one, we assume that
$Df^{-1}$
, we divide our approach into two cases. For the first one, we assume that
![]() $\dim \ker (Df_0)=r<\kappa $
. In this case, up to shrinking the neighborhood of
$\dim \ker (Df_0)=r<\kappa $
. In this case, up to shrinking the neighborhood of
![]() $f_0$
, we have that
$f_0$
, we have that
![]() $\dim \ker (Df)\leq r$
for every
$\dim \ker (Df)\leq r$
for every
![]() $f \in \mathcal {U}_0$
. Then, we can find a large
$f \in \mathcal {U}_0$
. Then, we can find a large
![]() $N>0$
such that
$N>0$
such that
for all
![]() $x \in M$
and all
$x \in M$
and all
![]() $\kappa $
-dimensional subspace
$\kappa $
-dimensional subspace
![]() $\Gamma $
of
$\Gamma $
of
![]() $T_xM$
. Then, we can conclude that
$T_xM$
. Then, we can conclude that
![]() $1/N \leq \|A_j\|,\|A_j^{-1}\|\leq N$
for each
$1/N \leq \|A_j\|,\|A_j^{-1}\|\leq N$
for each
![]() $1\leq j \leq \ell $
.
$1\leq j \leq \ell $
.
For the second case, we assume that
![]() $\dim \ker (Df_0)=\kappa $
. Then,
$\dim \ker (Df_0)=\kappa $
. Then,
![]() $\mathrm {Cr}_{\kappa }(f_0)=\{x \in M: \dim \ker ({Df_0}^{m_{f_0}}_x)=\kappa \}$
is non-empty and
$\mathrm {Cr}_{\kappa }(f_0)=\{x \in M: \dim \ker ({Df_0}^{m_{f_0}}_x)=\kappa \}$
is non-empty and
![]() $m_{f_0}=1$
.
$m_{f_0}=1$
.
This allows us to conclude that every
![]() $f \in \mathcal {F}$
satisfies that
$f \in \mathcal {F}$
satisfies that
![]() $m_f=1$
since
$m_f=1$
since
![]() $m_f\leq m_{f_0}$
. Then, to obtain the control of
$m_f\leq m_{f_0}$
. Then, to obtain the control of
![]() $\|A_j\|$
and
$\|A_j\|$
and
![]() $\|A_j^{-1}\|$
, we will show that there is a neighborhood U of
$\|A_j^{-1}\|$
, we will show that there is a neighborhood U of
![]() $\mathrm {Cr}_{\kappa }(f_0)$
in M such that if
$\mathrm {Cr}_{\kappa }(f_0)$
in M such that if
![]() $f \in \mathcal {F}$
, then
$f \in \mathcal {F}$
, then
![]() $\mathrm {Cr}_{\kappa }(f) \subseteq U$
and the piece of the orbit
$\mathrm {Cr}_{\kappa }(f) \subseteq U$
and the piece of the orbit
![]() $\{f^j(x):1\leq j \leq \ell \}$
along which there is a lack of domination property is away from U. This will imply a similar inequality as in (4.6) since
$\{f^j(x):1\leq j \leq \ell \}$
along which there is a lack of domination property is away from U. This will imply a similar inequality as in (4.6) since
![]() $\dim \ker (Df)<\kappa $
out of U.
$\dim \ker (Df)<\kappa $
out of U.
The next lemma deals with this subtle part of the proof.
Lemma 4.3. Assume that
![]() $\dim \ker (Df_0)=\kappa $
. Then, there exists a neighborhood
$\dim \ker (Df_0)=\kappa $
. Then, there exists a neighborhood
![]() $\mathcal {U} \subseteq \mathcal {U}_0$
of
$\mathcal {U} \subseteq \mathcal {U}_0$
of
![]() $f_0$
and another one U of
$f_0$
and another one U of
![]() $\mathrm {Cr}_{\kappa }(f_0)$
such that for any
$\mathrm {Cr}_{\kappa }(f_0)$
such that for any
![]() $f \in \mathcal {F}\cap \mathcal {U}$
, its critical point
$f \in \mathcal {F}\cap \mathcal {U}$
, its critical point
![]() $\mathrm {Cr}_{\kappa }(f)$
is contained in U, and if
$\mathrm {Cr}_{\kappa }(f)$
is contained in U, and if
![]() $(x_j)_j \in \Lambda _f$
satisfies
$(x_j)_j \in \Lambda _f$
satisfies
for each
![]() $1\leq j \leq l$
, then
$1\leq j \leq l$
, then
![]() $x_0,x_1,\ldots ,x_{l-1} \notin U$
.
$x_0,x_1,\ldots ,x_{l-1} \notin U$
.
4.1 Domination property near the critical points
Our goal here is to prove Lemma 4.3. For that, we will first make some preliminaries that will be needed in the proof.
Denote by
![]() $0\leq \sigma _{1}(x)\leq \sigma _{2}(x) \leq \cdots \leq \sigma _d(x)$
the singular values of
$0\leq \sigma _{1}(x)\leq \sigma _{2}(x) \leq \cdots \leq \sigma _d(x)$
the singular values of
![]() $Df$
at
$Df$
at
![]() $x \in M$
. Using that
$x \in M$
. Using that
![]() $\mathcal {F}$
accumulates at
$\mathcal {F}$
accumulates at
![]() $f_0$
(in
$f_0$
(in
![]() $C^1$
-topology) together with the fact that
$C^1$
-topology) together with the fact that
![]() $\ker (Df_0)$
at x is
$\ker (Df_0)$
at x is
![]() $\kappa $
-dimensional for each
$\kappa $
-dimensional for each
![]() $x \in \mathrm {Cr}_{\kappa }(f_0)$
, we can find a neighborhood
$x \in \mathrm {Cr}_{\kappa }(f_0)$
, we can find a neighborhood
![]() $\mathcal {U}_0$
of
$\mathcal {U}_0$
of
![]() $f_0$
and a neighborhood
$f_0$
and a neighborhood
![]() $U_0$
of
$U_0$
of
![]() $\mathrm {Cr}_{\kappa }(f_0)$
so that
$\mathrm {Cr}_{\kappa }(f_0)$
so that
![]() $\mathrm {Cr}_{\kappa }(f)$
is contained in
$\mathrm {Cr}_{\kappa }(f)$
is contained in
![]() $U_0$
for every f in
$U_0$
for every f in
![]() $\mathcal {F}\cap \mathcal {U}_0$
. In particular, the singular values of
$\mathcal {F}\cap \mathcal {U}_0$
. In particular, the singular values of
![]() $Df$
at
$Df$
at
![]() $x \in \mathrm {Cr}_{\kappa }(f)$
are the following:
$x \in \mathrm {Cr}_{\kappa }(f)$
are the following:
By continuity of
![]() $\sigma _i$
terms on M since f is a
$\sigma _i$
terms on M since f is a
![]() $C^1$
-endomorphism, we can assume that for all
$C^1$
-endomorphism, we can assume that for all
![]() $x \in U_0$
, one has that
$x \in U_0$
, one has that
Denote by
![]() $V_f(x)$
and
$V_f(x)$
and
![]() $W_f(x)$
the subspaces of
$W_f(x)$
the subspaces of
![]() $T_xM$
generated by the eigenvectors associated to
$T_xM$
generated by the eigenvectors associated to
![]() $\sigma _1(x),\ldots , \sigma _{\kappa }(x)$
and
$\sigma _1(x),\ldots , \sigma _{\kappa }(x)$
and
![]() $\sigma _{\kappa +1}(x), \ldots , \sigma _d(x)$
, respectively. These subspaces satisfy the following properties:
$\sigma _{\kappa +1}(x), \ldots , \sigma _d(x)$
, respectively. These subspaces satisfy the following properties:
-
(1)
 $V_f(x)\oplus W_f(x)=T_xM$
for every
$V_f(x)\oplus W_f(x)=T_xM$
for every
 $x \in U_0$
;
$x \in U_0$
; -
(2)
 $V_{f}(x)\perp W_{f}(x)$
and
$V_{f}(x)\perp W_{f}(x)$
and
 $Df(V_{f}(x))\perp Df(W_{f}(x))$
for every
$Df(V_{f}(x))\perp Df(W_{f}(x))$
for every
 $x \in U_0$
;
$x \in U_0$
; -
(3) if
 $f \in \mathcal {F}$
and
$f \in \mathcal {F}$
and
 $(x_i)_i \in \Lambda _f$
with
$(x_i)_i \in \Lambda _f$
with
 $x_i \in \mathrm {Cr}_{\kappa }(f)$
, then
$x_i \in \mathrm {Cr}_{\kappa }(f)$
, then
 $V_f(x_i)=\ker (Df_{x_i})=E(x_i)$
and
$V_f(x_i)=\ker (Df_{x_i})=E(x_i)$
and
 $Df_{x_i}(W_f(x_i))=\mathrm {Im}(Df_{x_i})=F(x_i)$
.
$Df_{x_i}(W_f(x_i))=\mathrm {Im}(Df_{x_i})=F(x_i)$
.
Furthermore, it follows from the continuous dependence on the singular values of
![]() $Df$
at x that the following maps are continuous:
$Df$
at x that the following maps are continuous:
Remark 4.4. In (4.9), the continuity is seen in
![]() $\mathrm {Grass}_r(TM)$
, the Grassmannian of the vector bundle
$\mathrm {Grass}_r(TM)$
, the Grassmannian of the vector bundle
![]() $TM$
, where its points are all the pairs
$TM$
, where its points are all the pairs
![]() $(x,\Gamma )$
such that
$(x,\Gamma )$
such that
![]() $\Gamma $
is an r-dimensional subspace of
$\Gamma $
is an r-dimensional subspace of
![]() $T_xM$
for
$T_xM$
for
![]() $r=\kappa $
and
$r=\kappa $
and
![]() $r=d-\kappa $
, respectively.
$r=d-\kappa $
, respectively.
For every
![]() $x \in U_0$
and
$x \in U_0$
and
![]() $\eta \in (0,\pi /2)$
, define the following cone-field:
$\eta \in (0,\pi /2)$
, define the following cone-field:
and so ![]() . Furthermore, it follows from 4.1 that
. Furthermore, it follows from 4.1 that
![]() $\mathscr {C}_{W_f}(x,\pi /2-\eta )=\mathscr {C}^{\kern2pt\ast }_{V_f}(x,\eta )$
.
$\mathscr {C}_{W_f}(x,\pi /2-\eta )=\mathscr {C}^{\kern2pt\ast }_{V_f}(x,\eta )$
.
Lemma 4.5. For all
![]() $\eta , \theta \in (0,\pi /2)$
small enough, up to shrinking the neighborhoods
$\eta , \theta \in (0,\pi /2)$
small enough, up to shrinking the neighborhoods
![]() $\mathcal {U}_0$
and
$\mathcal {U}_0$
and
![]() $U_0$
, we have that for every
$U_0$
, we have that for every
![]() $f \in \mathcal {U}_0$
and
$f \in \mathcal {U}_0$
and
![]() $x \in U_0$
, the following holds.
$x \in U_0$
, the following holds.
For every
![]() $u \in \mathscr {C}^{\kern2pt\ast }_{V_f}(x,\eta )$
, writing
$u \in \mathscr {C}^{\kern2pt\ast }_{V_f}(x,\eta )$
, writing
![]() $u=(v,w) \in V_f(x)\oplus W_f(x)$
, one has that
$u=(v,w) \in V_f(x)\oplus W_f(x)$
, one has that
Proof. We first notice that
![]() $V_{f_0}(x)=\ker (Df_0(x))$
and
$V_{f_0}(x)=\ker (Df_0(x))$
and
![]() $Df_0(T_xM)=Df_0(W_{f_0}(x))$
for every
$Df_0(T_xM)=Df_0(W_{f_0}(x))$
for every
![]() $x \in \mathrm {Cr}_{\kappa }(f_0)$
. Then, for every
$x \in \mathrm {Cr}_{\kappa }(f_0)$
. Then, for every
![]() $u\notin V_{f_0}$
, one decomposes
$u\notin V_{f_0}$
, one decomposes
![]() $u=(v,w)\in V_{f_0}(x)\oplus W_{f_0}(x)$
with
$u=(v,w)\in V_{f_0}(x)\oplus W_{f_0}(x)$
with
![]() $w\neq 0$
, implying that
$w\neq 0$
, implying that
![]() $Df_0(u)=Df_0(w)$
. In particular,
$Df_0(u)=Df_0(w)$
. In particular,
![]() $\mathbb {R}Df_0(u)$
is contained in
$\mathbb {R}Df_0(u)$
is contained in
![]() $Df_0(W_{f_0}(x))$
for all
$Df_0(W_{f_0}(x))$
for all
![]() $u \in \mathscr {C}^{\kern2pt\ast }_{V_{f_0}}(x,\eta )$
and
$u \in \mathscr {C}^{\kern2pt\ast }_{V_{f_0}}(x,\eta )$
and
![]() $x \in \mathrm {Cr}_{\kappa }(f_0)$
.
$x \in \mathrm {Cr}_{\kappa }(f_0)$
.
By the continuity in (4.9), we can shrink the neighborhoods
![]() $\mathcal {U}_0$
and
$\mathcal {U}_0$
and
![]() $U_0$
to get (4.10).
$U_0$
to get (4.10).
The next lemma provides a relation between the splittings
![]() $E\oplus F$
and
$E\oplus F$
and
![]() $V\oplus W$
, which guarantees a domination property around of a component of the critical set whose kernel is k-dimensional. For simplicity, the set
$V\oplus W$
, which guarantees a domination property around of a component of the critical set whose kernel is k-dimensional. For simplicity, the set
![]() $\mathcal {U}$
will denote a neighborhood of
$\mathcal {U}$
will denote a neighborhood of
![]() $f_0$
contained in
$f_0$
contained in
![]() $\mathcal {U}_0$
and U denotes a neighborhood of
$\mathcal {U}_0$
and U denotes a neighborhood of
![]() $\mathrm {Cr}_{\kappa }(f_0)$
contained
$\mathrm {Cr}_{\kappa }(f_0)$
contained
![]() $U_0$
.
$U_0$
.
Lemma 4.6. Given
![]() $\eta , \theta \in (0,\pi /2)$
small enough, there exist neighborhoods
$\eta , \theta \in (0,\pi /2)$
small enough, there exist neighborhoods
![]() $\mathcal {U}$
and U so that for each
$\mathcal {U}$
and U so that for each
![]() $f \in \mathcal {F}\cap \mathcal {U}$
and each
$f \in \mathcal {F}\cap \mathcal {U}$
and each
![]() $(x_i)_i \in \Lambda _f$
, one has that if
$(x_i)_i \in \Lambda _f$
, one has that if
![]() $x_i \in U$
, then for all
$x_i \in U$
, then for all
![]() $u_1 \in E(x_i)$
and
$u_1 \in E(x_i)$
and
![]() $u_2 \in F(x_i)$
, writing
$u_2 \in F(x_i)$
, writing
![]() $u_j=(v_j,w_j) \in V_f(x_i)\oplus W_f(x_i)$
for
$u_j=(v_j,w_j) \in V_f(x_i)\oplus W_f(x_i)$
for
![]() $j=1,2$
, the following hold:
$j=1,2$
, the following hold:
Proof. Recall that
![]() $\varepsilon _0>0$
and
$\varepsilon _0>0$
and
![]() $\alpha>0$
are fixed as in (4.5). Assume that
$\alpha>0$
are fixed as in (4.5). Assume that
![]() $2\eta , 2\theta <\min \{\varepsilon _0, \alpha \}/2$
. By Lemma 4.5, there exist neighborhoods
$2\eta , 2\theta <\min \{\varepsilon _0, \alpha \}/2$
. By Lemma 4.5, there exist neighborhoods
![]() $\mathcal {U}$
and U such that for every
$\mathcal {U}$
and U such that for every
![]() $f \in \mathcal {U}$
and
$f \in \mathcal {U}$
and
![]() $x \in U$
, the inequality (4.10) holds and moreover, for every
$x \in U$
, the inequality (4.10) holds and moreover, for every
![]() $f \in \mathcal {F}\cap \mathcal {U}$
, the component
$f \in \mathcal {F}\cap \mathcal {U}$
, the component
![]() $\mathrm {Cr}_{\kappa }(f)$
is contained in U.
$\mathrm {Cr}_{\kappa }(f)$
is contained in U.
We notice that from the inequality (4.10), it follows that to prove the lemma, it is sufficient to show that for every
![]() $(x_i)_i \in \Lambda _f$
whose
$(x_i)_i \in \Lambda _f$
whose
![]() $x_i \in U$
, we have
$x_i \in U$
, we have
Thus, our current goal is to prove (4.12). For that, observe that as ![]() , we have that the vectors of
, we have that the vectors of
![]() $E(x_i)$
and
$E(x_i)$
and
![]() $F(x_i)$
are neither in
$F(x_i)$
are neither in
![]() $\mathscr {C}_{V_f}(x_i,\eta )$
nor in
$\mathscr {C}_{V_f}(x_i,\eta )$
nor in
![]() $\mathscr {C}_{V_f}^{\kern2pt\ast }(x_i,\eta )$
simultaneously. Thus, only one of the following can happen:
$\mathscr {C}_{V_f}^{\kern2pt\ast }(x_i,\eta )$
simultaneously. Thus, only one of the following can happen:
-
• either
 $E(x_i) \subseteq \mathscr {C}_{V_f}(x_i,\eta ) \quad \mathrm {and} \quad F(x_i) \subseteq \mathscr {C}^{\kern2pt\ast }_{V_f}(x_i,\eta )$
; or
$E(x_i) \subseteq \mathscr {C}_{V_f}(x_i,\eta ) \quad \mathrm {and} \quad F(x_i) \subseteq \mathscr {C}^{\kern2pt\ast }_{V_f}(x_i,\eta )$
; or -
•
 $E(x) \subseteq \mathscr {C}^{\kern2pt\ast }_{V_f}(x_i,\eta ) \quad \mathrm {and} \quad F(x_i) \subseteq \mathscr {C}_{V_f}(x_i,\eta )$
.
$E(x) \subseteq \mathscr {C}^{\kern2pt\ast }_{V_f}(x_i,\eta ) \quad \mathrm {and} \quad F(x_i) \subseteq \mathscr {C}_{V_f}(x_i,\eta )$
.
If
![]() $E(x_i) \subseteq \mathscr {C}^{\kern2pt\ast }_{V_f}(x_i,\eta )$
and
$E(x_i) \subseteq \mathscr {C}^{\kern2pt\ast }_{V_f}(x_i,\eta )$
and
![]() $F(x_i) \subseteq \mathscr {C}_{V_f}(x_i,\eta )$
, then there is a vector
$F(x_i) \subseteq \mathscr {C}_{V_f}(x_i,\eta )$
, then there is a vector
![]() $u \in \mathscr {C}^{\kern2pt\ast }_{V_f}(x_i,\eta )$
, where
$u \in \mathscr {C}^{\kern2pt\ast }_{V_f}(x_i,\eta )$
, where ![]() and
and ![]() . Since
. Since
![]() $2\eta ,2\theta $
are smaller than
$2\eta ,2\theta $
are smaller than
![]() $\alpha $
, we can take two rotations
$\alpha $
, we can take two rotations
![]() $R_0$
and
$R_0$
and
![]() $R_1$
of angles less than
$R_1$
of angles less than
![]() $\alpha $
and
$\alpha $
and
![]() $u' \in F(x_i)$
satisfying
$u' \in F(x_i)$
satisfying
![]() $u \in R_0(F(x_i))$
and
$u \in R_0(F(x_i))$
and
![]() $R_1(Df_x(u))\in E(f(x_i))$
. Recall from the discussion in (4.5) to conclude that it is incompatible with (4.3).
$R_1(Df_x(u))\in E(f(x_i))$
. Recall from the discussion in (4.5) to conclude that it is incompatible with (4.3).
Therefore,
![]() $E(x_i) \subseteq \mathscr {C}_{V_f}(x_i,\eta )$
and
$E(x_i) \subseteq \mathscr {C}_{V_f}(x_i,\eta )$
and
![]() $F(x_i) \subseteq \mathscr {C}^{\kern2pt\ast }_{V_f}(x_i,\eta )$
, which concludes the proof.
$F(x_i) \subseteq \mathscr {C}^{\kern2pt\ast }_{V_f}(x_i,\eta )$
, which concludes the proof.
The previous lemma means that around
![]() $\Lambda $
, the subbundle E is
$\Lambda $
, the subbundle E is
![]() $\eta $
-close to
$\eta $
-close to
![]() $V_f$
, and that every
$V_f$
, and that every
![]() $(d-\kappa )$
-dimensional subspace contained in
$(d-\kappa )$
-dimensional subspace contained in
![]() $\mathscr {C}_{V_f}^{\kern2pt\ast }$
, which means it is away from
$\mathscr {C}_{V_f}^{\kern2pt\ast }$
, which means it is away from
![]() $V_f$
, is sent by
$V_f$
, is sent by
![]() $Df$
into a subspace
$Df$
into a subspace
![]() $\theta $
-close to
$\theta $
-close to
![]() $Df(W_f)$
. This will allows us to state the following.
$Df(W_f)$
. This will allows us to state the following.
Lemma 4.7. For each
![]() $\rho>0$
small enough, we can find
$\rho>0$
small enough, we can find
![]() $\eta , \theta>0$
and the neighborhoods
$\eta , \theta>0$
and the neighborhoods
![]() $\mathcal {U}$
and U satisfying Lemmas 4.5 and 4.6 such that for each
$\mathcal {U}$
and U satisfying Lemmas 4.5 and 4.6 such that for each
![]() $f \in \mathcal {F}\cap \mathcal {U}$
and
$f \in \mathcal {F}\cap \mathcal {U}$
and
![]() $(x_i)_i \in \Lambda _f$
, if
$(x_i)_i \in \Lambda _f$
, if
![]() $x_i \in U$
, then
$x_i \in U$
, then
Proof. Recall that the maps
![]() $\mathcal {U} \times U \ni (f,x) \mapsto V_f(x), \, W_f(x)$
are continuous, where
$\mathcal {U} \times U \ni (f,x) \mapsto V_f(x), \, W_f(x)$
are continuous, where
![]() $\mathcal {U}$
and U are neighborhoods of
$\mathcal {U}$
and U are neighborhoods of
![]() $f_0$
and
$f_0$
and
![]() $\mathrm {Cr}_{\kappa }(f_0)$
, respectively. Then, up to shrinking the neighborhoods
$\mathrm {Cr}_{\kappa }(f_0)$
, respectively. Then, up to shrinking the neighborhoods
![]() $\mathcal {U}$
and U, we can assume that
$\mathcal {U}$
and U, we can assume that
![]() $V_f$
and
$V_f$
and
![]() $V_{f_0}$
are
$V_{f_0}$
are
![]() $\eta $
-close to each other and, consequently,
$\eta $
-close to each other and, consequently,
![]() $W_f$
and
$W_f$
and
![]() $W_{f_0}$
are both contained in the dual-cone of each other.
$W_{f_0}$
are both contained in the dual-cone of each other.
Fix
![]() $\eta ,\theta>0$
small enough and take the neighborhoods
$\eta ,\theta>0$
small enough and take the neighborhoods
![]() $\mathcal {U}$
and U satisfying Lemmas 4.5 and 4.6. We observe that for every
$\mathcal {U}$
and U satisfying Lemmas 4.5 and 4.6. We observe that for every
![]() $u=(v,w) \in \mathscr {C}^{\kern2pt\ast }_{V_f}(x,\eta )$
, with
$u=(v,w) \in \mathscr {C}^{\kern2pt\ast }_{V_f}(x,\eta )$
, with
![]() $v \in V_f(x)$
and
$v \in V_f(x)$
and
![]() ${w\in W_f(x)}$
,
${w\in W_f(x)}$
,
and then
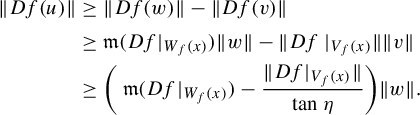 $$ \begin{align*} \|Df(u)\|&\geq \|Df(w)\|-\|Df(v)\|\\ &\geq \operatorname{{\mathfrak{m}}}(Df\!\mid_{W_f(x)})\|w\|-\|Df\mid_{V_f(x)}\!\|\|v\|\\ &\geq \bigg(\operatorname{{\mathfrak{m}}}(Df\!\mid_{W_f(x)})-\dfrac{\|Df\!\mid_{V_f(x)}\!\|}{\tan \eta}\bigg)\|w\|. \end{align*} $$
$$ \begin{align*} \|Df(u)\|&\geq \|Df(w)\|-\|Df(v)\|\\ &\geq \operatorname{{\mathfrak{m}}}(Df\!\mid_{W_f(x)})\|w\|-\|Df\mid_{V_f(x)}\!\|\|v\|\\ &\geq \bigg(\operatorname{{\mathfrak{m}}}(Df\!\mid_{W_f(x)})-\dfrac{\|Df\!\mid_{V_f(x)}\!\|}{\tan \eta}\bigg)\|w\|. \end{align*} $$
We now use that
![]() $(1+{1}/{\tan \eta })\|w\|\geq \|w\|+\|v\|\geq \|u\|$
to obtain that
$(1+{1}/{\tan \eta })\|w\|\geq \|w\|+\|v\|\geq \|u\|$
to obtain that
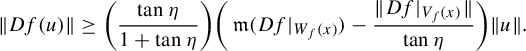 $$ \begin{align*} \|Df(u)\|\geq \bigg(\dfrac{\tan \eta}{1+\tan \eta}\bigg)\bigg(\operatorname{{\mathfrak{m}}}(Df\!\mid_{W_f(x)})-\dfrac{\|Df\!\mid_{V_f(x)}\!\|}{\tan \eta}\bigg)\|u\|. \end{align*} $$
$$ \begin{align*} \|Df(u)\|\geq \bigg(\dfrac{\tan \eta}{1+\tan \eta}\bigg)\bigg(\operatorname{{\mathfrak{m}}}(Df\!\mid_{W_f(x)})-\dfrac{\|Df\!\mid_{V_f(x)}\!\|}{\tan \eta}\bigg)\|u\|. \end{align*} $$
Since
![]() $V_{f_0}(x)=\ker (Df_0)$
and
$V_{f_0}(x)=\ker (Df_0)$
and
![]() $\operatorname {{\mathfrak {m}}}(Df\mid _{W_{f_0}(x)})$
is uniformly away from zero for each
$\operatorname {{\mathfrak {m}}}(Df\mid _{W_{f_0}(x)})$
is uniformly away from zero for each
![]() ${x \in \mathrm {Cr}_{\kappa }(f_0)}$
, we can shrink only the neighborhoods
${x \in \mathrm {Cr}_{\kappa }(f_0)}$
, we can shrink only the neighborhoods
![]() $\mathcal {U}$
and U to obtain that
$\mathcal {U}$
and U to obtain that
![]() $V_f(x)$
and
$V_f(x)$
and
![]() $W_f(x)$
are close to
$W_f(x)$
are close to
![]() $V_{f_0}(x)$
and
$V_{f_0}(x)$
and
![]() $W_{f_0}(x)$
for every
$W_{f_0}(x)$
for every
![]() $x \in U$
. Then, we can assume that
$x \in U$
. Then, we can assume that
![]() $\operatorname {{\mathfrak {m}}}(Df\mid _{W_f(x)})$
is uniformly away from zero and
$\operatorname {{\mathfrak {m}}}(Df\mid _{W_f(x)})$
is uniformly away from zero and
![]() $\|Df\mid _{V_f(x)}\|$
is so close to
$\|Df\mid _{V_f(x)}\|$
is so close to
![]() $0$
such that
$0$
such that
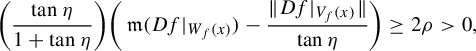 $$ \begin{align*}\bigg(\dfrac{\tan \eta}{1+\tan \eta}\bigg)\bigg(\operatorname{{\mathfrak{m}}}(Df\!\mid_{W_f(x)})-\dfrac{\|Df\!\mid_{V_f(x)}\!\|}{\tan \eta}\bigg)\geq 2\rho>0,\end{align*} $$
$$ \begin{align*}\bigg(\dfrac{\tan \eta}{1+\tan \eta}\bigg)\bigg(\operatorname{{\mathfrak{m}}}(Df\!\mid_{W_f(x)})-\dfrac{\|Df\!\mid_{V_f(x)}\!\|}{\tan \eta}\bigg)\geq 2\rho>0,\end{align*} $$
and hence
![]() $\|Df(u)\|\geq 2 \rho \|u\|$
for every
$\|Df(u)\|\geq 2 \rho \|u\|$
for every
![]() $x \in U$
.
$x \in U$
.
Finally, we take
![]() $f\in \mathcal {F}\cap \mathcal {U}$
, and use that
$f\in \mathcal {F}\cap \mathcal {U}$
, and use that
![]() $E(x)$
and
$E(x)$
and
![]() $V_f(x)$
depend continuously on x in U and are both identical on
$V_f(x)$
depend continuously on x in U and are both identical on
![]() $\mathrm {Cr}_{\kappa }(f)$
to conclude that
$\mathrm {Cr}_{\kappa }(f)$
to conclude that
![]() $\|Df\!\mid _{E(x)}\!\|\approx \|Df\!\mid _{V_f(x)}\!\|$
, which is close to
$\|Df\!\mid _{E(x)}\!\|\approx \|Df\!\mid _{V_f(x)}\!\|$
, which is close to
![]() $\|Df_0\!\mid {V_{f_0}}(x)\!\|\approx 0$
for each
$\|Df_0\!\mid {V_{f_0}}(x)\!\|\approx 0$
for each
![]() $x \in U$
. Therefore, up to shrinking the neighborhoods
$x \in U$
. Therefore, up to shrinking the neighborhoods
![]() $\mathcal {U}$
and U, we can get that
$\mathcal {U}$
and U, we can get that
![]() $\|Df\!\mid _{E(x)}\!\|<\rho $
for every
$\|Df\!\mid _{E(x)}\!\|<\rho $
for every
![]() $x \in U$
.
$x \in U$
.
Now we are able to prove Lemma 4.3.
4.2 Proof of Lemma 4.3
By Lemma 4.6, for all
![]() $\theta>0$
and all
$\theta>0$
and all
![]() $\eta> 0$
small, there exist neighborhoods
$\eta> 0$
small, there exist neighborhoods
![]() $\mathcal {U}$
and U so that for each
$\mathcal {U}$
and U so that for each
![]() $f \in \mathcal {F}\cap \mathcal {U}$
and each
$f \in \mathcal {F}\cap \mathcal {U}$
and each
![]() $(x_i)_i \in \Lambda _f$
, if
$(x_i)_i \in \Lambda _f$
, if
![]() $x_i \in U$
, then the following hold:
$x_i \in U$
, then the following hold:
In particular, ![]() for every
for every
![]() $v \in \mathscr {C}^{\kern2pt\ast }_{V_f}(x_i,\eta )$
.
$v \in \mathscr {C}^{\kern2pt\ast }_{V_f}(x_i,\eta )$
.
We consider the cone-field centered at F of length
![]() $\beta>0$
in coordinates
$\beta>0$
in coordinates
![]() $E\oplus F$
over
$E\oplus F$
over
![]() $(x_i)_i \in \Lambda _f$
by
$(x_i)_i \in \Lambda _f$
by
Choose
![]() $\beta>0$
so that
$\beta>0$
so that ![]() for every
for every
![]() $u \in \mathscr {C}_{F,E}(x_i,\beta )$
, where
$u \in \mathscr {C}_{F,E}(x_i,\beta )$
, where
![]() $\alpha>0$
was fixed in (4.5).
$\alpha>0$
was fixed in (4.5).
Remark 4.8. It should be emphasized that the cone-field above is not as the previous one defined in §2.2, where the length is the angle, since E and F are not necessary orthogonal.
Since the angle between E and F is uniformly away from zero, we can assume that
![]() $\theta , \eta>0$
above are chosen small enough so that for any
$\theta , \eta>0$
above are chosen small enough so that for any
![]() $(x_i)_i \in \Lambda _f$
, one has that if
$(x_i)_i \in \Lambda _f$
, one has that if
![]() $x_i \in U$
, then:
$x_i \in U$
, then:
-
(a)
 ;
; -
(b)
 .
.
Assume now that
![]() $(x_i)_i \in \Lambda $
satisfies the inequality (4.7). That is,
$(x_i)_i \in \Lambda $
satisfies the inequality (4.7). That is,
![]() $(x_i)_i$
satisfies:
$(x_i)_i$
satisfies:
In particular, it is immediate from Lemma 4.7 that
![]() $x_0 \notin U$
.
$x_0 \notin U$
.
It remains to prove that
![]() $x_1,\ldots , x_{l-1} \notin U$
. For that, we first observe that
$x_1,\ldots , x_{l-1} \notin U$
. For that, we first observe that
![]() $x_1,\ldots , x_{l-1}$
are pairwise distinct since, without loss of generality, if
$x_1,\ldots , x_{l-1}$
are pairwise distinct since, without loss of generality, if
![]() $x_l=x_0$
then, as the orbit hits on
$x_l=x_0$
then, as the orbit hits on
![]() $\mathrm {Cr}_{\kappa }(f)$
infinitely many times for the future, we have that
$\mathrm {Cr}_{\kappa }(f)$
infinitely many times for the future, we have that
![]() $x_j \in \mathrm {Cr}_{\kappa }(f)$
for some
$x_j \in \mathrm {Cr}_{\kappa }(f)$
for some
![]() $\leq 1\leq j\leq l-1$
and hence,
$\leq 1\leq j\leq l-1$
and hence,
![]() $\|Df\mid _{E(x_j)}\|=0$
. This contradicts the fact that
$\|Df\mid _{E(x_j)}\|=0$
. This contradicts the fact that
![]() $\|Df\mid _{F(x_j)}\|\neq 0$
.
$\|Df\mid _{F(x_j)}\|\neq 0$
.
Second, we suppose without loss of generality that
![]() $x_{l-1} \in U$
and take
$x_{l-1} \in U$
and take
![]() $v \in E(x_0)$
and
$v \in E(x_0)$
and
![]() $w \in F(x_0)$
the unit vectors, where
$w \in F(x_0)$
the unit vectors, where
Then, we have that
![]() $u=(v,\beta ^{-1}w) \in \partial \mathscr {C}_{F,E}(x_0,\beta )$
since
$u=(v,\beta ^{-1}w) \in \partial \mathscr {C}_{F,E}(x_0,\beta )$
since
![]() $\|v\|=1=\beta \|\beta ^{-1}w\|$
and hence,
$\|v\|=1=\beta \|\beta ^{-1}w\|$
and hence,
Taking
![]() $u_j=Df^j(v,\beta ^{-1}w)$
for each
$u_j=Df^j(v,\beta ^{-1}w)$
for each
![]() $1\leq j \leq l$
, we have that
$1\leq j \leq l$
, we have that
![]() $u_l=Df^l(v,\beta ^{-1}w)$
belongs to dual cone
$u_l=Df^l(v,\beta ^{-1}w)$
belongs to dual cone
![]() $\mathscr {C}_{F,E}^{\kern2pt\ast }(x_l,\beta /2)$
. This implies that
$\mathscr {C}_{F,E}^{\kern2pt\ast }(x_l,\beta /2)$
. This implies that
![]() $u_{l-1} \in \mathscr {C}_{V_f}(x_{l-1},\eta )$
. Otherwise, if
$u_{l-1} \in \mathscr {C}_{V_f}(x_{l-1},\eta )$
. Otherwise, if
![]() $u_{l-1} \notin \mathscr {C}^{\kern2pt\ast }_{V_f}(x_{l-1},\eta )$
, then writing
$u_{l-1} \notin \mathscr {C}^{\kern2pt\ast }_{V_f}(x_{l-1},\eta )$
, then writing
![]() $u_{l-1}=(v',w') \in V_f(x_{l-1})\oplus W_f(x_{l-1})$
and taking z in the intersection between
$u_{l-1}=(v',w') \in V_f(x_{l-1})\oplus W_f(x_{l-1})$
and taking z in the intersection between
![]() $F(x_{l-1})$
and the plane generated by
$F(x_{l-1})$
and the plane generated by
![]() $\{u_{l-1},w'\}$
, one can conclude that
$\{u_{l-1},w'\}$
, one can conclude that
![]() $z=av'+bw'$
and, by Lemma 4.6, one gets that
$z=av'+bw'$
and, by Lemma 4.6, one gets that
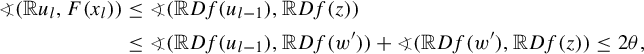
where by item (b), it implies that
![]() $u_l \in \mathscr {C}_{F,E}(x_l,\beta /2)$
, which is a contradiction.
$u_l \in \mathscr {C}_{F,E}(x_l,\beta /2)$
, which is a contradiction.
Thus, by item (a) and the choice of
![]() $\beta>0$
, one concludes that
$\beta>0$
, one concludes that ![]() and
and ![]() since
since
![]() $u \in \mathscr {C}_{F,E}(x_0,\beta )$
. Thus, we can find two rotations
$u \in \mathscr {C}_{F,E}(x_0,\beta )$
. Thus, we can find two rotations
![]() $R_0:T_{x_0}M \to T_{x_0}M$
and
$R_0:T_{x_0}M \to T_{x_0}M$
and
![]() $R_1:T_{x_{l-1}}M \to T_{x_{l-1}}M$
of angle smaller than
$R_1:T_{x_{l-1}}M \to T_{x_{l-1}}M$
of angle smaller than
![]() $\alpha $
and
$\alpha $
and
![]() $u_0 \in F(x_0)$
such that
$u_0 \in F(x_0)$
such that
Finally, we take that
![]() $\Sigma =\{x_{-1},\ldots ,x_{l-2}\}$
and
$\Sigma =\{x_{-1},\ldots ,x_{l-2}\}$
and
![]() $L_j:T_{x_{j-2}}M \to T_{x_{j-1}}M$
, defined by
$L_j:T_{x_{j-2}}M \to T_{x_{j-1}}M$
, defined by
![]() $L_1=R_0\circ Df_{x_{-1}},\, L_2=Df_0, \, \ldots ,\, L_{l-1}= Df_{x_{l-3}},\, \text {and } L_{l}=R_1\circ Df_{x_{l-2}}$
satisfy the hypothesis of Lemma 4.2 which is incompatible with (4.3).
$L_1=R_0\circ Df_{x_{-1}},\, L_2=Df_0, \, \ldots ,\, L_{l-1}= Df_{x_{l-3}},\, \text {and } L_{l}=R_1\circ Df_{x_{l-2}}$
satisfy the hypothesis of Lemma 4.2 which is incompatible with (4.3).
4.3 Proof of the uniform domination property
This section is devoted to conclude the proof of the uniform domination property. First of all, some preliminaries are needed.
Let us introduce a classical result about the lack of domination of matrices, where some proofs can be seen in [Reference Potrie23, Appendix A] and [Reference Bochi and Morris5, Lemma 3.1].
Lemma 4.9. For all
![]() $\delta>0$
and all
$\delta>0$
and all
![]() $N>1$
, there exists
$N>1$
, there exists
![]() $l> 1$
such that if
$l> 1$
such that if
![]() $A_1,\ldots , A_l$
are matrices in
$A_1,\ldots , A_l$
are matrices in
![]() ${\mathrm {GL}}(2,\mathbb {R})$
and
${\mathrm {GL}}(2,\mathbb {R})$
and
![]() $v, w \in \mathbb {R}^2$
are two unit vectors verifying
$v, w \in \mathbb {R}^2$
are two unit vectors verifying
for every
![]() $1\leq i \leq l$
, then there exist
$1\leq i \leq l$
, then there exist
![]() $R_i:V_i \to V_i$
rotation of angles smaller than
$R_i:V_i \to V_i$
rotation of angles smaller than
![]() $\delta $
such that
$\delta $
such that
![]() $R_lA_l\cdots R_1 A_1(w)$
and
$R_lA_l\cdots R_1 A_1(w)$
and
![]() $A_l\cdots A_1(v)$
are parallel.
$A_l\cdots A_1(v)$
are parallel.
Let us make some comments about what we have done so far. First, we have by Lemma 4.3 that if
![]() $\dim \ker (Df_0)=\kappa $
, then there exists a neighborhood
$\dim \ker (Df_0)=\kappa $
, then there exists a neighborhood
![]() $\mathcal {U}$
of
$\mathcal {U}$
of
![]() $f_0$
and a neighborhood U of
$f_0$
and a neighborhood U of
![]() $\mathrm {Cr}_{\kappa }(f_0)$
such that for every
$\mathrm {Cr}_{\kappa }(f_0)$
such that for every
![]() $f \in \mathcal {F}\cap \mathcal {U}$
and every
$f \in \mathcal {F}\cap \mathcal {U}$
and every
![]() $(x_i)_i \in \Lambda _{f}$
, we have that
$(x_i)_i \in \Lambda _{f}$
, we have that
![]() $\mathrm {Cr}_{\kappa }(f) \subseteq U$
and that the lack of domination property for the splitting
$\mathrm {Cr}_{\kappa }(f) \subseteq U$
and that the lack of domination property for the splitting
![]() $E\oplus F$
over
$E\oplus F$
over
![]() $\Lambda _f$
only might occur away from U. Then, we can get
$\Lambda _f$
only might occur away from U. Then, we can get
![]() $N \geq 1$
so that every
$N \geq 1$
so that every
![]() $f \in \mathcal {U}$
satisfies:
$f \in \mathcal {U}$
satisfies:
since
![]() $\ker (Df_x)$
for each
$\ker (Df_x)$
for each
![]() $x \notin U$
has dimension strictly smaller
$x \notin U$
has dimension strictly smaller
![]() $\kappa $
and
$\kappa $
and
![]() $Df$
on
$Df$
on
![]() $M\backslash U$
is a continuous map on a compact set. In particular,
$M\backslash U$
is a continuous map on a compact set. In particular,
![]() $1/N\leq \|Df\!\mid _{E(x)}\!\|\leq N$
for each
$1/N\leq \|Df\!\mid _{E(x)}\!\|\leq N$
for each
![]() $x \notin U$
and each
$x \notin U$
and each
![]() $f \in \mathcal {F}\cap \mathcal {U}$
.
$f \in \mathcal {F}\cap \mathcal {U}$
.
Recall that in the setting
![]() $\dim \ker (Df_0)=r<\kappa $
, we can suppose that for every
$\dim \ker (Df_0)=r<\kappa $
, we can suppose that for every
![]() $f \in \mathcal {U}$
, the following hold:
$f \in \mathcal {U}$
, the following hold:
We now fix
![]() $\ell _0\geq 1$
given by Lemma 4.9 for
$\ell _0\geq 1$
given by Lemma 4.9 for
![]() $\delta =\alpha $
and N above. In the following, we prove that the uniform domination property. In the first step, we assert that there are no large pieces of orbit without the domination property. More concretely, we have the following steps.
$\delta =\alpha $
and N above. In the following, we prove that the uniform domination property. In the first step, we assert that there are no large pieces of orbit without the domination property. More concretely, we have the following steps.
Step 1. For every
![]() $f \in \mathcal {F}\cap \mathcal {U}$
and every
$f \in \mathcal {F}\cap \mathcal {U}$
and every
![]() $(x_i)_i \in \Lambda _f$
, there is an integer
$(x_i)_i \in \Lambda _f$
, there is an integer
![]() $1\leq j \leq \ell _0$
which depends of the orbit
$1\leq j \leq \ell _0$
which depends of the orbit
![]() $(x_i)_i$
such that
$(x_i)_i$
such that
Proof of Step 1
The proof of this step will be by contradiction. That is, assume without loss of generality that for some
![]() $(x_i)_i \in \Lambda _f$
,
$(x_i)_i \in \Lambda _f$
,
for every
![]() $1\leq j \leq \ell _0$
. Then, there exist two unit vectors
$1\leq j \leq \ell _0$
. Then, there exist two unit vectors
![]() $v_j \in E(x_0)$
and
$v_j \in E(x_0)$
and
![]() $w_j \in F(x_0)$
so that
$w_j \in F(x_0)$
so that
for each
![]() $1\leq j \leq \ell _0$
. We notice that
$1\leq j \leq \ell _0$
. We notice that
![]() $Df^j(v_j)\neq 0$
for every
$Df^j(v_j)\neq 0$
for every
![]() $1 \leq j \leq \ell _0$
since
$1 \leq j \leq \ell _0$
since
![]() $Df^n(w_j)\neq 0$
for every
$Df^n(w_j)\neq 0$
for every
![]() $n\geq 1$
.
$n\geq 1$
.
It should also be noted that, in the particular setting that
![]() $|\ker (Df_0)|=\kappa $
, one has that
$|\ker (Df_0)|=\kappa $
, one has that
![]() $x_0, \ldots , \, x_{\ell _0-1} \notin U$
by Lemma 4.3.
$x_0, \ldots , \, x_{\ell _0-1} \notin U$
by Lemma 4.3.
Let us identify
![]() $T_{x_i}M$
with
$T_{x_i}M$
with
![]() $\mathbb {R}^d$
for
$\mathbb {R}^d$
for
![]() $0 \leq i \leq \ell _0$
, and fix the notation
$0 \leq i \leq \ell _0$
, and fix the notation
![]() $v=v_{\ell _0}$
and
$v=v_{\ell _0}$
and
![]() ${w=w_{\ell _0}}$
. Take the family of matrices
${w=w_{\ell _0}}$
. Take the family of matrices
![]() $A_1,\ldots ,A_m$
defined by
$A_1,\ldots ,A_m$
defined by
![]() $A_i=Df_{x_{i-1}}$
and the family of two-dimensional subspace
$A_i=Df_{x_{i-1}}$
and the family of two-dimensional subspace
![]() $V_i=A_i\cdots A_1(V_0)$
, where
$V_i=A_i\cdots A_1(V_0)$
, where
![]() $V_0$
denotes the subspace spanned by v and w. Then, denote by
$V_0$
denotes the subspace spanned by v and w. Then, denote by
![]() $\tilde {A}_i:V_{i-1}\to V_i$
the restriction of
$\tilde {A}_i:V_{i-1}\to V_i$
the restriction of
![]() $A_i$
to
$A_i$
to
![]() $V_{i-1}$
, which is an isomorphism and, by (4.15) and (4.16), verifies
$V_{i-1}$
, which is an isomorphism and, by (4.15) and (4.16), verifies
This family
![]() $\tilde {A}_1,\ldots ,\tilde {A}_{\ell _0}$
satisfies (4.14). Therefore, there exist
$\tilde {A}_1,\ldots ,\tilde {A}_{\ell _0}$
satisfies (4.14). Therefore, there exist
![]() $\tilde {R}_{\ell _0}\ldots , \tilde {R}_1$
rotations of angles less than
$\tilde {R}_{\ell _0}\ldots , \tilde {R}_1$
rotations of angles less than
![]() $\theta _0$
such that
$\theta _0$
such that
![]() $\tilde {R}_{\ell _0}\tilde {A}_{\ell _0}\cdots \tilde {R}_1\tilde {A}_1(w)$
and
$\tilde {R}_{\ell _0}\tilde {A}_{\ell _0}\cdots \tilde {R}_1\tilde {A}_1(w)$
and
![]() $\tilde {A}_{\ell _0}\cdots \tilde {A}_1(v)$
are parallel. Extending
$\tilde {A}_{\ell _0}\cdots \tilde {A}_1(v)$
are parallel. Extending
![]() $\tilde {R}_i$
to the linear map
$\tilde {R}_i$
to the linear map
![]() $R_i$
on
$R_i$
on
![]() $\mathbb {R}^d$
that equals the identity on the orthogonal complement of
$\mathbb {R}^d$
that equals the identity on the orthogonal complement of
![]() $V_i$
. Finally,
$V_i$
. Finally,
![]() $\Sigma =\{x_0,\ldots ,x_{\ell _0-1}\}$
and
$\Sigma =\{x_0,\ldots ,x_{\ell _0-1}\}$
and
![]() $L_i=R_i\circ A_i$
, for
$L_i=R_i\circ A_i$
, for
![]() $1\leq i \leq \ell _0$
, verify the hypothesis of Lemma 4.2 which is a contradiction. Therefore, one has that every
$1\leq i \leq \ell _0$
, verify the hypothesis of Lemma 4.2 which is a contradiction. Therefore, one has that every
![]() $f \in \mathcal {F}\cap \mathcal {U}$
verifies (4.17).
$f \in \mathcal {F}\cap \mathcal {U}$
verifies (4.17).
Finally, we can conclude the proof of the uniform domination property.
Step 2. There exists
![]() $\ell \geq 1$
so that for every
$\ell \geq 1$
so that for every
![]() $f \in \mathcal {F}\cap \mathcal {U}$
, the splitting
$f \in \mathcal {F}\cap \mathcal {U}$
, the splitting
![]() $E\oplus F$
over
$E\oplus F$
over
![]() $\Lambda _f$
satisfies
$\Lambda _f$
satisfies
![]() $E\prec _{\ell } F$
.
$E\prec _{\ell } F$
.
Proof of Step 2
By Step 1, let
![]() $\ell \geq \ell _0$
be very large. Then, for all
$\ell \geq \ell _0$
be very large. Then, for all
![]() $(x_i)_i \in \Lambda _f$
, there exists
$(x_i)_i \in \Lambda _f$
, there exists
![]() $1\leq j_0\leq \ell _0$
satisfying
$1\leq j_0\leq \ell _0$
satisfying
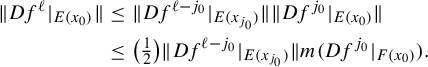 $$ \begin{align*} \|Df^{\ell}\!\mid_{E(x_0)}\!\|&\leq \|Df^{\ell-j_0}\!\mid_{E(x_{j_0})}\!\|\|Df^{j_0}\!\mid_{E(x_0)}\!\| \\ &\leq \big(\tfrac{1}{2}\big) \|Df^{\ell-j_0}\!\mid_{E(x_{j_0})}\!\|m(Df^{j_0}\!\mid_{F(x_0)}). \end{align*} $$
$$ \begin{align*} \|Df^{\ell}\!\mid_{E(x_0)}\!\|&\leq \|Df^{\ell-j_0}\!\mid_{E(x_{j_0})}\!\|\|Df^{j_0}\!\mid_{E(x_0)}\!\| \\ &\leq \big(\tfrac{1}{2}\big) \|Df^{\ell-j_0}\!\mid_{E(x_{j_0})}\!\|m(Df^{j_0}\!\mid_{F(x_0)}). \end{align*} $$
However, taking the point
![]() $(x_{j+j_0})_j$
, there exists
$(x_{j+j_0})_j$
, there exists
![]() $1 \leq j_1 \leq \ell _0$
such that
$1 \leq j_1 \leq \ell _0$
such that
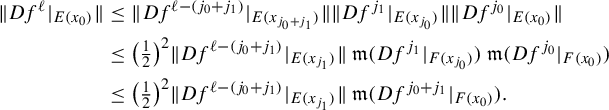 $$ \begin{align*} \|Df^{\ell}\!\mid_{E(x_0)}\!\|&\leq \|Df^{\ell-(j_0+j_1)}\!\mid_{E(x_{j_0+j_1})}\!\|\|Df^{j_1}\!\mid_{E(x_{j_0})}\!\|\|Df^{j_0}\!\mid_{E(x_0)}\!\| \\ &\leq \big(\tfrac{1}{2}\big)^2 \|Df^{\ell-(j_0+j_1)}\!\mid_{E(x_{j_1})}\!\|\operatorname{{\mathfrak{m}}}(Df^{j_1}\!\mid_{F(x_{j_0})})\operatorname{{\mathfrak{m}}}(Df^{j_0}\!\mid_{F(x_0)})\\ &\leq \big(\tfrac{1}{2}\big)^2 \|Df^{\ell-(j_0+j_1)}\!\mid_{E(x_{j_1})}\!\|\operatorname{{\mathfrak{m}}}(Df^{j_0+j_1}\!\mid_{F(x_0)}). \end{align*} $$
$$ \begin{align*} \|Df^{\ell}\!\mid_{E(x_0)}\!\|&\leq \|Df^{\ell-(j_0+j_1)}\!\mid_{E(x_{j_0+j_1})}\!\|\|Df^{j_1}\!\mid_{E(x_{j_0})}\!\|\|Df^{j_0}\!\mid_{E(x_0)}\!\| \\ &\leq \big(\tfrac{1}{2}\big)^2 \|Df^{\ell-(j_0+j_1)}\!\mid_{E(x_{j_1})}\!\|\operatorname{{\mathfrak{m}}}(Df^{j_1}\!\mid_{F(x_{j_0})})\operatorname{{\mathfrak{m}}}(Df^{j_0}\!\mid_{F(x_0)})\\ &\leq \big(\tfrac{1}{2}\big)^2 \|Df^{\ell-(j_0+j_1)}\!\mid_{E(x_{j_1})}\!\|\operatorname{{\mathfrak{m}}}(Df^{j_0+j_1}\!\mid_{F(x_0)}). \end{align*} $$
Repeating the process, we can find
![]() $n\geq 1$
so that
$n\geq 1$
so that
![]() $m_n=\ell -\sum _{i=0}^{n-1}j_i$
satisfies
$m_n=\ell -\sum _{i=0}^{n-1}j_i$
satisfies
![]() ${1 \leq m_n \leq \ell _0}$
; and
${1 \leq m_n \leq \ell _0}$
; and
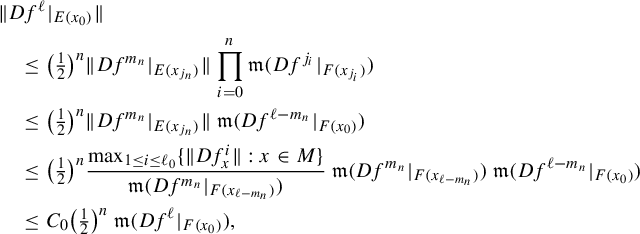 $$ \begin{align*} &\|Df^{\ell}\!\mid_{E(x_0)}\!\|\\ &\quad\leq\big(\tfrac{1}{2}\big)^n \|Df^{m_n}\!\mid_{E(x_{j_n})}\!\|\prod_{i=0}^{n}\operatorname{{\mathfrak{m}}}(Df^{j_i}\!\mid_{F(x_{j_i})}) \\ &\quad\leq \big(\tfrac{1}{2}\big)^n \|Df^{m_n}\!\mid_{E(x_{j_n})}\!\|\operatorname{{\mathfrak{m}}}(Df^{{\ell}-m_n}\!\mid_{F(x_0)})\\ &\quad\leq \big(\tfrac{1}{2}\big)^n \dfrac{\max_{1\leq i\leq \ell_0}\{\|Df^i_x\|:x\in M \}}{\operatorname{{\mathfrak{m}}}(Df^{m_n}\!\mid_{F(x_{\ell-m_n})})} \operatorname{{\mathfrak{m}}}(Df^{m_n}\!\mid_{F(x_{\ell-m_n})})\operatorname{{\mathfrak{m}}}(Df^{{\ell}-m_n}\!\mid_{F(x_0)})\\ &\quad\leq C_0 \big(\tfrac{1}{2}\big)^n\operatorname{{\mathfrak{m}}}(Df^{\ell}\!\mid_{F(x_0)}), \end{align*} $$
$$ \begin{align*} &\|Df^{\ell}\!\mid_{E(x_0)}\!\|\\ &\quad\leq\big(\tfrac{1}{2}\big)^n \|Df^{m_n}\!\mid_{E(x_{j_n})}\!\|\prod_{i=0}^{n}\operatorname{{\mathfrak{m}}}(Df^{j_i}\!\mid_{F(x_{j_i})}) \\ &\quad\leq \big(\tfrac{1}{2}\big)^n \|Df^{m_n}\!\mid_{E(x_{j_n})}\!\|\operatorname{{\mathfrak{m}}}(Df^{{\ell}-m_n}\!\mid_{F(x_0)})\\ &\quad\leq \big(\tfrac{1}{2}\big)^n \dfrac{\max_{1\leq i\leq \ell_0}\{\|Df^i_x\|:x\in M \}}{\operatorname{{\mathfrak{m}}}(Df^{m_n}\!\mid_{F(x_{\ell-m_n})})} \operatorname{{\mathfrak{m}}}(Df^{m_n}\!\mid_{F(x_{\ell-m_n})})\operatorname{{\mathfrak{m}}}(Df^{{\ell}-m_n}\!\mid_{F(x_0)})\\ &\quad\leq C_0 \big(\tfrac{1}{2}\big)^n\operatorname{{\mathfrak{m}}}(Df^{\ell}\!\mid_{F(x_0)}), \end{align*} $$
where
![]() $C_0$
is a constant satisfying
$C_0$
is a constant satisfying
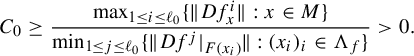 $$ \begin{align*} C_0 \geq \dfrac{\max_{1\leq i\leq \ell_0}\{\|Df^i_x\|:x\in M \}}{\min_{1\leq j \leq \ell_0}\{\|Df^j{\mid}_{F(x_i)}{\kern-1pt}\|: (x_i)_i \in \Lambda_f \}}>0. \end{align*} $$
$$ \begin{align*} C_0 \geq \dfrac{\max_{1\leq i\leq \ell_0}\{\|Df^i_x\|:x\in M \}}{\min_{1\leq j \leq \ell_0}\{\|Df^j{\mid}_{F(x_i)}{\kern-1pt}\|: (x_i)_i \in \Lambda_f \}}>0. \end{align*} $$
Note that
![]() $C_0$
is well defined and is uniform in
$C_0$
is well defined and is uniform in
![]() $\mathcal {F}\cap \mathcal {U}$
. Indeed, we can shrink
$\mathcal {F}\cap \mathcal {U}$
. Indeed, we can shrink
![]() $\mathcal {U}$
(if necessary) to obtain that
$\mathcal {U}$
(if necessary) to obtain that
![]() $\dim \ker (Df^j) \leq \dim \ker (Df^j_0)\leq \kappa $
at x and
$\dim \ker (Df^j) \leq \dim \ker (Df^j_0)\leq \kappa $
at x and
![]() $\ker (Df^j)$
is close to
$\ker (Df^j)$
is close to
![]() $\ker (Df^j_0)$
on
$\ker (Df^j_0)$
on
![]() $T_xM$
for each
$T_xM$
for each
![]() $x \in M, 1\leq j\leq \ell _0,$
and
$x \in M, 1\leq j\leq \ell _0,$
and
![]() $f \in \mathcal {U}$
. Then we assume that
$f \in \mathcal {U}$
. Then we assume that
![]() $\ker (Df^j_x)$
is contained in a cone
$\ker (Df^j_x)$
is contained in a cone
![]() $\mathscr {C}_{V}(x,\eta )$
, where V is the kernel of
$\mathscr {C}_{V}(x,\eta )$
, where V is the kernel of
![]() $Df_0^{\ell _0}$
at x and
$Df_0^{\ell _0}$
at x and
![]() $0<\eta <\alpha $
for each
$0<\eta <\alpha $
for each
![]() $x \in M$
and
$x \in M$
and
![]() $1\leq j \leq \ell _0$
. Since
$1\leq j \leq \ell _0$
. Since
![]() $\ker (Df^j_{x_i})\subseteq E(x_i)$
, for every
$\ker (Df^j_{x_i})\subseteq E(x_i)$
, for every
![]() $1\leq j \leq \ell _0$
, and
$1\leq j \leq \ell _0$
, and ![]() , for every
, for every
![]() $(x_i)_i \in \Lambda _f$
and
$(x_i)_i \in \Lambda _f$
and
![]() $f \in \mathcal {F}\cap \mathcal {U}$
, we conclude that
$f \in \mathcal {F}\cap \mathcal {U}$
, we conclude that
![]() $F(x_i)$
is contained in the complement cone of
$F(x_i)$
is contained in the complement cone of
![]() $\mathscr {C}_{V}(x, \eta )$
and that is enough to get that
$\mathscr {C}_{V}(x, \eta )$
and that is enough to get that
![]() $\min _{1\leq j \leq \ell _0}\{\|Df^j{\mid} _{F(x_i)}{\kern-1pt}\|: (x_i)_i \in \Lambda _f \}$
is uniformly away from zero.
$\min _{1\leq j \leq \ell _0}\{\|Df^j{\mid} _{F(x_i)}{\kern-1pt}\|: (x_i)_i \in \Lambda _f \}$
is uniformly away from zero.
Finally, we can choose
![]() $\ell>0$
large enough so that
$\ell>0$
large enough so that
![]() $n\geq 1$
satisfies
$n\geq 1$
satisfies
![]() $C_02^{-n}\leq 2^{-1}$
and so
$C_02^{-n}\leq 2^{-1}$
and so
![]() $E \prec _{\ell } F$
. This concludes the uniform domination property.
$E \prec _{\ell } F$
. This concludes the uniform domination property.
Therefore, we have just proved that every
![]() $f \in \mathcal {F}\cap \mathcal {U}$
admits
$f \in \mathcal {F}\cap \mathcal {U}$
admits
![]() $E\oplus F$
as an
$E\oplus F$
as an
![]() $(\alpha , \ell )$
- dominated splitting. This concludes the proof of Theorem C.
$(\alpha , \ell )$
- dominated splitting. This concludes the proof of Theorem C.
Acknowledgements
The authors thank the referee for her/his appropriate comments and suggestions. W.R. and R.P. were partially supported by CNPq/MCTI/FNDCT project 409198/2021-8, Brazil. R.P. was also partially funded by CSIC. C.L. and E.P. were partially supported by CNPq/MCTI/FNDCT project 406750/2021-1, Brazil. E.P. received support from NSF via grant DMS1956022.



