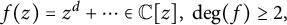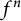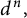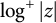Mahler measure of polynomial iterates

Abstract

Granville recently asked how the Mahler measure behaves in the context of polynomial dynamics. For a polynomial $f(z)=z^d+\cdots \in {\mathbb C}[z],\ \deg (f)\ge 2,$ we show that the Mahler measure of the iterates $f^n$ grows geometrically fast with the degree $d^n,$ and find the exact base of that exponential growth. This base is expressed via an integral of $\log ^+|z|$ with respect to the invariant measure of the Julia set for the polynomial $f.$ Moreover, we give sharp estimates for such an integral when the Julia set is connected.

1 Main results

For an arbitrary polynomial $P(z)=c_n\prod _{k=1}^{n}(z-z_k)\in {\mathbb C}[z]$ with $c_n\neq 0,$ the Mahler measure is given by

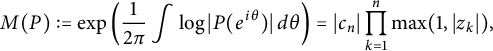(1.1) $$ \begin{align} M(P) := \exp\left(\frac{1}{2\pi}\int \log|P(e^{i\theta})|\,d\theta\right) = |c_n| \prod_{k=1}^{n} \max(1,|z_k|), \end{align} $$

where the second equality is a well-known consequence of Jensen’s formula (see [2, 7, 11] for background and applications).

Let $f(z)=z^d+\cdots \in {\mathbb C}[z],\ \deg (f)\ge 2,$ and consider the n-fold iterates for f denoted by $f^n$ , which are monic polynomials of degree $d^n,\ n\in {\mathbb N}.$ At a recent conference [9], Granville asked interesting questions on the behavior of the Mahler measure under composition of polynomials. In particular, how the Mahler measure of the polynomial iterates $f^n$ behaves as $n\to \infty .$ Our primary goal is to show that the Mahler measure of $f^n$ grows geometrically fast with the degree $d^n$ . In order to state a precise result, we need to introduce the Julia set of f denoted by J, which is a completely invariant compact set under iteration of f (see, e.g., [4] for details). It is also known that there is a unique unit Borel measure $\mu _J$ supported on J that is invariant under f. In fact, $\mu _J$ is the equilibrium measure of J in the sense of logarithmic potential theory (see [4, 13]), and it expresses the steady-state distribution of charge if J is viewed as conductor.

Theorem 1.1 If $f(z)=z^d+\cdots \in {\mathbb C}[z],\ \deg (f)\ge 2,$ is different from the monomial $z^d$ , then we have

(1.2) $$ \begin{align} \lim_{n\to\infty} d^{-n} \log M(f^n) = \int \log^+|z| d\mu_J(z)> 0, \end{align} $$

where $\mu _J$ is the invariant (equilibrium) measure of the Julia set J for f.

Remark 1.2 If $f(z)=z^d$ , then $f^n(z)=z^{d^n},\ n\in {\mathbb N},$ and $M(f^n) = 1,\ n\in {\mathbb N},$ by (1.1). Also note that the smallest value of $\int \log ^+|z| d\mu _J(z)$ is 0 that is attained for $f(z)=z^d$ with $J={\mathbb T}:=\{|z|=1\}$ and $d\mu _{\mathbb T}(e^{it})=dt/(2\pi ),\ t\in [0,2\pi ).$

In light of (1.2), we arrive at the question: How large can $\int \log ^+|z| d\mu _J(z)$ be? Since the location of the Julia set J varies with f in such a way that J can be essentially anywhere in the complex plane, the value of this integral can be arbitrarily large with the values of $\log ^+|z|.$ Indeed, if $J\subset \{z:|z|>R\}$ , then $\int \log ^+|z| d\mu _J(z) \ge \log {R}$ because $\mu _J$ is the unit measure, where $R>1$ can be arbitrarily large. However, if we make proper normalization assumptions, then we obtain some precise upper bounds stated below.

Let K be the filled-in Julia set that consists of the Julia set J and the union of the bounded components of its complement ${\mathbb C}\,{\backslash}\, J$ (see [4, p. 65]). It is clear that $J=\partial K$ , so that K is connected if and only if J is connected, which is known to hold if and only if all the critical points of f are contained in K (see [4, p. 66]). Moreover, J and K share the same equilibrium measure $\mu _J=\mu _K$ (cf. [3, 13]).

Theorem 1.3 If $f(z)=z^d+\cdots \in {\mathbb C}[z],\ \deg (f)\ge 2$ , J is connected, and $0\in K$ , then

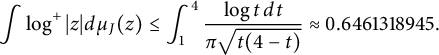(1.3) $$ \begin{align} \int \log^+|z| d\mu_J(z) \le \int_{1}^{4}\frac{\log{t}\,dt}{\pi \sqrt{t(4-t)}} \approx 0.6461318945. \end{align} $$

Equality holds above for $J=K=[0,4]$ and $f(z)=2\, T_d(z/2-1)$ , where $T_d(z)=\cos (d\arccos {z})$ is the classical Chebyshev polynomial.

Symmetry assumptions also produce interesting results such as the one below.

Theorem 1.4 If $f(z)=z^d+\cdots \in {\mathbb C}[z],\ \deg (f)\ge 2,$ is either an odd or an even function, and J is connected, then

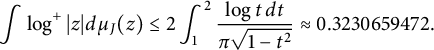(1.4) $$ \begin{align} \int \log^+|z| d\mu_J(z) \le 2 \int_{1}^{2}\frac{\log{t}\,dt}{\pi \sqrt{1-t^2}} \approx 0.3230659472. \end{align} $$

Equality holds above for $J=[-2,2]$ and $f(z)=2\, T_d(z/2)$ , where $T_d(z)=\cos (d\arccos {z})$ .

A classical example that satisfies the assumptions of Theorem 1.4 is given by the family of quadratic polynomials $f(z)=z^2+c$ with c from the Mandelbrot set (see Chapter VIII of [4]).

We remark that the growth of the Mahler measure for the iterates exhibited here is essentially due to the intrinsic connection of the Mahler measure to the unit circle. A more suitable version of the Mahler measure for the dynamical setting is known (see the recent papers [5, 6], where the first one surveys many developments in the area). Another related notion is dynamical (or canonical) height (see [14] for a comprehensive exposition). There are many other connections of the Mahler measure and its generalizations with polynomial dynamics. Thus, the integral of (1.2) can be interpreted as the Arakelov–Zhang pairing of f and $z^2$ that arises as a limit of average Weil heights in [12]. It is practically impossible to discuss all these interesting relations in detail in this short note.

For the proofs of Theorems 1.1, 1.3, and 1.4, we need the well-known result of Brolin [3, Theorem 16.1] on the equidistribution of preimages for the iterates $f^n$ :

Brolin’s Theorem. Let $w\in {\mathbb C}$ be any point with one possible exception. Consider the preimages of w under $f^n$ denoted by $\{z_{k,n}\}_{k=1}^{d^n},$ i.e., all solutions of the equation $f^n(z)=w$ listed according to multiplicities. Define the normalized counting measures in those preimages by

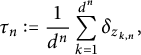(1.5) $$ \begin{align} \tau_n := \frac{1}{d^n} \sum_{k=1}^{d^n} \delta_{z_{k,n}}, \end{align} $$

where $\delta _z$ denotes a unit point mass at $z.$ Then we have the following weak^* convergence:

(1.6) $$ \begin{align} \tau_n \stackrel{*}{\rightarrow} \mu_J \quad\mbox{as }n\to\infty. \end{align} $$

Brolin’s result has the following implication, which is crucial for our purposes.

Corollary 1.5. If $f(z)=z^d+\cdots \in {\mathbb C}[z],\ \deg (f)\ge 2,$ is not the monomial $z^d$ , then we have for the zeros of $f^n$ denoted by $\{z_{k,n}\}_{k=1}^{d^n}$ that

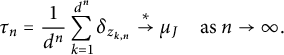(1.7) $$ \begin{align} \tau_n = \frac{1}{d^n} \sum_{k=1}^{d^n} \delta_{z_{k,n}} \stackrel{*}{\rightarrow} \mu_J \quad\mbox{as }n\to\infty. \end{align} $$

Proof The exceptional points in Brolin’s Theorem arise as values omitted by the family of iterates $\{f^n\}_{n=1}^\infty $ in a neighborhood of any point $\zeta \in J$ . It follows that there are at most two such omitted values by Montel’s theorem on normal families, for otherwise the family $\{f^n\}_{n=1}^\infty $ would be normal in that neighborhood, which contradicts the definition of the Julia set J for f. Moreover, Lemma 2.2 of [3] states that the exceptional values are the same for all points $\zeta \in J.$ Since f is a polynomial in our settings, it certainly omits the value $\infty $ in every disk $\{z:|z-\zeta |<r\},$ where $r>0,\ \zeta \in J,$ so that at most one exceptional value can occur in this case. For example, if $f(z)=z^d$ , then this exceptional value is $0$ in every disk $\{z:|z-\zeta |<1\},$ where $\zeta \in J={\mathbb T}$ the unit circumference. However, $0$ cannot be an exceptional value for any polynomial in Theorem 1.1. Indeed, since $\deg (f)\ge 2$ and f is not the monomial $z^d,$ there is a root $w_0\neq 0$ of f. If we assume that $0$ is an exceptional point for Brolin’s Theorem, equivalently an omitted value for the family $\{f^n\}_{n=1}^\infty $ in a neighborhood V of a point $\zeta \in J,$ then the same must be true for $w_0$ because $f^n(z_0)=w_0$ for a point $z_0\in V$ implies $f^{n+1}(z_0)=0$ . But two finite omitted values $0,w_0$ mean that the family $\{f^n\}_{n=1}^\infty $ must be normal in V, contradicting the definition of the Julia set $J.$ Thus, $0$ is not an exceptional point, and Corollary 1.5 is an immediate consequence of Brolin’s Theorem.

2 Proofs of the main results

We continue with the same notations as before.

Proof of Theorem 1.1

It is clear from (1.1) that

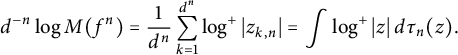$$\begin{align*}d^{-n} \log M(f^n) = \frac{1}{d^n} \sum_{k=1}^{d^n} \log^+|z_{k,n}| = \int \log^+|z|\,d\tau_n(z). \end{align*}$$

Since $\log ^+|z|$ is a continuous function in ${\mathbb C}$ , the limit relation in (1.2) follows from the weak^* convergence of (1.7). One only needs to observe here that the sets $\{z_{k,n}\}_{k=1}^{d^n}$ are uniformly bounded for all $n\in {\mathbb N},$ say belong to a fixed disk $D_R=\{z:|z|\le R\},$ so that $\log ^+|z|$ can be extended from $D_R$ to ${\mathbb C}\,{\backslash}\, D_R$ as a continuous function with compact support in ${\mathbb C}.$

The inequality in (1.2) follows from the work of Fernández [8], who showed that the Julia set J of f different from $z^d$ must have points in the domain $\Delta =\{z:|z|>1\}.$ It is well known that supp $\,\mu _J = J$ (see [3, Lemma 15.2] and [13, pp. 195–197]). Thus,

$$\begin{align*}\int \log^+|z| d\mu_J(z) = \int_{\Delta} \log|z| d\mu_J(z)> 0.\\[-42pt] \end{align*}$$

Proof of Theorem 1.3

Recall that the logarithmic capacity of the Julia set for a monic polynomial is equal to 1 (see Lemma 15.1 of [3] and Theorem 6.5.1 of [13] for a detailed proof). The book [13] contains a complete account on logarithmic potential theory, and on capacity in particular. Since $J=\partial K$ , the equilibrium measure of K is $\mu _K=\mu _J$ , and the capacity of K is 1 (cf. [13]). Clearly, K is a connected set because J is so. The conditions that the capacity of K is 1, $0\in K$ and K is connected introduce restrictions on the size of K and, consequently, on the size of the integral $\int \log ^+|z| d\mu _J(z)$ in (1.2). Theorem 6.2 of [1] (see also Corollary 6 of [10]) gives that the largest value of this integral is attained when $K=[0,4]=J$ , in which case it is well known [13] that

$$\begin{align*}d\mu_K(x) = d\mu_J(x) = \frac{dx}{\pi\sqrt{x(4-x)}}, \quad x\in(0,4). \end{align*}$$

To apply Theorem 6.2 of [1], we also need to note that $\log ^+|z| = \max (0,\log |z|)$ is clearly a convex function of $\log |z|.$ Thus, we have the upper bound (1.3)

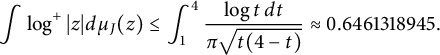$$\begin{align*}\int \log^+|z| d\mu_J(z) \le \int_{1}^{4}\frac{\log{t}\,dt}{\pi\sqrt{t(4-t)}} \approx 0.6461318945. \end{align*}$$

The case of equality for $J=[0,4]$ is attained by the polynomial $f(z)=2\, T_d(z/2-1)$ , where $T_d(z)=\cos (d\arccos {z})$ is the classical Chebyshev polynomial of the first kind (see Sections 1.6.2 and 6.2 of [14] for details).

Proof of Theorem 1.4

We proceed with a proof similar to the previous one, but use Corollary 6.3 of [1] instead of Theorem 6.2 of [1]. We have that capacity of J is 1 by Theorem 6.5.1 of [13], and J is connected by our assumption. Corollary 6.3 of [1] is applied to the filled-in Julia set K, so that $J=\partial K$ , where the equilibrium measure of K is $\mu _K=\mu _J$ , and the capacity of K is 1. Again, K is connected because J is so. Moreover, both J and K are symmetric with respect to the origin because f is even or odd. If f is odd, then 0 is a fixed point of f, implying that $0\in K.$ If f is even, then 0 is a critical point of f; hence, $0\in K$ because we assume that J is connected (cf. [4, p. 66]). Thus, $0\in K$ under our assumptions, and we obtain from Corollary 6.3 of [1] that the largest value of the integral in (1.4) is attained for $J=K=[-2,2] :$

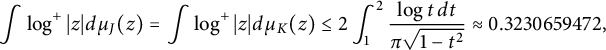$$\begin{align*}\int \log^+|z| d\mu_J(z) = \int \log^+|z| d\mu_K(z) \le 2 \int_{1}^{2}\frac{\log{t}\,dt}{\pi\sqrt{1-t^2}} \approx 0.3230659472, \end{align*}$$

where we used that the equilibrium measure for $J=K=[-2,2]$ is the Chebyshev distribution [13]

$$\begin{align*}d\mu_K(x) = d\mu_J(x) = \frac{dx}{\pi\sqrt{4-x^2}}, \quad x\in(-2,2). \end{align*}$$

It is well known that $J=[-2,2]$ for $f(z)=2\, T_d(z/2)$ , where $T_d(z)=\cos (d\arccos {z})$ (see Sections 1.6.2 and 6.2 of [14]).