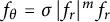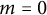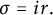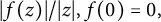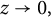1 Introduction
Recently, numerous nonlinear counterparts of the classical Beltrami equation are successfully studied by many mathematicians. The directional dilatation coefficients provide fruitful and flexible tools for investigating the main features of regular solutions to these equations (see [Reference Andreian Cazacu2, Reference Golberg9, Reference Ryazanov, Srebro and Yakubov26]).
In this paper, we estimate the ratio
![]() $|f(z)|/|z|$
under
$|f(z)|/|z|$
under
![]() $f(0)=0,$
which can be treated as asymptotic dilation or real differentiability condition (cf. [Reference Bojarski, Gutlyanskiĭ, Martio and Ryazanov6, Reference Golberg10]) at the origin and goes back to the classical Schwarz lemma bounds.
$f(0)=0,$
which can be treated as asymptotic dilation or real differentiability condition (cf. [Reference Bojarski, Gutlyanskiĭ, Martio and Ryazanov6, Reference Golberg10]) at the origin and goes back to the classical Schwarz lemma bounds.
Let
![]() $\mathbb {C}$
be the complex plane. In the complex notation
$\mathbb {C}$
be the complex plane. In the complex notation
![]() $f=u+iv$
and
$f=u+iv$
and
![]() $z=x+iy$
, the Beltrami equation in a domain
$z=x+iy$
, the Beltrami equation in a domain
![]() $G\subset \mathbb {C}$
has the form
$G\subset \mathbb {C}$
has the form
where
![]() $\mu \colon G\to \mathbb {C}$
is a measurable function and
$\mu \colon G\to \mathbb {C}$
is a measurable function and
are formal derivatives of f in
![]() $\overline {z}$
and z, while
$\overline {z}$
and z, while
![]() $f_{x}$
and
$f_{x}$
and
![]() $f_{y}$
are partial derivatives of f in the variables x and y, respectively.
$f_{y}$
are partial derivatives of f in the variables x and y, respectively.
Various existence theorems for solutions of the Sobolev class have been recently established applying the modulus approach for a quite wide class of linear and quasilinear degenerate Beltrami equations (see, e.g., [Reference Gutlyanskiĭ, Ryazanov, Srebro and Yakubov14, Reference Gutlyanskiĭ, Ryazanov, Srebro and Yakubov15, Reference Martio, Ryazanov, Srebro and Yakubov23, Reference Ryazanov, Srebro and Yakubov26, Reference Sevost’yanov34, Reference Srebro and Yakubov35]).
Let
![]() $\sigma \colon G \to \mathbb {C}$
be a measurable function and
$\sigma \colon G \to \mathbb {C}$
be a measurable function and
![]() $m\geqslant 0.$
We consider the following equation written in the polar coordinates
$m\geqslant 0.$
We consider the following equation written in the polar coordinates
![]() $(r,\theta )$
:
$(r,\theta )$
:
where
![]() $f_{\theta }$
and
$f_{\theta }$
and
![]() $f_{r}$
are the partial derivatives of f by
$f_{r}$
are the partial derivatives of f by
![]() $\theta $
and
$\theta $
and
![]() $r,$
respectively. The equations of this type were studied in the works [Reference Golberg and Salimov11, Reference Golberg, Salimov and Stefanchuk12, Reference Salimov and Stefanchuk30–Reference Salimov and Stefanchuk33].
$r,$
respectively. The equations of this type were studied in the works [Reference Golberg and Salimov11, Reference Golberg, Salimov and Stefanchuk12, Reference Salimov and Stefanchuk30–Reference Salimov and Stefanchuk33].
Applying the relations between these derivatives and the formal derivatives
(see, e.g., [Reference Astala, Iwaniec and Martin5, (21.51)]), one can rewrite equation (1.2) in the Cartesian form:
 $$ \begin{align} f_{\overline{z}}\,=\,\frac{z}{\overline{z}}\,\frac{\widetilde{\sigma}(z)\,|zf_{z}-\overline{z}f_{\overline{z}}|^{m}-1}{\widetilde{\sigma}(z)\,|zf_{z}-\overline{z}f_{\overline{z}}|^{m}+1}\, f_{z}\,, \end{align} $$
$$ \begin{align} f_{\overline{z}}\,=\,\frac{z}{\overline{z}}\,\frac{\widetilde{\sigma}(z)\,|zf_{z}-\overline{z}f_{\overline{z}}|^{m}-1}{\widetilde{\sigma}(z)\,|zf_{z}-\overline{z}f_{\overline{z}}|^{m}+1}\, f_{z}\,, \end{align} $$
where
![]() $\widetilde {\sigma }(z)=i\sigma (z)|z|$
.
$\widetilde {\sigma }(z)=i\sigma (z)|z|$
.
Under
![]() $m=0$
, equation (1.4) reduces to the standard linear Beltrami equation (1.1) with the complex coefficient
$m=0$
, equation (1.4) reduces to the standard linear Beltrami equation (1.1) with the complex coefficient
Picking
![]() $m=0$
and
$m=0$
and
![]() $\sigma =-i/|z|$
in (1.4), we arrive at the classical Cauchy–Riemann system. For
$\sigma =-i/|z|$
in (1.4), we arrive at the classical Cauchy–Riemann system. For
![]() $m>0$
, equation (1.4) provides a partial case of the general nonlinear system of equations (7.33) given in [Reference Astala, Iwaniec and Martin5, Section 7.7].
$m>0$
, equation (1.4) provides a partial case of the general nonlinear system of equations (7.33) given in [Reference Astala, Iwaniec and Martin5, Section 7.7].
Next, we consider an equation of another type, namely
Applying the relations (1.3), one can rewrite equation (1.5) by
 $$ \begin{align} f_{\overline{z}}\,=\,\frac{z}{\overline{z}}\,\frac{1+i\sigma(z)\,|z|^{-m-1}|zf_{z}+\overline{z}f_{\overline{z}}|^{m}}{1-i\sigma(z)\,|z|^{-m-1}|zf_{z}+\overline{z}f_{\overline{z}}|^{m}}\, f_{z}. \end{align} $$
$$ \begin{align} f_{\overline{z}}\,=\,\frac{z}{\overline{z}}\,\frac{1+i\sigma(z)\,|z|^{-m-1}|zf_{z}+\overline{z}f_{\overline{z}}|^{m}}{1-i\sigma(z)\,|z|^{-m-1}|zf_{z}+\overline{z}f_{\overline{z}}|^{m}}\, f_{z}. \end{align} $$
Assuming
![]() $m=0$
, equation (1.6) also becomes the standard linear Beltrami equation (1.1) with
$m=0$
, equation (1.6) also becomes the standard linear Beltrami equation (1.1) with
Choosing
![]() $m=0$
and
$m=0$
and
![]() $\sigma =i|z|$
in (1.6), we arrive again at the classical Cauchy–Riemann system. Later on, we assume that
$\sigma =i|z|$
in (1.6), we arrive again at the classical Cauchy–Riemann system. Later on, we assume that
![]() $m>0.$
$m>0.$
A mapping
![]() $f \colon G \to \mathbb C$
is called regular at a point
$f \colon G \to \mathbb C$
is called regular at a point
![]() $z_0\in G,$
if f has the total differential at this point and its Jacobian
$z_0\in G,$
if f has the total differential at this point and its Jacobian
![]() $J_f=|f_z|^{2}-|f_{\bar {z}}|^{2}$
does not vanish (cf. [Reference Lehto and Virtanen22, I.1.6]). A homeomorphism f of Sobolev class
$J_f=|f_z|^{2}-|f_{\bar {z}}|^{2}$
does not vanish (cf. [Reference Lehto and Virtanen22, I.1.6]). A homeomorphism f of Sobolev class
![]() $W_{\mathrm {{loc}}}^{1, 1}$
is called regular, if
$W_{\mathrm {{loc}}}^{1, 1}$
is called regular, if
![]() $J_{f}>0$
a.e. By a regular solution of equation (1.6), we call a regular homeomorphism
$J_{f}>0$
a.e. By a regular solution of equation (1.6), we call a regular homeomorphism
![]() $f \colon G \to \mathbb C,$
which satisfies (1.6) a.e. in
$f \colon G \to \mathbb C,$
which satisfies (1.6) a.e. in
![]() $G.$
$G.$
The nonlinear equations (1.4) and (1.6) provide partial cases of the nonlinear system of two real partial differential equations (see [Reference Lavrent’ev and Šabat21, (1)] and [Reference Lavrent’ev19, Reference Lavrent’ev20]). Note that various nonlinear systems of similar partial differential equations studied from different aspects and features can be found in [Reference Adamowicz1, Reference Aronsson3–Reference Astala, Iwaniec and Martin5, Reference Bojarski and Iwaniec7, Reference Carozza, Giannetti, di Napoli, Sbordone and Schiattarella8, Reference Guo and Kar13, Reference Kruschkal and Kühnau17–Reference Lavrent’ev and Šabat21, Reference Romanov25, Reference Šabat27, Reference Šabat28].
2 Auxiliary results
Later on, we use the following notations:
and
The area of set
![]() $f(B_r)$
we denote by
$f(B_r)$
we denote by
![]() $S_f(r)=|f(B_r)|.$
$S_f(r)=|f(B_r)|.$
Let
![]() $f:\mathbb {B}\to \mathbb {C}$
be a regular homeomorphism of the Sobolev class
$f:\mathbb {B}\to \mathbb {C}$
be a regular homeomorphism of the Sobolev class
![]() $W_{\mathrm {loc }}^{1,1}$
, and let
$W_{\mathrm {loc }}^{1,1}$
, and let
![]() $p>1$
. By the p-angular dilatation of the mapping f with respect to the point
$p>1$
. By the p-angular dilatation of the mapping f with respect to the point
![]() $z_0=0$
, we call a quantity
$z_0=0$
, we call a quantity
 $$ \begin{align*}D_{p,f}(z) = D_{p,f}(re^{i\theta}) = \frac{|f_{\theta}(re^{i\theta})|^p}{r^p J_f(re^{i\theta})}\,,\end{align*} $$
$$ \begin{align*}D_{p,f}(z) = D_{p,f}(re^{i\theta}) = \frac{|f_{\theta}(re^{i\theta})|^p}{r^p J_f(re^{i\theta})}\,,\end{align*} $$
where
![]() $z = re^{i\theta }$
and
$z = re^{i\theta }$
and
![]() $J_f$
is the Jacobian of f.
$J_f$
is the Jacobian of f.
For
![]() $D_{p,f}(z)$
and
$D_{p,f}(z)$
and
![]() $p>1$
, denote
$p>1$
, denote
 $$ \begin{align} d_{p,f}(r)=\left( \frac{1}{2\pi r} \int\limits_{\gamma_r}\, D_{p,f}^{\frac{1}{p-1}}(z) \, |dz| \right)^{p-1}\,. \end{align} $$
$$ \begin{align} d_{p,f}(r)=\left( \frac{1}{2\pi r} \int\limits_{\gamma_r}\, D_{p,f}^{\frac{1}{p-1}}(z) \, |dz| \right)^{p-1}\,. \end{align} $$
The following statement provides a differential inequality for the area functional
![]() $S_f(r)=|f(B_r)|$
(see Lemma 2.1 in [Reference Golberg, Salimov and Stefanchuk12]).
$S_f(r)=|f(B_r)|$
(see Lemma 2.1 in [Reference Golberg, Salimov and Stefanchuk12]).
Proposition 2.1 Let
![]() $f:\mathbb {B}\to \mathbb {C}$
be a regular homeomorphism of the Sobolev class
$f:\mathbb {B}\to \mathbb {C}$
be a regular homeomorphism of the Sobolev class
![]() $W_{\mathrm {loc }}^{1,1}$
that possesses the N-property, and let
$W_{\mathrm {loc }}^{1,1}$
that possesses the N-property, and let
![]() $p> 1$
. Then
$p> 1$
. Then
for almost all (a.a.)
![]() $r \in [0, 1)$
.
$r \in [0, 1)$
.
Proposition 2.2 Let
![]() $f:\mathbb {B}\to \mathbb {C}$
be a regular homeomorphism of the Sobolev class
$f:\mathbb {B}\to \mathbb {C}$
be a regular homeomorphism of the Sobolev class
![]() $W_{\mathrm {loc }}^{1,1}$
that possesses the N-property, and let
$W_{\mathrm {loc }}^{1,1}$
that possesses the N-property, and let
![]() $p> 1$
and
$p> 1$
and
![]() $K>0$
. If
$K>0$
. If
then
for a.a.
![]() $r\in [0,1).$
$r\in [0,1).$
Lemma 2.3 Let
![]() $f:\mathbb {B}\to \mathbb {C}$
be a regular homeomorphism of the Sobolev class
$f:\mathbb {B}\to \mathbb {C}$
be a regular homeomorphism of the Sobolev class
![]() $W_{\mathrm {loc }}^{1,1}$
that possesses the N-property,
$W_{\mathrm {loc }}^{1,1}$
that possesses the N-property,
![]() $1<p <2$
, and
$1<p <2$
, and
![]() $K>0$
. If
$K>0$
. If
![]() $d_{p,f}(r)\leqslant K$
for a.a.
$d_{p,f}(r)\leqslant K$
for a.a.
![]() $r\in (0,1)$
, then for
$r\in (0,1)$
, then for
![]() $r\in [0,1)$
,
$r\in [0,1)$
,
where
![]() $ C(p,K)=\pi K^{\frac {2}{p-2}} $
.
$ C(p,K)=\pi K^{\frac {2}{p-2}} $
.
Proof Let
![]() $0<\varepsilon <r<1$
. By (2.3), for a.a.
$0<\varepsilon <r<1$
. By (2.3), for a.a.
![]() $t\in [0,1)$
,
$t\in [0,1)$
,
 $$ \begin{align*}\frac{S'_f(t)\, dt }{S^{\frac{p}{2}}_f(t)}\geqslant 2\pi^{\frac{2-p}{2}}\, K^{-1}\, t^{1-p}\,dt, \end{align*} $$
$$ \begin{align*}\frac{S'_f(t)\, dt }{S^{\frac{p}{2}}_f(t)}\geqslant 2\pi^{\frac{2-p}{2}}\, K^{-1}\, t^{1-p}\,dt, \end{align*} $$
and integrating over the segment
![]() $[\varepsilon , r]$
, we obtain
$[\varepsilon , r]$
, we obtain
 $$ \begin{align*}\int\limits_\varepsilon^r \frac{S'_f(t) }{S^{\frac{p}{2}}_f(t)} \, dt \geqslant 2\pi^{\frac{2-p}{2}}\, K^{-1}\, \int\limits_\varepsilon^r t^{1-p}\,dt\,. \end{align*} $$
$$ \begin{align*}\int\limits_\varepsilon^r \frac{S'_f(t) }{S^{\frac{p}{2}}_f(t)} \, dt \geqslant 2\pi^{\frac{2-p}{2}}\, K^{-1}\, \int\limits_\varepsilon^r t^{1-p}\,dt\,. \end{align*} $$
Hence,
 $$ \begin{align*}\int\limits_\varepsilon^r \phi'_p(t)\, dt \geqslant \frac{2\pi^{\frac{2-p}{2}}\,}{(2-p)K} \left(r^{2-p}-\varepsilon^{2-p}\right), \end{align*} $$
$$ \begin{align*}\int\limits_\varepsilon^r \phi'_p(t)\, dt \geqslant \frac{2\pi^{\frac{2-p}{2}}\,}{(2-p)K} \left(r^{2-p}-\varepsilon^{2-p}\right), \end{align*} $$
where
![]() $\phi _p(t)=\frac {2}{2-p}\, S^{\frac {2-p}{2}}_f(t)\,.$
$\phi _p(t)=\frac {2}{2-p}\, S^{\frac {2-p}{2}}_f(t)\,.$
This function is nondecreasing on
![]() $[0, 1)$
, and
$[0, 1)$
, and
 $$ \begin{align*}\int\limits_\varepsilon^r \phi'_p(t)\, dt \leqslant \phi_p(r)- \phi_p(\varepsilon)\,=\frac{2}{2-p}\, \left(S^{\frac{2-p}{2}}_f(r)-S^{\frac{2-p}{2}}_f(\varepsilon)\right) \end{align*} $$
$$ \begin{align*}\int\limits_\varepsilon^r \phi'_p(t)\, dt \leqslant \phi_p(r)- \phi_p(\varepsilon)\,=\frac{2}{2-p}\, \left(S^{\frac{2-p}{2}}_f(r)-S^{\frac{2-p}{2}}_f(\varepsilon)\right) \end{align*} $$
(see Theorem IV.7.4 in [Reference Saks29]). Combining the last two inequalities, we have
 $$ \begin{align*}S^{\frac{2-p}{2}}_f(r)\geqslant S^{\frac{2-p}{2}}_f(r)-S^{\frac{2-p}{2}}_f(\varepsilon) \geqslant \frac{\pi^{\frac{2-p}{2}}\,}{K} \left(r^{2-p}-\varepsilon^{2-p}\right)\,. \end{align*} $$
$$ \begin{align*}S^{\frac{2-p}{2}}_f(r)\geqslant S^{\frac{2-p}{2}}_f(r)-S^{\frac{2-p}{2}}_f(\varepsilon) \geqslant \frac{\pi^{\frac{2-p}{2}}\,}{K} \left(r^{2-p}-\varepsilon^{2-p}\right)\,. \end{align*} $$
Finally, letting
![]() $\varepsilon \to 0$
, we get the estimate (2.4).
$\varepsilon \to 0$
, we get the estimate (2.4).
The following result is an analog of the well-known Ikoma–Schwartz lemma on estimating the limsup (see Corollary 3 in [Reference Ikoma16]).
Lemma 2.4 Let
![]() $f: \mathbb {B}\to \mathbb {C}$
be a regular homeomorphism of the Sobolev class
$f: \mathbb {B}\to \mathbb {C}$
be a regular homeomorphism of the Sobolev class
![]() $W_{\mathrm {loc }}^{1,1}$
that possesses the N-property and normalized by
$W_{\mathrm {loc }}^{1,1}$
that possesses the N-property and normalized by
![]() $f(0)= 0$
, and
$f(0)= 0$
, and
![]() $1<p <2$
and
$1<p <2$
and
![]() $K>0$
. If
$K>0$
. If
![]() $d_{p,f}(r)\leqslant K$
for a.a.
$d_{p,f}(r)\leqslant K$
for a.a.
![]() $r\in (0,1)$
, then
$r\in (0,1)$
, then
Proof Denote
![]() $\mathcal {M}_f(r)=\max \limits _{|z|=r}|f(z)|$
. Since
$\mathcal {M}_f(r)=\max \limits _{|z|=r}|f(z)|$
. Since
![]() $f(0)=0$
, we have
$f(0)=0$
, we have
Thus, applying Lemma 2.3, we obtain
 $$ \begin{align*}\limsup\limits_{z\to 0} \, \frac{|f(z)|}{|z|}=\limsup\limits_{r\to 0} \frac{\mathcal{M}_f(r)}{r}\geqslant \limsup\limits_{r\to 0} \sqrt{\frac{S_f(r)}{\pi r^2}}\geqslant K^{-\frac{1}{2-p}}\,.\\[-43pt] \end{align*} $$
$$ \begin{align*}\limsup\limits_{z\to 0} \, \frac{|f(z)|}{|z|}=\limsup\limits_{r\to 0} \frac{\mathcal{M}_f(r)}{r}\geqslant \limsup\limits_{r\to 0} \sqrt{\frac{S_f(r)}{\pi r^2}}\geqslant K^{-\frac{1}{2-p}}\,.\\[-43pt] \end{align*} $$
In particular, by Lemma 2.4, we come to the following statement.
Corollary 2.5 If
![]() $K>0$
and
$K>0$
and
![]() $D_{p,f}(z)\leqslant K$
for a.a.
$D_{p,f}(z)\leqslant K$
for a.a.
![]() $z\in \mathbb {B}$
, then
$z\in \mathbb {B}$
, then
![]() $ \limsup \limits _{z\to 0} \, \frac {|f(z)|}{|z|}\geqslant K^{-\frac {1}{2-p}}\,.$
$ \limsup \limits _{z\to 0} \, \frac {|f(z)|}{|z|}\geqslant K^{-\frac {1}{2-p}}\,.$
Next, we prove the following statement.
Theorem 2.6 Let
![]() $f: \mathbb {B}\to \mathbb {C}$
be a regular homeomorphism of the Sobolev class
$f: \mathbb {B}\to \mathbb {C}$
be a regular homeomorphism of the Sobolev class
![]() $W_{\mathrm {loc }}^{1,1}$
that possesses the N-property and normalized by
$W_{\mathrm {loc }}^{1,1}$
that possesses the N-property and normalized by
![]() $f(0)= 0$
, and let
$f(0)= 0$
, and let
![]() $1<p <2$
. Suppose that
$1<p <2$
. Suppose that
 $$ \begin{align*}\kappa_0=\liminf\limits_{\varepsilon\to 0} \left( \frac{1}{\pi\varepsilon^2}\int\limits_{B_{\varepsilon}}D_{p,f}^ {\frac{1}{p-1}}(z)\,dx\,dy\right)^{p-1}\,. \end{align*} $$
$$ \begin{align*}\kappa_0=\liminf\limits_{\varepsilon\to 0} \left( \frac{1}{\pi\varepsilon^2}\int\limits_{B_{\varepsilon}}D_{p,f}^ {\frac{1}{p-1}}(z)\,dx\,dy\right)^{p-1}\,. \end{align*} $$
1) If
![]() $\kappa _0\in (0, \infty )$
, then
$\kappa _0\in (0, \infty )$
, then
where
![]() $c_p$
is a positive constant depending on the parameter p.
$c_p$
is a positive constant depending on the parameter p.
2) If
![]() $\kappa _0=0$
, then
$\kappa _0=0$
, then
Proof Let
![]() $\varepsilon \in \left (0, 1 \right )$
. By Proposition 2.1, for a.a.
$\varepsilon \in \left (0, 1 \right )$
. By Proposition 2.1, for a.a.
![]() $r\in [0,1)$
,
$r\in [0,1)$
,
 $$ \begin{align*}\frac{S'_f(r)\, dr }{S^{\frac{p}{2}}_f(r)}\geqslant \frac{2\pi^{\frac{2-p}{2}}}{r^{p-1}d_{p,f}(r) }\,dr; \end{align*} $$
$$ \begin{align*}\frac{S'_f(r)\, dr }{S^{\frac{p}{2}}_f(r)}\geqslant \frac{2\pi^{\frac{2-p}{2}}}{r^{p-1}d_{p,f}(r) }\,dr; \end{align*} $$
therefore, integrating over the segment
![]() $[\frac {\varepsilon }{2}, \varepsilon ]$
, and arguing similarly to the proof of Lemma 2.3, we reach
$[\frac {\varepsilon }{2}, \varepsilon ]$
, and arguing similarly to the proof of Lemma 2.3, we reach
 $$ \begin{align*}S^{\frac{2-p}{2}}_f(\varepsilon)\geqslant S^{\frac{2-p}{2}}_f(\varepsilon)-S^{\frac{2-p}{2}}_f\left(\frac{\varepsilon}{2}\right) \geqslant \pi^{\frac{2-p}{2}}(2-p) \int\limits_{\frac{\varepsilon}{2}}^{\varepsilon} \frac{dr}{r^{p-1}d_{p,f}(r) }. \end{align*} $$
$$ \begin{align*}S^{\frac{2-p}{2}}_f(\varepsilon)\geqslant S^{\frac{2-p}{2}}_f(\varepsilon)-S^{\frac{2-p}{2}}_f\left(\frac{\varepsilon}{2}\right) \geqslant \pi^{\frac{2-p}{2}}(2-p) \int\limits_{\frac{\varepsilon}{2}}^{\varepsilon} \frac{dr}{r^{p-1}d_{p,f}(r) }. \end{align*} $$
Hence,
 $$ \begin{align} S_f(\varepsilon)\geqslant \pi(2-p)^{\frac{2}{2-p}} \left(\int\limits_{\frac{\varepsilon}{2}}^{\varepsilon} \frac{dr}{r^{p-1}d_{p,f}(r) } \right)^{\frac{2}{2-p}} \,. \end{align} $$
$$ \begin{align} S_f(\varepsilon)\geqslant \pi(2-p)^{\frac{2}{2-p}} \left(\int\limits_{\frac{\varepsilon}{2}}^{\varepsilon} \frac{dr}{r^{p-1}d_{p,f}(r) } \right)^{\frac{2}{2-p}} \,. \end{align} $$
Noting
 $$ \begin{align*}\frac{\varepsilon}{2}=\int\limits_{\frac{\varepsilon}{2}}^{\varepsilon} \frac{1}{\left(\int\limits_{\gamma_{r}}D_{p,f}^{\frac{1}{p-1}}(z)\,|dz|\right)^{\frac{p-1}{p}}} \left(\int\limits_{\gamma_{r}}D_{p,f}^{\frac{1}{p-1}}(z)\,|dz|\right)^{\frac{p-1}{p}}dr, \end{align*} $$
$$ \begin{align*}\frac{\varepsilon}{2}=\int\limits_{\frac{\varepsilon}{2}}^{\varepsilon} \frac{1}{\left(\int\limits_{\gamma_{r}}D_{p,f}^{\frac{1}{p-1}}(z)\,|dz|\right)^{\frac{p-1}{p}}} \left(\int\limits_{\gamma_{r}}D_{p,f}^{\frac{1}{p-1}}(z)\,|dz|\right)^{\frac{p-1}{p}}dr, \end{align*} $$
one obtains by Holder’s inequality with exponents p and
![]() $p^{'}=p/(p-1),$
$p^{'}=p/(p-1),$
 $$ \begin{align*}\left(\frac{\varepsilon}{2}\right)^{p}\leqslant\int\limits_{\frac{\varepsilon}{2}}^{\varepsilon} \frac{dr}{\left(\int\limits_{\gamma_{r}}D_{p,f}^{\frac{1}{p-1}}(z)\,|dz|\right)^{p-1}} \left(\int\limits_{\frac{\varepsilon}{2}}^{\varepsilon} \int\limits_{\gamma_{r}}D_{p,f}^{\frac{1}{p-1}}(z)\,|dz|\,dr\right)^{p-1}. \end{align*} $$
$$ \begin{align*}\left(\frac{\varepsilon}{2}\right)^{p}\leqslant\int\limits_{\frac{\varepsilon}{2}}^{\varepsilon} \frac{dr}{\left(\int\limits_{\gamma_{r}}D_{p,f}^{\frac{1}{p-1}}(z)\,|dz|\right)^{p-1}} \left(\int\limits_{\frac{\varepsilon}{2}}^{\varepsilon} \int\limits_{\gamma_{r}}D_{p,f}^{\frac{1}{p-1}}(z)\,|dz|\,dr\right)^{p-1}. \end{align*} $$
Due to (2.1), we rewrite the last inequality in the following form:
 $$ \begin{align*}\left(\frac{\varepsilon}{2}\right)^{p}\leqslant \frac{1}{(2\pi)^{p-1}} \int\limits_{\frac{\varepsilon}{2}}^{\varepsilon}\frac{dr}{r^{p-1}d_{p,f}(r)} \left(\int\limits_{\frac{\varepsilon}{2}}^{\varepsilon}\int\limits_{\gamma_{r}}D_{p,f}^{\frac{1}{p-1}}(z)\,|dz|\,dr\right)^{p-1}. \end{align*} $$
$$ \begin{align*}\left(\frac{\varepsilon}{2}\right)^{p}\leqslant \frac{1}{(2\pi)^{p-1}} \int\limits_{\frac{\varepsilon}{2}}^{\varepsilon}\frac{dr}{r^{p-1}d_{p,f}(r)} \left(\int\limits_{\frac{\varepsilon}{2}}^{\varepsilon}\int\limits_{\gamma_{r}}D_{p,f}^{\frac{1}{p-1}}(z)\,|dz|\,dr\right)^{p-1}. \end{align*} $$
Now, by the Fubini theorem, we have
 $$ \begin{align*}\int\limits_{\frac{\varepsilon}{2}}^{\varepsilon}\frac{dr}{r^{p-1}d_{p,f}(r)}\geqslant (2\pi)^{p-1}\left(\frac{\varepsilon}{2}\right)^p\left(\, \int\limits_{A(0, \frac{\varepsilon}{2}, \varepsilon)}D_{p,f}^ {\frac{1}{p-1}}(z)\,dx\,dy\right)^{1-p}\,. \end{align*} $$
$$ \begin{align*}\int\limits_{\frac{\varepsilon}{2}}^{\varepsilon}\frac{dr}{r^{p-1}d_{p,f}(r)}\geqslant (2\pi)^{p-1}\left(\frac{\varepsilon}{2}\right)^p\left(\, \int\limits_{A(0, \frac{\varepsilon}{2}, \varepsilon)}D_{p,f}^ {\frac{1}{p-1}}(z)\,dx\,dy\right)^{1-p}\,. \end{align*} $$
Since
![]() $ A(0, \frac {\varepsilon }{2}, \varepsilon )\subset B_{\varepsilon }$
,
$ A(0, \frac {\varepsilon }{2}, \varepsilon )\subset B_{\varepsilon }$
,
 $$ \begin{align} \int\limits_{\frac{\varepsilon}{2}}^{\varepsilon}\frac{dr}{r^{p-1}d_{p,f}(r)}\geqslant (2\pi)^{p-1}\left(\frac{\varepsilon}{2}\right)^p\left( \int\limits_{B_{\varepsilon}}D_{p,f}^ {\frac{1}{p-1}}(z)\,dx\,dy\right)^{1-p}. \end{align} $$
$$ \begin{align} \int\limits_{\frac{\varepsilon}{2}}^{\varepsilon}\frac{dr}{r^{p-1}d_{p,f}(r)}\geqslant (2\pi)^{p-1}\left(\frac{\varepsilon}{2}\right)^p\left( \int\limits_{B_{\varepsilon}}D_{p,f}^ {\frac{1}{p-1}}(z)\,dx\,dy\right)^{1-p}. \end{align} $$
Combining (2.6) and (2.7), we obtain
 $$ \begin{align*}S_f(\varepsilon)\geqslant \pi\left( \frac{2-p}{2} \right)^{\frac{2}{2-p}} \varepsilon^2 \left(\frac{1}{\pi\varepsilon^2}\int\limits_{B_{\varepsilon}}D_{p,f}^ {\frac{1}{p-1}}(z)\,dx\,dy\right)^{-\frac{2(p-1)}{2-p}} \,, \end{align*} $$
$$ \begin{align*}S_f(\varepsilon)\geqslant \pi\left( \frac{2-p}{2} \right)^{\frac{2}{2-p}} \varepsilon^2 \left(\frac{1}{\pi\varepsilon^2}\int\limits_{B_{\varepsilon}}D_{p,f}^ {\frac{1}{p-1}}(z)\,dx\,dy\right)^{-\frac{2(p-1)}{2-p}} \,, \end{align*} $$
and by (2.5),
 $$ \begin{align*}\frac{\mathcal{M}_f(\varepsilon)}{\varepsilon}\geqslant\sqrt{\frac{S_f(\varepsilon)}{\pi\varepsilon^2}}\geqslant c_p \left( \frac{1}{\pi\varepsilon^2}\int\limits_{B_{\varepsilon}}D_{p,f}^ {\frac{1}{p-1}}(z)\,dxdy\right)^{-\frac{p-1}{2-p}} \,, \end{align*} $$
$$ \begin{align*}\frac{\mathcal{M}_f(\varepsilon)}{\varepsilon}\geqslant\sqrt{\frac{S_f(\varepsilon)}{\pi\varepsilon^2}}\geqslant c_p \left( \frac{1}{\pi\varepsilon^2}\int\limits_{B_{\varepsilon}}D_{p,f}^ {\frac{1}{p-1}}(z)\,dxdy\right)^{-\frac{p-1}{2-p}} \,, \end{align*} $$
where
![]() $c_p=\left (\frac {2-p}{2}\right )^{\frac {1}{2-p}}$
.
$c_p=\left (\frac {2-p}{2}\right )^{\frac {1}{2-p}}$
.
Thus,
 $$ \begin{align*}\limsup\limits_{z\to 0} \, \frac{|f(z)|}{|z|}=\limsup\limits_{\varepsilon\to 0} \frac{\mathcal{M}_f(\varepsilon)}{\varepsilon}\geqslant c_p \, \kappa_0^{-\frac{1}{2-p}}. \end{align*} $$
$$ \begin{align*}\limsup\limits_{z\to 0} \, \frac{|f(z)|}{|z|}=\limsup\limits_{\varepsilon\to 0} \frac{\mathcal{M}_f(\varepsilon)}{\varepsilon}\geqslant c_p \, \kappa_0^{-\frac{1}{2-p}}. \end{align*} $$
This completes the proof of Theorem 2.6.
3 Application to nonlinear Beltrami equations
In this section, we present theorems on the asymptotic behavior of regular homeomorphic solutions to a nonlinear Beltrami equation of the form (1.6).
Theorem 3.1 Let
![]() $f: \mathbb {B}\to \mathbb {C}$
be a regular homeomorphic solution of equation (1.6) which belongs to Sobolev class
$f: \mathbb {B}\to \mathbb {C}$
be a regular homeomorphic solution of equation (1.6) which belongs to Sobolev class
![]() $W_{\mathrm {loc }}^{1,2}$
, and normalized by
$W_{\mathrm {loc }}^{1,2}$
, and normalized by
![]() $f(0) = 0$
. Assume that
$f(0) = 0$
. Assume that
![]() $C>0$
and the coefficient
$C>0$
and the coefficient
![]() $\sigma : \mathbb {B}\to \mathbb {C}$
satisfies the following condition:
$\sigma : \mathbb {B}\to \mathbb {C}$
satisfies the following condition:
 $$ \begin{align} \int\limits_{\gamma_r} \frac{|\sigma(z) |^{m+2} }{\, \left(\mathrm{Im}\,\sigma(z)\right)^{m+1} }\, |dz| \leqslant C\, r^{2} \end{align} $$
$$ \begin{align} \int\limits_{\gamma_r} \frac{|\sigma(z) |^{m+2} }{\, \left(\mathrm{Im}\,\sigma(z)\right)^{m+1} }\, |dz| \leqslant C\, r^{2} \end{align} $$
for a.a.
![]() $r\in (0,1)$
. Then
$r\in (0,1)$
. Then
 $$ \begin{align} \limsup\limits_{z\to 0} \, \frac{|f(z)|}{|z|}\geqslant \left(\frac{2\pi}{C}\right)^{\frac{1}{m}}\,. \end{align} $$
$$ \begin{align} \limsup\limits_{z\to 0} \, \frac{|f(z)|}{|z|}\geqslant \left(\frac{2\pi}{C}\right)^{\frac{1}{m}}\,. \end{align} $$
Proof Let
![]() $p=\frac {m+2}{m+1}$
,
$p=\frac {m+2}{m+1}$
,
![]() $1<p<2$
. It is well known that any homeomorphism
$1<p<2$
. It is well known that any homeomorphism
![]() $W_{\mathrm {loc }}^{1,2}$
possesses the N-property (see [Reference Martio and Ziemer24, Theorem 4.4]). Since f is a regular homeomorphic solution of equation (1.6), we get
$W_{\mathrm {loc }}^{1,2}$
possesses the N-property (see [Reference Martio and Ziemer24, Theorem 4.4]). Since f is a regular homeomorphic solution of equation (1.6), we get
and
 $$ \begin{align*}D_{p,f}(re^{i\theta}) = \frac{|f_{\theta}(re^{i\theta})|^p}{r^p J_f(re^{i\theta})}= \frac{|\sigma (re^{i\theta}) |^{\frac{m+2}{m+1}} }{r^{\frac{1}{m+1}} \, \mathrm{Im}\,\sigma (re^{i\theta})}\,. \end{align*} $$
$$ \begin{align*}D_{p,f}(re^{i\theta}) = \frac{|f_{\theta}(re^{i\theta})|^p}{r^p J_f(re^{i\theta})}= \frac{|\sigma (re^{i\theta}) |^{\frac{m+2}{m+1}} }{r^{\frac{1}{m+1}} \, \mathrm{Im}\,\sigma (re^{i\theta})}\,. \end{align*} $$
Therefore, in view of the condition (3.1), we have
 $$ \begin{align*}d_{p,f}(r)= \left( \frac{1}{2\pi r^2} \int\limits_{\gamma_r}\, \frac{|\sigma(z) |^{m+2} }{\, \left(\mathrm{Im}\,\sigma(z)\right)^{m+1} } \, |dz| \right)^{\frac{1}{m+1}} \leqslant \left(\frac{C}{2\pi}\right)^{\frac{1}{m+1}} \end{align*} $$
$$ \begin{align*}d_{p,f}(r)= \left( \frac{1}{2\pi r^2} \int\limits_{\gamma_r}\, \frac{|\sigma(z) |^{m+2} }{\, \left(\mathrm{Im}\,\sigma(z)\right)^{m+1} } \, |dz| \right)^{\frac{1}{m+1}} \leqslant \left(\frac{C}{2\pi}\right)^{\frac{1}{m+1}} \end{align*} $$
for a.a.
![]() $r\in (0,1)$
.
$r\in (0,1)$
.
Corollary 3.2 Let
![]() $f: \mathbb {B}\to \mathbb {C}$
be a regular homeomorphic solution of equation (1.6) which belongs to Sobolev class
$f: \mathbb {B}\to \mathbb {C}$
be a regular homeomorphic solution of equation (1.6) which belongs to Sobolev class
![]() $W_{\mathrm {loc }}^{1,2}$
, and normalized by
$W_{\mathrm {loc }}^{1,2}$
, and normalized by
![]() $f(0) = 0$
and
$f(0) = 0$
and
![]() $K>0$
. Assume that the coefficient
$K>0$
. Assume that the coefficient
![]() $\sigma : \mathbb {B}\to \mathbb {C}$
satisfies the following condition:
$\sigma : \mathbb {B}\to \mathbb {C}$
satisfies the following condition:
 $$ \begin{align} \frac{|\sigma (z) |^{m+2} }{\, \left(\mathrm{Im}\,\sigma(z)\right)^{m+1} }\, \leqslant K\, |z| \end{align} $$
$$ \begin{align} \frac{|\sigma (z) |^{m+2} }{\, \left(\mathrm{Im}\,\sigma(z)\right)^{m+1} }\, \leqslant K\, |z| \end{align} $$
for a.a.
![]() $z\in \mathbb {B}$
. Then
$z\in \mathbb {B}$
. Then
Proof Indeed, in view of the condition (3.3), we have
 $$ \begin{align*}\int\limits_{\gamma_r} \frac{|\sigma(z) |^{m+2} }{\, \left(\mathrm{Im}\,\sigma(z)\right)^{m+1} }\, |dz| \leqslant \int\limits_{\gamma_r} \, K|z|\, |dz|=2\pi K\, r^{2}\,.\end{align*} $$
$$ \begin{align*}\int\limits_{\gamma_r} \frac{|\sigma(z) |^{m+2} }{\, \left(\mathrm{Im}\,\sigma(z)\right)^{m+1} }\, |dz| \leqslant \int\limits_{\gamma_r} \, K|z|\, |dz|=2\pi K\, r^{2}\,.\end{align*} $$
Next, applying Theorem 3.1 with the parameter
![]() $C=2\pi K$
, we get the estimate (3.4).
$C=2\pi K$
, we get the estimate (3.4).
We illustrate the last bound by the following example.
Example 3.3 Fix
![]() $k>0$
and consider the equation
$k>0$
and consider the equation
in the unit disk
![]() $\mathbb {B}$
.
$\mathbb {B}$
.
Let
![]() $f=kre^{i\theta }$
. Obviously, the mapping f belongs to the Sobolev class
$f=kre^{i\theta }$
. Obviously, the mapping f belongs to the Sobolev class
![]() $W^{1,2}(\mathbb {B})$
. The partial derivatives of f with respect to
$W^{1,2}(\mathbb {B})$
. The partial derivatives of f with respect to
![]() $\theta $
and r are
$\theta $
and r are
and
![]() $J_f(re^{i\theta })= \frac {1}{r} \, \mathrm {Im}\, \left (\overline {f_r}\, f_\theta \right )=k^2>0\,. $
$J_f(re^{i\theta })= \frac {1}{r} \, \mathrm {Im}\, \left (\overline {f_r}\, f_\theta \right )=k^2>0\,. $
Now, we show that the mapping
![]() $f=k\, re^{i\theta }$
is a solution of equation (3.5). Clearly,
$f=k\, re^{i\theta }$
is a solution of equation (3.5). Clearly,
 $$ \begin{align*}\sigma=\frac{f_\theta}{|f_r|^m f_r}=\frac{i}{k^m}\,r \,.\end{align*} $$
$$ \begin{align*}\sigma=\frac{f_\theta}{|f_r|^m f_r}=\frac{i}{k^m}\,r \,.\end{align*} $$
Thus, (3.1) holds, since
 $$ \begin{align*}\int\limits_{\gamma_r} \frac{|\sigma(z) |^{m+2} }{\, \left(\mathrm{Im}\,\sigma(z)\right)^{m+1} }\, |dz| =C \, r^2\,, \end{align*} $$
$$ \begin{align*}\int\limits_{\gamma_r} \frac{|\sigma(z) |^{m+2} }{\, \left(\mathrm{Im}\,\sigma(z)\right)^{m+1} }\, |dz| =C \, r^2\,, \end{align*} $$
where
![]() $C=\frac {2\pi }{k^m}$
.
$C=\frac {2\pi }{k^m}$
.
On the other hand,
![]() $ \lim \limits _{z\to 0} \, \frac {|f(z)|}{|z|}=k\,.$
$ \lim \limits _{z\to 0} \, \frac {|f(z)|}{|z|}=k\,.$
Remark 3.4 The estimate (3.2) is sharp. It is easy to check that it is attained for a mapping
![]() $f=\left (\frac {2\pi }{C}\right )^{\frac {1}{m}}z$
.
$f=\left (\frac {2\pi }{C}\right )^{\frac {1}{m}}z$
.
By Theorem 2.6, similarly to the proof of Theorem 3.1, we obtain the following statement.
Theorem 3.5 Let
![]() $f\colon \mathbb {B}\to \mathbb {C}$
be a regular homeomorphic solution of equation (1.6) which belongs to Sobolev class
$f\colon \mathbb {B}\to \mathbb {C}$
be a regular homeomorphic solution of equation (1.6) which belongs to Sobolev class
![]() $W^{1,2}_{\mathrm {loc}},$
and normalized by
$W^{1,2}_{\mathrm {loc}},$
and normalized by
![]() $f(0)=0.$
Suppose that
$f(0)=0.$
Suppose that
 $$ \begin{align*}\sigma_{0}=\liminf\limits_{\varepsilon\rightarrow 0}\frac{1}{\pi \varepsilon^2}\int\limits_{B_{\varepsilon}} \frac{|\sigma(z)|^{m+2}}{|z| \left( \mathrm{Im}\, \sigma(z)\right)^{m+1}}\,dxdy. \end{align*} $$
$$ \begin{align*}\sigma_{0}=\liminf\limits_{\varepsilon\rightarrow 0}\frac{1}{\pi \varepsilon^2}\int\limits_{B_{\varepsilon}} \frac{|\sigma(z)|^{m+2}}{|z| \left( \mathrm{Im}\, \sigma(z)\right)^{m+1}}\,dxdy. \end{align*} $$
1) If
![]() $\sigma _{0}\in (0,\infty )$
, then
$\sigma _{0}\in (0,\infty )$
, then
where
![]() $c_{m}$
is a positive constant depending on the parameter
$c_{m}$
is a positive constant depending on the parameter
![]() $m.$
$m.$
2) If
![]() $\sigma _{0}=0$
, then
$\sigma _{0}=0$
, then
Example 3.6 Let
![]() $k>0$
and
$k>0$
and
![]() $\alpha \in (1,m+1)$
. Consider the equation
$\alpha \in (1,m+1)$
. Consider the equation
in the unit disk
![]() $\mathbb {B}.$
$\mathbb {B}.$
The mapping
belongs to the Sobolev class
![]() $W^{1,2}_{\mathrm {loc}}(\mathbb {B})$
. Its partial derivatives with respect to r and
$W^{1,2}_{\mathrm {loc}}(\mathbb {B})$
. Its partial derivatives with respect to r and
![]() $\theta $
are
$\theta $
are
It is easy to see that the mapping
![]() $f=k^{-\frac {1}{m}}\beta ^{\frac {m+1}{m}}r^{\frac {m+1-\alpha }{m}} e^{i\theta }$
is a regular homeomorphic solution of equation (3.6). Clearly,
$f=k^{-\frac {1}{m}}\beta ^{\frac {m+1}{m}}r^{\frac {m+1-\alpha }{m}} e^{i\theta }$
is a regular homeomorphic solution of equation (3.6). Clearly,
 $$ \begin{align*}\sigma=\frac{f_{\theta}}{|f_{r}|^{m}f_{r}}=i k r^{\alpha}.\end{align*} $$
$$ \begin{align*}\sigma=\frac{f_{\theta}}{|f_{r}|^{m}f_{r}}=i k r^{\alpha}.\end{align*} $$
The condition
![]() $\sigma _0=0$
in Theorem 3.5 is fulfilled, since
$\sigma _0=0$
in Theorem 3.5 is fulfilled, since
 $$ \begin{align*}\lim\limits_{\varepsilon\rightarrow 0}\frac{1}{\pi \varepsilon^2}\int\limits_{B_{\varepsilon}} \frac{|\sigma(z)|^{m+2}}{|z| \left( \mathrm{Im}\, \sigma(z)\right)^{m+1}}\,dxdy =0.\end{align*} $$
$$ \begin{align*}\lim\limits_{\varepsilon\rightarrow 0}\frac{1}{\pi \varepsilon^2}\int\limits_{B_{\varepsilon}} \frac{|\sigma(z)|^{m+2}}{|z| \left( \mathrm{Im}\, \sigma(z)\right)^{m+1}}\,dxdy =0.\end{align*} $$
By a direct calculation,
![]() $|f(z)|/|z|\to \infty $
as
$|f(z)|/|z|\to \infty $
as
![]() $z\to 0$
.
$z\to 0$
.