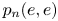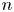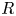Local limit theorems in relatively hyperbolic groups II: the non-spectrally degenerate case

Abstract

This is the second of a series of two papers dealing with local limit theorems in relatively hyperbolic groups. In this second paper, we restrict our attention to non-spectrally degenerate random walks and we prove precise asymptotics of the probability $p_n(e,e)$ of going back to the origin at time $n$. We combine techniques adapted from thermodynamic formalism with the rough estimates of the Green function given by part I to show that $p_n(e,e)\sim CR^{-n}n^{-3/2}$, where $R$ is the inverse of the spectral radius of the random walk. This both generalizes results of Woess for free products and results of Gouëzel for hyperbolic groups.

1. Introduction

Consider a finitely generated group $\Gamma$ and a probability measure $\mu$ on $\Gamma$. We define the $\mu$-random walk on $\Gamma$, starting at $\gamma \in \Gamma$, as $X_n^{\gamma }=\gamma g_1\dots g_n$, where $(g_k)$ are independent random variables of law $\mu$ in $\Gamma$. The law of $X_n^{\gamma }$ is denoted by $p_n(\gamma,\gamma ')$. For $\gamma =e$, it is given by the convolution powers $\mu ^{*n}$ of the measure $\mu$.

We say that $\mu$ is admissible if its support generates $\Gamma$ as a semigroup. We say that $\mu$ is symmetric if $\mu (\gamma )=\mu (\gamma ^{-1})$. Finally, if $\mu$ is admissible, we say that the random walk is aperiodic if $p_n(e,e)>0$ for large enough $n$. The local limit problem consists in finding asymptotics of $p_n(e,e)$ when $n$ goes to infinity. In many situations, if the $\mu$-random walk is aperiodic, one can prove a local limit theorem of the form

(1)\begin{equation} p_n(e,e)\sim C R^{-n}n^{-\alpha}, \end{equation}

where $C>0$ is a constant, $R\geq 1$, and $\alpha \in \mathbb {R}$.

If $\Gamma =\mathbb {Z}^{d}$ and $\mu$ is finitely supported and aperiodic, then classical Fourier computations show that $p_n(e,e)\sim Cn^{-d/2}$ if the random walk is centered and $p_n(e,e)\sim CR^{-n}n^{-d/2}$ with $R>1$ if the random walk is non-centered. If $\Gamma$ is a non-elementary Gromov-hyperbolic group and $\mu$ is finitely supported, symmetric and aperiodic, then one has $p_n(e,e)\sim CR^{-n}n^{-3/2}$, with $R>1$, see [Gou14] and references therein.

Free products are a great source of examples for various local limit theorems, see, for example, [Car88, Car89, CG12]. Woess proved in [Woe86] that for a special class of nearest-neighbor random walks on free products, called the ‘typical case’ in [Woe00], one has a local limit of the form (1), with $\alpha =3/2$. This ‘typical case’ should be considered informally as a situation where the random walk only sees the underlying tree structure of the free product, and not what happens inside the free factors. Thus, in some sense, this coefficient $3/2$ is consistent with the hyperbolic case [Gou14]. Our main goal in this series of two papers is to extend Woess’ results to any relatively hyperbolic group.

We give more details on relatively hyperbolic groups in § 2.1. Recall for now that a finitely generated group $\Gamma$ is relatively hyperbolic with respect to a collection of subgroups $\Omega$ if it acts via a geometrically finite action on a proper geodesic Gromov hyperbolic space $X$, such that $\Omega$ is exactly the set of stabilizers of parabolic limit points for this action. Let $\Omega _0$ be a set of representatives of conjugacy classes of elements of $\Omega$. Such a set $\Omega _0$ is finite.

Let $\mu$ be a probability measure on a relatively hyperbolic group $\Gamma$. Denote by $R_\mu$ the inverse of its spectral radius, that is, the radius of convergence of the Green function $G(x,y|r)$, defined as

\[ G(x,y|r)=\sum_{n\geq 0}p_n(x,y)r^{n}. \]

This radius of convergence is independent of $x,y$. Let $\mathcal {H}\in \Omega _0$ be a parabolic subgroup. Denote by $p_{\mathcal {H}}$ the first return kernel to $\mathcal {H}$ associated to the measure $R_\mu \mu$. Say that a probability measure $\mu$ is spectrally degenerate along $\mathcal {H}\in \Omega _0$ if the spectral radius of $p_{\mathcal {H}}$ is one and that $\mu$ is non-spectrally degenerate if, for every $\mathcal {H}\in \Omega _0$, it is not spectrally degenerate along $\mathcal {H}$. This definition is independent of the choice of $\Omega _0$. It was introduced in [DG21] and appeared to be crucial in the study of the stability of the Martin boundary of relatively hyperbolic groups.

In part I, we introduced the notion of spectral positive recurrence and proved a weaker form of (1) under this assumption, namely that there exists $C$ such that

\[ C^{-1}R^{-n}n^{-3/2}\leq p_n(e,e)\leq CR^{-n}n^{-3/2}. \]

In this part II, we prove a precise local limit theorem like (1), with $\alpha =3/2$, for non-spectrally degenerate measures on relatively hyperbolic groups. As it was proved in part I, non-spectrally degenerate random walks are spectrally positive recurrent, so our assumptions here are stronger, but we prove a more precise result. We insist on the fact that our methods in both papers are very different and that this paper is not an enhanced version of part I, as it uses the results of part I. We make further comments in § 2.3.

Our main goal is to prove the following.

Theorem 1.1 Let $\Gamma$ be a non-elementary relatively hyperbolic group. Let $\mu$ be a finitely supported, admissible, symmetric, and non-spectrally degenerate probability measure on $\Gamma$. Assume that the corresponding random walk is aperiodic. Then, for every $\gamma,\gamma '\in \Gamma$, there exists $C_{\gamma,\gamma '}>0$ such that

\[ p_n(\gamma,\gamma')\sim C_{\gamma,\gamma'}R_{\mu}^{-n}n^{-3/2}. \]

If the $\mu$-random walk is not aperiodic, similar asymptotics hold for $p_{2n}(\gamma,\gamma ')$ if the distance between $\gamma$ and $\gamma '$ is even and for $p_{2n+1}(\gamma,\gamma ')$ if this distance is odd.

This generalizes Woess's results [Woe86] on free products and known results on hyperbolic groups (see [GW86, Lal93, GL13, Gou14]). As a corollary, we also obtain the following.

Corollary 1.2 Let $\Gamma$ be a non-elementary relatively hyperbolic group. Let $\mu$ be a finitely supported, admissible, symmetric, and non-spectrally degenerate probability measure on $\Gamma$. Assume that the corresponding random walk is aperiodic. Denote by $q_n(x,y)$ the probability that the first visit in positive time at $y$ starting at $x$ is at time $n$. Then,

\[ q_n(\gamma,\gamma')\sim C_{\gamma,\gamma'}R_{\mu}^{-n}n^{-3/2}. \]

In [Ger81], Gerl conjectured that if a local limit of the form $p_n(e,e)\sim C R^{-n}n^{-\alpha }$ holds for a finitely supported random walk, then $\alpha$ is a group invariant. This conjecture was disproved by Cartwright in [Car89]. He gave examples of local limit theorems on $\mathbb {Z}^{d}*\mathbb {Z}^{d}$, with $\alpha =d/2$ and examples on the same groups with $\alpha =3/2$. Actually, if $d\neq 3$, then one can only get $\alpha =d/2$ if $d\geq 5$. There are some computations to explain why in [Car88] (see also [Woe00]). In [DG21, Proposition 6.1], we gave a geometric explanation of this fact and proved that if a parabolic subgroup $\mathcal {H}$ is virtually abelian of rank $d\leq 4$, the random walk cannot be spectrally degenerate along $\mathcal {H}$. As a particular case, we thus obtain the following corollary, for low-dimensional Kleinian groups.

Theorem 1.3 Let $\Gamma$ be the fundamental group of a geometrically finite hyperbolic manifold of dimension $n\leq 5$. Let $\mu$ be a finitely supported, admissible, and symmetric probability measure on $\Gamma$. Assume that the $\mu$-random walk is aperiodic. Then, for every $\gamma,\gamma '\in \Gamma$, there exists $C_{\gamma,\gamma '}>0$ such that

\[ p_n(\gamma,\gamma')\sim C_{\gamma,\gamma'}R_{\mu}^{-n}n^{-3/2}. \]

If the $\mu$-random walk is not aperiodic, similar asymptotics hold for $p_{2n}(\gamma,\gamma ')$ if the distance between $\gamma$ and $\gamma '$ is even and for $p_{2n+1}(\gamma,\gamma ')$ if it is odd.

Let us now give some details on the proofs. We have the same approach as Gouëzel and Lalley in [GL13, Gou14] and we begin by explaining their work.

The first step in both papers is to obtain an asymptotic differential equation satisfied by the Green function. Throughout this paper, we use the following notation: if two functions $f$ and $g$ satisfy that there exists some constant $C\geq 0$ such that $f\leq C g$, then we write $f\lesssim g$. In addition, if $f\lesssim g$ and $g\lesssim f$, then we write $f\asymp g$. Whenever we need to be specific about the constant, or about its dependence on some parameters, we write the full inequalities to avoid being unclear. In [GL13, Gou14], the authors proved that

(2)\begin{equation} \frac{d^{2}}{dr^{2}}G(e,e|r)\asymp \bigg(\frac{d}{dr}G(e,e|r)\bigg)^{3}, \end{equation}

the implicit constant not depending on $r$. Integrating these inequalities yields

\[ \bigg(\frac{d}{dr}G(e,e|r)\bigg)^{-2}-\bigg(\frac{d}{dr}G(e,e|R_{\mu})\bigg)^{-2}\asymp R_{\mu}-r, \]

so that, assuming $({d}/{dr})G(e,e|R_{\mu })=+\infty$ (which is proved in [GL13, Gou14]), one obtains

\[ \frac{d}{dr}G(e,e|r)\asymp \frac{1}{\sqrt{R_{\mu}-r}}. \]

The rigorous way to proceed is to transform these a priori estimates (2) into an equivalent when $r$ tends to $R_{\mu }$, that is,

(3)\begin{equation} \frac{d^{2}}{dr^{2}}G(e,e|r)\underset{r\rightarrow R_{\mu}}{\sim}C\bigg(\frac{d}{dr}G(e,e|r)\bigg)^{3}. \end{equation}

Once this is established, one can prove that

\[ \frac{d}{dr}G(e,e|r)\underset{r\rightarrow R_{\mu}}{\sim} \frac{C'}{\sqrt{R_{\mu}-r}}. \]

Finally, one can obtain asymptotics of $p_n(e,e)$ from asymptotics of $({d}/{dr})G(e,e|r)$ using Tauberian theorems and spectral theory. To go from (2) to (3), Lalley and Gouëzel used thermodynamic formalism. Precisely, they use Cannon's result and choose a finite automaton that encodes shortlex geodesics in the hyperbolic group $\Gamma$. They then define some potential function depending on $r$ on the path space of this automaton, using the Green function. To prove that this potential function is Hölder continuous, they use the strong Ancona inequalities (see § 2.4 for more details). They then apply the Ruelle–Perron–Frobenius theorem to the associated transfer operator to derive asymptotic properties of the first and second derivatives of the Green function, when $r$ tends to $R_\mu$, which, in turn, leads to (3).

Brief outline of the paper

We first compile in § 2 the tools and results that are needed in the following. We also review in § 3 the results of Sarig on thermodynamic formalism for countable shifts. The remaining sections are devoted to adapting the proofs of Lalley and Gouëzel to the relatively hyperbolic case.

Note that the first step, that is, obtaining an asymptotic differential equation satisfied by the Green function, is given by the results proved in part I. Precisely, [Dus22, Theorem 1.5] shows that (2) holds again in our situation. In the present paper, we mainly focus on the second step, that is deriving a precise equivalent such as (3) from the a priori estimates (2). We first give in §§ 4 and 5 an estimate for the first derivative of the Green function, in terms of the spectral data of a suited transfer operator. We then give in § 6 an estimate of the second derivative. Combining these two estimates leads to (3). There are several difficulties here.

First, we do not have a finite automaton encoding geodesics. Anyway, geodesics are not so much interesting for our purpose. Indeed, Ancona inequalities that are used in [GL13, Gou14] to prove Hölder continuity do not hold along geodesics, but along relative geodesics in relatively hyperbolic groups. On the other hand, we proved in part I that there exists an automaton with finite set of vertices and countable set of edges that encodes relative geodesics, see precisely [Dus22, Theorem 4.2]. We use this automaton instead.

However, the associated path space will not be finite but countable. We thus have to use thermodynamic formalism for countable Markov shifts, which is more delicate to handle than thermodynamic formalism for Markov shifts of finite type. For example, there are situations where Ruelle–Perron–Frobenius theorem, which is a crucial tool in [Gou14], does not hold for countable shifts. We thus prove that the Hölder continuous function analogous to that introduced in [GL13, Gou14] is positive recurrent (using the terminology of Sarig in [Sar99]), which is sufficient to mimic some of the arguments of Lalley and Gouëzel.

Another difficulty is that the family of transfer operators $(\mathcal {L}_r)_{r\leq R_\mu }$ we introduce does not vary continuously in $r$ for the operator norm. However, looking carefully at the proofs of [GL13, Gou14], one only needs continuity of the spectral data associated to this family of operators. We use an enhanced version of perturbations results due to Keller and Liverani [KL99] to prove this sort of continuity.

Finally, the last step, that is, getting the local limit theorem from the asymptotics of the Green function, is a combination of Tauberian theorems and spectral theory. We are able to use directly the results of [GL13] and so we have nothing to prove there to conclude. We also deduce Corollary 1.2 from Theorem 1.1 using directly results of [GL13]. We give more details in § 7.

2. Some background

2.1 Relatively hyperbolic groups

We first recall definitions and basic properties of relatively hyperbolic groups. More details are given in part I [Dus22]. Consider a finitely generated group $\Gamma$ acting discretely and by isometries on a proper and geodesic hyperbolic space $(X,d)$. We denote the limit set of $\Gamma$ by $\Lambda \Gamma$, that is, the set of accumulation points in the Gromov boundary $\partial X$ of an orbit $\Gamma \cdot o$, $o\in X$. A point $\xi \in \Lambda \Gamma$ is called conical if there is a sequence $(\gamma _{n})$ of $\Gamma$ and distinct points $\xi _1,\xi _2$ in $\Lambda \Gamma$ such that $\gamma _{n}\xi$ converges to $\xi _1$ and $\gamma _{n}\zeta$ converges to $\xi _2$ for all $\zeta \neq \xi$ in $\Lambda \Gamma$. A point $\xi \in \Lambda \Gamma$ is called parabolic if its stabilizer in $\Gamma$ is infinite, fixes exactly $\xi$ in $\Lambda \Gamma$ and contains no loxodromic element. The stabilizer of a parabolic limit point is called a (maximal) parabolic subgroup. A parabolic limit point $\xi$ in $\Lambda \Gamma$ is called bounded parabolic if is stabilizer in $\Gamma$ is infinite and acts cocompactly on $\Lambda \Gamma \setminus \{\xi \}$. Finally, the action is called geometrically finite if the limit set only consists of conical limit points and bounded parabolic limit points.

Definition 2.1 The group $\Gamma$ is relatively hyperbolic with respect to $\Omega$ if it acts geometrically finitely on such a hyperbolic space $(X,d)$ such that the stabilizers of the parabolic limit points are exactly the elements of $\Omega$. In this situation, $\Gamma$ is said to be non-elementary if its limit set is infinite.

One might choose different spaces $X$ on which $\Gamma$ can act geometrically finitely. However, different choices of $X$ give rise to equivariantly homeomorphic limit sets $\Lambda \Gamma$. We call this limit set the Bowditch boundary of $\Gamma$ and we denote it by $\partial _B\Gamma$.

Let $\Gamma$ be a relatively hyperbolic group with respect to a collection of subgroups $\Omega$. Let $\Omega _0$ be a set of representatives of conjugacy classes of elements of $\Omega$. Such a set $\Omega _0$ is necessarily finite, according to [Bow12, Proposition 6.15]. Fix a finite generating set $S$ for $\Gamma$. Denote by $\hat {\Gamma }$ the Cayley graph associated with the infinite generating set consisting of the union of $S$ and of all parabolic subgroups $\mathcal {H}\in \Omega _0$. Endowed with the graph distance, that we write $\hat {d}$, the graph $\hat {\Gamma }$ is hyperbolic.

A relative geodesic is a geodesic in the graph $\hat {\Gamma }$. A relative quasi-geodesic is a path of adjacent vertices in $\hat {\Gamma }$, which is a quasi-geodesic for the distance $\hat {d}$. Following Osin [Osi06], a path is called without backtracking if once it has left a coset $\gamma \mathcal {H}$, for $\mathcal {H}\in \Omega _0$, it never goes back to it. Relative geodesic and relative quasi-geodesic satisfy the following property, called the BCP property.

Proposition 2.1 (BCP property)

For all $\lambda \geq 1$ and $c\geq 0$, there exists a constant $C_{\lambda,c}$ such that for every pair $(\alpha _1,\alpha _2)$ of relative $(\lambda,c)$-quasi geodesic paths without backtracking, starting and ending at the same point in $\Gamma$, the following hold:

1. (i) if $\alpha _1$ travels more than $C_{\lambda,c}$ in a coset, then $\alpha _2$ enters this coset;

2. (ii) if $\alpha _1$ and $\alpha _2$ enter the same coset, the two entering points and the two exit points are $C_{\lambda,c}$-close to each other in $\operatorname {Cay}(\Gamma,S)$.

We need to study both geodesics in $\operatorname {Cay}(\Gamma,S)$ and relative geodesics in the following. We use the following terminology. Let $\alpha$ be a geodesic in $\operatorname {Cay}(\Gamma,S)$ and let $\eta _1,\eta _2\geq 0$. A point $\gamma$ on $\alpha$ is called an $(\eta _1,\eta _2)$-transition point if for any coset $\gamma _0\mathcal {H}$ of a parabolic subgroup, the part of $\alpha$ consisting of points at distance at most $\eta _2$ from $\gamma$ is not contained in the $\eta _1$-neighborhood of $\gamma _0\mathcal {H}$.

Transition points are of great importance in relatively hyperbolic groups. They stay close to points on relative geodesics in the following sense.

Lemma 2.2 [Hru10, Proposition 8.13]

Fix a generating set $S$. For every large enough $\eta _1,\eta _2>0$, there exists $r\geq 0$ such that the following holds. Let $\alpha$ be a geodesic in $\operatorname {Cay}(\Gamma,S)$ and let $\hat {\alpha }$ be a relative geodesic path with the same endpoints as $\alpha$. Then, for the distance in $\operatorname {Cay}(\Gamma,S)$, any $(\eta _1,\eta _2)$-transition point on $\alpha$ is within $r$ of a point on $\hat {\alpha }$ and, conversely, any point on $\hat {\alpha }$ is within $r$ of an $(\eta _1,\eta _2)$-transition point on $\alpha$.

2.2 Relatively automatic groups

Hyperbolic groups are known to be strongly automatic, meaning that for every generating set $S$, there exists a finite directed graph $\mathcal {G}=(V,E,v_*)$ encoding geodesics. It is quite implicit in Farb's work [Far94, Far98], although not formally stated, that relatively hyperbolic groups are relatively automatic in the following sense.

Let $\Gamma$ be a finitely generated group and let $\Omega$ be a collection of subgroups invariant by conjugacy and such that there is a finite set $\Omega _0$ of conjugacy classes representatives of subgroups in $\Omega$.

Definition 2.2 A relative automatic structure for $\Gamma$ with respect to the collection of subgroups $\Omega _0$ and with respect to some finite generating set $S$ is a directed graph $\mathcal {G}=(V,E,v_*)$ with distinguished vertex $v_*$ called the starting vertex, where the set of vertices $V$ is finite and with a labelling map $\phi :E\rightarrow S\cup \bigcup _{\mathcal {H}\in \Omega _0}\mathcal {H}$ such that the following holds. If $\omega =e_1,\ldots,e_n$ is a path of adjacent edges in $\mathcal {G}$, define $\phi (e_1,\ldots,e_n)=\phi (e_1)\dots \phi (e_n)\in \Gamma$. Then:

1. (i) no edge ends at $v_*$, except the trivial edge starting and ending at $v_*$;

2. (ii) every vertex $v\in V$ can be reached from $v_*$ in $\mathcal {G}$;

3. (iii) for every path $\omega =e_1,\ldots,e_n$, the path $e,\phi (e_1),\phi (e_1e_2),\ldots,\phi (\gamma )$ in $\Gamma$ is a relative geodesic from $e$ to $\phi (\gamma )$, that is, the image of $e,\phi (e_1),\phi (e_1e_2),\ldots,\phi (\gamma )$ in $\hat {\Gamma }$ is a geodesic for the metric $\hat {d}$;

4. (iv) the extended map $\phi$ is a bijection between paths in $\mathcal {G}$ starting at $v_*$ and elements of $\Gamma$.

Note that the union $S\cup \bigcup _{\mathcal {H}\in \Omega _0}\mathcal {H}$ is not required to be a disjoint union. Actually, the intersection of two distinct subgroups $\mathcal {H},\mathcal {H}'\in \Omega _0$ can be non-empty. Also note that we require the vertex set $V$ to be finite. However, the set of edges is infinite, except if all subgroups $\mathcal {H}$ in $\Omega _0$ are finite.

If there exists a relative automatic structure for $\Gamma$ with respect to $\Omega _0$ and $S$, we say that $\Gamma$ is automatic relative to $\Omega _0$ and $S$. The following was proved in part I.

Theorem 2.3 [Dus22, Theorem 4.2]

Let $\Gamma$ be a relatively hyperbolic group and let $\Omega _0$ be a finite set of representatives of conjugacy classes of the maximal parabolic subgroups. For every symmetric finite generating set $S$ of $\Gamma$, $\Gamma$ is automatic relative to $\Omega _0$ and $S$.

Along the proof of this theorem, a lot of technical lemmas about relative geodesics were proved in [Dus22]. We use some of them repeatedly in this paper, so we restate them for convenience. We use the same notation as previously and so we fix a relatively hyperbolic group $\Gamma$ and a finite set $\Omega _0$ of conjugacy classes of parabolic subgroups.

Lemma 2.4 [Dus22, Lemma 4.5]

For every $K\geq 0$, there exists $C\geq 0$ such that the following holds. Let $(x_1,\ldots,x_n,\ldots )$ and $(x_1',\ldots,x_m',\ldots )$ be two infinite relative geodesics such that $d(x_1,x'_1)\leq K$ and $x_n$ and $x_m'$ converge to the same conical limit point $\xi$. Then, for every $j\geq 1$, there exists $i_j$ such that $d(x_j,x_{i_j}')\leq C$.

Lemma 2.5 [Dus22, Lemma 4.16]

Let $(e,\gamma _1,\ldots,\gamma _n)$ and $(e,\gamma _1',\ldots,\gamma _m')$ be two relative geodesics. Assume that the nearest point projection of $\gamma '_m$ on $(e,\gamma _1,\ldots,\gamma _n)$ is at $\gamma _l$. If there are several such nearest point projection, choose the closest to $\gamma _n$. Then, any relative geodesic from $\gamma _m'$ to $\gamma _n$ passes within a bounded distance of $\gamma _{l}$ for the distance $d$. Moreover, if $\gamma _l\neq e$, then any relative geodesic from $e$ to $\gamma _m'$ passes within a bounded distance of $\gamma _{l-1}$.

2.3 Spectrally degenerate measures

We now consider a group $\Gamma$, hyperbolic relative to a collection of subgroups $\Omega$. We fix a finite collection $\Omega _0=\{\mathcal {H}_1,\ldots,\mathcal {H}_N\}$ of representatives of conjugacy classes of $\Omega$. We assume that $\Gamma$ is non-elementary. Let $\mu$ be a probability measure on $\Gamma$, $R_{\mu }$ the inverse of the spectral radius of the $\mu$-random walk and $G(\gamma,\gamma '|r)$ the associated Green function, evaluated at $r$, for $r\in [0,R_{\mu }]$. If $\gamma =\gamma '$, we simply use the notation $G(r)=G(\gamma,\gamma |r)=G(e,e|r)$.

We denote by $p_k$ the first return transition kernel to $\mathcal {H}_k$. Namely, if $h,h'\in \mathcal {H}_k$, then $p_k(h,h')$ is the probability that the $\mu$-random walk, starting at $h$, eventually comes back to $\mathcal {H}_k$ and that its first return to $\mathcal {H}_k$ is at $h'$. In other words,

\[ p_k(h,h')=\mathbb{P}_h(\exists n\geq 1, X_n=h',X_1,\ldots,X_{n-1}\notin \mathcal{H}_k). \]

More generally, for $r\in [0,R_{\mu }]$, we denote by $p_{k,r}$ the first return transition kernel to $\mathcal {H}_k$ for $r\mu$. Precisely, if $h,h'\in \mathcal {H}_k$, then

\[ p_{k,r}(h,h')=\sum_{n\geq 1}\sum_{\underset{\notin \mathcal{H}_k}{\gamma_1,\ldots,\gamma_{n-1}}}r^{n}\mu(h^{-1}\gamma_1)\mu(\gamma_1^{-1}\gamma_2)\dots\mu(\gamma_{n-2}^{-1}\gamma_{n-1})\mu(\gamma_{n-1}^{-1}h'). \]

We then denote by $p_{k,r}^{(n)}$ the convolution powers of this transition kernel, by $G_{k,r}(h,h'|t)$ the associated Green function, evaluated at $t$ and by $R_k(r)$ the inverse of the associated spectral radius, that is, the radius of convergence of the power series $t\mapsto G_{k,r}(h,h'|t)$. For simplicity, write $R_k=R_k(R_{\mu })$. If $h=h'$, we simply write $G_{k,r}(t)=G_{k,r}(h,h|t)=G_{k,r}(e,e|t)$.

According to [Dus22, Lemma 3.4], for any $r\in [0,R_{\mu }]$, for any $k\in \{1,\ldots,N\}$,

\[ G_{k,r}(h,h'|1)=G(h,h'|r). \]

In addition, because $\Gamma$ is non-elementary, it contains a free group and, hence, is non-amenable. It follows from a result of Guivarc'h (see [Gui80, p. 85, Remark b)]) that $G(R_{\mu })<+\infty$. Thus, $G_{k,R_{\mu }}(1)<+\infty$. In particular, $R_k\geq 1$.

Definition 2.3 We say that $\mu$ (or, equivalently, the random walk) is spectrally degenerate along $\mathcal {H}_k$ if $R_k=1$. We say it is non-spectrally degenerate if, for every $k$, $R_k>1$.

This definition was introduced in [DG21] to study the homeomorphism type of the Martin boundary at the spectral radius. As explained in [Dus22, § 3.3], it should be thought of as a notion of a spectral gap between the spectral radius of the random walk on the whole group and the spectral radii of the induced walks on the parabolic subgroups. Very roughly speaking, the random walk is not spectrally degenerate if the driving probability measure $\mu$ does not give too much weight to the parabolic subgroups. Let us give more details on this intuition now. For simplicity, we only consider the case of free products which was studied by Woess in [Woe86] and by Candellero and Gilch in [CG12]. We first need to introduce some notation.

Let $\Gamma =\Gamma _0*\Gamma _1$ be a free product of two groups. Then, $\Gamma$ is hyperbolic relative to the conjugates of the free factors $\Gamma _0$ and $\Gamma _1$. Consider a symmetric probability measure $\mu _0$, respectively $\mu _1$, whose finite support generates $\Gamma _0$, respectively $\Gamma _1$. For any $0< \beta < 1$, set

\[ \mu=\beta\mu_1+(1-\beta)\mu_0. \]

Then, $\mu$ is a symmetric probability measure whose finite support generates $\Gamma$. Such a probability measure is called adapted to the free product structure: the random walk driven by $\mu$ can only move inside one of the free factors at each step.

In this situation, the Green function $G_\mu$ of $\mu$ and the Green function $G_{\mu _0}$ of $\mu _0$ can be related by the following formula. For every $x,y\in \Gamma _0$, for every $r\leq R_\mu$,

(4)\begin{equation} \frac{G_\mu(x,y|r)}{G_\mu(e,e|r)}=\frac{G_{\mu_0}(x,y|\zeta_0(r))}{G_{\mu_0}(e,e|\zeta_0(r))}, \end{equation}

where $\zeta _0$ is a continuous function of $r$, see [Woe00, Proposition 9.18] for an explicit formula. We always have $\zeta _0(R_\mu )\leq R_{\mu _0}$. A similar formula holds for $x,y\in \Gamma _1$.

Actually, because $\mu$ is adapted to the free product structure, the first return kernel $p_{\Gamma _0,r}$ can be written as

\[ p_{\Gamma_0,r}(e,x)=(1-\beta)r\mu_0+w_0\delta_{e,x}, \]

where $w_0$ is the weight of the first return to $e$ associated to $r\mu$, starting with a step in $\Gamma _1$. Thus, [Woe00, Lemma 9.2] shows that for any $x,y\in \Gamma _0$,

(5)\begin{equation} G_{\Gamma_0,r}(x,y|t)=\frac{1}{1-w_0t}G_{\mu_0}\bigg(x,y \biggm| \frac{(1-\beta)rt}{1-w_0t}\bigg). \end{equation}

In particular, for $t=1$,

\[ G_{\Gamma_0,r}(x,y|1)=\frac{1}{1-w_0}G_{\mu_0}\bigg(x,y \biggm| \frac{(1-\beta)r}{1-w_0}\bigg) \]

and so we recover (4) with $\zeta (r)=({(1-\beta )r})/({1-w_0})$.

Following Woess [Woe00], we call the situation where $\zeta _i(R_\mu )< R_i$ (the inverse of the spectral radius of $\mu _i$) the ‘typical case’. We prove that the ‘typical case’ is exactly the case where the measure is not spectrally degenerate.

Proposition 2.6 Consider an adapted random walk on a free product $\Gamma =\Gamma _0*\Gamma _1$. The random walk is spectrally degenerate along $\Gamma _0$ if and only if $\zeta _0(R_\mu )=R_{\mu _0}$.

Proof. Applying (5) to $t=1+\epsilon$ and $r=R_\mu$, we obtain

\[ G_{\Gamma_0,R_\mu}(x,y|1+\epsilon)=\frac{1}{1-w_0(1+\epsilon)}G_{\mu_0}\bigg(x,y \biggm| \frac{(1-\beta)R_\mu(1+\epsilon)}{1-w_0(1+\epsilon)}\bigg). \]

If $\epsilon >0$, then

\[ \frac{(1-\beta)R_\mu(1+\epsilon)}{1-w_0(1+\epsilon)}>\frac{(1-\beta)R_\mu}{1-w_0}=\zeta_0(R_\mu). \]

Thus, there exists $t>1$ such that $G_{\Gamma _0,R_\mu }(x,y|t)$ is finite if and only if there exists $z>\zeta _0(R_\mu )$ such that $G_{\mu _0}(x,y|z)$ is finite, which concludes the proof.

Hence, in the context of adapted random walks on free products, to check whether the random walk is non-spectrally degenerate, one has to check whether $\zeta _i(R_\mu )< R_i$ or not. This problem was studied by Candellero and Gilch. More specifically, in [CG12, § 7], they construct both spectrally degenerate and non-spectrally degenerate measures. In particular, in their example A, $\Gamma _i=\mathbb {Z}^{d_i}$, where $d_i\geq 5$. Then, if $\beta$ is close enough to zero, the random walk is spectrally degenerate along $\Gamma _0$. Similarly, if $\beta$ is close enough to one, the random walk is spectrally degenerate along $\Gamma _1$. In the middle case, the random walk is not spectrally degenerate.

Let us also mention their example F, where $\Gamma _0=\mathbb {Z}^{5}$ and $\Gamma _1=\mathbb {Z}^{6}$. They construct measures $\mu _0$ and $\mu _1$ such that the adapted measure $\mu$ is spectrally degenerate for every $\beta$. More precisely, they show there exists a critical parameter $\beta _c$ such that the following classification holds. For $\beta <\beta _c$, $\mu$ is spectrally degenerate along $\Gamma _0$ and is not spectrally positive recurrent. For $\beta >\beta _c$, $\mu$ is spectrally degenerate along $\Gamma _1$ and is not spectrally positive recurrent. On the other hand, for $\beta =\beta _c$, $\mu$ is spectrally positive recurrent. This yields a random walk which is spectrally degenerate, but which is spectrally positive recurrent. In this situation, one has a local limit theorem of the form (1) with $\alpha =3/2$. This leads to the conjecture that spectral positive recurrence is a sufficient condition to obtain $\alpha =3/2$.

Unfortunately, it seems difficult to construct (non-)spectrally degenerate measures on general relatively hyperbolic groups, so we do not know yet any example beyond free products, except low-dimensional Kleinian groups, according to Theorem 1.3. A reasonable approach would be to try to adapt the method of Candellero and Gilch in the following way. Consider a relatively hyperbolic group $\Gamma$ and choose a parabolic subgroup $\mathcal {H}$. Start with an admissible, finitely supported and symmetric measure $\mu _0$ on $\Gamma$ and an admissible, finitely supported and symmetric measure $\mu _\mathcal {H}$ on $\mathcal {H}$. Define then $\mu =\beta \mu _0+(1-\beta )\mu _\mathcal {H}$. One would expect $\mu$ to be spectrally degenerate along $\mathcal {H}$ for small enough $\beta$. However, to actually prove that it is spectrally degenerate, one would need to prove a sort of continuity of the Green function and its derivatives with respect to the driving measure, which would, in turn, require some new material. Similar difficulties occur when trying to construct non-spectrally degenerate measures.

Finally, let us now recall some consequences of spectral degeneracy proved in [Dus22]. Let $\Gamma$ be a relatively hyperbolic group. We introduce the following notation. We write

\[ I^{(k)}(r)=\sum_{\gamma^{(1)},\ldots,\gamma^{(k)}\in \Gamma}G(\gamma,\gamma^{(1)}|r)G(\gamma^{(1)},\gamma^{(2)}|r)\dots G(\gamma^{(k-1)},\gamma^{(k)}|r)G(\gamma^{(k)},\gamma'|r). \]

Then, $I^{(k)}(r)$ is related to the $k$th derivative of the Green function. For a precise statement, we refer to [Dus22, Lemma 3.2]. For instance, we have the following.

Lemma 2.7 [Dus22, Lemma 3.1]

For every $\gamma,\gamma '\in \Gamma$, for every $r\in [0,R_{\mu }]$, we have

\[ \frac{d}{dr}(rG(\gamma_1,\gamma_2|r))=\sum_{\gamma\in \Gamma}G(\gamma_1,\gamma|r)G(\gamma,\gamma_2|r). \]

If $\mathcal {H}$ is a parabolic subgroup, we also write

\[ I^{(k)}_{\mathcal{H}}(r)=\sum_{\gamma^{(1)},\ldots,\gamma^{(k)}\in \mathcal{H}}G(\gamma,\gamma^{(1)}|r)G(\gamma^{(1)},\gamma^{(2)}|r)\dots G(\gamma^{(k-1)},\gamma^{(k)}|r)G(\gamma^{(k)},\gamma'|r). \]

Once $\Omega _0=\{\mathcal {H}_1,\ldots,\mathcal {H}_N\}$ is fixed, we also write $I^{(k)}_{j}(r)=I^{(k)}_{\mathcal {H}_j}(r)$ for simplicity.

One of the main results of part I is that whenever $I^{(2)}_{\mathcal {H}}(r)<+\infty$ for every parabolic subgroup $\mathcal {H}\in \Omega _0$, then

\[ I^{(2)}(r)\asymp ( I^{(1)}(r))^{3}. \]

This is a consequence of the following result.

Proposition 2.8 [Dus22, Proposition 5.6]

For every $r\in [0,R_{\mu })$, we have

\[ \frac{I^{(2)}(r)}{I^{(1)}(r))^{3}}\asymp 1+\sum_{j}I^{(2)}_{j}(r). \]

In particular, if $\mu$ is non-spectrally degenerate, then

\[ I^{(2)}(r)\asymp ( I^{(1)}(r))^{3}. \]

The following results were also proved in part I. Note that we do not need to assume that $\mu$ is non-spectrally degenerate.

Lemma 2.9 [Dus22, Lemma 5.4]

There exists some uniform $C\geq 0$ such that for every $r\in [0,R_{\mu }]$, for every $m$,

\[ \sum_{\gamma\in \hat{S}_m}H(e,\gamma|r)\leq C. \]

Corollary 2.10 [Dus22, Corollary 5.5]

For every parabolic subgroup $\mathcal {H}\in \Omega _0$ and every $r\in [0,R_{\mu }]$, we have $I^{(1)}_{\mathcal {H}}(r)<+\infty$.

Finally, we also use the following.

Proposition 2.11 [Dus22, Proposition 5.8]

If $\mu$ is non-spectrally degenerate, then

\[ \frac{d}{dr}_{|r=R_\mu}G(e,e|R_{\mu})=+\infty. \]

2.4 Relative Ancona inequalities

We consider a finitely generated group $\Gamma$, hyperbolic relative to a collection of subgroups $\Omega$. Let $\Omega _0$ be a finite set of representatives of conjugacy classes. We also consider a probability measure $\mu$ on $\Gamma$, whose finite support generates $\Gamma$ as a semigroup and denote by $R_{\mu }$ the inverse of its spectral radius. As soon as $\Gamma$ is non-elementary, it is non-amenable, so that $R_{\mu }>1$ according to Kesten's results [Kes59].

In the case where $\Gamma$ is hyperbolic, Ancona proved that the Green function $G$ is roughly multiplicative along geodesics. Precisely, there exists $C\geq 1$ such that if $x,y,z$ are elements along a geodesic in this order, then

(6)\begin{equation} \frac{1}{C}G(x,y)G(y,z)\leq G(x,z)\leq C G(x,y)G(y,z). \end{equation}

See [Anc88] for more details. The proof also works for the Green function evaluated at $r$, when $r< R_{\mu }$. Actually, the lower bound is always true, so that the content of Ancona inequalities really is

\[ G(x,z|r)\leq C G(x,y|r)G(y,z|r). \]

In [Gou14], Gouëzel proved that these inequalities still hold at $r=R_{\mu }$ and that the constant $C$ is uniform in $r$, when the measure is symmetric. He also gave a strengthened version of them. Namely, if $x,x',y,y'$ are four points such that geodesics $[x,y]$ from $x$ to $y$ and $[x',y']$ from $x'$ to $y'$ fellow travel for a time at least $n$, then for $r\in [1,R_{\mu }]$,

(7)\begin{equation} \bigg| \frac{G(x,y|r)G(x',y'|r)}{G(x',y|r)G(x,y'|r)} -1\bigg|\leq C\rho^{n}, \end{equation}

where $C\geq 0$ and $0<\rho <1$ are uniform (see [Gou14, Theorem 2.9]). This strengthened version of Ancona inequalities was proved at $r< R_{\mu }$ in [INO08]. It was also already proved at the spectral radius by Gouëzel and Lalley in the case of co-compact Fuchsian groups (see [GL13, Theorem 4.6]). It allowed the authors to obtain Hölder regularity for Martin kernels on the Martin boundary and then to use thermodynamic formalism to deduce local limit theorems in hyperbolic groups in [Gou14, GL13].

Back to relatively hyperbolic groups, inequalities similar to (6) were obtained by Gekhtman, Gerasimov, Potyagailo, and Yang in [GGPY21]. Recall that if $\alpha$ is a geodesic in the Cayley graph $\operatorname {Cay}(\Gamma,S)$, a point on $\alpha$ is called a transition point if it is not deep in a parabolic subgroup. It is proved in [GGPY21] that if $x,y,z$ are elements on a geodesic in this order and if $y$ is a transition point on this geodesic, then (6) holds. The proof actually works for $G(\cdot,\cdot |r)$ whenever $r< R_{\mu }$.

Because of our automatic structure, it is more convenient for us to work with relative geodesics rather than transition points on actual geodesics. We fix a generating set $S$ and consider the Cayley graph and the graph $\hat {\Gamma }$ associated with $S$.

Definition 2.4 Let $\Gamma$ be a relatively hyperbolic group and let $\mu$ be a probability measure on $\Gamma$ with Green function $G$. Let $R_\mu$ be the inverse of the spectral radius of $\mu$. If $r\in [1,R_{\mu }]$, say that $\mu$ satisfies the weak $r$-relative Ancona inequalities if there exists $C\geq 0$ (which depends on $r$) such that for every $x,y,z\in \Gamma$ such that their images in $\hat {\Gamma }$ lie in this order on a relative geodesic,

\[ \frac{1}{C}G(x,y|r)G(y,z|r)\leq G(x,z|r)\leq C G(x,y|r)G(y,z|r). \]

Say that $\mu$ satisfies the weak relative Ancona inequalities up to the spectral radius if it satisfies the $r$-relative Ancona inequalities for every $r\in [1,R_{\mu }]$ with a constant $C$ not depending on $r$.

We also need the following enhanced version of relative Ancona inequalities.

Definition 2.5 We say that two relative geodesics $[x,y]$ and $[x',y']$ $c$-fellow travel for a time $n$, for some $c\geq 0$, if there exist distinct points $\gamma _1,\ldots,\gamma _n$ which are at distance in $\operatorname {Cay}(\Gamma,S)$ at most $c$ from points on $[x,y]$ and points on $[x',y']$.

Definition 2.6 Let $\Gamma$ be a relatively hyperbolic group and let $\mu$ be a probability measure on $\Gamma$ with Green function $G$. Let $R_\mu$ be the inverse of the spectral radius of $\mu$. If $r\in [1,R_{\mu }]$, say that $\mu$ satisfies the strong $r$-relative Ancona inequalities if for every $c\geq 0$, there exist $C\geq 0$ and $0<\rho <1$ such that if $x,x',y,y'$ are four points such that relative geodesics $[x,y]$ from $x$ to $y$ and $[x',y']$ from $x'$ to $y'$ $c$-fellow travel for a time at least $n$, then

\[ \bigg| \frac{G(x,y|r)G(x',y'|r)}{G(x',y|r)G(x,y'|r)} -1\bigg|\leq C\rho^{n}. \]

Say that $\mu$ satisfies the strong relative Ancona inequalities up to the spectral radius if it satisfies the strong $r$-relative Ancona inequalities for every $r\in [1,R_{\mu }]$ with constants $C$ and $\rho$ not depending on $r$.

Remark 2.1 If $\mu$ satisfies the strong or weak relative Ancona inequalities, then the reflected measure $\check {\mu }$, defined by $\check {\mu }(\gamma )=\mu (\gamma ^{-1})$ also satisfies them. Indeed, if $\check {G}$ is the Green function of the reflected measure, then $\check {G}(x,y)=G(y,x)$.

The following is proved in [DG21].

Theorem 2.12 Let $\Gamma$ be a non-elementary relatively hyperbolic group and let $\mu$ be a symmetric probability measure on $\Gamma$ whose finite support generates $\Gamma$. Then $\mu$ satisfies both the weak and strong relative Ancona inequalities up to the spectral radius.

Actually, these inequalities are stated in [DG21] using the Floyd distance, which is a suitable rescaling of the distance in $\operatorname {Cay}(\Gamma,S)$. However, [GP16, Corollary 5.10] relates the Floyd distance with transition points and Lemma 2.2 relates transition points with points on a relative geodesic. We deduce the above theorem combining these two results with [DG21, Theorem 1.6].

3. Thermodynamic formalism

3.1 Transfer operators with countably many symbols

We follow here the terminology of Sarig and recall some facts proved in [Sar99, Sar03]. We consider a countable set $\Sigma$ (the set of symbols), and a matrix $A=(a_{s,s'})_{s,s'\in \Sigma }$, with entries zeros and ones (the transition matrix). We then define

\[ \Sigma_A^{*}=\{x=(x_1,\ldots,x_n), x_i\in \Sigma, n\geq 0,\forall i, a_{x_i,x_{i+1}}=1\} \]

and

\[ \partial \Sigma_A^{*}=\{x=(x_1,\ldots,x_n,\ldots), x_i\in \Sigma, \forall i, a_{x_i,x_{i+1}}=1\}. \]

Note that in the definition of $\Sigma _A^{*}$, $n$ can be zero, so that the empty sequence, that we denote by $\emptyset$, is in $\Sigma _A^{*}$. We also define

\[ \overline{\Sigma}_A=\Sigma_A^{*}\cup \partial \Sigma_A^{*}. \]

If $s_1,\ldots,s_k\in \Sigma$, we define the cylinder $[s_1,\ldots,s_k]$ as $\{x\in \overline {\Sigma }_A,x_1=s_1,\ldots,x_k=s_k\}$.

Let $T:\overline {\Sigma }_A\rightarrow \overline {\Sigma }_A$ be given by

\begin{align*} T((x_1,\ldots,x_n))=(x_2,\ldots,x_n) \end{align*}

if $(x_1,\ldots,x_n)\in \Sigma _A^{*}$ and

\begin{align*} T((x_1,\ldots,x_n,\ldots))=(x_2,\ldots,x_n,\ldots) \end{align*}

if $(x_1,\ldots,x_n,\ldots )\in \partial \Sigma _A^{*}$. We call $T$ the shift map and we call the pair $(\overline {\Sigma }_A,T)$ a Markov shift.

We say that the Markov shift is irreducible if for every $s,s'\in \Sigma$, there exists $N_{a,b}$ such that there exists $x\in \overline {\Sigma }_A$ with $x_1=s$ and $x'\in \overline {\Sigma }_A$ with $x'_1=s'$ such that $T^{N_{a,b}}x=x'$. In other words, one can reach any cylinder $[s']$ from any cylinder $[s]$ with a finite number of iterations of the shift. We say it is topologically mixing if for every $s,s'\in \Sigma$, there exists $N_{a,b}$ such that for every $n\geq N_{a,b}$, there exists $x\in \overline {\Sigma }_A$ with $x_1=s$ and $x'\in \overline {\Sigma }_A$ with $x'_1=s'$ such that $T^{n}x=x'$.

In [Sar99], everything is stated only using $\partial \Sigma _A^{*}$. However, up to considering a cemetery symbol $x_{{{\dagger}} }$, we can see finite sequences $(x_1,\ldots,x_n)$ in $\Sigma _A^{*}$ as infinite ones, of the form $(x_1,\ldots,x_n,x_{{{\dagger}} },\ldots,x_{{{\dagger}} },\ldots )$. Thus, we can apply the terminology and results of [Sar99] to $\overline {\Sigma }_A$. In addition, for technical reasons, it will be convenient to assume that the empty sequence is not a preimage of itself by the shift. This can be done, for example, using a second cemetery symbol.

We also define a metric on $\overline {\Sigma }_A$, setting $d(x,y)=2^{-n}$, where $n$ is the first time that the two sequences $x$ and $y$ differ.

If $\varphi : \overline {\Sigma }_A\rightarrow \mathbb {R}$ is a function, define

\[ V_n(\varphi)=\sup \{|\varphi(x)-\varphi(y)|,x_1=y_1,\ldots,x_n=y_n\}. \]

For $\rho \in (0,1)$, such a function $\varphi$ is called $\rho$-locally Hölder continuous if it satisfies

\[ \exists C, \forall n\geq 1, V_n(\varphi)\leq C\rho^{n}. \]

It is called locally Hölder continuous if it is $\rho$-locally Hölder continuous for some $\rho$. Note that nothing is required for $V_0(\varphi )$ and, in particular, $\varphi$ can be unbounded. We can always change the metric $d$ on $\overline {\Sigma }_A$, defining $d_{\rho }(x,y)=\rho ^{n}$, where $n$ is the first time that the two sequences $x$ and $y$ differ (and $0<\rho <1$). A $\rho$-locally Hölder continuous function is then a locally Lipschitz function for this new metric.

If $\varphi$ is locally Hölder continuous, we denote by $\varphi _n=\sum _{k=0}^{n-1}\varphi \circ T^{k}$ its $n$th Birkhoff sum. We also define its transfer operator $\mathcal {L}_{\varphi }$ as

\[ \mathcal{L}_{\varphi}f(x)=\sum_{Ty=x}{e}^{\varphi(y)}f(y). \]

It acts on several spaces of functions. We are interested in one in particular, described in the following, on which the transfer operator has a spectral gap. By definition, we have

\[ (\mathcal{L}_{\varphi}^{n}f)(x)=\sum_{T^{n}y=x}{e}^{\varphi_n(y)}f(y). \]

We also define, for $s\in \Sigma$,

\begin{align*} Z_n(\varphi,s)=\sum_{\underset{x_1=s}{T^{n}x=x}}{e}^{\varphi_n(x)}. \end{align*}

For every $s$, $({1}/{n})\log Z_n(\varphi,s)$ has a limit $P(\varphi,s)$. If the Markov shift is irreducible, then it is independent of $s$ and we denote it by $P(\varphi )$. Moreover, $P(\varphi,s)>-\infty$ and if $\|\mathcal {L}_{\varphi }1\|_{\infty }<+\infty$, then $P(\varphi,s)<+\infty$. We refer to [Sar99, Theorem 1] for a proof. Independence of $s$ is proved under the assumption that the Markov shift is topologically mixing, although the proof only requires that it is irreducible. We call $P(\varphi,s)$ the Gurevic pressure of $\varphi$ at $s$, or simply its pressure.

We say that $\varphi$ is positive recurrent if for every $s\in \Sigma$, there exist $M_{s}\geq 1$ and $\lambda _{s}>0$ such that for every large enough $n$, ${Z_n(\varphi,s)}/{\lambda _{s}^{n}}\in [M_{s}^{-1},M_{s}]$. If it is the case, then one necessarily has $\log \lambda _{s}=P(\varphi,s)$. The main result of [Sar99] is that positive recurrence is a necessary and sufficient condition for convergence of the iterates of the transfer operator $\mathcal {L}_{\varphi }^{n}$ (see [Sar99, Theorem 4] for a precise statement).

If the set of symbols $\Sigma$ is finite, then every Hölder continuous function is positive recurrent. Actually, we can say a little more in this case. The convergence of $\mathcal {L}_{\varphi }^{n}$ is exponentially fast. Precisely, if the Markov shift is topologically mixing, there exist $\lambda >0$, a positive function $h$ and a measure $\nu$ and constants $C\geq 0$ and $0<\theta <1$ satisfying, for all $\rho$-Hölder continuous function $f$ and all $n\in \mathbb {N}$,

\[ \bigg\|\lambda^{-n}\mathcal{L}_{\varphi}^{n}f-h\int f \,d\nu\bigg\|\leq C\theta^{n}\|f\|. \]

This is the so-called Ruelle–Perron–Frobenius theorem. Equivalently, $\lambda$ is a positive eigenvalue of the operator $\mathcal {L}_{\varphi }$ acting on the space of Hölder continuous functions and the remainder of the spectrum is contained in a disk of radius strictly smaller than $\lambda$. In other words, $\mathcal {L}_{\varphi }$ acts on this space with a spectral gap

When the set of symbols is countable, it can happen that the convergence is not exponentially fast (see [Sar99, Example 1]). However, there are sufficient conditions for this to hold, studied by Aaronson, Denker, and Urbański among others (see [ADU93, AD01]; see also [Gou04]).

Definition 3.1 Say that the Markov shift $(\overline {\Sigma }_A,T)$ has finitely many images if the set

\[ \{T[s],s \in \Sigma\} \]

is finite. Equivalently, there is only a finite number of different rows (and, thus, a finite number of different columns) in the matrix $A$.

Fix $0<\rho <1$. Let $\beta$ be the partition generated by the image sets, that is, $\beta$ is the $\sigma$-algebra generated by $\{T[s],s \in \Sigma \}$. Then, define for a $\rho$-locally Hölder continuous function $f$,

\[ D_{\rho,\beta} f=\sup_{b\in \beta}\sup_{x,y\in b}\frac{|f(x)-f(y)|}{d_{\rho}(x,y)}, \]

where we recall that $d_{\rho }(x,y)=\rho ^{n}$, where $n$ is the first time that the two sequences $x$ and $y$ differ. Denote then $\|f\|_{\rho,\beta }=\|f\|_{\infty }+D_{\rho,\beta }f$ and define

\[ \mathcal{B}_{\rho,\beta}=\{f, \|f\|_{\rho,\beta}<+\infty\}. \]

Then, $(\mathcal {B}_{\rho,\beta },\|\cdot \|_{\rho,\beta })$ is a Banach space.

Having finitely many images is a sufficient condition to have a spectral gap on $(\mathcal {B}_{\rho,\beta },\|\cdot \|_{\rho,\beta })$. Indeed, Mauldin and Urbański introduced in [MU01] the BIP property, which is automatically satisfied if the shift has finitely many images. Moreover, they proved that the BIP property is a sufficient condition for locally Hölder functions to have a Gibbs measure, whereas Sarig proved in [Sar99] that having a Gibbs measure is a sufficient condition to be positive recurrent and to have a spectral gap. In particular, we have the following two results.

Proposition 3.1 Let $(\overline {\Sigma }_A,T)$ be a topologically mixing countable Markov shift having finitely many images. Let $\varphi$ be a locally Hölder continuous function with finite pressure $P(\varphi )$. Then, $\varphi$ is positive recurrent.

Proof. As $\varphi$ is locally Hölder, the sum

\[ \sum_{n\geq 1} V_n(\varphi)=\sum_{n\geq 1}\sup \{|\varphi(x)-\varphi(y)|,x_1=y_1,\ldots,x_n=y_n\}\leq C\sum_{n\geq 1}\rho^{n} \]

is finite. Thus, [Sar03, Theorem 1] shows that $\varphi$ has a Gibbs measure. Consequently, [Sar99, Theorem 8] shows that $\varphi$ is positive recurrent.

Theorem 3.2 Sarig [Sar03, Corollary 3] and [Sar99, Theorem 4]

Let $(\overline {\Sigma }_A,T)$ be a topologically mixing countable Markov shift having finitely many images. Let $\varphi$ be a locally Hölder continuous function with finite pressure $P(\varphi )$. Then there exist a $\sigma$-finite measure $\nu$ and a function $h$ bounded away from zero and infinity such that $\mathcal {L}_{\varphi }^{*}\nu ={e}^{P(\varphi )}\nu$ and $\mathcal {L}_{\varphi }h={e}^{P(\varphi )}h$. There also exist $C\geq 0$ and $0<\theta <1$ such that for every $f\in \mathcal {B}_{\rho,\beta }$,

\[ \bigg\|{e}^{-nP(\varphi)}\mathcal{L}_{\varphi}^{n}f-h\int f \,d\nu\bigg\|_{\rho,\beta}\leq C\theta^{n}\|f\|_{\rho,\beta}. \]

Moreover, $\nu$ is supported on $\partial \Sigma _A^{*}$ and both measures $\nu$ and $m$ defined by $dm=h\,d\nu$ are ergodic.

The fact that $\nu$ is ergodic is not stated in Corollary 3 but in Corollary 2 of [Sar03]. Ergodicity of $m$ follows (see the remarks after [Sar99, Theorem 4]). Finally, the fact that $h$ is bounded away from zero and infinity is deduced from the fact that the shift has finitely many images, see [Sar99, Proposition 2].

Actually, we never really use the $\|\cdot \|_{\rho,\beta }$ norm and all our bounds in the following are on the $\rho$-Hölder norm, that is, we both bound $\|\cdot \|_{\infty }$ and $D_{\rho }$, which is defined by

\[ D_{\rho}f=\sup_{x,y\in \overline{\Sigma}_A}\frac{|f(x)-f(y)|}{d_{\rho}(x,y)}. \]

Obviously, a bound on $D_{\rho }$ is stronger than a bound $D_{\rho,\beta }$. Moreover, when bounding $D_{\rho }f$, we have to bound ${|f(x)-f(y)|}/{d_{\rho }(x,y)}$. We always assume that $x$ and $y$ start with the same element, otherwise $d(x,y)=\rho$ and one can, thus, bound ${|f(x)-f(y)|}/{d_{\rho }(x,y)}$ by $2\rho ^{-1}\|f\|_{\infty }$.

One issue we have to deal with, when applying these results to random walks on relatively hyperbolic groups in the next subsection, is that our Markov shift will not be topologically mixing. It will not even be irreducible (but will have only finitely many recurrent classes). This issue was already addressed in [Gou14] for a Markov shift with finitely many symbols, as we now explain.

In the following, we consider a countable Markov shift $(\overline {\Sigma }_A,T)$ with set of symbols $\Sigma$ and transition matrix $A$ and we assume that it has finitely many images. If the Markov shift is irreducible, but not topologically mixing, then there is a minimal period $p>1$ such that for any symbol $s \in \Sigma$, if $T^{-n}[s]\cap [s]\neq \emptyset$, then $n=pk$ for some $k\geq 0$. Then, one can decompose the set of symbols as a finite union $\Sigma =\Sigma _A^{(1)}\sqcup \Sigma _A^{(2)}\sqcup \cdots \sqcup \Sigma _A^{(p)}$, such that for $i\in \mathbb {Z}/p\mathbb {Z}$, if $a_{s,s'}=1$ and $s\in \Sigma ^{(i)}$, then $s'\in \Sigma ^{(i+1)}$. We call such a decomposition a cyclic decomposition. We denote by $\overline {\Sigma }_A^{(i)}$ the subset of $\overline {\Sigma }_A$ of sequences that begin with an element of $\Sigma _A^{(i)}$, so that the shift map $T$ maps $\overline {\Sigma }_A^{(i)}$ to $\overline {\Sigma }_A^{(i+1)}$. Moreover, in this case, $T^{p}$ acts on $\overline {\Sigma }_A^{(i)}$ and the induced Markov shift is topologically mixing. Using this decomposition together with Theorem 3.2, we get that if $\varphi$ is locally Hölder continuous function with finite pressure $P(\varphi )$ and if the Markov shift has finitely many images, then there are positive functions $h^{(i)}$ on $\overline {\Sigma }_A^{(i)}$ and probability measures $\nu ^{(i)}$ on $\overline {\Sigma }_A^{(i)}$ with $\int h^{(i)}d\nu ^{(i)}=1$ such that for $f\in \mathcal {B}_{\rho,\beta }$,

\[ \bigg\|{e}^{-nP(\varphi)}\mathcal{L}_{\varphi}^{n}f-\sum_{i=1}^{p}h^{(i)}\int f \,d\nu^{((i-n) \text{ mod } p)}\bigg\|_{\rho,\beta}\leq C\theta^{n}\|f\|_{\rho,\beta}. \]

Assume that the Markov shift is not irreducible. Then, because it has finitely many images, one can first decompose $\Sigma$ as $\Sigma =\Sigma _{A,0}\sqcup \Sigma _{A,1}\sqcup \cdots \Sigma _{A,q}$, such that if a path starts at $s\in \Sigma _{A,0}$, then it never reaches $s$ again and for $s,s'\in \Sigma$, one can reach $s'$ starting at $s$ and conversely if and only if $s$ and $s'$ are in the same subset $\Sigma _{A,j}$, $j\geq 1$. More formally, the decomposition of $\Sigma$ satisfies the following properties.

1. (i) If $s\in \Sigma _{A,0}$, then for all $n\geq 1$, $T^{-n}[s]\cap [s]=\emptyset$.

2. (ii) If there exist $n,n'$ such that $T^{-n}[s]\cap [s']\neq \emptyset$ and $T^{-n'}[s']\cap [s]\neq \emptyset$, then there exists $j\geq 1$ such that $s,s'\in \Sigma _{A,j}$.

3. (iii) Conversely, if $s,s'$ lie in the same $\Sigma _{A,j}$, $j\geq 1$, then there exist $n,n'$ such that $T^{-n}[s]\cap [s']\neq \emptyset$ and $T^{-n'}[s']\cap [s]\neq \emptyset$.

We call $\Sigma _{A,0}$ the transient component of $\Sigma$ and the sets $\Sigma _{A,j}$, $j\geq 1$, the biconnected components of $\Sigma$. All the non-trivial dynamical behavior of the Markov shift happens in the biconnected components. We denote by $\overline {\Sigma }_{A,j}$ the subset of $\overline {\Sigma }_A$ of sequences $x$ that stay in $\Sigma _{A,j}$, that is, for every $n$, $x_n\in \Sigma _{A,j}$. We similarly call the sets $\overline {\Sigma }_{A,j},j\geq 1$ the biconnected components of $\overline {\Sigma }_A$.

Then, $\overline {\Sigma }_{A,j}$ is stable under the shift map $T$ and we can apply the above discussion to $\overline {\Sigma }_{A,j}$. If $\varphi$ is a locally Hölder continuous function on $\overline {\Sigma }_A$, denote by $\varphi _j$ its restriction to the component $\overline {\Sigma }_{A,j}$, with associated transfer operator $\mathcal {L}_{\varphi _j}$. Denote the pressure of $\varphi _j$ by $P_j(\varphi )$. Then, $\mathcal {L}_{\varphi _j}$ has a spectral gap and ${e}^{P_j(\varphi )}$ is its dominant eigenvalue. Let $P(\varphi )$ be the maximum of all the $P_j(\varphi )$ and call a component $\overline {\Sigma }_{A,j}$ maximal if $P_j(\varphi )=P(\varphi )$.

Definition 3.2 We say that $\varphi$ is semisimple if one cannot reach a maximal component from another. That is, for every two maximal components $\overline {\Sigma }_{A,j}$, $\overline {\Sigma }_{A,j'}$, $j\neq j'$, for any two symbols $s\in \Sigma _{A,j}$, $s'\in \Sigma _{A,j'}$, for any $n\geq 1$, $T^{-n}[s]\cap [s']=\emptyset$.

Elaborating on ideas of Calegari and Fujiwara from [CF10], Gouëzel proved in [Gou14] a spectral gap theorem for the transfer operator of a semisimple Hölder continuous function, when the set of symbols is finite. His proof works for a countable set of symbols, if the Markov shift has finitely many images and the Hölder continuous function is positive recurrent, because it is based on a spectral decomposition over the sets $\overline {\Sigma }_{A,j}$, on which one applies the Ruelle–Perron–Frobenius theorem (that we replace here with Theorem 3.2). Thus, combining Theorem 3.2 and the proof of [Gou14, Theorem 3.8], we obtain the following.

Theorem 3.3 Let $(\overline {\Sigma }_A,T)$ be a countable Markov shift with finitely many images. Let $\varphi$ be a locally Hölder continuous function with finite maximal pressure $P(\varphi )$. Assume that $\varphi$ is semisimple. Denote by $\overline {\Sigma }_{A,1},\ldots \overline {\Sigma }_{A,k}$ the maximal components, with corresponding period $p_1,\ldots,p_k$ and consider a cyclic decomposition

\[ \Sigma_{A,j}=\Sigma_{A,j}^{(1)}\sqcup \cdots \Sigma_{A,j}^{(p_j)}. \]

Then, there exist functions $h_j^{(i)}$ and probability measures $\nu _j^{(i)}$ with $\int h_{j}^{(i)}d\nu _j^{(i)}=1$ and such that $\mathcal {L}_{\varphi }^{*}\nu _{j}^{(i)}=\nu _j^{(i-1) \text { mod } p_j}$ and $\mathcal {L}_{\varphi }h_{j}^{(i)}=h_j^{(i-1) \text { mod } p_j}$. Moreover, for $f\in \mathcal {B}_{\rho,\beta }$,

\[ \bigg\|{e}^{-nP(\varphi)}\mathcal{L}_{\varphi}^{n}f-\sum_{j=1}^{k}\sum_{i=1}^{p_j}h_j^{(i)}\int f\, d\nu_j^{((i-n) \text{ mod } p_j)}\bigg\|_{\rho,\beta}\leq C\theta^{n}\|f\|_{\rho,\beta}, \]

for some $C\geq 0$ and $0<\theta <1$. Finally, the functions $h_j^{(i)}$ are bounded away from zero and infinity on the support of $\nu _j^{(i)}$.

We also obtain the following result, again proved in [Gou14] for finite sets of symbols, which applies in our situation (see [Gou14, Lemma 3.7]).

Lemma 3.4 Let $(\overline {\Sigma }_A,T)$ be a countable Markov shift with finitely many images. Let $\varphi$ be a locally Hölder continuous function with finite maximal pressure $P(\varphi )$. Let $s\in \Sigma$ and assume that there is a path starting with $s$ that visits $k$ maximal components. Then, for any non-negative function $f$ with $f\geq 1$ on the set of paths starting with $s$, one has

\[ \mathcal{L}^{n}_{\varphi}f(\emptyset)\geq Cn^{k-1}{e}^{nP(\varphi)}, \]

where we recall that $\emptyset$ is the empty sequence in $\Sigma _A^{*}$. In particular, for $k=2$, if $\varphi$ is not semisimple, then

\[ \mathcal{L}^{n}_{\varphi}1(\emptyset)\geq Cn {e}^{nP(\varphi)}. \]

3.2 Perturbation of the pressure

In [Gou14], Gouëzel proves a perturbation theorem for finite sets of symbols (see precisely [Gou14, Proposition 3.10]). Its proof remains valid for countable shifts with finitely many images. Denote by $ |||{\cdot }|||_{\rho,\beta }$ the operator norm for operators acting on $(\mathcal {B}_{\rho,\beta },\|\cdot \|_{\rho,\beta })$. To apply Gouëzel's perturbation theorem, one needs to control $ |||{\mathcal {L}|||_{\varphi }-\mathcal {L}_{\psi }}_{\rho,\beta }$. However, estimating this norm will be very difficult in this paper, so we need finer results, that are based on the following theorem, proved by Keller and Liverani [KL99].

Consider a Banach $(V,\|\cdot \|)$ endowed with a norm $|\cdot |_w$, satisfying $|\cdot |_w\leq C \|\cdot \|$ for some uniform $C$. Letting $\mathcal {L}:V\to V$ be a linear operator, let

\[ |||{\mathcal{L}}|||=\sup \big\{\|\mathcal{L}v\|,\|v\|\leq 1\big\} \]

denote the operator norm of $\mathcal {L}$ associated with $\|\cdot \|$ and let

\[ |||{\mathcal{L}}|||_{s\to w}=\sup \big\{|\mathcal{L}v|_w,\|v\|\leq 1\big \} \]

be the operator norm of $\mathcal {L}:(V,\|\cdot \|)\to (V,|\cdot |_w)$.

Theorem 3.5 Consider a family of bounded operators $\mathcal {L}_r:(V,\|\cdot \|)\to (V,\|\cdot \|)$, with $r$ varying in $(0,R]$. Assume there exist $0<\sigma < M$ and $C\geq 0$ and there exists a function $\tau (r)$ converging to zero as $r$ tends to $R$ such that the following hold.

1. (i) For every $n$, for every $v\in V$, $|\mathcal {L}_R^{n}v|_w\leq CM^{n}|v|_w$.

2. (ii) For every $r\leq R$, for every $n$, for every $v\in V$, $\|\mathcal {L}_r^{n} v\|\leq C\sigma ^{n}\|v\|+CM^{n}|v|_w$.

3. (iii) For every $r\leq R$, $ |||{\mathcal {L}|||_r-\mathcal {L}_R}_{s\to w}\leq \tau (r)$.

For fixed $\rho >0$ and $\rho '>0$ let

\[ A_{\rho,\rho'}=\{z\in \mathbb{C},|z|\geq \sigma +\rho,d(z,\operatorname{spec}(\mathcal{L}_R))\geq \rho'\}. \]

Then, for any $\rho,\rho '>0$ there exist $\beta _0<1$ and $K_0\geq 0$ and there exists $r_0$ such that for every $\beta \leq \beta _0$, for every $r\in [r_0,R]$ for every z $z\in A_{\rho,\rho '}$:

1. (a) the operator $zI-\mathcal {L}_r:(V,\|\cdot \|)\to (V,\|\cdot \|)$ is invertible;

2. (b) the operator norm $ |||{(zI-\mathcal {L}_r)^{-1}}|||$ is bounded independently of $r$;

3. (c) the norm $ |||{\cdot }|||_{s\to w}$ satisfies $ |||{(zI-\mathcal {L}_r)^{-1}-(zI-\mathcal {L}_R)^{-1}}|||_{s\to w}\leq K_0 \tau (r)^{\beta }$.

Moreover, $\beta _0$ only depends on $\rho$ and can be explicitly computed whenever $\sigma +\rho \leq M$. Indeed, one can then choose

\[ \beta_0=\frac{\log(({\sigma+\rho})/{\sigma})}{\log({M}/{\sigma})}. \]

In particular, $\beta _0$ converges to zero as $\rho$ tends to zero and converges to one as $\rho$ tends to $M-\sigma$.

For a proof, we refer to [Bal18, A.3]. Note that it is asked there that for every $r$, $|\mathcal {L}_r^{n}v|_w\leq CM^{n}|v|_w$, whereas our condition (i) only requires that this holds for $r=R$. However, the proof in [Bal18, A.3] only uses this inequality for $r=R$.

Let us apply this to transfer operators. Consider a countable shift with finitely many images $(X_A,T)$ and a family of locally Hölder functions $f_r$, for $r\in (0,R]$. Let $\mathcal {L}_r=\mathcal {L}_{f_r}$ be the associated transfer operator. Assume that for every $r$, the maximal pressure $P_r$ of $f_r$ is finite and that $f_r$ is semisimple. Let $h_{j}^{(i)}$ and $\nu _j^{(i)}$ be the functions and measures given by Theorem 3.3, associated with $\mathcal {L}_{R}$. Define the measure $m_j$ as $dm_j= ({1}/{p_j})\sum _{i=1}^{p_j}h_{j}^{(i)}\,d\nu _j^{(i)}$.

Let $m=\sum m_j$. Consider the Banach space $(V=H_{\rho,\beta },\|\cdot \|=\|\cdot \|_{\rho,\beta })$ on $V=H_{\rho,\beta }$, endowed with the norm $|\cdot |_w=\|\cdot \|_{L^{1}(m)}$. As $m$ is finite, we have $|\cdot |_w\leq C \|\cdot \|$. We deduce from Theorem 3.5 the following.

Theorem 3.6 With the same notation as previously, assume there exists $\sigma$ such that $0<\sigma < e^{P_R}$ and that there exist $C\geq 0$ and a function $\tau (r)$ converging to zero as $r$ tends to $R$ such that the following hold.

1. (α) For every $r\leq R$, for every $n$, for every $v\in V$,

   \[ \|\mathcal{L}_r^{n} v\|\leq C\sigma^{n}\|v\|+C{e}^{nP_R}|v|_w. \]

2. (β) For every $r\leq R$, $ |||{\mathcal {L}_r-\mathcal {L}_R}|||_{s\to w}\leq \tau (r)$.

Then, for every $r$ which is close enough to $R$, there exist numbers $\tilde {P}_j(r)$ and eigenfunctions $\tilde {h}_{j,r}^{(i)}$ and eigenmeasures $\tilde {\nu }_{j,r}^{(i)}$ of $\mathcal {L}_r$ associated with the eigenvalue ${e}^{\tilde {P}_j(r)}$ such that

\[ \bigg\|{e}^{-nP_R}\mathcal{L}_{r}^{n}g-\sum_{j=1}^{k}{e}^{n(\tilde{P}_j(r)-P_R)}\sum_{i=1}^{p_j}\tilde{h}_{j,r}^{(i)}\int g \,d\tilde{\nu}_{j,r}^{((i-n) \text{ mod } p_j)}\bigg\|_{\rho,\beta}\leq C\theta^{n}\|g\|_{\rho,\beta}. \]

The functions $\tilde {h}_{j}^{(i)}$ and the measures $\tilde {\nu }_j^{(i)}$ have the same support as $h_j^{(i)}$ and $\nu _j^{(i)}$, respectively. Moreover, $\big \|\tilde {h}_{j,r}^{(i)}\big \|$ is uniformly bounded. Finally, $\big |\tilde {h}_{j,r}^{(i)}-h_j^{(i)}\big |_w$ converges to zero as $r$ tends to $R$ and $\tilde {\nu }_{j,r}^{(i)}$ weakly converges to $\nu _j^{(i)}$ as $r$ tends to $R$.

Proof. As $\mathcal {L}_R$ has a spectral gap according to Theorem 3.3, there exists $\sigma _0< e^{P_R}$ such that the spectrum of $\mathcal {L}_R$ outside of the disk of radius $\sigma _0$ exactly consists of the eigenvalue $e^{P_R}$, with eigenfunctions $h_j^{(i)}$ and eigenmeasures $\nu _j^{(i)}$. The result is then a consequence of Theorem 3.5, choosing $\rho$ such that $\sigma _0<\sigma +\rho <{e}^{P_R}$. Indeed, condition (i) there is satisfied with $M={e}^{P_R}$ because $\nu _j^{(i)}$ is an eigenmeasure of $\mathcal {L}_R$ associated with ${e}^{P_R}$. In addition, conditions (ii) and (iii) are direct consequences of assumptions ($\alpha$) and ($\beta$).

Note that $\int \tilde {h}_{j,r}^{(i)}\,d\nu _j^{(i)}\neq 0$ for $r$ close enough to $R$, because $\int h_j^{(i)}d\nu _j^{(i)}=1$ and $\big |\tilde {h}_{j,r}^{(i)}-h_j^{(i)}\big |_w$ converges to zero. One can, thus, normalize $\tilde {h}_{j,r}$ declaring $\int \tilde {h}_{j,r}^{(i)}\,d\nu _j^{(i)}=1$. We make this assumption in the following. We still have that $\big \|\tilde {h}_{j,r}^{(i)}\big \|$ is uniformly bounded and that $\big |\tilde {h}_{j,r}^{(i)}-h_j^{(i)}\big |_w$ converges to zero. The following result allows us to obtain a precise asymptotic of $\tilde {P}_{j,r}-P_R$ in the following sections.

Proposition 3.7 Under the assumptions of Theorem 3.6,

\[ {e}^{\tilde{P}_j(r)-P_R}-1= \int ({e}^{f_r-f_R}-1)\,dm_j+ \int ({e}^{f_r-f_R}-1)\frac{1}{p_j}\bigg(\sum_{i=0}^{p_j-1}h_j^{(i)}-\tilde{h}_{j,r}^{(i)}\bigg)\,d\nu_j^{(i)}, \]

where $dm_j= ({1}/{p_j})\sum _{i=1}^{p_j}h_{j}^{(i)}\,d\nu _j^{(i)}$.

Proof. As $\tilde {h}_{j,r}^{(i)}$ are eigenfunctions of $\mathcal {L}_r$ and $\tilde {h}_{j,r}$ is normalized, we have

\[ {e}^{\tilde{P}_j(r)}=\int \mathcal{L}_r \tilde{h}_{j,r}^{(i)}\,d\nu_j^{(i)}. \]

Consequently,

\[ {e}^{\tilde{P}_j(r)}-{e}^{P_R}=\int ( \mathcal{L}_r \tilde{h}_{j,r}^{(i)}-\mathcal{L}_Rh_j^{(i)})\,d\nu_j^{(i)}. \]

Note that for any function $g$, $\mathcal {L}_rg=\mathcal {L}_R ({e}^{f_r-f_R}g)$. In particular,

\[ {e}^{\tilde{P}_j(r)}-{e}^{P_R}=\int \mathcal{L}_R ( {e}^{f_r-f_R}\tilde{h}_{j,r}^{(i)}-h_j^{(i)})\,d\nu_j^{(i)}. \]

Using that $d\nu _j^{(i)}$ is an eigenmeasure of $\mathcal {L}_R$ associated with the eigenvalue ${e}^{P_R}$, we obtain

\begin{align*} {e}^{\tilde{P}_j(r)-P_R}-1&=\int ( {e}^{f_r-f_R}\tilde{h}_{j,r}^{(i)}-h_j^{(i)})\,d\nu_j^{(i)}\\ &=\int ( {e}^{f_r-f_R}-1) (\tilde{h}_{j,r}^{(i)}-h_j^{(i)})\,d\nu_j^{(i)} +\int \tilde{h}_{j,r}^{(i)}\,d\nu_j^{(i)}-\int {e}^{f_r-f_R}h_j^{(i)}\,d\nu_j^{(i)} . \end{align*}

As $\int h_j^{(i)}\,d\nu _j^{(i)}=\int \tilde {h}_{j,r}^{(i)}\,d\nu _j^{(i)}=1$, we thus obtain

\[ {e}^{\tilde{P}_j(r)-P_R}-1= \int ( {e}^{f_r-f_R}-1) (\tilde{h}_{j,r}^{(i)}-h_j^{(i)})\,d\nu_j^{(i)}+\int ({e}^{f_r-f_R}-1)h_j^{(i)}\,d\nu_j^{(i)}. \]

This holds for every $i$, which concludes the proof summing over $i$ and then dividing by $p_j$.

4. Asymptotic of the first derivative of the Green function

In this section, we assume that $\Gamma$ is hyperbolic relative to $\Omega$ and choose a system of representatives of conjugacy classes $\Omega _0=\{\mathcal {H}_1,\ldots,\mathcal {H}_N\}$ of elements of $\Omega$. We consider a probability measure $\mu$ on $\Gamma$ that satisfies weak and strong relative Ancona inequalities up to the spectral radius and we denote by $R_{\mu }$ the inverse of this spectral radius. Note that we do not need to assume that the measure $\mu$ is symmetric but only that relative Ancona inequalities are satisfied.

We assume that $\mu$ is not spectrally degenerate. According to Proposition 2.11, we have $ ({d}/{dr})_{|r=R_\mu }G(e,e|r)=+\infty$, or equivalently $I^{(1)}(R_\mu )=+\infty$ by Lemma 2.7. In addition, Proposition 2.8 shows that

\[ I^{(2)}(r)\asymp (I^{(1)}(r))^{3}. \]

Our goal in the following sections is to obtain a more precise statement, transforming $\asymp$ into $\sim$, when $r\to R_{\mu }$. Precisely, we prove the following.

Theorem 4.1 Under these assumptions, there exists $\xi >0$ such that

\[ I^{(2)}(r)\underset{r\to R_{\mu}}{\sim} \xi (I^{(1)}(r))^{3}. \]

To do so, we use thermodynamic formalism, adapting [Gou14, GL13].

4.1 Transfer operator for the Green function

We choose a generating set $S$ of $\Gamma$ as in Theorem 2.3, so that $\Gamma$ is automatic relative to $\Omega _0$ and $S$, where $\Omega _0$ is a finite set of representatives of conjugacy classes of the parabolic subgroups Let $\mathcal {G}=(V,E,v_*)$ be a graph and $\phi :E\rightarrow S\cup \bigcup _{\mathcal {H}\in \Omega _0}\mathcal {H}$ be a labelling map as in the definition of a relative automatic structure.

The set of vertices $V$ is finite. Moreover, if $\sigma \in \Sigma _0= S\cup \bigcup _{\mathcal {H}\in \Omega _0}\mathcal {H}$ and if $v\in V$, there is at most one edge that leaves $v$ and that is labelled with $\sigma$. Thus, the set of edges $E$ is countable. Set $\Sigma =E$ and consider the transition matrix $A=(a_{s,s'})_{s,s'\in \Sigma }$, defined by $a_{s,s'}=1$ if the edges $s$ and $s'$ are adjacent in $\mathcal {G}$ and $a_{s,s'}=0$ otherwise. We then define $\Sigma _A^{*}$, $\partial \Sigma _A$ and $\overline {\Sigma }_A$ as previously. According to the definition of a relative automatic structure, elements of $\overline {\Sigma }_A$ represent relative geodesics and relative geodesic rays.

We decompose $\Sigma _0= S\cup \bigcup _{\mathcal {H}\in \Omega _0}\mathcal {H}$ as follows. The sets $\mathcal {H}_j\cap \mathcal {H}_k$ are finite if $j\neq k$ (see, e.g., [DS05, Lemma 4.7]). We can, thus, consider $\mathcal {H}'_k=\mathcal {H}_k\setminus \cup _{j\neq k}\mathcal {H}_j$ and $\mathcal {H}'_0=\Sigma _0\setminus \cup _k \mathcal {H}'_k$. Then, $\mathcal {H}'_0$ remains finite and the sets $\mathcal {H}'_k$ are disjoint. By analogy with free factors in a free product, we introduce the following terminology.

Definition 4.1 We call the sets $\mathcal {H}'_k$ the factors of the relatively automatic structure

Paths of length $n$ in $\mathcal {G}$ beginning at $v_*$ are in bijection with the relative sphere $\hat {S}_n$. Moreover, infinite paths in $\mathcal {G}$ starting at $v_*$ give relative geodesic rays starting at $e$. Denote by $E_*\subset E$ the set of edges that starts at $v_*$. The labelling map $\phi$ can be extended to infinite paths. When restricted to infinite words starting in $E_*$, it gives a surjective map from paths beginning at $v_*$ to the Gromov boundary of the graph $\hat {\Gamma }$, which is by definition the set of conical limit points of $\Gamma$, included in the Bowditch boundary. Restricting the distance $d_\rho (x,y)=\rho ^{-n}$ to $E_*$, this induced map is continuous, endowing the Bowditch boundary with the usual topology. A formal way of restricting our attention to elements of the group and to conical limit points is to consider the function $1_{E_*}$ on $\overline {\Sigma }_A$ which takes value one on sequences in $\overline {\Sigma }_A$ beginning with an edge in $E_*$ and that takes value zero elsewhere. This function $1_{E_*}$ is locally Hölder continuous.

We have the following, which proves that every locally Hölder continuous function with finite pressure is positive recurrent, according to Proposition 3.1.

Lemma 4.2 The Markov shift $(\overline {\Sigma }_A,T)$ has finitely many images.

Proof. If an edge $s$ in $\Sigma$ ends at some vertex $v$ in $\mathcal {G}$, then the only edges $s'$ such that $a_{s,s'}=1$ are those that start at $v$. Thus, if two edges end at the same vertex $v$, they have the same row in the matrix $A$. The lemma follows, because there is only a finite number of vertices.

Recall that $R_{\mu }$ is the inverse of the spectral radius of the $\mu$-random walk on $\Gamma$. Also recall that for $r\in [0,R_{\mu }]$, we write $H(e,\gamma |r)=G(e,\gamma |r)G(\gamma,e|r)$. For $r\in [1,R_{\mu }]$, we define the function $\varphi _r$ on $\Sigma _A^{*}$ by $\varphi _r(\emptyset )=1$ and

\[ \varphi_r(x=x_1,\ldots,x_n)=\log \bigg(\frac{H(e,\phi(x)|r)}{H(e,\phi(T x)|r)}\bigg) = \log \bigg(\frac{H(e,\phi(x_1\dots x_n)|r)}{H(e,\phi(x_2\dots x_n)|r)}\bigg). \]

Using equivariance of the Green function, we also have

\[ \varphi_r(x=x_1,\ldots,x_n)=\log \bigg(\frac{H(e,\phi(x_1\dots x_n)|r)}{H(\phi(x_1),\phi(x_1\dots x_n)|r)}\bigg). \]

Lemma 4.3 For every $r\in [1,R_{\mu }]$, the function $\varphi _r$ can be extended to $\overline {\Sigma }_A$. It is then locally Hölder continuous on $\overline {\Sigma }_A$.

Proof. Let $n\geq 1$ and let $x,y\in \Sigma _A^{*}$ be such that $x_1=y_1,\ldots,x_n=y_n$. Hence, in $\Gamma$, we have $\phi (x_1)=\phi (y_1),\ldots,\phi (x_n)=\phi (y_n)$. This means that relative geodesics from $e$ to $\phi (x)$ and from $\phi (x_1)=\phi (y_1)$ to $\phi (y)$ fellow-travel for a time at least $n-1$. According to strong relative Ancona inequalities, we thus have, for some $C\geq 0$ and $0<\rho <1$,

\[ \bigg|\frac{G(e,\phi(x)|r)G(\phi(y_1),\phi(y)|r)}{G(\phi(x_1),\phi(x)|r)G(e,\phi(x)|r)} -1\bigg|\leq C\rho^{n}. \]

Weak relative Ancona inequalities also show that

\[ G(e,\phi(x)|r)G(\phi(y_1),\phi(y)|r)\geq \frac{1}{C}G(e,\phi(x_1)|r)G(\phi(x_1),\phi(x)|r)G(\phi(y_1),\phi(y)|r) \]

and because $x_1=y_1$, we obtain

\[ G(e,\phi(x)|r)G(\phi(y_1),\phi(y)|r)\geq \frac{1}{C^{2}}G(e,\phi(y)|r)G(\phi(x_1),\phi(x)|r). \]

Thus, ${G(e,\phi (x)|r)G(\phi (y_1),\phi (y)|r)}/{G(\phi (x_1),\phi (x)|r)G(e,\phi (x)|r)}$ is bounded away from zero, so that

(8)\begin{align} &\bigg| \log \bigg(\frac{H(e,\phi(x)|r)}{H(\phi(x_1),\phi(x)|r)}\bigg) - \log \bigg(\frac{H(e,\phi(y)|r)}{H(\phi(y_1),\phi(y)|r)}\bigg)\bigg|\nonumber\\ &\quad \leq C_1\bigg|\frac{G(e,\phi(x)|r)G(\phi(y_1),\phi(y)|r)}{G(\phi(x_1),\phi(x)|r)G(e,\phi(y)|r)} -1\bigg|\leq C\rho^{n}. \end{align}

This proves that if $x=(x_1,\ldots,x_n,\ldots )\in \partial \Sigma _A^{*}$, then the sequence $\varphi _r(x_1,\ldots,x_k)$ is Cauchy, so that it converges to some well-defined limit $\varphi _r(x)$. This extended function $\varphi _r$ on $\overline {\Sigma }_A$ still satisfies (8), so that it is locally Hölder continuous.

We denote by $\mathcal {L}_r$ the transfer operator associated with the function $\varphi _r$.

Lemma 4.4 For every $r\in [1,R_{\mu }]$, the function $\varphi _r$ has finite pressure and is positive recurrent.

Proof. As noted previously, because the Markov shift has finitely many images, Proposition 3.1 shows that any locally Hölder function with finite pressure is positive recurrent. Thus, we only need to prove that $\varphi$ has finite pressure, which is equivalent to proving that $\|\mathcal {L}_r1\|_\infty <+\infty$ by [Sar99, Theorem 1]. For $x\in \overline {\Sigma }_A$, let $X_x^{1}$ be the set of symbols that can precede $x$ in the automaton $\mathcal {G}$. Then, by weak relative Ancona inequalities,

\[ \mathcal{L}_r1(x)=\sum_{\sigma\in X_x^{1}}\frac{H(e,\sigma x|r)}{H(\sigma,\sigma x|r)}\lesssim \sum_{k=0}^{N}\sum_{\sigma\in \mathcal{H}_k'}H(e,\sigma|r). \]

This last sum is bounded by Corollary 2.10, which concludes the proof.

Let $P_j(r)$ be the pressure of the restriction of $\varphi _r$ to a component $\overline {\Sigma }_{A,j}$ of the Markov shift and let $P(r)$ be the maximal pressure, that is, the maximum of the $P_j(r)$. Recall that we declared that the empty sequence is not a preimage of the empty sequence. This will simplify the following.

The main reason for introducing this function $\varphi _r$ is that

\[ \mathcal{L}_r^{n}1_{E_*}(\emptyset)=\frac{1}{H(e,e|r)}\sum_{\gamma \in \hat{S}_n}H(e,\gamma|r), \]

where we recall that $1_{E_*}$ is the function on $\overline {\Sigma }_A$ that takes value one on paths that start at $v_*$ in the automaton $\mathcal {G}$ and zero elsewhere. Indeed, to prove Theorem 4.1, we want to understand $I^{(1)}(r)=\sum _{\gamma \in \Gamma }H(e,\gamma |r)$. Thus, we want to understand the behavior of $\sum _{\gamma \in \hat {S}_n}H(e,\gamma |r)$, which is thus the same as understanding the behavior of $\mathcal {L}_r^{n}1_{E_*}(\emptyset )$.

4.2 Continuity properties of the transfer operator

Our goal in this subsection is to prove that the map $r\mapsto \mathcal {L}_r$ is continuous in a weak sense. We begin by the following result.

Lemma 4.5 There exists $C>0$ such that for all $r\in [1,R_{\mu })$,

\[ \frac{1}{C}\frac{1}{\sqrt{R_{\mu}-r}}\leq \sum_{\gamma\in \Gamma}H(e,\gamma|r)\leq C \frac{1}{\sqrt{R_{\mu}-r}}. \]

Proof. Let $I_1(r)=\sum _\gamma H(e,\gamma |r)$ and $F(r)=r^{2}I_1(r)$. According to [Dus22, Lemma 3.2],

\[ F'(r)=2r\sum_{\gamma,\gamma'}G(e,\gamma'|r)G(\gamma',\gamma|r)G(\gamma,e|r). \]

Proposition 2.8 gives

\[ \frac{1}{C'}\leq \frac{F'(r)}{F(r)^{3}}\leq C' \]

and Proposition 2.11 gives $F(R_{\mu })=+\infty$. Thus, integrating the inequality above between $r$ and $R_{\mu }$, we obtain

\begin{align*} \frac{1}{C'}(R_{\mu}-r)\leq \frac{1}{F(r)^{2}}\leq C'(R_{\mu}-r), \end{align*}

which leads to the desired inequality.

We also prove the following.

Lemma 4.6 For any $r\in [1,R_{\mu }]$, $P(r)\leq 0$. Moreover, $P(R_{\mu })=0$ and $\varphi _{R_{\mu }}$ is semisimple.

Proof. If $P(r)$ were positive, then Theorem 3.3 would show that

\[ \mathcal{L}_r1_{E_*}(\emptyset)=\frac{1}{H(e,e|r)}\sum_{\gamma\in \hat{S}_n}H(e,\gamma|r) \]

tends to infinity. However, Lemma 2.9 shows that this quantity is bounded, so we obtain a contradiction.

If $P(R_{\mu })$ were negative, then $\sum _{\gamma \in \hat {S}_n}H(e,\gamma |r)$ would converge to zero exponentially fast, according to Theorem 3.3. In particular, $\sum _{\gamma \in \Gamma }H(e,\gamma |r)$ would be finite, that is, using Lemma 2.7, $ ({d}/{dr})_{|r=R_\mu }G(e,e|r)$ would be finite. This would be a contradiction with Proposition 2.11.

Finally, if $\varphi _{R_{\mu }}$ were not semisimple, then Lemma 3.4 would again show that $\sum _{\gamma \in \hat {S}_n}H(e,\gamma |r)$ would tend to infinity, because we already know that $P(R_{\mu })=0$. Again, Lemma 2.9 shows that this quantity is bounded.

Let $h_{j}^{(i)}$ and $\nu _j^{(i)}$ be the functions and measures given by Theorem 3.3, associated with $\mathcal {L}_{R_\mu }$. Let $m_j$ be the measure defined as $dm_j= ({1}/{p_j})\sum _{i=1}^{p_j}h_{j}^{(i)}\,d\nu _j^{(i)}$. According to [Sar99, Proposition 4], $m_j$ is a Gibbs measure. However, we have to apply this proposition to each component $\overline {\Sigma }_{A,j}$ of the shift, so that we do not have that $m_j([x_1,\ldots,x_n])\asymp H(e,x_1\dots x_n|R_\mu )$ for any cylinder $[x_1,\ldots,x_n]$. We still deduce that there exists $C\geq 0$ such that for any $n$, for any cylinder $[x_1,\ldots,x_n]$,

(9)\begin{align} m_j([x_1\dots x_n]) \leq C H(e,x_1\dots x_n|R_\mu). \end{align}

Furthermore, letting $m=\sum _j m_j$, there exists $C\geq 0$ such that for any $n$, for any cylinder $[x_1\dots x_n]$ in the support of one of the measures $m_j$,

(10)\begin{equation} \frac{1}{C} H(e,x_1\dots x_n|R_\mu)\leq m([x_1,\ldots,x_n]) \leq C H(e,x_1\dots x_n|R_\mu). \end{equation}

Proposition 4.7 There exists a non-negative function $\varphi$ on $\overline {X}_A$, possibly taking the value $+\infty$ on $\partial \Sigma _A$, which is integrable with respect to the measure $m$ and such that for every $x\in \Sigma _A$ and for every $1\leq r,r'\leq R_\mu$,

\begin{align*} |\varphi_r(x)-\varphi_{r'}(x)|\leq 2\varphi(x)\sqrt{|r-r'|}. \end{align*}

Integrating over $r$, this proposition is a direct consequence of the following lemma.

Lemma 4.8 There exists a non-negative function $\varphi$ on $\overline {X}_A$, possibly taking the value $+\infty$ on $\partial \Sigma _A$, which is integrable with respect to the measure $m$ and such that for every $x\in \Sigma _A$ and for every $1\leq r< R_\mu$,

\[ \bigg|\frac{d}{dr}\varphi_r(x)\bigg|\leq \varphi(x) \frac{1}{\sqrt{R_\mu-r}}. \]

Proof. Fix $x\in \Sigma _A$. We compute the derivative of $r\mapsto \varphi _r(x)$. To simplify the notation, we identify $x$ with $\phi (x)\in \Gamma$. We obtain

\[ \frac{d}{dr}\varphi_r(x)=\frac{d}{dr}\log \frac{H(e,x|r)}{H(x_1,x|r)}=\frac{d}{dr}\log r^{2}H(e,x|r)-\frac{d}{dr}\log r^{2}H(x_1,x|r). \]

In [Dus22, Lemma 3.2] we showed that

(11)\begin{align} \frac{d}{dr}\varphi_r(x)&=\sum_{y\in \Gamma}\frac{G(e,y|r)G(y,x|r)G(x,e|r)+G(e,x|r)G(x,y|r)G(y,e|r)}{rH(e,x|r)}\nonumber\\ &\quad -\sum_{y\in \Gamma}\frac{G(x_1,y|r)G(y,x|r)G(x,x_1|r)+G(x_1,x|r)G(x,y|r)G(y,x_1|r)}{rH(x_1,x|r)}. \end{align}

We first give an upper bound for

\[ \bigg|\frac{\sum_{y\in \Gamma}G(e,y|r)G(y,x|r)G(x,e|r)}{rH(e,x|r)}-\frac{\sum_{y\in \Gamma}G(x_1,y|r)G(y,x|r)G(x,x_1|r)}{rH(x_1,x|r)}\bigg|. \]

The remaining term in (11) will be bounded in the same way. Putting together these two sums, we obtain

\[ \frac{1}{rH(e,x|r)}\sum_{y\in \Gamma}G(e,y|r)G(y,x|r)G(x,e|r) -G(x_1,y|r)G(y,x|r)G(x,x_1|r)\frac{H(e,x|r)}{H(x_1,x|r)}. \]

We rewrite this as

\[ \frac{1}{rH(e,x|r)}\sum_{y\in \Gamma}G(e,y|r)G(y,x|r)G(x,e|r) \bigg( 1-\frac{G(x_1,y|r)G(e,x|r)}{G(x_1,x|r)G(e,y|r)}\bigg). \]

We decompose the sum over $\Gamma$ in the following way. Let $n=\hat {d}(e,x)$, so that the relative geodesic $[e,x]$ has length $n$. Denote by $e,x_1,\ldots,x_{n}$ successive points on this relative geodesic. In addition, for $0\leq k \leq n$, let $\Gamma _k$ be the set of $y\in \Gamma$ whose projection on $[e,x]$ which is closest to $x$ is exactly at $x_k$.

We use Lemma 2.5 several times. Let us first focus on the sum over $\Gamma _0$. If $y\in \Gamma _0$, then any relative geodesic from $y$ to $x$ passes within a bounded distance of $e$. Weak relative Ancona inequalities show that

\[ G(y,x|r)\lesssim G(y,e|r)G(e,x|r). \]

Similarly, any relative geodesic from $x_1$ to $y$ passes within a bounded distance of $e$, hence

\[ G(x_1,y|r)\lesssim G(x_1,e|r)G(e,y|r). \]

We also have

\[ G(e,x|r)\lesssim G(e,x_1|r)G(x_1,x|r), \]

so that

\begin{align*} &\bigg|\frac{1}{rH(e,x|r)}\sum_{y\in \Gamma_0}G(e,y|r)G(y,x|r)G(x,e|r) \bigg( 1-\frac{G(x_1,y|r)G(e,x|r)}{G(x_1,x|r)G(e,y|r)}\bigg)\bigg|\\ &\quad \lesssim \sum_{y\in \Gamma}H(e,y|r) (1+H(e,x_1|r)). \end{align*}

As $H(e,x_1|r)$ is uniformly bounded, we deduce from Lemma 4.5 that

\begin{align*} &\bigg|\frac{1}{rH(e,x|r)}\sum_{y\in \Gamma_0}G(e,y|r)G(y,x|r)G(x,e|r) \bigg( 1-\frac{G(x_1,y|r)G(e,x|r)}{G(x_1,x|r)G(e,y|r)}\bigg)\bigg |\\ &\quad \lesssim \frac{1}{\sqrt{R_\mu-r}}. \end{align*}

Let us focus on the sum over $\Gamma _1$ now. Let $\mathcal {H}_1$ be the union of parabolic subgroups containing $x_1$. Let $y\in \Gamma _1$ and denote by $\sigma$ its projection on $\mathcal {H}_1$. Then, any relative geodesic from $e$ to $y$ passes within a bounded distance of $\sigma$ and any relative geodesic from $y$ to $x$ passes first to a point within a bounded distance of $\sigma$, then to a point within bounded distance of $x_1$. We thus obtain

\[ G(e,y|r)\lesssim G(e,\sigma|r)G(\sigma,y|r) \]

and

\begin{align*} G(y,x|r)\lesssim G(y,\sigma|r)G(\sigma,x_1|r)G(x_1,x|r). \end{align*}

Similarly,

\[ \frac{G(x_1,y|r)G(e,x|r)}{G(x_1,x|r)G(e,y|r)}\lesssim \frac{G(x_1,\sigma|r)G(e,x_1|r)}{G(e,\sigma|r)}\lesssim 1. \]

Letting $\Gamma _1^{\sigma }$ be the set of $y$ whose projection on $\mathcal {H}_1$ is at $\sigma$, we obtain

\begin{align*} &\bigg|\frac{1}{rH(e,x|r)}\sum_{y\in \Gamma_1}G(e,y|r)G(y,x|r)G(x,e|r) \bigg( 1-\frac{G(x_1,y|r)G(e,x|r)}{G(x_1,x|r)G(e,y|r)}\bigg)\bigg|\\ &\quad\lesssim \sum_{\sigma\in \mathcal{H}_1}\sum_{y\in \Gamma_1^{\sigma}}\frac{G(e,\sigma|r)G(\sigma,x_1|r)}{G(e,x_1|r)}H(\sigma,y|r). \end{align*}

We bound the sum over $y\in \Gamma _1^{\sigma }$ by a sum over $y\in \Gamma$, so that

\begin{align*} &\bigg|\frac{1}{rH(e,x|r)}\sum_{y\in \Gamma_1}G(e,y|r)G(y,x|r)G(x,e|r) \bigg( 1-\frac{G(x_1,y|r)G(e,x|r)}{G(x_1,x|r)G(e,y|r)}\bigg)\bigg|\\ &\quad \lesssim \frac{1}{\sqrt{R_\mu-r}}\sum_{\sigma\in \mathcal{H}_1}\frac{G(e,\sigma|r)G(\sigma,x_1|r)}{G(e,x_1|r)}. \end{align*}

Suppose now that $k\geq 2$ and consider the sum over $\Gamma _k$. For any $y\in \Gamma _k$, relative geodesic from $x_1$ to $y$ and from $e$ to $x$ travel together for a time at least $k-1$. We deduce from strong relative Ancona inequalities that

\[ \bigg|1-\frac{G(x_1,y|r)G(e,x|r)}{G(x_1,x|r)G(e,y|r)}\bigg|\lesssim \rho^{k} \]

for some $0<\rho <1$. Letting $\mathcal {H}_k$ be the union of parabolic subgroups containing $x_{k-1}^{-1}x_{k}$, we also obtain

\begin{align*} &\bigg|\frac{1}{rH(e,x|r)}\sum_{y\in \Gamma_k}G(e,y|r)G(y,x|r)G(x,e|r) \bigg(1-\frac{G(x_1,y|r)G(e,x|r)}{G(x_1,x|r)G(e,y|r)}\bigg)\bigg|\\ &\quad \lesssim \rho^{k}\frac{1}{\sqrt{R_\mu-r}}\sum_{\sigma\in \mathcal{H}_k}\frac{G(x_{k-1},x_{k-1}\sigma|r)G(x_{k-1}\sigma,x_{k}|r)}{G(x_{k-1},x_{k}|r)}. \end{align*}

Putting everything together and letting $x_0=e$, we obtain

(12)\begin{align} &\bigg|\frac{1}{rH(e,x|r)}\sum_{y\in \Gamma}G(e,y|r)G(y,x|r)G(x,e|r) \bigg(1-\frac{G(x_1,y|r)G(e,x|r)}{G(x_1,x|r)G(e,y|r)}\bigg)\bigg|\nonumber\\ &\quad \lesssim \frac{1}{\sqrt{R_\mu-r}} \bigg(1+\sum_{k=0}^{n-1}\rho^{k}\sum_{\sigma\in \mathcal{H}_k}\frac{G(x_k,x_k\sigma|r)G(x_k\sigma,x_{k+1}|r)}{G(x_k,x_{k+1}|r)} \bigg). \end{align}

We now bound

\begin{align*} \sum_{k=0}^{n}\rho^{k}\sum_{\sigma\in \mathcal{H}_k}\frac{G(x_k,x_k\sigma|r)G(x_k\sigma,x_{k+1}|r)}{G(x_k,x_{k+1}|r)} \end{align*}

by an integrable function independently of $r$ and $n$. We first prove the following.

Lemma 4.9 There exists $\Lambda$ such that the following holds. Let $\mathcal {H}$ be a parabolic subgroup. For every $x$ in $\mathcal {H}$ and for any $1\leq r\leq R_\mu$, we have

\[ \sum_{y\in \mathcal{H}}G(e,y|r)G(y,x|r)\leq( \Lambda d(e,x)+\Lambda )G(e,x|r). \]

Proof. We write $G^{(1)}_{r}(e,x)= ({d}/{dt})_{|t=1} (G_{r}(e,x|t))$, where $G_r$ is the Green function associated with the first return kernel $p_{r}$ to $\mathcal {H}$. According to Lemma 2.7, it is enough to prove that

\[ G^{(1)}_{r}(e,x)\leq ( \Lambda d(e,x)+\Lambda )G(e,x|r). \]

As we are assuming that $\mu$ is non-spectrally degenerate along $\mathcal {H}$, there exists $\rho <1$ such that for any $x$, for any $n$,

\[ p_{r}^{(n)}(e,x)\leq p_{R_\mu}^{(n)}(e,x)\leq \rho^{n}, \]

where $p_{r}^{(n)}$ denotes the $n$th power of convolution of $p_{r}$. By definition,

\[ G^{(1)}_{r}(e,x)=\sum_{n\geq 0}np_{r}^{(n)}(e,x). \]

Note then that

\[ \sum_{n\geq \Lambda d(e,x)+\Lambda}np_{r}^{(n)}(e,x)\lesssim (\rho')^{\Lambda d(e,x)+\Lambda}. \]

As $r\geq 1$, for any $x$, $G(e,x|r)\geq p^{d(e,x)}$ for some $p<1$ and so

\[ G^{(1)}_{r}(e,x)\geq G(e,x|r)\geq p^{d(e,x)}. \]

If $\Lambda$ is large enough, we thus have

\[ \sum_{n\geq \Lambda d(e,x)+\Lambda}np_{r}^{(n)}(e,x)\leq \frac{1}{2}G^{(1)}_{r}(e,x), \]

so that

\[ G^{(1)}_{r}(e,x)\leq 2\sum_{n\leq \Lambda d(e,x)+\Lambda}np_{r}^{(n)}(e,x)\leq (2\Lambda d(e,x)+2\Lambda)G(e,x|r). \]

This concludes the proof.

Going back to the proof of Lemma 4.8, we obtain the upper bound

\[ \sum_{k=0}^{n}\rho^{k}\sum_{\sigma\in \mathcal{H}_k}\frac{G(x_k,x_k\sigma|r)G(x_k\sigma,x_{k+1}|r)}{G(x_k,x_{k+1}|r)}\leq \sum_{k=0}^{n}\rho^{k}(\Lambda d(x_{k},x_{k+1})+\Lambda). \]

We fix $N$ and define $\varphi _1^{(N)}$ by

(13)\begin{equation} \varphi_1^{(N)}(x)=1+\sum_{k=0}^{n-1}\rho^{k}(\Lambda d(x_{k},x_{k+1})+\Lambda) \end{equation}

for any word $x$ of length $n\leq N$. We extend $\varphi _1^{(N)}$ to a function on $\overline {\Sigma }_A$ declaring $\varphi _1^{(N)}$ to be constant on cylinders of length $N$. For fixed $x$, the sequence $\varphi _1^{(N)}(x)$ is non-decreasing. Let $\varphi _{1}(x)$ be its limit, possibly infinite if $x\in \partial \Sigma _A$. We now prove that $\varphi _1$ is integrable with respect to $m$. This is based on the following.

Letting $E$ be a set, a transition kernel $p$ is a function $p:E\times E\rightarrow [0,+\infty )$. We fix a base point $x_0\in E$. We say that $p$ is finite if its total mass is finite, that is,

\[ \sum_{x\in E}p(x_0,x)<+\infty. \]

If the total mass is one, then $p$ defines a Markov chain $Z_n$ on $E$. Otherwise, $p$ still defines a chain $Z_n$ with transition given by $p$. We let $z_n$ be the increments of this chain. Whenever $E$ is endowed with a distance $d$, we say that $p$ is $C$-quasi-invariant if there exists $C$ such that for any $k$,

\[ d(Z_k,Z_{k+1})\leq C d(e,z_{k+1}). \]

Lemma 4.10 Let $p$ be a finite $C$-quasi-invariant transition kernel on a countable metric space $(E,d)$. Let $x_0$ be a fixed point in $E$. Assume that $p$ has exponential moments in the sense that

\[ \sum_{x\in E}p(x_0,x){e}^{\alpha d(x_0,x)} \]

for some positive $\alpha$. Then, for any $\beta >0$, there exists $\lambda >0$ and $C_{\lambda }$ such that for any $x\in E$,

\[ \sum_{n\leq d(e,x)/\lambda}p^{(n)}(x_0,x)\leq C_{\lambda}{e}^{-\beta d(e,x)}, \]

where $p^{(n)}$ denotes the $n$th power of convolution of $p$.

Proof. The proof is contained in the proof of [BHM11, Lemma 3.6], although the statement and the assumptions there are different, so we rewrite it for convenience. To simplify the notation, we assume that the total mass of $p$ is one, so that $p$ defines a Markov chain $Z_n$. The general proof is the same. By assumption, we have

\[ \mathbb{E} ({e}^{\alpha d(x_0,Z_1)})=E<+\infty. \]

For any $\lambda$, Markov inequality shows that

\[ \mathbb{P}\bigg(\sup_{1\leq k\leq n}d(e,Z_k)\geq \lambda n\bigg)\leq {e}^{-({\alpha}/{C}) \lambda n}\mathbb{E} ({e}^{({\alpha}/{C}) \sup_{1\leq k\leq n}d(e,Z_k)}). \]

As $p$ is $C$-quasi-invariant, we have for any $k\leq n$, letting $Z_0=x_0$,

\[ d(x_0,Z_k)\leq \sum_{0\leq j\leq n-1}d(Z_j,Z_{j+1})\leq C \sum_{1\leq j\leq n}d(x_0,z_j). \]

As the $z_j$ are independent and follow the same law as $Z_1$, we obtain

\[ \mathbb{P}\bigg(\sup_{1\leq k\leq n}d(e,Z_k)\geq \lambda n\bigg)\leq {e}^{-({\alpha}/{C}) \lambda n}E^{n}\leq {e}^{n(-({\alpha}/{C}) \lambda +\log E)}. \]

We choose $\lambda$ large enough so that $- ({\alpha }/{C}) \lambda +\log E\leq -2\beta$. Then,

\[ \sum_{n\leq d(e,x)/\lambda}p^{(n)}(x_0,x)\leq \frac{d(e,x)}{\lambda}{e}^{-2\beta d(e,x)}\lesssim {e}^{-\beta d(e,x)}. \]

This concludes the proof.

We apply this in our situation. Let $\mathcal {H}$ be a parabolic subgroup. For any $\eta >0$, we let $p_{\eta,R_\mu }$ be the first return kernel associated with $R_\mu \mu$ to the $\eta$-neighborhood $\mathcal {N}_{\eta }(\mathcal {H})$ of $\mathcal {H}$. Then, [DG21, Lemma 4.6] shows that if $\eta$ is large enough, then $p_{\eta,R_\mu }$ has exponential moments. As it is defined as the first return associated with $R_\mu \mu$, it is $C$-quasi-invariant for the induced metric on $\mathcal {N}_{\eta }(\mathcal {H})$ (it is actually invariant for this distance). Thus, for any $\beta >0$, there exists $\lambda$ and $C_\lambda$ such that

\[ \sum_{n\leq d(e,x)/\lambda}p_{\eta,R_\mu}^{(n)}(e,x)\leq C_{\lambda}{e}^{-\beta d(e,x)}. \]

The Green function associated with $p_{\eta,R_\mu }$ coincides with the restriction of the Green function associated with $R_\mu \mu$ on $\mathcal {N}_{\eta }(\mathcal {H})$, see [Dus22, Lemma 3.4] for a proof. As there exists $q<1$ such that $G(e,x|R_\mu )\geq q^{d(e,x)}$, we can choose $\lambda$ so that

\[ \sum_{n\leq d(e,x)/\lambda}p_{\eta,R_\mu}^{(n)}(e,x)\leq \frac{1}{2}G(e,x|R_\mu) \]

and so

\[ G(e,x|R_\mu)\leq 2\sum_{n\geq d(e,x)/\lambda}p_{\eta,R_\mu}^{(n)}(e,x)\leq \frac{2\lambda}{d(e,x)}\sum_{n\geq d(e,x)}np_{\eta,R_\mu}^{(n)}(e,x). \]

According to Lemma 2.7,

\[ G(e,x|R_\mu)\leq \frac{2\lambda}{d(e,x)}\sum_{y\in \mathcal{N}_{\eta}(\mathcal{H})}G(e,y|R_\mu)G(y,x|R_\mu). \]

Finally, any point in $\mathcal {N}_\eta (\mathcal {H})$ is within $\eta$ of a point in $\mathcal {H}$, hence for any $x\in \mathcal {H}$,

(14)\begin{equation} d(e,x) G(e,x|R_\mu)\lesssim \sum_{y\in \mathcal{H}}G(e,y|R_\mu)G(y,x|R_\mu), \end{equation}

because $\eta$ is fixed.

Recall that we want to prove that $\varphi _1$ is integrable with respect to $m$. As $\varphi _1^{(n)}$ is non-decreasing, it is enough to show that there exists a uniform $C\geq 0$ such that for any $n$,

\begin{align*} \int \varphi_1^{(n)}\,dm\leq C. \end{align*}

By definition, $\varphi _1^{(n)}$ is constant on cylinders of the form $[x_1,\ldots,x_n]$. According to (9), we just need to show that for every $n$,

(15)\begin{equation} \sum_{x\in \hat{S}^{N}}H(e,x|R_\mu)\sum_{k=0}^{n-1}\rho^{k}d(x_k,x_{k+1}) \end{equation}

is uniformly bounded.

We decompose $x\in \hat {S}^{n}$ as $x=x_1\dots x_n$. For any $y\in \hat {S}^{k}$, denote by $X^{y}_1$ the set of symbols $\sigma$ which can follow $y$ in the automaton $\mathcal {G}$. More generally, denote by $X^{y}_j$ the set of words of length $j$ which can follow $y$. For fixed $k$ writing $\sigma _{k+1}=x_{k}^{-1}x_{k+1}$ and $y=x_{k+1}^{-1}x$, we have, using weak relative Ancona inequalities,

\begin{align*} &\sum_{x\in \hat{S}^{n}}H(e,x|R_\mu) d(x_k,x_{k+1})\\ &\quad\!\lesssim\! \sum_{x_k\in \hat{S}^{k}}\sum_{\sigma_{k+1} \in X^{x_k}_1}\sum_{y\in X^{x_{k+1}}_{n-k-1}}H(e,x_k|R_\mu)H(e,y|R_\mu) d(e,\sigma_{k+1})G(e,\sigma_{k+1}|R_\mu)G(\sigma_{k+1},e|R_\mu)\\ &\quad \!\lesssim\! \sum_{x_k\in \hat{S}^{k}}\sum_{\sigma_{k+1} \in X^{x_k}_1}\sum_{y\in X^{x_{k+1}}_{n-k-1}} H(e,x_k|R_\mu)H(e,y|R_\mu) \!\sum_{\sigma\in \mathcal{H}_k}G(e,\sigma|R_\mu)G(\sigma,\sigma_{k+1}|R_\mu)G(\sigma_{k+1},e|R_\mu). \end{align*}

Lemma 2.9 shows that

\[ \sum_{y\in X^{x_{k+1}}_{n-k-1}}H(e,y|R_\mu)\lesssim 1. \]

As $\mu$ is not spectrally degenerate,

\[ \sum_{\sigma\in \mathcal{H}_k}G(e,\sigma|R_\mu)G(\sigma,\sigma_{k+1}|R_\mu)G(\sigma_{k+1},e|R_\mu)\lesssim 1. \]

Using again Lemma 2.9,

\[ \sum_{x_k\in \hat{S}^{k}}H(e,x_k|R_\mu)\lesssim 1. \]

Finally, we find that (15) is bounded by $C\sum _{k=0}^{n-1}\rho ^{k}$ for some $C$. As $\rho <1$, this last sum is uniformly bounded.

To conclude, we give a similar bound for the remaining term in (11), with an integrable function $\varphi _2$. We set $\varphi =\varphi _1+\varphi _2$. This concludes the proof.

The function $\varphi$ is constructed as the non-decreasing limit of functions $\varphi ^{(n)}$ which are uniformly integrable and satisfy that for any word $x$ of length $n$,

(16)\begin{equation} \bigg|\frac{d}{dr}\varphi_r(x)\bigg|\leq \varphi^{(n)}(x) \frac{1}{\sqrt{R_\mu-r}}. \end{equation}

Let us note that we proved something a bit stronger than $\int \varphi ^{(n)}\,dm\lesssim 1$. Indeed, we proved there exists $C\geq 0$ such that for every $n$,

(17)\begin{equation} \sum_{x\in \hat{S}^{n}}H(e,x|R_\mu)\varphi^{(n)}(x)\leq C. \end{equation}

We both use (16) and (17) in the following. However, to simplify the notation, we only stated Lemma 4.8 using $\varphi$ and $m$.

We also prove the following result. We do not use in full generality, but only for $x=\emptyset$.

Proposition 4.11 For every $x\in \Sigma _A$, there exists $C_x$ such that for every $r,r'\leq R_{\mu }$ and for every bounded function $f$,

\[ \big|(\mathcal{L}_rf)(x)-(\mathcal{L}_{r'}f)(x)\big|\leq C_x\|f\|_{\infty}\sqrt{|r-r'|}. \]

Proof. Fix $x\in \Sigma _A$ and let $n=\hat {d}(e,x)$. Let $X_x^{1}$ be the set of symbols which can precede $x$ in the automaton $\mathcal {G}$. Then,

\[ (\mathcal{L}_rf)(x)-(\mathcal{L}_{r'}f)(x)=\sum_{\sigma\in X_x^{1}} ({e}^{\varphi_r(\sigma x)}-{e}^{\varphi_{r'}(\sigma x)})f(\sigma x). \]

Differentiating in $r$ the quantity

\[ \sum_{\sigma\in X_x^{1}}{e}^{\varphi_r(\sigma x)}f(\sigma x), \]

we obtain

\[ \sum_{\sigma\in X_x^{1}}\bigg(\frac{d}{dr}\varphi_r(\sigma x)\bigg){e}^{\varphi_r(\sigma x)}f(\sigma x). \]

Using Lemma 4.8, this is bounded by

\[ \|f\|_{\infty}\frac{1}{\sqrt{R_\mu-r}}\sum_{\sigma\in X_x^{1}}\varphi(\sigma x) {e}^{\varphi_r(\sigma x)}. \]

We deduce from weak relative Ancona inequalities that this is bounded by

\[ \|f\|_{\infty}\frac{1}{\sqrt{R_\mu-r}}\sum_{\sigma\in X_x^{1}}\varphi(\sigma x) H(e,\sigma|r). \]

As $\sum _{\sigma \in X_x^{1}}\varphi (\sigma x) H(e,\sigma |r)$ only depends on $x$, it is enough to show that this last sum is bounded independently of $r$. This is done exactly like showing that the sum (15) is bounded.

We want to apply Theorem 3.6, so we now prove that the assumptions of this theorem are satisfied, for $\tau (r)=\sqrt {R_\mu -r}$. Recall that $m=\sum _j m_j$.

Proposition 4.12 There exist constants $0<\sigma <1$ and $C\geq 0$ such that for every $1 \leq r\leq R_\mu$, for every $n$, for every function $f\in H_{\rho,\beta }$,

\[ \|\mathcal{L}_r^{n} f\|_{\rho,\beta}\leq C\sigma^{n}\|f\|_{\rho,\beta}+C\int |f| dm \]

and

\[ \int \big| (\mathcal{L}_r-\mathcal{L}_{R_\mu})f\big|dm\leq C\|f\|_{\rho,\beta}\sqrt{R_\mu-r}. \]

The proof of this proposition is postponed to the end of the section. We first state the following corollary which is deduced from Theorem 3.6.

Corollary 4.13 For every $r$ close enough of $R_\mu$, there exist numbers $\tilde {P}_j(r)$, eigenfunctions $\tilde {h}_{j,r}^{(i)}$, and eigenmeasures $\tilde {\nu }_{j,r}^{(i)}$ of $\mathcal {L}_r$ associated with the eigenvalue ${e}^{\tilde {P}_j(r)}$ such that for every $g\in H_{\rho,\beta }$,

\[ \bigg\|\mathcal{L}_{r}^{n}g-\sum_{j=1}^{k}{e}^{n(\tilde{P}_j(r))}\sum_{i=1}^{p_j}\tilde{h}_{j,r}^{(i)}\int g \,d\tilde{\nu}_{j,r}^{((i-n) \text{ mod } p_j)}\bigg\|_{\rho,\beta}\leq C\theta^{n}\|g\|_{\rho,\beta}, \]

where $C\geq 0$ and $0<\theta <1$. The functions $\tilde {h}_{j}^{(i)}$ and the measures $\tilde {\nu }_j^{(i)}$ have the same support as the functions $h_j^{(i)}$ and the measures $\nu _j^{(i)}$, respectively. Moreover, $\big \|\tilde {h}_{j,r}^{(i)}\big \|_{\rho,\beta }$ is uniformly bounded. Finally,

\[ \int \big|\tilde{h}_{j,r}^{(i)}-h_j^{(i)}\big|\,dm\underset{r\to R_\mu}{\longrightarrow}0 \]

and $\tilde {\nu }_{j,r}^{(i)}$ weakly converges to $\nu _j^{(i)}$ as $r$ tends to $R_\mu$.

To conclude, note that Proposition 4.11 yields

(18)\begin{equation} |\mathcal{L}_rf(\emptyset)-\mathcal{L}_{r'}f(\emptyset)|\lesssim \|f\|_{\rho,\beta}\sqrt{|r'-r|}. \end{equation}

Consequently,

(19)\begin{equation} |\tilde{h}_{j,r}^{(i)}(\emptyset)-h_j^{(i)}(\emptyset)|\underset{r\to R_\mu}{\longrightarrow}0. \end{equation}

Indeed, this last estimate (18) shows that we can replace the norm $|\cdot |_w$ when applying Theorem 3.6 with the norm $|\cdot |'_w$ defined by

\[ |f|'_w=|f(\emptyset)|+\int |f|\,dm. \]

Although we use (19) in the following, we preferred using the norm $|\cdot |_w$ in the statements and in the proofs for convenience.

We now prove Proposition 4.12. We use repeatedly strong relative Ancona inequalities to obtain stronger and stronger continuity statements. We first give an upper bound for $\|\mathcal {L}_r^{n} f\|_{\infty }$ and then one for $D_{\rho,\beta }(\mathcal {L}_r^{n} f)$, that actually use the first upper bound. This will conclude the proof of the first statement in the proposition. The proof of the second statement is similar but a bit more technically involved.

Proof. Let $f\in H_{\rho,\beta }$ and let $x\in \overline {\Sigma }_A$. Denote by $S_n\varphi _r$ the $n$th Birkhoff sum of $\varphi _r$ and let $X_x^{n}$ the set of words of length $n$ which can precede $x$ in the automaton $\mathcal {G}$. Then,

\[ \mathcal{L}_r^{n} f(x)=\sum_{\gamma\in X_x^{n}}{e}^{S_n\varphi_r(\gamma x)}f(\gamma x). \]

Let $f^{(n)}$ be the function which is constant on cylinders of length $n$ and which is equal to $f$ elsewhere. In particular,

\[ f^{(n)}(\gamma x)=f(\gamma) \]

for $x\in \overline {\Sigma }_A$ and $\gamma \in X_x^{n}$. As $f$ is $\rho$-locally Hölder,

\[ |f^{(n)}(\gamma x)-f(\gamma x)|\leq \rho^{n} D_{\rho,\beta}(f). \]

Hence,

\[ \big|\mathcal{L}_r^{n} f(x)\big|\leq \rho^{n}D_{\rho,\beta}(f)\sum_{\gamma\in X_x^{n}}{e}^{S_n\varphi_r(\gamma x)}+\sum_{\gamma\in X_x^{n}}{e}^{S_n\varphi_r(\gamma x)}|f^{(n)}(\gamma x)|. \]

To simplify, we identify an element $\gamma \in X_x^{1}$ with the corresponding element in $\hat {S}^{n}\subset \Gamma$. Note that ${e}^{S_n\varphi _r(\gamma x)}={H(e,\gamma x|r)}/{H(\gamma,\gamma x|r)}$. Using weak relative Ancona inequalities, we obtain

\[ \big|\mathcal{L}_r^{n} f(x)\big|\lesssim \rho^{n}D_{\rho,\beta}(f)\sum_{\gamma \in \hat{S}^{n}}H(e,\gamma|R_\mu) +\sum_{\gamma \in \hat{S}^{n}}H(e,\gamma|R_\mu) |f^{(n)}(\gamma x)|. \]

For every $\gamma \in \Gamma$, we can use the automaton $\mathcal {G}$ and choose a relative geodesic from $e$ to $\gamma$ whose increments we denote by $x_1,\ldots,x_n$. Let $[\gamma ]$ be the corresponding cylinder $[x_1,\ldots,x_n]$. Let $\hat {S}^{n}_{\mathrm {max}}$ be the set of $\gamma \in \hat {S}^{n}$ such that the cylinder $[\gamma ]$ is in a maximal component. As $f^{(n)}$ is constant on cylinders of length $n$, (10) shows that

\[ \sum_{\gamma \in \hat{S}^{n}_{\mathrm{max}}}H(e,\gamma|R_\mu) |f^{(n)}(\gamma x)|\lesssim \int |f^{(n)}|\,dm. \]

In addition, by the definition of maximal components, there exists $\rho '< e^{P(R_\mu )}=1$ such that

\[ \sum_{\gamma \in \hat{S}^{n}\setminus \hat{S}^{n}_{\mathrm{max}}}H(e,\gamma|R_\mu) |f^{(n)}(\gamma x)|\lesssim (\rho')^{n}\|f\|_\infty. \]

Using that $f$ is $\rho$-locally Hölder, we obtain

\[ \int |f^{(n)}|\,dm\lesssim \rho^{n} D_{\rho,\beta}(f)+\int |f|\,dm. \]

Lemma 2.9 shows that the sum $\sum _{\gamma \in \hat {S}^{n}}H(e,\gamma |R_\mu )$ is bounded independently of $n$. We thus obtain

(20)\begin{equation} \big|\mathcal{L}_r^{n} f(x)\big|\lesssim 2\rho^{n} D_{\rho,\beta}(f)+(\rho')^{n}\|f\|_\infty + \int |f|\,dm\lesssim \sigma^{n} \|f\|_{\rho,\beta}+\int |f|\,dm, \end{equation}

where $\sigma =\max (\rho,\rho ')$. We can thus control $\|\mathcal {L}_r^{n} f\|_\infty$.

We now focus on $D_{\rho,\beta }(\mathcal {L}_rf)$. Let $x,x'\in \overline {\Sigma }_A$ and let $\rho ^{m}=d_{\rho }(x,x')$, $m\geq 1$. We have

\begin{align*} \mathcal{L}_r^{n}f(x)-\mathcal{L}_r^{n}f(x')&= \sum_{\gamma\in X_x^{n}} ({e}^{S_n\varphi_r(\gamma x)}-{e}^{S_n\varphi_r(\gamma x')})f(\gamma x)\\ &\quad +\sum_{\gamma\in X_x^{n}}{e}^{S_n\varphi_r(\gamma x')}(f(\gamma x)-f(\gamma x')). \end{align*}

On the one hand, using that $f$ is $\rho$-locally Hölder and using weak relative Ancona inequalities to bound ${e}^{S_n\varphi _r(\gamma x)}$ by $H(e,\gamma |r)$ as previously, we obtain

\[ \sum_{\gamma\in X_x^{n}}{e}^{S_n\varphi_r(\gamma x')}|(f(\gamma x)-f(\gamma x'))|\lesssim \sum_{\gamma\in \hat{S}^{n}}H(e,\gamma|R_\mu) \rho^{n+m}D_{\rho,\beta}(f). \]

It follows from Lemma 2.9 that the sum $\sum _{\gamma \in \hat {S}^{n}}H(e,\gamma |R_\mu )$ is bounded and because $\rho ^{m}=d_\rho (x,x')$, we have

\[ \sum_{\gamma\in X_x^{n}}{e}^{S_n\varphi_r(\gamma x')}|(f(\gamma x)-f(\gamma x'))|\lesssim \rho^{n}\|f\|_{\rho,\beta}d_\rho(x,x'). \]

On the other hand,

\begin{align*} &\sum_{\gamma\in X_x^{n}} ({e}^{S_n\varphi_r(\gamma x)}-{e}^{S_n\varphi_r(\gamma x')})f(\gamma x)\\ &\quad =\sum_{\gamma\in X_x^{n}}{e}^{S_n\varphi_r(\gamma x)} (1-{e}^{S_n\varphi_r(\gamma x')-S_n\varphi_r(\gamma x)})f(\gamma x). \end{align*}

By definition,

\[ (1-{e}^{S_n\varphi_r(\gamma x')-S_n\varphi_r(\gamma x)})=\bigg(1-\frac{H(e,\gamma x|r)H(\gamma,\gamma x'|r)}{H(\gamma,\gamma x|r)H(e,\gamma x'|r)}\bigg). \]

As relative geodesics $[e,x]$ and $[e,x']$ fellow travel for a time at least $m$ and because $\gamma$ both precedes $x$ and $x'$ in the automaton $\mathcal {G}$, relative geodesics $[e,\gamma x]$ and $[\gamma,\gamma x']$ also fellow travel for a time at least $m$. Strong relative Ancona inequalities thus yield

\[ \big|1-{e}^{S_n\varphi_r(\gamma x')-S_n\varphi_r(\gamma x)}\big|\lesssim \rho^{m} \]

and so

\[ \bigg|\sum_{\gamma\in X_x^{n}} ({e}^{S_n\varphi_r(\gamma x)}-{e}^{S_n\varphi_r(\gamma x')})f(\gamma x)\bigg|\lesssim \rho^{m}\sum_{\gamma\in X_x^{n}}{e}^{S_n\varphi_r(\gamma x)}|f(\gamma x)|. \]

We bound $\sum _{\gamma \in X_x^{n}}{e}^{S_n\varphi _r(\gamma x)}|f(\gamma x)|$ by $\sigma ^{n}\|f\|_{\rho,\beta }+\int |f|\,dm$ as previously to obtain

(21)\begin{equation} \big|\mathcal{L}_rf(x)-\mathcal{L}_rf(x')\big|\lesssim \bigg(\sigma^{n}\|f\|_{\rho,\beta}+\int |f|\,dm\bigg)\,d_\rho(x,x'). \end{equation}

We deduce from (20) and (21) that

\[ \big\|\mathcal{L}_r^{n}f\big\|_{\rho,\beta}\lesssim \sigma^{n} \|f\|_{\rho,\beta}+\int |f|\,dm, \]

which concludes the first part of the proposition.

We now prove that

(22)\begin{equation} \int \big| (\mathcal{L}_r-\mathcal{L}_{R_\mu})f\big|\,dm\leq C\|f\|_{\rho,\beta}\sqrt{R_\mu-r}. \end{equation}

The function $f$ is $\rho$-locally Hölder. As the operator $\mathcal {L}_r-\mathcal {L}_{R_\mu }$ is bounded on $(H_{\rho,\beta },\|\cdot \|_{\rho,\beta })$, for every word $x=x_1\dots x_n$ of length $n$ and for every $y\in [x_1,\ldots,x_n]$,

\[ \big| (\mathcal{L}_r-\mathcal{L}_{R_\mu})f(y)- (\mathcal{L}_r-\mathcal{L}_{R_\mu})f(x)\big|\lesssim \rho^{n}\|f\|_{\rho,\beta}. \]

Hence,

\[ \big| (\mathcal{L}_r-\mathcal{L}_{R_\mu})f(y)\big|\lesssim \rho^{n}\|f\|_{\rho,\beta}+\big| (\mathcal{L}_r-\mathcal{L}_{R_\mu})f(x)\big|. \]

Fixing $r$, we choose $n$ large enough so that $\rho ^{n}\leq \sqrt {R_\mu -r}$. Let $\tilde {f}_r$ be the function which is constant on cylinders of length $n$ and which is equal to $(\mathcal {L}_r-\mathcal {L}_{R_\mu })f(x)$ elsewhere. To prove (22), we just need to show that

\[ \int \big|\tilde{f}_r\big|\,dm\lesssim \|f\|_{\rho,\beta}\sqrt{R_\mu-r}. \]

For every $x$ of length $n$ and for every $y$ in $[x_1,\ldots,x_n]$, we have

\[ \tilde{f}_r(y)=\sum_{\sigma\in X_x^{1}} ({e}^{\varphi_r(\sigma x)}-{e}^{\varphi_{R_\mu}(\sigma x)})f(\sigma x). \]

Differentiating this, we obtain

\[ \sum_{\sigma\in X_x^{1}}\bigg(\frac{d}{dr}\varphi_r(\sigma x)\bigg){e}^{\varphi_r(\sigma x)}f(\sigma x). \]

Using (16), we bound the absolute value of this term by

\[ \frac{1}{\sqrt{R_\mu-r}}\|f\|_{\infty}\sum_{\sigma\in X_x^{1}}\varphi^{(n+1)}(\sigma x){e}^{\varphi_r(\sigma x)}. \]

Inverting the sum and the derivative is legitimate because weak relative Ancona inequalities show that ${e}^{\varphi _r(\sigma x)}\lesssim H(e,\sigma )$. As in the proof of Lemma 4.8, we show that the sum

\[ \sum_{\sigma\in X_x^{1}}\varphi^{(n+1)}(\sigma x){e}^{\varphi_r(\sigma x)} \]

is finite. Therefore,

\[ \bigg|\frac{d}{dr}\tilde{f}_r(y)\bigg|\lesssim \frac{1}{\sqrt{R_\mu-r}}\|f\|_{\infty} \sum_{\sigma\in X_x^{1}}H(e,\sigma|R_\mu)\varphi^{(n+1)}(\sigma x). \]

Integrating this, we obtain

\[ \int \big|\tilde{f}_r\big|\,dm\lesssim \|f\|_{\rho,\beta}\sqrt{R_\mu-r}\int \sum_{\sigma\in X_x^{1}}H(e,\sigma|R_\mu)\varphi^{(n+1)}(\sigma x)\,dm(x). \]

As $x\mapsto \varphi ^{(n+1)}(\sigma x)$ is constant on cylinders of length $n$, (10) shows that

\begin{align*} \int \big|\tilde{f}_r\big|\,dm&\lesssim \|f\|_{\rho,\beta}\sqrt{R_\mu-r}\sum_{x\in \hat{S}^{n}}\sum_{\sigma\in X_x^{1}}H(e,\sigma|R_\mu)H(e,x|R_\mu)\varphi^{(n+1)}(\sigma x)\\ &\lesssim \|f\|_{\rho,\beta}\sqrt{R_\mu-r}\sum_{y\in \hat{S}^{n+1}}H(e,y|R_\mu)\varphi^{(n+1)}(y). \end{align*}

According to (17), we thus have

\[ \int \big|\tilde{f}_r\big|\,dm\lesssim \|f\|_{\rho,\beta}\sqrt{R_\mu-r}, \]

which concludes the proof.

5. Evaluating the pressure

Our goal in this section is to estimate the numbers $\tilde {P}_j(r)$ given by Corollary 4.13 and to compare them with the maximal pressure $P(r)$. This allows us to obtain a precise estimate of $I^{(1)}(r)$.

According to Corollary 4.13, if $R_{\mu }-r$ is small enough, then

\[ \mathcal{L}_{r}^{n}1_{E_*}(\emptyset)=\sum_{j=1}^{k}{e}^{n\tilde{P}_j(\varphi_r)}\sum_{i=1}^{p_j}\tilde{h}_j^{(i)}(\emptyset)\int 1_{E_*} \,d\tilde{\nu}_j^{((i-n) \text{ mod } p_j)}+O (\theta^{n}). \]

Here, $0<\theta <1$ and $k$ is the number of maximal components for the function $\varphi _{R_{\mu }}$. Denote by $p$ the least common multiple of the periods of these components, so that if $n\geq 0$ and $0\leq q < p$, then $d\tilde {\nu }_j^{((i-np+q) \text { mod } p_j)}$ only depends on $q$. In particular, we can write

\[ \mathcal{L}_{r}^{np+q}1_{E_*}(\emptyset)=\sum_{j=1}^{k} {e}^{(np+q)\tilde{P}_j(\varphi_r)}\xi_{q,j}(r)+O (\theta^{np+q}), \]

where $\xi _{q,j}$ is a non-negative function of $r$ defined on some fixed neighborhood of $R_{\mu }$. Note that $\xi _{q,j}(r)$ only depends on $\tilde {h}_{j,r}(\emptyset )$ and on $\int 1_{E_*}\,d\tilde {\nu }_{j,r}^{(i)}$ and that it is continuous in $r$ according to Corollary 4.13 and (19).

If $r< R_{\mu }$, then $\sum _{\gamma }H(e,\gamma |r)$ is finite, so the numbers $\tilde {P}_j(\varphi _r)$ are negative. Summing over $n$ and $q\in \{0,\ldots,p-1\}$, we obtain

(23)\begin{equation} \sum_{\gamma \in \Gamma}H(e,\gamma|r)=H(e,e|r)\sum_{n,q}\mathcal{L}_{r}^{np+q}1_{E_*}(\emptyset)=\sum_{j=1}^{k}\frac{\xi_j(r)}{|\tilde{P}_j(\varphi_r)|}+O(1), r\to R_{\mu}, \end{equation}

for some non-negative functions $\xi _j$, which are continuous in $r$ on some neighborhood of $R_{\mu }$.

We have the following result, which shows that the pressure is asymptotically independent of the maximal components. Its proof is postponed to the following subsections.

Proposition 5.1 For every $j\in \{1,\ldots,k\}$, $ {\tilde {P}_j(\varphi _r)}/{P(r)}$ tends to one when $r$ tends to $R_{\mu }$, where $P(r)$ is the maximal pressure of the function $\varphi _r$.

Combining Proposition 5.1 and (23), we obtain that

(24)\begin{equation} I^{(1)}(r)=\sum_{\gamma \in \Gamma}H(e,\gamma|r)=\frac{\xi(r)}{|P(r)|}+O(1), r\to R_{\mu}, \end{equation}

for some non-negative function $\xi$, which is continuous in $r$ on some neighborhood of $R_{\mu }$. Recall that $I^{(1)}(r)\asymp \sqrt {R_\mu -r}$ and $|P(r)|\asymp \sqrt {R_\mu -r}$. Therefore, $\xi (R_{\mu })>0$, so that $\xi (r)$ is bounded away from zero on a neighborhood of $R_{\mu }$.

The remainder of this section is devoted to proving Proposition 5.1. An analogous result is proved in [Gou14] for hyperbolic groups. This is done by showing the following.

Lemma 5.2 For $r\in [1,R_{\mu }]$, $\int \varphi _rdm_j$ does not depend on $j$, where $m_j$ is the measure in Proposition 3.7.

This lemma, in turn, is proved in several steps.

Step 1. Fix $c$ and define $U(c)\subset \partial \hat {\Gamma }$ as the set of points $\xi \in \partial \hat {\Gamma }$ such that if $x$ is an infinite sequence in $\partial \Sigma _A^{*}$ defining $\xi$ (that is, denoting $\gamma _n=x_1\dots x_n$, $e,\gamma _1,\ldots,\gamma _n,\ldots$ is a relative geodesic ray that converges to $\xi$ in $\partial \hat {\Gamma }$), then $\log H(e,\gamma _n|r)/\hat {d}(e,\gamma _n)$ converges to $c$. Then, the definition of $U(c)$ does not depend on the choice of the sequence $x_n$. Moreover, $U(c)$ is $\Gamma$-invariant, that is, for any $\gamma \in \Gamma$, $\gamma \cdot U(c)=U(c)$.

Step 2. Define the sequence of measures $\lambda _n=\sum _{\gamma \in \hat {S}_n}H(e,\gamma |R_{\mu })\delta _{\gamma }$ on $\Gamma$. Define $\tilde {\lambda }_N$ as

(25)\begin{equation} \tilde{\lambda}_N:=\left.\sum_{n=1}^{N}\lambda_n\right/\bigg(\sum_{n=1}^{N}\lambda_n(\Gamma)\bigg). \end{equation}

Then, up to a subsequence, $\tilde {\lambda }_N$ converges weakly to a probability measure on $\partial \hat {\Gamma }$, which we denote by $\lambda _{R_{\mu }}$.

Step 3. The limit measure $\lambda _{R_{\mu }}$ is ergodic for the action of $\Gamma$ on $\partial \hat {\Gamma }$.

Step 4. Let $c_j=\int \varphi _r\,dm_j$. Then, $\lambda _{R_{\mu }}(U(c_j))>0$. As $\lambda _{R_{\mu }}$ is ergodic and $U(c_i)$ is $\Gamma$-invariant, we thus have $\lambda _{R_{\mu }}(U(c_j))=1$ for all $j$. In particular, all the sets $U(c_j)$ intersect, which proves that $c_j$ is independent of $j$.

5.1 Proof of step 1

We prove here the following lemma.

Lemma 5.3 The sets $U(c)$ as previously are well defined and are $\Gamma$-invariant.

Step 1 is stated in [Gou14, § 3.5] using the Gromov boundary $\partial \Gamma$ of $\Gamma$ instead of $\partial \hat {\Gamma }$, because groups are hyperbolic in there and not relatively hyperbolic. It is a consequence of the fact that geodesics converging to $\xi \in \partial \Gamma$ in a hyperbolic group stay within a bounded distance of each other. This property still holds in our situation as we show in the proof of Lemma 5.3 that we now present.

Proof. First, let us show that the definition of $U(c)$ does not depend on the choice of the sequence $x$ defining $\xi$. Assume that $x$ and $x'$ are two sequences such that, setting $\gamma _n=x_1\dots x_n$ and $\gamma '_n=x_1'\dots x_n'$, both sequences $e,\gamma _1,\ldots,\gamma _n,\ldots$ and $e,\gamma _1',\ldots,\gamma _n',\ldots$ are relative geodesics converging to $\xi$. Then, according to Lemma 2.4, for every $n$, there exists $k_n$ such that $d(\gamma _n,\gamma _{k_n}')\leq C$, so that $H(e,\gamma _n|r)\asymp H(e,\gamma _{k_n}'|r)$. We thus have $|\log H(e,\gamma _n|r)-\log H(e,\gamma _{k_n}'|r)|\leq C'$. Moreover, because $d(\gamma _n,\gamma _{k_n}')\leq C$, $\hat {d}(\gamma _n,\gamma _{k_n}')\leq C$, so that $|n-k_n|\leq C''$ and, thus, $|\hat {d}(e,\gamma _n')-\hat {d}(e,\gamma _{k_n}')|\leq C''$. This proves that $\log H(e,\gamma _n|r)/\hat {d}(e,\gamma _n)$ and $\log H(e,\gamma _n'|r)/\hat {d}(e,\gamma _n')$ have the same limit.

Let $\gamma \in \Gamma$ and let $\xi \in U(c)$. We want to prove that $\gamma \cdot \xi \in U(c)$. Consider a sequence $x$ defining $\xi$ and a sequence $x'$ defining $\gamma \cdot \xi$, that is, setting $\gamma _n=x_1\dots x_n$ and $\gamma '_n=x_1'\dots x_n'$, the sequence $e,\gamma _1,\ldots,\gamma _n,\ldots$ is a relative geodesic converging to $\xi$ and the sequence $e,\gamma _1',\ldots,\gamma _n',\ldots$ is a relative geodesic converging to $\gamma \cdot \xi$. Then, $\gamma,\gamma \gamma _1,\ldots,\gamma \gamma _n,\ldots$ is a relative geodesic starting at $\gamma$ and converging to $\gamma \cdot \xi$. According to Lemma 2.4, for every $n$, there exists $k_n$ such that $d(\gamma \gamma _n,\gamma _{k_n}')\leq C$. This time, the bound $C$ depends on $\gamma$, but not on the sequences $\gamma _n$ and $\gamma '_n$. This shows that $H(\gamma ^{-1},\gamma _n|r)=H(e,\gamma \gamma _n|r)\asymp H(e,\gamma _{k_n}'|r)$, and because $\gamma$ is fixed, $H(\gamma ^{-1},\gamma _n|r)\asymp H(e,\gamma _n|r)$, so that $H(e,\gamma _n|r) \asymp H(e,\gamma _{k_n}'|r)$. The same proof then shows that $\log H(e,\gamma _n|r)/\hat {d}(e,\gamma _n)$ and $\log H(e,\gamma _n'|r)/\hat {d}(e,\gamma _n')$ have the same limit.

5.2 Proof of step 2

We prove here the following lemma.

Lemma 5.4 Up to a subsequence, $\tilde {\lambda }_N$ as defined in (25) converges weakly to a probability measure on $\partial \hat {\Gamma }$, which we denote by $\lambda _{R_{\mu }}$.

An analogous result follows directly from the convergence properties of the transfer operator $\mathcal {L}_r$ in [Gou14] and one does not need to extract a subsequence. However, in our situation, we can only prove convergence of $\int f \,d\lambda _n$ for functions $f\in \mathcal {B}_{\rho,\beta }$. As our space is not compact and not even locally compact, this set of functions is not dense in the set of all continuous and bounded functions for the $\|\cdot \|_{\infty }$ norm. To fix this problem, we need to consider a compact space that contains $\partial \hat {\Gamma }$ so that $\tilde {\lambda }_N$ converges to a measure on this compact space (up to a subsequence). We then prove that this limit measure gives full measure to $\partial \hat {\Gamma }$. The compact space in question is a version of the Martin boundary that we define. Actually, we deal both with the Martin boundary and the Bowditch boundary at the same time.

We first define the Green distance at the inverse of the spectral radius as

\[ d_G(\gamma,\gamma')=-\log F(\gamma,\gamma'|R_{\mu})F(\gamma',\gamma|R_{\mu}), \]

where $F(\gamma,\gamma '|R_{\mu })$ is the first visit Green function at $R_{\mu }$. More precisely, we have

(26)\begin{equation} F(\gamma,\gamma'|r)=\sum_{n\geq 0}r^{n} \mathbb{P}(X_0=\gamma,X_n=\gamma',X_k\neq \gamma', 1\leq k \leq n-1), \end{equation}

where $X_k$ is the position of the $\mu$-random walk at time $k$. Note that for $r=1$, $F(\gamma,\gamma '|1)$ is the probability of ever reaching $\gamma '$ starting at $\gamma$.

Using the relation

\[ G(\gamma,\gamma'|r)=F(\gamma,\gamma'|r)G(\gamma',\gamma'|r)=F(\gamma,\gamma'|r)G(e,e|r) \]

(see [Woe00, Lemma 1.13(b)]), we also have that

\[ d_G(\gamma,\gamma')=-\log G(\gamma,\gamma'|R_{\mu})-\log G(\gamma',\gamma|R_{\mu})+2G(e,e|R_{\mu}). \]

Actually, the Green distance was introduced by Blachère and Brofferio in [BB07] as $d_G(\gamma,\gamma ')=-\log F(\gamma,\gamma '|1)$. What we call the Green distance here is, thus, a symmetrized version at the spectral radius of what they call the Green distance.

In general, in any metric space $(X,d)$, one can consider a compactification given by the distance called the horofunction compactification. It was introduced by Kuratowski in [Kur35] and used a lot by Gromov (see, for example, [BGS85]). It is the smallest compact set $H$ such that the function $\phi :(x,y)\mapsto d(x,y)-d(x_0,y)$ extends continuously to $X\times H$, where $x_0$ is a base point. Its homeomorphism type does not depend on $x_0$. The horofunction boundary is the complement of $\Gamma$ in the horofunction compactification. We refer to [MT18, § 3] for a construction and many more details.

Define the Martin kernel as

\[ \tilde{K}(\gamma,\gamma')=\frac{G(\gamma,\gamma'|R_{\mu})G(\gamma',\gamma|R_{\mu})}{G(e,\gamma'|R_{\mu})G(\gamma',e|R_{\mu})}. \]

The Martin compactification is defined as the horofunction compactification for the Green distance. In other words, a sequence $\gamma _n$ in $\Gamma$ converges to a point $\xi$ in the Martin boundary if and only if the Martin kernel $\tilde {K}(\cdot,\gamma _n)$ converge pointwise to a limit function $\tilde {K}(\cdot,\xi )$. Usually, the Martin compactification is defined using the Martin kernel

\[ K(\gamma,\gamma')=\frac{G(\gamma,\gamma')}{G(e,\gamma')}. \]

Again, our Martin compactification is a symmetrized version of the usual Martin compactification.

It is proved in [GGPY21] that as soon as weak relative Ancona inequalities are satisfied, there is a one-to-one continuous map from $\Gamma \cup \partial \hat {\Gamma }$ to the Martin compactification, which is a homeomorphism on its image. Actually, this is proved for the usual definition of the Martin boundary. Although the proof still works for our symmetrized version, the terminology is a bit different and we give a proof for completeness.

Lemma 5.5 There is a one-to-one continuous map from $\Gamma \cup \partial \hat {\Gamma }$ to the Martin compactification, which is a homeomorphism on its image.

Proof. Let $\xi$ be a conical limit point and let $[e,\xi )$ be a relative geodesic ray from $e$ to $\xi$. Let $\gamma _n$ be a sequence along $[e,\xi )$ converging to $\xi$. Let $\gamma \in \Gamma$ and let $\tilde {\gamma }$ be its projection on $[e,\xi )$ in $\hat {\Gamma }$. Lemma 2.5 shows that for large enough $n$, a relative geodesic from $\gamma$ to $\gamma _n$ passes within a bounded distance of $\tilde {\gamma }$. In addition, [Dus22, Lemma 4.17] shows that for large enough $n$, relative geodesics from $e$ to $\gamma _n$ and from $\gamma$ to $\gamma _n$ fellow travel for an arbitrarily long time, when $n$ goes to infinity. Then, strong relative Ancona inequalities show that for every $\gamma$, $\tilde {K}(\gamma,\gamma _n)$ converges to some limit $\tilde {K}_{\xi }(\gamma )$, exactly as in the proof of Lemma 4.3. We thus proved that $\gamma _n$ converges to a limit that we still denote by $\xi$ in the Martin boundary.

More generally, let $\xi$ be a conical limit point and let $\xi _n$ be a sequence in $\Gamma \cup \partial \hat {\Gamma }$ converging to $\xi$. Let $\alpha$ be a relative geodesic ray from $e$ to $\xi$ and let $\alpha _n$ be a (finite or infinite) relative geodesic from $e$ to $\xi _n$. Let $d_\mu$ be an arbitrary distance on the Martin compactification. Then, there exists $\gamma _n\in \Gamma$ on $\alpha _n$ such that $d_{\mu }(\gamma _n,\xi _n)\leq {1}/{n}$. If $\xi _n\in \Gamma$, we can choose $\xi _n=\gamma _n$. Otherwise, we use what we just proved previously. Up to choosing $\hat {d}(e,\gamma _n)$ large enough, we can also assume that $\gamma _n$ converges to $\xi$ in $\Gamma \cup \partial \hat {\Gamma }$. Thus, there exists a sequence $k_n$ going to infinity such that the projection $\tilde {\gamma }_n$ of $\gamma _n$ on $\alpha$ in $\hat {\Gamma }$ satisfies $\hat {d}(e,\tilde {\gamma }_n)\geq k_n$. In particular, $\tilde {\gamma }_n$ converges to $\xi$ in the Martin boundary, that is, for any $\gamma$, $\tilde {K}(\gamma,\tilde {\gamma }_n)$ converges to $\tilde {K}_{\xi }(\gamma )$. Let $\gamma \in \Gamma$. Then, according to [Dus22, Lemma 4.17] applied twice, relative geodesics from $e$ to $\gamma _n$ and from $\gamma$ to $\tilde {\gamma }_n$ fellow-travel for an arbitrarily long time, when $n$ goes to infinity. Strong relative Ancona inequalities show that $\tilde {K}(\gamma,\gamma _n)$ also converges to $\tilde {K}_{\xi }(\gamma )$. Thus, $d_{\mu }(\xi,\gamma _n)$ goes to zero. As $d_{\mu }(\gamma _n,\xi _n)\leq {1}/{n}$, we also have that $\xi _n$ converges to $\xi$ in the Martin boundary.

We have, thus, constructed a map from $\Gamma \cup \partial \hat {\Gamma }$ to the Martin compactification. We also proved that this map is continuous. Let us prove that it is one-to-one. Let $\xi \neq \xi '$ be two conical limit points. We just need to prove that $\xi \neq \xi '$ in the Martin boundary. Consider two relative geodesics $[e,\xi )$ and $[e,\xi ')$ from $e$ to $\xi$ and from $e$ to $\xi '$. Let $\gamma _n$ and $\gamma _n'$ be a sequence on $[e,\xi )$ and $[e,\xi ')$, respectively, converging to $\xi$ and $\xi '$, respectively. As $\xi \neq \xi '$, the projection of $\gamma _n$ on $[e,\xi ')$ in $\hat {\Gamma }$ stays within a bounded distance of $e$. Thus, for large enough $n$ and $m$, a relative geodesic from $\gamma _n$ to $\gamma _m'$ passes within a bounded distance of $e$. Weak relative Ancona inequalities show that $\tilde {K}(\gamma _n,\gamma _m')\asymp H(\gamma _n,e|R_\mu )$. Letting $m$ tend to infinity, we thus have that $\tilde {K}_{\xi '}(\gamma _n)\asymp H(\gamma _n,e|R_\mu )$, so that $\tilde {K}_{\xi '}(\gamma _n)$ converges to zero. Weak relative Ancona inequalities also show that if $n< m$, we have $\tilde {K}(\gamma _n,\gamma _m)\asymp {1}/{H(e,\gamma _n|R_\mu )}$. Letting $m$ tend to infinity, we obtain $\tilde {K}_{\xi }(\gamma _n)\asymp {1}/{H(\gamma _n,e|R_\mu )}$, so that $\tilde {K}_{\xi }(\gamma _n)$ goes to infinity. We can thus find $n$ such that $\tilde {K}_{\xi }(\gamma _n)\neq \tilde {K}_{\xi '}(\gamma _n)$ and so $\xi \neq \xi '$ in the Martin boundary.

Finally, we prove that this map is a homeomorphism on its image. Let $\xi _n$ be a sequence in $\Gamma \cup \partial \hat {\Gamma }$ converging to $\xi$ in the Martin compactification. Assume by contradiction that it does not converge to $\xi$ in $\Gamma \cup \partial \hat {\Gamma }$. Fix a relative geodesic $\alpha$ from $e$ to $\xi$ and for every $n$, a relative geodesic $\alpha _n$ from $e$ to $\xi _n$. Then, up to choosing a subsequence, we can assume that the projection of $\alpha _n$ on $\alpha$ in $\hat {\Gamma }$ stays within a uniform bounded distance of $e$. In particular, if $\gamma _m$ is a sequence on $\alpha$ converging to $\xi$ and if $\gamma _k'$ is a sequence on $\alpha _n$ converging to $\xi _n$, then a relative geodesic from $\gamma _m$ to $\gamma _k'$ passes within a bounded distance of $e$, independently of $k,m,n$. Weak relative Ancona inequalities show that $\tilde {K}(\gamma _m,\gamma _k')\asymp H(\gamma _m,e|R_{\mu })$ so that letting $k$ tend to infinity, $\tilde {K}_{\xi _n}(\gamma _m)\asymp H(\gamma _m,e|R_{\mu })$. In particular, $\tilde {K}_{\xi _n}(\gamma _m)\leq C$ for some uniform $C$. However, as we saw above, $\tilde {K}_{\xi }(\gamma _m)$ tends to infinity, so there exists $m$ such that $\tilde {K}_{\xi }(\gamma _m)\geq C+1$. Fixing such an $m$, we obtain a contradiction, since $\tilde {K}_{\xi _n}(\gamma _m)$ converges to $\tilde {K}_{\xi }(\gamma _m)$ when $n$ tends to infinity.

We first prove that $\tilde {\lambda }_N$ converges to a probability measure on the Bowditch compactification. We then prove that it also converges to a probability measure on the Martin compactification.

Proposition 5.6 Up to a subsequence, the measure $\tilde {\lambda }_N$ weakly converges to a measure $\lambda _{R_\mu }$ on the Bowditch compactification. This limit measure gives full measure to the set of conical limit points.

Proof. Convergence up to a subsequence follows directly from compactness of the Bowditch compactification. We just need to prove that any limit measure of $\tilde {\lambda }_N$ gives full measure to the set of conical limit points. Recall that $\lambda _n=\sum _{\gamma \in \hat {S}_n}H(e,\gamma |R_{\mu })\delta _{\gamma }$ and $\tilde {\lambda }_N=\sum _{n=1}^{N}\lambda _n/ (\sum _{n=1}^{N}\lambda _n(\Gamma )).$

First, we prove that any limit measure $\lambda _{R_{\mu }}$ of $\tilde {\lambda }_N$ gives full mass to the Bowditch boundary. Let $K\subset \Gamma$ be a compact subset. Then, $K$ is finite, so that for any $N$, $\sum _{n=1}^{N}\lambda _n(K)$ is bounded, independently of $N$. Moreover, according to Proposition 2.11, $\sum _{n=1}^{N}\lambda _n(\Gamma )$ tends to infinity. This proves that for any subsequence $\tilde {\lambda }_{N_j}$ of $\tilde {\lambda }_N$, $\tilde {\lambda }_{N_j}(K)$ converges to zero when $j$ tends to infinity. As $K$ is both open and closed in the Bowditch compactification, the Portmanteau theorem shows that $\lambda _{R_{\mu }}(K)=0$.

Consider a parabolic limit point $\xi$ in the Bowditch boundary. As the set of parabolic limit points is countable, we just need to prove that $\lambda _{R_{\mu }}(\{\xi \})=0$ to conclude. Let $\mathcal {H}$ be the corresponding parabolic subgroup, that is, $\mathcal {H}$ is the stabilizer of $\xi$. Choose $\mathcal {H}_0\in \Omega _0$ so that $\mathcal {H}$ is conjugated to $\mathcal {H}_0$, say $\mathcal {H}=\gamma _0\mathcal {H}_0\gamma _0^{-1}$ Denote by $U_{\xi,n}$ the set of $\gamma \in \Gamma$ such that the projection of $\gamma$ on $\gamma _0 \mathcal {H}_0$ in the Cayley graph $\operatorname {Cay}(\Gamma,S)$ is at $d$-distance at least $n$ from $e$. Let $V(\xi,n)$ be the closure of $U(\xi,n)$ in the Bowditch compactification. Then, $V(\xi,n)$ contains $\{\xi \}$ so we only need to prove that $\lambda _{R_{\mu }}(V(\xi,n))$ converges to zero when $n$ tends to infinity.

According to the BCP property, if $\zeta \in V(\xi,n)$, then there exists $\gamma \in \mathcal {H}_0$ such that $\gamma _0\gamma$ is within a bounded distance of a relative geodesic from $e$ to $\zeta$. In particular, if $N$ is large enough, for every $\gamma '\in V(\xi,n)\cap \Gamma$ such that $\hat {d}(e,\gamma ')=N$, weak relative Ancona inequalities show that

\[ H(e,\gamma'|R_\mu)\lesssim H(e,\gamma_0|R_\mu)H(e,\gamma|R_\mu)H(\gamma_0\gamma,\gamma'|R_\mu). \]

Thus,

\[ \lambda_N(V(\xi,n))\lesssim \sum_{\gamma \in \mathcal{H}_0,d(e,\gamma_0\gamma)\geq n}H(e,\gamma|R_{\mu})\sum_{k=1}^{N}\lambda_k(\Gamma) \]

and so

\[ \tilde{\lambda}_N(V(\xi,n))\lesssim \sum_{\gamma \in \mathcal{H}_0,d(e,\gamma_0\gamma)\geq n}H(e,\gamma|R_{\mu}). \]

As $\gamma _0$ is fixed, this proves that

\[ \lambda_{R_{\mu}}(V(\xi,n))\lesssim \sum_{\gamma \in \mathcal{H}_0,d(e,\gamma)\geq n}H(e,\gamma|R_{\mu}). \]

According to Corollary 2.10, this last term converges to zero when $n$ tends to infinity, which concludes the proof.

We can thus see the measure $\lambda _{R_\mu }$ as a measure on $\partial \hat {\Gamma }$. We fix a subsequence $\tilde {\lambda }_{N_k}$ such that $\tilde {\lambda }_{N_k}$ weakly converges to $\lambda _{R_\mu }$. We can now prove Lemma 5.4.

Proof. There is a one-to-one and continuous map from $\Gamma \cup \partial \hat {\Gamma }$ to the Bowditch compactification, which is a homeomorphism on its image. As the limit measure $\lambda _{R_\mu }$ does not give any mass to the complement of $\Gamma \cup \partial \hat {\Gamma }$, the Portmanteau theorem shows that $\tilde {\lambda }_{N_k}$ also weakly converges to $\lambda _{R_\mu }$ on $\Gamma \cup \partial \hat {\Gamma }$.

We also prove the following corollary.

Lemma 5.7 The measure $\tilde {\lambda }_{N_k}$ also weakly converges to $\lambda _{R_\mu }$ on the Martin compactification.

Proof. There is a one-to-one and continuous map from $\Gamma \cup \partial \hat {\Gamma }$ to the Martin compactification, which is a homeomorphism on its image. Let $f$ be a bounded continuous function on the Martin compactification. Its restriction $\tilde {f}$ to $\Gamma \cup \partial \hat {\Gamma }$ also is bounded continuous, so $\tilde {\lambda }_{N_k}(f)=\tilde {\lambda }_{N_k}(\tilde {f})$ converges to $\lambda _{R_\mu }(\tilde {f})$. This proves that $\tilde {\lambda }_{N_k}$ also weakly converges to $\lambda _{R_\mu }$ on the Martin compactification.

5.3 Proof of step 3

We prove here the following.

Lemma 5.8 The limit measure $\lambda _{R_{\mu }}$ is ergodic for the action of $\Gamma$ on $\partial \hat {\Gamma }$.

This step is a bit more complicated. To show that $\lambda _{R_{\mu }}$ is ergodic, we follow the strategy of [MYJ20]. We first prove that $\lambda _{R_\mu }$ is conformal for the Green distance defined previously.

Let $\gamma \in \Gamma$ and let $L_{\gamma }$ the operator of multiplication by $\gamma$ on the left.

Lemma 5.9 For every $\gamma$, we have

\[ \frac{d(L_{\gamma})_*\lambda_{R_{\mu}}}{d\lambda_{R_{\mu}}}(\xi)=\tilde{K}_{\xi}(\gamma). \]

Proof. Direct computation shows that for fixed $\gamma _0$, one has, for any $\gamma$ and any $N$ such that $N\geq \hat {d}(e,\gamma _0)+\hat {d}(e,\gamma )$,

(27)\begin{equation} (L_{\gamma_0})_*\tilde{\lambda}_N(\gamma)=H(\gamma_0,\gamma|R_{\mu})/H(e,\gamma|R_{\mu})\tilde{\lambda}_N(\gamma)=\tilde{K}(\gamma_0,\gamma)\tilde{\lambda}_N(\gamma). \end{equation}

Lemma 2.9 shows that $\sum _{n=N-\hat {d}(e,\gamma _0)}^{N}\sum _{\gamma \in \hat {S}_n}H(e,\gamma |R_{\mu })$ is bounded. Thus, according to Proposition 2.11,

\[ \frac{\sum_{n=N-\hat{d}(e,\gamma_0)}^{N}H(e,\gamma|R_{\mu})}{\sum_{n\leq N}H(e,\gamma|R_{\mu})}\underset{N\to \infty}{\longrightarrow} 0. \]

Combined with (27), this shows that $((L_{\gamma _0})_*\tilde {\lambda }_N-\tilde {K}(\gamma _0,\cdot )\tilde {\lambda }_N)$ converges to zero in total variation norm.

By definition, for fixed $\gamma _0$, the function $\tilde {K}(\gamma _0,\cdot )$ is continuous and bounded on the Martin compactification. Thus, $\tilde {K}(\gamma _0,\cdot )\tilde {\lambda }_{N_k}$ weakly converges to $\tilde {K}(\gamma _0,\cdot )\lambda _{R_\mu }$. Moreover, left multiplication by $\gamma _0$ on $\Gamma$ extends to a homeomorphism on the Martin compactification, so that $(L_{\gamma _0})_*\tilde {\lambda }_{N_k}$ weakly converges to $(L_{\gamma _0})_*\lambda _{R_\mu }$. We have, thus, proved that $(L_{\gamma _0})_*\lambda _{R_\mu }=\tilde {K}(\gamma _0,\cdot )\lambda _{R_\mu }$.

We use this property to prove the following.

Lemma 5.10 The measure $\lambda _{R_\mu }$ on $\partial \hat {\Gamma }$ has no atom.

Proof. Assume in contrast that there exists $\xi \in \partial \hat {\Gamma }$ such that $\lambda _{R_\mu }(\xi )>0$. Consider a sequence $\gamma _n$ converging along a relative geodesic ray to $\xi$. Then, weak relative Ancona inequalities show that if $n\leq m$, then $\tilde {K}(\gamma _n,\gamma _m)\geq {C}/{H(e,\gamma _n|R_{\mu })}$. Consequently, letting $m$ tend to infinity, we see that $\tilde {K}_{\xi }(\gamma _n)\geq {C}/{H(e,\gamma _n|R_{\mu })}$. As $d(\gamma _n,e)$ tends to infinity, $H(e,\gamma _n|R_{\mu })$ converges to zero and so $\tilde {K}_{\xi }(\gamma _n)$ tends to infinity. Lemma 5.9 shows that $\lambda _{R_\mu }(\gamma _n^{-1}\xi )=\tilde {K}_{\xi }(\gamma _n)\lambda _{R_{\mu }}(\xi )$, which goes to infinity. This is a contradiction, because $\lambda _{R_{\mu }}$ is a probability measure.

In the following, it is simpler to see the measure $\lambda _{R_\mu }$ as a measure on the Bowditch boundary that gives full mass to the set of conical limit points. We used the symmetrized Martin boundary to prove Lemmas 5.9 and 5.10. In the hyperbolic setting, using results of Coornaert (see [Coo93]), conformal measures for hyperbolic distances are ergodic. Actually, [Coo93] only deals with geodesic distances and this was generalized by [BHM11] for distances that are hyperbolic and quasi-isometric to a word distance, such as the Green distance as long as weak Ancona inequalities hold (this is also proved in [BHM11]). Comparing a geodesic distance with the Green distance is more difficult here and we need another approach. We use instead the same strategy as in [MYJ20, Theorem 4.1] to prove Lemma 5.8, which generalizes Coornaert's result.

Before proving this proposition, let us introduce some notions of geometric measure theory from [MYJ20] and some constructions of [DG20] and [Yan22]. Let $\Lambda$ be a metric space. A covering relation $\mathcal {C}$ is a subset of the set of all pairs $(\xi,S)$ such that $\xi \in S\subset \Lambda$. A covering relation $\mathcal {C}$ is said to be fine at $\xi \in \Lambda$ if there exists a sequence $S_n$ of subsets of $\Lambda$ with $(\xi,S_n)\in \mathcal {C}$ and such that the diameter of $S_n$ converges to zero. Let $\mathcal {C}$ be a covering relation. For any measurable subset $E\subset \Lambda$, define $\mathcal {C}(E)$ to be the collection of subsets $S\subset \Lambda$ such that $(\xi,S)\in \mathcal {C}$ for some $\xi \in E$. A covering relation $\mathcal {C}$ is said to be a Vitali relation for a finite measure $\kappa$ on $\Lambda$ if it is fine at every point of $\Lambda$ and if the following holds: if $\mathcal {C}'\subset \mathcal {C}$ is fine at every point of $\Lambda$ then for every measurable subset $E$, $\mathcal {C}'(E)$ has a countable disjoint subfamily $\{S_n\}$ such that $\kappa (E\setminus \bigcup ^{\infty }_{n=1}S_{n})=0$. We use the letter $\mathcal {V}$ to denote a Vitali relation in the following.

Recall that an $(\eta _1,\eta _2)$-transition point on a geodesic $\alpha$ in the Cayley graph $\operatorname {Cay}(\Gamma,S)$ is a point $\gamma$ such that for any coset $\gamma _0\mathcal {H}$ of a parabolic subgroup, the part of $\alpha$ consisting of points at distance at most $\eta _2$ from $\gamma$ is not contained in the $\eta _1$-neighborhood of $\gamma _0\mathcal {H}$. Let $\xi$ be a conical limit point. Following Yang [Yan22], the partial shadow $\Omega _{\eta _1,\eta _2}(\gamma )$ at $\gamma \in \Gamma$ is the set of points $\xi$ in the Bowditch boundary such that there is a geodesic ray $[e,\xi )$ in $\operatorname {Cay}(\Gamma,S)$ containing an $(\eta _1,\eta _2)$-transition point in the ball $B(\gamma,2\eta _2)$.

We define the following relation $\mathcal {V}_{\eta _1,\eta _2}$ on the Bowditch boundary. For $\xi$ parabolic, we declare $(\xi,\{\xi \})\in \mathcal {V}_{\eta _1,\eta _2}$. For $\xi$ conical, we declare $(\xi, \Omega _{\eta _1,\eta _2}(\gamma ))\in \mathcal {V}_{\eta _1,\eta _2}$ whenever $\xi \in \Omega _{\eta _1, \eta _2}(\gamma )$. According to [DG20, Proposition 3.3], the relation $\mathcal {V}_{\eta _1,\eta _2}$ is fine at every limit point in the Bowditch boundary.

Let $\gamma \in \Gamma$ and let $\eta _1,\eta _2>0$. Consider a neighborhood $U$ of $\Omega _{\eta _1,\eta _2}(\gamma )$ in the Bowditch compactification. One can choose $U$ such that for any point $\xi$ in $U$, $\gamma$ is within a bounded distance of a transition point on a geodesic from $e$ to $\xi$. According to Lemma 2.2, $\gamma$ is within a bounded distance of a point on a relative geodesic from $e$ to $\xi$. In particular, weak relative Ancona inequalities imply that there exists a constant $C$ (depending on $\eta _2$) such that for $N$ large enough,

\[ \tilde{\lambda}_N(\Omega_{\eta_1,2\eta_2}(\gamma))\leq C \tilde{\lambda}_N(\Omega_{\eta_1,\eta_2}(\gamma)), \]

so that

\[ \lambda_{R_{\mu}}(\Omega_{\eta_1,2\eta_2}(\gamma))\leq C \lambda_{R_{\mu}}(\Omega_{\eta_1,\eta_2}(\gamma)). \]

The measure $\lambda _{R_{\mu }}$ on the Bowditch boundary gives full measure to the set of conical limit points. Thus, [DG20, Proposition 3.4] shows that the relation $\mathcal {V}_{\eta _1,\eta _2}$ is a Vitali relation for $\lambda _{R_{\mu }}$.

To prove Lemma 5.8, we need the following two results.

Lemma 5.11 [MYJ20, Theorem 4.2]

Let $E$ be a measurable subset of the Bowditch boundary. Then, for $\lambda _{R_{\mu }}$-almost every point $\xi \in E$, one has

\[ \frac{\lambda_{R_{\mu}}(E\cap S_n)}{\lambda_{R_{\mu}}(S_n)}\underset{n\to \infty}{\longrightarrow}1 \]

for every sequence $\{S_n\}$ such that $(\xi, S_n )\in \mathcal {V}_{\eta _1,\eta _2}$ for all $n$ and such that the diameter of $S_n$ converges to 0 when $n$ tends to infinity.

For the second result, we need to choose a distance on the Bowditch boundary. To simplify the argument, we choose the shortcut distance, so that the following holds. We refer to [Yan22, § 2.4] for the definition of the shortcut distance.

Lemma 5.12 For every $\epsilon >0$ and $\eta _1>0$, there exists $\eta _2>0$ such that for every $\gamma \in \Gamma$, the diameter of the complement of $\gamma ^{-1}\Omega _{\eta _1,\eta _2}(\gamma )$ is smaller than $\epsilon$.

Proof. This is exactly the content of the remark inside the proof of [Yan22, Lemma 4.1].

Actually, the choice of the distance is not relevant and with a bit of work, one could have proved the same result for a visual distance on the Bowditch boundary, adapting the arguments of [MYJ20, Proposition 2.10]. We only chose the shortcut distance to avoid reproving this technical claim.

We can finally prove Lemma 5.8. Everything is settled so that we can easily adapt the arguments of [MYJ20, Theorem 4.1]. We still rewrite the proof for convenience.

Proof. Denote by $\partial _B\Gamma$ the Bowditch boundary of $\Gamma$. Consider a $\Gamma$-invariant measurable subset $E$ of the Bowditch boundary, such that $\lambda _{R_{\mu }}(E)>0$. Assume, by contradiction, that $\lambda _{R_{\mu }}(E)<1$. We fix $\epsilon >0$ arbitrarily small. For technical reasons, we assume that $\lambda _{R_{\mu }}(\partial _B\Gamma )\geq 2\epsilon$, that is, $\epsilon \leq 1/2$.

According to Lemma 5.11, if $\eta _2$ is large enough, for $\lambda _{R_{\mu }}$-almost every $\xi$ in $E^{c}$,

\[ \frac{\lambda_{R_{\mu}}(E\cap \Omega_{\eta_1,\eta_2}(\gamma_n))}{\lambda_{R_{\mu}}(\Omega_{\eta_1,\eta_2}(\gamma_n))}\underset{n\to \infty}{\longrightarrow}0, \]

whenever $\gamma _n$ converges to $\xi$ along a relative geodesic ray. Take such a $\xi$ and such a sequence $\gamma _n$. Up to taking a subsequence, we can assume that $\gamma _n^{-1}$ converges to a point $\zeta$ in the Bowditch boundary. According to Lemma 5.10, $\lambda _{R_{\mu }}(\zeta )=0$.

Then, because the Bowditch boundary is compact, there exists $\delta >0$ (not depending on $\zeta$) such that the ball centered at $\zeta$ of radius $\delta$ has measure at most $\epsilon$. Moreover, according to Lemma 5.12, there exists $\eta _2>0$ such that the diameter of the complement of $\gamma _n^{-1}\Omega _{\eta _1,\eta _2}(\gamma _n)$ is smaller than $\delta$. Fixing such an $\eta _2>0$, for large enough $n$, we have that $\zeta \notin \gamma _n^{-1}\Omega _{\eta _1,\eta _2}(\gamma _n)$, so that the complement of $\gamma _n^{-1}\Omega _{\eta _1,\eta _2}(\gamma _n)$ is contained in the ball of center $\zeta$ and of radius $\delta$. In particular,

\[ \lambda_{R_{\mu}}(\partial_B\Gamma \setminus \gamma_n^{-1}\Omega_{\eta_1,\eta_2}(\gamma_n))\leq \epsilon. \]

As $\lambda _{R_{\mu }}(\partial _B\Gamma )\geq 2\epsilon$, we thus also have

\[ \lambda_{R_{\mu}}(\gamma_n^{-1}\Omega_{\eta_1,\eta_2}(\gamma_n))\geq \epsilon. \]

As $E$ is $\Gamma$-invariant, we have

\[ \lambda_{R_{\mu}}(E\cap \gamma_n^{-1}\Omega_{\eta_1,\eta_2}(\gamma_n))=(L_{\gamma_n})_*\lambda_{R_\mu}(E\cap \Omega_{\eta_1,\eta_2}(\gamma_n)). \]

Weak relative Ancona inequalities show that if $\xi '\in \Omega _{\eta _1,\eta _2}(\gamma _n)$, then

\[ \frac{1}{C(\eta_2)}\frac{1}{H(e,\gamma_n|R_{\mu})}\leq \tilde{K}_{\xi'}(\gamma_n)\leq C(\eta_2)\frac{1}{H(e,\gamma_n|R_{\mu})}. \]

In particular, Lemma 5.9 shows that

\[ \lambda_{R_{\mu}}(E\cap \gamma_n^{-1}\Omega_{\eta_1,\eta_2}(\gamma_n))\leq C(\eta_2)\frac{1}{H(e,\gamma_n|R_{\mu})}\lambda_{R_\mu}(E\cap \Omega_{\eta_1,\eta_2}(\gamma_n)). \]

Similarly, we have

\[ \lambda_{R_{\mu}}(\gamma_n^{-1}\Omega_{\eta_1,\eta_2}(\gamma_n))\geq \frac{1}{C(\eta_2)}\frac{1}{H(e,\gamma_n|R_{\mu})}\lambda_{R_\mu}(\Omega_{\eta_1,\eta_2}(\gamma_n)). \]

This proves that

\[ \frac{\lambda_{R_{\mu}}(E\cap \gamma_n^{-1}\Omega_{\eta_1,\eta_2}(\gamma_n))}{\lambda_{R_{\mu}}(\gamma_n^{-1}\Omega_{\eta_1,\eta_2}(\gamma_n))}\leq C'(\eta_2)\frac{\lambda_{R_{\mu}}(E\cap \Omega_{\eta_1,\eta_2}(\gamma_n))}{\lambda_{R_{\mu}}(\Omega_{\eta_1,\eta_2}(\gamma_n))}. \]

The right-hand side of this last equation converges to zero when $n$ tends to infinity. This proves that $\lambda _{R_{\mu }}(E\cap \gamma _n^{-1}\Omega _{\eta _1,\eta _2}(\gamma _n)))$ converges to zero when $n$ tends to infinity, because $\lambda _{R_{\mu }}(\gamma _n^{-1}\Omega _{\eta _1,\eta _2}(\gamma _n))\geq \epsilon$. Finally, recall that $\lambda _{R_{\mu }}(\partial _B\Gamma \setminus \gamma _n^{-1}\Omega _{\eta _1,\eta _2}(\gamma _n))\leq \epsilon$, so that $\lambda _{R_{\mu }}(E)\leq 2\epsilon$. As $\epsilon$ is arbitrarily small, we get that $\lambda _{R_{\mu }}(E)=0$, which is a contradiction.

5.4 Proof of step 4

We prove here the following.

Lemma 5.13 Let $c_j=\int \varphi _r\,dm_j$. With the notation as previously, we have

\[ \lambda_{R_\mu}(U(c_j))>0. \]

This lemma is a consequence of the two following results. We use the notation $\alpha _j=\sum _{i}\nu _j^{(i)}$, where the measures $\nu _j^{(i)}$ are given by Theorem 3.3.

Lemma 5.14 The measure $T_*\alpha _j$ is absolutely continuous with respect to the measure $\alpha _j$.

Proof. Since by Lemma 4.6 the maximal pressure at the spectral radius is zero, we have

\[ \mathcal{L}_{R_{\mu}}^{*}\alpha_j=\alpha_j. \]

Denote by $[x_1,\ldots,x_n]$ the cylinder consisting of elements of $\overline {\Sigma }_A$ starting with the symbols $x_1,\ldots,x_n$. Then, we have

\[ \alpha_j([x_1,\ldots,x_n])=\alpha_j(\mathcal{L}_{R_{\mu}}1_{[x_1,\ldots,x_n]}). \]

Moreover, weak Ancona inequalities show that

\[ \alpha_j(\mathcal{L}_{R_{\mu}}1_{[x_1,\ldots,x_n]})\leq C H(e,x_1|R_{\mu})\alpha_j([x_2,\ldots,x_n]). \]

Now, $T^{-1}[x_2,\ldots,x_n]$ is contained in the union of cylinders of the form $[x_1,\ldots,x_n]$, where $x_1\in S$ or $x_1\in \mathcal {H}$ for some parabolic subgroup. According to Corollary 2.10, the sum $\sum _{\sigma \in \mathcal {H}}H(e,\sigma |r)$ is uniformly bounded, so that

\[ \alpha_j(T^{-1}[x_2,\ldots,x_n])\leq C\alpha_j([x_2,\ldots,x_n]). \]

This is true for any cylinder $[x_2,\ldots,x_n]$. It follows that $\alpha _j(T^{-1}E)\leq C\alpha _j(E)$ for any measurable set $E\in \overline {\Sigma }_A$.

Recall that $\phi$ maps paths of $\overline {\Sigma }_A$ that start with $v_*$ to $\Gamma \cup \partial \hat {\Gamma }$. Let $\alpha _j(\cdot \cap E_*)$ be the measure $\alpha _j$ restricted to paths that start at $v_*$. Then, $\phi _*\alpha _j(\cdot \cap E_*)$ is a measure on $\partial \hat {\Gamma }$.

Lemma 5.15 The measure $\phi _*\alpha _j(\cdot \cap E_*)$ is absolutely continuous with respect to the measure $\lambda _{R_\mu }$.

Proof. The sequence of measures $\tilde {\lambda }_{N_k}$ weakly converges to $\lambda _{R_{\mu }}$ in the Bowditch compactification. Recall that according to Lemma 5.7, it also weakly converges to $\lambda _{R_\mu }$ in $\Gamma \cup \partial \hat {\Gamma }$.

If $f$ is a function defined on $\partial \hat {\Gamma }$, then $f\circ \phi$ is defined on $\overline {\Sigma }_A$ and it vanishes on the complement of $E_*$. We see $\partial \hat {\Gamma }$ as the Gromov boundary of the hyperbolic space $\hat {\Gamma }$ and we endow $\partial \hat {\Gamma }$ with a visual distance $d_v$, as in [GH90]. Then, there exists $\epsilon >0$ such that $d_v(\xi,\xi ')\leq {e}^{-\epsilon (\xi,\xi ')_e}$, where $(\xi,\xi ')_e$ is the Gromov product of $\xi$ and $\xi '$, based at $e$, see [GH90, Proposition 7.3.10]. In particular, if $f$ is a bounded locally Hölder continuous function on $\partial \hat {\Gamma }$, then $f\circ \phi$ is in $\mathcal {B}_{\rho,\beta }$. Theorem 3.3 shows that $\mathcal {L}_{R_{\mu }}^{np+q}(f\circ \phi )(\emptyset )$ converges to $\sum _{j=1}^{k}\sum _{i=1}^{p_j}h_j^{(i)}\int (f\circ \phi ) \,d\nu _j^{((i-n) \text { mod } p_j)}$. Also note that

\[ \sum_{\gamma \in \hat{S}_n}H(e,\gamma|R_\mu)=H(e,e|R_\mu)\mathcal{L}_{R_{\mu}}^{n}(1_{E_*}f\circ \phi)(\emptyset). \]

Let $\beta _j=\phi _*\alpha _j(\cdot \cap E_*)$. As the functions $h_j^{(i)}$ are bounded away from zero and infinity on the support of $\nu _j^{(i)}$, this proves that for any bounded locally hölder continuous function $f$ on $\partial \hat {\Gamma }$, we have

(28)\begin{equation} \beta_j(f)\leq C \lambda_{R_\mu}(f). \end{equation}

Bounded Hölder continuous functions are not dense in bounded continuous functions for the supremum norm, but they are dense in the space of integrable functions for the $L^{1}$-norm, see [AB06, Corollary 3.14]. Let $A\subset \partial \hat {\Gamma }$ be any measurable set. We want to prove that $\beta _j(A)\leq C \lambda _{R_{\mu }}(A)$. Let $\epsilon >0$. There exists a bounded locally Hölder continuous function $f$ such that

\[ \|f-1_A\|_{L^{1}(\partial \hat{\Gamma},\beta_j+\lambda_{R_\mu})}\leq \epsilon. \]

Then, $\beta _j(A)\leq \beta _j(|f|)+\epsilon$. As $|f|$ still is locally Hölder continuous, (28) shows that

\[ \beta_j(A)\leq C\lambda_{R_\mu}(|f|)+\epsilon\leq C\lambda_{R_\mu}(A)+(1+C)\epsilon. \]

As $\epsilon$ is arbitrary, this concludes the proof.

Those two lemmas allow us to conclude the proof of Lemma 5.13 We only outline the proof and refer to the end of the proof of [Gou14, Proposition 3.16] for the details. The probability measure $dm_j= ({1}/{p_j})\sum _{i=1}^{p_j}h_{j}^{(i)}\,d\nu _j^{(i)}$ is invariant and ergodic for the shift $T$ (see, for example, [Sar99, Lemma 11]). Fix $r$ close enough to $R_{\mu }$ so that the conclusions of Theorem 3.6 hold. Let $O_j$ be the set of points where the Birkhoff sums $ ({1}/{n})\sum _{1\leq k\leq n} \varphi _r\circ T^{k}$ converge to $c_j=\int \varphi _r dm_j$. By the Birkhoff ergodic theorem, $m_j(O_j)=1$. We first deduce that $\alpha _j(O_j\cap \overline {\Sigma }_{A,j})>0$. Using that $T_*\alpha _j$ is absolutely continuous with respect to $\alpha _j$, we then deduce that $\alpha _j(O_j)>0$. Then, using that $\phi _*\alpha _j(\cdot \cap E_*)$ is absolutely continuous with respect to $\lambda _{R_\mu }$, we deduce that $\lambda _{R_\mu }(\phi (O_j\cap E_*))>0$. Finally, direct computation shows that $\phi (O_j\cap E_*)\subset U(c_j)$. This proves that $\lambda _{R_\mu }(U(c_j))>0$.

We now conclude the proof of Lemma 5.2.

Proof. As $U(c_j)$ is invariant and $\lambda _{R_\mu }$ is ergodic, we thus have $\lambda _{R_\mu }(U(c_j))=1$. This holds for all $j$, so we finally obtain that every $U(c_j)$ intersect, so that $c_j$ does not depend on $j$.

5.5 End of the proof of Proposition 5.1

We want to prove that ${\tilde {P}_j(\varphi _r)}/{P(r)}$ tends to one when $r$ tends to $R_{\mu }$. According to Proposition 4.12, the assumptions of Proposition 3.7 are satisfied, so that

(29)\begin{align} {e}^{\tilde{P}_j(r)}-1&= \int ({e}^{\varphi_r-\varphi_{R_\mu}}-1)\,dm_j\nonumber\\ &\quad +\int ({e}^{\varphi_r-\varphi_{R_\mu}}-1)\frac{1}{p_j}\bigg( \sum_{i=0}^{p_j-1}h_j^{(i)}-\tilde{h}_{j,r}^{(i)}\bigg) \, d\nu_j^{(i)}. \end{align}

Lemma 4.5 and (23) show that $|P(r)|$ has order of magnitude $\sqrt {R_\mu -r}$. We actually show that

\[ {e}^{\tilde{P}_j(r)}-1= \int (\varphi_r-\varphi_{R_\mu})\,dm_j+o \big(\sqrt{R_\mu-r}\,\big). \]

We then combine this with Lemma 5.2 to complete the proof of Proposition 5.1.

Lemma 5.16 We have

\[ \int ({e}^{\varphi_r-\varphi_{R_\mu}}-1)\frac{1}{p_j} \bigg(\sum_{i=0}^{p_j-1}h_j^{(i)}-\tilde{h}_{j,r}^{(i)}\bigg)\,d\nu_j^{(i)}=o \big(\sqrt{R_\mu-r}\,\big). \]

Proof. According to Theorem 3.3, the functions $h_j^{(i)}$ are bounded away from zero and infinity on the support of $\nu _j^{(i)}$. We can thus replace $\nu _j^{(i)}$ with $m_j$, which is itself dominated by the measure $m$. Thus, we just need to show that for every $i$,

\[ \frac{1}{\sqrt{R_\mu-r}}\int \big|{e}^{\varphi_r-\varphi_{R_\mu}}-1\big |\big|h_j^{(i)}-\tilde{h}_{j,r}^{(i)}\big|\,dm\underset{r\to R_\mu}{\longrightarrow}0. \]

Let $r_n$ be a sequence converging to $R_\mu$ such that

\[ \frac{1}{\sqrt{R_\mu-r_n}}\int \big|{e}^{\varphi_{r_n}-\varphi_{R_\mu}}-1\big| \big|h_j^{(i)}-\tilde{h}_{j,r_n}^{(i)}\big|\,dm\underset{n\to +\infty}{\longrightarrow}\alpha \in [0,+\infty]. \]

According to Corollary 4.13,

\[ \int \big|h_j^{(i)}-\tilde{h}_{j,r_n}^{(i)}\big|\,dm\underset{n\to +\infty}{\longrightarrow} 0, \]

so up to taking a subsequence, $\big |h_j^{(i)}-\tilde {h}_{j,r_n}^{(i)}\big |$ converges to zero $m$-almost everywhere.

We now focus on $ {1}/{\sqrt {R_\mu -r_n}} \big |{e}^{\varphi _{r_n}-\varphi _{R_\mu }}-1\big |$. We show that

(30)\begin{equation} \frac{1}{\sqrt{R_\mu-r}}\int \big|{e}^{\varphi_{r}-\varphi_{R_\mu}}-1\big|\,dm\lesssim 1. \end{equation}

Differentiating the expression ${e}^{\varphi _{r}-\varphi _{R_\mu }}(x)$, we obtain

\[ \bigg(\frac{d}{dr}\varphi_r (x)\bigg){e}^{\varphi_{r}-\varphi_{R_\mu}}(x). \]

Weak relative Ancona inequalities yield

(31)\begin{equation} {e}^{\varphi_{r}-\varphi_{R_\mu}}(x)=\frac{H(e,x|r)/H(x_1,x|r)}{H(e,x|R_\mu)/H(x_1,x|R_\mu)}\lesssim \frac{H(e,x_1|r)}{H(e,x_1|R_\mu)}\lesssim 1. \end{equation}

Thus, Lemma 4.8 shows that

(32)\begin{equation} \bigg|\frac{d}{dr} ({e}^{\varphi_{r}-\varphi_{R_\mu}}(x))\bigg|\lesssim \frac{1}{\sqrt{R_\mu-r}}\varphi(x). \end{equation}

Integrating this inequality, we obtain

(33)\begin{equation} \big|{e}^{\varphi_{r}-\varphi_{R_\mu}}(x)-1\big|\lesssim \varphi(x)\sqrt{R_\mu-r}. \end{equation}

Integrating with respect to $m$, we finally obtain (30). In addition,

\[ \frac{1}{\sqrt{R_\mu-r_n}}\big|{e}^{\varphi_{r_n}-\varphi_{R_\mu}}-1\big|\big |h_j^{(i)}-\tilde{h}_{j,r_n}^{(i)}\big|\lesssim \varphi\big|h_j^{(i)}-\tilde{h}_{j,r_n}^{(i)}\big|, \]

so that

\[ \frac{1}{\sqrt{R_\mu-r_n}}\big|{e}^{\varphi_{r_n}-\varphi_{R_\mu}}-1\big |\big|h_j^{(i)}-\tilde{h}_{j,r_n}^{(i)}\big| \]

converges to zero $m$-almost everywhere.

Finally, we deduce from Corollary 4.13 that $\big |h_j^{(i)}-\tilde {h}_{j,r_n}^{(i)}\big |$ is uniformly bounded, hence

\[ \frac{1}{\sqrt{R_\mu-r_n}}\big|{e}^{\varphi_{r_n}-\varphi_{R_\mu}}-1\big| \big|h_j^{(i)}-\tilde{h}_{j,r_n}^{(i)}\big|\lesssim \varphi. \]

We apply the dominated convergence theorem, so that

\[ \frac{1}{\sqrt{R_\mu-r_n}}\int \big|{e}^{\varphi_{r_n}-\varphi_{R_\mu}}-1\big| \big|h_j^{(i)}-\tilde{h}_{j,r_n}^{(i)}\big|\,dm\underset{n\to +\infty}{\longrightarrow}0. \]

In other words, $\alpha =0$, which concludes the proof.

Lemma 5.17 We have

\[ \int ( ({e}^{\varphi_r-\varphi_{R_\mu}}-1)-(\varphi_r-\varphi_{R_\mu}))\,dm=o \big(\sqrt{R_\mu-r}\,\big). \]

Proof. Differentiating the integrand, we obtain

\[ \bigg(\frac{d}{dr}\varphi_r\bigg) ({e}^{\varphi_r-\varphi_{R_\mu}}-1). \]

Fix $R\leq R_\mu$ and let

\[ \overline{ \varphi}_R=\sup_{R\leq r\leq R_\mu}|{e}^{\varphi_r-\varphi_{R_\mu}}-1|. \]

For every $R\leq r\leq R_\mu$, according to Lemma 4.8,

\[ \bigg|\frac{d}{dr} \big[ ({e}^{\varphi_r-\varphi_{R_\mu}}-1)-(\varphi_r-\varphi_{R_\mu}) \big]\bigg|\leq \varphi \overline{\varphi}_R\frac{1}{\sqrt{R_\mu-r}}. \]

Integrating this inequality over $r$ varying between $R$ and $R_\mu$, we obtain

\[ \big| ({e}^{\varphi_R-\varphi_{R_\mu}}-1)-(\varphi_R-\varphi_{R_\mu}) \big|\leq \varphi \overline{\varphi}_R \sqrt{R_\mu-R}. \]

It is thus enough to prove that

\[ \int \varphi\overline{\varphi}_R\,dm\underset{R\to R_\mu}{\longrightarrow}0. \]

Consider a sequence $r_k$ converging to $R_\mu$ such that

\[ \int \varphi\overline{\varphi}_{r_k}\,dm\underset{k\to \infty}{\longrightarrow}\alpha. \]

According to (33), $\int \overline {\varphi }_R\,dm$ converges to zero, so up to taking a subsequence, $\overline {\varphi }_{r_k}$ converges to zero $m$-almost everywhere. Hence, $\varphi \overline {\varphi }_{r_k}$ converges to zero $m$-almost everywhere. In addition, according to (31), $\overline {\varphi }_r$ is uniformly bounded. We apply the dominated convergence theorem, so that

\[ \int \varphi\overline{\varphi}_{r_k}\,dm\underset{R\to R_\mu}{\longrightarrow}0. \]

In other words, $\alpha =0$, which concludes the proof.

We can now prove Proposition 5.1.

Proof. We combine Lemmas 5.16 and 5.17 and (29) to show that

\[ {e}^{\tilde{P}_j(r)}-1=\int (\varphi_r-\varphi_{R_\mu})\,dm_j + o \big( \sqrt{R_\mu-r}\,\big). \]

According to Lemma 5.2, the integral in the right member does not depend on $j$. Choose $j'$ so that the pressure is maximal. Then, for every $j$,

\[ {e}^{\tilde{P}_j(r)}-1={e}^{P(r)}-1+ o \big( \sqrt{R_\mu-r}\,\big), \]

hence,

\[ {e}^{\tilde{P}_j(r)}-1=P(r)+o (P(r))+o \big( \sqrt{R_\mu-r}\,\big). \]

We deduce from Lemma 4.5 and from (23) that $|P(r)|/\sqrt {R_{\mu }-r}$ is bounded away from zero and infinity. Thus,

\begin{align*} {e}^{\tilde{P}_j(r)}-1=P(r)+o (P(r)). \end{align*}

Consequently, for every $j$, $\tilde {P}_j(r)$ converges to zero as $r$ tends to $R_\mu$, so that

\[ \tilde{P}_j(r)\sim {e}^{\tilde{P}_j(r)}-1, \quad r\to R_\mu. \]

This also proves that

\begin{align*} \tilde{P}_j(r)\sim P(r), \quad r\to R_\mu, \end{align*}

which concludes the proof.

6. Asymptotic of the second derivative of the Green function

Our goal here is to prove the following proposition. We still assume that $\mu$ is not spectrally degenerate.

Proposition 6.1 When $r\to R_{\mu }$, we have

\begin{align*} I^{(2)}(r)=\xi I^{(1)}(r)^{3}+O (I^{(1)}(r)^{2}), \end{align*}

for some $\xi >0$.

We introduce some notation. We define for $r< R_{\mu }$ the function

\[ \Phi_r(\gamma)=\frac{\sum_{\gamma'}G(e,\gamma'|r)G(\gamma',\gamma|r)}{G(e,\gamma|r)}. \]

By definition,

\[ I^{(2)}(r)=\sum_{n\geq 0}\sum_{\gamma\in \hat{S}^{n}}H(e,\gamma|r)\Phi_r(\gamma)=H(e,e|r)\sum_{n\geq 0}\mathcal{L}_r^{n}(1_{E_*}\Phi_r\circ \phi) (\emptyset). \]

According to Theorem 3.3, for any $f:\Gamma \cup \partial \hat {\Gamma }\rightarrow \mathbb {R}$ such that $f\circ \phi :\overline {\Sigma }_A\rightarrow \mathbb {R}$ is in $H_{\rho,\beta }$,

\[ \sum_{n\geq 0}\mathcal{L}_r^{n}(1_{E_*}f\circ \phi)(\emptyset)=\sum_{j=1}^{k}\frac{c_f(j,r)}{|\tilde{P}_j(\varphi_r)|}+O(1),r\to R_{\mu}. \]

In addition, according to (24),

\[ I^{(1)}(r)\sim \frac{\xi(r)}{P(r)}, \quad r\to R_\mu. \]

Finally, Proposition 5.1, shows that $|\tilde {P}_j(\varphi _r)|/P(r)$ converges to one. Hence,

(34)\begin{equation} \sum_{n\geq 0}\mathcal{L}_r^{n}(1_{E_*}f\circ \phi)(\emptyset)\sim I^{(1)}(r) c_f, \quad r\to R_\mu, \end{equation}

where $c_f$ only depends on $f$. In other words $ ({1}/{I^{(1)}(r)})\sum _{n\geq 0}\mathcal {L}_r^{n}(1_{E_*}f\circ \phi )(\emptyset )$ converges. However, $\Phi _r\circ \phi \notin H_{\rho,\beta }$. The goal of the next subsection is to transform $\Phi _r$ in order to apply (34).

6.1 A partition of unity

We start with a rough study of $\Phi _r$. Let $\gamma \in \Gamma$ and let $[e,\gamma ]=(e,\gamma _1,\ldots,\gamma _{\hat {d}(e,\gamma )-1},\gamma )$ be a relative geodesic from $e$ to $\gamma$. For every $k\leq \hat {d}(e,\gamma )$, denote by $\Gamma _k$ the set of $\gamma '\in \Gamma$ whose projection on $[e,\gamma ]$ is at $\gamma _k$. If there are more than one such projections, we choose the closest to $\gamma$. Also denote by $\tilde {\gamma }_k$ the projection of $\gamma '$ on the union $\mathcal {H}_k$ of parabolic subgroups containing $\gamma _{k-1}^{-1}\gamma _k$. Lemma 2.5 shows that any relative geodesic from $e$ to $\gamma '$ passes within a bounded distance of $\gamma _{k-1}$. In addition, [Sis13, Lemma 1.13 (1)] shows that the exit point from $\mathcal {H}_k$ of any such relative geodesic is within a bounded distance of $\tilde {\gamma }_k$. Thus, any relative geodesic from $e$ to $\gamma$’ passes first within a bounded distance of $\gamma _{k-1}$ and then within a bounded distance of $\tilde {\gamma }_k$. In addition, any relative geodesic from $\gamma '$ to $\gamma$ passes within a bounded distance of $\tilde {\gamma }_k$, then of $\gamma _k$. Weak relative Ancona inequalities imply that for every $\gamma '\in \Gamma _k$,

\begin{align*} &\frac{G(e,\gamma'|r)G(\gamma',\gamma|r)}{G(e,\gamma|r)}\\ &\quad \asymp\frac{G(e,\gamma_{k-1}|r)G(\gamma_{k-1},\tilde{\gamma}_k|r)G(\tilde{\gamma}_k,\gamma'|r)G(\gamma',\tilde{\gamma}_k|r)G(\tilde{\gamma}_k,\gamma_k|r)G(\gamma_k,\gamma|r)}{G(e,\gamma_{k-1}|r)G(\gamma_{k-1},\gamma_k|r)G(\gamma_{k},\gamma|r)}. \end{align*}

We thus obtain that

\[ \frac{G(e,\gamma'|r)G(\gamma',\gamma|r)}{G(e,\gamma|r)}\asymp \frac{G(\gamma_{k-1},\tilde{\gamma}_k|r)G(\tilde{\gamma}_k,\gamma_k|r)}{G(\gamma_{k-1},\gamma_k|r)}G(\tilde{\gamma}_k,\gamma'|r)G(\gamma',\tilde{\gamma}_k|r). \]

We then sum over all $\gamma '\in \Gamma _k$. Let $\mathcal {H}_{\gamma _k}$ be the union of all parabolic subgroups in $\Omega _0$ containing $\gamma _{k-1}^{-1}\gamma _k$. Then $\gamma _{k-1}^{-1}\tilde {\gamma }_k\in \mathcal {H}_{\gamma _k}$. We can decompose the sum over $\gamma '\in \Gamma _k$ according to the projection on $\tilde {\gamma }_k\in \mathcal {H}_{\gamma _k}$. Bounding $\sum G(\tilde {\gamma }_k,\gamma '|r)G(\gamma ',\tilde {\gamma }_k|r)$ by $I^{(1)}(r)$, where $\tilde {\gamma }_k$ is fixed and the sum is over all $\gamma '$ projecting on $\tilde {\gamma }_k$, we finally obtain

\[ \sum_{\gamma'\in \Gamma_k}\frac{G(e,\gamma'|r)G(\gamma',\gamma|r)}{G(e,\gamma|r)}\lesssim I_1(r) \sum_{\tilde{\gamma}_k\in \mathcal{H}_{\gamma_k}}\frac{G(\gamma_{k-1},\tilde{\gamma}_k|r)G(\tilde{\gamma}_k,\gamma_k|r)}{G(\gamma_{k-1},\gamma_k|r)}. \]

We then construct a function $\Upsilon _r$ as follows. For every $\gamma \in \Gamma$, we choose a relative geodesic from $e$ to $\gamma$, using the automaton $\mathcal {G}$. Let $\gamma _1$ be the first point after $e$ on this relative geodesic. Note that $\gamma _1$ coincides with the first increment $\sigma _1$ on this relative geodesic. In general, we denote by $\sigma _k=\gamma _{k-1}^{-1}\gamma _k$ the $k$th increment. In addition, let $\mathcal {H}_{\sigma _1}$ be the union of all parabolic subgroups in $\Omega _0$ containing $\sigma _1$. We set

\[ \Upsilon_r(\gamma)=\sum_{\sigma\in \mathcal{H}_{\sigma_1}}\frac{G(e,\sigma|r)G(\sigma,\sigma_1|r)}{G(e,\sigma_1|r)}. \]

This function $\Upsilon _r$ only depends on the first element of the relative geodesic $[e,\gamma ]$. In other words, the function $\Upsilon _r\circ \phi (x)$ only depends on the first symbol of $x\in \overline {\Sigma }_A$. The estimate above yields

(35)\begin{equation} \Phi_r(\gamma)\lesssim I_1(r)\sum_{k=0}^{\hat{d}(e,\gamma)-1}\Upsilon_r \circ T^{k} ([e,\gamma]), \end{equation}

where $T$ is the left shift on relative geodesic, that is, $T([e,\gamma ])=(e,\gamma _1^{-1}\gamma _2,\ldots,\gamma _1^{-1}\gamma )$. Note that $\Upsilon _r$ is not bounded. Indeed, assuming that $\sigma _1$ is only in one parabolic subgroup $\mathcal {H}_1$ to simplify, then $\Upsilon _r(\gamma )$ is essentially given by

\[ \sum_{\sigma\in \mathcal{H}_{\sigma_1}}\frac{G^{(1)}_{1,r}(e,\sigma_1)}{G(e,\sigma_1|r)}. \]

This quantity is not bounded.

However, to prove Proposition 6.1, we need to estimate $\mathcal {L}_r(\Upsilon _r\circ \phi )(x)$. Recall that $X_x^{1}$ is the set of symbols $\sigma$ that can precede $x$ in $\Sigma _A$. Seeing $x$ and $\sigma$ as elements of $\Gamma$,

\[ \mathcal{L}_r(\Upsilon_r\circ \phi)(x)=\sum_{\sigma\in X_{\gamma}^{1}}\frac{H(e,\sigma x|r)}{H(e,x|r)}\sum_{\sigma '\in \mathcal{H}_{\sigma}}\frac{G(e,\sigma'|r)G(\sigma',\sigma|r)}{G(e,\sigma|r)}. \]

Therefore, weak relative Ancona inequalities show that

\[ \mathcal{L}_r(\Upsilon_r\circ \phi)(x)\lesssim \sum_{j}\sum_{\sigma,\sigma'\in \mathcal{H}_j}G(e,\sigma'|r)G(\sigma',\sigma|r)G(\sigma,e|r). \]

We rewrite this as

\begin{align*} \mathcal{L}_r(\Upsilon_r\circ \phi)(x)\lesssim \sum_{j} I_j^{(2)}(r). \end{align*}

As $\mu$ is not spectrally degenerate, we obtain

(36)\begin{equation} \mathcal{L}_r(\Upsilon_r\circ \phi)(x)\lesssim 1. \end{equation}

We only gave a rough estimate. To obtain a precise asymptotic, we replace the decomposition of $\Gamma$ into subsets $\Gamma _k$ as previously by a continuous decomposition, using a partition of unity. We construct such a partition of unity adapting the arguments of [GL13, Lemma 8.5].

We first introduce the following terminology. Consider a relative geodesic $\alpha$ that we write $\alpha =(\alpha _{-m},\ldots,\alpha _{-1},\alpha _0,\alpha _1,\ldots,\alpha _n)$. Let $\hat {l}(\alpha )=\hat {d}(\alpha _{-m},\alpha _n)$ be the relative length of $\alpha$ (here $n+m$) and let $l(\alpha )$ be its total length, defined by

\[ l(\alpha)=\sum_{k=-m+1}^{n}d(\alpha_{k-1},\alpha_k). \]

Note that if $\alpha,\alpha '$ are two relative geodesic with the same endpoints, we do not have $l(\alpha )=l(\alpha ')$ in general. However, the distance formula given by [Sis13, Theorem 3.1] shows that

\[ \frac{1}{\lambda_1}d(\alpha_{-m},\alpha_n)-c_1\leq l(\alpha)\leq \lambda_1 d(\alpha_{-m},\alpha_n)+c_1 \]

and so

\begin{align*} \frac{1}{\lambda_2}l(\alpha)-c_2\leq l(\alpha')\leq \lambda_2l(\alpha)+c_2. \end{align*}

Our goal is to construct a partition of unity $\kappa _{\alpha }$ associated to such a relative geodesic $\alpha$. Write $\alpha =(\alpha _{-m},\ldots,\alpha _{-1},\alpha _0,\alpha _1,\ldots,\alpha _n)$ and suppose that $\alpha _0=e$. To simplify, let $\alpha _-$ and $\alpha _+$ be the endpoints of $\alpha$, that is, $\alpha _-=\alpha _{-m}$ and $\alpha _+=\alpha _n$. Denote by $\alpha _l$ the sub-relative geodesic of $\alpha$ from $\alpha _{-}$ to $e$ and by $\alpha _r$ the sub-relative geodesic from $\alpha _1$ to $\alpha _+$.

Consider two constants $K_1$ and $K_2$ that we choose later. Assume that $l(\alpha _l)\geq 2K_1$ and $l(\alpha _r)\geq 2K_1$. Denote by $A(K_1)$ the set of $\gamma \in \Gamma$ such that:

1. (i) there either exists a relative geodesic from $\gamma$ to $\alpha _+$ whose distance from $\alpha _1$ is at least $K_1$; or

2. (ii) there exists a relative geodesic from $\alpha _-$ to $\gamma$ whose distance from $e$ is at least $K_1$.

Also denote by $B(K_2)$ the set of $\gamma \in \Gamma$ such that:

1. (i) any relative geodesic from $\gamma$ to $\alpha _+$ passes within $K_2$ of $\alpha _1$;

2. (ii) and any relative geodesic from $\alpha _-$ to $\gamma$ passes within $K_2$ of $e$.

In other words, $A(K_1)=B(K_1)^{c}$. Note that $B(K_2)$ is not empty and that $A(K_1)$ is not empty, for $l(\alpha _l)\geq 2K_1$ and $l(\alpha _r)\geq 2K_1$.

The following is a simple consequence of the fact that triangles are thin along transition points [DG20, Lemme 2.4] and that transition points are within a bounded distance of points on a relative geodesic [Hru10, Proposition 8.13].

Lemma 6.2 For fixed $K_2$, if $K_1$ is large enough, then the closures of $A(K_1)$ and $B(K_2)$ in the Bowditch compactification $\overline {\Gamma }_B$ are disjoint.

As $\overline {\Gamma }_B$ is compact, there exists a continuous function $f_{\alpha }$ on $\overline {\Gamma }_B$ taking values in $[0,1]$, that vanishes on $A(K_1)$ and which is equal to one on $B(K_2)$.

We now finish the construction of the partition of unity associated with $\alpha$. Let $n_1=n_1(\alpha )$ be the largest integer such that translating $n_1$ times the relative geodesic $\alpha$, on the right, the length on the left is still at least $K_1$. Formally,

(37)\begin{equation} n_1(\alpha)=\sup \{k\geq 0, l ((T^{-k}\alpha )_l)\geq K_1\}. \end{equation}

Similarly, let $n_2=n_2(\alpha )$ be the largest integer such that translating $n_2$ times $\alpha$ on the left, the length on the right is at least $K_1$. That is,

(38)\begin{align} n_2(\alpha)=\sup \{k\geq 0, l ((T^{k}\alpha )_r)\geq K_1\}. \end{align}

Let $A'(K_1)$ be the set of $\gamma$ such that for every $k\in [-n_1,n_2-1]$:

1. (i) there either exists a relative geodesic from $\gamma$ to $\alpha _+$ whose distance from $\alpha _{k+1}$ is at least $K_1$; or

2. (ii) there exists a relative geodesic from $\alpha _-$ to $\gamma$ whose distance from $\alpha _k$ is at least $K_1$.

Let $B'(K_2)$ be the set of $\gamma$ such that there exists $k\in [-n_1,n_2-1]$ such that:

1. (i) any relative geodesic from $\gamma$ to $\alpha _+$ passes within $K_2$ of $\alpha _{k+1}$;

2. (ii) and any relative geodesic from $\alpha _-$ to $\gamma$ passes within $K_2$ of $\alpha _k$.

Again, if $K_1$ is large enough, the closures of $A'(K_1)$ and $B'(K_2)$ in the Bowditch compactification are disjoint.

For technical reasons, we further need to truncate relative geodesics. Letting $\beta$ be any relative geodesic with $\beta _0=e$, denote by $\beta _{(2K_1)}$ the shortest sub-relative geodesic of $\beta$ such that $l((\beta _{(2K_1)})_l)\geq 2K_1$ and $l((\beta _{(2K_1)})_r)\geq 2K_1$. In other words, we truncate $\beta$ on the left (respectively, on the right) as soon as the length on the left (respectively, on the right) is at least $2K_1$. Note that if $K_1$ is large enough, whenever $\gamma \in B'(K_2)$, we have

(39)\begin{equation} \Sigma=\sum_{k=-n_1}^{n_2}f_{(T^{k}\alpha)_{(2K_1)}}(\alpha_k^{-1}\gamma)\geq 1. \end{equation}

Thus, there exists a function $g_{\alpha }$, which is continuous on the Bowditch compactification, which is equal to one on $A'(K_1)$, which is equal to the sum $\Sigma$ above on $B'(K_2)$ and whose values are between one and $\Sigma$. We set

\[ \kappa_{\alpha}=\frac{f_{\alpha_{(2K_1)}}}{g_{\alpha}}. \]

Denote by $\alpha '_+$ the right endpoint of $\alpha _{(2K_1)}$ and by $\alpha '_-$ the left endpoint of $\alpha _{(2K_1)}$. According to Lemma 2.5, the fact that a relative geodesic from $\gamma$ to $\alpha '_+$ passes within $K_2$ of $\alpha _1$ and a relative geodesic from $\alpha '_-$ to $\gamma$ passes within $K_2$ of $\alpha _0$ means that $\gamma$ projects on $\alpha$ approximately between $\alpha _0=e$ and $\alpha _1$. More precisely, the projections on $\alpha _{(2K_1)}$ which are the closest to $\alpha '_+$ and to $\alpha '_-$ are within a bounded distance of $\alpha _1$ and $e$, respectively. We deduce that the sum $\Sigma$ is bounded by some constant that only depends on $K_2$ and $K_1$. Roughly speaking, $\kappa _{\alpha }$ is a continuous function whose successive images by the shift mimics the decomposition of $\Gamma$ into the subsets $\Gamma _k$.

Let $\alpha =(\alpha _{-k},\ldots,\alpha _0,\alpha _1,\ldots,\alpha _l)$ be a relative geodesic, with $\alpha _0=e$. Whenever $l(\alpha _l)<2K_1$ or $l(\alpha _r)<2K_1$, we set $\Psi _r(\alpha )=0$. Otherwise, we set

(40)\begin{equation} \Psi_r(\alpha)=\frac{1}{I^{(1)}(r)}\sum_{\gamma\in \Gamma}\kappa_{\alpha}(\gamma)\frac{G(\alpha_-,\gamma|r)G(\gamma,\alpha_+|r)}{G(\alpha_-,\alpha_+|r)}. \end{equation}

This defines a function $\Psi _r$ on the set of relative geodesics $\alpha$ with $\alpha _0=e$.

According to the previous discussion, $\kappa _{\alpha }(\gamma )\neq 0$ can only happen if the projection of $\gamma$ on $\alpha _{(2K_1)}$ lies between $e$ and $\alpha _1$, up to a bounded distance. Choosing $K_1$ large enough, the same is true replacing $\alpha _{(2K_1)}$ with $\alpha$. Indeed, let $\alpha _-$ and $\alpha _+$ be the endpoints of $\alpha$ and let $\alpha '_-$ and $\alpha '_+$ the endpoints of $\alpha _{(2K_1)}$. If $K_1$ is large enough, then a relative geodesic from $\gamma$ to $\alpha '_-$ passes within a bounded distance of $e$ if and only if a relative geodesic from $\gamma$ to $\alpha _-$ also passes within a bounded distance of $e$. Similarly, a relative geodesic from $\gamma$ to $\alpha _+$ passes within a bounded distance of $\alpha _1$ if and only if the same is true for a relative geodesic from $\gamma$ to $\alpha '_+$. Weak relative Ancona inequalities thus show that for any $k$ large enough so that $\Psi _r(T^{k}[e,\gamma ])\neq 0$,

(41)\begin{equation} \Psi_r(T^{k}[e,\gamma])\asymp \Upsilon_r(T^{k}\gamma). \end{equation}

Hence, the function $\Psi _r$ will replace the function $\Upsilon _r$ in (35) to obtain a more accurate estimate.

Proposition 6.3 Let $\gamma \in \Gamma$ and let $\alpha _\gamma$ be the relative geodesic from $e$ to $\gamma$ given by the automaton $\mathcal {G}$. Then,

\[ \Phi_r(\gamma)=I^{(1)}(r)\sum_{k=0}^{\hat{d}(e,\gamma)-1}\Psi_r(T^{k}\alpha_\gamma)+O (I^{(1)}(r)). \]

Proof. Consider $\gamma \in \Gamma$. To simplify things, denote by $\alpha$ the relative geodesic from $e$ to $\gamma$. Let $m_1$ be the smallest integer such that $l ((T^{m_1}\alpha )_l)\geq K_1$ and $m_2$ the largest integer such that $l ((T^{m_2}\alpha )_r)\geq K_1$. By the definition of $\Psi _r$,

\begin{align*} \sum_{k=0}^{\hat{d}(e,\gamma)-1}\Psi_r(T^{k}\alpha)&=\sum_{k=m_1}^{m_2}\Psi_r(T^{k}\alpha)\\ &=\frac{1}{I^{(1)}(r)}\sum_{k=m_1}^{m_2}\sum_{\gamma'\in \Gamma}\kappa_{(T^{k}\alpha)}(\gamma')\frac{G(\alpha_k^{-1},\gamma'|r)G(\gamma',\alpha_k^{-1}\gamma|r)}{G(\alpha_k^{-1},\alpha_k^{-1}\gamma|r)}. \end{align*}

Translating on the left by $\alpha _k^{-1}$ and replacing $\gamma '$ with $\alpha _k^{-1}\gamma '$ in the sum, we obtain

\[ \sum_{k=0}^{\hat{d}(e,\gamma)-1}\Psi_r(T^{k}\alpha)=\frac{1}{I^{(1)}(r)}\sum_{\gamma'\in \Gamma}\bigg( \sum_{k=m_1}^{m_2}\kappa_{(T^{k}\alpha)}(\alpha_k^{-1}\gamma')\bigg) \frac{G(e,\gamma'|r)G(\gamma',\gamma|r)}{G(e,\gamma|r)}. \]

Recall that

\[ \Phi_r(\gamma)=\sum_{\gamma'\in \Gamma} \frac{G(e,\gamma'|r)G(\gamma',\gamma|r)}{G(e,\gamma|r)}. \]

We are thus looking for the elements $\gamma '\in \Gamma$ such that

(42)\begin{equation} \sum_{k=m_1}^{m_2}\kappa_{(T^{k}\alpha)}(\alpha_k^{-1}\gamma')\neq 1. \end{equation}

Suppose there exists $i\in [m_1,m_2-1]$ such that any relative geodesic from $\gamma '$ to $\gamma$ passes within $K_2$ of $\alpha _{i+1}$ and that any relative geodesic from $e$ to $\gamma '$ passes within $K_2$ of $\alpha _i$. Fix $k\in [m_1,m_2-1]$ and consider the translated relative geodesic $T^{k}\alpha$. Then, any relative geodesic from $\alpha _k^{-1}\gamma '$ to the right endpoint of $T^{k}\alpha$ passes within $K_2$ of $\alpha _k^{-1}\alpha _{i+1}$ and any relative geodesic from the left endpoint of $T^{k}\alpha$ to $\alpha _k^{-1}\gamma '$ passes within $K_2$ of $\alpha _k^{-1}\alpha _i$.

In particular, $\alpha _k^{-1}\gamma '\in B'(K_2)$, where $B'(K_2)$ is the set constructed as above, using the relative geodesic $T^{k}\alpha$. Hence,

\[ g_{T^{k}\alpha}(\alpha_k^{-1}\gamma')=\sum_{j=-n_1}^{n_2}f_{(T^{j}(T^{k}\alpha))_{(2K_1)}}((T^{k}\alpha)_j^{-1}\gamma'). \]

Note that $(T^{k}\alpha )_j=\alpha _{k+j}$, so that

\[ g_{T^{k}\alpha}(\alpha_k^{-1}\gamma')=\sum_{j=m_1-k}^{m_2-k}f_{(T^{k+j}\alpha)_{(2K_1)}}(\alpha_{k+j}^{-1}\gamma') =\sum_{j=m_1}^{m_2}f_{(T^{j}\alpha)_{(2K_1)}}(\alpha_j^{-1}\gamma'). \]

In particular, we see that

\[ \sum_{k=m_1}^{m_2}\kappa_{T^{k}\alpha}(\alpha_k^{-1}\gamma')= 1. \]

We proved that whenever (42) holds, then for every $i\in [m_1,m_2-1]$, either a relative geodesic from $\gamma '$ to $\gamma$ remains at a distance at least $K_2$ from $\alpha _{i+1}$ or a relative geodesic from $e$ to $\gamma '$ remains at distance at least $K_2$ from $\alpha _i$. We again use Lemma 2.5. Let $\alpha _{k+1}$ be the projection of $\gamma '$ the closest to $\gamma$ on $\alpha$. If $K_2$ was chosen large enough, then we necessarily have $k\geq m_2$ or $k\leq m_1-1$. Also let $\mathcal {H}_{\alpha _k}$ be the union of parabolic subgroups in $\Omega _0$ containing $\alpha _{k}^{-1}\alpha _{k+1}$ and let $\tilde {\alpha }_k$ be the projection of $\gamma '$ on $\mathcal {H}_{\alpha _k}$. According to [Sis13, Lemma 1.13(1)], the exit point from $\mathcal {H}_{\alpha _k}$ of any relative geodesic from $e$ to $\gamma '$ is within a bounded distance of $\tilde {\alpha }_k$. Thus, any such relative geodesic passes first within a bounded distance of $\alpha _k$ and then within a bounded distance of $\tilde {\alpha }_k$. Similarly, any relative geodesic from $\gamma '$ to $\gamma$ passes first within a bounded distance of $\tilde {\alpha }_k$ and then within a bounded distance of $\alpha _{k+1}$. Weak relative Ancona inequalities yield

\[ \frac{G(e,\gamma'|r)G(\gamma',\gamma|r)}{G(e,\gamma|r)}\lesssim I^{(1)}(r) \frac{G(\alpha_k,\tilde{\alpha}_k|r)G(\tilde{\alpha}_k,\alpha_{k+1}|r)}{G(\alpha_k,\alpha_{k+1}|r)}. \]

Also recall that (39) is uniformly bounded. Consequently, we have

\begin{align*} \bigg|\Phi_r(\gamma)-I^{(1)}(r)\sum_{k=0}^{\hat{d}(e,\gamma)-1}\Psi_r(T^{k}\alpha)\bigg| &\lesssim \ I^{(1)}(r)\sum_{0\leq k< m_1}\sum_{\sigma\in \mathcal{H}_{\alpha_k}}\frac{G(\alpha_k,\sigma|r)G(\sigma,\alpha_{k+1}|r)}{G(\alpha_k,\alpha_{k+1}|r)}\\ &\quad +I^{(1)}(r)\sum_{m_2\leq k\leq \hat{d}(e,\gamma)}\sum_{\sigma\in \mathcal{H}_{\alpha_k}}\frac{G(\alpha_k,\sigma|r)G(\sigma,\alpha_{k+1}|r)}{G(\alpha_k,\alpha_{k+1}|r)}. \end{align*}

By definition, $m_1$ and $\hat {d}(e,\gamma )-m_2$ are bounded by $K_1$ and $d(\alpha _{k},\alpha _{k+1})\leq K_1$. In particular,

\[ \sum_{\sigma\in \mathcal{H}_{\alpha_k}}\frac{G(\alpha_k,\sigma|r)G(\sigma,\alpha_{k+1}|r)}{G(\alpha_k,\alpha_{k+1}|r)} \]

is uniformly bounded. We thus have

\[ \Phi_r(\gamma)-I^{(1)}(r)\sum_{k=0}^{\hat{d}(e,\gamma)-1}\Psi_r(T^{k}\alpha)\lesssim I^{(1)}(r), \]

which concludes the proof.

6.2 Truncating $\Psi _r$

We say that a function $f$ defined on relative geodesic $\alpha$ satisfying $\alpha _0=e$ is locally Hölder if for every $n\geq 1$, as soon as $\alpha$ and $\alpha '$ coincide in the relative ball (for the distance $\hat {d}$) of center $e$ and radius $n$, $|f(\alpha )-f(\alpha ')|\leq C\rho ^{n}$, for some $C\geq 0$ and some $0<\rho <1$.

A similar function $\Psi _r$ is defined in [Gou14] for hyperbolic groups. It is proved there that for every $r$, $\Psi _r$ is continuous, locally Hölder and that $\Psi _r$ uniformly converges to a locally Hölder function $\Psi _{R_\mu }$, as $r$ tends to $R_\mu$. However, in our situation, such properties do not hold, so we cannot directly apply the strategy in [Gou14]. We are going instead to truncate $\Psi _r$ such that our new function only depends on a finite number of symbols.

Precisely, fix a constant $N\in \mathbb {N}$ and denote by $\alpha ^{(N)}$ the relative geodesic $\alpha$ restricted to $[-N,N]$. If $\hat {d}(e,\alpha _-)\leq N$ and $\hat {d}(e,\alpha _+)\leq N$, then $\alpha ^{(N)}=\alpha$. We set $\Psi _r^{(N)}(\alpha )=\Psi _r(\alpha ^{(N)})$. Let us fix another constant $D$ and define $\Psi _r^{(D,N)}(\alpha )$ as follows. If one of the increments $\alpha _{k-1}^{-1}\alpha _k$ of $\alpha$ satisfies $d(\alpha _{k-1}^{-1}\alpha _k)\geq D$, for some $k$ between $-N+1$ and $N$, then we set $\Psi _r^{(D,N)}(\alpha )=0$. Otherwise, we set $\Psi _r^{(D,N)}(\alpha )=\Psi _r^{(N)}(\alpha )$. To simplify notation, we use the following convention. Whenever $\hat {d}(e,\alpha _-)\leq N$, we set $\alpha _{-N}=\alpha _-$ and, similarly, whenever $\hat {d}(e,\alpha _+)\leq N$, we set $\alpha _N=\alpha _+$.

Our goal is to prove estimates that will allow us to replace $\Psi _r$ with $\Psi _r^{(D,N)}$. We start with the following lemma.

Lemma 6.4 If $N$ is large enough, depending on $K_1$ and $K_2$, then for every relative geodesic $\alpha$, we have $\kappa _{\alpha }=\kappa _{\alpha ^{(N)}}$.

Proof. First note that if $N\geq 2K_1$, $\alpha _{(2K_1)}^{(N)}=\alpha ^{(2K_1)}$, so that $f_{\alpha _{(2K_1)}}(\gamma )=0$ if and only if $f_{\alpha _{(2K_1)}^{(N)}}(\gamma )=0$. In particular, $\kappa _{\alpha }(\gamma )=0$ if and only if $\kappa _{\alpha ^{(N)}}(\gamma )=0$. Hence, we can assume that $f_{\alpha _{(2K_1)}}(\gamma )\neq 0$. We want to prove that if $N$ is large enough, then the sum $\Sigma$ defined by (39) is the same for $\alpha$ and for $\alpha ^{(N)}$. By the definition of $f$, the fact that $f_{\alpha _{(2K_1)}}(\gamma )\neq 0$ implies that any relative geodesic from $\gamma$ to the right endpoint of $\alpha _{(2K_1)}$ passes within a bounded distance of $\alpha _1$ and any relative geodesic from $\gamma$ to the left endpoint of $\alpha _{(2K_1)}$ passes within a bounded distance of $e$. Thus, the number of $k$ in the sum defining $\Sigma$ such that $f_{(T^{k}\alpha )_{(2K_1)}}(\alpha _k^{-1}\gamma )\neq 0$ is finite, with a bound depending only on $K_1$ and $K_2$. If $N$ is large enough, the same holds replacing $\alpha$ with $\alpha ^{(N)}$ and for any such $k$, $f_{(T^{k}\alpha )_{(2K_1)}}(\alpha _k^{-1}\gamma )=f_{(T^{k}\alpha ^{(N)})_{(2K_1)}}(\alpha _k^{-1}\gamma )$. This concludes the proof.

Thus,

\begin{align*} \Psi_r(\alpha^{(N)})=\frac{1}{I^{(1)}(r)}\sum_{\gamma\in \Gamma}\kappa_{\alpha}(\gamma)\frac{G(\alpha^{(N)}_-,\gamma|r)G(\gamma,\alpha^{(N)}_+|r)}{G(\alpha^{(N)}_-,\alpha^{(N)}_+|r)}. \end{align*}

In other words, when replacing $\Psi _r(\alpha )$ with $\Psi _r(\alpha ^{(N)})$, we do not have to replace $\kappa _{\alpha }$ with $\kappa _{\alpha ^{(N)}}$. This will be very convenient in the following.

Proposition 6.5 Let $\epsilon >0$. Then for $N$ large enough and for $D$ large enough (depending on $N$), for every $r\leq R_\mu$ and for every $n$,

\begin{align*} &\bigg|\sum_{k=0}^{n-1}\sum_{\gamma\in \hat{S}^{n}}H(e,\gamma|r) (\Psi_r \circ T^{k}([e,\gamma])-\Psi_r^{(D,N)}\circ T^{k}([e,\gamma]))\bigg|\\ &\quad\leq \epsilon \sum_{k=0}^{n-1}\sum_{\gamma\in \hat{S}^{n}}H(e,\gamma|r) \Psi_r \circ T^{k}([e,\gamma]). \end{align*}

Proof. We first show that we can replace $\Psi _r$ by $\Psi _r^{(N)}$, that is, we prove that if $N$ is large enough, then

(43)\begin{align} &\bigg|\sum_{k=0}^{n-1}\sum_{\gamma\in \hat{S}^{n}}H(e,\gamma|r) (\Psi_r \circ T^{k}([e,\gamma])-\Psi_r^{(N)}\circ T^{k}([e,\gamma]))\bigg|\nonumber\\ &\quad\lesssim \epsilon \sum_{k=0}^{n-1}\sum_{\gamma\in \hat{S}^{n}}H(e,\gamma|r) \Psi_r \circ T^{k}([e,\gamma]). \end{align}

Let $n$ and let $k\leq n-1$. Set $\alpha =T^{k}([e,\gamma ])$. Then, according to Lemma 6.4,

\begin{align*} &\sum_{\gamma\in \hat{S}^{n}}H(e,\gamma|r) (\Psi_r \circ T^{k}([e,\gamma])-\Psi_r^{(N)}\circ T^{k}([e,\gamma]))\\ &\quad =\frac{1}{I_1(r)}\sum_{\gamma\in \hat{S}^{n}}H(e,\gamma|r)\\ &\qquad \times\sum_{\gamma'\in \Gamma}\kappa_{\alpha}(\gamma')\bigg(\frac{G(\alpha_-,\gamma'|r)G(\gamma',\alpha_+|r)}{G(\alpha_-,\alpha_+|r)}-\frac{G(\alpha_{-N},\gamma'|r) G(\gamma',\alpha_N|r)}{G(\alpha_{-N},\alpha_N|r)}\bigg). \end{align*}

We rewrite

\begin{align*} &\bigg|\frac{G(\alpha_-,\gamma'|r)G(\gamma',\alpha_+|r)}{G(\alpha_-,\alpha_+|r)}-\frac{G(\alpha_{-N},\gamma'|r)G(\gamma',\alpha_N|r)}{G(\alpha_{-N},\alpha_N|r)}\bigg|\\ &\quad =\bigg(\frac{G(\alpha_{-},\gamma'|r)G(\gamma',\alpha_+|r)}{G(\alpha_{-},\alpha_+|r)}\bigg) \bigg|1-\frac{G(\alpha_{-N},\gamma'|r)G(\gamma',\alpha_N|r)G(\alpha_{-},\alpha_+|r)}{G(\alpha_{-N},\alpha_N|r)G(\alpha_-,\gamma'|r)G(\gamma',\alpha_+|r)}\bigg| \end{align*}

and

\begin{align*} &\bigg|1-\frac{G(\alpha_{-N},\gamma'|r)G(\gamma',\alpha_N|r)G(\alpha_{-},\alpha_+|r)}{G(\alpha_{-N},\alpha_N|r)G(\alpha_-,\gamma'|r)G(\gamma',\alpha_+|r)}\bigg|\\ &\quad = \bigg|1-\frac{G(\alpha_{-N},\gamma'|r)G(\alpha_{-},\alpha_+|r)}{G(\alpha_{-N},\alpha_+|r)G(\alpha_-,\gamma'|r)} \frac{G(\alpha_{-N},\alpha_+|r)G(\gamma',\alpha_N|r)}{G(\alpha_{-N},\alpha_N|r)G(\gamma',\alpha_+|r)}\bigg|. \end{align*}

We now show that

(44)\begin{equation} \bigg|1-\frac{G(\alpha_{-N},\gamma'|r)G(\alpha_{-},\alpha_+|r)}{G(\alpha_{-N},\alpha_+|r)G(\alpha_-,\gamma'|r)} \frac{G(\alpha_{-N},\alpha_+|r)G(\gamma',\alpha_N|r)}{G(\alpha_{-N},\alpha_N|r)G(\gamma',\alpha_+|r)}\bigg| \end{equation}

is arbitrary small when $N$ is large enough. Let

\[ u_N(\gamma')=\frac{G(\alpha_{-N},\gamma'|r)G(\alpha_{-},\alpha_+|r)}{G(\alpha_{-N},\alpha_+|r)G(\alpha_-,\gamma'|r)} \]

and

\[ v_N(\gamma')=\frac{G(\alpha_{-N},\alpha_+|r)G(\gamma',\alpha_N|r)}{G(\alpha_{-N},\alpha_N|r)G(\gamma',\alpha_+|r)}, \]

so that (44) can be written as $|1-u_N(\gamma ')v_N(\gamma ')|$. Assume that $\kappa _{\alpha }(\gamma ')\neq 0$. Then $f_{\alpha _{(2K_1)}}(\gamma ')\neq 0$ and so any relative geodesic from $\gamma '$ to the left endpoint of $\alpha _{(2K_1)}$ passes within $K_1$ of $e$. This implies that relative geodesics from $\alpha _{-N}$ to $\gamma '$ and from $\alpha _-$ to $\alpha _+$ fellow-travel for a time at least $N'$, where $N'$ tends to infinity as $N$ tends to infinity. Strong relative Ancona inequalities show that

\[ \big|1-u_N(\gamma')\big|\leq C\rho^{N'}. \]

Similarly, one can prove that

\[ \big|1-v_N(\gamma')\big|\leq C\rho^{N'}. \]

In addition, weak relative Ancona inequalities imply that $v_N(\gamma ')$ is bounded. This yields

\[ \big|1-u_N(\gamma')v_N(\gamma')\big|\leq v_N(\gamma')|1-u_N(\gamma')|+|1-v_N(\gamma')|\leq C'\rho^{N'}. \]

Hence,

\begin{align*} &\bigg|\sum_{\gamma\in \hat{S}^{n}}H(e,\gamma|r) (\Psi_r \circ T^{k}([e,\gamma])-\Psi_r^{(N)}\circ T^{k}([e,\gamma]))\bigg|\\ &\quad \leq C'\rho^{N'}\frac{1}{I^{(1)}(r)}\sum_{\gamma\in \hat{S}^{n}}H(e,\gamma|r)\sum_{\gamma'\in \Gamma}\kappa_{\alpha}(\gamma') \frac{G(\alpha_-,\gamma'|r)G(\gamma',\alpha_+|r)}{G(\alpha_-,\alpha_+|r)}\\ &\quad =C'\rho^{N'}\sum_{\gamma\in \hat{S}^{n}}H(e,\gamma|r)\Psi_r \circ T^{k}([e,\gamma]). \end{align*}

Thus, if $N$ is large enough, then (43) holds.

Let us compare $\Psi _r^{(D,N)} \circ T^{k}([e,\gamma ])$ and $\Psi _r^{(N)}\circ T^{k}([e,\gamma ])$ now. Let $\alpha =T^{k}[e,\gamma ]$. Then, $\Psi _r^{(D,N)} \circ T^{k}([e,\gamma ])-\Psi _r^{(N)}\circ T^{k}([e,\gamma ])$ is non-zero only for elements $\gamma$ such that there exists $j$ between $-N+1$ and $N$ such that $d(\alpha _{j-1},\alpha _{j})\geq D$. Denote by $\gamma _0=e,\gamma _1,\ldots,\gamma _n=\gamma$ successive elements on $[e,\gamma ]$, so that $\alpha _{j}=\gamma _k^{-1}\gamma _{j+k}$. Hence, $\Psi _r^{(D,N)} \circ T^{k}([e,\gamma ])-\Psi _r^{(N)}\circ T^{k}([e,\gamma ])$ is non-zero only for elements $\gamma$ such that there exists $j$ between $-N+k+1$ and $N+k$ such that $d(\gamma _{j-1},\gamma _{j})\geq D$.

Let $\hat {S}^{n}_{\geq D}$ be the set of $\gamma \in \hat {S}^{n}$ such that one of the increments of the relative geodesic $[e,\gamma ]$ between $-N+k+1$ and $N+k$ has length at least $D$. In addition, for a fixed $j$ between $-N+k+1$ and $N+k$, let $\hat {S}^{n,j}_{\geq D}$ be the subset of $\hat {S}^{n}_{\geq D}$ of elements $\gamma$ such that the first such increment is at step $j$. Then,

\begin{align*} &\sum_{\gamma\in \hat{S}^{n}}H(e,\gamma|r) (\Psi_r^{(N)} \circ T^{k}([e,\gamma])-\Psi_r^{(D,N)}\circ T^{k}([e,\gamma]))\\ &\quad =\frac{1}{I^{(1)}(r)}\sum_{\gamma\in \hat{S}^{n}_{\geq D}}H(e,\gamma|r)\sum_{\gamma'\in \Gamma}\kappa_{\alpha}(\gamma')\frac{G(\alpha_{-N},\gamma'|r)G(\gamma',\alpha_N|r)}{G(\alpha_{-N},\alpha_N|r)}\\ &\quad =\frac{1}{I^{(1)}(r)}\sum_{j=-N+k+1}^{N+k}\sum_{\gamma\in \hat{S}^{n,j}_{\geq D}}H(e,\gamma|r)\sum_{\gamma'\in \Gamma}\kappa_{\alpha}(\gamma')\frac{G(\alpha_{-N},\gamma'|r)G(\gamma',\alpha_N|r)}{G(\alpha_{-N},\alpha_N|r)}. \end{align*}

Fix $j$. For $\gamma \in \hat {S}^{n}$, we write $\gamma =\gamma _1\sigma \gamma _2$, where $\gamma _1\in \hat {S}^{j-1}$, $\sigma$ is in a factor $\mathcal {H}_k'$ and $\gamma '\in \hat {S}^{n-j}$. If $\gamma \in \hat {S}^{n,j}_{\geq D}$, then $d(e,\sigma )\geq D$. Weak relative Ancona inequalities show that

\[ H(e,\gamma|r)\lesssim H(e,\gamma_1|r)H(e,\sigma|r)H(e,\gamma_2|r). \]

In addition, using (41), we can replace $\Psi _r$ with $\Upsilon _r$ in the right member of the sum above. We obtain

(45)\begin{align} &\sum_{\gamma\in \hat{S}^{n}}H(e,\gamma|r) (\Psi_r^{(N)} \circ T^{k}([e,\gamma])-\Psi_r^{(D,N)}\circ T^{k}([e,\gamma]))\nonumber\\ &\quad \lesssim \sum_{j=-N+k+1}^{N+k}\sum_{\gamma\in \hat{S}^{n,j}_{\geq D}} H(e,\gamma_1|r)H(e,\sigma|r)H(e,\gamma_2|r)\Upsilon_r(T^{k}\alpha). \end{align}

Recall that $X_x^{1}$ is the set of symbols that can precede $x$ in $\Sigma _A$. More generally, $X_x^{m}$ is the set of words of length $m$ that can precede $x$. Decompose the sum over $\gamma$ as follows:

\begin{align*} &\sum_{\gamma\in \hat{S}^{n}}H(e,\gamma|r) (\Psi_r^{(N)} \circ T^{k}([e,\gamma])-\Psi_r^{(D,N)}\circ T^{k}([e,\gamma]))\\ &\quad \lesssim \sum_{j=-N+k+1}^{N+k}\sum_{\gamma_2\in \hat{S}^{n-j}}\sum_{\underset{d(e,\sigma)\geq D}{\sigma \in X_{\gamma_2}^{1}}}\sum_{\gamma_1\in X_{\sigma\gamma_2}^{j-1}} H(e,\gamma_1|r)H(e,\sigma|r)H(e,\gamma_2|r)\Upsilon_r(T^{k}\alpha). \end{align*}

Note that $\Upsilon _r(T^{k}\alpha )$ only depends on the $k$th increment of $[e,\gamma ]$. In particular, for $j\neq k$, we can factorize the sum over $\gamma _1,\sigma,\gamma _2$ by $\Upsilon _r(T^{k}\alpha )$. Hence, we can bound the terms $j\neq k$ by

\[ \Upsilon_r(T^{k}\alpha)\sum_{j=-N+k+1}^{N+k}\sum_{\gamma_2\in \hat{S}^{n-j}}H(e,\gamma_2|r)\sum_{\underset{d(e,\sigma)\geq D}{\sigma \in X_{\gamma_2}^{1}}}H(e,\sigma|r)\sum_{\gamma_1\in X_{\sigma\gamma_2}^{j-1}}H(e,\gamma_1|r). \]

Corollary 2.10 shows that

\[ \sum_{\sigma\in X_{\gamma_2}^{1}}H(e,\sigma|r) \]

is uniformly bounded. Thus, for large enough $D$,

(46)\begin{equation} \sum_{\underset{d(e,\sigma)\geq D}{\sigma \in X_{\gamma_2}^{1}}}H(e,\sigma|r)\leq \frac{\epsilon}{2N}\sum_{\sigma\in X_{\gamma_2}^{1}}H(e,\sigma|r). \end{equation}

Let us focus on the term $j=k$. We can still factorize the sum over $\gamma _1$ by $\Upsilon _r(T^{k}\alpha )$. We want to bound the sum over $\sigma$. According to the definition of $\Upsilon _r$, we thus need to bound

\begin{align*} &\sum_{\underset{d(e,\sigma)\geq D}{\sigma \in X_{\gamma_2}^{1}}}H(e,\sigma|r)\sum_{\sigma'\in \mathcal{H}_{\sigma}}\frac{G(e,\sigma'|r)G(\sigma',\sigma|r)}{G(e,\sigma|r)}\\ &\quad =\sum_{\underset{d(e,\sigma)\geq D}{\sigma \in X_{\gamma_2}^{1}}}\sum_{\sigma'\in \mathcal{H}_{\sigma}}G(e,\sigma'|r)G(\sigma',\sigma|r)G(\sigma,e|r). \end{align*}

As $\mu$ is not spectrally degenerate, the sum

\[ \sum_{\sigma \in X_{\gamma_2}^{1}}\sum_{\sigma'\in \mathcal{H}_{\sigma}}G(e,\sigma'|r)G(\sigma',\sigma|r)G(\sigma,e|r) \]

is uniformly bounded. Thus, for large enough $D$,

(47)\begin{align} &\sum_{\underset{d(e,\sigma)\geq D}{\sigma \in X_{\gamma_2}^{1}}}\sum_{\sigma'\in \mathcal{H}_{\sigma}}G(e,\sigma'|r)G(\sigma',\sigma|r)G(\sigma,e|r)\nonumber\\ &\quad \leq \frac{\epsilon}{2N}\sum_{\sigma \in X_{\gamma_2}^{1}}\sum_{\sigma'\in \mathcal{H}_{\sigma}}G(e,\sigma'|r)G(\sigma',\sigma|r)G(\sigma,e|r). \end{align}

When $j$ is fixed, there is a unique way of decomposing $\gamma$ as $\gamma _1\sigma \gamma _2$. Hence, combining (45), (46), and (47), we obtain

(48)\begin{align} &\sum_{\gamma\in \hat{S}^{n}}H(e,\gamma|r) (\Psi_r^{(N)} \circ T^{k}([e,\gamma])-\Psi_r^{(D,N)}\circ T^{k}([e,\gamma]))\nonumber\\ &\quad \lesssim \sum_{j=-N+k+1}^{N+k}\frac{\epsilon}{2N}\sum_{\gamma\in \hat{S}^{n}}H(e,\gamma|r)\Psi_r^{(N)} \circ T^{k}([e,\gamma])\nonumber\\ &\quad \leq \epsilon\sum_{\gamma\in \hat{S}^{n}}H(e,\gamma|r)\Psi_r^{(N)} \circ T^{k}([e,\gamma]). \end{align}

Finally, combining (43) and (48), we obtain the desired inequality.

Recall that we want to compare $I^{(2)}(r)$ and $I^{(1)}(r)$. As we saw,

\[ I^{(2)}(r)=\sum_{n\geq 0}\sum_{\gamma\in \hat{S}^{n}}H(e,\gamma|r)\Phi_r(\gamma). \]

Proposition 6.3 thus yields

\[ I^{(2)}(r)=I^{(1)}(r)\sum_{n\geq 0}\sum_{\gamma\in \hat{S}^{n}}\sum_{k=0}^{n-1}H(e,\gamma|r)\Psi_r(T^{k}[e,\gamma])+O (I^{(1)}(r)^{2}). \]

We want to prove that

\[ I^{(2)}(r)=\xi I^{(1)}(r)^{3}+O (I^{(1)}(r)^{2}), \]

so that we only have to deal with

\[ I^{(1)}(r)\sum_{n\geq 0}\sum_{\gamma\in \hat{S}^{n}}\sum_{k=0}^{n-1}H(e,\gamma|r)\Psi_r(T^{k}[e,\gamma]). \]

In view of Proposition 6.5, we can replace $\Psi _r$ with $\Psi _r^{(D,N)}$.

We now consider the set $\overline {\Sigma }_{A,\mathbb {Z}}$ of (finite or infinite) sequences $x=(x_n)$ indexed by $\mathbb {Z}$ such that $x_n\in \Sigma$ and for every $n$, $x_n$ and $x_{n+1}$ are adjacent edges in the automaton $\mathcal {G}$. The map $T$ still defines a shift on $\overline {\Sigma }_{A,\mathbb {Z}}$.

As $\Psi ^{(D,N)}(\alpha )$ only depends on the truncated geodesic $\alpha ^{(N)}$, $\Psi ^{(D,N)}$ can be extended to a function defined on finite or infinite relative geodesics. For any $x\in \overline {\Sigma }_{A,\mathbb {Z}}$, $(\ldots,x_{-n},\ldots,x_0,\ldots.x_n,\ldots )$ defines such a relative geodesic, so $\Psi ^{(D,N)}\circ \phi$ is a well-defined function on $\overline {\Sigma }_{A,\mathbb {Z}}$. We will omit the reference to $\phi$ and see $\Psi ^{(D,N)}$ as a function on $\overline {\Sigma }_{A,\mathbb {Z}}$ to simplify. In addition, because $\Psi ^{(D,N)}(\alpha )$ only depends on the truncated relative geodesic $\alpha ^{(N)}$ and vanishes on relative geodesics $\alpha$ whose increments are too long, the induced function on $\overline {\Sigma }_{A,\mathbb {Z}}$ only depends on a finite number of symbols.

For a continuous function $f:\overline {\Sigma }_{A,\mathbb {Z}}\rightarrow \mathbb {R}$, we define

\[ \tilde{V}_n(f)=\sup \{|f(x)-f(y)|,x_{-n}=y_{-n},\ldots,x_0=y_0,\ldots,x_n=y_n\}. \]

Letting $0<\rho <1$, we say that $f$ is $\rho$-locally Hölder if there exists $C\geq 0$ such that

\[ \forall n\geq 1, \quad V_n(f)\leq C\rho^{n}. \]

As before, we do not ask anything on $V_0(f)$ and $f$ can be unbounded. Say that $f$ is locally Hölder if it is $\rho$-locally Hölder for some $\rho$. Define the Hölder norm $D_{\rho }$ as

\[ D_{\rho}(f)=\sup_n \frac{\tilde{V}_n(f)}{\rho^{n}}. \]

In addition, let $H_{\rho }$ be the set of bounded $\rho$-locally Hölder functions and define the norm

\[ \|\cdot \|_{\rho}=D_{\rho}+\|\cdot \|_{\infty} \]

on this space. Then, $(H_{\rho },\|\cdot \|_{\rho })$ is a Banach space.

We want to use Proposition 6.3 and apply the transfer operator to $\Psi _r^{(D,N)}$. To apply this operator, we first need to transform $\Psi _r^{(D,N)}$ into a function only depending on the future, that is, a function on $\overline {\Sigma }_A$. We start by proving the following.

Lemma 6.6 Fix $D$ and $N$. The functions $\Psi _r^{(D,N)}$ are $\rho$-locally Hölder and uniformly bounded. They uniformly converge in $(H_{\rho,\beta },\|\cdot \|_{\rho,\beta })$ to a function $\Psi _{R_{\mu }}^{(D,N)}$, as $r$ tends to $R_{\mu }$.

Proof. We first show that $\Psi _r^{(D,N)}$ is uniformly bounded. Recall that

\[ \Psi_r^{(D,N)}(\alpha)=\frac{1}{I^{(1)}(r)}\sum_{\gamma\in \Gamma}\kappa_{\alpha}(\gamma)\frac{G(\alpha_{-N},\gamma|r)G(\gamma,\alpha_N|r)}{G(\alpha_{-N},\alpha_N|r)}. \]

Denote by $\Gamma _k$ the set of $\gamma$ whose projection on $\alpha ^{(N)}$ is on $\alpha _{k+1}$, where we choose the projection which is the closest to $\alpha _N$. In addition, let $\mathcal {H}_k$ be the union of parabolic subgroups containing $\alpha _k^{-1}\alpha _{k+1}$. Then, weak relative Ancona inequalities, together with Lemma 2.5 show that

\[ \sum_{\gamma\in \Gamma_k}\frac{G(\alpha_{-N},\gamma|r)G(\gamma,\alpha_N|r)}{G(\alpha_{-N},\alpha_N|r)}\lesssim I^{(1)}(r)\sum_{\sigma \in \mathcal{H}_k}\frac{G(\alpha_k,\sigma|r)G(\sigma,\alpha_{k+1}|r)}{G(\alpha_{k},\alpha_{k+1}|r)}. \]

As $\kappa _{\alpha }$ is bounded, we thus have

\begin{align*} \Psi_r^{(D,N)}(\alpha)\leq C_{\alpha}, \end{align*}

where $C_\alpha$ only depends on $\alpha$. Actually, because $\Psi _r^{(D,N)}(\alpha )$ is non-zero for a finite number of $\alpha$ which only depends on $N$ and $D$, $C_\alpha$ also only depends on $D$ and $N$. Moreover, $\Psi ^{(D,N)}(\alpha )$ only depends on $\alpha ^{(N)}$, so it is $\rho$-locally Hölder and $\|\Psi ^{(D,N)} \|_{\rho,\beta }$ is bounded by some number only depending on $D$ and $N$.

Finally, because $\Psi ^{(D,N)}(\alpha )$ only depends on a finite number of symbols, pointwise convergence is equivalent to convergence in $(H_{\rho,\beta },\|\cdot \|_{\rho,\beta })$. Let us fix $\alpha$ and prove that $\Psi _r^{(D,N)}(\alpha )$ converges to a function $\Psi _{R_\mu }^{(D,N)}(\alpha )$, as $r$ tends to $R_\mu$. To do so, we express $\Psi _r^{(D,N)}$ as a sum using the transfer operator. We introduce a function $\psi _r$ on $\Gamma$ as follows. We set

\[ \psi_r(\gamma)=\kappa_{\alpha}(\gamma)\frac{G(\alpha_{-N},\gamma|r)G(\gamma,\alpha_N|r)}{G(\alpha_{-N},\alpha_N|r)H(e,\gamma|r)} \]

for any relative geodesic $\alpha$ such that $\Psi _r^{(N,D)}(\alpha )\neq 0$. Otherwise, we set $\psi _r=0$. Weak relative Ancona inequalities imply that $\gamma \mapsto G(\alpha _{-N},\gamma |r)G(\gamma,\alpha _N|r)$ can be extended to $\partial \hat {\Gamma }$. As $\kappa$ is defined on the whole Bowditch compactification, $\psi _r$ can also be extended to $\Gamma \cup \partial \hat {\Gamma }$, so $\psi _r\circ \phi$ is a function on $\overline {\Sigma }_A$. Note that

(49)\begin{equation} \Psi_r^{(D,N)}(\alpha)=\frac{1}{I^{(1)}(r)}\frac{1}{H(e,e|r)}\sum_{n\geq 0}\mathcal{L}_r^{n}(1_{E_*}\psi_r\circ \phi)(\emptyset). \end{equation}

We want to apply 4.13 to prove that $\Psi _r$ converges, so we have to transform $\psi _r$ into a locally Hölder function. First, $\psi _{r}$ is defined using the function $\kappa _{\alpha }$ which is only continuous. We again have to truncate $\psi _r$ to conclude our proof.

Fix $N'$ and let $\gamma _{N'}$ be the $N'$th element on the relative geodesic $[e,\gamma ]$ whenever $\hat {d}(e,\gamma )\geq N'$ and $\gamma _{N'}=\gamma$ otherwise. Set then

\[ \psi_r^{(N')}=\kappa_{\alpha}(\gamma_{N'})\frac{G(\alpha_{-N},\gamma|r)G(\gamma,\alpha_N|r)}{G(\alpha_{-N},\alpha_N|r)H(e,\gamma|r)}. \]

The functions $\psi _r$ and $\psi _r^{(N')}$ implicitly depend on $\alpha$ and on $N$ and $D$. Actually, Lemma 6.4 shows that they do not depend on $\alpha$, but only on $\alpha ^{(N)}$.

Lemma 6.7 For every $\epsilon >0$, for every $N$, and every $D$, there exists $N'_0$ such that for every $N'\geq N'_0$, for every $\alpha$, and for every $r< R_\mu$,

\[ \big|\psi_r-\psi_r^{(N')}\big|\leq \epsilon. \]

Proof. Let $\epsilon >0$. The function $\kappa _{\alpha }$ is continuous on the Bowditch compactification. Endow this compactification with any distance $d$. We can extend the definition of $\gamma _{N'}$ to any infinite relative geodesic $\alpha$ declaring $\alpha _{N'}$ to be the $N'$th point on $\alpha$. Then $\alpha _{N'}$ uniformly converges to the conical limit point defined by $\alpha$, as $N'$ tends to infinity. Thus, for any $\delta >0$, if $N'$ is large enough, then $d(\gamma,\gamma _{N'})\leq \delta$. Note that this can be easily directly shown if one chooses the shortcut metric on the Bowditch compactification defined in [GP13, Definition 2.6]. By compactness, $\kappa _{\alpha }$ is uniformly continuous. Hence, for $N'$ large enough, $\big |\kappa _{\alpha }(\gamma _{N'})-\kappa _{\alpha }(\gamma )\big |\leq \epsilon$. Thus,

\[ \big|\psi_r(\gamma)-\psi_r^{(N')}(\gamma)\big|\leq \epsilon\frac{G(\alpha_{-N},\gamma|r)G(\gamma,\alpha_N|r)}{G(\alpha_{-N},\alpha_N|r)H(e,\gamma|r)}\lesssim C_\alpha\epsilon, \]

where $C_\alpha$ only depends on $\alpha$. The integer $N'_0$ a priori depends on $\alpha$, because of $C_\alpha$ in the upper-bounded above and because uniform continuity of $\kappa _{\alpha }$ depends on $\alpha$. However, $\psi _r$ and $\psi _r^{(N')}$ are the null function except for a finite number of relative geodesics $\alpha$ which only depends on $N$ and $D$. This concludes the proof.

To show that $\Psi _r^{(D,N)}(\alpha )$ converges, it is enough to prove it is Cauchy, that is for every $\epsilon >0$, there exists $r_0< R_\mu$ such that for any $r,r'\in [r_0,R_\mu )$,

\[ \big|\Psi_r^{(D,N)}(\alpha)-\Psi_{r'}^{(D,N)}(\alpha)\big|\leq \epsilon. \]

Fix $\epsilon >0$. Let $N'$ be given by Lemma 6.7 so that for every $r< R_\mu$,

\[ \big|\psi_r-\psi_r^{(N')}\big|\leq \epsilon. \]

According to (49),

\begin{align*} &\big|\Psi_r^{(D,N)}(\alpha)-\Psi_{r'}^{(D,N)}(\alpha)\big |\\ &\quad \lesssim 2\epsilon+\frac{1}{I^{(1)}(r)}\bigg|\sum_{n\geq 0}\mathcal{L}_{r}^{n}(1_{E_*}\psi^{(N')}_{r}\circ \phi)(\emptyset)-\sum_{n\geq 0}\mathcal{L}_{r'}^{n}(1_{E_*}\psi^{(N')}_{r'}\circ \phi)(\emptyset)\bigg|. \end{align*}

We thus only need to prove that

\[ \frac{1}{I^{(1)}(r)}\sum_{n\geq 0}\mathcal{L}_{r}^{n}(1_{E_*}\psi^{(N')}_{r}\circ \phi)(\emptyset) \]

converges, as $r$ tends $R_\mu$. Note that the functions $\gamma \mapsto {G(\alpha _{-N},\gamma |r)G(\gamma,\alpha _N|r)}/{G(\alpha _{-N},\alpha _N|r)}$ and $\gamma \mapsto \kappa _{\alpha _{(2K_1)}}(\gamma _{N'})$ are bounded and locally Hölder, so $\psi _r\circ \phi$ lies in $H_{\rho,\beta }$.

To prove that the above sum, we need to prove that $\psi _r\circ \phi$ uniformly converges to $\psi _{R_\mu }\circ \phi$. This is not obvious and so we truncate $\psi _r$ as we truncated $\Psi _r$. Fix another constant $D'$. For $\gamma \in \Gamma$ let $[e,\gamma ]=(e,\gamma _1,\ldots,\gamma _n=\gamma )$ be the relative geodesic from $e$ to $\gamma$ given by the automaton $\mathcal {G}$. If one of the increments of $[e,\gamma ]$ is at least $D'$, set $\psi _r^{(D',N')}(\gamma )=0$. Otherwise, set $\psi _r^{(D',N')}(\gamma )=\psi _r^{(N')}(\gamma _{N'})$. As $\psi _r\circ \phi$ is bounded and locally Hölder, the same proof as the proof of Proposition 6.5 shows that for every $\eta >0$, for large enough $N'$ and $D'$,

(50)\begin{equation} \frac{1}{I^{(1)}(r)}\sum_{n\geq 0}\mathcal{L}_{r}^{n} (1_{E_*}\big |\psi^{(N')}_{r}\circ \phi-\psi^{(N',D')}\circ \phi\big|)(\emptyset)\leq \eta. \end{equation}

Remark 6.1 It might seem strange that we first had to truncate $\kappa _{\alpha }$ when defining $\psi _r^{(N')}$, before truncating again to define $\psi _r^{(D',N')}$. However, to apply the same strategy as in Proposition 6.5, we needed to know a priori that our function was locally Hölder.

Once again, to prove that

\[ \frac{1}{I^{(1)}(r)}\sum_{n\geq 0}\mathcal{L}_{r}^{n}(1_{E_*}\psi^{(N')}_{r}\circ \phi)(\emptyset) \]

converges, it is enough to prove that this quantity is Cauchy, as $r$ tends to $R_\mu$. In view of (50), we thus only need to prove that

\[ \frac{1}{I^{(1)}(r)}\sum_{n\geq 0}\mathcal{L}_{r}^{n}(1_{E_*}\psi^{(N',D')}_{r}\circ \phi)(\emptyset) \]

converges. The function $\psi ^{(N',D')}_{r}\circ \phi$ is bounded and locally Hölder. Moreover, whenever $x,y,z$ are fixed, $r\mapsto {G(x,y|r)G(y,z|r)}/{G(x,z|r)H(e,y|r)}$ is a continuous function. It converges to $ {G(x,y|R_\mu )G(y,z|R_\mu )}/{G(x,z|R_\mu )H(e,y|R_\mu )}$, as $r$ tends to $R_\mu$. Hence, $\psi ^{(N',D')}_{r}\circ \phi$ converges to a function $\psi ^{(N',D')}_{R_\mu }\circ \phi$. In addition, $\psi ^{(N',D')}_{r}\circ \phi$ only depends on a finite number of symbols, so this convergence also holds in $(H_{\rho,\beta },\|\cdot \|_{\rho,\beta })$. Now that every parameter is fixed, we set $f=1_{E_*}\psi ^{(N',D')}_{R_\mu }\circ \phi$ for convenience. We are left to proving that

\[ \frac{1}{I^{(1)}(r)}\sum_{n\geq 0}\mathcal{L}_{r}^{n}f(\emptyset) \]

converges, as $r$ tends to $R_\mu$, which is a direct consequence of (34).

6.3 From the double-sided to the one-sided shift

As announced, to study

\[ \sum_{n\geq 0}\sum_{\gamma\in \hat{S}^{n}}\sum_{k=0}^{n-1}H(e,\gamma|r)\Psi_r^{(D,N)}(T^{k}[e,\gamma]), \]

we express this sum with the transfer operator and then use Theorem 3.3, exactly as in the proof of Lemma 6.6. However, we cannot apply the transfer operator to the function $\Psi _r^{(D,N)}$, which depends both on past and future.

We use the following trick.

Lemma 6.8 Let $f$ be a $\rho$-locally Hölder function on $\overline {\Sigma }_{A,\mathbb {Z}}$. Then, there exist $\rho ^{1/2}$-locally Hölder functions $g$ and $u$ on $\overline {\Sigma }_{A,\mathbb {Z}}$ such that

\[ f=g+u-u\circ T. \]

Moreover, $g(x)=g(y)$ as soon as $x_n=y_n$ for every non-negative $n$, so that $g$ induces a function on $\overline {\Sigma }_A$. In addition, if $f$ is bounded, then $g$ and $u$ also are bounded and the maps

\[ f\in (H_{\rho},\|\cdot\|_{\rho})\mapsto g\in (H_{\rho^{1/2}},\|\cdot\|_{\rho^{1/2}}), \quad f\in (H_{\rho},\|\cdot\|_{\rho})\mapsto u\in (H_{\rho^{1/2}},\|\cdot\|_{\rho^{1/2}}) \]

are continuous.

This is proved in [PP90, Proposition 1.2] for finite-type shifts. However, the proof does not use that the set of symbols is finite.

According to Lemma 6.6, the functions $\Psi _r^{(D,N)}$ are bounded and locally Hölder on $\overline {\Sigma }_{A,\mathbb {Z}}$ and they converge in $(H_{\rho,\beta },\|\cdot \|_{\rho,\beta })$ to a function $\Psi _{R_\mu }^{(D,N)}$. We thus obtain from Lemma 6.8 functions $\tilde {\Psi }_r^{(D,N)}$, $r\leq R_\mu$ defined on $\overline {\Sigma }_A$ and functions $u_r^{(D,N)}$ defined on $\overline {\Sigma }_{A,\mathbb {Z}}$ such that

\[ \Psi_r^{(D,N)}=\tilde{\Psi}_r^{(D,N)}+u_r^{(D,N)}-u_r^{(D,N)}\circ T. \]

For any $x\in \overline {\Sigma }_A$ of length $n$,

\[ \sum_{k=0}^{n-1}\Psi_r^{(D,N)}(T^{k}x)=\sum_{k=0}^{n-1}\tilde{\Psi}_r^{(D,N)}(T^{k}x)+u_r^{(D,N)}(x)-u_r^{(D,N)}(T^{n}x). \]

The functions $u_r^{(D,N)}$ are bounded by some number that only depends on $D$ and $N$, so

\[ \sum_{k=0}^{n-1}\Psi_r^{(D,N)}(T^{k}x)=\sum_{k=0}^{n-1}\tilde{\Psi}_r^{(D,N)}(T^{k}x)+O_{D,N}(1). \]

Thus,

(51)\begin{align} &\sum_{n\geq 0}\sum_{\gamma\in \hat{S}^{n}}\sum_{k=0}^{n-1}H(e,\gamma|r)\Psi_r^{(D,N)}(T^{k}[e,\gamma])\nonumber\\ &\quad =\sum_{n\geq 0}\sum_{\gamma\in \hat{S}^{n}}\sum_{k=0}^{n-1}H(e,\gamma|r)\tilde{\Psi}_r^{(D,N)}(T^{k}[e,\gamma])+O_{D,N} (I^{(1)}(r)). \end{align}

As $\tilde {\Psi }_r^{(D,N)}$ only depends on the future, we rewrite this as

(52)\begin{align} &\sum_{n\geq 0}\sum_{\gamma\in \hat{S}^{n}}\sum_{k=0}^{n-1}H(e,\gamma|r)\tilde{\Psi}_r^{(D,N)}(T^{k}[e,\gamma])\nonumber\\ &\quad =H(e,e|r)\sum_{n\geq 0}\mathcal{L}_r^{n} \bigg(1_{E_*}\sum_{k=0}^{n-1}\tilde{\Psi}_r^{(D,N)}\circ T^{k}\bigg)(\emptyset). \end{align}

6.4 Proof of Proposition 6.1: convergence of $I^{(2)}(r)/I^{(1)}(r)^{3}$

We first prove that the quantity (52) is asymptotic to $\xi _{D,N}I^{(1)}(r)^{2}$, as $r$ tends to $R_\mu$, where $\xi _{D,N}$ is some number only depending on $D$ and $N$. As $\Psi _r^{(D,N)}$ converges in $(H_{\rho,\beta },\|\cdot \|_{\rho,\beta })$ to $\Psi _{R_\mu }^{(D,N)}$, we deduce from Lemma 6.6, up to changing $\rho$, that $\tilde {\Psi }_r^{(D,N)}$ converges in $(H_{\rho,\beta },\|\cdot \|_{\rho,\beta })$ to $\tilde {\Psi }_{R_\mu }^{(D,N)}$. We thus only need to prove that

\[ \sum_{n\geq 0}\mathcal{L}_r^{n}\bigg(1_{E_*}\sum_{k=0}^{n-1}\tilde{\Psi}_{R_\mu}^{(D,N)}\circ T^{k}\bigg)(\emptyset) \]

is asymptotic to $\xi _{D,N}I^{(1)}(r)^{2}$. Recall that $\mathcal {L}_r(u\cdot v\circ T)=v\mathcal {L}_r(u)$, so that

(53)\begin{align} \sum_{n\geq 0}\mathcal{L}_r^{n} \bigg(1_{E_*}\sum_{k=0}^{n-1}\tilde{\Psi}_{R_\mu}^{(D,N)}\circ T^{k}\bigg)&= \sum_{n\geq 0}\sum_{k=1}^{n}\mathcal{L}_r^{k}(\tilde{\Psi}_{R_\mu}^{(D,N)}\mathcal{L}_r^{n-k}1_{E_*})\nonumber\\ &=\sum_{k\geq 1}\mathcal{L}_r^{k}\bigg(\tilde{\Psi}_{R_\mu}^{(D,N)}\sum_{n\geq 0}\mathcal{L}_r^{n}1_{E_*}\bigg). \end{align}

From Corollary 4.13, we deduce that for any $r$ close enough to $R_{\mu }$ and for any $x\in \overline {\Sigma }_A$,

(54)\begin{equation} \sum_{n\geq 0}\mathcal{L}_r^{n}1_{E_*}(x)=\sum_{j=1}^{k}\frac{1}{\tilde{P}_j(r)}\sum_{i=1}^{p_j}\tilde{h}_{j,r}^{(i)}(x)\int 1_{E_*} \,d\tilde{\nu}_{j,r}^{((i-n) \text{ mod } p_j)}+O(1). \end{equation}

Let

\[ \alpha_{i,j,r}=\int 1_{E_*} d\tilde{\nu}_{j,r}^{((i-n) \text{ mod } p_j)}, \]

so that $\alpha _{i,j,r}$ converges to $\alpha _{i,j}$, as $r$ tends to $R_\mu$. We now estimate

\[ \sum_{k\geq 1}\mathcal{L}_r^{k}\bigg(\tilde{\Psi}_{R_\mu}^{(D,N)}\sum_{j=1}^{k}\frac{1}{\tilde{P}_j(r)}\sum_{i=1}^{p_j}\alpha_{i,j,r}\tilde{h}_{j,r}^{(i)}\bigg)(\emptyset). \]

According to (19), $\tilde {h}_{j,r}^{(i)}(\emptyset )$ converges to $h_j^{(i)}(\emptyset )$, as $r$ tends to $R_\mu$, so we can start the above sum at $k=0$. Fix $j$ and let $1\leq i \leq p_j$. We use again Corollary 4.13 to obtain

(55)\begin{align} &\sum_{k\geq 0}\mathcal{L}_r^{k} (\tilde{\Psi}_{R_\mu}^{(D,N)}\tilde{h}_{j,r}^{(i)})(\emptyset)\nonumber\\ &\quad =\sum_{j'}\frac{1}{|\tilde{P}_{j'}(r)|}\sum_{i'=1}^{p_{j'}}\tilde{h}_{j',r}^{(i')}(\emptyset)\int \tilde{\Psi}_{R_\mu}^{(D,N)}\tilde{h}_{j,r}^{(i)} \,d\tilde{\nu}_{j',r}^{((i'-n) \text{ mod } p_{j'})}+O(1). \end{align}

We show that for every $j',i'$,

\[ \int \tilde{\Psi}_{R_\mu}^{(D,N)}\tilde{h}_{j',r}^{(i')} \,d\tilde{\nu}_{j',r}^{((i'-n) \text{ mod } p_{j'})} \]

converges, as $r$ tends to $R_\mu$. Write

\begin{align*} \int \tilde{\Psi}_{R_\mu}^{(D,N)}\tilde{h}_{j',r}^{(i')} \,d\tilde{\nu}_{j',r}^{((i'-n) \text{ mod } p_{j'})}&=\int \tilde{\Psi}_{R_\mu}^{(D,N)} (\tilde{h}_{j',r}^{(i')}-h_j^{(i)})\,d\tilde{\nu}_{j',r}^{((i'-n) \text{ mod } p_{j'})}\\ &\quad +\int \tilde{\Psi}_{R_\mu}^{(D,N)}h_j^{(i)}\,d\tilde{\nu}_{j',r}^{((i'-n) \text{ mod } p_{j'})}. \end{align*}

Corollary 4.13 shows that $\tilde {\nu }_{j',r}^{((i'-n) \text { mod } p_{j'})}$ weakly converges to $\nu _{j'}^{((i'-n) \text { mod } p_{j'})}$, so that the second integral in the right-hand term converges. We show that the first converges to zero. Let $m_{j',r}$ be the measure defined by $dm_{j',r}= ({1}/{p_{j'}})\sum _{i'=1}^{p_{j'}}h_{j',r}^{(i)}d\nu _{j',r}^{(i')}$. According to [Sar99, Proposition 4], $m_{j',r}$ is Gibbs and according to [Sar99, Proposition 2], the functions $h_{j',r}^{(i)}$ are bounded away from zero and infinity on the support of $\nu _{j',r}^{(i)}$, so that

\[ \nu_{j',r}^{(i')}([x_1\dots x_n]) \leq C H(e,x_1\dots x_n|r)\leq C H(e,x_1\dots x_n|R_\mu). \]

Using (10), we see that the measure $\nu _{j',r}^{(i')}$ is dominated by the measure $m$ on cylinders. As $\tilde {\Psi }_{R_\mu }^{(D,N)} (\tilde {h}_{j',r}^{(i')}-h_j^{(i)})$ is locally Hölder, we have

\[ \bigg|\int \tilde{\Psi}_{R_\mu}^{(D,N)} (\tilde{h}_{j',r}^{(i')}-h_j^{(i)})\,d\tilde{\nu}_{j',r}^{((i'-n) \text{ mod } p_{j'})}\bigg|\lesssim \int \bigg| \tilde{\Psi}_{R_\mu}^{(D,N)} (\tilde{h}_{j',r}^{(i')}-h_j^{(i)})\bigg|\,dm. \]

Finally, because $\tilde {\Psi }_{R_\mu }^{(D,N)}$ is bounded, we have

\[ \bigg|\int \tilde{\Psi}_{R_\mu}^{(D,N)} (\tilde{h}_{j',r}^{(i')}-h_j^{(i)})\,d\tilde{\nu}_{j',r}^{((i'-n) \text{ mod } p_{j'})}\bigg|\lesssim \int |\tilde{h}_{j,r}^{(i)}-h_j^{(i)}|\,dm. \]

According to Corollary 4.13, this last quantity converges to zero.

Now, (19) shows that $\tilde {h}_{j',r}^{(i')}(\emptyset )$ converges and so we deduce from (55) that

\[ \sum_{k\geq 0}\mathcal{L}_r^{k} (\tilde{\Psi}_{R_\mu}^{(D,N)}\tilde{h}_{j,r}^{(i)})(\emptyset)=\sum_{j'}\frac{\xi^{i,j}_{j',D,N,r}}{|\tilde{P}_{j'}(r)|}, \]

where $\xi ^{i,j}_{j',D,N,r}$ converges, as $r$ tends to $R_\mu$. Also recall that we proved in Proposition 5.1 that $\tilde {P}_{j}(r)\sim P(r)$ for every $j$, so (23) yields

\[ O\bigg(\sum_{j=1}^{k}\frac{1}{\tilde{P}_j(r)}\bigg)=O (I^{(1)}(r)). \]

Finally, we get from (53) and (54) that

\[ \sum_{n\geq 0}\mathcal{L}_r^{n} \bigg(1_{E_*}\sum_{k=0}^{n-1}\tilde{\Psi}_{R_\mu}^{(D,N)}\circ T^{k}\bigg)=\sum_{j,j'}\frac{\xi^{j,j'}_{D,N,r}}{|\tilde{P}_{j}(r)||\tilde{P}_{j'}(r)|}+O (I^{(1)}(r)), \]

where $\xi ^{j,j'}_{D,N,r}$ converges. Consequently,

\[ \sum_{n\geq 0}\mathcal{L}_r^{n} \bigg(1_{E_*}\sum_{k=0}^{n-1}\tilde{\Psi}_{R_\mu}^{(D,N)}\circ T^{k}\bigg)=\frac{\xi_{D,N,r}}{P(r)^{2}}+O (I^{(1)}(r)), \]

where $\xi _{D,N,r}$ converges to some $\xi _{D,N}$. Therefore,

\[ \sum_{n\geq 0}\mathcal{L}_r^{n}\bigg(1_{E_*}\sum_{k=0}^{n-1}\tilde{\Psi}_{R_\mu}^{(D,N)}\circ T^{k}\bigg)(\emptyset) \]

is asymptotic to $\xi _{D,N}I^{(1)}(r)^{2}$, as $r$ tends to $R_\mu$.

We thus deduce from (51) and (52) that

(56)\begin{equation} \sum_{n\geq 0}\sum_{\gamma\in \hat{S}^{n}}\sum_{k=0}^{n-1}H(e,\gamma|r)\Psi_r^{(D,N)}(T^{k}[e,\gamma])=\xi_{D,N}I^{(1)}(r)^{2}+o_{D,N} (I^{(1)}(r)^{2}). \end{equation}

Also note that we deduce from (53) that

\[ \sum_{n\geq 0}\mathcal{L}_r^{n} \bigg(1_{E_*}\sum_{k=0}^{n-1}\tilde{\Psi}_{R_\mu}^{(D,N)}\circ T^{k}\bigg)=\sum_{k\geq 1}\mathcal{L}_r^{k}\bigg(\tilde{\Psi}_{R_\mu}^{(D,N)}\sum_{n\geq 0}\mathcal{L}_r^{n}1_{E_*}\bigg) \]

and so according to (23), we have

\[ \sum_{n\geq 0}\mathcal{L}_r^{n} \bigg(1_{E_*}\sum_{k=0}^{n-1}\tilde{\Psi}_{R_\mu}^{(D,N)}\circ T^{k}\bigg)\lesssim I^{(1)}(r)\sum_{k\geq 1}\mathcal{L}_r^{k} \tilde{\Psi}_{R_\mu}^{(D,N)}. \]

Thus, (36) and (41) show that

\[ \sum_{n\geq 0}\mathcal{L}_r^{n} \bigg(1_{E_*}\sum_{k=0}^{n-1}\tilde{\Psi}_{R_\mu}^{(D,N)}\circ T^{k}\bigg)\lesssim I^{(1)}(r)^{2}. \]

Hence,

(57)\begin{equation} \xi_{D,N}\lesssim 1. \end{equation}

We finally conclude the proof of Proposition 6.1.

Proof. Recall that

\begin{align*} I^{(2)}(r)=\sum_{\gamma\in \Gamma}H(e,\gamma|r)\Phi_r(\gamma)=\sum_{n\geq 0}\sum_{\gamma\in \hat{S}^{n}}\Phi_r(\gamma). \end{align*}

According to Proposition 6.3,

\[ I^{(2)}(r)=I^{(1)}(r)\sum_{n\geq 0}\sum_{\gamma\in \hat{S}^{n}}\sum_{k=0}^{n-1}\Psi_r(T^{k}[e,\gamma])+O(I^{(1)}(r)). \]

We need to prove that $I^{(2)}(r)/I^{(1)}(r)^{3}$ converges, as $r$ tends to $R_\mu$. It is thus enough to show that

\[ \frac{1}{I^{(1)}(r)^{2}}\sum_{n\geq 0}\sum_{\gamma\in \hat{S}^{n}}\sum_{k=0}^{n-1}\Psi_r(T^{k}[e,\gamma]) \]

converges.

Fix $\epsilon >0$. Choose sequences $D_l$ and $N_l$ that tend to infinity, as $l$ tends to infinity. As we want to apply Proposition 6.5, the sequence $D_l$ will actually depend on the sequence $N_l$. According to (57), we can assume, up to taking a sub-sequence, that $\xi _{D_l,N_l}$ converges to some constant $\xi$. We show that the above sum also converges to $\xi$. According to Proposition 6.5, we can choose $N_l$ and $D_l$ so that for any $l$ large enough,

\begin{align*} &\frac{1}{I^{(1)}(r)^{2}}\bigg|\sum_{n\geq 0}\sum_{\gamma\in \hat{S}^{n}}\sum_{k=0}^{n-1}\Psi_r(T^{k}[e,\gamma])-\sum_{n\geq 0}\sum_{\gamma\in \hat{S}^{n}}\sum_{k=0}^{n-1}\Psi_r^{(D_l,N_l)}(T^{k}[e,\gamma])\bigg|\\ &\quad \leq \epsilon \frac{1}{I^{(1)}(r)^{2}}\sum_{n\geq 0}\sum_{\gamma\in \hat{S}^{n}}\sum_{k=0}^{n-1}\Psi_r(T^{k}[e,\gamma]). \end{align*}

Fix a large enough $l$ so that this inequality is satisfied and so that $|\xi _{D_l,N_l}-\xi |\leq \epsilon$. Now that $l$ is fixed, we set $D=D_l$ and $N=N_l$. We thus have

\begin{align*} &\frac{1}{I^{(1)}(r)^{2}}\sum_{n\geq 0}\sum_{\gamma\in \hat{S}^{n}}\sum_{k=0}^{n-1}\Psi_r(T^{k}[e,\gamma])-\xi\\ &\quad \leq \frac{1}{1-\epsilon}\frac{1}{I^{(1)}(r)^{2}}\sum_{n\geq 0}\sum_{\gamma\in \hat{S}^{n}}\sum_{k=0}^{n-1}\Psi_r^{(D,N)}(T^{k}[e,\gamma])-\xi. \end{align*}

Hence, (56) shows that whenever $r$ is close enough to $R_\mu$,

\[ \frac{1}{I^{(1)}(r)^{2}}\sum_{n\geq 0}\sum_{\gamma\in \hat{S}^{n}}\sum_{k=0}^{n-1}\Psi_r(T^{k}[e,\gamma])-\xi\leq \frac{1}{1-\epsilon}\xi_{D,N}-\xi\leq \frac{\epsilon}{1-\epsilon}+\xi\bigg(\frac{1}{1-\epsilon}-1\bigg). \]

Similarly

\begin{align*} &\xi-\frac{1}{I^{(1)}(r)^{2}}\sum_{n\geq 0}\sum_{\gamma\in \hat{S}^{n}}\sum_{k=0}^{n-1}\Psi_r(T^{k}[e,\gamma])\\ &\quad \leq \xi-\frac{1}{1+\epsilon}\frac{1}{I^{(1)}(r)^{2}}\sum_{n\geq 0}\sum_{\gamma\in \hat{S}^{n}}\sum_{k=0}^{n-1}\Psi_r^{(D,N)}(T^{k}[e,\gamma]) \end{align*}

and so whenever $r$ is close enough to $R_\mu$,

\[ \xi-\frac{1}{I^{(1)}(r)^{2}}\sum_{n\geq 0}\sum_{\gamma\in \hat{S}^{n}}\sum_{k=0}^{n-1}\Psi_r(T^{k}[e,\gamma]) \leq \xi \bigg(1-\frac{1}{1+\epsilon}\bigg)-\frac{\epsilon}{1+\epsilon}. \]

As $\epsilon$ is arbitrary, this shows that

\[ \frac{1}{I^{(1)}(r)^{2}}\sum_{n\geq 0}\sum_{\gamma\in \hat{S}^{n}}\sum_{k=0}^{n-1}\Psi_r(T^{k}[e,\gamma])\underset{r\to R_\mu}{\longrightarrow}\xi. \]

Finally, we already know that $I^{(2)}(r)/I^{(1)}(r)^{3}$ is bounded away from zero, independently of $r$, so that $\xi \neq 0$. This concludes the proof.

Theorem 4.1 is a direct consequence of Proposition 6.1.

7. From the Green asymptotics to the local limit theorem

We can finally prove Theorem 1.1. We first deduce from Theorem 4.1 the following.

Corollary 7.1 Let $\Gamma$ be a non-elementary relatively hyperbolic group. Let $\mu$ be a finitely supported, admissible, and symmetric probability measure on $\Gamma$. Assume that the corresponding random walk is non-spectrally degenerate along parabolic subgroups. Then, for every $\gamma _1,\gamma _2$, there exists $C_{\gamma _1,\gamma _2}>0$ such that

\[ \frac{d}{dr} (G(\gamma_1,\gamma_2|r))\underset{r\to R_{\mu}}{\sim} C_{\gamma_1,\gamma_2}\frac{1}{\sqrt{R_\mu-r}}. \]

Proof. For $\gamma _1=\gamma _2=e$, this is a direct consequence of Theorem 4.1, combined with [Dus22, Lemma 3.2] which relates the derivatives of the Green function with the sums $I^{(k)}(r)$. Note that by equivariance, we only need to prove the result with $\gamma _2=e$. According to Lemma 2.7, an asymptotic of $ {d}/{dr} (G(\gamma,e|r))$ is given by an asymptotic of

\[ \sum_{\gamma'\in \Gamma}G(\gamma,\gamma'|r)G(\gamma',e|r). \]

Consider $\gamma \in \Gamma$ and set

\[ f_r(\gamma')=\frac{G(\gamma,\gamma'|r)}{G(e,\gamma'|r)}. \]

Let $\tilde {f}_r=f_r\circ \phi$. Then,

\[ \sum_{\gamma'\in \Gamma}G(\gamma,\gamma'|r)G(\gamma',e|r)=H(e,e|r)\sum_{n\geq 0}\mathcal{L}_r^{n} \tilde{f}_r(\emptyset). \]

As $\gamma$ is fixed, $\tilde {f}_r$ is uniformly bounded. Strong relative Ancona inequalities also imply that $\tilde {f}_r$ can be extended to a function on $\overline {\Sigma }_A$ which lie in $H_{\rho,\beta }$. If $\tilde {f}_r$ were uniformly converging to a function $\tilde {f}$, as $r$ tends to $R_\mu$, then we could directly conclude the proof, using (23). However, exactly like for $\Psi _r$, this uniform convergence does not necessarily hold and we have to truncate $\tilde {f}_r$. We can apply the same strategy as for the proof of Proposition 6.1 to conclude.

Theorem 1.1 follows directly from Corollary 7.1 and [GL13, Theorem 9.1]. Corollary 1.2 thus follows from [Gou14, Proposition 4.1]. Beware that the symmetry assumption on the measure $\mu$ is needed here, see the remarks in [Gou14, Section 4].