INTRODUCTION
The value of geo-referenced data in veterinary surveillance of both endemic and exotic diseases is immense. Recent examples in the literature show that these data have been used not only to identify areas with excess disease [Reference Haine1, Reference Sanchez2] and target areas for further studies [Reference Graham3], but also to produce hypotheses about means of disease introduction [Reference Vigre4], identify likely sites of incursion of an exotic disease [Reference Stevenson5] and for predictive modelling of alternative control strategies [Reference Yoon6].
The geo-referenced locations of livestock farms can be considered a spatial point process [Reference Diggle7]. An underlying assumption in the analysis of these processes is that of stationarity or spatial homogeneity, i.e. the intensity of the process does not depend on the location in space [Reference Diggle7, Reference Banerjee, Carlin and Gelfand8]. A point pattern representing the location of livestock farms will typically not meet this assumption – farms will probably be distant from large urban centres and will often be located near areas that meet their needs for specific inputs, e.g. feed supply and market access. Furthermore, in developed countries legislation now dictates the location of intensive production units due to their effects on the environment such as emissions of ammonia and phosphorus and requirements regardinging the spread of slurry.
Statistically spatial point patterns can be partitioned into first- and second-order properties that capture their global and local behaviours respectively [Reference Banerjee, Carlin and Gelfand8]. If the pattern shows a global trend (i.e. is non-stationary or inhomogeneous) then it exhibits a first-order effect. A second-order effect is due to spatial dependency and results from the spatial correlation structure in the data; these are small-scale or local effects. Somewhat ambiguously, both first- and second-order effects produce point patterns that exhibit local concentrations of points and it can be difficult to clearly identify one from the other [Reference Diggle9].
Specifically viewing slaughter-pig production in intensive farming areas there are concentrated areas of pig production within which the distances between farms can be very small. Denmark, as the world's largest exporter of pig meat provides a good example of intensive pig farming. The first aim of this paper is to capture the spatial distribution of these farms with regard to first- and second-order effects using farm location data from the Danish Central Husbandry Register in 2003. Our second aim is to investigate the second-order spatial properties by marking the locations with disease status and with a random farm-effect value from a generalized linear mixed model. We then determined the implications for surveillance. This methodology could be used on suitable data from any national disease control programme. We used data from the Danish Swine Salmonellosis Control Programme (DSSCP) from 2003. Many other countries that intensively farm pigs look to the Danish control programme as a model, e.g. the Zoonoses Action Plan in the UK [Reference Armstrong10], Ireland [Reference Casey11] and the German QS system [Reference Blaha12]. The Danish programme was developed in 1993 in response to an increase in the incidence of salmonellosis in humans attributable to consumption of pork [Reference Alban, Stege and Dahl13, Reference Mousing14] and is based around the random testing of meat-juice samples from slaughtered pigs. All herds that produce >200 finishers per year are tested and then categorized into one of three levels of a ‘serological Salmonella index’ for intervention strategies [Reference Alban, Stege and Dahl13]. An in-depth review of the programme is given by Christensen [Reference Christensen and Salman15].
In Denmark the number of human salmonellosis cases due to pork consumption has substantially reduced from 1444 in 1993 to 164 in 2004 [Reference Nielsen16]. This reduction in the number of human cases provides some indication that interventions that have been applied have been effective but raises questions about where to go to next in terms of resource allocation within the programme [Reference Alban and Stärk17]. There have been a number of recent stochastic models, both Danish [Reference Alban and Stärk17] and from elsewhere [Reference van der Gaag18, Reference Miller19] which have addressed the question, with variable results. The North American model found higher cost–benefit ratios for improvements in the post-slaughter phase [Reference Miller19], while both the Danish [Reference Alban and Stärk17] and the Dutch [Reference van der Gaag18] models identified both pre- and post-slaughter interventions as being efficient.
In terms of pre-slaughter interventions little consideration has been given to small-scale spatial risk factors. Work on the Danish programme has described a strong first-order spatial effect with a higher prevalence of farm-level seropositivity in the north and south of Jutland, and in the west of the country compared with the east [Reference Mousing14, Reference Carstensen and Christensen20, Reference Benschop21]. Our recent work [Reference Benschop21] has identified that case farms tend to be spatially aggregated, but we are not aware of any work specifically investigating the second-order properties of the data. Both increased pig density within a region [Reference Fedorka-Cray, Gray, Wray, Wray and Wray22] and small distances to other pig farms [Reference Berends23, Reference Langvad24] have been identified as risk factors for Salmonella infections. Survival times of bacteria are lengthy in the environment [Reference Winfield and Groisman25] and contaminated faecal matter can act as a reservoir [Reference Gray and Fedorka-Cray26], so processes acting locally, such as sharing contaminated agricultural machinery or poor biosecurity between farms, make the small-scale spatial structure worthwhile investigating. This has the potential to inform models that may lead to improved resource allocation in the Danish and other similar programmes.
MATERIALS AND METHODS
The dataset
Two extracts of data from 1 January 2003 to 31 December 2003 were obtained from the DSSCP [Reference Alban, Stege and Dahl13, Reference Mousing14]. These extracts comprised pig- and farm-level data. We chose data from 2003 for analysis since this was the period with the highest proportion of geo-referenced farms in our dataset (96·2%).
Data were managed using a relational database (Microsoft Access 2002 for Windows; Microsoft Corporation, USA) and spreadsheet software (Microsoft Excel 2002 for Windows; Microsoft Corporation). Statistical analyses were performed using the R statistical package version 2.2.0 (R Foundation; http://www.r-project.org) and WinBUGS version 1.4.1 (Imperial College and MRC, UK). R packages spatstat [Reference Baddeley and Turner27], geoR [Reference Ribeiro and Diggle28], splancs [Reference Rowlingson and Diggle29] and sm [Reference Bowman and Azzalini30] were used.
Pig-level data
There were 578 268 individual finisher-pig meat-juice results. Each included the date of sampling, the central husbandry register number identifying the farm of origin, and the result of the Danish-mix ELISA. A result of >20 OD% was classified as positive. This is the cut-off for positivity that has been used by the DSSCP since 1 August 2001 [Reference Alban, Stege and Dahl13].
Farm-level data
Of the 10 571 farms for which individual pig results were available, 10 166 had easting and northing coordinates of the farm house. This represented 96·2% of the contributing farms. The 405 farms without coordinate information were excluded from the analyses. Each farm had its central husbandry register number which included a number indicating within which of the 15 Danish counties the farm was located. Because they contributed very few farms, the two counties that constituted the county of Copenhagen were merged.
Spatial analyses
To investigate the spatial distribution of slaughter-pig farms we used three techniques: kernel estimation, nearest-neighbour distance and the inhomogeneous K function.
We calculated kernel density estimates [Reference Diggle31] of farm locations to visualize the broad scale variability in farm density. Spatially adaptive smoothing was implemented by weighting the global bandwidth at each data-point with weights derived from a pilot estimate (J. C. Marshall and M. L. Hazelton, unpublished observations). Regions that are data rich (e.g. Jutland), therefore receive less smoothing so as to preserve fine detail, whereas regions where the data are sparse (e.g. Zealand) receive more smoothing. A linear boundary kernel, with a Gaussian base was used to reduce boundary bias, and a global smoothing bandwidth of 17 km was chosen using the normal optimal method [Reference Bowman and Azzalini30].
For each county we calculated the distance from every farm location to its nearest neighbour.
We estimated a non-stationary analogue of the standard K function, the inhomogeneous K function [Reference Baddeley, Moller and Waagepetersen32] to investigate for evidence of local aggregations of pig farms after allowing for their non-uniform density. The K function is defined as the expected number of further points within a distance r of an arbitrary point, divided by the overall density of the points [Reference Ripley33].
In equation (1) K(r) is the standard K function, N(r) is the expected number of neighbouring farms within a distance r of an arbitrary farm and λ is the farm density. Inhomogeneous K-function analysis was performed using five large, approximately square, areas that included 82% of the sampled farms (Fig. 1). Square areas were chosen to avoid the instability that may be associated with unusual window geometry [Reference Ripley34]. Analysis of the whole of the country was prevented by computational and geographical constraints. To reduce the instability due to edge effects Ripley's isotropic corrections were implemented [Reference Ripley34]. One hundred simulated realizations of an inhomogeneous Poisson process were generated and the inhomogeneous K functions of these were calculated to produce an envelope around the observed data. This provided a way of testing if the observed pattern of farms is aggregated even after allowing for its non-uniform density. The practical value of the inhomogeneous K function over the standard K function is that the former permits a more global measure of aggregation as it allows for spatial inhomogeneity of the pattern (a varying λ).
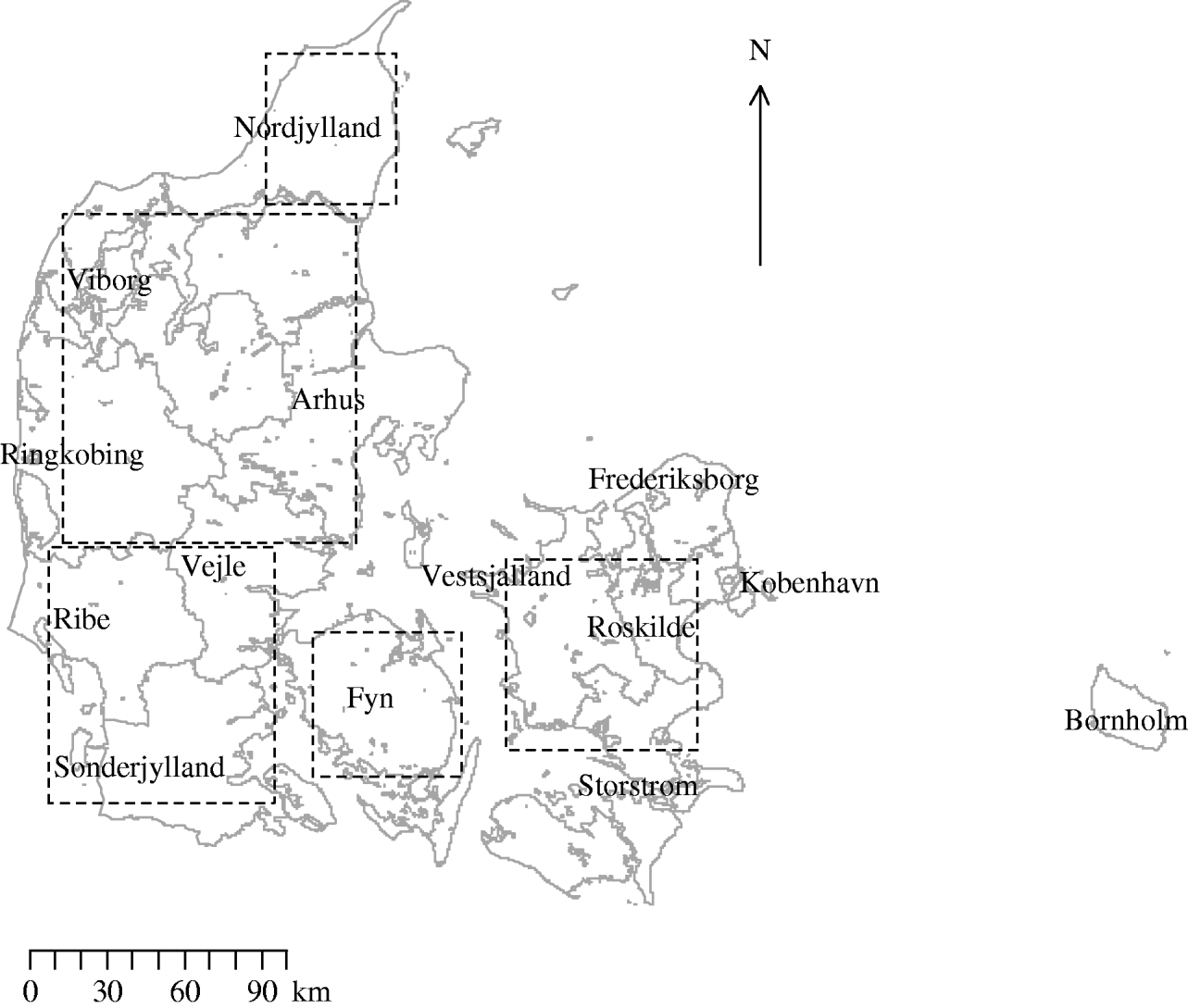
Fig. 1. Map of Denmark showing the location of counties and of the five areas used in the investigation of inhomogeneous K-function estimation.
To investigate if there were spatial aggregations of case farms over that of all farms the observed-difference K function was calculated. A farm was defined as a case if it had a proportion of positive pigs ⩾0·4. We chose this cut-off as it is the cut-off between levels 1 and 2 of the serological Salmonella finisher index. If herds are in levels 2 or 3 there are requirements placed upon them, e.g. pen faecal samples must be collected from the herd and there are penalty ‘Salmonella deductions’ reducing payments to these producers. Approximately 3% of herds were in levels 2 or 3 during 2003.
For each county separate K functions at distances r were calculated for both case farms, K case(r), and for all farms, K pop(r), and the observed difference function D(r) was calculated as follows:
The null hypothesis was of no extra aggregation of cases over that of the population corresponding to the cases being a random sample from the population. This permits the use of randomization tests which do not require the underlying point process to be stationary [Reference Diggle9]. Upper and lower permutation envelopes were produced by 99 random relabellings of the cases and population. Values of the observed-difference function were calculated for each permutation to investigate if there was any significant deviation of the observed-difference function from zero [Reference Chetwynd and Diggle35].
Our second approach to determine if there were any second-order effects was to investigate the hypothesis that geographically close farms were more similar than those geographically distant. The relationship between the outcome response (the proportion of pigs positive per farm) and the effect of herd size and farm was examined by fitting a generalized linear mixed model as follows:
In Equation (3) the logit of the observed probability of the jth pig from the ith farm being seropositive, p ij, was estimated as a function of a binary variable representing large herd-size category and a random effect term, U i, which was normally distributed with a mean of zero and variance σ2.
The model was applied to all farms in Denmark that had easting and northing coordinates supplied and were producing pigs for slaughter in 2003. The model was sequentially run for all Danish pig-producing counties as computational constraints prevented modelling all farms at once.
Model parameters were estimated using a Bayesian approach, implemented in WinBUGS version 1.4.1. Markov Chain Monte Carlo (MCMC) methods were applied to the observed data to simulate values from the joint conditional distributions of the unknown quantities. We chose non-informed prior and hyper-prior distributions for all model parameters: for the fixed-effects we chose Normal(0, 0·000001) and for σ2 (the variance of the farm random-effect term), we chose inverse Gamma(0·1, 0·001). Three chains were run and convergence was judged to have occurred on the basis of visual inspection of time-series and Gelman–Rubin plots [Reference Toft36]. The length of the chain was determined by running sufficient iterations to ensure the Monte Carlo standard errors for each parameter were <5% of the posterior standard deviation. A total of 30 000 iterations were run with a ‘burn in’ of 5000 iterations.
The farm-level random effects from the model were plotted on to county map outlines in an initial investigation into the presence or otherwise of second-order spatial effects. Then omni-directional binned semivariograms were plotted. These illustrate the difference between pairs of data-points (farm-level random effects) within a given spatial lag (the distance between pairs of farms) [Reference Isaaks and Srivastava37]. If there was spatial dependency between farms we would expect an upwards trend in the variogram. Conversely, little or no spatial autocorrelation would produce an essentially flat variogram. Directional semivariograms at angle sizes of 0°, 45°, 90° and 135° (tolerance of ±22·5°) were plotted to investigate if the spatial structure was anisotropic.
The significance of the spatial autocorrelation was determined by permuting the data values on the spatial locations to produce simulation envelopes. As permuted data should not exhibit spatial dependency any points lying outside these simulation envelopes indicate significant spatial autocorrelation. The magnitude of the spatial autocorrelation was determined by calculating the ratio of nugget to total semivariance. The nugget semivariance is the point at which an extrapolated fitted line would cross the vertical axis. A nugget to total semivariance ratio of <25% indicated strong spatial dependence, between 25% and 75% indicated moderate spatial dependence, and >75% indicated weak spatial dependence [Reference Cambardella38].
As we were interested in small-scale spatial dependency for both K function and semivariogram analysis the maximum distance investigated was 10 km.
RESULTS
There were 10 166 farms sampled in 2003 in the Danish programme with coordinate information. Figure 2 is the edge-corrected kernel-smoothed map of the farm density. Smoothed farm density was normally distributed with a mean of 0·20 and a standard deviation of 0·09 farms/km2. The range of smoothed densities varied throughout the country from zero in Copenhagen to 0·47 per in Viborg.
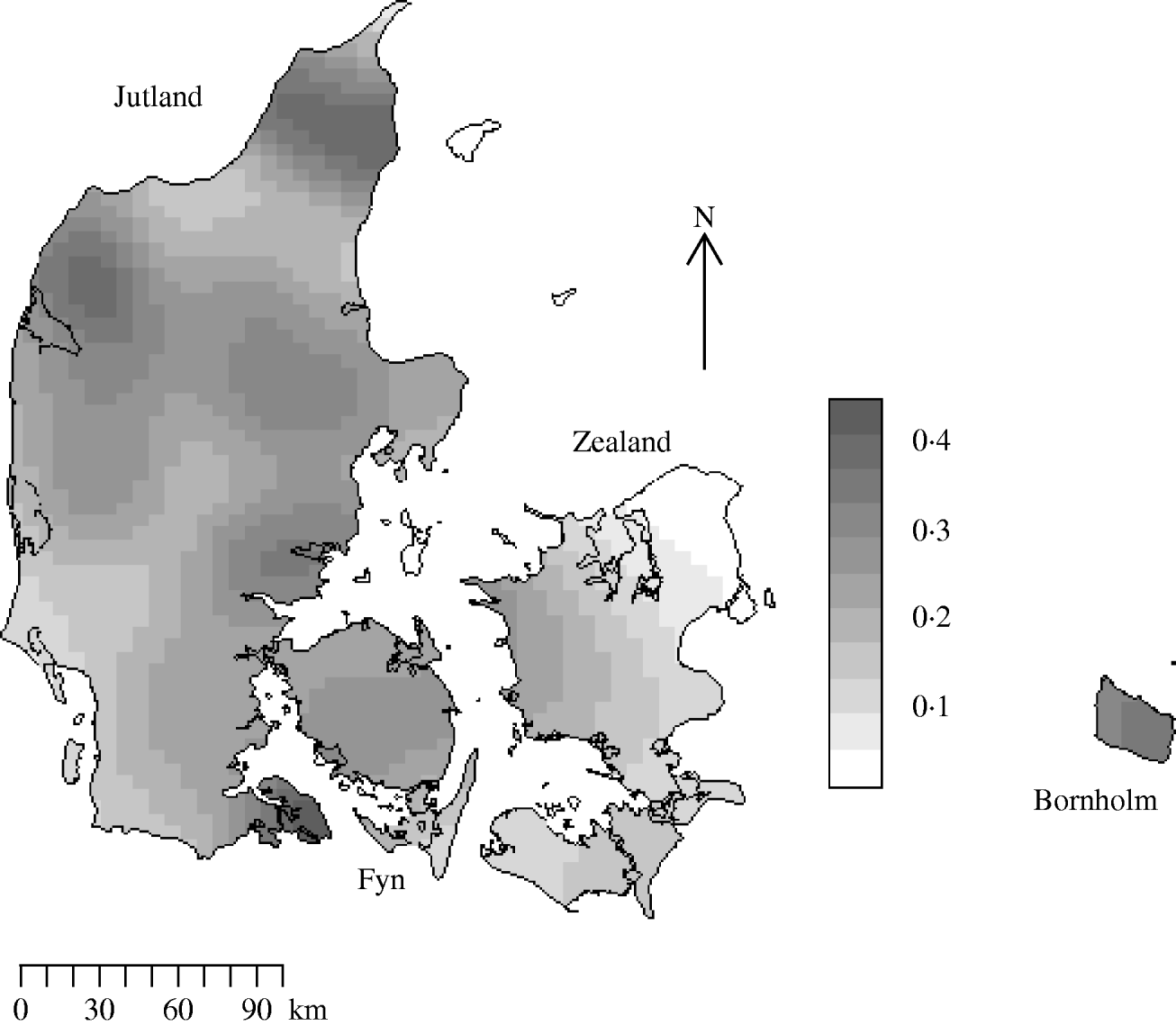
Fig. 2. Kernel-smoothed map showing variation in Salmonella meat-juice-tested slaughter herd densities across Denmark. The Jutland peninsula and main islands are labelled. Herds that produced <200 pigs for slaughter annually were not tested. Units are farms/km2.
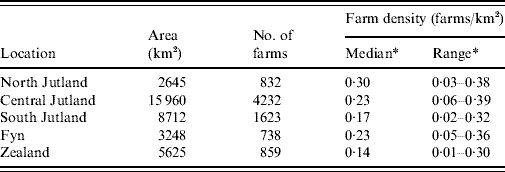
Figure 1 shows the location of counties and the five areas used in the investigation of inhomogeneous K-function estimation. Table 1 gives the area, number of farms and farm density for each of the five areas selected for inhomogeneous K-function analysis. In total the areas encompassed 8286/10 166 farms sampled for 2003. Over all five areas there was a wide range of farm densities from a median of 0·30 (range 0·03–0·38) farms/km2 in North Jutland to 0·14 (range 0·01–0·30) in Zealand.
Table 1. Area, number of farms, number of case farms and farm density for the five approximately square regions used in K-function analysis
* Calculated using the spatstat library in R.
The inhomogeneous K-function analysis of all large square areas showed that the observed pattern of farms was not aggregated (not shown). The median nearest-neighbour distance was 0·77 km (IQR 0·69, range 0·01–11·56 km).
Using the cut-off of ⩾40% meat-juice, ELISA-positive pigs in a herd produced 272 case farms. The case incidence risk was 3%. Figure 3 shows the observed-difference K function between case and population farms for the counties of Nordjylland, Arhus, Ringkobing and Sonderjylland. Nordjylland, Ringkobing and Arhus show evidence of local spatial aggregation of case farms over that of all farms. The extent of the aggregation was 1 km for Nordjylland and 4 km for Arhus. For Ringkobing it was statistically significant at 6 km with points beyond the simulation envelope. Together these three counties represented 40% of the Danish pig population in 2003. The results for the remaining counties were similar to that of Sonderjylland showing no evidence for local spatial aggregation of case farms over that of all farms.
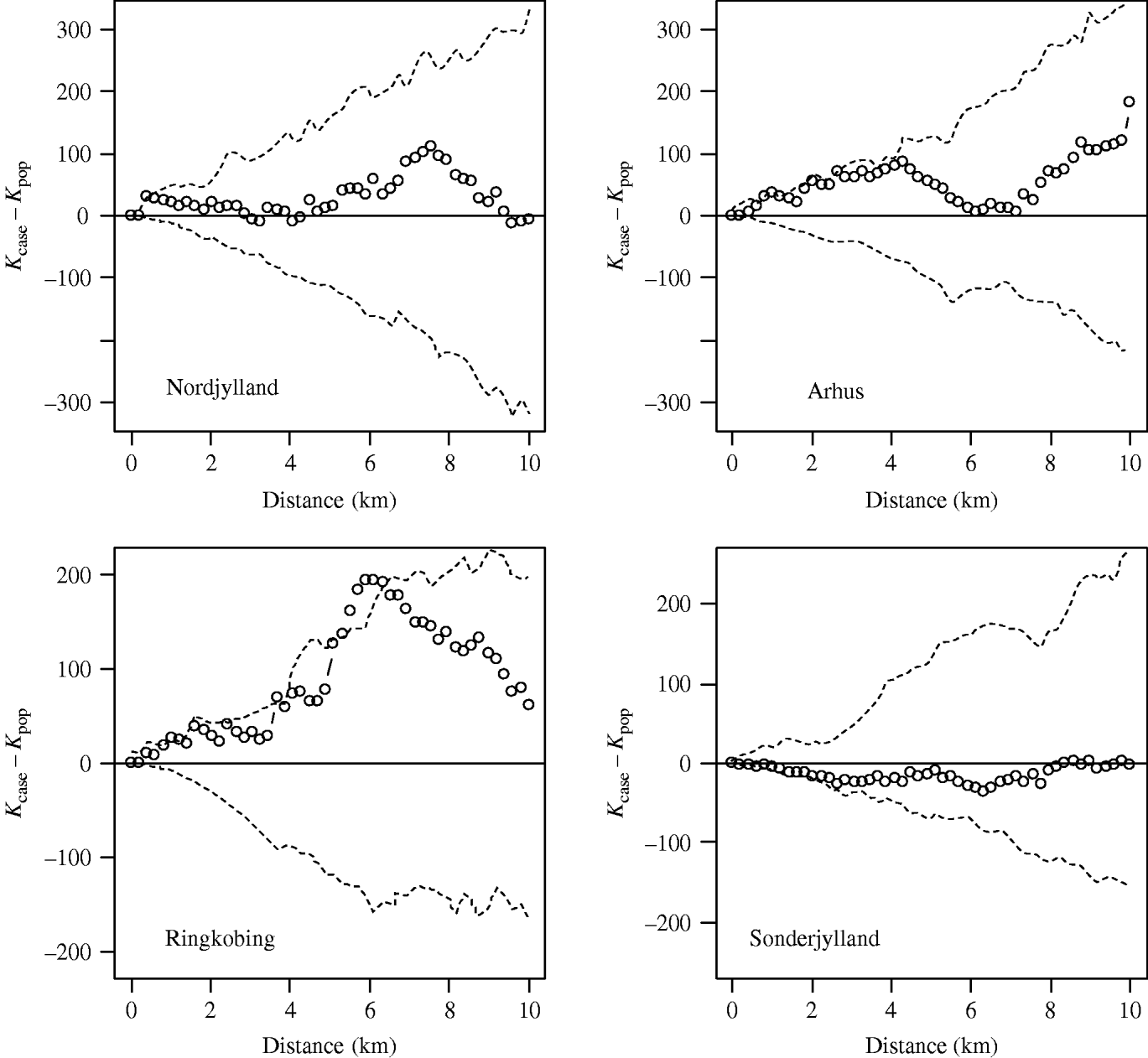
Fig. 3. Observed-difference K function between case and population farms for Nordjylland, Arhus, Ringkobing and Sonderjylland. The open symbols (○) represent the difference between the two K functions and the dashed lines (- - -) the simulation envelope based on 99 random relabellings of the cases and population. A farm was defined as a case if in 2003 the proportion of positive results was >40%.
When the farm-level random effects were plotted by their coordinates there were no apparent aggregations of similar-sized random effects. This pattern was seen in all counties. However, semivariograms (Fig. 4) for most large pig-producing counties showed evidence of spatial dependency with an upwards trend in the variogram at up to 4 km distance. Although most counties had all points lying within the simulation envelopes, the four main pig-producing counties Nordjylland, Viborg, Arhus and Sonderjylland had points below the envelopes indicating significant spatial autocorrelation from 2 km to 4 km. Together these four counties represented 50% of the Danish pig population in 2003. The nugget to total semivariance ratios of these four counties was ~70%, indicating moderate spatial autocorrelation. The strength of the dependency was proportional to slaughter-pig density with the exception of Fyn.
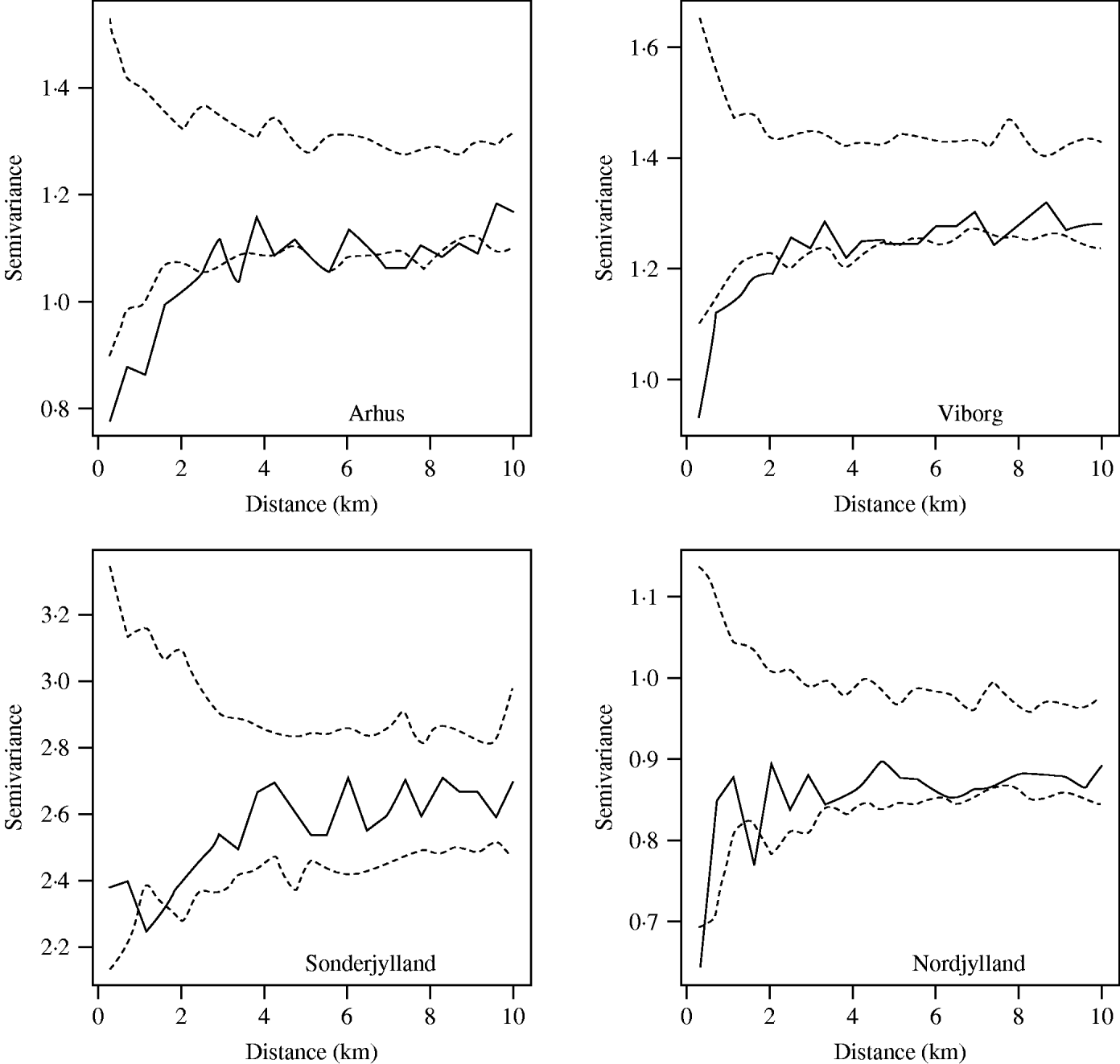
Fig. 4. Spatial semivariograms fitted to the herd-size adjusted farm-level random effects for the counties of Arhus, Viborg, Sonderjylland and Nordjylland. The open symbols (○) represent the semivariance and the dashed lines (- - -) the simulation envelopes obtained by permutation of the data on the spatial locations.
Table 2 shows the farm-level prevalence unadjusted for herd size, proportion of farms in the large herd-size category, odds ratios for large herd size and the variance of the random effects with 95% Bayesian credibility intervals for each county. The unadjusted farm-level prevalence was highest at ~5% in the north of Jutland (Nordjylland and Arhus) and lowest, at ~1%, in the east of Denmark (Bornholm and Roskilde). All counties in Jutland and Fyn had ⩾43% farms in the large herd-size category. Odds ratios for Nordjylland, Fyn, Ribe, Vejle and Viborg were significant suggesting that pigs in these counties were at more risk of being seropositive if herd size was large (>2000 finishers produced annually) than if it was medium (between 200 and 2000 finishers produced annually). The variance of the random effects was greatest in Sonderjylland indicating that farms in this county showed the most variation in farm-level prevalence of Salmonella.
Table 2. Unadjusted farm-level Salmonella seroprevalence, odds ratios, proportion of farms in the large herd-size category and variance of the farm-level random effects for Danish pig-producing counties in 2003
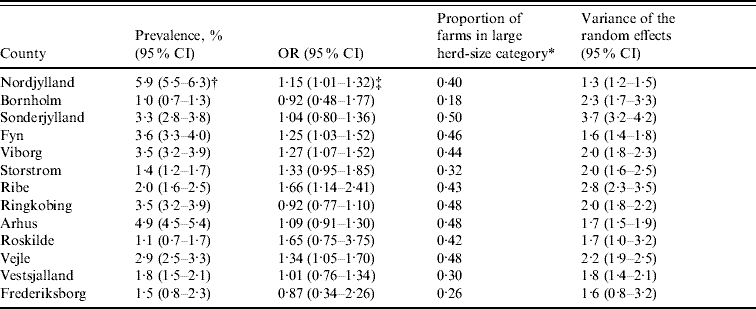
OR, Odds ratio; 95% CI, 95% Bayesian credible intervals.
* Farms with >60 pigs tested in 2003 (equates to an annual slaughter of >2000 finishers).
† Unadjusted farm-level prevalence.
‡ Interpretation: In Nordjylland the odds of a pig being seropositive was increased by a factor of 1·15 (95% Bayesian CI 1·01–1·32) if the pig was from a large (>2000 finishers produced annually) herd than if it was from a medium (between 200 and 2000 finishers produced annually) herd.
DISCUSSION
Slaughter-pig farm density showed large variation both at the country-wide and at the local level in Denmark in 2003. The areas of highest farm density are Viborg and Nordjylland on the Jutland peninsula (0·47 farms/km2); the lowest are on the island of Zealand. The distribution pattern of farms followed a random inhomogeneous Poisson process and although farms had near neighbours they did not spatially aggregate. With regard to Salmonella seropositivity we found consistent evidence for spatial dependency at distances of ~4 km. The strength of the spatial dependency varied throughout the country being proportional to farm density. Our findings were in accord with those reporting short distances between farms [Reference Berends23], being a neighbour of an infected farm [Reference Langvad24] and pig density [Reference Fedorka-Cray, Gray, Wray, Wray and Wray22] as potential risk factors for Salmonella infection in pigs.
This local spatial dependency adds to the current knowledge of the epidemiology of subclinical Salmonella in Danish slaughter-pig farms and can inform future strategies aimed at optimizing the control programme. For example, more intensive sampling of farms within a 4 km radius of identified problem farms, such as those in levels 2 or 3, on the Jutland peninsula is likely to capture more positive results, leading to interventions that may result in enhanced food safety. Similarly, we propose the concept of reduced sampling of farms that are near neighbours of ‘Salmonella-free’ farms. ‘Salmonella-free’ refers to farms enrolled in the ‘risk-based’ scheme which has been running since July 2005. This scheme requires one sample per month to be taken from herds with a Salmonella index level of 0 and a minimum of 10 negative meat-juice samples in the last 6 months. To date 50% of herds meet these criteria. Our study has identified that when spatial dependency is present, such as in Jutland, there are farms that provide essentially redundant information that could potentially be eliminated from the surveillance programme. Spatial sampling optimization for groundwater monitoring has been achieved using the variogram [Reference Ling39, Reference Cameron and Hunter40] and we propose using it to optimize sampling in the DSSCP. If spatial dependency is present in other disease programmes, both within and beyond Denmark, then these strategies could be applied to these programmes. For example, evidence for spatial dependency has been found between bulk milk tanks titres for Salmonella Typhimurium in Texas dairy herds [Reference Graham3] and between cattle herds in Denmark with regard to Salmonella Dublin infection [Reference Ersboll and Nielsen41].
Local farm density is a well recognized risk factor when investigating epidemics of animal disease [Reference Mintiens42–Reference Gibbens45]. The density of neighbouring herds was associated with so-called ‘neighbourhood infections’ during the 1994 classical swine fever epidemic in Belgium [Reference Mintiens42] and ‘local’ spread accounted for 79% of means of spread in the first 5 months of the 2001 foot-and-mouth disease epidemic in Great Britain [Reference Gibbens45]. High farm density implies that the distance between farms is short; in these examples a neighbourhood was an area of 1 km radius around an infected herd and local meant within 3 km of an infected place.
Although we are less familiar with farm-density investigation in relation to a subclinical endemic infection such as Salmonella in Danish finisher-pig herds there are compelling reasons to investigate it. If Salmonella is not already present, or if a novel serovar is in circulation, then pig herds are at risk from its introduction through many routes, the two main routes being the introduction of infected pigs and contaminated feed [Reference Lo Fo Wong46]. The latter is thought to be of minor importance as there are stringent controls on animal feed in Denmark; where in 2005 the prevalence of Salmonella in animal feed was low. There is much support for the theory that the introduction of infected pigs is a likely source of Salmonella for Danish pig farms [Reference Berends23, Reference Lo Fo Wong47–Reference Stärk49]. It is common farming practice to purchase stock from a geographically close supplier and this could lead to small-scale spatial dependency in the data. Denser farming areas probably offer more choice of supplier. Lo Fo Wong et al. reported that the odds of seropositivity increased significantly if greater than three suppliers were used [Reference Lo Fo Wong47].
The other ‘external’ sources of Salmonella such as visitors [Reference Funk, Davies and Gebreyes50], vermin [Reference Fedorka-Cray, Gray, Wray, Wray and Wray22, Reference Steinbach and Kroell51] and sharing of contaminated equipment [Reference Langvad24] can also be farm density-dependent. Rodents and flies have been found to carry Salmonella [Reference Letellier52, Reference Barber53] and the small distances between many of the Danish pig farms are well within the range of the brown rat [Reference Endepols54]. In addition airborne spread is possible at least over short experimental distances [Reference Oliveira, Carvalho and Garcia55, Reference Proux56]. Our findings of spatial dependency between farms with regard to Salmonella seropositivity, and aggregation of Salmonella case farms over that of all farms at distances of up to 4 km could be due to these locally acting processes or the contagious nature of the disease. Temporal studies would help elucidate this.
The inhomogeneous K function is a relatively new technique. It has been used to highlight significant differences in the spatial aggregation of vacuoles in mice brains infected with different transmissible spongiform encephalopathies [Reference Webster and Baddeley57]. The use of the inhomogeneous K function to summarize the spatial pattern of farms seems sensible. It allows for the spatial variation in intensity of the underlying point pattern which is likely to occur in animal production systems and is clearly seen in pig farm density in Denmark. By allowing for the non-uniform intensity of the spatial locations of farms it permits hypothesis testing for aggregation. Our results support the hypothesis that the farm distribution pattern follows a random inhomogeneous Poisson process with no aggregation beyond that.
Even though our dataset was effectively a census of Danish finisher swine herds in 2003 there was potential for selection, misclassification and confounder bias in our study. Selection bias may have occurred when we excluded 405 of 10 571 (4%) of farms because coordinate information was unavailable. As our database was drawn from herds registered in March 2004 the 10 571 farms with available coordinate information were still in production then and were likely to be different from the 405 that no longer were. However, this is likely to be of little importance as this group of farms represents only 4% of the total.
Further selection bias may have occurred in selecting the five large areas for the inhomogeneous K-function analysis. These were approximately square and excluded some areas of pig farms (notably Bornholm) and restricted the sites for consideration to those on large land masses. Nonetheless, we believe the coverage of farms within the five areas was suitably representative of all pig farms tested in 2003; 82% were included and the case incidence risk (3%) was the same as that for all farms.
The use of the farmhouse locations over that of the actual polygonal boundaries of the farm may potentially lead to an over-estimation of the distance between farms (misclassification bias). This would be of great significance in extensive sheep or beef cattle farming systems if farm sizes are large. However, it is likely to be of little consequence in intensive production systems such as the Danish pig farms we are investigating in the present study.
The adjustment for herd size in the geostatistical model was made as a number of earlier Danish studies [Reference Carstensen and Christensen20, Reference Baggesen48] and a recent Canadian study [Reference Farzan58] have reported large herd size as a risk factor for increased seropositivity in slaughter-pig herds. However, later studies in Denmark [Reference Stege59] and throughout Europe [Reference Lo Fo Wong47] showed no association and a Dutch study [Reference van der Wolf60] showed that large herd size was protective. In this study the effect of herd size was not investigated per se, but adjusting for herd size was undertaken in the context of its effect on spatial dependency. The odds ratios reported suggest increased risk in some counties as herd size increases. The reason for this may be that there are local practices, such as more movements of pigs between farms or higher within-farm pig density, which make large herd size more of a risk for increased Salmonella seroprevalence in these counties. Nevertheless these results must be interpreted with caution as the effect of herd size is probably confounded by other covariates, such as feeding and biosecurity practices that we have no information on.
Distance can be defined in different ways; Euclidean, time of travelling or in terms of social networks [Reference Haining61]. Ideally all three definitions should be considered in the spatial epidemiological investigations and we should not constrain ‘locality’ to only imply spatial proximity. However, this study focused on Euclidean distance between farmhouses but future studies in relation to social networks would appear to be a logical next step. This could be particularly helpful in tracing the dissemination of infected pigs.
We have outlined an approach to combine geo-referenced farm location information and routinely collected control programme data using techniques from spatial point patternandgeostatistical analysis. This has extended the current knowledge of the epidemiology of subclinical Salmonella in Danish slaughter-pig farms. Furthermore, we have demonstrated how our approach has the potential to optimize sampling strategies while maintaining consumer confidence in food safety. These techniques could be readily applied to data from other programmes in different countries.
ACKNOWLEDGEMENTS
We thank Adrian Baddeley from the University of Western Australia for his assistance with the inhomogeneous K-function analyses. We thank Jonathan Marshall from Massey University for his assistance with the spatially adaptive smoothing.
DECLARATION OF INTEREST
None.








