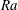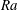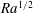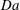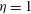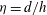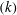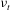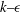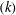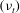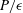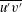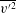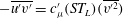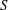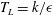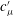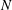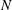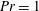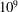Focus on Fluids
Soft suspensions: inertia cooperates with flexibility
-
- Published online by Cambridge University Press:
- 30 October 2014, pp. 1-4
-
- Article
-
- You have access
- HTML
- Export citation
Papers
Dynamics of sessile drops. Part 1. Inviscid theory
-
- Published online by Cambridge University Press:
- 31 October 2014, pp. 5-38
-
- Article
- Export citation
The effect of viscoelasticity on the turbulent kinetic energy cascade
-
- Published online by Cambridge University Press:
- 31 October 2014, pp. 39-62
-
- Article
- Export citation
The influence of harmonic wall motion on transitional boundary layers
-
- Published online by Cambridge University Press:
- 03 November 2014, pp. 63-94
-
- Article
- Export citation
High-Rayleigh-number convection of a reactive solute in a porous medium
-
- Published online by Cambridge University Press:
- 04 November 2014, pp. 95-126
-
- Article
- Export citation
Coevolution of width and sinuosity in meandering rivers
-
- Published online by Cambridge University Press:
- 04 November 2014, pp. 127-174
-
- Article
- Export citation
Investigation of the roughness-induced transition: global stability analyses and direct numerical simulations
-
- Published online by Cambridge University Press:
- 04 November 2014, pp. 175-211
-
- Article
- Export citation
Suction–shear–Coriolis instability in a flow between parallel plates
-
- Published online by Cambridge University Press:
- 04 November 2014, pp. 212-242
-
- Article
- Export citation
Two-phase filtered mass density function for LES of turbulent reacting flows
-
- Published online by Cambridge University Press:
- 05 November 2014, pp. 243-277
-
- Article
- Export citation
Linear and nonlinear evolution of a localized disturbance in polymeric channel flow
-
- Published online by Cambridge University Press:
- 05 November 2014, pp. 278-303
-
- Article
- Export citation
A revisit of the equilibrium assumption for predicting near-wall turbulence
-
- Published online by Cambridge University Press:
- 07 November 2014, pp. 304-312
-
- Article
- Export citation
Detonation in supersonic radial outflow
-
- Published online by Cambridge University Press:
- 07 November 2014, pp. 313-341
-
- Article
- Export citation
Structural and stability characteristics of jets in crossflow
-
- Published online by Cambridge University Press:
- 07 November 2014, pp. 342-367
-
- Article
- Export citation
Generalized Ertel’s theorem and infinite hierarchies of conserved quantities for three-dimensional time-dependent Euler and Navier–Stokes equations
-
- Published online by Cambridge University Press:
- 07 November 2014, pp. 368-386
-
- Article
- Export citation
Two-dimensional nonlinear travelling waves in magnetohydrodynamic channel flow
-
- Published online by Cambridge University Press:
- 11 November 2014, pp. 387-406
-
- Article
- Export citation
A pinned or free-floating rigid plate on a thin viscous film
-
- Published online by Cambridge University Press:
- 11 November 2014, pp. 407-430
-
- Article
- Export citation
Symmetry breaking of azimuthal thermo-acoustic modes in annular cavities: a theoretical study
-
- Published online by Cambridge University Press:
- 11 November 2014, pp. 431-465
-
- Article
- Export citation
Transition through Rayleigh–Taylor instabilities in a breaking internal lee wave
-
- Published online by Cambridge University Press:
- 11 November 2014, pp. 466-493
-
- Article
- Export citation
Direct numerical simulations of turbulent Ekman layers with increasing static stability: modifications to the bulk structure and second-order statistics
-
- Published online by Cambridge University Press:
- 11 November 2014, pp. 494-539
-
- Article
- Export citation
Stabilizing action of pressure in homogeneous compressible shear flows: effect of Mach number and perturbation obliqueness
-
- Published online by Cambridge University Press:
- 12 November 2014, pp. 540-566
-
- Article
- Export citation