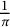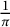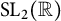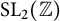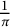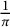1 Introduction
One of the best fortunes that Ramanujan left to his fellows might be the 17 extraordinary formulas for
![]() $\frac {1}{\pi }$
given in his seminal work [Reference Ramanujan10], one of which is the following striking formula:
$\frac {1}{\pi }$
given in his seminal work [Reference Ramanujan10], one of which is the following striking formula:
 $$ \begin{align} \frac{1}{\pi}=\frac{21}{8}\sum_{n=0}^{\infty}\binom{2n}{n}^{3}\left(n+\frac{5}{42}\right)\frac{1}{2^{12n}}, \end{align} $$
$$ \begin{align} \frac{1}{\pi}=\frac{21}{8}\sum_{n=0}^{\infty}\binom{2n}{n}^{3}\left(n+\frac{5}{42}\right)\frac{1}{2^{12n}}, \end{align} $$
which was derived from Jacobi’s complete elliptic integral of the first kind
 $$ \begin{align*}K(k)=\int_{0}^{\pi/2}\frac{d\theta}{\sqrt{1-k^{2}\sin(\theta)^{2}}}=\frac{\pi}{2}{}_{2}{F}_{1}\left(\frac{1}{2},\frac{1}{2};1;k^{2}\right) \end{align*} $$
$$ \begin{align*}K(k)=\int_{0}^{\pi/2}\frac{d\theta}{\sqrt{1-k^{2}\sin(\theta)^{2}}}=\frac{\pi}{2}{}_{2}{F}_{1}\left(\frac{1}{2},\frac{1}{2};1;k^{2}\right) \end{align*} $$
and its modular transformation, and a Clausen-type quadratic transformation
 $$ \begin{align} {}_{2}{F}_{1}\left(\frac{1}{2},\frac{1}{2};1;k^{2}\right)^{2}={}_{3}F_{2}\left(\frac{1}{2},\frac{1}{2},\frac{1}{2};1,1;4(1-k^{2})k^{2}\right). \end{align} $$
$$ \begin{align} {}_{2}{F}_{1}\left(\frac{1}{2},\frac{1}{2};1;k^{2}\right)^{2}={}_{3}F_{2}\left(\frac{1}{2},\frac{1}{2},\frac{1}{2};1,1;4(1-k^{2})k^{2}\right). \end{align} $$
After Ramanujan’s work, series for
![]() $\frac {1}{\pi }$
of the form
$\frac {1}{\pi }$
of the form
 $$ \begin{align} C\sum_{n=0}^{\infty}A(n)(n-B)t^{n} \end{align} $$
$$ \begin{align} C\sum_{n=0}^{\infty}A(n)(n-B)t^{n} \end{align} $$
with
![]() $A(n)$
, B, C algebraic numbers have been one of the central objects in related areas such as the theory of elliptic integrals, and have been extensively studied by many mathematicians, and now in the spirit of Ramanujan, we call a series convergent to
$A(n)$
, B, C algebraic numbers have been one of the central objects in related areas such as the theory of elliptic integrals, and have been extensively studied by many mathematicians, and now in the spirit of Ramanujan, we call a series convergent to
![]() $\frac {1}{\pi }$
of the form (1.3) a Ramanujan-type series for
$\frac {1}{\pi }$
of the form (1.3) a Ramanujan-type series for
![]() $\frac {1}{\pi }$
. In particular, when
$\frac {1}{\pi }$
. In particular, when
![]() $A(n)$
, B, and C are all rational, it is called a rational Ramanujan-type series. The reader is referred to [Reference Baruah, Berndt and Chan3] and the references therein for some studies on Ramanujan-type series.
$A(n)$
, B, and C are all rational, it is called a rational Ramanujan-type series. The reader is referred to [Reference Baruah, Berndt and Chan3] and the references therein for some studies on Ramanujan-type series.
One of the notable works on Ramanujan-type series is due to Chan, Chan, and Liu [Reference Chan, Chan and Liu5], in which they extend Ramanujan’s modular approach and invent a method for producing Ramanujan-type series via modular transformations and modular equations. Building upon Chan et al.’s work, Cooper and/or his collaborators (see, e.g., [Reference Cooper9] and the references therein) derived a number of families of explicit examples of Ramanujan-type series. Somewhat interestingly, if one takes a careful look at the derivations of Ramanujan’s series and Cooper’s work, one may note that they share some notable commonness, such as that:
-
• they are all somehow connected to some subgroups of
 $\mathrm {SL}_{2}(\mathbb {R})$
commensurable with
$\mathrm {SL}_{2}(\mathbb {R})$
commensurable with
 $\mathrm {SL}_{2}(\mathbb {Z})$
, whose associated modular curves are of genus zero,
$\mathrm {SL}_{2}(\mathbb {Z})$
, whose associated modular curves are of genus zero, -
• the coefficients
 $A(n)$
all satisfy some recurrence relation of the form
$A(n)$
all satisfy some recurrence relation of the form  $$ \begin{align*}(n+1)^{3}A(n+1)+c_{1}(n)A(n)+\cdots+c_{\ell}(n)A(n+1-\ell)=0 \end{align*} $$
$$ \begin{align*}(n+1)^{3}A(n+1)+c_{1}(n)A(n)+\cdots+c_{\ell}(n)A(n+1-\ell)=0 \end{align*} $$
for some
![]() $\ell \geq 2$
and cubic polynomials
$\ell \geq 2$
and cubic polynomials
![]() $c_{i}(n)$
in n, from which a number of questions may arise, such as:
$c_{i}(n)$
in n, from which a number of questions may arise, such as:
-
• how does a genus zero
 $\mathrm {SL}_{2}(\mathbb {R})$
-subgroup commensurable with
$\mathrm {SL}_{2}(\mathbb {R})$
-subgroup commensurable with
 $\mathrm {SL}_{2}(\mathbb {Z})$
give rise to a Ramanujan-type series?
$\mathrm {SL}_{2}(\mathbb {Z})$
give rise to a Ramanujan-type series? -
• does the order
 $\ell $
of the recurrence relation encode any particular information?
$\ell $
of the recurrence relation encode any particular information? -
• why is the coefficient of
 $A(n+1)$
always
$A(n+1)$
always
 $(n+1)^{3}$
?
$(n+1)^{3}$
?
In this note, all of these questions shall be addressed, and more generally, we shall show that all those Ramanujan-type series can be uniformly formulated as follows (throughout the remainder of this note, when we write
![]() $t(z_{0})$
, it is assumed to be finite, i.e.,
$t(z_{0})$
, it is assumed to be finite, i.e.,
![]() $z_{0}$
is assumed to not be a pole).
$z_{0}$
is assumed to not be a pole).
Theorem 1.1 Let
![]() $\Gamma $
be a subgroup of
$\Gamma $
be a subgroup of
![]() $\mathrm {SL}_{2}(\mathbb {R})$
commensurable with
$\mathrm {SL}_{2}(\mathbb {R})$
commensurable with
![]() $\mathrm {SL}_{2}(\mathbb {Z})$
such that the associated modular curve
$\mathrm {SL}_{2}(\mathbb {Z})$
such that the associated modular curve
![]() $X(\Gamma )=\overline {\Gamma \backslash \mathbb {H}}$
is of genus zero with a uniformizer
$X(\Gamma )=\overline {\Gamma \backslash \mathbb {H}}$
is of genus zero with a uniformizer
![]() $t=t(\tau )$
satisfying that:
$t=t(\tau )$
satisfying that:
-
• its Fourier coefficients at the cusp
 $[i\infty ]$
are algebraic numbers,
$[i\infty ]$
are algebraic numbers, -
• it has a zero at the cusp
 $[i\infty ]$
,
$[i\infty ]$
, -
• it has
-
– a pole at a cusp apart from
 $[i\infty ]$
, or at an elliptic point of period
$[i\infty ]$
, or at an elliptic point of period
 $h>2$
,
$h>2$
,or
-
– a pole at an elliptic point of period
 $h=2$
if there are no cusps other than
$h=2$
if there are no cusps other than
 $[i\infty ]$
or elliptic points of period
$[i\infty ]$
or elliptic points of period
 $h>2$
.
$h>2$
.
Then, for any imaginary quadratic point
![]() $\tau _{0}\in \mathbb {Q}[\sqrt {-d}]\cap \mathbb {H}$
such that
$\tau _{0}\in \mathbb {Q}[\sqrt {-d}]\cap \mathbb {H}$
such that
![]() $|t(\tau _{0})|<\mu (t)$
, where
$|t(\tau _{0})|<\mu (t)$
, where
one has that
 $$ \begin{align} \frac{1}{\pi}=C\sum_{n=0}^{\infty}A(n)\left(n-B\right)t(\tau_{0})^{n}, \end{align} $$
$$ \begin{align} \frac{1}{\pi}=C\sum_{n=0}^{\infty}A(n)\left(n-B\right)t(\tau_{0})^{n}, \end{align} $$
where
 $$ \begin{align*}B&=\left.t(\tau_{0})\left(\frac{1}{\pi i}\left.\frac{dy}{d\tau}\right|_{\tau_{0}}-\frac{1}{2\pi\mathrm{Im}(\tau_{0})}y(\tau_{0})\right)\right/\left(\frac{y(\tau_{0})}{2\pi i}\left.\frac{dt}{d\tau}\right|_{\tau_{0}}\right),\\ C&=\frac{2\mathrm{Im}(\tau_{0})}{t(\tau_{0})}\prod_{\substack{z_{0}\ \text{is a cusp}}}(t(\tau_{0})-t(z_0))\prod_{\substack{z_{0}\ \text{is an elliptic}\\ \text{ point of period}~h }}\left(t(\tau_{0})-t(z_{0})\right)^{\frac{h-1}{h}},\\ y(\tau)&=\prod_{\substack{z_{0}\ \text{is a cusp }}}(t-t(z_0))^{\frac{-1}{2}}\prod_{\substack{z_{0}\ \text{is an elliptic}\\ \text{ point of period}~h}}\left(t-t(z_{0})\right)^{\frac{1-h}{2h}}\left(\frac{1}{2\pi i}\frac{dt}{d\tau}\right)^{\frac{1}{2}}, \end{align*} $$
$$ \begin{align*}B&=\left.t(\tau_{0})\left(\frac{1}{\pi i}\left.\frac{dy}{d\tau}\right|_{\tau_{0}}-\frac{1}{2\pi\mathrm{Im}(\tau_{0})}y(\tau_{0})\right)\right/\left(\frac{y(\tau_{0})}{2\pi i}\left.\frac{dt}{d\tau}\right|_{\tau_{0}}\right),\\ C&=\frac{2\mathrm{Im}(\tau_{0})}{t(\tau_{0})}\prod_{\substack{z_{0}\ \text{is a cusp}}}(t(\tau_{0})-t(z_0))\prod_{\substack{z_{0}\ \text{is an elliptic}\\ \text{ point of period}~h }}\left(t(\tau_{0})-t(z_{0})\right)^{\frac{h-1}{h}},\\ y(\tau)&=\prod_{\substack{z_{0}\ \text{is a cusp }}}(t-t(z_0))^{\frac{-1}{2}}\prod_{\substack{z_{0}\ \text{is an elliptic}\\ \text{ point of period}~h}}\left(t-t(z_{0})\right)^{\frac{1-h}{2h}}\left(\frac{1}{2\pi i}\frac{dt}{d\tau}\right)^{\frac{1}{2}}, \end{align*} $$
and the coefficients
![]() $A(n)$
are defined by
$A(n)$
are defined by
and that
![]() $ \sum _{n=0}^{\infty }A(n)t^{n} $
is a solution of
$ \sum _{n=0}^{\infty }A(n)t^{n} $
is a solution of
which, as one shall see in Section 2, is the symmetric square of
where
 $$ \begin{align*}R_{1}(t)=\sum_{\substack{z_{0}\ \text{is a cusp}}}\frac{1}{t-t(z_{0})}+\sum_{\substack{z_{0}\ \text{is an elliptic }\\ \text{point of period}~h}}\frac{1-\frac{1}{h}}{t-t(z_{0})}, \end{align*} $$
$$ \begin{align*}R_{1}(t)=\sum_{\substack{z_{0}\ \text{is a cusp}}}\frac{1}{t-t(z_{0})}+\sum_{\substack{z_{0}\ \text{is an elliptic }\\ \text{point of period}~h}}\frac{1-\frac{1}{h}}{t-t(z_{0})}, \end{align*} $$
and
![]() $R_{2}(t)$
is a rational function in t such that
$R_{2}(t)$
is a rational function in t such that
![]() $R_{2}(t(\tau ))=\frac {3(t")^{2}-2t"'t'}{4(t')^{4}}+\frac {1}{2}R_{1}'(t(\tau ))+\frac {1}{4}R_{1}(t(\tau ))^{2}$
with
$R_{2}(t(\tau ))=\frac {3(t")^{2}-2t"'t'}{4(t')^{4}}+\frac {1}{2}R_{1}'(t(\tau ))+\frac {1}{4}R_{1}(t(\tau ))^{2}$
with
![]() $t'=\frac {dt}{d\tau }$
and
$t'=\frac {dt}{d\tau }$
and
![]() $R_{1}'(t)=\frac {dR_{1}}{dt}$
.
$R_{1}'(t)=\frac {dR_{1}}{dt}$
.
In particular, the coefficients
![]() $A(n)$
satisfy a linear homogeneous recurrence relation of the form
$A(n)$
satisfy a linear homogeneous recurrence relation of the form
for some cubic polynomials
![]() $c_{i}(n)$
in n, where
$c_{i}(n)$
in n, where
![]() $\nu (\Gamma )$
is defined by
$\nu (\Gamma )$
is defined by
 $$ \begin{align*}\nu(\Gamma)=\begin{cases}\displaystyle 2\left(\varepsilon_{\infty}+\sum_{h>2}\varepsilon_{h}-1\right)+\varepsilon_{2},&\mbox{if}\ \varepsilon_{\infty}+\sum_{h>2}\varepsilon_{h}\geq2,\\ \displaystyle \varepsilon_{2}+1,&\mbox{if}\ \varepsilon_{\infty}+\sum_{h>2}\varepsilon_{h}=1,\end{cases} \end{align*} $$
$$ \begin{align*}\nu(\Gamma)=\begin{cases}\displaystyle 2\left(\varepsilon_{\infty}+\sum_{h>2}\varepsilon_{h}-1\right)+\varepsilon_{2},&\mbox{if}\ \varepsilon_{\infty}+\sum_{h>2}\varepsilon_{h}\geq2,\\ \displaystyle \varepsilon_{2}+1,&\mbox{if}\ \varepsilon_{\infty}+\sum_{h>2}\varepsilon_{h}=1,\end{cases} \end{align*} $$
with
![]() $\varepsilon _{\infty }$
and
$\varepsilon _{\infty }$
and
![]() $\varepsilon _{h}$
, respectively, denoting the numbers of cusps and elliptic points of period h of
$\varepsilon _{h}$
, respectively, denoting the numbers of cusps and elliptic points of period h of
![]() $\Gamma $
.
$\Gamma $
.
Remark 1.2 Since
![]() $\Gamma $
is commensurable with
$\Gamma $
is commensurable with
![]() $\mathrm {SL}_{2}(\mathbb {Z})$
, then
$\mathrm {SL}_{2}(\mathbb {Z})$
, then
![]() $t(\tau )$
is algebraically related with
$t(\tau )$
is algebraically related with
![]() $j(\tau )$
. It is well known that for an imaginary quadratic point
$j(\tau )$
. It is well known that for an imaginary quadratic point
![]() $\tau _{0}\in \mathbb {H}$
,
$\tau _{0}\in \mathbb {H}$
,
![]() $j(\tau _{0})$
can be rigorously computed by a modular equation. As a result, one can indeed algebraically obtain the value of t at
$j(\tau _{0})$
can be rigorously computed by a modular equation. As a result, one can indeed algebraically obtain the value of t at
![]() $\tau _{0}$
, as well as the value of C. Similarly, the value of B can be algebraically computed using modular equations. See, e.g., [Reference Cohen and Strömberg8, Section 5.10].
$\tau _{0}$
, as well as the value of C. Similarly, the value of B can be algebraically computed using modular equations. See, e.g., [Reference Cohen and Strömberg8, Section 5.10].
Remark 1.3 As is seen in Theorem 1.1, the order of the recurrence relation in fact encodes some geometric information of
![]() $\Gamma $
by the conjugation-invariant
$\Gamma $
by the conjugation-invariant
![]() $\nu (\Gamma )$
. This answers one of the questions posed at the top of Theorem 1.1.
$\nu (\Gamma )$
. This answers one of the questions posed at the top of Theorem 1.1.
Remark 1.4 By [Reference Beardon4, Section 10.4], under the given assumptions, it is not hard to show that
![]() $\nu (\Gamma )>2$
.
$\nu (\Gamma )>2$
.
As an illustration, in the following example, we recover Ramanujan’s formula (1.1) from Theorem 1.1. Throughout the remainder of this note, we write
![]() $\eta (\tau )=q^{1/24}\prod _{n=1}^{\infty }(1-q^{n})$
with
$\eta (\tau )=q^{1/24}\prod _{n=1}^{\infty }(1-q^{n})$
with
![]() $q=\exp (2\pi i\tau )$
for the Dedekind eta function.
$q=\exp (2\pi i\tau )$
for the Dedekind eta function.
Example 1.5 (Ramanujan’s formula (1.1))
Let
 $\Gamma =\Gamma _{0}(4)+=\left \langle \Gamma _{0}(4),\begin {pmatrix}0&-1\\4&0\end {pmatrix}\right \rangle $
, the group generated by
$\Gamma =\Gamma _{0}(4)+=\left \langle \Gamma _{0}(4),\begin {pmatrix}0&-1\\4&0\end {pmatrix}\right \rangle $
, the group generated by
![]() $\Gamma _{0}(4)$
and its Fricke involution
$\Gamma _{0}(4)$
and its Fricke involution
 $\begin {pmatrix}0&-1\\4&0\end {pmatrix}$
, with
$\begin {pmatrix}0&-1\\4&0\end {pmatrix}$
, with
![]() $\varepsilon _{\infty }=2$
and
$\varepsilon _{\infty }=2$
and
![]() $\varepsilon _{2}=1$
and
$\varepsilon _{2}=1$
and
![]() $\varepsilon _{h}=0$
for
$\varepsilon _{h}=0$
for
![]() $h>2$
, and take the uniformizer
$h>2$
, and take the uniformizer
 $$ \begin{align*}t=t(\tau)=\frac{\eta(\tau)^{24}\eta(4\tau)^{24}}{\eta(2\tau)^{48}} \end{align*} $$
$$ \begin{align*}t=t(\tau)=\frac{\eta(\tau)^{24}\eta(4\tau)^{24}}{\eta(2\tau)^{48}} \end{align*} $$
with a zero at the cusp
![]() $[i\infty ]$
and a pole at the cusp
$[i\infty ]$
and a pole at the cusp
![]() $[\frac {1}{2}]$
and
$[\frac {1}{2}]$
and
![]() $\mu (t)=\frac {1}{64}$
. Then numerically, one can find that for
$\mu (t)=\frac {1}{64}$
. Then numerically, one can find that for
![]() $\tau _{0}=i\sqrt {7/4}$
, the coefficients
$\tau _{0}=i\sqrt {7/4}$
, the coefficients
![]() $B=-\frac {5}{42}$
,
$B=-\frac {5}{42}$
,
![]() $C=\frac {21i}{64}$
, and
$C=\frac {21i}{64}$
, and
![]() $t(\tau _{0})=\frac {1}{2^{12}}$
. Also, in this case, the coefficient
$t(\tau _{0})=\frac {1}{2^{12}}$
. Also, in this case, the coefficient
![]() $A(0)=-8i$
, and equation (1.5) can be specified as
$A(0)=-8i$
, and equation (1.5) can be specified as
 $$ \begin{align*}\frac{d^{3}Y}{dt^{3}}+\frac{3(96t-1)}{t(64t-1)}\frac{d^{2}Y}{dt^{2}}+\frac{208t-1}{t^{2}(64t-1)}\frac{dY}{dt}+\frac{8}{t^{2}(64t-1)}Y=0. \end{align*} $$
$$ \begin{align*}\frac{d^{3}Y}{dt^{3}}+\frac{3(96t-1)}{t(64t-1)}\frac{d^{2}Y}{dt^{2}}+\frac{208t-1}{t^{2}(64t-1)}\frac{dY}{dt}+\frac{8}{t^{2}(64t-1)}Y=0. \end{align*} $$
Substituting in
![]() $Y=\sum _{n=0}^{\infty }A(n)t^{n}$
and equating the coefficient of
$Y=\sum _{n=0}^{\infty }A(n)t^{n}$
and equating the coefficient of
![]() $t^{n}$
of the resulting series to 0, one finds that
$t^{n}$
of the resulting series to 0, one finds that
![]() $A(n)$
’s satisfy the following
$A(n)$
’s satisfy the following
![]() $2$
-term recurrence relation:
$2$
-term recurrence relation:
and it is easy to show that
 $$ \begin{align*}A(n)=A(0)\binom{2n}{n}^{3}=-8i\binom{2n}{n}^{3}. \end{align*} $$
$$ \begin{align*}A(n)=A(0)\binom{2n}{n}^{3}=-8i\binom{2n}{n}^{3}. \end{align*} $$
Substituting all these into (1.4), we reproduce Ramanujan’s striking formula (1.1)
 $$ \begin{align*}\frac{1}{\pi}=\frac{21}{8}\sum_{n=0}^{\infty}\binom{2n}{n}^{3}\left(n+\frac{5}{42}\right)\frac{1}{2^{12n}}. \end{align*} $$
$$ \begin{align*}\frac{1}{\pi}=\frac{21}{8}\sum_{n=0}^{\infty}\binom{2n}{n}^{3}\left(n+\frac{5}{42}\right)\frac{1}{2^{12n}}. \end{align*} $$
We also obtain the following example of a rational Ramanujan-type series for
![]() $\frac {1}{\pi }$
, which, to the best of our knowledge, has not appeared before in the literature.
$\frac {1}{\pi }$
, which, to the best of our knowledge, has not appeared before in the literature.
Example 1.6 Let
![]() $\Gamma =\gamma ^{-1}(\Gamma _{0}(4)\cap \Gamma (2))\gamma $
, where
$\Gamma =\gamma ^{-1}(\Gamma _{0}(4)\cap \Gamma (2))\gamma $
, where
 $\gamma =\begin {pmatrix}1&0\\1&1\end {pmatrix}$
, with
$\gamma =\begin {pmatrix}1&0\\1&1\end {pmatrix}$
, with
![]() $\varepsilon _{\infty }=4$
and
$\varepsilon _{\infty }=4$
and
![]() ${\varepsilon _{h}=0}$
for
${\varepsilon _{h}=0}$
for
![]() $h\geq 2$
, and take the uniformizer
$h\geq 2$
, and take the uniformizer
 $$ \begin{align*}t=t(\tau)=4\frac{\eta\left({2\tau}\right)^{8}\eta\left(\frac{\tau}{2}\right)^{4}}{\eta(\tau)^{12}} \end{align*} $$
$$ \begin{align*}t=t(\tau)=4\frac{\eta\left({2\tau}\right)^{8}\eta\left(\frac{\tau}{2}\right)^{4}}{\eta(\tau)^{12}} \end{align*} $$
with a zero at the cusp
![]() $[i\infty ]$
and a pole at the cusp
$[i\infty ]$
and a pole at the cusp
![]() $[1]$
and
$[1]$
and
![]() $\mu (t)=1$
. Then numerically, one can find that for
$\mu (t)=1$
. Then numerically, one can find that for
![]() $\tau _{0}=i$
, the coefficients
$\tau _{0}=i$
, the coefficients
![]() $B=0$
,
$B=0$
,
![]() $C=-1$
, and
$C=-1$
, and
![]() $t(\tau _{0})=\frac {\sqrt {2}}{2}$
. In this case, the coefficient
$t(\tau _{0})=\frac {\sqrt {2}}{2}$
. In this case, the coefficient
![]() $A(0)=-\frac {1}{4}$
, and equation (1.5) is given by
$A(0)=-\frac {1}{4}$
, and equation (1.5) is given by
 $$ \begin{align*}\frac{d^{3}Y}{dt^{3}}+\frac{3(3t^{2}-1)}{t^{3}-t}\frac{d^{2}Y}{dt^{2}}+\frac{19t^{4}-16t^{2}+1}{t^{2}(t^{2}-1)^{2}}\frac{dY}{dt}+\frac{4(2t^{2}-1)}{t(t^{2}-1)^{2}}Y=0. \end{align*} $$
$$ \begin{align*}\frac{d^{3}Y}{dt^{3}}+\frac{3(3t^{2}-1)}{t^{3}-t}\frac{d^{2}Y}{dt^{2}}+\frac{19t^{4}-16t^{2}+1}{t^{2}(t^{2}-1)^{2}}\frac{dY}{dt}+\frac{4(2t^{2}-1)}{t(t^{2}-1)^{2}}Y=0. \end{align*} $$
Thus, the coefficients
![]() $A(n)$
satisfy the
$A(n)$
satisfy the
![]() $3$
-term recurrence relation
$3$
-term recurrence relation
By Example 3.6, one can tell that
![]() $A(n)$
has the compact form
$A(n)$
has the compact form
 $$ \begin{align*}A(n)=\begin{cases}\displaystyle -\frac{1}{4}\left(\sum_{k}\binom{n-2k}{n/2-k}^{2}\binom{2k}{k}^{2}\right)4^{-n},&\mbox{if}\ n\ \mbox{is even,}\\ 0,&\mbox{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*}A(n)=\begin{cases}\displaystyle -\frac{1}{4}\left(\sum_{k}\binom{n-2k}{n/2-k}^{2}\binom{2k}{k}^{2}\right)4^{-n},&\mbox{if}\ n\ \mbox{is even,}\\ 0,&\mbox{otherwise.} \end{cases} \end{align*} $$
Substituting these into (1.4), one obtains a new, to the best of our knowledge, rational Ramanujan-type series
 $$ \begin{align*}\frac{1}{\pi}=\frac{1}{2}\sum_{n=0}^{\infty}\left(\sum_{k}\binom{2n-2k}{n-k}^{2}\binom{2k}{k}^{2}\right)n\frac{1}{2^{5n}}. \end{align*} $$
$$ \begin{align*}\frac{1}{\pi}=\frac{1}{2}\sum_{n=0}^{\infty}\left(\sum_{k}\binom{2n-2k}{n-k}^{2}\binom{2k}{k}^{2}\right)n\frac{1}{2^{5n}}. \end{align*} $$
Theorem 1.1 is mainly built upon properties of modular forms and a geometric notion called orbifold uniformization and relations between its attached differential forms called orbifold uniformizing differential equation, which is indeed a Fuchsian differential equation. In light of these, we organize the remainder of this note as follows. In Section 2, we review some basics of Fuchsian equations. In the first two subsections of Section 3, we briefly go over the notion of orbifold uniformization and relevant materials along with a few explicit examples, old and new, as illustrations, as well as establish a key lemma, Lemma 3.3, for Theorem 1.1. In the third subsection, we remark how a Clausen-type transformation formula in some general sense can be derived from the results of the preceding subsections as a byproduct, and recover the quadratic transformation (1.2) as an illustration. In the last section, we end this note with the proof of Theorem 1.1.
2 Fuchsian equations and their symmetric squares
In this section, we review Fuchsian equations and their basic properties, which we shall occasionally refer to. Most of the terminology and basic results are recalled from [Reference Yoshida12]. We start with a second-order linear differential equation
with
![]() $R_{i}(x)$
rational functions in x over
$R_{i}(x)$
rational functions in x over
![]() $\mathbb {C}$
. A point
$\mathbb {C}$
. A point
![]() $x_{0}$
is called a singular point for (2.1) if it is a pole of
$x_{0}$
is called a singular point for (2.1) if it is a pole of
![]() $R_{i}(x)$
for
$R_{i}(x)$
for
![]() $i=1$
or
$i=1$
or
![]() $2$
. A singular point
$2$
. A singular point
![]() $x_{0}$
is called regular if
$x_{0}$
is called regular if
![]() $(x-x_{0})R_{1}(x)$
and
$(x-x_{0})R_{1}(x)$
and
![]() $(x-x_{0})^{2}R_{2}(x)$
are holomorphic at
$(x-x_{0})^{2}R_{2}(x)$
are holomorphic at
![]() $x_{0}$
for
$x_{0}$
for
![]() $x_{0}\ne \infty $
, and
$x_{0}\ne \infty $
, and
![]() $R_{1}(1/x)/x$
and
$R_{1}(1/x)/x$
and
![]() $R_{2}(1/x)/x^{2}$
are holomorphic at
$R_{2}(1/x)/x^{2}$
are holomorphic at
![]() $x=0$
for
$x=0$
for
![]() $x_{0}=\infty $
. Equation (2.1) is called a Fuchsian equation if all of its singular points are regular. Moreover, a regular singular point
$x_{0}=\infty $
. Equation (2.1) is called a Fuchsian equation if all of its singular points are regular. Moreover, a regular singular point
![]() $x_{0}$
is called apparent if the Fuchsian equation has two linearly independent holomorphic solutions near
$x_{0}$
is called apparent if the Fuchsian equation has two linearly independent holomorphic solutions near
![]() $x_{0}$
. For a Fuchsian equation of the form (2.1) with a regular singular point
$x_{0}$
. For a Fuchsian equation of the form (2.1) with a regular singular point
![]() $x_{0}$
, the local solutions at
$x_{0}$
, the local solutions at
![]() $x_{0}$
to it may be characterized by a pair of so-called characteristic exponents
$x_{0}$
to it may be characterized by a pair of so-called characteristic exponents
![]() $s_{1}(x_{0})$
and
$s_{1}(x_{0})$
and
![]() $s_{2}(x_{0})$
defined to be the roots of
$s_{2}(x_{0})$
defined to be the roots of
![]() $s(s-1)+r_{1}s+r_{2}=0$
, where
$s(s-1)+r_{1}s+r_{2}=0$
, where
and
Several analytic properties [Reference Yoshida12, Section 2.5] of the solutions of (2.1) are characterized by the difference
![]() $s_{2}(x_{0})-s_{1}(x_{0})$
of the characteristic exponents. Moreover, the difference
$s_{2}(x_{0})-s_{1}(x_{0})$
of the characteristic exponents. Moreover, the difference
![]() $s_{2}(x_{0})-s_{1}(x_{0})$
of the characteristic exponents is a “projective” invariant, up to a sign, of a Fuchsian equation. One can actually transform (2.1) into a uniquely defined equation of the form
$s_{2}(x_{0})-s_{1}(x_{0})$
of the characteristic exponents is a “projective” invariant, up to a sign, of a Fuchsian equation. One can actually transform (2.1) into a uniquely defined equation of the form
so that the ratio of two of its linearly independent solutions remains, and such an equation is called the projective normal form of a Fuchsian equation of the form (2.1) defined by setting
![]() $R(x)=R_{2}(x)-\frac {1}{2}R_{1}'(x)-\frac {1}{4}R_{1}(x)^{2}$
. Such a differential equation has the same singular behavior as that of (2.1), i.e., they have the same (regular) singular points, whose solutions are projectively equivalent to that of (2.1) by a multiplier of
$R(x)=R_{2}(x)-\frac {1}{2}R_{1}'(x)-\frac {1}{4}R_{1}(x)^{2}$
. Such a differential equation has the same singular behavior as that of (2.1), i.e., they have the same (regular) singular points, whose solutions are projectively equivalent to that of (2.1) by a multiplier of
![]() $\exp \left (\int \frac {1}{2}R_{1}(x)dx\right )$
. As is just noted, the difference of characteristic exponents of the projective normal form differs from
$\exp \left (\int \frac {1}{2}R_{1}(x)dx\right )$
. As is just noted, the difference of characteristic exponents of the projective normal form differs from
![]() $s_{2}(x_{0})-s_{1}(x_{0})$
by a sign.
$s_{2}(x_{0})-s_{1}(x_{0})$
by a sign.
Finally, for a Fuchsian equation (2.1) with two linearly independent solutions
![]() $y_{1}=y_{1}(x)$
and
$y_{1}=y_{1}(x)$
and
![]() $y_{2}=y_{2}(x)$
, its symmetric square is defined by
$y_{2}=y_{2}(x)$
, its symmetric square is defined by
and a basis for the solutions to such a third-order linear differential equation consists of
![]() $y_{1}^{2},\, y_{1}y_{2},\, y_{2}^{2}$
. See, e.g., [Reference Singer11, Theorem 5.5]. So (1.5) defined in Theorem 1.1 is literally the symmetric square of some Fuchsian equation.
$y_{1}^{2},\, y_{1}y_{2},\, y_{2}^{2}$
. See, e.g., [Reference Singer11, Theorem 5.5]. So (1.5) defined in Theorem 1.1 is literally the symmetric square of some Fuchsian equation.
3 Orbifold uniformizations
In this section, we shall review the notion of orbifold uniformization and orbifold uniformizing differential equation used by Yoshida [Reference Yoshida12]. In particular, in Section 3, we establish a key lemma to Theorem 1.1 (see Lemma 3.3), wherein the question regarding the coefficient of
![]() $A(n+1)$
in the recurrence relation is answered. At the end, we remark how one may obtain Clausen-type transformation formulas via orbifold uniformizations.
$A(n+1)$
in the recurrence relation is answered. At the end, we remark how one may obtain Clausen-type transformation formulas via orbifold uniformizations.
3.1 Orbifolds
Recall that an orbifold is a triple
![]() $(X,Y,(b_{j}))$
consisting of a complex manifold X, a hypersurface
$(X,Y,(b_{j}))$
consisting of a complex manifold X, a hypersurface
![]() $Y\subset X$
which can be decomposed into irreducible components
$Y\subset X$
which can be decomposed into irreducible components
![]() $\cup _{j}Y_{j}$
, each of which is assigned with a number
$\cup _{j}Y_{j}$
, each of which is assigned with a number
![]() $b_{j}$
, either
$b_{j}$
, either
![]() $\infty $
or an integer greater than or equal to
$\infty $
or an integer greater than or equal to
![]() $2$
, called weight, so that for any point in
$2$
, called weight, so that for any point in
![]() $X-\cup _{j}\{Y_{j}|\,b_{j}=\infty \}$
, there is an open neighborhood U and a covering manifold which ramifies along
$X-\cup _{j}\{Y_{j}|\,b_{j}=\infty \}$
, there is an open neighborhood U and a covering manifold which ramifies along
![]() $U\cap Y$
with the given weights
$U\cap Y$
with the given weights
![]() $b_{j}$
. Moreover, an orbifold
$b_{j}$
. Moreover, an orbifold
![]() $(X,Y,(b_{j}))$
is called uniformizable if there is a simply connected global covering manifold of X with the given ramification data
$(X,Y,(b_{j}))$
is called uniformizable if there is a simply connected global covering manifold of X with the given ramification data
![]() $(Y,(b_{j}))$
. For example, the triple
$(Y,(b_{j}))$
. For example, the triple
![]() $(X,Y,(b_{j}))$
with
$(X,Y,(b_{j}))$
with
![]() $X=\mathbb {P}^{1}(\mathbb {C})$
,
$X=\mathbb {P}^{1}(\mathbb {C})$
,
![]() $Y=\{\infty \}\cup \{0\}\cup \{1\}$
and
$Y=\{\infty \}\cup \{0\}\cup \{1\}$
and
![]() $(b_{j})=(\infty ,3,2)$
is a uniformizable orbifold with the global covering map
$(b_{j})=(\infty ,3,2)$
is a uniformizable orbifold with the global covering map
![]() $J:\mathbb {H}\to \mathbb {P}^{1}(\mathbb {C})$
, where J is the modular j-invariant of the form
$J:\mathbb {H}\to \mathbb {P}^{1}(\mathbb {C})$
, where J is the modular j-invariant of the form
![]() $\frac {1}{1728q}+O(1)$
near
$\frac {1}{1728q}+O(1)$
near
![]() $i\infty $
.
$i\infty $
.
Note that for a modular curve
![]() $X(\Gamma )$
associated with an
$X(\Gamma )$
associated with an
![]() $\mathrm {SL}_{2}(\mathbb {R})$
-subgroup of genus zero commensurable with
$\mathrm {SL}_{2}(\mathbb {R})$
-subgroup of genus zero commensurable with
![]() $\mathrm {SL}_{2}(\mathbb {Z})$
,
$\mathrm {SL}_{2}(\mathbb {Z})$
,
![]() $(X(\Gamma ),S,(b_{j}))$
with S the set of cusps and elliptic points and
$(X(\Gamma ),S,(b_{j}))$
with S the set of cusps and elliptic points and
![]() $b_{j}$
being either
$b_{j}$
being either
![]() $\infty $
or the period of an elliptic point depending on its attached component being a cusp or an elliptic point is a uniformizable orbifold with the global covering manifold
$\infty $
or the period of an elliptic point depending on its attached component being a cusp or an elliptic point is a uniformizable orbifold with the global covering manifold
![]() $\pi _{\Gamma }:\mathbb {H}\to X(\Gamma )$
. This can also be identified with the orbifold
$\pi _{\Gamma }:\mathbb {H}\to X(\Gamma )$
. This can also be identified with the orbifold
![]() $(\mathbb {P}^{1}(\mathbb {C}),Y_{\Gamma },(b_{j}))$
through the uniformizer
$(\mathbb {P}^{1}(\mathbb {C}),Y_{\Gamma },(b_{j}))$
through the uniformizer
![]() $t:X(\Gamma )\to \mathbb {P}^{1}(\mathbb {C})$
, where
$t:X(\Gamma )\to \mathbb {P}^{1}(\mathbb {C})$
, where
![]() $Y_{\Gamma }=t(S)$
.
$Y_{\Gamma }=t(S)$
.
3.2 Orbifold uniformizing differential equations
Now, let
![]() $(X,Y,(b_{j}))$
be a uniformizable orbifold with
$(X,Y,(b_{j}))$
be a uniformizable orbifold with
![]() $X=\mathbb {P}^{1}(\mathbb {C})$
whose global covering manifold is
$X=\mathbb {P}^{1}(\mathbb {C})$
whose global covering manifold is
![]() $\mathbb {H}$
, and covering map is denoted by t. By the Galois theory of covering maps,
$\mathbb {H}$
, and covering map is denoted by t. By the Galois theory of covering maps,
![]() $X-\cup _{j}\{Y_{j}|\,b_{j}=\infty \}\cong \Gamma \backslash \mathbb {H}$
for some
$X-\cup _{j}\{Y_{j}|\,b_{j}=\infty \}\cong \Gamma \backslash \mathbb {H}$
for some
![]() $\Gamma \subset \mathrm {SL}_{2}(\mathbb {R})$
. Letting w be any local coordinate on
$\Gamma \subset \mathrm {SL}_{2}(\mathbb {R})$
. Letting w be any local coordinate on
![]() $\mathbb {H}$
, one can associate the orbifold with a differential equation called the orbifold uniformizing differential equation for X defined by
$\mathbb {H}$
, one can associate the orbifold with a differential equation called the orbifold uniformizing differential equation for X defined by
where
 $$ \begin{align*}\{w,t\}=\frac{3(w")^{2}-2w"'w'}{4(w')^{2}} \end{align*} $$
$$ \begin{align*}\{w,t\}=\frac{3(w")^{2}-2w"'w'}{4(w')^{2}} \end{align*} $$
with
![]() $w^{(n)}=\frac {d^{n}w}{dt^{n}}$
called the Schwarzian derivative. It is known [Reference Yoshida12, p. 50] that an orbifold uniformizing differential equation is a Fuchsian equation. Moreover, it is noteworthy to remark that the Schwarzian derivative is
$w^{(n)}=\frac {d^{n}w}{dt^{n}}$
called the Schwarzian derivative. It is known [Reference Yoshida12, p. 50] that an orbifold uniformizing differential equation is a Fuchsian equation. Moreover, it is noteworthy to remark that the Schwarzian derivative is
![]() $\mathrm {PSL}_{2}(\mathbb {C})$
invariant in w, i.e., for any
$\mathrm {PSL}_{2}(\mathbb {C})$
invariant in w, i.e., for any
![]() $\gamma \in \mathrm {PSL}_{2}(\mathbb {C})$
,
$\gamma \in \mathrm {PSL}_{2}(\mathbb {C})$
,
![]() $ \{w,t\}=\{\gamma \cdot w,t\}. $
$ \{w,t\}=\{\gamma \cdot w,t\}. $
Lemma 3.1 A solution to the orbifold uniformizing differential equation is given by
![]() $y(t)=\left (\frac {1}{dw/dt}\right )^{\frac {1}{2}}$
for a suitable choice of branch.
$y(t)=\left (\frac {1}{dw/dt}\right )^{\frac {1}{2}}$
for a suitable choice of branch.
Proof This follows from the Inverse Function Theorem and the simple relation
![]() $\{w,t\}=-\{t,w\}/(t')^{2}$
with
$\{w,t\}=-\{t,w\}/(t')^{2}$
with
![]() $t^{(n)}=\frac {d^{n}t}{dw^{n}}$
.
$t^{(n)}=\frac {d^{n}t}{dw^{n}}$
.
Suppose that
![]() $(X,Y,(b_{j}))$
is a uniformizable orbifold with
$(X,Y,(b_{j}))$
is a uniformizable orbifold with
![]() $X=\mathbb {P}^{1}(\mathbb {C})\cong X(\Gamma )$
for some
$X=\mathbb {P}^{1}(\mathbb {C})\cong X(\Gamma )$
for some
![]() $\mathrm {SL}_{2}(\mathbb {R})$
-subgroup
$\mathrm {SL}_{2}(\mathbb {R})$
-subgroup
![]() $\Gamma $
of genus zero commensurable with
$\Gamma $
of genus zero commensurable with
![]() $\mathrm { SL}_{2}(\mathbb {Z})$
. Clearly, every meromorphic function on
$\mathrm { SL}_{2}(\mathbb {Z})$
. Clearly, every meromorphic function on
![]() $X(\Gamma )$
is a rational function in t. With respect to the canonical local coordinate
$X(\Gamma )$
is a rational function in t. With respect to the canonical local coordinate
![]() $\tau $
on
$\tau $
on
![]() $\mathbb {H}$
, it is easy to check that
$\mathbb {H}$
, it is easy to check that
![]() $-\{t,\tau \}/(t')^{2}$
is a meromorphic function on
$-\{t,\tau \}/(t')^{2}$
is a meromorphic function on
![]() $X(\Gamma )$
by the fact that
$X(\Gamma )$
by the fact that
 $$ \begin{align*}\left.\frac{dt}{d\tau}\right|_{\tau\to\gamma\cdot\tau}=(c\tau+d)^{2}\frac{dt}{d\tau}, \end{align*} $$
$$ \begin{align*}\left.\frac{dt}{d\tau}\right|_{\tau\to\gamma\cdot\tau}=(c\tau+d)^{2}\frac{dt}{d\tau}, \end{align*} $$
where
 $\gamma =\begin {pmatrix}a&b\\c&d\end {pmatrix}\in \Gamma $
, and thus the orbifold uniformizing differential equation associated with
$\gamma =\begin {pmatrix}a&b\\c&d\end {pmatrix}\in \Gamma $
, and thus the orbifold uniformizing differential equation associated with
![]() $(\mathbb {P}^{1}(\mathbb {C}),Y_{\Gamma },(b_{j}))$
can be indeed rewritten as
$(\mathbb {P}^{1}(\mathbb {C}),Y_{\Gamma },(b_{j}))$
can be indeed rewritten as
for some rational function in t which can be determined when t in terms of
![]() $\tau $
is explicit.
$\tau $
is explicit.
Example 3.2 For
 $\Gamma =\Gamma _{0}(4)+=\left \langle \Gamma _{0}(4),\begin {pmatrix}0&-1\\4&0\end {pmatrix}\right \rangle $
, the group generated by
$\Gamma =\Gamma _{0}(4)+=\left \langle \Gamma _{0}(4),\begin {pmatrix}0&-1\\4&0\end {pmatrix}\right \rangle $
, the group generated by
![]() $\Gamma _{0}(4)$
and its Fricke involution
$\Gamma _{0}(4)$
and its Fricke involution
 $\begin {pmatrix}0&-1\\4&0\end {pmatrix}$
, as is seen in Example 1.5, a uniformizer, is given by
$\begin {pmatrix}0&-1\\4&0\end {pmatrix}$
, as is seen in Example 1.5, a uniformizer, is given by
 $$ \begin{align*}t(\tau)=\frac{\eta(4\tau)^{24}\eta(\tau)^{24}}{\eta(2\tau)^{48}}, \end{align*} $$
$$ \begin{align*}t(\tau)=\frac{\eta(4\tau)^{24}\eta(\tau)^{24}}{\eta(2\tau)^{48}}, \end{align*} $$
which has a simple zero at the cusp
![]() $[i\infty ]$
and a simple pole at the cusp
$[i\infty ]$
and a simple pole at the cusp
![]() $[\frac {1}{2}]$
. It is easy to check (or see Lemma 3.3) that
$[\frac {1}{2}]$
. It is easy to check (or see Lemma 3.3) that
 $$ \begin{align*}\frac{\{t,\tau\}}{(t')^{2}}=\frac{4096t^2-80t+1}{4t^2(64t-1)^2}, \end{align*} $$
$$ \begin{align*}\frac{\{t,\tau\}}{(t')^{2}}=\frac{4096t^2-80t+1}{4t^2(64t-1)^2}, \end{align*} $$
and thus by the remarks in Section 2, one can tell that a solution in terms of
![]() $\tau $
to the orbifold uniformizing differential equation
$\tau $
to the orbifold uniformizing differential equation
i.e.,
 $$ \begin{align*}\frac{d^{2}y}{dt^{2}}+\frac{4096t^2-80t+1}{4t^2(64t-1)^2}y=0, \end{align*} $$
$$ \begin{align*}\frac{d^{2}y}{dt^{2}}+\frac{4096t^2-80t+1}{4t^2(64t-1)^2}y=0, \end{align*} $$
is
![]() $y=\left (\frac {1}{2\pi i}\frac {d}{d\tau }\left (\frac {\eta (4\tau )^{24}\eta (\tau )^{24}}{\eta (2\tau )^{48}}\right )\right )^{\frac {1}{2}}$
for some choice of branch. Moreover, one can also check that the Fuchsian equation above is indeed the projective normal form of
$y=\left (\frac {1}{2\pi i}\frac {d}{d\tau }\left (\frac {\eta (4\tau )^{24}\eta (\tau )^{24}}{\eta (2\tau )^{48}}\right )\right )^{\frac {1}{2}}$
for some choice of branch. Moreover, one can also check that the Fuchsian equation above is indeed the projective normal form of
 $$ \begin{align} \frac{d^{2}y}{dt^{2}}+\frac{96t-1}{t(64t-1)}\frac{dy}{dt}+\frac{4}{t(64t-1)}y=0, \end{align} $$
$$ \begin{align} \frac{d^{2}y}{dt^{2}}+\frac{96t-1}{t(64t-1)}\frac{dy}{dt}+\frac{4}{t(64t-1)}y=0, \end{align} $$
and thus, in terms of
![]() $\tau $
, a solution to this equation is given by
$\tau $
, a solution to this equation is given by
 $$ \begin{align*}y=\left(\left(\frac{1}{64t^{3}-t^{2}}\right)^{\frac{1}{2}}\frac{1}{2\pi i}\frac{d}{d\tau}\left(\frac{\eta(4\tau)^{24}\eta(\tau)^{24}}{\eta(2\tau)^{48}}\right)\right)^{\frac{1}{2}}. \end{align*} $$
$$ \begin{align*}y=\left(\left(\frac{1}{64t^{3}-t^{2}}\right)^{\frac{1}{2}}\frac{1}{2\pi i}\frac{d}{d\tau}\left(\frac{\eta(4\tau)^{24}\eta(\tau)^{24}}{\eta(2\tau)^{48}}\right)\right)^{\frac{1}{2}}. \end{align*} $$
In the example above, we mention that the projective normal form of the Fuchsian equation (3.1) is exactly the orbifold uniformizing differential equation associated with
![]() $X(\Gamma _{0}(4)+)$
. Moreover, one may note that the denominators of its coefficients have lower degrees than that of the orbifold uniformizing differential equation does. In fact, for an orbifold uniformizing differential equation associated with an
$X(\Gamma _{0}(4)+)$
. Moreover, one may note that the denominators of its coefficients have lower degrees than that of the orbifold uniformizing differential equation does. In fact, for an orbifold uniformizing differential equation associated with an
![]() $\mathrm { SL}_{2}(\mathbb {R})$
-subgroup commensurable with
$\mathrm { SL}_{2}(\mathbb {R})$
-subgroup commensurable with
![]() $\mathrm {SL}_{2}(\mathbb {Z})$
, one can always “anti-projectivize” its orbifold uniformizing differential equation
$\mathrm {SL}_{2}(\mathbb {Z})$
, one can always “anti-projectivize” its orbifold uniformizing differential equation
to obtain a Fuchsian equation whose coefficients have denominators of lower degrees than that of
![]() $R(t)$
. We elaborate this in the following lemma.
$R(t)$
. We elaborate this in the following lemma.
Lemma 3.3 For a given genus zero modular curve
![]() $X(\Gamma )$
associated with an
$X(\Gamma )$
associated with an
![]() $\mathrm {SL}_{2}(\mathbb {R})$
-subgroup
$\mathrm {SL}_{2}(\mathbb {R})$
-subgroup
![]() $\Gamma $
commensurable with
$\Gamma $
commensurable with
![]() $\mathrm {SL}_{2}(\mathbb {Z})$
, choose a uniformizer
$\mathrm {SL}_{2}(\mathbb {Z})$
, choose a uniformizer
![]() $t=t(\tau )$
$t=t(\tau )$
-
• having a zero at the cusp
 $[i\infty ]$
$[i\infty ]$
-
• and
-
– a pole at a cusp apart from
 $[i\infty ]$
, or at an elliptic point of period
$[i\infty ]$
, or at an elliptic point of period
 $h>2$
,
$h>2$
,or
-
– a pole at an elliptic point of period
 $h=2$
if there are no cusps other than
$h=2$
if there are no cusps other than
 $[i\infty ]$
or elliptic points of period
$[i\infty ]$
or elliptic points of period
 $h>2$
.
$h>2$
.
Let
![]() $\nu (\Gamma )$
be defined as in Theorem 1.1 and denote by
$\nu (\Gamma )$
be defined as in Theorem 1.1 and denote by
![]() $\omega (\Gamma )$
the total number of cusps and elliptic points of
$\omega (\Gamma )$
the total number of cusps and elliptic points of
![]() $X(\Gamma )$
. Suppose that the orbifold uniformizing differential equation of
$X(\Gamma )$
. Suppose that the orbifold uniformizing differential equation of
![]() $X(\Gamma )$
is given by
$X(\Gamma )$
is given by
Then:
-
(1) this is the projective normal form of
(3.3)where $$ \begin{align} \frac{d^{2}y}{dt^{2}}+R_{1}(t)\frac{dy}{dt}+R_{2}(t)y=0, \end{align} $$
is of the form
$$ \begin{align} \frac{d^{2}y}{dt^{2}}+R_{1}(t)\frac{dy}{dt}+R_{2}(t)y=0, \end{align} $$
is of the form $$ \begin{align*}R_{1}(t)=\sum_{\substack{z_{0}\ \text{is a cusp}}}\frac{1}{t-t(z_{0})}+\sum_{\substack{z_{0}\ \text{is an elliptic }\\\text{point of period}~h}}\frac{1-\frac{1}{h}}{t-t(z_{0})} \end{align*} $$
for some polynomial
$$ \begin{align*}R_{1}(t)=\sum_{\substack{z_{0}\ \text{is a cusp}}}\frac{1}{t-t(z_{0})}+\sum_{\substack{z_{0}\ \text{is an elliptic }\\\text{point of period}~h}}\frac{1-\frac{1}{h}}{t-t(z_{0})} \end{align*} $$
for some polynomial $$ \begin{align*}P_{1}(t)\left/\left(\prod_{\substack{z_{0}\ \text{is a cusp or}\\ \text{an elliptic point}}}(t-t(z_{0}))\right)\right. \end{align*} $$
$$ \begin{align*}P_{1}(t)\left/\left(\prod_{\substack{z_{0}\ \text{is a cusp or}\\ \text{an elliptic point}}}(t-t(z_{0}))\right)\right. \end{align*} $$
 $P_{1}(t)$
of degree
$P_{1}(t)$
of degree
 $\omega (\Gamma )-2$
having no common factor with the denominator, and
$\omega (\Gamma )-2$
having no common factor with the denominator, and
 $R_{2}(t)=R(t)+\frac {1}{2}R_{1}'(t)+\frac {1}{4}R_{1}(t)^{2}$
,
$R_{2}(t)=R(t)+\frac {1}{2}R_{1}'(t)+\frac {1}{4}R_{1}(t)^{2}$
,
-
(2) for the symmetric square of (3.3)
(3.4)the coefficient $$ \begin{align} \frac{d^{3}Y}{dt^{3}}+3R_{1}(t)\frac{d^{2}Y}{dt^{2}}+\left(2R_{1}(t)^{2}+4R_{2}(t)+R_{1}'(t)\right)\frac{dY}{dt}+\left(4R_{1}(t)R_{2}(t)+2R_{2}'(t)\right)Y=0, \end{align} $$
$$ \begin{align} \frac{d^{3}Y}{dt^{3}}+3R_{1}(t)\frac{d^{2}Y}{dt^{2}}+\left(2R_{1}(t)^{2}+4R_{2}(t)+R_{1}'(t)\right)\frac{dY}{dt}+\left(4R_{1}(t)R_{2}(t)+2R_{2}'(t)\right)Y=0, \end{align} $$
 $2R_{1}(t)^{2}+4R_{2}(t)+R_{1}'(t)$
satisfies that is a polynomial in t of degree
$2R_{1}(t)^{2}+4R_{2}(t)+R_{1}'(t)$
satisfies that is a polynomial in t of degree $$ \begin{align*}\left(2R_{1}(t)^{2}+4R_{2}(t)+R_{1}'(t)\right)\times\left({\prod_{\substack{z_{0}\ \text{is a cusp or }\\\text{an elliptic point }\\\text{of period}~h>2}}}(t-t(z_{0}))^{2}\prod_{\substack{z_{0}\ \text{is an elliptic}\\\text{point of period}~2}}(t-t(z_{0}))\right) \end{align*} $$
$$ \begin{align*}\left(2R_{1}(t)^{2}+4R_{2}(t)+R_{1}'(t)\right)\times\left({\prod_{\substack{z_{0}\ \text{is a cusp or }\\\text{an elliptic point }\\\text{of period}~h>2}}}(t-t(z_{0}))^{2}\prod_{\substack{z_{0}\ \text{is an elliptic}\\\text{point of period}~2}}(t-t(z_{0}))\right) \end{align*} $$
 $\nu (\Gamma )-2$
coprime to and similarly the coefficient
$\nu (\Gamma )-2$
coprime to and similarly the coefficient $$ \begin{align*}\prod_{\substack{z_{0}\ \text{is a cusp or }\\\text{an elliptic point }\\\text{of period}~h>2}}(t-t(z_{0}))^{2}, \end{align*} $$
$$ \begin{align*}\prod_{\substack{z_{0}\ \text{is a cusp or }\\\text{an elliptic point }\\\text{of period}~h>2}}(t-t(z_{0}))^{2}, \end{align*} $$
 $4R_{1}(t)R_{2}(t)+2R_{2}'(t)$
satisfies that is a polynomial in t of degree
$4R_{1}(t)R_{2}(t)+2R_{2}'(t)$
satisfies that is a polynomial in t of degree $$ \begin{align*}\left(4R_{1}(t)R_{2}(t)+2R_{2}'(t)\right)\times\left({\prod_{\substack{z_{0}\ \text{is a cusp or }\\\text{an elliptic point }\\\text{of period}~h>2}}}(t-t(z_{0}))^{2}\prod_{\substack{z_{0}\ \text{is an elliptic}\\\text{point of period}~2}}(t-t(z_{0}))\right) \end{align*} $$
$$ \begin{align*}\left(4R_{1}(t)R_{2}(t)+2R_{2}'(t)\right)\times\left({\prod_{\substack{z_{0}\ \text{is a cusp or }\\\text{an elliptic point }\\\text{of period}~h>2}}}(t-t(z_{0}))^{2}\prod_{\substack{z_{0}\ \text{is an elliptic}\\\text{point of period}~2}}(t-t(z_{0}))\right) \end{align*} $$
 $\nu (\Gamma )-3$
,
$\nu (\Gamma )-3$
,
-
(3) a solution to (3.3) is given by
and a solution to (3.4) is given by $$ \begin{align*}y=\prod_{\substack{z_{0}\ \text{is a cusp}}}(t-t(z_0))^{\frac{-1}{2}}\prod_{\substack{z_{0}\ \text{is an elliptic }\\\text{point of period}~h}}\left(t-t(z_{0})\right)^{\frac{1-h}{2h}}\left(\frac{1}{2\pi i}\frac{1}{d\tau/dt}\right)^{\frac{1}{2}}, \end{align*} $$
and as functions in
$$ \begin{align*}y=\prod_{\substack{z_{0}\ \text{is a cusp}}}(t-t(z_0))^{\frac{-1}{2}}\prod_{\substack{z_{0}\ \text{is an elliptic }\\\text{point of period}~h}}\left(t-t(z_{0})\right)^{\frac{1-h}{2h}}\left(\frac{1}{2\pi i}\frac{1}{d\tau/dt}\right)^{\frac{1}{2}}, \end{align*} $$
and as functions in $$ \begin{align*}Y=\prod_{\substack{z_{0}\ \text{is a cusp}}}(t-t(z_0))^{-1}\prod_{\substack{z_{0}\ \text{is an elliptic }\\\text{point of period}~h}}\left(t-t(z_{0})\right)^{\frac{1-h}{h}}\frac{1}{2\pi i}\frac{1}{d\tau/dt}, \end{align*} $$
$$ \begin{align*}Y=\prod_{\substack{z_{0}\ \text{is a cusp}}}(t-t(z_0))^{-1}\prod_{\substack{z_{0}\ \text{is an elliptic }\\\text{point of period}~h}}\left(t-t(z_{0})\right)^{\frac{1-h}{h}}\frac{1}{2\pi i}\frac{1}{d\tau/dt}, \end{align*} $$
 $\tau $
, they are, respectively, modular forms of weights 1 and 2,
$\tau $
, they are, respectively, modular forms of weights 1 and 2,
-
(4) as a function in t, the solution
 $Y=Y(t)$
has a local holomorphic representation
$Y=Y(t)$
has a local holomorphic representation
 $\sum _{n=0}^{\infty }A(n)t^{n}$
at
$\sum _{n=0}^{\infty }A(n)t^{n}$
at
 $t=0$
converges for and the coefficients
$t=0$
converges for and the coefficients $$ \begin{align*}|t|<\mu(t)=\min\{|t(z_{0})|:\, z_{0}\ \mbox{is a cusp apart from}\ [i\infty],\ \mbox{or an elliptic point}\}, \end{align*} $$
$$ \begin{align*}|t|<\mu(t)=\min\{|t(z_{0})|:\, z_{0}\ \mbox{is a cusp apart from}\ [i\infty],\ \mbox{or an elliptic point}\}, \end{align*} $$
 $A(n)$
satisfy a linear homogeneous recurrence relation of the form for some cubic polynomials
$A(n)$
satisfy a linear homogeneous recurrence relation of the form for some cubic polynomials $$ \begin{align*}(n+1)^{3}A(n+1)+c_{1}(n)A(n)+\cdots+c_{\nu(\Gamma)-2}(n)A(n+3-\nu(\Gamma))=0 \end{align*} $$
$$ \begin{align*}(n+1)^{3}A(n+1)+c_{1}(n)A(n)+\cdots+c_{\nu(\Gamma)-2}(n)A(n+3-\nu(\Gamma))=0 \end{align*} $$
 $c_{i}(n)$
in n.
$c_{i}(n)$
in n.
Proof Throughout the proof, we write
 $$ \begin{align*}\alpha=\sum_{\substack{z\ \text{is a cusp}\\\text{not a pole}}}1+\sum_{\substack{z\ \text{is an elliptic}\\\text{point of period}~h}}\left(1-\frac{1}{h}\right). \end{align*} $$
$$ \begin{align*}\alpha=\sum_{\substack{z\ \text{is a cusp}\\\text{not a pole}}}1+\sum_{\substack{z\ \text{is an elliptic}\\\text{point of period}~h}}\left(1-\frac{1}{h}\right). \end{align*} $$
It is known by [Reference Beardon4, Section 10.4] together with the assumption that
![]() $X(\Gamma )$
is of genus zero and
$X(\Gamma )$
is of genus zero and
![]() $\Gamma $
is commensurable with
$\Gamma $
is commensurable with
![]() $\mathrm {SL}_{2}(\mathbb {Z})$
that
$\mathrm {SL}_{2}(\mathbb {Z})$
that
![]() $\alpha>1$
.
$\alpha>1$
.
Now, recall that
 $$ \begin{align*}R(t)=\frac{\{t,\tau\}}{(t')^{2}}=\frac{3(t")^{2}-2t"'t'}{4(t')^{4}}. \end{align*} $$
$$ \begin{align*}R(t)=\frac{\{t,\tau\}}{(t')^{2}}=\frac{3(t")^{2}-2t"'t'}{4(t')^{4}}. \end{align*} $$
Since the argument under other circumstance is similar, without loss of generality, suppose that
 $$ \begin{align*}t=\begin{cases}t(z_{0})+c_{1}(\tau-z_{0})+\cdots,&\mbox{if}\ z_{0}\ \mbox{is not a cusp or an elliptic point},\\\\ t(z_{0})+c_{1}(\tau-z_{0})^{h}+c_{2}(\tau-z_{0})^{h+1}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is an elliptic point of period}~h,\\\\ t(z_{0})+c_{1}q_{e}+c_{2}q_{e}^{2}+c_{3}q_{e}^{3}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is a cusp of width}~e\ \mbox{not a pole,}\\\\ \frac{1}{q_{e}}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is a cusp of width}~e\ \mbox{that is a pole,} \end{cases} \end{align*} $$
$$ \begin{align*}t=\begin{cases}t(z_{0})+c_{1}(\tau-z_{0})+\cdots,&\mbox{if}\ z_{0}\ \mbox{is not a cusp or an elliptic point},\\\\ t(z_{0})+c_{1}(\tau-z_{0})^{h}+c_{2}(\tau-z_{0})^{h+1}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is an elliptic point of period}~h,\\\\ t(z_{0})+c_{1}q_{e}+c_{2}q_{e}^{2}+c_{3}q_{e}^{3}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is a cusp of width}~e\ \mbox{not a pole,}\\\\ \frac{1}{q_{e}}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is a cusp of width}~e\ \mbox{that is a pole,} \end{cases} \end{align*} $$
where
![]() $c_{1}$
are all nonzero. One, therefore, can find that
$c_{1}$
are all nonzero. One, therefore, can find that
 $$ \begin{align*} &R(t(\tau))=\frac{\{t,\tau\}}{(t')^{2}}\\ &\quad=\begin{cases}O(1),&\mbox{if}\ z_{0}\ \mbox{is not a cusp or an elliptic point,}\\\\ \frac{h^{2}-1}{4h^{2}c_{1}^{2}}\frac{1}{(\tau-z_{0})^{2h}}-\frac{(h^{2}-1)c_{2}}{2h^{2}c_{1}^{3}}\frac{1}{(\tau-z_{0})^{2h-1}}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is an elliptic point of period}~h,\\\\ \frac{1}{4c_{1}^{2}}\frac{1}{q_{e}^{2}}-\frac{c_{2}}{c_{1}^{3}}\frac{1}{q_{e}}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is a cusp of width}~e\ \mbox{not a pole of}~t,\\\\ \frac{q_{e}^{2}}{4}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is a cusp of width}~e\ \mbox{that is a pole of}~t, \end{cases} \end{align*} $$
$$ \begin{align*} &R(t(\tau))=\frac{\{t,\tau\}}{(t')^{2}}\\ &\quad=\begin{cases}O(1),&\mbox{if}\ z_{0}\ \mbox{is not a cusp or an elliptic point,}\\\\ \frac{h^{2}-1}{4h^{2}c_{1}^{2}}\frac{1}{(\tau-z_{0})^{2h}}-\frac{(h^{2}-1)c_{2}}{2h^{2}c_{1}^{3}}\frac{1}{(\tau-z_{0})^{2h-1}}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is an elliptic point of period}~h,\\\\ \frac{1}{4c_{1}^{2}}\frac{1}{q_{e}^{2}}-\frac{c_{2}}{c_{1}^{3}}\frac{1}{q_{e}}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is a cusp of width}~e\ \mbox{not a pole of}~t,\\\\ \frac{q_{e}^{2}}{4}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is a cusp of width}~e\ \mbox{that is a pole of}~t, \end{cases} \end{align*} $$
and
 $$ \begin{align*} &R_{1}(t(\tau))=\begin{cases}O(1),&\mbox{if}\ z_{0}\ \mbox{is not a cusp or an elliptic point,}\\\\ \frac{h-1}{hc_{1}(\tau-z_{0})^{h}}-\frac{(h-1)c_{2}}{hc_{1}^{2}(\tau-z_0)^{h-1}}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is an elliptic point of period}~h,\\\\ \frac{1}{c_{1}q_{e}}-\frac{c_{2}}{c_{1}^{2}}+\cdots,&\mbox{if} z_{0}\ \mbox{is a cusp of width}~e\ \mbox{not a pole of}~t,\\\\ \alpha q_{e}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is a cusp of width}~e\ \mbox{that is a pole of}~t, \end{cases} \end{align*} $$
$$ \begin{align*} &R_{1}(t(\tau))=\begin{cases}O(1),&\mbox{if}\ z_{0}\ \mbox{is not a cusp or an elliptic point,}\\\\ \frac{h-1}{hc_{1}(\tau-z_{0})^{h}}-\frac{(h-1)c_{2}}{hc_{1}^{2}(\tau-z_0)^{h-1}}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is an elliptic point of period}~h,\\\\ \frac{1}{c_{1}q_{e}}-\frac{c_{2}}{c_{1}^{2}}+\cdots,&\mbox{if} z_{0}\ \mbox{is a cusp of width}~e\ \mbox{not a pole of}~t,\\\\ \alpha q_{e}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is a cusp of width}~e\ \mbox{that is a pole of}~t, \end{cases} \end{align*} $$
and
 $$ \begin{align*} &R_{2}(t(\tau))=\begin{cases}O(1),&\mbox{if}\ z_{0}\ \mbox{is not a cusp or an elliptic point,}\\\\ -\frac{3(h^{2}-1)c_{2}}{2h^{2}c_{1}^{3}(\tau-z_{0})^{h}}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is an elliptic point of period}~h,\\\\ -\frac{c_{2}}{2c_{1}^{3}q_{e}}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is a cusp of width}~e\ \mbox{not a pole of}~t,\\\\ \frac{1}{4}(\alpha-1)^{2} q_{e}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is a cusp of width}~e\ \mbox{that is a pole of}~t, \end{cases} \end{align*} $$
$$ \begin{align*} &R_{2}(t(\tau))=\begin{cases}O(1),&\mbox{if}\ z_{0}\ \mbox{is not a cusp or an elliptic point,}\\\\ -\frac{3(h^{2}-1)c_{2}}{2h^{2}c_{1}^{3}(\tau-z_{0})^{h}}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is an elliptic point of period}~h,\\\\ -\frac{c_{2}}{2c_{1}^{3}q_{e}}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is a cusp of width}~e\ \mbox{not a pole of}~t,\\\\ \frac{1}{4}(\alpha-1)^{2} q_{e}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is a cusp of width}~e\ \mbox{that is a pole of}~t, \end{cases} \end{align*} $$
which has at most a simple pole at a cusp that is not a pole of t and always has a double zero at the cusp
![]() $z_{0}$
that is a pole of t since
$z_{0}$
that is a pole of t since
![]() $\alpha>1$
. Building upon these, we are now ready to give proofs to our assertions.
$\alpha>1$
. Building upon these, we are now ready to give proofs to our assertions.
For (i), first, it is clear by definition that (3.2) is the projective normal form of (3.1). For the rational form of
![]() $R_{1}(t)$
, note that
$R_{1}(t)$
, note that
![]() $R_{1}(t)$
has simple poles at exactly that cusps and elliptic points that is not a pole of t, and a simple zero at the pole of t, and thus
$R_{1}(t)$
has simple poles at exactly that cusps and elliptic points that is not a pole of t, and a simple zero at the pole of t, and thus
 $$ \begin{align*}R_{1}(t)\times \prod_{\substack{z_{0}\ \text{is a cusp or}\\ \text{an elliptic point}}}(t-t(z_{0})) \end{align*} $$
$$ \begin{align*}R_{1}(t)\times \prod_{\substack{z_{0}\ \text{is a cusp or}\\ \text{an elliptic point}}}(t-t(z_{0})) \end{align*} $$
has a pole only at the cusp that is a pole of t, which is of order
![]() $\omega (\Gamma )-1$
, and no zeros at other cusps or elliptic points. As such, this must be a polynomial of degree
$\omega (\Gamma )-1$
, and no zeros at other cusps or elliptic points. As such, this must be a polynomial of degree
![]() $\omega (\Gamma )-1$
with no common factor with the multiplier. It is worth remarking that
$\omega (\Gamma )-1$
with no common factor with the multiplier. It is worth remarking that
![]() $R(t)$
is a rational function in t whose denominator is of degree
$R(t)$
is a rational function in t whose denominator is of degree
![]() $2\omega (\Gamma )-2>\omega (\Gamma )-1$
by [Reference Beardon4, Section 10.4].
$2\omega (\Gamma )-2>\omega (\Gamma )-1$
by [Reference Beardon4, Section 10.4].
For (ii), similarly, working through the computations, one can deduce that
 $$ \begin{align*} &2R_{1}(t)^{2}+4R_{2}(t)+R_{1}'(t)\\ &= \begin{cases}O(1),&\mbox{if}\ z_{0}\ \mbox{is not a cusp or an elliptic point,}\\\\ \frac{(h-2)(h-1)}{h^{2}c_{1}^{2}}\frac{1}{(\tau-z_{0})^{2h}}+\frac{(h-1)(2-4h)c_{2}}{h^{2}c_{1}^{3}}\frac{1}{(\tau-z_{0})^{2h-1}}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is an elliptic point of period}~h,\\\\ \frac{1}{c_{1}^{2}q_{e}^{2}}-\frac{4c_{2}}{c_{1}^{3}}\frac{1}{q_{e}}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is a cusp of width}~e\ \mbox{not a pole of}~t,\\\\ (\alpha^{2}-\alpha+1)q_{e}^{2}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is a cusp of width}~e\ \mbox{that is a pole of}~t, \end{cases} \end{align*} $$
$$ \begin{align*} &2R_{1}(t)^{2}+4R_{2}(t)+R_{1}'(t)\\ &= \begin{cases}O(1),&\mbox{if}\ z_{0}\ \mbox{is not a cusp or an elliptic point,}\\\\ \frac{(h-2)(h-1)}{h^{2}c_{1}^{2}}\frac{1}{(\tau-z_{0})^{2h}}+\frac{(h-1)(2-4h)c_{2}}{h^{2}c_{1}^{3}}\frac{1}{(\tau-z_{0})^{2h-1}}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is an elliptic point of period}~h,\\\\ \frac{1}{c_{1}^{2}q_{e}^{2}}-\frac{4c_{2}}{c_{1}^{3}}\frac{1}{q_{e}}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is a cusp of width}~e\ \mbox{not a pole of}~t,\\\\ (\alpha^{2}-\alpha+1)q_{e}^{2}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is a cusp of width}~e\ \mbox{that is a pole of}~t, \end{cases} \end{align*} $$
which has at most a simple pole at an elliptic point of period
![]() $2$
, and always has a double pole at an elliptic point of period
$2$
, and always has a double pole at an elliptic point of period
![]() $h>2$
and at a cusp that is not a pole of t, as well as a double zero at the cusp that is a pole of t since
$h>2$
and at a cusp that is not a pole of t, as well as a double zero at the cusp that is a pole of t since
![]() $\alpha>1$
, and
$\alpha>1$
, and
 $$ \begin{align*} &4R_{1}(t)R_{2}(t)+2R_{2}'(t)\\ &= \begin{cases}O(1),&\mbox{if}\ z_{0}\ \mbox{is not a cusp or an elliptic point,}\\\\ -\frac{3(h^{2}-1)(h-2)c_{2}}{h^{3}c_{1}^{4}}\frac{1}{(\tau-z_{0})^{2h}}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is an elliptic point of period}~h,\\\\ -\frac{c_{2}}{c_{1}^{4}}\frac{1}{q_{e}^{2}}+\frac{21c_{2}^{2}-16c_{1}c_{3}}{c_{1}^{5}}\frac{1}{q_{e}}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is a cusp of width}~e\ \mbox{not a pole,}\\\\ (\alpha-1)^{3}q_{e}^{3}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is a cusp of width}~e\ \mbox{that is a pole,} \end{cases} \end{align*} $$
$$ \begin{align*} &4R_{1}(t)R_{2}(t)+2R_{2}'(t)\\ &= \begin{cases}O(1),&\mbox{if}\ z_{0}\ \mbox{is not a cusp or an elliptic point,}\\\\ -\frac{3(h^{2}-1)(h-2)c_{2}}{h^{3}c_{1}^{4}}\frac{1}{(\tau-z_{0})^{2h}}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is an elliptic point of period}~h,\\\\ -\frac{c_{2}}{c_{1}^{4}}\frac{1}{q_{e}^{2}}+\frac{21c_{2}^{2}-16c_{1}c_{3}}{c_{1}^{5}}\frac{1}{q_{e}}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is a cusp of width}~e\ \mbox{not a pole,}\\\\ (\alpha-1)^{3}q_{e}^{3}+\cdots,&\mbox{if}\ z_{0}\ \mbox{is a cusp of width}~e\ \mbox{that is a pole,} \end{cases} \end{align*} $$
which has at most a simple pole at an elliptic point of period
![]() $2$
and at most a double pole at a cusp that is not a pole of t, and always has a double pole at an elliptic point of period
$2$
and at most a double pole at a cusp that is not a pole of t, and always has a double pole at an elliptic point of period
![]() $h>2$
and a zero of order 3 at the cusp
$h>2$
and a zero of order 3 at the cusp
![]() $z_{0}$
that is a pole of t.
$z_{0}$
that is a pole of t.
Then, clearly,
 $$ \begin{align*}\left(2R_{1}(t)^{2}+4R_{2}(t)+R_{1}'(t)\right)\times\left({\prod_{\substack{z_{0}\ \text{is a cusp or }\\\text{an elliptic point }\\\text{of period}~h>2}}}(t-t(z_{0}))^{2}\prod_{\substack{z_{0}\ \text{is an elliptic}\\\text{point of period}~2}}(t-t(z_{0}))\right) \end{align*} $$
$$ \begin{align*}\left(2R_{1}(t)^{2}+4R_{2}(t)+R_{1}'(t)\right)\times\left({\prod_{\substack{z_{0}\ \text{is a cusp or }\\\text{an elliptic point }\\\text{of period}~h>2}}}(t-t(z_{0}))^{2}\prod_{\substack{z_{0}\ \text{is an elliptic}\\\text{point of period}~2}}(t-t(z_{0}))\right) \end{align*} $$
has a pole only at the cusp that is a pole of t, which is order
![]() $\nu (\Gamma )-2$
, and thus a polynomial in t of degree
$\nu (\Gamma )-2$
, and thus a polynomial in t of degree
![]() $\nu (\Gamma )-2$
, which can possibly have a common factor with the multiplier in the case that
$\nu (\Gamma )-2$
, which can possibly have a common factor with the multiplier in the case that
![]() $t=t(z_{0})+c_{1}(\tau -z_{0})^{h}+O((\tau -z_{0})^{3h})$
at some elliptic point of period
$t=t(z_{0})+c_{1}(\tau -z_{0})^{h}+O((\tau -z_{0})^{3h})$
at some elliptic point of period
![]() $h=2$
. Argument for the case of
$h=2$
. Argument for the case of
![]() $4R_{1}(t)R_{2}(t)+2R_{2}'(t)$
is similar and thus omitted.
$4R_{1}(t)R_{2}(t)+2R_{2}'(t)$
is similar and thus omitted.
Item (iii) follows from the remarks given in Section 2 and Lemma 3.1.
For (iv), first, by items (i) and (ii), one can tell that the least common multiple of the denominators of
![]() $3R_{1}(t)$
,
$3R_{1}(t)$
,
![]() $2R_{1}(t)^{2}+4R_{2}(t)+R_{1}'(t)$
, and
$2R_{1}(t)^{2}+4R_{2}(t)+R_{1}'(t)$
, and
![]() $4R_{1}(t)R_{2}(t)+2R_{2}'(t)$
is exactly
$4R_{1}(t)R_{2}(t)+2R_{2}'(t)$
is exactly
 $$ \begin{align*}\mathcal{P}_{3}(t):= t^{2}\prod_{\substack{\tau_{0}\ \text{is a cusp apart}\\\text{from}\ [i\infty],\ \text{or an}\\\text{ elliptic point}\\\text{ of period}~h>2}}(t-t(z_{0}))^{2}\prod_{\substack{z_{0}\ \text{is an elliptic}\\\text{point of period}~2}}(t-t(z_{0})). \end{align*} $$
$$ \begin{align*}\mathcal{P}_{3}(t):= t^{2}\prod_{\substack{\tau_{0}\ \text{is a cusp apart}\\\text{from}\ [i\infty],\ \text{or an}\\\text{ elliptic point}\\\text{ of period}~h>2}}(t-t(z_{0}))^{2}\prod_{\substack{z_{0}\ \text{is an elliptic}\\\text{point of period}~2}}(t-t(z_{0})). \end{align*} $$
So clearing denominators, the symmetric square (3.4) is of the form
where
![]() $\mathcal {P}_{2}(t)$
is a polynomial of the form
$\mathcal {P}_{2}(t)$
is a polynomial of the form
![]() $t\tilde {\mathcal {P}}_{2}(t)$
with
$t\tilde {\mathcal {P}}_{2}(t)$
with
![]() $\tilde {\mathcal {P}}_{2}(t)$
of degree
$\tilde {\mathcal {P}}_{2}(t)$
of degree
![]() $\nu (\Gamma )-2$
coprime to
$\nu (\Gamma )-2$
coprime to
 $$ \begin{align*}\prod_{\substack{z_{0}\ \text{is an elliptic}\\\text{point of period}~2}}(t-t(z_{0})), \end{align*} $$
$$ \begin{align*}\prod_{\substack{z_{0}\ \text{is an elliptic}\\\text{point of period}~2}}(t-t(z_{0})), \end{align*} $$
![]() $\mathcal {P}_{1}(t)$
is a polynomial of degree
$\mathcal {P}_{1}(t)$
is a polynomial of degree
![]() $\nu (\Gamma )-2$
coprime to
$\nu (\Gamma )-2$
coprime to
 $$ \begin{align*}\prod_{\substack{\tau_{0}\ \text{is a cusp apart}\\ \text{from}\ [i\infty],\ \text{or an}\\\text{ elliptic point}\\\text{ of period}~h>2}}(t-t(z_{0}))^{2}, \end{align*} $$
$$ \begin{align*}\prod_{\substack{\tau_{0}\ \text{is a cusp apart}\\ \text{from}\ [i\infty],\ \text{or an}\\\text{ elliptic point}\\\text{ of period}~h>2}}(t-t(z_{0}))^{2}, \end{align*} $$
![]() $\mathcal {P}_{0}(t)$
is a polynomial of degree
$\mathcal {P}_{0}(t)$
is a polynomial of degree
![]() $\nu (\Gamma )-3$
, and
$\nu (\Gamma )-3$
, and
![]() $\mathcal {P}_{3}(t)/t^{2}$
is a polynomial in t of degree
$\mathcal {P}_{3}(t)/t^{2}$
is a polynomial in t of degree
![]() $\nu (\Gamma )-2$
with nonzero constant, that is to say, the greatest common divisor of
$\nu (\Gamma )-2$
with nonzero constant, that is to say, the greatest common divisor of
![]() $\mathcal {P}_{3}(t)/t^{2}$
and
$\mathcal {P}_{3}(t)/t^{2}$
and
![]() $\mathcal {P}_{i}(t)$
for
$\mathcal {P}_{i}(t)$
for
![]() $i\in \{0,1,2\}$
is 1. As a result, substituting
$i\in \{0,1,2\}$
is 1. As a result, substituting
![]() $\sum _{n=0}^{\infty }A(n)t^{n}$
into the left-hand side of the equation, one can deduce that for any m, the coefficient of
$\sum _{n=0}^{\infty }A(n)t^{n}$
into the left-hand side of the equation, one can deduce that for any m, the coefficient of
![]() $t^{m}$
is exactly a linear combination of
$t^{m}$
is exactly a linear combination of
![]() $A(m+1),\ldots ,A(m+3-\nu (\Gamma ))$
over
$A(m+1),\ldots ,A(m+3-\nu (\Gamma ))$
over
![]() $\overline {\mathbb {Q}}[m]$
, and the coefficient of
$\overline {\mathbb {Q}}[m]$
, and the coefficient of
![]() $A(m+1)$
is
$A(m+1)$
is
 $$ \begin{align*}\left(\lim_{t\to0}\frac{\mathcal{P}_{3}(t)}{t^{2}}\right) (m+1)m(m-1)+\tilde{\mathcal{P}}_{2}(0)(m+1)m+\mathcal{P}_{1}(0)(m+1), \end{align*} $$
$$ \begin{align*}\left(\lim_{t\to0}\frac{\mathcal{P}_{3}(t)}{t^{2}}\right) (m+1)m(m-1)+\tilde{\mathcal{P}}_{2}(0)(m+1)m+\mathcal{P}_{1}(0)(m+1), \end{align*} $$
where
 $$ \begin{align*}\lim_{t\to0}\frac{\mathcal{P}_{3}(t)}{t^{2}}=\prod_{\substack{\tau_{0}\ \text{is a cusp apart}\\\text{from }[i\infty],\ \text{or an}\\\text{ elliptic point}\\\text{ of period}~h>2}}t(z_{0})^{2}\prod_{\substack{z_{0}\ \text{is an elliptic}\\\text{point of period}~2}}(-t(z_{0}))\ne0. \end{align*} $$
$$ \begin{align*}\lim_{t\to0}\frac{\mathcal{P}_{3}(t)}{t^{2}}=\prod_{\substack{\tau_{0}\ \text{is a cusp apart}\\\text{from }[i\infty],\ \text{or an}\\\text{ elliptic point}\\\text{ of period}~h>2}}t(z_{0})^{2}\prod_{\substack{z_{0}\ \text{is an elliptic}\\\text{point of period}~2}}(-t(z_{0}))\ne0. \end{align*} $$
Note that by the proofs of (i) and (ii),
 $$ \begin{align*} \tilde{\mathcal{P}}_{2}(0)&=\lim_{t\to0}3R_{1}(t)t\frac{\mathcal{P}_{3}(t)}{t^{2}}=3\left(\lim_{t\to0}\frac{\mathcal{P}_{3}(t)}{t^{2}}\right) \end{align*} $$
$$ \begin{align*} \tilde{\mathcal{P}}_{2}(0)&=\lim_{t\to0}3R_{1}(t)t\frac{\mathcal{P}_{3}(t)}{t^{2}}=3\left(\lim_{t\to0}\frac{\mathcal{P}_{3}(t)}{t^{2}}\right) \end{align*} $$
and
Therefore, up to a multiplier of
![]() $\lim _{t\to 0}\frac {\mathcal {P}_{3}(t)}{t^{2}}$
, the coefficient of
$\lim _{t\to 0}\frac {\mathcal {P}_{3}(t)}{t^{2}}$
, the coefficient of
![]() $A(m+1)$
is exactly
$A(m+1)$
is exactly
Finally, setting the coefficient of
![]() $t^{m}$
to be 0 and cancelling the multiplier highlighted above, one obtains the desired linear homogeneous recurrence relation.
$t^{m}$
to be 0 and cancelling the multiplier highlighted above, one obtains the desired linear homogeneous recurrence relation.
The following example is recently discovered by Cooper et al. [Reference Anusha, Bhuvan, Cooper and Vasuki2, Theorem 6.2] using various q-series identities. We hereby provide a much simpler and more systematic derivation.
Example 3.4 For
![]() $\Gamma =\Gamma _{0}(21)+$
, the Fuchsian group generated by
$\Gamma =\Gamma _{0}(21)+$
, the Fuchsian group generated by
![]() $\Gamma _{0}(21)$
and all of its Atkin–Lehner involutions, with
$\Gamma _{0}(21)$
and all of its Atkin–Lehner involutions, with
where
![]() $u=\left (\frac {\eta (\tau )\eta (21\tau )}{\eta (3\tau )\eta (7\tau )}\right )^{2}$
, one can compute and find the associated orbifold uniformizing differential equation
$u=\left (\frac {\eta (\tau )\eta (21\tau )}{\eta (3\tau )\eta (7\tau )}\right )^{2}$
, one can compute and find the associated orbifold uniformizing differential equation
 $$ \begin{align*}\frac{d^{2}y}{dt^{2}}+\frac{11,340t^6+5,916t^5+1,705t^4+352t^3+30t^2+4t+1}{4t^2(4t+1)^2(27t^2+2t-1)^2}y=0, \end{align*} $$
$$ \begin{align*}\frac{d^{2}y}{dt^{2}}+\frac{11,340t^6+5,916t^5+1,705t^4+352t^3+30t^2+4t+1}{4t^2(4t+1)^2(27t^2+2t-1)^2}y=0, \end{align*} $$
whose “anti-projectivized” form is given by
 $$ \begin{align*}\frac{d^{2}y}{dt^{2}}+\frac{270t^3+70t^2-3t-1}{t(4t+1)(27t^{2}+2t-1)}\frac{dy}{dt}+\frac{240t^2+47t-2}{4t(4t+1)(27t^2+2t-1)}y=0. \end{align*} $$
$$ \begin{align*}\frac{d^{2}y}{dt^{2}}+\frac{270t^3+70t^2-3t-1}{t(4t+1)(27t^{2}+2t-1)}\frac{dy}{dt}+\frac{240t^2+47t-2}{4t(4t+1)(27t^2+2t-1)}y=0. \end{align*} $$
And thus, taking symmetric square, one obtains the third-order differential equation
 $$ \begin{align*}\frac{d^{3}Y}{dt^{3}}&+\frac{3(270t^3+70t^2-3t-1)}{t(4t+1)(27t^{2}+2t-1)}\frac{d^{2}Y}{dt^{2}}\\&+\frac{(15t-1)(88t^2+23t+1)}{t^2(4t+1)(27t^2+2t-1)}\frac{dY}{dt}+\frac{360t^2+47t-1}{t^2(4t+1)(27t^2+2t-1)}Y=0 \end{align*} $$
$$ \begin{align*}\frac{d^{3}Y}{dt^{3}}&+\frac{3(270t^3+70t^2-3t-1)}{t(4t+1)(27t^{2}+2t-1)}\frac{d^{2}Y}{dt^{2}}\\&+\frac{(15t-1)(88t^2+23t+1)}{t^2(4t+1)(27t^2+2t-1)}\frac{dY}{dt}+\frac{360t^2+47t-1}{t^2(4t+1)(27t^2+2t-1)}Y=0 \end{align*} $$
satisfied by
 $$ \begin{align*}Y=\frac{1}{t(4t+1)^{\frac{1}{2}}(27t^{2}+2t+1)^{\frac{1}{2}}}\frac{1}{2\pi i}\frac{dt}{d\tau}. \end{align*} $$
$$ \begin{align*}Y=\frac{1}{t(4t+1)^{\frac{1}{2}}(27t^{2}+2t+1)^{\frac{1}{2}}}\frac{1}{2\pi i}\frac{dt}{d\tau}. \end{align*} $$
Using the theory of modular forms or Sturm’s bound, one can check that
 $$ \begin{align*}\frac{1}{t(4t+1)^{\frac{1}{2}}(27t^{2}+2t+1)^{\frac{1}{2}}}\frac{1}{2\pi i}\frac{dt}{d\tau}=-i\frac{\eta(\tau)\eta(3\tau)\eta(7\tau)\eta(21\tau)}{t^{\frac{4}{3}}}, \end{align*} $$
$$ \begin{align*}\frac{1}{t(4t+1)^{\frac{1}{2}}(27t^{2}+2t+1)^{\frac{1}{2}}}\frac{1}{2\pi i}\frac{dt}{d\tau}=-i\frac{\eta(\tau)\eta(3\tau)\eta(7\tau)\eta(21\tau)}{t^{\frac{4}{3}}}, \end{align*} $$
which recovers [Reference Anusha, Bhuvan, Cooper and Vasuki2, Theorem 6.2].
3.3 Remark: Clausen-type transformations
As is noted at the beginning, a key ingredient of the derivation of Ramanujan’s formula (1.1) is the Clausen-type quadratic transformation formula
 $$ \begin{align} {}_{2}{F}_{1}\left(\frac{1}{2},\frac{1}{2};1;t\right)^{2}={}_{3}F_{2}\left(\frac{1}{2},\frac{1}{2},\frac{1}{2};1,1;4(1-t)t\right). \end{align} $$
$$ \begin{align} {}_{2}{F}_{1}\left(\frac{1}{2},\frac{1}{2};1;t\right)^{2}={}_{3}F_{2}\left(\frac{1}{2},\frac{1}{2},\frac{1}{2};1,1;4(1-t)t\right). \end{align} $$
In this subsection, one shall see that this can be regarded as a special case of a general Clausen-type transformation formula obtained by modular transformations between orbifold uniformizations associated with genus zero
![]() $\mathrm {SL}_{2}(\mathbb {R})$
-subgroups.
$\mathrm {SL}_{2}(\mathbb {R})$
-subgroups.
For any genus zero
![]() $\mathrm {SL}_{2}(\mathbb {R})$
-subgroups
$\mathrm {SL}_{2}(\mathbb {R})$
-subgroups
![]() $\Gamma _{1},\Gamma _{2}$
commensurable with
$\Gamma _{1},\Gamma _{2}$
commensurable with
![]() $\mathrm {SL}_{2}(\mathbb {Z})$
with
$\mathrm {SL}_{2}(\mathbb {Z})$
with
![]() $\Gamma _{1}<\Gamma _{2}$
, suppose that for
$\Gamma _{1}<\Gamma _{2}$
, suppose that for
![]() $i=1,2$
,
$i=1,2$
,
![]() $t_{i}$
is a uniformizer for
$t_{i}$
is a uniformizer for
![]() $X(\Gamma _{i})$
. Then there is a rational function
$X(\Gamma _{i})$
. Then there is a rational function
![]() $r(t_{1})$
in
$r(t_{1})$
in
![]() $t_{1}$
such that
$t_{1}$
such that
![]() $r(t_{1})=t_{2}$
. In addition, we have seen that
$r(t_{1})=t_{2}$
. In addition, we have seen that
 $$ \begin{align*}y_{i}=\prod_{\substack{z_{0}\ \text{is a cusp}}}(t_{i}-t_{i}(z_0))^{\frac{-1}{2}}\prod_{\substack{z_{0}\ \text{is an elliptic}\\\text{point of period}~h}}\left(t_{i}-t_{i}(z_{0})\right)^{\frac{1-h}{2h}}\left(\frac{1}{2\pi i}\frac{dt_{i}}{d\tau}\right)^{\frac{1}{2}} \end{align*} $$
$$ \begin{align*}y_{i}=\prod_{\substack{z_{0}\ \text{is a cusp}}}(t_{i}-t_{i}(z_0))^{\frac{-1}{2}}\prod_{\substack{z_{0}\ \text{is an elliptic}\\\text{point of period}~h}}\left(t_{i}-t_{i}(z_{0})\right)^{\frac{1-h}{2h}}\left(\frac{1}{2\pi i}\frac{dt_{i}}{d\tau}\right)^{\frac{1}{2}} \end{align*} $$
is a solution to
 $$ \begin{align*}\frac{d^{2}y}{dt_{i}^{2}}+R_{1}(t_{i})\frac{dy}{dt_{i}}+R_{2}(t_{i})y=0, \end{align*} $$
$$ \begin{align*}\frac{d^{2}y}{dt_{i}^{2}}+R_{1}(t_{i})\frac{dy}{dt_{i}}+R_{2}(t_{i})y=0, \end{align*} $$
where
 $$ \begin{align*}R_{1}(t_{i})=\sum_{\substack{z_{0}\ \text{is a cusp }}}\frac{1}{t_{i}-t_{i}(z_{0})}+\sum_{\substack{z_{0}\ \text{is an elliptic}\\\text{point of period}~h}}\frac{1-\frac{1}{h}}{t_{i}-t_{i}(z_{0})}, \end{align*} $$
$$ \begin{align*}R_{1}(t_{i})=\sum_{\substack{z_{0}\ \text{is a cusp }}}\frac{1}{t_{i}-t_{i}(z_{0})}+\sum_{\substack{z_{0}\ \text{is an elliptic}\\\text{point of period}~h}}\frac{1-\frac{1}{h}}{t_{i}-t_{i}(z_{0})}, \end{align*} $$
and
![]() $R_{2}(t)=\{t_{i},\tau \}/(t_{i}')^{2}+\frac {1}{2}R_{1}'(t_{i})+\frac {1}{4}R_{1}(t_{i})^{2}$
, and that
$R_{2}(t)=\{t_{i},\tau \}/(t_{i}')^{2}+\frac {1}{2}R_{1}'(t_{i})+\frac {1}{4}R_{1}(t_{i})^{2}$
, and that
 $$ \begin{align*}Y_{i}=\prod_{\substack{z_{0}\ \text{is a cusp }}}(t_{i}-t_{i}(z_0))^{-1}\prod_{\substack{z_{0}\ \text{is an elliptic}\\\text{point of period}~h}}\left(t_{i}-t_{i}(z_{0})\right)^{\frac{1-h}{h}}\frac{1}{2\pi i}\frac{dt_{i}}{d\tau} \end{align*} $$
$$ \begin{align*}Y_{i}=\prod_{\substack{z_{0}\ \text{is a cusp }}}(t_{i}-t_{i}(z_0))^{-1}\prod_{\substack{z_{0}\ \text{is an elliptic}\\\text{point of period}~h}}\left(t_{i}-t_{i}(z_{0})\right)^{\frac{1-h}{h}}\frac{1}{2\pi i}\frac{dt_{i}}{d\tau} \end{align*} $$
as a modular form for
![]() $\Gamma _{i}$
of weight 2 is a solution to the symmetric square of the Fuchsian equation above. Since
$\Gamma _{i}$
of weight 2 is a solution to the symmetric square of the Fuchsian equation above. Since
![]() $Y_{2}/Y_{1}$
is a modular function for
$Y_{2}/Y_{1}$
is a modular function for
![]() $\Gamma _{1}$
, there is a rational function in
$\Gamma _{1}$
, there is a rational function in
![]() $t_{1}$
such that
$t_{1}$
such that
![]() $Y_{2}=R(t_{1})Y_{1}$
. Suppose that near
$Y_{2}=R(t_{1})Y_{1}$
. Suppose that near
![]() $t_{i}=0$
, one has the following local expansions:
$t_{i}=0$
, one has the following local expansions:
 $$ \begin{align*}y_{i}=\sum_{n=0}^{\infty}a_{i}(n)t_{i}^{n}\quad\mbox{and}\quad Y_{i}=\sum_{n=0}^{\infty}A_{i}(n)t_{i}^{n} \end{align*} $$
$$ \begin{align*}y_{i}=\sum_{n=0}^{\infty}a_{i}(n)t_{i}^{n}\quad\mbox{and}\quad Y_{i}=\sum_{n=0}^{\infty}A_{i}(n)t_{i}^{n} \end{align*} $$
for
![]() $y_{i}$
and
$y_{i}$
and
![]() $Y_{i}$
. Then near
$Y_{i}$
. Then near
![]() $t_{1}=0$
such that
$t_{1}=0$
such that
![]() $r(t_{1})$
is also near 0, in this way, one obtains a Clausen-type transformation formula
$r(t_{1})$
is also near 0, in this way, one obtains a Clausen-type transformation formula
 $$ \begin{align} \sum_{n=0}^{\infty}A_{2}(n)r(t_{1})^{n}=R(t_{1})\left(\sum_{n=0}^{\infty}a_{1}(n)t_{1}^{n}\right)^{2}. \end{align} $$
$$ \begin{align} \sum_{n=0}^{\infty}A_{2}(n)r(t_{1})^{n}=R(t_{1})\left(\sum_{n=0}^{\infty}a_{1}(n)t_{1}^{n}\right)^{2}. \end{align} $$
In what follows, we exemplify this Clausen-type transformation by reproducing the quadratic transformation (3.6).
Example 3.5 Take
![]() $\Gamma _{1}=\gamma \Gamma (2)\gamma ^{-1}$
with
$\Gamma _{1}=\gamma \Gamma (2)\gamma ^{-1}$
with
 $\gamma =\begin {pmatrix}1&0\\0&2\end {pmatrix}$
, i.e.,
$\gamma =\begin {pmatrix}1&0\\0&2\end {pmatrix}$
, i.e.,
![]() $\Gamma _{1}=\Gamma _{0}(4)$
, and
$\Gamma _{1}=\Gamma _{0}(4)$
, and
![]() $\Gamma _{2}=\Gamma _{0}(4)+$
. Then correspondingly,
$\Gamma _{2}=\Gamma _{0}(4)+$
. Then correspondingly,
 $$ \begin{align*}t_{1}=16\frac{\eta(4\tau)^{16}\eta\left({\tau}\right)^{8}}{\eta(2\tau)^{24}}\quad\mbox{and}\quad t_{2}=\frac{\eta(4\tau)^{24}\eta(\tau)^{24}}{\eta(2\tau)^{48}}=\frac{t_{1}}{16}(1-t_{1}), \end{align*} $$
$$ \begin{align*}t_{1}=16\frac{\eta(4\tau)^{16}\eta\left({\tau}\right)^{8}}{\eta(2\tau)^{24}}\quad\mbox{and}\quad t_{2}=\frac{\eta(4\tau)^{24}\eta(\tau)^{24}}{\eta(2\tau)^{48}}=\frac{t_{1}}{16}(1-t_{1}), \end{align*} $$
and by properties of modular forms or Sturm’s bound, one can check that
 $$ \begin{align*}Y_{2}=\frac{1}{t_{2}\left(64t_{2}+1\right)^{\frac{1}{2}}}\frac{1}{2\pi i}\frac{dt_{2}}{d\tau}=\frac{1}{t_{1}(t_{1}-1)}\frac{1}{2\pi i}\frac{dt_{1}}{d\tau}=Y_{1}=y_{1}^{2}. \end{align*} $$
$$ \begin{align*}Y_{2}=\frac{1}{t_{2}\left(64t_{2}+1\right)^{\frac{1}{2}}}\frac{1}{2\pi i}\frac{dt_{2}}{d\tau}=\frac{1}{t_{1}(t_{1}-1)}\frac{1}{2\pi i}\frac{dt_{1}}{d\tau}=Y_{1}=y_{1}^{2}. \end{align*} $$
One can also deduce from the orbifold uniformizing differential equation satisfied by
![]() $y_{1}$
with respect to
$y_{1}$
with respect to
![]() $t_{1}$
and the symmetric square satisfied by
$t_{1}$
and the symmetric square satisfied by
![]() $Y_{2}$
with respect to
$Y_{2}$
with respect to
![]() $t_{2}$
that
$t_{2}$
that
 $$ \begin{align*}y_{1}=\sum_{n=0}^{\infty}\binom{2n}{n}^{2}\left(\frac{t_{1}}{4^{2}}\right)^{n}={}_{2}F_{1}\left(\frac{1}{2},\frac{1}{2};1;t_{1}\right) \end{align*} $$
$$ \begin{align*}y_{1}=\sum_{n=0}^{\infty}\binom{2n}{n}^{2}\left(\frac{t_{1}}{4^{2}}\right)^{n}={}_{2}F_{1}\left(\frac{1}{2},\frac{1}{2};1;t_{1}\right) \end{align*} $$
and
 $$ \begin{align*}Y_{2}=\sum_{n=0}^{\infty}\binom{2n}{n}^{3}t_{2}^{n}=\sum_{n=0}^{\infty}\binom{2n}{n}^{3}\left(\frac{4t_{1}(1-t_{1})}{4^{3}}\right)^{n}={}_{3}F_{2}\left(\frac{1}{2},\frac{1}{2},\frac{1}{2};1,1;4t_{1}(1-t_{1})\right). \end{align*} $$
$$ \begin{align*}Y_{2}=\sum_{n=0}^{\infty}\binom{2n}{n}^{3}t_{2}^{n}=\sum_{n=0}^{\infty}\binom{2n}{n}^{3}\left(\frac{4t_{1}(1-t_{1})}{4^{3}}\right)^{n}={}_{3}F_{2}\left(\frac{1}{2},\frac{1}{2},\frac{1}{2};1,1;4t_{1}(1-t_{1})\right). \end{align*} $$
Therefore, near
![]() $t_{1}=0$
,
$t_{1}=0$
,
 $$ \begin{align*}{}_{2}F_{1}\left(\frac{1}{2},\frac{1}{2};1;t_{1}\right)^{2}={}_{3}F_{2}\left(\frac{1}{2},\frac{1}{2},\frac{1}{2};1,1;4t_{1}(1-t_{1})\right). \end{align*} $$
$$ \begin{align*}{}_{2}F_{1}\left(\frac{1}{2},\frac{1}{2};1;t_{1}\right)^{2}={}_{3}F_{2}\left(\frac{1}{2},\frac{1}{2},\frac{1}{2};1,1;4t_{1}(1-t_{1})\right). \end{align*} $$
Another example given as follows plays an important role in the derivation of Example 1.6.
Example 3.6 Take
![]() $\Gamma _{1}=\gamma ^{-1}\left (\Gamma _{0}(4) \cap \Gamma (2)\right )\gamma $
with
$\Gamma _{1}=\gamma ^{-1}\left (\Gamma _{0}(4) \cap \Gamma (2)\right )\gamma $
with
 $\gamma =\begin {pmatrix}1&0\\1&1\end {pmatrix}$
and
$\gamma =\begin {pmatrix}1&0\\1&1\end {pmatrix}$
and
![]() $\Gamma _{2}=\Gamma (2)$
, and correspondingly
$\Gamma _{2}=\Gamma (2)$
, and correspondingly
 $$ \begin{align*}t_{1}=4\frac{\eta(2\tau)^{8}\eta\left(\frac{\tau}{2}\right)^{4}}{\eta(\tau)^{12}}\quad\mbox{and}\quad t_{2}=t_{1}^{2}, \end{align*} $$
$$ \begin{align*}t_{1}=4\frac{\eta(2\tau)^{8}\eta\left(\frac{\tau}{2}\right)^{4}}{\eta(\tau)^{12}}\quad\mbox{and}\quad t_{2}=t_{1}^{2}, \end{align*} $$
where
![]() $t_{2}$
is the well-known Lambda modular invariant. Following the remarks above, one first finds that
$t_{2}$
is the well-known Lambda modular invariant. Following the remarks above, one first finds that
 $$ \begin{align*}Y_{2}=\frac{1}{t_{2}^{2}-t_{2}}\frac{1}{2\pi i}\frac{dt_{2}}{d\tau}=\frac{2}{t_{1}^{3}-t_{1}}\frac{1}{2\pi i}\frac{dt_{1}}{d\tau}=2Y_{1}=2y_{1}^{2}. \end{align*} $$
$$ \begin{align*}Y_{2}=\frac{1}{t_{2}^{2}-t_{2}}\frac{1}{2\pi i}\frac{dt_{2}}{d\tau}=\frac{2}{t_{1}^{3}-t_{1}}\frac{1}{2\pi i}\frac{dt_{1}}{d\tau}=2Y_{1}=2y_{1}^{2}. \end{align*} $$
By [Reference Almkvist and Zudilin1, equation (n)] and [Reference Chan and Cooper6, p. 373], one can deduce by changes of variables that
 $$ \begin{align*}y_{1}^{2}=-\frac{1}{4}\left(\sum_{n=0}^{\infty}\left(\sum_{k}(-1)^{k}\binom{-1/2}{k}\binom{-1/2}{n-k}\binom{n}{k}\right)t_{1}^{n}\right)^{2} \end{align*} $$
$$ \begin{align*}y_{1}^{2}=-\frac{1}{4}\left(\sum_{n=0}^{\infty}\left(\sum_{k}(-1)^{k}\binom{-1/2}{k}\binom{-1/2}{n-k}\binom{n}{k}\right)t_{1}^{n}\right)^{2} \end{align*} $$
and
 $$ \begin{align*}Y_{2}=-\frac{1}{2}\sum_{n=0}^{\infty}\left(\sum_{k}\binom{2n-2k}{n-k}^{2}\binom{2k}{k}^{2}\right)16^{-n}t_{2}^{n}, \end{align*} $$
$$ \begin{align*}Y_{2}=-\frac{1}{2}\sum_{n=0}^{\infty}\left(\sum_{k}\binom{2n-2k}{n-k}^{2}\binom{2k}{k}^{2}\right)16^{-n}t_{2}^{n}, \end{align*} $$
and thus one has the following transformation identity near
![]() $t_{1}=0$
:
$t_{1}=0$
:
 $$ \begin{align*}\sum_{n=0}^{\infty}\left(\sum_{k}\binom{2n-2k}{n-k}^{2}\binom{2k}{k}^{2}\right)16^{-n}t_{1}^{2n} =\left(\sum_{n=0}^{\infty}\left(\sum_{k}(-1)^{k}\binom{-1/2}{k}\binom{-1/2}{n-k}\binom{n}{k}\right)t_{1}^{n}\right)^{2}. \end{align*} $$
$$ \begin{align*}\sum_{n=0}^{\infty}\left(\sum_{k}\binom{2n-2k}{n-k}^{2}\binom{2k}{k}^{2}\right)16^{-n}t_{1}^{2n} =\left(\sum_{n=0}^{\infty}\left(\sum_{k}(-1)^{k}\binom{-1/2}{k}\binom{-1/2}{n-k}\binom{n}{k}\right)t_{1}^{n}\right)^{2}. \end{align*} $$
Remark 3.7 The notion of Clausen-type transformation formulas arising from modular forms was first used in [Reference Chan, Tanigawa, Yang and Zudilin7] by Chan et al., in which they establish three examples that can be viewed as the specialization of (3.7) to the cases of
![]() $\Gamma _{1}=\Gamma _{0}(6)$
and
$\Gamma _{1}=\Gamma _{0}(6)$
and
![]() $\Gamma _{2}=\Gamma _{0}(6)+$
, where
$\Gamma _{2}=\Gamma _{0}(6)+$
, where
![]() $\Gamma _{0}(6)+$
is the group generated by
$\Gamma _{0}(6)+$
is the group generated by
![]() $\Gamma _{0}(6)$
and all its Atkin–Lehner involutions.
$\Gamma _{0}(6)$
and all its Atkin–Lehner involutions.
4 Proof of Theorem 1.1
We are now in a position to give a proof to our main theorem as a closing of this note.
Proof of Theorem 1.1
Under the given assumptions, write
 $$ \begin{align*}Y=Y(\tau)=\prod_{\substack{z_{0}\ \text{is a cusp}}}(t-t(z_0))^{-1}\prod_{\substack{z_{0}\ \text{is an elliptic }\\\text{point of period}~h}}\left(t-t(z_{0})\right)^{\frac{1-h}{h}}\frac{1}{2\pi i}\frac{dt}{d\tau}, \end{align*} $$
$$ \begin{align*}Y=Y(\tau)=\prod_{\substack{z_{0}\ \text{is a cusp}}}(t-t(z_0))^{-1}\prod_{\substack{z_{0}\ \text{is an elliptic }\\\text{point of period}~h}}\left(t-t(z_{0})\right)^{\frac{1-h}{h}}\frac{1}{2\pi i}\frac{dt}{d\tau}, \end{align*} $$
and start with the simple manipulation
 $$ \begin{align*}\frac{1}{2\pi i}\frac{dY}{d\tau}=\left(\frac{1}{2\pi i}\frac{dY}{d\tau}-\frac{2Y}{4\pi\mathrm{Im}(\tau)}\right)+\frac{2Y}{4\pi\mathrm{Im}(\tau)}. \end{align*} $$
$$ \begin{align*}\frac{1}{2\pi i}\frac{dY}{d\tau}=\left(\frac{1}{2\pi i}\frac{dY}{d\tau}-\frac{2Y}{4\pi\mathrm{Im}(\tau)}\right)+\frac{2Y}{4\pi\mathrm{Im}(\tau)}. \end{align*} $$
Writing
![]() $Y=y^{2}$
and multiplying both sides by y gives
$Y=y^{2}$
and multiplying both sides by y gives
 $$ \begin{align} y\frac{1}{2\pi i}\frac{dY}{d\tau}&=y\left(\frac{2y}{2\pi i}\frac{dy}{d\tau}-\frac{2y^{2}}{4\pi\mathrm{Im}(\tau)}\right)+y\frac{2Y}{4\pi\mathrm{Im}(\tau)}\nonumber\\ &= 2Y\left(\frac{1}{2\pi i}\frac{dy}{d\tau}-\frac{y}{4\pi\mathrm{Im}(\tau)}\right)+y\frac{2Y}{4\pi\mathrm{Im}(\tau)}. \end{align} $$
$$ \begin{align} y\frac{1}{2\pi i}\frac{dY}{d\tau}&=y\left(\frac{2y}{2\pi i}\frac{dy}{d\tau}-\frac{2y^{2}}{4\pi\mathrm{Im}(\tau)}\right)+y\frac{2Y}{4\pi\mathrm{Im}(\tau)}\nonumber\\ &= 2Y\left(\frac{1}{2\pi i}\frac{dy}{d\tau}-\frac{y}{4\pi\mathrm{Im}(\tau)}\right)+y\frac{2Y}{4\pi\mathrm{Im}(\tau)}. \end{align} $$
Recall by Lemma 3.3(iv) that
![]() $Y(\tau )=\sum _{n=0}^{\infty }A(n)t(\tau )^{n}$
with coefficients
$Y(\tau )=\sum _{n=0}^{\infty }A(n)t(\tau )^{n}$
with coefficients
![]() $A(n)$
satisfying a linear homogeneous recurrence relation of at most
$A(n)$
satisfying a linear homogeneous recurrence relation of at most
![]() $(\nu (\Gamma )-1)$
terms induced by (3.4) for
$(\nu (\Gamma )-1)$
terms induced by (3.4) for
Substitute this for the Y’s attached to the first two terms from left in (4.1) to get
 $$ \begin{align*} y\frac{1}{2\pi i}\frac{dt}{d\tau}\sum_{n=0}^{\infty}A(n)nt^{n-1}&=2\left(\frac{1}{2\pi i}\frac{dy}{d\tau}-\frac{y}{4\pi \mathrm{Im}(\tau)}\right)\sum_{n=0}^{\infty}A(n)t^{n}+y\frac{Y}{2\pi \mathrm{Im}(\tau)}. \end{align*} $$
$$ \begin{align*} y\frac{1}{2\pi i}\frac{dt}{d\tau}\sum_{n=0}^{\infty}A(n)nt^{n-1}&=2\left(\frac{1}{2\pi i}\frac{dy}{d\tau}-\frac{y}{4\pi \mathrm{Im}(\tau)}\right)\sum_{n=0}^{\infty}A(n)t^{n}+y\frac{Y}{2\pi \mathrm{Im}(\tau)}. \end{align*} $$
A simple manipulation gives the desired formula (1.4) for
![]() $\frac {1}{\pi }$
,
$\frac {1}{\pi }$
,
 $$ \begin{align*} \frac{1}{\pi}={C}\sum_{n=0}^{\infty}A(n)(n-{B})t^{n}, \end{align*} $$
$$ \begin{align*} \frac{1}{\pi}={C}\sum_{n=0}^{\infty}A(n)(n-{B})t^{n}, \end{align*} $$
where
 $$ \begin{align*} {B}&=t\left(\frac{1}{\pi i}\frac{dy}{d\tau}-\frac{y}{2\pi \mathrm{Im}(\tau)}\right)\left/\left(y\frac{1}{2\pi i}\frac{dt}{d\tau}\right)\right. \end{align*} $$
$$ \begin{align*} {B}&=t\left(\frac{1}{\pi i}\frac{dy}{d\tau}-\frac{y}{2\pi \mathrm{Im}(\tau)}\right)\left/\left(y\frac{1}{2\pi i}\frac{dt}{d\tau}\right)\right. \end{align*} $$
and
 $$ \begin{align*} {C}&=2\mathrm{Im}(\tau)\left.\frac{1}{2\pi i}\frac{dt}{d\tau}\right/\left(tY\right)\\ &=\frac{2\mathrm{Im}(\tau)}{t}\prod_{\substack{z_{0}\ \text{is a cusp}}}(t-t(z_0))\prod_{\substack{z_{0}\ \text{is an elliptic }\\\text{point of period}~h}}\left(t-t(z_{0})\right)^{\frac{h-1}{h}}. \end{align*} $$
$$ \begin{align*} {C}&=2\mathrm{Im}(\tau)\left.\frac{1}{2\pi i}\frac{dt}{d\tau}\right/\left(tY\right)\\ &=\frac{2\mathrm{Im}(\tau)}{t}\prod_{\substack{z_{0}\ \text{is a cusp}}}(t-t(z_0))\prod_{\substack{z_{0}\ \text{is an elliptic }\\\text{point of period}~h}}\left(t-t(z_{0})\right)^{\frac{h-1}{h}}. \end{align*} $$
Finally, since
![]() $y=y(\tau )$
is a meromorphic modular form of weight 1 and
$y=y(\tau )$
is a meromorphic modular form of weight 1 and
![]() $t=t(\tau )$
is a modular function for an
$t=t(\tau )$
is a modular function for an
![]() $\mathrm {SL}_{2}(\mathbb {R})$
-subgroup commensurable with
$\mathrm {SL}_{2}(\mathbb {R})$
-subgroup commensurable with
![]() $\mathrm {SL}_{2}(\mathbb {Z})$
, and both y and t have algebraic coefficients at
$\mathrm {SL}_{2}(\mathbb {Z})$
, and both y and t have algebraic coefficients at
![]() $[i\infty ]$
as assumed, by [Reference Cohen and Strömberg8, Corollary 5.10.7], one can conclude that both B and C are algebraic numbers for
$[i\infty ]$
as assumed, by [Reference Cohen and Strömberg8, Corollary 5.10.7], one can conclude that both B and C are algebraic numbers for
![]() $\tau $
an imaginary quadratic point in
$\tau $
an imaginary quadratic point in
![]() $\mathbb {H}$
.
$\mathbb {H}$
.
Acknowledgment
The author thanks the referee for his or her useful comments, corrections, and suggestions.