1. INTRODUCTION
The behaviour, evolution and potential instability of the West Antarctic ice sheet is one of the greatest sources of uncertainty in projections of future sea level (Stocker and others, Reference Stocker2013). The Amundsen Sea Embayment is the most rapidly changing sector in West Antarctica, containing both Thwaites and Pine Island Glaciers, the two leading contributors to Antarctic mass loss (Chen and others, Reference Chen, Wilson, Tapley, Blankenship and Young2008; Pritchard and others, Reference Pritchard, Arthen, Vaughan and Edwards2009; Mouginot and others, Reference Mouginot, Rignot and Scheuchl2014; Sutterley and others, Reference Sutterley2014). Although Pine Island Glacier has the larger contemporary negative mass balance, Thwaites Glacier is the only portion of Amundsen Sea sector with a landward-sloping bed that reaches from its current grounding position, on a series of bedrock highs, to the deep interior of the ice sheet (Holt and others, Reference Holt2006; Tinto and Bell, Reference Tinto and Bell2011; Schroeder and others, Reference Schroeder, Blankenship, Young, Witus and Anderson2014). This is a potentially unstable configuration (Weertman, 1974; Thomas and Bentley, Reference Thomas and Bentley1978; Schoof, Reference Schoof2007; Tsai and others, Reference Tsai, Stewart and Thompson2015) in which retreat initialized at its grounding zone could spread to the rest of the glacier catchment in a feedback process that may already be under way (Joughin and others, Reference Joughin, Smith and Medley2014; Rignot and others, Reference Rignot, Mouginot, Morlighem, Seroussi and Scheuchl2014). Because of this potential, efforts have been made to constrain projections of the rate and extent of such a retreat using numerical ice-sheet models (Parizek and others, Reference Parizek2013; Joughin and others, Reference Joughin, Smith and Medley2014; Pollard and others, Reference Pollard, DeConto and Alley2015). However, these models include ice flow laws and rheology values that are temperature dependent (Engelhardt, Reference Engelhardt2004; Cuffey and Paterson, Reference Cuffey and Paterson2010) yet largely unconstrained by glacier-scale observations of ice sheet temperatures (MacGregor and others, Reference MacGregor2015). As a result, poor knowledge of the englacial temperature structure of Thwaites Glacier may be a significant source of uncertainty in model-based projections of future sea-level contributions from the Amundsen Sea Embayment and West Antarctic ice sheet.
One of the most powerful and widely used geophysical tools for catchment-scale observation of subglacial and englacial ice-sheet properties is airborne radar sounding (Gudmandsen, Reference Gudmandsen and Wait1971; Corr and others, Reference Corr, Moore and Nicholls1993; Peters and others, Reference Peters, Blankenship and Morse2005; MacGregor and others, Reference MacGregor2007; Oswald and Gogineni, Reference Oswald and Gogineni2008; Carter and others, Reference Carter, Blankenship, Young and Holt2009; Dowdeswell and Evans, Reference Dowdeswell and Evans2004; Wright and others, Reference Wright2012; Schroeder and others, Reference Schroeder, Blankenship, Raney and Grima2015; Young and others, Reference Young, Schroeder, Blankenship, Kempf and Quartini2016). Radar-sounding bed echo strengths are influenced by a combination of englacial and subglacial properties (Boithias, Reference Boithias1987; Peters and others, Reference Peters, Blankenship and Morse2005; Matsuoka, Reference Matsuoka2011; MacGregor and others, Reference MacGregor2013). Therefore, correction for englacial attenuation is required in order to make inferences about the material and geometric properties of the bed from basal reflectivity. Variations in radar-sounding bed-echo strength have long been used to constrain and correct for englacial attenuation in areas where the depth-averaged attenuation rate could be assumed to be constant (Robin and others, Reference Robin, Evans and Bailey1969; Winebrenner and others, Reference Winebrenner, Smith, Catania, Conway and Raymond2003; Jacobel and others, Reference Jacobel, Welch, Osterhouse, Pettersson and MacGregor2009; Matsuoka and others, Reference Matsuoka, Morse and Raymond2010; Barrella and others, Reference Barrella, Barwick and Salzberg2011; Fujita and others, Reference Fujita2012; MacGregor and others, Reference MacGregor, Matsuoka, Waddington, Winebrenner and Pattyn2012) or to vary linearly with distance along flow (Schroeder and others, Reference Schroeder, Grima and Blankenship2016). However, these assumptions can limit the utility of such approaches to areas far below the scale of a glacier catchment (Jacobel and others, Reference Jacobel2010), making them unsuitable for observationally constraining larger-scale englacial temperature structure.
Recent work has demonstrated the use of radar reflections from englacial layers to constrain attenuation rates and temperatures as a function of depth within the upper portion of the Greenland ice sheet (MacGregor and others, Reference MacGregor2015). This technique exploits the dependence of radar attenuation on ice temperature (Gudmandsen, Reference Gudmandsen and Wait1971; Bogorodsky and others, Reference Bogorodsky, Bentley and Gudmandsen1985; Corr and others, Reference Corr, Moore and Nicholls1993; Wolff and others, Reference Wolff, Miners, Moore and Paren1997; MacGregor and others, Reference MacGregor2007) by assuming constant reflectivity values for internal layers (Drews and others, Reference Drews2009; MacGregor and others, Reference MacGregor2015). Although applicable at the ice-sheet scale, this approach requires extant, contiguous and undisturbed englacial layers, which excludes many fast-flowing and highly crevassed regions near grounding zones and shear margins as well as the deepest ~20% of the ice column (MacGregor and others, Reference MacGregor2015). It is these very regions, however, that can play a dominant role in ice-sheet dynamics and are likely to have the most heterogenous thermal signatures (Joughin and others, Reference Joughin2009; Matsuoka and others, Reference Matsuoka, MacGregor and Pattyn2012; Parizek and others, Reference Parizek2013). As a result, layer-based approaches can not be used to observe englacial temperatures in many of the areas most critical for ice-sheet modelling. To address this issue, we present a new radar-sounding analysis technique that uses unfocused bed echoes within an adaptive, empirical attenuation-fitting framework to provide catchment-scale estimates of englacial attenuation and temperature that can be applied to any radar-sounding system or survey orientation and are independent of the condition of englacial layers.
2. METHODS
Most existing techniques for constraining radar attenuation using bed echoes were developed to correct for rather than measure englacial attenuation (Jacobel and others, Reference Jacobel2010; Matsuoka and others, Reference Matsuoka, MacGregor and Pattyn2012; Schroeder and others, Reference Schroeder, Grima and Blankenship2016). As such, they either assume simplistic, constant or linearly varying attenuation rates for entire surveys (Jacobel and others, Reference Jacobel2010; Schroeder and others, Reference Schroeder, Grima and Blankenship2016) or rely on numerical ice-sheet models to predict attenuation rate values or gradients (Matsuoka and others, Reference Matsuoka, MacGregor and Pattyn2012; Jordan and others, Reference Jordan2016). While effective at improving estimates of basal reflectivity and therefore bed conditions, they do not resolve the pattern of englacial attenuation itself. In principle, improved spatial resolution could be achieved by fitting attenuation rates for sub-profile segments. In practice, however, such fitting requires sufficient variation in ice thickness and attenuation within a segment to accurately estimate the attenuation rate (Jacobel and others, Reference Jacobel2010), setting an effective lower bound on segment size. Further complicating matters, this bound, which results from the trade-off between spatial (segment length) and radiometric (attenuation estimate) resolution, varies as a function of local topography, ice thickness and the attenuation rate itself. Therefore, the optimum fitting-segment length will vary across a survey so that areas with larger ice thickness relief are fit with higher spatial resolution and areas with less ice thickness relief are fit with sufficiently long segments to achieve comparable radiometric resolution. To achieve this, we present a simple, adaptive, attenuation-fitting technique that can constrain spatial variations in the depth-averaged englacial attenuation rate and temperature at the glacier-catchment scale.
For radar sounding data, the geometrically-corrected bed-echo power
![]() $([P_{\rm g}])_{{\rm dB}}$
is given by
$([P_{\rm g}])_{{\rm dB}}$
is given by
where [P]dB is the received bed-echo power, h is the aircraft survey height above the surface, d is the ice thickness, ε is the real permittivity of ice and [ ]dB indicates power on a decibel scale (Matsuoka and others, Reference Matsuoka, MacGregor and Pattyn2012). This geometrically-corrected power is a function of instrument parameters (S), basal reflectivity (R), birefringence (B) and two-way englacial losses (L), so that
where [L]dB = 2d〈N〉 and 〈N〉 is the one-way depth-averaged attenuation rate (Matsuoka and others, Reference Matsuoka, MacGregor and Pattyn2012). Assuming that instrument parameters, reflectivity and birefringence are uncorrelated with ice thickness, the geometrically-corrected bed-echo power can be written as a linear function of thickness, so that
where P a is the attenuation-corrected bed-echo power, which includes the thickness-uncorrelated parameters. Then, for non-negligible values of 〈N〉, [P g]dB and d will be strongly anticorrelated. In the example profile (Fig. 1), this anticorrelation is easy to see in the ice thickness (Fig. 1c) and geometrically-corrected bed-echo power (Fig. 1d) profiles. By contrast, if the attenuation rate 〈N〉 was known, the attenuation-corrected bed-echo power (P a) could be calculated as
resulting in a [P a]dB profile that is uncorrelated with d. It is this difference in correlation behaviour between the corrected and uncorrected bed-echo power with ice thickness that we exploit to estimate the local englacial attenuation rate.

Fig. 1. (a) Airborne radar sounding survey (Holt and others, Reference Holt2006) of the Thwaites Glacier catchment (black boundary) in the context of ice-surface speed (Rignot and others, Reference Rignot, Mouginot and Scheuchl2011). Green boundary indicates ISSM modelling domain. (b) Example profile ‘THW/SJB2/DRP08a’ (red line in A) showing the length (W) of an attenuation fitting segment. The (c) ice thickness and (d) geometrically-corrected bed echo power for the example profile.
The attenuation-corrected bed echo power
![]() $([P_{\rm a}]_{{\rm dB}})$
and ice thickness (d) have a correlation-coefficient magnitude (C) of
$([P_{\rm a}]_{{\rm dB}})$
and ice thickness (d) have a correlation-coefficient magnitude (C) of
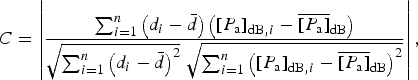 $$C = \left \vert {\displaystyle{{\sum\nolimits_{i = 1}^n {\left( {d_i - \bar d} \right)\left( {{\left[ {P_{\rm a}} \right]}_{{\rm dB},i} - {\overline {\left[ {P_{\rm a}} \right]}} _{{\rm dB}}} \right)}} \over {\sqrt {\sum\nolimits_{i = 1}^n {{\left( {d_i - \bar d} \right)}^2}} \;\sqrt {\sum\nolimits_{i = 1}^n {{\left( {{\left[ {P_{\rm a}} \right]}_{{\rm dB},i} - {\overline {\left[ {P_{\rm a}} \right]}} _{{\rm dB}}} \right)}^2}}}}} \right \vert, $$
$$C = \left \vert {\displaystyle{{\sum\nolimits_{i = 1}^n {\left( {d_i - \bar d} \right)\left( {{\left[ {P_{\rm a}} \right]}_{{\rm dB},i} - {\overline {\left[ {P_{\rm a}} \right]}} _{{\rm dB}}} \right)}} \over {\sqrt {\sum\nolimits_{i = 1}^n {{\left( {d_i - \bar d} \right)}^2}} \;\sqrt {\sum\nolimits_{i = 1}^n {{\left( {{\left[ {P_{\rm a}} \right]}_{{\rm dB},i} - {\overline {\left[ {P_{\rm a}} \right]}} _{{\rm dB}}} \right)}^2}}}}} \right \vert, $$
which will have a value closer to zero if corrected using the actual attenuation rate (〈N〉) and closer to one if corrected using a value of 〈N〉 that is either much larger or smaller than the actual value. This can be seen in Figure 2, which shows C as a function of the attenuation rate used in calculating P a for the example profile in Figure 1. Without attenuation correction (〈N〉 = 0), [P a]dB = [P g]dB and the uncorrected correlation-coefficient magnitude (C 0) is large (~0.8). As the attenuation-rate increases, the correlation-coefficient magnitude decreases to a minimum value of C 0 (~0) at an attenuation rate of 〈N m〉, which is the attenuation rate at the correlation minimum (C m) and our estimate for the local one-way depth-averaged attenuation rate. The value of C once again increases for actuation-rate values greater than 〈N m〉. We characterize the radiometric resolution of our attenuation-rate estimate by the half width (〈N h〉) of this correlation minimum that falls below a given correlation coefficient magnitude (C w) (Fig. 2).

Fig. 2. Correlation coefficient as a function of attenuation-rate correction 〈N〉 for the example profile (Fig. 1). Magnitude of the correlation coefficient (C) of ice thickness (d) and attenuation-corrected bed echo (P a) as a function of the attenuation rate (〈N〉) used in the correction. C 0 is the correlation coefficient magnitude without correction, C m is the minimum correlation coefficient magnitude, 〈N m〉 is the attenuation rate that produced the minimum correlation coefficient magnitude, C w is the correlation coefficient magnitude at which the width of the minimum is assessed, 〈N h〉 is the half-width of the correlation coefficient minimum.
In order to resolve the pattern of englacial attenuation at the finest spatial resolution possible while maintaining a target radiometric resolution, we perform this correlation-based fitting on sub-profile segments (Fig. 1b) and increase the length of that segment (W) until the target radiometric resolution is achieved (e.g.
![]() $\langle N_{\rm h}\rangle \le 1 \,{\rm dB}/{\rm km}$
for C
w = 0.1). This assumes that the thickness-correlated power-loss signal is an expression of englacial attenuation rather than basal conditions (MacGregor and others, Reference MacGregor2013; Schroeder and others, Reference Schroeder, Grima and Blankenship2016). We repeat this process for each location along a profile, discarding estimates for locations at which the target radiometric resolution can not be achieved. For the example profile in Figure 1, the resulting adaptively-fit attenuation rates (Fig. 3a) and fitting-segment lengths (Fig. 3b) show that, as expected, longer fitting segments occur in areas (e.g. along-track distances between 200 and 300 km) with less ice thickness relief (Fig. 1b). In this adaptive fitting, we require that 〈N
h〉 ≤ 1 dB/km, C
0 ≥ 0.5 and C
m ≤ 0.01 and use a C
w value of 0.1 (Fig. 2). Setting a minimum value on C
0 ensures that the window is long enough that there is an ice-thickness correlated attenuation signal that is meaningful to minimize. Setting a maximum value of C
m ensures that a meaningful minimization has been achieved. Figure 4 shows values of C
0 (A), C
m (B), 〈N
h〉 (C) and 〈N
m〉 (D) as a function of fitting segment length and along-track distance for the example profile in Figure 1. We can see that the values of the estimated attenuation rate (〈N
m〉, Fig. 4d) are most sensitive to C
0 (Fig. 4a). This is because the approach depends on having a depth-correlated attenuation signal to minimize. Segments that do not meet the minimum value for C
0 can lead to severe over- or under-estimations due to fitting signals other than the attenuation rate. Figure 4 also shows that some locations along the profile can achieve the target radiometric resolution (Fig. 4c) using much smaller segment lengths than others. Taking advantage of this heterogeneity to resolve the finer-scale details of attenuation-rate patterns is a major reason for pursuing an adaptive fitting approach.
$\langle N_{\rm h}\rangle \le 1 \,{\rm dB}/{\rm km}$
for C
w = 0.1). This assumes that the thickness-correlated power-loss signal is an expression of englacial attenuation rather than basal conditions (MacGregor and others, Reference MacGregor2013; Schroeder and others, Reference Schroeder, Grima and Blankenship2016). We repeat this process for each location along a profile, discarding estimates for locations at which the target radiometric resolution can not be achieved. For the example profile in Figure 1, the resulting adaptively-fit attenuation rates (Fig. 3a) and fitting-segment lengths (Fig. 3b) show that, as expected, longer fitting segments occur in areas (e.g. along-track distances between 200 and 300 km) with less ice thickness relief (Fig. 1b). In this adaptive fitting, we require that 〈N
h〉 ≤ 1 dB/km, C
0 ≥ 0.5 and C
m ≤ 0.01 and use a C
w value of 0.1 (Fig. 2). Setting a minimum value on C
0 ensures that the window is long enough that there is an ice-thickness correlated attenuation signal that is meaningful to minimize. Setting a maximum value of C
m ensures that a meaningful minimization has been achieved. Figure 4 shows values of C
0 (A), C
m (B), 〈N
h〉 (C) and 〈N
m〉 (D) as a function of fitting segment length and along-track distance for the example profile in Figure 1. We can see that the values of the estimated attenuation rate (〈N
m〉, Fig. 4d) are most sensitive to C
0 (Fig. 4a). This is because the approach depends on having a depth-correlated attenuation signal to minimize. Segments that do not meet the minimum value for C
0 can lead to severe over- or under-estimations due to fitting signals other than the attenuation rate. Figure 4 also shows that some locations along the profile can achieve the target radiometric resolution (Fig. 4c) using much smaller segment lengths than others. Taking advantage of this heterogeneity to resolve the finer-scale details of attenuation-rate patterns is a major reason for pursuing an adaptive fitting approach.

Fig. 3. Adaptively fit (a) estimated attenuation rate and (b) fitting segment lengths the example profile (Fig. 1).

Fig. 4. Results of the method applied to the example profile (Fig. 1), illustrating the effect of fitting window length. (a) correlation coefficient without correction (C 0), (b) minimum correlation coefficient value (C m), (c) half-width of the correlation coefficient minimum (〈N h〉), (d) estimated attenuation rate (〈N m〉).
We applied this approach to an airborne radar-sounding dataset collected across the Thwaites Glacier catchment using the High Capability Airborne Radar Sounder (HiCARS) as part of the Airborne Geophysical survey of the Amundsen Sea Embayment (AGASEA) (Holt and others, Reference Holt2006). These were processed using unfocused synthetic aperture radar for an along-track sampling rate of 4 Hz (Peters and others, Reference Peters, Blankenship and Morse2005). In estimating the attenuation rates for this survey, we require that C 0 ≥ 0.5, C m ≤ 0.01 and C w = 0.1 while setting the target radiometric resolution values of 〈N h〉 ≤ 1, 2 and 3 dB/km. This resulted in the estimated attenuation rate values shown in Figure 5 and the corresponding fitting-segment lengths shown in Figure 6. The resulting mean (μ) and standard deviation (σ) cross-over errors for each radiometric resolution are shown in Table 1. It is clear from Figures 4, 5 and 6 as well as Table 1 that more restrictive target radiometric resolutions will produce estimates with lower errors but degraded spatial resolution and coverage (more locations are discarded for failing to achieve the required radiometric resolution). In contrast, less restrictive target radiometric resolutions will achieve better spatial resolution and coverage at the cost of larger errors. It is also clear from Figure 4 that, in our approach, larger attenuation-rate areas require more permissive radiometric resolutions in order to be resolved. Therefore, in practice, the choice of target 〈N h〉 will depend on the glacier, region and process of interest.

Fig. 5. Estimated attenuation rates for target correlation coefficient half-widths of (a)
![]() $\langle N_{\rm h}\rangle \le 1\, {\rm dB}/\,{\rm km}$
, (b)
$\langle N_{\rm h}\rangle \le 1\, {\rm dB}/\,{\rm km}$
, (b)
![]() $\langle N_{\rm h}\rangle \le 2\, {\rm dB}/{\rm km}$
and (c)
$\langle N_{\rm h}\rangle \le 2\, {\rm dB}/{\rm km}$
and (c)
![]() $\langle N_{\rm h}\rangle \le 3 \,{\rm dB}/{\rm km}$
. Background contours are ice thickness (Fretwell and others, Reference Fretwell2013).
$\langle N_{\rm h}\rangle \le 3 \,{\rm dB}/{\rm km}$
. Background contours are ice thickness (Fretwell and others, Reference Fretwell2013).

Fig. 6. Fitting segment lengths (W) for target correlation coefficient half-widths of (a)
![]() $\langle N_{\rm h}\rangle \le 1\, {\rm dB}/{\rm km}$
, (b)
$\langle N_{\rm h}\rangle \le 1\, {\rm dB}/{\rm km}$
, (b)
![]() $\langle N_{\rm h}\rangle \le 2 \,{\rm dB}/{\rm km}$
and (c)
$\langle N_{\rm h}\rangle \le 2 \,{\rm dB}/{\rm km}$
and (c)
![]() $\langle N_{\rm h}\rangle \le 3\, {\rm dB}/{\rm km}$
. Background contours are ice thickness (Fretwell and others, Reference Fretwell2013).
$\langle N_{\rm h}\rangle \le 3\, {\rm dB}/{\rm km}$
. Background contours are ice thickness (Fretwell and others, Reference Fretwell2013).
Table 1. Mean (μ) and standard deviation (σ) cross-over errors for the estimated attenuation rates (Fig. 5) using correlation-minimum values of 〈N h〉 ≤ 1, 2, and 3 dB/km

3. RESULTS
In order to create a gridded estimate of englacial rates across the catchment of Thwaites Glacier for comparison with modelled values, we combine the profile-based estimates in Figure 4 by selecting the value at each location with the best radiometric resolution (〈N h〉). This allows us to take advantage of the more accurate estimates of Figure 4a without forfeiting the coverage of Figure 4c. This is especially relevant in the high-attenuation regions near the grounding zone and eastern shear margin where the same fractional variation in 〈N〉 would result in a larger value of 〈N h〉 relative to low-attenuation regions. Since the greatest cross-over errors occur near areas of steep relief in basal topography (Fig. 4), we exclude locations with basal slopes >3.5° (Fretwell and others, Reference Fretwell2013). We then interpolated both the 〈N m〉 and 〈N h〉 results onto a regular 5km × 5 km grid, weighting each value by its distance to the grid point using a Gaussian filter with a width of 7.5 km and scaling the 〈N h〉 values to the corresponding cross-over errors in Table 1. This interpolation results in gridded estimates of both attenuation rates (Fig. 7a) and fitting errors (Fig. 7b) across the catchment.

Fig. 7. (a) Gridded attenuation rates from combining the lowest error at each location (Fig. 5) and (b) estimated error for those gridded attenuation rates from scaling the correlation minimum half-widths (〈N h〉) to the resulting mean cross-over error (μ) (Table 1). Background contours are ice thickness (Fretwell and others, Reference Fretwell2013).
We compare the observation-based estimates of attenuation rates to values predicted using a numerical ice-sheet model of the same region. For this comparison, we use the Ice Sheet System model (ISSM, Morlighem and others, Reference Morlighem2010; Larour and others, Reference Larour, Seroussi, Morlighem and Rignot2012). The catchment of Thwaites Glacier (Fig. 1a) is modelled with a 1.5 km resolution horizontal mesh, extruded into 20 vertical layers. We use an enthalpy-based model (Aschwanden and others, Reference Aschwanden, Bueler, Khroulev and Blatter2012) that includes advection, conduction and deformational heat, and assume the ice to be in thermal steady state (Seroussi and others, Reference Seroussi2013). Surface temperatures from the regional atmospheric model RACMO2 (Lenaerts and others, Reference Lenaerts, Den Broeke, Berg, Meijgaard and Kuipers Munneke2012) are imposed at the surface and geothermal flux inferred from magnetic data (Fox Maule and others, Reference Fox Maule, Purucker, Olsen and Mosegard2005) are applied at the base. The full-Stokes equations are used to compute the stress balance. We infer the basal friction to match observed surface velocities (Rignot and others, Reference Rignot, Mouginot and Scheuchl2011) using an adjoint-based optimization and use it to compute the frictional heat at the base. We interpolate these results onto the same 5 km grid as the observed attenuation rates and use a temperature-dependent attenuation model for West Antarctica (MacGregor and others, Reference MacGregor2007; Matsuoka and others, Reference Matsuoka, MacGregor and Pattyn2012) to calculate the one-way attenuation rate for the entire ice column (Fig. 8a). Specifically, we use the Matsuoka and others (Reference Matsuoka, MacGregor and Pattyn2012) formulation of the MacGregor and others. (Reference MacGregor2007) Siple Dome model to calculate the one-way depth-averaged attenuation-rates. We estimate the uncertainty in the modelled attenuation-rate as the difference between these values (Fig. 7a) and those computed using a different temperature-dependent attenuation model from Wolff and others (Reference Wolff, Miners, Moore and Paren1997) (Fig. 8b). These relatively small uncertainty values (compared with the pattern in Fig. 8a) are conservative estimates since potential errors from assumed ice chemistry or surface temperature values are negligible compared with the difference between models (MacGregor and others, Reference MacGregor2015). Therefore, any comparison of the observed (Fig. 7) and modelled (Fig. 8) attenuation-rate patterns can be confidently interpreted as expressions of ice-sheet temperature structure rather than the details of a particular temperature-dependent attenuation-rate model.

Fig. 8. (a) Modelled attenuation rate using the ISSM numerical ice-sheet model (Larour and others, Reference Larour, Seroussi, Morlighem and Rignot2012) and a temperature-dependent attenuation model (MacGregor and others, Reference MacGregor2007). (b) Estimated uncertainty in the modelled englacial attenuation rate (Wolff and others, Reference Wolff, Miners, Moore and Paren1997; MacGregor and others, Reference MacGregor2015). Background contours are ice thickness (Fretwell and others, Reference Fretwell2013).
Our radar-derived estimates of one-way englacial attenuation rates (Fig. 7) reproduce the catchment-scale pattern of modelled attenuation (Fig. 8) across Thwaites Glacier. Figure 9 shows the difference between the modelled and estimated attenuation values. The greatest differences occur in regions with steep basal topography near the glacier's shear margins (Fig. 9), suggesting that some care should be taken when interpreting attenuation rates in these areas. Where such differences occur, one of two effects is likely at play: first, in some areas liquid basal water or thawed bed, and therefore radar reflectivity, can increase with increasing depth (Schroeder and others, Reference Schroeder, Grima and Blankenship2016), leading to an under-estimate of attenuation-rates. Second, the opposite effect can also occur in areas where roughness, and therefore scattering losses, increase with ice depth, leading to an over-estimate of attenuation rates (Peters and others, Reference Peters, Blankenship and Morse2005; MacGregor and others, Reference MacGregor2013; Young and others, Reference Young, Schroeder, Blankenship, Kempf and Quartini2016). Because steep slopes result in greater ice-thickness relief (and therefore large C 0 values) our adaptive-fitting algorithm will tend to expand fitting windows to include them in estimates of nearby attenuation rates (resulting in the observed pattern of over- and under- estimates in Fig. 9). Whatever their sign and cause, even these differences are less than both the attenuation signal itself (Fig. 7a) and the estimated fitting error produced by our technique (Fig. 7b). Overall, we find that our approach successfully captures gridded (Fig. 7) and profile-based (Fig. 5) variations in attenuation rate using only the information in radar bed echoes. Therefore, within the catchment, the pattern of englacial temperature from the ISSM model of Thwaites Glacier is consistent with the pattern of englacial attenuation from radar-sounding observations.

Fig. 9. Difference between estimated (Fig. 7a) and modelled (Fig. 8a) attenuation rates. Background contours are ice thickness (Fretwell and others, Reference Fretwell2013).
4. CONCLUSIONS
The technique we present directly constrains the spatially variable englacial attenuation rate in glaciers and ice sheets using only bed echoes. This approach can use lines in any orientation and data from any radar sounding system. It probes the full ice thickness (including warm ice at the bottom of the ice column) and operates in the fast-flowing regions of glaciers where the layers are disrupted. We find that this approach is capable of capturing the catchment-scale attenuation-rate structure predicted by the ISSM numerical ice-sheet model. The greatest difference between estimated and modelled values occurs in areas with large slopes in bed topography; however, even this difference falls within the estimated fitting error of the technique. While two-way attenuation rates cannot directly resolve vertical englacial temperature profiles, they place an observational constraint on those profiles through their net effect on signal power. For the first time, this approach provides the radio glaciology community with the capability to place direct observational constraints on the spatial variation in englacial attenuation rates and therefore temperatures using only radar bed echoes. This complements existing layer-based techniques, which can measure vertical gradients in attenuation, but do not probe the entire ice column. Together, these approaches stand to enable observation-based estimates of the entire vertical attenuation and temperature profile across entire ice sheets and glacier catchments.
ACKNOWLEDGEMENTS
The authors would like to thank N. Holschuh and an anonymous reviewer for their thoughtful comments. D.M.S. was supported by a grant from the NASA Cryospheric Sciences Program. H.S. was supported by grants from the NASA Cryospheric Sciences and Sea Level Rise Programs. W.C. was supported by a NASA Earth and Space Science Fellowship. Part of this work was carried out by the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration.












