1. Introduction
Over the past two decades, the Greenland ice sheet (GrIS) has been losing mass at an increasing rate due, in significant part, to increased discharge in the southern and northwestern sectors (Reference Rignot and KanagaratnamRignot and Kanagaratnam, 2006; Reference Van den BroekeVan den Broeke and others, 2009). Thinning at the margins occurs more on fast-moving glaciers and can reach many tens of kilometres into the ice sheet (Reference Pritchard, Arthern, Vaughan and EdwardsPritchard and others, 2009). The cause of this dynamic thinning is poorly understood and one approach is to study it through numerical modelling. For such a model to be credible, it must be able to reproduce the geometry and glacial discharge of the present-day GrIS. Only then will we have reliable initial conditions from which to assess future sea-level contributions from glacial dynamics (Reference Heimbach and BugnionHeimbach and Bugnion, 2009; Reference Arthern and GudmundssonArthern and Gudmundsson, 2010; Reference Yan, Zhang, Gao, Wang and JohannessenYan and others, 2013).
Initial conditions reflecting the present-day ice sheet can be generated in two main ways: (1) by solving an inverse problem to infer unknown parameters such as those related to basal drag and ice rheology, followed by relaxation of the surface of the ice for a relatively short period of a few decades using constant forcing (Reference Gillet-ChauletGillet-Chaulet and others, 2012), or (2) by spinning up a model over a glacial–interglacial cycle of >105 years (Reference Yan, Zhang, Gao, Wang and JohannessenYan and others, 2013). The latter approach has the advantage that the simulated ice sheet evolves freely, producing a self-consistent state, but it is difficult to obtain simulated surface elevation and velocity that match observations well. We take the former approach, which has the advantages of making fuller use of the available observations and of being able to use finer horizontal resolution because of the relatively short runs involved. We also compare our results with observations of ice discharge (Reference Rignot and KanagaratnamRignot and Kanagaratnam, 2006).
2. Model Description
We model GrIS using BISICLES, an ice-sheet model that uses a block-structured finite volume discretization with adaptive mesh refinement (Reference CornfordCornford and others, 2013). Adaptive mesh refinement allows fine resolution in areas of fast-flowing ice to capture the behaviour of the outlet glaciers, which are typically a few kilometres wide, and far coarser resolution over the bulk of the ice sheet where flow is relatively uniform. BISICLES is based on the vertically integrated stress balance of Reference Schoof and HindmarshSchoof and Hindmarsh (2010), which treats longitudinal and lateral stresses as depth-independent, but allows for vertical shear in the nonlinear rheology.
GrIS is assumed to be in hydrostatic equilibrium and flows with depth-independent horizontal velocity equal to the basal velocity u . Its thickness h evolves in time through
where M s is surface mass balance, M b is submarine melt rate and melting beneath grounded ice is neglected. The flow is governed by the approximate stress balance equations (Reference Schoof and HindmarshSchoof and Hindmarsh, 2010)
where I is the identity tensor, s is the ice surface elevation, g is the acceleration due to gravity and ρi is the density of ice. The horizontal rate-of-strain tensor ![]() is defined by
is defined by
Basal traction for grounded ice is modelled using a linear viscous friction law with coefficient C and is given by
where r is bedrock elevation and ρ
w is the density of sea water. We set ρ
i to 917 kg m−3 and ρ
w to 1027 kg m−3. The vertically integrated effective viscosity ![]() is computed from the vertically varying effective viscosity μ through
is computed from the vertically varying effective viscosity μ through
where μ includes a contribution from vertical shear and satisfies
where the flow rate exponent n = 3 and ø is a stiffening factor. The rate factor A(T) depends on the ice temperature T through the Arrhenius law described by Reference PatersonPaterson (1994). We use a three-dimensional (3-D), steady-state temperature field generated by a high-order, thermomechanical model (Reference Price, Payne, Howat and SmithPrice and others, 2011) as a background field, and the actual effective viscosity is found by solving the inverse problem.
At the lateral boundaries we assume that the normal stress across the calving front is equal to the pressure exerted by the sea water on the front, which gives the condition


where n = (nx , ny ) is the normal to the front. This condition is sufficient to close the stress balance equations (Eqn (2)) provided the basal traction coefficient C is nonzero within part of the domain, otherwise velocity would have to be prescribed somewhere. Equation (1) is closed provided that the flow is directed outwards at all the lateral boundaries and an initial thickness is specified, i.e. set to observations.
3. Inverse Problem
3.1. Description
The stress balance equations (Eqn (2)) for the ice-sheet model require the specification of two-dimensional (2-D) fields for both the stiffening factor ø and the basal traction coefficient C of the ice. These fields are unknown, but can be inferred from observations of surface elevation, bedrock topography and ice thickness (Reference BamberBamber and others, 2013) and surface velocity (Reference JoughinJoughin, 2002; Reference Joughin, Smith, Howat, Scambos and MoonJoughin and others, 2010) by solving an inverse problem. The inverse problem is solved using a gradient-based optimization method which uses the ice-sheet model’s adjoint stress balance equations (Reference MacAyealMacAyeal, 1993). We seek ø and C that minimize the cost function over the horizontal domain Ω
subject to
where u obs is the observed surface speed, u is the modelled vertically averaged speed for a fixed geometry and C 0 is an initial guess. The coefficient λ is set to 1 where we want to match the model, or 0 where there are no velocity observations or where a few observations may be spurious (e.g. in the southeast margin).
The cost function (Eqn (9)) is composed of two parts: a mismatch between observed and model speeds, J m, and a penalty function, αJ p. Ideally, the penalty function would not be required (so that α = 0) because it is tantamount to a claim to some prior knowledge of ø and C, and we do not have such information. In practice, though, we require α > 0, for two reasons. Firstly, J does not have a unique minimum with respect to both ø and C; in other words, the inverse problem would be under-determined, because we have one field of data and two fields of unknowns. Secondly, even if we were only seeking C, the inverse problem would be ill-conditioned, i.e. extremely sensitive to small changes in u obs. We callibrated α using the L-curve analysis described by Reference HansenHansen (1994) to provide a trade-off between the penalty function and the fit to the data. We choose α = 2:0 × 105, having found that lower values lead to faster growth in J p than reduction in J m, while larger values lead to the converse.
3.2. Adjusting input data
There are a few anomalies in the observed geometry data (Reference BamberBamber and others, 2013), and some discrepancies in the way the ice-sheet model interprets the data, that need to be addressed before the inverse problem is solved. In the observational data the surface of the ice shelves of the northeast glaciers was given as below sea level, so we raised ice surface elevation and bedrock topography data by 2 m. We then used the hydrostatic equilibrium to test for floating ice in the region surrounding the ice shelves of the northeast glaciers and update the ice mask supplied with geometry data.
During testing of the inverse problem we found that the model produced ice flow across, rather than along, the floating tongue of Petermann Glacier. We attributed this transverse velocity to erroneous steep ice-covered slopes adjacent to the floating tongue. To mitigate the flow error we used alternative thickness and bedrock topography named ‘IceThickness_unprocessed’ and ‘BedrockElevation_ unprocessed’ in Reference BamberBamber and others’ (2013) dataset in the region surrounding the tongue. We also altered the supplied ice mask by setting floating ice to grounded ice if the ice was observed to be moving at <10 m a−1. It was not necessary to alter the corresponding surface elevation or bedrock topography. However, we lowered bedrock topography below the remaining ice shelf, and all the other shelves, to guarantee a minimum water depth of 10 m under hydrostatic equilibrium.
3.3. Initial guess
The stiffness factor ø is initially set to 1.0 everywhere, while the basal traction coefficient is initialized with
where h
obs is the observed ice thickness and
![]() obs is the smoothed observed surface elevation. The speed of the ice, U, is made up of u
obs where observations exist, and balance velocities from the SeaRise dataset where they are missing (Reference Gillet-ChauletGillet-Chaulet and others, 2012). Values of C are restricted to between 20.0 and 1.0 × 105 Pa a m–1 beneath the ice and are set to 100.0 Pa a m–1 on ocean and bare land.
obs is the smoothed observed surface elevation. The speed of the ice, U, is made up of u
obs where observations exist, and balance velocities from the SeaRise dataset where they are missing (Reference Gillet-ChauletGillet-Chaulet and others, 2012). Values of C are restricted to between 20.0 and 1.0 × 105 Pa a m–1 beneath the ice and are set to 100.0 Pa a m–1 on ocean and bare land.
3.4. Weighted cost function
The inverse problem aims to minimize the largest misfits. Given that these will tend to be in areas with the highest observed speeds (e.g. near the terminus of outlet glaciers), the cost function is dominated by mismatches in these areas. We introduce a weighted cost function to increase the relative importance of the mismatches in the main trunk of the ice streams where speeds are moderate. We replace λ = 1 in Eqn (9) with a Gaussian function of the observed speed given by
where β = 50 and σ = 3000 m a−1. Typical values of λ at speeds of 1, 5 and 10 km a−1 are 47.4, 13.2 and 1.2, respectively. λ = 0 where observations are missing and balance velocities are used to set C.
3.5. Procedure for the inverse problem
The inverse problem was run until the rate of change in the L2-norm of the misfit between the observed and modelled speed with iteration appeared close to zero (Fig. 1a). The inverse problem is solved by carrying out iterations of the nonlinear conjugate gradient method with the descent direction computed by solving the adjoint stress balance equations. The stress balance equations are self-adjoint if we neglect the dependence of μ on u (Reference Goldberg and SergienkoGoldberg and Sergienko, 2011; Reference Morlighem, Seroussi, Larour and RignotMorlighem and others, 2013).

Fig. 1. (a) Convergence of inverse problem with λ = 1 (dashed) and weighted cost function (solid). (b) Scatter plot of modelled against observed speed for the initial guess of basal traction (blue) and after 64 iterations of the inverse problem using λ = 1 (purple) and using the weighted function (orange). The black line represents a perfect fit.
BISICLES used two levels of refinement to calculate velocity. The computational mesh consisted of a base grid of 4 km over the whole ice sheet, increasing in resolution to 1 km in blocks over the fast-moving outlet glaciers. The finest mesh matched the resolution of the observational data.
3.6. Results
3.6.1. General performance of the inverse problem and comparison of cost functions
Figure 1b shows how well the inverse problem improves the modelled speed compared to that calculated from the initial guess. Apart from the overall relatively poor match, the modelled speed from the initial guess cannot reproduce the very high observed values. The root-mean-square error (RMSE) of the modelled speed from the observed speed for the initial guess is 79.8 m a−1, while for the optimized solutions we obtain 37.0 m a−1 for λ = 1 and 17.8 m a−1 for the weighted function. Reference Price, Payne, Howat and SmithPrice and others (2011) obtained a value of 38 m a−1 using their thermomechanical, 3-D ice-sheet model on a mesh with spacing of 5 km.
The optimized model speed using the weighted function produces a better fit than that using λ = 1 for moderate observed values of a few hundred m a−1 to 5 km a−1. These values are typically found in the main trunk of the ice streams, so it is important that we capture them, in order to accurately calculate glacial discharge from the whole ice sheet. In particular, λ = 1 significantly underestimates the speed of the distinct ice streams feeding the northeast glaciers from inland. Both types of cost function capture the very high (8–12 km a−1) values equally well. However, the fit for the weighted function around 6 and 8 km a−1 tends to underestimate the observations relative to the λ = 1 case. Nonetheless, the fit only applies to a few observations located near the termini of Jakobshavn, Kangerdlugssuaq and Helheim glaciers rather than spread throughout the ice sheet. Therefore, the weighted function does not provide a perfect fit, but still performs better than λ = 1 on average.
3.6.2. Spatial pattern of the misfit
Figure 2 shows the spatial pattern of the mismatch between the observed speed and the optimized model speed using the weighted function. The model agrees well with observations in the interior of GrIS, with only 7% of the total area of observed surface speed having a misfit of >20 m a−1. Most of the mismatch occurs at the margins and along narrow outlet glaciers, with the largest absolute values near the fronts of Kangerdlugssuaq and Helheim Glaciers. The model tends to underestimate speed in the main trunk of a glacier while overestimating it at the edges. As we can see from the inserts in Figure 2, the relative misfit in the trunk of the glaciers is small. The model also overestimates speed around Rink Glacier and the southeast margin, where the ice is relatively thin, slow-moving and terminates on land.

Fig. 2. The mismatch between the observed and optimized model speed for the whole ice sheet (centre). The percentage misfits of the modelled speed relative to the observations are shown for the boxed regions of Petermann Glacier (top left), Rink and surrounding glaciers (centre left), Jakobshavn Isbræ (bottom left), the northeast glaciers (top right), Kangerdlussuaq Glacier (centre right) and Helheim Glacier (bottom right). The inserts have the same colour scale as the central figure, where underestimated (overestimated) model speed is represented by red (blue).
Observational data are relatively sparse along the southeast margin, and the mismatch can be high near patches with missing observations, for two reasons. Firstly, the basal traction coefficient can appear discontinuous in space near boundaries of missing observations, which will affect the modelled velocity. The initial guess of the coefficient (Eqn (11)) is not smooth because the balance and observed velocities do not necessarily match at the boundaries. The basal traction coefficient can adjust across the boundaries where the misfit is unknown, as the inverse problem is solved because the gradient of the cost function varies smoothly in space. However, if observational data are sparse, the reach of such adjustment is limited. For this reason, where there are blocks of missing observations (e.g. upstream of glaciers between Helheim and Kangerdlussuaq), the modelled velocity field appears patchy and disjointed. Secondly, observed speed in the gridcells next to a large area of missing data is consistently lower than neighbouring observations, which may be an artifact of interpolation on to the dataset’s uniform grid. The inverse problem artificially increases the basal traction coefficient and lowers the optimized modelled velocity near a boundary with the missing observations, making both fields appear discontinuous. This is particularly noticeable near large areas of missing observations in high-speed regions such as around the tributaries of Helheim Glacier (see insert in Fig. 2).
The close match for Petermann and the northeast glaciers is acceptable given uncertainties in the geometry of the ice shelves (see Section 3.2) and the inherent temporal mismatch between the observational datasets.
3.6.3. Spatial pattern of inferred parameters
Figure 3 shows the inferred stiffness factor and basal traction coefficient using the weighted cost function. The stiffness factor is close to 1 everywhere except around fast-moving glaciers, where the ice is softened along the shear margins and stiffened near the termini and edges of floating tongues. The basal traction coefficient appears disjointed around areas of missing observed velocity data, unsurprisingly, because the coefficient is initialized from two different input velocity fields that can only be modified by a short distance from observations during optimization.

Fig. 3. (a) The optimized stiffness factor and (b) basal traction coefficient.
The outlet glaciers are distinguishable by slippery regions (low C, blue) of basal traction among the sticky interior (high C, red). This spatial pattern is comparable to those of present-day GrIS basal temperature in Figure 4B and D of Reference RogozhinaRogozhina and others (2012). In that paper, basal temperatures were generated from palaeoclimatic simulations using a polythermal ice-sheet model with two different geothermal heat flux models. It appears that slippery regions in our basal traction coefficient correspond to basal temperatures close to the pressure-melting point, which could allow basal sliding. Also, sticky regions correspond to basal temperatures well below the pressure-melting point, which suggests that ice is frozen to the bed.

Fig. 4. Block structure of BISICLES at 200 years of relaxation overlying sector divisions. Blocks with grid spacings of 8 km are outlined in orange, 4 km in yellow, 2 km in green, 1 km in blue and 500 m in red.
4. Relaxation
We allow the surface elevation to diverge from observations in a time-dependent run forced by a temporal mean present-day surface mass balance (SMB) to obtain initial conditions for GrIS. This relaxation allows the surface to adjust to anomalies in horizontal ice flux due to inconsistencies in the observational dataset and the solution from the inverse problem.
4.1. Surface mass balance
We compared annual SMB from the regional climate models (RCM) HIRHAM5 (Reference Lucas-Picher, Wulff-Nielsen, Christensen, Aðalsgeirsdóttir, Mottram and SimonsenLucas-Picher and others, 2012), MAR and RACMO2 (Reference RaeRae and others, 2012), to an ideal SMB constructed from the inverse problem. The ideal field was set to the flux divergence used to calculate the optimized solution, under the assumption of a steady ice sheet and negligible basal melting (see Eqn (1)). The inverse problem should provide a reasonable approximation to the actual flux divergence because it attempts to match the modelled ice speed to the observed ice speed using observed ice thickness and bedrock topography. The ideal field was smoothed to remove high-resolution features and/or noise that are not present in the lower-resolution RCM data. The RCM data were interpolated to a uniform 1 km grid using MATLAB®’s TriScatteredInterp. Where our ice sheet extends beyond that of the RCMs’ ice mask we used extrapolated SMB values, if they existed, and filled the remaining cells with averaged SMB from neighbouring cells.
The match between annual SMB for each RCM and the ideal SMB was measured using a RMSE that was ranked for each sector of the ice sheet (Fig. 4) and for surface elevation above and below 2000 m. We chose the 2000 m contour because the interior of GrIS was close to steady state in the 1990s at high elevations (Reference ThomasThomas and others, 2000). We noted that the southeast sector was poorly matched by all the RCMs. A rolling average of 10 years was used to smooth the largest errors while maintaining some variability.
A time-averaged SMB was selected from each RCM, which was then used to force a 50 year long run (see Section 4.3) to test the match. We also forced a run with the mean present-day SMB field used for the ice2sea project (Reference EdwardsEdwards and others, 2014), which is the 1989–2008 mean of the ERA-Interim forced MAR simulation (Reference FettweisFettweis, 2007).
We found that the ice sheet increased in volume, and its grounded margin retreated, in all the experiments. The largest volume increase occurred in the RACMO2 experiment. The ice2sea experiment produced the smallest increase in volume but also produced retreat that was significantly larger than in any other experiment. The HIRHAM5 experiment produced the least retreat and a moderate increase in volume that appeared to be tending towards zero.
We selected the 1997–2006 mean of the HIRHAM5 simulation at 0.05° resolution forced at the lateral boundaries by ERA-Interim (Reference Lucas-Picher, Wulff-Nielsen, Christensen, Aðalsgeirsdóttir, Mottram and SimonsenLucas-Picher and others, 2012) as our SMB forcing.
4.2. Basal melting beneath floating ice
We approximate basal melt rates of floating ice using three piecewise linear functions of ice thickness. The rates are based on values inferred from observations (Reference Rignot and SteffenRignot and Steffen, 2008; Reference Motyka, Truffer, Fahnestock, Mortensen, Rysgaard and HowatMotyka and others, 2011), and the regions where the rates are applied are determined by the transport of water masses around Greenland (Reference StraneoStraneo and others, 2012).
In the north, whose coastline is fed by water from the Arctic (Reference StraneoStraneo and others, 2012), we assume that the floating ice begins melting when it is 60 m thick. The melt rate increases linearly to 25 m a−1 for a thickness of 450 m, which corresponds to the maximum melt rate inferred for Petermann Glacier (Reference Rignot and SteffenRignot and Steffen, 2008). It then remains constant as thickness increases. From the northeast, Polar Water, which is too cold to cause melting in winter, is carried by East and West Greenland currents in the top 180 m of the water column (Reference StraneoStraneo and others, 2012). Below the Polar Water, warm Atlantic Water is fed by the Nordic Seas from the north. In the northeast we assume no melting until the ice is 200 m thick. Melting increases linearly with increasing thickness to 25 m a−1 at 450 m and then remains constant. Warmer Atlantic Water, which is fed by the Subpolar Gyre from the southeast, travels around the rest of the coastline (Reference StraneoStraneo and others, 2012). In the southeast and west we assume no melting until the ice is 200 m thick. Melting increases linearly with increasing thickness to 182 m a−1 at 600 m and then increases linearly again to pass through 298 m a−1 at 800 m. These values correspond to those inferred for Jakobshavn Isbræ (Reference Motyka, Truffer, Fahnestock, Mortensen, Rysgaard and HowatMotyka and others, 2011).
4.3. Procedure for the relaxation problem
A fixed calving front boundary condition is applied, where Eqns (7) and (8) are used and mass flux is either added to mesh cells to keep the front at least 1 m thick or removed to prevent the ice sheet from advancing. We also lower the bathymetry below known ice shelves to prevent the ice from grounding.
The computational mesh for the time-dependent run consists of blocks with a uniform grid spacing that ranges between 8 km and 500 m. The mesh is dynamically refined in blocks around the margins of the grounded ice where ice speed is >20 m a−1 and the basal traction is <500 Pa a m−1, i.e. low. It is also refined where the Laplacian of the velocity multiplied by the square of the grid spacing is >50 m a−1 and basal traction is low. This criterion captures abrupt changes in shear strain (e.g. at the grounding line or at shear margins). The whole ice sheet may be refined to a grid spacing of 2 km, while regions surrounding the main outlet glaciers and large bedrock troughs feeding them can be refined to 500 m. These regions include Petermann, northeast, Kangerdlussauq, Helheim and Rink glaciers and Jakobshavn Isbræ. Figure 4 shows the instantaneous block structure for the relaxation run at 200 years with 8 km resolution in the slow-moving interior, and resolution of at least 2 km around the margins.
The time-dependent problem was run for 200 years during which the rate of change of the ice sheet’s volume (defined formally as the partial derivative of the ice thickness with respect to time integrated horizontally over the ice sheet) reaches zero around 145 years and remains small. At the end of the experiment the rate of change of ice thickness exceeds 5 m a−1 for <0.05% of the total ice-sheet area. The highest rates occur at the terminus of ice streams and on floating ice tongues.
4.4. Results
4.4.1. Volume and area change
The total ice volume is 2:97 × 106 km3 or 7.3 m of sea-level rise equivalent (SLE). The volume increases by 0.2% (17.6 mm SLE) during the 200 year relaxation run. Reference Gillet-ChauletGillet-Chaulet and others (2012) found that volume increased by 0.5% during their 50 year relaxation run using Elmer/Ice. Figure 5a shows that the largest increase occurs in the east. The area of grounded ice reduces by 0.4% during relaxation, and Figure 5b shows that reduction is most pronounced in the southeast. The area of floating ice has reduced very slightly (0.1%) during 200 years, indicating that the retreat is land-based. The ice sheet appears to advance in the north despite a fixed front boundary condition being applied. The advance is primarily an artefact of interpolating from coarse to finer meshes along a land-terminating front.

Fig. 5. Percentage increase in the ice sheet’s volume (a) and area of grounded ice (b) for each sector (Fig. 4) and the whole ice sheet (thick black line). All calculations were performed with data on a 1 km uniform mesh.
4.4.2. Spatial pattern of ice thickness and velocity
The spatial patterns of the ice speed and thickness remain similar to those of the observational data after relaxation. Glaciers tend to be slower near their outlets. Large relative thickness errors are concentrated along the east, southeast and northwest margins of the ice sheet. The northwest is thickening, while in the east in regions of high accumulation at the margins, and high bedrock elevation, ice streams have thickened and slow-moving ice has thinned. Relative velocity errors are also concentrated along the eastern margin south of the northeast glaciers to the southern tip, corresponding to high surface elevation error in the observations (Reference BamberBamber and others, 2013). Curiously, modelled ice has thinned above a trench in the bedrock running northward from the centre of Greenland to Petermann Glacier, but there is no associated signal in the modelled velocity field.
4.4.3. Mass budget for all of GrIS
Figure 6a shows that the modelled ice sheet has adjusted to anomalies and is close to a steady state. Its volume approaches a steady state around 145 years. After 200 years the rate of volume change is –5.8 km3 a−1, total SMB is 413.4 km3 a−1 and total basal melt is 52.0 km3 a−1. The discharge, which is the outward flux of solid ice across floating and land-terminating fronts, is 367.2 km3 a−1.

Fig. 6. Mass budget during the relaxation run for (a) the whole ice sheet, (b) floating ice and (c) the ice sheet for surface elevation above 2000 m. The dashed lines represent observations for 1996 or 2000 (Reference Rignot and KanagaratnamRignot and Kanagaratnam, 2006) for SMB (green), estimated discharge across the grounding line (orange; a) and flux upstream of the ice front (orange; c).
4.4.4. Floating ice
Figure 6b shows that floating ice is close to equilibrium, with a mean rate of change of ice thickness of –1.7 km3 a−1 averaged over the last 20 years of the relaxation experiment, which indicates that our piecewise linear functions of basal melt rates are reasonable approximations. Ice is lost through basal melting at a mean rate of 51.9 km3 a−1, negative SMB of 2.4 km3 a−1 and discharge from the front of 89.7 km3 a−1. The floating ice is kept close to equilibrium, with an inward flux of ice across the grounding line of 140.9 km3 a−1. The thinning of the floating ice is concentrated in the northeast sector. Almost 30% of the total discharge of ice across floating fronts comes from Jakobshavn Isbræ.
4.4.5. 2000 m surface elevation contour
At high elevations the ice sheet is close to equilibrium (Fig. 6c), with rate of volume change of –2.1 km3 a−1, SMB of 304.6 km3 a−1 and flux of ice across the 2000 m surface elevation contour of 342.7 km3 a−1 after 200 years. There is an initial adjustment period where the rate of thinning and flux across the contour decrease in the east and southeast sectors. In the mountainous region of the east the contour shifts towards the margin, where ice flow becomes more concentrated in narrower streams and the ice thins, whereas in the southeast the mean flow slows. It is unsurprising that the flow adjusts in these sectors since there are large areas of missing observational velocity data (Fig. 2). The interior ice sheet is thickening in the east and northeast while thinning elsewhere, with the southwest thinning the most.
Below 2000 m the southeast sector has thickened the most during the relaxation period, while the northeast has thinned the most. After 200 years the east is the only sector still thickening below 2000 m.
5. Comparison with Observations
In Tables 1 and 2 we compare our model results for sectors of GrIS and the main outlet glaciers, respectively, with observations from 1996 or 2000 by Reference Rignot and KanagaratnamRignot and Kanagaratnam (2006). These observations coincide with the end of the period of equilibrium for GrIS before sustained and increasing mass loss took hold (Reference ShepherdShepherd and others, 2012). The inverse problem uses observed surface velocity collected from two winter seasons in 2000/01 and 2005/06 (Reference Joughin, Smith, Howat, Scambos and MoonJoughin and others, 2010). Observed ice thickness and bedrock elevation, also used for the relaxation experiment, mostly comes from airborne surveys carried out between 2000 and 2012, with the rest of the data collected as far back as the 1970s (Reference BamberBamber and others, 2013). Some regions of GrIS change rapidly during the 2000s, so the difference in date might be important when comparing our model results to observations. Also, our SMB forcing in the relaxation experiment is a temporal mean of HIRHAM5 data (Reference Lucas-Picher, Wulff-Nielsen, Christensen, Aðalsgeirsdóttir, Mottram and SimonsenLucas-Picher and others, 2012) from 1997 to 2006.
Table 1. Comparison with observations, ‘Obs’, for 1996 or 2000 (Reference Rignot and KanagaratnamRignot and Kanagaratnam, 2006) partitioned into sectors in Figure 4. Discharge is the flux of ice from the ice sheet front. ‘Inv’ contains values calculated from the observed ice geometry (Reference BamberBamber and others, 2013) and optimized velocity from the inverse problem using the weighted cost function. ‘200 yr’ contains values calculated from modelled ice geometry and velocity at the end of the relaxation experiment. ![]() and
and ![]() are the ice thickness and the outward velocity averaged over the flow across the front, while W is the total width of the flow at the front. δV is equal to partial derivative of ice thickness with respect to time integrated horizontally over the sector. M is the total melt rate beneath floating ice and SMB is the total surface mass balance over the ice. All calculations were performed with data on a 1 km uniform mesh
are the ice thickness and the outward velocity averaged over the flow across the front, while W is the total width of the flow at the front. δV is equal to partial derivative of ice thickness with respect to time integrated horizontally over the sector. M is the total melt rate beneath floating ice and SMB is the total surface mass balance over the ice. All calculations were performed with data on a 1 km uniform mesh

Table 2. Comparison with observations for individual glaciers for 1996 or 2000 (Reference Rignot and KanagaratnamRignot and Kanagaratnam, 2006). Upstream flux from the inverse problem (‘Inv’) and relaxation (‘200 yr’) runs is defined as the outward flux of ice across gates specified in Reference Rignot and SteffenRignot and others (2008). ![]() and
and ![]() are the thickness and outward velocity averaged across the width of the glacier W passing through the gate. All post-processing calculations were performed on a 1 km uniform mesh for the inverse problem. Those for the relaxation run were performed on the finest mesh used over the glacier, which is a 500 m mesh for all except Daugaard Jensen, which is a 2 km mesh
are the thickness and outward velocity averaged across the width of the glacier W passing through the gate. All post-processing calculations were performed on a 1 km uniform mesh for the inverse problem. Those for the relaxation run were performed on the finest mesh used over the glacier, which is a 500 m mesh for all except Daugaard Jensen, which is a 2 km mesh
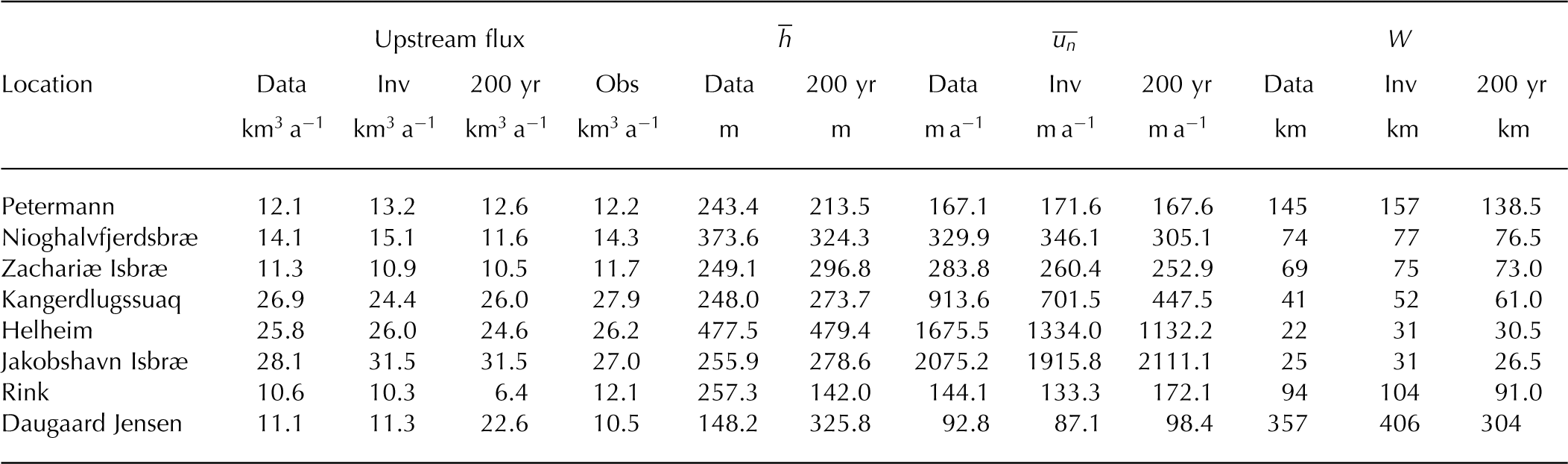
5.1. Whole ice sheet
The discharge or flux of ice across the front of the ice sheet to land or ocean is 342.4 km3 a−1 from the inverse problem with the weighted cost function, and 367.2 km3 a−1 at the end of the relaxation period, both of which compare reasonably well to Reference Rignot and KanagaratnamRignot and Kanagaratnam’s (2006) observed discharge of 357 km3 a−1 (Table 1). Modelled discharge appears to be underestimated in the northern and western sectors, but overestimated in the east. However, the observed value does not take into account melting, only SMB. If we add the melt to our discharge after relaxation and use Reference Rignot and KanagaratnamRignot and Kanagaratnam’s (2006) SMB rather than our own, then there is an extremely close match in the northern and western sectors. Our adjusted discharge in the east now underestimates the observed value by 49.6 km3 a−1.
Not all of GrIS is included by Reference Rignot and KanagaratnamRignot and Kanagaratnam (2006). Reference Van den BroekeVan den Broeke and others (2009) and Reference AndersenAndersen and others (2015) have greater coverage and estimate that discharge across the grounding line is 475–485 km3 a−1 and 558 ± 83 km3 a−1 (converted from Gt a−1 assuming constant ice density of 917.0 kg m−3), respectively. The corresponding value from the relaxation experiment is low, at 419 km3 a−1. However, our flux of ice across the SMB = 0 contour, 518.4 km3 a−1, does lie within Reference AndersenAndersen and others’ (2015) range.
The inverse problem is designed to produce a solution close to observations, so it should provide a reasonable reference against which to assess the effects of relaxing the free surface. Table 1 shows that relaxation reduces the discharge from the north, northeast and east, but increases it elsewhere, particularly in the southeast. The mean ice thickness of the flow across the front has increased in the southeast and northwest, while it has decreased elsewhere, particularly in the northern sectors where it has almost halved in the northeast. The mean outward velocity has increased in the eastern sectors, but has decreased by a quarter in the north. The total width of flow at the front has decreased everywhere, but this is most pronounced in the eastern sectors where it has nearly halved in the east.
For ice whose surface lies above 2000 m, the rate of volume change for the relaxation experiment is –2.1 km3 a−1 after 200 years, which agrees with Reference ThomasThomas and others’ (2000) observations for the 1990s that at high elevations GrIS was close to steady state. The rate of volume change is partitioned into the sectors as –1.4 km3 a−1 in the north, 6.8 km3 a−1 in the northeast, 11.0 km3 a−1 in the east, –5.3 km3 a−1 in the southeast, –10.2 km3 a−1 in the southwest and –3.0 km3 a−1 in the northwest. Taking these rates from those in Table 1 suggests that ice is thinning and/or retreating below 2000 m, except in the east where its volume is still increasing.
The flux across the 2000 m contour is 427.4 km3 a−1 for the inverse problem and 342.7 km3 a−1 at the end of the relaxation period. Both these values lie within the observed range of fluxes, 431 ± 74 km3 a−1, across a flux gate at an elevation of ~1700 m (Reference AndersenAndersen and others, 2015). The relaxation process has reduced the flux, particularly in the eastern sectors, where there are large regions of missing velocity observations and/or high uncertainties in the observed geometry around the 2000 m contour. The flux from the individual sectors after 200 years is partitioned as 16.1 km3 a−1 in the north, 25.0 km3 a−1 in the northeast, 47.2 km3 a−1 in the east, 86.6 km3 a−1 in the southeast, 113.6 km3 a−1 in the southwest and 54.2 km3 a−1 in the northwest. We find that the flux of ice has approximately halved at the front in the north and northeast, while it has increased by 73% at the front in the southeast (Table 1).
5.2. Discharge from the main outlet glaciers
We compare the outward flux of ice across gates specified in Reference Rignot and SteffenRignot and others (2008) to observed values (Reference Rignot and KanagaratnamRignot and Kanagaratnam, 2006) for individual glaciers. The mask used to locate the flux gates does not coincide with the glaciers in the observed data exactly, so we realigned the mask so that the fluxes calculated directly from the data matched the observed values. The match is within 5% for all the glaciers in Table 2 except Rink, where it is 12%.
Both the inverse problem and relaxation reproduce the flux from the main glaciers well. The two exceptions are Rink and Daugaard Jensen Glaciers for the relaxed experiment. The best match after relaxation is for Petermann. The flux in the inverse problem appears to be a near-perfect match for Helheim, but the modelled glacier flow is too slow and wide. The modelled flow for Kangerdlugssuaq is similarly too slow and wide. This worsens during relaxation, but the glacier also thickens, which increases the flux and improves the match. The inverse problem overestimates the flux for Jakobshavn Isbræ because the flow is too wide, and while this is corrected by relaxation the ice also thickens to give the same flux. Nioghalvfjerdsbræ thins, slows and the grounding line retreats around the flowline during relaxation. The flux calculated from the relaxation experiment for Rink is about half of the observed value. This is because the grounding line has retreated and the ice has speeded up and thinned significantly due to very high basal melting upstream of the flux gate. Clearly, the modelled melt rates are too high in this area of Greenland. The flux increases substantially across Daugaard Jensen during relaxation because the mean thickness along the gate has more than doubled. Daugaard Jensen is known to be in balance from observations (Reference Rignot and KanagaratnamRignot and Kanagaratnam, 2006), but the modelled ice stream still has a positive growth rate after relaxation. This imbalance may be due to too high SMB and/or an under-resolved outlet. The surrounding mesh is refined to 2 km, which has caused the outlet to be too narrow in places. We increased mesh refinement to 500 m in a separate test run, and the rate of thickening reduced.
6. Discussion
We discuss the limitations of both the inverse problem and the relaxation experiment. We noted in Section 3.6 that the modelled velocity for outlet glaciers tends to be underestimated compared to observations around the centre line of the flow but overestimated around the shear margins (Fig. 2). A lack of resolution is the most likely cause where the model tries to capture the abrupt change in ice velocity at the lateral boundaries of the ice streams with too few gridpoints. It is possible to further refine the model’s mesh to 500 m or less, but the inverse problem would have to use interpolated observational data in the cost function. The effects of under-resolution in the inverse problem appear to linger during relaxation even where resolution is greater. The mean flow of main outlet glaciers across the flux gates, for example, tends to be wider and slower compared to the observed flow (Table 2).
The inverse problem attempts to match observation by adjusting just two parameters. It may mask uncertainties in other parameters, data or model physics. The relatively large mismatch between the modelled speed and data near the ocean terminus of the outlet glaciers may be due to a lack of synchronicity of the datasets or to incorrect model assumptions. In particular, many glaciers have surged and retreated (Reference Howat, Joughin and ScambosHowat and others, 2007; Reference Joughin, Smith, Howat, Scambos and MoonJoughin and others, 2010). BISICLES parameterizes vertical stresses, but 3-D stress may be important near a terminus (Reference Morlighem, Rignot, Seroussi, Larour, Ben Dhia and AubryMorlighem and others, 2010; Reference FavierFavier and others, 2014). Also, BISICLES floats the front of many of the outlet glaciers, where the observational data indicate they should be grounded. This occurs because either hydrostatic equilibrium is invalid around the outlet and the vertical stresses keep ice that is above flotation grounded or there are errors in the initial geometry.
Modelled ice dynamics should be close to observations during the time-dependent run because the inverse problem gives basal traction and stiffness factor that will give model velocity that approximates observations. Figure 6 shows that the front of the ice sheet takes longer to adjust than the interior. A possible reason is that SMB has high errors at the front because the ice-sheet mask in the RCM does not exactly match our geometry. SMB from HIRHAM5 was chosen because the front retreated the least during relaxation. HIRHAM5 has the highest resolution of all RCMs tested, which reduces uncertainties at the front. We used crude extrapolation of SMB to fill missing values around the margins, whereas SMB used for the ice2sea project (Reference EdwardsEdwards and others, 2014) was extended beyond the ice sheet using a linear function with surface elevation. However, our ice-sheet margin retreated the most using the ice2sea forcing. Reference GoelzerGoelzer and others (2013), who also used ice2sea forcing, had to correct SMB during model initialization to keep the geometry close to observations. Given uncertainties at the front, comparing ice flux across a contour just inside the front with observations across the grounding line is more constructive. Our flux across the grounding line is too low compared to the observed value of 558 ± 83 km3 a−1 by Reference AndersenAndersen and others (2015), but our flux of 518.4 km3 a−1 across the SMB = 0 contour does lie within the range.
Discharge in the north and northeast is low compared to that of the inverse problem, which we take as a proxy for the observed value (Table 1). The outflowing ice has thinned on average during relaxation, particularly in the northeast, and it has also slowed in the north. Thinning and/or retreat of the ice front occurs below 2000 m for both sectors. Comparing the discharge with the observations of Reference Rignot and KanagaratnamRignot and Kanagaratnam (2006) suggests that basal melting of floating ice, which accounts for over half the total basal melt for GrIS, is responsible for the low relaxation value. However, the fronts of some floating tongues have eroded (ice thickness has reached its minimum allowable value), especially for Zachariæ Isbræ. Basal melting is switched off in the model when the ice thickness falls below 60 m or 200 m, which means that low SMB has eroded the fronts.
We noted that the inverse problem produced a good match between the optimized model speed and the observed speed for Petermann and the northeast glaciers despite problems with the observed geometry. After relaxation their floating tongues are noticeably different: Petermann’s is slower near the front and the fronts of the other two have partially retreated, while the remaining tongues are faster and thicker than the observations. However, the discharge across the upstream flux gates matches observations, with the exception of Nioghalvfjerdsbræ, after relaxation (Table 2). This may imply a minimal role of the ice tongue on grounded flow (Reference NickNick and others, 2012).
We found that the area of grounded ice retreated during relaxation (Fig. 5), but there was no clear pattern of grounding line movement. The grounding lines of Kangerdlugssuaq, Helheim and Zachariæ Isbræ advanced, while those of Rink and Nioghalvfjerdsbræ retreated. Petermann’s grounding line only adjusted, but Jakobshavn Isbræ’s line retreated in a complex way. The 500 m grid resolution across these grounding lines may be insufficient to resolve accurate movement (Reference Gladstone, Lee, Vieli and PayneGladstone and others, 2010). We should note that motion of the grounding line will affect the flux of ice, but the line has stopped migrating, on average, by the end of the relaxation experiment (Fig. 6b).
Ice found near the terminus of a number of glaciers that floats in the model but is grounded in reality could adversely affect discharge in the relaxation experiment because it has no basal traction and loses mass through basal melting. Some ice streams (e.g. Jakobshavn Isbræ and Helheim) are only lightly grounded, so small changes in ice thickness can float isolated gridcells upstream of the grounding line. Floating ice is in equilibrium except in the northeast, however, and modelled discharge from the main glaciers compares well with observations (Table 2), with the exceptions of Daugaard Jensen and Rink. More importantly, floating ice only accounts for a small proportion, 0.42% after 200 years, of the total area of ice, so any adverse effects will only be minor.
Overall the ice sheet is close to steady state, yet the east is still growing (Fig. 5a). Along the eastern margin between the northeast glaciers and Helheim the partial derivative of ice thickness with respect to time is positive. A possible explanation is that the SMB input is incorrect. The flux of ice from high elevations in the eastern sectors, including the southeast, is low compared to that of the inverse problem, though flux from the northeast and east in the relaxation experiment agrees well with observations (Reference AndersenAndersen and others, 2015). The apparent discrepancies may be due to the high uncertainties in the observed bedrock and surface elevation data (Reference BamberBamber and others, 2013). At the eastern front of the ice sheet, discharge is concentrated in narrower, faster-moving ice streams after relaxation (Table 1). North of Helheim this discharge is too low to balance the high SMB, but to the south the ice streams have also thickened during relaxation, which has increased discharge to bring the margin of the southeast into steady state.
Most of the growth of the ice sheet during the relaxation experiment is concentrated along the many outlet glaciers in the east, southeast and northwest. These glaciers are narrow and have complex geometry, which is poorly resolved by the 2 km mesh along the margin. The mesh over Kangerdlugssuaq and Helheim is refined to 500 m, and the tributaries and main trunk of both these glaciers are very close to steady state. While resolution is important, it is not clear that under-resolution leads to low discharge in the east (e.g. the modelled discharge from Daugaard Jensen is overestimated (Table 2)). In fact, the outlet glaciers in the southeast and northwest, where the margin is close to steady state, have thickened during relaxation to increase discharge above values in the inverse problem (Table 1).
7. Summary
We have presented an initial condition for the present-day GrIS. The unknown stiffness factor and basal traction coefficient are inferred from observations using an inverse problem. We use a cost function weighted with a Gaussian function of the observed ice speed, which increases the relative importance of moderate ice speeds that are typical of the main trunk of ice streams. The velocity and thickness of GrIS is found by relaxing the surface of the ice sheet over 200 years (Reference Gillet-ChauletGillet-Chaulet and others, 2012) forced by a 10 year mean SMB (Reference Lucas-Picher, Wulff-Nielsen, Christensen, Aðalsgeirsdóttir, Mottram and SimonsenLucas-Picher and others, 2012). We model submarine melt rates using piecewise linear functions of ice thickness based on the inferred rates for Petermann and Jakobshavn Isbræ (Reference Rignot and SteffenRignot and Steffen, 2008; Reference Motyka, Truffer, Fahnestock, Mortensen, Rysgaard and HowatMotyka and others, 2011) and the transport of water masses around Greenland’s coast (Reference StraneoStraneo and others, 2012).
The modelled ice sheet approaches a steady state around 145 years, and the rate of volume change is –5.8 km3 a−1 after the relaxation period. The ice is still thickening in the east after 200 years, which may be due to low resolution of the ice-sheet model and/or potentially incorrect SMB. However, the most likely cause is errors in the observed bedrock and ice surface elevations arising from interpolating sparse data because the east is poorly surveyed. The total discharge from the whole ice sheet is 367.2 km3 a−1, which is within 3% of the observed value by Reference Rignot and KanagaratnamRignot and Kanagaratnam (2006). The match is good, even though the observed surface velocity and ice-sheet geometry used in the inverse problem are not synchronous and the SMB forcing for the relaxation experiment is a mean spanning 10 years.
The modelled submarine melt rates generally perform well because the floating ice is close to equilibrium. The 180–200 year mean value is 51.9 km3 a−1. The rates for individual glaciers may be incorrect. For example, the rates for Rink Glacier appear to be far too high since the flux of ice near the terminus is almost half the observed value (Reference Rignot and KanagaratnamRignot and Kanagaratnam, 2006).
The outward flux of ice through fixed gates across the main outlet glaciers of Petermann, Nioghalvfjerdsbræ, Zachariæ Isbræ, Kangerdlugssuaq, Helheim and Jakobshavn Isbræ are within 20% of the observed values (Reference Rignot and KanagaratnamRignot and Kanagaratnam, 2006). The northern glaciers with floating tongues tend to be poorly matched in other models (Reference Price, Payne, Howat and SmithPrice and others, 2011; Reference Gillet-ChauletGillet-Chaulet and others, 2012). The match for Daugaard Jensen is relatively poor because the computational mesh is under-resolved. It is refined to 2 km, compared to 500 m around the main glaciers. The modelled glacier thickens because its flow is restricted by an outlet that is too narrow.
Acknowledgements
This work was funded by the UK Natural Environment Research Council (NERC) through the National Centre for Earth Observations and iGlass Consortium, NE/I010874/1. BISICLES development is led by D.F. Martin at Lawrence Berkeley National Laboratory, Berkeley, CA, USA, and S.L. Cornford at the University of Bristol, UK, with financial support provided by the UK Department of Energy and Climate Change and the NERC. Computing resources were provided by the Advanced Computing Research Centre, University of Bristol (http://www.bris.ac.uk/acrc/). We thank Stephen Price at Los Alamos National Laboratory, NM, USA, for providing the 3-D temperature field, and Ruth Mottram at the Danish Meteorological Institute for providing surface mass balance from HIRHAM5.










