Introduction
Snow layers that include graupel are relatively weak, and hence snow slab avalanches can fail on graupel layers (Reference McClung and SchaererMcClung and Schaerer, 1993). Graupel usually falls from the cumulus clouds of a cold front. In Japan, snow layers formed of graupel are sometimes responsible for avalanches (Abe, 2002). However, there are few data about the shear strength of graupel snow layers. Reference KaiharaKaihara (1998) reported time variations in the shear strength of a graupel layer. Reference Jamieson and JohnstonJamieson andJohnston (2001) reported measurements of shear strength for three graupel layers with different densities. In this paper, the shear strength and the angle of repose of graupel snow layers were obtained, and avalanches with graupel snow layers were characterized from these two parameters. Graupel usually has a diameter of up to 5 mm (Reference LudlumLudlum, 1991), but in this paper we also deal with graupel with a diameter that exceeds 5 mm.
Measurements
Shear strength
All measurements were carried out at Shinjo (38°470 N, 140°190 E; 127ma.s.l.) in the north part of Honshu island, Japan. The shear strength of graupel layers was measured using a shear frame with an area of 0.025 m2, as recommended by Reference SommerfeldSommerfeld (1984) (Fig. 1). In accordance with the shear-frame test procedure described by Reference Jamieson and JohnstonJamieson and Johnston (2001), the shear frame was inserted onto the weakest layer and pulled smoothly and quickly (in <1s). The attached force gauges had full load capacities of 10 and 100 N. The shear strength without an overburden load was determined by dividing the maximum load by the frame area of 0.025 m2. The weakest plane in each graupel layer was recognized from a pre-measurement, and was followed in a vertical cross-section by dyeing with blue ink (Fig. 2). The shear strength measured by this method is called the shear frame index (SFI; Reference Perla, Beck and ChengPerla and others, 1982). For statistical analysis, 11 measurements were conducted and the mean, maximum and minimum values were calculated. Temperature at the failure plane and density of the graupel snow layer were measured as well. Density was sampled from a 30 mm thick layer including the failure plane. The overburden snow load on the failed snow layer was also measured using a tube snow sampler with an area of 0.0042 m2.

Fig. 1. Shear frame tester with an area of 0.025 m2.

Fig. 2. Snow layer including graupel particles in a vertical cross-section. An arrow shows the failure plane.
Angle of repose
The angle of repose was measured using fresh graupel particles immediately after the snowfall. The graupel particles were caught and funneled via a cone made of thick paper onto a disk with a diameter of 0.2 m (Fig. 3). The angles of opposite slopes of the cone-shape debris formed by graupel particles were measured, and an average value was calculated. The temperature of the graupel particles was also measured. Two kinds of graupel particles were used to measure the angle of repose: random, unsieved particles; and sieved particles larger than 2.5 mm.

Fig. 3. Measurement of the angle of repose.
Results
Shear strength
As reported by Reference SommerfeldSommerfeld (1980), Reference Perla, Beck and ChengPerla and others (1982) and Reference FöhnFöhn (1987), shear strength decreases as the frame area increases. To calculate the actual values (without size effect), Reference FöhnFöhn (1987) compiled correction factors for frame areas of 0.01–0.25m2. According to Reference SommerfeldSommerfeld (1980) and Reference FöhnFöhn (1987), the correction factor for the 0.025 m2 shear frame is 0.65. However, the shear strength measured in this study was not converted with this coefficient because few data were available on the size effect for graupel layers.The shear strength of three different graupel layers was measured as shown inTable 1. The initial thicknesses of the three graupel layers were 80, 30 and 60 mm. After shear measurements had been taken, graupel particles with unchanged shape were identified in the failure plane. Figure 4 shows the graupel particles, including the failure plane, after the second measurement of the first graupel snowlayer (No.1-2 inTable 1). The diameter ranged from 1 to 5 mm, with an average of 2mm. The graupel was classified into R4a, b and c, as recommended by Reference Magono and LeeMagono and Lee (1966), and 1-f by Reference ColbeckColbeck and others (1990). Figure 5 shows the first graupel layer’s time variation of shear strength, density of the failure layer and overburden snow load on the failure layer over 3 days. The shear strength increased as the snow density increased.

Fig. 4. Plane view of the failure plane in a graupel layer after the shear frame test.

Fig. 5. Time variations in meteorological conditions, snow shear strength, density and overburden load.
Table 1. Shear strength (SFI), overburden load (L), density (ρ) and temperature (T) of three graupel layers

Angle of repose
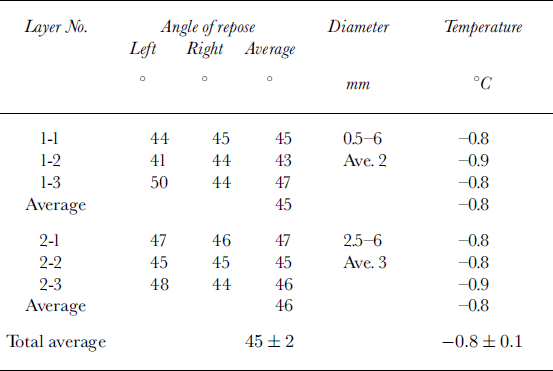
Six measurements of angle of repose were obtained after a snowstorm, and these are summarized inTable 2. The graupel particles were classified into R4b and c according to Reference Magono and LeeMagono and Lee (1966). The temperature of the graupel particles was –0.8 to –0.9°C, close to the melting point of ice, which suggests higher cohesion by capillarity. No difference was found between the two kinds of graupel particles relative to the angle of repose. The mean value of the angle of repose of both types of particles has been calculated to be 45±2°.
Table 2. Angle of repose. No. 1: unprocessed particles; No. 2: processed particles 42.5 mm in diameter
Discussion and Conclusions
The shear strength of graupel layers increased with snow density. Therefore SFI has been related to density as shown in Figure 6. The relation between shear strength, SFI (in kPa), and density, ρ (in kgm–3), of the first graupel layer (4 in Fig. 6) can be described by an exponential equation as follows:


Fig. 6. Relation between SFI and density for three graupel layers.The date refers to the date of formation. The thick solid line is a fit to the data of the graupel layer formed on 9 January 2002. Asterisk symbols (*) represent graupel measurements by Reference Jamieson and JohnstonJamieson and Johnston (2001). The thin solid line represents findings for dry new snow by Reference WatanabeWatanabe (1977). The dashed line represents findings for faceted crystals and depth hoar by Reference Jamieson and JohnstonJamieson and Johnston (2001).
Values for the other two graupel layers indicate high variation in strength. However, the mean values are distributed around Equation (1). Furthermore, three measurements of graupel layers reported by Reference Jamieson and JohnstonJamieson and Johnston (2001), converted from corrected values to raw values to compare with the present study, are also in fair agreement with Equation (1). The thin line in Figure 6 is for dry new snow (precipitation particles and decomposed and fragmented particles); it was established by Watanabe (1977) using a rotary vane apparatus with an area of 0.0018 m2.Reference WatanabeWatanabe’s (1977) relation was confirmed by Reference EndoEndo (1992) and Reference Yamanoi and EndoYamanoi and Endo (2002) using different types of apparatus (a shear frame (0.025m2) and a rotary vane (0.010m2), respectively). Reference Perla, Beck and ChengPerla and others (1982) reported a relation between SFI and density for six types of snow. The relation for initially metamorphosed snow with a density of 100–240 kgm–3 is close to the one by Reference WatanabeWatanabe (1977). The dashed line represents the relation established by Reference Jamieson and JohnstonJamieson and Johnston (2001) for faceted crystals and depth hoar, which has been converted to the same form as used in the present study.
The shear strength of graupel layers is approximately one-third that of dry new snow, and almost the same as that of faceted crystals and depth hoar with the same density. This result suggests that slab avalanches with weak layers of graupel, as well as of faceted crystals and depth hoar, may occur more easily than those with weak layers of dry new snow. In the present study, the shear strength of graupel layers with low density was measured. In mountainous areas at low temperature, a graupel layer may exist for long periods, and its density may become high, so the shear strength for high-density graupel layers should be investigated. Another subject for investigation is the effect of overburden load on graupel layers. Shear strength usually increases as the overburden load increases (Reference RochRoch, 1966; Reference Perla and BeckPerla and Beck, 1983). In the present study, the overburden load on the graupel layers was observed. However, the dependency of the overburden load on the shear strength is not discussed, and further investigation is required.
As reported by Reference Kuroiwa, Mizuno and TakeuchiKuroiwa and others (1967), the angle of repose increases as surface irregularities and/or the temperature of snow particles increase. They reported that the angle of repose for pulverized snow particles at temperatures of –35°C and –20°C is 45°, and that the angle of repose for wet snow can be considered to be nearly 90°. The angle of repose, θ, is related to the coefficient of internal friction between particles, μ (Reference Kuroiwa, Mizuno and TakeuchiKuroiwa and others, 1967), as
According to Equation (2), θ = 45° corresponds to μ = 1.0, which suggests that the particles have normal cohesion. The shape of the enlarged graupel particles analyzed here is almost spherical, with relatively few surface irregularities. This may explain why the angle of repose of these graupel particles was about 45° regardless of the high temperatures close to 0°C. This suggests that graupel layers cannot be formed on a slope exceeding 45°, and that a graupel-related avalanche cannot occur on such a slope. In the present study, however, all measurements were carried out at similar temperatures (close to the melting point of ice), and the temperature dependency of the angle of repose should be investigated.
Acknowledgements
The author would like to thank S. Mochizuki, K. Suzuki, T. Suzuki and N. Akiho for their support in collecting the data and in analysis, and J. Schweizer andT. Sato for their valuable comments on the manuscript.





