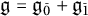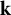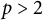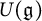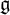1 Lie superalgebras in characteristic p
Since the works [Reference Brundan1–Reference Brundan and Kujawa3, Reference Cheng, Shu and Wang6, Reference Li and Shu13, Reference Shu and Wang21] etc. on irreducible representations of algebraic supergroups in odd characteristic, especially Wang–Zhao’s work [Reference Wang and Zhao29] focusing on irreducible representations of basic classical Lie superalgebras, the study of irreducible representations of finite-dimensional restricted Lie superalgebras in odd characteristic has found big progress. For instance, see [Reference Pan and Shu16, Reference Wang and Zhao30, Reference Yao33, Reference Zeng and Shu39–Reference Zheng and Shu43] etc. for determination of irreducible modules of classical Lie superalgebras; see [Reference Liu, Wang and Yuan14, Reference Shu and Yao22–Reference Shu and Zhang24, Reference Wang, Yuan and Liu28, Reference Yao32, Reference Yao34–Reference Yuan and Liu37] etc. for determination of irreducible modules of Cartan-type Lie superalgebras; and see [Reference Pan and Shu16, Reference Shu and Zhang23, Reference Wang and Zhao30, Reference Yao34, Reference Zeng and Shu39, Reference Zeng and Shu40, Reference Zhao42] etc. for dimensions or character formulas of irreducible modules. Nevertheless, their irreducible modules are not well-understood. The purpose of this article is to propose a formulation of maximal dimensions of their irreducible modules. In particular, we thoroughly investigate irreducible representations of finite-dimensional solvable Lie superalgebras.
Throughout the paper, the notions of vector spaces (resp. modules and subalgebras) mean vector superspaces (resp. super-modules and super-subalgebras). For simplicity, we will often omit the adjunct word “super.” All vector spaces are defined over
![]() $\mathbf {k}$
which is an algebraically closed field of characteristic
$\mathbf {k}$
which is an algebraically closed field of characteristic
![]() $p>2$
. For superspace
$p>2$
. For superspace
![]() $V=V_{\bar 0}+V_{\bar 1}$
, we will mention the super-dimension of V which means
$V=V_{\bar 0}+V_{\bar 1}$
, we will mention the super-dimension of V which means
![]() $\underline {\dim } V=(\dim V_{\bar 0}|\dim V_{\bar 1})$
, in the meanwhile, we mention the dimension of V which means
$\underline {\dim } V=(\dim V_{\bar 0}|\dim V_{\bar 1})$
, in the meanwhile, we mention the dimension of V which means
![]() $\dim _{\mathbf {k}} V:=\dim V_{\bar 0}+\dim V_{\bar 1}$
. As usual, we denote by
$\dim _{\mathbf {k}} V:=\dim V_{\bar 0}+\dim V_{\bar 1}$
. As usual, we denote by
![]() $V^{*}$
the linear dual space of V. Throughout the paper, all Lie (super)algebras are finite-dimensional unless other statements.
$V^{*}$
the linear dual space of V. Throughout the paper, all Lie (super)algebras are finite-dimensional unless other statements.
1.1 Restricted Lie superalgebras
A Lie superalgebra
![]() $\mathfrak {g}=\mathfrak {g}_{\bar 0}\oplus \mathfrak {g}_{\bar 1}$
is called a restricted one if
$\mathfrak {g}=\mathfrak {g}_{\bar 0}\oplus \mathfrak {g}_{\bar 1}$
is called a restricted one if
![]() $\mathfrak {g}_{\bar 0}$
is a restricted Lie algebra and
$\mathfrak {g}_{\bar 0}$
is a restricted Lie algebra and
![]() $\mathfrak {g}_{\bar 1}$
is a restricted module of
$\mathfrak {g}_{\bar 1}$
is a restricted module of
![]() $\mathfrak {g}_{\bar 0}$
, more precisely, there exists a p-mapping
$\mathfrak {g}_{\bar 0}$
, more precisely, there exists a p-mapping
![]() $[p]: \mathfrak {g}_{\bar 0}\rightarrow \mathfrak {g}_{\bar 0}$
satisfying:
$[p]: \mathfrak {g}_{\bar 0}\rightarrow \mathfrak {g}_{\bar 0}$
satisfying:
-
(a)
 $(kx)^{[p]} = k^px^{[p]}$
for all
$(kx)^{[p]} = k^px^{[p]}$
for all
 $k\in \mathbf {k}$
and
$k\in \mathbf {k}$
and
 $x\in \mathfrak {g}_{\bar 0}$
,
$x\in \mathfrak {g}_{\bar 0}$
, -
(b)
 $[x^{[p]}, y] = (\mathsf {ad} x)^p(y)$
for all
$[x^{[p]}, y] = (\mathsf {ad} x)^p(y)$
for all
 $x\in \mathfrak {g}_{\bar 0}$
and
$x\in \mathfrak {g}_{\bar 0}$
and
 $y\in \mathfrak {g}$
,
$y\in \mathfrak {g}$
, -
(c)
 $(x + y)^{[p]} = x^{[p]} + y^{[p]} + \sum _{i=1}^{p-1} s_i(x, y)$
for all
$(x + y)^{[p]} = x^{[p]} + y^{[p]} + \sum _{i=1}^{p-1} s_i(x, y)$
for all
 $x, y\in \mathfrak {g}_{\bar 0}$
, where
$x, y\in \mathfrak {g}_{\bar 0}$
, where
 $(\mathsf {ad} (x\otimes t + y\otimes 1))^{p-1}(x\otimes 1)=\sum _{i=1}^{p-1}is_i(x,y)\otimes t^{i-1}\in \mathfrak {g}_0\otimes _{\mathbf {k}} \mathbf {k}[t]$
. Here,
$(\mathsf {ad} (x\otimes t + y\otimes 1))^{p-1}(x\otimes 1)=\sum _{i=1}^{p-1}is_i(x,y)\otimes t^{i-1}\in \mathfrak {g}_0\otimes _{\mathbf {k}} \mathbf {k}[t]$
. Here,
 $\mathbf {k}[t]$
denotes the polynomial ring over
$\mathbf {k}[t]$
denotes the polynomial ring over
 $\mathbf {k}$
with indeterminant t.
$\mathbf {k}$
with indeterminant t.
With emphasis on the p-mapping
![]() $[p]$
, we sometimes denote the restricted Lie algebra
$[p]$
, we sometimes denote the restricted Lie algebra
![]() $\mathfrak {g}_{\bar 0}$
by
$\mathfrak {g}_{\bar 0}$
by
![]() $(\mathfrak {g}_{\bar 0},[p])$
. One can refer to [Reference Jacobson10, Section V.7] or [Reference Strade and Farnsteiner26, Chapter 2] for more details on restricted Lie algebras and restricted modules.
$(\mathfrak {g}_{\bar 0},[p])$
. One can refer to [Reference Jacobson10, Section V.7] or [Reference Strade and Farnsteiner26, Chapter 2] for more details on restricted Lie algebras and restricted modules.
Denote by
![]() $\mathcal {Z}(\mathfrak {g}),$
the center of
$\mathcal {Z}(\mathfrak {g}),$
the center of
![]() $U(\mathfrak {g})$
, i.e.,
$U(\mathfrak {g})$
, i.e.,
![]() $\mathcal {Z}(\mathfrak {g}):=\{u\in U(\mathfrak {g})\mid \mathsf {ad} x(u)=0\;\; \forall x\in \mathfrak {g}\}$
. For a restricted Lie superalgebra
$\mathcal {Z}(\mathfrak {g}):=\{u\in U(\mathfrak {g})\mid \mathsf {ad} x(u)=0\;\; \forall x\in \mathfrak {g}\}$
. For a restricted Lie superalgebra
![]() $\mathfrak {g}$
, the p-center
$\mathfrak {g}$
, the p-center
![]() $\mathcal {Z}_0$
of
$\mathcal {Z}_0$
of
![]() $U(\mathfrak {g}_{\bar 0})$
which is defined to be the subalgebra generated by
$U(\mathfrak {g}_{\bar 0})$
which is defined to be the subalgebra generated by
![]() $\{x^p-x^{[p]}\mid x\in \mathfrak {g}_{\bar 0}\}$
, lies in
$\{x^p-x^{[p]}\mid x\in \mathfrak {g}_{\bar 0}\}$
, lies in
![]() $\mathcal {Z}$
. Fix a basis
$\mathcal {Z}$
. Fix a basis
![]() $\{x_1,\ldots ,x_s\}$
of
$\{x_1,\ldots ,x_s\}$
of
![]() $\mathfrak {g}_{\bar 0}$
and a basis
$\mathfrak {g}_{\bar 0}$
and a basis
![]() $\{y_1,\ldots ,y_t\}$
of
$\{y_1,\ldots ,y_t\}$
of
![]() $\mathfrak {g}_{\bar 1}$
. Set
$\mathfrak {g}_{\bar 1}$
. Set
![]() $\xi _{i}=x_{i}^{p}-x_{i}^{[p]}, i=1,\ldots , s$
. The p-center
$\xi _{i}=x_{i}^{p}-x_{i}^{[p]}, i=1,\ldots , s$
. The p-center
![]() $\mathcal {Z}_0$
is a polynomial ring
$\mathcal {Z}_0$
is a polynomial ring
![]() $\mathbf {k}[\xi _{1},\ldots ,\xi _{s}]$
generated by
$\mathbf {k}[\xi _{1},\ldots ,\xi _{s}]$
generated by
![]() $\xi _{1},\ldots , \xi _{s}$
(see, for example, [Reference Wang and Zhao29, Section 2.3]).
$\xi _{1},\ldots , \xi _{s}$
(see, for example, [Reference Wang and Zhao29, Section 2.3]).
By the PBW theorem, one easily knows that the enveloping superalgebra
![]() $U(\mathfrak {g})$
is a free module over
$U(\mathfrak {g})$
is a free module over
![]() $\mathcal {Z}_0$
with basis
$\mathcal {Z}_0$
with basis
(see, for example, [Reference Wang and Zhao29, Section 2.3]).
1.2 Reduced enveloping algebras of restricted Lie superalgebras
Suppose V is an irreducible
![]() $U(\mathfrak {g})$
-module. By the above argument, for any
$U(\mathfrak {g})$
-module. By the above argument, for any
![]() $x\in \mathfrak {g}_{\bar 0}$
,
$x\in \mathfrak {g}_{\bar 0}$
,
![]() $x^p-x^{[p]}$
lies in the center of
$x^p-x^{[p]}$
lies in the center of
![]() $U(\mathfrak {g})$
. By definition,
$U(\mathfrak {g})$
. By definition,
![]() $x^p-x^{[p]}$
acts on V as an even linear transformation for
$x^p-x^{[p]}$
acts on V as an even linear transformation for
![]() $x\in \mathfrak {g}_{\bar 0}$
. Schur’s lemma entails that each
$x\in \mathfrak {g}_{\bar 0}$
. Schur’s lemma entails that each
![]() $x^p-x^{[p]}$
for
$x^p-x^{[p]}$
for
![]() $x\in \mathfrak {g}_{\bar 0}$
acts on V by scalar
$x\in \mathfrak {g}_{\bar 0}$
acts on V by scalar
![]() $\chi (x)^p$
for some
$\chi (x)^p$
for some
![]() $\chi \in {\mathfrak {g}_{\bar 0}}^{*}$
. Such
$\chi \in {\mathfrak {g}_{\bar 0}}^{*}$
. Such
![]() $\chi $
is called the p-character of V. Suppose
$\chi $
is called the p-character of V. Suppose
![]() $\chi \in {\mathfrak {g}_{\bar 0}}^{*}$
is given, which is naturally regarded in
$\chi \in {\mathfrak {g}_{\bar 0}}^{*}$
is given, which is naturally regarded in
![]() $\mathfrak {g}^{*}$
by trivial extension. Denote by
$\mathfrak {g}^{*}$
by trivial extension. Denote by
![]() $I_{\chi }$
, the ideal of
$I_{\chi }$
, the ideal of
![]() $U(\mathfrak {g})$
generated by the even central elements
$U(\mathfrak {g})$
generated by the even central elements
![]() $x^p-x^{[p]}-\chi (x)^p$
with x running over
$x^p-x^{[p]}-\chi (x)^p$
with x running over
![]() $\mathfrak {g}_{\bar 0}$
. More generally, we can say that a
$\mathfrak {g}_{\bar 0}$
. More generally, we can say that a
![]() $U(\mathfrak {g})$
-module M is a
$U(\mathfrak {g})$
-module M is a
![]() $\chi $
-reduced module for any given
$\chi $
-reduced module for any given
![]() $\chi \in \mathfrak {g}_{\bar 0}^{*}$
if for any
$\chi \in \mathfrak {g}_{\bar 0}^{*}$
if for any
![]() $x\in \mathfrak {g}_{\bar 0}$
,
$x\in \mathfrak {g}_{\bar 0}$
,
![]() $x^p-x^{[p]}$
acts by the scalar
$x^p-x^{[p]}$
acts by the scalar
![]() $\chi (x)^p$
. All
$\chi (x)^p$
. All
![]() $\chi $
-reduced modules for any given
$\chi $
-reduced modules for any given
![]() $\chi \in \mathfrak {g}_{\bar 0}^{*}$
constitute a full subcategory of the
$\chi \in \mathfrak {g}_{\bar 0}^{*}$
constitute a full subcategory of the
![]() $U(\mathfrak {g})$
-module category. The quotient algebra
$U(\mathfrak {g})$
-module category. The quotient algebra
![]() $U_{\chi }(\mathfrak {g}):=U(\mathfrak {g})/ I_{\chi }$
is called the reduced enveloping superalgebra of p-character
$U_{\chi }(\mathfrak {g}):=U(\mathfrak {g})/ I_{\chi }$
is called the reduced enveloping superalgebra of p-character
![]() $\chi $
. Then the
$\chi $
. Then the
![]() $\chi $
-reduced module category of
$\chi $
-reduced module category of
![]() $\mathfrak {g}$
coincides with the
$\mathfrak {g}$
coincides with the
![]() $U_{\chi }(\mathfrak {g})$
-module category. If
$U_{\chi }(\mathfrak {g})$
-module category. If
![]() $\mathfrak {h}$
is a restricted Lie subalgebra of
$\mathfrak {h}$
is a restricted Lie subalgebra of
![]() $\mathfrak {g}$
, we often make use of
$\mathfrak {g}$
, we often make use of
![]() $\chi |_{\mathfrak {h}_{{\bar 0}}}$
for
$\chi |_{\mathfrak {h}_{{\bar 0}}}$
for
![]() $\chi \in \mathfrak {g}^{*}_{\bar 0}$
when we consider the
$\chi \in \mathfrak {g}^{*}_{\bar 0}$
when we consider the
![]() $U_{\chi }(\mathfrak {g})$
-module category and its objects induced from
$U_{\chi }(\mathfrak {g})$
-module category and its objects induced from
![]() $\mathfrak {h}$
-modules. By abuse of notations, we will simply write
$\mathfrak {h}$
-modules. By abuse of notations, we will simply write
![]() $\chi |_{\mathfrak {h}_{{\bar 0}}}$
as
$\chi |_{\mathfrak {h}_{{\bar 0}}}$
as
![]() $\chi $
.
$\chi $
.
By the PBW theorem, the superalgebra
![]() $U_{\chi }(\mathfrak {g})$
has a basis
$U_{\chi }(\mathfrak {g})$
has a basis
and
![]() $\dim U_{\chi }(\mathfrak {g})=p^{\dim \mathfrak {g}_{\bar 0}}2^{\dim \mathfrak {g}_{\bar 1}}$
.
$\dim U_{\chi }(\mathfrak {g})=p^{\dim \mathfrak {g}_{\bar 0}}2^{\dim \mathfrak {g}_{\bar 1}}$
.
The reduced enveloping algebra corresponding to
![]() $\chi =0$
is
$\chi =0$
is
![]() $U_0(\mathfrak {g})$
. We call it the restricted enveloping algebra of
$U_0(\mathfrak {g})$
. We call it the restricted enveloping algebra of
![]() $\mathfrak {g}$
. The modules of
$\mathfrak {g}$
. The modules of
![]() $U_0(\mathfrak {g})$
are called restricted modules of
$U_0(\mathfrak {g})$
are called restricted modules of
![]() $\mathfrak {g}$
. The following observation is clear.
$\mathfrak {g}$
. The following observation is clear.
Lemma 1.1 The dimensions of irreducible modules of a restricted Lie algebra
![]() $\mathfrak {g}$
are not greater than
$\mathfrak {g}$
are not greater than
![]() $p^{\dim \mathfrak {g}_{\bar 0}}2^{\dim \mathfrak {g}_{\bar 1}}$
.
$p^{\dim \mathfrak {g}_{\bar 0}}2^{\dim \mathfrak {g}_{\bar 1}}$
.
1.3 Minimal p-envelopes of finite-dimensional Lie superalgebras
Any finite-dimensional Lie superalgebra can be embedded in a finite-dimensional restricted Lie superalgebra (see the appendix section). Let
![]() $\mathfrak {g}=\mathfrak {g}_{\bar 0}+\mathfrak {g}_{\bar 1}$
be any given Lie superalgebra. There is a minimal finite-dimensional restricted Lie superalgebra
$\mathfrak {g}=\mathfrak {g}_{\bar 0}+\mathfrak {g}_{\bar 1}$
be any given Lie superalgebra. There is a minimal finite-dimensional restricted Lie superalgebra
![]() $\mathfrak {g}_p$
such that
$\mathfrak {g}_p$
such that
![]() $\mathfrak {g}_p=(\mathfrak {g}_{\bar 0})_p+\mathfrak {g}_{\bar 1}$
is a p-envelope of
$\mathfrak {g}_p=(\mathfrak {g}_{\bar 0})_p+\mathfrak {g}_{\bar 1}$
is a p-envelope of
![]() $\mathfrak {g}$
, and
$\mathfrak {g}$
, and
![]() $(\mathfrak {g}_{\bar 0})_p$
a p-envelope of
$(\mathfrak {g}_{\bar 0})_p$
a p-envelope of
![]() $\mathfrak {g}_{\bar 0}$
(see Lemma A.3 in the appendix section). Then, one can still show that dimensions of all irreducible modules of
$\mathfrak {g}_{\bar 0}$
(see Lemma A.3 in the appendix section). Then, one can still show that dimensions of all irreducible modules of
![]() $\mathfrak {g}$
has unified upper-bound, by considering its minimal p-envelope. There is a natural question.
$\mathfrak {g}$
has unified upper-bound, by considering its minimal p-envelope. There is a natural question.
Question 1.2 What is the maximal dimension for irreducible modules over
![]() $\mathfrak {g}$
?
$\mathfrak {g}$
?
With aim at the above question, the purpose of the present paper is to formulate the maximal irreducible dimensions for finite-dimensional restricted Lie superalgebras over
![]() $\mathbf {k}$
, as a conjecture (see Conjecture 2.3). This conjecture is regarded a super version of the plausible first Kac–Weisfeiler conjecture (see Remark 2.4(2), or [Reference Kac12, Reference Weisfeiler and Kac31]). The progress of the work on the first Kac–Weisfeiler conjecture can be learnt from [Reference Martin, Stewart and Topley15, Reference Premet and Skryabin18].
$\mathbf {k}$
, as a conjecture (see Conjecture 2.3). This conjecture is regarded a super version of the plausible first Kac–Weisfeiler conjecture (see Remark 2.4(2), or [Reference Kac12, Reference Weisfeiler and Kac31]). The progress of the work on the first Kac–Weisfeiler conjecture can be learnt from [Reference Martin, Stewart and Topley15, Reference Premet and Skryabin18].
The main body of the text is devoted to the verification of the super first Kac–Weisfeiler conjecture in the case of basic classical Lie superalgebras and complete solvable Lie superalgebras.
2 Maximal dimensions of irreducible modules for a finite-dimensional restricted Lie superalgebra
Keep the notations and assumption as above. In particular,
![]() $\mathfrak {g}=\mathfrak {g}_{\bar 0}\oplus \mathfrak {g}_{\bar 1}$
is a finite-dimensional restricted Lie superalgebra over
$\mathfrak {g}=\mathfrak {g}_{\bar 0}\oplus \mathfrak {g}_{\bar 1}$
is a finite-dimensional restricted Lie superalgebra over
![]() $\mathbf {k}$
. For any given
$\mathbf {k}$
. For any given
![]() $\chi \in \mathfrak {g}_{\bar 0}^{*}$
, consider the bilinear form
$\chi \in \mathfrak {g}_{\bar 0}^{*}$
, consider the bilinear form
![]() $\textsf {B}_{\chi }$
on
$\textsf {B}_{\chi }$
on
![]() $\mathfrak {g}$
with regarding
$\mathfrak {g}$
with regarding
![]() $\chi \in \mathfrak {g}^{*}$
by trivial extension
$\chi \in \mathfrak {g}^{*}$
by trivial extension
Set
![]() $\ker (\textsf {B}_{\chi })=\{X\in \mathfrak {g}\mid \textsf {B}_{\chi }(X,\mathfrak {g})=0\}$
. Generally,
$\ker (\textsf {B}_{\chi })=\{X\in \mathfrak {g}\mid \textsf {B}_{\chi }(X,\mathfrak {g})=0\}$
. Generally,
![]() $\mathfrak {g}^{*}$
can be regarded a
$\mathfrak {g}^{*}$
can be regarded a
![]() $\mathfrak {g}$
-module via defining for
$\mathfrak {g}$
-module via defining for
![]() $X\in \mathfrak {g}_{|X|}, f\in \mathfrak {g}^{*}_{|f|}$
,
$X\in \mathfrak {g}_{|X|}, f\in \mathfrak {g}^{*}_{|f|}$
,
![]() $X.f:\mathfrak {g}\rightarrow \mathbf {k}$
with
$X.f:\mathfrak {g}\rightarrow \mathbf {k}$
with
![]() $(X.f)(Y)=-(-1)^{|X||f|}f{([X,Y])}, \forall Y\in \mathfrak {g}$
. Here,
$(X.f)(Y)=-(-1)^{|X||f|}f{([X,Y])}, \forall Y\in \mathfrak {g}$
. Here,
![]() $|X|$
and
$|X|$
and
![]() $|f|$
denote the parities of the
$|f|$
denote the parities of the
![]() $\mathbb {Z}_2$
-homogeneous element
$\mathbb {Z}_2$
-homogeneous element
![]() ${X\in \mathfrak {g}}$
and
${X\in \mathfrak {g}}$
and
![]() $f\in \mathfrak {g}^{*}$
, respectively. So we can define the centralizer of
$f\in \mathfrak {g}^{*}$
, respectively. So we can define the centralizer of
![]() $\chi $
in
$\chi $
in
![]() $\mathfrak {g}$
, which is denoted by
$\mathfrak {g}$
, which is denoted by
![]() $\mathfrak {z}^{\chi }$
. By definition,
$\mathfrak {z}^{\chi }$
. By definition,
Then this
![]() $\mathfrak {z}^{\chi }$
is exactly equal to
$\mathfrak {z}^{\chi }$
is exactly equal to
![]() $\ker (\textsf {B}_{\chi })$
. Furthermore, with
$\ker (\textsf {B}_{\chi })$
. Furthermore, with
![]() $\textsf {B}_{\chi }$
, we may define bilinear forms on the spaces
$\textsf {B}_{\chi }$
, we may define bilinear forms on the spaces
![]() $\tilde {\mathfrak {g}}:=\mathfrak {g}/ \mathfrak {z}^{\chi }$
,
$\tilde {\mathfrak {g}}:=\mathfrak {g}/ \mathfrak {z}^{\chi }$
,
![]() $\tilde {\mathfrak {g}}_{\bar 0}:=\mathfrak {g}_{\bar 0}/ \mathfrak {z}_{\bar 0}^{\chi }$
and
$\tilde {\mathfrak {g}}_{\bar 0}:=\mathfrak {g}_{\bar 0}/ \mathfrak {z}_{\bar 0}^{\chi }$
and
![]() $\tilde {\mathfrak {g}}_{\bar 1}:=\mathfrak {g}_{\bar 1}/ \mathfrak {z}_{\bar 1}^{\chi }$
, respectively. By abuse of notations, those bilinear forms are still denoted by
$\tilde {\mathfrak {g}}_{\bar 1}:=\mathfrak {g}_{\bar 1}/ \mathfrak {z}_{\bar 1}^{\chi }$
, respectively. By abuse of notations, those bilinear forms are still denoted by
![]() $\textsf {B}_{\chi }$
.
$\textsf {B}_{\chi }$
.
In the following arguments, we need some conventions and notations. Let
![]() $\lceil a\rceil $
denote the greatest integer lower bound of a for a real number
$\lceil a\rceil $
denote the greatest integer lower bound of a for a real number
![]() $a\in {\mathbb {R}}$
, and
$a\in {\mathbb {R}}$
, and
![]() $\lfloor a\rfloor $
denote the least integer upper bound of a.
$\lfloor a\rfloor $
denote the least integer upper bound of a.
Lemma 2.1 The following statements hold.
-
(1) The centralizer
 $\mathfrak {z}^{\chi }=\mathfrak {z}^{\chi }_{\bar 0}+\mathfrak {z}^{\chi }_{\bar 1}$
is a restricted subalgebra of
$\mathfrak {z}^{\chi }=\mathfrak {z}^{\chi }_{\bar 0}+\mathfrak {z}^{\chi }_{\bar 1}$
is a restricted subalgebra of
 $\mathfrak {g}$
if
$\mathfrak {g}$
if
 $\mathfrak {g}$
itself is a restricted Lie superalgebra.
$\mathfrak {g}$
itself is a restricted Lie superalgebra. -
(2)
 $\textsf {B}_{\chi }$
is a nondegenerate skew-symmetric bilinear form on
$\textsf {B}_{\chi }$
is a nondegenerate skew-symmetric bilinear form on
 $\tilde {\mathfrak {g}}_{\bar 0}$
, and a nondegenerate skew-symmetric bilinear form on
$\tilde {\mathfrak {g}}_{\bar 0}$
, and a nondegenerate skew-symmetric bilinear form on
 $\tilde {\mathfrak {g}}_{\bar 1}$
. Consequently,
$\tilde {\mathfrak {g}}_{\bar 1}$
. Consequently,
 $\dim (\mathfrak {g}_{\bar 0}-\mathfrak {z}_{\bar 0}^{\chi })$
is even.
$\dim (\mathfrak {g}_{\bar 0}-\mathfrak {z}_{\bar 0}^{\chi })$
is even. -
(3) Any maximal isotropic space in
 $\mathfrak {g}_{\bar 0}$
with respect to
$\mathfrak {g}_{\bar 0}$
with respect to
 $\textsf {B}_{\chi }$
has dimension
$\textsf {B}_{\chi }$
has dimension
 $\frac {\dim \mathfrak {g}_{\bar 0}+\dim \mathfrak {z}_{\bar 0}^{\chi }}{2}$
.
$\frac {\dim \mathfrak {g}_{\bar 0}+\dim \mathfrak {z}_{\bar 0}^{\chi }}{2}$
. -
(4) Any maximal isotropic space in
 $\mathfrak {g}_{\bar 1}$
with respect to
$\mathfrak {g}_{\bar 1}$
with respect to
 $\textsf {B}_{\chi }$
has dimension
$\textsf {B}_{\chi }$
has dimension
 $\frac {\dim \mathfrak {g}_{\bar 1}+\dim \mathfrak {z}^{\chi }_{\bar 1}}{2}$
if
$\frac {\dim \mathfrak {g}_{\bar 1}+\dim \mathfrak {z}^{\chi }_{\bar 1}}{2}$
if
 $\dim \mathfrak {g}_{\bar 1}-\dim \mathfrak {z}^{\chi }_{\bar 1}$
is even, and has dimension
$\dim \mathfrak {g}_{\bar 1}-\dim \mathfrak {z}^{\chi }_{\bar 1}$
is even, and has dimension
 $\frac {\dim \mathfrak {g}_{\bar 1}+\dim \mathfrak {z}^{\chi }_{\bar 1}-1}{2}$
if
$\frac {\dim \mathfrak {g}_{\bar 1}+\dim \mathfrak {z}^{\chi }_{\bar 1}-1}{2}$
if
 $\dim \mathfrak {g}_{\bar 1}-\dim \mathfrak {z}^{\chi }_{\bar 1}$
is odd.
$\dim \mathfrak {g}_{\bar 1}-\dim \mathfrak {z}^{\chi }_{\bar 1}$
is odd.
Proof The parts (1) and (2) directly follows from the definition. As to (3), we first note that
![]() $\mathfrak {z}^{\chi }$
is an isotropic subspace of
$\mathfrak {z}^{\chi }$
is an isotropic subspace of
![]() $\mathfrak {g}$
with respect to
$\mathfrak {g}$
with respect to
![]() $\textsf {B}_{\chi }$
. From the part (2), it follows that a maximal isotropic subspace
$\textsf {B}_{\chi }$
. From the part (2), it follows that a maximal isotropic subspace
![]() $\tilde V$
of
$\tilde V$
of
![]() $\tilde {\mathfrak {g}}_{\bar 0}$
has dimension
$\tilde {\mathfrak {g}}_{\bar 0}$
has dimension
![]() $\frac {\dim \mathfrak {g}_{\bar 0}-\dim \mathfrak {z}^{\chi }_{\bar 0}}{2}$
. So naturally, the preimage space of
$\frac {\dim \mathfrak {g}_{\bar 0}-\dim \mathfrak {z}^{\chi }_{\bar 0}}{2}$
. So naturally, the preimage space of
![]() $\tilde V$
in V which contains
$\tilde V$
in V which contains
![]() $\mathfrak {z}^{\chi }$
is a maximal isotropic subspace of
$\mathfrak {z}^{\chi }$
is a maximal isotropic subspace of
![]() $\mathfrak {g}_{\bar 0}$
. This maximal isotropic subspace has dimension
$\mathfrak {g}_{\bar 0}$
. This maximal isotropic subspace has dimension
![]() $\frac {\dim \mathfrak {g}_{\bar 0}+\dim \mathfrak {z}_{\bar 0}^{\chi }}{2}$
.
$\frac {\dim \mathfrak {g}_{\bar 0}+\dim \mathfrak {z}_{\bar 0}^{\chi }}{2}$
.
As to the part (4), from the part (2), again it follows that a maximal isotropic subspace
![]() $\tilde W$
of
$\tilde W$
of
![]() $\tilde {\mathfrak {g}}_{\bar 1}$
has dimension
$\tilde {\mathfrak {g}}_{\bar 1}$
has dimension
![]() $\lceil \frac {\dim \mathfrak {g}_{\bar 1}-\dim \mathfrak {z}^{\chi }_{\bar 1}}{2}\rceil $
. By the same reason, the preimage space of
$\lceil \frac {\dim \mathfrak {g}_{\bar 1}-\dim \mathfrak {z}^{\chi }_{\bar 1}}{2}\rceil $
. By the same reason, the preimage space of
![]() $\tilde W$
of
$\tilde W$
of
![]() $\tilde {\mathfrak {g}}_{\bar 1}$
which contains
$\tilde {\mathfrak {g}}_{\bar 1}$
which contains
![]() $\mathfrak {z}^{\chi }$
is a maximal isotropic subspace of
$\mathfrak {z}^{\chi }$
is a maximal isotropic subspace of
![]() $\mathfrak {g}_{\bar 1}$
. Consequently, this maximal isotropic subspace has dimension
$\mathfrak {g}_{\bar 1}$
. Consequently, this maximal isotropic subspace has dimension
![]() $\lceil \frac {\dim \mathfrak {g}_{\bar 1}+\dim \mathfrak {z}_{\bar 1}^{\chi }}{2}\rceil $
.
$\lceil \frac {\dim \mathfrak {g}_{\bar 1}+\dim \mathfrak {z}_{\bar 1}^{\chi }}{2}\rceil $
.
The proof is completed.
Remark 2.2 With the notations
![]() $\lceil a\rceil $
and
$\lceil a\rceil $
and
![]() $\lfloor a\rfloor $
for
$\lfloor a\rfloor $
for
![]() $a\in {\mathbb {R}}$
, Lemma 2.1(4) becomes that the maximal isotropic space with respect to
$a\in {\mathbb {R}}$
, Lemma 2.1(4) becomes that the maximal isotropic space with respect to
![]() $\textsf {B}_{\chi }$
in
$\textsf {B}_{\chi }$
in
![]() $\mathfrak {g}_{\bar 1}$
has dimension
$\mathfrak {g}_{\bar 1}$
has dimension
![]() $\lceil \frac {\dim \mathfrak {g}_{\bar 1}+\dim \mathfrak {z}^{\chi }_{\bar 1}}{2}\rceil $
. Set
$\lceil \frac {\dim \mathfrak {g}_{\bar 1}+\dim \mathfrak {z}^{\chi }_{\bar 1}}{2}\rceil $
. Set
 $$ \begin{align*}d(\mathfrak{g},\chi)=(\frac{\dim\mathfrak{g}_{\bar 0}+\dim\mathfrak{z}^{\chi}_{\bar 0}}{2}| \lceil\frac{\dim\mathfrak{g}_{\bar 1}+\dim\mathfrak{z}^{\chi}_{\bar 1}}{2}\rceil).\end{align*} $$
$$ \begin{align*}d(\mathfrak{g},\chi)=(\frac{\dim\mathfrak{g}_{\bar 0}+\dim\mathfrak{z}^{\chi}_{\bar 0}}{2}| \lceil\frac{\dim\mathfrak{g}_{\bar 1}+\dim\mathfrak{z}^{\chi}_{\bar 1}}{2}\rceil).\end{align*} $$
This
![]() $d(\mathfrak {g},\chi )$
is the maximal super-dimension of the isotropy subspaces of
$d(\mathfrak {g},\chi )$
is the maximal super-dimension of the isotropy subspaces of
![]() $\mathfrak {g}$
with respect to
$\mathfrak {g}$
with respect to
![]() $\textsf {B}_{\chi }$
. Set
$\textsf {B}_{\chi }$
. Set
![]() $i(\mathfrak {g},\chi )=\underline {\dim }\mathfrak {g}-d(\mathfrak {g},\chi )$
. Then
$i(\mathfrak {g},\chi )=\underline {\dim }\mathfrak {g}-d(\mathfrak {g},\chi )$
. Then
 $$ \begin{align*}i(\mathfrak{g},\chi)=(\frac{\dim \mathfrak{g}_{\bar 0}-\dim\mathfrak{z}^{\chi}_{\bar 0}}{2}| \lfloor\frac{\dim\mathfrak{g}_{\bar 1}-\dim\mathfrak{z}^{\chi}_{\bar 1}}{2}\rfloor). \end{align*} $$
$$ \begin{align*}i(\mathfrak{g},\chi)=(\frac{\dim \mathfrak{g}_{\bar 0}-\dim\mathfrak{z}^{\chi}_{\bar 0}}{2}| \lfloor\frac{\dim\mathfrak{g}_{\bar 1}-\dim\mathfrak{z}^{\chi}_{\bar 1}}{2}\rfloor). \end{align*} $$
2.1 The set
 $D(\mathfrak {g},\chi )$
of degraded subalgebras associated with
$D(\mathfrak {g},\chi )$
of degraded subalgebras associated with
 $\chi $
$\chi $
We regard
![]() $\chi \in \mathfrak {g}_{\bar 0}^{*}$
as a linear function on
$\chi \in \mathfrak {g}_{\bar 0}^{*}$
as a linear function on
![]() $\mathfrak {g}^{*}$
by trivial extension. Associated with
$\mathfrak {g}^{*}$
by trivial extension. Associated with
![]() $\chi $
, we say that a subalgebra
$\chi $
, we say that a subalgebra
![]() $\mathfrak {h}$
is degraded if
$\mathfrak {h}$
is degraded if
![]() $\underline \dim \mathfrak {h}=d(\mathfrak {g},\chi )$
and
$\underline \dim \mathfrak {h}=d(\mathfrak {g},\chi )$
and
![]() $\chi (\mathfrak {h}^{(1)})=0$
. Here and further,
$\chi (\mathfrak {h}^{(1)})=0$
. Here and further,
![]() $L^{(1)}$
for a Lie (super)algebra L denotes the derived subalgebra of L, i.e.,
$L^{(1)}$
for a Lie (super)algebra L denotes the derived subalgebra of L, i.e.,
![]() $L^{(1)}=[L,L]$
. Obviously, such subalgebras contain
$L^{(1)}=[L,L]$
. Obviously, such subalgebras contain
![]() $\mathfrak {z}^{\chi }$
if they exist. In this case, they are further restricted subalgebras whenever
$\mathfrak {z}^{\chi }$
if they exist. In this case, they are further restricted subalgebras whenever
![]() $\mathfrak {g}$
is a restricted Lie superalgebra.
$\mathfrak {g}$
is a restricted Lie superalgebra.
Denote by
![]() $D(\mathfrak {g},\chi ),$
the set of all degraded subalgebras
$D(\mathfrak {g},\chi ),$
the set of all degraded subalgebras
![]() $\mathfrak {h}$
of
$\mathfrak {h}$
of
![]() $\mathfrak {g}$
.
$\mathfrak {g}$
.
For the simplicity of arguments, we say that a pair of nonnegative integers
![]() $(a|b)$
is a super-datum. Call a and b its even entry and odd entry, respectively. For
$(a|b)$
is a super-datum. Call a and b its even entry and odd entry, respectively. For
![]() $\chi \in \mathfrak {g}^{*}_{\bar 0}\subset \mathfrak {g}^{*}$
, we set
$\chi \in \mathfrak {g}^{*}_{\bar 0}\subset \mathfrak {g}^{*}$
, we set
 $$ \begin{align*} &b^{\chi}_0=\dim\mathfrak{g}_{\bar 0}-\dim\mathfrak{z}^{\chi}_{\bar 0},\cr & b^{\chi}_1=\dim\mathfrak{g}_{\bar 1}-\dim\mathfrak{z}^{\chi}_{\bar 1}. \end{align*} $$
$$ \begin{align*} &b^{\chi}_0=\dim\mathfrak{g}_{\bar 0}-\dim\mathfrak{z}^{\chi}_{\bar 0},\cr & b^{\chi}_1=\dim\mathfrak{g}_{\bar 1}-\dim\mathfrak{z}^{\chi}_{\bar 1}. \end{align*} $$
Correspondingly,
![]() $i(\mathfrak {g},\chi )=(\frac {b^{\chi }_0}{2}| \lfloor \frac {b^{\chi }_1}{2}\rfloor )$
. Also set
$i(\mathfrak {g},\chi )=(\frac {b^{\chi }_0}{2}| \lfloor \frac {b^{\chi }_1}{2}\rfloor )$
. Also set
 $$ \begin{align*}\mathscr{M}(\mathfrak{g}) =\max_{\chi\in \mathfrak{g}_{\bar 0}^{*}}p^{\frac{b^{\chi}_0}{2}}2^{{\lfloor\frac{b^{\chi}_1}{2}\rfloor}}.\end{align*} $$
$$ \begin{align*}\mathscr{M}(\mathfrak{g}) =\max_{\chi\in \mathfrak{g}_{\bar 0}^{*}}p^{\frac{b^{\chi}_0}{2}}2^{{\lfloor\frac{b^{\chi}_1}{2}\rfloor}}.\end{align*} $$
Conjecture 2.3 Let
![]() $\mathfrak {g}$
be a finite-dimensional restricted Lie superalgebra over
$\mathfrak {g}$
be a finite-dimensional restricted Lie superalgebra over
![]() $\mathbf {k}$
. The maximal dimension of irreducible
$\mathbf {k}$
. The maximal dimension of irreducible
![]() $\mathfrak {g}$
-modules is
$\mathfrak {g}$
-modules is
![]() $\mathscr {M}(\mathfrak {g})$
.
$\mathscr {M}(\mathfrak {g})$
.
Remark 2.4 (1) Clearly, by definition,
![]() $\mathscr {M}(\mathfrak {g})$
can be expressed as
$\mathscr {M}(\mathfrak {g})$
can be expressed as
![]() $p^{\frac {b_0}{2}}2^{\lfloor \frac {b_1}{2}\rfloor }$
for some nonnegative integers
$p^{\frac {b_0}{2}}2^{\lfloor \frac {b_1}{2}\rfloor }$
for some nonnegative integers
![]() $b_0$
and
$b_0$
and
![]() $b_1$
. In general, such
$b_1$
. In general, such
![]() $b_0$
and
$b_0$
and
![]() $b_1$
are not necessarily unique. However, we will see that in many cases,
$b_1$
are not necessarily unique. However, we will see that in many cases,
![]() $b_0=\max _{\chi \in \mathfrak {g}_{\bar 0}^{*}}b_0^{\chi }$
and
$b_0=\max _{\chi \in \mathfrak {g}_{\bar 0}^{*}}b_0^{\chi }$
and
![]() $b_1=\max _{\chi \in \mathfrak {g}_{\bar 0}^{*}}b^{\chi }_1$
, which are unique.
$b_1=\max _{\chi \in \mathfrak {g}_{\bar 0}^{*}}b^{\chi }_1$
, which are unique.
(2) The formulation in the above conjecture becomes the first Kac–Weisfeiler conjecture when
![]() $\mathfrak {g}_{\bar 1}=0$
, i.e., a finite-dimensional restricted Lie algebra
$\mathfrak {g}_{\bar 1}=0$
, i.e., a finite-dimensional restricted Lie algebra
![]() $\mathfrak {g}_{\bar 0}$
is regarded a restricted Lie superalgebra with the odd part being zero.
$\mathfrak {g}_{\bar 0}$
is regarded a restricted Lie superalgebra with the odd part being zero.
(3) This conjecture is a super version of the first Kac–Weisfeiler conjecture on irreducible modules of restricted Lie algebras (see [Reference Kac12]).Footnote 1 For the latter, the study has been in a great progress, but the question is still open (see [Reference Martin, Stewart and Topley15, Reference Premet and Skryabin18]). There are remarkable works (see [Reference Kac12, Reference Premet17, Reference Wang and Zhao29]) concerning another (the second) Kac–Weisfeiler conjecture on irreducible modules of Lie algebras of reductive groups in prime characteristic and its super version. Some related progress can be found in [Reference Goodwin and Topley9, Reference Wang and Zhao30, Reference Zeng and Shu39, Reference Zeng and Shu40].
3 Irreducible modules of basic classical Lie superalgebras
In this section, we suppose
![]() $\mathfrak {g}$
is a basic classical Lie superalgebra over
$\mathfrak {g}$
is a basic classical Lie superalgebra over
![]() $\mathbf {k}$
. Then
$\mathbf {k}$
. Then
![]() $\mathfrak {g}=\mathfrak {g}_{\bar 0}\oplus \mathfrak {g}_{\bar 1}$
with even part being a reductive Lie algebra. As to classical Lie superalgebras of type P and Q, Conjecture 2.3 was very recently confirmed by taking quite different and nontrivial arguments (see [Reference Ren, Shu, Yang and Zhang19]).
$\mathfrak {g}=\mathfrak {g}_{\bar 0}\oplus \mathfrak {g}_{\bar 1}$
with even part being a reductive Lie algebra. As to classical Lie superalgebras of type P and Q, Conjecture 2.3 was very recently confirmed by taking quite different and nontrivial arguments (see [Reference Ren, Shu, Yang and Zhang19]).
3.1 Basic classical Lie superalgebras
We list basic classical Lie superalgebras and their even parts over
![]() $\mathbf {k}$
with the restriction on p (see, for example, [Reference Kac11, Reference Wang and Zhao29]). The restriction on p could be relaxed, but we always assume this restriction on p in this section). The most important feature is that each basic classical Lie superalgebra listed below admits a nondegenerate even supersymmetric bilinear form.
$\mathbf {k}$
with the restriction on p (see, for example, [Reference Kac11, Reference Wang and Zhao29]). The restriction on p could be relaxed, but we always assume this restriction on p in this section). The most important feature is that each basic classical Lie superalgebra listed below admits a nondegenerate even supersymmetric bilinear form.
3.1.1

For Lie superalgebra
![]() $\mathfrak {g}$
in the list, there is an algebraic supergroup G with
$\mathfrak {g}$
in the list, there is an algebraic supergroup G with
![]() $\mathsf {Lie}(G)=\mathfrak {g}$
satisfying:
$\mathsf {Lie}(G)=\mathfrak {g}$
satisfying:
-
(1) G has a purely-even subgroup scheme
 $G_{\text {ev}}$
which is an ordinary connected reductive algebraic group with
$G_{\text {ev}}$
which is an ordinary connected reductive algebraic group with
 $\mathsf {Lie}(G_{\text {ev}})=\mathfrak {g}_{\bar 0}$
.
$\mathsf {Lie}(G_{\text {ev}})=\mathfrak {g}_{\bar 0}$
. -
(2) There is a well-defined action of
 $G_{\text {ev}}$
on
$G_{\text {ev}}$
on
 $\mathfrak {g}$
, giving rise to the adjoint action of
$\mathfrak {g}$
, giving rise to the adjoint action of
 $\mathfrak {g}_{\bar 0}$
.
$\mathfrak {g}_{\bar 0}$
.
The above algebraic supergroup are usually called basic classical supergroups, which can be constructed as Chevalley supergroups (see [Reference Fioresi and Gavarini7, Reference Fioresi and Gavarini8]). Generally, for an algebraic supergroup G with
![]() $\mathfrak {g}=\mathsf {Lie}(G)$
,
$\mathfrak {g}=\mathsf {Lie}(G)$
,
![]() $\mathfrak {g}$
does not determine G. Instead, the theory of super groups shows that the pair
$\mathfrak {g}$
does not determine G. Instead, the theory of super groups shows that the pair
![]() $(G_{\text {ev}}, \mathfrak {g})$
determines G (see, for example, [Reference Carmeli, Caston and Fioresi4, Chapter 7]). The pair
$(G_{\text {ev}}, \mathfrak {g})$
determines G (see, for example, [Reference Carmeli, Caston and Fioresi4, Chapter 7]). The pair
![]() $(G_{\text {ev}},\mathfrak {g})$
is called a super Harish–Chandra pair (ibid.). More precisely, the category of algebraic supergroups is equivalent to the category of super Harish–Chandra pairs (ibid.).
$(G_{\text {ev}},\mathfrak {g})$
is called a super Harish–Chandra pair (ibid.). More precisely, the category of algebraic supergroups is equivalent to the category of super Harish–Chandra pairs (ibid.).
One easily knows that
![]() $\mathfrak {g}=\mathsf {Lie}(G)$
for an algebraic supergroup G is a restricted Lie superalgebra (cf. [Reference Shu and Wang21, Lemma 2.2] or [Reference Shu and Zheng25]).
$\mathfrak {g}=\mathsf {Lie}(G)$
for an algebraic supergroup G is a restricted Lie superalgebra (cf. [Reference Shu and Wang21, Lemma 2.2] or [Reference Shu and Zheng25]).
Let
![]() $\mathfrak {g}$
be a given basic classical Lie superalgebra. We fix a Cartan subalgebra
$\mathfrak {g}$
be a given basic classical Lie superalgebra. We fix a Cartan subalgebra
![]() $\mathfrak {h}$
in
$\mathfrak {h}$
in
![]() $\mathfrak {g}_{\bar 0}$
. Denote by
$\mathfrak {g}_{\bar 0}$
. Denote by
![]() $\Phi $
, the root system associate with
$\Phi $
, the root system associate with
![]() $\mathfrak {h}$
. Then
$\mathfrak {h}$
. Then
![]() $\Phi =\Phi _0\cup \Phi _1$
, where
$\Phi =\Phi _0\cup \Phi _1$
, where
![]() $\Phi _0$
stands for the set of even roots, and
$\Phi _0$
stands for the set of even roots, and
![]() $\Phi _1$
for the set of odd roots. Fix a triangular decomposition
$\Phi _1$
for the set of odd roots. Fix a triangular decomposition
![]() $\mathfrak {g} = \mathfrak {n}^-\oplus \mathfrak {h} \oplus \mathfrak {n}^+$
which is equivalent to say, fix a positive root system
$\mathfrak {g} = \mathfrak {n}^-\oplus \mathfrak {h} \oplus \mathfrak {n}^+$
which is equivalent to say, fix a positive root system
![]() $\Phi ^+$
, or to say fix a simple root system
$\Phi ^+$
, or to say fix a simple root system
![]() $\Delta $
. Here,
$\Delta $
. Here,
![]() $\mathfrak {n}^{\pm }$
stand the Lie subalgebras of positive and negative root vectors, respectively. Furthermore,
$\mathfrak {n}^{\pm }$
stand the Lie subalgebras of positive and negative root vectors, respectively. Furthermore,
![]() $\Phi ^-=-\Phi ^+$
, and
$\Phi ^-=-\Phi ^+$
, and
![]() $\Phi ^{\pm }=\Phi _1^{\pm }\cup \Phi _0^{\pm }$
. Moreover, without loss of generality we can assume
$\Phi ^{\pm }=\Phi _1^{\pm }\cup \Phi _0^{\pm }$
. Moreover, without loss of generality we can assume
![]() $\chi (\mathfrak {n}^+_{\bar 0})=0$
for any
$\chi (\mathfrak {n}^+_{\bar 0})=0$
for any
![]() $\chi \in \mathfrak {g}_{\bar 0}^{*}$
, up to
$\chi \in \mathfrak {g}_{\bar 0}^{*}$
, up to
![]() $G_{\text {ev}}$
-conjugation. Let
$G_{\text {ev}}$
-conjugation. Let
![]() $\mathfrak {b}= \mathfrak {h}\oplus \mathfrak {n}^+$
. Then any
$\mathfrak {b}= \mathfrak {h}\oplus \mathfrak {n}^+$
. Then any
![]() $\lambda \in \mathfrak {h}^{*}$
defines a one-dimensional
$\lambda \in \mathfrak {h}^{*}$
defines a one-dimensional
![]() $U_{\chi }(\mathfrak {h})$
-module
$U_{\chi }(\mathfrak {h})$
-module
![]() $\mathbf {k}_{\lambda }$
as long as
$\mathbf {k}_{\lambda }$
as long as
![]() $\lambda $
satisfies
$\lambda $
satisfies
![]() $\lambda (H)^p-\lambda (H^{[p]}) =\chi (H)^p$
for all
$\lambda (H)^p-\lambda (H^{[p]}) =\chi (H)^p$
for all
![]() $H\in \mathfrak {h}$
. Set
$H\in \mathfrak {h}$
. Set
which clearly contains
![]() $p^{\dim \mathfrak {h}}$
elements.
$p^{\dim \mathfrak {h}}$
elements.
The one-dimensional space
![]() $\mathbf {k}_{\lambda }$
can be regarded a
$\mathbf {k}_{\lambda }$
can be regarded a
![]() $U_{\chi }(\mathfrak {b})$
-module with trivial
$U_{\chi }(\mathfrak {b})$
-module with trivial
![]() $\mathfrak {n}^+$
-action, because of
$\mathfrak {n}^+$
-action, because of
![]() $\chi (\mathfrak {n}^+_{\bar 0})=0$
. Then we define an induced module (called a baby Verma module)
$\chi (\mathfrak {n}^+_{\bar 0})=0$
. Then we define an induced module (called a baby Verma module)
Obviously,
![]() $\dim Z_{\chi }(\lambda )=p^{\dim \mathfrak {n}_{\bar 0}^-} 2^{\dim \mathfrak {n}_{\bar 1}^-}$
. The following fact is clear.
$\dim Z_{\chi }(\lambda )=p^{\dim \mathfrak {n}_{\bar 0}^-} 2^{\dim \mathfrak {n}_{\bar 1}^-}$
. The following fact is clear.
Lemma 3.1 Any irreducible
![]() $U_{\chi }(\mathfrak {g})$
-module has dimension not bigger than
$U_{\chi }(\mathfrak {g})$
-module has dimension not bigger than
![]() $\dim Z_{\chi }(\lambda )$
.
$\dim Z_{\chi }(\lambda )$
.
The proof is standard. We give an account on it. By the above arguments, we only need to consider the case
![]() $\chi (\mathfrak {n}^+)=0$
. In this case, for any irreducible
$\chi (\mathfrak {n}^+)=0$
. In this case, for any irreducible
![]() $U_{\chi }(\mathfrak {g})$
-module V,
$U_{\chi }(\mathfrak {g})$
-module V,
![]() $\mathfrak {n}^+$
acts nilpotently on V. Hence, V admits one-dimensional
$\mathfrak {n}^+$
acts nilpotently on V. Hence, V admits one-dimensional
![]() $U_{\chi }(\mathfrak {b})$
-module
$U_{\chi }(\mathfrak {b})$
-module
![]() $\mathbf {k}_{\lambda }$
with
$\mathbf {k}_{\lambda }$
with
![]() $\mathfrak {n}^+$
-trivial action, and
$\mathfrak {n}^+$
-trivial action, and
![]() $U_{\chi }(\mathfrak {h})$
-action by some function
$U_{\chi }(\mathfrak {h})$
-action by some function
![]() $\lambda \in \Lambda (\chi )$
. So V coincides with
$\lambda \in \Lambda (\chi )$
. So V coincides with
![]() $U_{\chi }(\mathfrak {n}^-)\mathbf {k}_{\lambda }$
which is isomorphic to an irreducible quotient of
$U_{\chi }(\mathfrak {n}^-)\mathbf {k}_{\lambda }$
which is isomorphic to an irreducible quotient of
![]() $Z_{\chi }(\lambda )$
. The lemma follows.
$Z_{\chi }(\lambda )$
. The lemma follows.
Recall that
![]() $\mathfrak {g}_{\bar 0}=\mathsf {Lie}(G_{\text {ev}})$
, and any element
$\mathfrak {g}_{\bar 0}=\mathsf {Lie}(G_{\text {ev}})$
, and any element
![]() $X\in \mathfrak {g}_{\bar 0}$
admits Jordan–Chevalley decomposition
$X\in \mathfrak {g}_{\bar 0}$
admits Jordan–Chevalley decomposition
![]() $X=X_s+X_n$
with
$X=X_s+X_n$
with
![]() $X_s$
being semisimple and
$X_s$
being semisimple and
![]() $X_n$
nilpotent. Note that for a basic classical Lie algebra
$X_n$
nilpotent. Note that for a basic classical Lie algebra
![]() $\mathfrak {g}$
listed in 3.1.1, there is a nondegenerate
$\mathfrak {g}$
listed in 3.1.1, there is a nondegenerate
![]() $G_{\bar 0}$
-invariant symmetric bilinear form
$G_{\bar 0}$
-invariant symmetric bilinear form
![]() $(\cdot ,\cdot )$
on
$(\cdot ,\cdot )$
on
![]() $\mathfrak {g}_{\bar 0}$
. Hence, there is a G-equivariant isomorphism between
$\mathfrak {g}_{\bar 0}$
. Hence, there is a G-equivariant isomorphism between
![]() $\mathfrak {g}_{\bar 0}$
and
$\mathfrak {g}_{\bar 0}$
and
![]() $\mathfrak {g}_{\bar 0}^{*}$
. Consequently, for any
$\mathfrak {g}_{\bar 0}^{*}$
. Consequently, for any
![]() $\chi \in \mathfrak {g}_{\bar 0}^{*}$
, there exists a unique X such that
$\chi \in \mathfrak {g}_{\bar 0}^{*}$
, there exists a unique X such that
![]() $\chi =(X,-)$
, which leads to the Jordan–Chevalley decomposition
$\chi =(X,-)$
, which leads to the Jordan–Chevalley decomposition
![]() $\chi =\chi _s+\chi _n$
with
$\chi =\chi _s+\chi _n$
with
![]() $\chi _s=(X_s,-)$
and
$\chi _s=(X_s,-)$
and
![]() $\chi _n=(X_n,-)$
. Furthermore, there exists
$\chi _n=(X_n,-)$
. Furthermore, there exists
![]() $g\in G_{\text {ev}}$
such that
$g\in G_{\text {ev}}$
such that
![]() $(g.\chi _s)(\mathfrak {n}_{\bar 0}^{\pm })=0$
, and
$(g.\chi _s)(\mathfrak {n}_{\bar 0}^{\pm })=0$
, and
![]() $(g.\chi _n)(\mathfrak {b}_{\bar 0})=0,$
where the action of
$(g.\chi _n)(\mathfrak {b}_{\bar 0})=0,$
where the action of
![]() $g.$
means the coadjoint action. We say that
$g.$
means the coadjoint action. We say that
![]() $\chi $
is semisimple if
$\chi $
is semisimple if
![]() $\chi =\chi _s$
, and that
$\chi =\chi _s$
, and that
![]() $\chi $
is nilpotent if
$\chi $
is nilpotent if
![]() $\chi =\chi _n$
. For simplicity, we always assume that
$\chi =\chi _n$
. For simplicity, we always assume that
![]() $\chi =\chi _s+\chi _n$
with
$\chi =\chi _s+\chi _n$
with
![]() $\chi _s(\mathfrak {n}_{\bar 0}^{\pm })=0$
, and
$\chi _s(\mathfrak {n}_{\bar 0}^{\pm })=0$
, and
![]() $\chi _n(\mathfrak {b}_{\bar 0})=0$
in the following because the coadjoint action gives rise to an isomorphism between
$\chi _n(\mathfrak {b}_{\bar 0})=0$
in the following because the coadjoint action gives rise to an isomorphism between
![]() $U_{\chi }(\mathfrak {g})$
and
$U_{\chi }(\mathfrak {g})$
and
![]() $U_{g.\chi }(\mathfrak {g})$
.
$U_{g.\chi }(\mathfrak {g})$
.
For a semisimple p-character
![]() $\chi \in \mathfrak {g}_{\bar 0}^{*}$
, we say that
$\chi \in \mathfrak {g}_{\bar 0}^{*}$
, we say that
![]() $\chi $
is regular semisimple if
$\chi $
is regular semisimple if
![]() $\chi (H_{\alpha })$
are nonzero for all
$\chi (H_{\alpha })$
are nonzero for all
![]() $\alpha $
from
$\alpha $
from
![]() $\Phi $
, where
$\Phi $
, where
![]() $H_{\alpha }$
is the Cartan toral element corresponding to
$H_{\alpha }$
is the Cartan toral element corresponding to
![]() $\alpha $
. By Lei Zhao’s result, we have the following theorem.
$\alpha $
. By Lei Zhao’s result, we have the following theorem.
Theorem 3.2 [Reference Zhao42, Theorems 4.6 and 4.7]
Suppose
![]() $\chi $
is regular semisimple, and
$\chi $
is regular semisimple, and
![]() $\lambda \in \Lambda _{\chi }$
. Then
$\lambda \in \Lambda _{\chi }$
. Then
![]() $Z_{\chi }(\lambda )$
is irreducible.
$Z_{\chi }(\lambda )$
is irreducible.
For a regular semisimple p-character
![]() $\chi \in \mathfrak {g}_{\bar 0}^{*}$
, from the definition, it follows that
$\chi \in \mathfrak {g}_{\bar 0}^{*}$
, from the definition, it follows that
![]() $\mathfrak {z}^{\chi }=\mathfrak {h}$
. Hence,
$\mathfrak {z}^{\chi }=\mathfrak {h}$
. Hence,
![]() $(\frac {b_0^{\chi }}{2}\mid {\lfloor \frac {b_1^{\chi }}{2}\rfloor })=(\dim \mathfrak {n}^-_{\bar 0}\mid \dim \mathfrak {n}^-_{\bar 1})$
. Correspondingly,
$(\frac {b_0^{\chi }}{2}\mid {\lfloor \frac {b_1^{\chi }}{2}\rfloor })=(\dim \mathfrak {n}^-_{\bar 0}\mid \dim \mathfrak {n}^-_{\bar 1})$
. Correspondingly,
![]() $\dim Z_{\chi }(\lambda )= p^{\frac {b_0^{\chi }}{2}}2^{{\lfloor \frac {b_1^{\chi }}{2}\rfloor }}$
, which coincides with
$\dim Z_{\chi }(\lambda )= p^{\frac {b_0^{\chi }}{2}}2^{{\lfloor \frac {b_1^{\chi }}{2}\rfloor }}$
, which coincides with
![]() $p^{\frac {b_0}{2}}2^{{\lfloor \frac {b_1}{2}\rfloor }}$
. On the other hand, Wang–Zhao’s theorem concerning Kac–Weisfeiler property (see [Reference Wang and Zhao29, Theorem 4.3]) says that for any
$p^{\frac {b_0}{2}}2^{{\lfloor \frac {b_1}{2}\rfloor }}$
. On the other hand, Wang–Zhao’s theorem concerning Kac–Weisfeiler property (see [Reference Wang and Zhao29, Theorem 4.3]) says that for any
![]() $\chi \in \mathfrak {g}_{\bar 0}^{*}$
and any irreducible
$\chi \in \mathfrak {g}_{\bar 0}^{*}$
and any irreducible
![]() $U_{\chi }(\mathfrak {g})$
-module V,
$U_{\chi }(\mathfrak {g})$
-module V,
![]() $\dim V$
is divisible by
$\dim V$
is divisible by
![]() $p^{\frac {b_0^{\chi }}{2}}2^{{\lfloor \frac {b_1^{\chi }}{2}\rfloor }}$
. Hence, we have
$p^{\frac {b_0^{\chi }}{2}}2^{{\lfloor \frac {b_1^{\chi }}{2}\rfloor }}$
. Hence, we have
Combining the above with Lemma 3.1 and Theorem 3.2, we finally have the following result.
Corollary 3.3 Suppose
![]() $\mathfrak {g}$
is a basic classical Lie superalgebra over
$\mathfrak {g}$
is a basic classical Lie superalgebra over
![]() $\mathbf {k}$
. Then the maximal dimension of irreducible
$\mathbf {k}$
. Then the maximal dimension of irreducible
![]() $U(\mathfrak {g})$
-modules is exactly
$U(\mathfrak {g})$
-modules is exactly
![]() $\mathscr {M}(\mathfrak {g})$
. Moreover,
$\mathscr {M}(\mathfrak {g})$
. Moreover,
![]() $\mathscr {M}(\mathfrak {g})$
can be precisely described as
$\mathscr {M}(\mathfrak {g})$
can be precisely described as
![]() $p^{\frac {b_0}{2}}2^{{\lfloor \frac {b_1}{2}\rfloor }}$
for
$p^{\frac {b_0}{2}}2^{{\lfloor \frac {b_1}{2}\rfloor }}$
for
![]() $b_0=\max \{b^{\chi }_0|\chi \in \mathfrak {g}_{\bar 0}^{*}\}$
and
$b_0=\max \{b^{\chi }_0|\chi \in \mathfrak {g}_{\bar 0}^{*}\}$
and
![]() $b_1=\max \{b^{\chi }_1|\chi \in \mathfrak {g}_{\bar 0}^{*}\}$
.
$b_1=\max \{b^{\chi }_1|\chi \in \mathfrak {g}_{\bar 0}^{*}\}$
.
Consequently, the statement of Conjecture 2.3 is true for basic classical Lie superalgebras.
4 Irreducible modules of solvable Lie superalgebras
In the next two sections, we will study irreducible representations of finite-dimensional solvable Lie superalgebras over
![]() $\mathbf {k}$
, by exploiting the arguments for ordinary solvable Lie algebras (see [Reference Schue20, Reference Weisfeiler and Kac31] or [Reference Strade and Farnsteiner26, Chapter 5]). Keep the notations and assumptions as before. In particular, for a Lie (super)algebra L, we denote by
$\mathbf {k}$
, by exploiting the arguments for ordinary solvable Lie algebras (see [Reference Schue20, Reference Weisfeiler and Kac31] or [Reference Strade and Farnsteiner26, Chapter 5]). Keep the notations and assumptions as before. In particular, for a Lie (super)algebra L, we denote by
![]() $L^{(1)}$
the derived subalgebra of L, i.e.,
$L^{(1)}$
the derived subalgebra of L, i.e.,
![]() $L^{(1)}=[L,L]$
.
$L^{(1)}=[L,L]$
.
4.1 Basic properties on solvable Lie superalgebras
The following results are important for the later arguments.
Lemma 4.1 Let
![]() $\mathfrak {g}=\mathfrak {g}_{\bar 0}+\mathfrak {g}_{\bar 1}$
is a finite-dimensional Lie superalgebra over
$\mathfrak {g}=\mathfrak {g}_{\bar 0}+\mathfrak {g}_{\bar 1}$
is a finite-dimensional Lie superalgebra over
![]() $\mathbf {k}$
.
$\mathbf {k}$
.
-
(1) Suppose V is an irreducible module of
 $\mathfrak {g}$
. If all elements of
$\mathfrak {g}$
. If all elements of
 $[\mathfrak {g},\mathfrak {g}]$
act nilpotently on V, then V is one-dimensional.
$[\mathfrak {g},\mathfrak {g}]$
act nilpotently on V, then V is one-dimensional. -
(2) Suppose additionally,
 $\mathfrak {g}$
is solvable and non-abelian, then the center
$\mathfrak {g}$
is solvable and non-abelian, then the center
 $C(\mathfrak {g}):=\{X\in \mathfrak {g}\mid \mathsf {ad}(X)(\mathfrak {g})=0\}$
does not contain all abelian ideals of
$C(\mathfrak {g}):=\{X\in \mathfrak {g}\mid \mathsf {ad}(X)(\mathfrak {g})=0\}$
does not contain all abelian ideals of
 $\mathfrak {g}$
.
$\mathfrak {g}$
.
Proof (1) It is an obvious fact.
(2) We prove this statement by reductio ad absurdum. Suppose
![]() $C(\mathfrak {g})$
contains all abelian ideals. We intend to deduce a contradiction.
$C(\mathfrak {g})$
contains all abelian ideals. We intend to deduce a contradiction.
Note that
![]() $C(\mathfrak {g})$
is an ideal of
$C(\mathfrak {g})$
is an ideal of
![]() $\mathfrak {g}$
. Consider the natural surjective homomorphism of Lie superalgebras
$\mathfrak {g}$
. Consider the natural surjective homomorphism of Lie superalgebras
![]() $\bar {}:\mathfrak {g}\rightarrow \mathfrak {g}/ C(\mathfrak {g})$
. Of course,
$\bar {}:\mathfrak {g}\rightarrow \mathfrak {g}/ C(\mathfrak {g})$
. Of course,
![]() $\bar {\mathfrak {g}}= \mathfrak {g}/ C(\mathfrak {g})$
. By assumption,
$\bar {\mathfrak {g}}= \mathfrak {g}/ C(\mathfrak {g})$
. By assumption,
![]() $\bar {\mathfrak {g}}\ne 0$
which is still a solvable Lie superalgebra. Take a minimal ideal
$\bar {\mathfrak {g}}\ne 0$
which is still a solvable Lie superalgebra. Take a minimal ideal
![]() $I=I_{\bar 0}+I_{\bar 1}\lhd \mathfrak {g}$
containing
$I=I_{\bar 0}+I_{\bar 1}\lhd \mathfrak {g}$
containing
![]() $C(\mathfrak {g})$
properly. The solvableness of
$C(\mathfrak {g})$
properly. The solvableness of
![]() $\mathfrak {g}$
yields that I properly contains
$\mathfrak {g}$
yields that I properly contains
![]() $I^{(1)}$
. So
$I^{(1)}$
. So
![]() $I^{(1)}\subset C(\mathfrak {g})$
. Under the assumption of
$I^{(1)}\subset C(\mathfrak {g})$
. Under the assumption of
![]() $C(L)$
containing all abelian ideas, it follows that
$C(L)$
containing all abelian ideas, it follows that
![]() $I^{(1)}\ne 0$
. Consequently,
$I^{(1)}\ne 0$
. Consequently,
![]() $I_{\bar 0}\ne 0$
. Moreover, there exists a linear function
$I_{\bar 0}\ne 0$
. Moreover, there exists a linear function
![]() $\lambda \in C(\mathfrak {g})^{*}$
such that
$\lambda \in C(\mathfrak {g})^{*}$
such that
![]() $\lambda |_{I^{(1)}}\ne 0$
. Note that
$\lambda |_{I^{(1)}}\ne 0$
. Note that
![]() $\bar {I}\ne 0$
and it becomes an irreducible
$\bar {I}\ne 0$
and it becomes an irreducible
![]() $\mathfrak {g}$
-modules. This irreducible representation of
$\mathfrak {g}$
-modules. This irreducible representation of
![]() $\mathfrak {g}$
on
$\mathfrak {g}$
on
![]() $\bar {I}$
is denoted by
$\bar {I}$
is denoted by
![]() $(\rho ,\bar {I})$
. The linear function
$(\rho ,\bar {I})$
. The linear function
![]() $\lambda $
gives rise to a bilinear form
$\lambda $
gives rise to a bilinear form
![]() $\Lambda $
on
$\Lambda $
on
![]() $\bar {I}$
by defining
$\bar {I}$
by defining
![]() $\Lambda :\bar I\times \bar I\rightarrow \mathbf {k}$
via
$\Lambda :\bar I\times \bar I\rightarrow \mathbf {k}$
via
![]() $\Lambda (\bar v_1,\bar v_2)=\lambda ([\bar v_1,\bar v_2])$
for any
$\Lambda (\bar v_1,\bar v_2)=\lambda ([\bar v_1,\bar v_2])$
for any
![]() $v_1,v_2\in I$
. Then it is easily checked that
$v_1,v_2\in I$
. Then it is easily checked that
![]() $\Lambda $
satisfies
$\Lambda $
satisfies
![]() $\mathfrak {g}_{\bar 0}$
-invariant property in the sense that
$\mathfrak {g}_{\bar 0}$
-invariant property in the sense that
where
![]() $X.\bar v_i=\overline {[X,v_i]}$
. As
$X.\bar v_i=\overline {[X,v_i]}$
. As
![]() $\lambda \ne 0$
, we can take
$\lambda \ne 0$
, we can take
![]() $\bar v,\bar w$
such that
$\bar v,\bar w$
such that
![]() $\Lambda (\bar v,\bar w)\ne 0$
.
$\Lambda (\bar v,\bar w)\ne 0$
.
We claim
![]() $\rho (\mathfrak {g})=0$
, which means
$\rho (\mathfrak {g})=0$
, which means
![]() $\mathfrak {g}$
acts trivially on
$\mathfrak {g}$
acts trivially on
![]() $\bar I$
. Otherwise, if
$\bar I$
. Otherwise, if
![]() $\rho (\mathfrak {g})$
is nonzero, then there exists a nonzero abelian ideal J because
$\rho (\mathfrak {g})$
is nonzero, then there exists a nonzero abelian ideal J because
![]() $\rho (\mathfrak {g})$
is solvable. For any given nonzero
$\rho (\mathfrak {g})$
is solvable. For any given nonzero
![]() $Z\in J_{\bar 0}$
, consider the action of
$Z\in J_{\bar 0}$
, consider the action of
![]() $Z^p$
on
$Z^p$
on
![]() $\bar I$
. Note that for any
$\bar I$
. Note that for any
![]() $Y\in \rho (\mathfrak {g})$
,
$Y\in \rho (\mathfrak {g})$
,
![]() $[Z^p,Y]=\mathsf {ad}(Z)^p Y\in J^{(1)}=0$
. By Schur’s lemma, there exists
$[Z^p,Y]=\mathsf {ad}(Z)^p Y\in J^{(1)}=0$
. By Schur’s lemma, there exists
![]() $\alpha (Z)\in \mathbf {k}$
such that
$\alpha (Z)\in \mathbf {k}$
such that
![]() $Z^p.\bar v=\alpha (Z)\bar v$
for any
$Z^p.\bar v=\alpha (Z)\bar v$
for any
![]() $Z^p\bar v=\alpha (Z)\bar v$
. Comparing with (4.1), we have
$Z^p\bar v=\alpha (Z)\bar v$
. Comparing with (4.1), we have
Hence,
![]() $\alpha (Z)=0$
for all
$\alpha (Z)=0$
for all
![]() $Z\in J_{\bar 0}$
. Thus,
$Z\in J_{\bar 0}$
. Thus,
![]() $J_{\bar 0}$
acts nilpotently on
$J_{\bar 0}$
acts nilpotently on
![]() $\bar I$
, naturally so does
$\bar I$
, naturally so does
![]() $J_{\bar 1}$
. But
$J_{\bar 1}$
. But
![]() $\bar I$
is irreducible, which implies that J acts trivially on
$\bar I$
is irreducible, which implies that J acts trivially on
![]() $\bar I$
. This is to say
$\bar I$
. This is to say
![]() $J=0$
, a contraction.
$J=0$
, a contraction.
By the arguments, it is already deduced that
![]() $\rho (\mathfrak {g})=0$
and the irreducible
$\rho (\mathfrak {g})=0$
and the irreducible
![]() $\mathfrak {g}$
-module
$\mathfrak {g}$
-module
![]() $\bar I$
must be one-dimensional. This means,
$\bar I$
must be one-dimensional. This means,
![]() $I=\mathbf {k} v+C(\mathfrak {g})$
for
$I=\mathbf {k} v+C(\mathfrak {g})$
for
![]() $v\in \mathfrak {g}$
, which leads to a contradiction
$v\in \mathfrak {g}$
, which leads to a contradiction
![]() $I^{(1)}=0$
. The proof is completed.
$I^{(1)}=0$
. The proof is completed.
4.2 Induced modules for solvable restricted Lie superalgebras
Now, we begin to investigate irreducible modules of solvable restricted Lie superalgebras. In the following two subsections, we assume that
![]() $\mathfrak {g}=\mathfrak {g}_{\bar 0}+\mathfrak {g}_{\bar 1}$
is a finite-dimensional solvable restricted Lie superalgebra, and
$\mathfrak {g}=\mathfrak {g}_{\bar 0}+\mathfrak {g}_{\bar 1}$
is a finite-dimensional solvable restricted Lie superalgebra, and
![]() $\chi \in \mathfrak {g}_{\bar 0}^{*}$
which will be often regarded a linear function on
$\chi \in \mathfrak {g}_{\bar 0}^{*}$
which will be often regarded a linear function on
![]() $\mathfrak {g}$
by trivial extension. At first, Lemma 4.1(1) implies the following conclusion.
$\mathfrak {g}$
by trivial extension. At first, Lemma 4.1(1) implies the following conclusion.
Lemma 4.2 Let
![]() $\mathfrak {g}=\mathfrak {g}_{\bar 0}+\mathfrak {g}_{\bar 1}$
be a finite-dimensional solvable restricted Lie superalgebra, and
$\mathfrak {g}=\mathfrak {g}_{\bar 0}+\mathfrak {g}_{\bar 1}$
be a finite-dimensional solvable restricted Lie superalgebra, and
![]() $\chi \in \mathfrak {g}^{*}_{\bar 0}$
. If
$\chi \in \mathfrak {g}^{*}_{\bar 0}$
. If
![]() $\mathfrak {g}^{(1)}$
is nilpotent, and
$\mathfrak {g}^{(1)}$
is nilpotent, and
![]() $\chi (\mathfrak {g}^{(1)})=0$
, then any irreducible
$\chi (\mathfrak {g}^{(1)})=0$
, then any irreducible
![]() $U_{\chi }(\mathfrak {g})$
-module is one-dimensional.
$U_{\chi }(\mathfrak {g})$
-module is one-dimensional.
Next, let
![]() $\rho :\mathfrak {g}\rightarrow \mathfrak {gl}(V)$
be a finite-dimensional representation of
$\rho :\mathfrak {g}\rightarrow \mathfrak {gl}(V)$
be a finite-dimensional representation of
![]() $U_{\chi }(\mathfrak {g})$
. Suppose I is an ideal of
$U_{\chi }(\mathfrak {g})$
. Suppose I is an ideal of
![]() $\mathfrak {g}$
such that
$\mathfrak {g}$
such that
![]() $I^{(1)}\subset \ker \rho $
and
$I^{(1)}\subset \ker \rho $
and
![]() $[\mathfrak {g},I]\nsubseteq \ker \rho $
. So there is an irreducible I-submodule in V which is one-dimensional. This yields that
$[\mathfrak {g},I]\nsubseteq \ker \rho $
. So there is an irreducible I-submodule in V which is one-dimensional. This yields that
is nonzero. Consider
![]() $I^{\chi }:=\{X\in \mathfrak {g}\mid \chi ([X,I])=0\}$
. It is easily shown that
$I^{\chi }:=\{X\in \mathfrak {g}\mid \chi ([X,I])=0\}$
. It is easily shown that
![]() $I^{\chi }$
is a restricted subalgebra of
$I^{\chi }$
is a restricted subalgebra of
![]() $\mathfrak {g}$
containing I. Clearly,
$\mathfrak {g}$
containing I. Clearly,
![]() $I^{\chi }$
is still solvable, and
$I^{\chi }$
is still solvable, and
![]() $V_{I,\chi }$
becomes a module of
$V_{I,\chi }$
becomes a module of
![]() $U_{\chi }(I^{\chi })$
from which we will consider an induced module of
$U_{\chi }(I^{\chi })$
from which we will consider an induced module of
![]() $U_{\chi }(\mathfrak {g})$
.
$U_{\chi }(\mathfrak {g})$
.
We claim that
![]() $I^{\chi }$
is a proper subalgebra of
$I^{\chi }$
is a proper subalgebra of
![]() $\mathfrak {g}$
. We will show this by reductio ad absurdum. If
$\mathfrak {g}$
. We will show this by reductio ad absurdum. If
![]() $\mathfrak {g}=I^{\chi }$
, then
$\mathfrak {g}=I^{\chi }$
, then
![]() $V_{I,\chi }$
is a
$V_{I,\chi }$
is a
![]() $U_{\chi }(\mathfrak {g})$
-submodule and therefore coincides with V, which means
$U_{\chi }(\mathfrak {g})$
-submodule and therefore coincides with V, which means
![]() $\rho |_{[\mathfrak {g},I]}=\chi |_{[\mathfrak {g},I]}\mathsf {id}_V=0$
. Thus
$\rho |_{[\mathfrak {g},I]}=\chi |_{[\mathfrak {g},I]}\mathsf {id}_V=0$
. Thus
![]() $[\mathfrak {g},I]\subset \ker \rho $
, which contradicts the condition of I. So we can take a cobasis
$[\mathfrak {g},I]\subset \ker \rho $
, which contradicts the condition of I. So we can take a cobasis
![]() $\{e_1,\ldots ,e_s\}$
of
$\{e_1,\ldots ,e_s\}$
of
![]() $I^{\chi }_{\bar 0}$
in
$I^{\chi }_{\bar 0}$
in
![]() $\mathfrak {g}_{\bar 0}$
for
$\mathfrak {g}_{\bar 0}$
for
![]() $s=\dim \mathfrak {g}_{\bar 0}-\dim I^{\chi }_{\bar 0}$
, and a cobasis
$s=\dim \mathfrak {g}_{\bar 0}-\dim I^{\chi }_{\bar 0}$
, and a cobasis
![]() $\{f_1,\ldots ,f_t\}$
of
$\{f_1,\ldots ,f_t\}$
of
![]() $I^{\chi }_{\bar 1}$
in
$I^{\chi }_{\bar 1}$
in
![]() $\mathfrak {g}_{\bar 1}$
for
$\mathfrak {g}_{\bar 1}$
for
![]() $t=\dim \mathfrak {g}_{\bar 1}-\dim I^{\chi }_{\bar 1}$
, which means
$t=\dim \mathfrak {g}_{\bar 1}-\dim I^{\chi }_{\bar 1}$
, which means
Now, we consider the induced module
![]() $\mathcal {V}:=U_{\chi }(\mathfrak {g})\otimes _{U_{\chi }(I^{\chi })}V_{I,\chi }$
which can be expressed as a vector space
$\mathcal {V}:=U_{\chi }(\mathfrak {g})\otimes _{U_{\chi }(I^{\chi })}V_{I,\chi }$
which can be expressed as a vector space
where
![]() $\alpha =(a_1,\ldots ,a_s)\in \mathbb {Z}_{\geq 0}^s$
and
$\alpha =(a_1,\ldots ,a_s)\in \mathbb {Z}_{\geq 0}^s$
and
![]() $\gamma =(c_1,\ldots ,c_t)\in \mathbb {Z}_{\geq 0}^t$
are s-tuple and t-tuple of nonnegative integers, respectively,
$\gamma =(c_1,\ldots ,c_t)\in \mathbb {Z}_{\geq 0}^t$
are s-tuple and t-tuple of nonnegative integers, respectively,
![]() $\mathbf {e}^{\alpha }:=e_1^{a_1}\ldots e_s^{a_s}$
, and
$\mathbf {e}^{\alpha }:=e_1^{a_1}\ldots e_s^{a_s}$
, and
![]() ${\mathbf {f}}^{\gamma }=f_1^{c_1}\ldots f_t^{c_t}$
with
${\mathbf {f}}^{\gamma }=f_1^{c_1}\ldots f_t^{c_t}$
with
and
Set
and put
 $$ \begin{align*}\mathcal{V}_{(l)}=\sum_{\underset{ ||(\alpha,\gamma)||\leq l}{(\alpha,\gamma)\in P^s\times E^t}}\mathbf{k} \mathbf{e}^{\alpha}\mathbf{f}^{\gamma}\otimes V_{I,\chi}.\end{align*} $$
$$ \begin{align*}\mathcal{V}_{(l)}=\sum_{\underset{ ||(\alpha,\gamma)||\leq l}{(\alpha,\gamma)\in P^s\times E^t}}\mathbf{k} \mathbf{e}^{\alpha}\mathbf{f}^{\gamma}\otimes V_{I,\chi}.\end{align*} $$
Consider
![]() $U_{\bar 0}=\sum _{i=1}^s\mathbf {k} e_i$
and
$U_{\bar 0}=\sum _{i=1}^s\mathbf {k} e_i$
and
![]() $U_{\bar 1}=\sum _{j=1}^t\mathbf {k} f_j$
. Define a linear map
$U_{\bar 1}=\sum _{j=1}^t\mathbf {k} f_j$
. Define a linear map
![]() $\varphi $
from
$\varphi $
from
![]() $U_{\bar 0}$
to
$U_{\bar 0}$
to
![]() $I_{\bar 0}^{*}$
by sending any given
$I_{\bar 0}^{*}$
by sending any given
![]() $X\in I$
onto the function
$X\in I$
onto the function
![]() $\textsf {B}_{\chi }(X,-)$
on I. By the definition of
$\textsf {B}_{\chi }(X,-)$
on I. By the definition of
![]() $I^{\chi }$
, this
$I^{\chi }$
, this
![]() $\varphi $
is nondegenerate. Hence, there is a set
$\varphi $
is nondegenerate. Hence, there is a set
![]() $\{Z_1,\ldots ,Z_s\}\subset I_{\bar 0}$
such that
$\{Z_1,\ldots ,Z_s\}\subset I_{\bar 0}$
such that
![]() $\psi (e_j)(Z_i)=\delta _{ij}$
for
$\psi (e_j)(Z_i)=\delta _{ij}$
for
![]() $1\leq i,j\leq s$
. Here and further,
$1\leq i,j\leq s$
. Here and further,
![]() $\delta _{ij}$
denotes the Kronecker function whose value at
$\delta _{ij}$
denotes the Kronecker function whose value at
![]() $(i,j)$
is zero when
$(i,j)$
is zero when
![]() $i\ne j$
and
$i\ne j$
and
![]() $1$
when
$1$
when
![]() $i=j$
. Similarly, consider a linear map
$i=j$
. Similarly, consider a linear map
![]() $\psi $
from
$\psi $
from
![]() $U_{\bar 1}$
to
$U_{\bar 1}$
to
![]() $I^{*}_{\bar 1}$
sending Y onto the function
$I^{*}_{\bar 1}$
sending Y onto the function
![]() $\textsf {B}_{\chi }(Y,-)$
on
$\textsf {B}_{\chi }(Y,-)$
on
![]() $I_{\bar 1}$
, and this
$I_{\bar 1}$
, and this
![]() $\psi $
is nondegenerate too. We can choose
$\psi $
is nondegenerate too. We can choose
![]() $\{T_1,\ldots ,T_t\}\subset I_{\bar 1}$
such that
$\{T_1,\ldots ,T_t\}\subset I_{\bar 1}$
such that
![]() $\psi (f_j)(T_i)=\delta _{ij}$
for
$\psi (f_j)(T_i)=\delta _{ij}$
for
![]() $1\leq i,j\leq t$
.
$1\leq i,j\leq t$
.
Lemma 4.3 Keep the notations and assumptions as above. For
![]() $\mathbf{e}^{\alpha }\mathbf{f}^{\gamma }\otimes v\in \mathcal {V}_{(l)}$
with
$\mathbf{e}^{\alpha }\mathbf{f}^{\gamma }\otimes v\in \mathcal {V}_{(l)}$
with
![]() $v\in V_{I,\chi }$
, the following formula holds:
$v\in V_{I,\chi }$
, the following formula holds:
 $$ \begin{align} &(Z_i-\chi(Z_i)). \mathbf{e}^{\alpha}\mathbf{f}^{\gamma}\otimes v\equiv a_i\mathbf{e}^{\alpha-\epsilon_i}\mathbf{f}^{\gamma}\otimes v\quad\mod\mathcal{V}_{(l-2)} \;\text{ if }\alpha\ne 0; \text{ and }\cr &T_j. \mathbf{f}^{\gamma}\otimes v\equiv c_j\mathbf{f}^{\gamma-\epsilon_j}\otimes v\quad\mod\mathcal{V}_{(l-2)} \;\text{ if }\alpha= 0. \end{align} $$
$$ \begin{align} &(Z_i-\chi(Z_i)). \mathbf{e}^{\alpha}\mathbf{f}^{\gamma}\otimes v\equiv a_i\mathbf{e}^{\alpha-\epsilon_i}\mathbf{f}^{\gamma}\otimes v\quad\mod\mathcal{V}_{(l-2)} \;\text{ if }\alpha\ne 0; \text{ and }\cr &T_j. \mathbf{f}^{\gamma}\otimes v\equiv c_j\mathbf{f}^{\gamma-\epsilon_j}\otimes v\quad\mod\mathcal{V}_{(l-2)} \;\text{ if }\alpha= 0. \end{align} $$
Proof We first generally introduce an order relation
![]() $\preceq $
on
$\preceq $
on
![]() $\mathbb {Z}_{\geq 0}^q$
(the set of q-tuples of nonnegative integers) by defining
$\mathbb {Z}_{\geq 0}^q$
(the set of q-tuples of nonnegative integers) by defining
![]() $\kappa \preceq \alpha $
for any given
$\kappa \preceq \alpha $
for any given
![]() $\kappa '=(k^{\prime }_1,\ldots ,k^{\prime }_q)$
,
$\kappa '=(k^{\prime }_1,\ldots ,k^{\prime }_q)$
,
![]() $\alpha '=(a_1',\ldots ,a^{\prime }_q)\in \mathbb {Z}_{\geq 0}^q$
if and only if
$\alpha '=(a_1',\ldots ,a^{\prime }_q)\in \mathbb {Z}_{\geq 0}^q$
if and only if
![]() $k^{\prime }_i\leq a^{\prime }_i$
for all i.
$k^{\prime }_i\leq a^{\prime }_i$
for all i.
Now, we turn to the situation for the lemma. Set
![]() $\epsilon _k:=(\delta _{1k},\ldots , \delta _{sk})$
,
$\epsilon _k:=(\delta _{1k},\ldots , \delta _{sk})$
,
![]() $k=1,\ldots , s$
. Recall the following formula for
$k=1,\ldots , s$
. Recall the following formula for
![]() $Z\in I_{\bar 0}:$
$Z\in I_{\bar 0}:$
here and further, we set
 $$ \begin{align*}||\kappa||:=\sum_{i=1}^sk_i\end{align*} $$
$$ \begin{align*}||\kappa||:=\sum_{i=1}^sk_i\end{align*} $$
for
![]() $\kappa =(k_1,\ldots ,k_s)\in \mathbb {Z}_{\geq 0}^s$
, and set
$\kappa =(k_1,\ldots ,k_s)\in \mathbb {Z}_{\geq 0}^s$
, and set
 $$ \begin{align*}{\alpha\choose\kappa}:=\sum_{i=1}^s{a_i\choose k_i},\end{align*} $$
$$ \begin{align*}{\alpha\choose\kappa}:=\sum_{i=1}^s{a_i\choose k_i},\end{align*} $$
and for
![]() $T\in I_{\bar 1}$
$T\in I_{\bar 1}$
So in the case when
![]() $\alpha \ne 0$
, we have
$\alpha \ne 0$
, we have
Note that any elements from
![]() $I^{\chi }_{\bar 1}$
act trivially on v. So we can write
$I^{\chi }_{\bar 1}$
act trivially on v. So we can write
 $$ \begin{align*} (Z_i-\chi(Z_i).\mathbf{e}^{\alpha}\mathbf{f}^{\gamma}\otimes v &\equiv \mathbf{e}^{\alpha}\mathbf{f}^{\gamma}(Z_i-\chi(Z_i))\otimes v- \sum_{k=1}^s a_k\mathbf{e}^{\alpha-\epsilon_k}\mathbf{f}^{\gamma} [e_k,Z_i]\otimes v \quad\mod \mathcal{V}_{(l-2)}\cr &\equiv a_i\mathbf{e}^{\alpha-\epsilon_i}\mathbf{f}^{\gamma} \otimes v \quad\mod \mathcal{V}_{(l-2)}. \end{align*} $$
$$ \begin{align*} (Z_i-\chi(Z_i).\mathbf{e}^{\alpha}\mathbf{f}^{\gamma}\otimes v &\equiv \mathbf{e}^{\alpha}\mathbf{f}^{\gamma}(Z_i-\chi(Z_i))\otimes v- \sum_{k=1}^s a_k\mathbf{e}^{\alpha-\epsilon_k}\mathbf{f}^{\gamma} [e_k,Z_i]\otimes v \quad\mod \mathcal{V}_{(l-2)}\cr &\equiv a_i\mathbf{e}^{\alpha-\epsilon_i}\mathbf{f}^{\gamma} \otimes v \quad\mod \mathcal{V}_{(l-2)}. \end{align*} $$
By the same arguments, we can deal with the case when
![]() $\alpha =0$
. We finally have
$\alpha =0$
. We finally have
 $$ \begin{align*} T_j\mathbf{f}^{\gamma}\otimes v &\equiv \mathbf{f}^{\gamma} T_j\otimes v+ \sum_{k=1}^t \mathbf{f}^{\gamma-\epsilon_k}[f_k, T_j]\otimes v\quad\mod \mathcal{V}_{(l-2)}\cr &\equiv \mathbf{f}^{\gamma-\epsilon_j}\otimes v \quad\mod \mathcal{V}_{(l-2)}. \end{align*} $$
$$ \begin{align*} T_j\mathbf{f}^{\gamma}\otimes v &\equiv \mathbf{f}^{\gamma} T_j\otimes v+ \sum_{k=1}^t \mathbf{f}^{\gamma-\epsilon_k}[f_k, T_j]\otimes v\quad\mod \mathcal{V}_{(l-2)}\cr &\equiv \mathbf{f}^{\gamma-\epsilon_j}\otimes v \quad\mod \mathcal{V}_{(l-2)}. \end{align*} $$
The proof is completed.
Lemma 4.4 Keep the above notations and assumptions. In particular, let
![]() $\mathfrak {g}$
be a solvable restricted Lie superalgebra. Let
$\mathfrak {g}$
be a solvable restricted Lie superalgebra. Let
![]() $\rho : \mathfrak {g}\rightarrow \mathfrak {gl}(V)$
be an irreducible representation of
$\rho : \mathfrak {g}\rightarrow \mathfrak {gl}(V)$
be an irreducible representation of
![]() $U_{\chi }(\mathfrak {g})$
on V. The following statements hold.
$U_{\chi }(\mathfrak {g})$
on V. The following statements hold.
-
(1) The module
 $V_{I,\chi }$
defined in (4.2) is an irreducible
$V_{I,\chi }$
defined in (4.2) is an irreducible
 $U_{\chi }(I^{\chi })$
-module.
$U_{\chi }(I^{\chi })$
-module. -
(2) Furthermore, if we set
 $\mathcal {V}:=U_{\chi }(\mathfrak {g})\otimes _{U_{\chi }(I^{\chi })}V_{I,\chi }$
, then
$\mathcal {V}:=U_{\chi }(\mathfrak {g})\otimes _{U_{\chi }(I^{\chi })}V_{I,\chi }$
, then
 $V\cong \mathcal {V}$
.
$V\cong \mathcal {V}$
.
Proof (1) It is clear.
(2) Suppose W is a nonzero submodule of
![]() $U_{\chi }(\mathfrak {g})$
in
$U_{\chi }(\mathfrak {g})$
in
![]() $\mathcal {V}$
. Set
$\mathcal {V}$
. Set
![]() $W_0:=\{w\in V_{I,\chi }\mid 1\otimes w\in W\}$
. Obviously,
$W_0:=\{w\in V_{I,\chi }\mid 1\otimes w\in W\}$
. Obviously,
![]() $W_0$
is a
$W_0$
is a
![]() $U_{\chi }(I^{\chi })$
-submodule of
$U_{\chi }(I^{\chi })$
-submodule of
![]() $V_{I,\chi }$
. According to part (1),
$V_{I,\chi }$
. According to part (1),
![]() $V_{I,\chi }$
is an irreducible
$V_{I,\chi }$
is an irreducible
![]() $U_{\chi }(I^{\chi })$
-module. Hence
$U_{\chi }(I^{\chi })$
-module. Hence
![]() $W_0=V_{I,\chi }$
or
$W_0=V_{I,\chi }$
or
![]() $W_0=0$
. If the former case occurs, then
$W_0=0$
. If the former case occurs, then
![]() $W=\mathcal {V}$
. Hence it suffices to show that
$W=\mathcal {V}$
. Hence it suffices to show that
![]() $W_0$
is nonzero.
$W_0$
is nonzero.
Recall
![]() $\mathcal {V}=\sum _{(\alpha ,\gamma )\in P^s\times E^t}\mathbf {k} {\mathbf {e}}^{\alpha }{\mathbf {f}}^{\gamma }\otimes V_{I,\chi }$
. Obviously,
$\mathcal {V}=\sum _{(\alpha ,\gamma )\in P^s\times E^t}\mathbf {k} {\mathbf {e}}^{\alpha }{\mathbf {f}}^{\gamma }\otimes V_{I,\chi }$
. Obviously,
![]() $ W=\bigcup _{l\geq 0} (W\cap \mathcal {V}_{(l)})$
. On the other hand, we put
$ W=\bigcup _{l\geq 0} (W\cap \mathcal {V}_{(l)})$
. On the other hand, we put
![]() $W_{(l)}:=\sum _{\underset { ||(\alpha ,\gamma )||\leq l}{(\alpha ,\gamma )\in P^s\times E^t}}\mathbf {k} \mathbf {e}^{\alpha }\mathbf {f}^{\gamma }\otimes W_0$
. We claim that
$W_{(l)}:=\sum _{\underset { ||(\alpha ,\gamma )||\leq l}{(\alpha ,\gamma )\in P^s\times E^t}}\mathbf {k} \mathbf {e}^{\alpha }\mathbf {f}^{\gamma }\otimes W_0$
. We claim that
It yields that
![]() $W_0\ne 0$
, which is our purpose. In order to verify the claim, it suffices to show that
$W_0\ne 0$
, which is our purpose. In order to verify the claim, it suffices to show that
-
(*)
 $W_{(l)}=\mathcal {V}_{(l)}\cap W$
for all
$W_{(l)}=\mathcal {V}_{(l)}\cap W$
for all
 $l\geq 0$
.
$l\geq 0$
.
By definition, (*) is true for
![]() $l=0$
. We now prove that
$l=0$
. We now prove that
![]() $W\cap \mathcal {V}_{(l)}\subset W_{(l)}$
by induction on l. Let
$W\cap \mathcal {V}_{(l)}\subset W_{(l)}$
by induction on l. Let
![]() $l\geq 1$
and assume that
$l\geq 1$
and assume that
![]() $W\cap \mathcal {V}_{(l-1)}\subset W_{(l-1)}$
. Suppose that
$W\cap \mathcal {V}_{(l-1)}\subset W_{(l-1)}$
. Suppose that
![]() $v\in W\cap \mathcal {V}_{(l)}$
is arbitrarily given, we intend to show that
$v\in W\cap \mathcal {V}_{(l)}$
is arbitrarily given, we intend to show that
![]() $w\in W_{(l)}$
. Take a cobasis
$w\in W_{(l)}$
. Take a cobasis
![]() $\{v_1,\ldots , v_q\}$
of
$\{v_1,\ldots , v_q\}$
of
![]() $W_0$
in
$W_0$
in
![]() $V_{I,\chi }$
. Without loss of generality, we might as well assume
$V_{I,\chi }$
. Without loss of generality, we might as well assume
 $$ \begin{align*}v=\sum_{k=1}^q\sum_{\underset{ ||(\alpha,\gamma)||\leq l}{(\alpha,\gamma)\in P^s\times E^t}}C_{\alpha,\gamma,k}\mathbf{e}^{\alpha} \mathbf{f}^{\gamma}\otimes v_k\end{align*} $$
$$ \begin{align*}v=\sum_{k=1}^q\sum_{\underset{ ||(\alpha,\gamma)||\leq l}{(\alpha,\gamma)\in P^s\times E^t}}C_{\alpha,\gamma,k}\mathbf{e}^{\alpha} \mathbf{f}^{\gamma}\otimes v_k\end{align*} $$
with all
![]() $C_{\alpha ,\gamma ,k}\in \mathbf {k}$
. By (4.3), we have for
$C_{\alpha ,\gamma ,k}\in \mathbf {k}$
. By (4.3), we have for
![]() $i=1,\ldots ,s,$
$i=1,\ldots ,s,$
Thus
![]() $(Z_i-\chi (Z_i)).v\in W\cap \mathcal {V}_{(l-1)}$
. By the inductive hypothesis, it lies in
$(Z_i-\chi (Z_i)).v\in W\cap \mathcal {V}_{(l-1)}$
. By the inductive hypothesis, it lies in
![]() $W_{(l-1)}$
. Hence, all
$W_{(l-1)}$
. Hence, all
![]() $C_{\alpha ,\gamma ,k}=0$
as long as
$C_{\alpha ,\gamma ,k}=0$
as long as
![]() $||(\alpha ,\gamma )||=l$
and
$||(\alpha ,\gamma )||=l$
and
![]() $\alpha \ne 0$
. In the same way, let us deal with the case when
$\alpha \ne 0$
. In the same way, let us deal with the case when
![]() $|(\alpha ,\gamma )|=l$
and
$|(\alpha ,\gamma )|=l$
and
![]() $\alpha = 0$
. Multiplication by
$\alpha = 0$
. Multiplication by
![]() $T_j$
on v,
$T_j$
on v,
![]() $j=1,\ldots ,t$
yields
$j=1,\ldots ,t$
yields
For the same reason as the previous case, we have that
![]() $C_{0,\gamma ,k}=0$
for all
$C_{0,\gamma ,k}=0$
for all
![]() $\gamma $
with
$\gamma $
with
![]() $||(0,\gamma )||=l$
. Hence v must be zero. In summary,
$||(0,\gamma )||=l$
. Hence v must be zero. In summary,
![]() $W\cap \mathcal {V}_{(l)}\subset W_{(l)}$
. Finally, we have
$W\cap \mathcal {V}_{(l)}\subset W_{(l)}$
. Finally, we have
![]() $W\cap \mathcal {V}_{(l)}=W_{(l)}$
. This implies
$W\cap \mathcal {V}_{(l)}=W_{(l)}$
. This implies
![]() $W=\mathcal {V}$
. Consequently,
$W=\mathcal {V}$
. Consequently,
![]() $\mathcal {V}$
is an irreducible
$\mathcal {V}$
is an irreducible
![]() $U_{\chi }(\mathfrak {g})$
-module. On the other hand, there is a natural surjective
$U_{\chi }(\mathfrak {g})$
-module. On the other hand, there is a natural surjective
![]() $U_{\chi }(\mathfrak {g})$
-homomorphism from
$U_{\chi }(\mathfrak {g})$
-homomorphism from
![]() $\mathcal {V}$
onto V. The irreducibility of both V and
$\mathcal {V}$
onto V. The irreducibility of both V and
![]() $\mathcal {V}$
implies that the natural surjective homomorphism must be an isomorphism.
$\mathcal {V}$
implies that the natural surjective homomorphism must be an isomorphism.
4.3 Irreducible modules of solvable restricted Lie superalgebras
Furthermore, we have the following result.
Proposition 4.5 Keep the assumptions and notations as above. Suppose
![]() $\rho :\mathfrak {g}\rightarrow \mathfrak {gl}(V)$
is a finite-dimensional irreducible representation of
$\rho :\mathfrak {g}\rightarrow \mathfrak {gl}(V)$
is a finite-dimensional irreducible representation of
![]() $U_{\chi }(\mathfrak {g})$
. Then there is a subalgebra
$U_{\chi }(\mathfrak {g})$
. Then there is a subalgebra
![]() $\mathfrak {h}=\mathfrak {h}_{\bar 0}+\mathfrak {h}_{\bar 1}$
such that:
$\mathfrak {h}=\mathfrak {h}_{\bar 0}+\mathfrak {h}_{\bar 1}$
such that:
-
(i)
 $\dim V\geq p^{\dim \mathfrak {g}_{\bar 0}-\dim \mathfrak {h}_{\bar 0}}2^{\dim \mathfrak {g}_{\bar 1}-\dim \mathfrak {h}_{\bar 1}}$
, and
$\dim V\geq p^{\dim \mathfrak {g}_{\bar 0}-\dim \mathfrak {h}_{\bar 0}}2^{\dim \mathfrak {g}_{\bar 1}-\dim \mathfrak {h}_{\bar 1}}$
, and -
(ii) V contains a one-dimensional
 $\mathfrak {h}$
-submodule.
$\mathfrak {h}$
-submodule.
Proof Consider
![]() $\ker \rho $
(the kernel of
$\ker \rho $
(the kernel of
![]() $\rho $
) which is an ideal of
$\rho $
) which is an ideal of
![]() $\mathfrak {g}$
. If
$\mathfrak {g}$
. If
![]() $\mathfrak {g}/ \ker \rho $
is abelian, then
$\mathfrak {g}/ \ker \rho $
is abelian, then
![]() $[\mathfrak {g},\mathfrak {g}]$
acts trivially on V. Hence, V is certainly one-dimensional with trivial action of
$[\mathfrak {g},\mathfrak {g}]$
acts trivially on V. Hence, V is certainly one-dimensional with trivial action of
![]() $[\mathfrak {g}_{\bar 0},\mathfrak {g}_{\bar 0}]+\mathfrak {g}_{\bar 1}$
. So the proposition is true in this case while we take
$[\mathfrak {g}_{\bar 0},\mathfrak {g}_{\bar 0}]+\mathfrak {g}_{\bar 1}$
. So the proposition is true in this case while we take
![]() $\mathfrak {h}$
to be
$\mathfrak {h}$
to be
![]() $\mathfrak {g}$
itself.
$\mathfrak {g}$
itself.
In the following, we suppose that
![]() $\overline {\mathfrak {g}}:=\mathfrak {g}/ \ker \rho $
is not abelian. We will prove the proposition by induction on
$\overline {\mathfrak {g}}:=\mathfrak {g}/ \ker \rho $
is not abelian. We will prove the proposition by induction on
![]() $\dim \mathfrak {g}$
by steps.
$\dim \mathfrak {g}$
by steps.
(1) Keep in mind the assumption that
![]() $\overline {\mathfrak {g}}:=\mathfrak {g}/ \ker \rho $
is not abelian. So the center
$\overline {\mathfrak {g}}:=\mathfrak {g}/ \ker \rho $
is not abelian. So the center
![]() $C(\overline {\mathfrak {g}})$
is a proper subalgebra of
$C(\overline {\mathfrak {g}})$
is a proper subalgebra of
![]() $\overline {\mathfrak {g}}$
. So
$\overline {\mathfrak {g}}$
. So
![]() $C(\overline {\mathfrak {g}})$
does not contain all abelian ideal of
$C(\overline {\mathfrak {g}})$
does not contain all abelian ideal of
![]() $\mathfrak {g}$
, due to Lemma 4.1(2). So, there exists an ideal I of
$\mathfrak {g}$
, due to Lemma 4.1(2). So, there exists an ideal I of
![]() $\mathfrak {g}$
such that
$\mathfrak {g}$
such that
![]() $I^{(1)}\subset \ker \rho $
and
$I^{(1)}\subset \ker \rho $
and
![]() $[\mathfrak {g},I]\nsubseteq \ker \rho $
. Note that
$[\mathfrak {g},I]\nsubseteq \ker \rho $
. Note that
![]() $I^{(1)}$
acts trivially on V. So
$I^{(1)}$
acts trivially on V. So
![]() $\chi (I^{(1)})=0$
. Hence, there is an irreducible I-submodule in V which is one-dimensional. Still denote
$\chi (I^{(1)})=0$
. Hence, there is an irreducible I-submodule in V which is one-dimensional. Still denote
![]() $V_{I,\chi }=\{v\in V\mid X.v=\chi (X)v\;\forall X\in I\}$
. Then we have
$V_{I,\chi }=\{v\in V\mid X.v=\chi (X)v\;\forall X\in I\}$
. Then we have
![]() $V_{I,\chi }$
is nonzero. Keep the notation
$V_{I,\chi }$
is nonzero. Keep the notation
![]() $I^{\chi }=\{X\in \mathfrak {g}\mid \chi ([X,I])=0\}$
. It is already known that
$I^{\chi }=\{X\in \mathfrak {g}\mid \chi ([X,I])=0\}$
. It is already known that
![]() $I^{\chi }$
is a solvable restricted subalgebra of
$I^{\chi }$
is a solvable restricted subalgebra of
![]() $\mathfrak {g}$
. By the arguments in the first paragraph of Section 4.2,
$\mathfrak {g}$
. By the arguments in the first paragraph of Section 4.2,
![]() $I^{\chi }$
is a proper subalgebra of
$I^{\chi }$
is a proper subalgebra of
![]() $\mathfrak {g}$
. By Lemma 4.4,
$\mathfrak {g}$
. By Lemma 4.4,
![]() $V_{I,\chi }$
is an irreducible
$V_{I,\chi }$
is an irreducible
![]() $U_{\chi }(I^{\chi })$
-module, and
$U_{\chi }(I^{\chi })$
-module, and
Correspondingly,
(2) Note that
![]() $I^{\chi }$
already turns out to be a proper solvable restricted subalgebra. By the inductive hypothesis, there exits a solvable restricted subalgebra
$I^{\chi }$
already turns out to be a proper solvable restricted subalgebra. By the inductive hypothesis, there exits a solvable restricted subalgebra
![]() $\mathfrak {h}$
in
$\mathfrak {h}$
in
![]() $I^{\chi }$
such that the requirements (i) and (ii) are satisfied with respect to the irreducible
$I^{\chi }$
such that the requirements (i) and (ii) are satisfied with respect to the irreducible
![]() $U_{\chi }(I^{\chi })$
-module
$U_{\chi }(I^{\chi })$
-module
![]() $V_{I,\chi }$
. Hence, by (4.4), we finally have
$V_{I,\chi }$
. Hence, by (4.4), we finally have
![]() $\dim V\geq p^{\dim \mathfrak {g}_{\bar 0}-\dim \mathfrak {h}_{\bar 0}}2^{\dim \mathfrak {g}_{\bar 1}-\dim \mathfrak {h}_{\bar 1}}$
.
$\dim V\geq p^{\dim \mathfrak {g}_{\bar 0}-\dim \mathfrak {h}_{\bar 0}}2^{\dim \mathfrak {g}_{\bar 1}-\dim \mathfrak {h}_{\bar 1}}$
.
Combining Proposition 4.5 and Lemma 4.4(2), we conclude the following result.
Corollary 4.6 Let
![]() $\mathfrak {g}$
be a solvable restricted Lie superalgebra. Then any irreducible module of
$\mathfrak {g}$
be a solvable restricted Lie superalgebra. Then any irreducible module of
![]() $\mathfrak {g}$
must be isomorphic to
$\mathfrak {g}$
must be isomorphic to
![]() $U_{\chi }(\mathfrak {g})\otimes _{U_{\chi }(\mathfrak {h})}S$
for some restricted subalgebra
$U_{\chi }(\mathfrak {g})\otimes _{U_{\chi }(\mathfrak {h})}S$
for some restricted subalgebra
![]() $\mathfrak {h}$
with
$\mathfrak {h}$
with
![]() $\chi (\mathfrak {h}^{(1)})=0$
and for a one-dimensional
$\chi (\mathfrak {h}^{(1)})=0$
and for a one-dimensional
![]() $U_{\chi }(\mathfrak {h})$
-module S. Correspondingly, any irreducible module has dimension
$U_{\chi }(\mathfrak {h})$
-module S. Correspondingly, any irreducible module has dimension
![]() $p^m2^n$
for some
$p^m2^n$
for some
![]() $m,n\in \mathbb {N}$
.
$m,n\in \mathbb {N}$
.
4.4 Irreducible modules of general finite-dimensional solvable Lie superalgebras which are not necessarily restricted
In this section, we will extend the above results for solvable restricted Lie subalgebras to any solvable ones. Let
![]() $\mathfrak {g}=\mathfrak {g}_{\bar 0}+\mathfrak {g}_{\bar 1}$
be a given solvable Lie superalgebra. Recall that
$\mathfrak {g}=\mathfrak {g}_{\bar 0}+\mathfrak {g}_{\bar 1}$
be a given solvable Lie superalgebra. Recall that
![]() $\mathfrak {g}$
admits a minimal finite-dimensional p-envelope
$\mathfrak {g}$
admits a minimal finite-dimensional p-envelope
![]() $\mathfrak {g}_p$
, such that
$\mathfrak {g}_p$
, such that
![]() $\mathfrak {g}_p=(\mathfrak {g}_{\bar 0})_p\oplus \mathfrak {g}_{\bar 1}$
and
$\mathfrak {g}_p=(\mathfrak {g}_{\bar 0})_p\oplus \mathfrak {g}_{\bar 1}$
and
![]() $(\mathfrak {g}_{\bar 0})_p$
is a p-envelope of
$(\mathfrak {g}_{\bar 0})_p$
is a p-envelope of
![]() $\mathfrak {g}_{\bar 0}$
(see Lemma A.3 in the appendix). This
$\mathfrak {g}_{\bar 0}$
(see Lemma A.3 in the appendix). This
![]() $\mathfrak {g}_p$
becomes a solvable restricted Lie superalgebra. As mentioned in appendix,
$\mathfrak {g}_p$
becomes a solvable restricted Lie superalgebra. As mentioned in appendix,
![]() $\mathfrak {g}$
is an ideal of
$\mathfrak {g}$
is an ideal of
![]() $\mathfrak {g}_p$
. More precisely,
$\mathfrak {g}_p$
. More precisely,
![]() $\mathsf {ad}(\mathfrak {g}_{\bar 0})_p(\mathfrak {g}_{\bar 0})\subset \mathfrak {g}_{\bar 0}^{(1)}$
, and
$\mathsf {ad}(\mathfrak {g}_{\bar 0})_p(\mathfrak {g}_{\bar 0})\subset \mathfrak {g}_{\bar 0}^{(1)}$
, and
![]() $\mathsf {ad}(\mathfrak {g}_{\bar 0})_p\mathfrak {g}_{\bar 1}\subset \mathfrak {g}^{(1)}$
.
$\mathsf {ad}(\mathfrak {g}_{\bar 0})_p\mathfrak {g}_{\bar 1}\subset \mathfrak {g}^{(1)}$
.
For irreducible
![]() $\mathfrak {g}$
-module
$\mathfrak {g}$
-module
![]() $(V,\rho )$
,
$(V,\rho )$
,
![]() $\rho $
can extend to the one over
$\rho $
can extend to the one over
![]() $\mathfrak {g}_p$
(see, for example, [Reference Strade and Farnsteiner26, 2.5.3]). Hence, V becomes an irreducible
$\mathfrak {g}_p$
(see, for example, [Reference Strade and Farnsteiner26, 2.5.3]). Hence, V becomes an irreducible
![]() $\mathfrak {g}_p$
-modules. Hence, there exits a unique
$\mathfrak {g}_p$
-modules. Hence, there exits a unique
![]() $\Upsilon \in (\mathfrak {g}_{\bar 0})_p^{*}$
, with which the irreducible
$\Upsilon \in (\mathfrak {g}_{\bar 0})_p^{*}$
, with which the irreducible
![]() $\mathfrak {g}_p$
-module V is associated. Set
$\mathfrak {g}_p$
-module V is associated. Set
![]() $\chi =\Upsilon |_{\mathfrak {g}_{\bar 0}}$
. Then the irreducible
$\chi =\Upsilon |_{\mathfrak {g}_{\bar 0}}$
. Then the irreducible
![]() $\mathfrak {g}$
-module V is associated with a unique linear function
$\mathfrak {g}$
-module V is associated with a unique linear function
![]() $\chi \in \mathfrak {g}_{{\bar 0}}^{*}$
.
$\chi \in \mathfrak {g}_{{\bar 0}}^{*}$
.
Theorem 4.7 Let
![]() $\mathfrak {g}$
be a solvable Lie superalgebra. Any irreducible module of
$\mathfrak {g}$
be a solvable Lie superalgebra. Any irreducible module of
![]() $\mathfrak {g}$
is associated with some
$\mathfrak {g}$
is associated with some
![]() $\chi \in \mathfrak {g}_{\bar 0}^{*}$
, which has dimension
$\chi \in \mathfrak {g}_{\bar 0}^{*}$
, which has dimension
![]() $p^{\dim {\mathfrak {g}_{\bar 0}/ \mathfrak {h}_{\bar 0}}}2^{\dim {\mathfrak {g}_{\bar 1}/ \mathfrak {h}_{\bar 1}}}$
, where
$p^{\dim {\mathfrak {g}_{\bar 0}/ \mathfrak {h}_{\bar 0}}}2^{\dim {\mathfrak {g}_{\bar 1}/ \mathfrak {h}_{\bar 1}}}$
, where
![]() $\mathfrak {h}$
is a subalgebra with
$\mathfrak {h}$
is a subalgebra with
![]() $\chi (\mathfrak {h}^{(1)})=0$
and V contains a one-dimensional
$\chi (\mathfrak {h}^{(1)})=0$
and V contains a one-dimensional
![]() $\mathfrak {h}$
-module.
$\mathfrak {h}$
-module.
Proof For any given irreducible
![]() $\mathfrak {g}$
-module
$\mathfrak {g}$
-module
![]() $(V,\rho )$
, as arguments above, V becomes an irreducible
$(V,\rho )$
, as arguments above, V becomes an irreducible
![]() $\mathfrak {g}_p$
-modules associated with
$\mathfrak {g}_p$
-modules associated with
![]() $\Upsilon \in (\mathfrak {g}_{\bar 0})_p^{*}$
, and V is associated with
$\Upsilon \in (\mathfrak {g}_{\bar 0})_p^{*}$
, and V is associated with
![]() $\chi :=\Upsilon _{\mathfrak {g}_{\bar 0}}\in \mathfrak {g}^{*}_{\bar 0}$
. By Corollary 4.6, there exists a restricted subalgebra
$\chi :=\Upsilon _{\mathfrak {g}_{\bar 0}}\in \mathfrak {g}^{*}_{\bar 0}$
. By Corollary 4.6, there exists a restricted subalgebra
![]() $\frak {H}$
of
$\frak {H}$
of
![]() $\mathfrak {g}_p$
with
$\mathfrak {g}_p$
with
![]() $\Upsilon (\frak {H}^{(1)})=\chi (\frak {H}^{(1)})=0$
such that
$\Upsilon (\frak {H}^{(1)})=\chi (\frak {H}^{(1)})=0$
such that
![]() $V\cong U_{\chi }(\mathfrak {g}_p)\otimes _{U_{\chi }(\frak {H})}S$
, where
$V\cong U_{\chi }(\mathfrak {g}_p)\otimes _{U_{\chi }(\frak {H})}S$
, where
![]() $S\subset V$
is a one-dimensional
$S\subset V$
is a one-dimensional
![]() $\frak {H}$
-module. Correspondingly,
$\frak {H}$
-module. Correspondingly,
![]() $\dim V=p^{\dim {(\mathfrak {g}_{\bar 0})_p/ \frak {H}_{\bar 0}}}2^{\dim {\mathfrak {g}_{\bar 1}/ \frak {H}_{\bar 1}}}$
.
$\dim V=p^{\dim {(\mathfrak {g}_{\bar 0})_p/ \frak {H}_{\bar 0}}}2^{\dim {\mathfrak {g}_{\bar 1}/ \frak {H}_{\bar 1}}}$
.
Take
![]() $\mathfrak {h}{\kern-1pt}={\kern-1pt}\frak {H}\cap \mathfrak {g}$
. By definition,
$\mathfrak {h}{\kern-1pt}={\kern-1pt}\frak {H}\cap \mathfrak {g}$
. By definition,
![]() $\mathfrak {h}_{\bar 0}{\kern-1pt}={\kern-1pt}\frak {H}_{\bar 0}\cap \mathfrak {g}_{\bar 0}$
, and
$\mathfrak {h}_{\bar 0}{\kern-1pt}={\kern-1pt}\frak {H}_{\bar 0}\cap \mathfrak {g}_{\bar 0}$
, and
![]() $\mathfrak {h}_{\bar 1}{\kern-1pt}={\kern-1pt}\frak {H}_{\bar 1}\cap \mathfrak {g}_{\bar 1}{\kern-1pt}={\kern-1pt}\frak {H}_{\bar 1}$
. Then
$\mathfrak {h}_{\bar 1}{\kern-1pt}={\kern-1pt}\frak {H}_{\bar 1}\cap \mathfrak {g}_{\bar 1}{\kern-1pt}={\kern-1pt}\frak {H}_{\bar 1}$
. Then
![]() $\chi (\mathfrak {h}^{(1)})=0$
, and
$\chi (\mathfrak {h}^{(1)})=0$
, and
![]() $\mathfrak {h}$
has one-dimensional module S. Note that
$\mathfrak {h}$
has one-dimensional module S. Note that
![]() $(\mathfrak {g}_{\bar 0})_p/ \frak {H}_{\bar 0}\cong \mathfrak {g}_{\bar 0}/ \frak {H}_{\bar 0}\cap \mathfrak {g}_{\bar 0}$
, as vectors space. Hence
$(\mathfrak {g}_{\bar 0})_p/ \frak {H}_{\bar 0}\cong \mathfrak {g}_{\bar 0}/ \frak {H}_{\bar 0}\cap \mathfrak {g}_{\bar 0}$
, as vectors space. Hence
The proof is completed.
Remark 4.8 (1) The above theorem is an extension of the counterpart result on solvable Lie algebras (see [Reference Schue20] or [Reference Strade and Farnsteiner26, Section 5.8]).
(2) With the above theorem, we can propose the possibility that super KW property raised by Wang–Zhao in [Reference Wang and Zhao29] is satisfied with all finite-dimensional solvable Lie superalgebras over
![]() $\mathbf {k}$
.
$\mathbf {k}$
.
5 Irreducible modules of completely solvable Lie superalgebras
A Lie superalgebra
![]() $\mathfrak {g}$
is called completely solvable if
$\mathfrak {g}$
is called completely solvable if
![]() $\mathfrak {g}^{(1)}$
is nilpotent. Obviously, a completely solvable
$\mathfrak {g}^{(1)}$
is nilpotent. Obviously, a completely solvable
![]() $\mathfrak {g}$
is solvable and its even part
$\mathfrak {g}$
is solvable and its even part
![]() $\mathfrak {g}_{\bar 0}$
is a completely solvable Lie algebra.
$\mathfrak {g}_{\bar 0}$
is a completely solvable Lie algebra.
The following facts are very important to the subsequent arguments.
Lemma 5.1 Let
![]() $\mathfrak {g}=\mathfrak {g}_{\bar 0}+\mathfrak {g}_{\bar 1}$
be a completely solvable Lie superalgebra. The following statements hold.
$\mathfrak {g}=\mathfrak {g}_{\bar 0}+\mathfrak {g}_{\bar 1}$
be a completely solvable Lie superalgebra. The following statements hold.
-
(1) Any minimal ideal of
 $\mathfrak {g}$
is one-dimensional.
$\mathfrak {g}$
is one-dimensional. -
(2) There exists a sequence of ideals
 $\mathfrak {g}=\mathfrak {g}_0 \supset \mathfrak {g}_1\supset \cdots \supset \mathfrak {g}_{n-1}\supset \mathfrak {g}_{n}=0$
such that
$\mathfrak {g}=\mathfrak {g}_0 \supset \mathfrak {g}_1\supset \cdots \supset \mathfrak {g}_{n-1}\supset \mathfrak {g}_{n}=0$
such that
 $\dim _{\mathbf {k}} \mathfrak {g}_i=n-i$
.
$\dim _{\mathbf {k}} \mathfrak {g}_i=n-i$
. -
(3) For
 $\chi \in \mathfrak {g}_{{\bar 0}}^{*}$
, if
$\chi \in \mathfrak {g}_{{\bar 0}}^{*}$
, if
 $\mathfrak {h}$
is a subalgebra of codimension one which contains
$\mathfrak {h}$
is a subalgebra of codimension one which contains
 $\mathfrak {z}^{\chi }$
, then
$\mathfrak {z}^{\chi }$
, then
 $D(\mathfrak {h},\chi )\subset D(\mathfrak {g},\chi )$
.
$D(\mathfrak {h},\chi )\subset D(\mathfrak {g},\chi )$
. -
(4) Each proper subalgebra of
 $\mathfrak {g}$
is contained in a subalgebra of codimension one of
$\mathfrak {g}$
is contained in a subalgebra of codimension one of
 $\mathfrak {g}$
.
$\mathfrak {g}$
.
Proof By definition
![]() $\mathfrak {g}^{(1)}$
is nilpotent, it acts nilpotently on
$\mathfrak {g}^{(1)}$
is nilpotent, it acts nilpotently on
![]() $\mathfrak {g}$
under
$\mathfrak {g}$
under
![]() $\mathsf {ad}$
-action. By Lemma 4.1(1), the part (1) follows.
$\mathsf {ad}$
-action. By Lemma 4.1(1), the part (1) follows.
As to the part (2), by (1), there must be minimal ideals of
![]() $\mathfrak {g}$
which is
$\mathfrak {g}$
which is
![]() $\mathbb {Z}_2$
-homogeneous and one-dimensional. Notice that any subalgebras and quotients of
$\mathbb {Z}_2$
-homogeneous and one-dimensional. Notice that any subalgebras and quotients of
![]() $\mathfrak {g}$
are also completely solvable Lie superalgebras. By induction on dimension, the statement follows.
$\mathfrak {g}$
are also completely solvable Lie superalgebras. By induction on dimension, the statement follows.
As to (3), we are given
![]() $\mathfrak {m}\in D(\mathfrak {h},\chi )$
, intending to show
$\mathfrak {m}\in D(\mathfrak {h},\chi )$
, intending to show
![]() $\mathfrak {m}\in D(\mathfrak {g},\chi )$
. We first note that
$\mathfrak {m}\in D(\mathfrak {g},\chi )$
. We first note that
![]() $\underline {\dim }\mathfrak {m}=d(\mathfrak {h},\chi )$
. As
$\underline {\dim }\mathfrak {m}=d(\mathfrak {h},\chi )$
. As
![]() $\mathfrak {h}$
has codimension one, either
$\mathfrak {h}$
has codimension one, either
![]() $\mathfrak {h}_{\bar 0}$
has codimension one in
$\mathfrak {h}_{\bar 0}$
has codimension one in
![]() $\mathfrak {g}_{\bar 0}$
while
$\mathfrak {g}_{\bar 0}$
while
![]() $\mathfrak {h}_{\bar 1}=\mathfrak {g}_{\bar 1}$
, or
$\mathfrak {h}_{\bar 1}=\mathfrak {g}_{\bar 1}$
, or
![]() $\mathfrak {h}_{\bar 1}$
has codimension one in
$\mathfrak {h}_{\bar 1}$
has codimension one in
![]() $\mathfrak {g}_{\bar 1}$
while
$\mathfrak {g}_{\bar 1}$
while
![]() $\mathfrak {h}_{\bar 0}=\mathfrak {g}_{\bar 0}$
. For the first case,
$\mathfrak {h}_{\bar 0}=\mathfrak {g}_{\bar 0}$
. For the first case,
![]() $\dim \mathfrak {h}_{\bar 0}=\dim \mathfrak {g}_{\bar 0}-1$
. We have that the even entry of the super-datum
$\dim \mathfrak {h}_{\bar 0}=\dim \mathfrak {g}_{\bar 0}-1$
. We have that the even entry of the super-datum
![]() $d(\mathfrak {h},\chi )$
is not less than
$d(\mathfrak {h},\chi )$
is not less than
![]() $\frac {\dim \mathfrak {g}_{\bar 0}-1+\dim \mathfrak {z}_{\bar 0}^{\chi }}{2}=\frac {\dim \mathfrak {g}_{\bar 0}+\dim \mathfrak {z}_{\bar 0}^{\chi }}{2}-\frac {1}{2}$
, therefore, both are equal because both are integers and
$\frac {\dim \mathfrak {g}_{\bar 0}-1+\dim \mathfrak {z}_{\bar 0}^{\chi }}{2}=\frac {\dim \mathfrak {g}_{\bar 0}+\dim \mathfrak {z}_{\bar 0}^{\chi }}{2}-\frac {1}{2}$
, therefore, both are equal because both are integers and
![]() $\frac {\dim \mathfrak {g}_{\bar 0}+\dim \mathfrak {z}_{\bar 0}^{\chi }}{2}$
is already an integer. The odd entries of
$\frac {\dim \mathfrak {g}_{\bar 0}+\dim \mathfrak {z}_{\bar 0}^{\chi }}{2}$
is already an integer. The odd entries of
![]() $d(\mathfrak {h},\chi )$
and of
$d(\mathfrak {h},\chi )$
and of
![]() $d(\mathfrak {g},\chi )$
coincide. So in this case,
$d(\mathfrak {g},\chi )$
coincide. So in this case,
![]() $d(\mathfrak {h},\chi )=d(\mathfrak {g},\chi )$
.
$d(\mathfrak {h},\chi )=d(\mathfrak {g},\chi )$
.
For the second case,
![]() $\dim \mathfrak {h}_{\bar 1}=\dim \mathfrak {g}_{\bar 1}-1$
while
$\dim \mathfrak {h}_{\bar 1}=\dim \mathfrak {g}_{\bar 1}-1$
while
![]() $\mathfrak {h}_{\bar 0}=\mathfrak {g}_{\bar 0}$
. We can show by similar arguments as in the first case, that
$\mathfrak {h}_{\bar 0}=\mathfrak {g}_{\bar 0}$
. We can show by similar arguments as in the first case, that
![]() $d(\mathfrak {h},\chi )=d(\mathfrak {g},\chi )$
when
$d(\mathfrak {h},\chi )=d(\mathfrak {g},\chi )$
when
![]() $\frac {\dim \mathfrak {g}_{\bar 1}+\dim \mathfrak {z}_{\bar 1}^{\chi }}{2}$
is an integer. Suppose
$\frac {\dim \mathfrak {g}_{\bar 1}+\dim \mathfrak {z}_{\bar 1}^{\chi }}{2}$
is an integer. Suppose
![]() $\frac {\dim \mathfrak {g}_{\bar 1}+\dim \mathfrak {z}_{\bar 1}^{\chi }}{2}$
is not an integer. Then the odd entries of
$\frac {\dim \mathfrak {g}_{\bar 1}+\dim \mathfrak {z}_{\bar 1}^{\chi }}{2}$
is not an integer. Then the odd entries of
![]() $d(\mathfrak {h}, \chi )$
is equal to
$d(\mathfrak {h}, \chi )$
is equal to
![]() $\frac {\dim \mathfrak {h}_{\bar 1}+\dim \mathfrak {z}_{\bar 1}^{\chi }}{2}=\frac {\dim \mathfrak {g}_{\bar 1}-1+\dim \mathfrak {z}_{\bar 1}^{\chi }}{2}$
, which is exactly
$\frac {\dim \mathfrak {h}_{\bar 1}+\dim \mathfrak {z}_{\bar 1}^{\chi }}{2}=\frac {\dim \mathfrak {g}_{\bar 1}-1+\dim \mathfrak {z}_{\bar 1}^{\chi }}{2}$
, which is exactly
![]() $\lceil \frac {\dim \mathfrak {g}_{\bar 1}+\dim \mathfrak {z}_{\bar 1}^{\chi }}{2}\rceil $
, equal to the odd entry of
$\lceil \frac {\dim \mathfrak {g}_{\bar 1}+\dim \mathfrak {z}_{\bar 1}^{\chi }}{2}\rceil $
, equal to the odd entry of
![]() $d(\mathfrak {g},\chi )$
. And the even entries of
$d(\mathfrak {g},\chi )$
. And the even entries of
![]() $d(\mathfrak {h},\chi )$
and of
$d(\mathfrak {h},\chi )$
and of
![]() $d(\mathfrak {g},\chi )$
coincide already. Hence
$d(\mathfrak {g},\chi )$
coincide already. Hence
![]() $d(\mathfrak {h},\chi )=d(\mathfrak {g},\chi )$
in this case. Hence, we always have
$d(\mathfrak {h},\chi )=d(\mathfrak {g},\chi )$
in this case. Hence, we always have
![]() $D(\mathfrak {h},\chi )\subset D(\mathfrak {g},\chi )$
in any case. The proof of (3) is completed.
$D(\mathfrak {h},\chi )\subset D(\mathfrak {g},\chi )$
in any case. The proof of (3) is completed.
Now, we prove (4) by induction on dimension. Suppose
![]() $\mathfrak {h}$
is a proper subalgebra of
$\mathfrak {h}$
is a proper subalgebra of
![]() $\mathfrak {g}$
, and has codimension greater than one. Note that
$\mathfrak {g}$
, and has codimension greater than one. Note that
![]() $\mathfrak {g}_{n-1}$
is an ideal of dimension one. So
$\mathfrak {g}_{n-1}$
is an ideal of dimension one. So
![]() $\mathfrak {h}+\mathfrak {g}_{n-1}$
must be a proper subalgebra of
$\mathfrak {h}+\mathfrak {g}_{n-1}$
must be a proper subalgebra of
![]() $\mathfrak {g}$
. If
$\mathfrak {g}$
. If
![]() $\mathfrak {h}+\mathfrak {g}_{n-1}$
has codimension one, then we are done. If it has codimension greater than one, we consider
$\mathfrak {h}+\mathfrak {g}_{n-1}$
has codimension one, then we are done. If it has codimension greater than one, we consider
![]() $\phi : \mathfrak {g}\rightarrow \overline {\mathfrak {g}}:=\mathfrak {g}/ \mathfrak {g}_{n-1}$
. Then
$\phi : \mathfrak {g}\rightarrow \overline {\mathfrak {g}}:=\mathfrak {g}/ \mathfrak {g}_{n-1}$
. Then
![]() $\phi (\mathfrak {h}+\mathfrak {g}_{n-1})$
has codimension greater than one in
$\phi (\mathfrak {h}+\mathfrak {g}_{n-1})$
has codimension greater than one in
![]() $\overline {\mathfrak {g}}$
. Now,
$\overline {\mathfrak {g}}$
. Now,
![]() $\overline {\mathfrak {g}}$
has dimension less than
$\overline {\mathfrak {g}}$
has dimension less than
![]() $\dim _{\mathbf {k}} \mathfrak {g}$
. By the inductive hypothesis,
$\dim _{\mathbf {k}} \mathfrak {g}$
. By the inductive hypothesis,
![]() $\phi (\mathfrak {h}+\mathfrak {g}_{n-1})$
is contained in a subalgebra say
$\phi (\mathfrak {h}+\mathfrak {g}_{n-1})$
is contained in a subalgebra say
![]() $\mathfrak {p}$
, of codimension one in
$\mathfrak {p}$
, of codimension one in
![]() $\overline {\mathfrak {g}}$
. We take
$\overline {\mathfrak {g}}$
. We take
![]() $\phi ^{-1}(\mathfrak {p})$
the preimage of
$\phi ^{-1}(\mathfrak {p})$
the preimage of
![]() $\mathfrak {p}$
in
$\mathfrak {p}$
in
![]() $\mathfrak {g}$
. Then
$\mathfrak {g}$
. Then
![]() $\phi ^{-1}(\mathfrak {p})$
is a subalgebra of codimension one in
$\phi ^{-1}(\mathfrak {p})$
is a subalgebra of codimension one in
![]() $\mathfrak {g}$
, containing
$\mathfrak {g}$
, containing
![]() $\mathfrak {h}$
. This subalgebra is desired.
$\mathfrak {h}$
. This subalgebra is desired.
Corollary 5.2 For a completely solvable Lie superalgebra
![]() $\mathfrak {g}$
, the set
$\mathfrak {g}$
, the set
![]() $D(\mathfrak {g},\chi )$
is not empty.
$D(\mathfrak {g},\chi )$
is not empty.
Proof If
![]() $\mathfrak {z}^{\chi }=\mathfrak {g}$
, there is nothing to do because
$\mathfrak {z}^{\chi }=\mathfrak {g}$
, there is nothing to do because
![]() $\mathfrak {g}$
itself belongs to
$\mathfrak {g}$
itself belongs to
![]() $D(\mathfrak {g},\chi )$
. So we only need to consider the situation where
$D(\mathfrak {g},\chi )$
. So we only need to consider the situation where
![]() $\mathfrak {z}^{\chi }$
is a proper subalgebra of
$\mathfrak {z}^{\chi }$
is a proper subalgebra of
![]() $\mathfrak {g}$
in the following.
$\mathfrak {g}$
in the following.
By Lemma 5.1, it is easily deduced that there are minimal subalgebras in
![]() $\mathfrak {g}$
containing
$\mathfrak {g}$
containing
![]() $\mathfrak {z}^{\chi }$
and having super-dimension not less than
$\mathfrak {z}^{\chi }$
and having super-dimension not less than
![]() $d(\mathfrak {g},\chi )$
. We take one, say
$d(\mathfrak {g},\chi )$
. We take one, say
![]() $\mathfrak {p}$
. By Lemma 5.1 again, it is deduced that
$\mathfrak {p}$
. By Lemma 5.1 again, it is deduced that
![]() $D(\mathfrak {p},\chi )\subset D(\mathfrak {g},\chi )$
. We will show that this
$D(\mathfrak {p},\chi )\subset D(\mathfrak {g},\chi )$
. We will show that this
![]() $\mathfrak {p}$
exactly belongs to
$\mathfrak {p}$
exactly belongs to
![]() $D(\mathfrak {p},\chi )$
, therefore belongs to
$D(\mathfrak {p},\chi )$
, therefore belongs to
![]() $D(\mathfrak {g},\chi )$
.
$D(\mathfrak {g},\chi )$
.
(1) By applying Lemma 5.1(4) to the completely solvable superalgebra
![]() $\mathfrak {p}$
, it is concluded that the proper subalgebra
$\mathfrak {p}$
, it is concluded that the proper subalgebra
![]() $\mathfrak {z}^{\chi }$
is contained in a subalgebra of codimension one in
$\mathfrak {z}^{\chi }$
is contained in a subalgebra of codimension one in
![]() $\mathfrak {p}$
. Hence, the minimality of
$\mathfrak {p}$
. Hence, the minimality of
![]() $\mathfrak {p}$
yields that
$\mathfrak {p}$
yields that
![]() $\underline {\dim }\mathfrak {p}=d(\mathfrak {g},\chi )$
.
$\underline {\dim }\mathfrak {p}=d(\mathfrak {g},\chi )$
.
(2) By the above arguments, in
![]() $\mathfrak {p}_{\bar 0}$
(resp.
$\mathfrak {p}_{\bar 0}$
(resp.
![]() $\mathfrak {p}_{\bar 1}$
) the maximal isotropic space has dimension equal to
$\mathfrak {p}_{\bar 1}$
) the maximal isotropic space has dimension equal to
![]() $\dim \mathfrak {p}_{\bar 0}$
(resp.
$\dim \mathfrak {p}_{\bar 0}$
(resp.
![]() $\dim \mathfrak {p}_{\bar 1}$
). Hence,
$\dim \mathfrak {p}_{\bar 1}$
). Hence,
![]() $\mathfrak {p}$
itself is isotropic, which means
$\mathfrak {p}$
itself is isotropic, which means
![]() $\chi (\mathfrak {p}^{(1)})=0$
. Hence
$\chi (\mathfrak {p}^{(1)})=0$
. Hence
![]() $\mathfrak {p}\in D(\mathfrak {p},\chi )\subset D(\mathfrak {g},\chi )$
.
$\mathfrak {p}\in D(\mathfrak {p},\chi )\subset D(\mathfrak {g},\chi )$
.
Thus
![]() $D(\mathfrak {g},\chi )$
is not empty. The proof is completed.
$D(\mathfrak {g},\chi )$
is not empty. The proof is completed.
By Corollary 5.2, there exists
![]() $\mathfrak {h}\in D(\mathfrak {g},\chi )$
for any given
$\mathfrak {h}\in D(\mathfrak {g},\chi )$
for any given
![]() $\chi \in \mathfrak {g}_{\bar 0}^{*}$
.
$\chi \in \mathfrak {g}_{\bar 0}^{*}$
.
Proposition 5.3 Let
![]() $\mathfrak {g}=\mathfrak {g}_{\bar 0}+\mathfrak {g}_{\bar 1}$
be a completely solvable Lie superalgebra, and
$\mathfrak {g}=\mathfrak {g}_{\bar 0}+\mathfrak {g}_{\bar 1}$
be a completely solvable Lie superalgebra, and
![]() $\chi \in \mathfrak {g}_{\bar 0}^{*}$
given. Then there is an irreducible module V of
$\chi \in \mathfrak {g}_{\bar 0}^{*}$
given. Then there is an irreducible module V of
![]() $\mathfrak {g}$
such that
$\mathfrak {g}$
such that
![]() $\dim V=p^{\frac {b_0^{\chi }}{2}}2^{\lfloor \frac {b_1^{\chi }}{2}\rfloor }$
.
$\dim V=p^{\frac {b_0^{\chi }}{2}}2^{\lfloor \frac {b_1^{\chi }}{2}\rfloor }$
.
Proof By Corollary 5.2, there exists
![]() $\mathfrak {h}\in D(\mathfrak {g},\chi )$
. If
$\mathfrak {h}\in D(\mathfrak {g},\chi )$
. If
![]() $\mathfrak {g}$
coincides with
$\mathfrak {g}$
coincides with
![]() $\mathfrak {h}$
, then all irreducible modules are one-dimensional, we are done.
$\mathfrak {h}$
, then all irreducible modules are one-dimensional, we are done.
In the following, we suppose that
![]() $\mathfrak {h}$
is a proper subalgebra of
$\mathfrak {h}$
is a proper subalgebra of
![]() $\mathfrak {g}$
. We prove the statement by induction on
$\mathfrak {g}$
. We prove the statement by induction on
![]() $\dim \mathfrak {g}$
. By Lemma 5.1,
$\dim \mathfrak {g}$
. By Lemma 5.1,
![]() $\mathfrak {h}$
is contained in a subalgebra
$\mathfrak {h}$
is contained in a subalgebra
![]() $\mathfrak {p}$
of codimension one in
$\mathfrak {p}$
of codimension one in
![]() $\mathfrak {g}$
, and
$\mathfrak {g}$
, and
![]() $D(\mathfrak {p},\chi )\subset D(\mathfrak {g},\chi )$
. By the inductive hypothesis along with Remark 2.2(1), there is an irreducible
$D(\mathfrak {p},\chi )\subset D(\mathfrak {g},\chi )$
. By the inductive hypothesis along with Remark 2.2(1), there is an irreducible
![]() $\mathfrak {p}$
-module W with
$\mathfrak {p}$
-module W with
 $$ \begin{align} \dim W=\begin{cases} &p^{\frac{b_0^{\chi}}{2}-1}2^{\lfloor\frac{b_1^{\chi}}{2}\rfloor}\text{ if } \underline{\dim} \mathfrak{p}=(\dim\mathfrak{g}_{\bar 0}-1|\dim\mathfrak{g}_{\bar 1});\cr &p^{\frac{b_0^{\chi}}{2}}2^{\lfloor\frac{b_1^{\chi}}{2}\rfloor-1} \text{ if } \underline{\dim} \mathfrak{p}=(\dim\mathfrak{g}_{\bar 0}|\dim\mathfrak{g}_{\bar 1}-1). \end{cases} \end{align} $$
$$ \begin{align} \dim W=\begin{cases} &p^{\frac{b_0^{\chi}}{2}-1}2^{\lfloor\frac{b_1^{\chi}}{2}\rfloor}\text{ if } \underline{\dim} \mathfrak{p}=(\dim\mathfrak{g}_{\bar 0}-1|\dim\mathfrak{g}_{\bar 1});\cr &p^{\frac{b_0^{\chi}}{2}}2^{\lfloor\frac{b_1^{\chi}}{2}\rfloor-1} \text{ if } \underline{\dim} \mathfrak{p}=(\dim\mathfrak{g}_{\bar 0}|\dim\mathfrak{g}_{\bar 1}-1). \end{cases} \end{align} $$
There certainly exists an irreducible module V of
![]() $\mathfrak {g}$
such that V contains an irreducible
$\mathfrak {g}$
such that V contains an irreducible
![]() $\mathfrak {p}$
-submodule isomorphic to W. We claim that
$\mathfrak {p}$
-submodule isomorphic to W. We claim that
![]() $\dim V=p^{\frac {b_0^{\chi }}{2}}2^{\lfloor \frac {b_1^{\chi }}{2}\rfloor }$
.
$\dim V=p^{\frac {b_0^{\chi }}{2}}2^{\lfloor \frac {b_1^{\chi }}{2}\rfloor }$
.
Actually, by Proposition 4.5 and its proof, there is a subalgebra
![]() $\mathcal {H}$
such that
$\mathcal {H}$
such that
![]() $\chi (\mathcal {H}^{(1)})=0$
and the dimensions of W and of V are respectively formulated as
$\chi (\mathcal {H}^{(1)})=0$
and the dimensions of W and of V are respectively formulated as
![]() $\dim V=p^{\dim \mathfrak {g}_{\bar 0}/ \mathcal {H}_{\bar 0}}2^{\dim \mathfrak {g}_{\bar 1}/ \mathcal {H}_{\bar 1}}$
, and
$\dim V=p^{\dim \mathfrak {g}_{\bar 0}/ \mathcal {H}_{\bar 0}}2^{\dim \mathfrak {g}_{\bar 1}/ \mathcal {H}_{\bar 1}}$
, and
![]() $\dim W=p^{\dim \mathfrak {p}_{\bar 0}/ \mathcal {H}^{\prime }_{\bar 0}}2^{\dim \mathfrak {p}_{\bar 1}/ \mathcal {H}^{\prime }_{\bar 1}}$
, where
$\dim W=p^{\dim \mathfrak {p}_{\bar 0}/ \mathcal {H}^{\prime }_{\bar 0}}2^{\dim \mathfrak {p}_{\bar 1}/ \mathcal {H}^{\prime }_{\bar 1}}$
, where
![]() $\mathcal {H}^{\prime }_{\bar 0}=\mathfrak {g}_{\bar 0}\cap \mathcal {H}_{\bar 0}$
,
$\mathcal {H}^{\prime }_{\bar 0}=\mathfrak {g}_{\bar 0}\cap \mathcal {H}_{\bar 0}$
,
![]() $\mathcal {H}^{\prime }_{\bar 1}=\mathfrak {g}_{\bar 1}\cap \mathcal {H}_{\bar 1}$
. Note that
$\mathcal {H}^{\prime }_{\bar 1}=\mathfrak {g}_{\bar 1}\cap \mathcal {H}_{\bar 1}$
. Note that
![]() $(\mathfrak {p}_i+\mathcal {H}_i/ \mathcal {H}_i)\cong \mathfrak {p}_i/ \mathfrak {p}_i\cap \mathcal {H}_i$
,
$(\mathfrak {p}_i+\mathcal {H}_i/ \mathcal {H}_i)\cong \mathfrak {p}_i/ \mathfrak {p}_i\cap \mathcal {H}_i$
,
![]() $\forall i\in \mathbb {Z}_2$
, as vector spaces. From (5.1), it yields that
$\forall i\in \mathbb {Z}_2$
, as vector spaces. From (5.1), it yields that
![]() $\dim V=p^{\frac {b_0^{\chi }}{2}}2^{\lfloor \frac {b_1^{\chi }}{2}\rfloor }$
.
$\dim V=p^{\frac {b_0^{\chi }}{2}}2^{\lfloor \frac {b_1^{\chi }}{2}\rfloor }$
.
From now on, we turn to the situation of completely solvable restricted Lie superalgebras.
Proposition 5.4 Let
![]() $\mathfrak {g}$
be a completely solvable restricted Lie superalgebras with p-mapping
$\mathfrak {g}$
be a completely solvable restricted Lie superalgebras with p-mapping
![]() $[p]$
on
$[p]$
on
![]() $\mathfrak {g}_{\bar 0}$
, and
$\mathfrak {g}_{\bar 0}$
, and
![]() $\chi \in \mathfrak {g}^{*}_{\bar 0}$
any given p-character. Then the following statements hold.
$\chi \in \mathfrak {g}^{*}_{\bar 0}$
any given p-character. Then the following statements hold.
-
(1) Each irreducible
 $U_{\chi }(\mathfrak {g})$
-module V is associated with certain subalgebra
$U_{\chi }(\mathfrak {g})$
-module V is associated with certain subalgebra
 $\mathfrak {h}$
with
$\mathfrak {h}$
with
 $\chi (\mathfrak {h}^{(1)})=0$
, such that V has dimension and there is a one-dimensional
$\chi (\mathfrak {h}^{(1)})=0$
, such that V has dimension and there is a one-dimensional $$ \begin{align*}p^{\dim\mathfrak{g}_{\bar 0}/\mathfrak{h}_{\bar 0}}2^{\dim\mathfrak{g}_{\bar 0}/\mathfrak{h}_{\bar 0}}\end{align*} $$
$$ \begin{align*}p^{\dim\mathfrak{g}_{\bar 0}/\mathfrak{h}_{\bar 0}}2^{\dim\mathfrak{g}_{\bar 0}/\mathfrak{h}_{\bar 0}}\end{align*} $$
 $\mathfrak {h}$
-submodule in V.
$\mathfrak {h}$
-submodule in V.
-
(2) All irreducible modules of
 $U_{\chi }(\mathfrak {g})$
have the same dimension.
$U_{\chi }(\mathfrak {g})$
have the same dimension.
Proof (1) follows from Theorem 4.7.
For (2), we first notice that the even center
![]() $C(\mathfrak {g})_{\bar 0}$
is an ideal of
$C(\mathfrak {g})_{\bar 0}$
is an ideal of
![]() $\mathfrak {g}$
, and
$\mathfrak {g}$
, and
![]() $C(\mathfrak {g})_{\bar 0}=C(\mathfrak {g})\cap \mathfrak {g}_{\bar 0}\subset C(\mathfrak {g}_{\bar 0})$
. Then, we prove the proposition by different steps.
$C(\mathfrak {g})_{\bar 0}=C(\mathfrak {g})\cap \mathfrak {g}_{\bar 0}\subset C(\mathfrak {g}_{\bar 0})$
. Then, we prove the proposition by different steps.
(2.i) We claim that if
![]() $C(\mathfrak {g})_{\bar 0}^{[p]}=0$
, then every irreducible restricted representation of
$C(\mathfrak {g})_{\bar 0}^{[p]}=0$
, then every irreducible restricted representation of
![]() $\mathfrak {g}$
is one-dimensional. Note that by definition
$\mathfrak {g}$
is one-dimensional. Note that by definition
![]() $\mathfrak {g}^{(1)}$
is nilpotent, acting nilpotently on
$\mathfrak {g}^{(1)}$
is nilpotent, acting nilpotently on
![]() $\mathfrak {g}$
. Hence, there exists a positive integer k such that
$\mathfrak {g}$
. Hence, there exists a positive integer k such that
![]() $X^{[p]^k}\in C(\mathfrak {g})_{\bar 0}$
for all
$X^{[p]^k}\in C(\mathfrak {g})_{\bar 0}$
for all
![]() $X\in \mathfrak {g}_{\bar 0}$
. The assumption that
$X\in \mathfrak {g}_{\bar 0}$
. The assumption that
![]() $C(\mathfrak {g})_{\bar 0}^{[p]}=0$
entails that
$C(\mathfrak {g})_{\bar 0}^{[p]}=0$
entails that
![]() $\mathfrak {g}_{\bar 0}^{(1)}\subset \text {rad}_p(\mathfrak {g}_{\bar 0})$
, where
$\mathfrak {g}_{\bar 0}^{(1)}\subset \text {rad}_p(\mathfrak {g}_{\bar 0})$
, where
![]() $\text {rad}_p(\mathfrak {g}_{\bar 0})$
denotes p-radical which is the set of
$\text {rad}_p(\mathfrak {g}_{\bar 0})$
denotes p-radical which is the set of
![]() $X\in \mathfrak {g}_{\text {ev}}$
with
$X\in \mathfrak {g}_{\text {ev}}$
with
![]() $X^{[p]^n}=0$
for some positive integer
$X^{[p]^n}=0$
for some positive integer
![]() $n\in \mathbb {N}$
(here n is dependent on X). By the same arguments as in the proof [Reference Strade and Farnsteiner26, Lemma 5.8.6(1)], one has
$n\in \mathbb {N}$
(here n is dependent on X). By the same arguments as in the proof [Reference Strade and Farnsteiner26, Lemma 5.8.6(1)], one has
![]() $\mathfrak {g}_{\bar 0}=T\oplus \text {rad}_p(\mathfrak {g}_{\bar 0}),$
where T is a maximal torus of
$\mathfrak {g}_{\bar 0}=T\oplus \text {rad}_p(\mathfrak {g}_{\bar 0}),$
where T is a maximal torus of
![]() $\mathfrak {g}_{\bar 0}$
. In particular,
$\mathfrak {g}_{\bar 0}$
. In particular,
![]() $C(\mathfrak {g})_{\bar 0}\subset \text {rad}_p(\mathfrak {g}_{\bar 0})$
, and
$C(\mathfrak {g})_{\bar 0}\subset \text {rad}_p(\mathfrak {g}_{\bar 0})$
, and
![]() $\mathfrak {g}^{(1)}\subset \text {rad}_p(\mathfrak {g}_{\bar 0})+\mathfrak {g}_{\bar 1}$
while
$\mathfrak {g}^{(1)}\subset \text {rad}_p(\mathfrak {g}_{\bar 0})+\mathfrak {g}_{\bar 1}$
while
![]() $[\mathfrak {g}_{\bar 1},\mathfrak {g}_{\bar 1}]\subset \text {rad}_p(\mathfrak {g}_{\bar 0})$
. Hence
$[\mathfrak {g}_{\bar 1},\mathfrak {g}_{\bar 1}]\subset \text {rad}_p(\mathfrak {g}_{\bar 0})$
. Hence
![]() $\mathfrak {g}^{(1)}\subset \text {rad}(\mathfrak {g})$
. For any irreducible restricted representation
$\mathfrak {g}^{(1)}\subset \text {rad}(\mathfrak {g})$
. For any irreducible restricted representation
![]() $\rho : \mathfrak {g}\rightarrow \mathfrak {gl}(V)$
,
$\rho : \mathfrak {g}\rightarrow \mathfrak {gl}(V)$
,
![]() $\rho (\text {rad}_p(\mathfrak {g}_{\bar 0}))$
acts nilpotently on V, therefore acts trivially on V. So
$\rho (\text {rad}_p(\mathfrak {g}_{\bar 0}))$
acts nilpotently on V, therefore acts trivially on V. So
![]() $\rho (\mathfrak {g}^{(1)})$
acts trivially on V. By Lemma 4.2, V is one-dimensional, which is of parity
$\rho (\mathfrak {g}^{(1)})$
acts trivially on V. By Lemma 4.2, V is one-dimensional, which is of parity
![]() $0$
Footnote
2
. This V is completely decided by a function
$0$
Footnote
2
. This V is completely decided by a function
![]() $\lambda $
with
$\lambda $
with
![]() $\lambda (\mathfrak {g}^{(1)})=0$
and
$\lambda (\mathfrak {g}^{(1)})=0$
and
![]() $\lambda (X^{[p]})=\lambda (X)^p$
for
$\lambda (X^{[p]})=\lambda (X)^p$
for
![]() $X\in \mathfrak {g}_{\bar 0}$
.
$X\in \mathfrak {g}_{\bar 0}$
.
(2.ii) Suppose that
![]() $(W_i,\rho _i)$
(
$(W_i,\rho _i)$
(
![]() $i=1,2$
) are two irreducible modules of
$i=1,2$
) are two irreducible modules of
![]() $U_{\chi }(\mathfrak {g})$
with
$U_{\chi }(\mathfrak {g})$
with
![]() ${\rho _1}|_{C(\mathfrak {g})_{\bar 0}}={\rho _2}|_{C(\mathfrak {g})_{\bar 0}}$
. Consider
${\rho _1}|_{C(\mathfrak {g})_{\bar 0}}={\rho _2}|_{C(\mathfrak {g})_{\bar 0}}$
. Consider
![]() $\mathcal {H}:=\text {Hom}_{\mathbf {k}}(W_1,W_2)$
. Then
$\mathcal {H}:=\text {Hom}_{\mathbf {k}}(W_1,W_2)$
. Then
![]() $\mathcal {H}=\mathcal {H}_{\bar 0}+\mathcal {H}_{\bar 1}$
becomes a
$\mathcal {H}=\mathcal {H}_{\bar 0}+\mathcal {H}_{\bar 1}$
becomes a
![]() $\mathfrak {g}$
-module by defining via homogenous elements
$\mathfrak {g}$
-module by defining via homogenous elements
![]() $X\in \mathfrak {g}_{|X|}$
, and
$X\in \mathfrak {g}_{|X|}$
, and
![]() $\nu \in \mathcal {H}_{|\nu |}$
, where
$\nu \in \mathcal {H}_{|\nu |}$
, where
![]() $|X|, |\nu |\in \mathbb {Z}_2$
denote the parities of X and
$|X|, |\nu |\in \mathbb {Z}_2$
denote the parities of X and
![]() $\nu $
, respectively:
$\nu $
, respectively:
Furthermore, it is readily shown that
![]() $\mathcal {H}$
is a restricted
$\mathcal {H}$
is a restricted
![]() $\mathfrak {g}$
-module, on which the representation is denoted by
$\mathfrak {g}$
-module, on which the representation is denoted by
![]() $\vartheta $
. By definition,
$\vartheta $
. By definition,
![]() $\vartheta (\mathfrak {g})$
admits a p-mapping satisfying
$\vartheta (\mathfrak {g})$
admits a p-mapping satisfying
![]() $\vartheta (C(\mathfrak {g})_{\bar 0})^{[p]}=0$
because
$\vartheta (C(\mathfrak {g})_{\bar 0})^{[p]}=0$
because
![]() ${\rho _1}|_{C(\mathfrak {g})_{\bar 0}}={\rho _2}|_{C(\mathfrak {g})_{\bar 0}}$
and
${\rho _1}|_{C(\mathfrak {g})_{\bar 0}}={\rho _2}|_{C(\mathfrak {g})_{\bar 0}}$
and
![]() $C(\mathfrak {g})_{\bar 0}\subset C(\mathfrak {g}_{\bar 0})$
. Hence, there is an irreducible submodule of
$C(\mathfrak {g})_{\bar 0}\subset C(\mathfrak {g}_{\bar 0})$
. Hence, there is an irreducible submodule of
![]() $U_0(\mathfrak {g})$
in
$U_0(\mathfrak {g})$
in
![]() $\mathcal {H}$
, which must be one-dimensional by (2.i), admitting parity
$\mathcal {H}$
, which must be one-dimensional by (2.i), admitting parity
![]() $0$
. We take such one, for example,
$0$
. We take such one, for example,
![]() ${\mathbb {S}}:=\mathbf {k}\nu $
. Then
${\mathbb {S}}:=\mathbf {k}\nu $
. Then
![]() $\mathfrak {g}^{(1)}$
acts trivially on
$\mathfrak {g}^{(1)}$
acts trivially on
![]() $\nu $
, and
$\nu $
, and
![]() $\mathfrak {g}$
acts on
$\mathfrak {g}$
acts on
![]() $\nu $
by a scalar
$\nu $
by a scalar
![]() $\lambda \in \mathfrak {g}_{\bar 0}^{*}$
with
$\lambda \in \mathfrak {g}_{\bar 0}^{*}$
with
![]() $\lambda (\mathfrak {g}^{(1)})=0$
. Also
$\lambda (\mathfrak {g}^{(1)})=0$
. Also
![]() $\vartheta (X)\nu =\lambda (X)\nu $
for all
$\vartheta (X)\nu =\lambda (X)\nu $
for all
![]() $X\in \mathfrak {g}$
, consequently
$X\in \mathfrak {g}$
, consequently
![]() $\lambda (X^{[p]})=\lambda (X)^p$
for
$\lambda (X^{[p]})=\lambda (X)^p$
for
![]() $X\in \mathfrak {g}_{\bar 0}$
. By (5.2),
$X\in \mathfrak {g}_{\bar 0}$
. By (5.2),
![]() $\rho _2(X)(\vartheta (w))-\vartheta (\rho _1(X)w)=\lambda (X)\vartheta (w)$
for
$\rho _2(X)(\vartheta (w))-\vartheta (\rho _1(X)w)=\lambda (X)\vartheta (w)$
for
![]() $X\in \mathfrak {g}$
and
$X\in \mathfrak {g}$
and
![]() $w\in W_1$
. So the assignment
$w\in W_1$
. So the assignment
![]() $w\mapsto \vartheta (w)\otimes 1$
for
$w\mapsto \vartheta (w)\otimes 1$
for
![]() $w\in W_1$
defines a nontrivial
$w\in W_1$
defines a nontrivial
![]() $\mathfrak {g}$
-module homomorphism:
$\mathfrak {g}$
-module homomorphism:
![]() $W_1\rightarrow W_2\otimes _{\mathbf {k}} \mathbf {k}_{-\lambda }$
, which is even. By Schur’s lemma, this homomorphism must be an isomorphism. Hence
$W_1\rightarrow W_2\otimes _{\mathbf {k}} \mathbf {k}_{-\lambda }$
, which is even. By Schur’s lemma, this homomorphism must be an isomorphism. Hence
![]() $\dim W_1=\dim W_2$
.
$\dim W_1=\dim W_2$
.
(2.iii) Note that
![]() $C(\mathfrak {g})_{\bar 0}\subset C(\mathfrak {g}_{\bar 0})$
. So
$C(\mathfrak {g})_{\bar 0}\subset C(\mathfrak {g}_{\bar 0})$
. So
![]() $\mathfrak {g}_{\bar 0}$
possesses a p-mapping
$\mathfrak {g}_{\bar 0}$
possesses a p-mapping
![]() $[p]'$
with
$[p]'$
with
![]() $C(\mathfrak {g})_{\bar 0}^{[p]'}=0$
(see [Reference Strade and Farnsteiner26, Chapter 2]), and for any
$C(\mathfrak {g})_{\bar 0}^{[p]'}=0$
(see [Reference Strade and Farnsteiner26, Chapter 2]), and for any
![]() $y\in \mathfrak {g}_{\bar 0}$
,
$y\in \mathfrak {g}_{\bar 0}$
,
![]() $\xi (y):=y^{[p]}-y^{[p]'}$
belongs to
$\xi (y):=y^{[p]}-y^{[p]'}$
belongs to
![]() $C(\mathfrak {g})_{\bar 0}$
. So for any given irreducible representation
$C(\mathfrak {g})_{\bar 0}$
. So for any given irreducible representation
![]() $(\rho ,W)$
of
$(\rho ,W)$
of
![]() $\mathfrak {g}$
on the space W, by Schur’s lemma
$\mathfrak {g}$
on the space W, by Schur’s lemma
![]() $\xi (y)$
acts on W by scalar
$\xi (y)$
acts on W by scalar
![]() $c_W(y)^p$
, where
$c_W(y)^p$
, where
![]() $c_W$
is a linear function on
$c_W$
is a linear function on
![]() $C(\mathfrak {g})_{\bar 0}$
. Then, we have for any
$C(\mathfrak {g})_{\bar 0}$
. Then, we have for any
![]() $y\in C(\mathfrak {g})_{\bar 0,}$
$y\in C(\mathfrak {g})_{\bar 0,}$
Note that
![]() $c_W$
can extend to a function on
$c_W$
can extend to a function on
![]() $\mathfrak {g}_{\bar 0}$
which gives rise to a one-dimensional
$\mathfrak {g}_{\bar 0}$
which gives rise to a one-dimensional
![]() $U_{c_W}(\mathfrak {g})$
-module, with respect to
$U_{c_W}(\mathfrak {g})$
-module, with respect to
![]() $(\mathfrak {g},[p]')$
. So for any two irreducible
$(\mathfrak {g},[p]')$
. So for any two irreducible
![]() $U_{\chi }(\mathfrak {g})$
-modules
$U_{\chi }(\mathfrak {g})$
-modules
![]() $W_1$
and
$W_1$
and
![]() $W_2$
, we have two new irreducible representations
$W_2$
, we have two new irreducible representations
![]() $\overline {\rho }_i$
on
$\overline {\rho }_i$
on
![]() $\overline W_i:=W_i\otimes _{\mathbf {k}} \mathbf {k}_{-c_{W_i}}$
$\overline W_i:=W_i\otimes _{\mathbf {k}} \mathbf {k}_{-c_{W_i}}$
![]() $(i=1,2)$
, respectively. Then both of them become
$(i=1,2)$
, respectively. Then both of them become
![]() $U_{\chi }(\mathfrak {g})$
-modules with respect to
$U_{\chi }(\mathfrak {g})$
-modules with respect to
![]() $(\mathfrak {g},[p]')$
, and
$(\mathfrak {g},[p]')$
, and
![]() $\overline {\rho }_i|_{C(\mathfrak {g})_{\bar 0}}$
(
$\overline {\rho }_i|_{C(\mathfrak {g})_{\bar 0}}$
(
![]() $i=1,2$
) coincide. By (2.ii),
$i=1,2$
) coincide. By (2.ii),
![]() $\dim \overline {W}_i$
(
$\dim \overline {W}_i$
(
![]() $i=1,2$
) have the same dimension. Hence, both
$i=1,2$
) have the same dimension. Hence, both
![]() $W_1$
and
$W_1$
and
![]() $W_2$
have the same dimension.
$W_2$
have the same dimension.
The proof is completed.
Summing up Propositions 5.3 and 5.4 we have the following.
Theorem 5.5 Let
![]() $\mathfrak {g}=\mathfrak {g}_{\bar 0}+\mathfrak {g}_{\bar 1}$
be a finite-dimensional completely solvable restricted Lie superalgebra over
$\mathfrak {g}=\mathfrak {g}_{\bar 0}+\mathfrak {g}_{\bar 1}$
be a finite-dimensional completely solvable restricted Lie superalgebra over
![]() $\mathbf {k}$
. Then for any given
$\mathbf {k}$
. Then for any given
![]() $\chi \in \mathfrak {g}^{*}_{\bar 0}$
, all irreducible
$\chi \in \mathfrak {g}^{*}_{\bar 0}$
, all irreducible
![]() $\mathfrak {g}$
-modules associated with
$\mathfrak {g}$
-modules associated with
![]() $\chi $
have dimension
$\chi $
have dimension
The above theorem is an extension of Kac–Weisfeiler’s result on completely solvable restricted Lie algebras (see [Reference Weisfeiler and Kac31, Theorem 1]). As a corollary to Theorem 5.5, we have the following.
Corollary 5.6 Conjecture 2.3 holds for completely solvable restricted Lie superalgebras.
A Appendix: Minimal p-envelopes for a finite-dimensional Lie superalgebra over
 $\textbf {k}$
$\textbf {k}$
Let
![]() $\mathfrak {g}=\mathfrak {g}_{\bar 0}\oplus \mathfrak {g}_{\bar 1}$
be a finite-dimensional Lie superalgebra over
$\mathfrak {g}=\mathfrak {g}_{\bar 0}\oplus \mathfrak {g}_{\bar 1}$
be a finite-dimensional Lie superalgebra over
![]() $\mathbf {k}$
of characteristic
$\mathbf {k}$
of characteristic
![]() $p>2$
. In this appendix section, we introduce the properties of p-envelopes of
$p>2$
. In this appendix section, we introduce the properties of p-envelopes of
![]() $\mathfrak {g}$
. For more details on restricted Lie algebras, the reader may refer to [Reference Strade and Farnsteiner26, Section 2.5].
$\mathfrak {g}$
. For more details on restricted Lie algebras, the reader may refer to [Reference Strade and Farnsteiner26, Section 2.5].
A.1 Definition of p-envelopes
Definition A.1 Keep the notations and assumptions as above. A restricted Lie superalgebra
![]() $(\mathcal {G},[p])$
is said to be a p-envelope of
$(\mathcal {G},[p])$
is said to be a p-envelope of
![]() $\mathfrak {g}$
if there exists a homomorphism of Lie superalgebras
$\mathfrak {g}$
if there exists a homomorphism of Lie superalgebras
![]() $\mathbf {i}:\mathfrak {g}\rightarrow \mathcal {G}$
such that
$\mathbf {i}:\mathfrak {g}\rightarrow \mathcal {G}$
such that
![]() $\mathbf {i}$
is injective and the restricted Lie sub-superalgebra
$\mathbf {i}$
is injective and the restricted Lie sub-superalgebra
![]() $\mathbf {i}(\mathfrak {g})_p$
of
$\mathbf {i}(\mathfrak {g})_p$
of
![]() $\mathcal {G}$
generated by
$\mathcal {G}$
generated by
![]() $\mathfrak {g}$
coincides with
$\mathfrak {g}$
coincides with
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
In the following, we make an example of p-envelopes which is taken from the universal enveloping algebra
![]() $U(\mathfrak {g})$
. We first recall that an associative superalgebra
$U(\mathfrak {g})$
. We first recall that an associative superalgebra
![]() $\mathfrak {A}=\mathfrak {A}_{\bar 0}\oplus \mathfrak {A}_{\bar 1}$
can be endowed with structure of a restricted Lie superalgebra, which is denoted by
$\mathfrak {A}=\mathfrak {A}_{\bar 0}\oplus \mathfrak {A}_{\bar 1}$
can be endowed with structure of a restricted Lie superalgebra, which is denoted by
![]() $\mathfrak {A}^-$
, where the underline space of
$\mathfrak {A}^-$
, where the underline space of
![]() $\mathfrak {A}^-$
is
$\mathfrak {A}^-$
is
![]() $\mathfrak {A}$
itself, and the Lie bracket is defined via
$\mathfrak {A}$
itself, and the Lie bracket is defined via
![]() $[u_1,u_2]:=u_1u_2-(-1)^{|u_1||u_2|}u_2u_1$
for
$[u_1,u_2]:=u_1u_2-(-1)^{|u_1||u_2|}u_2u_1$
for
![]() $\mathbb {Z}_2$
-homogeneous elements
$\mathbb {Z}_2$
-homogeneous elements
![]() $u_i\in \mathfrak {A}_{|u_i|}$
,
$u_i\in \mathfrak {A}_{|u_i|}$
,
![]() $|u_i|\in \mathbb {Z}_2$
,
$|u_i|\in \mathbb {Z}_2$
,
![]() $i=1,2$
. And the p-mapping of
$i=1,2$
. And the p-mapping of
![]() $\mathfrak {A}_{\bar 0}$
is just the usual pth power in
$\mathfrak {A}_{\bar 0}$
is just the usual pth power in
![]() $\mathfrak {A}_{\bar 0}$
.
$\mathfrak {A}_{\bar 0}$
.
Example A.2 Let
![]() $\mathbf {i}:\mathfrak {g}\rightarrow U(\mathfrak {g})$
be the canonical imbedding of
$\mathbf {i}:\mathfrak {g}\rightarrow U(\mathfrak {g})$
be the canonical imbedding of
![]() $\mathfrak {g}$
into
$\mathfrak {g}$
into
![]() $U(\mathfrak {g})$
. Recall that in
$U(\mathfrak {g})$
. Recall that in
![]() $U(\mathfrak {g}_{\bar 0})^-\subset U(\mathfrak {g})^-$
, the Lie subalgebra
$U(\mathfrak {g}_{\bar 0})^-\subset U(\mathfrak {g})^-$
, the Lie subalgebra
![]() $\mathbf {i}(\mathfrak {g}_{\bar 0})$
generates a restricted Lie subalgebra
$\mathbf {i}(\mathfrak {g}_{\bar 0})$
generates a restricted Lie subalgebra
![]() $\mathbf {i}(\mathfrak {g}_{\bar 0})_p=\bigoplus _{i=0}^{\infty } \mathbf {i}(\mathfrak {g})^{p^i}$
of
$\mathbf {i}(\mathfrak {g}_{\bar 0})_p=\bigoplus _{i=0}^{\infty } \mathbf {i}(\mathfrak {g})^{p^i}$
of
![]() $U(\mathfrak {g}_{\bar 0})^-$
, where
$U(\mathfrak {g}_{\bar 0})^-$
, where
![]() $\mathbf {i}(\mathfrak {g})^{p^i}=\{\mathbf {i}(g)^{p^i}\mid g\in \mathfrak {g}_{\bar 0}\}$
(see [Reference Zassenhaus38] or [Reference Strade and Farnsteiner26, Section 5.2]). Take
$\mathbf {i}(\mathfrak {g})^{p^i}=\{\mathbf {i}(g)^{p^i}\mid g\in \mathfrak {g}_{\bar 0}\}$
(see [Reference Zassenhaus38] or [Reference Strade and Farnsteiner26, Section 5.2]). Take
Then
![]() $\mathcal {G}$
becomes a p-envelope of
$\mathcal {G}$
becomes a p-envelope of
![]() $\mathfrak {g}$
.
$\mathfrak {g}$
.
Such a p-envelope as above is usually called the universal p-envelope of
![]() $\mathfrak {g}$
, which we denote by
$\mathfrak {g}$
, which we denote by
![]() $\widehat {\mathfrak {g}}$
. By straightforward calculations, it is not hard to see that
$\widehat {\mathfrak {g}}$
. By straightforward calculations, it is not hard to see that
![]() $\mathbf {i}(\mathfrak {g})$
is an ideal of
$\mathbf {i}(\mathfrak {g})$
is an ideal of
![]() $\widehat {\mathfrak {g}}$
. Consider the superalgebra
$\widehat {\mathfrak {g}}$
. Consider the superalgebra
![]() $\text {SDer}(\mathfrak {g})$
of super derivations on
$\text {SDer}(\mathfrak {g})$
of super derivations on
![]() $\mathfrak {g}$
, and the homomorphism
$\mathfrak {g}$
, and the homomorphism
![]() $\mathsf {ad}: \widehat {\mathfrak {g}}\rightarrow \text {SDer}(\mathfrak {g})$
defined via sending
$\mathsf {ad}: \widehat {\mathfrak {g}}\rightarrow \text {SDer}(\mathfrak {g})$
defined via sending
![]() $x\mapsto \mathsf {ad} x|_{\mathbf {i}(\mathfrak {g})}$
. Then
$x\mapsto \mathsf {ad} x|_{\mathbf {i}(\mathfrak {g})}$
. Then
![]() $\ker (\mathsf {ad})$
coincides with the center
$\ker (\mathsf {ad})$
coincides with the center
![]() $C(\widehat {\mathfrak {g}})$
of
$C(\widehat {\mathfrak {g}})$
of
![]() $\widehat {\mathfrak {g}}$
.
$\widehat {\mathfrak {g}}$
.
By the same arguments as in the Lie algebras case (see [Reference Strade and Farnsteiner26, Section 2.5]), we have the following basic results.
Lemma A.3 The following statements hold.
-
(1) There is a finite-dimensional p-envelope
 $\mathcal {G}$
of
$\mathcal {G}$
of
 $\mathfrak {g}$
such that
$\mathfrak {g}$
such that
 $\mathcal {G}=(\mathfrak {g}_{\bar 0})_p\oplus \mathfrak {g}_{\bar 1}$
where
$\mathcal {G}=(\mathfrak {g}_{\bar 0})_p\oplus \mathfrak {g}_{\bar 1}$
where
 $(\mathfrak {g}_{\bar 0})_p$
is a p-envelope of
$(\mathfrak {g}_{\bar 0})_p$
is a p-envelope of
 $\mathfrak {g}_{\bar 0}$
.
$\mathfrak {g}_{\bar 0}$
. -
(2) There is a minimal finite-dimensional p-envelope
 $\mathcal {G}$
of
$\mathcal {G}$
of
 $\mathfrak {g}$
satisfying (1).
$\mathfrak {g}$
satisfying (1). -
(3) Any two minimal dimensional p-envelopes of
 $\mathfrak {g}$
are isomorphic, as Lie superalgebras.
$\mathfrak {g}$
are isomorphic, as Lie superalgebras.
Proof For the part (1), we choose a sub-superspace V in the center
![]() $C(\widehat {\mathfrak {g}})$
of
$C(\widehat {\mathfrak {g}})$
of
![]() $\widehat {\mathfrak {g}}$
such that
$\widehat {\mathfrak {g}}$
such that
![]() $C(\widehat {\mathfrak {g}})=V\oplus (C(\widehat {\mathfrak {g}})\cap \phi (\mathfrak {g}))$
. This V naturally becomes an ideal of
$C(\widehat {\mathfrak {g}})=V\oplus (C(\widehat {\mathfrak {g}})\cap \phi (\mathfrak {g}))$
. This V naturally becomes an ideal of
![]() $\hat {\mathfrak {g}}$
. Consider
$\hat {\mathfrak {g}}$
. Consider
![]() $\widetilde {\mathfrak {g}}:=\widehat {\mathfrak {g}}/ V$
. It is easily seen that
$\widetilde {\mathfrak {g}}:=\widehat {\mathfrak {g}}/ V$
. It is easily seen that
![]() $\widetilde {\mathfrak {g}}$
is endowed with structure of restricted Lie superalgebras arising from the one of
$\widetilde {\mathfrak {g}}$
is endowed with structure of restricted Lie superalgebras arising from the one of
![]() $\widehat {\mathfrak {g}}$
. Furthermore,
$\widehat {\mathfrak {g}}$
. Furthermore,
![]() $\dim \widetilde {\mathfrak {g}}=\dim \widehat {\mathfrak {g}}/ C(\widehat {\mathfrak {g}})+\dim C(\widehat {\mathfrak {g}}\cap \phi (\mathfrak {g})$
. Note that
$\dim \widetilde {\mathfrak {g}}=\dim \widehat {\mathfrak {g}}/ C(\widehat {\mathfrak {g}})+\dim C(\widehat {\mathfrak {g}}\cap \phi (\mathfrak {g})$
. Note that
![]() $\phi (\mathfrak {g})$
is an ideal of
$\phi (\mathfrak {g})$
is an ideal of
![]() $\widehat {\mathfrak {g}}$
, and the homomorphism
$\widehat {\mathfrak {g}}$
, and the homomorphism
![]() $\mathsf {ad}: \widehat {\mathfrak {g}}\rightarrow \text {SDer}(\mathfrak {g})$
defined via sending
$\mathsf {ad}: \widehat {\mathfrak {g}}\rightarrow \text {SDer}(\mathfrak {g})$
defined via sending
![]() $X\mapsto \mathsf {ad} X|_{\phi (\mathfrak {g})}$
, admits
$X\mapsto \mathsf {ad} X|_{\phi (\mathfrak {g})}$
, admits
![]() $\ker (\mathsf {ad})=C(\widehat {\mathfrak {g}})$
. Hence
$\ker (\mathsf {ad})=C(\widehat {\mathfrak {g}})$
. Hence
![]() $\dim \widehat {\mathfrak {g}}/ C(\widehat {\mathfrak {g}})\leq \dim \text {SDer}(\mathfrak {g})<\infty $
. Hence
$\dim \widehat {\mathfrak {g}}/ C(\widehat {\mathfrak {g}})\leq \dim \text {SDer}(\mathfrak {g})<\infty $
. Hence
![]() $\dim \widetilde {\mathfrak {g}}<\infty $
.
$\dim \widetilde {\mathfrak {g}}<\infty $
.
By the choice of V, there is an embedding
![]() $\psi $
of
$\psi $
of
![]() $\mathfrak {g}$
into
$\mathfrak {g}$
into
![]() $\widetilde {\mathfrak {g}}$
, i.e.
$\widetilde {\mathfrak {g}}$
, i.e.
![]() $\psi =\textsf {p}\circ \phi $
for the natural surjective homomorphism
$\psi =\textsf {p}\circ \phi $
for the natural surjective homomorphism
![]() $\textsf {p}:\widehat {\mathfrak {g}}\rightarrow \widetilde {\mathfrak {g}}$
. Consequently, it is readily known that
$\textsf {p}:\widehat {\mathfrak {g}}\rightarrow \widetilde {\mathfrak {g}}$
. Consequently, it is readily known that
![]() $\widetilde {\mathfrak {g}}$
is a p-envelope of
$\widetilde {\mathfrak {g}}$
is a p-envelope of
![]() $\mathfrak {g}$
. Such
$\mathfrak {g}$
. Such
![]() $\widetilde {\mathfrak {g}}$
satisfies the requirement that
$\widetilde {\mathfrak {g}}$
satisfies the requirement that
![]() $\widetilde {\mathfrak {g}}_{\bar 0}=\psi (\mathfrak {g}_{\bar 0})_p$
is a p-envelope of
$\widetilde {\mathfrak {g}}_{\bar 0}=\psi (\mathfrak {g}_{\bar 0})_p$
is a p-envelope of
![]() $\mathfrak {g}_{\bar 0}$
and
$\mathfrak {g}_{\bar 0}$
and
![]() $\widetilde {\mathfrak {g}}=\psi (\mathfrak {g}_{\bar 0})_p\oplus \psi (\mathfrak {g}_{\bar 1})$
.
$\widetilde {\mathfrak {g}}=\psi (\mathfrak {g}_{\bar 0})_p\oplus \psi (\mathfrak {g}_{\bar 1})$
.
As to (2), note that in the above arguments, the center of
![]() $\widetilde {\mathfrak {g}}$
lies in
$\widetilde {\mathfrak {g}}$
lies in
![]() $\psi (\mathfrak {g})$
. By an analog of the arguments in the proof of [Reference Strade and Farnsteiner26, Theorem 2.5.8], it can be proved that
$\psi (\mathfrak {g})$
. By an analog of the arguments in the proof of [Reference Strade and Farnsteiner26, Theorem 2.5.8], it can be proved that
![]() $\widetilde {\mathfrak {g}}$
is a minimal finite-dimensional p-envelope of
$\widetilde {\mathfrak {g}}$
is a minimal finite-dimensional p-envelope of
![]() $\mathfrak {g}$
satisfying (1).
$\mathfrak {g}$
satisfying (1).
The proof for (3) is also an analog of that of [Reference Strade and Farnsteiner26, Theorem 2.5.8]. We omit the details.
Acknowledgment
The author expresses his sincere thanks to the anonymous referee for his/her helpful comments and suggestions, and to Dr. Priyanshu Chakraborty for assistance in English expression.