1. INTRODUCTION
Global Navigation Satellite Systems (GNSS) have traditionally been used to investigate the spatio-temporal characteristics of the ionosphere Total Electron Content (TEC), both at the regional and the global levels. For precise estimation of the TEC, however, the Differential Code Bias (DCB) (i.e., difference in the code hardware delays at two different frequencies) for both of the satellites and the receiver must be accounted for. The satellite DCB values are stable over one day, while the receiver DCBs are not as stable (Sardon and Zarraoa, Reference Sardon and Zarraoa1997; Schaer, Reference Schaer1999).
Earlier studies focused on the estimation of Global Positioning System (GPS) differential code bias (e.g., Arikan et al., Reference Arikan, Nayir, Sezen and Arikan2008; Choi et al., Reference Choi, Cho and Lee2011; Jin et al., Reference Jin, Jin and Feng2012; Keshin, Reference Keshin2012; Kao et al., Reference Kao, Tu, Chen, Weng and Ji2013). Keshin (Reference Keshin2012) developed a model for receiver DCB estimation using vertical TEC values obtained from the IGS-GIM. The receiver DCBs and vertical residual ionospheric delays were computed using the least-squares estimation approach with linear constraints. The estimated values were compared with those of the IGS counterparts. The results showed agreement with the IGS values with differences less than 1 ns.
More recently, the DCBs for the new BeiDou and Galileo multi-GNSS signals were investigated by a number of researchers (e.g., Li et al., Reference Li, Yuan, Li, Ou and Huo.2012; Montenbruck et al., Reference Montenbruck, Hauschild and Steigenberger2014; Wei et al., Reference Wei, Zhang, Fan, Zhang, Huang and Chen2014; Zhang et al., Reference Zhang, Zhao, Zhang and Chen2014). Montenbruck et al. (Reference Montenbruck, Hauschild and Steigenberger2014) developed the multi-GNSS DCB estimation model for both the receivers and satellites. The DCBs for the legacy and modernised GPS, Galileo and BeiDou signals were determined using data collected from the IGS-MGEX network. The IGS-GIM was used in order to remove the ionospheric contribution from the dual frequency pseudorange differences. The estimated DCBs were compared with the group delay parameters transmitted through the GNSS broadcast ephemeris data. The findings showed good agreement with the broadcast parameters.
Ionospheric modelling using multi-GNSS measurements has been investigated by a number of researchers (e.g., Julien et al., Reference Julien, Issler and Lestarquit2012; Tu et al., Reference Tu, Ge, Zhang and Huang2013; Tang et al., Reference Tang, Jin and Xu2014; Zhang et al., Reference Zhang, Song, Yao, Shi, Lou and Yi2015). In Zhang et al. (Reference Zhang, Song, Yao, Shi, Lou and Yi2015), a regional ionosphere delay model is built over China using data from BeiDou only, GPS only, and combined GPS/BeiDou. The results show that the combined GPS/BeiDou model can significantly improve the accuracy of the estimated TEC and DCBs.
The objective of this research is to develop a multi-frequency multi-GNSS receiver differential code bias model. The receiver DCBs for the legacy and modernised GPS, Galileo and BeiDou signals are estimated based on ionosphere-corrected geometry-free linear combinations of the pseudorange observations. One way to remove the ionospheric delay from the pseudorange differences is to use the IGS-GIM model (Montenbruck et al., Reference Montenbruck, Hauschild and Steigenberger2014). Unfortunately, however, the IGS-GIM model has a limited spatiotemporal resolution. To overcome this problem, a Regional Ionospheric Model (RIM) over Europe is developed in this research. The developed RIM has spatial and temporal resolutions of 1° × 1° and 15 minutes, respectively. The accuracy of the developed RIM is validated for PPP applications. It is found that the positioning accuracy of the proposed RIM is superior to that of the IGS-GIM, where the RMSE values are reduced from ±0·325 to 0·25 m and from ±0·904 to 0·499 m, for the horizontal and height components, respectively (Abdelazeem et al., Reference Abdelazeem, Çelik and El-Rabbany2015). In order to produce the RIM, GPS observations from a regional network consisting of 60 International GNSS Service (IGS) and EUREF reference stations are processed in the Bernese-5·20 PPP module in order to estimate the VTEC values. The resulting MGR-DCB model is validated for receiver DCBs estimation for three IGS-MGEX stations on three different days. The estimated DCBs are compared with the publicly available IGS-MGEX values. The findings reveal that the estimated DCBs have good agreement with the MGEX values with mean difference and RMSE values less than 1 ns. In addition, the combined GPS, BeiDou and Galileo VTEC are assessed and compared with the IGS-GIM counterparts. It is shown that the combined VTEC values have mean difference and RMSE values less than 1 TECU with respect to the IGS-GIM counterparts.
2. PROPOSED MGR-DCB MODEL DEVELOPMENT
Firstly, a regional ionospheric model is developed in order to account for the effect of ionospheric delay in the pseudorange difference equations. The basic GPS observation equations can be expressed as follows (Kleusberg and Teunissen, Reference Kleusberg and Teunissen1998):
where P i and ϕ i are the pseudorange and carrier phase measurements in metres, respectively; ![]() $\rho _r^s $ is the satellite-receiver true geometric range; c is the speed of light in vacuum; dt r and dt s are the receiver and satellite clock errors, respectively;
$\rho _r^s $ is the satellite-receiver true geometric range; c is the speed of light in vacuum; dt r and dt s are the receiver and satellite clock errors, respectively; ![]() $I_{r,i}^s $ the ionospheric delay;
$I_{r,i}^s $ the ionospheric delay; ![]() $T_r^s $ the tropospheric delay; d r,i and
$T_r^s $ the tropospheric delay; d r,i and ![]() $\; d_i^s $ are the code hardware delays for the receiver and the satellite, respectively; δ r,i and
$\; d_i^s $ are the code hardware delays for the receiver and the satellite, respectively; δ r,i and ![]() $\delta _i^s $ are the carrier phase hardware delay for the receiver and the satellite, respectively; λ i is the wavelength of carrier phase; N i is the non-integer phase ambiguity, and ε p,i and ε ϕ,i are the code and phase un-modelled errors, including noise and multipath.
$\delta _i^s $ are the carrier phase hardware delay for the receiver and the satellite, respectively; λ i is the wavelength of carrier phase; N i is the non-integer phase ambiguity, and ε p,i and ε ϕ,i are the code and phase un-modelled errors, including noise and multipath.
Geometry-free linear combinations are formed using the un-differenced carrier-smoothed code observations, which eliminate the geometrical term, tropospheric delay, receiver and satellite clock errors as follows (Dach et al., Reference Dach, Hugentobler, Fridez and Meindl2007):
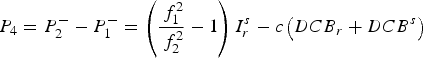 $$P_4 = P_2^ - - P_1^ - = \left( {\displaystyle{{\,f_1^2} \over {\,f_2^2}} - 1} \right)I_r^s - c\left( {DCB_r + DCB^s} \right)$$
$$P_4 = P_2^ - - P_1^ - = \left( {\displaystyle{{\,f_1^2} \over {\,f_2^2}} - 1} \right)I_r^s - c\left( {DCB_r + DCB^s} \right)$$
where ![]() ${\rm \;} P_i^ - $ are the smoothed code observables;
${\rm \;} P_i^ - $ are the smoothed code observables;![]() ${\rm \;} I_r^s {\rm \;} $ is the L1 ionospheric delay; DCB r and DCB s are the differential code bias for the receiver and the satellite, respectively.
${\rm \;} I_r^s {\rm \;} $ is the L1 ionospheric delay; DCB r and DCB s are the differential code bias for the receiver and the satellite, respectively.
Based on Equation (3), the Slant TEC (STEC) along the satellite-receiver path can be determined as follows:
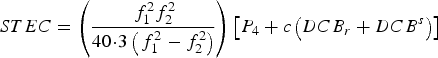 $$STEC = \left( {\displaystyle{{\,f_1^2 f_2^2} \over {40\!\cdot\!3\left( {\,f_1^2 - f_2^2} \right)}}} \right)\left[ {P_4 + c\left( {DCB_r + DCB^s} \right)} \right]$$
$$STEC = \left( {\displaystyle{{\,f_1^2 f_2^2} \over {40\!\cdot\!3\left( {\,f_1^2 - f_2^2} \right)}}} \right)\left[ {P_4 + c\left( {DCB_r + DCB^s} \right)} \right]$$The Vertical TEC (VTEC) can be estimated using the Modified Single Layer Model (MSLM) mapping function, which assumes that all free electrons are concentrated in a shell of infinitesimal thickness at height H. The effective height (H) corresponds to maximum electron density at the F2 peak ranges from 350 km to 450 km. The VTEC is determined at the Ionosphere Pierce Point (IPP), the point of intersection between the shell layer and satellite-receiver path, as given below (Schaer, Reference Schaer1999):
where z is the satellite's zenith distance at the receiver; R is the mean radius of the Earth, and α is a correction factor. Best fit of the MSLM with respect to the JPL Extended Slab Model (ESM) mapping function is achieved at H = 506·7 km and α = 0·9782, when using R = 6371 km and assuming a maximum zenith distance of 80° (Dach et al., Reference Dach, Hugentobler, Fridez and Meindl2007).
The VTEC can be modelled on a regional scale as a function E(β, s) of the geographic latitude (β) and the sun-fixed (s) longitude of the IPP, respectively. The regional VTEC is expressed as a spherical harmonic expansion, which takes the form (Schaer, Reference Schaer1999):
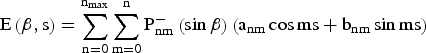 $${\rm E}\left( {{\rm \beta}, {\rm s}} \right) = \mathop \sum \limits_{{\rm n} = 0}^{{\rm n}_{{\rm max}}} \mathop \sum \limits_{{\rm m} = 0}^{\rm n} {\rm P}_{{\rm nm}}^ - \left( {\sin {\rm \beta}} \right)\left( {{\rm a}_{{\rm nm}} \cos {\rm ms} + {\rm b}_{{\rm nm}} \sin {\rm ms}} \right)$$
$${\rm E}\left( {{\rm \beta}, {\rm s}} \right) = \mathop \sum \limits_{{\rm n} = 0}^{{\rm n}_{{\rm max}}} \mathop \sum \limits_{{\rm m} = 0}^{\rm n} {\rm P}_{{\rm nm}}^ - \left( {\sin {\rm \beta}} \right)\left( {{\rm a}_{{\rm nm}} \cos {\rm ms} + {\rm b}_{{\rm nm}} \sin {\rm ms}} \right)$$
where n max is the maximum degree of the spherical harmonic expansion; ![]() $P_{nm}^ - $ are normalised associated Legendre functions of degree n and order m; a nm and b nm are the unknown coefficients of spherical harmonics.
$P_{nm}^ - $ are normalised associated Legendre functions of degree n and order m; a nm and b nm are the unknown coefficients of spherical harmonics.
Substituting Equations (4) and (5) into Equation (6), the ionospheric spherical harmonic model can be expressed as:
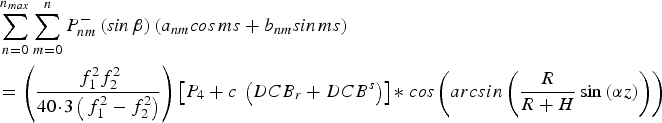 $$\eqalign{& \mathop \sum \limits_{n = 0}^{n_{max}} \mathop \sum \limits_{m = 0}^n P_{nm}^ - \left( {{\it sin} \,\beta} \right)\left( {a_{nm} {\it cos} \,ms + b_{nm} {\it sin} \,ms} \right) \cr & = \left( {\displaystyle{{\,f_1^2 f_2^2} \over {40\!\cdot\!3\left( {\,f_1^2 - f_2^2} \right)}}} \right)\left[ {P_4 + c\; \left( {DCB_r + DCB^s} \right)} \right]{\ast}\; {\it cos} \left( {arcsin\left( {\displaystyle{R \over {R + H}}\sin \left( {\alpha z} \right)} \right)} \right)}$$
$$\eqalign{& \mathop \sum \limits_{n = 0}^{n_{max}} \mathop \sum \limits_{m = 0}^n P_{nm}^ - \left( {{\it sin} \,\beta} \right)\left( {a_{nm} {\it cos} \,ms + b_{nm} {\it sin} \,ms} \right) \cr & = \left( {\displaystyle{{\,f_1^2 f_2^2} \over {40\!\cdot\!3\left( {\,f_1^2 - f_2^2} \right)}}} \right)\left[ {P_4 + c\; \left( {DCB_r + DCB^s} \right)} \right]{\ast}\; {\it cos} \left( {arcsin\left( {\displaystyle{R \over {R + H}}\sin \left( {\alpha z} \right)} \right)} \right)}$$where a nm, b nm, DCB r and DCB s are the unknown parameters to be computed.
In order to separate the DCBs of the receivers and satellites, an additional constraint must be used. This assumes that the sum of satellite DCBs is zero as follows (Dach et al., Reference Dach, Hugentobler, Fridez and Meindl2007):
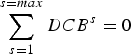 $$\mathop \sum \limits_{s = 1}^{s = max} DCB^s = 0$$
$$\mathop \sum \limits_{s = 1}^{s = max} DCB^s = 0$$After the development of the RIM, the multi-constellation GNSS receiver DCB can be estimated through the use of Equations (4) and (5) as follows:
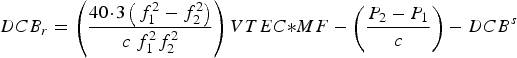 $$DCB_r = \left( {\displaystyle{{40\!\cdot\!3\left( {\,f_1^2 - f_2^2} \right)} \over {c\; f_1^2 f_2^2}}} \right)VTEC{\ast}MF - \left( {\displaystyle{{P_2 - P_1} \over c}} \right) - DCB^s $$
$$DCB_r = \left( {\displaystyle{{40\!\cdot\!3\left( {\,f_1^2 - f_2^2} \right)} \over {c\; f_1^2 f_2^2}}} \right)VTEC{\ast}MF - \left( {\displaystyle{{P_2 - P_1} \over c}} \right) - DCB^s $$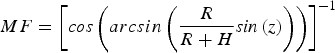 $$MF = \left[ {{\it cos} \left( {arcsin\left( {\displaystyle{R \over {R + H}}{\it sin} \left( z \right)} \right)} \right)} \right]^{ - 1} $$
$$MF = \left[ {{\it cos} \left( {arcsin\left( {\displaystyle{R \over {R + H}}{\it sin} \left( z \right)} \right)} \right)} \right]^{ - 1} $$where MF is the mapping function; P 1 and P 2 are the code observations on L 1 and L 2, respectively; f 1 and f 2 are the carrier phase frequencies on L 1 and L 2, respectively; the VTEC values are extracted from the RIM file for every 15 minutes. In addition, the satellite DCBs are obtained from the available MGEX file. The receiver DCBs is computed every 15 minutes, thus the daily average value can be obtained as follows:
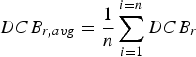 $$DCB_{r,avg} = \displaystyle{1 \over n}\mathop \sum \limits_{i = 1}^{i = n} DCB_r $$
$$DCB_{r,avg} = \displaystyle{1 \over n}\mathop \sum \limits_{i = 1}^{i = n} DCB_r $$The developed MGR-DCB model uses the unsmoothed code observations, where there is no effect of the noise level on the estimated daily mean differential code bias values (Montenbruck et al., Reference Montenbruck, Hauschild and Steigenberger2014).
In order to validate the developed MGR-DCB model, the combined VTEC is computed from the GPS, BeiDou and Galileo measurements by mapping the STEC from the high elevation satellites and assuming a single VTEC for each epoch. The combined VTEC can be obtained as follows (Tang et al., Reference Tang, Jin and Xu2014):
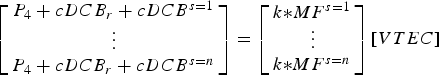 $$\left[ {\matrix{ {P_4 + cDCB_r + cDCB^{s = 1}} \cr \vdots \cr {P_4 + cDCB_r + cDCB^{s = n}} \cr}} \right] = \left[ {\matrix{ {k{\ast}MF^{s = 1}} \cr \vdots \cr {k{\ast}MF^{s = n}} \cr}} \right]\left[ {VTEC} \right]$$
$$\left[ {\matrix{ {P_4 + cDCB_r + cDCB^{s = 1}} \cr \vdots \cr {P_4 + cDCB_r + cDCB^{s = n}} \cr}} \right] = \left[ {\matrix{ {k{\ast}MF^{s = 1}} \cr \vdots \cr {k{\ast}MF^{s = n}} \cr}} \right]\left[ {VTEC} \right]$$
where n is the number of the observed GPS, BeiDou or Galileo satellites with high elevation angle into the single epoch; k is a frequency-dependent factor, 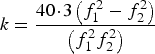 $k = \displaystyle{{40\!\cdot\!3\left( {f_1^2 - f_2^2} \right)} \over {\left( {f_1^2 f_2^2} \right)}}$ . It should be pointed out that the factor k has three different values for each of the GPS, BeiDou and Galileo systems.
$k = \displaystyle{{40\!\cdot\!3\left( {f_1^2 - f_2^2} \right)} \over {\left( {f_1^2 f_2^2} \right)}}$ . It should be pointed out that the factor k has three different values for each of the GPS, BeiDou and Galileo systems.
The combined VTEC is estimated from high elevation satellites under the assumption that the computed VTEC from those satellites are approximately equal to the VTEC values at the zenith above the receiver.
3. METHODOLOGY
A regional network consisting of 60 IGS and EUREF reference stations in Europe has been used to develop the regional ionospheric model (Figure 1). The stations are homogeneously distributed in different latitudes in order to reflect different ionospheric characteristics. GPS observations for three different days (Day of Year (DOY) 130, 200 and 362 in year 2014) have been downloaded (BKG, 2015) to represent the ionosphere seasonal variations in May, August and December, respectively. Each observation file has a 24-hour time span and a 30-second time interval. An elevation cut-off angle of 20° has been used. The files have been processed using the PPP module in the Bernese-5·20 software package. In order to produce the RIM, the IGS final satellite orbit, satellite clock and earth orientation parameters have been used (IGS, 2015) and then have been converted into the Bernese formats. The un-differenced code observations have been smoothed. In the parameters estimation process, the effective height has been selected to be 450 km. In addition, a maximum degree and order equal to six of the spherical harmonic expansions have been selected with a 15-minute interval. A group of 49 coefficients of the spherical harmonic model has been obtained each time epoch. Thereafter, to extract the VTEC maps a spatial and temporal resolution of 1° × 1° and 15 minutes, respectively, have been selected.

Figure 1. Reference stations distribution (with triangle shape) and examined stations (with asterisk shape).
In order to estimate the receiver differential code bias, The MGR-DCB model has been developed. A FORTRAN code has been written as per the flowchart shown in Figure 2. The VTEC values have been extracted from the RIM file at a 15-minute time interval. The estimation of the satellite DCB needs a well-distributed network, however, only three stations have been examined, therefore the satellite DCBs available from MGEX website (MGEX, 2015) has been used.

Figure 2. Flow chart of the developed MGR-DCB.
4. RESULTS AND ANALYSIS
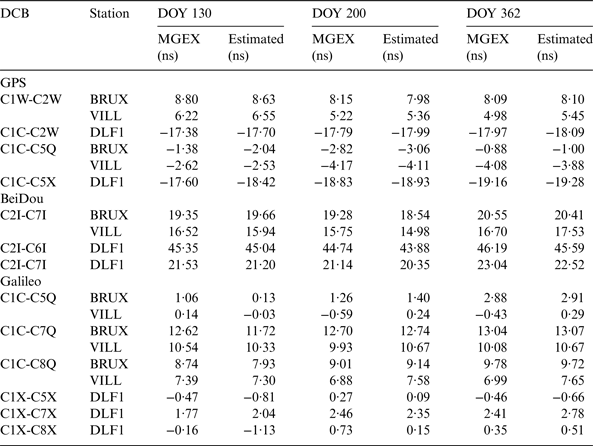
In order to assess the developed MGR-DCB model, the receiver DCBs for another set of reference stations was computed (Figure 1). The DCBs for the EUREF stations were not available, therefore only the MGEX stations were examined. The examined stations were selected to represent different latitudes and receiver types (Table 1). The legacy GPS DCBs for the P(Y)-code on the L1 and L2 tracking signals (C1W-C2W) was assessed. In addition, the DCBs for the GPS L1 C/A tracking and the L2 P(Y) tracking (C1C-C2W) was computed. Thereafter, the DCBs for the modernised GPS civil L5 signal with the different tracking mode used by the MGEX receivers (i.e., C1C-C5Q and C1C-C5X) were determined. For the BeiDou system, the DCBs for the three signals B1, B2 and B3 (C2I-C6I and C2I-C7I) were evaluated. For the Galileo E1, E5a, E5b and E5 signals, the DCBs for the receiver pilot-tracking mode, indicated by C1C-C5Q, C1C-C7Q and C1C-C8Q were determined. In addition, the C1X-C5X, C1X-C7X and C1X-C8X DCBs for the receiver combined (pilot and data) tracking mode were estimated.
Table 1. Examined stations characteristics.

Table 2 outlines the estimated multi-GNSS receiver DCBs for the examined stations in the three days and for the different receiver tracking modes. It is shown that the estimated DCBs from the MGR-DCB model have good agreement with the IGS-MGEX values.
Table 2. Estimated DCB values.

Figure 3 shows the mean difference and the RMSE of the receiver DCBs obtained from the MGR-DCB with respect to the IGS-MGEX DCBs values. For the legacy GPS C1W-C2W DCBs, it is shown that the mean difference is about -0·31 ns and 0·11 ns for station VILL and BRUX, respectively. For their RMSE values, they are about ±0·14 ns and 0·08 ns, respectively. The mean difference of the C1C-C2W DCB for station DLF1 is about 0·21 ns with ±0·08 ns RMSE value. For the modernised GPS L5 signal, the discrepancy between the estimated and MGEX is about -0·12 ns, 0·34 ns and 0·34 ns for station VILL, BRUX and DLF1, respectively. In addition, the RMSE values are about ±0·06, 0·23 and 0·33 ns for station VILL, BRUX and DLF1, respectively.

Figure 3. DCBs mean and RMSE values.
The BeiDou (C2I-C7I) differential code bias estimated from the MGR-DCB model show offsets from the MGEX values about 0·17, 0·19 and 0·55 ns with RMSE values about ±0·71, 0·43 and 0·19 ns for stations VILL, BRUX and DLF1, respectively. The BeiDou B3 signal can be tracked by station DLF1, thus its C2I-C6I DCB shows a mean difference of 0·59 ns with a RMSE value of ±0·22 ns.
The resulting Galileo E1-E5a differential code biases exhibit mean differences from the MGEX values about -0·46, 0·26 and 0·24 ns for stations VILL, BRUX and DLF1, respectively. In addition, the RMSE of the VILL, BRUX and DLF1 are ±0·45, 0·48 and 0·07 ns, respectively. For the resulting E1-E5b DCBs, the mean discrepancies are -0·37, 0·28 and -0·17 ns, while the RMSE values are ±0·42, 0·44 and 0·20 ns for stations VILL, BRUX and DLF1, respectively. The mean differences for the estimated E1-E5 DCBs are -0·42, 0·25 and 0·46 ns with RMSE values ±0·36, 0·41 and 0·47 ns for stations VILL, BRUX and DLF1, respectively.
It is shown from the above results that the mean difference between the estimated receiver DCBs and MGEX counterparts is less than 1 ns. In addition, the RMSE for the three examined stations is also less than 1 ns. This level of agreement means that the ionospheric correction values obtained through the developed regional ionospheric model are accurate. However, the station location contributes to the accuracy of the computed ionospheric value. This appears for station DLF1, where the mean difference is large (Figure 3). This is due to the fact that station DLF1 is located at the border of the developed ionospheric model as shown in Figure 1.
In order to validate the model, the Combined Vertical Total Electron Content (CVTEC) are computed from the GPS, Galileo and BeiDou measurements and then compared with the IGS-GIM counterparts. For illustration purposes, only the VTEC profiles for stations VILL, BRUX and DLF1, respectively on DOY 130 are given in Figure 4.

Figure 4. VTEC profiles on DOY 130.
Figure 5 illustrates the mean differences and RMSE values of the CVTEC with respect to the IGS-GIM counterparts for the three examined stations. It is shown that for station VILL the mean difference is about 0·4226 TECU with RMSE value about ±0·5833 TECU. For station BRUX, the mean discrepancy is -0·2454 TECU, while the RMSE is ±0·8528 TECU. In addition, the mean difference and RMSE values for station DLF1 are 0·8259 TECU and ±0·6881 TECU, respectively.

Figure 5. Statistical parameters for the CVTEC differences.
5. CONCLUSION
In this paper, a Multi-frequency multi-GNSS Receiver Differential Code Bias estimation model has been developed using the ionosphere-corrected geometry-free linear combinations of the pseudorange observations. In order to correct the pseudorange differences from the ionospheric delay, a Regional Ionospheric Model over Europe has been developed using GPS observations. The developed RIM has spatial and temporal resolutions of 1° × 1° and 15 minutes, respectively. To validate the proposed model, the receiver DCBs for GPS, Galileo and BeiDou signals have been estimated for three MGEX stations over three different days. It has been shown that the estimated DCBs have good agreement with the MGEX values, with mean difference and RMSE values less than 1 ns. In addition, the combined GPS, BeiDou and Galileo VTEC have been assessed and compared with the IGS-GIM counterparts. The findings showed good agreement with the IGS-GIM values with mean difference and RMSE values less than 1 TECU.