1. Introduction
Our objective is to study existence and uniqueness of two kinds of very weak solutions to nonlinear measure data problem

where $\Omega \subset {{\mathbb {R}^{n}}}$![]() is a bounded, $n\geq 2$
is a bounded, $n\geq 2$![]() , $\mu$
, $\mu$![]() is an arbitrary bounded measure on $\Omega$
is an arbitrary bounded measure on $\Omega$![]() , and $\mathcal {A}:\Omega \times {{\mathbb {R}^{n}}}\to {{\mathbb {R}^{n}}}$
, and $\mathcal {A}:\Omega \times {{\mathbb {R}^{n}}}\to {{\mathbb {R}^{n}}}$![]() has growth prescribed be the means of an inhomogeneous function $\varphi :\Omega \times {[0,\infty)}\to {[0,\infty)}$
has growth prescribed be the means of an inhomogeneous function $\varphi :\Omega \times {[0,\infty)}\to {[0,\infty)}$![]() of an Orlicz growth with respect to the second variable. Special cases of the leading part of the operator $\mathcal {A}$
of an Orlicz growth with respect to the second variable. Special cases of the leading part of the operator $\mathcal {A}$![]() include $p$
include $p$![]() -Laplacian, $p(x)$
-Laplacian, $p(x)$![]() -Laplacian, but we cover operators with Orlicz, double-phase growth, as well as weighted Orlicz or variable exponent double-phase one as long as it falls into the realm of Musielak–Orlicz spaces within the natural regime described in § 2. The existence of renormalized solutions to general measure data problem and uniqueness for measure data is new even in the reflexive Orlicz case. It was also not known in two cases enjoying lately particular attention – double-phase and variable exponent double-phase ones.
-Laplacian, but we cover operators with Orlicz, double-phase growth, as well as weighted Orlicz or variable exponent double-phase one as long as it falls into the realm of Musielak–Orlicz spaces within the natural regime described in § 2. The existence of renormalized solutions to general measure data problem and uniqueness for measure data is new even in the reflexive Orlicz case. It was also not known in two cases enjoying lately particular attention – double-phase and variable exponent double-phase ones.
Very weak solutions to measure data problems of the form (1.1) are already studied in depth in the classical setting of Sobolev spaces, that is when the growth of the leading part of the operator is governed by a power function with the celebrated special case of $p$![]() -Laplacian $\Delta _p u={{\rm div\,}}(|\nabla u|^{p-2}\nabla u)$
-Laplacian $\Delta _p u={{\rm div\,}}(|\nabla u|^{p-2}\nabla u)$![]() . To give a flavour let us mention e.g. [Reference Bénilan, Boccardo, Gallouët, Gariepy, Pierre and Vázquez12, Reference Boccardo, Gallouët and Orsina16, Reference Boccardo and Murat17, Reference Dal Maso and Malusa37, Reference Dal Maso, Murat, Orsina and Prignet38], where the existence is provided for various notions of very weak solutions for $L^{1}$
. To give a flavour let us mention e.g. [Reference Bénilan, Boccardo, Gallouët, Gariepy, Pierre and Vázquez12, Reference Boccardo, Gallouët and Orsina16, Reference Boccardo and Murat17, Reference Dal Maso and Malusa37, Reference Dal Maso, Murat, Orsina and Prignet38], where the existence is provided for various notions of very weak solutions for $L^{1}$![]() or measure data. Note that the notions in several cases coincide [Reference Dal Maso and Malusa37, Reference Dal Maso, Murat, Orsina and Prignet38, Reference Kilpeläinen, Kuusi and Tuhola–Kujanpää54]. In general, it is possible to find a proper notion enjoying existence, but sharp assumptions on $\mu$
or measure data. Note that the notions in several cases coincide [Reference Dal Maso and Malusa37, Reference Dal Maso, Murat, Orsina and Prignet38, Reference Kilpeläinen, Kuusi and Tuhola–Kujanpää54]. In general, it is possible to find a proper notion enjoying existence, but sharp assumptions on $\mu$![]() to ensure uniqueness for these type of problems are not known even when the operator $\mathcal {A}$
to ensure uniqueness for these type of problems are not known even when the operator $\mathcal {A}$![]() exposes the mentioned standard $p$
exposes the mentioned standard $p$![]() -growth. See counterexamples in [Reference Boccardo, Gallouët and Orsina16] showing non-uniqueness for concentrated measures. The natural sufficient condition in the standard case is that $\mu$
-growth. See counterexamples in [Reference Boccardo, Gallouët and Orsina16] showing non-uniqueness for concentrated measures. The natural sufficient condition in the standard case is that $\mu$![]() is so diffuse that it does not charge the sets of proper capacity zero and the proof of uniqueness essentially employs its characterization of the form of theorem 1.1.
is so diffuse that it does not charge the sets of proper capacity zero and the proof of uniqueness essentially employs its characterization of the form of theorem 1.1.
Analysis of problems exposing $(p,q)$![]() -growth, where the operator is trapped between polynomials $|\xi |^{p}\lesssim \mathcal {A}(x,\xi )\cdot \xi \lesssim 1+|\xi |^{q},$
-growth, where the operator is trapped between polynomials $|\xi |^{p}\lesssim \mathcal {A}(x,\xi )\cdot \xi \lesssim 1+|\xi |^{q},$![]() are already classical topic investigated since [Reference Gossez45, Reference Lavrentiev56, Reference Marcellini60, Reference Talenti67]. Nowadays, there is a great interest in analysis under nonstandard growth conditions that embraces more: problems with variable exponent growth used in modelling of electrorheological fluids [Reference Acerbi and Mingione1, Reference Ružička65], thermistor models [Reference Zhikov71] or image processing [Reference Chen, Levine and Rao19], with double-phase growth good for description of composite materials [Reference Colombo and Mingione34], as well as Orlicz one – engaged in modelling of non-Newtonian fluids [Reference Gwiazda and Świerczewska-Gwiazda46] and elasticity [Reference Ball7]. Studies on nonstandard growth problems form a solid stream in the modern nonlinear analysis [Reference Baroni, Colombo and Mingione9, Reference Chlebicka20, Reference Chlebicka and De Filippis23, Reference Chlebicka, Giannetti and Zatorska-Goldstein25, Reference Chlebicka and Karppinen29, Reference Chlebicka and Zatorska-Goldstein32, Reference Colombo and Mingione34, Reference De Filippis and Mingione39, Reference De Filippis and Oh40, Reference Harjulehto, Hästö and Lee50, Reference Harjulehto, Hästö and Toivanen51, Reference Marcellini61, Reference Yang, Yang and Yuan68]. The theory of existence of very weak solutions to problems with nonstandard growth and merely integrable data is under intensive investigation [Reference Aharouch and Bennouna3, Reference Bendahmane and Wittbold11, Reference Chlebicka and Nayar31, Reference Cianchi and Maz'ya33, Reference Gwiazda, Wittbold, Wróblewska and Zimmermann47, Reference Gwiazda, Skrzypczak and Zatorska-Goldstein48, Reference Sanchón and Urbano66, Reference Zhang69]. For the study on Musielak–Orlicz growth $L^{1}$
are already classical topic investigated since [Reference Gossez45, Reference Lavrentiev56, Reference Marcellini60, Reference Talenti67]. Nowadays, there is a great interest in analysis under nonstandard growth conditions that embraces more: problems with variable exponent growth used in modelling of electrorheological fluids [Reference Acerbi and Mingione1, Reference Ružička65], thermistor models [Reference Zhikov71] or image processing [Reference Chen, Levine and Rao19], with double-phase growth good for description of composite materials [Reference Colombo and Mingione34], as well as Orlicz one – engaged in modelling of non-Newtonian fluids [Reference Gwiazda and Świerczewska-Gwiazda46] and elasticity [Reference Ball7]. Studies on nonstandard growth problems form a solid stream in the modern nonlinear analysis [Reference Baroni, Colombo and Mingione9, Reference Chlebicka20, Reference Chlebicka and De Filippis23, Reference Chlebicka, Giannetti and Zatorska-Goldstein25, Reference Chlebicka and Karppinen29, Reference Chlebicka and Zatorska-Goldstein32, Reference Colombo and Mingione34, Reference De Filippis and Mingione39, Reference De Filippis and Oh40, Reference Harjulehto, Hästö and Lee50, Reference Harjulehto, Hästö and Toivanen51, Reference Marcellini61, Reference Yang, Yang and Yuan68]. The theory of existence of very weak solutions to problems with nonstandard growth and merely integrable data is under intensive investigation [Reference Aharouch and Bennouna3, Reference Bendahmane and Wittbold11, Reference Chlebicka and Nayar31, Reference Cianchi and Maz'ya33, Reference Gwiazda, Wittbold, Wróblewska and Zimmermann47, Reference Gwiazda, Skrzypczak and Zatorska-Goldstein48, Reference Sanchón and Urbano66, Reference Zhang69]. For the study on Musielak–Orlicz growth $L^{1}$![]() -data elliptic equations we refer to [Reference Gwiazda, Wittbold, Wróblewska and Zimmermann47] under growth restrictions on the conjugate of the modular function and to [Reference Gwiazda, Skrzypczak and Zatorska-Goldstein48, Reference Li, Yao and Zhou55], where existence is provided either in (all) reflexive spaces or when the growth of modular function is well-balanced (and the smooth functions are modularly dense, cf. also [Reference Ahmida, Chlebicka, Gwiazda and Youssfi4, Reference Borowski and Chlebicka18]). Analogous parabolic study can be found in [Reference Chlebicka, Gwiazda, Wróblewska-Kamińska and Świerczewska-Gwiazda26–Reference Chlebicka, Gwiazda and Zatorska-Goldstein28]. For measure data problems with Orlicz growth to our best knowledge we can refer only to [Reference Aissaoui Fqayeh, Benkirane, El Moumni and Youssfi6] for some class of measures, to [Reference Benkirane and Bennouna13, Reference Cianchi and Maz'ya33, Reference Dong and Fang43] for general measures in the reflexive case extended in [Reference Alberico, Chlebicka, Cianchi and Zatorska-Goldstein5, Reference Chlebicka, Giannetti and Zatorska-Goldstein24]. In [Reference Alberico, Chlebicka, Cianchi and Zatorska-Goldstein5, Reference Chlebicka, Giannetti and Zatorska-Goldstein24, Reference Cianchi and Maz'ya33], besides existence also regularity in the scale of Marcinkiewicz-type spaces is provided even for solutions to measure data problems, but therein the uniqueness is obtained only if the datum is integrable. In [Reference Chlebicka, Giannetti and Zatorska-Goldstein25], precise regularity results are provided recently extended in [Reference Chlebicka and Karppinen30]. On the other hand, existence of very weak solutions and uniqueness in the case of diffuse measures is studied in the variable exponent setting in [Reference Lv, Li and Zou57, Reference Maeda59, Reference Zhang69]. Here, two kinds of very weak solutions are proven to exist and coincide for arbitrary measure datum.
-data elliptic equations we refer to [Reference Gwiazda, Wittbold, Wróblewska and Zimmermann47] under growth restrictions on the conjugate of the modular function and to [Reference Gwiazda, Skrzypczak and Zatorska-Goldstein48, Reference Li, Yao and Zhou55], where existence is provided either in (all) reflexive spaces or when the growth of modular function is well-balanced (and the smooth functions are modularly dense, cf. also [Reference Ahmida, Chlebicka, Gwiazda and Youssfi4, Reference Borowski and Chlebicka18]). Analogous parabolic study can be found in [Reference Chlebicka, Gwiazda, Wróblewska-Kamińska and Świerczewska-Gwiazda26–Reference Chlebicka, Gwiazda and Zatorska-Goldstein28]. For measure data problems with Orlicz growth to our best knowledge we can refer only to [Reference Aissaoui Fqayeh, Benkirane, El Moumni and Youssfi6] for some class of measures, to [Reference Benkirane and Bennouna13, Reference Cianchi and Maz'ya33, Reference Dong and Fang43] for general measures in the reflexive case extended in [Reference Alberico, Chlebicka, Cianchi and Zatorska-Goldstein5, Reference Chlebicka, Giannetti and Zatorska-Goldstein24]. In [Reference Alberico, Chlebicka, Cianchi and Zatorska-Goldstein5, Reference Chlebicka, Giannetti and Zatorska-Goldstein24, Reference Cianchi and Maz'ya33], besides existence also regularity in the scale of Marcinkiewicz-type spaces is provided even for solutions to measure data problems, but therein the uniqueness is obtained only if the datum is integrable. In [Reference Chlebicka, Giannetti and Zatorska-Goldstein25], precise regularity results are provided recently extended in [Reference Chlebicka and Karppinen30]. On the other hand, existence of very weak solutions and uniqueness in the case of diffuse measures is studied in the variable exponent setting in [Reference Lv, Li and Zou57, Reference Maeda59, Reference Zhang69]. Here, two kinds of very weak solutions are proven to exist and coincide for arbitrary measure datum.
We consider (1.1) involving the leading part of the operator governed by a function $\varphi :\Omega \times {[0,\infty)}\to {[0,\infty)}$![]() and, thereby, placing our analysis in an unconventional functional setting, where the norm is defined by the means of the functional
and, thereby, placing our analysis in an unconventional functional setting, where the norm is defined by the means of the functional
Let us make an overview of the special cases of the functional framework we capture. The operator can be governed by power function variable in space, namely $\varphi (x,s)=|s|^{p(x)}$![]() , where $p:\Omega \to (1,\infty )$
, where $p:\Omega \to (1,\infty )$![]() is log-Hölder continuous, i.e. when there exists $c>0$
is log-Hölder continuous, i.e. when there exists $c>0$![]() such that $|p(x)-p(y)|\leq -{c}/{\log (|x-y|)}$
such that $|p(x)-p(y)|\leq -{c}/{\log (|x-y|)}$![]() for $|x-y|<{1}/{2}$
for $|x-y|<{1}/{2}$![]() , cf. [Reference Cruz-Uribe and Fiorenza36]. Another model example we cover is non-uniformly elliptic problems living in spaces with the double-phase energy, $\varphi (x,s)=|s|^{p}+a(x)|s|^{q}$
, cf. [Reference Cruz-Uribe and Fiorenza36]. Another model example we cover is non-uniformly elliptic problems living in spaces with the double-phase energy, $\varphi (x,s)=|s|^{p}+a(x)|s|^{q}$![]() , where $a\in C^{0,\alpha }(\Omega )$
, where $a\in C^{0,\alpha }(\Omega )$![]() is nonnegative and can vanish in some regions of $\Omega \subset {{\mathbb {R}^{n}}}$
is nonnegative and can vanish in some regions of $\Omega \subset {{\mathbb {R}^{n}}}$![]() , while exponents satisfy $1< p\leq q<\infty$
, while exponents satisfy $1< p\leq q<\infty$![]() and are close in the sense that $\frac {q}{p}\leq 1+\frac {\alpha }{n}$
and are close in the sense that $\frac {q}{p}\leq 1+\frac {\alpha }{n}$![]() necessary for density of smooth functions [Reference Ahmida, Chlebicka, Gwiazda and Youssfi4, Reference Colombo and Mingione34]. What is more, we admit problems posed in the reflexive Orlicz setting, when $\varphi$
necessary for density of smooth functions [Reference Ahmida, Chlebicka, Gwiazda and Youssfi4, Reference Colombo and Mingione34]. What is more, we admit problems posed in the reflexive Orlicz setting, when $\varphi$![]() is a doubling $N$
is a doubling $N$![]() -function $\varphi (x,s)=\varphi (s)\in \Delta _2\cap \nabla _2$
-function $\varphi (x,s)=\varphi (s)\in \Delta _2\cap \nabla _2$![]() , including Zygmund-type spaces where $\varphi _{p,\alpha }(s)=s^{p}\log ^{\alpha }(1+s),$
, including Zygmund-type spaces where $\varphi _{p,\alpha }(s)=s^{p}\log ^{\alpha }(1+s),$![]() $p>1,$
$p>1,$![]() $\alpha \in \mathbb {{R}}$
$\alpha \in \mathbb {{R}}$![]() or compositions and multiplications of functions from the family $\{\varphi _{\bar p,\bar \alpha }\}_{\bar {p},\bar {a}}$
or compositions and multiplications of functions from the family $\{\varphi _{\bar p,\bar \alpha }\}_{\bar {p},\bar {a}}$![]() with various parameters. More generally, under certain nondegeneracy and continuity conditions, given as (A0)-(A1) in § 2, we capture also general case (1.2). The remaining examples we can give here cover all weighted reflexive Orlicz functionals with non-degenerating weights, double-phase functions with variable exponents $\varphi (x,s)=|s|^{p(x)}+a(x)|s|^{q(x)}$
with various parameters. More generally, under certain nondegeneracy and continuity conditions, given as (A0)-(A1) in § 2, we capture also general case (1.2). The remaining examples we can give here cover all weighted reflexive Orlicz functionals with non-degenerating weights, double-phase functions with variable exponents $\varphi (x,s)=|s|^{p(x)}+a(x)|s|^{q(x)}$![]() , double phase with Orlicz phases $\varphi (x,s)=\varphi _1(s)+a(x)\varphi _2(s)$
, double phase with Orlicz phases $\varphi (x,s)=\varphi _1(s)+a(x)\varphi _2(s)$![]() or multi-phase cases $\varphi (x,s)=\sum _{i=1}^{k} a_i(x)\varphi _i(s)$
or multi-phase cases $\varphi (x,s)=\sum _{i=1}^{k} a_i(x)\varphi _i(s)$![]() (with appropriately regular weights) as long as conditions (A0)–(A1) are satisfied. We refer to [Reference Chlebicka20] for a more detailed overview of differential equations and to [Reference Harjulehto and Hästö49] for the fundamental properties of the functional framework.
(with appropriately regular weights) as long as conditions (A0)–(A1) are satisfied. We refer to [Reference Chlebicka20] for a more detailed overview of differential equations and to [Reference Harjulehto and Hästö49] for the fundamental properties of the functional framework.
Diffuse measures
The natural property of a measure to ensure uniqueness of very weak solutions to (1.1) is that $\mu$![]() is diffuse with respect to a relevant capacity. In order to characterize such measures, let us denote by ${{\mathcal {M}_b}}(\Omega )$
is diffuse with respect to a relevant capacity. In order to characterize such measures, let us denote by ${{\mathcal {M}_b}}(\Omega )$![]() the set of bounded measures on $\Omega \subset \mathbb {{R}}^{n}$
the set of bounded measures on $\Omega \subset \mathbb {{R}}^{n}$![]() and by $W^{1,\varphi (\cdot )}(\Omega )$
and by $W^{1,\varphi (\cdot )}(\Omega )$![]() the Musielak–Orlicz–Sobolev space. See § 2.3 for the introduction to the functional setting and all assumptions and § 2.5 for the capacity. By ${{\mathcal {M}^{\varphi (\cdot )}_b}}(\Omega )$
the Musielak–Orlicz–Sobolev space. See § 2.3 for the introduction to the functional setting and all assumptions and § 2.5 for the capacity. By ${{\mathcal {M}^{\varphi (\cdot )}_b}}(\Omega )$![]() we mean the set of $\varphi (\cdot )$
we mean the set of $\varphi (\cdot )$![]() -diffuse measures (or $\varphi (\cdot )$
-diffuse measures (or $\varphi (\cdot )$![]() -soft measures) consisting of such bounded measures ${{\mu _{\varphi (\cdot )}}}$
-soft measures) consisting of such bounded measures ${{\mu _{\varphi (\cdot )}}}$![]() that do not charge sets of $\varphi (\cdot )$
that do not charge sets of $\varphi (\cdot )$![]() -capacity zero (for every Borel set $E\subset \Omega$
-capacity zero (for every Borel set $E\subset \Omega$![]() such that ${{{\rm C}_{\varphi (\cdot )}}}(E)=0$
such that ${{{\rm C}_{\varphi (\cdot )}}}(E)=0$![]() it holds that ${{\mu _{\varphi (\cdot )}}}(E)=0$
it holds that ${{\mu _{\varphi (\cdot )}}}(E)=0$![]() ). One may think that a measure ${{\mu _{\varphi (\cdot )}}}\in {{\mathcal {M}^{\varphi (\cdot )}_b}}(\Omega )$
). One may think that a measure ${{\mu _{\varphi (\cdot )}}}\in {{\mathcal {M}^{\varphi (\cdot )}_b}}(\Omega )$![]() is ‘absolutely continuous with respect to ${{{\rm C}_{\varphi (\cdot )}}}$
is ‘absolutely continuous with respect to ${{{\rm C}_{\varphi (\cdot )}}}$![]() ’. Our first result is the following theorem.
’. Our first result is the following theorem.
Theorem 1.1 (Characterization of measures)
Suppose $\varphi \in \Phi _c(\Omega )$![]() on a bounded domain $\Omega \subset {{\mathbb {R}^{n}}},$
on a bounded domain $\Omega \subset {{\mathbb {R}^{n}}},$![]() $n\geq 2$
$n\geq 2$![]() . Assume that $\varphi$
. Assume that $\varphi$![]() satisfies (aInc)$_p,$
satisfies (aInc)$_p,$![]() (aDec)$_q,$
(aDec)$_q,$![]() (A0) and (A1). When $\mu \in {{\mathcal {M}_b}}(\Omega ),$
(A0) and (A1). When $\mu \in {{\mathcal {M}_b}}(\Omega ),$![]() then
then
i.e. there exist $f\in L^{1}(\Omega )$![]() and $G \in (L^{\widetilde \varphi (\cdot )}(\Omega ))^{n},$
and $G \in (L^{\widetilde \varphi (\cdot )}(\Omega ))^{n},$![]() such that $\mu =f-{{\rm div\,}}G$
such that $\mu =f-{{\rm div\,}}G$![]() in the sense of distributions.
in the sense of distributions.
Remark 1.2 Let us note that upon our assumptions $t^{p}\lesssim \varphi (\cdot,t)$![]() . If $p>n$
. If $p>n$![]() it holds that ${{\mathcal {M}_b}}(\Omega )\subset W^{-1,p'}(\Omega )\subset (W^{1,\varphi (\cdot )}_0(\Omega ))'.$
it holds that ${{\mathcal {M}_b}}(\Omega )\subset W^{-1,p'}(\Omega )\subset (W^{1,\varphi (\cdot )}_0(\Omega ))'.$![]() In this case, all measures are absolutely continuous with respect to the Lebesgue measure and, consequently, the result is really meaningful only for slowly growing functions $\varphi$
In this case, all measures are absolutely continuous with respect to the Lebesgue measure and, consequently, the result is really meaningful only for slowly growing functions $\varphi$![]() .
.
Remark 1.3 The decomposition of theorem 1.1
cannot be unique as $L^{1}(\Omega )\cap (W_0^{1,\varphi (\cdot )}(\Omega ))'\neq \{0\}.$![]() On the other hand, for every $\mu \in {{\mathcal {M}_b}}(\Omega )$
On the other hand, for every $\mu \in {{\mathcal {M}_b}}(\Omega )$![]() there exists a decomposition $\mu =\mu _{\varphi (\cdot )} +{{\mu ^{+}_{\rm sing}}}-{{\mu ^{-}_{\rm sing}}}$
there exists a decomposition $\mu =\mu _{\varphi (\cdot )} +{{\mu ^{+}_{\rm sing}}}-{{\mu ^{-}_{\rm sing}}}$![]() with some $\mu _{\varphi (\cdot )}$
with some $\mu _{\varphi (\cdot )}$![]() which is absolutely continuous with respect to ${\varphi (\cdot )}$
which is absolutely continuous with respect to ${\varphi (\cdot )}$![]() -capacity, while ${{\mu ^{+}_{\rm sing}}},{{\mu ^{-}_{\rm sing}}}\geq 0$
-capacity, while ${{\mu ^{+}_{\rm sing}}},{{\mu ^{-}_{\rm sing}}}\geq 0$![]() are singular with respect to the ${{{\rm C}_{\varphi (\cdot )}}}$
are singular with respect to the ${{{\rm C}_{\varphi (\cdot )}}}$![]() (concentrated on some set of $\varphi (\cdot )$
(concentrated on some set of $\varphi (\cdot )$![]() -capacity zero) and this decomposition is unique up to sets of $\varphi (\cdot )$
-capacity zero) and this decomposition is unique up to sets of $\varphi (\cdot )$![]() -capacity zero, see lemma 3.2. Consequently, any $\mu \in {{\mathcal {M}_b}}(\Omega )$
-capacity zero, see lemma 3.2. Consequently, any $\mu \in {{\mathcal {M}_b}}(\Omega )$![]() admits a decomposition $\mu =f+{{\rm div\,}}G +{{\mu ^{+}_{\rm sing}}}-{{\mu ^{-}_{\rm sing}}}$
admits a decomposition $\mu =f+{{\rm div\,}}G +{{\mu ^{+}_{\rm sing}}}-{{\mu ^{-}_{\rm sing}}}$![]() in the sense of distributions, with some $f\in L^{1}(\Omega )$
in the sense of distributions, with some $f\in L^{1}(\Omega )$![]() , $G \in (L^{\widetilde \varphi (\cdot )}(\Omega ))^{n}$
, $G \in (L^{\widetilde \varphi (\cdot )}(\Omega ))^{n}$![]() , and ${{{\rm C}_{\varphi (\cdot )}}}$
, and ${{{\rm C}_{\varphi (\cdot )}}}$![]() -singular ${{\mu ^{+}_{\rm sing}}},{{\mu ^{-}_{\rm sing}}}$
-singular ${{\mu ^{+}_{\rm sing}}},{{\mu ^{-}_{\rm sing}}}$![]() .
.
Let us point out a direct consequence of theorem 1.1 to the classical spaces.
Corollary 1.4 Orlicz case
Suppose $B:[0,\infty )\to [0,\infty )$![]() is a Young function, such that $B\in \Delta _2\cap \nabla _2$
is a Young function, such that $B\in \Delta _2\cap \nabla _2$![]() . Then $\mu _B\in {{\mathcal {M}_b}}(\Omega )$
. Then $\mu _B\in {{\mathcal {M}_b}}(\Omega )$![]() does not charge the sets of Sobolev $B$
does not charge the sets of Sobolev $B$![]() -capacity zero if and only if $\mu _B\in L^{1}(\Omega )+(W^{1,B}_0(\Omega ))',$
-capacity zero if and only if $\mu _B\in L^{1}(\Omega )+(W^{1,B}_0(\Omega ))',$![]() that is there exist $f\in L^{1}(\Omega )$
that is there exist $f\in L^{1}(\Omega )$![]() and $G \in (L^{\widetilde {B}}(\Omega ))^{n},$
and $G \in (L^{\widetilde {B}}(\Omega ))^{n},$![]() such that $\mu _B=f-{{\rm div\,}}G$
such that $\mu _B=f-{{\rm div\,}}G$![]() . In particular, the special case of this result is the classical measure characterization [Reference Boccardo, Gallouët and Orsina16]: if $p>1,$
. In particular, the special case of this result is the classical measure characterization [Reference Boccardo, Gallouët and Orsina16]: if $p>1,$![]() then $\mu _p\in {{\mathcal {M}_b}}(\Omega )$
then $\mu _p\in {{\mathcal {M}_b}}(\Omega )$![]() does not charge the sets of the Sobolev $p$
does not charge the sets of the Sobolev $p$![]() -capacity zero if and only if $\mu _p\in L^{1}(\Omega )+W^{-1,p'}(\Omega )$
-capacity zero if and only if $\mu _p\in L^{1}(\Omega )+W^{-1,p'}(\Omega )$![]() (there exist $f\in L^{1}(\Omega )$
(there exist $f\in L^{1}(\Omega )$![]() and $G \in (L^{p'}(\Omega ))^{n},$
and $G \in (L^{p'}(\Omega ))^{n},$![]() such that $\mu _p=f-{{\rm div\,}}G$
such that $\mu _p=f-{{\rm div\,}}G$![]() in the sense of distributions).
in the sense of distributions).
Corollary 1.5 Variable exponent case
Suppose $p:\Omega \to (1,\infty )$![]() with $1< p_-\leq p(\cdot )\leq p_+<\infty$
with $1< p_-\leq p(\cdot )\leq p_+<\infty$![]() is log-Hölder continuous and $p'(x):=p(x)/(p(x)-1)$
is log-Hölder continuous and $p'(x):=p(x)/(p(x)-1)$![]() . Then $\mu _{p(\cdot )}\in {{\mathcal {M}_b}}(\Omega )$
. Then $\mu _{p(\cdot )}\in {{\mathcal {M}_b}}(\Omega )$![]() does not charge the sets of Sobolev $p(\cdot )$
does not charge the sets of Sobolev $p(\cdot )$![]() -capacity zero if and only if $\mu _{p(\cdot )}\in L^{1}(\Omega )+W^{-1,p'(\cdot )}(\Omega ),$
-capacity zero if and only if $\mu _{p(\cdot )}\in L^{1}(\Omega )+W^{-1,p'(\cdot )}(\Omega ),$![]() i.e. there exist $f\in L^{1}(\Omega )$
i.e. there exist $f\in L^{1}(\Omega )$![]() and $G \in (L^{p'(\cdot )}(\Omega ))^{n},$
and $G \in (L^{p'(\cdot )}(\Omega ))^{n},$![]() such that $\mu _{p(\cdot )}=f-{{\rm div\,}}G$
such that $\mu _{p(\cdot )}=f-{{\rm div\,}}G$![]() in the sense of distributions, cf. [Reference Zhang and Zhou70].
in the sense of distributions, cf. [Reference Zhang and Zhou70].
Measure-data problems
Assumptions
Given $\varphi \in \Phi _c(\Omega )$![]() on a bounded domain $\Omega \subset {{\mathbb {R}^{n}}},$
on a bounded domain $\Omega \subset {{\mathbb {R}^{n}}},$![]() $n\geq 2$
$n\geq 2$![]() , such that $\varphi$
, such that $\varphi$![]() satisfies (aInc)$_p$
satisfies (aInc)$_p$![]() , (aDec)$_q$
, (aDec)$_q$![]() , (A0) and (A1), we shall study equation (1.1) where vector field $\mathcal {A}$
, (A0) and (A1), we shall study equation (1.1) where vector field $\mathcal {A}$![]() satisfies the following conditions:
satisfies the following conditions:
(𝒜1) $\mathcal {A}:\Omega \times {{\mathbb {R}^{n}}}\to {{\mathbb {R}^{n}}}$
 is Carathéodory function, i.e. it is measurable with respect to the first variable and continuous with respect to the last one;
is Carathéodory function, i.e. it is measurable with respect to the first variable and continuous with respect to the last one;(𝒜2) There exist numbers $c_1^{\varphi },c_2^{\varphi } >0$
 and a function $0\leq \gamma \in L^{\widetilde \varphi (\cdot )}(\Omega )$
and a function $0\leq \gamma \in L^{\widetilde \varphi (\cdot )}(\Omega )$ , such that for a.e. $x\in \Omega$
, such that for a.e. $x\in \Omega$ and all $\xi \in {{\mathbb {R}^{n}}}$
and all $\xi \in {{\mathbb {R}^{n}}}$ the following ellipticity and growth conditions are satisfied
\[ c_1^{\varphi} \varphi(x,|\xi|)\leq \mathcal{A}(x,\xi)\cdot\xi\quad\text{and}\quad |\mathcal{A}(x,\xi)|\leq c_2^{\varphi}\left(1+\gamma(x)+\varphi(x,|\xi|)/|\xi|\right). \]
the following ellipticity and growth conditions are satisfied
\[ c_1^{\varphi} \varphi(x,|\xi|)\leq \mathcal{A}(x,\xi)\cdot\xi\quad\text{and}\quad |\mathcal{A}(x,\xi)|\leq c_2^{\varphi}\left(1+\gamma(x)+\varphi(x,|\xi|)/|\xi|\right). \]
(𝒜3) $\mathcal {A}$
 is monotone, i.e. for a.e. $x\in \Omega$
is monotone, i.e. for a.e. $x\in \Omega$ and all $\eta \neq \xi \in {{\mathbb {R}^{n}}}$
and all $\eta \neq \xi \in {{\mathbb {R}^{n}}}$ \[ \big(\mathcal{A}(x,\eta)-\mathcal{A}(x,\xi)\big)\cdot(\eta-\xi)>0. \]
\[ \big(\mathcal{A}(x,\eta)-\mathcal{A}(x,\xi)\big)\cdot(\eta-\xi)>0. \]
(𝒜4) For a.e. $x\in \Omega$
 it holds that $\mathcal {A}(x,0)=0.$
it holds that $\mathcal {A}(x,0)=0.$
Special cases
Of course, $(\mathcal {A} 1)$![]() –$(\mathcal {A} 4)$
–$(\mathcal {A} 4)$![]() with $\varphi \in \Phi _c(\Omega )$
with $\varphi \in \Phi _c(\Omega )$![]() satisfying (aInc)$_p$
satisfying (aInc)$_p$![]() , (aDec)$_q$
, (aDec)$_q$![]() , (A0) and (A1) generalize not only classical conditions in the case when $\varphi (x,s)=s^{p}$
, (A0) and (A1) generalize not only classical conditions in the case when $\varphi (x,s)=s^{p}$![]() :
:
with $0\leq \gamma \in L^{p'}(\Omega )$![]() with the special case of $p$
with the special case of $p$![]() -Laplacian. When $\varphi (x,s)=s^{p(x)}$
-Laplacian. When $\varphi (x,s)=s^{p(x)}$![]() it covers
it covers
with $0\leq \gamma \in L^{p(\cdot )/(p(\cdot )-1)}(\Omega )$![]() with the special case of (possibly weighted) $p(x)$
with the special case of (possibly weighted) $p(x)$![]() -Laplacian. We allow for all $p:\Omega \to (1,\infty )$
-Laplacian. We allow for all $p:\Omega \to (1,\infty )$![]() under typical assumptions that $1< p_-\leq p(x)\leq p_+$
under typical assumptions that $1< p_-\leq p(x)\leq p_+$![]() and $p$
and $p$![]() is log-Hölder continuous. In the double-phase case $\varphi _{dp}(x,s)=s^{p}+a(x)s^{q}$
is log-Hölder continuous. In the double-phase case $\varphi _{dp}(x,s)=s^{p}+a(x)s^{q}$![]() , $0\leq a\in C^{0,\alpha }(\Omega )$
, $0\leq a\in C^{0,\alpha }(\Omega )$![]() , $q/p\leq 1 +\alpha /n$
, $q/p\leq 1 +\alpha /n$![]() , it covers non-uniformly elliptic operators satisfying
, it covers non-uniformly elliptic operators satisfying
with $0\leq \gamma \in L^{\widetilde \varphi _{dp}(\cdot )}(\Omega ).$![]() Finally, in Orlicz case when $B\in C^{1}({[0,\infty)})$
Finally, in Orlicz case when $B\in C^{1}({[0,\infty)})$![]() is a doubling $N$
is a doubling $N$![]() -function it also simplifies to typically considered conditions
-function it also simplifies to typically considered conditions

To give more examples one can consider problems in weighted Orlicz, double phase with variable exponents, or multi-phase Orlicz cases, as long as $\varphi (x,s)$![]() is comparable to a function doubling with respect to the second variable and satisfy nondegeneracy conditions (A0)–(A1).
is comparable to a function doubling with respect to the second variable and satisfy nondegeneracy conditions (A0)–(A1).
Problem
Distributional solutions to equation $-\Delta _p u=\mu$![]() when $p$
when $p$![]() is small ($1< p<2-1/n$
is small ($1< p<2-1/n$![]() ) do not necessarily belong to $W^{1,1}_{loc}(\Omega )$
) do not necessarily belong to $W^{1,1}_{loc}(\Omega )$![]() . The easiest example to give is the fundamental solution (when $\mu =\delta _0$
. The easiest example to give is the fundamental solution (when $\mu =\delta _0$![]() ). This restriction on the growth can be dispensed by the use of a weaker derivative. We make use of the symmetric truncation $T_k:\mathbb {{R}}\to \mathbb {{R}}$
). This restriction on the growth can be dispensed by the use of a weaker derivative. We make use of the symmetric truncation $T_k:\mathbb {{R}}\to \mathbb {{R}}$![]() defined as
defined as
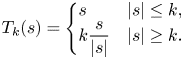
Note that as a consequence of [Reference Bénilan, Boccardo, Gallouët, Gariepy, Pierre and Vázquez12, lemma 2.1] for every function $u$![]() , such that $T_t(u)\in W^{1,\varphi (\cdot )}_0(\Omega )$
, such that $T_t(u)\in W^{1,\varphi (\cdot )}_0(\Omega )$![]() for every $t>0$
for every $t>0$![]() there exists a (unique) measurable function $Z_u : \Omega \to {{\mathbb {R}^{n}}}$
there exists a (unique) measurable function $Z_u : \Omega \to {{\mathbb {R}^{n}}}$![]() such that
such that
With an abuse of notation, we denote $Z_u$![]() simply by $\nabla u$
simply by $\nabla u$![]() and call it a generalized gradient.
and call it a generalized gradient.
In order to introduce definitions of very weak solutions we define the space
where $W^{1,\varphi (\cdot )}_0(\Omega )$![]() is the completion of $C_0^{\infty }(\Omega )$
is the completion of $C_0^{\infty }(\Omega )$![]() in norm of $W^{1,\varphi (\cdot )}(\Omega )$
in norm of $W^{1,\varphi (\cdot )}(\Omega )$![]() . In fact, $u\in W_0^{1,\varphi (\cdot )}(\Omega )$
. In fact, $u\in W_0^{1,\varphi (\cdot )}(\Omega )$![]() if and only if $u\in \mathcal {T}_0^{1, \varphi (\cdot )}(\Omega )$
if and only if $u\in \mathcal {T}_0^{1, \varphi (\cdot )}(\Omega )$![]() and $Z_u\in L^{\varphi (\cdot )}(\Omega ; {{\mathbb {R}^{n}}})$
and $Z_u\in L^{\varphi (\cdot )}(\Omega ; {{\mathbb {R}^{n}}})$![]() . In the latter case, $Z_u = \nabla u$
. In the latter case, $Z_u = \nabla u$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() .
.
Very weak solutions
We define two kinds of very weak solutions to problem (1.1) under assumptions $(\mathcal {A} 1)$![]() –$(\mathcal {A} 4)$
–$(\mathcal {A} 4)$![]() involving a measure $\mu \in {{\mathcal {M}_b}}(\Omega )$
involving a measure $\mu \in {{\mathcal {M}_b}}(\Omega )$![]() .
.
Inspired by [Reference Boccardo and Gallouët14, Reference Boccardo and Gallouët15, Reference Cianchi and Maz'ya33, Reference Dal Maso and Malusa37], we define solutions that can be reached in the limit of solutions to approximate problems.
Definition 1.6 A function $u\in \mathcal { T}_0^{1,\varphi (\cdot )}(\Omega )$![]() is called an approximable solution to problem (1.1) if $u$
is called an approximable solution to problem (1.1) if $u$![]() is an a.e. limit of a sequence of solutions $\{u_s\}_s\subset W_0^{1,\varphi (\cdot )}(\Omega )$
is an a.e. limit of a sequence of solutions $\{u_s\}_s\subset W_0^{1,\varphi (\cdot )}(\Omega )$![]() to
to
when $\{\mu ^{s}\}\subset C^{\infty }(\Omega )$![]() is a sequence of bounded functions that converges to $\mu$
is a sequence of bounded functions that converges to $\mu$![]() weakly-$*$
weakly-$*$![]() in the space of measures and such that
in the space of measures and such that
The definition seems very weak as we refrain from assuming any convergence of the gradients of $(u_s)$![]() . Nonetheless, this is enough to show in the proofs that for fixed $k$
. Nonetheless, this is enough to show in the proofs that for fixed $k$![]() also $\mathcal {A}(\cdot,\nabla (T_k u_s))\to \mathcal {A}(\cdot,\nabla (T_k u))$
also $\mathcal {A}(\cdot,\nabla (T_k u_s))\to \mathcal {A}(\cdot,\nabla (T_k u))$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() and thus it is justified to call $u$
and thus it is justified to call $u$![]() a solution (though in a very weak sense).
a solution (though in a very weak sense).
Having [Reference Dal Maso, Murat, Orsina and Prignet38] and remark 1.3 we consider renormalized solutions defined as follows.
Definition 1.7 A function $u\in \mathcal { T}_0^{1,\varphi (\cdot )}(\Omega )$![]() is called a renormalized solution to problem (1.1) with $\mu \in {{\mathcal {M}_b}}(\Omega )$
is called a renormalized solution to problem (1.1) with $\mu \in {{\mathcal {M}_b}}(\Omega )$![]() , if
, if
(i) for every $k>0$
 one has $\ \mathcal {A}(x,\nabla (T_k u))\in L^{\widetilde \varphi (\cdot )}(\Omega );$
one has $\ \mathcal {A}(x,\nabla (T_k u))\in L^{\widetilde \varphi (\cdot )}(\Omega );$
(ii) $\mu$
 is decomposed to $\mu ={{\mu _{\varphi (\cdot )}}}+{{\mu ^{+}_{\rm sing}}}-{{\mu ^{-}_{\rm sing}}}$
is decomposed to $\mu ={{\mu _{\varphi (\cdot )}}}+{{\mu ^{+}_{\rm sing}}}-{{\mu ^{-}_{\rm sing}}}$ , with ${{\mu _{\varphi (\cdot )}}}\in {{\mathcal {M}^{\varphi (\cdot )}_b}}(\Omega )$
, with ${{\mu _{\varphi (\cdot )}}}\in {{\mathcal {M}^{\varphi (\cdot )}_b}}(\Omega )$ and nonnegative ${{\mu ^{+}_{\rm sing}}} ,{{\mu ^{-}_{\rm sing}}} \in ( {{\mathcal {M}_b}}(\Omega )\setminus {{\mathcal {M}^{\varphi (\cdot )}_b}}(\Omega ))\cup \{0\}$
and nonnegative ${{\mu ^{+}_{\rm sing}}} ,{{\mu ^{-}_{\rm sing}}} \in ( {{\mathcal {M}_b}}(\Omega )\setminus {{\mathcal {M}^{\varphi (\cdot )}_b}}(\Omega ))\cup \{0\}$ , then
(1.8)\begin{align} & \int_\Omega \mathcal{A}(x,\nabla u)\cdot\nabla u\, h'(u)\phi\, {\rm d}x+\int_\Omega \mathcal{A}(x,\nabla u)\cdot\nabla\phi\, h(u)\, {\rm d}x\nonumber\\ & \quad=\int_\Omega h(u)\phi\,{\rm d}{{\mu_{\varphi({\cdot})}}}(x)+h(+\infty)\int_\Omega \phi\,{\rm d}{{\mu^{+}_{\rm sing}}} (x)-h(-\infty)\int_\Omega \phi\,{\rm d}{{\mu^{-}_{\rm sing}}} (x), \end{align}holds for any $h\in W^{1,\infty }(\mathbb {{R}})$
, then
(1.8)\begin{align} & \int_\Omega \mathcal{A}(x,\nabla u)\cdot\nabla u\, h'(u)\phi\, {\rm d}x+\int_\Omega \mathcal{A}(x,\nabla u)\cdot\nabla\phi\, h(u)\, {\rm d}x\nonumber\\ & \quad=\int_\Omega h(u)\phi\,{\rm d}{{\mu_{\varphi({\cdot})}}}(x)+h(+\infty)\int_\Omega \phi\,{\rm d}{{\mu^{+}_{\rm sing}}} (x)-h(-\infty)\int_\Omega \phi\,{\rm d}{{\mu^{-}_{\rm sing}}} (x), \end{align}holds for any $h\in W^{1,\infty }(\mathbb {{R}})$
 having $h'$
having $h'$ with compact support and for all $\phi \in C_0^{\infty }(\Omega )$
with compact support and for all $\phi \in C_0^{\infty }(\Omega )$ , where $h(+\infty ):=\lim _{r\to +\infty }h(r)$
, where $h(+\infty ):=\lim _{r\to +\infty }h(r)$ and $h(-\infty ):=\lim _{r\to +\infty }h(r)$
and $h(-\infty ):=\lim _{r\to +\infty }h(r)$ are well-defined as $h$
are well-defined as $h$ is constant close to infinities.
is constant close to infinities.
Our main result reads as follows.
Theorem 1.8 Let $\varphi \in \Phi _c(\Omega )$![]() on a bounded Lipschitz domain $\Omega \subset {{\mathbb {R}^{n}}},$
on a bounded Lipschitz domain $\Omega \subset {{\mathbb {R}^{n}}},$![]() $n\geq 2$
$n\geq 2$![]() . Suppose that $\varphi$
. Suppose that $\varphi$![]() satisfies (aInc)$_p,$
satisfies (aInc)$_p,$![]() (aDec)$_q,$
(aDec)$_q,$![]() (A0) and (A1), whereas a vector field $\mathcal {A}:\Omega \times {{\mathbb {R}^{n}}}\to {{\mathbb {R}^{n}}}$
(A0) and (A1), whereas a vector field $\mathcal {A}:\Omega \times {{\mathbb {R}^{n}}}\to {{\mathbb {R}^{n}}}$![]() satisfies ($\mathcal {A} 1$
satisfies ($\mathcal {A} 1$![]() )–($\mathcal {A} 4$
)–($\mathcal {A} 4$![]() ). When $\mu \in {{\mathcal {M}_b}}(\Omega ),$
). When $\mu \in {{\mathcal {M}_b}}(\Omega ),$![]() then the following claims hold true.
then the following claims hold true.
(i) There exists an approximable solution to problem (1.1).
(ii) There exists a renormalized solution to problem (1.1) satisfying (1.8) with measures such that ${\rm supp}\,{{\mu _{\varphi (\cdot )}}}\subset \{|u|<\infty \},$
 ${\rm supp}\,{{\mu ^{+}_{\rm sing}}}\subset \cap _{k>0}\{u>k\},$
${\rm supp}\,{{\mu ^{+}_{\rm sing}}}\subset \cap _{k>0}\{u>k\},$ and ${\rm supp}\,{{\mu ^{-}_{\rm sing}}}\subset \cap _{k>0}\{u<-k\}$
and ${\rm supp}\,{{\mu ^{-}_{\rm sing}}}\subset \cap _{k>0}\{u<-k\}$ .
.(iii) A function $u\in \mathcal {T}^{1,\varphi (\cdot )}_0(\Omega )$
 is an approximable solution from (i) if and only if it is a renormalized solution from (ii).
is an approximable solution from (i) if and only if it is a renormalized solution from (ii).
Uniqueness for approximable solution and renormalized solutions under additional assumption related to $\varphi (\cdot )$![]() -diffusivity of measure datum is provided in § 7.
-diffusivity of measure datum is provided in § 7.
As $h\equiv 1$![]() is an admissible choice in (1.8), we get the following remark.
is an admissible choice in (1.8), we get the following remark.
Remark 1.9 Under the assumptions of theorem 1.8 if $u$![]() is an approximable (equivalently, renormalized) solution, then
is an approximable (equivalently, renormalized) solution, then
so $u$![]() is then a solution in the distributional sense (which in particular is proven to exist).
is then a solution in the distributional sense (which in particular is proven to exist).
Moreover, for problems involving $\varphi (\cdot )$![]() -diffuse measures, by theorem 1.1 and proposition 6.1, we can formulate the following conclusion.
-diffuse measures, by theorem 1.1 and proposition 6.1, we can formulate the following conclusion.
Corollary 1.10 Under the assumptions of theorem 1.8 if $u$![]() is an approximable (equivalently, renormalized) solution and $\mu \in (L^{1}(\Omega )+(W^{1,\varphi (\cdot )}_0(\Omega ))')\cap {{\mathcal {M}_b}}(\Omega ),$
is an approximable (equivalently, renormalized) solution and $\mu \in (L^{1}(\Omega )+(W^{1,\varphi (\cdot )}_0(\Omega ))')\cap {{\mathcal {M}_b}}(\Omega ),$![]() then $u$
then $u$![]() exists, is unique, and satisfies
exists, is unique, and satisfies
As a direct consequence of theorem 1.8 we retrieve the already classical existence results of [Reference Boccardo, Gallouët and Orsina16, Reference Dal Maso, Murat, Orsina and Prignet38] involving $p$![]() -Laplace operator, as well as variable exponent ones [Reference Zhang69, Reference Zhang and Zhou70]. We extend the existence results for problems in reflexive Orlicz spaces proven in [Reference Cianchi and Maz'ya33] towards inhomogeneity of the spaces, as well as we extend the uniqueness result from $L^{1}$
-Laplace operator, as well as variable exponent ones [Reference Zhang69, Reference Zhang and Zhou70]. We extend the existence results for problems in reflexive Orlicz spaces proven in [Reference Cianchi and Maz'ya33] towards inhomogeneity of the spaces, as well as we extend the uniqueness result from $L^{1}$![]() to a class of diffuse measure data. It should be noted that renormalized solutions to general measure data problems with Orlicz growth were not studied so far. We also obtain the main goals of [Reference Gwiazda, Wittbold, Wróblewska and Zimmermann47, Reference Gwiazda, Skrzypczak and Zatorska-Goldstein48] within a different and a bit more restrictive functional framework (and slightly different kind of control on the modular function), but allowing for essentially broader class of data and providing uniqueness. To our best knowledge no results on equivalence of very weak solutions has been so far addressed in problems stated in generalized Orlicz spaces even in the $L^{1}$
to a class of diffuse measure data. It should be noted that renormalized solutions to general measure data problems with Orlicz growth were not studied so far. We also obtain the main goals of [Reference Gwiazda, Wittbold, Wróblewska and Zimmermann47, Reference Gwiazda, Skrzypczak and Zatorska-Goldstein48] within a different and a bit more restrictive functional framework (and slightly different kind of control on the modular function), but allowing for essentially broader class of data and providing uniqueness. To our best knowledge no results on equivalence of very weak solutions has been so far addressed in problems stated in generalized Orlicz spaces even in the $L^{1}$![]() -data case, for the $p$
-data case, for the $p$![]() -Laplace case we refer to [Reference Dal Maso, Murat, Orsina and Prignet38, Reference Kilpeläinen, Kuusi and Tuhola–Kujanpää54]. Finding a setting where they essentially do not coincide would be interesting. Given an interest one may expect developing our main goals further towards anisotropic or non-reflexive settings cf. [Reference Alberico, Chlebicka, Cianchi and Zatorska-Goldstein5, Reference Chlebicka, Giannetti and Zatorska-Goldstein24, Reference Gwiazda, Skrzypczak and Zatorska-Goldstein48], as well as by involving lower-order terms in (1.1) as in [Reference Gwiazda, Wittbold, Wróblewska and Zimmermann47], differential inclusions as in [Reference Denkowska, Gwiazda and Kalita41], or systems of equations.
-Laplace case we refer to [Reference Dal Maso, Murat, Orsina and Prignet38, Reference Kilpeläinen, Kuusi and Tuhola–Kujanpää54]. Finding a setting where they essentially do not coincide would be interesting. Given an interest one may expect developing our main goals further towards anisotropic or non-reflexive settings cf. [Reference Alberico, Chlebicka, Cianchi and Zatorska-Goldstein5, Reference Chlebicka, Giannetti and Zatorska-Goldstein24, Reference Gwiazda, Skrzypczak and Zatorska-Goldstein48], as well as by involving lower-order terms in (1.1) as in [Reference Gwiazda, Wittbold, Wróblewska and Zimmermann47], differential inclusions as in [Reference Denkowska, Gwiazda and Kalita41], or systems of equations.
There is some available information on the regularity of our very weak solutions following from comparison to solutions to problems with Orlicz growth. The conditions on $\varphi (\cdot )$![]() imply that there exists a Young function $B:{[0,\infty)}\to {[0,\infty)}$
imply that there exists a Young function $B:{[0,\infty)}\to {[0,\infty)}$![]() such that $B(s)\leq \varphi (x,s)$
such that $B(s)\leq \varphi (x,s)$![]() for a.a. $x\in \Omega$
for a.a. $x\in \Omega$![]() and all $s\geq 0$
and all $s\geq 0$![]() . Then any of the very weak solutions of theorem 1.8 belongs to $\mathcal {T}_0^{1,\varphi (\cdot )}(\Omega )\subset \mathcal {T}_0^{1,B}(\Omega )$
. Then any of the very weak solutions of theorem 1.8 belongs to $\mathcal {T}_0^{1,\varphi (\cdot )}(\Omega )\subset \mathcal {T}_0^{1,B}(\Omega )$![]() . Thus, we can get the same regularity of these solutions and their gradients expressed in Orlicz–Marcinkiewicz scale as in [Reference Cianchi and Maz'ya33, theorem 3.2]; see [Reference Cianchi and Maz'ya33, example 3.4] for applications with particular growth of $B$
. Thus, we can get the same regularity of these solutions and their gradients expressed in Orlicz–Marcinkiewicz scale as in [Reference Cianchi and Maz'ya33, theorem 3.2]; see [Reference Cianchi and Maz'ya33, example 3.4] for applications with particular growth of $B$![]() (including Zygmund-type ones). On the other hand, precise information on the local behaviour of solutions to problems with Orlicz growth obtained as a consequence of Wolff-potential estimates can be found in [Reference Chlebicka, Giannetti and Zatorska-Goldstein25] depending on the scale of datum (in Orlicz versions of Lorentz, Marcinkiewicz and Morrey scales). Furthermore, [Reference Chlebicka21] gives the Orlicz–Lorentz–Morrey-type regularity for gradients of solutions to problems involving related classes of measures, moreover, [Reference Chlebicka22] describes the regularizing effect of the lower-order term (in the same scale). For Riesz potential estimates for such problems see [Reference Baroni8]. For equations posed in the generalized Orlicz setting sharp conditions on a measure datum ensuring Hölder continuity of solutions has been recently provided via Wolff potential estimates [Reference Chlebicka and Karppinen30].
(including Zygmund-type ones). On the other hand, precise information on the local behaviour of solutions to problems with Orlicz growth obtained as a consequence of Wolff-potential estimates can be found in [Reference Chlebicka, Giannetti and Zatorska-Goldstein25] depending on the scale of datum (in Orlicz versions of Lorentz, Marcinkiewicz and Morrey scales). Furthermore, [Reference Chlebicka21] gives the Orlicz–Lorentz–Morrey-type regularity for gradients of solutions to problems involving related classes of measures, moreover, [Reference Chlebicka22] describes the regularizing effect of the lower-order term (in the same scale). For Riesz potential estimates for such problems see [Reference Baroni8]. For equations posed in the generalized Orlicz setting sharp conditions on a measure datum ensuring Hölder continuity of solutions has been recently provided via Wolff potential estimates [Reference Chlebicka and Karppinen30].
The main ideas of the proofs follow several seminal papers including [Reference Bénilan, Boccardo, Gallouët, Gariepy, Pierre and Vázquez12, Reference Boccardo, Gallouët and Orsina16, Reference Boccardo and Murat17, Reference Dal Maso, Murat, Orsina and Prignet38] and involve analysis of fine convergence of solutions of some approximate problems. Nonetheless, the functional setting is far more demanding. In fact, we employ a lot of very recent results on structural properties of the generalized Orlicz spaces and nonstandard capacities, see e.g. [Reference Baruah, Harjulehto and Hästo10, Reference De Filippis and Mingione39, Reference Harjulehto and Hästö49, Reference Harjulehto and Juusti52], and study properties of measures exposing certain capacitary properties.
As for organization – after preliminary part, the measure characterization is proven in § 3 and § 4 is devoted to approximate problems. Approximable solutions are investigated in § 5, while renormalized ones in § 6. Uniqueness is proven in § 7. The summary of the main proof is presented in § 8.
2. Preliminaries
2.1 Notation
By $\Omega$![]() we always mean a bounded set in ${{\mathbb {R}^{n}}}$
we always mean a bounded set in ${{\mathbb {R}^{n}}}$![]() , $n\geq 2$
, $n\geq 2$![]() . We shall make use of a Lipschitz continuous cut-off function $\psi _l:\mathbb {{R}}\to \mathbb {{R}}$
. We shall make use of a Lipschitz continuous cut-off function $\psi _l:\mathbb {{R}}\to \mathbb {{R}}$![]() by
by
By $\mu _1\ll \mu _2$![]() we denote we mean that $\mu _1$
we denote we mean that $\mu _1$![]() is absolutely continuous with respect to $\mu _2$
is absolutely continuous with respect to $\mu _2$![]() .
.
We study spaces of functions defined in $\Omega$![]() , $\mathbb {{R}}$
, $\mathbb {{R}}$![]() , or ${{\mathbb {R}^{n}}}$
, or ${{\mathbb {R}^{n}}}$![]() . $L^{0}(\Omega )$
. $L^{0}(\Omega )$![]() denotes the set of measurable functions defined on $\Omega$
denotes the set of measurable functions defined on $\Omega$![]() , $C_0(\Omega )$
, $C_0(\Omega )$![]() are continuous functions taking value zero on $\partial \Omega$
are continuous functions taking value zero on $\partial \Omega$![]() , while $C_b(\Omega )$
, while $C_b(\Omega )$![]() – continuous functions bounded on $\Omega$
– continuous functions bounded on $\Omega$![]() ; ${{\mathcal {M}_b}}(\Omega )$
; ${{\mathcal {M}_b}}(\Omega )$![]() are Radon measures with bounded total variation in $\Omega$
are Radon measures with bounded total variation in $\Omega$![]() ; ${{\mathcal {M}^{\varphi (\cdot )}_b}}(\Omega )$
; ${{\mathcal {M}^{\varphi (\cdot )}_b}}(\Omega )$![]() – bounded Radon measures diffuse with respect to $\varphi (\cdot )$
– bounded Radon measures diffuse with respect to $\varphi (\cdot )$![]() -capacity. If $\mu \in {{\mathcal {M}_b}}(\Omega )$
-capacity. If $\mu \in {{\mathcal {M}_b}}(\Omega )$![]() , $E$
, $E$![]() is a Borel set included in $\Omega$
is a Borel set included in $\Omega$![]() , the measure $\mu {\mathsf {L}} E$
, the measure $\mu {\mathsf {L}} E$![]() is defined by $(\mu {\mathsf {L}} E)(B)=\mu (E\cap B)$
is defined by $(\mu {\mathsf {L}} E)(B)=\mu (E\cap B)$![]() for any Borel set $B\subset \Omega$
for any Borel set $B\subset \Omega$![]() . If $\mu \in {{\mathcal {M}_b}}(\Omega )$
. If $\mu \in {{\mathcal {M}_b}}(\Omega )$![]() is such that $\mu =\mu {\mathsf {L}} E,$
is such that $\mu =\mu {\mathsf {L}} E,$![]() then we say that $\mu$
then we say that $\mu$![]() is concentrated on $E$
is concentrated on $E$![]() . In general, one cannot define the smallest set (in the sense of inclusion) where the measure is concentrated. By $L^{1}(\Omega,\mu )$
. In general, one cannot define the smallest set (in the sense of inclusion) where the measure is concentrated. By $L^{1}(\Omega,\mu )$![]() we denote classically functions with absolute value integrable with respect to $\mu$
we denote classically functions with absolute value integrable with respect to $\mu$![]() , shortened to $L^{1}(\Omega )$
, shortened to $L^{1}(\Omega )$![]() if $\mu$
if $\mu$![]() is Lebesgue's measure.
is Lebesgue's measure.
When $\mu _k,\mu \in {{\mathcal {M}_b}}(\Omega )$![]() , we say that $\mu _k\to \mu$
, we say that $\mu _k\to \mu$![]() weakly-$\ast$
weakly-$\ast$![]() in the space of measures if
in the space of measures if
Lemma 2.1 If $g_n:\Omega \to \mathbb {{R}}$![]() are measurable functions converging to $g$
are measurable functions converging to $g$![]() almost everywhere, then for each regular value $t$
almost everywhere, then for each regular value $t$![]() of the limit function $g$
of the limit function $g$![]() we have $\mathbb {1}_{\{t<|g_n|\}}\xrightarrow [n\to \infty ]{}\mathbb {1}_{\{t<|g|\}}$
we have $\mathbb {1}_{\{t<|g_n|\}}\xrightarrow [n\to \infty ]{}\mathbb {1}_{\{t<|g|\}}$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() .
.
Here, the term ‘regular value’ denotes a value $t$![]() such that $g^{-1}(t)$
such that $g^{-1}(t)$![]() has measure zero.
has measure zero.
Lemma 2.2 Suppose $w_n\to w$![]() in $L^{1}(\Omega ),$
in $L^{1}(\Omega ),$![]() $v_n,v\in L^{\infty }(\Omega ),$
$v_n,v\in L^{\infty }(\Omega ),$![]() and $v_n\to v$
and $v_n\to v$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() . Then $w_n v_n \to w v$
. Then $w_n v_n \to w v$![]() in $L^{1}(\Omega )$
in $L^{1}(\Omega )$![]() .
.
2.2 Generalized Orlicz functions
The framework we employ comes from the monograph [Reference Harjulehto and Hästö49]. For the classical treatment of the setting we refer to [Reference Musielak62, Reference Nakano63], while for recent developments within the related functional settings see [Reference Ahmida, Chlebicka, Gwiazda and Youssfi4, Reference Baruah, Harjulehto and Hästo10, Reference Borowski and Chlebicka18, Reference Chlebicka, Gwiazda, Wróblewska-Kamińska and Świerczewska-Gwiazda26, Reference Cruz-Uribe and Hästö35, Reference Harjulehto and Juusti52].
A real-valued function is $L$![]() -almost increasing, $L\geq 1$
-almost increasing, $L\geq 1$![]() , if $Lf(s) \geq f(t)$
, if $Lf(s) \geq f(t)$![]() for $s > t$
for $s > t$![]() . $L$
. $L$![]() -almost decreasing is defined analogously.
-almost decreasing is defined analogously.
Definition 2.3 We say that $\varphi :\Omega \times {[0,\infty)}\to [0,\infty ]$![]() is a convex $\Phi$
is a convex $\Phi$![]() –function, and write $\varphi \in \Phi _c(\Omega )$
–function, and write $\varphi \in \Phi _c(\Omega )$![]() , if the following conditions hold:
, if the following conditions hold:
(i) For every $s\in {[0,\infty)}$
 the function $x\mapsto \varphi (x, t)$
the function $x\mapsto \varphi (x, t)$ is measurable and for a.e. $x\in \Omega$
is measurable and for a.e. $x\in \Omega$ the function $s\mapsto \varphi (x, t)$
the function $s\mapsto \varphi (x, t)$ is increasing, convex, and left-continuous.
is increasing, convex, and left-continuous.(ii) $\varphi (x, 0) = \lim _{s\to 0^{+}} \varphi (x, s) = 0$
 and $\lim _{s\to \infty } \varphi (x, s) = \infty$
and $\lim _{s\to \infty } \varphi (x, s) = \infty$ for a.e. $x\in \Omega$
for a.e. $x\in \Omega$ .
.
Furthermore, we say that $\varphi \in \Phi _c(\Omega )$![]() satisfies
satisfies
(aInc)p if there exists $L_p\geq 1$
 such that $s\mapsto \varphi (x, s)/s^{p}$
such that $s\mapsto \varphi (x, s)/s^{p}$ is $L_p$
is $L_p$ -almost increasing in ${[0,\infty)}$
-almost increasing in ${[0,\infty)}$ for every $x\in \Omega$
for every $x\in \Omega$ ,
,(aDec)q if there exists $L_q\geq 1$
 such that $s\mapsto \varphi (x, s)/s^{q}$
such that $s\mapsto \varphi (x, s)/s^{q}$ is $L_q$
is $L_q$ -almost decreasing in ${[0,\infty)}$
-almost decreasing in ${[0,\infty)}$ for every $x\in \Omega$
for every $x\in \Omega$ .
.
We write (aInc), if there exist $p > 1$![]() such that (aInc)$_p$
such that (aInc)$_p$![]() holds and (aDec) if there exist $q > 1$
holds and (aDec) if there exist $q > 1$![]() such that (aDec)$_q$
such that (aDec)$_q$![]() holds. The corresponding conditions with $L = 1$
holds. The corresponding conditions with $L = 1$![]() are denoted by (Inc) or (Dec).
are denoted by (Inc) or (Dec).
We shall consider those $\varphi \in \Phi _c(\Omega )$![]() , which satisfy the following set of conditions.
, which satisfy the following set of conditions.
(A0) There exists $\beta _0\in (0, 1]$
 such that $\varphi (x, \beta _0) \leq 1$
such that $\varphi (x, \beta _0) \leq 1$ and $\varphi (x, 1/\beta _0) \geq 1$
and $\varphi (x, 1/\beta _0) \geq 1$ for all $x\in \Omega$
for all $x\in \Omega$ .
.(A1) There exists $\beta _1\in (0,1)$
 , such that for every ball $B$
, such that for every ball $B$ with $|B|\leq 1$
with $|B|\leq 1$ it holds that
\[ \beta_1\varphi^{{-}1}(x,s)\leq\varphi^{{-}1}(y,s)\quad\text{for every $s\in [1,1/|B|]$ and a.e. $x,y\in B\cap\Omega$}. \]
it holds that
\[ \beta_1\varphi^{{-}1}(x,s)\leq\varphi^{{-}1}(y,s)\quad\text{for every $s\in [1,1/|B|]$ and a.e. $x,y\in B\cap\Omega$}. \]
Condition (A0) is imposed in order to exclude degeneracy, while (A1) can be interpreted as local continuity.
We say that a function $\varphi$![]() satisfies $\Delta _2$
satisfies $\Delta _2$![]() -condition (and write $\varphi \in \Delta _2$
-condition (and write $\varphi \in \Delta _2$![]() ) if there exists a constant $c>0$
) if there exists a constant $c>0$![]() , such that for every $s\geq 0$
, such that for every $s\geq 0$![]() it holds $\varphi (x,2s)\leq c(\varphi (x,s)+1)$
it holds $\varphi (x,2s)\leq c(\varphi (x,s)+1)$![]() . When a function $\varphi \in \Phi _c(\Omega )$
. When a function $\varphi \in \Phi _c(\Omega )$![]() satisfies (aInc)p and (aDec)q, then $\varphi \in \Delta _2$
satisfies (aInc)p and (aDec)q, then $\varphi \in \Delta _2$![]() .
.
The Young conjugate of $\varphi \in \Phi _c(\Omega )$![]() is the function $\widetilde \varphi :\Omega \times {[0,\infty)}\to [0,\infty ]$
is the function $\widetilde \varphi :\Omega \times {[0,\infty)}\to [0,\infty ]$![]() defined as
defined as
The fact that Young conjugation is involute, i.e. $\widetilde {(\widetilde {\varphi } )}=\varphi$![]() is attributed to Fenchel and Moreau, see direct proof in [Reference Chlebicka, Gwiazda, Wróblewska-Kamińska and Świerczewska-Gwiazda26, theorem 2.1.41]. Moreover, if $\varphi \in \Phi _c(\Omega )$
is attributed to Fenchel and Moreau, see direct proof in [Reference Chlebicka, Gwiazda, Wróblewska-Kamińska and Świerczewska-Gwiazda26, theorem 2.1.41]. Moreover, if $\varphi \in \Phi _c(\Omega )$![]() , then $\widetilde \varphi \in \Phi _c(\Omega )$
, then $\widetilde \varphi \in \Phi _c(\Omega )$![]() . If $\widetilde \varphi \in \Delta _2,$
. If $\widetilde \varphi \in \Delta _2,$![]() we say that $\varphi$
we say that $\varphi$![]() satisfies $\nabla _2$
satisfies $\nabla _2$![]() -condition and denote it by $\varphi \in \nabla _2$
-condition and denote it by $\varphi \in \nabla _2$![]() . If $\varphi,\widetilde \varphi \in \Delta _2$
. If $\varphi,\widetilde \varphi \in \Delta _2$![]() , then we call $\varphi$
, then we call $\varphi$![]() a doubling function. If $\varphi \in \Phi _c(\Omega )$
a doubling function. If $\varphi \in \Phi _c(\Omega )$![]() satisfies (aInc)p and (aDec)q, then $\varphi,\widetilde \varphi \in \Delta _2$
satisfies (aInc)p and (aDec)q, then $\varphi,\widetilde \varphi \in \Delta _2$![]() , so within our framework $\varphi$
, so within our framework $\varphi$![]() is assumed to be doubling.
is assumed to be doubling.
For $\varphi \in \Phi _c(\Omega )$![]() , the following inequality of Fenchel–Young type holds true
, the following inequality of Fenchel–Young type holds true
In fact, within our framework with, since $\varphi$![]() is comparable to a doubling function there exist some constants depending only on $\varphi$
is comparable to a doubling function there exist some constants depending only on $\varphi$![]() for which we have
for which we have
2.3 Function spaces
We always deal with spaces generated by $\varphi \in \Phi _c(\Omega )$![]() satisfying (aInc)$_p$
satisfying (aInc)$_p$![]() , (aDec)$_q$
, (aDec)$_q$![]() , (A0) and (A1). For $f\in L^{0}(\Omega )$
, (A0) and (A1). For $f\in L^{0}(\Omega )$![]() we define the modular ${{\varrho }}_{\varphi (\cdot ),\Omega }$
we define the modular ${{\varrho }}_{\varphi (\cdot ),\Omega }$![]() by
by
When it is clear from the context we skip writing the domain.
Musielak–Orlicz space is defined as the set
endowed with the Luxemburg norm $\|f\|_{\varphi (\cdot )}=\inf \{\lambda > 0 : {{\varrho }}_{\varphi (\cdot )} (\tfrac 1\lambda f) \leq 1\} .$![]() For $\varphi \in \Phi _c(\Omega )$
For $\varphi \in \Phi _c(\Omega )$![]() , the space $L^{\varphi (\cdot )}(\Omega )$
, the space $L^{\varphi (\cdot )}(\Omega )$![]() is a Banach space [Reference Harjulehto and Hästö49, theorem 2.3.13]. Moreover, the following Hölder inequality holds true
is a Banach space [Reference Harjulehto and Hästö49, theorem 2.3.13]. Moreover, the following Hölder inequality holds true
If $a := \max \{L_p, L_q\}$![]() for constants from (aInc)$_p$
for constants from (aInc)$_p$![]() and (aDec)$_q$
and (aDec)$_q$![]() , then
, then
Sometimes it would be convenient for us to denote vector-valued functions integrable with the modular as $(L^{\varphi (\cdot )}(\Omega ))^{n}$![]() . Since there is no difference between claiming $H=(H_1,\dots,H_n)\in (L^{\varphi (\cdot )}(\Omega ))^{n}$
. Since there is no difference between claiming $H=(H_1,\dots,H_n)\in (L^{\varphi (\cdot )}(\Omega ))^{n}$![]() and $|H|\in L^{\varphi (\cdot )}(\Omega )$
and $|H|\in L^{\varphi (\cdot )}(\Omega )$![]() , we are not very careful with stressing it in the sequel. A function $f\in L^{\varphi (\cdot )} (\Omega )$
, we are not very careful with stressing it in the sequel. A function $f\in L^{\varphi (\cdot )} (\Omega )$![]() belongs to Musielak–Orlicz–Sobolev space $W^{1,\varphi (\cdot )} (\Omega )$
belongs to Musielak–Orlicz–Sobolev space $W^{1,\varphi (\cdot )} (\Omega )$![]() , if its distributional partial derivatives $\partial _1 f,\dots,\partial _n f$
, if its distributional partial derivatives $\partial _1 f,\dots,\partial _n f$![]() exist and belong to $L^{\varphi (\cdot )} (\Omega )$
exist and belong to $L^{\varphi (\cdot )} (\Omega )$![]() too. Because of the growth conditions $W^{1,\varphi (\cdot )}(\Omega )$
too. Because of the growth conditions $W^{1,\varphi (\cdot )}(\Omega )$![]() is a separable and reflexive space. Moreover, smooth functions are dense there. As a zero-trace space $W_0^{1,\varphi (\cdot )}(\Omega )$
is a separable and reflexive space. Moreover, smooth functions are dense there. As a zero-trace space $W_0^{1,\varphi (\cdot )}(\Omega )$![]() we mean the closure of $C_0^{\infty }(\Omega )$
we mean the closure of $C_0^{\infty }(\Omega )$![]() in $W^{1,\varphi (\cdot )}(\Omega )$
in $W^{1,\varphi (\cdot )}(\Omega )$![]() . In fact, due to [Reference Harjulehto and Hästö49, theorem 6.2.8] given a bounded domain $\Omega$
. In fact, due to [Reference Harjulehto and Hästö49, theorem 6.2.8] given a bounded domain $\Omega$![]() there exists a constant $c=c(n,\Omega )>0,$
there exists a constant $c=c(n,\Omega )>0,$![]() such that for any $u\in W_0^{1,\varphi (\cdot )}(\Omega )$
such that for any $u\in W_0^{1,\varphi (\cdot )}(\Omega )$![]() it holds that
it holds that
Moreover, [Reference Harjulehto and Hästö49, theorem 6.3.7] yields that
where ‘$\hookrightarrow \hookrightarrow$![]() ’ stands for a compact embedding.
’ stands for a compact embedding.
Remark 2.4 [Reference Harjulehto and Hästö49]
If $\varphi \in \Phi _c(\Omega )$![]() with $\Omega$
with $\Omega$![]() bounded, satisfies (aInc)p, (aDec)q, (A0) and (A1), then strong (norm) topology of $W^{1,\varphi (\cdot )}(\Omega )$
bounded, satisfies (aInc)p, (aDec)q, (A0) and (A1), then strong (norm) topology of $W^{1,\varphi (\cdot )}(\Omega )$![]() coincides with the modular topology. Moreover, smooth functions are dense in this space in both topologies. Thus, $W_0^{1,\varphi (\cdot )}(\Omega )$
coincides with the modular topology. Moreover, smooth functions are dense in this space in both topologies. Thus, $W_0^{1,\varphi (\cdot )}(\Omega )$![]() , under our assumptions, is a closure of $C_0^{\infty }(\Omega )$
, under our assumptions, is a closure of $C_0^{\infty }(\Omega )$![]() with respect to the modular topology of gradients in $L^{\varphi (\cdot )}(\Omega )$
with respect to the modular topology of gradients in $L^{\varphi (\cdot )}(\Omega )$![]() .
.
Space $(W^{1,\varphi (\cdot )}_0(\Omega ))'$![]() is considered endowed with the norm
is considered endowed with the norm

2.4 The operator
Let us motivate that the growth and coercivity conditions from $(\mathcal {A} 1)$![]() –$(\mathcal {A} 4)$
–$(\mathcal {A} 4)$![]() imply the expected proper definition of the operator involved in problem (1.1). We consider the operator ${{\mathfrak {A}_{\varphi (\cdot )}}} : W^{1,\varphi (\cdot )}_0(\Omega ) \to (W^{1,\varphi (\cdot )}_0(\Omega ))'$
imply the expected proper definition of the operator involved in problem (1.1). We consider the operator ${{\mathfrak {A}_{\varphi (\cdot )}}} : W^{1,\varphi (\cdot )}_0(\Omega ) \to (W^{1,\varphi (\cdot )}_0(\Omega ))'$![]() defined as
defined as
that is acting
where $\langle \cdot, \cdot \rangle$![]() denotes dual pairing between reflexive Banach spaces $W^{1,\varphi (\cdot )}(\Omega ))$
denotes dual pairing between reflexive Banach spaces $W^{1,\varphi (\cdot )}(\Omega ))$![]() and $(W^{1,\varphi (\cdot )}(\Omega ))'$
and $(W^{1,\varphi (\cdot )}(\Omega ))'$![]() is well-defined. Note that when $v\in W^{1,\varphi (\cdot )}(\Omega )$
is well-defined. Note that when $v\in W^{1,\varphi (\cdot )}(\Omega )$![]() and $w\in C_0^{\infty }(\Omega )$
and $w\in C_0^{\infty }(\Omega )$![]() , growth condition $(\mathcal {A} 2)$
, growth condition $(\mathcal {A} 2)$![]() , Hölder's inequality (2.4), equivalence (2.3) justify that
, Hölder's inequality (2.4), equivalence (2.3) justify that

Note that due to (2.3) the norm $\left \| {\varphi (\cdot,\lvert {\nabla v}\rvert )}/{\lvert {\nabla v}\rvert }\right \|_{L^{\widetilde \varphi (\cdot )}(\Omega )}< c$![]() with $c$
with $c$![]() depending on $\|\nabla v\|_{L^{\varphi (\cdot )}},p,q$
depending on $\|\nabla v\|_{L^{\varphi (\cdot )}},p,q$![]() only. Therefore
only. Therefore
By density argument, the operator is well-defined on $W^{1,\varphi (\cdot )}_0(\Omega )$![]() .
.
What is more, by ($\mathcal {A}$![]() 1)–($\mathcal {A}$
1)–($\mathcal {A}$![]() 2) and [Reference Chlebicka and Zatorska-Goldstein32, lemma 4.12] we have the following.
2) and [Reference Chlebicka and Zatorska-Goldstein32, lemma 4.12] we have the following.
Remark 2.5 For $u\in \mathcal {T}^{1,\varphi (\cdot )}(\Omega )$![]() , such that for some $M,k_0>0$
, such that for some $M,k_0>0$![]() it holds that ${{\varrho }}_{\varphi (\cdot ),\Omega }(\nabla T_k u)\leq Mk$
it holds that ${{\varrho }}_{\varphi (\cdot ),\Omega }(\nabla T_k u)\leq Mk$![]() for all $k>k_0$
for all $k>k_0$![]() , there exists a continuous function $\zeta :[0,|\Omega |]\to {[0,\infty)}$
, there exists a continuous function $\zeta :[0,|\Omega |]\to {[0,\infty)}$![]() , such that $\lim _{s\to 0^{+}}\zeta (s)=0$
, such that $\lim _{s\to 0^{+}}\zeta (s)=0$![]() and for any measurable $E\subset \Omega$
and for any measurable $E\subset \Omega$![]()
where ‘$\nabla$![]() ’ is understood as in (1.4). In particular, $\mathcal {A}(\cdot,\nabla u)\in (L^{1}(\Omega ))^{n}$
’ is understood as in (1.4). In particular, $\mathcal {A}(\cdot,\nabla u)\in (L^{1}(\Omega ))^{n}$![]() .
.
2.5 Capacities
Understanding capacities is needed to describe pointwise behaviour of Sobolev functions. We employ the generalization of classical notions of capacities, cf. [Reference Adams and Hedberg2, Reference Heinonen, Kilpeläinen and Martio53, Reference Reshetnyak64], as well as unconventional ones [Reference Diening, Harjulehto, Hästö and Ružička42, Reference Malý, Swanson and Ziemer58] to the Musielak–Orlicz–Sobolev setting according to [Reference Baruah, Harjulehto and Hästo10, Reference Harjulehto and Juusti52].
For a set $E\subset {{\mathbb {R}^{n}}}$![]() we define
we define
and its generalized Orlicz capacity of Sobolev type (called later $W^{1,\varphi (\cdot )}$![]() -capacity) by
-capacity) by
We shall consider generalized relative $\varphi (\cdot )$![]() -capacity ${{{\rm cap}_{\varphi (\cdot )}}}$
-capacity ${{{\rm cap}_{\varphi (\cdot )}}}$![]() . With this aim for every $K$
. With this aim for every $K$![]() compact in $\Omega \subset {{\mathbb {R}^{n}}}$
compact in $\Omega \subset {{\mathbb {R}^{n}}}$![]() let us denote
let us denote
and set
For open sets $A\subset \Omega$![]() we define
we define
and finally, if $E\subset \Omega$![]() is an arbitrary set
is an arbitrary set
This notion of capacity enjoys all fundamental properties of classical capacities [Reference Baruah, Harjulehto and Hästo10, Reference Harjulehto and Juusti52].
Let us pay some attention to sets of zero capacity. If $B_R$![]() is a ball in ${{\mathbb {R}^{n}}}$
is a ball in ${{\mathbb {R}^{n}}}$![]() , $E\subset B_R$
, $E\subset B_R$![]() and ${{{\rm cap}_{\varphi (\cdot )}}}(E,B_R)=0$
and ${{{\rm cap}_{\varphi (\cdot )}}}(E,B_R)=0$![]() , then $|E|=0$
, then $|E|=0$![]() . Having bounded $\Omega \subset {{\mathbb {R}^{n}}}$
. Having bounded $\Omega \subset {{\mathbb {R}^{n}}}$![]() for a set $E\subset \Omega$
for a set $E\subset \Omega$![]() we have ${{{\rm cap}_{\varphi (\cdot )}}}(E,\Omega )=0$
we have ${{{\rm cap}_{\varphi (\cdot )}}}(E,\Omega )=0$![]() if and only if ${{{\rm C}_{\varphi (\cdot )}}}(E)=0$
if and only if ${{{\rm C}_{\varphi (\cdot )}}}(E)=0$![]() . What is more, each set of $W^{1,\varphi (\cdot )}$
. What is more, each set of $W^{1,\varphi (\cdot )}$![]() -capacity zero is contained in a Borel set of $W^{1,\varphi (\cdot )}$
-capacity zero is contained in a Borel set of $W^{1,\varphi (\cdot )}$![]() -capacity zero. Countable union of sets of $W^{1,\varphi (\cdot )}$
-capacity zero. Countable union of sets of $W^{1,\varphi (\cdot )}$![]() -capacity zero has $W^{1,\varphi (\cdot )}$
-capacity zero has $W^{1,\varphi (\cdot )}$![]() -capacity zero.
-capacity zero.
Function $u$![]() is called ${{{\rm C}_{\varphi (\cdot )}}}$
is called ${{{\rm C}_{\varphi (\cdot )}}}$![]() -quasi-continuous if for every $\varepsilon >0$
-quasi-continuous if for every $\varepsilon >0$![]() there exists an open set $U$
there exists an open set $U$![]() with ${{{\rm C}_{\varphi (\cdot )}}} (U)<\varepsilon$
with ${{{\rm C}_{\varphi (\cdot )}}} (U)<\varepsilon$![]() , such that $f$
, such that $f$![]() restricted to $\Omega \setminus U$
restricted to $\Omega \setminus U$![]() is continuous. We say that a claim holds $\varphi (\cdot )$
is continuous. We say that a claim holds $\varphi (\cdot )$![]() -quasi-everywhere if it holds outside a set of Sobolev $\varphi (\cdot )$
-quasi-everywhere if it holds outside a set of Sobolev $\varphi (\cdot )$![]() -capacity zero. A set $E\subset \Omega$
-capacity zero. A set $E\subset \Omega$![]() is said to be ${{{\rm C}_{\varphi (\cdot )}}}$
is said to be ${{{\rm C}_{\varphi (\cdot )}}}$![]() -quasi-open if for every ${{\varepsilon }}>0$
-quasi-open if for every ${{\varepsilon }}>0$![]() there exists an open set $U$
there exists an open set $U$![]() such that $E\subset U\subset \Omega$
such that $E\subset U\subset \Omega$![]() and ${{{\rm C}_{\varphi (\cdot )}}}(U\setminus E)\leq {{\varepsilon }}$
and ${{{\rm C}_{\varphi (\cdot )}}}(U\setminus E)\leq {{\varepsilon }}$![]() .
.
Lemma 2.6 For every Cauchy sequence in $W^{1,\varphi (\cdot )} (\Omega )$![]() (equivalently under our regime, with respect to the $W^{1,\varphi (\cdot )} (\Omega )$
(equivalently under our regime, with respect to the $W^{1,\varphi (\cdot )} (\Omega )$![]() -modular topology) of functions from $C({{\mathbb {R}^{n}}})\cap W^{1,\varphi (\cdot )} (\Omega )$
-modular topology) of functions from $C({{\mathbb {R}^{n}}})\cap W^{1,\varphi (\cdot )} (\Omega )$![]() there is a subsequence which converges pointwise ${{{\rm C}_{\varphi (\cdot )}}}$
there is a subsequence which converges pointwise ${{{\rm C}_{\varphi (\cdot )}}}$![]() -quasi-everywhere in $\Omega$
-quasi-everywhere in $\Omega$![]() . Moreover, the convergence is uniform outside a set of arbitrary small capacity ${{{\rm C}_{\varphi (\cdot )}}}$
. Moreover, the convergence is uniform outside a set of arbitrary small capacity ${{{\rm C}_{\varphi (\cdot )}}}$![]() .
.
In the sequel, we shall always identify $u$![]() with its ${{{\rm C}_{\varphi (\cdot )}}}$
with its ${{{\rm C}_{\varphi (\cdot )}}}$![]() -quasi-continuous representative.
-quasi-continuous representative.
Lemma 2.7 For each $u\in \mathcal {T}^{1,\varphi (\cdot )}_0(\Omega )$![]() there exists a unique ${{{\rm C}_{\varphi (\cdot )}}}$
there exists a unique ${{{\rm C}_{\varphi (\cdot )}}}$![]() -quasi-continuous function $v \in \mathcal {T}^{1,\varphi (\cdot )}_0(\Omega )$
-quasi-continuous function $v \in \mathcal {T}^{1,\varphi (\cdot )}_0(\Omega )$![]() such that $u=v$
such that $u=v$![]() holds ${{{\rm C}_{\varphi (\cdot )}}}$
holds ${{{\rm C}_{\varphi (\cdot )}}}$![]() -quasi-everywhere in $\Omega$
-quasi-everywhere in $\Omega$![]() .
.
As a direct consequence of lemma 2.7, we have the following observations.
Lemma 2.8 For a ${{{\rm C}_{\varphi (\cdot )}}}$![]() -quasi-continuous function $u$
-quasi-continuous function $u$![]() and $k>0,$
and $k>0,$![]() the sets $\{|u|>k\}$
the sets $\{|u|>k\}$![]() and $\{|u|< k\}$
and $\{|u|< k\}$![]() are ${{{\rm C}_{\varphi (\cdot )}}}$
are ${{{\rm C}_{\varphi (\cdot )}}}$![]() -quasi-open.
-quasi-open.
Lemma 2.9 For every ${{{\rm C}_{\varphi (\cdot )}}}$![]() -quasi-open set $U\subset \Omega$
-quasi-open set $U\subset \Omega$![]() there exists an increasing sequence $\{v_n\}$
there exists an increasing sequence $\{v_n\}$![]() of nonnegative functions in $W^{1,\varphi (\cdot )}_0(\Omega )$
of nonnegative functions in $W^{1,\varphi (\cdot )}_0(\Omega )$![]() which converges to $\mathbb {1}_U$
which converges to $\mathbb {1}_U$![]() ${{{\rm C}_{\varphi (\cdot )}}}$
${{{\rm C}_{\varphi (\cdot )}}}$![]() -quasi-everywhere in $\Omega$
-quasi-everywhere in $\Omega$![]() .
.
Lemma 2.10 If ${{\mu _{\varphi (\cdot )}}}\in {{\mathcal {M}^{\varphi (\cdot )}_b}}(\Omega )$![]() and $u\in W^{1,\varphi (\cdot )}_0(\Omega ),$
and $u\in W^{1,\varphi (\cdot )}_0(\Omega ),$![]() then ${{{\rm C}_{\varphi (\cdot )}}}$
then ${{{\rm C}_{\varphi (\cdot )}}}$![]() -quasi-continuous representative $\widehat {u}$
-quasi-continuous representative $\widehat {u}$![]() of $u$
of $u$![]() is measurable with respect to ${{\mu _{\varphi (\cdot )}}}$
is measurable with respect to ${{\mu _{\varphi (\cdot )}}}$![]() . If additionally $u\in L^{\infty },$
. If additionally $u\in L^{\infty },$![]() then $\widehat {u}\in L^{\infty }(\Omega,{{\mu _{\varphi (\cdot )}}})\subset L^{1}(\Omega,{{\mu _{\varphi (\cdot )}}}).$
then $\widehat {u}\in L^{\infty }(\Omega,{{\mu _{\varphi (\cdot )}}})\subset L^{1}(\Omega,{{\mu _{\varphi (\cdot )}}}).$![]()
3. Measure characterization
In order to prove theorem 1.1 let us concentrate on the continuity of $\mu \in (L^{1}(\Omega )+(W^{1,{\varphi (\cdot )}}_0(\Omega ))')\cap {{\mathcal {M}_b}}(\Omega )$![]() with respect to the generalized capacity. Note that for a nonnegative measure having decomposition $\mu =f-{{\rm div\,}}G \in (L^{1}(\Omega )+(W^{1,{\varphi (\cdot )}}_0(\Omega ))')\cap {{\mathcal {M}_b}}(\Omega )$
with respect to the generalized capacity. Note that for a nonnegative measure having decomposition $\mu =f-{{\rm div\,}}G \in (L^{1}(\Omega )+(W^{1,{\varphi (\cdot )}}_0(\Omega ))')\cap {{\mathcal {M}_b}}(\Omega )$![]() with $f\in L^{1}(\Omega )$
with $f\in L^{1}(\Omega )$![]() and $G\in (L^{\widetilde \varphi (\cdot )}(\Omega ))^{n}$
and $G\in (L^{\widetilde \varphi (\cdot )}(\Omega ))^{n}$![]() and for an arbitrary set $E\subset \Omega$
and for an arbitrary set $E\subset \Omega$![]() , we have
, we have

for every ${\phi \in W^{1,{\varphi (\cdot )}}(\Omega )}.$![]() In general, it is possible that a set has zero measure, but positive capacity. This is excluded if the measure enjoys the above decomposition.
In general, it is possible that a set has zero measure, but positive capacity. This is excluded if the measure enjoys the above decomposition.
Lemma 3.1 If $\mu \in (L^{1}(\Omega )+(W^{1,{\varphi (\cdot )}}_0(\Omega ))')\cap {{\mathcal {M}_b}}(\Omega )$![]() and a set $E\subset \Omega$
and a set $E\subset \Omega$![]() is such that ${{{\rm cap}_{\varphi (\cdot )}}}(E,\Omega )=0,$
is such that ${{{\rm cap}_{\varphi (\cdot )}}}(E,\Omega )=0,$![]() then $\mu (E)=0$
then $\mu (E)=0$![]() .
.
Proof. By the assumption $\mu$![]() can be represented with the use of $f\in L^{1}(\Omega )$
can be represented with the use of $f\in L^{1}(\Omega )$![]() and $G\in (L^{\widetilde \varphi (\cdot )}(\Omega ))^{n}$
and $G\in (L^{\widetilde \varphi (\cdot )}(\Omega ))^{n}$![]() , such that $\mu =f-{{\rm div\,}}G$
, such that $\mu =f-{{\rm div\,}}G$![]() in the sense of distributions. Let us fix arbitrary (small) ${{\varepsilon }}>0$
in the sense of distributions. Let us fix arbitrary (small) ${{\varepsilon }}>0$![]() . We consider a sequence of truncations $\{T_\ell f\}_\ell$
. We consider a sequence of truncations $\{T_\ell f\}_\ell$![]() . Note that $\{T_\ell f\}_\ell$
. Note that $\{T_\ell f\}_\ell$![]() converges to $f$
converges to $f$![]() strongly in $L^{1}(\Omega )$
strongly in $L^{1}(\Omega )$![]() , so we can choose $k$
, so we can choose $k$![]() large enough for $\|T_kf-f\|_{L^{1}(\Omega )}<{{\varepsilon }}/2$
large enough for $\|T_kf-f\|_{L^{1}(\Omega )}<{{\varepsilon }}/2$![]() .
.
Note that for any $\widetilde {{\varepsilon }}>0$![]() there exists an open set $A\supset E$
there exists an open set $A\supset E$![]() with ${{{\rm cap}_{\varphi (\cdot )}}}(A,\Omega )<\widetilde {{\varepsilon }}$
with ${{{\rm cap}_{\varphi (\cdot )}}}(A,\Omega )<\widetilde {{\varepsilon }}$![]() . Parameter $\widetilde {{\varepsilon }}$
. Parameter $\widetilde {{\varepsilon }}$![]() will be chosen in a few lines. Let us fix a compact set $K\subset A$
will be chosen in a few lines. Let us fix a compact set $K\subset A$![]() . By definition of ${{{\rm cap}_{\varphi (\cdot )}}}$
. By definition of ${{{\rm cap}_{\varphi (\cdot )}}}$![]() there exists a sequence $\{\phi _j\}_j\subset C_0^{\infty }(A)$
there exists a sequence $\{\phi _j\}_j\subset C_0^{\infty }(A)$![]() of functions such that
of functions such that
Indeed to restrict to $\phi _j$![]() such that $0\leq \phi _j\leq 1$
such that $0\leq \phi _j\leq 1$![]() let us point out that the map $t\mapsto {\rm min}\{t,1\}$
let us point out that the map $t\mapsto {\rm min}\{t,1\}$![]() is Lipschitz, so $\widetilde f := {\rm min}\{ f,1\}\in \mathcal {R}_{\varphi (\cdot )}(K,\Omega )$
is Lipschitz, so $\widetilde f := {\rm min}\{ f,1\}\in \mathcal {R}_{\varphi (\cdot )}(K,\Omega )$![]() and ${{\varrho }}_{\varphi (\cdot ),K}(|\nabla \widetilde f|)\leq {{\varrho }}_{\varphi (\cdot ),K}(|\nabla f|)$
and ${{\varrho }}_{\varphi (\cdot ),K}(|\nabla \widetilde f|)\leq {{\varrho }}_{\varphi (\cdot ),K}(|\nabla f|)$![]() . On the other hand, we substituted the modular used in definition of ${{{\rm cap}_{\varphi (\cdot )}}}$
. On the other hand, we substituted the modular used in definition of ${{{\rm cap}_{\varphi (\cdot )}}}$![]() with the norm. This is justified by the fact that the sequence realizing the infimum converges also in norm topology, which follows from the doubling growth of $\varphi$
with the norm. This is justified by the fact that the sequence realizing the infimum converges also in norm topology, which follows from the doubling growth of $\varphi$![]() via (2.5).
via (2.5).
We note that
Due to Hölder inequality (2.4) and then the Poincaré inequality (2.6), we have

We pick $\widetilde {{\varepsilon }}={{\varepsilon }}/(8(2k + \|G\|_{(L^{\widetilde \varphi (\cdot )}(\Omega ))^{n}}))$![]() . Then $|\mu |(K)<{{\varepsilon }}$
. Then $|\mu |(K)<{{\varepsilon }}$![]() with arbitrary ${{\varepsilon }}>0$
with arbitrary ${{\varepsilon }}>0$![]() , so $|\mu |(K)=0$
, so $|\mu |(K)=0$![]() . Therefore
. Therefore
which ends the proof.
We are in position to prove theorem 1.1. We take basic ideas from [Reference Boccardo, Gallouët and Orsina16] with classical growth. Similar reasoning in variable exponent setting is given in [Reference Zhang69].
Proof of theorem 1.1. Lemma 3.1 provides the implication: if $\mu$![]() belongs to $( L^{1}(\Omega )+(W_0^{1,{\varphi (\cdot )}}(\Omega ))')\cap {{\mathcal {M}_b}}(\Omega )$
belongs to $( L^{1}(\Omega )+(W_0^{1,{\varphi (\cdot )}}(\Omega ))')\cap {{\mathcal {M}_b}}(\Omega )$![]() , then $\mu \in \mathcal {M}^{\varphi (\cdot )}_b(\Omega )$
, then $\mu \in \mathcal {M}^{\varphi (\cdot )}_b(\Omega )$![]() . Therefore, we concentrate now on the essentially more demanding converse, that is, if $\mu _{\varphi (\cdot )}\in \mathcal {M}^{\varphi (\cdot )}_b(\Omega )$
. Therefore, we concentrate now on the essentially more demanding converse, that is, if $\mu _{\varphi (\cdot )}\in \mathcal {M}^{\varphi (\cdot )}_b(\Omega )$![]() , then $\mu _{\varphi (\cdot )}\in L^{1}(\Omega ) + (W^{1,{\varphi (\cdot )}}_0(\Omega ))'$
, then $\mu _{\varphi (\cdot )}\in L^{1}(\Omega ) + (W^{1,{\varphi (\cdot )}}_0(\Omega ))'$![]() .
.
Step 1. Initial decomposition. We will show that for a nonnegative ${{\mu _{\varphi (\cdot )}}}\in {{\mathcal {M}^{\varphi (\cdot )}_b}}(\Omega )$![]() there exists a nonnegative measure ${{\gamma ^{\rm meas}}}\in (W_0^{1,{\varphi (\cdot )}}(\Omega ))'$
there exists a nonnegative measure ${{\gamma ^{\rm meas}}}\in (W_0^{1,{\varphi (\cdot )}}(\Omega ))'$![]() and nonnegative Borel measurable function $h\in L^{1}(\Omega,{{\gamma ^{\rm meas}}})$
and nonnegative Borel measurable function $h\in L^{1}(\Omega,{{\gamma ^{\rm meas}}})$![]() such that ${\rm d}{{\mu _{\varphi (\cdot )}}}=h\,{\rm d}{{\gamma ^{\rm meas}}}$
such that ${\rm d}{{\mu _{\varphi (\cdot )}}}=h\,{\rm d}{{\gamma ^{\rm meas}}}$![]() .
.
For any $\widetilde u\in W^{1,{\varphi (\cdot )}}(\Omega )$![]() we can find its ${{{\rm C}_{\varphi (\cdot )}}}$
we can find its ${{{\rm C}_{\varphi (\cdot )}}}$![]() -quasi-continuous representative denoted by $u$
-quasi-continuous representative denoted by $u$![]() (lemma 2.7). We define a functional $\mathcal {F}: W^{1,{\varphi (\cdot )}}_0(\Omega )\to [0,\infty ]$
(lemma 2.7). We define a functional $\mathcal {F}: W^{1,{\varphi (\cdot )}}_0(\Omega )\to [0,\infty ]$![]() by
by
and observe that it is convex and lower semicontinuous on a separable space $W^{1,{\varphi (\cdot )}}_0(\Omega )$![]() . Thus, $\mathcal {F}$
. Thus, $\mathcal {F}$![]() can be expressed as a supremum of a countable family of continuous affine functions [Reference Chlebicka, Gwiazda, Wróblewska-Kamińska and Świerczewska-Gwiazda26, lemma 2.1.11]. By its very definition $(W^{1,{\varphi (\cdot )}}_0(\Omega ))'$
can be expressed as a supremum of a countable family of continuous affine functions [Reference Chlebicka, Gwiazda, Wróblewska-Kamińska and Świerczewska-Gwiazda26, lemma 2.1.11]. By its very definition $(W^{1,{\varphi (\cdot )}}_0(\Omega ))'$![]() consists of all linear functionals on $W^{1,{\varphi (\cdot )}}_0(\Omega )$
consists of all linear functionals on $W^{1,{\varphi (\cdot )}}_0(\Omega )$![]() . Therefore, there exist sequences of functions $\{\xi _n\}_n\subset (W^{1,{\varphi (\cdot )}}_0(\Omega ))'$
. Therefore, there exist sequences of functions $\{\xi _n\}_n\subset (W^{1,{\varphi (\cdot )}}_0(\Omega ))'$![]() and numbers $\{a_n\}_n\subset {{\mathbb {R}^{n}}}$
and numbers $\{a_n\}_n\subset {{\mathbb {R}^{n}}}$![]() such that
such that
Then, for any $s>0$![]() , $s\mathcal {F}[u]=\mathcal {F}[su]\geq s\langle \xi _n,u\rangle -a_n$
, $s\mathcal {F}[u]=\mathcal {F}[su]\geq s\langle \xi _n,u\rangle -a_n$![]() for every $n$
for every $n$![]() . When we divide it by $s$
. When we divide it by $s$![]() and let $s\to \infty$
and let $s\to \infty$![]() we obtain that $\mathcal {F}[u]\geq \langle \xi _n,u\rangle$
we obtain that $\mathcal {F}[u]\geq \langle \xi _n,u\rangle$![]() for all $u\in W_0^{1,{\varphi (\cdot )}}(\Omega )$
for all $u\in W_0^{1,{\varphi (\cdot )}}(\Omega )$![]() . As $\mathcal {F}[0]= 0$
. As $\mathcal {F}[0]= 0$![]() we infer that $a_n\geq 0$
we infer that $a_n\geq 0$![]() . Therefore, $\mathcal {F}[u]\geq \sup _{n\in \mathbb {N}} \langle \xi _n,u\rangle \geq \sup _{n\in \mathbb {N}}\{\langle \xi _n,u\rangle -a_n\}=\mathcal {F}[u]$
. Therefore, $\mathcal {F}[u]\geq \sup _{n\in \mathbb {N}} \langle \xi _n,u\rangle \geq \sup _{n\in \mathbb {N}}\{\langle \xi _n,u\rangle -a_n\}=\mathcal {F}[u]$![]() and, in turn,
and, in turn,
This means that for all $\phi \in C_0^{\infty }(\Omega )$![]() we have
we have
By the same arguments for $-\varphi$![]() we get
we get
implying that $\xi _n\in (W^{1,{\varphi (\cdot )}}_0 (\Omega ))'\cap {{\mathcal {M}_b}}(\Omega ).$![]() By the Riesz representation theorem there exists nonnegative ${{\xi _n^{\rm meas}}}\in {{\mathcal {M}_b}}(\Omega )$
By the Riesz representation theorem there exists nonnegative ${{\xi _n^{\rm meas}}}\in {{\mathcal {M}_b}}(\Omega )$![]() , such that
, such that
Note that
Let us define

and observe that the series in absolutely convergent in $(W^{1,{\varphi (\cdot )}}_0(\Omega ))'$![]() . Therefore, for $\phi \in C_0^{\infty }(\Omega )$
. Therefore, for $\phi \in C_0^{\infty }(\Omega )$![]() we can write
we can write

and so $\eta \in (W^{1,{\varphi (\cdot )}}_0(\Omega ))'\cap {{\mathcal {M}_b}}(\Omega )$![]() too. We denote
too. We denote

and note that this is a series of positive elements that is absolutely convergent in ${{\mathcal {M}_b}}(\Omega )$![]() . Moreover, ${{\xi _n^{\rm meas}}}\ll {{\eta ^{\rm meas}}}$
. Moreover, ${{\xi _n^{\rm meas}}}\ll {{\eta ^{\rm meas}}}$![]() and thus for every $n$
and thus for every $n$![]() there exists a nonnegative function $h_n\in L^{1}(\Omega,{\rm d}{{\eta ^{\rm meas}}})$
there exists a nonnegative function $h_n\in L^{1}(\Omega,{\rm d}{{\eta ^{\rm meas}}})$![]() such that ${\rm d}{{\xi _n^{\rm meas}}}=h_n\, {\rm d}{{\eta ^{\rm meas}}}$
such that ${\rm d}{{\xi _n^{\rm meas}}}=h_n\, {\rm d}{{\eta ^{\rm meas}}}$![]() . Having (3.1) we deduce that
. Having (3.1) we deduce that

On the other hand, (3.2) ensures that $h_n{{\eta ^{\rm meas}}}\leq {{\mu _{\varphi (\cdot )}}}$![]() . This means that for any measurable set $E\subset \Omega$
. This means that for any measurable set $E\subset \Omega$![]() and every $n$
and every $n$![]() we have
we have
We denote $h_{\max }^{k}=\max \{h_1(x),\dots,h_k(x)\}$![]() and
and
Then $E^{j,k}$![]() for $i=1,\dots,k$
for $i=1,\dots,k$![]() are pairwise disjoint and $E=\cup _{j=1}^{k} E^{j,k}$
are pairwise disjoint and $E=\cup _{j=1}^{k} E^{j,k}$![]() , so
, so

Let us pass with $k\to \infty$![]() and take $h(x)=\sup _{l\in \mathbb {N}} h_l(x)$
and take $h(x)=\sup _{l\in \mathbb {N}} h_l(x)$![]() . We infer that for any measurable set $E\subset \Omega$
. We infer that for any measurable set $E\subset \Omega$![]()
According to (3.4), for every nonnegative $\phi \in C_0^{\infty }$![]() we have
we have
that is ${\rm d}{{\mu _{\varphi (\cdot )}}}=h\,{\rm d}{{\eta ^{\rm meas}}}.$![]() Since ${{\mu _{\varphi (\cdot )}}}(\Omega )\in {{\mathcal {M}_b}}(\Omega )$
Since ${{\mu _{\varphi (\cdot )}}}(\Omega )\in {{\mathcal {M}_b}}(\Omega )$![]() , we deduce that $h\in L^{1}(\Omega,{\rm d}{{\eta ^{\rm meas}}})$
, we deduce that $h\in L^{1}(\Omega,{\rm d}{{\eta ^{\rm meas}}})$![]() and the aim of this step is achieved with ${{\gamma ^{\rm meas}}}={{\eta ^{\rm meas}}}\in (W^{1,{\varphi (\cdot )}}_0(\Omega ))'$
and the aim of this step is achieved with ${{\gamma ^{\rm meas}}}={{\eta ^{\rm meas}}}\in (W^{1,{\varphi (\cdot )}}_0(\Omega ))'$![]() .
.
Step 2. Auxiliary sequence of measures. We take an increasing sequence of sets $\{K_i\}_i$![]() compact in $\Omega$
compact in $\Omega$![]() , such that $\cup _{i=1}^{\infty } K_i=\Omega$
, such that $\cup _{i=1}^{\infty } K_i=\Omega$![]() . We set
. We set
Then $\{\widetilde \mu _i\}_i$![]() is an increasing sequence of positive measures in $(W^{1,{\varphi (\cdot )}}_0(\Omega ))'$
is an increasing sequence of positive measures in $(W^{1,{\varphi (\cdot )}}_0(\Omega ))'$![]() with supports compact in $\Omega$
with supports compact in $\Omega$![]() . Let us denote
. Let us denote
Then $\sum _{i=1}^{k}\mu _i=T_k(h\mathbb {1}_{K_k}){{\gamma ^{\rm meas}}}\in {{\mathcal {M}_b}}(\Omega )$![]() . Since $\mu _i\geq 0$
. Since $\mu _i\geq 0$![]() , we have $\sum _{i=1}^{\infty } \|\mu _i\|_{\mathcal {M}(\Omega )}<\infty$
, we have $\sum _{i=1}^{\infty } \|\mu _i\|_{\mathcal {M}(\Omega )}<\infty$![]() . Furthermore, ${{\mu _{\varphi (\cdot )}}}=\sum _{i=1}^{\infty }\mu _i$
. Furthermore, ${{\mu _{\varphi (\cdot )}}}=\sum _{i=1}^{\infty }\mu _i$![]() and this series is absolutely convergent in ${{\mathcal {M}_b}}(\Omega )$
and this series is absolutely convergent in ${{\mathcal {M}_b}}(\Omega )$![]() .
.
Step 3. Construction of decomposition. Suppose ${{\varrho }}\in C_0^{\infty }(B(0,1))$![]() is a standard mollifier (nonnegative and symmetric function with $\int _{{\mathbb {R}^{n}}} {{\varrho }}\,{\rm d}x=1$
is a standard mollifier (nonnegative and symmetric function with $\int _{{\mathbb {R}^{n}}} {{\varrho }}\,{\rm d}x=1$![]() ) and set ${{\varrho }}_k(x)=k^{n}{{\varrho }}(kx)$
) and set ${{\varrho }}_k(x)=k^{n}{{\varrho }}(kx)$![]() . We consider mollification
. We consider mollification
For $k$![]() large enough, we can decompose $\mu _i=f_i+w_i$
large enough, we can decompose $\mu _i=f_i+w_i$![]() with
with
by choosing for every $i$![]() sufficiently large $k_0^{i}$
sufficiently large $k_0^{i}$![]() such that for $k_i>k_0^{i}$
such that for $k_i>k_0^{i}$![]() , $\mu _{i,k_i}^{{\varrho }}$
, $\mu _{i,k_i}^{{\varrho }}$![]() belongs to $C_0^{\infty }(\Omega )$
belongs to $C_0^{\infty }(\Omega )$![]() , so we restrict our attention to such $k_i$
, so we restrict our attention to such $k_i$![]() . Therefore, we get – up to a subsequence – convergence of $\{f_{i}\}_i=\{\mu _{i,k_i}^{{\varrho }}\}_i$
. Therefore, we get – up to a subsequence – convergence of $\{f_{i}\}_i=\{\mu _{i,k_i}^{{\varrho }}\}_i$![]() to ${{\mu _{\varphi (\cdot )}}}$
to ${{\mu _{\varphi (\cdot )}}}$![]() in measure and for every $i$
in measure and for every $i$![]() we have $\|f_i\|_{L^{1} (\Omega )}\leq \|{{\mu _{\varphi (\cdot )}}}\|_{{{\mathcal {M}_b}}(\Omega )}.$
we have $\|f_i\|_{L^{1} (\Omega )}\leq \|{{\mu _{\varphi (\cdot )}}}\|_{{{\mathcal {M}_b}}(\Omega )}.$![]() By step 2 the series $\sum _{i=1}^{\infty } f_i$
By step 2 the series $\sum _{i=1}^{\infty } f_i$![]() is convergent in $L^{1} (\Omega )$
is convergent in $L^{1} (\Omega )$![]() and there exists its limit $f^{0}=\sum _{i=1}^{\infty } f_i\in L^{1}(\Omega )$
and there exists its limit $f^{0}=\sum _{i=1}^{\infty } f_i\in L^{1}(\Omega )$![]() . As for convergence of $w_i$
. As for convergence of $w_i$![]() we observe first that due to [Reference Harjulehto and Hästö49, lemma 6.4.5] we get convergence of $\{\mu _{i,k}^{{\varrho }}\}_k$
we observe first that due to [Reference Harjulehto and Hästö49, lemma 6.4.5] we get convergence of $\{\mu _{i,k}^{{\varrho }}\}_k$![]() to $\mu _i$
to $\mu _i$![]() in $(W^{1,{\varphi (\cdot )}}_0(\Omega ))'$
in $(W^{1,{\varphi (\cdot )}}_0(\Omega ))'$![]() as $k\to \infty$
as $k\to \infty$![]() . We note that the series $\sum _{i=1}^{\infty } w_i$
. We note that the series $\sum _{i=1}^{\infty } w_i$![]() converges in $(W^{1,{\varphi (\cdot )}}_0(\Omega ))'$
converges in $(W^{1,{\varphi (\cdot )}}_0(\Omega ))'$![]() and there exists its limit $w^{0}=\sum _{i=1}^{\infty } w_i\in (W^{1,{\varphi (\cdot )}}_0(\Omega ))'$
and there exists its limit $w^{0}=\sum _{i=1}^{\infty } w_i\in (W^{1,{\varphi (\cdot )}}_0(\Omega ))'$![]() . Therefore, the three following series converge in the sense of distributions
. Therefore, the three following series converge in the sense of distributions

and, consequently, ${{\mu _{\varphi (\cdot )}}}=f^{0}+w^{0}$![]() .
.
Step 4. Summary. Let us recall that the proof starts with justification that for a nonnegative measure $\mu \in L^{1}(\Omega )+(W^{1,{\varphi (\cdot )}}_0(\Omega ))'\subset {{\mathcal {M}^{\varphi (\cdot )}_b}}(\Omega ) .$![]() Step 3 provides the reverse implication.
Step 3 provides the reverse implication.
If the measure was not nonnegative, we can write that ${{\mu _{\varphi (\cdot )}}}=(({{\mu _{\varphi (\cdot )}}})_++({{\mu _{\varphi (\cdot )}}})_-)$![]() and repeat the above reasoning separately for its positive and negative part. Note that by the monotonicity of capacity, if ${{{\rm cap}_{\varphi (\cdot )}}}(A,\Omega )=0$
and repeat the above reasoning separately for its positive and negative part. Note that by the monotonicity of capacity, if ${{{\rm cap}_{\varphi (\cdot )}}}(A,\Omega )=0$![]() , then $({{\mu _{\varphi (\cdot )}}})_+(A)=0=({{\mu _{\varphi (\cdot )}}})_-(A)$
, then $({{\mu _{\varphi (\cdot )}}})_+(A)=0=({{\mu _{\varphi (\cdot )}}})_-(A)$![]() ($\varphi (\cdot$
($\varphi (\cdot$![]() )-capacity can be exhausted over Borel sets included in $A$
)-capacity can be exhausted over Borel sets included in $A$![]() ), see [Reference Baruah, Harjulehto and Hästo10]. Note that if $\mu _{\varphi (\cdot )}$
), see [Reference Baruah, Harjulehto and Hästo10]. Note that if $\mu _{\varphi (\cdot )}$![]() is nonnegative, then $f\geq 0$
is nonnegative, then $f\geq 0$![]() . Hence, for a signed measure $\mu \in {{\mathcal {M}_b}}(\Omega )$
. Hence, for a signed measure $\mu \in {{\mathcal {M}_b}}(\Omega )$![]() we infer that $\mu \in {{\mathcal {M}^{\varphi (\cdot )}_b}}(\Omega )$
we infer that $\mu \in {{\mathcal {M}^{\varphi (\cdot )}_b}}(\Omega )$![]() if and only if $\mu \in ( L^{1}(\Omega )+(W^{1,{\varphi (\cdot )}}_0(\Omega ))')\cap {{\mathcal {M}_b}}(\Omega )$
if and only if $\mu \in ( L^{1}(\Omega )+(W^{1,{\varphi (\cdot )}}_0(\Omega ))')\cap {{\mathcal {M}_b}}(\Omega )$![]() , that is when there exists $f\in L^{1}(\Omega )$
, that is when there exists $f\in L^{1}(\Omega )$![]() and $G\in (L^{\widetilde \varphi (\cdot )}(\Omega ))^{n}$
and $G\in (L^{\widetilde \varphi (\cdot )}(\Omega ))^{n}$![]() , such that ${{\mu _{\varphi (\cdot )}}}=f-{{\rm div\,}}G\ \text { in the sense of distributions}.$
, such that ${{\mu _{\varphi (\cdot )}}}=f-{{\rm div\,}}G\ \text { in the sense of distributions}.$![]() Hence, the proof of the capacitary characterization is completed.
Hence, the proof of the capacitary characterization is completed.
To conclude remark 1.3 we need the following decomposition lemma. Its proof is essentially the one of [Reference Fukushima, Sato and Taniguchi44, lemma 2.1], but we find it valuable to present it for the sake of completeness.
Lemma 3.2 Suppose $\Omega$![]() is a bounded set in ${{\mathbb {R}^{n}}}$
is a bounded set in ${{\mathbb {R}^{n}}}$![]() and $\mathfrak {M}$
and $\mathfrak {M}$![]() is a family of its measurable subsets. Then for every $\mu \in {{\mathcal {M}_b}}(\Omega )$
is a family of its measurable subsets. Then for every $\mu \in {{\mathcal {M}_b}}(\Omega )$![]() there exist a decomposition $\mu =\mu _{ac}+{{\mu _{\rm sing}}},$
there exist a decomposition $\mu =\mu _{ac}+{{\mu _{\rm sing}}},$![]() such that
such that
(a) $\mu _{ac}(D)=0$
 for all sets $D\subset \mathfrak {M}$
for all sets $D\subset \mathfrak {M}$ with ${{{\rm C}_{\varphi (\cdot )}}}(D)=0,$
with ${{{\rm C}_{\varphi (\cdot )}}}(D)=0,$
(b) ${{\mu _{\rm sing}}}=\mu \mathbb {1}_{N}$
 for some set $N\subset \mathfrak {M}$
for some set $N\subset \mathfrak {M}$ with ${{{\rm C}_{\varphi (\cdot )}}}(N)=0$
with ${{{\rm C}_{\varphi (\cdot )}}}(N)=0$ .
.
Moreover, such decomposition is unique up to sets of $W^{1,\varphi (\cdot )}$![]() -capacity zero.
-capacity zero.
Proof. We fix an arbitrary sequence $D_1\subset D_2\subset \dots \subset \mathfrak {M}$![]() of sets with ${{{\rm C}_{\varphi (\cdot )}}}(D_i)=0$
of sets with ${{{\rm C}_{\varphi (\cdot )}}}(D_i)=0$![]() , such that
, such that
Denote $D_\infty =\bigcup _{i=1}^{\infty } D_i$![]() and note that $D_\infty \in \mathfrak {M}$
and note that $D_\infty \in \mathfrak {M}$![]() , ${{{\rm C}_{\varphi (\cdot )}}}(D_\infty )=0$
, ${{{\rm C}_{\varphi (\cdot )}}}(D_\infty )=0$![]() and $\mu (D_\infty )=\alpha$
and $\mu (D_\infty )=\alpha$![]() . Let us observe that $\mu (D\setminus D_\infty )=0$
. Let us observe that $\mu (D\setminus D_\infty )=0$![]() for every $D\in \mathfrak {M}$
for every $D\in \mathfrak {M}$![]() with ${{{\rm C}_{\varphi (\cdot )}}}(D)=0$
with ${{{\rm C}_{\varphi (\cdot )}}}(D)=0$![]() . By setting
. By setting
we get the decomposition of the desired properties. Due to [Reference Baruah, Harjulehto and Hästo10, proposition 7] countable sum of sets of $W^{1,\varphi (\cdot )}$![]() -capacity zero is of $W^{1,\varphi (\cdot )}$
-capacity zero is of $W^{1,\varphi (\cdot )}$![]() -capacity zero, so the uniqueness of the decomposition ${{{\rm C}_{\varphi (\cdot )}}}$
-capacity zero, so the uniqueness of the decomposition ${{{\rm C}_{\varphi (\cdot )}}}$![]() -quasi-everywhere is evident.
-quasi-everywhere is evident.
4. Approximate problems
This section is devoted to analysis of approximate problems with general datum.
In the case of a measure $\mu \in {{\mathcal {M}_b}}(\Omega )$![]() we shall consider an approximate sequence of bounded functions $\{\mu ^{s}\}\subset C^{\infty }(\Omega )$
we shall consider an approximate sequence of bounded functions $\{\mu ^{s}\}\subset C^{\infty }(\Omega )$![]() that converges to $\mu$
that converges to $\mu$![]() weakly-$*$
weakly-$*$![]() in the space of measures and satisfies (1.7). We study solutions to
in the space of measures and satisfies (1.7). We study solutions to

It is known that there exists at least one distributional solution $u_s\in W^{1,\varphi (\cdot )}(\Omega )$![]() to (4.1), see the proof by Galerkin approximation in [Reference Gwiazda, Wittbold, Wróblewska and Zimmermann47, § 5.1.1] under more general growth conditions embracing our case. In fact, since smooth functions are dense in the space where the solutions live i.e. $W_0^{1,\varphi (\cdot )}(\Omega )$
to (4.1), see the proof by Galerkin approximation in [Reference Gwiazda, Wittbold, Wróblewska and Zimmermann47, § 5.1.1] under more general growth conditions embracing our case. In fact, since smooth functions are dense in the space where the solutions live i.e. $W_0^{1,\varphi (\cdot )}(\Omega )$![]() , we can test the equation by the solution itself to get energy estimates and, consequently, the distributional solutions $u_s$
, we can test the equation by the solution itself to get energy estimates and, consequently, the distributional solutions $u_s$![]() are weak solutions.
are weak solutions.
Remark 4.1 Note that requiring regularity of $\mu ^{s}$![]() is not a restriction. In fact, the proof requires only $\mu ^{s}\in (W^{1,\varphi (\cdot )}_0(\Omega ))'\cap {{\mathcal {M}_b}}(\Omega )$
is not a restriction. In fact, the proof requires only $\mu ^{s}\in (W^{1,\varphi (\cdot )}_0(\Omega ))'\cap {{\mathcal {M}_b}}(\Omega )$![]() .
.
Proposition 4.2 (Basic a priori estimates)
Let $\Omega$![]() be bounded open domain in ${{\mathbb {R}^{n}}},$
be bounded open domain in ${{\mathbb {R}^{n}}},$![]() $\mathcal {A}:\Omega \times {{\mathbb {R}^{n}}}\to {{\mathbb {R}^{n}}}$
$\mathcal {A}:\Omega \times {{\mathbb {R}^{n}}}\to {{\mathbb {R}^{n}}}$![]() satisfy $(\mathcal {A} 1)$
satisfy $(\mathcal {A} 1)$![]() –$(\mathcal {A} 4),$
–$(\mathcal {A} 4),$![]() $\varphi \in \Phi _c(\Omega )$
$\varphi \in \Phi _c(\Omega )$![]() satisfy (aInc)$_p,$
satisfy (aInc)$_p,$![]() (aDec)$_q,$
(aDec)$_q,$![]() (A0), and (A1) and ${{\mu _{\varphi (\cdot )}}}\in {{\mathcal {M}_b}}(\Omega )$
(A0), and (A1) and ${{\mu _{\varphi (\cdot )}}}\in {{\mathcal {M}_b}}(\Omega )$![]() . Then, for a weak solutions $u_s$
. Then, for a weak solutions $u_s$![]() to (4.1) and $k>1,$
to (4.1) and $k>1,$![]() we have
we have
with constants $\bar {c}_1=2\|\mu \|_{\mathcal {M}_b(\Omega )} /{c_1^{\varphi }}, \bar {c}_2=c(c_1^{\varphi },c_2^{\varphi },c_{\Delta _2}(\varphi ),q,\|\mu \|_{\mathcal {M}_b(\Omega )}, \|1+\gamma \|_{L^{\widetilde \varphi (\cdot )}(\Omega )})>0$![]() . Furthermore, for some $\bar {c}_3=\bar {c}_3(\Omega,n)>0$
. Furthermore, for some $\bar {c}_3=\bar {c}_3(\Omega,n)>0$![]()
Since constants in the above estimates do not depend on $s$![]() , we can infer what follows.
, we can infer what follows.
Remark 4.3 Note that within our doubling regime this implies that for any fixed $k>0$![]() the sequence $\{\nabla T_k(u_s)\}_s$
the sequence $\{\nabla T_k(u_s)\}_s$![]() is uniformly bounded in $L^{\varphi (\cdot )}(\Omega )$
is uniformly bounded in $L^{\varphi (\cdot )}(\Omega )$![]() , $\{|\mathcal {A}(x,\nabla T_k(u_s))|\}_s$
, $\{|\mathcal {A}(x,\nabla T_k(u_s))|\}_s$![]() is uniformly bounded in $L^{\widetilde \varphi (\cdot )}(\Omega )$
is uniformly bounded in $L^{\widetilde \varphi (\cdot )}(\Omega )$![]() and the set $\{|u_s|\geq k\}$
and the set $\{|u_s|\geq k\}$![]() for increasing $k$
for increasing $k$![]() is shrinking uniformly in $s$
is shrinking uniformly in $s$![]() .
.
Proof of proposition 4.2. To get (4.2), we use first ($\mathcal {A}$![]() 2)$_1$
2)$_1$![]() , (4.1) tested by $T_k(u_s)\in W^{1,\varphi (\cdot )}_0(\Omega )$
, (4.1) tested by $T_k(u_s)\in W^{1,\varphi (\cdot )}_0(\Omega )$![]() , and the above remark, in the following way
, and the above remark, in the following way

We conclude the last inequality above because of the assumed properties of $\mu ^{s}$![]() .
.
In order to get (4.3), we use ($\mathcal {A}$![]() 2)$_2$
2)$_2$![]() , doubling growth (2.3), and finally (4.2) to conclude that for any $k>1$
, doubling growth (2.3), and finally (4.2) to conclude that for any $k>1$![]() we have
we have

where $c= c(c_1^{\varphi },c_2^{\varphi },c_{\Delta _2}(\varphi ),q,\|\mu \|_{\mathcal {M}_b(\Omega )}, \|1+\gamma \|_{L^{\widetilde \varphi (\cdot )}(\Omega )})$![]() .
.
To get (4.4) we start with observing that $|\{|u_s|\geq k\}|=|\{T_k(|u_s|)\geq k\}|$![]() . Then by Tchebyshev inequality, Poincaré inequality and (4.2) as follows
. Then by Tchebyshev inequality, Poincaré inequality and (4.2) as follows

5. Approximable solutions
Let us find the fundamental properties of limits of approximate problems.
Proposition 5.1 (Existence of approximable solutions and convergences)
Let $\Omega$![]() be bounded open domain in ${{\mathbb {R}^{n}}},$
be bounded open domain in ${{\mathbb {R}^{n}}},$![]() $\mathcal {A}:\Omega \times {{\mathbb {R}^{n}}}\to {{\mathbb {R}^{n}}}$
$\mathcal {A}:\Omega \times {{\mathbb {R}^{n}}}\to {{\mathbb {R}^{n}}}$![]() satisfy $(\mathcal {A} 1)$
satisfy $(\mathcal {A} 1)$![]() –$(\mathcal {A} 4),$
–$(\mathcal {A} 4),$![]() $\varphi \in \Phi _c(\Omega )$
$\varphi \in \Phi _c(\Omega )$![]() satisfy (aInc)$_p,$
satisfy (aInc)$_p,$![]() (aDec)$_q,$
(aDec)$_q,$![]() (A0) and (A1), and $\mu \in {{\mathcal {M}_b}}(\Omega )$
(A0) and (A1), and $\mu \in {{\mathcal {M}_b}}(\Omega )$![]() . Then there exists at least one approximable solution $u$
. Then there exists at least one approximable solution $u$![]() (see definition 1.6). Namely, up to a subsequence $\{u_s\}_{s}$
(see definition 1.6). Namely, up to a subsequence $\{u_s\}_{s}$![]() consisting of solutions to (4.1) , there exists a function $u\in \mathcal {T}^{1,\varphi (\cdot )}_0(\Omega ),$
consisting of solutions to (4.1) , there exists a function $u\in \mathcal {T}^{1,\varphi (\cdot )}_0(\Omega ),$![]() such that when $s\to 0$
such that when $s\to 0$![]() and $k>0$
and $k>0$![]() is fixed we have
is fixed we have
Moreover, for $k\to \infty$![]()
Proof. Having (4.2) we get that $\{T_k(u_s)\}_s$![]() is uniformly bounded in $W^{1,\varphi (\cdot )}_{0}(\Omega )$
is uniformly bounded in $W^{1,\varphi (\cdot )}_{0}(\Omega )$![]() . By recalling the Banach–Alaoglu theorem in the reflexive space, we infer that there exists a (non-relabelled) subsequence of $\{u_s\}$
. By recalling the Banach–Alaoglu theorem in the reflexive space, we infer that there exists a (non-relabelled) subsequence of $\{u_s\}$![]() and function $u\in \mathcal {T}^{1,\varphi (\cdot )}_0$
and function $u\in \mathcal {T}^{1,\varphi (\cdot )}_0$![]() such that for $s\to 0$
such that for $s\to 0$![]() we have (5.3). Note that in the general case we would have here weak-$\ast$
we have (5.3). Note that in the general case we would have here weak-$\ast$![]() convergence, but our space is reflexive and these notions of convergences coincide. Since embedding (2.7) is compact, up to a non-relabelled subsequence, for $s\to 0$
convergence, but our space is reflexive and these notions of convergences coincide. Since embedding (2.7) is compact, up to a non-relabelled subsequence, for $s\to 0$![]() also (5.2). Consequently, due to the Dunford–Pettis theorem, up to an (again) non-relabelled subsequence $\{T_k(u_s)\}_s$
also (5.2). Consequently, due to the Dunford–Pettis theorem, up to an (again) non-relabelled subsequence $\{T_k(u_s)\}_s$![]() is a Cauchy sequence in measure and (5.1) holds. By the same arguments, due to (4.3), there exists $\mathcal {A}_k^{\infty }\in (L^{\widetilde \varphi (\cdot )}(\Omega ))^{n}$
is a Cauchy sequence in measure and (5.1) holds. By the same arguments, due to (4.3), there exists $\mathcal {A}_k^{\infty }\in (L^{\widetilde \varphi (\cdot )}(\Omega ))^{n}$![]() such that for $s\to 0$
such that for $s\to 0$![]()
The effort will be put now in identification of the limit function
and proving that $u$![]() obtained in this procedure is a very weak solution. Recall that $\mathcal {A}$
obtained in this procedure is a very weak solution. Recall that $\mathcal {A}$![]() is continuous with respect to the last variable, we have the convergence (5.2) and what remains to prove is fine behaviour of $\{\nabla u_s\}_s$
is continuous with respect to the last variable, we have the convergence (5.2) and what remains to prove is fine behaviour of $\{\nabla u_s\}_s$![]() . In order to show that $\{\nabla u_s\}_s$
. In order to show that $\{\nabla u_s\}_s$![]() is a Cauchy sequence in measure we set ${{\epsilon }} >0$
is a Cauchy sequence in measure we set ${{\epsilon }} >0$![]() and $m,n\in \mathbb {N}$
and $m,n\in \mathbb {N}$![]() arbitrary (large). Given any $t, \tau, r >0$
arbitrary (large). Given any $t, \tau, r >0$![]() , one has that
, one has that
where
Note that (4.4) and arguments of the proof of [Reference Chlebicka and Zatorska-Goldstein32, lemma 4.12] enable to justify uniform integrability of $\{g(|\nabla u_k|)\}_k$![]() for some continuous and increasing function $g$
for some continuous and increasing function $g$![]() . Therefore, we can choose for any ${{\varepsilon }}>0$
. Therefore, we can choose for any ${{\varepsilon }}>0$![]() a number $\tau _{{\varepsilon }}$
a number $\tau _{{\varepsilon }}$![]() large enough so that for $\tau >\tau _{{\varepsilon }}$
large enough so that for $\tau >\tau _{{\varepsilon }}$![]() we obtain
we obtain
From now on we restrict ourselves to $\tau >\tau _{{\varepsilon }}$![]() . On the other hand, since $\{u_l\}$
. On the other hand, since $\{u_l\}$![]() is a Cauchy sequence in measure,
is a Cauchy sequence in measure,
What remains to prove is that there exists $\delta _{\tau,{{\varepsilon }}}>0$![]() , such that for every $\delta <\delta _{\tau,{{\varepsilon }}}$
, such that for every $\delta <\delta _{\tau,{{\varepsilon }}}$![]() , we get
, we get
Let us define a set
which is compact. Consider the function $\psi :\Omega \to [0,\infty )$![]() given by
given by
Monotonicity assumption ($\mathcal {A}3$![]() ) and the continuity of the function $\xi \mapsto \mathcal {A}(\cdot,\xi )$
) and the continuity of the function $\xi \mapsto \mathcal {A}(\cdot,\xi )$![]() a.e. in $S$
a.e. in $S$![]() ensure that $\psi \geq 0$
ensure that $\psi \geq 0$![]() in $\Omega$
in $\Omega$![]() . Furthermore, ($\mathcal {A} 4$
. Furthermore, ($\mathcal {A} 4$![]() ) implies that $|\{\mathcal {A}(x,0)=0\}|=0$
) implies that $|\{\mathcal {A}(x,0)=0\}|=0$![]() . Moreover,
. Moreover,

where the last but one equality follows on making use of the test function $T_r(u_l-u_m)$![]() and in the corresponding equation with $l$
and in the corresponding equation with $l$![]() replaced by $m$
replaced by $m$![]() , and subtracting the resultant equations. Estimate (5.15) and the properties of the function $\psi$
, and subtracting the resultant equations. Estimate (5.15) and the properties of the function $\psi$![]() ensure that, if $s$
ensure that, if $s$![]() is chosen sufficiently small, then (5.14) holds. From inequalities (5.10), (5.12), (5.14) and (5.13), we infer that $\{\nabla u_s\}_s$
is chosen sufficiently small, then (5.14) holds. From inequalities (5.10), (5.12), (5.14) and (5.13), we infer that $\{\nabla u_s\}_s$![]() is a Cauchy sequence in measure.
is a Cauchy sequence in measure.
To conclude that the function $u$![]() obtained in (5.3) and (5.2) is a desired approximable solution, we observe that it belongs to the class $\mathcal {T} ^{1,\varphi (\cdot )}_0(\Omega )$
obtained in (5.3) and (5.2) is a desired approximable solution, we observe that it belongs to the class $\mathcal {T} ^{1,\varphi (\cdot )}_0(\Omega )$![]() , and that $\nabla u_s \to \nabla u$
, and that $\nabla u_s \to \nabla u$![]() $\hbox {a.e. in} \Omega$
$\hbox {a.e. in} \Omega$![]() (up to subsequences), where $\nabla u$
(up to subsequences), where $\nabla u$![]() is understood in the sense of (1.4). Since $\{\nabla u_s\}$
is understood in the sense of (1.4). Since $\{\nabla u_s\}$![]() is a Cauchy sequence in measure, there exist a subsequence (still indexed by $s$
is a Cauchy sequence in measure, there exist a subsequence (still indexed by $s$![]() ) and a measurable function $W:\Omega \to {{\mathbb {R}^{n}}}$
) and a measurable function $W:\Omega \to {{\mathbb {R}^{n}}}$![]() such that $\nabla u_s\to W$
such that $\nabla u_s\to W$![]() a.e. in $\Omega.$
a.e. in $\Omega.$![]() To motivate that $\nabla u = W$
To motivate that $\nabla u = W$![]() and
and
it suffices to recall (5.3). Indeed, then for each fixed $k>0$![]() , there exists a subsequence of $\{u_s\}$
, there exists a subsequence of $\{u_s\}$![]() , still indexed by $s$
, still indexed by $s$![]() , such that
, such that
and $\lim _{s \to \infty } \nabla T_k(u_s) = \nabla T_k(u)$![]() weakly in $(L^{\varphi (\cdot )}(\Omega ))^{n}$
weakly in $(L^{\varphi (\cdot )}(\Omega ))^{n}$![]() . Therefore, $\nabla T_k(u) = \chi _{\{|u|< k\}} W$
. Therefore, $\nabla T_k(u) = \chi _{\{|u|< k\}} W$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() , whence (5.16) follows. Then, due to ($\mathcal {A} 1$
, whence (5.16) follows. Then, due to ($\mathcal {A} 1$![]() ) also (5.9) holds, that is we have (5.4) and (5.5). Due to remark 2.5 we get uniform integrability of $\{\mathcal {A}(x,\nabla T_k u)\}_k$
) also (5.9) holds, that is we have (5.4) and (5.5). Due to remark 2.5 we get uniform integrability of $\{\mathcal {A}(x,\nabla T_k u)\}_k$![]() , so Lebesgue's monotone convergence theorem justifies (5.7), where the limit is in $(L^{1}(\Omega ))^{n}$
, so Lebesgue's monotone convergence theorem justifies (5.7), where the limit is in $(L^{1}(\Omega ))^{n}$![]() by lemma 2.10. By (4.3) and Vitali's convergence theorem we infer (5.6).
by lemma 2.10. By (4.3) and Vitali's convergence theorem we infer (5.6).
6. Renormalized solutions
Our aim now is to analyse the measures generated by truncations of approximable solutions.
Proposition 6.1 If $u$![]() is an approximable solution under assumptions of proposition 5.1 and ${{\mathfrak {A}_{\varphi (\cdot )}}}$
is an approximable solution under assumptions of proposition 5.1 and ${{\mathfrak {A}_{\varphi (\cdot )}}}$![]() is given by (2.8), then for every $k>0$
is given by (2.8), then for every $k>0$![]() we have $\lambda _k:={{\mathfrak {A}_{\varphi (\cdot )}}}(T_ku)\in {{\mathcal {M}_b}}(\Omega )\cap (W^{1,\varphi (\cdot )}_0(\Omega ))'$
we have $\lambda _k:={{\mathfrak {A}_{\varphi (\cdot )}}}(T_ku)\in {{\mathcal {M}_b}}(\Omega )\cap (W^{1,\varphi (\cdot )}_0(\Omega ))'$![]() and
and
Then for $k\to \infty$![]() we have
we have
Moreover, for every $k>0$![]() it holds $|{{\mathfrak {A}_{\varphi (\cdot )}}}(T_ku)|(\{|u|>k\})=0$
it holds $|{{\mathfrak {A}_{\varphi (\cdot )}}}(T_ku)|(\{|u|>k\})=0$![]() and for every $\phi \in C_0(\Omega )$
and for every $\phi \in C_0(\Omega )$![]() we have
we have
with $\nu ^{+}_k={{\mathfrak {A}_{\varphi (\cdot )}}}(T_ku) {\mathsf {L}} \{u=k\}$![]() and $\nu ^{-}_k={{\mathfrak {A}_{\varphi (\cdot )}}}(T_ku) {\mathsf {L}} \{u=-k\}$
and $\nu ^{-}_k={{\mathfrak {A}_{\varphi (\cdot )}}}(T_ku) {\mathsf {L}} \{u=-k\}$![]() .
.
Proof. We prove first weak-$\ast$![]() convergence of measures generated by truncations of solutions and then their further properties.
convergence of measures generated by truncations of solutions and then their further properties.
Step 1. $\lambda _k\in {{\mathcal {M}_b}}(\Omega )$![]() and ${{\mathfrak {A}_{\varphi (\cdot )}}}(T_ku)\rightharpoonup {} {{\mathfrak {A}_{\varphi (\cdot )}}}(u)$
and ${{\mathfrak {A}_{\varphi (\cdot )}}}(T_ku)\rightharpoonup {} {{\mathfrak {A}_{\varphi (\cdot )}}}(u)$![]() weakly- $\ast$
weakly- $\ast$![]() in the space of measures.
in the space of measures.
For $k>\delta >0$![]() we define a Lipschitz functions $h_\delta,\sigma _\delta ^{+},\sigma _\delta ^{-}:\mathbb {{R}}\to \mathbb {{R}}$
we define a Lipschitz functions $h_\delta,\sigma _\delta ^{+},\sigma _\delta ^{-}:\mathbb {{R}}\to \mathbb {{R}}$![]() satisfying
satisfying

and $\sigma _\delta ^{-}(r)=\sigma _\delta ^{+}(-r)$![]() . We note that if $\{u_s\}$
. We note that if $\{u_s\}$![]() is an approximate sequence from definition 1.6 solving (4.1) with $\mu ^{s}$
is an approximate sequence from definition 1.6 solving (4.1) with $\mu ^{s}$![]() being bounded and smooth function, $\phi \in C_0^{\infty }(\Omega )$
being bounded and smooth function, $\phi \in C_0^{\infty }(\Omega )$![]() , then $h_\delta (u_s)\phi,\sigma _\delta ^{+}(u_s),\sigma _\delta ^{-}(u_s)\in W^{1,\varphi (\cdot )}_0(\Omega )\cap L^{\infty }(\Omega )$
, then $h_\delta (u_s)\phi,\sigma _\delta ^{+}(u_s),\sigma _\delta ^{-}(u_s)\in W^{1,\varphi (\cdot )}_0(\Omega )\cap L^{\infty }(\Omega )$![]() are admissible test functions in (1.6). By testing (4.1) by $h_\delta (u_s)\phi$
are admissible test functions in (1.6). By testing (4.1) by $h_\delta (u_s)\phi$![]() we get
we get

where

Observe that
Indeed,
To estimate $\|\nu _\delta ^{s,+}\|_{L^{1}(\Omega )}$![]() and $\|\nu _\delta ^{s,-}\|_{L^{1}(\Omega )}$
and $\|\nu _\delta ^{s,-}\|_{L^{1}(\Omega )}$![]() , we test (4.1) against $\sigma _\delta ^{+}(u_s)$
, we test (4.1) against $\sigma _\delta ^{+}(u_s)$![]() (respectively $\sigma _\delta ^{-}(u_s)$
(respectively $\sigma _\delta ^{-}(u_s)$![]() ) and obtain
) and obtain


In the end we have that
Due to remark 2.5 and ($\mathcal {A}$![]() 2) we get uniform integrability of $\{\mathcal {A}(x,\nabla (T_k (u_s)))\}_k$
2) we get uniform integrability of $\{\mathcal {A}(x,\nabla (T_k (u_s)))\}_k$![]() , so Lebesgue's monotone convergence theorem justifies we can let $\delta \to 0$
, so Lebesgue's monotone convergence theorem justifies we can let $\delta \to 0$![]() getting
getting
Therefore ${{\mathfrak {A}_{\varphi (\cdot )}}}(T_ku_s)\in {{\mathcal {M}_b}}(\Omega )$![]() and $\|{{\mathfrak {A}_{\varphi (\cdot )}}}(T_ku_s) \|_{{{\mathcal {M}_b}}(\Omega )}\leq 6\|\mu \|_{{{\mathcal {M}_b}}(\Omega )}$
and $\|{{\mathfrak {A}_{\varphi (\cdot )}}}(T_ku_s) \|_{{{\mathcal {M}_b}}(\Omega )}\leq 6\|\mu \|_{{{\mathcal {M}_b}}(\Omega )}$![]() , where the bound is uniform with respect to $s$
, where the bound is uniform with respect to $s$![]() and $k$
and $k$![]() . Consequently, the use of proposition 5.1 enables to infer that also that ${{\mathfrak {A}_{\varphi (\cdot )}}}(T_ku)\in {{\mathcal {M}_b}}(\Omega )$
. Consequently, the use of proposition 5.1 enables to infer that also that ${{\mathfrak {A}_{\varphi (\cdot )}}}(T_ku)\in {{\mathcal {M}_b}}(\Omega )$![]() , $\|{{\mathfrak {A}_{\varphi (\cdot )}}}(T_ku) \|_{{{\mathcal {M}_b}}(\Omega )}\leq 6\|\mu \|_{{{\mathcal {M}_b}}(\Omega )}$
, $\|{{\mathfrak {A}_{\varphi (\cdot )}}}(T_ku) \|_{{{\mathcal {M}_b}}(\Omega )}\leq 6\|\mu \|_{{{\mathcal {M}_b}}(\Omega )}$![]() , and – finally – (6.2). By remark 2.4 we can extend the family of admissible test functions to get (6.1) and conclusion that ${{\mathfrak {A}_{\varphi (\cdot )}}}(T_ku)\in {{\mathcal {M}_b}}(\Omega )\cap (W^{1,\varphi (\cdot )}_0(\Omega ))'$
, and – finally – (6.2). By remark 2.4 we can extend the family of admissible test functions to get (6.1) and conclusion that ${{\mathfrak {A}_{\varphi (\cdot )}}}(T_ku)\in {{\mathcal {M}_b}}(\Omega )\cap (W^{1,\varphi (\cdot )}_0(\Omega ))'$![]() .
.
Step 2. Existence of a diffuse measure $\vartheta \in {{\mathcal {M}^{\varphi (\cdot )}_b}}(\Omega )$![]() , such that
, such that
Lemma 2.10 ensures that $\phi \in W^{1,\varphi (\cdot )}_0(\Omega )\cap L^{\infty }(\Omega )$![]() belongs to $L^{1}(\Omega,\vartheta )$
belongs to $L^{1}(\Omega,\vartheta )$![]() with any $\vartheta \in {{\mathcal {M}^{\varphi (\cdot )}_b}}(\Omega )$
with any $\vartheta \in {{\mathcal {M}^{\varphi (\cdot )}_b}}(\Omega )$![]() .
.
Note that $\lambda _{l} {\mathsf {L}} \{|u|< k\}=\lambda _k {\mathsf {L}} \{|u|< k\}$![]() for every ${l} \geq k>0$
for every ${l} \geq k>0$![]() . Since the set $\{|u|< k\}$
. Since the set $\{|u|< k\}$![]() is ${{{\rm C}_{\varphi (\cdot )}}}$
is ${{{\rm C}_{\varphi (\cdot )}}}$![]() -quasi-open, lemmas 2.8 and 2.9 ensure that there exists an increasing sequence $\{w_j\}$
-quasi-open, lemmas 2.8 and 2.9 ensure that there exists an increasing sequence $\{w_j\}$![]() of nonnegative functions in $W^{1,\varphi (\cdot )}_0(\Omega )$
of nonnegative functions in $W^{1,\varphi (\cdot )}_0(\Omega )$![]() which converges to $\mathbb {1}_{\{|u|< k\}}$
which converges to $\mathbb {1}_{\{|u|< k\}}$![]() ${{{\rm C}_{\varphi (\cdot )}}}$
${{{\rm C}_{\varphi (\cdot )}}}$![]() -quasi-everywhere in $\Omega$
-quasi-everywhere in $\Omega$![]() . Then $w_j=0$
. Then $w_j=0$![]() a.e. in $\{|u|\geq k\}$
a.e. in $\{|u|\geq k\}$![]() . If $\psi \in C_0^{\infty }$
. If $\psi \in C_0^{\infty }$![]() , then $\phi =w_j\psi \in W^{1,\varphi (\cdot )}_0(\Omega )\cap L^{\infty }(\Omega )$
, then $\phi =w_j\psi \in W^{1,\varphi (\cdot )}_0(\Omega )\cap L^{\infty }(\Omega )$![]() is an admissible test function in (6.1), so for every ${l} \geq k$
is an admissible test function in (6.1), so for every ${l} \geq k$![]() we get
we get

Passing to the limit with $j\to \infty$![]() we get
we get
so of course $\lambda _{l} {\mathsf {L}} \{|u|< k\}=\lambda _k {\mathsf {L}} \{|u|< k\}$![]() . Consequently, there exists a unique (up to sets of $W^{1,\varphi (\cdot )}$
. Consequently, there exists a unique (up to sets of $W^{1,\varphi (\cdot )}$![]() -capacity zero) Borel measure $\vartheta$
-capacity zero) Borel measure $\vartheta$![]() , such that $\vartheta {\mathsf {L}} \{|u|=+\infty \}=0$
, such that $\vartheta {\mathsf {L}} \{|u|=+\infty \}=0$![]() and $\vartheta {\mathsf {L}} \{|u|< k\}=\lambda _{l} {\mathsf {L}} \{|u|< k\}$
and $\vartheta {\mathsf {L}} \{|u|< k\}=\lambda _{l} {\mathsf {L}} \{|u|< k\}$![]() for every $k>0$
for every $k>0$![]() and every ${l} \geq k$
and every ${l} \geq k$![]() . As $\lambda _k$
. As $\lambda _k$![]() vanishes on every set of zero capacity ${{{\rm C}_{\varphi (\cdot )}}}$
vanishes on every set of zero capacity ${{{\rm C}_{\varphi (\cdot )}}}$![]() , so does $\vartheta$
, so does $\vartheta$![]() . By (6.2) the measures $|\lambda _k|$
. By (6.2) the measures $|\lambda _k|$![]() are uniformly bounded with respect to $k$
are uniformly bounded with respect to $k$![]() , so $\{|\vartheta |(\{|u|< k\})\}_k$
, so $\{|\vartheta |(\{|u|< k\})\}_k$![]() is bounded. In turn, $|\vartheta |(\Omega )<\infty$
is bounded. In turn, $|\vartheta |(\Omega )<\infty$![]() and – finally – we infer that $\vartheta \in {{\mathcal {M}^{\varphi (\cdot )}_b}}(\Omega )$
and – finally – we infer that $\vartheta \in {{\mathcal {M}^{\varphi (\cdot )}_b}}(\Omega )$![]() .
.
Step 3. ${{\mathfrak {A}_{\varphi (\cdot )}}}(T_ku) {\mathsf {L}} \{|u|>k\}=0$![]() .
.
Lemma 2.7 gives that $u$![]() is ${{{\rm C}_{\varphi (\cdot )}}}$
is ${{{\rm C}_{\varphi (\cdot )}}}$![]() -quasi-continuous, thus the set $\{|u|>k\}$
-quasi-continuous, thus the set $\{|u|>k\}$![]() is ${{{\rm C}_{\varphi (\cdot )}}}$
is ${{{\rm C}_{\varphi (\cdot )}}}$![]() -quasi-open. Fix arbitrary open $V\subset \Omega$
-quasi-open. Fix arbitrary open $V\subset \Omega$![]() . By lemma 2.9, there exists an increasing sequence $\{\widehat w_j\}$
. By lemma 2.9, there exists an increasing sequence $\{\widehat w_j\}$![]() of nonnegative functions in $W^{1,\varphi (\cdot )}_0(\Omega )$
of nonnegative functions in $W^{1,\varphi (\cdot )}_0(\Omega )$![]() which converges to $\mathbb {1}_{V\cap \{|u|< k\}}$
which converges to $\mathbb {1}_{V\cap \{|u|< k\}}$![]() ${{{\rm C}_{\varphi (\cdot )}}}$
${{{\rm C}_{\varphi (\cdot )}}}$![]() -quasi-everywhere in $\Omega$
-quasi-everywhere in $\Omega$![]() . Then $\widehat w_j=0$
. Then $\widehat w_j=0$![]() a.e. in $\{|u|\leq k\}$
a.e. in $\{|u|\leq k\}$![]() and we can test (6.1) against $w_j \in W^{1,\varphi (\cdot )}_0(\Omega )\cap L^{\infty }(\Omega )$
and we can test (6.1) against $w_j \in W^{1,\varphi (\cdot )}_0(\Omega )\cap L^{\infty }(\Omega )$![]() . We obtain
. We obtain
Letting $j\to \infty$![]() we get that $(\lambda _k {\mathsf {L}} \{|u|>k\})(V)=0$
we get that $(\lambda _k {\mathsf {L}} \{|u|>k\})(V)=0$![]() . Since $V$
. Since $V$![]() was arbitrary open set, we have what was claimed.
was arbitrary open set, we have what was claimed.
Step 4. Limits. Since we have (6.7) and (6.8), we get (6.3) and (6.4) for any $\phi \in C_0(\Omega )$![]() , with some nonnegative $\nu _k^{+},\nu _k^{-}\in {{\mathcal {M}_b}}(\Omega )$
, with some nonnegative $\nu _k^{+},\nu _k^{-}\in {{\mathcal {M}_b}}(\Omega )$![]() . They have the form given in the claim, because ${{\mathfrak {A}_{\varphi (\cdot )}}}(T_ku)\in {{\mathcal {M}_b}}(\Omega )\cap (W^{1,\varphi (\cdot )}_0(\Omega ))'$
. They have the form given in the claim, because ${{\mathfrak {A}_{\varphi (\cdot )}}}(T_ku)\in {{\mathcal {M}_b}}(\Omega )\cap (W^{1,\varphi (\cdot )}_0(\Omega ))'$![]() has properties proven in steps 3 and 4.
has properties proven in steps 3 and 4.
Proposition 6.2 (Existence of renormalized solutions)
Let $\Omega$![]() be bounded open domain in ${{\mathbb {R}^{n}}},$
be bounded open domain in ${{\mathbb {R}^{n}}},$![]() $\mathcal {A}:\Omega \times {{\mathbb {R}^{n}}}\to {{\mathbb {R}^{n}}}$
$\mathcal {A}:\Omega \times {{\mathbb {R}^{n}}}\to {{\mathbb {R}^{n}}}$![]() satisfy $(\mathcal {A} 1)$
satisfy $(\mathcal {A} 1)$![]() –$(\mathcal {A} 4),$
–$(\mathcal {A} 4),$![]() $\varphi \in \Phi _c(\Omega )$
$\varphi \in \Phi _c(\Omega )$![]() satisfy (aInc)$_p,$
satisfy (aInc)$_p,$![]() (aDec)$_q,$
(aDec)$_q,$![]() (A0) and (A1), and $\mu \in {{\mathcal {M}_b}}(\Omega )$
(A0) and (A1), and $\mu \in {{\mathcal {M}_b}}(\Omega )$![]() . Then there exists at least one renormalized solution to (1.1) (definition 1.7).
. Then there exists at least one renormalized solution to (1.1) (definition 1.7).
Proof. By proposition 5.1 there exists an approximable solution $u\in \mathcal {T}^{1,\varphi (\cdot )}_0(\Omega )$![]() to (1.1). We shall show that actually it is also a renormalized solution. Due to proposition 6.1, measure $\mu$
to (1.1). We shall show that actually it is also a renormalized solution. Due to proposition 6.1, measure $\mu$![]() can be seen as the weak-$\ast$
can be seen as the weak-$\ast$![]() limit of $\{\lambda _k\}$
limit of $\{\lambda _k\}$![]() , which are expressed as
, which are expressed as
with $\vartheta \in {{\mathcal {M}^{\varphi (\cdot )}_b}}(\Omega )$![]() , $\nu _k^{+},\nu _k^{-}\in ( {{\mathcal {M}_b}}(\Omega )\setminus {{\mathcal {M}^{\varphi (\cdot )}_b}}(\Omega ))\cup \{0\}$
, $\nu _k^{+},\nu _k^{-}\in ( {{\mathcal {M}_b}}(\Omega )\setminus {{\mathcal {M}^{\varphi (\cdot )}_b}}(\Omega ))\cup \{0\}$![]() being such that $\nu _k^{+}=\nu _k^{+} {\mathsf {L}} \{u=k\}$
being such that $\nu _k^{+}=\nu _k^{+} {\mathsf {L}} \{u=k\}$![]() and $\nu _k^{-}=\nu _k^{-} {\mathsf {L}} \{u=-k\}$
and $\nu _k^{-}=\nu _k^{-} {\mathsf {L}} \{u=-k\}$![]() . Given $h\in W^{1,\infty }(\mathbb {{R}})$
. Given $h\in W^{1,\infty }(\mathbb {{R}})$![]() having $h'$
having $h'$![]() with compact support, $\phi \in C_0^{\infty }(\Omega )$
with compact support, $\phi \in C_0^{\infty }(\Omega )$![]() , and arbitrary $k>0$
, and arbitrary $k>0$![]() , function $h(T_{k+1}(u))\phi \in W^{1,\varphi (\cdot )}_0(\Omega )\cap L^{\infty }(\Omega )$
, function $h(T_{k+1}(u))\phi \in W^{1,\varphi (\cdot )}_0(\Omega )\cap L^{\infty }(\Omega )$![]() , so we can test equation (6.1) to get
, so we can test equation (6.1) to get
We need to justify letting $k\to \infty$![]() . We start with the left-hand side of (6.9) by having a look on
. We start with the left-hand side of (6.9) by having a look on
If we prove that both terms on the right-hand side in the last display are integrable, Lebesgue's monotone convergence theorem will give the desired conclusion. Recall that $u\in \mathcal {T}^{1,\varphi (\cdot )}_0(\Omega )$![]() and satisfy (4.2), so by proposition 4.2 and lemma 2.10, $\mathcal {A}(\cdot,\nabla u)\in (L^{1}(\Omega ))^{n}$
and satisfy (4.2), so by proposition 4.2 and lemma 2.10, $\mathcal {A}(\cdot,\nabla u)\in (L^{1}(\Omega ))^{n}$![]() . Moreover, $h'$
. Moreover, $h'$![]() is bounded and ${\rm supp}\,h'\subset [-M,M]$
is bounded and ${\rm supp}\,h'\subset [-M,M]$![]() for some $M>0$
for some $M>0$![]() , so
, so
is integrable by (4.2). For the second term we see that
so it suffices to use the same arguments as before. Therefore, (6.9) becomes the left-hand side of (1.8) in the limit. By remark 1.3 the following decomposition

is unique up to sets of $W^{1,\varphi (\cdot )}$![]() -capacity zero. By (6.2) it holds that $\vartheta {\mathsf {L}} \{|u|< k\}\rightharpoonup {{\mathfrak {A}_{\varphi (\cdot )}}}(u)$
-capacity zero. By (6.2) it holds that $\vartheta {\mathsf {L}} \{|u|< k\}\rightharpoonup {{\mathfrak {A}_{\varphi (\cdot )}}}(u)$![]() . Note that it is also (6.2) to justify testing against $W^{1,\varphi (\cdot )}_0(\Omega )\cap L^{\infty }(\Omega )$
. Note that it is also (6.2) to justify testing against $W^{1,\varphi (\cdot )}_0(\Omega )\cap L^{\infty }(\Omega )$![]() -function. To conclude we use Lebesgue's dominated convergence theorem in (6.10). To motivate the convergence of the first term we note that we can split the first term to positive and negative part, whose majorants are integrable due to lemma 2.10. For the remaining two terms it suffices to recall that $h$
-function. To conclude we use Lebesgue's dominated convergence theorem in (6.10). To motivate the convergence of the first term we note that we can split the first term to positive and negative part, whose majorants are integrable due to lemma 2.10. For the remaining two terms it suffices to recall that $h$![]() is bounded and constant in infinities. By (6.3) one has $\nu _k^{+}\rightharpoonup {{\mu ^{+}_{\rm sing}}}$
is bounded and constant in infinities. By (6.3) one has $\nu _k^{+}\rightharpoonup {{\mu ^{+}_{\rm sing}}}$![]() with ${\rm supp}\,{{\mu ^{+}_{\rm sing}}}\subset \cap _{k>0}\{u>k\}$
with ${\rm supp}\,{{\mu ^{+}_{\rm sing}}}\subset \cap _{k>0}\{u>k\}$![]() , and by (6.4) also $\nu _k^{-}\rightharpoonup {{\mu ^{-}_{\rm sing}}}$
, and by (6.4) also $\nu _k^{-}\rightharpoonup {{\mu ^{-}_{\rm sing}}}$![]() with ${\rm supp}\,{{\mu ^{-}_{\rm sing}}}\subset \cap _{k>0}\{u<-k\}$
with ${\rm supp}\,{{\mu ^{-}_{\rm sing}}}\subset \cap _{k>0}\{u<-k\}$![]() .
.
7. Uniqueness in problems with diffuse measure data
The previous results worked for a general measure data problems. Here, we restrict to a class of diffuse measure data to provide uniqueness.
Proposition 7.1 (Uniqueness of approximable solutions)
Let all assumptions of proposition 5.1 be satisfied. Assume that $f,G$![]() are obtained as limits of approximate sequences $\{f^{i}_s\}$
are obtained as limits of approximate sequences $\{f^{i}_s\}$![]() in $C^{\infty }(\Omega ),$
in $C^{\infty }(\Omega ),$![]() $i=1,2,$
$i=1,2,$![]() satisfying
satisfying
and $\{ {G^{i}_s}\}$![]() in $C^{\infty }(\Omega )$
in $C^{\infty }(\Omega )$![]() , $i=1,2$
, $i=1,2$![]() , such that
, such that
on measurable $E\subset \Omega$![]() . If $v^{i}$
. If $v^{i}$![]() is an approximable solution defined as an a.e. limit of weak solutions $v^{i}_s$
is an approximable solution defined as an a.e. limit of weak solutions $v^{i}_s$![]() to the approximate problems
to the approximate problems

then $v^{1}= v^{2}$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() .
.
Proof. We note first that the problem is well posed as $\mu ^{i,s}=f^{i}_s-{{\rm div\,}}G^{i}_s\rightharpoonup \mu _{\varphi (\cdot )}$![]() weakly-$*$
weakly-$*$![]() in the space of measures, $i=1,2$
in the space of measures, $i=1,2$![]() . We fix arbitrary $t,l>0$
. We fix arbitrary $t,l>0$![]() , use $\phi =T_t(T_l(v^{1}_s)-T_l(v^{2}_s))\in W_0^{1,\varphi (\cdot )}(\Omega )\cap L^{\infty }(\Omega )$
, use $\phi =T_t(T_l(v^{1}_s)-T_l(v^{2}_s))\in W_0^{1,\varphi (\cdot )}(\Omega )\cap L^{\infty }(\Omega )$![]() as a test function in both (1.6) and subtract the equations to obtain for every $s>0$
as a test function in both (1.6) and subtract the equations to obtain for every $s>0$![]()

The right-hand side above tends to $0$![]() . Indeed, the convergence of $R_s^{1}$
. Indeed, the convergence of $R_s^{1}$![]() holds because $|T_t(T_lv^{1}_s-T_lv^{2}_s)|\leq t$
holds because $|T_t(T_lv^{1}_s-T_lv^{2}_s)|\leq t$![]() and for $s\to 0$
and for $s\to 0$![]() we have $f^{1}_s-f^{2}_s\to 0$
we have $f^{1}_s-f^{2}_s\to 0$![]() in $L^{1}(\Omega )$
in $L^{1}(\Omega )$![]() . As for $R_s^{2}$
. As for $R_s^{2}$![]() it suffices to note that
it suffices to note that

where we used that weak convergence of the $\{\nabla T_l(v^{j}_s)\}_s$![]() $(j=1,2)$
$(j=1,2)$![]() in $(L^{\varphi (\cdot )}(\Omega ))^{n}$
in $(L^{\varphi (\cdot )}(\Omega ))^{n}$![]() , which in particular implies uniform boundedness of $\{\|\nabla T_l(v^{j}_s)\|_{L^{\varphi (\cdot )}(\Omega )}\}_s$
, which in particular implies uniform boundedness of $\{\|\nabla T_l(v^{j}_s)\|_{L^{\varphi (\cdot )}(\Omega )}\}_s$![]() $(j=1,2)$
$(j=1,2)$![]() and recalled that the strong convergence of $(G^{1}_s-G^{2}_s)\to 0$
and recalled that the strong convergence of $(G^{1}_s-G^{2}_s)\to 0$![]() in $(L^{\widetilde \varphi (\cdot )}(\Omega ))^{n}$
in $(L^{\widetilde \varphi (\cdot )}(\Omega ))^{n}$![]() . The left-hand side of (7.4) is nonnegative due to the monotonicity of $\mathcal {A}$
. The left-hand side of (7.4) is nonnegative due to the monotonicity of $\mathcal {A}$![]() . Moreover, as $R_s^{1}+R_s^{2}\to 0$
. Moreover, as $R_s^{1}+R_s^{2}\to 0$![]() , we get
, we get

Consequently, $\nabla v^{1} =\nabla v^{2}$![]() a.e. in $\{|T_l( v^{1}) -T_l( v^{2}) |\leq t\}$
a.e. in $\{|T_l( v^{1}) -T_l( v^{2}) |\leq t\}$![]() for every $t,l>0$
for every $t,l>0$![]() , and so
, and so
Given the boundary value also $v^{1}= v^{2}$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() .
.
8. Main proof
Proof of theorem 1.8. Existence of approximable solutions is provided in proposition 5.1. Proposition 6.2 yields that an approximable solution is a renormalized solutions. Proposition 6.1 actually localizes the support of singular measures. Approximable solutions can be achieved from renormalized ones by a choice of $h=T_k$![]() .
.
Acknowledgments
I. Chlebicka is supported by NCN grant no. 2016/23/D/ST1/01072.




