Estimating influenza-related excess mortality and reproduction numbers for seasonal influenza in Norway, 1975–2004

Summary

Influenza can be a serious, sometimes deadly, disease, especially for people in high-risk groups such as the elderly and patients with underlying, severe disease. In this paper we estimated the influenza-related excess mortality in Norway for 1975–2004, comparing it with dominant virus types and estimates of the reproduction number. Analysis was done using Poisson regression, explaining the weekly all-cause mortality by rates of reported influenza-like illness, together with markers for seasonal and year-to-year variation. The estimated excess mortality was the difference between the observed and predicted mortality, removing the influenza contribution from the prediction. We estimated the overall influenza-related excess mortality as 910 deaths per season, or 2·08% of the overall deaths. Age-grouped analyses indicated that the major part of the excess mortality occurred in the ⩾65 years age group, but that there was also a significant contribution to mortality in the 0–4 years age group. Estimates of the reproduction number R, ranged from about 1 to 1·69.

INTRODUCTION

Influenza is an infection of the respiratory tract caused by the influenza viruses; RNA viruses belonging to the family Orthomyxoviridae [1]. The disease is characterized by acute-onset fever, headache, myalgia, prostration, coryza, and a dry cough, and is usually self-limiting with recovery in 2–7 days [2, 3]. Primary viral, or secondary bacterial pneumonias are common complications of influenza. Most influenza patients recover without sequelae. Mortality is highest in the elderly and in patient groups with certain underlying, severe diseases [1–3]. For these risk groups annual influenza immunization is recommended in many countries.

In the northern hemisphere the virus usually causes annual outbreaks of varying length and severity during the winter seasons. When a new virus variant emerges to which no one is immune, larger epidemics – know as pandemics – may ensue. Last century three worldwide pandemics occurred; in 1918–1919 (Spanish flu), 1957–1958 (Asian flu), and 1968–1970 (Hong Kong flu) [2, 4].

Most developed countries have some sort of surveillance system for influenza measuring the number of patients seeking healthcare, virologically confirmed cases or some other marker for influenza-like illness (ILI) such as absence from school or work. No country has routine surveillance of influenza-related deaths.

It is difficult to discern if the cause of death is from influenza in patients with several other serious underlying illnesses. Influenza is rarely recorded as the cause of death on death certificates in Norway. Internationally many studies have been performed to estimate the mortality due to influenza [5–15], in Norway this has only been done for influenza pandemics [16].

The aim of this work was to estimate the excess mortality due to influenza in Norway by studying the relationship between the number of reported deaths and clinical influenza activity; and to compare these results with information on predominant influenza viruses and estimates of the reproduction number, R, for the different seasons.

METHODS

Data material

Information on clinical ILI was derived from The Norwegian Notification System for Infectious Diseases (MSIS). For the period 1975–1998 all general practices in primary healthcare and outpatient emergency clinics were obliged to report ILI along with other clinical diagnoses on a weekly basis to the Norwegian Institute of Public Health (NIPH). The average reporting coverage was about 60% of around 2000 practices. Rates of ILI were calculated as a proportion of the total population, without adjusting for the reporting coverage.

From autumn 1998 NIPH designated 201 sentinel reporting units based on geographical location, population size and previous reporting frequencies from the 2000 practices mentioned above. These formed about 10% of the practices but about 25% of the reported volume of ILI. The sentinels reported weekly, from week 40 in autumn to week 20 in spring, the number of ILI [using the case definition of ‘R80 Influenza’ from the International Classification of Primary Care (ICPC)]. The number of consultations and, from 2004–2005 when the information was available, the number of patients on the patient list of general practitioners, were used as denominators.

The weekly recording period was from Friday to Thursday, after which the report card was completed and sent to NIPH by post and entered into a database in EpiInfo 6·04d (CDC, USA). Quality checks for inconsistencies and improbable figures were performed.

Data on all-cause mortality per week by age group were derived from the Cause of Death Register at NIPH. The week number was obtained by defining week 1 as starting on 1 January each year, week 2 on 8 January and so on. Hence there may be a small discrepancy between the week numbering of ILI and deaths.

Information about dominant virus types and variants for each season was obtained from the virological influenza surveillance records in the Department of Virology, NIPH.

Estimating excess mortality

The number of overall deaths per week was modelled using a Poisson regression model, where the mortality rate was explained by the reported number of ILI cases, the week number and the season. For the ILI covariate, we considered different lagging, before choosing the type of lag which gave the best model fit (i.e. explained the most variability). The week number covariate, a factor numbered between 1 and 52, modelled the seasonality in the data, while the season covariate was a substitute for calendar year. Season was used instead of calendar year because a normal influenza season goes from autumn of one year to spring of the next.

To account for change in population size, the Norwegian population size at the beginning of each calendar year was used as an offset. The model is written as:

where _j,k is the predicted number of overall deaths in week number j and season k, j∊{1, 2, …, 52}, and k∊{spring 1975, 1975/1976, 1976/1977, …, 2003/2004, autumn 2004}. Population_j,k is the total population size of Norway on 1 January for the year containing week j in season k, β₀ is the intercept coefficient, β_ILI the coefficient to the ILI contribution (ILI_j,k being the reported number of ILI cases in week j in season k), the coefficient for the factor variable week at week j, and finally , the coefficient associated with season k. To account for any extra Poisson variation, a dispersion parameter was added, making the model a quasi-Poisson model. The analysis used the glm package in the open source statistical software R version 2.7.0 [17].

The model was fitted separately for the two datasets, one going from 1975 to 1998, the other from 1998 to 2004. The only weeks included in the analysis were the observed weeks and weeks where the ILI levels with the chosen lag were available. For the data from 1998 to 2004, no ILI figures were collected off-season, i.e. between week 20 and week 40.

The excess mortality was estimated by first considering the overall mortality once the influenza contribution had been removed. Rather than setting the influenza contribution to zero in this estimation, leaving the other parameters and covariates as they were, the influenza contribution was set to some threshold value accounting for the ever-present baseline of ILI cases, also observed off-season. As previously mentioned, off-season ILI numbers were not collected in the new reporting system, and one would expect these weeks (if measured) to represent the lowest ILI counts. We therefore removed the corresponding number of high ILI values, and then most of the outbreaks, to find this threshold. In other words, the threshold value was set to the mean of the remaining ILI values, excluding the 20 lowest and 20 highest values for each season. We expected this to give a conservative estimate of the off-season ILI level. The estimated excess mortality related to ILI was then calculated as the difference between the observed mortality and the predicted mortality leaving out the influenza contribution above this threshold.

Estimating the reproduction number

The reproduction number R, also known as the effective reproduction number, denotes the number of secondary infections caused on average by one infected individual being introduced into a population. R relates to R ₀, the reproduction number for an individual introduced into a population of only susceptibles. R ₀ serves as a threshold value for epidemic growth, where R ₀=1 is the threshold deciding whether an epidemic is possible or not [18, 19]. When a fraction p of a population is protected from infection, the relationship between R and R ₀ is given by R=(1−p)R ₀ [20, 21].

The reproduction number can be estimated through the initial growth rate of an epidemic r [18, 19, 21], which describes the growth of the epidemic in its initial phase, rather than the individual reproduction as with R.

When the initial growth of an epidemic is assumed to be exponential, r can be estimated by fitting a straight line to the natural logarithm of the number of infected individuals at each time point in the initial phase. The slope of this line is then the estimated initial growth rate r.

To determine the initial phase of an epidemic is a challenge, but one method is to consider the goodness of fit [20, 22]. We determined the initial phase by finding the starting point and the endpoint separately. The starting point was found by looking for structural change when modelling the natural logarithm of the number of infected individuals with linear regression, using data from the start of each season until the time of the influenza peak. If there was an influenza outbreak during this period, a breakpoint on the log scale of the ILI curve should exist. The breakpoint was found using the methods described in Zeileis et al. [23] (implemented in the R package strucchange). These methods test the null hypothesis of no change in regression parameters before and after each possible time point, and then choose the time point giving the lowest P value as the breakpoint, if this is significant. The endpoint, restricted to be at least three points later than the start point and no later than the peak, was chosen by the best goodness of fit in terms of R ².

Using the estimate of r we were able, by assuming a simple multistage model for the disease spread, to derive an expression for the reproduction number R [21, 24, 25]. Assuming a SEIR model (susceptible, exposed, infectious, recovered) for the spread of influenza, we obtained

where k ⁻¹ is the incubation time and γ⁻¹ the infectious period [24]. When calculating the R estimates for seasonal influenza we assumed a 2-day incubation time and a 4-day infectious period [20, 26]. A 95% confidence interval (CI) for the estimate of R was found using the lower and upper confidence limits for the estimate of r (derived from the linear regression model), and the formula for R above.

RESULTS

In the Poisson regression analysis, applying a lag of 1 week to the ILI variable gave the best model fit, when also adjusting for week and season variables. Figure 1 shows an overview of the data on ILI and all-cause mortality as used in the analysis.

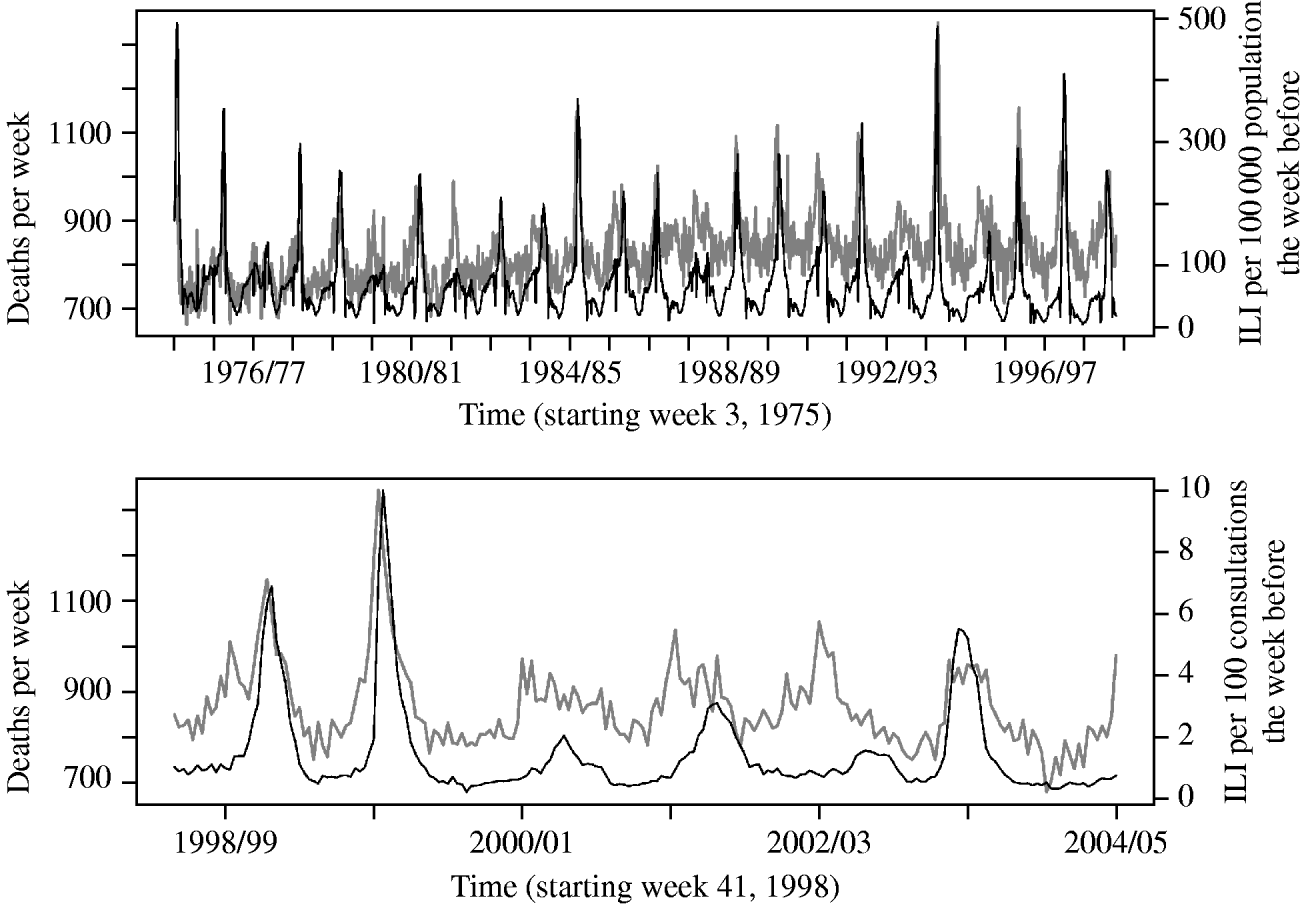
Fig. 1. Overall deaths per week (grey line) and reported number of influenza-like illness (ILI) cases the week before (black line), from the old (upper panel) and new (lower panel) reporting system.

The estimated excess mortality for season 1975/1976 to season 2003/2004 varied from 217 deaths (5·31/100 000 population or 0·53% of all deaths) in the 1976/1977 season, to 1802 deaths (41·45/100 000 population or 3·89% of all deaths) in the 1993/1994 season: this gave a mean estimated excess mortality of 910 deaths per season (21·25/100 000 population or 2·08% of all deaths), ignoring the two incomplete seasons of spring 1975 and autumn 2004.

Figure 2 shows the observed, overall deaths per week, the overall deaths per week modelled by Poisson regression, and the predicted mortality leaving the influenza contribution fixed at the defined threshold value, under both the old and new reporting systems. The threshold value was found to be 45·91/100 000 population in the data from the old reporting system, and 0·54/100 consultations for the data from the new reporting system. The agreement between the observed mortality and the predicted mortality suggests a good model fit. The estimated dispersion parameters in the analysis of the two datasets were 1·85 and 2·23, respectively. In Figure 2 the estimated excess mortality is the area between the line of the predicted mortality, where the influenza contribution is limited to the threshold value, and the line of the observed mortality (this is most visible in the lower panel).

Fig. 2. Observed overall deaths per week (grey line), predicted overall deaths (black line), and predicted mortality where the influenza-like illness (ILI) contribution is limited to a threshold value (dark grey dotted line), for the data from the old (upper panel) and new (lower panel) reporting system. The threshold value accounts for the ever-present baseline of ILI cases, also observed off-season.

The estimated excess mortality for each influenza season from 1975/1976 to 2003/2004 is listed in Table 1. This table also gives the total number of ILI cases/100 000 population for the old dataset, the mean number of ILI cases/100 consultations for the new dataset, estimates of R with 95% CIs and dominant virus type for each season. The R estimates range from close to 1, implying no outbreak, to 1·69 in the 1999/2000 season.

Table 1. Estimated excess mortality for each influenza season, together with numbers of reported ILI cases, estimated reproduction number R and dominant virus type

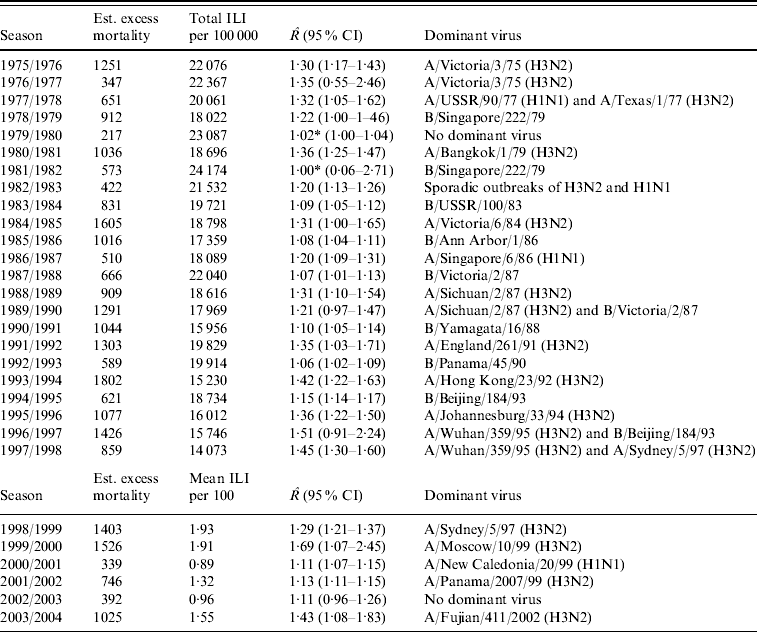
ILI, Influenza-like illness; CI, confidence interval.

* Estimated breakpoint not significant (no outbreak).

In Figure 3 we plotted the estimated excess mortality against estimates of R for each season, marked by groups of dominant virus type. It can be seen that influenza B seasons tended to have lower estimated excess mortality and R estimates than H3N2 seasons. For the other seasons, it can be seen that the two H1N1 seasons both had low estimates of excess mortality and R. Seasons with more than one dominant virus had varying estimates of excess mortality and R, while seasons with no dominant virus had low estimates. The mean estimated excess mortality in H3N2 seasons was 1169 deaths per season, compared to a mean estimated excess mortality of 781 deaths per season in B seasons. The mean estimated excess mortality in H1N1 seasons was 425 deaths per season, but there were only two seasons with H1N1 as the single dominant virus type. When testing the mean difference between estimated excess mortality in H3N2 and B seasons, using a standard two-sample t test, we found that the difference was significant at a 5% level (P value=0·01). When we did a similar test on the mean difference between estimated R in H3N2 and B seasons, again we found a significant difference (P value=0·00002).

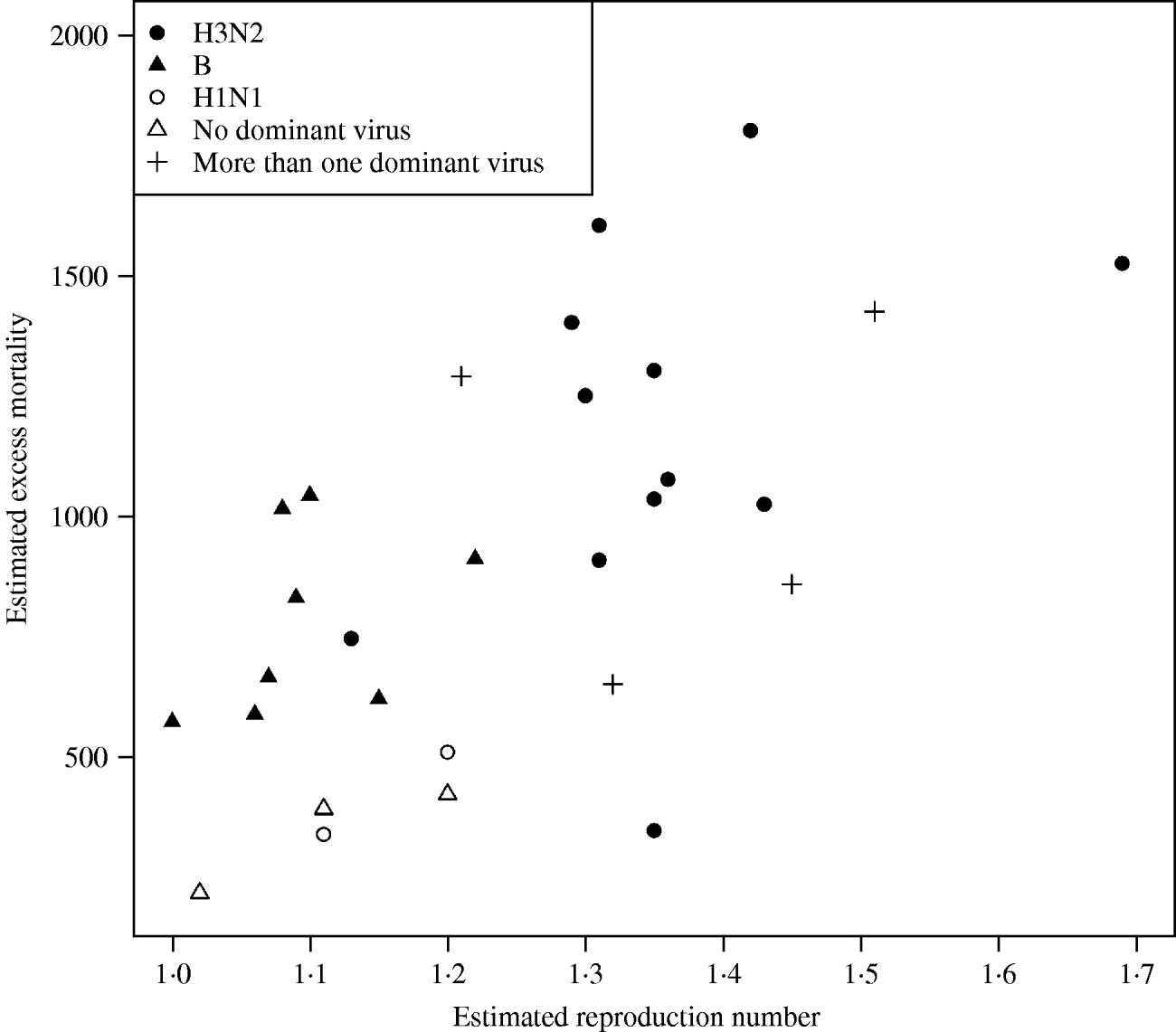
Fig. 3. Estimated excess mortality against R for each influenza season, marked by dominant virus type.

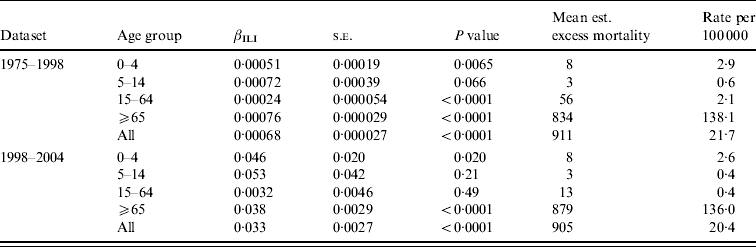
Table 2 shows estimates of β_ILI together with estimated excess mortality, for overall and age-grouped analyses. For the dataset going from 1975 to 1998 the level of ILI had a significant effect on the overall deaths in all ages except 5–14 years (using a 5% level of significance). It can also be seen that the highest (significant) effect is in the ⩾65 years age group, followed by the 0–4 and 15–64 years age groups. Most of the estimated excess mortality was found in the ⩾65 years age group. Considering the data going from 1998 to 2004 we saw the same patterns, but here the level of ILI had no significant effect on the overall mortality in either the 5–14 or 15–64 years age groups. The effect was higher in the 0–4 years group than in the ⩾65 years group, but almost all the excess mortality was in the oldest group. Note that the estimated β_ILI values for 1975–1998 and 1998–2004 cannot be compared to each other because of the different units for ILI level in the two periods.

Table 2. Regression results and estimated excess mortality for separate analyses on age groups, and for the overall analysis

DISCUSSION

Our model seems to give a good description of the observed mortality, capturing both the season-to-season change in the number of ILI cases, and the severity. This is also reflected when investigating estimates of the reproduction number R and dominant virus types for the different seasons. The H3N2 seasons had a significantly higher excess mortality and R estimates than the influenza B seasons. For the other strains, there were not many seasons in each group, but the trend was as expected. Seasons with H1N1 and no dominant virus had low impact in terms of excess mortality and R estimates, and the impact varied when there was more than one dominant virus.

ILI data divided into age groups were only available from the 2001 season and onwards, and have not been used in the analysis. Hiwever, age-grouped data for overall deaths were available for all years from 1975 to 2004. The analysis of these data showed that the effect of the influenza outbreaks on overall mortality was highest in the two lowest age groups, and in the ⩾65 years group. Most of the excess mortality was attributed to the ⩾65 years group.

Estimation of influenza-related excess mortality has been done in other countries using similar Poisson regression-based methods; for example on data from 1976 to 1999 in the USA [8], 1990–1999 in Canada [5], and 1996–1999 in Hong Kong [9]. The US study estimated that on average the number of influenza-related deaths formed 2·2% of all deaths, while in the Canadian study the corresponding estimate was 1·9%, compared to our estimate of 2·1%. In the Hong Kong study, the estimate of influenza-related excess mortality was 16·4 deaths/100 000 population, compared to our estimate of 21·3/100 000 in the Norwegian population. These findings are not dissimilar from European studies using different methods to estimate the excess mortality: a German study for 1985–2001 [10, 11] estimated the excess mortality as 16·1 and 17·4 deaths/100 000 population for two study periods, and a Czech study for 1982–2000 [15] estimated the excess mortality as 2·2% of all deaths. Our estimates for excess mortality in the ⩾65 years group of 140 and 158 deaths/100 000 are comparable with studies from Canada (108·8/100 000 population) [5], USA (132·5/100 000 population) [8], and Hong Kong (136·1/100 000 population) [9].

Most previous estimates of the reproduction number R have been made for pandemic influenza, but results from some studies are comparable to our estimates. Using a model based on the Asian 1957–1958 influenza A(H2N2) pandemic in the USA, R ₀ was estimated as 1·68 [26], while other studies estimated R for inter-pandemic years as 1·39 [27], or in the range between 1·2 and 1·8 [28]. These estimates correspond well to our estimates, which ranged from about 1 in seasons with no obvious influenza outbreak to a maximum of 1·69.

The Poisson regression-based models proved suitable, adjusting for available markfor influenza activity and seasonality in week-to-week data. In classic epidemic-threshold models, the excess mortality is defined as all deaths exceeding a seasonal baseline threshold, based on years with low influenza activity [5]. This baseline can be found for instance by cyclic regression [10, 12–14]. Although seemingly robust, these models do not utilize available influenza data as well as Poisson regression-based models [11]. The differences in the Poisson regression-based models are mostly due to the type of surveillance measurements available for influenza, the types of seasonal marker, and the resolution of the data. The Norwegian data differ from the other Poisson-regression based studies mentioned by using the rate of ILI consultations from general practitioners as the marker for influenza activity, instead of virological laboratory confirmations [8, 9] or influenza-certified deaths [5]. We found that the rate of ILI consultations, together with seasonal and year-to-year markers, modelled overall mortality satisfactorily.

In Poisson regression-based methods one can adjust for several variables in addition to different markers for influenza activity, e.g. other variables which influence mortality, and seasonal and year-to-year markers. Other possible explanatory variables include: dominant virus type, temperature, human respiratory syncytial virus (RSV) and other subcategories of overall death. Models with such additional explanatory variables and factor groups were explored.

Information about dominant virus types was better used as a supplement rather than including it in the model because viruses co-dominate and vary in magnitude between seasons. This leaves the year-to-year variability to be covered by the season variable. Temperature is often mentioned as an explanatory factor for overall death [29], but is unfeasible to use in Norway due to geographical and meteorological variability. Using the weekly average temperature in Oslo as a covariate gave a very small but significant impact; the reduction in over-dispersion was minimal and the results were broadly unchanged. For RSV infections, there are no consistent national data available, and RSV outbreaks rarely coincide with influenza outbreaks.

For our data a lag of 1 week between ILI activity and mortality gave the best model fit. A 1-week lag was also used in other similar analysis [5]. Using months instead of weeks to control for seasonality has been done in other studies [5], but in our case this weakened model fit.

Clinical surveillance data on ILI were collected from all general practices in primary care for 1975–1998 and from selected sentinels for the period 1998 onwards. Completeness of data may pose a problem for the first period for which we did not collect any denominator data. However, coverage has been estimated to be constant over the years with about 60% of the practices reporting every week. For the second period we did collect denominator data, and variability in completeness was not affected as much.

Clinically reported ILI, rather than laboratory confirmations, was chosen as a proxy for influenza activity. Laboratory diagnostics and their use have been developing over the study period and extensive data on laboratory confirmations in Norway are only available from 1999 onwards. These data show that the trends in the number of virus confirmations matched the ILI numbers well in seasons with obvious outbreaks, but in seasons with low influenza activity the fit is less good. In these seasons laboratory detections of influenza reflect not only influenza activity, but also laboratory testing activity due to outbreaks of other respiratory pathogens. As long as sampling in a population is representative, data on laboratory confirmations may serve well in some countries, but in Norway this information comes from a limited number of laboratories, and the testing practice and sensitivity varies widely from season to season and in the different laboratories. The ILI data are more robust for other factors, and the good agreement detected between ILI and mortality was not detected using laboratory data, as seen by a worse model fit when explaining mortality using laboratory data in the available period with a Poisson model. Although ILI consultation rates do not reflect the true rates of influenza in absolute numbers, they do reflect the epidemic curve. This is supported by the coincidence of peaks of ILI and excess mortality during seasons with large influenza outbreaks, as well as the agreement between peaks of ILI and the numbers of laboratory confirmations in such seasons, where data are available. The clinical definition of influenza has not changed in Norway over the years and is the same nationwide. Consequently regional and temporal biases are not expected. However, during each seasonal outbreak clinicians may be more inclined to use the R80 Influenza diagnosis when they know influenza virus is circulating, thereby enlarging the size of the peak, but the time period for the peak will not shift. Altered health-seeking behaviour over the years may affect the total number of ILI cases per season but would probably not change sufficiently quickly during a single season to alter the shape of the outbreak curve. Hence, we do not believe it would affect the relationship with mortality.

The ‘epidemiological week’ of the ILI surveillance was recorded from Friday to Thursday, 3 days earlier than the calendar week (in Norway: Monday–Sunday). As we tried different lag times between ILI and death, and found that 1 week gave the best fit, this should not influence the result.

The agreement of ILI and mortality in terms of peak and initial rise, and of ILI and laboratory data in seasons with obvious influenza outbreaks, suggests that ILI is also a suitable variable for estimating reproduction numbers. The Norwegian laboratory data are not sufficiently robust for such an estimation, and, where available, will tend towards overestimation (especially for seasons with low activity). However, the R estimates based on ILI data have some potential sources of bias. Unexpected decrease in ILI activity was found around Christmas and New Year in some seasons, probably due to lower registration in the holidays. These artefacts would be covered by the week-to-week markers when estimating excess mortality, but could cause some underestimation of R in seasons where the ILI peak is around New Year. There is a potential for overestimation due to clinicians being more inclined to use the influenza diagnosis during certain periods. Estimating R from the initial growth of the outbreak would not be as vulnerable for such bias as methods using the entire epidemic curve in the estimation. Asynchronous influenza epidemics across Norway would also be a source of bias, but surveillance data suggests that, for most seasons, epidemics are concurrent. At worst, epidemics may be displaced by 1–2 weeks for parts of the outbreak between the most distant regions. The assumptions of an incubation and infectious period also represent some uncertainty, while the uncertainty from the regression estimating the initial growth rate is quantified through 95% CIs for R. However, reproduction numbers are important quantities for measuring the impact of and comparing outbreaks, and they are central in modelling the impact of counter-measures. Few estimates for seasonal influenza are available in the literature, and the estimates from the Norwegian data serve as a useful addition. Our results fit well with existing estimates, which is an interesting finding in itself, and further proves that it is possible to estimate reproduction numbers using clinically reported ILI data.

In conclusion, the Poisson regression-based methods proved useful in explaining the number of overall deaths per week by reported ILI cases. Reproduction numbers R, estimated using reported ILI cases, ranged up to about 1·7, supporting results found by studies using different methods. Overall, influenza was estimated to contribute to more than 2% of all deaths in Norway.