1. Introduction
Melting of snow and ice at the surface of the Greenland ice sheet is an energy-balance problem. Snow or ice melt occurs when the snow or ice temperature reaches 0˚C, and is proportional to the amount of energy available for melt. However, the use of an energy-balance melt model for surface mass-balance predictions is limited in polar regions such as the Greenland ice sheet because the large set of data needed to calculate the surface energy balance must be accurate and available at a high horizontal and temporal resolution.
Observations on glaciers situated in the Alps, Scandinavia and on the Greenland ice sheet have revealed a strong correlation between melt rates and positive degree-days (Reference Finsterwalder and SchunkFinsterwalder and Schunk, 1887; Reference Braithwaite, Olesen. and OerlemansBraithwaite and Olesen, 1989; Reference Braithwaite and ZhangBraithwaite and Zhang, 2000). This correlation can be used to calculate ablation from only one parameter, i.e. the near-surface air temperature, with a positive degree-day melt model. Reference ReehReeh (1991) calculated the present climatological surface mass balance of the Greenland ice sheet with a positive degree-day melt model from parameterizations of the summer and mean annual air temperature assuming a cosine annual temperature evolution. Reference Huybrechts, Letréguilly and ReehHuybrechts and others (1991), Reference Letréguilly, Huybrechts and ReehLetréguilly and others (1991), Reference Fabre, Letréguilly, Ritz and MangeneyFabre and others (1995), Reference Calov and HutterCalov and Hutter (1996), Reference GreveGreve (1997) and Reference Ritz, Fabre and LetréguillyRitz and others (1997) have coupled a positive degree-day based melt model with a thermodynamic ice-sheet model to assess past, present and future evolution of the Greenland ice-sheet volume and its contribution to mean sea-level rise. Despite its simplicity, the positive degree-day surface mass-balance model is able to correctly represent the distribution of mass-balance zones and the altitude of the equilibrium line over the ice sheet. on the other hand, the positive degree-day melt model excludes the modelling of interactions and feedbacks between the atmosphere and the surface of the ice sheet. the positive degree-day melt model is computationally cheap and can be used in combination with the energy-balance method, for example, to complement run-off predictions from climatic-change scenarios.
Reference Van de WalVan de Wal (1996) performed simulations of the surface mass balance of the Greenland ice sheet with both a positive degree-day model and an energy-balance model. the number of long-term mass-balance measurements was insufficient to determine which of the approaches performed best.
First attempts to couple climate models with thermodynamic ice-sheet models have been made by Reference MarsiatMarsiat (1994), Reference De Wolde, Huybrechts, Oerlemans and van deWalDe Wolde and others (1997), Reference Calov and MarsiatCalov and Marsiat (1998), Reference Fabre, Ramstein, Ritz, Pinot and FournierFabre and others (1998) and Reference Huybrechts and Wolde.Huybrechts and de Wolde (1999). Depending on their approach (positive degree-day or energy-balance modelling), different climatologies were used to drive the models (e.g. surface air temperature, precipitation, cloudiness or vertical temperature lapse rates). to the authors’ knowledge, no long-term simulations have yet been performed with an atmosphere–ocean general circulation model (AOGCM) coupled with a three-dimensional thermodynamic ice-sheet model without the use of additional climatologies for the coupling of the two models.
Positive degree-day melt models are highly sensitive to their parameters. Themost sensitive parameters are the standard temperature deviation (see section 2.1) and the snow and ice degree-day factors (see section 2.2). In the literature, a wide range of values can be found for these parameters, which suggests a tuning range of the models. Reference BraithwaiteBraithwaite (1995) studied variations of the positive degree-day factors for two outlet glaciers in West Greenland by means of an energy-balance melt model over the period June–August 1979–86. the energy-balance melt model was driven by daily observations of air temperature, humidity, surface pressure, insolation and sunshine duration, as well as a prescribed albedo. Simulated values agreed with the observed ones, and sensitivity experiments to air temperature, surface albedo and wind speed showed important variations in the simulated snow and ice degree-day factors.
In this paper we explicitly model large-scale melt parameters with a regional climate model coupled to a thermodynamic multi-layered snow model for the southern part of the Greenland ice sheet at a high horizontal resolution of 20 km. the forcing is placed at the lateral boundaries of the regional climate model. Lateral boundary conditions are air-temperature, air-humidity and wind-speed components, taken from European Centre for Medium-Range Weather Forecasts (ECMWF) re-analyses. Regional climate model simulated near-surface atmospheric conditions (air temperature, air humidity, wind speed, short- and longwave incoming radiation, surface pressure as well as rain- and snowfall) are then used to force the snow-model subsurface energy–mass transfer model. In a first attempt, the 1991 ablation summer has been studied as a test case.
2. Large-Scale Positive Degree-Day Melt Model Parameters
2.1. Standard air-temperature deviation
Normally, large-scale melt models over Greenland calculate the amount of positive degree-days (PDD) by (Reference ReehReeh, 1991; Reference Huybrechts and Wolde.Huybrechts and de Wolde,1999):

assuming an annual sinusoidal evolution of the air temperature (Td in ˚C). σ is the standard air-temperature deviation and accounts for two different kinds of temperature variations that can contribute to positive temperatures, i.e. the deterministic daily temperature cycle and the stochastic weather fluctuations with a typical period of 5–7 days. It allows melt with negative air temperatures. PDD can be seen as a melt potential to melt snow and ice at the surface of the ice sheet. the 0 to ∞ temperature integration interval is mostly approximated by the interval (Td – 4σ; Td + 4σ) since the normal distribution function becomes very small outside this interval. PDD shows a very high sensitivity to the value of σ (personal communication from I. Reference Janssens and HuybrechtsJanssens, 2001). for example, for a mean annual temperature of 0˚C and a mean summer temperature of 5˚C, an increase of σ from 4.2˚C to 5.0˚C is equivalent to a yearly PDD increase of 10%. In the literature, σ values of 4.2–5.0˚C can be found.
2.2. Snow and ice degree-day factors
The amount of snow, superimposed ice and old ice melt at the surface of the ice sheet during the summer ablation season is proportional to the PDD. the proportionality factor used is the snow (ksnow) and ice (kice) degree-day factor.
Following Reference BraithwaiteBraithwaite (1995), the positive degree-day factor (k) for a N day period, with N* days with temperatures at or above the melting point, is defined as:
where A and PDD are the total ablation and the positive degree-day sum, respectively, for the N day period.
If daily ablation (ai) and daily average positive temperatures (Tpos,i) are available, k can also be expressed as:
with α and β equal to the linear fitting parameters (ai = α + β Tpos,i) to fit daily ablation (ai) and daily average positive temperatures (Tpos,i). the latter is defined from hourly temperatures (Tj) as (n = 24):
Reference Braithwaite and ZhangBraithwaite and Zhang (2000) provide an exhaustive list of snow and ice degree-day factors found in the literature and say that the reasons for the different degree-day factors are not immediately obvious. High values are found in cold situations such as the high-ablation zone in West Greenland during the Greenland Ice Margin Experiment (GIMEX-90, GIMEX-91) (Reference Oerlemans and VugtsOerlemans and Vugts, 1993) and Expéditions Glaciologiques Internationales au Groenland (EGIG) Camp IV (Reference Ambach, Thomsen, Søgaard and BraithwaiteAmbach, 1988) experimental campaigns. the measured positive degree-day factor for ice amounted, respectively, to 20.1, 22.2 and 18.6mm w.e. d–1 ˚C–1.
Snow and ice reflect downward solar radiation differently. the albedo of snow varies between 0.85 for fresh non-melting snow and 0.60 for old melting snow. the range of ice albedo can be even larger due to the presence of dust or volcanic matter.Very dirty ice can have an albedo as low as 0.10 (Reference Greuell, Genthon and BamberGreuell and Genthon, in press), while clean ice can have an albedo up to 0.58 (Reference Greuell and KonzelmannGreuell and Konzelmann, 1994). Therefore, degree-day factors are generally taken smaller for snow than for ice.
If runoff and ablation are needed at higher temporal and spatial resolutions, orientation, slope, aspect and horizon characteristics of the surface should be accounted for. Reference HockHock (1999) achieved this by including the potential clear-sky direct solar radiation in the melt calculations. for long-term ice-sheet mass-balance predictions this effect can be neglected; however, it is interesting to note that hourly simulated degree-day factors vary from 0.0 to 16.0 mm w.e. d–1 ˚C–1 (see Reference HockHock, 1999, fig. 9).
If one looks at temporal scales of multiple years and for larger geographical domains, the latitudinal and seasonal variation of daily potential solar radiation is expected to become important. Reference GreveGreve (2000) proposed a latitudinal variation at 60–80˚N of 7–10 mm w.e. d–1 ˚C–1 to simulate larger runoff in the northern part of the ice sheet.
3. Regional Climate Coupled Atmosphere– Snow Model
3.1. General description
The coupled atmosphere–snow regional climate model used is Modèle Atmosphérique Régional (MAR). the atmospheric part of MAR is fully described in Reference Gallée and SchayesGallée and Schayes (1994) and Reference GalléeGallée (1995). MAR is a hydrostatic primitive-equation model. A band of tundra points borders the inland ice sheet. the Reference DeardorffDeardorff (1978) force-restore model with a soil thermal conductivity of 0.65 Wm–1K–1 and an albedo of 0.20 is used to predict the tundra surface temperature evolution. In case of snow deposition upon the tundra area, the snow model (described below) is used.
MAR was originally developed for process studies in the polar regions (Reference GalléeGallée, 1995) but is now, besides Antarctica, also applied over temperate (Reference MarbaixMarbaix, 2000) and tropical (West Africa) regions for climatic studies (Reference Brasseur, Gallée, Creutin, Lebel and MarbaixBrasseur and others, 2001). the lateral boundary treatment consists in a buffer zone (width of 5 points) involving ``Newtonian’’ and ``diffusive’’ relaxation terms (Reference DaviesDavies,1983).
The MAR fine-grid 20 km resolution topography and soil type for Greenland are taken from the Reference EkholmEkholm (1996) Greenland topography and land masks.
3.2. Snow model
The snow model is part of the mesoscale atmospheric model MAR, as an interactive lower boundary. It is described in detail in Reference Gallée and DuynkerkeGallée and Duynkerke (1997) and Reference Lefebre, Gallée, vanYpersele and GreuellLefebre and others (in press). It feeds back to the atmosphere by means of a surface temperature, a specific humidity close to the surface, and surface properties (albedo, emissivity, roughness lengths). Surface albedo is a function of the simulated snow grain’s form and size, the depth of the snowpack upon year-old ice and the amount of meltwater accumulated upon the ice if all the snow has melted away. the snow model calculates both melt and refreezing, making it possible to distinguish the importance of internal meltwater refreezing and superimposed-ice formation.
3.3. Model set-up
The simulation starts on 1May 1991and lasts until the end of August, i.e. 123 days, corresponding to the major melting period over the ice sheet. the integration domain encompasses the southern part of Greenland and its neighbouring waters (Davis Strait, Atlantic Ocean and Denmark Strait). Sea surface temperatures and sea-ice distribution are prescribed from ECMWF re-analysis (ERA) fields. A 20 km horizontal resolution was used. This resolution may be insufficient to represent, for example, the small ablation zone in southeast Greenland in the presence of very steep ice-sheet margins, but is appropriate for the aim of our study.
A more detailed description of the model set-up and simulation can be found in Reference LefebreLefebre (2001) where the simulated near-surface atmospheric fields were compared and validated with observations from coastal and on-ice stations during summer 1991. A comparison between simulated and satellite-detected melt zones showed a good temporal and spatial correspondence between the two.
4. Modelled Large-Scalemelt Parameters
4.1. Positive degree-day factor
The equivalence between the MAR and the large-scale melt model’s variables and parameters is not so straightforward, because of the different time-scales considered but also because of the different vertical resolutions of the two types of model. the MAR multi-layered snow model has a snow-pack time-step of 6 min, while the large-scale positive degree-day based melt model can work with yearly time-steps provided the PDD melt potential is calculated with sufficient accuracy. Also, the large-scale positive degree-day melt models use vertically integrated quantities such as snow cover, superimposed ice, capillary water and run-off (see, e.g., Reference Janssens and HuybrechtsJanssens and Huybrechts, 2000). to discuss comparable variables, MAR vertically integrated melt has been calculated. In the model, melt equals the difference between the amount of melted snow or ice and the amount of refrozen internal meltwater or surface meltwater which are both calculated by the model. In case of snowmelt at temperatures near the melting point, the amount of refreezing considerably lowers the net amount of melt. Both daily average temperatures and daily average positive temperatures have been calculated from hourly model output (see Equation (4)).
Hereafter, the positive degree-day factor will be calculated for ETH Camp (Reference OhmuraOhmura and others, 1992) and the Kangerlussuaq K-transect (Reference Oerlemans and VugtsOerlemans and Vugts, 1993), which are both located in the model ablation area. the model ablation zone was taken from Reference ReehReeh’s (1991) mass-balance results. the model ablation-zone boundary can be seen in Figure 3 (shown later). It should be noted that due to the horizontal resolution of 20 km and the initialization procedure, model melt results are not always easily comparable with observed melt. the initialization procedure of the snowpack depth in the model ablation area at the beginning of the simulation was done by taking the ECMWF winter snow amount. Observations at ETH Camp and the K-transect showed, respectively, an under- and overestimation of the ECMWF amount of snow. the difference between ECMWF winter snow amount and the observed quantity is partly due to snowdrift which is estimated to be important. In the model, ice appears at the surface of ETH Camp while mass-balance measurements (Reference OhmuraOhmura and others, 1992) show that snow was present throughout the melting season. At the K-transect, an initial snowpack is present in the model close to the ice-sheet margin at the beginning of the simulation. In reality, all winter snow was blown away in the area close to the ice-sheet margin. Melt is mostly controlled by the surface albedo value, and thus depends strongly of the nature of the surface since snow and ice have different albedos. Finally, the positive degree-day analyses will be done for the whole integration domain, and distributions will be presented.
4.1.1. ETH Camp
The modelled positive degree-day factor at ETH Camp has been obtained separately when snow or ice was present at the surface. Figure 1 shows the modelled daily net ablation and daily average positive temperature together with the fitted linear relation for snow and ice melt for summer 1991. According to Equation (3), the slope of the line does not equal the positive degree-day factor. the first term in Equation (3) becomes less important for higher temperatures but cannot be neglected for locations close to the equilibrium line such as ETH Camp where melt appears at temperatures close to 0˚C.
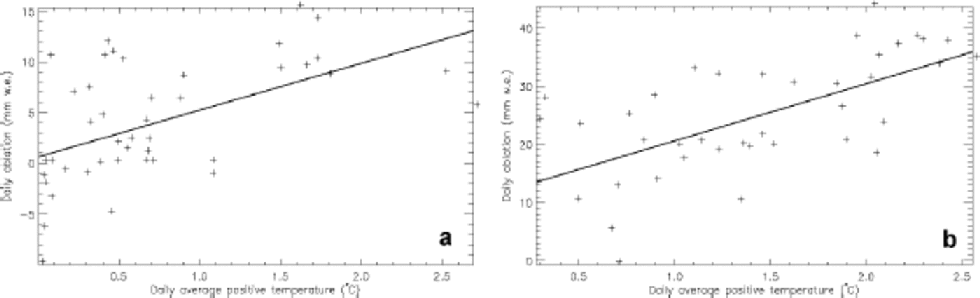
Fig. 1 Simulated daily net (melt – refreezing) ablation vs daily average positive temperature during summer 1991 at ETH Camp. (a) Snowmelt; (b) ice melt.
The calculated positive degree-day factor for snow and ice (Table 1) is 5.48 and 17.45 mm w.e. d–1 ˚C–1, respectively. the snow and ice values are somewhat larger than generally found in the literature but confirm the high values found along the K-transect, also situated in West Greenland. Refreezing of internal snow pack meltwater considerably lowers the amount of snowmelt and hence the positive degree-day factor.
Table 1. Modelled degree-day factor for ETH Camp during summer 1991 from daily net ablation and daily average positive temperature (calculated with hourly model output). the values in parentheses are calculated with daily melt without subtracting the amount of refreezing

If refreezing is excluded, a snow positive degree-day value of 13.04 mm w.e. d–1 ˚C–1 instead of 5.48 mm w.e. d–1 ˚C–1 is obtained (see Table 1). Also, superimposed-ice formation lowers the ice positive degree-day factor.
4.1.2. K-transect in model ablation zone
The positive degree-day factor is expected to vary drastically along a transect of the ice sheet because of the large variations in climatic conditions. the lower ablation zone is characterized by high temperatures. Higher up the ice sheet, temperatures are lower and radiation becomes more important because of the optically thinner atmospheric conditions. the K-transect (67˚N) has been chosen because it is well documented. Since 1990, continuous mass-balance measurements have been made in order to obtain a long-term mass-balance record and to study the origins and mechanisms behind the large interannual variations in surface melt. Positive degree-day factors for ice melt have been calculated for the model gridpoints situated along the K-transect. the calculations have been done for the whole model ablation zone. the snow degree-day factor (calculated from net ablation) increases from 4.95 mm w.e. d–1 ˚C–1 at the lowest model ice-sheet grid-point to 8.60 mm w.e. d–1 ˚C–1 at nearly 1600ma.s.l (see Fig. 2). the increase with altitude can be explained by the varying relative importance of global radiation fluxes compared to turbulent heat fluxes. Near the ice-sheet margin, more than half of the energy to melt snow comes from global radiation. Near 1600 m elevation, sensible- and latent-heat fluxes balance each other, and all of the energy to melt snow is provided by global radiation. the modelled snow albedo profile does not show significant variations along the transect. Its average value is 0.725, a typical value for well-developed melting snow with large snow grains. for ice melt, a very high ice positive degree-day factor of 43.57 mmw.e. d–1 ˚C–1 is found at 1600 ma.s.l. but from only 13 ice-melt days.
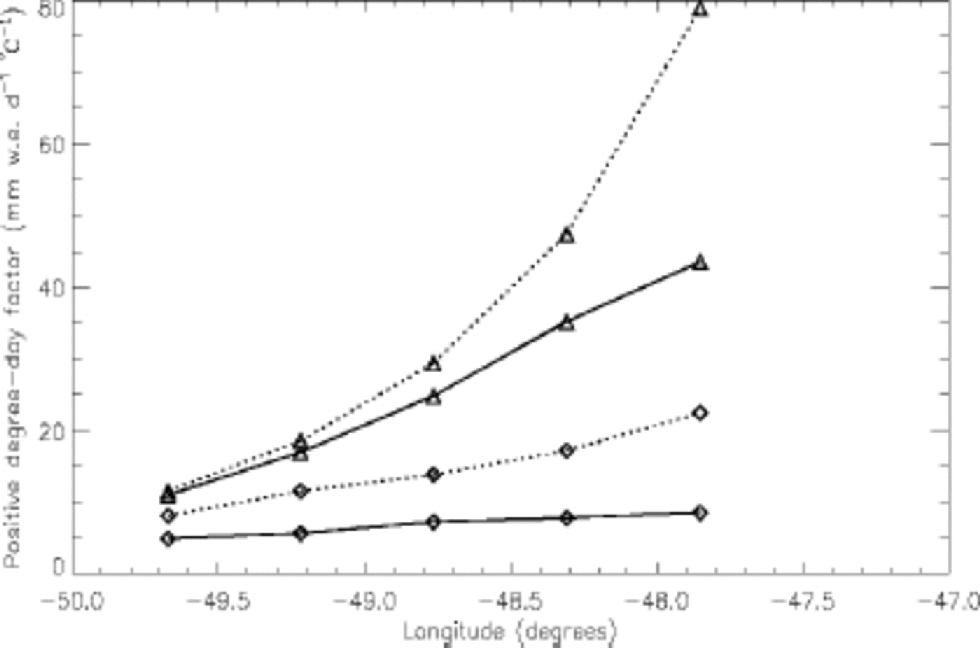
Fig. 2 Modelled snow (diamonds) and ice (triangles) positive degree-day factors for summer 1991 at the K-transect (approx. 67˚N), West Greenland. Dotted lines show melt without subtracting refreezing.
Refreezing of meltwater becomes more important higher on the ice sheet (see Fig. 2). the melt without refreezing-snow positive degree-day factor amounts to 22.52 mmw.e. d–1 ˚C–1 at the highest calculated point where 60% of the melt refreezes in the snowpack or as superimposed ice at the bottom of the snowpack upon the old ice. Close to the ice-sheetmargin, the ice degree-day factor, derived from ablation without refreezing, almost equals the ice degree-day factor from net ablation. At the highest model K-transect point, refreezing divides by two the amount of net ice ablation, which gives a very high ice degree-day factor of almost 79 mm w.e. d–1 ˚C–1 if refreezing is excluded.
4.1.3. Southern part of Greenland ice sheet
The same analysis has been done for the southern part of the Greenland ice sheet. Points with 510 days melt have been rejected. for snowmelt, positive degree-day factors (calculated with net ablation) of 5–7.5mm w.e. d–1 ˚C–1 are found in the model ablation zone inWest Greenland (see Fig. 3a). In the model ablation zone in East Greenland, somewhat lower snow values are found. Outside the model ablation zone, simulated positive degree-day values are higher inWest than in East Greenland although the northern regions generally have values of <2.5mmw.e. d–1 ˚C–1. It is also seen that around the model ablation-zone boundary, i.e. the line that separates the model ablation zone, characterized by snow lying upon ice, from the percolation zone where no ice is present in the snow model, a strong variation in snow positive degree-day factor is present. This is likely to be an artifact of the initialization procedure. the gradual transition between the ablation and percolation zone, within the superimposed-ice zone, the slush zone and the saturated-snow zone in between, was not present in the initial state which was completely homogeneous. This will only be possible after long-term (410 year) simulations can be performed. Outside the model ablation zone, simulated meltwater is able to percolate down the snowpack, which explains the lowering of the snow degree-day factor just above the model ablation boundary.
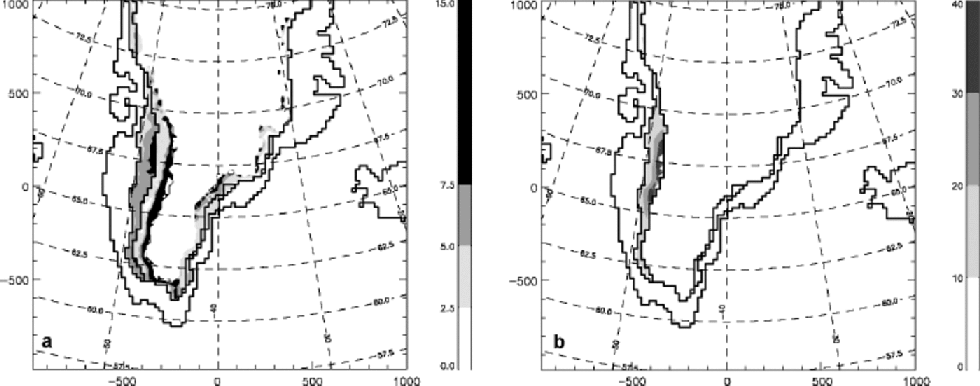
Fig. 3 (a) Modelled snow positive degree-day factor and (b) modelled ice positive degree-day factor (mm w.e. d–1˚C–1) for summer 1991 from net ablation. Only points with minimum 10 melting days have been selected.
The simulated ice positive degree-day factor gradually increases with altitude in West Greenland (see Fig. 3b). In East Greenland the summer snowfall balanced the snowmelt so that no ice appeared at the surface and no ice positive degree-day factors for East Greenland could be calculated.
The variation of the snow and ice PDD factors with latitude and surface height together with their histograms are shown in Figure 4. the strongest, most linear variation can be seen as a function of surface height. In case of snowmelt, a small decline can be seen as a function of latitude. Both the snow and ice histograms demonstrate that the most frequent simulated values agree with the generally accepted snow and ice positive degree-day factors of 3 and 8mm w.e. d–1 ˚C–1.

Fig. 4 Modelled (from net ablation) snow (upper panels) and ice (lower panels) positive degree-day factors during summer 1991 as a function of latitude and surface height. A histogram indicates 3 and 8 mm w.e. d–1˚C–1 as the most frequent values for snow and ice melt, respectively.
4.2. Standard air-temperature deviation
A monthly standard air-temperature deviation has been calculated from the model output by varying the standard air-temperature deviation (σ) in the righthand term of Equation (1) (with Td equal to the monthly simulated average temperature) so as to approach best the simulated monthly positive degree-day sum (left term of Equation (1)) which was calculated from hourly temperatures during the simulation. If the simulated positive degree-day sum was zero, the standard temperature deviation was not calculated and put to zero.
In Figure 5, the obtained standard deviations for May– August are plotted. In May, the highest values are found in West Greenland (3.0–5.0˚C), and the lowest in East Greenland. In June, the pattern is reversed, with lower values in West than in East Greenland. the lowest seasonal values are found in July (<3.0˚C). This seasonal cycle of temperature fluctuations is typical for northern latitudes, where the highest daily temperature fluctuations occur in the transition months such as April, May, August and September. In July, the melting surface reduces the near-surface air-temperature fluctuations, and the standard temperature deviation is 2.0–3.0˚C.
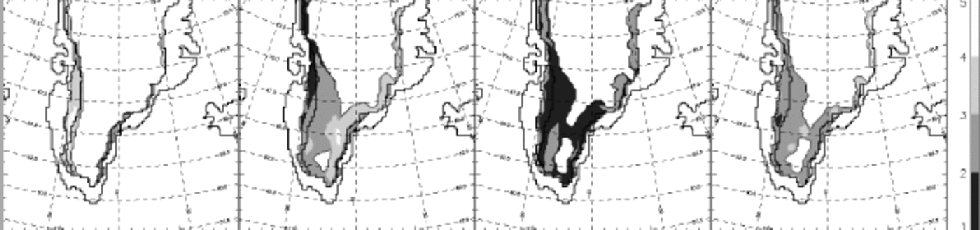
Fig. 5 Monthly (from left to right: May, June, July and August 1991) model-derived standard air-temperature deviation (˚C) (see section 4.2).
5. Conclusions
From the model results it is possible to distinguish net ablation and the amount of refreezing. Positive degree-day factors can be calculated from both the net ablation and the ablation without the subtracted amount of refreezing.
The measured positive-degree factors are derived from the net daily ablation, as it is impossible to measure the amount of refreezing in the field. In this paper, modelled degree-day factors show that close to the ice-sheet margin, refreezing is not so important, but that higher up the ice sheet a significant part of the daily melt refreezes in the snowpack or as superimposed ice. It should be noted that the measured ``net ablation’’ positive degree-day factors (Reference Braithwaite and ZhangBraithwaite and Zhang, 2000) are not equivalent to the positive degree-day factors used in the positive degree-day melt models. In the latter, melt and refreezing are calculated separately (see, e.g., Reference Janssens and HuybrechtsJanssens and Huybrechts, 2000). If refreezing is excluded, model results indicate higher snow and ice positive degree-day factors which suggest that the current positive-degree melt models probably underestimate the amount of melt in the higher parts of the ice sheet. Close to the ice-sheet margin, refreezing is of minor importance. the simulated frequency distribution of the snow and ice degree-day factors (from net ablation) peaks at the commonly observed and used values of 3 and 8mm w.e. d–1 ˚C–1.
The simulated temperature standard deviation is smaller than the generally uniformly used value of 4.2–5.0˚C. the highest values (3.0–5.0˚C) are found in May and June. the lowest values (<3.0˚C) occur in July. This seasonal cycle is typical for northern latitudes.
The presented results refer to the 1991 melt-season conditions and should therefore be treated with care as they only refer to one melting season. Longer simulations should be performed to assess the influence of varying subsurface conditions and interannual climate variability. Summer 1991 is considered a strong melting season (Reference Abdalati and SteffenAbdalati and Steffen, 1997). It would be interesting to look at the modelled melt parameters for a weak melting season, such as 1992.
Acknowledgements
F. Lefebre is financed by the Belgian Scientific Research Programme ``Global Change and Sustainable Development’’ (contract No. CG/10/09B) of the Prime Minister’s Science Policy Office. We are grateful to the Royal Meteorological Institute (KMI-IRM) for providing access to the ECMWF data services. D. Lucas (ECMWF, Reading) is thanked for help with the ERA data. the authors gratefully acknowledge the Belgian Fonds de la Recherche Fondamentale Collective, for providing computer facilities under project 2.4556.99 ``Simulation numérique et traitement de données’’.








