Introduction
In a previous study, finite-element modeling of fielddetermined velocity profiles across the southern margin of Ice Stream B has indicated that ice in the marginal shear zone must be softer than either the ice in the central part of the stream or the ice in the inter-ice-stream ridges (Echelmeyer and others,1994). That analysis also shows that there must be a weak deformable layer at the bed or greatly enhanced sliding there. Calculations for crosssections of Ice Stream B suggest that the total resistive force is partitioned almost equally between the margin and the bed, based on the model-inferred ice properties.
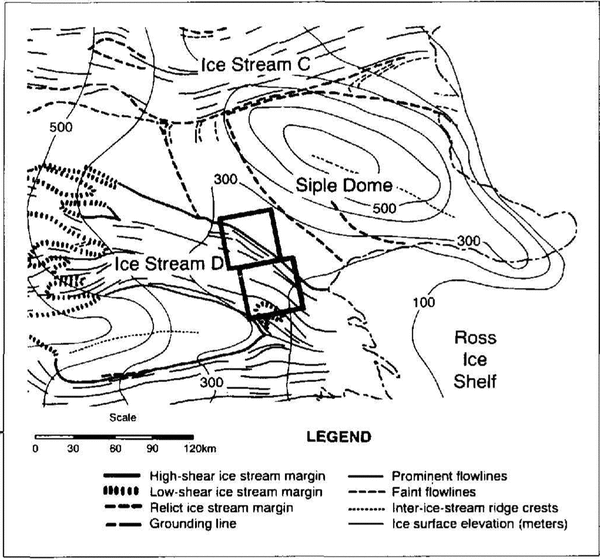
The margin of Ice Stream B is a well-developed shear margin of nearly uniform morphology in the study area of the previous paper. In this paper, we investigate a region of the southern Ice Stream D margin (see Figs I and Figs 2) where the morphology and surface velocity change over a relatively short longitudinal distance (60km). Morphologically, there is a gradual transition from a diffuse, weakly crevassed margin to one which is similar in appearance to the Ice Stream B southern margin. Feature mapping from Landsat TM imagery (Reference Scambos and BindschadlerScambos and Bindschadler 1991) shows that the width of the ice stream increases abruptly just upstream of this area, and that the margin in the study area appears to be developing from ice that does not inherit a history of prolonged, intense shear strain from upstream; rather, it is derived from the inter-ice-stream ice of ridge C/D. This mayor may not represent an ongoing margin migration or change in the ice dynamics of the area. In either case, this part of the southern margin of Ice Stream D offers a unique opportunity to study the development of an icestream margin, since it is a region where ice speeds and strain rates change significantly over a short longitudinal distance.

Fig. 1. Feature map of a part of the Siple Coast ice-stream area (modified from Scambos and Bindschadler, 1991), showing the study area and locatiun of images in Figure 2. South is towards the top.

Fig. 2. Landsat TAl sub-scenes showing the southern margin of Ice Stream D and the location of theJive ice-speed profiles discussed in the ted. Countours on the ice stream are ice speed in ma-1; the sub-scenes were computer-contoured separatly, thus the contours do not line up exactly across the gap in the two images.
Ice-speed profiles and shear-strain rate
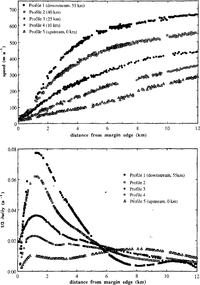
Ice velocities m the study area were determined using image-to-image cross-correlation techniques on two Landsat TM images of the region (two images of path 7, row 119, taken in January 1987 and December 1988; the method has been described by (Reference Scambos, Dutkicwicz, Wilson and BindschadlerScambos and others 1992). In earlier work (Reference Scambos, Dutkicwicz, Wilson and BindschadlerScambos and Bindschadler 1992), a general velocity field for this part of 1ce Stream D was determined from the same images, with spacing of velocity measurements at about 400 m (every 15 pixels on the Tyl images) using small image areas, or “chips”, of 32 ˣ 32 pixels. For the speed and strain-rate profiles of this study, supplemental velocity determinations were run at spacings of 50 100m (3–5 pixels). It should be noted that the individual velocity measurements are derived from image chips which overlap with chips for adjacent velocity measurements, and thus are not entirely independent. Image-to-image correlation software parameters were adjusted to address the high shear, and associated feature distortion, in the shearmargin area; this was done principally by using smaller (though still overlapping) image chips in the crosscorrelation comparison. All velocity measurements were edited to remove spurious matches inconsistent with the surrounding velocity field. Speed profiles were created by combining all valid velocity measurements within 1km wide strips oriented perpendicular to the margin; this is very nearly perpendicular to the flow direction in all cases. We define u as the velocity component in the direction parallel to the margin, defined as the . r, direction. The direction perpendicular to the margin is y. The profiles start from the morphological edge of the ice stream, that is, the outermost margin feature identifiable on the TM imagery. The near-margin part (within 12km from the margin)of the five profiles is shown in Figure 3a.

Fig. 3a Speed; b. Transverse speed gradient profiles of the southern margin of Ice Stream D.
Values of au/By for the profiles were calculated by taking the first derivative of fifth-order polynomial fits to the speed profiles. This had the effect of smoothing the gradient profiles, which is required because of a 35% random error in the determination ofu. To preserve aU the features of the speed profiles in the polynomial curves, two separate fits were applied to each profile, one incorporating only data within 4km of the margin edge and one incorporating all data. These were combined to yield the profiles shown in Figure 3b. Correlation indices for these fits(r2) were all above 0.9; most were above 0.995. Because the profiles are very nearly perpendicular to the flow direction, and because the longitudinal gradient of transverse velocity is small, the i∂u/∂y values are very nearly twice the shear strain rate. Plots of ∂u/∂y versus distance from margin edge are shown in Figure 3b.
The profiles clearly illustrate the rapid change in ice speed and shear strain rate that occurs along the southern margin area. Ice speed at mid-stream (see Fig. 2)increases from 420 to 670 ma' 1 between the upstream and downstream profiles, and speeds within the marginal zone also show a steady increase. The ∂u/∂y profiles show the formation of a zone of concentrated shear strain at about 1.3 km from the margin edge, with a maximum shear strain rate in the downstream profile (profile 1) ofO.08a 1. The upstream profile (profile .1) has a nearly constant shear strain rate of between 0.01 and 0.015 a-1. The zone of increased shear strain rate which develops in the downstream profiles remains at about 1.3km from the edge of the ice stream.
The speed and al1, profiles suggest that this pan of the southern margin of lce Stream D evolves as ice proceeds downstream from a case where the shear strain associated with ice-stream motion is distributed across a broad margin of stifTer ice to one in which the majority of the strain is taken up by a softer, high-strain zone located just inside the margin. To test this hypothesis, and to investigate the possibility that changes in the bed are associated with the evolution of the margin, finite-element modeling of the downstream and upstream profiles (profiles 1 and 5, respectively was conducted.
Finite-element modeling of the profiles
The finite-element ice-flow model we apply here requires several simplifying assumptions. The model calculates a velocity field for a cross-section of the ice stream, given the flow law for ice, a grid of estimated ice stiffi1esses, the driving; force and an ice-temperature profile with depth. The model has been developed in detail in Echelmeyer and others and (Reference EchelmeyerEchelmeyer 1983) The modeling scheme allows for flow in three dimensions within a twodimensional cross-section; hmvever, stress and velocity gradients out of the plane of the cross-section are taken to be zero. A power-law flow relation for ice (c= EAT“) is used, With n = 3, where c and T are the effective strain rate and effective stress, A is the temperature-dependent flow-law parameter and E is an enhancement factor dependent on crystal fahric and/or temperature variations other than those assumed at the start of the model run (Reference PatersonPaterson 1981);, (Reference Jacka and BuddJacka and Budd 1989). Only the southern half of the ice stream is modeled and zero transverse shear stress is assumed at the center line. The ice-stream cross-section is approximated by a rectangle with an ice thickness of 800m and a width of 23.2km for the downstream profile and 30km for the upstream profile (Ice Stream D changes in width in the study area from 46.4km in the downstream area to 59.7km in the upstream area). The 800 m thickness value is a guess based on a measured thickness of 800m at the grounding line approximately 15Okm downstream (personal communication from R. W. Jacobel). Modest errors in this thickness estimate (10%) will affect only the calculated parameters in the lowest layer of the model (the basal zone). The rectangular cross-sections are divided into grids of 264 quadrilateral elements with six horizontal layers, having boundaries at 0, 20, 100, 200, 400, 600 and 800m above the bed. Grid density increases near the margins, where high shear strain rates are expected.
A surface slope of 1.3 ˣ 10,-3 was used for calculating the driving force (estimated from (Reference RoseRose 1979). Ice speeds outside the ice stream at the margin arc assumed to be zero. The limit of ice speeds determinable by the imagebased velocity mapping is 10m a-1. It appears that the actual ice speed at the margin, extrapolating from the profiles to ˣ =0, is about 15ma' l; however, the possible error in image co-registration could account for roughly half this amount. A small non-zero velocity in the surrounding ice will have a modest eflect on the model results for the outermost vertical zone and no significant eHects elsewhere. An estimated ice-temperature profile is used, having a surface temperature of - 24ºC and a basal temperature of Oºc. This is similar to the temperature profile for lce Stream B determined by borehole measurements (Reference RoseEngelhardt and others 1990).
As discussed in (Echelmeyer and others), the high surface speed and small driving stress of the Siple Coast ice streams require that a highly deformable basal layer, or enhanced sliding at the bed, be incorporated into any plausible model of their flow. Simple ealeulations based on the flow law indicate that, ifno such basal layer is present, predicted center-line velocities are several orders of magnitude too low. Our assumption of a highly deformable layer at the base of Ice Stream D is consistent with the observation of very low-strength water-saturated till beneath Ice Stream B (Reference Engelhardt, Humphrey, Kamb and FahnestockEngelhardt and others 1990). This layer is treated in the model as an extremely deformable zone of 20m thickness with rheological properties governed by a power-law relation having very large “A” values. Although this assumption mimics the effects of a till layer in this model, the results for The basal layer should not be interpreted as predictive of the till properties. The model further assumes that there are no velocity discontinuities across any boundary in the system (i.e. no sliding); however, the very high deformation predicted within the basal layer (see model results below) may be interpreted as either deformation or enhanced sliding.
Several models of increasing complexity were made in order to investigate the ice and bed properties of the two profiles, and to determine the balance of drag forces. Model runs attempted to match both the center-line speed and marginal-zone speed and strain rate. The flow law parameter A is held constant in the transverse direction; it only varies with depth according to the input temperature profile. Each grid element is assigned a value of E. In a given series of model runs, the input values of E in the grid elements are changed to attempt to match the velocity profile. E =1 implies that the stiffness of ice within a grid clement is governed by the power-law relation and the temperature-dependent value of A. E > 1 represents softening of ice due to such factors as the development of a preferred crystal orientation or increased ice temperatures above the input temperature- profile values.
The model results for profile 1 are very similar to those of the profile at Ice Stream B (Fig. 4a; Echelmeyer and others, 1994). There, as here, it was determined that there is no physically reasonable distribution of basal shear stress which, by itself, can lead to the observed velocity profile. Furthermore, the ice cannot have uniform properties across the ice stream. This holds even if the flow-law parameter is in error by a factor of 10 or more. The strong curvature of the profile in the marginal zone requires soft ice in that area, i.e. E considerably greater than 1. A good fit to the observed center-line speed and the velocity profile is obtained if vertical zones with E values of,) and 12 are present near the margin, and E values in the basal zone are on the order of 106 (see (Figure 4a). A schematic of the model grid is shown as an inset to (Figure 4a, in which are shown only the grid-cell boundaries across which changes in the enhancement factor occur. The location of the E = 12 zone coincides with the most highly crevassed part of the margin in the imagery. A similar pattern and magnitude of E values generated the best fit for the Ice Stream B profile.
As discussed by Echelmeyer and others (1994), these model results are not quantitatively unique. They arc robust, however, in that the fundamental conclusions regarding softening of the ice in the marginal zone and high deformability or sliding at the bed are required by any physically reasonable version of the model, and ice properties near the center line of the stream must be fairly uniform. An exhaustive search for a distribution of E values to yield the best fit to the observed profiles has not been attempted, nor would it be a worthwhile pursuit without much more information on temperatures, ice thicknesses, longitudinal stress gradients, etc.
Basal and marginal shear stress are calculated as part of the finite-element analysis. The average basal shear stress at profile 1 is about 0.045 bar, and marginal shear stress reaches 1.50 bar near the surface. Integrating the shear stress along the side margin yields a value of 1.04 ˣ lO8Nm1. Integrating basal stress along the bed givens 1.08 = 108 Nm-1. Thus, for this model, 51 % of the total resistance to flow is attributable to basal drag and 49% to side-margin drag. Again, these results closely match those for the Ice Stream B profile.
For profile 5, where the shear margin does not appear to be well developed, the results are much different Fig. 4b. A model with E =1 everywhere in the ice and a non-uniform distrihution of basal shear stress, i.e. a variation in the enhancement factor E in the thin basal layer, yields a reasonable fit to the observed velocity profile. Thus, ice near the margin of profile 5 is not required to be softened relative to the center-line ice. This may mean that, at this location, the ice has not accumulated a large amount of shear strain, and a preferred fabric for shear strain or viscous heating in the marginal ice has not yet developed. Variations in E in the basal layer are required; specifically, basal shear stress must increase significantly ncar the margin, unless we attempt to match the velocity profile by using values of E 1, implying conditions we consider to be unlikely. E values for the marginal-zone bed layer are several orders of magnitude lower than for the central part of the profile, or profile 5. Thus, at this location, there is a distribution of basal shear stress which can, by itself given rise to the observed velocity profile. Again, the model is not a unique solution. A good fit might be obtained with some softening in the marginal-zone ice coupled with a larger increase in the basal shear stress in the near-margin bed. However, the magnitude of this softening would be much less than that inferred for profile 1

Fig. 4 Finite-element model results jor (a) downstream (Projile 1) and (b) upstream (profile 5) profiles.
For the profile 5 model, the marginal-shear stresses reach 1.45 bar and the mean basal shear stress is 0.065 0.07 bar. The integrated drag along the side margin is 0.9 ˣ10 Nm-1 and integrated basal drag is 2.0 ˣ 10 Nm-1 Total drag for profile 5 is greater than for profile 1 because of the increase in ice-stream width. The increase in basal drag is due to the higher stiffness of the bed near the margin of profile 5. In this model, 69% of the total resistance to flow is derived from the basal shear In profile 5; 31% is derived from side-margin shear satelliteimage- derived velocity-measuring technique will not work in most inter-ice-stream areas, because of the absence of small, sharp surface features to track.
Discussion
Several inferences may be drawn from the profile data and the results of the modeling. For the downstream profile (profile 1), the large enhancement factors found in the ice near the margin strongly suggest that ice in the margin is either very strain-softened or warmed through viscous heating, or both. Much of this strain-softening relative to normal ice may be the result of recrystallization of the near-margin ice into a fabric with an easyglide orientation, i.e. a fabric with caxes of the ice oriented normal to the transverse shear plane (Reference Jacka and Budde.g.Jacka and Budd 1989). Jacka and Budd reported that 15% total strain results in an increase in E to a value of 8. The total strain of the marginal ice is likely to be much larger than that of the experimentally deformed ice in Jacka and Budd's study; thus, the somewhat larger E values reported here, e.g. E = 12, are reasonahle.
Viscous heating under conditions of high strain rate and large shear stress as inferred for the marginal zone could lead to a warming of 2-10K at depth (Echelmeyer and others, 1994). This would result in an E value of 2-5 even in the ahsence of any fabric development. The critical parameter in any estimation of viscous heating is the residence time of a parcel of ice in the shear zone. Rapid influx from the inter-ice-stream ridges would greatly reduce the total heating experienced by a parcel of ice passing through the highest shear zone, because of the decrcase in residence time. At present, there is no way of estimating the rate of influx across the margin edge, because no field party has visited the area. The satelliteimage image- derived velocity-measuring technique will not work in most inter-ice-stream areas, because of the absence of small, sharp surface features to track.
For profile 5, the small, constant shear strain rate and absence of any required enhancement of ice flow in the marginal zone suggest that the residence time of the ice in the near-margin area has been too short for either recrystallization or strain heating to have taken place. This is consistent with satellite-image-based feature and velocity mapping of the area (Reference Scambos and BindschadlerScambos and Bindschadler 1991), (Reference Scambos and BindschadlerScambos and Bindschadler 1992), which suggests that the ice within this part of ice Stream D is derived from inter-ice-stream ice just upstream from the profile 5 transect.
The basal conditions inferred from the modeling may oIrer a plausible explanation for the development of a weak, water-saturated till layer at the bed beneath ice streams. In the marginal zone of profile 5, the effective strength or viscosity of the basal layer in the model is much higher than that of the bed farther in from the margin, or in the entire basal layer in profile 1. This may be due to a lower pore-water pressure or a lower liq uid-water content in the basal layer beneath this marginal zone relative to the other locations. A possible source of water in the profile I area is from melting due to viscous heating in the marginal zone ncar the bed. The central part of the profile 5 basal layer may receive water by transport from betterdeveloped marginal zones upstream of the study area.
Summary
This part of the margin of Ice Stream D undergoes rapid change over a relatively short longitudinal distance (55km), manifested by a significant increase in velocity and shear strain rate. A zone of concentrated shear strain approximately 1.3km in from the morphological edge of the ice stream develops in this distance. The model results presented here indicate that the ice in the marginal zone becomes progressively softer and the properties of the marginal bed change as one moves downstream. Ice-flow properties in the central region of the ice stream remain relatively constant, and are not required to be enhanced. The results derived for the downstream region of the study area (profile 1) are similar to those found along the wel1- developed shear margin at Ice Stream B. In the upstream region (profile 5), there is no high shear-strain zone, and no enhancement of ice-flow properties is required to match the velocity profile. There also appears to be a change in the distribution of basal drag between the two profiles as the_ shear margin develops, and as center-line speed increases
The model results are not unique but they are robust. Refinement of the quantitative aspects of the model results could be derived with better input values for profile ice thickness and ice temperature. However, the qualitative aspects of the results are relatively insensitive to modest errors in the flow-law parameter A, Ice thickness, surface slope or ice temperature.
Acknowledgements
Dr E. Waddington of the University of Washington and an anonymous reviewer made important contributions to the papcr via their questions and comments on the initial version. C. Larsen, of the Geophysical Institute at the Cniversity of Alaska, conducted the model runs for the profiles and his efforts are appreciated. This work was supported by U.S. National Science Foundation grant DPP-9018127 to R.A.B. at :"JASAjGocldard, and by the NASA Distributed Active Archive Center grant NAGW- 641 and contract :"JAS5-322392 to NSIDC.