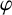1. Introduction
The problem of finding necessary and sufficient conditions for a composition operator to be bounded and compact has attracted much attention. The resolution of the boundedness and compactness of composition operators on Hardy and Bergman spaces on the unit disc
![]() $\mathbb {D}$
is a classical result in holomorphic function theory, treated by Shapiro in [Reference Shapiro9]. Since then, many other seminal works have provided characterisations of the holomorphic self maps
$\mathbb {D}$
is a classical result in holomorphic function theory, treated by Shapiro in [Reference Shapiro9]. Since then, many other seminal works have provided characterisations of the holomorphic self maps
![]() $\varphi :\mathbb {D}\to \mathbb {D}$
that induce a bounded composition operator. For instance, Pau and Perez [Reference Pau and Perez8, Theorem 3.1] gave necessary and sufficient conditions for both continuity and compactness of the composition operator on Dirichlet-type spaces. They used the Nevanlinna and generalised Nevanlinna counting functions to obtain these exceptional results. Their characterisation is obtained for specific exponents of the radial weight and not for all positive exponents.
$\varphi :\mathbb {D}\to \mathbb {D}$
that induce a bounded composition operator. For instance, Pau and Perez [Reference Pau and Perez8, Theorem 3.1] gave necessary and sufficient conditions for both continuity and compactness of the composition operator on Dirichlet-type spaces. They used the Nevanlinna and generalised Nevanlinna counting functions to obtain these exceptional results. Their characterisation is obtained for specific exponents of the radial weight and not for all positive exponents.
Compared with [Reference Pau and Perez8], we will not make use of such tools and we will follow a completely different and somewhat novel approach that combines results from multidimensional cases, namely the bi-disc case. The work of Kosinski [Reference Kosinski6] and Bayart [Reference Bayart2] dealt with the boundedness of composition operators in weighted Bergman spaces on the bi-disc and provided characterisations of symbols that induce bounded composition operators. We will provide only a sufficient condition, which works for all positive exponents of the radial weight of the Dirichlet space.
We exploit these multidimensional results to obtain bounded composition operators for the unit disc case. In particular, we give a sufficient condition for some symbols
![]() $\varphi $
to induce a bounded composition operator for the Dirichlet spaces
$\varphi $
to induce a bounded composition operator for the Dirichlet spaces
![]() $\mathcal {D}_p(\mathbb {D}), p>0,$
by applying one of the main results presented in [Reference Kosinski6], namely the rank sufficiency theorem for the weighted Bergman space on the bi-disc. Our approach can be described in a short manner as follows. Considering some holomorphic self map
$\mathcal {D}_p(\mathbb {D}), p>0,$
by applying one of the main results presented in [Reference Kosinski6], namely the rank sufficiency theorem for the weighted Bergman space on the bi-disc. Our approach can be described in a short manner as follows. Considering some holomorphic self map
![]() $\varphi $
of the unit disc, which is of class
$\varphi $
of the unit disc, which is of class
![]() $\mathcal {C}^1$
on the boundary of the disc
$\mathcal {C}^1$
on the boundary of the disc
![]() $\mathbb {T}$
, we induce a composition operator
$\mathbb {T}$
, we induce a composition operator
![]() $C_{\Psi }$
which is continuous on the weighted Bergman space
$C_{\Psi }$
which is continuous on the weighted Bergman space
![]() $A^p_{\beta }(\mathbb {D}^2)$
of the bi-disc, where
$A^p_{\beta }(\mathbb {D}^2)$
of the bi-disc, where
![]() $\Psi $
will be defined in terms of
$\Psi $
will be defined in terms of
![]() $\varphi .$
Then, by using the lift operator that we introduce in Section 2 and a recent double integral characterisation of the Dirichlet-type space
$\varphi .$
Then, by using the lift operator that we introduce in Section 2 and a recent double integral characterisation of the Dirichlet-type space
![]() $\mathcal {D}_p(\mathbb {D})$
that can be found in [Reference Balooch and Wu1], we give a sufficient condition for the composition operator
$\mathcal {D}_p(\mathbb {D})$
that can be found in [Reference Balooch and Wu1], we give a sufficient condition for the composition operator
![]() $C_{\varphi }$
to be bounded on
$C_{\varphi }$
to be bounded on
![]() $\mathcal {D}_p(\mathbb {D}).$
$\mathcal {D}_p(\mathbb {D}).$
2. Notation and tools
Throughout this note, we will denote by
![]() $\mathcal {O}(\mathbb {D},\mathbb {D})\cap \mathcal {C}^1(\overline {\mathbb {D}})$
the holomorphic self maps of the unit disc that are of class
$\mathcal {O}(\mathbb {D},\mathbb {D})\cap \mathcal {C}^1(\overline {\mathbb {D}})$
the holomorphic self maps of the unit disc that are of class
![]() $\mathcal {C}^1$
on the boundary. In the same notation, by replacing
$\mathcal {C}^1$
on the boundary. In the same notation, by replacing
![]() $\mathbb {D}$
with
$\mathbb {D}$
with
![]() $\mathbb {D}^2$
, we will talk about the holomorphic self maps of the bi-disc that are of class
$\mathbb {D}^2$
, we will talk about the holomorphic self maps of the bi-disc that are of class
![]() $\mathcal {C}^1$
at the (topological) boundary of the bi-disc, the bi-torus
$\mathcal {C}^1$
at the (topological) boundary of the bi-disc, the bi-torus
![]() $\mathbb {T}^2$
. Whenever we refer to a holomorphic function on the disc, we will simply write
$\mathbb {T}^2$
. Whenever we refer to a holomorphic function on the disc, we will simply write
![]() $f\in H(\mathbb {D}).$
Whenever the notation
$f\in H(\mathbb {D}).$
Whenever the notation
![]() $a\asymp b$
appears, it means that there exist two positive constants
$a\asymp b$
appears, it means that there exist two positive constants
![]() $C_1,C_2$
such that
$C_1,C_2$
such that
![]() $C_1a\leq b\leq C_2 a$
and whenever we encounter the notation
$C_1a\leq b\leq C_2 a$
and whenever we encounter the notation
![]() $a\lesssim b,$
it means that there is a positive constant
$a\lesssim b,$
it means that there is a positive constant
![]() $C>0$
such that
$C>0$
such that
![]() $a\leq Cb.$
We recall that for
$a\leq Cb.$
We recall that for
![]() $p>0$
, the Dirichlet type space of the unit disc, denoted by
$p>0$
, the Dirichlet type space of the unit disc, denoted by
![]() $\mathcal {D}_p(\mathbb {D}),$
consists of the holomorphic functions f on the unit disc
$\mathcal {D}_p(\mathbb {D}),$
consists of the holomorphic functions f on the unit disc
![]() $\mathbb {D},$
such that
$\mathbb {D},$
such that
By
![]() $A_{\beta }^p(\mathbb {D}^2)$
,
$A_{\beta }^p(\mathbb {D}^2)$
,
![]() $\beta \ge -1,$
we denote the classical weighted Bergman space of the bi-disc
$\beta \ge -1,$
we denote the classical weighted Bergman space of the bi-disc
![]() $\mathbb {D}^2,$
comprising the holomorphic functions on the bi-disc such that
$\mathbb {D}^2,$
comprising the holomorphic functions on the bi-disc such that
The measure
![]() $dA(z)={\pi }^{-1}\,dx\,dy$
is the normalised Lebesgue measure on the unit disc, while
$dA(z)={\pi }^{-1}\,dx\,dy$
is the normalised Lebesgue measure on the unit disc, while
![]() $dA_{\beta }(z)=c_{\beta }(1-|z|^2)^{\beta }\,dA(z)$
for
$dA_{\beta }(z)=c_{\beta }(1-|z|^2)^{\beta }\,dA(z)$
for
![]() $\beta \ge -1.$
The following recent result of Balooch and Wu [Reference Balooch and Wu1] will be of critical importance in our note.
$\beta \ge -1.$
The following recent result of Balooch and Wu [Reference Balooch and Wu1] will be of critical importance in our note.
Theorem 2.1. Let
![]() $\sigma , \tau \ge -1 $
and
$\sigma , \tau \ge -1 $
and
![]() $\beta \in \mathbb {R},$
with
$\beta \in \mathbb {R},$
with
![]() $\tfrac 12\max (\sigma ,\tau )-1<\beta \leq \tfrac 12 (\sigma +\tau ).$
Let
$\tfrac 12\max (\sigma ,\tau )-1<\beta \leq \tfrac 12 (\sigma +\tau ).$
Let
![]() $f\in H(\mathbb {D}).$
Then
$f\in H(\mathbb {D}).$
Then
 $$ \begin{align*}\int_{\mathbb{D}}\int_{\mathbb{D}}\frac{|f(z)-f(w)|^2}{|1-\overline{w}z|^{2(\beta+2)}}\,dA_{\sigma}(z)\,dA_{\tau}(w)\asymp ||f||^2_{\mathcal{D}_{\sigma+\tau-2\beta}(\mathbb{D})}.\end{align*} $$
$$ \begin{align*}\int_{\mathbb{D}}\int_{\mathbb{D}}\frac{|f(z)-f(w)|^2}{|1-\overline{w}z|^{2(\beta+2)}}\,dA_{\sigma}(z)\,dA_{\tau}(w)\asymp ||f||^2_{\mathcal{D}_{\sigma+\tau-2\beta}(\mathbb{D})}.\end{align*} $$
We now define a lift-type operator, similarly to [Reference Li, Wulan, Zhao and Zhu7], but with an exponent of two positive parameters
![]() $p,\gamma>0$
.
$p,\gamma>0$
.
Definition 2.2. Let
![]() $p,\gamma>0$
and
$p,\gamma>0$
and
![]() $f\in H(\mathbb {D}).$
The lift-type operator is defined by
$f\in H(\mathbb {D}).$
The lift-type operator is defined by
The first observation that one makes immediately is that the fraction that defines this operator appears in the characterisation of the Dirichlet-type spaces. The following proposition follows immediately.
Proposition 2.3. Let
![]() $f\in H(\mathbb {D})$
,
$f\in H(\mathbb {D})$
,
![]() $\sigma =\tau> -1$
and
$\sigma =\tau> -1$
and
![]() $\beta $
as in Theorem 2.1. The operator
$\beta $
as in Theorem 2.1. The operator
![]() $L^{2,2(\beta +2)}(f)$
maps
$L^{2,2(\beta +2)}(f)$
maps
![]() $\mathcal {D}_{2\sigma -2\beta }(\mathbb {D})$
into
$\mathcal {D}_{2\sigma -2\beta }(\mathbb {D})$
into
![]() $A^2_{\sigma }(\mathbb {D}^2).$
$A^2_{\sigma }(\mathbb {D}^2).$
Proof. The proof follows by a simple use of the asymptotic equality of Theorem 2.1 but we will write it down for convenience.
 $$ \begin{align*} ||L^{2,2(\beta+2)}(f)||^2_{A^2_{\sigma}(\mathbb{D}^2)}&=\int_{\mathbb{D}}\int_{\mathbb{D}}|L^{2,2(\beta+2)}(f)(z,w)|^2\,dA_{\sigma}(z)dA_{\sigma}(w) \\ &=\int_{\mathbb{D}}\int_{\mathbb{D}}\bigg|\frac{f(z)-f(w)}{(1-\overline{w}z)^{{2(\beta+2)}/{2}}}\bigg|^2\,dA_{\sigma}(z)dA_{\sigma}(w) \\ &\lesssim ||f||^2_{\mathcal{D}_{2\sigma-2\beta}(\mathbb{D})}.\\[-35pt] \end{align*} $$
$$ \begin{align*} ||L^{2,2(\beta+2)}(f)||^2_{A^2_{\sigma}(\mathbb{D}^2)}&=\int_{\mathbb{D}}\int_{\mathbb{D}}|L^{2,2(\beta+2)}(f)(z,w)|^2\,dA_{\sigma}(z)dA_{\sigma}(w) \\ &=\int_{\mathbb{D}}\int_{\mathbb{D}}\bigg|\frac{f(z)-f(w)}{(1-\overline{w}z)^{{2(\beta+2)}/{2}}}\bigg|^2\,dA_{\sigma}(z)dA_{\sigma}(w) \\ &\lesssim ||f||^2_{\mathcal{D}_{2\sigma-2\beta}(\mathbb{D})}.\\[-35pt] \end{align*} $$
The next theorem is a characterisation of the symbols
![]() $\Psi \in \mathcal {O}(\mathbb {D}^2,\mathbb {D}^2)\cap \mathcal {C}^1(\overline {\mathbb {D}^2})$
that induce a bounded composition operator on the weighted Bergman space
$\Psi \in \mathcal {O}(\mathbb {D}^2,\mathbb {D}^2)\cap \mathcal {C}^1(\overline {\mathbb {D}^2})$
that induce a bounded composition operator on the weighted Bergman space
![]() $A_{\beta }^2(\mathbb {D}^2)$
,
$A_{\beta }^2(\mathbb {D}^2)$
,
![]() $\beta>-1$
.
$\beta>-1$
.
Theorem 2.4 [Reference Kosinski6, Section 1, page 3]
Let
![]() $\Psi \in \mathcal {O}(\mathbb {D}^2,\mathbb {D}^2)\cap \mathcal {C}^1(\overline {\mathbb {D}^2}). $
Then the composition operator
$\Psi \in \mathcal {O}(\mathbb {D}^2,\mathbb {D}^2)\cap \mathcal {C}^1(\overline {\mathbb {D}^2}). $
Then the composition operator
![]() $C_{\Psi }:A_{\beta }^2(\mathbb {D}^2)\to A_{\beta }^2(\mathbb {D}^2)$
is bounded if and only if the derivative
$C_{\Psi }:A_{\beta }^2(\mathbb {D}^2)\to A_{\beta }^2(\mathbb {D}^2)$
is bounded if and only if the derivative
![]() $d_{\zeta }\Psi $
is invertible for all
$d_{\zeta }\Psi $
is invertible for all
![]() $\zeta \in \mathbb {T}^2$
with
$\zeta \in \mathbb {T}^2$
with
![]() $\Psi (\zeta )\in \mathbb {T}^2.$
$\Psi (\zeta )\in \mathbb {T}^2.$
Using this result, we can deduce the following lemma.
Lemma 2.5. Let
![]() $\varphi \in \mathcal {O}(\mathbb {D},\mathbb {D})\cap \mathcal {C}^1(\overline {\mathbb {D}}).$
Set
$\varphi \in \mathcal {O}(\mathbb {D},\mathbb {D})\cap \mathcal {C}^1(\overline {\mathbb {D}}).$
Set
![]() $\Phi (z_1,z_2)=(\varphi (z_1),\varphi (z_2)),z_1,z_2 \in \mathbb {D}.$
Then
$\Phi (z_1,z_2)=(\varphi (z_1),\varphi (z_2)),z_1,z_2 \in \mathbb {D}.$
Then
![]() $C_{\Phi }:A_{\beta }^2(\mathbb {D}^2)\to A_{\beta }^2(\mathbb {D}^2)$
is bounded.
$C_{\Phi }:A_{\beta }^2(\mathbb {D}^2)\to A_{\beta }^2(\mathbb {D}^2)$
is bounded.
Proof. It is quite obvious that
![]() $\Phi \in \mathcal {O}(\mathbb {D}^2,\mathbb {D}^2)\cap \mathcal {C}^1(\overline {\mathbb {D}^2}). $
We only have to show that the derivative
$\Phi \in \mathcal {O}(\mathbb {D}^2,\mathbb {D}^2)\cap \mathcal {C}^1(\overline {\mathbb {D}^2}). $
We only have to show that the derivative
![]() $d_{\zeta }\Phi $
is invertible for every
$d_{\zeta }\Phi $
is invertible for every
![]() $\zeta \in \mathbb {T}^2$
such that
$\zeta \in \mathbb {T}^2$
such that
![]() $\Phi (\zeta )\in \mathbb {T}^2$
. Let
$\Phi (\zeta )\in \mathbb {T}^2$
. Let
![]() ${\zeta =(\zeta _1,\zeta _2)}$
be such that
${\zeta =(\zeta _1,\zeta _2)}$
be such that
![]() $\Phi (\zeta _1,\zeta _2)=(\varphi (\zeta _1),\varphi (\zeta _2))\in \mathbb {T}^2.$
Of course, this only occurs for the points
$\Phi (\zeta _1,\zeta _2)=(\varphi (\zeta _1),\varphi (\zeta _2))\in \mathbb {T}^2.$
Of course, this only occurs for the points
![]() $\zeta _1,\zeta _2\in \mathbb {T}$
such that
$\zeta _1,\zeta _2\in \mathbb {T}$
such that
![]() $\varphi (\zeta _1),\varphi (\zeta _2)\in \mathbb {T},\zeta _1\neq \zeta _2.$
We calculate the Jacobian of the derivative
$\varphi (\zeta _1),\varphi (\zeta _2)\in \mathbb {T},\zeta _1\neq \zeta _2.$
We calculate the Jacobian of the derivative
![]() $d_{\zeta }\Phi $
for such points
$d_{\zeta }\Phi $
for such points
![]() $\zeta \in \mathbb {T}^2$
. It is an immediate observation that
$\zeta \in \mathbb {T}^2$
. It is an immediate observation that
So the Jacobian is
By the fact that
![]() $\varphi $
is of class
$\varphi $
is of class
![]() $\mathcal {C}^1$
, and hence continuous on the boundary, one can calculate the value of
$\mathcal {C}^1$
, and hence continuous on the boundary, one can calculate the value of
![]() $\varphi '$
at the boundary points
$\varphi '$
at the boundary points
![]() $\zeta _1,\zeta _2$
. By the Julia–Caratheodory theorem (see [Reference Caratheodory3]), it follows that the value of the derivative of
$\zeta _1,\zeta _2$
. By the Julia–Caratheodory theorem (see [Reference Caratheodory3]), it follows that the value of the derivative of
![]() $\varphi $
is nonzero. Hence, by Theorem 2.4,
$\varphi $
is nonzero. Hence, by Theorem 2.4,
![]() $C_{\Phi }$
defines a bounded composition operator on the weighted Bergman space
$C_{\Phi }$
defines a bounded composition operator on the weighted Bergman space
![]() $A_{\beta }^2(\mathbb {D}^2)$
and the proof is complete.
$A_{\beta }^2(\mathbb {D}^2)$
and the proof is complete.
3. Main result and proof
Here we state our main result and the proof of it. For what follows, we define
 $$ \begin{align*}k^{\varphi}(z,w)=\frac{1-\varphi(z)\overline{\varphi(w)}}{1-z\overline{w}}, \quad z,w\in \mathbb{D},\end{align*} $$
$$ \begin{align*}k^{\varphi}(z,w)=\frac{1-\varphi(z)\overline{\varphi(w)}}{1-z\overline{w}}, \quad z,w\in \mathbb{D},\end{align*} $$
for a function
![]() $\varphi \in \mathcal {O}(\mathbb {D},\mathbb {D})\cap \mathcal {C}^1(\overline {\mathbb {D}}),$
and denote by
$\varphi \in \mathcal {O}(\mathbb {D},\mathbb {D})\cap \mathcal {C}^1(\overline {\mathbb {D}}),$
and denote by
![]() $||\cdot ||_{\infty }$
the supremum norm over the bi-disc
$||\cdot ||_{\infty }$
the supremum norm over the bi-disc
![]() $\mathbb {D}^2,$
that is,
$\mathbb {D}^2,$
that is,
![]() $||k||_{\infty }=\sup _{(z,w)\in \mathbb {D}^2}|k(z,w)|$
.
$||k||_{\infty }=\sup _{(z,w)\in \mathbb {D}^2}|k(z,w)|$
.
Theorem 3.1. Let
![]() $\varphi \in \mathcal {O}(\mathbb {D},\mathbb {D})\cap \mathcal {C}^1(\overline {\mathbb {D}})$
such that
$\varphi \in \mathcal {O}(\mathbb {D},\mathbb {D})\cap \mathcal {C}^1(\overline {\mathbb {D}})$
such that
![]() $||k^{\varphi }(z,w)||_{\infty }<+\infty .$
Then the composition operator
$||k^{\varphi }(z,w)||_{\infty }<+\infty .$
Then the composition operator
![]() $C_{\varphi }:\mathcal {D}_p(\mathbb {D})\to \mathcal {D}_p(\mathbb {D})$
is bounded for
$C_{\varphi }:\mathcal {D}_p(\mathbb {D})\to \mathcal {D}_p(\mathbb {D})$
is bounded for
![]() $p=2\sigma -2\beta ,$
where
$p=2\sigma -2\beta ,$
where
![]() $\sigma>0$
and
$\sigma>0$
and
![]() $\tfrac 12\sigma -1<\beta <\sigma $
.
$\tfrac 12\sigma -1<\beta <\sigma $
.
Proof. Let
![]() $\sigma>0$
and
$\sigma>0$
and
![]() $\beta \in \mathbb {R}$
satisfy the conditions that we gave in our statement. For convenience, set
$\beta \in \mathbb {R}$
satisfy the conditions that we gave in our statement. For convenience, set
![]() $q=2(\beta +2).$
Then
$q=2(\beta +2).$
Then
 $$ \begin{align*} ||C_{\varphi}(f)||^2_{\mathcal{D}_{2\sigma-2\beta}(\mathbb{D})}&\asymp \int_{\mathbb{D}}\int_{\mathbb{D}}\frac{|f\circ\varphi(z)-f\circ \varphi(w)|^2}{|1-\overline{w}z|^{q}}\,dA_{\sigma}(z)\,dA_{\sigma}(w) \\ &=\int_{\mathbb{D}}\int_{\mathbb{D}}\frac{|f\circ\varphi(z)-f\circ \varphi(w)|^2}{|1-\overline{\varphi(w)}\varphi(z)|^{q}}\frac{|1-\overline{\varphi(w)}\varphi(z)|^{q}}{|1-\overline{w}z|^{q}}\,dA_{\sigma}(z)\,dA_{\sigma}(w) \\ &\leq \sup_{(z,w)\in \mathbb{D}^2}|k^{\varphi}(z,w)|^{q}\int_{\mathbb{D}}\int_{\mathbb{D}}\frac{|f\circ\varphi(z)-f\circ \varphi(w)|^2}{|1-\overline{\varphi(w)}\varphi(z)|^{q}}\,dA_{\sigma}(z)\,dA_{\sigma}(w). \end{align*} $$
$$ \begin{align*} ||C_{\varphi}(f)||^2_{\mathcal{D}_{2\sigma-2\beta}(\mathbb{D})}&\asymp \int_{\mathbb{D}}\int_{\mathbb{D}}\frac{|f\circ\varphi(z)-f\circ \varphi(w)|^2}{|1-\overline{w}z|^{q}}\,dA_{\sigma}(z)\,dA_{\sigma}(w) \\ &=\int_{\mathbb{D}}\int_{\mathbb{D}}\frac{|f\circ\varphi(z)-f\circ \varphi(w)|^2}{|1-\overline{\varphi(w)}\varphi(z)|^{q}}\frac{|1-\overline{\varphi(w)}\varphi(z)|^{q}}{|1-\overline{w}z|^{q}}\,dA_{\sigma}(z)\,dA_{\sigma}(w) \\ &\leq \sup_{(z,w)\in \mathbb{D}^2}|k^{\varphi}(z,w)|^{q}\int_{\mathbb{D}}\int_{\mathbb{D}}\frac{|f\circ\varphi(z)-f\circ \varphi(w)|^2}{|1-\overline{\varphi(w)}\varphi(z)|^{q}}\,dA_{\sigma}(z)\,dA_{\sigma}(w). \end{align*} $$
At this point, we observe that the integral on the right-hand side can be expressed as the norm of a composition operator
![]() $C_{\Phi }$
on the weighted Bergman space
$C_{\Phi }$
on the weighted Bergman space
![]() $A_{\sigma }^2(\mathbb {D}^2),$
where
$A_{\sigma }^2(\mathbb {D}^2),$
where
![]() $\Phi =\Phi (z_1,z_2)=(\varphi (z_1),\varphi (z_2)),z_1,z_2\in \mathbb {D}.$
To be precise,
$\Phi =\Phi (z_1,z_2)=(\varphi (z_1),\varphi (z_2)),z_1,z_2\in \mathbb {D}.$
To be precise,
 $$ \begin{align*}\int_{\mathbb{D}}\int_{\mathbb{D}}\frac{|f\circ\varphi(z)-f\circ \varphi(w)|^2}{|1-\overline{\varphi(w)}\varphi(z)|^{2(\beta+2)}}\,dA_{\sigma}(z)\,dA_{\sigma}(w)=||C_{\Phi}(L^{2,2(\beta+2)}(f))||^2_{A^2_{\sigma}(\mathbb{D}^2)}.\end{align*} $$
$$ \begin{align*}\int_{\mathbb{D}}\int_{\mathbb{D}}\frac{|f\circ\varphi(z)-f\circ \varphi(w)|^2}{|1-\overline{\varphi(w)}\varphi(z)|^{2(\beta+2)}}\,dA_{\sigma}(z)\,dA_{\sigma}(w)=||C_{\Phi}(L^{2,2(\beta+2)}(f))||^2_{A^2_{\sigma}(\mathbb{D}^2)}.\end{align*} $$
By Lemma 2.5,
![]() $C_\Phi :A^2_{\sigma }(\mathbb {D}^2)\to A^2_{\sigma }(\mathbb {D}^2)$
is bounded. Hence, by Proposition 2.3,
$C_\Phi :A^2_{\sigma }(\mathbb {D}^2)\to A^2_{\sigma }(\mathbb {D}^2)$
is bounded. Hence, by Proposition 2.3,
Summarising,
which, by our assumption that the supremum is bounded, gives the desired result.
4. Concluding remark
The significance of the main result of this note lies mainly in the fact that we managed to apply results for the bi-disc to the case of the unit disc. Another interesting aspect of the result is the appearance of the De Branges–Rovnyak kernel
![]() $k^\varphi $
that is induced by the symbol
$k^\varphi $
that is induced by the symbol
![]() $\varphi .$
Assuming that
$\varphi .$
Assuming that
![]() $\varphi \in \mathcal {O}(\mathbb {D},\mathbb {D})\cap \mathcal {C}^1(\overline {\mathbb {D}}),$
then it is known that
$\varphi \in \mathcal {O}(\mathbb {D},\mathbb {D})\cap \mathcal {C}^1(\overline {\mathbb {D}}),$
then it is known that
![]() $\varphi \in H^{\infty }(\mathbb {D})$
and also
$\varphi \in H^{\infty }(\mathbb {D})$
and also
![]() $||\varphi ||_{H^{\infty }(\mathbb {D})}\leq 1$
which means that the function
$||\varphi ||_{H^{\infty }(\mathbb {D})}\leq 1$
which means that the function
 $$ \begin{align*}k^{\varphi}(z,w)=\frac{1-\varphi(z)\overline{\varphi(w)}}{1-z\overline{w}},\quad z,w\in \mathbb{D}\end{align*} $$
$$ \begin{align*}k^{\varphi}(z,w)=\frac{1-\varphi(z)\overline{\varphi(w)}}{1-z\overline{w}},\quad z,w\in \mathbb{D}\end{align*} $$
is the De Branges–Rovnyak reproducing kernel associated with
![]() $\varphi .$
We can reformulate the main result of the note in the following manner.
$\varphi .$
We can reformulate the main result of the note in the following manner.
Corollary 4.1. Let
![]() $\varphi \in \mathcal {O}(\mathbb {D},\mathbb {D})\cap \mathcal {C}^1(\overline {\mathbb {D}})$
and assume that
$\varphi \in \mathcal {O}(\mathbb {D},\mathbb {D})\cap \mathcal {C}^1(\overline {\mathbb {D}})$
and assume that
![]() $|k^{\varphi }|$
is a bounded function on the bi-disc. Then, the composition operator
$|k^{\varphi }|$
is a bounded function on the bi-disc. Then, the composition operator
![]() $C_{\varphi }:\mathcal {D}_p(\mathbb {D})\to \mathcal {D}_p(\mathbb {D}), p>0, $
is bounded.
$C_{\varphi }:\mathcal {D}_p(\mathbb {D})\to \mathcal {D}_p(\mathbb {D}), p>0, $
is bounded.
For more details about the De Branges–Rovnyak spaces and kernel, see [Reference de Branges and Rovnyak4]. Also, in the work of Jury (see [Reference Jury5]), one can study the connections of the De Branges–Rovnyak kernel associated to a holomorphic self map of the unit disc, and the corresponding composition operators in the Hardy and Bergman spaces of the unit disc and also of the unit ball of
![]() $\mathbb {C}^n.$
$\mathbb {C}^n.$
Acknowledgements
The author would like to thank the following people: Prof. Łukasz Kosinski for his valuable help; Dr. D. Vavitsas, Dr. A. Kouroupis and A. Tsiri for their friendship; and his family for their support. Also, the author would like to thank the anonymous referee for the useful comments and the careful reading of the paper.