1. Introduction
It is well known that automobiles emit harmful pollutants and that exposure to air pollution substantially harms public health. A World Health Organization (WHO) study estimated that urban air pollution accounts for 6.4 million years of life lost annually worldwide (Cohen et al., Reference Cohen, Anderson, Ostro, Ezzati, Lopez, Rodgers and Christopher2004). Besides air pollution, traffic congestion caused by the wide use of automobiles also has negative effects on public welfare. To reduce the congestion and air pollution caused by automobiles, metropolitan areas worldwide are investing heavily in building or extending urban rail transit systems. Whether congestion and pollution can be reduced through such projects depends on which travel modes commuters reduce when they use more rail transit. This remains an open question in practice.
This study investigates the change in transportation mode usage in Beijing, a megacity unique in the speed of its subway development. With a US$30bn (200bn Chinese Yuan) investment in building new subway lines, Beijing's subway system grew from a small system with 39 stations in 2002 to more than 300 stations by 2014. The rollout of new subway lines creates a series of contrasts between commuters who experienced rail accessibility improvements and those that did not. In this paper, this rollout is utilized to estimate, ex post, how the completion of new rail transit lines affected the kilometers traveled by rail transit, autos, buses, and walking and bicycling, respectively.
Investment in commuter rail transit is a worldwide phenomenon, driven by a belief in its benefits, including less congestion, less air pollution and improved labor market access for the poor (Kain, Reference Kain1968; Vickrey, Reference Vickrey1969; Chen and Whalley, Reference Chen and Whalley2012). Transit authorities believe that the benefit is large; hence, the investment in rail transit is large (Cervero, Reference Cervero1998). For the same reason, passenger fares for public transportation are usually heavily subsidized (Kenworthy and Laube, Reference Kenworthy and Laube2001; Parry and Small, Reference Parry and Small2009). However, some researchers argue that the cost of building and maintaining new transit is higher than the measured benefit, and point out that the optimistic view of the rail transit benefit was based partially on an overestimation of ridership (Gordon and Willson, Reference Gordon and Willson1984; Allport and Thomson, Reference Allport and Thomson1990; Kain, Reference Kain1990, Reference Kain1992, Reference Kain1997; Pickrell, Reference Pickrell1992).
Besides the unsettled question concerning rail ridership, another equally important question is from which alternative travel modes rail transit riders are diverted. The rail benefit will be higher if rail transit ridership comes at the expense of more polluting modes of transportation such as automobiles, rather than less polluting modes such as bicycles. Besides traffic diversion effects, investments in rail transit may also create traffic by inducing demand for travel (Vickrey, Reference Vickrey1969). This study addresses the three questions simultaneously by looking into the changes in distance traveled by various modes and changes in travel quantity.
This paper is the first study to use a (pseudo) panel of individual trips to estimate the ex post effect of rail transit provision on mode usage in the context of a city in the developing world. An estimation of the ex post effect is preferred in terms of causal inference, given the difficulty in predicting the market share of a new rail system by an ex ante study (McFadden et al., Reference McFadden and Talvitie1977; Train, Reference Train1978). Discrete choice models, widely used in the travel mode choice literature,Footnote 1 require accurately constructing the attributes of alternatives, especially the alternative specific constants. Inaccurate construction of the alternatives tends to result in inaccurate prediction. In this study, households are observed before and after the coverage changes, taking advantage of three rounds of detailed individual travel diaries in Beijing, with new subway lines completed between the rounds. Households that are affected and those that are not affected are also observed. This is possible because the rail expansion improved accessibility for the households residing along the new lines, but not for the rest. The main estimation strategy is the differences-in-differences (DID) method. The double differencing removes two types of biases (Imbens and Wooldridge, Reference Imbens and Wooldridge2009). One bias comes from the comparison between the treatment group and the control group, which could be the result of permanent differences between these groups. People who prefer rail transit tend to choose to live in areas near rail stations. Cross-sectional studies (Gordon and Willson, Reference Gordon and Willson1984; Kain and Liu, Reference Kain, Liu, Glaeser and Meyer1994; Wardman, Reference Wardman1997; Winston and Shirley, Reference Winston and Shirley1998; Petitte, Reference Petitte2001) comparing commuters in nearby areas to those in farther areas usually suffer from this self-selection bias. The other bias comes from the comparison over time, which could be the result of time trends unrelated to the treatment. Macro-economic shocks and transport policies can be the sources of such bias, from which time-series studies (Gaudry, Reference Gaudry1975; Greene, Reference Greene1992; Gomez-Ibanez, 1996) tend to suffer.
To address the cross-area externality, which may dampen the validity of the DID method, the indirect effects of rail expansion are estimated as well. The cross-area externality comes from the fact that the areas without subway expansion can benefit from congestion alleviation when commuters in the affected area travel more by subway and less by automobile. Using rich information on individual trips, a measure of the intensity of spillover from affected areas is constructed. By including the spillover intensity in the regressions, the cross-area externality is estimated and the bias caused by the externality is removed.
This paper also differs from previous literature in the following two ways. First, this paper defines a continuous dependent variable, which is unusual in previous individual data studies.Footnote 2 This continuous definition, the percentage distance traveled by each mode in an individual trip, avoids the arbitrary definition of the main mode when a trip involves more than one mode, which is almost always the case in practice. Secondly, this study takes advantage of the higher frequency of the data – an annual survey as opposed to studies based on decadal census data – to alleviate the self-selection bias caused by migration. Baum-Snow and Kahn (Reference Baum-Snow and Kahn2000) used aggregate data at the census tract level with data points 10 years apart, thus accounting for migration with a predetermined migration rate. While built upon their research design, this paper uses very different data, and the short time frame limits the bias caused by migration. This potential source of endogeneity is tested in a later section.
The central result shows that rail transit usage doubled, on average, for commuters who experienced the improvement in rail transit accessibility, compared to the commuters who did not experience such improvement. Auto usage significantly decreased, by 16 per cent, while the impact on bus usage was small and not statistically significant, indicating that the new subway lines in this study diverted auto users instead of bus passengers. The results also show that the spillover effects of subway expansion are not large enough (yet) to affect the travel behavior of commuters residing in the areas without the rail transit accessibility improvement. Furthermore, this paper finds that changes in auto usage and rail transit usage vary with distance to the nearest rail station, traffic infrastructure conditions, and commuters’ auto ownership and income. Finally, this paper examines the effect of transit expansion on travel quantity, and finds that neither the number of commute work trips nor their length increased, indicating that little additional travel is induced by the subway expansion.
The remainder of the paper is organized as follows. Section 2 describes the data. Section 3 describes the empirical estimation strategy, presents the results on the effects on distance traveled by various modes, and investigates heterogeneities in the treatment and treatment effects. Section 4 studies the effects on travel quantity. Section 5 concludes.
2. Data
This study uses travel diary data from 2007, 2008 and 2009, covering periods before and after the opening of line 5, line 8 and line 10, as shown in figure 1. Line 5, opened in October 2007, goes north and south. It runs for 28 km and has 23 stations. Lines 8 and 10, opened in July 2008, go from west to east and then turn south. They run for 29 km and have 26 stations. There are two reasons why the three lines are of particular interest. One reason is that these three lines go in different directions and cover wide areas which are geographically representative. Beijing's development is based on the expansion of ring roads, all centered at Tiananmen Square. Residential areas within the inner rings tend to be wealthier. As shown in figure 2, lines 5, 8 and 10 cut vertically and horizontally across several rings. Therefore, the areas covered by these three lines are representative of different income levels. The other reason is that these three lines operate mainly within urban Beijing, an area that is highly populated and developed. Restricted by the land available for new housing projects, the migration rate in this area is relatively low. Renters can migrate without new housing projects, but this is limited by the supply in rental markets. Therefore, the self-selective bias is limited. This hypothesis is tested indirectly in a later section.

Figure 1. Beijing subway system expansion history and 2015 plan

Figure 2. Map of Beijing and subway lines 5, 8, and 10
The travel diary data are from the Beijing Household Travel Survey (BHTS) done by the Beijing Transportation Center (BTC) every year since the 1980s. In each of the eight urban districts, households are randomly selected, stratified by traffic analysis zone (TAZ). TAZs are geocoded areas, divided by the BTC for the purpose of traffic analysis. Each administrative district has 16–238 TAZs, based on the size of the area and the population of a district. In each TAZ, about 25 households are randomly selected for interviews in person to collect data on trips taken during a designated 24-hour period. In this paper, the sample is restricted to the 71 TAZs that are surveyed in all three years, which is referred to as the TAZ panel. This restriction is to ensure the comparability of the commuters across years, because the data are repeatedly cross-sectional at the commuter level, although they are panel data at the TAZ level.
The survey gathers: (1) information about each segment of a trip taken during the household's travel day, including travel purpose (e.g., going to work, shopping, transferringFootnote 3 ), travel mode (e.g., auto, bus, subway), travel distance, time when the travel began and ended and the TAZ code of the origin and the destination; (2) household information, including the TAZ code of the residence, vehicle ownership and monthly household income (levels 1–8); and (3) household member information, including gender, age, occupation, possession of a driver's license, and the TAZ code of the school (if a student) or the place of work (if an employee). Fourteen modes in the surveys are aggregated into four broader categories: (1) subway; (2) bus (including regular bus, minibus and shuttle); (3) auto (including driving/riding in a private/company auto, and taxi); and (4) walking and bicycling.
To measure the improvement in rail transit accessibility, each TAZ's proximity to rail transit is calculated in 2007, 2008 and 2009, using the digital map of TAZs from the BTC and the map of subway stations from the OpenStreetMap database. The proximity is measured as the distance between a TAZ's centroid and its nearest rail station. All households from the same TAZ are treated as residing at the same point.Footnote 4 This approximation is acceptable, because TAZs in urban Beijing are small. The average area of a TAZ is less than 1.5 km2.
A TAZ is defined as ‘treated’ if its distance to the nearest subway station decreased in 2008 (after the opening of line 5) or 2009 (after the opening of lines 8 and 10). All treated TAZs are referred to as the treatment group, and all untreated TAZs as the control group. There are 31 and 40 TAZs in the two groups, respectively. In the treatment group, 19 TAZs are treated after the first round of surveys, while the other 12 TAZs are not treated until after the first two rounds of surveys. They are referred to as the early treatment group and the late treatment group, respectively.
Focus is placed on work trips, defined to include going to work and going to school, for two reasons. First, most road congestion happens during rush hours. Secondly, decisions about the destination and the travel mode are usually made jointly, especially for trips for which the destinations are easy to change, such as shopping trips. It takes much longer to change the place of work or school. Therefore, the mode choice is isolated from the destination choice by restricting the sample to work trips.
The mode usage of a trip is measured as the percentage distance traveled using that mode.Footnote 5 Therefore, the mode usage of a trip is characterized by four continuous variables (percentage distance by subway, auto, bus, and walking and bicycling). As shown in table 1, the average percentage distance in work trips traveled by auto is around 30 per cent, which is the second largest share, next to the distance by walking and bicycling. Although subway usage is a small share of work trips, the share increased from year to year in the treatment group.
Table 1. Summary statistics

Notes: The summary statistics of the work trips from the balanced sample of TAZs (71 TAZs that are surveyed in all three years) are reported. Mode usage variables are calculated by dividing the reported distances of a mode by the total trip distance, which is the summation of reported distances of all trip segments (variable: reported trip distance). The reported distances could be subject to reporting bias. Therefore, the point-to-point distance between the centroids of the origin and destination TAZs (variable: measured trip distance) is also measured. We see that the two trip distance variables evolve differently. Therefore, to limit the effect of reporting bias on the results, I experiment with an alternative definition of mode usage (the main mode of a trip) in section 3.1. The results remain stable to this alternative definition.
In addition to the mode usage of a work trip, the number of work trips and the trip distance are also of interest. One way to measure trip distance is to add up the reported distances of the trip segments. The reported distance is affected by the choices of routes and travel modes and might be subject to reporting bias. To avoid these confounding factors, the point-to-point distance between the centroids of the origin and destination TAZs is also measured. For all trips traveling within a TAZ, the measured trip distance is zero.
A TAZ which is not treated directly may also be affected by the subway expansion through congestion alleviation. The intensity of the spillover from TAZ i to TAZ j is measured by the number of trips from TAZ i to TAZ j.Footnote 6 Therefore, the complete indirect effect on TAZ j is measured as the summation of the number of trips from all TAZs, and the indirect effect on TAZ j from the treatment is measured as the summation of the number of trips from treated TAZs.
In addition to accessibility of rail transit, mode usage is also influenced by traffic infrastructure characteristics, such as road coverage and number of bus stops. The spatial distribution of roads and bus stops in Beijing is taken from the OpenStreetMap database. Using this information, together with the digital map of TAZs, the road coverage and the number of bus stops for each TAZ are calculated.
Table 1 provides summary statistics of dependent variables (i.e., mode usage for work trips, number of trips and trip distance), variables to measure indirect effects, variables characterizing traffic infrastructure conditions, and demographic variables by group in 2007, 2008 and 2009.
3. Estimation strategies and results
In this section, the effect of the subway expansion on percentage distance traveled by various modes is estimated. The plausibility of some key assumptions is then tested.
3.1. Estimation of the subway expansion effect
Interest is centered primarily on estimating the sample average treatment effect on the treated (SATT) for each mode m, using the DID estimator:
where
![]() $\bar{Y}_{st}^{m}={1\over {N_{st}}}{\mathop \sum \nolimits_{i}} Y_{ist}^{m}$
; s equals 1 for the treatment group, and 0 for the control group; t equals 0 when the observation is before the treatment, and 1 after the treatment. Y
ist
m
is the percentage distance traveled in mode m by commuter i in group s at time t.
$\bar{Y}_{st}^{m}={1\over {N_{st}}}{\mathop \sum \nolimits_{i}} Y_{ist}^{m}$
; s equals 1 for the treatment group, and 0 for the control group; t equals 0 when the observation is before the treatment, and 1 after the treatment. Y
ist
m
is the percentage distance traveled in mode m by commuter i in group s at time t.
In order to reduce the bias potentially introduced by observable differences between residents in the treatment and control groups, a regression-based conditioning strategy is employed. With multiple time periods (three years, including 30 survey dates) and multiple groups (71 TAZs), a natural extension of the two-group-two-time-period model (Imbens and Wooldridge, Reference Imbens and Wooldridge2009) is used.
This regression-based DID estimator will be biased if travel behaviors of the control group are affected by the subway expansion. One potential channel through which an indirect effect could work is traffic congestion alleviation. This could occur if subway expansion diverts autos from the treated area. If so, congestion would be alleviated not only in the treated area, but also in the control area; commuters in the control area would then respond to the improved traffic conditions by driving more. Such cross-area externality is addressed by taking advantage of variation in the intensity of the spillover from the treated areas. The spillover intensity from treated area i to area j is measured, ex ante, as the number of trips from area i to area j.
The average treatment effects of subway expansion on the treated, as well as cross-area treatment externality, is estimated as:
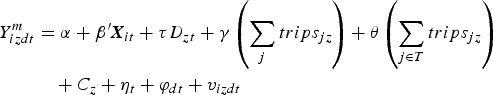 $$\eqalign{Y_{izdt}^{m}&=\alpha+{\bi \beta}'{\bi X}_{it}+\tau D_{zt}+ \gamma\left(\sum_{j}trips_{jz}\right)+\theta\left(\sum_{j\in T}trips_{jz}\right)\cr & \quad + C_z + \eta_t+\varphi_{dt}+v_{izdt}}$$
$$\eqalign{Y_{izdt}^{m}&=\alpha+{\bi \beta}'{\bi X}_{it}+\tau D_{zt}+ \gamma\left(\sum_{j}trips_{jz}\right)+\theta\left(\sum_{j\in T}trips_{jz}\right)\cr & \quad + C_z + \eta_t+\varphi_{dt}+v_{izdt}}$$
where Y
izdt
m
is the percentage distance traveled in mode m by commuter i residing in TAZ z at district d and observed at time t;
X
it
is a vector of observable covariates for commuter i observed at time t; D
zt
is the treatment indicator, which equals 1 if TAZ z is treated at time t, 0 otherwise;
![]() ${\mathop \sum \nolimits_{j}}{trips}_{jz}$
is the total number of trips, scaled by the length of roads in TAZ z, from all TAZs to TAZ z, and
${\mathop \sum \nolimits_{j}}{trips}_{jz}$
is the total number of trips, scaled by the length of roads in TAZ z, from all TAZs to TAZ z, and
![]() ${\mathop \sum \nolimits_{j\in T}}{trips}_{jz}$
is the number of trips from all treated TAZs to TAZ z; c
z
are TAZ dummies; η
t
are time dummies; φ
dt
are district-by-year dummies; and v
izdt
is the residual.
${\mathop \sum \nolimits_{j\in T}}{trips}_{jz}$
is the number of trips from all treated TAZs to TAZ z; c
z
are TAZ dummies; η
t
are time dummies; φ
dt
are district-by-year dummies; and v
izdt
is the residual.
Given the total number of trips from all TAZs to TAZ z, the number of trips from the treated TAZs to TAZ z is exogenous, since the treatment is exogenous to the characteristics of TAZ z.Footnote 7 The parameter τ captures the average effect of the subway expansion on changes in individual-level travel mode usage over time, conditional on variables in X . The parameter θ captures the cross-area treatment externality on the untreated TAZs.
Results are reported in table 2. In column (1), the basic specification, the mode usage is regressed on the treatment indicator, the group indicator and year dummies. The group indicator equals 1 if the commuter is residing in a treated TAZ, 0 otherwise. In column (2), TAZ dummies and survey date dummies are used, which are finer dummies than the group indicator and the year dummies. In the following columns, demographic variables are added in, which are related to mode usage. Extra caution is exercised when including auto ownership in X , because it is influenced by the treatment. When subway accessibility is improved, auto ownership may become less attractive. Therefore, subway expansion affects the mode usage not only directly by diverting commuters, but also indirectly by decreasing the demand for auto ownership. The coefficient of the treatment indicator catches both of the effects when not controlling for auto ownership, while it catches only the direct effect if controlling for auto ownership. In columns (3) and (4), the regression is run without and with auto ownership, respectively. In column (5), the measure of spillover intensities is added in.
Table 2. Effect of subway expansion on mode usage

Notes: Observations are at individual trip level. Only work trips are studied in this paper. The specification in each column is indicated in the lower part of the table. The full results are available in appendix A. Standard errors are clustered at the TAZ level. *, **, *** indicate 10%, 5% and 1% significance level, respectively.
Table 2 shows evidence of a positive and statistically significant effect of the subway expansion on subway usage and a negative and statistically significant effect on auto usage in all five specifications. The effect on bus usage is not statistically significant. The effect on walking and bicycling is statistically significant when controlling for demographic variables. A comparison of columns (3) and (4) shows that the effects remain stable to the control for auto ownership. This indicates that the indirect effect of the subway expansion on mode usage through changing the demand for auto ownership is small. This finding is confirmed by comparing the auto ownership trajectories between the treatment group and the control group. The graphic analysis and the regression results on auto ownership are available upon request.
Column (5) is the full specification and shows the main result. Panel A indicates that a decrease in the distance to the station increased the percentage distance traveled by subway by 0.0273 (from 0.0254 to 0.0527), which is a 107 per cent change. Panel B shows that the percentage distance traveled by auto decreased by 0.0489 (from 0.3031 to 0.2542), which is a 16 per cent change. Panel C shows that the effect on the percentage distance traveled by bus is 0.0189 (from 0.2622 to 0.2433), which is a 7 per cent decrease and not statistically significant. Panel D shows that the percentage distance traveled by walking and bicycling increased by 0.0406 (from 0.409 to 0.4496), which is a 10 per cent increase. These results indicate that the subway expansion diverted commuters from auto towards subway, while having no significant effect on bus passengers. The increase in the walking and bicycling distance indicates that walking and bicycling are complements to subway travel, rather than substitutes. The estimated coefficients of number of trips from the treated are small and not statistically significant. This suggests that the cross-area externality is not large enough within the studied areas and the time span studied to affect the travel behaviors of commuters in the control areas. This finding is consistent with Yang et al. (Reference Yang, Chen, Qin and Lu2015). They investigated the impact of subway expansion in Beijing from 2009 to 2013 on traffic congestion and found that congestion was not significantly alleviated. The full results of the main regression are available in appendix A.
I also experiment with the definition of mode usage. Now, mode usage is defined as a binary variable which equals 1 if subway, bus, auto, or walking and bicycling is the main mode of the trip, and equals 0 otherwise. The main mode is defined as the mode covering the greatest distance of a trip. The regression results, which are available upon request, show that the estimates remain stable to the alternative definition of mode usage.
3.2. Evaluating the underlying assumptions
In order to interpret these estimates as an unbiased measure of the subway expansion impacts, some important assumptions must hold – in particular, conditional unconfoundedness and stable unit treatment values.
3.2.1. Assessing unconfoundedness
The above analysis assumes that the mode usage has similar trajectories for the two groups over time, absent any treatment effect, conditional on observable individual characteristics. This assumption is not observable and therefore not testable in principle. One possible way to assess the plausibility of this assumption is to test whether the two groups had similar usage trajectories before the treatment. Due to data availability, the full sample is observed only once before the treatments. Therefore, the pre-treatment trajectories of the late treatment group, instead of the full treatment group, are compared to those of the control group. If the pre-treatment usage trajectories indeed are similar, the double difference
![]() $(\bar{Y}_{g_{2,2008}}^{m}-\bar{Y}_{g_{2,2007}}^{m})- (\bar{Y}_{g_{1,2008}}^{m}-\bar{Y}_{g_{1,2007}}^{m})$
should be 0, where g
1 is the control group, and g
2 is the late treatment group. A fake treatment indicator is defined, which equals 1 for the late treatment group in 2008, 0 otherwise. The sample is restricted to the two groups in 2007 and 2008, and the mode usage is regressed on the fake treatment indicator, year dummies, TAZ dummies, district by year dummies and demographic variables. The coefficient of the fake treatment indicator is expected to be 0. As shown in panel A of table 3, the estimates for all four modes are indeed small and not statistically significant.
$(\bar{Y}_{g_{2,2008}}^{m}-\bar{Y}_{g_{2,2007}}^{m})- (\bar{Y}_{g_{1,2008}}^{m}-\bar{Y}_{g_{1,2007}}^{m})$
should be 0, where g
1 is the control group, and g
2 is the late treatment group. A fake treatment indicator is defined, which equals 1 for the late treatment group in 2008, 0 otherwise. The sample is restricted to the two groups in 2007 and 2008, and the mode usage is regressed on the fake treatment indicator, year dummies, TAZ dummies, district by year dummies and demographic variables. The coefficient of the fake treatment indicator is expected to be 0. As shown in panel A of table 3, the estimates for all four modes are indeed small and not statistically significant.
Table 3. Indirect test of unconfoundedness

Notes: Panel A tests whether the pre-treatment mode usage trajectories are similar between the late treatment group and the control group. The sample is restricted to those in the control group and the late treatment group in 2007 and 2008. Panel B tests the plausibility of the SUTVA assumption. The control group is restricted to the TAZs that are within a 2-km radius circle of a subway station. The specifications in both panels are the same as the main regression. Standard errors are clustered at the TAZ level. *, **, *** indicate 10%, 5% and 1% significance level, respectively.
3.2.2. Assessing the stability of unit treatment values
The estimation strategy also requires that the potential mode usage of one individual is independent of the treatment status of other individuals. There are two potential ways in which this assumption might be violated. One way is through traffic congestion alleviation, which we have addressed by including the cross-area externality in the regressions. The second potential violation of the assumption is through self-selective migration. If untreated commuters who prefer the subway are attracted to the treated TAZs, this would decrease the average subway usage of the control group, and exaggerate the estimates of the subway expansion impacts. Lacking migration data or panel data at the household level, the violation of the assumption is not empirically tractable, unless we generate a specific hypothesis regarding how the violation would manifest itself. The hypothesis is as follows: some commuters prefer the subway, but live farther away for reasons such as the high housing prices and limited housing supply in the nearby areas. The new lines put more areas within walking distance, and therefore may induce the migration of these commuters. If this kind of migration exists, we would expect to find smaller treatment effects when the control group is restricted to nearby TAZs. Panel B of table 3 reports SATT estimates obtained using only data from TAZs within a 2-km distance of a subway station as controls. They are similar to the results from the main regressions. This suggests that self-selective migration, if any, is not large enough to bias the estimated expansion effects significantly. This is as expected, as mentioned in the data section. In highly populated urban Beijing, without excess housing supply, large migration is not likely to happen within a one-year time span.
3.3. Treatment effect heterogeneity
In this subsection, four types of treatment effect heterogeneity are investigated. First, continuous treatment is considered. Next, variation of the effects across areas with different traffic infrastructure conditions is investigated. Then, the question of whether the effects are correlated with demographics is explored. Finally, the effects of the rail accessibility improvement at the destination are studied.
3.3.1. Continuous treatment
Both the distance reduction and the resultant distance to the nearest subway station are continuous. We expect to see different mode usage changes across the groups that experienced different reductions in distance and different distances as a result. To allow for such differences,
![]() $\varphi D_{zt}\ast {dist}_{zt}+\mu {dist}_{zt}$
is added in equation (2), where dist
zt
is the distance between TAZ z and its nearest subway station at time t. Denoting the distance before and after the subway expansion as d
0 and d
1, respectively, the effect of subway expansion can then be expressed as
$\varphi D_{zt}\ast {dist}_{zt}+\mu {dist}_{zt}$
is added in equation (2), where dist
zt
is the distance between TAZ z and its nearest subway station at time t. Denoting the distance before and after the subway expansion as d
0 and d
1, respectively, the effect of subway expansion can then be expressed as
![]() $\tau+\varphi d_{1}+\mu(d_{1}+d_{0})$
, where d
1+d
0 measures distance reduction. As shown in table 4, panel A, φ is estimated as negative in the subway regression, and positive in the auto regression; μ is estimated as small and not statistically significant in all regressions. This suggests that the diversion effect of subway expansion depends on whether the expansion brings a subway station to commuters’ residential places, rather than how large the distance reduction was; that is, the resultant distance matters, while the magnitude of improvement does not.
$\tau+\varphi d_{1}+\mu(d_{1}+d_{0})$
, where d
1+d
0 measures distance reduction. As shown in table 4, panel A, φ is estimated as negative in the subway regression, and positive in the auto regression; μ is estimated as small and not statistically significant in all regressions. This suggests that the diversion effect of subway expansion depends on whether the expansion brings a subway station to commuters’ residential places, rather than how large the distance reduction was; that is, the resultant distance matters, while the magnitude of improvement does not.
Table 4. Heterogeneity in treatment and treatment effect

Notes: Each panel has the same specification as the main regression, except for additional interaction terms for panels A through C and the additional treatment indicator (treatment at destination) for panel D. Standard errors are clustered at the TAZ level. *, **, *** indicate 10%, 5% and 1% significance level, respectively.
3.3.2. Heterogeneous treatment effects across traffic infrastructure conditions
To investigate the heterogeneous treatment effects across TAZs with different traffic infrastructure conditions,
![]() ${\bf{\delta'Z}}_{zt}D_{zt}$
is added in equation (2), where
Z
zt
is a vector, including road coverage and the number of bus stops in TAZ z at time t. As shown in table 4, panel B, the estimated coefficient of treatment × road coverage is negative for subway, positive for auto and negative for bus. It suggests that, in the areas with an extensive road system, a new subway line is less attractive, compared to areas with less road coverage. In an area with more road coverage, the additional subway passengers are less likely to be commuters who previously drove to work and more likely to be previous bus passengers. This is expected, because commuters in areas with more road coverage are likely to have had good experiences when driving, so they will not bother to switch from driving to subway when there is a new subway line. The coefficient of treatment × number of bus stops is positive for subway and auto, while it is negative for bus. This suggests that a new line in areas with a large public transit system is more attractive, compared to an isolated line. Its passengers are more likely to be previous bus passengers, while they are less likely to be auto drivers. To summarize, a new subway line in an area with a smaller road system but a larger public transit system will have better ridership; however, if the goal of this new line is to attract as many auto drivers as possible, it is better to place the new line in areas with less road coverage and fewer bus stops.
${\bf{\delta'Z}}_{zt}D_{zt}$
is added in equation (2), where
Z
zt
is a vector, including road coverage and the number of bus stops in TAZ z at time t. As shown in table 4, panel B, the estimated coefficient of treatment × road coverage is negative for subway, positive for auto and negative for bus. It suggests that, in the areas with an extensive road system, a new subway line is less attractive, compared to areas with less road coverage. In an area with more road coverage, the additional subway passengers are less likely to be commuters who previously drove to work and more likely to be previous bus passengers. This is expected, because commuters in areas with more road coverage are likely to have had good experiences when driving, so they will not bother to switch from driving to subway when there is a new subway line. The coefficient of treatment × number of bus stops is positive for subway and auto, while it is negative for bus. This suggests that a new line in areas with a large public transit system is more attractive, compared to an isolated line. Its passengers are more likely to be previous bus passengers, while they are less likely to be auto drivers. To summarize, a new subway line in an area with a smaller road system but a larger public transit system will have better ridership; however, if the goal of this new line is to attract as many auto drivers as possible, it is better to place the new line in areas with less road coverage and fewer bus stops.
3.3.3. Heterogeneous treatment effects across demographics
To investigate the effect of heterogeneity across auto ownership,
![]() ${\bf {\delta'X}}_{it}D_{zt}$
is added in equation (2), where auto ownership, driver's license, interaction of auto ownership and driver's license, and income are included in
X
. An auto owner is defined as an individual who has a driver's license and is a member of a household that has one or more autos. As shown in table 4, panel C, the estimated coefficient of treatment × auto ownership × driver's license and that of treatment × income are negative in the auto regression, indicating that auto usage by auto owners and commuters with higher income decreased more, compared to commuters without an auto or a driver's license and those with lower income. This is straightforward because auto owners and commuters with higher income have much greater auto usage to begin with. This finding is consistent with the finding of Yang et al. (Reference Yang, Chen, Qin and Lu2015) that new subway lines in outer Beijing, where the residents have a lower income than those of urban Beijing, have little effect on traffic congestion. Therefore, the impacts are also measured as percentage changes, and it is found that auto owners and commuters with a higher income are less likely to be diverted from autos towards the subway. The calculation and comparison are available in appendix B.
${\bf {\delta'X}}_{it}D_{zt}$
is added in equation (2), where auto ownership, driver's license, interaction of auto ownership and driver's license, and income are included in
X
. An auto owner is defined as an individual who has a driver's license and is a member of a household that has one or more autos. As shown in table 4, panel C, the estimated coefficient of treatment × auto ownership × driver's license and that of treatment × income are negative in the auto regression, indicating that auto usage by auto owners and commuters with higher income decreased more, compared to commuters without an auto or a driver's license and those with lower income. This is straightforward because auto owners and commuters with higher income have much greater auto usage to begin with. This finding is consistent with the finding of Yang et al. (Reference Yang, Chen, Qin and Lu2015) that new subway lines in outer Beijing, where the residents have a lower income than those of urban Beijing, have little effect on traffic congestion. Therefore, the impacts are also measured as percentage changes, and it is found that auto owners and commuters with a higher income are less likely to be diverted from autos towards the subway. The calculation and comparison are available in appendix B.
3.3.4. Treatment at destination
Rail accessibility is also improved when the distance between the place of work and a subway station is decreased. The effect of the treatment at destination is estimated by adding
![]() $\tau^{d}D^{d}_{zt}$
in equation (2).
$\tau^{d}D^{d}_{zt}$
in equation (2).
![]() $D^{d}_{zt}$
is the indicator of treatment at destination, which equals 1 if the distance between the work TAZ and the nearest subway station is decreased at time t, 0 otherwise. As shown in table 4, panel D, the estimated coefficient of treatment at destination is small and not statistically significant in all regressions, and the estimated impacts of the treatment at origin are not changed significantly by the additional treatment indicator. This indicates that, conditional on the treatment at the origin, treatment at the destination has a minor impact on mode usage. A possible reason is that the main business areas are covered by the old subway lines. The main function of the new lines (lines 5, 8, and 10) is to collect and bring commuters to those major destinations. Therefore, the effect of treatment at origin is large, while the effect of treatment at destination is small. When all of urban Beijing is covered by subway lines, as in the 2015 Plan, we expect to see the effect of treatment at the destination for the additional lines.
$D^{d}_{zt}$
is the indicator of treatment at destination, which equals 1 if the distance between the work TAZ and the nearest subway station is decreased at time t, 0 otherwise. As shown in table 4, panel D, the estimated coefficient of treatment at destination is small and not statistically significant in all regressions, and the estimated impacts of the treatment at origin are not changed significantly by the additional treatment indicator. This indicates that, conditional on the treatment at the origin, treatment at the destination has a minor impact on mode usage. A possible reason is that the main business areas are covered by the old subway lines. The main function of the new lines (lines 5, 8, and 10) is to collect and bring commuters to those major destinations. Therefore, the effect of treatment at origin is large, while the effect of treatment at destination is small. When all of urban Beijing is covered by subway lines, as in the 2015 Plan, we expect to see the effect of treatment at the destination for the additional lines.
4. Effect on trip quantity
As the expansion makes commuting faster and more convenient, commuters in the treatment group may respond to the convenience by making more or longer trips.Footnote 8 In this section, the question is asked as to whether the subway expansion increased the number of trips and the trip length. Table 5 summarizes the results of estimating equation (2) with different dependent variables. In column (1), the dependent variable is the number of work trips taken by a commuter on a weekday. The estimate is small and not statistically significant. This indicates that commuters did not increase the frequency of work trips in response to the accessibility improvement. Columns (2) through (5) measure the effect of the expansion on trip distances. In columns (2) and (4), the trip distance is measured as the sum of reported distances of trip segments and the point-to-point distance measured on digital maps, respectively. Columns (3) and (5) take the natural logarithm of the reported distances and the measured distances, respectively. The estimates are small and not statistically significant in columns (2) through (5). This indicates that commuters did not travel farther to work when rail transit accessibility was improved.
Table 5. Effects of subway expansion on number of trips and trip distance

Notes: All columns have the same specification as the main regression but different dependent variables. Standard errors are clustered at the TAZ level. *, **, *** indicate 10%, 5% and 1% significance level, respectively.
5. Conclusion
In this paper, the rapid rollout of new subway lines in urban Beijing is used to test whether the improvement of subway accessibility diverted commuters toward the subway, and from which modes travel was diverted. The main methodology is a DID method which compares changes in the travel behaviors of commuters who reside in the areas with rail accessibility improvement to those who did not experience such improvement. To solve the potential estimation bias posed by the fact that rail expansion may affect commuters residing in areas without rail accessibility improvement through congestion alleviation, due to less driving by the commuters who experienced the subway improvement, the intensity of spillover from the treated is measured and the cross-area externality is estimated as well.
The results indicate that the new subway lines increased the percentage distance traveled by subway by 107 per cent, and decreased the percentage distance traveled by autos on average by 16 per cent in the treated areas relative to the untreated areas. The percentage distance traveled by buses decreased by 7 per cent and is not statistically significant. Along with the increase in subway usage, walking and bicycling distance increased by 10 per cent. The results also show that commuters residing in areas closer to subway stations, rather than those in areas which experienced greater improvement in rail accessibility, were more likely to divert toward the subway; new subway lines built in areas with less road coverage but more bus stops diverted more commuters to the subway; and auto owners and commuters with higher income were less likely to switch from auto use toward subway use. Furthermore, it is found that neither trip length nor number of trips increased with rail expansion. As for the cross-area externality, the spillover effects are found to be small and not statistically significant. This implies that the congestion alleviation effects were not large enough, within the areas and time span of the study, to affect the travel behaviors of the commuters residing in areas which did not experience rail accessibility improvements.
Now let us find out what the 16 per cent decrease in auto usage (auto usage decreased from 0.30 of the distance traveled in a trip to 0.25) means in economic terms. Many studies have shown that automobile exhaust substantially harms public health. Particulate matter, one of the main pollutants from diesel automobiles, is linked to cardiopulmonary diseases, respiratory infections, lung cancers and infant mortality; other automobile emissions, such as carbon monoxide and nitrogen oxides, are also linked to infant mortality and childhood asthma (Chay and Greenstone, Reference Chay and Greenstone2003; EPA, 2004; Neidell, Reference Neidell2004; Currie and Neidell, Reference Currie and Neidell2005). The externalities caused by auto use also include greenhouse gas emissions, congestion, traffic accidents, noise, and so on. Parry and Small (Reference Parry and Small2009) estimated the externality cost of driving for several large cities over the world, and found that the cost varies from US$0.46 per mile for Washington, DC to US$2.42 per mile for London. Although the value of time and value of statistical life are possibly lower in urban Beijing than in Washington, DC because of the lower average wage, the cost of air pollution is not necessarily lower, given the higher population density in urban Beijing.Footnote 9 So this cost range is adopted for the following calculation.
The average work trip distance in the sample is 8 km, and therefore about 0.4 km is diverted from autos per trip. When the 2015 Plan is completed, all the residents in urban Beijing (11.7 million in 2010) will be within walking distance of at least one subway station. Supposing that two-thirds of them make one round trip per day for work (based on the sample statistics), the total distance saved in auto usage will be 6.27 million km per day. Therefore, the cost saved by diverting commuters from autos will be US$1.80m to US$9.49m per day. Assuming that there are 250 week days per year, US$0.45bn–US$2.37bn will be saved in the first year of completion of the 2015 Plan. Regardless of the precise numbers used to interpret the magnitude of the air quality and congestion alleviation benefits, the calculation indicates that the effects of rail transit infrastructure are economically substantial.
Notice that the 16 per cent decrease in auto usage is neither a guarantee nor an upper bound of the effect of rail expansion, because, as shown in this paper, the impacts of rail expansion on mode usage depend on the distance of a new subway station to commuters’ residences, the road coverage and bus systems of the areas where the subway stations are built, and the income and auto ownership of the commuters in those areas. A subway line with stations close to residential places in areas with limited road coverage and undeveloped bus services, or in areas where the residents have relatively lower income and less auto ownership, is likely to have a large diversion effect on autos.
Appendix A: Full list of the main results
Table A1. Effect of subway expansion on mode usage

Appendix B: Measuring treatment effect heterogeneity in percentage change
Table B1. Measuring treatment effect heterogeneity in percentage change












