1. Introduction
Although there is no single, agreed-upon definition of commonsense, most definitions include the notion that commonsense is a shared human ability of understanding and judging everyday matters (Davis & Marcus, Reference Davis and Marcus2015; Minsky, Reference Minsky2006). Commonsense reasoning in AI is about the development of computational agents that are capable of achieving human-like performance when presented with tasks that involve commonsense judgements (e.g. “True or False: If you throw a wine glass against a wooden floor, it will probably shatter”, from the CycIC-entangled task). In recent years, significant computational progress has been achieved on this problem due to the advent of techniques such as transformer-based language representation models, of which Bidirectional Encoder Representations from Transformers (BERT) is an example (Devlin et al., Reference Devlin, Chang, Lee and Toutanova2019). Other examples include models such as Generative Pre-trained Transformer 3 (GPT-3) (Floridi & Chiriatti, Reference Floridi and Chiriatti2020), as well as recently released question-answering models such as UnifiedQA (Khashabi et al., Reference Khashabi, Min, Khot, Sabharwal, Tafjord, Clark and Hajishirzi2020). Other enabling technologies include ensemble applications of symbolic and sub-symbolic AI approaches (Besold et al., Reference Besold, Garcez, Bader, Bowman, Domingos, Hitzler, Kühnberger, Lamb, Lowd, Lima, de Penning, Pinkas, Poon and Zaverucha2017; Calegari et al., Reference Calegari, Ciatto, Denti and Omicini2020; Cambria et al., Reference Cambria, Li, Xing, Poria and Kwok2020), which have also been successfully applied to difficult problems in AI, such as commonsense reasoning.
Because commonsense is broad, there is interest in both AI and cognitive science to better categorize the different kinds of commonsense reasoning that humans often rely on to navigate everyday life. While the problem of how humans categorize things in the world has been extensively studied (Mervis & Rosch, Reference Mervis and Rosch1981), recent literature has made considerable progress on the axiomatization of commonsense reasoning (Gordon & Hobbs, Reference Gordon and Hobbs2017). Specifically, Gordon and Hobbs performed a comprehensive study of representational requirements for strategic planning. Planning strategies were collected in ten different domains, and formally represented. They found that 988 concepts could be considered common in all analyzed domains. These 988 concepts were then clustered into 48 representational areas. Eight of these areas (the ones selected for our experiment) were judged by the authors to be examples of foundational categories that are involved in human commonsense reasoning and are also commonly used in knowledge representation research. Our interest in these foundational categories is their potential to support the development of a formal logic for commonsense reasoning.
Our objective in this paper is to experimentally test the hypothesis of whether these 8 identified categories can be used by humans to reliably classify sentences into one or more of these categories. We test this hypothesis by designing and conducting an experiment where trained human annotators are tasked with independently classifying 200 commonsense sentences. To prove reliability, we robustly analyze the results to test for agreement among the annotators on their classifications. An annotation-driven experiment that, in structure, is similar to the one we propose is the work by Clinciu et al. (Reference Clinciu, Gkatzia and Mahamood2021), where multiple annotators annotate papers published on commonsense reasoning, followed by a set of recommendations based on analysis. In contrast, we propose annotation of sentences from a commonsense reasoning benchmark into categories. Our end-goal is similar in that we draw on the results of this study to advocate for better design of commonsense benchmarks.
We note that such a reliable categorization, if it is found to exist, can facilitate several important purposes in the AI sub-community that investigates commonsense reasoning. First, it may help to design more comprehensive benchmarks (covering all the categories in the Gordon-Hobbs theory) for evaluating AI commonsense reasoners. Second, it may help to better understand the reasoners themselves, e.g., if one reasoner is doing better than another on some category (like time), but not some other category (like world states). In contrast, if the null hypothesis of human agreement underlying the hypothesis can be rejected with high significance, then it begs the question of whether the proposed axiomatization of commonsense is under-specified and needs further refinement. Our results show that, for some categories, this is indeed the case, while for others, there is agreement among human annotators.
2. Methods
Participants were asked to annotate a set of 200 sentences or ‘prompts’ that compose the CycIC-entangled (CycIC3) development dataset (described below), into one or more of the 8 categories (time, space, physical entities, classes and instances, sets, world states, and values and quantities) that have been identified by Gordon and Hobbs (Reference Gordon and Hobbs2004) as relevant to most real-world commonsense reasoning tasks. Definitions for those categories are detailed, with references, in a recent book by the same authors (Gordon & Hobbs, Reference Gordon and Hobbs2017). Cyc was originally proposed by Lenat and Guha (Reference Lenat and Guha1989), and has been discussed in a number of publications over the decades (Lenat et al., Reference Lenat, Guha, Pittman, Pratt and Shepherd1990; Reference Lenat, Witbrock, Baxter, Blackstone, Deaton, Schneider, Scott and Shepard2010). Recently, Cyc released a benchmark dataset for use in evaluating natural-language-based AI agents on commonsense prompts that only require a True/False response. In its newest release, the CycIC3 development set (which is publicly available) contains 200 sentences that were designed to cover a reasonably representative set of commonsense concepts. Although CycIC3 provides some limited metadata about each of the sentences (including a category directly derived from the Cyc platform), the metadata is not directly aligned with a formal set of commonsense categories, since CycIC3’s sentences were designed independently of the Gordon-Hobbs categories. Hence, these sentences/prompts provide a reasonable and independent corpus for acquiring annotations on those categories, without incurring bias in task construction.
2.1. Annotators and annotation guidelines
Five members actively working under the DARPA Machine Common Sense program participated as annotators in the experiment. While four out of the five annotators have computer science backgrounds, they have varying degrees of expertise. Prior to the experiment, the annotators received written instructions that included a brief description of each category, 2-5 example prompts per category, and annotation-scoring directions. The annotators were asked to provide a score, on a 5-point scale (with 1 being the least relevant, to 5 being the most relevant), for each of the 8 categories per prompt. Our goal in using this 5-point scale was to capture nuances in categorization that binary scores may have been incapable of capturing, and to ensure that annotators thought about the suitability of each category per prompt. Furthermore, by asking for a score for each category, rather than asking annotators to ‘name’ the most suitable category or categories per prompt, we mitigated the potential problem where annotators may have forgotten about some of the more difficult categories.
To elicit annotations, a spreadsheet was set up and shared on the Web with the five annotators. This spreadsheet contained the full set of 200 prompts, with a column for each of the 8 categories. The original spreadsheet, without annotations, is provided in the supplementary material.
In an effort to normalize the understanding of the categories, and to calibrate the scoring process with respect to the 5-point scale, the annotators were first instructed to independently annotate only the first 20 prompts. Once all participants completed this ‘preliminary experiment’, they met collectively to review and discuss the results. As a result of this discussion, the scale for scoring the relevance of each category was changed from 1-5 to 0-5, where a score of 0 was used to indicate that a category is not relevant. Each participant was then instructed to complete, from the very beginning, the entire spreadsheet, containing the full set of 200 prompts, by scoring each prompt on a scale of 0-5 for each of the 8 categories. Note that the 20 prompts used during the preliminary experiment were included in the final spreadsheet, although annotators were asked to fill in the entire spreadsheet from scratch. Post-annotation comments were also solicited from all annotators to understand task difficulty.
3. Metrics
To quantify annotator agreement across the 8 categories, we used the balanced accuracy metric by treating, in turn, each annotator’s categorization as the gold standard against which the other annotators’ judgments would be evaluated. For binary judgments, balanced accuracy is the weighted proportion of correct answers (with respect to a given gold standard). In the supplementary material, we also provide the simple accuracy (unweighted proportion of correct answers). While a multi-class version of balanced accuracy is also available, we used the binary version of this metric to ensure robustness, since we wanted to ignore small scoring differences across annotators. We did this by using a threshold to convert the scaled annotations (on the 0-5 point scale) across 8 categories into a binary judgment per category, for each prompt. For example, a threshold of 3 (that we use for our main results) indicates that a prompt scored as 0, 1, or 2 for some category by an annotator is not considered to belong to the category by that annotator (and hence is assigned a ‘binary’ label of 0), whereas prompts scored as 3, 4 or 5 are considered to belong to that category (binary label of 1). For each category, therefore, we can always recover a binary signal per prompt per annotator. We also consider the thresholds 1, 2, 4, and 5 and report additional results in the supplementary results. However, there is little qualitative difference when using these different thresholds, attesting to the robustness of our results.
We illustrate the process using an example. Suppose that the judgments of annotator A are treated as the gold standard (or ‘ground-truth’). For a given category C (say, time) and threshold 3, we obtain a balanced accuracy for each of the other four annotators (G, H, M and R) by first ‘binarizing’ their original scaled annotation and then computing a single, balanced accuracy metric per annotator for C.
Since there are 8 categories, and 5 annotators, a total of
![]() $ 5\times 4\times 8=160 $
balanced accuracy measurements are obtained and reported in Results. Assuming the null hypothesis that the binarized annotations of the ground-truth annotator and the annotator being evaluated are equally distributed, we can compute a p-value for each such pair of comparisons. For each category there are
$ 5\times 4\times 8=160 $
balanced accuracy measurements are obtained and reported in Results. Assuming the null hypothesis that the binarized annotations of the ground-truth annotator and the annotator being evaluated are equally distributed, we can compute a p-value for each such pair of comparisons. For each category there are
![]() $ 5\times 4/2=10 $
comparisons, due to symmetry. Other works (Agresti, Reference Agresti1992) that have conducted similar categorization experiments to identify agreement or disagreement among subjects have used Cohen’s Kappa statistic to compute agreement and to check for chance agreement. Although we report the p-value scores in this paper, Cohen’s Kappa statistic and the Kendall’s
$ 5\times 4/2=10 $
comparisons, due to symmetry. Other works (Agresti, Reference Agresti1992) that have conducted similar categorization experiments to identify agreement or disagreement among subjects have used Cohen’s Kappa statistic to compute agreement and to check for chance agreement. Although we report the p-value scores in this paper, Cohen’s Kappa statistic and the Kendall’s
![]() $ \tau $
scores are provided in the supplementary material.
$ \tau $
scores are provided in the supplementary material.
4. Results
Our key experimental results are displayed in Tables 1, 2, and 3. In each table, the set of binarized annotations (using a threshold of 3) provided by the annotator in the first column is assumed to be the gold standard for that row, and all other annotators (listed in five major columns) are evaluated using the balanced accuracy metric described earlier. Since the balanced accuracy for an annotator (on any category) is trivially 1.0 when evaluated against itself, the cells falling along the diagonal are blank in each table.
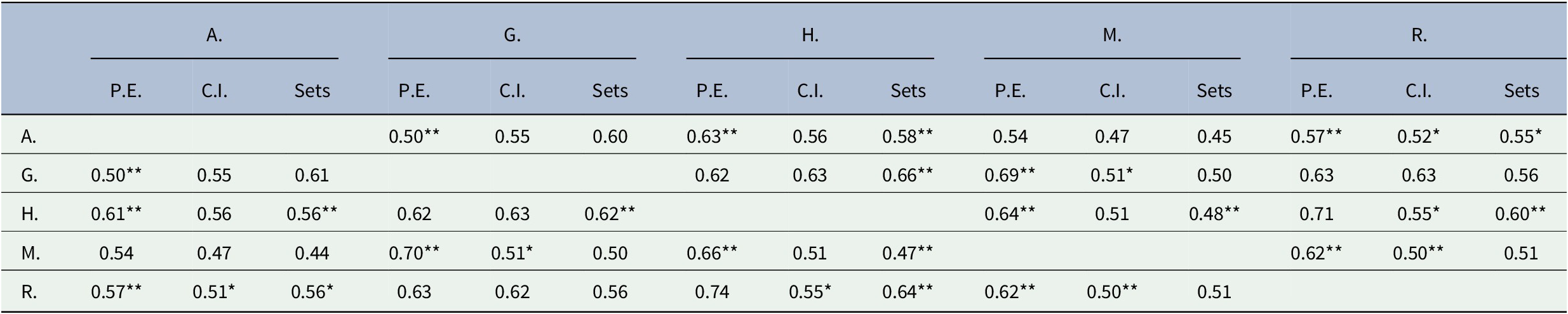
Table 1. Balanced accuracy scores and p-value levels for each annotator pair for the Physical Entities (P.E.), Classes and Instances (C.I.), and Sets categories. A, G, H, M and R designate the five annotators.
Note: *0.01 <
![]() $ p $
<= 0.05 **
$ p $
<= 0.05 **
![]() $ p $
<= 0.01
$ p $
<= 0.01
Table 2. Balanced accuracy scores and p-value levels for each annotator pair for the World States (W.S.), and Values and Quantities (V.Q.) categories. A, G, H, M and R designate the five annotators.

Note: *0.01 <
![]() $ p $
<= 0.05 **
$ p $
<= 0.05 **
![]() $ p $
<= 0.01
$ p $
<= 0.01
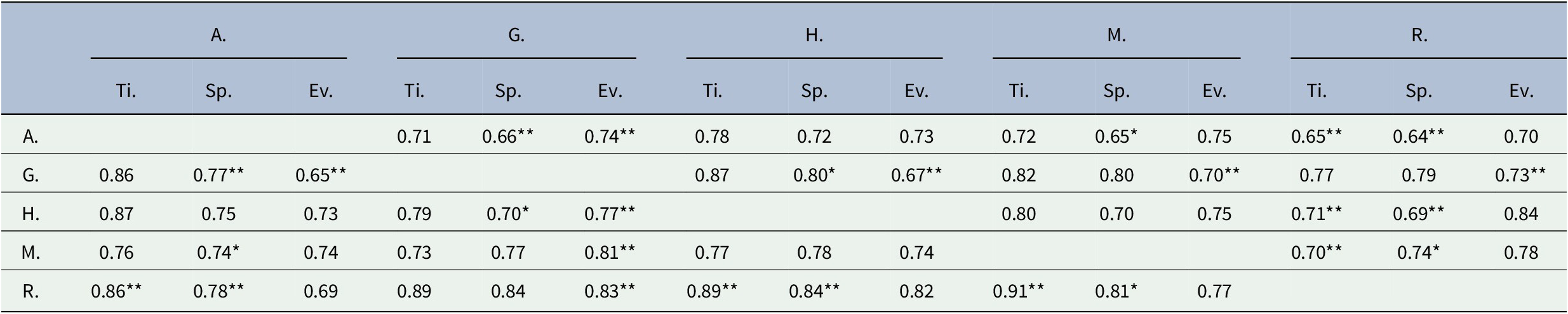
Table 3. Balanced accuracy scores and p-value levels for each annotator pair for the Time (Ti.), Space (Sp.), and Events (Ev.) categories. A, G, H, M and R designate the five annotators.
Note: *0.01 <
![]() $ p $
<= 0.05 **
$ p $
<= 0.05 **
![]() $ p $
<= 0.01
$ p $
<= 0.01
Specifically, Table 1 reports results for the categories that are relatively general, i.e., Physical Entities (P.E), Classes and Instances (C.I), and Sets, and were used most often by the annotators (often in conjunction with other, less general categories). Compared to the categories in the other tables, there was considerable disagreement among annotators on the three categories in Table 1. With only two exceptions, balanced accuracy is below 70%, even though two sets of commonsense, human judgments are being compared. For most results, the p-value is well below 0.01 (indicated with a **), meaning that the null hypothesis of annotator agreement can be rejected with high significance.
In complete contrast with Table 1, there is much more agreement among the annotators on the more deterministic categories in Table 3, such as Time (Ti.), Space (Sp.), and Events (Ev.). For instance, there are very few balanced accuracies that are below 70% in Table 3, and although the null hypothesis of agreement can be rejected for some pairs of annotators (for a category), there is weak or no significance for many others.
Results in Table 2 fall between the extremes in Tables 1 and 3. We find that balanced accuracies for categories that are considered less broad are higher, on average, than for those reported in Table 1. The two categories in this table, which include World States (W.S.) and Values and Quantities (V.Q.), have some degree of non-determinism, but are not as narrowly defined as the categories in Table 3.
During our data analysis, we varied the threshold to test if it leads to more agreement. The data for this additional analysis is included in the supplementary material. Results were largely consistent with those shown in Tables 1, 2, and 3, attesting to the robustness of the experiment and its conclusions.
5. Discussion
While our main results suggest that the more deterministic subset (Time, Space, and Events) of the 8 categories identified by Gordon and Hobbs (Reference Gordon and Hobbs2004) can potentially be used to categorize sentences in commonsense benchmarks, the same results also show that there is much more annotator disagreement among the most general categories, such as Classes and Instances, and Sets.
To understand the difference more qualitatively, it is useful to consider two examples. For the first example, consider the prompt “If a chicken lays an egg, then the chicken existed before the egg”. In our experiment, Time and Events were the categories that were consistently used to classify this prompt (using any threshold) by all of the annotators, indicating high agreement. Alternatively, the sentence prompt “Stabbing someone typically expresses love” could not reach agreement among all annotators for
![]() $ threshold>=3 $
. Only the Events category was used by all annotators for this prompt, and only when considering
$ threshold>=3 $
. Only the Events category was used by all annotators for this prompt, and only when considering
![]() $ threshold<3 $
. While this prompt was also categorized into other categories such as Sets or Classes and Instances, annotators were not consistent among themselves. While reasons for this lack of consistency are not completely evident, for the second prompt, the annotators reported difficulty in classifying sentences about emotions and human preferences into any of the 8 presented categories. Some annotators also commented that they did not find much difference between some categories (e.g., Sets and Classes and Instances), implying that these categories may have been used interchangeably.
$ threshold<3 $
. While this prompt was also categorized into other categories such as Sets or Classes and Instances, annotators were not consistent among themselves. While reasons for this lack of consistency are not completely evident, for the second prompt, the annotators reported difficulty in classifying sentences about emotions and human preferences into any of the 8 presented categories. Some annotators also commented that they did not find much difference between some categories (e.g., Sets and Classes and Instances), implying that these categories may have been used interchangeably.
Sentence structure and language usage do not seem to be predictive of disagreement. Disagreement on categorization is also not correlated with difficulty in answering the prompt itself. For example, Cyc has claimed a human performance baseline of 100% for the CycIC3 benchmark, meaning that humans were able to answer each prompt correctly (true or false), despite significant disagreement in categorizing the prompts.
Earlier we noted that the Gordon-Hobbs theory contains 48 categories. We focused on the 8 that were identified as foundational. An important question that we hope to address in future work is whether the methodology presented in this paper can be successfully replicated on those categories. While a similar annotation exercise can be designed, some experimental caveats need to be borne in mind. First, as evidenced by annotator-feedback, annotators can sometimes get confused between categories and what they mean, even with eight categories. The problem is likely to get much worse if all 48 categories are presented to the annotators at the same time. Second, choice paralysis is a real issue that cannot be neglected when too many choices are presented to annotators. Other aspects are also important, such as the order in which the choices are presented. Cognitive fatigue may lead to less meaningful scores as annotators provide scores per sentence on increasing numbers of categories. Finally, at least some of the other 40 categories may fall in the ‘abstract’ or broad categories on which significant disagreement was observed even with 8 categories. Therefore, more annotators may be required to obtain statistically valid scores on those categories. While laying out an experimental study for all 48 categories is beyond the scope of this work, we believe that even formulating such a design would be a valuable area for future research.
Our long-term goal is to determine if a set of categories could reliably be used within a metadata layer to analyze the content of commonsense benchmarks. Potentially, a text classification algorithm might be able to automatically generate characterization for prompts in those benchmarks, as initially explored in Santos et al. (Reference Santos, Gordon, Liang, Forbush and McGuinness2021). The development of such an automated method will leverage the results discussed in this paper, and other results produced by researchers involved in the DARPA Machine Common Sense program. However, before such a classifier can be developed, methods for reducing human disagreement need to be devised. For example, annotation guidelines for the 8 categories may need to be better enumerated in future such exercises, and additional categories may be necessary for reducing ambiguity.
Acknowledgments
The authors thank the DARPA Machine Common Sense Program for supporting this research. We also acknowledge and thank Minor Gordon for conducting preliminary experiments leading up to the primary experiments reported herein, and Rebecca Cowan for contributing to the definitions of the identified categories.
Supplementary Materials
To view supplementary material for this article, please visit http://dx.doi.org/10.1017/exp.2021.9.
Author Contributions
Mayank Kejriwal and Henrique Santos conceived and designed the experiment. Alice M. Mulvehill and Henrique Santos established the methodology. Gretchen Forbush and Henrique Santos performed the data analysis. Henrique Santos, Alice M. Mulvehill, and Gretchen Forbush wrote the article. Mayank Kejriwal and Deborah L. McGuinness co-led the team effort and co-authored the article.
Funding Information
This work is funded through the DARPA MCS program under award number N660011924033.
Data Availability Statement
The CycIC-entangled (CycIC3) dataset is available at https://github.com/steeter-cyclist/CycIC3. The code used to compute scores is available at https://github.com/tetherless-world/mcs-formalization.
Conflict of Interest
None to declare.





Comments
Comments to the Author: The paper presents empirical results showing agreement of human annotations for 8 of 48 representational areas of commonsense concepts proposed by Gordon and Hobbs. This line of work is important for the field of artificial intelligence because the manually created categories can fit what people treat as “common” but sometimes the proposed categorization is not as universal as its creators assume. However, there are several issues with the research and its presentation:
[evaluation depth] Common sense evaluation is problematic (see e.g. Clinciu et al. latest paper “It’s Common Sense, isn’t it? Demystifying Human Evaluations in Commonsense-enhanced NLG systems”); references about similar experiments might be missing.
[evaluation method] No explanation why the classic Kendall’s τ, Kolmogorov-Smirnov’s D, or Cohen’s Kappa (free-marginal kappa?) couldn’t be used
[annotators info] Only five annotators with almost identical background (no information about sex or gender, probable problems with representativeness)
[data origin] CycIC dataset test set only has 3,000 sentences, where the 200 questions were taken from? No reference, probable problem with reproducibility.
[data choice] Why CycIC or widely used ConceptNet categories couldn’t be used instead or compared?
[probable overstatement] The authors have chosen 8 areas of common sense and claim that their work can be helpful to evaluate remaining 40 (but as Gordon and Hobbs note, “the difference between these areas is in the degrees of interdependency that theories in these two groups require - these first eight representational areas can be developed in isolation from each other, whereas the latter forty cannot”.