Introduction
Leads and polynyas play important roles in coupling the atmosphere with the Arctic Ocean. Reference Maykut and PerovichMaykut and Perovich (1987) showed that the solar flux into leads is important for heating the ocean and melting sea ice. Not all of the solar flux impinging on the ocean surface is retained within the ocean. The ratio of the upwelling to downwelling shortwave radiation just above the surface is called the albedo. The albedo is used to estimate the amount of radiation retained in the ocean. Upwelling shortwave radiation is a combination of the light reflected from the surface and the emergent light field from within the ocean. The emergent upwelling irradiance is typically a small fraction (0.5%) of the light entering the ocean. The downwelling light field can be separated into diffuse skylight and a direct solar beam. Under cloudy conditions the light field is primarily diffuse, and under clear-sky conditions it is a mixture of diffuse and direct components. The reflectance of the direct beam at the air/ocean interface is dependent on the solar zenith angle, wind speed and relative direction between the waves and the sun (Reference Preisendorfer and MobleyPreisendorfer and Mobley, 1986). Reflections from the ice edge may also affect the albedo. As part of the Surface Heat Budget of the Arctic (SHEBA) field experiment, we collected downwelling and upwelling shortwave radiation measurements to determine the albedo at a lead near the SHEBA camp.
In most work a simple albedo parameterization has been used to study the role of leads in melting ice; either a constant value (Reference Maykut and PerovichMaykut and Perovich, 1987), or a parameterization of the direct component that varies as a function of solar zenith angle (Reference Ebert and CurryEbert and Curry, 1993). The parameterization used by Ebert and Curry was originally presented by Reference Briegleb, Minnis, Ramanathan and HarrisonBriegleb and others (1986). The work of Briegleb and others is based on the values presented by Reference PaynePayne (1972) that were an extrapolation of measurements collected in the coastal ocean at mid-latitudes. The data in Reference PaynePayne (1972) are averaged and are based on an average wind speed (3.7 ms−1). The relationship between albedo and wind speed has been clearly demonstrated (Reference SaundersSaunders, 1967; Reference Preisendorfer and MobleyPreisendorfer and Mobley, 1986). The effect of wind speed is significant at solar zenith angles > 50°. Since solar zenith angles > 50° are common in the Arctic, it would be preferable to include wind speed in a parameterization of lead albedo.
In this paper we examine measurements of lead albedo collected during summer 1998 in the central Arctic. We also expand the parameterization of Reference Briegleb, Minnis, Ramanathan and HarrisonBriegleb and others (1986) to include the effects of wind speed.
Method
Upwelling and downwelling irradiance measurements were collected between 8 June and 28 July 1998 with two Eppley radiometers, a PSP and a Model 8−48 black-and-white pyranometer. Both radiometers are sensitive to radiation between 285 and 2800 nm. The PSP was calibrated prior to deployment in the Arctic. The 8−48 pyranometer was intercalibrated with the PSP at the beginning and end of our observation program by placing both sensors facing upward and recording data for a period of lday No change in the intercalibration was found between the beginning and end of the experiment. Dark measurements were made by wrapping the sensors in a black cloth and recording the values. Samples were recorded every 30 s using a Campbell Scientific data logger. The sampling periods lasted between 4 hours and 1 day. Downwelling irradiance measured at the lead and at the meteorological tower by the SHEBA project office were found to be in good agreement.
Several methods were used to deploy the radiometers. Early in June we used a frame that was attached to the ice. It held the radiometers approximately 1 m from the ice edge and about 1 m above the water. As the summer heating became more pronounced, it became difficult to maintain the alignment of the sensors, so the wooden boom was attached to a spare skiff During short measurement periods the boat would be launched and tied to the ice. This method put the radiometers about 1.5 m from the boat and 0.5 m above the water. It also placed the radiometers further out into the lead, reducing ice-edge effects (reflectance and damped waves). For longer deployment periods it was necessary to place the boat on the ice to prevent it from being damaged by floes drifting in the lead. In this case the radiometers were about 1.5 m from the ice edge and 1 m above the water. A second skiff was used to allow an operator to access the leveling screws for leveling the radiometers. There was no noticeable difference in measurements based on deployment technique.
Several factors make albedo measurements of open water within the ice pack difficult. These factors include self-shadowing, leveling, icing and lack of cosine response of the sensors at large solar zenith. Icing of the sensors deployed at the lead continued to occur throughout the summer, and it is a bit more difficult to level sensors over water than those mounted on a platform on the ice. Difficulties also include reflections from the ice edge, viewing the submerged ice shelf, the lack of capillary waves at the upwind edge, brash ice and floes passing the sensors, the lead closing and the freezing of the sea surface. Some of these difficulties can be overcome by deploying the sensors from a boat. However, ice movement can be very rapid, so we only deployed the boat when someone was present.
Results
The albedo was calculated as the ratio of the upwelling irradiance to the downwelling irradiance. For each sampling period, a 1 h section was selected and the albedo measurements during that hour were averaged. From long sampling periods the interval chosen was normally near the beginning of the record because rime ice tended to form on the sensors as time progressed. We selected a time when the albedo was not fluctuating by more than ±0.01. Large fluctuations in the albedo were observed to be caused by brash and pans of ice passing under the sensor and when the sky was partly cloudy, especially when the sun was near the horizon. This selection criterion favors times with complete cloud cover or clear-sky conditions. The atmospheric transmission of the data presented had a range of 0.25−0.72 with a mean of 0.52 and standard deviation of 0.16. The atmospheric transmission was calculated as the downwelling irradiance divided by the solar constant and the cosine of the solar zenith angle. Because we selected time periods near the beginning of the record, our results are biased towards the albedo near solar noon (solar zenith angle mm. = 53.7, max. = 79.4). The hourly averaged albedo data are shown in Figure 1. The mean value of the albedo data is 0.066 with a standard deviation of 0.007. The 24 data points include 2 clear-sky cases and 22 from overcast periods.
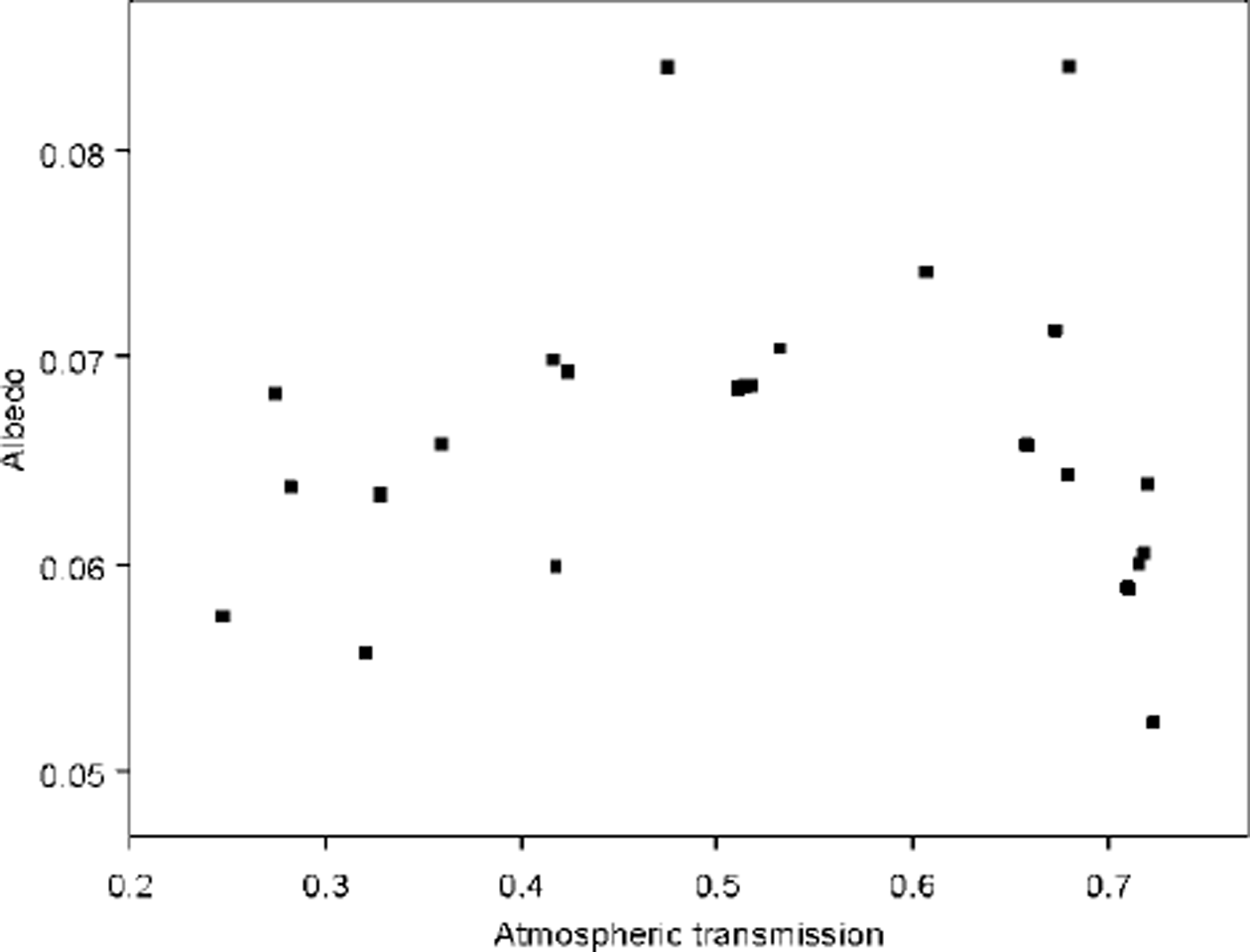
Fig. 1. The albedo calculated for 1 h intervals from the sampling periods as a function of atmospheric transmittance.
On cloudy days no consistent dependence on solar zenith angle or wind speed was observed. Small changes in albedo were observed within a sampling period, but these appear to be primarily related to changes in the cloud cover. Changes in albedo of 0.02 were coincident with changes in cloudiness and are consistent with the observations of Reference Grenfell and PerovichGrenfell and Perovich (1984). The change in albedo may be associated with the change in the incoming light spectrum, as suggested by Reference Grenfell and PerovichGrenfell and Perovich (1984), or a change in the distribution of the downwelling light field. The observed values still remain near the mean value of 0.066 independent of the cause of the change in albedo (Fig. 1), and no relationship was found between the albedo and atmospheric transmittance.
The largest variations in the albedo were observed on clear days. The measurements include one very clear day (23 June) and at least one occasion with mostly clear sky (12 June). A portion of these measurements is shown in Figure 2, along with the albedo values presented by Reference PaynePayne (1972) for the same atmospheric transmittance and solar zenith angle. Under clear-sky conditions the albedo steadily increased with increasing zenith angle to a value > 0.15. At large zenith angles the albedo is expected to be strongly dependent on wind speed (Reference PaynePayne, 1972; Reference Preisendorfer and MobleyPreisendorfer and Mobley 1986). On 12 June the wind speed at 2 m was ∼ 4 .5 m s−1 , and on 23 June it was 3.5 m s"1 and decreased to < 2 m s−1 during the time interval displayed. The difference in wind speed may explain the observed difference in albedo on the two occasions.
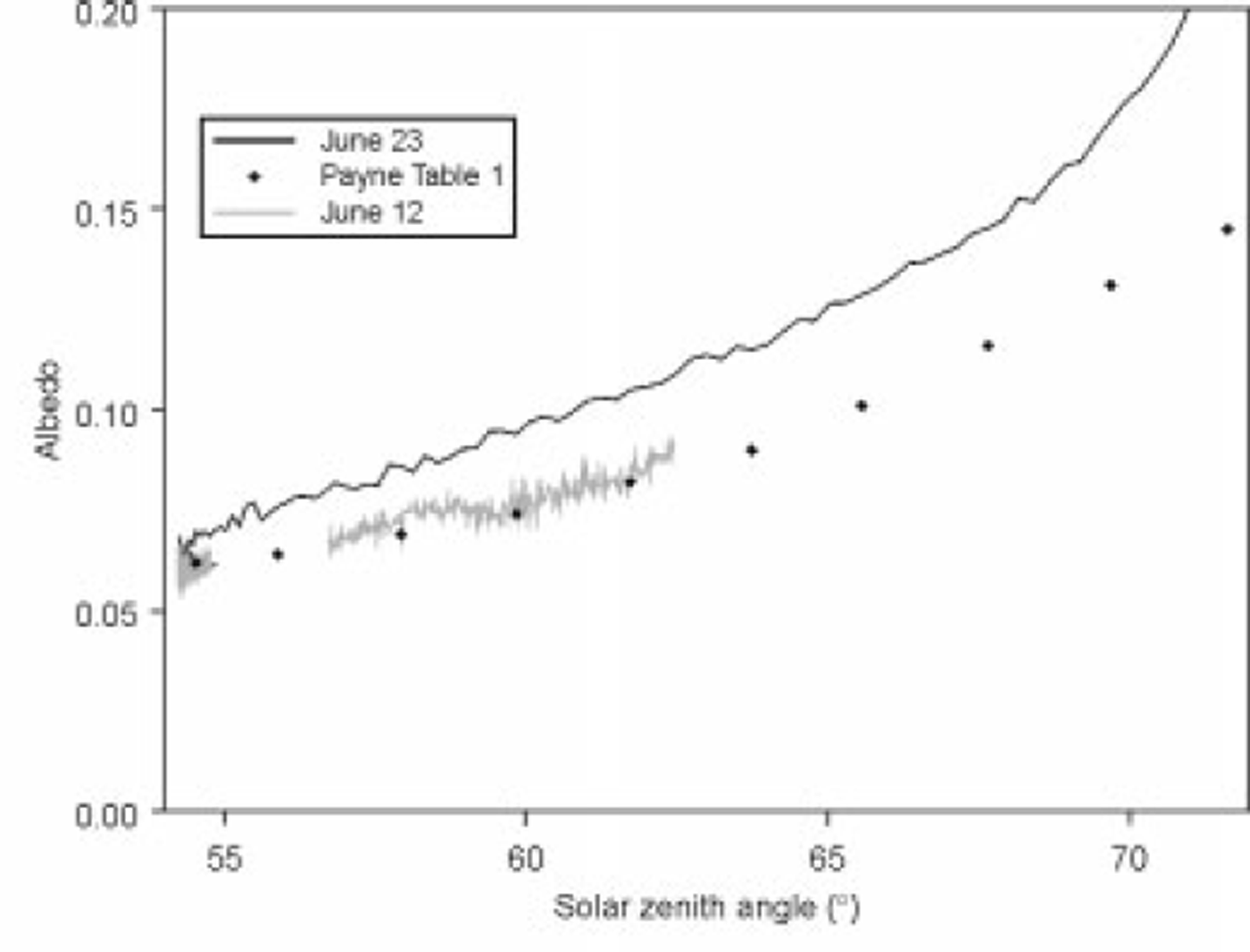
Fig. 2. Measured albedo values on 23 and 12 june presented with those found in table 1 of Reference PaynePayne (1972) for the appropriate solar zenith angle and atmospheric transmittance.
Discussion
The mean albedo was 0.066 [0.007], which matches the open-ocean value observed by Reference Simpson and PaulsonSimpson and Paulson (1979) when the atmospheric transmittance was small (0 ≤ Tr ≤ 0.3, indicative of cloudy conditions) and is not significantly different from the albedo for similar conditions presented by Payne (0.061). The albedo measurements from the time intervals presented did not have a dependence on atmospheric transmittance. This is because the clear-sky albedo, at the mean solar zenith angle of our measurements, is nearly the same as the albedo of diffuse light.
Variations in cloudiness affected the observed albedo within a narrow range about the mean value (0.05−0.07). In contrast to the results presented in Reference Katsaros, McMurdie, Lind and DeVaultKatsaros and others (1985), we did not observe a dependence of the albedo on atmospheric transmission (Fig. 1). This may be due to the small range of solar zenith angles during our measurements.
Variations in wind speed and reflections from the ice may be responsible for the differences evident in Figure 2 between the observed albedos and those from Reference PaynePayne (1972). The average wind speed during Payne’s measurements was near 3.7 ms−1, which may explain the agreement between his values and our observations on 12 June when the wind speeds were similar. At the lower wind speeds present on 23 June, we expect higher albedos than those reported by Payne, since the dependence of the albedo on wind speed is greatest at low wind speeds and large solar zenith angles; however, we were unable to provide a model that can describe the observed albedo (Fig. 2).
The reflectivity of a direct beam incident on the lead surface at a zenith angle of 90° changes from 1.0 at zero wind speed to ∼0.24 with a 20 ms−1 wind (Reference Preisendorfer and MobleyPreisendorfer and Mobley, 1986). Because the albedo at the solar zenith angles prevalent in the Arctic is strongly dependent on wind speed, it is important to characterize the dependence. The albedo depends on the optical properties of the water in addition to surface reflectance. However, when surface reflectance is high, which occurs at large solar zenith angles, the surface reflectance is > 10 times the water-leaving irradiance so that the reflectance model is an adequate representation of the total albedo. It is possible to devise a parameterization that incorporates the modeled variations in reflectance due to wind speed presented by Reference Preisendorfer and MobleyPreisendorfer and Mobley (1986). A modification of the formula of Reference Briegleb, Minnis, Ramanathan and HarrisonBriegleb and others (1986) results in a simple parameterization of the albedo of the direct beam that includes the effects of wind speed from 0 to 20 m s−1. The parameterization that we suggest substitutes the constant in the denominator of the Reference Briegleb, Minnis, Ramanathan and HarrisonBriegleb and others (1986) equation with a polynomial equation with wind speed as the variable:

where a is the albedo, μ is the cosine of the solar zenith angle and w is the wind speed in meters per second. The predictions of this equation are presented in Figure 3. This parameterization provides a good representation of the change in albedo with wind speed when compared to the results of Reference Preisendorfer and MobleyPreisendorfer and Mobley (1986), although it does not precisely reproduce the Fresnel reflectance function at zero wind speed. When developing the parameterization, we used the mean of the modeled values of the reflectance with the waves parallel and perpendicular to the direction of the sun (Reference Preisendorfer and MobleyPreisendorfer and Mobley, 1986). Preisendorfer and Mobley showed that the albedo is a function of wind speed for both cloudy and clear-sky conditions. However, variations in the albedo due to types of clouds and the distribution of sky radiance are as large as the wind-speed dependence, and the variation in albedo due to wind is small compared to the direct sun case (0.02 vs 0.7), so one may neglect the wind-speed dependence under cloudy conditions.

Fig. 3. The albedo of the direct beam calculated using the parameterization presented in this paper. wind speed (w) is given in ms−1. the open symbols with lines are the model results; the solid symbols represent the values from Reference Preisendorfer and MobleyPreisendorfer and Mobley (1986). the symbol shape is the same for a given wind speed with a + symbol for w = 0 from preisendorfer and mobley. the direct beam values in Reference PaynePayne (1972) are also presented.
The parameterizations cannot reproduce the albedos measured on 23 June (Fig. 2). This is most likely due to not accounting for reflections of sunlight from the ice edge to the sea surface. On calm days like 23 June, the reflection from the ice edge was clearly visible and could be seen to extend a significant distance within the lead. This reflection provides a downwelling light source below our instruments and may add significant amounts of radiance at large zenith angles where the reflectance of water is large. Light reflected downward from the lead edge at large zenith angles tends to increase the measured albedo. Reflection from the snow and ice also contributes to the measured upwelling light and increases the calculated albedo.
Limited fetch within the leads may also affect albedos. The limited fetch does not allow the wave field to develop, so the wave field within leads may not be representative of the open ocean at the same wind speed. This is especially true of the albedo near the upwind edge of the lead where fetch is small. Often waves were not seen in the first meter or two adjacent to the ice edge. The effect of fetch could be an important factor in small leads.
Conclusions
Much of the summer the sky is overcast, so a single value of the albedo (0.066) may be sufficient for modeling during that time. In the spring when the sky is clearer and the sun is lower, it is important to account for the effect of wind speed on albedo. We have suggested a simple modification to the direct-beam albedo parameterization of Reference Briegleb, Minnis, Ramanathan and HarrisonBriegleb and others (1986) that includes the effect of wind speed. Parameterizations that can recreate the Fresnel reflectance at zero wind speed and that include a factor describing the light emerging from the ocean are logical next steps in continuing this effort.
Acknowledgements
We are grateful to S. Searson for her efforts in obtaining the summer lead data. We thank the crews of the N.G.C.C. des groseilliers and the SHEBA logistics personnel for their efforts to ensure a safe, enjoyable, and successful experiment. This project is funded by the Office of Naval Research High Latitude Program as part of SHEBA. The solar zenith angles used to determine atmospheric transmittance were calculated from the routines on the Applied Astronomy portion of the U.S. Navy Observatory web site.





