Quantifying air–water turbulence with moment field equations

Abstract

Energy transfer in turbulent fluids is non-Gaussian. We quantify non-Gaussian energy transfer between the atmosphere and bodies of water using a turbulent diffusion operator coupled with temporally self-affine velocity distributions and a recursive integration method that produce multifractal measures. The measures serve as input to a system of moment field equations (derived from Navier–Stokes) that generate and track high-frequency gravity waves that propagate through the water surface (as a result of the air–water interactions). The dimension of the support of the air–water turbulence produced by our methods falls within the range of theory and observation, and correspondingly, hindcast statistical measures of the water-wave surface such as significant water-wave height and wave period are well correlated to observational buoy data. Further, our recursive integration method can be used by spectral resolving phase-averaged models to interpolate temporal wind data to smaller scales to capture the non-Gaussian behaviour of the air–water interaction.

1. Introduction and motivation

The energy spectrum associated with water waves encompasses a vast range of frequencies. On one end of the spectrum are low-frequency tidal waves generated by the mutual attraction of the Sun, Moon and Earth while on the other end are high-frequency ripples, the periods of which are fractions of a second (see figure 1 in Conroy et al. (2018)). A significant portion of energy contained within this spectrum resides in a high-frequency band of water waves generated by air–water interactions known as the wind sea. When a wind sea is created by a large storm – such as a hurricane – it can wreak havoc among coastal communities. In total, 210 billion US dollars was spent on the recoveries of Hurricane Katrina and Superstorm Sandy (e.g. Blake 2013; GSO 2015).

As time progresses into the twenty-first century, the probability of an increase in the intensity of global tropical cyclones along with their destruction potential is likely (probability $>$66 %) (GFDL 2020). A recent report by the World Meteorological Organization task team (Knutson et al. 2020) also concludes that it is likely that rainfall rates associated with these cyclones will increase and sea level rise caused by anthropogenic warming should cause higher inundation levels when tropical cyclones do occur, which can lead to an increase in coastal community damages (GFDL 2020). In an effort to adapt to this situation and create coastal communities that are resilient to hurricane storm surge, researchers and coastal managers are attempting to use ensemble storm surge studies and real time forecast guidance to gauge how coastal flood dynamics responds to variations in storm strength, track and duration. Both approaches can employ hundreds to thousands of storm surge computer simulations to quantify the risk of a particular storm event. The computer simulations rely on two distinct mathematical models that share information in terms of stress to quantify the total storm surge inundation. These models consist of a long wave model that quantifies storm surge dynamics due to (i) the tides (waves with a period of 12 h or 24 h) and (ii) waves created by the large pressure gradient at the sea surface associated with the storm (waves with a period greater than 2.5 min). The long wave model is coupled to a short wave model (high-frequency gravity water waves with a period between 1 and 30 s), which quantifies the wind sea that forms in conjunction with the long waves. Advanced short wave models (see WAMDI 1988; Booij, Ris & Holthuijsen 1999; Tolman 2009; Smit, Janssen & Herbers 2015) can capture a multitude of surface water-wave phenomena on a wide variety of scales. This complexity, however, comes at a steep computational cost. ‘Operational’ short wave ocean models typically increase the computational load by a factor of three for coupled models using an unstructured mesh (Dietrich et al. 2012), and can run up to $86$ times as slow as a structured grid long wave model (Mellor, Donelan & Oey 2008). Due to the expense of the short wave component, ensemble storm surge studies routinely disregard (Liberto et al. 2011) or relax the convergence criteria of the short wave numerical solution (Ning, Emanuel & Vanmarcke 2014), which can have a negative impact in terms of the reliability of model results. Beyond danger of inaccuracy during disaster scenarios, these ‘quick’ fixes can ultimately perpetuate a public distrust in the validity of such computational tools.

The primary goal of this investigation is to leverage the 60-plus years of wind, water-wave and turbulence research to develop a rigorous framework to quantify the wind sea in a fashion that is computationally efficient and extendable (in terms of future work) to incorporate swell and coastal effects. To achieve this goal we focus our efforts on two main parts: (i) the development of a mathematical model to quantify the generation and propagation of various conservative quantities (momentum, energy, etc.) of the wind sea and (ii) the development of a statistical method to quantify the input in terms of the cause and effect of air–water interactions that transfer energy and grow the wind sea.

The secondary goal is to introduce a recursive integration method that extracts a measure of nonlinearity of the air–water interaction from observational wind speed data measured at 10 m above the sea surface, denoted by $U_{10}$, and uses this measure to interpolate $U_{10}$ to shorter time scales. The measure is known as the Hurst exponent (Hurst 1951, 1955; Mandelbrot 1977) and it is an important measure in terms of quantifying dependence driven variability of the wind data (see the details provided in § 3, as well as our companion paper Conroy, Kubatko & Mandli (2021) and Mandelbrot (1977)). When the Hurst exponent is set to $H = 1/2$, the water surface is composed of linear waves. However, numerical findings indicate that for a wind sea created by air–water interactions the Hurst exponent falls within the bounds $0.33 < H < 0.45$ and varies at a given spatial coordinate in time. The fact that $H < 1/2$ for the wind sea is significant because it corresponds to anti-persistent behaviour. Physically, this can be attributed to vortices that form in the turbulent air–water interaction which store information and give the flow field a ‘memory’ of the generator of the turbulence. The cyclonic nature of the vortices leads to the anti-correlated motion and vortex stretching leads to singular regions of energy dissipation at small scales that have a multifractal (statistical) distribution (Frisch 1996; Yakhot 2006). Balanced source terms for wave generation in spectral resolving phase-averaged wave models are a function of $U_{10}$. It is rare to have access to observational data for $U_{10}$ that are observed at the time scales necessary to integrate the action balance equation in time. Therefore, $U_{10}$ must be interpolated to smaller time scales. This is predominantly accomplished via linear interpolation, which does not capture non-Gaussian behaviour. The recursive integration methods presented in § 3 can be used in spectral resolving phase-averaged models to capture the non-Gaussian behaviour of $U_{10}$. In fact, Cavaleri (2009) draws attention to the fact that phase-averaged water-wave models typically under-predict peak wave heights and peak wave periods in strong storms unless ‘strong, but effective tuning’ is used. In our companion paper (Conroy et al. 2021) we show that this effect can be alleviated with our recursive integration methods and we conjecture that using our recursive integration methods to generate $U_{10}$ coupled with a source term such as, for example, the Zakharov–Resio–Pushkarev wind input source term (Zakharov, Resio & Pushkarev 2017), will help remedy this effect in spectral resolving wave models. Details for obtaining the numerical code for the recursive integration method can be found in Appendix A.

1.1. Background

Before we delve into the specifics of the mathematical treatment of our investigation it seems prudent that we provide the reader with some background information in regard to how our investigation leverages water-wave research and fits in with existing water-wave models and theories.

More specifically, our model fits into the phase-averaging classification of water-wave models that seeks to quantify the bulk movement of the short waves of the sea surface. Due to the large range of scales (both spatial and temporal) that span water-wave dynamics (see Salmon 1998) it is impossible to resolve all of the individual wave trains that comprise the water surface. Phase-averaging models circumvent this issue by characterizing the water-wave environment in a statistical sense, and make use of a probability density function to determine the water-wave dynamics that is most likely to occur at a specific geographic coordinate of interest under a given physical condition. Many short wave models quantify the water-wave heights and frequencies generated by air–water interactions by solving an energy balance equation (or action balance equation if the wind sea forms in the presence of currents). The energy balance equation involves operators in both geographic space and spectral space, and results in a five-dimensional equation whose solution is exacerbated by its spectral resolving source term, which is a function of atmospheric input, nonlinear wave–wave interactions and dissipation (see Hasselmann et al. 1973; Janssen 2004).

Rather than solve the action balance equation, we solve a system of balance equations derived from the Navier–Stokes equations (see Appendix B). These equations preserve statistical moments of quantities of interest (e.g. momentum, energy, energy flux) of the short water waves and can be described as moment field equations. The main advantage of our approach is twofold: (i) the final form of the system of equations we solve to quantify air–water turbulence consists of conservative hyperbolic partial differential equations (PDEs) with source terms, which are amenable to advanced discretization methods and are relatively easy to solve numerically, and (ii) the air–water energy transfer terms allow for non-Gaussian energy transfer (non-Gaussian loosely means that events in the tails of the distribution play an important role in the process). In other words, we do not assume a priori that the stochastic random variables that quantify the turbulent energy of the atmosphere are Gaussian. Indeed, there are some near-Gaussian features of turbulence but energy transfer is not one of them. Further, it should be emphasized that near Gaussian is not synonymous with Gaussian; if the turbulent velocity were truly Gaussian then the energy flux through the wavenumber $k$ would identically vanish (Frisch 1996).

Due to the fact that the moment field equations consist of moments of the Navier–Stokes equation we have to deal with the issue of moment closure (each equation for the $n$th-order moment involves terms of the $(n+1)$th-order moment which means the equations cannot be solved without some kind of closure scheme, see Friedrich & Peinke (2020), for example). Previous water-wave investigations make use of the Reynolds-averaged Navier–Stokes (RANS) equation to quantify air–water turbulence (Janssen 2004). Many of these investigations used variations of an eddy viscosity mixing length approach to close the RANS equation. However, these efforts were more focused on investigating critical layer dynamics and largely did not attempt to track the water waves after they were created (Janssen 2004).

Because we are concerned with generating and tracking the water waves, we close the moment field equations with a novel approach that transforms the turbulent diffusion operator to a wave propagation term. The wave propagation term quantifies energy transfer between the wind and water in terms of a pulsation – a pulsation in the energy of the atmosphere creates a corresponding pulsation of energy in the water surface – whether or not the energy pulsation transferred from the wind to the water surface grows into a longer wave depends on the strength of the pulsation and the speed of the water wave and the duration (or fetch) of the wind. More specifically, because we model air and water as inviscid fluids, if the physical conditions are such that an inflection point exists between the speed of the wind and water wave then at least one instability exists and the water wave will grow if the wind continues to blow at the same speed (see Moreland, Saffman & Yuen 1991). Rather than explicitly calculate these instabilities we quantify the probability of an instability occurring via a parameter that we denote by $q$, and use this information in a statistical operator that generates the expected energy pulse in the water surface.

We define the exact quantitative relation connecting the wind velocity to the corresponding energy pulse (created in the water surface) via the original energy transfer parameterization of Hasselmann et al. (1975), which takes into account atmospheric input, nonlinear wave interactions and dissipation, and has been verified by the direct numerical simulations of Tanaka (2001). It can be noted that Hasselmann's original nonlinear energy parameterization is only valid for growing wind seas and is not applicable to swell waves, and therefore, we limit the current investigation to water waves with a non-dimensional frequency $\nu = f_m U_{10}/g > 14$, where $f_m$ is the peak frequency of the water waves, $U_{10}$ is the wind speed measured at $10$ m from the water surface and $g$ is acceleration due to gravity.

The resonance mechanism described above is originally due to Phillips (1957) and Miles (1957), who both independently conjectured that resonance between the wind and the water surface generates water waves. Phillips considers a resonance mechanism involving turbulent pressure fluctuations while the Miles theory takes into account the resonance between wave induced pressure fluctuations and the free surface of the water (Janssen 2004). The Phillips mechanism leads to a linear growth rate while the Miles mechanism leads to an exponential growth rate caused by shear flow instability. Recent laboratory experiments by Liberzon & Shemer (2011) show that wave growth is exponential, however, these same experiments invalidate some of the consequences of Miles’ theory, although it has received support from experiments examining longer waves (Janssen 2004).

In this investigation, we assume that the wave growth is exponential, however, we do not explicitly resolve the shear flow instability mechanism posited by Miles. Instead, we consider the probability of the likeliness of an instability occurring based on the current physical state of the atmosphere and body of water and quantify the temporal distribution of these instabilities. Because we neglect viscosity effects in our model, these instabilities take the form of singularities.

As in the work of Phillips, we also develop the resonance mechanism in terms of a reference frame that moves in tandem with the water surface and transfers energy via pressure and shear stress. Rather than characterize the frame of reference of this energy transfer (between air and water) with the speed of the stress distribution, however, we characterize the frame of reference using a speed, $\|\boldsymbol {u}_0\|$, linked to the flow of energy in the wind-sea spectrum. Further, unlike Phillips, who assumes that the stress fluctuations are random, we utilize a formulation such that the characteristic speed of each stress pulsation depends on the previous stress pulsation, so that all of the turbulent pulsations are connected to a generating event. In other words, the stress pulsations have a memory of the event that generated the turbulence.

To illustrate this point, consider the simple example of a laminar fluid flowing past a dense screen mesh. As the fluid flows past the screen mesh turbulence will be created and energy dissipation will occur nearly everywhere within the fluid. The turbulence in this case is nearly space filling (to the extent that the screen mesh is space filling) and the energy transfer can be quantified (in terms of low-order moments) using the famous theory of Kolmogorov (1941).

For wind flowing over a body of water the generating event of the turbulence, for example, could be due to the wind initially flowing over rough topography before flowing over a rough coastline and then over the body of water. The energy dissipation caused by these generating events result in a distribution of eddies that is not space filling but is fractal (Frisch 1996; Mandelbrot 1974); the dimension of the statistical signature of energy transfer lies between a dimension of 2 and 3. In this case, the turbulence is said to be intermittent, and Kolmogorov's 1941 theory is no longer applicable (Yakhot 2006). In fact, turbulence observed in nature is multifractal (Frisch 1996; Mandelbrot 1998), there is a spectrum of fractal dimensions associated with a given flow field which it acquires through interactions with its environment. In the example of the wind flowing over a body of water, the spectrum of fractal dimensions (in terms of the eddy distribution) results from the wind's interaction with the topography, coastline and body of water where each event injects a different statistical pattern into the flow field. The recursive integration method we introduce in § 3 is general enough to extract the statistical distribution of energy transfer from the flow field regardless of the generating event.

More specifically, we generate multifractal measures of the eddy distribution in the wind by decomposing observational wind data into a series of duration limited pulses where the temporal distribution of the wind speed and direction are modelled using a power law. The characteristic speed/direction of each pulse can change with each duration. The power law exponent also changes with each pulsation, and measures the extent of the turbulence associated with each pulse. In particular, a large absolute value of the exponent indicates a greater probability that an instability will occur and is associated with either injection or dissipation of energy/momentum at the air–water interface.

It can be noted that when we refer to air–water turbulence we refer to small scale, high-frequency turbulence where the period of the turbulence is less than the period of the water waves. In this case the small scale turbulence is so fast that it is always in equilibrium with the shear flow which generates an instability and transfers energy between the air and water (Janssen 2004). Large scale turbulence (classified as having a period greater than the water waves) is excluded from the current investigation.

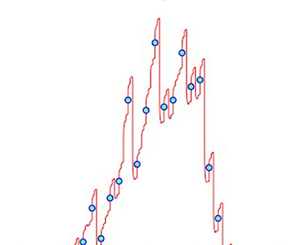
Due to the fact that wind data are typically presented in hourly averages, and because we are concerned with small scale turbulence, we introduce a recursive integration procedure that generates a refined distribution of the wind turbulence for shorter time scales. The method leverages the fact that the Navier–Stokes equations are invariant under scaling transformations in the form of self-affine power laws that hold for small viscosity values (Frisch 1996). Typically, such scaling properties only hold over a range of scales delineated by an inner cutoff and outer cutoff. The outer cutoff is usually specified in terms of the integral length scale while the inner cutoff is typically associated with molecular diffusion. Because of this fact, scaling laws can typically can only be employed over 3–5 decades of refinement.

The recursive integration method we develop herein proceeds in a similar iterative fashion as cascade models such as the $p$ model (Meneveau & Sreenivasan 1987) and $\beta$ model (Frisch 1996), and was originally inspired by the curdling models of Mandelbrot (1974), however, there are some important distinctions. In the $p$ model, the probabilities of a binomial distribution were chosen so as to reproduce the generalized dimensions of the multifractal spectrum of the dissipation field of several fully developed turbulent flows. The $\beta$ model (which was introduced by Mandelbrot (1974) and popularized by Frisch (1996)) also uses a pre-determined value for $\beta$ that determines the fractal dimension of the energy dissipation, and the weighted curdling model of Mandelbrot is typically used by prescribing the distribution of the weights using a priori considerations.

In our approach, rather than use a priori considerations, we use a conditional probability and determine the weights based on the current state and previous state of the dynamics of the wind field. We achieve this by preserving the area and endpoint values of the data over each time interval that the average wind data are reported, and calculate the characteristic velocity, $\|\boldsymbol {u}_0\|$, and power law exponent, $q$, that defines the velocity distribution. Each successive iteration is initialized by integrating over a sub-region of the distribution to determine a new set of averages that are used to determine the velocity distribution over a shorter duration of time. An important component of our recursive integration concerns the fact that we are able to cut out temporal regions during the integration process to produce a fractal support of the measure which falls within the range of observations with each recursion. This is markedly different than most cascade models that begin from a uniform measure and require a number of recursions before the fractal measure of the dissipation falls within the range of observations. In this respect, our recursive integration procedure can generate what Mandelbrot (1974) refers to as conservative and non-conservative cascades. The recursive integration method coupled with the source terms developed in § 2.1 are the key to capturing the non-Gaussian behaviour of the energy transfer. Further, we would like to emphasize that the recursive integration method presented herein is by no means meant to represent a physical mechanism of energy transfer in a turbulent fluid; it is purely a mathematical construct to interpolate the data in a non-Gaussian fashion.

The remainder of this paper is organized as follows; in § 2 we introduce the moment field equations and derive source terms that quantify air–water energy transfer. We close these source terms in § 3 and introduce our recursive integration method and the corresponding energy measures. Finally, in § 4 we apply our methods to air–water turbulence over Lake Erie and measure the fractal dimension of the turbulent energy as well as the generating and propagating of short water waves over Lake Erie. We compare numerical results to observations and close the paper with a discussion of conclusions and future work.

2. Moment field equations

Let $\varOmega$ be a bounded domain in $\mathbb {R}^3$. We track energy associated with the short water waves generated by air–water interactions within $\varOmega$ by solving a set of moment field equations,

(2.1)\begin{equation} \frac{\partial m_n}{\partial t} + \nabla_{xy} \cdot \left(m_n \boldsymbol{c}_0+ \sum_{i=0}^n m_{n-i}\boldsymbol{c}_{i+1}\right) = \mu_n \varDelta_{xy} m_n,\quad n = 0,1,\ldots ,N, \end{equation}

where c ₀ is the group speed of the long wave that the short gravity waves are travelling with, c ₁ is the speed associated with the short wave group, c ₂ is the acceleration of the short wave group, etc., $\mu$ is a diffusion coefficient, $\nabla _{xy} = \partial / \partial x \hat {i} + \partial / \partial y\hat {j}$, $\varDelta _{xy} = \partial ^2 / \partial x^2 + \partial ^2 / \partial y^2$ and $n$ corresponds to the order of the moment, $m_n$, of the one-dimensional density ($F(\boldsymbol {x}_0,k,t)$) of the short water waves at the geographic point $\boldsymbol {x}_0$,

(2.2)\begin{equation} m_n =\int_{k_i}^{k_f}{k^n F(\boldsymbol{x}_0,k,t)\,{\rm d}k},\quad n = 0,1,\ldots ,N. \end{equation}

Here, $k = \| \boldsymbol {k} \|$ is the magnitude of the water wavenumber vector with mean direction $\bar {\theta }$ and $k_i$ and $k_f$ are the low and high wavenumber cutoffs of the wind sea. The mean direction satisfies the differential equation,

(2.3)\begin{equation} \frac{\partial \bar{\theta}}{\partial t}=f\left(\frac{\partial \bar{\theta}}{\partial x}; D(\boldsymbol{x},t)\right), \end{equation}

where $D(\boldsymbol {x},t)$ parameterizes the inhomogeneities of the medium of propagation, see Salmon (1998), for example. It can be noted that $D$ incorporates atmospheric input, fluid depths, etc.; the $\boldsymbol {c}_{i}$ are coefficients that represent the velocity, acceleration, etc. of the water-wave group (see Appendix B), and are functions of a dispersion relation,

(2.4)\begin{equation} G(\bar{k}_{n+1},\bar{\omega}_{n+1})=0, \end{equation}

which relates the angular frequencies ($\bar {\omega }_{n+1} = 2{\rm \pi} \bar {f}_{n+1}$) to the characteristic wavenumbers, $\bar {k}_{n+1}$, defined as

(2.5)\begin{equation} \bar{k}_{n+1}=\frac{\displaystyle\int{k^{n+1} F(\boldsymbol{x}_0,k,t)\,\textrm{d}k}}{ \displaystyle\int{k^n F(\boldsymbol{x}_0,k,t)\,\textrm{d}k}}=\frac{m_{n+1}}{m_n}, \end{equation}

where the bounds of integration in (2.5) are from $k_i$ to $k_f$. The number of moments preserved in (2.1) is a function of the water-wave dynamics under consideration. In this initial investigation, we set $N = 1$ and solve the system of equations,

(2.6)\begin{gather} \frac{\partial m_0}{\partial t}+\nabla_{xy} \cdot ((\boldsymbol{c}_0+\boldsymbol{c}_1) m_0)= \tilde{\mu}_0\frac{\partial }{\partial x}\left( \frac{\partial m_0}{\partial x}\right) , \end{gather}

(2.7)\begin{gather}\frac{\partial m_1}{\partial t}+\nabla_{xy} \cdot ((\boldsymbol{c}_0+\boldsymbol{c}_1) m_1)=\tilde{\mu}_1\frac{\partial }{\partial x}\left( \frac{\partial m_1}{\partial x}\right) , \end{gather}

(2.8)\begin{gather}\frac{\partial \bar{\theta}}{\partial t}=D(\bar{\theta},\bar{\theta}_w,\mathcal{E}), \end{gather}

where $\mathcal {E}$ is energy supplied to the water waves from the atmosphere, $\bar {\theta }_w$ is the mean direction of the atmospheric velocity in the boundary layer, $m_0$ is a characteristic quantity (momentum, energy or energy flux) of the short water-wave group, $m_1$ is a measure of the representative water wavenumber and $\tilde {\mu }_0$ and $\tilde {\mu }_1$ are diffusion coefficients to be defined in the next subsection. It can be noted that in this work we neglect the high-order wave group acceleration term (c ₂)m ₀ in (2.7) and assume that $\boldsymbol {c}_0 = 0$ (the air–water interactions create a wind sea in the absence of any ambient current).

2.1. Air–water energy transfer

The physical model described by (2.1) can be enunciated in the following fashion; we have a set of moment ‘masses’ that characterize the energy of a group of water waves propagating through a medium at a velocity that depends on the specific properties of the medium as well as the water-wave group itself. In the case of air–water turbulence, pressure pulsations in the local atmosphere tend to transfer energy to the moment masses causing them to deviate from their reference energy level – this is the energy transfer that we wish to quantify – the scales of the problem, however, render the inner workings of this process opaque, giving it the appearance of a random process. Classically, this process is modelled with a diffusive operator that attempts to quantify the potential for a space–time region to deviate from its current energy configuration due to subscale energy transfer. Let us leverage this diffusive operator to derive an air–water energy transfer term.

Choosing a reference frame that moves with the velocity of the water-wave group, the propensity for the moment field to fluctuate from its spectral configuration is

(2.9)\begin{equation} \frac{\partial m_n}{\partial t}=\bar{\mu}_n\varDelta_{xy} m_n,\quad n = 0,1, \end{equation}

where $\bar {\mu }_n$ is a function of the variance supplied by the atmospheric turbulence. Equation (2.9) gives the probability that a certain measure of moment mass lies within the interval $[\boldsymbol {x}_0-\delta \boldsymbol {x}/2,\boldsymbol {x}_0+\delta \boldsymbol {x}/2]$ at a given instant in time $t$. However, we are interested in the energy transfer along a path that is fixed in space and interval in time, so what we really require is an expression that gives the probability that a certain measure of moment mass lies in the interval $[t_i,t_f]$ (where $t_f - t_i \equiv l \equiv \varDelta t$) at the spatial point $\boldsymbol {x}_0$. In other words, we need an expression for diffusion in time. We can achieve this through the use of the wave equation along with a relation due to Kolmogorov. In particular, the wave equation is

(2.10)\begin{equation} \frac{\partial ^2 m_n}{\partial t^2}=\|\boldsymbol{c}_{g_f}\|^2 \varDelta_{xy} m_n, \end{equation}

where $\|\boldsymbol {c}_{g_f}\|$ is the speed of a group of fluctuations in the moment field that results from pressure pulsations in the atmosphere. It can be noted that in the previous equation and the remainder of this subsection, $n = 0,1$. We assume a relation exists between $\bar {\mu }_n$ and $\|\boldsymbol {c}_{g_f}\|^2$ so that we can make use of (2.9) and (2.10) to write,

(2.11)\begin{equation} \frac{\partial m_n}{\partial t}=\tilde{\mu}_n \varDelta_{xy} \mathcal{E}_n = \mathcal{A}\frac{\partial ^2\mathcal{E}_n}{\partial t^2}, \end{equation}

where we have rewritten $m_n$ on the right-hand side of (2.9) and (2.10) as $\mathcal {E}_n$ to emphasize that this corresponds to moments of the water-wave energy pulsation generated by pulsations in the wind. We then utilize the idea of probability space–time paths from No. 9 in Kolmogorov (1992) to rewrite this expression solely as a function of the separation in time. Specifically, we have

(2.12)\begin{equation} \frac{\partial m_n}{\partial t}=\tilde{\mu}_n\varDelta_{xy} \mathcal{E}_n = \mathcal{A}\frac{\partial ^2\mathcal{E}_n}{\partial t^2} = \sum_{i} A_{in} \frac{{\rm d} \mathcal{E}_n}{{\rm d}t}, \end{equation}

where the last term follows from the general result presented in § 10 in No. 9 of Kolmogorov (1992). It can be emphasized that ${\rm d} \mathcal {E}_n/{\rm d}t$ is the change in the local energy field due to changes in the atmospheric velocity in the boundary layer (or energy transfer) over a duration limited interval $\varDelta t$. In other words, ${{\rm d} \mathcal {E}_n}/{\rm d}t$ represents the energy pulsation generated in the water by a stress pulsation in the wind. What remains is to determine the $A_{nk}$ that measure the probability for the water-wave field to pass from state $\varrho _j$ to state $\varrho _k$ in the local (temporal) neighbourhood under consideration (Kolmogorov 1992). Assuming that the energy transfer travels with the group velocity of the fluctuation in the moment field, $\|\boldsymbol {c}_{g_f}\|$, we can write

(2.13)\begin{gather} \frac{\partial m_n}{\partial t}=\tilde{\mu}_n\left(\frac{\partial ^2\mathcal{E}_n}{\partial x^2}+\frac{\partial ^2\mathcal{E}_n}{\partial y^2}\right) =\tilde{\mu}_n\left(\frac{{\rm d}^2\mathcal{E}_n}{(c_{g_{f_x}}\,{\rm d}t)^2} +\frac{{\rm d}^2\mathcal{E}_n}{(c_{g_{f_y}}\,{\rm d}t)^2}\right), \end{gather}

(2.14)\begin{gather}\frac{\partial m_n}{\partial t}=\frac{\tilde{\mu}_n}{\|\boldsymbol{c}_{g_f}\|^2\cos^2\theta} \frac{{\rm d}^2\mathcal{E}_n}{{\rm d}t^2}+\frac{\tilde{\mu}_n}{\|\boldsymbol{c}_{g_f}\|^2\sin^2\theta} \frac{{\rm d}^2\mathcal{E}_n}{{\rm d}t^2}. \end{gather}

Substitution of the general relation (74) in No. 9 of Kolmogorov (1992) gives,

(2.15)\begin{equation} \frac{\partial m_n}{\partial t}=\frac{\tilde{\mu}_n}{\|\boldsymbol{c}_{g_f}\|^2\cos^2\theta}\left(\sum A_{xn}\frac{{\rm d}\mathcal{E}_n}{{\rm d}t}\right)+\frac{\tilde{\mu}_n}{\|\boldsymbol{c}_{g_f}\|^2\sin^2\theta} \left(\sum A_{yn}\frac{{\rm d}\mathcal{E}_n}{{\rm d}t}\right). \end{equation}

For expression (2.15) to hold true, we must set

(2.16)\begin{gather} \sum A_{xn}=\frac{\mathcal{C}_n}{2\tilde{\mu}_n}\|\boldsymbol{c}_{g_f}\|^2\cos^2\theta, \end{gather}

(2.17)\begin{gather}\sum A_{yn} = \frac{\mathcal{C}_n}{2\tilde{\mu}_n}\|\boldsymbol{c}_{g_f}\|^2\sin^2\theta, \end{gather}

where the $\mathcal {C}_n$ terms relate $\partial m_n / \partial t$ to ${\rm d}\mathcal {E} / {\rm d}t$. The final air–sea transfer source terms ($S_n$) are,

(2.18)\begin{gather} S_n = \sum A_{in} \frac{{\rm d}\mathcal{E}_n}{{\rm d}t}, \end{gather}

(2.19)\begin{gather}S_n=\left(\frac{\mathcal{C}_n}{2\tilde{\mu}_n}\|\boldsymbol{c}_{g_f}\|^2\cos^2\theta + \frac{\mathcal{C}_n}{2\tilde{\mu}_n}\|\boldsymbol{c}_{g_f}\|^2\sin^2\theta\right) \frac{{\rm d}\mathcal{E}_n}{{\rm d}t}, \end{gather}

(2.20)\begin{gather}S_n=\frac{\mathcal{C}_n}{2\tilde{\mu}_n}\|\boldsymbol{c}_{g_f}\|^2\frac{{\rm d}\mathcal{E}_n}{{\rm d}t}. \end{gather}

The $\tilde {\mu }_n$ term in (2.20) scales the spectral transfer of the local neighbourhood under consideration and is simply equal to $1/2\|\boldsymbol {c}_{g_f}\|^2$. The exact value of $\mathcal {C}_0$ will depend on the specific density function being conserved by the moment field equations. For instance, if the density function quantifies momentum ($P = \mathcal {E}/c_p$ where $c_p= \omega / k$ is the phase speed of the water waves), then, for $n = 0$, we have,

(2.21)\begin{equation} \mathcal{C}_0 = \frac{1}{\|\boldsymbol{c}_{p_f}\|}, \end{equation}

where $\|\boldsymbol {c}_{p_f}\|$ is the phase speed of the water-wave pulsation. If the density function quantifies water-wave energy, then for $n=0$, $\mathcal {C}_0$ is set to,

(2.22)\begin{equation} \mathcal{C}_0=\frac{\|\boldsymbol{c}_{p_f}\|}{\|\boldsymbol{c}_{p_f}\|}=1. \end{equation}

Finally, in the case of energy flux we have,

(2.23)\begin{equation} \mathcal{C}_0= \frac{\|\boldsymbol{c}_{p_f}\|^2}{\|\boldsymbol{c}_{p_f}\|}=\|\boldsymbol{c}_{p_f}\|. \end{equation}

Regardless of the probability density quantified by the moment field equations, the $\mathcal {C}_1$ term takes the form,

(2.24)\begin{equation} \mathcal{C}_1= \frac{\|\boldsymbol{c}_{g_f}\|}{\|\boldsymbol{c}_{p}\|}, \end{equation}

which qualitatively is similar to the inverse of the wave age $\chi _{10} = c_p / U_{10}$. The key difference between expression (2.24) and the inverse wave age involves the fact that expression (2.24) is written in terms of the speed of the water-wave pulsation generated in the water surface by the wind rather than being written in terms of the wind speed $U_{10}$. Substitution of (2.23) and (2.24) into (2.20), for example, yields the source terms for the moment field equations that quantify the energy flux transferred from the wind to the water waves,

(2.25)\begin{equation} S_0 = \|\boldsymbol{c}_{p_f}\|\frac{{\rm d}\mathcal{E}_0}{{\rm d}t}, \end{equation}

and

(2.26)\begin{equation} S_1 = \left(\frac{\|\boldsymbol{c}_{g_f}\|}{\|\boldsymbol{c}_{p}\|}\right) \frac{{\rm d}\mathcal{E}_1}{{\rm d}t}. \end{equation}

Here, we emphasize the fact that the ${{\rm d}\mathcal {E}_n}/{{\rm d}t}$ terms are explicit functions of the wind speed. More specifically, the ${{\rm d}\mathcal {E}_n}/{{\rm d}t}$ terms are duration limited pulsations in the local energy field of the water-wave group that result from air–water interactions in the atmospheric boundary layer and satisfy the energy balance equation of nonlinear energy transfer that accounts for atmospheric input, nonlinear wave interactions and dissipation as quantified by Hasselmann et al. (1975). We define these terms as well as the explicit form of the duration limited wind velocity in the next section.

3. The wind-sea generator: air–water interactions

We define the atmospheric turbulence that generates the wind sea by considering the incompressible Navier–Stokes equations,

(3.1)\begin{equation} \frac{\partial \boldsymbol{u}}{\partial t}+(\boldsymbol{u}\boldsymbol{\cdot} \boldsymbol{\nabla}) \boldsymbol{u}={-}\frac{1}{\rho_a}\boldsymbol{\nabla} p + \mu \varDelta \boldsymbol{u}, \end{equation}

where $p$ is the pressure, $\rho _a$ is the density of air and $\mu$ is the fluid viscosity. Rather than attempt to explicitly solve these equations we leverage scaling properties of (3.1) to measure the energy transfer associated with the air–sea turbulence. That is, in the limit $\mu \rightarrow 0$ the Navier–Stokes equations are invariant under scaling transformations (Frisch 1996),

(3.2a–c)\begin{equation} \boldsymbol{u} \rightarrow \lambda^h\boldsymbol{u},\quad t \rightarrow \lambda^{1-h}t,\quad r \rightarrow \lambda r,\quad \lambda > 0. \end{equation}

The scaling also holds at small viscosity (see Frisch 1996) if,

(3.3)\begin{equation} \mu= \lambda^{h-1}\mu, \end{equation}

which implies that the dissipation, defined as $\epsilon = \mu \langle (\boldsymbol {\nabla } \boldsymbol {u})^2\rangle$ ($\langle \cdot \rangle$ denotes ensemble averages), scales as,

(3.4)\begin{equation} \epsilon \rightarrow \lambda^{3h-1}\epsilon. \end{equation}

From this, it follows that the absolute probability of encountering an active region of turbulence is,

(3.5)\begin{equation} \delta u \sim \left(\frac{r}{L}\right)^h, \end{equation}

for $\ell _{\eta } < r \ll L$, where $\ell _{\eta }$ is a dissipation cutoff, $L$ is the integral length scale and $r$ is a spatial distance, see Frisch (1996) for more details. It can be noted that scaling exponent ($h$) of the Navier–Stokes equation is related to the Hurst exponent ($H$) via

(3.6)\begin{equation} H=\frac{1}{3h+2}. \end{equation}

In the case $h \geq 1/3$ energy is conserved, however, if $h < 1/3$ then the scaling relations are non-conservative and energy is lost to due to a loss of regularity (Frisch 1996).

The Hurst exponent is important in a statistical context because it measures the extent of the memory of the process (Mandelbrot 1977). If a process is random and Gaussian then the variance of the process is connected to the square root of the period and the process is ‘memoryless’; past events have no influence on future events and $H = 1/2$ (the variance is tied to the square root operator). To illustrate this point further, imagine we are studying the time series of a variable with temporal movements that are generated by a process that is unknown to the observer. Let us denote these movements by $B_{H}(t)$. If the expectation of the motion is zero for all time $t$, then the expected variance of the motion over a period $T$ can be expressed in terms of the Hurst exponent (Mandelbrot 1977),

(3.7)\begin{equation} \mathbb{V}[ B_{H}(t + T) - B_{H}(t)]=T^{2H}, \end{equation}

where $\mathbb {V}[\cdot ]$ is the expected variance and $0 < H < 1$ (Mandelbrot 1977). When $H < 1/2$ the motion is antipersistent; it has a tendency to return to some past condition, whereas if $H > 1/2$ the motion is persistent and a given condition tends to persist for long intervals of time (Mandelbrot 1977). It can be noted that the graph dimension of the corresponding time series is $D_G = 2 - H$ and is always greater than the topological dimension. There is a self-similar trail ($(X(t),Y(t))=f(B_H(t))$) connected to the graph dimension that corresponds to the spatial path of the motion and the dimension of this trail is given by $D_E = 1/H > D_G$, and corresponds to the dimension that the trail is embedded in. If the trail occurs in Cartesian space and ‘fills’ all three dimensions, for instance, then the trail is said to be space filling. However, $D_E$ does not have to be an integer. In the case it is a non-integer, $D_E$, is known as the fractal dimension. When a process is multifractal there is a spectrum of fractal dimensions associated with the flow and $D_E > D_G$, however, the relation $D_E = 1/H$ no longer holds, see Mandelbrot (1997, 1998) for more details. In this case the dimension of the self-similar support of the multifractal measure is determined via other considerations, see § 3.5.3.

It is interesting to note that Kolmogorov (1941) assumes energy interactions are local in wavenumber space; energy transfer concentrates on a singular set of points with $H = 1/3$. Clearly, the motion has a memory of the generating event because $H < 1/2$ and the set is also space filling because we have $D_E = 1/(1/3) = 3$. Experiments and observations, however, tend to point to the fact that energy transfer in a turbulent fluid is not space filling but is intermittent at small scales (Frisch 1996).

3.1. Distribution of the wind velocity

Rather than utilize the absolute probability given by (3.5) (which is highly dependent on $L$) we utilize a conditional probability to generate measures of the velocity and energy transfer connected to air–water interactions. That is, given the condition that an active region of turbulence occurs within the period $l_{d_{\eta }} \ll l_{d_{\epsilon }} < t_l < l_0 \ll L_T$ ($l_{d_{\eta }}$ is the molecule length scale, $l_{d_{\epsilon }} \approx 1 \times 10^{-6}$ and $L_T$ is the temporal integral length scale), then we assume that the local distribution of the atmospheric velocity at the spatial point $\boldsymbol {x}_0$ is temporally hyperbolic, with magnitude,

(3.8)\begin{equation} \|\boldsymbol{u}\|=\|\boldsymbol{u}_0\|\left[\frac{g}{\|\boldsymbol{u}_0\|}(t_{l})\right]^q, \end{equation}

and direction,

(3.9)\begin{equation} \theta_w=\theta_0\left[\frac{\omega_{\theta}}{\theta_0}(t_{l})\right]^{\varUpsilon}, \end{equation}

where $t_{l}$ is the local time, $g$ is acceleration due to gravity, $(\|\boldsymbol {u}_0\|,\theta _0)$ are local constants and $\omega _{\theta }$ is the minimum turning frequency of the characteristic reference velocity ($\boldsymbol {u}_0$),

(3.10)\begin{equation} \boldsymbol{u}_0=\| \boldsymbol{u}_0 \|\textrm{e}^{\textrm{i} \theta_0}, \end{equation}

i.e. the representative velocity of the large scale flow field of the space–time region under consideration. It can be noted that the exponents $(q,\varUpsilon )$ quantify the amount of change (from the reference velocity field $\boldsymbol {u}_0$) that $\boldsymbol {u}$ undergoes over the time interval $l_0 - l_{d_{\epsilon }}$ (if $q = 0$ and $\varUpsilon = 0$ then $\boldsymbol {u} = \boldsymbol {u}_0$). For a given time series the global distribution of the atmospheric turbulent velocity consists of the union of all the local regions used to pave the temporal velocity curve, i.e.

(3.11)\begin{equation} \boldsymbol{u}_{l}=\mathop{\bigcup}\limits_{j=1}^{\mathcal{N}}\boldsymbol{u}^{(\,j)} =\mathop{\bigcup}\limits_{j=1}^{\mathcal{N}}\{\|\boldsymbol{u}^{(\,j)}\|\, \textrm{e}^{{\rm i}\theta_w^{(\,j)}}\}, \end{equation}

where the magnitude $\|\boldsymbol {u}^{(\,j)}\|$ and direction $\theta ^{(\,j)}_w$ are functions of the spatial coordinate $\boldsymbol {x}_0$ and global time $t$, and $\mathcal {N}$ is the total number of local regions used to pave the temporal velocity curve. It can be noted that the $l$ attached to $\boldsymbol {u}_{l}$ indicates that the temporal continuity of the representation of the distribution of the atmospheric velocity depends on the inner cutoff of the kernel. More specifically, we define a temporal region $\mathcal {R}^{(\,j)}$ located at the geographical coordinate $\boldsymbol {x}_0$ of height,

(3.12)\begin{equation} u_{\epsilon}(\boldsymbol{x}_0,l_0)= \sup_{l \in \mathcal{L}_{\epsilon (l)}} \| \boldsymbol{u}^{(\,j)} \| - \inf_{l \in \mathcal{L}_{\epsilon (l)}} \| \boldsymbol{u}^{(\,j)} \|, \end{equation}

and length,

(3.13)\begin{equation} \mathcal{L}_{\epsilon} = [l_{d_{\epsilon}},l_0]. \end{equation}

Each $\mathcal {R}^{(\,j)}$ is a local reference frame that wholly contains the dynamic perturbations of the flow field in the time interval $l_0$ (at the point $\boldsymbol {x}_0$). Embedded within each $\mathcal {R}^{(\,j)}$ is a cut out region $]l_{d_{\epsilon }}, l_{d}[$ where functions (3.8) and (3.9) are no longer valid. This region corresponds to a measure of uncertainty in terms of the measure of the turbulent velocity on the length scale, $l_0$, and therefore, we would like to make $l_d$ as small as possible. We address this issue in § 3.5.

3.1.1. Determination of characteristic pressure

To complete the description of the atmospheric flow field we need to determine the pressure field associated with the velocity distribution given by (3.11). In the limit $\mu \rightarrow 0$ local accelerations along a space–time path in the atmosphere are solely due to pressure gradients,

(3.14)\begin{equation} \frac{\mathrm{D}\boldsymbol{u}}{\mathrm{D}t} ={-} \frac{1}{\rho_a} \boldsymbol{\nabla} p, \end{equation}

where ${\mathrm {D}\cdot }/{(\mathrm {D}t)}$ is the total derivative. In general, the total pressure will vary in both the $x$ and $y$ directions of the domain,

(3.15)\begin{equation} \mathrm{d}p=\frac{\partial p}{\partial x}\,\mathrm{d} x+\frac{\partial p}{\partial y}\,\mathrm{d} y. \end{equation}

Substituting (3.14) into (3.15) and rearranging gives

(3.16)\begin{equation} \mathrm{d}p ={-}\rho_a \left(\frac{\mathrm{d} x}{\mathrm{d}t} \,\mathrm{d}u + \frac{\mathrm{d}y}{\mathrm{d}t}\,\mathrm{d}v\right). \end{equation}

Integrating yields the total pressure,

(3.17)\begin{equation} p_T = p_0 - \frac{\rho_a}{2}(u^2+v^2), \end{equation}

where $p_0$ is the characteristic reference pressure associated with the large scale flow field. In general, $p_0$ is a function of the large scale thermodynamic properties of the atmosphere as well as the topography and boundary of the domain. If we make use of the fact that $u = \| \boldsymbol {u}^{(\,j)}\| \cos (\theta )$ and $v = \| \boldsymbol {u}^{(\,j)} \| \sin (\theta )$ over a given $\mathcal {R}^{(\,j)}$, then (3.17) simplifies to,

(3.18)\begin{equation} p_T^{(\,j)} = p_0^{(\,j)} - \frac{\rho_a}{2}\|\boldsymbol{u}^{(\,j)}\|^2, \end{equation}

and it becomes apparent that the pressure fluctuations in the local atmosphere with respect to $p_0$ are equivalent to the kinetic energy of the atmosphere.

We close the description of the turbulent flow field by relating $p_0^{(\,j)}$ to the average pressure (or expected pressure) $\bar {p}^{(\,j)}$ over a given $\mathcal {R}^{(\,j)}$. In particular, the average pressure ($\bar {p}^{(\,j)}$) can be expressed in terms of the total pressure ($p_T^{(\,j)}$) as,

(3.19)\begin{equation} \bar{p}^{(\,j)}=\frac{1}{(l_0-l_{d_{\epsilon}})}\int_{l_{d_{\epsilon}}}^{l_0}{p_T^{(\,j)}\,\mathrm{d}t_l} =\frac{1}{(l_0-l_{d_{\epsilon}})}\int_{l_{d_{\epsilon}}}^{l_0}\left(p_0^{(\,j)}-\underbrace{\frac{\rho_a}{2}\|\boldsymbol{u}^{(\,j)}\|^2}_{{\equiv} p'^{(\,j)}}\right)\mathrm{d}t_l. \end{equation}

Inserting (3.8) into (3.19) while evaluating the integral yields,

(3.20)\begin{align} \bar{p}^{(\,j)}&=p_0^{(\,j)}-\frac{1}{(l_0-l_{d_{\epsilon}})} \int_{l_{d_{\epsilon}}}^{l_0}{\frac{\rho_a}{2}\|\boldsymbol{u}^{(\,j)}\|^2\,\mathrm{d}t_l}\nonumber\\ &=p_0^{(\,j)}-\left(\frac{\rho_a \|\boldsymbol{u}_0^{(\,j)}\|^2}{2(2q^{(\,j)}+1)}\left(\frac{g(l_0)}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{2q^{(\,j)}+1} -\frac{\rho_a\|\boldsymbol{u}_0^{(\,j)}\|^2}{2(2q^{(\,j)}+1)}\left(\frac{g(l_{d_{\epsilon}})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{2q^{(\,j)}+1}\right). \end{align}

Re-arranging the latter expression gives the relation for $p_0^{(\,j)}$ in terms of $\bar {p}^{(\,j)}$,

(3.21)\begin{equation} p_0^{(\,j)} = \bar{p}^{(\,j)}+\left(\frac{\rho_a \|\boldsymbol{u}_0^{(\,j)}\|^2}{2(2q^{(\,j)}+1)}\left(\frac{g(l_0)}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{2q^{(\,j)}+1} -\frac{\rho_a\|\boldsymbol{u}_0^{(\,j)}\|^2}{2(2q^{(\,j)}+1)} \left(\frac{g(l_{d_{\epsilon}})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{2q^{(\,j)}+1}\right). \end{equation}

The local distribution of the total pressure, $p_T^{(\,j)} = p_0^{(\,j)} - p^{'(\,j)}$, over a given $\mathcal {R}^{(\,j)}$ is then

(3.22)\begin{align} p_T^{(\,j)}&=\bar{p}^{(\,j)}+\frac{\rho_a}{2}\left[\frac{\|\boldsymbol{u}_0^{(\,j)}\|^2}{(2q^{(\,j)}+1)} \left(\frac{g(l_0)}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{2q^{(\,j)}+1}-\frac{\rho_a \|\boldsymbol{u}_0^{(\,j)}\|^2}{2(2q^{(\,j)}+1)}\left(\frac{g(l_{d_{\epsilon}})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{2q^{(\,j)}+1}\right. \nonumber\\ &\quad \left. -\|\boldsymbol{u}_0^{(\,j)}\|^2\left(\frac{g(t_{l})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{2q^{(\,j)}}\right], \end{align}

and the global distribution of the total pressure is the union of the pressure kernels associated with each $\mathcal {R}^{(\,j)}$,

(3.23)\begin{equation} p_{l} =\mathop{\bigcup}\limits_{j=1}^{\mathcal{N}} p_T^{(\,j)}. \end{equation}

3.2. Group velocity of water-wave pulsations

To close the energy transfer source terms, we assume that the water-wave pulsations generated by the turbulent pressure pulsations of the wind are small amplitude waves. This allows us to use linear wave theory (see figure 1) to define the group velocity of the water-wave pulsations created by the wind. We acknowledge that the process through which momentum and energy is fluxed into the water column is significantly more complicated than the linear model depicted in figure 1, see Fedorov & Melville (1998) for a more rigorous theoretical description. However, the goal of this section is not to accurately quantify the complicated momentum and energy flux between the air and water surface, but rather, to show in simple terms how the singularity (or instability) that is associated with energy transfer arises within our statistical formulation. More specifically, the mathematical model described in figure 1 can be solved over the local duration, $t_l\in (l_{d_{\epsilon }},l_0)$, using a velocity potential of the form,

(3.24)\begin{equation} \phi = \hat{\phi}\cos(\omega t_l - kx), \end{equation}

with amplitude,

(3.25)\begin{equation} \hat{\phi} = \frac{\omega a}{k} \tanh^{{-}1}(kd), \end{equation}

and surface elevation,

(3.26)\begin{equation} \eta = a\sin(\omega t_l - kx), \end{equation}

where $\rho _w$ is the density of water, $k = \|\boldsymbol {k}\|$ is the magnitude of the wavenumber, and $a = f(z,t)$ is a coefficient that ensures the solution, $\phi (x,z,t)$, satisfies the top and bottom boundary conditions. The dispersion relation for the advection of the energy pulsation created in the water waves by the turbulent pressure of the wind over the duration, $t_l\in (l_{d_{\epsilon }},l_0)$, is determined using the dynamic boundary condition. At time $t=0$, before the fluctuation in the atmospheric pressure begins, the pressure of the water and atmosphere at the free surface is in balance and is equal to $p_0$. When $t>0$, the pressure fluctuation in the atmosphere begins to transfer energy to the water waves and the pressure at the free surface dynamically adjusts. Therefore, at $z = \eta$ the dynamic boundary condition becomes,

(3.27)\begin{equation} \frac{\partial \phi}{\partial t}+g\eta+\frac{p}{\rho_w}-\frac{\mathcal{T}}{\rho_w}\eta_{xx}=0, \end{equation}

where $\mathcal {T}\eta _{xx}$ is the net normal force per unit area that represents the surface tension of the water. Substitution of $\phi$ along with the dynamic pressure (3.18) into (3.27) while rearranging and simplifying gives the dispersion relation,

(3.28)\begin{equation} \omega^2= gk\tanh(kd)\left(1-\frac{\rho_a/2 \|\boldsymbol{u}\|^2 }{\rho_w g\eta}-\frac{\mathcal{T}}{g\rho_w}k^2\right). \end{equation}

Equation (3.28) is singular when $\eta = 0$. The singularity arises in our mathematical formulation from the pressure pulsation in the wind due to its kinetic energy and corresponds to a potential instability in the water surface; it is a relic of our simple mathematical approach. It can be noted that the pressure adjustment at the free surface is of the order $10^{-3}$ and is only relevant when the surface elevation of the water is a relatively ‘small’ value but larger than an inner cutoff (say, $10^{-6}$). Making use of (3.28) the phase speed of the water wave pulsation is,

(3.29)\begin{equation} \|\boldsymbol{c}_{p_f}\|=c_{p_f} = \frac{\omega}{k}= \sqrt{\frac{g}{k}\tanh(kd)\left(1-\frac{\rho_a/2 \|\boldsymbol{u}\|^2 }{\rho_w g\eta}-\frac{\mathcal{T}}{\rho_w}k^2\right)}, \end{equation}

while an expression for the group velocity can be derived via,

(3.30)\begin{equation} \|\boldsymbol{c}_{g_f}\|=c_{g_f} = \frac{\partial \omega}{\partial k}, \end{equation}

which ends up being a function of $\partial \eta / \partial k$. Clearly, the phase speed of the water-wave pulsation as defined by (3.29) depends on the ratio of kinetic energy of the wind to the potential energy of the sea surface. Another important consequence that immediately can be seen is that at the moment $t_l > 0$, just as the energy transfer begins and before an appreciable change in the velocity of the water pulsation forms (where the singularity exists in our representation of the wind velocity), the surface elevation of the water waves is the solution to a partial differential equation involving the pressure and the surface tension of the free surface,

(3.31)\begin{equation} \eta - \frac{\mathcal{T}}{g\rho_w}\eta_{xx} ={-}\frac{\rho_a/2 \|\boldsymbol{u}\|^2}{g\rho_w}, \end{equation}

which demonstrates the role that the pressure pulsation plays in the initial generation of the water waves. For instance, substitution of the expression $\eta$ into the PDE above would give the dependence of the amplitude of $\eta$ on the pressure pulsation, which is a function of time. The initial excitation of the surface elevation will be controlled by the absolute value of the exponent $q$ in expression (3.8). The larger the absolute value of the exponent, the larger the jump that will occur in the surface elevation at time $t_l > 0$, see figure $3$ in our companion paper (Conroy et al. 2021) for an illustration of the jumps in $\|\boldsymbol {u}\|$. Because we are not explicitly concerned with resolving the initial water waves of the air–water transfer (and because the local pressure term is ${\approx }10^{-3}$), we ignore the pressure term and the surface tension term in the calculations of $c_{p_f}$ and $c_{g_f}$ in our numerical simulations. It can be noted that the above analysis does not examine the effect of the water surface on the atmosphere, however, in this investigation we only make use of observational wind data which already have this effect built in. Finally, there is ample evidence that the water-wave generation mechanism should make use of the friction wind speed $u_{*}$ as opposed to the wind speed $U_{10}$ (see Janssen (2004), for example). We utilize $U_{10}$ in this work simply because the closure scheme developed by Hasselmann et al. (1975) uses $U_{10}$.

Figure 1. Model problem of linear wave theory.

3.3. Duration limited solutions to the energy balance equation

When the speed of the wind can be represented locally by the power law given by (3.8) then closed form solutions exist to a parameterized form of the energy balance equation. More specifically, Hasselmann et al. (1975) derived a rigorous parameterization of the spectral energy balance that takes into account nonlinear wave–wave interactions, dissipation and atmospheric input, and has been verified by the direct numerical simulations of Tanaka (2001). For duration limited wind waves, the non-dimensional representative frequency and energy of the corresponding water-wave pulsations can be expressed solely in terms of the characteristic constants (see Hasselmann et al. (1975) for details),

(3.32)\begin{equation} \left.\begin{array}{c} \nu^{(\,j)} =a^{(\,j)}\left[\dfrac{g}{\|\boldsymbol{u}_0^{(\,j)}\|}(t_{l})\right]^{\varphi^{(\,j)}},\quad \varphi^{(\,j)}=3/7(q^{(\,j)}-1),\\ \epsilon^{(\,j)} = d^{(\,j)}(\nu^{(\,j)})^{{-}10/3}, \end{array}\right\} \end{equation}

where

(3.33)\begin{equation} \left.\begin{array}{c} a^{(\,j)} = 16.8(1+1.51q^{(\,j)})^{3/7}, \\ b^{(\,j)} = 0.031\left(\dfrac{1+1.33q^{(\,j)}}{1+1.51q^{(\,j)}}\right)^{1/2}, \end{array}\right\} \end{equation}

and

(3.34)\begin{equation} d^{(\,j)} = b^{(\,j)}\varLambda. \end{equation}

The shape parameter, $\varLambda$, relates the representative frequency, energy and dissipation parameter, $\alpha ^{(\,j)}$, via

(3.35)\begin{equation} \varLambda = \frac{\epsilon^{(\,j)} (\nu^{(\,j)})^4}{\alpha^{(\,j)}} = {\rm constant}, \end{equation}

where $\varLambda = 1.60 (\pm 0.02) (10^{-4})$ arises from wind-wave observations (Hasselmann et al. 1973) and is directly proportional to the graph dimension of the atmospheric turbulent velocity in the air–sea boundary layer. The measure of the high-frequency spectral cutoff, $\alpha ^{(\,j)}$, which parameterizes dissipation, is proportional to the fourth-order moment but can be expressed in terms of $\|\boldsymbol {u}_0^{(\,j)}\|$ and $q^{(\,j)}$ as,

(3.36)\begin{equation} \alpha^{(\,j)}=b^{(\,j)}(\nu^{(\,j)})^{2/3}, \end{equation}

where $b^{(\,j)}$ is given by (3.33), and $\nu ^{(\,j)}$ by (3.32). The global distributions of the representative non-dimensional frequency and energy of the wind sea are,

(3.37)\begin{equation} \nu_{l} =\mathop{\bigcup}\limits_{j=1}^{\mathcal{N}} \nu^{(\,j)}, \end{equation}

and

(3.38)\begin{equation} \mathcal{\epsilon}_{l} =\mathop{\bigcup}\limits_{j=1}^{\mathcal{N}} \mathcal{\epsilon}^{(\,j)}, \end{equation}

where $\nu = f_m U_{10}/g$ and $\epsilon = \mathcal {E} g^2/ U_{10}^4$. It can be noted that other closure schemes besides Hasselmann et al. (1975) can be used to define the duration limited pulsations in the water surface. For instance, the Zakharov–Resio–Pushkarev wind input source term (Zakharov et al. 2017) can be used as well. When the short water waves are not duration limited then we can use (3.32) to determine the ${\rm d} \mathcal {E}_0 / {\rm d}t$ and ${\rm d} \mathcal {E}_1 / {\rm d}t$ terms needed for the air–water energy transfer source terms (2.25) and (2.26). Making use of (3.32) and differentiating with respect to time yields,

(3.39)\begin{equation} \frac{{\rm d} \mathcal{E}_0^{(\,j)}}{ {\rm d}t} = \frac{C_0 \varLambda \|\boldsymbol{u}_0^{(\,j)}\|^4\mathcal{Q}^{(\,j)}(9q^{(\,j)}+5)(151q^{(\,j)}+100)^{3/7} \left(\dfrac{g}{\|\boldsymbol{u}_0^{(\,j)}\|}(t_{l})\right)^{(31/7)q^{(\,j)}-3/7}} {g^2(t_{l})\left[(151q^{(\,j)}+100)^{3/7}\left(\dfrac{g}{\|\boldsymbol{u}_0^{(\,j)}\|}(t_{l})\right)^{(3/7)q^{(\,j)}-3/7}\right]^{13/3}}, \end{equation}

and

(3.40)\begin{equation} \frac{{\rm d} \mathcal{E}_1^{(\,j)}}{ {\rm d}t} = \frac{C_1\varLambda \|\boldsymbol{u}_0^{(\,j)}\|^3\mathcal{Q}^{(\,j)}(2q^{(\,j)}+1)(151q^{(\,j)}+100)^{6/7} \left(\dfrac{g}{\|\boldsymbol{u}_0^{(\,j)}\|}(t_{l})\right)^{(27/7)q^{(\,j)}-6/7}} {g(t_{l})\left[(151q^{(\,j)}+100)^{3/7}\left(\dfrac{g}{\|\boldsymbol{u}_0^{(\,j)}\|}(t_{l})\right)^{(3/7)q^{(\,j)}-3/7}\right]^{13/3}}, \end{equation}

where

(3.41)\begin{equation} \mathcal{Q}^{(\,j)} =\left(\frac{133q^{(\,j)}+100}{151q^{(\,j)}+100}\right)^{1/2}, \end{equation}

and $C_0 = 5.25(10^{-4})$ and $C_1 = 4.20(10^{-3})$. Due to the fact that the pulsations ${\rm d} \mathcal {E}_0 / {\rm d}t$ and ${\rm d} \mathcal {E}_1 / {\rm d}t$ correspond to high frequency pulsations that are typically of a much shorter wavelength than the water depth, the fluctuations travel with a deep water-wave phase speed,

(3.42)\begin{equation} \|\boldsymbol{c}_{p_f}\|_{l} =\mathop{\bigcup}\limits_{j=1}^{\mathcal{N}} \frac{g}{2 {\rm \pi}f_m^{(\,j)}}, \end{equation}

and group speed,

(3.43)\begin{equation} \|\boldsymbol{c}_{g_f}\|_{l} =\mathop{\bigcup}\limits_{j=1}^{\mathcal{N}} \frac{g}{4 {\rm \pi}f_m^{(\,j)}}, \end{equation}

where we have neglected the high-order term of (3.29). Substitution of (3.40) and (3.43) into (2.20) reduces the closure of the moment field equations to the calculation of the characteristic constants that define the distribution of the wind velocity.

3.4. Calculation of characteristic constants

We calculate the set of characteristic constants $\{ \|\boldsymbol {u}_0^{(\,j)}\|, \theta _0^{(\,j)}, q^{(\,j)}, \varUpsilon ^{(\,j)} \}_{j=1}^{\mathcal {N}}$ that define the velocity kernels and the corresponding duration limited water-wave pulsations through preservation of large scale averages of observational atmospheric velocity data combined with some reconstruction of the endpoint values of each $\mathcal {R}^{(\,j)}$. We denote these reconstructed endpoint values as $u^{(\,j)}_i$ and $u^{(\,j)}_f$. For a given $\mathcal {R}^{(\,j)}$ located at $\boldsymbol {x}_0$ of length $l_0$ the initial and final speed values are,

(3.44) \begin{equation} \left.\begin{array}{c} \|\boldsymbol{u}^{(\,j)}(t_{l}=l_{d_{\epsilon}})\| = \|\boldsymbol{u}_0^{(\,j)}\|\left(\dfrac{g(l_{d_{\epsilon}})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{q^{(\,j)}}=u_i^{(\,j)},\\ \|\boldsymbol{u}^{(\,j)}(t_{l}=l_0)\| = \|\boldsymbol{u}_0^{(\,j)}\| \left(\dfrac{g (l_0)}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{q^{(\,j)}}=u_f^{(\,j)}. \end{array}\right\} \end{equation}

Solving for $q^{(\,j)}$ we have,

(3.45)\begin{equation} q^{(\,j)} =\log\left(\frac{u_i^{(\,j)}}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)\left/\,\log \left(\frac{g(l_{d_{\epsilon}})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right), \right. \end{equation}

(3.46)\begin{equation}q^{(\,j)}=\log\left(\frac{u_f^{(\,j)}}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)\left/\,\log \left(\frac{g(l_0)}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)\right. . \end{equation}

Setting these equations equal to one another and simplifying leads to an expression that can be solved for $\|\boldsymbol {u}_0^{(\,j)}\|$,

(3.47)\begin{equation} \log\left(\frac{u_i^{(\,j)}}{\|\boldsymbol{u}_0^{(\,j)}\|}\right) \log\left(\frac{g(l_0)}{\|\boldsymbol{u}_0^{(\,j)}\|}\right) - \log\left(\frac{u_f^{(\,j)}}{\|\boldsymbol{u}_0^{(\,j)}\|}\right) \log\left(\frac{g(l_{d_{\epsilon}})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right) = 0. \end{equation}

The exponent $q^{(\,j)}$ can be determined by preserving large scale averages of observational wind data, i.e. the area. In particular, the integral of (3.8) is

(3.48)\begin{equation} \left.\begin{aligned} \underbrace{\int_{l_{d_{\epsilon}}}^{l_0}{\|\boldsymbol{u}_0^{(\,j)}\| \left(\frac{g(t_{l})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{q^{(\,j)}}\,{\rm d}t_{l}}} & =\left.\frac{(\|\boldsymbol{u}_0^{(\,j)}\|)^2}{g(q^{(\,j)}+1)}\left(\frac{g(t_{\ell})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{q^{(\,j)}+1} \right|_{l_{d_{\epsilon}}}^{l_0},\\ \bar{u}^{(\,j)}(l_0-l_{d_{\epsilon}}) & =\left[ \frac{(\|\boldsymbol{u}_0^{(\,j)}\|)^2}{g(q^{(\,j)}+1)}\left(\frac{g(l_0)}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{q^{(\,j)}+1}\right.\\ & \quad \left.-\, \frac{(\|\boldsymbol{u}_0^{(\,j)}\|)^2}{g(q^{(\,j)}+1)} \left(\frac{g(l_{d_{\epsilon}})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{q^{(\,j)}+1}\right], \end{aligned}\right\} \end{equation}

where $t_{l}$ is the local time, $\bar {u}^{(\,j)}$ is the average wind speed over the region $\mathcal {R}^{(\,j)}$. We solve (3.47) and (3.48) simultaneously with the help of a Newton solver, see our companion paper (Conroy et al. 2021) for details.

Here, we emphasize that our solution method for the characteristic constants introduces a dependency between distributions, where the explicit dependence is a function of the chosen reconstruction scheme. For instance, if an upwind reconstruction scheme is used then the distribution $\boldsymbol {u}^{(\,j)}$ over a given $\mathcal {R}^{(\,j)}$ will be conditioned by past expectations ($\bar {u}^{(j-1)}$), however, if any other reconstruction scheme is utilized then the distribution will depend on past and future expectations ($\bar {u}^{(j+1)}$) in a ratio defined by the reconstruction.

Because we are concerned with small scale turbulence a major question concerns the optimal length of the local $\mathcal {R}^{(\,j)}$ over which the velocity kernels are well defined in terms of transferring momentum to the water and in terms of numerical consistency. That is, the calculation of the characteristic constants depends on time averaged values of velocity and pressure which in some instances could be defined on a scale whose region of uncertainty, $] l_{d_{\epsilon }}, l_{d} [$, is too large to correspond to small scale turbulence and too large to consistently integrate the moment field equations (this corresponds to the case where the numerical time step necessary to integrate (2.1) is less than the length of the region of uncertainty, see Conroy et al. (2021) for details). We address this issue and shrink the region of uncertainty through a recursive integration process to construct a refined distribution of the velocity of the turbulent medium so that $] l_{d_{\epsilon }}, l_{d} [ < {\rm d}t$ where ${\rm d}t$ is the time step of the numerical integrator of (2.1).

3.5. Recursive integration and energy measures

The goal of the recursive integration process is to shrink the region of uncertainty associated with each velocity distribution $\boldsymbol {u}^{(\,j)}$ in a manner such that $] l_{d_{\epsilon }}, l_{d} [ < {\rm d}t$. We proceed by first subdividing each $\mathcal {R}^{(\,j)}$ into two subregions $\mathcal {R}^{(\,j)}_{1}$ and $\mathcal {R}^{(\,j)}_{2}$ ; we then calculate the expected velocity of each subregion and pair these values with the nonlinear solution method described in Conroy et al. (2021) to create a new set of velocity kernels. This new set is composed of twice as many $\mathcal {R}^{(\,j)}$ as the original set and adds cut outs along the space–time path while shrinking the region of uncertainty $] l_{d_{\epsilon }}, l_{d_{i}} [$ associated with these cut outs toward zero, see Conroy et al. (2021) for the full algorithm.

3.5.1. Velocity measure

Consider the discrete sequence of lengths associated with a given $\mathcal {R}^{(\,j)}$,

(3.49)\begin{equation} l_{i}=l_0 2^{{-}i},\quad i=0,1,2,\ldots M. \end{equation}

The average, or expected speed of each subregion of level $i+1$ is connected to the expectation of level $i$ via

(3.50)\begin{equation} \bar{u}^{(\,j)}_{i} = \frac{1}{C_{i+1}}\sum_{s = 1}^{C_{i+1}} w^{(\,j)}_{s} \bar{u}^{(\,j)}_{s}, \end{equation}

where $C_{i+1}$ is the number of sub-regions of level $i+1$ and the $w^{(\,j)}_{s}$ correspond to the measure (or weights) of each subregion $s$, which are defined as,

(3.51)\begin{equation} w^{(\,j)}_{s} = \frac{\bar{u}^{(\,j)}_{i}}{\bar{u}^{(\,j)}_{s}}. \end{equation}

The expectation of the parent kernel $\bar {u}^{(\,j)}_{i}$ is

(3.52)\begin{equation} \bar{u}^{(\,j)}_{i}=\frac{1}{(l_{i}-l_{d_{\epsilon}})} \int^{l_{i}}_{l_{d_{\epsilon}}}{\| \boldsymbol{u}_0^{(\,j)} \| \left(\frac{g}{\| \boldsymbol{u}_0^{(\,j)} \|}t_{l}\right)^{q^{(\,j)}}\,{\rm d}t_{l}}, \end{equation}

and the offspring, $\bar {u}^{(\,j)}_{s}$, corresponds to the expected speed of the turbulent velocity over an interior time interval, $l_{d_{\epsilon }} < (l_{s+1} - l_{s}) < l_{i}$,

(3.53)\begin{align} \bar{u}^{(\,j)}_{s} &=\frac{1}{(l_{s+1} - l_{s})} \int_{l_{s}}^{l_{s+1}} {\| \boldsymbol{u}_0^{(\,j)} \| \left(\frac{g}{\| \boldsymbol{u}_0^{(\,j)} \|}t_{l}\right)^{q^{(\,j)}}\,{\rm d}t_{l}},\nonumber\\ & = \left[\frac{\| \boldsymbol{u}_0^{(\,j)} \|^2}{g(l_{s+1} - l_{s})(q^{(\,j)}+1)}\left(\frac{g}{\| \boldsymbol{u}_0^{(\,j)} \|}l_{s+1}\right)^{q^{(\,j)}+1}\right.\nonumber\\ &\quad - \left. \frac{\| \boldsymbol{u}_0 \|^2}{g(l_{s+1} - l_{s})(q^{(\,j)}+1)}\left(\frac{g}{\| \boldsymbol{u}_0^{(\,j)} \|}l_{s}\right)^{q^{(\,j)}+1}\right]. \end{align}

When dyadic intervals serve as the refinement mechanism, the averages used to initiate the next level of integration are,

(3.54)\begin{equation} \bar{u}_1^{(\,j)}= \frac{1}{(l_{i}/2 - l_{d_i})} \int_{l_{d_i}}^{l_{i}/2} {\| \boldsymbol{u}_0^{(\,j)} \| \left(\frac{g}{\| \boldsymbol{u}_0^{(\,j)} \|}t_{l}\right)^{q^{(\,j)}}\,\textrm{d}t_{l}}, \end{equation}

and

(3.55)\begin{equation} \bar{u}_2^{(\,j)}= \frac{1}{(l_{i} - l_{i}/2)} \int_{l_{i}/2}^{l_{i}} {\| \boldsymbol{u}_0^{(\,j)} \| \left(\frac{g}{\| \boldsymbol{u}_0^{(\,j)} \|}t_{l}\right)^{q^{(\,j)}}\,\textrm{d}t_{l}}. \end{equation}

It can be noted that the interval $] l_{d_{\epsilon }},l_{d_i} [$ is cut out of the integration. The manner in which this interval is handled during the recursion process leads to markedly different measures and dimensions of the support. More specifically, when the length of the cut out is set to a relatively small number, such as $1 \times 10^{-7}$ and kept constant with each level of integration, the sum of the weights equals $C_{i+1}$ and the refinement cascade is said to be conservative, or microcanonical (Mandelbrot 1974). In this case $] l_{d_{\epsilon }},l_{d_i} [$ is always less than ${\rm d}t$, however, the graph dimension of the resulting velocity distribution will not be in a range that matches theory and observation until after five levels of recursive integration. The dimension of the support in this case is approximately equal to the embedding dimension $E$ (the resulting measure of the turbulence is $E$-filling). Conversely, if we allow the cut out $] l_{d_{\epsilon }},l_{d_i} [$ to vary in length (more specifically to shrink or become thinner) with each integration, then the sum of the weights only equals $C_{i+1}$ on average, local conservation is not maintained and the recursion is said to be canonical (Mandelbrot 1974). In this scenario, the graph dimension of the velocity distribution is in the range of observations and theory with each recursion and we can re-write (3.50) as

(3.56)\begin{equation} \bar{u}^{(\,j)}_i = \frac{1}{C_{i+1}}\sum_{s=1}^{C_{i+1}}\bar{u}^{(\,j)}_s + \bar{u}^{(\,j)}_{\bar{\epsilon}}, \end{equation}

where $\bar {u}^{(\,j)}_{\bar {\epsilon }}$ is the value of velocity cut out from the refinement of level $i$. This cut out represents a loss of regularity in the velocity field in the spirit of Onsager (1949).

3.5.2. Energy measures

We measure the distribution of turbulent energy in the wind by defining the following measure (or weight),

(3.57)\begin{equation} w^{(\,j)}_{\mathcal{E}s}=\frac{(\bar{u}^{(\,j)}_i)^2}{(\bar{u}_s^{(\,j)})^2}, \end{equation}

where $\bar {u}^{(\,j)}_i$ and $\bar {u}_s^{(\,j)}$ correspond to the measures of the parent and offspring kernels presented in the previous subsection. The weights, $w_{\mathcal {E}s}$, measure the redistribution of energy across temporal scales,

(3.58)\begin{equation} \langle \mathcal{E} \rangle^{(\,j)}_i = \frac{1}{C_{i+1}}\sum_{s = 1}^{C_{i+1}} w^{(\,j)}_{\mathcal{E}s} \mathcal{E}_s^{(\,j)}, \end{equation}

and the total ensemble averages of the energy measure are,

(3.59)\begin{equation} \langle \mathcal{E} \rangle_l= \frac{1}{\mathcal{N}}\sum_{j = 1}^{\mathcal{N}} \langle \mathcal{E} \rangle^{(\,j)}_M. \end{equation}

It can be noted that when definitions (3.52) and (3.53) are substituted into (3.57), then (3.57) is qualitatively similar to the expressions used in She & Leveque (1994) to measure the hierarchy of dissipation structures within a turbulent fluid. The energy transfer moments take the form,

(3.60)\begin{equation} \langle \mathcal{E}^n \rangle_l = (l)^{\tau(n)+1 }, \end{equation}

where the exponent function of the moments, $\tau (n)$, are defined as in Mandelbrot (1998),

(3.61)\begin{equation} \tau(n) = \frac{3}{E}\varPsi(n) - (n -1). \end{equation}

Here, $E$ is the dimension of the embedding space and the determining function is,

(3.62)\begin{equation} \varPsi(n) = \log_{C_{i+1}} \langle (w_{\mathcal{E}s}^{(\,j)}) ^n \rangle, \end{equation}

where the ensemble average is over the indices $s$ and $j$ (see Mandelbrot (1998) for more details). It can be noted that the $\tau$-functions (and therefore the moments) remain bounded below some critical value $n_{crit}$. For values greater than $n_{crit}$, however, values for the $\tau$-functions become large and tend toward infinity as $n \rightarrow \infty$. This critical $n$-value serves as a scale factor for the velocity structure functions (Mandelbrot 1974, 1997),

(3.63)\begin{equation} \langle (\delta u)^n\rangle^{1/n}= l ^{\zeta(n)},\quad \text{where}\ \zeta(n)=\frac{1+\tau(n)}{n_{crit}}, \end{equation}

and determines the length of the virtual cut out of the velocity in the canonical case at each scale length $l_i$. That is, the slope of the graph of $\log {(l_{d_i})}$ vs $\log {(l_i)}$ has a slope equal to $n_{crit}$, and we have,

(3.64)\begin{equation} l_{d_i} \propto( l_i)^{{-}n_{crit}}. \end{equation}

This relationship was revealed in our numerical studies of the recursive integration, where we find that $n_{{\rm crit}} \approx 5$. This is significant because $n_{{\rm crit}}$ corresponds to the asymptotically scaling tail of the distribution of the energy weights of our multifractal measures, the value of which ($n_{{\rm crit}} \approx 5$) happens to be equal to the high-frequency tail representing dissipation of the water-wave spectrum; see Zakharov et al. (2017), for instance. It can be noted that we choose the initial inner cutoff, $l_{d_0}$, of the recursive integration process in a manner such that the structure function of the velocity distribution lies in the range of theory and observation, see figures 2 and 3 and our companion paper (Conroy et al. 2021) for details.

Figure 2. Velocity structure function exponents at Lake Erie Buoy 45005 vs experimental data of Anselmet et al. (1984) and Benzi et al. (1993) and theoretical relation of She & Leveque (1994) (black dashed line). Diamonds correspond to average structure functions (May–October) of the recursive integration methods, black crosses ($+$) correspond to the data of Benzi et al. (1993) and all other markers correspond to data of Anselmet et al. (1984).

Figure 3. Velocity structure function exponents at Lake Erie Buoy 45005 vs experimental data of Anselmet et al. (1984) and Benzi et al. (1993) and theoretical relation of She & Leveque (1994) (black dashed line). Diamonds correspond to average structure functions (May–October) of the recursive integration methods, black crosses ($+$) correspond to the data of Benzi et al. (1993) and all other markers correspond to data of Anselmet et al. (1984).

3.5.3. Dimension of the support of the measure

The slopes of the $\tau$-functions for $n = 1$ are (Mandelbrot 1974),

(3.65)\begin{equation} D_E ={-}E\tau'(1)={-}3\langle w_s \log_C w_s\rangle+E. \end{equation}

When $D_E > 0$, $D_E$ is the intrinsic dimension of the support of the measure $w_s$ in the $E-$dimension embedding space. In the case $E = 3$, $D_E$ corresponds to the fractal dimension of the spatial trail of the self-affine measure of the turbulent energy transfer (Mandelbrot 1974). It is a measure of how the local variation of a function grows as the characteristic length scale over which the function is defined shrinks towards a relative zero (inner cutoff) (Mandelbrot 1977, 1985; Dubuc et al. 1989). It can be noted that, in the turbulence literature, $D_E$ typically lies in the range $2.95 \geq D_E \geq 2.27$ (Mandelbrot 1974; Schertzer & Lovejoy 1985; Frisch 1996).

4. Quantifying air–water turbulence over Lake Erie

We apply our quantitative methods to air–water turbulence over Lake Erie, the tenth largest lake in the world and the fourth largest lake (by surface area) of the Great Lakes. Lake Erie commerce generates approximately $10.7$ billion US dollars in annual revenue (OEC 2015), and due to its orientation, large surface area and (relatively) shallow water depth, is extremely susceptible to wind water-wave generation, with seiches known to form on the lake of up to $5$ m (NOAA 2016). Tidal ranges on the lake are less than $5$ cm, and thus, the main driver of the circulation of the system is due to gravity water waves generated by air–water interactions.

4.1. Air–water interactions

To quantify air–water interactions over Lake Erie and generate input data for the moment field equations, we apply the nonlinear solution method outlined in § 3.4 to observational atmospheric data obtained from 27 meteorological stations owned and operated by the National Oceanic and Atmospheric Association (NOAA); the positions of the 27 stations are illustrated in figure 7 in Conroy et al. (2018). The exponents of the structure functions of the velocity measure (3.51) are shown in figures 2 and 3 while the dimension of the support of the energy measures are shown in table 1. In general, our methods produce structure functions and a fractal embedding dimension, $D_E$, that match theory and analysis of experimental data. The value of $D_E$ lies in the range $2.82 \geq D_E \geq 2.27$ with an average value $D_E = 2.58$. Analysis of atmospheric boundary layer data puts a lower bound on the graph dimension of the velocity of $D_G = 1.56$ (Syu & Kirchoff 1993), which in the uniscaling case gives an embedding dimension $D_E = 2.27$. This is a reflection of the fact that atmospheric turbulence can be very intermittent. It can be noted that, after four recursive integrations, the length of each $\mathcal {R}^{(\,j)}$ is $\varDelta t_l = l_3= 3.75$ min, and the average exponent in the velocity distribution (3.8) is $\bar {q} \approx 5.0 \times 10^{-4}$. In other words, on average, at relatively small scales the energy transfer as measured by $q^{(\,j)}$ is rather negligible and the bulk of the energy transfer (at these scales) is due to a few ‘rare’ events (typical minimum and maximum values of $q^{(\,j)}$ are $\approx \pm 0.03$ which is $\approx 13$ times the standard deviation). This highlights the intermittency of the turbulence at relatively small scales which is a phenomenon that is well documented in the literature (Frisch 1996; Hentschel & Procaccia 1982, 1983; Schertzer & Lovejoy 1985). See Conroy et al. (2021) for a complete numerical investigation of the recursive integration process.

Table 1. Fractal dimension ($D_E$) of measure (3.57) using data from NDBC Buoy 45005 (NDBC 2016) on Lake Erie.

4.2. Short water waves on Lake Erie

We perform hindcast simulations of the short water-wave energy over Lake Erie for the month of August 2011 using the input data detailed in the previous subsection. We begin by simply using the duration limited relation given by (3.33) coupled with our recursive integration method and calculate significant wave height over the lake associated with the velocity distributions (3.8). It can be noted that significant wave height is the average wave height of the third highest waves of the wind sea, which we define as,

(4.1)\begin{equation} H_{s} \approx 4 (\mathcal{E}_l)^H, \end{equation}

where $H = 0.43$ is the Hurst exponent calculated via the methods presented in our companion paper (Conroy et al. 2021) and $\mathcal {E}_l$ is given by (3.32). Results are shown in figures 4 and 5, where numerical results match the observational significant water-wave height quantitatively well. In fact, the root-mean-square (r.m.s.) error in this case is $0.132$ m and the correlation coefficient is $R = 0.91$. The agreement between observed and calculated significant water-wave height using the duration limited kernel (3.32) coupled with the recursive integration method of § 3.5 is satisfactory, however, it can be noted that there are certain events in figure 4 that indicate the wave field cannot be fully approximated by a duration limited kernel. In other words, there is some advection effect that needs to be included in the model, for instance, see the events from 4 August to 7 August and the event just before 15 August.

Figure 4. Significant wave height over Lake Erie at Buoy 45005 (NDBC 2016) during the month of August 2011. Significant wave height in this case was modelled using only the duration limited kernel (3.32) coupled with our recursive integration methods.

Figure 5. August 2011 linear regression at Lake Erie Buoy 45005 (NDBC 2016) for modelled results using the duration limited kernel (3.32) coupled with our recursive integration methods.

To account for advection of water-wave energy through Lake Erie we solve the moment field equations and perform hindcast simulations for the months of August 2011 and July 2011. We use a deep water-wave dispersion relation for (2.4),

(4.2)\begin{equation} \bar{\omega}_1^2=g \bar{k}_1, \end{equation}

and set the moment field to quantify the energy flux so that the variance of the sea surface is calculated via,

(4.3)\begin{equation} \sigma^2 = \left(\frac{m_0}{\| \boldsymbol{c}_1 \|}\right), \end{equation}

where $\| \boldsymbol {c}_1\|$ corresponds to the peak phase speed of the water waves and calculate significant wave height via the approximation $H_s \approx 4\sqrt {\sigma ^2}$ (Holthuijsen 2007). The moment field equations are discretized with an unstructured discontinuous Galerkin (DG) finite element method (see Conroy et al. (2021) for details). Model simulations were performed with $\mathbb {P}^0$ polynomials using a time step ${\rm d}t = 2$ min, which on average took $5$ min (of CPU time) to execute on an Apple laptop. With ${\rm d}t = 2$ min the numerical results generated by the model are ‘noisy’, just as any physical wave record observed at such a frequency would be. Therefore, to compare model output to buoy observations we correspondingly average the model output over hourly time windows. Results are shown in figures 6–9 and tables 2 and 3.

Figure 6. Hourly averaged significant water-wave height (a) and average water-wave period (b) at NDBC Buoy 45005 (NDBC 2016) in Lake Erie for August 2011. Note how, qualitatively, both SWAN (blue line) and the moment field model (red line) are well correlated to the buoy data (black line) in panel (a).

Figure 7. August 2011 linear regression of the moment field model results at Buoy 45005 (NDBC 2016) in Lake Erie. Panel (a) shows the regression for significant water-wave height while (b) is average water-wave period, ($T_{avg}=1/\bar {f}_0$) of the moment field model.

Figure 8. Hourly averaged significant water-wave height (a) and average water-wave period (b) at NDBC Buoy 45005 (NDBC 2016) in Lake Erie for July 2011. Note how qualitatively, both SWAN (blue line) and the moment field model (red line) are well correlated to the buoy data (black line) in panel (a)

Figure 9. July 2011 linear regression of the moment field model results at Buoy 45005 (NDBC 2016) in Lake Erie. Panel (a) shows the regression for significant water-wave height while (b) is average water-wave period, ($T_{avg}=1/\bar {f}_0$) of the moment field model.

Table 2. Statistical comparison of moment field model (MFM) and SWAN with Lake Erie Buoy 45005 (NDBC 2016) for significant water-wave height.

Table 3. Statistical comparison of moment field model with Lake Erie Buoy 45005 (NDBC 2016) for average water-wave period.

In general, model output is well correlated to the buoy observations and to the water wave model known as Simulating WAves Nearshore (SWAN) (SWAN 2015). SWAN solves the action balance equation and on average took $3$ h to execute a monthly simulation. In fact, the moment field model executes almost $40$ times as fast as SWAN while producing similar error measures in terms of significant wave height – the r.m.s. error for the moment field model was $0.100$ m in August 2011 and $0.095$ m for July 2011, while SWAN produced r.m.s. errors of $0.097$ and $0.092$ m, respectively. It can be noted that the moment field equations produce lower error measures in terms of matching the mean and standard deviation of the buoy data as compared to SWAN. However, there are durations in the water-wave record where both SWAN and the moment field equations over or under-predict buoy observations (there does not seem to be any discernible bias in either case). One observation to make note of is the fact that the moment field model slightly misses the timing in the local minimum that occurs in significant wave height on 17 August 2011 and 30 August 2011, an issue that we will explore in future work.

To emphasize the fact that our model captures nonlinear energy transfer we calculate the graph dimension $D_G$ of the pulsation group velocity of the water waves used in the model source terms at NDBC Buoy 45005. We calculate $D_G$ using the method described in our companion paper (Conroy et al. 2021) where the slope of the best fit line in figure 10 corresponds to the graph dimension of the pulsation velocity, which has a value of $1.57$ ($H = 0.43$) and mirrors the graph dimension of the wind, see Conroy et al. (2021) for more details.

Figure 10. Least squares approximation of the graph dimension, $D_G$, of the pulsation group velocity of the water waves, $\boldsymbol {c}_{g_f}$, for August 2011.

The correlation between the model output of water-wave period and observed water-wave period is not as high of a value as the correlation of significant wave height, and the r.m.s. error is also a higher value for the water-wave period as compared to significant wave height. This is a common theme among short wave models (Holthuijsen 2007), and ultimately, high numerical resolution via $p$-refinement and $h$-refinement (or adaptation) needs to be used in spatial areas where the peak frequency is rapidly changing to accurately resolve the water-wave period (Conroy et al. 2021).

5. Conclusions

Energy transfer in turbulent fluids is non-Gaussian. We quantify this non-Gaussian transfer between wind and water using self-affine velocity distributions and a recursive integration method that redistributes and concentrates this transfer in time. The resulting energy measures are multifractal and the dimension of the support of the energy distribution is consistent with theory and observation. The self-affine velocity distributions satisfy a parametrized form of the energy balance equation for water waves as well as invariant properties of the Navier–Stokes equation and are used to construct source terms for a system of moment field equations that track and propagate the short water waves created by air–water interactions.

Our methods are accurate and efficient; application to Lake Erie produces embedding dimensions that lie in the range $2.82 \geq D_E \geq 2.27$, and correspondingly, water-wave periods and significant water-wave heights are well correlated with observational buoy data and the water-wave model known as SWAN. Further, our methods execute almost 40 times as quickly as SWAN.

The recursive integration method presented herein can be used by a full spectral model to interpolate the wind data ($U_{10}$) in a non-Gaussian fashion. Typical short water-wave models interpolate the wind input to smaller time scales using linear interpolation, which does not extend the variability dependence of the observational data to small scales (hourly averaged data down to minutes or seconds), and can distort the timing of how energy flows within the water-wave spectrum. In fact, this could be part of the reason why phase-averaged water-wave models have had trouble capturing peak water-wave heights and periods in strong storms, as described by Cavaleri (2009).

Future work could follow a number of different paths (for instance, in regards to the recursive integration), but our ultimate goal is to utilize the model in ensemble storm surge studies. To fully depict the short water-wave field in this case an additional swell phase needs to be included in the moment field equations as well as the appropriate transfer and dissipation terms. One can argue that swell dissipation is the largest source of error in phase-averaging water-wave models (Stopa et al. 2016) and we plan to collaborate with scientists (see Zappa et al. (2008) for instance) to obtain more accurate estimates of swell decay. In addition to modelling swell and its dissipation, we will need to develop source terms that account for coastal effects as the short water waves propagate into coastal regions, which we could base on the work of Holthuijsen, Booij & Herbers (1989). This work is well under way and future investigations will examine how to consistently transfer energy between the wind-sea and swell phases, as well as the longer circulation waves that the short water waves form on.