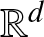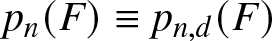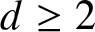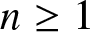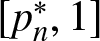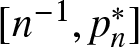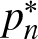1. Introduction, background, and main results
1.1. Introduction, notation, and definitions
We begin with some definitions, including the Definition 1.2 of (multivariate) records as studied in this paper. For ![]() $\mathbf x, \mathbf y \in \mathbb R^d$, we write
$\mathbf x, \mathbf y \in \mathbb R^d$, we write ![]() $\mathbf x \leq \mathbf y$ or
$\mathbf x \leq \mathbf y$ or ![]() $\mathbf y \geq \mathbf x$ to mean that
$\mathbf y \geq \mathbf x$ to mean that ![]() $x_j \leq y_j$ for
$x_j \leq y_j$ for ![]() $1 \leq j \leq d$, and we write
$1 \leq j \leq d$, and we write ![]() $\mathbf x \prec \mathbf y$ or
$\mathbf x \prec \mathbf y$ or ![]() $\mathbf y \succ \mathbf x$ to mean that
$\mathbf y \succ \mathbf x$ to mean that ![]() $x_j \lt y_j$ for
$x_j \lt y_j$ for ![]() $1 \leq j \leq d$. For
$1 \leq j \leq d$. For ![]() $\mathbf x \in \mathbb R^d$, we use the usual notation
$\mathbf x \in \mathbb R^d$, we use the usual notation  $\|\mathbf x\|_1 := \sum_{j = 1}^d |x_j|$. We use the standard notation
$\|\mathbf x\|_1 := \sum_{j = 1}^d |x_j|$. We use the standard notation ![]() $\implies$ for weak convergence of probability measures in Euclidean spaces (or their distribution functions).
$\implies$ for weak convergence of probability measures in Euclidean spaces (or their distribution functions).
Throughout this paper, ![]() $\mathbf X^{(1)}, \mathbf X^{(2)}, \dots$ are assumed to be i.i.d. (independent and identically distributed) copies of a d-dimensional random vector
$\mathbf X^{(1)}, \mathbf X^{(2)}, \dots$ are assumed to be i.i.d. (independent and identically distributed) copies of a d-dimensional random vector ![]() $\mathbf X$ with distribution function F and law (or distribution) denoted by
$\mathbf X$ with distribution function F and law (or distribution) denoted by ![]() ${\mathcal L}(\mathbf X)$. Throughout the paper we restrict attention to continuous F, mainly to avoid the complicating mathematical nuisance of ties, as explained in Remark 1.1(d).
${\mathcal L}(\mathbf X)$. Throughout the paper we restrict attention to continuous F, mainly to avoid the complicating mathematical nuisance of ties, as explained in Remark 1.1(d).
(a) As noted by a reviewer of a previous draft, a distribution function F on
 $\mathbb R^d$ is continuous if and only if each of its d univariate marginals is. This is easy to prove from the observation in [Reference Billingsley4, Sect. 3 (only in first edition)] that F corresponding to random vector
$\mathbb R^d$ is continuous if and only if each of its d univariate marginals is. This is easy to prove from the observation in [Reference Billingsley4, Sect. 3 (only in first edition)] that F corresponding to random vector  $\mathbf X$ is continuous at
$\mathbf X$ is continuous at  $\mathbf x \in \mathbb R^d$ if and only if
$\mathbf x \in \mathbb R^d$ if and only if  $F(\mathbf x) = \operatorname{\mathbb P{}}(\mathbf X \prec \mathbf x)$.
$F(\mathbf x) = \operatorname{\mathbb P{}}(\mathbf X \prec \mathbf x)$.(b) Specializing (a) to d = 1, the distribution function of a random variable Y is continuous if and only if
 $\operatorname{\mathbb P{}}(Y = y) = 0$ for each
$\operatorname{\mathbb P{}}(Y = y) = 0$ for each  $y \in \mathbb R$.
$y \in \mathbb R$.(c) We note in passing, however, that, in contradistinction to (b), atomlessness of a random vector does not imply continuity of the distribution function in dimensions 2 and higher; see, for example, [Reference Chow and Teicher6, Sect. 8.5].
(d) Combining (a)–(b), it follows that, if the d-dimensional random vector
 $\mathbf X$ has continuous distribution function F, then almost surely for every
$\mathbf X$ has continuous distribution function F, then almost surely for every  $1 \leq j \leq d$ there are no ties among
$1 \leq j \leq d$ there are no ties among  $X^{(1)}_j, X^{(2)}_j, \ldots$.
$X^{(1)}_j, X^{(2)}_j, \ldots$.
(a) For
 $n \geq 1$, we say that
$n \geq 1$, we say that  $\mathbf X^{(n)}$ is a (Pareto) record (or that it sets a record at time n) if
$\mathbf X^{(n)}$ is a (Pareto) record (or that it sets a record at time n) if  $\mathbf X^{(n)} \leq \mathbf X^{(i)}$ fails for all
$\mathbf X^{(n)} \leq \mathbf X^{(i)}$ fails for all  $1 \leq i \lt n$.
$1 \leq i \lt n$.(b) If
 $1 \leq k \leq n$, we say that
$1 \leq k \leq n$, we say that  $\mathbf X^{(k)}$ is a current record (or remaining record, or maximum) at time n if
$\mathbf X^{(k)}$ is a current record (or remaining record, or maximum) at time n if  $\mathbf X^{(k)} \leq \mathbf X^{(i)}$ fails for all
$\mathbf X^{(k)} \leq \mathbf X^{(i)}$ fails for all  $1 \leq i \leq n$ with i ≠ k.
$1 \leq i \leq n$ with i ≠ k.(c) For
 $n \geq 1$ we let Rn denote the number of records
$n \geq 1$ we let Rn denote the number of records  $\mathbf X^{(k)}$ with
$\mathbf X^{(k)}$ with  $1 \leq k \leq n$ and let rn denote the number of remaining records at time n.
$1 \leq k \leq n$ and let rn denote the number of remaining records at time n.
Remark 1.3. It is clear from Definition 1.2 that if ![]() ${\widetilde {\mathbf X}} = (g_1(X_1), \ldots, g_d(X_d))$ where
${\widetilde {\mathbf X}} = (g_1(X_1), \ldots, g_d(X_d))$ where ![]() $g_1, \ldots, g_d$ are strictly increasing transformations, then the stochastic processes
$g_1, \ldots, g_d$ are strictly increasing transformations, then the stochastic processes ![]() $(R_n)$ and
$(R_n)$ and ![]() $(r_n)$ are the same for the i.i.d. sequence
$(r_n)$ are the same for the i.i.d. sequence ![]() ${\widetilde {\mathbf X}}^{(1)}, {\widetilde {\mathbf X}}^{(2)}, \ldots$ as for
${\widetilde {\mathbf X}}^{(1)}, {\widetilde {\mathbf X}}^{(2)}, \ldots$ as for ![]() $\mathbf X^{(1)}, \mathbf X^{(2)}, \ldots$. Further, since we assume that F is continuous, it follows from Remark 1.1 that the distribution function
$\mathbf X^{(1)}, \mathbf X^{(2)}, \ldots$. Further, since we assume that F is continuous, it follows from Remark 1.1 that the distribution function ![]() $\widetilde{F}$ of
$\widetilde{F}$ of ![]() ${\widetilde {\mathbf X}}$ is also continuous.
${\widetilde {\mathbf X}}$ is also continuous.
Remark 1.4. We note that the expected number rn of maxima at time n is n times the probability that ![]() $\mathbf X^{(n)}$ sets a record. Thus our main Theorems 1.11–1.12 about record-setting probabilities also give information about the expected number of maxima when i.i.d. vectors are sampled.
$\mathbf X^{(n)}$ sets a record. Thus our main Theorems 1.11–1.12 about record-setting probabilities also give information about the expected number of maxima when i.i.d. vectors are sampled.
Omitting, for now, any dependence on F or d from the notation, the probability pn that ![]() $\mathbf X^{(n)}$ sets a record is given by
$\mathbf X^{(n)}$ sets a record is given by
 \begin{align}
p_n &= \int\!\operatorname{\mathbb P{}}(\mathbf X \in \mathrm{d} \mathbf x) [1 - \operatorname{\mathbb P{}}(\mathbf X \geq \mathbf x)]^{n - 1}
= \int\!\mathrm{d} F(\mathbf x) [1 - H(-\mathbf x)]^{n - 1} \nonumber \\
&= \int\!\mathrm{d} H(\mathbf y) [1 - H(\mathbf y)]^{n - 1}
= \operatorname{\mathbb E{}}[1 - H(-\mathbf X)]^{n - 1},
\end{align}
\begin{align}
p_n &= \int\!\operatorname{\mathbb P{}}(\mathbf X \in \mathrm{d} \mathbf x) [1 - \operatorname{\mathbb P{}}(\mathbf X \geq \mathbf x)]^{n - 1}
= \int\!\mathrm{d} F(\mathbf x) [1 - H(-\mathbf x)]^{n - 1} \nonumber \\
&= \int\!\mathrm{d} H(\mathbf y) [1 - H(\mathbf y)]^{n - 1}
= \operatorname{\mathbb E{}}[1 - H(-\mathbf X)]^{n - 1},
\end{align} where H denotes the distribution function corresponding to ![]() $- \mathbf X$.
$- \mathbf X$.
Remark 1.5. For fixed d and n, the mapping from F (equivalently, from H) to pn is many-to-one; recall Remark 1.3. In particular, pn has the same value for all continuous F such that the coordinates of ![]() $\mathbf X$ are independent.
$\mathbf X$ are independent.
1.2. RP equivalence classes, RP ordering, and the main results
We see from (1) that the sequence ![]() $(p_n)_{n \geq 1}$ of record-setting probabilities is determined by
$(p_n)_{n \geq 1}$ of record-setting probabilities is determined by ![]() ${\mathcal L}(H(-\mathbf X))$. Conversely, since the distribution of a bounded random variable is determined by its moments,
${\mathcal L}(H(-\mathbf X))$. Conversely, since the distribution of a bounded random variable is determined by its moments, ![]() ${\mathcal L}(H(-\mathbf X))$ is determined by
${\mathcal L}(H(-\mathbf X))$ is determined by ![]() $(p_n)_{n \geq 1}$. We are thus led to define an equivalence relation on (continuous) d-dimensional distribution functions F (for each fixed d) by declaring that
$(p_n)_{n \geq 1}$. We are thus led to define an equivalence relation on (continuous) d-dimensional distribution functions F (for each fixed d) by declaring that ![]() $F \sim {\widetilde F}$ if
$F \sim {\widetilde F}$ if ![]() $H(-\mathbf X)$ and
$H(-\mathbf X)$ and ![]() ${\widetilde H}(-{\widetilde {\mathbf X}})$ have the same distribution, where F,
${\widetilde H}(-{\widetilde {\mathbf X}})$ have the same distribution, where F, ![]() $\widetilde{F}$, H, and
$\widetilde{F}$, H, and ![]() ${\widetilde H}$ are the distribution functions of
${\widetilde H}$ are the distribution functions of ![]() $\mathbf X$,
$\mathbf X$, ![]() $ - \mathbf X$,
$ - \mathbf X$, ![]() ${\widetilde {\mathbf X}}$, and
${\widetilde {\mathbf X}}$, and ![]() $ - {\widetilde {\mathbf X}}$, respectively; we call this the record-setting probability (RP) equivalence.
$ - {\widetilde {\mathbf X}}$, respectively; we call this the record-setting probability (RP) equivalence.
We are now prepared to define a partial order on the RP equivalence classes.
Definition 1.6. Let C and ![]() ${\widetilde C}$ be RP equivalence classes with (arbitrarily chosen) respective representatives F and
${\widetilde C}$ be RP equivalence classes with (arbitrarily chosen) respective representatives F and ![]() ${\widetilde F}$. We say that
${\widetilde F}$. We say that ![]() $C \leq {\widetilde C}$ in the RP ordering (or, by abuse of terminology, that
$C \leq {\widetilde C}$ in the RP ordering (or, by abuse of terminology, that ![]() $F \leq {\widetilde F}$ in the RP ordering) if
$F \leq {\widetilde F}$ in the RP ordering) if ![]() $H(-\mathbf X) \geq {\widetilde H}(-{\widetilde {\mathbf X}})$ stochastically.
$H(-\mathbf X) \geq {\widetilde H}(-{\widetilde {\mathbf X}})$ stochastically.
Remark 1.7. From (1) it follows immediately that if ![]() $F \leq {\widetilde F}$ in the RP ordering, then
$F \leq {\widetilde F}$ in the RP ordering, then ![]() $p_n \leq \tilde p_n$ for every n.
$p_n \leq \tilde p_n$ for every n.
Let ![]() $C^*$ denote the RP equivalence class corresponding to independent coordinates. We next introduce new notions of negative dependence and positive dependence; we relate these notions to more standard notions later, in Section 4.
$C^*$ denote the RP equivalence class corresponding to independent coordinates. We next introduce new notions of negative dependence and positive dependence; we relate these notions to more standard notions later, in Section 4.
Definition 1.8. We will say that F is negatively record-setting probability dependent (NRPD) if its RP equivalence class C satisfies ![]() $C \geq C^*$ in the RP ordering.
$C \geq C^*$ in the RP ordering.
Definition 1.9. We will say that F is positively record-setting probability dependent (PRPD) if its RP equivalence class C satisfies ![]() $C \leq C^*$ in the RP ordering.
$C \leq C^*$ in the RP ordering.
Remark 1.10. Thus any F having independent coordinates is both NRPD and PRPD.
We can now state our two main results. For both, let ![]() $p_n(F) \equiv p_{n, d}(F)$ denote the probability that the
$p_n(F) \equiv p_{n, d}(F)$ denote the probability that the ![]() $n^{\rm \scriptsize}$th observation
$n^{\rm \scriptsize}$th observation ![]() $\mathbf X^{(n)}$ from the (continuous) distribution F sets a record, and let
$\mathbf X^{(n)}$ from the (continuous) distribution F sets a record, and let ![]() $p^*_n$ denote the value when
$p^*_n$ denote the value when ![]() $F \in C^*$.
$F \in C^*$.
Theorem 1.11 For each fixed ![]() $d \geq 2$ and
$d \geq 2$ and ![]() $n \geq 1$ the image of the mapping pn on the domain of NRPD distributions is precisely the interval
$n \geq 1$ the image of the mapping pn on the domain of NRPD distributions is precisely the interval ![]() $[p^*_n, 1]$.
$[p^*_n, 1]$.
Theorem 1.12 For each fixed ![]() $d \geq 1$ and
$d \geq 1$ and ![]() $n \geq 1$ the image of the mapping pn on the domain of PRPD distributions is precisely the interval
$n \geq 1$ the image of the mapping pn on the domain of PRPD distributions is precisely the interval ![]() $[n^{-1}, p^*_n]$.
$[n^{-1}, p^*_n]$.
(a) For d = 1 and
 $n \geq 2$ the conclusion of Theorem 1.11 is false, since then
$n \geq 2$ the conclusion of Theorem 1.11 is false, since then  $p_{n, 1}(F) \equiv n^{-1}$.
$p_{n, 1}(F) \equiv n^{-1}$.(b) For n = 1 the results of Theorems 1.11–1.12 are trivial, since we have
 $p_{1, d}(F) \equiv 1$; so in proving the theorems we may assume
$p_{1, d}(F) \equiv 1$; so in proving the theorems we may assume  $n \geq 2$.
$n \geq 2$.
Corollary 1.14. For fixed ![]() $d \geq 2$ and
$d \geq 2$ and ![]() $n \geq 1$ the image of the mapping pn on the domain of all continuous distributions F is precisely the interval
$n \geq 1$ the image of the mapping pn on the domain of all continuous distributions F is precisely the interval ![]() $[n^{-1}, 1]$, irrespective of d.
$[n^{-1}, 1]$, irrespective of d.
We outline here the strategy, as illustrated in Figure 1 and carried out in Section 7, for proving Theorems 1.11–1.12 (and subsequently Corollary 1.14). Let ![]() $\mathcal{R}_{{\rm N}}$ and
$\mathcal{R}_{{\rm N}}$ and ![]() $\mathcal{R}_{{\rm P}}$ denote the respective images. It is immediate from our definitions that
$\mathcal{R}_{{\rm P}}$ denote the respective images. It is immediate from our definitions that ![]() $\mathcal{R}_{{\rm N}} \subseteq [p^*_n, 1]$ and
$\mathcal{R}_{{\rm N}} \subseteq [p^*_n, 1]$ and ![]() $\mathcal{R}_{{\rm P}} \subseteq [0, p^*_n]$, and by considering just first coordinates (see Lemma 2.2) we quickly narrow the latter to
$\mathcal{R}_{{\rm P}} \subseteq [0, p^*_n]$, and by considering just first coordinates (see Lemma 2.2) we quickly narrow the latter to ![]() $\mathcal{R}_{{\rm P}} \subseteq [n^{-1}, p^*_n]$. To show the reverse containments, we then fill the interval
$\mathcal{R}_{{\rm P}} \subseteq [n^{-1}, p^*_n]$. To show the reverse containments, we then fill the interval ![]() $[p^*_n, 1]$ with elements of
$[p^*_n, 1]$ with elements of ![]() $\mathcal{R}_{{\rm N}}$ by choosing distribution functions F from a certain class of marginalized-Dirichlet distributions and their weak limits, and we fill the interval
$\mathcal{R}_{{\rm N}}$ by choosing distribution functions F from a certain class of marginalized-Dirichlet distributions and their weak limits, and we fill the interval ![]() $[n^{-1}, p^*_n]$ with elements of
$[n^{-1}, p^*_n]$ with elements of ![]() $\mathcal{R}_{{\rm P}}$ by choosing distribution functions F from a certain class of distributions with positively associated (PA) coordinates (more specifically, certain scale mixtures of i.i.d. Exponential distributions) and their weak limits.
$\mathcal{R}_{{\rm P}}$ by choosing distribution functions F from a certain class of distributions with positively associated (PA) coordinates (more specifically, certain scale mixtures of i.i.d. Exponential distributions) and their weak limits.

Figure 1. The strategy for proving Theorems 1.11–1.12; here the random variable “PAa” has the PA distribution ![]() $\widehat F_a$ described in Section 6.
$\widehat F_a$ described in Section 6.
1.3. Brief literature review
Let us mention some related literature concerning Pareto records; we continue to assume F is continuous throughout this review. The book [Reference Arnold, Balakrishnan and Nagaraja1] is a standard reference for univariate records (the case d = 1). For multivariate records in the case of independent coordinates, we have already remarked that the record-setting probability ![]() $p_n = p^*_n$ does not depend on the distributions of the individual coordinates, but other aspects (such as the location of remaining records) do. Usually, as in [Reference Bai, Devroye, Hwang and Tsai2] (see also the references therein), the coordinates are taken to be i.i.d., either Uniform(0, 1) or standard Exponential. Bai et al. [Reference Bai, Devroye, Hwang and Tsai2] obtain, for fixed d and for both Rn and rn, asymptotic expansions as
$p_n = p^*_n$ does not depend on the distributions of the individual coordinates, but other aspects (such as the location of remaining records) do. Usually, as in [Reference Bai, Devroye, Hwang and Tsai2] (see also the references therein), the coordinates are taken to be i.i.d., either Uniform(0, 1) or standard Exponential. Bai et al. [Reference Bai, Devroye, Hwang and Tsai2] obtain, for fixed d and for both Rn and rn, asymptotic expansions as ![]() $n \to \infty$ for the expected value and variance and a central limit theorem with a Berry–Esseen bound. The main contributions of Fill and Naiman [Reference Fill and Naiman12] are localization theorems for the Pareto frontier—that is, the topological boundary between the record-setting region and its complement when coordinates are i.i.d. standard Exponential—and some of those theorems are substantially sharpened in [Reference Fill, Naiman and Sun13]. An importance-sampling algorithm for sampling records is presented, and partially analyzed, in [Reference Fill and Naiman11]. A limiting distribution (again, for fixed d as
$n \to \infty$ for the expected value and variance and a central limit theorem with a Berry–Esseen bound. The main contributions of Fill and Naiman [Reference Fill and Naiman12] are localization theorems for the Pareto frontier—that is, the topological boundary between the record-setting region and its complement when coordinates are i.i.d. standard Exponential—and some of those theorems are substantially sharpened in [Reference Fill, Naiman and Sun13]. An importance-sampling algorithm for sampling records is presented, and partially analyzed, in [Reference Fill and Naiman11]. A limiting distribution (again, for fixed d as ![]() $n \to \infty$) is established for the number
$n \to \infty$) is established for the number ![]() $r_{n - 1} + 1 - r_n$ of remaining records broken by
$r_{n - 1} + 1 - r_n$ of remaining records broken by ![]() $\mathbf X^{(n)}$ conditionally given that
$\mathbf X^{(n)}$ conditionally given that ![]() $\mathbf X^{(n)}$ sets a record, for d = 2 in [Reference Fill9] and for general d in [Reference Fill10].
$\mathbf X^{(n)}$ sets a record, for d = 2 in [Reference Fill9] and for general d in [Reference Fill10].
An underlying theme of the present paper is that it is interesting to see how results (for example, concerning asymptotics for moments and distributions for Rn and rn and localization of the frontier) vary with F. When F is the uniform distribution on the d-dimensional simplex, Hwang and Tsai [Reference Hwang and Tsai14] (see also the references therein, especially Bai et al. [Reference Bai, Hwang and Tsai3]) proceed in a fashion similar to that in [Reference Bai, Devroye, Hwang and Tsai2] to obtain analogues of the asymptotic results of that earlier paper. It is worth noting that the computations are more involved in the simplex case than in [Reference Bai, Devroye, Hwang and Tsai2], in part because results about rn no longer translate immediately to results about Rn since the use of so-called concomitants (see Remark 3.1) becomes more involved, and that the results are enormously different; indeed, for example, as noted in the last line of the table on p. 1,867 of [Reference Hwang and Tsai14], we have ![]() $\operatorname{\mathbb E{}} r_n \sim (\ln n)^{d - 1} / (d - 1)!$ for independent coordinates while
$\operatorname{\mathbb E{}} r_n \sim (\ln n)^{d - 1} / (d - 1)!$ for independent coordinates while ![]() $\operatorname{\mathbb E{}} r_n \sim \Gamma(1/d)\,n^{(d - 1) / d}$ for uniform sampling from the d-simplex.
$\operatorname{\mathbb E{}} r_n \sim \Gamma(1/d)\,n^{(d - 1) / d}$ for uniform sampling from the d-simplex.
1.4. Organization
In Section 2, we record two simple but very useful general observations about the record-breaking probability pn. In Section 3, we briefly review the special case of independent coordinates. In Section 4, we relate the notions of NRPD and PRPD to existing notions of negative and positive dependence. In Section 5, we introduce and treat a class of examples of NRPD distributions F closely related to Dirichlet distributions and in Section 6 we introduce and treat a class of PRPD examples that are scale mixtures of i.i.d. Exponential coordinates. Finally, in Section 7 we prove Theorems 1.11–1.12 and Corollary 1.14 and make a few additional remarks concerning the variability of ![]() $p_n$.
$p_n$.
1.5. Manifesto
In light of Theorems 1.11–1.12 (see also Figure 1 and the proof strategy discussed at the end of Section 1.2), we regard the marginalized-Dirichlet NRPD distributions and the scale-mixture PRPD distributions we will use to prove the theorems, if not as canonical examples, then at least as standard examples worthy of thorough consideration—in particular, to study how the behaviors of these examples vary with their associated parameter values. Accordingly, we regard this paper as a pilot study of sorts, and we are presently working to extend (most of) the results of references [Reference Bai, Devroye, Hwang and Tsai2], [Reference Hwang and Tsai14], [Reference Fill and Naiman12]–[Reference Fill, Naiman and Sun13], [Reference Fill and Naiman11], [Reference Fill9], and [Reference Fill10] to these two classes of examples.
2. The record-breaking probability pn: general information
To carry out our proof strategy for Theorems 1.11–1.12, we first need a result that pn is continuous as a function of ![]() ${\mathcal L}(\mathbf X)$ at any continuous distribution on
${\mathcal L}(\mathbf X)$ at any continuous distribution on ![]() $\mathbb R^d$. For this result (Proposition 2.1), we do not need to assume that the distributions of the random vectors
$\mathbb R^d$. For this result (Proposition 2.1), we do not need to assume that the distributions of the random vectors ![]() $\mathbf X(m)$ are continuous.
$\mathbf X(m)$ are continuous.
Proposition 2.1. Fix ![]() $d \geq 1$ and
$d \geq 1$ and ![]() $n \geq 1$. If
$n \geq 1$. If ![]() $\mathbf X(m)$ converges in distribution to
$\mathbf X(m)$ converges in distribution to ![]() $\mathbf X$ having a continuous distribution, then the corresponding record-setting probabilities satisfy
$\mathbf X$ having a continuous distribution, then the corresponding record-setting probabilities satisfy ![]() $p_n(m) \to p_n$ as
$p_n(m) \to p_n$ as ![]() $m \to \infty$.
$m \to \infty$.
Proof. The distribution functions Hm of ![]() $- \mathbf X(m)$ and H of
$- \mathbf X(m)$ and H of ![]() $- \mathbf X$ satisfy
$- \mathbf X$ satisfy ![]() $H_m\!\implies\!H$. Moreover, H is continuous, so
$H_m\!\implies\!H$. Moreover, H is continuous, so ![]() $H_m(\mathbf y)$ converges to
$H_m(\mathbf y)$ converges to ![]() $H(\mathbf y)$ uniformly in
$H(\mathbf y)$ uniformly in ![]() $\mathbf y$ [Reference Billingsley4, Problem 3 in Sect. 3 (only in first edition)] and hence (recalling that n here is fixed)
$\mathbf y$ [Reference Billingsley4, Problem 3 in Sect. 3 (only in first edition)] and hence (recalling that n here is fixed) ![]() $[1 - H_m(\mathbf y)]^{n - 1}$ converges to
$[1 - H_m(\mathbf y)]^{n - 1}$ converges to ![]() $[1 - H(\mathbf y)]^{n - 1}$ uniformly in
$[1 - H(\mathbf y)]^{n - 1}$ uniformly in ![]() $\mathbf y$. It follows that as
$\mathbf y$. It follows that as ![]() $m \to \infty$ we have
$m \to \infty$ we have
 \begin{equation*}
p_n(m) = \int\!\mathrm{d} H_m(\mathbf y) [1 - H_m(\mathbf y)]^{n - 1} \to \int\!\mathrm{d} H(\mathbf y) [1 - H(\mathbf y)]^{n - 1} = p_n.]
\end{equation*}
\begin{equation*}
p_n(m) = \int\!\mathrm{d} H_m(\mathbf y) [1 - H_m(\mathbf y)]^{n - 1} \to \int\!\mathrm{d} H(\mathbf y) [1 - H(\mathbf y)]^{n - 1} = p_n.]
\end{equation*}Our next result exhibits the smallest and largest possible values of pn.
Lemma 2.2. Fix ![]() $d \geq 2$ and
$d \geq 2$ and ![]() $n \geq 1$. We always have
$n \geq 1$. We always have ![]() $p_n \in [n^{-1}, 1]$, and
$p_n \in [n^{-1}, 1]$, and ![]() $p_n = n^{-1}$ and
$p_n = n^{-1}$ and ![]() $p_n = 1$ are both possible.
$p_n = 1$ are both possible.
Proof. If  $X^{(n)}_1$ sets a one-dimensional record (which has probability n −1), then
$X^{(n)}_1$ sets a one-dimensional record (which has probability n −1), then ![]() $\mathbf X^{(n)}$ sets a d-dimensional record. Thus
$\mathbf X^{(n)}$ sets a d-dimensional record. Thus ![]() $p_n \geq n^{-1}$, and equality holds if Y has any continuous distribution on
$p_n \geq n^{-1}$, and equality holds if Y has any continuous distribution on ![]() $\mathbb R$ and
$\mathbb R$ and ![]() $\mathbf X = (Y, \ldots, Y)$.
$\mathbf X = (Y, \ldots, Y)$.
At the other extreme, if ![]() $d \geq 2$ and (for example)
$d \geq 2$ and (for example) ![]() $\mathbf X \geq \textbf{0}$ has any continuous distribution (such as any Dirichlet distribution) satisfying
$\mathbf X \geq \textbf{0}$ has any continuous distribution (such as any Dirichlet distribution) satisfying ![]() $\|\mathbf X\|_1 = 1$, then
$\|\mathbf X\|_1 = 1$, then ![]() $\mathbf X^{(1)}, \mathbf X^{(2)}, \ldots$ form an antichain in the partial order ≤ on
$\mathbf X^{(1)}, \mathbf X^{(2)}, \ldots$ form an antichain in the partial order ≤ on ![]() $\mathbb R^d$, so
$\mathbb R^d$, so ![]() $p_n = 1$.
$p_n = 1$.
For further general information about pn (in addition to Theorems 1.11–1.12, of course), see Remark 7.1.
3. Independent coordinates:  $p_n^*$
$p_n^*$
This brief section concerns the case where the coordinates of each observation are independent. As noted in Remark 1.5, pn doesn’t otherwise depend on F in this setting, so we may as well assume that the coordinates are i.i.d. Exponential(1). Then (writing ![]() $p^*_n$ for pn in this special case)
$p^*_n$ for pn in this special case)
 \begin{align*}
p^*_n
&= \int\!\operatorname{\mathbb P{}}(\mathbf X \in \mathrm{d} \mathbf x) [1 - \operatorname{\mathbb P{}}(\mathbf X \geq \mathbf x)]^{n - 1}
= \int_{\textbf{0} \leq \mathbf x \in \mathbb R^d}\!e^{- \|\mathbf x\|_1} \left( 1 - e^{- \|\mathbf x\|_1} \right)^{n - 1} \,\mathrm{d} \mathbf x \\
&= \int_0^{\infty}\!\frac{y^{d - 1}}{(d - 1)!} e^{-y} (1 - e^{-y})^{n - 1} \,\mathrm{d} y \\
&= n^{-1} \sum_{j = 1}^n (-1)^{j - 1} \binom{n}{j}\,\, j^{- (d - 1)}
=: n^{-1} {\widehat H}^{(d - 1)}_n ( = n^{-1}\ \mbox{when}\ d = 1).
\end{align*}
\begin{align*}
p^*_n
&= \int\!\operatorname{\mathbb P{}}(\mathbf X \in \mathrm{d} \mathbf x) [1 - \operatorname{\mathbb P{}}(\mathbf X \geq \mathbf x)]^{n - 1}
= \int_{\textbf{0} \leq \mathbf x \in \mathbb R^d}\!e^{- \|\mathbf x\|_1} \left( 1 - e^{- \|\mathbf x\|_1} \right)^{n - 1} \,\mathrm{d} \mathbf x \\
&= \int_0^{\infty}\!\frac{y^{d - 1}}{(d - 1)!} e^{-y} (1 - e^{-y})^{n - 1} \,\mathrm{d} y \\
&= n^{-1} \sum_{j = 1}^n (-1)^{j - 1} \binom{n}{j}\,\, j^{- (d - 1)}
=: n^{-1} {\widehat H}^{(d - 1)}_n ( = n^{-1}\ \mbox{when}\ d = 1).
\end{align*} Alternatively, as pointed out by a reviewer of a previous draft, the same expression can be obtained for ![]() $p^*_n$ by applying the principle of inclusion–exclusion to
$p^*_n$ by applying the principle of inclusion–exclusion to  $\operatorname{\mathbb P{}}\left( \bigcup_{i = 1}^{n - 1} \{\mathbf X^{(n)} \leq \mathbf X^{(i)}\} \right)$.
$\operatorname{\mathbb P{}}\left( \bigcup_{i = 1}^{n - 1} \{\mathbf X^{(n)} \leq \mathbf X^{(i)}\} \right)$.
The numbers
 \begin{equation*}
{\widehat H}^{(k)}_n = \sum_{j = 1}^n (-1)^{j - 1} \binom{n}{j} j^{- k}
\end{equation*}
\begin{equation*}
{\widehat H}^{(k)}_n = \sum_{j = 1}^n (-1)^{j - 1} \binom{n}{j} j^{- k}
\end{equation*} appearing in the expression for ![]() $p^*_n$ are called Roman harmonic numbers, studied in [Reference Loeb and Rota17], [Reference Roman18], and [Reference Sesma20]. This
$p^*_n$ are called Roman harmonic numbers, studied in [Reference Loeb and Rota17], [Reference Roman18], and [Reference Sesma20]. This  ${\widehat H}^{(k)}_n$ can be written as a positive linear combination of products of generalized harmonic numbers
${\widehat H}^{(k)}_n$ can be written as a positive linear combination of products of generalized harmonic numbers  $H^{(r)}_n := \sum_{j = 1}^n j^{-r}$. In particular,
$H^{(r)}_n := \sum_{j = 1}^n j^{-r}$. In particular,  ${\widehat H}^{(1)}_n = H^{(1)}_n$.
${\widehat H}^{(1)}_n = H^{(1)}_n$.
(a) In obvious notation, the numbers
 $\operatorname{\mathbb E{}} r^*_{n, d} = n p^*_{n, d} = \operatorname{\mathbb E{}} R^*_{n, d - 1}$ increase strictly in n for fixed
$\operatorname{\mathbb E{}} r^*_{n, d} = n p^*_{n, d} = \operatorname{\mathbb E{}} R^*_{n, d - 1}$ increase strictly in n for fixed  $d \geq 2$, with limit
$d \geq 2$, with limit  $\infty$ as
$\infty$ as  $n \to \infty$. (Note: The equality in distribution of the random variables
$n \to \infty$. (Note: The equality in distribution of the random variables  $r_{n, d}$ and
$r_{n, d}$ and  $R_{n, d - 1}$ for general continuous F follows by standard consideration of concomitants: Consider
$R_{n, d - 1}$ for general continuous F follows by standard consideration of concomitants: Consider  $\mathbf X^{(1)}, \ldots, \mathbf X^{(n)}$ sorted according to the value of the
$\mathbf X^{(1)}, \ldots, \mathbf X^{(n)}$ sorted according to the value of the  $d^{\rm \scriptsize}$th coordinate.) Further, the numbers
$d^{\rm \scriptsize}$th coordinate.) Further, the numbers  $p^*_{n, d}$ increase strictly in d for fixed
$p^*_{n, d}$ increase strictly in d for fixed  $n \geq 2$, with limit 1 as
$n \geq 2$, with limit 1 as  $d \to \infty$; and decrease strictly in n for fixed
$d \to \infty$; and decrease strictly in n for fixed  $d \geq 1$, with limit 0 as
$d \geq 1$, with limit 0 as  $n \to \infty$.
$n \to \infty$.(b) For fixed d we have
 \begin{equation*}
p^*_{n, d} \sim n^{-1} \frac{(\ln n)^{d - 1}}{(d - 1)!}\ \mbox{as}\ n \to \infty.
\end{equation*}
\begin{equation*}
p^*_{n, d} \sim n^{-1} \frac{(\ln n)^{d - 1}}{(d - 1)!}\ \mbox{as}\ n \to \infty.
\end{equation*}Bai et al. [Reference Bai, Devroye, Hwang and Tsai2] give a more extensive asymptotic expansion.
4. Negative dependence (including NRPD) and positive dependence (including PRPD)
In this section, we review existing notions of negative and positive dependence in Subsections 4.1–4.2 and relate our new notions of NRPD and PRPD to them in Subsection 4.3.
4.1. Negative dependence
For a discussion of several notions of negative dependence, see [Reference Joag-Dev and Proschan15]. The first two notions in the next definition can be found there, with focus on the first notion (NA); we have created the third by interpolating between the first two.
(a) Random variables
 $X_1, \ldots, X_k$ are said to be negatively associated (NA) if for every pair of disjoint subsets A 1 and A 2 of
$X_1, \ldots, X_k$ are said to be negatively associated (NA) if for every pair of disjoint subsets A 1 and A 2 of  $\{1, \ldots, k\}$ we have
$\{1, \ldots, k\}$ we have
 \begin{equation*}
\operatorname{Cov}\{f_1(X_i:i \in A_1),\,f_2(X_j:j \in A_2)\} \leq 0
\end{equation*}
\begin{equation*}
\operatorname{Cov}\{f_1(X_i:i \in A_1),\,f_2(X_j:j \in A_2)\} \leq 0
\end{equation*}whenever f 1 and f 2 are nondecreasing (in each argument) and the covariance is defined.
(b) Random variables
 $X_1, \ldots, X_k$ are said to be negatively upper orthant dependent (NUOD) if for all real numbers
$X_1, \ldots, X_k$ are said to be negatively upper orthant dependent (NUOD) if for all real numbers  $x_1, \ldots, x_k$ we have
$x_1, \ldots, x_k$ we have
 \begin{equation*}
\operatorname{\mathbb P{}}(X_i \gt x_i,\ i = 1, \ldots, k) \leq \prod_{i = 1}^k \operatorname{\mathbb P{}}(X_i \gt x_i).
\end{equation*}
\begin{equation*}
\operatorname{\mathbb P{}}(X_i \gt x_i,\ i = 1, \ldots, k) \leq \prod_{i = 1}^k \operatorname{\mathbb P{}}(X_i \gt x_i).
\end{equation*}(c) We say that random variables
 $X_1, \ldots, X_k$ are negatively upper orthant associated (NUOA) if for every pair of disjoint subsets A 1 and A 2 of
$X_1, \ldots, X_k$ are negatively upper orthant associated (NUOA) if for every pair of disjoint subsets A 1 and A 2 of  $\{1, \ldots, k\}$ and all real numbers
$\{1, \ldots, k\}$ and all real numbers  $x_1, \ldots, x_k$ we have
$x_1, \ldots, x_k$ we have
 \begin{equation*}
\operatorname{\mathbb P{}}(X_i \gt x_i,\ i = 1, \ldots, k) \leq \operatorname{\mathbb P{}}(X_i \gt x_i,\ i \in A_1)\,\operatorname{\mathbb P{}}(X_j \gt x_j,\ j \in A_2).
\end{equation*}
\begin{equation*}
\operatorname{\mathbb P{}}(X_i \gt x_i,\ i = 1, \ldots, k) \leq \operatorname{\mathbb P{}}(X_i \gt x_i,\ i \in A_1)\,\operatorname{\mathbb P{}}(X_j \gt x_j,\ j \in A_2).
\end{equation*}
(a) NA implies NUOA, which implies NUOD.
(b) Theorem 2.8 in [Reference Joag-Dev and Proschan15] gives a way of constructing NA
 $(X_1, \ldots, X_k)$, namely, if
$(X_1, \ldots, X_k)$, namely, if  $G_1, \ldots, G_k$ are independent random variables with log-concave densities, then the conditional distribution of
$G_1, \ldots, G_k$ are independent random variables with log-concave densities, then the conditional distribution of  $\textstyle\mathbf G=(G_1,\dots,G_k)$ given
$\textstyle\mathbf G=(G_1,\dots,G_k)$ given  $\sum_{j = 1}^k G_j$ is NA almost surely.
$\sum_{j = 1}^k G_j$ is NA almost surely.
4.2. Positive dependence
For a general discussion of various notions of positive dependence focusing on the one in the next definition, see [Reference Esary, Proschan and Walkup8].
Definition 4.3. Random variables ![]() $\textbf{X} = (X_1, \ldots, X_k)$ are said to be positively associated (PA) (or simply associated) if
$\textbf{X} = (X_1, \ldots, X_k)$ are said to be positively associated (PA) (or simply associated) if
whenever f 1 and f 2 are nondecreasing (in each argument) and the covariance is defined.
Remark 4.4. It is easy to show that if Z and ![]() $G_1, \ldots, G_d$ are independent positive random variables, then the scale mixture
$G_1, \ldots, G_d$ are independent positive random variables, then the scale mixture
is PA. The proof uses the law of total covariance (conditioning on Z), the fact [Reference Esary, Proschan and Walkup8, Thm. 2.1] that independent random variables are PA (applied to the conditional covariance), and the fact ([Reference Esary, Proschan and Walkup8, Property P3], due to Chebyshev) that the set consisting of a single random variable is PA (applied to the covariance of the conditional expectations).
4.3. Relation with NRPD and PRPD
Our motivation for regarding NRPD and PRPD of respective Definitions 1.8 and 1.9 as notions of negative and positive dependence, respectively, is the following observation. One might suspect that NA implies NRPD and that PA implies PRPD; we are unable to prove either implication, but we can prove the weaker results (recall Remark 1.7) that NA implies ![]() $p_2 \geq p^*_2$ and PA implies
$p_2 \geq p^*_2$ and PA implies ![]() $p_2 \leq p^*_2$.
$p_2 \leq p^*_2$.
To establish the claimed inequalities, in the following proof replace ![]() $*$ by ≤ if the observations are PA, by = if they have independent coordinates, and by ≥ if they are NA. The claim is that
$*$ by ≤ if the observations are PA, by = if they have independent coordinates, and by ≥ if they are NA. The claim is that ![]() $p_2 * 1 - 2^{-d}$. To see this, recall (1). We then have
$p_2 * 1 - 2^{-d}$. To see this, recall (1). We then have
 \begin{align*}
p_2
&= \int \operatorname{\mathbb P{}}(\mathbf X \in \mathrm{d} \mathbf x) [1 - \operatorname{\mathbb P{}}(\mathbf X \geq \mathbf x)] = 1 - \int \operatorname{\mathbb P{}}(\mathbf X \in \mathrm{d} \mathbf x) \operatorname{\mathbb P{}}(\mathbf X \geq \mathbf x) \\
&* 1 - \int \operatorname{\mathbb P{}}(\mathbf X \in \mathrm{d} \mathbf x) \prod_{j = 1}^d \operatorname{\mathbb P{}}(X_j \geq x_j) \\
&* 1 - \int \prod_{j = 1}^d [\operatorname{\mathbb P{}}(X_j \in \mathrm{d} x_j) \operatorname{\mathbb P{}}(X_j \geq x_j)] \\
&= 1 - \prod_{j = 1}^d \int [\operatorname{\mathbb P{}}(X_j \in \mathrm{d} x) \operatorname{\mathbb P{}}(X_j \geq x)] \\
&= 1 - \prod_{j = 1}^d \int [\operatorname{\mathbb P{}}(X_j \in \mathrm{d} x) \operatorname{\mathbb P{}}(X^*_j \geq x | X_j = x))] \\
&{} \qquad \qquad \mbox{where}\ X^*_j\ \mbox{is an independent copy of}\ X_j \\
&= 1 - \prod_{j = 1}^d \int [\operatorname{\mathbb P{}}(X_j \in \mathrm{d} x) \operatorname{\mathbb P{}}(X^*_j \geq X_j | X_j = x))] \\
&= 1 - \prod_{j = 1}^d \operatorname{\mathbb P{}}(X^*_j \geq X_j) = 1 - \prod_{j = 1}^d 2^{-1} = 1 - 2^{-d}.
\end{align*}
\begin{align*}
p_2
&= \int \operatorname{\mathbb P{}}(\mathbf X \in \mathrm{d} \mathbf x) [1 - \operatorname{\mathbb P{}}(\mathbf X \geq \mathbf x)] = 1 - \int \operatorname{\mathbb P{}}(\mathbf X \in \mathrm{d} \mathbf x) \operatorname{\mathbb P{}}(\mathbf X \geq \mathbf x) \\
&* 1 - \int \operatorname{\mathbb P{}}(\mathbf X \in \mathrm{d} \mathbf x) \prod_{j = 1}^d \operatorname{\mathbb P{}}(X_j \geq x_j) \\
&* 1 - \int \prod_{j = 1}^d [\operatorname{\mathbb P{}}(X_j \in \mathrm{d} x_j) \operatorname{\mathbb P{}}(X_j \geq x_j)] \\
&= 1 - \prod_{j = 1}^d \int [\operatorname{\mathbb P{}}(X_j \in \mathrm{d} x) \operatorname{\mathbb P{}}(X_j \geq x)] \\
&= 1 - \prod_{j = 1}^d \int [\operatorname{\mathbb P{}}(X_j \in \mathrm{d} x) \operatorname{\mathbb P{}}(X^*_j \geq x | X_j = x))] \\
&{} \qquad \qquad \mbox{where}\ X^*_j\ \mbox{is an independent copy of}\ X_j \\
&= 1 - \prod_{j = 1}^d \int [\operatorname{\mathbb P{}}(X_j \in \mathrm{d} x) \operatorname{\mathbb P{}}(X^*_j \geq X_j | X_j = x))] \\
&= 1 - \prod_{j = 1}^d \operatorname{\mathbb P{}}(X^*_j \geq X_j) = 1 - \prod_{j = 1}^d 2^{-1} = 1 - 2^{-d}.
\end{align*}5. Marginalized-Dirichlet distributions Fa: strict decreasing monotonicity in the RP ordering
The following is the usual definition of Dirichlet distribution, where the normalizing constant is the multivariate beta-function value  ${\mathrm B}(\mathrm b) := \frac{\prod_{j = 1}^k \Gamma(b_j)}{\Gamma(\|\mathbf b\|_1)}$.
${\mathrm B}(\mathrm b) := \frac{\prod_{j = 1}^k \Gamma(b_j)}{\Gamma(\|\mathbf b\|_1)}$.
Definition 5.1. Let ![]() $k \geq 2$ and
$k \geq 2$ and ![]() $\mathbf b = (b_1, \ldots, b_k) \succ {\mathbf{0}}$. If
$\mathbf b = (b_1, \ldots, b_k) \succ {\mathbf{0}}$. If ![]() $\mathbf Y = (Y_1, \ldots, Y_k) \succ {\mathbf{0}}$ satisfies
$\mathbf Y = (Y_1, \ldots, Y_k) \succ {\mathbf{0}}$ satisfies ![]() $\|\mathbf Y\|_1 = 1$ and
$\|\mathbf Y\|_1 = 1$ and ![]() $(Y_1, \ldots, Y_{k - 1})$ has
$(Y_1, \ldots, Y_{k - 1})$ has ![]() $(k - 1)$-dimensional density (with respect to Lebesgue measure)
$(k - 1)$-dimensional density (with respect to Lebesgue measure)
 \begin{equation*}
\frac{1}{{\mathrm B}(\mathrm b)} y_1^{b_1 - 1} \cdots y_k^{b_k - 1}\,{\mathbf{1}}\,(y_1 \gt 0, \ldots, y_k \gt 0)
\end{equation*}
\begin{equation*}
\frac{1}{{\mathrm B}(\mathrm b)} y_1^{b_1 - 1} \cdots y_k^{b_k - 1}\,{\mathbf{1}}\,(y_1 \gt 0, \ldots, y_k \gt 0)
\end{equation*} with  $y_k := 1 - \sum_{j = 1}^{k - 1} y_j$, then we say that
$y_k := 1 - \sum_{j = 1}^{k - 1} y_j$, then we say that ![]() $\mathbf Y$ has the Dirichlet
$\mathbf Y$ has the Dirichlet ![]() $(\mathbf b)$ distribution.
$(\mathbf b)$ distribution.
We will have special interest in taking ![]() $\mathbf X = (X_1, \ldots, X_d)$ to be the first d coordinates of
$\mathbf X = (X_1, \ldots, X_d)$ to be the first d coordinates of ![]() $(Y_1, \ldots, Y_{d + 1}) \sim$ Dirichlet
$(Y_1, \ldots, Y_{d + 1}) \sim$ Dirichlet ![]() $(1, \ldots, 1, a)$; we denote the distribution of
$(1, \ldots, 1, a)$; we denote the distribution of ![]() $\mathbf X$ in this case by
$\mathbf X$ in this case by ![]() $\mbox{Dir}_a$ and the corresponding distribution function by Fa; we refer to the distributions
$\mbox{Dir}_a$ and the corresponding distribution function by Fa; we refer to the distributions ![]() $\mbox{Dir}_a$ as marginalized-Dirichlet distributions. We will have occasional interest in taking
$\mbox{Dir}_a$ as marginalized-Dirichlet distributions. We will have occasional interest in taking
(a) When a = 1, the vector
 $\mathbf X$ is uniformly distributed in the (open) d-dimensional unit simplex
(3)
$\mathbf X$ is uniformly distributed in the (open) d-dimensional unit simplex
(3) \begin{equation}
{\mathcal S}_d := \{\mathbf x = (x_1, \ldots, x_d):\,x_j \gt 0\ \mbox{for}\ j = 1, \ldots, d\ \mbox{and}\ \|\mathbf x\|_1 \lt 1 \}.
\end{equation}
\begin{equation}
{\mathcal S}_d := \{\mathbf x = (x_1, \ldots, x_d):\,x_j \gt 0\ \mbox{for}\ j = 1, \ldots, d\ \mbox{and}\ \|\mathbf x\|_1 \lt 1 \}.
\end{equation}This special case is the focus of [Reference Hwang and Tsai14].
(b) We find explicit computation (exact or asymptotic) of pn intractable for general Dirichlet distributions.
Dirichlet distributions exhibit negative dependence among the coordinates according to standard notions [Reference Joag-Dev and Proschan15]:
(a) The distribution Fa is NUOA (recall Definition 4.1(c)) for every
 $a \in (0, \infty)$, by a simple calculation.
$a \in (0, \infty)$, by a simple calculation.(b) The distribution Fa is NA if
 $a \geq 1$. Indeed, as in Definition 5.1, let
$a \geq 1$. Indeed, as in Definition 5.1, let  $\mathbf b = (b_1, \ldots, b_k) \succ \textbf{0}$. The proof (recall Remark 4.2(b)) that Dirichlet
$\mathbf b = (b_1, \ldots, b_k) \succ \textbf{0}$. The proof (recall Remark 4.2(b)) that Dirichlet $(\mathbf b)$ is NA when
$(\mathbf b)$ is NA when  $b_j \geq 1$ for every j relies on the following two standard facts:
$b_j \geq 1$ for every j relies on the following two standard facts:(i) If
 $G_j \sim$ Gamma
$G_j \sim$ Gamma $(b_j)$ are independent random variables (
$(b_j)$ are independent random variables ( $\,j = 1, \ldots, k$), then
$\,j = 1, \ldots, k$), then  $\Arrowvert\mathbf G\Arrowvert_1\sim$ Gamma
$\Arrowvert\mathbf G\Arrowvert_1\sim$ Gamma $(\|\mathbf b\|_1)$ and
$(\|\mathbf b\|_1)$ and
 \begin{equation*}
\mathbf Y := \left( \frac{G_1}{\|{\boldsymbol{G}}\|_1}, \ldots, \frac{G_k}{{\|\boldsymbol{G}}\|_1} \right) \sim \mbox{Dirichlet}(\mathbf b)
\end{equation*}
\begin{equation*}
\mathbf Y := \left( \frac{G_1}{\|{\boldsymbol{G}}\|_1}, \ldots, \frac{G_k}{{\|\boldsymbol{G}}\|_1} \right) \sim \mbox{Dirichlet}(\mathbf b)
\end{equation*}are independent.
(ii) For any
 $b \geq 1$, the Gamma(b) density is log-concave.
$b \geq 1$, the Gamma(b) density is log-concave.
Consider ![]() $F = F_a$. The cases n = 1 (with
$F = F_a$. The cases n = 1 (with ![]() $p_n \equiv 1$) and d = 1 (where the choice of a is irrelevant) being trivial, in the following monotonicity result we consider only
$p_n \equiv 1$) and d = 1 (where the choice of a is irrelevant) being trivial, in the following monotonicity result we consider only ![]() $n \geq 2$ and
$n \geq 2$ and ![]() $d \geq 2$.
$d \geq 2$.
Proposition 5.4. Fix ![]() $d \geq 2$ and
$d \geq 2$ and ![]() $n \geq 2$, and let
$n \geq 2$, and let ![]() $F = F_a$, that is,
$F = F_a$, that is, ![]() $\mathbf X \sim {\rm Dir}_a$. Then Fa is strictly decreasing in the RP ordering and therefore the probability
$\mathbf X \sim {\rm Dir}_a$. Then Fa is strictly decreasing in the RP ordering and therefore the probability ![]() $p_n(a) := p_n(F_a)$ that
$p_n(a) := p_n(F_a)$ that ![]() $\mathbf X^{(n)}$ sets a record is strictly decreasing in a.
$\mathbf X^{(n)}$ sets a record is strictly decreasing in a.
Proof. By successive integrations one finds
thus ![]() $H_a(-\mathbf X) = (1 - \|\mathbf X\|_1)^{d + a - 1}$. Further,
$H_a(-\mathbf X) = (1 - \|\mathbf X\|_1)^{d + a - 1}$. Further, ![]() $1 - \|\mathbf X\|_1 \sim$ Beta(a, d), so the first assertion is an immediate consequence of Lemma 5.6 below, and the second assertion follows from Remark 1.7.
$1 - \|\mathbf X\|_1 \sim$ Beta(a, d), so the first assertion is an immediate consequence of Lemma 5.6 below, and the second assertion follows from Remark 1.7.
Before proceeding to Lemma 5.6, we remind the reader of the definition of the likelihood ratio partial ordering (specialized to our setting of random variables taking values in the unit interval) and its connection to the well-known stochastic ordering.
Definition 5.5. Given two real-valued random variables S and T with respective everywhere strictly positive densities f and g with respect to Lebesgue measure on ![]() $(0, 1)$, we say that
$(0, 1)$, we say that ![]() $S \leq T$ in the likelihood ratio (LR) ordering if
$S \leq T$ in the likelihood ratio (LR) ordering if ![]() $g(u) / f(u)$ is nondecreasing in
$g(u) / f(u)$ is nondecreasing in ![]() $u \in (0, 1)$.
$u \in (0, 1)$.
As noted (for example) in [Reference Ross19, Sect. 9.4], if ![]() $S \leq T$ in the LR ordering, then
$S \leq T$ in the LR ordering, then ![]() $S \leq T$ stochastically.
$S \leq T$ stochastically.
Lemma 5.6. Fix a real number d > 1, and let Za have the Beta(a, d) distribution. Then ![]() $W_{a} := Z_{a}^{d + a - 1}$ is strictly increasing in the LR ordering, and therefore also in the stochastic ordering, as
$W_{a} := Z_{a}^{d + a - 1}$ is strictly increasing in the LR ordering, and therefore also in the stochastic ordering, as ![]() $a \in (0, \infty)$ increases.
$a \in (0, \infty)$ increases.
Proof. By elementary calculation, Wa has density ga on ![]() $(0, 1)$ given by the following expression, with
$(0, 1)$ given by the following expression, with ![]() $c_{a} := (d + a - 1) {\rm B}(a, d)$:
$c_{a} := (d + a - 1) {\rm B}(a, d)$:
 \begin{align*}
g_{a}(w)
&= c_{a}^{-1} w^{- (d - 1) / (d + a - 1)} \left( 1 - w^{1 / (d + a - 1)} \right)^{d - 1} \\
&= c_{a}^{-1} \left( w^{- 1 / (d + a - 1)} - 1 \right)^{d - 1}.
\end{align*}
\begin{align*}
g_{a}(w)
&= c_{a}^{-1} w^{- (d - 1) / (d + a - 1)} \left( 1 - w^{1 / (d + a - 1)} \right)^{d - 1} \\
&= c_{a}^{-1} \left( w^{- 1 / (d + a - 1)} - 1 \right)^{d - 1}.
\end{align*} Letting ![]() $0 \lt a \lt b \lt \infty$ and setting
$0 \lt a \lt b \lt \infty$ and setting ![]() $v := w^{- 1 / (d + b - 1)}$ and
$v := w^{- 1 / (d + b - 1)}$ and
it then suffices to show for any fixed t > 1 that the ratio ![]() $(v - 1) / (v^t - 1)$ decreases strictly as v increases over
$(v - 1) / (v^t - 1)$ decreases strictly as v increases over ![]() $(1, \infty)$.
$(1, \infty)$.
For this, we consider the log-ratio, whose derivative is ![]() $h(v) / [(v - 1) (v^t - 1)]$, where
$h(v) / [(v - 1) (v^t - 1)]$, where
so we need only show that ![]() $h(v) \lt 0$ for
$h(v) \lt 0$ for ![]() $v \in (1, \infty)$. Indeed, since
$v \in (1, \infty)$. Indeed, since
for ![]() $v \in (1, \infty)$, we see that
$v \in (1, \infty)$, we see that ![]() $h(v) \lt h(1) = 0$ for
$h(v) \lt h(1) = 0$ for ![]() $v \in (1, \infty)$.
$v \in (1, \infty)$.
6. Positively associated  $\widehat F_a$: strict increasing monotonicity in the RP ordering
$\widehat F_a$: strict increasing monotonicity in the RP ordering
Distributions on ![]() $\mathbb R^d$ with PA coordinates can be constructed in similar fashion to the marginalized-Dirichlet distributions Fa (recall Remarks 4.4 and 5.3(b)). Given a > 0, let
$\mathbb R^d$ with PA coordinates can be constructed in similar fashion to the marginalized-Dirichlet distributions Fa (recall Remarks 4.4 and 5.3(b)). Given a > 0, let ![]() $\widehat F_a$ denote the PA distribution of
$\widehat F_a$ denote the PA distribution of
 \begin{equation*}
\mathbf X = \left( \frac{G_1}{G}, \ldots, \frac{G_d}{G} \right)\ \mbox{(scale mixture of i.i.d. Exponentials)},
\end{equation*}
\begin{equation*}
\mathbf X = \left( \frac{G_1}{G}, \ldots, \frac{G_d}{G} \right)\ \mbox{(scale mixture of i.i.d. Exponentials)},
\end{equation*} where the random variables ![]() $G, G_1, \ldots, G_d$ are independent,
$G, G_1, \ldots, G_d$ are independent, ![]() $G \sim \mbox{Gamma$(a)$}$, and
$G \sim \mbox{Gamma$(a)$}$, and ![]() $G_j \sim \mbox{Exponential}(1) \equiv \mbox{Gamma$(1)$}$ for
$G_j \sim \mbox{Exponential}(1) \equiv \mbox{Gamma$(1)$}$ for ![]() $j = 1, \ldots, d$.
$j = 1, \ldots, d$.
(a) Scale mixtures of a finite number of i.i.d. Exponential random variables appear in a study of finite versions of de Finetti’s theorem [Reference Diaconis and Freedman7, (3.11)].
(b) We find explicit computation (exact or asymptotic) of pn intractable for general scale mixtures, let alone for general PA distributions.
Similarly to Proposition 5.4, in our positive-association example we have the following claim:
Proposition 6.2. Fix ![]() $d \geq 2$ and
$d \geq 2$ and ![]() $n \geq 2$, and let
$n \geq 2$, and let ![]() $F = \widehat F_a$. Then
$F = \widehat F_a$. Then ![]() $\widehat F_a$ is strictly increasing in the RP ordering and therefore the probability
$\widehat F_a$ is strictly increasing in the RP ordering and therefore the probability ![]() $\hat{p}_n(a) := p_n(\widehat F_a)$ that
$\hat{p}_n(a) := p_n(\widehat F_a)$ that ![]() $\mathbf X^{(n)}$ sets a record is strictly increasing in a.
$\mathbf X^{(n)}$ sets a record is strictly increasing in a.
Proof. A simple computation for ![]() $\mathbf x \geq \textbf{0}$ gives
$\mathbf x \geq \textbf{0}$ gives
and thus ![]() $H_a(-\mathbf X) = (1 + \|\mathbf X\|_1)^{-a}$. Further,
$H_a(-\mathbf X) = (1 + \|\mathbf X\|_1)^{-a}$. Further, ![]() $(1+\Arrowvert\mathbf X\Arrowvert_1)^{-1}=G/(G+\Arrowvert\mathbf G\Arrowvert_1)\sim\text{Beta}(a,d)$, so the first assertion is an immediate consequence of the following lemma, and the second assertion follows from Remark 1.7.
$(1+\Arrowvert\mathbf X\Arrowvert_1)^{-1}=G/(G+\Arrowvert\mathbf G\Arrowvert_1)\sim\text{Beta}(a,d)$, so the first assertion is an immediate consequence of the following lemma, and the second assertion follows from Remark 1.7.
Lemma 6.3. Fix a real number d > 1, and let Za have the Beta(a, d) distribution. Then  $\widehat W_{a} := Z_{a}^{a}$ is strictly decreasing in the LR ordering, and therefore also in the stochastic ordering, as
$\widehat W_{a} := Z_{a}^{a}$ is strictly decreasing in the LR ordering, and therefore also in the stochastic ordering, as ![]() $a \in (0, \infty)$ increases.
$a \in (0, \infty)$ increases.
Proof. By elementary calculation, ![]() $\widehat W_{a}$ has density
$\widehat W_{a}$ has density ![]() $\hat{g}_{a}$ on
$\hat{g}_{a}$ on ![]() $(0, 1)$ given by the following expression, with
$(0, 1)$ given by the following expression, with ![]() $c_{a} := a {\rm B}(a, d)$:
$c_{a} := a {\rm B}(a, d)$:
 \begin{equation*}
\hat{g}_{a}(w)
= c_{a}^{-1} \left( 1 - w^{1 / a} \right)^{d - 1}.
\end{equation*}
\begin{equation*}
\hat{g}_{a}(w)
= c_{a}^{-1} \left( 1 - w^{1 / a} \right)^{d - 1}.
\end{equation*} Letting ![]() $0 \lt a \lt b \lt \infty$ and setting
$0 \lt a \lt b \lt \infty$ and setting ![]() $v := w^{1 / a}$ and
$v := w^{1 / a}$ and ![]() $t := a / b$, it then suffices to show for any fixed
$t := a / b$, it then suffices to show for any fixed ![]() $t \in (0, 1)$ that the ratio
$t \in (0, 1)$ that the ratio ![]() $(1 - v^t) / (1 - v)$ decreases strictly as v increases over
$(1 - v^t) / (1 - v)$ decreases strictly as v increases over ![]() $(0, 1)$.
$(0, 1)$.
For this, we consider the log-ratio, whose derivative is
where we again use the definition (4), but now for ![]() $v \in (0, 1]$ (and with
$v \in (0, 1]$ (and with ![]() $t \in (0, 1)$); so we need only show that
$t \in (0, 1)$); so we need only show that ![]() $h(v) \gt 0$ for
$h(v) \gt 0$ for ![]() $v \in (0, 1)$. Indeed, since
$v \in (0, 1)$. Indeed, since
for ![]() $v \in (0, 1)$, we see that
$v \in (0, 1)$, we see that ![]() $h(v) \gt h(1) = 0$ for
$h(v) \gt h(1) = 0$ for ![]() $v \in (0, 1)$.
$v \in (0, 1)$.
7. Proofs of Theorems 1.11–1.12 and Corollary 1.14
We are now prepared to prove Theorems 1.11–1.12 and Corollary 1.14 according to the outline provided at the end of Section 1.2; see Figure 1.
Proof of Theorem 1.11
In light of Lemma 2.2, it suffices to show that the image of pn on the domain of our marginalized-Dirichlet examples Fa is ![]() $(p^*_n, 1)$.
$(p^*_n, 1)$.
We can regard ![]() $p_n \equiv p_n(a)$ as a function on the domain
$p_n \equiv p_n(a)$ as a function on the domain ![]() $(0, \infty)$ corresponding to our Dirichlet index a. Since the density
$(0, \infty)$ corresponding to our Dirichlet index a. Since the density ![]() $f_a(x)$ corresponding to Fa at each fixed argument x is a continuous function of a, it follows from Scheffé’s theorem (e.g., [Reference Billingsley5, Thm. 16.12]) that the corresponding distribution functions Fa are continuous in a in the topology of weak convergence. It then follows from Propositions 2.1 and 5.4 that the image in question is
$f_a(x)$ corresponding to Fa at each fixed argument x is a continuous function of a, it follows from Scheffé’s theorem (e.g., [Reference Billingsley5, Thm. 16.12]) that the corresponding distribution functions Fa are continuous in a in the topology of weak convergence. It then follows from Propositions 2.1 and 5.4 that the image in question is ![]() $(p_n(\infty-), p_n(0+))$.
$(p_n(\infty-), p_n(0+))$.
But, as ![]() $a \to \infty$, it is easy to see that the density of a times an observation converges pointwise to the density for independent Exponentials. By Scheffé’s theorem and Proposition 2.1, therefore,
$a \to \infty$, it is easy to see that the density of a times an observation converges pointwise to the density for independent Exponentials. By Scheffé’s theorem and Proposition 2.1, therefore, ![]() $p_n(\infty-) = p^*_n$.
$p_n(\infty-) = p^*_n$.
To compute ![]() $p_n(0+)$, we first observe that the distribution of an observation
$p_n(0+)$, we first observe that the distribution of an observation ![]() $\mathbf X(a)$ from Fa is that of
$\mathbf X(a)$ from Fa is that of
 \begin{equation*}
\left( \frac{Y_1}{\|\mathbf Y\|_1 + G_{a}}, \ldots, \frac{Y_d}{\|\mathbf Y\|_1 + G_{a}} \right),
\end{equation*}
\begin{equation*}
\left( \frac{Y_1}{\|\mathbf Y\|_1 + G_{a}}, \ldots, \frac{Y_d}{\|\mathbf Y\|_1 + G_{a}} \right),
\end{equation*} where ![]() $Y_1, \dots, Y_d$ are standard Exponential random variables, Ga is distributed (unit-scale) Gamma(a), and all d + 1 random variables are independent. It follows easily that
$Y_1, \dots, Y_d$ are standard Exponential random variables, Ga is distributed (unit-scale) Gamma(a), and all d + 1 random variables are independent. It follows easily that ![]() $\mathbf X(a)$ converges in distribution to the distribution Dir
$\mathbf X(a)$ converges in distribution to the distribution Dir![]() $(\textbf{1})$ mentioned at (2) (for which
$(\textbf{1})$ mentioned at (2) (for which ![]() $p_n = 1$, as mentioned in the proof of Lemma 2.2) as a → 0. Thus, by Proposition 2.1,
$p_n = 1$, as mentioned in the proof of Lemma 2.2) as a → 0. Thus, by Proposition 2.1, ![]() $p_n(0+) = 1$.
$p_n(0+) = 1$.
Proof of Theorem 1.12
In light of Lemma 2.2, it suffices to show that the image on the domain of our PA examples ![]() $\widehat F_a$ is
$\widehat F_a$ is ![]() $(n^{-1}, p^*_n)$.
$(n^{-1}, p^*_n)$.
In this case we can regard ![]() $p_n \equiv \hat{p}_n(a)$ as a function on the domain
$p_n \equiv \hat{p}_n(a)$ as a function on the domain ![]() $(0, \infty)$ corresponding to our Gamma index parameter a. The value of the density of an observation at a given point
$(0, \infty)$ corresponding to our Gamma index parameter a. The value of the density of an observation at a given point ![]() $\mathbf x \geq \textbf{0}$ in
$\mathbf x \geq \textbf{0}$ in ![]() $\mathbb R^d$ is
$\mathbb R^d$ is
 \begin{equation*}
\frac{\Gamma(d + a)}{\Gamma(a)} (1 + \|\mathbf x\|_1)^{- (d + a)},
\end{equation*}
\begin{equation*}
\frac{\Gamma(d + a)}{\Gamma(a)} (1 + \|\mathbf x\|_1)^{- (d + a)},
\end{equation*} which is a continuous function of ![]() $a \in (0, \infty)$. It follows from Scheffé’s theorem that the corresponding distribution functions
$a \in (0, \infty)$. It follows from Scheffé’s theorem that the corresponding distribution functions ![]() $\widehat F_a$ are continuous in the topology of weak convergence. It then follows from Propositions 2.1 and 6.2 that the image in question is
$\widehat F_a$ are continuous in the topology of weak convergence. It then follows from Propositions 2.1 and 6.2 that the image in question is ![]() $(\hat{p}_n(0+), \hat{p}_n(\infty -))$.
$(\hat{p}_n(0+), \hat{p}_n(\infty -))$.
But, as ![]() $a \to \infty$, it’s easy to see that the density of a times an observation converges pointwise to the density for independent standard Exponentials. By Scheffé’s theorem and Proposition 2.1, therefore,
$a \to \infty$, it’s easy to see that the density of a times an observation converges pointwise to the density for independent standard Exponentials. By Scheffé’s theorem and Proposition 2.1, therefore, ![]() $\hat{p}_n(\infty -) = p^*_n$.
$\hat{p}_n(\infty -) = p^*_n$.
To compute ![]() $\hat{p}_n(0+)$, we can without changing
$\hat{p}_n(0+)$, we can without changing ![]() $\hat{p}_n(a)$ take an observation
$\hat{p}_n(a)$ take an observation  $\widehat {\mathbf X}(a)$ to have coordinates that are a times the logarithms of those described in our PA example. According to [Reference Liu, Martin and Syring16, Thm. 1] and Slutsky’s theorem,
$\widehat {\mathbf X}(a)$ to have coordinates that are a times the logarithms of those described in our PA example. According to [Reference Liu, Martin and Syring16, Thm. 1] and Slutsky’s theorem, ![]() $\mathbf X(a)$ converges in distribution to
$\mathbf X(a)$ converges in distribution to ![]() $(Y, \ldots, Y)$, where Y is standard Exponential. By Proposition 2.1, therefore,
$(Y, \ldots, Y)$, where Y is standard Exponential. By Proposition 2.1, therefore, ![]() $\hat{p}_n(0+) = n^{-1}$.
$\hat{p}_n(0+) = n^{-1}$.
Proof of Corollary 1.14
The corollary follows immediately from Lemma 2.2 and Theorems 1.11–1.12. For a considerably simpler proof, one can use the fact (from Lemma 2.2) that there are distributions F 0 and F 1 satisfying ![]() $p_n(F_0) = n^{-1}$ and
$p_n(F_0) = n^{-1}$ and ![]() $p_n(F_1) = 1$ for every n. By defining Fq to be the
$p_n(F_1) = 1$ for every n. By defining Fq to be the ![]() $(1 - q, q)$ mixture of F 0 and F 1 for
$(1 - q, q)$ mixture of F 0 and F 1 for ![]() $q \in [0, 1]$, we see from Proposition 2.1 (since Fq is clearly continuous in q in the weak topology) and the intermediate value theorem that the image of pn on the domain
$q \in [0, 1]$, we see from Proposition 2.1 (since Fq is clearly continuous in q in the weak topology) and the intermediate value theorem that the image of pn on the domain ![]() $\{F_q: q \in [0, 1]\}$ contains (and therefore by Lemma 2.2 equals)
$\{F_q: q \in [0, 1]\}$ contains (and therefore by Lemma 2.2 equals) ![]() $[n^{-1}, 1]$.
$[n^{-1}, 1]$.
Remark 7.1. We have now learned from Theorems 1.11–1.12 information about how pn behaves as a function of the (continuous) distribution of ![]() $\mathbf X$. As a complement, we conclude this paper with general (and rather more mundane) information about how pn behaves as a function of n and as a function of d.
$\mathbf X$. As a complement, we conclude this paper with general (and rather more mundane) information about how pn behaves as a function of n and as a function of d.
(a) As already noted, from (1) it is apparent that pn is nonincreasing in n. By the dominated convergence theorem,
 \begin{equation*}
p_n \downarrow p_{\infty} := \int_{\mathbf x:\,\operatorname{\mathbb P{}}(\mathbf X \geq \mathbf x) = 0}\!\operatorname{\mathbb P{}}(\mathbf X \in \mathrm{d} \mathbf x)
\end{equation*}
\begin{equation*}
p_n \downarrow p_{\infty} := \int_{\mathbf x:\,\operatorname{\mathbb P{}}(\mathbf X \geq \mathbf x) = 0}\!\operatorname{\mathbb P{}}(\mathbf X \in \mathrm{d} \mathbf x)
\end{equation*}as
 $n \uparrow \infty$. For each fixed
$n \uparrow \infty$. For each fixed  $d \geq 2$, the image of the mapping
$d \geq 2$, the image of the mapping  $p_{\infty}$ on the domain of all continuous distributions on
$p_{\infty}$ on the domain of all continuous distributions on  $\mathbb R^d$ is the entire interval
$\mathbb R^d$ is the entire interval  $[0, 1]$. To see by example that
$[0, 1]$. To see by example that  $q \in [0, 1]$ is in the image, choose the distribution F of
$q \in [0, 1]$ is in the image, choose the distribution F of  $\mathbf X$ to be the
$\mathbf X$ to be the  $(q, 1- q)$-mixture of any Dirichlet distribution and any of our marginalized-Dirichlet distributions Fa.
$(q, 1- q)$-mixture of any Dirichlet distribution and any of our marginalized-Dirichlet distributions Fa.(b) To make sense of the question of how pn varies as a function of
 $d \in \{1, 2, \ldots\}$, one should specify a sequence of distributions, with the
$d \in \{1, 2, \ldots\}$, one should specify a sequence of distributions, with the  $d^{\rm \scriptsize}$th distribution being over
$d^{\rm \scriptsize}$th distribution being over  $\mathbb R^d$. It is rather obvious that if
$\mathbb R^d$. It is rather obvious that if  $d' \lt d$ and
$d' \lt d$ and  $\mathbf X(d')$ is obtained by selecting any deterministic set of dʹ coordinates from
$\mathbf X(d')$ is obtained by selecting any deterministic set of dʹ coordinates from  $\mathbf X(d)$, then
$\mathbf X(d)$, then  $p_n(d') \leq p_n(d)$; in this sense,
$p_n(d') \leq p_n(d)$; in this sense,  $p_n(d)$ is nondecreasing in the dimension d.
$p_n(d)$ is nondecreasing in the dimension d.Fix
 $n \geq 1$, and for any specified sequence (in d) of distributions of
$n \geq 1$, and for any specified sequence (in d) of distributions of  $\mathbf X(d)$ let
$\mathbf X(d)$ let  $p_n(\infty) := \lim_{d \to \infty} p_n(d)$. The image of the mapping
$p_n(\infty) := \lim_{d \to \infty} p_n(d)$. The image of the mapping  $p_n(\infty)$ on the domain of all sequences of continuous distributions is
$p_n(\infty)$ on the domain of all sequences of continuous distributions is  $[n^{-1}, 1]$. This follows easily from Corollary 1.14. Indeed, given
$[n^{-1}, 1]$. This follows easily from Corollary 1.14. Indeed, given  $q \in [n^{-1}, 1]$, one can choose
$q \in [n^{-1}, 1]$, one can choose  $\mathbf X = \mathbf X(2) = (X_1, X_2)$ giving
$\mathbf X = \mathbf X(2) = (X_1, X_2)$ giving  $p_n(2) = q$ and then take
$p_n(2) = q$ and then take  $\mathbf X(d) = (X_1, X_1, \ldots, X_1, X_2)$ for every d.
$\mathbf X(d) = (X_1, X_1, \ldots, X_1, X_2)$ for every d.For all of our standard examples (independent coordinates, our marginalized-Dirichlet distributions Fa, and our PA examples
 $\widehat F_a$) we have
$\widehat F_a$) we have  $p_n(\infty) = 1$. In light of our earlier results, it is sufficient to prove this for the PA examples. For that, since the Beta(a, d) distributions converge weakly to unit mass at 0 as
$p_n(\infty) = 1$. In light of our earlier results, it is sufficient to prove this for the PA examples. For that, since the Beta(a, d) distributions converge weakly to unit mass at 0 as  $d \to \infty$, it follows from the consequence
(5)
$d \to \infty$, it follows from the consequence
(5) \begin{equation}
\hat{p}_n(a) = \operatorname{\mathbb E{}}(1 - Z_{a, d}^a)^{n - 1}\ \mbox{where}\ Z_{a, d} \sim\ \mbox{Beta}\ (a, d)
\end{equation}
\begin{equation}
\hat{p}_n(a) = \operatorname{\mathbb E{}}(1 - Z_{a, d}^a)^{n - 1}\ \mbox{where}\ Z_{a, d} \sim\ \mbox{Beta}\ (a, d)
\end{equation}of the proof of Proposition 6.2 that
 $p_n(\infty) = 1$.
$p_n(\infty) = 1$.
Acknowledgments
We thank three anonymous reviewers for helpful comments.
Competing interests
The authors declare none.