Can nonexperts really emulate statistical learning methods? A comment on “The accuracy, fairness, and limits of predicting recidivism”

Abstract

Recent research has questioned the value of statistical learning methods for producing accurate predictions in the criminal justice context. Using results from respondents on Amazon Mechanical Turk (MTurkers) who were asked to predict recidivism, Dressel and Farid (2018) argue that nonexperts can achieve predictive accuracy and fairness on par with algorithmic approaches that employ statistical learning models. Analyzing the same data from the original study, this comment employs additional techniques and compares the quality of the predicted probabilities output from statistical learning procedures versus the MTurkers’ evaluations. The metrics presented indicate that statistical approaches do, in fact, outperform the nonexperts in important ways. Based on these new analyses, it is difficult to accept the conclusion presented in Dressel and Farid (2018) that their results “cast significant doubt on the entire effort of algorithmic recidivism prediction.”

1 Introduction

With machine learning becoming more pervasive and data availability improving over time, the value of predictive algorithms for public policy optimization has received growing attention in recent years (Kleinberg et al. 2017; Bansak et al. 2018; Milgrom and Tadelis 2018). One policy area that has cast a particularly large spotlight on such algorithms is criminal justice, where statistical learning procedures are often used to predict things like a criminal defendant’s likelihood of failing to appear at court or reoffending in the future. These predictions are then used as risk assessments to inform decisions on a defendant’s bail, sentencing, and parole. Policymakers, academic researchers, and the popular media alike have scrutinized the increasing deployment of such tools (James 2015). In particular, the use of predictive algorithms in the criminal justice system has been extensively critiqued on fairness grounds, with claims that they may exhibit racial biases and hence perpetuate preexisting social inequities (Angwin et al. 2016), though the nature and extent of any such biases in these algorithms has been contested (Corbett-Davies, Goel, and González-Bailón 2017). In addition, recent research (Dressel and Farid 2018) has also cast doubt on something more fundamental to such algorithms, the accuracy with which they can actually make predictions, which will be the focus here.

Using aggregated results from respondents on Amazon Mechanical Turk (MTurkers) who were asked to predict whether or not individual criminal defendants would recidivate within two years, Dressel and Farid (2018) argue that groups of nonexperts making collective determinations can achieve predictive accuracy and fairness on par with algorithmic approaches that employ statistical learning models. Specifically, according to the performance metrics and algorithmic approaches they assess, the algorithmic results they report are not statistically significantly different from the MTurkers’ performance when pooling the predictions of groups of MTurkers. They interpret their findings as results that “cast significant doubt on the entire effort of algorithmic recidivism prediction.” In reporting on this research, a wide variety of media outlets echoed this conclusion into the popular realm with headlines like “Can software predict crime? Maybe so, but no better than a human” (Chokshi 2018), “Software ‘no more accurate than untrained humans’ at judging reoffending risk” (Devlin 2018), and “Courts use algorithms to help determine sentencing, but random people get the same results” (Chodosh 2018). Additional analyses presented here, however, suggest that such conclusions may be exaggerated.

Employing additional techniques and analyses of the same data used in the original study, this comment shows that the MTurkers’ evaluations are not as comparable to statistical learning methods as suggested by the study, but are rather outperformed by statistical methods in important ways. In presenting these new analyses, this comment highlights important evaluative metrics and potential strengths of statistical learning techniques for policy optimization that were overlooked by the original study and its subsequent media coverage. As social scientists become increasingly involved in the design and evaluation of policy optimization algorithms, it is vital that they have a comprehensive perspective on how and when to use competing evaluative metrics.

2 Original Study

Dressel and Farid (2018) draw on a data set of 7214 pretrial criminal defendants in Broward County, Florida from 2013 to 2014, which included the defendants’ demographic information, criminal history, and whether or not they recidivated within the following two years. They randomly sampled 1000 defendants from the data set to use as profiles that they recruited two waves of MTurkers to evaluate. For each evaluation, MTurkers were presented with the defendant’s age, sex, criminal charge and degree, and past criminal record; in addition, MTurkers in the second wave were also given the defendant’s race. MTurkers were then asked to predict whether the defendant in question would or would not recidivate within the next two years, and they were told whether they were correct after each evaluation. Each MTurker evaluated 50 profiles, and each of the 1000 sampled defendant profiles was evaluated by 20 separate MTurkers in each wave, thereby allowing for analysis of both individual MTurkers’ performance and the pooled performance of groups of MTurkers evaluating an individual defendant.

Figure 1. Variation in MTurkers’ individual performance. The figure displays a histogram of the proportion of correct predictions for each individual MTurker, when not presented with race (results for MTurkers presented with race are similar). The vertical lines denote the mean and median proportion correct.

As shown in Figure 1, there is large variation in the accuracy of the nonexpert predictions when looking at the proportion of correct responses across individual MTurkers, ranging from $0.38$ for the worst performing MTurkers to $0.80$ for the best, with a mean and median of $0.62$ and $0.64$ . This variation highlights the risks of relying on any single individual’s evaluations. Hence, the original study’s results focus on the MTurkers’ pooled predictions; as each defendant was evaluated by 20 MTurkers, a final prediction for each defendant was computed based on a majority-vote procedure. Like the original study, this comment also focuses on those pooled results. Unlike the original study, however, the analysis presented here finds evidence that these nonexperts’ pooled evaluations are outperformed by statistical learning approaches.

3 Probability Calibration and New Analyses

This comment identifies an important gap in the original study’s analysis of the pooled results. That study’s results focus mainly on the accuracy of binary predictions output by the statistical learning approaches compared to the MTurkers’ pooled evaluations. In contrast, the study does not fully analyze the quality of the probabilistic outputs of these various methods. In practice, statistical learning models are often employed in policy processes not simply to perform discrete classification but rather to generate more fine-grained probabilistic outputs that can then be considered and used by (usually human expert) decision-making authorities, and the usefulness of such outputs to inform cost-efficient decisions often depends upon the reliability of the underlying predicted probabilities (Brier 1950; Cohen and Goldszmidt 2004; Steyerberg et al. 2010). Accordingly, any evaluation of such models or their comparison with alternative prediction methods should consider these predicted probabilities.

Indeed, in the criminal justice case in question, statistical learning models have been used to generate risk scores that are functions of the predicted probabilities naturally output from those models, and policy and human decision-making processes (e.g. judge decisions) can then be informed by these scores (Monahan and Skeem 2016). As discussed elsewhere, rigorously balancing security and justice considerations involves determining the appropriate decision points along the probability line (Corbett-Davies et al. 2017). In doing so, a well-designed policy process must consider the balance of various factors, such as the financial, fairness, and long-term social costs of incarceration, as well as the public safety costs of releasing defendants with varying levels of risk of reoffending. Taking all of these considerations into account, it is not necessarily desirable to use a predetermined probability criterion or cut point, such as $0.5$ , for any decision rule. In addition, it may also not be desirable to utilize a single fixed cut point if the decision space is multidimensional. Such multidimensionality could be present if there exist more than two decision options (e.g. imprisonment, supervised release, or no incapacitation at all) or if the expected costs associated with a decision option can vary (e.g. in the case of differential risk of releasing separate defendants who may have the same likelihood of reoffending but whose likely type of reoffense differs in severity and danger to public safety).

Crucial to recognize is that the task of determining efficient decision rules requires not only that predicted probabilities are available but also that those predicted probabilities closely reflect actual probabilities (Zadrozny and Elkan 2001; Cohen and Goldszmidt 2004). That is, groups of individuals given a predicted probability of $p$ should, in reality, have a probability of $p$ . In general, the greater the divergence between the predicted and true probabilities, the more likely it is that decisions will not result in the intended consequences or distribution of costs. Accordingly, the reliability of predicted probabilities should be assessed as part of the evaluation of recidivism prediction methods, though such an assessment is not performed in Dressel and Farid (2018).

Figure 2. Probability calibration across methods (MTurkers not told defendant race), using Sample approach to model uncertainty. The top two panels display probability calibration plots. Each point and interval in the upper two panels correspond to a bin of predicted probabilities. The black triangles comprise the MTurkers’ calibration points for the evaluations where MTurkers were not provided with the defendants’ race. Each point’s position along the $x$ -axis signifies the mean predicted probability within the bin, while its position on the $y$ -axis signifies the actual proportion of positives among the units contained within the bin. The gray points represent the mean proportion of positives within each bin across 1000 evaluations of each of the statistical learning methods, while the error bars provide 95% confidence intervals for the proportion of positives within each bin, with uncertainty modeled using the Sample approach. The three bottom panels display histograms of the predicted probabilities for each method.

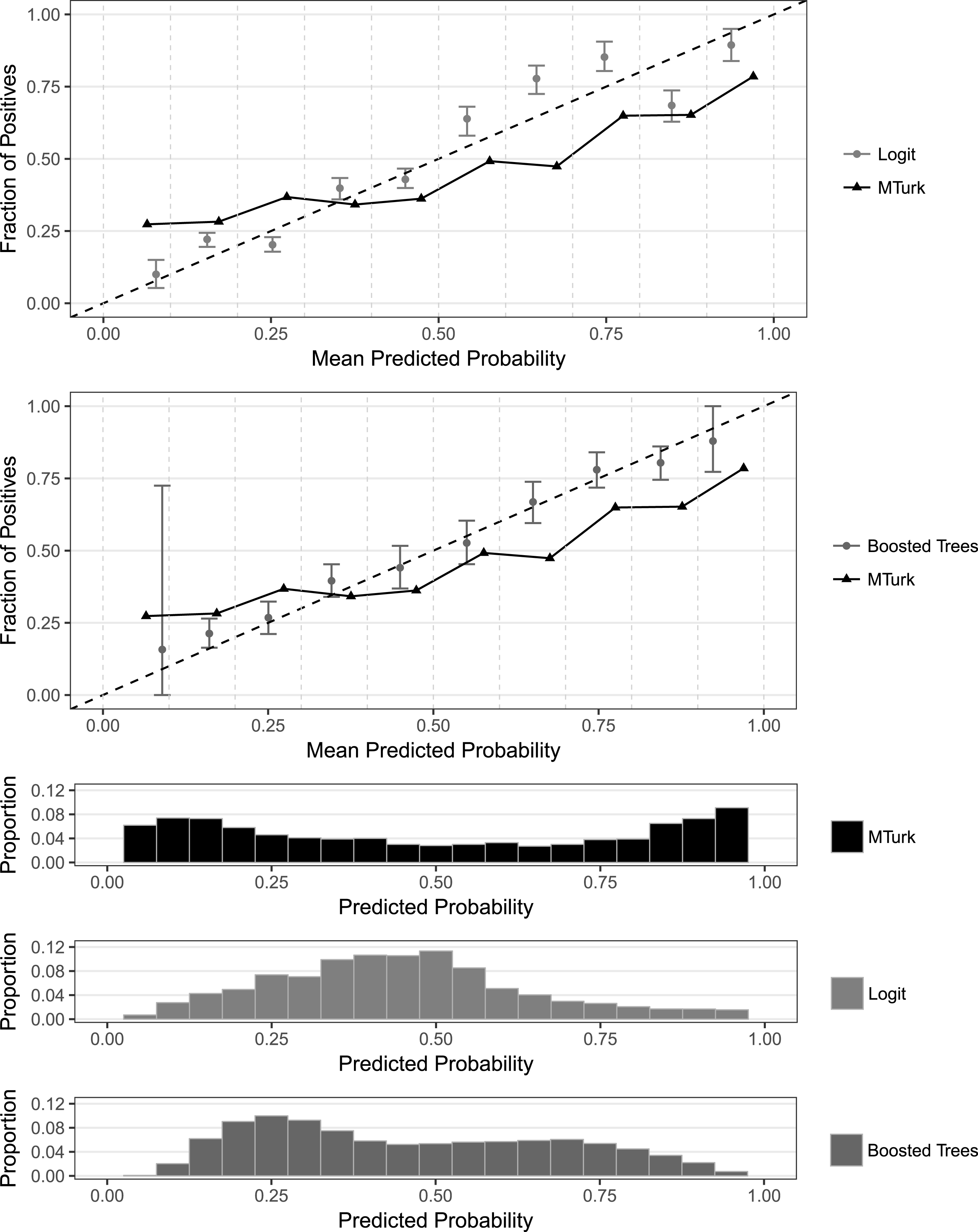
Figure 3. Probability calibration across methods (MTurkers not told defendant race), using Bootstrap approach to model uncertainty. The top two panels display probability calibration plots. Each point and interval in the upper two panels correspond to a bin of predicted probabilities. The black triangles comprise the MTurkers’ calibration points for the evaluations where MTurkers were not provided with the defendants’ race. Each point’s position along the $x$ -axis signifies the mean predicted probability within the bin, while its position on the $y$ -axis signifies the actual proportion of positives among the units contained within the bin. The gray points represent the mean proportion of positives within each bin across 1000 evaluations of each of the statistical learning methods, while the error bars provide 95% confidence intervals for the proportion of positives within each bin, with uncertainty modeled using the Bootstrap approach. The three bottom panels display histograms of the predicted probabilities for each method.

This comment presents a calibration analysis to compare the reliability of the probabilistic outputs generated by the MTurkers’ pooled evaluations (i.e. the fraction of MTurkers who predicted recidivism for a given defendant) and those generated by a simple and more complex statistical learning procedure: a logistic regression and a stochastic gradient boosted trees model, both of which employ the seven predictors available in the data that were used in the original study’s analysis. The predictors include age, sex, number of juvenile misdemeanors, number of juvenile felonies, number of prior (nonjuvenile) crimes, crime degree (misdemeanor vs. felony), and crime charge. The supplementary materials (SM) present additional technical details on the model fitting procedures used in this study. The results, shown in Figures 2 and 3, provide evidence that both statistical learning procedures outperform the MTurkers’ evaluations, with the more complex procedure appearing to produce the most reliable predicted probabilities. ¹

For a model or method to be perfectly calibrated, its predicted probabilities should equal the true probabilities (Hernández-Orallo, Flach, and Ferri 2012). With empirical data, this can be evaluated by aggregating the data into bins. The top two panels in Figures 2 and 3 display calibration plots, which bin the predicted probabilities output from each method into ten intervals of equal width along the $x$ -axis. For each bin, the $y$ -axis displays the actual proportion of positives (i.e. empirical probability in that bin). Hence, for well-calibrated predicted probabilities, the mean predicted probability within each bin should be close to the actual proportion of positives in that bin, tracing along the identity line. In the top two panels of Figures 2 and 3, the black triangles correspond to the probability calibration points for the MTurkers’ pooled evaluations of the 1000 defendants, when MTurkers were not provided with the defendants’ race. This MTurker calibration curve is compared to probability calibration results from the two statistical learning methods.

To model the uncertainty in the calibration results associated with the two statistical learning methods, 1000 test-set evaluations are performed for each method. In Figures 2 and 3, the gray points represent the mean proportion of positives within each bin for the test data across the 1000 evaluations, while the error bars provide 95% confidence intervals for the proportion of positives within each bin. The difference between the results in Figures 2 and 3 lies in the approach to modeling the uncertainty. Specifically, there are at least two possible approaches to modeling the uncertainty which adopt different statistical perspectives on the underlying data. The first approach is to treat the full data set of 7214 defendants as the fixed, full population and the sampling of 1000 test units as the random process, which mimics the actual procedure used by the authors of the original study. To apply this approach to the statistical methods assessed here, for each of the 1000 evaluations, 1000 test units are randomly sampled (without replacement), and the remaining data are used as the training set. The results of this Sample approach are displayed in Figure 2.

The alternative approach is to treat the original study’s 1000 evaluated units as the fixed test set, and to treat the remainder of the data as though they are a random sample from an underlying population distribution. To apply this approach, for each of the 1000 evaluations, the same 1000 units that were evaluated by the MTurkers are used as a fixed test set, and the training data are comprised of a bootstrapped resample from the remaining data. The results of this Bootstrap approach are displayed in Figure 3.

As the results in both Figures 2 and 3 show, the statistical methods appear to handily outperform the MTurkers’ pooled predictions, with slightly better performance displayed by the boosted trees models. Not only are the statistical methods’ mean calibration points consistently closer to the identity line across the bins, but the MTurkers’ calibration points actually fall outside of the statistical methods’ confidence intervals for most bins. For the boosted trees models, this occurs in 5 and 6 of the bins for the Sample and Bootstrap approaches, respectively. Further, the boosted trees models’ calibration points increase with near-perfect monotonicity (the one exception is the first bin for the Sample method, where the predicted probabilities are extremely sparse). In contrast, the nonmonotonicity of the MTurker calibration curve shows noticeably imperfect rank ordering of the bins, though this is of course subject to finite-sample variation.

The bottom three panels of Figures 2 and 3 show the distribution of predicted probabilities across the three methods, and they shed light on where things are likely going wrong in the MTurkers’ pooled predictions. Specifically, there is substantial mass in the tails for the MTurkers, indicating that MTurkers as a crowd tend toward overconfidence. In contrast, the statistical learning methods do not display this tail behavior. This sparsity in the tails for the statistical methods also explains their irregular confidence interval behavior in the tails, though this would not be a concern if policy processes do not employ decision points at these extremes.

The SM also includes the same results when MTurkers were shown the race of the defendants. In this condition, the MTurkers’ calibration appears to be even worse, with starker nonmonotonicity. While finite-sample noise may have contributed to this result, it still calls into question not only whether pooled nonexpert evaluations directly yield well-calibrated probabilities but also whether they are likely to even provide well-behaved and properly ranked scores that can then be effectively transformed into well-calibrated probabilities via standard techniques (Platt 2000; Zadrozny and Elkan 2001; Niculescu-Mizil and Caruana 2005a,b).

The poor calibration of the MTurkers’ pooled evaluations is also reflected in their aggregate performance metrics. A wide variety of metrics exist for evaluating and comparing the performance of predictive models for binary outcomes. As discussed elsewhere, there are complicated mathematical relationships between these metrics, the metrics do not always produce consistent conclusions as to which model is best, and the instrumental value of each individual metric for informing model choice depends upon the context and objectives of a model’s ultimate deployment (Hernández-Orallo, Flach, and Ferri 2012; Hofman, Sharma, and Watts 2017). In other words, these metrics are not arbitrarily interchangeable. Table 1 compares the performance of the MTurkers to that of the statistical learning methods across a variety of these metrics, including the commonly used metrics reported in Dressel and Farid (2018), namely the percent correctly classified (PCC) using the standard cut point of $0.5$ and the area under the receiver operating characteristic (ROC) curve (AUC-ROC).

The MTurkers’ pooled evaluations without (with) race presented achieve values of $0.670$ ( $0.665$ ) and $0.709$ ( $0.709$ ) for the PCC and AUC-ROC, respectively, which fall inside the statistical learning methods’ 95% confidence intervals for the Sample approach but outside of the intervals for the Bootstrap approach, providing limited though perhaps inconclusive evidence for the superior performance of the statistical learning methods. However, metrics like the PCC and AUC-ROC have several properties that make them problematic for model comparison. For instance, the PCC employs a single arbitrary cut point, and the value of the computed PCC will vary depending upon that criterion. The usefulness of the AUC-ROC as a metric for comparing the performance of classifiers has also been called into question by previous research on various grounds (Hand 2009; Hanczar et al. 2010). A key problem is that these metrics are not based on strictly proper scoring rules: their mathematical properties are such that they do not fully incentivize a forecaster to make predictions based on the true underlying data-generating process, and similar or better scores can be achieved by forecasting false beliefs (Winkler and Murphy 1968). Metrics that are not strictly proper are known to lead to practical problems for both prediction and estimation goals (Gneiting and Raftery 2007).

Table 1. Model performance results. The table displays several performance metrics for the statistical learning methods—gradient boosted trees (GBM) and logistic regression (Logit)—under both approaches to modeling uncertainty (Sample and Bootstrap), along with the results for the MTurkers’ pooled evaluations both without and with race presented. For the statistical learning methods, 95% confidence intervals are displayed. A cut point of $0.5$ is employed for the PCC, FPR, and FNR.

a See SM for details on the log score calculations.

In contrast, the Brier score is an error metric that can be used to more directly measure the relative aggregate accuracy of predicted probabilities across different methods. The term “Brier score” is used in the binary classification context to denote the mean squared error (MSE), $1/n\sum _{i=1}^{n}(\hat{p}_{i}-y_{i})^{2}$ , where $y_{i}$ is an indicator that denotes whether the outcome for unit $i$ is a success, and $\hat{p}_{i}$ denotes the predicted probability of success for unit $i$ . It is based on a strictly proper scoring rule, and it can be decomposed into multiple components, where one of the components is calibration (also called reliability), measuring the extent to which predicted probabilities reflect realized probabilities (Murphy 1973; Blattenberger and Lad 1985). The results shown in Table 1 comparing the Brier score for the MTurkers’ pooled evaluations against the statistical learning methods confirm the visual results from Figures 2 and 3. That is, the statistical learning methods dominate the MTurkers’ evaluations across the board: the Brier score for the MTurkers is $0.240$ , which falls outside of and higher (signifying worse performance) than the Brier score 95% confidence intervals for both statistical learning methods under both approaches to modeling their uncertainty. The superior performance of the statistical learning methods is also exhibited under an alternative strictly proper scoring rule, the logarithmic scoring rule, with the MTurkers’ pooled evaluations achieving mean logarithmic scores that fall outside of and are more negative (signifying worse performance) than the statistical methods’ 95% confidence intervals.

Finally, Table 1 also reports false positive rates (FPRs) and false negative rates (FNRs), based upon a standard cut point of $0.5$ . As can be seen, using $0.5$ as the cut point, the statistical learning methods have consistently lower FPRs but higher FNRs than the MTurkers’ pooled evaluations. Two important points should be noted with respect to these results. First, because these metrics are constructed as a function of an adjustable cut point, that cut point can be increased (decreased) to reduce the false positive (negative) rate at the expense of the false negative (positive) rate. For illustrative purposes, the SM displays results for each statistical learning method when specifying a cut point that balances the FPR and FNR. As the results show, such balance can be achieved in this case at the cost of only modestly decreasing the PCC. In contrast, the AUC-ROC, Brier score, and log score are not computed as a function of a particular cut point, and hence are unaffected by altering the binary classification criterion.

The second important point, however, is that perfect parity between FPR and FNR is not necessarily desirable. Instead, whether it is preferable for a binary classification rule to yield an FPR that is higher than, lower than, or equal to the FNR depends upon the classifier’s deployment context and the relative costs between false positives and negatives. As already explained, the classification criterion can be easily modified to achieve the specific balance between FPR and FNR deemed optimal by policymakers or experts in charge of the classifier’s deployment—that is, if the classifier is even being used to produce binary classification outputs, as opposed to predicted probabilities or risk scores.

Dressel and Farid (2018) also report performance metrics for their competing methods across racial groups, namely Black and White defendants. The SM reports the results of the analyses presented in this study, subsetted to Black and White defendants. Despite the reduced sample sizes, with few exceptions, the statistical learning methods’ Brier score and log score confidence intervals indicate superior performance over the MTurkers’ pooled evaluations for both Black and White defendants. In addition, the statistical learning methods’ bootstrap-based confidence intervals for the AUC-ROC also beat the MTurkers’ pooled evaluations for both Black and White defendants.

However, there is a discrepancy in the balance between the FPR and FNR across Black and White defendants when employing the cut point of $0.5$ , for both the statistical learning methods and MTurkers’ evaluations. Specifically, the FPRs appear roughly similar to or greater than the FNRs for Black defendants, but for White defendants the FPRs are consistently lower than the FNRs. Relatedly, the false positive (negative) rates are consistently higher for Black (White) defendants, relative to White (Black) defendants. This potential for imbalance in predicting recidivism across racial groups is an important issue that has been investigated in the existing literature, with some highlighting this imbalance as evidence of bias (Angwin et al. 2016; Dressel and Farid 2018), and others showing how it is an inherent mathematical byproduct of applying common classification rules to subpopulations with distinct underlying risk distributions (Corbett-Davies et al. 2017; Kleinberg, Mullainathan, and Raghavan 2017). ² As already described above, it is possible to induce parity in FPR and FNR by changing the binary classification criterion. This could be performed separately across subgroups, and results presented in the SM provide an illustration. Whether it would be preferable, ethical, or even legal to apply distinct classification rules across different racial groups to achieve such parity in a real-world deployment is a separate issue, however, and one that would need to be carefully considered by the relevant policymakers and legal authorities.

4 Conclusions

In many applications, probabilities are the underlying inputs into a policy process, making the ability to generate well-calibrated predicted probabilities extremely valuable. In their defense, Dressel and Farid (2018) do not explicitly claim the MTurkers’ pooled vote proportions to represent probabilities, they do not make any claims about the calibration of the MTurkers’ probabilistic outputs, nor is it necessarily reasonable to expect that outputs (whether proper probabilities or scores more generally) generated via such a crowd-based method should be well-calibrated. In contrast, however, the results presented here show that this is precisely an area in which statistical learning methods can excel. These results, of course, do not guarantee that automated classifiers will always outperform other approaches, yet the results do indicate that the potential value of statistical learning methods in the criminal justice realm should not merely be dismissed. That is, it is difficult to accept the conclusion presented in Dressel and Farid (2018) that their results “cast significant doubt on the entire effort of algorithmic recidivism prediction.”

Dressel and Farid (2018) do raise a number of additional important issues not addressed here on the use of predictive algorithms in criminal justice. First, they directly assess the performance of one specific criminal risk assessment tool in deployment, the Correctional Offender Management Profiling for Alternative Sanctions (COMPAS). As the focus here is on the possible value of statistical learning methods in general, rather than a specific deployment instance, the evidence presented here does not aim to either refute or buttress the authors’ critiques of COMPAS itself. However, the evidence and discussion presented here can be used in concert with that of the original study to inform how specific deployments may be improved in the future. Second, the authors of the original study also highlight how most of the power in predicting recidivism appears to come from two specific predictors, age and number of prior charges. Indeed, in the analyses presented here, age and number of prior charges exhibit the greatest predictive importance, followed by crime charge. This observation highlights a key question, ubiquitous across prediction problems, on whether the outcome is fundamentally difficult to predict or whether data on other important variables are not yet being collected and observed. Finally, the authors also highlight the various other fairness-related critiques existing in the literature on the use of statistical algorithms in criminal justice.