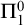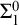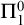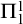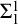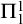1 Introduction
The motivation for this project come from two sources: Gödel’s second incompleteness theorem and Gentzen’s consistency proof of arithmetic. These results are complementary in many ways. In the first place, they jointly form a complicated and ambiguous resolution of Hilbert’s problem of proving the consistency of arithmetic. Moreover, Gentzen’s proof refines Gödel’s result by exhibiting the first example of a non-meta-mathematical arithmetic statement—namely, the statement that
![]() $\varepsilon _0$
lacks primitive recursive descending sequences—that is not provable from the Peano axioms. Though Gödel’s result is highly general, his proof relies on self-reference, rendering it opaque and mysterious [Reference Kotlarski6, Reference Salehi15, Reference Visser16]. By contrast, Gentzen’s proof is concrete but his results are specific to the case of Peano arithmetic. In this paper we prove a version of the second incompleteness theorem that is general like Gödel’s but with a proof that is concrete like Gentzen’s; in particular, we use the methods of ordinal analysis and do not rely on diagonalization or self-reference.
$\varepsilon _0$
lacks primitive recursive descending sequences—that is not provable from the Peano axioms. Though Gödel’s result is highly general, his proof relies on self-reference, rendering it opaque and mysterious [Reference Kotlarski6, Reference Salehi15, Reference Visser16]. By contrast, Gentzen’s proof is concrete but his results are specific to the case of Peano arithmetic. In this paper we prove a version of the second incompleteness theorem that is general like Gödel’s but with a proof that is concrete like Gentzen’s; in particular, we use the methods of ordinal analysis and do not rely on diagonalization or self-reference.
Let’s start by giving a typical statement Gödel’s second incompleteness theorem:
Theorem 1.1 (Gödel)
No consistent and recursively axiomatizable extension of elementary arithmetic proves its own consistency.
Recursive axiomatizability is equivalent to
![]() $\Sigma ^0_1$
-definability by Craig’s Trick. Moreover, consistency is provably equivalent (in elementary arithmetic) to
$\Sigma ^0_1$
-definability by Craig’s Trick. Moreover, consistency is provably equivalent (in elementary arithmetic) to
![]() $\Pi ^0_1$
-soundness. Hence, we may restate Gödel’s Theorem as follows:
$\Pi ^0_1$
-soundness. Hence, we may restate Gödel’s Theorem as follows:
Theorem 1.2 (Gödel)
If T is a
![]() $\Pi ^0_1$
-sound and
$\Pi ^0_1$
-sound and
![]() $\Sigma ^0_1$
-definable extension of elementary arithmetic, then T does not prove its own
$\Sigma ^0_1$
-definable extension of elementary arithmetic, then T does not prove its own
![]() $\Pi ^0_1$
-soundness.
$\Pi ^0_1$
-soundness.
We prove the following analogous result for systems of second-order arithmetic:
Theorem 1.3. If T is a
![]() $\Pi ^1_1$
-sound and
$\Pi ^1_1$
-sound and
![]() $\Sigma ^1_1$
-definable extension of
$\Sigma ^1_1$
-definable extension of
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
, then T does not prove its own
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
, then T does not prove its own
![]() $\Pi ^1_1$
-soundness.
$\Pi ^1_1$
-soundness.
![]() $\Pi ^1_1$
-soundness is a strictly stronger condition than
$\Pi ^1_1$
-soundness is a strictly stronger condition than
![]() $\Pi ^0_1$
-soundness. However,
$\Pi ^0_1$
-soundness. However,
![]() $\Sigma ^1_1$
-definability is a strictly weaker condition than
$\Sigma ^1_1$
-definability is a strictly weaker condition than
![]() $\Sigma ^0_1$
-definability. Hence, Theorem 1.3 is neither weaker nor stronger than Gödel’s Theorem but incomparable with it.
$\Sigma ^0_1$
-definability. Hence, Theorem 1.3 is neither weaker nor stronger than Gödel’s Theorem but incomparable with it.
Let’s take a brief look at the ideas motivating the proof. In what follows
![]() $\mathsf {WF}(\prec )$
is a sentence expressing the well-foundedness of
$\mathsf {WF}(\prec )$
is a sentence expressing the well-foundedness of
![]() $\prec $
:
$\prec $
:
![]() $\mathsf {RFN}_{\Pi ^1_1}(T)$
is a sentence naturally expressing the
$\mathsf {RFN}_{\Pi ^1_1}(T)$
is a sentence naturally expressing the
![]() $\Pi ^1_1$
-soundness of T:
$\Pi ^1_1$
-soundness of T:
and the proof-theoretic ordinal
![]() $|T|_{\mathsf {AN}}$
of a theory T is the supremum of the ordinals
$|T|_{\mathsf {AN}}$
of a theory T is the supremum of the ordinals
![]() $\alpha $
for which there is some
$\alpha $
for which there is some
![]() $\Sigma ^1_1$
presentation
$\Sigma ^1_1$
presentation
![]() $\prec $
of
$\prec $
of
![]() $\alpha $
such that
$\alpha $
such that
![]() $T\vdash \mathsf {WF}(\prec )$
.
$T\vdash \mathsf {WF}(\prec )$
.
Assuming that T is
![]() $\Pi ^1_1$
-sound and
$\Pi ^1_1$
-sound and
![]() $\Sigma ^1_1$
-definable, Spector’s
$\Sigma ^1_1$
-definable, Spector’s
![]() $\Sigma ^1_1$
-bounding theorem implies that
$\Sigma ^1_1$
-bounding theorem implies that
![]() $|T|_{\mathsf {AN}}$
is strictly less than
$|T|_{\mathsf {AN}}$
is strictly less than
![]() , whence
, whence
![]() $|T|_{\mathsf {AN}}$
has some
$|T|_{\mathsf {AN}}$
has some
![]() $\Sigma ^1_1$
presentation. For any
$\Sigma ^1_1$
presentation. For any
![]() $\Sigma ^1_1$
-presentation
$\Sigma ^1_1$
-presentation
![]() $\prec $
of
$\prec $
of
![]() $|T|_{\mathsf {AN}}$
, the following is true by definition:
$|T|_{\mathsf {AN}}$
, the following is true by definition:
We then need to show that there is at least one
![]() $\Sigma ^1_1$
-presentation
$\Sigma ^1_1$
-presentation
![]() $\prec $
of
$\prec $
of
![]() $|T|_{\mathsf {AN}}$
such that:
$|T|_{\mathsf {AN}}$
such that:
For then, from claims (1) and (2), we infer that
![]() $T\nvdash \mathsf {RFN}_{\Pi ^1_1}(T)$
.
$T\nvdash \mathsf {RFN}_{\Pi ^1_1}(T)$
.
This proof is analogous to a folklore proof of a different version of the second incompleteness theorem, namely, that no
![]() $\Pi ^0_2$
-sound and
$\Pi ^0_2$
-sound and
![]() $\Sigma ^0_1$
-definable theory T proves its own
$\Sigma ^0_1$
-definable theory T proves its own
![]() $\Pi ^0_2$
-soundness. In this folklore proof one first defines a recursive function
$\Pi ^0_2$
-soundness. In this folklore proof one first defines a recursive function
![]() $f_T$
that is not provably total in T by diagonalizing against the set of provably total recursive functions of T; one then shows that the totality of
$f_T$
that is not provably total in T by diagonalizing against the set of provably total recursive functions of T; one then shows that the totality of
![]() $f_T$
is T-provably equivalent to the
$f_T$
is T-provably equivalent to the
![]() $\Pi ^0_2$
-soundness of T. See [Reference Beklemishev3] for a detailed proof. Just as the class of the provably total recursive functions of T is the canonical “invariant” measuring the
$\Pi ^0_2$
-soundness of T. See [Reference Beklemishev3] for a detailed proof. Just as the class of the provably total recursive functions of T is the canonical “invariant” measuring the
![]() $\Pi ^0_2$
-strength of T, the proof-theoretic ordinal of T is the canonical “invariant” measuring the
$\Pi ^0_2$
-strength of T, the proof-theoretic ordinal of T is the canonical “invariant” measuring the
![]() $\Pi ^1_1$
-strength of T. And just as the non-provability of
$\Pi ^1_1$
-strength of T. And just as the non-provability of
![]() $\Pi ^0_2$
-soundness is derived by defining a total recursive function in terms of the canonical
$\Pi ^0_2$
-soundness is derived by defining a total recursive function in terms of the canonical
![]() $\Pi ^0_2$
-invariant, we derive Theorem 1.3 by defining a well-ordering in terms of the canonical
$\Pi ^0_2$
-invariant, we derive Theorem 1.3 by defining a well-ordering in terms of the canonical
![]() $\Pi ^1_1$
-invariant.
$\Pi ^1_1$
-invariant.
A slight modification of our proof of Theorem 1.3 delivers a stronger result:
Theorem 1.4. There is no sequence
![]() of
of
![]() $\Pi ^1_1$
-sound and
$\Pi ^1_1$
-sound and
![]() $\Sigma ^1_1$
-definable extensions of
$\Sigma ^1_1$
-definable extensions of
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
such that for each n,
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
such that for each n,
![]() $T_n \vdash \mathsf {RFN}_{\Pi ^1_1}(T_{n+1})$
.
$T_n \vdash \mathsf {RFN}_{\Pi ^1_1}(T_{n+1})$
.
To see that Theorem 1.4 implies Theorem 1.3, note that if T were a counter-example to Theorem 1.3 then we would get a counter-example to Theorem 1.4 by letting
![]() $T=T_n$
for each n. Theorem 1.4 extends earlier work [Reference Pakhomov and Walsh8, Reference Pakhomov and Walsh9] of Pakhomov and the author, who proved the following:
$T=T_n$
for each n. Theorem 1.4 extends earlier work [Reference Pakhomov and Walsh8, Reference Pakhomov and Walsh9] of Pakhomov and the author, who proved the following:
Theorem 1.5 (Pakhomov–W.)
There is no sequence
![]() of
of
![]() $\Pi ^1_1$
-sound and
$\Pi ^1_1$
-sound and
![]() $\Sigma ^0_1$
-definable extensions of
$\Sigma ^0_1$
-definable extensions of
![]() $\mathsf {ACA}_0$
such that for each n,
$\mathsf {ACA}_0$
such that for each n,
![]() $T_n \vdash \mathsf {RFN}_{\Pi ^1_1}(T_{n+1})$
.
$T_n \vdash \mathsf {RFN}_{\Pi ^1_1}(T_{n+1})$
.
Pakhomov and the author proved Theorem 1.5 to provide an explanation for the apparent pre-well-ordering of natural theories by proof-theoretic strength; see [Reference Walsh17] for a discussion of this phenomenon. Theorem 1.4 extends this explanation to the new setting of
![]() $\Sigma ^1_1$
-definable theories. Whereas the proof of Theorem 1.5 appeals to the second incompleteness theorem and makes no mention of proof-theoretic ordinals, our proof of Theorem 1.4 uses ordinal analysis and does not appeal to any version of the second incompleteness theorem. Note that Theorem 1.4 is neither stronger nor weaker than Theorem 1.5; the former requires the stronger hypothesis that T extend
$\Sigma ^1_1$
-definable theories. Whereas the proof of Theorem 1.5 appeals to the second incompleteness theorem and makes no mention of proof-theoretic ordinals, our proof of Theorem 1.4 uses ordinal analysis and does not appeal to any version of the second incompleteness theorem. Note that Theorem 1.4 is neither stronger nor weaker than Theorem 1.5; the former requires the stronger hypothesis that T extend
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
but only the weaker hypothesis that T be
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
but only the weaker hypothesis that T be
![]() $\Sigma ^1_1$
-definable.
$\Sigma ^1_1$
-definable.
The main tool that we use to derive Theorems 1.3 and 1.4 is Spector’s
![]() $\Sigma ^1_1$
-bounding theorem. Though the standard proofs (e.g., [Reference Sacks14, Chapter 1, Corollary 5.5]) of Spector’s theorem rely on diagonalization, there is an alternate diagonalization-free proof due to Beckmann and Pohlers [Reference Beckmann and Pohlers2]. This latter proof derives
$\Sigma ^1_1$
-bounding theorem. Though the standard proofs (e.g., [Reference Sacks14, Chapter 1, Corollary 5.5]) of Spector’s theorem rely on diagonalization, there is an alternate diagonalization-free proof due to Beckmann and Pohlers [Reference Beckmann and Pohlers2]. This latter proof derives
![]() $\Sigma ^1_1$
-bounding from an analysis of cut-free infinitary derivations. In particular,
$\Sigma ^1_1$
-bounding from an analysis of cut-free infinitary derivations. In particular,
![]() $\Sigma ^1_1$
-bounding is derived from a result known as “the boundedness theorem,” which roughly states that for arithmetically definable well-orders
$\Sigma ^1_1$
-bounding is derived from a result known as “the boundedness theorem,” which roughly states that for arithmetically definable well-orders
![]() $\prec $
, the order-type of
$\prec $
, the order-type of
![]() $\prec $
cannot exceed the depth of the shortest proof of the well-foundedness of
$\prec $
cannot exceed the depth of the shortest proof of the well-foundedness of
![]() $\prec $
in
$\prec $
in
![]() -logic. Versions of the boundedness theorem are already implicit in Gentzen’s proof [Reference Gentzen5] that
-logic. Versions of the boundedness theorem are already implicit in Gentzen’s proof [Reference Gentzen5] that
![]() $\mathsf {PA}$
does not prove the primitive recursive well-foundedness of
$\mathsf {PA}$
does not prove the primitive recursive well-foundedness of
![]() $\varepsilon _0$
. Note that Gentzen’s proof of this independence result does not appeal to Gödel’s second incompleteness theorem and does not rely on self-reference but rather involves a combinatorial analysis of proofs in
$\varepsilon _0$
. Note that Gentzen’s proof of this independence result does not appeal to Gödel’s second incompleteness theorem and does not rely on self-reference but rather involves a combinatorial analysis of proofs in
![]() $\mathsf {PA}$
.
$\mathsf {PA}$
.
We also rely on a formalized version of Spector’s theorem. Roughly, the formalized version says that for any
![]() $\Sigma ^1_1$
predicate H, if
$\Sigma ^1_1$
predicate H, if
![]() $\mathsf {ACA}_0$
proves “H is a set of recursive ordinals,” then for some e,
$\mathsf {ACA}_0$
proves “H is a set of recursive ordinals,” then for some e,
![]() $\mathsf {ACA}_0$
proves “e is a recursive ordinal but
$\mathsf {ACA}_0$
proves “e is a recursive ordinal but
![]() $\neg H(e)$
.” The standard proof of the formalized version of
$\neg H(e)$
.” The standard proof of the formalized version of
![]() $\Sigma ^1_1$
-bounding uses the recursion theorem to define a recursive function. Though this is not exactly the construction of a self-referential sentence, definitions using the recursion theorem share the opacity of constructions of sentences using the fixed point lemma. Accordingly, we provide a new proof of this formalized version of Spector’s theorem. The new proof uses the same techniques Gentzen used to prove the boundedness theorem and that Beckmann and Pohlers used to prove the
$\Sigma ^1_1$
-bounding uses the recursion theorem to define a recursive function. Though this is not exactly the construction of a self-referential sentence, definitions using the recursion theorem share the opacity of constructions of sentences using the fixed point lemma. Accordingly, we provide a new proof of this formalized version of Spector’s theorem. The new proof uses the same techniques Gentzen used to prove the boundedness theorem and that Beckmann and Pohlers used to prove the
![]() $\Sigma ^1_1$
-bounding theorem. Thus, we do not rely on self-reference or diagonalization in any form.
$\Sigma ^1_1$
-bounding theorem. Thus, we do not rely on self-reference or diagonalization in any form.
Here is our plan for the rest of the paper. In Section 2 we cover some preliminary material, including definitions and notation; we also discuss two folklore results that we use to prove the main theorems. In Section 3 we provide proofs of Theorems 1.3 and 1.4. In Section 4 we provide an alternate proof using infinitary derivations of the formalized version of Spector’s
![]() $\Sigma ^1_1$
-bounding theorem. Finally, in Section 5 we present some open problems concerning the optimality of Theorem 1.3.
$\Sigma ^1_1$
-bounding theorem. Finally, in Section 5 we present some open problems concerning the optimality of Theorem 1.3.
2 Preliminaries
One of the central concepts in proof theory is that of a proof-theoretic ordinal. To say what proof-theoretic ordinals are, we must say what a presentation of an ordinal is.
Definition 2.1. For a syntactic complexity class
![]() $\Gamma $
, a
$\Gamma $
, a
![]() $\Gamma $
presentation of an ordinal
$\Gamma $
presentation of an ordinal
![]() $\alpha $
is a
$\alpha $
is a
![]() $\Gamma $
formula that defines an ordering of order-type
$\Gamma $
formula that defines an ordering of order-type
![]() $\alpha $
over the standard structure
$\alpha $
over the standard structure
![]() $\big (\mathbb {N},\mathcal {P}(\mathbb {N})\big )$
.
$\big (\mathbb {N},\mathcal {P}(\mathbb {N})\big )$
.
We now present two definitions of “proof-theoretic ordinal,” both of which are necessary for our proof.
Definition 2.2. Let
![]() $|T|_{\mathsf {RE}}$
be the supremum of the ordinals
$|T|_{\mathsf {RE}}$
be the supremum of the ordinals
![]() $\alpha $
for which there is some
$\alpha $
for which there is some
![]() $\Sigma ^0_1$
presentation
$\Sigma ^0_1$
presentation
![]() $\prec $
of
$\prec $
of
![]() $\alpha $
such that
$\alpha $
such that
![]() $T\vdash \mathsf {WF}(\prec )$
.
$T\vdash \mathsf {WF}(\prec )$
.
Definition 2.3. Let
![]() $|T|_{\mathsf {AN}}$
be the supremum of the ordinals
$|T|_{\mathsf {AN}}$
be the supremum of the ordinals
![]() $\alpha $
for which there is some
$\alpha $
for which there is some
![]() $\Sigma ^1_1$
presentation
$\Sigma ^1_1$
presentation
![]() $\prec $
of
$\prec $
of
![]() $\alpha $
such that
$\alpha $
such that
![]() $T\vdash \mathsf {WF}(\prec )$
.
$T\vdash \mathsf {WF}(\prec )$
.
The
![]() $\mathsf {AN}$
in the notation
$\mathsf {AN}$
in the notation
![]() $|T|_{\mathsf {AN}}$
means analytic. Indeed,
$|T|_{\mathsf {AN}}$
means analytic. Indeed,
![]() $|T|_{\mathsf {AN}}$
is the supremum of the T-provably well-founded analytic linear orders, where analytic means lightface
$|T|_{\mathsf {AN}}$
is the supremum of the T-provably well-founded analytic linear orders, where analytic means lightface
![]() $\Sigma ^1_1$
.
$\Sigma ^1_1$
.
By definition,
![]() . However, we can say more about the relationship between these three values if we make some assumptions about T. In the following subsections we will describe these results, which belong to mathematical folklore.
. However, we can say more about the relationship between these three values if we make some assumptions about T. In the following subsections we will describe these results, which belong to mathematical folklore.
2.1 The first folklore result
If T is
![]() $\Pi ^1_1$
-sound and
$\Pi ^1_1$
-sound and
![]() $\Sigma ^1_1$
-definable, we can say more about the relationship between
$\Sigma ^1_1$
-definable, we can say more about the relationship between
![]() $|T|_{\mathsf {AN}}$
and
$|T|_{\mathsf {AN}}$
and
![]() .
.
Theorem 2.4 (Folklore)
If T is
![]() $\Pi ^1_1$
-sound and
$\Pi ^1_1$
-sound and
![]() $\Sigma ^1_1$
-definable, then
$\Sigma ^1_1$
-definable, then
![]() .
.
Theorem 2.4 follows immediately from Spector’s
![]() $\Sigma ^1_1$
-bounding theorem:
$\Sigma ^1_1$
-bounding theorem:
Theorem 2.5 (Spector)
For any
![]() $\Sigma ^1_1$
presentation
$\Sigma ^1_1$
presentation
![]() $\prec $
of an ordinal,
$\prec $
of an ordinal,
![]() .
.
Standard proofs of Spector’s
![]() $\Sigma ^1_1$
-bounding appeal to the fact that Kleene’s
$\Sigma ^1_1$
-bounding appeal to the fact that Kleene’s
![]() $\mathcal {O}$
is not
$\mathcal {O}$
is not
![]() $\Sigma ^1_1$
-definable. Note that the latter is typically proved using an ordinary diagonalization argument; see, e.g., [Reference Sacks14, Chapter 1, Theorem 5.4].
$\Sigma ^1_1$
-definable. Note that the latter is typically proved using an ordinary diagonalization argument; see, e.g., [Reference Sacks14, Chapter 1, Theorem 5.4].
However, there is an alternate proof due to Beckmann and Pohlers [Reference Beckmann and Pohlers2] of Spector’s Theorem that does not use diagonalization. The Beckmann–Pohlers proof proceeds by analyzing the structure of infinitary cut-free derivations. Beckmann and Pohlers derive
![]() $\Sigma ^1_1$
-bounding a result known as “the boundedness lemma,” which they claim is essentially implicit in Gentzen’s proof of the
$\Sigma ^1_1$
-bounding a result known as “the boundedness lemma,” which they claim is essentially implicit in Gentzen’s proof of the
![]() $\mathsf {PA}$
non-derivability of
$\mathsf {PA}$
non-derivability of
![]() $\varepsilon _0$
-induction. Accordingly, when we appeal to Theorem 2.4, we are appeal to a result that has a Gentzen-style non-diagonalization proof.
$\varepsilon _0$
-induction. Accordingly, when we appeal to Theorem 2.4, we are appeal to a result that has a Gentzen-style non-diagonalization proof.
2.2 The second folklore result
We can say more about the relationship between
![]() $|T|_{\mathsf {RE}}$
and
$|T|_{\mathsf {RE}}$
and
![]() $|T|_{\mathsf {AN}}$
for all
$|T|_{\mathsf {AN}}$
for all
![]() $\Pi ^1_1$
-sound T that extend
$\Pi ^1_1$
-sound T that extend
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
. Recall that
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
. Recall that
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
is the theory whose axioms are those of
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
is the theory whose axioms are those of
![]() $\mathsf {ACA}_0$
plus each instance of the schema:
$\mathsf {ACA}_0$
plus each instance of the schema:
where
![]() $\varphi (n,X)$
is a
$\varphi (n,X)$
is a
![]() $\Sigma ^1_1$
formula in which Y does not occur and where
$\Sigma ^1_1$
formula in which Y does not occur and where
Theorem 2.6 (Folklore)
If T is a
![]() $\Pi ^1_1$
-sound extension of
$\Pi ^1_1$
-sound extension of
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
, then
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
, then
![]() $|T|_{\mathsf {RE}}=|T|_{\mathsf {AN}}$
.
$|T|_{\mathsf {RE}}=|T|_{\mathsf {AN}}$
.
The main tool for proving Theorem 2.6 is a formalized version of Spector’s theorem. To state this formalized result, we first introduce some notation.
Definition 2.7. Let
![]() $Rec:=\{e\in \mathbb {N} \mid e \text { is an index of a total recursive function}\}$
. With each
$Rec:=\{e\in \mathbb {N} \mid e \text { is an index of a total recursive function}\}$
. With each
![]() $e\in Rec$
there is an associated relation
$e\in Rec$
there is an associated relation
![]() $\prec _e$
where
$\prec _e$
where
where
![]() $\langle , \rangle $
is a primitive recursive pairing function.
$\langle , \rangle $
is a primitive recursive pairing function.
Definition 2.8. Let
![]() $\mathfrak {W}_{Rec} : = \{e\in \mathbb {N} \mid e\in Rec \wedge \mathsf {WO}(\prec _e)\}$
.
$\mathfrak {W}_{Rec} : = \{e\in \mathbb {N} \mid e\in Rec \wedge \mathsf {WO}(\prec _e)\}$
.
In [Reference Rathjen13] (see Proposition 2.19), Rathjen derives Theorem 2.6 from the following lemma, which is a formalized version of Spector’s
![]() $\Sigma ^1_1$
-bounding theorem:
$\Sigma ^1_1$
-bounding theorem:
Lemma 2.9 (Rathjen)
Suppose
![]() $H(x)$
is a
$H(x)$
is a
![]() $\Sigma ^1_1$
formula such that:
$\Sigma ^1_1$
formula such that:
Then, for some
![]() $e\in Rec$
,
$e\in Rec$
,
Theorem 2.6 is straightforwardly derived from Lemma 2.9. Rathjen provides a proof of Lemma 1.1 in [Reference Rathjen12]. Note that this proof of Lemma 2.9 makes use of the recursion theorem. In Section 4 we will present an alternative proof of Lemma 2.9 that does not make any use of the recursion theorem or other diagonalization.
2.3 Remarks
Before continuing, let’s highlight some features of these folklore results and their relationship to the main theorems.
First, note the role that
![]() $\Sigma ^1_1$
-bounding plays in the proofs of the folklore results. We will not mention
$\Sigma ^1_1$
-bounding plays in the proofs of the folklore results. We will not mention
![]() $\Sigma ^1_1$
-bounding explicitly in the proofs of the main theorems, but we will still rely on it insofar as it is used to prove these folklore results. We feel that the role of
$\Sigma ^1_1$
-bounding explicitly in the proofs of the main theorems, but we will still rely on it insofar as it is used to prove these folklore results. We feel that the role of
![]() $\Sigma ^1_1$
-bounding is so important that it is worth explicitly highlighting where it is being used.
$\Sigma ^1_1$
-bounding is so important that it is worth explicitly highlighting where it is being used.
Second, note that in the proofs of both folklore results, we must appeal to the
![]() $\Pi ^1_1$
-soundness of T. We will not appeal to
$\Pi ^1_1$
-soundness of T. We will not appeal to
![]() $\Pi ^1_1$
-soundness explicitly in the proofs of the main theorems; we will only rely on it insofar as we invoke these folklore results.
$\Pi ^1_1$
-soundness explicitly in the proofs of the main theorems; we will only rely on it insofar as we invoke these folklore results.
One can find proofs of Theorems 2.4 and 2.6 in [Reference Rathjen13].
3 The main theorems
In this section we prove our main theorem, an analogue of Gödel’s second incompleteness theorem. We start by introducing two formulas and make a remark about their syntactic complexity. We will use these formulas and appeal to the remark many times, so it is worth isolating them here.
Definition 3.1. For a binary formula
![]() $\triangleleft $
, let
$\triangleleft $
, let
![]() $\mathsf {LO}(\triangleleft )$
stand for the conjunction of the following clauses:
$\mathsf {LO}(\triangleleft )$
stand for the conjunction of the following clauses:
-
(1)
 $\neg \exists x \mathsf {True}_{\Sigma ^0_1}(x\triangleleft x).$
$\neg \exists x \mathsf {True}_{\Sigma ^0_1}(x\triangleleft x).$
-
(2)
 $\forall x \forall y \big ( \mathsf {True}_{\Sigma ^0_1}(x\triangleleft y) \vee \mathsf {True}_{\Sigma ^0_1}(y\triangleleft x) \vee x=y \big ).$
$\forall x \forall y \big ( \mathsf {True}_{\Sigma ^0_1}(x\triangleleft y) \vee \mathsf {True}_{\Sigma ^0_1}(y\triangleleft x) \vee x=y \big ).$
-
(3)
 $\forall x \forall y \forall z \Big ( \big ( \mathsf {True}_{\Sigma ^0_1}(x\triangleleft y) \wedge \mathsf {True}_{\Sigma ^0_1}(y\triangleleft z) \big ) \to \mathsf {True}_{\Sigma ^0_1}(x\triangleleft z) \Big ).$
$\forall x \forall y \forall z \Big ( \big ( \mathsf {True}_{\Sigma ^0_1}(x\triangleleft y) \wedge \mathsf {True}_{\Sigma ^0_1}(y\triangleleft z) \big ) \to \mathsf {True}_{\Sigma ^0_1}(x\triangleleft z) \Big ).$
Definition 3.2. For a binary formula
![]() $\triangleleft $
, let
$\triangleleft $
, let
![]() $\mathsf {WF}(\triangleleft )$
stand for
$\mathsf {WF}(\triangleleft )$
stand for
Remark 3.3. Note the use of the
![]() $\Sigma ^0_1$
truth-predicate in Definitions 3.1 and 3.2. Thus, for any formula
$\Sigma ^0_1$
truth-predicate in Definitions 3.1 and 3.2. Thus, for any formula
![]() $\triangleleft $
,
$\triangleleft $
,
![]() $\mathsf {LO}(\triangleleft )$
is arithmetic and
$\mathsf {LO}(\triangleleft )$
is arithmetic and
![]() $\mathsf {WF}(\triangleleft )$
is
$\mathsf {WF}(\triangleleft )$
is
![]() $\Pi ^1_1$
. Of course,
$\Pi ^1_1$
. Of course,
![]() $\mathsf {LO}(\triangleleft )$
and
$\mathsf {LO}(\triangleleft )$
and
![]() $\mathsf {WF}(\triangleleft )$
will make the most sense when applied to
$\mathsf {WF}(\triangleleft )$
will make the most sense when applied to
![]() $\Sigma ^0_1$
formulas or in quantified statements about
$\Sigma ^0_1$
formulas or in quantified statements about
![]() $\Sigma ^0_1$
formulas. We shall use it in the latter way.
$\Sigma ^0_1$
formulas. We shall use it in the latter way.
3.1 The key lemma
The key to the proofs of Theorems 1.3 and 1.4 is the following lemma:
Lemma 3.4. If T is
![]() $\Pi ^1_1$
-sound and
$\Pi ^1_1$
-sound and
![]() $\Sigma ^1_1$
-definable, then there is a
$\Sigma ^1_1$
-definable, then there is a
![]() $\Sigma ^1_1$
presentation
$\Sigma ^1_1$
presentation
![]() $\prec _T$
of
$\prec _T$
of
![]() $|T|_{\mathsf {RE}}$
such that
$|T|_{\mathsf {RE}}$
such that
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0\vdash \mathsf {RFN}_{\Pi ^1_1}(T) \to \mathsf {WF}(\prec _T).$
$\Sigma ^1_1\text {-}\mathsf {AC}_0\vdash \mathsf {RFN}_{\Pi ^1_1}(T) \to \mathsf {WF}(\prec _T).$
Proof Let T be
![]() $\Pi ^1_1$
-sound and
$\Pi ^1_1$
-sound and
![]() $\Sigma ^1_1$
-definable. By Theorem 2.4,
$\Sigma ^1_1$
-definable. By Theorem 2.4,
![]() , whence there is some
, whence there is some
![]() $\Sigma ^0_1$
-definable
$\Sigma ^0_1$
-definable
![]() $\prec _\star $
such that
$\prec _\star $
such that
![]() $|T|_{\mathsf {RE}}=\mathsf {otyp}(\prec _\star )$
.
$|T|_{\mathsf {RE}}=\mathsf {otyp}(\prec _\star )$
.
We are now going to define an alternate presentation
![]() $\prec _T$
of
$\prec _T$
of
![]() $|T|_{\mathsf {RE}}$
. Informally, the formula
$|T|_{\mathsf {RE}}$
. Informally, the formula
![]() $\alpha \prec _T \beta $
says that
$\alpha \prec _T \beta $
says that
![]() $\alpha $
is less than
$\alpha $
is less than
![]() $\beta $
in an initial segment of the
$\beta $
in an initial segment of the
![]() $\prec _\star $
ordering that embeds into a
$\prec _\star $
ordering that embeds into a
![]() $\Sigma ^0_1$
-definable linear order
$\Sigma ^0_1$
-definable linear order
![]() $\triangleleft $
such that T proves the well-foundedness of
$\triangleleft $
such that T proves the well-foundedness of
![]() $\triangleleft $
. More formally, we define
$\triangleleft $
. More formally, we define
![]() $\alpha \prec _T \beta $
as the conjunction of
$\alpha \prec _T \beta $
as the conjunction of
-
(1)
 $\alpha \prec _\star \beta $
,
$\alpha \prec _\star \beta $
, -
(2)
 $\exists \triangleleft \in \Sigma ^0_1 \; \exists f \; \Big ( \mathsf {Emb}(f,\prec _\star \restriction \beta , \triangleleft ) \; \wedge \mathsf {LO}(\triangleleft ) \; \wedge \; \mathsf {Pr}_T\big (\mathsf {WF}(\triangleleft )\big ) \Big ),$
$\exists \triangleleft \in \Sigma ^0_1 \; \exists f \; \Big ( \mathsf {Emb}(f,\prec _\star \restriction \beta , \triangleleft ) \; \wedge \mathsf {LO}(\triangleleft ) \; \wedge \; \mathsf {Pr}_T\big (\mathsf {WF}(\triangleleft )\big ) \Big ),$
where
![]() $\mathsf {Emb}(f,\prec _\star \restriction \beta ,\triangleleft )$
stands for
$\mathsf {Emb}(f,\prec _\star \restriction \beta ,\triangleleft )$
stands for
and where
![]() $\mathsf {LO}(\triangleleft )$
and
$\mathsf {LO}(\triangleleft )$
and
![]() $\mathsf {WF}(\triangleleft )$
are as in Definitions 3.1 and 3.2.
$\mathsf {WF}(\triangleleft )$
are as in Definitions 3.1 and 3.2.
Claim.
![]() $\prec _T$
is
$\prec _T$
is
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
-provably equivalent to a
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
-provably equivalent to a
![]() $\Sigma ^1_1$
formula.
$\Sigma ^1_1$
formula.
Clearly
![]() $\alpha \prec _\star \beta $
is
$\alpha \prec _\star \beta $
is
![]() $\Sigma ^0_1$
. Now let’s look at the second conjunct of
$\Sigma ^0_1$
. Now let’s look at the second conjunct of
![]() $\alpha \prec _T\beta $
. Note that
$\alpha \prec _T\beta $
. Note that
![]() $\mathsf {Emb}(f,\prec _\star \restriction \beta ,\triangleleft )$
and
$\mathsf {Emb}(f,\prec _\star \restriction \beta ,\triangleleft )$
and
![]() $\mathsf {LO}(\triangleleft )$
are both arithmetic. On the other hand,
$\mathsf {LO}(\triangleleft )$
are both arithmetic. On the other hand,
![]() $\mathsf {Pr}_T\big ( \mathsf {WF}(\triangleleft )\big )$
is
$\mathsf {Pr}_T\big ( \mathsf {WF}(\triangleleft )\big )$
is
![]() $\Sigma ^1_1$
, since T is
$\Sigma ^1_1$
, since T is
![]() $\Sigma ^1_1$
-definable. So the conjunction
$\Sigma ^1_1$
-definable. So the conjunction
is provably equivalent in
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
to a
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
to a
![]() $\Sigma ^1_1$
formula. Thus, the second conjunct of
$\Sigma ^1_1$
formula. Thus, the second conjunct of
![]() $\alpha \prec _T\beta $
is given by an existential number quantifier before an existential set quantifier before a (formula that is
$\alpha \prec _T\beta $
is given by an existential number quantifier before an existential set quantifier before a (formula that is
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
-provably equivalent to a)
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
-provably equivalent to a)
![]() $\Sigma ^1_1$
formula. It follows that
$\Sigma ^1_1$
formula. It follows that
![]() $\prec _T$
is
$\prec _T$
is
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
-provably equivalent to a
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
-provably equivalent to a
![]() $\Sigma ^1_1$
formula.
$\Sigma ^1_1$
formula.
Claim.
![]() $\prec _T$
is a presentation of
$\prec _T$
is a presentation of
![]() $|T|_{\mathsf {RE}}$
.
$|T|_{\mathsf {RE}}$
.
![]() $\mathsf {otyp}(\prec _T) \leqslant |T|_{\mathsf {RE}}$
: The first conjunct in the definition of
$\mathsf {otyp}(\prec _T) \leqslant |T|_{\mathsf {RE}}$
: The first conjunct in the definition of
![]() $\prec _T$
ensures that
$\prec _T$
ensures that
![]() $\mathsf {otyp}(\prec _T)\leqslant \mathsf {otyp}(\prec _\star )$
. To finish the argument, recall that
$\mathsf {otyp}(\prec _T)\leqslant \mathsf {otyp}(\prec _\star )$
. To finish the argument, recall that
![]() $\mathsf {otyp}(\prec _\star )=|T|_{\mathsf {RE}}$
.
$\mathsf {otyp}(\prec _\star )=|T|_{\mathsf {RE}}$
.
![]() $\mathsf {otyp}(\prec _T) \geqslant |T|_{\mathsf {RE}}$
: Let
$\mathsf {otyp}(\prec _T) \geqslant |T|_{\mathsf {RE}}$
: Let
![]() $\alpha <|T|_{\mathsf {RE}}=\mathsf {otyp}(\prec _\star )$
. We need to see that
$\alpha <|T|_{\mathsf {RE}}=\mathsf {otyp}(\prec _\star )$
. We need to see that
![]() $\alpha <\mathsf {otyp}(\prec _T)$
.
$\alpha <\mathsf {otyp}(\prec _T)$
.
Since
![]() $\alpha <\mathsf {otyp}(\prec _\star )$
and
$\alpha <\mathsf {otyp}(\prec _\star )$
and
![]() $\alpha <|T|_{\mathsf {RE}}$
, there is an embedding of an initial segment of
$\alpha <|T|_{\mathsf {RE}}$
, there is an embedding of an initial segment of
![]() $\prec _\star $
that includes the
$\prec _\star $
that includes the
![]() $\prec _\star $
representation of
$\prec _\star $
representation of
![]() $\alpha $
into a
$\alpha $
into a
![]() $\Sigma ^0_1$
-definable well-order that is T-provably well-founded. It is then immediate from the definition of
$\Sigma ^0_1$
-definable well-order that is T-provably well-founded. It is then immediate from the definition of
![]() $\prec _T$
that
$\prec _T$
that
![]() $\alpha <\mathsf {otyp}(\prec _T)$
.
$\alpha <\mathsf {otyp}(\prec _T)$
.
Claim.
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0\vdash \mathsf {RFN}_{\Pi ^1_1}(T) \to \mathsf {WF}(\prec _T).$
$\Sigma ^1_1\text {-}\mathsf {AC}_0\vdash \mathsf {RFN}_{\Pi ^1_1}(T) \to \mathsf {WF}(\prec _T).$
Reason in
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
: Suppose that
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
: Suppose that
![]() $\prec _T$
is ill-founded. Then, by the definition of
$\prec _T$
is ill-founded. Then, by the definition of
![]() $\prec _T$
, there is some infinite descending sequence in
$\prec _T$
, there is some infinite descending sequence in
![]() $\prec _\star $
that embeds into a
$\prec _\star $
that embeds into a
![]() $\Sigma ^0_1$
-definable linear order
$\Sigma ^0_1$
-definable linear order
![]() $\triangleleft $
such that
$\triangleleft $
such that
![]() $T\vdash \mathsf {WF}(\triangleleft )$
. Since
$T\vdash \mathsf {WF}(\triangleleft )$
. Since
![]() $\triangleleft $
embeds an ill-founded linear order,
$\triangleleft $
embeds an ill-founded linear order,
![]() $\triangleleft $
is ill-founded. So T proves a false
$\triangleleft $
is ill-founded. So T proves a false
![]() $\Pi ^1_1$
sentence, namely,
$\Pi ^1_1$
sentence, namely,
![]() $\mathsf {WF}(\triangleleft )$
.
$\mathsf {WF}(\triangleleft )$
.
3.2 An incompleteness theorem
We now present a proof of Theorem 1.3, restated here:
Theorem 3.5. If T is a
![]() $\Pi ^1_1$
-sound and
$\Pi ^1_1$
-sound and
![]() $\Sigma ^1_1$
-definable extension of
$\Sigma ^1_1$
-definable extension of
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
, then T does not prove its own
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
, then T does not prove its own
![]() $\Pi ^1_1$
-soundness.
$\Pi ^1_1$
-soundness.
Proof By Lemma 3.4, there is a
![]() $\Sigma ^1_1$
presentation
$\Sigma ^1_1$
presentation
![]() $\prec _T$
of
$\prec _T$
of
![]() $|T|_{\mathsf {RE}}$
such that
$|T|_{\mathsf {RE}}$
such that
Since T extends
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
, we infer that
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
, we infer that
Claim.
![]() $T\nvdash \mathsf {WF}(\prec _T)$
.
$T\nvdash \mathsf {WF}(\prec _T)$
.
Since T extends
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
, by Theorem 2.6,
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
, by Theorem 2.6,
![]() $|T|_{\mathsf {RE}}=|T|_{\mathsf {AN}}$
. Moreover, since T extends
$|T|_{\mathsf {RE}}=|T|_{\mathsf {AN}}$
. Moreover, since T extends
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
, we infer that
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
, we infer that
![]() $\prec _T$
is T-provably equivalent to a
$\prec _T$
is T-provably equivalent to a
![]() $\Sigma ^1_1$
formula. So
$\Sigma ^1_1$
formula. So
![]() $\prec _T$
is a presentation of
$\prec _T$
is a presentation of
![]() $|T|_{\mathsf {AN}}$
that is T-provably equivalent to a
$|T|_{\mathsf {AN}}$
that is T-provably equivalent to a
![]() $\Sigma ^1_1$
formula, whence
$\Sigma ^1_1$
formula, whence
![]() $T\nvdash \mathsf {WF}(\prec _T)$
.
$T\nvdash \mathsf {WF}(\prec _T)$
.
It follows immediately from (3) and from the claim that
![]() $T\nvdash \mathsf {RFN}_{\Pi ^1_1}(T)$
.
$T\nvdash \mathsf {RFN}_{\Pi ^1_1}(T)$
.
3.3 Well-foundedness
In this subsection we prove a strengthening of Theorem 3.5 that is of independent interest. The following result is proved in [Reference Pakhomov and Walsh8, Reference Pakhomov and Walsh9]:
Theorem 3.6 (Pakhomov–W.)
There is no sequence
![]() of
of
![]() $\Pi ^1_1$
-sound and
$\Pi ^1_1$
-sound and
![]() $\Sigma ^0_1$
-definable extensions of
$\Sigma ^0_1$
-definable extensions of
![]() $\mathsf {ACA}_0$
such that for each n,
$\mathsf {ACA}_0$
such that for each n,
![]() $T_n\vdash \mathsf {RFN}_{\Pi ^1_1}(T_{n+1})$
.
$T_n\vdash \mathsf {RFN}_{\Pi ^1_1}(T_{n+1})$
.
Pakhomov and the author proved Theorem 3.6 to provide an explanation of the apparent pre-well-ordering of natural theories by proof-theoretic strength; see [Reference Walsh17] for a discussion of this phenomenon. In [Reference Pakhomov and Walsh8, Reference Pakhomov and Walsh9], Theorem 3.6 is proved using Gödel’s second incompleteness theorem. In particular, we show that the theory
![]() $\mathsf {ACA}_0+\varphi $
, where
$\mathsf {ACA}_0+\varphi $
, where
![]() $\varphi $
states that Theorem 3.6 is false, proves its own consistency. In [Reference Lutz and Walsh7] it is claimed that such a result “could be proved by showing that a descending sequence
$\varphi $
states that Theorem 3.6 is false, proves its own consistency. In [Reference Lutz and Walsh7] it is claimed that such a result “could be proved by showing that a descending sequence
![]() of theories would induce a descending sequence in the ordinals (namely, the associated sequence of proof-theoretic ordinals).” We now present such a proof (though for
of theories would induce a descending sequence in the ordinals (namely, the associated sequence of proof-theoretic ordinals).” We now present such a proof (though for
![]() $\Sigma ^1_1$
-definable extensions of
$\Sigma ^1_1$
-definable extensions of
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
rather than for
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
rather than for
![]() $\Sigma ^0_1$
-definable extensions of
$\Sigma ^0_1$
-definable extensions of
![]() $\mathsf {ACA}_0$
).
$\mathsf {ACA}_0$
).
What follows is a restatement of Theorem 1.4:
Theorem 3.7. There is no sequence
![]() of
of
![]() $\Pi ^1_1$
-sound and
$\Pi ^1_1$
-sound and
![]() $\Sigma ^1_1$
-definable extensions of
$\Sigma ^1_1$
-definable extensions of
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
such that for each n,
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
such that for each n,
![]() $T_n \vdash \mathsf {RFN}_{\Pi ^1_1}(T_{n+1})$
.
$T_n \vdash \mathsf {RFN}_{\Pi ^1_1}(T_{n+1})$
.
Proof Suppose that there is such a sequence
![]() . From Lemma 3.4 we infer that, for each n, there is a
. From Lemma 3.4 we infer that, for each n, there is a
![]() $\Sigma ^1_1$
presentation
$\Sigma ^1_1$
presentation
![]() $\prec _{T_n}$
of
$\prec _{T_n}$
of
![]() $|T_{n}|_{\mathsf {RE}}$
such that
$|T_{n}|_{\mathsf {RE}}$
such that
Since each
![]() $T_n$
extends
$T_n$
extends
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
, Theorem 2.6 entails that, for each n, there is a
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
, Theorem 2.6 entails that, for each n, there is a
![]() $\Sigma ^1_1$
presentation
$\Sigma ^1_1$
presentation
![]() $\prec _{T_n}$
of
$\prec _{T_n}$
of
![]() $|T_{n}|_{\mathsf {AN}}$
such that
$|T_{n}|_{\mathsf {AN}}$
such that
Since each
![]() $T_n$
extends
$T_n$
extends
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
, for each n,
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
, for each n,
By assumption, for each n,
![]() $T_n\vdash \mathsf {RFN}_{\Pi ^1_1}(T_{n+1})$
, so we infer that, for each n,
$T_n\vdash \mathsf {RFN}_{\Pi ^1_1}(T_{n+1})$
, so we infer that, for each n,
Whence
![]() $|T_n|_{\mathsf {AN}}>|T_{n+1}|_{\mathsf {AN}}$
for each n. Yet
$|T_n|_{\mathsf {AN}}>|T_{n+1}|_{\mathsf {AN}}$
for each n. Yet
![]() $|T_n|_{\mathsf {AN}}$
is an ordinal for each n. So
$|T_n|_{\mathsf {AN}}$
is an ordinal for each n. So
![]() is a descending sequence in the ordinals.
is a descending sequence in the ordinals.
Note that Theorem 3.7 entails Theorem 3.5. Indeed, if T were a counter-example to Theorem 3.5 then we would get a counter-example to Theorem 3.7 by letting
![]() $T=T_n$
for each n.
$T=T_n$
for each n.
4 Avoiding diagonalization
Considering the motivations outlined in Section 1, it is desirable to avoid diagoanlization in the proofs of Theorems 2.4 and 2.6.
As discussed in Section 2.1, the standard proofs of Spector’s
![]() $\Sigma ^1_1$
-bounding theorem rely on diagonalization. However, there is already an alternate proof of Spector’s theorem due to Beckmann and Pohlers [Reference Beckmann and Pohlers2] that uses Gentzen’s methods and avoids diagonalization.
$\Sigma ^1_1$
-bounding theorem rely on diagonalization. However, there is already an alternate proof of Spector’s theorem due to Beckmann and Pohlers [Reference Beckmann and Pohlers2] that uses Gentzen’s methods and avoids diagonalization.
Theorem 2.6, on the other hand, relies on Lemma 2.9, which is a formalized version of
![]() $\Sigma ^1_1$
-bounding. Rathjen’s proof of Lemma 2.9 uses the recursion theorem to formalize the standard proof of
$\Sigma ^1_1$
-bounding. Rathjen’s proof of Lemma 2.9 uses the recursion theorem to formalize the standard proof of
![]() $\Sigma ^1_1$
-bounding. In this section we develop an alternate proof of Lemma 2.9. Rather than an attempt to formalize the diagonalization proof of
$\Sigma ^1_1$
-bounding. In this section we develop an alternate proof of Lemma 2.9. Rather than an attempt to formalize the diagonalization proof of
![]() $\Sigma ^1_1$
-bounding in a different way, we instead formalize the Beckmann–Pohlers proof.
$\Sigma ^1_1$
-bounding in a different way, we instead formalize the Beckmann–Pohlers proof.
4.1 Infinitary derivations
The Beckmann–Pohlers proof of
![]() $\Sigma ^1_1$
-bounding involves the analysis of derivations in a cut-free infinitary proof system. We provide here a standard definition of such a proof system; for other discussion of such proof systems, see [Reference Pohlers10, Reference Pohlers and Buss11]. Note that this proof system is a version of the Tait calculus. Thus, our proof system deals with formulas within which negation is only appended to atomic formulas; this is possible due to the normal form theorems available in classical logic. In what follows, let
$\Sigma ^1_1$
-bounding involves the analysis of derivations in a cut-free infinitary proof system. We provide here a standard definition of such a proof system; for other discussion of such proof systems, see [Reference Pohlers10, Reference Pohlers and Buss11]. Note that this proof system is a version of the Tait calculus. Thus, our proof system deals with formulas within which negation is only appended to atomic formulas; this is possible due to the normal form theorems available in classical logic. In what follows, let
![]() $\mathsf {Diag}(\mathbb {N})$
be the atomic diagram of
$\mathsf {Diag}(\mathbb {N})$
be the atomic diagram of
![]() $\mathbb {N}$
in the signature
$\mathbb {N}$
in the signature
![]() $(0,1,+,\times )$
.
$(0,1,+,\times )$
.
Definition 4.1. We define
![]() $\vdash ^\alpha \Delta $
inductively by the following clauses:
$\vdash ^\alpha \Delta $
inductively by the following clauses:
-
(AxM) If
 $\Delta \cap \mathsf {Diag}(\mathbb {N})\neq \emptyset $
, then
$\Delta \cap \mathsf {Diag}(\mathbb {N})\neq \emptyset $
, then
 $\vdash ^\alpha \Delta $
for all ordinals
$\vdash ^\alpha \Delta $
for all ordinals
 $\alpha $
.
$\alpha $
. -
(AxL) If
 $t^{\mathbb {N}}=s^{\mathbb {N}}$
, then
$t^{\mathbb {N}}=s^{\mathbb {N}}$
, then
 $\vdash ^\alpha \Delta ,s\notin X,t\in X$
for all ordinals
$\vdash ^\alpha \Delta ,s\notin X,t\in X$
for all ordinals
 $\alpha $
.
$\alpha $
. -
(∧) If
 $\vdash ^{\alpha _i}\Delta ,A_i$
and
$\vdash ^{\alpha _i}\Delta ,A_i$
and
 $\alpha _i<\alpha $
for
$\alpha _i<\alpha $
for
 $i=1,2$
, then
$i=1,2$
, then
 $\vdash ^\alpha \Delta , A_1\wedge A_2$
.
$\vdash ^\alpha \Delta , A_1\wedge A_2$
. -
(∨) If
 $\vdash ^{\alpha _i}\Delta ,A_i$
and
$\vdash ^{\alpha _i}\Delta ,A_i$
and
 $\alpha _i<\alpha $
for some
$\alpha _i<\alpha $
for some
 $i\in \{1,2\}$
, then
$i\in \{1,2\}$
, then
 $\vdash ^\alpha \Delta , A_1\vee A_2$
.
$\vdash ^\alpha \Delta , A_1\vee A_2$
. -
(∀) If
 $\vdash ^{\alpha _i}\Delta ,A(i)$
and
$\vdash ^{\alpha _i}\Delta ,A(i)$
and
 $\alpha _i<\alpha $
for all
$\alpha _i<\alpha $
for all
 $i\in \mathbb {N}$
, then
$i\in \mathbb {N}$
, then
 $\vdash ^\alpha \Delta , \forall x A(x)$
.
$\vdash ^\alpha \Delta , \forall x A(x)$
. -
(∃) If
 $\vdash ^{\alpha _i}\Delta ,A(i)$
and
$\vdash ^{\alpha _i}\Delta ,A(i)$
and
 $\alpha _i<\alpha $
for some
$\alpha _i<\alpha $
for some
 $i\in \mathbb {N}$
, then
$i\in \mathbb {N}$
, then
 $\vdash ^\alpha \Delta , \exists x A(x)$
.
$\vdash ^\alpha \Delta , \exists x A(x)$
.
The relation
![]() $\vdash ^\alpha \Delta $
is to be read that there is an infinite proof tree of
$\vdash ^\alpha \Delta $
is to be read that there is an infinite proof tree of
![]() $\bigvee \Delta $
whose depth is bounded by the ordinal
$\bigvee \Delta $
whose depth is bounded by the ordinal
![]() $\alpha $
.
$\alpha $
.
Let’s briefly record two lemmas that we will make use of. First we state the “monotonicity lemma,” which follows immediately from the definition of
![]() $\vdash ^\alpha \Delta $
:
$\vdash ^\alpha \Delta $
:
Lemma 4.2. If
![]() $\vdash ^\alpha \Delta $
,
$\vdash ^\alpha \Delta $
,
![]() $\alpha \leqslant \beta $
, and
$\alpha \leqslant \beta $
, and
![]() $\Delta \subseteq \Gamma $
, then
$\Delta \subseteq \Gamma $
, then
![]() $\vdash ^\beta \Gamma $
.
$\vdash ^\beta \Gamma $
.
Second, we state the
![]() $\wedge $
-inversion rule. For a proof of the
$\wedge $
-inversion rule. For a proof of the
![]() $\wedge $
-inversion rule, see [Reference Pohlers10, Theorem 10.7].
$\wedge $
-inversion rule, see [Reference Pohlers10, Theorem 10.7].
Lemma 4.3. If
![]() $\vdash ^\alpha \Delta ,\bigwedge \{A_i \mid i\in I\}$
then, for all
$\vdash ^\alpha \Delta ,\bigwedge \{A_i \mid i\in I\}$
then, for all
![]() $i\in I$
,
$i\in I$
,
![]() $\vdash ^\alpha A_i$
.
$\vdash ^\alpha A_i$
.
The infinitary proof calculus is sound and complete for
![]() $\Pi ^1_1$
sentences of arithmetic:
$\Pi ^1_1$
sentences of arithmetic:
Theorem 4.4. For any
![]() $\Pi ^1_1$
sentence
$\Pi ^1_1$
sentence
![]() $\forall \vec {X}\varphi (\vec {X})$
,
$\forall \vec {X}\varphi (\vec {X})$
,
In fact, there is a sharp restricted version of the completeness half of the theorem relating consequences of
![]() $\mathsf {ACA}_0$
and proofs of height less than
$\mathsf {ACA}_0$
and proofs of height less than
![]() $\varepsilon _0$
:
$\varepsilon _0$
:
Theorem 4.5. For any
![]() $\Pi ^1_1$
sentence
$\Pi ^1_1$
sentence
![]() $\forall \vec {X} \varphi (\vec {X})$
,
$\forall \vec {X} \varphi (\vec {X})$
,
Note that the definition of infinitary derivations makes use of transfinite recursion and is beyond the scope
![]() $\mathsf {ACA}_0$
. Nevertheless, there are many methods for formalizing infinitary derivations in such a way that appropriate versions of Lemmas 4.2, 4.3 and Theorem 4.5 are provable in
$\mathsf {ACA}_0$
. Nevertheless, there are many methods for formalizing infinitary derivations in such a way that appropriate versions of Lemmas 4.2, 4.3 and Theorem 4.5 are provable in
![]() $\mathsf {ACA}_0$
, all without recourse to the fixed point lemma or recursion theorem. For present purposes, we will need to formalize only those infinitary derivations whose depth is less than
$\mathsf {ACA}_0$
, all without recourse to the fixed point lemma or recursion theorem. For present purposes, we will need to formalize only those infinitary derivations whose depth is less than
![]() $\varepsilon _0$
, a rather meager class of infinitary derivations. We will turn to the specifics in the next subsection.
$\varepsilon _0$
, a rather meager class of infinitary derivations. We will turn to the specifics in the next subsection.
4.2 Formalizing infinitary derivations
In this subsection we turn to the task of formalization in
![]() $\mathsf {ACA}_0$
. This task has two components. First, we must describe how it is that we define infinitary proofs in
$\mathsf {ACA}_0$
. This task has two components. First, we must describe how it is that we define infinitary proofs in
![]() $\mathsf {ACA}_0$
. Second, we must describe how it is that we reason about infinitary proofs in
$\mathsf {ACA}_0$
. Second, we must describe how it is that we reason about infinitary proofs in
![]() $\mathsf {ACA}_0$
. A necessary pre-condition for completing both tasks is fixing an ordinal notation system.
$\mathsf {ACA}_0$
. A necessary pre-condition for completing both tasks is fixing an ordinal notation system.
Remark 4.6. We fix a nice ordinal notation system for ordinals up to and including (at least)
![]() $2^{\varepsilon _0}+1$
. We use the symbols
$2^{\varepsilon _0}+1$
. We use the symbols
![]() $\{\boldsymbol {<},\boldsymbol {>},\boldsymbol {\leqslant },\boldsymbol {\geqslant }\}$
for this ordinal notation system. In the remainder of this section of the paper, when we use these symbols we are using them to refer to this fixed ordinal notation system.
$\{\boldsymbol {<},\boldsymbol {>},\boldsymbol {\leqslant },\boldsymbol {\geqslant }\}$
for this ordinal notation system. In the remainder of this section of the paper, when we use these symbols we are using them to refer to this fixed ordinal notation system.
The basic idea behind our definition of infinitary proofs in
![]() $\mathsf {ACA}_0$
is that infinitary proofs are
$\mathsf {ACA}_0$
is that infinitary proofs are
![]() -branching trees. Each node in the proof is tagged with a sequent, ordinal notation, and a rule:
-branching trees. Each node in the proof is tagged with a sequent, ordinal notation, and a rule:
Definition 4.7. Let
![]() $\mathsf {SEQ}$
be the set of finite sequents, i.e., sets of formulas in (Tait calculus) normal form in the signature
$\mathsf {SEQ}$
be the set of finite sequents, i.e., sets of formulas in (Tait calculus) normal form in the signature
![]() $(0,1,+,\times )$
. Let
$(0,1,+,\times )$
. Let
We demand that the trees satisfy local correctness conditions. The local correctness conditions merely say that if a node is tagged with a sequent
![]() $\Delta $
and rule R, then the premises of that node are tagged with sequents that are correct for the rule R. Buchholz essentially introduces these local correctness conditions (changed only slightly here) in [Reference Buchholz4, Definitions 2.1–2.3].
$\Delta $
and rule R, then the premises of that node are tagged with sequents that are correct for the rule R. Buchholz essentially introduces these local correctness conditions (changed only slightly here) in [Reference Buchholz4, Definitions 2.1–2.3].
Definition 4.8. Let
![]() $(\Delta ,R)\subseteq \mathsf {SEQ}\times \mathsf {RULE}$
and let
$(\Delta ,R)\subseteq \mathsf {SEQ}\times \mathsf {RULE}$
and let
![]() $(\Delta )_{i\in I}$
be a sequence of sequents (the premises of
$(\Delta )_{i\in I}$
be a sequence of sequents (the premises of
![]() $\Delta $
). We say that
$\Delta $
). We say that
![]() $(\Delta ,R)$
and
$(\Delta ,R)$
and
![]() $(\Delta )_{i\in I}$
jointly satisfy the local correctness conditions if each of the following holds:
$(\Delta )_{i\in I}$
jointly satisfy the local correctness conditions if each of the following holds:
-
(AxM) If
 $R=\mathsf {AxM}$
then
$R=\mathsf {AxM}$
then

-
(AxL) If
 $R=\mathsf {AxL}$
then there are
$R=\mathsf {AxL}$
then there are
 $t^{\mathbb {N}}=s^{\mathbb {N}}$
such that
$t^{\mathbb {N}}=s^{\mathbb {N}}$
such that
 $s\notin X,t\in X\in \Delta $
.
$s\notin X,t\in X\in \Delta $
. -
(∧) If
 $R=\wedge $
then
$R=\wedge $
then
 $I=\{1,2\}$
and for some
$I=\{1,2\}$
and for some
 $A_1$
and
$A_1$
and
 $A_2$
:
$A_2$
:  $$ \begin{align*} A_1\wedge A_2\in\Delta\ \text{and for all}\ i\in\{1,2\}, \Delta_i \subseteq \Delta,A_i.\end{align*} $$
$$ \begin{align*} A_1\wedge A_2\in\Delta\ \text{and for all}\ i\in\{1,2\}, \Delta_i \subseteq \Delta,A_i.\end{align*} $$
-
(∧) If
 $R=\vee $
then
$R=\vee $
then
 $I\subseteq \{1,2\}$
and for some
$I\subseteq \{1,2\}$
and for some
 $A_1$
and
$A_1$
and
 $A_2$
,
$A_2$
,  $$ \begin{align*}A_1\vee A_2\in\Delta\ \text{and for some}\ i\in\{1,2\}, \Delta_i \subseteq \Delta,A_i.\end{align*} $$
$$ \begin{align*}A_1\vee A_2\in\Delta\ \text{and for some}\ i\in\{1,2\}, \Delta_i \subseteq \Delta,A_i.\end{align*} $$
-
(∀) If
 $R=\forall $
then
$R=\forall $
then
 $I=\mathbb {N}$
and for some
$I=\mathbb {N}$
and for some
 $\forall xA(x)$
,
$\forall xA(x)$
,  $$ \begin{align*}\forall xA(x)\in\Delta\ \text{and for all}\ i\in \mathbb{N}, \Delta_i \subseteq \Delta,A(i).\end{align*} $$
$$ \begin{align*}\forall xA(x)\in\Delta\ \text{and for all}\ i\in \mathbb{N}, \Delta_i \subseteq \Delta,A(i).\end{align*} $$
-
(∃) If
 $R=\exists $
then
$R=\exists $
then
 $I\subseteq \mathbb {N}$
and for some
$I\subseteq \mathbb {N}$
and for some
 $\exists xA(x)$
,
$\exists xA(x)$
,  $$ \begin{align*}\exists xA(x)\in\Delta\ \text{and for some}\ i\in \mathbb{N}, \Delta_i \subseteq \Delta,A(i).\end{align*} $$
$$ \begin{align*}\exists xA(x)\in\Delta\ \text{and for some}\ i\in \mathbb{N}, \Delta_i \subseteq \Delta,A(i).\end{align*} $$
-
(CUT) If
 $R=\mathsf {CUT}$
then
$R=\mathsf {CUT}$
then
 $I=\{1,2 \}$
and for some A,
$I=\{1,2 \}$
and for some A,  $$ \begin{align*}\Delta_1 \subseteq \Delta,A\ \text{and}\ \Delta_2\subseteq \Delta,\neg A.\end{align*} $$
$$ \begin{align*}\Delta_1 \subseteq \Delta,A\ \text{and}\ \Delta_2\subseteq \Delta,\neg A.\end{align*} $$
-
(REP) If
 $R=\mathsf {REP}$
then
$R=\mathsf {REP}$
then
 $I=\{1\}$
and
$I=\{1\}$
and
 $\Delta _1 = \Delta $
.
$\Delta _1 = \Delta $
.
Definition 4.9 (
 $\mathsf {ACA}_0$
)
$\mathsf {ACA}_0$
)
An infinitary proof is an
![]() -branching tree where each node is labeled by a triple
-branching tree where each node is labeled by a triple
![]() $(\Delta ,R,\alpha )$
consisting of a sequent
$(\Delta ,R,\alpha )$
consisting of a sequent
![]() $\Delta $
, rule R, and ordinal notation
$\Delta $
, rule R, and ordinal notation
![]() $\alpha $
such that:
$\alpha $
such that:
-
(1) The ordinal labels strictly descend from the root towards the axioms.
-
(2) The local correctness conditions from Definition 4.8 are satisfied.
Note that (1) does not force the ordinal tags to be exact but merely to give bounds.
We are particular interested in those infinitary proofs in which the rule
![]() $\mathsf {CUT}$
is not applied. We write
$\mathsf {CUT}$
is not applied. We write
![]() $\vdash ^\alpha _\Delta $
if the sequent
$\vdash ^\alpha _\Delta $
if the sequent
![]() $\Delta $
has such an infinitary proof wherein the root has ordinal tag
$\Delta $
has such an infinitary proof wherein the root has ordinal tag
![]() $\alpha $
.
$\alpha $
.
Now we turn to the task of formalizing reasoning about infinitary derivations in
![]() $\mathsf {ACA}_0$
. One particularly elegant way of formalizing such reasoning is due to Buchholz [Reference Buchholz4]. We fix a standard embedding f of proofs of
$\mathsf {ACA}_0$
. One particularly elegant way of formalizing such reasoning is due to Buchholz [Reference Buchholz4]. We fix a standard embedding f of proofs of
![]() $\Pi ^1_1$
statements in
$\Pi ^1_1$
statements in
![]() $\mathsf {ACA}_0$
into infinitary derivations in
$\mathsf {ACA}_0$
into infinitary derivations in
![]() -logic. Using our ordinal notation system
-logic. Using our ordinal notation system
![]() $\boldsymbol <$
that includes a representation of
$\boldsymbol <$
that includes a representation of
![]() $\varepsilon _0$
, we can define a term system for those infinitary derivations that arise from f. The term of a proof in this term system encodes the information in its root, i.e., its sequent, the rule it was inferred with, and an ordinal bound. The definition of this term system for infinitary derivations uses primitive recursion but does not use the fixed point lemma or recursion theorem.
$\varepsilon _0$
, we can define a term system for those infinitary derivations that arise from f. The term of a proof in this term system encodes the information in its root, i.e., its sequent, the rule it was inferred with, and an ordinal bound. The definition of this term system for infinitary derivations uses primitive recursion but does not use the fixed point lemma or recursion theorem.
Remark 4.10. An infinitary proof is coded by the label of its root. Buchholz shows that there are primitive recursive functions that can be used to compute, from the code of (the root of) a proof P, the codes of P’s subtrees. Accordingly, we can use
![]() $\mathsf {ACA}_0$
(and even
$\mathsf {ACA}_0$
(and even
![]() $\mathsf {RCA}_0$
) to construct a proof tree from its code. Moreover, we will be able to prove in
$\mathsf {RCA}_0$
) to construct a proof tree from its code. Moreover, we will be able to prove in
![]() $\mathsf {ACA}_0$
that the defined tree satisfies the definition of an infinitary proof by the way Buchholz sets up his term system for infinitary derivations.
$\mathsf {ACA}_0$
that the defined tree satisfies the definition of an infinitary proof by the way Buchholz sets up his term system for infinitary derivations.
In Definition 4.9 we did not require that the ordinal tags are exact but merely that they are bounds. Hence, the new version of Lemma 4.2 is trivial:
Lemma 4.11. For any
![]() $\alpha \boldsymbol {<}\varepsilon _0$
,
$\alpha \boldsymbol {<}\varepsilon _0$
,
![]() $\mathsf {ACA}_0$
proves “if
$\mathsf {ACA}_0$
proves “if
![]() $\vdash ^\alpha \Delta $
,
$\vdash ^\alpha \Delta $
,
![]() $\alpha \boldsymbol {\leqslant }\beta $
, and
$\alpha \boldsymbol {\leqslant }\beta $
, and
![]() $\Delta \subseteq \Gamma $
, then
$\Delta \subseteq \Gamma $
, then
![]() $\vdash ^\beta \Gamma $
.”
$\vdash ^\beta \Gamma $
.”
For the analogue of Lemma 4.3, we refer the reader to the proof of Theorem 10.7 in [Reference Pohlers10]. Note that Pohlers proves Theorem 10.7 by induction along
![]() $\alpha $
. In the following we can follow suit since we are assuming
$\alpha $
. In the following we can follow suit since we are assuming
![]() $\alpha \boldsymbol <\varepsilon _0$
.
$\alpha \boldsymbol <\varepsilon _0$
.
Lemma 4.12. For any
![]() $\alpha \boldsymbol {<}\varepsilon _0$
,
$\alpha \boldsymbol {<}\varepsilon _0$
,
![]() $\mathsf {ACA}_0$
proves “if
$\mathsf {ACA}_0$
proves “if
![]() $\vdash ^\alpha \Delta ,\bigwedge \{A_i \mid i\in I\}$
then, for all
$\vdash ^\alpha \Delta ,\bigwedge \{A_i \mid i\in I\}$
then, for all
![]() $i\in I$
,
$i\in I$
,
![]() $\vdash ^\alpha A_i$
.”
$\vdash ^\alpha A_i$
.”
Finally, we note that the following version of Theorem 4.5 follows easily given how we have set things up:
Theorem 4.13. For any
![]() $\Pi ^1_1$
sentence
$\Pi ^1_1$
sentence
![]() $\forall \vec {X} \varphi (\vec {X})$
, if
$\forall \vec {X} \varphi (\vec {X})$
, if
![]() $\mathsf {ACA}_0\vdash \forall \vec {X}\varphi (\vec {X})$
then for some
$\mathsf {ACA}_0\vdash \forall \vec {X}\varphi (\vec {X})$
then for some
![]() $\alpha \boldsymbol {<}\varepsilon _0$
,
$\alpha \boldsymbol {<}\varepsilon _0$
,
![]() $ \mathsf {ACA}_0$
proves that
$ \mathsf {ACA}_0$
proves that
![]() $\vdash ^\alpha \varphi (\vec {X}).$
$\vdash ^\alpha \varphi (\vec {X}).$
Indeed, if
![]() $\mathsf {ACA}_0\vdash \forall \vec {X}\varphi (\vec {X})$
then, through the usual embedding f of
$\mathsf {ACA}_0\vdash \forall \vec {X}\varphi (\vec {X})$
then, through the usual embedding f of
![]() $\mathsf {ACA}_0$
proofs into
$\mathsf {ACA}_0$
proofs into
![]() -logic,
-logic,
![]() $\mathsf {ACA}_0$
can prove that there is an infinitary derivation with height
$\mathsf {ACA}_0$
can prove that there is an infinitary derivation with height
![]() $\boldsymbol <\varepsilon _0$
of
$\boldsymbol <\varepsilon _0$
of
![]() $\varphi (\vec {X})$
. We get a term for this proof in Buchholz’s term system and then, by Remark 4.10, we use it to construct an
$\varphi (\vec {X})$
. We get a term for this proof in Buchholz’s term system and then, by Remark 4.10, we use it to construct an
![]() -proof of height
-proof of height
![]() $\alpha $
of
$\alpha $
of
![]() $\varphi (\vec {X})$
, all in
$\varphi (\vec {X})$
, all in
![]() $\mathsf {ACA}_0$
.
$\mathsf {ACA}_0$
.
Before continuing, we want to note that Lemmas 4.11 and 4.12 and Theorem 4.13 are all proved without recourse to the recursion theorem or self-reference.
4.3 The boundedness lemma
We need to check that a version of what is called “the boundedness lemma” is provable in
![]() $\mathsf {ACA}_0$
. Beckmann and Pohlers claim that a version of the boundedness lemma is already implicit in Gentzen’s [Reference Gentzen5] proof of the
$\mathsf {ACA}_0$
. Beckmann and Pohlers claim that a version of the boundedness lemma is already implicit in Gentzen’s [Reference Gentzen5] proof of the
![]() $\mathsf {PA}$
non-derivability of
$\mathsf {PA}$
non-derivability of
![]() $\varepsilon _0$
-induction. To state this result, let us recall one definition that occurs frequently in the work of Pohlers.Footnote
1
$\varepsilon _0$
-induction. To state this result, let us recall one definition that occurs frequently in the work of Pohlers.Footnote
1
Definition 4.14. The truth complexity
![]() $\mathsf {tc}\big (\forall \vec {X}\varphi (\vec {X})\big )$
of a
$\mathsf {tc}\big (\forall \vec {X}\varphi (\vec {X})\big )$
of a
![]() $\Pi ^1_1$
statement
$\Pi ^1_1$
statement
![]() $\forall \vec {X}\varphi (\vec {X})$
is the least
$\forall \vec {X}\varphi (\vec {X})$
is the least
![]() $\alpha $
such that
$\alpha $
such that
![]() $\vdash ^\alpha \varphi (\vec {X})$
.
$\vdash ^\alpha \varphi (\vec {X})$
.
Before continuing we will also fix some notation. We let
Note that
![]() $\mathsf {TI}(\prec )$
expresses transfinite induction along
$\mathsf {TI}(\prec )$
expresses transfinite induction along
![]() $\prec $
and for arithmetically definable
$\prec $
and for arithmetically definable
![]() $\prec $
the sentence
$\prec $
the sentence
![]() $\mathsf {TI}(\prec )$
is
$\mathsf {TI}(\prec )$
is
![]() $\Pi ^1_1$
. An upshot of the boundedness lemma is the boundedness theorem, which establishes a tight connection between
$\Pi ^1_1$
. An upshot of the boundedness lemma is the boundedness theorem, which establishes a tight connection between
![]() $\mathsf {otyp}(\prec )$
and
$\mathsf {otyp}(\prec )$
and
![]() $\mathsf {tc}\big (\mathsf {TI}(\prec )\big )$
. Beckmann and Pohlers attribute the following consequence of the boundedness theorem to Gentzen:
$\mathsf {tc}\big (\mathsf {TI}(\prec )\big )$
. Beckmann and Pohlers attribute the following consequence of the boundedness theorem to Gentzen:
Theorem 4.15 (Gentzen)
For any arithmetic well-ordering
![]() $\prec $
,
$\prec $
,
Beckmann [Reference Beckmann and Pohlers2] has sharpened Gentzen’s result to show that
![]() $\mathsf {otyp}(\prec )\leqslant \mathsf {tc}\big (\mathsf {TI}(\prec )\big )$
, which he derives from a sharp version of the boundedness lemma. For present purposes, we will not need the sharp version. To state the version that we will need, we need to cover some definitions.
$\mathsf {otyp}(\prec )\leqslant \mathsf {tc}\big (\mathsf {TI}(\prec )\big )$
, which he derives from a sharp version of the boundedness lemma. For present purposes, we will not need the sharp version. To state the version that we will need, we need to cover some definitions.
Definition 4.16. A formula
![]() $\varphi $
is X-positive if
$\varphi $
is X-positive if
![]() $\varphi $
has no occurrences of X of the form
$\varphi $
has no occurrences of X of the form
![]() $t\notin X$
.
$t\notin X$
.
Definition 4.17. If
![]() $\varphi $
is a formula, then
$\varphi $
is a formula, then
![]() $\varphi [X\mapsto \psi ]$
is the set of formulas we get by replacing each occurrence of
$\varphi [X\mapsto \psi ]$
is the set of formulas we get by replacing each occurrence of
![]() $t\in X$
in
$t\in X$
in
![]() $\varphi $
with
$\varphi $
with
![]() $\psi (t)$
. If
$\psi (t)$
. If
![]() $\Delta =\{\varphi _1,\dots ,\varphi _n\}$
is a set of formulas, then
$\Delta =\{\varphi _1,\dots ,\varphi _n\}$
is a set of formulas, then
![]() $\Delta [X\mapsto \psi ]=\{\varphi _1[X\mapsto \psi ],\dots ,\varphi _n[X\mapsto \psi ]\}$
.
$\Delta [X\mapsto \psi ]=\{\varphi _1[X\mapsto \psi ],\dots ,\varphi _n[X\mapsto \psi ]\}$
.
Definition 4.18. For any well-ordering
![]() $\prec $
:
$\prec $
:
-
(1)
 $|n|_\prec $
is the rank of n in
$|n|_\prec $
is the rank of n in
 $\prec $
.
$\prec $
. -
(2)
 $\prec _\alpha = \{n\mid |n|_\prec \boldsymbol <\alpha \}.$
$\prec _\alpha = \{n\mid |n|_\prec \boldsymbol <\alpha \}.$
Remark 4.19. Note that
![]() $y\in X[X\mapsto \prec _\alpha ] = |y|_\prec \boldsymbol <\alpha $
.
$y\in X[X\mapsto \prec _\alpha ] = |y|_\prec \boldsymbol <\alpha $
.
The following lemma—the boundedness lemma—is a version of Lemma 13.9 in [Reference Pohlers10]. Our proof is essentially the same as that in Pohlers, except that Pohlers relies on some notions that are not formalizable in
![]() $\mathsf {ACA}_0$
. In particular, we are careful to use partial truth-predicates rather than speak of satisfaction in
$\mathsf {ACA}_0$
. In particular, we are careful to use partial truth-predicates rather than speak of satisfaction in
![]() $\mathbb {N}$
.
$\mathbb {N}$
.
Lemma 4.20 (
 $\mathsf {ACA}_0$
)
$\mathsf {ACA}_0$
)
Let
![]() $\alpha \boldsymbol {<}\varepsilon _0$
be well-founded. Let
$\alpha \boldsymbol {<}\varepsilon _0$
be well-founded. Let
![]() $\prec $
be an arithmetic well-ordering. Let
$\prec $
be an arithmetic well-ordering. Let
![]() $\Delta $
be a finite set of X-positive formulas. Suppose that
$\Delta $
be a finite set of X-positive formulas. Suppose that
Then it follows that
where
![]() $\gamma =\beta +2^\alpha $
and
$\gamma =\beta +2^\alpha $
and
![]() $\beta =\mathsf {max}\{|t_1|_\prec ,\dots ,|t_n|_{\prec }\}$
.
$\beta =\mathsf {max}\{|t_1|_\prec ,\dots ,|t_n|_{\prec }\}$
.
Proof We prove the claim by induction on
![]() $\alpha $
; note that this is licit since we are assuming that
$\alpha $
; note that this is licit since we are assuming that
![]() $\alpha $
is well-founded. We split into cases based on the final inference in the derivation that yields
$\alpha $
is well-founded. We split into cases based on the final inference in the derivation that yields
![]() $\vdash ^\alpha \neg \mathsf {Prog}(\prec ,X),t_1\notin X,\dots ,t_n\notin X,\Delta $
. Note that we do not have to consider the inference
$\vdash ^\alpha \neg \mathsf {Prog}(\prec ,X),t_1\notin X,\dots ,t_n\notin X,\Delta $
. Note that we do not have to consider the inference
![]() $\mathsf {CUT}$
since the derivation is cut-free. Note that we also do not have to consider the inference
$\mathsf {CUT}$
since the derivation is cut-free. Note that we also do not have to consider the inference
![]() $\mathsf {REP}$
; if the given proof ends with repetition we simply look at some smaller proof of the same sequent that does not end with repetition.
$\mathsf {REP}$
; if the given proof ends with repetition we simply look at some smaller proof of the same sequent that does not end with repetition.
Case 1: The sequent
![]() $\neg \mathsf {Prog}(\prec ,X),t_1\notin X,\dots ,t_n\notin X,\Delta $
is an axiom according to (AxM). The set
$\neg \mathsf {Prog}(\prec ,X),t_1\notin X,\dots ,t_n\notin X,\Delta $
is an axiom according to (AxM). The set
![]() $\Delta $
contains a true atomic formula
$\Delta $
contains a true atomic formula
![]() $\varphi $
. Then
$\varphi $
. Then
![]() $\varphi =\varphi [X\mapsto \prec _{\gamma }]$
. So
$\varphi =\varphi [X\mapsto \prec _{\gamma }]$
. So
![]() $\Delta [X\mapsto \prec _{\gamma }]$
contains a true formula, namely
$\Delta [X\mapsto \prec _{\gamma }]$
contains a true formula, namely
![]() $\varphi =\varphi [X\mapsto \prec _{\gamma }]$
.
$\varphi =\varphi [X\mapsto \prec _{\gamma }]$
.
Case 2: The sequent
![]() $\neg \mathsf {Prog}(\prec ,X),t_1\notin X,\dots ,t_n\notin X,\Delta $
is an axiom according to (AxL).
$\neg \mathsf {Prog}(\prec ,X),t_1\notin X,\dots ,t_n\notin X,\Delta $
is an axiom according to (AxL).
![]() $\Delta $
contains a formula
$\Delta $
contains a formula
![]() $t_i\in X$
for some
$t_i\in X$
for some
![]() $i\leqslant n$
. If
$i\leqslant n$
. If
![]() $\beta _i =|t_i|_{\prec }$
, then
$\beta _i =|t_i|_{\prec }$
, then
![]() $\beta _i\leqslant \beta <\gamma $
and
$\beta _i\leqslant \beta <\gamma $
and
![]() $\mathsf {True}_{\Pi ^1_1}\big ( (t_i\in X)[X\mapsto \prec _\gamma ] \big )$
since
$\mathsf {True}_{\Pi ^1_1}\big ( (t_i\in X)[X\mapsto \prec _\gamma ] \big )$
since
![]() $\beta _i<\gamma $
. Hence
$\beta _i<\gamma $
. Hence
![]() $\mathsf {True}_{\Pi ^1_1}\big ( \bigvee \Delta [X\mapsto \prec _\gamma ] \big )$
.
$\mathsf {True}_{\Pi ^1_1}\big ( \bigvee \Delta [X\mapsto \prec _\gamma ] \big )$
.
Case 3: The final inference yields
![]() $\Delta $
. Assume that the main formula of the final inference belongs to
$\Delta $
. Assume that the main formula of the final inference belongs to
![]() $\Delta $
. Then we have the premises
$\Delta $
. Then we have the premises
where
![]() $\Delta _i$
contains only X-positive formulas. From the induction hypothesis we infer that
$\Delta _i$
contains only X-positive formulas. From the induction hypothesis we infer that
![]() $\forall i \; \mathsf {True}_{\Pi ^1_1}\Big ( \forall X \big (\bigvee \Delta _i[X\mapsto \prec _{\gamma _i}] \big ) \Big )$
where
$\forall i \; \mathsf {True}_{\Pi ^1_1}\Big ( \forall X \big (\bigvee \Delta _i[X\mapsto \prec _{\gamma _i}] \big ) \Big )$
where
![]() $\gamma _i=\beta +2^{\alpha _i}$
. Lemma 4.11, i.e., the monotonicity lemma, delivers
$\gamma _i=\beta +2^{\alpha _i}$
. Lemma 4.11, i.e., the monotonicity lemma, delivers
Appealing to Lemma 4.11 once again we infer that
since validity is preserved by all inferences.
Case 4: The final inference yields
![]() $\neg \mathsf {Prog}(\prec ,X)$
. The main formula of the final inference is
$\neg \mathsf {Prog}(\prec ,X)$
. The main formula of the final inference is
Then we have the premise:
By
![]() $\wedge $
-inversion, i.e., Lemma 4.12, we obtain
$\wedge $
-inversion, i.e., Lemma 4.12, we obtain
and also
Assume towards a contradiction that
![]() $\neg \mathsf {True}_{\Pi ^1_1}\Big ( \forall X \big (\bigvee \Delta [X\mapsto \prec _{\gamma }] \big ) \Big ).$
$\neg \mathsf {True}_{\Pi ^1_1}\Big ( \forall X \big (\bigvee \Delta [X\mapsto \prec _{\gamma }] \big ) \Big ).$
Applying the induction hypothesis to (4) we obtain
where
![]() $\gamma _0=\beta +2^{\alpha _0}$
.
$\gamma _0=\beta +2^{\alpha _0}$
.
By Lemma 4.11
By (6) we then obtain that
![]() $y\in \prec _{2^{\gamma _0}}$
for all
$y\in \prec _{2^{\gamma _0}}$
for all
![]() $y\prec t$
, i.e.,
$y\prec t$
, i.e.,
![]() $|t|_{\prec }\boldsymbol \leqslant 2^{\gamma _0}$
. Letting
$|t|_{\prec }\boldsymbol \leqslant 2^{\gamma _0}$
. Letting
![]() $\beta _0:=\mathsf {max}\{|t|_\prec ,\beta \}$
, then we have
$\beta _0:=\mathsf {max}\{|t|_\prec ,\beta \}$
, then we have
![]() $\beta _0\boldsymbol \leqslant \gamma _0$
. Applying the induction hypothesis to (5), we obtain
$\beta _0\boldsymbol \leqslant \gamma _0$
. Applying the induction hypothesis to (5), we obtain
Note that
![]() $\beta _0\boldsymbol \leqslant \beta + 2^{\alpha _0}$
and also
$\beta _0\boldsymbol \leqslant \beta + 2^{\alpha _0}$
and also
![]() $2^{\alpha _0}+2^{\alpha _0} \boldsymbol \leqslant 2^\alpha $
. Hence,
$2^{\alpha _0}+2^{\alpha _0} \boldsymbol \leqslant 2^\alpha $
. Hence,
Lemma 4.11 then yields
contradicting our initial assumption.
For the purposes of the present paper, we will appeal only to the following special case of the previous lemma:
Corollary 4.21 (
 $\mathsf {ACA}_0$
)
$\mathsf {ACA}_0$
)
Let
![]() $\alpha \boldsymbol < \varepsilon _0$
be well-founded. Let
$\alpha \boldsymbol < \varepsilon _0$
be well-founded. Let
![]() $\prec $
be an arithmetic well-ordering. Let
$\prec $
be an arithmetic well-ordering. Let
![]() $\Delta $
be a finite set of X-positive formulas. Suppose that
$\Delta $
be a finite set of X-positive formulas. Suppose that
Then it follows that
4.4 Formalizing
 $\Sigma ^1_1$
-bounding
$\Sigma ^1_1$
-bounding
We are now ready to provide a diagonalization-free proof of Lemma 2.9, restated here:
Lemma 4.22 (Rathjen)
Suppose
![]() $H(x)$
is a
$H(x)$
is a
![]() $\Sigma ^1_1$
formula such that
$\Sigma ^1_1$
formula such that
Then, for some
![]() $e\in Rec$
,
$e\in Rec$
,
Proof Let
![]() $H(x)$
be a
$H(x)$
be a
![]() $\Sigma ^1_1$
formula satisfying the hypothesis of the lemma. Then
$\Sigma ^1_1$
formula satisfying the hypothesis of the lemma. Then
![]() $H(x)$
is of the form
$H(x)$
is of the form
![]() $\exists Y\theta (x,Y)$
for some arithmetic formula
$\exists Y\theta (x,Y)$
for some arithmetic formula
![]() $\theta $
. For an
$\theta $
. For an
![]() $x\in \mathfrak {W}_{Rec}$
, let
$x\in \mathfrak {W}_{Rec}$
, let
![]() $\prec ^x$
be the well-ordering encoded by x.
$\prec ^x$
be the well-ordering encoded by x.
We reason as follows:
 $$\begin{align*} \mathsf{ACA}_0 &\vdash \forall x \big(\exists Y\theta(x,Y) \to x\in \mathfrak{W}_{Rec} \big),\\ \mathsf{ACA}_0 &\vdash \forall x \big( \neg \exists Y\theta(x,Y) \vee \forall X\mathsf{TI}(\prec^x,X) \big),\\ \mathsf{ACA}_0 &\vdash \forall x \Big( \neg \exists Y\theta(x,Y) \vee \forall X\big( \neg\mathsf{Prog}(\prec^x,X) \vee \forall y \in\mathsf{field}(\prec^x)\; y\in X \big) \Big),\\ \mathsf{ACA}_0 &\vdash \forall X \forall Y \forall x \big( \neg \theta(x,Y) \vee \neg\mathsf{Prog}(\prec^x,X) \vee \forall y \in\mathsf{field}(\prec^x) \; y\in X \big). \end{align*}$$
$$\begin{align*} \mathsf{ACA}_0 &\vdash \forall x \big(\exists Y\theta(x,Y) \to x\in \mathfrak{W}_{Rec} \big),\\ \mathsf{ACA}_0 &\vdash \forall x \big( \neg \exists Y\theta(x,Y) \vee \forall X\mathsf{TI}(\prec^x,X) \big),\\ \mathsf{ACA}_0 &\vdash \forall x \Big( \neg \exists Y\theta(x,Y) \vee \forall X\big( \neg\mathsf{Prog}(\prec^x,X) \vee \forall y \in\mathsf{field}(\prec^x)\; y\in X \big) \Big),\\ \mathsf{ACA}_0 &\vdash \forall X \forall Y \forall x \big( \neg \theta(x,Y) \vee \neg\mathsf{Prog}(\prec^x,X) \vee \forall y \in\mathsf{field}(\prec^x) \; y\in X \big). \end{align*}$$
By Theorem 4.13, there is an
![]() $\alpha \boldsymbol <\varepsilon _0$
such that the following is provable in
$\alpha \boldsymbol <\varepsilon _0$
such that the following is provable in
![]() $\mathsf {ACA}_0$
:
$\mathsf {ACA}_0$
:
We now switch to reasoning in
![]() $\mathsf {ACA}_0$
. Suppose that
$\mathsf {ACA}_0$
. Suppose that
![]() $H(n)$
holds. That is,
$H(n)$
holds. That is,
Applying Corollary 4.21 to (7) we infer that
Which, by definition of
![]() $\prec ^x_{2^\alpha }$
, is just to say
$\prec ^x_{2^\alpha }$
, is just to say
Which is just to say that
Combining (8) and (9) we see that
![]() $\forall y\in \mathsf {field}(\prec ^n) \; |y|_{\prec ^n} \boldsymbol < 2^\alpha $
.
$\forall y\in \mathsf {field}(\prec ^n) \; |y|_{\prec ^n} \boldsymbol < 2^\alpha $
.
This is just to say that
![]() $\mathsf {otyp}(\prec ^n) \boldsymbol < 2^\alpha $
. We infer that
$\mathsf {otyp}(\prec ^n) \boldsymbol < 2^\alpha $
. We infer that
Whence
![]() $2^\alpha +1\in \mathfrak {W}_{Rec}$
but
$2^\alpha +1\in \mathfrak {W}_{Rec}$
but
![]() $\neg H(2^\alpha +1)$
.
$\neg H(2^\alpha +1)$
.
5 Open problems
We will conclude with open problem concerning the sharpness of these theorems. That is, can any of the hypotheses in the statement of these theorems be weakened? There are three hypotheses that can be tweaked in interesting ways. First, there is the question of relaxing the definability condition.
Question 5.1. Is there a
![]() $\Pi ^1_1$
-sound and
$\Pi ^1_1$
-sound and
![]() $\Pi ^1_1$
-definable extension of
$\Pi ^1_1$
-definable extension of
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
that proves its own
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
that proves its own
![]() $\Pi ^1_1$
-soundness?
$\Pi ^1_1$
-soundness?
Note that a positive answer to this question would imply that Theorem 3.5 is sharp, at least along the dimension of the descriptive complexity of T.
If we do not demand that the theory extends
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
, then we can get a positive answer of sorts by considering the set of
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
, then we can get a positive answer of sorts by considering the set of
![]() $\Pi ^1_1$
truths. This theory is
$\Pi ^1_1$
truths. This theory is
![]() $\Pi ^1_1$
-sound and definable by the
$\Pi ^1_1$
-sound and definable by the
![]() $\Pi ^1_1$
predicate
$\Pi ^1_1$
predicate
![]() $\mathsf {True}_{\Pi ^1_1}(x)$
, which says that x encodes a sentence that is
$\mathsf {True}_{\Pi ^1_1}(x)$
, which says that x encodes a sentence that is
![]() $\mathsf {ACA}_0$
-provably equivalent to a
$\mathsf {ACA}_0$
-provably equivalent to a
![]() $\Pi ^1_1$
sentence. This theory proves its own
$\Pi ^1_1$
sentence. This theory proves its own
![]() $\Pi ^1_1$
-reflection statement:
$\Pi ^1_1$
-reflection statement:
which is a logical truth. However, note that this depends on treating
![]() $\Pi ^1_1$
-reflection as a single statement, which is arguably inappropriate for a theory that does not extend
$\Pi ^1_1$
-reflection as a single statement, which is arguably inappropriate for a theory that does not extend
![]() $\mathsf {ACA}_0$
. If we treated
$\mathsf {ACA}_0$
. If we treated
![]() $\Pi ^1_1$
-reflection as a schema
$\Pi ^1_1$
-reflection as a schema
 $$ \begin{align*}\Bigg\{ \forall \vec{x} \Big( \mathsf{True}_{\Pi^1_1}\big(\varphi(\vec{x})\big) \to \varphi(\vec{x}) \Big) \mid \varphi(\vec{x}) \in \Pi^1_1 \Bigg\},\end{align*} $$
$$ \begin{align*}\Bigg\{ \forall \vec{x} \Big( \mathsf{True}_{\Pi^1_1}\big(\varphi(\vec{x})\big) \to \varphi(\vec{x}) \Big) \mid \varphi(\vec{x}) \in \Pi^1_1 \Bigg\},\end{align*} $$
then the theory in question might not prove instances of this schema since
![]() $\mathsf {ACA}_0$
is required to transform arbitrary
$\mathsf {ACA}_0$
is required to transform arbitrary
![]() $\Pi ^1_1$
statements into normal form.
$\Pi ^1_1$
statements into normal form.
If we define T as the union of
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
with the set of all
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
with the set of all
![]() $\Pi ^1_1$
truths, then the
$\Pi ^1_1$
truths, then the
![]() $\Pi ^1_1$
-reflection statement
$\Pi ^1_1$
-reflection statement
is not a
![]() $\Pi ^1_1$
statement, since the antecedent is
$\Pi ^1_1$
statement, since the antecedent is
![]() $\Pi ^1_1$
, so it does not trivially follow from T.
$\Pi ^1_1$
, so it does not trivially follow from T.
Second, there is the question of relaxing the soundness condition.
Question 5.2. Is there a
![]() $\Sigma ^1_1$
-sound and
$\Sigma ^1_1$
-sound and
![]() $\Sigma ^1_1$
-definable extension of
$\Sigma ^1_1$
-definable extension of
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
that proves its own
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
that proves its own
![]() $\Pi ^1_1$
-soundness?
$\Pi ^1_1$
-soundness?
If we demand in addition that the theory proves Theorem 3.5 and provably extends
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
, then we get a strong negative answer. Suppose that:
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
, then we get a strong negative answer. Suppose that:
-
(1) T is definable by a
 $\Sigma ^1_1$
formula
$\Sigma ^1_1$
formula
 $\tau $
.
$\tau $
. -
(2) T proves that
 $\tau $
extends
$\tau $
extends
 $\Sigma ^1_1\text {-}\mathsf {AC}_0$
.
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
. -
(3) T proves the
 $\Pi ^1_1$
-soundness of
$\Pi ^1_1$
-soundness of
 $\tau $
.
$\tau $
.
Then, since T proves Theorem 3.5, T proves that
![]() $\tau $
is not
$\tau $
is not
![]() $\Pi ^1_1$
-sound. Hence, T proves both that
$\Pi ^1_1$
-sound. Hence, T proves both that
![]() $\tau $
is and is not
$\tau $
is and is not
![]() $\Pi ^1_1$
-sound, i.e., T is inconsistent, whence T is not
$\Pi ^1_1$
-sound, i.e., T is inconsistent, whence T is not
![]() $\Sigma ^1_1$
-sound.
$\Sigma ^1_1$
-sound.
Finally, there is the question of relaxing the condition that T extend
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
.
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
.
Question 5.3. Is there a
![]() $\Pi ^1_1$
-sound and
$\Pi ^1_1$
-sound and
![]() $\Sigma ^1_1$
-definable extension of
$\Sigma ^1_1$
-definable extension of
![]() $\mathsf {ACA}_0$
that proves its own
$\mathsf {ACA}_0$
that proves its own
![]() $\Pi ^1_1$
-soundness?
$\Pi ^1_1$
-soundness?
Regarding this question there are reasons to expect a negative answer. In a recent preprint [Reference Aguilera and Pakhomov1], Aguilera and Pakhomov have introduced
![]() $|T|_{\Pi ^1_2}$
, the
$|T|_{\Pi ^1_2}$
, the
![]() $\Pi ^1_2$
norm of T.
$\Pi ^1_2$
norm of T.
![]() $|T|_{\Pi ^1_2}$
is a dilator associated with T that is in some ways analogous to the proof-theoretic ordinal of T, except that it measures the
$|T|_{\Pi ^1_2}$
is a dilator associated with T that is in some ways analogous to the proof-theoretic ordinal of T, except that it measures the
![]() $\Pi ^1_2$
consequences of T. Aguilera and Pakhomov prove that
$\Pi ^1_2$
consequences of T. Aguilera and Pakhomov prove that
![]() $\Pi ^1_2$
-reflection for T is equivalent to the statement “
$\Pi ^1_2$
-reflection for T is equivalent to the statement “
![]() $|T|_{\Pi ^1_2}$
is a dilator” [Reference Aguilera and Pakhomov1, Theorem 7]; this is an analogue of Lemma 3.4. The important point is that this result is proved for T extending
$|T|_{\Pi ^1_2}$
is a dilator” [Reference Aguilera and Pakhomov1, Theorem 7]; this is an analogue of Lemma 3.4. The important point is that this result is proved for T extending
![]() $\mathsf {ACA}_0$
. An appropriate reformulation of their proof of Theorem 7 may deliver a negative answer to Question 5.3, which would strengthen Theorem 3.5.
$\mathsf {ACA}_0$
. An appropriate reformulation of their proof of Theorem 7 may deliver a negative answer to Question 5.3, which would strengthen Theorem 3.5.