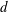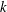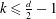Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wang, Zhenjian
2020.
On Homogeneous Polynomials Determined by their Partial Derivatives – CORRIGENDUM.
Canadian Mathematical Bulletin,
Vol. 63,
Issue. 2,
p.
479.