The mechanism of switching direction of swirling sloshing waves

Abstract

Swirling waves frequently occur in a three-dimensional tank under a nearly resonant excitation with oblique excitation angle. The oblique excitation produces two excitation components and the secondary component triggers rotational waves. The detailed mechanism of the switch in circular direction is clearly described in this study. The evolution of the hydrodynamic forces (F_z) on the tank walls presents a beating phenomenon and the switch direction always occurs at the peak and trough of the envelope of the F_z history. The external excitation moment changes the circulation intensity, and finally the swirling wave becomes a single-direction wave, but only for a short time. The profile of the single-direction wave was determined by the dominant sloshing mode and the instantaneous tank motion was found to be a key factor to determine the consequent swirling flow circulating direction.

1. Introduction

Sloshing flows occur in liquid tanks in moving vehicles, aircraft and ships, and in reservoirs during earthquakes. They may cause impact loads and there is a mutual interaction between global sloshing loads and the dynamics of the structure. It is of significant importance in the design of such containers that the physical behaviours of liquid sloshing, especially in terms of the kinematic and dynamic responses, are well understood. Excitation with frequencies in the vicinity of the lowest natural frequencies of the liquid motion is of primary practical interest.

Sloshing waves in tanks have been studied experimentally, analytically and numerically in recent decades. A comprehensive review of early analytical and experimental studies of liquid sloshing with application to the aerospace industry was reported by Abramson (1966). If the interior of the tank is smooth with no breaking waves, an inviscid/irrotational potential flow solution in combination with viscous boundary layer flow is suitable for describing sloshing (Faltinsen & Timokha 2009) and resonant sloshing (Faltinsen & Timokha 2021). For a comprehensive review of methods and results of asymptotic sloshing analysis, readers are referred to Ibrahim (2005). A three-dimensional analysis of nonlinear sloshing waves in a rectangular tank with finite water depth was reported by Faltinsen, Rognebakke & Timokha (2005). In addition to the potential flow approaches, many numerical studies in solving sloshing problems with primitive variables have been made, particularly when the fully nonlinear effects of the waves on the free surface are included. Papers that describe the modelling of two-dimensional sloshing include Frandsen (2004), and Chen & Nokes (2005).

The analysis of sloshing in three-dimensional (3-D) tanks is relatively rare in the literature. Liu & Lin (2008) developed a numerical model (Numerical Wave Tank) to study 3-D nonlinear liquid sloshing with breaking waves and liquid fragmentation. The volume of fluid (VOF) method was used, and large-eddy simulation was adopted to model the turbulence effect. Wu & Chen (2009) extended the time-independent finite-difference method to study sloshing in a 3-D tank, a spectral analysis identified the resonant frequencies of each type of wave and the results show a strong correlation between resonant modes and the occurrence of the sloshing wave types. Wu, Chen & Hung (2013) analysed the detailed hydrodynamic force components induced by transient sloshing in a 3-D tank subjected to oblique horizontal excitation.

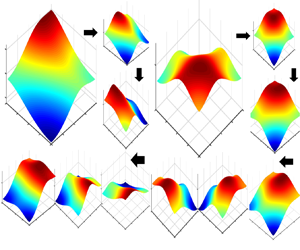
The angular frequencies, ${\omega _{i,j}}$, of the natural modes of a square base tank, can be given as (given by Faltinsen & Timokha 2009) ${\lambda _{i,j}} = {\rm \pi}\sqrt {{i^2} + {j^2}} ,\omega _{i,j}^2 = g{\lambda _{i,j}}\tanh ({\lambda _{i,j}}{d_0})$, where g is the gravitational acceleration, $d_0$ is the liquid depth of the tank and the natural modes are ${f_{i,j}} = f_i^{(1)}f_j^{(2)};\,f_i^{(1)}(x) = \cos ({\rm \pi} i(x + 1/2)),i \ge 0$ and $f_j^{(2)}(z) = \cos ({\rm \pi} j(z + 1/2)),\,j \ge 0$. Sloshing mode f_i,j shows the natural mode components triggered in the surge and sway directions; f _1,0 and f _0,1 mean pure sway (z-axis) and surge (x-axis) motions, respectively, as depicted in figure 1. Under external forcing, the swirling mode occurs when the forcing frequency is close to the first natural frequency of the liquid tank. Under a pure surge or sway motion, the swirling modes, however, can be triggered by the resonant sloshing with wave breaking and tank roof impact on the free surface (Faltinsen & Timokha 2009). For self-excited sloshing, the complex sloshing phenomenon is caused by the nonlinear interactions relating to the geometry of the tank, inlet–outlet flow directions, sloshing modes at the free surface and jet fluctuations (Saeki, Madarame & Okamoto 2001; Hua et al. 2017). Besides, once sloshing waves are triggered, the phenomenon of the complex interaction of sloshing modes at the free surface occurs. In this scenario, if the sloshing oscillation frequency is close to the first resonant frequency of the tank, resonant sloshing occurs, and it might trigger swirling modes to generate swirling waves. In this work, we only focus on the swirling waves triggered by external forcing.

Figure 1. Sketch of sloshing modes (a) f _1,0; (b) f _0,1.

In the present study, the beating swirling waves are analysed in the context of the effect of various excitation angles. The hydrodynamic forces are correlated with momentum flux-type integrals along the free surface. The momentum and angular momentum of the swirling waves are explored and analysed in detail in relation to the tank motion and types of sloshing waves. The mechanism of switching direction of swirling waves is elucidated. Section 2 introduces the equations of motion written in a moving frame of reference attached to the accelerating tank. Section 3 presents the detailed results and provides a comprehensive discussion of all phenomena found in this study. Although the governing equations incorporate excitations with six degrees of freedom, only coupled surge and sway motions are included in the present simulations. Section 4 summarizes the key conclusions.

2. Mathematical formulation

In this work, a rigid tank with an unsteady velocity and partially filled with liquid is considered. As illustrated in figure 2, the tank breadth is L, the tank width is B and d ₀ is the undisturbed liquid depth.

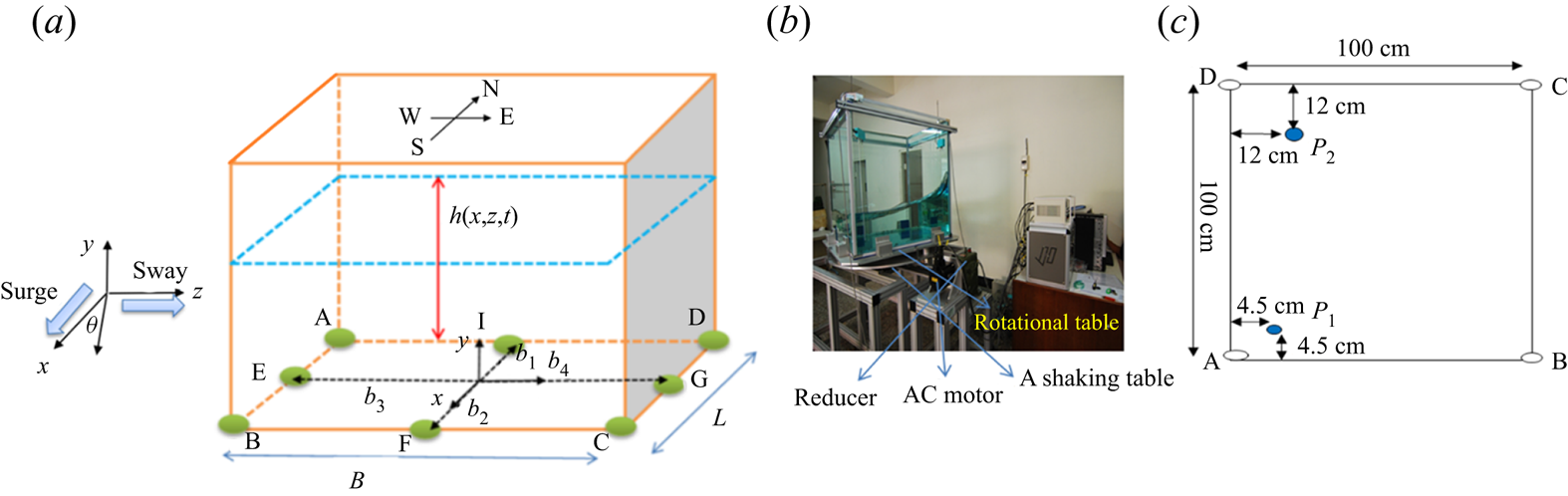
Figure 2. (a) Definition of the sketch; (b) experimental set-up; (c) positions of the wave probes from the top view of the tank.

For a tank excited at coupled surge and sway motion with the tank-fixed coordinate, the Navier–Stokes equations can be expressed as

(2.1)\begin{gather}\frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} + w\frac{{\partial u}}{{\partial z}} ={-} \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} - {\ddot{x}_C} + \upsilon {\nabla ^2}u,\end{gather}

(2.2)\begin{gather}\frac{{\partial v}}{{\partial t}} + u\frac{{\partial v}}{{\partial x}} + v\frac{{\partial v}}{{\partial y}} + w\frac{{\partial v}}{{\partial z}} ={-} g - \frac{1}{\rho }\frac{{\partial p}}{{\partial y}} + \upsilon {\nabla ^2}v,\end{gather}

(2.3)\begin{gather}\frac{{\partial w}}{{\partial t}} + u\frac{{\partial w}}{{\partial x}} + v\frac{{\partial w}}{{\partial y}} + w\frac{{\partial w}}{{\partial z}} ={-} \frac{1}{\rho }\frac{{\partial p}}{{\partial z}} - {\ddot{z}_C} + \upsilon {\nabla ^2}w,\end{gather}

where u, v and w are the liquid velocity components in the x, y and z directions relative to the tank, g is the gravitational acceleration, p is the pressure, $\rho $ is the liquid density and $\upsilon$ is the kinematic viscosity coefficient. Further, the terms ${\ddot{x}_C}$ and ${\ddot{z}_C}$ are the acceleration components of the tank in the x- and z-directions, respectively. The continuity equation for incompressible flow is

(2.4)\begin{equation}\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0.\end{equation}

The kinematic boundary condition on the free surface is

(2.5)\begin{equation}\frac{{\partial \eta }}{{\partial t}} + u\frac{{\partial \eta }}{{\partial x}} + w\frac{{\partial \eta }}{{\partial z}} = v.\end{equation}

Here, $\eta (x,z,t) = h(x,z,t) - {d_0}$ is the wave elevation measured from the liquid surface at rest. The dynamic conditions can be expressed as follows:

(2.6)\begin{gather}{n_i}{\sigma _{ij}}{n_j} ={-} {p_{atm}} = 0,\end{gather}

(2.7)\begin{gather}{\tau _i}{\sigma _{ij}}{n_j} = 0,\end{gather}

(2.8)\begin{gather}{\sigma _{ij}} ={-} p{\delta _{ij}} + \mu \left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right),\end{gather}

where ${n_i}$ and ${\tau _i}$ are the normal and tangential unit vectors to the free surface, and ${\sigma _{ij}}$ is the ith component of the stress tensor acting on the surface. Also, ${\delta _{ij}}$ is the Kronecker delta. The no-slip condition is applied at the boundary between the liquid and the tank surface except at the intersection line between the free surface and the tank surface. For the initial condition, all parameters implemented in the study are set to zero at the beginning of the simulations.

In the present study, we employ simple mapping functions to remove the time dependence of the free surface in the fluid domain. The irregular boundary, including the time-varying fluid surface, non-vertical walls and non-horizontal bottom, can be mapped onto a cubic coordinates $({x^\ast },{y^\ast },{z^\ast })$ by the proper coordinate transformations (Hung & Wang 1987; Chen & Nokes 2005). In this work, the coordinates $({x^\ast },{y^\ast },{z^\ast })$ can be further transformed such that the layers near the wall and free surface boundaries are stretched to capture sharp local velocity gradients and free surface profile. The above governing equations were solved in dimensionless forms. The detailed coordinate transformation and the dimensionless equations implemented in the study are tedious and have already been reported in Wu & Chen (2009). The Crank–Nicholson second-order finite-difference scheme and the Gauss–Seidel point successive overrelaxation iterative procedure are implemented to calculate fluid velocity and pressure, respectively. The detailed finite-difference method can be found in Appendix A and also in Wu (2009).

3. Results and discussion

The convergence study of the present numerical model was extensively validated in the reported papers (Wu & Chen 2009; Wu et al. 2013). Figure 3 compares the wave elevations at probe 1 (H_A: wave elevation at probe 1) and probe 2 (H_D: wave elevation at probe 2) of swirling waves at θ = 15°. The agreements of the comparison are very good, and more numerical validation can be found in Wu (2009) and Wu et al. (2013). The tank size of the following simulations is fixed as B/L = 1. Based on the definition of the excitation angle θ, the components of the excitation amplitude in surge (x-axis) and sway (z-axis) directions are ${a_0}\sin ({\omega _f}t)\cos (\theta )$ and ${a_0}\sin ({\omega _f}t)\sin (\theta )$, respectively, where a ₀ is the excitation amplitude of the tank and ω_f is the external forcing frequency. The numerical and experimental results show an excellent agreement. The phenomenon of switching of the direction of swirling waves was also observed in the experiment, which will be elucidated in this study.

Figure 3. Comparison between the present results of experiment and numerical simulation. The measured data at (a) wave probe P ₁; (b) wave probe P ₂; T = 0–60 s, B/L = 1, d ₀/L = 0.25, a ₀/L = 0.005, ω_f = 0.97ω _1,0, θ = 15°.

3.1. Beating phenomenon with various excitation angles

The sloshing amplitude function is a combination of an amplitude-modulated harmonic function with a frequency equal to the difference of the forced frequency (ω_f) and the fundamental frequency of liquid in tank (ω ₁) and the amplitude varying with a frequency of sum of ω_f and ω ₁. For a tank under harmonic excitation, the sloshing amplitude function may have a factor of $(\cos ({\omega _f}t)-\cos ({\omega _0}t))$ or $\sin (({\omega _0}-{\omega _f})t/2)\sin (({\omega _0} + {\omega _f}) t/2)$. If the natural and forced frequencies are similar, i.e. $|{\omega _0}-{\omega _f}|$ is small, then the amplitude function is a low-frequency function multiplying a high-frequency function. This phenomenon is known as beating. The ‘beating’ phenomenon of swirling waves is well known from experimental studies on sloshing motions in circular and spherical tanks. In particular, Abramson (1966, p. 99) noted: ‘The motion is even more complicated as a type of “beating” also exists; the first anti-symmetric liquid-sloshing mode first begins to transform itself into a rotational motion increasing in angular velocity in, say, the counterclockwise direction, which reaches a maximum and then decreases essentially to zero and then reverses and increases in the clockwise direction, and so on alternatively’.

The swirling waves only occur within a range of excitation frequencies close to the resonant excitations, and swirling behaviour is seldom seen when the excitation angle θ is larger than 30° or close to 0°. Figure 4 depicts the wave history of H_A with various excitation angles and shows different beating periods of sloshing waves. The dimensionless time T is defined as $T = t\sqrt {g/{d_0}} $. The first beating period of point A (H_A) increases as does the excitation angle. Besides, the distinct first beating period of swirling waves at various excitation angles may stem from the effect of wave nonlinearity, which is defined as the ratio of wave elevation of the maximum peak η_max to the maximum trough η_min. The nonlinearity of wave elevations of θ = 5°, 10°, 15° and 30° is 2.265, 2.312, 2.464 and 3.196, respectively, which increases with the excitation angle. The nonlinearity is also correlated deeply with water depth, excitation amplitude and excitation frequency of the tank. For more investigations of wave nonlinearity the reader referred to Wu et al. (2013).

Figure 4. Wave history (H_A) of swirling waves with various excitation angles; d ₀/L = 0.25, a ₀/L = 0.005, ω_f = 0.97ω _1,0. Solid line: θ = 5°; dash line: θ = 10°; dotted line: θ = 15°; dash-dotted line: θ = 30°.

3.2. Flow momentum and angular momentum of swirling waves

Physically, the circulatory flow motion in the tank can be correlated with the fluid momentum in the x and z axes. The dimensionless horizontal momentum of the fluid (Mo) in the tank can be obtained by

(3.1)\begin{equation}Mo = {{\left( {\rho \left[ {\iint\!\!\!\int {{u_a}\,\textrm{d}\kern0.06em x\,\textrm{d}y\,\textrm{d}z} + \iint\!\!\!\int {{w_a}\,\textrm{d}\kern0.06em x\,\textrm{d}y\,\textrm{d}z} } \right]} \right)} / {\rho \sqrt {g{d_0}} d_0^3}} = M{o_x} + M{o_z},\end{equation}

where Mo_x and Mo_z are the components of the fluid momentum contributed by velocity components u_a and w_a (global system), respectively. To investigate the rotation of swirling waves, we further define the angular momentum of the circulatory flow to the x, y and z axes in the tank, respectively, as

(3.2)\begin{gather}{M_{\theta x}} = {{\left( {\rho \left[ {\iint\!\!\!\int {{w_a}\,\textrm{d}\kern0.06em x\,\textrm{d}y\,\textrm{d}z} \times {r_y} + \iint\!\!\!\int {{v_a}\,\textrm{d}\kern0.06em x\,\textrm{d}y\,\textrm{d}z \times {r_z}} } \right]} \right)} / {\rho \sqrt {g{d_0}} d_0^4}},\end{gather}

(3.3)\begin{gather}{M_{\theta y}} = {{\left( {\rho \left[ {\iint\!\!\!\int {{u_a}\,\textrm{d}\kern0.06em x\,\textrm{d}y\,\textrm{d}z} \times {r_z} + \iint\!\!\!\int {{w_a}\,\textrm{d}\kern0.06em x\,\textrm{d}y\,\textrm{d}z \times {r_x}} } \right]} \right)} / {\rho \sqrt {g{d_0}} d_0^4}},\end{gather}

(3.4)\begin{gather}{M_{\theta z}} = {{\left( {\rho \left[ {\iint\!\!\!\int {{u_a}\,\textrm{d}\kern0.06em x\,\textrm{d}y\,\textrm{d}z} \times {r_y} + \iint\!\!\!\int {{v_a}\,\textrm{d}\kern0.06em x\,\textrm{d}y\,\textrm{d}z \times {r_x}} } \right]} \right)} / {\rho \sqrt {g{d_0}} d_0^4}},\end{gather}

where r is the horizontal distance from the tank centre to the position of the liquid element and the subscript of r is the direction to the designated axis. The swirling direction of the sloshing waves is presented by M_θy. The rate of change of angular momentum at a fixed reference point is equal to the external forces (moments) acting on the body. In other words, the external forces acting on the tank are transferred to the rate of change of angular momentum of fluid particles in the tank. The rate of change of angular momentum of sloshing waves (M_T) about the tank centre, therefore, is equal to the external moments acting on the tank

(3.5) \begin{align} {M_T} & = \dfrac{{\textrm{d}{M_{\theta y}}}}{{\textrm{d}t}} = {{\left( {\rho \left[ {\iint\!\!\!\int {\dfrac{{\textrm{d}{u_a}}}{{\textrm{d}t}}\,\textrm{d}\kern0.06em x\,\textrm{d}y\,\textrm{d}z} \times {r_z} + \iint\!\!\!\int {\dfrac{{\textrm{d}{w_a}}}{{\textrm{d}t}}\,\textrm{d}\kern0.06em x\,\textrm{d}y\,\textrm{d}z \times {r_x}} } \right]} \right)} / {\rho gd_0^4}}\\ & = \sum {r \times {F_{ext}}} . \end{align}

Angular moment M_θy tells the direction and strength of the swirling waves. We, therefore, only consider the rate of change of angular momentum in the y-axis. In this study, we define the positive and negative M_T as indicating, respectively, the counterclockwise and clockwise moments acting on the fluid by the external forcing. Figure 5 shows the time histories of the momentum of the flow and the wave elevation at point A. The total energy of sloshing waves is a combination of kinetic energy and potential energy. The maximum kinetic energy of the waves appears when the free surface is nearly flat. The peaks of Mo_x and Mo_z occur at H_A close to 0. Oppositely, as Mo_x and Mo_z are almost zero and, therefore, the peaks of H_A are presented.

Figure 5. Momentum of the waves in the x-direction (Mo_x: solid line) and in the z-direction (Mo_z: dash line) and the dimensionless elevation (H_A): dotted line; d ₀/L = 0.25, a ₀/L = 0.005, ω_f = 0.97ω _1,0, θ = 15°.

The momentum of the liquid in the tank is deeply correlated with the tank motion. As illustrated in figure 6, the motion of the tank (dotted line) will cause the liquid to move in the opposite direction to the tank motion due to the inertial effect. In other words, the forward tank motion (figure 6a, see time interval from point A to point B) results in the tendency of the backward movement of the liquid and, therefore, the original forward movement of the fluid (Mo_x and Mo_z > 0) is gradually influenced by the tank motion and then turns into the backward motion at T = 17.5 (Mo_x and Mo_z < 0). The inverse phenomenon is shown when the tank motion becomes backward (see the time interval from point B to point C). Since an inclined excitation (θ = 15°) was applied, Mo_x is initially larger than Mo_z. This indicates that the flow in the tank moves faster in the North–South direction than in the East–West direction. The phenomenon of flow motion is opposite when Mo_x < Mo_z. Besides, the travel direction of the flow in the tank can be estimated by the phase difference between Mo_x and Mo_z. As depicted in figure 6(b), the phases of Mo_x and Mo_z are almost identical during T = 0 ~ 40. This means the flow motion in the tank is travelling in a constant back-and-forth direction, referred to as ‘single-directional’ waves (Chen & Wu 2011). It is known that swirling motion occurs due to the simultaneous appearance of the f _(1,0) and f _(0,1) modes and their phase angles have some differences. That is, as the phase lag between Mo_x and Mo_z occurs, the direction of flow motion is no longer fixed, it is varied with time instead and then the circulatory flow (swirling waves) appears. The envelope of the liquid momentum increases with time (T = 0 ~ 100) as well as the strength of the flow motion inside the tank. After T > 100, the peaks of Mo_x decrease with time, whereas the peaks of Mo_z continually increase. As T = 155 ~ 165, the phase lag between Mo_x and Mo_z nearly disappears and the magnitudes of Mo_x and Mo_z are almost equal. In other words, a nearly diagonal wave appears during this period (T = 155–165). The reason the strength of the swirling waves is reduced and replaced by the diagonal-like waves can be associated with the tank motion and the fluid momentum Mo_x. The swirling waves occur when T > 40, the circulatory flow motion in the tank has its own oscillating period and the flow motion in the tank is no longer dominated by the tank motion. The phase difference between Mo_x and the tank motion gradually becomes apparent. When the phase lag of Mo_x is approximately 1/4 period later than that of the tank motion (see point D to point E), the forward tank motion encounters the instantaneous backward flow movement in the surge direction (Mo_x < 0). The strength of swirling waves gradually reduces to zero and the sloshing wave turns into a single-directional wave. In short, the evolution of sloshing waves during the first beating period includes single-directional waves (T = 0 ~ 40) → counterclockwise swirling waves (T = 40 ~ 155) → nearly single-directional waves (T = 155 ~ 165)→ clockwise swirling waves (T > 170).

Figure 6. Momentum of the waves in the x direction (Mo_x: solid line) and in the z-direction (Mo_z: dash line) and the dimensionless excitation displacement of the tank (a ₀/d ₀): dotted line; d ₀/L = 0.25, a ₀/L = 0.005, ω_f = 0.97ω _1,0, θ = 15°.

3.3. The switch of swirling directions

Faltinsen et al. (2005) indicated ‘The switching of the rotational direction of swirling waves was most probably affected by random perturbations occurring due to the local phenomena including the steepness of the wave pattern and local breaking phenomena’. However, the detailed physical mechanism by which the switching direction of swirling waves is still not clear.

Figure 7 portrays the time histories of the components of angular momentum (M_θ) of the liquid in the tank; M_θy presents the swirling direction of the waves, and positive and negative M_θy indicate counterclockwise and clockwise flow motions, respectively. As depicted in figure 7(a), M_θy apparently increases after T = 40, and so does the strength of counterclockwise swirling waves. At T = 170, M_θy decreases to become negative and the swirling wave switches from counterclockwise to clockwise. From T = 0 to 1380, there are five switches. As illustrated in figure 7(b), we found that the swirling direction switches from counterclockwise to clockwise when M_θx and M_θz are out of phase (mode (1,0), f _(1,0), is dominant) and it switches from clockwise to counterclockwise when M_θx and M_θz are in phase (mode (0,1), f _(0,1), is dominant). Besides, at the moment of switching direction, M_θx, M_θy and M_θz are all close to 0. In other words, the sloshing waves become nearly single-directional waves at the time of switch.

Figure 7. Angular momentum M_θ of swirling waves: (a) M_θx and M_θy; (b) swirling wave switch from counterclockwise to clockwise when M_θx and M_θz are out of phase; switch from clockwise to counter-clockwise when M_θx and M_θz are in phase; (c,d) zoom in of the circular parts of (b); d ₀/L = 0.25, a ₀/L = 0.005, ω_f = 0.97ω _1,0, θ = 15°.

Based on the momentum balance (Wu et al. 2013), the velocity component ‘w’ is mainly generated by external forcing components in the z-axis and can be represented by sloshing-induced force in the z direction (F_z)

(3.6)\begin{equation}{F_z} = {{\left[ {\int_{ - L/2}^{L/2} {\int_0^h {{P_W}\,\textrm{d}y\,\textrm{d}\kern0.06em x} } + \int_{ - L/2}^{L/2} {\int_0^h {{P_E}\,\textrm{d}y\,\textrm{d}\kern0.06em x} } } \right]} / {\rho gd_0^3}},\end{equation}

in which the subscripts E and W represent the pressure integrations on the east and west walls of the tank. The beating phenomenon can be found in the time history of F_z shown in figure 8 and we can connect each peak and trough of F_z for generating F_z-envelope. As depicted in figure 8, the counterclockwise swirling wave occurs as F_z increases, whereas the clockwise swirling wave appears as F_z decreases during each swirling period. At the peak and trough of F_z-envelope, the single-directional waves and the switch occur. Similar behaviours were found (figure 9) in the varied cases with different excitation angles and frequencies.

Figure 8. Horizontal sloshing-induced force component F_z; d ₀/L = 0.25, a ₀/L = 0.005, ω_f = 0.97ω _1,0 and θ = 15°. The switch direction from counterclockwise to clockwise always occurs at F_z-peak, whereas and the switch direction from clockwise to counterclockwise always occurs at F_z-trough.

Figure 9. Angular momentum components, M_θy, of swirling waves: (a) ω_f = 1.05ω _1,0, θ = 10°; (b) ω_f = 0.95ω _1,0, θ = 30°; d ₀/L = 0.25, a ₀/L = 0.005.

The question remains: Why is the swirling period of the sloshing wave related to the sloshing-induced force F_z? This can be found from the effect of the secondary mode. As the excitation angle is close to 0, the swirling wave is hard to generate unless by the influence of some other disturbances, such as breaking waves. As the excitation angle increases, the tank motion has two components which can be divided into primary and secondary components. For θ = 15°, the primary and secondary components are in the x (surge) and z (sway) directions, respectively. The primary component of tank motion excites fluid sloshing, while the secondary component of tank motion is to trigger swirling flow. As a result, the swirling period of the wave is almost identical to that of the z-component of induced force F_z, which is attributed to the secondary component of tank excitation.

In addition, the beating period of F_z can be used to estimate the swirling period of the waves. Since F_z is related to the secondary tank motion, its beating period can be approximately calculated by the 2-D beating wave period from an analytic solution

(3.7)\begin{equation}{T_a} = 2{\rm \pi}/(|{\omega _f}-{\omega _1}|)\times \sqrt {g/{d_0}} ,\end{equation}

where ω_f and ω ₁ are, respectively, the excitation frequency and the first natural frequency of liquid in tank. The mean value of the swirling period (up to T = 1500) was compared with the analytic solution, as shown in figure 10. The difference between our simulated results and the analytical solution is less than 10 % and the empirical swirling period of sloshing wave (T_s) may be expressed as

(3.8) \begin{equation}{T_s} = (1 \pm 0.1)\times 2{\rm \pi}/(|{\omega _f}-{\omega _1}|)\times \sqrt {g/{d_0}}.\end{equation}

As excitation angle θ increases, the difference between T_a and T_s increases as well, which is related to sloshing nonlinearity due to various excitation angles (Chen & Wu 2011).

Figure 10. Comparison of dimensionless swirling period of waves between the analytic result and the present simulations; d ₀/L = 0.25, a ₀/L = 0.005.

As mentioned earlier, tank displacement plays an important role in increasing or decreasing the liquid momentum (M_O) and liquid angular momentum (M_θ). The rate change of angular momentum (M_T) is equal to the sum of the external force moments acting on the fluid in the tank, as shown in (3.5). According to the definition direction of angular momentum M_θy in this study, M_T > 0 means that the external forcing moment triggers counterclockwise moments to the fluid inside the tank. On the other hand, the clockwise moment of the fluid was triggered by the external forcing moment when M_T < 0. Figure 11 depicts the time history of M_T of the swirling waves and the associated variation of M_θy. As T < 120, M_T is positive, the external forcing generates a counterclockwise moment to the fluid, which results in the increase of M_θy; M_θy gradually diminishes as T > 120 and the strength of counterclockwise flow is reduced because the external forcing induces clockwise moments (M_T < 0) to the fluid. As the counterclockwise flow strength decreases to almost 0 (M_θy ~ 0), there is no circulatory flow in the tank. As a result, single-directional waves occur. The external forcing moment varies the flow circulation strength and direction, and the switch between swirling and single-directional waves occurs. At T = 170, M_θy becomes negative and swirling flow changes to clockwise flow. As T > 200, the dominant moment induced by external forcing becomes counterclockwise (M_T > 0), which reduces the strength of the clockwise flow. Afterwards, the clockwise swirling wave shifts its direction to the counterclockwise direction (M_θy > 0) at T ~ 270. We clearly found that the external excitation forcing affects the strength of the swirling motion of the fluid in the tank.

Figure 11. The rate of change of angular momentum (M_T), and we can see how M_T (dark line) affects the increase and decrease of M_θy (orange line) and switches swirling direction; d ₀/L = 0.25, a ₀/L = 0.005, ω_f = 0.97ω _1,0, θ = 15°.

Figure 12 demonstrates one of the switch point occurring at the peak of F_z-envelope at which M_θx and M_θz are out of phase (figure 7b). At the time, M_θx-envelope is at its peak, which implies the single-direction wave is primarily attributed to f _(1,0) and the trajectory of the mass centre is biased towards the surge direction (see snapshots). The other switch point occurs at the trough of F_z-envelope at which M_θx-envelope is at its trough and f _(0,1) has more effect than f _(1,0) on the single-direction wave and the trajectory of the mass centre is biased more towards the sway direction. As an example, at T = 395.9 to 401.63, the trajectory of the flow mass centre is in a South–Westerly direction and, at the same time, the tank is moving in the South–East direction and the inertia (gravitational) effect results in switching of the swirling direction to a clockwise direction. Oppositely, at T = 521.16 to 526.62, the trajectory of the flow mass centre is moving North–Easterly and the instantaneous tank motion results in switching of the swirling direction to a counterclockwise direction. The movie of the phenomena mentioned above for swirling waves is provided as supplementary material (available at https://doi.org/10.1017/jfm.2022.896).

Figure 12. (a) Single-directional waves always occur at the peak and trough of F_z-envelope (snapshots: arrow sign in blue colour indicates the tank motion direction, arrow sign in green colour indicates the trajectory of mass volume centre); (b) snapshots of clockwise swirling waves (upper subplot in sequential order 1→2→3→4) and counterclockwise swirling waves (lower subplot in sequential order 1→2→3→4).

3.4. Frequency domain of swirling waves

The frequency domain of swirling waves would be good information to estimate the occurrence of the swirling phenomenon. We simulated more cases at various excitation angles, excitation amplitudes and water depths to find the frequency range of swirling waves and the result is depicted in figure 13. The results of Faltinsen & Timokha (2009) are also shown in the figure, their results are, however, limited to a fixed excitation direction (i.e. in the surge direction). As the tank has a shallow liquid depth, the frequency domain of swirling waves becomes wider, especially for a tank exited with a larger excitation amplitude (a ₀/L = 0.0078). On the contrary, the frequency domain of swirling waves is limited to a small range for the tank with finite liquid depths. The corresponding maximum sloshing amplitudes (η_max) of the cases of $\theta = 10\mathrm{^\circ }$ and 30° in figure 13 are depicted in figure 14, and the wave nonlinearity $\textrm{(}{\eta _{max}}/{\eta _{min}}\textrm{)}\ \textrm{at}\ \theta = 30\mathrm{^\circ }$ is illustrated in figure 15. According to the assumption of the proposed numerical model, we cannot consider the phenomena of wave breaking, wave run-up and tank roof impact in the simulations. In other words, η_max is captured before the simulation diverges at nearly resonant sloshing. In figure 14, the soft-spring and hard-spring responses of η_max are presented near the first resonant excitation frequency (ω _1,0) in a shallow liquid (d ₀/L ≤ 0.25) and at finite liquid depths (d ₀/L ≥ 0.4), respectively. In addition, the effect of excitation angle on η_max is more significant as the liquid depth decreases, especially for the shallow liquid depth. Increasing the excitation amplitude (a ₀/L = 0.0078) of the tank results in larger η_max and sloshing nonlinearity (figure 15). As the liquid depth decreases from the finite to shallow depths, the nonlinearity of sloshing waves increases significantly. As we know, the wave travel speed decreases with the liquid depth. The increased nonlinearity of sloshing waves diminishes the travel speed of sloshing waves resulting in the hysteresis phenomenon on the resonant frequency (ω _1,0) in shallow liquid depths. Thus, the soft-spring phenomenon is presented for shallow water depths.

Figure 13. The frequency domain of swirling waves under various water depths, excitation angles and excitation amplitudes.

Figure 14. Maximum sloshing amplitude under various water depths, excitation angles and excitation amplitudes; (a) a ₀/L = 0.005; (b) a ₀/L = 0.0078.

Figure 15. Nonlinearity of sloshing waves under different water depths and excitation amplitudes; θ = 30°.

The effect of excitation angle on the shift of the frequency domain of swirling waves is clearly seen by comparing with the results of Faltinsen & Timokha (2009) for a tank under 0-degree excitation (surge motion). Although different beat periods and sloshing displacements of swirling waves are presented due to the effect of excitation angle, the corresponding frequency domains are nearly the same when the excitation angle is in the range of 5° ≤ θ < 30°. The frequency domain of swirling waves slightly reduces as θ = 30°, which might be caused by the effect of the nonlinearity of sloshing waves. In short, the evolutions of swirling waves are very sensitive to physical conditions, including liquid depth, excitation angle, excitation amplitude and frequency of external forcing.

4. Conclusion

The sloshing displacement of liquid in a tank is a combination of the standing wave and forced (progressive) wave. When a 3-D tank is under a near-resonant excitation, the beat phenomenon occurs, and a secondary excitation force creates swirling flow. In our study, the following concluding remarks can be given:

1. (i) The period of a swirling wave in a tank is closely related to the beat period, while the swirling behaviour is seldom seen when θ is larger than 30° or close to 0°. The oblique excitation produces two excitation components and the secondary component triggers rotational waves.

2. (ii) The excitation moment enhances or reduces the circulation strength, and the instantaneous tank motion finally switches the circulation direction. The magnitude of the components of liquid angular momentum, M_θx and M_θz, and their phase difference are the key factors in determining the quantity of fluid movement and the direction of the circulatory flow.

3. (iii) Further, the phase difference between the tank motion and the fluid momentum is significant in influencing the strength of the circulatory flow. The angular momentum of the liquid M_θy represents the strength and the rotational direction of the circulatory flow in the tank. The sum of the moment made by an external force acting on the fluid is equal to the rate of change of angular momentum of the fluid, and plays an important role in affecting the strength of rotation of swirling waves.

4. (iv) The evolutions of swirling waves are very sensitive to physical conditions, including liquid depth, excitation angle, excitation amplitude and frequency of external forcing.

5. (v) The switch of the swirling direction always occurs at the peak or trough of F_z-envelope. The external excitation moment varies the circulation strength, and the swirling wave becomes a single-directional wave, but it is only sustained for a short period of time. The instantaneous tank motion at the time finally switches the consequent circulation direction.