1. Introduction
Synchronisation of the wake behind a bluff body to its structural vibration is of interest for various engineering applications. Such synchronisation can cause detrimental effects, such as structural fatigue and resonance induced by vortex-induced vibrations (Sarpkaya Reference Sarpkaya2004; Williamson & Govardhan Reference Williamson and Govardhan2004). Alternatively, promoting synchronisation can enhance the performance in other engineering systems, such as the molecular mixing rate in chemical reactors (Celik & Beskok Reference Celik and Beskok2009), the heat transfer rate of heat exchangers (Gau, Wu & Su Reference Gau, Wu and Su2001) and the efficiency of energy-harvesting systems (Wang et al. Reference Wang, Geng, Ding, Zhu and Yurchenko2020). The importance of accurately predicting synchronisation conditions in engineering systems cannot be emphasised enough (Bearman Reference Bearman1984; Naudascher & Rockwell Reference Naudascher and Rockwell2005).
Previous studies have investigated the synchronisation between the vortex shedding frequency from a bluff body, mainly for a circular cylinder and its oscillatory motion. For various types of oscillation motions and Reynolds numbers, synchronisation regimes and vortex patterns have been identified and classified in both experimental and numerical studies (Olinger & Sreenivasan Reference Olinger and Sreenivasan1988; Ongoren & Rockwell Reference Ongoren and Rockwell1988; Williamson & Roshko Reference Williamson and Roshko1988; Woo Reference Woo1999; Ponta & Aref Reference Ponta and Aref2005; Perdikaris, Kaiktsis & Triantafyllou Reference Perdikaris, Kaiktsis and Triantafyllou2009; Jacono et al. Reference Jacono, Leontini, Thompson and Sheridan2010; Leontini, Jacono & Thompson Reference Leontini, Jacono and Thompson2011). These studies are based on time-consuming sweeps of the parametric space in the amplitude-frequency domain using forced motion of a bluff body. Moreover, the synchronisation boundaries are identified differently depending on the identification criteria used (Kumar, Navrose & Mittal Reference Kumar, Navrose and Mittal2016) and the wake measurement location (Kumar et al. Reference Kumar, Lopez, Probst, Francisco, Askari and Yang2013). These subtle difficulties in the identification of precise synchronisation conditions, as well as a lack of understanding the underlying physics, highlight some weaknesses of previous experimental and numerical approaches. Therefore, a theoretical approach to investigate synchronisation is desirable.
The theoretical approach we consider is phase-reduction analysis, which describes the dynamics of high-dimensional periodic flows in terms of a single scalar variable ‘phase’. Phase-reduction analysis has been applied to nonlinear oscillators in a wide range of studies, including those on biological rhythms (Winfree Reference Winfree1967; Shiogai, Stefanovska & McClintock Reference Shiogai, Stefanovska and McClintock2010) and chemical oscillators (Kuramoto Reference Kuramoto2003; Pietras & Daffertshofer Reference Pietras and Daffertshofer2019). This technique enables us to examine synchronisation without extensive parametric sweeps by identifying the phase response of flows to external perturbations (Taira & Nakao Reference Taira and Nakao2018; Khodkar & Taira Reference Khodkar and Taira2020; Khodkar, Klamo & Taira Reference Khodkar, Klamo and Taira2021; Loe et al. Reference Loe, Nakao, Jimbo and Kotani2021). Furthermore, phase-reduction analysis has been used to guide flow control of periodic flows (Nair et al. Reference Nair, Taira, Brunton and Brunton2021; Godavarthi, Kawamura & Taira Reference Godavarthi, Kawamura and Taira2023; Loe et al. Reference Loe, Zheng, Kotani and Jimbo2023; Fukami, Nakao & Taira Reference Fukami, Nakao and Taira2024). However, all previous applications of phase-reduction analysis were focused on two-dimensional periodic flows, even though synchronisation in real engineering systems often involves three-dimensional flows. The three-dimensionality of a flow creates added richness compared with its two-dimensional counterpart, which influences the synchronisation properties. Hence, it is important to identify the influence of three-dimensionality on synchronisation. However, the implementation of phase-reduction analysis is not straightforward for three-dimensional wakes since, generally, they are not perfectly periodic.
In this study, we examine the effect of three-dimensionality on the synchronisation of a cylinder's wake to the motion of the cylinder. We consider rotational, cross-flow translational and streamwise translational oscillations, which are the bases of in-plane cylinder oscillation. We extend the phase reduction analysis to characterise the perturbation dynamics of three-dimensional flows. Since the underlying three-dimensionality adds fluctuations to the limit cycle, we leverage an ensemble-averaging technique to obtain mean responses of the three-dimensional wake.
This paper is organised as follows. Physical characteristics of three-dimensional wakes are presented in § 2. Fundamentals of phase-reduction analysis for periodic flows are introduced in § 3 with a new technique to measure the phase response of three-dimensional flows. The results of the present phase-reduction analysis are provided in § 4, revealing the influence of three-dimensionality within the flow on the synchronisation. Conclusions are offered in § 5.
2. Numerical simulation of cylinder wakes
2.1. Problem description and numerical set-ups
We consider two- and three-dimensional incompressible wakes past a circular cylinder using direct numerical simulations (DNS). The Reynolds number in this study is selected as ![]() ${\textit {Re}} = U_{\infty }D/\nu = 300$, where
${\textit {Re}} = U_{\infty }D/\nu = 300$, where ![]() $U_{\infty }$ is the free-stream velocity,
$U_{\infty }$ is the free-stream velocity, ![]() $D$ is the diameter of the cylinder and
$D$ is the diameter of the cylinder and ![]() $\nu$ is the kinematic viscosity. The Reynolds number is selected such that the cylinder wake develops three-dimensional structures, which is discussed in more detail in § 2.2. A finite-volume formulation (Ham & Iaccarino Reference Ham and Iaccarino2004; Ham, Mattsson & Iaccarino Reference Ham, Mattsson and Iaccarino2006) and a fractional-step method (Kim & Moin Reference Kim and Moin1985) with second-order accuracy are adopted for spatial discretisation and time stepping, respectively. The computational domain is extended to
$\nu$ is the kinematic viscosity. The Reynolds number is selected such that the cylinder wake develops three-dimensional structures, which is discussed in more detail in § 2.2. A finite-volume formulation (Ham & Iaccarino Reference Ham and Iaccarino2004; Ham, Mattsson & Iaccarino Reference Ham, Mattsson and Iaccarino2006) and a fractional-step method (Kim & Moin Reference Kim and Moin1985) with second-order accuracy are adopted for spatial discretisation and time stepping, respectively. The computational domain is extended to ![]() $(x,y)/D \in [-20,30] \times [-40,40]$ from the centre of the cylinder shown in figure 1. To simulate the three-dimensional wake, the spanwise extension of the computational domain is set to
$(x,y)/D \in [-20,30] \times [-40,40]$ from the centre of the cylinder shown in figure 1. To simulate the three-dimensional wake, the spanwise extension of the computational domain is set to ![]() $z/D \in [-2,2]$ with the spanwise extent of the cylinder being
$z/D \in [-2,2]$ with the spanwise extent of the cylinder being ![]() $L_{z}/D = 4$, which allows us to capture the three-dimensional features related to mode A and mode B instabilities (Barkley & Henderson Reference Barkley and Henderson1996). Structured grids are generated near the cylinder and in the downstream region with the uniform grid size
$L_{z}/D = 4$, which allows us to capture the three-dimensional features related to mode A and mode B instabilities (Barkley & Henderson Reference Barkley and Henderson1996). Structured grids are generated near the cylinder and in the downstream region with the uniform grid size ![]() $\Delta z/D = 0.05$ in the spanwise direction, which sufficiently resolves flow structures of mode A and B (
$\Delta z/D = 0.05$ in the spanwise direction, which sufficiently resolves flow structures of mode A and B (![]() $\lambda _{A}/D \approx 4$ and
$\lambda _{A}/D \approx 4$ and ![]() $\lambda _{B}/D \approx 0.8$). To reduce computational costs, hybrid-typed grids with approximately 0.1 million and 7.3 million volume cells are used for two- and three-dimensional wakes, respectively. Grid distributions in other directions are stretched to cluster cells near the cylinder surface. Far-field regions are discretised in an unstructured manner. The time step size of
$\lambda _{B}/D \approx 0.8$). To reduce computational costs, hybrid-typed grids with approximately 0.1 million and 7.3 million volume cells are used for two- and three-dimensional wakes, respectively. Grid distributions in other directions are stretched to cluster cells near the cylinder surface. Far-field regions are discretised in an unstructured manner. The time step size of ![]() $U_\infty \Delta t /D = 0.005$ guarantees the Courant–Friedrichs–Lewy (CFL) number remains small,
$U_\infty \Delta t /D = 0.005$ guarantees the Courant–Friedrichs–Lewy (CFL) number remains small, ![]() $U_\infty \Delta t/\Delta x < 1$, during computations.
$U_\infty \Delta t/\Delta x < 1$, during computations.
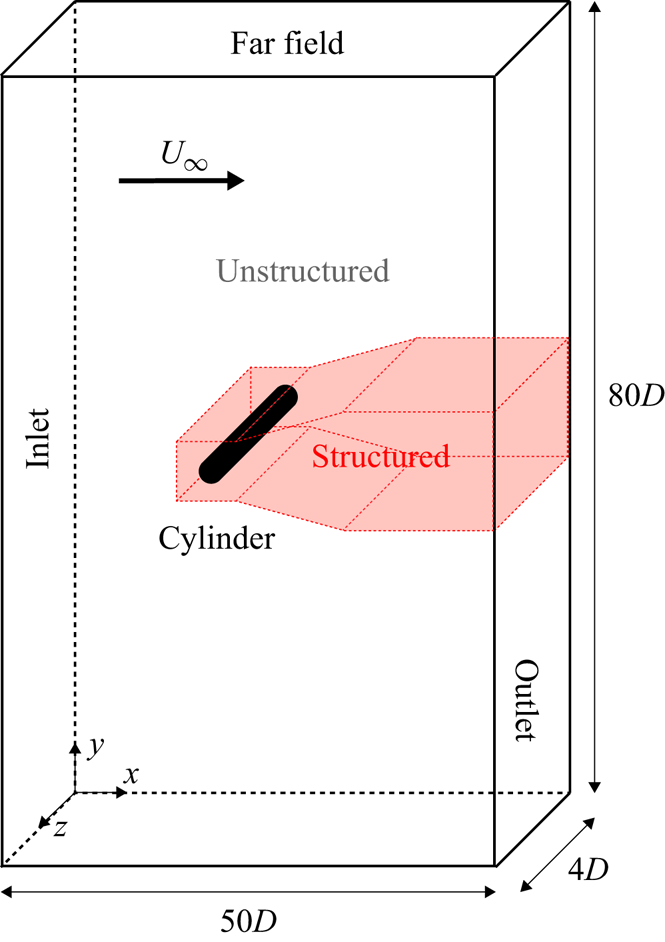
Figure 1. Computational domain for DNS of three-dimensional cylinder wakes.
For the DNS of the flow over a stationary cylinder, Dirichlet boundary conditions are given to the inlet boundary with the free-stream velocity ![]() $\boldsymbol {u}=(U_{\infty },0,0)$ and the cylinder surface with
$\boldsymbol {u}=(U_{\infty },0,0)$ and the cylinder surface with ![]() $\boldsymbol {u}=\boldsymbol {0}$, respectively. The far-field boundary is prescribed with a Neumann condition of
$\boldsymbol {u}=\boldsymbol {0}$, respectively. The far-field boundary is prescribed with a Neumann condition of ![]() $\partial \boldsymbol {u}/\partial n = \boldsymbol {0}$. The periodic boundary condition is enforced in the spanwise direction, and a convective outlet condition is given to the outflow boundary. Our numerical solutions are validated through a comparison of the Strouhal number,
$\partial \boldsymbol {u}/\partial n = \boldsymbol {0}$. The periodic boundary condition is enforced in the spanwise direction, and a convective outlet condition is given to the outflow boundary. Our numerical solutions are validated through a comparison of the Strouhal number, ![]() ${\textit {St}}$, the lift coefficient,
${\textit {St}}$, the lift coefficient, ![]() $C_{L}$, and the drag coefficient,
$C_{L}$, and the drag coefficient, ![]() $C_{D}$, respectively, defined as
$C_{D}$, respectively, defined as
where ![]() $\rho$ denotes the fluid density,
$\rho$ denotes the fluid density, ![]() $F_L$ and
$F_L$ and ![]() $F_D$ represent the lift and drag acting on the cylinder and
$F_D$ represent the lift and drag acting on the cylinder and ![]() $f_L$ is the frequency of the lift fluctuations that contains the maximum energy. Table 1 summarises the validation of the current simulation.
$f_L$ is the frequency of the lift fluctuations that contains the maximum energy. Table 1 summarises the validation of the current simulation.
Table 1. Comparison of the Strouhal number (![]() ${\textit {St}}$), root-mean-squared lift coefficient (
${\textit {St}}$), root-mean-squared lift coefficient (![]() $C^{\prime }_{L}$) and time-averaged drag coefficients (
$C^{\prime }_{L}$) and time-averaged drag coefficients (![]() $\bar {C}_D$) based on 200 shedding cycles for two- and three-dimensional cylinder flows at
$\bar {C}_D$) based on 200 shedding cycles for two- and three-dimensional cylinder flows at ![]() ${\textit {Re}} = 300$.
${\textit {Re}} = 300$.

To measure the phase-response and identify the synchronisation boundaries of the cylinder wake, we introduce impulsive and oscillatory motion for the cylinder in the DNS. The motions of the cylinder are prescribed with the instantaneous translational or rotational speed of the cylinder, ![]() $U(t)$. The impulsive motion is approximated with a Gaussian function
$U(t)$. The impulsive motion is approximated with a Gaussian function
 \begin{equation} U(t) = \varepsilon\delta(t-t_{0}) \simeq \frac{\varepsilon}{\sqrt{2{\rm \pi}}\sigma}\exp\left[-\frac{1}{2}\left(\frac{t-t_0}{\sigma}\right)^2\right], \end{equation}
\begin{equation} U(t) = \varepsilon\delta(t-t_{0}) \simeq \frac{\varepsilon}{\sqrt{2{\rm \pi}}\sigma}\exp\left[-\frac{1}{2}\left(\frac{t-t_0}{\sigma}\right)^2\right], \end{equation}
where ![]() $\varepsilon$ is the magnitude of the impulsive motion and
$\varepsilon$ is the magnitude of the impulsive motion and ![]() $\sigma$ determines the width of the Gaussian function, which is set to
$\sigma$ determines the width of the Gaussian function, which is set to ![]() $\sigma =10\Delta t$ in this study. Similarly, the oscillatory cylinder motion is modelled using the sinusoidal form
$\sigma =10\Delta t$ in this study. Similarly, the oscillatory cylinder motion is modelled using the sinusoidal form
where ![]() $U_{f}$ and
$U_{f}$ and ![]() $\varOmega _{f}$ are the oscillation amplitude and angular frequency. Cylinder motions are incorporated in the DNS by modifying the boundary conditions depending on the type of motion (Khodkar et al. Reference Khodkar, Klamo and Taira2021). For the rotating cylinder,
$\varOmega _{f}$ are the oscillation amplitude and angular frequency. Cylinder motions are incorporated in the DNS by modifying the boundary conditions depending on the type of motion (Khodkar et al. Reference Khodkar, Klamo and Taira2021). For the rotating cylinder, ![]() $U(t)$ is assigned to the tangential velocity at the cylinder surface, replacing the no-slip condition. Cross-flow and streamwise translations are realised by moving the reference frame, subtracting
$U(t)$ is assigned to the tangential velocity at the cylinder surface, replacing the no-slip condition. Cross-flow and streamwise translations are realised by moving the reference frame, subtracting ![]() $U(t)$ from the velocity at the inlet and far-field boundary.
$U(t)$ from the velocity at the inlet and far-field boundary.
2.2. Wake characteristics of a stationary cylinder
We analyse the fundamental flow physics of the three-dimensional wake of a stationary cylinder at ![]() ${\textit {Re}} = 300$ focusing on its representation in the phase plane. We start by providing a definition of the phase,
${\textit {Re}} = 300$ focusing on its representation in the phase plane. We start by providing a definition of the phase, ![]() $\theta$, and the amplitude,
$\theta$, and the amplitude, ![]() $r$, of a cylinder's wake based on the lift coefficient
$r$, of a cylinder's wake based on the lift coefficient ![]() $C_{L}$ and its Hilbert transform
$C_{L}$ and its Hilbert transform ![]() $\tilde {C}_{L}$ (Rosenblum, Pikovsky & Kurths Reference Rosenblum, Pikovsky and Kurths1996; Pikovsky et al. Reference Pikovsky, Rosenblum, Osipov and Kurths1997) as
$\tilde {C}_{L}$ (Rosenblum, Pikovsky & Kurths Reference Rosenblum, Pikovsky and Kurths1996; Pikovsky et al. Reference Pikovsky, Rosenblum, Osipov and Kurths1997) as
where ![]() $\textrm {p.v.}$ denotes the Cauchy principal value, and
$\textrm {p.v.}$ denotes the Cauchy principal value, and ![]() $\theta _{0}$ is determined as
$\theta _{0}$ is determined as ![]() ${\rm \pi} /2$ to be consistent with earlier studies (Taira & Nakao Reference Taira and Nakao2018; Khodkar & Taira Reference Khodkar and Taira2020).
${\rm \pi} /2$ to be consistent with earlier studies (Taira & Nakao Reference Taira and Nakao2018; Khodkar & Taira Reference Khodkar and Taira2020).
The wake behind a circular cylinder undergoes the first bifurcation at ![]() ${\textit {Re}} \approx 47$ caused by the primary instability. It triggers the wake transition from a flow with two steady counter-rotating vortices to a two-dimensional periodic flow with von Kármán vortex shedding (Jackson Reference Jackson1987; Provansal, Mathis & Boyer Reference Provansal, Mathis and Boyer1987). However, at
${\textit {Re}} \approx 47$ caused by the primary instability. It triggers the wake transition from a flow with two steady counter-rotating vortices to a two-dimensional periodic flow with von Kármán vortex shedding (Jackson Reference Jackson1987; Provansal, Mathis & Boyer Reference Provansal, Mathis and Boyer1987). However, at ![]() ${\textit {Re}} = 300$, since the computational domain is restricted to only be two-dimensional for the left-hand side graphic of figure 2(a), it qualitatively shows this primary instability. The two-dimensional wake presents a strong single peak in the corresponding frequency spectrum shown in figure 2(c), indicating the perfect periodicity of the two-dimensional wake. In the phase plane, the two-dimensional wake is represented by the limit cycle as shown in figure 2(d). By increasing the Reynolds number further, or in our case by making the computational domain three-dimensional in the case of the right-hand side graphic of figure 2(a), the second bifurcation occurs and the wake becomes three-dimensional. This transition to the three-dimensional flow is due to the emergence of two distinct instabilities (Williamson & Roshko Reference Williamson and Roshko1988; Barkley & Henderson Reference Barkley and Henderson1996; Williamson Reference Williamson1996; Posdziech & Grundmann Reference Posdziech and Grundmann2001; Rolandi et al. Reference Rolandi, Fontane, Jardin, Gressier and Joly2023). The mode A instability occurs at
${\textit {Re}} = 300$, since the computational domain is restricted to only be two-dimensional for the left-hand side graphic of figure 2(a), it qualitatively shows this primary instability. The two-dimensional wake presents a strong single peak in the corresponding frequency spectrum shown in figure 2(c), indicating the perfect periodicity of the two-dimensional wake. In the phase plane, the two-dimensional wake is represented by the limit cycle as shown in figure 2(d). By increasing the Reynolds number further, or in our case by making the computational domain three-dimensional in the case of the right-hand side graphic of figure 2(a), the second bifurcation occurs and the wake becomes three-dimensional. This transition to the three-dimensional flow is due to the emergence of two distinct instabilities (Williamson & Roshko Reference Williamson and Roshko1988; Barkley & Henderson Reference Barkley and Henderson1996; Williamson Reference Williamson1996; Posdziech & Grundmann Reference Posdziech and Grundmann2001; Rolandi et al. Reference Rolandi, Fontane, Jardin, Gressier and Joly2023). The mode A instability occurs at ![]() ${\textit {Re}} \approx 190$ with the spanwise wavelength
${\textit {Re}} \approx 190$ with the spanwise wavelength ![]() $\lambda _{A}/D \approx 4$ which deforms the primary vortices. The mode B instability starts to appear at the higher Reynolds number of
$\lambda _{A}/D \approx 4$ which deforms the primary vortices. The mode B instability starts to appear at the higher Reynolds number of ![]() ${\textit {Re}}\approx 240$ with the spanwise wavelength
${\textit {Re}}\approx 240$ with the spanwise wavelength ![]() $\lambda _{B}/D \approx 0.8$. This instability mode is associated with secondary fine structures in the braid region, stretched in the streamwise direction and connecting the primary vortices. These instability modes create time-varying lift fluctuations associated with the more broadband frequency spectrum and a corresponding shift in the peak frequency, as shown in figure 2(b,c). The three-dimensional wake exhibits an unclosed trajectory with the amplitude variation in the phase plane, depicted in figure 2(d).
$\lambda _{B}/D \approx 0.8$. This instability mode is associated with secondary fine structures in the braid region, stretched in the streamwise direction and connecting the primary vortices. These instability modes create time-varying lift fluctuations associated with the more broadband frequency spectrum and a corresponding shift in the peak frequency, as shown in figure 2(b,c). The three-dimensional wake exhibits an unclosed trajectory with the amplitude variation in the phase plane, depicted in figure 2(d).

Figure 2. Comparison of two- and three-dimensional wakes at ![]() ${\textit {Re}} = 300$. (a) Contours of spanwise vorticity of the two-dimensional wake and flow structures of three-dimensional wake visualised by the isosurface of the
${\textit {Re}} = 300$. (a) Contours of spanwise vorticity of the two-dimensional wake and flow structures of three-dimensional wake visualised by the isosurface of the ![]() $Q$-criterion at
$Q$-criterion at ![]() $Q=0.05$ coloured by spanwise vorticity. (b) Temporal variation of the lift coefficient, (c) power spectra,
$Q=0.05$ coloured by spanwise vorticity. (b) Temporal variation of the lift coefficient, (c) power spectra, ![]() $\hat {C}_{L}$, of the lift coefficient and (d) phase plane representation of the lift coefficient.
$\hat {C}_{L}$, of the lift coefficient and (d) phase plane representation of the lift coefficient.
Two instantaneous flow snapshots corresponding to lower and higher amplitudes, ![]() $r=0.44$ and
$r=0.44$ and ![]() $0.73$, at the same phase, are visualised in figures 3(a) and 3(b), respectively. The visualisations distinctly emphasise the primary and secondary vortical structures by colouring the spanwise vorticity,
$0.73$, at the same phase, are visualised in figures 3(a) and 3(b), respectively. The visualisations distinctly emphasise the primary and secondary vortical structures by colouring the spanwise vorticity, ![]() $\omega _{z}$, and streamwise vorticity,
$\omega _{z}$, and streamwise vorticity, ![]() $\omega _{x}$. We observe that the secondary vortical structures are more uniformly arranged and aligned with each other in the higher amplitude cycle with
$\omega _{x}$. We observe that the secondary vortical structures are more uniformly arranged and aligned with each other in the higher amplitude cycle with ![]() $r = 0.73$. Moreover, the primary vortices are more coherent along the spanwise direction. In contrast, in the lower-amplitude cycle with
$r = 0.73$. Moreover, the primary vortices are more coherent along the spanwise direction. In contrast, in the lower-amplitude cycle with ![]() $r = 0.44$, the streamwise stretched vortical structures appear less organised, and the primary vortex cores exhibit greater dislocations and deformation along the spanwise direction.
$r = 0.44$, the streamwise stretched vortical structures appear less organised, and the primary vortex cores exhibit greater dislocations and deformation along the spanwise direction.

Figure 3. Instantaneous wake from a stationary cylinder visualised by isosurfaces of the ![]() $Q$-criterion (
$Q$-criterion (![]() $Q=0.05$) coloured with (i)
$Q=0.05$) coloured with (i) ![]() $\omega _z$ and (ii)
$\omega _z$ and (ii) ![]() $\omega _x$ corresponding to (a)
$\omega _x$ corresponding to (a) ![]() $r=0.44$ and (b)
$r=0.44$ and (b) ![]() $0.73$.
$0.73$.
Similar trends are seen more clearly in scale-decomposed flow structures (Fujino, Motoori & Goto Reference Fujino, Motoori and Goto2023). We apply a spatial band-pass filter to the velocity field based on a two-dimensional Gaussian kernel, ![]() $G$, in the
$G$, in the ![]() $x$ and
$x$ and ![]() $y$ directions with the length scale range of
$y$ directions with the length scale range of ![]() $[\sigma _{1},\sigma _{2}]$ as
$[\sigma _{1},\sigma _{2}]$ as
where
and the integration window ![]() $\mathcal {S}$ covers the whole computational domain in the
$\mathcal {S}$ covers the whole computational domain in the ![]() $x$ and
$x$ and ![]() $y$ directions. Large- and small-scale flow structures with a length scale range of
$y$ directions. Large- and small-scale flow structures with a length scale range of ![]() $[\sigma _{max},2\sigma _{max}]$ and
$[\sigma _{max},2\sigma _{max}]$ and ![]() $[\sigma _{max}/4,\sigma _{max}/2]$ are visualised in figure 4, where the cutoff length scale is
$[\sigma _{max}/4,\sigma _{max}/2]$ are visualised in figure 4, where the cutoff length scale is ![]() $\sigma _{max}=D/(2{\rm \pi} {\textit {St}})$ (Yasuda, Goto & Vassilicos Reference Yasuda, Goto and Vassilicos2020). We observe more large-scale structures as the amplitude
$\sigma _{max}=D/(2{\rm \pi} {\textit {St}})$ (Yasuda, Goto & Vassilicos Reference Yasuda, Goto and Vassilicos2020). We observe more large-scale structures as the amplitude ![]() $r$ increases, whereas the small-scale structures diminish. These observations tell us that the cylinder wake is more irregular as the amplitude
$r$ increases, whereas the small-scale structures diminish. These observations tell us that the cylinder wake is more irregular as the amplitude ![]() $r$ decreases.
$r$ decreases.

Figure 4. Instantaneous visualisation of scale-decomposed flows by isosurfaces of the ![]() $Q$-criterion (
$Q$-criterion (![]() $Q=0.05$) corresponding to (a)
$Q=0.05$) corresponding to (a) ![]() $r=$ 0.44 and (b) 0.73. Panels (i) and (ii) capture large-scale
$r=$ 0.44 and (b) 0.73. Panels (i) and (ii) capture large-scale ![]() $[\sigma _{max},2\sigma _{max}]$ and small-scale
$[\sigma _{max},2\sigma _{max}]$ and small-scale ![]() $[\sigma _{max}/4,\sigma _{max}/2]$ structures, respectively.
$[\sigma _{max}/4,\sigma _{max}/2]$ structures, respectively.
These patterns can also be quantitatively identified by enstrophies defined as
where ![]() $\omega _{i}$ denotes the vorticity component in each direction (
$\omega _{i}$ denotes the vorticity component in each direction (![]() $i=x$,
$i=x$, ![]() $y$ and
$y$ and ![]() $z$). The non-spanwise enstrophy
$z$). The non-spanwise enstrophy ![]() $\mathcal {E}_{x}+\mathcal {E}_{y}$ characterises the three-dimensionality of the wake induced by the spanwise mixing. The integration window
$\mathcal {E}_{x}+\mathcal {E}_{y}$ characterises the three-dimensionality of the wake induced by the spanwise mixing. The integration window ![]() $\mathcal {V}$ is set to
$\mathcal {V}$ is set to ![]() $(x,y,z)/D \in [-1,4] \times [-3,3]\times [-2,2]$ to examine flow structures formed within one shedding period. The variation in the non-spanwise enstrophy,
$(x,y,z)/D \in [-1,4] \times [-3,3]\times [-2,2]$ to examine flow structures formed within one shedding period. The variation in the non-spanwise enstrophy, ![]() $\mathcal {E}_x+\mathcal {E}_y$, and spanwise enstrophy,
$\mathcal {E}_x+\mathcal {E}_y$, and spanwise enstrophy, ![]() $\mathcal {E}_z$, with
$\mathcal {E}_z$, with ![]() $r$ is shown in figure 5(a). A decrease in
$r$ is shown in figure 5(a). A decrease in ![]() $r$ corresponds to a decrease in
$r$ corresponds to a decrease in ![]() $\mathcal {E}_z$ and an increase in
$\mathcal {E}_z$ and an increase in ![]() $\mathcal {E}_x+\mathcal {E}_y$. This indicates that larger spanwise mixing occurs when
$\mathcal {E}_x+\mathcal {E}_y$. This indicates that larger spanwise mixing occurs when ![]() $r$ is smaller and induces enhancement in three-dimensional flow structures. Moreover, weaker spanwise vortices are reflected as portions of smaller fluctuation amplitude in the
$r$ is smaller and induces enhancement in three-dimensional flow structures. Moreover, weaker spanwise vortices are reflected as portions of smaller fluctuation amplitude in the ![]() $C_L$ time history, which corresponds to smaller
$C_L$ time history, which corresponds to smaller ![]() $r$ in the phase plane.
$r$ in the phase plane.

Figure 5. Variation of enstrophies with ![]() $r$. (a) Spanwise enstrophy
$r$. (a) Spanwise enstrophy ![]() $\mathcal {E}_z$ and non-spanwise enstrophy
$\mathcal {E}_z$ and non-spanwise enstrophy ![]() $\mathcal {E}_x+\mathcal {E}_y$. (b) Enstrophies of spanwise-averaged vorticity
$\mathcal {E}_x+\mathcal {E}_y$. (b) Enstrophies of spanwise-averaged vorticity ![]() $\mathcal {E}^{0}$, mode A
$\mathcal {E}^{0}$, mode A ![]() $\mathcal {E}^{A}$ and mode B
$\mathcal {E}^{A}$ and mode B ![]() $\mathcal {E}^{B}$.
$\mathcal {E}^{B}$.
To identify the dependencies between the instabilities and phase-amplitude variations of the three-dimensional wake, we apply the discrete Fourier transform (DFT) in the spanwise direction, which leads to the decomposition of the vorticity field as
 \begin{equation} \boldsymbol{\omega}(\boldsymbol{x},t) = \sum_{m=0}^{N_z/2} \hat{\boldsymbol{\omega}}(x,y,t,m){\rm e}^{2{\rm \pi} {\rm i}mz/L_{z} } = \boldsymbol{\omega}^{0}(\boldsymbol{x},t) + \boldsymbol{\omega}^{A}(\boldsymbol{x},t) + \boldsymbol{\omega}^{B}(\boldsymbol{x},t), \end{equation}
\begin{equation} \boldsymbol{\omega}(\boldsymbol{x},t) = \sum_{m=0}^{N_z/2} \hat{\boldsymbol{\omega}}(x,y,t,m){\rm e}^{2{\rm \pi} {\rm i}mz/L_{z} } = \boldsymbol{\omega}^{0}(\boldsymbol{x},t) + \boldsymbol{\omega}^{A}(\boldsymbol{x},t) + \boldsymbol{\omega}^{B}(\boldsymbol{x},t), \end{equation}
where ![]() $\hat {\boldsymbol {\omega }}$ denotes the coefficient of each Fourier mode and
$\hat {\boldsymbol {\omega }}$ denotes the coefficient of each Fourier mode and ![]() $N_z = L_z / \Delta z$ is the number of grid points in the spanwise direction. We categorise the Fourier modes into three vorticity components corresponding to the spanwise average (
$N_z = L_z / \Delta z$ is the number of grid points in the spanwise direction. We categorise the Fourier modes into three vorticity components corresponding to the spanwise average (![]() $\boldsymbol {\omega }^{0}$), mode A (
$\boldsymbol {\omega }^{0}$), mode A (![]() $\boldsymbol {\omega }^{A}$) and mode B (
$\boldsymbol {\omega }^{A}$) and mode B (![]() $\boldsymbol {\omega }^{B}$). In other words, Fourier modes with large wavelengths, such that
$\boldsymbol {\omega }^{B}$). In other words, Fourier modes with large wavelengths, such that ![]() $\lambda /D \geq 2$, are considered mode A, and the remaining Fourier modes, with shorter wavelengths, are classified as mode B. This wavelength threshold is chosen to fall within a range of stable wavelengths that separate the range of unstable wavelengths of mode A and mode B (Leontini, Jacono & Thompson Reference Leontini, Jacono and Thompson2015; Rolandi et al. Reference Rolandi, Fontane, Jardin, Gressier and Joly2023).
$\lambda /D \geq 2$, are considered mode A, and the remaining Fourier modes, with shorter wavelengths, are classified as mode B. This wavelength threshold is chosen to fall within a range of stable wavelengths that separate the range of unstable wavelengths of mode A and mode B (Leontini, Jacono & Thompson Reference Leontini, Jacono and Thompson2015; Rolandi et al. Reference Rolandi, Fontane, Jardin, Gressier and Joly2023).
As in the previous analysis, we quantify the contribution of each vorticity component by evaluating total enstrophy as shown in figure 5(b). Attributing to the orthogonality of Fourier modes, the total enstrophy, ![]() $\mathcal {E}$, is also decomposed into three parts as
$\mathcal {E}$, is also decomposed into three parts as ![]() $\mathcal {E} = \mathcal {E}^{0} + \mathcal {E}^{A} + \mathcal {E}^{B}$. Mode B surpasses mode A through the entire range of
$\mathcal {E} = \mathcal {E}^{0} + \mathcal {E}^{A} + \mathcal {E}^{B}$. Mode B surpasses mode A through the entire range of ![]() $r$, which implies the finer structures from the mode B instability are more prominent than large-scale structures from mode A. Both
$r$, which implies the finer structures from the mode B instability are more prominent than large-scale structures from mode A. Both ![]() $\mathcal {E}^{A}$ and
$\mathcal {E}^{A}$ and ![]() $\mathcal {E}^{B}$ become larger as
$\mathcal {E}^{B}$ become larger as ![]() $r$ decreases, whereas
$r$ decreases, whereas ![]() $\mathcal {E}^{0}$ shows the opposite trend. Thus, it can be argued that secondary instabilities convert two-dimensional flow features in the wake to three-dimensional structures as
$\mathcal {E}^{0}$ shows the opposite trend. Thus, it can be argued that secondary instabilities convert two-dimensional flow features in the wake to three-dimensional structures as ![]() $r$ decreases.
$r$ decreases.
We also identify regions where each instability mode actively grows by plotting the magnitudes of each vorticity component in figure 6. For the shedding cycle with ![]() $r = 0.73$, the mode A vorticity component highlights primary vortex cores, whereas mode B structures reside in the shear layers connecting two primary vortices. Flow structures of mode A last longer in the downstream region than mode B structures which implicates a faster decay rate of the mode B structures (Jiang et al. Reference Jiang, Cheng, Draper, An and Tong2016). Moreover, smooth isocontour lines of
$r = 0.73$, the mode A vorticity component highlights primary vortex cores, whereas mode B structures reside in the shear layers connecting two primary vortices. Flow structures of mode A last longer in the downstream region than mode B structures which implicates a faster decay rate of the mode B structures (Jiang et al. Reference Jiang, Cheng, Draper, An and Tong2016). Moreover, smooth isocontour lines of ![]() $\omega _{z}^{0}$ in figure 3(b) reflect the coherence of primary vortices in the spanwise direction. These trends are generally maintained in shedding cycles with smaller
$\omega _{z}^{0}$ in figure 3(b) reflect the coherence of primary vortices in the spanwise direction. These trends are generally maintained in shedding cycles with smaller ![]() $r$, although the distributions of instability modes become more irregular due to the enhanced spanwise mixing. In particular, we observe that the mode A vorticity component at smaller
$r$, although the distributions of instability modes become more irregular due to the enhanced spanwise mixing. In particular, we observe that the mode A vorticity component at smaller ![]() $r$ no longer only highlights primary vortex core regions but it is also present in the braid region. Flow structures associated with the mode B vorticity component are stronger and thickened in the braid regions, which gives rise to larger elongated vortical structures in this region. This can also be seen in figure 3. These originate from the thickening of the shear layers in the braid region connecting the two primary vortices, which now allows flow structures with the larger wavelength to be amplified within this region.
$r$ no longer only highlights primary vortex core regions but it is also present in the braid region. Flow structures associated with the mode B vorticity component are stronger and thickened in the braid regions, which gives rise to larger elongated vortical structures in this region. This can also be seen in figure 3. These originate from the thickening of the shear layers in the braid region connecting the two primary vortices, which now allows flow structures with the larger wavelength to be amplified within this region.
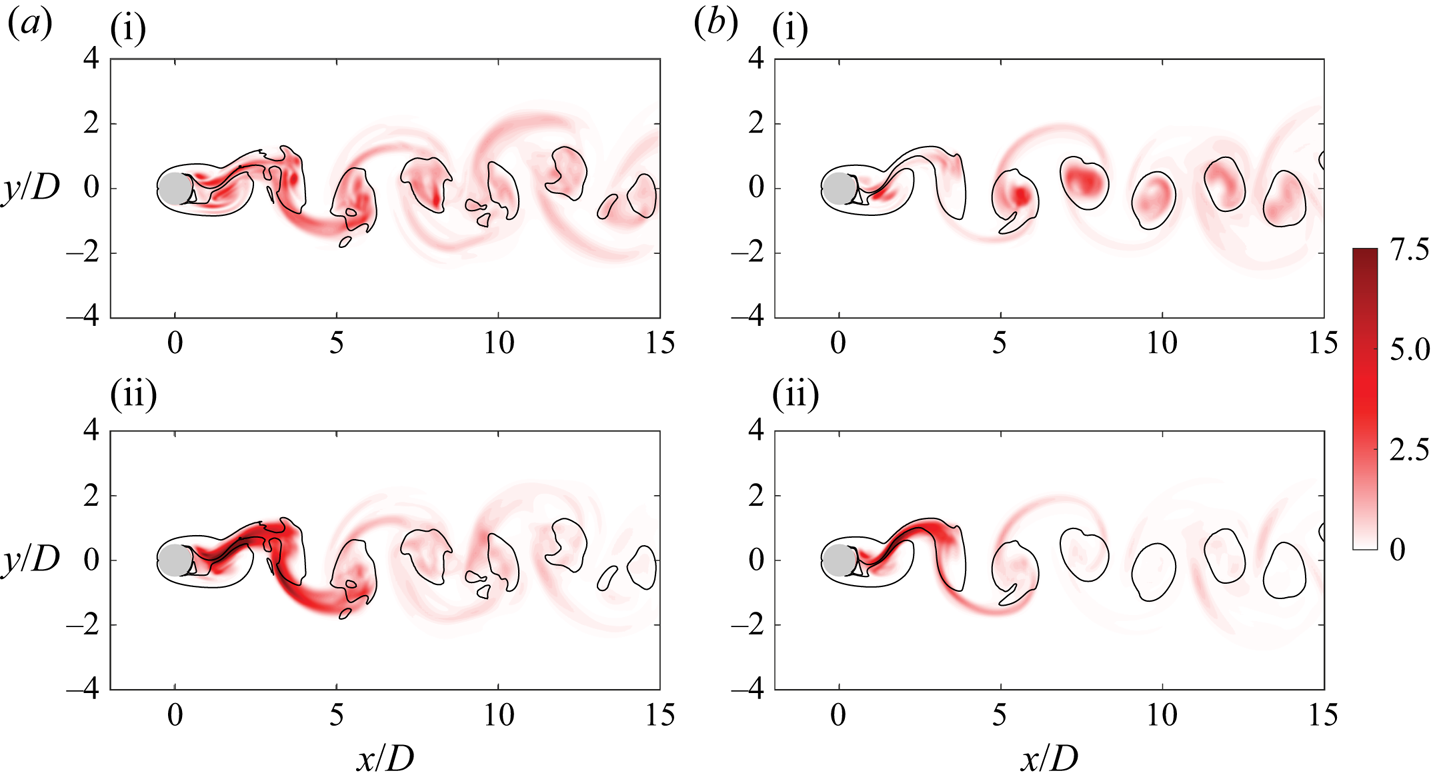
Figure 6. Contours of spanwise-averaged (i) ![]() $\boldsymbol {\omega }^{A} \boldsymbol {\cdot } \boldsymbol {\omega }^{A}$ and (ii)
$\boldsymbol {\omega }^{A} \boldsymbol {\cdot } \boldsymbol {\omega }^{A}$ and (ii) ![]() $\boldsymbol {\omega }^{B} \boldsymbol {\cdot } \boldsymbol {\omega }^{B}$ for (a)
$\boldsymbol {\omega }^{B} \boldsymbol {\cdot } \boldsymbol {\omega }^{B}$ for (a) ![]() $r=0.44$ and (b)
$r=0.44$ and (b) ![]() $0.73$. The black lines represent the contour lines of
$0.73$. The black lines represent the contour lines of ![]() $\omega ^{0}_{z} = \pm 0.5$.
$\omega ^{0}_{z} = \pm 0.5$.
3. Phase-reduction analysis of fluid flows
3.1. Phase-reduction analysis of periodic flows
The dynamics of incompressible flows governed by the Navier–Stokes (NS) equations can be expressed with the state vector ![]() $\boldsymbol {q}$ and the NS operator
$\boldsymbol {q}$ and the NS operator ![]() $\boldsymbol {\mathcal {N}}$ as
$\boldsymbol {\mathcal {N}}$ as
where ![]() $\boldsymbol {x}$ and
$\boldsymbol {x}$ and ![]() $t$ denote dimensionless space and time, respectively. A periodic flow can be described as a limit cycle solution
$t$ denote dimensionless space and time, respectively. A periodic flow can be described as a limit cycle solution ![]() $\boldsymbol {q}_0$ of the governing equation (3.1) with phase
$\boldsymbol {q}_0$ of the governing equation (3.1) with phase ![]() $\theta$. Since
$\theta$. Since ![]() $\boldsymbol {q}_0$ is periodic,
$\boldsymbol {q}_0$ is periodic, ![]() $\boldsymbol {q}_0(\boldsymbol {x},t) = \boldsymbol {q}_0(\boldsymbol {x},t+2{\rm \pi} /\varOmega _{n})$ where
$\boldsymbol {q}_0(\boldsymbol {x},t) = \boldsymbol {q}_0(\boldsymbol {x},t+2{\rm \pi} /\varOmega _{n})$ where ![]() $\varOmega _n$ is the natural angular frequency of the flow. Here, we consider the phase functional
$\varOmega _n$ is the natural angular frequency of the flow. Here, we consider the phase functional ![]() $\varTheta (\boldsymbol {q})$ that allows us to relate the high-dimensional instantaneous flow field
$\varTheta (\boldsymbol {q})$ that allows us to relate the high-dimensional instantaneous flow field ![]() $\boldsymbol {q}$ to its phase variable
$\boldsymbol {q}$ to its phase variable ![]() $\theta$. The concept of phase,
$\theta$. The concept of phase, ![]() $\varTheta (\boldsymbol {q})$, is then extended to the vicinity of the limit cycle to describe weakly perturbed flows. More specifically, if the flow
$\varTheta (\boldsymbol {q})$, is then extended to the vicinity of the limit cycle to describe weakly perturbed flows. More specifically, if the flow ![]() $\boldsymbol {q}(\boldsymbol {x},t)$ asymptotically converges to the limit cycle solution
$\boldsymbol {q}(\boldsymbol {x},t)$ asymptotically converges to the limit cycle solution ![]() $\boldsymbol {q}_{0}(\boldsymbol {x},t)$ as it develops, the phase of
$\boldsymbol {q}_{0}(\boldsymbol {x},t)$ as it develops, the phase of ![]() $\boldsymbol {q}$ is defined as
$\boldsymbol {q}$ is defined as ![]() $\varTheta (\boldsymbol {q}(\boldsymbol {x},t)) = \varTheta (\boldsymbol {q}_{0}(\boldsymbol {x},t))$. Combined with the governing equation (3.1), the phase dynamics of the unperturbed periodic flow can be described using functional derivatives of
$\varTheta (\boldsymbol {q}(\boldsymbol {x},t)) = \varTheta (\boldsymbol {q}_{0}(\boldsymbol {x},t))$. Combined with the governing equation (3.1), the phase dynamics of the unperturbed periodic flow can be described using functional derivatives of ![]() $\varTheta (\boldsymbol {q})$ as
$\varTheta (\boldsymbol {q})$ as
where ![]() $\mathcal {V}_f$ denotes the control volume.
$\mathcal {V}_f$ denotes the control volume.
Now, suppose a small perturbation term, with magnitude ![]() $\varepsilon <1$ and spatiotemporal profile
$\varepsilon <1$ and spatiotemporal profile ![]() $\boldsymbol {p}(\boldsymbol {x},t)$ such that
$\boldsymbol {p}(\boldsymbol {x},t)$ such that ![]() $\lVert \boldsymbol {p}(\boldsymbol {x},t) \rVert = 1$, is added to (3.1) to analyse the dynamics of perturbed flows,
$\lVert \boldsymbol {p}(\boldsymbol {x},t) \rVert = 1$, is added to (3.1) to analyse the dynamics of perturbed flows,
This leads to the phase dynamics of weakly perturbed flows,
For a weak perturbation, the functional derivative ![]() $\delta \varTheta /\delta \boldsymbol {q}$ can be linearly approximated with respect to the limit cycle
$\delta \varTheta /\delta \boldsymbol {q}$ can be linearly approximated with respect to the limit cycle ![]() $\boldsymbol {q}=\boldsymbol {q}_{0}$. This yields the spatial phase-sensitivity function
$\boldsymbol {q}=\boldsymbol {q}_{0}$. This yields the spatial phase-sensitivity function
 \begin{equation} \boldsymbol{Z}(\boldsymbol{x};\theta) \equiv \left. \frac{\delta\varTheta(\boldsymbol{q})}{\delta\boldsymbol{q}}\right|_{ \boldsymbol{q}=\boldsymbol{q}_{0}}, \end{equation}
\begin{equation} \boldsymbol{Z}(\boldsymbol{x};\theta) \equiv \left. \frac{\delta\varTheta(\boldsymbol{q})}{\delta\boldsymbol{q}}\right|_{ \boldsymbol{q}=\boldsymbol{q}_{0}}, \end{equation}
which provides the linear phase response of fluid flows to small external perturbations. In particular, (3.4) is further simplified by introducing the phase-sensitivity function ![]() $\zeta (\theta )$ associated with the spatial forcing profile
$\zeta (\theta )$ associated with the spatial forcing profile ![]() $\boldsymbol {f}(\boldsymbol {x})$ as
$\boldsymbol {f}(\boldsymbol {x})$ as
when the perturbation can be decomposed as ![]() $\boldsymbol {p}(\boldsymbol {x},t) = \eta (t)\boldsymbol {f}(\boldsymbol {x})$.
$\boldsymbol {p}(\boldsymbol {x},t) = \eta (t)\boldsymbol {f}(\boldsymbol {x})$.
Among the various approaches to determine the phase-sensitivity function ![]() $\zeta (\theta )$ (Nakao Reference Nakao2016; Iima Reference Iima2019; Kawamura, Godavarthi & Taira Reference Kawamura, Godavarthi and Taira2022), we employ the direct method which can be performed in both numerical and experimental studies (Taira & Nakao Reference Taira and Nakao2018). For this method, a weak impulsive perturbation
$\zeta (\theta )$ (Nakao Reference Nakao2016; Iima Reference Iima2019; Kawamura, Godavarthi & Taira Reference Kawamura, Godavarthi and Taira2022), we employ the direct method which can be performed in both numerical and experimental studies (Taira & Nakao Reference Taira and Nakao2018). For this method, a weak impulsive perturbation ![]() $\eta (t) = \delta (t-t_{0})$ is applied to the flow at different phases, where
$\eta (t) = \delta (t-t_{0})$ is applied to the flow at different phases, where ![]() $\delta (t-t_{0})$ is a Dirac-delta function centred at
$\delta (t-t_{0})$ is a Dirac-delta function centred at ![]() $t=t_{0}$. When the transient effects of the impulsive perturbation settle, the perturbed flow returns to a stable state on the limit cycle, leaving an asymptotic phase shift. The asymptotic phase shift is often referred to as the phase-response function
$t=t_{0}$. When the transient effects of the impulsive perturbation settle, the perturbed flow returns to a stable state on the limit cycle, leaving an asymptotic phase shift. The asymptotic phase shift is often referred to as the phase-response function ![]() $g(\theta ;\varepsilon ) = \lim _{t\to \infty } [\varTheta (\boldsymbol {q}_{\delta }(\boldsymbol {x},t)) - \varTheta (\boldsymbol {q}_{0}(\boldsymbol {x},t))]$, where
$g(\theta ;\varepsilon ) = \lim _{t\to \infty } [\varTheta (\boldsymbol {q}_{\delta }(\boldsymbol {x},t)) - \varTheta (\boldsymbol {q}_{0}(\boldsymbol {x},t))]$, where ![]() $\boldsymbol {q}_{\delta }$ denotes the state vector of the flow perturbed impulsively at
$\boldsymbol {q}_{\delta }$ denotes the state vector of the flow perturbed impulsively at ![]() $\theta$. The phase-sensitivity function,
$\theta$. The phase-sensitivity function, ![]() $\zeta (\theta )$, is calculated by integrating (3.6a,b) with an impulsive perturbation and results in
$\zeta (\theta )$, is calculated by integrating (3.6a,b) with an impulsive perturbation and results in ![]() $\zeta (\theta ) \approx g(\theta ;\varepsilon )/\varepsilon$ through the first-order approximation (Nakao Reference Nakao2016). Based on this perspective, the phase-sensitivity function can be interpreted physically as how much phase advancement, or delay, would be induced by imposing an external impulsive perturbation at a particular phase of the system.
$\zeta (\theta ) \approx g(\theta ;\varepsilon )/\varepsilon$ through the first-order approximation (Nakao Reference Nakao2016). Based on this perspective, the phase-sensitivity function can be interpreted physically as how much phase advancement, or delay, would be induced by imposing an external impulsive perturbation at a particular phase of the system.
Using (3.6a,b), the synchronisation of wake dynamics to any periodic forcing, with angular frequency ![]() $\varOmega _f$, can be investigated theoretically. Synchronisation between the flow and the periodic forcing is achieved when the relative phase
$\varOmega _f$, can be investigated theoretically. Synchronisation between the flow and the periodic forcing is achieved when the relative phase ![]() $\phi (t) \equiv \theta (t) - \varOmega _{f}t/m$ converges to a constant value, i.e.
$\phi (t) \equiv \theta (t) - \varOmega _{f}t/m$ converges to a constant value, i.e.
where the natural number ![]() $m$ denotes the subharmonic number of interest. This expression can be rewritten in an autonomous form by averaging over a period of the perturbation
$m$ denotes the subharmonic number of interest. This expression can be rewritten in an autonomous form by averaging over a period of the perturbation ![]() $T_{f} = 2{\rm \pi} /\varOmega _{f}$ (Kuramoto Reference Kuramoto2003; Ermentrout & Terman Reference Ermentrout and Terman2010),
$T_{f} = 2{\rm \pi} /\varOmega _{f}$ (Kuramoto Reference Kuramoto2003; Ermentrout & Terman Reference Ermentrout and Terman2010),
where ![]() $\varGamma (\phi )$ is the phase-coupling function given by
$\varGamma (\phi )$ is the phase-coupling function given by
 \begin{equation} \varGamma(\phi) = \frac{1}{T_{f}} \int _{-{\rm \pi}/\varOmega_{f}} ^{{\rm \pi}/\varOmega_{f}} \zeta\left(\phi + \frac{\varOmega_{f}}{m}\tau \right) \eta(\tau) \, \mathrm{d}\tau = \frac{1}{2{\rm \pi} } \int _{-{\rm \pi}} ^{\rm \pi} \zeta\left(\phi + \frac{\varphi}{m}\right) \eta\left(\frac{\varphi}{\varOmega_{f}}\right) \, \mathrm{d}\varphi. \end{equation}
\begin{equation} \varGamma(\phi) = \frac{1}{T_{f}} \int _{-{\rm \pi}/\varOmega_{f}} ^{{\rm \pi}/\varOmega_{f}} \zeta\left(\phi + \frac{\varOmega_{f}}{m}\tau \right) \eta(\tau) \, \mathrm{d}\tau = \frac{1}{2{\rm \pi} } \int _{-{\rm \pi}} ^{\rm \pi} \zeta\left(\phi + \frac{\varphi}{m}\right) \eta\left(\frac{\varphi}{\varOmega_{f}}\right) \, \mathrm{d}\varphi. \end{equation}Considering the stable solution of (3.8), the condition for synchronisation can be derived theoretically as
and the synchronisability is defined as ![]() $S = \max \varGamma - \min \varGamma$. The condition described by (3.10) theoretically identifies the possible combination map of the forcing angular frequency,
$S = \max \varGamma - \min \varGamma$. The condition described by (3.10) theoretically identifies the possible combination map of the forcing angular frequency, ![]() $\varOmega _{f}$, and magnitude,
$\varOmega _{f}$, and magnitude, ![]() $\varepsilon$, that can achieve synchronisation, known as the Arnold tongue. The synchronisability,
$\varepsilon$, that can achieve synchronisation, known as the Arnold tongue. The synchronisability, ![]() $S$, conveys the ease by which synchronisation is achieved for a specific periodic perturbation at a different forcing frequency. A larger
$S$, conveys the ease by which synchronisation is achieved for a specific periodic perturbation at a different forcing frequency. A larger ![]() $S$ indicates that a smaller motion is sufficient for the flow to be synchronised with external forcing at angular frequency
$S$ indicates that a smaller motion is sufficient for the flow to be synchronised with external forcing at angular frequency ![]() $\varOmega _f$.
$\varOmega _f$.
3.2. Ensemble-based phase-reduction framework
Strictly speaking, the phase-reduction framework is only valid for perfectly periodic flows. However, as discussed in § 2, three-dimensional flows do not exhibit perfect limit-cyclic behaviour which requires care when performing phase-reduction analysis. In recent years, a few studies have worked on extending the phase-reduction approach to chaotic oscillators (Josić & Mar Reference Josić and Mar2001; Kurebayashi et al. Reference Kurebayashi, Fujiwara, Nakao and Ikeguchi2012; Schwabedal et al. Reference Schwabedal, Pikovsky, Kralemann and Rosenblum2012; Imai, Suetani & Aoyagi Reference Imai, Suetani and Aoyagi2022; Tönjes & Kori Reference Tönjes and Kori2022). Inspired by these works, we extend the phase-based description to three-dimensional flows.
The phase dynamics of three-dimensional flows can be expressed as
where the term ![]() $F(\boldsymbol {q}(\boldsymbol {x},t))$ represents the instantaneous frequency fluctuation from the natural angular frequency
$F(\boldsymbol {q}(\boldsymbol {x},t))$ represents the instantaneous frequency fluctuation from the natural angular frequency ![]() $\varOmega _{n}$, which stems from the phase diffusion of systems (Josić & Mar Reference Josić and Mar2001; Kurebayashi et al. Reference Kurebayashi, Fujiwara, Nakao and Ikeguchi2012). Following the same procedure provided in § 3.1, the phase dynamics of the weakly perturbed three-dimensional flows are modelled as
$\varOmega _{n}$, which stems from the phase diffusion of systems (Josić & Mar Reference Josić and Mar2001; Kurebayashi et al. Reference Kurebayashi, Fujiwara, Nakao and Ikeguchi2012). Following the same procedure provided in § 3.1, the phase dynamics of the weakly perturbed three-dimensional flows are modelled as
Since we are more interested in the long-term dynamics when investigating synchronisation, observing the mean phase dynamics of the flow is more valuable than the instantaneous dynamics. Hence, we apply an ensemble-averaging to (3.12) which can be expressed as
 \begin{equation} \langle X \rangle = \lim_{K\to\infty} \frac{1}{K}\sum_{k=1}^{K} X^{(k)}, \end{equation}
\begin{equation} \langle X \rangle = \lim_{K\to\infty} \frac{1}{K}\sum_{k=1}^{K} X^{(k)}, \end{equation}
where ![]() $\langle \cdot \rangle$ denotes the ensemble-averaging operator and
$\langle \cdot \rangle$ denotes the ensemble-averaging operator and ![]() $X^{(k)}$ is the
$X^{(k)}$ is the ![]() $k$th realisation of a variable
$k$th realisation of a variable ![]() $X$. This yields
$X$. This yields
which has the same form as (3.4). Thus, we define the spatial phase-sensitivity function of three-dimensional flows as
 \begin{equation} \boldsymbol{Z}(\boldsymbol{x};\theta) = \left\langle \left. \frac{\delta\varTheta(\boldsymbol{q})}{\delta\boldsymbol{q}} \right|_{\scriptscriptstyle \boldsymbol{q}=\boldsymbol{q}_{0}} \right\rangle, \end{equation}
\begin{equation} \boldsymbol{Z}(\boldsymbol{x};\theta) = \left\langle \left. \frac{\delta\varTheta(\boldsymbol{q})}{\delta\boldsymbol{q}} \right|_{\scriptscriptstyle \boldsymbol{q}=\boldsymbol{q}_{0}} \right\rangle, \end{equation}
which evaluates ![]() $\langle \delta \varTheta /\delta \boldsymbol {q} \rangle$ from (3.14) with respect to the unperturbed flow
$\langle \delta \varTheta /\delta \boldsymbol {q} \rangle$ from (3.14) with respect to the unperturbed flow ![]() $\boldsymbol {q}_{0}(\boldsymbol {x},t)$. We then obtain the phase-sensitivity function
$\boldsymbol {q}_{0}(\boldsymbol {x},t)$. We then obtain the phase-sensitivity function ![]() $\zeta (\theta )$ of three-dimensional flows for a given spatial forcing profile
$\zeta (\theta )$ of three-dimensional flows for a given spatial forcing profile ![]() $\boldsymbol {f}(\boldsymbol {x})$ according to (3.6a,b). This leads us to the identical formulation of phase-coupling functions and synchronisation conditions provided in (3.9) and 3.10 for three-dimensional flows.
$\boldsymbol {f}(\boldsymbol {x})$ according to (3.6a,b). This leads us to the identical formulation of phase-coupling functions and synchronisation conditions provided in (3.9) and 3.10 for three-dimensional flows.
For practical implementation of the ensemble-based framework, we consider a finite number of sample cycles to estimate the phase-sensitivity function. We note that sample cycles are extracted based on the observed probabilistic distribution of their occurrence in three-dimensional flows to avoid biased sampling. In this study, since the amplitude variable, ![]() $r$, in the phase plane captures the three-dimensionality of the cylinder wake, we construct the probability density function of this cycle amplitude using a kernel density estimation with the Gaussian function (Bowman & Azzalini Reference Bowman and Azzalini1997) as shown in figure 7(a). We then divide
$r$, in the phase plane captures the three-dimensionality of the cylinder wake, we construct the probability density function of this cycle amplitude using a kernel density estimation with the Gaussian function (Bowman & Azzalini Reference Bowman and Azzalini1997) as shown in figure 7(a). We then divide ![]() $P(r)$ into subdivisions that have an equal probability, and sample cycles are extracted from each subdivision. We then apply the direct method to obtain the phase-response functions on these selected samples. Extracted sample cycles are perturbed impulsively at various phases to measure the phase-response function as shown in figure 8(a). Finally, the phase-sensitivity function is calculated by averaging and normalising with the impulse magnitude,
$P(r)$ into subdivisions that have an equal probability, and sample cycles are extracted from each subdivision. We then apply the direct method to obtain the phase-response functions on these selected samples. Extracted sample cycles are perturbed impulsively at various phases to measure the phase-response function as shown in figure 8(a). Finally, the phase-sensitivity function is calculated by averaging and normalising with the impulse magnitude, ![]() $\varepsilon$, yielding
$\varepsilon$, yielding
 \begin{equation} \zeta(\theta) \approx \frac{1}{\varepsilon K} \sum_{k=1}^{K} g^{(k)}(\theta;\varepsilon), \end{equation}
\begin{equation} \zeta(\theta) \approx \frac{1}{\varepsilon K} \sum_{k=1}^{K} g^{(k)}(\theta;\varepsilon), \end{equation}
where ![]() $g^{(k)}(\theta ;\varepsilon )$ denotes the phase-response function of the
$g^{(k)}(\theta ;\varepsilon )$ denotes the phase-response function of the ![]() $k$th sample cycle from among a total of
$k$th sample cycle from among a total of ![]() $K$ cycles.
$K$ cycles.

Figure 7. (a) Probability density function of cycle amplitude ![]() $r$ for extraction and (b) 10 selected sample cycles.
$r$ for extraction and (b) 10 selected sample cycles.

Figure 8. (a) Representation in the phase plane of three sample cycles, each with different amplitudes, perturbed at ![]() $\theta =0.6{\rm \pi}$ with rotary impulsive cylinder motion (solid) and the corresponding unperturbed sample cycles (dashed). (b) Estimation of
$\theta =0.6{\rm \pi}$ with rotary impulsive cylinder motion (solid) and the corresponding unperturbed sample cycles (dashed). (b) Estimation of ![]() $g^{(k)}(\theta,\varepsilon )$ and
$g^{(k)}(\theta,\varepsilon )$ and ![]() $h^{(k)}(\theta,\varepsilon )$ for ensemble-based phase-reduction analysis.
$h^{(k)}(\theta,\varepsilon )$ for ensemble-based phase-reduction analysis.
Determination of the phase-response function poses another challenge in the phase-reduction analysis of three-dimensional flows. Unlike for two-dimensional flows, the perturbed three-dimensional flow does not exactly return to the unperturbed trajectory due to its chaotic nature negating the concept of an asymptotic phase shift. This requires careful assessment of the phase-response function. We observe that when the perturbation is sufficiently weak, there exists a finite time interval where the dynamics of the perturbed flow remain analogous to the unperturbed flow. Within this finite time interval, the perturbed flow initially deviates from the unperturbed flow due to the transient effect of the perturbation. The perturbed flow then approaches the unperturbed flow on the phase plane as the transient effect of the perturbation dies out. After this time horizon, the perturbed flow starts to deviate again from the unperturbed flow due to the chaotic nature of three-dimensional flows.
Based on this perspective, we use the time ![]() $t^{*}$, when the perturbed flow is closest to the unperturbed flow, to estimate the phase-response functions of three-dimensional flows. To determine
$t^{*}$, when the perturbed flow is closest to the unperturbed flow, to estimate the phase-response functions of three-dimensional flows. To determine ![]() $t^{*}$, we monitor the distance function
$t^{*}$, we monitor the distance function ![]() $d$ between the unperturbed and perturbed flows on the phase plane as shown in figure 8(b), which is defined as
$d$ between the unperturbed and perturbed flows on the phase plane as shown in figure 8(b), which is defined as
 \begin{align} d^{(k)}(t;\theta,\varepsilon) = \left[ \left(R(\boldsymbol{q}_{\delta}^{(k)})\right)^2 + \left(R(\boldsymbol{q}_{0}^{(k)})\right)^2 - 2R(\boldsymbol{q}_{\delta}^{(k)})R(\boldsymbol{q}_{0}^{(k)})\cos\left(\varTheta(\boldsymbol{q}_{\delta}^{(k)}) - \varTheta(\boldsymbol{q}_{0}^{(k)})\right)\right]^{1/2} \end{align}
\begin{align} d^{(k)}(t;\theta,\varepsilon) = \left[ \left(R(\boldsymbol{q}_{\delta}^{(k)})\right)^2 + \left(R(\boldsymbol{q}_{0}^{(k)})\right)^2 - 2R(\boldsymbol{q}_{\delta}^{(k)})R(\boldsymbol{q}_{0}^{(k)})\cos\left(\varTheta(\boldsymbol{q}_{\delta}^{(k)}) - \varTheta(\boldsymbol{q}_{0}^{(k)})\right)\right]^{1/2} \end{align}
using the law of cosines. Similar to the way we denote the phase functional ![]() $\varTheta$ as returning the phase
$\varTheta$ as returning the phase ![]() $\theta (t) = \varTheta (\boldsymbol {q}(\boldsymbol {x},t))$ for a particular flow
$\theta (t) = \varTheta (\boldsymbol {q}(\boldsymbol {x},t))$ for a particular flow ![]() $\boldsymbol {q}(\boldsymbol {x},t)$, the amplitude functional
$\boldsymbol {q}(\boldsymbol {x},t)$, the amplitude functional ![]() $R$ returns the amplitude of that flow field as
$R$ returns the amplitude of that flow field as ![]() $r(t) = R(\boldsymbol {q}(\boldsymbol {x},t))$. We now seek the time
$r(t) = R(\boldsymbol {q}(\boldsymbol {x},t))$. We now seek the time ![]() $t^{*}$ such that
$t^{*}$ such that ![]() $d$ is minimised after the impulse perturbation and before it starts to grow again. To not be affected by the local fluctuations of
$d$ is minimised after the impulse perturbation and before it starts to grow again. To not be affected by the local fluctuations of ![]() $d$, we mainly track the variation of local minimum and maximum values of
$d$, we mainly track the variation of local minimum and maximum values of ![]() $d$. Both local maximum and minimum values of the distance function
$d$. Both local maximum and minimum values of the distance function ![]() $d$ keep decreasing as the transient effects of the perturbation diminish. When either the local minimum or maximum value of
$d$ keep decreasing as the transient effects of the perturbation diminish. When either the local minimum or maximum value of ![]() $d$ increases, we can presume that the perturbed flow has started to deviate from the unperturbed flow. Thus, we take the time
$d$ increases, we can presume that the perturbed flow has started to deviate from the unperturbed flow. Thus, we take the time ![]() $t^{*}$ to be when we observe the minimum value in the function
$t^{*}$ to be when we observe the minimum value in the function ![]() $d$ before either of the extrema values start to increase. Finally, the phase-response function is measured as
$d$ before either of the extrema values start to increase. Finally, the phase-response function is measured as ![]() $g^{(k)}(\theta ;\varepsilon ) = \varTheta (\boldsymbol {q}_{\delta }^{(k)}(\boldsymbol {x},t^{*})) - \varTheta (\boldsymbol {q}_{0}^{(k)}(\boldsymbol {x},t^{*}))$ for each sample cycle, as shown in figure 8(b).
$g^{(k)}(\theta ;\varepsilon ) = \varTheta (\boldsymbol {q}_{\delta }^{(k)}(\boldsymbol {x},t^{*})) - \varTheta (\boldsymbol {q}_{0}^{(k)}(\boldsymbol {x},t^{*}))$ for each sample cycle, as shown in figure 8(b).
In addition to the phase-response and phase-sensitivity functions, we can similarly measure the amplitude variation introduced by the weak impulsive perturbation. Since ![]() $r$ denotes the three-dimensional characteristics of the wake, the deviation of the amplitude in the phase plane trajectory at
$r$ denotes the three-dimensional characteristics of the wake, the deviation of the amplitude in the phase plane trajectory at ![]() $t^*$ represents a modification of underlying three-dimensional characteristics. In this context, we also quantify the function
$t^*$ represents a modification of underlying three-dimensional characteristics. In this context, we also quantify the function ![]() $h^{(k)}(\theta ;\varepsilon ) = R(\boldsymbol {q}_{\delta }^{(k)}(\boldsymbol {x},t^{*})) - R(\boldsymbol {q}_{0}^{(k)}(\boldsymbol {x},t^{*}))$ in addition to the phase-response functions as shown in figure 8(b). Similar to the phase-sensitivity function
$h^{(k)}(\theta ;\varepsilon ) = R(\boldsymbol {q}_{\delta }^{(k)}(\boldsymbol {x},t^{*})) - R(\boldsymbol {q}_{0}^{(k)}(\boldsymbol {x},t^{*}))$ in addition to the phase-response functions as shown in figure 8(b). Similar to the phase-sensitivity function ![]() $\zeta (\theta )$, the function
$\zeta (\theta )$, the function ![]() $h$ is averaged and normalised with the impulse magnitude,
$h$ is averaged and normalised with the impulse magnitude, ![]() $\varepsilon$, to give the function
$\varepsilon$, to give the function ![]() $\xi (\theta )$ defined as
$\xi (\theta )$ defined as
 \begin{equation} \xi(\theta) \equiv \frac{1}{\varepsilon K} \sum_{k=1}^{K} h^{(k)}(\theta;\varepsilon). \end{equation}
\begin{equation} \xi(\theta) \equiv \frac{1}{\varepsilon K} \sum_{k=1}^{K} h^{(k)}(\theta;\varepsilon). \end{equation}
This function represents the mean normalised variation of ![]() $r$ made by the impulsive perturbations.
$r$ made by the impulsive perturbations.
4. Synchronisation characteristics of three-dimensional wake
Let us numerically investigate the synchronisation between oscillations of a circular cylinder and its wake based on phase-reduction analysis. In order to study the influence of the three-dimensionality in the wake, we compare the three-dimensional wake synchronisation characteristics with the imposed two-dimensional wake ones at the same Reynolds number. As mentioned in § 1, we consider three types of in-plane cylinder motions, streamwise translation, cross-flow translation and rotation. While the two-dimensional wake is analysed as presented in § 3.1, the three-dimensional wake is studied using the ensemble-based phase-reduction analysis with 10 sample cycles as shown in figure 7(b). The sample cycles are extracted based on the probability density function constructed with 200 shedding cycles provided in figure 7(a), which is identified to be of sufficient length for the convergence of the cumulative distribution function. We apply the impulsive cylinder motion with a magnitude of ![]() $\varepsilon /U_{\infty } = 0.025$, which is identified as being sufficiently small to satisfy the linearity assumption, to measure the phase-sensitivity functions. This identification is performed by testing successively smaller impulse magnitudes and noting that corresponding decreases occurred in the phase or amplitude difference between the perturbed and unperturbed flows. However, decreasing the impulse magnitude from 0.025 to 0.0125 does not produce meaningful changes in the phase or amplitude difference for either of the three types of motions used.
$\varepsilon /U_{\infty } = 0.025$, which is identified as being sufficiently small to satisfy the linearity assumption, to measure the phase-sensitivity functions. This identification is performed by testing successively smaller impulse magnitudes and noting that corresponding decreases occurred in the phase or amplitude difference between the perturbed and unperturbed flows. However, decreasing the impulse magnitude from 0.025 to 0.0125 does not produce meaningful changes in the phase or amplitude difference for either of the three types of motions used.
Two- and three-dimensional wake phase-sensitivity functions for rotary, cross-flow translation and streamwise translation motions are compared in figure 9. The ensemble-averaged ![]() $\zeta (\theta )$ for three-dimensional flows are shown in blue and the light blue regions show the 95 % confidence intervals obtained from the samples. We note that the overall trend of three-dimensional wake phase-sensitivity functions resembles those from two-dimensional wakes. This is because the two-dimensional coherent structures in von Kármán vortex shedding are predominant, even in three-dimensional wakes at
$\zeta (\theta )$ for three-dimensional flows are shown in blue and the light blue regions show the 95 % confidence intervals obtained from the samples. We note that the overall trend of three-dimensional wake phase-sensitivity functions resembles those from two-dimensional wakes. This is because the two-dimensional coherent structures in von Kármán vortex shedding are predominant, even in three-dimensional wakes at ![]() ${\textit {Re}}=300$, over the secondary instabilities. Hence, the perturbation dynamics of the flow follow the shedding of spanwise vortices. This implies that the potential exists to use two-dimensional flows from low to moderate Reynolds numbers to capture phase-sensitivity functions and perturbation dynamics for three-dimensional flows at the equivalent Reynolds number.
${\textit {Re}}=300$, over the secondary instabilities. Hence, the perturbation dynamics of the flow follow the shedding of spanwise vortices. This implies that the potential exists to use two-dimensional flows from low to moderate Reynolds numbers to capture phase-sensitivity functions and perturbation dynamics for three-dimensional flows at the equivalent Reynolds number.

Figure 9. Comparison of phase-sensitivity functions of two- and three-dimensional wakes, denoted as ![]() $\zeta_{2D}(\theta)$ and
$\zeta_{2D}(\theta)$ and ![]() $\zeta_{3D}(\theta)$ respectively, at
$\zeta_{3D}(\theta)$ respectively, at ![]() ${\textit{Re}} =300$ for each perturbation type: (a) rotary, (b) cross-flow and (c) streamwise. The shaded area displays the 95 % confidence interval of
${\textit{Re}} =300$ for each perturbation type: (a) rotary, (b) cross-flow and (c) streamwise. The shaded area displays the 95 % confidence interval of ![]() $\zeta_{3D}(\theta)$.
$\zeta_{3D}(\theta)$.
We find that the three-dimensional wake is less sensitive than the two-dimensional wake to all three types of external perturbation in terms of the phase. The magnitudes of the phase-sensitivity functions for a three-dimensional wake are decreased significantly for the rotary and cross-flow perturbations. In contrast, the phase-sensitivity function for the streamwise perturbation is much less affected by the three-dimensionality. When the cylinder translates in the streamwise direction, it moves towards or away from the vortices behind it. Thus, a phase shift by the streamwise motion is largely associated with the adjustment of distance between the cylinder and the spanwise vortices. This distance is less affected by the spanwise three-dimensionality of the wake.
Using the phase-sensitivity functions, we determine the synchronisability of the wake to steady sinusoidal oscillations using the phase-coupling functions, ![]() $\varGamma (\phi )$. Phase-coupling functions of two- and three-dimensional wakes are evaluated and shown in figure 10. Since the synchronisation of the cylinder wake to streamwise oscillations mainly occurs when
$\varGamma (\phi )$. Phase-coupling functions of two- and three-dimensional wakes are evaluated and shown in figure 10. Since the synchronisation of the cylinder wake to streamwise oscillations mainly occurs when ![]() $\varOmega _{f} \approx 2\varOmega _{n}$ (Al-Mdallal, Lawrence & Kocabiyik Reference Al-Mdallal, Lawrence and Kocabiyik2007; Marzouk & Nayfeh Reference Marzouk and Nayfeh2009), the second harmonic (
$\varOmega _{f} \approx 2\varOmega _{n}$ (Al-Mdallal, Lawrence & Kocabiyik Reference Al-Mdallal, Lawrence and Kocabiyik2007; Marzouk & Nayfeh Reference Marzouk and Nayfeh2009), the second harmonic (![]() $m = 2$) is investigated for the streamwise translation. In fact, the phase coupling function with
$m = 2$) is investigated for the streamwise translation. In fact, the phase coupling function with ![]() $m = 1$ for streamwise oscillations is zero valued (
$m = 1$ for streamwise oscillations is zero valued (![]() $\varGamma (\phi ) = 0$) due to the
$\varGamma (\phi ) = 0$) due to the ![]() ${\rm \pi}$ periodicity of the phase-sensitivity function as shown in figure 9, indicating that synchronisation to the first harmonic is hardly seen. However, synchronisation to the first harmonic of streamwise cylinder oscillations can occur for large enough oscillation amplitudes (Leontini, Jacono & Thompson Reference Leontini, Jacono and Thompson2013; Konstantinidis & Bouris Reference Konstantinidis and Bouris2016).
${\rm \pi}$ periodicity of the phase-sensitivity function as shown in figure 9, indicating that synchronisation to the first harmonic is hardly seen. However, synchronisation to the first harmonic of streamwise cylinder oscillations can occur for large enough oscillation amplitudes (Leontini, Jacono & Thompson Reference Leontini, Jacono and Thompson2013; Konstantinidis & Bouris Reference Konstantinidis and Bouris2016).

Figure 10. Phase-coupling functions, ![]() $\varGamma _{2D}(\phi )$ and
$\varGamma _{2D}(\phi )$ and ![]() $\varGamma _{3D}(\phi )$, and synchronisability,
$\varGamma _{3D}(\phi )$, and synchronisability, ![]() $S_{2D}$ and
$S_{2D}$ and ![]() $S_{3D}$, evaluation of two- and three-dimensional wakes for each perturbation type: (a) rotary; (b) cross-flow; (c) streamwise.
$S_{3D}$, evaluation of two- and three-dimensional wakes for each perturbation type: (a) rotary; (b) cross-flow; (c) streamwise.
On the other hand, the first harmonic (![]() $m = 1$) is targeted for rotation and cross-flow translation. Similar to the phase-sensitivity function results, we again observe that three-dimensionality within the wake imposes a higher resistance to synchronisation. Synchronisability to rotary and cross-flow oscillations shows a large reduction (39.1 % and 44.6 %, respectively) compared with the two-dimensional flow. The synchronisability to streamwise oscillation showed only a 10.1 % decrease.
$m = 1$) is targeted for rotation and cross-flow translation. Similar to the phase-sensitivity function results, we again observe that three-dimensionality within the wake imposes a higher resistance to synchronisation. Synchronisability to rotary and cross-flow oscillations shows a large reduction (39.1 % and 44.6 %, respectively) compared with the two-dimensional flow. The synchronisability to streamwise oscillation showed only a 10.1 % decrease.
To understand the source of the difference between the phase-sensitivity functions of two- and three-dimensional wakes at the same Reynolds number, we consider the effect of impulsive cylinder motion in an additional degree of freedom of the three-dimensional wake, the amplitude ![]() $r$. We compare
$r$. We compare ![]() $\xi (\theta )$ with the difference in phase sensitivities,
$\xi (\theta )$ with the difference in phase sensitivities, ![]() $\zeta _{2D}(\theta ) - \zeta _{3D}(\theta )$, for the three perturbation motions as shown in figure 11. We observe that the function
$\zeta _{2D}(\theta ) - \zeta _{3D}(\theta )$, for the three perturbation motions as shown in figure 11. We observe that the function ![]() $\xi (\theta )$ generally becomes larger at phases where the phase-sensitivity function of the three-dimensional wake exhibits a relatively large difference from the corresponding two-dimensional one. Correlation coefficients,
$\xi (\theta )$ generally becomes larger at phases where the phase-sensitivity function of the three-dimensional wake exhibits a relatively large difference from the corresponding two-dimensional one. Correlation coefficients, ![]() $\rho$, between
$\rho$, between ![]() $\xi (\theta )$ and
$\xi (\theta )$ and ![]() $\zeta _{2D}(\theta ) - \zeta _{3D}(\theta )$ are also evaluated and have values higher than 0.9. This indicates that the energy given by the cylinder motion changes both the instantaneous phase and the amplitude in the phase plane. Recalling that the amplitude variable
$\zeta _{2D}(\theta ) - \zeta _{3D}(\theta )$ are also evaluated and have values higher than 0.9. This indicates that the energy given by the cylinder motion changes both the instantaneous phase and the amplitude in the phase plane. Recalling that the amplitude variable ![]() $r$ reflects the instantaneous three-dimensional properties of the wake, it can be argued that the portion of energy transferred, in the amplitude direction, from the cylinder to the wake modifies the three-dimensional characteristics of the flow. However, since only the energy transferred in the instantaneous phase direction supports synchronisation, three-dimensional wakes require larger energy to achieve synchronisation as observed in the synchronisability estimations.
$r$ reflects the instantaneous three-dimensional properties of the wake, it can be argued that the portion of energy transferred, in the amplitude direction, from the cylinder to the wake modifies the three-dimensional characteristics of the flow. However, since only the energy transferred in the instantaneous phase direction supports synchronisation, three-dimensional wakes require larger energy to achieve synchronisation as observed in the synchronisability estimations.

Figure 11. Amplitude variation, ![]() $\xi (\theta )$, for three-dimensional wakes normalised by the magnitude of impulsive cylinder motion along with 95 % confidence intervals: (a) rotary; (b) cross-flow; (c) streamwise. Differences between the phase-sensitivity functions of two- and three-dimensional wakes,
$\xi (\theta )$, for three-dimensional wakes normalised by the magnitude of impulsive cylinder motion along with 95 % confidence intervals: (a) rotary; (b) cross-flow; (c) streamwise. Differences between the phase-sensitivity functions of two- and three-dimensional wakes, ![]() $\zeta _{2D}(\theta ) - \zeta _{3D}(\theta )$, are also provided for comparison.
$\zeta _{2D}(\theta ) - \zeta _{3D}(\theta )$, are also provided for comparison.
Based on (3.10), the synchronisation conditions of the non-dimensional forcing amplitude, ![]() $U^{*}_{f} = U_f/U_\infty$, and frequency,
$U^{*}_{f} = U_f/U_\infty$, and frequency, ![]() $\varOmega ^{*}_{f}=\varOmega _{f}D/(2{\rm \pi} U_{\infty })$, can be theoretically predicted based on the phase-coupling functions and shown in figure 12. We validate our methodology and results by comparing the predicted synchronisation boundaries from phase-reduction analysis to DNS parametric studies. The region between the solid lines is predicted to be synchronised to the external forcing while the two regions outside the lines are predicted to be asynchronous. The circles indicate the synchronisation bounds determined by performing DNS with the cylinder undergoing steady and continuous oscillations at the corresponding forcing amplitude and frequency. Horizontal error bars represent the uncertainty in the identification of synchronisation boundaries associated with the nonuniform and finite resolution of the DNS parametric sweeps. Synchronisation in DNS is determined by monitoring the temporal variation of the phase difference,
$\varOmega ^{*}_{f}=\varOmega _{f}D/(2{\rm \pi} U_{\infty })$, can be theoretically predicted based on the phase-coupling functions and shown in figure 12. We validate our methodology and results by comparing the predicted synchronisation boundaries from phase-reduction analysis to DNS parametric studies. The region between the solid lines is predicted to be synchronised to the external forcing while the two regions outside the lines are predicted to be asynchronous. The circles indicate the synchronisation bounds determined by performing DNS with the cylinder undergoing steady and continuous oscillations at the corresponding forcing amplitude and frequency. Horizontal error bars represent the uncertainty in the identification of synchronisation boundaries associated with the nonuniform and finite resolution of the DNS parametric sweeps. Synchronisation in DNS is determined by monitoring the temporal variation of the phase difference, ![]() $\phi (t)$, between the sinusoidally forced cylinder oscillation and the wake, defined in (3.7). When
$\phi (t)$, between the sinusoidally forced cylinder oscillation and the wake, defined in (3.7). When ![]() $\phi (t)$ converges to a certain value with a small standard deviation,
$\phi (t)$ converges to a certain value with a small standard deviation, ![]() $\sigma (\phi (t)) < 0.1{\rm \pi}$, we classify the case as synchronised.
$\sigma (\phi (t)) < 0.1{\rm \pi}$, we classify the case as synchronised.

Figure 12. Synchronisation condition (Arnold tongue) for each type of oscillation motion predicted using phase-reduction analysis (solid lines) and identified using DNS (circles): (a) rotary; (b) cross-flow; (c) streamwise. Horizontal bars represent the uncertainty in the identification of synchronisation boundaries by DNS.
From figure 12, we observe that phase-reduction analysis is able to predict the synchronisation conditions for both two- and three-dimensional wakes for ![]() $U^{*}_{f} < 0.1$, indicating that the linear assumption is valid for oscillations with small amplitudes. As the oscillation amplitude of the non-dimensional velocity increases, the DNS results deviate from the predictions due to the stronger nonlinearity. In addition, synchronisation to rotary and cross-flow oscillations are not observed when the oscillation amplitude is weak, classified as
$U^{*}_{f} < 0.1$, indicating that the linear assumption is valid for oscillations with small amplitudes. As the oscillation amplitude of the non-dimensional velocity increases, the DNS results deviate from the predictions due to the stronger nonlinearity. In addition, synchronisation to rotary and cross-flow oscillations are not observed when the oscillation amplitude is weak, classified as ![]() $U^{*}_{f} = 0.025$ and
$U^{*}_{f} = 0.025$ and ![]() $0.05$ for each type of motion, respectively, and denoted as cross- symbols in the figure. As discussed in Pikovsky et al. (Reference Pikovsky, Rosenblum, Osipov and Kurths1997), chaotic oscillators with phase diffusion do not show synchronisation when the oscillation is not strong enough to suppress the phase diffusion.
$0.05$ for each type of motion, respectively, and denoted as cross- symbols in the figure. As discussed in Pikovsky et al. (Reference Pikovsky, Rosenblum, Osipov and Kurths1997), chaotic oscillators with phase diffusion do not show synchronisation when the oscillation is not strong enough to suppress the phase diffusion.
To elaborate on this point theoretically, we look into the temporal variation of the instantaneous phase difference ![]() $\phi (t)$, which can be expressed approximately as
$\phi (t)$, which can be expressed approximately as
derived from (3.12). Let us now compare the scales of each term on the right-hand side of this equation under the assumption that the oscillation amplitude, ![]() $U^{*}_{f}$, is small and approaches zero. Since
$U^{*}_{f}$, is small and approaches zero. Since ![]() $\varOmega _{f}/m$ should be very close to
$\varOmega _{f}/m$ should be very close to ![]() $\varOmega _{n}$ to synchronise the wake to small-amplitude oscillations, the first term is negligible. The third term is also negligible because of the linear proportionality to
$\varOmega _{n}$ to synchronise the wake to small-amplitude oscillations, the first term is negligible. The third term is also negligible because of the linear proportionality to ![]() $U^{*}_{f}$. However, the second term
$U^{*}_{f}$. However, the second term ![]() $F$ is independent of the external forcing because it is an inherent property of the three-dimensional wake. Thus, the first and third terms disappear for small-amplitude oscillation conditions, and the dynamics of
$F$ is independent of the external forcing because it is an inherent property of the three-dimensional wake. Thus, the first and third terms disappear for small-amplitude oscillation conditions, and the dynamics of ![]() $\phi$ are governed predominantly by
$\phi$ are governed predominantly by ![]() $F$ as
$F$ as ![]() $\dot {\phi }(t) \simeq F(\boldsymbol {q}(\boldsymbol {x},t))$. As a result, if instantaneous fluctuations
$\dot {\phi }(t) \simeq F(\boldsymbol {q}(\boldsymbol {x},t))$. As a result, if instantaneous fluctuations ![]() $F$ in three-dimensional flows are not sufficiently small, it prevents the convergence of
$F$ in three-dimensional flows are not sufficiently small, it prevents the convergence of ![]() $\phi$ unless
$\phi$ unless ![]() $F$ is restrained by relatively large oscillations. Thus, the oscillation amplitude has to exceed a certain threshold to facilitate synchronisation regardless of the forcing frequency. Furthermore, the third term is also proportional to the phase-sensitivity function, which implies a larger threshold for
$F$ is restrained by relatively large oscillations. Thus, the oscillation amplitude has to exceed a certain threshold to facilitate synchronisation regardless of the forcing frequency. Furthermore, the third term is also proportional to the phase-sensitivity function, which implies a larger threshold for ![]() $U^{*}_{f}$ when the magnitude of the phase-sensitivity function
$U^{*}_{f}$ when the magnitude of the phase-sensitivity function ![]() $\zeta (\theta )$ is smaller. This is seen in the largest threshold for
$\zeta (\theta )$ is smaller. This is seen in the largest threshold for ![]() $U^{*}_{f}$ for the cross-flow oscillation and no threshold appearing within
$U^{*}_{f}$ for the cross-flow oscillation and no threshold appearing within ![]() $U^{*}_f \geq 0.025$ for the streamwise oscillation, which correspond to the smallest and largest phase-sensitivity function magnitudes among oscillation types as shown in figure 9.
$U^{*}_f \geq 0.025$ for the streamwise oscillation, which correspond to the smallest and largest phase-sensitivity function magnitudes among oscillation types as shown in figure 9.
We also note that the left synchronisation boundaries obtained from the three-dimensional wake DNS results are located inside the two-dimensional wake results. This indicates the added difficulty in synchronising the three-dimensional wake as predicted by phase-reduction analysis. On the other hand, the right synchronisation boundaries, representing high-frequency oscillations, exhibit different trends depending on the oscillation type which deviates from the theoretical predictions.
For two-dimensional wakes, we commonly see deviations of the DNS identified right boundaries from the predictions by phase-reduction analysis, which is also observed in the previous study of Khodkar et al. (Reference Khodkar, Klamo and Taira2021). They identified that synchronisation to higher frequencies is more restrictive than lower frequencies, attributing it to the physical constraint of the vortex formation region behind the cylinder. Synchronisation to high-frequency oscillations requires the vortex formation region to be compact. However, it is impossible to shorten the vortex formation region beyond a certain limit. This is reflected in the asymmetry of the DNS-based Arnold tongue and its inward deflection at the right branch for two-dimensional wakes. This hypothesis, however, only applies to two-dimensional wakes as we observe that three-dimensional wakes exhibit a longer vortex formation region than the corresponding two-dimensional wake, as visualised in figure 13. Since a three-dimensional wake initially has a longer vortex formation region, it holds a greater capacity for shortening the vortex formation region. This offers an easier path to synchronisation for high-frequency oscillations in a three-dimensional wake compared with a two-dimensional wake, resulting in no inward deflection of the Arnold tongue at the right synchronisation boundary.

Figure 13. Contours of mean spanwise vorticity of the (a) two-dimensional and (b) three-dimensional wakes.
For the rotary oscillations, while the left synchronisation boundary agrees with the prediction, we find that the right synchronisation boundary of the three-dimensional wake obtained from DNS results deflects outward as the oscillation amplitude increases. This results in the three-dimensional wake having a larger upper bound than the two-dimensional wake when ![]() $U^{*}_{f} \geq 0.075$. Two instantaneous flow structures of cases on the right boundary with
$U^{*}_{f} \geq 0.075$. Two instantaneous flow structures of cases on the right boundary with ![]() $U^{*}_{f} = 0.05$ and
$U^{*}_{f} = 0.05$ and ![]() $0.075$ for rotary motion are compared in figures 14(a) and 14(b). It is observed that secondary vortical structures disappear when
$0.075$ for rotary motion are compared in figures 14(a) and 14(b). It is observed that secondary vortical structures disappear when ![]() $U^{*}_{f} \geq 0.075$, showing that high-frequency rotary oscillations largely suppress the three-dimensionality of the wake. The suppression of secondary instabilities and the two-dimensionalisation of the wake by oscillatory cylinder motion are observed in previous studies as well (Poncet Reference Poncet2002; Deng, Shao & Ren Reference Deng, Shao and Ren2007; Kim et al. Reference Kim, Park, Park, Bae and Yoo2009). This demonstrates the existence of a transition from a three-dimensional to a two-dimensional wake as the oscillation amplitude increases along the right branch. Due to this transition, cylinder wakes with high-frequency rotary oscillation deviate significantly from the unperturbed three-dimensional wake, which gives rise to the strong nonlinear response. Since phase reduction analysis adopts a first-order approximation to estimate the phase-sensitivity function, these nonlinear effects and the transition from a three-dimensional flow to a two-dimensional flow are not captured and are attributed to higher-order effects. On the other hand, such an outward deflection is not observed at the right boundary for cross-flow oscillations since the wake transition does not occur for this type of motion as shown in figure 14(c) and 14(d).
$U^{*}_{f} \geq 0.075$, showing that high-frequency rotary oscillations largely suppress the three-dimensionality of the wake. The suppression of secondary instabilities and the two-dimensionalisation of the wake by oscillatory cylinder motion are observed in previous studies as well (Poncet Reference Poncet2002; Deng, Shao & Ren Reference Deng, Shao and Ren2007; Kim et al. Reference Kim, Park, Park, Bae and Yoo2009). This demonstrates the existence of a transition from a three-dimensional to a two-dimensional wake as the oscillation amplitude increases along the right branch. Due to this transition, cylinder wakes with high-frequency rotary oscillation deviate significantly from the unperturbed three-dimensional wake, which gives rise to the strong nonlinear response. Since phase reduction analysis adopts a first-order approximation to estimate the phase-sensitivity function, these nonlinear effects and the transition from a three-dimensional flow to a two-dimensional flow are not captured and are attributed to higher-order effects. On the other hand, such an outward deflection is not observed at the right boundary for cross-flow oscillations since the wake transition does not occur for this type of motion as shown in figure 14(c) and 14(d).

Figure 14. Wake visualisation with isosurfaces of the ![]() $Q$-criterion (
$Q$-criterion (![]() $Q=0.05$) coloured by
$Q=0.05$) coloured by ![]() $\omega _{x}$ for cases on the right synchronisation boundaries.
$\omega _{x}$ for cases on the right synchronisation boundaries.
Regardless of the oscillation amplitude, the DNS-based right synchronisation boundary of the three-dimensional wake is always outside of the two-dimensional wake for the streamwise oscillations. Similar to the rotary oscillations, streamwise oscillations with ![]() $U^{*}_{f}=0.05$ are able to two-dimensionalise the cylinder wake, while the three-dimensionality still remains at the oscillation amplitude of
$U^{*}_{f}=0.05$ are able to two-dimensionalise the cylinder wake, while the three-dimensionality still remains at the oscillation amplitude of ![]() $U^{*}_{f}=0.025$, shown in figure 14(e) and 14(f). To identify differences between the wakes and understand this observation further, we additionally examine scale-decomposed flow structures for this case on the right boundary, plotted in figure 15, and compare them with the unperturbed three-dimensional wakes provided in figure 4. We find that both large- and small-scale structures resemble the unperturbed three-dimensional wake with large
$U^{*}_{f}=0.025$, shown in figure 14(e) and 14(f). To identify differences between the wakes and understand this observation further, we additionally examine scale-decomposed flow structures for this case on the right boundary, plotted in figure 15, and compare them with the unperturbed three-dimensional wakes provided in figure 4. We find that both large- and small-scale structures resemble the unperturbed three-dimensional wake with large ![]() $r$. This indicates that the three-dimensionality of the wake can be partially suppressed by the streamwise oscillation even though the oscillation amplitude is small. Due to the stronger nonlinear response of the wake to the streamwise motion, discrepancies between the synchronisation boundaries of the DNS results and the phase-reduction analysis can be large for this type of oscillation.
$r$. This indicates that the three-dimensionality of the wake can be partially suppressed by the streamwise oscillation even though the oscillation amplitude is small. Due to the stronger nonlinear response of the wake to the streamwise motion, discrepancies between the synchronisation boundaries of the DNS results and the phase-reduction analysis can be large for this type of oscillation.

Figure 15. Scale-decomposed flow structures by isosurfaces of the ![]() $Q$-criterion (
$Q$-criterion (![]() $Q=0.05$) corresponding to streamwise oscillation with
$Q=0.05$) corresponding to streamwise oscillation with ![]() $U^{*}_{f}=0.025$ and
$U^{*}_{f}=0.025$ and ![]() $\varOmega ^{*}_f=0.4262$ on the right synchronisation boundary: (a) large-scale structures and (b) small-scale structures.
$\varOmega ^{*}_f=0.4262$ on the right synchronisation boundary: (a) large-scale structures and (b) small-scale structures.
5. Conclusions
We have examined the influence of the three-dimensionality of the wake on its ability to synchronise to cylinder oscillations at ![]() ${\textit {Re}} = 300$. Phase-reduction analysis was used for the theoretical analysis of wake synchronisation. Even though the ability of phase-reduction analysis to study the synchronisation of two-dimensional flows has been shown in previous studies, the chaotic nature of three-dimensional wakes makes its implementation for these realistic flows challenging. To address this difficulty, we introduced an ensemble-averaging technique to extend phase-reduction analysis to three-dimensional flows. In addition, we provided a guideline to perform the ensemble-averaged phase-reduction analysis based on the direct method, which includes sample cycle extractions and measurements of phase-sensitivity functions. We applied phase-reduction analysis to both two- and three-dimensional cylinder wakes to understand the effect of three-dimensionality on synchronisation.
${\textit {Re}} = 300$. Phase-reduction analysis was used for the theoretical analysis of wake synchronisation. Even though the ability of phase-reduction analysis to study the synchronisation of two-dimensional flows has been shown in previous studies, the chaotic nature of three-dimensional wakes makes its implementation for these realistic flows challenging. To address this difficulty, we introduced an ensemble-averaging technique to extend phase-reduction analysis to three-dimensional flows. In addition, we provided a guideline to perform the ensemble-averaged phase-reduction analysis based on the direct method, which includes sample cycle extractions and measurements of phase-sensitivity functions. We applied phase-reduction analysis to both two- and three-dimensional cylinder wakes to understand the effect of three-dimensionality on synchronisation.
While the behaviour of the phase-sensitivity functions for two- and three-dimensional wakes are similar, due to two-dimensional von Kármán vortex shedding being the dominant feature in the wake dynamics of both, there is still a significant decrease in the phase-sensitivity of three-dimensional wake. This decrease is especially large for the cross-flow and rotary cylinder motions. This ultimately leads to reduced synchronisability and results in narrower Arnold tongues compared with the two-dimensional wake cases. Observing the amplitude variations from impulsive motions, the reduction of synchronisability was attributed to the energy transferred to the wake partially going into the amplitude direction. We have identified that the synchronisation conditions derived by phase-reduction analysis are valid for cylinder oscillations with velocities that are smaller than 10 % of the free-stream velocity. In addition, the parametric examination showed that there exists a minimum required oscillation amplitude to overcome the phase diffusion of the three-dimensional wake and achieve synchronisation. Nonlinear effects from wake three-dimensionality, which are associated with the vortex formation and transition from three- to two-dimensional flow, are also identified by analysing flow structures of synchronised wakes. To sum up, the phase-reduction analysis predicts the synchronisation conditions with reasonable accuracy, especially for small oscillation amplitudes when nonlinear effects are fairly small.
The present study has not only revealed synchronisation conditions of the three-dimensional cylinder wake but has also provided a systematic way to predict and analyse the synchronisation characteristics of more complex flows. Previous experimental studies observed that turbulent cylinder wakes at high Reynolds numbers (up to ![]() ${\textit {Re}} \thicksim 10^5$) also exhibit rhythmic behaviours with a single dominant frequency, according to their energy spectrum, similar to the low-Reynolds-number wakes (Szepessy & Bearman Reference Szepessy and Bearman1992; Braza, Perrin & Hoarau Reference Braza, Perrin and Hoarau2006). Therefore, it is anticipated that phase characterisation of the flow is still valid, and the ensemble-based phase-reduction framework would be applicable, to turbulent flows with a high Reynolds number. Considering the sizable computational costs or experimental resources required to perform parametric studies, phase-reduction analysis gives an effective prediction of the synchronisation with reasonable precision.
${\textit {Re}} \thicksim 10^5$) also exhibit rhythmic behaviours with a single dominant frequency, according to their energy spectrum, similar to the low-Reynolds-number wakes (Szepessy & Bearman Reference Szepessy and Bearman1992; Braza, Perrin & Hoarau Reference Braza, Perrin and Hoarau2006). Therefore, it is anticipated that phase characterisation of the flow is still valid, and the ensemble-based phase-reduction framework would be applicable, to turbulent flows with a high Reynolds number. Considering the sizable computational costs or experimental resources required to perform parametric studies, phase-reduction analysis gives an effective prediction of the synchronisation with reasonable precision.
Acknowledgement
The authors are very grateful to Dr K. Fukami for his insight and suggestions during this work.
Funding
This work was supported by the National Science Foundation (NPS Award 2129638; UCLA Award 2129639). This work used Expanse at the San Diego Supercomputing Center (SDSC) through allocation PHY230016 from the Advanced Cyberinfrastructure Coordination Ecosystem: Services and Support (ACCESS) program and Hoffman2 provided by UCLA Office of Advanced Research Computing's Research Technology Group.
Declaration of interests
The authors report no conflict of interest.