Plucking as an Effect of Water-Pressure Variations at the Glacier Bed

Abstract

A rapid displacement of glaciers occurs at times when the water supply from melting or lake drainage surmounts the capacity of the subglacial drainage system. It is explained by the hydraulic action of water at high pressure in cavities which open up on the lee side of undulations or steps of the glacier bed. It is suggested that, because of pressure-induced temperature fluctuations, rock fragments may freeze on to the glacier sole and be lifted out into an opening cavity. Laboratory experiments have shown that small pressure fluctuations of a few bars* only are sufficient for rock slabs of a considerable thickness to be moved in this way.

Introduction

Plucking and abrasion are traditionally considered to be the two main fundamental erosive processes, but for a more thorough understanding of erosion it is helpful to sub divide these basic processes further (Sugden and John 1976: 151 ff). Indeed plucking is usually the result of more than one mechanism. A rock fragment has first to become loose, then it has to be evacuated from the bed, and finally it has to be entrained by the ice. In this complex series of events, water pressure at the bed can be important in more than one respect. Lliboutry (1962) has pointed out that variable water pressure in cavities which form in relation to basal slip can cause rock fatigue, and, in general terms, has linked plucking to regelation (Lliboutry 1964-65(2): 681). Robin (1976) has discussed a heat-pump effect causing a layer of basal ice to be locally below the pressure melting point. He suggests that, during water pressure induced changes of stress distribution, the ice can freeze to the rock in patches, whereupon plucking may occur. No details of the extraction of rock fragments are given, however. It is the object of this study to add a few specific ideas on the mechanism of plucking.

Water pressure and basal slip

The mode of motion to be considered is best understood by means of a simple model, in which the glacier is assumed to consist of a rigid body resting on a frictionless bed. The bed further more is formed of uniform steps tilted backward at the angle ψ (Fig. 1). The mean slope of the bed is equal to the surface slope α. For the mean ice thickness h cos α, the mean overburden pressure at the bed is readily found to be P_o = ρ gh cos² α, where ρ is the density of the ice and g is the acceleration due to gravity. It is now assumed that water at the pressure p_w acts at the bed, and that the water has unlimited access at all points. Simple geometrical considerations show that above a critical water pressure

(1)

Fig. 1. Basic rigid-body model of translatory glacier displacement by high water pressure in cavities (hydraulic-jack effect).

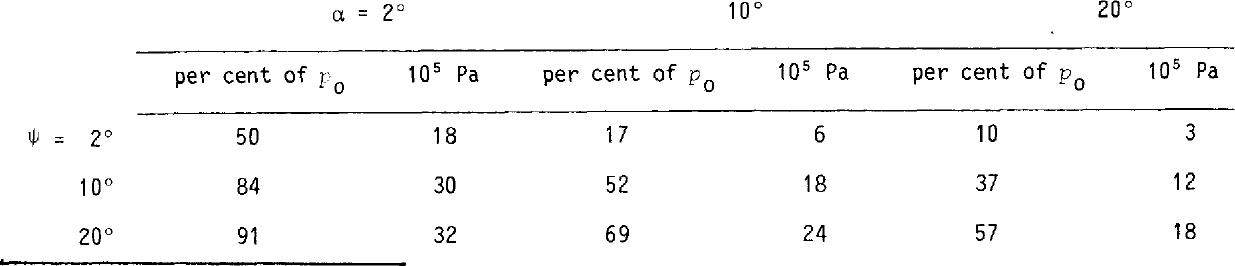
where τ is the basal shear stress, the glacier will be pushed forward at an accelerating rate, independently of the inclination δ of the steep side of the steps, while nothing happens at a lower water pressure. A derivation is given in a paper by Iken (in press); the second, more general, form of the equation was suggested by C.F. Raymond (personal communication). The action of the water can be compared to that in a hydraulic jack (Lliboutry, 1964-65(2):648). The critical pressure p_c is proportional to the overburden pressure and depends on the angles α.and ψ. The smaller the reverse dip ψ of the steps is. the smaller the critical water pressure will be, as can be expected; and the smaller α. is for a given dip , the closer p_c will approach p_o . Table I gives examples of critical water pressure for a variety of combinations of α. and ψ.

Table I. Critical pressure p_c in per cent of overburden pressurep_o and in p_a for a 400 m-thick and infinitely wide glacier for various combinations ofαandψ

When the glacier moves forward, it is simultaneously raised because of the reverse inclination of the steps. The observed growth in thickness d of the glacier must be equal to the volume of cavities per unit area.

The rigid ice and the frictionless bed are equally unrealistic in this model. Furthermore, an unlimited supply of water to the bed cannot be expected to exist at the beginning of the acceleration phase because of the lack of communicating channels, while at an advanced stage drainage connections would be too well developed for a high water pressure to persist, taking into account that steps with a uniform angle and uniform length will hardly be found in normal conditions. The situation is different with deformable ice, which will adjust to the bed in areas of concentrated stress (e.g. the tips of the steps) and thereby tend to reduce, if not to seal off, the drainage of the water. Friction at the bed reduces the acceleration as compared to the frictionless bed, so that a higher water pressure will be required to cause an appreciable effect.

Comprehensive sliding theories exist for smaller water pressures than those which are considered here (e.g. Lliboutry 1968, Kamb 1970). They show that, if ice deforms according to a linear or power law, cavities can open up below the critical pressure p_c . The limit below which no cavities form at all is called the separation pressure. Steady-state solutions have been almost exclusively considered in this theoretical work. Iken (in press), on the contrary, has concentrated on the transient stages in a recent study with an idealized numerical model, dealing with the range between separation pressure and critical pressure. This study shows that in the process of cavity formation much higher velocities are initially reached than in the steady state when stable cavities are fully developed. The opening and closure of cavities is caused by relatively small variations of water pressure, but the velocity variations are quite spectacular (including backsliding), and so are the variations of ice pressure at the bed.

There is ample observational evidence of the direct influence of water on glacier movement. Short-term fluctuations of surface velocity and water pressure following the daily cycle or after rain-fall have been reported by Iken (1978) from polar and Alpine glaciers. Furthermore, in spring and early summer an uplift of the glacier surface can be observed as well as the enhanced horizontal displacement on typical flat valley glaciers. Flotron (1973) has reported a rise of 0.5 m in 4 weeks, followed by some fluctuations and a slower lowering of the surface during the following 3 to 4 months, on Unteraargletscher in 1970-71. The horizontal velocity showed short peaks of about 150 to 300 mm d^-1 (in intervals of 4 d) as against a mean velocity of some 50 mm d^-1 during winter. Among various explanations considered, the one based on the formation of large water-filled cavities at the bed is more satisfactory than the others (Iken and others 1979).

A sudden formation of numerous crevasses was observed, also on Unteraargletscher, during a period of rain and intense snow-melt in the spring of 1977. At the same time, the local seismicity from crevassing was extremely high (Deichmann and others 1979), and a number of ponds and the water-soaked snow layer were drained suddenly by the freshly-formed crevasses. It seems probable that a feedback mechanism was active so that the opening of crevasses, down to the bed where they were filled with water, increased the drainage from the surface to the bed; there the water acted in the suggested manner, and the displacement of the glacier by the water caused, in turn, more crevasses to form, thus leading to still faster drainage. The end of the cycle was soon reached, however, probably because of the limited amount of water stored at the surface, and because of the fast development of the subglacial drainage channels. Very high piezometric water pressures were observed by the authors on Gornergletscher in drill holes and moulins, both during the early melt season and in relation to the drainage of an ice-dammed 1ake; fresh crevasses could usually be noticed as well, and enhanced glacier movement and concurrent lifting of the surface were measured.

These observations support the concept of a temporary fast displacement of the glacier by basal slip on the up-stream facets of bed undulations, while water-filled cavities open up on the lee side of the waves or mounds. The movement is very fast when the water pressure rises above the critical value p_c , and more moderate, though still well above the steady-state flow, for an increasing water pressure between the separation pressure and the critical water pressure. Under natural conditions, a considerable local variation of the angle ψ, and hence of the value of p_c , is to be expected. The glacier will show the average behaviour caused by the sum of the water action in a large number of cavities differing in size and shape.

Plucking Mechanism

At first sight, one of the main difficulties in understanding how a glacier removes rocks from the substratum at a large ice depth seems to lie in the high overburden pressure. Although its importance is only relative, depending on the water pressure acting in the joints of the bedrock, it is not easy to visualize how appreciable pieces of bedrock may become dislodged as long as a firm contact between ice and rock persists. The concept of the hydraulic-jack mechanism depicted above, by which large cavities are being formed, offers a ready answer. Fragments from the bed can fall off on the lee side of roches moutonnées in the classical manner when cavities are open, irrespective of overburden pressure, and furthermore the edge of the steps may be broken off and pushed into the openings-by• the sliding glacier. The mechanism is particularly effective in conjunction with Robin's heat-pump effect (Robin 1976).

The heat-pump effect is the consequence of spontaneous melting in temperate ice when the pressure rises, followed by drainage of part of the melt water through veins. The temperature immediately falls to the new pressure-melting point. When the pressure decreases again, the temperature cannot adjust fully because only part of the water is left to supply, when freezing, the heat necessary to reach equilibrium; the rest of the heat has to come from conduction (or internal friction). The idea has been tested in the laboratory on small samples (Goodman and others 1979), and it was found that at a pressure of 5 ⨯ 10⁶ Pa about half the free water produced by compression was expelled from the samples.

The heat-pump effect can take place in two cases: wherever ice moves from hign to low pressure, and also when the pressure decreases because of a change in stress distribution with time, e.g. when sudden changes of water pressure occur in the interconnecting drainage system at the glacier bed. The consequences of the heat-pump effect are, according to Robin, that dry friction occurs in certain areas of the bed, with certain implications for abrasion, and the formation of cold patches leading to stick-slip motion.

Cold patches form in places where the pressure decreases. They should therefore not occur in the developing cavities of the basic model of the previous section, where an increase of water pressure causes the glacier to shift. However, if one assumes that water at a high pressure has access to some cavities only, while others open passively with a concurrent drop in pressure, then freezing and adhesion of rocks can take place in the passive cavities. The pressure in the active cavities, of course, will have to become correspondingly higher for the hydrau1icjack action of the water to become effective. In nature, it is not unlikely that a sudden strong increase of water pressure takes place in part of the cavities only, depending on the proximity of subg1acia1 channels as well as water-filled crevasses reaching the bed in the process of surface drainage. Figure 2 illustrates the situation. While the ice becomes separated from the rock face in the active cavity (a), a previously jointed fragment is pulled out of the glacier bed in the passive one (b). Bottom freezing may still occur if the water stays at an intermediate pressure slightly less than the previous pressure of the ice to the rock (c).

Fig. 2. Extraction of fragments from the rock bed:

• (a) active cavity with hydraulic driving force,

• (b) passive cavity in which a rock fragment is frozen to the ice as a result of the Robin heat-pump effect,

• (c) combination of freezing and driving force at intermediate water pressure.

A more detailed picture of the plucking process than that inferred from the rigid body can be obtained with an idealized numerical model in which it is assumed that linear viscous ice slides on a frictionless bed given by a sine wave (for details of the model see Iken, in press). Figure 3 gives an example. The waves are 20 m long and 3 m high (double amplitude). The cavity shown is approximately stable at a water pressure of 24.1 ⨯ 10⁵ Pa. It is contracting in the upper and expanding in the lower graph when the water pressure is decreased by 0.5 ⨯ 10⁵ Pa and increased by as little as 0.2 ⨯ 10⁵ Pa, respectively, relative to the pressure for the stable cavity. The water and ice pressures at the bed are given together with the flow field for both situations. The total pressure changes for a sudden increase from the low to the high water pressure are also shown (bold-face numbers). In the model the mean normal pressure on the bed is kept constant, so that an increase or decrease of water pressure in the cavity is balanced by a respective decrease or increase of ice pressure between the cavities. The very large pressure gradients between some points indicate that the accuracy of the analysis is limited. but the order of magnitude is believed to be realistic.

Fig. 3. Pressure distribution on a sinusoidal bed with water-filled cavities (small light numbers). (a) Cavities shrinking at a water pressure of 23.6 ⨯ 10⁵ Pa. (b) Cavities expanding at a water pressure of 24.3 ⨯ 10⁵ Pa. The pressure changes on the bed, corresponding to the variation of water pressure, are given with large heavy numbers. (The difference in the last digit at the crest of the waves is due to the inaccuracy of the numerical treatment.) Arrows represent velocity vectors; the scale refers to a viscosity of η = 2.27 ⨯ 10¹⁴ P and a basal shear stress τ = 1.03 ⨯ 10⁵ Pa; p_o = 27.2 ⨯ 10⁵ Pa = mean pressure at the glacier sole in both plots. Cavities as shown would be stable at 24.1 ⨯ 10⁵ Pa.

Of particular interest is the fact that although the water pressure in the cavity increases by a minor amount of 0.7 ⨯ 10⁵ Pa (7 m of water column) only. the ice pressure changes locally by some 13 ⨯ 10⁵ Pa! The amplification of the pressure variation lies in this case in the order of magnitude anticipated by Robin (1976), who indicates a factor of 10 on an average scale. dealing, however. with much larger changes of water pressure: 13 ⨯ 10⁵ Pa water pressure, 13 ⨯ 10⁶ Pa ice pressure. The detailed information on the distribution of the pressure changes contained in Figure 3 (boldface numbers) can be interpreted in terms of temperature. Areas with negative numbers are those where the water film at the ice-rock interface may freeze and where the cold patches envisaged by Robin are located. It is noteworthy that, in addition to the cold-patch area at the apex of the undulation, an additional one forms near the bottom of the trough. What the figure does not show is that the cavity shrinks at low and expands at high water pressure. The ice is therefore moving away from the bed at the upper edge of an opening cavity (and also at the lower edge if the pressure increase is sufficiently large). Rock fragments adhering to the ice where the cold patches form can be moved out into the cavity. The area of potential plucking will be larger as the water pressure increases. It should be pointed out here that under natural conditions the water pressure is not confined below the critical pressure. and that above the critical pressure viscous and rigid bodies show similar acceleration. In this situation the whole ice body moves almost parallel to the tangent at the inflection point of the sine wave, and rock fragments could be lifted up over the full width of the respective cold patches at the crest as well as at the bottom of the waves. As in the case of the rigid body. one can expect that not all the cavities are connected to the subglacial drainage system, so that passive cavities with a higher plucking potential open up beside active ones. This is not a mandatory condition, however. for plucking to occur. The main difference between the viscous and the rigid model where plucking is concerned is that the mechanism operates in a much more general way with the viscous model.

It is, perhaps, unnecessary to say that cold patches, leading to either enhanced friction or stick-slip motion immediately up-stream from cavities, provide an effective means of pushing off rock at the down-stream edge of the crest of a roche moutonnée. The mechanism depicted here. in addition, shows how fragments may be removed from other sections of a wavy bed. The forces one can expect to act are likely to be sufficient to overcome not only the weight of the fragments, but also to extract them from surrounding bedrock, but they will hardly be sufficient to break the rock.

Once rock fragments have been extracted from the rock bed into the cavities it is easy to visualize how they become incorporated into the ice when the water pressure drops and the cavities close (Fig. 3a). Naturally these fragments represent grinding stones when the ice continues to slide on the bed.

Plucking Experiment

In order to demonstrate the basic ability of the glacier sole to lift up rock fragments from the bed, the following experiment was carried out (Fig. 4). Three ice plates about 40 by 40 mm² and 10 to 15 mm thick were placed between two rock specimens and put under pressure. The ice bond between the two rocks was then checked by lifting up the top slab and pushing down the bottom one. The experiment was carried out under water in a cold room kept at an average temperature of about 0°C.

Fig. 4. "Plucking experiment" to demonstrate the heat-pump effect.

In two successful experiments carried out so far, it was shown that slabs of porphyry with a rough surface could be picked up after application of the weight for a few hours to one day. The mean uniaxial stress was 1.5 and 3 ⨯ 10⁵ Pa. A tension of 0.03 and 0.07 ⨯ 10⁵ Pa was afterwards supported for 1 to 2 min, and breakage was produced at the higher tension of 0.06 and 0.13 ⨯ 10⁵ Pa, respectively. Since the stress distribution was poorly controlled (i.e. the tensile stress was probably quite different from one ice plate to the other, in particular with a concentration at the edge of one of the plates). these results indicate that the adhesion would be stronger under more favourable conditions. It is important to note further that the stresses applied in the experiment were small when compared to the ones occurring under natural conditions at the glacier bed.

The experiment was carried out with commercial ice in tap water, and the observed effect may have been influenced by the melting point depression caused by the chemical impurity of the water. It is estimated that the depression amounted to about 0.01 deg, inferred from a measured electric conductivity of 25 mS m^-1. The lowering of the temperature caused by the compression of the ice was, at 74 ⨯ 10^-9 deg Pa^-1, slightly greater. so that an additional cooling to the one already brought about by the water bath took place. This supposition is borne out by the observation of ice spicules forming along the edge of the ice plates as well as by considerable thinning of the ice plates with time. There is no doubt that pressure melting occurred and that. during this process, not only the ice but also the rock cooled down. It is concluded that melting at the ice-rock interface caused by the heat flow from the rock to the boundary plays a role in the heat-pump process which may be equally or even more important than the immediate cooling of the ice by pressure melting. This is so because the melt water will be squeezed out more readily from the interface than from within the ice. The experiment also demonstrated that the "brine" of the surrounding water bath did not immediately penetrate along the ice-rock interface when compression changed to tension. These observations suggest that the water film at the ice-rock boundaries froze when the pressure was removed, and that the interfaces represented cold patches in Robin's sense. It can be added that some of the ice plates remained firmly frozen to the rock surface after the rock slabs had come apart. Further experiments with better control of salinity of the water bath, the purity of the ice samples, and the stress distribution could tell us more about the formation and strength of cold patches.

Discussion

A pertinent question asked by the referee of this paper concerns the conditions for freezing rock onto the base of a glacier. The problem involves (1) the presence of water to freeze, (2) the heat sink, and (3) the movement of the water in the freezing layer.

(1) Existence of a water layer which can freeze

The assumption of a pressure fluctuation at the ice-rock interface (which is governed by the pressure variation in the subglacial drainage system) automatically means that phases of pressure melting alternate with phases of freezing. The thickness of the water layer, when the switch from melting to freezing occurs, depends on local conditions and on the intensity and duration of pressure melting. The water in the layer may originate from within the ice from where it becomes squeezed out if a pressure gradient exists towards the interface. More important is the melting caused by the heat conduction from the rock to the interface. As the rock cools down, the production rate of water decays with time, and the layer becomes thinner when the water drains away.

(2) Potential thickness of a freezing layer

The question of how thick a water layer can be in order to freeze is easier to answer. A pressure change of 13 ⨯ 10⁶ Pa is connected to a change of the pressure-melting point by 1 deg, and the compensation of the latent heat involved causes 0.6% of the ice to melt, or the same quantity of water to freeze, depending on whether the pressure increases or decreases. Assuming equal heat capacity and thermal conductivity for ice and rock, and using the temperature distribution charts from Robin (1976, fig. 4), it is found that, when the pressure in the ice decreases suddenly by 13 ⨯ 10⁶ Pa, the water that will freeze at the ice-rock interface amounts to a layer about 0.06 mm thick after 20 sand 2 mm thick after 6 h, provided that the ice is free of water. The freezing potential is halved if the ice contains the exact amount, or an excess, of water to provide the latent heat necessary for the temperature increase of 1 deg in the ice. In the case of the experiment described above, with a pressure change of 3 ⨯ 10⁵ Pa only, the thickness of the water layer that could have frozen in 1 min is estimated to be about 1.5 μm if no water was squeezed out of the ice specimens, or 3.0 μm if all the water was squeezed out prior to the pressure release.

(3) Movement in the water layer

The models used here to find pressure distributions are based on the assumption of an immediate flow of water to and from the interface, hence the movement of water in the freezing layer cannot be treated, by definition. (Similarly, nothing can be said about the behaviour of cold patches, since the assumption of a frictionless bed immediately breaks down with the formation of such patches.) Intuitively it can be surmised that the freezing of ice to rock is most likely to take place when a rapid pressure drop occurs after an extended period of pressure melting. The existence of a network of small drainage channels cutting across ice pressure barriers would also favour a very thin water film which could easily freeze.

The notion that cold patches form when the water pressure rises, while observation shows that the velocity increases, is a paradox. A possible explanation is that at very high water pressure, when the ice moves in a tangential direction to the inflection points of the sine waves of Figure 3, the cold patches break easily under tension. The retardation caused by the cold patches before breakage may be too short to be detected.

Conclusions

The combination of the rapid opening of large-scale water-filled cavities under high water pressure with the heat-pump effect proposed by Robin (1976) represents a plausible mechanism by which rock fragments and even large slabs of rock can be extracted by the glacier from its bed. The prerequisite for this plucking process to become effective is that the rock is sufficiently and suitably jointed. Apart from the bedrock condition, a large amplitude of the water-pressure fluctuations inducing the heat-pump effect, and a high basal shear stress helping the cavities to form, are likewise important. Spring (1980) has shown by model computation that the pressure amplitude of the main subglacial drainage channel increases with distance from the terminus. The probability that the plucking process takes place in the form depicted here increases therefore also with that distance. However, fluctuations of run-off decrease in the accumulation area. A place where plucking is particularly likely to occur because of a combination of large water-pressure amplitudes and high basal shear stress is the section of the glacier at the foot of an ice fall, where overdeepened basins are known to be located.