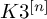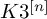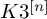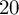1 Introduction
1.1 Background
A prominent rôle in the theory of
![]() $K3$
surfaces is played by spherical (i.e. rigid and simple) vector bundles. In [Reference O’GradyO’G22], we have proved existence and uniqueness results for stable vector bundles on general polarized hyperkähler (HK) variety of type
$K3$
surfaces is played by spherical (i.e. rigid and simple) vector bundles. In [Reference O’GradyO’G22], we have proved existence and uniqueness results for stable vector bundles on general polarized hyperkähler (HK) variety of type
![]() $K3^{[2]}$
with certain discrete invariants (of the polarization and of the vector bundle). In the present paper, we show that the main result in [Reference O’GradyO’G22] extends to HK varieties of type
$K3^{[2]}$
with certain discrete invariants (of the polarization and of the vector bundle). In the present paper, we show that the main result in [Reference O’GradyO’G22] extends to HK varieties of type
![]() $K3^{[n]}$
of arbitrary (even) dimension. More precisely, we prove that for certain choices of rank and first two Chern classes on a polarized HK variety
$K3^{[n]}$
of arbitrary (even) dimension. More precisely, we prove that for certain choices of rank and first two Chern classes on a polarized HK variety
![]() $(X,h)$
of type
$(X,h)$
of type
![]() $K3^{[n]}$
, there exists one and only one stable vector bundle with the assigned rank and first two Chern classes provided the moduli point of
$K3^{[n]}$
, there exists one and only one stable vector bundle with the assigned rank and first two Chern classes provided the moduli point of
![]() $(X,h)$
is a general point of a certain irreducible component of the relevant moduli space of polarized
$(X,h)$
is a general point of a certain irreducible component of the relevant moduli space of polarized
![]() $HK$
varieties.
$HK$
varieties.
We like to think of this result as evidence in favour of the following slogan: stable vector bundles on higher dimensional HK manifolds behave as well as stable sheaves on
![]() $K3$
surfaces, provided one restricts to (stable) vector bundles whose projectivization extends to all small deformations of the base HK manifold (i.e. projectively hyperhomolomorphic vector bundles).
$K3$
surfaces, provided one restricts to (stable) vector bundles whose projectivization extends to all small deformations of the base HK manifold (i.e. projectively hyperhomolomorphic vector bundles).
1.2 The main result
Let
![]() ${\mathscr K}^d_e(2n)$
be the moduli space of polarized HK varieties of type
${\mathscr K}^d_e(2n)$
be the moduli space of polarized HK varieties of type
![]() $K3^{[n]}$
of degree e and divisibility d. Thus,
$K3^{[n]}$
of degree e and divisibility d. Thus,
![]() ${\mathscr K}^d_e(2n)$
parametrizes isomorphism classes of couples
${\mathscr K}^d_e(2n)$
parametrizes isomorphism classes of couples
![]() $(X,h)$
, where X is an HK manifold of type
$(X,h)$
, where X is an HK manifold of type
![]() $K3^{[n]}$
,
$K3^{[n]}$
,
![]() $h\in \operatorname {\mathrm {NS}}(X)$
is the class of an ample divisor class (we assume that h is primitive), such that
$h\in \operatorname {\mathrm {NS}}(X)$
is the class of an ample divisor class (we assume that h is primitive), such that
![]() $q_X(h)=e$
and
$q_X(h)=e$
and
![]() $\operatorname {\mathrm {div}}(h)=d$
, where
$\operatorname {\mathrm {div}}(h)=d$
, where
![]() $q_X$
is the Beauville-Bogomolov-Fujiki (BBF) quadratic form of X and
$q_X$
is the Beauville-Bogomolov-Fujiki (BBF) quadratic form of X and
![]() $\operatorname {\mathrm {div}}(h)$
is the divisibility of h, that is the positive generator of
$\operatorname {\mathrm {div}}(h)$
is the divisibility of h, that is the positive generator of
![]() $q_X(h,H^2(X;{\mathbb Z}))$
. Note that
$q_X(h,H^2(X;{\mathbb Z}))$
. Note that
![]() $\operatorname {\mathrm {div}}(h)$
divides
$\operatorname {\mathrm {div}}(h)$
divides
![]() $2(n-1)$
. It is known under which hypotheses
$2(n-1)$
. It is known under which hypotheses
![]() ${\mathscr K}^d_e(2n)$
is not empty. If that is the case, then it is a quasi-projective variety (not necessarily irreducible) of pure dimension
${\mathscr K}^d_e(2n)$
is not empty. If that is the case, then it is a quasi-projective variety (not necessarily irreducible) of pure dimension
![]() $20$
.
$20$
.
We recall that if
![]() ${\mathscr F}$
is a (coherent) sheaf on a complex smooth variety, the discriminant of
${\mathscr F}$
is a (coherent) sheaf on a complex smooth variety, the discriminant of
![]() ${\mathscr F}$
is defined to be the Betti cohomology class
${\mathscr F}$
is defined to be the Betti cohomology class
Theorem 1.1. Let
![]() $n,r_0,g,l,e\in {\mathbb N}_{+}$
, with
$n,r_0,g,l,e\in {\mathbb N}_{+}$
, with
![]() $n\ge 2$
, and let
$n\ge 2$
, and let
 $$ \begin{align*} \overline{e}:= \begin{cases} e\ \text{if}\ r_0\ \text{is even,} \\ 4e\ \text{if}\ r_0\ \text{is odd.} \end{cases} \end{align*} $$
$$ \begin{align*} \overline{e}:= \begin{cases} e\ \text{if}\ r_0\ \text{is even,} \\ 4e\ \text{if}\ r_0\ \text{is odd.} \end{cases} \end{align*} $$
Assume that
 $$ \begin{align} g\ \text{divides} \begin{cases} (r_0-1)\ \text{if}\ r_0\ \text{is even,} \\ (r_0-1)/2\ \text{ if}\ r_0\ \text{is odd,} \end{cases} \end{align} $$
$$ \begin{align} g\ \text{divides} \begin{cases} (r_0-1)\ \text{if}\ r_0\ \text{is even,} \\ (r_0-1)/2\ \text{ if}\ r_0\ \text{is odd,} \end{cases} \end{align} $$
that
 $$ \begin{align} l|(n-1),\quad \gcd\{l, r_0\}=1,\quad \gcd\left\{l, \frac{r_0-1}{g}\right\}=1, \end{align} $$
$$ \begin{align} l|(n-1),\quad \gcd\{l, r_0\}=1,\quad \gcd\left\{l, \frac{r_0-1}{g}\right\}=1, \end{align} $$
that
and that
 $$ \begin{align} \overline{e}+\frac{2(n-1)(r_0-1)^2}{g^2}\equiv 0\quad \pmod{8l^2}. \end{align} $$
$$ \begin{align} \overline{e}+\frac{2(n-1)(r_0-1)^2}{g^2}\equiv 0\quad \pmod{8l^2}. \end{align} $$
Let
![]() $i\in \{1,2\}$
be such that
$i\in \{1,2\}$
be such that
![]() $i\equiv r_0\ \pmod {2}$
. Then there exists an irreducible component of
$i\equiv r_0\ \pmod {2}$
. Then there exists an irreducible component of
![]() ${\mathscr K}^{il}_e(2n)$
, denoted by
${\mathscr K}^{il}_e(2n)$
, denoted by
![]() ${\mathscr K}^{il}_e(2n)^{\mathrm {good}}$
(see Definition 5.3), such that for a general
${\mathscr K}^{il}_e(2n)^{\mathrm {good}}$
(see Definition 5.3), such that for a general
![]() $[(X,h)]\in {\mathscr K}^{il}_e(2n)^{\mathrm {good}}$
, there exists one and only one (up to isomorphism) h slope-stable vector bundle
$[(X,h)]\in {\mathscr K}^{il}_e(2n)^{\mathrm {good}}$
, there exists one and only one (up to isomorphism) h slope-stable vector bundle
![]() ${\mathscr E}$
on X, such that
${\mathscr E}$
on X, such that
Moreover, for such a vector bundle,
![]() $H^p(X,End^0({\mathscr E}))=0$
for all p.
$H^p(X,End^0({\mathscr E}))=0$
for all p.
1.3 Comments
1.3.1 Special cases
Let
![]() $g=l=1$
in Theorem 1.1. Then the hypotheses reduce to the following congruences:
$g=l=1$
in Theorem 1.1. Then the hypotheses reduce to the following congruences:
 $$ \begin{align} e\equiv \begin{cases} 4(n-1)r_0-2n-6\quad \pmod{8r_0} & \text{if}\ r_0\equiv 0\quad \pmod{4}, \\ \frac{1}{2}((n-1)r_0-n-3)\quad \pmod{2r_0} & \text{if}\ r_0\equiv 1\quad \pmod{4}, \\ -2n-6\quad \pmod{8r_0} & \text{if}\ r_0\equiv 2\quad \pmod{4}, \\ -\frac{1}{2}((n-1)r_0+n+3)\quad \pmod{2r_0} & \text{if}\ r_0\equiv 3\quad \pmod{4}. \end{cases} \end{align} $$
$$ \begin{align} e\equiv \begin{cases} 4(n-1)r_0-2n-6\quad \pmod{8r_0} & \text{if}\ r_0\equiv 0\quad \pmod{4}, \\ \frac{1}{2}((n-1)r_0-n-3)\quad \pmod{2r_0} & \text{if}\ r_0\equiv 1\quad \pmod{4}, \\ -2n-6\quad \pmod{8r_0} & \text{if}\ r_0\equiv 2\quad \pmod{4}, \\ -\frac{1}{2}((n-1)r_0+n+3)\quad \pmod{2r_0} & \text{if}\ r_0\equiv 3\quad \pmod{4}. \end{cases} \end{align} $$
In particular, for
![]() $n=2$
(and
$n=2$
(and
![]() $g=l=1$
), Theorem 1.1 reduces to the main result in [Reference O’GradyO’G22]. Note also that in this case,
$g=l=1$
), Theorem 1.1 reduces to the main result in [Reference O’GradyO’G22]. Note also that in this case,
![]() ${\mathscr K}^{il}_e(2n)$
is irreducible by [Reference DebarreDeb22, Theorem 3.5], and hence
${\mathscr K}^{il}_e(2n)$
is irreducible by [Reference DebarreDeb22, Theorem 3.5], and hence
![]() ${\mathscr K}^{il}_e(2n)^{\mathrm {good}}={\mathscr K}^{il}_e(2n)$
.
${\mathscr K}^{il}_e(2n)^{\mathrm {good}}={\mathscr K}^{il}_e(2n)$
.
1.3.2 Rank and Chern classes
The choice of rank and first two Chern classes in Theorem 1.1 is not as special as one would think. Let us first consider a rigid stable vector bundle
![]() ${\mathscr E}$
on a polarized
${\mathscr E}$
on a polarized
![]() $K3$
surface
$K3$
surface
![]() $(S,h)$
of rank r with
$(S,h)$
of rank r with
![]() $c_1({\mathscr E})=ah$
. Since
$c_1({\mathscr E})=ah$
. Since
![]() $\chi (S,End\,{\mathscr E})=2$
, we have
$\chi (S,End\,{\mathscr E})=2$
, we have
It follows that
![]() $\gcd \{r,a\}=1$
. The following result is a (weak) extension to higher dimensions.
$\gcd \{r,a\}=1$
. The following result is a (weak) extension to higher dimensions.
Proposition 1.2. Let
![]() $(X,h)$
be a polarized HK variety of type
$(X,h)$
be a polarized HK variety of type
![]() $K3^{[n]}$
, and let
$K3^{[n]}$
, and let
![]() ${\mathscr F}$
be a slope-stable vector bundle on X. Suppose that
${\mathscr F}$
be a slope-stable vector bundle on X. Suppose that
![]() $c_1({\mathscr F})=ah$
and that the natural morphism
$c_1({\mathscr F})=ah$
and that the natural morphism
![]() $\operatorname {\mathrm {Def}}(X,{\mathscr F})\to \operatorname {\mathrm {Def}}(X,h)$
is surjective. Then
$\operatorname {\mathrm {Def}}(X,{\mathscr F})\to \operatorname {\mathrm {Def}}(X,h)$
is surjective. Then
where
![]() $r_0,m,b_0'$
are integers, and
$r_0,m,b_0'$
are integers, and
![]() $\gcd \{r_0,b_0'\}=1$
.
$\gcd \{r_0,b_0'\}=1$
.
Note that in Proposition 1.2, we do not assume that
![]() ${\mathscr F}$
is rigid. There are examples of slope-stable projectively hyperholomorphic vector bundles for which
${\mathscr F}$
is rigid. There are examples of slope-stable projectively hyperholomorphic vector bundles for which
![]() $m>1$
which are not rigid (see [Reference MarkmanMar21, Reference BottiniBot22] and [Reference FatighentiFat23]). The tangent vector bundle of an HK manifold of type
$m>1$
which are not rigid (see [Reference MarkmanMar21, Reference BottiniBot22] and [Reference FatighentiFat23]). The tangent vector bundle of an HK manifold of type
![]() $K3^{[2]}$
is an example of a rigid slope-stable projectively hyperholomorphic vector bundle with
$K3^{[2]}$
is an example of a rigid slope-stable projectively hyperholomorphic vector bundle with
![]() $m>1$
(in fact,
$m>1$
(in fact,
![]() $m=4$
) (see [Reference GavranGav21]). There are no other examples of the latter type that I am aware of.
$m=4$
) (see [Reference GavranGav21]). There are no other examples of the latter type that I am aware of.
The stable vector bundles in Theorem 1.1, together with those obtained by tensoring with powers of the polarization, cover many of the choices of rank and first Chern class with
![]() $m=1$
which are a priori possible according to Proposition 1.2.
$m=1$
which are a priori possible according to Proposition 1.2.
Regarding the discriminant of the vector bundle(s)
![]() ${\mathscr E}$
in Theorem 1.1, we note the following. First, the formula for the discriminant in (1.2.6) for
${\mathscr E}$
in Theorem 1.1, we note the following. First, the formula for the discriminant in (1.2.6) for
![]() $n=1$
is exactly the formula in (1.3.2). Next, since
$n=1$
is exactly the formula in (1.3.2). Next, since
![]() $-\Delta ({\mathscr E})$
is the second Chern class of the pushforward to X of the relative tangent bundle of
$-\Delta ({\mathscr E})$
is the second Chern class of the pushforward to X of the relative tangent bundle of
![]() ${\mathbb P}({\mathscr E})\to X$
, and
${\mathbb P}({\mathscr E})\to X$
, and
![]() ${\mathbb P}({\mathscr E})$
extends to all small deformations of X (because
${\mathbb P}({\mathscr E})$
extends to all small deformations of X (because
![]() $H^2(X,End^0({\mathscr E}))=0$
), the cohomology class
$H^2(X,End^0({\mathscr E}))=0$
), the cohomology class
![]() $\Delta ({\mathscr E})$
remains of type
$\Delta ({\mathscr E})$
remains of type
![]() $(2,2)$
for all deformations of X. It follows that
$(2,2)$
for all deformations of X. It follows that
![]() $\Delta ({\mathscr E})$
is a linear combination of
$\Delta ({\mathscr E})$
is a linear combination of
![]() $c_2(X)$
and
$c_2(X)$
and
![]() $q_X^{\vee }$
(see the main result in [Reference ZhangZha15]). If
$q_X^{\vee }$
(see the main result in [Reference ZhangZha15]). If
![]() $n\in \{2,3\}$
, then
$n\in \{2,3\}$
, then
![]() $c_2(X)$
and
$c_2(X)$
and
![]() $q_X^{\vee }$
are linearly dependent, and hence, it follows (without doing any computation) that
$q_X^{\vee }$
are linearly dependent, and hence, it follows (without doing any computation) that
![]() $\Delta ({\mathscr E})$
is a multiple of
$\Delta ({\mathscr E})$
is a multiple of
![]() $c_2(X)$
. If
$c_2(X)$
. If
![]() $n>3$
, then
$n>3$
, then
![]() $c_2(X)$
and
$c_2(X)$
and
![]() $q_X^{\vee }$
are linearly independent, hence, there is no ‘a priori’reason why
$q_X^{\vee }$
are linearly independent, hence, there is no ‘a priori’reason why
![]() $\Delta ({\mathscr E})$
should be a multiple of
$\Delta ({\mathscr E})$
should be a multiple of
![]() $c_2(X)$
. In fact, I know of no examples of stable projectively hyperholomorphic vector bundles on HK varieties of type
$c_2(X)$
. In fact, I know of no examples of stable projectively hyperholomorphic vector bundles on HK varieties of type
![]() $K3^{[n]}$
whose discriminant is not a multiple of the second Chern class.
$K3^{[n]}$
whose discriminant is not a multiple of the second Chern class.
The vector bundles
![]() ${\mathscr E}$
in Theorem 1.1 are atomic, in fact, they are in the
${\mathscr E}$
in Theorem 1.1 are atomic, in fact, they are in the
![]() ${\mathscr O}_X$
-orbit (see [Reference MarkmanMar21]), and hence, the Beckmann-Markman extended Mukai vector
${\mathscr O}_X$
-orbit (see [Reference MarkmanMar21]), and hence, the Beckmann-Markman extended Mukai vector
![]() $\widetilde {v}({\mathscr E})$
(see [Reference MarkmanMar21, Theorem 6.13], [Reference BeckmannBec23, Definition 4.16], [Reference BeckmannBec22, Definition 1.1]) is determined uniquely (if we require that its first entry equals
$\widetilde {v}({\mathscr E})$
(see [Reference MarkmanMar21, Theorem 6.13], [Reference BeckmannBec23, Definition 4.16], [Reference BeckmannBec22, Definition 1.1]) is determined uniquely (if we require that its first entry equals
![]() $r({\mathscr E})$
), in particular,
$r({\mathscr E})$
), in particular,
![]() $\widetilde {q}(\widetilde {v}({\mathscr E}))=-(n+3)r_0^{2n-2}/2$
by [Reference BeckmannBec23, Lemma 4.8]. By the formula relating the projection of the discriminant
$\widetilde {q}(\widetilde {v}({\mathscr E}))=-(n+3)r_0^{2n-2}/2$
by [Reference BeckmannBec23, Lemma 4.8]. By the formula relating the projection of the discriminant
![]() $\Delta ({\mathscr E})$
on the Verbitsky subalgebra and the square
$\Delta ({\mathscr E})$
on the Verbitsky subalgebra and the square
![]() $\widetilde {q}(\widetilde {v}({\mathscr E}))$
in [Reference BottiniBot22, Proposition 3.11], we get that if
$\widetilde {q}(\widetilde {v}({\mathscr E}))$
in [Reference BottiniBot22, Proposition 3.11], we get that if
![]() $\Delta ({\mathscr E})$
is a multiple of
$\Delta ({\mathscr E})$
is a multiple of
![]() $c_2(X)$
, then it is given by the formula in (1.2.6).
$c_2(X)$
, then it is given by the formula in (1.2.6).
The natural question to ask is the following: Are we close to having listed all slope-stable rigid vector bundles on a polarized HK variety of type
![]() $K3^{[n]}$
with
$K3^{[n]}$
with
![]() $20$
moduli?
$20$
moduli?
1.3.3 Projective bundles
Let X and
![]() ${\mathscr E}$
be as in Theorem 1.1. The projectivization
${\mathscr E}$
be as in Theorem 1.1. The projectivization
![]() ${\mathbb P}({\mathscr E})$
extends (uniquely) to a projective bundle on all (small) deformations of X because
${\mathbb P}({\mathscr E})$
extends (uniquely) to a projective bundle on all (small) deformations of X because
![]() $H^2(X,End^0({\mathscr E}))=0$
. Actually, Markman [Reference MarkmanMar21, Theorem 1.4] shows that
$H^2(X,End^0({\mathscr E}))=0$
. Actually, Markman [Reference MarkmanMar21, Theorem 1.4] shows that
![]() ${\mathbb P}({\mathscr E})$
extends to a projective bundle on all deformations of X (it is projectively hyperholomorphic). In fact, the (possibly twisted) locally free sheaf E on
${\mathbb P}({\mathscr E})$
extends to a projective bundle on all deformations of X (it is projectively hyperholomorphic). In fact, the (possibly twisted) locally free sheaf E on
![]() $S^{[n]}$
appearing in Markman loc. cit. is obtained by deforming the vector bundle
$S^{[n]}$
appearing in Markman loc. cit. is obtained by deforming the vector bundle
![]() ${\mathscr F}[n]^{+}$
associated to a spherical vector bundle
${\mathscr F}[n]^{+}$
associated to a spherical vector bundle
![]() ${\mathscr F}$
on S, see Definition 3.1 (or Definition 5.1 in [Reference O’GradyO’G22]), and likewise the vector bundles in Theorem 1.1 are obtained by deforming
${\mathscr F}$
on S, see Definition 3.1 (or Definition 5.1 in [Reference O’GradyO’G22]), and likewise the vector bundles in Theorem 1.1 are obtained by deforming
![]() ${\mathscr F}[n]^{+}$
. Theorem 1.1 should provide a uniqueness result for stable projective bundles
${\mathscr F}[n]^{+}$
. Theorem 1.1 should provide a uniqueness result for stable projective bundles
![]() $\mathbf P$
of dimension
$\mathbf P$
of dimension
![]() $(r_0^n-1)$
with characteristic class given by the third equality in (1.2.6) (i.e.
$(r_0^n-1)$
with characteristic class given by the third equality in (1.2.6) (i.e.
![]() $-c_2(\Theta _{{\mathbf P}/X})$
, where
$-c_2(\Theta _{{\mathbf P}/X})$
, where
![]() $\Theta _{{\mathbf P}/X}$
is the relative tangent bundle of
$\Theta _{{\mathbf P}/X}$
is the relative tangent bundle of
![]() ${\mathbf P}\to X$
) on a general HK manifold of type
${\mathbf P}\to X$
) on a general HK manifold of type
![]() $K3^{[n]}$
. In order to turn this into a precise statement, one would need to specify with respect to which Kähler classes the projective bundle is supposed to be stable. The zoo of conditions in Theorem 1.1 would then correspond to the cases in which the projective bundle is the projectivization of a vector bundle, that is to the vanishing of the relevant Brauer class.
$K3^{[n]}$
. In order to turn this into a precise statement, one would need to specify with respect to which Kähler classes the projective bundle is supposed to be stable. The zoo of conditions in Theorem 1.1 would then correspond to the cases in which the projective bundle is the projectivization of a vector bundle, that is to the vanishing of the relevant Brauer class.
1.3.4 Franchetta property
Let
![]() ${\mathscr U}^{il}_e(2n)\subset {\mathscr K}^{il}_e(2n)$
be an open nonempty subset with the property that there exists one and only one stable vector bundle
${\mathscr U}^{il}_e(2n)\subset {\mathscr K}^{il}_e(2n)$
be an open nonempty subset with the property that there exists one and only one stable vector bundle
![]() ${\mathscr E}$
on
${\mathscr E}$
on
![]() $[(X,h)]\in {\mathscr U}^{il}_e(2n)$
, such that the equations in (1.2.6) hold, and let
$[(X,h)]\in {\mathscr U}^{il}_e(2n)$
, such that the equations in (1.2.6) hold, and let
![]() ${\mathscr X}\to {\mathscr U}^{il}_e(2n)$
be the tautological family of HK (polarized) varieties (we might need to pass to the moduli stack). By Theorem A.5 in [Reference MukaiMuk87], there exists a quasitautological vector bundle
${\mathscr X}\to {\mathscr U}^{il}_e(2n)$
be the tautological family of HK (polarized) varieties (we might need to pass to the moduli stack). By Theorem A.5 in [Reference MukaiMuk87], there exists a quasitautological vector bundle
![]() $\mathsf E$
on
$\mathsf E$
on
![]() ${\mathscr X}$
, that is a vector bundle whose restriction to a fibre
${\mathscr X}$
, that is a vector bundle whose restriction to a fibre
![]() $(X,h)$
of
$(X,h)$
of
![]() ${\mathscr X}\to {\mathscr U}^{il}_e(2n)$
is isomorphic to
${\mathscr X}\to {\mathscr U}^{il}_e(2n)$
is isomorphic to
![]() ${\mathscr E}^{\oplus d}$
for some
${\mathscr E}^{\oplus d}$
for some
![]() $d>0$
, where
$d>0$
, where
![]() ${\mathscr E}$
is the vector bundle of Theorem 1.1. If
${\mathscr E}$
is the vector bundle of Theorem 1.1. If
![]() $[(X,h)]\in {\mathscr U}^{il}_e(2n)$
, the generalized Franchetta conjecture, see [Reference Fu, Laterveer and VialFLV19], predicts that the restriction to
$[(X,h)]\in {\mathscr U}^{il}_e(2n)$
, the generalized Franchetta conjecture, see [Reference Fu, Laterveer and VialFLV19], predicts that the restriction to
![]() $\operatorname {\mathrm {CH}}^2(X)_{{\mathbb Q}}$
of
$\operatorname {\mathrm {CH}}^2(X)_{{\mathbb Q}}$
of
![]() $\operatorname {\mathrm {ch}}_2({\mathsf E})\in \operatorname {\mathrm {CH}}({\mathscr X})_{{\mathbb Q}}$
is equal to
$\operatorname {\mathrm {ch}}_2({\mathsf E})\in \operatorname {\mathrm {CH}}({\mathscr X})_{{\mathbb Q}}$
is equal to
![]() $-d\frac {r_0^{2n-2}(r_0^2-1)}{12}c_2(X)$
. In other words, it predicts that the third equality in (1.2.6) holds at the level of (rational) Chow groups. In general, it is not easy to give a rationally defined algebraic cycle class on a nonempty open subset of the moduli stack of polarized HK varieties. Theorem 1.1 produces such a cycle, and hence, it provides a good test for the generalized Franchetta conjecture.
$-d\frac {r_0^{2n-2}(r_0^2-1)}{12}c_2(X)$
. In other words, it predicts that the third equality in (1.2.6) holds at the level of (rational) Chow groups. In general, it is not easy to give a rationally defined algebraic cycle class on a nonempty open subset of the moduli stack of polarized HK varieties. Theorem 1.1 produces such a cycle, and hence, it provides a good test for the generalized Franchetta conjecture.
1.4 Basic ideas
The key elements in the proof of the main result are the following. First, there is the extension to modular sheaves (defined in [Reference O’GradyO’G22]) on higher dimensional HK manifolds of the decomposition of the (real) ample cone of a smooth projective surface into open chambers for which slope stability of sheaves with fixed numerical characters does not change (see [Reference O’GradyO’G22]).
The second element is the behaviour of modular vector bundles on a Lagrangian HK manifold. If the polarization is very close to the pullback of an ample line bundle from the base, then the restriction of a slope-stable vector bundle to a general Lagrangian fibre is slope semistable, and if it is slope-stable, then it is a semihomogeneous vector bundle, in particular, it has no nontrivial infinitesimal deformations keeping the determinant fixed. In the reverse direction, if the restriction of a vector bundle to a general Lagrangian fibre is slope-stable, then the vector bundle is slope-stable (provided the polarization is very close to the pullback of abrn ample line bundle from the base). The key element in the proof of existence is a construction discussed in [Reference O’GradyO’G22] (and in [Reference MarkmanMar21]) which associates to a vector bundle
![]() ${\mathscr F}$
on a
${\mathscr F}$
on a
![]() $K3$
surface S a sheaf
$K3$
surface S a sheaf
![]() ${\mathscr F}[n]^{+}$
on
${\mathscr F}[n]^{+}$
on
![]() $S^{[n]}$
. The sheaf
$S^{[n]}$
. The sheaf
![]() ${\mathscr F}[n]^{+}$
is locally free by Haiman’s highly nontrivial results in [Reference HaimanHai01]. If
${\mathscr F}[n]^{+}$
is locally free by Haiman’s highly nontrivial results in [Reference HaimanHai01]. If
![]() ${\mathscr F}$
is a spherical vector bundle, then
${\mathscr F}$
is a spherical vector bundle, then
![]() $\operatorname {\mathrm {End}}^0({\mathscr F}[n]^{+})$
has no nonzero cohomology by Bridgeland-King-Reid’s derived version of the McKay correspondence. This gives that
$\operatorname {\mathrm {End}}^0({\mathscr F}[n]^{+})$
has no nonzero cohomology by Bridgeland-King-Reid’s derived version of the McKay correspondence. This gives that
![]() ${\mathscr F}[n]^{+}$
extends to all (small) deformations of
${\mathscr F}[n]^{+}$
extends to all (small) deformations of
![]() $(S^{[n]},\det {\mathscr F}[n]^{+})$
, and that the projectivization
$(S^{[n]},\det {\mathscr F}[n]^{+})$
, and that the projectivization
![]() ${\mathbb P}({\mathscr F}[n]^{+})$
extends to all (small) deformations of
${\mathbb P}({\mathscr F}[n]^{+})$
extends to all (small) deformations of
![]() $S^{[n]}$
(the last result follows from a classical result of Horikawa). We prove slope stability of
$S^{[n]}$
(the last result follows from a classical result of Horikawa). We prove slope stability of
![]() ${\mathscr F}[n]^{+}$
in the case of an elliptic
${\mathscr F}[n]^{+}$
in the case of an elliptic
![]() $K3$
surface S by using our results on vector bundles on Lagrangian HK manifolds. In fact, if S is an elliptic
$K3$
surface S by using our results on vector bundles on Lagrangian HK manifolds. In fact, if S is an elliptic
![]() $K3$
surface, then there is a Lagrangian fibration
$K3$
surface, then there is a Lagrangian fibration
![]() $S^{[n]}\to ({\mathbb P}^1)^{(n)}\cong {\mathbb P}^n$
, whose general fibre is the product of n fibres of the elliptic fibration. If
$S^{[n]}\to ({\mathbb P}^1)^{(n)}\cong {\mathbb P}^n$
, whose general fibre is the product of n fibres of the elliptic fibration. If
![]() ${\mathscr F}$
is a slope-stable rigid vector bundle on S, then the restriction to an elliptic fibre is slope-stable. It follows that the restriction of
${\mathscr F}$
is a slope-stable rigid vector bundle on S, then the restriction to an elliptic fibre is slope-stable. It follows that the restriction of
![]() ${\mathscr F}[n]^{+}$
to a general fibre of the Lagrangian fibration
${\mathscr F}[n]^{+}$
to a general fibre of the Lagrangian fibration
![]() $S^{[n]}\to {\mathbb P}^n$
is slope-stable. From this, one gets that the (unique) extension of
$S^{[n]}\to {\mathbb P}^n$
is slope-stable. From this, one gets that the (unique) extension of
![]() ${\mathscr F}[n]^{+}$
to a general Lagrangian deformation of
${\mathscr F}[n]^{+}$
to a general Lagrangian deformation of
![]() $(S^{[n]},\det {\mathscr F}[n]^{+})$
is slope-stable with respect to
$(S^{[n]},\det {\mathscr F}[n]^{+})$
is slope-stable with respect to
![]() $\det {\mathscr F}[n]^{+}$
(provided we move in a Noether-Lefschetz locus with high enough discriminant). Uniqueness of a general slope-stable vector bundle with the given numerical invariants is obtained by proving uniqueness for vector bundles on (polarized) HK varieties with Lagrangian fibrations (with discriminant high enough and almost coprime to the rank). The main points in the proof of the latter result are the following. Let
$\det {\mathscr F}[n]^{+}$
(provided we move in a Noether-Lefschetz locus with high enough discriminant). Uniqueness of a general slope-stable vector bundle with the given numerical invariants is obtained by proving uniqueness for vector bundles on (polarized) HK varieties with Lagrangian fibrations (with discriminant high enough and almost coprime to the rank). The main points in the proof of the latter result are the following. Let
![]() ${\mathscr F}$
be a spherical vector bundle on an elliptic
${\mathscr F}$
be a spherical vector bundle on an elliptic
![]() $K3$
surface S: the vector bundle
$K3$
surface S: the vector bundle
![]() ${\mathscr E}_X$
on a (small) Lagrangian deformation X of
${\mathscr E}_X$
on a (small) Lagrangian deformation X of
![]() $S^{[n]}$
obtained by extension of
$S^{[n]}$
obtained by extension of
![]() ${\mathscr F}[n]^{+}$
restricts to slope-stable semihomogeneous vector bundles on Lagrangian fibres parametrized by a large open subset of the base (the complement has codimension at least
${\mathscr F}[n]^{+}$
restricts to slope-stable semihomogeneous vector bundles on Lagrangian fibres parametrized by a large open subset of the base (the complement has codimension at least
![]() $2$
). Any slope-stable vector bundle
$2$
). Any slope-stable vector bundle
![]() ${\mathscr E}$
on X with the same rank
${\mathscr E}$
on X with the same rank
![]() $c_1$
and
$c_1$
and
![]() $c_2$
as
$c_2$
as
![]() ${\mathscr E}_X$
restricts to a slope-stable semihomogeneous vector bundle on a general Lagrangian fibre. Any two simple semihomogeneous vector bundles on an Abelian variety with the same rank and determinant are obtained one from the other via tensorization with a (torsion) line bundle. This, together with a monodromy argument, gives that
${\mathscr E}_X$
restricts to a slope-stable semihomogeneous vector bundle on a general Lagrangian fibre. Any two simple semihomogeneous vector bundles on an Abelian variety with the same rank and determinant are obtained one from the other via tensorization with a (torsion) line bundle. This, together with a monodromy argument, gives that
![]() ${\mathscr E}_X$
and
${\mathscr E}_X$
and
![]() ${\mathscr E}$
restrict to isomorphic vector bundles on a general Lagrangian fibre. Since the set of Lagrangian fibres for which the restriction of
${\mathscr E}$
restrict to isomorphic vector bundles on a general Lagrangian fibre. Since the set of Lagrangian fibres for which the restriction of
![]() ${\mathscr E}_X$
is slope-stable has the complement of codimension at least
${\mathscr E}_X$
is slope-stable has the complement of codimension at least
![]() $2$
, one concludes that
$2$
, one concludes that
![]() ${\mathscr E}_X$
and
${\mathscr E}_X$
and
![]() ${\mathscr E}$
are isomorphic.
${\mathscr E}$
are isomorphic.
1.5 Outline of the paper
Sections 2 and 3 are devoted to the computation of the discriminant of the vector bundle
![]() ${\mathscr F}[n]^{+}$
on
${\mathscr F}[n]^{+}$
on
![]() $S^{[n]}$
, provided
$S^{[n]}$
, provided
![]() ${\mathscr F}$
is a spherical vector bundle on the
${\mathscr F}$
is a spherical vector bundle on the
![]() $K3$
surface S. Since
$K3$
surface S. Since
![]() ${\mathbb P}({\mathscr F}[n]^{+})$
extends to all (small) deformations of
${\mathbb P}({\mathscr F}[n]^{+})$
extends to all (small) deformations of
![]() $S^{[n]}$
, one knows a priori that the discriminant is a linear combination of
$S^{[n]}$
, one knows a priori that the discriminant is a linear combination of
![]() $c_2(S^{[n]})$
and the inverse
$c_2(S^{[n]})$
and the inverse
![]() $q^{\vee }_{S^{[n]}}$
of the BBF quadratic form. From this, it follows that one can work on the open subset of
$q^{\vee }_{S^{[n]}}$
of the BBF quadratic form. From this, it follows that one can work on the open subset of
![]() $S^{[n]}$
parametrizing subschemes whose support has cardinality at least
$S^{[n]}$
parametrizing subschemes whose support has cardinality at least
![]() $n-1$
, and then a straightforward computation gives that the discriminant is as in (1.2.6).
$n-1$
, and then a straightforward computation gives that the discriminant is as in (1.2.6).
In Section 4, we show that by starting from slope-stable spherical vector bundles
![]() ${\mathscr F}$
on an elliptic surface
${\mathscr F}$
on an elliptic surface
![]() $S\to {\mathbb P}^1$
, we can produce vector bundles
$S\to {\mathbb P}^1$
, we can produce vector bundles
![]() ${\mathscr F}[n]^{+}$
on
${\mathscr F}[n]^{+}$
on
![]() $S^{[n]}$
with rank and first two Chern classes covering all the cases in Theorem 1.1. Moreover, we study the restriction of such an
$S^{[n]}$
with rank and first two Chern classes covering all the cases in Theorem 1.1. Moreover, we study the restriction of such an
![]() ${\mathscr F}[n]^{+}$
to fibres of the Lagrangian fibration
${\mathscr F}[n]^{+}$
to fibres of the Lagrangian fibration
![]() $S^{[n]}\to ({\mathbb P}^1)^{(n)}\cong {\mathbb P}^n$
.
$S^{[n]}\to ({\mathbb P}^1)^{(n)}\cong {\mathbb P}^n$
.
Section 5 is the most demanding part of the paper. The key ideas, outlined in Section 1.4, are combined together in order to give the proof of Theorem 1.1 (and of Proposition 1.2).
2 The isospectral Hilbert scheme
2.1 Summary of results
We start by introducing notation and recalling known results. Let S be a
![]() $K3$
surface. The isospectral Hilbert scheme of n points on S, denoted by
$K3$
surface. The isospectral Hilbert scheme of n points on S, denoted by
![]() $X_n=X_n(S)$
, was introduced and studied by Haiman (see Definition 3.2.4 in [Reference HaimanHai01]). We have a commutative diagram
$X_n=X_n(S)$
, was introduced and studied by Haiman (see Definition 3.2.4 in [Reference HaimanHai01]). We have a commutative diagram

In fact,
![]() $X_n(S)$
is the reduced scheme associated to the fibre product of
$X_n(S)$
is the reduced scheme associated to the fibre product of
![]() $S^n$
and
$S^n$
and
![]() $S^{[n]}$
over
$S^{[n]}$
over
![]() $S^{(n)}$
. Moreover, the map
$S^{(n)}$
. Moreover, the map
![]() $\tau $
is identified with the blow up of
$\tau $
is identified with the blow up of
![]() $S^n$
with centre the big diagonal (see Corollary 3.8.3 in [Reference HaimanHai01]). Let
$S^n$
with centre the big diagonal (see Corollary 3.8.3 in [Reference HaimanHai01]). Let
![]() $\operatorname {\mathrm {pr}}_i\colon S^n\to S$
be the i-th projection, and let
$\operatorname {\mathrm {pr}}_i\colon S^n\to S$
be the i-th projection, and let
![]() $\tau _i\colon X_n(S)\to S$
be the composition
$\tau _i\colon X_n(S)\to S$
be the composition
![]() $\tau _i:=\operatorname {\mathrm {pr}}_i\circ \tau $
. Let
$\tau _i:=\operatorname {\mathrm {pr}}_i\circ \tau $
. Let
and let
![]() $X_n(S)_{*}:=\tau ^{-1}((S^n)_{*})$
. Let
$X_n(S)_{*}:=\tau ^{-1}((S^n)_{*})$
. Let
![]() $E_n\subset X_n(S)_{*}$
be the exceptional divisor of
$E_n\subset X_n(S)_{*}$
be the exceptional divisor of
![]() $X_n(S)_{*}\to (S^n)_{*}$
. Then
$X_n(S)_{*}\to (S^n)_{*}$
. Then
![]() $E_n$
is smooth because the restriction of the big diagonal to
$E_n$
is smooth because the restriction of the big diagonal to
![]() $(S^n)_{*}$
is smooth. We let
$(S^n)_{*}$
is smooth. We let
Let
![]() $\eta \in H^4(S;{\mathbb Q})$
be the fundamental class.
$\eta \in H^4(S;{\mathbb Q})$
be the fundamental class.
If X is an HK manifold, the nondegenerate BBF symmetric bilinear form
![]() $H^2(X)\times H^2(X)\to {\mathbb C}$
defines a symmetric bilinear form
$H^2(X)\times H^2(X)\to {\mathbb C}$
defines a symmetric bilinear form
![]() $H^2(X)^{\vee }\times H^2(X)^{\vee }\to {\mathbb C}$
, that is a symmetric element of
$H^2(X)^{\vee }\times H^2(X)^{\vee }\to {\mathbb C}$
, that is a symmetric element of
![]() $H^2(X)\otimes H^2(X)$
, whose image in
$H^2(X)\otimes H^2(X)$
, whose image in
![]() $H^4(X)$
via the cup product map is a rational Hodge class
$H^4(X)$
via the cup product map is a rational Hodge class
![]() $q^{\vee }_X$
.
$q^{\vee }_X$
.
Below are the results obtained in the present section.
Proposition 2.1. Let
![]() $n\ge 2$
. We have the following equalities in the rational cohomology of
$n\ge 2$
. We have the following equalities in the rational cohomology of
![]() $X_n(S)_{*}$
:
$X_n(S)_{*}$
:
 $$ \begin{align} \rho^{*}\left(\operatorname{\mathrm{ch}}_2(S^{[n]}\right)_{|X_n(S)_{*}} = &-24\sum_{l=1}^n\tau_l^{*}(\eta)_{|X_n(S)_{*}}+3 e_n^2, \end{align} $$
$$ \begin{align} \rho^{*}\left(\operatorname{\mathrm{ch}}_2(S^{[n]}\right)_{|X_n(S)_{*}} = &-24\sum_{l=1}^n\tau_l^{*}(\eta)_{|X_n(S)_{*}}+3 e_n^2, \end{align} $$
 $$ \begin{align} \rho^{*}(q^{\vee})_{|X_n(S)_{*}} = & -(2n-24)\sum_{l=1}^n \tau_l^{*}(\eta)-\frac{4n-3}{2n-2}e_n^2. \end{align} $$
$$ \begin{align} \rho^{*}(q^{\vee})_{|X_n(S)_{*}} = & -(2n-24)\sum_{l=1}^n \tau_l^{*}(\eta)-\frac{4n-3}{2n-2}e_n^2. \end{align} $$
Before stating the next result, we note that while
![]() $q^{\vee }_X$
is a rational cohomology class,
$q^{\vee }_X$
is a rational cohomology class,
![]() $(2n-2)q^{\vee }_X$
lifts to an integral class (uniquely because the group
$(2n-2)q^{\vee }_X$
lifts to an integral class (uniquely because the group
![]() $H^*(S^{[n]};{\mathbb Z})$
is torsion-free by the main result in [Reference MarkmanMar07]).
$H^*(S^{[n]};{\mathbb Z})$
is torsion-free by the main result in [Reference MarkmanMar07]).
Proposition 2.2. Let
![]() $n\ge 4$
, and let
$n\ge 4$
, and let
![]() $T_n\subset H^4(S^{[n]};{\mathbb Z})$
be the saturation of the subgroup spanned by
$T_n\subset H^4(S^{[n]};{\mathbb Z})$
be the saturation of the subgroup spanned by
![]() $c_2(S^{[n]})$
and
$c_2(S^{[n]})$
and
![]() $(2n-2)q_X^{\vee }$
. The map
$(2n-2)q_X^{\vee }$
. The map
 $$ \begin{align} \begin{matrix} T_n & \longrightarrow & H^4(X_n(S)_{*};{\mathbb Z}) \\ a & \mapsto & \rho^{*}(a)_{|X_n(S)_{*}} \end{matrix} \end{align} $$
$$ \begin{align} \begin{matrix} T_n & \longrightarrow & H^4(X_n(S)_{*};{\mathbb Z}) \\ a & \mapsto & \rho^{*}(a)_{|X_n(S)_{*}} \end{matrix} \end{align} $$
is injective.
The proof of Propositions 2.1 and 2.2 are, respectively, in Sections 2.2 and 2.3.
2.2 Proof of Proposition 2.1
We start by recalling a couple of formulae. First, suppose that
![]() $j\colon D\hookrightarrow W$
is the embedding of a smooth divisor in a smooth ambient variety, and that
$j\colon D\hookrightarrow W$
is the embedding of a smooth divisor in a smooth ambient variety, and that
![]() ${\mathscr F}$
is a sheaf on D. Then, by Grothendieck-Riemann-Roch and the push-pull formula, we have
${\mathscr F}$
is a sheaf on D. Then, by Grothendieck-Riemann-Roch and the push-pull formula, we have
Next, we recall how one computes the Chern classes of a blow up. Let Z be a smooth variety, and let
![]() $Y\subset Z$
be a smooth subvariety of pure codimension c. Let
$Y\subset Z$
be a smooth subvariety of pure codimension c. Let
![]() $f\colon \widetilde {Z}\to Z$
be the blow up of Y. Let
$f\colon \widetilde {Z}\to Z$
be the blow up of Y. Let
![]() $j\colon E\hookrightarrow \widetilde {Z}$
be the inclusion of the exceptional divisor of f, and let
$j\colon E\hookrightarrow \widetilde {Z}$
be the inclusion of the exceptional divisor of f, and let
![]() $e\in H^2(\widetilde {Z};{\mathbb Q})$
be the class of E. If
$e\in H^2(\widetilde {Z};{\mathbb Q})$
be the class of E. If
![]() ${\mathscr N}_{Y/Z}$
is the normal bundle of Y in Z, then
${\mathscr N}_{Y/Z}$
is the normal bundle of Y in Z, then
![]() $E\cong {\mathbb P}({\mathscr N}_{Y/Z})$
, and the restriction of
$E\cong {\mathbb P}({\mathscr N}_{Y/Z})$
, and the restriction of
![]() ${\mathscr O}_{ \widetilde {Z}}(E)$
to E is isomorphic to the tautological subline bundle
${\mathscr O}_{ \widetilde {Z}}(E)$
to E is isomorphic to the tautological subline bundle
![]() ${\mathscr O}_E(-1)$
. Let
${\mathscr O}_E(-1)$
. Let
![]() ${\mathscr Q}$
be the quotient bundle on E, that is the vector bundle fitting into the exact sequence
${\mathscr Q}$
be the quotient bundle on E, that is the vector bundle fitting into the exact sequence
where
![]() $f_E\colon E\to Y$
is the restriction of f. The differential of f gives the exact sequence
$f_E\colon E\to Y$
is the restriction of f. The differential of f gives the exact sequence
Taking Chern characters, and applying the formula in (2.2.1) to the inclusion
![]() $j\colon E\hookrightarrow \widetilde {Z}$
and the sheaf
$j\colon E\hookrightarrow \widetilde {Z}$
and the sheaf
![]() ${\mathscr Q}$
, we get the formula
${\mathscr Q}$
, we get the formula
 $$ \begin{align} \operatorname{\mathrm{ch}}(\widetilde{Z})=f^{*}(\operatorname{\mathrm{ch}}(Z))-\operatorname{\mathrm{ch}}( j_{*}({\mathscr Q}) )=f^{*}(\operatorname{\mathrm{ch}}(Z))-j_{*}(\operatorname{\mathrm{ch}}( ({\mathscr Q}) )\cdot\left(1-\frac{e}{2}+\ldots\right)= \nonumber\\ =f^{*}(\operatorname{\mathrm{ch}}(Z))-j_{*}\left((c-1)+f_E^{*}(c_1({\mathscr N}_{Y/Z})-j^{*}(e)\right)\cdot\left(1-\frac{e}{2}+\ldots\right)\equiv \nonumber\\ \equiv f^{*}(\operatorname{\mathrm{ch}}(Z))- j_{*}\left(f_E^{*}(c_1({\mathscr N}_{Y/Z})\right)-(c-1)e+\frac{c+1}{2}e^2\quad\pmod{H^6(\widetilde{Z};{\mathbb Q})} .\end{align} $$
$$ \begin{align} \operatorname{\mathrm{ch}}(\widetilde{Z})=f^{*}(\operatorname{\mathrm{ch}}(Z))-\operatorname{\mathrm{ch}}( j_{*}({\mathscr Q}) )=f^{*}(\operatorname{\mathrm{ch}}(Z))-j_{*}(\operatorname{\mathrm{ch}}( ({\mathscr Q}) )\cdot\left(1-\frac{e}{2}+\ldots\right)= \nonumber\\ =f^{*}(\operatorname{\mathrm{ch}}(Z))-j_{*}\left((c-1)+f_E^{*}(c_1({\mathscr N}_{Y/Z})-j^{*}(e)\right)\cdot\left(1-\frac{e}{2}+\ldots\right)\equiv \nonumber\\ \equiv f^{*}(\operatorname{\mathrm{ch}}(Z))- j_{*}\left(f_E^{*}(c_1({\mathscr N}_{Y/Z})\right)-(c-1)e+\frac{c+1}{2}e^2\quad\pmod{H^6(\widetilde{Z};{\mathbb Q})} .\end{align} $$
Proof of the equality in (2.1.4).
Since
![]() $X_n(S)_{*}$
is the blow up of
$X_n(S)_{*}$
is the blow up of
![]() $(S^n)_{*}$
with centre the smooth locus of the big diagonal, we can relate the Chern characters of
$(S^n)_{*}$
with centre the smooth locus of the big diagonal, we can relate the Chern characters of
![]() $X_n(S)_{*}$
and
$X_n(S)_{*}$
and
![]() $(S^n)_{*}$
via the equality in (2.2.4). Since
$(S^n)_{*}$
via the equality in (2.2.4). Since
![]() $\operatorname {\mathrm {ch}}_2(S^n)=-24\sum _{i=1}^n\tau _i^{*}(\eta )$
, and the normal bundle of the big diagonal in
$\operatorname {\mathrm {ch}}_2(S^n)=-24\sum _{i=1}^n\tau _i^{*}(\eta )$
, and the normal bundle of the big diagonal in
![]() $S^n$
has trivial first Chern class, the equation in (2.2.4) gives that
$S^n$
has trivial first Chern class, the equation in (2.2.4) gives that
 $$ \begin{align} \operatorname{\mathrm{ch}}_2(X_n(S)_{*})=\frac{3}{2}e_n^2 -24\sum_{l=1}^n\tau_l^{*}(\eta)_{|X_n(S)_{*}}. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{ch}}_2(X_n(S)_{*})=\frac{3}{2}e_n^2 -24\sum_{l=1}^n\tau_l^{*}(\eta)_{|X_n(S)_{*}}. \end{align} $$
The differential of the map
![]() $\rho \colon X_n(S)\to S^{[n]}$
gives the exact sequence
$\rho \colon X_n(S)\to S^{[n]}$
gives the exact sequence
where
![]() $\iota \colon E_n\hookrightarrow X_n(S)_{*}$
is the inclusion map. Taking Chern characters, we get that
$\iota \colon E_n\hookrightarrow X_n(S)_{*}$
is the inclusion map. Taking Chern characters, we get that
The equality in (2.1.4) follows from the equalities in (2.2.5) and (2.2.7).
Proof of the equality in (2.1.5).
Let
![]() $\{\alpha _1,\ldots ,\alpha _{22}\}$
be an orthonormal basis of
$\{\alpha _1,\ldots ,\alpha _{22}\}$
be an orthonormal basis of
![]() $H^2(S;{\mathbb C})$
. Then
$H^2(S;{\mathbb C})$
. Then
 $$ \begin{align} q^{\vee}=\sum_{i=1}^{22}\mu(\alpha_i)^2-\frac{1}{2n-2}\delta_n^2, \end{align} $$
$$ \begin{align} q^{\vee}=\sum_{i=1}^{22}\mu(\alpha_i)^2-\frac{1}{2n-2}\delta_n^2, \end{align} $$
and hence
 $$ \begin{align} \rho^{*}(q^{\vee})_{|X_n(S)_{*}}=\sum_{i=1}^{22}\left(\sum_{l=1}^n \tau_l^{*}(\alpha_i)\right)^2-\frac{1}{2n-2}e_n^2= \nonumber\\ =22\sum_{l=1}^n \tau_l^{*}(\eta)+2\sum_{1\le l<m\le n}\left(\sum_{i=1}^{22}\tau_l^{*}(\alpha_i)\cdot \tau_m^{*}(\alpha_i)\right)-\frac{1}{2n-2}e^2. \end{align} $$
$$ \begin{align} \rho^{*}(q^{\vee})_{|X_n(S)_{*}}=\sum_{i=1}^{22}\left(\sum_{l=1}^n \tau_l^{*}(\alpha_i)\right)^2-\frac{1}{2n-2}e_n^2= \nonumber\\ =22\sum_{l=1}^n \tau_l^{*}(\eta)+2\sum_{1\le l<m\le n}\left(\sum_{i=1}^{22}\tau_l^{*}(\alpha_i)\cdot \tau_m^{*}(\alpha_i)\right)-\frac{1}{2n-2}e^2. \end{align} $$
Let
![]() $D_n\subset S^n$
be the big diagonal. Then
$D_n\subset S^n$
be the big diagonal. Then
 $$ \begin{align} \operatorname{\mathrm{cl}}(D_n)=(n-1)\sum_{l=1}^n \tau_l^{*}(\eta)+\sum_{1\le l<m\le n}\left(\sum_{i=1}^{22}\tau_l^{*}(\alpha_i)\cdot \tau_m^{*}(\alpha_i)\right). \end{align} $$
$$ \begin{align} \operatorname{\mathrm{cl}}(D_n)=(n-1)\sum_{l=1}^n \tau_l^{*}(\eta)+\sum_{1\le l<m\le n}\left(\sum_{i=1}^{22}\tau_l^{*}(\alpha_i)\cdot \tau_m^{*}(\alpha_i)\right). \end{align} $$
Moreover, it follows from the “Key Formula”(see, for example, Proposition 6.7 in [Reference FultonFul84]) that we have the relation
The equality in (2.1.5) follows at once from the equalities in (2.2.3) and (2.2.4).
2.3 Proof of Proposition 2.2.
Lemma 2.3. Let
![]() $n\ge 2$
. Then the classes
$n\ge 2$
. Then the classes
![]() $\alpha _n:=\sum _{l=1}^n\tau _l^{*}(\eta )_{|X_n(S)_{*}}$
and
$\alpha _n:=\sum _{l=1}^n\tau _l^{*}(\eta )_{|X_n(S)_{*}}$
and
![]() $e_n^2$
are linearly independent in
$e_n^2$
are linearly independent in
![]() $H^4(X_n(S)_{*};{\mathbb Z})$
.
$H^4(X_n(S)_{*};{\mathbb Z})$
.
Proof. We prove the lemma by integrating
![]() $\alpha _n$
and
$\alpha _n$
and
![]() $e_n^2$
over algebraic
$e_n^2$
over algebraic
![]() $2$
cycles on
$2$
cycles on
![]() $X_n(S)_{*}$
defined as follows. Let
$X_n(S)_{*}$
defined as follows. Let
![]() $p_1,\ldots ,p_{n-1}\subset S$
be
$p_1,\ldots ,p_{n-1}\subset S$
be
![]() $n-1$
distinct points, and let
$n-1$
distinct points, and let
Clearly,
![]() $\Gamma \subset X_n(S)_{*}$
, and it is isomorphic to the blow up of S at
$\Gamma \subset X_n(S)_{*}$
, and it is isomorphic to the blow up of S at
![]() $p_1,\ldots ,p_{n-1}$
. In order to define the second
$p_1,\ldots ,p_{n-1}$
. In order to define the second
![]() $2$
cycle, we assume (as we may) that S contains two smooth curves
$2$
cycle, we assume (as we may) that S contains two smooth curves
![]() $C_1,C_2$
intersecting with transverse intersection of cardinality
$C_1,C_2$
intersecting with transverse intersection of cardinality
![]() $d>0$
. Let
$d>0$
. Let
![]() $q_1,\ldots ,q_{n-2}\subset (S\setminus C_1\setminus C_2)$
be
$q_1,\ldots ,q_{n-2}\subset (S\setminus C_1\setminus C_2)$
be
![]() $n-2$
distinct points, and let
$n-2$
distinct points, and let
Clearly,
![]() $\Omega \subset X_n(S)_{*}$
, and it is isomorphic to the blow up of
$\Omega \subset X_n(S)_{*}$
, and it is isomorphic to the blow up of
![]() $C_1\times C_2$
at the d points
$C_1\times C_2$
at the d points
![]() $(x,x)$
for
$(x,x)$
for
![]() $x\in C_1\cap C_2$
.
$x\in C_1\cap C_2$
.
It makes sense to integrate
![]() $\alpha _n$
and
$\alpha _n$
and
![]() $e_n^2$
over
$e_n^2$
over
![]() $\Gamma ,\Omega $
because the latter are compact (complex) surfaces contained in
$\Gamma ,\Omega $
because the latter are compact (complex) surfaces contained in
![]() $X_n(S)_{*}$
. One checks easily that the
$X_n(S)_{*}$
. One checks easily that the
![]() $2\times 2$
“Gram matrix” of the integrals of
$2\times 2$
“Gram matrix” of the integrals of
![]() $\alpha _n$
and
$\alpha _n$
and
![]() $e_n^2$
over
$e_n^2$
over
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Omega $
is given by Table 1. It follows that
$\Omega $
is given by Table 1. It follows that
![]() $\alpha _n$
and
$\alpha _n$
and
![]() $e_n^2$
are linearly independent.
$e_n^2$
are linearly independent.
Table 1 Integrals of
![]() $\alpha _n,e_n^2$
over
$\alpha _n,e_n^2$
over
![]() $\Gamma ,\Omega $
.
$\Gamma ,\Omega $
.

Now we can prove Proposition 2.2. Proposition 2.1 expresses the restriction to
![]() $X_n(S)_{*}$
of
$X_n(S)_{*}$
of
![]() $\rho ^{*}(c_2(S^{[n]})$
and
$\rho ^{*}(c_2(S^{[n]})$
and
![]() $q^{\vee }$
as linear combinations of
$q^{\vee }$
as linear combinations of
![]() $\alpha _n$
and
$\alpha _n$
and
![]() $e_n$
. The determinant of the
$e_n$
. The determinant of the
![]() $2\times 2$
matrix with entries the corresponding coefficients is nonsingular if and only if
$2\times 2$
matrix with entries the corresponding coefficients is nonsingular if and only if
![]() $n\notin \{2,3\}$
, hence, Proposition 2.2 follows from Lemma 2.3.
$n\notin \{2,3\}$
, hence, Proposition 2.2 follows from Lemma 2.3.
Remark 2.4. Let
![]() $n\in \{2,3\}$
. By Proposition 2.1, the classes
$n\in \{2,3\}$
. By Proposition 2.1, the classes
![]() $\rho ^{*}\left (\operatorname {\mathrm {ch}}_2(S^{[n]}\right )_{|X_n(S)_{*}}$
and
$\rho ^{*}\left (\operatorname {\mathrm {ch}}_2(S^{[n]}\right )_{|X_n(S)_{*}}$
and
![]() $\rho ^{*}(q^{\vee })_{|X_n(S)_{*}}$
are linearly dependent. This agrees with known results. In fact, if X is an HK of type
$\rho ^{*}(q^{\vee })_{|X_n(S)_{*}}$
are linearly dependent. This agrees with known results. In fact, if X is an HK of type
![]() $K3^{[2]}$
, then
$K3^{[2]}$
, then
![]() $c_2(X)$
and
$c_2(X)$
and
![]() $q^{\vee }_X$
are linearly dependent because
$q^{\vee }_X$
are linearly dependent because
![]() $\operatorname {\mathrm {Sym}}^2 H^2(X;{\mathbb Q})=H^4(X;{\mathbb Q})$
, and if X is an HK of type
$\operatorname {\mathrm {Sym}}^2 H^2(X;{\mathbb Q})=H^4(X;{\mathbb Q})$
, and if X is an HK of type
![]() $K3^{[3]}$
, then
$K3^{[3]}$
, then
![]() $c_2(X)$
and
$c_2(X)$
and
![]() $q^{\vee }_X$
are linearly dependent although
$q^{\vee }_X$
are linearly dependent although
![]() $\operatorname {\mathrm {Sym}}^2 H^2(X;{\mathbb Q})$
is strictly contained in
$\operatorname {\mathrm {Sym}}^2 H^2(X;{\mathbb Q})$
is strictly contained in
![]() $H^4(X;{\mathbb Q})$
(see Example 14 in [Reference MarkmanMar02], or Remark 3.3 in [Reference Green, Kim, Laza and RoblesGKLR22]).
$H^4(X;{\mathbb Q})$
(see Example 14 in [Reference MarkmanMar02], or Remark 3.3 in [Reference Green, Kim, Laza and RoblesGKLR22]).
3 Basic modular vector bundles on
 $S^{[n]}$
$S^{[n]}$
3.1 Summary of results
Let S be a
![]() $K3$
surface. We maintain the notation introduced in Section 2.1. Let
$K3$
surface. We maintain the notation introduced in Section 2.1. Let
![]() ${\mathscr F}$
be a locally free sheaf on S. Then
${\mathscr F}$
be a locally free sheaf on S. Then
is a locally free sheaf on
![]() $X_n(S)$
. The map
$X_n(S)$
. The map
![]() $\rho $
in (2.1.1) is finite, and moreover, it is flat because
$\rho $
in (2.1.1) is finite, and moreover, it is flat because
![]() $X_n(S)$
is Cohen–Macaulay (CM) by Theorem 3.1 in [Reference HaimanHai01]. It follows that the pushforward
$X_n(S)$
is Cohen–Macaulay (CM) by Theorem 3.1 in [Reference HaimanHai01]. It follows that the pushforward
![]() $\rho _{*}(X_n({\mathscr F}))$
is also locally free. The symmetric group
$\rho _{*}(X_n({\mathscr F}))$
is also locally free. The symmetric group
![]() ${\mathscr S}_n$
acts on
${\mathscr S}_n$
acts on
![]() $X_n(S)$
compatibly with its permutation action on
$X_n(S)$
compatibly with its permutation action on
![]() $S^n$
, and hence, the action lifts to an action
$S^n$
, and hence, the action lifts to an action
![]() $\mu _n^{+}$
on
$\mu _n^{+}$
on
![]() $X_n({\mathscr F})$
. Since
$X_n({\mathscr F})$
. Since
![]() $\mu _n$
maps to itself any fibre of
$\mu _n$
maps to itself any fibre of
![]() $\rho \colon X_n(S)\to S^{[n]}$
, we get an action
$\rho \colon X_n(S)\to S^{[n]}$
, we get an action
![]() $\overline {\mu }_n^{+}\colon {\mathscr S}_n \to \operatorname {\mathrm {Aut}}(\rho _{*}X_n({\mathscr F}))$
.
$\overline {\mu }_n^{+}\colon {\mathscr S}_n \to \operatorname {\mathrm {Aut}}(\rho _{*}X_n({\mathscr F}))$
.
Definition 3.1. Let
![]() ${\mathscr F}[n]^{+}\subset \rho _{*}X_n({\mathscr F})$
be the sheaf of
${\mathscr F}[n]^{+}\subset \rho _{*}X_n({\mathscr F})$
be the sheaf of
![]() ${\mathscr S}_n$
-invariants for
${\mathscr S}_n$
-invariants for
![]() $\overline {\mu }_n^{+}$
.
$\overline {\mu }_n^{+}$
.
Since
![]() $\rho _{*}X_n({\mathscr F})$
is locally free, so is
$\rho _{*}X_n({\mathscr F})$
is locally free, so is
![]() ${\mathscr F}[n]^{+}$
.
${\mathscr F}[n]^{+}$
.
Let
![]() $r_0$
be the rank of
$r_0$
be the rank of
![]() ${\mathscr F}$
. Below is the main result of the present section.
${\mathscr F}$
. Below is the main result of the present section.
Proposition 3.2. Suppose that
![]() ${\mathscr F}$
is spherical, that is
${\mathscr F}$
is spherical, that is
![]() $h^p(S,\operatorname {\mathrm {End}}^0({\mathscr F}))=0$
for all p. Let
$h^p(S,\operatorname {\mathrm {End}}^0({\mathscr F}))=0$
for all p. Let
![]() $n\ge 2$
. Then
$n\ge 2$
. Then
 $$ \begin{align} c_1({\mathscr F}[n]^{+}) & = r_0^{n-1} \left(\mu(c_1({\mathscr F}))-\frac{r_0- 1}{2}\delta_n\right), \end{align} $$
$$ \begin{align} c_1({\mathscr F}[n]^{+}) & = r_0^{n-1} \left(\mu(c_1({\mathscr F}))-\frac{r_0- 1}{2}\delta_n\right), \end{align} $$
Remark 3.3. The notation in (3.1.3) and (3.1.4) is unambiguous because the group
![]() $H^*(S^{[n]};{\mathbb Z})$
is torsion-free by the main result in [Reference MarkmanMar07] (see also [Reference TotaroTot20]). Notice that Proposition 3.2 holds also (trivially) for
$H^*(S^{[n]};{\mathbb Z})$
is torsion-free by the main result in [Reference MarkmanMar07] (see also [Reference TotaroTot20]). Notice that Proposition 3.2 holds also (trivially) for
![]() $n=1$
, provided we set
$n=1$
, provided we set
![]() $\delta _1=0$
.
$\delta _1=0$
.
If
![]() ${\mathscr F}$
is spherical, then the vector bundle
${\mathscr F}$
is spherical, then the vector bundle
![]() ${\mathscr F}[n]^{+}$
is modular by Proposition 3.2, and we refer to it as a basic modular vector bundle. The proof of Proposition 3.2 is in Section 3.4.
${\mathscr F}[n]^{+}$
is modular by Proposition 3.2, and we refer to it as a basic modular vector bundle. The proof of Proposition 3.2 is in Section 3.4.
Remark 3.4. The equalities in Proposition 3.2 should hold with the weaker hypothesis
![]() $\chi (S,\operatorname {\mathrm {End}}^0({\mathscr F}))=0$
. To prove this, it would suffice to show that such a vector bundle is the limit of spherical vector bundles.
$\chi (S,\operatorname {\mathrm {End}}^0({\mathscr F}))=0$
. To prove this, it would suffice to show that such a vector bundle is the limit of spherical vector bundles.
3.2 Chern classes of
 $\rho ^{*}{\mathscr F}[n]^{+}$
restricted to
$\rho ^{*}{\mathscr F}[n]^{+}$
restricted to
 $X_n(S)_{*}$
$X_n(S)_{*}$
Let
![]() $h_{+}\in H^{1,1}_{{\mathbb Q}}(S^{[n]})$
be given by
$h_{+}\in H^{1,1}_{{\mathbb Q}}(S^{[n]})$
be given by
In the present subsection, we prove the following result.
Proposition 3.5. Let S be a
![]() $K3$
surface, and let
$K3$
surface, and let
![]() ${\mathscr F}$
be a vector bundle on S, such that
${\mathscr F}$
be a vector bundle on S, such that
![]() $\chi (S,End^0 ({\mathscr F}))=2$
. Let
$\chi (S,End^0 ({\mathscr F}))=2$
. Let
![]() $r_0$
be the rank of S, and let
$r_0$
be the rank of S, and let
![]() $h^{+}\in H^{1,1}_{{\mathbb Q}}(S^{[2]})$
be as in (3.2.1). Then the following equalities hold:
$h^{+}\in H^{1,1}_{{\mathbb Q}}(S^{[2]})$
be as in (3.2.1). Then the following equalities hold:
 $$ \begin{align} \operatorname{\mathrm{ch}}_2(\rho^{*}{\mathscr F}[n]^{+})_{|X_n(S)_{*}} & = r_0^{n-2}\rho^{*} \left(\frac{(r_0^2-1)}{24}\operatorname{\mathrm{ch}}_2(S^{[n]})+\frac{1}{2}h_{+}^2\right)_{|X_n(S)_{*}.} \end{align} $$
$$ \begin{align} \operatorname{\mathrm{ch}}_2(\rho^{*}{\mathscr F}[n]^{+})_{|X_n(S)_{*}} & = r_0^{n-2}\rho^{*} \left(\frac{(r_0^2-1)}{24}\operatorname{\mathrm{ch}}_2(S^{[n]})+\frac{1}{2}h_{+}^2\right)_{|X_n(S)_{*}.} \end{align} $$
Proof. Let
![]() $D_n\subset (S^n)_{*}$
be the (intersection of
$D_n\subset (S^n)_{*}$
be the (intersection of
![]() $(S^n)_{*}$
with the) big diagonal. For
$(S^n)_{*}$
with the) big diagonal. For
![]() $1\le j<k\le n$
, let
$1\le j<k\le n$
, let
![]() $D_n(j,k)\subset D_n$
be the set of points
$D_n(j,k)\subset D_n$
be the set of points
![]() $(x_1,\ldots ,x_n)$
, such that
$(x_1,\ldots ,x_n)$
, such that
![]() $x_j=x_k$
. We have the open embedding
$x_j=x_k$
. We have the open embedding
 $$ \begin{align} \begin{matrix} D_n(j,k) & \overset{\overline{\epsilon}_{j,k}}{\hookrightarrow} & S^{n-1} \\ (x_1,\ldots,x_n) & \mapsto & (x_j,x_1,\ldots,x_{j-1},\widehat{x_j},x_{j+1},\ldots,x_{k-1},\widehat{x_k},x_{k+1},\ldots,x_n). \end{matrix} \end{align} $$
$$ \begin{align} \begin{matrix} D_n(j,k) & \overset{\overline{\epsilon}_{j,k}}{\hookrightarrow} & S^{n-1} \\ (x_1,\ldots,x_n) & \mapsto & (x_j,x_1,\ldots,x_{j-1},\widehat{x_j},x_{j+1},\ldots,x_{k-1},\widehat{x_k},x_{k+1},\ldots,x_n). \end{matrix} \end{align} $$
Let
![]() $\tau _{E_{n}}\colon E_{n}\to D_n$
be the restriction of
$\tau _{E_{n}}\colon E_{n}\to D_n$
be the restriction of
![]() $\tau $
to
$\tau $
to
![]() $E_{n}$
, and let
$E_{n}$
, and let
![]() $E_n(j,k):=\tau _{E_{n}}^{-1}(D_n(j,k))$
. Then
$E_n(j,k):=\tau _{E_{n}}^{-1}(D_n(j,k))$
. Then
![]() $E_{n}=\coprod E_n(j,k)$
. Let
$E_{n}=\coprod E_n(j,k)$
. Let
![]() $\tau _{j,k}\colon E_n(j,k)\to D_n(j,k)$
be defined by the restriction of
$\tau _{j,k}\colon E_n(j,k)\to D_n(j,k)$
be defined by the restriction of
![]() $\tau _{E_{n}}$
, and let
$\tau _{E_{n}}$
, and let
 $$ \begin{align} \begin{matrix} E_n(j,k) & \overset{\epsilon_{j,k}}{\longrightarrow} & S^{n-1} \\ y & \mapsto & \overline{\epsilon}_{j,k}(\tau_{j,k}(y)). \end{matrix} \end{align} $$
$$ \begin{align} \begin{matrix} E_n(j,k) & \overset{\epsilon_{j,k}}{\longrightarrow} & S^{n-1} \\ y & \mapsto & \overline{\epsilon}_{j,k}(\tau_{j,k}(y)). \end{matrix} \end{align} $$
Let
![]() ${\mathscr Q}_{j,k}$
be the locally free sheaf on
${\mathscr Q}_{j,k}$
be the locally free sheaf on
![]() $E_n(j,k)$
defined by
$E_n(j,k)$
defined by
 $$ \begin{align} {\mathscr Q}_{j,k}:=\epsilon_{j,k}^{*}\left(\bigwedge^2{\mathscr F}\boxtimes {\mathscr F}\boxtimes\ldots\boxtimes{\mathscr F}\right). \end{align} $$
$$ \begin{align} {\mathscr Q}_{j,k}:=\epsilon_{j,k}^{*}\left(\bigwedge^2{\mathscr F}\boxtimes {\mathscr F}\boxtimes\ldots\boxtimes{\mathscr F}\right). \end{align} $$
Let
![]() $\iota _{j,k}\colon E_n(j,k)\hookrightarrow X_n(S)_{*}$
be the inclusion map. We have an exact sequence
$\iota _{j,k}\colon E_n(j,k)\hookrightarrow X_n(S)_{*}$
be the inclusion map. We have an exact sequence
It follows that
Since
![]() $\chi (S,End^0 ({\mathscr F}))=2$
, the Hirzebruch-Riemann-Roch theorem gives that
$\chi (S,End^0 ({\mathscr F}))=2$
, the Hirzebruch-Riemann-Roch theorem gives that
Using the above equality, one gets that modulo
![]() $H^6(X_n(S)_{*};{\mathbb Q})$
, we have
$H^6(X_n(S)_{*};{\mathbb Q})$
, we have
 $$ \begin{align} &\tau_1^*(\operatorname{\mathrm{ch}}({\mathscr F}))\cdot\ldots\cdot \tau_n^*(\operatorname{\mathrm{ch}}({\mathscr F}))= r_0^n+r_0^{n-1}\sum_{l=1}^n\tau_{l}^{*}(c_1({\mathscr F}))+ \nonumber\\ &+\frac{1}{2} r_0^{n-2}\sum_{l=1}^n\tau_{l}^{*}(c_1({\mathscr F})^2-2(r_0^2-1)\eta)+ \nonumber\\ &+ r_0^{n-2}\sum_{1\le l<m\le n}\tau_{l}^{*}(c_1({\mathscr F}))\cdot \tau_{m}^{*}(c_1({\mathscr F})). \end{align} $$
$$ \begin{align} &\tau_1^*(\operatorname{\mathrm{ch}}({\mathscr F}))\cdot\ldots\cdot \tau_n^*(\operatorname{\mathrm{ch}}({\mathscr F}))= r_0^n+r_0^{n-1}\sum_{l=1}^n\tau_{l}^{*}(c_1({\mathscr F}))+ \nonumber\\ &+\frac{1}{2} r_0^{n-2}\sum_{l=1}^n\tau_{l}^{*}(c_1({\mathscr F})^2-2(r_0^2-1)\eta)+ \nonumber\\ &+ r_0^{n-2}\sum_{1\le l<m\le n}\tau_{l}^{*}(c_1({\mathscr F}))\cdot \tau_{m}^{*}(c_1({\mathscr F})). \end{align} $$
Let
![]() $e_n(j,k)=\operatorname {\mathrm {cl}}(E_n(j,k))$
. Using the equality in (2.2.1), one gets that modulo
$e_n(j,k)=\operatorname {\mathrm {cl}}(E_n(j,k))$
. Using the equality in (2.2.1), one gets that modulo
![]() $H^6(X_n(S)_{*};{\mathbb Q})$
, we have
$H^6(X_n(S)_{*};{\mathbb Q})$
, we have
 $$ \begin{align*} &\operatorname{\mathrm{ch}}(\iota_{j,k,*}({\mathscr Q}_{j,k})) = \iota_{j,k,*}(\operatorname{\mathrm{ch}}({\mathscr Q}_{j,k}))\cdot \left(1-\frac{e_n(j,k)}{2}\right)=\\ &= \iota_{j,k,*}\left(\iota_{j,k}^{*}\left({r_0\choose 2}r_0^{n-2}+\frac{1}{2}(r_0-1)r_0^{n-2}\sum_{l=1}^n\tau_l^{*}c_1({\mathscr F}) \right)\right) \cdot \left(1-\frac{e_n(i,j)}{2}\right)=\\ &= {r_0\choose 2}r_0^{n-2} e_n(j,k)+\frac{1}{2}(r_0-1)r_0^{n-2} e_n(j,k)\cdot \sum_{l=1}^n\tau_l^{*}c_1({\mathscr F})- \frac{1}{2}{r_0\choose 2}r_0^{n-2} e_n(j,k)^2. \end{align*} $$
$$ \begin{align*} &\operatorname{\mathrm{ch}}(\iota_{j,k,*}({\mathscr Q}_{j,k})) = \iota_{j,k,*}(\operatorname{\mathrm{ch}}({\mathscr Q}_{j,k}))\cdot \left(1-\frac{e_n(j,k)}{2}\right)=\\ &= \iota_{j,k,*}\left(\iota_{j,k}^{*}\left({r_0\choose 2}r_0^{n-2}+\frac{1}{2}(r_0-1)r_0^{n-2}\sum_{l=1}^n\tau_l^{*}c_1({\mathscr F}) \right)\right) \cdot \left(1-\frac{e_n(i,j)}{2}\right)=\\ &= {r_0\choose 2}r_0^{n-2} e_n(j,k)+\frac{1}{2}(r_0-1)r_0^{n-2} e_n(j,k)\cdot \sum_{l=1}^n\tau_l^{*}c_1({\mathscr F})- \frac{1}{2}{r_0\choose 2}r_0^{n-2} e_n(j,k)^2. \end{align*} $$
The equalities in (3.2.2), (3.2.3) and (3.2.4) follow at once from the equalities in (3.2.9), (3.2.11) and the above equality.
3.3 Deformations of
 $(S^{[n]},{\mathbb P}({\mathscr F}[n]^{+}))$
$(S^{[n]},{\mathbb P}({\mathscr F}[n]^{+}))$
Let
![]() ${\mathscr F}$
be a vector bundle on S, and let
${\mathscr F}$
be a vector bundle on S, and let
![]() $f\colon {\mathbb P}({\mathscr F}[n]^{+})\to S^{[n]}$
be the structure map. We let
$f\colon {\mathbb P}({\mathscr F}[n]^{+})\to S^{[n]}$
be the structure map. We let
![]() $\operatorname {\mathrm {Def}}({\mathbb P}({\mathscr F}[n]^{+}),f, S^{[n]})$
be the deformation functor of the map f (see Definition 8.2.7 in [Reference ManettiMan22]).
$\operatorname {\mathrm {Def}}({\mathbb P}({\mathscr F}[n]^{+}),f, S^{[n]})$
be the deformation functor of the map f (see Definition 8.2.7 in [Reference ManettiMan22]).
Proposition 3.6. Suppose that the
![]() $K3$
surface S is projective and that
$K3$
surface S is projective and that
![]() ${\mathscr F}$
is a spherical vector bundle on S. Then the natural map
${\mathscr F}$
is a spherical vector bundle on S. Then the natural map
![]() $\operatorname {\mathrm {Def}}({\mathbb P}({\mathscr F}[n]^{+}),f, S^{[n]})\to \operatorname {\mathrm {Def}}(S^{[n]})$
is smooth.
$\operatorname {\mathrm {Def}}({\mathbb P}({\mathscr F}[n]^{+}),f, S^{[n]})\to \operatorname {\mathrm {Def}}(S^{[n]})$
is smooth.
Proof. The result follows from a theorem of Horikawa. In fact, let
![]() $X:={\mathbb P}({\mathscr F}[n]^{+})$
,
$X:={\mathbb P}({\mathscr F}[n]^{+})$
,
![]() $Y:=S^{[n]}$
, and consider the exact sequence of locally free sheaves on X
$Y:=S^{[n]}$
, and consider the exact sequence of locally free sheaves on X
By [Reference HorikawaHor74, Theorem 6.1] (see also Corollary 8.2.14 in [Reference ManettiMan22]), it suffices to prove that the map
![]() $H^1(X,\Theta _X)\to H^1(X,f^{*}\Theta _Y)$
is surjective and the map
$H^1(X,\Theta _X)\to H^1(X,f^{*}\Theta _Y)$
is surjective and the map
![]() $H^2(X,\Theta _X)\to H^2(X,f^{*}\Theta _Y)$
is injective. By the exact sequence in (3.3.1), it suffices to show that
$H^2(X,\Theta _X)\to H^2(X,f^{*}\Theta _Y)$
is injective. By the exact sequence in (3.3.1), it suffices to show that
![]() $H^2(X,\Theta _{X/Y})=0$
. By the local-to-global spectral sequence abutting to
$H^2(X,\Theta _{X/Y})=0$
. By the local-to-global spectral sequence abutting to
![]() $H^2(X,\Theta _{X/Y})$
, we are done if we prove that
$H^2(X,\Theta _{X/Y})$
, we are done if we prove that
We have
 $$ \begin{align} R^q f_{*}(\Theta_{X/Y}))\cong \begin{cases} End^0 {\mathscr F}[n]^{+} & \text{if}\ q=0, \\ 0 & \text{if}\ q>0. \end{cases} \end{align} $$
$$ \begin{align} R^q f_{*}(\Theta_{X/Y}))\cong \begin{cases} End^0 {\mathscr F}[n]^{+} & \text{if}\ q=0, \\ 0 & \text{if}\ q>0. \end{cases} \end{align} $$
It follows from the McKay correspondence (see Proposition 5.4 in [Reference O’GradyO’G22]) that
and this finishes the proof.
Corollary 3.7. Suppose that the
![]() $K3$
surface S is projective and that
$K3$
surface S is projective and that
![]() ${\mathscr F}$
is a spherical vector bundle on S. If
${\mathscr F}$
is a spherical vector bundle on S. If
![]() $n\le 3$
, then
$n\le 3$
, then
![]() $\Delta ({\mathscr F}[n]^{+})$
belongs to the saturation of
$\Delta ({\mathscr F}[n]^{+})$
belongs to the saturation of
![]() $c_2(S^{[n]})$
, if
$c_2(S^{[n]})$
, if
![]() $n\ge 4$
, then
$n\ge 4$
, then
![]() $\Delta ({\mathscr F}[n]^{+})$
belongs to the saturation of the span of
$\Delta ({\mathscr F}[n]^{+})$
belongs to the saturation of the span of
![]() $c_2(S^{[n]})$
and
$c_2(S^{[n]})$
and
![]() $q^{\vee }$
.
$q^{\vee }$
.
Proof. Let
![]() ${\mathscr X}\overset {F}{\longrightarrow }{\mathscr Y}\overset {G}{\longrightarrow } T$
be representative of
${\mathscr X}\overset {F}{\longrightarrow }{\mathscr Y}\overset {G}{\longrightarrow } T$
be representative of
![]() $\operatorname {\mathrm {Def}}({\mathbb P}({\mathscr F}[n]^{+}),f, S^{[n]})$
. Thus both F and G are proper holomorphic maps of analytic spaces, there exists
$\operatorname {\mathrm {Def}}({\mathbb P}({\mathscr F}[n]^{+}),f, S^{[n]})$
. Thus both F and G are proper holomorphic maps of analytic spaces, there exists
![]() $0\in T$
, such that
$0\in T$
, such that
![]() $F^{-1}(G^{-1}(0))\to G^{-1}(0)$
is identified with
$F^{-1}(G^{-1}(0))\to G^{-1}(0)$
is identified with
![]() $f\colon {\mathbb P}({\mathscr F}[n]^{+})\to S^{[n]}$
, and every (small) deformation of f is identified with
$f\colon {\mathbb P}({\mathscr F}[n]^{+})\to S^{[n]}$
, and every (small) deformation of f is identified with
![]() $F^{-1}(G^{-1}(t))\to G^{-1}(t)$
for some
$F^{-1}(G^{-1}(t))\to G^{-1}(t)$
for some
![]() $t\in T$
(close to
$t\in T$
(close to
![]() $0$
). For
$0$
). For
![]() $t\in T$
(close to
$t\in T$
(close to
![]() $0$
), the map
$0$
), the map
![]() $F^{-1}(G^{-1}(t))\to G^{-1}(t)$
is a
$F^{-1}(G^{-1}(t))\to G^{-1}(t)$
is a
![]() ${\mathbb P}^{r-1}$
fibration, where
${\mathbb P}^{r-1}$
fibration, where
![]() $r=\operatorname {\mathrm {rk}}({\mathscr F}[n]^{+})$
, and hence, the pushforward
$r=\operatorname {\mathrm {rk}}({\mathscr F}[n]^{+})$
, and hence, the pushforward
![]() $F_{*}(\Theta _{{\mathscr X}/{\mathscr Y}})$
is a vector bundle on
$F_{*}(\Theta _{{\mathscr X}/{\mathscr Y}})$
is a vector bundle on
![]() ${\mathscr Y}$
(of rank
${\mathscr Y}$
(of rank
![]() $r^2-1$
). By Proposition 3.6, the family
$r^2-1$
). By Proposition 3.6, the family
![]() $G\colon {\mathscr Y}\to T$
is versal at
$G\colon {\mathscr Y}\to T$
is versal at
![]() $t=0$
, and hence, the characteristic class
$t=0$
, and hence, the characteristic class
![]() $c_2(F_{*}(\Theta _{X_0/Y_0})$
(here,
$c_2(F_{*}(\Theta _{X_0/Y_0})$
(here,
![]() $X_0=F^{-1}(G^{-1}(0))$
and
$X_0=F^{-1}(G^{-1}(0))$
and
![]() $Y_0= G^{-1}(0)$
) remains of type
$Y_0= G^{-1}(0)$
) remains of type
![]() $(2,2)$
for all small deformation of
$(2,2)$
for all small deformation of
![]() $Y_0=S^{[n]}$
. If
$Y_0=S^{[n]}$
. If
![]() $n\le 3$
, it follows that
$n\le 3$
, it follows that
![]() $c_2(F_{*}(\Theta _{X_0/Y_0})$
belongs to the saturation of
$c_2(F_{*}(\Theta _{X_0/Y_0})$
belongs to the saturation of
![]() $c_2(S^{[n]})$
, and if
$c_2(S^{[n]})$
, and if
![]() $n\ge 4$
, it follows that
$n\ge 4$
, it follows that
![]() $c_2(F_{*}(\Theta _{X_0/Y_0})$
belongs to the saturation of the span of
$c_2(F_{*}(\Theta _{X_0/Y_0})$
belongs to the saturation of the span of
![]() $c_2(S^{[n]})$
and
$c_2(S^{[n]})$
and
![]() $q^{\vee }$
(see [Reference ZhangZha15]). We are done because
$q^{\vee }$
(see [Reference ZhangZha15]). We are done because
Remark 3.8. Let
![]() $\operatorname {\mathrm {Def}}(S^{[n]},\det {\mathscr F}[n]^{+}))$
be the deformation functor of the couple
$\operatorname {\mathrm {Def}}(S^{[n]},\det {\mathscr F}[n]^{+}))$
be the deformation functor of the couple
![]() $(S^{[n]},\det {\mathscr F}[n]^{+}))$
. The natural map
$(S^{[n]},\det {\mathscr F}[n]^{+}))$
. The natural map
![]() $\operatorname {\mathrm {Def}}({\mathscr F}[n]^{+})\to \operatorname {\mathrm {Def}}(S^{[n]},c_1({\mathscr F}[n]^{+}))$
is an isomorphism, by the Artamkin-Mukai theorem [Reference MukaiMuk84, Reference ArtamkinArt88] (see also [Reference Iacono and ManettiIM19]) and by the vanishing in (3.3.4). Hence,
$\operatorname {\mathrm {Def}}({\mathscr F}[n]^{+})\to \operatorname {\mathrm {Def}}(S^{[n]},c_1({\mathscr F}[n]^{+}))$
is an isomorphism, by the Artamkin-Mukai theorem [Reference MukaiMuk84, Reference ArtamkinArt88] (see also [Reference Iacono and ManettiIM19]) and by the vanishing in (3.3.4). Hence,
![]() ${\mathscr F}[n]^{+}$
extends (uniquely) to a vector bundle on any small deformation of
${\mathscr F}[n]^{+}$
extends (uniquely) to a vector bundle on any small deformation of
![]() $S^{[n]}$
keeping
$S^{[n]}$
keeping
![]() $c_1({\mathscr F}[n]^{+})$
of type
$c_1({\mathscr F}[n]^{+})$
of type
![]() $(1,1)$
.
$(1,1)$
.
3.4 Proof of Proposition 3.2
The equality in (3.1.2) follows at once from the equality in (3.2.2). Similarly, the equality in (3.1.3) follows at once from the equality in (3.2.3), because the restriction map
![]() $H^2(S^{[n]};{\mathbb Z})\to H^2(\rho (X_n(S)_{*}))$
is an isomorphism (the complement of
$H^2(S^{[n]};{\mathbb Z})\to H^2(\rho (X_n(S)_{*}))$
is an isomorphism (the complement of
![]() $\rho (X_n(S)_{*})$
in
$\rho (X_n(S)_{*})$
in
![]() $S^{[n]}$
has codimension greater than one). Lastly, we prove the equality in (3.1.4). Proposition 3.5 and a straightforward computation give that
$S^{[n]}$
has codimension greater than one). Lastly, we prove the equality in (3.1.4). Proposition 3.5 and a straightforward computation give that
 $$ \begin{align*} \rho^{*}\Delta({\mathscr F}[n]^{+})_{|X_n(S)_{*}}=\rho^{*}\left(\frac{r_0^{2n-2}(r_0^2-1)}{12}c_2\left(S^{[n]}\right)\right)_{|X_n(S)_{*}}. \end{align*} $$
$$ \begin{align*} \rho^{*}\Delta({\mathscr F}[n]^{+})_{|X_n(S)_{*}}=\rho^{*}\left(\frac{r_0^{2n-2}(r_0^2-1)}{12}c_2\left(S^{[n]}\right)\right)_{|X_n(S)_{*}}. \end{align*} $$
If
![]() $n\le 3$
, then by Proposition 3.7 (note: we may assume that S is projective),
$n\le 3$
, then by Proposition 3.7 (note: we may assume that S is projective),
![]() $\Delta ({\mathscr F}[n]^{+})$
is a (possibly rational) multiple of
$\Delta ({\mathscr F}[n]^{+})$
is a (possibly rational) multiple of
![]() $c_2\left (S^{[n]}\right )$
. Since the restriction of
$c_2\left (S^{[n]}\right )$
. Since the restriction of
![]() $\rho ^{*}c_2\left (S^{[n]}\right )$
to
$\rho ^{*}c_2\left (S^{[n]}\right )$
to
![]() $X_n(S)_{*}$
is nonzero (by the equality in (2.1.4) and Lemma 2.3), the equality in (3.1.4) follows. If
$X_n(S)_{*}$
is nonzero (by the equality in (2.1.4) and Lemma 2.3), the equality in (3.1.4) follows. If
![]() $n\ge 4$
, then by Proposition 3.7
$n\ge 4$
, then by Proposition 3.7
![]() $\Delta ({\mathscr F}[n]^{+})$
is a linear combination (possibly with rational coefficients) of
$\Delta ({\mathscr F}[n]^{+})$
is a linear combination (possibly with rational coefficients) of
![]() $c_2\left (S^{[n]}\right )$
and
$c_2\left (S^{[n]}\right )$
and
![]() $q^{\vee }$
, and the equality follows from Proposition 2.2.
$q^{\vee }$
, and the equality follows from Proposition 2.2.
4 Basic modular vector bundles on
 $S^{[n]}$
for S an elliptic
$S^{[n]}$
for S an elliptic
 $K3$
surface
$K3$
surface
4.1 Contents of the section
We show that by starting from slope-stable spherical vector bundles
![]() ${\mathscr F}$
on an elliptic surface S, we can produce vector bundles
${\mathscr F}$
on an elliptic surface S, we can produce vector bundles
![]() ${\mathscr F}[n]^{+}$
on
${\mathscr F}[n]^{+}$
on
![]() $S^{[n]}$
with rank and first two Chern classes covering all the cases in Theorem 1.1. We also study the restriction of such an
$S^{[n]}$
with rank and first two Chern classes covering all the cases in Theorem 1.1. We also study the restriction of such an
![]() ${\mathscr F}[n]^{+}$
to fibres of the Lagrangian fibration
${\mathscr F}[n]^{+}$
to fibres of the Lagrangian fibration
![]() $S^{[n]}\to {\mathbb P}^n$
.
$S^{[n]}\to {\mathbb P}^n$
.
4.2 Basic modular sheaves with the required topology
The present section contains analogues of the results in Sections 6.2 and 6.3 of [Reference O’GradyO’G22]. Let S be a
![]() $K3$
surface with an elliptic fibration
$K3$
surface with an elliptic fibration
![]() $S\to {\mathbb P}^1$
; we let C be a fibre of the elliptic fibration. The claim below follows from surjectivity of the period map for
$S\to {\mathbb P}^1$
; we let C be a fibre of the elliptic fibration. The claim below follows from surjectivity of the period map for
![]() $K3$
surfaces.
$K3$
surfaces.
Claim 4.1. Let
![]() $m_0,d_0$
be positive natural numbers. There exist
$m_0,d_0$
be positive natural numbers. There exist
![]() $K3$
surfaces S with an elliptic fibration
$K3$
surfaces S with an elliptic fibration
![]() $S\to {\mathbb P}^1$
, such that
$S\to {\mathbb P}^1$
, such that
The following result is a (slight) extension of Proposition 6.2 in [Reference O’GradyO’G22] (and is more or less well-known by experts).
Proposition 4.2. Let
![]() $m_0,r_0,s_0\in {\mathbb N}_{+}$
, and let
$m_0,r_0,s_0\in {\mathbb N}_{+}$
, and let
![]() $t,d_0\in {\mathbb Z}$
. Suppose that
$t,d_0\in {\mathbb Z}$
. Suppose that
-
(a)
 $t^2 m_0=r_0s_0-1$
,
$t^2 m_0=r_0s_0-1$
, -
(b)
 $d_0$
is coprime to
$d_0$
is coprime to
 $r_0$
,
$r_0$
, -
(c) we have
(4.2.2) $$ \begin{align} d_0>\frac{(2m_0+1)r_0^2(r_0^2-1)}{4}. \end{align} $$
$$ \begin{align} d_0>\frac{(2m_0+1)r_0^2(r_0^2-1)}{4}. \end{align} $$
Let S be an elliptic
![]() $K3$
surface as in Claim 4.1. Then there exists a vector bundle
$K3$
surface as in Claim 4.1. Then there exists a vector bundle
![]() ${\mathscr F}$
on S, such that the following hold:
${\mathscr F}$
on S, such that the following hold:
-
(1)
 $v({\mathscr F})=(r_0,tD,s_0)$
,
$v({\mathscr F})=(r_0,tD,s_0)$
, -
(2)
 $\chi (S,End({\mathscr F}))=2$
,
$\chi (S,End({\mathscr F}))=2$
, -
(3)
 ${\mathscr F}$
is L slope-stable for any polarization L of S,
${\mathscr F}$
is L slope-stable for any polarization L of S, -
(4) and the restriction of
 ${\mathscr F}$
to every fibre of the elliptic fibration
${\mathscr F}$
to every fibre of the elliptic fibration
 $S\to {\mathbb P}^1$
is slope-stable.
$S\to {\mathbb P}^1$
is slope-stable.
(Notice that every fibre is irreducible by our assumptions on
![]() $\operatorname {\mathrm {NS}}(S)$
, hence, slope-stability of a sheaf on a fibre is well-defined, i.e. independent of the choice of a polarization.)
$\operatorname {\mathrm {NS}}(S)$
, hence, slope-stability of a sheaf on a fibre is well-defined, i.e. independent of the choice of a polarization.)
Proof. One proceeds, literally, as in the proof of Proposition 6.2 in [Reference O’GradyO’G22].
Assume that
![]() $n,r_0,g,l,e\in {\mathbb N}_{+}$
, and that the equalities in (1.2.3), (1.2.4) and(1.2.5) (in Theorem 1.1) hold. Let
$n,r_0,g,l,e\in {\mathbb N}_{+}$
, and that the equalities in (1.2.3), (1.2.4) and(1.2.5) (in Theorem 1.1) hold. Let
 $$ \begin{align} s_0:=\frac{g^2\overline{e}+ (2n-2)(r_0-1)^2+8}{8r_0},\quad m_0:=\frac{ g^2 \overline{e}+ 2(n-1)(r_0-1)^2}{8g^2 l^2}. \end{align} $$
$$ \begin{align} s_0:=\frac{g^2\overline{e}+ (2n-2)(r_0-1)^2+8}{8r_0},\quad m_0:=\frac{ g^2 \overline{e}+ 2(n-1)(r_0-1)^2}{8g^2 l^2}. \end{align} $$
Then
![]() $s_0, m_0$
are integers by the equalities in (1.2.4) and in (1.2.5). A straightforward computation gives that
$s_0, m_0$
are integers by the equalities in (1.2.4) and in (1.2.5). A straightforward computation gives that
Let S be a
![]() $K3$
surface as in Claim 4.1, where
$K3$
surface as in Claim 4.1, where
![]() $m_0$
is as in (4.2.3), and
$m_0$
is as in (4.2.3), and
![]() $d_0$
is an integer coprime to
$d_0$
is an integer coprime to
![]() $r_0$
, such that the inequality in (4.2.2) holds. By Proposition 4.2, there exists a vector bundle
$r_0$
, such that the inequality in (4.2.2) holds. By Proposition 4.2, there exists a vector bundle
![]() ${\mathscr F}$
on S, such that
${\mathscr F}$
on S, such that
and Items (2)–(4) of that same proposition hold.
Claim 4.3. Keep notation and hypotheses as above, in particular,
![]() ${\mathscr F}$
is the vector bundle on S, such that the equation in (4.2.5) and Items (2)–(4) of Proposition 4.2 hold. Let
${\mathscr F}$
is the vector bundle on S, such that the equation in (4.2.5) and Items (2)–(4) of Proposition 4.2 hold. Let
![]() ${\mathscr E}:={\mathscr F}[n]^{+}$
. Then we have
${\mathscr E}:={\mathscr F}[n]^{+}$
. Then we have
where
![]() $h\in \operatorname {\mathrm {NS}}(S^{[n]})$
is primitive,
$h\in \operatorname {\mathrm {NS}}(S^{[n]})$
is primitive,
![]() $q(h)=e$
and
$q(h)=e$
and
![]() $\operatorname {\mathrm {div}}(h)=il$
.
$\operatorname {\mathrm {div}}(h)=il$
.
Proof. Let
Then h is integral by the hypothesis in (1.2.2), primitive by the third equality in (1.2.3),
![]() $q(h)=e$
by the second equality in (4.2.3) and
$q(h)=e$
by the second equality in (4.2.3) and
![]() $\operatorname {\mathrm {div}}(h)=il$
. The equalities in (4.2.6) hold by Proposition 3.2.
$\operatorname {\mathrm {div}}(h)=il$
. The equalities in (4.2.6) hold by Proposition 3.2.
4.3 Restriction of
 ${\mathscr F}[n]^{+}$
to Lagrangian fibres
${\mathscr F}[n]^{+}$
to Lagrangian fibres
Definition 4.4. Let
![]() $S\to {\mathbb P}^1$
be an elliptically fibred
$S\to {\mathbb P}^1$
be an elliptically fibred
![]() $K3$
surface. If
$K3$
surface. If
![]() $x\in {\mathbb P}^1$
, we let
$x\in {\mathbb P}^1$
, we let
![]() $C_x$
be the (scheme theoretic) elliptic fibre over x. Let
$C_x$
be the (scheme theoretic) elliptic fibre over x. Let
![]() $B=\{b_1,\ldots ,b_m\}\subset {\mathbb P}^1$
be the set of x, such that
$B=\{b_1,\ldots ,b_m\}\subset {\mathbb P}^1$
be the set of x, such that
![]() $C_x$
is singular. Then B is not empty (generically,
$C_x$
is singular. Then B is not empty (generically,
![]() $m=24$
). The Lagrangian fibration associated to
$m=24$
). The Lagrangian fibration associated to
![]() $S\to {\mathbb P}^1$
is the map
$S\to {\mathbb P}^1$
is the map
![]() $\pi \colon S^{[n]}\to {\mathbb P}^n$
given by the composition
$\pi \colon S^{[n]}\to {\mathbb P}^n$
given by the composition
We record a few facts regarding the (scheme theoretic) fibres of
![]() $\pi $
. Let
$\pi $
. Let
![]() $x_1,\ldots ,x_n\in {\mathbb P}^1$
be pairwise distinct: then
$x_1,\ldots ,x_n\in {\mathbb P}^1$
be pairwise distinct: then
Next, we describe the discriminant locus of
![]() $\pi \colon S^{[n]}\to ({\mathbb P}^1)^{(n)}$
, that is the subset
$\pi \colon S^{[n]}\to ({\mathbb P}^1)^{(n)}$
, that is the subset
![]() ${\mathscr D}\subset ({\mathbb P}^1)^{(n)}$
parametrizing cycles
${\mathscr D}\subset ({\mathbb P}^1)^{(n)}$
parametrizing cycles
![]() $x_1+\ldots +x_n$
, such that
$x_1+\ldots +x_n$
, such that
![]() $\pi ^{-1}(x_1+\ldots +x_n)$
is singular. For
$\pi ^{-1}(x_1+\ldots +x_n)$
is singular. For
![]() $b_j\in B$
, let
$b_j\in B$
, let
![]() ${\mathscr D}(b_j)\subset ({\mathbb P}^1)^{(n)}$
be the irreducible divisor parametrizing cycles
${\mathscr D}(b_j)\subset ({\mathbb P}^1)^{(n)}$
be the irreducible divisor parametrizing cycles
![]() $x_1+\ldots +x_n$
, such that
$x_1+\ldots +x_n$
, such that
![]() $x_i=b_j$
for some
$x_i=b_j$
for some
![]() $i\in \{1,\ldots ,n\}$
. Let
$i\in \{1,\ldots ,n\}$
. Let
Note that the fibres of
![]() $\pi $
over points of
$\pi $
over points of
![]() ${\mathscr T}$
are reducible and nonreduced.
${\mathscr T}$
are reducible and nonreduced.
Proposition 4.5. The irreducible decomposition of the discriminant locus
![]() ${\mathscr D}$
of
${\mathscr D}$
of
![]() $\pi \colon S^{[n]}\to {\mathbb P}^n$
is given by
$\pi \colon S^{[n]}\to {\mathbb P}^n$
is given by
 $$ \begin{align} {\mathscr D}={\mathscr T}\cup\bigcup\limits_{j=1}^m {\mathscr D}(b_j). \end{align} $$
$$ \begin{align} {\mathscr D}={\mathscr T}\cup\bigcup\limits_{j=1}^m {\mathscr D}(b_j). \end{align} $$
Below is the main result of the present subsection.
Proposition 4.6. Let S be a
![]() $K3$
surface with an elliptic fibration
$K3$
surface with an elliptic fibration
![]() $S\to {\mathbb P}^1$
as in Claim 4.1, and let
$S\to {\mathbb P}^1$
as in Claim 4.1, and let
![]() $\pi \colon S^{[n]}\to {\mathbb P}^n$
be the associated Lagrangian fibration. Let
$\pi \colon S^{[n]}\to {\mathbb P}^n$
be the associated Lagrangian fibration. Let
![]() ${\mathscr F}$
be a vector bundle on S as in Proposition 4.2. Then the following hold:
${\mathscr F}$
be a vector bundle on S as in Proposition 4.2. Then the following hold:
-
(a) If
 $x_1,\ldots ,x_n\in {\mathbb P}^1$
are pairwise distinct, then the restriction of
$x_1,\ldots ,x_n\in {\mathbb P}^1$
are pairwise distinct, then the restriction of
 ${\mathscr F}[n]^{+}$
to
${\mathscr F}[n]^{+}$
to
 $\pi ^{-1}(x_1+\ldots +x_n)$
is slope-stable for any product polarization (this makes sense by the isomorphism in (4.3.2)).
$\pi ^{-1}(x_1+\ldots +x_n)$
is slope-stable for any product polarization (this makes sense by the isomorphism in (4.3.2)). -
(b) Let
 $U\subset ({\mathbb P}^1)^{(n)}$
be the open subset parametrizing cycles
$U\subset ({\mathbb P}^1)^{(n)}$
be the open subset parametrizing cycles
 $x_1+\ldots +x_n$
, such that the restriction of
$x_1+\ldots +x_n$
, such that the restriction of
 ${\mathscr F}[n]^{+}$
to
${\mathscr F}[n]^{+}$
to
 $\pi ^{-1}(x_1+\ldots +x_n)$
is a simple sheaf. The complement of U has codimension at least
$\pi ^{-1}(x_1+\ldots +x_n)$
is a simple sheaf. The complement of U has codimension at least
 $2$
.
$2$
.
Before proving Proposition 4.6, we notice that Proposition 6.10 in [Reference O’GradyO’G22] holds for products of projective varieties of arbitrary dimension.
Lemma 4.7. For
![]() $i\in \{1,2\}$
, let
$i\in \{1,2\}$
, let
![]() $(X_i,L_i)$
be an irreducible polarized projective variety of dimension
$(X_i,L_i)$
be an irreducible polarized projective variety of dimension
![]() $d_i$
, and let
$d_i$
, and let
![]() ${\mathscr V}_i$
be a slope-stable vector bundle on
${\mathscr V}_i$
be a slope-stable vector bundle on
![]() $X_i$
. Then
$X_i$
. Then
![]() ${\mathscr V}_1\boxtimes {\mathscr V}_2$
is slope-stable for any product polarization
${\mathscr V}_1\boxtimes {\mathscr V}_2$
is slope-stable for any product polarization
![]() ${\mathscr L}:=L_1^{m_1}\boxtimes L_2^{m_2}$
(of course,
${\mathscr L}:=L_1^{m_1}\boxtimes L_2^{m_2}$
(of course,
![]() $m_1,m_2\in {\mathbb N}_{+}$
).
$m_1,m_2\in {\mathbb N}_{+}$
).
Proof. Suppose that there exists an injection
![]() $\alpha \colon {\mathscr E}\to {\mathscr V}_1\boxtimes {\mathscr V}_2$
with torsion-free cokernel, such that
$\alpha \colon {\mathscr E}\to {\mathscr V}_1\boxtimes {\mathscr V}_2$
with torsion-free cokernel, such that
![]() $0<r({\mathscr E})<r({\mathscr V}_1\boxtimes {\mathscr V}_2)$
and
$0<r({\mathscr E})<r({\mathscr V}_1\boxtimes {\mathscr V}_2)$
and
The open subset
![]() $U\subset X_1\times X_2$
of points p at which
$U\subset X_1\times X_2$
of points p at which
![]() $\alpha $
is an injection of vector bundles (i.e. the stalk of
$\alpha $
is an injection of vector bundles (i.e. the stalk of
![]() ${\mathscr E}$
at p is free and
${\mathscr E}$
at p is free and
![]() $\alpha $
defines an injection of the fibre of
$\alpha $
defines an injection of the fibre of
![]() ${\mathscr E}$
at p to the fibre of
${\mathscr E}$
at p to the fibre of
![]() ${\mathscr V}_1\boxtimes {\mathscr V}_2$
at p) has the complement of codimension at least
${\mathscr V}_1\boxtimes {\mathscr V}_2$
at p) has the complement of codimension at least
![]() $2$
. Let
$2$
. Let
![]() $p=(x_1,x_2)\in U$
. The restrictions of
$p=(x_1,x_2)\in U$
. The restrictions of
![]() $\alpha $
to
$\alpha $
to
![]() $\{x_1\}\times X_2$
and to
$\{x_1\}\times X_2$
and to
![]() $X_1\times \{x_2\}$
are generically injective maps of vector bundles. Let
$X_1\times \{x_2\}$
are generically injective maps of vector bundles. Let
 $$ \begin{align*} A_1:=m_1^{d_1-1} m_2^{d_2}\deg X_2 {d_1+d_2-1\choose d_2},\quad A_2:=m_1^{d_1} m_2^{d_2-1}\deg X_1 {d_1+d_2-1\choose d_1}. \end{align*} $$
$$ \begin{align*} A_1:=m_1^{d_1-1} m_2^{d_2}\deg X_2 {d_1+d_2-1\choose d_2},\quad A_2:=m_1^{d_1} m_2^{d_2-1}\deg X_1 {d_1+d_2-1\choose d_1}. \end{align*} $$
We have
and
Since the restrictions of
![]() ${\mathscr V}_1\boxtimes {\mathscr V}_2$
to
${\mathscr V}_1\boxtimes {\mathscr V}_2$
to
![]() $X_1\times \{x_2\}$
and to
$X_1\times \{x_2\}$
and to
![]() $\{x_1\}\times X_2$
are isomorphic to the polystable vector bundles
$\{x_1\}\times X_2$
are isomorphic to the polystable vector bundles
![]() ${\mathscr V}_1\otimes _{{\mathbb C}}{\mathbb C}^{r({\mathscr V}_2)}$
and
${\mathscr V}_1\otimes _{{\mathbb C}}{\mathbb C}^{r({\mathscr V}_2)}$
and
![]() ${\mathscr V}_1\otimes _{{\mathbb C}}{\mathbb C}^{r({\mathscr V}_1)}$
, respectively, it follows from (4.3.5), (4.3.6) and (4.3.7) that
${\mathscr V}_1\otimes _{{\mathbb C}}{\mathbb C}^{r({\mathscr V}_1)}$
, respectively, it follows from (4.3.5), (4.3.6) and (4.3.7) that
![]() $\mu ({\mathscr E}_{|X_1\times \{x_2\}})=\mu ({\mathscr V}_1)$
and
$\mu ({\mathscr E}_{|X_1\times \{x_2\}})=\mu ({\mathscr V}_1)$
and
![]() $\mu ({\mathscr E}_{|\{x_1\}\times X_2})=\mu ({\mathscr V}_2)$
. In turn, these equalities give that there exist vector subspaces
$\mu ({\mathscr E}_{|\{x_1\}\times X_2})=\mu ({\mathscr V}_2)$
. In turn, these equalities give that there exist vector subspaces
![]() $0\not =W_i\subset {\mathbb C}^{r({\mathscr V}_i)}$
, such that
$0\not =W_i\subset {\mathbb C}^{r({\mathscr V}_i)}$
, such that
![]() ${\mathscr E}_{|X_1\times \{x_2\}}={\mathscr V}_1\otimes _{{\mathbb C}} W_2$
on
${\mathscr E}_{|X_1\times \{x_2\}}={\mathscr V}_1\otimes _{{\mathbb C}} W_2$
on
![]() $U\cap (X_1\times \{x_2\})$
and
$U\cap (X_1\times \{x_2\})$
and
![]() ${\mathscr E}_{|\{x_1\}\times X_2}=W_1\otimes _{{\mathbb C}}{\mathscr V}_2$
on
${\mathscr E}_{|\{x_1\}\times X_2}=W_1\otimes _{{\mathbb C}}{\mathscr V}_2$
on
![]() $U\cap (\{x\}_1\times X_2)$
. It follows that
$U\cap (\{x\}_1\times X_2)$
. It follows that
![]() $\operatorname {\mathrm {Im}}\alpha _{|U}=({\mathscr V}_1\boxtimes {\mathscr V}_2)_{|U}$
. This is a contradiction.
$\operatorname {\mathrm {Im}}\alpha _{|U}=({\mathscr V}_1\boxtimes {\mathscr V}_2)_{|U}$
. This is a contradiction.
Proof of Proposition 4.6.
(a): Follows from the stability of the restriction of
![]() ${\mathscr F}$
to any elliptic fibre of
${\mathscr F}$
to any elliptic fibre of
![]() $S\to {\mathbb P}^1$
(Proposition 4.2), and Lemma 4.7.
$S\to {\mathbb P}^1$
(Proposition 4.2), and Lemma 4.7.
(b): Let
![]() $V\subset ({\mathbb P}^1)^{(n)}$
be the open subset parametrizing cycles
$V\subset ({\mathbb P}^1)^{(n)}$
be the open subset parametrizing cycles
![]() $\Gamma :=d_1 x_1+\ldots + d_m x_m$
, such that
$\Gamma :=d_1 x_1+\ldots + d_m x_m$
, such that
![]() $d_j\le 2$
for all
$d_j\le 2$
for all
![]() $j\in \{1,\ldots ,m\}$
, and
$j\in \{1,\ldots ,m\}$
, and
![]() $C_{x_j}$
is smooth if
$C_{x_j}$
is smooth if
![]() $d_j=2$
. If
$d_j=2$
. If
![]() $\Gamma $
is such a cycle, then the restriction of
$\Gamma $
is such a cycle, then the restriction of
![]() ${\mathscr F}[n]^{+}$
to
${\mathscr F}[n]^{+}$
to
![]() $\pi ^{-1}(\Gamma )$
is a simple sheaf. In fact,
$\pi ^{-1}(\Gamma )$
is a simple sheaf. In fact,
![]() $\pi ^{-1}(\Gamma )$
is a product of schemes
$\pi ^{-1}(\Gamma )$
is a product of schemes
![]() $\boldsymbol{C}_1\times \ldots \times \boldsymbol{C}_m$
, where
$\boldsymbol{C}_1\times \ldots \times \boldsymbol{C}_m$
, where
![]() $ \boldsymbol{C}_j=C_{x_j}$
if
$ \boldsymbol{C}_j=C_{x_j}$
if
![]() $d_j=1$
, while if
$d_j=1$
, while if
![]() $d_j=2$
, then
$d_j=2$
, then
![]() $ \boldsymbol{C}_j$
is identified with the scheme theoretic fibre over
$ \boldsymbol{C}_j$
is identified with the scheme theoretic fibre over
![]() $2x_j\in ({\mathbb P}^1)^{(2)}$
of the Lagrangian fibration
$2x_j\in ({\mathbb P}^1)^{(2)}$
of the Lagrangian fibration
![]() $S^{[2]}\to ({\mathbb P}^1)^{(2)}$
. Moreover
$S^{[2]}\to ({\mathbb P}^1)^{(2)}$
. Moreover
If
![]() $d_j=1$
, then
$d_j=1$
, then
![]() $ \boldsymbol{C}_j=C_{x_j}$
and
$ \boldsymbol{C}_j=C_{x_j}$
and
![]() ${\mathscr F}_{|\boldsymbol{C}_j}$
is simple by Proposition 4.2. If
${\mathscr F}_{|\boldsymbol{C}_j}$
is simple by Proposition 4.2. If
![]() $d_j=2$
, then
$d_j=2$
, then
![]() $ \boldsymbol{C}_j$
is the scheme considered in [Reference O’GradyO’G22, Section 6.4], and
$ \boldsymbol{C}_j$
is the scheme considered in [Reference O’GradyO’G22, Section 6.4], and
![]() ${\mathscr F}_{|\boldsymbol{C}_j}$
is simple by [Reference O’GradyO’G22, Proposition 6.13]. By the isomorphism in (4.3.8), it follows that
${\mathscr F}_{|\boldsymbol{C}_j}$
is simple by [Reference O’GradyO’G22, Proposition 6.13]. By the isomorphism in (4.3.8), it follows that
![]() ${\mathscr F}[n]^{+}_{|\pi ^{-1}(\Gamma )}$
is simple. Since the complement of V in
${\mathscr F}[n]^{+}_{|\pi ^{-1}(\Gamma )}$
is simple. Since the complement of V in
![]() $({\mathbb P}^1)^{(n)}$
is a (closed) subset of codimension at least
$({\mathbb P}^1)^{(n)}$
is a (closed) subset of codimension at least
![]() $2$
, this proves Item (b).
$2$
, this proves Item (b).
Remark 4.8. By Item (a) of Proposition 4.6, the restriction of
![]() ${\mathscr F}[n]^{+}$
to a (singular) Lagrangian fibre
${\mathscr F}[n]^{+}$
to a (singular) Lagrangian fibre
![]() $X_t$
parametrized by a general point
$X_t$
parametrized by a general point
![]() $t\in {\mathscr D}(b_j)$
(notation as in (4.3.4)) is slope-stable for any product polarization.
$t\in {\mathscr D}(b_j)$
(notation as in (4.3.4)) is slope-stable for any product polarization.
The following remarks place Item (a) of Proposition 4.6 in the context of known results.
Remark 4.9. Let
![]() $X\to {\mathbb P}^n$
be a Lagrangian fibration of an HK manifold. For
$X\to {\mathbb P}^n$
be a Lagrangian fibration of an HK manifold. For
![]() $t\in {\mathbb P}^n$
, let
$t\in {\mathbb P}^n$
, let
![]() $X_t:=\pi ^{-1}(t)$
be the schematic fibre of
$X_t:=\pi ^{-1}(t)$
be the schematic fibre of
![]() $X\to {\mathbb P}^n$
over t. If
$X\to {\mathbb P}^n$
over t. If
![]() $X_t$
is smooth, there exists an ample primitive class
$X_t$
is smooth, there exists an ample primitive class
![]() $\theta _t\in H^{1,1}_{{\mathbb Z}}(X_t)$
, such that the image of the restriction map
$\theta _t\in H^{1,1}_{{\mathbb Z}}(X_t)$
, such that the image of the restriction map
![]() $H^2(X;{\mathbb Z})\to H^2(X_t;{\mathbb Z})$
is contained in
$H^2(X;{\mathbb Z})\to H^2(X_t;{\mathbb Z})$
is contained in
![]() ${\mathbb Z}\theta _t$
(see [Reference WieneckWie16]). If
${\mathbb Z}\theta _t$
(see [Reference WieneckWie16]). If
![]() ${\mathscr F}$
is a sheaf on
${\mathscr F}$
is a sheaf on
![]() $X_t$
, slope-(semi)stability of
$X_t$
, slope-(semi)stability of
![]() ${\mathscr F}$
will always mean
${\mathscr F}$
will always mean
![]() $\theta _t$
slope-(semi)stability.
$\theta _t$
slope-(semi)stability.
Remark 4.10. Let
![]() $X\to {\mathbb P}^n$
be a Lagrangian fibration of an HK manifold of type
$X\to {\mathbb P}^n$
be a Lagrangian fibration of an HK manifold of type
![]() $K3^{[n]}$
, and let
$K3^{[n]}$
, and let
![]() $X_t$
be a smooth Lagrangian fibre. Then the primitive ample class
$X_t$
be a smooth Lagrangian fibre. Then the primitive ample class
![]() $\theta _t\in H^{1,1}_{{\mathbb Z}}(X_t)$
is a principal polarization of
$\theta _t\in H^{1,1}_{{\mathbb Z}}(X_t)$
is a principal polarization of
![]() $X_t$
(see [Reference WieneckWie16]). If
$X_t$
(see [Reference WieneckWie16]). If
![]() $S^{[n]}\to {\mathbb P}^n$
is the Lagrangian fibration in (4.3.1), and
$S^{[n]}\to {\mathbb P}^n$
is the Lagrangian fibration in (4.3.1), and
![]() $\pi ^{-1}(x_1+\ldots +x_n)\cong C_{x_1}\times \ldots C_{x_n}$
is a smooth Lagrangian fibre, then
$\pi ^{-1}(x_1+\ldots +x_n)\cong C_{x_1}\times \ldots C_{x_n}$
is a smooth Lagrangian fibre, then
![]() $\theta _{x_1+\ldots +x_n}$
is the product principal polarization.
$\theta _{x_1+\ldots +x_n}$
is the product principal polarization.
5 Proof of Theorem 1.1 and Proposition 1.2
5.1 Contents of the section
In the present section, we prove the following two statements.
Proposition 5.1. Let
![]() $n,r_0,g,l,e,i$
be as in Theorem 1.1. There exists an irreducible component
$n,r_0,g,l,e,i$
be as in Theorem 1.1. There exists an irreducible component
![]() ${\mathscr K}^{il}_e(2n)^{\mathrm {good}}$
of
${\mathscr K}^{il}_e(2n)^{\mathrm {good}}$
of
![]() ${\mathscr K}^{il}_e(2n)$
, such that for a general polarized HK variety
${\mathscr K}^{il}_e(2n)$
, such that for a general polarized HK variety
![]() $(X,h)$
parametrized by
$(X,h)$
parametrized by
![]() ${\mathscr K}^{il}_e(2n)^{\mathrm {good}}$
, there exists an h slope-stable vector bundle
${\mathscr K}^{il}_e(2n)^{\mathrm {good}}$
, there exists an h slope-stable vector bundle
![]() ${\mathscr E}$
on X, such that the equalities in (1.2.6) hold, and moreover,
${\mathscr E}$
on X, such that the equalities in (1.2.6) hold, and moreover,
![]() $H^p(X,End^0({\mathscr E}))=0$
for all p.
$H^p(X,End^0({\mathscr E}))=0$
for all p.
Proposition 5.2. Let
![]() $n,r_0,g,l,e,i$
be as in Theorem 1.1. If
$n,r_0,g,l,e,i$
be as in Theorem 1.1. If
![]() $[(X,h)]\in {\mathscr K}^{il}_e(2n)^{\mathrm {good}}$
is a general point, then there exists a unique h slope-stable vector bundle
$[(X,h)]\in {\mathscr K}^{il}_e(2n)^{\mathrm {good}}$
is a general point, then there exists a unique h slope-stable vector bundle
![]() ${\mathscr E}$
on X, such that the equalities in (1.2.6) hold.
${\mathscr E}$
on X, such that the equalities in (1.2.6) hold.
The same exact argument given in the “Proof of Theorem 1.4” on p. 30 of [Reference O’GradyO’G22] shows that Theorem 1.1 follows from Propositions 5.1 and 5.2.
In Sections 5.2 and 5.3, we prove results that are used in the proof of Propositions 5.1 and 5.2. Proposition 5.1 is proved in Section 5.4. Sections 5.5 and 5.6 contain results that are used in the proof of Proposition 5.2. Propositions 5.2 and 1.2 are proved in Sections 5.7 and 5.8, respectively.
5.2 The relevant component of
 ${\mathscr K}^{il}_e(2n)$
, and Noether-Lefschetz divisors
${\mathscr K}^{il}_e(2n)$
, and Noether-Lefschetz divisors
Let S be an elliptic
![]() $K3$
surface as in Claim 4.3, and let
$K3$
surface as in Claim 4.3, and let
![]() $C,D$
be divisor classes generating
$C,D$
be divisor classes generating
![]() $\operatorname {\mathrm {NS}}(S)$
as in loc. cit. Let
$\operatorname {\mathrm {NS}}(S)$
as in loc. cit. Let
![]() $X_0=S^{[n]}$
, and let
$X_0=S^{[n]}$
, and let
be the Lagrangian fibration associated to the elliptic fibration of S (see (4.3.1)). Let
Definition 5.3. Let
![]() ${\mathscr K}^{il}_e(2n)^{\mathrm {good}}\subset {\mathscr K}^{il}_e(2n)$
be the irreducible component containing
${\mathscr K}^{il}_e(2n)^{\mathrm {good}}\subset {\mathscr K}^{il}_e(2n)$
be the irreducible component containing
![]() $[(S^{[n]},h_0)]$
.
$[(S^{[n]},h_0)]$
.
Let
![]() $d_0=C\cdot D$
(see (4.2.1)). The sublattice
$d_0=C\cdot D$
(see (4.2.1)). The sublattice
![]() $\langle f_0,h_0\rangle \subset H^{1,1}_{{\mathbb Z}}(X_0)$
is saturated and
$\langle f_0,h_0\rangle \subset H^{1,1}_{{\mathbb Z}}(X_0)$
is saturated and
(the last equality follows from (4.2.3)). Let
![]() $L_0,F_0$
be the line bundles on
$L_0,F_0$
be the line bundles on
![]() $X_0$
, such that
$X_0$
, such that
![]() $c_1(L_0)=h_0$
and
$c_1(L_0)=h_0$
and
![]() $c_1(F_0)=f_0$
.
$c_1(F_0)=f_0$
.
Definition 5.4. Let
![]() $\varphi \colon {\mathscr X}\to B$
be an (analytic) contractible representative of the functor
$\varphi \colon {\mathscr X}\to B$
be an (analytic) contractible representative of the functor
![]() $\operatorname {\mathrm {Def}}(X_0,L_0,F_0)$
. Let
$\operatorname {\mathrm {Def}}(X_0,L_0,F_0)$
. Let
![]() $0\in B$
be the base point, so that
$0\in B$
be the base point, so that
![]() $X_0=\varphi ^{-1}(0)\cong S^{[n]}$
. For
$X_0=\varphi ^{-1}(0)\cong S^{[n]}$
. For
![]() $b\in B$
, we let
$b\in B$
, we let
![]() $X_b:=\varphi ^{-1}(b)$
, and we let
$X_b:=\varphi ^{-1}(b)$
, and we let
![]() $L_b,F_b$
be the line bundles on
$L_b,F_b$
be the line bundles on
![]() $X_b$
which are deformations of
$X_b$
which are deformations of
![]() $L_0,F_0$
, respectively. We let
$L_0,F_0$
, respectively. We let
![]() $h_b:=c_1(L_b)$
and
$h_b:=c_1(L_b)$
and
![]() $f_b:=c_1(F_b)$
.
$f_b:=c_1(F_b)$
.
Our first observation is that if
![]() $d_0$
is large enough, then
$d_0$
is large enough, then
![]() $h_b$
is ample for a general
$h_b$
is ample for a general
![]() $b\in B$
. Before proving this, we recall the following elementary result.
$b\in B$
. Before proving this, we recall the following elementary result.
Lemma 5.5 (Lemma 4.3 in [Reference O’GradyO’G22]).
Let
![]() $(\Lambda ,q)$
be a nondegenerate rank
$(\Lambda ,q)$
be a nondegenerate rank
![]() $2$
lattice which represents
$2$
lattice which represents
![]() $0$
, and hence,
$0$
, and hence,
![]() $\operatorname {\mathrm {disc}}(\Lambda )=-d^2$
, where d is a strictly positive integer. Let
$\operatorname {\mathrm {disc}}(\Lambda )=-d^2$
, where d is a strictly positive integer. Let
![]() $\alpha \in \Lambda $
be primitive isotropic, and complete it to a basis
$\alpha \in \Lambda $
be primitive isotropic, and complete it to a basis
![]() $\{\alpha ,\beta \}$
, such that
$\{\alpha ,\beta \}$
, such that
![]() $q(\beta )\ge 0$
. If
$q(\beta )\ge 0$
. If
![]() $\gamma \in \Lambda $
has strictly negative square (i.e.
$\gamma \in \Lambda $
has strictly negative square (i.e.
![]() $q(\gamma )<0$
), then
$q(\gamma )<0$
), then
 $$ \begin{align} q(\gamma)\le -\frac{2d}{1+q(\beta)}. \end{align} $$
$$ \begin{align} q(\gamma)\le -\frac{2d}{1+q(\beta)}. \end{align} $$
Proposition 5.6. Keep notation as above, and assume that
Then
![]() $L_b$
is ample on
$L_b$
is ample on
![]() $X_b$
for a general
$X_b$
for a general
![]() $b\in B$
.
$b\in B$
.
Proof. Let
![]() $b\in B$
be a very general point, in the sense that
$b\in B$
be a very general point, in the sense that
![]() $\operatorname {\mathrm {NS}}(X_b)=\langle h_b,f_b\rangle $
. By the inequality in (5.2.5) and Lemma 5.5, there are no
$\operatorname {\mathrm {NS}}(X_b)=\langle h_b,f_b\rangle $
. By the inequality in (5.2.5) and Lemma 5.5, there are no
![]() $\xi \in \operatorname {\mathrm {NS}}(X_b)$
, such that
$\xi \in \operatorname {\mathrm {NS}}(X_b)$
, such that
![]() $-2(n-1)^2(n+3)\le q(\xi )<0$
. By [Reference MongardiMon15, Corollary 2.7], it follows that the ample cone of
$-2(n-1)^2(n+3)\le q(\xi )<0$
. By [Reference MongardiMon15, Corollary 2.7], it follows that the ample cone of
![]() $X_b$
is equal to the intersection of
$X_b$
is equal to the intersection of
![]() $\operatorname {\mathrm {NS}}(X_b)$
and the positive cone (if R is the integral generator of an extremal ray, then, viewed by duality as an element of
$\operatorname {\mathrm {NS}}(X_b)$
and the positive cone (if R is the integral generator of an extremal ray, then, viewed by duality as an element of
![]() $H^2(K3^{[n]},{\mathbb Q})$
, the multiple
$H^2(K3^{[n]},{\mathbb Q})$
, the multiple
![]() $2(n-1) R$
is integral because the divisibility of any element of
$2(n-1) R$
is integral because the divisibility of any element of
![]() $H^2(X_b,{\mathbb Z})$
is a divisor of
$H^2(X_b,{\mathbb Z})$
is a divisor of
![]() $2n-2$
). Hence, either
$2n-2$
). Hence, either
![]() $h_b$
or
$h_b$
or
![]() $-h_b$
is ample. By considering the limit case
$-h_b$
is ample. By considering the limit case
![]() $b=0$
, we get that
$b=0$
, we get that
![]() $h_b$
is ample. This proves that
$h_b$
is ample. This proves that
![]() $h_b$
is ample for b very general. Since
$h_b$
is ample for b very general. Since
![]() $h_b$
is ample for b in the complement of an analytic subset of B, we are done.
$h_b$
is ample for b in the complement of an analytic subset of B, we are done.
Assume that the inequality in (5.2.5) holds. By Proposition 5.6, we have the moduli map
 $$ \begin{align} \begin{matrix} B & \longrightarrow & {\mathscr K}^{il}_e(2n) \\ b & \mapsto & [(X_b,h_b)]. \end{matrix} \end{align} $$
$$ \begin{align} \begin{matrix} B & \longrightarrow & {\mathscr K}^{il}_e(2n) \\ b & \mapsto & [(X_b,h_b)]. \end{matrix} \end{align} $$
Note that the image of the above period map is contained in a unique (irreducible) Noether-Lefschetz divisor in
![]() ${\mathscr K}^{il}_e(2n)^{\mathrm {good}}$
.
${\mathscr K}^{il}_e(2n)^{\mathrm {good}}$
.
Definition 5.7. If the inequality in (5.2.5) holds, we let
![]() $\operatorname {\mathrm {\mathit {NL}}}(d_0)\subset {\mathscr K}^{il}_e(2n)^{\mathrm {good}}$
be the unique irreducible Noether-Lefschetz divisor containing the image of the moduli map in (5.2.6).
$\operatorname {\mathrm {\mathit {NL}}}(d_0)\subset {\mathscr K}^{il}_e(2n)^{\mathrm {good}}$
be the unique irreducible Noether-Lefschetz divisor containing the image of the moduli map in (5.2.6).
Remark 5.8. Let
![]() $[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)$
be a general point. Then there exists a well-defined rank two subspace
$[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)$
be a general point. Then there exists a well-defined rank two subspace
![]() $V\subset \operatorname {\mathrm {NS}}(X)$
, such that
$V\subset \operatorname {\mathrm {NS}}(X)$
, such that
![]() $V=\langle h,f\rangle $
, where
$V=\langle h,f\rangle $
, where
(for
![]() $[(X,h)]$
in a proper Zariski closed subset of
$[(X,h)]$
in a proper Zariski closed subset of
![]() $\operatorname {\mathrm {\mathit {NL}}}(d_0)$
, there might be more than one such rank two subspace). For almost all choices (of
$\operatorname {\mathrm {\mathit {NL}}}(d_0)$
, there might be more than one such rank two subspace). For almost all choices (of
![]() $n,r_0,g,l,e,i$
and
$n,r_0,g,l,e,i$
and
![]() $d_0$
), there is a unique class
$d_0$
), there is a unique class
![]() $f\in V$
, such that
$f\in V$
, such that
![]() $V=\langle h,f\rangle $
and the equalities in (5.2.7) hold, while for special choices, there are two such classes. If monodromy exchanges these two isotropic classes, there is no intrinsic way of distinguishing them. Abusing language, we will speak of “the class f”. If
$V=\langle h,f\rangle $
and the equalities in (5.2.7) hold, while for special choices, there are two such classes. If monodromy exchanges these two isotropic classes, there is no intrinsic way of distinguishing them. Abusing language, we will speak of “the class f”. If
![]() $(X,h)=(X_0,h_0)$
(recall that
$(X,h)=(X_0,h_0)$
(recall that
![]() $X_0=S^{[n]}$
, where S is our elliptic
$X_0=S^{[n]}$
, where S is our elliptic
![]() $K3$
surface), then
$K3$
surface), then
![]() $f_0=c_1(\pi _0^{*}{\mathscr O}_{{\mathbb P}^n}(1))$
, where
$f_0=c_1(\pi _0^{*}{\mathscr O}_{{\mathbb P}^n}(1))$
, where
![]() $\pi _0$
is the Lagrangian fibration given in (5.2.1). By [Reference MatsushitaMat17, Theorem 1.2], it follows that if
$\pi _0$
is the Lagrangian fibration given in (5.2.1). By [Reference MatsushitaMat17, Theorem 1.2], it follows that if
![]() $[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)$
is a general point, then there exists a Lagrangian fibration
$[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)$
is a general point, then there exists a Lagrangian fibration
![]() $\pi _X\colon {\mathscr X}\to {\mathbb P}^n$
, such that
$\pi _X\colon {\mathscr X}\to {\mathbb P}^n$
, such that
![]() $f=c_1(\pi _X^{*}{\mathscr O}_{{\mathbb P}^n}(1))$
.
$f=c_1(\pi _X^{*}{\mathscr O}_{{\mathbb P}^n}(1))$
.
Proposition 5.9. Keep notation as above, and assume that the inequality in (5.2.5) holds, and that
![]() $d_0$
is coprime to
$d_0$
is coprime to
![]() $r_0$
. Let
$r_0$
. Let
![]() $\operatorname {\mathrm {\mathit {NL}}}(d_0)\subset {\mathscr K}^{il}_e(2n)^{\mathrm {good}}$
be the Noether-Lefschetz divisor of Definition 5.7. There exist an open dense
$\operatorname {\mathrm {\mathit {NL}}}(d_0)\subset {\mathscr K}^{il}_e(2n)^{\mathrm {good}}$
be the Noether-Lefschetz divisor of Definition 5.7. There exist an open dense
![]() $\operatorname {\mathrm {\mathit {NL}}}(d_0)^*\subset \operatorname {\mathrm {\mathit {NL}}}(d_0)$
, and for each
$\operatorname {\mathrm {\mathit {NL}}}(d_0)^*\subset \operatorname {\mathrm {\mathit {NL}}}(d_0)$
, and for each
![]() $[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)^*$
, a vector bundle
$[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)^*$
, a vector bundle
![]() ${\mathscr E}_X$
on X, such that
${\mathscr E}_X$
on X, such that
![]() $H^p(X,End^0({\mathscr E}_X))=0$
for all p, and the restriction of
$H^p(X,End^0({\mathscr E}_X))=0$
for all p, and the restriction of
![]() ${\mathscr E}_X$
to a general smooth fibre of the Lagrangian fibration
${\mathscr E}_X$
to a general smooth fibre of the Lagrangian fibration
![]() $X\to {\mathbb P}^n$
(see Remark 5.8) is slope-stable.
$X\to {\mathbb P}^n$
(see Remark 5.8) is slope-stable.
Proof. Let
![]() ${\mathscr E}_0:={\mathscr F}[n]^{+}$
be the vector bundle on
${\mathscr E}_0:={\mathscr F}[n]^{+}$
be the vector bundle on
![]() $X_0$
of Claim 4.3. Note that
$X_0$
of Claim 4.3. Note that
![]() $c_1({\mathscr E}_0)=h_0$
by loc.cit. If B is small enough, then by Remark 3.8, the vector bundle
$c_1({\mathscr E}_0)=h_0$
by loc.cit. If B is small enough, then by Remark 3.8, the vector bundle
![]() ${\mathscr E}_0$
on
${\mathscr E}_0$
on
![]() $X_0$
deforms uniquely to a vector bundle
$X_0$
deforms uniquely to a vector bundle
![]() ${\mathscr E}_b$
on
${\mathscr E}_b$
on
![]() $X_b$
, and hence, we get a vector bundle
$X_b$
, and hence, we get a vector bundle
![]() ${\mathscr E}_X$
on X for
${\mathscr E}_X$
on X for
![]() $[(X,h)]$
in a dense open subset
$[(X,h)]$
in a dense open subset
![]() ${\mathscr U}\subset \operatorname {\mathrm {\mathit {NL}}}(d_0)$
. The equations in (5.2.8) hold by the equations in (4.2.6). Since
${\mathscr U}\subset \operatorname {\mathrm {\mathit {NL}}}(d_0)$
. The equations in (5.2.8) hold by the equations in (4.2.6). Since
![]() $H^p(X,End^0({\mathscr E}_0))=0$
for all p (see (3.3.4)), it follows from upper semicontinuity of the dimension of cohomology sheaves that for
$H^p(X,End^0({\mathscr E}_0))=0$
for all p (see (3.3.4)), it follows from upper semicontinuity of the dimension of cohomology sheaves that for
![]() $[(X,h)]$
in a smaller dense open subset
$[(X,h)]$
in a smaller dense open subset
![]() ${\mathscr U}'\subset {\mathscr U}$
, we have
${\mathscr U}'\subset {\mathscr U}$
, we have
![]() $H^p(X,End^0({\mathscr E}_X))=0$
for all p. Lastly, it follows from Item (a) of Proposition 4.6 and Remark 4.10 that for
$H^p(X,End^0({\mathscr E}_X))=0$
for all p. Lastly, it follows from Item (a) of Proposition 4.6 and Remark 4.10 that for
![]() $[(X,h)]$
in a smaller dense open subset
$[(X,h)]$
in a smaller dense open subset
![]() ${\mathscr U}"\subset {\mathscr U}'$
, the restriction of
${\mathscr U}"\subset {\mathscr U}'$
, the restriction of
![]() ${\mathscr E}_X$
to a general fibre of the Lagrangian fibration
${\mathscr E}_X$
to a general fibre of the Lagrangian fibration
![]() $X\to {\mathbb P}^n$
(see Remark 5.8) is slope-stable. We set
$X\to {\mathbb P}^n$
(see Remark 5.8) is slope-stable. We set
![]() $\operatorname {\mathrm {\mathit {NL}}}(d_0)^*:={\mathscr U}"$
.
$\operatorname {\mathrm {\mathit {NL}}}(d_0)^*:={\mathscr U}"$
.
5.3 Suitable polarizations
We recall that if h is a-suitable (see [Reference O’GradyO’G22, Definition 3.5]) and
![]() ${\mathscr E}$
is a vector bundle on X with
${\mathscr E}$
is a vector bundle on X with
![]() $a({\mathscr E})\le a$
(see (3.1.1) loc.cit. for the definition of
$a({\mathscr E})\le a$
(see (3.1.1) loc.cit. for the definition of
![]() $a({\mathscr E})$
), then slope stability of the restriction of
$a({\mathscr E})$
), then slope stability of the restriction of
![]() ${\mathscr E}$
to a general Lagrangian fibre (there is a canonical choice of polarization of any smooth Lagrangian fibre, see Remark 4.9) implies slope stability of
${\mathscr E}$
to a general Lagrangian fibre (there is a canonical choice of polarization of any smooth Lagrangian fibre, see Remark 4.9) implies slope stability of
![]() ${\mathscr E}$
, and the following weak converse holds: slope stability of
${\mathscr E}$
, and the following weak converse holds: slope stability of
![]() ${\mathscr E}$
implies that the restriction of
${\mathscr E}$
implies that the restriction of
![]() ${\mathscr E}$
to a general Lagrangian fibre is slope semistable.
${\mathscr E}$
to a general Lagrangian fibre is slope semistable.
Lemma 5.10. Keep assumptions and notation as above, and let
![]() $a>0$
. Suppose that
$a>0$
. Suppose that
Let
![]() $[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)$
be a general point, and let
$[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)$
be a general point, and let
![]() $f\in V\subset \operatorname {\mathrm {NS}}(X)$
be as in Remark 5.8. Then there does not exist
$f\in V\subset \operatorname {\mathrm {NS}}(X)$
be as in Remark 5.8. Then there does not exist
![]() $\xi \in \operatorname {\mathrm {NS}}(X)$
, such that
$\xi \in \operatorname {\mathrm {NS}}(X)$
, such that
Proof. Let
![]() $\langle h,f\rangle =V\subset \operatorname {\mathrm {NS}}(X)$
be as in Remark 5.8. Applying Lemma 5.5 to
$\langle h,f\rangle =V\subset \operatorname {\mathrm {NS}}(X)$
be as in Remark 5.8. Applying Lemma 5.5 to
![]() $\Lambda :=V$
,
$\Lambda :=V$
,
![]() $\alpha =f$
and
$\alpha =f$
and
![]() $\beta =h$
, one gets that there are no
$\beta =h$
, one gets that there are no
![]() $\xi \in V$
, such that
$\xi \in V$
, such that
![]() $-a\le q_X(\xi )<0$
. In particular, if
$-a\le q_X(\xi )<0$
. In particular, if
![]() $\operatorname {\mathrm {NS}}(X)=\langle h,f\rangle $
(as is the case for very general
$\operatorname {\mathrm {NS}}(X)=\langle h,f\rangle $
(as is the case for very general
![]() $[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)$
), then there is no
$[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)$
), then there is no
![]() $\xi \in V$
, such that the inequalities in (5.3.2) hold.
$\xi \in V$
, such that the inequalities in (5.3.2) hold.
It follows that the set of
![]() $[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)$
for which there exists
$[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)$
for which there exists
![]() $\xi \in \operatorname {\mathrm {NS}}(X)$
, such that the inequalities in (5.3.2) hold, is the intersection of
$\xi \in \operatorname {\mathrm {NS}}(X)$
, such that the inequalities in (5.3.2) hold, is the intersection of
![]() $\operatorname {\mathrm {\mathit {NL}}}(d_0)$
with a finite union of Noether-Lefschetz divisors in
$\operatorname {\mathrm {\mathit {NL}}}(d_0)$
with a finite union of Noether-Lefschetz divisors in
![]() ${\mathscr K}^{il}_e(2n)$
, each of which does not contain
${\mathscr K}^{il}_e(2n)$
, each of which does not contain
![]() $\operatorname {\mathrm {\mathit {NL}}}(d_0)$
. In fact, suppose that the inequalities in (5.3.2) hold. Let D be the (finite) index of
$\operatorname {\mathrm {\mathit {NL}}}(d_0)$
. In fact, suppose that the inequalities in (5.3.2) hold. Let D be the (finite) index of
![]() $\langle h,f\rangle \oplus (\langle h,f\rangle ^{\bot }\cap \operatorname {\mathrm {NS}}(X))$
in
$\langle h,f\rangle \oplus (\langle h,f\rangle ^{\bot }\cap \operatorname {\mathrm {NS}}(X))$
in
![]() $\operatorname {\mathrm {NS}}(X)$
. It is crucial to note that D has an upper bound which only depends on the discriminant of the restrictions of
$\operatorname {\mathrm {NS}}(X)$
. It is crucial to note that D has an upper bound which only depends on the discriminant of the restrictions of
![]() $q_X$
to V (i.e.
$q_X$
to V (i.e.
![]() $-(ild_0)^2$
) and to
$-(ild_0)^2$
) and to
![]() $V^{\bot }$
, and the latter has an upper bound depending only on the discriminant of V and the discriminant of
$V^{\bot }$
, and the latter has an upper bound depending only on the discriminant of V and the discriminant of
![]() $q_X$
(i.e.
$q_X$
(i.e.
![]() $2n-2$
). Then
$2n-2$
). Then
Moreover, we have just proved that
![]() $\xi _2$
is nonzero. Since the restriction of
$\xi _2$
is nonzero. Since the restriction of
![]() $q_X$
to
$q_X$
to
![]() $h^{\bot }\cap \operatorname {\mathrm {NS}}(X)$
is negative definite, we get that
$h^{\bot }\cap \operatorname {\mathrm {NS}}(X)$
is negative definite, we get that
![]() $q(\xi _2)<0$
. We also have
$q(\xi _2)<0$
. We also have
![]() $q(\xi _1)<0$
by the last two inequalities in (5.3.2).
$q(\xi _1)<0$
by the last two inequalities in (5.3.2).
Hence, by the first inequality in (5.3.2), there exists a positive M independent of
![]() $(X,h)$
, such that
$(X,h)$
, such that
![]() $-M\le q(\xi _2)<0$
(here, it is crucial that D has an upper bound which only depends on
$-M\le q(\xi _2)<0$
(here, it is crucial that D has an upper bound which only depends on
![]() $(ild_0)^2$
) and
$(ild_0)^2$
) and
![]() $2n-2$
). Hence, the moduli point of
$2n-2$
). Hence, the moduli point of
![]() $(X,h)$
belongs to the intersection of
$(X,h)$
belongs to the intersection of
![]() $\operatorname {\mathrm {\mathit {NL}}}(d_0)$
with a finite union of Noether-Lefschetz divisors in
$\operatorname {\mathrm {\mathit {NL}}}(d_0)$
with a finite union of Noether-Lefschetz divisors in
![]() ${\mathscr K}^{il}_e(2n)$
, and none of them contains
${\mathscr K}^{il}_e(2n)$
, and none of them contains
![]() $\operatorname {\mathrm {\mathit {NL}}}(d_0)$
because if
$\operatorname {\mathrm {\mathit {NL}}}(d_0)$
because if
![]() $\rho (X)=2$
, then
$\rho (X)=2$
, then
![]() $[(X,h)]$
is not contained in any of these Noether-Lefschetz divisors.
$[(X,h)]$
is not contained in any of these Noether-Lefschetz divisors.
Proposition 5.11. Keep notation as above, and assume that
Let
![]() $[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)$
(the inequality in (5.3.4) implies that the inequality in (5.2.5) holds, and hence, the Noether-Lefschetz divisor
$[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)$
(the inequality in (5.3.4) implies that the inequality in (5.2.5) holds, and hence, the Noether-Lefschetz divisor
![]() $\operatorname {\mathrm {\mathit {NL}}}(d_0)\subset {\mathscr K}^{il}_e(2n)^{\mathrm {good}}$
is defined). If
$\operatorname {\mathrm {\mathit {NL}}}(d_0)\subset {\mathscr K}^{il}_e(2n)^{\mathrm {good}}$
is defined). If
![]() ${\mathscr E}$
is a vector bundle on X, such that the equalities in (1.2.6) hold, then h is
${\mathscr E}$
is a vector bundle on X, such that the equalities in (1.2.6) hold, then h is
![]() $a({\mathscr E})$
-suitable (relative to the associated Lagrangian fibration
$a({\mathscr E})$
-suitable (relative to the associated Lagrangian fibration
![]() $\pi \colon {\mathscr X}\to {\mathbb P}^n$
).
$\pi \colon {\mathscr X}\to {\mathbb P}^n$
).
Proof. If
![]() $\alpha \in H^2(X)$
, we have
$\alpha \in H^2(X)$
, we have
(the equality above can be obtained from the known Hirzebruch-Huybrechts-Riemann-Roch formula for HK manifolds of Type
![]() $K3^{[n]}$
) gives that
$K3^{[n]}$
) gives that
![]() $d({\mathscr E}_X)=r_0^{2n-2}(r_0^2-1)(n+3)/2$
(the definition of
$d({\mathscr E}_X)=r_0^{2n-2}(r_0^2-1)(n+3)/2$
(the definition of
![]() $d({\mathscr E}_X)$
is in [Reference O’GradyO’G22, (1.2.2)]), and hence
$d({\mathscr E}_X)$
is in [Reference O’GradyO’G22, (1.2.2)]), and hence
The inequality in (5.3.4) and Lemma 5.10 give that h is
![]() $a({\mathscr E})$
-suitable.
$a({\mathscr E})$
-suitable.
5.4 Proof of Proposition 5.1
Keep notation and assumptions as above, and assume, in addition, that
![]() $d_0$
is coprime to
$d_0$
is coprime to
![]() $r_0$
and that the inequality in (5.3.4) holds (note that the set of such
$r_0$
and that the inequality in (5.3.4) holds (note that the set of such
![]() $d_0$
is infinite). Let
$d_0$
is infinite). Let
![]() $[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)^*$
, and let
$[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)^*$
, and let
![]() ${\mathscr E}_X$
be a vector bundle on X as in Proposition 5.9. By Proposition 5.11, the polarization h is
${\mathscr E}_X$
be a vector bundle on X as in Proposition 5.9. By Proposition 5.11, the polarization h is
![]() $a({\mathscr E}_X)$
-suitable relative to the Lagrangian fibration
$a({\mathscr E}_X)$
-suitable relative to the Lagrangian fibration
![]() $\pi _X\colon {\mathscr X}\to {\mathbb P}^n$
. By Proposition 5.9, the restriction of
$\pi _X\colon {\mathscr X}\to {\mathbb P}^n$
. By Proposition 5.9, the restriction of
![]() ${\mathscr E}_X$
to a general fibre of
${\mathscr E}_X$
to a general fibre of
![]() $\pi _X\colon {\mathscr X}\to {\mathbb P}^n$
is slope-stable. Since h is
$\pi _X\colon {\mathscr X}\to {\mathbb P}^n$
is slope-stable. Since h is
![]() $a({\mathscr E}_X)$
-suitable, the vector bundle
$a({\mathscr E}_X)$
-suitable, the vector bundle
![]() ${\mathscr E}_X$
is h slope-stable by [Reference O’GradyO’G22, Proposition 3.6]. We have
${\mathscr E}_X$
is h slope-stable by [Reference O’GradyO’G22, Proposition 3.6]. We have
![]() $H^p(X,End^0({\mathscr E}_X))=0$
for all p, and hence,
$H^p(X,End^0({\mathscr E}_X))=0$
for all p, and hence,
![]() ${\mathscr E}_X$
extends (uniquely) to all small deformations of
${\mathscr E}_X$
extends (uniquely) to all small deformations of
![]() $(X,\det {\mathscr E}_X)$
by Remark 3.8. Since
$(X,\det {\mathscr E}_X)$
by Remark 3.8. Since
![]() $c_1({\mathscr E}_X)$
is a multiple of h, we get that
$c_1({\mathscr E}_X)$
is a multiple of h, we get that
![]() ${\mathscr E}_X$
extends to a vector bundle
${\mathscr E}_X$
extends to a vector bundle
![]() ${\mathscr E}'$
on a general deformation
${\mathscr E}'$
on a general deformation
![]() $(X',h')$
of
$(X',h')$
of
![]() $(X,h)$
. By openness of slope stability,
$(X,h)$
. By openness of slope stability,
![]() ${\mathscr E}'$
is slope-stable, and by upper semicontinuity of cohomology dimension,
${\mathscr E}'$
is slope-stable, and by upper semicontinuity of cohomology dimension,
![]() $H^p(X,End^0({\mathscr E}'))=0$
for all p.
$H^p(X,End^0({\mathscr E}'))=0$
for all p.
5.5 Tate-Shafarevich twists
A basic example of Lagrangian fibration is obtained as follows. Let
![]() $(S,h_S)$
be a polarized
$(S,h_S)$
be a polarized
![]() $K3$
surface of genus n. Let
$K3$
surface of genus n. Let
![]() ${\mathscr J}(S)$
be the moduli space of rank
${\mathscr J}(S)$
be the moduli space of rank
![]() $0$
pure
$0$
pure
![]() ${\mathscr O}_S(1)$
semistable sheaves
${\mathscr O}_S(1)$
semistable sheaves
![]() $\xi $
with
$\xi $
with
![]() $\chi (\xi )=1-n$
, that is sheaves with Mukai vector
$\chi (\xi )=1-n$
, that is sheaves with Mukai vector
![]() $(0,h_S,1-n)$
. The generic point of
$(0,h_S,1-n)$
. The generic point of
![]() ${\mathscr J}(S)$
is represented by
${\mathscr J}(S)$
is represented by
![]() $i_{*}{\mathscr L}$
, where
$i_{*}{\mathscr L}$
, where
![]() $i\colon C\hookrightarrow S$
is the inclusion of a smooth
$i\colon C\hookrightarrow S$
is the inclusion of a smooth
![]() $C\in {\mathscr O}_S(1)$
, and
$C\in {\mathscr O}_S(1)$
, and
![]() ${\mathscr L}$
is a line bundle of degree
${\mathscr L}$
is a line bundle of degree
![]() $0$
. Suppose that all divisors in the complete linear system
$0$
. Suppose that all divisors in the complete linear system
![]() $|{\mathscr O}_S(1)|$
are irreducible and reduced. Then every semistable sheaf parametrized by
$|{\mathscr O}_S(1)|$
are irreducible and reduced. Then every semistable sheaf parametrized by
![]() ${\mathscr J}(S)$
is stable, and
${\mathscr J}(S)$
is stable, and
![]() ${\mathscr J}(S)$
is an HK projective variety of Type
${\mathscr J}(S)$
is an HK projective variety of Type
![]() $K3^{[n]}$
. Moreover, the support map
$K3^{[n]}$
. Moreover, the support map
![]() ${\mathscr J}(S)\to |{\mathscr O}_S(1)|\cong {\mathbb P}^n$
is a Lagrangian fibration. Let
${\mathscr J}(S)\to |{\mathscr O}_S(1)|\cong {\mathbb P}^n$
is a Lagrangian fibration. Let
![]() $\operatorname {\mathrm {\mathit {NL}}}(d_0)\subset {\mathscr K}^{il}_e(2n)^{\mathrm {good}}$
be the Noether-Lefschetz divisor of Definition 5.7, and let
$\operatorname {\mathrm {\mathit {NL}}}(d_0)\subset {\mathscr K}^{il}_e(2n)^{\mathrm {good}}$
be the Noether-Lefschetz divisor of Definition 5.7, and let
![]() $[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)$
be a general point. Then the associated Lagrangian fibration
$[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)$
be a general point. Then the associated Lagrangian fibration
![]() $\pi \colon X\to {\mathbb P}^n$
is related to a (general) moduli space
$\pi \colon X\to {\mathbb P}^n$
is related to a (general) moduli space
![]() ${\mathscr J}(S)$
via a Tate-Shafarevich twist. In order to be more precise, we recall a result of Markman. First, if
${\mathscr J}(S)$
via a Tate-Shafarevich twist. In order to be more precise, we recall a result of Markman. First, if
![]() $[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)$
is a general point, then there is an associated polarized
$[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)$
is a general point, then there is an associated polarized
![]() $K3$
surface
$K3$
surface
![]() $(S,D)$
of genus n, and moreover,
$(S,D)$
of genus n, and moreover,
![]() $(S,D)$
is a general such polarized surface (see [Reference MarkmanMar14, Section 4.1]).
$(S,D)$
is a general such polarized surface (see [Reference MarkmanMar14, Section 4.1]).
Proposition 5.12. Keep notation as above, and assume that the inequality in (5.2.5) holds. Let
![]() $[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)$
be a general point, let
$[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)$
be a general point, let
![]() $X\to {\mathbb P}^n$
be the associated Lagrangian fibration and let
$X\to {\mathbb P}^n$
be the associated Lagrangian fibration and let
![]() $(S,D)$
be the associated polarized
$(S,D)$
be the associated polarized
![]() $K3$
surface (which is a general polarized
$K3$
surface (which is a general polarized
![]() $K3$
surface of genus n). Then
$K3$
surface of genus n). Then
![]() $ X\to {\mathbb P}^n$
is isomorphic to a Tate-Shafarevich twist of
$ X\to {\mathbb P}^n$
is isomorphic to a Tate-Shafarevich twist of
![]() ${\mathscr J}(S)\to |D|$
via an identification
${\mathscr J}(S)\to |D|$
via an identification
![]() ${\mathbb P}^n\overset {\sim }{\longrightarrow }|D|$
.
${\mathbb P}^n\overset {\sim }{\longrightarrow }|D|$
.
Proof. Suppose first that
![]() $\rho (X)=2$
. Then, as shown in the proof of Proposition 5.6, the ample cone of X is equal to the positive cone (because of the inequality in (5.2.5)), and hence, every bimeromorphic map
$\rho (X)=2$
. Then, as shown in the proof of Proposition 5.6, the ample cone of X is equal to the positive cone (because of the inequality in (5.2.5)), and hence, every bimeromorphic map
![]() $X\dashrightarrow X'$
, where
$X\dashrightarrow X'$
, where
![]() $X'$
is an
$X'$
is an
![]() $HK$
, is actually an isomorphism. It follows that X is isomorphic to a Tate-Shafarevich twist of
$HK$
, is actually an isomorphism. It follows that X is isomorphic to a Tate-Shafarevich twist of
![]() ${\mathscr J}(S)\to |D|$
by Theorem 7.13 in [Reference MarkmanMar14]. The result follows from this because the locus in
${\mathscr J}(S)\to |D|$
by Theorem 7.13 in [Reference MarkmanMar14]. The result follows from this because the locus in
![]() $\operatorname {\mathrm {\mathit {NL}}}(d_0)$
parametrizing
$\operatorname {\mathrm {\mathit {NL}}}(d_0)$
parametrizing
![]() $(X,h)$
, such that
$(X,h)$
, such that
![]() $\rho (X)=2$
is dense.
$\rho (X)=2$
is dense.
Let
![]() $\operatorname {\mathrm {Pic}}^0(X/{\mathbb P}^n)$
be the relative Picard scheme of the Lagrangian fibration
$\operatorname {\mathrm {Pic}}^0(X/{\mathbb P}^n)$
be the relative Picard scheme of the Lagrangian fibration
![]() $ X\to {\mathbb P}^n$
(notice that all fibres of
$ X\to {\mathbb P}^n$
(notice that all fibres of
![]() $X\to {\mathbb P}^n$
are irreducible by Proposition 5.12). Let
$X\to {\mathbb P}^n$
are irreducible by Proposition 5.12). Let
![]() $U\subset {\mathbb P}^n$
be the open dense set of regular values of
$U\subset {\mathbb P}^n$
be the open dense set of regular values of
![]() $X\to {\mathbb P}^n$
. If
$X\to {\mathbb P}^n$
. If
![]() $t\in U$
, the fibre of
$t\in U$
, the fibre of
![]() $\operatorname {\mathrm {Pic}}^0(X/{\mathbb P}^n)\to {\mathbb P}^n$
over t is an Abelian variety
$\operatorname {\mathrm {Pic}}^0(X/{\mathbb P}^n)\to {\mathbb P}^n$
over t is an Abelian variety
![]() $A_t$
(of dimension n) and the fundamental group
$A_t$
(of dimension n) and the fundamental group
![]() $\pi _1(U,t)$
acts by monodromy on the subgroup
$\pi _1(U,t)$
acts by monodromy on the subgroup
![]() $A_{t,tors}$
of torsion points.
$A_{t,tors}$
of torsion points.
Corollary 5.13. Keep hypotheses and notation as above, and suppose that
![]() $V\subset A_t[r_0^n]$
is a coset (of a subgroup of
$V\subset A_t[r_0^n]$
is a coset (of a subgroup of
![]() $ A_t[r_0^n]$
) of cardinality
$ A_t[r_0^n]$
) of cardinality
![]() $r_0^{2n}$
invariant under the action of monodromy. Then
$r_0^{2n}$
invariant under the action of monodromy. Then
![]() $V= A_t[r_0]$
.
$V= A_t[r_0]$
.
Proof. Let
![]() $(S,D)$
be the polarized
$(S,D)$
be the polarized
![]() $K3$
surface of genus n associated to X following Markman. Let
$K3$
surface of genus n associated to X following Markman. Let
![]() ${\mathscr J}(S)_0\subset {\mathscr J}(S)$
be the open dense subset of smooth points (i.e. smooth points of
${\mathscr J}(S)_0\subset {\mathscr J}(S)$
be the open dense subset of smooth points (i.e. smooth points of
![]() ${\mathscr J}(S)$
with surjective differential) of the map
${\mathscr J}(S)$
with surjective differential) of the map
![]() ${\mathscr J}(S)\to |D|$
. By Proposition 5.12,
${\mathscr J}(S)\to |D|$
. By Proposition 5.12,
![]() $\operatorname {\mathrm {Pic}}^0(X/{\mathbb P}^n)\to {\mathbb P}^n$
is isomorphic to
$\operatorname {\mathrm {Pic}}^0(X/{\mathbb P}^n)\to {\mathbb P}^n$
is isomorphic to
![]() ${\mathscr J}(S)_0\to |D|$
, for a certain identification
${\mathscr J}(S)_0\to |D|$
, for a certain identification
![]() ${\mathbb P}^n\overset {\sim }{\longrightarrow } |D|$
. Under this identification,
${\mathbb P}^n\overset {\sim }{\longrightarrow } |D|$
. Under this identification,
![]() $t\in {\mathbb P}^n$
corresponds to a smooth curve
$t\in {\mathbb P}^n$
corresponds to a smooth curve
![]() $C\in |D|$
, and the corresponding Lagrangian fibre
$C\in |D|$
, and the corresponding Lagrangian fibre
![]() $A_t$
is the Jacobian of C. Hence, we have a natural isomorphism
$A_t$
is the Jacobian of C. Hence, we have a natural isomorphism
and the identification is compatible with the monodromy actions.
First, we prove the result under the assumption that V is a subgroup G. By the structure theorem for finite Abelian groups,
![]() $G\cong {\mathbb Z}/(d_1)\oplus \ldots \oplus {\mathbb Z}/(d_r)$
, where
$G\cong {\mathbb Z}/(d_1)\oplus \ldots \oplus {\mathbb Z}/(d_r)$
, where
![]() $r\le 2n$
(because
$r\le 2n$
(because
![]() $A_t[r_0^n]\cong {\mathbb Z}/(r_0^n)^{\oplus 2n}$
) and
$A_t[r_0^n]\cong {\mathbb Z}/(r_0^n)^{\oplus 2n}$
) and
![]() $d_i| r_0^n$
for all i. The monodromy action on
$d_i| r_0^n$
for all i. The monodromy action on
![]() $H_1(C;{\mathbb Z})$
is transitive on nonzero elements by [Reference Flapan, Macrì, O’Grady and SaccàFMOS22, Proposition 4.4] (if
$H_1(C;{\mathbb Z})$
is transitive on nonzero elements by [Reference Flapan, Macrì, O’Grady and SaccàFMOS22, Proposition 4.4] (if
![]() $n\ge 3$
, if
$n\ge 3$
, if
![]() $n=2$
transitivity is proved by hand). It follows from the isomorphism in (5.5.1) that
$n=2$
transitivity is proved by hand). It follows from the isomorphism in (5.5.1) that
![]() $r=2n$
and
$r=2n$
and
![]() $d_1=\ldots =d_r$
. Thus,
$d_1=\ldots =d_r$
. Thus,
![]() $d_i=r_0$
for all
$d_i=r_0$
for all
![]() $i\in \{1,\ldots ,2n\}$
because
$i\in \{1,\ldots ,2n\}$
because
![]() $|G|=r_0^{2n}$
. This proves the result under the assumption that V is a subgroup. Now let V be a translate of a group G. Then
$|G|=r_0^{2n}$
. This proves the result under the assumption that V is a subgroup. Now let V be a translate of a group G. Then
![]() $G=\{a-b \mid a,b\in V\}$
, and hence, G is also invariant for the monodromy action. Thus,
$G=\{a-b \mid a,b\in V\}$
, and hence, G is also invariant for the monodromy action. Thus,
![]() $G= A_t[r_0]$
by what we have just proved, and the coset V gives a point of the quotient
$G= A_t[r_0]$
by what we have just proved, and the coset V gives a point of the quotient
![]() $A_t[r_0^{2n}]/A_t[r_0^n]\cong A_t[r_0^n]$
which is invariant for the monodromy action. There is a unique invariant element, namely
$A_t[r_0^{2n}]/A_t[r_0^n]\cong A_t[r_0^n]$
which is invariant for the monodromy action. There is a unique invariant element, namely
![]() $0$
, because of the isomorphism in (5.5.1) and the transitivity of the monodromy action on nonzero elements of
$0$
, because of the isomorphism in (5.5.1) and the transitivity of the monodromy action on nonzero elements of
![]() $H_1(C;{\mathbb Z})$
. Hence,
$H_1(C;{\mathbb Z})$
. Hence,
![]() $V=A_t[r_0]$
.
$V=A_t[r_0]$
.
5.6 More properties of
 ${\mathscr E}_X$
for
${\mathscr E}_X$
for
 $[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)^*$
a general point
$[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)^*$
a general point
The main result of the present subsection is the following improved version of Proposition 5.9.
Proposition 5.14. Keep notation as in Section 5.2, and assume that
![]() $d_0$
is coprime to
$d_0$
is coprime to
![]() $r_0$
, and that the inequality in (5.3.4) holds. There exist an open dense subset
$r_0$
, and that the inequality in (5.3.4) holds. There exist an open dense subset
![]() $\operatorname {\mathrm {\mathit {NL}}}(d_0)^{**}\subset \operatorname {\mathrm {\mathit {NL}}}(d_0)^*$
, and for each
$\operatorname {\mathrm {\mathit {NL}}}(d_0)^{**}\subset \operatorname {\mathrm {\mathit {NL}}}(d_0)^*$
, and for each
![]() $[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)^{**}$
, an h slope-stable vector bundle
$[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)^{**}$
, an h slope-stable vector bundle
![]() ${\mathscr E}_X$
on X, such that the following hold:
${\mathscr E}_X$
on X, such that the following hold:
-
(1) The equalities in (5.2.8) hold.
-
(2)
 $H^p(X,End^0({\mathscr E}_X))=0$
for all p.
$H^p(X,End^0({\mathscr E}_X))=0$
for all p. -
(3) There exists an open
 ${\mathscr U}_X\subset {\mathbb P}^n$
, whose complement has codimension at least
${\mathscr U}_X\subset {\mathbb P}^n$
, whose complement has codimension at least
 $2$
, such that for every
$2$
, such that for every
 $t\in {\mathscr U}_X$
, the restriction of
$t\in {\mathscr U}_X$
, the restriction of
 ${\mathscr E}_X$
to the fibre
${\mathscr E}_X$
to the fibre
 $X_t$
over t of the Lagrangian fibration
$X_t$
over t of the Lagrangian fibration
 $X\to {\mathbb P}^n$
is slope-stable for the restriction of h to
$X\to {\mathbb P}^n$
is slope-stable for the restriction of h to
 $X_t$
.
$X_t$
.
Before proving Proposition 5.14, we need to go through a couple of results. The result below for Abelian surfaces is [Reference O’GradyO’G22, Proposition 4.4]. Part of the proof below is literally taken from the proof of Proposition 4.4 in [Reference O’GradyO’G22], but there is a crucial extra input (not needed in dimension
![]() $2$
), namely [Reference SimpsonSim92, Theorem 2].
$2$
), namely [Reference SimpsonSim92, Theorem 2].
Proposition 5.15. Let
![]() $(A,\theta )$
be a principally polarized Abelian variety of dimension n, and let
$(A,\theta )$
be a principally polarized Abelian variety of dimension n, and let
![]() ${\mathscr F}$
be a slope semistable vector bundle on A, such that
${\mathscr F}$
be a slope semistable vector bundle on A, such that
![]() $c_1({\mathscr F})$
is a multiple of
$c_1({\mathscr F})$
is a multiple of
![]() $\theta $
and
$\theta $
and
![]() $\Delta ({\mathscr F})\cdot \theta ^{n-2}=0$
. Then there exist integers
$\Delta ({\mathscr F})\cdot \theta ^{n-2}=0$
. Then there exist integers
![]() $r_0,m,b_0$
with
$r_0,m,b_0$
with
![]() $r_0,m\in {\mathbb N}_{+}$
and
$r_0,m\in {\mathbb N}_{+}$
and
![]() $\gcd \{r_0,b_0\}=1$
, such that
$\gcd \{r_0,b_0\}=1$
, such that
If
![]() ${\mathscr F}$
is not
${\mathscr F}$
is not
![]() $\theta $
slope-stable, then we may assume that
$\theta $
slope-stable, then we may assume that
![]() $m>1$
.
$m>1$
.
Proof. If
![]() ${\mathscr F}$
is slope-stable, then it is simple semihomogeneous by [Reference O’GradyO’G22, Proposition A.2], and hence, we may write (5.6.1) with
${\mathscr F}$
is slope-stable, then it is simple semihomogeneous by [Reference O’GradyO’G22, Proposition A.2], and hence, we may write (5.6.1) with
![]() $m=1$
by [Reference O’GradyO’G22, Proposition A.3].
$m=1$
by [Reference O’GradyO’G22, Proposition A.3].
Suppose that
![]() ${\mathscr F}$
is strictly
${\mathscr F}$
is strictly
![]() $\theta $
slope-semistable, that is there exists a destabilizing exact sequence of torsion-free sheaves
$\theta $
slope-semistable, that is there exists a destabilizing exact sequence of torsion-free sheaves
with
![]() ${\mathscr G}$
slope-stable. Arguing as in the proof of [Reference O’GradyO’G22, Proposition 4.4], one proves that
${\mathscr G}$
slope-stable. Arguing as in the proof of [Reference O’GradyO’G22, Proposition 4.4], one proves that
Let us prove that
![]() ${\mathscr G}$
and
${\mathscr G}$
and
![]() ${\mathscr H}$
are locally free. Let
${\mathscr H}$
are locally free. Let
![]() $r:=r({\mathscr F})$
, and let
$r:=r({\mathscr F})$
, and let
![]() $m_r\colon A\to A$
be the multiplication by r map. Let
$m_r\colon A\to A$
be the multiplication by r map. Let
![]() ${\mathscr L}$
be a line bundle on A, such that
${\mathscr L}$
be a line bundle on A, such that
![]() $c_1({\mathscr L})=-ra\theta $
, and let
$c_1({\mathscr L})=-ra\theta $
, and let
![]() ${\mathscr E}:=m_r^{*}({\mathscr F})\otimes {\mathscr L}$
. Then
${\mathscr E}:=m_r^{*}({\mathscr F})\otimes {\mathscr L}$
. Then
![]() ${\mathscr E}$
is slope-semistable (because
${\mathscr E}$
is slope-semistable (because
![]() ${\mathscr F}$
is) and
${\mathscr F}$
is) and
By [Reference SimpsonSim92, Theorem 2], it follows that every quotient of the (slope) Jordan-Hölder filtration of
![]() ${\mathscr E}$
is locally free. Since
${\mathscr E}$
is locally free. Since
![]() $m_r^{*}({\mathscr G})\otimes {\mathscr L}$
is a polystable subsheaf of
$m_r^{*}({\mathscr G})\otimes {\mathscr L}$
is a polystable subsheaf of
![]() ${\mathscr E}$
, we get that it is locally free. Thus,
${\mathscr E}$
, we get that it is locally free. Thus,
![]() $m_r^{*}({\mathscr G})$
is locally free, and hence, also
$m_r^{*}({\mathscr G})$
is locally free, and hence, also
![]() ${\mathscr G}$
is locally free. By the equalities in (5.6.3), we may iterate this argument to show that also
${\mathscr G}$
is locally free. By the equalities in (5.6.3), we may iterate this argument to show that also
![]() ${\mathscr H}$
is locally free.
${\mathscr H}$
is locally free.
It follows that if
is a (slope) Jordan-Hölder filtration of
![]() ${\mathscr F}$
, then each quotient
${\mathscr F}$
, then each quotient
![]() ${\mathscr Q}_i:={\mathscr G}_i/{\mathscr G}_{i-1}$
is a slope-stable locally free sheaf with
${\mathscr Q}_i:={\mathscr G}_i/{\mathscr G}_{i-1}$
is a slope-stable locally free sheaf with
 $$ \begin{align} \frac{c_1({\mathscr Q}_i)}{\operatorname{\mathrm{rk}}({\mathscr Q}_i)}=\frac{c_1({\mathscr F})}{r({\mathscr F})},\quad \Delta({\mathscr Q}_i)\cdot \theta^{n-2}=0. \end{align} $$
$$ \begin{align} \frac{c_1({\mathscr Q}_i)}{\operatorname{\mathrm{rk}}({\mathscr Q}_i)}=\frac{c_1({\mathscr F})}{r({\mathscr F})},\quad \Delta({\mathscr Q}_i)\cdot \theta^{n-2}=0. \end{align} $$
Hence, each
![]() ${\mathscr Q}_i$
is simple semihomogeneous by [Reference O’GradyO’G22, Proposition A.2], and therefore, by [Reference O’GradyO’G22, Proposition A.3] (see also [Reference MukaiMuk78, Remark 7.13]), there exist coprime integers
${\mathscr Q}_i$
is simple semihomogeneous by [Reference O’GradyO’G22, Proposition A.2], and therefore, by [Reference O’GradyO’G22, Proposition A.3] (see also [Reference MukaiMuk78, Remark 7.13]), there exist coprime integers
![]() $r_i,b_i$
, with
$r_i,b_i$
, with
![]() $r_i>0$
, such that
$r_i>0$
, such that
![]() $r({\mathscr Q}_i)=r_i^n$
and
$r({\mathscr Q}_i)=r_i^n$
and
![]() $c_1({\mathscr Q}_i)=r_i^{n-1}b_i\theta $
. Let
$c_1({\mathscr Q}_i)=r_i^{n-1}b_i\theta $
. Let
![]() $i,j\in \{1,\ldots ,m\}$
; since the slopes of
$i,j\in \{1,\ldots ,m\}$
; since the slopes of
![]() ${\mathscr Q}_i$
and
${\mathscr Q}_i$
and
![]() ${\mathscr Q}_j$
are equal, we get that
${\mathscr Q}_j$
are equal, we get that
![]() $b_i r_j=b_j r_i$
. It follows that
$b_i r_j=b_j r_i$
. It follows that
![]() $r_i=r_j$
and
$r_i=r_j$
and
![]() $b_i=b_j$
because
$b_i=b_j$
because
![]() $\gcd \{r_i,b_i\}=\gcd \{r_j,b_j\}=1$
. Thus,
$\gcd \{r_i,b_i\}=\gcd \{r_j,b_j\}=1$
. Thus,
![]() $r({\mathscr F})=m r_0^n$
and
$r({\mathscr F})=m r_0^n$
and
![]() $c_1({\mathscr F})=m r^{n-1}_0 b_0\theta $
, where
$c_1({\mathscr F})=m r^{n-1}_0 b_0\theta $
, where
![]() $r_0=r_i$
and
$r_0=r_i$
and
![]() $b_0=b_i$
for all
$b_0=b_i$
for all
![]() $i\in \{1,\ldots ,m\}$
. We have
$i\in \{1,\ldots ,m\}$
. We have
![]() $m\ge 2$
because we assumed that
$m\ge 2$
because we assumed that
![]() ${\mathscr F}$
is strictly slope-semistable.
${\mathscr F}$
is strictly slope-semistable.
Corollary 5.16. Let
![]() $(A,\theta )$
be a principally polarized Abelian variety of dimension n, and let
$(A,\theta )$
be a principally polarized Abelian variety of dimension n, and let
![]() ${\mathscr F}$
be a
${\mathscr F}$
be a
![]() $\theta $
slope-semistable vector bundle on A, such that
$\theta $
slope-semistable vector bundle on A, such that
![]() $\Delta ({\mathscr F})\cdot \theta ^{n-2}=0$
. If
$\Delta ({\mathscr F})\cdot \theta ^{n-2}=0$
. If
![]() $r({\mathscr F})=r_0^n$
and
$r({\mathscr F})=r_0^n$
and
![]() $c_1({\mathscr F})=r_0^{n-1} b_0 \theta $
, where
$c_1({\mathscr F})=r_0^{n-1} b_0 \theta $
, where
![]() $r_0, b_0$
are coprime integers, then
$r_0, b_0$
are coprime integers, then
![]() ${\mathscr F}$
is
${\mathscr F}$
is
![]() $\theta $
slope-stable.
$\theta $
slope-stable.
Proof. By contradiction, suppose that
![]() ${\mathscr F}$
is not
${\mathscr F}$
is not
![]() $\theta $
slope-stable. By Proposition 5.15, we may write
$\theta $
slope-stable. By Proposition 5.15, we may write
![]() $r({\mathscr F})=s_0^n m$
,
$r({\mathscr F})=s_0^n m$
,
![]() $c_1({\mathscr F})=s_0^{n-1} c_0 m\theta $
, where
$c_1({\mathscr F})=s_0^{n-1} c_0 m\theta $
, where
![]() $s_0,m,c_0$
are integers (with
$s_0,m,c_0$
are integers (with
![]() $s_0,m>0$
),
$s_0,m>0$
),
![]() $s_0,c_0$
are coprime and
$s_0,c_0$
are coprime and
![]() $m>1$
. It follows that
$m>1$
. It follows that
![]() $s_0 b_0=c_0 r_0$
. Since
$s_0 b_0=c_0 r_0$
. Since
![]() $\gcd \{r_0,b_0\}=1$
and
$\gcd \{r_0,b_0\}=1$
and
![]() $\gcd \{s_0,c_0\}=1$
, we get that
$\gcd \{s_0,c_0\}=1$
, we get that
![]() $r_0=s_0$
, and hence,
$r_0=s_0$
, and hence,
![]() $m=1$
. This is a contradiction.
$m=1$
. This is a contradiction.
Proof of Proposition 5.14.
Let
![]() $\varphi \colon {\mathscr X}\to B$
be as in Definition 5.4. Recall that
$\varphi \colon {\mathscr X}\to B$
be as in Definition 5.4. Recall that
![]() $X_0=\varphi ^{-1}(0)\cong S^{[n]}$
, where S is an elliptic
$X_0=\varphi ^{-1}(0)\cong S^{[n]}$
, where S is an elliptic
![]() $K3$
surface as in Claim 4.3. Let
$K3$
surface as in Claim 4.3. Let
![]() ${\mathscr E}_0:={\mathscr F}[n]^{+}$
be the vector bundle on
${\mathscr E}_0:={\mathscr F}[n]^{+}$
be the vector bundle on
![]() $X_0$
of Claim 4.3. If B is small enough, the vector bundle
$X_0$
of Claim 4.3. If B is small enough, the vector bundle
![]() ${\mathscr E}_0$
on
${\mathscr E}_0$
on
![]() $X_0$
deforms uniquely to a vector bundle
$X_0$
deforms uniquely to a vector bundle
![]() ${\mathscr E}_b$
on
${\mathscr E}_b$
on
![]() $X_b$
, hence, we get a vector bundle
$X_b$
, hence, we get a vector bundle
![]() ${\mathscr E}_X$
on X for
${\mathscr E}_X$
on X for
![]() $[(X,h)]$
in a dense open subset
$[(X,h)]$
in a dense open subset
![]() ${\mathscr U}\subset \operatorname {\mathrm {\mathit {NL}}}(d_0)$
. Moreover,
${\mathscr U}\subset \operatorname {\mathrm {\mathit {NL}}}(d_0)$
. Moreover,
![]() ${\mathscr E}_X$
is h slope stable and Items (1) and (2) of Proposition 5.14 hold (see the proof of Proposition 5.1). For
${\mathscr E}_X$
is h slope stable and Items (1) and (2) of Proposition 5.14 hold (see the proof of Proposition 5.1). For
![]() $[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)^*$
, where
$[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)^*$
, where
![]() $\operatorname {\mathrm {\mathit {NL}}}(d_0)^*\subset {\mathscr U}$
is an open dense subset, the restriction of
$\operatorname {\mathrm {\mathit {NL}}}(d_0)^*\subset {\mathscr U}$
is an open dense subset, the restriction of
![]() ${\mathscr E}_X$
to a general smooth fibre of the Lagrangian fibration
${\mathscr E}_X$
to a general smooth fibre of the Lagrangian fibration
![]() $X\to {\mathbb P}^n$
is slope-stable (see Proposition 5.1).
$X\to {\mathbb P}^n$
is slope-stable (see Proposition 5.1).
Let
![]() ${\mathscr V}_0\subset {\mathbb P}^n$
be the set of t, such that the restriction of
${\mathscr V}_0\subset {\mathbb P}^n$
be the set of t, such that the restriction of
![]() ${\mathscr E}_0$
to the fibre over t of the Lagrangian fibration
${\mathscr E}_0$
to the fibre over t of the Lagrangian fibration
![]() $S^{[n]}\to {\mathbb P}^n$
is simple. By Item (b) of Proposition 4.6,
$S^{[n]}\to {\mathbb P}^n$
is simple. By Item (b) of Proposition 4.6,
![]() ${\mathscr V}_0$
is an open subset whose complement has codimension (in
${\mathscr V}_0$
is an open subset whose complement has codimension (in
![]() ${\mathbb P}^n$
) at least
${\mathbb P}^n$
) at least
![]() $2$
. It follows that there exists an open dense subset
$2$
. It follows that there exists an open dense subset
![]() $\operatorname {\mathrm {\mathit {NL}}}(d_0)^*_s\subset \operatorname {\mathrm {\mathit {NL}}}(d_0)^*$
with the following property: if
$\operatorname {\mathrm {\mathit {NL}}}(d_0)^*_s\subset \operatorname {\mathrm {\mathit {NL}}}(d_0)^*$
with the following property: if
![]() $[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)^*_s$
, the subset
$[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)^*_s$
, the subset
![]() ${\mathscr V}_X\subset {\mathbb P}^n$
has parametrizing fibres
${\mathscr V}_X\subset {\mathbb P}^n$
has parametrizing fibres
![]() $X_t$
of the Lagrangian fibration
$X_t$
of the Lagrangian fibration
![]() $X\to {\mathbb P}^n$
, such that the restriction of
$X\to {\mathbb P}^n$
, such that the restriction of
![]() ${\mathscr E}_X$
to
${\mathscr E}_X$
to
![]() $X_t$
is simple and has complement of codimension (in
$X_t$
is simple and has complement of codimension (in
![]() ${\mathbb P}^n$
) at least
${\mathbb P}^n$
) at least
![]() $2$
.
$2$
.
Let
![]() $[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)^*_s$
. We claim that if
$[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)^*_s$
. We claim that if
![]() $t\in {\mathscr V}_X$
and
$t\in {\mathscr V}_X$
and
![]() $X_t$
is smooth, then the restriction
$X_t$
is smooth, then the restriction
![]() ${\mathscr E}_{X|X_t}$
is slope-stable. In order to prove this, we start by noting that for any Lagrangian (scheme-theoretic) fibre
${\mathscr E}_{X|X_t}$
is slope-stable. In order to prove this, we start by noting that for any Lagrangian (scheme-theoretic) fibre
![]() $X_t$
, we have
$X_t$
, we have
 $$ \begin{align} \int_{[X_t]}\Delta({\mathscr E}_{X|X_t})\cdot \left(h_{|X_t}\right)^{n-2}=0. \end{align} $$
$$ \begin{align} \int_{[X_t]}\Delta({\mathscr E}_{X|X_t})\cdot \left(h_{|X_t}\right)^{n-2}=0. \end{align} $$
In fact, the above equality is an easy consequence of the modularity of
![]() ${\mathscr E}_X$
(see [Reference O’GradyO’G22, Lemma 2.5]). Let
${\mathscr E}_X$
(see [Reference O’GradyO’G22, Lemma 2.5]). Let
![]() $X_t$
be a general smooth Lagrangian fibre. By Proposition 5.9, the restriction of
$X_t$
be a general smooth Lagrangian fibre. By Proposition 5.9, the restriction of
![]() ${\mathscr E}_X$
to
${\mathscr E}_X$
to
![]() $X_t$
is slope-stable, hence,
$X_t$
is slope-stable, hence,
![]() ${\mathscr E}_{X|X_t}$
is semihomogeneous because of the equality in (5.6.5) (see [Reference O’GradyO’G22, Lemma 2.5]). It follows that if
${\mathscr E}_{X|X_t}$
is semihomogeneous because of the equality in (5.6.5) (see [Reference O’GradyO’G22, Lemma 2.5]). It follows that if
![]() $t_0\in {\mathscr V}_X$
and
$t_0\in {\mathscr V}_X$
and
![]() $X_{t_0}$
is smooth, then
$X_{t_0}$
is smooth, then
![]() ${\mathscr E}_{X|X_{t_0}}$
is (simple) semihomogeneous. To prove this, we introduce some notation. For
${\mathscr E}_{X|X_{t_0}}$
is (simple) semihomogeneous. To prove this, we introduce some notation. For
![]() $t\in {\mathbb P}^n$
, such that
$t\in {\mathbb P}^n$
, such that
![]() $X_t$
is smooth, let
$X_t$
is smooth, let
 $$ \begin{align*} \Phi^0({\mathscr E}_{X|X_t}) & := \{(x,[\xi])\in X_t\times \widehat{X}_t \mid \exists\ T_x^{*}({\mathscr E}_{X|X_t})\overset{\sim}{\longrightarrow} ({\mathscr E}_{X|X_t})\otimes\xi\}, \\ \Psi^0({\mathscr E}_{X|X_t}) & := \{(x,[\xi])\in X_t\times \widehat{X}_t \mid \operatorname{\mathrm{Hom}}(T_x^{*}({\mathscr E}_{X|X_t}),({\mathscr E}_{X|X_t})\otimes\xi)\not=0\}, \end{align*} $$
$$ \begin{align*} \Phi^0({\mathscr E}_{X|X_t}) & := \{(x,[\xi])\in X_t\times \widehat{X}_t \mid \exists\ T_x^{*}({\mathscr E}_{X|X_t})\overset{\sim}{\longrightarrow} ({\mathscr E}_{X|X_t})\otimes\xi\}, \\ \Psi^0({\mathscr E}_{X|X_t}) & := \{(x,[\xi])\in X_t\times \widehat{X}_t \mid \operatorname{\mathrm{Hom}}(T_x^{*}({\mathscr E}_{X|X_t}),({\mathscr E}_{X|X_t})\otimes\xi)\not=0\}, \end{align*} $$
where
![]() $T_x\colon X_t\to X_t$
is translated by
$T_x\colon X_t\to X_t$
is translated by
![]() $x\in X_t$
(locally, in t, we may assume that
$x\in X_t$
(locally, in t, we may assume that
![]() $X_t$
is a family of Abelian varieties rather than torsors over Abelian varieties). Recall that
$X_t$
is a family of Abelian varieties rather than torsors over Abelian varieties). Recall that
![]() ${\mathscr E}_{X|X_t}$
is semihomogeneous if and only if
${\mathscr E}_{X|X_t}$
is semihomogeneous if and only if
![]() $\Phi ^0({\mathscr E}_{X|X_t})$
has dimension at least n, and that if that is the case, then the group
$\Phi ^0({\mathscr E}_{X|X_t})$
has dimension at least n, and that if that is the case, then the group
![]() $\Phi ^0({\mathscr E}_{X|X_t})$
has pure dimension n. Let
$\Phi ^0({\mathscr E}_{X|X_t})$
has pure dimension n. Let
![]() $X_t$
be a general smooth Lagrangian fibre, so that
$X_t$
be a general smooth Lagrangian fibre, so that
![]() ${\mathscr E}_{X|X_t}$
is slope-stable and semihomogeneous. Then
${\mathscr E}_{X|X_t}$
is slope-stable and semihomogeneous. Then
![]() $\Phi ^0({\mathscr E}_{X|X_t})$
has pure dimension n, and moreover, (by slope stability)
$\Phi ^0({\mathscr E}_{X|X_t})$
has pure dimension n, and moreover, (by slope stability)
![]() $\Phi ^0({\mathscr E}_{X|X_t})=\Psi ^0({\mathscr E}_{X|X_t})$
. By upper semicontinuity of cohomology dimension, it follows that every irreducible component of
$\Phi ^0({\mathscr E}_{X|X_t})=\Psi ^0({\mathscr E}_{X|X_t})$
. By upper semicontinuity of cohomology dimension, it follows that every irreducible component of
![]() $\Psi ^0({\mathscr E}_{X|X_{t_0}})$
has dimension at least n. Now,
$\Psi ^0({\mathscr E}_{X|X_{t_0}})$
has dimension at least n. Now,
![]() $(0,[{\mathscr O}_{X_{t_0}}])\in \Psi ^0({\mathscr E}_{X|X_{t_0}})$
and, since
$(0,[{\mathscr O}_{X_{t_0}}])\in \Psi ^0({\mathscr E}_{X|X_{t_0}})$
and, since
![]() ${\mathscr E}_{X|X_{t_0}}$
is simple, every nonzero homomorphism
${\mathscr E}_{X|X_{t_0}}$
is simple, every nonzero homomorphism
![]() ${\mathscr E}_{X|X_{t_0}}\to {\mathscr E}_{X|X_{t_0}}$
is an isomorphism. It follows that
${\mathscr E}_{X|X_{t_0}}\to {\mathscr E}_{X|X_{t_0}}$
is an isomorphism. It follows that
![]() $\Phi ^0({\mathscr E}_{X|X_{t_0}})$
has dimension at least n, and hence,
$\Phi ^0({\mathscr E}_{X|X_{t_0}})$
has dimension at least n, and hence,
![]() ${\mathscr E}_{X|X_{t_0}}$
is semihomogeneous. By [Reference MukaiMuk78, Proposition 6.13], we get that
${\mathscr E}_{X|X_{t_0}}$
is semihomogeneous. By [Reference MukaiMuk78, Proposition 6.13], we get that
![]() ${\mathscr E}_{X|X_{t_0}}$
is slope-semistable (actually, it is Gieseker stable, see Proposition 6.16 loc.cit.). Lastly, we prove that
${\mathscr E}_{X|X_{t_0}}$
is slope-semistable (actually, it is Gieseker stable, see Proposition 6.16 loc.cit.). Lastly, we prove that
![]() ${\mathscr E}_{X|X_{t_0}}$
is slope-stable. Let
${\mathscr E}_{X|X_{t_0}}$
is slope-stable. Let
![]() $\theta _{t_0}$
be the principal polarization of
$\theta _{t_0}$
be the principal polarization of
![]() $X_{t_0}$
(see Remark 4.9). Since
$X_{t_0}$
(see Remark 4.9). Since
![]() $q_{X_{t_0}}(h,f)=ild_0$
(see (5.2.7)), we have
$q_{X_{t_0}}(h,f)=ild_0$
(see (5.2.7)), we have
![]() $h_{|X_{t_0}}=ild_0\theta _{t_0}$
. Hence
$h_{|X_{t_0}}=ild_0\theta _{t_0}$
. Hence
By hypothesis g, l and
![]() $d_0$
are coprime to
$d_0$
are coprime to
![]() $r_0$
. By Corollary 5.16, we get that
$r_0$
. By Corollary 5.16, we get that
![]() ${\mathscr E}_{X|X_{t_0}}$
is slope-stable.
${\mathscr E}_{X|X_{t_0}}$
is slope-stable.
We finish the proof by showing that if
![]() $[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)^*_s$
is general, then the restriction of
$[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)^*_s$
is general, then the restriction of
![]() ${\mathscr E}_X$
to a general singular Lagrangian fibre is slope-stable. Since
${\mathscr E}_X$
to a general singular Lagrangian fibre is slope-stable. Since
![]() $[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)^*_s$
is general, the discriminant divisor
$[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)^*_s$
is general, the discriminant divisor
![]() ${\mathscr D}_X\subset {\mathbb P}^n$
parametrizing singular Lagrangian fibres of
${\mathscr D}_X\subset {\mathbb P}^n$
parametrizing singular Lagrangian fibres of
![]() $X\to {\mathbb P}^n$
is the dual of an embedded
$X\to {\mathbb P}^n$
is the dual of an embedded
![]() $K3$
surface
$K3$
surface
![]() $S\subset ({\mathbb P}^n)^{\vee }$
. In fact, this holds by Proposition 5.12. Hence,
$S\subset ({\mathbb P}^n)^{\vee }$
. In fact, this holds by Proposition 5.12. Hence,
![]() ${\mathscr D}_X$
is an irreducible divisor. Thus, it suffices to prove that there exist
${\mathscr D}_X$
is an irreducible divisor. Thus, it suffices to prove that there exist
![]() $t\in {\mathscr D}_X$
, such that
$t\in {\mathscr D}_X$
, such that
![]() ${\mathscr E}_{X|X_t}$
is slope-stable (for the restriction of h to
${\mathscr E}_{X|X_t}$
is slope-stable (for the restriction of h to
![]() $X_t$
). This follows from Remark 4.8 and openness of slope stability.
$X_t$
). This follows from Remark 4.8 and openness of slope stability.
5.7 Proof of Proposition 5.2
The key result is the following.
Proposition 5.17. Keep notation as in Section 5.2. Assume, in addition, that
![]() $d_0$
is coprime to
$d_0$
is coprime to
![]() $r_0$
, and that the inequality in (5.3.4) holds. Let
$r_0$
, and that the inequality in (5.3.4) holds. Let
![]() $[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)^{**}$
be a general point. Then (up to isomorphism) there exists one and only one h slope-stable vector bundle
$[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)^{**}$
be a general point. Then (up to isomorphism) there exists one and only one h slope-stable vector bundle
![]() ${\mathscr E}$
on X, such that the equalities in (1.2.6) hold.
${\mathscr E}$
on X, such that the equalities in (1.2.6) hold.
Proof. Let
![]() ${\mathscr E}_X$
be a vector bundle on X as in Proposition 5.14, and let
${\mathscr E}_X$
be a vector bundle on X as in Proposition 5.14, and let
![]() ${\mathscr E}$
be an h slope-stable vector bundle on X, such that the equalities in (1.2.6) hold. We prove that
${\mathscr E}$
be an h slope-stable vector bundle on X, such that the equalities in (1.2.6) hold. We prove that
![]() ${\mathscr E}_X$
and
${\mathscr E}_X$
and
![]() ${\mathscr E}$
are isomorphic.
${\mathscr E}$
are isomorphic.
Let
![]() $\pi \colon X\to {\mathbb P}^n$
be the associated Lagrangian fibration. By Proposition 5.11, the polarization h is
$\pi \colon X\to {\mathbb P}^n$
be the associated Lagrangian fibration. By Proposition 5.11, the polarization h is
![]() $a({\mathscr E})$
-suitable, and hence, the restriction of
$a({\mathscr E})$
-suitable, and hence, the restriction of
![]() ${\mathscr E}$
to a general Lagrangian fibre is slope-semistable. We claim that if
${\mathscr E}$
to a general Lagrangian fibre is slope-semistable. We claim that if
![]() $X_t$
is a smooth Lagrangian fibre and
$X_t$
is a smooth Lagrangian fibre and
![]() ${\mathscr E}_{|X_{t}}$
is slope-semistable, then it is actually slope-stable. In fact, this follows from Corollary 5.16 — the computations showing that the hypotheses of Corollary 5.16 are satisfied have already been done (see (5.6.6)). The upshot is that there exists a dense open subset
${\mathscr E}_{|X_{t}}$
is slope-semistable, then it is actually slope-stable. In fact, this follows from Corollary 5.16 — the computations showing that the hypotheses of Corollary 5.16 are satisfied have already been done (see (5.6.6)). The upshot is that there exists a dense open subset
![]() ${\mathscr U}_X^0\subset {\mathbb P}^n$
, contained in the set of regular values of the Lagrangian fibration, with the property that for all
${\mathscr U}_X^0\subset {\mathbb P}^n$
, contained in the set of regular values of the Lagrangian fibration, with the property that for all
![]() $t\in {\mathscr U}_X^0$
, the restrictions
$t\in {\mathscr U}_X^0$
, the restrictions
![]() ${\mathscr E}_{X|X_t}$
and
${\mathscr E}_{X|X_t}$
and
![]() ${\mathscr E}_{|X_t}$
are simple semihomogeneous vector bundles (since they are slope-stable vector bundles and
${\mathscr E}_{|X_t}$
are simple semihomogeneous vector bundles (since they are slope-stable vector bundles and
![]() $\Delta ({\mathscr E}_{X|X_t})\cdot \theta _t^{n-2}=\Delta ({\mathscr E}_{|X_t})\cdot \theta _t^{n-2}=0$
, they are semihomogeneous by [Reference O’GradyO’G22, Proposition A.2]).
$\Delta ({\mathscr E}_{X|X_t})\cdot \theta _t^{n-2}=\Delta ({\mathscr E}_{|X_t})\cdot \theta _t^{n-2}=0$
, they are semihomogeneous by [Reference O’GradyO’G22, Proposition A.2]).
We claim that if
![]() $t\in {\mathscr U}_X^0$
, then
$t\in {\mathscr U}_X^0$
, then
![]() ${\mathscr E}_{X|X_t}$
and
${\mathscr E}_{X|X_t}$
and
![]() ${\mathscr E}_{|X_t}$
are isomorphic. First, note that, since they are simple semihomogenous vector bundles with same rank and
${\mathscr E}_{|X_t}$
are isomorphic. First, note that, since they are simple semihomogenous vector bundles with same rank and
![]() $c_1$
, the set
$c_1$
, the set
is not empty by [Reference MukaiMuk78, Theorem 7.11], and it has cardinality
![]() $r_0^{2n}$
by Proposition 7.1 op. cit. Note that
$r_0^{2n}$
by Proposition 7.1 op. cit. Note that
![]() $V_t\subset X_t[r_0^{n}]$
because
$V_t\subset X_t[r_0^{n}]$
because
![]() ${\mathscr E}_{X|X_t}$
and
${\mathscr E}_{X|X_t}$
and
![]() ${\mathscr E}_{|X_t}$
have rank
${\mathscr E}_{|X_t}$
have rank
![]() $r_0^n$
and isomorphic determinants. Next, we claim that
$r_0^n$
and isomorphic determinants. Next, we claim that
![]() $V_t$
is invariant under the monodromy action of
$V_t$
is invariant under the monodromy action of
![]() $\pi _1({\mathscr U}_X^0,t)$
. In fact, let
$\pi _1({\mathscr U}_X^0,t)$
. In fact, let
 $$ \begin{align} {\mathscr V}:=\bigcup\limits_{t\in{\mathscr U}_X^0}V_t. \end{align} $$
$$ \begin{align} {\mathscr V}:=\bigcup\limits_{t\in{\mathscr U}_X^0}V_t. \end{align} $$
We show that the forgetful map
is a topological covering. Let
![]() $t_1\in {\mathscr U}_X^0$
, and let
$t_1\in {\mathscr U}_X^0$
, and let
![]() $\xi _{t_1}\in V_{t_1}$
. Let
$\xi _{t_1}\in V_{t_1}$
. Let
![]() $B\subset {\mathscr U}_X^0$
be an open (in the classical topology) neighbourhood of
$B\subset {\mathscr U}_X^0$
be an open (in the classical topology) neighbourhood of
![]() $t_1$
which is contractible. For each
$t_1$
which is contractible. For each
![]() $t\in B$
, let
$t\in B$
, let
![]() $\xi _t\subset X_t[r_0^{n}]$
be obtained from
$\xi _t\subset X_t[r_0^{n}]$
be obtained from
![]() $\xi _{t_1}$
by parallel transport. We claim that
$\xi _{t_1}$
by parallel transport. We claim that
In fact, the traceless endomorphism bundles of the right and left sides of (5.7.3) have vanishing cohomologies (see Theorem 5.8 in [Reference MukaiMuk78]). Since their determinants remain of type
![]() $(1,1)$
on
$(1,1)$
on
![]() $X_t$
for all
$X_t$
for all
![]() $t\in B$
(actually, for all
$t\in B$
(actually, for all
![]() $t\in {\mathscr U}_X^0$
), it follows that each of them extends uniquely to all
$t\in {\mathscr U}_X^0$
), it follows that each of them extends uniquely to all
![]() $X_{t'}$
for
$X_{t'}$
for
![]() $t'\in B$
close enough to t. Since they are isomorphic for
$t'\in B$
close enough to t. Since they are isomorphic for
![]() $t=t_1$
, we get that they are isomorphic for all
$t=t_1$
, we get that they are isomorphic for all
![]() $t\in B$
. This shows that the map in (5.7.2) is a topological covering. The proof shows also that monodromy takes
$t\in B$
. This shows that the map in (5.7.2) is a topological covering. The proof shows also that monodromy takes
![]() $V_t$
to itself.
$V_t$
to itself.
Since
![]() $V_t$
is invariant under the monodromy action of
$V_t$
is invariant under the monodromy action of
![]() $\pi _1({\mathscr U}_X^0,t)$
, it follows from Corollary 5.13 that
$\pi _1({\mathscr U}_X^0,t)$
, it follows from Corollary 5.13 that
![]() $V_t=A[r_0]$
. Thus,
$V_t=A[r_0]$
. Thus,
![]() $0\in V_t$
, and therefore,
$0\in V_t$
, and therefore,
![]() ${\mathscr E}_{X|X_t}\cong {\mathscr E}_{|X_t}$
.
${\mathscr E}_{X|X_t}\cong {\mathscr E}_{|X_t}$
.
Now, we use the hypothesis that
![]() $[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)^{**}$
is a general point. Then the polarized
$[(X,h)]\in \operatorname {\mathrm {\mathit {NL}}}(d_0)^{**}$
is a general point. Then the polarized
![]() $K3$
surface
$K3$
surface
![]() $(S,D)$
is a general surface of genus n (see Section 5.5), and by Proposition 5.12, the Lagrangian fibration
$(S,D)$
is a general surface of genus n (see Section 5.5), and by Proposition 5.12, the Lagrangian fibration
![]() $\pi \colon X\to {\mathbb P}^n$
is a Tate-Shafarevich twist of the relative Jacobian
$\pi \colon X\to {\mathbb P}^n$
is a Tate-Shafarevich twist of the relative Jacobian
![]() ${\mathscr J}(S)\to |D|$
. It follows that the discriminant curve
${\mathscr J}(S)\to |D|$
. It follows that the discriminant curve
![]() $B\subset {\mathbb P}^n$
is isomorphic to the dual of
$B\subset {\mathbb P}^n$
is isomorphic to the dual of
![]() $S\subset |D|^{\vee }$
, and hence is reduced. Let
$S\subset |D|^{\vee }$
, and hence is reduced. Let
![]() ${\mathscr U}_X^{\dagger }:={\mathscr U}_X\setminus \operatorname {\mathrm {sing}} B$
, where
${\mathscr U}_X^{\dagger }:={\mathscr U}_X\setminus \operatorname {\mathrm {sing}} B$
, where
![]() ${\mathscr U}_X$
is as in Proposition 5.14. Note that
${\mathscr U}_X$
is as in Proposition 5.14. Note that
![]() ${\mathscr U}_X^{\dagger }$
is an open subset of
${\mathscr U}_X^{\dagger }$
is an open subset of
![]() ${\mathbb P}^n$
whose complement has codimension at least
${\mathbb P}^n$
whose complement has codimension at least
![]() $2$
. One proves that
$2$
. One proves that
proceeding as in the proof of [Reference O’GradyO’G22, Proposition 7.4]. More precisely, there exists a smooth projective curve
![]() $T\subset {\mathscr U}_X^{\dagger }$
containing t and transverse to B (recall that the complement of
$T\subset {\mathscr U}_X^{\dagger }$
containing t and transverse to B (recall that the complement of
![]() ${\mathscr U}_X^{\dagger }$
in
${\mathscr U}_X^{\dagger }$
in
![]() ${\mathbb P}^n$
has codimension at least
${\mathbb P}^n$
has codimension at least
![]() $2$
). Then
$2$
). Then
![]() $Y:=\pi ^{-1}(T)$
is a smooth projective (integral) variety of dimension
$Y:=\pi ^{-1}(T)$
is a smooth projective (integral) variety of dimension
![]() $n+1$
and the sheaves
$n+1$
and the sheaves
![]() ${\mathscr F}:={\mathscr E}_{X|Y}$
and
${\mathscr F}:={\mathscr E}_{X|Y}$
and
![]() ${\mathscr G}:={\mathscr E}_{|Y}$
satisfy the hypotheses of [Reference O’GradyO’G22, Lemma 7.5], and hence, the isomorphism in (5.7.4) holds by the quoted lemma.
${\mathscr G}:={\mathscr E}_{|Y}$
satisfy the hypotheses of [Reference O’GradyO’G22, Lemma 7.5], and hence, the isomorphism in (5.7.4) holds by the quoted lemma.
Since
![]() ${\mathscr E}_{X|X_t}$
and
${\mathscr E}_{X|X_t}$
and
![]() ${\mathscr E}_{|X_t}$
are simple for all
${\mathscr E}_{|X_t}$
are simple for all
![]() $t\in {\mathscr U}_X^{\dagger }$
, and since
$t\in {\mathscr U}_X^{\dagger }$
, and since
![]() $c_1({\mathscr E}_X)=c_1({\mathscr E})$
, it follows that the restrictions of
$c_1({\mathscr E}_X)=c_1({\mathscr E})$
, it follows that the restrictions of
![]() ${\mathscr E}_X$
and
${\mathscr E}_X$
and
![]() ${\mathscr E}$
to
${\mathscr E}$
to
![]() $\pi ^{-1}({\mathscr U}_X^{\dagger })$
are isomorphic (see the proof of Proposition 7.4 in [Reference O’GradyO’G22], in particular, the beginning of the proof of Lemma 7.5). The complement of
$\pi ^{-1}({\mathscr U}_X^{\dagger })$
are isomorphic (see the proof of Proposition 7.4 in [Reference O’GradyO’G22], in particular, the beginning of the proof of Lemma 7.5). The complement of
![]() $\pi ^{-1}({\mathscr U}_X^{\dagger })$
in X has codimension at least
$\pi ^{-1}({\mathscr U}_X^{\dagger })$
in X has codimension at least
![]() $2$
because
$2$
because
![]() $\pi $
is equidimensional, and hence, the isomorphism
$\pi $
is equidimensional, and hence, the isomorphism
![]() ${\mathscr E}_{X|\pi ^{-1}({\mathscr U}_X^{\dagger })}\overset {\sim }{\longrightarrow } {\mathscr E}_{|\pi ^{-1}({\mathscr U}_X^{\dagger })}$
extends to an isomorphism
${\mathscr E}_{X|\pi ^{-1}({\mathscr U}_X^{\dagger })}\overset {\sim }{\longrightarrow } {\mathscr E}_{|\pi ^{-1}({\mathscr U}_X^{\dagger })}$
extends to an isomorphism
![]() ${\mathscr E}_X\overset {\sim }{\longrightarrow } {\mathscr E}$
.
${\mathscr E}_X\overset {\sim }{\longrightarrow } {\mathscr E}$
.
We are ready to prove Proposition 5.2. Let
![]() $n,r_0,g,l,e$
be as in Theorem 1.1. Since the result is trivially true for
$n,r_0,g,l,e$
be as in Theorem 1.1. Since the result is trivially true for
![]() $r_0=1$
, we assume that
$r_0=1$
, we assume that
![]() $r_0\ge 2$
. Let
$r_0\ge 2$
. Let
![]() ${\mathscr X}\to T_{e}^{il}(2n)$
be a complete family of polarized HK varieties of Type
${\mathscr X}\to T_{e}^{il}(2n)$
be a complete family of polarized HK varieties of Type
![]() $K3^{[n]}$
parametrized by
$K3^{[n]}$
parametrized by
![]() ${\mathscr K}_{e}^{il}(2n)^{\mathrm {good}}$
. Since
${\mathscr K}_{e}^{il}(2n)^{\mathrm {good}}$
. Since
![]() ${\mathscr K}_{e}^{il}(2n)^{\mathrm {good}}$
is irreducible, we may, and will, assume that
${\mathscr K}_{e}^{il}(2n)^{\mathrm {good}}$
is irreducible, we may, and will, assume that
![]() $T_{e}^{il}(2n)$
is irreducible. For
$T_{e}^{il}(2n)$
is irreducible. For
![]() $t\in T_{e}^{il}(2n)$
, we let
$t\in T_{e}^{il}(2n)$
, we let
![]() $(X_t,h_t)$
be the corresponding polarized HK of Type
$(X_t,h_t)$
be the corresponding polarized HK of Type
![]() $K3^{[n]}$
. Let
$K3^{[n]}$
. Let
![]() $m\colon T_{e}^{il}(2n)\to {\mathscr K}_{e}^{il}(2n)^{\mathrm {good}}$
be the moduli map sending t to
$m\colon T_{e}^{il}(2n)\to {\mathscr K}_{e}^{il}(2n)^{\mathrm {good}}$
be the moduli map sending t to
![]() $[(X_t,h_t)]$
.
$[(X_t,h_t)]$
.
By Gieseker and Maruyama, there exists a relative moduli space
such that for every
![]() $t\in T_{e}^{il}(2n)$
, the (scheme theoretic) fibre
$t\in T_{e}^{il}(2n)$
, the (scheme theoretic) fibre
![]() $f^{-1}(t)$
is isomorphic to the (coarse) moduli space of
$f^{-1}(t)$
is isomorphic to the (coarse) moduli space of
![]() $h_t$
slope-stable vector bundles
$h_t$
slope-stable vector bundles
![]() ${\mathscr E}$
on
${\mathscr E}$
on
![]() $X_t$
, such that (1.2.6) holds. Moreover, the morphism f is of finite type by Maruyama [Reference MaruyamaMar81], and hence,
$X_t$
, such that (1.2.6) holds. Moreover, the morphism f is of finite type by Maruyama [Reference MaruyamaMar81], and hence,
![]() $f({\mathscr M}(r_0,g))$
is a constructible subset of
$f({\mathscr M}(r_0,g))$
is a constructible subset of
![]() $T_{e}^{il}(2n)$
.
$T_{e}^{il}(2n)$
.
Let
![]() $d(r_0,e,l)$
be the right-hand side of the inequality in (5.3.4). For t in a dense subset of
$d(r_0,e,l)$
be the right-hand side of the inequality in (5.3.4). For t in a dense subset of
![]() $\bigcup \limits _{d> d(r_0,e,l)}m^{-1}(\operatorname {\mathrm {\mathit {NL}}}(d)^{\text {good}})$
, the preimage
$\bigcup \limits _{d> d(r_0,e,l)}m^{-1}(\operatorname {\mathrm {\mathit {NL}}}(d)^{\text {good}})$
, the preimage
![]() $f^{-1}(t)$
is a singleton by Proposition 5.17. Since
$f^{-1}(t)$
is a singleton by Proposition 5.17. Since
![]() $\bigcup \limits _{d> d(r_0,e,l)}m^{-1}(\operatorname {\mathrm {\mathit {NL}}}(d)^{\text {good}})$
is Zariski dense in
$\bigcup \limits _{d> d(r_0,e,l)}m^{-1}(\operatorname {\mathrm {\mathit {NL}}}(d)^{\text {good}})$
is Zariski dense in
![]() $T_{e}^{il}(2n)$
(it is the union of an infinite collection of pairwise distinct divisors), and since
$T_{e}^{il}(2n)$
(it is the union of an infinite collection of pairwise distinct divisors), and since
![]() $f({\mathscr M}(r_0,g))$
is a constructible subset of
$f({\mathscr M}(r_0,g))$
is a constructible subset of
![]() $T_{e}^{il}(2n)$
, it follows that for general
$T_{e}^{il}(2n)$
, it follows that for general
![]() $t\in T_{e}^{il}(2n)$
, the fibre
$t\in T_{e}^{il}(2n)$
, the fibre
![]() $f^{-1}(t)$
is a singleton.
$f^{-1}(t)$
is a singleton.
Let
![]() $[{\mathscr E}]$
be the unique point of
$[{\mathscr E}]$
be the unique point of
![]() $f^{-1}(t)$
for t a generic point of
$f^{-1}(t)$
for t a generic point of
![]() $m^{-1}(\operatorname {\mathrm {\mathit {NL}}}(d)^{\text {good}})$
, where
$m^{-1}(\operatorname {\mathrm {\mathit {NL}}}(d)^{\text {good}})$
, where
![]() $d> d(r_0,e,l)$
. Then
$d> d(r_0,e,l)$
. Then
![]() $H^p(X_t, End^0({\mathscr E}))=0$
by Proposition 5.14. Hence, the last sentence of Theorem 1.1 follows from upper semicontinuity of cohomology.
$H^p(X_t, End^0({\mathscr E}))=0$
by Proposition 5.14. Hence, the last sentence of Theorem 1.1 follows from upper semicontinuity of cohomology.
5.8 Proof of Proposition 1.2
Since the natural morphism
![]() $\operatorname {\mathrm {Def}}(X,{\mathscr F})\to \operatorname {\mathrm {Def}}(X,h)$
is surjective, for
$\operatorname {\mathrm {Def}}(X,{\mathscr F})\to \operatorname {\mathrm {Def}}(X,h)$
is surjective, for
![]() $d_0\gg 0$
, there exist extensions of
$d_0\gg 0$
, there exist extensions of
![]() ${\mathscr F}$
to polarized HK varieties
${\mathscr F}$
to polarized HK varieties
![]() $(Y,h)$
of type
$(Y,h)$
of type
![]() $K3^{[n]}$
with a Lagrangian fibration
$K3^{[n]}$
with a Lagrangian fibration
![]() $\pi \colon Y\to {\mathbb P}^n$
, such that
$\pi \colon Y\to {\mathbb P}^n$
, such that
(as usual,
![]() $f:=c_1(\pi ^{*}{\mathscr O}_{{\mathbb P}^n}(1))$
). Let
$f:=c_1(\pi ^{*}{\mathscr O}_{{\mathbb P}^n}(1))$
). Let
![]() $X_t$
be a smooth (Lagrangian) fibre of
$X_t$
be a smooth (Lagrangian) fibre of
![]() $\pi $
, and let
$\pi $
, and let
![]() $\theta _t$
be the principal polarization of
$\theta _t$
be the principal polarization of
![]() $X_t$
induced by the Lagrangian fibration (see Remark 4.10). We claim that
$X_t$
induced by the Lagrangian fibration (see Remark 4.10). We claim that
In fact, the above equality follows from the equalities
By the equality in (5.8.2), we get that
By Proposition 5.15, we may write
where
![]() $r_0,m,b_0$
are integers,
$r_0,m,b_0$
are integers,
![]() $r_0,m\in {\mathbb N}_{+}$
and
$r_0,m\in {\mathbb N}_{+}$
and
![]() $\gcd \{r_0,b_0\}=1$
. Choose
$\gcd \{r_0,b_0\}=1$
. Choose
![]() $d_0$
coprime to
$d_0$
coprime to
![]() $r({\mathscr E})$
: then
$r({\mathscr E})$
: then
![]() $d_0$
divides
$d_0$
divides
![]() $b_0$
, and the equation in (1.3.3) holds with
$b_0$
, and the equation in (1.3.3) holds with
![]() $b_0'=b_0/d_0$
.
$b_0'=b_0/d_0$
.
Acknowledgments
Thanks to Marco Manetti for explaining Horikawa’s classical result [Reference HorikawaHor74, Theorem 6.1], and to Emanuele Macrì for helping me out by introducing me to the powerful [Reference SimpsonSim92, Theorem 2]. This work was partially supported by PRIN 2017YRA3LK.
Competing interests
The authors have no competing interest to declare.