1. Introduction
1.1 Deep nets: Method of choice
Following Devlin et al. (Reference Devlin, Chang, Lee and Toutanova2019), deep nets have become the method of choice for a number of tasks in:
1. Natural language: fill-mask, question answering, sentence similarity, summarization, text classification, text generation, token classification, translation
2. Audio: audio classification, audio-to-audio, automatic speech recognition, text-to-speech (speech synthesis)
3. Computer vision: image classification, image segmentation, object detection.
There are dozens/thousands of models on HuggingFace for each of these tasks.Footnote a There are also many secondary sources on deep nets and machine learning including:
1. text books (Bishop Reference Bishop2016; Goodfellow et al., Reference Goodfellow, Bengio and Courville2016),
2. more practical books (Géron Reference Géron2019; Chollet Reference Chollet2021),
3. surveysFootnote b (LeCun et al., Reference LeCun, Bengio and Hinton2015; Pouyanfar et al., Reference Pouyanfar, Sadiq, Yan, Tian, Tao, Reyes, Shyu, Chen and Iyengar2018; Kumar et al., Reference Kumar, Verma and Mangla2018; Liu et al., Reference Liu, Ouyang, Wang, Fieguth, Chen, Liu and Pietikäinen2020; Qiu et al., Reference Qiu, Sun, Xu, Shao, Dai and Huang2020; Dong et al., Reference Dong, Wang and Abbas2021), and
4. tutorials: ACL-2022 (Church et al., Reference Church, Kordoni, Marcus, Davis, Ma and Chen2022a), plus three articles in the Emerging Trends column in this journal (Church et al., Reference Church, Yuan, Guo, Wu, Yang and Chen2021b, Reference Church, Chen and Ma2021a, Reference Church, Cai, Ying, Chen, Xun and Bian2022b).
1.2 Growth is out of control
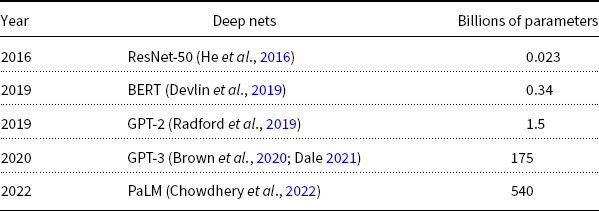
As illustrated in Table 1, deep nets are becoming larger and larger (for better or for worse). There have been dramatic increases in size over time, where size can be measured in a variety of different ways:
Table 1. Deep nets are becoming larger and larger over time.
1. model size,
 $m$ (number of parameters),
$m$ (number of parameters),2. number of dimensions,
 $d$ (problem size),
$d$ (problem size),3. size of (annotated and unannotated) training data,
4. staff (authors per paper),
5. hardware (number of CPUs, GPUs, TPUs, and data centers), and
6. costs (including externalities such as global warming).
The consensus in industry, at least for practical applications, is that bigger nets are better, especially if one cares about performance on test sets (and little else). It is not clear why bigger is better, or even that it is, or that it is a good thing,Footnote c though there are quite a few blogs on this topic. Social media may not be a good way to judge consensus; social media can easily become an echo chamber with multiple blogs promoting the same paper (Bubeck and Sellke Reference Bubeck and Sellke2021).Footnote d, Footnote e
Most of these larger models are coming from industry; training large models has become too expensive for academia (Bommasani et al., Reference Bommasani, Hudson, Adeli, Altman, Arora, von Arx, Bernstein, Bohg, Bosselut, Brunskill, Brynjolfsson, Buch, Card, Castellon, Chatterji, Chen, Creel, Davis, Demszky, Donahue, Doumbouya, Durmus, Ermon, Etchemendy, Ethayarajh, Fei-Fei, Finn, Gale, Gillespie, Goel, Goodman, Grossman, Guha, Hashimoto, Henderson, Hewitt, Ho, Hong, Hsu, Huang, Icard, Jain, Jurafsky, Kalluri, Karamcheti, Keeling, Khani, Khattab, Kohd, Krass, Krishna, Kuditipudi, Kumar, Ladhak, Lee, Lee, Leskovec, Levent, Li, Li, Ma, Malik, Manning, Mirchandani, Mitchell, Munyikwa, Nair, Narayan, Narayanan, Newman, Nie, Niebles, Nilforoshan, Nyarko, Ogut, Orr, Papadimitriou, Park, Piech, Portelance, Potts, Raghunathan, Reich, Ren, Rong, Roohani, Ruiz, Ryan, Ré, Sadigh, Sagawa, Santhanam, Shih, Srinivasan, Tamkin, Taori, Thomas, Tramèr, Wang, Wang, Wu, Wu, Wu, Xie, Yasunaga, You, Zaharia, Zhang, Zhang, Zhang, Zhang, Zheng, Zhou and Liang2021). A recent model from Google, PaLM (Chowdhery et al., Reference Chowdhery, Narang, Devlin, Bosma, Mishra, Roberts, Barham, Chung, Sutton, Gehrmann, Schuh, Shi, Tsvyashchenko, Maynez, Rao, Barnes, Tay, Shazeer, Prabhakaran, Reif, Du, Hutchinson, Pope, Bradbury, Austin, Isard, Gur-Ari, Yin, Duke, Levskaya, Ghemawat, Dev, Michalewski, Garcia, Misra, Robinson, Fedus, Zhou, Ippolito, Luan, Lim, Zoph, Spiridonov, Sepassi, Dohan, Agrawal, Omernick, Dai, Pillai, Pellat, Lewkowycz, Moreira, Child, Polozov, Lee, Zhou, Wang, Saeta, Diaz, Firat, Catasta, Wei, Meier-Hellstern, Eck, Dean, Petrov and Fiedel2022), for example, produces impressive results, but the size of the investment is, perhaps, even more impressive. The model was trained on thousands of TPUs, too many for a single data center. The PaLM paper has dozens of authors. Suffice it to say: PaLM is big in every imaginable way.
PaLM’s contribution is more in Systems Research than Computational Linguistics. It is an amazing engineering and logistical feat to make productive use of so much hardware. Before PaLM, efficiency had been declining. Previous attempts to scale training tended to increase waste (idle time). PaLM not only produced a larger net (at greater expense), but perhaps more importantly, they found a more effective approach to scaling, opening a path toward even larger (and even more expensive) nets, coming soon to an application on a phone near you.
2. Factors that ought to limit growth
There are a number of factors that one might expect to limit growth on deep nets. Of course, none of these factors matter, as evidenced by the fact that growth is out of control. This paper will focus on the last (non)-factor: the so-called curse of dimensionality (CoD).
1. budget constraints (including externalities such as global warming),
2. constraints imposed by deployment platforms (such as phones),
3. availability of (annotated and unannotated) training data (including externalities such as concerns for invisible workers),
4. overfitting, and
5. the CoD.
2.1 Budget constraints and global warming
Budgets are not unlimited, of course, even in industry. Industry would not train such large (and expensive) nets without compelling motivations to do so.
Budget constraints include capital and expense, as well as less obvious factors such as carbon emissions. Following Strubell et al. (Reference Strubell, Ganesh and McCallum2019),Footnote f there have been concerns about accounting and externalities. One might hope that more appropriate taxes on carbon emissions would discourage industry from training larger and larger nets, though we have our doubts. The cost of training is a one-time upfront cost. If a net is used by millions of users every day for years, then recurring costs (inference) dominate one-time costs (training). As a result, it has become standard practice in industry to train larger and larger nets but reduce costs just in time with compression methods such as distillation (DistilBERT)Footnote g, Footnote h (Sanh et al., Reference Sanh, Debut, Chaumond and Wolf2019). Compression makes it possible to train larger nets but reduce costs before deployment (where costs matter).
2.2 Deployment platforms (phones)
The same just-in-time compression technology will become important as nets migrate to phones. In the past, most of the computation tended to be in the cloud (at the center of the network), but more and more computation will likely migrate to edge devices (phones). Given resource limitations on phones (power, memory, CPU/GPU cycles), one might expect this migration to limit growth.Footnote i However, the same compression methods mentioned above are also being used to address these migration issues. Thus, constraints on deployment (cost, power, etc.) have important consequences for compression technology, but less so for training, where out-of-control growth is likely to continue for the foreseeable future.
2.3 Training data are not unlimited
Another non-factor mentioned above is training data. There are many use cases with limitations on training data. Annotated data are particularly expensive, both in monetary terms and other terms (impacts on invisible workers).Footnote j Because of concerns such as these, there is more and more interest in prompting (Liu et al., Reference Liu, Yuan, Fu, Jiang, Hayashi and Neubig2021), zero-shot learning and few-shot learning. These methods reduce demand for annotated (and unannotated) training data. However, many of the most successful such methods make use of extremely large pretrained models such as GPT-3 and PaLM. Thus, it is unlikely that limitations on annotated (and unannotated) training data will stem the out-of-control growth (for pretrained models).
2.4 Overfitting
With many traditional methods, such as regression, if we have too many parameters, we are likely to overfit the training set. A number of traditional methods for addressing overfitting will be mentioned in Section 3 such as feature selection and regularization. It is widely believed that deep nets do not suffer from overfitting, even when heavily over-parameterized.Footnote k Deep nets have developed methods such as stochastic gradient descent with random restarts. There are a few theoretical suggestions that such methods are effective (Li and Liang Reference Li and Liang2018) and over-parameterization does not lead to overfitting (Brutzkus et al., Reference Brutzkus, Globerson, Malach and Shalev-Shwartz2018; Allen-Zhu et al., Reference Allen-Zhu, Li and Liang2019; Oymak and Soltanolkotabi Reference Oymak and Soltanolkotabi2020).
Overfitting can be viewed as a special case of the CoD.
2.5 Curse of dimensionality (COD)
One might expect the CoD to limit out-of-control growth. Donoho (Reference Donoho2000) provides some hints why this might not be the case. He introduces a novel perspective, suggesting that large ![]() $d$ (dimensions) can be both a blessing and a curse. Donoho starts with Bellman’s original argument (Bellman Reference Bellman1966). Bellman’s argument introduced the term, CoD, to motivate his work on dynamic programming:
$d$ (dimensions) can be both a blessing and a curse. Donoho starts with Bellman’s original argument (Bellman Reference Bellman1966). Bellman’s argument introduced the term, CoD, to motivate his work on dynamic programming:
Bellman reminded us that, if we consider a cartesian grid of spacing 1/10 on the unit cube in 10 dimensions, we have ![]() $10^{10}$ points; if the cube in 20 dimensions was considered, we would have of course
$10^{10}$ points; if the cube in 20 dimensions was considered, we would have of course ![]() $10^{20}$ points. His interpretation: if our goal is to optimize a function over a continuous product domain of a few dozen variables by exhaustively searching a discrete search space defined by a crude discretization, we could easily be faced with the problem of making tens of trillions of evaluations of the function. Bellman argued that this curse precluded, under almost any computational scheme then foreseeable, the use of exhaustive enumeration strategies, and argued in favor of his method of dynamic programming. (Donoho Reference Donoho2000)
$10^{20}$ points. His interpretation: if our goal is to optimize a function over a continuous product domain of a few dozen variables by exhaustively searching a discrete search space defined by a crude discretization, we could easily be faced with the problem of making tens of trillions of evaluations of the function. Bellman argued that this curse precluded, under almost any computational scheme then foreseeable, the use of exhaustive enumeration strategies, and argued in favor of his method of dynamic programming. (Donoho Reference Donoho2000)
How can CoD be a blessing? While it may be easy to find examples where large ![]() $d$ causes trouble, there are also examples where large
$d$ causes trouble, there are also examples where large ![]() $d$ is a blessing. Donoho calls out concentration of measure (Ledoux Reference Ledoux2001) as one of the better examples of a blessing.
$d$ is a blessing. Donoho calls out concentration of measure (Ledoux Reference Ledoux2001) as one of the better examples of a blessing.
The concentration of measure phenomenon in product spaces roughly states that, if a set ![]() $A$ in a product
$A$ in a product ![]() $\Omega ^N$ of probability spaces has measure at least one half, “most” of the points of
$\Omega ^N$ of probability spaces has measure at least one half, “most” of the points of ![]() $\Omega ^N$ are “close” to
$\Omega ^N$ are “close” to ![]() $A$. (Talagrand Reference Talagrand1995)
$A$. (Talagrand Reference Talagrand1995)
This observation has many applications. Donoho, for example, uses the concentration of measure in a widely cited paper on compressed sensing (Donoho Reference Donoho2006).
Blessings show up in many practical applications. Consider web search, for example. Web search is more effective in larger networks. Enterprise search can be frustrating. Why is it easier to find good stuff on the web than on a small website for a company or a university? Larger networks can be a blessing because there are more links to what you are looking for in larger communities. Page rank (Page et al., Reference Page, Brin, Motwani and Winograd1999), for example, has more dynamic range on larger graphs.
Under Metcalfe’s Law,Footnote l larger graphs have advantages because edges scale faster than vertices. A telephone network is a popular example of Metcalfe’s Law. The cost of adding another cell phone to the network is a constant, but the benefits scale with the number of other phones already in the network. It is said that Metcalfe’s Law makes it hard for second movers to challenge an establish incumbent with a dominant position in the market. When benefits scale with edges and costs scale with vertices, then the rich get richer.
There are many examples of methods that thrive on scale such as approximate nearest neighborsFootnote m (Indyk and Motwani Reference Indyk and Motwani1998), random projections (Li et al., Reference Li, Hastie and Church2006), and sketches (a method originally designed to remove near duplicate web pages from large crawls (Broder Reference Broder2000), but has many generalizations (Li and Church Reference Li and Church2007)).
Consider eigenvector and node2vec-like embeddings of graphs (Grover and Leskovec Reference Grover and Leskovec2016; Zhou et al., Reference Zhou, Cui, Hu, Zhang, Yang, Liu, Wang, Li and Sun2020). Again, larger graphs have advantages. If we use vectors to represent vertices in a graph (such as a telephone network or web pages), and we estimate similarity of two vertices as a cosine of two vectors, then estimates of similarity improve with larger graphs and longer vectors with more hidden dimensions.
This paper is more concerned with deep nets. Are there reasons to believe that scale could be a blessing for deep nets? Before addressing that question, we will discuss some historical background. Why did we used to believe that scale was a problem?
3. What is our problem with scale?
Researchers today have become comfortable with scale, but we used to feel differently. It is common practice these days to use models with more parameters than observations, especially when discussing topics such as zero-shot and few-shot learning.
It is hard for people from our generation to get used to this new world order. We used to assume, as a matter of faith, that we need more observations than parameters. By Occam’s razor, we preferred models with fewer degrees of freedom. At least in the case of regression, if there are too many degrees of freedom, and not enough training data, then regression coefficients will not reach significance. Even when the coefficients reach significance, if there are too many parameters, then overfitting is likely, producing large errors on the test set.
We used to assume that concepts such as degrees of freedom, significance, and feature selection were important for most models under consideration, not just regression. Much has been written on methods to avoid over-parameterization such as feature selection (LeCun et al., Reference LeCun, Denker and Solla1989; Dash and Liu Reference Dash and Liu1997; Guyon and Elisseeff Reference Guyon and Elisseeff2003; Fan and Lv Reference Fan and Lv2010; Kumar and Minz Reference Kumar and Minz2014; Reference Li, Cheng, Wang, Morstatter, Trevino, Tang and LiuLi et al., 2017), ANOVA (Scheffe Reference Scheffe1999), regularization (Tibshirani Reference Tibshirani1996; Reference Bickel, Li, Tsybakov, van de Geer, Yu, Valdés, Rivero, Fan and van der VaartBickel et al., 2006, Reference Bickel, Ritov and Tsybakov2009), invariant features (Fant Reference Fant1973; Stevens and Blumstein Reference Stevens and Blumstein1981; Acero and Stern Reference Acero and Stern1991; Lowe Reference Lowe1999; Brown and Lowe Reference Brown and Lowe2002), feature engineering (Scott and Matwin Reference Scott and Matwin1999), and term weighting (Salton and Buckley Reference Salton and Buckley1988). Over-parameterization is problematic for many/most traditional methods (Fan and Lv Reference Fan and Lv2008), though there may be a few exceptions (Bartlett et al., Reference Bartlett, Long, Lugosi and Tsigler2020).
These days, hill-climbing is the method of choice for fitting deep nets. But we were warned by our teachers that hill-climbing cannot possibly scale up to problems with large ![]() $d$ and rich (non-convex) structure (with many local minima)Footnote n (Minsky Reference Minsky1961; Minsky and Papert Reference Minsky and Papert1969). Bishop rejects our teachers’ concerns as “incorrect conjecture” on page 193 (Bishop Reference Bishop2006), but it took the field many decades to appreciate that hill-climbing is feasible in high dimensions, and we are still trying to figure out why that is the case.
$d$ and rich (non-convex) structure (with many local minima)Footnote n (Minsky Reference Minsky1961; Minsky and Papert Reference Minsky and Papert1969). Bishop rejects our teachers’ concerns as “incorrect conjecture” on page 193 (Bishop Reference Bishop2006), but it took the field many decades to appreciate that hill-climbing is feasible in high dimensions, and we are still trying to figure out why that is the case.
It has been claimed that certain methods such as support vector machines (Cortes and Vapnik Reference Cortes and Vapnik1995; Hearst et al., Reference Hearst, Dumais, Osuna, Platt and Scholkopf1998) work relatively well in high dimensional spaces (Joachims Reference Joachims1998), but those technologies did not lead to out-of-control growth like we are seeing for deep nets. Apparently, deep nets are not merely robust to high dimensions, but they thrive on them. How can that be?
4. Weinan E: A mathematical perspective on machine learning
It is generally accepted, at least among practitioners, that deep nets thrive on scale. The big question is: why. Is there a theoretical justification for what we are all doing?
Weinan E recently gave a theoretical talk on recent progress on somewhat related questions.Footnote o, Footnote p The discussion below will use slide numbers and page numbers to refer to the talkFootnote q and an overview article (E, 2020), respectively.
This work is very much a work in progress. Currently, their results are better for two-level nets; extensions to multi-layer networks are “unsatisfactory” (slide 37). Of course, much work remains to be done, as explained in a paper with a brutally honest title that ends with: what we know and what we don’t (E et al., Reference Ma, Wojtowytsch and Wu2020). Actually, the theory community has a long tradition of sharing lists of promising open problems with their students. Our field would have less (pointless) SOTA-chasing (Church and Kordoni Reference Church and Kordoni2022) if we produced more brutally honest papers like this. Such papers help students find good projects to work on.
Weinan E’s talk is divided into three sections:
1. Introduction (slides 1–20): Apparently, deep nets are better than alternatives (polynomials) in high dimensions
2. Theoretical discussion of errors
(a) Approximation error,
 $E_a$ (slides 21–37; pp. 17–19): errors due to the choice of the hypothesis space
$E_a$ (slides 21–37; pp. 17–19): errors due to the choice of the hypothesis space(b) Estimation error,
 $E_e$ (slides 38–45; pp. 19–21): additional errors due to finiteness of data
$E_e$ (slides 38–45; pp. 19–21): additional errors due to finiteness of data(c) Optimization error,
 $E_o$ (slides 46–54): additional errors caused by training
$E_o$ (slides 46–54): additional errors caused by training
3. Applications of deep nets to solve problems in high dimensions (slides 56–70).
The discussion of errors starts with an example of the CoD (slide 13). Suppose we want to approximate a function ![]() $f^*$ with
$f^*$ with ![]() $f_m$ using a classical method such as piecewise linear functions over a mesh of size
$f_m$ using a classical method such as piecewise linear functions over a mesh of size ![]() $h$. Assuming
$h$. Assuming ![]() $h \sim m^{1/d}$, where
$h \sim m^{1/d}$, where ![]() $d$ is the dimensionality of the problem and
$d$ is the dimensionality of the problem and ![]() $m$ is the size of the model (in terms of free parameters), then computational costs grow exponentially with
$m$ is the size of the model (in terms of free parameters), then computational costs grow exponentially with ![]() $d$. That is, errors,
$d$. That is, errors, ![]() $E = |f^* - f_m|$, scale in a nasty way with
$E = |f^* - f_m|$, scale in a nasty way with ![]() $d$:
$d$:
Thus, to reduce the error by a factor of 10, we need to increase ![]() $m$ by a factor of
$m$ by a factor of ![]() $10^{d/2}$.
$10^{d/2}$.
Weinan E concludes with the observation:
Compared with polynomials, neural networks provide a much more effective tool for approximating functions in high dimension. (slide 68)
Similar comments probably hold for regression-like methods and other traditional methods that are being replaced by neural nets.
The crux of Weinan E’s talk is to replace grid-based methods with Monte Carlo estimation. Slide 24 suggests that newer methods (based on Monte Carlo estimation) have error rates that are independent of dimensions ![]() $d$, in contrast to older methods (slide 23) based on uniform grids.
$d$, in contrast to older methods (slide 23) based on uniform grids.
Much of the Weinan E’s talk attempts to make this intuition more rigorous and more general. The discussion on slides 23 and 24 is specific to a number of particulars: a particular type of error (approximation error), and a particular type of network (a two-layer network), and a particular method on a particular grid.
They are making great progress, with many recent promising results, and there will be more results in the future. The discussion of approximation errors, ![]() $E_a$, is relatively long (16 slides on
$E_a$, is relatively long (16 slides on ![]() $E_a$ versus 7 slides on
$E_a$ versus 7 slides on ![]() $E_e$ and 8 slides on
$E_e$ and 8 slides on ![]() $E_o$), suggesting there has been more progress on approximation errors.
$E_o$), suggesting there has been more progress on approximation errors.
The three types of errors are defined on slide 20. Weinan E splits the error, ![]() $E = |f^* - \hat{f}|$, into three sub-errors,
$E = |f^* - \hat{f}|$, into three sub-errors, ![]() $E = E_a + E_e + E_o$, by introducing two milestones between
$E = E_a + E_e + E_o$, by introducing two milestones between ![]() $f^*$ and
$f^*$ and ![]() $\hat{f}$:
$\hat{f}$:
1. milestone
 $f_m$: best approximation of
$f_m$: best approximation of  $f^*$ in a hypothesis space,
$f^*$ in a hypothesis space,  $\mathcal{H}$
$\mathcal{H}$2. milestone
 $\tilde{f}_{n,m}$: best approximation of
$\tilde{f}_{n,m}$: best approximation of  $f_m$ using only the dataset,
$f_m$ using only the dataset,  $S$.
$S$.
The three sub-errors defined in terms of these milestones:
• Approximation error: gap from goal,
 $f^*$, to first milestone,
$f^*$, to first milestone,• Estimation error: gap between two milestones, and
• Optimization error: gap from last milestone to approximation,
 $\hat{f}$.
$\hat{f}$.
The discussion of these errors mentions CoD, but in different ways:
1. Approximation error (slide 23; on p. 17): CoD is challenging for grid-based approximation methods, where errors scale in a nasty way with
 $d$.
$d$.2. Estimation error (slide 43; p. 18): size of training data grows exponentially quickly with
 $d$.
$d$.3. Optimization error (slide 48): convergence rate for gradient-based training algorithms must suffer from CoD.
One of the more exciting results is a bound on approximation errors that is independent of ![]() $d$ (E Reference Ma and Wu2022) (slide 34; p. 19). This result establishes that certain types of nets are immune to CoD, though there is some fine-print. This result is currently limited to two-layer nets, and it only covers one type of error (approximation errors).
$d$ (E Reference Ma and Wu2022) (slide 34; p. 19). This result establishes that certain types of nets are immune to CoD, though there is some fine-print. This result is currently limited to two-layer nets, and it only covers one type of error (approximation errors).
5. Conclusions
As mentioned above, current practice is well ahead of theory; some even compare what we do to alchemy (Church and Liberman Reference Church and Liberman2021).Footnote r Over the last few years, industry has been producing deep nets that are bigger in every imaginable way (for better and for worse): model size (![]() $m$), dimensions (
$m$), dimensions (![]() $d$), cost, training data, staff, hardware, carbon emissions, negative impacts on invisible workers, etc. Recent progress on the theory side is not able to keep up with practice in industry, but there are some exciting theoretical results suggesting that approximation errors for two-layer nets may be independent of
$d$), cost, training data, staff, hardware, carbon emissions, negative impacts on invisible workers, etc. Recent progress on the theory side is not able to keep up with practice in industry, but there are some exciting theoretical results suggesting that approximation errors for two-layer nets may be independent of ![]() $d$. There will likely be more progress on the theory side, relaxing much of the fine-print.
$d$. There will likely be more progress on the theory side, relaxing much of the fine-print.
Eventually, theory will catch up to practice and explain why it makes sense for industry to do what it is doing. Theory is on a path toward explaining why deep nets might be immune to the CoD, but the out-of-control growth suggests a more bullish conjecture: deep nets are succeeding because of scale (West Reference West2018), not in spite of scale.





