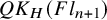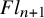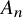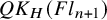1 Introduction
Let
![]() $Fl_{n+1}$
denote the (full) flag manifold
$Fl_{n+1}$
denote the (full) flag manifold
![]() $G/B$
of type
$G/B$
of type
![]() $A_{n}$
, where
$A_{n}$
, where
![]() $G = SL_{n+1}(\mathbb {C})$
is the special linear group of rank n, with Borel subgroup B consisting of the upper triangular matrices in
$G = SL_{n+1}(\mathbb {C})$
is the special linear group of rank n, with Borel subgroup B consisting of the upper triangular matrices in
![]() $G = SL_{n+1}(\mathbb {C})$
and maximal torus
$G = SL_{n+1}(\mathbb {C})$
and maximal torus
![]() $H \subset B$
consisting of the diagonal matrices in
$H \subset B$
consisting of the diagonal matrices in
![]() $G = SL_{n+1}(\mathbb {C})$
. Let
$G = SL_{n+1}(\mathbb {C})$
. Let
![]() $R(H)$
denote the representation ring of H, which we identify with the group algebra
$R(H)$
denote the representation ring of H, which we identify with the group algebra
![]() $\mathbb {Z}[P] = \bigoplus _{\nu \in P} \mathbb {Z} \mathbf {e}^{\nu }$
of the weight lattice
$\mathbb {Z}[P] = \bigoplus _{\nu \in P} \mathbb {Z} \mathbf {e}^{\nu }$
of the weight lattice
![]() $P = \sum _{i =1}^{n} \mathbb {Z} \varpi _{i}$
of
$P = \sum _{i =1}^{n} \mathbb {Z} \varpi _{i}$
of
![]() $G = SL_{n+1}(\mathbb {C})$
, where
$G = SL_{n+1}(\mathbb {C})$
, where
![]() $\varpi _{i}$
,
$\varpi _{i}$
,
![]() $1 \leq i \leq n$
, are the fundamental weights; we set
$1 \leq i \leq n$
, are the fundamental weights; we set
![]() $\varpi _{0} := 0$
and
$\varpi _{0} := 0$
and
![]() $\varpi _{n+1} := 0$
by convention. We denote by
$\varpi _{n+1} := 0$
by convention. We denote by
![]() $QK_{H}(Fl_{n+1}) := K_{H}(Fl_{n+1}) \otimes _{R(H)} R(H)[\![Q]\!]$
the H-equivariant (small) quantum K-theory ring, defined by Givental [Reference GiventalGiv] and Lee [Reference LeeLee], where
$QK_{H}(Fl_{n+1}) := K_{H}(Fl_{n+1}) \otimes _{R(H)} R(H)[\![Q]\!]$
the H-equivariant (small) quantum K-theory ring, defined by Givental [Reference GiventalGiv] and Lee [Reference LeeLee], where
![]() $K_{H}(Fl_{n+1}) = \bigoplus _{w \in W} R(H)[\mathcal{O}^{w}]$
denotes the H-equivariant (ordinary) K-theory ring of
$K_{H}(Fl_{n+1}) = \bigoplus _{w \in W} R(H)[\mathcal{O}^{w}]$
denotes the H-equivariant (ordinary) K-theory ring of
![]() $Fl_{n+1}$
with the (opposite) Schubert classes
$Fl_{n+1}$
with the (opposite) Schubert classes
![]() $[\mathcal{O}^{w}]$
indexed by the elements w of the finite Weyl group
$[\mathcal{O}^{w}]$
indexed by the elements w of the finite Weyl group
![]() $W = S_{n+1}$
of
$W = S_{n+1}$
of
![]() $G = SL_{n+1}(\mathbb {C})$
as a basis over
$G = SL_{n+1}(\mathbb {C})$
as a basis over
![]() $R(H)$
, and where
$R(H)$
, and where
![]() $R(H)[\![Q]\!] = R(H)[\![Q_1, \ldots , Q_{n}]\!]$
denotes the ring of formal power series in the Novikov variables
$R(H)[\![Q]\!] = R(H)[\![Q_1, \ldots , Q_{n}]\!]$
denotes the ring of formal power series in the Novikov variables
![]() $Q_{i} := Q^{\alpha _i^{\vee }}$
corresponding to the simple coroots
$Q_{i} := Q^{\alpha _i^{\vee }}$
corresponding to the simple coroots
![]() $\alpha _i^{\vee }$
,
$\alpha _i^{\vee }$
,
![]() $1 \leq i \leq n$
, with coefficients in
$1 \leq i \leq n$
, with coefficients in
![]() $R(H)$
.
$R(H)$
.
In our previous paper [Reference Maeno, Naito and SagakiMaNS], we proved that there exists an
![]() $R(H)[\![Q]\!]$
-algebra isomorphism
$R(H)[\![Q]\!]$
-algebra isomorphism
where
![]() $\mathcal{I}^{Q}$
is the ideal of
$\mathcal{I}^{Q}$
is the ideal of
![]() $(R(H)[\![Q]\!])[x_{1},\dots ,x_{n},x_{n+1}]$
generated by
$(R(H)[\![Q]\!])[x_{1},\dots ,x_{n},x_{n+1}]$
generated by
 $$ \begin{align*} \sum_{ \begin{subarray}{c} J \subset [n+1] \\[1mm] |J|=l \end{subarray}} \, \prod_{j \in J, j+1 \notin J} (1-Q_{j}) \prod_{j \in J} (1-x_{j}) - \sum_{ \begin{subarray}{c} J \subset [n+1] \\[1mm] |J|=l \end{subarray}}\mathbf{e}^{\epsilon_{J}}, \qquad 1 \le l \le n+1, \end{align*} $$
$$ \begin{align*} \sum_{ \begin{subarray}{c} J \subset [n+1] \\[1mm] |J|=l \end{subarray}} \, \prod_{j \in J, j+1 \notin J} (1-Q_{j}) \prod_{j \in J} (1-x_{j}) - \sum_{ \begin{subarray}{c} J \subset [n+1] \\[1mm] |J|=l \end{subarray}}\mathbf{e}^{\epsilon_{J}}, \qquad 1 \le l \le n+1, \end{align*} $$
with
![]() $[n+1] := \{1,2,\dots ,n+1\}$
; here, we understand that
$[n+1] := \{1,2,\dots ,n+1\}$
; here, we understand that
![]() $Q_{n+1} = 0$
, and for a subset
$Q_{n+1} = 0$
, and for a subset
![]() $J \subset [n+1]$
, we set
$J \subset [n+1]$
, we set
![]() $\epsilon _{J} := \sum _{j \in J} \epsilon _{j}$
, where
$\epsilon _{J} := \sum _{j \in J} \epsilon _{j}$
, where
![]() $\epsilon _{j} = \varpi _{j} - \varpi _{j-1}$
for
$\epsilon _{j} = \varpi _{j} - \varpi _{j-1}$
for
![]() $1 \leq j \leq n+1$
. Also,
$1 \leq j \leq n+1$
. Also,
![]() $\Psi ^{Q}$
maps the residue class of
$\Psi ^{Q}$
maps the residue class of
![]() $(1-Q_j)(1-x_{j})$
modulo
$(1-Q_j)(1-x_{j})$
modulo
![]() $\mathcal{I}^{Q}$
to
$\mathcal{I}^{Q}$
to
![]() $[\mathcal{O}_{Fl_{n+1}}(-\epsilon _{j})]$
for
$[\mathcal{O}_{Fl_{n+1}}(-\epsilon _{j})]$
for
![]() $1 \le j \le n$
, and the residue class of
$1 \le j \le n$
, and the residue class of
![]() $(1 - x_{n+1})$
modulo
$(1 - x_{n+1})$
modulo
![]() $\mathcal{I}^{Q}$
to
$\mathcal{I}^{Q}$
to
![]() $[\mathcal{O}_{Fl_{n+1}}(-\epsilon _{n+1})]$
; note that
$[\mathcal{O}_{Fl_{n+1}}(-\epsilon _{n+1})]$
; note that
![]() $-\epsilon _{n+1} = \epsilon _{1} + \cdots + \epsilon _{n}$
. Here, for
$-\epsilon _{n+1} = \epsilon _{1} + \cdots + \epsilon _{n}$
. Here, for
![]() $1 \leq j \leq n+1$
,
$1 \leq j \leq n+1$
,
![]() $\mathcal{O}_{Fl_{n+1}}(-\epsilon _{j})$
denotes the quotient (line) bundle
$\mathcal{O}_{Fl_{n+1}}(-\epsilon _{j})$
denotes the quotient (line) bundle
![]() $\mathcal{U}_{j}/\mathcal{U}_{j-1}$
over
$\mathcal{U}_{j}/\mathcal{U}_{j-1}$
over
![]() $Fl_{n+1}$
, where
$Fl_{n+1}$
, where
![]() $0 = \mathcal{U}_{0} \subset \mathcal{U}_{1} \subset \cdots \subset \mathcal{U}_{n} \subset \mathcal{U}_{n+1} = Fl_{n+1} \times \mathbb {C}^{n+1}$
is the universal, or tautological, flag of subvector bundles of the trivial bundle
$0 = \mathcal{U}_{0} \subset \mathcal{U}_{1} \subset \cdots \subset \mathcal{U}_{n} \subset \mathcal{U}_{n+1} = Fl_{n+1} \times \mathbb {C}^{n+1}$
is the universal, or tautological, flag of subvector bundles of the trivial bundle
![]() $Fl_{n+1} \times \mathbb {C}^{n+1}$
.
$Fl_{n+1} \times \mathbb {C}^{n+1}$
.
The purpose of this paper is to prove that quantum double Grothendieck polynomials, introduced in [Reference Lenart and MaenoLM, Section 8], represent (opposite) Schubert classes in
![]() $QK_{H}(Fl_{n+1})$
under the presentation above. This result can be thought of as the H-equivariant analog of [Reference Lenart, Naito and SagakiLNS, Theorem 51], in which it is proved that quantum Grothendieck polynomials represent (opposite) Schubert classes in the non-equivariant quantum K-theory ring
$QK_{H}(Fl_{n+1})$
under the presentation above. This result can be thought of as the H-equivariant analog of [Reference Lenart, Naito and SagakiLNS, Theorem 51], in which it is proved that quantum Grothendieck polynomials represent (opposite) Schubert classes in the non-equivariant quantum K-theory ring
![]() $QK(Fl_{n})$
. However, the strategy of our proof in the H-equivariant case is quite different from that in the non-equivariant case in that we can reduce the proof to the case of the longest element by using quantum (dual) left Demazure operators introduced in [Reference Mihalcea, Naruse and SuMNS], which act only on equivariant parameters.
$QK(Fl_{n})$
. However, the strategy of our proof in the H-equivariant case is quite different from that in the non-equivariant case in that we can reduce the proof to the case of the longest element by using quantum (dual) left Demazure operators introduced in [Reference Mihalcea, Naruse and SuMNS], which act only on equivariant parameters.
To be more precise, for the longest element
![]() $w_{\circ } \in W=S_{n+1}$
, the associated quantum double Grothendieck polynomial
$w_{\circ } \in W=S_{n+1}$
, the associated quantum double Grothendieck polynomial
![]() $\mathfrak {G}_{w_{\circ }}^{Q}(x,y)$
is defined as
$\mathfrak {G}_{w_{\circ }}^{Q}(x,y)$
is defined as
 $$ \begin{align*} \mathfrak{G}_{w_{\circ}}^{Q}(x,y) = \prod_{k=1}^{n}\Bigg( \sum_{l=0}^{k}(-1)^{l}(1-y_{n+1-k})^{l}F_{l}^{k}(x_{1},\dots,x_{n},x_{n+1}) \Bigg), \end{align*} $$
$$ \begin{align*} \mathfrak{G}_{w_{\circ}}^{Q}(x,y) = \prod_{k=1}^{n}\Bigg( \sum_{l=0}^{k}(-1)^{l}(1-y_{n+1-k})^{l}F_{l}^{k}(x_{1},\dots,x_{n},x_{n+1}) \Bigg), \end{align*} $$
where
 $$ \begin{align*} F_{l}^{k}(x_{1},\dots,x_{n},x_{n+1}):= \sum_{ \begin{subarray}{c} J \subset [k] \\[1mm] |J|=l \end{subarray}} \, \prod_{j \in J, j+1 \notin J} (1-Q_{j}) \prod_{j \in J}(1-x_{j}) \end{align*} $$
$$ \begin{align*} F_{l}^{k}(x_{1},\dots,x_{n},x_{n+1}):= \sum_{ \begin{subarray}{c} J \subset [k] \\[1mm] |J|=l \end{subarray}} \, \prod_{j \in J, j+1 \notin J} (1-Q_{j}) \prod_{j \in J}(1-x_{j}) \end{align*} $$
for
![]() $0 \le l \le k \le n$
, with
$0 \le l \le k \le n$
, with
![]() $[k] := \{1, 2, \ldots , k\}$
; note that
$[k] := \{1, 2, \ldots , k\}$
; note that
![]() $\mathfrak {G}_{w_{\circ }}^{Q}(x,y)$
is an element of
$\mathfrak {G}_{w_{\circ }}^{Q}(x,y)$
is an element of
![]() $\mathbb {Z}[\![Q]\!][x_{1}, \ldots , x_{n},x_{n+1}][(1-y_{1})^{\pm 1}, \ldots , (1-y_{n})^{\pm 1}]$
, which can be thought of as a subring of
$\mathbb {Z}[\![Q]\!][x_{1}, \ldots , x_{n},x_{n+1}][(1-y_{1})^{\pm 1}, \ldots , (1-y_{n})^{\pm 1}]$
, which can be thought of as a subring of
![]() $(\mathbb {Z}[(1-y_{1})^{\pm 1}, \ldots , (1-y_{n})^{\pm 1}][\![Q]\!])[x_{1}, \ldots , x_{n},x_{n+1}]$
, where we identify
$(\mathbb {Z}[(1-y_{1})^{\pm 1}, \ldots , (1-y_{n})^{\pm 1}][\![Q]\!])[x_{1}, \ldots , x_{n},x_{n+1}]$
, where we identify
![]() $R(H) \cong \mathbb {Z}[\mathbf {e}^{\pm \epsilon _{1}}, \ldots , \mathbf {e}^{\pm \epsilon _{n}}]$
with
$R(H) \cong \mathbb {Z}[\mathbf {e}^{\pm \epsilon _{1}}, \ldots , \mathbf {e}^{\pm \epsilon _{n}}]$
with
![]() $\mathbb {Z}[(1-y_{1})^{\pm 1}, \ldots , (1-y_{n})^{\pm 1}]$
by
$\mathbb {Z}[(1-y_{1})^{\pm 1}, \ldots , (1-y_{n})^{\pm 1}]$
by
![]() $1 - y_{j}=\mathbf {e}^{-\epsilon _{j}}$
for
$1 - y_{j}=\mathbf {e}^{-\epsilon _{j}}$
for
![]() $1 \le j \le n$
, and then identify
$1 \le j \le n$
, and then identify
![]() $(R(H)[\![Q]\!])[x_{1}, \ldots , x_{n},x_{n+1}]$
with
$(R(H)[\![Q]\!])[x_{1}, \ldots , x_{n},x_{n+1}]$
with
![]() $(\mathbb {Z}[(1-y_{1})^{\pm 1}, \ldots , (1-y_{n})^{\pm 1}][\![Q]\!])[x_{1}, \ldots , x_{n},x_{n+1}]$
. For an arbitrary
$(\mathbb {Z}[(1-y_{1})^{\pm 1}, \ldots , (1-y_{n})^{\pm 1}][\![Q]\!])[x_{1}, \ldots , x_{n},x_{n+1}]$
. For an arbitrary
![]() $w \in W = S_{n+1}$
, the associated quantum double Grothendieck polynomial
$w \in W = S_{n+1}$
, the associated quantum double Grothendieck polynomial
![]() $\mathfrak {G}_{w}^{Q}(x,y)$
is defined as
$\mathfrak {G}_{w}^{Q}(x,y)$
is defined as
where
![]() $\pi _{ww_{\circ }}^{(y)}$
denotes the Demazure operator acting on the y variables (see Section 4.1 for details). Since we can show that the Demazure operators
$\pi _{ww_{\circ }}^{(y)}$
denotes the Demazure operator acting on the y variables (see Section 4.1 for details). Since we can show that the Demazure operators
![]() $\pi _{i}^{(y)}$
for
$\pi _{i}^{(y)}$
for
![]() $1 \leq i \leq n$
on the quotient ring
$1 \leq i \leq n$
on the quotient ring
![]() $(R(H)[\![Q]\!])[x_{1}, \ldots , x_{n},x_{n+1}]/\mathcal{I}^{Q}$
coincide with the quantum (dual) left Demazure operators
$(R(H)[\![Q]\!])[x_{1}, \ldots , x_{n},x_{n+1}]/\mathcal{I}^{Q}$
coincide with the quantum (dual) left Demazure operators
![]() $\delta _{i}^{\vee }$
for
$\delta _{i}^{\vee }$
for
![]() $1 \leq i \leq n$
on
$1 \leq i \leq n$
on
![]() $QK_{H}(Fl_{n+1})$
(see the commutative diagram in (4.5)) under the
$QK_{H}(Fl_{n+1})$
(see the commutative diagram in (4.5)) under the
![]() $R(H)[\![Q]\!]$
-algebra isomorphism
$R(H)[\![Q]\!]$
-algebra isomorphism
we need only consider the case of the longest element
![]() $w_{\circ } \in W = S_{n+1}$
; this line of argument is indeed proposed in [Reference Mihalcea, Naruse and SuMNS, Section 8].
$w_{\circ } \in W = S_{n+1}$
; this line of argument is indeed proposed in [Reference Mihalcea, Naruse and SuMNS, Section 8].
Now, we are ready to state the main result of this paper.
Theorem 1. Let w be an arbitrary element of
![]() $W = S_{n+1}$
. Then, under the isomorphism (1.1), the following equality holds in
$W = S_{n+1}$
. Then, under the isomorphism (1.1), the following equality holds in
![]() $QK_{H}(Fl_{n+1})$
:
$QK_{H}(Fl_{n+1})$
:
where we identify
![]() $R(H) \cong \mathbb {Z}[\mathbf {e}^{\pm \epsilon _{1}}, \ldots , \mathbf {e}^{\pm \epsilon _{n}}]$
with
$R(H) \cong \mathbb {Z}[\mathbf {e}^{\pm \epsilon _{1}}, \ldots , \mathbf {e}^{\pm \epsilon _{n}}]$
with
![]() $\mathbb {Z}[(1-y_{1})^{\pm 1}, \ldots , (1-y_{n})^{\pm 1}]$
, and then
$\mathbb {Z}[(1-y_{1})^{\pm 1}, \ldots , (1-y_{n})^{\pm 1}]$
, and then
![]() $(R(H)[\![Q]\!])[x_{1}, \ldots , x_{n},x_{n+1}]$
with
$(R(H)[\![Q]\!])[x_{1}, \ldots , x_{n},x_{n+1}]$
with
![]() $(\mathbb {Z}[(1-y_{1})^{\pm 1}, \ldots , (1-y_{n})^{\pm 1}][\![Q]\!])[x_{1}, \ldots , x_{n},x_{n+1}]$
by
$(\mathbb {Z}[(1-y_{1})^{\pm 1}, \ldots , (1-y_{n})^{\pm 1}][\![Q]\!])[x_{1}, \ldots , x_{n},x_{n+1}]$
by
![]() $1 - y_{j}=\mathbf {e}^{-\epsilon _{j}}$
for
$1 - y_{j}=\mathbf {e}^{-\epsilon _{j}}$
for
![]() $1 \le j \le n$
.
$1 \le j \le n$
.
Here, we should mention that the result above for the (essential) case of the longest element
![]() $w_{\circ } \in W = S_{n+1}$
is obtained, via the
$w_{\circ } \in W = S_{n+1}$
is obtained, via the
![]() $R(H)$
-module isomorphism between
$R(H)$
-module isomorphism between
![]() $QK_{H}(Fl_{n+1})$
and the H-equivariant K-group
$QK_{H}(Fl_{n+1})$
and the H-equivariant K-group
![]() $K_{H}(\mathbf {Q}_{G})$
of the semi-infinite flag manifold
$K_{H}(\mathbf {Q}_{G})$
of the semi-infinite flag manifold
![]() $\mathbf {Q}_{G}$
associated to
$\mathbf {Q}_{G}$
associated to
![]() $G = SL_{n+1}(\mathbb {C})$
(established in [Reference KatoKat1]), from an explicit formula (Corollary 2.5) expressing the semi-infinite Schubert class
$G = SL_{n+1}(\mathbb {C})$
(established in [Reference KatoKat1]), from an explicit formula (Corollary 2.5) expressing the semi-infinite Schubert class
![]() $[\mathcal{O}_{\mathbf {Q}_{G}(w_{\circ })}]$
in
$[\mathcal{O}_{\mathbf {Q}_{G}(w_{\circ })}]$
in
![]() $K_{H}(\mathbf {Q}_{G})$
, with
$K_{H}(\mathbf {Q}_{G})$
, with
![]() $G = SL_{n+1}(\mathbb {C})$
; see Section 3 for details. Also, we prove Corollary 2.5 (or Proposition 2.4) first by applying the general Chevalley formula for
$G = SL_{n+1}(\mathbb {C})$
; see Section 3 for details. Also, we prove Corollary 2.5 (or Proposition 2.4) first by applying the general Chevalley formula for
![]() $K_{H}(\mathbf {Q}_{G})$
in [Reference Lenart, Naito and SagakiLNS] and then by constructing a sign-reversing involution on a certain set of directed paths in the quantum Bruhat graph associated to
$K_{H}(\mathbf {Q}_{G})$
in [Reference Lenart, Naito and SagakiLNS] and then by constructing a sign-reversing involution on a certain set of directed paths in the quantum Bruhat graph associated to
![]() $W = S_{n+1}$
which appear in the resulting expansion; see Section 5 for details.
$W = S_{n+1}$
which appear in the resulting expansion; see Section 5 for details.
This paper is organized as follows. In Section 2, we first fix the basic notation for root systems (in particular, for the root system of type A) and then recall the definition of the quantum Bruhat graph. Also, we recall the definitions of the
![]() $(H \times \mathbb {C}^{*})$
-equivariant K-group
$(H \times \mathbb {C}^{*})$
-equivariant K-group
![]() $K_{H \times \mathbb {C}^{*}}(\mathbf {Q}_{G})$
and H-equivariant K-group
$K_{H \times \mathbb {C}^{*}}(\mathbf {Q}_{G})$
and H-equivariant K-group
![]() $K_{H}(\mathbf {Q}_{G})$
of the semi-infinite flag manifold
$K_{H}(\mathbf {Q}_{G})$
of the semi-infinite flag manifold
![]() $\mathbf {Q}_{G}$
, and state the key proposition (Proposition 2.4), deferring its proof to Section 5. In Section 3, we briefly review the relationship of
$\mathbf {Q}_{G}$
, and state the key proposition (Proposition 2.4), deferring its proof to Section 5. In Section 3, we briefly review the relationship of
![]() $K_{H}(\mathbf {Q}_{G})$
with the H-equivariant quantum K-theory ring
$K_{H}(\mathbf {Q}_{G})$
with the H-equivariant quantum K-theory ring
![]() $QK_{H}(G/B)$
of the flag manifold
$QK_{H}(G/B)$
of the flag manifold
![]() $G/B$
and prove our main result (Theorem 1) for the (essential) case of the longest element
$G/B$
and prove our main result (Theorem 1) for the (essential) case of the longest element
![]() $w_{\circ } \in W = S_{n+1}$
. In Section 4, we prove our main result (Theorem 1) for an arbitrary
$w_{\circ } \in W = S_{n+1}$
. In Section 4, we prove our main result (Theorem 1) for an arbitrary
![]() $w \in W = S_{n+1}$
through the strategy explained above. Section 5 is entirely devoted to the proof of Proposition 2.4.
$w \in W = S_{n+1}$
through the strategy explained above. Section 5 is entirely devoted to the proof of Proposition 2.4.
2 An explicit formula expressing the semi-infinite Schubert class associated to
 $w_{\circ }$
$w_{\circ }$
2.1 Notation for root systems
Let G be a connected, simply-connected, simple algebraic group over
![]() $\mathbb {C}$
, H a maximal torus of G. We set
$\mathbb {C}$
, H a maximal torus of G. We set
![]() $\mathfrak {g} := \mathrm {Lie}(G)$
and
$\mathfrak {g} := \mathrm {Lie}(G)$
and
![]() $\mathfrak {h} := \mathrm {Lie}(H)$
. Thus,
$\mathfrak {h} := \mathrm {Lie}(H)$
. Thus,
![]() $\mathfrak {g}$
is a finite-dimensional simple Lie algebra over
$\mathfrak {g}$
is a finite-dimensional simple Lie algebra over
![]() $\mathbb {C}$
, and
$\mathbb {C}$
, and
![]() $\mathfrak {h}$
is a Cartan subalgebra of
$\mathfrak {h}$
is a Cartan subalgebra of
![]() $\mathfrak {g}$
. We denote by
$\mathfrak {g}$
. We denote by
![]() $\langle \cdot \,, \cdot \rangle : \mathfrak {h}^{\ast } \times \mathfrak {h} \rightarrow \mathbb {C}$
the canonical pairing, where
$\langle \cdot \,, \cdot \rangle : \mathfrak {h}^{\ast } \times \mathfrak {h} \rightarrow \mathbb {C}$
the canonical pairing, where
![]() $\mathfrak {h}^{\ast } = \mathrm {Hom}_{\mathbb {C}}(\mathfrak {h}, \mathbb {C})$
.
$\mathfrak {h}^{\ast } = \mathrm {Hom}_{\mathbb {C}}(\mathfrak {h}, \mathbb {C})$
.
Let
![]() $\Delta \subset \mathfrak {h}^{\ast }$
be the root system of
$\Delta \subset \mathfrak {h}^{\ast }$
be the root system of
![]() $\mathfrak {g}$
,
$\mathfrak {g}$
,
![]() $\Delta ^{+} \subset \Delta $
the set of positive roots, and
$\Delta ^{+} \subset \Delta $
the set of positive roots, and
![]() $\{ \alpha _{i} \}_{i \in I} \subset \Delta ^{+}$
the set of simple roots. We denote by
$\{ \alpha _{i} \}_{i \in I} \subset \Delta ^{+}$
the set of simple roots. We denote by
![]() $\alpha ^{\vee } \in \mathfrak {h}$
the coroot corresponding to
$\alpha ^{\vee } \in \mathfrak {h}$
the coroot corresponding to
![]() $\alpha \in \Delta $
. Also, we denote by
$\alpha \in \Delta $
. Also, we denote by
![]() $\theta \in \Delta ^+$
the highest root of
$\theta \in \Delta ^+$
the highest root of
![]() $\Delta $
and set
$\Delta $
and set
![]() $\rho := (1/2) \sum _{\alpha \in \Delta ^{+}} \alpha $
. The root lattice Q and the coroot lattice
$\rho := (1/2) \sum _{\alpha \in \Delta ^{+}} \alpha $
. The root lattice Q and the coroot lattice
![]() $Q^{\vee }$
of
$Q^{\vee }$
of
![]() $\mathfrak {g}$
are defined by
$\mathfrak {g}$
are defined by
![]() $Q := \sum _{i \in I} \mathbb {Z} \alpha _{i}$
and
$Q := \sum _{i \in I} \mathbb {Z} \alpha _{i}$
and
![]() $Q^{\vee } := \sum _{i \in I} \mathbb {Z} \alpha _{i}^{\vee }$
. In addition, for
$Q^{\vee } := \sum _{i \in I} \mathbb {Z} \alpha _{i}^{\vee }$
. In addition, for
![]() $\alpha \in \Delta $
, we set
$\alpha \in \Delta $
, we set
 $$ \begin{align*} \operatorname{\mathrm{sgn}}(\alpha):= \begin{cases} 1 & \text{if } \alpha \in \Delta^{+}, \\ -1 & \text{if } \alpha \in \Delta^{-}, \end{cases} \qquad |\alpha|:=\operatorname{\mathrm{sgn}}(\alpha)\alpha \in \Delta^{+}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{sgn}}(\alpha):= \begin{cases} 1 & \text{if } \alpha \in \Delta^{+}, \\ -1 & \text{if } \alpha \in \Delta^{-}, \end{cases} \qquad |\alpha|:=\operatorname{\mathrm{sgn}}(\alpha)\alpha \in \Delta^{+}. \end{align*} $$
For
![]() $i \in I$
, the weight
$i \in I$
, the weight
![]() $\varpi _{i} \in \mathfrak {h}^{\ast }$
given by
$\varpi _{i} \in \mathfrak {h}^{\ast }$
given by
![]() $\langle \varpi _{i}, \alpha _{j}^{\vee } \rangle = \delta _{i,j}$
for all
$\langle \varpi _{i}, \alpha _{j}^{\vee } \rangle = \delta _{i,j}$
for all
![]() $j \in I$
, where
$j \in I$
, where
![]() $\delta _{i,j}$
denotes the Kronecker delta, is called the i-th fundamental weight. The weight lattice P of
$\delta _{i,j}$
denotes the Kronecker delta, is called the i-th fundamental weight. The weight lattice P of
![]() $\mathfrak {g}$
is defined by
$\mathfrak {g}$
is defined by
![]() $P := \sum _{i \in I} \mathbb {Z} \varpi _{i}$
. We denote by
$P := \sum _{i \in I} \mathbb {Z} \varpi _{i}$
. We denote by
![]() $\mathbb {Z}[P]$
the group algebra of P, which is the associative algebra generated by formal elements
$\mathbb {Z}[P]$
the group algebra of P, which is the associative algebra generated by formal elements
![]() $\mathbf {e}^{\nu }$
,
$\mathbf {e}^{\nu }$
,
![]() $\nu \in P$
, where the product is defined by
$\nu \in P$
, where the product is defined by
![]() $\mathbf {e}^{\mu } \mathbf {e}^{\nu } := \mathbf {e}^{\mu + \nu }$
for
$\mathbf {e}^{\mu } \mathbf {e}^{\nu } := \mathbf {e}^{\mu + \nu }$
for
![]() $\mu , \nu \in P$
; we identify the group algebra
$\mu , \nu \in P$
; we identify the group algebra
![]() $\mathbb {Z}[P]$
with the representation ring
$\mathbb {Z}[P]$
with the representation ring
![]() $R(H)$
of H.
$R(H)$
of H.
A reflection
![]() $s_{\alpha } \in GL(\mathfrak {h}^{\ast })$
,
$s_{\alpha } \in GL(\mathfrak {h}^{\ast })$
,
![]() $\alpha \in \Delta $
, is defined by
$\alpha \in \Delta $
, is defined by
![]() $s_{\alpha } \mu := \mu - \langle \mu , \alpha ^{\vee } \rangle \alpha $
for
$s_{\alpha } \mu := \mu - \langle \mu , \alpha ^{\vee } \rangle \alpha $
for
![]() $\mu \in \mathfrak {h}^{\ast }$
. We write
$\mu \in \mathfrak {h}^{\ast }$
. We write
![]() $s_{i} := s_{\alpha _{i}}$
for
$s_{i} := s_{\alpha _{i}}$
for
![]() $i \in I$
. Then the (finite) Weyl group W of
$i \in I$
. Then the (finite) Weyl group W of
![]() $\mathfrak {g}$
is defined to be the subgroup of
$\mathfrak {g}$
is defined to be the subgroup of
![]() $GL(\mathfrak {h}^{\ast })$
generated by
$GL(\mathfrak {h}^{\ast })$
generated by
![]() $\{ s_{i} \}_{i \in I}$
; that is,
$\{ s_{i} \}_{i \in I}$
; that is,
![]() $W := \langle s_{i} \mid i \in I \rangle $
. For
$W := \langle s_{i} \mid i \in I \rangle $
. For
![]() $w \in W$
, there exist
$w \in W$
, there exist
![]() $i_{1}, \ldots , i_{r} \in I$
such that
$i_{1}, \ldots , i_{r} \in I$
such that
![]() $w = s_{i_{1}} \cdots s_{i_{r}}$
. If r is minimal, then the product
$w = s_{i_{1}} \cdots s_{i_{r}}$
. If r is minimal, then the product
![]() $s_{i_{1}} \cdots s_{i_{r}}$
is called a reduced expression for w, and r is called the length of w; we denote by
$s_{i_{1}} \cdots s_{i_{r}}$
is called a reduced expression for w, and r is called the length of w; we denote by
![]() $\ell (w)$
the length of w. Note that a reduced expression for w is not unique, but the length
$\ell (w)$
the length of w. Note that a reduced expression for w is not unique, but the length
![]() $\ell (w)$
is uniquely determined. Also, the affine Weyl group
$\ell (w)$
is uniquely determined. Also, the affine Weyl group
![]() $W_{\mathrm {af}}$
of
$W_{\mathrm {af}}$
of
![]() $\mathfrak {g}$
is, by definition, the semi-direct product group
$\mathfrak {g}$
is, by definition, the semi-direct product group
![]() $W \ltimes \{ t_{\xi } \mid \xi \in Q^{\vee } \}$
of W and the abelian group
$W \ltimes \{ t_{\xi } \mid \xi \in Q^{\vee } \}$
of W and the abelian group
![]() $\{ t_{\xi } \mid \xi \in Q^{\vee } \} \cong Q^{\vee }$
, where
$\{ t_{\xi } \mid \xi \in Q^{\vee } \} \cong Q^{\vee }$
, where
![]() $t_{\xi }$
denotes the translation in
$t_{\xi }$
denotes the translation in
![]() $\mathfrak {h}^{\ast }$
corresponding to
$\mathfrak {h}^{\ast }$
corresponding to
![]() $\xi \in Q^{\vee }$
.
$\xi \in Q^{\vee }$
.
Definition 2.1. The quantum Bruhat graph of W, denoted by
![]() $\mathrm {QBG}(W)$
, is the
$\mathrm {QBG}(W)$
, is the
![]() $\Delta ^{+}$
-labeled directed graph whose vertices are the elements of W and whose edges are of the following form:
$\Delta ^{+}$
-labeled directed graph whose vertices are the elements of W and whose edges are of the following form:
![]() $x \xrightarrow {\hspace {2pt}\alpha \hspace {2pt}} y$
, with
$x \xrightarrow {\hspace {2pt}\alpha \hspace {2pt}} y$
, with
![]() $x, y \in W$
and
$x, y \in W$
and
![]() $\alpha \in \Delta ^{+}$
, such that
$\alpha \in \Delta ^{+}$
, such that
![]() $y = x s_{\alpha }$
and either of the following holds: (B)
$y = x s_{\alpha }$
and either of the following holds: (B)
![]() $\ell (y) = \ell (x) + 1$
, or (Q)
$\ell (y) = \ell (x) + 1$
, or (Q)
![]() $\ell (y) = \ell (x) + 1 - 2 \langle \rho , \alpha ^{\vee } \rangle $
. An edge satisfying (B) (resp., (Q)) is called a Bruhat edge (resp., quantum edge).
$\ell (y) = \ell (x) + 1 - 2 \langle \rho , \alpha ^{\vee } \rangle $
. An edge satisfying (B) (resp., (Q)) is called a Bruhat edge (resp., quantum edge).
For an edge
![]() $x \xrightarrow {\hspace {2pt}\alpha \hspace {2pt}} y$
in
$x \xrightarrow {\hspace {2pt}\alpha \hspace {2pt}} y$
in
![]() $\mathrm {QBG}(W)$
, we sometimes write
$\mathrm {QBG}(W)$
, we sometimes write
![]() $x \xrightarrow [\mathsf {B}]{\hspace {2pt}\alpha \hspace {2pt}} y$
(resp.,
$x \xrightarrow [\mathsf {B}]{\hspace {2pt}\alpha \hspace {2pt}} y$
(resp.,
![]() $x \xrightarrow [\mathsf {Q}]{\hspace {2pt}\alpha \hspace {2pt}} y$
) to indicate that the edge is a Bruhat (resp., quantum) edge.
$x \xrightarrow [\mathsf {Q}]{\hspace {2pt}\alpha \hspace {2pt}} y$
) to indicate that the edge is a Bruhat (resp., quantum) edge.
2.2 The root system of type A
We recall the root system of type A. In the rest of this paper, when G is of type A, we use the notation introduced in this subsection. Also, we set
![]() $[m]:=\{ 1,2,\dots ,m \}$
for
$[m]:=\{ 1,2,\dots ,m \}$
for
![]() $m \in \mathbb {Z}_{\ge 0}$
.
$m \in \mathbb {Z}_{\ge 0}$
.
Assume that G is of type
![]() $A_{n}$
(i.e.,
$A_{n}$
(i.e.,
![]() $G = SL_{n+1}(\mathbb {C})$
). Then
$G = SL_{n+1}(\mathbb {C})$
). Then
![]() $\mathfrak {g} = \mathfrak {sl}_{n+1}(\mathbb {C})$
, and
$\mathfrak {g} = \mathfrak {sl}_{n+1}(\mathbb {C})$
, and
![]() $\mathfrak {h} := \{ h \in \mathfrak {g} \mid h \text { is a diagonal matrix}\}$
is a Cartan subalgebra of
$\mathfrak {h} := \{ h \in \mathfrak {g} \mid h \text { is a diagonal matrix}\}$
is a Cartan subalgebra of
![]() $\mathfrak {g}$
. We let
$\mathfrak {g}$
. We let
![]() $\{\epsilon _{k} \mid k \in [n+1] \}$
be the standard basis of
$\{\epsilon _{k} \mid k \in [n+1] \}$
be the standard basis of
![]() $\mathbb {Z}^{n+1}$
and realize the weight lattice as
$\mathbb {Z}^{n+1}$
and realize the weight lattice as
![]() $P=\mathbb {Z}^{n+1}/\mathbb {Z}(\epsilon _1+\cdots +\epsilon _{n+1})$
. By abuse of notation, we continue to denote the image of
$P=\mathbb {Z}^{n+1}/\mathbb {Z}(\epsilon _1+\cdots +\epsilon _{n+1})$
. By abuse of notation, we continue to denote the image of
![]() $\epsilon _k$
in P by the same symbol. Thus,
$\epsilon _k$
in P by the same symbol. Thus,
![]() $\varpi _k := \epsilon _1+\dotsm +\epsilon _k$
, for
$\varpi _k := \epsilon _1+\dotsm +\epsilon _k$
, for
![]() $k \in I = [n]$
, are the fundamental weights of
$k \in I = [n]$
, are the fundamental weights of
![]() $\mathfrak {g}$
, and
$\mathfrak {g}$
, and
![]() $\epsilon _1 + \cdots + \epsilon _n + \epsilon _{n+1} = 0$
. We set
$\epsilon _1 + \cdots + \epsilon _n + \epsilon _{n+1} = 0$
. We set
![]() $\alpha _{i} := \epsilon _{i} - \epsilon _{i+1}$
for
$\alpha _{i} := \epsilon _{i} - \epsilon _{i+1}$
for
![]() $i \in I = [n]$
and
$i \in I = [n]$
and
![]() $\alpha _{i, j} := \alpha _{i} + \alpha _{i+1} + \cdots + \alpha _{j}=\epsilon _{i}-\epsilon _{j+1}$
for
$\alpha _{i, j} := \alpha _{i} + \alpha _{i+1} + \cdots + \alpha _{j}=\epsilon _{i}-\epsilon _{j+1}$
for
![]() $i, j \in [n]$
with
$i, j \in [n]$
with
![]() $i \le j$
. Then
$i \le j$
. Then
![]() $\Delta = \{ \pm \alpha _{i,j} \mid 1 \le i \le j \le n \}$
forms a root system of
$\Delta = \{ \pm \alpha _{i,j} \mid 1 \le i \le j \le n \}$
forms a root system of
![]() $\mathfrak {g}$
, with the set of positive roots
$\mathfrak {g}$
, with the set of positive roots
![]() $\Delta ^+ = \{ \alpha _{i,j} \mid 1 \le i \le j \le n \}$
and the set of simple roots
$\Delta ^+ = \{ \alpha _{i,j} \mid 1 \le i \le j \le n \}$
and the set of simple roots
![]() $\{ \alpha _{1}, \ldots , \alpha _{n} \}$
.
$\{ \alpha _{1}, \ldots , \alpha _{n} \}$
.
The Weyl group of
![]() $\mathfrak {g}=\mathfrak {sl}_{n+1}(\mathbb {C})$
is, by definition, the subgroup
$\mathfrak {g}=\mathfrak {sl}_{n+1}(\mathbb {C})$
is, by definition, the subgroup
![]() $W = \langle s_{1}, \ldots , s_{n} \rangle $
of
$W = \langle s_{1}, \ldots , s_{n} \rangle $
of
![]() $GL(\mathfrak {h}^{\ast })$
, where
$GL(\mathfrak {h}^{\ast })$
, where
![]() $s_{1}, \ldots , s_{n}$
are the simple reflections. For
$s_{1}, \ldots , s_{n}$
are the simple reflections. For
![]() $i,j \in [n+1]$
with
$i,j \in [n+1]$
with
![]() $i < j$
, we denote by
$i < j$
, we denote by
![]() $(i,j)$
the transposition of i and j. It is known that the assignment
$(i,j)$
the transposition of i and j. It is known that the assignment
![]() $s_{1} \mapsto (1, 2),\, s_{2} \mapsto (2, 3),\,\dots ,\, s_{n} \mapsto (n, n+1)$
induces a group isomorphism
$s_{1} \mapsto (1, 2),\, s_{2} \mapsto (2, 3),\,\dots ,\, s_{n} \mapsto (n, n+1)$
induces a group isomorphism
![]() $W \xrightarrow {\sim } S_{n+1}$
, where
$W \xrightarrow {\sim } S_{n+1}$
, where
![]() $S_{n+1}$
denotes the symmetric group of degree
$S_{n+1}$
denotes the symmetric group of degree
![]() $n+1$
. By this isomorphism, we regard
$n+1$
. By this isomorphism, we regard
![]() $x \in W$
as a permutation on
$x \in W$
as a permutation on
![]() $[n+1]=\{ 1, \ldots , n+1 \}$
; in addition, it follows that
$[n+1]=\{ 1, \ldots , n+1 \}$
; in addition, it follows that
![]() $x \epsilon _{i} = \epsilon _{x(i)}$
for
$x \epsilon _{i} = \epsilon _{x(i)}$
for
![]() $i \in [n+1]$
. Also, the longest element of W, denoted by
$i \in [n+1]$
. Also, the longest element of W, denoted by
![]() $w_{\circ }$
, is regarded as the permutation
$w_{\circ }$
, is regarded as the permutation
 $$ \begin{align*} \begin{pmatrix} 1 & 2 & \cdots & n & n+1 \\ n+1 & n & \cdots & 2 & 1 \end{pmatrix}; \end{align*} $$
$$ \begin{align*} \begin{pmatrix} 1 & 2 & \cdots & n & n+1 \\ n+1 & n & \cdots & 2 & 1 \end{pmatrix}; \end{align*} $$
that is,
![]() $w_{\circ }$
is considered as the permutation defined by
$w_{\circ }$
is considered as the permutation defined by
![]() $w_{\circ }(k) = n+2-k$
for
$w_{\circ }(k) = n+2-k$
for
![]() $k \in [n+1]$
.
$k \in [n+1]$
.
We know from [Reference LenartLen, Proposition 3.6] the following.
Lemma 2.2. Let
![]() $x \in W \cong S_{n+1}$
, and
$x \in W \cong S_{n+1}$
, and
![]() $1 \le a < b \le n+1$
.
$1 \le a < b \le n+1$
.
-
(B) We have a Bruhat edge
 $x \xrightarrow {\hspace {2pt}(a,b)\hspace {2pt}} x \cdot (a,b)$
in
$x \xrightarrow {\hspace {2pt}(a,b)\hspace {2pt}} x \cdot (a,b)$
in
 $\mathrm {QBG}(W) = \mathrm {QBG}(S_{n+1})$
if and only if
$\mathrm {QBG}(W) = \mathrm {QBG}(S_{n+1})$
if and only if
 $x(a) < x(b)$
, and either
$x(a) < x(b)$
, and either
 $x(c) < x(a)$
or
$x(c) < x(a)$
or
 $x(b) < x(c)$
holds for each
$x(b) < x(c)$
holds for each
 $a < c < b$
.
$a < c < b$
. -
(Q) We have a quantum edge
 $x \xrightarrow {\hspace {2pt}(a,b)\hspace {2pt}} x \cdot (a,b)$
in
$x \xrightarrow {\hspace {2pt}(a,b)\hspace {2pt}} x \cdot (a,b)$
in
 $\mathrm {QBG}(W) = \mathrm {QBG}(S_{n+1})$
if and only if
$\mathrm {QBG}(W) = \mathrm {QBG}(S_{n+1})$
if and only if
 $x(a)> x(b)$
, and
$x(a)> x(b)$
, and
 $x(b) < x(c) < x(a)$
for all
$x(b) < x(c) < x(a)$
for all
 $a < c < b$
.
$a < c < b$
.
2.3 Equivariant K-groups of semi-infinite flag manifolds
Let
![]() $\mathbf {Q}_{G}^{\mathrm {rat}}$
denote the semi-infinite flag manifold associated to G, which is a (reduced) ind-scheme of ind-infinite type whose set of
$\mathbf {Q}_{G}^{\mathrm {rat}}$
denote the semi-infinite flag manifold associated to G, which is a (reduced) ind-scheme of ind-infinite type whose set of
![]() $\mathbb {C}$
-valued points is
$\mathbb {C}$
-valued points is
![]() $G(\mathbb {C}(\!(z)\!))/(H(\mathbb {C}) \cdot N(\mathbb {C}(\!(z)\!)))$
(see [Reference Kato, Naito and SagakiKaNS, Reference KatoKat2] for details), where G is a connected, simply-connected, simple algebraic group over
$G(\mathbb {C}(\!(z)\!))/(H(\mathbb {C}) \cdot N(\mathbb {C}(\!(z)\!)))$
(see [Reference Kato, Naito and SagakiKaNS, Reference KatoKat2] for details), where G is a connected, simply-connected, simple algebraic group over
![]() $\mathbb {C}$
,
$\mathbb {C}$
,
![]() $B=HN$
is a Borel subgroup, H is a maximal torus, and N is the unipotent radical of B; note that
$B=HN$
is a Borel subgroup, H is a maximal torus, and N is the unipotent radical of B; note that
![]() $\mathbf {Q}_{G}^{\mathrm {rat}}$
can be thought of as an inductive limit of copies of the (reduced) closed subscheme
$\mathbf {Q}_{G}^{\mathrm {rat}}$
can be thought of as an inductive limit of copies of the (reduced) closed subscheme
![]() $\mathbf {Q}_{G} \subset \prod _{i \in I} \mathbb {P}(L(\varpi _{i}) \otimes _{\mathbb {C}} \mathbb {C}[\![z]\!])$
of infinite type, introduced in [Reference Finkelberg and MirkovicFM, Section 4.1], where
$\mathbf {Q}_{G} \subset \prod _{i \in I} \mathbb {P}(L(\varpi _{i}) \otimes _{\mathbb {C}} \mathbb {C}[\![z]\!])$
of infinite type, introduced in [Reference Finkelberg and MirkovicFM, Section 4.1], where
![]() $L(\varpi _{i})$
is the irreducible highest weight G-module of highest weight
$L(\varpi _{i})$
is the irreducible highest weight G-module of highest weight
![]() $\varpi _{i}$
. One has the semi-infinite Schubert (sub)variety
$\varpi _{i}$
. One has the semi-infinite Schubert (sub)variety
![]() $\mathbf {Q}_{G}(x) \subset \mathbf {Q}_{G}^{\mathrm {rat}}$
associated to each element x of the affine Weyl group
$\mathbf {Q}_{G}(x) \subset \mathbf {Q}_{G}^{\mathrm {rat}}$
associated to each element x of the affine Weyl group
![]() $W_{\mathrm {af}} \cong W \ltimes Q^{\vee }$
, with
$W_{\mathrm {af}} \cong W \ltimes Q^{\vee }$
, with
![]() $W = \langle s_i \mid i \in I \rangle $
the (finite) Weyl group and
$W = \langle s_i \mid i \in I \rangle $
the (finite) Weyl group and
![]() $Q^{\vee } = \sum _{i \in I} \mathbb {Z} \alpha _i^{\vee }$
the coroot lattice of G; note that
$Q^{\vee } = \sum _{i \in I} \mathbb {Z} \alpha _i^{\vee }$
the coroot lattice of G; note that
![]() $\mathbf {Q}_{G}(x)$
is, by definition, the closure of the orbit under the Iwahori subgroup
$\mathbf {Q}_{G}(x)$
is, by definition, the closure of the orbit under the Iwahori subgroup
![]() $\mathbf {I} := (\mathrm {ev}_{z = 0})^{-1}(B) \subset G(\mathbb {C}[\![z]\!])$
through the (
$\mathbf {I} := (\mathrm {ev}_{z = 0})^{-1}(B) \subset G(\mathbb {C}[\![z]\!])$
through the (
![]() $H \times \mathbb {C}^{*}$
)-fixed point labeled by
$H \times \mathbb {C}^{*}$
)-fixed point labeled by
![]() $x \in W_{\mathrm {af}}$
in exactly the same way as in [Reference Kato, Naito and SagakiKaNS, Section 4.2] and [Reference OrrO, Section 2.3], and that
$x \in W_{\mathrm {af}}$
in exactly the same way as in [Reference Kato, Naito and SagakiKaNS, Section 4.2] and [Reference OrrO, Section 2.3], and that
![]() $\mathbf {Q}_{G}(x)$
is contained in
$\mathbf {Q}_{G}(x)$
is contained in
![]() $\mathbf {Q}_{G}(e) = \mathbf {Q}_{G}$
for all
$\mathbf {Q}_{G}(e) = \mathbf {Q}_{G}$
for all
![]() $x \in W_{\mathrm {af}}^{\geq 0} := \{ x = w t_{\xi } \in W_{\mathrm {af}} \mid w \in W, \xi \in Q^{\vee ,+} \}$
, where
$x \in W_{\mathrm {af}}^{\geq 0} := \{ x = w t_{\xi } \in W_{\mathrm {af}} \mid w \in W, \xi \in Q^{\vee ,+} \}$
, where
![]() $Q^{\vee , +} := \sum _{i \in I} \mathbb {Z}_{\geq 0} \alpha _{i}^{\vee } \subset Q^{\vee }$
. Also, for each weight
$Q^{\vee , +} := \sum _{i \in I} \mathbb {Z}_{\geq 0} \alpha _{i}^{\vee } \subset Q^{\vee }$
. Also, for each weight
![]() $\nu = \sum _{i \in I} m_{i} \varpi _{i} \in P$
with
$\nu = \sum _{i \in I} m_{i} \varpi _{i} \in P$
with
![]() $m_{i} \in \mathbb {Z}$
, we have a (
$m_{i} \in \mathbb {Z}$
, we have a (
![]() $G(\mathbb {C}[\![z]\!]) \rtimes \mathbb {C}^{*}$
)-equivariant line bundle
$G(\mathbb {C}[\![z]\!]) \rtimes \mathbb {C}^{*}$
)-equivariant line bundle
![]() $\mathcal{O}_{\mathbf {Q}_{G}}(\nu )$
over
$\mathcal{O}_{\mathbf {Q}_{G}}(\nu )$
over
![]() $\mathbf {Q}_{G}$
, which is given by the restriction of the line bundle
$\mathbf {Q}_{G}$
, which is given by the restriction of the line bundle
![]() $\boxtimes _{i \in I} \mathcal{O}(m_{i})$
over
$\boxtimes _{i \in I} \mathcal{O}(m_{i})$
over
![]() $\prod _{i \in I} \mathbb {P}(L(\varpi _{i}) \otimes _{\mathbb {C}} \mathbb {C}[\![z]\!])$
.
$\prod _{i \in I} \mathbb {P}(L(\varpi _{i}) \otimes _{\mathbb {C}} \mathbb {C}[\![z]\!])$
.
The
![]() $(H \times \mathbb {C}^{*})$
-equivariant K-group
$(H \times \mathbb {C}^{*})$
-equivariant K-group
![]() $K_{H \times \mathbb {C}^{\ast }}(\mathbf {Q}_{G})$
is a module over
$K_{H \times \mathbb {C}^{\ast }}(\mathbf {Q}_{G})$
is a module over
![]() $\mathbb {Z}[q,q^{-1}][P]$
(equivariant parameters) and has the semi-infinite Schubert classes
$\mathbb {Z}[q,q^{-1}][P]$
(equivariant parameters) and has the semi-infinite Schubert classes
![]() $[\mathcal{O}_{\mathbf {Q}_{G}(x)}]$
associated to
$[\mathcal{O}_{\mathbf {Q}_{G}(x)}]$
associated to
![]() $x \in W_{\mathrm {af}}^{\geq 0} \simeq W \times Q^{\vee ,+}$
as a topological basis (in the sense of [Reference Kato, Naito and SagakiKaNS, Proposition 5.11]) over
$x \in W_{\mathrm {af}}^{\geq 0} \simeq W \times Q^{\vee ,+}$
as a topological basis (in the sense of [Reference Kato, Naito and SagakiKaNS, Proposition 5.11]) over
![]() $\mathbb {Z}[q,q^{-1}][P]$
, where
$\mathbb {Z}[q,q^{-1}][P]$
, where
![]() $P = \sum _{i \in I} \mathbb {Z} \varpi _{i}$
is the weight lattice of G whose group algebra
$P = \sum _{i \in I} \mathbb {Z} \varpi _{i}$
is the weight lattice of G whose group algebra
![]() $\mathbb {Z}[P] = \bigoplus _{\nu \in P} \mathbb {Z}\mathbf {e}^{\nu }$
is identified with the representation ring
$\mathbb {Z}[P] = \bigoplus _{\nu \in P} \mathbb {Z}\mathbf {e}^{\nu }$
is identified with the representation ring
![]() $R(H)$
of H, and
$R(H)$
of H, and
![]() $q \in R(\mathbb {C}^{*})$
corresponds to the loop rotation action of
$q \in R(\mathbb {C}^{*})$
corresponds to the loop rotation action of
![]() $\mathbb {C}^{*}$
. More precisely, the K-group
$\mathbb {C}^{*}$
. More precisely, the K-group
![]() $K_{H \times \mathbb {C}^{*}}(\mathbf {Q}_{G})$
is defined to be the
$K_{H \times \mathbb {C}^{*}}(\mathbf {Q}_{G})$
is defined to be the
![]() $\mathbb {Z}[q, q^{-1}][P]$
-submodule of the equivariant K-group
$\mathbb {Z}[q, q^{-1}][P]$
-submodule of the equivariant K-group
![]() $\widetilde {K}^{\prime }(\mathbf {Q}_{G})$
of
$\widetilde {K}^{\prime }(\mathbf {Q}_{G})$
of
![]() $\mathbf {Q}_{G}$
, introduced in [Reference KatoKat1, Section 1.5], consisting of all those convergent (in the sense of [Reference Kato, Naito and SagakiKaNS, Proposition 5.11]) formal infinite linear combinations of the classes
$\mathbf {Q}_{G}$
, introduced in [Reference KatoKat1, Section 1.5], consisting of all those convergent (in the sense of [Reference Kato, Naito and SagakiKaNS, Proposition 5.11]) formal infinite linear combinations of the classes
![]() $[\mathcal{O}_{\mathbf {Q}_{G}(x)}]$
,
$[\mathcal{O}_{\mathbf {Q}_{G}(x)}]$
,
![]() $x \in W_{\mathrm {af}}^{\geq 0}$
, of the structure sheaves
$x \in W_{\mathrm {af}}^{\geq 0}$
, of the structure sheaves
![]() $\mathcal{O}_{\mathbf {Q}_{G}(x)}$
of the semi-infinite Schubert varieties
$\mathcal{O}_{\mathbf {Q}_{G}(x)}$
of the semi-infinite Schubert varieties
![]() $\mathbf {Q}_{G}(x) \subset \mathbf {Q}_{G}$
with coefficients
$\mathbf {Q}_{G}(x) \subset \mathbf {Q}_{G}$
with coefficients
![]() $a_{x} \in \mathbb {Z}[q, q^{-1}][P]$
; briefly speaking, convergence holds if the sum
$a_{x} \in \mathbb {Z}[q, q^{-1}][P]$
; briefly speaking, convergence holds if the sum
![]() $\sum _{x \in W_{\mathrm {af}}^{\geq 0}} \vert a_{x} \vert $
of the absolute values
$\sum _{x \in W_{\mathrm {af}}^{\geq 0}} \vert a_{x} \vert $
of the absolute values
![]() $|a_{x}|$
lies in
$|a_{x}|$
lies in
![]() $\mathbb {Z}[P](\!( q^{-1} )\!)$
. For each
$\mathbb {Z}[P](\!( q^{-1} )\!)$
. For each
![]() $x \in W_{\mathrm {af}}^{\geq 0}$
and
$x \in W_{\mathrm {af}}^{\geq 0}$
and
![]() $\nu \in P$
, it follows from [Reference Kouno, Lenart and NaitoKoLN, Theorem 5.16] and (the proof of) [Reference Kato, Naito and SagakiKaNS, Corollary 5.12] that the twisted semi-infinite Schubert class
$\nu \in P$
, it follows from [Reference Kouno, Lenart and NaitoKoLN, Theorem 5.16] and (the proof of) [Reference Kato, Naito and SagakiKaNS, Corollary 5.12] that the twisted semi-infinite Schubert class
![]() $[\mathcal{O}_{\mathbf {Q}_{G}(x)}(\nu )] := [\mathcal{O}_{\mathbf {Q}_{G}(x)}] \otimes [\mathcal{O}_{\mathbf {Q}_{G}}(\nu )]$
, defined by the tensor product in
$[\mathcal{O}_{\mathbf {Q}_{G}(x)}(\nu )] := [\mathcal{O}_{\mathbf {Q}_{G}(x)}] \otimes [\mathcal{O}_{\mathbf {Q}_{G}}(\nu )]$
, defined by the tensor product in
![]() $\widetilde {K}^{\prime }(\mathbf {Q}_{G})$
(see [Reference KatoKat1, Theorem 1.25]), indeed lies in
$\widetilde {K}^{\prime }(\mathbf {Q}_{G})$
(see [Reference KatoKat1, Theorem 1.25]), indeed lies in
![]() $K_{H \times \mathbb {C}^{\ast }}(\mathbf {Q}_{G})$
; in particular, we have
$K_{H \times \mathbb {C}^{\ast }}(\mathbf {Q}_{G})$
; in particular, we have
![]() $[\mathcal{O}_{\mathbf {Q}_{G}}(\nu )] = [\mathcal{O}_{\mathbf {Q}_{G}}] \otimes [\mathcal{O}_{\mathbf {Q}_{G}}(\nu )] \in K_{H \times \mathbb {C}^{\ast }}(\mathbf {Q}_{G})$
for all
$[\mathcal{O}_{\mathbf {Q}_{G}}(\nu )] = [\mathcal{O}_{\mathbf {Q}_{G}}] \otimes [\mathcal{O}_{\mathbf {Q}_{G}}(\nu )] \in K_{H \times \mathbb {C}^{\ast }}(\mathbf {Q}_{G})$
for all
![]() $\nu \in P$
.
$\nu \in P$
.
Also, following [Reference KatoKat1, Section 1.5], we define the H-equivariant K-group
![]() $K_{H}(\mathbf {Q}_{G})$
of
$K_{H}(\mathbf {Q}_{G})$
of
![]() $\mathbf {Q}_{G}$
to be the specialization (of coefficients) at
$\mathbf {Q}_{G}$
to be the specialization (of coefficients) at
![]() $q = 1$
of
$q = 1$
of
![]() $\widetilde {K}^{\prime }(\mathbf {Q}_{G})$
(or equivalently, of
$\widetilde {K}^{\prime }(\mathbf {Q}_{G})$
(or equivalently, of
![]() $K_{H \times \mathbb {C}^{*}}(\mathbf {Q}_{G})$
), which turns out to be (cf. [Reference KatoKat1, Lemma 1.22]) the
$K_{H \times \mathbb {C}^{*}}(\mathbf {Q}_{G})$
), which turns out to be (cf. [Reference KatoKat1, Lemma 1.22]) the
![]() $\mathbb {Z}[P]$
-module
$\mathbb {Z}[P]$
-module
![]() $\prod _{x \in W_{\mathrm {af}}^{\geq 0}} \mathbb {Z}[P][\mathcal{O}_{\mathbf {Q}_{G}(x)}]$
(direct product). Namely, the K-group
$\prod _{x \in W_{\mathrm {af}}^{\geq 0}} \mathbb {Z}[P][\mathcal{O}_{\mathbf {Q}_{G}(x)}]$
(direct product). Namely, the K-group
![]() $K_{H}(\mathbf {Q}_{G})$
consists of all infinite linear combinations of the semi-infinite Schubert classes
$K_{H}(\mathbf {Q}_{G})$
consists of all infinite linear combinations of the semi-infinite Schubert classes
![]() $[\mathcal{O}_{\mathbf {Q}_{G}(x)}]$
,
$[\mathcal{O}_{\mathbf {Q}_{G}(x)}]$
,
![]() $x \in W_{\mathrm {af}}^{\geq 0}$
, with coefficients in
$x \in W_{\mathrm {af}}^{\geq 0}$
, with coefficients in
![]() $\mathbb {Z}[P]$
; the semi-infinite Schubert classes
$\mathbb {Z}[P]$
; the semi-infinite Schubert classes
![]() $[\mathcal{O}_{\mathbf {Q}_{G}(x)}]$
,
$[\mathcal{O}_{\mathbf {Q}_{G}(x)}]$
,
![]() $x \in W_{\mathrm {af}}^{\geq 0}$
, form a topological basis of
$x \in W_{\mathrm {af}}^{\geq 0}$
, form a topological basis of
![]() $K_{H}(\mathbf {Q}_{G})$
over
$K_{H}(\mathbf {Q}_{G})$
over
![]() $\mathbb {Z}[P]$
. Then, for each
$\mathbb {Z}[P]$
. Then, for each
![]() $\nu \in P$
, a
$\nu \in P$
, a
![]() $\mathbb {Z}[P]$
-linear endomorphism
$\mathbb {Z}[P]$
-linear endomorphism
![]() $\bullet \otimes [\mathcal{O}_{\mathbf {Q}_{G}}(\nu )]$
of
$\bullet \otimes [\mathcal{O}_{\mathbf {Q}_{G}}(\nu )]$
of
![]() $K_{H}(\mathbf {Q}_{G})$
is induced from the
$K_{H}(\mathbf {Q}_{G})$
is induced from the
![]() $\mathbb {Z}[q, q^{-1}][P]$
-linear endomorphism
$\mathbb {Z}[q, q^{-1}][P]$
-linear endomorphism
![]() $\bullet \otimes [\mathcal{O}_{\mathbf {Q}_{G}}(\nu )]$
of
$\bullet \otimes [\mathcal{O}_{\mathbf {Q}_{G}}(\nu )]$
of
![]() $K_{H \times \mathbb {C}^{*}}(\mathbf {Q}_{G})$
by the specialization (of coefficients) at
$K_{H \times \mathbb {C}^{*}}(\mathbf {Q}_{G})$
by the specialization (of coefficients) at
![]() $q = 1$
(see [Reference KatoKat1, Theorem 1.26]); thus, we have
$q = 1$
(see [Reference KatoKat1, Theorem 1.26]); thus, we have
![]() $[\mathcal{O}_{\mathbf {Q}_{G}}(\nu )] = [\mathcal{O}_{\mathbf {Q}_{G}}] \otimes [\mathcal{O}_{\mathbf {Q}_{G}}(\nu )] \in K_{H}(\mathbf {Q}_{G})$
for
$[\mathcal{O}_{\mathbf {Q}_{G}}(\nu )] = [\mathcal{O}_{\mathbf {Q}_{G}}] \otimes [\mathcal{O}_{\mathbf {Q}_{G}}(\nu )] \in K_{H}(\mathbf {Q}_{G})$
for
![]() $\nu \in P$
. In addition, for
$\nu \in P$
. In addition, for
![]() $\xi \in Q^{\vee ,+}$
, a
$\xi \in Q^{\vee ,+}$
, a
![]() $\mathbb {Z}[P]$
-linear endomorphism
$\mathbb {Z}[P]$
-linear endomorphism
![]() $\mathsf {t}_{\xi }$
on
$\mathsf {t}_{\xi }$
on
![]() $K_{H}(\mathbf {Q}_{G})$
, given by
$K_{H}(\mathbf {Q}_{G})$
, given by
![]() $\mathsf {t}_{\xi }[\mathcal{O}_{\mathbf {Q}_{G}(x)}] := [\mathcal{O}_{\mathbf {Q}_{G}(x t_{\xi })}]$
for
$\mathsf {t}_{\xi }[\mathcal{O}_{\mathbf {Q}_{G}(x)}] := [\mathcal{O}_{\mathbf {Q}_{G}(x t_{\xi })}]$
for
![]() $x \in W_{\mathrm {af}}^{\geq 0}$
, is induced by the right action of
$x \in W_{\mathrm {af}}^{\geq 0}$
, is induced by the right action of
![]() $Q^{\vee } \subset H(\mathbb {C}(\!(z)\!))/H(\mathbb {C})$
on
$Q^{\vee } \subset H(\mathbb {C}(\!(z)\!))/H(\mathbb {C})$
on
![]() $\mathbf {Q}_{G}^{\mathrm {rat}}$
(see [Reference KatoKat1, equation (1.20)]); the
$\mathbf {Q}_{G}^{\mathrm {rat}}$
(see [Reference KatoKat1, equation (1.20)]); the
![]() $\mathbb {Z}[P]$
-linear endomorphism
$\mathbb {Z}[P]$
-linear endomorphism
![]() $\mathsf {t}_{\xi }$
of
$\mathsf {t}_{\xi }$
of
![]() $K_{H}(\mathbf {Q}_{G})$
is also obtained by the specialization at
$K_{H}(\mathbf {Q}_{G})$
is also obtained by the specialization at
![]() $q = 1$
from the
$q = 1$
from the
![]() $\mathbb {Z}[q, q^{-1}]$
-linear endomorphism of
$\mathbb {Z}[q, q^{-1}]$
-linear endomorphism of
![]() $K_{H \times \mathbb {C}^{*}}(\mathbf {Q}_{G})$
given by the same formula. We know from [Reference KatoKat1, Theorem 1.26] (cf. [Reference OrrO, Proposition 2.4])
$K_{H \times \mathbb {C}^{*}}(\mathbf {Q}_{G})$
given by the same formula. We know from [Reference KatoKat1, Theorem 1.26] (cf. [Reference OrrO, Proposition 2.4])
for
![]() $x \in W_{\mathrm {af}}^{\geq 0}$
,
$x \in W_{\mathrm {af}}^{\geq 0}$
,
![]() $\xi \in Q^{\vee ,+}$
, and
$\xi \in Q^{\vee ,+}$
, and
![]() $\nu \in P$
; for
$\nu \in P$
; for
![]() $j \in I$
, we set
$j \in I$
, we set
![]() $\mathsf {t}_{j} := \mathsf {t}_{\alpha _j^{\vee }}$
. Since the semi-infinite Schubert classes
$\mathsf {t}_{j} := \mathsf {t}_{\alpha _j^{\vee }}$
. Since the semi-infinite Schubert classes
![]() $[\mathcal{O}_{\mathbf {Q}_{G}(x)}]$
,
$[\mathcal{O}_{\mathbf {Q}_{G}(x)}]$
,
![]() $x \in W_{\mathrm {af}}^{\geq 0}$
, form a topological basis of
$x \in W_{\mathrm {af}}^{\geq 0}$
, form a topological basis of
![]() $K_{H}(\mathbf {Q}_{G})$
over
$K_{H}(\mathbf {Q}_{G})$
over
![]() $\mathbb {Z}[P]$
, it follows that
$\mathbb {Z}[P]$
, it follows that
for an arbitrary element
![]() $\bullet \in K_{H}(\mathbf {Q}_{G})$
and
$\bullet \in K_{H}(\mathbf {Q}_{G})$
and
![]() $\xi \in Q^{\vee ,+}$
,
$\xi \in Q^{\vee ,+}$
,
![]() $\nu \in P$
.
$\nu \in P$
.
Remark 2.3. Let
![]() $\mathsf {F}_{1},\dots ,\mathsf {F}_{N}$
be polynomials in
$\mathsf {F}_{1},\dots ,\mathsf {F}_{N}$
be polynomials in
![]() $\mathsf {t}_{i}$
,
$\mathsf {t}_{i}$
,
![]() $i \in I$
, and let
$i \in I$
, and let
![]() $\nu _{1},\dots ,\nu _{N} \in P$
. When we write
$\nu _{1},\dots ,\nu _{N} \in P$
. When we write
![]() $(\mathsf {F}_{1}[\mathcal{O}_{\mathbf {Q}_{G}}( \nu _{1} )]) \otimes (\mathsf {F}_{2}[\mathcal{O}_{\mathbf {Q}_{G}}( \nu _{2} )]) \otimes \cdots \otimes (\mathsf {F}_{N}[\mathcal{O}_{\mathbf {Q}_{G}}( \nu _{N} )]) \otimes \bullet $
for
$(\mathsf {F}_{1}[\mathcal{O}_{\mathbf {Q}_{G}}( \nu _{1} )]) \otimes (\mathsf {F}_{2}[\mathcal{O}_{\mathbf {Q}_{G}}( \nu _{2} )]) \otimes \cdots \otimes (\mathsf {F}_{N}[\mathcal{O}_{\mathbf {Q}_{G}}( \nu _{N} )]) \otimes \bullet $
for
![]() $\bullet \in K_{H}(\mathbf {Q}_{G})$
, it is always understood to be the element
$\bullet \in K_{H}(\mathbf {Q}_{G})$
, it is always understood to be the element
![]() $(\mathsf {F}_{1}\mathsf {F}_{2} \cdots \mathsf {F}_{N})([\mathcal{O}_{\mathbf {Q}_{G}}( \nu _{1} + \nu _{2} + \cdots + \nu _{N} )] \otimes \bullet )$
in
$(\mathsf {F}_{1}\mathsf {F}_{2} \cdots \mathsf {F}_{N})([\mathcal{O}_{\mathbf {Q}_{G}}( \nu _{1} + \nu _{2} + \cdots + \nu _{N} )] \otimes \bullet )$
in
![]() $K_{H}(\mathbf {Q}_{G})$
. Namely, for
$K_{H}(\mathbf {Q}_{G})$
. Namely, for
![]() $\bullet \in K_{H}(\mathbf {Q}_{G})$
, we always understand that
$\bullet \in K_{H}(\mathbf {Q}_{G})$
, we always understand that
 $$ \begin{align*} \begin{aligned} & (\mathsf{F}_{1}[\mathcal{O}_{\mathbf{Q}_{G}}( \nu_{1} )]) \otimes (\mathsf{F}_{2}[\mathcal{O}_{\mathbf{Q}_{G}}( \nu_{2} )]) \otimes \cdots \otimes (\mathsf{F}_{N}[\mathcal{O}_{\mathbf{Q}_{G}}( \nu_{N} )]) \otimes \bullet \\ &\quad = (\mathsf{F}_{1}\mathsf{F}_{2} \cdots \mathsf{F}_{N}) ([\mathcal{O}_{\mathbf{Q}_{G}}( \nu_{1} + \nu_{2} + \cdots + \nu_{N} )] \otimes \bullet). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} & (\mathsf{F}_{1}[\mathcal{O}_{\mathbf{Q}_{G}}( \nu_{1} )]) \otimes (\mathsf{F}_{2}[\mathcal{O}_{\mathbf{Q}_{G}}( \nu_{2} )]) \otimes \cdots \otimes (\mathsf{F}_{N}[\mathcal{O}_{\mathbf{Q}_{G}}( \nu_{N} )]) \otimes \bullet \\ &\quad = (\mathsf{F}_{1}\mathsf{F}_{2} \cdots \mathsf{F}_{N}) ([\mathcal{O}_{\mathbf{Q}_{G}}( \nu_{1} + \nu_{2} + \cdots + \nu_{N} )] \otimes \bullet). \end{aligned} \end{align*} $$
2.4 An explicit formula expressing the semi-infinite Schubert class associated to
 $w_{\circ }$
$w_{\circ }$
In this subsection, we assume that
![]() $G = SL_{n+1}(\mathbb {C})$
and hence
$G = SL_{n+1}(\mathbb {C})$
and hence
![]() $\mathfrak {g} = \mathfrak {sl}_{n+1}(\mathbb {C})$
, which is of type
$\mathfrak {g} = \mathfrak {sl}_{n+1}(\mathbb {C})$
, which is of type
![]() $A_{n}$
. For
$A_{n}$
. For
![]() $1 \le k \le n$
, we set
$1 \le k \le n$
, we set
 $$ \begin{align*} \begin{aligned} w_{k} &:= (s_{1}s_{2} \cdots s_{n}) (s_{1}s_{2} \cdots s_{n-1}) \cdots (s_{1}s_{2} \cdots s_{k+1}) (s_{1}s_{2} \cdots s_{k}) \\ & = (1,2,\dots,n+1)(1,2,\dots,n) \cdots (1,2,\dots,k+2)(1,2,\dots,k+1) \\[1.5mm] & = \begin{pmatrix} 1 & 2 & \cdots & k-1 & k & k+1 & \cdots & n & n+1 \\ n-k+2 & n-k+3 & \cdots & n & n+1 & n-k+1 & \cdots & 2 & 1 \end{pmatrix}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} w_{k} &:= (s_{1}s_{2} \cdots s_{n}) (s_{1}s_{2} \cdots s_{n-1}) \cdots (s_{1}s_{2} \cdots s_{k+1}) (s_{1}s_{2} \cdots s_{k}) \\ & = (1,2,\dots,n+1)(1,2,\dots,n) \cdots (1,2,\dots,k+2)(1,2,\dots,k+1) \\[1.5mm] & = \begin{pmatrix} 1 & 2 & \cdots & k-1 & k & k+1 & \cdots & n & n+1 \\ n-k+2 & n-k+3 & \cdots & n & n+1 & n-k+1 & \cdots & 2 & 1 \end{pmatrix}, \end{aligned} \end{align*} $$
which is an element of the Weyl group
![]() $W = S_{n+1}$
of
$W = S_{n+1}$
of
![]() $\mathfrak {g} = \mathfrak {sl}_{n+1}(\mathbb {C})$
; we set
$\mathfrak {g} = \mathfrak {sl}_{n+1}(\mathbb {C})$
; we set
![]() $w_{n+1}:=e$
by convention. Note that
$w_{n+1}:=e$
by convention. Note that
![]() $w_{1} = w_{\circ }$
, the longest element of W. Also, for a subset J of
$w_{1} = w_{\circ }$
, the longest element of W. Also, for a subset J of
![]() $[n+1]=\big \{1,2,\dots ,n+1\big \}$
, we set
$[n+1]=\big \{1,2,\dots ,n+1\big \}$
, we set
 $$ \begin{align} \epsilon_{J}:=\sum_{j \in J} \epsilon_{j}. \end{align} $$
$$ \begin{align} \epsilon_{J}:=\sum_{j \in J} \epsilon_{j}. \end{align} $$
We have
![]() $\epsilon _{J} \in W\varpi _{|J|}$
, where
$\epsilon _{J} \in W\varpi _{|J|}$
, where
![]() $\varpi _{0}=\varpi _{n+1}:=0$
by convention. In particular,
$\varpi _{0}=\varpi _{n+1}:=0$
by convention. In particular,
![]() $\epsilon _{J}$
is a minuscule weight (i.e.,
$\epsilon _{J}$
is a minuscule weight (i.e.,
![]() $\langle \epsilon _{J}, \alpha _{j}^{\vee } \rangle \in \{-1,0,1\}$
for all
$\langle \epsilon _{J}, \alpha _{j}^{\vee } \rangle \in \{-1,0,1\}$
for all
![]() $1 \le j \le n$
). We set
$1 \le j \le n$
). We set
 $$ \begin{align} J^{-} & := \big\{1 \le j \le n \mid j \notin J,\,j+1 \in J \big\} \nonumber \\ & = \big\{ 1 \le j \le n \mid \langle \epsilon_{J}, \alpha_{j}^{\vee} \rangle < 0 \big\} \nonumber \\ & = \big\{ 1 \le j \le n \mid \langle \epsilon_{J}, \alpha_{j}^{\vee} \rangle = -1 \big\}; \end{align} $$
$$ \begin{align} J^{-} & := \big\{1 \le j \le n \mid j \notin J,\,j+1 \in J \big\} \nonumber \\ & = \big\{ 1 \le j \le n \mid \langle \epsilon_{J}, \alpha_{j}^{\vee} \rangle < 0 \big\} \nonumber \\ & = \big\{ 1 \le j \le n \mid \langle \epsilon_{J}, \alpha_{j}^{\vee} \rangle = -1 \big\}; \end{align} $$
recall that
![]() $\alpha _{j} = \epsilon _{j}-\epsilon _{j+1}$
. For
$\alpha _{j} = \epsilon _{j}-\epsilon _{j+1}$
. For
![]() $0 \le p \le k \le n+1$
, we set
$0 \le p \le k \le n+1$
, we set
 $$ \begin{align} \mathfrak{F}^{k}_{p} := \sum_{ \begin{subarray}{c} J \subset [k] \\[1mm] |J|=p \end{subarray}} \left(\prod_{ j \in J^{-} } (1-\mathsf{t}_{j})\right)[\mathcal{O}_{\mathbf{Q}_{G}}( w_{\circ} \epsilon_{J} )] \in K_{H}(\mathbf{Q}_{G}), \end{align} $$
$$ \begin{align} \mathfrak{F}^{k}_{p} := \sum_{ \begin{subarray}{c} J \subset [k] \\[1mm] |J|=p \end{subarray}} \left(\prod_{ j \in J^{-} } (1-\mathsf{t}_{j})\right)[\mathcal{O}_{\mathbf{Q}_{G}}( w_{\circ} \epsilon_{J} )] \in K_{H}(\mathbf{Q}_{G}), \end{align} $$
where
![]() $[k]=\big \{1,2,\dots ,k\big \}$
; note that
$[k]=\big \{1,2,\dots ,k\big \}$
; note that
![]() $\mathfrak {F}^{k}_{0}=1$
. The proof of the following proposition will be given in Section 5.
$\mathfrak {F}^{k}_{0}=1$
. The proof of the following proposition will be given in Section 5.
Proposition 2.4. For
![]() $1 \leq k \leq n$
, the following equality holds in
$1 \leq k \leq n$
, the following equality holds in
![]() $K_{H}(\mathbf {Q}_{G})$
:
$K_{H}(\mathbf {Q}_{G})$
:
 $$ \begin{align} \left( \sum_{p=0}^{k}(-1)^{p} \mathbf{e}^{p \epsilon_{n+1-k}} \mathfrak{F}^{k}_{p} \right) \otimes [\mathcal{O}_{\mathbf{Q}_{G}(w_{k+1})}] = [\mathcal{O}_{\mathbf{Q}_{G}(w_{k})}]. \end{align} $$
$$ \begin{align} \left( \sum_{p=0}^{k}(-1)^{p} \mathbf{e}^{p \epsilon_{n+1-k}} \mathfrak{F}^{k}_{p} \right) \otimes [\mathcal{O}_{\mathbf{Q}_{G}(w_{k+1})}] = [\mathcal{O}_{\mathbf{Q}_{G}(w_{k})}]. \end{align} $$
Noting that
![]() $w_{1}=w_{\circ }$
and
$w_{1}=w_{\circ }$
and
![]() $w_{n+1}=e$
, we obtain the following.
$w_{n+1}=e$
, we obtain the following.
Corollary 2.5. The following equality holds in
![]() $K_{H}(\mathbf {Q}_{G})$
:
$K_{H}(\mathbf {Q}_{G})$
:
 $$ \begin{align} [\mathcal{O}_{\mathbf{Q}_{G}(w_{\circ})}] = \bigotimes_{k=1}^{n} \left( \sum_{p=0}^{k}(-1)^{p} \mathbf{e}^{p \epsilon_{n+1-k}} \mathfrak{F}^{k}_{p} \right). \end{align} $$
$$ \begin{align} [\mathcal{O}_{\mathbf{Q}_{G}(w_{\circ})}] = \bigotimes_{k=1}^{n} \left( \sum_{p=0}^{k}(-1)^{p} \mathbf{e}^{p \epsilon_{n+1-k}} \mathfrak{F}^{k}_{p} \right). \end{align} $$
3 Proof of the main result for
 $w = w_{\circ }$
$w = w_{\circ }$
3.1 Relationship between
 $K_{H}(\mathbf {Q}_{G})$
and
$K_{H}(\mathbf {Q}_{G})$
and
 $QK_{H}(G/B)$
$QK_{H}(G/B)$
Let G be a connected, simply-connected, simple algebraic group over
![]() $\mathbb {C}$
, with Borel subgroup
$\mathbb {C}$
, with Borel subgroup
![]() $B \subset G$
and maximal torus
$B \subset G$
and maximal torus
![]() $H \subset B$
. Let
$H \subset B$
. Let
![]() $QK_{H}(G/B) := K_{H}(G/B) \otimes _{R(H)} R(H)[\![Q^{\vee ,+}]\!]$
denote the H-equivariant (small) quantum K-theory ring of the ordinary flag manifold
$QK_{H}(G/B) := K_{H}(G/B) \otimes _{R(H)} R(H)[\![Q^{\vee ,+}]\!]$
denote the H-equivariant (small) quantum K-theory ring of the ordinary flag manifold
![]() $G/B$
, defined by Givental [Reference GiventalGiv] and Lee [Reference LeeLee], where
$G/B$
, defined by Givental [Reference GiventalGiv] and Lee [Reference LeeLee], where
![]() $R(H)[\![Q^{\vee ,+}]\!]$
is the ring of formal power series in the Novikov variables
$R(H)[\![Q^{\vee ,+}]\!]$
is the ring of formal power series in the Novikov variables
![]() $Q_i = Q^{\alpha _i^{\vee }}$
,
$Q_i = Q^{\alpha _i^{\vee }}$
,
![]() $i \in I$
, with coefficients in the representation ring
$i \in I$
, with coefficients in the representation ring
![]() $R(H)$
of H; for
$R(H)$
of H; for
![]() $\xi = \sum _{i \in I} k_i \alpha _i^{\vee } \in Q^{\vee ,+} = \sum _{i \in I} \mathbb {Z}_{\geq 0} \alpha _i^{\vee }$
, we set
$\xi = \sum _{i \in I} k_i \alpha _i^{\vee } \in Q^{\vee ,+} = \sum _{i \in I} \mathbb {Z}_{\geq 0} \alpha _i^{\vee }$
, we set
![]() $Q^{\xi } := \prod _{i \in I} Q_i^{k_i} \in R(H)[\![Q^{\vee ,+}]\!]$
. The quantum K-theory ring
$Q^{\xi } := \prod _{i \in I} Q_i^{k_i} \in R(H)[\![Q^{\vee ,+}]\!]$
. The quantum K-theory ring
![]() $QK_{H}(G/B)$
is a free module over
$QK_{H}(G/B)$
is a free module over
![]() $R(H)[\![Q^{\vee ,+}]\!]$
having the (opposite) Schubert classes
$R(H)[\![Q^{\vee ,+}]\!]$
having the (opposite) Schubert classes
![]() $[\mathcal{O}^{w}]$
,
$[\mathcal{O}^{w}]$
,
![]() $w \in W$
, as a basis; also, the quantum multiplication
$w \in W$
, as a basis; also, the quantum multiplication
![]() $\star $
in
$\star $
in
![]() $QK_{H}(G/B)$
is a deformation of the classical tensor product in
$QK_{H}(G/B)$
is a deformation of the classical tensor product in
![]() $K_{H}(G/B)$
and is defined in terms of the
$K_{H}(G/B)$
and is defined in terms of the
![]() $2$
-point and
$2$
-point and
![]() $3$
-point (genus zero, equivariant) K-theoretic Gromov-Witten invariants; see [Reference GiventalGiv] and [Reference LeeLee] for details.
$3$
-point (genus zero, equivariant) K-theoretic Gromov-Witten invariants; see [Reference GiventalGiv] and [Reference LeeLee] for details.
In [Reference KatoKat1, Reference KatoKat3], based on [Reference Givental and LeeGL, Reference Braverman and FinkelbergBF, Reference Iritani, Milano and TonitaIMT] (see also [Reference Anderson, Chen and TsengACT]), Kato established an
![]() $R(H)$
-module isomorphism
$R(H)$
-module isomorphism
![]() $\Phi $
from
$\Phi $
from
![]() $QK_{H}(G/B)$
onto the H-equivariant K-group
$QK_{H}(G/B)$
onto the H-equivariant K-group
![]() $K_{H}(\mathbf {Q}_{G})$
of the semi-infinite flag manifold
$K_{H}(\mathbf {Q}_{G})$
of the semi-infinite flag manifold
![]() $\mathbf {Q}_{G}$
, in which tensor product operation with an arbitrary line bundle class is induced from that in
$\mathbf {Q}_{G}$
, in which tensor product operation with an arbitrary line bundle class is induced from that in
![]() $K_{H\times \mathbb {C}^*}(\mathbf {Q}_{G})$
by the specialization at
$K_{H\times \mathbb {C}^*}(\mathbf {Q}_{G})$
by the specialization at
![]() $q = 1$
; in our notation, the map
$q = 1$
; in our notation, the map
![]() $\Phi $
sends the (opposite) Schubert class
$\Phi $
sends the (opposite) Schubert class
![]() $\mathbf {e}^{\mu }[\mathcal{O}^{w}] Q^{\xi }$
in
$\mathbf {e}^{\mu }[\mathcal{O}^{w}] Q^{\xi }$
in
![]() $QK_{H}(G/B)$
to the corresponding semi-infinite Schubert class
$QK_{H}(G/B)$
to the corresponding semi-infinite Schubert class
![]() $\mathbf {e}^{-\mu }[\mathcal{O}_{\mathbf {Q}_{G}(wt_{\xi })}]$
in
$\mathbf {e}^{-\mu }[\mathcal{O}_{\mathbf {Q}_{G}(wt_{\xi })}]$
in
![]() $K_{H}(\mathbf {Q}_{G})$
for
$K_{H}(\mathbf {Q}_{G})$
for
![]() $\mu \in P$
,
$\mu \in P$
,
![]() $w \in W$
and
$w \in W$
and
![]() $\xi \in Q^{\vee ,+}$
. The isomorphism
$\xi \in Q^{\vee ,+}$
. The isomorphism
![]() $\Phi $
also respects, in a sense, quantum multiplication
$\Phi $
also respects, in a sense, quantum multiplication
![]() $\star $
in
$\star $
in
![]() $QK_{H}(G/B)$
and tensor product in
$QK_{H}(G/B)$
and tensor product in
![]() $K_{H}(\mathbf {Q}_{G})$
. More precisely, one has the commutative diagram
$K_{H}(\mathbf {Q}_{G})$
. More precisely, one has the commutative diagram

where for
![]() $\nu \in P$
, the line bundle
$\nu \in P$
, the line bundle
![]() $\mathcal{O}_{G/B}(-\nu )$
over
$\mathcal{O}_{G/B}(-\nu )$
over
![]() $G/B$
denotes the G-equivariant line bundle constructed as the quotient space
$G/B$
denotes the G-equivariant line bundle constructed as the quotient space
![]() $G \times ^{B} \mathbb {C}_{\nu }$
of the product space
$G \times ^{B} \mathbb {C}_{\nu }$
of the product space
![]() $G \times \mathbb {C}_{\nu }$
by the usual (free) left action of the Borel subgroup B of G corresponding to the positive roots, with
$G \times \mathbb {C}_{\nu }$
by the usual (free) left action of the Borel subgroup B of G corresponding to the positive roots, with
![]() $\mathbb {C}_{\nu }$
the one-dimensional B-module of weight
$\mathbb {C}_{\nu }$
the one-dimensional B-module of weight
![]() $\nu $
. (Here, we warn the reader that the convention of [Reference KatoKat1] differs from that of [Reference Kato, Naito and SagakiKaNS] and this paper, by the twist coming from the involution
$\nu $
. (Here, we warn the reader that the convention of [Reference KatoKat1] differs from that of [Reference Kato, Naito and SagakiKaNS] and this paper, by the twist coming from the involution
![]() $-w_{\circ }$
.) Also, we know from [Reference KatoKat1] that for
$-w_{\circ }$
.) Also, we know from [Reference KatoKat1] that for
![]() $w \in W$
and
$w \in W$
and
![]() $\xi \in Q^{\vee ,+}$
, the equality
$\xi \in Q^{\vee ,+}$
, the equality
![]() $\Phi ([\mathcal{O}^{w}] Q^{\xi }) = \mathsf {t}_{\xi } \, \Phi ([\mathcal{O}^{w}])$
holds, and hence that for an arbitrary element
$\Phi ([\mathcal{O}^{w}] Q^{\xi }) = \mathsf {t}_{\xi } \, \Phi ([\mathcal{O}^{w}])$
holds, and hence that for an arbitrary element
![]() $\bullet $
of
$\bullet $
of
![]() $QK_{H}(G/B)$
and
$QK_{H}(G/B)$
and
![]() $\xi \in Q^{\vee ,+}$
, the equality
$\xi \in Q^{\vee ,+}$
, the equality
holds.
We know from [Reference Buch, Chaput, Mihalcea and PerrinBCMP, Corollary 5.14] that the quantum multiplicative structure over
![]() $R(H)[\![Q^{\vee ,+}]\!]$
of
$R(H)[\![Q^{\vee ,+}]\!]$
of
![]() $QK_{H}(G/B)$
is completely determined by the quantum multiplication with the line bundle classes
$QK_{H}(G/B)$
is completely determined by the quantum multiplication with the line bundle classes
![]() $[\mathcal{O}_{G/B}(-\varpi _{i})]$
,
$[\mathcal{O}_{G/B}(-\varpi _{i})]$
,
![]() $i \in I$
; in fact, by using Nakayama’s Lemma (i.e., [Reference EisenbudE, Corollary 4.8 b]) together with [Reference EisenbudE, Exercise 7.3], we can show that
$i \in I$
; in fact, by using Nakayama’s Lemma (i.e., [Reference EisenbudE, Corollary 4.8 b]) together with [Reference EisenbudE, Exercise 7.3], we can show that
![]() $QK_{H}(G/B)$
is generated as an algebra (with quantum multiplication
$QK_{H}(G/B)$
is generated as an algebra (with quantum multiplication
![]() $\star $
) over
$\star $
) over
![]() $R(H)[\![Q^{\vee ,+}]\!]$
by the line bundle classes
$R(H)[\![Q^{\vee ,+}]\!]$
by the line bundle classes
![]() $[\mathcal{O}_{G/B}(-\varpi _{i})]$
,
$[\mathcal{O}_{G/B}(-\varpi _{i})]$
,
![]() $i \in I$
, since
$i \in I$
, since
![]() $K_{H}(G/B)$
is known to be generated by the same line bundle classes as an algebra (with tensor product
$K_{H}(G/B)$
is known to be generated by the same line bundle classes as an algebra (with tensor product
![]() $\otimes $
) over
$\otimes $
) over
![]() $R(H)$
([Reference MihalceaMi]). Therefore, if G is of type
$R(H)$
([Reference MihalceaMi]). Therefore, if G is of type
![]() $A_{n}$
(i.e.,
$A_{n}$
(i.e.,
![]() $G = SL_{n+1}(\mathbb {C})$
), then we deduce from [Reference Maeno, Naito and SagakiMaNS, Propositions 5.1 and 5.2], together with the comments following them, that
$G = SL_{n+1}(\mathbb {C})$
), then we deduce from [Reference Maeno, Naito and SagakiMaNS, Propositions 5.1 and 5.2], together with the comments following them, that
![]() $QK_{H}(Fl_{n+1})$
is generated as an algebra over
$QK_{H}(Fl_{n+1})$
is generated as an algebra over
![]() $R(H)[\![Q^{\vee ,+}]\!] = R(H)[\![Q]\!] = R(H)[\![Q_1, \ldots , Q_{n}]\!]$
by the line bundle classes
$R(H)[\![Q^{\vee ,+}]\!] = R(H)[\![Q]\!] = R(H)[\![Q_1, \ldots , Q_{n}]\!]$
by the line bundle classes
![]() $[\mathcal{O}_{Fl_{n+1}}(-\epsilon _{j})]$
,
$[\mathcal{O}_{Fl_{n+1}}(-\epsilon _{j})]$
,
![]() $1 \leq j \leq n$
; indeed, for
$1 \leq j \leq n$
; indeed, for
![]() $1 \leq j \leq n$
and an arbitrary element
$1 \leq j \leq n$
and an arbitrary element
![]() $\bullet \in QK_{H}(Fl_{n+1})$
, we have
$\bullet \in QK_{H}(Fl_{n+1})$
, we have
3.2 An explicit formula expressing the Schubert class associated to
 $w_{\circ }$
$w_{\circ }$
In this subsection, we assume that G is of type
![]() $A_{n}$
(i.e.,
$A_{n}$
(i.e.,
![]() $G = SL_{n+1}(\mathbb {C})$
). Now, for
$G = SL_{n+1}(\mathbb {C})$
). Now, for
![]() $0 \le p \le k \le n+1$
, we set
$0 \le p \le k \le n+1$
, we set
 $$ \begin{align} \mathcal{F}^{k}_{p}:= \sum_{ \begin{subarray}{c} J \subset [k] \\[1mm] |J|=p \end{subarray}} \, \prod_{ \begin{subarray}{c} 1 \le j \le k \\[1mm] j,\,j+1 \in J \end{subarray} } \frac{1}{1-Q_{j}} \sideset{}{^\star}\prod_{j \in J} [\mathcal{O}_{Fl_{n+1}}(-\epsilon_{j})] \in QK_{H}(Fl_{n+1}), \end{align} $$
$$ \begin{align} \mathcal{F}^{k}_{p}:= \sum_{ \begin{subarray}{c} J \subset [k] \\[1mm] |J|=p \end{subarray}} \, \prod_{ \begin{subarray}{c} 1 \le j \le k \\[1mm] j,\,j+1 \in J \end{subarray} } \frac{1}{1-Q_{j}} \sideset{}{^\star}\prod_{j \in J} [\mathcal{O}_{Fl_{n+1}}(-\epsilon_{j})] \in QK_{H}(Fl_{n+1}), \end{align} $$
with
![]() $[k]=\big \{1,2,\dots ,k\big \}$
, where
$[k]=\big \{1,2,\dots ,k\big \}$
, where
![]() $\prod ^{\star }$
denotes the product with respect to the quantum multiplication
$\prod ^{\star }$
denotes the product with respect to the quantum multiplication
![]() $\star $
; note that
$\star $
; note that
![]() $\mathcal{F}^{k}_{0} = 1$
for
$\mathcal{F}^{k}_{0} = 1$
for
![]() $0 \le k \le n+1$
. Also, recall from (2.5) that for
$0 \le k \le n+1$
. Also, recall from (2.5) that for
![]() $0 \leq p \leq k \leq n+1$
, the element
$0 \leq p \leq k \leq n+1$
, the element
![]() $\mathfrak {F}^{k}_{p} \in K_{H}(\mathbf {Q}_{G})$
is defined by
$\mathfrak {F}^{k}_{p} \in K_{H}(\mathbf {Q}_{G})$
is defined by
 $$ \begin{align} \mathfrak{F}^{k}_{p} = \sum_{ \begin{subarray}{c} J \subset [k] \\[1mm] |J|=p \end{subarray}} \left( \prod_{ \begin{subarray}{c} 1 \le j \le k \\[1mm] j \notin J,\,j+1 \in J \end{subarray}} (1-\mathsf{t}_{j}) \right)[\mathcal{O}_{\mathbf{Q}_{G}}(w_{\circ} \epsilon_{J})]. \end{align} $$
$$ \begin{align} \mathfrak{F}^{k}_{p} = \sum_{ \begin{subarray}{c} J \subset [k] \\[1mm] |J|=p \end{subarray}} \left( \prod_{ \begin{subarray}{c} 1 \le j \le k \\[1mm] j \notin J,\,j+1 \in J \end{subarray}} (1-\mathsf{t}_{j}) \right)[\mathcal{O}_{\mathbf{Q}_{G}}(w_{\circ} \epsilon_{J})]. \end{align} $$
Here, since
![]() $- \epsilon _j = \varpi _{j-1} - \varpi _j$
for
$- \epsilon _j = \varpi _{j-1} - \varpi _j$
for
![]() $1 \leq j \leq n+1$
(
$1 \leq j \leq n+1$
(
![]() $\varpi _0 = \varpi _{n+1} := 0$
by convention), we see from [Reference Maeno, Naito and SagakiMaNS, Proposition 5.2] that
$\varpi _0 = \varpi _{n+1} := 0$
by convention), we see from [Reference Maeno, Naito and SagakiMaNS, Proposition 5.2] that
 $$ \begin{align} \Phi \left(\bullet \star \frac{1}{1 - Q_{j-1}}[\mathcal{O}_{Fl_{n+1}}(- \epsilon_{j})]\right) = \Phi(\bullet) \otimes [\mathcal{O}_{\mathbf{Q}_{G}}(w_{\circ} \epsilon_{j})] \end{align} $$
$$ \begin{align} \Phi \left(\bullet \star \frac{1}{1 - Q_{j-1}}[\mathcal{O}_{Fl_{n+1}}(- \epsilon_{j})]\right) = \Phi(\bullet) \otimes [\mathcal{O}_{\mathbf{Q}_{G}}(w_{\circ} \epsilon_{j})] \end{align} $$
for
![]() $1 \leq j \leq n+1$
and an arbitrary element
$1 \leq j \leq n+1$
and an arbitrary element
![]() $\bullet \in QK_{H}(Fl_{n+1})$
, where
$\bullet \in QK_{H}(Fl_{n+1})$
, where
![]() $G = SL_{n+1}(\mathbb {C})$
, and
$G = SL_{n+1}(\mathbb {C})$
, and
![]() $Q_{0} = Q_{n+1} := 0$
by convention.
$Q_{0} = Q_{n+1} := 0$
by convention.
Proposition 3.1. For
![]() $0 \leq p \leq k \leq n+1$
, the following equality holds in
$0 \leq p \leq k \leq n+1$
, the following equality holds in
![]() $K_{H}(\mathbf {Q}_{G})$
:
$K_{H}(\mathbf {Q}_{G})$
:
Proof. First note that for a subset
![]() $J \subset [k]$
, the equality
$J \subset [k]$
, the equality
![]() $[\mathcal{O}_{\mathbf {Q}_{G}}(w_{\circ } \epsilon _{J})] = \bigotimes _{j \in J} [\mathcal{O}_{\mathbf {Q}_{G}}(w_{\circ } \epsilon _{j})]$
holds since
$[\mathcal{O}_{\mathbf {Q}_{G}}(w_{\circ } \epsilon _{J})] = \bigotimes _{j \in J} [\mathcal{O}_{\mathbf {Q}_{G}}(w_{\circ } \epsilon _{j})]$
holds since
![]() $\epsilon _{J} = \sum _{j \in J} \epsilon _{j}$
. Therefore, by repeated application of equation (3.5), together with equations (2.2) and (3.2), we deduce that the image
$\epsilon _{J} = \sum _{j \in J} \epsilon _{j}$
. Therefore, by repeated application of equation (3.5), together with equations (2.2) and (3.2), we deduce that the image
![]() $\Phi ^{-1}(\mathfrak {F}^{k}_{p})$
of
$\Phi ^{-1}(\mathfrak {F}^{k}_{p})$
of
![]() $\mathfrak {F}^{k}_{p}$
under the inverse mapping
$\mathfrak {F}^{k}_{p}$
under the inverse mapping
![]() $\Phi ^{-1}$
of the
$\Phi ^{-1}$
of the
![]() $R(H)$
-module isomorphism
$R(H)$
-module isomorphism
![]() $\Phi $
is
$\Phi $
is
 $$ \begin{align} \sum_{ \begin{subarray}{c} J \subset [k] \\[1mm] |J|=p \end{subarray}} \, \prod_{ \begin{subarray}{c} 1 \le j \le k \\[1mm] j \notin J,\,j+1 \in J \end{subarray} } (1-Q_{j}) \prod_{j \in J} \frac{1}{1 - Q_{j-1}} \sideset{}{^\star}\prod_{j \in J} [\mathcal{O}_{Fl_{n+1}}(-\epsilon_{j})], \end{align} $$
$$ \begin{align} \sum_{ \begin{subarray}{c} J \subset [k] \\[1mm] |J|=p \end{subarray}} \, \prod_{ \begin{subarray}{c} 1 \le j \le k \\[1mm] j \notin J,\,j+1 \in J \end{subarray} } (1-Q_{j}) \prod_{j \in J} \frac{1}{1 - Q_{j-1}} \sideset{}{^\star}\prod_{j \in J} [\mathcal{O}_{Fl_{n+1}}(-\epsilon_{j})], \end{align} $$
which is easily seen to be identical to
![]() $\mathcal{F}^{k}_{p}$
. This proves the proposition.
$\mathcal{F}^{k}_{p}$
. This proves the proposition.
Also, from Corollary 2.5, we obtain the following, again by repeated application of equation (3.5), together with relations (2.2) and (3.2).
Proposition 3.2. Let
![]() $w_{\circ } \in W = S_{n+1}$
be the longest element. Then, the following equality holds in
$w_{\circ } \in W = S_{n+1}$
be the longest element. Then, the following equality holds in
![]() $QK_{H}(Fl_{n+1})$
:
$QK_{H}(Fl_{n+1})$
:
 $$ \begin{align} [\mathcal{O}^{w_{\circ}}] = \sideset{}{^\star}\prod_{k=1}^{n} \Bigg( \sum_{p=0}^{k}(-1)^{p} \mathbf{e}^{-p \epsilon_{n+1-k}} \mathcal{F}^{k}_{p}\Bigg) \in QK_{H}(Fl_{n+1}). \end{align} $$
$$ \begin{align} [\mathcal{O}^{w_{\circ}}] = \sideset{}{^\star}\prod_{k=1}^{n} \Bigg( \sum_{p=0}^{k}(-1)^{p} \mathbf{e}^{-p \epsilon_{n+1-k}} \mathcal{F}^{k}_{p}\Bigg) \in QK_{H}(Fl_{n+1}). \end{align} $$
3.3 Proof of the main result for
 $w = w_{\circ }$
$w = w_{\circ }$
We know from [Reference Maeno, Naito and SagakiMaNS, Section 6] that there exists an
![]() $R(H)[\![Q]\!]$
-algebra isomorphism
$R(H)[\![Q]\!]$
-algebra isomorphism
where
![]() $\mathcal{I}^{Q}$
denotes the ideal of
$\mathcal{I}^{Q}$
denotes the ideal of
![]() $(R(H)[\![Q]\!])[x_{1},\dots ,x_{n},x_{n+1}]$
generated by
$(R(H)[\![Q]\!])[x_{1},\dots ,x_{n},x_{n+1}]$
generated by
 $$ \begin{align} \sum_{ \begin{subarray}{c} J \subset [n+1] \\[1mm] |J|=l \end{subarray}} \, \prod_{j \in J, j+1 \notin J} (1-Q_{j}) \prod_{j \in J} (1-x_{j}) - \sum_{ \begin{subarray}{c} J \subset [n+1] \\[1mm] |J|=l \end{subarray}}\mathbf{e}^{\epsilon_{J}}, \qquad 1 \le l \le n+1, \end{align} $$
$$ \begin{align} \sum_{ \begin{subarray}{c} J \subset [n+1] \\[1mm] |J|=l \end{subarray}} \, \prod_{j \in J, j+1 \notin J} (1-Q_{j}) \prod_{j \in J} (1-x_{j}) - \sum_{ \begin{subarray}{c} J \subset [n+1] \\[1mm] |J|=l \end{subarray}}\mathbf{e}^{\epsilon_{J}}, \qquad 1 \le l \le n+1, \end{align} $$
with
![]() $[n+1]=\big \{1,2,\dots ,n+1\big \}$
; here, we understand that
$[n+1]=\big \{1,2,\dots ,n+1\big \}$
; here, we understand that
![]() $Q_{n+1} = 0$
. Also, we know that the isomorphism
$Q_{n+1} = 0$
. Also, we know that the isomorphism
![]() $\Psi ^{Q}$
maps the residue class
$\Psi ^{Q}$
maps the residue class
![]() $(1-Q_j)(1-x_{j}) \ \mathrm {mod} \ \mathcal{I}^{Q}$
to
$(1-Q_j)(1-x_{j}) \ \mathrm {mod} \ \mathcal{I}^{Q}$
to
![]() $[\mathcal{O}_{Fl_{n+1}}(-\epsilon _{j})]$
for
$[\mathcal{O}_{Fl_{n+1}}(-\epsilon _{j})]$
for
![]() $1 \le j \le n$
, and the residue class
$1 \le j \le n$
, and the residue class
![]() $(1-x_{n+1}) \ \mathrm {mod} \ \mathcal{I}^{Q}$
to
$(1-x_{n+1}) \ \mathrm {mod} \ \mathcal{I}^{Q}$
to
![]() $[\mathcal{O}_{Fl_{n+1}}(-\epsilon _{n+1})]$
; note that
$[\mathcal{O}_{Fl_{n+1}}(-\epsilon _{n+1})]$
; note that
![]() $-\epsilon _{n+1} = \epsilon _1 + \cdots + \epsilon _n$
.
$-\epsilon _{n+1} = \epsilon _1 + \cdots + \epsilon _n$
.
In the following, by
![]() $1 - y_{j} = \mathbf {e}^{-\epsilon _{j}}$
for
$1 - y_{j} = \mathbf {e}^{-\epsilon _{j}}$
for
![]() $1 \le j \le n$
, we identify
$1 \le j \le n$
, we identify
-
(ID1)
 $R(H) \cong \mathbb {Z}[\mathbf {e}^{\pm \epsilon _{1}},\dots ,\mathbf {e}^{\pm \epsilon _{n}}]$
with
$R(H) \cong \mathbb {Z}[\mathbf {e}^{\pm \epsilon _{1}},\dots ,\mathbf {e}^{\pm \epsilon _{n}}]$
with
 $\mathbb {Z}[(1-y_{1})^{\pm 1},\dots ,(1-y_{n})^{\pm 1}]$
, and
$\mathbb {Z}[(1-y_{1})^{\pm 1},\dots ,(1-y_{n})^{\pm 1}]$
, and -
(ID2)
 $(R(H)[\![Q]\!])[x_{1},\dots ,x_{n},x_{n+1}]$
with
$(R(H)[\![Q]\!])[x_{1},\dots ,x_{n},x_{n+1}]$
with
 $(\mathbb{Z}[(1-y_{1})^{\pm 1},\dots,(1-y_{n})^{\pm 1}][\![Q]\!])[x_{1},\dots,x_{n},x_{n+1}]$
.
$(\mathbb{Z}[(1-y_{1})^{\pm 1},\dots,(1-y_{n})^{\pm 1}][\![Q]\!])[x_{1},\dots,x_{n},x_{n+1}]$
.
For
![]() $0 \le p \le k \le n$
, we define
$0 \le p \le k \le n$
, we define
 $$ \begin{align} F_{p}^{k}(x_{1},\dots,x_{n},x_{n+1}):= \sum_{ \begin{subarray}{c} J \subset [k] \\[1mm] |J|=p \end{subarray}} \, \prod_{j \in J, j+1 \notin J} (1-Q_{j}) \prod_{j \in J} (1-x_{j}) \in \mathbb{Z}[\![Q]\!][x_{1},\dots,x_{n},x_{n+1}]. \end{align} $$
$$ \begin{align} F_{p}^{k}(x_{1},\dots,x_{n},x_{n+1}):= \sum_{ \begin{subarray}{c} J \subset [k] \\[1mm] |J|=p \end{subarray}} \, \prod_{j \in J, j+1 \notin J} (1-Q_{j}) \prod_{j \in J} (1-x_{j}) \in \mathbb{Z}[\![Q]\!][x_{1},\dots,x_{n},x_{n+1}]. \end{align} $$
Then, we can easily verify that for
![]() $0 \le p \le k \le n$
,
$0 \le p \le k \le n$
,
Therefore, we deduce from Proposition 3.2 that the residue class
 $$ \begin{align*} \prod_{k=1}^{n} \Bigg( \sum_{p=0}^{k}(-1)^{p}(1-y_{n+1-k})^{p}F_{p}^{k}(x_{1},\dots,x_{n},x_{n+1}) \Bigg)\ \mod \mathcal{I}^{Q} \end{align*} $$
$$ \begin{align*} \prod_{k=1}^{n} \Bigg( \sum_{p=0}^{k}(-1)^{p}(1-y_{n+1-k})^{p}F_{p}^{k}(x_{1},\dots,x_{n},x_{n+1}) \Bigg)\ \mod \mathcal{I}^{Q} \end{align*} $$
is mapped under the
![]() $R(H)[\![Q]\!]$
-algebra isomorphism
$R(H)[\![Q]\!]$
-algebra isomorphism
![]() $\Psi ^{Q}$
to
$\Psi ^{Q}$
to
 $$ \begin{align*} \sideset{}{^\star}\prod_{k=1}^{n} \Bigg( \sum_{p=0}^{k}(-1)^{p}\mathbf{e}^{-p \epsilon_{n+1-k}} \mathcal{F}^{k}_{p} \Bigg) = [\mathcal{O}^{w_{\circ}}] \in QK_{H}(Fl_{n+1}); \end{align*} $$
$$ \begin{align*} \sideset{}{^\star}\prod_{k=1}^{n} \Bigg( \sum_{p=0}^{k}(-1)^{p}\mathbf{e}^{-p \epsilon_{n+1-k}} \mathcal{F}^{k}_{p} \Bigg) = [\mathcal{O}^{w_{\circ}}] \in QK_{H}(Fl_{n+1}); \end{align*} $$
recall the identification
![]() $1-y_{j} = \mathbf {e}^{-\epsilon _{j}}$
for
$1-y_{j} = \mathbf {e}^{-\epsilon _{j}}$
for
![]() $1 \le j \le n$
.
$1 \le j \le n$
.
Now, let us set
 $$ \begin{align} \begin{aligned} \mathfrak{G}_{w_{\circ}}^{Q}(x,y) & := \prod_{k=1}^{n}\Bigg( \sum_{l=0}^{k}(-1)^{l}(1-y_{n+1-k})^{l}F_{l}^{k}(x_{1},\dots,x_{n},x_{n+1}) \Bigg) \\ & \in \mathbb{Z}[\![Q]\!][x_{1},\dots,x_{n},x_{n+1}][(1-y_{1})^{\pm 1},\dots,(1-y_{n})^{\pm 1}], \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathfrak{G}_{w_{\circ}}^{Q}(x,y) & := \prod_{k=1}^{n}\Bigg( \sum_{l=0}^{k}(-1)^{l}(1-y_{n+1-k})^{l}F_{l}^{k}(x_{1},\dots,x_{n},x_{n+1}) \Bigg) \\ & \in \mathbb{Z}[\![Q]\!][x_{1},\dots,x_{n},x_{n+1}][(1-y_{1})^{\pm 1},\dots,(1-y_{n})^{\pm 1}], \end{aligned} \end{align} $$
which can be thought of as a subring of
![]() $(\mathbb {Z}[(1-y_{1})^{\pm 1},\dots ,(1-y_{n})^{\pm 1}][\![Q]\!])[x_{1},\dots ,x_{n},x_{n+1}]$
; see Section 4.1 below. Then, from the above, we obtain the following.
$(\mathbb {Z}[(1-y_{1})^{\pm 1},\dots ,(1-y_{n})^{\pm 1}][\![Q]\!])[x_{1},\dots ,x_{n},x_{n+1}]$
; see Section 4.1 below. Then, from the above, we obtain the following.
Theorem 3.3. Let
![]() $w_{\circ } \in W=S_{n+1}$
be the longest element. Then, under the identification (ID2), the following equality holds in
$w_{\circ } \in W=S_{n+1}$
be the longest element. Then, under the identification (ID2), the following equality holds in
![]() $QK_{H}(Fl_{n+1})$
:
$QK_{H}(Fl_{n+1})$
:
where
![]() $\Psi ^{Q}$
is the
$\Psi ^{Q}$
is the
![]() $R(H)[\![Q]\!]$
-algebra isomorphism in (3.9).
$R(H)[\![Q]\!]$
-algebra isomorphism in (3.9).
4 Proof of the main result for an arbitrary w
4.1 Quantum double Grothendieck polynomials
First we recall from [Reference Lenart and MaenoLM, Section 8] the Demazure operators
![]() $\pi ^{(y)}_{i}$
acting on the y variables; note that we use Demazure operators acting on the y variables, while in [Reference Lenart and MaenoLM], they are acting on the x variables. Let
$\pi ^{(y)}_{i}$
acting on the y variables; note that we use Demazure operators acting on the y variables, while in [Reference Lenart and MaenoLM], they are acting on the x variables. Let
![]() $i \in [n]=\{1,2,\dots ,n\}$
. We define the Demazure operator
$i \in [n]=\{1,2,\dots ,n\}$
. We define the Demazure operator
![]() $\pi ^{(y)}_{i}$
(with respect to the y variables) on
$\pi ^{(y)}_{i}$
(with respect to the y variables) on
![]() $\mathbb {Z}[(1 - y_1)^{\pm 1},\ldots ,(1 - y_n)^{\pm 1}]$
by
$\mathbb {Z}[(1 - y_1)^{\pm 1},\ldots ,(1 - y_n)^{\pm 1}]$
by
where we identify the Laurent polynomial ring
![]() $\mathbb {Z}[(1-y_1)^{\pm 1}, \ldots , (1-y_{n})^{\pm 1}]$
with the quotient of the polynomial ring
$\mathbb {Z}[(1-y_1)^{\pm 1}, \ldots , (1-y_{n})^{\pm 1}]$
with the quotient of the polynomial ring
![]() $\mathbb {Z}[(1-y_1), \ldots , (1-y_{n}), (1-y_{n+1})]$
by the relation
$\mathbb {Z}[(1-y_1), \ldots , (1-y_{n}), (1-y_{n+1})]$
by the relation
![]() $(1-y_1) \cdots (1-y_{n})(1-y_{n+1}) = 1$
; we extend it to
$(1-y_1) \cdots (1-y_{n})(1-y_{n+1}) = 1$
; we extend it to
![]() $\mathbb {Z}[\![Q]\!][x_{1},\dots ,x_{n},x_{n+1}][(1-y_{1})^{\pm 1},\dots ,(1-y_{n})^{\pm 1}]$
by
$\mathbb {Z}[\![Q]\!][x_{1},\dots ,x_{n},x_{n+1}][(1-y_{1})^{\pm 1},\dots ,(1-y_{n})^{\pm 1}]$
by
![]() $\mathbb {Z}[\![Q]\!][x_{1},\dots ,x_{n},x_{n+1}]$
-linearity, and also to
$\mathbb {Z}[\![Q]\!][x_{1},\dots ,x_{n},x_{n+1}]$
-linearity, and also to
![]() $(\mathbb {Z}[(1-y_{1})^{\pm 1},\dots ,(1-y_{n})^{\pm 1}][\![Q]\!])[x_{1},\dots ,x_{n},x_{n+1}]$
by letting it act trivially on the elements of
$(\mathbb {Z}[(1-y_{1})^{\pm 1},\dots ,(1-y_{n})^{\pm 1}][\![Q]\!])[x_{1},\dots ,x_{n},x_{n+1}]$
by letting it act trivially on the elements of
![]() $\mathbb {Z}[\![Q]\!][x_{1}. \ldots , x_{n}, x_{n+1}]$
. Also, for
$\mathbb {Z}[\![Q]\!][x_{1}. \ldots , x_{n}, x_{n+1}]$
. Also, for
![]() $w \in W=S_{n+1}$
with reduced expression
$w \in W=S_{n+1}$
with reduced expression
![]() $w = s_{i_{1}} \cdots s_{i_{l}}$
, we define
$w = s_{i_{1}} \cdots s_{i_{l}}$
, we define
![]() $\pi ^{(y)}_{w}:=\pi ^{(y)}_{i_1} \cdots \pi ^{(y)}_{i_l}$
; it is well-known that this definition does not depend on the choice of a reduced expression for w.
$\pi ^{(y)}_{w}:=\pi ^{(y)}_{i_1} \cdots \pi ^{(y)}_{i_l}$
; it is well-known that this definition does not depend on the choice of a reduced expression for w.
Now, let us recall from [Reference Lenart and MaenoLM, Section 8] the definition of quantum double Grothendieck polynomials. For the longest element
![]() $w_{\circ } \in W=S_{n+1}$
, we define
$w_{\circ } \in W=S_{n+1}$
, we define
![]() $\mathfrak {G}_{w_{\circ }}^{Q}(x,y)$
as in (3.12). Note that the polynomial
$\mathfrak {G}_{w_{\circ }}^{Q}(x,y)$
as in (3.12). Note that the polynomial
![]() $\mathfrak {G}_{w_{\circ }}^{Q}(x,y)$
is the image under the quantization map
$\mathfrak {G}_{w_{\circ }}^{Q}(x,y)$
is the image under the quantization map
![]() $\mathscr {Q}$
(with respect to the x variables) of the ordinary double Grothendieck polynomial
$\mathscr {Q}$
(with respect to the x variables) of the ordinary double Grothendieck polynomial
 $$ \begin{align*} \mathfrak{G}_{w_{\circ}}(x,y):= \prod_{k=1}^{n}\Bigg( \sum_{l=0}^{k} (-1)^{l}(1-y_{n+1-k})^{l}f_{l}^{k}(x_{1},\dots,x_{n},x_{n+1}) \Bigg), \end{align*} $$
$$ \begin{align*} \mathfrak{G}_{w_{\circ}}(x,y):= \prod_{k=1}^{n}\Bigg( \sum_{l=0}^{k} (-1)^{l}(1-y_{n+1-k})^{l}f_{l}^{k}(x_{1},\dots,x_{n},x_{n+1}) \Bigg), \end{align*} $$
where
 $$ \begin{align*} f_{l}^{k}(x_{1},\dots,x_{n},x_{n+1}):= \sum_{ \begin{subarray}{c} J \subset [k] \\[1mm] |J|=l \end{subarray}} \, \prod_{j \in J}(1-x_{j}), \end{align*} $$
$$ \begin{align*} f_{l}^{k}(x_{1},\dots,x_{n},x_{n+1}):= \sum_{ \begin{subarray}{c} J \subset [k] \\[1mm] |J|=l \end{subarray}} \, \prod_{j \in J}(1-x_{j}), \end{align*} $$
with
![]() $[k] = \{1, 2, \ldots , k\}$
; for more details on the quantization map
$[k] = \{1, 2, \ldots , k\}$
; for more details on the quantization map
![]() $\mathscr {Q}$
, we refer the reader to [Reference Lenart and MaenoLM, Sections 3 and 5]. For an arbitrary
$\mathscr {Q}$
, we refer the reader to [Reference Lenart and MaenoLM, Sections 3 and 5]. For an arbitrary
![]() $w \in W=S_{n+1}$
, the quantum double Grothendieck polynomial
$w \in W=S_{n+1}$
, the quantum double Grothendieck polynomial
![]() $\mathfrak {G}_{w}^{Q}(x,y)$
is defined by
$\mathfrak {G}_{w}^{Q}(x,y)$
is defined by
which is a subring of
![]() $(\mathbb {Z}[(1-y_{1})^{\pm 1},\dots ,(1-y_{n})^{\pm 1}][\![Q]\!])[x_{1},\dots ,x_{n},x_{n+1}]$
.
$(\mathbb {Z}[(1-y_{1})^{\pm 1},\dots ,(1-y_{n})^{\pm 1}][\![Q]\!])[x_{1},\dots ,x_{n},x_{n+1}]$
.
Remark 4.1. In our definition of quantum double Grothendieck polynomials
![]() $\mathfrak {G}_{w}^{Q}(x,y)$
, the roles of the variables x and y are interchanged from those in [Reference Lenart and MaenoLM, Section 8]. In addition, we use the Demazure operator
$\mathfrak {G}_{w}^{Q}(x,y)$
, the roles of the variables x and y are interchanged from those in [Reference Lenart and MaenoLM, Section 8]. In addition, we use the Demazure operator
![]() $\pi ^{(y)}_{ww_{\circ }}$
instead of
$\pi ^{(y)}_{ww_{\circ }}$
instead of
![]() $\pi ^{(y)}_{w^{-1}w_{\circ }}$
. Hence, our polynomial
$\pi ^{(y)}_{w^{-1}w_{\circ }}$
. Hence, our polynomial
![]() $\mathfrak {G}_{w}^{Q}(x,y)$
coincides with
$\mathfrak {G}_{w}^{Q}(x,y)$
coincides with
![]() $\mathfrak {G}_{w^{-1}}^{q}(y,x)$
in the notation of [Reference Lenart and MaenoLM, Section 8].
$\mathfrak {G}_{w^{-1}}^{q}(y,x)$
in the notation of [Reference Lenart and MaenoLM, Section 8].
Remark 4.2. Our polynomial
![]() $\mathfrak {G}_{w}^{Q}(x,y)$
coincides with the one in [Reference Maeno, Naito and SagakiMaNS, Appendix B]; this is because the quantization map
$\mathfrak {G}_{w}^{Q}(x,y)$
coincides with the one in [Reference Maeno, Naito and SagakiMaNS, Appendix B]; this is because the quantization map
![]() $\mathscr {Q}$
(with respect to the x variables) commutes with the Demazure operators
$\mathscr {Q}$
(with respect to the x variables) commutes with the Demazure operators
![]() $\pi ^{(y)}_{i}$
,
$\pi ^{(y)}_{i}$
,
![]() $1 \leq i \leq n$
, and we have
$1 \leq i \leq n$
, and we have
![]() $\mathfrak {G}_{w}(y,x) = \mathfrak {G}_{w^{-1}}(x,y)$
for ordinary double Grothendieck polynomials.
$\mathfrak {G}_{w}(y,x) = \mathfrak {G}_{w^{-1}}(x,y)$
for ordinary double Grothendieck polynomials.
4.2 Quantum left Demazure operators
Let
![]() $K_{H}(Fl_{n+1})$
be the H-equivariant (ordinary) K-theory ring of the (full) flag manifold
$K_{H}(Fl_{n+1})$
be the H-equivariant (ordinary) K-theory ring of the (full) flag manifold
![]() $Fl_{n+1}$
of type
$Fl_{n+1}$
of type
![]() $A_{n}$
. The ring
$A_{n}$
. The ring
![]() $K_{H}(Fl_{n+1})$
admits a left action of the Weyl group
$K_{H}(Fl_{n+1})$
admits a left action of the Weyl group
![]() $W=S_{n+1}$
, given by the left multiplication on the flag manifold
$W=S_{n+1}$
, given by the left multiplication on the flag manifold
![]() $Fl_{n+1}= SL_{n+1}(\mathbb {C})/B$
, where B is the Borel subgroup of
$Fl_{n+1}= SL_{n+1}(\mathbb {C})/B$
, where B is the Borel subgroup of
![]() $G = SL_{n+1}(\mathbb {C})$
consisting of the upper triangular matrices in
$G = SL_{n+1}(\mathbb {C})$
consisting of the upper triangular matrices in
![]() $G = SL_{n+1}(\mathbb {C})$
; for each
$G = SL_{n+1}(\mathbb {C})$
; for each
![]() $w \in W = S_{n+1}$
, let
$w \in W = S_{n+1}$
, let
![]() $w^{L}$
denote the corresponding ring automorphism of
$w^{L}$
denote the corresponding ring automorphism of
![]() $K_{H}(Fl_{n+1})$
. By using the ring automorphisms
$K_{H}(Fl_{n+1})$
. By using the ring automorphisms
![]() $s_{i}^{L}$
,
$s_{i}^{L}$
,
![]() $i \in [n]$
, of
$i \in [n]$
, of
![]() $K_{H}(Fl_{n+1})$
, one can define the (dual) left Demazure operators
$K_{H}(Fl_{n+1})$
, one can define the (dual) left Demazure operators
![]() $\delta _{i}^{\vee }$
,
$\delta _{i}^{\vee }$
,
![]() $i \in [n]$
, on
$i \in [n]$
, on
![]() $K_{H}(Fl_{n+1})$
by
$K_{H}(Fl_{n+1})$
by
Here, we recall the well-known presentation
where
![]() $\mathcal{I}$
is the ideal of
$\mathcal{I}$
is the ideal of
![]() $\mathbb {Z}[\mathbf {e}^{\pm \epsilon _1},\dots ,\mathbf {e}^{\pm \epsilon _n}] \otimes \mathbb {Z}[x_{1}^{\pm 1},\dots ,x_{n}^{\pm 1}]$
generated by
$\mathbb {Z}[\mathbf {e}^{\pm \epsilon _1},\dots ,\mathbf {e}^{\pm \epsilon _n}] \otimes \mathbb {Z}[x_{1}^{\pm 1},\dots ,x_{n}^{\pm 1}]$
generated by
![]() $\iota (f) \otimes 1 - 1 \otimes f$
,
$\iota (f) \otimes 1 - 1 \otimes f$
,
![]() $f \in \mathbb {Z}[x_{1}^{\pm 1},\dots ,x_{n}^{\pm 1}]^{S_{n+1}}$
, with
$f \in \mathbb {Z}[x_{1}^{\pm 1},\dots ,x_{n}^{\pm 1}]^{S_{n+1}}$
, with
![]() $\iota :\mathbb {Z}[x_{1}^{\pm 1},\dots ,x_{n}^{\pm 1}] \rightarrow \mathbb {Z}[\mathbf {e}^{\pm \epsilon _1},\dots ,\mathbf {e}^{\pm \epsilon _n}]$
the natural isomorphism given by
$\iota :\mathbb {Z}[x_{1}^{\pm 1},\dots ,x_{n}^{\pm 1}] \rightarrow \mathbb {Z}[\mathbf {e}^{\pm \epsilon _1},\dots ,\mathbf {e}^{\pm \epsilon _n}]$
the natural isomorphism given by
![]() $\iota (x_{i}^{\pm 1}) = \mathbf {e}^{\pm \epsilon _i}$
,
$\iota (x_{i}^{\pm 1}) = \mathbf {e}^{\pm \epsilon _i}$
,
![]() $1 \le i \le n$
; we identify the Laurent polynomial ring
$1 \le i \le n$
; we identify the Laurent polynomial ring
![]() $\mathbb {Z}[x_{1}^{\pm 1}, \ldots , x_{n}^{\pm 1}]$
with the quotient of
$\mathbb {Z}[x_{1}^{\pm 1}, \ldots , x_{n}^{\pm 1}]$
with the quotient of
![]() $\mathbb {Z}[x_{1}, \ldots , x_{n}, x_{n+1}]$
by the relation
$\mathbb {Z}[x_{1}, \ldots , x_{n}, x_{n+1}]$
by the relation
![]() $x_{1} \cdots x_{n} x_{n+1} = 1$
, and the Laurent polynomial ring
$x_{1} \cdots x_{n} x_{n+1} = 1$
, and the Laurent polynomial ring
![]() $\mathbb {Z}[\mathbf {e}^{\pm \epsilon _1}, \ldots , \mathbf {e}^{\pm \epsilon _n}]$
with the quotient of
$\mathbb {Z}[\mathbf {e}^{\pm \epsilon _1}, \ldots , \mathbf {e}^{\pm \epsilon _n}]$
with the quotient of
![]() $\mathbb {Z}[\mathbf {e}^{\epsilon _1}, \ldots , \mathbf {e}^{\epsilon _n}, \mathbf {e}^{\epsilon _{n+1}}]$
by the relation
$\mathbb {Z}[\mathbf {e}^{\epsilon _1}, \ldots , \mathbf {e}^{\epsilon _n}, \mathbf {e}^{\epsilon _{n+1}}]$
by the relation
![]() $\mathbf {e}^{\epsilon _1} \cdots \mathbf {e}^{\epsilon _n} \mathbf {e}^{\epsilon _{n+1}} = 1$
. We know from (the dual version of) [Reference Mihalcea, Naruse and SuMNS, Proposition 9.5] that under the presentation above of
$\mathbf {e}^{\epsilon _1} \cdots \mathbf {e}^{\epsilon _n} \mathbf {e}^{\epsilon _{n+1}} = 1$
. We know from (the dual version of) [Reference Mihalcea, Naruse and SuMNS, Proposition 9.5] that under the presentation above of
![]() $K_{H}(Fl_{n+1})$
, the action of the (dual) left Demazure operator
$K_{H}(Fl_{n+1})$
, the action of the (dual) left Demazure operator
![]() $\delta _{i}^{\vee }$
on
$\delta _{i}^{\vee }$
on
![]() $K_{H}(Fl_{n+1})$
coincides with that on the quotient ring
$K_{H}(Fl_{n+1})$
coincides with that on the quotient ring
![]() $(\mathbb {Z}[\mathbf {e}^{\pm \epsilon _1},\dots ,\mathbf {e}^{\pm \epsilon _n}] \otimes \mathbb {Z}[x_{1}^{\pm 1},\dots ,x_{n}^{\pm 1}])/\mathcal{I}$
induced by the (dual) Demazure operator on the left factor
$(\mathbb {Z}[\mathbf {e}^{\pm \epsilon _1},\dots ,\mathbf {e}^{\pm \epsilon _n}] \otimes \mathbb {Z}[x_{1}^{\pm 1},\dots ,x_{n}^{\pm 1}])/\mathcal{I}$
induced by the (dual) Demazure operator on the left factor
![]() $\mathbb {Z}[\mathbf {e}^{\pm \epsilon _1},\dots ,\mathbf {e}^{\pm \epsilon _n}]$
, given by
$\mathbb {Z}[\mathbf {e}^{\pm \epsilon _1},\dots ,\mathbf {e}^{\pm \epsilon _n}]$
, given by
where
![]() $s_{i}$
denotes the natural action of the simple reflection
$s_{i}$
denotes the natural action of the simple reflection
![]() $s_{i} \in W=S_{n+1}$
on
$s_{i} \in W=S_{n+1}$
on
![]() $R(H) \cong \mathbb {Z}[\mathbf {e}^{\pm \epsilon _1},\dots ,\mathbf {e}^{\pm \epsilon _n}]$
.
$R(H) \cong \mathbb {Z}[\mathbf {e}^{\pm \epsilon _1},\dots ,\mathbf {e}^{\pm \epsilon _n}]$
.
Remark 4.3. It is easy to see that under the identification (ID1) in Section 3.3, the action of the operator (4.2) on
![]() $\mathbb {Z}[\mathbf {e}^{\pm \epsilon _1},\dots ,\mathbf {e}^{\pm \epsilon _n}]$
coincides with that of the Demazure operator
$\mathbb {Z}[\mathbf {e}^{\pm \epsilon _1},\dots ,\mathbf {e}^{\pm \epsilon _n}]$
coincides with that of the Demazure operator
![]() $\pi ^{(y)}_{i}$
on
$\pi ^{(y)}_{i}$
on
![]() $\mathbb {Z}[(1-y_{1})^{\pm 1},\dots ,(1-y_{n})^{\pm 1}]$
.
$\mathbb {Z}[(1-y_{1})^{\pm 1},\dots ,(1-y_{n})^{\pm 1}]$
.
Let
![]() $QK_{H}(Fl_{n+1})=K_{H}(Fl_{n+1}) \otimes _{R(H)} R(H)[\![Q]\!]$
be the H-equivariant (small) quantum K-theory ring of
$QK_{H}(Fl_{n+1})=K_{H}(Fl_{n+1}) \otimes _{R(H)} R(H)[\![Q]\!]$
be the H-equivariant (small) quantum K-theory ring of
![]() $Fl_{n+1}$
. We know from [Reference Mihalcea, Naruse and SuMNS, Section 8] that for each
$Fl_{n+1}$
. We know from [Reference Mihalcea, Naruse and SuMNS, Section 8] that for each
![]() $w \in W = S_{n+1}$
, the ring automorphism
$w \in W = S_{n+1}$
, the ring automorphism
![]() $w^{L}$
of
$w^{L}$
of
![]() $K_{H}(Fl_{n+1})$
extends by
$K_{H}(Fl_{n+1})$
extends by
![]() $\mathbb {Z}[\![Q]\!]$
-linearity to the ring automorphism of
$\mathbb {Z}[\![Q]\!]$
-linearity to the ring automorphism of
![]() $QK_{H}(Fl_{n+1})$
, and hence, the (dual) left Demazure operators
$QK_{H}(Fl_{n+1})$
, and hence, the (dual) left Demazure operators
![]() $\delta _{i}^{\vee }$
,
$\delta _{i}^{\vee }$
,
![]() $1 \leq i \leq n$
, on
$1 \leq i \leq n$
, on
![]() $K_{H}(Fl_{n+1})$
extend by
$K_{H}(Fl_{n+1})$
extend by
![]() $\mathbb {Z}[\![Q]\!]$
-linearity to
$\mathbb {Z}[\![Q]\!]$
-linearity to
![]() $QK_{H}(Fl_{n+1})$
. Moreover, we know from [Reference Mihalcea, Naruse and SuMNS, Proposition 8.3] that the following equalities hold in
$QK_{H}(Fl_{n+1})$
. Moreover, we know from [Reference Mihalcea, Naruse and SuMNS, Proposition 8.3] that the following equalities hold in
![]() $QK_{H}(Fl_{n+1})$
for
$QK_{H}(Fl_{n+1})$
for
![]() $1 \leq i \leq n$
:
$1 \leq i \leq n$
:
for
![]() $\nu \in P$
and
$\nu \in P$
and
![]() $\bullet \in QK_{H}(Fl_{n+1})$
, and
$\bullet \in QK_{H}(Fl_{n+1})$
, and
 $$ \begin{align} \delta_{i}^{\vee}([\mathcal{O}^{w}])= \begin{cases} [\mathcal{O}^{s_iw}] & \text{if } s_{i}w < w, \\ [\mathcal{O}^{w}] & \text{if } s_{i}w> w \end{cases} \end{align} $$
$$ \begin{align} \delta_{i}^{\vee}([\mathcal{O}^{w}])= \begin{cases} [\mathcal{O}^{s_iw}] & \text{if } s_{i}w < w, \\ [\mathcal{O}^{w}] & \text{if } s_{i}w> w \end{cases} \end{align} $$
for
![]() $w \in W = S_{n+1}$
.
$w \in W = S_{n+1}$
.
4.3 Proof of the main result for an arbitrary w
Recall the
![]() $R(H)[\![Q]\!]$
-algebra isomorphism
$R(H)[\![Q]\!]$
-algebra isomorphism
![]() $\Psi ^{Q}$
from (3.9). Also, recall the identification (ID1) and (ID2) from Section 3.3. Let
$\Psi ^{Q}$
from (3.9). Also, recall the identification (ID1) and (ID2) from Section 3.3. Let
![]() $i \in [n] = \{1, \ldots , n\}$
. If we extend the Demazure operator
$i \in [n] = \{1, \ldots , n\}$
. If we extend the Demazure operator
![]() $\pi ^{(y)}_{i}$
on
$\pi ^{(y)}_{i}$
on
![]() $\mathbb {Z}[(1-y_{1})^{\pm 1},\dots ,(1-y_{n})^{\pm 1}] \text{ by }\mathbb{Z}[\![Q]\!]$
-linearly to
$\mathbb {Z}[(1-y_{1})^{\pm 1},\dots ,(1-y_{n})^{\pm 1}] \text{ by }\mathbb{Z}[\![Q]\!]$
-linearly to
![]() $(\mathbb {Z}[(1-y_{1})^{\pm 1},\dots ,(1-y_{n})^{\pm 1}][\![Q]\!])[x_{1},\dots ,x_{n},x_{n+1}]$
by letting it act trivially on the elements of
$(\mathbb {Z}[(1-y_{1})^{\pm 1},\dots ,(1-y_{n})^{\pm 1}][\![Q]\!])[x_{1},\dots ,x_{n},x_{n+1}]$
by letting it act trivially on the elements of
![]() $\mathbb {Z}[x_{1}, \ldots , x_{n}, x_{n+1}]$
, then the (resulting) Demazure operator
$\mathbb {Z}[x_{1}, \ldots , x_{n}, x_{n+1}]$
, then the (resulting) Demazure operator
![]() $\pi ^{(y)}_{i}$
stabilizes the ideal
$\pi ^{(y)}_{i}$
stabilizes the ideal
![]() $\mathcal{I}^{Q}$
generated by the elements in (3.10), since the elementary symmetric functions
$\mathcal{I}^{Q}$
generated by the elements in (3.10), since the elementary symmetric functions
![]() $\sum _{J \subset [n+1], \, |J|=l} \, \mathbf {e}^{\epsilon _{J}}$
,
$\sum _{J \subset [n+1], \, |J|=l} \, \mathbf {e}^{\epsilon _{J}}$
,
![]() $1 \leq l \leq n+1$
, are invariant under the natural action of
$1 \leq l \leq n+1$
, are invariant under the natural action of
![]() $s_i$
and the Demazure operator
$s_i$
and the Demazure operator
![]() $\pi ^{(y)}_{i}$
satisfies the (twisted) Leibniz rule. Hence, it induces a
$\pi ^{(y)}_{i}$
satisfies the (twisted) Leibniz rule. Hence, it induces a
![]() $\mathbb {Z}[\![Q]\!]$
-linear operator, also denoted by
$\mathbb {Z}[\![Q]\!]$
-linear operator, also denoted by
![]() $\pi_{i}^{(y)}$
, acting trivially on the (residue classes of the) variables
$\pi_{i}^{(y)}$
, acting trivially on the (residue classes of the) variables
![]() $x_{i}$
for
$x_{i}$
for
![]() $1 \leq i \leq n+1$
on the quotient ring
$1 \leq i \leq n+1$
on the quotient ring
![]() $(\mathbb {Z}[(1-y_{1})^{\pm 1},\dots ,(1-y_{n})^{\pm 1}][\![Q]\!])[x_{1},\dots ,x_{n},x_{n+1}]/\mathcal{I}^{Q}$
. Also, by (4.3) and the fact that
$(\mathbb {Z}[(1-y_{1})^{\pm 1},\dots ,(1-y_{n})^{\pm 1}][\![Q]\!])[x_{1},\dots ,x_{n},x_{n+1}]/\mathcal{I}^{Q}$
. Also, by (4.3) and the fact that
![]() $\Psi ^{Q}$
maps the residue class of
$\Psi ^{Q}$
maps the residue class of
![]() $(1-Q_{j})(1-x_{j})$
modulo
$(1-Q_{j})(1-x_{j})$
modulo
![]() $\mathcal{I}^{Q}$
to
$\mathcal{I}^{Q}$
to
![]() $[\mathcal{O}_{Fl_{n+1}}(-\epsilon _{j})]$
for
$[\mathcal{O}_{Fl_{n+1}}(-\epsilon _{j})]$
for
![]() $1 \le j \le n+1$
(recall that
$1 \le j \le n+1$
(recall that
![]() $Q_{n+1} = 0$
by convention), it follows that the quantum (dual) left Demazure operator
$Q_{n+1} = 0$
by convention), it follows that the quantum (dual) left Demazure operator
![]() $\delta _{i}^{\vee }$
on
$\delta _{i}^{\vee }$
on
![]() $QK_{H}(Fl_{n+1})$
is a
$QK_{H}(Fl_{n+1})$
is a
![]() $\mathbb {Z}[\![Q]\!]$
-linear operator acting trivially on the variables
$\mathbb {Z}[\![Q]\!]$
-linear operator acting trivially on the variables
![]() $x_{i}$
for
$x_{i}$
for
![]() $1 \leq i \leq n+1$
. Since
$1 \leq i \leq n+1$
. Since
![]() $QK_{H}(Fl_{n+1})$
and the quotient ring
$QK_{H}(Fl_{n+1})$
and the quotient ring
![]() $(\mathbb {Z}[(1-y_{1})^{\pm 1},\dots ,(1-y_{n})^{\pm 1}][\![Q]\!])[x_{1},\dots ,x_{n},x_{n+1}]/\mathcal{I}^{Q}$
are both generated by the (image under the quotient map of the) elements of
$(\mathbb {Z}[(1-y_{1})^{\pm 1},\dots ,(1-y_{n})^{\pm 1}][\![Q]\!])[x_{1},\dots ,x_{n},x_{n+1}]/\mathcal{I}^{Q}$
are both generated by the (image under the quotient map of the) elements of
![]() $\mathbb {Z}[x_{1}, \ldots , x_{n}, x_{n+1}]$
over
$\mathbb {Z}[x_{1}, \ldots , x_{n}, x_{n+1}]$
over
![]() $\mathbb {Z}[\mathbf {e}^{\pm \epsilon _{1}},\dots ,\mathbf {e}^{\pm \epsilon _{n}}][\![Q]\!] \cong \mathbb {Z}[(1-y_{1})^{\pm 1},\dots ,(1-y_{n})^{\pm 1}][\![Q]\!]$
, and since the (dual) left Demazure operator
$\mathbb {Z}[\mathbf {e}^{\pm \epsilon _{1}},\dots ,\mathbf {e}^{\pm \epsilon _{n}}][\![Q]\!] \cong \mathbb {Z}[(1-y_{1})^{\pm 1},\dots ,(1-y_{n})^{\pm 1}][\![Q]\!]$
, and since the (dual) left Demazure operator
![]() $\delta _{i}^{\vee }$
and the Demazure operator
$\delta _{i}^{\vee }$
and the Demazure operator
![]() $\pi ^{(y)}_{i}$
coincide on
$\pi ^{(y)}_{i}$
coincide on
![]() $\mathbb {Z}[\mathbf {e}^{\pm \epsilon _{1}},\dots ,\mathbf {e}^{\pm \epsilon _{n}}] \cong \mathbb {Z}[(1-y_{1})^{\pm 1},\dots ,(1-y_{n})^{\pm 1}]$
by Remark 4.3, together with the comment on
$\mathbb {Z}[\mathbf {e}^{\pm \epsilon _{1}},\dots ,\mathbf {e}^{\pm \epsilon _{n}}] \cong \mathbb {Z}[(1-y_{1})^{\pm 1},\dots ,(1-y_{n})^{\pm 1}]$
by Remark 4.3, together with the comment on
![]() $\delta _{i}^{\vee }$
preceding it, we deduce that the operators
$\delta _{i}^{\vee }$
preceding it, we deduce that the operators
![]() $\delta _{i}^{\vee }$
and
$\delta _{i}^{\vee }$
and
![]() $\pi ^{(y)}_{i}$
coincide on
$\pi ^{(y)}_{i}$
coincide on
recall the identification (ID2). Namely, we obtain the following commutative diagram for all
![]() $1 \leq i \leq n$
:
$1 \leq i \leq n$
:

Now, we are ready to state and prove the main result of this paper.
Theorem 4.4. Let w be an arbitrary element of
![]() $W = S_{n+1}$
. Then, under the identification (ID2), the following equality holds in
$W = S_{n+1}$
. Then, under the identification (ID2), the following equality holds in
![]() $QK_{H}(Fl_{n+1})$
:
$QK_{H}(Fl_{n+1})$
:
where
![]() $\Psi ^{Q}$
is the
$\Psi ^{Q}$
is the
![]() $R(H)[\![Q]\!]$
-algebra isomorphism in (3.9).
$R(H)[\![Q]\!]$
-algebra isomorphism in (3.9).
Proof. The assertion of the theorem is already proved for
![]() $w = w_{\circ } \in W=S_{n+1}$
by Theorem 3.3:
$w = w_{\circ } \in W=S_{n+1}$
by Theorem 3.3:
For an arbitrary
![]() $w \in W=S_{n+1}$
, let
$w \in W=S_{n+1}$
, let
![]() $ww_{\circ } = s_{i_{1}} \cdots s_{i_{l}}$
be a reduced expression; notice that
$ww_{\circ } = s_{i_{1}} \cdots s_{i_{l}}$
be a reduced expression; notice that
![]() $l = \ell (w_{\circ })-\ell (w)$
. Then, by the definition of quantum double Grothendieck polynomials, we have
$l = \ell (w_{\circ })-\ell (w)$
. Then, by the definition of quantum double Grothendieck polynomials, we have
Here, note that
![]() $w = s_{i_1} \cdots s_{i_l} w_{\circ }$
, and that
$w = s_{i_1} \cdots s_{i_l} w_{\circ }$
, and that
![]() $w < s_{i_2} \cdots s_{i_l} w_{\circ } < \cdots < s_{i_l}w_{\circ } < w_{\circ }$
in the Bruhat order
$w < s_{i_2} \cdots s_{i_l} w_{\circ } < \cdots < s_{i_l}w_{\circ } < w_{\circ }$
in the Bruhat order
![]() $<$
on
$<$
on
![]() $W = S_{n+1}$
, since
$W = S_{n+1}$
, since
![]() $\ell (w) = \ell (w_{\circ }) - l$
. Therefore, by the property (4.4) of quantum (dual) left Demazure operators
$\ell (w) = \ell (w_{\circ }) - l$
. Therefore, by the property (4.4) of quantum (dual) left Demazure operators
![]() $\delta _{i}^{\vee }$
, we deduce that
$\delta _{i}^{\vee }$
, we deduce that
From the equalities (4.6), (4.7) and (4.8), using the commutative diagram (4.5), we conclude that
![]() $\Psi ^{Q}(\mathfrak {G}_{w}^{Q}(x,y) \ \mathrm {mod} \ \mathcal{I}^{Q}) = [\mathcal{O}^{w}] \in QK_{H}(Fl_{n+1})$
. This proves the theorem.
$\Psi ^{Q}(\mathfrak {G}_{w}^{Q}(x,y) \ \mathrm {mod} \ \mathcal{I}^{Q}) = [\mathcal{O}^{w}] \in QK_{H}(Fl_{n+1})$
. This proves the theorem.
Remark 4.5. Let
![]() $R(H)[Q]_{\mathrm {loc}}$
denote the localization of the polynomial ring
$R(H)[Q]_{\mathrm {loc}}$
denote the localization of the polynomial ring
![]() $R(H)[Q] := R(H)[Q_1, \ldots , Q_n]$
with respect to the multiplicative set
$R(H)[Q] := R(H)[Q_1, \ldots , Q_n]$
with respect to the multiplicative set
![]() $1 + (Q_1, \ldots , Q_n)$
, where
$1 + (Q_1, \ldots , Q_n)$
, where
![]() $(Q_{1}, \ldots , Q_{n})$
is the ideal of
$(Q_{1}, \ldots , Q_{n})$
is the ideal of
![]() $R(H)[Q]$
generated by the variables
$R(H)[Q]$
generated by the variables
![]() $Q_{1}, \ldots , Q_{n}$
. Also, let
$Q_{1}, \ldots , Q_{n}$
. Also, let
![]() $\mathcal{I}^{Q}_{\mathrm {loc}}$
denote the ideal of
$\mathcal{I}^{Q}_{\mathrm {loc}}$
denote the ideal of
![]() $(R(H)[Q]_{\mathrm {loc}})[x_1, \ldots , x_n, x_{n+1}]$
generated by the same elements as for the ideal
$(R(H)[Q]_{\mathrm {loc}})[x_1, \ldots , x_n, x_{n+1}]$
generated by the same elements as for the ideal
![]() $\mathcal{I}^{Q}$
. In [Reference Maeno, Naito and SagakiMaNS, Remark 6.3], we stated that the quotient ring
$\mathcal{I}^{Q}$
. In [Reference Maeno, Naito and SagakiMaNS, Remark 6.3], we stated that the quotient ring
![]() $(R(H)[Q]_{\mathrm {loc}})[x_{1},\ldots ,x_{n},x_{n+1}]/\mathcal{I}^{Q}_{\mathrm {loc}}$
is isomorphic to the subring
$(R(H)[Q]_{\mathrm {loc}})[x_{1},\ldots ,x_{n},x_{n+1}]/\mathcal{I}^{Q}_{\mathrm {loc}}$
is isomorphic to the subring
![]() $QK_{H}(Fl_{n+1})_{\mathrm {loc}} := K_{H}(Fl_{n+1}) \otimes _{R(H)} R(H)[Q]_{\mathrm {loc}}$
of
$QK_{H}(Fl_{n+1})_{\mathrm {loc}} := K_{H}(Fl_{n+1}) \otimes _{R(H)} R(H)[Q]_{\mathrm {loc}}$
of
![]() $QK_{H}(Fl_{n+1})$
$QK_{H}(Fl_{n+1})$
![]() $= K_{H}(Fl_{n+1}) \otimes _{R(H)} R(H)[\![Q]\!]$
. Based on this result, by the same line of argument as for the proof of Theorem 4.4, we can prove that the assertion of Theorem 4.4 still holds in this setting (i.e., in the setting where we use
$= K_{H}(Fl_{n+1}) \otimes _{R(H)} R(H)[\![Q]\!]$
. Based on this result, by the same line of argument as for the proof of Theorem 4.4, we can prove that the assertion of Theorem 4.4 still holds in this setting (i.e., in the setting where we use
![]() $R(H)[Q]_{\mathrm {loc}}$
in place of
$R(H)[Q]_{\mathrm {loc}}$
in place of
![]() $R(H)[\![Q]\!]$
).
$R(H)[\![Q]\!]$
).
5 Proof of Proposition 2.4
5.1 General Chevalley formula
We briefly review the general Chevalley formula for
![]() $K_{H}(\mathbf {Q}_{G})$
, following [Reference Lenart, Naito and SagakiLNS] (cf. [Reference Kouno, Lenart and NaitoKoLN, Theorem 5.16]); this formula plays an important role in the proof of Proposition 2.4. We use the notation and setting of Section 2.4. Recall that
$K_{H}(\mathbf {Q}_{G})$
, following [Reference Lenart, Naito and SagakiLNS] (cf. [Reference Kouno, Lenart and NaitoKoLN, Theorem 5.16]); this formula plays an important role in the proof of Proposition 2.4. We use the notation and setting of Section 2.4. Recall that
![]() $\mathfrak {g}$
is an (arbitrary) finite-dimensional simple Lie algebra over
$\mathfrak {g}$
is an (arbitrary) finite-dimensional simple Lie algebra over
![]() $\mathbb {C}$
. Let
$\mathbb {C}$
. Let
![]() $\mathfrak {h}^{\ast }_{\mathbb {R}} :=\mathbb {R} \otimes _{\mathbb {Z}} P$
be a real form of
$\mathfrak {h}^{\ast }_{\mathbb {R}} :=\mathbb {R} \otimes _{\mathbb {Z}} P$
be a real form of
![]() $\mathfrak {h}^{\ast }$
, and set
$\mathfrak {h}^{\ast }$
, and set
We denote by
![]() $s_{\beta ,l}$
the affine reflection in the affine hyperplane
$s_{\beta ,l}$
the affine reflection in the affine hyperplane
![]() $H_{\beta ,l}$
. The affine hyperplanes
$H_{\beta ,l}$
. The affine hyperplanes
![]() $H_{\beta ,l}$
,
$H_{\beta ,l}$
,
![]() $\beta \in \Delta $
,
$\beta \in \Delta $
,
![]() $l \in \mathbb {Z}$
, divide the real vector space
$l \in \mathbb {Z}$
, divide the real vector space
![]() $\mathfrak {h}^{\ast }_{\mathbb {R}}$
into open regions, called alcoves; the fundamental alcove is defined as
$\mathfrak {h}^{\ast }_{\mathbb {R}}$
into open regions, called alcoves; the fundamental alcove is defined as
We say that two alcoves are adjacent if they are distinct and have a common wall. Given a pair of adjacent alcoves A and B, we write
![]() $A \xrightarrow {\hspace {2pt}\beta \hspace {2pt}} B$
for
$A \xrightarrow {\hspace {2pt}\beta \hspace {2pt}} B$
for
![]() $\beta \in \Delta $
if the common wall is orthogonal to
$\beta \in \Delta $
if the common wall is orthogonal to
![]() $\beta $
and
$\beta $
and
![]() $\beta $
points in the direction from A to B.
$\beta $
points in the direction from A to B.
Definition 5.1 [Reference Lenart and PostnikovLP]
An alcove path is a sequence of alcoves
![]() $(A_0, A_1, \ldots , A_m)$
such that
$(A_0, A_1, \ldots , A_m)$
such that
![]() $A_{j-1}$
and
$A_{j-1}$
and
![]() $A_j$
are adjacent for
$A_j$
are adjacent for
![]() $j=1,\ldots ,m$
. We say that
$j=1,\ldots ,m$
. We say that
![]() $(A_0, A_1, \ldots , A_m)$
is reduced if it has minimal length among all alcove paths from
$(A_0, A_1, \ldots , A_m)$
is reduced if it has minimal length among all alcove paths from
![]() $A_0$
to
$A_0$
to
![]() $A_m$
.
$A_m$
.
Let
![]() $\lambda \in P$
, and let
$\lambda \in P$
, and let
![]() $A_{\lambda }=A_{\circ }+\lambda $
be the translation of the fundamental alcove
$A_{\lambda }=A_{\circ }+\lambda $
be the translation of the fundamental alcove
![]() $A_{\circ }$
by the weight
$A_{\circ }$
by the weight
![]() $\lambda $
.
$\lambda $
.
Definition 5.2 [Reference Lenart and PostnikovLP]
Let
![]() $\lambda \in P$
. A sequence
$\lambda \in P$
. A sequence
![]() $(\beta _1, \beta _2, \dots , \beta _m)$
of roots is called a reduced
$(\beta _1, \beta _2, \dots , \beta _m)$
of roots is called a reduced
![]() $\lambda $
-chain (of roots) if
$\lambda $
-chain (of roots) if
is a reduced alcove path.
A reduced alcove path
![]() $(A_0=A_{\circ },A_1,\ldots ,A_m=A_{-\lambda })$
can be identified with the corresponding total order on the hyperplanes, to be called
$(A_0=A_{\circ },A_1,\ldots ,A_m=A_{-\lambda })$
can be identified with the corresponding total order on the hyperplanes, to be called
![]() $\lambda $
-hyperplanes, which separate
$\lambda $
-hyperplanes, which separate
![]() $A_\circ $
from
$A_\circ $
from
![]() $A_{-\lambda }$
. This total order is given by the sequence
$A_{-\lambda }$
. This total order is given by the sequence
![]() $H_{\beta _i,-l_i}$
for
$H_{\beta _i,-l_i}$
for
![]() $i=1,\ldots ,m$
, where
$i=1,\ldots ,m$
, where
![]() $H_{\beta _i,-l_i}$
contains the common wall of
$H_{\beta _i,-l_i}$
contains the common wall of
![]() $A_{i-1}$
and
$A_{i-1}$
and
![]() $A_i$
. Note that
$A_i$
. Note that
![]() $\langle \lambda , \beta _i^\vee \rangle \ge 0$
, and that the integers
$\langle \lambda , \beta _i^\vee \rangle \ge 0$
, and that the integers
![]() $l_i$
, called heights, have the following ranges:
$l_i$
, called heights, have the following ranges:
 $$ \begin{align*} \begin{aligned} & 0 \le l_i \le \langle \lambda, \beta_i^\vee \rangle-1 \quad \text{if} \quad \beta_i \in \Delta^+, \\ & 1 \le l_i \le \langle \lambda, \beta_i^\vee \rangle \quad \text{if} \quad \beta_i \in \Delta^- = - \Delta^+. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} & 0 \le l_i \le \langle \lambda, \beta_i^\vee \rangle-1 \quad \text{if} \quad \beta_i \in \Delta^+, \\ & 1 \le l_i \le \langle \lambda, \beta_i^\vee \rangle \quad \text{if} \quad \beta_i \in \Delta^- = - \Delta^+. \end{aligned} \end{align*} $$
Note also that a reduced
![]() $\lambda $
-chain
$\lambda $
-chain
![]() $(\beta _1, \ldots , \beta _m)$
determines the corresponding reduced alcove path, and hence we can identify them.
$(\beta _1, \ldots , \beta _m)$
determines the corresponding reduced alcove path, and hence we can identify them.
Let
![]() $\lambda \in P$
, and fix a reduced
$\lambda \in P$
, and fix a reduced
![]() $\lambda $
-chain, which we denote by
$\lambda $
-chain, which we denote by
![]() $\Gamma (\lambda )=(\beta _1,\,\ldots ,\,\beta _m)$
; later in Section 5.2, for
$\Gamma (\lambda )=(\beta _1,\,\ldots ,\,\beta _m)$
; later in Section 5.2, for
![]() $\lambda = - \epsilon _{J} \in P$
with
$\lambda = - \epsilon _{J} \in P$
with
![]() $J \subset [k]$
, we make a specific choice of reduced
$J \subset [k]$
, we make a specific choice of reduced
![]() $\lambda $
-chain and denote it by
$\lambda $
-chain and denote it by
![]() $\Gamma _{J}$
. Let
$\Gamma _{J}$
. Let
![]() $w \in W$
.
$w \in W$
.
Definition 5.3 [Reference Lenart and LubovskyLL]
A (possibly empty) subset
![]() $A=\left \{ j_1 < j_2 < \cdots < j_s \right \}$
of
$A=\left \{ j_1 < j_2 < \cdots < j_s \right \}$
of
![]() $[m]=\{1,\ldots ,m\}$
is called a w-admissible subset if we have the following directed path in the quantum Bruhat graph
$[m]=\{1,\ldots ,m\}$
is called a w-admissible subset if we have the following directed path in the quantum Bruhat graph
![]() $\mathrm {QBG}(W)$
:
$\mathrm {QBG}(W)$
:
 $$ \begin{align} \begin{aligned} & \Pi(w,A): w \xrightarrow{\hspace{2pt}|\beta_{j_1}|\hspace{2pt}} w s_{\beta_{j_1}} \xrightarrow{\hspace{2pt}|\beta_{j_2}|\hspace{2pt}} ws_{\beta_{j_1}}s_{\beta_{j_2}} \xrightarrow{\hspace{2pt}|\beta_{j_3}|\hspace{2pt}} \cdots \\ & \hspace{30mm} \cdots \xrightarrow{\hspace{2pt}|\beta_{j_s}|\hspace{2pt}} ws_{\beta_{j_1}}s_{\beta_{j_2}} \cdots s_{\beta_{j_s}}=:\operatorname{\mathrm{end}}(A). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & \Pi(w,A): w \xrightarrow{\hspace{2pt}|\beta_{j_1}|\hspace{2pt}} w s_{\beta_{j_1}} \xrightarrow{\hspace{2pt}|\beta_{j_2}|\hspace{2pt}} ws_{\beta_{j_1}}s_{\beta_{j_2}} \xrightarrow{\hspace{2pt}|\beta_{j_3}|\hspace{2pt}} \cdots \\ & \hspace{30mm} \cdots \xrightarrow{\hspace{2pt}|\beta_{j_s}|\hspace{2pt}} ws_{\beta_{j_1}}s_{\beta_{j_2}} \cdots s_{\beta_{j_s}}=:\operatorname{\mathrm{end}}(A). \end{aligned} \end{align} $$
Let
![]() $\mathcal{A}(w,\Gamma (\lambda ))$
denote the collection of all w-admissible subsets of
$\mathcal{A}(w,\Gamma (\lambda ))$
denote the collection of all w-admissible subsets of
![]() $[m] = \{1, \ldots , m\}$
.
$[m] = \{1, \ldots , m\}$
.
Let
![]() $A=\{ j_1 < \cdots < j_s\} \in \mathcal{A}(w,\Gamma (\lambda ))$
. The weight of A is defined by
$A=\{ j_1 < \cdots < j_s\} \in \mathcal{A}(w,\Gamma (\lambda ))$
. The weight of A is defined by
Also, we set
 $$ \begin{align} A^{-}:=\left\{j_i \in A \ \biggm| \ \begin{array}{l} ws_{\beta_{j_1}} \cdots s_{\beta_{j_{i-1}}} \xrightarrow{\hspace{2pt}|\beta_i|\hspace{2pt}} ws_{\beta_{j_1}} \cdots s_{\beta_{j_{i-1}}}s_{\beta_{j_{i}}} \\[2mm] \text{is a quantum edge} \end{array} \right\},\end{align} $$
$$ \begin{align} A^{-}:=\left\{j_i \in A \ \biggm| \ \begin{array}{l} ws_{\beta_{j_1}} \cdots s_{\beta_{j_{i-1}}} \xrightarrow{\hspace{2pt}|\beta_i|\hspace{2pt}} ws_{\beta_{j_1}} \cdots s_{\beta_{j_{i-1}}}s_{\beta_{j_{i}}} \\[2mm] \text{is a quantum edge} \end{array} \right\},\end{align} $$
 $$ \begin{align} \operatorname{\mathrm{down}}(A):=\sum_{j\in A^-}|\beta_j|^\vee\in Q^{\vee,+}. \qquad\qquad\qquad\qquad\qquad\qquad \end{align} $$
$$ \begin{align} \operatorname{\mathrm{down}}(A):=\sum_{j\in A^-}|\beta_j|^\vee\in Q^{\vee,+}. \qquad\qquad\qquad\qquad\qquad\qquad \end{align} $$
We write
![]() $\lambda \in P$
as
$\lambda \in P$
as
![]() $\lambda =\sum _{i\in I}\lambda _i\varpi _i \in P$
, with
$\lambda =\sum _{i\in I}\lambda _i\varpi _i \in P$
, with
![]() $\lambda _{i} \in \mathbb {Z}$
for
$\lambda _{i} \in \mathbb {Z}$
for
![]() $i \in I$
. Following [Reference Lenart, Naito and SagakiLNS, Section 4.1], let
$i \in I$
. Following [Reference Lenart, Naito and SagakiLNS, Section 4.1], let
![]() $\overline {\mathrm {Par}(\lambda )}$
denote the set of I-tuples of partitions
$\overline {\mathrm {Par}(\lambda )}$
denote the set of I-tuples of partitions
![]() $\boldsymbol {\chi }=(\chi ^{(i)})_{i\in I}$
such that
$\boldsymbol {\chi }=(\chi ^{(i)})_{i\in I}$
such that
![]() $\chi ^{(i)}$
is a partition of length at most
$\chi ^{(i)}$
is a partition of length at most
![]() $\max (\lambda _i,0)$
; in [Reference Naito and SagakiNS1, Section 2.5], for
$\max (\lambda _i,0)$
; in [Reference Naito and SagakiNS1, Section 2.5], for
![]() $\lambda \in P^{+}$
, we introduced the set
$\lambda \in P^{+}$
, we introduced the set
![]() $\mathrm {Par}(\lambda )$
of I-tuples of partitions
$\mathrm {Par}(\lambda )$
of I-tuples of partitions
![]() $\boldsymbol {\chi }=(\chi ^{(i)})_{i\in I}$
such that
$\boldsymbol {\chi }=(\chi ^{(i)})_{i\in I}$
such that
![]() $\chi ^{(i)}$
is a partition of length less than
$\chi ^{(i)}$
is a partition of length less than
![]() $\lambda _i$
(which we do not use in this paper). For
$\lambda _i$
(which we do not use in this paper). For
![]() $\boldsymbol {\chi } = (\chi ^{(i)})_{i \in I} \in \overline {\mathrm {Par}(\lambda )}$
, we set
$\boldsymbol {\chi } = (\chi ^{(i)})_{i \in I} \in \overline {\mathrm {Par}(\lambda )}$
, we set
![]() $\iota (\boldsymbol {\chi }) := \sum _{i \in I} \chi ^{(i)}_1 \alpha _i^{\vee } \in Q^{\vee ,+}$
, with
$\iota (\boldsymbol {\chi }) := \sum _{i \in I} \chi ^{(i)}_1 \alpha _i^{\vee } \in Q^{\vee ,+}$
, with
![]() $\chi ^{(i)}_1$
the first part of the partition
$\chi ^{(i)}_1$
the first part of the partition
![]() $\chi ^{(i)}$
for each
$\chi ^{(i)}$
for each
![]() $i \in I$
.
$i \in I$
.
By specializing at
![]() $q = 1$
in [Reference Lenart, Naito and SagakiLNS, Theorem 33] (cf. [Reference Kouno, Lenart and NaitoKoLN, Theorem 5.16]), we obtain the following general Chevalley formula for
$q = 1$
in [Reference Lenart, Naito and SagakiLNS, Theorem 33] (cf. [Reference Kouno, Lenart and NaitoKoLN, Theorem 5.16]), we obtain the following general Chevalley formula for
![]() $K_{H}(\mathbf {Q}_{G})$
.
$K_{H}(\mathbf {Q}_{G})$
.
Theorem 5.4. Let
![]() $\lambda =\sum _{i\in I}\lambda _i\varpi _i \in P$
be an arbitrary weight,
$\lambda =\sum _{i\in I}\lambda _i\varpi _i \in P$
be an arbitrary weight,
![]() $\Gamma (\lambda )$
an arbitrary reduced
$\Gamma (\lambda )$
an arbitrary reduced
![]() $\lambda $
-chain, and
$\lambda $
-chain, and
![]() $x=wt_{\xi }\in W_{\mathrm {af}}^{\ge 0} \simeq W \times Q^{\vee ,+}$
. Then, the following equality holds in
$x=wt_{\xi }\in W_{\mathrm {af}}^{\ge 0} \simeq W \times Q^{\vee ,+}$
. Then, the following equality holds in
![]() $K_{H}(\mathbf {Q}_{G})$
:
$K_{H}(\mathbf {Q}_{G})$
:
 $$ \begin{align} & [\mathcal{O}_{\mathbf{Q}_{G}}(-w_{\circ} \lambda)] \otimes [\mathcal{O}_{\mathbf{Q}_{G}(x)}] \nonumber \\[3mm] & \quad = \sum_{A \in \mathcal{A}(w,\Gamma(\lambda))} \sum_{ \boldsymbol{\chi} \in \overline{\mathrm{Par}(\lambda)} } (-1)^{n(A)} \mathbf{e}^{\operatorname{\mathrm{wt}}(A)} [\mathcal{O}_{\mathbf{Q}_{G}( \operatorname{\mathrm{end}}(A)t_{\xi+\operatorname{\mathrm{down}}(A)+\iota(\boldsymbol{\chi})} )}]. \end{align} $$
$$ \begin{align} & [\mathcal{O}_{\mathbf{Q}_{G}}(-w_{\circ} \lambda)] \otimes [\mathcal{O}_{\mathbf{Q}_{G}(x)}] \nonumber \\[3mm] & \quad = \sum_{A \in \mathcal{A}(w,\Gamma(\lambda))} \sum_{ \boldsymbol{\chi} \in \overline{\mathrm{Par}(\lambda)} } (-1)^{n(A)} \mathbf{e}^{\operatorname{\mathrm{wt}}(A)} [\mathcal{O}_{\mathbf{Q}_{G}( \operatorname{\mathrm{end}}(A)t_{\xi+\operatorname{\mathrm{down}}(A)+\iota(\boldsymbol{\chi})} )}]. \end{align} $$
In order to prove equation (2.6), we compute
 $$ \begin{align} \left( \left(\prod_{ j \in J^{-} } (1-\mathsf{t}_{j})\right) [\mathcal{O}_{\mathbf{Q}_{G}}( w_{\circ} \epsilon_{J} )] \right) \otimes [\mathcal{O}_{\mathbf{Q}_{G}(w_{k+1})}] \in K_{H}(\mathbf{Q}_{G}) \end{align} $$
$$ \begin{align} \left( \left(\prod_{ j \in J^{-} } (1-\mathsf{t}_{j})\right) [\mathcal{O}_{\mathbf{Q}_{G}}( w_{\circ} \epsilon_{J} )] \right) \otimes [\mathcal{O}_{\mathbf{Q}_{G}(w_{k+1})}] \in K_{H}(\mathbf{Q}_{G}) \end{align} $$
for
![]() $J = \big \{ j_{1},j_{2},\dots ,j_{p} \big \} \subset [k] =\big \{1,2,\ldots ,k\big \}$
, with
$J = \big \{ j_{1},j_{2},\dots ,j_{p} \big \} \subset [k] =\big \{1,2,\ldots ,k\big \}$
, with
![]() $1 \le j_{1} < j_{2} < \cdots < j_{p} \le k$
; recall Remark 2.3 and the definition of
$1 \le j_{1} < j_{2} < \cdots < j_{p} \le k$
; recall Remark 2.3 and the definition of
![]() $J^{-}$
from (2.4).
$J^{-}$
from (2.4).
Lemma 5.5. Keep the setting above. The following equality holds in
![]() $K_{H}(\mathbf {Q}_{G})$
:
$K_{H}(\mathbf {Q}_{G})$
:
 $$ \begin{align} & \left( \left(\prod_{ j \in J^{-} } (1-\mathsf{t}_{j})\right) [\mathcal{O}_{\mathbf{Q}_{G}}( w_{\circ} \epsilon_{J} )] \right) \otimes [\mathcal{O}_{\mathbf{Q}_{G}(w_{k+1})}] \nonumber \\[3mm] & \qquad = \sum_{A \in \mathcal{A}(w_{k+1},\Gamma(-\epsilon_{J}))} (-1)^{n(A)} \mathbf{e}^{\operatorname{\mathrm{wt}}(A)} [\mathcal{O}_{\mathbf{Q}_{G}( \operatorname{\mathrm{end}}(A)t_{\operatorname{\mathrm{down}}(A)} )}]. \end{align} $$
$$ \begin{align} & \left( \left(\prod_{ j \in J^{-} } (1-\mathsf{t}_{j})\right) [\mathcal{O}_{\mathbf{Q}_{G}}( w_{\circ} \epsilon_{J} )] \right) \otimes [\mathcal{O}_{\mathbf{Q}_{G}(w_{k+1})}] \nonumber \\[3mm] & \qquad = \sum_{A \in \mathcal{A}(w_{k+1},\Gamma(-\epsilon_{J}))} (-1)^{n(A)} \mathbf{e}^{\operatorname{\mathrm{wt}}(A)} [\mathcal{O}_{\mathbf{Q}_{G}( \operatorname{\mathrm{end}}(A)t_{\operatorname{\mathrm{down}}(A)} )}]. \end{align} $$
Proof. Applying Theorem 5.4 to the case that
![]() $\lambda =-\epsilon _{J}$
and
$\lambda =-\epsilon _{J}$
and
![]() $x = w_{k+1}$
, we obtain
$x = w_{k+1}$
, we obtain
 $$ \begin{align*} & [\mathcal{O}_{\mathbf{Q}_{G}}(w_{\circ} \epsilon_{J})] \otimes [\mathcal{O}_{\mathbf{Q}_{G}(w_{k+1})}] = \sum_{A \in \mathcal{A}(w_{k+1},\Gamma(-\epsilon_{J}))} \, \sum_{ \boldsymbol{\chi} \in \overline{\mathrm{Par}(-\epsilon_{J})} } (-1)^{n(A)} \mathbf{e}^{\operatorname{\mathrm{wt}}(A)} [\mathcal{O}_{\mathbf{Q}_{G}( \operatorname{\mathrm{end}}(A)t_{\operatorname{\mathrm{down}}(A)+\iota(\boldsymbol{\chi})} )}]. \end{align*} $$
$$ \begin{align*} & [\mathcal{O}_{\mathbf{Q}_{G}}(w_{\circ} \epsilon_{J})] \otimes [\mathcal{O}_{\mathbf{Q}_{G}(w_{k+1})}] = \sum_{A \in \mathcal{A}(w_{k+1},\Gamma(-\epsilon_{J}))} \, \sum_{ \boldsymbol{\chi} \in \overline{\mathrm{Par}(-\epsilon_{J})} } (-1)^{n(A)} \mathbf{e}^{\operatorname{\mathrm{wt}}(A)} [\mathcal{O}_{\mathbf{Q}_{G}( \operatorname{\mathrm{end}}(A)t_{\operatorname{\mathrm{down}}(A)+\iota(\boldsymbol{\chi})} )}]. \end{align*} $$
Here, observe that for
![]() $1 \le j \le n$
, we have
$1 \le j \le n$
, we have
![]() $\langle -\epsilon _{J}, \alpha _{j}^{\vee } \rangle \in \{-1,0,1\}$
, and that the equality
$\langle -\epsilon _{J}, \alpha _{j}^{\vee } \rangle \in \{-1,0,1\}$
, and that the equality
![]() $\langle -\epsilon _{J}, \alpha _{j}^{\vee } \rangle = 1$
holds if and only if
$\langle -\epsilon _{J}, \alpha _{j}^{\vee } \rangle = 1$
holds if and only if
![]() $j \in J^{-}$
. This implies that
$j \in J^{-}$
. This implies that
![]() $-\epsilon _{J}=\sum _{i \in J^{-}} \varpi _{i}$
. Hence,
$-\epsilon _{J}=\sum _{i \in J^{-}} \varpi _{i}$
. Hence,
![]() $\boldsymbol {\chi } = (\chi ^{(i)})_{i \in I} \in \overline {\mathrm {Par}(-\epsilon _{J})}$
if and only if
$\boldsymbol {\chi } = (\chi ^{(i)})_{i \in I} \in \overline {\mathrm {Par}(-\epsilon _{J})}$
if and only if
![]() $\chi ^{(i)}$
is a partition of length at most one for all
$\chi ^{(i)}$
is a partition of length at most one for all
![]() $i \in J^{-}$
and the empty partition for all
$i \in J^{-}$
and the empty partition for all
![]() $i \notin J^{-}$
. By the definition of
$i \notin J^{-}$
. By the definition of
![]() $\iota (\boldsymbol {\chi })$
, we deduce that the map
$\iota (\boldsymbol {\chi })$
, we deduce that the map
![]() $\boldsymbol {\chi } \mapsto \iota (\boldsymbol {\chi })$
gives a bijection from
$\boldsymbol {\chi } \mapsto \iota (\boldsymbol {\chi })$
gives a bijection from
![]() $\overline {\mathrm {Par}(-\epsilon _{J})}$
onto
$\overline {\mathrm {Par}(-\epsilon _{J})}$
onto
![]() $\sum _{j \in J^{-}}\mathbb {Z}_{\ge 0}\alpha _{j}^{\vee }$
. Therefore, we see that
$\sum _{j \in J^{-}}\mathbb {Z}_{\ge 0}\alpha _{j}^{\vee }$
. Therefore, we see that
 $$ \begin{align*} & \sum_{A \in \mathcal{A}(w_{k+1},\Gamma(-\epsilon_{J}))} \, \sum_{ \boldsymbol{\chi} \in \overline{\mathrm{Par}(-\epsilon_{J})} } (-1)^{n(A)} \mathbf{e}^{\operatorname{\mathrm{wt}}(A)} [\mathcal{O}_{\mathbf{Q}_{G}( \operatorname{\mathrm{end}}(A)t_{\operatorname{\mathrm{down}}(A)+\iota(\boldsymbol{\chi})} )}] \\[3mm] & \quad = \sum_{A \in \mathcal{A}(w_{k+1},\Gamma(-\epsilon_{J}))} \, \sum_{ \zeta \in \sum_{j \in J^{-}}\mathbb{Z}_{\ge 0}\alpha_{j}^{\vee} } (-1)^{n(A)} \mathbf{e}^{\operatorname{\mathrm{wt}}(A)} [\mathcal{O}_{\mathbf{Q}_{G}( \operatorname{\mathrm{end}}(A)t_{\operatorname{\mathrm{down}}(A)+\zeta} )}] \\[3mm] & \quad = \left(\prod_{j \in J^{-}} \frac{1}{1-\mathsf{t}_{j}}\right) \sum_{A \in \mathcal{A}(w_{k+1},\Gamma(-\epsilon_{J}))} (-1)^{n(A)} \mathbf{e}^{\operatorname{\mathrm{wt}}(A)} [\mathcal{O}_{\mathbf{Q}_{G}( \operatorname{\mathrm{end}}(A)t_{\operatorname{\mathrm{down}}(A)} )}]. \end{align*} $$
$$ \begin{align*} & \sum_{A \in \mathcal{A}(w_{k+1},\Gamma(-\epsilon_{J}))} \, \sum_{ \boldsymbol{\chi} \in \overline{\mathrm{Par}(-\epsilon_{J})} } (-1)^{n(A)} \mathbf{e}^{\operatorname{\mathrm{wt}}(A)} [\mathcal{O}_{\mathbf{Q}_{G}( \operatorname{\mathrm{end}}(A)t_{\operatorname{\mathrm{down}}(A)+\iota(\boldsymbol{\chi})} )}] \\[3mm] & \quad = \sum_{A \in \mathcal{A}(w_{k+1},\Gamma(-\epsilon_{J}))} \, \sum_{ \zeta \in \sum_{j \in J^{-}}\mathbb{Z}_{\ge 0}\alpha_{j}^{\vee} } (-1)^{n(A)} \mathbf{e}^{\operatorname{\mathrm{wt}}(A)} [\mathcal{O}_{\mathbf{Q}_{G}( \operatorname{\mathrm{end}}(A)t_{\operatorname{\mathrm{down}}(A)+\zeta} )}] \\[3mm] & \quad = \left(\prod_{j \in J^{-}} \frac{1}{1-\mathsf{t}_{j}}\right) \sum_{A \in \mathcal{A}(w_{k+1},\Gamma(-\epsilon_{J}))} (-1)^{n(A)} \mathbf{e}^{\operatorname{\mathrm{wt}}(A)} [\mathcal{O}_{\mathbf{Q}_{G}( \operatorname{\mathrm{end}}(A)t_{\operatorname{\mathrm{down}}(A)} )}]. \end{align*} $$
From this, we deduce that in
![]() $K_{H}(\mathbf {Q}_{G})$
,
$K_{H}(\mathbf {Q}_{G})$
,
 $$ \begin{align*} & \left( \left(\prod_{ j \in J^{-} } (1-\mathsf{t}_{j})\right) [\mathcal{O}_{\mathbf{Q}_{G}}( w_{\circ} \epsilon_{J} )] \right) \otimes [\mathcal{O}_{\mathbf{Q}_{G}(w_{k+1})}] \\[3mm] & \hspace{5mm} = \left(\prod_{ j \in J^{-} } (1-\mathsf{t}_{j})\right) \big( [\mathcal{O}_{\mathbf{Q}_{G}}( w_{\circ} \epsilon_{J} )] \otimes [\mathcal{O}_{\mathbf{Q}_{G}(w_{k+1})}] \big) \quad \text{(see Remark~2.3)} \\[3mm] & \hspace{5mm} = \left(\prod_{ j \in J^{-} } (1-\mathsf{t}_{j})\right) \left( \left(\prod_{ j \in J^{-} } \frac{1}{1-\mathsf{t}_{j}}\right) \sum_{A \in \mathcal{A}(w_{k+1},\Gamma(-\epsilon_{J}))} (-1)^{n(A)} \mathbf{e}^{\operatorname{\mathrm{wt}}(A)} [\mathcal{O}_{\mathbf{Q}_{G}( \operatorname{\mathrm{end}}(A)t_{\operatorname{\mathrm{down}}(A)} )}] \right) \\[3mm] & \hspace{5mm} = \sum_{A \in \mathcal{A}(w_{k+1},\Gamma(-\epsilon_{J}))} (-1)^{n(A)} \mathbf{e}^{\operatorname{\mathrm{wt}}(A)} [\mathcal{O}_{\mathbf{Q}_{G}( \operatorname{\mathrm{end}}(A)t_{\operatorname{\mathrm{down}}(A)} )}], \end{align*} $$
$$ \begin{align*} & \left( \left(\prod_{ j \in J^{-} } (1-\mathsf{t}_{j})\right) [\mathcal{O}_{\mathbf{Q}_{G}}( w_{\circ} \epsilon_{J} )] \right) \otimes [\mathcal{O}_{\mathbf{Q}_{G}(w_{k+1})}] \\[3mm] & \hspace{5mm} = \left(\prod_{ j \in J^{-} } (1-\mathsf{t}_{j})\right) \big( [\mathcal{O}_{\mathbf{Q}_{G}}( w_{\circ} \epsilon_{J} )] \otimes [\mathcal{O}_{\mathbf{Q}_{G}(w_{k+1})}] \big) \quad \text{(see Remark~2.3)} \\[3mm] & \hspace{5mm} = \left(\prod_{ j \in J^{-} } (1-\mathsf{t}_{j})\right) \left( \left(\prod_{ j \in J^{-} } \frac{1}{1-\mathsf{t}_{j}}\right) \sum_{A \in \mathcal{A}(w_{k+1},\Gamma(-\epsilon_{J}))} (-1)^{n(A)} \mathbf{e}^{\operatorname{\mathrm{wt}}(A)} [\mathcal{O}_{\mathbf{Q}_{G}( \operatorname{\mathrm{end}}(A)t_{\operatorname{\mathrm{down}}(A)} )}] \right) \\[3mm] & \hspace{5mm} = \sum_{A \in \mathcal{A}(w_{k+1},\Gamma(-\epsilon_{J}))} (-1)^{n(A)} \mathbf{e}^{\operatorname{\mathrm{wt}}(A)} [\mathcal{O}_{\mathbf{Q}_{G}( \operatorname{\mathrm{end}}(A)t_{\operatorname{\mathrm{down}}(A)} )}], \end{align*} $$
as desired. This proves the lemma.
5.2 A special reduced chain (of roots)
Let us fix
![]() $J = \big \{ j_{1},j_{2},\dots ,j_{p} \big \} \subset [k]$
, with
$J = \big \{ j_{1},j_{2},\dots ,j_{p} \big \} \subset [k]$
, with
![]() $1 \le j_{1} < j_{2} < \cdots < j_{p} \le k$
. Following [Reference Lenart, Naito, Orr and SagakiLNOS, Lemma 4.1], we take a special reduced
$1 \le j_{1} < j_{2} < \cdots < j_{p} \le k$
. Following [Reference Lenart, Naito, Orr and SagakiLNOS, Lemma 4.1], we take a special reduced
![]() $(-\epsilon _{J})$
-chain (of roots) from
$(-\epsilon _{J})$
-chain (of roots) from
![]() $A_{\circ }$
to
$A_{\circ }$
to
![]() $A_{\epsilon _{J}}$
(see Definition 5.2) as follows. Notice that
$A_{\epsilon _{J}}$
(see Definition 5.2) as follows. Notice that
![]() $\epsilon _{J} \in W\varpi _{p}$
. Let
$\epsilon _{J} \in W\varpi _{p}$
. Let
![]() $x_{J}$
be the (unique) minimal-length element in
$x_{J}$
be the (unique) minimal-length element in
![]() $\big \{ w \in W \mid w \varpi _{p} = \epsilon _{J} \big \}$
, and let
$\big \{ w \in W \mid w \varpi _{p} = \epsilon _{J} \big \}$
, and let
![]() $x_{J} = s_{i_{a}} \cdots s_{i_{1}}$
, with
$x_{J} = s_{i_{a}} \cdots s_{i_{1}}$
, with
![]() $a:=\ell (x_{J})$
, be the reduced expression of the following form:
$a:=\ell (x_{J})$
, be the reduced expression of the following form:
 $$ \begin{align} \begin{aligned} x_{J} & = s_{i_{a}} \cdots s_{i_{1}} \\ & = \underbrace{(s_{j_1-1} \cdots s_{2}s_{1})}_{\text{mapping }\epsilon_{1} \text{ to } \epsilon_{j_{1}}.} \underbrace{(s_{j_2-1} \cdots s_{3}s_{2})}_{\text{mapping } \epsilon_{2} \text{ to } \epsilon_{j_{2}}.} \cdots \\[2mm] & \qquad \cdots \underbrace{(s_{j_{p-1}-1} \cdots s_{p}s_{p-1})}_{\text{mapping } \epsilon_{p-1} \text{ to } \epsilon_{j_{p-1}}.} \underbrace{(s_{j_{p}-1} \cdots s_{p+1}s_{p}).}_{\text{mapping } \epsilon_{p} \text{ to } \epsilon_{j_p}.} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} x_{J} & = s_{i_{a}} \cdots s_{i_{1}} \\ & = \underbrace{(s_{j_1-1} \cdots s_{2}s_{1})}_{\text{mapping }\epsilon_{1} \text{ to } \epsilon_{j_{1}}.} \underbrace{(s_{j_2-1} \cdots s_{3}s_{2})}_{\text{mapping } \epsilon_{2} \text{ to } \epsilon_{j_{2}}.} \cdots \\[2mm] & \qquad \cdots \underbrace{(s_{j_{p-1}-1} \cdots s_{p}s_{p-1})}_{\text{mapping } \epsilon_{p-1} \text{ to } \epsilon_{j_{p-1}}.} \underbrace{(s_{j_{p}-1} \cdots s_{p+1}s_{p}).}_{\text{mapping } \epsilon_{p} \text{ to } \epsilon_{j_p}.} \end{aligned} \end{align} $$
Also, let
![]() $y_{J}$
be the (unique) element such that
$y_{J}$
be the (unique) element such that
![]() $y_{J}x_{J}$
is the (unique) minimal-length element in
$y_{J}x_{J}$
is the (unique) minimal-length element in
![]() $\big \{ w \in W \mid w \varpi _{p} = w_{\circ } \varpi _{p} \big \}$
, and let
$\big \{ w \in W \mid w \varpi _{p} = w_{\circ } \varpi _{p} \big \}$
, and let
![]() $y_{J} = s_{k_{1}} \cdots s_{k_{b}}$
, with
$y_{J} = s_{k_{1}} \cdots s_{k_{b}}$
, with
![]() $b:=\ell (y_{J})$
, be the reduced expression of the following form:
$b:=\ell (y_{J})$
, be the reduced expression of the following form:
 $$ \begin{align} \begin{aligned} y_{J} & = s_{k_{1}} \cdots s_{k_{b}} \\ & = \underbrace{(s_{n-p+1} \cdots s_{j_{1}+1}s_{j_{1}})}_{\text{mapping } \epsilon_{j_1} \text{ to } \epsilon_{n-p+2}.} \underbrace{(s_{n-p+2} \cdots s_{j_{2}+1}s_{j_{2}})}_{\text{mapping } \epsilon_{j_2} \text{ to } \epsilon_{n-p+3}.} \cdots \\[2mm] & \qquad \cdots \underbrace{(s_{n-1} \cdots s_{j_{p-1}+1}s_{j_{p-1}}) }_{\text{mapping } \epsilon_{j_{p-1}} \text{ to } \epsilon_{n}.} \underbrace{(s_{n} \cdots s_{j_{p}+1}s_{j_{p}}).}_{\text{mapping } \epsilon_{j_p} \text{ to } \epsilon_{n+1}.} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} y_{J} & = s_{k_{1}} \cdots s_{k_{b}} \\ & = \underbrace{(s_{n-p+1} \cdots s_{j_{1}+1}s_{j_{1}})}_{\text{mapping } \epsilon_{j_1} \text{ to } \epsilon_{n-p+2}.} \underbrace{(s_{n-p+2} \cdots s_{j_{2}+1}s_{j_{2}})}_{\text{mapping } \epsilon_{j_2} \text{ to } \epsilon_{n-p+3}.} \cdots \\[2mm] & \qquad \cdots \underbrace{(s_{n-1} \cdots s_{j_{p-1}+1}s_{j_{p-1}}) }_{\text{mapping } \epsilon_{j_{p-1}} \text{ to } \epsilon_{n}.} \underbrace{(s_{n} \cdots s_{j_{p}+1}s_{j_{p}}).}_{\text{mapping } \epsilon_{j_p} \text{ to } \epsilon_{n+1}.} \end{aligned} \end{align} $$
We set
We call the sequences
![]() $\boldsymbol {\beta }:=(\beta _{a},\dots ,\beta _{1})$
and
$\boldsymbol {\beta }:=(\beta _{a},\dots ,\beta _{1})$
and
![]() $\boldsymbol {\gamma }:=(\gamma _{1},\dots ,\gamma _{b})$
the
$\boldsymbol {\gamma }:=(\gamma _{1},\dots ,\gamma _{b})$
the
![]() $\boldsymbol {\beta }$
-sequence and
$\boldsymbol {\beta }$
-sequence and
![]() $\boldsymbol {\gamma }$
-sequence for J, respectively.
$\boldsymbol {\gamma }$
-sequence for J, respectively.
Proposition 5.6 [Reference Lenart, Naito, Orr and SagakiLNOS, Lemma 4.1]
If we set
then
![]() $\Gamma _{J}$
is a reduced
$\Gamma _{J}$
is a reduced
![]() $(-\epsilon _{J})$
-chain from
$(-\epsilon _{J})$
-chain from
![]() $A_{\circ }$
to
$A_{\circ }$
to
![]() $A_{\epsilon _{J}}$
. Moreover, for
$A_{\epsilon _{J}}$
. Moreover, for
![]() $1 \le c \le a$
, the affine hyperplane between the
$1 \le c \le a$
, the affine hyperplane between the
![]() $(c-1)$
-th alcove and the c-th alcove in
$(c-1)$
-th alcove and the c-th alcove in
![]() $\Gamma _{J}$
is
$\Gamma _{J}$
is
![]() $H_{-\beta _{a-c+1},0}$
, and for
$H_{-\beta _{a-c+1},0}$
, and for
![]() $1 \le d \le b$
, the affine hyperplane between the
$1 \le d \le b$
, the affine hyperplane between the
![]() $(a+d-1)$
-th alcove and the
$(a+d-1)$
-th alcove and the
![]() $(a+d)$
-th alcove in
$(a+d)$
-th alcove in
![]() $\Gamma _{J}$
is
$\Gamma _{J}$
is
![]() $H_{\gamma _{d},1}$
; remark that
$H_{\gamma _{d},1}$
; remark that
![]() $\epsilon _{J} \in H_{\gamma _{d},1}$
, and hence,
$\epsilon _{J} \in H_{\gamma _{d},1}$
, and hence,
![]() $s_{\gamma _{d},1}(\epsilon _{J}) = \epsilon _{J}$
for all
$s_{\gamma _{d},1}(\epsilon _{J}) = \epsilon _{J}$
for all
![]() $1 \le d \le b$
(see also Remark 5.11 below).
$1 \le d \le b$
(see also Remark 5.11 below).
Example 5.7. Assume that
![]() $n = 5$
,
$n = 5$
,
![]() $k=4$
and
$k=4$
and
![]() $J=\{2,4\}$
. In this case, we see that
$J=\{2,4\}$
. In this case, we see that
in particular,
![]() $a=\ell (x_{J})=3$
and
$a=\ell (x_{J})=3$
and
![]() $b = \ell (y_{J})=5$
. We have
$b = \ell (y_{J})=5$
. We have
 $$ \begin{align*} \beta_{3} & = \alpha_{1} = (1,2), \\ \beta_{2} & = s_1\alpha_3 = \alpha_{3} = (3,4), \\ \beta_{1} & = s_1s_3\alpha_2 = \alpha_{1}+\alpha_{2}+\alpha_{3} = (1,4), \\ \gamma_{1} & = s_4s_5s_2s_3\alpha_{4} = \alpha_{2}+\alpha_{3}+\alpha_{4}+\alpha_{5} = (2,6), \\ \gamma_{2} & = s_4s_5s_2\alpha_{3} = \alpha_{2}+\alpha_{3}+\alpha_{4} = (2,5), \\ \gamma_{3} & = s_4s_5\alpha_{2} = \alpha_{2} = (2,3), \\ \gamma_{4} & = s_4\alpha_{5} = \alpha_{4} + \alpha_{5} = (4,6), \\ \gamma_{5} & = \alpha_{4} = (4,5). \end{align*} $$
$$ \begin{align*} \beta_{3} & = \alpha_{1} = (1,2), \\ \beta_{2} & = s_1\alpha_3 = \alpha_{3} = (3,4), \\ \beta_{1} & = s_1s_3\alpha_2 = \alpha_{1}+\alpha_{2}+\alpha_{3} = (1,4), \\ \gamma_{1} & = s_4s_5s_2s_3\alpha_{4} = \alpha_{2}+\alpha_{3}+\alpha_{4}+\alpha_{5} = (2,6), \\ \gamma_{2} & = s_4s_5s_2\alpha_{3} = \alpha_{2}+\alpha_{3}+\alpha_{4} = (2,5), \\ \gamma_{3} & = s_4s_5\alpha_{2} = \alpha_{2} = (2,3), \\ \gamma_{4} & = s_4\alpha_{5} = \alpha_{4} + \alpha_{5} = (4,6), \\ \gamma_{5} & = \alpha_{4} = (4,5). \end{align*} $$
Thus,
 $$ \begin{align*} \Gamma_{J} & =(-\alpha_{1}, -\alpha_{3}, -(\alpha_{1}+\alpha_{2}+\alpha_{3}), \\ & \qquad \qquad \alpha_{2}+\alpha_{3}+\alpha_{4}+\alpha_{5}, \alpha_{2}+\alpha_{3}+\alpha_{4}, \alpha_{2}, \alpha_{4} + \alpha_{5}, \alpha_{4}) \end{align*} $$
$$ \begin{align*} \Gamma_{J} & =(-\alpha_{1}, -\alpha_{3}, -(\alpha_{1}+\alpha_{2}+\alpha_{3}), \\ & \qquad \qquad \alpha_{2}+\alpha_{3}+\alpha_{4}+\alpha_{5}, \alpha_{2}+\alpha_{3}+\alpha_{4}, \alpha_{2}, \alpha_{4} + \alpha_{5}, \alpha_{4}) \end{align*} $$
is a reduced
![]() $(-\epsilon _{J})$
-chain from
$(-\epsilon _{J})$
-chain from
![]() $A_{\circ }$
to
$A_{\circ }$
to
![]() $A_{\epsilon _{J}}$
.
$A_{\epsilon _{J}}$
.
Let us compute
![]() $\beta _{c} \in \Delta ^{+}$
,
$\beta _{c} \in \Delta ^{+}$
,
![]() $1 \le c \le a$
, more explicitly. For
$1 \le c \le a$
, more explicitly. For
![]() $1 \le u \le p$
and
$1 \le u \le p$
and
![]() $u \le t \le j_{u}-1$
, we set
$u \le t \le j_{u}-1$
, we set
notice that the sequence
![]() $\boldsymbol {\beta }=(\beta _{a},\dots ,\beta _{1})$
is identical to
$\boldsymbol {\beta }=(\beta _{a},\dots ,\beta _{1})$
is identical to
 $$ \begin{align} \begin{aligned} & (\beta_{1,j_{1}-1},\dots,\beta_{1,2},\beta_{1,1},\ \beta_{2,j_{2}-1},\dots,\beta_{2,3},\beta_{2,2},\ \dots\dots, \\ & \ \beta_{p-1,j_{p-1}-1},\dots,\beta_{p-1,p},\beta_{p-1,p-1},\ \beta_{p,j_{p}-1},\dots,\beta_{p,p+1},\beta_{p,p}). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & (\beta_{1,j_{1}-1},\dots,\beta_{1,2},\beta_{1,1},\ \beta_{2,j_{2}-1},\dots,\beta_{2,3},\beta_{2,2},\ \dots\dots, \\ & \ \beta_{p-1,j_{p-1}-1},\dots,\beta_{p-1,p},\beta_{p-1,p-1},\ \beta_{p,j_{p}-1},\dots,\beta_{p,p+1},\beta_{p,p}). \end{aligned} \end{align} $$
We set
![]() $\tau (u,t):= |\big \{1 \le r \le u-1 \mid t-r+1 \le j_{u-r} \big \}|$
.
$\tau (u,t):= |\big \{1 \le r \le u-1 \mid t-r+1 \le j_{u-r} \big \}|$
.
Lemma 5.8. The equality
![]() $\beta _{u,t}=\epsilon _{t-\tau (u,t)}-\epsilon _{j_{u}}$
holds for
$\beta _{u,t}=\epsilon _{t-\tau (u,t)}-\epsilon _{j_{u}}$
holds for
![]() $1 \le u \le p$
and
$1 \le u \le p$
and
![]() $u \le t \le j_{u}-1$
.
$u \le t \le j_{u}-1$
.
Proof. For
![]() $1 \le u \le p$
and
$1 \le u \le p$
and
![]() $u \le t \le j_{u}-1$
, we have
$u \le t \le j_{u}-1$
, we have
 $$ \begin{align*} \beta_{u,t} & := (s_{j_1-1} \cdots s_{2}s_{1}) \cdots (s_{j_{u-1}-1} \cdots s_{u}s_{u-1}) (s_{j_{u}-1} \cdots s_{t+1})(\epsilon_{t}-\epsilon_{t+1}) \\ & = (s_{j_1-1} \cdots s_{2}s_{1}) \cdots (s_{j_{u-1}-1} \cdots s_{u}s_{u-1}) (\epsilon_{t}-\epsilon_{j_{u}}) \\ & = \begin{cases} \epsilon_{t}-\epsilon_{j_{u}} & \text{if } t> j_{u-1}, \\ (s_{j_1-1} \cdots s_{2}s_{1}) \cdots (s_{j_{u-2}-1} \cdots s_{u-1}s_{u-2})(\epsilon_{t-1}-\epsilon_{j_{u}}) & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \beta_{u,t} & := (s_{j_1-1} \cdots s_{2}s_{1}) \cdots (s_{j_{u-1}-1} \cdots s_{u}s_{u-1}) (s_{j_{u}-1} \cdots s_{t+1})(\epsilon_{t}-\epsilon_{t+1}) \\ & = (s_{j_1-1} \cdots s_{2}s_{1}) \cdots (s_{j_{u-1}-1} \cdots s_{u}s_{u-1}) (\epsilon_{t}-\epsilon_{j_{u}}) \\ & = \begin{cases} \epsilon_{t}-\epsilon_{j_{u}} & \text{if } t> j_{u-1}, \\ (s_{j_1-1} \cdots s_{2}s_{1}) \cdots (s_{j_{u-2}-1} \cdots s_{u-1}s_{u-2})(\epsilon_{t-1}-\epsilon_{j_{u}}) & \text{otherwise}. \end{cases} \end{align*} $$
In the case
![]() $t \le j_{u-1}$
, we have
$t \le j_{u-1}$
, we have
 $$ \begin{align*} & (s_{j_1-1} \cdots s_{2}s_{1}) \cdots (s_{j_{u-2}-1} \cdots s_{u-1}s_{u-2})(\epsilon_{t-1}-\epsilon_{j_{u}}) \\ & = \begin{cases} \epsilon_{t-1}-\epsilon_{j_{u}} & \text{if } t-1> j_{u-2}, \\ (s_{j_1-1} \cdots s_{2}s_{1}) \cdots (s_{j_{u-3}-1} \cdots s_{u-2}s_{u-3})(\epsilon_{t-2}-\epsilon_{j_{u}}) & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} & (s_{j_1-1} \cdots s_{2}s_{1}) \cdots (s_{j_{u-2}-1} \cdots s_{u-1}s_{u-2})(\epsilon_{t-1}-\epsilon_{j_{u}}) \\ & = \begin{cases} \epsilon_{t-1}-\epsilon_{j_{u}} & \text{if } t-1> j_{u-2}, \\ (s_{j_1-1} \cdots s_{2}s_{1}) \cdots (s_{j_{u-3}-1} \cdots s_{u-2}s_{u-3})(\epsilon_{t-2}-\epsilon_{j_{u}}) & \text{otherwise}. \end{cases} \end{align*} $$
Repeating this computation, we deduce that
![]() $\beta _{u,t}=\epsilon _{t-\tau (u,t)}-\epsilon _{j_{u}}$
. This proves the lemma.
$\beta _{u,t}=\epsilon _{t-\tau (u,t)}-\epsilon _{j_{u}}$
. This proves the lemma.
Remark 5.9. Let
![]() $1 \le u \le p$
, and write
$1 \le u \le p$
, and write
where
![]() $m_{u}=(j_{u}-1)-(u-1) = j_{u}-u$
; we set
$m_{u}=(j_{u}-1)-(u-1) = j_{u}-u$
; we set
![]() $t_{u,m_{u}+1}:=j_{u}$
by convention. Then, we have
$t_{u,m_{u}+1}:=j_{u}$
by convention. Then, we have
Hence, the sequence
![]() $\boldsymbol {\beta }=(\beta _{a},\dots ,\beta _{1})$
is of the form
$\boldsymbol {\beta }=(\beta _{a},\dots ,\beta _{1})$
is of the form

where
![]() $(j_{r},j_{s})$
does not appear in the sequence above for any
$(j_{r},j_{s})$
does not appear in the sequence above for any
![]() $1 \le r < s \le p$
.
$1 \le r < s \le p$
.
Similarly, let us compute
![]() $\gamma _{d} \in \Delta ^{+}$
,
$\gamma _{d} \in \Delta ^{+}$
,
![]() $1 \le d \le b$
, more explicitly. For
$1 \le d \le b$
, more explicitly. For
![]() $1 \le u \le p$
and
$1 \le u \le p$
and
![]() $j_{u} \le t \le n-p+u$
, we set
$j_{u} \le t \le n-p+u$
, we set
notice that the sequence
![]() $\boldsymbol {\gamma }=(\gamma _{1},\dots ,\gamma _{b})$
is identical to
$\boldsymbol {\gamma }=(\gamma _{1},\dots ,\gamma _{b})$
is identical to
 $$ \begin{align} \begin{aligned} & (\gamma_{1,n-p+1},\dots,\gamma_{1,j_{1}+1},\gamma_{1,j_{1}}, \ \gamma_{2,n-p+2},\dots,\gamma_{2,j_{2}+1},\gamma_{2,j_{2}}, \ \dots\dots, \\ & \ \gamma_{p-1,n-1},\dots,\gamma_{p-1,j_{p-1}+1},\gamma_{p-1,j_{p-1}}, \ \gamma_{p,n},\dots,\gamma_{p,j_{p}+1},\gamma_{p,j_{p}} ). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & (\gamma_{1,n-p+1},\dots,\gamma_{1,j_{1}+1},\gamma_{1,j_{1}}, \ \gamma_{2,n-p+2},\dots,\gamma_{2,j_{2}+1},\gamma_{2,j_{2}}, \ \dots\dots, \\ & \ \gamma_{p-1,n-1},\dots,\gamma_{p-1,j_{p-1}+1},\gamma_{p-1,j_{p-1}}, \ \gamma_{p,n},\dots,\gamma_{p,j_{p}+1},\gamma_{p,j_{p}} ). \end{aligned} \end{align} $$
We set
![]() $\sigma (u,t):= |\big \{ u+1 \le r \le p \mid t+r-u \ge j_{r} \big \}|$
. The proof of the following lemma is similar to that of Lemma 5.8.
$\sigma (u,t):= |\big \{ u+1 \le r \le p \mid t+r-u \ge j_{r} \big \}|$
. The proof of the following lemma is similar to that of Lemma 5.8.
Lemma 5.10. The equality
![]() $\gamma _{u,t} = \epsilon _{j_{u}}-\epsilon _{t+1+\sigma (u,t)}$
holds for
$\gamma _{u,t} = \epsilon _{j_{u}}-\epsilon _{t+1+\sigma (u,t)}$
holds for
![]() $1 \le u \le p$
and
$1 \le u \le p$
and
![]() $j_{u} \le t \le n-p+u$
.
$j_{u} \le t \le n-p+u$
.
Remark 5.11. Let
![]() $1 \le u \le p$
, and write
$1 \le u \le p$
, and write
where
![]() $m=(n+1-j_{u})-(p-u) = n + 1 - p - j_{u}+u$
. Then, we have
$m=(n+1-j_{u})-(p-u) = n + 1 - p - j_{u}+u$
. Then, we have
 $$ \begin{align*} \begin{aligned} & (\gamma_{u,n-p+u},\dots,\gamma_{u,j_{u}+1},\gamma_{u,j_{u}}) \\ & = \big( \epsilon_{j_{u}}-\epsilon_{t_{m}}, \ \epsilon_{j_{u}}-\epsilon_{t_{m-1}}, \ \dots, \ \epsilon_{j_{u}}-\epsilon_{t_{2}}, \ \epsilon_{j_{u}}-\epsilon_{t_{1}} \big). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} & (\gamma_{u,n-p+u},\dots,\gamma_{u,j_{u}+1},\gamma_{u,j_{u}}) \\ & = \big( \epsilon_{j_{u}}-\epsilon_{t_{m}}, \ \epsilon_{j_{u}}-\epsilon_{t_{m-1}}, \ \dots, \ \epsilon_{j_{u}}-\epsilon_{t_{2}}, \ \epsilon_{j_{u}}-\epsilon_{t_{1}} \big). \end{aligned} \end{align*} $$
Hence, the sequence
![]() $\boldsymbol {\gamma }=(\gamma _{1},\dots ,\gamma _{b})$
is of the form
$\boldsymbol {\gamma }=(\gamma _{1},\dots ,\gamma _{b})$
is of the form

where
![]() $(j_{r},j_{s})$
does not appear in the sequence above for any
$(j_{r},j_{s})$
does not appear in the sequence above for any
![]() $1 \le r < s \le p$
.
$1 \le r < s \le p$
.
5.3 Proof of Proposition 2.4
For each
![]() $J = \big \{ j_{1},j_{2},\dots ,j_{p} \big \} \subset [k]$
, let
$J = \big \{ j_{1},j_{2},\dots ,j_{p} \big \} \subset [k]$
, let
![]() $\mathbf {D}_{J}$
be the set of directed paths in
$\mathbf {D}_{J}$
be the set of directed paths in
![]() $\mathrm {QBG}(W)$
of the form
$\mathrm {QBG}(W)$
of the form
 $$ \begin{align} \begin{aligned} & \mathbf{p}:w_{k+1} = \underbrace{ x_{s} \xrightarrow{\hspace{2pt}\beta_{a_s}\hspace{2pt}} \cdots \xrightarrow{\hspace{2pt}\beta_{a_1}\hspace{2pt}} x_{0}}_{ =:\,\mathbf{p}_{\beta}, \text{ the } \beta\text{-part of } \mathbf{p}} = \underbrace{ y_{0} \xrightarrow{\hspace{2pt}\gamma_{b_1}\hspace{2pt}} \cdots \xrightarrow{\hspace{2pt}\gamma_{b_t}\hspace{2pt}} y_{t}}_{ =:\,\mathbf{p}_{\gamma}, \text{ the } \gamma\text{-part of } \mathbf{p}} = : \operatorname{\mathrm{end}}(\mathbf{p}), \\ & \textrm{with } s \ge 0, a \ge a_{s}> \cdots > a_{1} \ge 1, \\ & \textrm{and } t \ge 0, 1 \le b_{1} < b_{2} < \cdots < b_{t} \le b. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & \mathbf{p}:w_{k+1} = \underbrace{ x_{s} \xrightarrow{\hspace{2pt}\beta_{a_s}\hspace{2pt}} \cdots \xrightarrow{\hspace{2pt}\beta_{a_1}\hspace{2pt}} x_{0}}_{ =:\,\mathbf{p}_{\beta}, \text{ the } \beta\text{-part of } \mathbf{p}} = \underbrace{ y_{0} \xrightarrow{\hspace{2pt}\gamma_{b_1}\hspace{2pt}} \cdots \xrightarrow{\hspace{2pt}\gamma_{b_t}\hspace{2pt}} y_{t}}_{ =:\,\mathbf{p}_{\gamma}, \text{ the } \gamma\text{-part of } \mathbf{p}} = : \operatorname{\mathrm{end}}(\mathbf{p}), \\ & \textrm{with } s \ge 0, a \ge a_{s}> \cdots > a_{1} \ge 1, \\ & \textrm{and } t \ge 0, 1 \le b_{1} < b_{2} < \cdots < b_{t} \le b. \end{aligned} \end{align} $$
We call the directed subpath
![]() $w_{k+1} = x_{s} \xrightarrow {\hspace {2pt}\beta _{a_s}\hspace {2pt}} \cdots \xrightarrow {\hspace {2pt}\beta _{a_1}\hspace {2pt}} x_{0}$
of
$w_{k+1} = x_{s} \xrightarrow {\hspace {2pt}\beta _{a_s}\hspace {2pt}} \cdots \xrightarrow {\hspace {2pt}\beta _{a_1}\hspace {2pt}} x_{0}$
of
![]() $\mathbf {p}$
the
$\mathbf {p}$
the
![]() $\boldsymbol {\beta }$
-part of
$\boldsymbol {\beta }$
-part of
![]() $\mathbf {p}$
and denote it by
$\mathbf {p}$
and denote it by
![]() $\mathbf {p}_{\boldsymbol {\beta }}$
. Notice that the label sequence
$\mathbf {p}_{\boldsymbol {\beta }}$
. Notice that the label sequence
![]() $(\beta _{a_s},\dots ,\beta _{a_1})$
of
$(\beta _{a_s},\dots ,\beta _{a_1})$
of
![]() $\mathbf {p}_{\boldsymbol {\beta }}$
is a subsequence of
$\mathbf {p}_{\boldsymbol {\beta }}$
is a subsequence of
![]() $\boldsymbol {\beta }=(\beta _{a},\dots ,\beta _{1})$
, described in Lemma 5.8 and Remark 5.9, with
$\boldsymbol {\beta }=(\beta _{a},\dots ,\beta _{1})$
, described in Lemma 5.8 and Remark 5.9, with
![]() $a = \ell (x_{J})$
; the subscript
$a = \ell (x_{J})$
; the subscript
![]() $\boldsymbol {\beta }$
of
$\boldsymbol {\beta }$
of
![]() $\mathbf {p}_{\boldsymbol {\beta }}$
indicates that
$\mathbf {p}_{\boldsymbol {\beta }}$
indicates that
![]() $\mathbf {p}_{\boldsymbol {\beta }}$
is obtained from
$\mathbf {p}_{\boldsymbol {\beta }}$
is obtained from
![]() $\mathbf {p}$
by taking the first consecutive edges whose labels are contained in the
$\mathbf {p}$
by taking the first consecutive edges whose labels are contained in the
![]() $\boldsymbol {\beta }$
-sequence. Similarly, we call the directed subpath
$\boldsymbol {\beta }$
-sequence. Similarly, we call the directed subpath
![]() $y_{0} \xrightarrow {\hspace {2pt}\gamma _{b_1}\hspace {2pt}} \cdots \xrightarrow {\hspace {2pt}\gamma _{b_t}\hspace {2pt}} y_{t} = \operatorname {\mathrm {end}}(\mathbf {p})$
of
$y_{0} \xrightarrow {\hspace {2pt}\gamma _{b_1}\hspace {2pt}} \cdots \xrightarrow {\hspace {2pt}\gamma _{b_t}\hspace {2pt}} y_{t} = \operatorname {\mathrm {end}}(\mathbf {p})$
of
![]() $\mathbf {p}$
the
$\mathbf {p}$
the
![]() $\boldsymbol {\gamma }$
-part of
$\boldsymbol {\gamma }$
-part of
![]() $\mathbf {p}$
and denote it by
$\mathbf {p}$
and denote it by
![]() $\mathbf {p}_{\boldsymbol {\gamma }}$
. Notice that the label sequence
$\mathbf {p}_{\boldsymbol {\gamma }}$
. Notice that the label sequence
![]() $(\gamma _{b_1},\dots ,\gamma _{b_t})$
is a subsequence of
$(\gamma _{b_1},\dots ,\gamma _{b_t})$
is a subsequence of
![]() $\boldsymbol {\gamma }=(\gamma _{1},\dots ,\gamma _{b})$
, described in Lemma 5.15 and Remark 5.11, with
$\boldsymbol {\gamma }=(\gamma _{1},\dots ,\gamma _{b})$
, described in Lemma 5.15 and Remark 5.11, with
![]() $b = \ell (y_{J})$
; the subscript
$b = \ell (y_{J})$
; the subscript
![]() $\boldsymbol {\gamma }$
of
$\boldsymbol {\gamma }$
of
![]() $\mathbf {p}_{\boldsymbol {\gamma }}$
indicates that
$\mathbf {p}_{\boldsymbol {\gamma }}$
indicates that
![]() $\mathbf {p}_{\boldsymbol {\gamma }}$
is obtained from
$\mathbf {p}_{\boldsymbol {\gamma }}$
is obtained from
![]() $\mathbf {p}$
by taking the second consecutive edges whose labels are contained in the
$\mathbf {p}$
by taking the second consecutive edges whose labels are contained in the
![]() $\boldsymbol {\gamma }$
-sequence.
$\boldsymbol {\gamma }$
-sequence.
Proposition 5.13. The following equality holds in
![]() $K_{H}(\mathbf {Q}_{G})$
:
$K_{H}(\mathbf {Q}_{G})$
:
 $$ \begin{align} & \overbrace{ \left( \sum_{p=0}^{k}(-1)^{p} \mathbf{e}^{p \epsilon_{n+1-k}} \mathfrak{F}^{k}_{p} \right) \otimes [\mathcal{O}_{\mathbf{Q}_{G}( w_{k+1} )}] }^{ \mathrm{LHS\ of\ (2.6)} } \nonumber \\[3mm] & = \sum_{J \subset [k]} \sum_{\mathbf{p} \in \mathbf{D}_{J}} \mathbf{e}^{|J| \epsilon_{n+1-k}-\operatorname{\mathrm{end}}(\mathbf{p}_{\boldsymbol{\beta}})\epsilon_{J}} (-1)^{|J|+\ell(\mathbf{p}_{\boldsymbol{\gamma}})} [\mathcal{O}_{\mathbf{Q}_{G}( \operatorname{\mathrm{end}}(\mathbf{p})t_{\operatorname{\mathrm{wt}}(\mathbf{p})} )}]. \end{align} $$
$$ \begin{align} & \overbrace{ \left( \sum_{p=0}^{k}(-1)^{p} \mathbf{e}^{p \epsilon_{n+1-k}} \mathfrak{F}^{k}_{p} \right) \otimes [\mathcal{O}_{\mathbf{Q}_{G}( w_{k+1} )}] }^{ \mathrm{LHS\ of\ (2.6)} } \nonumber \\[3mm] & = \sum_{J \subset [k]} \sum_{\mathbf{p} \in \mathbf{D}_{J}} \mathbf{e}^{|J| \epsilon_{n+1-k}-\operatorname{\mathrm{end}}(\mathbf{p}_{\boldsymbol{\beta}})\epsilon_{J}} (-1)^{|J|+\ell(\mathbf{p}_{\boldsymbol{\gamma}})} [\mathcal{O}_{\mathbf{Q}_{G}( \operatorname{\mathrm{end}}(\mathbf{p})t_{\operatorname{\mathrm{wt}}(\mathbf{p})} )}]. \end{align} $$
Proof. First recall Lemma 5.5. It is easy to see that there exists a bijection between the sets
![]() $\mathbf {D}_{J}$
and
$\mathbf {D}_{J}$
and
![]() $\mathcal{A}(w_{k+1},\Gamma _{J})$
. Indeed, for a subset
$\mathcal{A}(w_{k+1},\Gamma _{J})$
. Indeed, for a subset
![]() $A=\big \{p_{1},\dots ,p_{u}\}$
of
$A=\big \{p_{1},\dots ,p_{u}\}$
of
![]() $[a+b]=\{1,2,\dots ,a+b\}$
, A is an element of
$[a+b]=\{1,2,\dots ,a+b\}$
, A is an element of
![]() $\mathcal{A}(w_{k+1},\Gamma _{J})$
if and only if
$\mathcal{A}(w_{k+1},\Gamma _{J})$
if and only if
is an element of
![]() $\mathbf {D}_{J}$
. Notice that
$\mathbf {D}_{J}$
. Notice that
![]() $\operatorname {\mathrm {end}}(A)=\operatorname {\mathrm {end}}(\mathbf {p}(A))$
and
$\operatorname {\mathrm {end}}(A)=\operatorname {\mathrm {end}}(\mathbf {p}(A))$
and
![]() $\operatorname {\mathrm {down}}(A)=\operatorname {\mathrm {wt}}(\mathbf {p})$
. For
$\operatorname {\mathrm {down}}(A)=\operatorname {\mathrm {wt}}(\mathbf {p})$
. For
![]() $\mathbf {p} \in \mathbf {D}_{J}$
of the form (5.18), we set
$\mathbf {p} \in \mathbf {D}_{J}$
of the form (5.18), we set
![]() $\operatorname {\mathrm {end}}(\mathbf {p}_{\boldsymbol {\beta }}):=x_{0}$
and
$\operatorname {\mathrm {end}}(\mathbf {p}_{\boldsymbol {\beta }}):=x_{0}$
and
![]() $\ell (\mathbf {p}_{\boldsymbol {\gamma }}):=t$
; we see that for
$\ell (\mathbf {p}_{\boldsymbol {\gamma }}):=t$
; we see that for
![]() $A \in \mathcal{A}(w_{k+1},\Gamma _{J})$
,
$A \in \mathcal{A}(w_{k+1},\Gamma _{J})$
,
![]() $\operatorname {\mathrm {wt}}(A)=-\operatorname {\mathrm {end}}(\mathbf {p}(A)_{\boldsymbol {\beta }})\epsilon _{J}$
and
$\operatorname {\mathrm {wt}}(A)=-\operatorname {\mathrm {end}}(\mathbf {p}(A)_{\boldsymbol {\beta }})\epsilon _{J}$
and
![]() $n(A)=\ell (\mathbf {p}(A)_{\boldsymbol {\gamma }})$
. Therefore, we deduce that in
$n(A)=\ell (\mathbf {p}(A)_{\boldsymbol {\gamma }})$
. Therefore, we deduce that in
![]() $K_{H}(\mathbf {Q}_{G})$
,
$K_{H}(\mathbf {Q}_{G})$
,
 $$ \begin{align*} & \left( \left(\prod_{ j \in J^{-} } (1-\mathsf{t}_{j})\right) [\mathcal{O}_{\mathbf{Q}_{G}}( w_{\circ} \epsilon_{J} )] \right) \otimes [\mathcal{O}_{\mathbf{Q}_{G}(w_{k+1})}] \\[3mm] & \hspace{5mm} = \sum_{A \in \mathcal{A}(w_{k+1},\Gamma(-\epsilon_{J}))} (-1)^{n(A)} \mathbf{e}^{\operatorname{\mathrm{wt}}(A)} [\mathcal{O}_{\mathbf{Q}_{G}( \operatorname{\mathrm{end}}(A)t_{\operatorname{\mathrm{down}}(A)} )}] \qquad \text{by (5.9)} \\[3mm] & \hspace{5mm} = \sum_{\mathbf{p} \in \mathbf{D}_{J}} \mathbf{e}^{-\operatorname{\mathrm{end}}(\mathbf{p}_{\boldsymbol{\beta}})\epsilon_{J}} (-1)^{\ell(\mathbf{p}_{\boldsymbol{\gamma}})} [\mathcal{O}_{\mathbf{Q}_{G}( \operatorname{\mathrm{end}}(\mathbf{p})t_{\operatorname{\mathrm{wt}}(\mathbf{p})} )}], \end{align*} $$
$$ \begin{align*} & \left( \left(\prod_{ j \in J^{-} } (1-\mathsf{t}_{j})\right) [\mathcal{O}_{\mathbf{Q}_{G}}( w_{\circ} \epsilon_{J} )] \right) \otimes [\mathcal{O}_{\mathbf{Q}_{G}(w_{k+1})}] \\[3mm] & \hspace{5mm} = \sum_{A \in \mathcal{A}(w_{k+1},\Gamma(-\epsilon_{J}))} (-1)^{n(A)} \mathbf{e}^{\operatorname{\mathrm{wt}}(A)} [\mathcal{O}_{\mathbf{Q}_{G}( \operatorname{\mathrm{end}}(A)t_{\operatorname{\mathrm{down}}(A)} )}] \qquad \text{by (5.9)} \\[3mm] & \hspace{5mm} = \sum_{\mathbf{p} \in \mathbf{D}_{J}} \mathbf{e}^{-\operatorname{\mathrm{end}}(\mathbf{p}_{\boldsymbol{\beta}})\epsilon_{J}} (-1)^{\ell(\mathbf{p}_{\boldsymbol{\gamma}})} [\mathcal{O}_{\mathbf{Q}_{G}( \operatorname{\mathrm{end}}(\mathbf{p})t_{\operatorname{\mathrm{wt}}(\mathbf{p})} )}], \end{align*} $$
and hence that
 $$ \begin{align*} & \left( \sum_{p=0}^{k}(-1)^{p} \mathbf{e}^{p \epsilon_{n+1-k}} \mathfrak{F}^{k}_{p} \right) \otimes [\mathcal{O}_{\mathbf{Q}_{G}( w_{k+1} )}] \nonumber \\[3mm] & = \sum_{p=0}^{k}(-1)^{p} \mathbf{e}^{p \epsilon_{n+1-k}} \sum_{ \begin{subarray}{c} J \subset [k] \\[1mm] |J|=p \end{subarray}} \left( \left(\prod_{ j \in J^{-} } (1-\mathsf{t}_{j})\right)[\mathcal{O}_{\mathbf{Q}_{G}}( w_{\circ} \epsilon_{J} )] \right) \otimes [\mathcal{O}_{\mathbf{Q}_{G}( w_{k+1} )}] \nonumber \\[3mm] & = \sum_{J \subset [k]} (-1)^{|J|} \mathbf{e}^{|J| \epsilon_{n+1-k}} \left( \left(\prod_{ j \in J^{-} } (1-\mathsf{t}_{j})\right)[\mathcal{O}_{\mathbf{Q}_{G}}( w_{\circ} \epsilon_{J} )] \right) \otimes [\mathcal{O}_{\mathbf{Q}_{G}( w_{k+1} )}] \nonumber \\[3mm] & = \sum_{J \subset [k]} \sum_{\mathbf{p} \in \mathbf{D}_{J}} \mathbf{e}^{|J| \epsilon_{n+1-k}-\operatorname{\mathrm{end}}(\mathbf{p}_{\boldsymbol{\beta}})\epsilon_{J}} (-1)^{|J|+\ell(\mathbf{p}_{\boldsymbol{\gamma}})} [\mathcal{O}_{\mathbf{Q}_{G}( \operatorname{\mathrm{end}}(\mathbf{p})t_{\operatorname{\mathrm{wt}}(\mathbf{p})} )}]. \end{align*} $$
$$ \begin{align*} & \left( \sum_{p=0}^{k}(-1)^{p} \mathbf{e}^{p \epsilon_{n+1-k}} \mathfrak{F}^{k}_{p} \right) \otimes [\mathcal{O}_{\mathbf{Q}_{G}( w_{k+1} )}] \nonumber \\[3mm] & = \sum_{p=0}^{k}(-1)^{p} \mathbf{e}^{p \epsilon_{n+1-k}} \sum_{ \begin{subarray}{c} J \subset [k] \\[1mm] |J|=p \end{subarray}} \left( \left(\prod_{ j \in J^{-} } (1-\mathsf{t}_{j})\right)[\mathcal{O}_{\mathbf{Q}_{G}}( w_{\circ} \epsilon_{J} )] \right) \otimes [\mathcal{O}_{\mathbf{Q}_{G}( w_{k+1} )}] \nonumber \\[3mm] & = \sum_{J \subset [k]} (-1)^{|J|} \mathbf{e}^{|J| \epsilon_{n+1-k}} \left( \left(\prod_{ j \in J^{-} } (1-\mathsf{t}_{j})\right)[\mathcal{O}_{\mathbf{Q}_{G}}( w_{\circ} \epsilon_{J} )] \right) \otimes [\mathcal{O}_{\mathbf{Q}_{G}( w_{k+1} )}] \nonumber \\[3mm] & = \sum_{J \subset [k]} \sum_{\mathbf{p} \in \mathbf{D}_{J}} \mathbf{e}^{|J| \epsilon_{n+1-k}-\operatorname{\mathrm{end}}(\mathbf{p}_{\boldsymbol{\beta}})\epsilon_{J}} (-1)^{|J|+\ell(\mathbf{p}_{\boldsymbol{\gamma}})} [\mathcal{O}_{\mathbf{Q}_{G}( \operatorname{\mathrm{end}}(\mathbf{p})t_{\operatorname{\mathrm{wt}}(\mathbf{p})} )}]. \end{align*} $$
This proves the proposition.
Recall that
 $$ \begin{align*} \begin{aligned} & w_{k+1} := (s_{1}s_{2} \cdots s_{n}) (s_{1}s_{2} \cdots s_{n-1}) \cdots (s_{1}s_{2} \cdots s_{k+1}) \\ & = (1,2,\dots,n+1)(1,2,\dots,n) \cdots (1,2,\dots,k+2) \\[1.5mm] & = \begin{pmatrix} 1 & 2 & \cdots & k & k+1 & k+2 & \cdots & n & n+1 \\ n-k+1 & n-k+2 & \cdots & n & n+1 & n-k & \cdots & 2 & 1 \end{pmatrix}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} & w_{k+1} := (s_{1}s_{2} \cdots s_{n}) (s_{1}s_{2} \cdots s_{n-1}) \cdots (s_{1}s_{2} \cdots s_{k+1}) \\ & = (1,2,\dots,n+1)(1,2,\dots,n) \cdots (1,2,\dots,k+2) \\[1.5mm] & = \begin{pmatrix} 1 & 2 & \cdots & k & k+1 & k+2 & \cdots & n & n+1 \\ n-k+1 & n-k+2 & \cdots & n & n+1 & n-k & \cdots & 2 & 1 \end{pmatrix}. \end{aligned} \end{align*} $$
Also, recall that
![]() $J = \big \{ j_{1},j_{2},\dots ,j_{p} \big \} \subset [k]$
, with
$J = \big \{ j_{1},j_{2},\dots ,j_{p} \big \} \subset [k]$
, with
![]() $1 \le j_{1} < j_{2} < \cdots < j_{p} \le k$
, and recall from (5.14) that
$1 \le j_{1} < j_{2} < \cdots < j_{p} \le k$
, and recall from (5.14) that
![]() $\Gamma _{J}=(-\beta _{a},\ldots ,-\beta _{1},\gamma _{1},\dots ,\gamma _{b})$
. Let
$\Gamma _{J}=(-\beta _{a},\ldots ,-\beta _{1},\gamma _{1},\dots ,\gamma _{b})$
. Let
![]() $\mathbf {p} \in \mathbf {D}_{J}$
. We see from Remark 5.9 that the (label sequence of the)
$\mathbf {p} \in \mathbf {D}_{J}$
. We see from Remark 5.9 that the (label sequence of the)
![]() $\boldsymbol {\beta }$
-part
$\boldsymbol {\beta }$
-part
![]() $\mathbf {p}_{\boldsymbol {\beta }}$
of
$\mathbf {p}_{\boldsymbol {\beta }}$
of
![]() $\mathbf {p}$
is of the following form:
$\mathbf {p}$
is of the following form:
 $$ \begin{align} \begin{aligned} w_{k+1} & \xrightarrow{\hspace{2pt}(t_{1,m_{1}},j_{1})\hspace{2pt}} \bullet \xrightarrow{\hspace{2pt}(t_{1,m_{1}-1},j_{1})\hspace{2pt}} \cdots \xrightarrow{\hspace{2pt}(t_{1,m_{1}-r_{1}+1},j_{1})\hspace{2pt}} \bullet \\& \xrightarrow{\hspace{2pt}(t_{2,m_{2}},j_{2})\hspace{2pt}} \bullet \xrightarrow{\hspace{2pt}(t_{2,m_{2}-1},j_{2})\hspace{2pt}} \cdots \xrightarrow{\hspace{2pt}(t_{2,m_{2}-r_{2}+1},j_{2})\hspace{2pt}} \bullet \\& \cdots \cdots\\& \xrightarrow{\hspace{2pt}(t_{p,m_{p}},j_{p})\hspace{2pt}} \bullet \xrightarrow{\hspace{2pt}(t_{p,m_{p}-1},j_{p})\hspace{2pt}} \cdots \xrightarrow{\hspace{2pt}(t_{p,m_{p}-r_{p}+1},j_{p})\hspace{2pt}} \bullet, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} w_{k+1} & \xrightarrow{\hspace{2pt}(t_{1,m_{1}},j_{1})\hspace{2pt}} \bullet \xrightarrow{\hspace{2pt}(t_{1,m_{1}-1},j_{1})\hspace{2pt}} \cdots \xrightarrow{\hspace{2pt}(t_{1,m_{1}-r_{1}+1},j_{1})\hspace{2pt}} \bullet \\& \xrightarrow{\hspace{2pt}(t_{2,m_{2}},j_{2})\hspace{2pt}} \bullet \xrightarrow{\hspace{2pt}(t_{2,m_{2}-1},j_{2})\hspace{2pt}} \cdots \xrightarrow{\hspace{2pt}(t_{2,m_{2}-r_{2}+1},j_{2})\hspace{2pt}} \bullet \\& \cdots \cdots\\& \xrightarrow{\hspace{2pt}(t_{p,m_{p}},j_{p})\hspace{2pt}} \bullet \xrightarrow{\hspace{2pt}(t_{p,m_{p}-1},j_{p})\hspace{2pt}} \cdots \xrightarrow{\hspace{2pt}(t_{p,m_{p}-r_{p}+1},j_{p})\hspace{2pt}} \bullet, \end{aligned} \end{align} $$
where
![]() $m_{q} \ge r_{q} \ge 0$
for
$m_{q} \ge r_{q} \ge 0$
for
![]() $1 \le q \le p$
; for each
$1 \le q \le p$
; for each
![]() $1 \le q \le p$
such that
$1 \le q \le p$
such that
![]() $r_{q} \ge 1$
, we have
$r_{q} \ge 1$
, we have
 $$ \begin{align} \begin{aligned} & j_{q}> t_{q,m_{q}} > t_{q,m_{q}-1} > \cdots > t_{q,m_{q}-r_{q}+1} \ge 1, \\ & \hspace{30mm} \text{with } t_{q,m_{q}-r+1} \ne j_{1},j_{2},\dots,j_{q-1} \text{ for } 1 \le r \le r_{q}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & j_{q}> t_{q,m_{q}} > t_{q,m_{q}-1} > \cdots > t_{q,m_{q}-r_{q}+1} \ge 1, \\ & \hspace{30mm} \text{with } t_{q,m_{q}-r+1} \ne j_{1},j_{2},\dots,j_{q-1} \text{ for } 1 \le r \le r_{q}. \end{aligned} \end{align} $$
By convention, we set
![]() $t_{q,m_{q}+1}:=j_{q}$
for
$t_{q,m_{q}+1}:=j_{q}$
for
![]() $1 \le q \le p$
.
$1 \le q \le p$
.
Lemma 5.14. Keep the setting above. If (5.21) is the
![]() $\boldsymbol {\beta }$
-part of an element
$\boldsymbol {\beta }$
-part of an element
![]() $\mathbf {p} \in \mathbf {D}_{J}$
, then the following are satisfied:
$\mathbf {p} \in \mathbf {D}_{J}$
, then the following are satisfied:
-
(i)
 $t_{p,m_{p}-r_{p}+1} \ge \cdots \ge t_{2,m_{2}-r_{2}+1} \ge t_{1,m_{1}-r_{1}+1}$
;
$t_{p,m_{p}-r_{p}+1} \ge \cdots \ge t_{2,m_{2}-r_{2}+1} \ge t_{1,m_{1}-r_{1}+1}$
; -
(ii) for each
 $1 \le q \le p$
such that
$1 \le q \le p$
such that
 $r_{q} \ge 1$
, the sequence
$r_{q} \ge 1$
, the sequence
 $t_{q,m_{q}}> t_{q,m_{q}-1} > \cdots > t_{q,m_{q}-r_{q}+1}$
is identical to the largest
$t_{q,m_{q}}> t_{q,m_{q}-1} > \cdots > t_{q,m_{q}-r_{q}+1}$
is identical to the largest
 $r_{q}$
elements in
$r_{q}$
elements in
 $\{1,2,\dots ,j_{q}-1\} \setminus \{j_{1},j_{2},\dots ,j_{q-1}\}$
.
$\{1,2,\dots ,j_{q}-1\} \setminus \{j_{1},j_{2},\dots ,j_{q-1}\}$
.
Moreover, all the edges in (5.21) are Bruhat edges. Conversely, let
![]() $0 \le r_{q} \le m_{q}$
for
$0 \le r_{q} \le m_{q}$
for
![]() $1 \le q \le p$
, and assume that
$1 \le q \le p$
, and assume that
![]() $\{ t_{q,m_{q}-r+1} \mid 1 \le q \le p,\,1 \le r \le r_{q} \}$
satisfy (5.22), and (i), (ii) above. Then, (5.21) is a directed path in
$\{ t_{q,m_{q}-r+1} \mid 1 \le q \le p,\,1 \le r \le r_{q} \}$
satisfy (5.22), and (i), (ii) above. Then, (5.21) is a directed path in
![]() $\mathrm {QBG}(W)$
whose edges are all Bruhat edges; in particular, there exists an element
$\mathrm {QBG}(W)$
whose edges are all Bruhat edges; in particular, there exists an element
![]() $\mathbf {p}$
whose
$\mathbf {p}$
whose
![]() $\boldsymbol {\beta }$
-part
$\boldsymbol {\beta }$
-part
![]() $\mathbf {p}_{\boldsymbol {\beta }}$
is of the form (5.21).
$\mathbf {p}_{\boldsymbol {\beta }}$
is of the form (5.21).
Proof. It follows from Lemma 2.2 that
is a directed path in
![]() $\mathrm {QBG}(W)$
, where
$\mathrm {QBG}(W)$
, where
![]() $r \ge 0$
and
$r \ge 0$
and
![]() $j_{1}-1 \ge k_{1}> k_{2} > \cdots > k_{r} \ge 1$
, if and only if
$j_{1}-1 \ge k_{1}> k_{2} > \cdots > k_{r} \ge 1$
, if and only if
![]() $k_{1}=j_{1}-1$
,
$k_{1}=j_{1}-1$
,
![]() $k_{2}=j_{1}-2$
,
$k_{2}=j_{1}-2$
,
![]() $\dots $
,
$\dots $
,
![]() $k_{r}=j_{1}-r$
; in this case, all the edges in (5.23) are Bruhat edges.
$k_{r}=j_{1}-r$
; in this case, all the edges in (5.23) are Bruhat edges.
Also, it follows from Lemma 2.2 that
 $$ \begin{align} \begin{aligned} w_{k+1} = x_{0} & \xrightarrow{\hspace{2pt}(j_{1}-1,j_{1})\hspace{2pt}} x_{1} \xrightarrow{\hspace{2pt}(j_{1}-2,j_{1})\hspace{2pt}} \cdots \xrightarrow{\hspace{2pt}(j_{1}-r_{1},j_{1})\hspace{2pt}} x_{r_{1}} \\ & \xrightarrow{\hspace{2pt}(k_{1},j_{2})\hspace{2pt}} x_{r_{1}+1} \xrightarrow{\hspace{2pt}(k_{2},j_{2})\hspace{2pt}} \cdots \xrightarrow{\hspace{2pt}(k_{r},j_{2})\hspace{2pt}} x_{r_{1}+r} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} w_{k+1} = x_{0} & \xrightarrow{\hspace{2pt}(j_{1}-1,j_{1})\hspace{2pt}} x_{1} \xrightarrow{\hspace{2pt}(j_{1}-2,j_{1})\hspace{2pt}} \cdots \xrightarrow{\hspace{2pt}(j_{1}-r_{1},j_{1})\hspace{2pt}} x_{r_{1}} \\ & \xrightarrow{\hspace{2pt}(k_{1},j_{2})\hspace{2pt}} x_{r_{1}+1} \xrightarrow{\hspace{2pt}(k_{2},j_{2})\hspace{2pt}} \cdots \xrightarrow{\hspace{2pt}(k_{r},j_{2})\hspace{2pt}} x_{r_{1}+r} \end{aligned} \end{align} $$
is a directed path in
![]() $\mathrm {QBG}(W)$
, where
$\mathrm {QBG}(W)$
, where
![]() $r_{1},r \ge 0$
and
$r_{1},r \ge 0$
and
![]() $j_{2}-1 \ge k_{1}> k_{2} > \cdots > k_{r} \ge 1$
with
$j_{2}-1 \ge k_{1}> k_{2} > \cdots > k_{r} \ge 1$
with
![]() $k_{r'} \ne j_{1}$
for any
$k_{r'} \ne j_{1}$
for any
![]() $1 \le r ' \le r$
, if and only if
$1 \le r ' \le r$
, if and only if
![]() $\{k_{1},k_{2},\dots .k_{r}\}$
is identical to the largest r elements in
$\{k_{1},k_{2},\dots .k_{r}\}$
is identical to the largest r elements in
![]() $\{1,2,\dots ,j_{2}-1\} \setminus \{j_{1}\}$
and
$\{1,2,\dots ,j_{2}-1\} \setminus \{j_{1}\}$
and
![]() $k_{r} \ge j_{1}-r_{1}$
; in this case, all the edges in (5.24) are Bruhat edges.
$k_{r} \ge j_{1}-r_{1}$
; in this case, all the edges in (5.24) are Bruhat edges.
Similarly, it follows from Lemma 2.2 that
 $$ \begin{align} \begin{aligned} w_{k+1} = x_{0} & \xrightarrow{\hspace{2pt}(j_{1}-1,j_{1})\hspace{2pt}} x_{1} \xrightarrow{\hspace{2pt}(j_{1}-2,j_{1})\hspace{2pt}} \cdots \xrightarrow{\hspace{2pt}(j_{1}-r_{1},j_{1})\hspace{2pt}} x_{r_{1}} \\ & \xrightarrow{\hspace{2pt}(t_{2,m_{2}},j_{2})\hspace{2pt}} x_{r_{1}+1} \xrightarrow{\hspace{2pt}(t_{2,m_{2}-1},j_{2})\hspace{2pt}} \cdots \xrightarrow{\hspace{2pt}(t_{2,m_{2}-r_{2}+1},j_{2})\hspace{2pt}} x_{r_{1}+r_{2}} \\ & \xrightarrow{\hspace{2pt}(k_{1},j_{3})\hspace{2pt}} x_{r_{1}+r_{2}+1} \xrightarrow{\hspace{2pt}(k_{2},j_{3})\hspace{2pt}} \cdots \xrightarrow{\hspace{2pt}(k_{r},j_{3})\hspace{2pt}} x_{r_{1}+r_{2}+r} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} w_{k+1} = x_{0} & \xrightarrow{\hspace{2pt}(j_{1}-1,j_{1})\hspace{2pt}} x_{1} \xrightarrow{\hspace{2pt}(j_{1}-2,j_{1})\hspace{2pt}} \cdots \xrightarrow{\hspace{2pt}(j_{1}-r_{1},j_{1})\hspace{2pt}} x_{r_{1}} \\ & \xrightarrow{\hspace{2pt}(t_{2,m_{2}},j_{2})\hspace{2pt}} x_{r_{1}+1} \xrightarrow{\hspace{2pt}(t_{2,m_{2}-1},j_{2})\hspace{2pt}} \cdots \xrightarrow{\hspace{2pt}(t_{2,m_{2}-r_{2}+1},j_{2})\hspace{2pt}} x_{r_{1}+r_{2}} \\ & \xrightarrow{\hspace{2pt}(k_{1},j_{3})\hspace{2pt}} x_{r_{1}+r_{2}+1} \xrightarrow{\hspace{2pt}(k_{2},j_{3})\hspace{2pt}} \cdots \xrightarrow{\hspace{2pt}(k_{r},j_{3})\hspace{2pt}} x_{r_{1}+r_{2}+r} \end{aligned} \end{align} $$
is a directed path in
![]() $\mathrm {QBG}(W)$
, where
$\mathrm {QBG}(W)$
, where
![]() $r_{1},r_{2},r \ge 0$
,
$r_{1},r_{2},r \ge 0$
,
![]() $t_{2,m_{2}-r_{2}+1} \ge j_{1}-r_{1}$
, and
$t_{2,m_{2}-r_{2}+1} \ge j_{1}-r_{1}$
, and
![]() $j_{3}-1 \ge k_{1}> k_{2} > \cdots > k_{r} \ge 1$
with
$j_{3}-1 \ge k_{1}> k_{2} > \cdots > k_{r} \ge 1$
with
![]() $k_{r'} \ne j_{1},j_{2}$
for any
$k_{r'} \ne j_{1},j_{2}$
for any
![]() $1 \le r ' \le r$
, if and only if
$1 \le r ' \le r$
, if and only if
![]() $\{k_{1},k_{2},\dots .k_{r}\}$
is identical to the largest r elements in
$\{k_{1},k_{2},\dots .k_{r}\}$
is identical to the largest r elements in
![]() $\{1,2,\dots ,j_{3}-1\} \setminus \{j_{1},j_{2}\}$
and
$\{1,2,\dots ,j_{3}-1\} \setminus \{j_{1},j_{2}\}$
and
![]() $k_{r} \ge t_{2,m_{2}-r_{2}+1}$
; in this case, all the edges in (5.25) are Bruhat edges.
$k_{r} \ge t_{2,m_{2}-r_{2}+1}$
; in this case, all the edges in (5.25) are Bruhat edges.
Repeating the argument above, we can verify the assertions of the lemma.
We now define
Let
![]() $J = \big \{ j_{1},j_{2},\dots ,j_{p} \big \} \subset [k]$
, and let
$J = \big \{ j_{1},j_{2},\dots ,j_{p} \big \} \subset [k]$
, and let
![]() $\mathbf {p} \in \mathbf {D}$
be of the form (5.18); for simplicity of notation, we will henceforth write as
$\mathbf {p} \in \mathbf {D}$
be of the form (5.18); for simplicity of notation, we will henceforth write as
 $$ \begin{align*} \mathbf{p} & = [\beta_{a_s},\,\dots,\,\beta_{a_1} \mid \gamma_{b_1},\,\dots,\gamma_{b_t}], \\ \mathbf{p}_{\boldsymbol{\beta}} & = [\beta_{a_s},\,\dots,\,\beta_{a_1}], \quad \mathbf{p}_{\boldsymbol{\gamma}} = [\gamma_{b_1},\,\dots,\gamma_{b_t}]. \end{align*} $$
$$ \begin{align*} \mathbf{p} & = [\beta_{a_s},\,\dots,\,\beta_{a_1} \mid \gamma_{b_1},\,\dots,\gamma_{b_t}], \\ \mathbf{p}_{\boldsymbol{\beta}} & = [\beta_{a_s},\,\dots,\,\beta_{a_1}], \quad \mathbf{p}_{\boldsymbol{\gamma}} = [\gamma_{b_1},\,\dots,\gamma_{b_t}]. \end{align*} $$
Then we define subsets
![]() $\mathbf {D}_{J}^{\mathrm {A}}$
,
$\mathbf {D}_{J}^{\mathrm {A}}$
,
![]() $\mathbf {D}_{J}^{\mathrm {B}}$
, and
$\mathbf {D}_{J}^{\mathrm {B}}$
, and
![]() $\mathbf {D}_{J}^{\mathrm {C}}$
of
$\mathbf {D}_{J}^{\mathrm {C}}$
of
![]() $\mathbf {D}_{J}$
as follows (recall (5.21), (5.22) and Lemma 5.14):
$\mathbf {D}_{J}$
as follows (recall (5.21), (5.22) and Lemma 5.14):
-
(A) When
 $J \ne \emptyset $
and
$J \ne \emptyset $
and
 $j_{1} = \min J \ge 2$
(and hence
$j_{1} = \min J \ge 2$
(and hence
 $1 \notin J$
), we define
$1 \notin J$
), we define
 $\mathbf {D}_{J}^{\mathrm {A}}$
to be the subset of
$\mathbf {D}_{J}^{\mathrm {A}}$
to be the subset of
 $\mathbf {D}_{J}$
consisting of all those elements
$\mathbf {D}_{J}$
consisting of all those elements
 $\mathbf {p} \in \mathbf {D}_{J}$
whose
$\mathbf {p} \in \mathbf {D}_{J}$
whose
 $\boldsymbol {\beta }$
-part
$\boldsymbol {\beta }$
-part
 $\mathbf {p}_{\boldsymbol {\beta }}$
is of the form (5.27)
$\mathbf {p}_{\boldsymbol {\beta }}$
is of the form (5.27) $$ \begin{align} \mathbf{p}_{\boldsymbol{\beta}} & = [ (j_{1}-1,j_{1}), (j_{1}-2,j_{1}),\dots,(2,j_{1}),(1,j_{1}), \nonumber \\ & \underbrace{ (t_{2,m_{2}},j_{2}),\dots,(t_{2,m_{2}-r_{2}+1},j_{2}), \dots\dots, (t_{p,m_{p}},j_{p}),\dots,(t_{p,m_{p}-r_{p}+1},j_{p})}_{=:\,\mathbf{s}}]. \end{align} $$
$$ \begin{align} \mathbf{p}_{\boldsymbol{\beta}} & = [ (j_{1}-1,j_{1}), (j_{1}-2,j_{1}),\dots,(2,j_{1}),(1,j_{1}), \nonumber \\ & \underbrace{ (t_{2,m_{2}},j_{2}),\dots,(t_{2,m_{2}-r_{2}+1},j_{2}), \dots\dots, (t_{p,m_{p}},j_{p}),\dots,(t_{p,m_{p}-r_{p}+1},j_{p})}_{=:\,\mathbf{s}}]. \end{align} $$
-
(B) When
 $J \ne \emptyset $
and
$J \ne \emptyset $
and
 $j_{1}=\min J$
is equal to
$j_{1}=\min J$
is equal to
 $1$
, we set
$1$
, we set
 $\mathbf {D}_{J}^{\mathrm {B}}:=\mathbf {D}_{J}$
; note that the
$\mathbf {D}_{J}^{\mathrm {B}}:=\mathbf {D}_{J}$
; note that the
 $\boldsymbol {\beta }$
-part
$\boldsymbol {\beta }$
-part
 $\mathbf {p}_{\boldsymbol {\beta }}$
of
$\mathbf {p}_{\boldsymbol {\beta }}$
of
 $\mathbf {p} \in \mathbf {D}_{J}^{\mathrm {B}}$
is of the form (5.28)
$\mathbf {p} \in \mathbf {D}_{J}^{\mathrm {B}}$
is of the form (5.28) $$ \begin{align} \mathbf{p}_{\boldsymbol{\beta}} & = [ (t_{2,m_{2}},j_{2}),\dots,(t_{2,m_{2}-r_{2}+1},j_{2}), \nonumber \\ & \qquad \qquad \dots\dots, (t_{p,m_{p}},j_{p}),\dots,(t_{p,m_{p}-r_{p}+1},j_{p})]. \end{align} $$
$$ \begin{align} \mathbf{p}_{\boldsymbol{\beta}} & = [ (t_{2,m_{2}},j_{2}),\dots,(t_{2,m_{2}-r_{2}+1},j_{2}), \nonumber \\ & \qquad \qquad \dots\dots, (t_{p,m_{p}},j_{p}),\dots,(t_{p,m_{p}-r_{p}+1},j_{p})]. \end{align} $$
-
(C) When
 $J = \emptyset $
, we set
$J = \emptyset $
, we set
 $\mathbf {D}_{J}^{\mathrm {C}}:=\mathbf {D}_{J}$
. Also, when
$\mathbf {D}_{J}^{\mathrm {C}}:=\mathbf {D}_{J}$
. Also, when
 $J \ne \emptyset $
and
$J \ne \emptyset $
and
 $j_{1}=\min J \ge 2$
, we define
$j_{1}=\min J \ge 2$
, we define
 $\mathbf {D}_{J}^{\mathrm {C}}$
to be the subset of
$\mathbf {D}_{J}^{\mathrm {C}}$
to be the subset of
 $\mathbf {D}_{J}$
consisting of all those elements
$\mathbf {D}_{J}$
consisting of all those elements
 $\mathbf {p} \in \mathbf {D}_{J}$
whose
$\mathbf {p} \in \mathbf {D}_{J}$
whose
 $\boldsymbol {\beta }$
-part
$\boldsymbol {\beta }$
-part
 $\mathbf {p}_{\boldsymbol {\beta }}$
is of the form (5.29)
$\mathbf {p}_{\boldsymbol {\beta }}$
is of the form (5.29) $$ \begin{align} \mathbf{p}_{\boldsymbol{\beta}} & = [ (j_{1}-1,j_{1}), (j_{1}-2,j_{1}),\dots,(j_{1}-r_{1}+1,j_{1}),(j_{1}-r_{1},j_{1}), \nonumber \\ & (t_{2,m_{2}},j_{2}),\dots,(t_{2,m_{2}-r_{2}+1},j_{2}), \dots\dots, (t_{p,m_{p}},j_{p}),\dots,(t_{p,m_{p}-r_{p}+1},j_{p})], \end{align} $$
$$ \begin{align} \mathbf{p}_{\boldsymbol{\beta}} & = [ (j_{1}-1,j_{1}), (j_{1}-2,j_{1}),\dots,(j_{1}-r_{1}+1,j_{1}),(j_{1}-r_{1},j_{1}), \nonumber \\ & (t_{2,m_{2}},j_{2}),\dots,(t_{2,m_{2}-r_{2}+1},j_{2}), \dots\dots, (t_{p,m_{p}},j_{p}),\dots,(t_{p,m_{p}-r_{p}+1},j_{p})], \end{align} $$
where
 $r_{1} = 0$
, or
$r_{1} = 0$
, or
 $r_{1} \ge 1$
and
$r_{1} \ge 1$
and
 $j_{1} - r_{1} \ge 2$
.
$j_{1} - r_{1} \ge 2$
.
It is easily seen that
![]() $\mathbf {D}_{J} = \mathbf {D}_{J}^{\mathrm {A}} \sqcup \mathbf {D}_{J}^{\mathrm {B}} \sqcup \mathbf {D}_{J}^{\mathrm {C}}$
.
$\mathbf {D}_{J} = \mathbf {D}_{J}^{\mathrm {A}} \sqcup \mathbf {D}_{J}^{\mathrm {B}} \sqcup \mathbf {D}_{J}^{\mathrm {C}}$
.
Lemma 5.15. Let
![]() $\mathbf {p} \in \mathbf {D}_{J}^{\mathrm {A}} \sqcup \mathbf {D}_{J}^{\mathrm {B}}$
, and assume that the
$\mathbf {p} \in \mathbf {D}_{J}^{\mathrm {A}} \sqcup \mathbf {D}_{J}^{\mathrm {B}}$
, and assume that the
![]() $\boldsymbol {\gamma }$
-part
$\boldsymbol {\gamma }$
-part
![]() $\mathbf {p}_{\boldsymbol {\gamma }}$
of
$\mathbf {p}_{\boldsymbol {\gamma }}$
of
![]() $\mathbf {p}$
is of the form
$\mathbf {p}$
is of the form
 $$ \begin{align*} \begin{aligned} \operatorname{\mathrm{end}}(\mathbf{p}_{\boldsymbol{\beta}}) & \xrightarrow{\hspace{2pt}(j_{1},k_{r})\hspace{2pt}} \bullet \xrightarrow{\hspace{2pt}(j_{1},k_{r-1})\hspace{2pt}} \cdots \xrightarrow{\hspace{2pt}(j_{1},k_{2})\hspace{2pt}} \bullet \xrightarrow{\hspace{2pt}(j_{1},k_{1})\hspace{2pt}} \bullet \\ & \cdots \cdots, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \operatorname{\mathrm{end}}(\mathbf{p}_{\boldsymbol{\beta}}) & \xrightarrow{\hspace{2pt}(j_{1},k_{r})\hspace{2pt}} \bullet \xrightarrow{\hspace{2pt}(j_{1},k_{r-1})\hspace{2pt}} \cdots \xrightarrow{\hspace{2pt}(j_{1},k_{2})\hspace{2pt}} \bullet \xrightarrow{\hspace{2pt}(j_{1},k_{1})\hspace{2pt}} \bullet \\ & \cdots \cdots, \end{aligned} \end{align*} $$
where
![]() $r \ge 0$
, and
$r \ge 0$
, and
![]() $n+1 \ge k_{r}> k_{r-1} > \cdots > k_{1} \ge j_{1}+1$
with
$n+1 \ge k_{r}> k_{r-1} > \cdots > k_{1} \ge j_{1}+1$
with
![]() $k_{u} \notin \{j_{2},\dots ,j_{p}\}$
for any
$k_{u} \notin \{j_{2},\dots ,j_{p}\}$
for any
![]() $1 \le u \le r$
. Then, either of the following holds: (i)
$1 \le u \le r$
. Then, either of the following holds: (i)
![]() $r = 0$
, or (ii)
$r = 0$
, or (ii)
![]() $r = 1$
and
$r = 1$
and
![]() $k_{1}=j_{1}+1$
; note that case (ii) does not occur if
$k_{1}=j_{1}+1$
; note that case (ii) does not occur if
![]() $j_{1}+1 \in J$
. In case (ii), the edge
$j_{1}+1 \in J$
. In case (ii), the edge
![]() $\operatorname {\mathrm {end}}(\mathbf {p}_{\boldsymbol {\beta }}) \xrightarrow {\hspace {2pt}(j_{1},j_{1}+1)\hspace {2pt}} \bullet $
is a Bruhat edge.
$\operatorname {\mathrm {end}}(\mathbf {p}_{\boldsymbol {\beta }}) \xrightarrow {\hspace {2pt}(j_{1},j_{1}+1)\hspace {2pt}} \bullet $
is a Bruhat edge.
Proof. Assume that
![]() $r> 0$
. Note that
$r> 0$
. Note that
![]() $\operatorname {\mathrm {end}}(\mathbf {p}_{\boldsymbol {\beta }})(j_{1}) = w_{k+1}(1) = n-k+1$
; see (5.27) and (5.28). If
$\operatorname {\mathrm {end}}(\mathbf {p}_{\boldsymbol {\beta }})(j_{1}) = w_{k+1}(1) = n-k+1$
; see (5.27) and (5.28). If
![]() $k_{r} \ge k+2$
, then
$k_{r} \ge k+2$
, then
However,
![]() $j_{1} < k+1 < k_{r}$
, and
$j_{1} < k+1 < k_{r}$
, and
![]() $\operatorname {\mathrm {end}}(\mathbf {p}_{\boldsymbol {\beta }})(k+1) = n+1$
is greater than both
$\operatorname {\mathrm {end}}(\mathbf {p}_{\boldsymbol {\beta }})(k+1) = n+1$
is greater than both
![]() $\operatorname {\mathrm {end}}(\mathbf {p}_{\boldsymbol {\beta }})(k_{r})$
and
$\operatorname {\mathrm {end}}(\mathbf {p}_{\boldsymbol {\beta }})(k_{r})$
and
![]() $\operatorname {\mathrm {end}}(\mathbf {p}_{\boldsymbol {\beta }})(j_{1})$
, which is a contradiction (see Lemma 2.2). Thus, we see that
$\operatorname {\mathrm {end}}(\mathbf {p}_{\boldsymbol {\beta }})(j_{1})$
, which is a contradiction (see Lemma 2.2). Thus, we see that
![]() $k_{r} \le k+1$
.
$k_{r} \le k+1$
.
Suppose, for a contradiction, that
![]() $j_{1}+1=j_{2} \in J$
; note that
$j_{1}+1=j_{2} \in J$
; note that
![]() $j_{2} < k_{r} \le k+1$
and
$j_{2} < k_{r} \le k+1$
and
![]() $k_{r} \notin \{j_{3},\dots ,j_{p}\}$
. In this case, it follows rom Lemma 5.14 and (5.27), (5.28) that
$k_{r} \notin \{j_{3},\dots ,j_{p}\}$
. In this case, it follows rom Lemma 5.14 and (5.27), (5.28) that
![]() $\operatorname {\mathrm {end}}(\mathbf {p}_{\boldsymbol {\beta }})(j_{2}) = w_{k+1}(t_1) = n-k+t_1$
for some
$\operatorname {\mathrm {end}}(\mathbf {p}_{\boldsymbol {\beta }})(j_{2}) = w_{k+1}(t_1) = n-k+t_1$
for some
![]() $1 \le t_{1} \le j_{2}$
, and hence that
$1 \le t_{1} \le j_{2}$
, and hence that
Since
![]() $j_{2} < k_{r} \le k+1$
and
$j_{2} < k_{r} \le k+1$
and
![]() $k_{r} \notin \{j_{3},\dots ,j_{p}\}$
, we deduce by Lemma 5.14 and (5.27), (5.28) that
$k_{r} \notin \{j_{3},\dots ,j_{p}\}$
, we deduce by Lemma 5.14 and (5.27), (5.28) that
![]() $\operatorname {\mathrm {end}}(\mathbf {p}_{\boldsymbol {\beta }})(k_{r}) = w_{k+1}(t_{2})=n-k+t_{2}$
for some
$\operatorname {\mathrm {end}}(\mathbf {p}_{\boldsymbol {\beta }})(k_{r}) = w_{k+1}(t_{2})=n-k+t_{2}$
for some
![]() $j_{2} < t_{2} \le k+1$
. Hence, we obtain
$j_{2} < t_{2} \le k+1$
. Hence, we obtain
 $$ \begin{align*} \underbrace{ \operatorname{\mathrm{end}}(\mathbf{p}_{\boldsymbol{\beta}})(j_{1}) }_{=\, n-k+1} < \underbrace{ \operatorname{\mathrm{end}}(\mathbf{p}_{\boldsymbol{\beta}})(j_{2}) }_{=\, n-k+t_1} < \underbrace{ \operatorname{\mathrm{end}}(\mathbf{p}_{\boldsymbol{\beta}})(k_{r}) }_{=\, n-k+t_2}, \end{align*} $$
$$ \begin{align*} \underbrace{ \operatorname{\mathrm{end}}(\mathbf{p}_{\boldsymbol{\beta}})(j_{1}) }_{=\, n-k+1} < \underbrace{ \operatorname{\mathrm{end}}(\mathbf{p}_{\boldsymbol{\beta}})(j_{2}) }_{=\, n-k+t_1} < \underbrace{ \operatorname{\mathrm{end}}(\mathbf{p}_{\boldsymbol{\beta}})(k_{r}) }_{=\, n-k+t_2}, \end{align*} $$
which is a contradiction (see Lemma 2.2). Thus, we see that
![]() $j_{1}+1 \not \in J$
.
$j_{1}+1 \not \in J$
.
Suppose, for a contradiction, that
![]() $j_{1}+1 \notin J$
and
$j_{1}+1 \notin J$
and
![]() $j_{1}+1 < k_{r} \le k+1$
; recall that
$j_{1}+1 < k_{r} \le k+1$
; recall that
![]() $k_{r} \notin \{j_{2},\dots ,j_{p}\}$
. In this case, we deduce by (5.27) and (5.28) that
$k_{r} \notin \{j_{2},\dots ,j_{p}\}$
. In this case, we deduce by (5.27) and (5.28) that
which is a contradiction (see Lemma 2.2). Thus, we see that
![]() $k_{r}=j_{1}+1$
; since
$k_{r}=j_{1}+1$
; since
![]() $\operatorname {\mathrm {end}}(\mathbf {p}_{\boldsymbol {\beta }})(j_{1}) < \operatorname {\mathrm {end}}(\mathbf {p}_{\boldsymbol {\beta }})(j_{1}+1)$
, the edge
$\operatorname {\mathrm {end}}(\mathbf {p}_{\boldsymbol {\beta }})(j_{1}) < \operatorname {\mathrm {end}}(\mathbf {p}_{\boldsymbol {\beta }})(j_{1}+1)$
, the edge
![]() $\operatorname {\mathrm {end}}(\mathbf {p}_{\boldsymbol {\beta }}) \xrightarrow {\hspace {2pt}(j_{1},j_{1}+1)\hspace {2pt}} \bullet $
is a Bruhat edge. This proves the lemma.
$\operatorname {\mathrm {end}}(\mathbf {p}_{\boldsymbol {\beta }}) \xrightarrow {\hspace {2pt}(j_{1},j_{1}+1)\hspace {2pt}} \bullet $
is a Bruhat edge. This proves the lemma.
Let
![]() $\mathbf {D}_{J}^{\mathrm {A}_1}$
(resp.,
$\mathbf {D}_{J}^{\mathrm {A}_1}$
(resp.,
![]() $\mathbf {D}_{J}^{\mathrm {A}_2}$
) denote the subset of
$\mathbf {D}_{J}^{\mathrm {A}_2}$
) denote the subset of
![]() $\mathbf {D}_{J}^{\mathrm {A}}$
consisting of all those elements
$\mathbf {D}_{J}^{\mathrm {A}}$
consisting of all those elements
![]() $\mathbf {p} \in \mathbf {D}_{J}^{\mathrm {A}}$
whose initial label of the
$\mathbf {p} \in \mathbf {D}_{J}^{\mathrm {A}}$
whose initial label of the
![]() $\boldsymbol {\gamma }$
-part
$\boldsymbol {\gamma }$
-part
![]() $\mathbf {p}_{\boldsymbol {\gamma }}$
is (resp., is not)
$\mathbf {p}_{\boldsymbol {\gamma }}$
is (resp., is not)
![]() $(j_{1},j_{1}+1)$
; see Lemma 5.15. Similarly, let
$(j_{1},j_{1}+1)$
; see Lemma 5.15. Similarly, let
![]() $\mathbf {D}_{J}^{\mathrm {B}_1}$
(resp.,
$\mathbf {D}_{J}^{\mathrm {B}_1}$
(resp.,
![]() $\mathbf {D}_{J}^{\mathrm {B}_2}$
) denote the subset of
$\mathbf {D}_{J}^{\mathrm {B}_2}$
) denote the subset of
![]() $\mathbf {D}_{J}^{\mathrm {B}}$
consisting of all those elements
$\mathbf {D}_{J}^{\mathrm {B}}$
consisting of all those elements
![]() $\mathbf {p} \in \mathbf {D}_{J}^{\mathrm {B}}$
whose initial label of the
$\mathbf {p} \in \mathbf {D}_{J}^{\mathrm {B}}$
whose initial label of the
![]() $\boldsymbol {\gamma }$
-part
$\boldsymbol {\gamma }$
-part
![]() $\mathbf {p}_{\boldsymbol {\gamma }}$
is (resp., is not)
$\mathbf {p}_{\boldsymbol {\gamma }}$
is (resp., is not)
![]() $(1,2)$
.
$(1,2)$
.
We can easily show the following; the element
![]() $\mathbf {q}$
in this lemma is a unique element of
$\mathbf {q}$
in this lemma is a unique element of
![]() $\mathbf {D}$
fixed by our ‘sijection’ (i.e., a bijection between signed sets) defined below.
$\mathbf {D}$
fixed by our ‘sijection’ (i.e., a bijection between signed sets) defined below.
Lemma 5.16. We have
note that
![]() $\{k\} \subset [k]$
is a unique subset
$\{k\} \subset [k]$
is a unique subset
![]() $J \subset [k]$
such that
$J \subset [k]$
such that
![]() $\mathbf {q} \in \mathbf {D}_{J}^{\mathrm {A}_1}$
. Also, we have
$\mathbf {q} \in \mathbf {D}_{J}^{\mathrm {A}_1}$
. Also, we have
Let us complete the proof of Proposition 2.4. For this purpose, we define a ‘sijection’ (i.e., a bijection between signed sets)
![]() $\Phi :\mathbf {D} \rightarrow \mathbf {D}$
as follows. We set
$\Phi :\mathbf {D} \rightarrow \mathbf {D}$
as follows. We set
![]() $\Phi (\mathbf {q}):=\mathbf {q}$
(see Lemma 5.16). Let
$\Phi (\mathbf {q}):=\mathbf {q}$
(see Lemma 5.16). Let
![]() $\mathbf {p} \in \mathbf {D}_{J}^{\mathrm {A}_2}$
; note that
$\mathbf {p} \in \mathbf {D}_{J}^{\mathrm {A}_2}$
; note that
![]() $j_{1}=\min J \ge 2$
and
$j_{1}=\min J \ge 2$
and
![]() $j_{1}-1 \notin J$
. We set
$j_{1}-1 \notin J$
. We set
![]() $\Phi (J):=(J \setminus \{j_{1}\}) \sqcup \{j_{1}-1\}$
and then define
$\Phi (J):=(J \setminus \{j_{1}\}) \sqcup \{j_{1}-1\}$
and then define
![]() $\Phi (\mathbf {p}) \in \mathbf {D}_{\Phi (J)}^{\mathrm {A}_1} \sqcup \mathbf {D}_{\Phi (J)}^{\mathrm {B}_1}$
as follows. Recall that the
$\Phi (\mathbf {p}) \in \mathbf {D}_{\Phi (J)}^{\mathrm {A}_1} \sqcup \mathbf {D}_{\Phi (J)}^{\mathrm {B}_1}$
as follows. Recall that the
![]() $\boldsymbol {\beta }$
-part
$\boldsymbol {\beta }$
-part
![]() $\mathbf {p}_{\boldsymbol {\beta }}$
of
$\mathbf {p}_{\boldsymbol {\beta }}$
of
![]() $\mathbf {p}$
is of the form (5.27), and that if the
$\mathbf {p}$
is of the form (5.27), and that if the
![]() $\boldsymbol {\gamma }$
-part
$\boldsymbol {\gamma }$
-part
![]() $\mathbf {p}_{\boldsymbol {\gamma }}$
of
$\mathbf {p}_{\boldsymbol {\gamma }}$
of
![]() $\mathbf {p}$
is nontrivial, then it starts at the edge whose label is
$\mathbf {p}$
is nontrivial, then it starts at the edge whose label is
![]() $(j_{u},t)$
for some
$(j_{u},t)$
for some
![]() $2 \le u \le p$
and
$2 \le u \le p$
and
![]() $j_{u} \le t \le n+1$
, with
$j_{u} \le t \le n+1$
, with
![]() $t \notin \{j_{u+1},\dots ,j_{p}\}$
(see Lemma 5.15). We define
$t \notin \{j_{u+1},\dots ,j_{p}\}$
(see Lemma 5.15). We define
![]() $\Phi (\mathbf {p})$
by
$\Phi (\mathbf {p})$
by
where
![]() $\mathbf {s}'$
is obtained from
$\mathbf {s}'$
is obtained from
![]() $\mathbf {s}$
by replacing
$\mathbf {s}$
by replacing
![]() $(j_{1}-1,j_{u})$
appearing in
$(j_{1}-1,j_{u})$
appearing in
![]() $\mathbf {p}_{\boldsymbol {\beta }}$
with
$\mathbf {p}_{\boldsymbol {\beta }}$
with
![]() $(j_{1},j_{u})$
for each
$(j_{1},j_{u})$
for each
![]() $2 \le u \le p$
; by [Reference Naito and SagakiNS2, Lemma 2.3 (2)] and Lemma 5.14, we deduce that
$2 \le u \le p$
; by [Reference Naito and SagakiNS2, Lemma 2.3 (2)] and Lemma 5.14, we deduce that
![]() $\Phi (\mathbf {p}) \in \mathbf {D}_{\Phi (J)}^{\mathrm {A}_1} \sqcup \mathbf {D}_{\Phi (J)}^{\mathrm {B}_1}$
(note that
$\Phi (\mathbf {p}) \in \mathbf {D}_{\Phi (J)}^{\mathrm {A}_1} \sqcup \mathbf {D}_{\Phi (J)}^{\mathrm {B}_1}$
(note that
![]() $\Phi (\mathbf {p}) \in \mathbf {D}_{\Phi (J)}^{\mathrm {B}_1}$
if and only if
$\Phi (\mathbf {p}) \in \mathbf {D}_{\Phi (J)}^{\mathrm {B}_1}$
if and only if
![]() $j_{1}=2$
). Also, it follows that
$j_{1}=2$
). Also, it follows that
 $$ \begin{align} \begin{aligned} & |\Phi(J)|=|J|, \\ & |\Phi(J)|\epsilon_{n+1-k}-\operatorname{\mathrm{end}}(\Phi(\mathbf{p})_{\boldsymbol{\beta}})\epsilon_{\Phi(J)} = |J|\epsilon_{n+1-k}-\operatorname{\mathrm{end}}(\mathbf{p}_{\boldsymbol{\beta}})\epsilon_{J}, \\ & \ell(\Phi(\mathbf{p})_{\boldsymbol{\gamma}})=\ell(\mathbf{p}_{\boldsymbol{\gamma}})+1, \quad \operatorname{\mathrm{end}}(\Phi(\mathbf{p}))t_{\operatorname{\mathrm{wt}}(\Phi(\mathbf{p}))} = \operatorname{\mathrm{end}}(\mathbf{p})t_{\operatorname{\mathrm{wt}}(\mathbf{p})}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & |\Phi(J)|=|J|, \\ & |\Phi(J)|\epsilon_{n+1-k}-\operatorname{\mathrm{end}}(\Phi(\mathbf{p})_{\boldsymbol{\beta}})\epsilon_{\Phi(J)} = |J|\epsilon_{n+1-k}-\operatorname{\mathrm{end}}(\mathbf{p}_{\boldsymbol{\beta}})\epsilon_{J}, \\ & \ell(\Phi(\mathbf{p})_{\boldsymbol{\gamma}})=\ell(\mathbf{p}_{\boldsymbol{\gamma}})+1, \quad \operatorname{\mathrm{end}}(\Phi(\mathbf{p}))t_{\operatorname{\mathrm{wt}}(\Phi(\mathbf{p}))} = \operatorname{\mathrm{end}}(\mathbf{p})t_{\operatorname{\mathrm{wt}}(\mathbf{p})}. \end{aligned} \end{align} $$
Let
![]() $\mathbf {p} \in \mathbf {D}_{J}^{\mathrm {A}_1} \sqcup \mathbf {D}_{J}^{\mathrm {B}_1}$
, with
$\mathbf {p} \in \mathbf {D}_{J}^{\mathrm {A}_1} \sqcup \mathbf {D}_{J}^{\mathrm {B}_1}$
, with
![]() $J \ne \{k\}$
; recall that
$J \ne \{k\}$
; recall that
![]() $\mathbf {D}_{ \{ k \} }^{\mathrm {A}_1} \sqcup \mathbf {D}_{ \{ k \} }^{\mathrm {B}_1} = \{\mathbf {q}\}$
, and note that
$\mathbf {D}_{ \{ k \} }^{\mathrm {A}_1} \sqcup \mathbf {D}_{ \{ k \} }^{\mathrm {B}_1} = \{\mathbf {q}\}$
, and note that
![]() $j_{1}+1 \notin [k] \setminus J$
. We set
$j_{1}+1 \notin [k] \setminus J$
. We set
![]() $\Phi (J):= (J \setminus \{j_{1}\}) \sqcup \{j_{1}+1\}$
and then define
$\Phi (J):= (J \setminus \{j_{1}\}) \sqcup \{j_{1}+1\}$
and then define
![]() $\Phi (\mathbf {p}) \in \mathbf {D}_{\Phi (J)}^{\mathrm {A}_1}$
as follows. Recall that the
$\Phi (\mathbf {p}) \in \mathbf {D}_{\Phi (J)}^{\mathrm {A}_1}$
as follows. Recall that the
![]() $\boldsymbol {\beta }$
-part
$\boldsymbol {\beta }$
-part
![]() $\mathbf {p}_{\boldsymbol {\beta }}$
of
$\mathbf {p}_{\boldsymbol {\beta }}$
of
![]() $\mathbf {p}$
is of the form (5.27) or (5.28), and that the
$\mathbf {p}$
is of the form (5.27) or (5.28), and that the
![]() $\boldsymbol {\gamma }$
-part
$\boldsymbol {\gamma }$
-part
![]() $\mathbf {p}_{\boldsymbol {\gamma }}$
of
$\mathbf {p}_{\boldsymbol {\gamma }}$
of
![]() $\mathbf {p}$
starts at the edge whose label is
$\mathbf {p}$
starts at the edge whose label is
![]() $(j_{1},j_{1}+1)$
(see Lemma 5.15). We define
$(j_{1},j_{1}+1)$
(see Lemma 5.15). We define
![]() $\Phi (\mathbf {p})$
by
$\Phi (\mathbf {p})$
by
where
![]() $\mathbf {s}"$
is obtained from
$\mathbf {s}"$
is obtained from
![]() $\mathbf {s}$
by replacing
$\mathbf {s}$
by replacing
![]() $(j_{1}+1,j_{u})$
appearing in
$(j_{1}+1,j_{u})$
appearing in
![]() $\mathbf {p}_{\beta }$
with
$\mathbf {p}_{\beta }$
with
![]() $(j_{1},j_{u})$
for each
$(j_{1},j_{u})$
for each
![]() $2 \le u \le p$
, and
$2 \le u \le p$
, and
![]() $\mathbf {p}_{\gamma } \setminus (j_{1},j_{1}+1)$
is the sequence obtained form
$\mathbf {p}_{\gamma } \setminus (j_{1},j_{1}+1)$
is the sequence obtained form
![]() $\mathbf {p}_{\gamma }$
by removing the initial label
$\mathbf {p}_{\gamma }$
by removing the initial label
![]() $(j_{1},j_{1}+1)$
; by [Reference Naito and SagakiNS2, Lemma 2.3 (4)] and Lemma 5.14, we deduce that
$(j_{1},j_{1}+1)$
; by [Reference Naito and SagakiNS2, Lemma 2.3 (4)] and Lemma 5.14, we deduce that
![]() $\Phi (\mathbf {p}) \in \mathbf {D}_{\Phi (J)}^{\mathrm {A}_2}$
. Also, it follows that
$\Phi (\mathbf {p}) \in \mathbf {D}_{\Phi (J)}^{\mathrm {A}_2}$
. Also, it follows that
 $$ \begin{align} \begin{aligned} & |\Phi(J)|=|J|, \\ & |\Phi(J)|\epsilon_{n+1-k}-\operatorname{\mathrm{end}}(\Phi(\mathbf{p})_{\beta})\epsilon_{\Phi(J)} = |J|\epsilon_{n+1-k}-\operatorname{\mathrm{end}}(\mathbf{p}_{\beta})\epsilon_{J}, \\ & \ell(\Phi(\mathbf{p})_{\gamma})=\ell(\mathbf{p}_{\gamma})-1, \quad \operatorname{\mathrm{end}}(\Phi(\mathbf{p}))t_{\operatorname{\mathrm{wt}}(\Phi(\mathbf{p}))} = \operatorname{\mathrm{end}}(\mathbf{p})t_{\operatorname{\mathrm{wt}}(\mathbf{p})}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & |\Phi(J)|=|J|, \\ & |\Phi(J)|\epsilon_{n+1-k}-\operatorname{\mathrm{end}}(\Phi(\mathbf{p})_{\beta})\epsilon_{\Phi(J)} = |J|\epsilon_{n+1-k}-\operatorname{\mathrm{end}}(\mathbf{p}_{\beta})\epsilon_{J}, \\ & \ell(\Phi(\mathbf{p})_{\gamma})=\ell(\mathbf{p}_{\gamma})-1, \quad \operatorname{\mathrm{end}}(\Phi(\mathbf{p}))t_{\operatorname{\mathrm{wt}}(\Phi(\mathbf{p}))} = \operatorname{\mathrm{end}}(\mathbf{p})t_{\operatorname{\mathrm{wt}}(\mathbf{p})}. \end{aligned} \end{align} $$
If
![]() $\mathbf {p} \in \mathbf {D}_{J}^{\mathrm {B}_2}$
, then
$\mathbf {p} \in \mathbf {D}_{J}^{\mathrm {B}_2}$
, then
![]() $\mathbf {p} \in \mathbf {D}_{\Phi (J)}^{\mathrm {C}}$
with
$\mathbf {p} \in \mathbf {D}_{\Phi (J)}^{\mathrm {C}}$
with
![]() $\Phi (J):=J \setminus \{1\}$
. We define
$\Phi (J):=J \setminus \{1\}$
. We define
![]() $\Phi (\mathbf {p}):=\mathbf {p} \in \mathbf {D}_{\Phi (J)}^{\mathrm {C}}$
for
$\Phi (\mathbf {p}):=\mathbf {p} \in \mathbf {D}_{\Phi (J)}^{\mathrm {C}}$
for
![]() $\mathbf {p} \in \mathbf {D}_{J}^{\mathrm {B}_2}$
. It follows that
$\mathbf {p} \in \mathbf {D}_{J}^{\mathrm {B}_2}$
. It follows that
 $$ \begin{align} \begin{aligned} & |\Phi(J)|=|J|-1, \\ & |\Phi(J)|\epsilon_{n+1-k}-\operatorname{\mathrm{end}}(\Phi(\mathbf{p})_{\beta})\epsilon_{\Phi(J)} = |J|\epsilon_{n+1-k}-\operatorname{\mathrm{end}}(\mathbf{p}_{\beta})\epsilon_{J}, \\ & \ell(\Phi(\mathbf{p})_{\gamma})=\ell(\mathbf{p}_{\gamma}), \qquad \operatorname{\mathrm{end}}(\Phi(\mathbf{p}))t_{\operatorname{\mathrm{wt}}(\Phi(\mathbf{p}))} = \operatorname{\mathrm{end}}(\mathbf{p})t_{\operatorname{\mathrm{wt}}(\mathbf{p})}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & |\Phi(J)|=|J|-1, \\ & |\Phi(J)|\epsilon_{n+1-k}-\operatorname{\mathrm{end}}(\Phi(\mathbf{p})_{\beta})\epsilon_{\Phi(J)} = |J|\epsilon_{n+1-k}-\operatorname{\mathrm{end}}(\mathbf{p}_{\beta})\epsilon_{J}, \\ & \ell(\Phi(\mathbf{p})_{\gamma})=\ell(\mathbf{p}_{\gamma}), \qquad \operatorname{\mathrm{end}}(\Phi(\mathbf{p}))t_{\operatorname{\mathrm{wt}}(\Phi(\mathbf{p}))} = \operatorname{\mathrm{end}}(\mathbf{p})t_{\operatorname{\mathrm{wt}}(\mathbf{p})}. \end{aligned} \end{align} $$
Similarly, if
![]() $\mathbf {p} \in \mathbf {D}_{J}^{\mathrm {C}}$
, then
$\mathbf {p} \in \mathbf {D}_{J}^{\mathrm {C}}$
, then
![]() $\mathbf {p} \in \mathbf {D}_{\Phi (J)}^{\mathrm {B}_2}$
with
$\mathbf {p} \in \mathbf {D}_{\Phi (J)}^{\mathrm {B}_2}$
with
![]() $\Phi (J):=J \sqcup \{1\}$
. We define
$\Phi (J):=J \sqcup \{1\}$
. We define
![]() $\Phi (\mathbf {p}):=\mathbf {p} \in \mathbf {D}_{\Phi (J)}^{\mathrm {B}_2}$
for
$\Phi (\mathbf {p}):=\mathbf {p} \in \mathbf {D}_{\Phi (J)}^{\mathrm {B}_2}$
for
![]() $\mathbf {p} \in \mathbf {D}_{J}^{\mathrm {C}}$
. It follows that
$\mathbf {p} \in \mathbf {D}_{J}^{\mathrm {C}}$
. It follows that
 $$ \begin{align} \begin{aligned} & |\Phi(J)|=|J|+1, \\ & |\Phi(J)|\epsilon_{n+1-k}-\operatorname{\mathrm{end}}(\Phi(\mathbf{p})_{\beta})\epsilon_{\Phi(J)} = |J|\epsilon_{n+1-k}-\operatorname{\mathrm{end}}(\mathbf{p}_{\beta})\epsilon_{J}, \\ & \ell(\Phi(\mathbf{p})_{\gamma})=\ell(\mathbf{p}_{\gamma}), \qquad \operatorname{\mathrm{end}}(\Phi(\mathbf{p}))t_{\operatorname{\mathrm{wt}}(\Phi(\mathbf{p}))} = \operatorname{\mathrm{end}}(\mathbf{p})t_{\operatorname{\mathrm{wt}}(\mathbf{p})}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & |\Phi(J)|=|J|+1, \\ & |\Phi(J)|\epsilon_{n+1-k}-\operatorname{\mathrm{end}}(\Phi(\mathbf{p})_{\beta})\epsilon_{\Phi(J)} = |J|\epsilon_{n+1-k}-\operatorname{\mathrm{end}}(\mathbf{p}_{\beta})\epsilon_{J}, \\ & \ell(\Phi(\mathbf{p})_{\gamma})=\ell(\mathbf{p}_{\gamma}), \qquad \operatorname{\mathrm{end}}(\Phi(\mathbf{p}))t_{\operatorname{\mathrm{wt}}(\Phi(\mathbf{p}))} = \operatorname{\mathrm{end}}(\mathbf{p})t_{\operatorname{\mathrm{wt}}(\mathbf{p})}. \end{aligned} \end{align} $$
Thus, we have obtained a bijection
![]() $\Phi :\mathbf {D} \rightarrow \mathbf {D}$
such that (i)
$\Phi :\mathbf {D} \rightarrow \mathbf {D}$
such that (i)
![]() $\Phi (\mathbf {q})=\mathbf {q}$
, (ii)
$\Phi (\mathbf {q})=\mathbf {q}$
, (ii)
![]() $\Phi (\mathbf {p}) \ne \mathbf {p}$
,
$\Phi (\mathbf {p}) \ne \mathbf {p}$
,
![]() $\Phi (\Phi (\mathbf {p}))=\mathbf {p}$
, and such that
$\Phi (\Phi (\mathbf {p}))=\mathbf {p}$
, and such that
 $$ \begin{align*} \begin{aligned} & \mathbf{e}^{|\Phi(J)| \epsilon_{n+1-k}-\operatorname{\mathrm{end}}(\Phi(\mathbf{p})_{\beta})\epsilon_{\Phi(J)}} (-1)^{|\Phi(J)|+\ell(\Phi(\mathbf{p})_{\gamma})} [\mathcal{O}_{\mathbf{Q}_{G}(\operatorname{\mathrm{end}}(\Phi(\mathbf{p}))t_{\operatorname{\mathrm{wt}}(\Phi(\mathbf{p}))})}] \\ & = - \mathbf{e}^{|J| \epsilon_{n+1-k}-\operatorname{\mathrm{end}}(\mathbf{p}_{\beta})\epsilon_{J}} (-1)^{|J|+\ell(\mathbf{p}_{\gamma})} [\mathcal{O}_{\mathbf{Q}_{G}(\operatorname{\mathrm{end}}(\mathbf{p})t_{\operatorname{\mathrm{wt}}(\mathbf{p})})}] \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} & \mathbf{e}^{|\Phi(J)| \epsilon_{n+1-k}-\operatorname{\mathrm{end}}(\Phi(\mathbf{p})_{\beta})\epsilon_{\Phi(J)}} (-1)^{|\Phi(J)|+\ell(\Phi(\mathbf{p})_{\gamma})} [\mathcal{O}_{\mathbf{Q}_{G}(\operatorname{\mathrm{end}}(\Phi(\mathbf{p}))t_{\operatorname{\mathrm{wt}}(\Phi(\mathbf{p}))})}] \\ & = - \mathbf{e}^{|J| \epsilon_{n+1-k}-\operatorname{\mathrm{end}}(\mathbf{p}_{\beta})\epsilon_{J}} (-1)^{|J|+\ell(\mathbf{p}_{\gamma})} [\mathcal{O}_{\mathbf{Q}_{G}(\operatorname{\mathrm{end}}(\mathbf{p})t_{\operatorname{\mathrm{wt}}(\mathbf{p})})}] \end{aligned} \end{align*} $$
for all
![]() $\mathbf {p} \in \mathbf {D}_{J} \setminus \{\mathbf {q}\}$
with
$\mathbf {p} \in \mathbf {D}_{J} \setminus \{\mathbf {q}\}$
with
![]() $J \subset [k]$
. Therefore, the right-hand side of equation (5.19) becomes
$J \subset [k]$
. Therefore, the right-hand side of equation (5.19) becomes
as desired. This completes the proof of Proposition 2.4.
Acknowledgements
The second and third authors would like to thank Cristian Lenart and Daniel Orr for related collaborations.
Funding statement
S.N. was partly supported by JSPS Grant-in-Aid for Scientific Research (C) 21K03198. D.S. was partly supported by JSPS Grants-in-Aid for Scientific Research (C) 19K03145 and 23K03045.
Competing interest
The authors have no competing interest to declare.