I. INTRODUCTION
In the Earth's mantle, with increasing depth, pressure increases rapidly, reaching values as high as 136 GPa at the base of the mantle. Reference Karki, Stixrude and Wentzcovitch1 These ultrahigh pressures have profound implications on the rheology of the Earth's constituents that can be quite different from that observed at ordinary pressure. Therefore, it is of primary importance to investigate the mechanical behavior of the high-pressure phases of the deep Earth to understand the structure and dynamics of the Earth's interior.
Below 670 km, the phase assemblages present in the Earth's transition zone decompose into a mixture of silicates with the perovskite structure and magnesium oxides (containing some iron). The high-pressure behavior of periclase (MgO) is thus of major importance in the rheology of the Earth's interior. MgO is an ionic solid, which is chemically and physically stable at high temperatures and pressures. It can keep its NaCl-type structure up to 227 GPa confining pressure. Reference Duffy, Hemley and Mao2 This unique structural stability makes MgO an ideal benchmark for investigating the behavior of solids at extreme pressure conditions. The structure and elasticity of MgO at high pressure have been widely studied by using first-principles calculations. Indeed, pressure-induced variation of the elastic moduli arises from changes in the structure and nature of atomic bondings under pressure and from phase transformations. Reference Karki, Stixrude and Wentzcovitch1 For instance, the individual elastic moduli of MgO throughout Earth's mantle pressure regime have been obtained with density functional theory. It was found that the pressure-induced elastic anisotropy is preserved down to the Earth's lowest mantle. Reference Karki, Wentzcovitch, de Gironcoli and Baroni3 The pressure-induced phase transformation of MgO was compared with that of other ionic and solids. Reference Karki, Ackland and Crain4 The elastic moduli, the intrinsic anharmonic parameters, and the B1–B2 transition pressure of MgO were determined from ab initio calculations. Simulation results show that MgO keeps its NaCl-type B1 structure at all pressures existing within the Earth, and that the critical pressure at which MgO transforms into the CsCl-type B2 structure is 509 GPa. Reference Oganov and Dorogokupets5,Reference Karki, Stixrude, Clark, Warren, Ackland and Crain6
In the Earth's mantle, MgO is present in the form of polycrystalline aggregates, which exhibit various grain sizes and grain boundary (GB) misorientation angles. GBs in MgO significantly influence polycrystal elasticity and plasticity, and have attracted intensive research interest among high-pressure experimentalists. Merkel et al. used diamond anvil cell coupled with in situ synchrotron x-ray diffraction measurements to investigate the evolution of yield strength and deformation mechanisms of MgO polycrystals at pressures up to 47 GPa. Reference Merkel, Wenk, Shu, Shen, Gillet, Mao and Hemley7 Marquardt et al. carried out Brillouin scattering experiments on MgO nanocrystals to characterize their elastic properties and GBs at high pressures. Reference Marquardt, Gleason, Marquardt, Speziale, Miyagi, Neusser, Wenk and Jeanloz8 It was found that at high pressures, the small grain sizes have profound effects on the elastic properties. Van Orman et al. performed high-pressure diffusion experiments in MgO to investigate the rheological and chemical transport properties within the lower mantle. Reference Van Orman, Fei, Hauri and Wang9 Recent deformation experiments performed under lower mantle conditions by Girard et al. Reference Girard, Amulele, Farla, Mohiuddin and Karato10 on bridgmanite and (Mg, Fe)O aggregates have shown that the rheology contrast between the two phases leads to phase separation and shear localization within oxide-rich domains. Hence, the mechanical properties of GBs in MgO at high-pressure are expected to contribute significantly to the rheology of the deep mantle.
First-principles methods and molecular dynamics simulations are efficient modeling tools that allow studying the physical properties of GBs in MgO at the atomic scale Reference Harris, Watson and Parker11–Reference Verma and Karki14 under high pressures. The atomic and electronic structures of three {n10}/[001] MgO tilt GBs (n = 2, 3, and 4) were investigated as a function of pressure by using the density functional theory. Reference Verma and Karki14 Using a similar method, the ability of MgO GBs to accommodate point defects and enhance diffusion rates was explored. Results show that defects and impurities (Ca, Al, and proton) segregate preferentially within the boundary area and that the segregation susceptibility considerably increases with pressure. Reference Karki, Ghosh and Verma15
Continuous modeling of the structure of GBs using smooth first order/second order distortion fields and crystal defect density fields at interatomic scale is attractive because it provides the basis for a mechanical description of the lattice defects. Attractiveness of continuous modeling at this scale derives further from its ability to serve as a basis for coarse-grained representations of polycrystalline media. Within a recent elasto-plastic framework proposed by Fressengeas et al. Reference Fressengeas, Taupin and Capolungo16 and Acharya–Fressengeas, Reference Acharya and Fressengeas17 it was shown that dislocation, disclination and generalized-disclination (g-disclination) density fields were appropriate mathematical objects for a consistent continuous description of the atomic defected structures, energetics, and dynamics of GBs. Reference Fressengeas, Taupin and Capolungo18–Reference Sun, Taupin, Fressengeas and Cordier20 For instance, disclinations were found to decorate GBs in minerals and were proposed as good candidates at providing plastic accommodation mechanisms in dislocation slip-deprived rocks in the upper mantle. Reference Cordier, Demouchy, Beausir, Taupin, Barou and Fressengeas19 Here we focus on how pressure influences the dislocation, disclination, and g-disclination structures of a MgO {310}/[001] tilt GB. At first, the discrete atomic positions simulated by first-principles calculations are used to derive the strain and rotation fields in the boundary area at different pressures. Then, the dislocation, disclination and g-disclination density fields are calculated to study the influence of pressure on the defected structure of GBs, in terms of discontinuities of elastic displacement, rotation, and strain fields.
II. MODELING METHODS
A. MgO boundaries from first principles calculations
The MgO GB studied here is a {310}/[001] (misorientation θ = 36.8°) tilt boundary, which was constructed in a previous work.
Reference Verma and Karki14
The initial configuration of the GB before self-relaxation was created by the following two steps. At first, two blocks of MgO single crystals are cut along
![]() $\left( {310} \right)$
and
$\left( {310} \right)$
and
![]() $\left( {3\bar 10} \right)$
surfaces, respectively, and rotated about the [001] axis. Then, the two MgO cut blocks are joined together and the initial unrelaxed GB is formed. After the initial configuration of the GB was generated, the structure was relaxed using the Vienna ab-initio simulation package with local density approximation and projector-augmented-wave method.
Reference Sun, Cordier, Taupin, Fressengeas and Jahn21
A plane wave cutoff energy of 450 eV and Gamma-point Brillouin zone sampling were used. Both cell parameters and atomic positions were optimized for the boundary supercell containing 560 atoms according to pressure in the range 0–150 GPa. Doubling the supercell did not affect the calculated boundary structure significantly.
$\left( {3\bar 10} \right)$
surfaces, respectively, and rotated about the [001] axis. Then, the two MgO cut blocks are joined together and the initial unrelaxed GB is formed. After the initial configuration of the GB was generated, the structure was relaxed using the Vienna ab-initio simulation package with local density approximation and projector-augmented-wave method.
Reference Sun, Cordier, Taupin, Fressengeas and Jahn21
A plane wave cutoff energy of 450 eV and Gamma-point Brillouin zone sampling were used. Both cell parameters and atomic positions were optimized for the boundary supercell containing 560 atoms according to pressure in the range 0–150 GPa. Doubling the supercell did not affect the calculated boundary structure significantly.
The relaxed configurations of asymmetric MgO {310}/[001] GBs at 0, 50, 100, and 150 GPa pressures are shown in Figs. 1(a), 1(b), 1(c), and 1(d), respectively. Atoms are represented by black dots, and the atomic structural units composing the boundaries are delineated by blue lines. As can be seen in Fig. 1(a), the GB structure at 0 GPa is made of hexagon-like atomic structural units, which are similar to those at 50 GPa [see Fig. 1(b)]. However, as far as the pressure reaches 100 or 150 GPa, the hexagon-like structural units evolve toward more triangular and thin shapes [Fig. 1(c)].
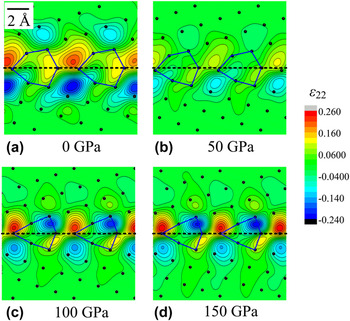
FIG. 1. Close-up showing the tilt strain ε 22 fields on top of the relaxed atomic structure of the simulated {310}/[001] MgO tilt boundary under pressures (a) 0, (b) 50, (c) 100, and (d) 150 GPa.
B. From atomic to continuous description of GB structures
The atomic structures of the relaxed and unrelaxed configurations obtained from first-principles calculations are now used to derive the continuous dislocation/disclination/g-disclination fields characterizing the lattice incompatibility in the defected area of the GB. The following steps are performed:
-
(i) Local values of the transformation gradient tensor at each atomic position are computed by using the atomic positions in the reference and deformed configurations. As it is less energetic, the reference configuration is taken as the relaxed GB structure and the current configuration is the initial unrelaxed GB structure.
-
(ii) Elastic strain, rotation, curvature tensor fields and then dislocation, disclination, and g-disclination density field values are calculated at each atomic position by following the methods recently introduced Reference Sun, Taupin, Fressengeas and Cordier20 (see also the Appendix).
-
(iii) Linear interpolation is used to generate spatial field distributions in between atoms from local values at atoms. In the linear interpolation of fields, the mesh size is 0.5 angstrom.
This method has been applied to a 18.9° and a 60.8° symmetrical tilt boundary in copper and forsterite, respectively, Reference Sun, Taupin, Fressengeas and Cordier20,Reference Kresse and Furthmüller22 and its accuracy/reliability was checked by comparison with recent similar techniques. Reference Gullett, Horstemeyer, Baskes and Fang23,Reference Zimmerman, Bammann and Gao24
III. RESULTS AND DISCUSSION
A. Elastic fields
Strain is a measure of the deformation of the body with respect to a reference configuration. The ε 22 strain fields of the MgO boundary at 0, 50, 100, and 150 GPa pressures are displayed in Figs. 1(a), 1(b), 1(c), and 1(d), respectively. The strains ε 11 and ε 12 are shown in the Supplementary Materials. The ε 22 component (strain normal to the GB plane) is larger than the others and is chosen to characterize the influence of pressure. As plotted in Fig. 1(a), the strain field ε 22 at 0 GPa is located along the boundary with alternate signs across the GB interface. The extreme values of the contractions and extensions form dipoles, and they are located in areas in between the structural units and are extremely close to the interface. Figure 1(b) shows the strain ε 22 of the boundary at 50 GPa. The shape of dipoles in Fig. 1(b) is quite close to that at 0 GPa, but the magnitude of strains is about 0.15, which is only 60% of that at 0 GPa. The ε 22 strain fields at 100 and 150 GPa are displayed in Figs. 1(c) and 1(d), respectively. The extreme values of the contractions and extensions of ε 22 at 100 or 150 GPa are also located along the interface with alternate signs across the boundary. However, as compared with the ε 22 strain fields at 0 and 50 GPa, strain quadrupoles, rather than dipoles, are seen.
The elastic tilt rotation field ω of the boundaries at 0, 50, 100, and 150 GPa are plotted in Figs. 2(a), 2(b), 2(c), and 2(d), respectively (rotation around the axis perpendicular to the figures). For the four pressures studied, tilt rotation dipoles are observed and are located within a 6 Å thick layer along the interface. It is observed that the shapes of rotation fields at 0 and 50 GPa are very similar. Just like the strain field shown in Fig. 1, ω has relatively smaller values at 50 GPa than at 0 GPa. However, at 100 and 150 GPa, the dipolar structure of the rotation fields significantly differs: At 100 or 150 GPa, the dipole arms are arranged along a straight line subparallel to the boundary plane. At 0 and 50 GPa, they are inclined with respect to the GB plane, and subsequent dipoles tend to form a zigzag pattern.
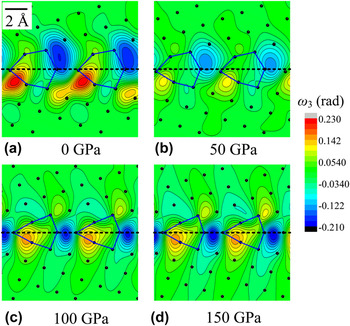
FIG. 2. Close-up showing the tilt rotation
![]() $\omega$
field on top of the relaxed atomic structure of the simulated {310}/[001] MgO tilt boundary under pressures (a) 0, (b) 50, (c) 100, and (d) 150 GPa.
$\omega$
field on top of the relaxed atomic structure of the simulated {310}/[001] MgO tilt boundary under pressures (a) 0, (b) 50, (c) 100, and (d) 150 GPa.
B. Dislocation and disclination density fields
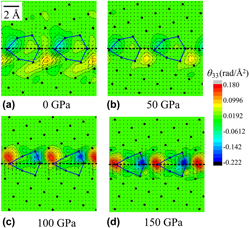
The discontinuities of the displacement and rotation fields in the GB interface area can be described by using Volterra's model defects, i.e., dislocations and disclinations, respectively. By using the elasto-plastic model of dislocation and disclination fields, Reference Fressengeas, Taupin and Capolungo16 the disclination density θ 33 and dislocation density (α 13, α 23) fields are used to characterize the discontinuity of tilt elastic rotation and of the in-plane displacements (displacements in the plane of the figures). The calculated defect densities are displayed in Fig. 3 for the four pressures studied. The defect topology reflected by the wedge disclination density θ 33 is an elastic rotation discontinuity around the axis perpendicular to the figure, supported by a defect line aligned with that same axis. The edge dislocation densities (α 13, α 23), respectively, render horizontal and vertical Burgers vectors, supported by the same defect line parallel to the GB tilt axis (axis perpendicular to the figure plane). In this figure, the disclination density is color-coded and the dislocation densities are represented by the associated in-plane components of the Burgers vector field per unit surface (arrows). It can be seen that the disclination and dislocation distributions are confined to a thin 6 Å layer along the interface.

FIG. 3. Disclination density field θ33 and Burgers vector fields for pressures (a) 0, (b) 50, (c) 100, and (d) 150 GPa. The arrows represent the local Burgers vector, whose components are the edge dislocation densities (α 13 and α 23) per unit surface.
The disclination dipole structures (shape and strength) are very similar at 0 GPa [Fig. 3(a)] and at 50 GPa [Fig. 3(b)]. In both cases, the disclination dipoles are subsequently arranged in a zigzag manner, just like the rotation fields. It is indeed seen that the disclination dipoles accommodate the strong rotation variations (jumps) along the GB interface. However, the disclination density field at 100 GPa is radically different from that at 50 GPa. In Fig. 3(c), the disclination dipoles at 100 GPa are arranged along a straight line parallel to the GB plane, the positive (resp. negative) pole being at the left (resp. right) end of the structural units. The maximum local magnitude of disclination densities at 100 GPa is 0.18 rad/Å2, almost two times larger than that at 50 GPa. Similarly, the local dislocation density values (α 13, α 23) are larger at 100 GPa than at 50 GPa. The disclination dipoles at 150 GPa are plotted in Fig. 3(d). The shape and strength of disclination dipoles slightly differs from 100 GPa to 150 GPa, except that the position of disclination dipoles at 150 GPa is more symmetrical with respect to the boundary plane, while dipoles at 100 GPa are a little offset downward.
The Burgers vector components associated with the (α 13, α 23) dislocation density distribution are now computed, together with the Frank vector component associated with the wedge disclination density field θ 33. The Frank vector Ω is defined as the angular closure defect, which can be obtained by integrating the elastic curvature tensor along a closed circuit C, and equivalently by:
where S is the surface of unit normal n delimited by C. In the present MgO case, the Frank vector resulting from the distribution of the disclination density θ 33 over a surface S in the plane (e 1, e 2) is
As the pressure increases from 0 to 50 GPa, the
![]() $\left\langle {001} \right\rangle$
Frank vector component decreases from 1.02 to 0.63 radian (58° to 36°). However, the
$\left\langle {001} \right\rangle$
Frank vector component decreases from 1.02 to 0.63 radian (58° to 36°). However, the
![]() $\left\langle {001} \right\rangle$
Frank vector component increases up to 0.96 radian (55°) at 100 GPa, and reaches to 1.10 radian (63°) at 150 GPa. This variation trend is consistent with the evolution of disclination spatial distributions for the four pressures (Fig. 3).
$\left\langle {001} \right\rangle$
Frank vector component increases up to 0.96 radian (55°) at 100 GPa, and reaches to 1.10 radian (63°) at 150 GPa. This variation trend is consistent with the evolution of disclination spatial distributions for the four pressures (Fig. 3).
The Burgers vector is now defined as
In the above, r is the position vector and the disclination densities have a nonlocal impact on the Burgers vector. In the plane (e 1, e 2), Eq. (3) reduces to
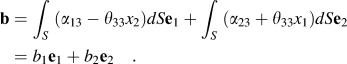 $${\bf {b}} = \int_S {\left( {{\alpha _{13}} - {\theta _{33}}{x_2}} \right)} {d}S{\bf{e}}_1 + \int_S {\left( {{\alpha _{23}} + {\theta _{33}}{x_1}} \right)} {d}S{\bf{e}}_2 = {b_1}{\bf{e}}_1 + {b_2}{\bf{e}}_2\quad .$$
$${\bf {b}} = \int_S {\left( {{\alpha _{13}} - {\theta _{33}}{x_2}} \right)} {d}S{\bf{e}}_1 + \int_S {\left( {{\alpha _{23}} + {\theta _{33}}{x_1}} \right)} {d}S{\bf{e}}_2 = {b_1}{\bf{e}}_1 + {b_2}{\bf{e}}_2\quad .$$
We find that the magnitude of the in-plane Burgers vector (in the plane of the figures) changes from b = 0.83 Å at 0 GPa to b = 0.39 Å at 50 GPa, then it increases to b = 1.27 Å at 100 GPa, and finally equals b = 1.15 Å at 150 GPa. Again, the relationship between the magnitude of the Burgers vector and pressure is consistent with the variation of the dislocation density fields with pressure.
C. G-disclination density fields
As evidenced above, the boundaries exhibit discontinuities of the elastic displacement and rotation fields in the GB interface area, which can be described by a distribution of dislocation and disclination densities. However, it is also observed that the GB exhibits discontinuities of the elastic strain tensor. As recently discussed, Reference Acharya and Fressengeas17 the discontinuity of the elastic distortion (rotation plus strain) can be smoothly described by g-disclination densities. The g-disclination densities complement standard disclinations by rendering the discontinuity of strain in addition to the discontinuity of rotation.
The strain ε 22 (see Fig. 1) shows a more discontinuous spatial distribution than other strain components, (see Supplementary Materials). The g-disclination density field ξ 223, which reflects the discontinuity of strain ε 22 supported by a defect line parallel to the GB tilt axis, is plotted in Fig. 4 for the four pressures investigated. Similarly to the disclination field, all the g-disclination density fields show a positive (resp. negative) pole at the left (resp. right) end of the structural units. However, the g-disclination densities ξ 223 at 100 or 150 GPa are much higher in magnitude than in the two other cases, implying discontinuities of strain ε 22.

FIG. 4. Close-up showing the g-disclination density field ξ 233 on top of the relaxed atomic structure of the simulated {310}/[001] MgO tilt boundary under pressures (a) 0, (b) 50, (c) 100, and (d) 150 GPa.
IV. CONCLUSIONS
By using an atomistic-to-continuum crossover method, we provide a continuous description of the defect density fields within a MgO {310}/[001] tilt GB at different pressures. The elastic fields such as strain and rotation fields at each pressure are calculated in the boundary area from discrete atomic positions. Then dislocation, disclination and g-disclination density fields are calculated and used to describe discontinuities in the fields of displacement, rotation, and strain in the GB area at each pressure. Results show that as the pressure increases from 0 to 50 GPa, the intensities of all elastic fields (displacement, rotation, and strain) and the intensity of all defect density fields decrease while then, they increase when the pressure reaches 100 GPa. We show here that pressure has a strong effect on the defected structure of GBs, and the evolution does not follow a simple tendency of compacting structures with increasing pressure. Indeed, the defect structure of the boundary is significantly modified, which has potential implications on its elastic energy level and mobility under stress, with consequences in particular on the plasticity of polycrystalline aggregates. Further work is in progress to quantify these effects.
Supplementary Material
To view supplementary material for this article, please visit http://dx.doi.org/10.1557/jmr.2016.346.
ACKNOWLEDGMENT
This work was supported by funding from the European Research Council under the ERC Grant No. 290424—RheoMan.
APPENDIX
In this appendix, the kinematics of the elasto-plastic incompatibility associated with crystal defect fields is briefly recalled. Since compatible plastic processes are not envisioned in the present paper, compatibility is about elastic deformation measures only.
A.1. Displacement gradient
A fixed Cartesian coordinate system is assumed to describe the changes in the shape, size, and orientation of a simply connected continuous crystalline body containing defects. For each point, the Lagrange and Euler coordinates X and x label the positions of a material element in the reference and deformed state, respectively. x is a function of X, and the transformation gradient of x(X) is defined as the second order tensor
The total displacement field u = x − X describes the changes in position of matter. This field is assumed to be single valued and continuous, possibly between atoms and below interatomic distances. Thus, matter is assumed to be able to transmit stresses and couple stresses at this scale. The displacement gradient, also referred to as the distortion tensor, is
where I is the second order identity tensor and
![]() ${\delta _{ij}}$
is Kronecker delta,
${\delta _{ij}}$
is Kronecker delta,
A.2. Strain, rotation, and curvature tensors
Strain is a measure of the deformation of the body with respect to a reference configuration. The strain tensor
![]() ${\bf{\varepsilon }}$
is the symmetric part of the distortion grad u,
${\bf{\varepsilon }}$
is the symmetric part of the distortion grad u,
The rotation tensor ω is the skew-symmetric part of the distortion grad u,
and the associated rotation vector
![]() $\vec \omega$
reads
$\vec \omega$
reads
where
![]() ${e_{ijk}}$
is the alternating Levi-Civita tensor,
${e_{ijk}}$
is the alternating Levi-Civita tensor,
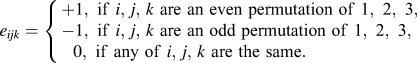 $${e_{ijk}} = \left\{ {\matrix{ { + 1,{\rm{\ if\ }}i{\rm{,\ }}j{\rm{,\ }}k{\rm{\ are\ an\ even\ permutation\ of\ 1,\ 2,\ 3,\ }}} \hfill \cr { - 1,{\rm{\ if\ }}i{\rm{,\ }}j{\rm{,\ }}k{\rm{\ are\ an\ odd\ permutation\ of\ 1,\ 2,\ 3,}}} \hfill \cr {{\rm{\ \ }}0,{\rm{\ if\ any\ of\ }}i{\rm{,\ }}j{\rm{,\ }}k{\rm{\ are\ the\ same}}{\rm{.}}} \hfill \cr} } \right.$$
$${e_{ijk}} = \left\{ {\matrix{ { + 1,{\rm{\ if\ }}i{\rm{,\ }}j{\rm{,\ }}k{\rm{\ are\ an\ even\ permutation\ of\ 1,\ 2,\ 3,\ }}} \hfill \cr { - 1,{\rm{\ if\ }}i{\rm{,\ }}j{\rm{,\ }}k{\rm{\ are\ an\ odd\ permutation\ of\ 1,\ 2,\ 3,}}} \hfill \cr {{\rm{\ \ }}0,{\rm{\ if\ any\ of\ }}i{\rm{,\ }}j{\rm{,\ }}k{\rm{\ are\ the\ same}}{\rm{.}}} \hfill \cr} } \right.$$
From the rotation vector
![]() $\vec \omega$
, the curvature tensor κ can be defined as
$\vec \omega$
, the curvature tensor κ can be defined as
A.3. Disclination, dislocation, and g-disclination density tensors
In the absence of plasticity, the curvature tensor
![]() ${\bf{\kappa }}$
can be identified with its compatible elastic component
${\bf{\kappa }}$
can be identified with its compatible elastic component
![]() $\kappa _{\rm{e}}^{//}$
. However, the elastic curvature tensor also comprises an incompatible part
$\kappa _{\rm{e}}^{//}$
. However, the elastic curvature tensor also comprises an incompatible part
![]() $\kappa _{\rm{e}}^ \bot$
, which counter-balances the incompatible plastic curvature
$\kappa _{\rm{e}}^ \bot$
, which counter-balances the incompatible plastic curvature
![]() $\kappa _{\rm{p}}^ \bot$
arising from the presence of crystal defects because continuity of the body is maintained. As a result, the elastic curvature tensor
$\kappa _{\rm{p}}^ \bot$
arising from the presence of crystal defects because continuity of the body is maintained. As a result, the elastic curvature tensor
![]() ${\kappa} _{\rm{e}}} = \kappa _{\rm{e}}^ \bot + \kappa _{\rm{e}}^{//}$
may not be curl-free, even if the total curvature tensor κ is compatible. This rotational incompatibility is conveniently described by the continuous disclination density tensor
${\kappa} _{\rm{e}}} = \kappa _{\rm{e}}^ \bot + \kappa _{\rm{e}}^{//}$
may not be curl-free, even if the total curvature tensor κ is compatible. This rotational incompatibility is conveniently described by the continuous disclination density tensor
deriving from the incompatible part
![]() $\kappa _{\rm{e}}^ \bot$
of the elastic curvature. The same line of reasoning applies to the elastic strain tensor, which results in defining Nye's dislocation density tensor α from the incompatible elastic strain field and curvature field through
$\kappa _{\rm{e}}^ \bot$
of the elastic curvature. The same line of reasoning applies to the elastic strain tensor, which results in defining Nye's dislocation density tensor α from the incompatible elastic strain field and curvature field through
In the finite strain assumption, the dislocation density tensor α is obtained from the elastic transformation tensor F e through the relation
To describe the strain discontinuity, the third-order tensor ξ is defined as
where
![]() $G_{ijm}^{{\rm{e,sym}}} = {1 \over 2}{\Big( {u_{i,j}^{\rm{e}} + u_{j,i}^{\rm{e}}} \Big)_{{\!\!,}m}} = \varepsilon _{ij,m}^{\rm{e}}$
is a component of the symmetric part of the elastic second distortion tensor.
$G_{ijm}^{{\rm{e,sym}}} = {1 \over 2}{\Big( {u_{i,j}^{\rm{e}} + u_{j,i}^{\rm{e}}} \Big)_{{\!\!,}m}} = \varepsilon _{ij,m}^{\rm{e}}$
is a component of the symmetric part of the elastic second distortion tensor.