Introduction
Fimbulisen is an ice shelf fringing Dronning Maud Land, Antarctica, located at 69.5–71.5° S and 3° W to 7.5° E (Fig. 1). It is the largest ice shelf in the Haakon VII Sea, with an area of ~39 400 km2. The ice stream Jutulstraumen, the largest outlet glacier in Dronning Maud Land, feeds the central part of the ice shelf. The inflow of this large ice stream builds up an ice tongue inside the ice shelf, the Trolltunga, which divides the ice shelf into a fast- and a slow-moving part. As it is the only ice shelf extended beyond the continental shelf, it is more prone than any other ice shelf to the Warm Deep Water (WDW) located just 100 km north of the ice front (Reference Smedsrud, Jenkin, Holland and NøstSmedsrud and others, 2006) which flows underneath the ice shelf. However, the extent to which this warm water can access the sub-ice-shelf cavity remains unclear (Reference NøstNøst, 2004; Reference NichollsNicholls and others, 2006; Reference Smedsrud, Jenkin, Holland and NøstSmedsrud and others, 2006; Reference Price, Heywood and NichollsPrice and others, 2007).

Fig. 1. Map of Fimbulisen showing the model margin (white line) and several ice rises inside the model domain (black line). Background image: Moderate Resolution Imaging Spectroradiometer (MODIS) image from 2003, courtesy of US National Snow and Ice Data Center.
The increase of ocean temperature along the Greenwich meridian between the Antarctic continent and the Maud Rise at 64° S during 1977–2001 is comparable to a surface heat flux of 4 Wm−2, which is ten times larger than the global ocean warming (Reference SmedsrudSmedsrud, 2005). This suggests that Fimbulisen might be prone to the effect of warming ocean more than other ice shelves around the Antarctic continent, since WDW has a potential to enhance melting at the ice base.
Fimbulisen is, on the other hand, a rather cold ice shelf, particularly at its fast-flowing part. The temperature profile measurement by the Norwegian Antarctic Expedition (Reference Orheim, Hagen, Österhus and SætrangOrheim and others, 1990b,a) over 1991/92 at 70°58.72’S, 0°11.93’E (referred to as S1) is shown in Figure 2. The accuracy of the measurement was ±0.05°C and the thermistor string was measured again 2 and 3 years after the deployment; the temperature profile is therefore assumed to be very accurate.
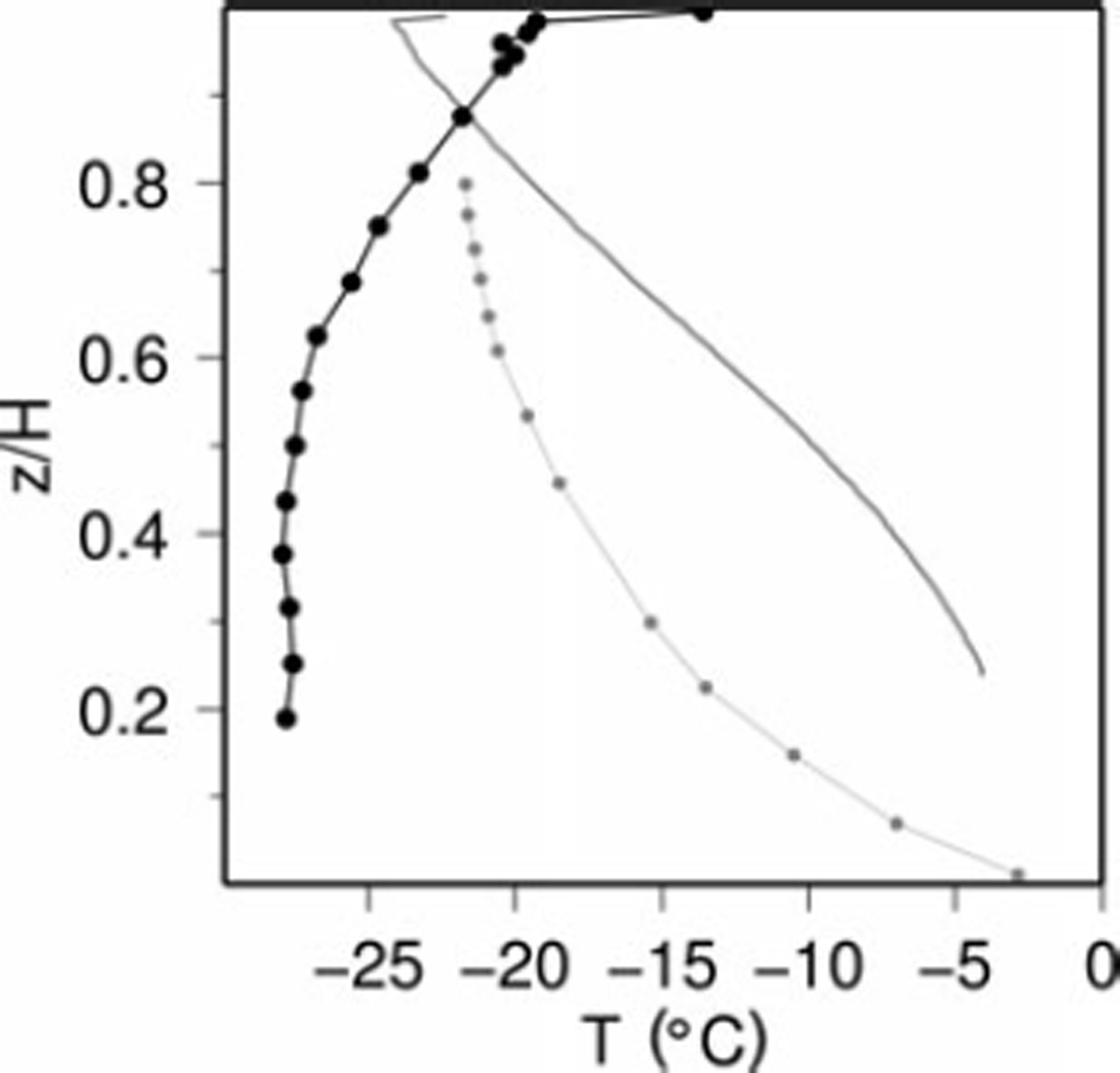
Fig. 2. Measured temperature profile at S1 in black (Reference Orheim, Hagen, Österhus and SætrangOrheim and others, 1990b,a). For comparison, temperature profiles from Ross Ice Shelf at Little America V (grey dots; Reference GowGow 1963) and from the Filchner–Ronne Ice Shelf at B15 (grey line; Reference Eicken, Oerter, Miller, Graf and KipfstuhlEicken and others 1994) are included.
Only a few temperature profiles were measured on Antarctic ice shelves, however, and none of them are comparable to the S1 profile. The temperature at S1 decreases with increasing depth: for 80% of the depth of ~400 m the ice is 8°C colder than at 10m depth. Reference HumbertHumbert (2006) shows that this decrease results in ice that is unusually stiff for ice shelves. Only small strain rates may therefore be present, which contrasts with the large flow of speeds.
Ice shelves are sensitive elements of the climate system as they are sandwiched between two potentially varying boundary conditions: ocean and atmosphere. In order to assess the response of the mass balance to global warming, the thermomechanical behaviour has to be investigated. Basal melting at the ice/ocean transition strongly affects the thermal regime of the ice and hence its viscosity. To understand the dynamics of Fimbulisen, its thermal statemust be determined. Consequently, this study aims to derive the three-dimensional (3-D) temperature field of Fimbulisen.
Theory
The temperature evolution equation can be derived by combining the constitutive equation for ice deformation, internal energy and the heat flux of polycrystalline ice (Fourier’s law of heat conduction) with the balance of internal energy. Following the terminology of Reference Weis, Greve and HutterWeis and others (1999), which neglects horizontal heat conduction, the resulting temperature evolution equation for meteoric ice is:

where vx , vy are the horizontal velocities, vz is the vertical velocity, ρ ice is the ice density, c ice is the specific heat capacity of ice and K ice is the heat conductivity of ice. The last term on the right-hand side represents the strain heating where η is the viscosity and d e is the effective strain rate (second invariant of the strain-rate tensor), defined:

The viscosity is determined by the effective strain and flow rate factor B(T) and the exponent n of Glen’s flow law of ice:
Reference HookeHooke (1981) parameterized the rate factor as a function of the type exp(a/T+b/Tc ). Adjustment of the parameters to laboratory and field measurements of stress and strain rates resulted in:
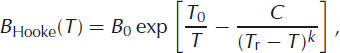
where the constants B 0, T 0, C, T r and k are as listed in Table 1. This parameterization was chosen since it avoids the kink at –10°C present in the more widely used parameterization (Reference PatersonPaterson, 1994).
Table 1. Standard physical parameters of the ice-shelf temperature model

Vertical integration of the mass balance leads to the vertical velocity Vz (Reference Greve and BlatterGreve and Blatter, 2009, equation (5.95)):

where ![]() is the vertical velocity at the ice base h
b, obtained by applying the ice-thickness evolution equation and the kinematic boundary condition at the ice-ocean transition to the shallow-shelf approximation, including a time-dependent sea-level height (Reference WeisWeis, 2001). The vertical velocity then becomes
is the vertical velocity at the ice base h
b, obtained by applying the ice-thickness evolution equation and the kinematic boundary condition at the ice-ocean transition to the shallow-shelf approximation, including a time-dependent sea-level height (Reference WeisWeis, 2001). The vertical velocity then becomes

and is a function of the surface accumulation rate a s, the basal melt rate a b (positive for melting), the densities of sea water and ice (ρ sw, ρ ice), the surface elevation h s and the gradients of the horizontal velocities.
Since the horizontal velocities are independent of depth, Vz is a linear function of the depth. As the vertical velocity is the only variable that depends on the basal melt rate, it represents the ice–ocean interaction.
The energy jump condition at the ice base (Reference Greve and BlatterGreve and Blatter, 2009), which includes the latent heat of melting and the frictional dissipation at the ice base, cannot be taken into account here as it would lead to an overdetermined system of equations. The basal melt rate a b is, however, computed in ocean models by solving the energy jump condition at the ice base. Although this requires the gradient of the ice temperature at the base, the derived basal melt rates are largely dominated by the latent heat of melting ice and the oceanic heat flux.
In Equations (1) and (6) the ice shelf is assumed to consist entirely of consolidated ice (density pi
ce) and a firn layer is neglected. The firn layer is only taken into account in deriving the geometry of the ice shelf, where a mean density ![]() is applied (described below).
is applied (described below).
Here we assume that the present-day geometry of the ice shelf is preserved and that the ice shelf is in steady state. The processes at the ice-ocean transition need to balance the horizontal divergence of the volume flux and surface accumulation:

These equations have been solved using the commercial finite-element software COMSOL assuming steady state; the time derivatives in Equations (1) and (6) are assumed to vanish.
Model Set-Up
Modelling domain and its vertical geometry
For a suitable meshed 3-D geometry of Fimbulisen, observed ice-thickness data, a surface elevation digital elevation model (DEM) and the location of the grounding line and calving front have been used. The grounding line and calving front of Fimbulisen was detected by means of satellite imagery. Moderate Resolution Imaging Spectroradiometer (MODIS, http://nsidc.org/data/iceshelves_images), Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) and Advanced Synthetic Aperture Radar (ASAR) imagery were visually analysed. The latter two sources were particularly useful in the identification of several tiny ice rises along the calving front.
Ice-thickness data H obs from radio-echo soundings by Reference Steinhage, Nixdorf, Meyer and MillerSteinhage and others (1999) (5166 data points) as well as from seismic measurements by Reference Nøst, Goodwin, Rønstad and ThorsenNøst and others (2002) and Reference NøstNøst (2004) (169 data points) were used to derive an ice-shelf thickness distribution H(x,y). The radio-echo sounding dataset covers the western area, the inflow area of Jutulstraumen and the vicinity of the grounding line, whereas the seismic data span a grid from the western margin to ∼5.5° E. The ice-thickness distribution east of this range has been assumed to have the same pattern as at 4 – 5.5° E. Interpolation of all data led to an ice-thickness grid H(x,y), depicted in Figure 3a.

Fig. 3. Set-up of the 3-D geometry of Fimbulisen. (a) Derived ice-thickness grid; (b) calculated ice surface elevation grid.
The tracks along which the ice surface elevation is observed by the Ice, Cloud and land Elevation Satellite (ICESat) Geoscience Laser Altimeter System (GLAS) only correspond to the location of ice-thickness measurements at a few points. The ICESat GLAS DEM (http://nsidc.org/data/nsidc-0304.html) freeboard heights h
s
ob have therefore been used to evaluate the surface elevation at all locations of ice-thickness measurements. Areas of elevation artefacts have been eliminated manually. From the resulting set of ice-thickness and ice surface elevation data, the mean ice density ![]() has been estimated using the flotation criterion, i.e.
has been estimated using the flotation criterion, i.e.
The resulting mean ice density ![]() has also been interpolated in order to obtain
has also been interpolated in order to obtain ![]() The greatest densities arise at the inflow from Jutulstraumen. Lower densities along the ice front are due to the fact that melting of the lower part of the ice shelf (highest densities) increases the effect of the less dense firn layer at the top. It should be noted that the mean ice density distribution
The greatest densities arise at the inflow from Jutulstraumen. Lower densities along the ice front are due to the fact that melting of the lower part of the ice shelf (highest densities) increases the effect of the less dense firn layer at the top. It should be noted that the mean ice density distribution ![]() has been used in this study only to derive the 3-D geometry; in all other circumstances the ice was assumed to have a constant density ρ
ice.
has been used in this study only to derive the 3-D geometry; in all other circumstances the ice was assumed to have a constant density ρ
ice.
Using the ice thickness and mean ice density distribution and applying ![]() an ice surface elevation grid h
s(x,y) was obtained. The resulting ice draft hb and the surface elevation hs
distribution define the 3-D geometry of the model. Ice rises have been removed from the ice-shelf model domain as they form small ice sheets which are independent of the surrounding ice shelf. The only ice rumple has been included in the modelling domain; however, its effect on the temperature field is negligible.
an ice surface elevation grid h
s(x,y) was obtained. The resulting ice draft hb and the surface elevation hs
distribution define the 3-D geometry of the model. Ice rises have been removed from the ice-shelf model domain as they form small ice sheets which are independent of the surrounding ice shelf. The only ice rumple has been included in the modelling domain; however, its effect on the temperature field is negligible.
The 3-D geometry has been interpolated with a mesh of 40 vertical layers of prism elements, resulting in 88 560 prism elements with variable side lengths between 1.4 and 11.9 km. Some transects have been included as interior boundaries in order to refine the mesh and for later analysis purposes.
Temperature boundary conditions
The heat equation requires boundary conditions at all model domain boundaries: (1) the temperature at the surface of the entire ice shelf T s(x, y); (2) the temperature at the ice base T b(x,y); (3) vertical temperature profiles at the transition from inland ice to ice shelf T IN(z) ; (4) vertical temperature profiles at the transition from ice rises to ice shelf T IR(z); (5) ice-shelf transitions (between Blaskimen Ice Rise and Novyy Island and Novyy Island and the grounding line); and (6) no heat flux through the ice front.
The surface temperature was treated either as (1) constant, with T s(x, y) = 253.5 K (as indicated by the S1 temperature profile at 10 m depth) or (2) to be the mean annual surface temperature derived from twice-daily Advanced Very High Resolution Radiometer (AVHRR) surface skin temperatures. A cloud detection algorithm which performs logical operations of the thermal image data time series (personal communication from T. Scambos and T. Haran, 2005) was applied to eliminate cloud pixels. This algorithm appeared to provide good results for the Ross Ice Shelf (Reference HumbertHumbert, 2005). We reordered the remaining clear-sky pixels to time series for each pixel. Assuming that the temperature follows a sine curve as a function of time, a fit was made to the equation
where c 1, c 2, c 3 and c 4 are adjustable parameters. The mean annual surface temperature is consequently T s(x,y)=c 4(x, y). This has been calculated for the years 1992, 1995, 1997 and 1998.
The arithmetic average of these data was compared with 10 m temperatures from shallow cores. As well as the temperature profile at S1, there are shallow cores along the ice front (some of this ice has now calved) by Reference Du PlessisDu Plessis (1973) and a 30 m core (square in Fig. 4) by Reference Melvold, Hagen, Laumann and RolstadMelvold and others (1997). The offset is about +6˚C, except along the ice front. There, the AVHRR-based temperature shows a larger variation in horizontal directions than the 10 m temperatures. Figure 4 depicts the mean annual surface temperature with this spatially constant offset of 6 K and 10 m temperatures.

Fig. 4. Mean annual ice surface temperature distribution from AVHRR averaged over 1992, 1995, 1997 and 1998 plus an additional offset of 6 K. The symbols represent 10 m temperatures from various cores. Circles denote measurements by Reference Du PlessisDu Plessis (1973), squares represent measurements by Reference Melvold, Hagen, Laumann and RolstadMelvold and others (1997) and the triangle represents S1 (Reference Orheim, Hagen, Österhus and SætrangOrheim and others, 1990b,a).
At the ice base, the temperature is set to the freezing point of sea water. This can be estimated from the salinity and the hydrostatic pressure, which both lower the temperature of freezing. Reference Fujino, Lewis and PerkinFujino and others (1974) obtained the freezing/melting temperature from experiments performed with sea water and pressure values up to 100 bars:

where T f is in ˚C and S is the salinity in ppt. According to Reference Smedsrud, Jenkin, Holland and NøstSmedsrud and others (2006), the salinity in the mixed layer below the ice shelf is 34.25 ppt. The resulting temperature of the ice base Tb (x,y) ranges from 270.6 to 271.2 K.
The vertical temperature profile along the grounding line between inland ice and ice shelf T IN(z) has a strong influence on the temperature field, as it is dominated by advection. Care therefore has to be taken in choosing the upstream boundary condition. Results from the ice-sheet model SICOPOLIS (SImulation COde for POLythermal Ice Sheets; http://eprints.lib.hokudai.ac.jp/dspace/handle/2115/34433) show that the temperature profile in the inflow area of Jutulstraumen and at ±40 km west and east has a cold core. The shape of this temperature profile has been parameterized as a piecewise linear function:

where Tc is the coldest temperature, r 1 , r 2 are the adjustable parameters and hb = hs – H. Figure 5 depicts this temperature profile for selected parameter combinations of r 1 and r 2 .
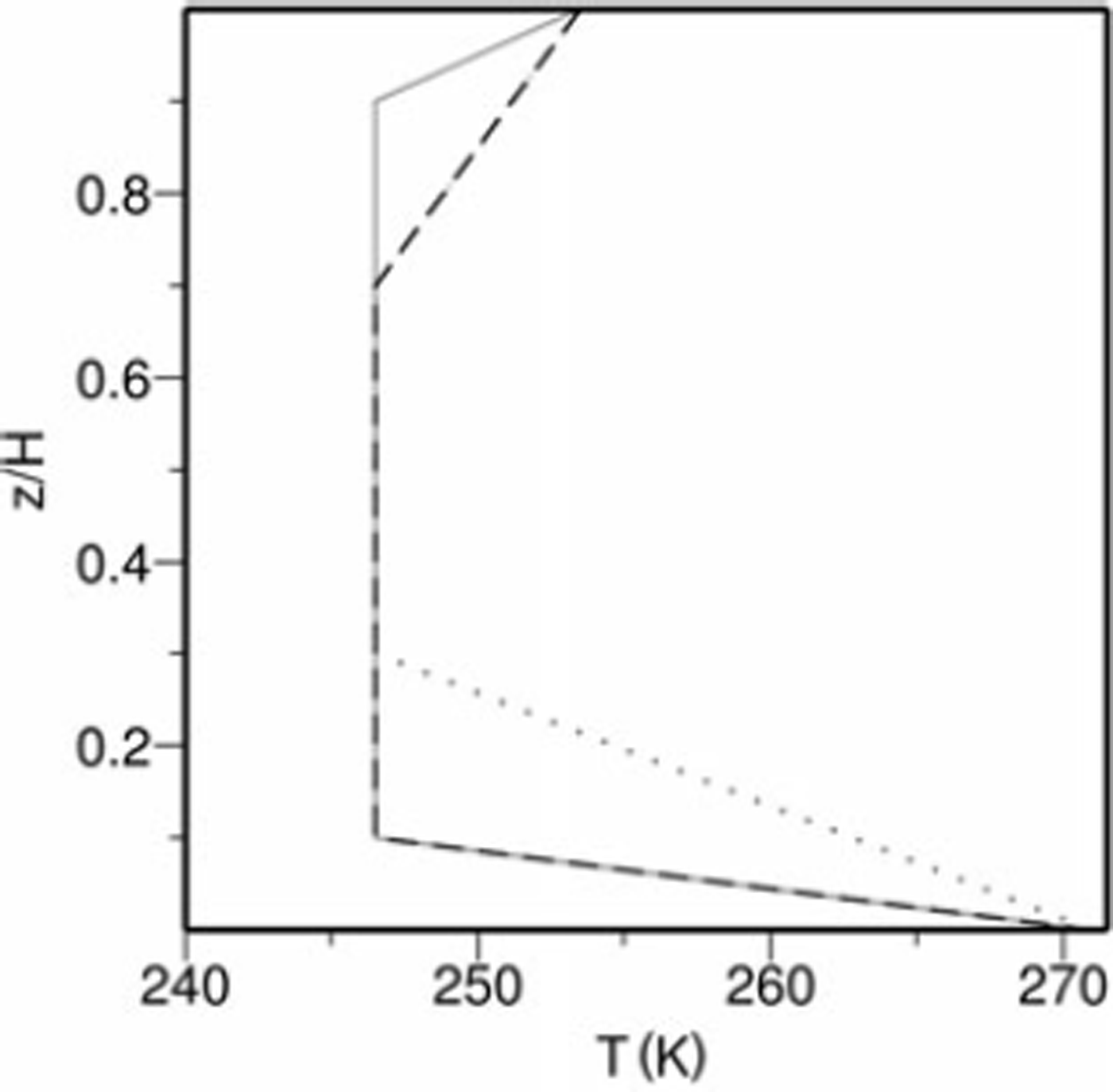
Fig. 5. Shape of the inflowing temperature profile along the grounding line towards Dronning Maud Land. Three different settings for the piecewise linear inflow profiles were chosen: r 1 = 0.1, r 2 = 0.9 (solid grey), r 1 = 0.3, r 2 = 0.7 (dotted grey) and r1 = 0.1, r 2 = 0.7 (dashed black).
There are several ice rises on Fimbulisen; however, an inflow from the ice rise into the ice shelf was only found at a few ice rises. In general, ice rises divide the ice flow. We therefore assume that there is no heat flux out of the ice shelf along the margins of those ice rises which are entirely separated from the ice-shelf flow regime.
At the grounding line of Blaskimen Ice Rise and Novyy Island we found inflow from the ice rise into the ice shelf. Measurements on Crary Ice Rise, Ross Ice Shelf (Reference Bindschadler, Roberts and IkenBindschadler and others, 1990), and on Berkner Island, Filchner Ice Shelf (personal communication from R. Mulvaney, 2008), showed that the vertical temperature profile on the ice rise is nearly linear. T IR(z) is therefore assumed to be of the form:
The basal temperature ![]() was found to be ∼–4˚ C (Reference Bindschadler, Roberts and IkenBindschadler and others, 1990).
was found to be ∼–4˚ C (Reference Bindschadler, Roberts and IkenBindschadler and others, 1990).
Input quantities
Surface velocities for Fimbulisen have been estimated by means of radar interferometry by Reference RignotRignot and others (2008) and W. Rack (personal communication, 2008). The former dataset covers about 60% of the area, including the fast-flowing extension of Jutulstraumen and the western side. The latter dataset gives a high-resolution velocity distribution at the inflow gate of Jutulstraumen in the vicinity of the grounding line. The ice in the centre moves with speeds of 600–800 m a−1, separated from ice masses by shear margins flowing at a maximum velocity of 100 m a−1. The two datasets have been interpolated and smoothed to form a single horizontal velocity distribution used for the modelling. Figure 6 displays the resulting speed distribution. Short-scale variations in the vertical velocity arise from the distribution of the derivatives of the horizontal velocities. For the estimation of vz, the derivatives of the horizontal velocity field (Equation (6)) were additionally smoothed. The strain-heating term in Equation (1) was calculated without smoothing.

Fig. 6. Distribution of horizontal velocities after adjustment.
The surface accumulation was estimated by Reference Arthern, Winebrenner and VaughanArthern and others (2006) and Reference RotschkyRotschky and others (2007). The former estimates the snow accumulation from passive microwaves, while the latter uses point measurements including shallow firn cores and snow pits. The accumulation distribution by Reference Arthern, Winebrenner and VaughanArthern and others (2006) ranges from 0.19 to 0.25ma−1 while that of Reference RotschkyRotschky and others (2007) varies from 0.15 to 0.45 m a−1, i.e. almost double the accumulation in some areas. The datasets differ considerably in the northwestern area of Fimbulisen. The area in which we expect the largest basal melt rates along the inflow gate of Jutulstraumen is therefore not affected by the choice of dataset. Based on the assumption that the dataset from the point measurements represents the local conditions best, the surface accumulation dataset of Reference RotschkyRotschky and others (2007) was used.
Basal melt rates
Since we assume the ice shelf to be in a steady state, the basal melt rate distribution was computed by applying Equation (7). The area of shear margins along the sides of the fast-flowing ice stream were excluded and the short distance variations in the fast-flowing area were spatially averaged in order to obtain a smooth distribution. The resulting distribution (Fig. 7a) includes large basal melt along the inflow gate of Jutulstraumen; values of up to 15 m a−1 were reached, and pronounced melting took place at Trolltunga. The western and eastern areas are prone to small basal melt only.

Fig. 7. Basal melt rate distributions: (a) computed basal melt rate distribution arising from the mass-balance and steady-state assumption; (b) difference between the basal melt rate distribution from B. Smith (personal communication, 2009) and that shown in (a); (c) difference between (a) and basal melt rate from ocean modelling by Reference Smedsrud, Jenkin, Holland and NøstSmedsrud and others (2006); and (d) difference between (a) and basal melt rate from ocean modelling by Reference Nicholls, Abrahamsen, Heywood, Stansfield and ØsterhusNicholls and others (2008).
Based on the same assumptions, W. Rack, D. Steinhage and S. Vey (personal communication, 2008) estimated the mass flux of the inflow of Jutulstraumen in the first 33 km after the crossing of the grounding line. The average basal melt rate determined by them is 10 m a−1.
B. Smith (personal communication, 2009) also derived the basal melt rate distribution from the assumption of steady state. In contrast to the current study, Smith’s horizontal velocity distribution is very accurate and thus his results are more reliable. The differences in the basal melt rate distribution derived here generally arise in the areas close to the grounding line, where Smith retrieved basal melt rates in the range of 1.1 m a−1 (western areas) to 2.6 m a−1 (eastern areas). The inflow of Jutulstraumen is the area with the largest basal melt rate (17 m a−1) . The differences in the basal melt rates derived here are displayed in Figure 7b.
The basal melt rate distribution derived here is also compared to two ocean modelling studies by Reference Smedsrud, Jenkin, Holland and NøstSmedsrud and others (2006) and Reference Nicholls, Abrahamsen, Heywood, Stansfield and ØsterhusNicholls and others (2008).
Reference Smedsrud, Jenkin, Holland and NøstSmedsrud and others (2006) applied the POLAIR (Polar Ocean Land Atmostphere Ice Regional) modeling system (Reference Holland and JenkinsHolland and Jenkins, 2001) to Fimbulisen. Their computed basal melt rates even exceed 15 m a−1 in some areas along the extension of Jutulstraumen and generally indicate large melt rates along the thicker, central part towards Trolltunga. Strong melting also occurs in the vicinity of a large ice rise at the ice front. In all other areas moderate basal melting, up to slight freezing, is suggested. The difference between the basal melt distribution derived here and this distribution is shown in Figure 7c.
Reference Nicholls, Abrahamsen, Heywood, Stansfield and ØsterhusNicholls and others (2008) extended the study of Reference Smedsrud, Jenkin, Holland and NøstSmedsrud and others (2006) by improving the time-stepping procedure, using a varying surface forcing and improvements of the climatology. These authors generally found the basal melt rates to be moderate, i.e. below 1 m a−1, in most areas and only increasing along the ice front. The considerably thicker extension of Jutulstraumen does not result in enhanced melt; melt rates are small even at the grounding line of Jutulstraumen. In Figure 7d the difference between this basal melt rate and the basal melt distribution derived here can be found.
Simulated Temperature Field
Inflowing temperature profile
The inflowing temperature profile includes a cold core with a temperature T c (see Equation (11)). Different simulations have been carried out by varying the coldest temperature T c. The value has been chosen in order to minimize the difference between the simulated and measured temperature at S1. Using this value, the shape of the temperature profile has been varied by changing the location of the kink locations r 1 and r 2. The results of three different settings, [r 1 = 0.1,r 2 = 0.9], [r 1 = 0.3,r 2 = 0.7] and [r 1 = 0.1, r 2 = 0.7], are depicted in Figure 8. Each figure shows the temperature profile at a single location for all three settings. The locations denoted in each figure correspond to those in Figure 9.
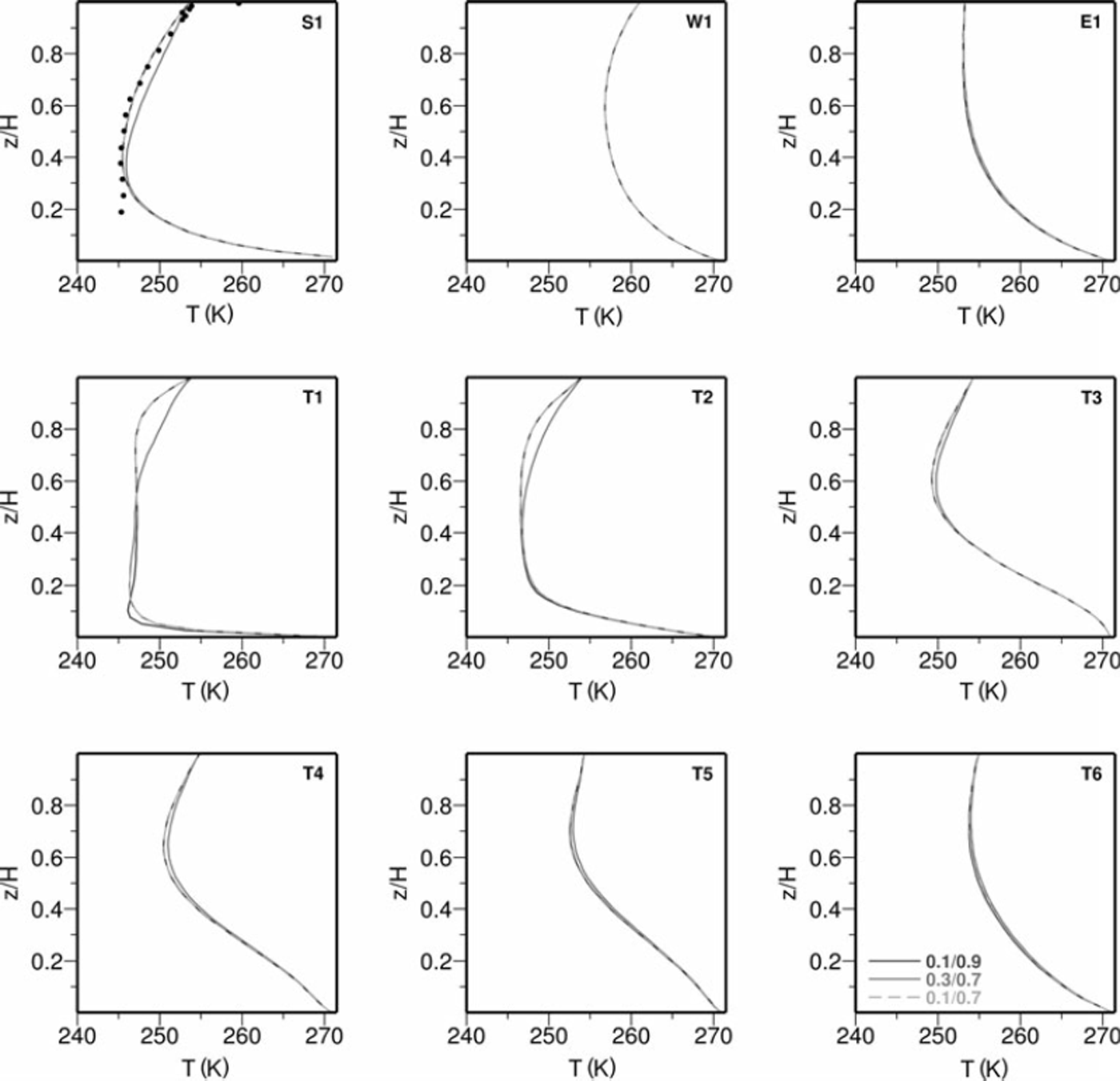
Fig. 8. Vertical temperature profile at nine locations (see Fig. 9) for different values of r 1 and r 2. In panel S1, the measured temperatures are shown as black dots.

Fig. 9. Location of nine temperature profiles (see Fig. 8).
The temperature profiles calculated using the former and latter settings show minor differences. We therefore conclude that the choice of r 2 is of minor importance for the resulting temperature field. The parameter r 1, which defines the upper part of the inflowing temperature profile, has a greater effect on the results; results show that the gradient of the temperature profiles decreased and the ice in the upper part became warmer.
In comparison to the measured temperature profile at S1 and the model output of SICOPOLIS, the parameter combination [r 1 = 0.1, r 2 = 0.7] and the coldest temperature T c = 247 K have been chosen as inflowing temperature profile. As the simulated temperature profile at S1 and the measured temperature profile agree to a considerable extent, we conclude that the inflowing temperature profile from the inland ice sheet was parameterized reasonably well.
All the panels in Figure 8 are drawn with a vertical axis that shows the relative depth only. The ice thickness varies considerably along the flowline of the extension of Jutulstraumen, as can be seen in Figure 3. The thinning, which is to a large extent due to basal melting, has to be taken into account when interpreting the shape of the temperature profile.
Profiles T1–T6 demonstrate how the cold bulk ice is transported through the ice shelf and how it is warmed during the flow. Close to the ice front at T6, the temperature profile no longer exhibits the history of the cold ice from the interior ice sheet. The influence from the boundary condition is still quite strong at T1, while at T3 this influence has already vanished. We therefore do not consider much of the computed temperature field to be greatly affected by the choice of the shape of the boundary condition. The simulations suggest that the warmest ice masses exist at the ice front and in the western and eastern areas.
For the simulation using values [r 1 = 0.1, r 2 = 0.7], further investigations have been performed. Figure 10c shows the location of two cross-sections: one along and one across a flowline from Jutulstraumen to Trolltunga. The temperature field at several points was extracted and interpolated; the results are shown in Figure 10a and b. Each tick on the x axis represents one extracted vertical temperature profile, beginning from the grounding line.

Fig. 10. (a, b) Vertical temperatures along (a) and across (b) a flowline from Jutulstraumen to Trolltunga. (c) Map showing the locations of the points along (northwards) or across (eastwards) the flowline.
The relative z coordinate is shown on the vertical axis of the diagram. The profile along the flowline (Fig. 10a) exhibits the warming of the cold bulk ice mass flowing from the ice sheet into Fimbulisen on its way towards the ice front. A temperature profile taken across the flowline clearly exhibits the different ice masses in the western area, Jutulstraumen and the eastern areas. The slow-moving parts in the east and the west are considerably warmer than Jutulstraumen. The cross-section also shows that the margin on the western side is wider than the margin on the eastern side. This is consistent with the observed shear zones. In the western area, the transition zone between the slow- and fast-moving parts has a large width and includes major rift zones. On the other hand, the transition zone on the eastern side is comparable with a narrow shear margin. The ice in the fast-moving part is coldest in the east. This may be a consequence of the ice-flow direction, as the inflowing cold ice forms a zone of compressive stress on the eastern margin while it spreads on the western side.
As the temperature profiles in Figure 8 and the cross-sections in Figure 10 show, the temperature change in the lowest part of the ice shelf is quite large. In most ocean models the basal melt rate is computed by solving an equation for the heat transfer at the ice/ocean transition, including the term ∂T/∂z|b (temperature gradient at the ice base). As the simulations show, this term is highly influenced by the advective contribution to the temperature field. Estimating it from the atmospheric temperature and the basal temperature of the ice without solving the temperature field of the ice can lead to considerable underestimation of this term.
As the temperature gradient at the ice–ocean transition is largest along the grounding line and at the first few hundred kilometres of the extension of Jutulstraumen, its effect on the basal melt rate distribution is assumed to be largest there. As Figure 7c and d show, the differences in the basal melt rate distributions resulting from the mass-balance and ocean models is greatest in this area. This demonstrates the need for coupled ice-shelf/ocean models.
The flow rate factor B(T) of Glen’s flow law has a strong influence on the ice viscosity. The depth-averaged flow rate factor B m is shown in Figure 11 . The distribution exhibits high values for B m where Jutulstraumen flows into Fimbulisen. The transport of the cold ice also leads to high B values for ice in the fast-flowing part. Along the grounding line in the west and east, cold ice moves from the interior ice sheet into the ice shelf. The slower flow allows the ice to warm considerably, so that the mean flow rate factor reaches lower values. The 3-D field B(x, y, z) serves as input for future ice-flow modelling studies.

Fig. 11. Depth-averaged flow rate factor B m.
Atmospheric warming
In order to study how surface warming arising from climate change might affect the temperature distribution of Fimbulisen, the surface temperature was stepwise increased. We assume that the system had time to adjust to the variation in the climate forcing and is in steady state once more. These simulation results therefore only serve as a long-term tendency. The surface temperature boundary condition has been increased in 1 K steps, so that an offset of + 1 K to +4 K was added to the surface temperature distribution shown in Figure 4. As ice shelves are flat and have a low surface elevation, the atmospheric warming is assumed to influence the ice shelves before the interior ice sheet (at a higher elevation) will be affected. The inflowing temperature profile was therefore kept at its present state.
The resulting temperature profiles at S1 and close to the ice front in the western and eastern area are displayed in Figure 12. At S1, the temperature profile is mainly influenced by the cold ice which is transported from the interior ice sheet; the increase in surface temperature only affects the relatively small upper fraction of the ice shelf. In the slower-moving areas, the atmospheric warming influences the largest part of the ice shelf and only a small fraction at the base of the ice shelf remains unaffected. We infer that the slower-moving areas soften proportionally much more than the faster-moving areas. This will have an effect on the shear margin on the eastern side of Jutulstraumen and on the rift system on its western side.

Fig. 12. Response of the ice-shelf temperature to atmospheric warming: vertical temperature profile for temperature increases of 1 K, 2 K, 3K and 4K.
Conclusions
Knowledge of the thermal state of Fimbulisen is a mandatory requirement in understanding its dynamics, as the temperature–depth profile is influenced strongly by advected cold ice. The resulting variability in ice temperatures implies strong variability in ice stiffness.
This study provides numerical solutions for the 3-D steady-state temperature field. These were computed using horizontal flow velocities and surface accumulation rates from observations, as well as a basal melt rate distribution arising from the mass balance. The resulting 3-D temperature field is intended to serve as input for the modelling of ice-flow dynamics and the ocean.
The basal melt rate distribution was calculated from the mass balance. At the inflow gate from Jutulstraumen, the basal melt rates were highest at up to 15 m a−1. In the slower-moving areas in the western and eastern parts, a b was smaller (<0.6 m a At the northern tip of Trolltunga, where the ice shelf overhangs the continental shelf, the basal melt rate increased to values of 1.2 m a−1. This compares well with the basal melt rate distribution obtained by mass-balance estimations from B. Smith (personal communication, 2009) but differs from the results of ocean modelling carried out by Reference Smedsrud, Jenkin, Holland and NøstSmedsrud and others (2006) and Reference Nicholls, Abrahamsen, Heywood, Stansfield and ØsterhusNicholls and others (2008). A conceivable reason might be that ocean modelling does not take into account the ice temperature gradient arising from the advection of cold ice masses from the inland ice.
The computed temperature field consists of areas in which the temperature regime is dominated by advection, leading to a cold bulk ice mass. In the slower-moving areas, the ice is considerably warmer. At the ice front, the temperature– depth profiles are parabolic in all regions. The computed and measured temperature profiles agree reasonably well at S1, suggesting that the boundary conditions were chosen appropriately.
The atmospheric temperature forcing has been varied in further simulations, with an offset added to the surface temperature distribution. The results suggest that the warming effectively increases the temperatures throughout the ice column in the slower-moving parts. In areas where advection dominates the ice temperature, however, only the upper part of the ice shelf is affected. A surface temperature increase will therefore affect the shear between the fast- and slow-moving areas.
Acknowledgements
This study was supported by the German Research Foundation (DFG) under grants HU 1570/2–1. The author thanks C. Schoof, E. Bueler and two anonymous reviewers for helpful comments. R. Greve supported this study with temperature profiles from the ice-sheet model SICOPOLIS and helpful discussions. P. Abrahamsen (British Antarctic Survey, UK) and L.H. Smedsrud (University of Bergen, Norway) kindly provided their datasets of the basal melt rate. ASTER and ASAR images were provided by the European Space Agency under project IPY AOPOL. 4032. E. Rignot (Jet Propulsion Laboratory, USA) and W. Rack (University of Canterbury, New Zealand) made their surface velocity dataset available. The ice-thickness data were provided courtesy of O. Anders Nøst (Norsk Polarinstitut, Norway), D. Steinhage (Alfred Wegener Institute, Germany) and W. Rack.















