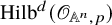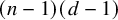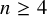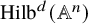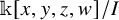Small elementary components of Hilbert schemes of points

Abstract

We answer an open problem posed by Iarrobino, Hilbert scheme of points: Overview of last ten years. Proceedings of Symposia in Pure Mathematics, 46 (American Mathematical Society, Providence, RI, 1987), 297–320: Is there a component of the punctual Hilbert scheme [Grothendieck, Techniques de construction et théorèmes d'existence en géométrie algébrique. IV. Les schémas de Hilbert', in Séminaire Bourbaki, 6 (Societe Mathematique de France, Paris, 1995), 221, 249–276] $\operatorname {\mathrm {Hilb}}^d({\mathscr {O}}_{\mathbb {A}^n,p})$ with dimension less than $(n-1)(d-1)$ ? For each $n\geq 4$ , we construct an infinite class of elementary components in $\operatorname {\mathrm {Hilb}}^d(\mathbb {A}^n)$ producing such examples. Our techniques also allow us to construct an explicit example of a local Artinian ring [Iarrobino and Kanev, Power sums, Gorenstein algebras, and determinantal loci (Springer-Verlag, Berlin, 1999), 221–226] of the form with trivial negative tangents, vanishing nonnegative obstruction space, and socle-dimension $2$ .

1 Introduction

Hilbert schemes of points are moduli spaces of fundamental importance in algebraic geometry, commutative algebra, and algebraic combinatorics. Since their construction by Grothendieck [14], they have seen broad-ranging applications, from the McKay correspondence [6, 28] to Haiman’s proof of the Macdonald positivity conjecture [17]. In 1968, Fogarty [11] proved the irreducibility of the Hilbert scheme of points on a smooth surface. A few years later, Iarrobino [22, 23] and Iarrobino–Emsalem [26] showed that, in contrast, for $n\geq 3$ and d sufficiently large, the Hilbert scheme of points $\operatorname {\mathrm {Hilb}}^d(\mathbb {A}^n)$ is reducible. Since then, it has remained a notoriously difficult problem to describe the structure of the irreducible components of $\operatorname {\mathrm {Hilb}}^d(\mathbb {A}^n)$ .

Only a handful of explicit constructions of irreducible components exist in the literature, many of these constructions involving clever new insights [4, 8, 10, 20, 21, 24, 27, 29, 30, 34]. Even less is known about elementary components, namely, irreducible components parametrizing subschemes supported at a point. The study of all irreducible components may be reduced to that of elementary ones due to the fact that, generically, every component is étale-locally the product of elementary ones. Nearly all elementary components constructed thus far have dimensions larger than that of the main component of $\operatorname {\mathrm {Hilb}}^d(\mathbb {A}^n)$ , namely, $nd$ . The only elementary components in the literature with dimensions shown to be less than $nd$ are examples with Hilbert functions $(1, 4, 3)$ and $(1, 6, 6, 1)$ due to Iarrobino–Emsalem [26], $(1, 5, 3)$ and $(1, 5, 4)$ due to Shafarevich [34], $(1, 5, 3, 4)$ , $(1, 5, 3, 4, 5, 6)$ , and $(1, 5, 5, 7)$ due to Huibregtse [20, 21], $(1,4,10,16,17,8)$ due to Jelisiejew [29], and finally, one infinite family also constructed by Jelisiejew [29, Theorem 1.4].

In the case of the punctual Hilbert scheme $\operatorname {\mathrm {Hilb}}^d({\mathscr {O}}_{\mathbb {A}^n,p})$ at a point p, there is a sharp lower bound on the dimensions of its smoothable components. Specifically, the smoothable locus U of $\operatorname {\mathrm {Hilb}}^d(\mathbb {A}^n)$ determines a smoothable locus $U_p = U \cap \operatorname {\mathrm {Hilb}}^d({\mathscr {O}}_{\mathbb {A}^n,p})$ in the punctual Hilbert scheme. Here, $U_p$ can be reducible, unlike the case of $\operatorname {\mathrm {Hilb}}^d(\mathbb {A}^n)$ . Gaffney proved [12, Theorem 3.5] that all irreducible components of $U_p$ have dimension at least $(n-1)(d-1)$ . Moreover, Iarrobino identified an irreducible component realizing this lower bound, consisting of the curvilinear points. It has remained an open problem for over 30 years to determine whether Gaffney’s bound extends to all irreducible components of $\operatorname {\mathrm {Hilb}}^d({\mathscr {O}}_{\mathbb {A}^n,p})$ :

Question 1.1 [25, p. 310], cf. [26, p. 186].

Let $p\in \mathbb {A}^n$ be a point. Does there exist an irreducible component of $\operatorname {\mathrm {Hilb}}^d({\mathscr {O}}_{\mathbb {A}^n,p})$ of dimension less than $(n-1)(d-1)$ ?

The goal of this paper is to answer Question 1.1. We produce an infinite family of elementary components in $\operatorname {\mathrm {Hilb}}^d(\mathbb {A}^4)$ with dimension less than $3(d-1)$ , which turns out to generalize the original example presented in [26], making key use of Jelisiejew’s criterion [29]. Moreover, the examples we produce are flexible in the sense that our elementary components $Z\subset \operatorname {\mathrm {Hilb}}^d(\mathbb {A}^4)$ also frequently yield new components $Z_i\subset \operatorname {\mathrm {Hilb}}^{d-i}(\mathbb {A}^n)$ for small i (see Theorem 1.5).

We work throughout over an algebraically closed field of characteristic $0$ .

Theorem 1.2. Let

$$ \begin{align*} d=\frac{1}{2}ab(a+b) \end{align*} $$

with $a,b\in \mathbb {Z}$ and $a,b \ge 2$ . If $(a,b)\neq (2,2)$ , then $\operatorname {\mathrm {Hilb}}^d({\mathscr {O}}_{\mathbb {A}^4,p})$ contains an irreducible component of dimension less than $3(d-1)$ .

Specifically, we prove Theorem 1.2 by showing:

Theorem 1.3. Every ideal in of the form

$$ \begin{align*} I := \langle x,y \rangle ^{n_1} + \langle z,w \rangle ^{n_2} + \langle xz-yw \rangle , \end{align*} $$

for $n_1, n_2 \ge 2$ , determines a smooth point $[I]$ of the Hilbert scheme of points $\operatorname {\mathrm {Hilb}}^{d}(\mathbb {A}^4)$ , where

$$ \begin{align*} d = d(n_1,n_2) := \frac{n_1n_2(n_1+n_2)}{2}. \end{align*} $$

The unique component containing $[I]$ is elementary of dimension

$$ \begin{align*} D = \frac{1}{3}m^3 + mM^2 + m^2 + 2mM + M^2 - \frac{1}{3}m -1, \end{align*} $$

where $m=\min (n_1,n_2)$ and $M=\max (n_1,n_2)$ . This dimension is less than $4d$ for all $n_1,n_2\geq 2$ , and less than $3(d-1)$ for $(m,M)\notin \{(2,2),(2,3),(2,4)\}$ .

Using our ideals from Theorem 1.3, one easily bootstraps to $\operatorname {\mathrm {Hilb}}^d(\mathbb {A}^n)$ for $n\geq 4$ , thereby resolving Question 1.1 for all such n:

Corollary 1.4. Let S, I, $n_1$ , $n_2$ , d, and D be as in Theorem 1.3. Let $\widetilde {S} = S[u_1,u_2\dotsc ,u_r]$ be the polynomial ring in $n = 4+r$ variables, and let $\widetilde {I} = I + \langle u_1,u_2,\dotsc ,u_r \rangle $ . Then $[\widetilde {I}]\in \operatorname {\mathrm {Hilb}}^d(\mathbb {A}^n)$ is a smooth point. The unique component containing $[\widetilde {I}]$ is elementary of dimension $D+rd$ .

Moreover, for $n_1$ and $n_2$ sufficiently large, this elementary component has dimension strictly less than $(n-1)(d-1)$ (see Remark 8.1 for specific bounds needed on $n_1$ and $n_2$ , e.g., $n_1=2$ and $n_2>\frac {r}{2}+4$ suffices).

Additionally, by enlarging I by socle elements from $S/I$ , we obtain secondary families of elementary components arising from our primary components constructed in Theorem 1.3. This behavior of elementary components is not uncommon and yet was previously unobserved (see the last paragraph of subsection 1.1 for further details). Specifically, for any I as in Theorem 1.3 and any nonzero $s\in \operatorname {\mathrm {Soc}}(S/I)$ , we prove that $I+ \langle s \rangle $ also defines a smooth point of $\operatorname {\mathrm {Hilb}}^{d-1}(\mathbb {A}^4)$ belonging to a unique elementary component. We show that one may even iterate this construction to produce smooth points $I+ \langle s_1,s_2,\dots ,s_r \rangle $ on unique elementary components provided that a particular constraint holds which relates socles to bidegrees. Notice that the ideals in Theorem 1.3 are bigraded, where the bidegree of a monomial $x^{u_1}y^{u_2}z^{u_3}w^{u_4} \in S$ is defined here to be $(u_1+u_2, u_3+u_4) \in \mathbb {N}^2$ . Then we have:

Theorem 1.5. Let I be as in Theorem 1.3 with $n_1,n_2 \ge 3$ . Let $s_1, s_2, \dotsc , s_{r} \in S$ define elements in $\operatorname {\mathrm {Soc}}(S/I)$ , and let

$$ \begin{align*} J = I + \langle s_1,\dots,s_r \rangle \end{align*} $$

and $B=S/J$ . If either

1. (i) $r=1$ , or

2. (ii) $\operatorname {\mathrm {Soc}} B = B_{(n_1-1, n_2-1)}$ ,

then $[J]$ is a smooth point of $\operatorname {\mathrm {Hilb}}^{d-r}(\mathbb {A}^4)$ , belonging to a unique elementary component.

Remark 1.6. The proof of Theorem 1.5 shows that J has trivial negative tangents, namely, that , as well as vanishing nonnegative obstruction space, that is, (see subsection 2.2 for the definitions of the $T^i$ -modules).

Let us briefly discuss some further applications of our techniques. First, consider the following folklore question, an affirmative answer to which would distinguish cactus and secant varieties [5, Proposition 7.4] (see also [3], [13]).

Question 1.7. Does there exist a Gorenstein local Artinian algebra of the form with trivial negative tangents?

Theorem 1.5 and Remark 1.6 show that

(1) $$ \begin{align} I = \langle x,y \rangle ^{3} + \langle z,w \rangle ^{3} + \langle xz-yw,x^2z^2,x^2w^2,y^2z^2 \rangle \end{align} $$

has trivial negative tangents and vanishing nonnegative obstruction space; while $S/I$ is not Gorenstein (socle-dimension $1$ ), it does have socle-dimension $2$ . It is possible that variants of the ideals considered in Theorem 1.5 may yield an answer to Question 1.7 (see Example 8.6 for further details and Remark 8.7 for similar examples).

It is also interesting to note that our techniques yield examples of Hilbert schemes with at least two elementary components. ¹ Theorem 1.3 shows, for instance, that the ideal $ \langle x,y \rangle ^2 + \langle z,w \rangle ^4 + \langle xz-yw \rangle $ defines a smooth point of an elementary component of $\operatorname {\mathrm {Hilb}}^{24}(\mathbb {A}^4)$ , while Theorem 1.5 shows that the ideal in (1) also defines a smooth point on an elementary component of $\operatorname {\mathrm {Hilb}}^{24}(\mathbb {A}^4)$ ; an explicit check shows that the tangent space dimensions at these two points are different (see Examples 8.3 and 8.4).

1.1 Technique of proof and comparison with [29]

On the face of it, our infinite family of examples looks similar to the one given by Jelisiejew in [29]. However, our examples differ in several significant ways. The first notable difference is that, although we both produce infinite families of smooth points on elementary components of $\operatorname {\mathrm {Hilb}}^d(\mathbb {A}^4)$ , Jelisiejew’s examples occur in much sparser degrees: the first few degrees in his examples are $d = 8, 35, 99, 224, \dotsc $ , whereas our first few examples occur in degrees $d=8, 15, 24,25,26,27, 35, 39,40,41,42, 48,56, 57,58,59, 60 \dotsc $ (note our algebra of degree $35$ differs from the one in [29], see Example 8.2.).

Second, the algebras $A=S/I$ that we produce have vanishing nonnegative obstructions , whereas Jelisiejew’s examples do not, for example, when $s=\sum _i (xz)^i(yw)^{3-i}$ , his algebra $R(4)$ has nonvanishing $T^2$ in degree $0$ . Showing the vanishing of $T^2_{\geq 0}$ is the key step in our proof that $[I]$ defines a smooth point of the Hilbert scheme.

Third, a highly important distinction between our work and [29] involves our techniques of proof. In order to understand this distinction, let us briefly describe Jelisiejew’s proof. In showing trivial negative tangents and smoothness, he reduces the number of explicit calculations by considering a Białynicki-Birula decomposition of the flag Hilbert scheme, which is a moduli space parametrizing pairs of ideals $I \supset M$ in S. To compare this decomposition of the flag Hilbert scheme with $\operatorname {\mathrm {Hilb}}^+_{pts}(\mathbb {A}^4)$ , and to produce useful dimension counts, his approach requires showing surjectivity of graded pieces of certain maps $\partial ,\psi $ (see the commutative diagram [29, Diagram 2.1]). Specifically, Jelisiejew uses surjectivity of $\partial _{\geq 0}$ in [29, Corollary 4.13] to prove smoothness and surjectivity of $\psi _{<0}$ in the proof of [29, Theorem 1.4] to show trivial negative tangents.

We emphasize that Jelisiejew’s flag Hilbert scheme techniques do not apply to our examples. Indeed, we prove in Proposition 9.1 that for our examples, $\psi _{<0}$ is never surjective; furthermore, if $\min (n_1,n_2)\geq 4$ , then $\partial _{\ge 0}$ is also never surjective. As a result, it is not possible to prove smoothness of $[I]$ using the flag Hilbert scheme as in [29, Corollary 4.13], and not possible to show trivial negative tangents by a dimension count as in [29, Proof of Theorem 1.4]. In fact, one can see immediately that the condition used to ensure $\partial _{\ge 0}$ is surjective described in [29, Remark 4.15] is not true for our examples, as $q = xz-yw$ is of low degree. Hence, our proof relies on explicit computations with the cotangent complex in order to prove trivial negative tangents (Proposition 3.1) and vanishing nonnegative obstructions (Proposition 4.1).

Lastly, although the examples constructed in Theorem 1.3 are the primary focus of our paper, one of the novel features of our work is Theorem 1.5, which produces secondary families of elementary components, derived from our main ones by adding generators from the socle. The idea of producing new elementary components from old ones via socle elements appears to have gone unnoticed, and yet it is far from an isolated phenomenon. In fact, one can check that this same behavior occurs in many of Jelisiejew’s examples as well as variants of our main examples given in Remark 8.7. Furthermore, we observe analogous socle behavior in a follow-up paper [36], where we construct a new infinite family of elementary components; our new examples given in [36] are constructed by rather different means, making use of the so-called Galois closure operation for ring extensions, introduced by the first author and Bhargava [7].

1.2 How we found our examples

The family of elementary components in Theorem 1.3 generalizes the original example of Iarrobino–Emsalem, which is recovered when $n_1=n_2=2$ . Our examples, however, were arrived at by different methods, and can be best understood in terms of the T-graph of the Hilbert scheme $\operatorname {\mathrm {Hilb}}^{d}(\mathbb {A}^n)$ ; this is the graph whose vertices correspond to torus-fixed points of $\operatorname {\mathrm {Hilb}}^{d}(\mathbb {A}^n)$ , and whose edges correspond to torus-invariant curves linking these fixed points. The T-graph was defined in [2] and studied further in [19, 32, 35], mostly in dimension $n=2$ . To produce our examples, we constructed edges of the T-graph corresponding to curves in $\operatorname {\mathrm {Hilb}}^{d}(\mathbb {A}^4)$ whose general point is a smooth point with small tangent space dimension. The examples in Theorem 1.3 correspond to the T-invariant curves $ \langle x,y \rangle ^{n_1}+ \langle z,w \rangle ^{n_2}+ \langle \lambda xz + \mu zw \rangle $ with $(\lambda : \mu )\in \mathbb {P}^1$ .

Our method to construct such curves is inspired by Haiman’s work [16, Section 2]. In rough terms, we start with a T-fixed point corresponding to a monomial ideal and aim to perturb by a tangent vector in the direction of another monomial ideal. In more detail, we devised the following procedure, which we implemented in Macaulay2 [15]:

1. (i) Consider a monomial ideal of colength d;

2. (ii) compute an explicit basis of the tangent space $T_{[K]}\operatorname {\mathrm {Hilb}}^d(\mathbb {A}^n)$ ; by default in Macaulay2, these are vectors with monomial entries, hence, they perturb K in the direction of another monomial ideal;

3. (iii) each basis vector determines a first-order flat deformation of K, that is, an ideal $K_{\varepsilon }$ of ;

4. (iv) fix generators $g_1+\varepsilon g^{\prime }_1,\dots ,g_m+\varepsilon g^{\prime }_m$ for $K_{\varepsilon }$ , and consider the ideal $I_t:= \langle g_1+t g^{\prime }_1,\dots ,g_m+t g^{\prime }_m \rangle $ of ; if $S_t/I_t$ has no t-torsion, then specialize t to any value in to obtain a new ideal $K'\subset S$ which also lives in $\operatorname {\mathrm {Hilb}}^d(\mathbb {A}^n)$ ;

5. (v) if , then $[K']$ does not lie on the smoothable component, meaning a small-dimensional nonsmoothable irreducible component of $\operatorname {\mathrm {Hilb}}^d(\mathbb {A}^n)$ has been detected;

6. (vi) check to see if $K'$ has trivial negative tangents.

For instance, setting $K = \langle x,y \rangle ^{n_1}+ \langle z,w \rangle ^{n_2} + \langle xz \rangle $ , we can find the first-order deformation $K_{\varepsilon } = \langle x,y \rangle ^{n_1}+ \langle z,w \rangle ^{n_2} + \langle xz + \varepsilon yw \rangle $ , which yields the new ideal $K' = \langle x,y \rangle ^{n_1}+ \langle z,w \rangle ^{n_2} + \langle xz + yw \rangle $ .

Interestingly, by iteratively applying our above algorithm, we also obtain some of Jelisiejew’s examples. For instance, a smooth point on Jelisiejew’s family $\mathcal {Z}(3) \subset \operatorname {\mathrm {Hilb}}^{35}(\mathbb {A}^4)$ is given by $I = \langle x,y \rangle ^3+ \langle z,w \rangle ^3+ \langle x^2z^2+xyzw+y^2w^2 \rangle $ . Setting $K = \langle x,y \rangle ^3+ \langle z,w \rangle ^3+ \langle x^2z^2 \rangle $ , one obtains a first-order deformation $K_{\varepsilon } = \langle x,y \rangle ^3+ \langle z,w \rangle ^3+ \langle x^2z^2+\varepsilon xyzw \rangle $ of K. This yields the ideal $K' = \langle x,y \rangle ^3+ \langle z,w \rangle ^3+ \langle x^2z^2+xyzw \rangle \subset S$ which has a small tangent space but fails to have trivial negative tangents. However, if we repeat the procedure starting from $K'$ , we find the first-order deformation $K^{\prime }_{\varepsilon } = \langle x,y \rangle ^3+ \langle z,w \rangle ^3+ \langle x^2z^2+xyzw + \varepsilon y^2w^2 \rangle $ , from which our algorithm outputs Jelisiejew’s ideal I.

Lastly, it is worth mentioning that one may also view our examples from the perspective of singularity theory; namely, one starts with a simple singularity, such as $xz-yw$ and takes a suitable fat point centered at the singular point. Although this is not the point of view that led us to our infinite class of examples, we imagine this perspective is a useful one. Indeed, variations of this construction were given by Erman in [9] to prove Murphy’s law for certain strata of the Hilbert scheme.

2 Preliminaries

We set some notation and highlight a useful tool for studying Hilbert schemes of points.

2.1 Basic set-up

Let be the coordinate ring of affine space $\mathbb {A}^4$ , where is an algebraically closed field of characteristic $0$ . For a vector $\boldsymbol {u} = (u_1,u_2,u_3,u_4) \in \mathbb {N}^4$ , let $\boldsymbol {x}^{\boldsymbol {u}} := x^{u_1}y^{u_2}z^{u_3}w^{u_4}$ , denote the corresponding monomial in S and denote its degree in the standard grading by $|\boldsymbol {x}^{\boldsymbol {u}}| = |\boldsymbol {u}| := u_1+u_2+u_3+u_4$ ; more generally, we use $|f|$ to denote the degree of any homogeneous element f in the standard grading. This grading can be refined to a bigrading on S, defined on monomials by $\operatorname {\mathrm {bideg}}(\boldsymbol {x}^{\boldsymbol {u}}) := (u_1+u_2,u_3+u_4) \in \mathbb {N}^2$ . All of the ideals I and J mentioned in Theorems 1.3 and 1.5 are bigraded, and thus, standard graded. If R is a $\mathbb {Z}$ -graded ring, M is a graded R-module, and $j \in \mathbb {Z}$ , then the jth twist of M is the graded R-module $M(j)$ satisfying $M(j)_i := M_{j+i}$ , for all $i \in \mathbb {Z}$ .

2.2 The truncated cotangent complex

Our approach to proving Theorems 1.3 and 1.5 requires computing certain $T^i$ -modules, so we review the construction of the truncated cotangent complex. We follow [18, Section 3] closely, which itself follows [31].

To obtain a model of the truncated cotangent complex of a ring homomorphism $A \to B$ , we choose surjections $R_{B/A} \twoheadrightarrow B$ , with kernel denoted I, and $F_{B/A} \twoheadrightarrow I$ , where $R_{B/A}$ is a polynomial ring over A and $F_{B/A}$ is a free $R_{B/A}$ -module. We then set $Q_{B/A}$ to be the kernel of $F_{B/A} \twoheadrightarrow I$ and $\operatorname {\mathrm {Kos}}_{B/A}$ to be its submodule of Koszul relations [18, Section 3]. We drop the subscripts when no confusion should arise. The truncated cotangent complex of B over A is the complex $L_{B/A,\bullet }$ concentrated in homological degrees $0,1,2$ , with terms

$$ \begin{align*} L_{B/A,\bullet} \colon \Omega_{R/A} \otimes_{R} B \stackrel{\ d_1^{B/A}}{\longleftarrow} F \otimes_{R} B \stackrel{\ d_2^{B/A}}{\longleftarrow} Q/\operatorname{\mathrm{Kos}}, \end{align*} $$

where $d_2^{B/A}$ is induced by the inclusion $Q \subseteq F$ and $d_1^{B/A}$ is obtained by composing the map $L_1 = F \otimes _{R} B \twoheadrightarrow I/I^2$ with the map induced by the derivation $R \to \Omega _{R/A}$ . We sometimes use $d_i^L$ to denote the differentials. One derives from this the $T^i$ -modules

$$ \begin{align*} T^i(B/A, M) := H^i(\operatorname{\mathrm{Hom}}_B(L_{B/A,\bullet}, M)), \end{align*} $$

for any B-module M and $0 \le i \le 2$ (we also call these tangent cohomology modules when convenient). The notation $T^i_{B/A}$ is often used when $M = B$ , or simply $T^i_{B}$ , if is the base field. When viewed as an element of the derived category, the complex $L_{B/A,\bullet }$ is independent of the choices of $R_{B/A}$ and $F_{B/A}$ (see, e.g. [18, Remark 3.3.1]). Hence, the tangent cohomology modules depend only on the map $A \to B$ .

Remark 2.1. When A and B are both graded by an abelian group G and the map $A \to B$ is a graded homomorphism, all choices in the construction of the truncated cotangent complex can be made to respect the grading. If the cotangent modules $L_{B/A,i}$ are all finite over B and M is a graded B-module, then $T^i(B/A,M)$ is also graded. Importantly, the nine-term long exact sequences described in [18, Theorems 3.4–3.5] also respect the grading. This holds for our examples, where we only need $G = \mathbb {Z}$ or $\mathbb {Z}^2$ and the gradings mentioned in subsection 2.1.

2.3 A comparison theorem

We briefly describe a theorem of Jelisiejew. Let I be any ideal in defining a local Artinian quotient supported at $0 \in \mathbb {A}^4$ . Motivated by the Białynicki-Birula decomposition, Jelisiejew defines a scheme $\operatorname {\mathrm {Hilb}}^+_{pts}(\mathbb {A}^4)$ and constructs a map

$$ \begin{align*} \theta\colon\operatorname{\mathrm{Hilb}}^+_{pts}(\mathbb{A}^4) \times \mathbb{A}^4 \to \operatorname{\mathrm{Hilb}}^{pts}(\mathbb{A}^4) \end{align*} $$

with the following properties. First, $\theta |_{\operatorname {\mathrm {Hilb}}^+_{pts}(\mathbb {A}^4)\times \{0\}}$ is a monomorphism and maps -points bijectively to subschemes of $\mathbb {A}^4$ supported at $0$ . Second, on the level of -points, if $[J]$ is supported at $0$ , then $\theta ([J],v)$ is the point supported at v obtained by translating $[J]$ .

Theorem 2.2 [29, Theorem 4.5].

If I is supported at the origin and has trivial negative tangents, then $\theta $ defines an open immersion of a local neighborhood of $([I],0)$ into $\operatorname {\mathrm {Hilb}}^{pts}(\mathbb {A}^4)$ . In particular, if , then all components of $\operatorname {\mathrm {Hilb}}^{pts}(\mathbb {A}^4)$ containing $[I]$ are elementary.

Proposition 2.3. Suppose I is supported at the origin with trivial negative tangents, $A=S/I$ , and . Then I defines a smooth point on $\operatorname {\mathrm {Hilb}}^{pts}(\mathbb {A}^4)$ .

Proof. By Theorem 2.2, it suffices to show that $[I]$ defines a smooth point of $\operatorname {\mathrm {Hilb}}^+_{pts}(\mathbb {A}^4)$ . By [29, Theorem 4.2], the obstruction space for $(\operatorname {\mathrm {Hilb}}^+_{pts}(\mathbb {A}^4), [I])$ is given by , which vanishes by assumption. Therefore, obstructions to all higher-order deformations vanish, showing smoothness of $[I]$ in $\operatorname {\mathrm {Hilb}}^+_{pts}(\mathbb {A}^4)$ .

3 Trivial negative tangents, I

Our goal in this section is to understand the tangent space of the point $[I] \in \operatorname {\mathrm {Hilb}}^{pts}(\mathbb {A}^4)$ corresponding to an ideal of the form

for some $n_1, n_2 \ge 2$ . The ideal I is $\mathfrak {m}$ -primary, where $\mathfrak {m} := \langle x,y,z,w \rangle \subset S$ is the ideal of the origin $0 \in \mathbb {A}^4$ . We will prove:

Proposition 3.1. The ideal I has trivial negative tangents, hence, every irreducible component of $\operatorname {\mathrm {Hilb}}^{pts}(\mathbb {A}^4)$ containing $[I]$ must be elementary by [29, Theorem 1.2].

The ensuing proof explicitly calculates the form of tangent vectors. One may wonder whether the approach of [29, Proof of Theorem 1.4] can be taken to reduce the number of explicit calculations. In Proposition 9.1, we show that key hypotheses for this alternate approach fail for our examples (see subsection 1.1 for further details).

Let $\varphi \in \operatorname {\mathrm {Hom}}_S(I, S/I) \cong T_{[I]} \operatorname {\mathrm {Hilb}}^{pts}(\mathbb {A}^4)$ , so that $\varphi $ is determined by its values on the generators

$$ \begin{align*} x^{n_1}, x^{n_1-1}y, \dotsc, y^{n_1}, z^{n_2}, z^{n_2-1}w, \dotsc, w^{n_2}, xz-yw \end{align*} $$

of I. These values lie in the -vector space $A := S/I$ spanned by the cosets $x^{u_1}y^{u_2}z^{u_3}w^{u_4} + I$ , where $u_1+u_2 < n_1$ and $u_3+u_4 < n_2$ ; a basis of $S/I$ is obtained by ignoring any such monomial divisible by $yw$ , that is, setting

$$ \begin{align*} \mathcal{B} := \{ x^{u_1}y^{u_2}z^{u_3}w^{u_4} + I \mid u_1+u_2 < n_1,\ u_3+u_4< n_2,\ u_2u_4 = 0 \}, \end{align*} $$

yields a monomial basis for $S/I$ . In order for $\varphi $ to be S-linear, it must vanish on the syzygies of I, that is, the following relations must hold:

(2) $$ \begin{align} & & y \varphi(x^{n_1-k}y^k) = x \varphi(x^{n_1-k-1}y^{k+1}), &\text{for all } 0 \le k < n_1, \end{align} $$

(3) $$ \begin{align} & w \varphi(z^{n_2-\ell}w^{\ell}) = z \varphi(z^{n_2-\ell-1}w^{\ell+1}), &\text{for all } 0 \le \ell < n_2, \end{align} $$

(4) $$ \begin{align} & x^{n_1-1-k}y^k \varphi(xz-yw) = z \varphi(x^{n_1-k}y^k) - w \varphi(x^{n_1-1-k}y^{k+1}), &\text{for all } 0 \le k < n_1,\end{align} $$

(5) $$ \begin{align}& z^{n_2-1-\ell}w^{\ell} \varphi(xz-yw) = x \varphi(z^{n_2-\ell}w^{\ell}) - y \varphi(z^{n_2-1-\ell}w^{\ell+1}), &\text{for all } 0 \le \ell < n_2.\end{align} $$

Our proof of Proposition 3.1 will proceed as follows. To prove that the tangent space $\operatorname {\mathrm {Hom}}_S(I, S/I)$ vanishes in degrees at most $-2$ , we will (essentially) only need to use relations (2) and (3). Then, to see that $\operatorname {\mathrm {Hom}}_S(I, S/I)_{-1}$ is exactly the -span of the trivial tangent vectors, we will rely on relations (4) and (5).

3.1 Preliminary lemmas

We collect several helpful lemmas that will be used throughout this paper. Given $p\in S/I$ , we may expand it in the basis $\mathcal {B}$ . We refer to the support of p as the set of basis elements with nonzero coefficients showing up in the expansion of p—the support of $0$ is $\varnothing $ . Note that $\operatorname {\mathrm {Ann}}_{x,y}:=\operatorname {\mathrm {Ann}}(x)=\operatorname {\mathrm {Ann}}(y)$ and $\operatorname {\mathrm {Ann}}_{z,w}:=\operatorname {\mathrm {Ann}}(z)=\operatorname {\mathrm {Ann}}(w)$ are spanned by basis vectors, so it makes sense to say whether the support of p intersects $\operatorname {\mathrm {Ann}}_{x,y}$ or $\operatorname {\mathrm {Ann}}_{z,w}$ . Note also that if $p,q\in S/I$ have disjoint support, then $p=q$ forces $p=q=0$ .

Lemma 3.2. If $p\in S/I$ , then it may be decomposed as

$$ \begin{align*} p=\sum_{0<i<n_1}y^ip_{i,0}+\sum_{0<j<n_2}w^jp_{0,j}+p_{0,0}, \end{align*} $$

where

1. (i) each $p_{i,j}$ is a polynomial in $x,z$ ,

2. (ii) for $i\geq 0$ , $p_{i,0}$ has x-degree less than $n_1-i$ and z-degree less than $n_2$ ,

3. (iii) for $j\geq 0$ , $p_{0,j}$ has x-degree less than $n_1$ and z-degree less than $n_2-j$ , and

4. (iv) all of the terms in the sum have disjoint support.

Furthermore, we have

Proof. Expressing p as a linear combination of elements of $\mathcal {B}$ and grouping basis vectors by their y- and w-exponents, we obtain our desired decomposition of p with properties (i)–(iv).

Because $p_{i,0}$ has $(n_1-i)n_2$ monomials in x and z, and $p_{0,j}$ has $n_1(n_2-j)$ monomials in x and z, we see $S/I$ has dimension

$$ \begin{align*} \bigl( (n_1-1)n_2 + (n_1-2)n_2 + \dotsb + n_2 \bigr) + (n_1n_2) &+ \bigl( (n_2-1)n_1 + (n_2-2)n_1 + \dotsb + n_1 \bigr) \\ &=\frac{(n_1-1)n_1}{2}n_2 + n_1n_2 + n_1\frac{(n_2-1)n_2}{2} \\ &= \frac{n_1n_2}{2}(n_1+n_2).\\[-34pt] \end{align*} $$

Lemma 3.3. If $p,q\in S/I$ satisfy

$$ \begin{align*} yp=xq,\\[-18pt] \end{align*} $$

then we may write

$$ \begin{align*} p=p'+xr_y+wr_w,\quad\quad q=q'+yr_y+zr_w,\\[-18pt] \end{align*} $$

such that

1. (i) $r_y$ is a polynomial in $x,y,z$ and $r_w$ is a polynomial in $x,z,w$ ,

2. (ii) $p',q'\in \operatorname {\mathrm {Ann}}_{x,y}$ , while $p-p'$ and $q-q'$ are supported away from $\operatorname {\mathrm {Ann}}_{x,y}$ ,

3. (iii) $p'$ , $xr_y$ , and $wr_w$ , have mutually disjoint support, and

4. (iv) $q'$ , $yr_y$ , and $zr_w$ have mutually disjoint support.

Furthermore, $p'$ and $q'$ are unique, the image of $r_y$ in $S/\operatorname {\mathrm {Ann}}_{x,y}$ is unique, and the image of $r_w$ in $S/\operatorname {\mathrm {Ann}}_{z,w}$ is unique.

Proof. Expanding p in the basis $\mathcal {B}$ , let $p'$ be the sum of all monomial terms of p which are annihilated by x (equivalently, y). This gives a decomposition analogous to Lemma 3.2, where we write

$$ \begin{align*} p=p'+\sum_{0<i<n_1-1}y^ip_{i,0}+\sum_{0<j<n_2}w^jp_{0,j}+p_{0,0} \end{align*} $$

and

$$ \begin{align*} q=q'+\sum_{0<i<n_1-1}y^iq_{i,0}+\sum_{0<j<n_2}w^jq_{0,j}+q_{0,0}, \end{align*} $$

and where no monomial terms of any of the terms $y^ip_{i,0}$ , $w^jp_{0,j}$ , $p_{0,0}$ , $y^iq_{i,0}$ , $w^jq_{0,j}$ , $q_{0,0}$ are annihilated by y (equivalently, x). Then

$$ \begin{align*} yp=\sum_{0<i<n_1-1}y^{i+1}p_{i,0}+\sum_{0<j<n_2}w^{j-1}xzp_{0,j}+yp_{0,0} \end{align*} $$

and

$$ \begin{align*} xq=\sum_{0<i<n_1-1}y^ixq_{i,0}+\sum_{0<j<n_2}w^jxq_{0,j}+xq_{0,0}. \end{align*} $$

Since none of the terms in the sum are zero (by hypothesis), equating terms with the same $y^iw^j$ -powers, we see

$$ \begin{align*} \begin{cases} \begin{aligned} p_{i,0} =xq_{i+1,0} && 0\leq i\leq n_1-3,\\ p_{n_1-2,0} = 0, &&\\ zp_{0,j+1} =q_{0,j} && 0\leq j\leq n_2-2,\\ q_{0,n_2-1} =0. && \end{aligned} \end{cases} \end{align*} $$

Therefore, letting

$$ \begin{align*} r_y=\sum_{0\leq i\leq n_1-3}y^iq_{i+1,0} \quad\textrm{and}\quad r_w=\sum_{0\leq j\leq n_2-2}w^jp_{0,j+1}, \end{align*} $$

we have the desired decompositions $p=p'+xr_y+wr_w$ and $q=q'+yr_y+zr_w$ .

It remains to prove the uniqueness properties. First, since $xr_y$ and $wr_w$ have supports disjoint from $\operatorname {\mathrm {Ann}}_{x,y}$ , we see $p'$ is uniquely determined. Now suppose we have different choices $r^{\prime }_y$ and $r^{\prime }_w$ with properties (i)–(iv). Since $p'$ is uniquely determined, we have

$$ \begin{align*} xr_y+wr_w=xr^{\prime}_y+wr^{\prime}_w. \end{align*} $$

Let $r_y=r_{y,0}+ys_y$ and $r^{\prime }_y=r^{\prime }_{y,0}+ys^{\prime }_y$ , where $r_{y,0}$ and $r^{\prime }_{y,0}$ have no y-terms. Expanding, we have

$$ \begin{align*} xr_{y,0}+xys_y+wr_w=xr^{\prime}_{y,0}+xys^{\prime}_y+wr^{\prime}_w. \end{align*} $$

Then collecting terms with $y^0w^0$ -powers, we see $xr_{y,0}=xr^{\prime }_{y,0}$ , so the image of $r_{y,0}$ in $S/\operatorname {\mathrm {Ann}}_{x,y}$ is uniquely determined. Similarly, collecting terms with $y^iw^0$ -powers for $i>0$ , we have $xys_y=xys^{\prime }_y$ , so the image of $ys_y$ in $S/\operatorname {\mathrm {Ann}}_{x,y}$ is also uniquely determined. Therefore, the image of $r_y$ in $S/\operatorname {\mathrm {Ann}}_{x,y}$ is uniquely determined. Finally, collecting terms with $y^0w^j$ -powers for $j>0$ , we see $wr_w=wr^{\prime }_w$ , so the image of $r_w$ in $S/\operatorname {\mathrm {Ann}}_{z,w}$ is uniquely determined.

More generally, we have the following result.

Corollary 3.4. Let $p_0, p_1, \dotsc , p_n\in S/I$ satisfy the property

$$ \begin{align*} yp_k=xp_{k+1}, \end{align*} $$

for all $0\leq k<n$ , where $n \le n_1$ . Then there exist $t_0, t_1, \dotsc , t_n \in S/I$ , such that we may write

$$ \begin{align*} p_k = p^{\prime}_k+\sum_{i=0}^kx^{n-k}y^{k-i}z^it_i + \sum_{i=k+1}^nx^{n-i}z^kw^{i-k}t_i, \end{align*} $$

for all $0 \le k \le n$ , where

1. (i) $p^{\prime }_k\in \operatorname {\mathrm {Ann}}_{x,y}$ and $p_k-p^{\prime }_k$ is supported away from $\operatorname {\mathrm {Ann}}_{x,y}$ ,

2. (ii) $t_0$ is a polynomial in $x,y,z$ and $t_n$ is a polynomial in $x,z,w$ ,

3. (iii) $t_i$ is a polynomial in $x,z$ for $0<i<n$ ,

4. (iv) if $(j_{1},j_{2})$ denotes the bidegree of any element in the support of $t_i$ , then the bounds $0\le j_1<n_1-1-n+i$ and $0\le j_{2}<n_2-i$ both hold, and

5. (v) for every k, all terms $p^{\prime }_k$ , $\{x^{n-k}y^{k-i}z^it_i\}_{0\leq i\leq k}$ , and $\{x^{n-i}z^kw^{i-k}t_i\}_{k<i\leq n}$ have mutually disjoint support.

Proof. Lemma 3.3 handles the case when $n=1$ . When $n=2=n_1$ , applying Lemma 3.3 to the pairs $p_0,p_1$ and $p_1,p_2$ yields

$$ \begin{align*} p_0 = p_0' +wr_w, \qquad p_1 = p_1' + zr_w = p_1' +w\rho_w, \qquad p_2 = p_2' +z\rho_w; \end{align*} $$

here, $r_y = \rho _y = 0$ follows from Lemma 3.3(ii) and $r_w$ , $\rho _w$ are polynomials in $z,w$ . Write $r_w = r_{w,0} + wr_{w,+}$ , where $r_{w,0}$ is a polynomial in z and $r_{w,+}$ is a polynomial in $z,w$ . Comparing w-terms in $p_1$ , we find

$$ \begin{align*} zr_{w,0} = 0 \qquad\text{and}\qquad wzr_{w,+} = w\rho_w. \end{align*} $$

As $zr_{w,0}=0$ if and only if $wr_{w,0}=0$ , we may assume $r_{w,0} = 0$ . Let $u_0 = u_1 = 0$ and $u_2 = r_{w,+}$ . This implies

$$ \begin{align*} p_0 = p_0' +w^2u_2, \qquad p_1 = p_1' + zwu_2, \qquad p_2 = p_2' +z^2u_2, \end{align*} $$

giving the desired expressions; properties (i)–(v) can easily be verified in this case (if, in addition, $n_2 = 2$ , then we take $u_2=0$ ). A similar proof works whenever $n=2$ , where $r_y, \rho _y \neq 0$ are allowed if $n_1>2$ . In these cases, starting with

$$ \begin{align*} p_0 = p_0' +xr_y +wr_w, \qquad p_1 = p_1' +yr_y +zr_w = p_1' +x\rho_y +w\rho_w, \qquad p_2 = p_2' +y\rho_y +z\rho_w \end{align*} $$

and additionally writing $\rho _y = \rho _{y,0} + y\rho _{y,+}$ , we find the desired expressions

$$ \begin{align*} p_0 &= p_0' +x^2u_0 +xwu_1 +w^2u_2, \\ p_1 &= p_1' +xyu_0 +xzu_1 +zwu_2, \\ p_2 &= p_2' +y^2u_0 +yzu_1 +z^2u_2. \end{align*} $$

Here we take $u_i=0$ if the resulting term would be $0$ or land in $\operatorname {\mathrm {Ann}}_{x,y}$ .

Now assume $n>2$ . Considering the tuples $(p_0,\dots ,p_{n-1})$ and $(p_1,\dots ,p_n)$ , by induction, we have $t_i$ and $\tau _i$ satisfying properties (i)–(v) (with n replaced by $n-1$ ) and such that

$$ \begin{align*} p_k=p^{\prime}_k+\sum_{i=0}^kx^{n-1-k}y^{k-i}z^it_i + \sum_{i=k+1}^{n-1}x^{n-1-i}z^kw^{i-k}t_i \end{align*} $$

for $k<n$ , and

$$ \begin{align*} p_k = p^{\prime}_k + \sum_{i=0}^{k-1}x^{n-k}y^{k-i-1}z^i\tau_i + \sum_{i=k}^{n-1}x^{n-1-i}z^{k-1}w^{i-k+1}\tau_i \end{align*} $$

for $k>0$ . Since the basis vectors appearing in $p_k$ that are in the support of $\operatorname {\mathrm {Ann}}_{x,y}$ are uniquely determined, the $p^{\prime }_k$ terms are the same in the two expressions for $p_k$ .

For each $1 < i < n-1$ , comparing the two expressions for the $y^{k-i}$ - or $w^{i-k}$ -terms, we have

(6) $$ \begin{align} x^{n-1-k}y^{k-i}z^it_i = x^{n-k}y^{k-i}z^{i-1}\tau_{i-1}, \quad\text{ if } i\le k, \end{align} $$

(7) $$ \begin{align} x^{n-1-i}z^kw^{i-k}t_i = x^{n-i}z^{k-1}w^{i-k}\tau_{i-1}, \quad\text{ if } i> k, \end{align} $$

for all $0<k<n$ . By our inductive assumption on the bidegrees of $t_i$ and $\tau _{i-1}$ , if $i<n_2$ , then none of the terms appearing in (6) or (7) is zero, and hence, there exists a polynomial $u_i$ in $x,z$ , such that

$$ \begin{align*} t_i=xu_i\quad\textrm{and}\quad \tau_{i-1}=zu_i; \end{align*} $$

observe that any monomial in the support of $u_i$ has bidegree $(j_1,j_2)$ with $0\le j_1<n_1-1-n+i$ and $0\le j_2<n_2-i$ . If, on the other hand, $i>n_2$ , then both $t_i$ and $\tau _{i-1}$ vanish, so we may take $u_i=0$ . Finally, if $i=n_2$ , then $t_i=0$ ; by our assumption on the bidegree of $\tau _{i-1}$ , the only way (6) or (7) can hold is if $\tau _{i-1}=0$ as well, so we may take $u_i=0$ .

Let

$$ \begin{align*} \tau_0=\tau_{0,0}+y\tau_{0,+}, \end{align*} $$

where $\tau _{0,0}$ is a polynomial in $x,z$ and $\tau _{0,+}$ is a polynomial in $x,y,z$ . Similarly, let

$$ \begin{align*} t_{n-1}=t_{n-1,0}+wt_{n-1,+}, \end{align*} $$

where $t_{n-1,0}$ is a polynomial in $x,z$ and $t_{n-1,+}$ is a polynomial in $x,z,w$ .

Next, by comparing the $y^0w^0$ -terms in the expression for $p_1$ , we see $x^{n-2}zt_1=x^{n-1}\tau _{0,0}$ . If $n=n_1$ , then we take $u_1 = 0$ . Otherwise, by our assumptions on the bidegrees of $t_1$ and $\tau _0$ , no terms in the two sides of the equation are zero, so there exists a polynomial $u_1$ in $x,z$ , such that

$$ \begin{align*} t_1=xu_1\quad\textrm{and}\quad \tau_{0,0}=zu_1. \end{align*} $$

We then see that any monomial in the support of $u_1$ has bidegree $(j_1,j_2)$ with $0\le j_1<n_1-n$ and $0\le j_2<n_2-1$ . Comparing the terms in $p_1$ with a power of y, we see

$$ \begin{align*} x^{n-2}yt_0=x^{n-1}y\tau_{0,+}. \end{align*} $$

Since $\operatorname {\mathrm {Ann}}(x)=\operatorname {\mathrm {Ann}}(y)$ , this implies

$$ \begin{align*} x^{n-1-\ell}y^\ell t_0=x^{n-\ell}y^\ell \tau_{0,+}, \end{align*} $$

for all $0\leq \ell \leq n-1$ . If $n \ge n_1-1$ , then we take $u_0 = 0$ . Otherwise, any monomial in the support of $\tau _{0,+}$ has bidegree $(j_1,j_2)$ with $0\le j_1<n_1-1-n$ and $0\le j_2<n_2$ .

Next, comparing the $w^{n-2}$ -terms in $p_1$ yields $zw^{n-2}t_{n-1,0}=w^{n-2}x\tau _{n-2}$ . Arguing in the same manner as we did with (6) and (7), we see

$$ \begin{align*} t_{n-1,0}=xu_{n-1} \quad\textrm{and}\quad \tau_{n-2}=zu_{n-1}, \end{align*} $$

for some polynomial $u_{n-1}$ in $x,z$ , where $u_{n-1}=0$ , if $n-1\geq n_2$ . Comparing the $w^j$ -terms in $p_1$ with $j\geq n-1$ , we have $zw^{n-1}t_{n-1,+}=w^{n-1}\tau _{n-1}$ , and since $\operatorname {\mathrm {Ann}}(z)=\operatorname {\mathrm {Ann}}(w)$ , we have

$$ \begin{align*} z^{\ell+1}w^{n-1-\ell}t_{n-1,+}=w^{n-1-\ell}z^\ell \tau_{n-1}, \end{align*} $$

for $0\leq \ell \leq n-1$ .

Let

$$ \begin{align*} u_0=\tau_{0,+} \quad\textrm{and}\quad u_n=t_{n-1,+}. \end{align*} $$

For $k<n$ , using that $t_i=xu_i$ for $1\leq i\leq n-2$ , we see

$$ \begin{align*} p_k =p^{\prime}_k+x^{n-1-k}y^kt_0 + \sum_{i=1}^k x^{n-k}y^{k-i}z^iu_i + \sum_{i=k+1}^{n-2}x^{n-i}z^kw^{i-k}u_i+z^kw^{n-1-k}t_{n-1}. \end{align*} $$

Next, we have

$$ \begin{align*} z^kw^{n-1-k}t_{n-1} = z^kw^{n-1-k}t_{n-1,0}+z^kw^{n-k}t_{n-1,+} = z^kw^{n-1-k}xu_{n-1}+z^kw^{n-k}u_n. \end{align*} $$

Combining this with the fact that $x^{n-1-k}y^kt_0 = x^{n-k}y^k\tau _{0,+} = x^{n-k}y^ku_0$ , we see

$$ \begin{align*} p_k = p^{\prime}_k + \sum_{i=0}^k x^{n-k}y^{k-i}z^iu_i + \sum_{i=k+1}^n x^{n-i}z^kw^{i-k}u_i, \end{align*} $$

which is the desired expression for $p_k$ with $k<n$ .

For $k=n$ , we have

$$ \begin{align*} p_n &=p^{\prime}_n+\sum_{i=0}^{n-1}y^{n-1-i}z^i\tau_i\\ &=p^{\prime}_n+y^{n-1}(\tau_{0,0}+y\tau_{0,+}) + \sum_{i=1}^{n-1}y^{n-1-i}z^i(zu_{i+1})\\ &=p^{\prime}_n+y^{n-1}(zu_1+yu_0)+\sum_{i=2}^{n}y^{n-i}z^iu_i\\ &=p^{\prime}_n+\sum_{i=0}^{n}y^{n-i}z^iu_i, \end{align*} $$

which is the desired expression.

We have now shown that $u_0, u_1, \dotsc , u_n$ satisfy properties (i)–(iv). For (v), let $0\le k<n$ . If $0\leq i\leq k$ , then $x^{n-k}y^{k-i}z^iu_i$ and $x^{n-1-k}y^{k-i}z^it_i$ have the same support, and if $i>k$ , then $x^{n-i}z^kw^{i-k}u_i$ and $x^{n-1-i}z^kw^{i-k}t_i$ have the same support; furthermore, the support of $z^{k}w^{n-1-k}t_{n-1}$ is partitioned into the supports of $xz^kw^{n-1-k}u_{n-1}$ and $z^kw^{n-k}u_n$ for $k<n-1$ , and similarly for $k=n-1$ . When $k=n$ , $y^{n-i}z^iu_i$ and $y^{n-1-i}z^i\tau _{i-1}$ have the same support for $i\ge 2$ , while the support of $y^{n-1}\tau _0$ partitions into the support of $y^{n-1}zu_1$ and the support of $y^nu_0$ . Hence, property (v) holds too.

3.2 Proof of Proposition 3.1

Recall that $\varphi \in \operatorname {\mathrm {Hom}}_S(I,S/I)$ is a tangent vector. The trivial tangents are the tangent vectors corresponding to the homomorphisms $\partial _x, \partial _y, \partial _z, \partial _w$ , where

$$ \begin{align*} \partial_x(f) := \frac{\partial f}{\partial x} + I, \text{ for } f \in I, \end{align*} $$

and $\partial _y, \partial _z, \partial _w$ are defined analogously. As I is homogeneous, the module $\operatorname {\mathrm {Hom}}_S(I, S/I)$ inherits the grading (and the bigrading), so that

$$ \begin{align*} \operatorname{\mathrm{Hom}}_S(I, S/I) = \bigoplus_{i \in \mathbb{Z}} \operatorname{\mathrm{Hom}}_S(I, S/I)_i \end{align*} $$

with $\operatorname {\mathrm {Hom}}_S(I, S/I)_i = \{ \varphi \in \operatorname {\mathrm {Hom}}_S(I, S/I) \mid \varphi (I_j) \subseteq (S/I)_{i+j}, \text { for all } j \in \mathbb {N} \}$ (and similarly for the bigrading). The trivial tangents have degree $-1$ in the standard grading.

Let us assume that $\varphi $ is graded of degree $j < 0$ . Let

$$ \begin{align*} p_k := \varphi(x^{n_1-k}y^k), \end{align*} $$

for all $0 \le k \le n_1$ . Relation (2) says that $yp_k = xp_{k+1}$ , for all $0 \le k < n_1$ . Corollary 3.4 then applies to these values of $\varphi $ , with $n = n_1$ , giving expressions

$$ \begin{align*} p_0 &= p^{\prime}_0 + \sum_{i=2}^{n_1} x^{n_1-i}z^kw^{i-k}t_i \quad\text{and} \\ p_k &= p^{\prime}_k + \sum_{i=2}^k x^{n_1-k}y^{k-i}z^it_i + \sum_{i=k+1}^{n_1} x^{n_1-i}z^kw^{i-k}t_i, \quad\text{for } 0<k\le n_1 \end{align*} $$

( $i=0$ gives a zero term and $i=1$ gives a term in $\operatorname {\mathrm {Ann}}_{x,y}$ ). Observe that the degrees of all of the terms $x^{n_1-k}y^{k-i}z^it_i$ and $x^{n_1-i}z^kw^{i-k}t_i$ equal $n_1+|t_i| \ge n_1$ . Because $j<0$ , we must then have $t_i = 0$ for all i, by Corollary 3.4(v). Moreover, as $p_k' \in \operatorname {\mathrm {Ann}}_{x,y}$ , any nonzero term of $p_k'$ must have degree at least $n_1-1$ . This implies $p_k'$ , and hence $p_k$ , is zero, if $j<-1$ . By symmetry, $\varphi (z^{n_2-\ell }w^{\ell })$ is also zero, if $j<-1$ . Relation (4) then implies that $\varphi (xz-yw) = 0$ , if $j<-1$ . This shows that $\operatorname {\mathrm {Hom}}_S(I,S/I)_{j} = 0$ , for $j<-1$ .

Suppose that $j = -1$ . We still know that all $t_i = 0$ and so $p_k = p_k'$ , for all k. Thus, we now have expressions

$$ \begin{align*} p_k = \sum_{0 \le i < n_1} a^{(k)}_i x^{n_1-1-i}y^i +I, \end{align*} $$

where each , by Lemma 3.2. Also, we have

$$ \begin{align*} \varphi(xz-yw) = c_0x + c_1y + c_3z + c_4w +I, \end{align*} $$

where all .

Proposition 3.1 now reduces to the following:

Proposition 3.5. Any S-linear map $\varphi \colon I \to S/I$ of degree $-1$ is a -linear combination of the trivial tangents $\partial _x, \partial _y, \partial _z, \partial _w$ .

Proof. Relation (4) can now be written

$$ \begin{align*} c_{3} x^{n_1-1-k}y^k z + c_{4} x^{n_1-1-k}y^k w + I &= \sum_{0 \le i < n_1} a_{i}^{(k)} x^{n_1-1-i} y^{i} z - \sum_{0\le i<n_1} a_{i}^{(k+1)} x^{n_1-1-i} y^{i} w + I \\ &= \sum_{0\le i< n_1} a_{i}^{(k)} x^{n_1-1-i} y^{i} z - a_{0}^{(k+1)} x^{n_1-1} w \\ &\qquad \qquad \qquad \qquad - \sum_{0<i<n_1} a_{i}^{(k+1)} x^{n_1-i} y^{i-1} z + I, \end{align*} $$

as $yw + I = xz + I$ .

When $k = 0$ , this becomes

$$ \begin{align*} c_{3} x^{n_1-1} z + c_{4} x^{n_1-1} w + I &= \sum_{0\le i<n_1} a_{i}^{(0)} x^{n_1-1-i} y^{i} z - a_{0}^{(1)} x^{n_1-1} w \\ &\qquad \qquad \qquad \qquad - \sum_{0<i<n_1} a_{i}^{(1)} x^{n_1-i} y^{i-1} z + I, \end{align*} $$

which implies $c_3 = a_{0}^{(0)} - a_{1}^{(1)}$ , $c_4 = -a_{0}^{(1)}$ , $a_{n_1-1}^{(0)} = 0$ , and $a_{i}^{(0)} = a_{i+1}^{(1)}$ , for all $0<i<n_1-1$ . When $0 < k < n_1 -1$ , this becomes

$$ \begin{align*} c_{3} x^{n_1-1-k}y^k z + c_{4} x^{n_1-k}y^{k-1} z + I &= \sum_{0\le i< n_1} a_{i}^{(k)} x^{n_1-1-i} y^{i} z - a_{0}^{(k+1)} x^{n_1-1} w \\ &\qquad \qquad \qquad \qquad - \sum_{0<i<n_1} a_{i}^{(k+1)} x^{n_1-i} y^{i-1} z + I, \end{align*} $$

which shows $c_3 = a_{k}^{(k)} - a_{k+1}^{(k+1)}$ , $c_4 = a_{k-1}^{(k)} - a_{k}^{(k+1)}$ , $a_{n_1-1}^{(k)} = a_{0}^{(k+1)} = 0$ , and $a_{i}^{(k)} = a_{i+1}^{(k+1)}$ , for all the remaining coefficients. And when $k = n_1 -1$ , this becomes

$$ \begin{align*} c_{3} y^{n_1-1} z + c_{4} x y^{n_1-2} z + I &= \sum_{0\le i< n_1} a_{i}^{(n_1-1)} x^{n_1-1-i} y^{i} z - a_{0}^{(n_1)} x^{n_1-1} w \\ &\qquad \qquad \qquad \qquad - \sum_{0<i<n_1} a_{i}^{(n_1)} x^{n_1-i} y^{i-1} z + I, \end{align*} $$

showing that $c_3 = a_{n_1-1}^{(n_1-1)}$ , $c_4 = a_{n_1-2}^{(n_1-1)} - a_{n_1-1}^{(n_1)}$ , $a_{0}^{(n_1)} = 0$ , and $a_{i}^{(n_1-1)} = a_{i+1}^{(n_1)}$ , for all the remaining coefficients. This shows that

$$ \begin{align*} c_3 = a_{0}^{(0)} - a_{1}^{(1)} = a_{1}^{(1)} - a_{2}^{(2)} = \dotsb = a_{n_1-2}^{(n_1-2)} - a_{n_1-1}^{(n_1-1)} = a_{n_1-1}^{(n_1-1)} \end{align*} $$

and

$$ \begin{align*} c_4 = -a_{0}^{(1)} = a_{0}^{(1)} - a_{1}^{(2)} = \dotsb = a_{n_1-3}^{(n_1-2)} - a_{n_1-2}^{(n_1-1)} = a_{n_1-2}^{(n_1-1)} - a_{n_1-1}^{(n_1)}, \end{align*} $$

while the remaining coefficients $a_{k}^{(j)}$ vanish. Letting $a := c_3$ and $a' := -c_4$ , this yields

$$ \begin{align*} \varphi(x^{n_1}) &= a n_1 x^{n_1-1} + I, \\ \varphi(x^{n_1-k}y^k) &= a (n_1-k) x^{n_1-k-1}y^k + a' k x^{n_1-k}y^{k-1} + I, \quad\text{for } 0<k<n_1 \\ \varphi(y^{n_1}) &= a' n_1 y^{n_1-1} + I, \text{ and } \\ \varphi(xz-yw) &= c_{1}x + c_{2}y + az - a'w + I. \end{align*} $$

Adjusting the argument for the remaining generators of I yields

$$ \begin{align*} \varphi(z^{n_2}) &= b n_2 z^{n_2-1} + I, \\ \varphi(z^{n_2-\ell}w^{\ell}) &= b (n_2-\ell) z^{n_2-\ell-1}w^{\ell} + b' \ell z^{n_2-\ell}w^{\ell-1} + I, \quad\text{for } 0<\ell<n_1 \\ \varphi(w^{n_2}) &= b' n_2 w^{n_2-1} + I, \text{ and } \\ \varphi(xz-yw) &= bx - b'y + az - a'w + I, \end{align*} $$

where $b := c_1$ and $b' = - c_2$ . Hence, we find $\varphi = a\partial _x + a'\partial _y + b\partial _z + b'\partial _w$ , as desired.

This demonstrates that I only has trivial negative tangents and finishes the proof of Proposition 3.1.

4 Vanishing nonnegative obstruction spaces, I

Continuing with the notation from Section 3, our goal in this section is to prove the following:

Proposition 4.1. $[I]\in \operatorname {\mathrm {Hilb}}^{d}(\mathbb {A}^4)$ is a smooth point.

Let $A=S/I$ and . By Proposition 2.3, it is enough to show $T^2_{A, \ge 0} = 0$ . Let $\mathcal {F}_{\bullet }$ be a minimal free resolution of A over S,

$$ \begin{align*} \mathcal{F}_{\bullet} \colon S \stackrel{\ d_{1}^{\mathcal{F}}}{\longleftarrow} S(-n_1)^{n_1+1} \oplus S(-n_2)^{n_2+1} \oplus S(-2) \stackrel{\ d_{2}^{\mathcal{F}}}{\longleftarrow} \mathcal{F}_{2} \longleftarrow \dotsb, \end{align*} $$

and set $F := \mathcal {F}_{1}$ . The truncated cotangent complex of the map has terms $L_2 = Q/\operatorname {\mathrm {Kos}}$ , $L_1 = F/IF = F \otimes _S A$ , and , where $Q = \ker d_{1}^{\mathcal {F}}$ and $\operatorname {\mathrm {Kos}} \subset Q$ is the submodule of Koszul relations. Note that $L_2 \cong \mathcal {F}_{2} / \operatorname {\mathrm {Kos}}'$ , where $\operatorname {\mathrm {Kos}}'$ is the preimage of $\operatorname {\mathrm {Kos}}$ under $d_{2}^{\mathcal {F}}$ . So $L_{\bullet }$ equals

(cot_A/k )

Observe that $\mathcal {F}_{\bullet }$ inherits the bigrading, and moreover, $L_{\bullet }$ is bigraded, as is seen from the generators and the definition of the differential.

We denote generators of F by

$$ \begin{align*} (x^{n_1-k}y^k;),\quad (z^{n_2-\ell}w^{\ell};), \quad (q;), \end{align*} $$

for $0 \le k \le n_1$ , $0 \le \ell \le n_2$ , and

$$ \begin{align*} q := xz-yw, \end{align*} $$

so that $d_{1}^{\mathcal {F}}(g;) = g$ , for a generator $g \in I$ . Albeit odd at first glance, this notation conveniently extends to encode syzygies, where $(g;h)$ is used to denote a syzygy obtained from multiplication of a generator g by an element h. Thus, among the generators of $\mathcal {F}_{2}$ are $(x^{n_1-k}y^k; x)$ and $(z^{n_2-\ell }w^{\ell }; z)$ , for $k,\ell> 0$ —these elements map to the (minimal) syzygies

$$ \begin{align*} y(x^{n_1-k+1}y^{k-1};) - x(x^{n_1-k}y^k;) \quad \text{ and } \quad w(z^{n_2-\ell+1}w^{\ell-1};) - z(z^{n_2-\ell}w^{\ell};) \end{align*} $$

obtained, respectively, by multiplying $x^{n_1-k}y^k$ by x, and $z^{n_2-\ell }w^{\ell }$ by z (the ideals $ \langle x,y \rangle ^{n_1}$ and $ \langle z,w \rangle ^{n_2}$ are minimally resolved (individually) by the Eliahou–Kervaire resolution, which applies more generally to stable ideals and can be completely described in notation generalizing this; see [33, Section 28] for details). In addition, $\mathcal {F}_{2}$ has generators we shall denote $(q; x^{n_1-k}y^{k-1})$ and $(q; z^{n_2-\ell }w^{\ell -1})$ , for $1 \le k \le n_1$ and $1 \le \ell \le n_2$ —these map to the (minimal) syzygies

$$ \begin{align*} z (x^{n_1-k+1}y^{k-1};) - w (x^{n_1-k}y^{k};) - x^{n_1-k}y^{k-1} (q;) \end{align*} $$

and

$$ \begin{align*} x (z^{n_2-\ell+1}w^{\ell-1};) - y (z^{n_2-\ell}w^{\ell};) - z^{n_2-\ell}w^{\ell-1} (q;), \end{align*} $$

respectively (cf. relations (2)–(5)).

Lemma 4.2. The cotangent module $L_2$ is generated by the aforementioned syzygies, namely, by $(x^{n_1-k}y^k; x)$ , $(z^{n_2-\ell }w^{\ell }; z)$ , $(q; x^{n_1-k}y^{k-1})$ , and $(q; z^{n_2-\ell }w^{\ell -1})$ , for appropriate $k,\ell $ .

Proof. Minimality of the Eliahou–Kervaire resolution produces the generators $(x^{n_1-k}y^k; x)$ and $(z^{n_2-\ell }w^{\ell }; z)$ of $\mathcal {F}_{2}$ , while the syzygies $(q; x^{n_1-k}y^{k-1})$ and $(q; z^{n_2-\ell }w^{\ell -1})$ are minimal between $(q;)$ and either $(x^{n_1-k}y^k;)$ or $(z^{n_2-\ell }w^{\ell };)$ . Finally, any minimal syzygies between $(x^{n_1-k}y^k;)$ and $(z^{n_2-\ell }w^{\ell };)$ must be Koszul relations, as the corresponding generators of I have no variables in common.

By definition, $T^2_{A}$ is the quotient of $L^2 := \operatorname {\mathrm {Hom}}_{A}(L_2, A)$ by the image of $d^1_L := - \circ d_2^L$ , where $d_2^L \colon L_2 \to L_1$ is induced by $d_{2}^{\mathcal {F}}$ . We aim to understand $L^2_{\ge 0}$ , specifically showing the following.

Proposition 4.3. Given the preceding set-up, we have $L^2_{\ge 0} = d^1_L(L^1_{\ge 0})$ , i.e. $T^2_{A, \ge 0} = 0$ .

In other words, any A-linear map $\psi \colon L_2 \to A$ of nonnegative degree extends over the differential $d_2^{L} \colon L_2 \to L_1$ to a compatible A-linear map $\psi ' \colon L_1 \to A$ . Before proving this, we set some notation and record a helpful lemma. According to Lemma 4.2, $\psi $ is determined by its values on $(x^{n_1-k}y^k; x)$ , $(z^{n_2-\ell }w^{\ell }; z)$ , $(q; x^{n_1-k}y^{k-1})$ , and $(q; z^{n_2-\ell }w^{\ell -1})$ , for $1 \le k \le n_1$ and $1 \le \ell \le n_2$ . Lemma 3.2 yields expressions

$$ \begin{align*} \psi(x^{n_1-k}y^k; x) &=: P_k = \sum_{0<i<n_1} y^i(P_k)_{i,0} + (P_k)_{0,0} + \sum_{0<j<n_2} w^j(P_k)_{0,j} \quad\text{ and } \\ \psi(q; x^{n_1-k}y^{k-1}) &=: Q_k = \sum_{0<i<n_1} y^i (Q_k)_{i,0} + (Q_k)_{0,0} + \sum_{0<j<n_2} w^j(Q_k)_{0,j} ,\end{align*} $$

along with similar expressions for $\psi (z^{n_2-\ell }w^{\ell }; z)$ and $\psi (q; z^{n_2-\ell }w^{\ell -1})$ .

Lemma 4.4. Any homomorphism $\psi \colon L_2 \to A$ as above satisfies the following:

1. (i) all terms of $(P_k)_{0,j}$ are divisible by x, for $0 \le j < n_2$ , and

2. (ii) the equalities $x Q_k = w P_{k}$ and $y Q_k = z P_{k}$ hold.

The analogous statements for $\psi (z^{n_2-\ell }w^{\ell }; z)$ and $\psi (q; z^{n_2-\ell }w^{\ell -1})$ are also true.

Proof. Observe that $x^{n_1-k}y^{k-1} (x^{n_1-k}y^k; x) \in \operatorname {\mathrm {Kos}}'$ , so that

$$ \begin{align*} 0 &= x^{n_1-k}y^{k-1} \psi(x^{n_1-k}y^k; x) = x^{n_1-k}y^{k-1}(P_k)_{0,0} + x^{n_1-k}y^{k-1}\sum_{0<j<n_2} w^j(P_k)_{0,j} \\ &= y^{k-1}x^{n_1-k}(P_k)_{0,0} + \sum_{0<j<k} y^{k-1-j} x^{n_1-k+j} z^j (P_k)_{0,j} + \sum_{k\le j<n_2} w^{j-k+1} x^{n_1-1} z^{k-1} (P_k)_{0,j} \\ &= \sum_{0<j<k} y^{j} x^{n_1-1-j} z^{k-1-j} (P_k)_{0,k-1-j} + x^{n_1-1} z^{k-1} (P_k)_{0,k-1} + \sum_{0<j\le n_2-k} w^{j} x^{n_1-1} z^{k-1} (P_k)_{0,k-1+j} \\ &= \sum_{0<j<k} y^{j} x^{n_1-1-j} z^{k-1-j} (P_k)_{0,k-1-j}^z + x^{n_1-1} z^{k-1} (P_k)_{0,k-1}^z + \sum_{0<j\le n_2-k} w^{j} x^{n_1-1} z^{k-1} (P_k)_{0,k-1+j}^z, \end{align*} $$

where $(P_k)_{0,j}^z$ is the $x^0z^{\ge 0}$ -part of $(P_k)_{0,j}$ . Since the z-degree of $(P_k)_{0,j}^z$ is less than $n_2-j$ , this shows $(P_k)_{0,j}^z = 0$ , for all $0 \le j < n_2$ , proving (i). To prove the first equality in (ii), simply observe that $x(q; x^{n_1-k}y^{k-1}) - w(x^{n_1-k}y^{k}; x) \in \operatorname {\mathrm {Kos}}'$ ; the second equality is similarly proved. The analogous statements for $\psi (z^{n_2-\ell }w^{\ell }; z)$ and $\psi (q; z^{n_2-\ell }w^{\ell -1})$ are obtained by switching the roles of $x,y$ and $z,w$ .

Lemma 4.4(i) says that all terms of $\psi (x^{n_1-k}y^k; x)$ are divisible by x or y. Part (ii) imposes further restrictions on the values of $\psi $ . We can now proceed with the proof of Proposition 4.3.

Proof of Proposition 4.3.

The goal is to find compatible values $\psi '(x^{n_1-k}y^k;)$ , $\psi '(z^{n_2-\ell }w^{\ell };)$ , and $\psi '(q;)$ for the generators of $L_1$ in order to define an extension $\psi ' \colon L_1 \to A$ , such that $\psi = \psi ' \circ d_2^L$ , that is, we require values $\pi _k := \psi '(x^{n_1-k}y^k;)$ and $\rho := \psi '(q;)$ in A, such that the equalities

(8) $$ \begin{align} P_k &= \ y\pi_{k-1} - x\pi_k \quad\text{ and } \end{align} $$

(9) $$ \begin{align} Q_k &= z \pi_{k-1} - w \pi_{k} - x^{n_1-k}y^{k-1} \rho \end{align} $$

hold when $k>0$ , along with analogous equalities involving $\psi (z^{n_2-\ell }w^{\ell }; z)$ , $\psi (q; z^{n_2-\ell }w^{\ell -1})$ , $\psi '(z^{n_2-\ell }w^{\ell };)$ , and $\rho $ . As $T^2_A$ is bigraded and graded, we simplify by assuming that $\psi $ and $\psi '$ are bihomogeneous of bidegree $(-d_1,d_2)$ and total degree $d_2-d_1 \ge 0$ .

To begin, suppose that $P_k = 0$ for all k. If all $Q_k = 0$ , then (8) and (9) are solved by setting all $\pi _k = 0$ and $\rho = 0$ .

Next, assume that some $Q_\ell \neq 0$ . Lemma 4.4(ii) then tells us $Q_\ell $ is a nonzero element of $\operatorname {\mathrm {Ann}}_{x,y}$ ; since $\operatorname {\mathrm {bideg}}(Q_{\ell }) = (n_1-d_1,1+d_2)$ , this forces $d_1 = 1$ and $0 < d_2 < n_2 -1$ . We will solve (9) by choosing $\rho =0$ and $\pi _0, \pi _1, \dotsc , \pi _{n_1}\in \operatorname {\mathrm {Ann}}_{x,y}$ ; hence, (8) is trivially satisfied. Then, for all k, we have

$$ \begin{align*} Q_k &= \sum_{0<i<n_1} y^i (Q_k)_{i,0} + (Q_k)_{0,0} + \sum_{0<j<n_1} w^j (Q_k)_{0,j} \\ &= \sum_{0<i<n_1} y^i x^{n_1-1-i} z^{d_2+1} b^{(k)}_{i,0} + x^{n_1-1} z^{d_2+1} b^{(k)}_{0,0} + \sum_{0<j\le d_2+1} w^j x^{n_1-1} z^{d_2+1-j} b^{(k)}_{0,j}, \end{align*} $$

where each . Similarly, we have

$$ \begin{align*} z\pi_{k-1} &= z \left( \sum_{0<i<n_1} y^i (\pi_{k-1})_{i,0} + (\pi_{k-1})_{0,0} + \sum_{0<j<n_2} w^j (\pi_{k-1})_{0,j} \right) \\ &= z \left( \sum_{0<i<n_1} y^i x^{n_1-1-i} z^{d_2} \mu^{(k-1)}_{i,0} + x^{n_1-1} z^{d_2} \mu^{(k-1)}_{0,0} + \sum_{0<j\le d_2} w^j x^{n_1-1} z^{d_2-j} \mu^{(k-1)}_{0,j} \right) \\ &= \sum_{0<i<n_1} y^i x^{n_1-1-i} z^{d_2+1} \mu^{(k-1)}_{i,0} + x^{n_1-1} z^{d_2+1} \mu^{(k-1)}_{0,0} + \sum_{0<j\le d_2} w^j x^{n_1-1} z^{d_2+1-j} \mu^{(k-1)}_{0,j}, \end{align*} $$

along with

$$ \begin{align*} w\pi_{k} &= w \left( \sum_{0<i<n_1} y^i (\pi_{k})_{i,0} + (\pi_{k})_{0,0} + \sum_{0<j<n_2} w^j (\pi_{k})_{0,j} \right) \\ &= w \left( \sum_{0<i<n_1} y^i x^{n_1-1-i} z^{d_2} \mu^{(k)}_{i,0} + x^{n_1-1} z^{d_2} \mu^{(k)}_{0,0} + \sum_{0<j\le d_2} w^j x^{n_1-1} z^{d_2-j} \mu^{(k)}_{0,j} \right) \\ &= \sum_{0<i<n_1} y^{i-1} x^{n_1-i} z^{d_2+1} \mu^{(k)}_{i,0} + w x^{n_1-1} z^{d_2} \mu^{(k)}_{0,0} + \sum_{0<j\le d_2} w^{j+1} x^{n_1-1} z^{d_2-j} \mu^{(k)}_{0,j} \\ &= \sum_{0<i<n_1-1} y^{i} x^{n_1-1-i} z^{d_2+1} \mu^{(k)}_{i+1,0} + x^{n_1-1} z^{d_2+1} \mu^{(k)}_{1,0} + \sum_{0<j\le d_2+1} w^{j} x^{n_1-1} z^{d_2+1-j} \mu^{(k)}_{0,j-1}, \end{align*} $$

where each . Thus, (9) reduces to the system

(‡) $$ \begin{align} \begin{cases} \begin{aligned} b^{(k)}_{n_1-1,0} &= \mu^{(k-1)}_{n_1-1,0} &&\text{ if } i = n_1-1, \\ b^{(k)}_{i,0} &= \mu^{(k-1)}_{i,0} - \mu^{(k)}_{i+1,0} &&\text{ if } 0 \le i \le n_1-2, \\ b^{(k)}_{0,j} &= \mu^{(k-1)}_{0,j} - \mu^{(k)}_{0,j-1} &&\text{ if } 0 < j \le d_2, \text{ and } \\ b^{(k)}_{0,d_2+1} &= - \mu^{(k)}_{0,d_2} &&\text{ if } j = d_2+1. \end{aligned} \end{cases} \end{align} $$

This gives a system of linear equations in the variables $\mu _{i,j}^{(k)}$ which splits into two independent subsystems:

1. (i) all equations involving $\mu _{i,j}^{(k)}$ ’s with $k -i +j \le d_2$ ,

2. (ii) all equations involving $\mu _{i,j}^{(k)}$ ’s with $k -i +j> d_2$

(the quantity $k -i +j$ is constant among $\mu _{i,j}^{(k)}$ ’s in each equation). If $i = n_1-1$ , then $k - i \le d_2$ holds, because $k \le n_1$ and $d_2 \ge 1$ , so the first equation of (‡) belongs to (i). Also, $j = d_2$ implies $k + j> d_2$ exactly when $k> 0$ , so the fourth equation of (‡) belongs to (ii). For (i), after fixing the $\mu _{i,0}^{(n_1)}$ and $\mu _{0,j}^{(n_1)}$ arbitrarily, there is a unique solution given by

$$ \begin{align*} \mu_{i,0}^{(k)} &= \begin{cases} b_{i,0}^{(k+1)} + b_{i+1,0}^{(k+2)} + \dots +b_{n_1-1,0}^{(k+n_1-i)} & \text{if }i\geq k,\\ b_{i,0}^{(k+1)} +b_{i+1,0}^{(k+2)} +\dots +b_{i+n_1-k-1,0}^{(n_1)}+\mu_{i+n_1-k,0}^{(n_1)} & \text{if }i<k, \end{cases} \\ \mu_{0,j}^{(k)} &= \begin{cases} b_{0,j}^{(k+1)} + b_{0,j-1}^{(k+2)} + \dotsb + b_{0,j-n_1+k+1}^{(n_1)} + \mu_{0,j-n_1+k}^{(n_1)} &\text{if } j \ge n_1-k, \\ b_{0,j}^{(k+1)} + \dotsb + b_{0,1}^{(k+j)} + b_{0,0}^{(k+j+1)} + b_{1,0}^{(k+j+2)} \dotsb + b_{n_1-1-k-j,0}^{(n_1)} + \mu_{n_1-k-j,0}^{(n_1)} &\text{if } j < n_1-k. \end{cases} \end{align*} $$

For (ii), there is a unique solution given by

$$ \begin{align*} \mu_{i,0}^{(k)} &= -b_{i-1,0}^{(k)} -b_{i-2,0}^{(k-1)} - \dotsb -b_{0,0}^{(k-i+1)} -b_{0,1}^{(k-i)} -\dotsb -b_{0,d_2+1}^{(k-i-d_2)} \quad \text{ and } \\ \mu_{0,j}^{(k)} &= - b_{0,j+1}^{(k)} - b_{0,j+2}^{(k-1)} - \dotsb -b_{0,d_2+1}^{(k+j-d_2)}. \end{align*} $$

This proves that (‡), and thus (9), can be solved under the assumption that all $P_k = 0$ , and therefore that (8) and (9) can be solved under this assumption.

Lastly, we turn to the case where some $P_\ell \neq 0$ . Since $\operatorname {\mathrm {bideg}}(P_\ell ) = (n_1+1-d_1, d_2)$ , we must have $d_1> 1$ and $d_2<n_2$ . Applying Lemma 4.4(i), we see $0 < n_1+1-d_1<n_1$ . Now, for all k, we have

$$ \begin{align*} P_k &= \sum_{0<i<n_1} y^i (P_k)_{i,0} + (P_k)_{0,0} + \sum_{0<j<n_1} w^j (P_k)_{0,j} \\ &= \sum_{0<i\le n_1-d_1+1} y^i x^{n_1+1-d_1-i} z^{d_2} c^{(k)}_{i,0} + x^{n_1+1-d_1} z^{d_2} c^{(k)}_{0,0} + \sum_{0<j\le d_2} w^j x^{n_1+1-d_1} z^{d_2-j} c^{(k)}_{0,j}, \end{align*} $$

where each . Similarly, we have

$$ \begin{align*} \!\! y\pi_{k-1} &= y \left( \sum_{0<i<n_1} y^i (\pi_{k-1})_{i,0} + (\pi_{k-1})_{0,0} + \sum_{0<j<n_2} w^j (\pi_{k-1})_{0,j} \right) \\ &= y \left( \sum_{0<i\le n_1-d_1} y^i x^{n_1-d_1-i} z^{d_2} \lambda^{(k-1)}_{i,0} + x^{n_1-d_1} z^{d_2} \lambda^{(k-1)}_{0,0} + \sum_{0<j\le d_2} w^j x^{n_1-d_1} z^{d_2-j} \lambda^{(k-1)}_{0,j} \right) \\ &= \sum_{0<i\le n_1-d_1} y^{i+1} x^{n_1-d_1-i} z^{d_2} \lambda^{(k-1)}_{i,0} + yx^{n_1-d_1} z^{d_2} \lambda^{(k-1)}_{0,0} + \sum_{0<j\le d_2} w^{j-1} x^{n_1+1-d_1} z^{d_2-j+1} \lambda^{(k-1)}_{0,j} \\ &= \sum_{0<i\le n_1+1-d_1} y^{i} x^{n_1+1-d_1-i} z^{d_2} \lambda^{(k-1)}_{i-1,0} + x^{n_1+1-d_1} z^{d_2} \lambda^{(k-1)}_{0,1} + \sum_{0<j<d_2} w^{j} x^{n_1+1-d_1} z^{d_2-j} \lambda^{(k-1)}_{0,j+1} ,\end{align*} $$

along with

$$ \begin{align*} x\pi_{k} &= x \left( \sum_{0<i<n_1} y^i (\pi_{k})_{i,0} + (\pi_{k})_{0,0} + \sum_{0<j<n_2} w^j (\pi_{k})_{0,j} \right) \\ &= x \left( \sum_{0<i\le n_1-d_1} y^i x^{n_1-d_1-i} z^{d_2} \lambda^{(k)}_{i,0} + x^{n_1-d_1} z^{d_2} \lambda^{(k)}_{0,0} + \sum_{0<j\le d_2} w^j x^{n_1-d_1} z^{d_2-j} \lambda^{(k)}_{0,j} \right) \\ &= \sum_{0<i\le n_1-d_1} y^i x^{n_1+1-d_1-i} z^{d_2} \lambda^{(k)}_{i,0} + x^{n_1+1-d_1} z^{d_2} \lambda^{(k)}_{0,0} + \sum_{0<j\le d_2} w^j x^{n_1+1-d_1} z^{d_2-j} \lambda^{(k)}_{0,j}, \end{align*} $$

where each . Thus, (8) reduces to the following system:

(†) $$ \begin{align} \begin{cases} \begin{aligned} c^{(k)}_{n_1-d_1+1,0} &= \lambda^{(k-1)}_{n_1-d_1,0} &&\text{ if } i = n_1-d_1+1, \\ c^{(k)}_{i,0} &= \lambda^{(k-1)}_{i-1,0} - \lambda^{(k)}_{i,0} &&\text{ if } 0 < i \le n_1-d_1, \\ c^{(k)}_{0,j} &= \lambda^{(k-1)}_{0,j+1} - \lambda^{(k)}_{0,j} &&\text{ if } 0 \le j < d_2, \text{ and } \\ c^{(k)}_{0,d_2} &= - \lambda^{(k)}_{0,d_2} &&\text{ if } j = d_2. \end{aligned} \end{cases} \end{align} $$

This system has the same general form as (‡) and can be solved in exactly the same way.

Therefore, the system (†), and thus (8), can be solved when some $P_\ell \neq 0$ , and we may proceed to studying equality (9). It is easily seen from the basis $\mathcal {B}$ that multiplication-by-x defines an injective -linear map $A_{(i_1,i_2)} \to A_{(i_1+1,i_2)}$ between bigraded pieces of A when $0 \le i_1 < n_1-1$ . But $d_1 \ge 2$ , so Lemma 4.4 gives

$$ \begin{align*} xQ_k = wP_k = w(y\pi_{k-1} - x\pi_k) = xz\pi_{k-1} - xw\pi_k = x(z\pi_{k-1} - w\pi_k - x^{n_1-k}y^{k-1}\rho), \end{align*} $$

which implies that $\pi _0, \pi _1, \dotsc , \pi _{n_1}$ and $\rho $ satisfy (9), for any choice of $\rho $ .

To finish, we observe that by symmetry, the same approach solves the analogous equations (8 ^′) and (9 ^′) obtained from (8) and (9), where the roles of $x,y$ and $z,w$ are switched. To see that the solutions we obtain are consistent, note that $\rho $ is the only term appearing in both sets of equations (8), (9) and (8 ^′), (9 ^′), and that in every case, we can solve these equations with $\rho = 0$ . Hence, $\psi \colon L_2 \to A$ factors through a map $\psi ' \colon L_1 \to A$ .

Proof of Proposition 4.1.

Combine Propositions 4.3 and 2.3.

5 Trivial negative tangents, II

In this section, we study a new socle phenomenon of elementary components. We continue our study of negative tangents, focusing on the family of ideals described in Theorem 1.5. As before, let $I := \langle x,y \rangle ^{n_1} + \langle z,w \rangle ^{n_2} + \langle q \rangle $ , where $q := xz - yw$ and now $n_1, n_2 \ge 3$ , and set $A := S/I$ . We begin with a simple observation.

Lemma 5.1. The socle $\operatorname {\mathrm {Soc}} A$ is bigraded and equals $A_{(n_1-1,n_2-1)} = A_{n_1+n_2-2}$ .

In other words, Lemma 5.1 says that the socle of A equals the bidegree $(n_1-1,n_2-1)$ piece of A, which coincides with the total degree $n_1+n_2-2$ piece of A.

Proof. Since $\mathfrak {m}_A$ is bigraded, $\operatorname {\mathrm {Soc}} A$ is as well. When $i_1 \le n_1-2$ , multiplication-by-x gives an injective map $A_{(i_1,i_2)} \to A_{(i_1+1,i_2)}$ ; when $i_2 \le n_2-2$ , the multiplication-by-z map $A_{(i_1,i_2)} \to A_{(i_1,i_2+1)}$ is injective. It is clear that $x,y,z,w$ kill $A_{(n_1-1,n_2-1)}$ , thus, we find that $\operatorname {\mathrm {Soc}} A = A_{(n_1-1,n_2-1)} = A_{n_1+n_2-2}$ .

Let $J := I + \langle s \rangle $ , where $s \in S_{(n_1-1,n_2-1)} \smallsetminus I$ , and $B := S/J$ , so there is a short exact sequence

$$ \begin{align*} 0 \longrightarrow J/I \longrightarrow A \stackrel{\pi}{\longrightarrow} B \longrightarrow 0. \end{align*} $$

By Proposition 3.5, we know that I has trivial negative tangents—we wish to show that J has trivial negative tangents too. We could proceed directly as in Section 3, performing elementary computations; instead, we apply a standard long exact sequence in tangent cohomology (see Remark 2.1 and [18, Theorem 3.5]). Namely, the pair of natural ring maps leads to a long exact sequence containing the following portion:

(10)

which we use to show that .

Lemma 5.2. We have $T^1(B/A,B)_{<0} = 0$ and .

Proof. We examine first, using the notation of Section 4. The truncated cotangent complex of is described by ( ). As $L_0 \cong A(-1)^4$ in the standard grading, the B-dual is

$$ \begin{align*} \operatorname{\mathrm{Hom}}_A(L_{\bullet},B) \colon B(1)^4 \longrightarrow \operatorname{\mathrm{Hom}}_{A}(F/IF,B) \longrightarrow \operatorname{\mathrm{Hom}}_A(\mathcal{F}_{2}/\operatorname{\mathrm{Kos}}',B). \end{align*} $$

Let $\psi \colon L_1 = F/IF \to B$ represent an element of with $i < 0$ ; $\psi $ is determined by its values on the generators $(g;)$ of $L_1$ (listed just after ( )). Because the degrees satisfy $|\psi (g;)| = |g|+i < n_1+n_2-2 = |s|$ , the map $\pi $ identifies $A_{|\psi (g;)|}$ with $B_{|\psi (g;)|}$ . This allows us to define an A-linear map $\widetilde {\psi } \colon L_1 \to A$ satisfying $\psi = \pi \circ \widetilde {\psi }$ via $\widetilde {\psi }(g;) := \psi (g;)$ , for each g. Checking degrees also shows that $\widetilde {\psi } \circ d_2^{L} = 0$ : for instance, $|\psi \circ d_2^L(x^{n_1-k}y^k;x)| = n_1+1+i < n_1+n_2-2$ implies $\widetilde {\psi } \circ d_2^{L}(x^{n_1-k}y^k;x) = \psi \circ d_2^{L}(x^{n_1-k}y^k;x) = 0$ ; other generators similarly vanish. This means $\widetilde {\psi }$ defines an element of . We know , by Proposition 3.5, so $\widetilde {\psi }$ is a -linear combination of the trivial tangents $\partial _x, \partial _y, \partial _z, \partial _w$ . The identification of $\widetilde {\psi }(g;)$ with $\psi (g;)$ , for each g, then implies $\psi $ is a -linear combination of the trivial tangents. Thus, we have .

We examine $T^1(B/A,B)$ next, forming the truncated cotangent complex of $\pi $ . As $\pi $ is surjective, we set $R_{B/A} = A$ ; then we may choose $F_{B/A} = A(-n_1-n_2+2)$ as $J/I = \langle s +I \rangle $ is principal. Next, $Q_{B/A} = \mathfrak {m}_A(-n_1-n_2+2)$ holds, because $s +I \in \operatorname {\mathrm {Soc}} A$ ; this also guarantees that $\operatorname {\mathrm {Kos}}_{B/A} = 0$ . Finally, $\Omega _{R_{B/A}/A} = \Omega _{A/A} = 0$ , so we see that the truncated cotangent complex equals

$$ \begin{align*} L_{B/A,\bullet} \colon 0 \longleftarrow B(-n_1-n_2+2) \longleftarrow \mathfrak{m}_A(-n_1-n_2+2), \end{align*} $$

where the differential $d_2^{B/A}$ is a twist of $\pi |_{\mathfrak {m}_A} \colon \mathfrak {m}_A \to B$ . This implies

$$ \begin{align*} T^1(B/A,B) = \ker d_{B/A}^1 &= \{ \varphi \colon B(-n_1-n_2+2) \to B \mid \varphi \circ d_2^{B/A} = 0 \} \\ &= \{ \varphi \colon B(-n_1-n_2+2) \to B \mid \varphi|_{\mathfrak{m}_B} = 0 \} \cong (\operatorname{\mathrm{Soc}} B)(n_1+n_2-2), \end{align*} $$

so that $T^1(B/A,B)_{<0} = 0$ holds by the following lemma.

Lemma 5.3. The socle $\operatorname {\mathrm {Soc}} B$ is bigraded and equals $B_{(n_1-1,n_2-1)} = B_{n_1+n_2-2}$ .

Proof. As B and $\mathfrak {m}_B$ are bigraded, so $\operatorname {\mathrm {Soc}} B$ is bigraded. When $i_1 \le n_1-2$ and $i_2 \le n_2-2$ , the multiplication-by-x and -y maps $[x], [y] \colon B_{(i_1,i_2)} \to B_{(i_1+1,i_2)}$ and the multiplication maps $[z],[w] \colon B_{(i_1,i_2)} \to B_{(i_1,i_2+1)}$ are injective. When $(i_1,i_2) = (n_1-2,n_2-1)$ , the kernels of $[x]$ and $[y]$ have dimension at most $1$ . Suppose that $b \in B_{(n_1-2,n_2-1)}$ satisfies $xb = yb = 0$ ; treating b as an element of A, this means $xb$ and $yb$ are scalar multiples of s and thus of each other; a direct computation in the basis $\mathcal {B}$ then shows that $b=0$ . A similar occurrence holds for $[z]$ and $[w]$ , when $(i_1,i_2) = (n_1-1,n_2-2)$ . Thus, we find that $\operatorname {\mathrm {Soc}} B = B_{(n_1-1,n_2-1)} = B_{n_1+n_2-2}$ .

This proves the following.

Proposition 5.4. The ideal J has trivial negative tangents.

Proof. Lemmas 5.1, 5.2, and 5.3 show that , proving that via the long exact sequence (10).

We show next that the above arguments can oftentimes be iterated. This is done after a preliminary lemma.

Lemma 5.5. Let $s_1, s_2, \dotsc , s_r \in \operatorname {\mathrm {Soc}} A$ and $A^{(i)} = A / \langle s_1, s_2, \dotsc , s_i \rangle $ . If the socle of $A^{(r)}$ satisfies $\operatorname {\mathrm {Soc}} A^{(r)} = A^{(r)}_{(n_1-1, n_2-1)}$ , then $\operatorname {\mathrm {Soc}} A^{(i)} = A^{(i)}_{(n_1-1, n_2-1)}$ holds, for all $1 \leq i \leq r$ .

Proof. We have surjections

$$ \begin{align*} A = A^{(0)}\xrightarrow{\pi_0} A^{(1)}\xrightarrow{\pi_1}\dotsb \xrightarrow{\pi_{r-1}} A^{(r)}. \end{align*} $$

We already know $\operatorname {\mathrm {Soc}} A = A_{(n_1-1, n_2-1)}$ by Lemma 5.1. In particular, for all i, the image of $s_i$ in $A^{(i-1)}$ is contained in $A^{(i-1)}_{(n_1-1, n_2-1)}$ .

We prove the lemma by backwards induction on i. We have the following diagram

If $A^{(i)}_{(n_1-1,n_2-1)} \neq \operatorname {\mathrm {Soc}} A^{(i)}$ , then there exists $s \in \operatorname {\mathrm {Soc}} A^{(i)}$ with bidegree $(k,\ell ) \neq (n_1-1,n_2-1)$ . But then $\pi _i(s)\in A^{(i+1)}_{(k,\ell )}\cap \operatorname {\mathrm {Soc}} A^{(i+1)} = 0$ . Therefore, s is a scalar multiple of the image of $s_{i+1}$ , which we know is in $A^{(i)}_{(n_1-1, n_2-1)}$ , giving a contradiction.

Corollary 5.6. Let $s_1, s_2, \dotsc , s_{r} \in S$ ,

$$ \begin{align*} J' = I + \langle s_1, s_2, \dotsc, s_{r} \rangle, \end{align*} $$

and $B' = S/J'$ . Assume every $s_i+I\in \operatorname {\mathrm {Soc}} A$ and $\operatorname {\mathrm {Soc}} B' = B^{\prime }_{(n_1-1,n_2-1)}$ . Then $J'$ has trivial negative tangents.

Proof. We prove the result by induction on r. Proposition 5.4 handles the case $r = 1$ , so let $r> 1$ . Let $I^{(0)} := I$ , $I^{(i)} := I + \langle s_1, s_2, \dotsc , s_i \rangle $ , and $A^{(i)}=S/I^{(i)}$ for $1 \le i \le r$ . We may further suppose that $s_{i+1} + I^{(i)} \in \operatorname {\mathrm {Soc}} A^{(i)}$ is nonzero. Note that, by Lemma 5.5, $\operatorname {\mathrm {Soc}} A^{(i)} = A^{(i)}_{(n_1-1, n_2-1)}$ for all $1 \leq i \leq r$ .

Set $I' = I^{(r-1)}$ , $A' = S/I'$ , and $\pi ' \colon A' \to B'$ . We use the long exact sequence of the pair of ring maps

, studying the portion

To understand

, we use the truncated cotangent complex $L^{\prime }_{\bullet }$ of

. Let $\mathcal {F}^{\prime }_{\bullet }$ be the minimal free resolution of $A'$ ; we have

$$ \begin{align*} F' := \mathcal{F}^{\prime}_{1} = \mathcal{F}_1\oplus \bigoplus_{i = 1}^{r-1} S(s_i;), \end{align*} $$

where $(s_i;) \mapsto s_i$ and where $\mathcal {F}_{\bullet }$ is the minimal free resolution of A. Let

. We further assume that $\psi '$ is bigraded.

First, assume that $j<-1$ . Like in the proof of Lemma 5.2, we wish to lift a class to . We have $|\psi '(s_i;)| = n_1+n_2-2 +j < n_1+n_2-2$ , so we can define a map $\widetilde {\psi '} \colon F'/I'F' \to A'$ via $\widetilde {\psi '}(g;) := \psi '(g;)$ , for our generators $g \in I'$ . For this to define an element $[\widetilde {\psi '}]$ in cohomology, we need to show $\widetilde {\psi '} \circ d_2^{L'} = 0$ . Observe that $\mathcal {F}^{\prime }_2$ has the form

$$ \begin{align*} \mathcal{F}^{\prime}_2 = \mathcal{F}_2 \oplus \bigoplus_{i=1}^{r-1} S(s_i;x) \oplus S(s_i;y) \oplus S(s_i;z) \oplus S(s_i;w), \end{align*} $$

where $(s_i;x)$ maps to a choice of minimal syzygy arising from the fact that $xs_i \in I^{(i-1)}$ , and similarly for $(s_i;y)$ , $(s_i;z)$ , and $(s_i;w)$ (recall that $0 \neq s_i +I^{(i-1)} \in \operatorname {\mathrm {Soc}} A^{(i-1)}$ ). All generators of the form $(s_i;x)$ or $(s_i;y)$ have bidegree $(n_1, n_2-1)$ , while the generators of the form $(s_i;z)$ or $(s_i;w)$ have bidegree $(n_1-1, n_2)$ . Since $j<-1$ , we see $\operatorname {\mathrm {bideg}}(\psi ') \notin \{ (-1,0), (0,-1) \}$ . Then identifying (bi)graded pieces of B and A—like in the proof of Lemma 5.2—shows that $\widetilde {\psi '} \circ d_2^{L'} = 0$ , and therefore that $[\psi ']=0$ .

It remains to show that $[\psi ']$ is trivial when $\operatorname {\mathrm {bideg}}(\psi ') \in \{(-1,0), (0,-1)\}$ . We show this directly rather than lifting to $\widetilde {\psi '}$ . Suppose $\operatorname {\mathrm {bideg}}(\psi ') = (-1,0)$ . Note that $\psi ' \colon F'/I'F' \to B'$ is an $A'$ -linear map satisfying $\psi ' \circ d_2^{L'} = 0$ and so factors through $I'/I^{\prime 2}$ ; for simplicity, we work with the corresponding S-linear map $\varphi ' \colon I' \to B'$ . Considering $\operatorname {\mathrm {bideg}}(\psi ')$ , the generators of $I \subset I'$ have values

$$ \begin{align*} \varphi'(x^{n_1-k}y^k) = \sum_{0\le i<n_1} y^ix^{n_1-1-i}a^{(k)}_{i,0}, \quad \varphi'(z^{n_2-\ell}w^{\ell}) = 0, \quad \text{ and } \quad \varphi'(q) = az - a'w, \end{align*} $$

where , for all $0 \le k \le n_1$ . Observe that relation (4) holds for $\varphi '$ and takes place in $B^{\prime }_{(n_1-1,1)} = A^{\prime }_{(n_1-1,1)} = A_{(n_1-1,1)}$ . This implies that the proof of Proposition 3.5 applies verbatim to these values of $\varphi '$ ; in other words, $\varphi '$ acts as a derivative map on the generators of I, and so $\varphi '|_{I} = \delta |_{I}$ , where $\delta := \pi ' \circ (a\partial _x + a'\partial _y)$ and $a\partial _x + a'\partial _y \colon I' \to A'$ . As $xs_1, ys_1 \in I$ , we have $x\varphi '(s_1) = x\delta (s_1)$ and $y\varphi '(s_1) = y\delta (s_1)$ , and we see that $\varphi '(s_1) - \delta (s_1) \in (\operatorname {\mathrm {Soc}} B')_{(n_1-2, n_2-1)} = 0$ , which means $\varphi '(s_1) = \delta (s_1)$ . Thus, $\varphi '|_{I^{(1)}} = \delta |_{I^{(1)}}$ holds. Repeating this for $xs_2, ys_2 \in I^{(1)}$ now shows that $\varphi '|_{I^{(2)}} = \delta |_{I^{(2)}}$ holds, and continuing, we eventually obtain $\varphi ' = \delta $ . In other words, $\psi '$ is a trivial negative tangent vector, and a symmetric argument applies to the case $\operatorname {\mathrm {bideg}}(\psi ') = (0,-1)$ . Therefore, we have .

The argument to show $T^1(B'/A',B')_{<0} = 0$ mirrors the proof of Proposition 5.4, as $\pi ' \colon A' \to B'$ is a surjection, and we are assuming that $\operatorname {\mathrm {Soc}} B' = B^{\prime }_{(n_1-1, n_2-1)}$ . Hence, the long exact sequence proves that .

6 Vanishing nonnegative obstruction spaces, II

Continuing with the notation from Section 5, our goal here is to prove that . As before, the pair of natural ring maps yields a long exact sequence, which terminates as follows:

(11)

Let us first examine $T^2(B/A,B)$ . The truncated cotangent complex of $\pi \colon A \to B$ is described in the proof of Lemma 5.2; it is

$$ \begin{align*} L_{B/A,\bullet} \colon 0 \longleftarrow B(-n_1-n_2+2) \longleftarrow \mathfrak{m}_A(-n_1-n_2+2), \end{align*} $$

where the differential is a twist of $\mathfrak {m}_A \subset A \to B$ . By definition, this implies $T^2(B/A,B)$ is a quotient of $\operatorname {\mathrm {Hom}}_{B}(\mathfrak {m}_A(-n_1-n_2+2), B)$ , the latter being trivial in nonnegative degrees—that is, $\mathfrak {m}_A(-n_1-n_2+2)$ is generated in degree $n_1+n_2-1$ while $B_i = 0$ , for all $ i> n_1+n_2-2$ . This shows that

(12) $$ \begin{align} T^2(B/A,B)_{\ge 0} = 0. \end{align} $$

Recall that the truncated cotangent complex of is described in ( ) and equals

$$ \begin{align*} L_{\bullet} \colon A(-1)^4 \longleftarrow \mathcal{F}_{1} \otimes_S A \longleftarrow \mathcal{F}_{2}/\operatorname{\mathrm{Kos}}'. \end{align*} $$

We show the following.

Proposition 6.1. Let $B := S/J$ , where J is as in Section 5. We have .

Proof. We must examine . Suppose we are given an A-linear homomorphism $\psi \colon \mathcal {F}_{2}/\operatorname {\mathrm {Kos}}' \to B$ of nonnegative degree; decomposing $\psi $ , we may assume that $\psi $ has $\operatorname {\mathrm {bideg}}(\psi ) = (j_1,j_2) \in \mathbb {Z}^2$ , such that $j_1+j_2 \ge 0$ . We may think of $\psi $ as an S-linear map $\mathcal {F}_{2} \to B$ vanishing on $\operatorname {\mathrm {Kos}}'$ . As $\mathcal {F}_{2}$ is free, there is a bigraded lifting $\widetilde {\psi } \colon \mathcal {F}_{2} \to A$ , such that $\pi \circ \widetilde \psi = \psi $ . If $\widetilde \psi |_{\operatorname {\mathrm {Kos}}'} = 0$ , then $\widetilde \psi $ defines an element of , so $\widetilde \psi $ factors through $d_2^{L}$ ; then $\psi $ also factors through $d_2^L$ , showing that $\psi $ is trivial in .

So it remains to show that $\widetilde \psi |_{\operatorname {\mathrm {Kos}}'} = 0$ . Let $G \in \operatorname {\mathrm {Kos}}'$ be a minimal generator, and set $(i_1,i_2) := \operatorname {\mathrm {bideg}}(G)$ so that

$$ \begin{align*} (i_1,i_2) \in \{ (2n_1,0), (0,2n_2), (n_1,n_2), (n_1+1,1), (1,n_2+1) \}. \end{align*} $$

That is, the Koszul relation $x^{n_1-i}y^i (x^{n_1-i'}y^{i'};) - x^{n_1-i'}y^{i'} (x^{n_1-i}y^{i};)$ has bidegree $(2n_1,0)$ ; the Koszul relation $x^{n_1-i}y^i (q;) - q (x^{n_1-i}y^{i};)$ has bidegree $(n_1+1,1)$ ; etc. Without loss of generality, assume $n_1 \le n_2$ . Since $\pi \circ \widetilde \psi = \psi $ , we have

$$ \begin{align*} \widetilde\psi(G) \in J/I \subset A_{(n_1-1,n_2-1)}. \end{align*} $$

As $\widetilde \psi (G) \in A_{(i_1+j_1,i_2+j_2)}$ and $j_1+j_2 \ge 0$ , we immediately find that

$$ \begin{align*} (j_1,j_2) \notin \{ (-n_1-1,n_2-1), (-2,n_2-2), (n_1-2,-2)\}\quad\Longrightarrow\quad \widetilde\psi(G)=0. \end{align*} $$

In particular, for such $(j_1,j_2)$ , we have ; combining this with (11) and (12), we find .

To complete the proof, we must show that

for $(j_1,j_2)$ belonging to $\{ (-n_1-1,n_2-1), (-2,n_2-2), (n_1-2,-2)\}$ . Consider the long exact sequence induced by the ring maps

, which contains the following portion:

Because

is surjective, we have

since $j_1$ or $j_2$ is at most $-2$ (cf. [18, Proposition 3.8]). Since

$$ \begin{align*} T^2(B/A,B)_{(j_1,j_2)} = 0 \end{align*} $$

holds by (12), restricting this long exact sequence to the bidegree $(j_1,j_2)$ part shows that

. Hence, we have

.

Again, the argument iterates.

Corollary 6.2. Let $s_1, s_2, \dotsc , s_{r} \in S$ ,

$$ \begin{align*} J' = I + \langle s_1, s_2, \dotsc, s_{r} \rangle ,\end{align*} $$

and $B' = S/J'$ . Assume every $s_i+I\in \operatorname {\mathrm {Soc}} A$ and $\operatorname {\mathrm {Soc}} B' = B^{\prime }_{(n_1-1,n_2-1)}$ . Then $J'$ has vanishing nonnegative obstruction space.

Proof. We prove the result by induction on r. Proposition 6.1 handles the case $r = 1$ , so we take $r> 1$ . Let $I^{(0)} := I$ , $I^{(i)} := I + \langle s_1, s_2, \dotsc , s_i \rangle $ , and $A^{(i)}=S/I^{(i)}$ for $1 \le i \le r$ . We may further suppose that $s_{i+1} + I^{(i)} \in \operatorname {\mathrm {Soc}} A^{(i)}$ is nonzero. Note that, by Lemma 5.5, $\operatorname {\mathrm {Soc}} A^{(i)} = A^{(i)}_{(n_1-1, n_2-1)}$ for all $1 \leq i \leq r$ .

Set $I' = I^{(r-1)}$ , $A' = S/I'$ , and $\pi ' \colon A' \to B'$ . We use the long exact sequence of the pair of ring maps

, studying the portion

Our assumptions guarantee that the proof of the equality $T^2(B'/A',B')_{\ge 0} = 0$ follows exactly as in the case $r = 1$ .

As mentioned in the proof of Corollary 5.6, the minimal free resolution of $A'$ over S has terms

$$ \begin{align*} \mathcal{F}^{\prime}_{\bullet} \colon S \longleftarrow \mathcal{F}_1 \oplus \bigoplus_{i = 1}^{r-1} S(s_i;) \longleftarrow \mathcal{F}_2 \oplus \bigoplus_{i=1}^{r-1} \bigl( S(s_i;x) \oplus S(s_i;y) \oplus S(s_i;z) \oplus S(s_i;w) \bigr) \longleftarrow \dotsb. \end{align*} $$

We wish to apply the proof of Proposition 6.1 to an $A'$ -linear map $\psi ' \colon \mathcal {F}^{\prime }_2 / \operatorname {\mathrm {Kos}}" \to B'$ . Note that the generators of $\mathcal {F}^{\prime }_2$ not belonging to $\mathcal {F}_2$ all have degree $n_1+n_2-1$ . This implies that any $\psi '$ of nonnegative degree must vanish on these generators and any syzygies involving them. The same analysis of bidegrees as in the proof of Proposition 6.1 then holds, showing that . Hence, we have by the long exact sequence.

7 Dimensions of components

Let I be as in Theorem 1.3. Having now shown that $[I]$ is a smooth point of the Hilbert scheme and that the irreducible component containing $[I]$ is elementary, we compute the dimension of this component (see Corollary 7.3). This is achieved by explicitly computing the dimension of the tangent space $\operatorname {\mathrm {Hom}}_S(I,S/I)$ .

Let $\varphi \in \operatorname {\mathrm {Hom}}_S(I,S/I)$ . Our starting point is to reexamine relation (4), namely

$$ \begin{align*} x^{n_1-1-k}y^k \varphi(xz-yw) = z \varphi(x^{n_1-k}y^k) - w \varphi(x^{n_1-1-k}y^{k+1}), \end{align*} $$

where $0 \le k \le n_1-1$ .

Proposition 7.1. Let $q:=xz-yw$ , $r := \varphi (q)$ , and $p_k := \varphi (x^{n_1-k}y^k)$ , for $0 \le k \le n_1$ . Let $p^{\prime }_k \in \operatorname {\mathrm {Ann}}_{x,y}$ be such that $p_k-p^{\prime }_k$ is supported away from $\operatorname {\mathrm {Ann}}_{x,y}$ . For any $f\in S/I$ , let $f_{i,j}$ be as in Lemma 3.2. Each $(p^{\prime }_k)_{i,j}$ factors as $x^{n_1-1-i} (p^{\prime }_k)_{i,j}^z$ , where $(p^{\prime }_k)_{i,j}^z$ is some polynomial in z. Let $r_{0,j}^z$ denote the $x^0z^{\ge 0}$ -part of $r_{0,j}$ .

Then relation (4) is equivalent to the equations

(⋆ ^z ) $$\begin{align} \begin{cases} z(p_{k}')_{i,0}^z = (n_1-k)z^{k-i} r_{0,k-i}^z, &\text{ for } k \le i < n_1, \\ z(p_{k+1}')_{i+1,0}^z = z^{k-i} \left( z (p_{0}')_{0,k-i}^z - (k+1)r_{0,k-i}^z \right), &\text{ for } 0 \le i < k, \\ z^j(p_{k+1}')_{0,j-1}^z = z^{k+j} \left( z(p_0')_{0,k+j}^z - (k+1) r_{0,k+j}^z \right), &\text{ for } 0 < j < n_2. \end{cases} \end{align}$$

Note that terms in (⋆ ^z ) may vanish per Lemma 3.2, for example, if $k<i$ , then $r_{0,k-i}^z = 0$ .

Proof. In this notation, (4) becomes

$$ \begin{align*} x^{n_1-1-k}y^k r = z p_k - w p_{k+1}, \end{align*} $$

where $0\le k < n_1$ . Applying Lemma 3.2 to the left-hand side, we have

$$ \begin{align*} x^{n_1-1-k}y^kr &= x^{n_1-1-k}y^k \left( \sum_{0<i<n_1} y^i r_{i,0} + \sum_{0<j<n_2} w^j r_{0,j} + r_{0,0}\right) \\ &= \sum_{0<j<n_2} x^{n_1-1-k}y^k w^j r_{0,j}^z + x^{n_1-1-k}y^kr_{0,0}^z, \end{align*} $$

where $r_{0,j}^z$ denotes the $x^0z^{\ge 0}$ -part of the polynomial $r_{0,j} = r_{0,j}(x,z)$ , for $j \ge 0$ . This equals

$$ \begin{align*} &= \sum_{0<j\le k} y^{k-j} x^{n_1-1-k+j} z^j r_{0,j}^z + \sum_{k<j<n_2} w^{j-k} x^{n_1-1} z^k r_{0,j}^z + x^{n_1-1-k} y^k r_{0,0}^z \\ &= \sum_{0 \le i < k} y^i x^{n_1-1-i} z^{k-i} r_{0,k-i}^z + y^k x^{n_1-1-k} r_{0,0}^z + \sum_{0<j<n_2-k} w^j x^{n_1-1} z^k r_{0,k+j}^z \\ &= \sum_{0<i\le k} y^i x^{n_1-1-i} z^{k-i} r_{0,k-i}^z + \sum_{0<j<n_2-k} w^j x^{n_1-1} z^k r_{0,k+j}^z + x^{n_1-1} z^k r_{0,k}^z, \end{align*} $$

which is the expression guaranteed by Lemma 3.2 for the element $x^{n_1-1-k}y^k r \in A = S/I$ .

Now consider the right-hand side $zp_k - wp_{k+1}$ . A straightforward calculation with the expressions from Corollary 3.4 shows that $z p_k - w p_{k+1} = z p_k' - w p_{k+1}'$ , where $p_k'$ is the part of $p_k$ annihilated by x and y. For any element $f = \sum _{i>0} y^i f_{i,0} + \sum _{j>0} w^j f_{0,j} + f_{0,0}$ expressed using Lemma 3.2 and belonging to $\operatorname {\mathrm {Ann}}_{x,y} = A_{(n_1-1,*)}$ , we may assume $f_{i,j}$ has the form $x^{n_1-1-i} f_{i,j}^z$ , where $f_{i,j}^z$ is a polynomial in z. Thus, we have

$$ \begin{align*} zp_k' &= z\left( \sum_{0<i<n_1} y^i (p_k')_{i,0} + \sum_{0<j<n_2} w^j (p_k')_{0,j} + (p_k')_{0,0} \right) \\ &= z\left( \sum_{0<i<n_1} y^i x^{n_1-1-i} (p_k')_{i,0}^z + \sum_{0<j<n_2} w^j x^{n_1-1} (p_k')_{0,j}^z + x^{n_1-1} (p_k')_{0,0}^z \right) \\ &= \sum_{0<i<n_1} y^i x^{n_1-1-i} z (p_k')_{i,0}^z + \sum_{0<j<n_2-1} w^j x^{n_1-1} z (p_k')_{0,j}^z + x^{n_1-1} z (p_k')_{0,0}^z. \end{align*} $$

We also have

$$ \begin{align*} wp_{k+1}' &= w\left( \sum_{0<i<n_1} y^i (p_{k+1}')_{i,0} + \sum_{0<j<n_2} w^j (p_{k+1}')_{0,j} + (p_{k+1}')_{0,0} \right) \\ &= w\left( \sum_{0<i<n_1} y^i x^{n_1-1-i} (p_{k+1}')_{i,0}^z + \sum_{0<j<n_2} w^j x^{n_1-1} (p_{k+1}')_{0,j}^z + x^{n_1-1} (p_{k+1}')_{0,0}^z \right) \\ &= \sum_{0<i<n_1} y^{i-1} x^{n_1-i} z (p_{k+1}')_{i,0}^z + \sum_{0<j<n_2-1} w^{j+1} x^{n_1-1} (p_{k+1}')_{0,j}^z + w x^{n_1-1} (p_{k+1}')_{0,0}^z \\ &= \sum_{0<i<n_1-1} y^{i} x^{n_1-1-i} z (p_{k+1}')_{i+1,0}^z + \sum_{0<j<n_2} w^{j} x^{n_1-1} (p_{k+1}')_{0,j-1}^z + x^{n_1-1} z (p_{k+1}')_{1,0}^z ,\end{align*} $$

and combining these gives

$$ \begin{align*} zp_k' - wp_{k+1}' &= \sum_{0<i<n_1} y^i x^{n_1-1-i} z \left( (p_k')_{i,0}^z - (p_{k+1}')_{i+1,0}^z \right) \\ &\qquad\qquad + \sum_{0<j<n_2} w^j x^{n_1-1} \left( z (p_k')_{0,j}^z - (p_{k+1}')_{0,j-1}^z \right) + x^{n_1-1} z \left( (p_k')_{0,0}^z - (p_{k+1}')_{1,0}^z \right) \!, \end{align*} $$

where $i = n_1-1$ implies $(p_{k+1}')_{i+1,0}^z$ and $j = n_2-1$ implies $w^j z = 0$ . Thus, (4) is equivalent to the conditions

$$ \begin{align*} \begin{cases} z^{k-i} r_{0,k-i}^z = z (p_k')_{i,0}^z - z (p_{k+1}')_{i+1,0}^z, &\text{ for } 0 \le i < n_1 \\ w^j z^k r_{0,k+j}^z = w^j z (p_k')_{0,j}^z - w^j (p_{k+1}')_{0,j-1}^z, &\text{ for } 0 < j < n_2, \end{cases} \end{align*} $$

where terms may vanish for certain values of their indices (as indicated in the preceding summation notation). Moreover, these conditions are unchanged when w is replaced by z. When $i \ge k$ , we rewrite the first condition as

$$ \begin{align*} z (p_{k}')_{i,0}^z &= z (p_{k+1}')_{i+1,0}^z + z^{k-i} r_{0,k-i}^z = z (p_{k+2}')_{i+2,0}^z + 2z^{k-i} r_{0,k-i}^z = \dotsb \\ &= z (p_{n_1}')_{i+n_1-k,0}^z + (n_1-k)z^{k-i} r_{0,k-i}^z = (n_1-k)z^{k-i} r_{0,k-i}^z, \end{align*} $$

as $(p_{n_1}')_{n_1+i-k,0}^z = 0$ by definition. When $0 \le i < k$ , we rewrite the first condition differently as

$$ \begin{align*} z (p_{k+1}')_{i+1,0}^z &= z (p_{k}')_{i,0}^z - z^{k-i} r_{0,k-i}^z = z (p_{k-1}')_{i-1,0}^z - 2z^{k-i} r_{0,k-i}^z = \dotsb \\ &= z (p_{k-i}')_{0,0}^z - (i+1)z^{k-i} r_{0,k-i}^z \\ &= z^{k-i} \left( z (p_0')_{0,k-i}^z - (k-i)r_{0,k-i}^z \right) - (i+1)z^{k-i} r_{0,k-i}^z \\ &= z^{k-i} \left( z(p_0')_{0,k-i}^z - (k+1)r_{0,k-i}^z \right), \end{align*} $$

assuming the third condition in the statement of the proposition holds. To obtain the latter, we rewrite the second condition above as

$$ \begin{align*} z^j (p_{k+1}')_{0,j-1}^z &= z^{j+1} (p_k')_{0,j}^z - z^{k+j} r_{0,k+j}^z = z^{j+2} (p_{k-1}')_{0,j+1}^z - 2z^{k+j} r_{0,k+j}^z = \dotsb \\ &= z^{j+k+1} (p_{0}')_{0,j+k}^z - (k+1)z^{k+j} r_{0,k+j}^z. \end{align*} $$

Hence, we obtain the desired conditions.

Corollary 7.2. The unique irreducible component of $\operatorname {\mathrm {Hilb}}^{d}(\mathbb {A}^4)$ containing $[I]$ has dimension

$$ \begin{align*} D = D(n_1,n_2) := F(n_1,n_2) + F(n_2,n_1) + d(n_1,n_2) -1, \end{align*} $$

where

$$ \begin{align*} F(a,b) := \sum_{i=2}^{a-1} (i-1)\binom{b-i}{1} + (a-1)\binom{b-a+1}{2} + (a+1)(a+b-1) + \binom{b-1}{2}, \end{align*} $$

$d = d(n_1,n_2) = \frac {n_1n_2}{2}(n_1+n_2)$ , and $\binom {j}{k}$ denotes $\frac {j!}{k!(j-k)!}$ if $j \ge k \ge 0$ and is $0$ otherwise.

Proof. We shall compute the dimension of the tangent space $\operatorname {\mathrm {Hom}}_S(I, A)$ at the smooth point $[I]$ rather directly. A homomorphism $\varphi \colon I \to A$ is determined by its values

$$ \begin{align*} r = \varphi(xz-yw), p_k = \varphi(x^{n_1-k}y^k), q_{\ell} = \varphi(z^{n_2-\ell}w^{\ell}), \text{ for } 0 \le k \le n_1 \text{ and } 0 \le \ell \le n_2. \end{align*} $$

There are four kinds of relations that put restrictions on coefficients, namely:

1. (i) relations among $p_0, p_1, \dotsc , p_{n_1}$ described in Corollary 3.4;

2. (ii) relations among $q_0, q_1, \dotsc , q_{n_2}$ described in Corollary 3.4 with $n_1$ and $n_2$ swapped;

3. (iii) relations among $p_0, p_1, \dotsc , p_{n_1}$ and r described in Proposition 7.1;

4. (iv) relations among $q_0, q_1, \dotsc , q_{n_2}$ and r described in Proposition 7.1 with $n_1$ and $n_2$ swapped.

Moreover, these conditions are independent, in the sense that (i) only restricts the coefficients of the $p_k-p^{\prime }_k$ , whereas (iii) only restricts the coefficients of the $p_k'$ ’s and uses the coefficients of r as parameters (ensuring (iii) and (iv) are independent).

Starting with (i), we apply Corollary 3.4 to the sequence $p_0, p_1, \dotsc , p_{n_1}$ to show

$$ \begin{align*} p_k &= p_k' + \sum_{i=0}^{k} x^{n_1-k}y^{k-i}z^it_i + \sum_{i=k+1}^{n_1} x^{n_1-i}z^kw^{i-k}t_i \\ &= p_k' + \sum_{i=2}^{k} x^{n_1-k}y^{k-i}z^it_i + \sum_{i=k+1}^{n_1} x^{n_1-i}z^kw^{i-k}t_i, \end{align*} $$

where $p_k'$ is the part of $p_k$ annihilated by x (equivalently, y); the second equality follows as $i=0$ implies $x^{n_1-k}y^{k-0} = 0$ and $i=1$ gives either the term $x^{n_1-1}z^0w^{1-0}t_1 \in \operatorname {\mathrm {Ann}}(x)$ for $k=0$ or the term $x^{n_1-k}y^{k-1}z^1t_1 \in \operatorname {\mathrm {Ann}}(x)$ for $k> 0$ . Observe that the term containing $t_i$ also has a monomial of bidegree $(n_1-i,i)$ . Corollary 3.4 states that $t_i$ is a polynomial in $x,z$ for $2 \le i < n_1$ , so the x-degree satisfies $\deg _{x}(t_i) < i-1$ (a term of x-degree $i-1$ would produce an element of $\operatorname {\mathrm {Ann}}(x)$ ) and the z-degree satisfies $\deg _z(t_i) < n_2-i$ . These imply that $t_i$ has $(i-1)(n_2-i)$ free coefficients, if $i < n_2$ , and $0$ free coefficients, if $i \ge n_2$ ; we denote this number by $(i-1)\binom {n_2-i}{1}$ . Similarly, $t_{n_1}$ is a polynomial in $x,z,w$ and $\deg _x(t_{n_1}) < n_1-1$ and $\deg _{z,w}(t_{n_1}) < n_2-n_1$ . This gives $(n_1-1) \binom {2+n_2-n_1-1}{2} = (n_1-1) \binom {n_2-n_1+1}{2}$ free coefficients. Thus, a formula for the contribution of $t_2, \dotsc , t_{n_1}$ to the dimension is

(t _i -count) $$\begin{align} \sum_{i=2}^{n_1-1} (i-1)\binom{n_2-i}{1} + (n_1-1)\binom{n_2-n_1+1}{2}. \end{align} $$

The analogous count using (ii) is obtained by swapping $n_1$ and $n_2$ .

For (iii), we use Proposition 7.1 to find free parameters in each $p_k'$ . The first condition of (⋆ ^z ) says that the coefficients $f_0, f_1, \dotsc , f_{n_2-2}$ of $f_0 + f_1z + \dotsb + f_{n_2-1}z^{n_2-1} := (p_k')_{i,0}^z$ are determined by those of $r_{0,k-i}^z$ ; only the coefficient $f_{n_2-1}$ is free, so $(p_k')_{i,0}^z$ contributes exactly one degree of freedom (when $k < i$ , we have $r_{0,k-i}^z := 0$ ; when $k = i$ , we get $z(p_k')_{k,0}^z = (n_1-k)r_{0,0}^z$ , further implying $r_{0,0}^z$ (and in turn r) has trivial constant term—this is expected as I has trivial negative tangents and $\deg q = 2$ ). The second condition of (⋆ ^z ) says that the coefficients $f_0, f_1, \dotsc , f_{n_2-2}$ of $f_0 + f_1z + \dotsb + f_{n_2-1}z^{n_2-1} := (p_{k+1}')_{i+1,0}^z$ are determined by those of $(p_0')_{0,k-i}^z$ and $r_{0,k-i}^z$ ; the coefficient $f_{n_2-1}$ is free. The third condition of (⋆ ^z ) says that the coefficients $f_0, f_1, \dotsc , f_{n_2-j-1}$ of $f_0 + f_1z + \dotsb + f_{n_2-j}z^{n_2-j} := (p_{k+1}')_{0,j-1}^z$ are determined by those of $(p_0')_{0,k+j}^z$ and $r_{0,k+j}^z$ ; the coefficient $f_{n_2-j}$ is free. In other words, letting $0 < \kappa \le n_1$ , every term in the following expansion contributes a single degree of freedom:

$$ \begin{align*} p_{\kappa}' &= \sum_{0<\iota<n_1} y^{\iota}x^{n_1-1-\iota}(p_{\kappa}')_{\iota,0}^z + x^{n_1-1}(p_{\kappa}')_{0,0}^z + \sum_{0<\eta<n_2} w^{\eta}x^{n_1-1}(p_{\kappa}')_{0,\eta}^z, \\ &= \sum_{0<\iota<\kappa} y^{\iota}x^{n_1-1-\iota}(p_{\kappa}')_{\iota,0}^z + \sum_{\kappa\le \iota<n_1} y^{\iota}x^{n_1-1-\iota}(p_{\kappa}')_{\iota,0}^z \\ &\qquad\qquad\qquad\qquad + x^{n_1-1}(p_{\kappa}')_{0,0}^z + \sum_{0<\eta<n_2} w^{\eta}x^{n_1-1}(p_{\kappa}')_{0,\eta}^z, \\ &= \sum_{0\le i<k} y^{i+1}x^{n_1-2-i}(p_{k+1}')_{i+1,0}^z + \sum_{\kappa\le \iota<n_1} y^{\iota}x^{n_1-1-\iota}(p_{\kappa}')_{\iota,0}^z \\ &\qquad\qquad\qquad\qquad + x^{n_1-1}(p_{k+1}')_{0,0}^z + \sum_{1<j<n_2+1} w^{j-1}x^{n_1-1}(p_{k+1}')_{0,j-1}^z, \end{align*} $$

where $k = \kappa -1$ , $i = \iota -1$ , and $j = \eta +1$ ; the only term here not covered by (⋆ ^z ) is $(p_{k+1}')_{0,n_2-1}^z$ , which is therefore a free constant. As each term contributes one degree of freedom, the contribution by $p_1', p_2', \dotsc , p_{n_1}'$ equals $n_1(n_1+n_2-1)$ . Now considering

$$ \begin{align*} p_{0}' &= \sum_{0<i<n_1} y^{i}x^{n_1-1-i}(p_{0}')_{i,0}^z + x^{n_1-1}(p_{0}')_{0,0}^z + \sum_{0<j<n_2} w^{j}x^{n_1-1}(p_{0}')_{0,j}^z, \end{align*} $$

we find that each $(p_{0}')_{i,0}^z$ contributes one degree of freedom, for $i \ge 0$ , giving $n_1$ . Each $(p_{0}')_{0,j}^z$ is free and contributes $n_2-j$ degrees of freedom, for $0 < j < n_2$ , giving $\sum _{j=1}^{n_2-1} n_2-j = \binom {n_2}{2}$ . Thus, a formula for the contribution to the dimension by $p_0', p_1', \dotsc , p_{n_1}'$ is

(p ^′ _κ-count) $$\begin{align} n_1(n_1 + n_2) + \binom{n_2}{2}. \end{align} $$

The analogous count for (iv) is obtained by swapping $n_1$ and $n_2$ , and neither (iii) nor (iv) restricts the coefficients of r.

The total contribution by $p_0, p_1, \dotsc , p_{n_1}$ to the dimension is therefore the sum of ( t _i -count) and ( p ^′ _κ-count), which equals

$$ \begin{align*} F(n_1,n_2) := \sum_{i=2}^{n_1-1} (i-1)\binom{n_2-i}{1} + (n_1-1)\binom{n_2-n_1+1}{2} + n_1(n_1+n_2) + \binom{n_2}{2}. \end{align*} $$

Symmetrically, the contribution by $q_0, q_1, \dotsc , q_{n_2}$ is $F(n_2,n_1)$ . To finish, we need the contribution by r. The only condition on r, imposed by (⋆ ^z ) when $k=i$ , is of having a trivial constant term. Thus, r contributes dimensions.

Hence, combining with the dimension formula in Lemma 3.2, we see

as desired.

Corollary 7.3. The dimension D simplifies to

$$ \begin{align*} D = \frac{1}{3}m^3 + mM^2 + m^2 + 2mM + M^2 - \frac{1}{3}m -1, \end{align*} $$

where $m := \min \{n_1,n_2\}$ and $M := \max \{n_1,n_2\}$ . In particular, the dimension D of the irreducible component of $\operatorname {\mathrm {Hilb}}^{d}(\mathbb {A}^4)$ containing the point $[I]$ satisfies $D<4d$ , and moreover, if $(m,M) \notin \{(2,2), (2,3), (2,4)\}$ , then $D<3(d-1)$ .

Proof. Let $a=n_1, b=n_2$ , and assume $a \le b$ without loss of generality. We first simplify the summations in $F(a,b)$ and $F(b,a)$ coming from ( t _i -count). For $F(a,b)$ , we have

$$ \begin{align*} \sum_{i=2}^{a-1} (i-1)\binom{b-i}{1} &= \sum_{i=2}^{a-1} (i-1)(b-i) = \sum_{i=1}^{a-2} i(b-1-i) = (b-1)\sum_{i=1}^{a-2} i - \sum_{i=1}^{a-2} i^2 \\ &= (b-1)\binom{a-1}{2} - \binom{a-1}{2}\frac{2(a-2)+1}{3} = \binom{a-1}{2} \left( b - \frac{2}{3}a \right) \end{align*} $$

so that

$$ \begin{align*} F(a,b) = \binom{a-1}{2} \left( b - \frac{2}{3}a \right) + (a-1)\binom{b-a+1}{2} + a(a+b) + \binom{b}{2}. \end{align*} $$

For $F(b,a)$ , we have

$$ \begin{align*} \sum_{i=2}^{b-1} (i-1)\binom{a-i}{1} &= \sum_{i=2}^{a-1} (i-1)(a-i) = \sum_{i=1}^{a-2} i(a-1-i) = (a-1)\sum_{i=1}^{a-2} i - \sum_{i=1}^{a-2} i^2 \\ &= (a-1)\binom{a-1}{2} - \binom{a-1}{2}\frac{2a-3}{3} = \binom{a-1}{2} \frac{1}{3}a \end{align*} $$

so that

$$ \begin{align*} F(b,a) = \binom{a-1}{2} \frac{1}{3}a + 0 + b(a+b) + \binom{a}{2}, \text{ as } (b-1)\binom{a-b+1}{2} = 0. \end{align*} $$

Therefore, we find that

$$ \begin{align*} D &= F(a,b) + F(b,a) + d(a,b) -1 \\ &= \binom{a-1}{2} \left( b - \frac{1}{3}a \right) + (a-1)\binom{b-a+1}{2} + (a+b)^2 + \binom{a}{2} + \binom{b}{2} + \frac{ab(a+b)}{2} -1, \end{align*} $$

which gives the desired expression $\frac {1}{3}a^3 + ab^2 + a^2 + 2ab + b^2 - \frac {1}{3}a -1$ when expanded.

Now we examine when $3(d-1)> D$ , or rather

$$ \begin{align*} 3(d-1) - D &= 3\frac{ab(a+b)}{2} -3 - \left( \frac{1}{3}a^3 + ab^2 + a^2 + 2ab + b^2 - \frac{1}{3}a -1 \right) \\ &= -\frac{1}{3}a^3 +\frac{3}{2}a^2b + \frac{1}{2}ab^2 -a^2 -2ab -b^2 +\frac{1}{3}a -2 \\ &= \left(\frac{1}{2}a-1\right)b^2 + \left(\frac{3}{2}a^2 -2a\right)b -\frac{1}{3}a^3 -a^2 +\frac{1}{3}a -2>0. \end{align*} $$

If $a=2$ , then this reduces to $2b - 8> 0$ , so the inequality is satisfied if and only if $b> 4$ . Now let $a> 2$ . Then $3(d-1)-D$ is quadratic in b with roots

$$ \begin{align*} r_{\pm}(a) = \frac{2a-\frac{3}{2}a^2 \pm \sqrt{\left(\frac{3}{2}a^2 -2a\right)^2 - 4\left(\frac{1}{2}a-1\right)\left(-\frac{1}{3}a^3 -a^2 +\frac{1}{3}a -2 \right)}}{a-2} \end{align*} $$

and discriminant simplifying to $\frac {35}{12}a^4 -\frac {16}{3}a^3 -\frac {2}{3}a^2 +\frac {16}{3}a -8$ ; the discriminant is positive for $a>2$ . If both roots satisfy $r_{\pm }(a) < a$ , then $a \le b$ implies $3(d-1) - D> 0$ , as the $b^2$ -term in the expression for $3(d-1) - D$ has a positive coefficient. We check

$$ \begin{align*} a> r_{\pm}(a) &\Longleftrightarrow a^2-2a > 2a-\frac{3}{2}a^2 \pm \sqrt{\frac{35}{12}a^4 -\frac{16}{3}a^3 -\frac{2}{3}a^2 +\frac{16}{3}a -8} \\ &\Longleftrightarrow \left(\frac{5}{2}a^2 -4a\right)^2 > \frac{35}{12}a^4 -\frac{16}{3}a^3 -\frac{2}{3}a^2 +\frac{16}{3}a -8 \\ &\Longleftrightarrow \frac{10}{3}a^4 -\frac{44}{3}a^3 +\frac{50}{3}a^2 -\frac{16}{3}a +8 > 0. \end{align*} $$

The latter factors as $\frac {2}{3}(a-2)(5a^3 -12a^2 +a -6)$ and is positive for $a\ge 3$ . Hence, the point $[I] \in \operatorname {\mathrm {Hilb}}^d(\mathbb {A}^4)$ lies on a component of dimension $D < 3(d-1)$ .

When $(a,b) \in \{(2,2), (2,3), (2,4)\}$ , we immediately find $D(a,b) < 4d(a,b)$ . Hence, here the point $[I] \in \operatorname {\mathrm {Hilb}}^d(\mathbb {A}^4)$ lies on a component of dimension $D < 4d$ .

Remark 7.4. When $n_1 = n_2 = n$ , we obtain $D = \frac {4}{3}n^3 + 4n^2 - \frac {1}{3}n -1$ and $4d = 4n^3$ .

8 Compendium of elementary components

Collecting the results from Sections 3–7, we prove the theorems from the Introduction.

Proof of Theorems 1.3 and 1.5.

Let I be as in Theorem 1.3. Proposition 3.1 shows that every irreducible component containing $[I]$ is elementary. Proposition 4.1 then shows that $[I]$ is a smooth point, so it must lie on a unique irreducible component. The formula for is given in Lemma 3.2. Lastly, the formula for the dimension D of the irreducible component containing $[I]$ is given in Corollary 7.3, where it is also shown that $D<4d$ and if $(m,M)\notin \{(2,2),(2,3),(2,4)\}$ , then $D<3(d-1)$ . This proves Theorem 1.3.

Finally, let J be as in Theorem 1.5. Corollary 5.6 shows that J has trivial negative tangents, so every component containing it is elementary by [29, Theorem 1.2]. Corollary 6.2 then proves that $[J]$ is a smooth point, so it must lie on a unique irreducible component. Lastly, Lemma 5.3 shows that the condition on the socle is automatic when $r=1$ . This proves Theorem 1.5.

Proof of Theorem 1.2.

Let I, d, and D be as in Theorem 1.3. By Theorem 2.2, there is an open subset $U\subset X:=\operatorname {\mathrm {Hilb}}^+_{d}(\mathbb {A}^4) \times \mathbb {A}^4$ , such that $\theta |_U\colon U\to \operatorname {\mathrm {Hilb}}^d(\mathbb {A}^4)$ is an open immersion with $\theta |_U\bigl (([I],0)\bigr )=[I]$ . Consider the Cartesian diagram

where $\mathcal {Z}$ is the reduced closed subscheme of points $[J]$ supported at the origin. By Theorem 1.3, we know $[I]$ is a smooth point contained on a unique elementary component, so shrinking U if necessary, we may assume U is smooth, irreducible, and of dimension D.

We show that every irreducible component of V containing $([I],0)$ has dimension exactly equal to $D-4$ . For the purposes of computing dimensions, it suffices to replace V by its reduction $V_{\textrm {red}}$ . Since $V\subset Z$ is open, $V_{\textrm {red}}=V\times _Z Z_{\textrm {red}}$ , and so we may replace Z by any closed subscheme of X whose reduction agrees with $Z_{\textrm {red}}$ . By definition of $\theta $ , the -points of Z are precisely those of $X_0:=\operatorname {\mathrm {Hilb}}^+_{d}(\mathbb {A}^4) \times \{0\}$ . Thus, $X_0$ and Z have the same reduction. We have therefore reduced to showing that $\dim (U\cap X_0)=D-4$ .

Since $U\subset X$ is open and $X=\operatorname {\mathrm {Hilb}}^+_{d}(\mathbb {A}^4)\times \mathbb {A}^4 \to \mathbb {A}^4$ is flat, we have a flat map $f\colon U\to \mathbb {A}^4$ . Then $U\cap X_0$ is the fiber of f over $0$ . As U and $\mathbb {A}^4$ are smooth and irreducible -schemes, we see $\dim (U\cap X_0)= \dim (U)-4=D-4$ .

Hence, this shows that every irreducible component of $\mathcal {Z}$ containing $[I]$ has dimension at most $D-4$ . Theorem 1.3 tells us $D<3(d-1)$ for $(m,M)\notin \{(2,2),(2,3),(2,4)\}$ , and one verifies $D-4 < 3(d-1)$ when $(m,M) \in \{(2,3),(2,4)\}$ .

Proof of Corollary 1.4.

First, $\widetilde {A} := \widetilde {S}/\widetilde {I} \cong A$ so

. Next, we compute the dimension of the tangent space of $\operatorname {\mathrm {Hilb}}^d(\mathbb {A}^n)$ at $[\widetilde {I}]$ . Note that if $\widetilde {\varphi } \in \operatorname {\mathrm {Hom}}_{\widetilde {S}}(\widetilde {I},\widetilde {A})$ , then $\widetilde {\varphi }|_I\in \operatorname {\mathrm {Hom}}_S(I,A)$ . Since every minimal syzygy involving some $u_i$ is Koszul, $\widetilde {\varphi }(u_i)$ can take any value in $\widetilde {A}$ . In particular, $\widetilde {I}$ has trivial negative tangents, and moreover, we find

Since $\widetilde {A}$ is isomorphic to A as

-algebras, the vanishing of

follows from that of

. Hence, by Proposition 2.3, $[\widetilde {I}]$ is a smooth point and therefore lives on a unique component which is elementary.

This component has dimension strictly less than $(n-1)(d-1) = (3+r)(d-1)$ if $D < 3(d-1)-r$ . The proof of Corollary 7.3 shows that this inequality is always satisfied for sufficiently large $n_1$ and $n_2$ . Indeed, letting $a=\min (n_1,n_2)$ and $b=\max (n_1,n_2)$ , we see

(13) $$ \begin{align} 3(d-1)-r-D=\left(\frac{1}{2}a-1\right)b^2 + \left(\frac{3}{2}a^2 -2a\right)b -\frac{1}{3}a^3 -a^2 +\frac{1}{3}a -2-r. \end{align} $$

For $a>2$ , this is a quadratic in b with positive leading term; for $a=2$ , this is a linear expression in b with positive leading term. In either case, for fixed a, and b sufficiently large, this expression is positive.

Remark 8.1. Let $m=\min (n_1,n_2)$ and $M=\max (n_1,n_2)$ . By considering the quadratic (13), we see the unique component containing $[\widetilde {I}]\in \operatorname {\mathrm {Hilb}}^d(\mathbb {A}^n)$ has dimension strictly less than $(n-1)(d-1)$ if

$$ \begin{align*} m=2\quad\quad\textrm{and}\quad\quad M>\frac{r}{2}+4. \end{align*} $$

If $m>2$ , then one computes that the discriminant of the quadratic in b is positive and so (13) is positive whenever M is strictly larger than the positive root of the quadratic. That is, letting

$$ \begin{align*} r_+:= \frac{2m-\frac{3}{2}m^2 \pm \sqrt{\left(\frac{3}{2}m^2 -2m\right)^2 - 4\left(\frac{1}{2}m-1\right)\left(-\frac{1}{3}m^3 -m^2 +\frac{1}{3}m -2 -r\right)}}{m-2} ,\end{align*} $$

we see if

$$ \begin{align*} m>2\quad\quad\textrm{and}\quad\quad M>r_+ ,\end{align*} $$

then the unique component containing $[\widetilde {I}]\in \operatorname {\mathrm {Hilb}}^d(\mathbb {A}^n)$ has dimension strictly less than $(n-1)(d-1)$ .

We end the paper by discussing some examples and variations of Theorems 1.3 and 1.5. For a survey of the known elementary components prior to our work, see [29, Remark 6.10] and the section on smoothability in [1, Appendix B].

Example 8.2. Plugging in some values of $(n_1,n_2)$ to define I, we obtain the following:

• • for $(n_1,n_2) = (2,2)$ , the point $[I] \in \operatorname {\mathrm {Hilb}}^8(\mathbb {A}^4)$ lies on the $25$ -dimensional component first discovered by Iarrobino–Emsalem [26, Section 2.2];

• • for $(n_1,n_2) = (2,3)$ , the point $[I] \in \operatorname {\mathrm {Hilb}}^{15}(\mathbb {A}^4)$ is smooth on a $44$ -dimensional component;

• • for $(n_1,n_2) = (2,4)$ , the point $[I] \in \operatorname {\mathrm {Hilb}}^{24}(\mathbb {A}^4)$ is smooth on a $69$ -dimensional component;

• • for $(n_1,n_2) = (2,5)$ , the point $[I] \in \operatorname {\mathrm {Hilb}}^{35}(\mathbb {A}^4)$ is smooth on a $100$ -dimensional component;

• • for $(n_1,n_2) = (3,3)$ , the point $[I] \in \operatorname {\mathrm {Hilb}}^{27}(\mathbb {A}^4)$ is smooth on a $70$ -dimensional component;

• • for $(n_1,n_2) = (3,4)$ , the point $[I] \in \operatorname {\mathrm {Hilb}}^{42}(\mathbb {A}^4)$ is smooth on a $104$ -dimensional component.

The scheme $\operatorname {\mathrm {Hilb}}^{35}(\mathbb {A}^4)$ is already known to have a $124$ -dimensional elementary component, denoted $\mathcal {Z}(3)$ in [29]. Thus, this Hilbert scheme has at least two elementary components.

Example 8.3. Consider the following example, where Theorem 1.5 holds. Define I using $(n_1, n_2) = (3,3)$ , and set $s_1 := x^2z^2$ , $s_2 := x^2w^2$ , and $s_3 := y^2z^2$ . For $0\leq i\leq 3$ , let $I^{(i)} := I + \langle s_1, \dotsc , s_i \rangle $ and $A^{(i)}=S/I^{(i)}$ . One can verify that

• • the point $[I^{(0)}] \in \operatorname {\mathrm {Hilb}}^{27}(\mathbb {A}^4)$ is smooth on a $70$ -dimensional component (as above);

• • the point $[I^{(1)}] \in \operatorname {\mathrm {Hilb}}^{26}(\mathbb {A}^4)$ is smooth on a $77$ -dimensional component;

• • the point $[I^{(2)}] \in \operatorname {\mathrm {Hilb}}^{25}(\mathbb {A}^4)$ is smooth on an $82$ -dimensional component;

• • the point $[I^{(3)}] \in \operatorname {\mathrm {Hilb}}^{24}(\mathbb {A}^4)$ is smooth on an $85$ -dimensional component.

That is, each $[I^{(i)}] \in \operatorname {\mathrm {Hilb}}^{27-i}(\mathbb {A}^4)$ is a smooth point on an elementary component of dimension less than that of the main component, namely, $4(27-i)$ . Furthermore, we see that $\operatorname {\mathrm {Hilb}}^{24}(\mathbb {A}^4)$ has at least two elementary components, by comparing with Example 8.2.

Example 8.4. Further examples similar to Example 8.3 can be found. For instance, the ideals

$$ \begin{align*} I &= \langle x,y \rangle ^4 + \langle z,w \rangle ^4 + \langle xz-yw, xy^2w^3, x^3w^3, y^3zw^2, y^3z^3 \rangle \quad\text{and} \\ I &= \langle x,y \rangle ^3 + \langle z,w \rangle ^5 + \langle xz-yw \rangle \end{align*} $$

lie on distinct elementary components of $\operatorname {\mathrm {Hilb}}^{60}(\mathbb {A}^4)$ of respective dimensions $179$ and $146$ .

Example 8.5. It is an amusing coincidence that the point $[I] \in \operatorname {\mathrm {Hilb}}^{10^3}(\mathbb {A}^4)$ defined by

$$ \begin{align*} I = \langle x,y \rangle ^{10} + \langle z,w \rangle ^{10} + \langle xz-yw \rangle \end{align*} $$

lies on an elementary component of dimension $1729$ . The dimension $1729$ is the second taxicab number, that is, the minimal positive integer expressible as a sum of two distinct cubes in two different ways: $1729 = 9^3+10^3 = 1^3+12^3$ .

Example 8.6. As mentioned in the Introduction (see Question 1.7), producing a local, zero-dimensional Gorenstein quotient of S with trivial negative tangents gives a way to distinguish cactus and secant varieties (see [5, Proposition 7.4]). Our techniques allow us to produce an example with socle-dimension $2$ (as opposed to socle-dimension $1$ ).

Let us return to the setting of Example 8.3. Letting $(n_1, n_2) = (3,3)$ , we find that

$$ \begin{align*} \operatorname{\mathrm{Soc}} A = \langle x^2z^2 +I, x^2zw +I, x^2w^2 +I, xyz^2 +I, y^2z^2 +I \rangle \end{align*} $$

is $5$ -dimensional.

Then,

$$ \begin{align*}\operatorname{\mathrm{Soc}} A^{(3)} = \langle x^2zw +I^{(2)}, xyz^2 +I^{(2)} \rangle\end{align*} $$

is $2$ -dimensional. By Theorem 1.5 and Remark 1.6, $A^{(3)}$ has trivial negative tangents and vanishing nonnegative obstruction space.

Remark 8.7. Natural variants of the ideals in Theorem 1.3 also produce trivial negative tangents. For instance, Table 1 displays some triples $(n_1,n_2,n_3)$ that determine ideals

$$ \begin{align*} J := \langle x,y \rangle ^{n_1} + \langle z,w \rangle ^{n_2} + \langle xz-yw, (xz)^{n_3} \rangle \end{align*} $$

with trivial negative tangents, verified by direct computations in Macaulay2 [15] (for any ideal, it suffices to check that $T^1_{A,i} = 0$ for finitely many $i<0$ ; e.g., if I is homogeneous, then $\operatorname {\mathrm {Hom}}(I,S/I)_{<-N} = 0$ , where N is the highest degree of a generator of I). Letting $B := S/J$ for $(n_1,n_2,n_3) = (4,4,2)$ , one can verify that the quotient $B/ \langle s_1,s_2,s_3,s_4 \rangle $ has trivial negative tangents and socle-dimension $2$ , where each $s_i$ is sufficiently general inside the socle of $B/ \langle s_1,s_2,\dotsc ,s_{i-1} \rangle $ .

Furthermore, setting

, the examples in Table 1 satisfy the inequality

. For $(n_1,n_2,n_3) \neq (4,4,2)$ , we have the stronger inequality

These examples may define singular points $[J]$ , however, since the obstruction spaces

are nontrivial. Thus, the examples from Table 1 define (possibly singular) points which lie exclusively on elementary components of $\operatorname {\mathrm {Hilb}}^{d_B}(\mathbb {A}^4)$ with dimensions less than that of the main component; moreover, with the exception of $(4,4,2)$ , Table 1 provides additional examples which answer Question 1.1.

Table 1 Triples defining further ideals with trivial negative tangents

Remark 8.8. Theorem 1.5 also allows one to produce natural points on the nested Hilbert scheme, which parametrizes flags of ideals. Specifically, letting $I^{(i)}=I+ \langle s_1,\dots ,s_i \rangle $ , we see that

$$ \begin{align*} [I^{(r)}\supset\dotsb\supset I^{(1)}\supset I] \in \operatorname{\mathrm{Hilb}}^{(d-r,\dots,d-1,d)}(\mathbb{A}^4). \end{align*} $$

Preliminary investigations suggest the points $[J\supset I] \in \operatorname {\mathrm {Hilb}}^{(d-1,d)}(\mathbb {A}^4)$ are smooth. This raises the question: Does $[I^{(r)}\supset \dotsb \supset I^{(1)}\supset I]$ always define a smooth point of $\operatorname {\mathrm {Hilb}}^{(d-r,\dots ,d-1,d)}(\mathbb {A}^4)$ ?

9 Failure of surjectivity for $\partial _{\geq 0}$ and $\psi _{<0}$

As mentioned in subsection 1.1 of the Introduction, Jelisiejew [29] circumvents the need for explicit computations by making use of the flag Hilbert scheme. To do so, he needs surjectivity of two particular maps, $\partial _{\geq 0}$ and $\psi _{<0}$ (see [29, Diagram 2.1]). In this section, we prove that both of these maps fail to be surjective for our examples, and hence, one cannot apply arguments as in [29, Corollary 4.13] and [29, Proof of Theorem 1.4] to prove smoothness and trivial negative tangents of $[I]$ .

Proposition 9.1. Keep the notation as in Theorem 1.3. Then:

• • $\psi _{<0}$ is not surjective, and

• • if $\min (n_1,n_2)\geq 4$ , then $\partial _{\geq 0}$ is not surjective.

Proof. Let $M = \langle x,y \rangle ^{n_1}+ \langle z,w \rangle ^{n_2}$ . Then $I = M+ \langle q \rangle $ with $q = xz-yw$ . Without loss of generality, $n_1\le n_2$ . The exact sequences

$$ \begin{align*} 0 \to M \to I \to I/M \to 0 \end{align*} $$

and

$$ \begin{align*} 0 \to I/M \to S/M \to A \to 0 \end{align*} $$

with $A=S/I$ induce homomorphisms

We first show that if $n_1\geq 4$ , then the degree $0$ piece $\partial _0$ is not surjective. As $I/M$ is generated by q, we have $I/M \cong (S/M')(-2)$ , where $M'= \langle x,y \rangle ^{n_1-1}+ \langle z,w \rangle ^{n_2-1}$ ; applying $\operatorname {\mathrm {Hom}}_S(-,A)$ to

$$ \begin{align*} 0\to M'\to S\to S/M'\to 0 \end{align*} $$

shows that elements of $\operatorname {\mathrm {Ext}}_S^1(I/M,A)$ are homomorphisms $h'\colon M'\to A$ modulo those induced by multiplication by an element of S.

Denote the generators of $M'$ by $f_k' = x^{n_1-k}y^{k-1}$ , for $1\le k\le n_1$ , and $g_{\ell }' = z^{n_2-\ell }w^{\ell -1}$ , for $1\le \ell \le n_2$ . Similarly, write $f_k = x^{n_1-k}y^{k}$ , for $0\le k\le n_1$ , and $g_{\ell } = z^{n_2-\ell }w^{\ell }$ , for $0\le \ell \le n_2$ . Given a homomorphism $h\colon M\to A$ , by rewriting the product $f_k'q \in M'$ in terms of the generators of M, one sees that the homomorphism $\widetilde {\partial h}$ is given by

$$ \begin{align*} \widetilde{\partial h}\colon M'\to A \end{align*} $$

$$ \begin{align*} \widetilde{\partial h}(f_k')=zh(f_{k-1}) - wh(f_k)\quad\textrm{and}\quad\widetilde{\partial h}(g_{\ell}') = xh(g_{\ell-1})-yh(g_{\ell}). \end{align*} $$

In particular, any such map satisfies

$$ \begin{align*} y\widetilde{\partial h}(f^{\prime}_k) = y\bigl( zh(f_{k-1}) - wh(f_k) \bigr) = zh(yf_{k-1}) - ywh(f_k) = zh(xf_k) - xzh(f_k) = 0 ,\end{align*} $$

and moreover, $y\bigl ([a](f_k')\bigr ) = ayf_k' = af_k = 0$ in A, where $[a]\colon S\to A$ denotes multiplication by $a\in A$ .

To see that $\partial _0$ is not surjective, we produce a map $h'\colon M'\to A$ of degree $2$ (to account for the twist) not of the form $\widetilde {\partial h} + [a]$ . Define

$$ \begin{align*} h'(f_k') = y^2z^{k-1}w^{n_1-k}\quad\textrm{and}\quad h'(g_{\ell}') = 0 \end{align*} $$

for each k and $\ell $ . The map $h'$ is well-defined, as the relation $yw=xz$ in A ensures $yh'(f^{\prime }_k) = xh'(f^{\prime }_{k+1})$ . Examining the $zw$ -degree shows $g^{\prime }_{\ell }h'(f^{\prime }_k) = f^{\prime }_kh'(g^{\prime }_{\ell }) = 0$ , for all $k,\ell $ . Moreover,

$$ \begin{align*} yh'(f^{\prime}_1) = y(y^2w^{n_1-1}) \neq 0 \;\text{ when }\; n_1 \ge 4. \end{align*} $$

Hence, $\partial _0$ is not surjective.

Second, we show that the degree $-1$ piece $\psi _{-1}$ is not surjective; here we simply assume $n_1\geq 2$ , that is, we are no longer assuming $n_1$ is at least $4$ . Using $I/M \cong (S/M')(-2)$ and applying $\operatorname {\mathrm {Hom}}_S(-,S/M)$ to the exact sequence

$$ \begin{align*} 0\to M'\to S\to S/M' \to 0 \end{align*} $$

shows that elements of $\operatorname {\mathrm {Ext}}^1_S(I/M,S/M)$ are homomorphisms $h'\colon M'\to S/M$ modulo those induced by a single element. As before, given a homomorphism $h\colon M\to S/M$ , we obtain $\widetilde {\psi h}\colon M'\to S/M$ with values

$$ \begin{align*} \widetilde{\psi h}(f_k') = zh(f_{k-1}) - wh(f_k) \quad\text{ and }\quad \widetilde{\psi h}(g_{\ell}') = xh(g_{\ell-1})-yh(g_{\ell}). \end{align*} $$

Define

$$ \begin{align*} h'\colon M'\to S/M \end{align*} $$

$$ \begin{align*} h'(f_1') = -y^{n_1-1}w\quad\textrm{and}\quad h'(f_k')=h'(g_{\ell}') = 0, \end{align*} $$

for all $k>1$ and all $\ell $ . Then $h'$ is well-defined, as $yh'(f_1') = 0$ and $g_{\ell }'h'(f_1') = -y^{n_1-1}wg_{\ell '} = -y^{n_1-1}g_{\ell } = 0$ in $S/M$ , for all $\ell $ . Since this is a map of degree $1$ , after accounting for the twist, it yields a class of degree $-1$ in $\operatorname {\mathrm {Ext}}^1_S(I/M,S/M)$ .

We wish to show $h'$ is not of the form $\widetilde {\psi h} + [v]$ , for any degree $-1$ homomorphism h and $v\in (S/M)_1$ . If $h' = \widetilde {\psi h} + [v]$ , then evaluating on $f^{\prime }_1$ ,

(14) $$ \begin{align} -y^{n_1-1}w = zh(f_{0}) - wh(f_1) + vx^{n_1-1} \end{align} $$

holds, and we see v is a linear form in z and w, that is, $v = cz+dw$ for . One solution to Equation (14) is given by $h(f_0)=0$ , $h(f_1)=y^{n_1-1}$ and $v=0$ ; thus, any other solution differs from this by a syzygy among $z,w,x^{n_1-1}$ . As a result, every solution is of the form

$$ \begin{align*} h(f_0) = wb - cx^{n_1-1}, \quad h(f_1) = y^{n_1-1} + zb + dx^{n_1-1}, \quad v = cz + dw, \end{align*} $$

where $b\in (S/M)_{n_1-2}$ . Using that $xf_1=yf_0$ , we see

$$ \begin{align*} 0 = xh(f_1) - yh(f_0) = qb, \end{align*} $$

where, recall, the equality takes place in $S/M$ . As a result, b arises from a syzygy between the generators of $I = M+ \langle q \rangle $ . But the minimal degree of such a syzygy is $n_1+1$ , putting b in degree $n_1-1$ (after accounting for the twist), and so $b=0$ . To finish the proof, we evaluate $h'$ at $f_2' = x^{n_1-2}y$ , which shows

$$ \begin{align*} 0 = h'(f_2') = zh(f_1) - wh(f_2) + vf_2' = (y^{n_1-1}z+dx^{n_1-1}z) - wh(f_2) + (cz+dw)x^{n_1-2}y. \end{align*} $$

Reducing modulo w gives

$$ \begin{align*} 0 = y^{n_1-1}z + dx^{n_1-1}z + cx^{n_1-2}yz. \end{align*} $$

But this is impossible, as all three monomials here are basis elements of $S/(M+ \langle w \rangle )$ . Hence, $h'$ cannot equal $\widetilde {\psi h} + [v]$ , which implies $\psi _{-1}$ is not surjective.