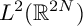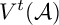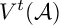1 Introduction
For the past two decades, shift-invariant spaces on
![]() $\mathbb {R}^{n}$
have been studied extensively and applied in various fields such as time–frequency analysis, sampling theory, approximation theory, numerical analysis, and electrical engineering. In the recent past, these spaces have been studied on several locally compact groups. The main problem deals with obtaining characterization theorems for the system of translates to form a frame sequence or a Riesz sequence.
$\mathbb {R}^{n}$
have been studied extensively and applied in various fields such as time–frequency analysis, sampling theory, approximation theory, numerical analysis, and electrical engineering. In the recent past, these spaces have been studied on several locally compact groups. The main problem deals with obtaining characterization theorems for the system of translates to form a frame sequence or a Riesz sequence.
Bownik in [Reference Bownik4] characterized shift-invariant spaces on
![]() ${\mathbb {R}}^n$
in terms of range functions and obtained characterization for a system of translates on
${\mathbb {R}}^n$
in terms of range functions and obtained characterization for a system of translates on
![]() ${\mathbb {R}}^n$
to be a frame sequence and a Riesz sequence. Later shift-invariant spaces were studied on locally compact abelian groups in [Reference Bownik and Ross5], [Reference Cabrelli and Paternostro6], [Reference Kamyabi Gol and Tousi17] and on a non-abelian compact group in [Reference Radha and Kumar20].
${\mathbb {R}}^n$
to be a frame sequence and a Riesz sequence. Later shift-invariant spaces were studied on locally compact abelian groups in [Reference Bownik and Ross5], [Reference Cabrelli and Paternostro6], [Reference Kamyabi Gol and Tousi17] and on a non-abelian compact group in [Reference Radha and Kumar20].
Currey et al. in [Reference Currey, Mayeli and Oussa9] characterized a shift-invariant system in terms of range function for SI/Z-type groups. In [Reference Iverson16], Iverson studied frames of the form
![]() $\{\rho (\xi )f_{i}\}_{\xi \in K,i\in I}$
, where
$\{\rho (\xi )f_{i}\}_{\xi \in K,i\in I}$
, where
![]() $\rho $
is a representation of a non-abelian compact group K on a Hilbert space
$\rho $
is a representation of a non-abelian compact group K on a Hilbert space
![]() $H_{\rho }$
using operator-valued Zak transform. There are several interesting characterization theorems for frames and Riesz sequences in connection with shift-invariant spaces on various types of Heisenberg groups such as polarized Heisenberg group, standard Heisenberg group, and A. Weil’s abstract Heisenberg group. We refer to [Reference Arati and Radha1], [Reference Barbieri, Hernández and Mayeli2], [Reference Radha and Adhikari19] in this connection. Recently, in [Reference Das and Radha11], characterization theorems for frame sequences and Riesz sequences have been studied for the shift-invariant system in terms of Gramian and dual Gramian, respectively, on the Heisenberg group. In [Reference Barbieri, Hernández and Paternostro3], Barbieri et al. investigated the structure of subspaces of a Hilbert space which are invariant under unitary representations of a discrete group. Here, they generalized the concepts of bracket map, fiberization map, dual integrability, and obtained characterization of frames and Riesz bases in a more general setting.
$H_{\rho }$
using operator-valued Zak transform. There are several interesting characterization theorems for frames and Riesz sequences in connection with shift-invariant spaces on various types of Heisenberg groups such as polarized Heisenberg group, standard Heisenberg group, and A. Weil’s abstract Heisenberg group. We refer to [Reference Arati and Radha1], [Reference Barbieri, Hernández and Mayeli2], [Reference Radha and Adhikari19] in this connection. Recently, in [Reference Das and Radha11], characterization theorems for frame sequences and Riesz sequences have been studied for the shift-invariant system in terms of Gramian and dual Gramian, respectively, on the Heisenberg group. In [Reference Barbieri, Hernández and Paternostro3], Barbieri et al. investigated the structure of subspaces of a Hilbert space which are invariant under unitary representations of a discrete group. Here, they generalized the concepts of bracket map, fiberization map, dual integrability, and obtained characterization of frames and Riesz bases in a more general setting.
In [Reference Radha and Adhikari18], Radha and Saswata introduced twisted shift-invariant spaces
![]() $V^{t}({\phi })$
in
$V^{t}({\phi })$
in
![]() $L^{2}(\mathbb {R}^{2n})$
and studied the problem of finding a characterization for the system of twisted translates to form a frame sequence or a Riesz sequence. The characterizations were obtained using certain “Condition C.” On the other hand, Das et al. in [Reference Das, Massopust and Radha10] introduced twisted
$L^{2}(\mathbb {R}^{2n})$
and studied the problem of finding a characterization for the system of twisted translates to form a frame sequence or a Riesz sequence. The characterizations were obtained using certain “Condition C.” On the other hand, Das et al. in [Reference Das, Massopust and Radha10] introduced twisted
![]() $B-$
splines
$B-$
splines
![]() $B_{n}$
and studied various properties. It was observed that for
$B_{n}$
and studied various properties. It was observed that for
![]() $n\geq 2$
, these splines do not satisfy “Condition C.” For
$n\geq 2$
, these splines do not satisfy “Condition C.” For
![]() $n=2$
, it was shown that the twisted translates of
$n=2$
, it was shown that the twisted translates of
![]() $B_{n}$
form a Riesz sequence using certain specific numerical computations. But, for
$B_{n}$
form a Riesz sequence using certain specific numerical computations. But, for
![]() $n>2$
, such computations could not be extended. They were also not successful in proving the result for
$n>2$
, such computations could not be extended. They were also not successful in proving the result for
![]() $n=2$
analytically. Hence, it becomes necessary to obtain a characterization for a system of twisted translates to form a Riesz sequence (also a frame sequence) without using “Condition C.” In this paper, as a first step, we attempt to find such a characterization which can help us to verify these results for some simple examples. This is the motivation of this paper.
$n=2$
analytically. Hence, it becomes necessary to obtain a characterization for a system of twisted translates to form a Riesz sequence (also a frame sequence) without using “Condition C.” In this paper, as a first step, we attempt to find such a characterization which can help us to verify these results for some simple examples. This is the motivation of this paper.
In this paper, we focus on a twisted shift-invariant system of the form
![]() $E^{t}(\mathcal {A}):=\{{T_{(k,l)}^t} {\phi }_{s} : k,l \in {\mathbb {Z}^n}, s\in {\mathbb {Z}}\}$
for a countable collection of functions
$E^{t}(\mathcal {A}):=\{{T_{(k,l)}^t} {\phi }_{s} : k,l \in {\mathbb {Z}^n}, s\in {\mathbb {Z}}\}$
for a countable collection of functions
![]() $\mathcal {A}:=\{{\phi }_{s} : s\in {\mathbb {Z}}\}$
in
$\mathcal {A}:=\{{\phi }_{s} : s\in {\mathbb {Z}}\}$
in
![]() $L^{2}({\mathbb {R}}^{2n})$
, where
$L^{2}({\mathbb {R}}^{2n})$
, where
![]() ${T_{(k,l)}^t}{\phi }$
denotes the twisted translation of
${T_{(k,l)}^t}{\phi }$
denotes the twisted translation of
![]() ${\phi }\in L^{2}(\mathbb {R}^{2n})$
. (There exist different versions of twisted translations depending on the definition of the Schrödinger representation [see, e.g., [Reference Debrouwere and Prangoski12] for a different choice].) We define a class of operators
${\phi }\in L^{2}(\mathbb {R}^{2n})$
. (There exist different versions of twisted translations depending on the definition of the Schrödinger representation [see, e.g., [Reference Debrouwere and Prangoski12] for a different choice].) We define a class of operators
![]() $\{H_{l}(\xi ) : l\in {\mathbb {Z}^n},\xi \in {\mathbb {T}^{n}}\}$
using the fiber map associated with the system
$\{H_{l}(\xi ) : l\in {\mathbb {Z}^n},\xi \in {\mathbb {T}^{n}}\}$
using the fiber map associated with the system
![]() $E^{t}(\mathcal {A})$
. We obtain a characterization for the system
$E^{t}(\mathcal {A})$
. We obtain a characterization for the system
![]() $E^{t}(\mathcal {A})$
to be a frame sequence in terms of the operators
$E^{t}(\mathcal {A})$
to be a frame sequence in terms of the operators
![]() $H_{l}(\xi )$
and their adjoints. We obtain the corresponding Riesz sequence characterization in terms of the Gramian associated with
$H_{l}(\xi )$
and their adjoints. We obtain the corresponding Riesz sequence characterization in terms of the Gramian associated with
![]() $E^{t}(\mathcal {A})$
. We also prove that the system
$E^{t}(\mathcal {A})$
. We also prove that the system
![]() $E^{t}(\mathcal {A})$
is a frame sequence (Riesz sequence) if and only if the system
$E^{t}(\mathcal {A})$
is a frame sequence (Riesz sequence) if and only if the system
![]() $\{\tau {\phi }_{s}(\xi +l) : l\in {\mathbb {Z}^n}, s\in {\mathbb {Z}}\}$
is a frame sequence (Riesz sequence) for a.e.
$\{\tau {\phi }_{s}(\xi +l) : l\in {\mathbb {Z}^n}, s\in {\mathbb {Z}}\}$
is a frame sequence (Riesz sequence) for a.e.
![]() $\xi \in {\mathbb {T}^{n}}$
, using the fiber map
$\xi \in {\mathbb {T}^{n}}$
, using the fiber map
![]() $\tau $
. When
$\tau $
. When
![]() $A=\{{\phi }\}$
, we prove that if
$A=\{{\phi }\}$
, we prove that if
![]() $E^{t}(\mathcal {A})$
is a frame sequence, then the weight function
$E^{t}(\mathcal {A})$
is a frame sequence, then the weight function
![]() $W_{{\phi }}(\xi )$
is bounded above and below
$W_{{\phi }}(\xi )$
is bounded above and below
![]() $a.e.~\xi \in \mathbb {T}^{n}\setminus N$
, where
$a.e.~\xi \in \mathbb {T}^{n}\setminus N$
, where
![]() $N=:\{\xi \in \mathbb {T}^{n} : \omega _{\phi }(\xi )=0\}$
. We also prove a similar result when
$N=:\{\xi \in \mathbb {T}^{n} : \omega _{\phi }(\xi )=0\}$
. We also prove a similar result when
![]() $E^{t}(\mathcal {A})$
is a Riesz sequence. We illustrate these results with examples. However, the converse need not be true. We provide a counter example.
$E^{t}(\mathcal {A})$
is a Riesz sequence. We illustrate these results with examples. However, the converse need not be true. We provide a counter example.
We then study the problem of dual twisted shift-invariant system. We consider two twisted shift-invariant systems
![]() $E^{t}(\mathcal {A})$
and
$E^{t}(\mathcal {A})$
and
![]() $E^{t}(\mathcal {D})$
. We assume that they are Bessel sequences. Then we obtain a characterization of
$E^{t}(\mathcal {D})$
. We assume that they are Bessel sequences. Then we obtain a characterization of
![]() $E^{t}(\mathcal {A})$
and
$E^{t}(\mathcal {A})$
and
![]() $E^{t}(\mathcal {D})$
to be dual frames. As a consequence, we show that if
$E^{t}(\mathcal {D})$
to be dual frames. As a consequence, we show that if
![]() ${\phi }$
satisfies “Condition C,” then as in the classical case, the canonical dual frame is the only dual frame that consists of twisted translations of a single function. In the final part of the paper, we show that if the system of twisted translates
${\phi }$
satisfies “Condition C,” then as in the classical case, the canonical dual frame is the only dual frame that consists of twisted translations of a single function. In the final part of the paper, we show that if the system of twisted translates
![]() $\{{T_{(k,l)}^t} {\phi } : k,l\in \mathbb {Z}^{n}\}$
is a Riesz sequence in
$\{{T_{(k,l)}^t} {\phi } : k,l\in \mathbb {Z}^{n}\}$
is a Riesz sequence in
![]() $L^{2}(\mathbb {R}^{2n})$
, where
$L^{2}(\mathbb {R}^{2n})$
, where
![]() ${\phi }\in L^{2}(\mathbb {R}^{2n})$
such that it satisfies “Condition C,” then there exists a
${\phi }\in L^{2}(\mathbb {R}^{2n})$
such that it satisfies “Condition C,” then there exists a
![]() ${\phi }^{\sharp }\in V^{t}({\phi })$
such that
${\phi }^{\sharp }\in V^{t}({\phi })$
such that
![]() $\{{T_{(k,l)}^t} {\phi }^{\sharp } : k,l\in \mathbb {Z}^{n}\}$
is an orthonormal system in
$\{{T_{(k,l)}^t} {\phi }^{\sharp } : k,l\in \mathbb {Z}^{n}\}$
is an orthonormal system in
![]() $L^{2}(\mathbb {R}^{2n})$
and
$L^{2}(\mathbb {R}^{2n})$
and
![]() $V^{t}({\phi })=V^{t}({\phi }^{\sharp })$
. We illustrate this with an example.
$V^{t}({\phi })=V^{t}({\phi }^{\sharp })$
. We illustrate this with an example.
2 Notation and background
Let
![]() ${\mathcal {H}}\neq 0$
be a separable Hilbert space.
${\mathcal {H}}\neq 0$
be a separable Hilbert space.
Definition 2.1. A sequence
![]() $\{f_{k} : k\in {\mathbb {Z}}\}$
in
$\{f_{k} : k\in {\mathbb {Z}}\}$
in
![]() ${\mathcal {H}}$
is called a frame for
${\mathcal {H}}$
is called a frame for
![]() ${\mathcal {H}}$
if there exist two constants
${\mathcal {H}}$
if there exist two constants
![]() $A,B>0$
such that
$A,B>0$
such that
 $$ \begin{align} A\|f\|^{2}\leq \sum_{k\in {\mathbb{Z}}}|\langle f,f_{k}\rangle|^{2} \leq B\|f\|^{2},\qquad \forall\ f\in {\mathcal{H}}. \end{align} $$
$$ \begin{align} A\|f\|^{2}\leq \sum_{k\in {\mathbb{Z}}}|\langle f,f_{k}\rangle|^{2} \leq B\|f\|^{2},\qquad \forall\ f\in {\mathcal{H}}. \end{align} $$
If only the right-hand side inequality of (2.1) holds, then
![]() $\{f_{k} : k\in {\mathbb {Z}}\}$
is called a Bessel sequence. If
$\{f_{k} : k\in {\mathbb {Z}}\}$
is called a Bessel sequence. If
![]() $A=B$
in (2.1), then
$A=B$
in (2.1), then
![]() $\{f_{k} : k\in {\mathbb {Z}}\}$
is called a tight frame. If (2.1) holds with
$\{f_{k} : k\in {\mathbb {Z}}\}$
is called a tight frame. If (2.1) holds with
![]() $A=B=1$
, then
$A=B=1$
, then
![]() $\{f_{k} : k\in {\mathbb {Z}}\}$
is called a Parseval frame. If
$\{f_{k} : k\in {\mathbb {Z}}\}$
is called a Parseval frame. If
![]() $\{f_{k} : k\in {\mathbb {Z}}\}$
is a frame for
$\{f_{k} : k\in {\mathbb {Z}}\}$
is a frame for
![]() $\overline {\operatorname {\mathrm {span}}\{f_{k} : k\in {\mathbb {Z}}\}}$
, then it is called a frame sequence. The frame operator
$\overline {\operatorname {\mathrm {span}}\{f_{k} : k\in {\mathbb {Z}}\}}$
, then it is called a frame sequence. The frame operator
![]() $S:{\mathcal {H}}\rightarrow {\mathcal {H}}$
associated with a frame
$S:{\mathcal {H}}\rightarrow {\mathcal {H}}$
associated with a frame
![]() $\{f_{k} : k\in {\mathbb {Z}}\}$
is defined by
$\{f_{k} : k\in {\mathbb {Z}}\}$
is defined by
 $$ \begin{align*} Sf:=\sum\limits_{k\in {\mathbb{Z}}}\langle f,f_{k}\rangle f_{k},\qquad\forall\ f\in {\mathcal{H}}. \end{align*} $$
$$ \begin{align*} Sf:=\sum\limits_{k\in {\mathbb{Z}}}\langle f,f_{k}\rangle f_{k},\qquad\forall\ f\in {\mathcal{H}}. \end{align*} $$
It can be shown that S is a bounded, invertible, self-adjoint, and positive operator on
![]() ${\mathcal {H}}$
. In addition,
${\mathcal {H}}$
. In addition,
![]() $\{S^{-1}f_{k} : k\in {\mathbb {Z}}\}$
is also a frame with frame operator
$\{S^{-1}f_{k} : k\in {\mathbb {Z}}\}$
is also a frame with frame operator
![]() $S^{-1}$
and frame bounds
$S^{-1}$
and frame bounds
![]() $B^{-1}, A^{-1}$
.
$B^{-1}, A^{-1}$
.
Definition 2.2. Let
![]() $\{f_{k} : k\in {\mathbb {Z}}\}$
be a frame for
$\{f_{k} : k\in {\mathbb {Z}}\}$
be a frame for
![]() ${\mathcal {H}}$
, and let S be the corresponding frame operator. Then the collection
${\mathcal {H}}$
, and let S be the corresponding frame operator. Then the collection
![]() $\{S^{-1}f_{k} : k\in {\mathbb {Z}}\}$
is called the canonical dual frame of
$\{S^{-1}f_{k} : k\in {\mathbb {Z}}\}$
is called the canonical dual frame of
![]() $\{f_{k} : k\in {\mathbb {Z}}\}$
.
$\{f_{k} : k\in {\mathbb {Z}}\}$
.
Definition 2.3. Let
![]() $\{f_{k} : k\in {\mathbb {Z}}\}$
and
$\{f_{k} : k\in {\mathbb {Z}}\}$
and
![]() $\{g_{k} : k\in {\mathbb {Z}}\}$
be two frames for
$\{g_{k} : k\in {\mathbb {Z}}\}$
be two frames for
![]() ${\mathcal {H}}$
. Then
${\mathcal {H}}$
. Then
![]() $\{g_{k} : k\in {\mathbb {Z}}\}$
is said to be a dual frame of
$\{g_{k} : k\in {\mathbb {Z}}\}$
is said to be a dual frame of
![]() $\{f_{k} : k\in {\mathbb {Z}}\}$
if
$\{f_{k} : k\in {\mathbb {Z}}\}$
if
 $$ \begin{align*} f=\sum_{k\in{\mathbb{Z}}}\langle f, g_k\rangle f_k,\ \ \ \ \ \ \ \forall\ f\in{\mathcal{H}}. \end{align*} $$
$$ \begin{align*} f=\sum_{k\in{\mathbb{Z}}}\langle f, g_k\rangle f_k,\ \ \ \ \ \ \ \forall\ f\in{\mathcal{H}}. \end{align*} $$
Theorem 2.4. Assume that
![]() $\{f_k:k\in {\mathbb {Z}}\}$
and
$\{f_k:k\in {\mathbb {Z}}\}$
and
![]() $\{g_k:k\in {\mathbb {Z}}\}$
are Bessel sequences in
$\{g_k:k\in {\mathbb {Z}}\}$
are Bessel sequences in
![]() ${\mathcal {H}}$
. Then the following are equivalent:
${\mathcal {H}}$
. Then the following are equivalent:
-
(i)
 $f=\sum \limits _{k\in {\mathbb {Z}}}\langle f,g_k\rangle f_k,\quad \forall \ f\in {\mathcal {H}}$
.
$f=\sum \limits _{k\in {\mathbb {Z}}}\langle f,g_k\rangle f_k,\quad \forall \ f\in {\mathcal {H}}$
. -
(ii)
 $f=\sum \limits _{k\in {\mathbb {Z}}}\langle f,f_k\rangle g_k,\quad \forall \ f\in {\mathcal {H}}$
.
$f=\sum \limits _{k\in {\mathbb {Z}}}\langle f,f_k\rangle g_k,\quad \forall \ f\in {\mathcal {H}}$
. -
(iii)
 $\langle f,g\rangle =\sum \limits _{k\in {\mathbb {Z}}}\langle f,f_k\rangle \langle g_k,g\rangle ,\quad \forall \ f,g\in {\mathcal {H}}.$
$\langle f,g\rangle =\sum \limits _{k\in {\mathbb {Z}}}\langle f,f_k\rangle \langle g_k,g\rangle ,\quad \forall \ f,g\in {\mathcal {H}}.$
When one of the above equivalent conditions is satisfied,
![]() $\{f_k:k\in {\mathbb {Z}}\}$
and
$\{f_k:k\in {\mathbb {Z}}\}$
and
![]() $\{g_k:k\in {\mathbb {Z}}\}$
are dual frames for
$\{g_k:k\in {\mathbb {Z}}\}$
are dual frames for
![]() ${\mathcal {H}}$
. If B denotes an upper frame bound for
${\mathcal {H}}$
. If B denotes an upper frame bound for
![]() $\{f_k:~k\in {\mathbb {Z}}\}$
, then
$\{f_k:~k\in {\mathbb {Z}}\}$
, then
![]() $B^{-1}$
is a lower frame bound for
$B^{-1}$
is a lower frame bound for
![]() $\{g_k:~k\in {\mathbb {Z}}\}$
.
$\{g_k:~k\in {\mathbb {Z}}\}$
.
Definition 2.5. A sequence
![]() $\{f_{k} : k\in {\mathbb {Z}}\}$
in
$\{f_{k} : k\in {\mathbb {Z}}\}$
in
![]() ${\mathcal {H}}$
is called a Riesz basis for
${\mathcal {H}}$
is called a Riesz basis for
![]() ${\mathcal {H}}$
if there exists a bounded invertible operator U on
${\mathcal {H}}$
if there exists a bounded invertible operator U on
![]() ${\mathcal {H}}$
and an orthonormal basis
${\mathcal {H}}$
and an orthonormal basis
![]() $\{e_{k} : k\in {\mathbb {Z}}\}$
of
$\{e_{k} : k\in {\mathbb {Z}}\}$
of
![]() ${\mathcal {H}}$
such that
${\mathcal {H}}$
such that
![]() $U(e_{k})=f_{k},\ \forall \ k\in {\mathbb {Z}}$
. If
$U(e_{k})=f_{k},\ \forall \ k\in {\mathbb {Z}}$
. If
![]() $\{f_{k} : k\in {\mathbb {Z}}\}$
is a Riesz basis for
$\{f_{k} : k\in {\mathbb {Z}}\}$
is a Riesz basis for
![]() $\overline {\operatorname {\mathrm {span}}\{f_{k} : k\in {\mathbb {Z}}\}}$
, then it is called a Riesz sequence.
$\overline {\operatorname {\mathrm {span}}\{f_{k} : k\in {\mathbb {Z}}\}}$
, then it is called a Riesz sequence.
Theorem 2.6. For a sequence
![]() $\{f_{k} : k\in {\mathbb {Z}}\}$
in
$\{f_{k} : k\in {\mathbb {Z}}\}$
in
![]() ${\mathcal {H}}$
, the following conditions are equivalent:
${\mathcal {H}}$
, the following conditions are equivalent:
-
(i)
 $\{f_{k}\}$
is a Riesz basis for
$\{f_{k}\}$
is a Riesz basis for
 ${\mathcal {H}}$
.
${\mathcal {H}}$
. -
(ii)
 $\{f_{k}\}$
is complete in
$\{f_{k}\}$
is complete in
 ${\mathcal {H}}$
, and there exist constants
${\mathcal {H}}$
, and there exist constants
 $A,B>0$
such that for every finite scalar sequence
$A,B>0$
such that for every finite scalar sequence
 $\{c_{k}\}$
, one has
$\{c_{k}\}$
, one has  $$ \begin{align*}A\sum_{k}|c_{k}|^{2}\leq \big\|\sum_{k} c_{k}f_{k}\big\|^{2}\leq B\sum_{k} |c_{k}|^{2}.\end{align*} $$
$$ \begin{align*}A\sum_{k}|c_{k}|^{2}\leq \big\|\sum_{k} c_{k}f_{k}\big\|^{2}\leq B\sum_{k} |c_{k}|^{2}.\end{align*} $$
For further study of frames and Riesz bases, we refer to [Reference Christensen8].
The Heisenberg group
![]() $\mathbb {H}^{n}$
is a nilpotent Lie group whose underlying manifold is
$\mathbb {H}^{n}$
is a nilpotent Lie group whose underlying manifold is
![]() $\mathbb {R}^{n}\times \mathbb {R}^{n}\times {\mathbb {R}}$
with the group operation defined by
$\mathbb {R}^{n}\times \mathbb {R}^{n}\times {\mathbb {R}}$
with the group operation defined by
![]() $(x,y,t)(u,v,s)=(x+u,y+v,t+s+\frac {1}{2}(u\cdot y-v\cdot x))$
and the Haar measure is the Lebesgue measure
$(x,y,t)(u,v,s)=(x+u,y+v,t+s+\frac {1}{2}(u\cdot y-v\cdot x))$
and the Haar measure is the Lebesgue measure
![]() $dxdydt$
on
$dxdydt$
on
![]() $\mathbb {R}^{n}\times \mathbb {R}^{n}\times {\mathbb {R}}$
. Using the Schrödinger representation
$\mathbb {R}^{n}\times \mathbb {R}^{n}\times {\mathbb {R}}$
. Using the Schrödinger representation
![]() $\pi _{\lambda }$
,
$\pi _{\lambda }$
,
![]() $\lambda \in {\mathbb {R}}^{\ast },$
given by
$\lambda \in {\mathbb {R}}^{\ast },$
given by
we define the group Fourier transform of
![]() $f\in L^{1}(\mathbb {H}^{n})$
as
$f\in L^{1}(\mathbb {H}^{n})$
as
 $$ \begin{align*} \widehat{f}(\lambda)=\int_{\mathbb{H}^{n}}f(z,t)\pi_{\lambda}(z,t)\,dzdt,~\text{where}~\lambda\in{\mathbb{R}}^{\ast}, \end{align*} $$
$$ \begin{align*} \widehat{f}(\lambda)=\int_{\mathbb{H}^{n}}f(z,t)\pi_{\lambda}(z,t)\,dzdt,~\text{where}~\lambda\in{\mathbb{R}}^{\ast}, \end{align*} $$
which is a bounded operator on
![]() $L^{2}(\mathbb {R}^{n})$
. In other words, for
$L^{2}(\mathbb {R}^{n})$
. In other words, for
![]() ${\phi }\in L^{2}(\mathbb {R}^{n})$
, we have
${\phi }\in L^{2}(\mathbb {R}^{n})$
, we have
 $$ \begin{align*} \widehat{f}(\lambda){\phi}=\int_{\mathbb{H}^{n}}f(z,t)\pi_{\lambda}(z,t){\phi}\,dzdt, \end{align*} $$
$$ \begin{align*} \widehat{f}(\lambda){\phi}=\int_{\mathbb{H}^{n}}f(z,t)\pi_{\lambda}(z,t){\phi}\,dzdt, \end{align*} $$
where the integral is a Bochner integral taking values in
![]() $L^{2}({\mathbb {R}}^{n}).$
If f is also in
$L^{2}({\mathbb {R}}^{n}).$
If f is also in
![]() $L^{2}(\mathbb {H}^{n})$
, then
$L^{2}(\mathbb {H}^{n})$
, then
![]() $\widehat {f}(\lambda )$
is a Hilbert–Schmidt operator. Define
$\widehat {f}(\lambda )$
is a Hilbert–Schmidt operator. Define
 $$ \begin{align*} f^{\lambda}(z)=\int_{{\mathbb{R}}}e^{2\pi i\lambda t}f(z,t)\,dt, \end{align*} $$
$$ \begin{align*} f^{\lambda}(z)=\int_{{\mathbb{R}}}e^{2\pi i\lambda t}f(z,t)\,dt, \end{align*} $$
which is the inverse Fourier transform of f in the t variable. Then we can write
 $$ \begin{align*} \widehat{f}(\lambda)=\int_{\mathbb{C}^{n}}f^{\lambda}(z)\pi_{\lambda}(z,0)dz. \end{align*} $$
$$ \begin{align*} \widehat{f}(\lambda)=\int_{\mathbb{C}^{n}}f^{\lambda}(z)\pi_{\lambda}(z,0)dz. \end{align*} $$
Let
![]() $g\in L^{1}(\mathbb {C}^{n})$
. Define
$g\in L^{1}(\mathbb {C}^{n})$
. Define
 $$ \begin{align*} W_{\lambda}(g)=\int_{\mathbb{C}^{n}}g(z)\pi_{\lambda}(z,0)\,dz. \end{align*} $$
$$ \begin{align*} W_{\lambda}(g)=\int_{\mathbb{C}^{n}}g(z)\pi_{\lambda}(z,0)\,dz. \end{align*} $$
When
![]() $\lambda =1$
, it is called the Weyl transform of g, denoted by
$\lambda =1$
, it is called the Weyl transform of g, denoted by
![]() $W(g)$
. This can be explicitly written as
$W(g)$
. This can be explicitly written as
 $$ \begin{align*} W(g){\phi}(\xi)=\int_{\mathbb{R}^{2n}}g(x,y)e^{2\pi i(x\cdot\xi+\frac{1}{2}x\cdot y)}{\phi}(\xi+y)\,dxdy,~{\phi}\in L^{2}({\mathbb{R}}^{n}). \end{align*} $$
$$ \begin{align*} W(g){\phi}(\xi)=\int_{\mathbb{R}^{2n}}g(x,y)e^{2\pi i(x\cdot\xi+\frac{1}{2}x\cdot y)}{\phi}(\xi+y)\,dxdy,~{\phi}\in L^{2}({\mathbb{R}}^{n}). \end{align*} $$
The Weyl transform is an integral operator with kernel
![]() $K_{g}(\xi ,\eta )=\int _{{\mathbb {R}}^{n}}g(x,\eta -\xi )e^{\pi ix\cdot (\xi +\eta )}dx$
. If
$K_{g}(\xi ,\eta )=\int _{{\mathbb {R}}^{n}}g(x,\eta -\xi )e^{\pi ix\cdot (\xi +\eta )}dx$
. If
![]() $g\in L^{1}\cap L^{2}(\mathbb {C}^{n})$
, then
$g\in L^{1}\cap L^{2}(\mathbb {C}^{n})$
, then
![]() $K_{g}\in L^{2}({\mathbb {R}}^{2n})$
, which implies that
$K_{g}\in L^{2}({\mathbb {R}}^{2n})$
, which implies that
![]() $W(g)$
is a Hilbert–Schmidt operator whose norm is given by
$W(g)$
is a Hilbert–Schmidt operator whose norm is given by
![]() $\|W(g)\|^{2}_{\mathcal {B}_{2}}=\|K_{g}\|^{2}_{L^{2}({\mathbb {R}}^{2n})}$
, where
$\|W(g)\|^{2}_{\mathcal {B}_{2}}=\|K_{g}\|^{2}_{L^{2}({\mathbb {R}}^{2n})}$
, where
![]() $\mathcal {B}_{2}$
is the Hilbert space of Hilbert–Schmidt operators on
$\mathcal {B}_{2}$
is the Hilbert space of Hilbert–Schmidt operators on
![]() $L^{2}({\mathbb {R}}^{n})$
with inner product
$L^{2}({\mathbb {R}}^{n})$
with inner product
![]() $(T,S)=\operatorname {\mathrm {tr}}(TS^{\ast })$
. The Plancherel formula and the inversion formula for the Weyl transform are given by
$(T,S)=\operatorname {\mathrm {tr}}(TS^{\ast })$
. The Plancherel formula and the inversion formula for the Weyl transform are given by
![]() $\|W(g)\|^{2}_{\mathcal {B}_{2}}=\|g\|^{2}_{L^{2}(\mathbb {C}^{n})}$
and
$\|W(g)\|^{2}_{\mathcal {B}_{2}}=\|g\|^{2}_{L^{2}(\mathbb {C}^{n})}$
and
![]() $g(w)=\operatorname {\mathrm {tr}}(\pi (w)^{\ast }W(g))$
,
$g(w)=\operatorname {\mathrm {tr}}(\pi (w)^{\ast }W(g))$
,
![]() $w\in \mathbb {C}^{n}$
, respectively. For a detailed study of analysis on the Heisenberg group, we refer to [Reference Folland14], [Reference Thangavelu21].
$w\in \mathbb {C}^{n}$
, respectively. For a detailed study of analysis on the Heisenberg group, we refer to [Reference Folland14], [Reference Thangavelu21].
Definition 2.7 [Reference Radha and Adhikari18].
Let
![]() ${\phi } \in {L^2(\mathbb {R}^{2n})}$
. For
${\phi } \in {L^2(\mathbb {R}^{2n})}$
. For
![]() $(k,l)\in {\mathbb {Z}}^{2n},$
the twisted translation
$(k,l)\in {\mathbb {Z}}^{2n},$
the twisted translation
![]() ${T_{(k,l)}^t}{\phi }$
of
${T_{(k,l)}^t}{\phi }$
of
![]() ${\phi }$
is defined by
${\phi }$
is defined by
Using the definition of twisted translation, we have
Remark 2.8. Let G be a locally compact group. Let
![]() $\Pi $
be a unitary irreducible representation of G on
$\Pi $
be a unitary irreducible representation of G on
![]() $\mathcal {H}$
. Let
$\mathcal {H}$
. Let
![]() $V_{g}$
denote the matrix coefficient of
$V_{g}$
denote the matrix coefficient of
![]() $\Pi $
, namely
$\Pi $
, namely
![]() ${V_{g}f(x)=\langle \Pi (x)g, f\rangle }$
,
${V_{g}f(x)=\langle \Pi (x)g, f\rangle }$
,
![]() $f,g\in \mathcal {H}$
. Then it is well known that
$f,g\in \mathcal {H}$
. Then it is well known that
![]() $V_{g}$
is the intertwining operator between
$V_{g}$
is the intertwining operator between
![]() $\Pi $
and the left regular representation L. More precisely
$\Pi $
and the left regular representation L. More precisely
![]() $V_{g}(\Pi (x)f)=L_{x}V_{g}(f)$
,
$V_{g}(\Pi (x)f)=L_{x}V_{g}(f)$
,
![]() $x\in G$
(see [Reference Feichtinger and Gröchenig13]). In particular, if G is taken to be the Heisenberg group
$x\in G$
(see [Reference Feichtinger and Gröchenig13]). In particular, if G is taken to be the Heisenberg group
![]() $\mathbb {H}^{n}$
,
$\mathbb {H}^{n}$
,
![]() $\pi _{1}$
, the Schrödinger representation of
$\pi _{1}$
, the Schrödinger representation of
![]() $\mathbb {H}^{n}$
on
$\mathbb {H}^{n}$
on
![]() $L^{2}(\mathbb {R}^{n})$
,
$L^{2}(\mathbb {R}^{n})$
,
![]() $L_{(x,y,t)}$
, the left translation on
$L_{(x,y,t)}$
, the left translation on
![]() $\mathbb {H}^{n}$
, then we get the corresponding intertwining operator
$\mathbb {H}^{n}$
, then we get the corresponding intertwining operator
![]() $V_{g}$
. However, since the definition of twisted translation
$V_{g}$
. However, since the definition of twisted translation
![]() $T^{t}_{(k,l)}$
, mentioned in this paper, is a projective representation, we obtain the following relation:
$T^{t}_{(k,l)}$
, mentioned in this paper, is a projective representation, we obtain the following relation:
![]() $|V_{g}\pi _{1}(x,y,0)f|=|T^{t}_{(x,y)}V_{g}f|$
.
$|V_{g}\pi _{1}(x,y,0)f|=|T^{t}_{(x,y)}V_{g}f|$
.
Lemma 2.9 [Reference Radha and Adhikari18].
Let
![]() ${\phi } \in {L^2(\mathbb {R}^{2n})}$
. Then the kernel of the Weyl transform of
${\phi } \in {L^2(\mathbb {R}^{2n})}$
. Then the kernel of the Weyl transform of
![]() ${T_{(k,l)}^t}{\phi }$
satisfies
${T_{(k,l)}^t}{\phi }$
satisfies
Definition 2.10 [Reference Radha and Adhikari18].
For
![]() ${\phi } \in {L^2(\mathbb {R}^{2n})}$
and
${\phi } \in {L^2(\mathbb {R}^{2n})}$
and
![]() $\xi \in {\mathbb {R}}^{n}$
, the function
$\xi \in {\mathbb {R}}^{n}$
, the function
![]() $\omega _{{\phi }}$
is defined by
$\omega _{{\phi }}$
is defined by
 $$ \begin{align*} \omega_{{\phi}}(\xi)&:=\sum\limits_{m\in {\mathbb{Z}^n}}\int_{{\mathbb{R}}^{n}}|K_{{\phi}}(\xi+m,\eta)|^{2}\,d\eta. \end{align*} $$
$$ \begin{align*} \omega_{{\phi}}(\xi)&:=\sum\limits_{m\in {\mathbb{Z}^n}}\int_{{\mathbb{R}}^{n}}|K_{{\phi}}(\xi+m,\eta)|^{2}\,d\eta. \end{align*} $$
In [Reference Radha and Adhikari18], the characterization theorems such as the system of twisted translates forming a frame sequence or a Riesz sequence are given in terms of the function
![]() $\omega _{{\phi }}.$
$\omega _{{\phi }}.$
Definition 2.11 [Reference Radha and Adhikari18].
A function
![]() ${\phi } \in {L^2(\mathbb {R}^{2n})}$
is said to satisfy “Condition C” if
${\phi } \in {L^2(\mathbb {R}^{2n})}$
is said to satisfy “Condition C” if
 $$ \begin{align*}\sum_{m\in {\mathbb{Z}^n}}\int_{{\mathbb{R}}^{n}}K_{{\phi}}(\xi+m,\eta)\overline{K_{{\phi}}(\xi+m+l,\eta)}\,d\eta=0,~a.e.~\xi\in {\mathbb{T}^{n}},~\forall~l\in {\mathbb{Z}^n}\setminus\{0\}.\end{align*} $$
$$ \begin{align*}\sum_{m\in {\mathbb{Z}^n}}\int_{{\mathbb{R}}^{n}}K_{{\phi}}(\xi+m,\eta)\overline{K_{{\phi}}(\xi+m+l,\eta)}\,d\eta=0,~a.e.~\xi\in {\mathbb{T}^{n}},~\forall~l\in {\mathbb{Z}^n}\setminus\{0\}.\end{align*} $$
3 Frame sequence in a twisted shift-invariant space
Let
![]() $\mathcal {A}:=\{{\phi }_{s} : s\in {\mathbb {Z}}\}$
be the countable collection of functions in
$\mathcal {A}:=\{{\phi }_{s} : s\in {\mathbb {Z}}\}$
be the countable collection of functions in
![]() $L^{2}(\mathbb {R}^{2n})$
and
$L^{2}(\mathbb {R}^{2n})$
and
![]() ${E^{t}(\mathcal {A}):=\{{T_{(k,l)}^t} {\phi }_{s} : k,l\in {\mathbb {Z}^n}, s\in {\mathbb {Z}}\}}$
. We shall denote
${E^{t}(\mathcal {A}):=\{{T_{(k,l)}^t} {\phi }_{s} : k,l\in {\mathbb {Z}^n}, s\in {\mathbb {Z}}\}}$
. We shall denote
![]() $\operatorname {\mathrm {span}}( E^{t}(\mathcal {A}))$
by
$\operatorname {\mathrm {span}}( E^{t}(\mathcal {A}))$
by
![]() $U^t(\mathcal {A})$
and
$U^t(\mathcal {A})$
and
![]() $\overline {U^t(\mathcal {A})}$
by
$\overline {U^t(\mathcal {A})}$
by
![]() $V^{t}(\mathcal {A})$
. The space
$V^{t}(\mathcal {A})$
. The space
![]() $V^{t}(\mathcal {A})$
is called a twisted shift-invariant space. When
$V^{t}(\mathcal {A})$
is called a twisted shift-invariant space. When
![]() $A=\{{\phi }\}$
, it is called a twisted (principal) shift-invariant space. We define
$A=\{{\phi }\}$
, it is called a twisted (principal) shift-invariant space. We define
![]() $\tau : L^{2}(\mathbb {R}^{2n})\rightarrow L^{2}({\mathbb {T}^{n}},{L^{2}(\mathbb {R}^{n},\ell ^{2}(\mathbb {Z}^{n}))})$
by
$\tau : L^{2}(\mathbb {R}^{2n})\rightarrow L^{2}({\mathbb {T}^{n}},{L^{2}(\mathbb {R}^{n},\ell ^{2}(\mathbb {Z}^{n}))})$
by
The map
![]() $\tau $
is called the fiber map. It can be shown that
$\tau $
is called the fiber map. It can be shown that
![]() $L^{2}(\mathbb {R}^{2n})$
is isometric isomorphic to
$L^{2}(\mathbb {R}^{2n})$
is isometric isomorphic to
![]() $L^{2}(\mathbb {T}^{n},L^{2}(\mathbb {R}^{n}, \ell ^{2}(\mathbb {Z}^{n})))$
via the fiber map
$L^{2}(\mathbb {T}^{n},L^{2}(\mathbb {R}^{n}, \ell ^{2}(\mathbb {Z}^{n})))$
via the fiber map
![]() $\tau $
. Using Lemma 2.9, the image of
$\tau $
. Using Lemma 2.9, the image of
![]() ${T_{(k,l)}^t} f$
under the fiber map
${T_{(k,l)}^t} f$
under the fiber map
![]() $\tau $
is given by
$\tau $
is given by
Define
![]() $J : {\mathbb {T}^{n}}\rightarrow \{\text {closed subspaces of}~ L^{2}({\mathbb {R}}^{n},\ell ^{2}({\mathbb {Z}^n}))\}$
by
$J : {\mathbb {T}^{n}}\rightarrow \{\text {closed subspaces of}~ L^{2}({\mathbb {R}}^{n},\ell ^{2}({\mathbb {Z}^n}))\}$
by
![]() $J(\xi ):=\overline {\operatorname {\mathrm {span}}\{\tau {\phi }_{s}(\xi +l) : l\in \mathbb {Z}^{n}, s\in \mathbb {Z}\}}$
. Then J is called a range function. For
$J(\xi ):=\overline {\operatorname {\mathrm {span}}\{\tau {\phi }_{s}(\xi +l) : l\in \mathbb {Z}^{n}, s\in \mathbb {Z}\}}$
. Then J is called a range function. For
![]() $\xi \in {\mathbb {T}^{n}}$
, let
$\xi \in {\mathbb {T}^{n}}$
, let
![]() $P(\xi )$
denote the orthogonal projection of
$P(\xi )$
denote the orthogonal projection of
![]() $L^{2}({\mathbb {R}}^{n},\ell ^{2}({\mathbb {Z}^n}))$
onto
$L^{2}({\mathbb {R}}^{n},\ell ^{2}({\mathbb {Z}^n}))$
onto
![]() $J(\xi )$
. Then the range function J is said to be measurable if
$J(\xi )$
. Then the range function J is said to be measurable if
![]() $\xi \mapsto \big <P(\xi )\Lambda _1,\Lambda _2\big>$
is measurable for each
$\xi \mapsto \big <P(\xi )\Lambda _1,\Lambda _2\big>$
is measurable for each
![]() $\Lambda _1,\Lambda _2 \in L^{2}({\mathbb {R}}^{n},\ell ^{2}({\mathbb {Z}^n}))$
. The following proposition gives the connection between the image of
$\Lambda _1,\Lambda _2 \in L^{2}({\mathbb {R}}^{n},\ell ^{2}({\mathbb {Z}^n}))$
. The following proposition gives the connection between the image of
![]() $V^{t}({\mathcal {A}})$
under the fiber map and the range function.
$V^{t}({\mathcal {A}})$
under the fiber map and the range function.
Proposition 3.1. For a measurable range function J, define
![]() $M_{J}:=\{\Phi \in L^{2}(\mathbb {T}^{n},L^{2}(\mathbb {R}^{n},\ell ^{2}(\mathbb {Z}^{n}))) : \Phi (\xi )\in J(\xi )~\text {for a.e.}~\xi \in \mathbb {T}^{n}\}$
. Then
$M_{J}:=\{\Phi \in L^{2}(\mathbb {T}^{n},L^{2}(\mathbb {R}^{n},\ell ^{2}(\mathbb {Z}^{n}))) : \Phi (\xi )\in J(\xi )~\text {for a.e.}~\xi \in \mathbb {T}^{n}\}$
. Then
![]() $M_{J}$
and
$M_{J}$
and
![]() $\tau (V^{t}(\mathcal {A}))$
satisfy the following properties.
$\tau (V^{t}(\mathcal {A}))$
satisfy the following properties.
-
(i)
 $M_{J}$
is a closed subspace of
$M_{J}$
is a closed subspace of
 $L^{2}(\mathbb {T}^{n},L^{2}(\mathbb {R}^{n},\ell ^{2}(\mathbb {Z}^{n})))$
.
$L^{2}(\mathbb {T}^{n},L^{2}(\mathbb {R}^{n},\ell ^{2}(\mathbb {Z}^{n})))$
. -
(ii)
 $\tau (V^{t}(\mathcal {A}))$
is a closed subspace of
$\tau (V^{t}(\mathcal {A}))$
is a closed subspace of
 $L^{2}(\mathbb {T}^{n},L^{2}(\mathbb {R}^{n},\ell ^{2}(\mathbb {Z}^{n})))$
. Moreover
$L^{2}(\mathbb {T}^{n},L^{2}(\mathbb {R}^{n},\ell ^{2}(\mathbb {Z}^{n})))$
. Moreover
 $\tau (V^{t}(\mathcal {A}))$
is closed under multiplication by exponentials. In other words,
$\tau (V^{t}(\mathcal {A}))$
is closed under multiplication by exponentials. In other words,
 $\Phi \in \tau (V^{t}(\mathcal {A}))$
implies
$\Phi \in \tau (V^{t}(\mathcal {A}))$
implies
 $e^{2\pi i\langle \cdot ,k\rangle }\Phi (\cdot )\in \tau (V^{t}(\mathcal {A}))$
,
$e^{2\pi i\langle \cdot ,k\rangle }\Phi (\cdot )\in \tau (V^{t}(\mathcal {A}))$
,
 $\forall \ k\in \mathbb {Z}^{n}$
.
$\forall \ k\in \mathbb {Z}^{n}$
. -
(iii)
 $M_{J}=\tau (V^{t}(\mathcal {A}))$
.
$M_{J}=\tau (V^{t}(\mathcal {A}))$
.
The proof follows similar lines as in the proof of Proposition
![]() $1.5$
in [Reference Bownik4].
$1.5$
in [Reference Bownik4].
For
![]() $\xi \in \mathbb {T}^{n}, l\in \mathbb {Z}^{n}$
, define
$\xi \in \mathbb {T}^{n}, l\in \mathbb {Z}^{n}$
, define
![]() $H_{l}(\xi ) : \ell ^{2}(\mathbb {Z})\rightarrow L^{2}(\mathbb {R}^{n},\ell ^{2}(\mathbb {Z}^{n}))$
by
$H_{l}(\xi ) : \ell ^{2}(\mathbb {Z})\rightarrow L^{2}(\mathbb {R}^{n},\ell ^{2}(\mathbb {Z}^{n}))$
by
 $$ \begin{align*}H_{l}(\xi)(\{c_{s}\})=\sum\limits_{s\in \mathbb{Z}}c_{s}\tau {\phi}_{s}(\xi+l).\end{align*} $$
$$ \begin{align*}H_{l}(\xi)(\{c_{s}\})=\sum\limits_{s\in \mathbb{Z}}c_{s}\tau {\phi}_{s}(\xi+l).\end{align*} $$
Suppose
![]() $H_{l}(\xi )$
is a bounded linear operator. Then we find its adjoint using the relation
$H_{l}(\xi )$
is a bounded linear operator. Then we find its adjoint using the relation
![]() $\forall \ \{c_{s}\}\in \ell ^{2}(\mathbb {Z})$
and
$\forall \ \{c_{s}\}\in \ell ^{2}(\mathbb {Z})$
and
![]() $ {\phi }\in L^{2}(\mathbb {R}^{n},\ell ^{2}(\mathbb {Z}^{n}))$
. Thus,
$ {\phi }\in L^{2}(\mathbb {R}^{n},\ell ^{2}(\mathbb {Z}^{n}))$
. Thus,
 $$ \begin{align*} \big\langle H_{l}(\xi)(\{c_{s}\}_{n\in \mathbb{Z}}),{\phi}\big\rangle_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}&=\bigg\langle \sum\limits_{s\in \mathbb{Z}}c_{s}\tau {\phi}_{s}(\xi+l),{\phi}\bigg\rangle_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\\ &=\sum\limits_{s\in \mathbb{Z}}c_{s}\big\langle \tau {\phi}_{s}(\xi+l),{\phi}\big\rangle _{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\\ &=\sum\limits_{s\in \mathbb{Z}}c_{s}\overline{\big\langle {\phi},\tau {\phi}_{s}(\xi+l)\big\rangle }_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\\ &=\big<\{c_{s}\}_{s\in \mathbb{Z}},\{\big\langle {\phi},\tau {\phi}_{s}(\xi+l)\big\rangle \}_{s\in \mathbb{Z}}\big>_{\ell^{2}({\mathbb{Z}})}. \end{align*} $$
$$ \begin{align*} \big\langle H_{l}(\xi)(\{c_{s}\}_{n\in \mathbb{Z}}),{\phi}\big\rangle_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}&=\bigg\langle \sum\limits_{s\in \mathbb{Z}}c_{s}\tau {\phi}_{s}(\xi+l),{\phi}\bigg\rangle_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\\ &=\sum\limits_{s\in \mathbb{Z}}c_{s}\big\langle \tau {\phi}_{s}(\xi+l),{\phi}\big\rangle _{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\\ &=\sum\limits_{s\in \mathbb{Z}}c_{s}\overline{\big\langle {\phi},\tau {\phi}_{s}(\xi+l)\big\rangle }_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\\ &=\big<\{c_{s}\}_{s\in \mathbb{Z}},\{\big\langle {\phi},\tau {\phi}_{s}(\xi+l)\big\rangle \}_{s\in \mathbb{Z}}\big>_{\ell^{2}({\mathbb{Z}})}. \end{align*} $$
Hence, by the uniqueness of adjoint of an operator, we get
Now, we make use of the following result in order to obtain a characterization for the system of twisted translates to form a frame sequence.
Lemma 3.2. Let
![]() $f\in L^{2}(\mathbb {R}^{2n})$
, and let
$f\in L^{2}(\mathbb {R}^{2n})$
, and let
![]() $H_{l}(\xi )$
be a bounded linear operator from
$H_{l}(\xi )$
be a bounded linear operator from
![]() $\ell ^{2}(\mathbb {Z})$
into
$\ell ^{2}(\mathbb {Z})$
into
![]() $ L^{2}(\mathbb {R}^{n},\ell ^{2}(\mathbb {Z}^{n}))$
for each
$ L^{2}(\mathbb {R}^{n},\ell ^{2}(\mathbb {Z}^{n}))$
for each
![]() $l\in \mathbb {Z}^{n},~\xi \in \mathbb {T}^{n}$
. Then
$l\in \mathbb {Z}^{n},~\xi \in \mathbb {T}^{n}$
. Then
![]() $H_{l}(\xi )^{\ast }$
satisfies
$H_{l}(\xi )^{\ast }$
satisfies
 $$ \begin{align} \sum\limits_{(k,s)\in \mathbb{Z}^{n+1}}\big|\big<f,T^{t}_{(k,l)}{\phi}_{s}\big>\big|^{2}=\int_{\mathbb{T}^{n}}\|H_{l}(\xi)^{\ast}\tau f(\xi)\|_{L^{2}(\mathbb{R}^{n},\ell^{2}(\mathbb{Z}^{n}))}^{2}\,d\xi\ , \end{align} $$
$$ \begin{align} \sum\limits_{(k,s)\in \mathbb{Z}^{n+1}}\big|\big<f,T^{t}_{(k,l)}{\phi}_{s}\big>\big|^{2}=\int_{\mathbb{T}^{n}}\|H_{l}(\xi)^{\ast}\tau f(\xi)\|_{L^{2}(\mathbb{R}^{n},\ell^{2}(\mathbb{Z}^{n}))}^{2}\,d\xi\ , \end{align} $$
for each
![]() $l\in {\mathbb {Z}^n}$
.
$l\in {\mathbb {Z}^n}$
.
Proof. Consider
 $$ \begin{align} \big<f,T^{t}_{(k,l)}{\phi}_{s}\big>_{L^{2}(\mathbb{R}^{2n})}&=\big<\tau f, \tau (T^{t}_{(k,l)}{\phi}_{s})\big>_{L^{2}({\mathbb{T}^{n}},{L^{2}(\mathbb{R}^{n},\ell^{2}(\mathbb{Z}^{n}))})}\nonumber\\ &=\int_{\mathbb{T}^{n}}\big<\tau f(\xi),\tau (T^{t}_{(k,l)}{\phi}_{s})(\xi)\big>_{{L^{2}(\mathbb{R}^{n},\ell^{2}(\mathbb{Z}^{n}))}}\,d\xi\nonumber\\ &=\int_{\mathbb{T}^{n}}\int_{\mathbb{R}^{n}}\big<\tau f(\xi)(\eta),\tau (T^{t}_{(k,l)}{\phi}_{s})(\xi)(\eta)\big>_{\ell^{2}({\mathbb{Z}^n})}d\eta\, d\xi\nonumber\\ &=e^{-\pi ik\cdot l}\int_{\mathbb{T}^{n}}\int_{\mathbb{R}^{n}}\big<\tau f(\xi)(\eta),\tau {\phi}_{s}(\xi+l)(\eta)\big>_{\ell^{2}({\mathbb{Z}^n})}e^{-2\pi ik\cdot\xi}d\eta\, d\xi\nonumber\\ &=e^{-\pi ik\cdot l}\int_{\mathbb{T}^{n}}\big<\tau f(\xi),\tau {\phi}_{s}(\xi+l)\big>_{{L^{2}(\mathbb{R}^{n},\ell^{2}(\mathbb{Z}^{n}))}}e^{-2\pi ik\cdot \xi}\,d\xi\nonumber\\ &=e^{-\pi ik\cdot l}\int_{\mathbb{T}^{n}}F_{l,s}(\xi)e^{-2\pi ik\cdot\xi}\,d\xi\nonumber\\ &=e^{-\pi ik\cdot l}\widehat{F_{l,s}}(k), \end{align} $$
$$ \begin{align} \big<f,T^{t}_{(k,l)}{\phi}_{s}\big>_{L^{2}(\mathbb{R}^{2n})}&=\big<\tau f, \tau (T^{t}_{(k,l)}{\phi}_{s})\big>_{L^{2}({\mathbb{T}^{n}},{L^{2}(\mathbb{R}^{n},\ell^{2}(\mathbb{Z}^{n}))})}\nonumber\\ &=\int_{\mathbb{T}^{n}}\big<\tau f(\xi),\tau (T^{t}_{(k,l)}{\phi}_{s})(\xi)\big>_{{L^{2}(\mathbb{R}^{n},\ell^{2}(\mathbb{Z}^{n}))}}\,d\xi\nonumber\\ &=\int_{\mathbb{T}^{n}}\int_{\mathbb{R}^{n}}\big<\tau f(\xi)(\eta),\tau (T^{t}_{(k,l)}{\phi}_{s})(\xi)(\eta)\big>_{\ell^{2}({\mathbb{Z}^n})}d\eta\, d\xi\nonumber\\ &=e^{-\pi ik\cdot l}\int_{\mathbb{T}^{n}}\int_{\mathbb{R}^{n}}\big<\tau f(\xi)(\eta),\tau {\phi}_{s}(\xi+l)(\eta)\big>_{\ell^{2}({\mathbb{Z}^n})}e^{-2\pi ik\cdot\xi}d\eta\, d\xi\nonumber\\ &=e^{-\pi ik\cdot l}\int_{\mathbb{T}^{n}}\big<\tau f(\xi),\tau {\phi}_{s}(\xi+l)\big>_{{L^{2}(\mathbb{R}^{n},\ell^{2}(\mathbb{Z}^{n}))}}e^{-2\pi ik\cdot \xi}\,d\xi\nonumber\\ &=e^{-\pi ik\cdot l}\int_{\mathbb{T}^{n}}F_{l,s}(\xi)e^{-2\pi ik\cdot\xi}\,d\xi\nonumber\\ &=e^{-\pi ik\cdot l}\widehat{F_{l,s}}(k), \end{align} $$
where
![]() $F_{l,s}(\xi )=\big <\tau f(\xi ),\tau {\phi }_{s}(\xi +l)\big>_{{L^{2}(\mathbb {R}^{n},\ell ^{2}(\mathbb {Z}^{n}))}}$
. Hence, we get
$F_{l,s}(\xi )=\big <\tau f(\xi ),\tau {\phi }_{s}(\xi +l)\big>_{{L^{2}(\mathbb {R}^{n},\ell ^{2}(\mathbb {Z}^{n}))}}$
. Hence, we get
 $$ \begin{align} \sum\limits_{k\in \mathbb{Z}^{n}}\big|\big<f,T^{t}_{(k,l)}{\phi}_{s}\big>\big|^{2}&=\sum\limits_{k\in \mathbb{Z}^{n}}|\widehat{F_{l,s}}(k)|^{2}\nonumber\\ &=\|F_{l,s}\|_{L^{2}(\mathbb{T}^{n})}^{2}\nonumber\\ &=\int_{\mathbb{T}^{n}}|F_{l,s}(\xi)|^{2}\,d\xi, \end{align} $$
$$ \begin{align} \sum\limits_{k\in \mathbb{Z}^{n}}\big|\big<f,T^{t}_{(k,l)}{\phi}_{s}\big>\big|^{2}&=\sum\limits_{k\in \mathbb{Z}^{n}}|\widehat{F_{l,s}}(k)|^{2}\nonumber\\ &=\|F_{l,s}\|_{L^{2}(\mathbb{T}^{n})}^{2}\nonumber\\ &=\int_{\mathbb{T}^{n}}|F_{l,s}(\xi)|^{2}\,d\xi, \end{align} $$
by applying the Plancherel formula for the Fourier series. Now, using the definition of
![]() $H_{l}(\xi )^{\ast }$
, we obtain
$H_{l}(\xi )^{\ast }$
, we obtain
 $$ \begin{align*} \sum\limits_{(k,s)\in \mathbb{Z}^{n+1}}\big|\big<f,T^{t}_{(k,l)}{\phi}_{s}\big>\big|^{2}&=\int_{\mathbb{T}^{n}}\sum\limits_{s\in\mathbb{Z}}\big|\big<\tau f(\xi), \tau {\phi}_{s}(\xi+l)\big>_{L^{2}({\mathbb{R}}^{n},l^{2}({\mathbb{Z}^n}))}\big|^{2}\,d\xi\\ &=\int_{\mathbb{T}^{n}}\|H_{l}(\xi)^{\ast}\tau f(\xi)\|^{2}\,d\xi, \end{align*} $$
$$ \begin{align*} \sum\limits_{(k,s)\in \mathbb{Z}^{n+1}}\big|\big<f,T^{t}_{(k,l)}{\phi}_{s}\big>\big|^{2}&=\int_{\mathbb{T}^{n}}\sum\limits_{s\in\mathbb{Z}}\big|\big<\tau f(\xi), \tau {\phi}_{s}(\xi+l)\big>_{L^{2}({\mathbb{R}}^{n},l^{2}({\mathbb{Z}^n}))}\big|^{2}\,d\xi\\ &=\int_{\mathbb{T}^{n}}\|H_{l}(\xi)^{\ast}\tau f(\xi)\|^{2}\,d\xi, \end{align*} $$
proving our assertion.
Theorem 3.3. The collection
![]() $E^{t}(\mathcal {A})$
is a frame sequence with frame bounds
$E^{t}(\mathcal {A})$
is a frame sequence with frame bounds
![]() $A,B>0$
if and only if
$A,B>0$
if and only if
 $$ \begin{align} AP(\xi)\leq \sum\limits_{l\in \mathbb{Z}^{n}}H_{l}(\xi)H_{l}(\xi)^{\ast}\leq BP(\xi),~for~a.e.~\xi\in\mathbb{T}^{n}. \end{align} $$
$$ \begin{align} AP(\xi)\leq \sum\limits_{l\in \mathbb{Z}^{n}}H_{l}(\xi)H_{l}(\xi)^{\ast}\leq BP(\xi),~for~a.e.~\xi\in\mathbb{T}^{n}. \end{align} $$
Proof. Suppose
![]() $E^{t}(\mathcal {A})$
is a frame sequence with frame bounds
$E^{t}(\mathcal {A})$
is a frame sequence with frame bounds
![]() $A,B>0$
. In other words,
$A,B>0$
. In other words,
 $$ \begin{align} A\|f\|^2\leq \sum_{(k,l,s)\in\mathbb{Z}^{2n+1}}\big|\big\langle f,T^{t}_{(k,l)}{\phi}_{s}\big\rangle \big|^{2}\leq B \|f\|^2,\ \ \ \ \ \ \ \forall\ f\in V^t(\mathcal{A}). \end{align} $$
$$ \begin{align} A\|f\|^2\leq \sum_{(k,l,s)\in\mathbb{Z}^{2n+1}}\big|\big\langle f,T^{t}_{(k,l)}{\phi}_{s}\big\rangle \big|^{2}\leq B \|f\|^2,\ \ \ \ \ \ \ \forall\ f\in V^t(\mathcal{A}). \end{align} $$
Let
![]() $\Phi (\xi )\in ~J(\xi ),\ \ \xi \in \mathbb {T}^{n}.$
Consider a trigonometric polynomial
$\Phi (\xi )\in ~J(\xi ),\ \ \xi \in \mathbb {T}^{n}.$
Consider a trigonometric polynomial
 $$ \begin{align*} \psi(\xi)=\sum_{k\in \mathcal{F}}c_{k}e^{2\pi ik\cdot \xi}, \end{align*} $$
$$ \begin{align*} \psi(\xi)=\sum_{k\in \mathcal{F}}c_{k}e^{2\pi ik\cdot \xi}, \end{align*} $$
where
![]() $\mathcal {F}$
is a finite subset of
$\mathcal {F}$
is a finite subset of
![]() $\mathbb {Z}^{n}$
. Define
$\mathbb {Z}^{n}$
. Define
![]() $f\in L^{2}(\mathbb {R}^{2n})$
by
$f\in L^{2}(\mathbb {R}^{2n})$
by
![]() $\tau f(\xi )=\psi (\xi )\Phi (\xi ),~\xi \in \mathbb {T}^{n}$
. More explicitly, it can be written as
$\tau f(\xi )=\psi (\xi )\Phi (\xi ),~\xi \in \mathbb {T}^{n}$
. More explicitly, it can be written as
 $$ \begin{align*} \tau f(\xi)&=\sum\limits_{k\in\mathcal{F}}c_{k}e^{2\pi ik\cdot \xi}\Phi(\xi). \end{align*} $$
$$ \begin{align*} \tau f(\xi)&=\sum\limits_{k\in\mathcal{F}}c_{k}e^{2\pi ik\cdot \xi}\Phi(\xi). \end{align*} $$
By using Proposition 3.1, we can show that
![]() $\tau f(\xi )\in J(\xi ),$
which implies that
$\tau f(\xi )\in J(\xi ),$
which implies that
![]() $f\in V^{t}(\mathcal {A}).$
Further, we have
$f\in V^{t}(\mathcal {A}).$
Further, we have
![]() $H_{l}(\xi )^{\ast }\tau f(\xi )=\psi (\xi )H_{l}(\xi )^{\ast }\Phi (\xi )$
. Now, from Lemma 3.2, we get
$H_{l}(\xi )^{\ast }\tau f(\xi )=\psi (\xi )H_{l}(\xi )^{\ast }\Phi (\xi )$
. Now, from Lemma 3.2, we get
 $$ \begin{align} \sum\limits_{(k,l,s)\in \mathbb{Z}^{2n+1}}\big|\big<f,T^{t}_{(k,l)}{\phi}_{s}\big>\big|^{2}&=\int_{\mathbb{T}^{n}}\sum\limits_{l\in \mathbb{Z}^{n}}\|H_{l}(\xi)^{\ast}\tau f(\xi)\|^{2}\,d\xi\nonumber\\ &=\int_{\mathbb{T}^{n}}\sum\limits_{l\in \mathbb{Z}^{n}}\|\psi(\xi)H_{l}(\xi)^{\ast}\Phi(\xi)\|^{2}\,d\xi\nonumber\\ &=\int_{\mathbb{T}^{n}}|\psi(\xi)|^{2}\sum\limits_{l\in \mathbb{Z}^{n}}\|H_{l}(\xi)^{\ast}\Phi(\xi)\|^{2}\,d\xi. \end{align} $$
$$ \begin{align} \sum\limits_{(k,l,s)\in \mathbb{Z}^{2n+1}}\big|\big<f,T^{t}_{(k,l)}{\phi}_{s}\big>\big|^{2}&=\int_{\mathbb{T}^{n}}\sum\limits_{l\in \mathbb{Z}^{n}}\|H_{l}(\xi)^{\ast}\tau f(\xi)\|^{2}\,d\xi\nonumber\\ &=\int_{\mathbb{T}^{n}}\sum\limits_{l\in \mathbb{Z}^{n}}\|\psi(\xi)H_{l}(\xi)^{\ast}\Phi(\xi)\|^{2}\,d\xi\nonumber\\ &=\int_{\mathbb{T}^{n}}|\psi(\xi)|^{2}\sum\limits_{l\in \mathbb{Z}^{n}}\|H_{l}(\xi)^{\ast}\Phi(\xi)\|^{2}\,d\xi. \end{align} $$
On the other hand,
 $$ \begin{align} \|f\|^{2}&=\|\tau f\|^{2}\nonumber\\ &=\int_{\mathbb{T}^{n}}\|\tau f(\xi)\|^{2}\,d\xi\nonumber\\ &=\int_{\mathbb{T}^{n}}\|\psi(\xi)\Phi(\xi)\|^{2}\,d\xi\nonumber\\ &=\int_{\mathbb{T}^{n}}|\psi(\xi)|^{2}\|\Phi(\xi)\|^{2}\,d\xi. \end{align} $$
$$ \begin{align} \|f\|^{2}&=\|\tau f\|^{2}\nonumber\\ &=\int_{\mathbb{T}^{n}}\|\tau f(\xi)\|^{2}\,d\xi\nonumber\\ &=\int_{\mathbb{T}^{n}}\|\psi(\xi)\Phi(\xi)\|^{2}\,d\xi\nonumber\\ &=\int_{\mathbb{T}^{n}}|\psi(\xi)|^{2}\|\Phi(\xi)\|^{2}\,d\xi. \end{align} $$
Using (3.7) and (3.8) in (3.6), we get
 $$ \begin{align} A\int_{{\mathbb{T}^{n}}}|\psi(\xi)|^{2}\|\Phi(\xi)\|^{2}\,d\xi\leq \int_{{\mathbb{T}^{n}}}|\psi(\xi)|^{2}\sum\limits_{l\in{\mathbb{Z}^n}}\|H_{l}(\xi)^{\ast}\Phi(\xi)\|^{2}\,d\xi\leq B\int_{{\mathbb{T}^{n}}}|\psi(\xi)|^2\|\Phi(\xi)\|^{2}\,d\xi. \end{align} $$
$$ \begin{align} A\int_{{\mathbb{T}^{n}}}|\psi(\xi)|^{2}\|\Phi(\xi)\|^{2}\,d\xi\leq \int_{{\mathbb{T}^{n}}}|\psi(\xi)|^{2}\sum\limits_{l\in{\mathbb{Z}^n}}\|H_{l}(\xi)^{\ast}\Phi(\xi)\|^{2}\,d\xi\leq B\int_{{\mathbb{T}^{n}}}|\psi(\xi)|^2\|\Phi(\xi)\|^{2}\,d\xi. \end{align} $$
Since (3.9) holds for any trigonometric polynomial
![]() $\psi \in L^{2}({\mathbb {T}^{n}})$
, we arrive at
$\psi \in L^{2}({\mathbb {T}^{n}})$
, we arrive at
 $$ \begin{align} A\|\Phi(\xi)\|^{2}\leq\sum\limits_{l\in{\mathbb{Z}^n}}\|H_{l}(\xi)^{\ast}\Phi(\xi)\|^{2}\leq B\|\Phi(\xi)\|^{2},\ \text{for}\ a.e.~\xi\in{\mathbb{T}^{n}}. \end{align} $$
$$ \begin{align} A\|\Phi(\xi)\|^{2}\leq\sum\limits_{l\in{\mathbb{Z}^n}}\|H_{l}(\xi)^{\ast}\Phi(\xi)\|^{2}\leq B\|\Phi(\xi)\|^{2},\ \text{for}\ a.e.~\xi\in{\mathbb{T}^{n}}. \end{align} $$
Now, the above equation together with
 $\ker \bigg (\sum \limits _{l\in {\mathbb {Z}^n}}H_{l}(\xi )H_{l}(\xi )^{\ast }\bigg )=J(\xi )^{\perp }$
leads to (3.5). Conversely, assume that (3.5) holds. Let
$\ker \bigg (\sum \limits _{l\in {\mathbb {Z}^n}}H_{l}(\xi )H_{l}(\xi )^{\ast }\bigg )=J(\xi )^{\perp }$
leads to (3.5). Conversely, assume that (3.5) holds. Let
![]() $f\in V^{t}(\mathcal {A})$
. Then,
$f\in V^{t}(\mathcal {A})$
. Then,
![]() $\tau f(\xi )\in J(\xi )$
by using Proposition 3.1. Hence, (3.5) reduces to
$\tau f(\xi )\in J(\xi )$
by using Proposition 3.1. Hence, (3.5) reduces to
 $$ \begin{align*} A\|\tau f(\xi)\|^{2}\leq \sum\limits_{l\in{\mathbb{Z}^n}}\|H_{l}(\xi)^{\ast}\tau f(\xi)\|^{2}\leq B\|\tau f(\xi)\|^{2},~\text{for}\ a.e.~\xi\in{\mathbb{T}^{n}}. \end{align*} $$
$$ \begin{align*} A\|\tau f(\xi)\|^{2}\leq \sum\limits_{l\in{\mathbb{Z}^n}}\|H_{l}(\xi)^{\ast}\tau f(\xi)\|^{2}\leq B\|\tau f(\xi)\|^{2},~\text{for}\ a.e.~\xi\in{\mathbb{T}^{n}}. \end{align*} $$
Taking integral with respect to
![]() $\xi $
in the above inequality, we get
$\xi $
in the above inequality, we get
 $$ \begin{align*} A\int_{{\mathbb{T}^{n}}}\|\tau f(\xi)\|^{2}d\xi\leq \int_{{\mathbb{T}^{n}}}\sum\limits_{l\in {\mathbb{Z}^n}}\|H_{l}(\xi)^{\ast}\tau f(\xi)\|^{2}d\xi\leq B\int_{{\mathbb{T}^{n}}}\|\tau f(\xi)\|^{2}d\xi. \end{align*} $$
$$ \begin{align*} A\int_{{\mathbb{T}^{n}}}\|\tau f(\xi)\|^{2}d\xi\leq \int_{{\mathbb{T}^{n}}}\sum\limits_{l\in {\mathbb{Z}^n}}\|H_{l}(\xi)^{\ast}\tau f(\xi)\|^{2}d\xi\leq B\int_{{\mathbb{T}^{n}}}\|\tau f(\xi)\|^{2}d\xi. \end{align*} $$
Now, using Lemma 3.2 and the isometry of
![]() $\tau $
in the above inequality, we get
$\tau $
in the above inequality, we get
 $$ \begin{align*} A\|f\|^2\leq \sum_{(k,l,s)\in\mathbb{Z}^{2n+1}}\big|\big\langle f,T^{t}_{(k,l)}{\phi}_{s}\big\rangle \big|^{2}\leq B \|f\|^2. \end{align*} $$
$$ \begin{align*} A\|f\|^2\leq \sum_{(k,l,s)\in\mathbb{Z}^{2n+1}}\big|\big\langle f,T^{t}_{(k,l)}{\phi}_{s}\big\rangle \big|^{2}\leq B \|f\|^2. \end{align*} $$
Since
![]() $f\in V^{t}(\mathcal {A})$
is arbitrary, the assertion follows.
$f\in V^{t}(\mathcal {A})$
is arbitrary, the assertion follows.
Now, we obtain the following corollaries as a consequence of Theorem 3.3.
Corollary 3.4. The collection
![]() $E^{t}(\mathcal {A})$
is a Parseval frame sequence if and only if
$E^{t}(\mathcal {A})$
is a Parseval frame sequence if and only if
 $$ \begin{align*}\sum\limits_{l\in{\mathbb{Z}^n}}H_{l}(\xi)H_{l}(\xi)^{\ast}=P(\xi),\ \ \ \ \ \text{for}\ a.e.\ \xi\in{\mathbb{T}^{n}}.\end{align*} $$
$$ \begin{align*}\sum\limits_{l\in{\mathbb{Z}^n}}H_{l}(\xi)H_{l}(\xi)^{\ast}=P(\xi),\ \ \ \ \ \text{for}\ a.e.\ \xi\in{\mathbb{T}^{n}}.\end{align*} $$
Corollary 3.5. The collection
![]() $E^{t}(\mathcal {A})$
is a frame sequence with frame bounds A and B if and only if the collection
$E^{t}(\mathcal {A})$
is a frame sequence with frame bounds A and B if and only if the collection
![]() $\{\tau {\phi }_{s}(\xi +l) : s\in {\mathbb {Z}},l\in {\mathbb {Z}^n}\}$
is a frame sequence with the same bounds, for
$\{\tau {\phi }_{s}(\xi +l) : s\in {\mathbb {Z}},l\in {\mathbb {Z}^n}\}$
is a frame sequence with the same bounds, for
![]() $a.e$
.
$a.e$
.
![]() $\xi \in {\mathbb {T}^{n}}$
.
$\xi \in {\mathbb {T}^{n}}$
.
Proof. Assume that
![]() $E^{t}(\mathcal {A})$
is a frame sequence with frame bounds A and B. Now, by Theorem 3.3, it is equivalent to
$E^{t}(\mathcal {A})$
is a frame sequence with frame bounds A and B. Now, by Theorem 3.3, it is equivalent to
 $$ \begin{align*} A\|\tau f(\xi)\|^{2}\leq\sum\limits_{(l,s)\in \mathbb{Z}^{n+1}}|\big<\tau f(\xi),\tau {\phi}_{s}(\xi+l)\big>|^{2}\leq B \|\tau f(\xi)\|^{2} \end{align*} $$
$$ \begin{align*} A\|\tau f(\xi)\|^{2}\leq\sum\limits_{(l,s)\in \mathbb{Z}^{n+1}}|\big<\tau f(\xi),\tau {\phi}_{s}(\xi+l)\big>|^{2}\leq B \|\tau f(\xi)\|^{2} \end{align*} $$
![]() $\forall \ f\in V^{t}(\mathcal {A})$
and for
$\forall \ f\in V^{t}(\mathcal {A})$
and for
![]() $a.e$
.
$a.e$
.
![]() $\xi \in {\mathbb {T}^{n}}$
, which proves our assertion.
$\xi \in {\mathbb {T}^{n}}$
, which proves our assertion.
Theorem 3.6. The collection
![]() $E^{t}(\mathcal {A})$
is a frame sequence with frame bounds A and B if and only if
$E^{t}(\mathcal {A})$
is a frame sequence with frame bounds A and B if and only if
![]() $\forall \ f\in V^{t}(\mathcal {A})$
and for
$\forall \ f\in V^{t}(\mathcal {A})$
and for
![]() $a.e.\ \xi \in {\mathbb {T}^{n}}$
, where S is the frame operator associated with the system
$a.e.\ \xi \in {\mathbb {T}^{n}}$
, where S is the frame operator associated with the system
![]() $E^{t}(\mathcal {A})$
.
$E^{t}(\mathcal {A})$
.
Proof. The frame operator S associated with
![]() $E^{t}(\mathcal {A})$
is given by
$E^{t}(\mathcal {A})$
is given by
 $$ \begin{align*} Sf=\sum\limits_{(k,l,s)\in \mathbb{Z}^{2n+1}}\big<f,{T_{(k,l)}^t} {\phi}_{s}\big>{T_{(k,l)}^t} {\phi}_{s},\ \ \ \ \ \forall\ f\in V^t({\mathcal{A}}). \end{align*} $$
$$ \begin{align*} Sf=\sum\limits_{(k,l,s)\in \mathbb{Z}^{2n+1}}\big<f,{T_{(k,l)}^t} {\phi}_{s}\big>{T_{(k,l)}^t} {\phi}_{s},\ \ \ \ \ \forall\ f\in V^t({\mathcal{A}}). \end{align*} $$
 $$ \begin{align*} \tau(Sf)(\xi)=&\sum\limits_{(k,l,s)\in \mathbb{Z}^{2n+1}}\big<f,{T_{(k,l)}^t} {\phi}_{s}\big>\tau({T_{(k,l)}^t} {\phi}_{s})(\xi) \\ =&\sum\limits_{(k,l,s)\in \mathbb{Z}^{2n+1}}\big<f,{T_{(k,l)}^t} {\phi}_{s}\big>e^{\pi ik\cdot(2\xi+l)}\tau {\phi}_{s}(\xi+l) \\ =&\sum\limits_{(l,s)\in \mathbb{Z}^{n+1}}\Big(\sum\limits_{k\in{\mathbb{Z}^n}}\big<f,{T_{(k,l)}^t} {\phi}_{s}\big>e^{\pi ik\cdot(2\xi+l)}\Big)\tau {\phi}_{s}(\xi+l) \\ =&\sum\limits_{(l,s)\in \mathbb{Z}^{n+1}}\Big(\sum\limits_{k\in{\mathbb{Z}^n}} \widehat{F}_{l,s}(k)e^{2\pi ik\cdot\xi} \Big) \tau {\phi}_{s}(\xi+l) \\ =&\sum\limits_{(l,s)\in\mathbb{Z}^{n+1}}F_{l,s}(\xi)\ \tau {\phi}_{s}(\xi+l) \\ =&\sum\limits_{(l,s)\in\mathbb{Z}^{n+1}}\big<\tau f(\xi),\tau {\phi}_{s}(\xi+l)\big>_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\tau {\phi}_{s}(\xi+l), \end{align*} $$
$$ \begin{align*} \tau(Sf)(\xi)=&\sum\limits_{(k,l,s)\in \mathbb{Z}^{2n+1}}\big<f,{T_{(k,l)}^t} {\phi}_{s}\big>\tau({T_{(k,l)}^t} {\phi}_{s})(\xi) \\ =&\sum\limits_{(k,l,s)\in \mathbb{Z}^{2n+1}}\big<f,{T_{(k,l)}^t} {\phi}_{s}\big>e^{\pi ik\cdot(2\xi+l)}\tau {\phi}_{s}(\xi+l) \\ =&\sum\limits_{(l,s)\in \mathbb{Z}^{n+1}}\Big(\sum\limits_{k\in{\mathbb{Z}^n}}\big<f,{T_{(k,l)}^t} {\phi}_{s}\big>e^{\pi ik\cdot(2\xi+l)}\Big)\tau {\phi}_{s}(\xi+l) \\ =&\sum\limits_{(l,s)\in \mathbb{Z}^{n+1}}\Big(\sum\limits_{k\in{\mathbb{Z}^n}} \widehat{F}_{l,s}(k)e^{2\pi ik\cdot\xi} \Big) \tau {\phi}_{s}(\xi+l) \\ =&\sum\limits_{(l,s)\in\mathbb{Z}^{n+1}}F_{l,s}(\xi)\ \tau {\phi}_{s}(\xi+l) \\ =&\sum\limits_{(l,s)\in\mathbb{Z}^{n+1}}\big<\tau f(\xi),\tau {\phi}_{s}(\xi+l)\big>_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\tau {\phi}_{s}(\xi+l), \end{align*} $$
by applying the Fourier series of
![]() $F_{l,s}$
. Now, using the definition of
$F_{l,s}$
. Now, using the definition of
![]() $H_{l}(\xi )$
and its adjoint, we have
$H_{l}(\xi )$
and its adjoint, we have
 $$ \begin{align} \sum\limits_{l\in{\mathbb{Z}^n}}H_{l}(\xi)H_{l}(\xi)^{\ast}\tau f(\xi)&=\sum\limits_{(l,s)\in \mathbb{Z}^{n+1}}\big<\tau f(\xi),\tau {\phi}_{s}(\xi+l)\big>_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\tau {\phi}_{s}(\xi+l)\nonumber \\ &=\tau(Sf)(\xi). \end{align} $$
$$ \begin{align} \sum\limits_{l\in{\mathbb{Z}^n}}H_{l}(\xi)H_{l}(\xi)^{\ast}\tau f(\xi)&=\sum\limits_{(l,s)\in \mathbb{Z}^{n+1}}\big<\tau f(\xi),\tau {\phi}_{s}(\xi+l)\big>_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\tau {\phi}_{s}(\xi+l)\nonumber \\ &=\tau(Sf)(\xi). \end{align} $$
By Theorem 3.3, the system
![]() $E^{t}(\mathcal {A})$
is a frame sequence with frame bounds A and B if and only if
$E^{t}(\mathcal {A})$
is a frame sequence with frame bounds A and B if and only if
 $$ \begin{align*} A\|\tau f(\xi)\|^{2}\leq \Big\langle\sum\limits_{l\in{\mathbb{Z}^n}}H_{l}(\xi)H_{l}(\xi)^{\ast}\tau f(\xi), \tau f(\xi)\Big \rangle\leq B\|\tau f(\xi)\|^{2}, \end{align*} $$
$$ \begin{align*} A\|\tau f(\xi)\|^{2}\leq \Big\langle\sum\limits_{l\in{\mathbb{Z}^n}}H_{l}(\xi)H_{l}(\xi)^{\ast}\tau f(\xi), \tau f(\xi)\Big \rangle\leq B\|\tau f(\xi)\|^{2}, \end{align*} $$
for
![]() $a.e.\ \xi \in {\mathbb {T}^{n}}$
. Now, using (3.12) in the above inequality, we arrive at the required result.
$a.e.\ \xi \in {\mathbb {T}^{n}}$
. Now, using (3.12) in the above inequality, we arrive at the required result.
For
![]() ${\phi }\in L^2({\mathbb {R}}^{2n})$
and
${\phi }\in L^2({\mathbb {R}}^{2n})$
and
![]() $\xi \in {\mathbb {T}^{n}}$
, we define
$\xi \in {\mathbb {T}^{n}}$
, we define
 $$ \begin{align*} W_{{\phi}}(\xi)&:=\frac{1}{\omega_{{\phi}}(\xi)} \sum\limits_{l\in {\mathbb{Z}^n}}\big|\sum\limits_{m\in {\mathbb{Z}^n}}\int_{{\mathbb{R}}^{n}}K_{{\phi}}(\xi+m,\eta)\overline{K_{\phi}(\xi+m+l,\eta)}\,d\eta\big|^{2},~\text{whenever}~\omega_{\phi}(\xi)\neq 0. \end{align*} $$
$$ \begin{align*} W_{{\phi}}(\xi)&:=\frac{1}{\omega_{{\phi}}(\xi)} \sum\limits_{l\in {\mathbb{Z}^n}}\big|\sum\limits_{m\in {\mathbb{Z}^n}}\int_{{\mathbb{R}}^{n}}K_{{\phi}}(\xi+m,\eta)\overline{K_{\phi}(\xi+m+l,\eta)}\,d\eta\big|^{2},~\text{whenever}~\omega_{\phi}(\xi)\neq 0. \end{align*} $$
Theorem 3.7. Let
![]() $\mathcal {A}=\{{\phi }\}$
, and let
$\mathcal {A}=\{{\phi }\}$
, and let
![]() $E^{t}(\mathcal {A})$
be a frame sequence with frame bounds A and B. Then
$E^{t}(\mathcal {A})$
be a frame sequence with frame bounds A and B. Then
![]() $A\leq W_{{\phi }}(\xi )\leq B$
for
$A\leq W_{{\phi }}(\xi )\leq B$
for
![]() $a.e$
.
$a.e$
.
![]() $\xi \in {\mathbb {T}^{n}}\setminus N$
, where
$\xi \in {\mathbb {T}^{n}}\setminus N$
, where
![]() $N:=\{\xi \in {\mathbb {T}^{n}} : w_{{\phi }}(\xi )=0\}$
.
$N:=\{\xi \in {\mathbb {T}^{n}} : w_{{\phi }}(\xi )=0\}$
.
Proof. Using Corollary 3.5, we have
 $$ \begin{align*} A\|\Phi(\xi)\|^{2}\leq \sum\limits_{l\in{\mathbb{Z}^n}}|\big<\Phi(\xi),\tau {\phi}(\xi+l)\big>|^{2}\leq B\|\Phi(\xi)\|^{2}, \end{align*} $$
$$ \begin{align*} A\|\Phi(\xi)\|^{2}\leq \sum\limits_{l\in{\mathbb{Z}^n}}|\big<\Phi(\xi),\tau {\phi}(\xi+l)\big>|^{2}\leq B\|\Phi(\xi)\|^{2}, \end{align*} $$
![]() $\forall \ \Phi (\xi )\in J(\xi )$
and for
$\forall \ \Phi (\xi )\in J(\xi )$
and for
![]() $a.e.\ \xi \in {\mathbb {T}^{n}}$
. Taking
$a.e.\ \xi \in {\mathbb {T}^{n}}$
. Taking
![]() $\Phi (\xi )=\tau {\phi }(\xi )\in J(\xi )$
in the above inequality, we obtain
$\Phi (\xi )=\tau {\phi }(\xi )\in J(\xi )$
in the above inequality, we obtain
 $$ \begin{align*} A\|\tau {\phi}(\xi)\|^{2}\leq \sum\limits_{l\in{\mathbb{Z}^n}}|\big<\tau {\phi}(\xi),\tau {\phi}(\xi+l)\big>|^{2}\leq B\|\tau {\phi}(\xi)\|^{2}, \end{align*} $$
$$ \begin{align*} A\|\tau {\phi}(\xi)\|^{2}\leq \sum\limits_{l\in{\mathbb{Z}^n}}|\big<\tau {\phi}(\xi),\tau {\phi}(\xi+l)\big>|^{2}\leq B\|\tau {\phi}(\xi)\|^{2}, \end{align*} $$
for
![]() $a.e.\ \xi \in {\mathbb {T}^{n}}$
. Now, using the definition of the fiber map
$a.e.\ \xi \in {\mathbb {T}^{n}}$
. Now, using the definition of the fiber map
![]() $\tau $
, we have
$\tau $
, we have
 $$ \begin{align*} A\sum\limits_{m\in{\mathbb{Z}^n}}\int_{{\mathbb{R}}^{n}}|K_{{\phi}}(\xi+m,\eta)|^{2}d\eta&\leq \sum\limits_{l\in{\mathbb{Z}^n}}\big|\sum\limits_{m\in{\mathbb{Z}^n}}\int_{{\mathbb{R}}^{n}}K_{{\phi}}(\xi+m,\eta)K_{{\phi}}(\xi+m+l,\eta)d\eta\big|^{2}\\ &\leq B\sum\limits_{m\in{\mathbb{Z}^n}}\int_{{\mathbb{R}}^{n}}|K_{{\phi}}(\xi+m,\eta)|^{2}d\eta, \end{align*} $$
$$ \begin{align*} A\sum\limits_{m\in{\mathbb{Z}^n}}\int_{{\mathbb{R}}^{n}}|K_{{\phi}}(\xi+m,\eta)|^{2}d\eta&\leq \sum\limits_{l\in{\mathbb{Z}^n}}\big|\sum\limits_{m\in{\mathbb{Z}^n}}\int_{{\mathbb{R}}^{n}}K_{{\phi}}(\xi+m,\eta)K_{{\phi}}(\xi+m+l,\eta)d\eta\big|^{2}\\ &\leq B\sum\limits_{m\in{\mathbb{Z}^n}}\int_{{\mathbb{R}}^{n}}|K_{{\phi}}(\xi+m,\eta)|^{2}d\eta, \end{align*} $$
which in turn implies that
![]() $A\leq W_{{\phi }}(\xi )\leq B$
for
$A\leq W_{{\phi }}(\xi )\leq B$
for
![]() $a.e.\ \xi \in {\mathbb {T}^{n}}\setminus N$
.
$a.e.\ \xi \in {\mathbb {T}^{n}}\setminus N$
.
For
![]() $l_1,l_2\in {\mathbb {Z}^n}$
and
$l_1,l_2\in {\mathbb {Z}^n}$
and
![]() $\xi \in {\mathbb {T}^{n}}$
, using the definition of the fiber map
$\xi \in {\mathbb {T}^{n}}$
, using the definition of the fiber map
![]() $\tau $
, we have
$\tau $
, we have
 $$ \begin{align} \big<\tau{\phi}(\xi+l_{1}),\tau{\phi}(\xi+l_{2})\big>_{L^{2}({\mathbb{R}}^{n}, \ell^{2}({\mathbb{Z}^n}))}&=\int_{{\mathbb{R}}^{n}}\sum\limits_{m\in{\mathbb{Z}^n}}K_{{\phi}}(\xi+m+l_{1},\eta) \overline{K_{{\phi}}(\xi+m+l_{2},\eta)}\,d\eta \nonumber \\ &=\int_{{\mathbb{R}}^{n}}\sum\limits_{m\in{\mathbb{Z}^n}}K_{{\phi}}(\xi+m,\eta)\overline{K_{{\phi}}(\xi+m+l_{2}-l_1,\eta)}\,d\eta. \end{align} $$
$$ \begin{align} \big<\tau{\phi}(\xi+l_{1}),\tau{\phi}(\xi+l_{2})\big>_{L^{2}({\mathbb{R}}^{n}, \ell^{2}({\mathbb{Z}^n}))}&=\int_{{\mathbb{R}}^{n}}\sum\limits_{m\in{\mathbb{Z}^n}}K_{{\phi}}(\xi+m+l_{1},\eta) \overline{K_{{\phi}}(\xi+m+l_{2},\eta)}\,d\eta \nonumber \\ &=\int_{{\mathbb{R}}^{n}}\sum\limits_{m\in{\mathbb{Z}^n}}K_{{\phi}}(\xi+m,\eta)\overline{K_{{\phi}}(\xi+m+l_{2}-l_1,\eta)}\,d\eta. \end{align} $$
Corollary 3.8 [Reference Radha and Adhikari18].
Let
![]() ${\mathcal {A}}=\{{\phi }\}$
and
${\mathcal {A}}=\{{\phi }\}$
and
![]() ${\phi }$
satisfy “Condition C.” Then
${\phi }$
satisfy “Condition C.” Then
![]() $E^t({\mathcal {A}})$
is a frame sequence with frame bounds A and B if and only if
$E^t({\mathcal {A}})$
is a frame sequence with frame bounds A and B if and only if
Proof. Let
![]() $E^t({\mathcal {A}})$
be a frame sequence with frame bounds A and B. Then, by Theorem 3.7, we have
$E^t({\mathcal {A}})$
be a frame sequence with frame bounds A and B. Then, by Theorem 3.7, we have
![]() $A\leq W_{{\phi }}(\xi )\leq B$
, for
$A\leq W_{{\phi }}(\xi )\leq B$
, for
![]() $a.e$
.
$a.e$
.
![]() $\xi \in {\mathbb {T}^{n}}\setminus N$
. Since
$\xi \in {\mathbb {T}^{n}}\setminus N$
. Since
![]() ${\phi }$
satisfies “Condition C,” we get
${\phi }$
satisfies “Condition C,” we get
 $$ \begin{align} W_{{\phi}}(\xi)&=\frac{1}{\omega_{{\phi}}(\xi)}\Big| \sum\limits_{m\in{\mathbb{Z}^n}} \int_{{\mathbb{R}}^{n}}|K_{{\phi}}(\xi+m,\eta)|^{2}\,d\eta\Big|^2 \notag \\ &=\frac{1}{\omega_{{\phi}}(\xi)}\ \omega_{{\phi}}^2(\xi)\notag \\ &=\omega_{{\phi}}(\xi)\ , \end{align} $$
$$ \begin{align} W_{{\phi}}(\xi)&=\frac{1}{\omega_{{\phi}}(\xi)}\Big| \sum\limits_{m\in{\mathbb{Z}^n}} \int_{{\mathbb{R}}^{n}}|K_{{\phi}}(\xi+m,\eta)|^{2}\,d\eta\Big|^2 \notag \\ &=\frac{1}{\omega_{{\phi}}(\xi)}\ \omega_{{\phi}}^2(\xi)\notag \\ &=\omega_{{\phi}}(\xi)\ , \end{align} $$
for
![]() $\xi \in {\mathbb {T}^{n}}\setminus N$
, which in turn implies (3.14). Conversely, assume that (3.14) holds. Let
$\xi \in {\mathbb {T}^{n}}\setminus N$
, which in turn implies (3.14). Conversely, assume that (3.14) holds. Let
![]() $\Phi (\xi )=\sum \limits _{l^{\prime }\in {\mathbb {Z}^n}}\alpha _{l^{\prime }}(\xi )\tau \phi (\xi +l^{\prime })\in J(\xi )$
. Then, using (3.13), we have
$\Phi (\xi )=\sum \limits _{l^{\prime }\in {\mathbb {Z}^n}}\alpha _{l^{\prime }}(\xi )\tau \phi (\xi +l^{\prime })\in J(\xi )$
. Then, using (3.13), we have
 $$ \begin{align} \big<\Phi(\xi),\tau {\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}=&\sum\limits_{l^{\prime}\in{\mathbb{Z}^n}}\alpha_{l^{\prime}}(\xi)\big<\tau {\phi}(\xi+l^{\prime}),\tau {\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\nonumber\\ =&\sum\limits_{l^{\prime}\in{\mathbb{Z}^n}}\alpha_{l^{\prime}}(\xi) \int_{{\mathbb{R}}^{n}}\sum\limits_{m\in{\mathbb{Z}^n}}K_{{\phi}}(\xi+m,\eta)\overline{K_{{\phi}}(\xi+m+l-l^{\prime},\eta)}\,d\eta \end{align} $$
$$ \begin{align} \big<\Phi(\xi),\tau {\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}=&\sum\limits_{l^{\prime}\in{\mathbb{Z}^n}}\alpha_{l^{\prime}}(\xi)\big<\tau {\phi}(\xi+l^{\prime}),\tau {\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\nonumber\\ =&\sum\limits_{l^{\prime}\in{\mathbb{Z}^n}}\alpha_{l^{\prime}}(\xi) \int_{{\mathbb{R}}^{n}}\sum\limits_{m\in{\mathbb{Z}^n}}K_{{\phi}}(\xi+m,\eta)\overline{K_{{\phi}}(\xi+m+l-l^{\prime},\eta)}\,d\eta \end{align} $$
and
 $$ \begin{align} \|\Phi(\xi)\|_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}^2 &=\big<\Phi(\xi),\Phi(\xi)\big>_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\nonumber \\ =&\sum\limits_{l_{1},l_{2}\in{\mathbb{Z}^n}}\alpha_{l_{1}}(\xi)\overline{\alpha_{l_{2}}(\xi)}\big<\tau {\phi}(\xi+l_{1},\tau {\phi}(\xi+l_{2}))\big>_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\nonumber\\ =&\sum\limits_{l_{1},l_{2}\in{\mathbb{Z}^n}}\alpha_{l_{1}}(\xi)\overline{\alpha_{l_{2}}(\xi)}\int_{{\mathbb{R}}^{n}}\sum\limits_{m\in{\mathbb{Z}^n}}K_{{\phi}}(\xi+m,\eta)\overline{K_{{\phi}}(\xi+m+l_{2}-l_{1},\eta)}\,d\eta. \end{align} $$
$$ \begin{align} \|\Phi(\xi)\|_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}^2 &=\big<\Phi(\xi),\Phi(\xi)\big>_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\nonumber \\ =&\sum\limits_{l_{1},l_{2}\in{\mathbb{Z}^n}}\alpha_{l_{1}}(\xi)\overline{\alpha_{l_{2}}(\xi)}\big<\tau {\phi}(\xi+l_{1},\tau {\phi}(\xi+l_{2}))\big>_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\nonumber\\ =&\sum\limits_{l_{1},l_{2}\in{\mathbb{Z}^n}}\alpha_{l_{1}}(\xi)\overline{\alpha_{l_{2}}(\xi)}\int_{{\mathbb{R}}^{n}}\sum\limits_{m\in{\mathbb{Z}^n}}K_{{\phi}}(\xi+m,\eta)\overline{K_{{\phi}}(\xi+m+l_{2}-l_{1},\eta)}\,d\eta. \end{align} $$
Since
![]() ${\phi }$
satisfies “Condition C,” (3.16) reduces to
${\phi }$
satisfies “Condition C,” (3.16) reduces to
 $$ \begin{align} \big<\Phi(\xi),\tau {\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))} &=\alpha_{l}(\xi)\int_{{\mathbb{R}}^{n}}\sum\limits_{m\in{\mathbb{Z}^n}}|K_{{\phi}}(\xi+m,\eta)|^{2}\,d\eta \nonumber \\ =&\alpha_{l}(\xi)\ \omega_{{\phi}}(\xi) \end{align} $$
$$ \begin{align} \big<\Phi(\xi),\tau {\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))} &=\alpha_{l}(\xi)\int_{{\mathbb{R}}^{n}}\sum\limits_{m\in{\mathbb{Z}^n}}|K_{{\phi}}(\xi+m,\eta)|^{2}\,d\eta \nonumber \\ =&\alpha_{l}(\xi)\ \omega_{{\phi}}(\xi) \end{align} $$
and (3.17) reduces to
 $$ \begin{align} \|\Phi(\xi)\|_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}^2 &=\sum\limits_{l_{1}\in{\mathbb{Z}^n}}|\alpha_{l_{1}}(\xi)|^{2} \int_{{\mathbb{R}}^{n}} \sum\limits_{m\in{\mathbb{Z}^n}}|K_{{\phi}}(\xi+m,\eta)|^{2}\,d\eta \nonumber \\ =&\omega_{{\phi}}(\xi) \sum\limits_{l_{1}\in{\mathbb{Z}^n}}|\alpha_{l_{1}}(\xi)|^{2}. \end{align} $$
$$ \begin{align} \|\Phi(\xi)\|_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}^2 &=\sum\limits_{l_{1}\in{\mathbb{Z}^n}}|\alpha_{l_{1}}(\xi)|^{2} \int_{{\mathbb{R}}^{n}} \sum\limits_{m\in{\mathbb{Z}^n}}|K_{{\phi}}(\xi+m,\eta)|^{2}\,d\eta \nonumber \\ =&\omega_{{\phi}}(\xi) \sum\limits_{l_{1}\in{\mathbb{Z}^n}}|\alpha_{l_{1}}(\xi)|^{2}. \end{align} $$
Now, using (3.18) and (3.19), we obtain
 $$ \begin{align} \sum\limits_{l\in{\mathbb{Z}^n}}|\big<\Phi(\xi),\tau {\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}|^{2}=&\sum\limits_{l\in{\mathbb{Z}^n}}|\alpha_{l}(\xi)|^{2}\ \omega_{{\phi}}^2(\xi)\notag \\ =&\omega_{{\phi}}(\xi) \bigg( \omega_{{\phi}}(\xi) \sum\limits_{l\in{\mathbb{Z}^n}}|\alpha_{l}(\xi)|^{2}\bigg) \notag \\ =& \omega_{{\phi}}(\xi)\ \|\Phi(\xi)\|_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}^{2}. \end{align} $$
$$ \begin{align} \sum\limits_{l\in{\mathbb{Z}^n}}|\big<\Phi(\xi),\tau {\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}|^{2}=&\sum\limits_{l\in{\mathbb{Z}^n}}|\alpha_{l}(\xi)|^{2}\ \omega_{{\phi}}^2(\xi)\notag \\ =&\omega_{{\phi}}(\xi) \bigg( \omega_{{\phi}}(\xi) \sum\limits_{l\in{\mathbb{Z}^n}}|\alpha_{l}(\xi)|^{2}\bigg) \notag \\ =& \omega_{{\phi}}(\xi)\ \|\Phi(\xi)\|_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}^{2}. \end{align} $$
Now, making use of (3.14), we have
for
![]() $a.e.\ \xi \in {\mathbb {T}^{n}}\setminus N$
. Hence, (3.20) gives
$a.e.\ \xi \in {\mathbb {T}^{n}}\setminus N$
. Hence, (3.20) gives
 $$ \begin{align} A\|\Phi(\xi)\|_{L^{2}({\mathbb{R}}^{n},l^{2}({\mathbb{Z}^n}))}^{2}\leq \sum\limits_{l\in{\mathbb{Z}^n}}|\big<\Phi(\xi),\tau {\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}}^{n},l^{2}({\mathbb{Z}^n}))}|^{2}\leq B\|\Phi(\xi)\|_{L^{2}({\mathbb{R}}^{n},l^{2}({\mathbb{Z}^n}))}^{2}, \end{align} $$
$$ \begin{align} A\|\Phi(\xi)\|_{L^{2}({\mathbb{R}}^{n},l^{2}({\mathbb{Z}^n}))}^{2}\leq \sum\limits_{l\in{\mathbb{Z}^n}}|\big<\Phi(\xi),\tau {\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}}^{n},l^{2}({\mathbb{Z}^n}))}|^{2}\leq B\|\Phi(\xi)\|_{L^{2}({\mathbb{R}}^{n},l^{2}({\mathbb{Z}^n}))}^{2}, \end{align} $$
for
![]() $a.e.\ \xi \in {\mathbb {T}^{n}}\setminus N$
. Moreover, from (3.19) and (3.20), we have
$a.e.\ \xi \in {\mathbb {T}^{n}}\setminus N$
. Moreover, from (3.19) and (3.20), we have
 $$ \begin{align*} \|\Phi(\xi)\|_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}^2=0\ \ \ \ \text{and}\ \ \ \ \sum\limits_{l\in{\mathbb{Z}^n}}|\big<\Phi(\xi),\tau {\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}|^{2}=0,\ \ \ \ \ \forall\ \xi\in N. \end{align*} $$
$$ \begin{align*} \|\Phi(\xi)\|_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}^2=0\ \ \ \ \text{and}\ \ \ \ \sum\limits_{l\in{\mathbb{Z}^n}}|\big<\Phi(\xi),\tau {\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}|^{2}=0,\ \ \ \ \ \forall\ \xi\in N. \end{align*} $$
Thus, (3.21) holds for all
![]() $\xi \in N$
, all sides being equal to zero. Therefore, using Corollary 3.5, we obtain the required result.
$\xi \in N$
, all sides being equal to zero. Therefore, using Corollary 3.5, we obtain the required result.
Now, we provide an example of a function
![]() ${\phi }\in L^2(\mathbb {R}^{2})$
such that the system
${\phi }\in L^2(\mathbb {R}^{2})$
such that the system
![]() $\{{T_{(k,l)}^t}{\phi } : k,l\in \mathbb {Z}\}$
forms a frame sequence (i) when
$\{{T_{(k,l)}^t}{\phi } : k,l\in \mathbb {Z}\}$
forms a frame sequence (i) when
![]() ${\phi }$
satisfies “Condition C” and (ii)
${\phi }$
satisfies “Condition C” and (ii)
![]() ${\phi }$
does not satisfy “Condition C.” Before stating the example, we observe the following.
${\phi }$
does not satisfy “Condition C.” Before stating the example, we observe the following.
Let
![]() $f,g\in L^{2}(\mathbb {R}^{2n})$
and
$f,g\in L^{2}(\mathbb {R}^{2n})$
and
![]() $l\in {\mathbb {Z}^n}$
. Then using a similar calculation as in (3.3), we get
$l\in {\mathbb {Z}^n}$
. Then using a similar calculation as in (3.3), we get
where
![]() $F_{l}(\xi )=\big \langle \tau f(\xi ),\tau g(\xi +l)\big \rangle _{{L^{2}(\mathbb {R}^{n},\ell ^{2}(\mathbb {Z}^{n}))}}$
. Making use of the Fourier series of
$F_{l}(\xi )=\big \langle \tau f(\xi ),\tau g(\xi +l)\big \rangle _{{L^{2}(\mathbb {R}^{n},\ell ^{2}(\mathbb {Z}^{n}))}}$
. Making use of the Fourier series of
![]() $F_l$
, we get
$F_l$
, we get
 $$ \begin{align} F_{l}(\xi)=\sum\limits_{k\in{\mathbb{Z}^n}}\big\langle f,{T_{(k,l)}^t} g\big\rangle e^{\pi ik\cdot(2\xi+l)}. \end{align} $$
$$ \begin{align} F_{l}(\xi)=\sum\limits_{k\in{\mathbb{Z}^n}}\big\langle f,{T_{(k,l)}^t} g\big\rangle e^{\pi ik\cdot(2\xi+l)}. \end{align} $$
On the other hand, using the definition of the map
![]() $\tau $
, we have
$\tau $
, we have
 $$ \begin{align} F_{l}(\xi)=\sum\limits_{m\in{\mathbb{Z}^n}}\int_{\mathbb{R}^{n}}K_{f}(\xi+m,\eta)\overline{K_{g}(\xi+m+l,\eta)}\,d\eta. \end{align} $$
$$ \begin{align} F_{l}(\xi)=\sum\limits_{m\in{\mathbb{Z}^n}}\int_{\mathbb{R}^{n}}K_{f}(\xi+m,\eta)\overline{K_{g}(\xi+m+l,\eta)}\,d\eta. \end{align} $$
Therefore, from (3.22) and (3.23), we get
 $$ \begin{align} \sum\limits_{m\in{\mathbb{Z}^n}}\int_{\mathbb{R}^{n}}K_{f}(\xi+m,\eta)\overline{K_{g}(\xi+m+l,\eta)}\,d\eta=\sum\limits_{k\in{\mathbb{Z}^n}}\big\langle f,{T_{(k,l)}^t} g\big\rangle e^{\pi ik\cdot(2\xi+l)}. \end{align} $$
$$ \begin{align} \sum\limits_{m\in{\mathbb{Z}^n}}\int_{\mathbb{R}^{n}}K_{f}(\xi+m,\eta)\overline{K_{g}(\xi+m+l,\eta)}\,d\eta=\sum\limits_{k\in{\mathbb{Z}^n}}\big\langle f,{T_{(k,l)}^t} g\big\rangle e^{\pi ik\cdot(2\xi+l)}. \end{align} $$
Let
![]() $f=g={\phi }$
(say) in (3.24). Then the identity (3.24) can be used to verify “Condition C” for the function
$f=g={\phi }$
(say) in (3.24). Then the identity (3.24) can be used to verify “Condition C” for the function
![]() ${\phi }$
.
${\phi }$
.
Example 3.9. Define
![]() ${\phi }:=\chi _{[0,2]\times [0,1]}$
. For
${\phi }:=\chi _{[0,2]\times [0,1]}$
. For
![]() $k,l\in {\mathbb {Z}}$
, consider
$k,l\in {\mathbb {Z}}$
, consider
 $$ \begin{align} \big<{\phi},T^{t}_{(k,l)}{\phi}\big>=&\int_{{\mathbb{R}}^{2}}{\phi}(x,y)\overline{T^{t}_{(k,l)}{\phi}(x,y)}dydx\nonumber \\ =&\int_{0}^{2}\int_{0}^{1}e^{-\pi i(xl-yk)}\overline{{\phi}(x-k,y-l)}dydx \nonumber \\ =&\int_{-k}^{2-k}\int_{-l}^{1-l}e^{-\pi i((x+k)l-(y+l)k)}{\phi}(x,y)dydx \nonumber \\ =&\int_{[-k,2-k]\cap [0,2]}\int_{[-l,1-l]\cap[0,1]}e^{-\pi i(xl-ky)}dydx. \end{align} $$
$$ \begin{align} \big<{\phi},T^{t}_{(k,l)}{\phi}\big>=&\int_{{\mathbb{R}}^{2}}{\phi}(x,y)\overline{T^{t}_{(k,l)}{\phi}(x,y)}dydx\nonumber \\ =&\int_{0}^{2}\int_{0}^{1}e^{-\pi i(xl-yk)}\overline{{\phi}(x-k,y-l)}dydx \nonumber \\ =&\int_{-k}^{2-k}\int_{-l}^{1-l}e^{-\pi i((x+k)l-(y+l)k)}{\phi}(x,y)dydx \nonumber \\ =&\int_{[-k,2-k]\cap [0,2]}\int_{[-l,1-l]\cap[0,1]}e^{-\pi i(xl-ky)}dydx. \end{align} $$
From the range of the above two integrals, we see that
![]() $\big <{\phi },T^{t}_{(k,l)}{\phi }\big>\neq 0$
only when
$\big <{\phi },T^{t}_{(k,l)}{\phi }\big>\neq 0$
only when
![]() $k=-1,0,1$
and
$k=-1,0,1$
and
![]() $l=0$
. Hence, using (3.24) for
$l=0$
. Hence, using (3.24) for
![]() $l\neq 0$
and
$l\neq 0$
and
![]() $f=g={\phi }$
, we have
$f=g={\phi }$
, we have
 $$ \begin{align*} \sum\limits_{m\in{\mathbb{Z}}}\int_{{\mathbb{R}}}K_{{\phi}}(\xi+m,\eta)\overline{K_{{\phi}}(\xi+m+l,\eta)}d\eta =&\sum\limits_{k\in{\mathbb{Z}}}\big<{\phi},T^{t}_{(k,l)}{\phi}\big>e^{\pi ik(2\xi+l)}\\ =\ &0, \end{align*} $$
$$ \begin{align*} \sum\limits_{m\in{\mathbb{Z}}}\int_{{\mathbb{R}}}K_{{\phi}}(\xi+m,\eta)\overline{K_{{\phi}}(\xi+m+l,\eta)}d\eta =&\sum\limits_{k\in{\mathbb{Z}}}\big<{\phi},T^{t}_{(k,l)}{\phi}\big>e^{\pi ik(2\xi+l)}\\ =\ &0, \end{align*} $$
for all
![]() $\xi \in \mathbb {T}$
, showing that
$\xi \in \mathbb {T}$
, showing that
![]() ${\phi }$
satisfies “Condition C.” Further, simplifying (3.25), we get
${\phi }$
satisfies “Condition C.” Further, simplifying (3.25), we get
 $$ \begin{align*} \big<{\phi},T^{t}_{(k,l)}{\phi}\big>=\begin{cases} \frac{2}{\pi i}, & (k,l)=(-1,0),\\ 2, & (k,l)=(0,0),\\ -\frac{2}{\pi i}, & (k,l)=(1,0),\\ 0, & otherwise. \end{cases} \end{align*} $$
$$ \begin{align*} \big<{\phi},T^{t}_{(k,l)}{\phi}\big>=\begin{cases} \frac{2}{\pi i}, & (k,l)=(-1,0),\\ 2, & (k,l)=(0,0),\\ -\frac{2}{\pi i}, & (k,l)=(1,0),\\ 0, & otherwise. \end{cases} \end{align*} $$
Using (3.24) for
![]() $f=g={\phi }$
and
$f=g={\phi }$
and
![]() $l=0$
, we obtain
$l=0$
, we obtain
 $$ \begin{align*} \omega_{{\phi}}(\xi)=\ &\sum\limits_{m\in{\mathbb{Z}}}\int_{{\mathbb{R}}}|K_{{\phi}}(\xi+m,\eta)|^{2}\,d\eta\\[4pt] =\ &\sum\limits_{k\in{\mathbb{Z}}}\big<{\phi},T^{t}_{(k,0)}{\phi}\big>e^{2\pi ik\xi}\\[4pt] =\ &\frac{2}{\pi i}e^{-2\pi i\xi}+2-\frac{2}{\pi i}e^{2\pi i\xi}\\[4pt] =\ &2-\frac{2}{\pi i}(e^{2\pi i\xi}-e^{-2\pi i\xi})\\[4pt] =\ &2-\frac{4}{\pi}\sin (2\pi\xi). \end{align*} $$
$$ \begin{align*} \omega_{{\phi}}(\xi)=\ &\sum\limits_{m\in{\mathbb{Z}}}\int_{{\mathbb{R}}}|K_{{\phi}}(\xi+m,\eta)|^{2}\,d\eta\\[4pt] =\ &\sum\limits_{k\in{\mathbb{Z}}}\big<{\phi},T^{t}_{(k,0)}{\phi}\big>e^{2\pi ik\xi}\\[4pt] =\ &\frac{2}{\pi i}e^{-2\pi i\xi}+2-\frac{2}{\pi i}e^{2\pi i\xi}\\[4pt] =\ &2-\frac{2}{\pi i}(e^{2\pi i\xi}-e^{-2\pi i\xi})\\[4pt] =\ &2-\frac{4}{\pi}\sin (2\pi\xi). \end{align*} $$
Since
![]() $|\frac {4}{\pi }\sin (2\pi \xi )|<\frac {4}{3}$
,
$|\frac {4}{\pi }\sin (2\pi \xi )|<\frac {4}{3}$
,
![]() $\forall \ \xi \in (0,1)$
, we get
$\forall \ \xi \in (0,1)$
, we get
![]() $\frac {2}{3}\leq \omega _{{\phi }}(\xi )\leq \frac {10}{3}$
, for
$\frac {2}{3}\leq \omega _{{\phi }}(\xi )\leq \frac {10}{3}$
, for
![]() $a.e$
.
$a.e$
.
![]() $\xi \in \mathbb {T}$
. Therefore, using Corollary 3.8, we conclude that the system
$\xi \in \mathbb {T}$
. Therefore, using Corollary 3.8, we conclude that the system
![]() $\{{T_{(k,l)}^t} {\phi }:k,l\in {\mathbb {Z}}\}$
is a frame sequence with frame bounds
$\{{T_{(k,l)}^t} {\phi }:k,l\in {\mathbb {Z}}\}$
is a frame sequence with frame bounds
![]() $\frac {2}{3}$
and
$\frac {2}{3}$
and
![]() $\frac {10}{3}$
.
$\frac {10}{3}$
.
Example 3.10. Let
![]() ${\phi }:=\chi _{[0,1]\times [0,2]}$
. For
${\phi }:=\chi _{[0,1]\times [0,2]}$
. For
![]() $k,l\in {\mathbb {Z}},$
$k,l\in {\mathbb {Z}},$
 $$ \begin{align*} \big<{\phi},T^{t}_{(k,l)}{\phi}\big>=&\int_{{\mathbb{R}}^{2}}{\phi}(x,y)\overline{T^{t}_{(k,l)}{\phi}}\,dydx\\[4pt] =&\int_{0}^{1}\int_{0}^{2}e^{-\pi i(xl-yk)}\overline{{\phi}(x-k,y-l)}\,dydx\\[4pt] =&\int_{-k}^{1-k}\int_{-l}^{2-l}e^{-\pi i((x+k)l-(y+l)k)}{\phi}(x,y)\,dydx\\[4pt] =&\int_{x\in [-k,1-k]\cap [0,1]}\int_{y\in [-l,2-l]\cap[0,2]}e^{-\pi i(xl-ky)}\,dydx. \end{align*} $$
$$ \begin{align*} \big<{\phi},T^{t}_{(k,l)}{\phi}\big>=&\int_{{\mathbb{R}}^{2}}{\phi}(x,y)\overline{T^{t}_{(k,l)}{\phi}}\,dydx\\[4pt] =&\int_{0}^{1}\int_{0}^{2}e^{-\pi i(xl-yk)}\overline{{\phi}(x-k,y-l)}\,dydx\\[4pt] =&\int_{-k}^{1-k}\int_{-l}^{2-l}e^{-\pi i((x+k)l-(y+l)k)}{\phi}(x,y)\,dydx\\[4pt] =&\int_{x\in [-k,1-k]\cap [0,1]}\int_{y\in [-l,2-l]\cap[0,2]}e^{-\pi i(xl-ky)}\,dydx. \end{align*} $$
From the range of the above integrals, we see that
![]() $\big <{\phi },T^{t}_{(k,l)}{\phi }\big>\neq 0$
only when
$\big <{\phi },T^{t}_{(k,l)}{\phi }\big>\neq 0$
only when
![]() $k=0$
and
$k=0$
and
![]() $l=-1,0,1$
. Computing explicitly, we get
$l=-1,0,1$
. Computing explicitly, we get
 $$ \begin{align} \big<{\phi},T^{t}_{(k,l)}{\phi}\big>=\begin{cases} \frac{-2}{\pi i}, & (k,l)=(0,-1),\\ 2, & (k,l)=(0,0),\\ \frac{2}{\pi i}, & (k,l)=(0,1),\\ 0, & otherwise. \end{cases} \end{align} $$
$$ \begin{align} \big<{\phi},T^{t}_{(k,l)}{\phi}\big>=\begin{cases} \frac{-2}{\pi i}, & (k,l)=(0,-1),\\ 2, & (k,l)=(0,0),\\ \frac{2}{\pi i}, & (k,l)=(0,1),\\ 0, & otherwise. \end{cases} \end{align} $$
Using (3.24) for
![]() $f=g={\phi }$
and
$f=g={\phi }$
and
![]() $l=1$
, we get
$l=1$
, we get
 $$ \begin{align*} \sum\limits_{m\in{\mathbb{Z}}}\int_{\mathbb{R}}K_{{\phi}}(\xi+m,\eta)\overline{K_{{\phi}}(\xi+m+1,\eta)}d\eta=&\sum\limits_{k\in{\mathbb{Z}}}\big<{\phi},T^{t}_{(k,1)}{\phi}\big>e^{\pi ik(2\xi+1)}\\ =&\big<{\phi},T^{t}_{(0,1)}{\phi}\big>\\ =&\frac{2}{\pi i}\neq 0, \end{align*} $$
$$ \begin{align*} \sum\limits_{m\in{\mathbb{Z}}}\int_{\mathbb{R}}K_{{\phi}}(\xi+m,\eta)\overline{K_{{\phi}}(\xi+m+1,\eta)}d\eta=&\sum\limits_{k\in{\mathbb{Z}}}\big<{\phi},T^{t}_{(k,1)}{\phi}\big>e^{\pi ik(2\xi+1)}\\ =&\big<{\phi},T^{t}_{(0,1)}{\phi}\big>\\ =&\frac{2}{\pi i}\neq 0, \end{align*} $$
for all
![]() $\xi \in \mathbb {T}$
, showing that
$\xi \in \mathbb {T}$
, showing that
![]() ${\phi }$
does not satisfy “Condition C.” Now, using Corollary 3.5, we aim to prove that the system
${\phi }$
does not satisfy “Condition C.” Now, using Corollary 3.5, we aim to prove that the system
![]() $\{{T_{(k,l)}^t}{\phi } : k,l\in {\mathbb {Z}}\}$
forms a frame sequence. Let
$\{{T_{(k,l)}^t}{\phi } : k,l\in {\mathbb {Z}}\}$
forms a frame sequence. Let
![]() ${\Phi (\xi )=\sum \limits _{l\in {\mathbb {Z}}}\alpha _{l}(\xi )\tau {\phi }(\xi +l)\in J(\xi )}$
for some
${\Phi (\xi )=\sum \limits _{l\in {\mathbb {Z}}}\alpha _{l}(\xi )\tau {\phi }(\xi +l)\in J(\xi )}$
for some
![]() $\{\alpha _l(\xi )\}_{l\in {\mathbb {Z}}}\in c_{00}({\mathbb {Z}})$
, for
$\{\alpha _l(\xi )\}_{l\in {\mathbb {Z}}}\in c_{00}({\mathbb {Z}})$
, for
![]() $\xi \in \mathbb {T}$
. Then, using (3.13) and (3.24), we get
$\xi \in \mathbb {T}$
. Then, using (3.13) and (3.24), we get
 $$ \begin{align} \|\Phi(\xi)\|^{2}_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}=&\sum\limits_{l_{1},l_{2}\in{\mathbb{Z}}}\alpha_{l_{1}}(\xi)\overline{\alpha_{l_{2}}(\xi)}\big<\tau{\phi}(\xi+l_{1}),\tau{\phi}(\xi+l_{2})\big>_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))} \nonumber\\ =&\sum\limits_{l_{1},l_{2}\in{\mathbb{Z}}}\alpha_{l_{1}}(\xi)\overline{\alpha_{l_{2}}(\xi)}\int_{{\mathbb{R}}}\sum\limits_{m\in{\mathbb{Z}}}K_{{\phi}}(\xi+m,\eta)\overline{K_{{\phi}}(\xi+m+l_{2}-l_1,\eta)}\,d\eta \nonumber\\ =&\sum\limits_{l_{1},l_{2}\in{\mathbb{Z}}}\alpha_{l_{1}}(\xi)\overline{\alpha_{l_{2}}(\xi)}\sum\limits_{k\in{\mathbb{Z}}}\big\langle {\phi},T_{(k,l_2-l_1)}^t {\phi}\big\rangle e^{\pi ik(2\xi+l_2-l_1)}. \end{align} $$
$$ \begin{align} \|\Phi(\xi)\|^{2}_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}=&\sum\limits_{l_{1},l_{2}\in{\mathbb{Z}}}\alpha_{l_{1}}(\xi)\overline{\alpha_{l_{2}}(\xi)}\big<\tau{\phi}(\xi+l_{1}),\tau{\phi}(\xi+l_{2})\big>_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))} \nonumber\\ =&\sum\limits_{l_{1},l_{2}\in{\mathbb{Z}}}\alpha_{l_{1}}(\xi)\overline{\alpha_{l_{2}}(\xi)}\int_{{\mathbb{R}}}\sum\limits_{m\in{\mathbb{Z}}}K_{{\phi}}(\xi+m,\eta)\overline{K_{{\phi}}(\xi+m+l_{2}-l_1,\eta)}\,d\eta \nonumber\\ =&\sum\limits_{l_{1},l_{2}\in{\mathbb{Z}}}\alpha_{l_{1}}(\xi)\overline{\alpha_{l_{2}}(\xi)}\sum\limits_{k\in{\mathbb{Z}}}\big\langle {\phi},T_{(k,l_2-l_1)}^t {\phi}\big\rangle e^{\pi ik(2\xi+l_2-l_1)}. \end{align} $$
Now, applying (3.26) in (3.27), we get
 $$ \begin{align} \|\Phi(\xi)\|^{2}_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}=&\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)(2\overline{\alpha_{l}(\xi)}+\frac{2}{\pi i}\overline{\alpha_{l+1}(\xi)}-\frac{2}{\pi i}\overline{\alpha_{l-1}(\xi)})\nonumber\\ =&\frac{2}{\pi i}\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)(\overline{\alpha_{l+1}(\xi)}- \overline{\alpha_{l-1}(\xi)})+2\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}\nonumber\\ =&\frac{2}{\pi i}\left(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l+1}(\xi)}- \overline{\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l+1}(\xi)}}\right)+2\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}\nonumber\\ =&\frac{2}{\pi i}\left( 2i \operatorname{\mathrm{Im}}\left(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l+1}(\xi)}\right)\right)+2 \sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}\nonumber\\ =&\frac{4}{\pi} \operatorname{\mathrm{Im}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi) \overline{\alpha_{l+1}(\xi)}\Bigg)+2\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}. \end{align} $$
$$ \begin{align} \|\Phi(\xi)\|^{2}_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}=&\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)(2\overline{\alpha_{l}(\xi)}+\frac{2}{\pi i}\overline{\alpha_{l+1}(\xi)}-\frac{2}{\pi i}\overline{\alpha_{l-1}(\xi)})\nonumber\\ =&\frac{2}{\pi i}\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)(\overline{\alpha_{l+1}(\xi)}- \overline{\alpha_{l-1}(\xi)})+2\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}\nonumber\\ =&\frac{2}{\pi i}\left(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l+1}(\xi)}- \overline{\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l+1}(\xi)}}\right)+2\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}\nonumber\\ =&\frac{2}{\pi i}\left( 2i \operatorname{\mathrm{Im}}\left(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l+1}(\xi)}\right)\right)+2 \sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}\nonumber\\ =&\frac{4}{\pi} \operatorname{\mathrm{Im}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi) \overline{\alpha_{l+1}(\xi)}\Bigg)+2\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}. \end{align} $$
Again using (3.13) and (3.24), we have
 $$ \begin{align} \big<\Phi(\xi),\tau{\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}=&\sum\limits_{l_1\in{\mathbb{Z}}} \alpha_{l_1}(\xi)\big<\tau{\phi}(\xi+l_{1}),\tau {\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))} \notag\\ =&\sum\limits_{l_1\in{\mathbb{Z}}}\alpha_{l_1}(\xi)\int_{{\mathbb{R}}} \sum\limits_{m\in{\mathbb{Z}}}K_{{\phi}}(\xi+m,\eta)\overline{K_{{\phi}}(\xi+m+l-l_1,\eta)}\,d\eta \nonumber\\ =&\sum\limits_{l_1\in{\mathbb{Z}}}\alpha_{l_1}(\xi)\sum\limits_{k\in{\mathbb{Z}}}\big\langle {\phi},T_{(k,l-l_1)}^t {\phi}\big\rangle e^{\pi ik(2\xi+l-l_1)}. \end{align} $$
$$ \begin{align} \big<\Phi(\xi),\tau{\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}=&\sum\limits_{l_1\in{\mathbb{Z}}} \alpha_{l_1}(\xi)\big<\tau{\phi}(\xi+l_{1}),\tau {\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))} \notag\\ =&\sum\limits_{l_1\in{\mathbb{Z}}}\alpha_{l_1}(\xi)\int_{{\mathbb{R}}} \sum\limits_{m\in{\mathbb{Z}}}K_{{\phi}}(\xi+m,\eta)\overline{K_{{\phi}}(\xi+m+l-l_1,\eta)}\,d\eta \nonumber\\ =&\sum\limits_{l_1\in{\mathbb{Z}}}\alpha_{l_1}(\xi)\sum\limits_{k\in{\mathbb{Z}}}\big\langle {\phi},T_{(k,l-l_1)}^t {\phi}\big\rangle e^{\pi ik(2\xi+l-l_1)}. \end{align} $$
Now, using (3.26) in (3.29), we get
 $$ \begin{align*} \big<\Phi(\xi),\tau{\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}&=2\alpha_{l}(\xi)+\frac{2}{\pi i}\alpha_{l-1}(\xi)-\frac{2}{\pi i}\alpha_{l+1}(\xi)\\ &=\frac{2}{\pi i}(\alpha_{l-1}(\xi)-\alpha_{l+1}(\xi))+2\alpha_{l}(\xi). \end{align*} $$
$$ \begin{align*} \big<\Phi(\xi),\tau{\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}&=2\alpha_{l}(\xi)+\frac{2}{\pi i}\alpha_{l-1}(\xi)-\frac{2}{\pi i}\alpha_{l+1}(\xi)\\ &=\frac{2}{\pi i}(\alpha_{l-1}(\xi)-\alpha_{l+1}(\xi))+2\alpha_{l}(\xi). \end{align*} $$
Hence,
 $$ \begin{align} &\sum\limits_{l\in{\mathbb{Z}}}|\big<\Phi(\xi),\tau{\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}|^{2}\nonumber\\ &\quad=\sum\limits_{l\in{\mathbb{Z}}}\Big|\frac{2}{\pi i}(\alpha_{l-1}(\xi)-\alpha_{l+1}(\xi))+2\alpha_{l}(\xi)\Big|^{2}\nonumber\\ &\quad=\sum\limits_{l\in{\mathbb{Z}}}\frac{4}{\pi^{2}}|\alpha_{l-1}(\xi)-\alpha_{l+1}(\xi)|^{2}+\sum\limits_{l\in{\mathbb{Z}}}4|\alpha_{l}(\xi)|^{2}+\sum\limits_{l\in{\mathbb{Z}}}2 \operatorname{\mathrm{Re}}\Bigg(\frac{4}{\pi i}\overline{\alpha_{l}(\xi)}(\alpha_{l-1}(\xi)-\alpha_{l+1}(\xi))\Bigg)\nonumber\\ &\quad=\frac{4}{\pi^2}S_{1}+4\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}+8S_{2}, \end{align} $$
$$ \begin{align} &\sum\limits_{l\in{\mathbb{Z}}}|\big<\Phi(\xi),\tau{\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}|^{2}\nonumber\\ &\quad=\sum\limits_{l\in{\mathbb{Z}}}\Big|\frac{2}{\pi i}(\alpha_{l-1}(\xi)-\alpha_{l+1}(\xi))+2\alpha_{l}(\xi)\Big|^{2}\nonumber\\ &\quad=\sum\limits_{l\in{\mathbb{Z}}}\frac{4}{\pi^{2}}|\alpha_{l-1}(\xi)-\alpha_{l+1}(\xi)|^{2}+\sum\limits_{l\in{\mathbb{Z}}}4|\alpha_{l}(\xi)|^{2}+\sum\limits_{l\in{\mathbb{Z}}}2 \operatorname{\mathrm{Re}}\Bigg(\frac{4}{\pi i}\overline{\alpha_{l}(\xi)}(\alpha_{l-1}(\xi)-\alpha_{l+1}(\xi))\Bigg)\nonumber\\ &\quad=\frac{4}{\pi^2}S_{1}+4\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}+8S_{2}, \end{align} $$
where
 $$ \begin{align*} S_1:=\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l-1}(\xi)-\alpha_{l+1}(\xi)|^{2}\ \ \ \ \ \text{and}\ \ \ \ \ S_2:=\sum\limits_{l\in{\mathbb{Z}}} \operatorname{\mathrm{Re}}\big(\frac{1}{\pi i}\overline{\alpha_{l}(\xi)}(\alpha_{l-1}(\xi)-\alpha_{l+1}(\xi))\big). \end{align*} $$
$$ \begin{align*} S_1:=\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l-1}(\xi)-\alpha_{l+1}(\xi)|^{2}\ \ \ \ \ \text{and}\ \ \ \ \ S_2:=\sum\limits_{l\in{\mathbb{Z}}} \operatorname{\mathrm{Re}}\big(\frac{1}{\pi i}\overline{\alpha_{l}(\xi)}(\alpha_{l-1}(\xi)-\alpha_{l+1}(\xi))\big). \end{align*} $$
But
 $$ \begin{align} S_{1}=&\sum\limits_{l\in{\mathbb{Z}}}\big(|\alpha_{l-1}(\xi)|^{2}+|\alpha_{l+1}(\xi)|^{2}-2\operatorname{\mathrm{Re}}(\alpha_{l-1}(\xi)\overline{\alpha_{l+1}(\xi)})\big)\nonumber\\ =&2\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}-2\operatorname{\mathrm{Re}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l-1}(\xi)\overline{\alpha_{l+1}(\xi)}\Bigg) \end{align} $$
$$ \begin{align} S_{1}=&\sum\limits_{l\in{\mathbb{Z}}}\big(|\alpha_{l-1}(\xi)|^{2}+|\alpha_{l+1}(\xi)|^{2}-2\operatorname{\mathrm{Re}}(\alpha_{l-1}(\xi)\overline{\alpha_{l+1}(\xi)})\big)\nonumber\\ =&2\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}-2\operatorname{\mathrm{Re}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l-1}(\xi)\overline{\alpha_{l+1}(\xi)}\Bigg) \end{align} $$
and
 $$ \begin{align} S_{2}=&\sum\limits_{l\in{\mathbb{Z}}}\operatorname{\mathrm{Re}}\left(-\frac{i}{\pi}\overline{\alpha_{l}(\xi)}(\alpha_{l-1}(\xi)-\alpha_{l+1}(\xi))\right)\nonumber\\ =&\sum\limits_{l\in{\mathbb{Z}}}\frac{-1}{\pi}\operatorname{\mathrm{Im}}\left(\alpha_{l}(\xi)(\overline{\alpha_{l-1}(\xi)}-\overline{\alpha_{l+1}(\xi)})\right)\nonumber\\ =&\frac{-1}{\pi}\operatorname{\mathrm{Im}}\left(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l-1}(\xi)}-\overline{\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l-1}(\xi)}}\right)\nonumber\\ =&\frac{-1}{\pi}\operatorname{\mathrm{Im}}\Bigg(2i\operatorname{\mathrm{Im}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l-1}(\xi)}\Bigg)\Bigg)\nonumber\\ =&\frac{-2}{\pi}\operatorname{\mathrm{Im}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l-1}(\xi)}\Bigg). \end{align} $$
$$ \begin{align} S_{2}=&\sum\limits_{l\in{\mathbb{Z}}}\operatorname{\mathrm{Re}}\left(-\frac{i}{\pi}\overline{\alpha_{l}(\xi)}(\alpha_{l-1}(\xi)-\alpha_{l+1}(\xi))\right)\nonumber\\ =&\sum\limits_{l\in{\mathbb{Z}}}\frac{-1}{\pi}\operatorname{\mathrm{Im}}\left(\alpha_{l}(\xi)(\overline{\alpha_{l-1}(\xi)}-\overline{\alpha_{l+1}(\xi)})\right)\nonumber\\ =&\frac{-1}{\pi}\operatorname{\mathrm{Im}}\left(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l-1}(\xi)}-\overline{\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l-1}(\xi)}}\right)\nonumber\\ =&\frac{-1}{\pi}\operatorname{\mathrm{Im}}\Bigg(2i\operatorname{\mathrm{Im}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l-1}(\xi)}\Bigg)\Bigg)\nonumber\\ =&\frac{-2}{\pi}\operatorname{\mathrm{Im}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l-1}(\xi)}\Bigg). \end{align} $$
Using (3.32) and (3.31) in (3.30), we get
 $$ \begin{align} &\sum\limits_{l\in{\mathbb{Z}}}|\big<\Phi(\xi),\tau {\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}|^{2}\nonumber \\ =&\frac{8}{\pi^{2}}\sum_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}-\frac{8}{\pi^{2}}\operatorname{\mathrm{Re}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l-1}(\xi)\overline{\alpha_{l+1}(\xi)}\Bigg)+4\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}-\frac{16}{\pi}\operatorname{\mathrm{Im}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l-1}(\xi)}\Bigg)\nonumber\\ =&\Bigg(4+\frac{8}{\pi^{2}}\Bigg)\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}-\frac{16}{\pi}\operatorname{\mathrm{Im}}\Bigg(\overline{\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l+1}(\xi)}}\Bigg)-\frac{8}{\pi^{2}}\operatorname{\mathrm{Re}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l-1}(\xi)\overline{\alpha_{l+1}(\xi)}\Bigg)\nonumber\\ =&\Bigg(4+\frac{8}{\pi^{2}}\Bigg)\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}+\frac{16}{\pi}\operatorname{\mathrm{Im}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l+1}(\xi)}\Bigg)-\frac{8}{\pi^{2}}\operatorname{\mathrm{Re}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l-1}(\xi)\overline{\alpha_{l+1}(\xi)}\Bigg). \end{align} $$
$$ \begin{align} &\sum\limits_{l\in{\mathbb{Z}}}|\big<\Phi(\xi),\tau {\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}|^{2}\nonumber \\ =&\frac{8}{\pi^{2}}\sum_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}-\frac{8}{\pi^{2}}\operatorname{\mathrm{Re}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l-1}(\xi)\overline{\alpha_{l+1}(\xi)}\Bigg)+4\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}-\frac{16}{\pi}\operatorname{\mathrm{Im}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l-1}(\xi)}\Bigg)\nonumber\\ =&\Bigg(4+\frac{8}{\pi^{2}}\Bigg)\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}-\frac{16}{\pi}\operatorname{\mathrm{Im}}\Bigg(\overline{\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l+1}(\xi)}}\Bigg)-\frac{8}{\pi^{2}}\operatorname{\mathrm{Re}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l-1}(\xi)\overline{\alpha_{l+1}(\xi)}\Bigg)\nonumber\\ =&\Bigg(4+\frac{8}{\pi^{2}}\Bigg)\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}+\frac{16}{\pi}\operatorname{\mathrm{Im}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l+1}(\xi)}\Bigg)-\frac{8}{\pi^{2}}\operatorname{\mathrm{Re}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l-1}(\xi)\overline{\alpha_{l+1}(\xi)}\Bigg). \end{align} $$
But
 $$ \begin{align*} \Bigg|\operatorname{\mathrm{Re}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l-1}(\xi)\overline{\alpha_{l+1}(\xi)}\Bigg)\Bigg|\leq \Bigg|\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l-1}(\xi)\overline{\alpha_{l+1}(\xi)}\Bigg|\leq \sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}. \end{align*} $$
$$ \begin{align*} \Bigg|\operatorname{\mathrm{Re}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l-1}(\xi)\overline{\alpha_{l+1}(\xi)}\Bigg)\Bigg|\leq \Bigg|\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l-1}(\xi)\overline{\alpha_{l+1}(\xi)}\Bigg|\leq \sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}. \end{align*} $$
Hence,
 $$ \begin{align} -\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2} \leq \operatorname{\mathrm{Re}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l-1}(\xi)\overline{\alpha_{l+1}(\xi)}\Bigg)\leq \sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}. \end{align} $$
$$ \begin{align} -\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2} \leq \operatorname{\mathrm{Re}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l-1}(\xi)\overline{\alpha_{l+1}(\xi)}\Bigg)\leq \sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}. \end{align} $$
Now, using (3.34) and (3.28) in (3.33), we get
 $$ \begin{align} \sum\limits_{l\in{\mathbb{Z}}}|\big<\Phi(\xi),\tau {\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}|^{2}\leq&\bigg(4+\frac{8}{\pi^{2}}\bigg) \sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}+\frac{16}{\pi}\operatorname{\mathrm{Im}}\bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi) \overline{\alpha_{l+1}(\xi)}\bigg)+\frac{8}{\pi^{2}}\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2} \notag\\ =&\bigg(4+\frac{16}{\pi^{2}}\bigg)\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}+\frac{16}{\pi}\operatorname{\mathrm{Im}} \bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l+1}(\xi)}\bigg)\notag\\ <&8\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}+\frac{16}{\pi}\operatorname{\mathrm{Im}} \bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l+1}(\xi)}\bigg)\notag\\ =&4\Bigg(2\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}+ \frac{4}{\pi} \operatorname{\mathrm{Im}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l+1}(\xi)}\Bigg)\Bigg) \notag \\ =&4\|\Phi(\xi)\|^{2}_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}, \end{align} $$
$$ \begin{align} \sum\limits_{l\in{\mathbb{Z}}}|\big<\Phi(\xi),\tau {\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}|^{2}\leq&\bigg(4+\frac{8}{\pi^{2}}\bigg) \sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}+\frac{16}{\pi}\operatorname{\mathrm{Im}}\bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi) \overline{\alpha_{l+1}(\xi)}\bigg)+\frac{8}{\pi^{2}}\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2} \notag\\ =&\bigg(4+\frac{16}{\pi^{2}}\bigg)\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}+\frac{16}{\pi}\operatorname{\mathrm{Im}} \bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l+1}(\xi)}\bigg)\notag\\ <&8\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}+\frac{16}{\pi}\operatorname{\mathrm{Im}} \bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l+1}(\xi)}\bigg)\notag\\ =&4\Bigg(2\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}+ \frac{4}{\pi} \operatorname{\mathrm{Im}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l+1}(\xi)}\Bigg)\Bigg) \notag \\ =&4\|\Phi(\xi)\|^{2}_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}, \end{align} $$
for all
![]() $\xi \in (0,1]$
and
$\xi \in (0,1]$
and
 $$ \begin{align} \sum\limits_{l\in{\mathbb{Z}}}|\big<\Phi(\xi),\tau {\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}|^{2}\geq&\big(4+\frac{8}{\pi^{2}}\big) \sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}+\frac{16}{\pi} \operatorname{\mathrm{Im}}\bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi) \overline{\alpha_{l+1}(\xi)}\bigg)-\frac{8}{\pi^{2}} \sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2} \nonumber \\ =&4\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}+\frac{16}{\pi} \operatorname{\mathrm{Im}}\bigg(\sum\limits_{l\in{\mathbb{Z}}} \alpha_{l}(\xi)\overline{\alpha_{l+1}(\xi)}\bigg) \nonumber \\ >&4\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}+\frac{8}{\pi} \operatorname{\mathrm{Im}}\bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l+1}(\xi)}\bigg) \nonumber \\ =&2\Bigg(2\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}+ \frac{4}{\pi} \operatorname{\mathrm{Im}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi) \overline{\alpha_{l+1}(\xi)}\Bigg)\Bigg) \nonumber \\ =&2\|\Phi(\xi)\|^{2}_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}, \end{align} $$
$$ \begin{align} \sum\limits_{l\in{\mathbb{Z}}}|\big<\Phi(\xi),\tau {\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}|^{2}\geq&\big(4+\frac{8}{\pi^{2}}\big) \sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}+\frac{16}{\pi} \operatorname{\mathrm{Im}}\bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi) \overline{\alpha_{l+1}(\xi)}\bigg)-\frac{8}{\pi^{2}} \sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2} \nonumber \\ =&4\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}+\frac{16}{\pi} \operatorname{\mathrm{Im}}\bigg(\sum\limits_{l\in{\mathbb{Z}}} \alpha_{l}(\xi)\overline{\alpha_{l+1}(\xi)}\bigg) \nonumber \\ >&4\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}+\frac{8}{\pi} \operatorname{\mathrm{Im}}\bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi)\overline{\alpha_{l+1}(\xi)}\bigg) \nonumber \\ =&2\Bigg(2\sum\limits_{l\in{\mathbb{Z}}}|\alpha_{l}(\xi)|^{2}+ \frac{4}{\pi} \operatorname{\mathrm{Im}}\Bigg(\sum\limits_{l\in{\mathbb{Z}}}\alpha_{l}(\xi) \overline{\alpha_{l+1}(\xi)}\Bigg)\Bigg) \nonumber \\ =&2\|\Phi(\xi)\|^{2}_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}, \end{align} $$
for all
![]() $\xi \in (0,1]$
. Combining (3.35) and (3.36), we get
$\xi \in (0,1]$
. Combining (3.35) and (3.36), we get
 $$ \begin{align*} 2\|\Phi(\xi)\|^{2}_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}\leq \sum\limits_{l\in{\mathbb{Z}}}|\big<\Phi(\xi),\tau {\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}|^{2}\leq 4\|\Phi(\xi)\|^{2}_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}, \end{align*} $$
$$ \begin{align*} 2\|\Phi(\xi)\|^{2}_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}\leq \sum\limits_{l\in{\mathbb{Z}}}|\big<\Phi(\xi),\tau {\phi}(\xi+l)\big>_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}|^{2}\leq 4\|\Phi(\xi)\|^{2}_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}, \end{align*} $$
for all
![]() $\xi \in (0,1]$
. Then it follows from Corollary 3.5 that
$\xi \in (0,1]$
. Then it follows from Corollary 3.5 that
![]() $\{{T_{(k,l)}^t}{\phi } : k,l\in {\mathbb {Z}}\}$
is a frame sequence with frame bounds
$\{{T_{(k,l)}^t}{\phi } : k,l\in {\mathbb {Z}}\}$
is a frame sequence with frame bounds
![]() $2$
and
$2$
and
![]() $4$
.
$4$
.
4 Riesz sequence in a twisted shift-invariant space
For
![]() $\xi \in {\mathbb {T}^{n}}$
, define
$\xi \in {\mathbb {T}^{n}}$
, define
![]() $H(\xi ) : \ell ^{2}(\mathbb {Z}^{n+1})\rightarrow L^{2}({\mathbb {R}}^{n},\ell ^{2}({\mathbb {Z}^n}))$
by
$H(\xi ) : \ell ^{2}(\mathbb {Z}^{n+1})\rightarrow L^{2}({\mathbb {R}}^{n},\ell ^{2}({\mathbb {Z}^n}))$
by
 $$ \begin{align*} H(\xi)(\{c_{l,s}\})=\sum\limits_{(l,s)\in\mathbb{Z}^{n+1}}c_{l,s}\tau {\phi}_{s}(\xi+l). \end{align*} $$
$$ \begin{align*} H(\xi)(\{c_{l,s}\})=\sum\limits_{(l,s)\in\mathbb{Z}^{n+1}}c_{l,s}\tau {\phi}_{s}(\xi+l). \end{align*} $$
If
![]() $H(\xi )$
defines a bounded operator from
$H(\xi )$
defines a bounded operator from
![]() $\ell ^{2}(\mathbb {Z}^{n+1})$
into
$\ell ^{2}(\mathbb {Z}^{n+1})$
into
![]() $L^{2}({\mathbb {R}}^{n},\ell ^{2}({\mathbb {Z}^n}))$
, then its adjoint
$L^{2}({\mathbb {R}}^{n},\ell ^{2}({\mathbb {Z}^n}))$
, then its adjoint
![]() $H(\xi )^{\ast }:L^{2}({\mathbb {R}}^{n},\ell ^{2}({\mathbb {Z}^n}))\rightarrow \ell ^{2}(\mathbb {Z}^{n+1})$
is given by
$H(\xi )^{\ast }:L^{2}({\mathbb {R}}^{n},\ell ^{2}({\mathbb {Z}^n}))\rightarrow \ell ^{2}(\mathbb {Z}^{n+1})$
is given by
The Gramian associated with the system
![]() $\{\tau {\phi }_{s}(\xi +l) : (l,s)\in \mathbb {Z}^{n+1}\}$
, denoted by
$\{\tau {\phi }_{s}(\xi +l) : (l,s)\in \mathbb {Z}^{n+1}\}$
, denoted by
![]() $G(\xi )$
, is defined by
$G(\xi )$
, is defined by
![]() $G(\xi )=H(\xi )^{\ast }H(\xi )$
, and the corresponding dual Gramian, denoted by
$G(\xi )=H(\xi )^{\ast }H(\xi )$
, and the corresponding dual Gramian, denoted by
![]() $\widetilde {G}(\xi )$
, is defined by
$\widetilde {G}(\xi )$
, is defined by
![]() $\widetilde {G}(\xi )=H(\xi )H(\xi )^{\ast }$
.
$\widetilde {G}(\xi )=H(\xi )H(\xi )^{\ast }$
.
Theorem 4.1. The family
![]() $E^{t}(\mathcal {A})$
is a Riesz sequence with Riesz bounds A and B if and only if
$E^{t}(\mathcal {A})$
is a Riesz sequence with Riesz bounds A and B if and only if
where I is the identity operator on
![]() $\ell ^{2}(\mathbb {Z}^{n+1})$
.
$\ell ^{2}(\mathbb {Z}^{n+1})$
.
Proof. Let
![]() $E^{t}(\mathcal {A})$
be a Riesz sequence with Riesz bounds A and B. Then,
$E^{t}(\mathcal {A})$
be a Riesz sequence with Riesz bounds A and B. Then,
 $$ \begin{align} A\|\{c_{k,l,s}\}\|^{2}_{\ell^{2}(\mathbb{Z}^{2n+1})}\leq \|\sum\limits_{k,(l,s)\in\mathcal{F}\times\mathcal{F}^{\prime}}c_{k,l,s}{T_{(k,l)}^t} {\phi}_{s}\|^{2}_{L^{2}(\mathbb{R}^{2n})}\leq B\|c_{k,l,s}\|^{2}_{\ell^{2}(\mathbb{Z}^{2n+1})}, \end{align} $$
$$ \begin{align} A\|\{c_{k,l,s}\}\|^{2}_{\ell^{2}(\mathbb{Z}^{2n+1})}\leq \|\sum\limits_{k,(l,s)\in\mathcal{F}\times\mathcal{F}^{\prime}}c_{k,l,s}{T_{(k,l)}^t} {\phi}_{s}\|^{2}_{L^{2}(\mathbb{R}^{2n})}\leq B\|c_{k,l,s}\|^{2}_{\ell^{2}(\mathbb{Z}^{2n+1})}, \end{align} $$
![]() $\forall \ \{c_{k,l,s}\}_{(k,(l,s))\in \mathcal {F}\times \mathcal {F}^{\prime }}\in c_{00}(\mathbb {Z}^{2n+1})$
, where
$\forall \ \{c_{k,l,s}\}_{(k,(l,s))\in \mathcal {F}\times \mathcal {F}^{\prime }}\in c_{00}(\mathbb {Z}^{2n+1})$
, where
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {F}^{\prime }$
are finite subsets of
$\mathcal {F}^{\prime }$
are finite subsets of
![]() ${\mathbb {Z}^n}$
and
${\mathbb {Z}^n}$
and
![]() $\mathbb {Z}^{n+1}$
, respectively. By isometry of
$\mathbb {Z}^{n+1}$
, respectively. By isometry of
![]() $\tau $
and (3.1), we have
$\tau $
and (3.1), we have
 $$ \begin{align} \bigg\|\sum\limits_{(k,(l,s))\in\mathcal{F}\times\mathcal{F^{\prime}}}c_{k,l,s}{T_{(k,l)}^t} {\phi}_{s}\bigg\|^{2}_{L^{2}(\mathbb{R}^{2n})}=&\bigg\|\sum\limits_{(k,(l,s))\in\mathcal{F}\times\mathcal{F^{\prime}}}c_{k,l,s}\tau({T_{(k,l)}^t} {\phi}_{s})\bigg\|^{2}_{L^{2}({\mathbb{T}^{n}},L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n})))}\nonumber\\ =&\int_{{\mathbb{T}^{n}}}\Big\|\sum\limits_{(k,(l,s))\in\mathcal{F}\times\mathcal{F^{\prime}}}c_{k,l,s}\tau ({T_{(k,l)}^t} {\phi}_{s})(\xi)\Big\|^{2}_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\,d\xi\nonumber\\ =&\int_{{\mathbb{T}^{n}}}\Big\|\sum\limits_{(k,(l,s))\in\mathcal{F}\times\mathcal{F^{\prime}}}c_{k,l,s}e^{\pi ik\cdot(2\xi+l)}\tau {\phi}_{s}(\xi+l)\Big\|^{2}_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\,d\xi\nonumber\\ =&\int_{{\mathbb{T}^{n}}}\Big\|\sum\limits_{(l,s)\in\mathcal{F^{\prime}}}p_{l,s}(\xi)\tau {\phi}_{s}(\xi+l)\Big\|^{2}_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\,d\xi, \end{align} $$
$$ \begin{align} \bigg\|\sum\limits_{(k,(l,s))\in\mathcal{F}\times\mathcal{F^{\prime}}}c_{k,l,s}{T_{(k,l)}^t} {\phi}_{s}\bigg\|^{2}_{L^{2}(\mathbb{R}^{2n})}=&\bigg\|\sum\limits_{(k,(l,s))\in\mathcal{F}\times\mathcal{F^{\prime}}}c_{k,l,s}\tau({T_{(k,l)}^t} {\phi}_{s})\bigg\|^{2}_{L^{2}({\mathbb{T}^{n}},L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n})))}\nonumber\\ =&\int_{{\mathbb{T}^{n}}}\Big\|\sum\limits_{(k,(l,s))\in\mathcal{F}\times\mathcal{F^{\prime}}}c_{k,l,s}\tau ({T_{(k,l)}^t} {\phi}_{s})(\xi)\Big\|^{2}_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\,d\xi\nonumber\\ =&\int_{{\mathbb{T}^{n}}}\Big\|\sum\limits_{(k,(l,s))\in\mathcal{F}\times\mathcal{F^{\prime}}}c_{k,l,s}e^{\pi ik\cdot(2\xi+l)}\tau {\phi}_{s}(\xi+l)\Big\|^{2}_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\,d\xi\nonumber\\ =&\int_{{\mathbb{T}^{n}}}\Big\|\sum\limits_{(l,s)\in\mathcal{F^{\prime}}}p_{l,s}(\xi)\tau {\phi}_{s}(\xi+l)\Big\|^{2}_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\,d\xi, \end{align} $$
where
![]() $p_{l,s}(\xi )=\sum \limits _{k\in \mathcal {F}}c_{k,l,s}e^{\pi ik\cdot (2\xi +l)}$
is a trigonometric polynomial in
$p_{l,s}(\xi )=\sum \limits _{k\in \mathcal {F}}c_{k,l,s}e^{\pi ik\cdot (2\xi +l)}$
is a trigonometric polynomial in
![]() $L^{2}({\mathbb {T}^{n}})$
. Now, for
$L^{2}({\mathbb {T}^{n}})$
. Now, for
![]() $k^{\prime }\in {\mathbb {Z}^n}$
,
$k^{\prime }\in {\mathbb {Z}^n}$
,
 $$ \begin{align} \widehat{p_{l,s}}(k^{\prime})=&\int_{{\mathbb{T}^{n}}}p_{l,s}(\xi)e^{-2\pi ik^{\prime}\cdot\xi}d\xi\nonumber\\ =&\int_{{\mathbb{T}^{n}}}\Bigg(\sum\limits_{k\in\mathcal{F}}c_{k,l,s}e^{\pi ik\cdot(2\xi+l)}\Bigg)e^{-2\pi ik^{\prime}\cdot\xi}d\xi\nonumber\\ =&\sum\limits_{k\in\mathcal{F}}c_{k,l,s}e^{\pi ik\cdot l}\int_{{\mathbb{T}^{n}}}e^{-2\pi i(k^{\prime}-k)\cdot \xi} d\xi\nonumber\\ =&\sum\limits_{k\in\mathcal{F}}c_{k,l,s}e^{\pi ik\cdot l}\delta_{k,k^{\prime}}\nonumber\\ =&c_{k^{\prime},l,s}e^{\pi ik^{\prime}\cdot l}. \end{align} $$
$$ \begin{align} \widehat{p_{l,s}}(k^{\prime})=&\int_{{\mathbb{T}^{n}}}p_{l,s}(\xi)e^{-2\pi ik^{\prime}\cdot\xi}d\xi\nonumber\\ =&\int_{{\mathbb{T}^{n}}}\Bigg(\sum\limits_{k\in\mathcal{F}}c_{k,l,s}e^{\pi ik\cdot(2\xi+l)}\Bigg)e^{-2\pi ik^{\prime}\cdot\xi}d\xi\nonumber\\ =&\sum\limits_{k\in\mathcal{F}}c_{k,l,s}e^{\pi ik\cdot l}\int_{{\mathbb{T}^{n}}}e^{-2\pi i(k^{\prime}-k)\cdot \xi} d\xi\nonumber\\ =&\sum\limits_{k\in\mathcal{F}}c_{k,l,s}e^{\pi ik\cdot l}\delta_{k,k^{\prime}}\nonumber\\ =&c_{k^{\prime},l,s}e^{\pi ik^{\prime}\cdot l}. \end{align} $$
Hence, we get
 $$ \begin{align} \sum\limits_{(k,(l,s))\in\mathcal{F}\times \mathcal{F^{\prime}}}|c_{k,l,s}|^{2}=&\sum\limits_{k,(l,s)\in\mathcal{F}\times\mathcal{F^{\prime}}}|\widehat{p_{l,s}}(k)|^{2}\nonumber\\ =&\sum\limits_{(l,s)\in\mathcal{F^{\prime}}}\left(\sum_{k\in\mathcal{F}}|\widehat{p_{l,s}}(k)|^{2}\right)\nonumber\\ =&\sum_{(l,s)\in\mathcal{F^{\prime}}}\|p_{l,s}\|_{L^2({\mathbb{T}^{n}})}^{2}\nonumber\\ =&\sum_{(l,s)\in\mathcal{F^{\prime}}}\int_{{\mathbb{T}^{n}}}|p_{l,s}(\xi)|^{2}\,d\xi, \end{align} $$
$$ \begin{align} \sum\limits_{(k,(l,s))\in\mathcal{F}\times \mathcal{F^{\prime}}}|c_{k,l,s}|^{2}=&\sum\limits_{k,(l,s)\in\mathcal{F}\times\mathcal{F^{\prime}}}|\widehat{p_{l,s}}(k)|^{2}\nonumber\\ =&\sum\limits_{(l,s)\in\mathcal{F^{\prime}}}\left(\sum_{k\in\mathcal{F}}|\widehat{p_{l,s}}(k)|^{2}\right)\nonumber\\ =&\sum_{(l,s)\in\mathcal{F^{\prime}}}\|p_{l,s}\|_{L^2({\mathbb{T}^{n}})}^{2}\nonumber\\ =&\sum_{(l,s)\in\mathcal{F^{\prime}}}\int_{{\mathbb{T}^{n}}}|p_{l,s}(\xi)|^{2}\,d\xi, \end{align} $$
by applying the Plancherel formula for the Fourier series of
![]() $p_{l,s}$
. Using (4.3) and (4.5) in (4.2), we get
$p_{l,s}$
. Using (4.3) and (4.5) in (4.2), we get
 $$ \begin{align} A\sum\limits_{(l,s)\in\mathcal{F^{\prime}}}\int_{{\mathbb{T}^{n}}}|p_{l,s}(\xi)|^{2}\,d\xi\leq \int_{{\mathbb{T}^{n}}}\Big\|\sum_{(l,s)\in\mathcal{F^{\prime}}}p_{l,s}(\xi)\tau {\phi}_{s}(\xi+l)\Big\|^{2}\,d\xi\leq B\sum_{(l,s)\in\mathcal{F^{\prime}}}\int_{{\mathbb{T}^{n}}}|p_{l,s}(\xi)|^{2}\,d\xi. \end{align} $$
$$ \begin{align} A\sum\limits_{(l,s)\in\mathcal{F^{\prime}}}\int_{{\mathbb{T}^{n}}}|p_{l,s}(\xi)|^{2}\,d\xi\leq \int_{{\mathbb{T}^{n}}}\Big\|\sum_{(l,s)\in\mathcal{F^{\prime}}}p_{l,s}(\xi)\tau {\phi}_{s}(\xi+l)\Big\|^{2}\,d\xi\leq B\sum_{(l,s)\in\mathcal{F^{\prime}}}\int_{{\mathbb{T}^{n}}}|p_{l,s}(\xi)|^{2}\,d\xi. \end{align} $$
Consider a family
![]() $\mathcal {C}:=\{m_{l,s}\in L^{\infty }({\mathbb {T}^{n}}) : (l,s)\in \mathbb {Z}^{n+1}\}$
. Then, by Lusin’s theorem, there exists a sequence of trigonometric polynomials
$\mathcal {C}:=\{m_{l,s}\in L^{\infty }({\mathbb {T}^{n}}) : (l,s)\in \mathbb {Z}^{n+1}\}$
. Then, by Lusin’s theorem, there exists a sequence of trigonometric polynomials
![]() $\{p^{(i)}_{l,s}\}_{i\in \mathbb {N}}$
such that
$\{p^{(i)}_{l,s}\}_{i\in \mathbb {N}}$
such that
![]() $\|p^{(i)}_{l,s}\|_{L^\infty ({\mathbb {T}^{n}})}\leq \|m_{l,s}\|_{L^\infty ({\mathbb {T}^{n}})}$
, for all
$\|p^{(i)}_{l,s}\|_{L^\infty ({\mathbb {T}^{n}})}\leq \|m_{l,s}\|_{L^\infty ({\mathbb {T}^{n}})}$
, for all
![]() $i\in \mathbb {N}$
, and
$i\in \mathbb {N}$
, and
![]() $p^{i}_{l,s}(\xi )\rightarrow m_{l,s}(\xi )$
as
$p^{i}_{l,s}(\xi )\rightarrow m_{l,s}(\xi )$
as
![]() $i\rightarrow \infty $
for
$i\rightarrow \infty $
for
![]() $a.e.\ \xi \in {\mathbb {T}^{n}}$
. Now, using (4.6), we have
$a.e.\ \xi \in {\mathbb {T}^{n}}$
. Now, using (4.6), we have
 $$ \begin{align*} A\sum\limits_{(l,s)\in\mathcal{F^{\prime}}}\int_{{\mathbb{T}^{n}}}|p^{(i)}_{l,s}(\xi)|^{2}\,d\xi\leq \int_{{\mathbb{T}^{n}}}\Big\|\sum_{(l,s)\in\mathcal{F^{\prime}}}p^{(i)}_{l,s}(\xi)\tau {\phi}_{s}(\xi+l)\Big\|^{2}\,d\xi\leq B\sum_{(l,s)\in\mathcal{F^{\prime}}}\int_{{\mathbb{T}^{n}}}|p^{(i)}_{l,s}(\xi)|^{2}\,d\xi, \end{align*} $$
$$ \begin{align*} A\sum\limits_{(l,s)\in\mathcal{F^{\prime}}}\int_{{\mathbb{T}^{n}}}|p^{(i)}_{l,s}(\xi)|^{2}\,d\xi\leq \int_{{\mathbb{T}^{n}}}\Big\|\sum_{(l,s)\in\mathcal{F^{\prime}}}p^{(i)}_{l,s}(\xi)\tau {\phi}_{s}(\xi+l)\Big\|^{2}\,d\xi\leq B\sum_{(l,s)\in\mathcal{F^{\prime}}}\int_{{\mathbb{T}^{n}}}|p^{(i)}_{l,s}(\xi)|^{2}\,d\xi, \end{align*} $$
![]() $\forall \ i\in {\mathbb {N}}$
. Taking limit as
$\forall \ i\in {\mathbb {N}}$
. Taking limit as
![]() $i\rightarrow \infty $
and then applying Lebesgue dominated convergence theorem in the above inequality, we obtain
$i\rightarrow \infty $
and then applying Lebesgue dominated convergence theorem in the above inequality, we obtain
 $$ \begin{align} A\sum\limits_{(l,s)\in\mathcal{F^{\prime}}}\int_{{\mathbb{T}^{n}}}|m_{l,s}(\xi)|^{2}\,d\xi\leq \int_{{\mathbb{T}^{n}}}\Big\|\sum_{(l,s)\in\mathcal{F^{\prime}}}m_{l,s}(\xi)\tau {\phi}_{s}(\xi+l)\Big\|^{2}\,d\xi\leq B\sum_{(l,s)\in\mathcal{F^{\prime}}}\int_{{\mathbb{T}^{n}}}|m_{l,s}(\xi)|^{2}\,d\xi. \end{align} $$
$$ \begin{align} A\sum\limits_{(l,s)\in\mathcal{F^{\prime}}}\int_{{\mathbb{T}^{n}}}|m_{l,s}(\xi)|^{2}\,d\xi\leq \int_{{\mathbb{T}^{n}}}\Big\|\sum_{(l,s)\in\mathcal{F^{\prime}}}m_{l,s}(\xi)\tau {\phi}_{s}(\xi+l)\Big\|^{2}\,d\xi\leq B\sum_{(l,s)\in\mathcal{F^{\prime}}}\int_{{\mathbb{T}^{n}}}|m_{l,s}(\xi)|^{2}\,d\xi. \end{align} $$
Now, (4.1) is equivalent to
 $$ \begin{align} A\sum\limits_{(l,s)\in\mathcal{E}}|c_{l,s}|^{2}\leq \bigg\|\sum\limits_{(l,s)\in\mathcal{E}}c_{l,s}\tau {\phi}_{s}(\xi+l)\bigg\|^{2}\leq B\sum\limits_{(l,s)\in\mathcal{E}}|c_{l,s}|^{2} \end{align} $$
$$ \begin{align} A\sum\limits_{(l,s)\in\mathcal{E}}|c_{l,s}|^{2}\leq \bigg\|\sum\limits_{(l,s)\in\mathcal{E}}c_{l,s}\tau {\phi}_{s}(\xi+l)\bigg\|^{2}\leq B\sum\limits_{(l,s)\in\mathcal{E}}|c_{l,s}|^{2} \end{align} $$
for
![]() $a.e.\ \xi \in {\mathbb {T}^{n}}$
and for every finite set
$a.e.\ \xi \in {\mathbb {T}^{n}}$
and for every finite set
![]() $\mathcal {E}\subset \mathbb {Z}^{n+1}$
. Thus, we aim to prove (4.8). Suppose (4.8) were not true. Then there would exist a Lebesgue measurable set
$\mathcal {E}\subset \mathbb {Z}^{n+1}$
. Thus, we aim to prove (4.8). Suppose (4.8) were not true. Then there would exist a Lebesgue measurable set
![]() $D\subset {\mathbb {T}^{n}}$
with positive Lebesgue measure such that at least one of the following inequalities holds:
$D\subset {\mathbb {T}^{n}}$
with positive Lebesgue measure such that at least one of the following inequalities holds:
 $$ \begin{align} \bigg\|\sum\limits_{(l,s)\in\mathcal{E}}c^{\prime}_{l,s}\tau {\phi}_{s}(\xi+l)\bigg\|^{2}&> B\sum\limits_{(l,s)\in\mathcal{E}}|c^{\prime}_{l,s}|^{2},\ \ \ \forall\ \xi\in D, \end{align} $$
$$ \begin{align} \bigg\|\sum\limits_{(l,s)\in\mathcal{E}}c^{\prime}_{l,s}\tau {\phi}_{s}(\xi+l)\bigg\|^{2}&> B\sum\limits_{(l,s)\in\mathcal{E}}|c^{\prime}_{l,s}|^{2},\ \ \ \forall\ \xi\in D, \end{align} $$
 $$ \begin{align} \bigg\|\sum\limits_{(l,s)\in\mathcal{E}}c^{\prime}_{l,s}\tau {\phi}_{s}(\xi+l)\bigg\|^{2}&< A\sum\limits_{(l,s)\in\mathcal{E}}|c^{\prime}_{l,s}|^{2},\ \ \ \forall\ \xi\in D. \end{align} $$
$$ \begin{align} \bigg\|\sum\limits_{(l,s)\in\mathcal{E}}c^{\prime}_{l,s}\tau {\phi}_{s}(\xi+l)\bigg\|^{2}&< A\sum\limits_{(l,s)\in\mathcal{E}}|c^{\prime}_{l,s}|^{2},\ \ \ \forall\ \xi\in D. \end{align} $$
Assume that (4.9) holds. Define
![]() $m^{\prime }_{l,s}(\xi ):=\frac {c^{\prime }_{l,s}}{\sqrt {\mu (D)}}\chi _{D}(\xi )$
, where
$m^{\prime }_{l,s}(\xi ):=\frac {c^{\prime }_{l,s}}{\sqrt {\mu (D)}}\chi _{D}(\xi )$
, where
![]() $\mu (D)$
denotes the Lebesgue measure of D. Then
$\mu (D)$
denotes the Lebesgue measure of D. Then
![]() $m^{\prime }_{l,s}\in \mathcal {C}$
and
$m^{\prime }_{l,s}\in \mathcal {C}$
and
 $$ \begin{align*} \int_{{\mathbb{T}^{n}}}\Big\|\sum_{(l,s)\in\mathcal{E}}m^{\prime}_{l,s}(\xi)\tau {\phi}_{s}(\xi+l)\Big\|^{2}\,d\xi=&\int_{D}\Big\|\sum_{(l,s)\in\mathcal{E}}\frac{c^{\prime}_{l,s}}{\sqrt{\mu(D)}}\tau {\phi}_{s}(\xi+l)\Big\|^{2}\,d\xi\\ =&\frac{1}{\mu(D)}\int_{D}\Big\|\sum_{(l,s)\in\mathcal{E}}c^{\prime}_{l,s}\tau {\phi}_{s}(\xi+l)\Big\|^{2}\,d\xi\\>&\frac{1}{\mu(D)}B\sum_{(l,s)\in\mathcal{E}}|c^{\prime}_{l,s}|^{2}\int_{D}\,d\xi\\ =&B\sum_{(l,s)\in\mathcal{E}}|c^{\prime}_{l,s}|^{2}, \end{align*} $$
$$ \begin{align*} \int_{{\mathbb{T}^{n}}}\Big\|\sum_{(l,s)\in\mathcal{E}}m^{\prime}_{l,s}(\xi)\tau {\phi}_{s}(\xi+l)\Big\|^{2}\,d\xi=&\int_{D}\Big\|\sum_{(l,s)\in\mathcal{E}}\frac{c^{\prime}_{l,s}}{\sqrt{\mu(D)}}\tau {\phi}_{s}(\xi+l)\Big\|^{2}\,d\xi\\ =&\frac{1}{\mu(D)}\int_{D}\Big\|\sum_{(l,s)\in\mathcal{E}}c^{\prime}_{l,s}\tau {\phi}_{s}(\xi+l)\Big\|^{2}\,d\xi\\>&\frac{1}{\mu(D)}B\sum_{(l,s)\in\mathcal{E}}|c^{\prime}_{l,s}|^{2}\int_{D}\,d\xi\\ =&B\sum_{(l,s)\in\mathcal{E}}|c^{\prime}_{l,s}|^{2}, \end{align*} $$
which is a contradiction to (4.7). Similarly, if we assume (4.10), we will get a contradiction to (4.7) again. Therefore, we obtain (4.1).
Conversely, assume that (4.1) holds. We need to prove (4.2). So let
![]() $\{c_{k,l,s}\}_{(k,(l,s))\in \mathcal {F}\times \mathcal {F}^{\prime }}\in c_{00}(\mathbb {Z}^{2n+1})$
. For
$\{c_{k,l,s}\}_{(k,(l,s))\in \mathcal {F}\times \mathcal {F}^{\prime }}\in c_{00}(\mathbb {Z}^{2n+1})$
. For
![]() $\xi \in {\mathbb {T}^{n}}$
, we define
$\xi \in {\mathbb {T}^{n}}$
, we define
 $$ \begin{align*} p_{l,s}(\xi)=\sum\limits_{k\in \mathcal{F}}c_{k,l,s}e^{\pi ik\cdot(2\xi+l)}. \end{align*} $$
$$ \begin{align*} p_{l,s}(\xi)=\sum\limits_{k\in \mathcal{F}}c_{k,l,s}e^{\pi ik\cdot(2\xi+l)}. \end{align*} $$
Using (4.1), we have
 $$ \begin{align*} A\sum\limits_{(l,s)\in\mathcal{E}}|p_{l,s}(\xi)|^{2}\leq \bigg\|\sum\limits_{(l,s)\in\mathcal{E}}p_{l,s}(\xi)\tau {\phi}_{s}(\xi+l)\bigg\|^{2}\leq B\sum\limits_{(l,s)\in\mathcal{E}}|p_{l,s}(\xi)|^{2}, \end{align*} $$
$$ \begin{align*} A\sum\limits_{(l,s)\in\mathcal{E}}|p_{l,s}(\xi)|^{2}\leq \bigg\|\sum\limits_{(l,s)\in\mathcal{E}}p_{l,s}(\xi)\tau {\phi}_{s}(\xi+l)\bigg\|^{2}\leq B\sum\limits_{(l,s)\in\mathcal{E}}|p_{l,s}(\xi)|^{2}, \end{align*} $$
for
![]() $a.e.\ \xi \in {\mathbb {T}^{n}}$
. Now, integrating with respect to
$a.e.\ \xi \in {\mathbb {T}^{n}}$
. Now, integrating with respect to
![]() $\xi $
over
$\xi $
over
![]() ${\mathbb {T}^{n}}$
, we obtain
${\mathbb {T}^{n}}$
, we obtain
 $$ \begin{align*} A\sum\limits_{(l,s)\in\mathcal{E}}\int_{{\mathbb{T}^{n}}}|p_{l,s}(\xi)|^{2}\leq \int_{{\mathbb{T}^{n}}}\bigg\|\sum\limits_{(l,s)\in\mathcal{E}}p_{l,s}(\xi)\tau {\phi}_{s}(\xi+l)\bigg\|^{2}\leq B\sum\limits_{(l,s)\in\mathcal{E}}\int_{{\mathbb{T}^{n}}}|p_{l,s}(\xi)|^{2}, \end{align*} $$
$$ \begin{align*} A\sum\limits_{(l,s)\in\mathcal{E}}\int_{{\mathbb{T}^{n}}}|p_{l,s}(\xi)|^{2}\leq \int_{{\mathbb{T}^{n}}}\bigg\|\sum\limits_{(l,s)\in\mathcal{E}}p_{l,s}(\xi)\tau {\phi}_{s}(\xi+l)\bigg\|^{2}\leq B\sum\limits_{(l,s)\in\mathcal{E}}\int_{{\mathbb{T}^{n}}}|p_{l,s}(\xi)|^{2}, \end{align*} $$
which together with (4.3) and (4.5) gives the required result.
Corollary 4.2. The family
![]() $E^{t}(\mathcal {A})$
is a Riesz sequence with bounds A and B if and only if the family
$E^{t}(\mathcal {A})$
is a Riesz sequence with bounds A and B if and only if the family
![]() $\{\tau {\phi }_{s}(\xi +l) : (l,s)\in \mathbb {Z}^{n+1}\}$
is a Riesz sequence with the same bounds, for
$\{\tau {\phi }_{s}(\xi +l) : (l,s)\in \mathbb {Z}^{n+1}\}$
is a Riesz sequence with the same bounds, for
![]() $a.e.\ \xi \in {\mathbb {T}^{n}}$
.
$a.e.\ \xi \in {\mathbb {T}^{n}}$
.
Proof. Let the family
![]() $E^{t}(\mathcal {A})$
be a Riesz sequence with bounds A and B. Then, by Theorem 4.1, it is equivalent to (4.1), which in turn is equivalent to
$E^{t}(\mathcal {A})$
be a Riesz sequence with bounds A and B. Then, by Theorem 4.1, it is equivalent to (4.1), which in turn is equivalent to
 $$ \begin{align*} A\sum\limits_{(l,s)\in{\mathbb{Z}}^{n+1}}|c_{l,s}|^{2}\leq \bigg\|\sum\limits_{(l,s)\in{\mathbb{Z}}^{n+1}}c_{l,s}\tau {\phi}_{s}(\xi+l)\bigg\|^{2}\leq B\sum\limits_{(l,s)\in{\mathbb{Z}}^{n+1}}|c_{l,s}|^{2}, \end{align*} $$
$$ \begin{align*} A\sum\limits_{(l,s)\in{\mathbb{Z}}^{n+1}}|c_{l,s}|^{2}\leq \bigg\|\sum\limits_{(l,s)\in{\mathbb{Z}}^{n+1}}c_{l,s}\tau {\phi}_{s}(\xi+l)\bigg\|^{2}\leq B\sum\limits_{(l,s)\in{\mathbb{Z}}^{n+1}}|c_{l,s}|^{2}, \end{align*} $$
![]() $\forall \ \{c_{l,s}\}\in \ell ^2({\mathbb {Z}}^{n+1})$
and for
$\forall \ \{c_{l,s}\}\in \ell ^2({\mathbb {Z}}^{n+1})$
and for
![]() $a.e.\ \xi \in {\mathbb {T}^{n}}$
, proving our assertion.
$a.e.\ \xi \in {\mathbb {T}^{n}}$
, proving our assertion.
Corollary 4.3. Let
![]() ${\mathcal {A}}=\{{\phi }\}$
, and let
${\mathcal {A}}=\{{\phi }\}$
, and let
![]() $E^{t}({\mathcal {A}})$
be a Riesz sequence with bounds A and B. Then
$E^{t}({\mathcal {A}})$
be a Riesz sequence with bounds A and B. Then
![]() $A\leq W_{{\phi }}(\xi )\leq B$
, for
$A\leq W_{{\phi }}(\xi )\leq B$
, for
![]() $a.e.\ \xi \in {\mathbb {T}^{n}}$
.
$a.e.\ \xi \in {\mathbb {T}^{n}}$
.
Proof. Since the system
![]() $E^{t}({\mathcal {A}})$
is a Riesz sequence with bounds A and B, it is a frame sequence with the same bounds. Thus, by Theorem 3.7, we have
$E^{t}({\mathcal {A}})$
is a Riesz sequence with bounds A and B, it is a frame sequence with the same bounds. Thus, by Theorem 3.7, we have
![]() $A\leq W_{{\phi }}(\xi )\leq B$
, for
$A\leq W_{{\phi }}(\xi )\leq B$
, for
![]() $a.e. \xi \in {\mathbb {T}^{n}}\setminus N$
. Now, in order to obtain the required result, it is enough to show that
$a.e. \xi \in {\mathbb {T}^{n}}\setminus N$
. Now, in order to obtain the required result, it is enough to show that
![]() $\mu (N)=0$
. By Corollary 4.2, we have
$\mu (N)=0$
. By Corollary 4.2, we have
 $$ \begin{align*} A\|\{c_{l,s}\}\|^{2}_{\ell^{2}(\mathbb{Z}^{n+1})}\leq \bigg\|\sum\limits_{(l,s)\in\mathbb{Z}^{n+1}}c_{l,s}\tau {\phi}(\xi+l)\bigg\|^{2}_{L^{2}({\mathbb{R}^{n}},\ell^{2}({\mathbb{Z}^n}))}, \end{align*} $$
$$ \begin{align*} A\|\{c_{l,s}\}\|^{2}_{\ell^{2}(\mathbb{Z}^{n+1})}\leq \bigg\|\sum\limits_{(l,s)\in\mathbb{Z}^{n+1}}c_{l,s}\tau {\phi}(\xi+l)\bigg\|^{2}_{L^{2}({\mathbb{R}^{n}},\ell^{2}({\mathbb{Z}^n}))}, \end{align*} $$
![]() $\forall \ \{c_{l,s}\}\in \ell ^{2}(\mathbb {Z}^{n+1})$
and for
$\forall \ \{c_{l,s}\}\in \ell ^{2}(\mathbb {Z}^{n+1})$
and for
![]() $a.e.\ \xi \in {\mathbb {T}^{n}}$
. In particular, by choosing
$a.e.\ \xi \in {\mathbb {T}^{n}}$
. In particular, by choosing
![]() $c_{l,s}=\delta _{((l,s),(0,0))},\forall \ (l,s)\in {\mathbb {Z}}^{n+1}$
, in the above inequality, we get
$c_{l,s}=\delta _{((l,s),(0,0))},\forall \ (l,s)\in {\mathbb {Z}}^{n+1}$
, in the above inequality, we get
![]() $0<A\leq \|\tau {\phi }(\xi )\|^{2}$
, for
$0<A\leq \|\tau {\phi }(\xi )\|^{2}$
, for
![]() $a.e.\ \xi \in {\mathbb {T}^{n}}$
. Hence,
$a.e.\ \xi \in {\mathbb {T}^{n}}$
. Hence,
![]() $w_{\phi }(\xi )=\|\tau {\phi }(\xi )\|^{2}>0$
, for
$w_{\phi }(\xi )=\|\tau {\phi }(\xi )\|^{2}>0$
, for
![]() $a.e.\ \xi \in {\mathbb {T}^{n}}$
, showing that
$a.e.\ \xi \in {\mathbb {T}^{n}}$
, showing that
![]() $\mu (N)=0$
.
$\mu (N)=0$
.
But the converse need not be true. We illustrate it with a counter example.
Example 4.4. We define
![]() $\phi \in L^{2}(\mathbb {R}^{2})$
by
$\phi \in L^{2}(\mathbb {R}^{2})$
by
![]() $K_{\phi }(\xi ,\eta )=\chi _{[0,2)\times [0,1)}(\xi ,\eta ),\ (\xi ,\eta )\in \mathbb {R}^{2}$
. Then, for
$K_{\phi }(\xi ,\eta )=\chi _{[0,2)\times [0,1)}(\xi ,\eta ),\ (\xi ,\eta )\in \mathbb {R}^{2}$
. Then, for
![]() $\xi ,\eta \in [0,1)$
, we have
$\xi ,\eta \in [0,1)$
, we have
 $$ \begin{align*} K_{\phi}(\xi+m,\eta)= \begin{cases} 1, & m=0,1,\\ 0, & otherwise, \end{cases} \ \ \ \ \ \ \ \text{and}\ \ \ \ \ \ \ K_{\phi}(\xi+m+1,\eta)= \begin{cases} 1, & m=-1,0,\\ 0, & otherwise. \end{cases} \end{align*} $$
$$ \begin{align*} K_{\phi}(\xi+m,\eta)= \begin{cases} 1, & m=0,1,\\ 0, & otherwise, \end{cases} \ \ \ \ \ \ \ \text{and}\ \ \ \ \ \ \ K_{\phi}(\xi+m+1,\eta)= \begin{cases} 1, & m=-1,0,\\ 0, & otherwise. \end{cases} \end{align*} $$
Hence, we get
 $$ \begin{align*} \sum_{m\in\mathbb{Z}}\int_{\mathbb{R}}K_{\phi}(m+\xi,\eta)\overline{K_{\phi}(m+\xi+1,\eta)}d\eta =& \sum_{m\in\mathbb{Z}}\int_{0}^{1}K_{\phi}(m+\xi,\eta)K_{\phi}(m+\xi+1,\eta)d\eta\\ =&1,\ \ \ \ \ \ \ \ \forall\ \xi\in [0,1), \end{align*} $$
$$ \begin{align*} \sum_{m\in\mathbb{Z}}\int_{\mathbb{R}}K_{\phi}(m+\xi,\eta)\overline{K_{\phi}(m+\xi+1,\eta)}d\eta =& \sum_{m\in\mathbb{Z}}\int_{0}^{1}K_{\phi}(m+\xi,\eta)K_{\phi}(m+\xi+1,\eta)d\eta\\ =&1,\ \ \ \ \ \ \ \ \forall\ \xi\in [0,1), \end{align*} $$
showing that
![]() $\phi $
does not satisfy “Condition C.” Now,
$\phi $
does not satisfy “Condition C.” Now,
 $$ \begin{align} \omega_\phi(\xi)=&\sum_{m\in\mathbb{Z}}\int_{\mathbb{R}}|K_{\phi}(m+\xi,\eta)|^{2}\,d\eta\nonumber\\ =&\sum_{m\in\mathbb{Z}}\int_{0}^{1}|K_{\phi}(m+\xi,\eta)|^{2}\,d\eta\nonumber\\ =&2,\ \ \ \ \ \ \ \ \forall\ \xi\in [0,1). \end{align} $$
$$ \begin{align} \omega_\phi(\xi)=&\sum_{m\in\mathbb{Z}}\int_{\mathbb{R}}|K_{\phi}(m+\xi,\eta)|^{2}\,d\eta\nonumber\\ =&\sum_{m\in\mathbb{Z}}\int_{0}^{1}|K_{\phi}(m+\xi,\eta)|^{2}\,d\eta\nonumber\\ =&2,\ \ \ \ \ \ \ \ \forall\ \xi\in [0,1). \end{align} $$
Hence, for
![]() $\xi \in [0,1)$
, we get
$\xi \in [0,1)$
, we get
 $$ \begin{align} W_\phi(\xi)=&\frac{1}{\omega_\phi(\xi)}\sum_{l\in\mathbb{Z}}\big|\sum_{m\in\mathbb{Z}}\int_{\mathbb{R}}K_{\phi}(m+\xi,\eta)\overline{K_{\phi}(\xi+m+l,\eta)}\,d\eta\big|^{2} \nonumber\\ =&\frac{1}{2}\sum_{l\in\mathbb{Z}}\big|\sum_{m\in\mathbb{Z}}\int_{0}^{1}K_{\phi}(m+\xi,\eta)\overline{K_{\phi}(\xi+m+l,\eta)}\,d\eta\big|^{2}\nonumber\\ =&\frac{1}{2}\sum_{l\in\mathbb{Z}}\big|\int_0^1 K_{\phi}(\xi+l,\eta)+K_{\phi}(\xi+1+l,\eta)\,d\eta\big|^{2}\nonumber\\ =& \frac{1}{2}\sum_{l=-1,0,1}\big|\int_0^1 K_{\phi}(\xi+l,\eta)+K_{\phi}(\xi+1+l,\eta)\,d\eta\big|^{2} \nonumber\\ =&\frac{1}{2}\times 6\nonumber\\ =& 3, \end{align} $$
$$ \begin{align} W_\phi(\xi)=&\frac{1}{\omega_\phi(\xi)}\sum_{l\in\mathbb{Z}}\big|\sum_{m\in\mathbb{Z}}\int_{\mathbb{R}}K_{\phi}(m+\xi,\eta)\overline{K_{\phi}(\xi+m+l,\eta)}\,d\eta\big|^{2} \nonumber\\ =&\frac{1}{2}\sum_{l\in\mathbb{Z}}\big|\sum_{m\in\mathbb{Z}}\int_{0}^{1}K_{\phi}(m+\xi,\eta)\overline{K_{\phi}(\xi+m+l,\eta)}\,d\eta\big|^{2}\nonumber\\ =&\frac{1}{2}\sum_{l\in\mathbb{Z}}\big|\int_0^1 K_{\phi}(\xi+l,\eta)+K_{\phi}(\xi+1+l,\eta)\,d\eta\big|^{2}\nonumber\\ =& \frac{1}{2}\sum_{l=-1,0,1}\big|\int_0^1 K_{\phi}(\xi+l,\eta)+K_{\phi}(\xi+1+l,\eta)\,d\eta\big|^{2} \nonumber\\ =&\frac{1}{2}\times 6\nonumber\\ =& 3, \end{align} $$
showing that the weight function is bounded above and below for
![]() $a.e.\ \xi \in [0,1)$
. Now, we shall make use of Corollary
$a.e.\ \xi \in [0,1)$
. Now, we shall make use of Corollary
![]() $4.2$
in order to prove that the system
$4.2$
in order to prove that the system
![]() $\{T_{(k,l)}^t\phi :k,l\in \mathbb {Z}\}$
does not form a Riesz sequence. For
$\{T_{(k,l)}^t\phi :k,l\in \mathbb {Z}\}$
does not form a Riesz sequence. For
![]() $\{c_{l}\}\in \ell ^{2}(\mathbb {Z})$
and
$\{c_{l}\}\in \ell ^{2}(\mathbb {Z})$
and
![]() $\xi \in [0,1)$
, we have
$\xi \in [0,1)$
, we have
 $$ \begin{align} \Big\|\sum_{l}c_{l}\tau\phi(\xi+l)\Big\|^{2}_{L^{2}(\mathbb{R},\ell^{2}(\mathbb{Z}))} =&\sum_{l,l^{\prime}}c_{l}\overline{c_{l^{\prime}}}\big<\tau\phi(\xi+l),\tau\phi(\xi+l^{\prime})\big>_{L^{2}(\mathbb{R},\ell^{2}(\mathbb{Z}))}\nonumber\\ =&\sum_{l,l^{\prime}}c_{l}\overline{c_{l^{\prime}}}\bigg(\sum_{m\in\mathbb{Z}}\int_{\mathbb{R}}K_{\phi}(m+\xi,\eta)\overline{K_{\phi}(m+\xi+l^{\prime}-l,\eta)}\,d\eta\bigg)\nonumber\\ =&\sum_{l,l^{\prime}}c_{l}\overline{c_{l^{\prime}}}\bigg(\sum_{m\in\mathbb{Z}}\int_{0}^1K_{\phi}(m+\xi,\eta)\overline{K_{\phi}(m+\xi+l^{\prime}-l,\eta)}\,d\eta\bigg)\nonumber\\ =&\sum_{l,l^{\prime}}c_{l}\overline{c_{l^{\prime}}}\bigg(\int_0^1K_{\phi}(\xi+l^{\prime}-l,\eta)+K_{\phi}(1+\xi+l^{\prime}-l,\eta)\,d\eta\bigg)\nonumber\\ =&\sum_{l}c_{l}\overline{c_{l}}+\sum_{l}c_{l}\overline{c_{l+1}}+\sum_{l}c_{l}\overline{c_{l-1}}+\sum_{l}c_{l}\overline{c_{l}}\nonumber\\ =&2\sum_{l}|c_{l}|^{2}+2\operatorname{\mathrm{Re}}\left(\sum_{l}c_{l}\overline{c_{l+1}}\right). \end{align} $$
$$ \begin{align} \Big\|\sum_{l}c_{l}\tau\phi(\xi+l)\Big\|^{2}_{L^{2}(\mathbb{R},\ell^{2}(\mathbb{Z}))} =&\sum_{l,l^{\prime}}c_{l}\overline{c_{l^{\prime}}}\big<\tau\phi(\xi+l),\tau\phi(\xi+l^{\prime})\big>_{L^{2}(\mathbb{R},\ell^{2}(\mathbb{Z}))}\nonumber\\ =&\sum_{l,l^{\prime}}c_{l}\overline{c_{l^{\prime}}}\bigg(\sum_{m\in\mathbb{Z}}\int_{\mathbb{R}}K_{\phi}(m+\xi,\eta)\overline{K_{\phi}(m+\xi+l^{\prime}-l,\eta)}\,d\eta\bigg)\nonumber\\ =&\sum_{l,l^{\prime}}c_{l}\overline{c_{l^{\prime}}}\bigg(\sum_{m\in\mathbb{Z}}\int_{0}^1K_{\phi}(m+\xi,\eta)\overline{K_{\phi}(m+\xi+l^{\prime}-l,\eta)}\,d\eta\bigg)\nonumber\\ =&\sum_{l,l^{\prime}}c_{l}\overline{c_{l^{\prime}}}\bigg(\int_0^1K_{\phi}(\xi+l^{\prime}-l,\eta)+K_{\phi}(1+\xi+l^{\prime}-l,\eta)\,d\eta\bigg)\nonumber\\ =&\sum_{l}c_{l}\overline{c_{l}}+\sum_{l}c_{l}\overline{c_{l+1}}+\sum_{l}c_{l}\overline{c_{l-1}}+\sum_{l}c_{l}\overline{c_{l}}\nonumber\\ =&2\sum_{l}|c_{l}|^{2}+2\operatorname{\mathrm{Re}}\left(\sum_{l}c_{l}\overline{c_{l+1}}\right). \end{align} $$
For each
![]() $n\in \mathbb {N}$
, we define
$n\in \mathbb {N}$
, we define
![]() $X^{(n)}\in \ell ^2(\mathbb {Z})$
by
$X^{(n)}\in \ell ^2(\mathbb {Z})$
by
 $$ \begin{align*} X^{(n)}_l&= \begin{cases} \frac{(-1)^l}{\sqrt{2n}}, & l=1,2,\ldots,2n,\\ 0, & otherwise. \end{cases} \end{align*} $$
$$ \begin{align*} X^{(n)}_l&= \begin{cases} \frac{(-1)^l}{\sqrt{2n}}, & l=1,2,\ldots,2n,\\ 0, & otherwise. \end{cases} \end{align*} $$
It is easy to see that
![]() $\|X^{(n)}\|_{\ell ^2(\mathbb {Z})}=1$
,
$\|X^{(n)}\|_{\ell ^2(\mathbb {Z})}=1$
,
![]() $\forall \ n\in \mathbb {N}$
. For each
$\forall \ n\in \mathbb {N}$
. For each
![]() $n\in \mathbb {N}$
, by taking
$n\in \mathbb {N}$
, by taking
![]() $c_{l}=X^{(n)}_l$
in (4.13), we obtain
$c_{l}=X^{(n)}_l$
in (4.13), we obtain
 $$ \begin{align} \Big\|\sum_{l}X^{(n)}_l\tau\phi(\xi+l)\Big\|^{2}_{L^{2}(\mathbb{R},\ell^{2}(\mathbb{Z}))} &=2\sum_{l}|X^{(n)}_l|^{2}+2\operatorname{\mathrm{Re}}\left(\sum_{l}X^{(n)}_l\overline{X^{(n)}_{l+1}}\right)\notag\\ &=2+2\operatorname{\mathrm{Re}}\left(\sum_{l}X^{(n)}_l\overline{X^{(n)}_{l+1}}\right). \end{align} $$
$$ \begin{align} \Big\|\sum_{l}X^{(n)}_l\tau\phi(\xi+l)\Big\|^{2}_{L^{2}(\mathbb{R},\ell^{2}(\mathbb{Z}))} &=2\sum_{l}|X^{(n)}_l|^{2}+2\operatorname{\mathrm{Re}}\left(\sum_{l}X^{(n)}_l\overline{X^{(n)}_{l+1}}\right)\notag\\ &=2+2\operatorname{\mathrm{Re}}\left(\sum_{l}X^{(n)}_l\overline{X^{(n)}_{l+1}}\right). \end{align} $$
But
 $$ \begin{align*} \sum_{l\in\mathbb{Z}}X^{(n)}_l\overline{X^{(n)}_{l+1}}&=\sum_{l=1}^{2n-1}\frac{(-1)^l}{\sqrt{2n}}\times \frac{(-1)^{l+1}}{\sqrt{2n}}\\ &=-\frac{1}{2n}\sum_{l=1}^{2n-1}(1)\\ &=-\frac{1}{2n} (2n-1)\\ &=\frac{1}{2n}-1. \end{align*} $$
$$ \begin{align*} \sum_{l\in\mathbb{Z}}X^{(n)}_l\overline{X^{(n)}_{l+1}}&=\sum_{l=1}^{2n-1}\frac{(-1)^l}{\sqrt{2n}}\times \frac{(-1)^{l+1}}{\sqrt{2n}}\\ &=-\frac{1}{2n}\sum_{l=1}^{2n-1}(1)\\ &=-\frac{1}{2n} (2n-1)\\ &=\frac{1}{2n}-1. \end{align*} $$
Hence, (4.14) reduces to
 $$ \begin{align*} \Big\|\sum_{l}X^{(n)}_l\tau\phi(\xi+l)\Big\|^{2}_{L^{2}(\mathbb{R},\ell^{2}(\mathbb{Z}))}&=2+2\Big(\frac{1}{2n}-1\Big)=\frac{1}{n}=\frac{1}{n}\|X^{(n)}\|_{\ell^2(\mathbb{Z})}^2,\ \forall\ n\in\mathbb{N}. \end{align*} $$
$$ \begin{align*} \Big\|\sum_{l}X^{(n)}_l\tau\phi(\xi+l)\Big\|^{2}_{L^{2}(\mathbb{R},\ell^{2}(\mathbb{Z}))}&=2+2\Big(\frac{1}{2n}-1\Big)=\frac{1}{n}=\frac{1}{n}\|X^{(n)}\|_{\ell^2(\mathbb{Z})}^2,\ \forall\ n\in\mathbb{N}. \end{align*} $$
Since the above equation holds for all
![]() $n\in \mathbb {N}$
, using Corollary
$n\in \mathbb {N}$
, using Corollary
![]() $4.2$
, we deduce that the system
$4.2$
, we deduce that the system
![]() $\{T_{(k,l)}^t\phi :k,l\in \mathbb {Z}\}$
does not satisfy the lower Riesz condition.
$\{T_{(k,l)}^t\phi :k,l\in \mathbb {Z}\}$
does not satisfy the lower Riesz condition.
Corollary 4.5 [Reference Radha and Adhikari18].
Let
![]() ${\mathcal {A}}=\{{\phi }\}$
and
${\mathcal {A}}=\{{\phi }\}$
and
![]() ${\phi }$
satisfy “Condition C.” Then
${\phi }$
satisfy “Condition C.” Then
![]() $E^{t}({\phi })$
is a Riesz sequence with bounds A and B if and only if
$E^{t}({\phi })$
is a Riesz sequence with bounds A and B if and only if
Proof. Let the system
![]() $E^{t}({\mathcal {A}})$
be a Riesz sequence with bounds A and B. Then, from Corollary 4.3, we have
$E^{t}({\mathcal {A}})$
be a Riesz sequence with bounds A and B. Then, from Corollary 4.3, we have
![]() $A\leq W_{{\phi }}(\xi )\leq B$
, for
$A\leq W_{{\phi }}(\xi )\leq B$
, for
![]() $a.e.\ \xi \in {\mathbb {T}^{n}}$
. Since
$a.e.\ \xi \in {\mathbb {T}^{n}}$
. Since
![]() ${\phi }$
satisfies “Condition C,” by (3.15), we have
${\phi }$
satisfies “Condition C,” by (3.15), we have
![]() $W_{{\phi }}(\xi )=w_{{\phi }}(\xi )$
, for
$W_{{\phi }}(\xi )=w_{{\phi }}(\xi )$
, for
![]() $a.e.\ \xi \in {\mathbb {T}^{n}}$
, which proves (4.15).
$a.e.\ \xi \in {\mathbb {T}^{n}}$
, which proves (4.15).
Conversely, assume that (4.15) holds. Since
![]() ${\phi }$
satisfies “Condition C,” using the similar steps in obtaining (3.19), we can get
${\phi }$
satisfies “Condition C,” using the similar steps in obtaining (3.19), we can get
 $$ \begin{align*} \bigg\|\sum_{l\in{\mathbb{Z}^n}}c_{l}\tau{\phi}(\xi+l)\bigg\|^{2}_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}&=\omega_{\phi}(\xi)\sum_{l\in{\mathbb{Z}^n}}|c_{l}|^{2}, \end{align*} $$
$$ \begin{align*} \bigg\|\sum_{l\in{\mathbb{Z}^n}}c_{l}\tau{\phi}(\xi+l)\bigg\|^{2}_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}&=\omega_{\phi}(\xi)\sum_{l\in{\mathbb{Z}^n}}|c_{l}|^{2}, \end{align*} $$
![]() $\forall \ \{c_{l}\}\in c_{00}({\mathbb {Z}^n})$
and
$\forall \ \{c_{l}\}\in c_{00}({\mathbb {Z}^n})$
and
![]() $\xi \in {\mathbb {T}^{n}}$
. Now, applying (4.15) in the above equation, we have
$\xi \in {\mathbb {T}^{n}}$
. Now, applying (4.15) in the above equation, we have
 $$ \begin{align*} A\|\{c_{l}\}\|^{2}_{\ell^{2}(\mathbb{Z}^{n})}\leq \bigg\|\sum\limits_{l\in{\mathbb{Z}^n}}c_{l}\tau {\phi}(\xi+l)\bigg\|^{2}_{L^{2}({\mathbb{R}^{n}},\ell^{2}({\mathbb{Z}^n}))}\leq B\|\{c_{l}\}\|^{2}_{\ell^{2}(\mathbb{Z}^{n})}, \end{align*} $$
$$ \begin{align*} A\|\{c_{l}\}\|^{2}_{\ell^{2}(\mathbb{Z}^{n})}\leq \bigg\|\sum\limits_{l\in{\mathbb{Z}^n}}c_{l}\tau {\phi}(\xi+l)\bigg\|^{2}_{L^{2}({\mathbb{R}^{n}},\ell^{2}({\mathbb{Z}^n}))}\leq B\|\{c_{l}\}\|^{2}_{\ell^{2}(\mathbb{Z}^{n})}, \end{align*} $$
![]() $\forall \ \{c_{l}\}\in c_{00}({\mathbb {Z}^n})$
and for
$\forall \ \{c_{l}\}\in c_{00}({\mathbb {Z}^n})$
and for
![]() $a.e.\ \xi \in {\mathbb {T}^{n}}$
. Hence, the system
$a.e.\ \xi \in {\mathbb {T}^{n}}$
. Hence, the system
![]() $\{\tau \phi(\xi +l) : (l \in \mathbb {Z}^{n}\}$
is a Riesz sequence with bounds A and B, for
$\{\tau \phi(\xi +l) : (l \in \mathbb {Z}^{n}\}$
is a Riesz sequence with bounds A and B, for
![]() $a.e.\ \xi \in {\mathbb {T}^{n}}$
. Therefore, using Corollary 4.2, we obtain the required result.
$a.e.\ \xi \in {\mathbb {T}^{n}}$
. Therefore, using Corollary 4.2, we obtain the required result.
Now, we provide an example of a function
![]() ${\phi }\in L^2(\mathbb {R}^{2})$
which does not satisfy “Condition C” and the system
${\phi }\in L^2(\mathbb {R}^{2})$
which does not satisfy “Condition C” and the system
![]() $\{{T_{(k,l)}^t}{\phi }:k,l\in {\mathbb {Z}}\}$
is a Riesz sequence.
$\{{T_{(k,l)}^t}{\phi }:k,l\in {\mathbb {Z}}\}$
is a Riesz sequence.
Example 4.6. We define
![]() ${\phi }\in L^2(\mathbb {R}^{2})$
by
${\phi }\in L^2(\mathbb {R}^{2})$
by
For
![]() $\xi ,\eta \in [0,1)$
, using the definition of
$\xi ,\eta \in [0,1)$
, using the definition of
![]() $K_{{\phi }}$
, we observe that
$K_{{\phi }}$
, we observe that
 $$ \begin{align*} K_{{\phi}}(\xi+m,\eta)= \begin{cases} 2, & m=0,\\ 1, & m=1,\\ 0, & otherwise, \end{cases} \ \ \ \ \ \ \ \text{and}\ \ \ \ \ \ \ K_{{\phi}}(\xi+m+1,\eta)= \begin{cases} 2, & m=-1,\\ 1, & m=0,\\ 0, & otherwise. \end{cases} \end{align*} $$
$$ \begin{align*} K_{{\phi}}(\xi+m,\eta)= \begin{cases} 2, & m=0,\\ 1, & m=1,\\ 0, & otherwise, \end{cases} \ \ \ \ \ \ \ \text{and}\ \ \ \ \ \ \ K_{{\phi}}(\xi+m+1,\eta)= \begin{cases} 2, & m=-1,\\ 1, & m=0,\\ 0, & otherwise. \end{cases} \end{align*} $$
Hence, for
![]() $\xi ,\eta \in [0,1)$
, we get
$\xi ,\eta \in [0,1)$
, we get
 $$ \begin{align*} K_{\phi}(\xi+m,\eta)\overline{K_{\phi}(\xi+m+1,\eta)}= \begin{cases} 2, & m=0,\\ 0, & otherwise, \end{cases} \end{align*} $$
$$ \begin{align*} K_{\phi}(\xi+m,\eta)\overline{K_{\phi}(\xi+m+1,\eta)}= \begin{cases} 2, & m=0,\\ 0, & otherwise, \end{cases} \end{align*} $$
showing that
 $$ \begin{align*} \sum_{m\in{\mathbb{Z}}}\int_{{\mathbb{R}}}K_{\phi}(\xi+m,\eta)\overline{K_{\phi}(\xi+m+1,\eta)}d\eta=& \sum_{m\in{\mathbb{Z}}}\int_{0}^{1}K_{\phi}(\xi+m,\eta)K_{\phi}(\xi+m+1,\eta)d\eta.\\ =&2. \end{align*} $$
$$ \begin{align*} \sum_{m\in{\mathbb{Z}}}\int_{{\mathbb{R}}}K_{\phi}(\xi+m,\eta)\overline{K_{\phi}(\xi+m+1,\eta)}d\eta=& \sum_{m\in{\mathbb{Z}}}\int_{0}^{1}K_{\phi}(\xi+m,\eta)K_{\phi}(\xi+m+1,\eta)d\eta.\\ =&2. \end{align*} $$
Thus,
![]() ${\phi }$
does not satisfy “Condition C.” We shall make use of Corollary 4.2 in order to show that the system
${\phi }$
does not satisfy “Condition C.” We shall make use of Corollary 4.2 in order to show that the system
![]() $\{{T_{(k,l)}^t}{\phi } : k,l\in {\mathbb {Z}}\}$
is a Riesz sequence. For
$\{{T_{(k,l)}^t}{\phi } : k,l\in {\mathbb {Z}}\}$
is a Riesz sequence. For
![]() $\{c_{l}\}\in \ell ^{2}({\mathbb {Z}^n})$
, using (3.13), we have
$\{c_{l}\}\in \ell ^{2}({\mathbb {Z}^n})$
, using (3.13), we have
 $$ \begin{align*} \Big\|\sum_{l}c_{l}\tau{\phi}(\xi+l)\Big\|^{2}_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}=&\sum_{l,l^{\prime}}c_{l}\overline{c_{l^{\prime}}}\big<\tau{\phi}(\xi+l),\tau{\phi}(\xi+l^{\prime})\big>_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}\\ =&\sum_{l,l^{\prime}}c_{l}\overline{c_{l^{\prime}}}\bigg(\sum_{m\in{\mathbb{Z}}}\int_{{\mathbb{R}}}K_{{\phi}}(\xi+m,\eta)\overline{K_{{\phi}}(\xi+m+l^{\prime}-l,\eta)}\,d\eta\bigg)\\ =&\sum_{l,l^{\prime}}c_{l}\overline{c_{l^{\prime}}}\bigg(\sum_{m\in{\mathbb{Z}}}\int_{0}^1K_{{\phi}}(\xi+m,\eta)\overline{K_{{\phi}}(\xi+m+l^{\prime}-l,\eta)}\,d\eta\bigg). \end{align*} $$
$$ \begin{align*} \Big\|\sum_{l}c_{l}\tau{\phi}(\xi+l)\Big\|^{2}_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}=&\sum_{l,l^{\prime}}c_{l}\overline{c_{l^{\prime}}}\big<\tau{\phi}(\xi+l),\tau{\phi}(\xi+l^{\prime})\big>_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}\\ =&\sum_{l,l^{\prime}}c_{l}\overline{c_{l^{\prime}}}\bigg(\sum_{m\in{\mathbb{Z}}}\int_{{\mathbb{R}}}K_{{\phi}}(\xi+m,\eta)\overline{K_{{\phi}}(\xi+m+l^{\prime}-l,\eta)}\,d\eta\bigg)\\ =&\sum_{l,l^{\prime}}c_{l}\overline{c_{l^{\prime}}}\bigg(\sum_{m\in{\mathbb{Z}}}\int_{0}^1K_{{\phi}}(\xi+m,\eta)\overline{K_{{\phi}}(\xi+m+l^{\prime}-l,\eta)}\,d\eta\bigg). \end{align*} $$
The possible values of m and
![]() $l^{\prime }-l$
that can survive in the sum are
$l^{\prime }-l$
that can survive in the sum are
![]() $m=0$
and
$m=0$
and
![]() $l^{\prime }-l=-1,0,1$
. Therefore, for
$l^{\prime }-l=-1,0,1$
. Therefore, for
![]() $\xi \in [0,1)$
, we get
$\xi \in [0,1)$
, we get
 $$ \begin{align*} \Big\|\sum_{l}c_{l}\tau{\phi}(\xi+l)\Big\|^{2}_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}=&5\sum_{l}|c_{l}|^{2}+2\sum_{l}\overline{c_{l+1}}c_{l}+2\sum_{l}\overline{c_{l-1}}c_{l}\\ =&5\sum_{l}|c_{l}|^{2}+2\sum_{l}\overline{c_{l+1}}c_{l}+2\overline{\sum_{l}\overline{c_{l+1}}c_{l}}\\ =&5\sum_{l}|c_{l}|^{2}+4\operatorname{\mathrm{Re}}\Big(\sum_{l}\overline{c_{l+1}}c_{l}\Big). \end{align*} $$
$$ \begin{align*} \Big\|\sum_{l}c_{l}\tau{\phi}(\xi+l)\Big\|^{2}_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}=&5\sum_{l}|c_{l}|^{2}+2\sum_{l}\overline{c_{l+1}}c_{l}+2\sum_{l}\overline{c_{l-1}}c_{l}\\ =&5\sum_{l}|c_{l}|^{2}+2\sum_{l}\overline{c_{l+1}}c_{l}+2\overline{\sum_{l}\overline{c_{l+1}}c_{l}}\\ =&5\sum_{l}|c_{l}|^{2}+4\operatorname{\mathrm{Re}}\Big(\sum_{l}\overline{c_{l+1}}c_{l}\Big). \end{align*} $$
Now, using
![]() $\big |\operatorname {\mathrm {Re}}\big (\sum _{l}\overline {c_{l+1}}c_{l}\big )\big |\leq \sum _{l}|c_{l}|^{2}$
, we can show that
$\big |\operatorname {\mathrm {Re}}\big (\sum _{l}\overline {c_{l+1}}c_{l}\big )\big |\leq \sum _{l}|c_{l}|^{2}$
, we can show that
 $$ \begin{align*} \sum_{l}|c_{l}|^{2}\leq \Big\|\sum_{l}c_{l}\tau{\phi}(\xi+l)\Big\|^{2}_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}&\leq 9\sum_{l}|c_{l}|^{2},\ \ \ \ \ \forall\ \xi\in[0,1), \end{align*} $$
$$ \begin{align*} \sum_{l}|c_{l}|^{2}\leq \Big\|\sum_{l}c_{l}\tau{\phi}(\xi+l)\Big\|^{2}_{L^{2}({\mathbb{R}},\ell^{2}({\mathbb{Z}}))}&\leq 9\sum_{l}|c_{l}|^{2},\ \ \ \ \ \forall\ \xi\in[0,1), \end{align*} $$
proving our assertion.
5 Dual twisted shift-invariant system
Let
![]() $\mathcal {D}=\{\varphi _{s} : s\in {\mathbb {Z}}\}$
be a collection of functions in
$\mathcal {D}=\{\varphi _{s} : s\in {\mathbb {Z}}\}$
be a collection of functions in
![]() $L^{2}(\mathbb {R}^{2n})$
. As we defined
$L^{2}(\mathbb {R}^{2n})$
. As we defined
![]() $E^{t}(\mathcal {A})$
,
$E^{t}(\mathcal {A})$
,
![]() $U^{t}(\mathcal {A})$
,
$U^{t}(\mathcal {A})$
,
![]() $V^{t}(\mathcal {A})$
, and
$V^{t}(\mathcal {A})$
, and
![]() $H_{l}(\xi )$
for the collection
$H_{l}(\xi )$
for the collection
![]() ${\mathcal {A}}$
, we define
${\mathcal {A}}$
, we define
![]() $E^{t}(\mathcal {D})$
,
$E^{t}(\mathcal {D})$
,
![]() $U^{t}(\mathcal {D})$
,
$U^{t}(\mathcal {D})$
,
![]() $V^{t}(\mathcal {D})$
, and
$V^{t}(\mathcal {D})$
, and
![]() $T_{l}(\xi )$
, respectively, for the collection
$T_{l}(\xi )$
, respectively, for the collection
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
Proposition 5.1. Let
![]() $E^{t}(\mathcal {A})$
and
$E^{t}(\mathcal {A})$
and
![]() $E^{t}(\mathcal {D})$
be two Bessel sequences. Then, for
$E^{t}(\mathcal {D})$
be two Bessel sequences. Then, for
![]() ${{\phi },\varphi \in L^{2}(\mathbb {R}^{2n})}$
, we have the following identity:
${{\phi },\varphi \in L^{2}(\mathbb {R}^{2n})}$
, we have the following identity:
 $$ \begin{align} \sum_{(k,s)\in\mathbb{Z}^{n+1}}\big<{\phi},{T_{(k,l)}^t} {\phi}_{s}\big>\big<{T_{(k,l)}^t} \varphi_{s}, \varphi\big>=\int_{{\mathbb{T}^{n}}}\big<H_{l}(\xi)^{\ast}\tau {\phi}(\xi), T_{l}(\xi)^{\ast}\tau \varphi(\xi)\big>_{\ell^2({\mathbb{Z}})}\,d\xi, \end{align} $$
$$ \begin{align} \sum_{(k,s)\in\mathbb{Z}^{n+1}}\big<{\phi},{T_{(k,l)}^t} {\phi}_{s}\big>\big<{T_{(k,l)}^t} \varphi_{s}, \varphi\big>=\int_{{\mathbb{T}^{n}}}\big<H_{l}(\xi)^{\ast}\tau {\phi}(\xi), T_{l}(\xi)^{\ast}\tau \varphi(\xi)\big>_{\ell^2({\mathbb{Z}})}\,d\xi, \end{align} $$
for each
![]() $l\in {\mathbb {Z}^n}$
.
$l\in {\mathbb {Z}^n}$
.
Proof. For
![]() ${\phi }\in L^{2}(\mathbb {R}^{2n})$
, using (3.1), we have
${\phi }\in L^{2}(\mathbb {R}^{2n})$
, using (3.1), we have
 $$ \begin{align} \big<{\phi},{T_{(k,l)}^t} {\phi}_{s}\big>_{L^{2}(\mathbb{R}^{2n})}=&\big<\tau {\phi},\tau{T_{(k,l)}^t} {\phi}_{s}\big>_{L^{2}({\mathbb{T}^{n}},L^{2}({\mathbb{R}^{n}},\ell^{2}({\mathbb{Z}^n})))}\nonumber\\=&\int_{{\mathbb{T}^{n}}}e^{-\pi ik\cdot(2\xi+l)}\big<\tau {\phi}(\xi),\tau {\phi}_{s}(\xi+l)\big>_{L^{2}({\mathbb{R}^{n}},\ell^{2}({\mathbb{Z}^n}))}\,d\xi\nonumber\\=&e^{-\pi ik\cdot l}\widehat{F}_{l,s}(k), \end{align} $$
$$ \begin{align} \big<{\phi},{T_{(k,l)}^t} {\phi}_{s}\big>_{L^{2}(\mathbb{R}^{2n})}=&\big<\tau {\phi},\tau{T_{(k,l)}^t} {\phi}_{s}\big>_{L^{2}({\mathbb{T}^{n}},L^{2}({\mathbb{R}^{n}},\ell^{2}({\mathbb{Z}^n})))}\nonumber\\=&\int_{{\mathbb{T}^{n}}}e^{-\pi ik\cdot(2\xi+l)}\big<\tau {\phi}(\xi),\tau {\phi}_{s}(\xi+l)\big>_{L^{2}({\mathbb{R}^{n}},\ell^{2}({\mathbb{Z}^n}))}\,d\xi\nonumber\\=&e^{-\pi ik\cdot l}\widehat{F}_{l,s}(k), \end{align} $$
where
![]() $F_{l,s}(\xi )=\big <\tau {\phi }(\xi ), \tau {\phi }_{s}(\xi +l)\big>_{L^{2}({\mathbb {R}}^{n},\ell ^{2}({\mathbb {Z}^n}))}$
. Similarly, for
$F_{l,s}(\xi )=\big <\tau {\phi }(\xi ), \tau {\phi }_{s}(\xi +l)\big>_{L^{2}({\mathbb {R}}^{n},\ell ^{2}({\mathbb {Z}^n}))}$
. Similarly, for
![]() $\varphi \in L^{2}(\mathbb {R}^{2n})$
, we can show that
$\varphi \in L^{2}(\mathbb {R}^{2n})$
, we can show that
where
![]() $G_{l,s}(\xi )=\big <\tau \varphi (\xi ), \tau \varphi _{s}(\xi +l)\big>_{L^{2}({\mathbb {R}}^{n},\ell ^{2}({\mathbb {Z}^n}))}$
. We notice that
$G_{l,s}(\xi )=\big <\tau \varphi (\xi ), \tau \varphi _{s}(\xi +l)\big>_{L^{2}({\mathbb {R}}^{n},\ell ^{2}({\mathbb {Z}^n}))}$
. We notice that
![]() $H_{l}(\xi )^{\ast }\tau {\phi }(\xi )=\{F_{l,s}(\xi )\}_{s\in {\mathbb {Z}}}$
and
$H_{l}(\xi )^{\ast }\tau {\phi }(\xi )=\{F_{l,s}(\xi )\}_{s\in {\mathbb {Z}}}$
and
![]() $T_{l}(\xi )^{\ast }\tau \varphi (\xi )=\{G_{l,s}(\xi )\}_{s\in {\mathbb {Z}}}$
. Now, making use of (5.2) and (5.3), we obtain
$T_{l}(\xi )^{\ast }\tau \varphi (\xi )=\{G_{l,s}(\xi )\}_{s\in {\mathbb {Z}}}$
. Now, making use of (5.2) and (5.3), we obtain
 $$ \begin{align*} \sum_{(k,s)\in\mathbb{Z}^{n+1}}\big<{\phi},{T_{(k,l)}^t} {\phi}_{s}\big>\big<{T_{(k,l)}^t} \varphi_{s}, \varphi\big>=&\sum_{s\in{\mathbb{Z}}}\Big(\sum_{k\in{\mathbb{Z}^n}}\widehat{F}_{l,s}(k)\overline{\widehat{G}_{l,s}(k)}\Big)\\ =&\sum_{s\in{\mathbb{Z}}}\big<\widehat{F}_{l,s},\widehat{G}_{l,s}\big>_{\ell^2({\mathbb{Z}^n})}\\ =& \sum_{s\in{\mathbb{Z}}}\langle {F}_{l,s}, {G}_{l,s}\rangle_{L^2({\mathbb{T}^{n}})} \\ =&\sum_{s\in{\mathbb{Z}}}\int_{{\mathbb{T}^{n}}}F_{l,s}(\xi)\overline{G_{l,s}(\xi)}\,d\xi\\ =&\int_{{\mathbb{T}^{n}}}\big\langle \{F_{l,s}(\xi)\}_{s\in{\mathbb{Z}}},\{G_{l,s}(\xi)\}_{s\in{\mathbb{Z}}}\big\rangle_{\ell^2({\mathbb{Z}})}\,d\xi\\ =&\int_{{\mathbb{T}^{n}}}\big<H_{l}(\xi)^{\ast}\tau {\phi}(\xi), T_{l}(\xi)^{\ast}\tau \varphi(\xi)\big>_{\ell^2({\mathbb{Z}})}\,d\xi, \end{align*} $$
$$ \begin{align*} \sum_{(k,s)\in\mathbb{Z}^{n+1}}\big<{\phi},{T_{(k,l)}^t} {\phi}_{s}\big>\big<{T_{(k,l)}^t} \varphi_{s}, \varphi\big>=&\sum_{s\in{\mathbb{Z}}}\Big(\sum_{k\in{\mathbb{Z}^n}}\widehat{F}_{l,s}(k)\overline{\widehat{G}_{l,s}(k)}\Big)\\ =&\sum_{s\in{\mathbb{Z}}}\big<\widehat{F}_{l,s},\widehat{G}_{l,s}\big>_{\ell^2({\mathbb{Z}^n})}\\ =& \sum_{s\in{\mathbb{Z}}}\langle {F}_{l,s}, {G}_{l,s}\rangle_{L^2({\mathbb{T}^{n}})} \\ =&\sum_{s\in{\mathbb{Z}}}\int_{{\mathbb{T}^{n}}}F_{l,s}(\xi)\overline{G_{l,s}(\xi)}\,d\xi\\ =&\int_{{\mathbb{T}^{n}}}\big\langle \{F_{l,s}(\xi)\}_{s\in{\mathbb{Z}}},\{G_{l,s}(\xi)\}_{s\in{\mathbb{Z}}}\big\rangle_{\ell^2({\mathbb{Z}})}\,d\xi\\ =&\int_{{\mathbb{T}^{n}}}\big<H_{l}(\xi)^{\ast}\tau {\phi}(\xi), T_{l}(\xi)^{\ast}\tau \varphi(\xi)\big>_{\ell^2({\mathbb{Z}})}\,d\xi, \end{align*} $$
for each
![]() $l\in {\mathbb {Z}^n}$
, proving (5.1).
$l\in {\mathbb {Z}^n}$
, proving (5.1).
Theorem 5.2. Let
![]() $E^{t}(\mathcal {A})$
and
$E^{t}(\mathcal {A})$
and
![]() $E^{t}(\mathcal {D})$
be two Bessel sequences. Then
$E^{t}(\mathcal {D})$
be two Bessel sequences. Then
![]() $E^{t}(\mathcal {A})$
and
$E^{t}(\mathcal {A})$
and
![]() $E^{t}(\mathcal {D})$
are dual frames if and only if
$E^{t}(\mathcal {D})$
are dual frames if and only if
 $$ \begin{align} \sum_{l\in{\mathbb{Z}^n}}T_{l}(\xi)H_{l}(\xi)^{\ast}=I,\ \ \ \ \ for\ a.e.~\xi\in {\mathbb{T}^{n}}, \end{align} $$
$$ \begin{align} \sum_{l\in{\mathbb{Z}^n}}T_{l}(\xi)H_{l}(\xi)^{\ast}=I,\ \ \ \ \ for\ a.e.~\xi\in {\mathbb{T}^{n}}, \end{align} $$
where I is the identity operator on
![]() $L^2({\mathbb {R}}^n,\ell ^{2}({\mathbb {Z}^n}))$
.
$L^2({\mathbb {R}}^n,\ell ^{2}({\mathbb {Z}^n}))$
.
Proof. Assume that
![]() $E^{t}(\mathcal {A})$
and
$E^{t}(\mathcal {A})$
and
![]() $E^{t}(\mathcal {D})$
are dual frames. Then, by Theorem 2.4, we have
$E^{t}(\mathcal {D})$
are dual frames. Then, by Theorem 2.4, we have
 $$ \begin{align} \sum\limits_{(k,l,s)\in\mathbb{Z}^{2n+1}}\big<{\phi},{T_{(k,l)}^t} {\phi}_{s}\big>\big<{T_{(k,l)}^t} \varphi_{s}, \varphi\big>=\big<{\phi},\varphi\big> \end{align} $$
$$ \begin{align} \sum\limits_{(k,l,s)\in\mathbb{Z}^{2n+1}}\big<{\phi},{T_{(k,l)}^t} {\phi}_{s}\big>\big<{T_{(k,l)}^t} \varphi_{s}, \varphi\big>=\big<{\phi},\varphi\big> \end{align} $$
for all
![]() ${\phi },\varphi \in L^{2}(\mathbb {R}^{2n})$
. In particular, by taking
${\phi },\varphi \in L^{2}(\mathbb {R}^{2n})$
. In particular, by taking
![]() ${\phi }=\varphi =\psi $
in (5.5), we get
${\phi }=\varphi =\psi $
in (5.5), we get
 $$ \begin{align} \sum\limits_{(k,l,s)\in\mathbb{Z}^{2n+1}}\big<\psi,{T_{(k,l)}^t} {\phi}_{s}\big>\big<{T_{(k,l)}^t} \varphi_{s}, \psi\big>=\|\psi\|^{2},\ \ \ \ \ \forall\ \psi\in L^{2}(\mathbb{R}^{2n}). \end{align} $$
$$ \begin{align} \sum\limits_{(k,l,s)\in\mathbb{Z}^{2n+1}}\big<\psi,{T_{(k,l)}^t} {\phi}_{s}\big>\big<{T_{(k,l)}^t} \varphi_{s}, \psi\big>=\|\psi\|^{2},\ \ \ \ \ \forall\ \psi\in L^{2}(\mathbb{R}^{2n}). \end{align} $$
By using Proposition 5.1, we can rewrite (5.6) as
 $$ \begin{align} \int_{{\mathbb{T}^{n}}}\sum_{l\in{\mathbb{Z}^n}}\big<H_{l}(\xi)^{\ast}\tau \psi(\xi), T_{l}(\xi)^{\ast}\tau \psi(\xi)\big>_{\ell^2({\mathbb{Z}})}\,d\xi&=\|\psi\|^{2},\ \ \ \ \ \forall\ \psi\in L^{2}(\mathbb{R}^{2n}). \end{align} $$
$$ \begin{align} \int_{{\mathbb{T}^{n}}}\sum_{l\in{\mathbb{Z}^n}}\big<H_{l}(\xi)^{\ast}\tau \psi(\xi), T_{l}(\xi)^{\ast}\tau \psi(\xi)\big>_{\ell^2({\mathbb{Z}})}\,d\xi&=\|\psi\|^{2},\ \ \ \ \ \forall\ \psi\in L^{2}(\mathbb{R}^{2n}). \end{align} $$
Now, we aim to prove (5.4), which is equivalent to
 $$ \begin{align} \sum\limits_{l\in{\mathbb{Z}^n}}\big<H_{l}(\xi)^{\ast}\Phi,T_{l}(\xi)^{\ast}\Phi\big>=\|\Phi\|^{2},~\text{for}\ a.e.~\xi\in {\mathbb{T}^{n}},\quad \forall\ \Phi\in L^{2}({\mathbb{R}}^n,\ell^{2}({\mathbb{Z}^n})). \end{align} $$
$$ \begin{align} \sum\limits_{l\in{\mathbb{Z}^n}}\big<H_{l}(\xi)^{\ast}\Phi,T_{l}(\xi)^{\ast}\Phi\big>=\|\Phi\|^{2},~\text{for}\ a.e.~\xi\in {\mathbb{T}^{n}},\quad \forall\ \Phi\in L^{2}({\mathbb{R}}^n,\ell^{2}({\mathbb{Z}^n})). \end{align} $$
Let
![]() $\Phi \in L^{2}({\mathbb {R}}^n,\ell ^{2}({\mathbb {Z}^n}))$
. Then, we can write
$\Phi \in L^{2}({\mathbb {R}}^n,\ell ^{2}({\mathbb {Z}^n}))$
. Then, we can write
![]() $\Phi (\eta )=\{C^{\eta }_{m}\}_{m\in {\mathbb {Z}}^n}\in \ell ^2({\mathbb {Z}^n})$
, for
$\Phi (\eta )=\{C^{\eta }_{m}\}_{m\in {\mathbb {Z}}^n}\in \ell ^2({\mathbb {Z}^n})$
, for
![]() $a.e.\ \eta \in {\mathbb {R}}^n$
. For
$a.e.\ \eta \in {\mathbb {R}}^n$
. For
![]() $p\in L^{2}({\mathbb {T}^{n}})$
, we define
$p\in L^{2}({\mathbb {T}^{n}})$
, we define
![]() $\psi \in L^{2}(\mathbb {R}^{2n})$
by
$\psi \in L^{2}(\mathbb {R}^{2n})$
by
![]() $K_{\psi }(\xi ,\eta )=p(\xi -m)C^{\eta }_{m},$
where m is that unique element in
$K_{\psi }(\xi ,\eta )=p(\xi -m)C^{\eta }_{m},$
where m is that unique element in
![]() ${\mathbb {Z}^n}$
for which
${\mathbb {Z}^n}$
for which
![]() $\xi -m\in {\mathbb {T}^{n}}$
. Then, for
$\xi -m\in {\mathbb {T}^{n}}$
. Then, for
![]() $\xi \in {\mathbb {T}^{n}}$
, we have
$\xi \in {\mathbb {T}^{n}}$
, we have
![]() $K_{\psi }(\xi +m,\eta )=p(\xi )C^{\eta }_{m}$
,
$K_{\psi }(\xi +m,\eta )=p(\xi )C^{\eta }_{m}$
,
![]() $\forall \ m\in {\mathbb {Z}^n}$
. Hence, for
$\forall \ m\in {\mathbb {Z}^n}$
. Hence, for
![]() $\xi \in {\mathbb {T}^{n}},\eta \in {\mathbb {R}}^n$
, we get
$\xi \in {\mathbb {T}^{n}},\eta \in {\mathbb {R}}^n$
, we get
 $$ \begin{align*} \tau \psi(\xi)(\eta)&=\{K_{\psi}(\xi+m,\eta)\}_{m\in{\mathbb{Z}^n}}\\ &=p(\xi)\{C^{\eta}_{m}\}_{m\in{\mathbb{Z}^n}}\\ &=p(\xi)\Phi(\eta), \end{align*} $$
$$ \begin{align*} \tau \psi(\xi)(\eta)&=\{K_{\psi}(\xi+m,\eta)\}_{m\in{\mathbb{Z}^n}}\\ &=p(\xi)\{C^{\eta}_{m}\}_{m\in{\mathbb{Z}^n}}\\ &=p(\xi)\Phi(\eta), \end{align*} $$
showing that
![]() $\tau \psi (\xi )=p(\xi )\Phi $
. Consequently, we get
$\tau \psi (\xi )=p(\xi )\Phi $
. Consequently, we get
 $$ \begin{align} \|\psi\|_{L^{2}(\mathbb{R}^{2n})}^2&=\|\tau \psi\|_{L^{2}({\mathbb{T}^{n}},{L^{2}(\mathbb{R}^{n},\ell^{2}(\mathbb{Z}^{n}))})}^{2}\notag \\ &=\int_{{\mathbb{T}^{n}}}\|\tau \psi(\xi)\|_{{L^{2}(\mathbb{R}^{n},\ell^{2}(\mathbb{Z}^{n}))}}^{2}\,d\xi \notag \\ &=\int_{{\mathbb{T}^{n}}}|p(\xi)|^{2}\|\Phi\|^{2}_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\,d\xi \end{align} $$
$$ \begin{align} \|\psi\|_{L^{2}(\mathbb{R}^{2n})}^2&=\|\tau \psi\|_{L^{2}({\mathbb{T}^{n}},{L^{2}(\mathbb{R}^{n},\ell^{2}(\mathbb{Z}^{n}))})}^{2}\notag \\ &=\int_{{\mathbb{T}^{n}}}\|\tau \psi(\xi)\|_{{L^{2}(\mathbb{R}^{n},\ell^{2}(\mathbb{Z}^{n}))}}^{2}\,d\xi \notag \\ &=\int_{{\mathbb{T}^{n}}}|p(\xi)|^{2}\|\Phi\|^{2}_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\,d\xi \end{align} $$
and
 $$ \begin{align} \int_{{\mathbb{T}^{n}}}\sum_{l\in{\mathbb{Z}^n}}\big<H_{l}(\xi)^{\ast}\tau \psi(\xi),T_{l}(\xi)^{\ast}\tau \psi(\xi)\big>=&\int_{{\mathbb{T}^{n}}}|p(\xi)|^{2}\sum_{l\in{\mathbb{Z}^n}}\big<H_{l}(\xi)^{\ast}\Phi,T_{l}(\xi)^{\ast}\Phi\big>\,d\xi. \end{align} $$
$$ \begin{align} \int_{{\mathbb{T}^{n}}}\sum_{l\in{\mathbb{Z}^n}}\big<H_{l}(\xi)^{\ast}\tau \psi(\xi),T_{l}(\xi)^{\ast}\tau \psi(\xi)\big>=&\int_{{\mathbb{T}^{n}}}|p(\xi)|^{2}\sum_{l\in{\mathbb{Z}^n}}\big<H_{l}(\xi)^{\ast}\Phi,T_{l}(\xi)^{\ast}\Phi\big>\,d\xi. \end{align} $$
By making use of (5.9) and (5.10) in (5.7), we obtain
 $$ \begin{align*} \int_{{\mathbb{T}^{n}}}|p(\xi)|^{2}\sum_{l\in{\mathbb{Z}^n}}\big<H_{l}(\xi)^{\ast}\Phi,T_{l}(\xi)^{\ast}\Phi\big>\,d\xi = \int_{{\mathbb{T}^{n}}}|p(\xi)|^{2}\|\Phi\|^{2}_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\,d\xi. \end{align*} $$
$$ \begin{align*} \int_{{\mathbb{T}^{n}}}|p(\xi)|^{2}\sum_{l\in{\mathbb{Z}^n}}\big<H_{l}(\xi)^{\ast}\Phi,T_{l}(\xi)^{\ast}\Phi\big>\,d\xi = \int_{{\mathbb{T}^{n}}}|p(\xi)|^{2}\|\Phi\|^{2}_{L^{2}({\mathbb{R}}^{n},\ell^{2}({\mathbb{Z}^n}))}\,d\xi. \end{align*} $$
Since this is true for all
![]() $p\in L^{2}({\mathbb {T}^{n}})$
, we arrive at (5.8).
$p\in L^{2}({\mathbb {T}^{n}})$
, we arrive at (5.8).
Conversely, assume that (5.4) holds. Then, for
![]() ${\phi },\varphi \in L^{2}(\mathbb {R}^{2n})$
using Proposition 5.1, we have
${\phi },\varphi \in L^{2}(\mathbb {R}^{2n})$
using Proposition 5.1, we have
 $$ \begin{align*} \sum_{(k,l,s)\in\mathbb{Z}^{2n+1}}\big<{\phi},{T_{(k,l)}^t} \phi_{s}\big>\big<{T_{(k,l)}^t} \varphi_{s}, \varphi\big>&=\int_{{\mathbb{T}^{n}}}\big<\sum_{l\in{\mathbb{Z}^n}}T_{l}(\xi)H_{l}(\xi)^{\ast}\tau {\phi}(\xi), \tau \varphi(\xi)\big>_{{L^{2}(\mathbb{R}^{n},\ell^{2}(\mathbb{Z}^{n}))}}\,d\xi\\ &=\int_{{\mathbb{T}^{n}}}\big<\tau {\phi}(\xi), \tau \varphi(\xi)\big>_{{L^{2}(\mathbb{R}^{n},\ell^{2}(\mathbb{Z}^{n}))}}\,d\xi\\ &=\langle \tau {\phi},\tau \varphi\rangle_{L^{2}({\mathbb{T}^{n}},{L^{2}(\mathbb{R}^{n},\ell^{2}(\mathbb{Z}^{n}))})}\\ &=\langle {\phi},\varphi\rangle_{L^{2}(\mathbb{R}^{2n})}. \end{align*} $$
$$ \begin{align*} \sum_{(k,l,s)\in\mathbb{Z}^{2n+1}}\big<{\phi},{T_{(k,l)}^t} \phi_{s}\big>\big<{T_{(k,l)}^t} \varphi_{s}, \varphi\big>&=\int_{{\mathbb{T}^{n}}}\big<\sum_{l\in{\mathbb{Z}^n}}T_{l}(\xi)H_{l}(\xi)^{\ast}\tau {\phi}(\xi), \tau \varphi(\xi)\big>_{{L^{2}(\mathbb{R}^{n},\ell^{2}(\mathbb{Z}^{n}))}}\,d\xi\\ &=\int_{{\mathbb{T}^{n}}}\big<\tau {\phi}(\xi), \tau \varphi(\xi)\big>_{{L^{2}(\mathbb{R}^{n},\ell^{2}(\mathbb{Z}^{n}))}}\,d\xi\\ &=\langle \tau {\phi},\tau \varphi\rangle_{L^{2}({\mathbb{T}^{n}},{L^{2}(\mathbb{R}^{n},\ell^{2}(\mathbb{Z}^{n}))})}\\ &=\langle {\phi},\varphi\rangle_{L^{2}(\mathbb{R}^{2n})}. \end{align*} $$
Then the result follows by using Theorem 2.4.
Now, let
![]() ${\mathcal {A}}=\{ {\phi }\}$
, and let
${\mathcal {A}}=\{ {\phi }\}$
, and let
![]() $E^t({\mathcal {A}})$
be a frame sequence. In other words, the system
$E^t({\mathcal {A}})$
be a frame sequence. In other words, the system
![]() $E^t({\mathcal {A}})$
is a frame for
$E^t({\mathcal {A}})$
is a frame for
Let
![]() $\mathcal {D}=\{ \widetilde {{\phi }}\}$
, for some
$\mathcal {D}=\{ \widetilde {{\phi }}\}$
, for some
![]() $\widetilde {{\phi }}\in L^2(\mathbb {R}^{2n})$
. Then, the system
$\widetilde {{\phi }}\in L^2(\mathbb {R}^{2n})$
. Then, the system
![]() $E^t(\mathcal {D})$
is said to be an oblique dual of
$E^t(\mathcal {D})$
is said to be an oblique dual of
![]() $E^t({\mathcal {A}})$
if
$E^t({\mathcal {A}})$
if
 $$ \begin{align*} f=\sum_{k,l\in{\mathbb{Z}^n}}\langle f,{T_{(k,l)}^t}\widetilde{{\phi}}\rangle{T_{(k,l)}^t}{\phi},\ \ \ \ \ \ \ \forall\ f\in V^t({\mathcal{A}}). \end{align*} $$
$$ \begin{align*} f=\sum_{k,l\in{\mathbb{Z}^n}}\langle f,{T_{(k,l)}^t}\widetilde{{\phi}}\rangle{T_{(k,l)}^t}{\phi},\ \ \ \ \ \ \ \forall\ f\in V^t({\mathcal{A}}). \end{align*} $$
Then we have the following theorem.
Theorem 5.3. Let
![]() $E^{t}({\mathcal {A}})$
and
$E^{t}({\mathcal {A}})$
and
![]() $E^{t}(\mathcal {D})$
be two Bessel sequences. Then
$E^{t}(\mathcal {D})$
be two Bessel sequences. Then
![]() $E^t(\mathcal {D})$
is an oblique dual of
$E^t(\mathcal {D})$
is an oblique dual of
![]() $E^t({\mathcal {A}})$
if and only if
$E^t({\mathcal {A}})$
if and only if
 $$ \begin{align} \sum\limits_{l\in{\mathbb{Z}^n}}H_{l}(\xi)T_{l}(\xi)^{\ast}=I_{\xi},~for\ a.e.~\xi\in{\mathbb{T}^{n}}, \end{align} $$
$$ \begin{align} \sum\limits_{l\in{\mathbb{Z}^n}}H_{l}(\xi)T_{l}(\xi)^{\ast}=I_{\xi},~for\ a.e.~\xi\in{\mathbb{T}^{n}}, \end{align} $$
where
![]() $I_{\xi }$
is the identity operator on
$I_{\xi }$
is the identity operator on
![]() $J(\xi )$
.
$J(\xi )$
.
The proof follows similar lines as that of Theorem 5.2.
In addition, if we assume that
![]() ${\phi }$
satisfies “Condition C,” then as in the classical case (Corollary 7.4.2 in [Reference Christensen7]), we can show that the canonical dual frame is the only dual frame that consists of twisted translations of a single function. Toward this end, we make use of the following results.
${\phi }$
satisfies “Condition C,” then as in the classical case (Corollary 7.4.2 in [Reference Christensen7]), we can show that the canonical dual frame is the only dual frame that consists of twisted translations of a single function. Toward this end, we make use of the following results.
Proposition 5.4 [Reference Radha and Adhikari18].
Let
![]() ${\phi }\in {L^2(\mathbb {R}^{2n})}$
be such that
${\phi }\in {L^2(\mathbb {R}^{2n})}$
be such that
![]() $\phi $
satisfies “Condition C.” Then the map
$\phi $
satisfies “Condition C.” Then the map
![]() $f\mapsto r$
initially defined on
$f\mapsto r$
initially defined on
![]() $U^t(\mathcal {A})$
can be extended to an isometric isomorphism of
$U^t(\mathcal {A})$
can be extended to an isometric isomorphism of
![]() $V^{t}(\phi )$
onto
$V^{t}(\phi )$
onto
![]() $L^{2}({\mathbb {T}^{n}},\ell ^{2}({\mathbb {Z}^n});\omega _{{\phi }})$
.
$L^{2}({\mathbb {T}^{n}},\ell ^{2}({\mathbb {Z}^n});\omega _{{\phi }})$
.
Theorem 5.5 [Reference Radha and Adhikari18].
Let
![]() ${\phi }\in L^{2}(\mathbb {R}^{2n})$
and
${\phi }\in L^{2}(\mathbb {R}^{2n})$
and
![]() $a,b>0$
. Suppose
$a,b>0$
. Suppose
![]() $\{T^{t}_{(bk,al)}{\phi } : (k,l)\in \mathbb {Z}^{2n}\}$
is a frame for
$\{T^{t}_{(bk,al)}{\phi } : (k,l)\in \mathbb {Z}^{2n}\}$
is a frame for
![]() $L^{2}(\mathbb {R}^{2n})$
with frame operator S. Then the canonical dual frame also has the same structure and is given by
$L^{2}(\mathbb {R}^{2n})$
with frame operator S. Then the canonical dual frame also has the same structure and is given by
![]() $T^{t}_{(bk,al)}S^{-1}{\phi }$
.
$T^{t}_{(bk,al)}S^{-1}{\phi }$
.
Corollary 5.6. Let
![]() ${\phi }\in L^{2}(\mathbb {R}^{2n})$
be such that
${\phi }\in L^{2}(\mathbb {R}^{2n})$
be such that
![]() ${\phi }$
satisfies “Condition C.” Let
${\phi }$
satisfies “Condition C.” Let
![]() $\{{T_{(k,l)}^t} {\phi } : k,l\in \mathbb {Z}^{n}\}$
be a frame sequence. Then there exists unique
$\{{T_{(k,l)}^t} {\phi } : k,l\in \mathbb {Z}^{n}\}$
be a frame sequence. Then there exists unique
![]() $\tilde {{\phi }}\in V^{t}({\phi })$
such that
$\tilde {{\phi }}\in V^{t}({\phi })$
such that
![]() ${f=\sum \limits _{k,l\in \mathbb {Z}^{n}}\big <f,{T_{(k,l)}^t} \tilde {{\phi }}\big>{T_{(k,l)}^t} {\phi } \ \ \forall \, f\in V^{t}({\phi })}$
with
${f=\sum \limits _{k,l\in \mathbb {Z}^{n}}\big <f,{T_{(k,l)}^t} \tilde {{\phi }}\big>{T_{(k,l)}^t} {\phi } \ \ \forall \, f\in V^{t}({\phi })}$
with
![]() $\widetilde {{\phi }}=S^{-1}{\phi }$
$\widetilde {{\phi }}=S^{-1}{\phi }$
Proof. Let S be the frame operator associated with
![]() $\{{T_{(k,l)}^t} {\phi } : k,l\in \mathbb {Z}^{n}\}$
. Then, for all
$\{{T_{(k,l)}^t} {\phi } : k,l\in \mathbb {Z}^{n}\}$
. Then, for all
![]() $f\in V^{t}({\phi })$
, we have
$f\in V^{t}({\phi })$
, we have
![]() $f=\sum \limits _{k,l\in \mathbb {Z}^{n}}\big <f,{T_{(k,l)}^t} S^{-1}{\phi }\big>{T_{(k,l)}^t} {\phi }$
, by Theorem 5.5. Let
$f=\sum \limits _{k,l\in \mathbb {Z}^{n}}\big <f,{T_{(k,l)}^t} S^{-1}{\phi }\big>{T_{(k,l)}^t} {\phi }$
, by Theorem 5.5. Let
![]() $\widetilde {{\phi }}\in V^{t}({\phi })$
. We have
$\widetilde {{\phi }}\in V^{t}({\phi })$
. We have
![]() $\widetilde {{\phi }}=\sum \limits _{k,l\in {\mathbb {Z}^n}}\alpha _{k,l}{T_{(k,l)}^t}{\phi }$
, for some
$\widetilde {{\phi }}=\sum \limits _{k,l\in {\mathbb {Z}^n}}\alpha _{k,l}{T_{(k,l)}^t}{\phi }$
, for some
![]() $\{\alpha _{k,l}\}\in \ell ^2({\mathbb {Z}}^{2n})$
. For
$\{\alpha _{k,l}\}\in \ell ^2({\mathbb {Z}}^{2n})$
. For
![]() $\xi \in {\mathbb {T}^{n}}$
, using (3.1), we get
$\xi \in {\mathbb {T}^{n}}$
, using (3.1), we get
 $$ \begin{align} \tau \tilde{{\phi}}(\xi)=&\sum\limits_{k,l\in{\mathbb{Z}^n}}\alpha_{k,l}\tau({T_{(k,l)}^t}{\phi})(\xi)\nonumber\\ =&\sum\limits_{k,l\in{\mathbb{Z}^n}}\alpha_{k,l}e^{\pi ik\cdot(2\xi+l)}\tau{\phi}(\xi+l)\nonumber\\ =&\sum\limits_{l\in{\mathbb{Z}^n}}r_{l}(\xi)\tau{\phi}(\xi+l), \end{align} $$
$$ \begin{align} \tau \tilde{{\phi}}(\xi)=&\sum\limits_{k,l\in{\mathbb{Z}^n}}\alpha_{k,l}\tau({T_{(k,l)}^t}{\phi})(\xi)\nonumber\\ =&\sum\limits_{k,l\in{\mathbb{Z}^n}}\alpha_{k,l}e^{\pi ik\cdot(2\xi+l)}\tau{\phi}(\xi+l)\nonumber\\ =&\sum\limits_{l\in{\mathbb{Z}^n}}r_{l}(\xi)\tau{\phi}(\xi+l), \end{align} $$
where
![]() $r_{l}(\xi )=\sum _{k\in {\mathbb {Z}^n}}\alpha _{k,l}e^{\pi ik\cdot (2\xi +l)}$
. Since
$r_{l}(\xi )=\sum _{k\in {\mathbb {Z}^n}}\alpha _{k,l}e^{\pi ik\cdot (2\xi +l)}$
. Since
![]() ${\phi }$
satisfies “Condition C,” using the similar steps as in obtaining (3.19), we can show that
${\phi }$
satisfies “Condition C,” using the similar steps as in obtaining (3.19), we can show that
 $$ \begin{align*} \|\tau \widetilde{{\phi}}(\xi)\|_{{L^{2}(\mathbb{R}^{n},\ell^{2}(\mathbb{Z}^{n}))}}^{2}&=\omega_{{\phi}}(\xi) \sum\limits_{l\in{\mathbb{Z}^n}}|r_{l}(\xi)|^{2}. \end{align*} $$
$$ \begin{align*} \|\tau \widetilde{{\phi}}(\xi)\|_{{L^{2}(\mathbb{R}^{n},\ell^{2}(\mathbb{Z}^{n}))}}^{2}&=\omega_{{\phi}}(\xi) \sum\limits_{l\in{\mathbb{Z}^n}}|r_{l}(\xi)|^{2}. \end{align*} $$
Hence, using isometry of the fiber map
![]() $\tau $
, we get
$\tau $
, we get
 $$ \begin{align} \|\widetilde{{\phi}}\|_{L^2(\mathbb{R}^{2n})}^2&=\int_{{\mathbb{T}^{n}}}\|\tau \widetilde{{\phi}}(\xi)\|_{{L^{2}(\mathbb{R}^{n},\ell^{2}(\mathbb{Z}^{n}))}}^{2}\,d\xi \nonumber \\ &=\int_{{\mathbb{T}^{n}}}\omega_{{\phi}}(\xi) \sum\limits_{l\in{\mathbb{Z}^n}}|r_{l}(\xi)|^{2}\,d\xi \nonumber \\ &=\|r\|_{L^{2}({\mathbb{T}^{n}},\ell^{2}({\mathbb{Z}^n});\omega_{{\phi}})}^2, \end{align} $$
$$ \begin{align} \|\widetilde{{\phi}}\|_{L^2(\mathbb{R}^{2n})}^2&=\int_{{\mathbb{T}^{n}}}\|\tau \widetilde{{\phi}}(\xi)\|_{{L^{2}(\mathbb{R}^{n},\ell^{2}(\mathbb{Z}^{n}))}}^{2}\,d\xi \nonumber \\ &=\int_{{\mathbb{T}^{n}}}\omega_{{\phi}}(\xi) \sum\limits_{l\in{\mathbb{Z}^n}}|r_{l}(\xi)|^{2}\,d\xi \nonumber \\ &=\|r\|_{L^{2}({\mathbb{T}^{n}},\ell^{2}({\mathbb{Z}^n});\omega_{{\phi}})}^2, \end{align} $$
where
![]() $r(\xi )=\{r_{l}(\xi )\}_{l\in {\mathbb {Z}^n}}$
,
$r(\xi )=\{r_{l}(\xi )\}_{l\in {\mathbb {Z}^n}}$
,
![]() $\xi \in {\mathbb {T}^{n}}$
. Further, by Theorem 5.3, we have
$\xi \in {\mathbb {T}^{n}}$
. Further, by Theorem 5.3, we have
 $$ \begin{align} \tau {\phi}(\xi)=&\sum_{l\in{\mathbb{Z}^n}}H_{l}(\xi)T_{l}(\xi)^{\ast}\tau {\phi}(\xi)\nonumber \\ =&\sum_{l\in{\mathbb{Z}^n}}\big<\tau{\phi}(\xi),\tau\tilde{{\phi}}(\xi+l)\big>\tau {\phi}(\xi+l) \nonumber \\ =&\sum_{l\in{\mathbb{Z}^n}}\bigg<\tau{\phi}(\xi),\sum\limits_{l^{\prime}\in{\mathbb{Z}^n}}r_{l^{\prime}}(\xi)\tau{\phi}(\xi+l+l^{\prime})\bigg>\tau {\phi}(\xi+l) \nonumber \\ =&\sum_{l,l^{\prime}\in{\mathbb{Z}^n}}\overline{r_{l^{\prime}}(\xi)}\big<\tau{\phi}(\xi),\tau{\phi}(\xi+l+l^{\prime})\big>\tau {\phi}(\xi+l), \end{align} $$
$$ \begin{align} \tau {\phi}(\xi)=&\sum_{l\in{\mathbb{Z}^n}}H_{l}(\xi)T_{l}(\xi)^{\ast}\tau {\phi}(\xi)\nonumber \\ =&\sum_{l\in{\mathbb{Z}^n}}\big<\tau{\phi}(\xi),\tau\tilde{{\phi}}(\xi+l)\big>\tau {\phi}(\xi+l) \nonumber \\ =&\sum_{l\in{\mathbb{Z}^n}}\bigg<\tau{\phi}(\xi),\sum\limits_{l^{\prime}\in{\mathbb{Z}^n}}r_{l^{\prime}}(\xi)\tau{\phi}(\xi+l+l^{\prime})\bigg>\tau {\phi}(\xi+l) \nonumber \\ =&\sum_{l,l^{\prime}\in{\mathbb{Z}^n}}\overline{r_{l^{\prime}}(\xi)}\big<\tau{\phi}(\xi),\tau{\phi}(\xi+l+l^{\prime})\big>\tau {\phi}(\xi+l), \end{align} $$
for
![]() $a.e.\ \xi \in {\mathbb {T}^{n}}$
. Since
$a.e.\ \xi \in {\mathbb {T}^{n}}$
. Since
![]() ${\phi }$
satisfies “Condition C,” using (3.13), we get
${\phi }$
satisfies “Condition C,” using (3.13), we get
 $$ \begin{align*} \big<\tau{\phi}(\xi),\tau{\phi}(\xi+l+l^{\prime})\big>&=\int_{{\mathbb{R}}^{n}}\sum\limits_{m\in{\mathbb{Z}^n}}K_{{\phi}}(\xi+m,\eta)\overline{K_{{\phi}}(\xi+m+l+l^{\prime},\eta)}\,d\eta\\ &=0, \end{align*} $$
$$ \begin{align*} \big<\tau{\phi}(\xi),\tau{\phi}(\xi+l+l^{\prime})\big>&=\int_{{\mathbb{R}}^{n}}\sum\limits_{m\in{\mathbb{Z}^n}}K_{{\phi}}(\xi+m,\eta)\overline{K_{{\phi}}(\xi+m+l+l^{\prime},\eta)}\,d\eta\\ &=0, \end{align*} $$
whenever
![]() $l+l^{\prime }\neq 0$
. Hence, (5.14) reduces to
$l+l^{\prime }\neq 0$
. Hence, (5.14) reduces to
 $$ \begin{align*} \tau {\phi}(\xi)&=\sum\limits_{l\in{\mathbb{Z}^n}} \overline{r_{-l}(\xi)}\omega_{{\phi}}(\xi)\tau{\phi}(\xi+l)\\ &=\sum\limits_{l\in{\mathbb{Z}^n}}r^{\prime}_{-l}(\xi)\tau{\phi}(\xi+l), \end{align*} $$
$$ \begin{align*} \tau {\phi}(\xi)&=\sum\limits_{l\in{\mathbb{Z}^n}} \overline{r_{-l}(\xi)}\omega_{{\phi}}(\xi)\tau{\phi}(\xi+l)\\ &=\sum\limits_{l\in{\mathbb{Z}^n}}r^{\prime}_{-l}(\xi)\tau{\phi}(\xi+l), \end{align*} $$
where
Hence,
 $$ \begin{align*} \|{\phi}\|_{L^2(\mathbb{C}^n)}^2&=\int_{{\mathbb{T}^{n}}}\|\tau {\phi}(\xi)\|_{{L^{2}(\mathbb{R}^{n},\ell^{2}(\mathbb{Z}^{n}))}}^{2}\,d\xi\\ &=\int_{{\mathbb{T}^{n}}}\omega_{{\phi}}(\xi) \sum\limits_{l\in{\mathbb{Z}^n}}|r_{l}^{\prime}(\xi)|^{2}\,d\xi\\ &=\|r^{\prime}\|_{L^{2}({\mathbb{T}^{n}},\ell^{2}({\mathbb{Z}^n});\omega_{{\phi}})}^2, \end{align*} $$
$$ \begin{align*} \|{\phi}\|_{L^2(\mathbb{C}^n)}^2&=\int_{{\mathbb{T}^{n}}}\|\tau {\phi}(\xi)\|_{{L^{2}(\mathbb{R}^{n},\ell^{2}(\mathbb{Z}^{n}))}}^{2}\,d\xi\\ &=\int_{{\mathbb{T}^{n}}}\omega_{{\phi}}(\xi) \sum\limits_{l\in{\mathbb{Z}^n}}|r_{l}^{\prime}(\xi)|^{2}\,d\xi\\ &=\|r^{\prime}\|_{L^{2}({\mathbb{T}^{n}},\ell^{2}({\mathbb{Z}^n});\omega_{{\phi}})}^2, \end{align*} $$
where
![]() $r^{\prime }(\xi )=\{r_{l}^{\prime }(\xi )\}_{l\in {\mathbb {Z}^n}}$
. Using (5.15), we notice that
$r^{\prime }(\xi )=\{r_{l}^{\prime }(\xi )\}_{l\in {\mathbb {Z}^n}}$
. Using (5.15), we notice that
Thus, by using Proposition 5.4,
![]() $r^{\prime }\in L^{2}({\mathbb {T}^{n}},\ell ^{2}({\mathbb {Z}^n});\omega _{{\phi }})$
is uniquely determined. Hence,
$r^{\prime }\in L^{2}({\mathbb {T}^{n}},\ell ^{2}({\mathbb {Z}^n});\omega _{{\phi }})$
is uniquely determined. Hence,
![]() $r\in L^{2}({\mathbb {T}^{n}},\ell ^{2}({\mathbb {Z}^n});\omega _{{\phi }})$
can be uniquely determined via (5.15). Therefore, by Proposition 5.4, we obtain the uniqueness of
$r\in L^{2}({\mathbb {T}^{n}},\ell ^{2}({\mathbb {Z}^n});\omega _{{\phi }})$
can be uniquely determined via (5.15). Therefore, by Proposition 5.4, we obtain the uniqueness of
![]() $\widetilde {{\phi }}$
from (5.13).
$\widetilde {{\phi }}$
from (5.13).
6 Orthogonalization in a twisted shift-invariant space
It is well known that if
![]() $\{T_{k}{\phi } : k\in \mathbb {Z}\}$
is a Riesz sequence in
$\{T_{k}{\phi } : k\in \mathbb {Z}\}$
is a Riesz sequence in
![]() $L^{2}(\mathbb {R})$
, then there exists
$L^{2}(\mathbb {R})$
, then there exists
![]() ${\phi }^{\sharp }\in V({\phi })$
such that
${\phi }^{\sharp }\in V({\phi })$
such that
![]() $\{T_{k} {\phi }^{\sharp } : k\in \mathbb {Z}\}$
is an orthonormal system for
$\{T_{k} {\phi }^{\sharp } : k\in \mathbb {Z}\}$
is an orthonormal system for
![]() $V({\phi })$
. This is a useful criterion in wavelet literature (see Lemma 1.8 in [Reference Hernández and Weiss15]). We wish to prove a similar result for the system of twisted translates on
$V({\phi })$
. This is a useful criterion in wavelet literature (see Lemma 1.8 in [Reference Hernández and Weiss15]). We wish to prove a similar result for the system of twisted translates on
![]() $L^{2}(\mathbb {R}^{2n})$
. Toward this end, we have the following result.
$L^{2}(\mathbb {R}^{2n})$
. Toward this end, we have the following result.
Theorem 6.1 [Reference Radha and Adhikari18].
Let
![]() ${\phi }\in {L^2(\mathbb {R}^{2n})}$
. Then
${\phi }\in {L^2(\mathbb {R}^{2n})}$
. Then
![]() $\{{T_{(k,l)}^t}{\phi } : (k,l)\in {\mathbb {Z}}^{2n}\}$
is an orthonormal system in
$\{{T_{(k,l)}^t}{\phi } : (k,l)\in {\mathbb {Z}}^{2n}\}$
is an orthonormal system in
![]() ${L^2(\mathbb {R}^{2n})}$
if and only if
${L^2(\mathbb {R}^{2n})}$
if and only if
![]() $\omega _{{\phi }}(\xi )=1~for\ a.e.~\xi \in {\mathbb {T}^{n}}~\text {and}~{\phi }$
satisfies “Condition C.”
$\omega _{{\phi }}(\xi )=1~for\ a.e.~\xi \in {\mathbb {T}^{n}}~\text {and}~{\phi }$
satisfies “Condition C.”
It is clear from the statement of Theorem 6.1 that it is mandatory to assume “Condition C,” when we talk about the orthonormality of the system of twisted translates. With this comment, we are ready to state our result.
Theorem 6.2. Let
![]() $\phi \in L^2(\mathbb {R}^{2n})$
such that
$\phi \in L^2(\mathbb {R}^{2n})$
such that
![]() $\phi $
satisfies “Condition C.” Let
$\phi $
satisfies “Condition C.” Let
![]() $E^t({\phi })$
be a Riesz sequence. Then there exists
$E^t({\phi })$
be a Riesz sequence. Then there exists
![]() $\phi ^{\sharp }\in L^{2}(\mathbb {R}^{2n})$
such that the system
$\phi ^{\sharp }\in L^{2}(\mathbb {R}^{2n})$
such that the system
![]() $E^t({\phi }^{\sharp })$
is an orthonormal system in
$E^t({\phi }^{\sharp })$
is an orthonormal system in
![]() $L^{2}(\mathbb {R}^{2n})$
with
$L^{2}(\mathbb {R}^{2n})$
with
![]() $V^{t}({\phi })=V^{t}({\phi }^{\sharp })$
.
$V^{t}({\phi })=V^{t}({\phi }^{\sharp })$
.
Proof. Since
![]() $E^t({\phi })$
is a Riesz sequence, by Corollary 4.5, there exists
$E^t({\phi })$
is a Riesz sequence, by Corollary 4.5, there exists
![]() $A,B>0$
such that
$A,B>0$
such that
![]() $A\leq \omega _{\phi }(\xi )\leq B$
, for
$A\leq \omega _{\phi }(\xi )\leq B$
, for
![]() $a.e.\ \xi \in \mathbb {T}^{n}$
. Hence, using the periodicity of
$a.e.\ \xi \in \mathbb {T}^{n}$
. Hence, using the periodicity of
![]() $\omega _{\phi }$
, we have
$\omega _{\phi }$
, we have
![]() $A\leq \omega _{\phi }(\xi )\leq B$
, for
$A\leq \omega _{\phi }(\xi )\leq B$
, for
![]() $a.e.\ \xi \in {\mathbb {R}}^{n}$
. We define
$a.e.\ \xi \in {\mathbb {R}}^{n}$
. We define
 $$ \begin{align} K(\xi,\eta):=\frac{K_{\phi}(\xi,\eta)}{\sqrt{\omega_{\phi}(\xi)}}, \end{align} $$
$$ \begin{align} K(\xi,\eta):=\frac{K_{\phi}(\xi,\eta)}{\sqrt{\omega_{\phi}(\xi)}}, \end{align} $$
for
![]() $\eta \in {\mathbb {R}}^n$
and for
$\eta \in {\mathbb {R}}^n$
and for
![]() $a.e.\ \xi \in {\mathbb {R}}^n$
. Now,
$a.e.\ \xi \in {\mathbb {R}}^n$
. Now,
 $$ \begin{align*} \int_{\mathbb{R}^{n}}\int_{\mathbb{R}^{n}}|K(\xi,\eta)|^{2}\,d\xi d\eta&=\int_{\mathbb{R}^{n}}\int_{\mathbb{R}^{n}}\bigg|\frac{K_{\phi}(\xi,\eta)}{\sqrt{\omega_{\phi}(\xi)}}\bigg|^{2}\,d\xi d\eta\\ &\leq\frac{1}{A}\int_{\mathbb{R}^{n}}\int_{\mathbb{R}^{n}}|K_{\phi}(\xi,\eta)|^{2}\,d\xi d\eta\\ &= \frac{1}{A}\|K_{\phi}\|_{L^2(\mathbb{R}^{2n})}^2\\ &= \frac{1}{A} \|{\phi}\|_{L^2(\mathbb{R}^{2n})}^2\\ &<\infty, \end{align*} $$
$$ \begin{align*} \int_{\mathbb{R}^{n}}\int_{\mathbb{R}^{n}}|K(\xi,\eta)|^{2}\,d\xi d\eta&=\int_{\mathbb{R}^{n}}\int_{\mathbb{R}^{n}}\bigg|\frac{K_{\phi}(\xi,\eta)}{\sqrt{\omega_{\phi}(\xi)}}\bigg|^{2}\,d\xi d\eta\\ &\leq\frac{1}{A}\int_{\mathbb{R}^{n}}\int_{\mathbb{R}^{n}}|K_{\phi}(\xi,\eta)|^{2}\,d\xi d\eta\\ &= \frac{1}{A}\|K_{\phi}\|_{L^2(\mathbb{R}^{2n})}^2\\ &= \frac{1}{A} \|{\phi}\|_{L^2(\mathbb{R}^{2n})}^2\\ &<\infty, \end{align*} $$
proving that
![]() $K\in L^{2}(\mathbb {R}^{2n})$
. Define
$K\in L^{2}(\mathbb {R}^{2n})$
. Define
![]() $\Theta :L^2({\mathbb {R}}^n)\rightarrow L^2({\mathbb {R}}^n)$
by
$\Theta :L^2({\mathbb {R}}^n)\rightarrow L^2({\mathbb {R}}^n)$
by
 $$ \begin{align*} (\Theta f)(x)=\int_{{\mathbb{R}}^{n}}K(x,y)f(y)\,dy,\ \ \ \ \ \ \forall\ f\in L^2({\mathbb{R}}^n). \end{align*} $$
$$ \begin{align*} (\Theta f)(x)=\int_{{\mathbb{R}}^{n}}K(x,y)f(y)\,dy,\ \ \ \ \ \ \forall\ f\in L^2({\mathbb{R}}^n). \end{align*} $$
Here,
![]() $\Theta $
is an integral operator with kernel K in
$\Theta $
is an integral operator with kernel K in
![]() $L^{2}(\mathbb {R}^{2n})$
. Thus,
$L^{2}(\mathbb {R}^{2n})$
. Thus,
![]() $\Theta \in \mathcal {B}_2$
. Since the Weyl transform
$\Theta \in \mathcal {B}_2$
. Since the Weyl transform
![]() $W:L^2({\mathbb {R}}^{2n})\rightarrow \mathcal {B}_2$
is an isometric isomorphism, there exists unique
$W:L^2({\mathbb {R}}^{2n})\rightarrow \mathcal {B}_2$
is an isometric isomorphism, there exists unique
![]() ${\phi }^{\sharp }\in L^2({\mathbb {R}}^{2n})$
such that
${\phi }^{\sharp }\in L^2({\mathbb {R}}^{2n})$
such that
![]() $W{\phi }^{\sharp }=\Theta $
. Hence, we obtain
$W{\phi }^{\sharp }=\Theta $
. Hence, we obtain
 $$ \begin{align} K_{{\phi}^{\sharp}}(\xi,\eta)&=K(\xi,\eta)\notag\\ &=\frac{K_{\phi}(\xi,\eta)}{\sqrt{\omega_{\phi}(\xi)}}. \end{align} $$
$$ \begin{align} K_{{\phi}^{\sharp}}(\xi,\eta)&=K(\xi,\eta)\notag\\ &=\frac{K_{\phi}(\xi,\eta)}{\sqrt{\omega_{\phi}(\xi)}}. \end{align} $$
Since
![]() ${\phi }$
satisfies “Condition C,” for
${\phi }$
satisfies “Condition C,” for
![]() $l\in \mathbb {Z}^{n}\setminus \{0\}$
, we have
$l\in \mathbb {Z}^{n}\setminus \{0\}$
, we have
 $$ \begin{align*} \sum_{m \in \mathbb{Z}^n}\int_{\mathbb{R}^n}K_{\phi^{\sharp}}(\xi+m, \eta)\overline{K_{\phi^{\sharp}}(\xi+m+l, \eta)}\,d\eta=&\sum_{m \in \mathbb{Z}^n}\int_{\mathbb{R}^n}\frac{K_{\phi}(\xi+m,\eta)}{\sqrt{\omega_{\phi}(\xi+m)}}\overline{\frac{K_{\phi}(\xi+m+l,\eta)}{\sqrt{\omega_{\phi}(\xi+m+l)}}}\,d\eta\\ =&\frac{1}{\omega_{\phi}(\xi)}\sum_{m \in \mathbb{Z}^n}\int_{\mathbb{R}^n}K_{\phi}(\xi+m,\eta)\overline{K_{\phi}(\xi+m+l,\eta)}\,d\eta\\ =&\ 0, \end{align*} $$
$$ \begin{align*} \sum_{m \in \mathbb{Z}^n}\int_{\mathbb{R}^n}K_{\phi^{\sharp}}(\xi+m, \eta)\overline{K_{\phi^{\sharp}}(\xi+m+l, \eta)}\,d\eta=&\sum_{m \in \mathbb{Z}^n}\int_{\mathbb{R}^n}\frac{K_{\phi}(\xi+m,\eta)}{\sqrt{\omega_{\phi}(\xi+m)}}\overline{\frac{K_{\phi}(\xi+m+l,\eta)}{\sqrt{\omega_{\phi}(\xi+m+l)}}}\,d\eta\\ =&\frac{1}{\omega_{\phi}(\xi)}\sum_{m \in \mathbb{Z}^n}\int_{\mathbb{R}^n}K_{\phi}(\xi+m,\eta)\overline{K_{\phi}(\xi+m+l,\eta)}\,d\eta\\ =&\ 0, \end{align*} $$
for
![]() $a.e.\ \xi \in \mathbb {T}^{n}$
, showing that
$a.e.\ \xi \in \mathbb {T}^{n}$
, showing that
![]() $\phi ^{\sharp }$
satisfies “Condition C.” Moreover,
$\phi ^{\sharp }$
satisfies “Condition C.” Moreover,
 $$ \begin{align*} \omega_{\phi^{\sharp}}(\xi)&=\sum_{m\in \mathbb{Z}^n}\int_{\mathbb{R}^n}|K_{\phi^{\sharp}}(\xi+m, \eta)|^2d\eta\\ &=\sum_{m\in \mathbb{Z}^n}\int_{\mathbb{R}^n}\bigg|\frac{K_{\phi}(\xi+m,\eta)}{\sqrt{\omega_{\phi}(\xi+m)}}\bigg|^{2}d\eta\\ &=\frac{1}{\omega_{\phi}(\xi)}\sum_{m\in \mathbb{Z}^n}\int_{\mathbb{R}^n}|K_{\phi}(\xi+m,\eta)|^{2}d\eta\\ &=1, \end{align*} $$
$$ \begin{align*} \omega_{\phi^{\sharp}}(\xi)&=\sum_{m\in \mathbb{Z}^n}\int_{\mathbb{R}^n}|K_{\phi^{\sharp}}(\xi+m, \eta)|^2d\eta\\ &=\sum_{m\in \mathbb{Z}^n}\int_{\mathbb{R}^n}\bigg|\frac{K_{\phi}(\xi+m,\eta)}{\sqrt{\omega_{\phi}(\xi+m)}}\bigg|^{2}d\eta\\ &=\frac{1}{\omega_{\phi}(\xi)}\sum_{m\in \mathbb{Z}^n}\int_{\mathbb{R}^n}|K_{\phi}(\xi+m,\eta)|^{2}d\eta\\ &=1, \end{align*} $$
for
![]() $a.e.\ \xi \in \mathbb {T}^{n}$
. Hence, by Theorem 6.1, the system
$a.e.\ \xi \in \mathbb {T}^{n}$
. Hence, by Theorem 6.1, the system
![]() $E^t({\phi }^{\sharp })$
is an orthonormal system. Now, it remains to prove that
$E^t({\phi }^{\sharp })$
is an orthonormal system. Now, it remains to prove that
![]() $V^{t}({\phi })=V^{t}({\phi }^{\sharp })$
. Let
$V^{t}({\phi })=V^{t}({\phi }^{\sharp })$
. Let
![]() $\sqrt {\omega _{\phi }(\xi )}=\sum \limits _{k\in \mathbb {Z}^{n}}a_{k}e^{2\pi ik\cdot \xi }$
be the Fourier series of
$\sqrt {\omega _{\phi }(\xi )}=\sum \limits _{k\in \mathbb {Z}^{n}}a_{k}e^{2\pi ik\cdot \xi }$
be the Fourier series of
![]() $\sqrt {\omega _{\phi }(\xi )}$
. Then, by using (6.2) and Lemma 2.9, we get
$\sqrt {\omega _{\phi }(\xi )}$
. Then, by using (6.2) and Lemma 2.9, we get
 $$ \begin{align*} K_{\phi}(\xi,\eta)&=\sqrt{\omega_{\phi}(\xi,\eta)}K_{\phi^{\sharp}}(\xi,\eta)\\ &=\sum_{k\in \mathbb{Z}^n}a_{k}e^{2\pi ik\cdot \xi}K_{\phi^{\sharp}}(\xi,\eta)\\ &=\sum_{k\in \mathbb{Z}^n}a_{k}K_{T^{t}_{(k,0)}\phi^{\sharp}}(\xi,\eta)\\ &=\sum_{k\in \mathbb{Z}^n}a_{k}\int_{\mathbb{R}^n}T^{t}_{(k,0)}\phi^{\sharp}(x,\eta-\xi)e^{\pi ix\cdot(\xi+\eta)}dx\\ &=\int_{\mathbb{R}^n}\sum_{k\in \mathbb{Z}^n}a_{k}T^{t}_{(k,0)}\phi^{\sharp}(x,\eta-\xi)e^{\pi ix\cdot(\xi+\eta)}dx\\ &=K_{\sum\limits_{k\in \mathbb{Z}^n}a_{k}T^{t}_{(k,0)}\phi^{\sharp}}(\xi,\eta), \end{align*} $$
$$ \begin{align*} K_{\phi}(\xi,\eta)&=\sqrt{\omega_{\phi}(\xi,\eta)}K_{\phi^{\sharp}}(\xi,\eta)\\ &=\sum_{k\in \mathbb{Z}^n}a_{k}e^{2\pi ik\cdot \xi}K_{\phi^{\sharp}}(\xi,\eta)\\ &=\sum_{k\in \mathbb{Z}^n}a_{k}K_{T^{t}_{(k,0)}\phi^{\sharp}}(\xi,\eta)\\ &=\sum_{k\in \mathbb{Z}^n}a_{k}\int_{\mathbb{R}^n}T^{t}_{(k,0)}\phi^{\sharp}(x,\eta-\xi)e^{\pi ix\cdot(\xi+\eta)}dx\\ &=\int_{\mathbb{R}^n}\sum_{k\in \mathbb{Z}^n}a_{k}T^{t}_{(k,0)}\phi^{\sharp}(x,\eta-\xi)e^{\pi ix\cdot(\xi+\eta)}dx\\ &=K_{\sum\limits_{k\in \mathbb{Z}^n}a_{k}T^{t}_{(k,0)}\phi^{\sharp}}(\xi,\eta), \end{align*} $$
which, by the uniqueness of the kernel, implies that
![]() $\phi =\sum \limits _{k\in \mathbb {Z}^{n}}a_{k}T^{t}_{(k,0)}\phi ^{\sharp }$
. Thus, using (2.2), we get
$\phi =\sum \limits _{k\in \mathbb {Z}^{n}}a_{k}T^{t}_{(k,0)}\phi ^{\sharp }$
. Thus, using (2.2), we get
 $$ \begin{align*} T^{t}_{(k^{\prime},l^{\prime})}\phi(x,y)&=\sum_{k\in\mathbb{Z}^n}a_{k}T^{t}_{(k^{\prime},l^{\prime})}T^{t}_{(k,0)}\phi^{\sharp}(x,y)\\ &=\sum_{k\in\mathbb{Z}^n}a_{k}e^{\pi il^{\prime}\cdot k}T^{t}_{((k^{\prime}+k),l^{\prime})}\phi^{\sharp}(x,y), \end{align*} $$
$$ \begin{align*} T^{t}_{(k^{\prime},l^{\prime})}\phi(x,y)&=\sum_{k\in\mathbb{Z}^n}a_{k}T^{t}_{(k^{\prime},l^{\prime})}T^{t}_{(k,0)}\phi^{\sharp}(x,y)\\ &=\sum_{k\in\mathbb{Z}^n}a_{k}e^{\pi il^{\prime}\cdot k}T^{t}_{((k^{\prime}+k),l^{\prime})}\phi^{\sharp}(x,y), \end{align*} $$
showing that
![]() $V^{t}({\phi })\subset V^{t}({\phi }^{\sharp })$
. Similarly, we can prove
$V^{t}({\phi })\subset V^{t}({\phi }^{\sharp })$
. Similarly, we can prove
![]() $V^{t}({\phi }^{\sharp })\subset V^{t}({\phi })$
, by using the Fourier series of
$V^{t}({\phi }^{\sharp })\subset V^{t}({\phi })$
, by using the Fourier series of
![]() $\frac {1}{\sqrt {\omega _{{\phi }}}}$
in (6.2).
$\frac {1}{\sqrt {\omega _{{\phi }}}}$
in (6.2).
Now, we illustrate this theorem with an example. Recall that for
![]() $f,g\in L^{2}(\mathbb {R}^{2n})$
, we have (3.24).
$f,g\in L^{2}(\mathbb {R}^{2n})$
, we have (3.24).
Example 6.3. Let
![]() ${\phi }(x,y)=\sum \limits _{m\in {\mathbb {Z}}}\frac {1}{10^{|m|}}\chi _{[m,m+1)\times [0,1)}(x,y),\ \ \ \ (x,y)\in {\mathbb {R}}^2.$
Then, for
${\phi }(x,y)=\sum \limits _{m\in {\mathbb {Z}}}\frac {1}{10^{|m|}}\chi _{[m,m+1)\times [0,1)}(x,y),\ \ \ \ (x,y)\in {\mathbb {R}}^2.$
Then, for
![]() ${k,l\in {\mathbb {Z}},}$
we have
${k,l\in {\mathbb {Z}},}$
we have
 $$ \begin{align} \big<{\phi},{T_{(k,l)}^t}{\phi}\big>=&\int_{{\mathbb{R}}^{2}}{\phi}(x,y)\overline{{T_{(k,l)}^t}{\phi}(x,y)}\,dydx\nonumber\\ =&\int_{0}^{1}\int_{{\mathbb{R}}}{\phi}(x,y)e^{-\pi i(xl-yk)}{\phi}(x-k,y-l)\,dxdy. \end{align} $$
$$ \begin{align} \big<{\phi},{T_{(k,l)}^t}{\phi}\big>=&\int_{{\mathbb{R}}^{2}}{\phi}(x,y)\overline{{T_{(k,l)}^t}{\phi}(x,y)}\,dydx\nonumber\\ =&\int_{0}^{1}\int_{{\mathbb{R}}}{\phi}(x,y)e^{-\pi i(xl-yk)}{\phi}(x-k,y-l)\,dxdy. \end{align} $$
It is easy to see that
![]() $\operatorname {\mathrm {supp}}{\phi }={\mathbb {R}}\times [0,1]$
and
$\operatorname {\mathrm {supp}}{\phi }={\mathbb {R}}\times [0,1]$
and
![]() $ \operatorname {\mathrm {supp}}{T_{(k,l)}^t} {\phi }={\mathbb {R}}\times [l,l+1]$
. Hence,
$ \operatorname {\mathrm {supp}}{T_{(k,l)}^t} {\phi }={\mathbb {R}}\times [l,l+1]$
. Hence,
![]() $\big <{\phi },{T_{(k,l)}^t}{\phi }\big>=0$
, whenever
$\big <{\phi },{T_{(k,l)}^t}{\phi }\big>=0$
, whenever
![]() $l\neq 0$
. Consequently, using (3.24), we obtain
$l\neq 0$
. Consequently, using (3.24), we obtain
 $$ \begin{align*} \sum\limits_{m\in{\mathbb{Z}^n}}\int_{\mathbb{R}^{n}}K_{{\phi}}(\xi+m,\eta)\overline{K_{{\phi}}(\xi+m+l,\eta)}\,d\eta&=\sum\limits_{k\in{\mathbb{Z}^n}}\big\langle {\phi},{T_{(k,l)}^t} {\phi}\big\rangle e^{\pi ik(2\xi+l)}\\ &=0,\ \ \ \ \forall\ l\neq 0, \end{align*} $$
$$ \begin{align*} \sum\limits_{m\in{\mathbb{Z}^n}}\int_{\mathbb{R}^{n}}K_{{\phi}}(\xi+m,\eta)\overline{K_{{\phi}}(\xi+m+l,\eta)}\,d\eta&=\sum\limits_{k\in{\mathbb{Z}^n}}\big\langle {\phi},{T_{(k,l)}^t} {\phi}\big\rangle e^{\pi ik(2\xi+l)}\\ &=0,\ \ \ \ \forall\ l\neq 0, \end{align*} $$
showing that
![]() ${\phi }$
satisfies “Condition C.” Now, we make use of Corollary (4.5) to show that the system
${\phi }$
satisfies “Condition C.” Now, we make use of Corollary (4.5) to show that the system
![]() $E^{t}({\phi })$
forms a Riesz sequence. From the definition of
$E^{t}({\phi })$
forms a Riesz sequence. From the definition of
![]() ${\phi }$
, we get
${\phi }$
, we get
 $$ \begin{align*} \|{\phi}\|_{L^2({\mathbb{R}}^{2n})}^2=&\int_{{\mathbb{R}}^{2}}|{\phi}(x,y)|^{2}dxdy\\ =&\int_{{\mathbb{R}}}\int_{0}^{1}|{\phi}(x,y)|^{2}dydx\\ =&\sum\limits_{m\in{\mathbb{Z}}}\int_{m}^{m+1}|{\phi}(x,y)|^{2}dx\\ =&\sum\limits_{m\in{\mathbb{Z}}}\int_{m}^{m+1}\frac{1}{100^{|m|}}dx\\ =&\sum\limits_{m\in{\mathbb{Z}}}\frac{1}{100^{|m|}}\\ =&\frac{101}{99}, \end{align*} $$
$$ \begin{align*} \|{\phi}\|_{L^2({\mathbb{R}}^{2n})}^2=&\int_{{\mathbb{R}}^{2}}|{\phi}(x,y)|^{2}dxdy\\ =&\int_{{\mathbb{R}}}\int_{0}^{1}|{\phi}(x,y)|^{2}dydx\\ =&\sum\limits_{m\in{\mathbb{Z}}}\int_{m}^{m+1}|{\phi}(x,y)|^{2}dx\\ =&\sum\limits_{m\in{\mathbb{Z}}}\int_{m}^{m+1}\frac{1}{100^{|m|}}dx\\ =&\sum\limits_{m\in{\mathbb{Z}}}\frac{1}{100^{|m|}}\\ =&\frac{101}{99}, \end{align*} $$
and, for
![]() $k\neq 0$
and
$k\neq 0$
and
![]() $l=0$
in (6.3), we get
$l=0$
in (6.3), we get
 $$ \begin{align} \big<{\phi},T^{t}_{(k,0)}{\phi}\big>=&\int_{0}^{1}\bigg(\sum\limits_{m\in{\mathbb{Z}}}\int_{m}^{m+1}{\phi}(x,y){\phi}(x-k,y)\,dx\bigg)e^{\pi iyk}\,dy\nonumber\\ =&\int_{0}^{1}\bigg(\sum\limits_{m\in{\mathbb{Z}}}\int_{m}^{m+1}\frac{1}{10^{|m|}}{\phi}(x-k,y)\,dx\bigg)e^{\pi iyk}\,dy\nonumber\\ =&\int_{0}^{1}\bigg(\sum\limits_{m\in{\mathbb{Z}}}\int_{m-k}^{m+1-k}\frac{1}{10^{|m|}}{\phi}(x,y)\,dx\bigg)e^{\pi iyk}\,dy\nonumber\\ =&\int_{0}^{1}\bigg(\sum\limits_{m\in{\mathbb{Z}}}\int_{m-k}^{m+1-k}\frac{1}{10^{|m|}}\frac{1}{10^{|m-k|}}\,dx\bigg)e^{\pi iyk}\,dy \nonumber\\ =&\bigg( \sum\limits_{m\in{\mathbb{Z}}}\frac{1}{10^{|m|}}\frac{1}{10^{|m-k|}}\bigg)\bigg(\int_{0}^{1}e^{\pi iyk}\,dy\bigg). \end{align} $$
$$ \begin{align} \big<{\phi},T^{t}_{(k,0)}{\phi}\big>=&\int_{0}^{1}\bigg(\sum\limits_{m\in{\mathbb{Z}}}\int_{m}^{m+1}{\phi}(x,y){\phi}(x-k,y)\,dx\bigg)e^{\pi iyk}\,dy\nonumber\\ =&\int_{0}^{1}\bigg(\sum\limits_{m\in{\mathbb{Z}}}\int_{m}^{m+1}\frac{1}{10^{|m|}}{\phi}(x-k,y)\,dx\bigg)e^{\pi iyk}\,dy\nonumber\\ =&\int_{0}^{1}\bigg(\sum\limits_{m\in{\mathbb{Z}}}\int_{m-k}^{m+1-k}\frac{1}{10^{|m|}}{\phi}(x,y)\,dx\bigg)e^{\pi iyk}\,dy\nonumber\\ =&\int_{0}^{1}\bigg(\sum\limits_{m\in{\mathbb{Z}}}\int_{m-k}^{m+1-k}\frac{1}{10^{|m|}}\frac{1}{10^{|m-k|}}\,dx\bigg)e^{\pi iyk}\,dy \nonumber\\ =&\bigg( \sum\limits_{m\in{\mathbb{Z}}}\frac{1}{10^{|m|}}\frac{1}{10^{|m-k|}}\bigg)\bigg(\int_{0}^{1}e^{\pi iyk}\,dy\bigg). \end{align} $$
But
 $$ \begin{align*} \int_{0}^{1}e^{\pi iyk}\,dy&= \begin{cases} 0, & \mbox{if } k \text{ is even,}\\ -\frac{2}{\pi ik}, & \mbox{if } k \text{ is odd}. \end{cases} \end{align*} $$
$$ \begin{align*} \int_{0}^{1}e^{\pi iyk}\,dy&= \begin{cases} 0, & \mbox{if } k \text{ is even,}\\ -\frac{2}{\pi ik}, & \mbox{if } k \text{ is odd}. \end{cases} \end{align*} $$
Hence, (6.4) gives
 $$ \begin{align} \big<{\phi},T^{t}_{(k,0)}{\phi}\big>=& \begin{cases} 0, & \mbox{if } k \text{ is even,}\\ -\frac{2}{\pi ik}\sum\limits_{m\in{\mathbb{Z}}}\frac{1}{10^{|m|}}\frac{1}{10^{|m-k|}}, & \mbox{if } k \text{ is odd}. \end{cases} \end{align} $$
$$ \begin{align} \big<{\phi},T^{t}_{(k,0)}{\phi}\big>=& \begin{cases} 0, & \mbox{if } k \text{ is even,}\\ -\frac{2}{\pi ik}\sum\limits_{m\in{\mathbb{Z}}}\frac{1}{10^{|m|}}\frac{1}{10^{|m-k|}}, & \mbox{if } k \text{ is odd}. \end{cases} \end{align} $$
Now, we aim to compute
![]() $\sum \limits _{m\in {\mathbb {Z}}}\frac {1}{10^{|m|}}\frac {1}{10^{|m-k|}}$
explicitly for odd k.
$\sum \limits _{m\in {\mathbb {Z}}}\frac {1}{10^{|m|}}\frac {1}{10^{|m-k|}}$
explicitly for odd k.
First, we assume that k is an odd positive integer. Then
 $$ \begin{align} \sum\limits_{m\in{\mathbb{Z}}}\frac{1}{10^{|m|}}\frac{1}{10^{|m-k|}}=&\sum_{m=0}^{\infty}\frac{1}{10^{m}}\frac{1}{10^{|m-k|}}+\sum_{m=-\infty}^{-1}\frac{1}{10^{-m}}\frac{1}{10^{|m-k|}}\nonumber\\ =&\sum_{m=0}^{k}\frac{1}{10^{m}}\frac{1}{10^{k-m}}+\sum_{m=k+1}^{\infty}\frac{1}{10^{m}}\frac{1}{10^{m-k}}+\sum_{m=1}^{\infty}\frac{1}{10^{m}}\frac{1}{10^{|-m-k|}}\nonumber\\ =&\sum\limits_{m=0}^{k}\frac{1}{10^{k}}+2\sum_{m=1}^{\infty}\frac{1}{10^{m}}\frac{1}{10^{m+k}}\nonumber\\ =&\frac{k+1}{10^{k}}+\frac{2}{10^{k}}\sum_{m=1}^{\infty}\frac{1}{100^{m}}\nonumber\\ =&\frac{k}{10^{k}}+\frac{101}{99}\frac{1}{10^{k}}. \end{align} $$
$$ \begin{align} \sum\limits_{m\in{\mathbb{Z}}}\frac{1}{10^{|m|}}\frac{1}{10^{|m-k|}}=&\sum_{m=0}^{\infty}\frac{1}{10^{m}}\frac{1}{10^{|m-k|}}+\sum_{m=-\infty}^{-1}\frac{1}{10^{-m}}\frac{1}{10^{|m-k|}}\nonumber\\ =&\sum_{m=0}^{k}\frac{1}{10^{m}}\frac{1}{10^{k-m}}+\sum_{m=k+1}^{\infty}\frac{1}{10^{m}}\frac{1}{10^{m-k}}+\sum_{m=1}^{\infty}\frac{1}{10^{m}}\frac{1}{10^{|-m-k|}}\nonumber\\ =&\sum\limits_{m=0}^{k}\frac{1}{10^{k}}+2\sum_{m=1}^{\infty}\frac{1}{10^{m}}\frac{1}{10^{m+k}}\nonumber\\ =&\frac{k+1}{10^{k}}+\frac{2}{10^{k}}\sum_{m=1}^{\infty}\frac{1}{100^{m}}\nonumber\\ =&\frac{k}{10^{k}}+\frac{101}{99}\frac{1}{10^{k}}. \end{align} $$
Similarly, if k is a negative odd integer, we can show that
 $$ \begin{align} \sum\limits_{m\in{\mathbb{Z}}}\frac{1}{10^{|m|}}\frac{1}{10^{|m-k|}}=&\frac{-k}{10^{-k}}+\frac{101}{99}\frac{1}{10^{-k}}. \end{align} $$
$$ \begin{align} \sum\limits_{m\in{\mathbb{Z}}}\frac{1}{10^{|m|}}\frac{1}{10^{|m-k|}}=&\frac{-k}{10^{-k}}+\frac{101}{99}\frac{1}{10^{-k}}. \end{align} $$
Using (6.6) and (6.7) in (6.5), we get
 $$ \begin{align*} \big<{\phi},T^{t}_{(k,0)}{\phi}\big>=\begin{cases} 0, & \mbox{if } k\in 2{\mathbb{Z}}\setminus\{0\},\\ -\frac{2}{\pi i}\big(\frac{1}{10^{k}}+\frac{101}{99}\frac{1}{k10^{k}}\big), & \mbox{if } k\in 2\mathbb{N}-1,\\ \frac{2}{\pi i}\big(\frac{1}{10^{-k}}+\frac{101}{99}\frac{1}{(-k)10^{-k}}\big), & \mbox{if } k\in 1-2\mathbb{N}. \end{cases} \end{align*} $$
$$ \begin{align*} \big<{\phi},T^{t}_{(k,0)}{\phi}\big>=\begin{cases} 0, & \mbox{if } k\in 2{\mathbb{Z}}\setminus\{0\},\\ -\frac{2}{\pi i}\big(\frac{1}{10^{k}}+\frac{101}{99}\frac{1}{k10^{k}}\big), & \mbox{if } k\in 2\mathbb{N}-1,\\ \frac{2}{\pi i}\big(\frac{1}{10^{-k}}+\frac{101}{99}\frac{1}{(-k)10^{-k}}\big), & \mbox{if } k\in 1-2\mathbb{N}. \end{cases} \end{align*} $$
Now, using (3.24), we have
 $$ \begin{align} \omega_{{\phi}}(\xi)&=\sum\limits_{m\in {\mathbb{Z}}}\int_{{\mathbb{R}}}|K_{{\phi}}(\xi+m,\eta)|^{2}\,d\eta \nonumber\\ &=\sum\limits_{k\in{\mathbb{Z}}}\big\langle {\phi},T^{t}_{(k,0)}{\phi}\big\rangle e^{2\pi ik\xi} \nonumber \\ &=\|{\phi}\|^2+\sum_{k\in 2\mathbb{N}-1}\big\langle {\phi},T^{t}_{(k,0)}{\phi}\big\rangle e^{2\pi ik\xi}+\sum_{k\in 1-2\mathbb{N}}\big\langle {\phi},T^{t}_{(k,0)}{\phi}\big\rangle e^{2\pi ik\xi} \nonumber \\ &=\frac{101}{99}-\frac{2}{\pi i}\sum_{k\in 2\mathbb{N}-1} \!\Big(\frac{1}{10^{k}}+\frac{101}{99}\frac{1}{k10^{k}}\Big)e^{2\pi ik\xi}+\frac{2}{\pi i}\sum_{k\in 1-2\mathbb{N}}\!\Big(\frac{1}{10^{-k}}+\frac{101}{99}\frac{1}{(-k)10^{-k}}\Big)e^{2\pi ik\xi} \nonumber \\ &=\frac{101}{99}-\frac{2}{\pi i}\sum_{k\in 2\mathbb{N}-1} \Big(\frac{1}{10^{k}}+\frac{101}{99}\frac{1}{k10^{k}}\Big)e^{2\pi ik\xi}+\frac{2}{\pi i}\sum_{k\in 2\mathbb{N}-1}\Big(\frac{1}{10^{k}}+\frac{101}{99}\frac{1}{k10^{k}}\Big)e^{-2\pi ik\xi} \nonumber \\ &=\frac{101}{99}-\frac{2}{\pi i}\sum_{k\in 2\mathbb{N}-1} \Big(\frac{1}{10^{k}}+\frac{101}{99}\frac{1}{k10^{k}}\Big)(e^{2\pi ik\xi}-e^{-2\pi ik\xi}) \nonumber \\ &=\frac{101}{99}-\frac{4}{\pi}\sum_{k\in 2\mathbb{N}-1} \Big(\frac{1}{10^{k}}+\frac{101}{99}\frac{1}{k10^{k}}\Big)\sin (2\pi k\xi)\nonumber \\ &=\frac{101}{99}-R(\xi), \end{align} $$
$$ \begin{align} \omega_{{\phi}}(\xi)&=\sum\limits_{m\in {\mathbb{Z}}}\int_{{\mathbb{R}}}|K_{{\phi}}(\xi+m,\eta)|^{2}\,d\eta \nonumber\\ &=\sum\limits_{k\in{\mathbb{Z}}}\big\langle {\phi},T^{t}_{(k,0)}{\phi}\big\rangle e^{2\pi ik\xi} \nonumber \\ &=\|{\phi}\|^2+\sum_{k\in 2\mathbb{N}-1}\big\langle {\phi},T^{t}_{(k,0)}{\phi}\big\rangle e^{2\pi ik\xi}+\sum_{k\in 1-2\mathbb{N}}\big\langle {\phi},T^{t}_{(k,0)}{\phi}\big\rangle e^{2\pi ik\xi} \nonumber \\ &=\frac{101}{99}-\frac{2}{\pi i}\sum_{k\in 2\mathbb{N}-1} \!\Big(\frac{1}{10^{k}}+\frac{101}{99}\frac{1}{k10^{k}}\Big)e^{2\pi ik\xi}+\frac{2}{\pi i}\sum_{k\in 1-2\mathbb{N}}\!\Big(\frac{1}{10^{-k}}+\frac{101}{99}\frac{1}{(-k)10^{-k}}\Big)e^{2\pi ik\xi} \nonumber \\ &=\frac{101}{99}-\frac{2}{\pi i}\sum_{k\in 2\mathbb{N}-1} \Big(\frac{1}{10^{k}}+\frac{101}{99}\frac{1}{k10^{k}}\Big)e^{2\pi ik\xi}+\frac{2}{\pi i}\sum_{k\in 2\mathbb{N}-1}\Big(\frac{1}{10^{k}}+\frac{101}{99}\frac{1}{k10^{k}}\Big)e^{-2\pi ik\xi} \nonumber \\ &=\frac{101}{99}-\frac{2}{\pi i}\sum_{k\in 2\mathbb{N}-1} \Big(\frac{1}{10^{k}}+\frac{101}{99}\frac{1}{k10^{k}}\Big)(e^{2\pi ik\xi}-e^{-2\pi ik\xi}) \nonumber \\ &=\frac{101}{99}-\frac{4}{\pi}\sum_{k\in 2\mathbb{N}-1} \Big(\frac{1}{10^{k}}+\frac{101}{99}\frac{1}{k10^{k}}\Big)\sin (2\pi k\xi)\nonumber \\ &=\frac{101}{99}-R(\xi), \end{align} $$
where
 $$ \begin{align*} R(\xi):=\frac{4}{\pi}\sum_{k\in 2\mathbb{N}-1} \Big(\frac{1}{10^{k}}+\frac{101}{99}\frac{1}{k10^{k}}\Big)\sin (2\pi k\xi). \end{align*} $$
$$ \begin{align*} R(\xi):=\frac{4}{\pi}\sum_{k\in 2\mathbb{N}-1} \Big(\frac{1}{10^{k}}+\frac{101}{99}\frac{1}{k10^{k}}\Big)\sin (2\pi k\xi). \end{align*} $$
Now, we have
 $$ \begin{align} |R(\xi)|&\leq \frac{4}{\pi}\sum_{k\in 2\mathbb{N}-1} \Big(\frac{1}{10^{k}}+\frac{101}{99}\frac{1}{k10^{k}}\Big)\notag \\ &=\frac{4}{\pi}\bigg[\sum_{k\in 2\mathbb{N}-1}\frac{1}{10^{k}}+\frac{101}{99}\sum_{k\in 2\mathbb{N}-1}\frac{1}{k10^{k}} \bigg],\ \ \ \ \ \ \forall\ \xi\in [0,1). \end{align} $$
$$ \begin{align} |R(\xi)|&\leq \frac{4}{\pi}\sum_{k\in 2\mathbb{N}-1} \Big(\frac{1}{10^{k}}+\frac{101}{99}\frac{1}{k10^{k}}\Big)\notag \\ &=\frac{4}{\pi}\bigg[\sum_{k\in 2\mathbb{N}-1}\frac{1}{10^{k}}+\frac{101}{99}\sum_{k\in 2\mathbb{N}-1}\frac{1}{k10^{k}} \bigg],\ \ \ \ \ \ \forall\ \xi\in [0,1). \end{align} $$
Decomposing
 $$ \begin{align*} \sum_{k=1}^{\infty}\frac{1}{10^{k}}=\sum\limits_{k\in 2\mathbb{N}-1}\frac{1}{10^{k}}+\sum_{k=1}^{\infty}\frac{1}{10^{2k}}\ \ \ \ \ \ \text{and}\ \ \ \ \ \ \sum_{k=1}^{\infty}\frac{1}{k10^{k}}=\sum\limits_{k\in 2\mathbb{N}-1}\frac{1}{k10^{k}}+\frac{1}{2}\sum_{k=1}^{\infty}\frac{1}{k10^{2k}}, \end{align*} $$
$$ \begin{align*} \sum_{k=1}^{\infty}\frac{1}{10^{k}}=\sum\limits_{k\in 2\mathbb{N}-1}\frac{1}{10^{k}}+\sum_{k=1}^{\infty}\frac{1}{10^{2k}}\ \ \ \ \ \ \text{and}\ \ \ \ \ \ \sum_{k=1}^{\infty}\frac{1}{k10^{k}}=\sum\limits_{k\in 2\mathbb{N}-1}\frac{1}{k10^{k}}+\frac{1}{2}\sum_{k=1}^{\infty}\frac{1}{k10^{2k}}, \end{align*} $$
we can show that
 $$ \begin{align*} \sum\limits_{k\in 2\mathbb{N}-1}\frac{1}{10^{k}}=\frac{10}{99}\ \ \ \ \ \ \ \text{and}\ \ \ \ \ \ \ \sum\limits_{k\in 2\mathbb{N}-1}\frac{1}{k10^{k}}=-\ln\left(\frac{9}{10}\right)+\frac{1}{2}\ln\left(\frac{99}{100}\right). \end{align*} $$
$$ \begin{align*} \sum\limits_{k\in 2\mathbb{N}-1}\frac{1}{10^{k}}=\frac{10}{99}\ \ \ \ \ \ \ \text{and}\ \ \ \ \ \ \ \sum\limits_{k\in 2\mathbb{N}-1}\frac{1}{k10^{k}}=-\ln\left(\frac{9}{10}\right)+\frac{1}{2}\ln\left(\frac{99}{100}\right). \end{align*} $$
Hence, from (6.9), we obtain
 $$ \begin{align*} |R(\xi)|&\leq\frac{4}{\pi}\Bigg[\frac{10}{99}+\frac{101}{99} \Bigg(-\ln\left(\frac{9}{10}\right)+\frac{1}{2}\ln\left(\frac{99}{100}\right)\Bigg)\Bigg]\\ &<0.26,\ \ \ \ \ \ \forall\ \xi\in [0,1). \end{align*} $$
$$ \begin{align*} |R(\xi)|&\leq\frac{4}{\pi}\Bigg[\frac{10}{99}+\frac{101}{99} \Bigg(-\ln\left(\frac{9}{10}\right)+\frac{1}{2}\ln\left(\frac{99}{100}\right)\Bigg)\Bigg]\\ &<0.26,\ \ \ \ \ \ \forall\ \xi\in [0,1). \end{align*} $$
Thus, from (6.8), we get
and
Therefore, by Corollary 4.5, the system
![]() $E^t({\phi })$
is a Riesz sequence with bounds
$E^t({\phi })$
is a Riesz sequence with bounds
![]() $0.7$
and
$0.7$
and
![]() $1.3$
. Now, by Theorem
$1.3$
. Now, by Theorem
![]() $5.1$
, there exists
$5.1$
, there exists
![]() ${\phi }^{\sharp }\in L^2({\mathbb {R}}^{2})$
, given by
${\phi }^{\sharp }\in L^2({\mathbb {R}}^{2})$
, given by
 $$ \begin{align} K_{{\phi}^{\sharp}}(\xi,\eta)&=\frac{K_{\phi}(\xi,\eta)}{\sqrt{\omega_\phi(\xi)}},\ \ \ \ \ \ (\xi,\eta)\in{\mathbb{R}}^2, \end{align} $$
$$ \begin{align} K_{{\phi}^{\sharp}}(\xi,\eta)&=\frac{K_{\phi}(\xi,\eta)}{\sqrt{\omega_\phi(\xi)}},\ \ \ \ \ \ (\xi,\eta)\in{\mathbb{R}}^2, \end{align} $$
such that the system
![]() $E^t({\phi }^{\sharp })$
is an orthonormal system in
$E^t({\phi }^{\sharp })$
is an orthonormal system in
![]() $L^2({\mathbb {R}}^{2})$
with
$L^2({\mathbb {R}}^{2})$
with
![]() $V^{t}({\phi })=V^{t}({\phi }^{\sharp })$
.
$V^{t}({\phi })=V^{t}({\phi }^{\sharp })$
.
Acknowledgment
We would like to thank the referee for meticulously reading the manuscript and giving us the valuable suggestions.