Introduction
Many polythermal valley glaciers and ice sheets have a cold surface layer in the ablation zone that meets the bed near the terminus. Ice is assumed to be frozen to the substrate in these marginal areas, and is usually assumed to inhibit basal slip there (e.g. Reference Hutter and OlunloyoHutter and Olunloyo, 1981; Reference EvansEvans, 2009). Where wet-based ice in the interior moving by basal sliding or bed deformation meets cold-based ice closer to the margins (referred to as the basal thermal transition or BTT), large longitudinal stress gradients are therefore expected (e.g. Reference Hutter and OlunloyoHutter and Olunloyo, 1980). A common inference is that these stress gradients cause folding or thrust faulting of the glacier, resulting in uplift of basal debris to the ice surface (e.g. Reference Hambrey, Bennett, Dowdeswell, Glasser and HuddartHambrey and others, 1999). With deglaciation, surface accumulations of this debris may result in belts of high-relief hummocky topography. Such landscapes have therefore sometimes been interpreted as indicating past climatic regimes that supported polythermal glaciers (Reference Hambrey, Bennett and GlasserHambrey and others, 1997).
The relationship between the BTT of a polythermal glacier and the resulting stress field (and by extension, sediment transport processes) is largely conjectural. Although the transition between cold and temperate ice layers has been determined in numerous glaciers using ground-penetrating radar (GPR) (e.g. Reference BjørnssonBjörnsson and others, 1996; Reference Jansson, Näslund, Pettersson, Richardson-Näslund and HolmlundJansson and others, 2000; Reference MurrayMurray and others, 2000), extensive measurements of flow kinematics in ice spanning the BTT have been made in only two glaciers: Trapridge Glacier in Canada (Reference Clarke and BlakeClarke and Blake, 1991) and Bakaninbreen in Svalbard (e.g. Reference MurrayMurray and others, 2000). At both of these glaciers, the BTT separates ice moving by sliding and bed deformation up-glacier from nearly stagnant terminal ice. Bulges in the ice surface over the BTT attest to strong longitudinal compression there.
Storglaciären is a small, non-surge-type, polythermal glacier in Sweden (Fig. 1) whose terminus contains structures consistent with longitudinal compression but displays no surface bulge. The cold surface layer has been studied in detail by Reference Holmlund and ErikssonHolmlund and Eriksson (1989) and Reference Pettersson, Jansson and HolmlundPettersson and others (2003, Reference Pettersson, Jansson and Blatter2004, Reference Pettersson, Jansson, Huwald and Blatter2007). As of 2003, this layer of subfreezing ice varied in thickness in the ablation zone from 25 to 70 m. Based on this cold-layer thickness, the rim of cold-based ice near the lateral margins and terminus is expected to be ∼50–200 m wide. Up-glacier, basal ice is temperate and moves by both sliding and bed deformation (e.g. Reference Iverson, Hanson, Hooke and JanssonIverson and others, 1995).
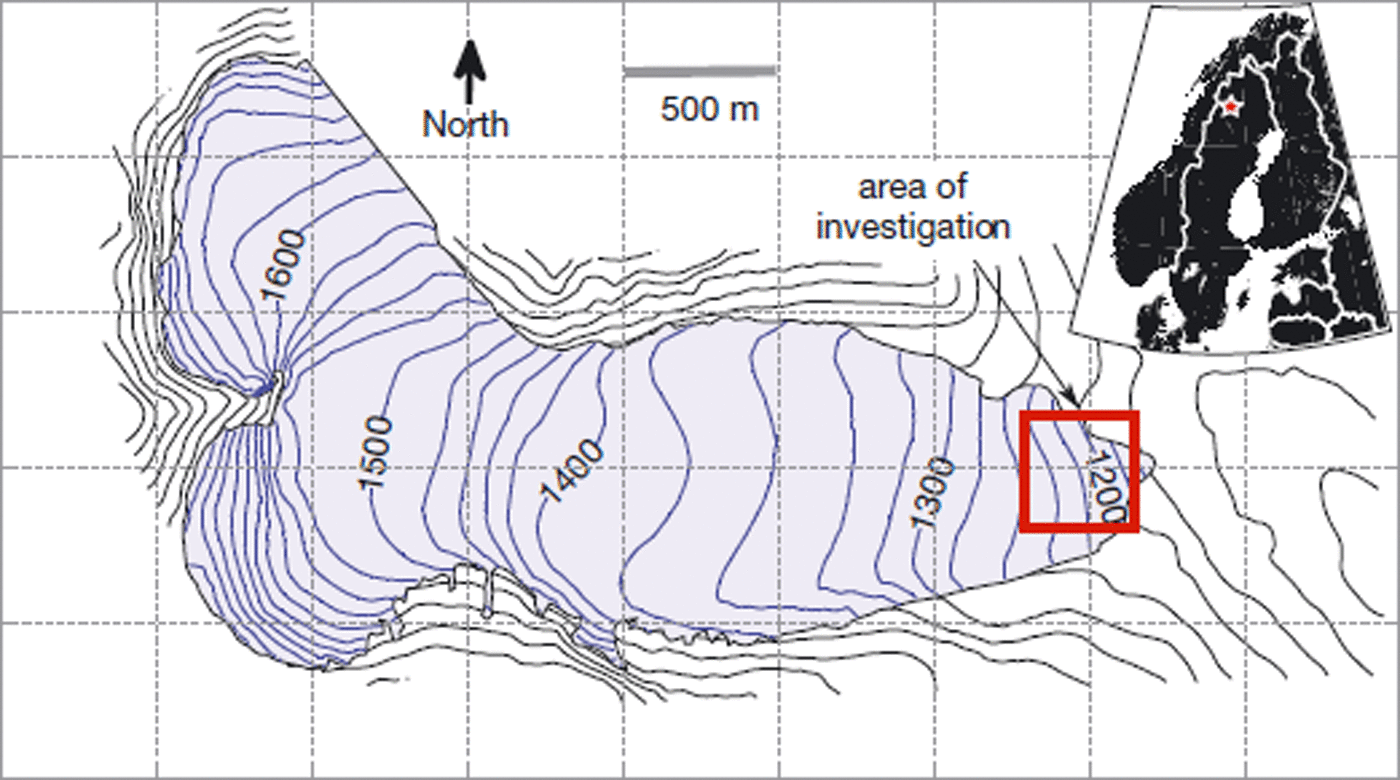
Fig. 1. Map of Storglaciären showing the area of interest at the terminus. Elevation in metres.
An arcuate, up-glacier-dipping debris band emerged on the northern side of the terminus of Storglaciären in 1994. Differential ablation at the surface has caused this structure to form a debris-mantled ridge of ice that extends about one-third of the way across the terminus. Reference Jansson, Näslund, Pettersson, Richardson-Näslund and HolmlundJansson and others (2000) observed englacial reflections in GPR surveys that appeared to represent the continuation at depth of this debris band. Projecting this reflection towards the glacier bed suggested that it emanated from the transition between warm-based and cold-based ice. These observations, along with sedimentological and geochemical analyses, led Reference Glasser, Hambrey, Etienne, Jansson and PetterssonGlasser and others (2003) to interpret that thrust faulting due to longitudinal compression across the BTT was responsible for the debris band.
Past velocity measurements near the terminus provide conflicting evidence for longitudinal compression across the BTT. Using extensive stake networks that overlap the up-glacier portion of our study area, Reference Brzozowski and HookeBrzozowski and Hooke (1981) and Reference Hedfors, Peyaud, Pohjola, Jansson and PetterssonHedfors and others (2003) inferred that basal velocity was relatively high and drag was low near the inferred BTT of Reference Jansson, Näslund, Pettersson, Richardson-Näslund and HolmlundJansson and others (2000), thus limiting the longitudinal compression there. In contrast, Reference Jansson, Näslund, Pettersson, Richardson-Näslund and HolmlundJansson and others (2000) found that surface velocity along a transect crossing the debris ridge in the northern part of the terminus declined by >50% across the ridge. However, this reduction was measured in stakes separated by 50 m, so the distribution of velocity closer to the debris band was unknown. Nevertheless, they inferred that the longitudinal compression was due to the change from warm- to cold-bed conditions across the BTT. Using two velocity stakes closer to the glacier centre line and up-glacier from the BTT, Reference Hanson, Hooke and GraceHanson and others (1998) found that surface velocities near the terminus were insensitive to local water pressure fluctuations. These measurements were interpreted as indicating that ice motion in the terminus was driven largely by longitudinal compression from ice up-glacier, and that the magnitude of this compression was controlled by up-glacier velocity fluctuations.
In this paper, we attempt to characterize the kinematics and mechanics of ice flow near the margin of Storglaciären using diverse field measurements and numerical modelling. We test the hypothesis that the BTT is a slip/no-slip transition and hence the site of substantial longitudinal compression.
Methods
Field methods
Field measurements were focused along two flow-parallel transects that were expected to span the BTT (Fig. 2). One of these, which we refer to as the ‘south transect’, was at the approximate centre line of the glacier and was where most of the instrumentation was installed. The other transect was ∼85 m to the north and intersected the southern end of the prominent debris ridge. Our coordinate system begins with zero at the initial position of the uppermost surface velocity stake in each transect.
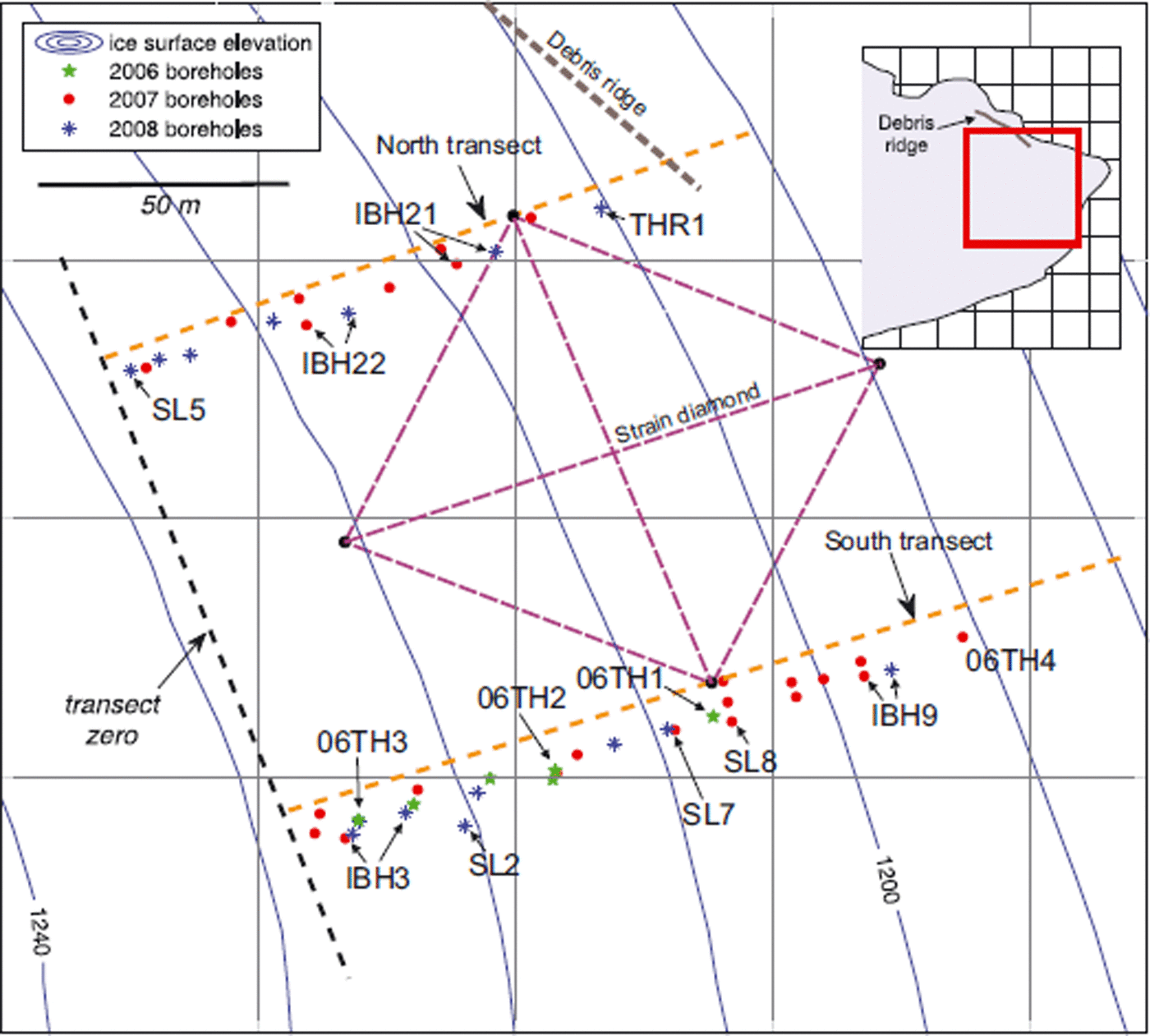
Fig. 2. Map of the terminus showing instrumented borehole locations and the location of the velocity stake network and strain diamond. Abbreviations next to boreholes correspond to instrument names used in the text. Elevation is in metres.
The transition between cold-based and warm-based ice was studied with thermistor strings and GPR surveys. A Mali ProEx GPR system with 100 MHz centre-frequency antennae was used for surveys in April and August 2008. The system was used in constant-offset mode with a 1 m antenna separation. The antennae were pulled on sleds during spring and pushed on a wheeled cart in summer. A hand-held GPS (Garmin 12 XL) was used to locate GPR profiles. A dewow filter and linear time gain function were used to reduce noise and enhance visibility of deeper structures in the radargrams. Time traces were then converted to depth profiles assuming a uniform radar velocity of 0.168 m ns−1 and were georeferenced and elevation-adjusted according to ice surface topography measured with differential GPS.
Thermistor strings were assembled with Fenwal Uni-Curve thermistors (5 kΩ, sn.192-502LET-A01) which were spliced onto and sealed into multiconductor cables at intervals of 1 m where the cold–temperate transition was expected to be, and at 5 m intervals elsewhere. At the bottom end of each thermistor string, a high-precision temperature-insensitive resistor (Vishay PTF56, 5 kΩ) was included as a means of isolating any changes in resistance resulting from cable stretching (Reference Pettersson, Jansson and HolmlundPettersson and others, 2003). The thermistors have a factory uncertainty of ±0.2°C, but laboratory calibration with a high-precision (±0.01°C) reference thermistor reduced this value to ±0.03°C. The thermistors were configured in half-bridges and logged at 30 m in intervals with a Campbell CR10X data logger and two Campbell AM-64 multiplexers.
Mean annual ice surface velocity was measured in 2006 and 2007 with a differential GPS (Trimble 4600 LS and 4000 SSI) and in 2007 and 2008 with a total station (Geodimeter 610). Aluminium stakes (5 m) were drilled vertically into the ice at 20 m intervals along each of the longitudinal transects. Most of the 20 stakes installed in 2006 were nearly melted out by late July 2007, so a new stake array was installed in 2007 using the same longitudinal transects as well as two new transverse transects. The new array was used for total station measurements in both 2007 and 2008. Four of the new stakes, arranged in a diamond that spanned the two transects (Fig. 2), were also used as a strain net to compute local strain rates. With atmospheric and stake-lean corrections, position errors are estimated to be of the order of 1–2 cm, yielding velocity uncertainties less than 1% of surface velocity at most stakes.
Basal motion was measured in 2007 and 2008 using ‘slidometers’ (conceptually like the ‘drag spools’ of Reference Blake, Fischer and ClarkeBlake and others (1994)). These consisted of miniature string potentiometers (Micro-Epsilon WPS1250-MK46-P) potted in dielectric grease-filled PVC containers. Anchors were stainless-steel cones, custom-machined to fit loosely on the tip of a cable-drawn insertion tool. When deployed through a borehole, a slidometer anchor was hammered into the glacier substrate with the potentiometer held in the borehole just above the bed. Any subsequent displacement of the ice enclosing the potentiometer relative to the anchor was then measured. Anchors were hammered as deeply as possible into the subglacial sediment layer to capture basal displacement due to both bed deformation and sliding.
Before installing slidometers, the bed was probed with a penetration tool allowing estimation of the thickness of basal till. Minimum till thicknesses varied from a few centimetres to a few decimetres; slidometers were deployed only where sediment was sufficiently thick to completely bury the anchor (≥5 cm). Some anchors may have been above the base of the till layer, causing basal displacement to be underestimated by not recording some deformation of the bed at depth.
One slidometer was used to measure fault motion across an englacial debris band (and therefore called a ‘thrustometer’). The instrument was deployed in a borehole along the north stake transect, ∼10 m up-glacier from the debris ridge (Fig. 2). Beginning at ∼9.5 m depth, drilling of this borehole proceeded unusually slowly for 20 cm, culminating in gushing of silt-laden water. Subsequent drilling was through clean ice. After the silty discharge from the borehole mouth ceased, a nearly buoyant anchor (steel hex nuts embedded in a block of wood) was attached to the end of 1.25 m of wire extending from the end of the potentiometer housing. The device was lowered into the borehole so that the anchor was suspended below the depth where debris was encountered and the potentiometer housing was above the debris. The instrument was then allowed to freeze in place.
Englacial velocity was investigated by repeat borehole inclinometry in four boreholes, two in each transect (labelled IBH in Fig. 2). A complete inclinometry survey was performed in new boreholes in August 2007, then repeated in the same holes after 1 year had elapsed. Between surveys, a wire rope was allowed to freeze into the borehole, after which it was presumed to behave passively as the ice deformed. In 2008, a special attachment for the drill stem allowed the nozzle to follow the wire while drilling. The borehole inclinometer (made by Geokon Inc., Lebanon, NH, USA, model 6000X) contained two orthogonally mounted accelerometers (in a plane normal to the long axis of the inclinometer casing) and a digital compass.
Following Reference Harper, Humphrey, Pfeffer, Huzurbazar, Bahr and WelchHarper and others (2001), the inclinometer had centring springs on each end of the 1.5 m long casing, allowing it to be deployed in an uncased borehole. After a borehole was drilled, the inclinometer was lowered in 1 m increments to the bottom of the hole. Voltage outputs for the two axes of tilt and the digital compass were recorded with a Campbell CR10X data logger at 2 s intervals. The instrument was then raised incrementally out of the borehole to obtain a second set of readings. This down-and-up sequence was repeated in a few boreholes to assess the measurement error. The instrumental uncertainty was ±0.02° in tilt and ±0.07° in azimuth, resulting in a maximum position error for each increment of ∼1 mm.
However, Reference Blake and ClarkeBlake and Clarke (1992) demonstrated that inclinometry may underestimate borehole tilt due to tension in the inclinometer cable, which tends to pull the top of the instrument into a more vertical orientation than the hole itself. As a result, inclinometry data provided minimum estimates of internal ice deformation and therefore yielded maximum estimates of basal velocities. Furthermore, because the position of only the borehole top was known, misalignment and instrumental error could propagate down the hole. Using the methods described by Reference Harper, Humphrey, Pfeffer, Huzurbazar, Bahr and WelchHarper and others (2001), the total uncertainty in our inclinometry-derived estimate of basal velocity was ∼±2.7 mm d−1 for a 25 m deep borehole.
Modelling approach
A two-dimensional (2-D) finite element model was applied to each of the two instrumented longitudinal transects, with the goal of exploring how conditions near the BTT affect surface velocity. Ice flow was idealized as steady. The finite element method was implemented using ELMER (www.csc.fi/elmer), a free multiphysics package developed by the Finnish IT Center for Science (e.g. Reference Gagliardini and ZwingerGagliardini and Zwinger, 2008).
Ice flow was modelled with the Stokes equations for an incompressible, non-inertial, power-law fluid:
where P is pressure, ρ i is the density of ice, g is the gravity vector, B is a viscosity parameter, n is the power-law exponent and v is the velocity vector. The viscosity parameter B was treated as a function of temperature using a form of the Arrhenius relationship:
where B 0 is a reference value for B, Q is the activation energy for ice creep, R g is the universal gas constant and T is temperature (Reference HookeHooke, 2005). Temperature fields in the domains were assumed to be steady. The value of B 0, a constant independent of temperature but not independent of n, was adjusted to yield favourable fits between measured and simulated englacial and ice-surface velocities.
Model domains were generated using ice-surface geometries derived from differential GPS surveys in 2008 and bed geometry derived from GPR bed reflections, adjusted according to measured borehole depths. Surface and bed topography were simplified to smooth third- or fourth-order polynomials (fitted with r 2 > 0.99) to eliminate corners that cause numerical artefacts. The geometries (especially at the bed) of the down-glacier edges of each domain were uncertain due to incomplete GPR coverage and late-season snow cover and were extrapolated from patterns established in the better-constrained portions of the terminus. These domains are shown in Figure 3, along with the boundary conditions and temperature fields.
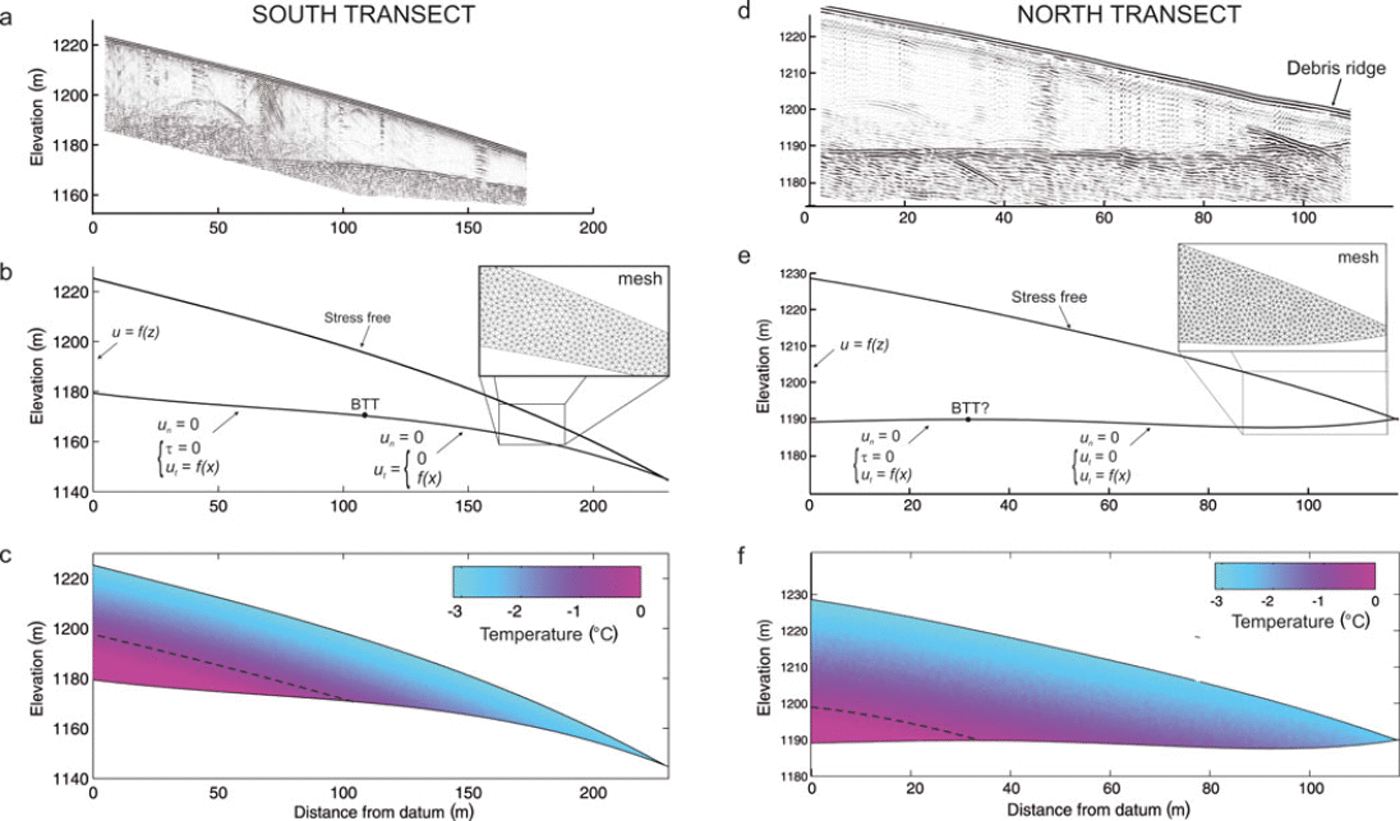
Fig. 3. Processed radargrams, boundary conditions and temperature fields for the two model domains: (a–c) south transect and (d–f) north transect. (a) GPR survey results from August 2008 along the south transect. (b) Domain boundary and boundary conditions, with an inset showing a portion of the computational mesh. Bracketed boundary conditions changed depending on which case (maximum or minimum basal velocity) was used. (c) Temperature field derived from thermistor measurements and radar results, simplified to a 2-D polynomial function. Nodal temperatures were interpolated from the temperature field to define the viscosity parameter using Equation (3).
Ice flow was driven by the gravitational body force and by velocity conditions at the left (inflow) boundary and the bed (Fig. 3). Plane strain was assumed. For both model domains, the inflow condition was varied between maximum and minimum conditions, based on bounds for englacial and subglacial velocities derived from inclinometer and slidometer measurements. In all cases, the inflow condition was set so that velocity at the upper-left corner (i.e. the boundary node at the top of the inflow boundary) was equal to the measured mean annual velocity there.
The basal boundary condition was defined in two ways to explore the effect of the basal velocity distribution on surface velocity. In one case a slip/no-slip condition was imposed at the point, inferred from GPR and thermistor measurements, where the glacier becomes cold-based. Up-glacier from that point, the bed was assumed to support zero shear stress, and down-glacier from the BTT no slip was permitted (cf. Reference Moore, Iverson and CohenMoore and others, 2009). In the second case, a polynomial function describing basal slip velocity was prescribed across the bed in accordance with field measurements. The ice surface in all cases was stress-free and fixed, implying that ice flux across the upper surface should be balanced by ablation to retain a steady-state geometry.
Initial model runs were used to test the sensitivity of the results to variations in rheological parameters B 0 and n (Table 1). Initial values of B0 were chosen to yield B values for n = 3 similar to published values for Storglaciären (∼7.0 × 27 Pa s1/3; e.g. Reference HansonHanson 1995). Since field measurements were concentrated in the south transect, sensitivity analysis was confined to that transect. Basal and inflow boundary conditions were then adjusted as described above, within the bounds allowed by field measurements of englacial and subglacial velocity. Resulting horizontal and vertical components of ice surface velocity were compared with measured values to determine sets of boundary conditions that best reproduced measured velocity components in both domains.
Table 1. Parameter values used in Storglaciären simulations

Results
Field data
Measured temperatures show that the cold surface layer at the terminus near the glacier centre line is 20–30 m thick (Fig. 4). All three thermistor strings installed in 2006 were apparently in temperate-based ice, so a string was installed in 2007 (06TH4) further down-glacier to verify that there was cold-based ice in the terminus. The lowest thermistor in that string recorded −0.022°C before it failed. This temperature is slightly less than the expected pressure-melting temperature (−0.017°C), but the measurement uncertainty exceeds this difference. The basal temperature gradient at 06TH4 remained steady at ∼−0.1°C m−1 over the course of an entire year. Extrapolation of a temperature field from the thermistors suggests that the BTT in the southern transect is at x = 108 ± ∼10 m (in the transect coordinate system). A smoothed representation of this temperature field is shown in Figure 3c.
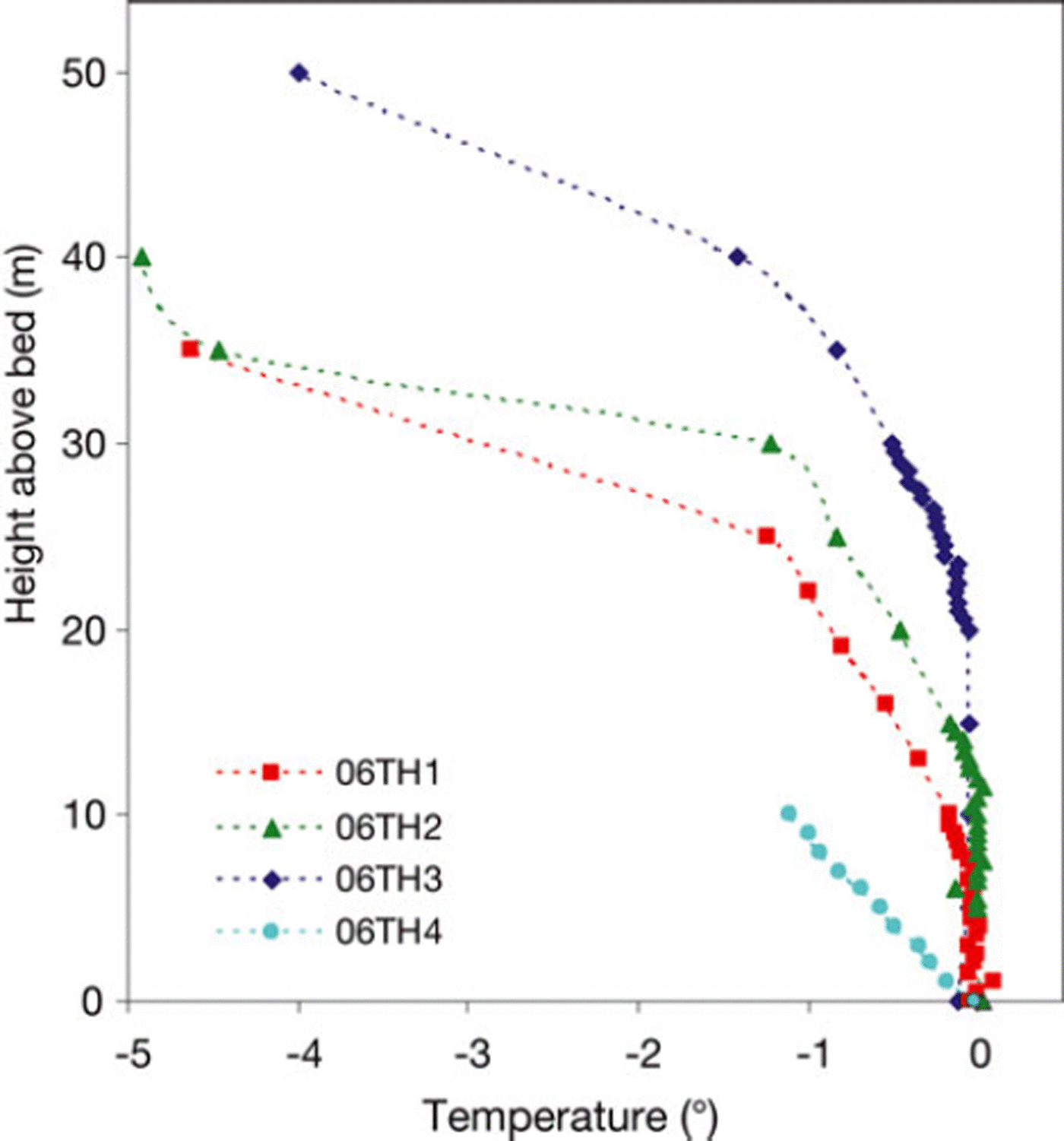
Fig. 4. Thermistor temperatures in the south transect as of November 2007. Thermistor strings 06TH1–06TH3 were installed in July 2006, while 06TH4 was installed in July 2007. Thermistor string 06TH3 is furthest up-glacier near x = 0, and 06TH4 is closest to the terminus. See Figure 2 for locations.
GPR results verify that both temperate-based and cold-based ice were present in the study area (Fig. 3a and d). Temperate ice is clearly visible in the south transect as a zone of diffuse, low-energy reflections that obscures the bed reflection. In the north transect these diffuse reflections are less prominent but visible to x = 30 m. Cold ice is largely transparent to the radar. Bed geometry is somewhat convex-up in the south transect and slightly concave-up at the lower end of the north transect. A strong down-glacier-dipping reflector of unknown origin is visible in the lower part of the north profile (appearing in surveys of the area in both April and August 2008; Fig. 3d). No up-glacier-dipping structure is evident in this profile at the expected location of the debris band, but a survey in the same area in late summer 2008 revealed a faint up-glacier-dipping reflection there (Reference MooreMoore, 2009). No distinct englacial planar reflections are visible in the south transect (Fig. 3a).
The horizontal component of ice surface velocity (as measured in 2007–08 with the total station) declined smoothly in both transects with proximity to the ice margin (Fig. 5), and roughly parallels the stake transects. Mean surface velocity was ∼25 mm d−1 at the upper end of each transect (Fig. 5). Horizontal velocities at stakes S1 and N1, the lowest in each transect, were non-negligible, particularly in the north where velocity was ∼9.5 mm d−1 in ice that is only ∼5 m thick. Vertical velocities in the south transect were negligible but approached 2.5 mm d−1 in the lower half of the north transect (Fig. 5).
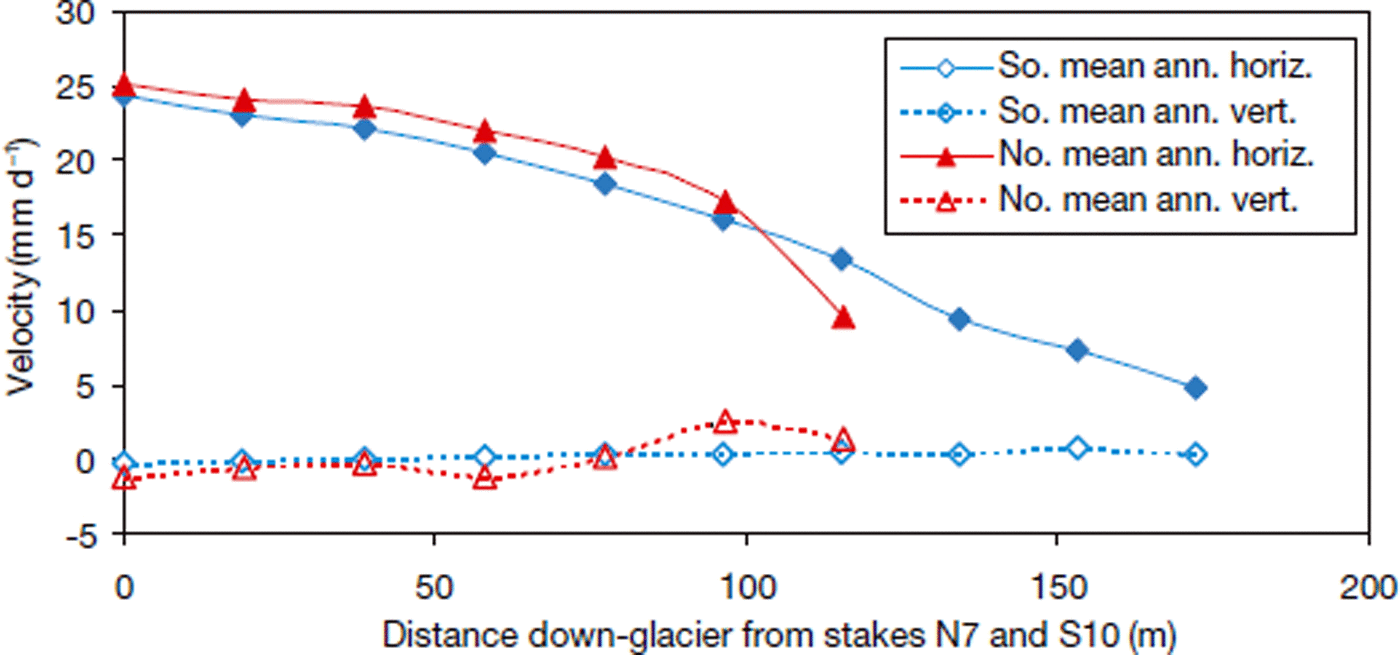
Fig. 5. Mean annual surface velocity components in both transects derived from total station measurements in 2007 and 2008.
Strain rates computed from the strain net indicate that longitudinal and vertical components of strain rate were an order of magnitude larger than transverse components. The mean annual longitudinal strain rate was 1.11 × 10−4 d−1, and the transverse component was 1.78 × 10−5 d−1 (compressive strains are positive). These results indicate that the model assumption of two-dimensional flow (plane strain) is reasonable in the terminus region. They also verify that the ice in the terminus region is under longitudinal compression.
Two of the four slidometers installed in 2007 yielded clear basal motion signals in early fall 2007, one for 2 months and the other for 1 month (Fig. 6a and b; SL7 and SL8). Both exhibited subtle diurnal signals but recorded fairly steady displacement rates when averaged over longer periods. These instruments were located close to the inferred BTT and up-glacier from it; during October 2007, the closer instrument recorded a smaller speed (∼1.4 mm d−1) than the instrument located 12 m further up-glacier (∼3.0 mm d−1).
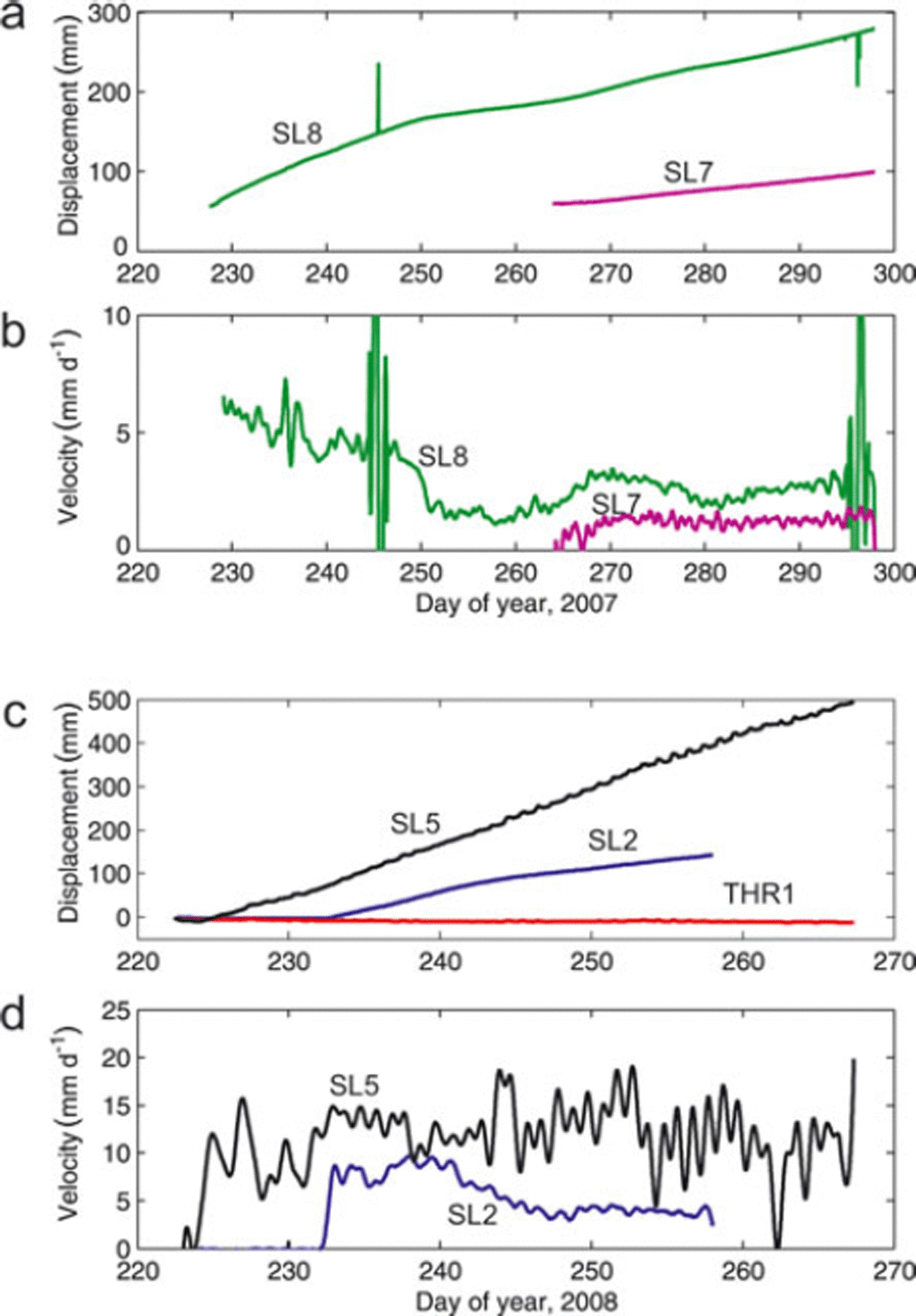
Fig. 6. Slidometer measurements from the terminus of Storglaciären in fall 2007 and 2008. Velocities were computed by applying a smoothing filter (third order Savitzky–Golay, 24 hour window) to numerically differentiated displacement records. (a) Displacement and (b) velocity from two slidometers (SL7 and SL8) along the south transect in 2007. (c) Displacement and (d) velocity from two slidometers and one ‘thrustometer’ in 2008. SL2 was in the upper part of the south transect, SL5 at the up-glacier end of the north transect. THR1 spanned the debris band in a borehole drilled near the down-glacier end of the north transect. See Figure 2 for locations.
In 2008 two slidometers, each near the up-glacier end of a transect, recorded continuous movement for more than 1 month (Fig. 6c and d, SL5 and SL2). In the south transect, SL2 recorded a long-term average displacement rate of 7.5 mm d−1 while SL5 in the north transect recorded average displacement rates of 11.2 mm d−1 with large diurnal variations. The instrument deployed as a thrustometer at the lower end of the north transect recorded no discernible displacement over 40 days of record.
Inclinometry results in four boreholes (two in each transect) indicate that internal ice deformation in the terminus was small, accounting for 0–23% of the total displacement of the borehole top measured with the total station (Fig. 7). The greatest internal deformation (23% of surface velocity) was recorded in BH9, which was located within a few metres of the inferred BTT in the south transect (Fig. 7b). A gentle quasi-parabolic profile is evident in the trajectory of BH9, but each of the three other boreholes (Fig. 7a, c and d) exhibits a plug-flow profile with surface and bed velocity almost equal. Maximum slip velocities derived from inclinometry range from 11.5 to 24.0 mm d−1, two to eight times larger than slip speeds from slidometer measurements in the same area.
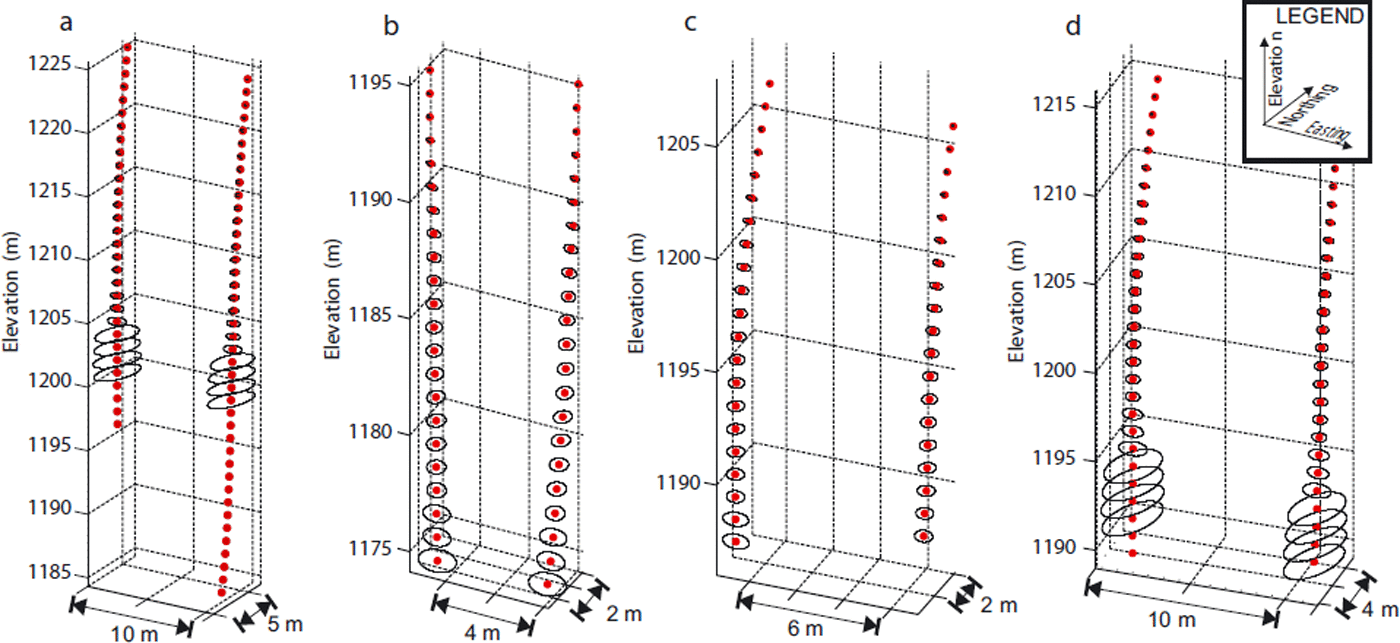
Fig. 7. Results from repeat inclinometry of boreholes (a) IBH3, (b) IBH9, (c) IBH21 and (d) IBH22 (see Fig. 2 for locations). One year elapsed between data collected in 2007 (left) and 2008 (right). Red circles denote the mean locations from multiple resurveys. Error ellipses were generated using the method outlined by Reference Harper, Humphrey, Pfeffer, Huzurbazar, Bahr and WelchHarper and others (2001), and are omitted for depths greater than 25 m due to the small datasets (and consequent large uncertainties) there. Net displacement at the base of the borehole corresponds to approximate basal velocity. Data deeper than 30 m from the first survey of IBH3 are missing because the survey was impeded by a borehole obstruction.
Model results
Model results were obtained using inflow and basal boundaryconditions derived from our measurements of surface velocity (velocity stakes), englacial velocity profiles (inclinometry) and basal slip velocity (inclinometry and slidometers). As mentioned previously, slidometer measurements probably underestimate basal velocities whereas inclinometry tends to underestimate borehole deformation, thereby overestimating basal velocity. Therefore, in driving the finite element model, we considered end-member cases in which slidometer and inclinometer data were considered to provide minimum and maximum basal velocities, respectively (Fig. 8). A crucial distinction between these cases is that for the minimum prescribed basal velocity there is a slip/no-slip transition. For the maximum-velocity case, however, velocity decreases smoothly towards the glacier margin. The slip/no-slip transition for the minimum-velocity case in the south transect is prescribed at x = 108 m, consistent with GPR, thermistor and slidometer measurements. Minimum and maximum basal velocity estimates in the north transect suggest that a slip/no-slip transition, if present at all, probably does not appear at the location of the BTT suggested by interpretation of GPR (x ∼ 30 m); rather, it appears over the strong internal reflection near the margin (x ∼ 90 m, Fig. 3d). Both a slip/no-slip transition at x = 90 m and a prescribed basal velocity that decreases nonlinearly towards the margin (Fig. 8b) are therefore considered in north-transect simulations.
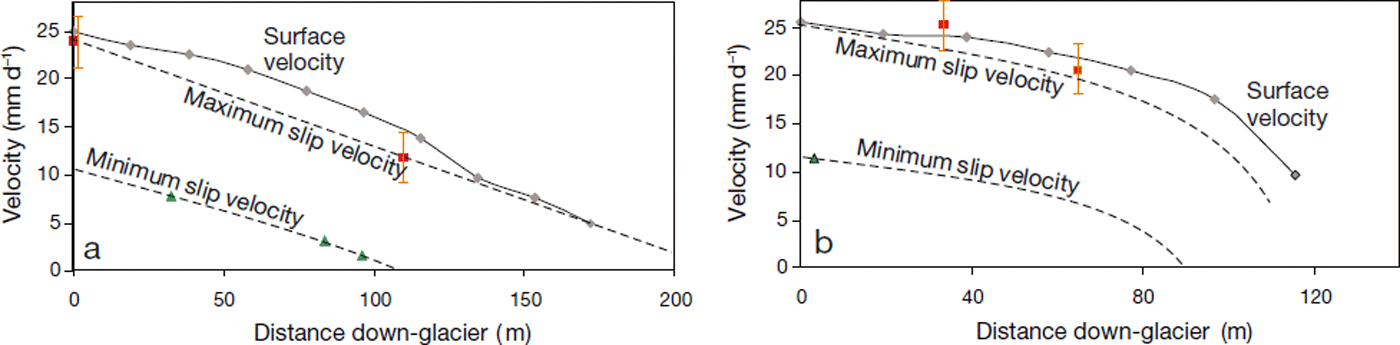
Fig. 8. Constraints on basal slip velocity in (a) south and (b) north transects. Maximum estimates are derived from inclinometry, whereas minimum estimates are derived from slidometers. Polynomial approximations of the trends shown as maxima and minima were used to drive the numerical models.
Modelled surface velocities for the south transect, using best estimates of B 0 and n (n = 3 and B 0 = 0.1 Pa s1/3) and the case of maximum basal velocity, are similar to measured surface velocities (Figs 9 and 10). Consistent with inclinometry, the inflow condition is plug flow with basal and surface velocity equal at the upper end of the domain. Basal velocity is prescribed as a linear function of distance along the transect, reaching zero only at the ice edge and therefore representing a case in which the cold base at the margin is mobile. The results are only subtly sensitive to prescribed values of B 0 and n (Fig. 10). Several combinations of rheological parameters produce surface velocities qualitatively similar to measured values, but stiffer parameter combinations (lower n or higher B 0) provide a better quantitative match of measurements.
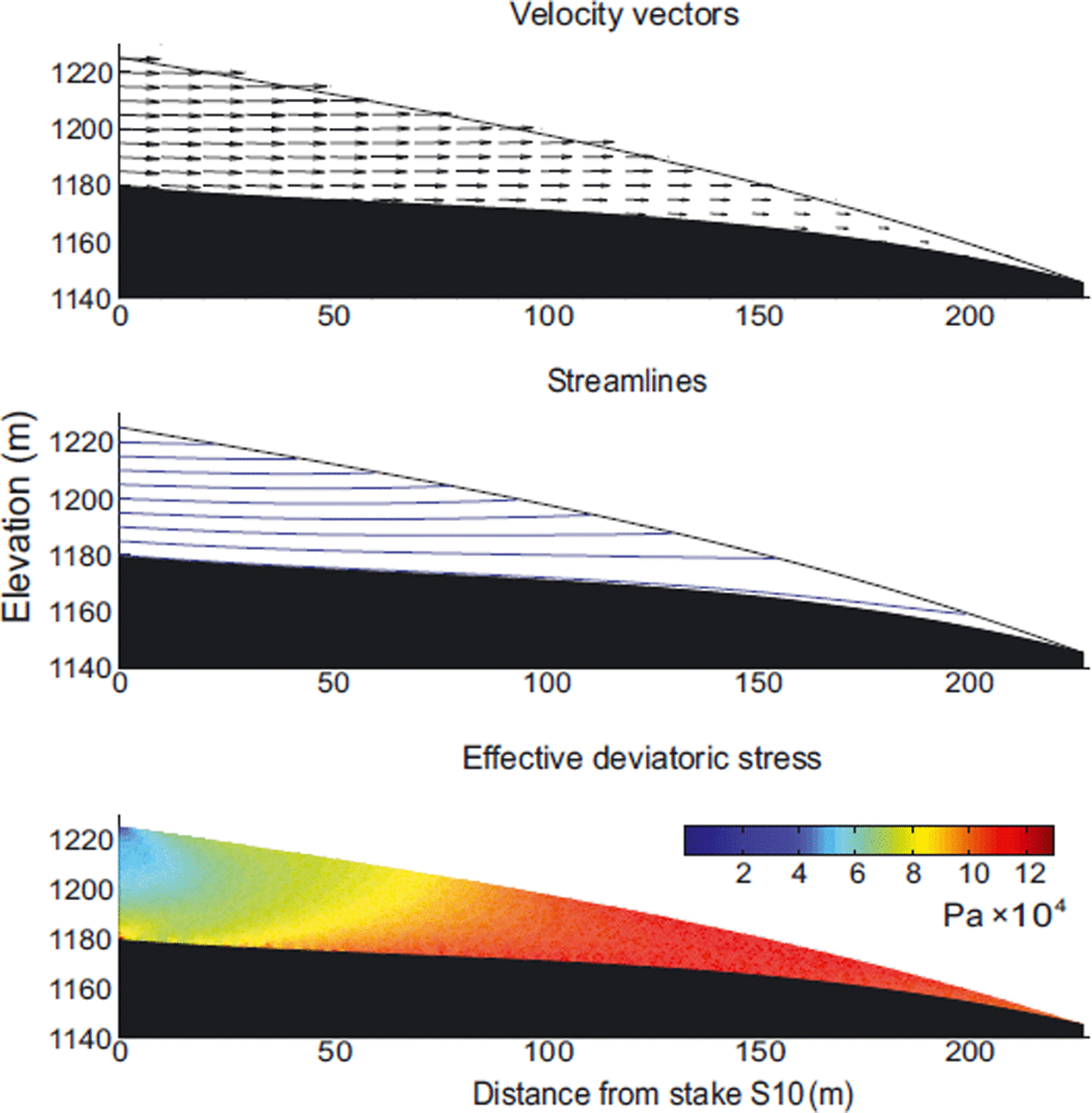
Fig. 9. Simulated velocity and stress fields in the south transect driven with a linear function describing basal slip velocity.
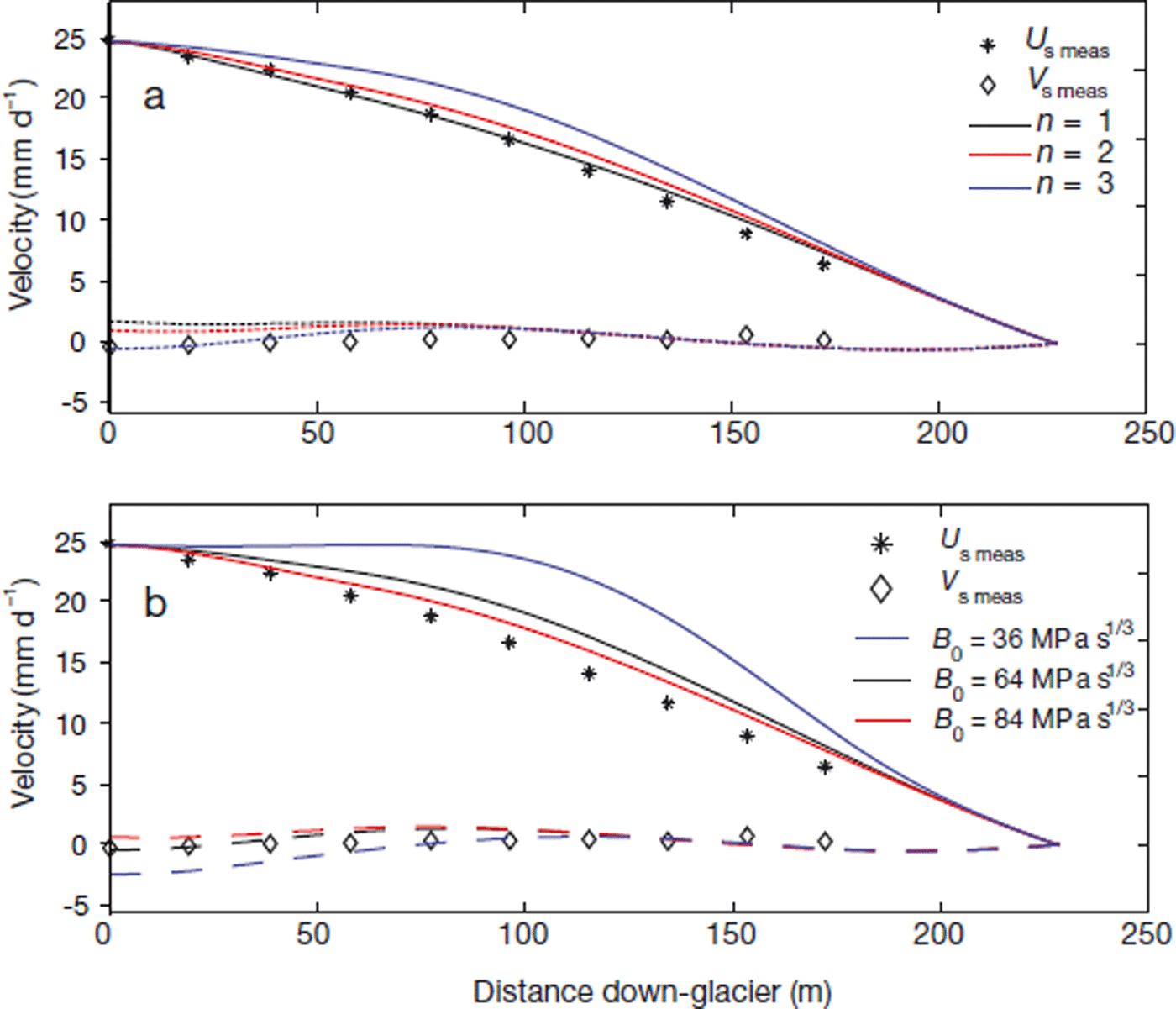
Fig. 10. Comparison between measured and modelled surface velocity components for south transect simulations and the sensitivity of model output to rheological parameters: (a) n and (b) B 0. Solid and dashed curves are the modelled horizontal and vertical component of surface velocity, respectively. Symbols are measured velocity components.
Changing the basal velocity conditions in the south transect to the minimum-slip velocity case with a slip/noslip transition significantly alters the ice flow and stress distribution (Fig. 11). Stresses are concentrated at the slip/noslip transition near x = 108 m, reaching >0.4 MPa; the ice is diverted to the surface, leaving stagnant ice closer to the margin. Surface velocity components for this simulation are inconsistent with measurements (Fig. 12). In this case, as with any simulation that contains a transition from slip to no-slip beneath the terminus, there is a steep decline in horizontal velocity and a peak in vertical velocity centred over the slip/no-slip transition that is not indicated by field measurements of the south transect.
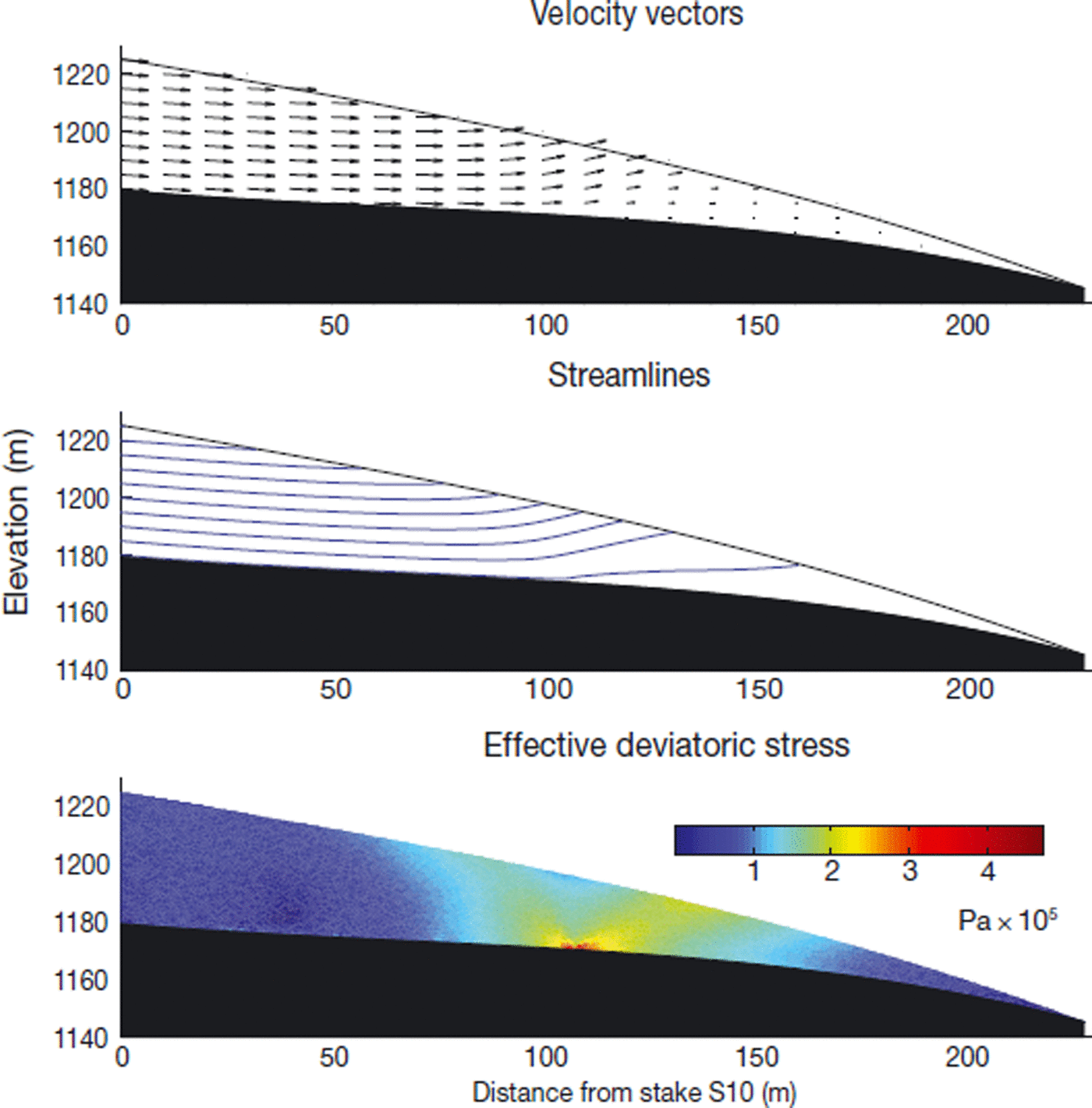
Fig. 11. Simulated velocity and stress fields in the south transect over a slip/no-slip transition in the bed at x = 108 m.
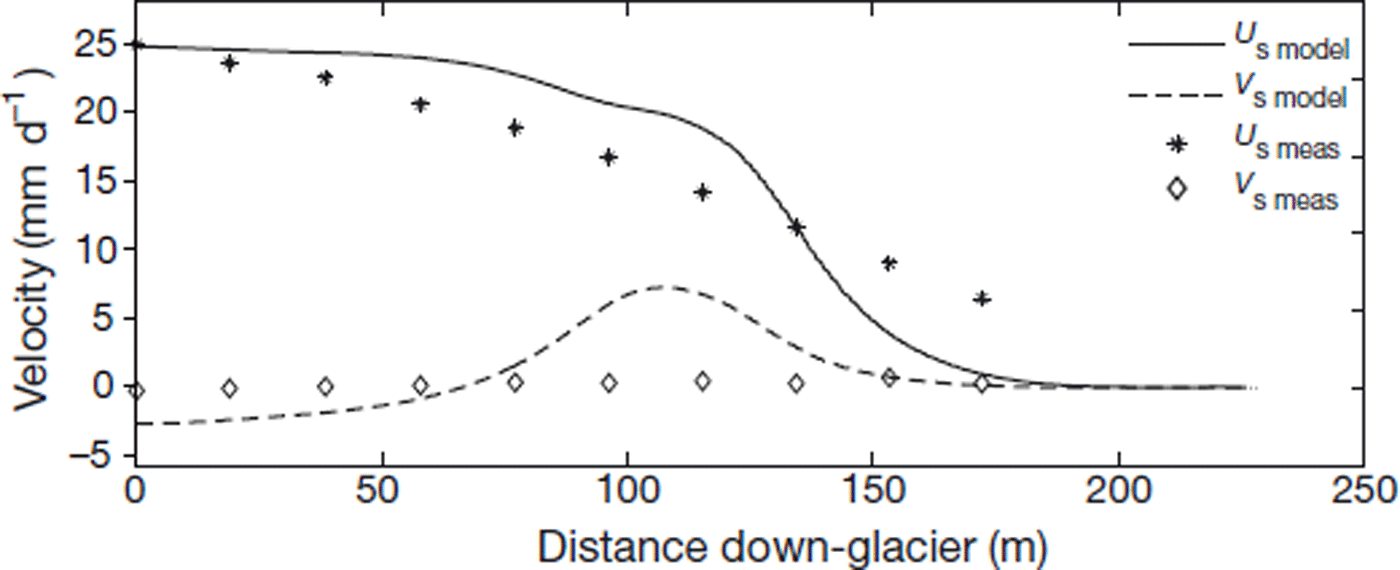
Fig. 12. Surface velocity in the south transect with flow over a slip/no-slip transition in the bed at x = 108 m. Measured surface velocity components are shown for comparison.
The results of numerical modelling of the south transect therefore indicate that a slip/no-slip transition is not present at x = 108 m or elsewhere. Simulated surface velocity components are best matched for high basal velocities if the ice is rheologically stiff, subject to some longitudinal push from up-glacier, and able to slip over the bed along the entire length of the transect. In contrast, for any simulation in which basal velocity is set to zero before the ice margin, there is a pronounced decrease in horizontal surface velocity accompanied by a local maximum in vertical surface velocity that is inconsistent with field measurements.
In the north transect also, a slip/no-slip transition results in surface velocities that are not consistent with measured values (Fig. 13). A slip/no-slip transition causes a large symmetrical peak in the vertical component of surface velocity and an abrupt decline in the horizontal component as ice is diverted away from the bed. Consequent horizontal velocities down-glacier from the slip transition are small compared to measurements, suggesting that a slip/no-slip transition is too extreme. In contrast, basal velocities that decrease smoothly towards the margin, in accordance with the polynomial function shown for the case of maximum slip velocity in Figure 8b, provide a good fit to measured surface velocities.
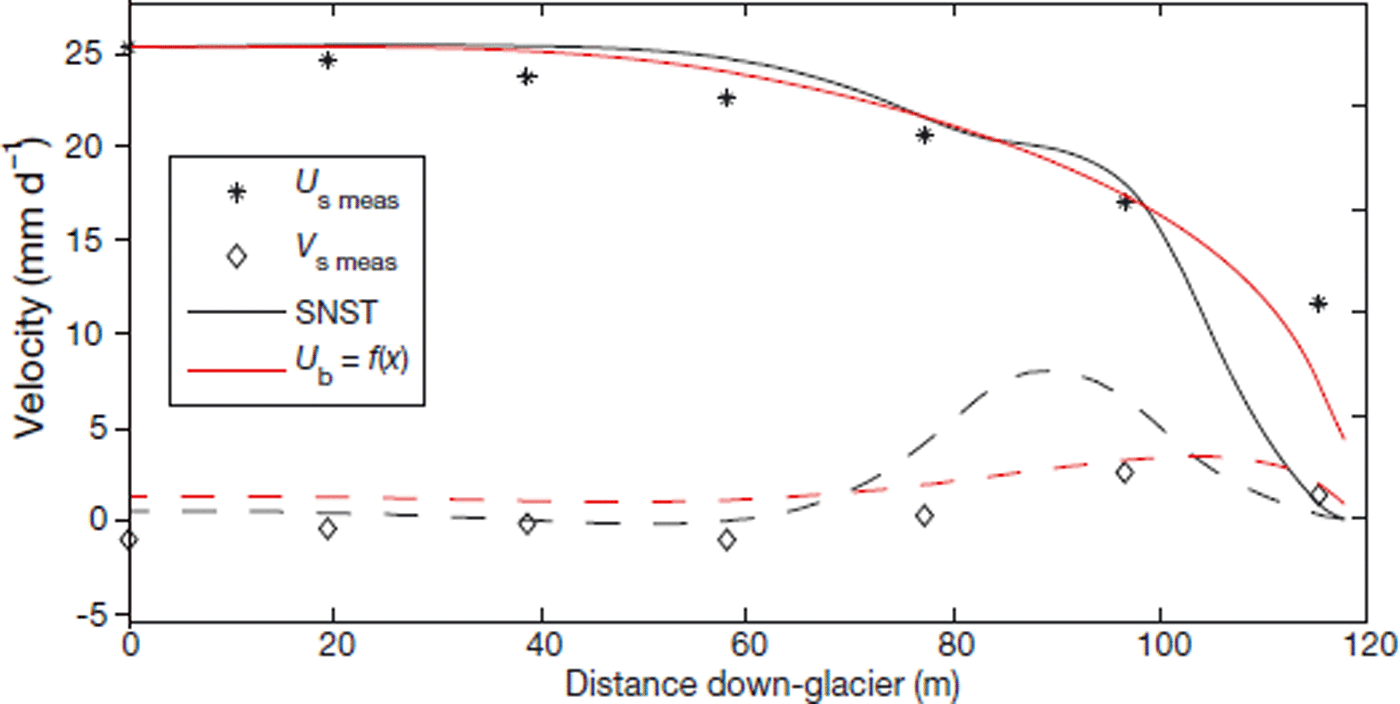
Fig. 13. Comparison of measured surface velocity components in the north transect with modelled surface velocity components. Curves correspond to horizontal (solid) and vertical (dashed) components of modelled velocity. Black curves represent the minimum basal velocity case in which a slip/no-slip transition (SNST) is assumed, whereas red curves represent the maximum basal velocity case in which a polynomial basal velocity function is prescribed all the way to the terminus.
Discussion
Thermistors and GPR indicate that the cold surface layer in the terminus of Storglaciären is 20–30 m thick and that a basal temperate ice layer is absent where ice is thinner than 20 m. In the south transect the BTT appears to be near x = 108 m based on extrapolation of the thermistor temperature field, although the deepest thermistor in 06TH4 (the furthest down-glacier thermistor string) is within measurement uncertainty of the melting temperature. Most of the ice within the study area along the north transect appears to be cold, although a thin wedge of temperate ice at the bed may be present as far down-glacier as x = 30 m. There is no evidence for isolated patches of temperate ice at the base as inferred at Bakaninbreen by Reference MurrayMurray and others (2000) and Reference Smith, Murray, Davison, Clough, Woodward and JiskootSmith and others (2002), although variable reflection strength may indicate differences in bed moisture content or bed composition. However, a bright englacial or subglacial reflector in the north transect (Fig. 3d) indicates that unfrozen and perhaps wet subglacial sediments may form a basal structure near the terminus, close to the expected downwards projection of the debris band. The bright reflector is not clearly separate from the bed and could therefore be a till mound at the bed or, alternatively, a persistent englacial or subglacial drainage structure filled with sediment.
Longitudinal compression across the BTT
Ice surface velocities do not exhibit any significant expression of a slip/no-slip transition at the BTT, as would be predicted based on model results presented here and in Reference Moore, Iverson and CohenMoore and others (2009, figs 4 and 5). Horizontal velocities decline steadily toward the terminus but remain substantial (e.g. ∼9.5 mm d−1 at stake N1) even at the lowest stake positions where ice is <10 m thick, showing that the terminus is not stagnant. The vertical component of ice surface velocity is near zero everywhere except near the ice margin in the north transect, several tens of metres (and thus several ice thicknesses) downstream from the BTT. These velocity patterns indicate that the BTT does not represent an abrupt change in basal slip resistance.
Slidometer measurements yielded consistently smaller basal slip velocities than the repeated inclinometry surveys: 10–40% compared to 70–100% of surface velocity, respectively. Model results driven with slidometer-derived basal slip velocities –the case of minimum slip velocity (Fig. 8) –do not produce surface velocity patterns that match measurements (Fig. 12). If the ice is stiff (high B0, consistent with cold ice), model results driven with the inclinometry derived basal slip extrapolated to the terminus (the case of maximum slip velocity; see Fig. 8) agree better with measurements (Fig. 10).
Basal motion, either by sliding or bed deformation, therefore must account for most of the ice motion across the terminus, even down-glacier from the BTT where the ice is cold at the bed. One explanation for the under-representation of basal motion by the slidometers is that some motion occurred deeper within the substrate than the slidometer anchors were inserted, or perhaps at a till–bedrock interface (Reference Truffer, Harrison and EchelmeyerTruffer and others, 2000). An alternative explanation is that some slidometer anchors were partly incorporated into the moving glacier base, either by freeze-on or by squeezing of till into the base of the boreholes through which the slidometers were installed.
A force-balance analysis (outlined in the Appendix) based on our surface velocity measurements yields results that are qualitatively similar to those of Reference Brzozowski and HookeBrzozowski and Hooke (1981) and Reference Hedfors, Peyaud, Pohjola, Jansson and PetterssonHedfors and others (2003). Depth- and time-averaged longitudinal stresses are expected to impose ∼25 kPa of additional basal shear stress at the terminus. This is less than half of the local driving stresses estimated from f ρ i gh i sin α s (∼60 kPa for a shape factor f = 0.65) and is small compared to the stresses predicted by models of ice flowing over a slip/no-slip boundary (Reference Moore, Iverson and CohenMoore and others, 2009). Nevertheless, this estimate implies that the terminus (or part of it) is more strongly coupled to the bed than the ice up-glacier. Inspection of Figure 5 indicates that the local longitudinal strain rate at the down-glacier end of the north transect is probably greater than anywhere else in the study area. There is no evidence of a significant thermal transition in this region. However, the gentle adverse bed slope shown in Figure 3d does change in the same part of the north domain where velocity gradients change, suggesting that longitudinal stress is more strongly affected by bed geometry than thermal regime.
Character of the frozen margin
Model results indicate that the cold ice must be able to move over the bed to account for observed surface velocities in both the north and south transects. This implies that the BTT (defined by thermistor measurements and GPR surveys as the pointwhere the basal layer of temperate ice disappears) is not a slip/no-slip transition. Two interpretations are possible: (1) the freezing isotherm meets the bed where we have identified the BTT, but down-glacier the glacier base remains at the melting temperature; or (2) the freezing isotherm descends into the bed, resulting in ice and sediment accretion, and there is slip along the isotherm or deformation in the till below it. The second scenario requires a widespread subglacial sediment layer, a constraint that is met beneath the margin of Storglaciären (Reference Baker, Hooyer and JanssonBaker and Hooyer, 1996).
The character of the freezing isotherm where it encounters the bed is not well known at any polythermal glacier. Theoretical considerations suggest that there are three distinct thermal zones surrounding the BTT (Fig. 14). Where the base of a glacier contains a temperate ice layer (T-zone), no heat may be conducted away from the ice–bed interface and any heating of the glacier base may melt ice only at the interface (Reference Blatter and HutterBlatter and Hutter, 1991; Reference Fowler, Murray and NgFowler and others, 2001). Where a glacier is cold throughout its thickness but reaches the melting temperature at the bed, a heat flux qc = −kdT/dz is conducted upwards, where k is the thermal conductivity of ice, T is temperature and z is vertical distance. Any additional heat supplied to the base of the ice that cannot be conducted upwards may be used for melting (warm (W) zone). If the heat that can be conducted away from the bed exceeds that supplied by heat sources (e.g. geothermal heat), subglacial water must supply the deficit by freezing at the ice–bed interface or within the pore spaces of subglacial sediment (cold (C) zone). The heat-balance inequality that distinguishes the W and C zones determines whether the freezing isotherm remains at the bed or descends into it. This inequality therefore also determines whether sliding of clean ice over the substrate can accommodate motion or whether motion must occur within a subglacial sediment layer.
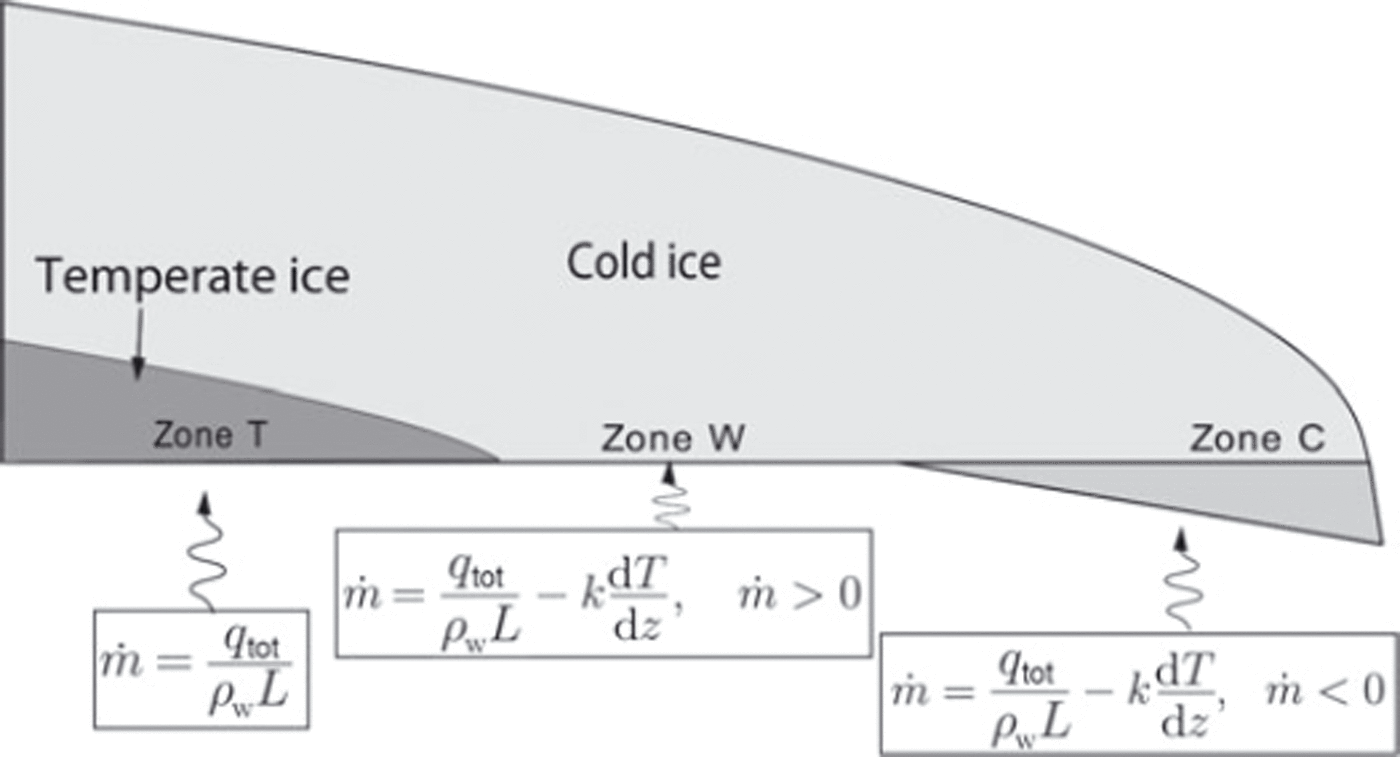
Fig. 14. Schematic illustration of three thermal zones at the basal thermal transition (BTT). See text for descriptions of zones T, W and C. q tot is the sum of basal heat fluxes due to geothermal heat, friction and pore-water flow. All other variables are defined in the Appendix.
Thermistor measurements from the furthest down-glacier thermistor string (06TH4) indicate a basal temperature gradient near the BTT of −0.1°Cm−1 (Fig. 4), implying a basal heat flux of 0.210 W m−2. This basal heat flux is about four times larger than typical continental geothermal fluxes and also four times larger than the flux inferred from a deep permafrost borehole across the valley from Storglaciären (Reference Isaksen, Holmlund, Sollid and HarrisIsaksen and others, 2001). Thus, additional heat sources are required to explain the measured temperature gradient. Possible sources include heat from sliding friction, dissipated energy from basal water flow and latent heat from basal freezing (Reference Clarke, Collins and ThompsonClarke and others, 1984; Reference PatersonPaterson, 1994).
Basal velocities of Storglaciären are small, so frictional heating is insignificant (∼0.005 W m−2 compared to a geothermal flux of ∼0.05 W m−2). Storglaciären is underlain by a layer of till that could act both as a porous meltwater passage and as accommodation space for subglacial freezing, so basal water flow and freeze-on may both contribute. However, only latent heat from basal freezing can produce a heat supply that increases down-glacier. A down-glacierincreasing heat source is required if the vertical temperature gradient steepens due to thinning ice towards the margin.
A one-dimensional energy balance (see Appendix) indicates that a freeze-on rate of a few centimetres to a few decimetres per year can account for the needed heat flux. No englacial temperature data are available in the north transect, so we cannot perform a similar energy balance there. However, textural and geochemical analyses indicate that bands of debris outcropping at the ice surface there were entrained from the bed a short distance from the terminus by freeze-on (Reference MooreMoore, 2009).
Results of Reference Echelmeyer and WangEchelmeyer and Wang (1987) and Reference MaohuanMaohuan (1992) from the subpolar Ürümqi glacier No. 1, China, may be relevant to our observations. From a tunnel excavated into the cold-based terminus, Reference Echelmeyer and WangEchelmeyer and Wang (1987) measured basal motion that accounted for nearly all of the surface velocity, despite basal temperatures less than −1 °C. Internal pervasive shear of frozen subglacial till accounted for ∼60% of the surface motion while the remainder of basal motion was accommodated by slip along discrete surfaces within the basal ice and frozen till. The authors also measured steep vertical basal temperature gradients (−0.3°C m−1), and attributed the excess basal heat flux to subglacial water flow.
An alternative explanation for our observations is therefore that basal motion is accommodated within a frozen basal or subglacial debris layer. Subsequent work at Ürümqi glacier No. 1 by Reference MaohuanMaohuan (1992), however, indicated that the 0°C isotherm was sufficiently deep near the terminus that it was within sub-till bedrock, thereby bonding the glacier and till to a rigid substrate. Bedrock reflections are not apparent in radar surveys in the central part of the terminus of Storglaciären, and a trench excavated in the ice margin in 1995 encountered no bedrock within 1.25 m of the glacier sole (Reference Baker, Hooyer and JanssonBaker and Hooyer, 1996). Therefore, unfrozen till likely underlies frozen-on till under the terminus. This unfrozen till should be more susceptible to shear than its overlying frozen counterpart. Furthermore, a permeable subglacial layer must be available if pore-water flow and freeze-on supply the excess basal heat required by the steep vertical temperature gradient. These circumstantial lines of evidence support the hypothesis that the glacier terminus and accreted debris-bearing basal ice move over a weak, unfrozen substrate.
Sediment transport paths in glaciers are controlled largely by ice flow trajectories. Conditions that affect ice flow vectors will therefore also dictate transport paths until the sediment is released by the glacier. Near the margin of Storglaciären, longitudinal compression (and thus departure from bed-parallel flow) appears to correlate with changes in bed topography more strongly than with basal thermal regime. Sediment already entrained in the glacier is therefore more readily elevated from low-level to high-level transport where basal motion is impeded by an adverse bed slope or basal obstacle. This may help to explain why supraglacial accumulation of basally derived sediment is limited to the northern part of the margin of Storglaciären, even though the BTT extends across the entire terminus (Reference MooreMoore, 2009).
Conclusions
Radar and thermistor measurements indicate that the cold surface layer of Storglaciären meets the bed ∼100 m from the terminus. Basal freezing likely occurs where this cold ice thins towards the glacier margin. However, model evaluation of basal and surface velocities indicates that basal sliding or bed deformation must occur beneath the cold-based margin. Therefore, the BTT does not represent a slip/no-slip transition. Rather, weak unfrozen till beneath the freezing isotherm likely allows basal motion beneath cold ice all the way to the terminus. The deformability of this unfrozen basal layer therefore limits the magnitude of longitudinal compression caused by the cold margin. Indeed, local longitudinal strain rates in the glacier appear to be influenced more strongly by the topography of the glacier bed than by changes in basal thermal regime. Thus, where the margins of polythermal glaciers rest on soft beds, sediment transport paths (and therefore ultimately landform assemblages) can be insensitive to basal thermal regime.
Acknowledgements
We thank J. Byers, M. Dettinger and particularly R. Pettersson for field assistance. We thank S. Cook for a thorough review that led to improvements in the paper. This work was supported by US National Science Foundation grant EAR-0541918 to N.R.I. and D.C.
Appendix
Force balance in the terminus
Longitudinal stress gradients can be estimated from velocities measured at the glacier surface using the force-balance method (Reference Van der Veen and WhillansVan der Veen and Whillans, 1989). A necessary assumption is that strain rates at the surface are representative of depth-averaged values, which is broadly consistent with our inclinometry measurements. In the study area, ice is 10–40 m thick. We consider average stresses over longitudinal distances of 100 m. Following Reference HookeHooke (2005), the relationship between the dominant terms in a balance of stresses is
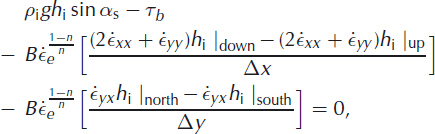
where α
s is ice surface slope, h
i is local ice thickness, ![]() ,
, ![]() and
and ![]() are longitudinal, transverse and shearstrain-rate components, respectively, and subscripts up, down, north and south refer to the vertical faces of the ice volume of interest. Significant simplification can be achieved if all strain rates with y-components are neglected. The force balance then reduces to
are longitudinal, transverse and shearstrain-rate components, respectively, and subscripts up, down, north and south refer to the vertical faces of the ice volume of interest. Significant simplification can be achieved if all strain rates with y-components are neglected. The force balance then reduces to
where the third term on the left-hand side is often called the G-term.
Using measured ice thicknesses and velocities for stakes N6–7, N1–2, S2–3 and S9–10, computed values of the G-term indicate that the terminus in both north and south transects supports ∼20–25 kPa of basal shear stress in excess of local driving stress. A drawback of using an averaging length of 100 m is that the along-flow variation in strain rates observed in the north transect is eliminated. If shorter averaging lengths were used, the lower part of the north transect would likely stand out as a site of locally enhanced stress gradients.
Energy balance beneath the terminus
The heat balance at the bed of a glacier can be written:
where the terms on the left-hand side correspond to geothermal heat flux, heat production or consumption due to freezing or melting at the bed, heat dissipation due to groundwater flow, frictional heat and heat conducted away from the bed. As mentioned in the main text, the frictional term for Storglaciären is expected to be small and is therefore neglected. The second term, q
m, is of a different sign depending on whether ice is freezing onto or melting from the base of the glacier. Defining ![]() as the rate of basal melting (where a negative value indicates freeze-on), the heat flux from this source is
as the rate of basal melting (where a negative value indicates freeze-on), the heat flux from this source is
where n t is the porosity of the subglacial till, ρ i is ice density and L is the latent heat of fusion. The heat flux dissipated by till pore-water flow (e.g. Reference Clarke, Collins and ThompsonClarke and others, 1984; Reference Manga and KirchnerManga and Kirchner, 2004) is
where Q/w is discharge per unit width and the hydraulic potential ϕ h = ρ w gH t where ρ w is the density of water, g is acceleration due to gravity and H t is the total hydraulic head. Combining this with Darcy’s law, we obtain the heat flux:
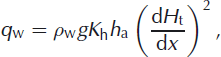
where K h h a is the hydraulic transmissivity of the subglacial aquifer. If the possible effect of aquifer blockage by ice on the hydraulic gradient is neglected, then Equations (A3–A6) with q c = −kdT/dz yield:
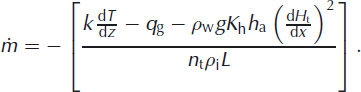
Assuming that the mean hydraulic gradient across the cold margin is proportional to ice surface slope and estimating the vertical temperature gradient down-glacier from 06TH4 from terminus geometry, the basal freezing rate needed to account for ice thinning towards the terminus is of the order of 10−1−10−2 m a−1.

















