Article contents
Conditional analysis on extreme wall shear stress and heat flux events in compressible turbulent boundary layers
Published online by Cambridge University Press: 03 November 2023
Abstract
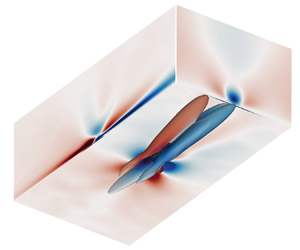
This study presents a comprehensive analysis on the extreme positive and negative events of wall shear stress and heat flux fluctuations in compressible turbulent boundary layers (TBLs) solved by direct numerical simulations. To examine the compressibility effects, we focus on the extreme events in two representative cases, i.e. a supersonic TBL of Mach number  $M=2$ and a hypersonic TBL of
$M=2$ and a hypersonic TBL of  $M=8$, by scrutinizing the coherent structures and their correlated dynamics based on conditional analysis. As characterized by the spatial distribution of wall shear stress and heat flux, the extreme events are indicated to be closely related to the structural organization of wall streaks, in addition to the occurrence of the alternating positive and negative structures (APNSs) in the hypersonic TBL. These two types of coherent structures are strikingly different, namely the nature of wall streaks and APNSs are shown to be related to the solenoidal and dilatational fluid motions, respectively. Quantitative analysis using a volumetric conditional average is performed to identify and extract the coherent structures that directly account for the extreme events. It is found that in the supersonic TBL, the essential ingredients of the conditional field are hairpin-like vortices, whose combinations can induce wall streaks, whereas in the hypersonic TBL, the essential ingredients become hairpin-like vortices as well as near-wall APNSs. To quantify the momentum and energy transport mechanisms underlying the extreme events, we proposed a novel decomposition method for extreme skin friction and heat flux, based on the integral identities of conditionally averaged governing equations. Taking advantage of this decomposition method, the dominant transport mechanisms of the hairpin-like vortices and APNSs are revealed. Specifically, the momentum and energy transports undertaken by the hairpin-like vortices are attributed to multiple comparable mechanisms, whereas those by the APNSs are convection dominated. In that, the dominant transport mechanisms in extreme events between the supersonic and hypersonic TBLs are indicated to be totally different.
$M=8$, by scrutinizing the coherent structures and their correlated dynamics based on conditional analysis. As characterized by the spatial distribution of wall shear stress and heat flux, the extreme events are indicated to be closely related to the structural organization of wall streaks, in addition to the occurrence of the alternating positive and negative structures (APNSs) in the hypersonic TBL. These two types of coherent structures are strikingly different, namely the nature of wall streaks and APNSs are shown to be related to the solenoidal and dilatational fluid motions, respectively. Quantitative analysis using a volumetric conditional average is performed to identify and extract the coherent structures that directly account for the extreme events. It is found that in the supersonic TBL, the essential ingredients of the conditional field are hairpin-like vortices, whose combinations can induce wall streaks, whereas in the hypersonic TBL, the essential ingredients become hairpin-like vortices as well as near-wall APNSs. To quantify the momentum and energy transport mechanisms underlying the extreme events, we proposed a novel decomposition method for extreme skin friction and heat flux, based on the integral identities of conditionally averaged governing equations. Taking advantage of this decomposition method, the dominant transport mechanisms of the hairpin-like vortices and APNSs are revealed. Specifically, the momentum and energy transports undertaken by the hairpin-like vortices are attributed to multiple comparable mechanisms, whereas those by the APNSs are convection dominated. In that, the dominant transport mechanisms in extreme events between the supersonic and hypersonic TBLs are indicated to be totally different.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 9
- Cited by



