Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T17:39:05.187Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized Cesàro Matrices

Published online by Cambridge University Press:  20 November 2018

H. C. Rhaly Jr
H. C. Rhaly Jr*
Affiliation:
Department of Mathematics, University of Mississippi, University, Mississippi 38677
*
Current Address: Department of Mathematics, Millsaps College, Jackson, Mississippi 39210
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For α ∈ [0, 1] the operator 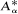is the operator formally defined on the Hardy space H2 by

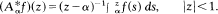
If α = 1, then the usual identification of H2 with l2 takes A1 onto the discrete Cesàro operator. Here we see that {Aα: α ∈ [0, 1]} is not arcwise connected, that Re Aα ≥ 0, that Aα is a Hilbert-Schmidt operator if α ∈[0, 1), and that Aα is neither normaloid nor spectraloid if α ∈(0, 1).

Keywords

47B9947A1247B1047B38Cesàro operatorHilbert-Schmidt operatornumerical range
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 27 , Issue 4 , 01 December 1984 , pp. 417 - 422
Copyright
Copyright © Canadian Mathematical Society 1984

References

1. Brown, A., Halmos, P. R. and Shields, A. L., Cesàro operators, Acta Sci. Math. (Szeged) 26 (1965), 125-137.Google Scholar
2. Donoghue, W. F., On the numerical range of a bounded operator, Michigan Math. J. 4 (1957), 261-263.CrossRefGoogle Scholar
3. Halmos, P. R., A Hubert Space Problem Book, Van Nostrand, Princeton, 1967.Google Scholar
4. Halmos, P. R. and Sunder, V. S., Bounded Integral Operators on L2 Spaces, Springer-Verlag, New York, 1978.CrossRefGoogle Scholar
5. Lancaster, P., Theory of Matrices, Academic Press, New York, 1969.Google Scholar
6. Rhaly, H. C., Discrete generalized Cesàro operators, Proc. Amer. Math. Soc. 86 (1982), 405-409.Google Scholar