1. Introduction
The time-dependent motion of small particles immersed in viscous fluids has been studied extensively, providing the foundations for a multitude of applications and technologies. One prominent application is in microrheology where the characterisation of particle dynamics forms the basis for measurement (Squires & Mason Reference Squires and Mason2010). Examples include the optical trapping of small spherical particles (Atakhorrami et al. Reference Atakhorrami, Koenderink, Schmidt and MacKintosh2005, Reference Atakhorrami, Mizuno, Koenderink, Liverpool, MacKintosh and Schmidt2008) through to monitoring of the rotational diffusion of highly non-spherical microdisks (Cheng & Mason Reference Cheng and Mason2003). Particle motion in such microrheological measurements can be induced either passively (e.g. via Brownian fluctuations) or through active forcing (e.g. using an electric/magnetic field).
Another example where unsteady particle motion can be used to advantage is in the autonomous propulsion of non-spherical particles in acoustic fields. It is known that when small particles, with either shape or density asymmetries, are trapped at the pressure node of an acoustic standing wave, they can undergo autonomous (self-induced) propulsion (e.g. see Wang et al. Reference Wang, Castro, Hoyos and Mallouk2012; Rao et al. Reference Rao, Li, Meng, Zheng, Cai and Wang2015; Ahmed et al. Reference Ahmed, Wang, Bai, Gentekos, Hoyos and Mallouk2016). The primary mechanism proposed for this experimentally observed propulsion is (nonlinear) acoustic streaming, driven by (linear) small-amplitude oscillatory motion of the particle itself (Nadal & Lauga Reference Nadal and Lauga2014; Collis, Chakraborty & Sader Reference Collis, Chakraborty and Sader2017; Nadal & Michelin Reference Nadal and Michelin2020). In this application, coupling of translational and rotational motion of the particle drives directed streaming, producing a jet which propels the particle (Collis et al. Reference Collis, Chakraborty and Sader2017; Nadal & Michelin Reference Nadal and Michelin2020; Collis, Chakraborty & Sader Reference Collis, Chakraborty and Sader2022). Interestingly, Lippera et al. (Reference Lippera, Dauchot, Michelin and Benzaquen2019) proved that no propulsion occurs to first order in the radial shape perturbation of nearly spherical particles. This established that higher-order effects drive propulsion of these particles.
Such applications of unsteady particle motion are not limited to rigid particles. For example, Pelton et al. (Reference Pelton, Chakraborty, Malachosky, Guyot-Sionnest and Sader2013) studied the small-amplitude (oscillatory) elastic vibration of bipyramidal gold nanoparticles that are performing ultra-high-frequency (gigahertz) elastic vibrations in fluid. The short time scale of the generated unsteady flow (in the picosecond regime) naturally interrogates molecular relaxation processes in simple liquids (Slie, Donfor & Litovitz Reference Slie, Donfor and Litovitz1966; O'Sullivan et al. Reference O'Sullivan, Kannam, Chakraborty, Todd and Sader2019). This allows for direct interrogation of the viscoelastic response of these liquids (Chakraborty et al. Reference Chakraborty, Hartland, Pelton and Sader2018), which constitutes an application of nanorheology (Canale et al. Reference Canale, Comtet, Niguès, Cohen, Clanet, Siria and Bocquet2019). An understanding of the hydrodynamic interaction of small particles is essential for interpreting measurements in all of the applications mentioned above.
Perfect solid spheres are a rare occurrence in nature, yet are used ubiquitously to model real-world phenomena including some of the applications listed above. A canonical example in fluid mechanics is the drag experienced by a perfect solid sphere moving steadily in a viscous fluid at low Reynolds number, i.e. Stokes’ law (Stokes Reference Stokes1851). The resulting formula, and its variants as a function of geometry, have found broad-ranging applications that include the sedimentation of dilute particulate suspensions (Richardson & Zaki Reference Richardson and Zaki1954) through to the characterisation of optical laser traps (Perkins Reference Perkins2009).
Viscous flows generated by the motion of small particles occur precisely in this low-Reynolds-number regime. Consequently, they are often treated under the framework of the unsteady Stokes equations (that naturally encompass the steady case), which neglect the fluid's convective inertia while retaining its local inertia. This simplified approach is justified in a range of applications, including the small-amplitude oscillatory motion of micro- and nanoparticles. Neglect of the fluid's convective inertia greatly simplifies calculation of the flow field, leading to results that are linear in the particle velocity while generally retaining the dominant physical processes (Batchelor Reference Batchelor2000). A well-known exception is ‘Stokes’ paradox’ for the steady, two-dimensional flow generated by a cylinder in an unbounded fluid, where convective inertial effects balance viscous effects in the particle's far field. Importantly, such exceptions do not occur in unsteady flows, flows generated by three-dimensional bodies or in bounded fluid domains.
Because particles are often modelled as perfect spheres, knowledge of the effects of (any degree of) non-sphericity is important for practical implementation. A key contribution to this understanding was reported by Zhang & Stone (Reference Zhang and Stone1998) who developed an analytical theory that considers the radial degree of non-sphericity to be asymptotically small, quantified by the small non-dimensional parameter ![]() $\epsilon$. That previous work examined the effect of non-sphericity on the force and torque experienced by a nearly spherical particle undergoing arbitrary translational and rotational motion.
$\epsilon$. That previous work examined the effect of non-sphericity on the force and torque experienced by a nearly spherical particle undergoing arbitrary translational and rotational motion.
The theory of Zhang & Stone (Reference Zhang and Stone1998) is derived to first order in the non-spherical shape parameter ![]() $\epsilon$, i.e. it is correct to
$\epsilon$, i.e. it is correct to ![]() $O(\epsilon )$. While accounting for much of the fluid physics of nearly spherical particles, this first-order approach does not capture several phenomena exhibited by non-spherical particles. For example, non-spherical particles undergoing pure steady translation experience finite torque. The first-order theory of Zhang & Stone (Reference Zhang and Stone1998) predicts that this torque (about the particle's geometric centre) is identically zero to
$O(\epsilon )$. While accounting for much of the fluid physics of nearly spherical particles, this first-order approach does not capture several phenomena exhibited by non-spherical particles. For example, non-spherical particles undergoing pure steady translation experience finite torque. The first-order theory of Zhang & Stone (Reference Zhang and Stone1998) predicts that this torque (about the particle's geometric centre) is identically zero to ![]() $O(\epsilon )$, regardless of the particle's shape and orientation. A prediction of zero torque does not coincide with observations of non-spherical particles. For illustrative purposes, consider the extreme case of a particle consisting of a slender rod attached to a sphere at one of its ends, moving at finite angle of attack to its principal geometric axis. The particle naturally experiences a non-zero torque about its geometric centre. This torque–translation coupling phenomenon is not restricted to highly non-spherical particles (as per this example). We therefore conclude that any such coupling between translational motion and (rotation-inducing) torque for nearly spherical particles must occur at higher order in
$O(\epsilon )$, regardless of the particle's shape and orientation. A prediction of zero torque does not coincide with observations of non-spherical particles. For illustrative purposes, consider the extreme case of a particle consisting of a slender rod attached to a sphere at one of its ends, moving at finite angle of attack to its principal geometric axis. The particle naturally experiences a non-zero torque about its geometric centre. This torque–translation coupling phenomenon is not restricted to highly non-spherical particles (as per this example). We therefore conclude that any such coupling between translational motion and (rotation-inducing) torque for nearly spherical particles must occur at higher order in ![]() $\epsilon$, i.e.
$\epsilon$, i.e. ![]() $O(\epsilon ^2)$. Another illustration of this phenomenon is exhibited by the flagellum of bacteria. Many bacteria swim by rotating a helical flagellum (Berg & Anderson Reference Berg and Anderson1973). This conversion of rotation into linear translation is only possible due to rotation–force coupling. A nearly spherical analogue of such a particle will exhibit force–rotation and torque–translation coupling at
$O(\epsilon ^2)$. Another illustration of this phenomenon is exhibited by the flagellum of bacteria. Many bacteria swim by rotating a helical flagellum (Berg & Anderson Reference Berg and Anderson1973). This conversion of rotation into linear translation is only possible due to rotation–force coupling. A nearly spherical analogue of such a particle will exhibit force–rotation and torque–translation coupling at ![]() $O(\epsilon ^2)$.
$O(\epsilon ^2)$.
Another practical situation arises when examining the orientation-averaged force experienced by non-spherical particles in flow. For example, Cheng & Mason (Reference Cheng and Mason2003) studied the rotational diffusion of highly non-spherical solid microdisks to determine the shear moduli of a surrounding viscoelastic fluid. This required the orientation average of the hydrodynamic force/torque experienced by the disks (Hubbard & Douglas Reference Hubbard and Douglas1993). The above-mentioned ![]() $O(\epsilon )$ theory predicts that the orientation average of the force experienced by a nearly spherical particle in its direction of motion is identical to that of a perfect sphere. This demonstrates that the existing first-order theory for nearly spherical particles does not capture the effect of particle non-sphericity in such measurements. A third phenomena is the non-zero torque experienced by a non-spherical particle undergoing oscillatory rotation in the (high-frequency) inviscid flow limit, for which the first-order theory predicts zero torque.
$O(\epsilon )$ theory predicts that the orientation average of the force experienced by a nearly spherical particle in its direction of motion is identical to that of a perfect sphere. This demonstrates that the existing first-order theory for nearly spherical particles does not capture the effect of particle non-sphericity in such measurements. A third phenomena is the non-zero torque experienced by a non-spherical particle undergoing oscillatory rotation in the (high-frequency) inviscid flow limit, for which the first-order theory predicts zero torque.
A higher-order theory is required to capture these key phenomena. This forms the aim of the present work, which develops theory for nearly spherical particles to second order in the non-spherical shape parameter ![]() $\epsilon$, i.e. to
$\epsilon$, i.e. to ![]() $O(\epsilon ^2)$. The theory is derived for nearly spherical particles of arbitrary shape, by performing a regular perturbation expansion in small
$O(\epsilon ^2)$. The theory is derived for nearly spherical particles of arbitrary shape, by performing a regular perturbation expansion in small ![]() $\epsilon$. The first-order flow field is required for the second-order solution, which is obtained using a general solution to the unsteady Stokes equations in vector spherical harmonics. An explicit analytical form for the second-order solution is derived, requiring the shape of the particle surface only. The utility of this general theory is demonstrated through its application to three example nearly spherical particles: (1) a prolate spheroid, (2) a ‘pear-shaped’ particle that exhibits force–rotation and torque–translation coupling and (3) a ‘harmonic virion’. The latter particle is a simple model for a SARS-CoV-2 virion, which is used to study how the number of ‘spiky’ surface protrusions affect the virion's hydrodynamics. In all cases, formulae are presented for generally unsteady, non-axisymmetric particle motion. A Mathematica notebook is provided in the supplementary material available at https://doi.org/10.1017/jfm.2024.1075 (with user notes in Appendix A), facilitating implementation of the derived theory for particle shapes of the user's choosing. An additional comparison is made with an anisotropic Brownian particle studied by Kraft et al. (Reference Kraft, Wittkowski, Ten Hagen, Edmond, Pine and Löwen2013), which demonstrates good agreement of the developed theory with existing results in the case of translation–rotation coupling.
$\epsilon$. The first-order flow field is required for the second-order solution, which is obtained using a general solution to the unsteady Stokes equations in vector spherical harmonics. An explicit analytical form for the second-order solution is derived, requiring the shape of the particle surface only. The utility of this general theory is demonstrated through its application to three example nearly spherical particles: (1) a prolate spheroid, (2) a ‘pear-shaped’ particle that exhibits force–rotation and torque–translation coupling and (3) a ‘harmonic virion’. The latter particle is a simple model for a SARS-CoV-2 virion, which is used to study how the number of ‘spiky’ surface protrusions affect the virion's hydrodynamics. In all cases, formulae are presented for generally unsteady, non-axisymmetric particle motion. A Mathematica notebook is provided in the supplementary material available at https://doi.org/10.1017/jfm.2024.1075 (with user notes in Appendix A), facilitating implementation of the derived theory for particle shapes of the user's choosing. An additional comparison is made with an anisotropic Brownian particle studied by Kraft et al. (Reference Kraft, Wittkowski, Ten Hagen, Edmond, Pine and Löwen2013), which demonstrates good agreement of the developed theory with existing results in the case of translation–rotation coupling.
We begin in § 2 by deriving the general theoretical framework for an arbitrary nearly spherical particle immersed in an unbounded and quiescent viscous fluid, to second order in ![]() $\epsilon$. This gives the force and torque experienced by the particle in terms of its motion and resulting fluid stress tensors; the latter are specified by the fluid velocity at the particle surface, via the Lorentz reciprocal theorem. Results of the implementation of this framework are given in § 3 where general and explicit analytical expressions for the force and torque, solely in terms of the particle motion, are reported. The above-mentioned example particles are then studied in § 4 using the derived general expressions from § 3. This includes analytical formulae for the force and torque experienced by these example particles, their orientation-averaged expressions and their limits of zero- and high-frequency motion. To demonstrate the validity of the derived formulae, their predictions are compared with three-dimensional finite-amplitude direct numerical simulations (DNS) of the (nonlinear) Navier–Stokes equations in § 5. Details of the theoretical and numerical calculations are relegated to appendices, which also contain information on the Mathematica notebook (supplementary material; information in Appendix A).
$\epsilon$. This gives the force and torque experienced by the particle in terms of its motion and resulting fluid stress tensors; the latter are specified by the fluid velocity at the particle surface, via the Lorentz reciprocal theorem. Results of the implementation of this framework are given in § 3 where general and explicit analytical expressions for the force and torque, solely in terms of the particle motion, are reported. The above-mentioned example particles are then studied in § 4 using the derived general expressions from § 3. This includes analytical formulae for the force and torque experienced by these example particles, their orientation-averaged expressions and their limits of zero- and high-frequency motion. To demonstrate the validity of the derived formulae, their predictions are compared with three-dimensional finite-amplitude direct numerical simulations (DNS) of the (nonlinear) Navier–Stokes equations in § 5. Details of the theoretical and numerical calculations are relegated to appendices, which also contain information on the Mathematica notebook (supplementary material; information in Appendix A).
2. Theoretical framework
We consider a nearly spherical particle that executes small-amplitude, oscillatory rigid-body motion at a single angular frequency, ![]() $\omega$, and amplitude,
$\omega$, and amplitude, ![]() $a$, in a quiescent and unbounded viscous fluid. The following non-dimensionalisation is performed: all distance variables are scaled by the radius of an equivalent-volume sphere,
$a$, in a quiescent and unbounded viscous fluid. The following non-dimensionalisation is performed: all distance variables are scaled by the radius of an equivalent-volume sphere, ![]() $R_{eq}$, time by
$R_{eq}$, time by ![]() $\omega ^{-1}$, velocity by
$\omega ^{-1}$, velocity by ![]() $\omega a$, angular velocity by
$\omega a$, angular velocity by ![]() $\omega a/R_{eq}$ and pressure by
$\omega a/R_{eq}$ and pressure by ![]() $\omega \mu a / R_{eq}$, where
$\omega \mu a / R_{eq}$, where ![]() $\mu$ is the fluid's shear viscosity; this specifies the force and torque scales of
$\mu$ is the fluid's shear viscosity; this specifies the force and torque scales of ![]() $\omega \mu a R_{eq}$ and
$\omega \mu a R_{eq}$ and ![]() $\omega \mu a R_{eq}^2$, respectively. Henceforth, all variables refer to their non-dimensional counterparts. The non-dimensional oscillation amplitude is
$\omega \mu a R_{eq}^2$, respectively. Henceforth, all variables refer to their non-dimensional counterparts. The non-dimensional oscillation amplitude is ![]() $\delta \equiv a/R_{eq}$, and the governing Navier–Stokes equations is
$\delta \equiv a/R_{eq}$, and the governing Navier–Stokes equations is
where ![]() $\beta = \rho R^{2}_{eq}\omega /\mu$ is the oscillatory Reynolds number of the flow and
$\beta = \rho R^{2}_{eq}\omega /\mu$ is the oscillatory Reynolds number of the flow and ![]() $\rho$ is the fluid density. The fluid boundary conditions are
$\rho$ is the fluid density. The fluid boundary conditions are
where ![]() $S_p$ is the (time-varying) location of the particle surface, the constant vectors
$S_p$ is the (time-varying) location of the particle surface, the constant vectors ![]() $\boldsymbol{U}$ and
$\boldsymbol{U}$ and ![]() $\boldsymbol{\varOmega }$ specify the rigid-body (dimensionless) translational and angular velocities of the particle, respectively, and
$\boldsymbol{\varOmega }$ specify the rigid-body (dimensionless) translational and angular velocities of the particle, respectively, and ![]() ${\rm Re}$ gives the real part of the expression. Figure 1 gives graphical illustrations of three nearly spherical particles that are studied in § 4 (with exaggerated shape perturbation, for clarity).
${\rm Re}$ gives the real part of the expression. Figure 1 gives graphical illustrations of three nearly spherical particles that are studied in § 4 (with exaggerated shape perturbation, for clarity).

Figure 1. Examples of three nearly spherical particles generated using the radial coordinate specified by (2.5). The degree of (infinitesimal) non-sphericity is exaggerated for clarity. (a) Prolate spheroid with a major-axis length of ![]() $1+\epsilon$, with radial shape perturbation functions
$1+\epsilon$, with radial shape perturbation functions ![]() $f$ and
$f$ and ![]() $g$ specified in (4.3). (b) ‘Pear-shaped’ particle, with
$g$ specified in (4.3). (b) ‘Pear-shaped’ particle, with ![]() $f$ and
$f$ and ![]() $g$ specified in (4.11b). (c) ‘Harmonic virion’ where
$g$ specified in (4.11b). (c) ‘Harmonic virion’ where ![]() $f$ is specified by a linear combination of
$f$ is specified by a linear combination of ![]() $(l,m) = (20,\pm 10)$ spherical harmonics, see (4.18a) with
$(l,m) = (20,\pm 10)$ spherical harmonics, see (4.18a) with ![]() $n = 10$, and
$n = 10$, and ![]() $g$ is specified in (4.18b).
$g$ is specified in (4.18b).
2.1. Small-oscillation-amplitude limit
The nearly spherical particle executes small-amplitude motion such that the scaled Lagrangian displacements of all material points on its surface are of ![]() $O(\delta )$. Consequently, the scaled angular displacements of these material points are also of
$O(\delta )$. Consequently, the scaled angular displacements of these material points are also of ![]() $O(\delta )$.
$O(\delta )$.
Expanding (2.1) to linear order in small ![]() $\delta$ gives the (linear) unsteady Stokes equations. This has the consequence that all effects due to nonlinear interactions of either fluid or particle motion (including Lagrangian boundary corrections) are removed, i.e. there are no time-averaged effects or mixing at different frequencies. Due to this linearity, all dependent variables (denoted by
$\delta$ gives the (linear) unsteady Stokes equations. This has the consequence that all effects due to nonlinear interactions of either fluid or particle motion (including Lagrangian boundary corrections) are removed, i.e. there are no time-averaged effects or mixing at different frequencies. Due to this linearity, all dependent variables (denoted by ![]() $X$) exhibit the explicit time dependence
$X$) exhibit the explicit time dependence ![]() $X(\boldsymbol{r}, t) = {\rm Re}[\tilde {X}(\boldsymbol{r}) \,{\rm e}^{-\mathrm{i} t}]$, where
$X(\boldsymbol{r}, t) = {\rm Re}[\tilde {X}(\boldsymbol{r}) \,{\rm e}^{-\mathrm{i} t}]$, where ![]() $\boldsymbol{r}$ is the position vector from the particle's geometric centre, ‘
$\boldsymbol{r}$ is the position vector from the particle's geometric centre, ‘![]() $\mathrm{i}$’ is the imaginary unit and
$\mathrm{i}$’ is the imaginary unit and ![]() $t$ is time. The superfluous
$t$ is time. The superfluous ![]() $\sim$ notation is omitted for convenience and henceforth all dependent variables refer to their quantities in the frequency domain; note that as per (2.4),
$\sim$ notation is omitted for convenience and henceforth all dependent variables refer to their quantities in the frequency domain; note that as per (2.4), ![]() $\boldsymbol{U}$ and
$\boldsymbol{U}$ and ![]() $\boldsymbol{\varOmega }$ are both quantities in the frequency domain. The unsteady Stokes equations are therefore
$\boldsymbol{\varOmega }$ are both quantities in the frequency domain. The unsteady Stokes equations are therefore
where ![]() $\lambda = (1-\mathrm{i})\sqrt {\beta /2}$. In this linear limit, the flow boundary conditions are the velocity of the particle mapped onto the stationary particle surface, i.e.
$\lambda = (1-\mathrm{i})\sqrt {\beta /2}$. In this linear limit, the flow boundary conditions are the velocity of the particle mapped onto the stationary particle surface, i.e.
where ![]() $S$ is the (stationary) surface of the nearly spherical particle, together with decay of the velocity field to zero far from the particle, i.e. (2.2b) holds. Figure 2 shows a cross-section of the particles defined in figure 1, illustrating the difference between the nearly spherical surface,
$S$ is the (stationary) surface of the nearly spherical particle, together with decay of the velocity field to zero far from the particle, i.e. (2.2b) holds. Figure 2 shows a cross-section of the particles defined in figure 1, illustrating the difference between the nearly spherical surface, ![]() $S$, and the surface of the unit sphere,
$S$, and the surface of the unit sphere, ![]() $\hat {S}$, which is equivalent to the surface of the equivalent-volume sphere after non-dimensionalising by
$\hat {S}$, which is equivalent to the surface of the equivalent-volume sphere after non-dimensionalising by ![]() $R_{{eq}}$. Due to linearity of the governing equations/boundary conditions, all results in this study can be trivially extended to arbitrary time-dependent motions of the particle through the use of Fourier/Laplace transforms.
$R_{{eq}}$. Due to linearity of the governing equations/boundary conditions, all results in this study can be trivially extended to arbitrary time-dependent motions of the particle through the use of Fourier/Laplace transforms.
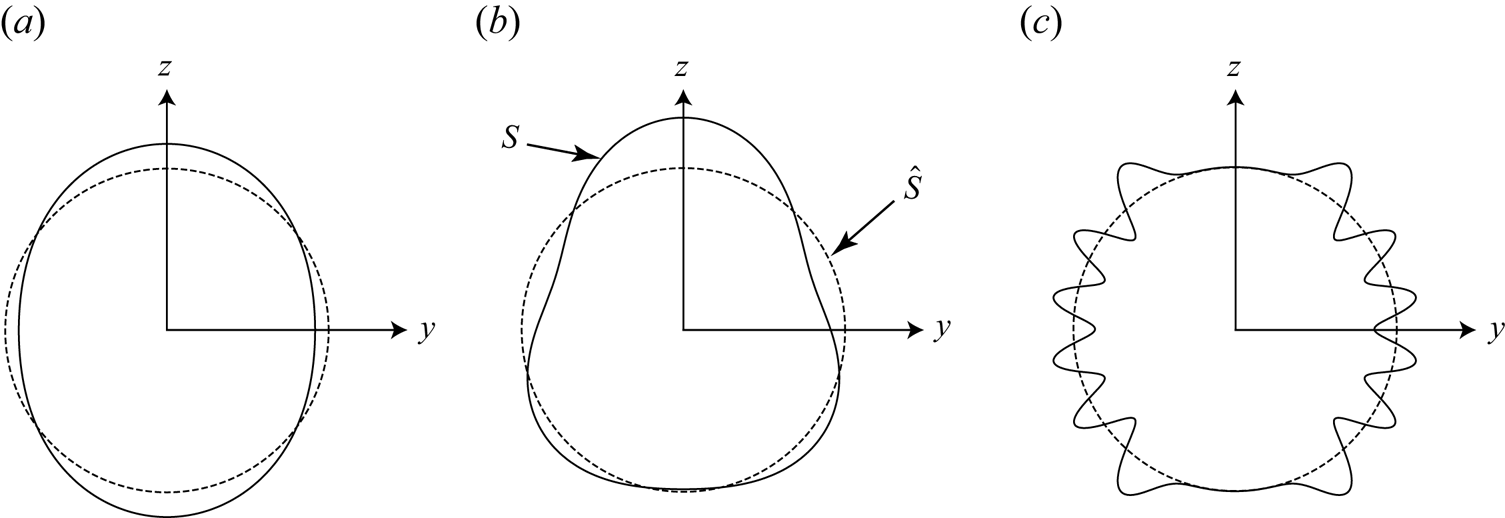
Figure 2. Cross-sections in the ![]() $y_1$–
$y_1$–![]() $z_1$,
$z_1$, ![]() $y_2$–
$y_2$–![]() $z_2$ and
$z_2$ and ![]() $y_3$–
$y_3$–![]() $z_3$ Cartesian planes of the three particles in figure 1. Solid lines correspond to
$z_3$ Cartesian planes of the three particles in figure 1. Solid lines correspond to ![]() $S$, the surface of the nearly spherical particle (non-dimensionalised by the radius of an equivalent-volume sphere), and dashed lines correspond to
$S$, the surface of the nearly spherical particle (non-dimensionalised by the radius of an equivalent-volume sphere), and dashed lines correspond to ![]() $\hat {S}$, the surface of the unit sphere. See (4.3), (4.11b) and (4.18), with
$\hat {S}$, the surface of the unit sphere. See (4.3), (4.11b) and (4.18), with ![]() $i=2$, for the shape perturbation functions,
$i=2$, for the shape perturbation functions, ![]() $f$ and
$f$ and ![]() $g$, that generate
$g$, that generate ![]() $S$ in (a)–(c), respectively. The (infinitesimal) degree of non-sphericity is exaggerated for clarity.
$S$ in (a)–(c), respectively. The (infinitesimal) degree of non-sphericity is exaggerated for clarity.
2.2. Nearly spherical particle
The particle is ‘nearly spherical’ and of arbitrary shape with a surface that is specified by the dimensionless radial coordinate:
We remind the reader that ![]() $R$ and all spatial variables are scaled by the radius of an equivalent-volume sphere,
$R$ and all spatial variables are scaled by the radius of an equivalent-volume sphere, ![]() $R_{eq}$. Equation (2.5) defines the shape of the particle and is independent of its motion. The
$R_{eq}$. Equation (2.5) defines the shape of the particle and is independent of its motion. The ![]() $O(1)$ dimensionless functions
$O(1)$ dimensionless functions ![]() $f(\theta, \phi )$ and
$f(\theta, \phi )$ and ![]() $g(\theta, \phi )$ define the radial shape perturbation correct to
$g(\theta, \phi )$ define the radial shape perturbation correct to ![]() $O(\epsilon ^2)$. The variables
$O(\epsilon ^2)$. The variables ![]() $\theta$ and
$\theta$ and ![]() $\phi$ are the usual polar and azimuthal angles, respectively, of the particle's fixed spherical coordinate system (see figure 1) whose origin is at the particle's geometric centre. The parameter
$\phi$ are the usual polar and azimuthal angles, respectively, of the particle's fixed spherical coordinate system (see figure 1) whose origin is at the particle's geometric centre. The parameter ![]() $\epsilon$ is the asymptotically small ‘non-spherical parameter’ which is identical to that used by Zhang & Stone (Reference Zhang and Stone1998). The relationship between the two radial shape perturbation functions,
$\epsilon$ is the asymptotically small ‘non-spherical parameter’ which is identical to that used by Zhang & Stone (Reference Zhang and Stone1998). The relationship between the two radial shape perturbation functions, ![]() $f$ and
$f$ and ![]() $g$, is discussed below. Note that for a particle with an inhomogeneous mass density distribution, the particle's geometric centre and centre of mass may not coincide.
$g$, is discussed below. Note that for a particle with an inhomogeneous mass density distribution, the particle's geometric centre and centre of mass may not coincide.
The equivalent-volume sphere constraint is
where ![]() $R$ is defined in (2.5). When (2.6) is expanded to first and second order in
$R$ is defined in (2.5). When (2.6) is expanded to first and second order in ![]() $\epsilon$, we obtain the respective results
$\epsilon$, we obtain the respective results
where ![]() $\hat {S}$ is the surface of the unit sphere; see § 2.1. Requiring that the origin of the coordinate system is at the particle's geometric centre provides the additional constraint
$\hat {S}$ is the surface of the unit sphere; see § 2.1. Requiring that the origin of the coordinate system is at the particle's geometric centre provides the additional constraint
which when evaluated to first and second order in ![]() $\epsilon$ respectively gives
$\epsilon$ respectively gives
where ![]() $\boldsymbol{n}$ is the unit normal to
$\boldsymbol{n}$ is the unit normal to ![]() $\hat {S}$, directed into the fluid domain. Directives for specifying the functions
$\hat {S}$, directed into the fluid domain. Directives for specifying the functions ![]() $f$ and
$f$ and ![]() $g$ to ensure satisfaction of (2.7) and (2.9) are given in Appendix B.
$g$ to ensure satisfaction of (2.7) and (2.9) are given in Appendix B.
We note that the surface perturbation in (2.5) could alternatively be described using ![]() $R(\theta,\phi ) = 1+f(\theta,\phi )$. This would generate a different but equivalent asymptotic theory. However, the benefit of using (2.5) is that it naturally enables a spherical harmonic expansion of the surface at each order of
$R(\theta,\phi ) = 1+f(\theta,\phi )$. This would generate a different but equivalent asymptotic theory. However, the benefit of using (2.5) is that it naturally enables a spherical harmonic expansion of the surface at each order of ![]() $\epsilon$. This is specifically advantageous for particle shapes described using a finite number of terms in their spherical harmonic expansion.
$\epsilon$. This is specifically advantageous for particle shapes described using a finite number of terms in their spherical harmonic expansion.
Regime of validity: Importantly, the small-oscillation-amplitude asymptotic expansion to ![]() $O(\delta )$ is taken before the near-spherical-particle asymptotic expansion to
$O(\delta )$ is taken before the near-spherical-particle asymptotic expansion to ![]() $O(\epsilon ^2)$. It follows that the results reported in this study apply rigorously when the oscillation amplitude,
$O(\epsilon ^2)$. It follows that the results reported in this study apply rigorously when the oscillation amplitude, ![]() $\delta$, is much smaller than the height of any surface perturbation on the particle, i.e.
$\delta$, is much smaller than the height of any surface perturbation on the particle, i.e. ![]() $\delta \ll \epsilon$. We note that the opposite limit (
$\delta \ll \epsilon$. We note that the opposite limit (![]() $\delta \gg \epsilon$) requires inclusion of nonlinear convective inertial effects in the flow – it will generate nonlinear flow phenomena such as acoustic streaming – which is not the focus of this study; a brief illustration of this effect is reported in § 5.
$\delta \gg \epsilon$) requires inclusion of nonlinear convective inertial effects in the flow – it will generate nonlinear flow phenomena such as acoustic streaming – which is not the focus of this study; a brief illustration of this effect is reported in § 5.
2.3. Flow generated by a nearly spherical particle
We expand the flow variables in the (infinitesimal) non-spherical parameter ![]() $\epsilon$:
$\epsilon$:
Substituting (2.10) into (2.4), and performing a Taylor expansion about ![]() $r = 1$, then gives
$r = 1$, then gives
 \begin{align} &\boldsymbol{u}^{(0)}|_{r=1} +\epsilon(\boldsymbol{u}^{(1)}|_{r=1} + f \partial_r \boldsymbol{u}^{(0)}|_{r=1} ) \nonumber\\ &\qquad + \epsilon^2\left(\boldsymbol{u}^{(2)}|_{r=1} + g \partial_r \boldsymbol{u}^{(0)}|_{r=1} + f \partial_r \boldsymbol{u}^{(1)}|_{r=1} + \frac{f^2}{2} \partial^2_r \boldsymbol{u}^{(0)}|_{r=1} \right) + O(\epsilon^3) \nonumber\\ &\quad =\boldsymbol{U} + \boldsymbol{\varOmega}\times\boldsymbol{n} + \epsilon f \boldsymbol{\varOmega}\times\boldsymbol{n} + \epsilon^2 g \boldsymbol{\varOmega}\times\boldsymbol{n} + O(\epsilon^3), \end{align}
\begin{align} &\boldsymbol{u}^{(0)}|_{r=1} +\epsilon(\boldsymbol{u}^{(1)}|_{r=1} + f \partial_r \boldsymbol{u}^{(0)}|_{r=1} ) \nonumber\\ &\qquad + \epsilon^2\left(\boldsymbol{u}^{(2)}|_{r=1} + g \partial_r \boldsymbol{u}^{(0)}|_{r=1} + f \partial_r \boldsymbol{u}^{(1)}|_{r=1} + \frac{f^2}{2} \partial^2_r \boldsymbol{u}^{(0)}|_{r=1} \right) + O(\epsilon^3) \nonumber\\ &\quad =\boldsymbol{U} + \boldsymbol{\varOmega}\times\boldsymbol{n} + \epsilon f \boldsymbol{\varOmega}\times\boldsymbol{n} + \epsilon^2 g \boldsymbol{\varOmega}\times\boldsymbol{n} + O(\epsilon^3), \end{align}
where ![]() $\partial _r$ and
$\partial _r$ and ![]() $\partial ^2_r$ are the first and second partial derivatives with respect to the radial coordinate,
$\partial ^2_r$ are the first and second partial derivatives with respect to the radial coordinate, ![]() $r$, respectively. Note that the position vector,
$r$, respectively. Note that the position vector, ![]() $\boldsymbol{r}$, is identical to the unit normal vector,
$\boldsymbol{r}$, is identical to the unit normal vector, ![]() $\boldsymbol{n}$, when evaluation occurs on the surface of the unit sphere,
$\boldsymbol{n}$, when evaluation occurs on the surface of the unit sphere, ![]() $\hat {S}$. Equation (2.11) then specifies the required flow boundary conditions on the nearly spherical particle surface (evaluated at the sphere surface,
$\hat {S}$. Equation (2.11) then specifies the required flow boundary conditions on the nearly spherical particle surface (evaluated at the sphere surface, ![]() $r=1$), at each order in
$r=1$), at each order in ![]() $\epsilon$:
$\epsilon$:
with the individual flows vanishing far from the particle, as per (2.2b).
2.4. Force and torque acting on a nearly spherical particle
For a steady Stokes flow, the resulting force and torque acting on a body can be evaluated by integrating the stress tensor, ![]() $\boldsymbol{\sigma }$, on any surface that encloses the body (including any singular points of the flow), because the stress tensor is divergence free (Brenner Reference Brenner1964a). The situation is more involved for unsteady Stokes flows where the stress tensor is not divergence free; the stress tensor must be integrated on the body's surface. Extending the approach of Zhang & Stone (Reference Zhang and Stone1998) to
$\boldsymbol{\sigma }$, on any surface that encloses the body (including any singular points of the flow), because the stress tensor is divergence free (Brenner Reference Brenner1964a). The situation is more involved for unsteady Stokes flows where the stress tensor is not divergence free; the stress tensor must be integrated on the body's surface. Extending the approach of Zhang & Stone (Reference Zhang and Stone1998) to ![]() $O(\epsilon ^2)$ gives the following respective expressions for the force and torque exerted by the fluid on the nearly spherical particle:
$O(\epsilon ^2)$ gives the following respective expressions for the force and torque exerted by the fluid on the nearly spherical particle:
with
and
where the individual stress tensors, ![]() $\boldsymbol{\sigma }^{(0)}$,
$\boldsymbol{\sigma }^{(0)}$, ![]() $\boldsymbol{\sigma }^{(1)}$,
$\boldsymbol{\sigma }^{(1)}$, ![]() $\boldsymbol{\sigma }^{(2)}$, are defined by the flows generated by the boundary conditions in (2.12a), (2.12b), (2.12c), respectively. As required, all the integrals in (2.14) are specified over
$\boldsymbol{\sigma }^{(2)}$, are defined by the flows generated by the boundary conditions in (2.12a), (2.12b), (2.12c), respectively. As required, all the integrals in (2.14) are specified over ![]() $\hat {S};$ see Appendix C for the derivation of the above results.
$\hat {S};$ see Appendix C for the derivation of the above results.
In principle, (2.14) requires knowledge of the above-mentioned individual stress tensors. Use of the Lorentz reciprocal theorem bypasses this requirement by enabling determination of the integrals in (2.14) using only their respective velocity fields. For an arbitrary unsteady Stokes flow, ![]() $(\boldsymbol{u}', \boldsymbol{\sigma }')$, this gives
$(\boldsymbol{u}', \boldsymbol{\sigma }')$, this gives
which are derived by substituting this arbitrary flow, and flows generated by the translation and rotation (of unitary velocity magnitude) of a unit sphere, into the Lorentz reciprocal theorem.
3. Force and torque in terms of the particle motion
We use the general theoretical framework in § 2 to derive analytical expressions for the force and torque on an arbitrary nearly spherical particle. The torque is evaluated with respect to the particle's geometric centre (about which the angular velocity is also specified).
3.1. Zeroth-order solution
The zeroth-order solution in ![]() $\epsilon$, i.e.
$\epsilon$, i.e. ![]() $O(1)$, corresponds to the force and torque experienced by a perfect sphere (Stokes Reference Stokes1851). The fluid's velocity field and its radial gradients at the sphere's surface, to be used in the subsequent first- and second-order solutions, are
$O(1)$, corresponds to the force and torque experienced by a perfect sphere (Stokes Reference Stokes1851). The fluid's velocity field and its radial gradients at the sphere's surface, to be used in the subsequent first- and second-order solutions, are
 \begin{gather} \partial^2_r \boldsymbol{u}^{(0)}|_{r=1} = \left(\frac{3}{2}(3+3\lambda+\lambda^2) (\boldsymbol{I}-\boldsymbol{n}\boldsymbol{n}) - 3(1+\lambda)\boldsymbol{n}\boldsymbol{n}\right) \boldsymbol{\cdot}\boldsymbol{U} \nonumber\\ +\, \frac{6+6\lambda + 3\lambda^2 + \lambda^3}{1+\lambda}\boldsymbol{\varOmega}\times\boldsymbol{n}. \end{gather}
\begin{gather} \partial^2_r \boldsymbol{u}^{(0)}|_{r=1} = \left(\frac{3}{2}(3+3\lambda+\lambda^2) (\boldsymbol{I}-\boldsymbol{n}\boldsymbol{n}) - 3(1+\lambda)\boldsymbol{n}\boldsymbol{n}\right) \boldsymbol{\cdot}\boldsymbol{U} \nonumber\\ +\, \frac{6+6\lambda + 3\lambda^2 + \lambda^3}{1+\lambda}\boldsymbol{\varOmega}\times\boldsymbol{n}. \end{gather}The force and torque are evaluated directly using (2.15) and yield the well known results
 $$\begin{gather}\boldsymbol{T}^{(0)} ={-}8{\rm \pi} \left(\frac{1+\lambda+\dfrac{\lambda^2}{3}}{1+\lambda}\right)\boldsymbol{\varOmega}. \end{gather}$$
$$\begin{gather}\boldsymbol{T}^{(0)} ={-}8{\rm \pi} \left(\frac{1+\lambda+\dfrac{\lambda^2}{3}}{1+\lambda}\right)\boldsymbol{\varOmega}. \end{gather}$$3.2. First-order solution
The first-order velocity boundary condition in ![]() $\epsilon$ is obtained by substituting (3.1b) into (2.12b):
$\epsilon$ is obtained by substituting (3.1b) into (2.12b):
Equations (2.14b), (2.15a) and (3.3) then give
while (2.14e), (2.15b), (3.1a) and (3.3) yield
The formulae in (3.4) and (3.5) coincide with those of Zhang & Stone (Reference Zhang and Stone1998). Expressing ![]() $f (\theta, \phi )$ generally as a series involving spherical harmonics (see Appendix B) establishes that only the spherical harmonics of degree
$f (\theta, \phi )$ generally as a series involving spherical harmonics (see Appendix B) establishes that only the spherical harmonics of degree ![]() $l = 2$ provide a non-zero contribution to both (3.4) and (3.5). That is, the force and torque to
$l = 2$ provide a non-zero contribution to both (3.4) and (3.5). That is, the force and torque to ![]() $O(\epsilon )$ experienced by a nearly spherical particle are dictated by those of an equivalent ellipsoid (Zhang & Stone Reference Zhang and Stone1998).
$O(\epsilon )$ experienced by a nearly spherical particle are dictated by those of an equivalent ellipsoid (Zhang & Stone Reference Zhang and Stone1998).
Equations (3.4) and (3.5) show that the force and torque (about the particle's geometric centre) are decoupled. The particle experiences no drag force due to its rotational motion, and no torque due to its linear translation. This does not agree with general physical reality and, as such, coupling between translational and rotational motion/forces must occur at higher order in ![]() $\epsilon$, as discussed in § 1. Additionally, the
$\epsilon$, as discussed in § 1. Additionally, the ![]() $\lambda ^2$ coefficient of
$\lambda ^2$ coefficient of ![]() $\boldsymbol{T}^{(1)}$ is zero as
$\boldsymbol{T}^{(1)}$ is zero as ![]() $|\lambda |\rightarrow \infty$, again in disagreement with reality, i.e. the high-frequency limit mentioned in § 1.
$|\lambda |\rightarrow \infty$, again in disagreement with reality, i.e. the high-frequency limit mentioned in § 1.
3.3. Second-order solution
We now evaluate the second-order solution in ![]() $\epsilon$ for the force and torque, which is the principal aim of this study. Details of this derivation are relegated to Appendix D. These solutions are decomposed into two components: (1) a component involving only
$\epsilon$ for the force and torque, which is the principal aim of this study. Details of this derivation are relegated to Appendix D. These solutions are decomposed into two components: (1) a component involving only ![]() $\boldsymbol{u}^{(0)}$ and (2) a component that depends on
$\boldsymbol{u}^{(0)}$ and (2) a component that depends on ![]() $\partial _r \boldsymbol{u}^{(1)}$ which is expressed as an infinite series involving the shape perturbation function,
$\partial _r \boldsymbol{u}^{(1)}$ which is expressed as an infinite series involving the shape perturbation function, ![]() $f$. These two components are denoted by subscripts 1 and 2, respectively:
$f$. These two components are denoted by subscripts 1 and 2, respectively:
where expressions for each component of ![]() $\boldsymbol{F}^{(2)}$ and
$\boldsymbol{F}^{(2)}$ and ![]() $\boldsymbol{T}^{(2)}$ follow from (2.12c), (2.14c) and (2.14f), and are detailed in (D4a), (D4b), (D5a) and (D5b). The first components, that involve only
$\boldsymbol{T}^{(2)}$ follow from (2.12c), (2.14c) and (2.14f), and are detailed in (D4a), (D4b), (D5a) and (D5b). The first components, that involve only ![]() $\boldsymbol{u}^{(0)}$, are easily evaluated and give
$\boldsymbol{u}^{(0)}$, are easily evaluated and give
 \begin{align} \boldsymbol{F}^{(2)}_1 &= \left[ \frac{3}{8}(1+\lambda)(9 + 9\lambda + 5\lambda^2) \int_{\hat{S}} f^2 (\boldsymbol{I} - \boldsymbol{n}\boldsymbol{n}) \, \mathrm{d}S \right. \nonumber\\ & \quad \left. -\,\frac{3}{4}(1+\lambda)(3 + 3\lambda + \lambda^2) \int_{\hat{S}} f^2 \boldsymbol{n}\boldsymbol{n} \, \mathrm{d}S - \frac{9}{4}(1+\lambda)^2 \int_{\hat{S}} g (\boldsymbol{I} - \boldsymbol{n}\boldsymbol{n}) \, \mathrm{d}S \right] \boldsymbol{\cdot}\boldsymbol{U} \nonumber\\ & \quad - \frac{45 + 90\lambda + 69\lambda^2 + 27\lambda^3 + 5\lambda^4}{4(1+\lambda)}\int_{\hat{S}} f^2 \boldsymbol{n} \, \mathrm{d}S\times\boldsymbol{\varOmega} \end{align}
\begin{align} \boldsymbol{F}^{(2)}_1 &= \left[ \frac{3}{8}(1+\lambda)(9 + 9\lambda + 5\lambda^2) \int_{\hat{S}} f^2 (\boldsymbol{I} - \boldsymbol{n}\boldsymbol{n}) \, \mathrm{d}S \right. \nonumber\\ & \quad \left. -\,\frac{3}{4}(1+\lambda)(3 + 3\lambda + \lambda^2) \int_{\hat{S}} f^2 \boldsymbol{n}\boldsymbol{n} \, \mathrm{d}S - \frac{9}{4}(1+\lambda)^2 \int_{\hat{S}} g (\boldsymbol{I} - \boldsymbol{n}\boldsymbol{n}) \, \mathrm{d}S \right] \boldsymbol{\cdot}\boldsymbol{U} \nonumber\\ & \quad - \frac{45 + 90\lambda + 69\lambda^2 + 27\lambda^3 + 5\lambda^4}{4(1+\lambda)}\int_{\hat{S}} f^2 \boldsymbol{n} \, \mathrm{d}S\times\boldsymbol{\varOmega} \end{align}and
 \begin{align} \boldsymbol{T}^{(2)}_1 &= \frac{3(3+2\lambda)(6+ 8\lambda + 4\lambda^2 + \lambda^3)}{4(1+\lambda)}\int_{\hat{S}} f^2 \boldsymbol{n} \, \mathrm{d}S \times \boldsymbol{U} \nonumber\\ &\quad + \left[\frac{9 + 18\lambda + 20\lambda^2 + 16\lambda^3 + 7\lambda^4 + \lambda^5}{(1+\lambda)^2}\int_{\hat{S}} f^2 (\boldsymbol{I} - \boldsymbol{n}\boldsymbol{n}) \, \mathrm{d}S \right.\nonumber\\ &\quad \left. -\,\frac{(3+2\lambda)(3+4\lambda+2\lambda^2)}{(1+\lambda)^2}\int_{\hat{S}} g (\boldsymbol{I} - \boldsymbol{n}\boldsymbol{n}) \, \mathrm{d}S \right]\boldsymbol{\cdot}\boldsymbol{\varOmega}. \end{align}
\begin{align} \boldsymbol{T}^{(2)}_1 &= \frac{3(3+2\lambda)(6+ 8\lambda + 4\lambda^2 + \lambda^3)}{4(1+\lambda)}\int_{\hat{S}} f^2 \boldsymbol{n} \, \mathrm{d}S \times \boldsymbol{U} \nonumber\\ &\quad + \left[\frac{9 + 18\lambda + 20\lambda^2 + 16\lambda^3 + 7\lambda^4 + \lambda^5}{(1+\lambda)^2}\int_{\hat{S}} f^2 (\boldsymbol{I} - \boldsymbol{n}\boldsymbol{n}) \, \mathrm{d}S \right.\nonumber\\ &\quad \left. -\,\frac{(3+2\lambda)(3+4\lambda+2\lambda^2)}{(1+\lambda)^2}\int_{\hat{S}} g (\boldsymbol{I} - \boldsymbol{n}\boldsymbol{n}) \, \mathrm{d}S \right]\boldsymbol{\cdot}\boldsymbol{\varOmega}. \end{align} Derivations of the corresponding second components, that depend on ![]() $\partial _r \boldsymbol{u}^{(1)}$, are more involved and yield
$\partial _r \boldsymbol{u}^{(1)}$, are more involved and yield
 \begin{align} \boldsymbol{F}^{(2)}_2 &= \sum_{l=1}^{\infty}\sum_{m={-}l}^{l} \left[ \kappa_1 \kappa_2 \gamma_l^{(1)} \int_{\hat{S}} f\boldsymbol{R}_{lm}\, \mathrm{d}S \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm}^{*} \, \mathrm{d}S\right. \nonumber\\ & \quad \left. +\, \kappa_2^2 \gamma_l^{(2)} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm} \, \mathrm{d}S \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm}^{*} \, \mathrm{d}S + \kappa_2^2 \gamma_l^{(3)} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}_{lm} \, \mathrm{d}S \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}_{lm}^{*} \, \mathrm{d}S \right] \boldsymbol{\cdot} \boldsymbol{U} \nonumber\\ & \quad + \left[ \kappa_1 \kappa_3 \gamma_l^{(1)} \int_{\hat{S}} f \boldsymbol{R}_{lm} \, \mathrm{d}S \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}_{lm}^{*} \, \mathrm{d}S + \kappa_2 \kappa_3 \gamma_l^{(2)} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm} \, \mathrm{d}S \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}_{lm}^{*} \, \mathrm{d}S \right. \nonumber\\ & \quad \left. -\, \kappa_2 \kappa_3 \gamma_l^{(3)} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}_{lm} \, \mathrm{d}S \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm}^{*}\, \mathrm{d}S\right] \boldsymbol{\cdot} \boldsymbol{\varOmega} \end{align}
\begin{align} \boldsymbol{F}^{(2)}_2 &= \sum_{l=1}^{\infty}\sum_{m={-}l}^{l} \left[ \kappa_1 \kappa_2 \gamma_l^{(1)} \int_{\hat{S}} f\boldsymbol{R}_{lm}\, \mathrm{d}S \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm}^{*} \, \mathrm{d}S\right. \nonumber\\ & \quad \left. +\, \kappa_2^2 \gamma_l^{(2)} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm} \, \mathrm{d}S \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm}^{*} \, \mathrm{d}S + \kappa_2^2 \gamma_l^{(3)} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}_{lm} \, \mathrm{d}S \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}_{lm}^{*} \, \mathrm{d}S \right] \boldsymbol{\cdot} \boldsymbol{U} \nonumber\\ & \quad + \left[ \kappa_1 \kappa_3 \gamma_l^{(1)} \int_{\hat{S}} f \boldsymbol{R}_{lm} \, \mathrm{d}S \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}_{lm}^{*} \, \mathrm{d}S + \kappa_2 \kappa_3 \gamma_l^{(2)} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm} \, \mathrm{d}S \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}_{lm}^{*} \, \mathrm{d}S \right. \nonumber\\ & \quad \left. -\, \kappa_2 \kappa_3 \gamma_l^{(3)} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}_{lm} \, \mathrm{d}S \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm}^{*}\, \mathrm{d}S\right] \boldsymbol{\cdot} \boldsymbol{\varOmega} \end{align}and
 \begin{align} \boldsymbol{T}^{(2)}_2 &= \sum_{l=1}^{\infty} \sum_{m={-}l}^{l} \left[ - \kappa_2 \kappa_3 \gamma_l^{(3)} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm} \, \mathrm{d}S \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}_{lm}^{*} \, \mathrm{d}S + \kappa_2 \kappa_3 \gamma_l^{(2)} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}_{lm} \, \mathrm{d}S \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm}^{*} \, \mathrm{d}S \right]\boldsymbol{\cdot}\boldsymbol{U}\nonumber\\ & \quad + \left[ \kappa_3^2 \gamma_l^{(3)} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm} \, \mathrm{d}S \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm}^{*} \, \mathrm{d}S + \kappa_3^2 \gamma_l^{(2)} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}_{lm} \, \mathrm{d}S \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}^{*}_{lm} \, \mathrm{d}S \right]\boldsymbol{\cdot} \boldsymbol{\varOmega}, \end{align}
\begin{align} \boldsymbol{T}^{(2)}_2 &= \sum_{l=1}^{\infty} \sum_{m={-}l}^{l} \left[ - \kappa_2 \kappa_3 \gamma_l^{(3)} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm} \, \mathrm{d}S \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}_{lm}^{*} \, \mathrm{d}S + \kappa_2 \kappa_3 \gamma_l^{(2)} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}_{lm} \, \mathrm{d}S \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm}^{*} \, \mathrm{d}S \right]\boldsymbol{\cdot}\boldsymbol{U}\nonumber\\ & \quad + \left[ \kappa_3^2 \gamma_l^{(3)} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm} \, \mathrm{d}S \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm}^{*} \, \mathrm{d}S + \kappa_3^2 \gamma_l^{(2)} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}_{lm} \, \mathrm{d}S \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}^{*}_{lm} \, \mathrm{d}S \right]\boldsymbol{\cdot} \boldsymbol{\varOmega}, \end{align}
where ![]() $\boldsymbol{R}_{lm}$,
$\boldsymbol{R}_{lm}$, ![]() $\boldsymbol{\boldsymbol{\varTheta }}_{lm}$,
$\boldsymbol{\boldsymbol{\varTheta }}_{lm}$, ![]() $\boldsymbol{\boldsymbol{\varPhi }}_{lm}$ are vector spherical harmonics defined in Appendix D; the outer product is implied between the pairs of integrals in (3.9) and (3.10); the coefficients are
$\boldsymbol{\boldsymbol{\varPhi }}_{lm}$ are vector spherical harmonics defined in Appendix D; the outer product is implied between the pairs of integrals in (3.9) and (3.10); the coefficients are
 \begin{equation}
\left.\begin{array}{c@{}} \displaystyle\gamma_l^{(1)} =
\sqrt{l(l+1)},\\ \displaystyle \gamma_l^{(2)} =
\dfrac{\lambda^2}{2l+1}\left[1 +
\dfrac{\mathrm{h}^{(1)}_{l+1}(\mathrm{i}\lambda)}{\mathrm{h}^{(1)}_{l-1}(\mathrm{i}\lambda)}\right]-
1, \\ \displaystyle \gamma_l^{(3)} = l -
\mathrm{i}\lambda\dfrac{\mathrm{h}^{(1)}_{l+1}(\mathrm{i}\lambda)}{\mathrm{h}^{(1)}_{l}(\mathrm{i}\lambda)},
\end{array}\right\}
\end{equation}
\begin{equation}
\left.\begin{array}{c@{}} \displaystyle\gamma_l^{(1)} =
\sqrt{l(l+1)},\\ \displaystyle \gamma_l^{(2)} =
\dfrac{\lambda^2}{2l+1}\left[1 +
\dfrac{\mathrm{h}^{(1)}_{l+1}(\mathrm{i}\lambda)}{\mathrm{h}^{(1)}_{l-1}(\mathrm{i}\lambda)}\right]-
1, \\ \displaystyle \gamma_l^{(3)} = l -
\mathrm{i}\lambda\dfrac{\mathrm{h}^{(1)}_{l+1}(\mathrm{i}\lambda)}{\mathrm{h}^{(1)}_{l}(\mathrm{i}\lambda)},
\end{array}\right\}
\end{equation}
where ![]() $\mathrm{h}^{(1)}_l$ is the spherical Hankel function of the first kind of degree
$\mathrm{h}^{(1)}_l$ is the spherical Hankel function of the first kind of degree ![]() $l$; and
$l$; and
The (first) infinite sums in (3.9) and (3.10) begin with ![]() $l = 1$ because the
$l = 1$ because the ![]() $l = 0$ terms are identically zero, due to the respective equivalent-volume and geometric-centre requirements in (2.7a) and (2.9a). Equations (3.6)–(3.12) specify the complete second-order solution and require only the shape perturbation functions,
$l = 0$ terms are identically zero, due to the respective equivalent-volume and geometric-centre requirements in (2.7a) and (2.9a). Equations (3.6)–(3.12) specify the complete second-order solution and require only the shape perturbation functions, ![]() $f (\theta, \phi )$ and
$f (\theta, \phi )$ and ![]() $g(\theta, \phi )$. In contrast to the first-order solution in the previous section, where only the
$g(\theta, \phi )$. In contrast to the first-order solution in the previous section, where only the ![]() $l=2$ spherical harmonics of
$l=2$ spherical harmonics of ![]() $f(\theta, \phi )$ contribute, all spherical harmonics with
$f(\theta, \phi )$ contribute, all spherical harmonics with ![]() $l \ge 2$ can affect the second-order solution; see § B.1.
$l \ge 2$ can affect the second-order solution; see § B.1.
3.3.1. Infinite series in (3.9) and (3.10)
The number of non-zero terms in the (first) infinite series, over index ![]() $l$, in (3.9) and (3.10), is dictated by the nature of the shape perturbation function,
$l$, in (3.9) and (3.10), is dictated by the nature of the shape perturbation function, ![]() $f$. Suppose,
$f$. Suppose, ![]() $f$ can be expressed as a finite linear combination of
$f$ can be expressed as a finite linear combination of ![]() $k$ spherical harmonics:
$k$ spherical harmonics:
 \begin{equation} f(\theta, \phi) = \sum_{i = 1}^k f_{l_i m_i} Y_{l_i m_i}(\theta,\phi), \end{equation}
\begin{equation} f(\theta, \phi) = \sum_{i = 1}^k f_{l_i m_i} Y_{l_i m_i}(\theta,\phi), \end{equation}
where ![]() $l_i$ and
$l_i$ and ![]() $m_i$ are specified integers, i.e. the number of non-zero terms in (B1a) is finite. For each
$m_i$ are specified integers, i.e. the number of non-zero terms in (B1a) is finite. For each ![]() $i$ in (3.13), the only terms in (3.9) and (3.10) that may be non-zero are
$i$ in (3.13), the only terms in (3.9) and (3.10) that may be non-zero are
with
Moreover, let ![]() $l = l_{max}$ be the largest degree,
$l = l_{max}$ be the largest degree, ![]() $l$, in (3.13). It follows from (3.14) that all terms in (3.9) and (3.10) for
$l$, in (3.13). It follows from (3.14) that all terms in (3.9) and (3.10) for ![]() $l > l_{max}+1$ are identically zero. The infinite series in (3.9) and (3.10) then become finite series from
$l > l_{max}+1$ are identically zero. The infinite series in (3.9) and (3.10) then become finite series from ![]() $l = 1$ to
$l = 1$ to ![]() $l_{maxsum}\, (\equiv l_{max} +1)$. This property is used in the Mathematica notebook provided in the supplementary material, with the notebook variable
$l_{maxsum}\, (\equiv l_{max} +1)$. This property is used in the Mathematica notebook provided in the supplementary material, with the notebook variable ![]() $\textrm{MAXNUM} \equiv l_{maxsum}$; see Appendix A.
$\textrm{MAXNUM} \equiv l_{maxsum}$; see Appendix A.
3.4. Orientation-averaged solution
It is of practical relevance to study the orientation-averaged force and torque experienced by nearly spherical particles, i.e. the expected value of the force (or torque) exerted by the fluid on a particle that is oscillating along (or around) a random axis. This can arise in experiments when the particle orientation is not controlled, e.g. measurements of the particle's Brownian motion, where all particle orientations are sampled equally. The orientation-averaged force, ![]() $\bar {\boldsymbol{F}}$, and torque,
$\bar {\boldsymbol{F}}$, and torque, ![]() $\bar {\boldsymbol{T}}$, are determined by taking a uniformly distributed ensemble of all possible orientations, and calculating the average of the resulting forces and torques, i.e. for given
$\bar {\boldsymbol{T}}$, are determined by taking a uniformly distributed ensemble of all possible orientations, and calculating the average of the resulting forces and torques, i.e. for given ![]() $\boldsymbol{U}$ and
$\boldsymbol{U}$ and ![]() $\boldsymbol{\varOmega }$,
$\boldsymbol{\varOmega }$,
where ![]() $(\psi ',\theta ',\phi ')$ are a set of Euler angles with respect to the laboratory frame. It can be shown that this procedure gives
$(\psi ',\theta ',\phi ')$ are a set of Euler angles with respect to the laboratory frame. It can be shown that this procedure gives
 $$\begin{gather}\bar{\boldsymbol{T}} = \left[{-}8{\rm \pi} \left(\frac{1+\lambda+\dfrac{\lambda^2}{3}}{1+\lambda}\right) + \frac{\epsilon^2}{3}\, \mathrm{tr} \, \boldsymbol{C}^{(2)}\right]\boldsymbol{\varOmega} + O(\epsilon^3), \end{gather}$$
$$\begin{gather}\bar{\boldsymbol{T}} = \left[{-}8{\rm \pi} \left(\frac{1+\lambda+\dfrac{\lambda^2}{3}}{1+\lambda}\right) + \frac{\epsilon^2}{3}\, \mathrm{tr} \, \boldsymbol{C}^{(2)}\right]\boldsymbol{\varOmega} + O(\epsilon^3), \end{gather}$$
where ![]() $\mathrm{tr}\,\boldsymbol{A}^{(2)}$ and
$\mathrm{tr}\,\boldsymbol{A}^{(2)}$ and ![]() $\mathrm{tr}\,\boldsymbol{C}^{(2)}$ are the trace of the tensorial coefficients of
$\mathrm{tr}\,\boldsymbol{C}^{(2)}$ are the trace of the tensorial coefficients of ![]() $\boldsymbol{U}$ in (3.6a) and
$\boldsymbol{U}$ in (3.6a) and ![]() $\boldsymbol{\varOmega }$ in (3.6b), respectively. Explicit forms for
$\boldsymbol{\varOmega }$ in (3.6b), respectively. Explicit forms for ![]() $\mathrm{tr}\,\boldsymbol{A}^{(2)}$ and
$\mathrm{tr}\,\boldsymbol{A}^{(2)}$ and ![]() $\mathrm{tr}\,\boldsymbol{C}^{(2)}$ are given by (D16a) and (D16b), respectively; see § D.3. As discussed in § 1, particle non-sphericity enters into the orientation averages at
$\mathrm{tr}\,\boldsymbol{C}^{(2)}$ are given by (D16a) and (D16b), respectively; see § D.3. As discussed in § 1, particle non-sphericity enters into the orientation averages at ![]() $O(\epsilon ^2)$.
$O(\epsilon ^2)$.
4. Application to example nearly spherical particles
In this section, we illustrate the utility of the force and torque formulae in § 3 for three particle geometries: (a) a prolate spheroid, (b) a ‘pear-shaped’ particle and (c) a ‘harmonic virion’; see figure 1. These examples serve to demonstrate the emergence of non-zero orientation-averaged forces and torques, and the coupling between translational/rotational particle motion and torque/force, the expressions for which may find use in practice. Analytical formulae for a pear-shaped particle in § 4.2 are compared with independent DNS of the Navier–Stokes equations in § 5. Additionally, a comparison is made with a Brownian motion study by Kraft et al. (Reference Kraft, Wittkowski, Ten Hagen, Edmond, Pine and Löwen2013) to examine the validity of the presented solution for the case of translation–rotation coupling.
4.1. Spheroidal particle
First, we consider a prolate spheroid (illustrated in figures 1a and 2a) with its axis of rotational symmetry aligned along the Cartesian ![]() $z$ axis, with basis vector
$z$ axis, with basis vector ![]() $\hat {\boldsymbol{z}}$. The dimensionless length of the spheroid's major axis is chosen to be
$\hat {\boldsymbol{z}}$. The dimensionless length of the spheroid's major axis is chosen to be ![]() $1+\epsilon$. Requiring that its volume is independent of
$1+\epsilon$. Requiring that its volume is independent of ![]() $\epsilon$ and equal to that of an equivalent-volume sphere, i.e.
$\epsilon$ and equal to that of an equivalent-volume sphere, i.e. ![]() $4{\rm \pi} /3$ as per (2.5) and (2.7), gives a minor-axis length of
$4{\rm \pi} /3$ as per (2.5) and (2.7), gives a minor-axis length of ![]() $1/\sqrt {1+\epsilon }$. The corresponding radial coordinate, for arbitrary
$1/\sqrt {1+\epsilon }$. The corresponding radial coordinate, for arbitrary ![]() $\epsilon$, of the spheroid's surface is then
$\epsilon$, of the spheroid's surface is then
 \begin{equation} R = \frac{1+\epsilon}{\sqrt{\cos^2\theta + (1+\epsilon)^3\sin^2\theta}} , \end{equation}
\begin{equation} R = \frac{1+\epsilon}{\sqrt{\cos^2\theta + (1+\epsilon)^3\sin^2\theta}} , \end{equation}
which when expanded in small ![]() $\epsilon$ gives
$\epsilon$ gives
with
where ![]() $Y_{l,m} (\theta, \phi )$ is the scalar spherical harmonic defined in Appendix D. Note that
$Y_{l,m} (\theta, \phi )$ is the scalar spherical harmonic defined in Appendix D. Note that ![]() $g(\theta,\phi )$ contains an
$g(\theta,\phi )$ contains an ![]() $(l,m) = (4,0)$ spherical harmonic to exactly represent the spheroid; this does not affect the force and torque, as discussed in § B.1.
$(l,m) = (4,0)$ spherical harmonic to exactly represent the spheroid; this does not affect the force and torque, as discussed in § B.1.
4.1.1. First-order solution
The leading-order effects of non-sphericity are given by the first-order solutions in ![]() $\epsilon$ for the force and torque, which follow directly from (3.4) and (3.5):
$\epsilon$ for the force and torque, which follow directly from (3.4) and (3.5):
It is evident that the corresponding orientation-averaged first-order solutions are zero for both the force and the torque, as expected.
4.1.2. Second-order solution
The two components of the second-order solution in ![]() $\epsilon$ (defined in § 3.3), denoted by subscripts 1 and 2, are now determined. These are evaluated using the Mathematica notebook (supplementary material and Appendix A), which can be used for particle geometries of the user's choosing. Consequently, the results in this section serve as benchmarks for this future usage.
$\epsilon$ (defined in § 3.3), denoted by subscripts 1 and 2, are now determined. These are evaluated using the Mathematica notebook (supplementary material and Appendix A), which can be used for particle geometries of the user's choosing. Consequently, the results in this section serve as benchmarks for this future usage.
Force
The first component of the second-order force follows immediately from (3.7):
The radial shape perturbation function, ![]() $f$, in (4.3) involves spherical harmonics of degree
$f$, in (4.3) involves spherical harmonics of degree ![]() $l \le l_{max} = 2$. This facilitates exact evaluation (with
$l \le l_{max} = 2$. This facilitates exact evaluation (with ![]() $l_{maxsum} \equiv l_{max}+1=3$; see § 3.3.1) of the second component of the force in (3.9), giving
$l_{maxsum} \equiv l_{max}+1=3$; see § 3.3.1) of the second component of the force in (3.9), giving
 \begin{align} \boldsymbol{F}^{(2)}_2 &={-}\frac{{\rm \pi} (1+\lambda)}{350(3+3\lambda + \lambda^2)}[(4383 + 8829\lambda + 6039\lambda^2 + 2073\lambda^3 + 350\lambda^4)(\boldsymbol{I} - \hat{\boldsymbol{z}}\hat{\boldsymbol{z}}) \nonumber\\ &\quad + (2952 + 6156\lambda + 4176\lambda^2 + 1272\lambda^3 + 140\lambda^4)\hat{\boldsymbol{z}}\hat{\boldsymbol{z}}]\boldsymbol{\cdot} \boldsymbol{U}. \end{align}
\begin{align} \boldsymbol{F}^{(2)}_2 &={-}\frac{{\rm \pi} (1+\lambda)}{350(3+3\lambda + \lambda^2)}[(4383 + 8829\lambda + 6039\lambda^2 + 2073\lambda^3 + 350\lambda^4)(\boldsymbol{I} - \hat{\boldsymbol{z}}\hat{\boldsymbol{z}}) \nonumber\\ &\quad + (2952 + 6156\lambda + 4176\lambda^2 + 1272\lambda^3 + 140\lambda^4)\hat{\boldsymbol{z}}\hat{\boldsymbol{z}}]\boldsymbol{\cdot} \boldsymbol{U}. \end{align}The second-order solution for the force is then obtained by substituting (4.5) and (4.6) into (3.6), yielding the required result:
 \begin{align} \boldsymbol{F}^{(2)} &={-}\frac{3{\rm \pi} (1+\lambda)}{350(3+3\lambda + \lambda^2)}[(351 + 723\lambda + 183\lambda^2 - 29\lambda^3)(\boldsymbol{I} - \hat{\boldsymbol{z}}\hat{\boldsymbol{z}} )\nonumber\\ &\quad + (684 + 1452\lambda + 852\lambda^2 + 184\lambda^3)\hat{\boldsymbol{z}}\hat{\boldsymbol{z}}]\boldsymbol{\cdot} \boldsymbol{U}. \end{align}
\begin{align} \boldsymbol{F}^{(2)} &={-}\frac{3{\rm \pi} (1+\lambda)}{350(3+3\lambda + \lambda^2)}[(351 + 723\lambda + 183\lambda^2 - 29\lambda^3)(\boldsymbol{I} - \hat{\boldsymbol{z}}\hat{\boldsymbol{z}} )\nonumber\\ &\quad + (684 + 1452\lambda + 852\lambda^2 + 184\lambda^3)\hat{\boldsymbol{z}}\hat{\boldsymbol{z}}]\boldsymbol{\cdot} \boldsymbol{U}. \end{align} Equation (4.7) is to be compared with known limiting cases from the literature. Namely, Chwang & Wu (Reference Chwang and Wu1975) calculated the second-order force and torque experienced by a prolate spheroid undergoing steady, but arbitrary, translation and rotation. In the steady limit, i.e. ![]() $|\lambda | \rightarrow 0$, (4.7) coincides with the exact solution of Chwang & Wu (Reference Chwang and Wu1975). Moreover, for translational motion of the spheroid along its major axis – which extracts the
$|\lambda | \rightarrow 0$, (4.7) coincides with the exact solution of Chwang & Wu (Reference Chwang and Wu1975). Moreover, for translational motion of the spheroid along its major axis – which extracts the ![]() $\hat {\boldsymbol{z}}\hat {\boldsymbol{z}}$ component of (4.7) – the solution here agrees with the corresponding result reported by Lawrence & Weinbaum (Reference Lawrence and Weinbaum1986).
$\hat {\boldsymbol{z}}\hat {\boldsymbol{z}}$ component of (4.7) – the solution here agrees with the corresponding result reported by Lawrence & Weinbaum (Reference Lawrence and Weinbaum1986).
Torque
Repeating this calculation for the torque in (3.6) gives
 \begin{align} \boldsymbol{T}^{(2)} &={-}\frac{4{\rm \pi} }{105(1+\lambda)^3(15+15\lambda+6\lambda^2+\lambda^3)} [(3861 + 15444\lambda + 27996\lambda^2 + 29391\lambda^3 \nonumber\\ &\quad + 19311\lambda^4 + 8107\lambda^5 + 2130\lambda^6 + 321\lambda^7 + 21\lambda^8)(\boldsymbol{I} - \hat{\boldsymbol{z}}\hat{\boldsymbol{z}}) + 2(1242 + 4968\lambda \nonumber\\ &\quad + 8733\lambda^2 + 8661\lambda^3 + 5196\lambda^4 + 1889\lambda^5 + 390\lambda^6 + 36\lambda^7)\hat{\boldsymbol{z}}\hat{\boldsymbol{z}} ]\boldsymbol{\cdot}\boldsymbol{\varOmega}. \end{align}
\begin{align} \boldsymbol{T}^{(2)} &={-}\frac{4{\rm \pi} }{105(1+\lambda)^3(15+15\lambda+6\lambda^2+\lambda^3)} [(3861 + 15444\lambda + 27996\lambda^2 + 29391\lambda^3 \nonumber\\ &\quad + 19311\lambda^4 + 8107\lambda^5 + 2130\lambda^6 + 321\lambda^7 + 21\lambda^8)(\boldsymbol{I} - \hat{\boldsymbol{z}}\hat{\boldsymbol{z}}) + 2(1242 + 4968\lambda \nonumber\\ &\quad + 8733\lambda^2 + 8661\lambda^3 + 5196\lambda^4 + 1889\lambda^5 + 390\lambda^6 + 36\lambda^7)\hat{\boldsymbol{z}}\hat{\boldsymbol{z}} ]\boldsymbol{\cdot}\boldsymbol{\varOmega}. \end{align}
We again find that the exact solution of Chwang & Wu (Reference Chwang and Wu1975) is recovered from (4.8) in the steady limit, ![]() $|\lambda | \rightarrow 0$, as required.
$|\lambda | \rightarrow 0$, as required.
It is notable that the particle's translation–rotation and its resulting torque–force do not couple, respectively, at first or second order in ![]() $\epsilon$. That is, the force depends only on the translational velocity of the particle whereas the torque (about the particle's geometric centre) relies only on its angular velocity. Indeed, this special result is true for all orders in
$\epsilon$. That is, the force depends only on the translational velocity of the particle whereas the torque (about the particle's geometric centre) relies only on its angular velocity. Indeed, this special result is true for all orders in ![]() $\epsilon$, and is due to the particle's fore–aft geometric symmetry.
$\epsilon$, and is due to the particle's fore–aft geometric symmetry.
4.1.3. Orientation-averaged force and torque
The orientation-averaged force and torque (defined in § 3.4) are calculated using (3.17), (4.7) and (4.8), giving
 \begin{align} & \boldsymbol{\bar{T}} ={-}8{\rm \pi} \boldsymbol{\varOmega} \left[\frac{1+\lambda+\dfrac{\lambda^2}{3}}{1+\lambda}\right. \nonumber\\ &\qquad \left. +\, \epsilon^2 \frac{243 + 972\lambda + 1749\lambda^2 + 1812\lambda^3 + 1167\lambda^4 + 476\lambda^5 + 120\lambda^6 + 17\lambda^7 + \lambda^8}{15(1+\lambda)^3(15+15\lambda+6\lambda^2+\lambda^3)} \vphantom{\boldsymbol{\bar{T}} ={-}8{\rm \pi} \boldsymbol{\varOmega} \left[\frac{1+\lambda+\dfrac{\lambda^2}{3}}{1+\lambda}\right.}\right] + O(\epsilon^3). \end{align}
\begin{align} & \boldsymbol{\bar{T}} ={-}8{\rm \pi} \boldsymbol{\varOmega} \left[\frac{1+\lambda+\dfrac{\lambda^2}{3}}{1+\lambda}\right. \nonumber\\ &\qquad \left. +\, \epsilon^2 \frac{243 + 972\lambda + 1749\lambda^2 + 1812\lambda^3 + 1167\lambda^4 + 476\lambda^5 + 120\lambda^6 + 17\lambda^7 + \lambda^8}{15(1+\lambda)^3(15+15\lambda+6\lambda^2+\lambda^3)} \vphantom{\boldsymbol{\bar{T}} ={-}8{\rm \pi} \boldsymbol{\varOmega} \left[\frac{1+\lambda+\dfrac{\lambda^2}{3}}{1+\lambda}\right.}\right] + O(\epsilon^3). \end{align}Interestingly, we observe that particle non-sphericity increases the magnitude of the orientation-averaged force and torque.
4.2. ‘Pear-shaped’ particle
Next, we examine a particle that does not possess fore–aft symmetry which, in principle, enables coupling of the translational force that the particle experiences with its rotational motion. The shape perturbation function, ![]() $f$, is specified using a linear combination of
$f$, is specified using a linear combination of ![]() $l = 2$ and 3 spherical harmonics, with
$l = 2$ and 3 spherical harmonics, with ![]() $m = 0$ for each harmonic; this produces an axisymmetric particle. The result is a particle that resembles a pear; see figures 1(b) and 2(b).
$m = 0$ for each harmonic; this produces an axisymmetric particle. The result is a particle that resembles a pear; see figures 1(b) and 2(b).
The coefficient of the ![]() $l = 2$ spherical harmonic of
$l = 2$ spherical harmonic of ![]() $f$ is chosen to be identical to that of the spheroid studied in § 4.1. The first-order forces and torques here are identical between the two particles and given by (4.4a) and (4.4b), respectively. The corresponding coefficient of the
$f$ is chosen to be identical to that of the spheroid studied in § 4.1. The first-order forces and torques here are identical between the two particles and given by (4.4a) and (4.4b), respectively. The corresponding coefficient of the ![]() $l = 3$ harmonic is then chosen to be equal to that of the
$l = 3$ harmonic is then chosen to be equal to that of the ![]() $l = 2$ harmonic. The second-order shape perturbation function,
$l = 2$ harmonic. The second-order shape perturbation function, ![]() $g$, is specified using the result in Appendix B with coefficients of the
$g$, is specified using the result in Appendix B with coefficients of the ![]() $l=2$ components set to zero. This gives the radial coordinate of the particle's surface:
$l=2$ components set to zero. This gives the radial coordinate of the particle's surface:
with
 $$\begin{gather}g(\theta, \phi) ={-}\frac{2\sqrt{{\rm \pi} }}{5}\left(2{Y}_{0,0}(\theta, \phi) + 9\sqrt{\frac{3}{35}}{Y}_{1,0}(\theta, \phi)\right) , \end{gather}$$
$$\begin{gather}g(\theta, \phi) ={-}\frac{2\sqrt{{\rm \pi} }}{5}\left(2{Y}_{0,0}(\theta, \phi) + 9\sqrt{\frac{3}{35}}{Y}_{1,0}(\theta, \phi)\right) , \end{gather}$$where the spherical harmonics are defined in Appendix D.
4.2.1. Second-order solution
The second-order contributions to the force and torque are evaluated from (3.6)–(3.12), again using the Mathematica notebook (supplementary material and Appendix A), giving
where ![]() $a_1 (\lambda ),\ldots, a_5(\lambda ), b_1(\lambda ),\ldots, b_5(\lambda )$ are polynomials specified in Appendix E. Here, the maximum degree of spherical harmonics defining the shape perturbation function,
$a_1 (\lambda ),\ldots, a_5(\lambda ), b_1(\lambda ),\ldots, b_5(\lambda )$ are polynomials specified in Appendix E. Here, the maximum degree of spherical harmonics defining the shape perturbation function, ![]() $f$, in (4.11b) is
$f$, in (4.11b) is ![]() $l_{max}=3$. This gives
$l_{max}=3$. This gives ![]() $l_{maxsum} \equiv l_{max}+1=4$, as per § 3.3.1.
$l_{maxsum} \equiv l_{max}+1=4$, as per § 3.3.1.
Coupling between translational and rotational motion is evident in (4.12) and appears at ![]() $O(\epsilon ^2)$, as anticipated in § 1. Moreover, the derived solution in (4.12) possesses the well-known, and required, symmetry relation in the coupling of force/rotation and torque/translation (Brenner Reference Brenner1964b). Namely, the tensorial coefficient of
$O(\epsilon ^2)$, as anticipated in § 1. Moreover, the derived solution in (4.12) possesses the well-known, and required, symmetry relation in the coupling of force/rotation and torque/translation (Brenner Reference Brenner1964b). Namely, the tensorial coefficient of ![]() $\boldsymbol{\varOmega }$ in (4.12a) is the transpose of the coefficient of
$\boldsymbol{\varOmega }$ in (4.12a) is the transpose of the coefficient of ![]() $\boldsymbol{U}$ in (4.12b).
$\boldsymbol{U}$ in (4.12b).
4.2.2. Orientation-averaged force and torque
The orientation-averaged force and torque (§ 3.4) are derived from (3.17), (4.12a) and (4.12b):
 $$\begin{gather}\bar{\boldsymbol{T}} ={-}8{\rm \pi} \boldsymbol{\varOmega} \left[\frac{1+\lambda+\dfrac{\lambda^2}{3}}{1+\lambda} + \epsilon^2 \frac{a_7(\lambda)}{b_7(\lambda)}\right] + O(\epsilon^3), \end{gather}$$
$$\begin{gather}\bar{\boldsymbol{T}} ={-}8{\rm \pi} \boldsymbol{\varOmega} \left[\frac{1+\lambda+\dfrac{\lambda^2}{3}}{1+\lambda} + \epsilon^2 \frac{a_7(\lambda)}{b_7(\lambda)}\right] + O(\epsilon^3), \end{gather}$$
where the polynomials ![]() $a_6(\lambda )$,
$a_6(\lambda )$, ![]() $b_6(\lambda )$,
$b_6(\lambda )$, ![]() $a_7(\lambda )$ and
$a_7(\lambda )$ and ![]() $b_7(\lambda )$ are given in Appendix E. As for the prolate spheroid studied in § 4.1, non-sphericity enhances the magnitude of the orientation-averaged force and torque experienced by the particle.
$b_7(\lambda )$ are given in Appendix E. As for the prolate spheroid studied in § 4.1, non-sphericity enhances the magnitude of the orientation-averaged force and torque experienced by the particle.
4.2.3. Steady and high-frequency limits
Due to the complexity of (4.12), we provide its results in the steady and (high-frequency) inviscid limits, i.e. ![]() $|\lambda | \rightarrow 0$ and
$|\lambda | \rightarrow 0$ and ![]() $|\lambda | \rightarrow \infty$, respectively. These may be useful in practice, e.g. in applications involving Brownian motion. The force and torque in the steady limit are
$|\lambda | \rightarrow \infty$, respectively. These may be useful in practice, e.g. in applications involving Brownian motion. The force and torque in the steady limit are
 \begin{align} \boldsymbol{F}_{|\lambda|\rightarrow 0} &={-}6{\rm \pi} \left[1 + \epsilon\frac{1}{10}\left(\boldsymbol{I} - 3\hat{\boldsymbol{z}}\hat{\boldsymbol{z}}\right) + \epsilon^2 \left( \frac{501}{700} \left(\boldsymbol{I} - \hat{\boldsymbol{z}}\hat{\boldsymbol{z}}\right) + \frac{24}{35}\hat{\boldsymbol{z}}\hat{\boldsymbol{z}} \right)\right]\boldsymbol{\cdot} \boldsymbol{U} \nonumber\\ & \quad +\epsilon^2\frac{162{\rm \pi} }{5\sqrt{35}}\left(\hat{\boldsymbol{y}}\hat{\boldsymbol{x}} - \hat{\boldsymbol{x}}\hat{\boldsymbol{y}}\right)\boldsymbol{\cdot} \boldsymbol{\varOmega} + O(\epsilon^3), \end{align}
\begin{align} \boldsymbol{F}_{|\lambda|\rightarrow 0} &={-}6{\rm \pi} \left[1 + \epsilon\frac{1}{10}\left(\boldsymbol{I} - 3\hat{\boldsymbol{z}}\hat{\boldsymbol{z}}\right) + \epsilon^2 \left( \frac{501}{700} \left(\boldsymbol{I} - \hat{\boldsymbol{z}}\hat{\boldsymbol{z}}\right) + \frac{24}{35}\hat{\boldsymbol{z}}\hat{\boldsymbol{z}} \right)\right]\boldsymbol{\cdot} \boldsymbol{U} \nonumber\\ & \quad +\epsilon^2\frac{162{\rm \pi} }{5\sqrt{35}}\left(\hat{\boldsymbol{y}}\hat{\boldsymbol{x}} - \hat{\boldsymbol{x}}\hat{\boldsymbol{y}}\right)\boldsymbol{\cdot} \boldsymbol{\varOmega} + O(\epsilon^3), \end{align} \begin{align} \boldsymbol{T}_{|\lambda|\rightarrow 0} &={-} 8{\rm \pi} \left[1 + \epsilon \frac{3}{10}\left(\boldsymbol{I} - 3\hat{\boldsymbol{z}}\hat{\boldsymbol{z}}\right) + \epsilon^2 \left(\frac{541}{140}(\boldsymbol{I} - \hat{\boldsymbol{z}}\hat{\boldsymbol{z}}) + \frac{227}{175}\hat{\boldsymbol{z}}\hat{\boldsymbol{z}}\right) \right]\boldsymbol{\cdot}\boldsymbol{\varOmega} \nonumber\\ &\quad + \epsilon^2\frac{162{\rm \pi} }{5\sqrt{35}}(\hat{\boldsymbol{x}}\hat{\boldsymbol{y}} - \hat{\boldsymbol{y}}\hat{\boldsymbol{x}})\boldsymbol{\cdot} \boldsymbol{U} + O(\epsilon^3), \end{align}
\begin{align} \boldsymbol{T}_{|\lambda|\rightarrow 0} &={-} 8{\rm \pi} \left[1 + \epsilon \frac{3}{10}\left(\boldsymbol{I} - 3\hat{\boldsymbol{z}}\hat{\boldsymbol{z}}\right) + \epsilon^2 \left(\frac{541}{140}(\boldsymbol{I} - \hat{\boldsymbol{z}}\hat{\boldsymbol{z}}) + \frac{227}{175}\hat{\boldsymbol{z}}\hat{\boldsymbol{z}}\right) \right]\boldsymbol{\cdot}\boldsymbol{\varOmega} \nonumber\\ &\quad + \epsilon^2\frac{162{\rm \pi} }{5\sqrt{35}}(\hat{\boldsymbol{x}}\hat{\boldsymbol{y}} - \hat{\boldsymbol{y}}\hat{\boldsymbol{x}})\boldsymbol{\cdot} \boldsymbol{U} + O(\epsilon^3), \end{align}
while the corresponding inviscid results, i.e. ![]() $|\lambda | \rightarrow \infty$, are
$|\lambda | \rightarrow \infty$, are
 \begin{align} \boldsymbol{F}_{|\lambda|\rightarrow \infty} &={-}\frac{2{\rm \pi} }{3}\lambda^2\left[1 + \epsilon\frac{9}{10}(\boldsymbol{I} - 3\hat{\boldsymbol{z}}\hat{\boldsymbol{z}}) + \epsilon^2 \left( \frac{111}{140} (\boldsymbol{I} - \hat{\boldsymbol{z}}\hat{\boldsymbol{z}}) + \frac{681}{175}\hat{\boldsymbol{z}}\hat{\boldsymbol{z}} \right)\right]\boldsymbol{\cdot} \boldsymbol{U} \nonumber\\ & \quad +\epsilon^2\lambda^2\frac{6{\rm \pi} }{\sqrt{35}}(\kern 1.5pt\hat{\boldsymbol{y}}\hat{\boldsymbol{x}} - \hat{\boldsymbol{x}}\hat{\boldsymbol{y}})\boldsymbol{\cdot} \boldsymbol{\varOmega} + O(\epsilon^3), \end{align}
\begin{align} \boldsymbol{F}_{|\lambda|\rightarrow \infty} &={-}\frac{2{\rm \pi} }{3}\lambda^2\left[1 + \epsilon\frac{9}{10}(\boldsymbol{I} - 3\hat{\boldsymbol{z}}\hat{\boldsymbol{z}}) + \epsilon^2 \left( \frac{111}{140} (\boldsymbol{I} - \hat{\boldsymbol{z}}\hat{\boldsymbol{z}}) + \frac{681}{175}\hat{\boldsymbol{z}}\hat{\boldsymbol{z}} \right)\right]\boldsymbol{\cdot} \boldsymbol{U} \nonumber\\ & \quad +\epsilon^2\lambda^2\frac{6{\rm \pi} }{\sqrt{35}}(\kern 1.5pt\hat{\boldsymbol{y}}\hat{\boldsymbol{x}} - \hat{\boldsymbol{x}}\hat{\boldsymbol{y}})\boldsymbol{\cdot} \boldsymbol{\varOmega} + O(\epsilon^3), \end{align}The resultant orientation-averaged forces and torques in the steady and inviscid limits, derived from (4.13), are
We observe that the ![]() $O(\epsilon ^2)$ term provides the leading-order contribution to the torque in the inviscid limit, as eluded to in § 1. Again, particle non-sphericity enhances the magnitudes of the force and torque.
$O(\epsilon ^2)$ term provides the leading-order contribution to the torque in the inviscid limit, as eluded to in § 1. Again, particle non-sphericity enhances the magnitudes of the force and torque.
It remains to be established if the above-mentioned enhancements due to particle non-sphericity, in the magnitude of the orientation-averaged force and torque experienced by the spheroid and ‘pear-shaped’ particles, hold true for all particle shapes. Note that the surface area of a nearly spherical particle always exceeds that of its equivalent-volume sphere, which is consistent with this enhancement.
4.3. ‘Harmonic virion’
Virions are often studied via acoustic techniques (see e.g. Robach et al. Reference Robach, Michels, Cerf, Braunwald and Tripier-Darcy1983; Babincová, Sourivong & Babinec Reference Babincová, Sourivong and Babinec2000; Yang et al. Reference Yang, Lin, Liu, Lu, Hung, Huang, Tsai, Kao, Chen and Sun2015), corresponding to the small-amplitude, unsteady Stokes limit in the present study. The following model provides insight into the hydrodynamics of virions when a spherical geometry cannot be assumed, such as SARS-CoV-2 virions, which exhibit ‘spiky’ protrusions; see figure 3(a). This model may also prove useful in studying the hydrodynamics of SARS-CoV-2 virions in aerosols, which is one of their methods of transmission (Van Doremalen et al. Reference Van Doremalen2020). Rather than consider the true geometry of the virion, its shape is modelled using a single spherical harmonic to facilitate analysis and interpretation. This model is also applicable to other virions and is termed a ‘harmonic virion’; see figure 3(b–d). In this section, we study how the size and number of ‘spiky’ protrusions of the particles affect their hydrodynamics.
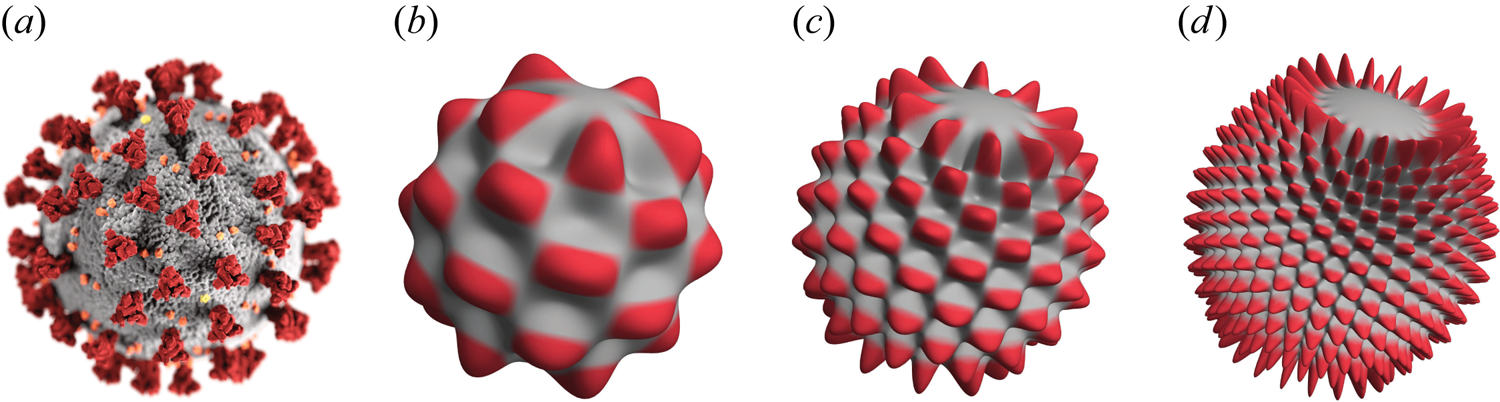
Figure 3. (a) Illustration of a SARS-CoV-2 virion (Eckert & Higgins Reference Eckert and Higgins2020). (b–d) ‘Harmonic virions’ which provide a simple hydrodynamic model for a SARS-CoV-2 virion. The nearly spherical particles are constructed with linear combinations of (b) ![]() $(l,m)=(10,\pm 5)$, (c)
$(l,m)=(10,\pm 5)$, (c) ![]() $(l,m)=(20,\pm 10)$ and (d)
$(l,m)=(20,\pm 10)$ and (d) ![]() $(l,m)=(40,\pm 20)$ for the first-order shape perturbation function
$(l,m)=(40,\pm 20)$ for the first-order shape perturbation function ![]() $f$ in (4.18a).
$f$ in (4.18a).
Three different ‘harmonic virions’ are studied, representing a progressively rougher and ‘spikier’ virion. The shape perturbation functions for these particles are
with ![]() $n \in \{5,\, 10,\, 20\}$, and
$n \in \{5,\, 10,\, 20\}$, and
We calculate the orientation-averaged forces and torques experienced by these particles, which may be practically relevant due to the randomising effects of Brownian motion. The resulting analytical expressions are complicated and in this section we focus on the (numericised) asymptotic limits of small and large ![]() $|\lambda |$, reported to three significant figures; exact formulae for all
$|\lambda |$, reported to three significant figures; exact formulae for all ![]() $\lambda$ are contained in the Mathematica notebook (supplementary material). The resulting orientation-averaged force is
$\lambda$ are contained in the Mathematica notebook (supplementary material). The resulting orientation-averaged force is
with the subscript ![]() $n$ specified in (4.18), and
$n$ specified in (4.18), and
The corresponding formula for the orientation-averaged torque is
with
Figure 4 gives results for the orientation-averaged forces and torques, as a function of dimensionless frequency, ![]() $\lambda$; exact formulae from the Mathematica notebook (supplementary material) are used. The most pronounced difference between these results and that for a perfect sphere is observed for the orientation-averaged torque when
$\lambda$; exact formulae from the Mathematica notebook (supplementary material) are used. The most pronounced difference between these results and that for a perfect sphere is observed for the orientation-averaged torque when ![]() $|\lambda | \gg 1$. The torque experienced by a perfect sphere scales as
$|\lambda | \gg 1$. The torque experienced by a perfect sphere scales as ![]() $\lambda$ for
$\lambda$ for ![]() $|\lambda | \gg 1$ due to the vanishingly small influence of the no-slip boundary condition; see (4.22a). In contrast, the harmonic virion's orientation-averaged torque varies as
$|\lambda | \gg 1$ due to the vanishingly small influence of the no-slip boundary condition; see (4.22a). In contrast, the harmonic virion's orientation-averaged torque varies as ![]() $\lambda ^2$ due to its protrusions producing non-zero added mass in this inviscid limit; see (4.22b)–(4.22d). It is also evident that the orientation-averaged force and torque magnitudes increase as the degree and order of the spherical harmonics increase, i.e. the particles become spikier. This is not unexpected due to the increase in particle surface area.
$\lambda ^2$ due to its protrusions producing non-zero added mass in this inviscid limit; see (4.22b)–(4.22d). It is also evident that the orientation-averaged force and torque magnitudes increase as the degree and order of the spherical harmonics increase, i.e. the particles become spikier. This is not unexpected due to the increase in particle surface area.

Figure 4. Orientation-averaged force and torque for the three ‘harmonic virions’ in figure 3. Magnitudes of the second-order orientation-averaged (a) force and (c) torque monotonically increase with ![]() $|\lambda |$. Also shown is the ratio of the magnitude of the second-order orientation-averaged (b) force and (d) torque to their leading-order counterparts (i.e. results for a perfect sphere).
$|\lambda |$. Also shown is the ratio of the magnitude of the second-order orientation-averaged (b) force and (d) torque to their leading-order counterparts (i.e. results for a perfect sphere).
The ratio of the second-order to leading-order solutions in figure 4(b,d) reveals intriguing behaviour. This ratio is not constant, as may be naively anticipated, establishing that no perfect sphere can mimic the frequency-dependent – or equivalently, time-dependent – orientation-averaged force and torque experienced by a harmonic virion. Interestingly, this ratio for the force is maximised for intermediate ![]() $|\lambda |$, the value of which increases with increasing
$|\lambda |$, the value of which increases with increasing ![]() $(l, m)$. This maximum occurs when the viscous penetration depth, over which vorticity diffuses, matches the spacing of the protrusions. In this case, the force becomes sensitively dependent on the precise shape and spacing of the protrusions. No such maxima occur for the torque due to the different dependencies on
$(l, m)$. This maximum occurs when the viscous penetration depth, over which vorticity diffuses, matches the spacing of the protrusions. In this case, the force becomes sensitively dependent on the precise shape and spacing of the protrusions. No such maxima occur for the torque due to the different dependencies on ![]() $\lambda$ in the high-frequency limit discussed above.
$\lambda$ in the high-frequency limit discussed above.
4.4. Comparison with the Brownian motion of anisotropic particles studied by Kraft et al. (Reference Kraft, Wittkowski, Ten Hagen, Edmond, Pine and Löwen2013)
Kraft et al. (Reference Kraft, Wittkowski, Ten Hagen, Edmond, Pine and Löwen2013) studied the motion of anisotropic particles constructed by fusing together spheres of different radii. They measured the friction tensors of the particles by monitoring their Brownian trajectories. For a particle consisting of three fused spheres of different radii (see figure 5), they observed coupling between the translational and rotational motion of the Brownian particles in both experiments and numerical simulations performed in the steady Stokes limit.

Figure 5. (a) Geometry and numerical results for the resistance of an anisotropic Brownian particle studied by Kraft et al. (Reference Kraft, Wittkowski, Ten Hagen, Edmond, Pine and Löwen2013). The Brownian particle is constructed by fusing together three spheres of radii 2.1, 1.7 and 1.3 ![]() $\mathrm{\mu }$m, respectively. The resistance matrix,
$\mathrm{\mu }$m, respectively. The resistance matrix, ![]() $\boldsymbol{M}$, relates the force and torque via
$\boldsymbol{M}$, relates the force and torque via ![]() $(\boldsymbol{F}, \boldsymbol{T}) = \boldsymbol{M}* (\boldsymbol{U}, \boldsymbol{\varOmega })$. Note that the resistance matrix is given in dimensional form where the units of the first, second, third and fourth 3
$(\boldsymbol{F}, \boldsymbol{T}) = \boldsymbol{M}* (\boldsymbol{U}, \boldsymbol{\varOmega })$. Note that the resistance matrix is given in dimensional form where the units of the first, second, third and fourth 3![]() $\times$3 submatrices are
$\times$3 submatrices are ![]() $\mathrm{\mu }$m,
$\mathrm{\mu }$m, ![]() $\mathrm{\mu }$m
$\mathrm{\mu }$m![]() $^2$,
$^2$, ![]() $\mathrm{\mu }$m
$\mathrm{\mu }$m![]() $^2$ and
$^2$ and ![]() $\mathrm{\mu }$m
$\mathrm{\mu }$m![]() $^3$, respectively. (b) Present theory. Nearly spherical reconstruction of the anisotropic Brownian particle using spherical harmonics with
$^3$, respectively. (b) Present theory. Nearly spherical reconstruction of the anisotropic Brownian particle using spherical harmonics with ![]() $l \le 5$. The radius of the equivalent-volume sphere is calculated from the combined volumes of the three fused spheres and results in
$l \le 5$. The radius of the equivalent-volume sphere is calculated from the combined volumes of the three fused spheres and results in ![]() $R_{eq} = 2.5$
$R_{eq} = 2.5$ ![]() $\mathrm{\mu }$m. The resistance matrix is constructed from the theory in § 3 in the limit
$\mathrm{\mu }$m. The resistance matrix is constructed from the theory in § 3 in the limit ![]() $\lambda \rightarrow 0$ and then cast into dimensional form using
$\lambda \rightarrow 0$ and then cast into dimensional form using ![]() $R_{eq}$ and the dimensions above. This matrix is to be compared with the literature data of Kraft et al. (Reference Kraft, Wittkowski, Ten Hagen, Edmond, Pine and Löwen2013) reported in (a).
$R_{eq}$ and the dimensions above. This matrix is to be compared with the literature data of Kraft et al. (Reference Kraft, Wittkowski, Ten Hagen, Edmond, Pine and Löwen2013) reported in (a).
We reconstruct this particle using spherical harmonics up to order ![]() $l \le 5$, resulting in the shape given in figure 5(b). Using the force and torque formulae in § 3, and taking the limit as
$l \le 5$, resulting in the shape given in figure 5(b). Using the force and torque formulae in § 3, and taking the limit as ![]() $\lambda \rightarrow 0$, we calculate the force and torque reported in figure 5(b). Critically, the only information used from Kraft et al. (Reference Kraft, Wittkowski, Ten Hagen, Edmond, Pine and Löwen2013) is the radii of the three spheres and the origin of the coordinate system as approximated from figure 5(a); no other fitting parameters are used. We observe excellent agreement between our nearly spherical theory and the numerical results of Kraft et al. (Reference Kraft, Wittkowski, Ten Hagen, Edmond, Pine and Löwen2013). Agreement between the components of the coupling tensor are particularly relevant because they arise exclusively from the
$\lambda \rightarrow 0$, we calculate the force and torque reported in figure 5(b). Critically, the only information used from Kraft et al. (Reference Kraft, Wittkowski, Ten Hagen, Edmond, Pine and Löwen2013) is the radii of the three spheres and the origin of the coordinate system as approximated from figure 5(a); no other fitting parameters are used. We observe excellent agreement between our nearly spherical theory and the numerical results of Kraft et al. (Reference Kraft, Wittkowski, Ten Hagen, Edmond, Pine and Löwen2013). Agreement between the components of the coupling tensor are particularly relevant because they arise exclusively from the ![]() $O(\epsilon ^2)$ terms reported in this study.
$O(\epsilon ^2)$ terms reported in this study.
5. Direct numerical simulations at finite amplitude
In this section, we validate the (infinitesimally) small-amplitude theory reported in § 3 by comparison with finite-amplitude, time-dependent DNS of the (nonlinear) incompressible Navier–Stokes equations, (2.1) and (2.2). The DNS are performed using COMSOL Multiphysics![]() . Details are reported in Appendix F.
. Details are reported in Appendix F.
The ‘pear-shaped’ particle described in § 4.2 is used for this validation, together with a normalised frequency of ![]() $\beta = 1$; other frequencies lead to similar conclusions (data not shown). The linear and angular oscillatory velocities are set to
$\beta = 1$; other frequencies lead to similar conclusions (data not shown). The linear and angular oscillatory velocities are set to ![]() $\boldsymbol{U} = \delta \hat {\boldsymbol{z}}$ and
$\boldsymbol{U} = \delta \hat {\boldsymbol{z}}$ and ![]() $\boldsymbol{\varOmega } = \delta \hat {\boldsymbol{y}}$, respectively. The values of
$\boldsymbol{\varOmega } = \delta \hat {\boldsymbol{y}}$, respectively. The values of ![]() $\delta$ and
$\delta$ and ![]() $\epsilon$ are varied to examine the combined effects of non-sphericity and oscillation amplitude, respectively. For each set of these values, time series of the force and torque experienced by the particle are computed from which their complex Fourier series are determined. This uses a fundamental angular frequency of
$\epsilon$ are varied to examine the combined effects of non-sphericity and oscillation amplitude, respectively. For each set of these values, time series of the force and torque experienced by the particle are computed from which their complex Fourier series are determined. This uses a fundamental angular frequency of ![]() $\omega = 1$, as dictated by the above non-dimensionalisation. All DNS are converged to at least 98 % with respect to the magnitude of the largest non-zero
$\omega = 1$, as dictated by the above non-dimensionalisation. All DNS are converged to at least 98 % with respect to the magnitude of the largest non-zero ![]() $\textrm{e}^{-\textrm{i}t}$ Fourier coefficient of the force/torque; this coincides with the particle's oscillatory motion. Results for this fundamental Fourier coefficient of the DNS provide the finite-amplitude counterpart to the small-amplitude theory which is a solution of the (linear) unsteady Stokes equation. This enables direct comparison between the DNS and the small-amplitude theory. Symmetries in the ‘pear-shaped’ particle and oscillatory velocities produce non-zero results for (i) the force in the
$\textrm{e}^{-\textrm{i}t}$ Fourier coefficient of the force/torque; this coincides with the particle's oscillatory motion. Results for this fundamental Fourier coefficient of the DNS provide the finite-amplitude counterpart to the small-amplitude theory which is a solution of the (linear) unsteady Stokes equation. This enables direct comparison between the DNS and the small-amplitude theory. Symmetries in the ‘pear-shaped’ particle and oscillatory velocities produce non-zero results for (i) the force in the ![]() $x$ direction, denoted
$x$ direction, denoted ![]() $F_x$, (ii) force in the
$F_x$, (ii) force in the ![]() $z$ direction, denoted
$z$ direction, denoted ![]() $F_z$, and (iii) torque about the
$F_z$, and (iii) torque about the ![]() $y$ axis, denoted
$y$ axis, denoted ![]() $T_y$. Results for these components from the DNS and small-amplitude theory are reported in figure 6. Details of the DNS and their convergence, including validation on a perfect sphere, are relegated to Appendix F.
$T_y$. Results for these components from the DNS and small-amplitude theory are reported in figure 6. Details of the DNS and their convergence, including validation on a perfect sphere, are relegated to Appendix F.
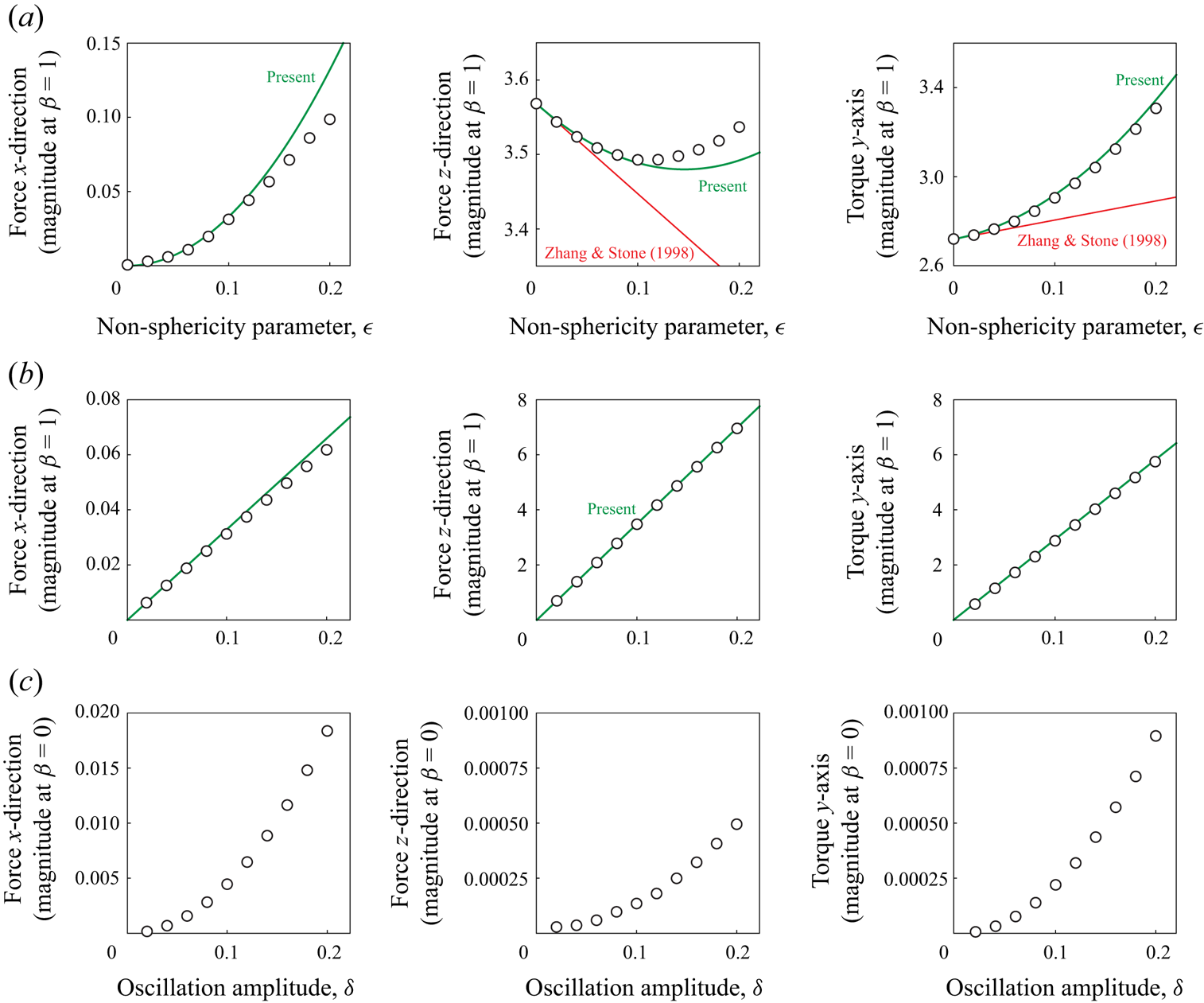
Figure 6. Force and torque components of the ‘pear-shaped’ particle, with ![]() $\boldsymbol{U} = \delta \hat {\boldsymbol{z}}$ and
$\boldsymbol{U} = \delta \hat {\boldsymbol{z}}$ and ![]() $\boldsymbol{\varOmega } = \delta \hat {\boldsymbol{y}}$. Nearly spherical theory (solid lines); DNS (circles). Results for magnitudes of
$\boldsymbol{\varOmega } = \delta \hat {\boldsymbol{y}}$. Nearly spherical theory (solid lines); DNS (circles). Results for magnitudes of ![]() $F_x$,
$F_x$, ![]() $F_z$ and
$F_z$ and ![]() $T_y$, for particle motion at
$T_y$, for particle motion at ![]() $\beta = 1$. (a) Force/torque components at
$\beta = 1$. (a) Force/torque components at ![]() $\beta =1$ (fundamental frequency), for oscillation amplitude,
$\beta =1$ (fundamental frequency), for oscillation amplitude, ![]() $\delta = 0.1$, as non-spherical parameter
$\delta = 0.1$, as non-spherical parameter ![]() $\epsilon$ is varied. (b) Force/torque components at
$\epsilon$ is varied. (b) Force/torque components at ![]() $\beta =1$ (fundamental frequency), for non-spherical parameter,
$\beta =1$ (fundamental frequency), for non-spherical parameter, ![]() $\epsilon = 0.1$, as oscillation amplitude
$\epsilon = 0.1$, as oscillation amplitude ![]() $\delta$ is varied. (c) Force/torque components at
$\delta$ is varied. (c) Force/torque components at ![]() $\beta =0$ (steady streaming), for non-spherical parameter,
$\beta =0$ (steady streaming), for non-spherical parameter, ![]() $\epsilon = 0.1$, as oscillation amplitude
$\epsilon = 0.1$, as oscillation amplitude ![]() $\delta$ is varied.
$\delta$ is varied.
We first assess the validity of the second-order solution in the developed nearly spherical theory. For this purpose, the dimensionless oscillation amplitude is set to ![]() $\delta = 0.1$ and the non-spherical parameter
$\delta = 0.1$ and the non-spherical parameter ![]() $\epsilon$ is varied; note that
$\epsilon$ is varied; note that ![]() $\epsilon =0$ corresponds to a perfect sphere. It is evident from figure 6(a) that the DNS and small-amplitude theory agree for smaller values of
$\epsilon =0$ corresponds to a perfect sphere. It is evident from figure 6(a) that the DNS and small-amplitude theory agree for smaller values of ![]() $\epsilon$, i.e.
$\epsilon$, i.e. ![]() $\epsilon \lesssim 0.1$. This provides independent validation of the nearly spherical theory. Specifically, the DNS force in the
$\epsilon \lesssim 0.1$. This provides independent validation of the nearly spherical theory. Specifically, the DNS force in the ![]() $x$ direction,
$x$ direction, ![]() $F_x$, coincides precisely with the nearly spherical theory for smaller values of
$F_x$, coincides precisely with the nearly spherical theory for smaller values of ![]() $\epsilon$. A quadratic variation in
$\epsilon$. A quadratic variation in ![]() $\epsilon$ is predicted by the nearly spherical theory and observed in the DNS. A deviation emerges at larger values of
$\epsilon$ is predicted by the nearly spherical theory and observed in the DNS. A deviation emerges at larger values of ![]() $\epsilon$, which is not unexpected given the asymptotic nature of the nearly spherical theory. Similar agreement is observed for
$\epsilon$, which is not unexpected given the asymptotic nature of the nearly spherical theory. Similar agreement is observed for ![]() $F_z$ and
$F_z$ and ![]() $T_y$ with the second-order solution correctly capturing the DNS trends as the non-spherical parameter
$T_y$ with the second-order solution correctly capturing the DNS trends as the non-spherical parameter ![]() $\epsilon$ is increased. Results for the phase of these force and torque components exhibit similar agreement (data not shown). Critically, the DNS shows that the force in the
$\epsilon$ is increased. Results for the phase of these force and torque components exhibit similar agreement (data not shown). Critically, the DNS shows that the force in the ![]() $x$ direction,
$x$ direction, ![]() $F_x$, is coupled to the particle's angular velocity around the
$F_x$, is coupled to the particle's angular velocity around the ![]() $y$ axis. This behaviour is captured correctly by the second-order solution; the first-order theory of Zhang & Stone (Reference Zhang and Stone1998) predicts
$y$ axis. This behaviour is captured correctly by the second-order solution; the first-order theory of Zhang & Stone (Reference Zhang and Stone1998) predicts ![]() $F_x=0 + O(\epsilon ^2)$.
$F_x=0 + O(\epsilon ^2)$.
Next, we investigate the validity of the (leading-order) small-![]() $\delta$ expansion employed in the nearly spherical theory, i.e. its foundational use of the unsteady Stokes equations. As noted at the end of § 2.2, this theory is expected to be valid provided the dimensionless oscillation amplitude is much smaller than the non-spherical parameter, i.e.
$\delta$ expansion employed in the nearly spherical theory, i.e. its foundational use of the unsteady Stokes equations. As noted at the end of § 2.2, this theory is expected to be valid provided the dimensionless oscillation amplitude is much smaller than the non-spherical parameter, i.e. ![]() $\delta \ll \epsilon$. For this purpose, we now fix the non-spherical parameter to be
$\delta \ll \epsilon$. For this purpose, we now fix the non-spherical parameter to be ![]() $\epsilon = 0.1$ and vary the oscillation amplitude,
$\epsilon = 0.1$ and vary the oscillation amplitude, ![]() $\delta$. Results for the magnitude of the force and torque are reported in figure 6(b); similar results are found for the phase (data not shown). Linear dependence on the oscillation amplitude,
$\delta$. Results for the magnitude of the force and torque are reported in figure 6(b); similar results are found for the phase (data not shown). Linear dependence on the oscillation amplitude, ![]() $\delta$, for
$\delta$, for ![]() $\delta < \epsilon$ is evident in all results, as required. A deviation from linearity emerges for
$\delta < \epsilon$ is evident in all results, as required. A deviation from linearity emerges for ![]() $\delta > \epsilon$ which is again not unexpected. This is due to the significant effect of nonlinear convective inertia in this regime (explored below). Note that the force component in the
$\delta > \epsilon$ which is again not unexpected. This is due to the significant effect of nonlinear convective inertia in this regime (explored below). Note that the force component in the ![]() $x$ direction,
$x$ direction, ![]() $F_x$, is zero for a perfect sphere and depends quadratically on the non-spherical parameter
$F_x$, is zero for a perfect sphere and depends quadratically on the non-spherical parameter ![]() $\epsilon$. The predictions of the nearly spherical theory precisely coincide with the DNS for this purely non-spherical force component. This comparison validates use of the unsteady Stokes equations as the foundation of the nearly spherical theory, and demonstrates its predicted regime of validity,
$\epsilon$. The predictions of the nearly spherical theory precisely coincide with the DNS for this purely non-spherical force component. This comparison validates use of the unsteady Stokes equations as the foundation of the nearly spherical theory, and demonstrates its predicted regime of validity, ![]() $\delta \ll \epsilon$, given in § 2.2.
$\delta \ll \epsilon$, given in § 2.2.
Increasing the oscillation amplitude, ![]() $\delta$, is expected to produce non-zero steady components of the force and torque. This is due to the effect of nonlinear convective inertia, which is absent from the nearly spherical theory. The DNS data for these steady components are reported in figure 6(c) and exhibit the expected nonlinear variation in oscillation amplitude,
$\delta$, is expected to produce non-zero steady components of the force and torque. This is due to the effect of nonlinear convective inertia, which is absent from the nearly spherical theory. The DNS data for these steady components are reported in figure 6(c) and exhibit the expected nonlinear variation in oscillation amplitude, ![]() $\delta$. These steady components are generally much smaller than the fundamental frequency components reported in figure 6(b). However, we observe that when the steady component of
$\delta$. These steady components are generally much smaller than the fundamental frequency components reported in figure 6(b). However, we observe that when the steady component of ![]() $F_x$ in figure 6(b) is similar in magnitude to the fundamental frequency component in figure 6(c), i.e.
$F_x$ in figure 6(b) is similar in magnitude to the fundamental frequency component in figure 6(c), i.e. ![]() $\delta \gtrsim \epsilon = 0.1$, the latter component no longer tracks linearly with the oscillation amplitude,
$\delta \gtrsim \epsilon = 0.1$, the latter component no longer tracks linearly with the oscillation amplitude, ![]() $\delta$. This confirms that the nearly spherical theory – based on the (linear) unsteady Stokes equations – is valid provided the effect of nonlinear convective inertia is negligible. This occurs when
$\delta$. This confirms that the nearly spherical theory – based on the (linear) unsteady Stokes equations – is valid provided the effect of nonlinear convective inertia is negligible. This occurs when ![]() $\delta \ll \epsilon$, as predicted in § 2.2. Analytical calculation of this streaming flow is beyond the scope of this study.
$\delta \ll \epsilon$, as predicted in § 2.2. Analytical calculation of this streaming flow is beyond the scope of this study.
The present theory requires the oscillation amplitude, ![]() $\delta$, to be smaller than all other length scales, including the non-spherical shape parameter,
$\delta$, to be smaller than all other length scales, including the non-spherical shape parameter, ![]() $\epsilon$. This means that (strictly) the theory is not valid when
$\epsilon$. This means that (strictly) the theory is not valid when ![]() $\epsilon \ll \delta$. However, the left-hand panel of figure 6(a) appears to show agreement in this regime. This is because the force in the
$\epsilon \ll \delta$. However, the left-hand panel of figure 6(a) appears to show agreement in this regime. This is because the force in the ![]() $x$ direction is constrained to (i) zero as
$x$ direction is constrained to (i) zero as ![]() $\epsilon \rightarrow 0$ (the result for a sphere) and (ii) the derived non-spherical
$\epsilon \rightarrow 0$ (the result for a sphere) and (ii) the derived non-spherical ![]() $O(\epsilon ^2)$ result for
$O(\epsilon ^2)$ result for ![]() $\epsilon \gg \delta$. The intermediate regime of
$\epsilon \gg \delta$. The intermediate regime of ![]() $0< \delta < \epsilon$ smoothly connects these two results, with any deviation from the theory not resolvable with the accuracy of our numerical simulations.
$0< \delta < \epsilon$ smoothly connects these two results, with any deviation from the theory not resolvable with the accuracy of our numerical simulations.
6. Conclusions
We have examined the force and torque experienced by a nearly spherical particle of arbitrary shape moving in a quiescent and unbounded viscous fluid. This builds on the previous work of Zhang & Stone (Reference Zhang and Stone1998), by providing an asymptotic solution in the small non-sphericity parameter correct to ![]() $O(\epsilon ^2)$. In so doing, the derived general formulae enable analytical calculations of important fluid physical phenomena of arbitrary nearly spherical particles. These include hydrodynamic coupling between the particle's translational and rotational motion, and the effect of particle non-sphericity on the orientation-averaged force and torque that it experiences. General unsteady linear motion was considered according to the unsteady Stokes equations. Strictly, the derived general formulae apply when the oscillation amplitude is far smaller than the height of the particle's non-sphericity, i.e.
$O(\epsilon ^2)$. In so doing, the derived general formulae enable analytical calculations of important fluid physical phenomena of arbitrary nearly spherical particles. These include hydrodynamic coupling between the particle's translational and rotational motion, and the effect of particle non-sphericity on the orientation-averaged force and torque that it experiences. General unsteady linear motion was considered according to the unsteady Stokes equations. Strictly, the derived general formulae apply when the oscillation amplitude is far smaller than the height of the particle's non-sphericity, i.e. ![]() $\delta \ll \epsilon$.
$\delta \ll \epsilon$.
To illustrate the utility of these general formulae, we used them to explore the hydrodynamic forces experienced by three particles: (1) a spheroidal particle that exhibits fore–aft symmetry, (2) a ‘pear-shaped’ particle that does not possess this high degree of symmetry and (3) a ‘harmonic virion’ which models the SARS-CoV-2 virion. Closed-form expressions for the force and torque experienced by these particles were derived correct to ![]() $O(\epsilon ^2)$, together with their orientation-averaged formulae. This showed that a perfect sphere cannot be generally used to model the time-dependent, orientation-averaged forces experienced by a nearly spherical particle. Additionally, it was observed that non-sphericity enhances the magnitude of the orientation-averaged force and torque experienced by these three particles, a result whose applicability to general particles is yet to be established. It is envisaged that the general formulae in § 3 will find utility in the analytical solution of flow problems that have previously been inaccessible. This may be useful, for example, in improving the efficiency of computational simulations of particle suspensions that may rely on single particle results.
$O(\epsilon ^2)$, together with their orientation-averaged formulae. This showed that a perfect sphere cannot be generally used to model the time-dependent, orientation-averaged forces experienced by a nearly spherical particle. Additionally, it was observed that non-sphericity enhances the magnitude of the orientation-averaged force and torque experienced by these three particles, a result whose applicability to general particles is yet to be established. It is envisaged that the general formulae in § 3 will find utility in the analytical solution of flow problems that have previously been inaccessible. This may be useful, for example, in improving the efficiency of computational simulations of particle suspensions that may rely on single particle results.
It is anticipated that the present theory will find use in studying the Brownian motion of nearly spherical particles. Because non-sphericity enters into the orientation-averaged forces at ![]() $O(\epsilon ^2)$, non-sphericity is also expected to affect orientationally averaged diffusivities at this order. Unsteady effects may also couple with the effects of non-sphericity to modify the velocity autocorrelation functions relative to those of a perfect sphere.
$O(\epsilon ^2)$, non-sphericity is also expected to affect orientationally averaged diffusivities at this order. Unsteady effects may also couple with the effects of non-sphericity to modify the velocity autocorrelation functions relative to those of a perfect sphere.
The derived nearly spherical theory was validated against independent finite-amplitude time-domain simulations of the (nonlinear) Navier–Stokes equations. Agreement with the DNS was observed when ![]() $\delta \lesssim \epsilon$, which aligns with the regime of validity of the derived theory; see above.
$\delta \lesssim \epsilon$, which aligns with the regime of validity of the derived theory; see above.
A Mathematica notebook is included in the supplementary material, which applies the general formulae in § 3 to nearly spherical particles with an arbitrary shape perturbation function. Usage details are discussed in Appendix A.
Supplementary material
Supplementary material is available at https://doi.org/10.1017/jfm.2024.1075.
Declaration of interests
The authors report no conflict of interest.
Data availability statement
All data are reported in this paper.
Appendix A. Mathematica notebook for arbitrary particle shapes (supplementary material)
The Mathematica notebook provided in the supplementary material implements the theory in § 3 to analytically evaluate the force and torque acting on a nearly spherical particle. This notebook requires the following inputs:
1. The shape perturbation functions,
 $f$ and
$f$ and  $g$. These functions must be specified as linear combinations of spherical harmonics, as per (B1).
$g$. These functions must be specified as linear combinations of spherical harmonics, as per (B1).2. The positive integer,
 $\textrm{MAXSUM} \equiv l_{maxsum}$. This is the largest (truncation) index,
$\textrm{MAXSUM} \equiv l_{maxsum}$. This is the largest (truncation) index,  $l$, used in evaluation of the infinite series in (3.9) and (3.10).
$l$, used in evaluation of the infinite series in (3.9) and (3.10).
An exact analytical solution is recovered when ![]() $\mathrm{MAXSUM} = l_{max}+1$, where
$\mathrm{MAXSUM} = l_{max}+1$, where ![]() $l_{max}$ is the highest degree of all spherical harmonics defining
$l_{max}$ is the highest degree of all spherical harmonics defining ![]() $f$. If
$f$. If ![]() $f$ involves an infinite sum of spherical harmonics (i.e. of all degrees),
$f$ involves an infinite sum of spherical harmonics (i.e. of all degrees), ![]() $\mathrm{MAXSUM}$ should be chosen to balance accuracy with computational expense.
$\mathrm{MAXSUM}$ should be chosen to balance accuracy with computational expense.
Appendix B. How to choose  $f (\theta, \phi )$ and
$f (\theta, \phi )$ and  $g(\theta, \phi )$
$g(\theta, \phi )$
Here, we describe how to choose the radial shape perturbation functions, ![]() $f(\theta, \phi )$ and
$f(\theta, \phi )$ and ![]() $g(\theta, \phi )$, to ensure the requirements in (2.7) and (2.9) are satisfied. Consider the general spherical harmonic decompositions:
$g(\theta, \phi )$, to ensure the requirements in (2.7) and (2.9) are satisfied. Consider the general spherical harmonic decompositions:
 $$\begin{gather} f(\theta, \phi) = \sum_{l=0}^{\infty}\sum_{m={-}l}^{m=l} f_{lm} {Y}_{lm}(\theta,\phi), \end{gather}$$
$$\begin{gather} f(\theta, \phi) = \sum_{l=0}^{\infty}\sum_{m={-}l}^{m=l} f_{lm} {Y}_{lm}(\theta,\phi), \end{gather}$$ $$\begin{gather}g(\theta, \phi) = \sum_{l=0}^{\infty}\sum_{m={-}l}^{m=l} g_{lm} {Y}_{lm}(\theta,\phi), \end{gather}$$
$$\begin{gather}g(\theta, \phi) = \sum_{l=0}^{\infty}\sum_{m={-}l}^{m=l} g_{lm} {Y}_{lm}(\theta,\phi), \end{gather}$$
where ![]() $f_{lm}$ and
$f_{lm}$ and ![]() $g_{lm}$ are constants and the scalar spherical harmonic,
$g_{lm}$ are constants and the scalar spherical harmonic, ![]() ${Y}_{lm}(\theta,\phi )$, is given in (D7); the indices
${Y}_{lm}(\theta,\phi )$, is given in (D7); the indices ![]() $l$ and
$l$ and ![]() $m$ of
$m$ of ![]() ${Y}_{lm}(\theta,\phi )$ are its ‘degree’ and ‘order’, respectively.
${Y}_{lm}(\theta,\phi )$ are its ‘degree’ and ‘order’, respectively.
Substituting (B1a) into (2.7a) and (2.9a) yields the respective results
while substituting (B1b) into (2.7b) and (2.9b) respectively gives
where ![]() $\hat {\boldsymbol{x}}$,
$\hat {\boldsymbol{x}}$, ![]() $\hat {\boldsymbol{y}}$ and
$\hat {\boldsymbol{y}}$ and ![]() $\hat {\boldsymbol{z}}$ are the usual Cartesian basis vectors. While (B3a) shows that
$\hat {\boldsymbol{z}}$ are the usual Cartesian basis vectors. While (B3a) shows that ![]() $g_{0,0}$ is always negative, it does not reduce the particle size as would usually be the case for the
$g_{0,0}$ is always negative, it does not reduce the particle size as would usually be the case for the ![]() $l=0$,
$l=0$, ![]() $m=0$ spherical harmonic. This is because the effect of
$m=0$ spherical harmonic. This is because the effect of ![]() $f^2$ in isolation is to increase the size of the particle at
$f^2$ in isolation is to increase the size of the particle at ![]() $O(\epsilon ^2)$. The negative
$O(\epsilon ^2)$. The negative ![]() $g_{0,0}$ coefficient therefore counteracts the effect of
$g_{0,0}$ coefficient therefore counteracts the effect of ![]() $f^2$ to ensure the equivalent-volume sphere constraint is satisfied to
$f^2$ to ensure the equivalent-volume sphere constraint is satisfied to ![]() $O(\epsilon ^2)$.
$O(\epsilon ^2)$.
All other coefficients, ![]() $f_{lm}$ and
$f_{lm}$ and ![]() $g_{lm}$, in (B1) are unconstrained and may be set freely to achieve the desired nearly spherical particle shape.
$g_{lm}$, in (B1) are unconstrained and may be set freely to achieve the desired nearly spherical particle shape.
B.1. Contributions to the force and torque
Importantly, only components of ![]() $f(\theta, \phi )$ in (B1a) with
$f(\theta, \phi )$ in (B1a) with ![]() $l = 2$ contribute to the force and torque at
$l = 2$ contribute to the force and torque at ![]() $O(\epsilon )$; however, its components with
$O(\epsilon )$; however, its components with ![]() $l\ge 2$ must be considered at
$l\ge 2$ must be considered at ![]() $O(\epsilon ^2)$. In contrast, only components of
$O(\epsilon ^2)$. In contrast, only components of ![]() $g$ with
$g$ with ![]() $l \le 2$ contribute to the force and torque at
$l \le 2$ contribute to the force and torque at ![]() $O(\epsilon ^2)$.
$O(\epsilon ^2)$.
Appendix C. Derivation of the general formulae in (2.14)
The surfaces of the nearly spherical particle and the corresponding equivalent-volume sphere are each enclosed by an arbitrary, but identical, reference surface, ![]() $S_{ref}$. The resulting volumetric fluid region contained between the surface of the nearly spherical particle,
$S_{ref}$. The resulting volumetric fluid region contained between the surface of the nearly spherical particle, ![]() $S$, and the reference surface,
$S$, and the reference surface, ![]() $S_{ref}$, is denoted
$S_{ref}$, is denoted ![]() $V_f$; similarly, the fluid volume for the corresponding equivalent-volume perfect sphere is
$V_f$; similarly, the fluid volume for the corresponding equivalent-volume perfect sphere is ![]() $\hat {V}_f$. Note that
$\hat {V}_f$. Note that ![]() $V_f$ and
$V_f$ and ![]() $\hat {V}_f$ are finite subsets of the entire (unbounded) fluid domains and
$\hat {V}_f$ are finite subsets of the entire (unbounded) fluid domains and ![]() $S_{{ref}}$ must enclose both
$S_{{ref}}$ must enclose both ![]() $S$ and
$S$ and ![]() $\hat {S}$. An example of these regions for the ‘pear-shaped’ particle (figure 1b) studied in § 4 is given in figure 7.
$\hat {S}$. An example of these regions for the ‘pear-shaped’ particle (figure 1b) studied in § 4 is given in figure 7.

Figure 7. Example of the surface and volumetric regions used with the divergence theorem in Appendix C, for the ‘pear-shaped’ particle defined in § 4.2. The same (arbitrary) surface, ![]() $S_{ref}$, has finite area and encloses surfaces of the nearly spherical particle,
$S_{ref}$, has finite area and encloses surfaces of the nearly spherical particle, ![]() $S$, and its equivalent-volume sphere,
$S$, and its equivalent-volume sphere, ![]() $\hat {S}$; the finite area requirement of
$\hat {S}$; the finite area requirement of ![]() $S_{ref}$ guarantees existence of (C4). (a) Surface
$S_{ref}$ guarantees existence of (C4). (a) Surface ![]() $S$ is the surface of the nearly spherical particle and
$S$ is the surface of the nearly spherical particle and ![]() $V_f$ is the volumetric region between
$V_f$ is the volumetric region between ![]() $S$ and
$S$ and ![]() $S_{ref}$. (b) Surface
$S_{ref}$. (b) Surface ![]() $\hat {S}$ is the surface of the equivalent-volume sphere and
$\hat {S}$ is the surface of the equivalent-volume sphere and ![]() $\hat {V}_f$ is the region between
$\hat {V}_f$ is the region between ![]() $\hat {S}$ and
$\hat {S}$ and ![]() $S_{ref}$.
$S_{ref}$.
C.1. Force acting on the particle
Applying the divergence theorem to ![]() $V_f$ and
$V_f$ and ![]() $\hat {V}_f$ gives
$\hat {V}_f$ gives
where the same stress tensor, ![]() $\boldsymbol{\sigma }$, is used in both (C1a) and (C1b), and chosen to be that of the nearly spherical particle. While the unbounded fluid domain bounded by the surface at infinity could have been used here, the choice of a finite bounding surface is necessary for the torque calculation below and so is also used here for consistency; note there are no restrictions on
$\boldsymbol{\sigma }$, is used in both (C1a) and (C1b), and chosen to be that of the nearly spherical particle. While the unbounded fluid domain bounded by the surface at infinity could have been used here, the choice of a finite bounding surface is necessary for the torque calculation below and so is also used here for consistency; note there are no restrictions on ![]() $\boldsymbol{u}$ or
$\boldsymbol{u}$ or ![]() $\boldsymbol{\sigma }$ over
$\boldsymbol{\sigma }$ over ![]() $S_{{ref}}$. Formally, the fluid velocity field,
$S_{{ref}}$. Formally, the fluid velocity field, ![]() $\boldsymbol{u}$, generated by the nearly spherical particle may be analytically continued into its solid domain, allowing for use of the divergence theorem in (C1b). Because
$\boldsymbol{u}$, generated by the nearly spherical particle may be analytically continued into its solid domain, allowing for use of the divergence theorem in (C1b). Because ![]() $\boldsymbol{\nabla }\boldsymbol{\cdot }\boldsymbol{\sigma } = \lambda ^2 \boldsymbol{u}$, (C1) can then be rearranged to give the force exerted by the fluid on the nearly spherical particle:
$\boldsymbol{\nabla }\boldsymbol{\cdot }\boldsymbol{\sigma } = \lambda ^2 \boldsymbol{u}$, (C1) can then be rearranged to give the force exerted by the fluid on the nearly spherical particle:
Substituting (2.5) and (2.10) into (C2), taking a Taylor expansion about ![]() $r=1$ (retaining terms to
$r=1$ (retaining terms to ![]() $O(\epsilon ^2)$) and performing the
$O(\epsilon ^2)$) and performing the ![]() $r$-integration in the volume integral, gives
$r$-integration in the volume integral, gives
Then, substituting (2.12a) and (2.12b) into (C3) and simplifying through use of properties of the radial shape perturbation functions in (2.7) and (2.9) gives the force acting on the nearly spherical particle correct to ![]() $O(\epsilon ^2)$, i.e. (2.13a).
$O(\epsilon ^2)$, i.e. (2.13a).
C.2. Torque acting on the particle
A similar calculation follows for the torque. The ‘divergence-like’ relationship relevant for torque calculations, which invokes symmetry of the stress tensor, ![]() $\boldsymbol{\sigma }$, is
$\boldsymbol{\sigma }$, is
for some volume, ![]() $V'$, with bounding surface,
$V'$, with bounding surface, ![]() $S'$. Note that, in general, the surface and volume integrals in (C4) do not exist for an unsteady Stokes flow in an unbounded fluid domain. Evaluation of (C4) must therefore take place on a bounded domain. Similar to the force calculation in § C.1, the torque exerted by the fluid on the nearly spherical particle is
$S'$. Note that, in general, the surface and volume integrals in (C4) do not exist for an unsteady Stokes flow in an unbounded fluid domain. Evaluation of (C4) must therefore take place on a bounded domain. Similar to the force calculation in § C.1, the torque exerted by the fluid on the nearly spherical particle is
where ![]() $\boldsymbol{\sigma }$ is the fluid stress tensor generated by the nearly spherical particle,
$\boldsymbol{\sigma }$ is the fluid stress tensor generated by the nearly spherical particle, ![]() $\boldsymbol{u}$ is its corresponding velocity field and
$\boldsymbol{u}$ is its corresponding velocity field and ![]() $S_{ref}$ has been chosen to have finite area in the derivation of (C5) to ensure existence of the integrals in (C4). Performing the same procedure as the force calculation in § C.1 gives
$S_{ref}$ has been chosen to have finite area in the derivation of (C5) to ensure existence of the integrals in (C4). Performing the same procedure as the force calculation in § C.1 gives
 \begin{align} \lambda^2 \int_{\hat{V}_f - V_f} \boldsymbol{r}\times\boldsymbol{u} \, \mathrm{d}V &= \lambda^2 \int_{\hat{S}} \epsilon f \boldsymbol{n}\times \boldsymbol{u}^{(0)} \nonumber\\ &\quad +\epsilon^2 \boldsymbol{n} \times \left[\left(f^2 + \frac{3}{2} g\right) \boldsymbol{u}^{(0)} + f \boldsymbol{u}^{(1)} + \frac{f^2}{2}\partial_r \boldsymbol{u}^{(0)}\right] \mathrm{d}S + O(\epsilon^3), \end{align}
\begin{align} \lambda^2 \int_{\hat{V}_f - V_f} \boldsymbol{r}\times\boldsymbol{u} \, \mathrm{d}V &= \lambda^2 \int_{\hat{S}} \epsilon f \boldsymbol{n}\times \boldsymbol{u}^{(0)} \nonumber\\ &\quad +\epsilon^2 \boldsymbol{n} \times \left[\left(f^2 + \frac{3}{2} g\right) \boldsymbol{u}^{(0)} + f \boldsymbol{u}^{(1)} + \frac{f^2}{2}\partial_r \boldsymbol{u}^{(0)}\right] \mathrm{d}S + O(\epsilon^3), \end{align}
where ![]() $\boldsymbol{u}$ is the fluid velocity field due to the nearly spherical particle. Substituting (2.12a) and (2.12b) into (C6) gives the torque acting on the nearly spherical particle correct to
$\boldsymbol{u}$ is the fluid velocity field due to the nearly spherical particle. Substituting (2.12a) and (2.12b) into (C6) gives the torque acting on the nearly spherical particle correct to ![]() $O(\epsilon ^2)$, i.e. (2.13b).
$O(\epsilon ^2)$, i.e. (2.13b).
Appendix D. Derivation of the second-order solution in § 3.3
Derivation of the second-order solution in § 3.3 is detailed in this appendix. First, we decompose the boundary condition in (2.12c) as
where
The stress tensors resulting from the two velocity fields in (D1) are denoted ![]() $\boldsymbol{\sigma }^{(2)}_1$ and
$\boldsymbol{\sigma }^{(2)}_1$ and ![]() $\boldsymbol{\sigma }^{(2)}_2$, respectively. Substituting (3.1b) and (3.1c) into (D2a) gives
$\boldsymbol{\sigma }^{(2)}_2$, respectively. Substituting (3.1b) and (3.1c) into (D2a) gives
 \begin{align} \boldsymbol{u}^{(2)}_1|_{r=1} &= g \left(\frac{3}{2}(1+\lambda)(\boldsymbol{I} - \boldsymbol{n}\boldsymbol{n})\boldsymbol{\cdot}\boldsymbol{U} + \frac{3+3\lambda + \lambda^2}{1+\lambda}\boldsymbol{\varOmega}\times\boldsymbol{n}\right) \nonumber\\ &\quad +\frac{f^2}{2}\left(3\left[-\frac{1}{2}(3+3\lambda+\lambda^2)(\boldsymbol{I}-\boldsymbol{n}\boldsymbol{n}) + (1+\lambda)\boldsymbol{n}\boldsymbol{n}\right]\boldsymbol{\cdot}\boldsymbol{U}\right. \nonumber\\ &\quad -\left. \frac{6+6\lambda + 3\lambda^2 + \lambda^3}{1+\lambda}\boldsymbol{\varOmega}\times\boldsymbol{n}\right) . \end{align}
\begin{align} \boldsymbol{u}^{(2)}_1|_{r=1} &= g \left(\frac{3}{2}(1+\lambda)(\boldsymbol{I} - \boldsymbol{n}\boldsymbol{n})\boldsymbol{\cdot}\boldsymbol{U} + \frac{3+3\lambda + \lambda^2}{1+\lambda}\boldsymbol{\varOmega}\times\boldsymbol{n}\right) \nonumber\\ &\quad +\frac{f^2}{2}\left(3\left[-\frac{1}{2}(3+3\lambda+\lambda^2)(\boldsymbol{I}-\boldsymbol{n}\boldsymbol{n}) + (1+\lambda)\boldsymbol{n}\boldsymbol{n}\right]\boldsymbol{\cdot}\boldsymbol{U}\right. \nonumber\\ &\quad -\left. \frac{6+6\lambda + 3\lambda^2 + \lambda^3}{1+\lambda}\boldsymbol{\varOmega}\times\boldsymbol{n}\right) . \end{align}From (2.14c) and (2.14f), it follows that the respective contributions to the force and torque experienced by the spherical particle are
and
D.1. Solutions for  $\boldsymbol{F}^{(2)}_1$ and
$\boldsymbol{F}^{(2)}_1$ and  $\boldsymbol{T}^{(2)}_1$
$\boldsymbol{T}^{(2)}_1$
Equations (D4a) and (D5a) for ![]() $\boldsymbol{F}^{(2)}_1$ and
$\boldsymbol{F}^{(2)}_1$ and ![]() $\boldsymbol{T}^{(2)}_1$, respectively, are evaluated using (2.15) together with (D3) to bypass direct evaluation of the stress tensor. This leads to the required results in (3.7) and (3.8).
$\boldsymbol{T}^{(2)}_1$, respectively, are evaluated using (2.15) together with (D3) to bypass direct evaluation of the stress tensor. This leads to the required results in (3.7) and (3.8).
D.2. Solutions for  $\boldsymbol{F}^{(2)}_2$ and
$\boldsymbol{F}^{(2)}_2$ and  $\boldsymbol{T}^{(2)}_2$
$\boldsymbol{T}^{(2)}_2$
Because the radial gradient of the first-order velocity field appears in (D2b), an analytical solution for ![]() $\boldsymbol{u}^{(1)}$ is required to evaluate the second-order force and torque. This is acheived using a general solution to the unsteady Stokes equations (Miller & Scriven Reference Miller and Scriven1968; Lippera et al. Reference Lippera, Dauchot, Michelin and Benzaquen2019) expressed in terms of vector spherical harmonics (Barrera, Estevez & Giraldo Reference Barrera, Estevez and Giraldo1985). The vector spherical harmonics are
$\boldsymbol{u}^{(1)}$ is required to evaluate the second-order force and torque. This is acheived using a general solution to the unsteady Stokes equations (Miller & Scriven Reference Miller and Scriven1968; Lippera et al. Reference Lippera, Dauchot, Michelin and Benzaquen2019) expressed in terms of vector spherical harmonics (Barrera, Estevez & Giraldo Reference Barrera, Estevez and Giraldo1985). The vector spherical harmonics are
where
 \begin{equation} {Y}_{lm} (\theta, \phi) = \sqrt{\frac{(2l+1)}{4{\rm \pi} }\frac{(l-m)!}{(l+m)!}} \, \mathrm{P}^m_l (\cos\theta)\,\mathrm{e}^{\mathrm{i}m\phi} \end{equation}
\begin{equation} {Y}_{lm} (\theta, \phi) = \sqrt{\frac{(2l+1)}{4{\rm \pi} }\frac{(l-m)!}{(l+m)!}} \, \mathrm{P}^m_l (\cos\theta)\,\mathrm{e}^{\mathrm{i}m\phi} \end{equation}
are the scalar spherical harmonics, with ![]() $\mathrm{P}^m_l$ the associated Legendre polynomials; the ‘degree’ and ‘order’ of both the vector and scalar spherical harmonics, and associated Legendre polynomials are
$\mathrm{P}^m_l$ the associated Legendre polynomials; the ‘degree’ and ‘order’ of both the vector and scalar spherical harmonics, and associated Legendre polynomials are ![]() $l$ and
$l$ and ![]() $m$, respectively. The first-order velocity field is then
$m$, respectively. The first-order velocity field is then
 \begin{equation} \boldsymbol{u}^{(1)} (r, \theta, \phi) = \sum_{l=0}^{\infty}\sum_{m={-}l}^{m=l}u_{lm}(r)\boldsymbol{R}_{lm} (\theta, \phi) + v_{lm}(r)\boldsymbol{\boldsymbol{\varTheta}}_{lm} (\theta, \phi) + w_{lm}(r)\boldsymbol{\boldsymbol{\varPhi}}_{lm} (\theta, \phi), \end{equation}
\begin{equation} \boldsymbol{u}^{(1)} (r, \theta, \phi) = \sum_{l=0}^{\infty}\sum_{m={-}l}^{m=l}u_{lm}(r)\boldsymbol{R}_{lm} (\theta, \phi) + v_{lm}(r)\boldsymbol{\boldsymbol{\varTheta}}_{lm} (\theta, \phi) + w_{lm}(r)\boldsymbol{\boldsymbol{\varPhi}}_{lm} (\theta, \phi), \end{equation}where
 $$\begin{gather} u_{lm}(r) =\alpha_{lm} \frac{\mathrm{h}^{(1)}_{l-1}(\mathrm{i} \lambda r) + \mathrm{h}^{(1)}_{l+1}(\mathrm{i} \lambda r)}{\mathrm{h}^{(1)}_{l-1}(\mathrm{i}\lambda)} + p_{lm}\frac{l+1}{\lambda^2 r^{l+2}}, \end{gather}$$
$$\begin{gather} u_{lm}(r) =\alpha_{lm} \frac{\mathrm{h}^{(1)}_{l-1}(\mathrm{i} \lambda r) + \mathrm{h}^{(1)}_{l+1}(\mathrm{i} \lambda r)}{\mathrm{h}^{(1)}_{l-1}(\mathrm{i}\lambda)} + p_{lm}\frac{l+1}{\lambda^2 r^{l+2}}, \end{gather}$$ $$\begin{gather}v_{lm}(r) = \alpha_{lm} \frac{(l + 1)\mathrm{h}^{(1)}_{l-1}(\mathrm{i} \lambda r) - l \, \mathrm{h}^{(1)}_{l+1}(\mathrm{i}\lambda r) }{\sqrt{l(l+1)} \, \mathrm{h}^{(1)}_{l-1}(\mathrm{i}\lambda)} - p_{lm}\frac{\sqrt{l(l+1)}}{\lambda^2 r^{l+2}}, \end{gather}$$
$$\begin{gather}v_{lm}(r) = \alpha_{lm} \frac{(l + 1)\mathrm{h}^{(1)}_{l-1}(\mathrm{i} \lambda r) - l \, \mathrm{h}^{(1)}_{l+1}(\mathrm{i}\lambda r) }{\sqrt{l(l+1)} \, \mathrm{h}^{(1)}_{l-1}(\mathrm{i}\lambda)} - p_{lm}\frac{\sqrt{l(l+1)}}{\lambda^2 r^{l+2}}, \end{gather}$$ $$\begin{gather}w_{lm}(r) = W_{lm} \frac{\mathrm{h}^{(1)}_{l}(\mathrm{i} \lambda r)}{\mathrm{h}^{(1)}_{l}(\mathrm{i} \lambda)}, \end{gather}$$
$$\begin{gather}w_{lm}(r) = W_{lm} \frac{\mathrm{h}^{(1)}_{l}(\mathrm{i} \lambda r)}{\mathrm{h}^{(1)}_{l}(\mathrm{i} \lambda)}, \end{gather}$$
where ![]() $\mathrm{h}^{(1)}_{l}$ is the spherical Hankel function of the first kind (that vanishes as
$\mathrm{h}^{(1)}_{l}$ is the spherical Hankel function of the first kind (that vanishes as ![]() $r\rightarrow \infty$),
$r\rightarrow \infty$),
 $$\begin{gather}p_{lm} =\lambda^2 \frac{((l+1)U_{lm}-\sqrt{l(l+1)}V_{lm})\, \mathrm{h}^{(1)}_{l-1}(\mathrm{i}\lambda) - (l U_{lm} + \sqrt{l(l+1)}V_{lm})\,\mathrm{h}^{(1)}_{l+1}(\mathrm{i}\lambda)}{(l+1)(2l+1)\mathrm{h}^{(1)}_{l-1} (\mathrm{i}\lambda)} \end{gather}$$
$$\begin{gather}p_{lm} =\lambda^2 \frac{((l+1)U_{lm}-\sqrt{l(l+1)}V_{lm})\, \mathrm{h}^{(1)}_{l-1}(\mathrm{i}\lambda) - (l U_{lm} + \sqrt{l(l+1)}V_{lm})\,\mathrm{h}^{(1)}_{l+1}(\mathrm{i}\lambda)}{(l+1)(2l+1)\mathrm{h}^{(1)}_{l-1} (\mathrm{i}\lambda)} \end{gather}$$and
with the superscript * denoting the complex conjugate and ![]() $\boldsymbol{u}^{(1)}|_{r=1}$ defined in (3.3).
$\boldsymbol{u}^{(1)}|_{r=1}$ defined in (3.3).
The required radial gradient is then
 \begin{align} \partial_r\boldsymbol{u}^{(1)}|_{r=1} &= \sum_{l=0}^{\infty}\sum_{m={-}l}^{l} \sqrt{l(l+1)} \, V_{lm} \boldsymbol{R}_{lm} + \left(l - \mathrm{i}\lambda\frac{\mathrm{h}^{(1)}_{l+1}(\mathrm{i}\lambda)}{\mathrm{h}^{(1)}_{l}(\mathrm{i}\lambda)}\right)W_{lm}\boldsymbol{\boldsymbol{\varPhi}}_{lm} \nonumber\\ &\quad + \left(\frac{\lambda^2}{2l+1}\left[1 + \frac{\mathrm{h}^{(1)}_{l+1}(\mathrm{i}\lambda)}{\mathrm{h}^{(1)}_{l-1}(\mathrm{i}\lambda)}\right] - 1\right) V_{lm}\boldsymbol{\boldsymbol{\varTheta}}_{lm}, \end{align}
\begin{align} \partial_r\boldsymbol{u}^{(1)}|_{r=1} &= \sum_{l=0}^{\infty}\sum_{m={-}l}^{l} \sqrt{l(l+1)} \, V_{lm} \boldsymbol{R}_{lm} + \left(l - \mathrm{i}\lambda\frac{\mathrm{h}^{(1)}_{l+1}(\mathrm{i}\lambda)}{\mathrm{h}^{(1)}_{l}(\mathrm{i}\lambda)}\right)W_{lm}\boldsymbol{\boldsymbol{\varPhi}}_{lm} \nonumber\\ &\quad + \left(\frac{\lambda^2}{2l+1}\left[1 + \frac{\mathrm{h}^{(1)}_{l+1}(\mathrm{i}\lambda)}{\mathrm{h}^{(1)}_{l-1}(\mathrm{i}\lambda)}\right] - 1\right) V_{lm}\boldsymbol{\boldsymbol{\varTheta}}_{lm}, \end{align}where
 \begin{align} V_{lm} &\equiv \int_{\hat{S}}\boldsymbol{u}^{(1)} \boldsymbol{\cdot} \boldsymbol{\boldsymbol{\varTheta}}_{lm}^* \,\mathrm{d}S \nonumber\\ &= \frac{3}{2}(1+\lambda)\int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}^{*}_{lm} \,\mathrm{d}S \boldsymbol{\cdot} \boldsymbol{U} + \frac{3+3\lambda+\lambda^2}{1+\lambda}\int_{\hat{S}} f \boldsymbol{n}\times\boldsymbol{\boldsymbol{\varTheta}}^{*}_{lm} \,\mathrm{d}S \boldsymbol{\cdot} \boldsymbol{\varOmega}, \end{align}
\begin{align} V_{lm} &\equiv \int_{\hat{S}}\boldsymbol{u}^{(1)} \boldsymbol{\cdot} \boldsymbol{\boldsymbol{\varTheta}}_{lm}^* \,\mathrm{d}S \nonumber\\ &= \frac{3}{2}(1+\lambda)\int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}^{*}_{lm} \,\mathrm{d}S \boldsymbol{\cdot} \boldsymbol{U} + \frac{3+3\lambda+\lambda^2}{1+\lambda}\int_{\hat{S}} f \boldsymbol{n}\times\boldsymbol{\boldsymbol{\varTheta}}^{*}_{lm} \,\mathrm{d}S \boldsymbol{\cdot} \boldsymbol{\varOmega}, \end{align} \begin{align} W_{lm} &\equiv \int_{\hat{S}}\boldsymbol{u}^{(1)} \boldsymbol{\cdot} \boldsymbol{\boldsymbol{\varPhi}}_{lm}^* \,\mathrm{d}S \nonumber\\ &= \frac{3}{2}(1+\lambda)\int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}^{*}_{lm}\, \mathrm{d}S \boldsymbol{\cdot} \boldsymbol{U} + \frac{3+3\lambda+\lambda^2}{1+\lambda}\int_{\hat{S}} f \boldsymbol{n}\times\boldsymbol{\boldsymbol{\varPhi}}^{*}_{lm} \,\mathrm{d}S \boldsymbol{\cdot} \boldsymbol{\varOmega}. \end{align}
\begin{align} W_{lm} &\equiv \int_{\hat{S}}\boldsymbol{u}^{(1)} \boldsymbol{\cdot} \boldsymbol{\boldsymbol{\varPhi}}_{lm}^* \,\mathrm{d}S \nonumber\\ &= \frac{3}{2}(1+\lambda)\int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}^{*}_{lm}\, \mathrm{d}S \boldsymbol{\cdot} \boldsymbol{U} + \frac{3+3\lambda+\lambda^2}{1+\lambda}\int_{\hat{S}} f \boldsymbol{n}\times\boldsymbol{\boldsymbol{\varPhi}}^{*}_{lm} \,\mathrm{d}S \boldsymbol{\cdot} \boldsymbol{\varOmega}. \end{align}The corresponding contribution to the force is
while for the torque is
Substituting (D12) into (D14) and (D15) gives the required expressions in (3.9) and (3.10), respectively.
D.3. Trace of the second-order tensorial coefficients in § 3.4
The traces of the tensorial coefficients of ![]() $\boldsymbol{U}$ and
$\boldsymbol{U}$ and ![]() $\boldsymbol{\varOmega }$ in the second-order solution, as used in (3.17a) and (3.17b), are
$\boldsymbol{\varOmega }$ in the second-order solution, as used in (3.17a) and (3.17b), are
 \begin{align} \mathrm{tr}\,\boldsymbol{A}^{(2)} &= 3(1+\lambda)(3+3\lambda+\lambda^2)\int_{\hat{S}} f^2 \, \mathrm{d}S +\sum_{l=1}^{\infty}\sum_{m={-}l}^{l} \left[ \kappa_1 \kappa_2 \gamma_l^{(1)} \int_{\hat{S}} f\boldsymbol{R}_{lm}\, \mathrm{d}S \boldsymbol{\cdot} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm}^{*} \, \mathrm{d}S\right. \nonumber\\ & \quad + \left.\kappa_2^2 \gamma_l^{(2)} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm} \, \mathrm{d}S \boldsymbol{\cdot} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm}^{*} \, \mathrm{d}S + \kappa_2^2 \gamma_l^{(3)} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}_{lm} \, \mathrm{d}S \boldsymbol{\cdot}\int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}_{lm}^{*} \, \mathrm{d}S \right], \end{align}
\begin{align} \mathrm{tr}\,\boldsymbol{A}^{(2)} &= 3(1+\lambda)(3+3\lambda+\lambda^2)\int_{\hat{S}} f^2 \, \mathrm{d}S +\sum_{l=1}^{\infty}\sum_{m={-}l}^{l} \left[ \kappa_1 \kappa_2 \gamma_l^{(1)} \int_{\hat{S}} f\boldsymbol{R}_{lm}\, \mathrm{d}S \boldsymbol{\cdot} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm}^{*} \, \mathrm{d}S\right. \nonumber\\ & \quad + \left.\kappa_2^2 \gamma_l^{(2)} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm} \, \mathrm{d}S \boldsymbol{\cdot} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm}^{*} \, \mathrm{d}S + \kappa_2^2 \gamma_l^{(3)} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}_{lm} \, \mathrm{d}S \boldsymbol{\cdot}\int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}_{lm}^{*} \, \mathrm{d}S \right], \end{align} \begin{align} \mathrm{tr}\,\boldsymbol{C}^{(2)} & = \frac{2(3+\lambda)(6+10\lambda+8\lambda^2+4\lambda^3+\lambda^5)}{(1+\lambda)^2}\int_{\hat{S}} f^2 \, \mathrm{d}S \nonumber\\ & \quad + \!\sum_{l=1}^{\infty}\sum_{m={-}l}^{l}\left[ \kappa_3^2 \gamma_l^{(3)} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm} \, \mathrm{d}S \boldsymbol{\cdot} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm}^{*} \, \mathrm{d}S + \kappa_3^2 \gamma_l^{(2)} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}_{lm} \, \mathrm{d}S \boldsymbol{\cdot}\!\int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}^{*}_{lm} \, \mathrm{d}S\! \right]\!, \end{align}
\begin{align} \mathrm{tr}\,\boldsymbol{C}^{(2)} & = \frac{2(3+\lambda)(6+10\lambda+8\lambda^2+4\lambda^3+\lambda^5)}{(1+\lambda)^2}\int_{\hat{S}} f^2 \, \mathrm{d}S \nonumber\\ & \quad + \!\sum_{l=1}^{\infty}\sum_{m={-}l}^{l}\left[ \kappa_3^2 \gamma_l^{(3)} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm} \, \mathrm{d}S \boldsymbol{\cdot} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varTheta}}_{lm}^{*} \, \mathrm{d}S + \kappa_3^2 \gamma_l^{(2)} \int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}_{lm} \, \mathrm{d}S \boldsymbol{\cdot}\!\int_{\hat{S}} f \boldsymbol{\boldsymbol{\varPhi}}^{*}_{lm} \, \mathrm{d}S\! \right]\!, \end{align}
where the identities ![]() $\mathrm{tr}\, \boldsymbol{n}\boldsymbol{n} = 1$ and
$\mathrm{tr}\, \boldsymbol{n}\boldsymbol{n} = 1$ and ![]() $\mathrm{tr}\,(\boldsymbol{I} - \boldsymbol{n}\boldsymbol{n}) = 2$ and (2.7b) are used to simplify these results. Contractions arise between pairs of integrals due to taking the trace of the tensorial quantities.
$\mathrm{tr}\,(\boldsymbol{I} - \boldsymbol{n}\boldsymbol{n}) = 2$ and (2.7b) are used to simplify these results. Contractions arise between pairs of integrals due to taking the trace of the tensorial quantities.
Appendix E. Polynomials
The following polynomials appear in the second-order solutions for the ‘pear-shaped’ particle in (4.12) and (4.13):
 $$\begin{align} a_1(\lambda) & = (1+\lambda)(67\,635 + 203\,850\lambda + 224\,784\lambda^2 +124\,605\lambda^3 + 36\,198\lambda^4 \nonumber\\ &\quad + 4947\lambda^5 + 185\lambda^6), \end{align}$$
$$\begin{align} a_1(\lambda) & = (1+\lambda)(67\,635 + 203\,850\lambda + 224\,784\lambda^2 +124\,605\lambda^3 + 36\,198\lambda^4 \nonumber\\ &\quad + 4947\lambda^5 + 185\lambda^6), \end{align}$$ $$\begin{align}a_2(\lambda) & = 2(1+\lambda)(16\,200 + 49\,545\lambda + 58\,950\lambda^2 + 37\,098\lambda^3 + 13\,248\lambda^4\nonumber\\ &\quad + 2607\lambda^5 + 227\lambda^6), \end{align}$$
$$\begin{align}a_2(\lambda) & = 2(1+\lambda)(16\,200 + 49\,545\lambda + 58\,950\lambda^2 + 37\,098\lambda^3 + 13\,248\lambda^4\nonumber\\ &\quad + 2607\lambda^5 + 227\lambda^6), \end{align}$$ \begin{align} a_4(\lambda) &= 2(38\,343\,375 + 191\,716\,875\lambda + 441\,643\,365\lambda^2 + 618\,594\,525\lambda^3 + 585\,998\,235\lambda^4 \nonumber\\ &\quad + 395\,720\,610\lambda^5 + 195\,716\,763\lambda^6 + 71\,630\,007\lambda^7 + 19\,312\,973\lambda^8 + 3\,752\,990\lambda^9 \nonumber\\ &\quad + 500\,349\lambda^{10} + 41\,148\lambda^{11} + 1575\lambda^{12}), \end{align}
\begin{align} a_4(\lambda) &= 2(38\,343\,375 + 191\,716\,875\lambda + 441\,643\,365\lambda^2 + 618\,594\,525\lambda^3 + 585\,998\,235\lambda^4 \nonumber\\ &\quad + 395\,720\,610\lambda^5 + 195\,716\,763\lambda^6 + 71\,630\,007\lambda^7 + 19\,312\,973\lambda^8 + 3\,752\,990\lambda^9 \nonumber\\ &\quad + 500\,349\lambda^{10} + 41\,148\lambda^{11} + 1575\lambda^{12}), \end{align} \begin{align} a_5(\lambda) &= 8(3\,217\,725 + 16\,088\,625\lambda + 36\,801\,855\lambda^2 + 50\,712\,300\lambda^3 +46\,703\,340\lambda^4 \nonumber\\ &\quad + 30\,205\,050\lambda^5 + 14\,034\,816\lambda^6 + 4\,703\,289\lambda^7 + 1\,119\,191\lambda^8 + 181\,085\lambda^9 \nonumber\\ &\quad + 18\,048 \lambda^{10} + 846\lambda^{11}), \end{align}
\begin{align} a_5(\lambda) &= 8(3\,217\,725 + 16\,088\,625\lambda + 36\,801\,855\lambda^2 + 50\,712\,300\lambda^3 +46\,703\,340\lambda^4 \nonumber\\ &\quad + 30\,205\,050\lambda^5 + 14\,034\,816\lambda^6 + 4\,703\,289\lambda^7 + 1\,119\,191\lambda^8 + 181\,085\lambda^9 \nonumber\\ &\quad + 18\,048 \lambda^{10} + 846\lambda^{11}), \end{align} \begin{gather} a_7(\lambda) = 142\,155 + 710\,775\lambda + 1\,635\,705 \lambda^2 + 2\,285\,775 \lambda^3 + 2\,156\,841 \lambda^4 + 1\,448\,034\lambda^5 , \nonumber\\ \quad +\, 710\,433 \lambda^6 + 257\,259 \lambda^7 + 68\,417 \lambda^8 + 13\,064 \lambda^9 + 1703\lambda^{10} + 136 \lambda^{11} + 5\lambda^{12} , \end{gather}
\begin{gather} a_7(\lambda) = 142\,155 + 710\,775\lambda + 1\,635\,705 \lambda^2 + 2\,285\,775 \lambda^3 + 2\,156\,841 \lambda^4 + 1\,448\,034\lambda^5 , \nonumber\\ \quad +\, 710\,433 \lambda^6 + 257\,259 \lambda^7 + 68\,417 \lambda^8 + 13\,064 \lambda^9 + 1703\lambda^{10} + 136 \lambda^{11} + 5\lambda^{12} , \end{gather}Appendix F. The DNS details and validation study
Finite-amplitude time-domain simulations are performed with the finite-element-analysis software COMSOL Multiphysics (version 5.6), using the incompressible Navier–Stokes equations. A three-dimensional domain is used with an inner boundary specified by the particle shape, i.e. (2.5), and a spherical outer boundary of dimensionless radius ![]() $R_{\infty } \gg 1$. Due to symmetry in the ‘pear-shaped’ particle geometry and its boundary conditions, we simulate half the flow domain, i.e.
$R_{\infty } \gg 1$. Due to symmetry in the ‘pear-shaped’ particle geometry and its boundary conditions, we simulate half the flow domain, i.e. ![]() $y>0$, and apply the appropriate symmetry boundary condition at
$y>0$, and apply the appropriate symmetry boundary condition at ![]() $y=0$. Details of the ‘pear-shaped’ particle geometry are given in § 4.2. A translational velocity of
$y=0$. Details of the ‘pear-shaped’ particle geometry are given in § 4.2. A translational velocity of ![]() $\delta \cos t \,\hat {\boldsymbol{z}}$ and a rotational velocity of
$\delta \cos t \,\hat {\boldsymbol{z}}$ and a rotational velocity of ![]() $\delta \cos t\,\hat {\boldsymbol{y}}$ are specified for the particle.
$\delta \cos t\,\hat {\boldsymbol{y}}$ are specified for the particle.
The velocity boundary condition at the particle surface, (2.2a), is rescaled using ![]() $\boldsymbol{u}_N \equiv \boldsymbol{u} \delta$; the subscript
$\boldsymbol{u}_N \equiv \boldsymbol{u} \delta$; the subscript ![]() $N$ refers to the value in COMSOL. This allows the dimensional Navier–Stokes equations to simulate their corresponding dimensionless form by setting
$N$ refers to the value in COMSOL. This allows the dimensional Navier–Stokes equations to simulate their corresponding dimensionless form by setting ![]() $\rho _N = \beta$ and
$\rho _N = \beta$ and ![]() $\mu _N = 1$. Thus, velocity fields prescribed at
$\mu _N = 1$. Thus, velocity fields prescribed at ![]() $\boldsymbol{u}_N = O(\delta )$ in the DNS correspond to
$\boldsymbol{u}_N = O(\delta )$ in the DNS correspond to ![]() $\boldsymbol{u} = O(1)$ in the asymptotic theory. Validity of the asymptotic theory will then produce an error in the force relative to the DNS of
$\boldsymbol{u} = O(1)$ in the asymptotic theory. Validity of the asymptotic theory will then produce an error in the force relative to the DNS of ![]() $O(\delta ^2)$, i.e.
$O(\delta ^2)$, i.e. ![]() $\boldsymbol{F}_N - \boldsymbol{F} \delta = O(\delta ^2)$.
$\boldsymbol{F}_N - \boldsymbol{F} \delta = O(\delta ^2)$.
The numerical procedure is validated for a perfect sphere using the above parameters; results are given in figure 8. At the fundamental oscillation frequency, the force in the ![]() $y$ direction, and the torque around both the
$y$ direction, and the torque around both the ![]() $x$ and
$x$ and ![]() $z$ axes, must be zero (by symmetry). The fundamental frequency component, i.e. at an angular frequency of unity, recovers the expected results for (i) the force in the
$z$ axes, must be zero (by symmetry). The fundamental frequency component, i.e. at an angular frequency of unity, recovers the expected results for (i) the force in the ![]() $z$ direction and (ii) the torque around the
$z$ direction and (ii) the torque around the ![]() $y$ axis (Stokes Reference Stokes1851). The force component in the
$y$ axis (Stokes Reference Stokes1851). The force component in the ![]() $x$ direction at the fundamental frequency should be zero to
$x$ direction at the fundamental frequency should be zero to ![]() $O(\delta ^2)$, and thus the DNS data in figure 8(a) are representative of the error in the numerical procedure, which is at the 0.01 % level. The steady component of the force in the
$O(\delta ^2)$, and thus the DNS data in figure 8(a) are representative of the error in the numerical procedure, which is at the 0.01 % level. The steady component of the force in the ![]() $x$ direction, denoted
$x$ direction, denoted ![]() $F_{{stream}}$, is expected to be non-zero for finite-amplitude oscillations, due to the combined translational and rotational motion of the perfect sphere; this produces a streaming flow. Using (1.11) and (1.10) with
$F_{{stream}}$, is expected to be non-zero for finite-amplitude oscillations, due to the combined translational and rotational motion of the perfect sphere; this produces a streaming flow. Using (1.11) and (1.10) with ![]() $U_{{prop}} = 0$ from Collis et al. (Reference Collis, Chakraborty and Sader2022), we arrive at
$U_{{prop}} = 0$ from Collis et al. (Reference Collis, Chakraborty and Sader2022), we arrive at
 \begin{align} F_{{stream}} &={-}\frac{\beta}{4}\int_{\hat{V}} \boldsymbol{u}'\boldsymbol{\cdot} (\boldsymbol{u}^{(0)}\boldsymbol{\cdot}\boldsymbol{\nabla}\boldsymbol{u}^{(0)*})\,{\rm d}V +\frac{1}{4}\int_{\hat{S}}(\boldsymbol{n}\boldsymbol{\cdot}\boldsymbol{\sigma}') \boldsymbol{\cdot}(\boldsymbol{r}_1\boldsymbol{\cdot}\boldsymbol{\nabla}\boldsymbol{u}^{(0)*})\nonumber\\ &\quad -\boldsymbol{i}\boldsymbol{\cdot}[\boldsymbol{n} \boldsymbol{\cdot} (\boldsymbol{r}_1\boldsymbol{\cdot}\boldsymbol{\nabla}\boldsymbol{\sigma}^{(0)*}) +\text{i}(\boldsymbol{n}\times\boldsymbol{\varOmega})\boldsymbol{\cdot}\boldsymbol{\sigma}^{(0)*} ]\, {\rm d}S + {\rm c.c.}, \end{align}
\begin{align} F_{{stream}} &={-}\frac{\beta}{4}\int_{\hat{V}} \boldsymbol{u}'\boldsymbol{\cdot} (\boldsymbol{u}^{(0)}\boldsymbol{\cdot}\boldsymbol{\nabla}\boldsymbol{u}^{(0)*})\,{\rm d}V +\frac{1}{4}\int_{\hat{S}}(\boldsymbol{n}\boldsymbol{\cdot}\boldsymbol{\sigma}') \boldsymbol{\cdot}(\boldsymbol{r}_1\boldsymbol{\cdot}\boldsymbol{\nabla}\boldsymbol{u}^{(0)*})\nonumber\\ &\quad -\boldsymbol{i}\boldsymbol{\cdot}[\boldsymbol{n} \boldsymbol{\cdot} (\boldsymbol{r}_1\boldsymbol{\cdot}\boldsymbol{\nabla}\boldsymbol{\sigma}^{(0)*}) +\text{i}(\boldsymbol{n}\times\boldsymbol{\varOmega})\boldsymbol{\cdot}\boldsymbol{\sigma}^{(0)*} ]\, {\rm d}S + {\rm c.c.}, \end{align}
where all symbols are as defined in the main text and additionally ![]() $\hat {V}$ is the (unbounded) fluid domain outside the unit sphere,
$\hat {V}$ is the (unbounded) fluid domain outside the unit sphere, ![]() $(\boldsymbol{u}', \boldsymbol{\sigma }')$ are auxiliary fields for the velocity and stress tensor for a unit sphere translating with unitary velocity in the
$(\boldsymbol{u}', \boldsymbol{\sigma }')$ are auxiliary fields for the velocity and stress tensor for a unit sphere translating with unitary velocity in the ![]() $x$ direction in a steady Stokes flow,
$x$ direction in a steady Stokes flow, ![]() $\boldsymbol{r}_1 = \textrm{i}(\boldsymbol{U}+\boldsymbol{\varOmega }\times \boldsymbol{r})$, the symbol
$\boldsymbol{r}_1 = \textrm{i}(\boldsymbol{U}+\boldsymbol{\varOmega }\times \boldsymbol{r})$, the symbol ![]() $^*$ denotes the complex conjugate and c.c. is the complex conjugate of the entire preceding expression. The steady part of the force in the
$^*$ denotes the complex conjugate and c.c. is the complex conjugate of the entire preceding expression. The steady part of the force in the ![]() $x$ direction is hence
$x$ direction is hence ![]() $\delta F_{stream}$. Equation (F1) is in excellent agreement with the DNS data; see left-hand panel of figure 8(b). Other components of the force and torque are expected to be zero by symmetry, and the results in figure 8(b) are due to numerical error; they are two orders of magnitude smaller and due to the three-dimensional discretisation of the particle surface.
$\delta F_{stream}$. Equation (F1) is in excellent agreement with the DNS data; see left-hand panel of figure 8(b). Other components of the force and torque are expected to be zero by symmetry, and the results in figure 8(b) are due to numerical error; they are two orders of magnitude smaller and due to the three-dimensional discretisation of the particle surface.

Figure 8. Translating and rotating perfect sphere, with ![]() $\boldsymbol{U} = \delta \hat {\boldsymbol{z}}$ and
$\boldsymbol{U} = \delta \hat {\boldsymbol{z}}$ and ![]() $\boldsymbol{\varOmega } = \delta \hat {\boldsymbol{y}}$. Magnitudes of
$\boldsymbol{\varOmega } = \delta \hat {\boldsymbol{y}}$. Magnitudes of ![]() $F_x$,
$F_x$, ![]() $F_z$ and
$F_z$ and ![]() $T_y$, for particle motion at
$T_y$, for particle motion at ![]() $\beta =1$. The DNS data (circles). (a) Force/torque components at
$\beta =1$. The DNS data (circles). (a) Force/torque components at ![]() $\beta =1$ (fundamental frequency), as oscillation amplitude
$\beta =1$ (fundamental frequency), as oscillation amplitude ![]() $\delta$ is varied. Unsteady Stokes formulae (lines) for force, (3.2a), and torque, (3.2b). (b) Force/torque components at
$\delta$ is varied. Unsteady Stokes formulae (lines) for force, (3.2a), and torque, (3.2b). (b) Force/torque components at ![]() $\beta =0$ (steady streaming), as oscillation amplitude
$\beta =0$ (steady streaming), as oscillation amplitude ![]() $\delta$ is varied. Analytical formula for
$\delta$ is varied. Analytical formula for ![]() $F_x$ (line) given by (F1).
$F_x$ (line) given by (F1).
































































































